1 Serie di Taylor di una funzione
|
|
|
- Filomena Valenti
- 8 anni fa
- Visualizzazioni
Transcript
1 Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita in un intervallo I e supponiamo che essa sia di classe C (I). Fissiamo un punto x 0 I. In tal caso si puó considerare per ogni n 0 la derivata n-ma della funzione in x 0, f (n) (x 0 ). Si puó dunque considerare la serie di potenze, di punto iniziale x 0, i cui coefficienti sono cioè la serie a n = f (n) (x 0 ), n 0, f (n) (x 0 ) (x x 0 ) n. Questa serie prende il nome di serie di Taylor di punto iniziale x 0 per la funzione f(x). Per quanto dimostrato sulle serie di potenze nel capitolo 6, si osserva che non solo la serie di Taylor di una funzione data f(x) è una serie di potenze, ma ogni serie di potenze è la serie di Taylor della sua somma. Pertanto se, per una funzione assegnata f(x) si conosce una serie di potenze, di punto iniziale x 0, che converge alla funzione data, nel suo intervallo di convergenza, allora la serie è la serie di Taylor, di punto iniziale x 0, per la funzione data. Esempi. Abbiamo provato nel capitolo 6 che. x = + xn, x (, ). 2. +x = + ( )n x n, x (, ). 3. +x 2 = + ( )n x 2n, x (, ). 4. ln( x) = + n= xn n, x [, ). ln( + x) = + n= ( )n xn n, x (, ]. 5. arctan x = + x2n+ ( )n 2n+, x [, ] 6. ( x) 2 = + n= n xn, x (, ). In ogni caso la serie a secondo membro è la serie di Taylor di punto iniziale 0 per la funzione a primo membro.
2 Analisi Matematica Convergenza di una serie di Taylor La serie di Taylor di una funzione è, almeno per il momento, una serie formale, per cui non sappiamo nulla riguardo alla convergenza. Se peró teniamo conto che si tratta di una serie di potenze, di punto iniziale x 0, si puó affermare che la serie di Taylor di una funzione f(x) converge sempre in x 0 ; ha un raggio di convergenza 0 R + ; (se R > 0) converge puntualmente e assolutamente in un intervallo (x 0 R, x 0 + R), simmetrico rispetto al punto iniziale (estremi compresi o no a seconda dei casi); (se R > 0) converge totalmente e uniformemente in ogni intervallo [x 0 K, x 0 + K] (x 0 R, x 0 + R). È peró intuitivamente naturale porsi la seguente domanda Domanda. La somma di una serie di Taylor è proprio la funzione f(x)? Osserviamo anzitutto che non ci si puó aspettare che la convergenza della serie alla funzione sia in tutto il campo di definizione della funzione stessa, in quanto questo insieme potrebbe non essere simmetrico rispetto a x 0. Quindi ci si chiede Domanda 2. Se f(x) è una funzione di classe C (x 0 δ, x 0 + δ), si puó affermare che il raggio di convergenza della sua serie di Taylor sia R = δ? la somma della serie sia f(x) in (x 0 δ, x 0 + δ)? Si puó verificare facilmente che la risposta a entrambe le domande è NO. Puó cioè capitare che sia la serie abbia raggio di convergenza R < δ (anche se la somma della serie è proprio f(x) in (x 0 R, x 0 + R)); il raggio della serie sia R = δ, ma sia S(x) f(x). Esempio. Sia f(x) = + x 2. La funzione è di classe C (R) e si verifica che { f (n) 0, se n = 2k +, (0) = ( ) k, se n = 2k. Pertanto la serie di Taylor di punto iniziale 0 è ( ) n x 2n.
3 Analisi Matematica 2 3 Sappiamo che questa serie ha raggio di convergenza R = e che la somma delle serie è f(x) per ogni x (, ), ma solo in questo intervallo, nonostante che la funzione sia di classe C (R). Esempio 2. Sia f(x) = {e x 2, x 0 0, x = 0. È immediato osservare che la funzione è continua in R e derivabile n volte in ogni x 0, essendo ( ) f (n) (x) = Q 3n e x x 2, se Q 3n (t) è un polinomio di grado 3n nella variabile t. Ne consegue che lim x 0 f (n) (x) = 0, n > 0. Ció assicura che la funzione ha derivata di ordine n, per ogni n > 0, anche in x 0 = 0 e che f (n) (0) = 0, n > 0. Pertanto f(x) è di classe C (R). Si puó scrivere quindi la serie di Taylor di punto iniziale 0 per la funzione ed è 0 xn. Questa serie, avendo nullo ogni coefficiente, converge su tutto R alla funzione g(x) identicamente nulla su R. Pertanto la serie converge su tutto R ma la somma non è la funzione f(x). Quindi ci si chiede Domanda 3. Se f(x) è una funzione di classe C (x 0 δ, x 0 + δ), quali condizioni sulla funzione f(x) assicurano che il raggio di convergenza della sua serie di Taylor sia R = δ? la somma della serie sia f(x) in (x 0 δ, x 0 + δ)? Diciamo che la funzione f(x) è sviluppabile in serie di Taylor di punto iniziale x 0 se esiste un intervallo (x 0 δ, x 0 + δ) in cui la serie converge alla funzione. Teorema (Criterio di sviluppabilitá in serie di Taylor). Sia f(x) una funzione di classe C (x 0 δ, x 0 + δ). Se M > 0 tale che, per ogni n 0, f (n) (x) M δ n, x (x 0 δ, x 0 + δ), allora f(x) è sviluppabile in serie di Taylor di punto iniziale x 0 in (x 0 δ, x 0 + δ) e R = δ. Omettiamo, almeno per il momento, la dimostrazione di questo teorema, che puó essere fatta solo dopo la sezione 5. Dal teorema segue facilmente il seguente corollario
4 Analisi Matematica 2 4 Corollario. (Criterio di sviluppabilitá in serie di Taylor). Sia f(x) una funzione di classe C (x 0 δ, x 0 + δ). Se M > 0 tale che, per ogni n 0, f (n) (x) M, x (x 0 δ, x 0 + δ), allora f(x) è sviluppabile in serie di Taylor di punto iniziale x 0 in (x 0 δ, x 0 + δ) e R = δ. Dimostrazione. Osserviamo che, per ogni n > 0, δ n > 0, lim δ n = +. Allora esiste C > 0 tale che δ n C, per ogni n, cioè tale che C δ n, Da ció segue, per l ipotesi fatta, che, per ogni n 0, n. f (n) (x) M M C Dunque il teorema garantisce la tesi. δ n, x (x 0 δ, x 0 + δ). La condizione di sviluppabilitá espressa dal corollario ha il vantaggio di non dipendere da δ; peró è piú restrittiva di quella fornita dal teorema. È importante sapere che la serie di Taylor di punto iniziale x 0 converge a una funzione data, almeno in un intorno di x 0, perchè ció consente di approssimare la funzione, almeno vicino al punto iniziale, mediante le somme parziali della serie, che sono polinomi. Esempi.. Sia f(x) = e x. Fissiamo x 0 = 0. È banale osservare che, per ogni n > 0, si ha f (n) (x) = e x, e quindi f (n) (0) = 0, n 0. La serie di Taylor della funzione di punto iniziale 0 è allora xn. La serie ha raggio di convergenza R = + ; inoltre essa converge alla funzione, per ogni x reale. Infatti, fissato δ > 0, si ha f (n) (x) = e x e δ, x ( δ, δ) e quindi vale l ipotesi del corollario, se M = e δ.
5 Analisi Matematica Sia f(x) = sin x. Fissiamo x 0 = 0. Si ha e cosí via. Pertanto f(x) = sin x, f (x) = cos x, f (x) = sin x, f (x) = cos x, f(0) = 0, f (0) =, f (0) = 0, f (0) =, e cosí via. La serie di Taylor della funzione di punto iniziale 0 è allora ( ) n (2n + )! x2n+. La serie ha raggio di convergenza R = + ; inoltre essa converge alla funzione, per ogni x reale. Infatti, fissato δ > 0, si ha f (n) (x), x ( δ, δ) e quindi vale l ipotesi del corollario, se M =. 3. Sia f(x) = cos x. Fissiamo x 0 = 0. Si ha e cosí via. Pertanto f(x) = cos x, f (x) = sin x, f (x) = cos x, f (x) = sin x, f(0) =, f (0) = 0, f (0) =, f (0) = 0, e cosí via. La serie di Taylor della funzione di punto iniziale 0 è allora ( ) n (2n)! x2n. La serie ha raggio di convergenza R = + ; inoltre essa converge alla funzione, per ogni x reale. Infatti, fissato δ > 0, si ha f (n) (x), x ( δ, δ) e quindi vale l ipotesi del corollario, se M =.
6 Analisi Matematica 2 6 Osservazione. Per le funzioni x, + x, + x 2, ln( x), ln( + x), arctan x, ( x) 2 si sa che ciascuna è la somma della propria serie di Taylor, nell intervallo di convergenza della serie. Come giá detto nella sezione, ció è conseguenza del fatto che ciascuna di queste funzioni è la somma di una serie di potenze nota, nell intervallo di convergenza dlla serie. Lo stesso si puó dire per ogni funzione che si sa essere la somma di una serie di potenze nel relativo intervallo di convergenza. 2 Sviluppi notevoli Elenchiamo alcune osservazioni utili per determinare la sviluppabilitá in serie di taylor di una funzione nota (con un punto inioziale fissato). Come giá detto, ogni funzione che si sa essere la somma di una serie di potenze nell intervallo di convergenza è sviluppabile nella serie di Taylor in tutto l intervallo di convergenza della serie. Se una funzione f(x) è sviluppabile in serie di Taylor e si sostituisce x con αx k, per α e k fissati, la funzione composta g(x) = f(αx k ) è sviluppabile nella serie di Taylor, che è ottenuta dalla serie di Taylor della funzione f(x) sostituendo x con αx k. L intervallo di convergenza si deduce con la stessa sostituzione. Se una funzione f(x) è sviluppabile in serie di Taylor e si considera una sua derivata e la sua primitiva che vale 0 nel punto iniziale, allora anche la derivata e la primitiva sono sviluppabili nella serie di Taylor, che si ottiene da quella di f(x) derivando e integrando termine a termine rispettivamente. Tenendo conto di queste considerazioni e degli esempi trattati in precedenza elenchiamo i principali sviluppi in serie di Taylor, specificando per quali x essi valgono.. e x = + x n, x R. 2. e ax = + an x n, x R. 3. e ax2 = + an x 2n, x R. 4. sin x = + ( )n (2n+)! x 2n+, x R. 5. sin x x = + ( )n (2n+)! x 2n, x R. In realtá la funzione a primo membro non è definita in 0, ma si puó prolungare per continuitá e la formula segue dalla formula 4, dividendo per x entrambi i membri. Si noti che dall uguaglianza segue, senza fare nessun conto, che la funzione a primo membro è C (R).
7 Analisi Matematica cos x = + ( )n (2n)! x 2n, x R. 7. x = + xn, x (, ). 8. +x = + ( )n x n, x (, ). 9. +x 2 = + ( )n x 2n, x (, ). 0. ln( x) = + xn+ n+, x [, ).. ln( + x) = + xn+ ( )n n+, x (, ]. 2. arctan x = + x2n+ ( )n 2n+, x [, ]. 3. ( x) 2 = + n= n xn, x (, ). 4. ( + x) α = + ( n ) α x n, x (, ), se ( ) { α(α ) (α n+) n = se n, α se n = 0. La serie a secondo membro si chiama serie binomiale. Come casi particolari, per α = /2 e α = /2 si hanno le due formule seguenti x = + ( /2 ) α x n, x (, ), 6. +x = + ( /2 ) α x n, x (, ), 3 Polinomi di Taylor di una funzione Sia f(x)una funzione sviluppabile in serie di Taylor di punto iniziale x 0 in (x 0 δ, x 0 + δ). Per definizione di serie, si ha f(x) = lim n T n (x), x (x 0 δ, x 0 + δ), se T n (x) è la somma parziale n-ma della serie, cioè T n (x) = n k=0 k! f (k) (x 0 ) (x x 0 ) k. Allora T n (x) è un polinomio nella variabile x x 0, di grado T n n, che chiamiamo polinomio di Taylor di punto iniziale x 0 e ordine n per la funzione data.
8 Analisi Matematica 2 8 Pertanto, dire che f(x) è sviluppabile nella sua serie di Taylor di punto iniziale x 0 in (x 0 δ, x 0 +δ) equivale a dire che, in (x 0 δ, x 0 + δ), la funzione è limite per n + dell n-mo polinomio di Taylor (di punto iniziale x 0 ), cioè che puó essere approssimata in tale intervallo mediante un polinomio di Taylor, con un approssimazione tanto migliore quanto piú grande è n. Piú in generale, se f(x) è una funzione di classe C (I) e se x 0 è un punto fissato di I, si puó considerare, per ogni n, il polinomio di Taylor di punto iniziale x 0 e ordine n per la funzione data, con l obiettivo di trovare n (il piú piccolo possibile) in modo tale che il polinomio approssimi la funzione, in un intervallo fissato (x 0 δ, x 0 + δ), o in un punto fissato, con un errore al di sotto di una soglia accettabile. È banale osservare che, piú piccolo è δ o piú vicino a x 0 è il punto fissato, migliore sará l approssimazione, a paritá di n. Infatti, risulta dal momento che lim f(x) T n (x) 0, x x 0 lim f(x) = lim T n (x) = f(x 0 ). x x 0 x x 0 Quindi se, data una funzione f(x) di classe C (I), se ne considerano polinomi di Taylor di punto iniziale x 0, con x 0 fissato in I, un fatto fondamentale è valutare, per n fissato e in un intervallo fissato (x 0 δ, x 0 + δ), o in un punto fissato, l errore n-mo (o resto n-mo) E n (x) = f(x) T n (x). Se siamo in grado di fare, ció saremo in grado di affrontare (e risolvere) i due di approssimazione seguenti:. trovare n (il piú piccolo possibile) in modo tale che il polinomio T n (x) approssimi la funzione, in un intervallo fissato (x 0 δ, x 0 + δ), o in un punto fissato, con un errore (in modulo) al di sotto di una soglia accettabile; 2. trovare δ (il piú grande possibile) in modo tale che il polinomio T n (x) di ordine fissato n approssimi la funzione in (x 0 δ, x 0 + δ), con un errore (in modulo) al di sotto di una soglia accettabile. Per valutare E n (x) sará necessario avere una formula che lo esprima in modo esplicito, o almeno un metodo per maggiorarlo. Prima di affrontare il problema della valutazione dell errore, vediamo quale è il significato dei polinomi di Taylor; cioè rispondiamo alla domanda perché, se vogliamo approssimare una funzione, vicino a un punto x 0, mediante un polinomio (di grado n) nella variabile x x 0, scegliamo proprio il polinomio di Taylor di punto iniziale x 0 e ordine n?
9 Analisi Matematica 2 9 La risposta alla domanda è la seguente: perché il polinomio di Taylor di punto iniziale x 0 e ordine n è, tra tutti i polinomi di grado n nella variabile x x 0, quello che meglio approssima la funzione vicino a x 0. Ma cosa significa l espressione migliore approssimazione? Ci sono due modi possibili di dare un senso all espressione migliore approssimazione.. Il polinomio P (x) di grado n che meglio approssima la funzione f(x) vicino a x 0 è quello che ha un contatto di ordine n con la funzione f(x) in x 0., nel senso che P (k) (x 0 ) = f (k) (x 0 ), k = 0,, n. 2. Il polinomio P (x) di grado n che meglio approssima la funzione f(x) vicino a x 0 è quello che differisce dalla funzione vicino a x 0 per un infinitesimo di ordine superiore a (x x 0 ) n, cioè quello tale che f(x) P (x) = o((x x 0 ) n ) per x x 0 nel senso che lim f(x) P (x) (x x 0 ) n = 0. In effetti si prova che i due criteri precedenti sono equivalenti e caratterizzano entrambi proprio il polinomio di Taylor della funzione di punto iniziale x 0 e ordine n. È quanto afferma il seguente teorema. Teorema. Sia f(x) una funzione f(x) di classe C (I) e sia x 0 I. Sono fatti equivalenti:. P (x) è il polinomio nella variabile x x 0 di grado n che ha un contatto di ordine n con la funzione in x 0 ; 2. P (x) è il polinomio nella variabile x x 0 di grado n tale che f(x) P (x) = o((x x 0 ) n ) per x x 0 ; 3. P (x) è il polinomio di Taylor di punto iniziale x 0 e ordine n per f(x). Dimostrazione. Proviamo che () (2) e che () (3). () (2). Supponiamo che P (k) (x 0 ) = f (k) (x 0 ), per ogni k = 0,, n. f(x) P (x) Proviamo che lim x xo (x x 0 ) = 0. n Per calcolare il limite si usa il teorema di de l Hospital n volte successivamente e si ottiene che lim f(x) P (x) (x x 0 ) n = lim = lim f (x) P (x) n (x x 0 ) n = f (n ) (x) P (n ) (x) (x x 0 ) = lim f (n) (x) P (n) (x) = 0.
10 Analisi Matematica 2 0 Viceversa, se lim x xo ogni k = 0,, n. f(x) P (x) (x x 0 ) n = 0, proviamo per assurdo che P (k) (x 0 ) = f (k) (x 0 ), per A questo scopo supponiamo che esista un k per cui P (k) (x 0 ) f (k) (x 0 ); se k 0 è il piú piccolo di tali k, risulterebbe lim f(x) P (x) (x x 0 ) k 0 = lim = lim f (x) P (x) k 0 (x x 0 ) k 0 = f (k0 ) (x) P (k0 ) (x) k 0! (x x 0 ) = lim f (k0) (x) P (k0) (x) k 0! 0 e ció è assurdo per l ipotesi fatta. () (3). Se P (x) è il polinomio di Taylor di punto iniziale x 0 e ordine n per f(x), allora P (x) ha un contatto di ordine n con la funzione in x 0. Infatti un conto diretto mostra che P (k) (x 0 ) = f (k) (x 0 ), k = 0,, n. D altra parte se P (x) = n k=0 a k (x x 0 ) k è un polinomio nella variabile x x 0 di grado n e ha un contatto di ordine n con la funzione f(x) in x 0, allora per ogni k = 0,, n, k! a k = P (k) (x 0 ) = f (k) (x 0 ) e quindi P (x) è il polinomio di Taylor di punto iniziale x 0 e ordine n per f(x). Il teorema precedente fornisce una descrizione dell errore o resto n-mo E n (x). In effetti il teorema stabilisce che E n (x) = o((x x 0 ) n ) (x x 0 ), cioè f(x) = T n (x) + o((x x 0 ) n ) (x x 0 ). Questa formula è detta formula di Peano per l errore E n (x). Essa non fornisce una misura quantitativa dell errore, peró assicura che vicino a x 0 si puó sostituire la funzione con il polinomio, se si possono trascurare gli infinitesimi di ordine maggiore di n. La formula di Peano puó ad esempio essere utile nel calcolo di limiti di forme indeterminate Formula di Lagrange per l errore n-mo. Sia f(x) una funzione f(x) di classe C (I) e sia x 0 I. Se consideriamo il suo polinomio di Taylor di punto iniziale x 0 e ordine n, e vogliamo dare una valutazione quantitativa dell errore E n (x) in un intervallo (x 0 δ, x 0 + δ), è utile il seguente teorema, che fornisce una formula esplicita per l errore. Teorema. (Formula di Lagrange per il resto n-mo). Sia f(x) una funzione f(x) di classe C (I) e sia x 0 I. Per n 0, si consideri il polinomio di Taylor T n (x) di punto iniziale x 0 e sia E n (x) = f(x) T n (x). Allora
11 Analisi Matematica 2 per ogni x in un intervallo (x 0 δ, x 0 + δ), esiste c compreso tra x 0 e x tale che E n (x) = (n + )! f (n+) (c) (x x 0 ) n+. Dimostrazione. Diamo la dimostrazione per n =. Supponiamo x > x 0 e applichiamo il teorema di Cauchy nell intervallo [x 0, x] alle funzioni r(x) = E (x) = f(x) T (x), g(x) = (x x 0 ) 2. Osservando che r(x 0 ) = g(x 0 ) = 0, il teorema afferma che esiste x [x 0, x], tale che r(x) g(x) = r(x) r(x 0) g(x) g(x 0 ) = r (x ) g (x ). Applichiamo ancora una volta il teorema di Cauchy nell intervallo [x 0, x ] alle funzioni r (x) = f (x) T (x), g (x) = 2 (x x 0 ). Osservando che r (x 0 ) = g (x 0 ) = 0, il teorema afferma che esiste c [x 0, x ], tale che r (x ) g (x ) = r (x ) r (x 0 ) g (x ) g (x 0 ) = r (c) g (c). Poiché r (x) = f (x) T (x) = f (x) e g (x) = 2, si conclude che cioè che che è la formula richiesta. E (x) (x x 0 ) 2 = f (c) 2 E (x) = f (c) 2 (x x 0 ) 2, 5 Appendice. Possiamo ora dare la dimostrazione del Teorema di Sezione.2. Fissiamo x in (x 0 δ, x 0 + δ) e n > 0. La differenza f(x) T n (x) si puó esprimere mediante la formula di Lagrange per il resto n-mo, cioè f(x) T n (x) = (n + )! f (n+) (c n ) (x x 0 ) n+, per un opportuno c n compreso tra x 0 e x. Se facciamo l ipotesi che f (n) (x) M δ n, si ha allora f(x) T n (x) = (n + )! f (n+) (c) x x 0 n+ (n + )! M (n + )! δ n+ x x 0 n+ = M ( ) x x0 n+. δ Se osserviamo che x x 0 δ <, sará ( ) x x0 n+ 0 δ cioè f(x) T n (x) 0.
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI
 CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
Docente: Anna Valeria Germinario. Università di Bari. A.V.Germinario (Università di Bari) Analisi Matematica ITPS 1 / 22
 Laurea in Informatica e Tecnologie per la Produzione del Software Corso di Analisi Matematica Calcolo differenziale e approssimazioni, formula di Taylor Docente: Anna Valeria Germinario Università di Bari
Laurea in Informatica e Tecnologie per la Produzione del Software Corso di Analisi Matematica Calcolo differenziale e approssimazioni, formula di Taylor Docente: Anna Valeria Germinario Università di Bari
Corso di Analisi Matematica. Polinomi e serie di Taylor
 a.a. 2013/14 Laurea triennale in Informatica Corso di Analisi Matematica Polinomi e serie di Taylor Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli
a.a. 2013/14 Laurea triennale in Informatica Corso di Analisi Matematica Polinomi e serie di Taylor Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli
u 1 u k che rappresenta formalmente la somma degli infiniti numeri (14.1), ordinati al crescere del loro indice. I numeri u k
 Capitolo 4 Serie numeriche 4. Serie convergenti, divergenti, indeterminate Data una successione di numeri reali si chiama serie ad essa relativa il simbolo u +... + u +... u, u 2,..., u,..., (4.) oppure
Capitolo 4 Serie numeriche 4. Serie convergenti, divergenti, indeterminate Data una successione di numeri reali si chiama serie ad essa relativa il simbolo u +... + u +... u, u 2,..., u,..., (4.) oppure
Indice. 1 Introduzione alle Equazioni Differenziali 1 1.1 Esempio introduttivo... 1 1.2 Nomenclatura e Teoremi di Esistenza ed Unicità...
 Indice 1 Introduzione alle Equazioni Differenziali 1 1.1 Esempio introduttivo............................. 1 1.2 Nomenclatura e Teoremi di Esistenza ed Unicità.............. 5 i Capitolo 1 Introduzione
Indice 1 Introduzione alle Equazioni Differenziali 1 1.1 Esempio introduttivo............................. 1 1.2 Nomenclatura e Teoremi di Esistenza ed Unicità.............. 5 i Capitolo 1 Introduzione
Matematica generale CTF
 Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
SUCCESSIONI NUMERICHE
 SUCCESSIONI NUMERICHE Una funzione reale di una variabile reale f di dominio A è una legge che ad ogni x A associa un numero reale che denotiamo con f(x). Se A = N, la f è detta successione di numeri reali.
SUCCESSIONI NUMERICHE Una funzione reale di una variabile reale f di dominio A è una legge che ad ogni x A associa un numero reale che denotiamo con f(x). Se A = N, la f è detta successione di numeri reali.
Successioni di funzioni reali
 E-school di Arrigo Amadori Analisi I Successioni di funzioni reali 01 Introduzione. In questo capitolo applicheremo i concetti di successione e di serie alle funzioni numeriche reali. Una successione di
E-school di Arrigo Amadori Analisi I Successioni di funzioni reali 01 Introduzione. In questo capitolo applicheremo i concetti di successione e di serie alle funzioni numeriche reali. Una successione di
Applicazioni del calcolo differenziale allo studio delle funzioni
 Capitolo 9 9.1 Crescenza e decrescenza in piccolo; massimi e minimi relativi Sia y = f(x) una funzione definita nell intervallo A; su di essa non facciamo, per ora, alcuna particolare ipotesi (né di continuità,
Capitolo 9 9.1 Crescenza e decrescenza in piccolo; massimi e minimi relativi Sia y = f(x) una funzione definita nell intervallo A; su di essa non facciamo, per ora, alcuna particolare ipotesi (né di continuità,
EQUAZIONI DIFFERENZIALI Esercizi svolti. y = xy. y(2) = 1.
 EQUAZIONI DIFFERENZIALI Esercizi svolti 1. Determinare la soluzione dell equazione differenziale (x 2 + 1)y + y 2 =. y + x tan y = 2. Risolvere il problema di Cauchy y() = 1 2 π. 3. Risolvere il problema
EQUAZIONI DIFFERENZIALI Esercizi svolti 1. Determinare la soluzione dell equazione differenziale (x 2 + 1)y + y 2 =. y + x tan y = 2. Risolvere il problema di Cauchy y() = 1 2 π. 3. Risolvere il problema
Per lo svolgimento del corso risulta particolarmente utile considerare l insieme
 1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
LEZIONE 23. Esempio 23.1.3. Si consideri la matrice (si veda l Esempio 22.2.5) A = 1 2 2 3 3 0
 LEZIONE 23 231 Diagonalizzazione di matrici Abbiamo visto nella precedente lezione che, in generale, non è immediato che, data una matrice A k n,n con k = R, C, esista sempre una base costituita da suoi
LEZIONE 23 231 Diagonalizzazione di matrici Abbiamo visto nella precedente lezione che, in generale, non è immediato che, data una matrice A k n,n con k = R, C, esista sempre una base costituita da suoi
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria).
 Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
Sviluppi di Taylor Esercizi risolti
 Esercizio 1 Sviluppi di Taylor Esercizi risolti Utilizzando gli sviluppi fondamentali, calcolare gli sviluppi di McLaurin con resto di Peano delle funzioni seguenti fino all ordine n indicato: 1. fx ln1
Esercizio 1 Sviluppi di Taylor Esercizi risolti Utilizzando gli sviluppi fondamentali, calcolare gli sviluppi di McLaurin con resto di Peano delle funzioni seguenti fino all ordine n indicato: 1. fx ln1
FUNZIONI CONVESSE. + e x 0
 FUNZIONI CONVESSE Sia I un intervallo aperto di R (limitato o illimitato) e sia f(x) una funzione definita in I. Dato x 0 I, la retta r passante per il punto P 0 (x 0, f(x 0 )) di equazione y = f(x 0 )
FUNZIONI CONVESSE Sia I un intervallo aperto di R (limitato o illimitato) e sia f(x) una funzione definita in I. Dato x 0 I, la retta r passante per il punto P 0 (x 0, f(x 0 )) di equazione y = f(x 0 )
CONCETTO DI LIMITE DI UNA FUNZIONE REALE
 CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
5. La teoria astratta della misura.
 5. La teoria astratta della misura. 5.1. σ-algebre. 5.1.1. σ-algebre e loro proprietà. Sia Ω un insieme non vuoto. Indichiamo con P(Ω la famiglia di tutti i sottoinsiemi di Ω. Inoltre, per ogni insieme
5. La teoria astratta della misura. 5.1. σ-algebre. 5.1.1. σ-algebre e loro proprietà. Sia Ω un insieme non vuoto. Indichiamo con P(Ω la famiglia di tutti i sottoinsiemi di Ω. Inoltre, per ogni insieme
Schemi delle Lezioni di Matematica Generale. Pierpaolo Montana
 Schemi delle Lezioni di Matematica Generale Pierpaolo Montana A volte i fenomeni economici che ci interessano non variano con continuitá oppure non possono essere osservati con continuitá, ma solo a intervalli
Schemi delle Lezioni di Matematica Generale Pierpaolo Montana A volte i fenomeni economici che ci interessano non variano con continuitá oppure non possono essere osservati con continuitá, ma solo a intervalli
Corso di Analisi Matematica Serie numeriche
 Corso di Analisi Matematica Serie numeriche Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 25 1 Definizione e primi esempi 2 Serie a
Corso di Analisi Matematica Serie numeriche Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 25 1 Definizione e primi esempi 2 Serie a
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI
 FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
Esercizi svolti su serie di Fourier
 Esercizi svolti su serie di Fourier Esercizio. (Onda quadra. Determinare i coefficienti di Fourier della funzione x [, f(x = x [, prolungata a una funzione -periodica su R (d ora in poi denoteremo con
Esercizi svolti su serie di Fourier Esercizio. (Onda quadra. Determinare i coefficienti di Fourier della funzione x [, f(x = x [, prolungata a una funzione -periodica su R (d ora in poi denoteremo con
Capitolo 1 ANALISI COMPLESSA
 Capitolo 1 ANALISI COMPLESSA 1 1.4 Serie in campo complesso 1.4.1 Serie di potenze Una serie di potenze è una serie del tipo a k (z z 0 ) k. Per le serie di potenze in campo complesso valgono teoremi analoghi
Capitolo 1 ANALISI COMPLESSA 1 1.4 Serie in campo complesso 1.4.1 Serie di potenze Una serie di potenze è una serie del tipo a k (z z 0 ) k. Per le serie di potenze in campo complesso valgono teoremi analoghi
Dimensione di uno Spazio vettoriale
 Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Sulla monotonia delle funzioni reali di una variabile reale
 Liceo G. B. Vico - Napoli Sulla monotonia delle funzioni reali di una variabile reale Prof. Giuseppe Caputo Premetto due teoremi come prerequisiti necessari per la comprensione di quanto verrà esposto
Liceo G. B. Vico - Napoli Sulla monotonia delle funzioni reali di una variabile reale Prof. Giuseppe Caputo Premetto due teoremi come prerequisiti necessari per la comprensione di quanto verrà esposto
risulta (x) = 1 se x < 0.
 Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
f(x) = 1 x. Il dominio di questa funzione è il sottoinsieme proprio di R dato da
 Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Limiti e continuità delle funzioni reali a variabile reale
 Limiti e continuità delle funzioni reali a variabile reale Roberto Boggiani Versione 4.0 9 dicembre 2003 1 Esempi che inducono al concetto di ite Per introdurre il concetto di ite consideriamo i seguenti
Limiti e continuità delle funzioni reali a variabile reale Roberto Boggiani Versione 4.0 9 dicembre 2003 1 Esempi che inducono al concetto di ite Per introdurre il concetto di ite consideriamo i seguenti
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI
 APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
Quesiti di Analisi Matematica A
 Quesiti di Analisi Matematica A Presentiamo una raccolta di quesiti per la preparazione alla prova orale del modulo di Analisi Matematica A. Per una buona preparazione é consigliabile rispondere ad alta
Quesiti di Analisi Matematica A Presentiamo una raccolta di quesiti per la preparazione alla prova orale del modulo di Analisi Matematica A. Per una buona preparazione é consigliabile rispondere ad alta
E naturale chiedersi alcune cose sulla media campionaria x n
 Supponiamo che un fabbricante stia introducendo un nuovo tipo di batteria per un automobile elettrica. La durata osservata x i delle i-esima batteria è la realizzazione (valore assunto) di una variabile
Supponiamo che un fabbricante stia introducendo un nuovo tipo di batteria per un automobile elettrica. La durata osservata x i delle i-esima batteria è la realizzazione (valore assunto) di una variabile
SUCCESSIONI NUMERICHE
 SUCCESSIONI NUMERICHE Definizione: Si chiama successione numerica una funzione definita su IN a valori in IR, cioè una legge che associa ad ogni intero n un numero reale a n. Per abuso di linguaggio, si
SUCCESSIONI NUMERICHE Definizione: Si chiama successione numerica una funzione definita su IN a valori in IR, cioè una legge che associa ad ogni intero n un numero reale a n. Per abuso di linguaggio, si
SIMULAZIONE TEST ESAME - 1
 SIMULAZIONE TEST ESAME - 1 1. Il dominio della funzione f(x) = log (x2 + 1)(4 x 2 ) (x 2 2x + 1) è: (a) ( 2, 2) (b) ( 2, 1) (1, 2) (c) (, 2) (2, + ) (d) [ 2, 1) (1, 2] (e) R \{1} 2. La funzione f : R R
SIMULAZIONE TEST ESAME - 1 1. Il dominio della funzione f(x) = log (x2 + 1)(4 x 2 ) (x 2 2x + 1) è: (a) ( 2, 2) (b) ( 2, 1) (1, 2) (c) (, 2) (2, + ) (d) [ 2, 1) (1, 2] (e) R \{1} 2. La funzione f : R R
3.1 Successioni. R Definizione (Successione numerica) E Esempio 3.1 CAPITOLO 3
 CAPITOLO 3 Successioni e serie 3. Successioni Un caso particolare di applicazione da un insieme numerico ad un altro insieme numerico è quello delle successioni, che risultano essere definite nell insieme
CAPITOLO 3 Successioni e serie 3. Successioni Un caso particolare di applicazione da un insieme numerico ad un altro insieme numerico è quello delle successioni, che risultano essere definite nell insieme
Matematica generale CTF
 Equazioni differenziali 9 dicembre 2015 Si chiamano equazioni differenziali quelle equazioni le cui incognite non sono variabili reali ma funzioni di una o più variabili. Le equazioni differenziali possono
Equazioni differenziali 9 dicembre 2015 Si chiamano equazioni differenziali quelle equazioni le cui incognite non sono variabili reali ma funzioni di una o più variabili. Le equazioni differenziali possono
EQUAZIONI DIFFERENZIALI. 1. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x 2 log t (d) x = e t x log x (e) y = y2 5y+6
 EQUAZIONI DIFFERENZIALI.. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x log t (d) x = e t x log x (e) y = y 5y+6 (f) y = ty +t t +y (g) y = y (h) xy = y (i) y y y = 0 (j) x = x (k)
EQUAZIONI DIFFERENZIALI.. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x log t (d) x = e t x log x (e) y = y 5y+6 (f) y = ty +t t +y (g) y = y (h) xy = y (i) y y y = 0 (j) x = x (k)
Alcuni complementi sulle successioni
 Alcuni complementi sulle successioni 1 (Teorema del confronto) Siano {a n } e {b n } due successioni regolari tali che si abbia a n b n n N. (1) Allora: a n b n. (2) Dim. Sia L = a n ed L = b n. Se L =
Alcuni complementi sulle successioni 1 (Teorema del confronto) Siano {a n } e {b n } due successioni regolari tali che si abbia a n b n n N. (1) Allora: a n b n. (2) Dim. Sia L = a n ed L = b n. Se L =
Proposta di soluzione della prova di matematica Liceo scientifico di Ordinamento - 2014
 Proposta di soluzione della prova di matematica Liceo scientifico di Ordinamento - 14 Problema 1 Punto a) Osserviamo che g (x) = f(x) e pertanto g () = f() = in quanto Γ è tangente all asse delle ascisse,
Proposta di soluzione della prova di matematica Liceo scientifico di Ordinamento - 14 Problema 1 Punto a) Osserviamo che g (x) = f(x) e pertanto g () = f() = in quanto Γ è tangente all asse delle ascisse,
I appello - 24 Marzo 2006
 Facoltà di Ingegneria - Corso di Laurea in Ing. Energetica e Gestionale A.A.2005/2006 I appello - 24 Marzo 2006 Risolvere gli esercizi motivando tutte le risposte. I.) Studiare la convergenza puntuale,
Facoltà di Ingegneria - Corso di Laurea in Ing. Energetica e Gestionale A.A.2005/2006 I appello - 24 Marzo 2006 Risolvere gli esercizi motivando tutte le risposte. I.) Studiare la convergenza puntuale,
10. Insiemi non misurabili secondo Lebesgue.
 10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
SERIE NUMERICHE. prof. Antonio Greco 6-11-2013
 SERIE NUMERICHE prof. Antonio Greco 6--203 Indice Motivazioni........... 3 Definizione........... 3 Errore tipico........... 3 Un osservazione utile...... 3 Condizione necessaria...... 4 Serie armonica.........
SERIE NUMERICHE prof. Antonio Greco 6--203 Indice Motivazioni........... 3 Definizione........... 3 Errore tipico........... 3 Un osservazione utile...... 3 Condizione necessaria...... 4 Serie armonica.........
19. Inclusioni tra spazi L p.
 19. Inclusioni tra spazi L p. Nel n. 15.1 abbiamo provato (Teorema 15.1.1) che, se la misura µ è finita, allora tra i corispondenti spazi L p (µ) si hanno le seguenti inclusioni: ( ) p, r ]0, + [ : p
19. Inclusioni tra spazi L p. Nel n. 15.1 abbiamo provato (Teorema 15.1.1) che, se la misura µ è finita, allora tra i corispondenti spazi L p (µ) si hanno le seguenti inclusioni: ( ) p, r ]0, + [ : p
APPLICAZIONI LINEARI
 APPLICAZIONI LINEARI 1. Esercizi Esercizio 1. Date le seguenti applicazioni lineari (1) f : R 2 R 3 definita da f(x, y) = (x 2y, x + y, x + y); (2) g : R 3 R 2 definita da g(x, y, z) = (x + y, x y); (3)
APPLICAZIONI LINEARI 1. Esercizi Esercizio 1. Date le seguenti applicazioni lineari (1) f : R 2 R 3 definita da f(x, y) = (x 2y, x + y, x + y); (2) g : R 3 R 2 definita da g(x, y, z) = (x + y, x y); (3)
Ottimizazione vincolata
 Ottimizazione vincolata Ricordiamo alcuni risultati provati nella scheda sulla Teoria di Dini per una funzione F : R N+M R M di classe C 1 con (x 0, y 0 ) F 1 (a), a = (a 1,, a M ), punto in cui vale l
Ottimizazione vincolata Ricordiamo alcuni risultati provati nella scheda sulla Teoria di Dini per una funzione F : R N+M R M di classe C 1 con (x 0, y 0 ) F 1 (a), a = (a 1,, a M ), punto in cui vale l
Introduzione al MATLAB c Parte 2
 Introduzione al MATLAB c Parte 2 Lucia Gastaldi Dipartimento di Matematica, http://dm.ing.unibs.it/gastaldi/ 18 gennaio 2008 Outline 1 M-file di tipo Script e Function Script Function 2 Costrutti di programmazione
Introduzione al MATLAB c Parte 2 Lucia Gastaldi Dipartimento di Matematica, http://dm.ing.unibs.it/gastaldi/ 18 gennaio 2008 Outline 1 M-file di tipo Script e Function Script Function 2 Costrutti di programmazione
Osservazioni sulla continuità per le funzioni reali di variabile reale
 Corso di Matematica, I modulo, Università di Udine, Osservazioni sulla continuità Osservazioni sulla continuità per le funzioni reali di variabile reale Come è noto una funzione è continua in un punto
Corso di Matematica, I modulo, Università di Udine, Osservazioni sulla continuità Osservazioni sulla continuità per le funzioni reali di variabile reale Come è noto una funzione è continua in un punto
Esercizi su lineare indipendenza e generatori
 Esercizi su lineare indipendenza e generatori Per tutto il seguito, se non specificato esplicitamente K indicherà un campo e V uno spazio vettoriale su K Cose da ricordare Definizione Dei vettori v,,v
Esercizi su lineare indipendenza e generatori Per tutto il seguito, se non specificato esplicitamente K indicherà un campo e V uno spazio vettoriale su K Cose da ricordare Definizione Dei vettori v,,v
STRUTTURE ALGEBRICHE
 STRUTTURE ALGEBRICHE Operazioni in un insieme Sia A un insieme non vuoto; una funzione f : A A A si dice operazione binaria (o semplicemente operazione), oppure legge di composizione interna. Per definizione
STRUTTURE ALGEBRICHE Operazioni in un insieme Sia A un insieme non vuoto; una funzione f : A A A si dice operazione binaria (o semplicemente operazione), oppure legge di composizione interna. Per definizione
Corso di Analisi Matematica. Successioni e serie numeriche
 a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Successioni e serie numeriche Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità
a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Successioni e serie numeriche Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità
x 2 + y2 4 = 1 x = cos(t), y = 2 sin(t), t [0, 2π] Al crescere di t l ellisse viene percorsa in senso antiorario.
![x 2 + y2 4 = 1 x = cos(t), y = 2 sin(t), t [0, 2π] Al crescere di t l ellisse viene percorsa in senso antiorario. x 2 + y2 4 = 1 x = cos(t), y = 2 sin(t), t [0, 2π] Al crescere di t l ellisse viene percorsa in senso antiorario.](/thumbs/39/18585741.jpg) Le soluzioni del foglio 2. Esercizio Calcolare il lavoro compiuto dal campo vettoriale F = (y + 3x, 2y x) per far compiere ad una particella un giro dell ellisse 4x 2 + y 2 = 4 in senso orario... Soluzione.
Le soluzioni del foglio 2. Esercizio Calcolare il lavoro compiuto dal campo vettoriale F = (y + 3x, 2y x) per far compiere ad una particella un giro dell ellisse 4x 2 + y 2 = 4 in senso orario... Soluzione.
CRITERI DI CONVERGENZA PER LE SERIE. lim a n = 0. (1) s n+1 = s n + a n+1. (2) CRITERI PER LE SERIE A TERMINI NON NEGATIVI
 Il criterio più semplice è il seguente. CRITERI DI CONVERGENZA PER LE SERIE Teorema(condizione necessaria per la convergenza). Sia a 0, a 1, a 2,... una successione di numeri reali. Se la serie a k è convergente,
Il criterio più semplice è il seguente. CRITERI DI CONVERGENZA PER LE SERIE Teorema(condizione necessaria per la convergenza). Sia a 0, a 1, a 2,... una successione di numeri reali. Se la serie a k è convergente,
1 Applicazioni Lineari tra Spazi Vettoriali
 1 Applicazioni Lineari tra Spazi Vettoriali Definizione 1 (Applicazioni lineari) Si chiama applicazione lineare una applicazione tra uno spazio vettoriale ed uno spazio vettoriale sul campo tale che "!$%!
1 Applicazioni Lineari tra Spazi Vettoriali Definizione 1 (Applicazioni lineari) Si chiama applicazione lineare una applicazione tra uno spazio vettoriale ed uno spazio vettoriale sul campo tale che "!$%!
Convessità e derivabilità
 Convessità e derivabilità Definizione 1 (convessità per funzioni derivabili) Sia f : (a, b) R derivabile su (a, b). Diremo che f è convessa o concava su (a, b) se per ogni 0 (a,b) il grafico di f sta tutto
Convessità e derivabilità Definizione 1 (convessità per funzioni derivabili) Sia f : (a, b) R derivabile su (a, b). Diremo che f è convessa o concava su (a, b) se per ogni 0 (a,b) il grafico di f sta tutto
1. Distribuzioni campionarie
 Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 3 e 6 giugno 2013 - di Massimo Cristallo - 1. Distribuzioni campionarie
Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 3 e 6 giugno 2013 - di Massimo Cristallo - 1. Distribuzioni campionarie
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
1 Alcuni criteri di convergenza per serie a termini non negativi
 Alcuni criteri di convergenza per serie a termini non negativi (Criterio del rapporto.) Consideriamo la serie a (.) a termini positivi (ossia a > 0, =, 2,...). Supponiamo che esista il seguente ite a +
Alcuni criteri di convergenza per serie a termini non negativi (Criterio del rapporto.) Consideriamo la serie a (.) a termini positivi (ossia a > 0, =, 2,...). Supponiamo che esista il seguente ite a +
Esercizi svolti. 1. Si consideri la funzione f(x) = 4 x 2. a) Verificare che la funzione F(x) = x 2 4 x2 + 2 arcsin x è una primitiva di
 Esercizi svolti. Si consideri la funzione f() 4. a) Verificare che la funzione F() 4 + arcsin è una primitiva di f() sull intervallo (, ). b) Verificare che la funzione G() 4 + arcsin π è la primitiva
Esercizi svolti. Si consideri la funzione f() 4. a) Verificare che la funzione F() 4 + arcsin è una primitiva di f() sull intervallo (, ). b) Verificare che la funzione G() 4 + arcsin π è la primitiva
Capitolo 2. Operazione di limite
 Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
FUNZIONE REALE DI UNA VARIABILE
 FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
Pertanto la formula per una prima approssimazione del tasso di rendimento a scadenza fornisce
 A. Peretti Svolgimento dei temi d esame di MDEF A.A. 015/16 1 PROVA CONCLUSIVA DI MATEMATICA per le DECISIONI ECONOMICO-FINANZIARIE Vicenza, 9/01/016 ESERCIZIO 1. Data l obbligazione con le seguenti caratteristiche:
A. Peretti Svolgimento dei temi d esame di MDEF A.A. 015/16 1 PROVA CONCLUSIVA DI MATEMATICA per le DECISIONI ECONOMICO-FINANZIARIE Vicenza, 9/01/016 ESERCIZIO 1. Data l obbligazione con le seguenti caratteristiche:
A i è un aperto in E. i=1
 Proposizione 1. A è aperto se e solo se A c è chiuso. Dimostrazione. = : se x o A c, allora x o A = A o e quindi esiste r > 0 tale che B(x o, r) A; allora x o non può essere di accumulazione per A c. Dunque
Proposizione 1. A è aperto se e solo se A c è chiuso. Dimostrazione. = : se x o A c, allora x o A = A o e quindi esiste r > 0 tale che B(x o, r) A; allora x o non può essere di accumulazione per A c. Dunque
8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica.
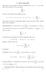 8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica la nuova successione {s n } definita come s 1 = a 1, s 2 = a 1 + a 2, s 3
8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica la nuova successione {s n } definita come s 1 = a 1, s 2 = a 1 + a 2, s 3
Università degli Studi di Catania A.A. 2012-2013. Corso di laurea in Ingegneria Industriale
 Università degli Studi di Catania A.A. 2012-2013 Corso di laurea in Ingegneria Industriale Corso di Analisi Matematica I (A-E) (Prof. A.Villani) Elenco delle dimostrazioni che possono essere richieste
Università degli Studi di Catania A.A. 2012-2013 Corso di laurea in Ingegneria Industriale Corso di Analisi Matematica I (A-E) (Prof. A.Villani) Elenco delle dimostrazioni che possono essere richieste
Funzioni. Parte prima. Daniele Serra
 Funzioni Parte prima Daniele Serra Nota: questi appunti non sostituiscono in alcun modo le lezioni del prof. Favilli, né alcun libro di testo. Sono piuttosto da intendersi a integrazione di entrambi. 1
Funzioni Parte prima Daniele Serra Nota: questi appunti non sostituiscono in alcun modo le lezioni del prof. Favilli, né alcun libro di testo. Sono piuttosto da intendersi a integrazione di entrambi. 1
Serie numeriche e serie di potenze
 Serie numeriche e serie di potenze Sommare un numero finito di numeri reali è senza dubbio un operazione che non può riservare molte sorprese Cosa succede però se ne sommiamo un numero infinito? Prima
Serie numeriche e serie di potenze Sommare un numero finito di numeri reali è senza dubbio un operazione che non può riservare molte sorprese Cosa succede però se ne sommiamo un numero infinito? Prima
Limiti e continuità di funzioni reali di una variabile
 di funzioni reali di una variabile Corso di Analisi Matematica - capitolo VI Facoltà di Economia, UER Maria Caterina Bramati Université Libre de Bruxelles ECARES 22 Novembre 2006 Intuizione di ite di funzione
di funzioni reali di una variabile Corso di Analisi Matematica - capitolo VI Facoltà di Economia, UER Maria Caterina Bramati Université Libre de Bruxelles ECARES 22 Novembre 2006 Intuizione di ite di funzione
Teoria in sintesi 10. Attività di sportello 1, 24 - Attività di sportello 2, 24 - Verifica conclusiva, 25. Teoria in sintesi 26
 Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8. Cognome:... Nome:... Matricola:...
 Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8 Cognome:................ Nome:................ Matricola:................ (Dare una dimostrazione esauriente di tutte le
Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8 Cognome:................ Nome:................ Matricola:................ (Dare una dimostrazione esauriente di tutte le
Proof. Dimostrazione per assurdo. Consideriamo l insieme complementare di P nell insieme
 G Pareschi Principio di induzione Il Principio di Induzione (che dovreste anche avere incontrato nel Corso di Analisi I) consente di dimostrare Proposizioni il cui enunciato è in funzione di un numero
G Pareschi Principio di induzione Il Principio di Induzione (che dovreste anche avere incontrato nel Corso di Analisi I) consente di dimostrare Proposizioni il cui enunciato è in funzione di un numero
Parte 2. Determinante e matrice inversa
 Parte. Determinante e matrice inversa A. Savo Appunti del Corso di Geometria 013-14 Indice delle sezioni 1 Determinante di una matrice, 1 Teorema di Cramer (caso particolare), 3 3 Determinante di una matrice
Parte. Determinante e matrice inversa A. Savo Appunti del Corso di Geometria 013-14 Indice delle sezioni 1 Determinante di una matrice, 1 Teorema di Cramer (caso particolare), 3 3 Determinante di una matrice
Matematica 1 - Corso di Laurea in Ingegneria Meccanica
 Matematica 1 - Corso di Laurea in Ingegneria Meccanica Esercitazione su massimi e minimi vincolati 9 dicembre 005 Esercizio 1. Considerare l insieme C = {(x,y) R : (x + y ) = x } e dire se è una curva
Matematica 1 - Corso di Laurea in Ingegneria Meccanica Esercitazione su massimi e minimi vincolati 9 dicembre 005 Esercizio 1. Considerare l insieme C = {(x,y) R : (x + y ) = x } e dire se è una curva
Basi di matematica per il corso di micro
 Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
4 Dispense di Matematica per il biennio dell Istituto I.S.I.S. Gaetano Filangieri di Frattamaggiore EQUAZIONI FRATTE E SISTEMI DI EQUAZIONI
 119 4 Dispense di Matematica per il biennio dell Istituto I.S.I.S. Gaetano Filangieri di Frattamaggiore EQUAZIONI FRATTE E SISTEMI DI EQUAZIONI Indice degli Argomenti: TEMA N. 1 : INSIEMI NUMERICI E CALCOLO
119 4 Dispense di Matematica per il biennio dell Istituto I.S.I.S. Gaetano Filangieri di Frattamaggiore EQUAZIONI FRATTE E SISTEMI DI EQUAZIONI Indice degli Argomenti: TEMA N. 1 : INSIEMI NUMERICI E CALCOLO
La funzione è continua nel suo dominio perchè y = f(x) è composizione di funzioni continue. Il punto x = 0 è un punto isolato per D f.
 FUNZIONI CONTINUE - ALCUNI ESERCIZI SVOLTI SIMONE ALGHISI 1. Continuità di una funzione Dati un insieme D R, una funzione f : D R e x 0 R, si è detto che f è continua in x 0 se sono soddisfatte le seguenti
FUNZIONI CONTINUE - ALCUNI ESERCIZI SVOLTI SIMONE ALGHISI 1. Continuità di una funzione Dati un insieme D R, una funzione f : D R e x 0 R, si è detto che f è continua in x 0 se sono soddisfatte le seguenti
1 Definizione: lunghezza di una curva.
 Abstract Qui viene affrontato lo studio delle curve nel piano e nello spazio, con particolare interesse verso due invarianti: la curvatura e la torsione Il primo ci dice quanto la curva si allontana dall
Abstract Qui viene affrontato lo studio delle curve nel piano e nello spazio, con particolare interesse verso due invarianti: la curvatura e la torsione Il primo ci dice quanto la curva si allontana dall
+ P a n n=1 + X. a n = a m 3. n=1. m=4. Per poter dare un significato alla somma (formale) di infiniti termini, ricorriamo al seguente procedimento:
 Capitolo 3 Serie 3. Definizione Sia { } una successione di numeri reali. Ci proponiamo di dare significato, quando possibile, alla somma a + a 2 +... + +... di tutti i termini della successione. Questa
Capitolo 3 Serie 3. Definizione Sia { } una successione di numeri reali. Ci proponiamo di dare significato, quando possibile, alla somma a + a 2 +... + +... di tutti i termini della successione. Questa
Quando troncare uno sviluppo in serie di Taylor
 Quando troncare uno sviluppo in serie di Taylor Marco Robutti October 13, 2014 Lo sviluppo in serie di Taylor di una funzione è uno strumento matematico davvero molto utile, e viene spesso utilizzato in
Quando troncare uno sviluppo in serie di Taylor Marco Robutti October 13, 2014 Lo sviluppo in serie di Taylor di una funzione è uno strumento matematico davvero molto utile, e viene spesso utilizzato in
Le derivate versione 4
 Le derivate versione 4 Roberto Boggiani 2 luglio 2003 Riciami di geometria analitica Dalla geometria analitica sulla retta sappiamo ce dati due punti del piano A(x, y ) e B(x 2, y 2 ) con x x 2 la retta
Le derivate versione 4 Roberto Boggiani 2 luglio 2003 Riciami di geometria analitica Dalla geometria analitica sulla retta sappiamo ce dati due punti del piano A(x, y ) e B(x 2, y 2 ) con x x 2 la retta
F (x) = f(x) per ogni x I. Per esempio:
 Funzioni Primitive (Integrali Indefiniti) (l.v.) Pur essendo un argomento che fa parte del Calcolo Differenziale, molti autori inseriscono funzioni primitive nel capitolo sul Calcolo Integrale, in quanto
Funzioni Primitive (Integrali Indefiniti) (l.v.) Pur essendo un argomento che fa parte del Calcolo Differenziale, molti autori inseriscono funzioni primitive nel capitolo sul Calcolo Integrale, in quanto
Successioni e serie di funzioni
 Successioni e serie di funzioni A. Albanese, A. Leaci, D. Pallara In questa dispensa generalizzeremo la trattazione delle successioni e delle serie al caso in cui i termini delle stesse siano non numeri
Successioni e serie di funzioni A. Albanese, A. Leaci, D. Pallara In questa dispensa generalizzeremo la trattazione delle successioni e delle serie al caso in cui i termini delle stesse siano non numeri
Lezione 6 (16/10/2014)
 Lezione 6 (16/10/2014) Esercizi svolti a lezione Esercizio 1. La funzione f : R R data da f(x) = 10x 5 x è crescente? Perché? Soluzione Se f fosse crescente avrebbe derivata prima (strettamente) positiva.
Lezione 6 (16/10/2014) Esercizi svolti a lezione Esercizio 1. La funzione f : R R data da f(x) = 10x 5 x è crescente? Perché? Soluzione Se f fosse crescente avrebbe derivata prima (strettamente) positiva.
Insiemi di livello e limiti in più variabili
 Insiemi di livello e iti in più variabili Insiemi di livello Si consideri una funzione f : A R, con A R n. Un modo per poter studiare il comportamento di una funzione in più variabili potrebbe essere quello
Insiemi di livello e iti in più variabili Insiemi di livello Si consideri una funzione f : A R, con A R n. Un modo per poter studiare il comportamento di una funzione in più variabili potrebbe essere quello
1. PRIME PROPRIETÀ 2
 RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
La curva grafico della funzione, partendo dal punto A(a,f(a)), si snoda con continuità, senza interruzioni, fino ad approdare nel punto B(b,f(b)).
 Calcolo differenziale Il teorema di Rolle TEOREMA DI ROLLE Ipotesi f continua su [a, b] f derivabile per lo meno su (a,b) f(a) = f(b) Tesi Esiste almeno un punto c in (a, b) tale che Giustificazione con
Calcolo differenziale Il teorema di Rolle TEOREMA DI ROLLE Ipotesi f continua su [a, b] f derivabile per lo meno su (a,b) f(a) = f(b) Tesi Esiste almeno un punto c in (a, b) tale che Giustificazione con
CONTINUITÀ E DERIVABILITÀ Esercizi proposti. 1. Determinare lim M(sinx) (M(t) denota la mantissa di t)
 CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
PROBLEMI TRADIZIONALI SIMULAZIONE DELLA PROVA DI MATEMATICA
 Simulazione 01/15 ANNO SCOLASTICO 01/15 PROBLEMI TRADIZIONALI SIMULAZIONE DELLA PROVA DI MATEMATICA DELL ESAME DI STATO PER IL LICEO SCIENTIFICO Il candidato risolva uno dei due problemi Problema 1 Nella
Simulazione 01/15 ANNO SCOLASTICO 01/15 PROBLEMI TRADIZIONALI SIMULAZIONE DELLA PROVA DI MATEMATICA DELL ESAME DI STATO PER IL LICEO SCIENTIFICO Il candidato risolva uno dei due problemi Problema 1 Nella
INTEGRALI DEFINITI. Tale superficie viene detta trapezoide e la misura della sua area si ottiene utilizzando il calcolo di un integrale definito.
 INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
Applicazioni lineari
 Applicazioni lineari Esempi di applicazioni lineari Definizione. Se V e W sono spazi vettoriali, una applicazione lineare è una funzione f: V W tale che, per ogni v, w V e per ogni a, b R si abbia f(av
Applicazioni lineari Esempi di applicazioni lineari Definizione. Se V e W sono spazi vettoriali, una applicazione lineare è una funzione f: V W tale che, per ogni v, w V e per ogni a, b R si abbia f(av
Appunti sul corso di Complementi di Matematica - prof. B.Bacchelli. 03 - Equazioni differenziali lineari omogenee a coefficienti costanti.
 Appunti sul corso di Complementi di Matematica - prof. B.Bacchelli 03 - Equazioni differenziali lineari omogenee a coefficienti costanti. Def. Si dice equazione differenziale lineare del secondo ordine
Appunti sul corso di Complementi di Matematica - prof. B.Bacchelli 03 - Equazioni differenziali lineari omogenee a coefficienti costanti. Def. Si dice equazione differenziale lineare del secondo ordine
4 3 4 = 4 x 10 2 + 3 x 10 1 + 4 x 10 0 aaa 10 2 10 1 10 0
 Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
LEZIONE 7. Esercizio 7.1. Quale delle seguenti funzioni è decrescente in ( 3, 0) e ha derivata prima in 3 che vale 0? x 3 3 + x2. 2, x3 +2x +3.
 7 LEZIONE 7 Esercizio 7.1. Quale delle seguenti funzioni è decrescente in ( 3, 0) e ha derivata prima in 3 che vale 0? x 3 3 + x2 2 6x, x3 +2x 2 6x, 3x + x2 2, x3 +2x +3. Le derivate sono rispettivamente,
7 LEZIONE 7 Esercizio 7.1. Quale delle seguenti funzioni è decrescente in ( 3, 0) e ha derivata prima in 3 che vale 0? x 3 3 + x2 2 6x, x3 +2x 2 6x, 3x + x2 2, x3 +2x +3. Le derivate sono rispettivamente,
Le funzioni continue. A. Pisani Liceo Classico Dante Alighieri A.S. 2002-03. A. Pisani, appunti di Matematica 1
 Le funzioni continue A. Pisani Liceo Classico Dante Alighieri A.S. -3 A. Pisani, appunti di Matematica 1 Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato
Le funzioni continue A. Pisani Liceo Classico Dante Alighieri A.S. -3 A. Pisani, appunti di Matematica 1 Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato
Grafico qualitativo di una funzione reale di variabile reale
 Grafico qualitativo di una funzione reale di variabile reale Mauro Saita 1 Per commenti o segnalazioni di errori scrivere, per favore, a: maurosaita@tiscalinet.it Dicembre 2014 Indice 1 Qualè il grafico
Grafico qualitativo di una funzione reale di variabile reale Mauro Saita 1 Per commenti o segnalazioni di errori scrivere, per favore, a: maurosaita@tiscalinet.it Dicembre 2014 Indice 1 Qualè il grafico
Alcune note sulle serie di potenze 1
 Alcune note sulle serie di potenze Contents G. Falqui Preliminari 2 Serie di potenze 3 3 Rappresentazione di funzioni mediante serie di potenze 7 3. Esempi notevoli........................... 9 3.2 Formula
Alcune note sulle serie di potenze Contents G. Falqui Preliminari 2 Serie di potenze 3 3 Rappresentazione di funzioni mediante serie di potenze 7 3. Esempi notevoli........................... 9 3.2 Formula
11) convenzioni sulla rappresentazione grafica delle soluzioni
 2 PARAGRAFI TRATTATI 1)La funzione esponenziale 2) grafici della funzione esponenziale 3) proprietá delle potenze 4) i logaritmi 5) grafici della funzione logaritmica 6) principali proprietá dei logaritmi
2 PARAGRAFI TRATTATI 1)La funzione esponenziale 2) grafici della funzione esponenziale 3) proprietá delle potenze 4) i logaritmi 5) grafici della funzione logaritmica 6) principali proprietá dei logaritmi
2 Argomenti introduttivi e generali
 1 Note Oltre agli esercizi di questa lista si consiglia di svolgere quelli segnalati o assegnati sul registro e genericamente quelli presentati dal libro come esercizio o come esempio sugli argomenti svolti
1 Note Oltre agli esercizi di questa lista si consiglia di svolgere quelli segnalati o assegnati sul registro e genericamente quelli presentati dal libro come esercizio o come esempio sugli argomenti svolti
4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale
 4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale Spazi Metrici Ricordiamo che uno spazio metrico è una coppia (X, d) dove X è un insieme e d : X X [0, + [ è una funzione, detta metrica,
4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale Spazi Metrici Ricordiamo che uno spazio metrico è una coppia (X, d) dove X è un insieme e d : X X [0, + [ è una funzione, detta metrica,
Serie numeriche. 1 Definizioni e proprietà elementari
 Serie numeriche Definizioni e proprietà elementari Sia { } una successione, definita per ogni numero naturale n n. Per ogni n n, consideriamo la somma s n degli elementi della successione di posto d s
Serie numeriche Definizioni e proprietà elementari Sia { } una successione, definita per ogni numero naturale n n. Per ogni n n, consideriamo la somma s n degli elementi della successione di posto d s
Sulle funzioni di W 1,p (Ω) a traccia nulla
 Sulle funzioni di W 1,p () a traccia nulla Sia u W 1,p (R n ) e supponiamo che il supp u, essendo un aperto di R n. Possiamo approssimare u con una successione di funzioni C il cui supporto è contenuto
Sulle funzioni di W 1,p () a traccia nulla Sia u W 1,p (R n ) e supponiamo che il supp u, essendo un aperto di R n. Possiamo approssimare u con una successione di funzioni C il cui supporto è contenuto
Anelli a fattorizzazione unica. Domini ad ideali principali. Anelli Euclidei
 Capitolo 5: Anelli speciali: Introduzione: Gli anelli speciali sono anelli dotati di ulteriori proprietà molto forti che ne rendono agevole lo studio. Anelli euclidei Domini ad ideali principali Anelli
Capitolo 5: Anelli speciali: Introduzione: Gli anelli speciali sono anelli dotati di ulteriori proprietà molto forti che ne rendono agevole lo studio. Anelli euclidei Domini ad ideali principali Anelli
La distribuzione Normale. La distribuzione Normale
 La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
