Corso di Analisi Matematica. Successioni e serie numeriche
|
|
|
- Leonzio Pesce
- 8 anni fa
- Visualizzazioni
Transcript
1 a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Successioni e serie numeriche Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli studenti. Parte del materiale presentato è tratto dai libri di testo consigliati, la cui consultazione è vivamente incoraggiata. 1 / 60
2 Successioni numeriche Si chiama successione numerica ogni funzione reale definita in un insieme del tipo {n N n n 0 }, con n 0 numero naturale. Esempio: la relazione f (x) = x 2, la relazione f (x) = x 2, x [0, + ), definisce una funzione; x N, definisce una successione. Parlando di successioni, solitamente denotiamo la variabile indipendente con n il valore che la successione assume in un numero naturale n con il simbolo a n (oppure b n, x n,... ), chiamato termine n-esimo della successione l immagine della successione con {a n } n N (oppure {a n }) Il grafico di una successione è costituito da infiniti punti isolati di coordinate (n, a n ), con n N, n n 0. 2 / 60
3 Esempi di successioni numeriche (1) a n = 1 n a_n n 1.2 (2) a n = n 1 n a_n n 3 / 60
4 1 (3) a n = ( 1)n n a_n n (4) a n = ( 1) n a_n n / 60
5 0 n (5) a n = n 2 a_n (6) a n = n! a_n n 5 / 60
6 Prolungamento di una successione Diciamo che una funzione f è un prolungamento della successione {a n } se f è definita nell intervallo [n 0, + ) e si ha f (n) = a n per ogni n n 0. Esempi La funzione f : [1, + ) R tale che f (x) = 1/x è il prolungamento naturale della successione a n = 1/n, ottenuto sostituendo la variabile discreta n con la variabile continua x a_n 0.6 f(x) n x La successione a n = ( 1) n non ammette prolungamento naturale (perché?) ma ammette prolungamento; per esempio, la funzione f : [1, + ) R tale che f (x) = cos(πx). 6 / 60
7 Successioni limitate Dato che ogni successione è una funzione, ha senso parlare di successioni limitate inferiormente limitate superiormente limitate nonché di estremo inferiore ed estremo superiore minimo e massimo di una successione. Esempio Stabilire per ognuna delle successioni (1) (6) se è limitata e determinarne estremo inferiore e superiore, precisando se sono minimo e massimo. 7 / 60
8 Successioni monotone Rileggendo la definizione di funzione monotona nel caso di una successione otteniamo, per esempio, che una successione è crescente se per ogni m, n interi, con m < n, si ha a m a n. In realtà, per verificare se una successione è monotona basta confrontare tra loro termini consecutivi. Precisamente, una successione {a n } è crescente se e solo se a n a n+1 per ogni n strettamente crescente se e solo se a n < a n+1 per ogni n decrescente se e solo se a n a n+1 per ogni n strettamente decrescente se e solo se a n > a n+1 per ogni n Esempio Studiare la monotonia delle successioni (1) (6). 8 / 60
9 Osservazioni Se una funzione prolungamento di una successione è monotona, anche la successione lo è. Vale il viceversa? Si potrebbe erroneamente pensare che la presenza del termine oscillante ( 1) n implichi mancanza di monotonia; non è detto che sia così. Esempio: a n = n + ( 1)n n. Verificare... Per farsi un idea dell andamento di una successione è utile esplicitarne i primi termini; tuttavia, ciò non è sufficiente a stabilire che la successione sia monotona. Esempio: a n = 10n n! Vedi pagina seguente 9 / 60
10 n 10 n 10 n n n! n! (I valori di 10 n n! sono arrotondati alla seconda cifra decimale.) 10 / 60
11 Proprietà vere definitivamente Diciamo che una proprietà P n è vera definitivamente se P n è vera per tutti gli n sufficientemente grandi, cioè se esiste ν N tale che la proprietà P n sia vera per ogni n ν. Esempi I termini della successione {n 5} sono definitivamente positivi. I termini della successione {( 1) n } non sono definitivamente positivi. I termini della successione { } {n 2 } sono definitivamente maggiori di n La successione è definitivamente decrescente. n! Osservazione Se le proprietà P n e P n sono entrambe vere definitivamente, allora anche la proprietà P n P n è vera definitivamente. Spiegare / 60
12 Successioni infinitesime Una successione {a n } di numeri positivi si dice infinitesima se per ogni ε > 0 la disuguaglianza a n < ε è vera definitivamente. Esplicitare... Esempi La successione costante a n 0 è infinitesima. Se p > 0, la successione a n = 1 n p è infinitesima. { } 3n + 1 La successione non è infinitesima. 2n Una successione {a n } di numeri qualsiasi si dice infinitesima se la successione { a n } è infinitesima. Esplicitare... Esempio La successione { } ( 1) n n 2 è infinitesima. 12 / 60
13 Successioni convergenti La successione {a n } si dice convergente se esiste a R tale che la successione {a n a} sia infinitesima. Esplicitare... In tal caso diciamo che {a n } converge ad a. Esempi La successione costante a n a converge ad a. { } n 1 La successione converge a 1. n Osservazione Una successione non può convergere a due numeri distinti. Verifica... Osservazione Ogni successione infinitesima è convergente. A quale numero? 13 / 60
14 Interpretazione grafica Esplicitiamo ulteriormente la definizione della pagina precedente: {a n } converge ad a se per ogni ε > 0 esiste ν ε N tale che la disuguaglianza a ε < a n < a + ε sia vera per ogni n ν ε. Da un punto di vista grafico, la disuguaglianza significa che il punto (n, a n ) si trova nella striscia orizzontale S a,ε delimitata dalle rette di equazione y = a ε e y = a + ε. Pertanto, la successione {a n } converge ad a se e solo se, per ogni ε > 0, il suo grafico è racchiuso nella striscia S a,ε, a partire da un certo punto in poi a_n a_n ε = 0.3 ν ε = 4 ε = 0.15 ν ε = n n 14 / 60
15 Successioni divergenti Si dice che la successione {a n } diverge positivamente se per ogni M > 0 la disuguaglianza a n > M è vera definitivamente. Si dice che la successione {a n } diverge negativamente se per ogni M > 0 la disuguaglianza a n < M è vera definitivamente. Interpretazione grafica? Esempi { } n + 1 La successione non diverge positivamente. n Se p > 0, la successione {n p } diverge positivamente. La successione { ln ( 1 n)} diverge negativamente. 15 / 60
16 Successioni regolari e loro limiti Una successione si dice regolare se è convergente oppure divergente. Una successione non regolare si dice irregolare o indeterminata. Se la successione {a n } è regolare, diciamo che {a n } ha limite e scriviamo a se {a n } è convergente e converge ad a lim a n = + se {a n } diverge positivamente n + se {a n } diverge negativamente si legge: limite per n che tende a più infinito di a n Notazione alternativa: a n l (si legge: a n tende a l) Osservazione Il limite di una successione regolare è un elemento di R. Precisare / 60
17 Esempio (da ricordare) Sia q R. La successione {q n } n N si chiama progressione geometrica di ragione q. (Per q = 0 si pone il primo termine uguale a 1.) Se q 1, la progressione geometrica è irregolare. Se q > 1, la progressione geometrica è regolare e si ha 0 se 1 < q < 1 lim n + qn = 1 se q = 1 + se q > 1 Verifica / 60
18 Proposizione (Limiti e limitatezza) Sia {a n } una successione regolare. {a n } converge = {a n } è limitata {a n } diverge positivamente = {a n } è illimitata superiormente {a n } diverge negativamente = {a n } è illimitata inferiormente Dimostrazione: immediata Osservazione Le implicazioni precedenti non possono essere invertite, in quanto esistono successioni limitate che non convergono, esistono successioni illimitate superiormente che non divergono positivamente, esistono successioni illimitate inferiormente che non divergono negativamente. Esempi? 18 / 60
19 Teorema (Regolarità delle successioni monotone) Ogni successione monotona è regolare. Precisamente: (1) {a n } crescente = lim n + a n = sup a n (2) {a n } decrescente = lim n + a n = inf a n Dimostrazione di (1)... Corollario del teorema RSM Supponiamo che la successione {a n } sia monotona. Allora: {a n } converge {a n } è limitata {a n } diverge {a n } è illimitata Confrontare con la proposizione di pagina / 60
20 Osservazioni La monotonia è una condizione sufficiente ma non necessaria affinché una successione sia regolare. Esempio? Se una successione è definitivamente monotona, essa è regolare; non è detto però che il limite coincida con l estremo superiore [inferiore] se la successione è definitivamente crescente [decrescente]. Il teorema RSM e il suo corollario dipendono dalla proprietà dell estremo superiore e non valgono in Q. In particolare, non è detto che una successione monotona e limitata di numeri razionali abbia limite razionale. Esempi (vedere anche pagina 32) x 1 = 0.1 x 2 = x 3 = x 4 = ( lim ) n =: e n + n numero di Nepero 20 / 60
21 Limiti e operazioni algebriche Teorema (Operazioni con successioni convergenti) Supponiamo a n a R e b n b R. Allora: a n + b n a + b regola della somma a n b n a b regola della differenza λ a n λ a (λ R) regola del multiplo a n b n a b regola del prodotto 1 a n 1 a a n b n a b (a 0) regola del reciproco (b 0) regola del rapporto Dimostrazione della regola della somma e del prodotto / 60
22 Esempi Verificare che le seguenti successioni sono convergenti e determinarne i rispettivi limiti. a n = b n = ( ) n 1 n 4 n ( ) n n n c n = 3 n + 2n 3 n 22 / 60
23 Proposizione (Reciproco di una successione infinitesima) Sia {a n } una successione infinitesima. Allora: {a n } ha segno costante (definitivamente) {a n } non ha segno costante (definitivamente) Verifica... = = { 1 } diverge, a n positivamente o negativamente a seconda del segno di a n { 1 } non ha limite a n Esempi / 60
24 Teorema (Operazioni con successioni divergenti) Siano {a n } e {b n } successioni divergenti. Se le due successioni divergono con lo stesso segno, la successione somma {a n + b n } diverge con lo stesso segno. E la differenza? Se λ 0, la successione multiplo {λ a n } diverge, con lo stesso segno di {a n } se λ > 0, con segno opposto se λ < 0. La successione prodotto {a n b n } diverge, positivamente se le due successioni divergono con lo stesso segno, negativamente se le due successioni divergono con segni opposti. { 1 } La successione reciproco è infinitesima. E il rapporto? a n Verifica... Esempi Calcolare i limiti di {n n }, {n 3 2 n }, { 4n 3 }, { 1 } n n 24 / 60
25 Limiti e relazione d ordine Teorema (Permanenza del segno) Sia {a n } una successione, sia a R e si supponga a n a. (1) a > 0 = a n > 0 definitivamente a < 0 = a n < 0 definitivamente (2) a n 0 definitivamente = a 0 a n 0 definitivamente = a 0 Dimostrazione... Osservazioni Le implicazioni in (1) valgono anche se a = + e a =, rispettivamente. Le conclusioni in (2) sono le stesse anche se si suppone definitivamente a n > 0 e a n < 0, rispettivamente. Esempio? 25 / 60
26 Esercizio Dimostrare la seguente generalizzazione del teorema PS-(2): Siano {a n } e {b n } due successioni e siano a, b R. Allora: a n a b n b = a b. a n b n definitivamente Suggerimento: applicare il teorema PS e la regola della differenza alla successione c n := a n b n. 26 / 60
27 Teorema (Confronto, o convergenza obbligata, o dei Carabinieri) Siano {a n }, {b n }, {c n } tre successioni tali che a n b n c n definitivamente, {a n } e {c n } convergono a uno stesso limite a. Allora: anche {b n } converge ad a. Dimostrazione... Esempi Calcolare il limite delle successioni sin(n), n 3 + ( 1) n n 2, 2 ( 1)n n 2 n 3 Generalizzando: {a n } limitata, {b n } infinitesima = {a n b n } infinitesima { an } {a n } limitata, {b n } divergente = infinitesima b n Perché? 27 / 60
28 Teorema (Divergenza obbligata) Siano {a n } e {b n } successioni tali che a n b n definitivamente. Allora: {a n } diverge positivamente = {b n } diverge positivamente, {b n } diverge negativamente = {a n } diverge negativamente. Dimostrazione: immediata Esempi Calcolare il limite delle successioni n 3 + sin(n), ( 1) n n 4, (n 2 4) (2 + ( 1)n n ), 2n 3 5 cos(n) n Generalizzando: {a n } divergente, {b n } limitata = {a n ± b n } divergente {a n } divergente, {b n } convergente e non infinitesima = {a n b n }, {a n /b n } divergenti Perché? 28 / 60
29 Esempi Calcolare il limite delle successioni (n 3 + n)(2 + cos(n)), 2n 3 5 sin(n) 3 Generalizzando: {a n } divergente, {b n } lontana da 0 = {a n b n }, {a n /b n } divergenti Perché? Esempio Calcolare il limite della successione 2n3 + n 2 5 sin(n) 2 Generalizzando: {a n } divergente {b n } infinitesima con segno costante Perché? n 2 = { an b n } divergente 29 / 60
30 Forme di indecisione Né le regole algebriche né le loro generalizzazioni permettono di determinare a priori il limite nei seguenti casi, che chiamiamo forme di indecisione: differenza di successioni che divergono con lo stesso segno (forma + ) prodotto di una successione infinitesima per una divergente (forma 0 ) rapporto di due successioni divergenti (forma / ) rapporto di due successioni infinitesime (forma 0/0) Le forme di indecisione vengono in genere risolte manipolando algebricamente le espressioni assegnate per ricondursi a successioni alle quali sia possibile applicare le regole algebriche e le loro generalizzazioni. 30 / 60
31 Esempi Per ciascuno dei seguenti limiti, individuare e risolvere la forma di indecisione: ( lim 3n 4 2n 3 n ) arctan(n) ( lim n + n + n 4 n ) n (2n + 1)(n + 2) lim n + 3n 2 + 3n ( ) lim n + 1 n n + lim n + arctan(n) (n 4 n ) + 1 n n n lim n + n! + 3 n??? 31 / 60
32 Successioni definite per ricorrenza (1) Verificare che la successione {a n } definita ponendo a 1 = 1 a n+1 = a n + 1 a 2 n è strettamente crescente e diverge positivamente. (2) Verificare che la successione {a n } definita ponendo a 1 = 2 a n+1 = a n a n è limitata e strettamente decrescente. Determinarne il limite. 32 / 60
33 Serie numeriche Sia {a n } n N una successione di numeri reali. Definiamo la somma parziale (o ridotta) n-esima ponendo S 0 := a 0 S 1 := a 0 + a 1. S n := a 0 + a a n (= n a k ). k=0 In alternativa, per ricorrenza: S 0 := a 0 S n := S n 1 + a n n 1 La successione {S n } si chiama serie di termine a n. Nota Se la successione {a n } è definita solo per n n 0, conveniamo di porre a n = 0 per n < n 0. Ne segue che in quanto diremo non sarà restrittivo supporre che la successione {a n } sia sempre definita per ogni n N. 33 / 60
34 Per definizione, la serie di termine a n non è altro che la successione delle somme parziali S n costruite a partire da a n. Pertanto, la locuzione convergente divergente positivamente la serie di termine a n è divergente negativamente regolare indeterminata equivale alla locuzione convergente la successione delle divergente positivamente somme parziali S n è divergente negativamente costruite a partire da a n regolare indeterminata Se la serie è regolare, il limite della successione {S n } prende il nome di somma della serie e si denota con il simbolo + n=0 a n. Motivazione? 34 / 60
35 Terminologia e osservazioni generali Studiare il carattere di una serie significa stabilire se essa converge, diverge o è indeterminata. Se a n = b n definitivamente, le serie di termine a n e b n hanno lo stesso carattere. Tuttavia, se entrambe convergono, in genere le rispettive somme non sono uguali. Nella pratica si usano i simboli + a n, n=0 per denotare la serie di termine a n, indipendentemente dal fatto che essa sia regolare o no. n a n 35 / 60
36 !!! Attenzione a non confondere la convergenza della serie di termine a n con la convergenza della successione {a n }, la somma della serie con il limite della successione {a n }. Le due nozioni sono legate tramite la seguente Proposizione (Condizione necessaria per la convergenza di una serie) Se la serie di termine a n converge, allora la successione {a n } è infinitesima; l implicazione contraria è falsa. (In altre parole: la condizione a n 0 è necessaria ma non sufficiente per la convergenza della serie di termine a n.) Verifica... Esempi Le serie di termine ( 1) n e n 1 non convergono. n La serie di termine 1 potrebbe convergere; per stabilire se converge n oppure no, occorre indagare ulteriormente. 36 / 60
37 Serie telescopiche Una serie si dice telescopica se il suo termine può essere scritto nella forma a n = b n b n+1, oppure a n = b n+1 b n. In entrambi i casi, la somma parziale n-esima si ottiene facilmente: S n = (b 0 b 1 ) + (b 1 b 2 ) (b n b n+1 ) = b 0 b n+1, oppure S n = (b 1 b 0 ) + (b 2 b 1 ) (b n+1 b n ) = b n+1 b 0. Esempi La serie di termine a n = 1, detta serie di Mengoli, converge e n(n + 1) ha somma uguale a 1. ( La serie di termine a n = ln ) diverge positivamente. n Cf. la proposizione di pagina / 60
38 La serie geometrica Sia q R. Si chiama serie geometrica di ragione q la serie di termine a n = q n, con n 0. (Per q = 0 si pone il primo termine uguale a 1.) Proposizione La serie geometrica di ragione q è indeterminata per q 1; diverge positivamente per q 1; converge per 1 < q < 1 e la sua somma è q ( 1, 1) = Verifica... + n=0 q n = 1 1 q. 1 ; in simboli: 1 q Esempi: studiare il carattere delle serie n ( 1) n ( 3) n n=0 n=1 n=0 4 n + n=2 ( 3) n 4 n 38 / 60
39 Operazioni con le serie Dai teoremi sulle operazioni algebriche per successioni si deducono le seguenti proprietà: Somma di serie Se la serie di termine a n converge e ha somma A e la serie di termine b n converge e ha somma B, la serie di termine a n + b n converge e ha somma A + B. Se la serie di termine a n diverge positivamente e la serie di termine b n converge o diverge positivamente, la serie di termine a n + b n diverge positivamente. Multiplo di serie Se la serie di termine a n converge e ha somma A e λ è una costante, la serie di termine λ a n converge e ha somma λ A. Se la serie di termine a n diverge e λ 0 è una costante, la serie di termine λ a n diverge, positivamente o negativamente a seconda del modo in cui la serie di termine a n diverge e del segno di λ. 39 / 60
40 Esempi La serie La serie La serie + n=1 + n=1 + n=1 ( ( ln ) ) + 2 n n ( ( ) 1 n(n + 1) 3n+1 2 n ) 1 n(n + 1) + 2n 3 n+1 diverge positivamente. diverge negativamente. converge e ha somma 5 3. Nota Sotto opportune condizioni, si può definire il prodotto di due serie (che non è la serie di termine a n b n ); non ce ne occuperemo. 40 / 60
41 Cosa sono i criteri di convergenza e a che servono? Siano S n := n k=1 1 k e T n := n k=1 1 k 2. La seguente tabella mostra i valori (troncati e arrotondati alla quinta cifra decimale) di S n e T n per alcuni valori di n: n S n T n Si intuisce che le serie di termini n e 1 hanno caratteri diversi; n2 per verificarlo attraverso la definizione, occorre determinare l espressione esplicita di S n e T n. Ma come si fa? 41 / 60
42 Problema generale: se non si riesce a scrivere esplicitamente la somma parziale n-esima costruita a partire da una successione a n, non si può applicare la definizione di serie convergente, divergente, indeterminata per stabilire il carattere della serie di termine a n ; ammesso che la serie sia convergente, non è possibile determinarne la somma. Soluzione: si stabilisce il carattere della serie attraverso un argomento indiretto ( criterio ); stabilito che la serie è convergente, si calcola un valore approssimato della somma (mediante una stima del resto ). 42 / 60
43 Resto n-esimo di una serie Supponiamo che la serie di termine a n converga. Siano S n e S, rispettivamente, la somma parziale n-esima e la somma della serie. Definiamo il resto n-esimo: R n := S S n ( = an+1 + a n ) Esso rappresenta l errore che si commette sostituendo alla somma S la somma parziale S n. Osservazione Il resto n-esimo di una serie convergente tende a 0 per n. Esempio Sia q < 1. Il resto n-esimo della serie geometrica di ragione q è + n R n := q n q k = 1 1 q 1 qn+1 = qn+1 1 q 1 q. n=0 k=0 43 / 60
44 Stima del resto n-esimo In generale non siamo in grado di scrivere esplicitamente il resto n-esimo di una serie convergente. In alcuni casi riusciamo però a stimarlo in termini di una quantità nota; ciò è sufficiente ad approssimare la somma della serie convergente commettendo un errore controllato. Precisamente: se per un certo intero N si ha R N α, allora S S N α, ossia S N α S S N + α. Dato che S N è esplicitamente calcolabile, ( ) fornisce un intervallo al quale la somma S, incognita, appartiene. Se riusciamo a stabilire in qualche modo che S N approssima S per difetto [per eccesso], otteniamo una approssimazione migliore di S, cioè un intervallo di ampiezza minore al quale S appartiene: S N S S N + α [S N α S S N ] ( ) 44 / 60
45 Serie a termini positivi La serie di termine a n si dice a termini positivi se a n 0 per ogni n; si dice a termini strettamente positivi se a n > 0 per ogni n. Esempi? Osservazione Sia S n la somma parziale n-esima costruita a partire da una successione a n 0. Risulta: S n = S n 1 + a n S n 1, cioè la successione delle somme parziali {S n } è monotona crescente. Conseguenze: una serie a termini positivi può solo convergere oppure divergere positivamente; (teorema RSM) se la serie converge, la somma parziale S n approssima per difetto la somma S e il resto R n è positivo. 45 / 60
46 Proposizione La serie (a termini positivi) + n=1 1 n p ( ) converge se e solo se p > 1; in tal caso si ha 1 0 R n (p 1)n p 1. Lo dimostreremo in seguito, nel capitolo sul calcolo integrale. Per p = 1 la serie ( ) si chiama serie armonica; per p 1 si chiama serie armonica generalizzata di esponente p. 46 / 60
47 Esercizio Per ciascuna delle seguenti serie, stabilire se essa converge. In caso affermativo, scrivere una maggiorazione del resto n-esimo e utilizzarla per determinare un intero N tale che approssimando la somma della serie con la somma parziale S N si commetta un errore inferiore a (a) + n=1 1 n (c) + n=1 1 n 2 n (b) + n=1 1 n n (d) + n=1 1 n 5 47 / 60
48 Soluzione dell esercizio precedente p carattere stima del resto minimo N S N della serie e condizione per cui vale da imporre la condizione 1 diverge 3/2 converge R n 2 n 1/2 < N = S /2 converge R n 2 3n 3/2 < N = 17 S converge R n 1 4n 4 < N = 3 S / 60
49 Confronto tra gli esercizi (c) e (d): velocità di convergenza 1 n 5/2 1 n 5 n S n stima di R n S n stima di R n / 60
50 Teorema (Criterio del confronto) Siano {a n } e {b n } due successioni tali che 0 a n b n per ogni n ν. Vedremo anche il criterio del confronto asintotico Se la serie di termine b n converge, anche la serie di termine a n converge e si ha + + a n b n ; n=ν n=ν inoltre, detti R n e R n il resto n-esimo della serie di termine a n e b n, rispettivamente, risulta 0 R n R n. Se la serie di termine a n diverge, anche la serie di termine b n diverge. 50 / 60
51 Esempi Stabilire se la serie assegnata converge. In caso affermativo, scrivere una maggiorazione per il resto n-esimo e utilizzarla per calcolare un valore approssimato della somma della serie con un errore inferiore a (a) + n=1 n + ln(n) 2 n n (d) + n=1 ( ) 1 n sin n 4 sin(t) t per ogni t R (b) + n=1 n n (e) + n=1 3 n 2 n n (c) + n=1 n sin(n) 2 5n (f) + n=1 2 n 5 n / 60
52 Digressione: serie numeriche e rappresentazione decimale Ricordiamo che un numero decimale è un espressione della forma ± c 0. c 1 c 2 c 3... ( ) dove c 0 è un intero naturale e c 1, c 2,... {0, 1, 2,..., 8, 9}. Se il numero decimale è infinito, ( ) va intesa come ( ± c 0 + c c c ) ; l espressione tra parentesi è la somma della serie numerica di termine a n := c n 10 n. Questa serie converge? Se il numero decimale è periodico, la somma è un numero razionale? Quale? Verifichiamo (e saldiamo un debito in sospeso, vedi L insieme dei numeri reali ) / 60
53 Serie a segni alterni Teorema (Criterio di Leibniz) Supponiamo che la serie di termine a n sia a segni alterni, cioè che con b n 0. a n = ( 1) n b n, oppure a n = ( 1) n 1 b n = ( 1) n+1 b n, Se la successione {b n } è decrescente e infinitesima, allora la serie di termine a n è convergente. Inoltre, detto R n il resto n-esimo della serie, si ha Idea della dimostrazione... R n b n / 60
54 Esempio (da ricordare!) La serie armonica alternata + ( 1) n 1 1 n = converge. n=1 Esempio Stabilire in base al criterio di Leibniz che la serie + ( 1) n+1 2 n + 1 n=0 converge. Scrivere una maggiorazione per il resto n-esimo e utilizzarla per determinare un intero N tale che la somma parziale S N approssimi la somma S a meno di Stabilire se S N è una approssimazione per eccesso o per difetto di S. Scrivere un intervallo al quale S appartiene. 54 / 60
55 Osservazioni sulle ipotesi del criterio di Leibniz Se le ipotesi b n 0 e b n+1 b n sono soddisfatte definitivamente, ossia per n ν, si può ancora concludere che la serie di termine ( 1) n b n converge. Inoltre, la stima del resto è valida per n ν. Se i termini b n non sono (definitivamente) positivi, oppure la successione {b n } non è (definitivamente) decrescente, il criterio non è applicabile e la serie va studiata con altri strumenti. Se {b n } non è infinitesima, neppure {a n } lo è (perché?) e quindi si può concludere che la serie di termine a n non converge. Per provare la monotonia di {b n } non basta guardare i primi termini! Possibili strategie: ricorrere alla definizione, cioè verificare che la disuguaglianza b n+1 b n è vera (definitivamente), oppure applicare il test di monotonia a una funzione prolungamento di {b n }. lo vedremo in seguito 55 / 60
56 Convergenza assoluta Si dice che la serie di termine a n converge assolutamente se la serie di termine a n converge. Osservazione Per le serie a termini di segno costante la nozione di convergenza assoluta coincide con quella di convergenza. Teorema (Legame tra convergenza e convergenza assoluta) Se la serie di termine a n è convergente, anche la serie di termine a n lo è e si ha + + disuguaglianza triangolare a n a n con infiniti addendi n=0 n=0 Il viceversa non è vero, cioè esistono serie che convergono ma non convergono assolutamente. Esse si chiamano condizionalmente convergenti. Dimostrazione / 60
57 Esempi Stabilire se le serie assegnate sono assolutamente convergenti, condizionalmente convergenti, non convergenti. + n=1 sin(n) n n=1 ( 1) n 1 n Osservazione Per studiare la assoluta convergenza della serie di termine a n possiamo applicare alla serie di termine a n i criteri per le serie a termini positivi (del confronto, già visto; del confronto asintotico e dell integrale, che vedremo). Se, in base a questi criteri, la serie di termine a n non converge, la serie di termine a n potrebbe convergere o meno; ciò va stabilito caso per caso tramite opportune considerazioni. In alcuni casi il carattere della serie può essere determinato tramite il criterio del rapporto. Vedere pagina seguente / 60
58 Teorema (Criterio del rapporto) Sia a n 0 definitivamente e supponiamo che esista (finito o infinito) a n+1 lim =: L. n + a n Se L [0, 1), la serie di termine a n converge assolutamente. Se L (1, + ) {+ }, la serie di termine a n non converge. Dimostrazione... Esempio Studiare la convergenza delle serie + n=1 ( 2) n 3 n + n + n=1 ( 3) n 2 n + n 58 / 60
59 Osservazione Il criterio del rapporto può ovviamente essere applicato anche alle serie a termini positivi. In questo caso, le conclusioni diventano: se L [0, 1), la serie di termine a n converge; se L (1, + ) {+ }, la serie di termine a n diverge positivamente. Esempio: studiare la convergenza delle serie + n=1 2 n e n n + n=1 2 n n 2 + n Osservazione (Caso di indecisione nel criterio del rapporto) Se nel criterio del rapporto è L = 1, non si può concludere nulla sul carattere della serie. Per esempio, per la serie armonica generalizzata 1 si ha L = 1 np indipendentemente da p ; tuttavia, per alcuni valori di p essa converge e per altri diverge. 59 / 60
60 Un criterio per determinare se una successione è infinitesima Corollario del criterio del rapporto Sia {a n } una successione tale che a n 0 definitivamente. Se a n+1 lim < 1, n + a n allora la successione {a n } è infinitesima. Esempi (da ricordare) Le seguenti successioni sono infinitesime: { n p } { a n } a n (p R, a > 1) n! { n p a n} { n p } (p R, a < 1) n! (a R) (p R) { n! n n } Risolviamo la forma di indecisione in sospeso di pagina / 60
Matematica generale CTF
 Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Corso di Analisi Matematica Serie numeriche
 Corso di Analisi Matematica Serie numeriche Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 25 1 Definizione e primi esempi 2 Serie a
Corso di Analisi Matematica Serie numeriche Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 25 1 Definizione e primi esempi 2 Serie a
SUCCESSIONI NUMERICHE
 SUCCESSIONI NUMERICHE Definizione: Si chiama successione numerica una funzione definita su IN a valori in IR, cioè una legge che associa ad ogni intero n un numero reale a n. Per abuso di linguaggio, si
SUCCESSIONI NUMERICHE Definizione: Si chiama successione numerica una funzione definita su IN a valori in IR, cioè una legge che associa ad ogni intero n un numero reale a n. Per abuso di linguaggio, si
u 1 u k che rappresenta formalmente la somma degli infiniti numeri (14.1), ordinati al crescere del loro indice. I numeri u k
 Capitolo 4 Serie numeriche 4. Serie convergenti, divergenti, indeterminate Data una successione di numeri reali si chiama serie ad essa relativa il simbolo u +... + u +... u, u 2,..., u,..., (4.) oppure
Capitolo 4 Serie numeriche 4. Serie convergenti, divergenti, indeterminate Data una successione di numeri reali si chiama serie ad essa relativa il simbolo u +... + u +... u, u 2,..., u,..., (4.) oppure
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria).
 Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica.
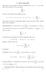 8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica la nuova successione {s n } definita come s 1 = a 1, s 2 = a 1 + a 2, s 3
8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica la nuova successione {s n } definita come s 1 = a 1, s 2 = a 1 + a 2, s 3
Corso di Analisi Matematica. Polinomi e serie di Taylor
 a.a. 2013/14 Laurea triennale in Informatica Corso di Analisi Matematica Polinomi e serie di Taylor Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli
a.a. 2013/14 Laurea triennale in Informatica Corso di Analisi Matematica Polinomi e serie di Taylor Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli
3.1 Successioni. R Definizione (Successione numerica) E Esempio 3.1 CAPITOLO 3
 CAPITOLO 3 Successioni e serie 3. Successioni Un caso particolare di applicazione da un insieme numerico ad un altro insieme numerico è quello delle successioni, che risultano essere definite nell insieme
CAPITOLO 3 Successioni e serie 3. Successioni Un caso particolare di applicazione da un insieme numerico ad un altro insieme numerico è quello delle successioni, che risultano essere definite nell insieme
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE
 LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
SUCCESSIONI NUMERICHE
 SUCCESSIONI NUMERICHE Una funzione reale di una variabile reale f di dominio A è una legge che ad ogni x A associa un numero reale che denotiamo con f(x). Se A = N, la f è detta successione di numeri reali.
SUCCESSIONI NUMERICHE Una funzione reale di una variabile reale f di dominio A è una legge che ad ogni x A associa un numero reale che denotiamo con f(x). Se A = N, la f è detta successione di numeri reali.
1 Serie di Taylor di una funzione
 Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI
 CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
Serie numeriche. 1 Definizioni e proprietà elementari
 Serie numeriche Definizioni e proprietà elementari Sia { } una successione, definita per ogni numero naturale n n. Per ogni n n, consideriamo la somma s n degli elementi della successione di posto d s
Serie numeriche Definizioni e proprietà elementari Sia { } una successione, definita per ogni numero naturale n n. Per ogni n n, consideriamo la somma s n degli elementi della successione di posto d s
CRITERI DI CONVERGENZA PER LE SERIE. lim a n = 0. (1) s n+1 = s n + a n+1. (2) CRITERI PER LE SERIE A TERMINI NON NEGATIVI
 Il criterio più semplice è il seguente. CRITERI DI CONVERGENZA PER LE SERIE Teorema(condizione necessaria per la convergenza). Sia a 0, a 1, a 2,... una successione di numeri reali. Se la serie a k è convergente,
Il criterio più semplice è il seguente. CRITERI DI CONVERGENZA PER LE SERIE Teorema(condizione necessaria per la convergenza). Sia a 0, a 1, a 2,... una successione di numeri reali. Se la serie a k è convergente,
1 Alcuni criteri di convergenza per serie a termini non negativi
 Alcuni criteri di convergenza per serie a termini non negativi (Criterio del rapporto.) Consideriamo la serie a (.) a termini positivi (ossia a > 0, =, 2,...). Supponiamo che esista il seguente ite a +
Alcuni criteri di convergenza per serie a termini non negativi (Criterio del rapporto.) Consideriamo la serie a (.) a termini positivi (ossia a > 0, =, 2,...). Supponiamo che esista il seguente ite a +
Per lo svolgimento del corso risulta particolarmente utile considerare l insieme
 1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
+ P a n n=1 + X. a n = a m 3. n=1. m=4. Per poter dare un significato alla somma (formale) di infiniti termini, ricorriamo al seguente procedimento:
 Capitolo 3 Serie 3. Definizione Sia { } una successione di numeri reali. Ci proponiamo di dare significato, quando possibile, alla somma a + a 2 +... + +... di tutti i termini della successione. Questa
Capitolo 3 Serie 3. Definizione Sia { } una successione di numeri reali. Ci proponiamo di dare significato, quando possibile, alla somma a + a 2 +... + +... di tutti i termini della successione. Questa
SERIE NUMERICHE. prof. Antonio Greco 6-11-2013
 SERIE NUMERICHE prof. Antonio Greco 6--203 Indice Motivazioni........... 3 Definizione........... 3 Errore tipico........... 3 Un osservazione utile...... 3 Condizione necessaria...... 4 Serie armonica.........
SERIE NUMERICHE prof. Antonio Greco 6--203 Indice Motivazioni........... 3 Definizione........... 3 Errore tipico........... 3 Un osservazione utile...... 3 Condizione necessaria...... 4 Serie armonica.........
Corso di Analisi Matematica. Funzioni continue
 a.a. 203/204 Laurea triennale in Informatica Corso di Analisi Matematica Funzioni continue Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli studenti.
a.a. 203/204 Laurea triennale in Informatica Corso di Analisi Matematica Funzioni continue Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli studenti.
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI
 FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
Limiti e continuità delle funzioni reali a variabile reale
 Limiti e continuità delle funzioni reali a variabile reale Roberto Boggiani Versione 4.0 9 dicembre 2003 1 Esempi che inducono al concetto di ite Per introdurre il concetto di ite consideriamo i seguenti
Limiti e continuità delle funzioni reali a variabile reale Roberto Boggiani Versione 4.0 9 dicembre 2003 1 Esempi che inducono al concetto di ite Per introdurre il concetto di ite consideriamo i seguenti
CONCETTO DI LIMITE DI UNA FUNZIONE REALE
 CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
Capitolo 2. Operazione di limite
 Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Serie numeriche e serie di potenze
 Serie numeriche e serie di potenze Sommare un numero finito di numeri reali è senza dubbio un operazione che non può riservare molte sorprese Cosa succede però se ne sommiamo un numero infinito? Prima
Serie numeriche e serie di potenze Sommare un numero finito di numeri reali è senza dubbio un operazione che non può riservare molte sorprese Cosa succede però se ne sommiamo un numero infinito? Prima
Schemi delle Lezioni di Matematica Generale. Pierpaolo Montana
 Schemi delle Lezioni di Matematica Generale Pierpaolo Montana A volte i fenomeni economici che ci interessano non variano con continuitá oppure non possono essere osservati con continuitá, ma solo a intervalli
Schemi delle Lezioni di Matematica Generale Pierpaolo Montana A volte i fenomeni economici che ci interessano non variano con continuitá oppure non possono essere osservati con continuitá, ma solo a intervalli
Teoria in sintesi 10. Attività di sportello 1, 24 - Attività di sportello 2, 24 - Verifica conclusiva, 25. Teoria in sintesi 26
 Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
Appunti di Analisi Matematica 1. Docente: Klaus Engel. Università degli Studi dell Aquila Facoltà di Ingegneria A.A. 2011/12
 Appunti di Analisi Matematica Docente: Klaus Engel Università degli Studi dell Aquila Facoltà di Ingegneria A.A. / http://univaq.it/~engel ( = %7E) (Versione del 4 dicembre ) Note scritte in collaborazione
Appunti di Analisi Matematica Docente: Klaus Engel Università degli Studi dell Aquila Facoltà di Ingegneria A.A. / http://univaq.it/~engel ( = %7E) (Versione del 4 dicembre ) Note scritte in collaborazione
I appello - 26 Gennaio 2007
 Facoltà di Ingegneria - Corso di Laurea in Ing. Informatica e delle Telecom. A.A.006/007 I appello - 6 Gennaio 007 Risolvere gli esercizi motivando tutte le risposte. (N.B. il quesito teorico è obbligatorio)
Facoltà di Ingegneria - Corso di Laurea in Ing. Informatica e delle Telecom. A.A.006/007 I appello - 6 Gennaio 007 Risolvere gli esercizi motivando tutte le risposte. (N.B. il quesito teorico è obbligatorio)
10. Insiemi non misurabili secondo Lebesgue.
 10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
l insieme Y è detto codominio (è l insieme di tutti i valori che la funzione può assumere)
 Che cos è una funzione? Assegnati due insiemi X e Y si ha una funzione elemento di X uno e un solo elemento di Y. f : X Y se esiste una corrispondenza che associa ad ogni Osservazioni: l insieme X è detto
Che cos è una funzione? Assegnati due insiemi X e Y si ha una funzione elemento di X uno e un solo elemento di Y. f : X Y se esiste una corrispondenza che associa ad ogni Osservazioni: l insieme X è detto
Le funzioni continue. A. Pisani Liceo Classico Dante Alighieri A.S. 2002-03. A. Pisani, appunti di Matematica 1
 Le funzioni continue A. Pisani Liceo Classico Dante Alighieri A.S. -3 A. Pisani, appunti di Matematica 1 Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato
Le funzioni continue A. Pisani Liceo Classico Dante Alighieri A.S. -3 A. Pisani, appunti di Matematica 1 Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato
Insiemi di livello e limiti in più variabili
 Insiemi di livello e iti in più variabili Insiemi di livello Si consideri una funzione f : A R, con A R n. Un modo per poter studiare il comportamento di una funzione in più variabili potrebbe essere quello
Insiemi di livello e iti in più variabili Insiemi di livello Si consideri una funzione f : A R, con A R n. Un modo per poter studiare il comportamento di una funzione in più variabili potrebbe essere quello
1. Distribuzioni campionarie
 Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 3 e 6 giugno 2013 - di Massimo Cristallo - 1. Distribuzioni campionarie
Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 3 e 6 giugno 2013 - di Massimo Cristallo - 1. Distribuzioni campionarie
INTEGRALI DEFINITI. Tale superficie viene detta trapezoide e la misura della sua area si ottiene utilizzando il calcolo di un integrale definito.
 INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
CONTINUITÀ E DERIVABILITÀ Esercizi risolti
 CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
Università degli Studi di Catania A.A. 2012-2013. Corso di laurea in Ingegneria Industriale
 Università degli Studi di Catania A.A. 2012-2013 Corso di laurea in Ingegneria Industriale Corso di Analisi Matematica I (A-E) (Prof. A.Villani) Elenco delle dimostrazioni che possono essere richieste
Università degli Studi di Catania A.A. 2012-2013 Corso di laurea in Ingegneria Industriale Corso di Analisi Matematica I (A-E) (Prof. A.Villani) Elenco delle dimostrazioni che possono essere richieste
Applicazioni del calcolo differenziale allo studio delle funzioni
 Capitolo 9 9.1 Crescenza e decrescenza in piccolo; massimi e minimi relativi Sia y = f(x) una funzione definita nell intervallo A; su di essa non facciamo, per ora, alcuna particolare ipotesi (né di continuità,
Capitolo 9 9.1 Crescenza e decrescenza in piccolo; massimi e minimi relativi Sia y = f(x) una funzione definita nell intervallo A; su di essa non facciamo, per ora, alcuna particolare ipotesi (né di continuità,
3 GRAFICI DI FUNZIONI
 3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
Alcuni complementi sulle successioni
 Alcuni complementi sulle successioni 1 (Teorema del confronto) Siano {a n } e {b n } due successioni regolari tali che si abbia a n b n n N. (1) Allora: a n b n. (2) Dim. Sia L = a n ed L = b n. Se L =
Alcuni complementi sulle successioni 1 (Teorema del confronto) Siano {a n } e {b n } due successioni regolari tali che si abbia a n b n n N. (1) Allora: a n b n. (2) Dim. Sia L = a n ed L = b n. Se L =
5. La teoria astratta della misura.
 5. La teoria astratta della misura. 5.1. σ-algebre. 5.1.1. σ-algebre e loro proprietà. Sia Ω un insieme non vuoto. Indichiamo con P(Ω la famiglia di tutti i sottoinsiemi di Ω. Inoltre, per ogni insieme
5. La teoria astratta della misura. 5.1. σ-algebre. 5.1.1. σ-algebre e loro proprietà. Sia Ω un insieme non vuoto. Indichiamo con P(Ω la famiglia di tutti i sottoinsiemi di Ω. Inoltre, per ogni insieme
Una ricetta per il calcolo dell asintoto obliquo. Se f(x) è asintotica a mx+q allora abbiamo f(x) mx q = o(1), da cui (dividendo per x) + o(1), m =
 Una ricetta per il calcolo dell asintoto obliquo Se f() è asintotica a m+q allora abbiamo f() m q = o(1), da cui (dividendo per ) m = f() q + 1 f() o(1) = + o(1), mentre q = f() m = o(1). Dunque si ha
Una ricetta per il calcolo dell asintoto obliquo Se f() è asintotica a m+q allora abbiamo f() m q = o(1), da cui (dividendo per ) m = f() q + 1 f() o(1) = + o(1), mentre q = f() m = o(1). Dunque si ha
Sulla monotonia delle funzioni reali di una variabile reale
 Liceo G. B. Vico - Napoli Sulla monotonia delle funzioni reali di una variabile reale Prof. Giuseppe Caputo Premetto due teoremi come prerequisiti necessari per la comprensione di quanto verrà esposto
Liceo G. B. Vico - Napoli Sulla monotonia delle funzioni reali di una variabile reale Prof. Giuseppe Caputo Premetto due teoremi come prerequisiti necessari per la comprensione di quanto verrà esposto
Docente: Anna Valeria Germinario. Università di Bari. A.V.Germinario (Università di Bari) Analisi Matematica ITPS 1 / 22
 Laurea in Informatica e Tecnologie per la Produzione del Software Corso di Analisi Matematica Calcolo differenziale e approssimazioni, formula di Taylor Docente: Anna Valeria Germinario Università di Bari
Laurea in Informatica e Tecnologie per la Produzione del Software Corso di Analisi Matematica Calcolo differenziale e approssimazioni, formula di Taylor Docente: Anna Valeria Germinario Università di Bari
Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata, Matematica
 DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
Limiti e continuità di funzioni reali di una variabile
 di funzioni reali di una variabile Corso di Analisi Matematica - capitolo VI Facoltà di Economia, UER Maria Caterina Bramati Université Libre de Bruxelles ECARES 22 Novembre 2006 Intuizione di ite di funzione
di funzioni reali di una variabile Corso di Analisi Matematica - capitolo VI Facoltà di Economia, UER Maria Caterina Bramati Université Libre de Bruxelles ECARES 22 Novembre 2006 Intuizione di ite di funzione
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
CONTINUITÀ E DERIVABILITÀ Esercizi proposti. 1. Determinare lim M(sinx) (M(t) denota la mantissa di t)
 CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
Esercizi di Analisi Matematica I
 Esercizi di Analisi Matematica I Andrea Corli e Alessia Ascanelli gennaio 9 Indice Introduzione iii Nozioni preliminari. Fattoriali e binomiali..................................... Progressioni..........................................
Esercizi di Analisi Matematica I Andrea Corli e Alessia Ascanelli gennaio 9 Indice Introduzione iii Nozioni preliminari. Fattoriali e binomiali..................................... Progressioni..........................................
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI
 APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
Capitolo 2. Serie Numeriche
 Capitolo 2 Serie Numeriche Iniziamo ricordando la nozione di successione e le operazioni definibili tra successioni. Questo permetterà di poter definire, con una certa semplicità la nozione di somma infinita
Capitolo 2 Serie Numeriche Iniziamo ricordando la nozione di successione e le operazioni definibili tra successioni. Questo permetterà di poter definire, con una certa semplicità la nozione di somma infinita
Esponenziali elogaritmi
 Esponenziali elogaritmi Potenze ad esponente reale Ricordiamo che per un qualsiasi numero razionale m n prendere n>0) si pone a m n = n a m (in cui si può sempre a patto che a sia un numero reale positivo.
Esponenziali elogaritmi Potenze ad esponente reale Ricordiamo che per un qualsiasi numero razionale m n prendere n>0) si pone a m n = n a m (in cui si può sempre a patto che a sia un numero reale positivo.
19. Inclusioni tra spazi L p.
 19. Inclusioni tra spazi L p. Nel n. 15.1 abbiamo provato (Teorema 15.1.1) che, se la misura µ è finita, allora tra i corispondenti spazi L p (µ) si hanno le seguenti inclusioni: ( ) p, r ]0, + [ : p
19. Inclusioni tra spazi L p. Nel n. 15.1 abbiamo provato (Teorema 15.1.1) che, se la misura µ è finita, allora tra i corispondenti spazi L p (µ) si hanno le seguenti inclusioni: ( ) p, r ]0, + [ : p
risulta (x) = 1 se x < 0.
 Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
SIMULAZIONE TEST ESAME - 1
 SIMULAZIONE TEST ESAME - 1 1. Il dominio della funzione f(x) = log (x2 + 1)(4 x 2 ) (x 2 2x + 1) è: (a) ( 2, 2) (b) ( 2, 1) (1, 2) (c) (, 2) (2, + ) (d) [ 2, 1) (1, 2] (e) R \{1} 2. La funzione f : R R
SIMULAZIONE TEST ESAME - 1 1. Il dominio della funzione f(x) = log (x2 + 1)(4 x 2 ) (x 2 2x + 1) è: (a) ( 2, 2) (b) ( 2, 1) (1, 2) (c) (, 2) (2, + ) (d) [ 2, 1) (1, 2] (e) R \{1} 2. La funzione f : R R
Equazioni alle differenze finite (cenni).
 AL 011. Equazioni alle differenze finite (cenni). Sia a n } n IN una successione di numeri reali. (Qui usiamo la convenzione IN = 0, 1,,...}). Diremo che è una successione ricorsiva o definita per ricorrenza
AL 011. Equazioni alle differenze finite (cenni). Sia a n } n IN una successione di numeri reali. (Qui usiamo la convenzione IN = 0, 1,,...}). Diremo che è una successione ricorsiva o definita per ricorrenza
Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8. Cognome:... Nome:... Matricola:...
 Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8 Cognome:................ Nome:................ Matricola:................ (Dare una dimostrazione esauriente di tutte le
Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8 Cognome:................ Nome:................ Matricola:................ (Dare una dimostrazione esauriente di tutte le
Esame di Analisi Matematica prova scritta del 23 settembre 2013
 Esame di Analisi Matematica prova scritta del 23 settembre 2013 1. Determinare dominio, limiti significativi, intervalli di monotonia della funzione f (x) = (2x + 3) 2 e x/2 e tracciarne il grafico. In
Esame di Analisi Matematica prova scritta del 23 settembre 2013 1. Determinare dominio, limiti significativi, intervalli di monotonia della funzione f (x) = (2x + 3) 2 e x/2 e tracciarne il grafico. In
Parte 2. Determinante e matrice inversa
 Parte. Determinante e matrice inversa A. Savo Appunti del Corso di Geometria 013-14 Indice delle sezioni 1 Determinante di una matrice, 1 Teorema di Cramer (caso particolare), 3 3 Determinante di una matrice
Parte. Determinante e matrice inversa A. Savo Appunti del Corso di Geometria 013-14 Indice delle sezioni 1 Determinante di una matrice, 1 Teorema di Cramer (caso particolare), 3 3 Determinante di una matrice
4 3 4 = 4 x 10 2 + 3 x 10 1 + 4 x 10 0 aaa 10 2 10 1 10 0
 Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Slide Cerbara parte1 5. Le distribuzioni teoriche
 Slide Cerbara parte1 5 Le distribuzioni teoriche I fenomeni biologici, demografici, sociali ed economici, che sono il principale oggetto della statistica, non sono retti da leggi matematiche. Però dalle
Slide Cerbara parte1 5 Le distribuzioni teoriche I fenomeni biologici, demografici, sociali ed economici, che sono il principale oggetto della statistica, non sono retti da leggi matematiche. Però dalle
11) convenzioni sulla rappresentazione grafica delle soluzioni
 2 PARAGRAFI TRATTATI 1)La funzione esponenziale 2) grafici della funzione esponenziale 3) proprietá delle potenze 4) i logaritmi 5) grafici della funzione logaritmica 6) principali proprietá dei logaritmi
2 PARAGRAFI TRATTATI 1)La funzione esponenziale 2) grafici della funzione esponenziale 3) proprietá delle potenze 4) i logaritmi 5) grafici della funzione logaritmica 6) principali proprietá dei logaritmi
COGNOME e NOME: FIRMA: MATRICOLA:
 Anno Accademico 04/ 05 Corsi di Analisi Matematica I Proff. A. Villani, R. Cirmi e F. Faraci) Prova d Esame del giorno 6 febbraio 05 Prima prova scritta compito A) Non sono consentiti formulari, appunti,
Anno Accademico 04/ 05 Corsi di Analisi Matematica I Proff. A. Villani, R. Cirmi e F. Faraci) Prova d Esame del giorno 6 febbraio 05 Prima prova scritta compito A) Non sono consentiti formulari, appunti,
MATEMATICA. { 2 x =12 y 3 y +8 x =0, si pone il problema di trovare, se esistono, un numero x ed un numero y che risolvano entrambe le equazioni.
 MATEMATICA. Sistemi lineari in due equazioni due incognite. Date due equazioni lineari nelle due incognite x, y come ad esempio { 2 x =12 y 3 y +8 x =0, si pone il problema di trovare, se esistono, un
MATEMATICA. Sistemi lineari in due equazioni due incognite. Date due equazioni lineari nelle due incognite x, y come ad esempio { 2 x =12 y 3 y +8 x =0, si pone il problema di trovare, se esistono, un
Alcune nozioni di base di Logica Matematica
 Alcune nozioni di base di Logica Matematica Ad uso del corsi di Programmazione I e II Nicola Galesi Dipartimento di Informatica Sapienza Universitá Roma November 1, 2007 Questa é una breve raccolta di
Alcune nozioni di base di Logica Matematica Ad uso del corsi di Programmazione I e II Nicola Galesi Dipartimento di Informatica Sapienza Universitá Roma November 1, 2007 Questa é una breve raccolta di
EQUAZIONI DIFFERENZIALI. 1. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x 2 log t (d) x = e t x log x (e) y = y2 5y+6
 EQUAZIONI DIFFERENZIALI.. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x log t (d) x = e t x log x (e) y = y 5y+6 (f) y = ty +t t +y (g) y = y (h) xy = y (i) y y y = 0 (j) x = x (k)
EQUAZIONI DIFFERENZIALI.. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x log t (d) x = e t x log x (e) y = y 5y+6 (f) y = ty +t t +y (g) y = y (h) xy = y (i) y y y = 0 (j) x = x (k)
Limiti di Successione
 Nicola Rossi Limiti di Successione Argomento di Portfolio IX Ciclo SSIS, Classe A049, Indirizzo F.I.M. A.A. 2008/2009 2 Introduzione Il concetto di limite è senza dubbio uno dei più importanti di tutta
Nicola Rossi Limiti di Successione Argomento di Portfolio IX Ciclo SSIS, Classe A049, Indirizzo F.I.M. A.A. 2008/2009 2 Introduzione Il concetto di limite è senza dubbio uno dei più importanti di tutta
Funzione reale di variabile reale
 Funzione reale di variabile reale Siano A e B due sottoinsiemi non vuoti di. Si chiama funzione reale di variabile reale, di A in B, una qualsiasi legge che faccia corrispondere, a ogni elemento A x A
Funzione reale di variabile reale Siano A e B due sottoinsiemi non vuoti di. Si chiama funzione reale di variabile reale, di A in B, una qualsiasi legge che faccia corrispondere, a ogni elemento A x A
21. Studio del grafico di una funzione: esercizi
 1. Studio del grafico di una funzione: esercizi Esercizio 1.6. Studiare ciascuna delle seguenti funzioni in base allo schema di pagina 194, eseguendo anche il computo della derivata seconda e lo studio
1. Studio del grafico di una funzione: esercizi Esercizio 1.6. Studiare ciascuna delle seguenti funzioni in base allo schema di pagina 194, eseguendo anche il computo della derivata seconda e lo studio
Le equazioni. Diapositive riassemblate e rielaborate da prof. Antonio Manca da materiali offerti dalla rete.
 Le equazioni Diapositive riassemblate e rielaborate da prof. Antonio Manca da materiali offerti dalla rete. Definizione e caratteristiche Chiamiamo equazione l uguaglianza tra due espressioni algebriche,
Le equazioni Diapositive riassemblate e rielaborate da prof. Antonio Manca da materiali offerti dalla rete. Definizione e caratteristiche Chiamiamo equazione l uguaglianza tra due espressioni algebriche,
Lezioni di Matematica 1 - I modulo
 Lezioni di Matematica 1 - I modulo Luciano Battaia 16 ottobre 2008 Luciano Battaia - http://www.batmath.it Matematica 1 - I modulo. Lezione del 16/10/2008 1 / 13 L introduzione dei numeri reali si può
Lezioni di Matematica 1 - I modulo Luciano Battaia 16 ottobre 2008 Luciano Battaia - http://www.batmath.it Matematica 1 - I modulo. Lezione del 16/10/2008 1 / 13 L introduzione dei numeri reali si può
FUNZIONI / ESERCIZI SVOLTI
 ANALISI MATEMATICA I - A.A. 0/0 FUNZIONI / ESERCIZI SVOLTI ESERCIZIO. Data la funzione f () = determinare l insieme f (( +)). Svolgimento. Poiché f (( +)) = { dom f : f () ( +)} = { dom f : f () > } si
ANALISI MATEMATICA I - A.A. 0/0 FUNZIONI / ESERCIZI SVOLTI ESERCIZIO. Data la funzione f () = determinare l insieme f (( +)). Svolgimento. Poiché f (( +)) = { dom f : f () ( +)} = { dom f : f () > } si
Proof. Dimostrazione per assurdo. Consideriamo l insieme complementare di P nell insieme
 G Pareschi Principio di induzione Il Principio di Induzione (che dovreste anche avere incontrato nel Corso di Analisi I) consente di dimostrare Proposizioni il cui enunciato è in funzione di un numero
G Pareschi Principio di induzione Il Principio di Induzione (che dovreste anche avere incontrato nel Corso di Analisi I) consente di dimostrare Proposizioni il cui enunciato è in funzione di un numero
Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R
 Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Quesiti di Analisi Matematica A
 Quesiti di Analisi Matematica A Presentiamo una raccolta di quesiti per la preparazione alla prova orale del modulo di Analisi Matematica A. Per una buona preparazione é consigliabile rispondere ad alta
Quesiti di Analisi Matematica A Presentiamo una raccolta di quesiti per la preparazione alla prova orale del modulo di Analisi Matematica A. Per una buona preparazione é consigliabile rispondere ad alta
Funzioni. Parte prima. Daniele Serra
 Funzioni Parte prima Daniele Serra Nota: questi appunti non sostituiscono in alcun modo le lezioni del prof. Favilli, né alcun libro di testo. Sono piuttosto da intendersi a integrazione di entrambi. 1
Funzioni Parte prima Daniele Serra Nota: questi appunti non sostituiscono in alcun modo le lezioni del prof. Favilli, né alcun libro di testo. Sono piuttosto da intendersi a integrazione di entrambi. 1
La Programmazione Lineare
 4 La Programmazione Lineare 4.1 INTERPRETAZIONE GEOMETRICA DI UN PROBLEMA DI PROGRAMMAZIONE LINEARE Esercizio 4.1.1 Fornire una rappresentazione geometrica e risolvere graficamente i seguenti problemi
4 La Programmazione Lineare 4.1 INTERPRETAZIONE GEOMETRICA DI UN PROBLEMA DI PROGRAMMAZIONE LINEARE Esercizio 4.1.1 Fornire una rappresentazione geometrica e risolvere graficamente i seguenti problemi
Il concetto di valore medio in generale
 Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
2 FUNZIONI REALI DI VARIABILE REALE
 2 FUNZIONI REALI DI VARIABILE REALE 2.1 CONCETTO DI FUNZIONE Definizione 2.1 Siano A e B due insiemi. Una funzione (o applicazione) f con dominio A a valori in B è una legge che associa ad ogni elemento
2 FUNZIONI REALI DI VARIABILE REALE 2.1 CONCETTO DI FUNZIONE Definizione 2.1 Siano A e B due insiemi. Una funzione (o applicazione) f con dominio A a valori in B è una legge che associa ad ogni elemento
x 1 + x 2 3x 4 = 0 x1 + x 2 + x 3 = 0 x 1 + x 2 3x 4 = 0.
 Problema. Sia W il sottospazio dello spazio vettoriale R 4 dato da tutte le soluzioni dell equazione x + x 2 + x = 0. (a. Sia U R 4 il sottospazio dato da tutte le soluzioni dell equazione Si determini
Problema. Sia W il sottospazio dello spazio vettoriale R 4 dato da tutte le soluzioni dell equazione x + x 2 + x = 0. (a. Sia U R 4 il sottospazio dato da tutte le soluzioni dell equazione Si determini
Capitolo 1 ANALISI COMPLESSA
 Capitolo 1 ANALISI COMPLESSA 1 1.4 Serie in campo complesso 1.4.1 Serie di potenze Una serie di potenze è una serie del tipo a k (z z 0 ) k. Per le serie di potenze in campo complesso valgono teoremi analoghi
Capitolo 1 ANALISI COMPLESSA 1 1.4 Serie in campo complesso 1.4.1 Serie di potenze Una serie di potenze è una serie del tipo a k (z z 0 ) k. Per le serie di potenze in campo complesso valgono teoremi analoghi
Criterio del rapporto. Sia n a n una successione in [0, + ) ]0, + ) ]0, 1[ Criterio del rapporto. Sia n a n una successione in ]0, + ).
![Criterio del rapporto. Sia n a n una successione in [0, + ) ]0, + ) ]0, 1[ Criterio del rapporto. Sia n a n una successione in ]0, + ). Criterio del rapporto. Sia n a n una successione in [0, + ) ]0, + ) ]0, 1[ Criterio del rapporto. Sia n a n una successione in ]0, + ).](/thumbs/39/18159842.jpg) Criterio del rapporto. Si una successione in IR [0, + ) ]0, + ) ]0, [ Criterio del rapporto. Si una successione in ]0, + ). Se esiste k [0, ] ]0, [ [0, [ ]0, ] Criterio del rapporto. Si una successione
Criterio del rapporto. Si una successione in IR [0, + ) ]0, + ) ]0, [ Criterio del rapporto. Si una successione in ]0, + ). Se esiste k [0, ] ]0, [ [0, [ ]0, ] Criterio del rapporto. Si una successione
G. Pareschi ALGEBRE DI BOOLE. 1. Algebre di Boole
 G. Pareschi ALGEBRE DI BOOLE 1. Algebre di Boole Nel file precedente abbiamo incontrato la definizione di algebra di Boole come reticolo: un algebra di Boole e un reticolo limitato, complementato e distributivo.
G. Pareschi ALGEBRE DI BOOLE 1. Algebre di Boole Nel file precedente abbiamo incontrato la definizione di algebra di Boole come reticolo: un algebra di Boole e un reticolo limitato, complementato e distributivo.
Intorni Fissato un punto sull' asse reale, si definisce intorno del punto, un intervallo aperto contenente e tutto contenuto in
 Intorni Fissato un punto sull' asse reale, si definisce intorno del punto, un intervallo aperto contenente e tutto contenuto in Solitamente si fa riferimento ad intorni simmetrici =, + + Definizione: dato
Intorni Fissato un punto sull' asse reale, si definisce intorno del punto, un intervallo aperto contenente e tutto contenuto in Solitamente si fa riferimento ad intorni simmetrici =, + + Definizione: dato
f(x) = 1 x. Il dominio di questa funzione è il sottoinsieme proprio di R dato da
 Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
1. PRIME PROPRIETÀ 2
 RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
FUNZIONE REALE DI UNA VARIABILE
 FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
Convessità e derivabilità
 Convessità e derivabilità Definizione 1 (convessità per funzioni derivabili) Sia f : (a, b) R derivabile su (a, b). Diremo che f è convessa o concava su (a, b) se per ogni 0 (a,b) il grafico di f sta tutto
Convessità e derivabilità Definizione 1 (convessità per funzioni derivabili) Sia f : (a, b) R derivabile su (a, b). Diremo che f è convessa o concava su (a, b) se per ogni 0 (a,b) il grafico di f sta tutto
Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 2011/2012
 Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 211/212 Ricordare: una funzione lipschitziana tra spazi metrici manda insiemi limitati in insiemi limitati; se il dominio di una funzione
Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 211/212 Ricordare: una funzione lipschitziana tra spazi metrici manda insiemi limitati in insiemi limitati; se il dominio di una funzione
x 2 + y2 4 = 1 x = cos(t), y = 2 sin(t), t [0, 2π] Al crescere di t l ellisse viene percorsa in senso antiorario.
![x 2 + y2 4 = 1 x = cos(t), y = 2 sin(t), t [0, 2π] Al crescere di t l ellisse viene percorsa in senso antiorario. x 2 + y2 4 = 1 x = cos(t), y = 2 sin(t), t [0, 2π] Al crescere di t l ellisse viene percorsa in senso antiorario.](/thumbs/39/18585741.jpg) Le soluzioni del foglio 2. Esercizio Calcolare il lavoro compiuto dal campo vettoriale F = (y + 3x, 2y x) per far compiere ad una particella un giro dell ellisse 4x 2 + y 2 = 4 in senso orario... Soluzione.
Le soluzioni del foglio 2. Esercizio Calcolare il lavoro compiuto dal campo vettoriale F = (y + 3x, 2y x) per far compiere ad una particella un giro dell ellisse 4x 2 + y 2 = 4 in senso orario... Soluzione.
SUCCESSIONI E SERIE NUMERICHE
 Prof Lonzi Marco Dispense per il Corso di ANALISI MATEMATICA SUCCESSIONI E SERIE NUMERICHE AA 2015/16 1 SUCCESSIONI Dicesi Successione a valori reali ogni funzione 0À Ä, avente cioè per dominio l'insieme
Prof Lonzi Marco Dispense per il Corso di ANALISI MATEMATICA SUCCESSIONI E SERIE NUMERICHE AA 2015/16 1 SUCCESSIONI Dicesi Successione a valori reali ogni funzione 0À Ä, avente cioè per dominio l'insieme
Applicazioni lineari
 Applicazioni lineari Esempi di applicazioni lineari Definizione. Se V e W sono spazi vettoriali, una applicazione lineare è una funzione f: V W tale che, per ogni v, w V e per ogni a, b R si abbia f(av
Applicazioni lineari Esempi di applicazioni lineari Definizione. Se V e W sono spazi vettoriali, una applicazione lineare è una funzione f: V W tale che, per ogni v, w V e per ogni a, b R si abbia f(av
Indice. 1 Introduzione alle Equazioni Differenziali 1 1.1 Esempio introduttivo... 1 1.2 Nomenclatura e Teoremi di Esistenza ed Unicità...
 Indice 1 Introduzione alle Equazioni Differenziali 1 1.1 Esempio introduttivo............................. 1 1.2 Nomenclatura e Teoremi di Esistenza ed Unicità.............. 5 i Capitolo 1 Introduzione
Indice 1 Introduzione alle Equazioni Differenziali 1 1.1 Esempio introduttivo............................. 1 1.2 Nomenclatura e Teoremi di Esistenza ed Unicità.............. 5 i Capitolo 1 Introduzione
2.1 Definizione di applicazione lineare. Siano V e W due spazi vettoriali su R. Un applicazione
 Capitolo 2 MATRICI Fra tutte le applicazioni su uno spazio vettoriale interessa esaminare quelle che mantengono la struttura di spazio vettoriale e che, per questo, vengono dette lineari La loro importanza
Capitolo 2 MATRICI Fra tutte le applicazioni su uno spazio vettoriale interessa esaminare quelle che mantengono la struttura di spazio vettoriale e che, per questo, vengono dette lineari La loro importanza
Esami d Analisi Matematica 1. Filippo De Mari e Marina Venturino
 Esami d Analisi Matematica 1 Filippo De Mari e Marina Venturino Indice Parte 1. ANNO ACCADEMICO 1999-000 5 1. Corso di Studi in Ingegneria Meccanica 5 Parte. ANNO ACCADEMICO 001-00 15 1. Corso di Studi
Esami d Analisi Matematica 1 Filippo De Mari e Marina Venturino Indice Parte 1. ANNO ACCADEMICO 1999-000 5 1. Corso di Studi in Ingegneria Meccanica 5 Parte. ANNO ACCADEMICO 001-00 15 1. Corso di Studi
Basi di matematica per il corso di micro
 Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
ESERCITAZIONI DI ANALISI 1 FOGLIO 1 FOGLIO 2 FOGLIO 3 FOGLIO 4 FOGLIO 5 FOGLIO 6 FOGLIO 7 SVOLTI. Marco Pezzulla
 ESERCITAZIONI DI ANALISI FOGLIO FOGLIO FOGLIO 3 FOGLIO 4 FOGLIO 5 FOGLIO 6 FOGLIO 7 SVOLTI Marco Pezzulla gennaio 05 FOGLIO. Determinare il dominio e il segno della funzione ( ) f(x) arccos x x + π/3.
ESERCITAZIONI DI ANALISI FOGLIO FOGLIO FOGLIO 3 FOGLIO 4 FOGLIO 5 FOGLIO 6 FOGLIO 7 SVOLTI Marco Pezzulla gennaio 05 FOGLIO. Determinare il dominio e il segno della funzione ( ) f(x) arccos x x + π/3.
Calcolo differenziale Test di autovalutazione
 Test di autovalutazione 1. Sia f : R R iniettiva, derivabile e tale che f(1) = 3, f (1) = 2, f (3) = 5. Allora (a) (f 1 ) (3) = 1 5 (b) (f 1 ) (3) = 1 2 (c) (f 1 ) (1) = 1 2 (d) (f 1 ) (1) = 1 3 2. Sia
Test di autovalutazione 1. Sia f : R R iniettiva, derivabile e tale che f(1) = 3, f (1) = 2, f (3) = 5. Allora (a) (f 1 ) (3) = 1 5 (b) (f 1 ) (3) = 1 2 (c) (f 1 ) (1) = 1 2 (d) (f 1 ) (1) = 1 3 2. Sia
Esercizi svolti. 1. Si consideri la funzione f(x) = 4 x 2. a) Verificare che la funzione F(x) = x 2 4 x2 + 2 arcsin x è una primitiva di
 Esercizi svolti. Si consideri la funzione f() 4. a) Verificare che la funzione F() 4 + arcsin è una primitiva di f() sull intervallo (, ). b) Verificare che la funzione G() 4 + arcsin π è la primitiva
Esercizi svolti. Si consideri la funzione f() 4. a) Verificare che la funzione F() 4 + arcsin è una primitiva di f() sull intervallo (, ). b) Verificare che la funzione G() 4 + arcsin π è la primitiva
2. Leggi finanziarie di capitalizzazione
 2. Leggi finanziarie di capitalizzazione Si chiama legge finanziaria di capitalizzazione una funzione atta a definire il montante M(t accumulato al tempo generico t da un capitale C: M(t = F(C, t C t M
2. Leggi finanziarie di capitalizzazione Si chiama legge finanziaria di capitalizzazione una funzione atta a definire il montante M(t accumulato al tempo generico t da un capitale C: M(t = F(C, t C t M
La funzione è continua nel suo dominio perchè y = f(x) è composizione di funzioni continue. Il punto x = 0 è un punto isolato per D f.
 FUNZIONI CONTINUE - ALCUNI ESERCIZI SVOLTI SIMONE ALGHISI 1. Continuità di una funzione Dati un insieme D R, una funzione f : D R e x 0 R, si è detto che f è continua in x 0 se sono soddisfatte le seguenti
FUNZIONI CONTINUE - ALCUNI ESERCIZI SVOLTI SIMONE ALGHISI 1. Continuità di una funzione Dati un insieme D R, una funzione f : D R e x 0 R, si è detto che f è continua in x 0 se sono soddisfatte le seguenti
