Parallelogrammi, trapezi e poligoni regolari
|
|
|
- Raffaella Cirillo
- 9 anni fa
- Просмотров:
Транскрипт
1 CAPITOLO 5 Paraeogrammi, trapezi e poigoni regoari 1. I PARALLELOGRAMMI CON GEOGEBRA Esercitazione 1. Costruire un paraeogramma dati tre vertici consecutivi Per risovere questo probema usiamo a definizione di paraeogramma; i passi dea costruzione sono i seguenti: 1. si disegnano tre punti A, B, C ne piano eucideo 2. si costruisce a retta che passa per A e B 3. si costruisce a retta che passa per B e C 4. da A si traccia a paraea ad BC 5. da C si traccia a paraea ad AB 6. si trova i punto D di intersezione dee rette ai punti 4. e si disegna i poigono ABCD. Ma quanti paraeogrammi possiamo costruire con tre punti? Otre a queo trovato, che eá stato costruito a partire da vertice B, ne esistono atri due percheâ possiamo ripetere a stessa costruzione a partire da vertice A oppure da vertice C. Otteniamo cosõá i paraeogrammi ABCD, ABEC, ACBF. Dunque, a meno di fissare 'ordine con cui si devono susseguire e ettere: tre punti non aineati definiscono sempre tre paraeogrammi. Poiche eá di uso frequente a costruzione di un paraeogramma noti tre dei suoi vertici, conviene memorizzare a costruzione in uno strumento, come abbiamo fatto per i trasporto di un segmento. Ricordiamo a procedura: attiviamo i comando Strumenti/Crea nuovo strumento indichiamo come oggetti finai i quarto vertice e i paraeogramma (attenzione a'ordine dei punti) Q Re Fraschini - Grazzi, Atas SpA Tema 5 - Cap. 5: PARALLELOGRAMMI, TRAPEZI E POLIGONI REGOLARI 1
2 indichiamo come oggetti iniziai i tre punti diamo nome paraeogramma tre vertici ao strumento e saviamo in un fie. Esercitazione 2. Dividere un segmento in n parti congruenti Dividere un segmento in 2 parti congruenti significa trovare i suo punto medio, dividere in 4 parti significa trovare i punto medio di ciascuno dei segmenti individuati, dividere in 8 parti significa trovare i punto medio di ciascuno dei segmenti ottenuti ne caso precedente; in sostanza se n eá una potenza di 2 i probema non presenta particoari difficotaá percheâ si appica piuá vote i concetto di punto medio. Dividere un segmento in un numero di parti che non eá una potenza de 2 comporta una procedura diversa che appica i teorema dea corrispondenza di Taete; questa procedura ha comunque carattere generae e si puoá appicare per un n quasiasi, quindi anche una potenza de 2. Per eseguira ci serviremo deo strumento di trasporto dei segmenti che deve quindi essere reso disponibie aprendo i fie corrispondente da menu Fie/Apri. Disegniamo dunque un segmento AB e supponiamo di voero dividere in 5 parti congruenti; i passi sono i seguenti: 1. disegniamo un segmento PQ (per questioni di visuaizzazione de'immagine non deve essere troppo ungo); 2. disegniamo una semiretta r avente origine in A; 3. trasportiamo i segmento PQ su r in modo che i primo estremo sia in A; 4. ripetiamo i trasporto atre quattro vote scegiendo come primo estremo ogni vota 'utimo punto disegnato; 5. da'utimo punto ottenuto su r tracciamo a retta s che passa per B; 6. da ciascuno dei punti estremi dei segmenti trasportati tracciamo a paraea aa retta s; 7. determiniamo i punti di intersezione con i segmento AB di ciascuna retta de fascio di paraee costruito; 8. usando o strumento 3-Segmento tra due punti tracciamo i segmenti in cui AB rimane suddiviso (eventuamente modifichiamo i coore di questi segmenti per renderi piuá visibii). EÁ adesso possibie verificare con o strumento 10-Reazione tra due oggetti che i cinque segmenti ottenuti sono congruenti. In questa costruzione i segmento AB e a semiretta r rappresentano e due trasversai de fascio di rette paraee; avendo disegnato segmenti congruenti su r, anche quei individuati su segmento AB o sono. 2. I PARALLELOGRAMMI CON CABRI Un paraeogramma puoá essere costruito se si conoscono acuni eementi; vediamo i casi principai e memorizziamo e costruzioni in una macro in modo da potere poi utiizzare. Esercitazione 1. Sono noti i centro di simmetria e due vertici consecutivi Disegna tre punti ne fogio di avoro e chiama A e B i due vertici, O i centro di simmetria che, come sappiamo, eá i punto di intersezione dee diagonai. Con o strumento Simmetria centrae trova adesso i simmetrici dei punti A e B rispetto ad O e, con o strumen- 2 Tema 5 - Cap. 5: PARALLELOGRAMMI, TRAPEZI E POLIGONI REGOLARI Q Re Fraschini - Grazzi, Atas SpA
3 to Poigono de'icona Rette costruisci i poigono che ha per vertici i punti A e B ed i oro simmetrici (ricorda che devi chiudere i poigono ciccando aa fine su primo punto). Memorizza adesso a costruzione in una macro; ricordiamo a procedura: scegi Oggetti iniziai da'icona Macro e seeziona i tre punti A, B, O scegi Oggetti finai e seeziona i paraeogramma scegi Definizione dea macro e competa a finestra ricordando di inserire i messaggio di aiuto che descrive a macro nea casea di testo Messaggio di aiuto e di spuntare a casea Sava come fie (assegna aa macro i nome Paraeogramma centro e vertici). Dopo aver confermato con OK, dai i nome a fie e memorizzao nea ibreria. Esercitazione 2. Sono noti tre vertici Disegna tre punti ne fogio di avoro e chiamai A, B, C; per costruire i paraeogramma che i ha come vertici, devi prima trovare i quarto vertice D. Osserviamo subito che i probema ha piuá di una souzione percheâ esistono tre paraeogrammi che hanno vertici nei punti dati (osserva a figura 1); eá quindi necessario indicare quae sia 'ordine con cui devono essere presi i punti. Supponiamo che i paraeogramma che dobbiamo disegnare sia ABCD (gi atri due sono ACBD e BACD); a procedura da seguire eá sempice e si basa sua proprietaá dei paraeogrammi di avere i ati opposti paraei: traccia dapprima e semirette BA e BC traccia da A a paraea r aa semiretta BC traccia da C a paraea s aa semiretta AB trova i punto di intersezione dee due rette r e s e chiamao D disegna i poigono ABCD. Memorizza a costruzione in una macro (i tre punti sono gi Oggetti iniziai, i paraeogramma eá 'Oggetto finae, dai nome Paraeogramma tre vertici aa macro). Ricordati poi che, quando a usi per disegnare un paraeogramma, verranno uniti con dei segmenti i primo punto con i secondo e i secondo punto con i terzo. Prova dunque a costruire i tre paraeogrammi dea figura 1: per disegnare i paraeogramma ABCD indica ne'ordine i punti A, B, C per disegnare i paraeogramma ACBD indica ne'ordine i punti A, C, B per disegnare i paraeogramma BACD indica ne'ordine i punti B, A, C. Figura 1 ESERCIZI 1. Costruisci un paraeogramma ABCD, prendi un punto S su ato AB ed un punto T su ato CD in modo che AS CT; verifica che SBTD eá un paraeogramma. Q Re Fraschini - Grazzi, Atas SpA Tema 5 - Cap. 5: PARALLELOGRAMMI, TRAPEZI E POLIGONI REGOLARI 3
4 2. Disegna: a. un rettangoo note e unghezze dei suoi ati b. un rombo note e sue diagonai c. un quadrato nota a unghezza de suo ato. 3. Disegna un paraeogramma e traccia i segmento che unisce i punti medi di due ati opposti; verifica che tae segmento eá congruente agi atri due ati de paraeogramma. 4. Dopo aver disegnato un paraeogramma, trova i punto O di intersezione dee sue diagonai; verifica che ogni segmento che passa per O e che ha gi estremi sui ati de paraeogramma ha O come punto medio. 5. Due paraeogrammi hanno un ato in comune e si trovano in semipiani opposti rispetto a tae ato; verifica che anche i quadriatero che si ottiene congiungendo i vertici non comuni eá un paraeogramma. 6. Dopo aver disegnato un quadriatero quasiasi, trova i punti medi dei suoi ati e costruisci i quadriatero che i ha come vertici; verifica che tae quadriatero eá un paraeogramma. 7. Dopo aver costruito un rombo: a. verifica che e sue diagonai sono bisettrici degi angoi; b. traccia e bisettrici degi angoi formati dae diagonai e determina i oro punti di intersezione con i ati de rombo; c. verifica che tai punti sono i vertici di un quadrato. 8. Un segmento AB eá a base di un trapezio ABCD, rettangoo in A e D, de quae eá data 'ampiezza de'angoo di vertice B e a misura dea base minore CD. Trova una procedura per costruire tae trapezio. 9. Disegna: a. un trapezio quasiasi b. un trapezio isoscee e verifica che gi angoi adiacenti ae due basi sono congruenti c. un trapezio rettangoo. 10. Dati tre segmenti, disegna un trapezio isoscee in modo che due di essi siano e basi e i terzo ato sia i ato obiquo. 11. Disegna un triangoo ABC e prendi un punto P su ato AC; traccia a retta PM, dove M eá i punto medio de ato BC e indica con Q i punto di intersezione dea retta PM con a retta de ato AB. Stabiisci quando i punto Q esiste e quando non esiste motivando a tua risposta in base ae conoscenze acquisite in questo capitoo. 12. Disegna un paraeogramma ABCD di centro O e indica con M i punto medio de ato AB e con N i punto medio de ato CD; trova i punto D 0 simmetrico de vertice D rispetto a M e i punto A 0 simmetrico di A rispetto a N. Verifica che: a. i punti A 0, C, B, D 0 sono aineati b. i punti M, O, N sono aineati c. i quadriateri ADBD 0 e ACA 0 D sono paraeogrammi. 13. Costruisci un quadrato e trova una procedura per circoscrivere ad esso un atro quadrato che abbia un ato paraeo aa diagonae de primo. 14. Disegna un rombo ABCD edaiverticib e D traccia e rette paraee aa diagonae AC. Sua paraea per B prendi due punti P e Q simmetrici rispetto a B e sua paraea per D due punti simmetrici R e S rispetto a D. a. Verifica che i quadriatero convesso di vertici P, Q, S, R eá un trapezio isoscee. b. Stabiisci come devono essere presi i punti P, Q, S, R in modo che i quadriatero sia un rettangoo oppure un quadrato. 4 Tema 5 - Cap. 5: PARALLELOGRAMMI, TRAPEZI E POLIGONI REGOLARI Q Re Fraschini - Grazzi, Atas SpA
5 1 Un giardino quadrato di 20m di ato viene innaffiato con irrigatori puntiformi.ciascun irrigatore innaffia tutti i punti che distano da esso a piuá 10 metri.qua eá i minimo numero di irrigatori necessario per innaffiare tutto i giardino? a. 1 b. 2 c. 4 d. 4 e. 5 d: Š 2 In un frutteto rettangoare c'eá un abero ogni 4 metri (come in figura).sapendo che ci sono 391 aberi, quanto misura i perimetro de rettangoo che ha per vertici i punti in cui ci sono gi aberi A, B, C, D? a. 136m b. 208m c. 304m d. 320m e. non si puoá determinare univocamente c: Š 3 Nea figura a fianco i rettangoi (tutti uguai) hanno atezza a ebaseb.i perimetro dea figura a. eá 15a 15b b. eá 10a 10b c. eá 15a 30b d. eá 30a 30b e. non eá nessuno dei precedenti b: Š 4 ABCD eá un quadrato ed EBC eá un triangoo equiatero.qua eá 'ampiezza in gradi de'angoo AED? d a. 120 b. 135 c. 150 d. 160 e. nessuno dei precedenti c: Š 5 Nea figura 'angoo DCE d vae 70 e ABCD e DEFG sono quadrati uguai.l'angoo convesso ADG d vae: a. 110 b. 120 c. 130 d. 140 e. 160 d: Š La parete dea camera Camia e Leo sono due gemei; frequentano a stessa scuoa, in cassi diverse, ma hanno a stessa insegnante di matematica.e' pomeriggio e da quache ora Camia si eá chiusa nea sua camera; suo frateo, che si trova nea stanza a fianco, sente strani rumori e, incuriosito, apre uno spiragio nea camera di sua sorea. Q Re Fraschini - Grazzi, Atas SpA Tema 5 - Cap. 5: PARALLELOGRAMMI, TRAPEZI E POLIGONI REGOLARI 5
6 Leo: Camia: Leo: Camia: "Camia, ma che cosa diavoo stai facendo?" "Ho ridipinto una parete dea mia camera usando i teoremi di geometria studiati a scuoa". "Ma sei fuori di testa? Guarda che se vai avanti cosõá ti fisso un appuntamento con o psicoogo". "Ma dai, non sono diventata matta.e' soo che non mi piaceva piuá a parete dietro a mio etto tutta bianca e ho cominciato a tirare quache riga su un fogio per vedere se mi veniva quacosa di carino. Dai vieni a vedere che cosa ho fatto". Leo apre a porta ed entra in camera senza evare gi occhi daa parete che sta di fronte a etto. Camia: "Aora, che cosa ne dici?" Leo: "Beo, mi sembra originae.invece dei soiti fiori, nuvoe e farfae, hai usato dei disegni geometrici, anche i coori mi piacciono, danno un senso di aegria.ma che cosa c'entra con i teoremi sui paraeogrammi?" Camia: "E' percheâ tu non guardi mai con attenzione; vieni che ti faccio vedere". EcosõÁ Camia comincia a indicare inee e figure e a spiegare quai teoremi ha usato per costruire que disegno.per riuscire a seguire i discorso dea nostra amica dobbiamo mettere dee ettere sua parete dipinta; osserva aora a figura e giustifica e affermazioni degi esercizi che seguono tenendo presente i teoremi che hai studiato, ma soprattutto gi esercizi che hai fatto. 1 Osserva i paraeogrammi inscritti ne rettangoo che abbiamo staccato con un tratteggio nea parte in ato a sinistra dea parete; essi hanno tutti o stesso perimetro. 2 Neo stesso rettangoo a parte centrae in azzurro, che eá data da'intersezione di tutti i paraeogrammi eá un rombo. 3 Nea parte superiore di destra si individuano i triangoi isoscei ABC, BDE, BFG e acuni paraeogrammi; a caratteristica di questi paraeogrammi eá che i oro perimetro eá uguae aa somma dei ati congruenti dei triangoi a cui si riferiscono. 4 I triangoo isoscee ACM ha a caratteristica di avere a base CM che eá congruente a'atezza uscente da vertice A.Quanto eá ungo i ato de quadrato inscritto ne triangoo? Che cosa si ottiene unendo i punti medi dei ati di questo quadrato? 5 Osserviamo adesso a parte in basso a sinistra reativa a triangoo PQR ne quae PN eá a mediana.i segmento che esce da vertice Q e passa per i punto medio di PN interseca i ato PR in un punto S. Che caratteristiche ha questo punto? 6 Guardiamo da utimo a parte in basso a destra dove eá raffigurato i rombo APRM di centro O; per costruire a figura interna, Camia ha mandato da O e perpendicoari ai ati de rombo.che figura ha ottenuto e percheâ? 1 I ati dei paraeogrammi sono paraei ae diagonai de rettangoo; i perimetri sono tutti i doppio di una diagonae 2 I vertici dei paraeogrammi sono simmetrici rispetto agi assi di simmetria de rettangoo 3 Per esempio DE AD AC 4 ` 1 2 CM; un atro quadrato 5 divide PR in modo che SR 2PS 6 Un rettangoo, diagonai congruenti di centro O 6 Tema 5 - Cap. 5: PARALLELOGRAMMI, TRAPEZI E POLIGONI REGOLARI Q Re Fraschini - Grazzi, Atas SpA
I primi elementi e i triangoli
 MATEMATICAperTUTTI I triangoi 1 ESERCIZIO SVOLTO I primo criterio di congruenza. I confronto fra figure geometriche è un operazione che ricorre spesso in geometria, speciamente i confronto fra triangoi.
MATEMATICAperTUTTI I triangoi 1 ESERCIZIO SVOLTO I primo criterio di congruenza. I confronto fra figure geometriche è un operazione che ricorre spesso in geometria, speciamente i confronto fra triangoi.
CONOSCENZE 1. il concetto di parallelismo e. e perpendicolari. 2. la proiezione di un segmento
 GEOMETRIA PREREQUISITI conoscere e caratteristiche de sistema decimae conoscere e proprietaá dee quattro operazioni e operare con esse operare con e misure angoari conoscere gi enti dea geometria e e oro
GEOMETRIA PREREQUISITI conoscere e caratteristiche de sistema decimae conoscere e proprietaá dee quattro operazioni e operare con esse operare con e misure angoari conoscere gi enti dea geometria e e oro
Parallelogrammi e trapezi 1
 Paraeogrammi e trapezi riconoscere un paraeogramma e individuarne e proprietaá riconoscere paraeogrammi particoari e individuarne e proprietaá riconoscere trapezi e individuarne e proprietaá individuare
Paraeogrammi e trapezi riconoscere un paraeogramma e individuarne e proprietaá riconoscere paraeogrammi particoari e individuarne e proprietaá riconoscere trapezi e individuarne e proprietaá individuare
GEOMETRIA PIANA. Legenda: l = lato. a, b, c = dimensioni d1, d2 oppure d, D = diagonali 2P = perimetro r = raggio π (pi greco) = 3,14 b
 GEOMETRIA PIANA Legenda: A = area h = atezza = ato = ase o ase minore B = ase maggiore a,, c = dimensioni d1, d oppure d, D = diagonai P = perimetro r = raggio π (pi greco) = 3,14 d a A P d h r B D d c
GEOMETRIA PIANA Legenda: A = area h = atezza = ato = ase o ase minore B = ase maggiore a,, c = dimensioni d1, d oppure d, D = diagonai P = perimetro r = raggio π (pi greco) = 3,14 d a A P d h r B D d c
MAPPA 1 FIGURE. Figure geometriche: idee, misure, strumenti. Figure geometriche Una figura geometrica è un insieme di punti.
 MPP 1 Figure Figure geometriche Una figura geometrica è un insieme di punti. Figure piane e figure soide Una figura i cui punti appartengono tutti ao stesso piano si chiama piana. Una figura i cui punti
MPP 1 Figure Figure geometriche Una figura geometrica è un insieme di punti. Figure piane e figure soide Una figura i cui punti appartengono tutti ao stesso piano si chiama piana. Una figura i cui punti
VERIFICA DI GEOMETRIA
 NOME...T... VERIFI I GEOMETRI 1) Indica con una crocetta se vero o faso: I trapezi anno tutti i ati opposti paraei. I paraeogrammi anno i ati opposti uguai e paraei. Un triangoo equiatero è un poigono
NOME...T... VERIFI I GEOMETRI 1) Indica con una crocetta se vero o faso: I trapezi anno tutti i ati opposti paraei. I paraeogrammi anno i ati opposti uguai e paraei. Un triangoo equiatero è un poigono
Le funzioni goniometriche
 CAPITOLO 1 MATEMATICA PER LA FISICA Le funzioni goniometriche Obiettivi definire e funzioni goniometriche fondamentai in riferimento ai triangoi rettangoi e aa circonferenza goniometrica risovere triangoi
CAPITOLO 1 MATEMATICA PER LA FISICA Le funzioni goniometriche Obiettivi definire e funzioni goniometriche fondamentai in riferimento ai triangoi rettangoi e aa circonferenza goniometrica risovere triangoi
Il piano cartesiano, la retta e le funzioni di proporzionalità
 MATEMATICAperTUTTI I piano cartesiano, a retta e e funzioni di proporzionaità ESERCIZIO SVOLTO I piano cartesiano. Per fissare un sistema di riferimento ne piano si considerano due rette orientate fra
MATEMATICAperTUTTI I piano cartesiano, a retta e e funzioni di proporzionaità ESERCIZIO SVOLTO I piano cartesiano. Per fissare un sistema di riferimento ne piano si considerano due rette orientate fra
Parallelismo e perpendicolaritaá nel piano
 CAPITOLO 3 Paraeismo e perpendicoaritaá ne piano 1. L'UTILIZZO DEGLI SLIDER E IL PARALLELISMO CON GEOGEBRA Uno sider eá un numero, oppure un angoo, i cui vaore puoá variare in un fissato intervao a, bš
CAPITOLO 3 Paraeismo e perpendicoaritaá ne piano 1. L'UTILIZZO DEGLI SLIDER E IL PARALLELISMO CON GEOGEBRA Uno sider eá un numero, oppure un angoo, i cui vaore puoá variare in un fissato intervao a, bš
Triangolo rettangolo
 Triangoo rettangoo Le paroe dea matematica Cateto minore C i ipotenusa C1 Cateto maggiore Verificiamo i teorema di Pitagora Enunciato: In un triangoo rettangoo area de quadrato costruito su ipotenusa è
Triangoo rettangoo Le paroe dea matematica Cateto minore C i ipotenusa C1 Cateto maggiore Verificiamo i teorema di Pitagora Enunciato: In un triangoo rettangoo area de quadrato costruito su ipotenusa è
I poligoni e la circonferenza
 CAPITOLO 2 I poigoni e a circonferenza 1. POLIGONI INSCRITTI E CIRCOSCRITTI CON GEOGEBRA Esercitazione 1. I teoremi sui quadriateri con GeoGebra Facciamo a seguente costruzione: disegniamo un triangoo
CAPITOLO 2 I poigoni e a circonferenza 1. POLIGONI INSCRITTI E CIRCOSCRITTI CON GEOGEBRA Esercitazione 1. I teoremi sui quadriateri con GeoGebra Facciamo a seguente costruzione: disegniamo un triangoo
1. LA PARABOLA CON GEOGEBRA
 1. LA PARABOLA CON GEOGEBRA Dopo aver avviato i programma, chiudiamo a Vista Agebra, togiamo gi assi cartesiani e a grigia da quea grafica in modo da avorare iniziamente ne piano eucideo. Affrontiamo poi
1. LA PARABOLA CON GEOGEBRA Dopo aver avviato i programma, chiudiamo a Vista Agebra, togiamo gi assi cartesiani e a grigia da quea grafica in modo da avorare iniziamente ne piano eucideo. Affrontiamo poi
Luoghi di punti e funzioni non lineari
 CAPITOLO 3 Luoghi di punti e funzioni non ineari 1. LE FUNZIONI NON LINEARI CON DERIVE Per costruire i grafico di una paraboa o di un'iperboe si usa a stessa procedura usata per a retta: si scrive 'equazione
CAPITOLO 3 Luoghi di punti e funzioni non ineari 1. LE FUNZIONI NON LINEARI CON DERIVE Per costruire i grafico di una paraboa o di un'iperboe si usa a stessa procedura usata per a retta: si scrive 'equazione
Costruzioni geometriche. (Teoria pag , esercizi )
 Costruzioni geometriche. (Teoria pag. 81-96, esercizi 141-153 ) 1) Costruzione con squadra e riga. a) Rette parallele. Ricorda: due rette sono parallele quando.... oppure quando hanno la stessa. Matematicamente
Costruzioni geometriche. (Teoria pag. 81-96, esercizi 141-153 ) 1) Costruzione con squadra e riga. a) Rette parallele. Ricorda: due rette sono parallele quando.... oppure quando hanno la stessa. Matematicamente
Costruzioni geometriche. ( Teoria pag , esercizi 141 )
 Costruzioni geometriche. ( Teoria pag. 81-96, esercizi 141 ) 1) Costruzione con squadra e riga. a) Rette parallele. Ricorda ; due rette sono parallele quando.... oppure quando hanno la stessa. Matematicamente
Costruzioni geometriche. ( Teoria pag. 81-96, esercizi 141 ) 1) Costruzione con squadra e riga. a) Rette parallele. Ricorda ; due rette sono parallele quando.... oppure quando hanno la stessa. Matematicamente
1 La traslazione. 2 La composizione di traslazioni. 3 La rotazione
 1 La traslazione Per poter applicare una traslazione ad una generica figura geometrica si deve: ± creare il vettore di traslazione AB mediante il comando Vettore tra due punti; ± cliccare con il mouse
1 La traslazione Per poter applicare una traslazione ad una generica figura geometrica si deve: ± creare il vettore di traslazione AB mediante il comando Vettore tra due punti; ± cliccare con il mouse
Lunghezza della circonferenza e area del cerchio
 3 GEMETRI Lunghezza dea circonferenza e area de cerchio Esercizi suppementari di verifica Esercizio 1 Metti una crocetta su vero (V) o faso (F) accanto ad ogni formua reativa aa unghezza dea circonferenza
3 GEMETRI Lunghezza dea circonferenza e area de cerchio Esercizi suppementari di verifica Esercizio 1 Metti una crocetta su vero (V) o faso (F) accanto ad ogni formua reativa aa unghezza dea circonferenza
Figure piane. Due figure sono congruenti se sovrapposte coincidono perfettamente. figure a contorno mistilineo
 Figure piane poigoni cerci figure a contorno curviineo figure a contorno mistiineo I due poigoni sono congruenti I due cerci non sono congruenti ue figure sono congruenti se sovrapposte coincidono perfettamente
Figure piane poigoni cerci figure a contorno curviineo figure a contorno mistiineo I due poigoni sono congruenti I due cerci non sono congruenti ue figure sono congruenti se sovrapposte coincidono perfettamente
Grafici di particolari funzioni lineari
 A Grafici di particoari funzioni ineari Vogiamo tracciare i grafico dea funzione y ˆ jxj. x quando x 0 Sappiamo che jxj significa x quando x < 0 Possiamo aora riscrivere 'equazione di questa funzione in
A Grafici di particoari funzioni ineari Vogiamo tracciare i grafico dea funzione y ˆ jxj. x quando x 0 Sappiamo che jxj significa x quando x < 0 Possiamo aora riscrivere 'equazione di questa funzione in
Cap 1. I PRIMI ELEMENTI
 Cap 1. I PRIMI ELEMENTI Rivedi a teoria I termini primitivi In quasiasi discipina non si puoá definire tutto e non si puoá dimostrare tutto; eá necessario introdurre acuni oggetti (termini primitivi) e
Cap 1. I PRIMI ELEMENTI Rivedi a teoria I termini primitivi In quasiasi discipina non si puoá definire tutto e non si puoá dimostrare tutto; eá necessario introdurre acuni oggetti (termini primitivi) e
I quadrilateri Punti notevoli di un triangolo
 I quadrilateri Capitolo Quadrilateri 1 erifica per la classe prima COGME............................... ME............................. Quesiti 1.a ero o falso? 1. La somma degli angoli interni di un ottagono
I quadrilateri Capitolo Quadrilateri 1 erifica per la classe prima COGME............................... ME............................. Quesiti 1.a ero o falso? 1. La somma degli angoli interni di un ottagono
LA GEOMETRIA NELLO SPAZIO
 LA GEOMETRIA NELLO SPAZIO n.1 Un eemento primitivo: o spazio. Lo spazio è caratterizzato dai seguenti assiomi: Lo spazio contiene infiniti punti, infinite rette, infiniti piani. Ogni piano divide o spazio
LA GEOMETRIA NELLO SPAZIO n.1 Un eemento primitivo: o spazio. Lo spazio è caratterizzato dai seguenti assiomi: Lo spazio contiene infiniti punti, infinite rette, infiniti piani. Ogni piano divide o spazio
Cap 1. LA CIRCONFERENZA
 Cap 1. LA CIRCONERENZA Rivedi a teoria I uoghi geometrici Un uogo eá 'insieme di tutti e soi gi oggetti geometrici che possiedono una proprietaá P; se gi oggetti sono punti, si para di uogo di punti. Esempi
Cap 1. LA CIRCONERENZA Rivedi a teoria I uoghi geometrici Un uogo eá 'insieme di tutti e soi gi oggetti geometrici che possiedono una proprietaá P; se gi oggetti sono punti, si para di uogo di punti. Esempi
Il Tetraedro regolare
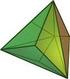 I Tetraedro regoare E i soido che ha per facce 4 triangoi equiateri, (F = 4) Ha 6 spigoi (S = 6) e 4 vertici (V = 4) I suo sviuppo è i seguente: Chiuso diventa: Le proiezioni possibii sono: I suoi assi
I Tetraedro regoare E i soido che ha per facce 4 triangoi equiateri, (F = 4) Ha 6 spigoi (S = 6) e 4 vertici (V = 4) I suo sviuppo è i seguente: Chiuso diventa: Le proiezioni possibii sono: I suoi assi
RAPPRESENTARE LA TERRA
 CPIA 1 FOGGIA VOLUME MODULO D 2 LE VENTI CAPITOLO REGIONI ITALIANE 0 RAPPRESENTARE LA TERRA 1. Paroe per capire Aa fine de capitoo scrivi i significato di queste paroe nuove: panisfero...... paraeo......
CPIA 1 FOGGIA VOLUME MODULO D 2 LE VENTI CAPITOLO REGIONI ITALIANE 0 RAPPRESENTARE LA TERRA 1. Paroe per capire Aa fine de capitoo scrivi i significato di queste paroe nuove: panisfero...... paraeo......
GEOMETRIA EUCLIDEA L equivalenza delle superfici piane
 GEOMETRIA EUCLIDEA Superficie piana Il concetto di superficie piana è un concetto primitivo: i poligoni, i cerchi o in generale regioni di piano delimitate da una linea chiusa o da più linee chiuse che
GEOMETRIA EUCLIDEA Superficie piana Il concetto di superficie piana è un concetto primitivo: i poligoni, i cerchi o in generale regioni di piano delimitate da una linea chiusa o da più linee chiuse che
GEOMETRIA EUCLIDEA I teoremi di Euclide e Pitagora
 GEOMETRIA EUCLIDEA I teoremi di Euclide e Pitagora Vediamo tre importanti teoremi che riguardano i triangoli rettangoli e che si dimostrano utilizzando l equivalenza delle superfici piane. Primo teorema
GEOMETRIA EUCLIDEA I teoremi di Euclide e Pitagora Vediamo tre importanti teoremi che riguardano i triangoli rettangoli e che si dimostrano utilizzando l equivalenza delle superfici piane. Primo teorema
1. MISURIAMO GLI ANGOLI CON GEOGEBRA
 . MISURIAMO GLI ANGOLI CON GEOGEBRA Nascondiamo gi assi cartesiani in modo da usare a finestra grafica come piano eucideo. Disegniamo un punto C che rappresenti i centro di una circonferenza e creiamo
. MISURIAMO GLI ANGOLI CON GEOGEBRA Nascondiamo gi assi cartesiani in modo da usare a finestra grafica come piano eucideo. Disegniamo un punto C che rappresenti i centro di una circonferenza e creiamo
La circonferenza e i poligoni
 MATEMATICAperTUTTI 1 ESERCIZIO GUIDATO Dimostriamo che due corde congruenti di una circonferenza hanno la stessa distanza dal centro. Disegniamo una circonferenza, le due corde AB e CD fra loro congruenti
MATEMATICAperTUTTI 1 ESERCIZIO GUIDATO Dimostriamo che due corde congruenti di una circonferenza hanno la stessa distanza dal centro. Disegniamo una circonferenza, le due corde AB e CD fra loro congruenti
C2 Congruenza - Esercizi
 C Congruenza - Esercizi COSTRUZIONI 1) Disegnare un segmento congruente al segmento dato contando i quadretti. ) Disegnare un segmento congruente al segmento dato utilizzando riga e compasso (costruzione
C Congruenza - Esercizi COSTRUZIONI 1) Disegnare un segmento congruente al segmento dato contando i quadretti. ) Disegnare un segmento congruente al segmento dato utilizzando riga e compasso (costruzione
Nicola De Rosa, Liceo scientifico di ordinamento sessione straordinaria 2012, matematicamente.it
 Nicoa De Rosa, Liceo scientifico di ordinamento sessione straordinaria, matematicamente.it PROBLEMA I triangoo ABC, rettangoo in A, ha ipotenusa BC a ; sia P i punto medio di AC, Q a sua proiezione ortogonae
Nicoa De Rosa, Liceo scientifico di ordinamento sessione straordinaria, matematicamente.it PROBLEMA I triangoo ABC, rettangoo in A, ha ipotenusa BC a ; sia P i punto medio di AC, Q a sua proiezione ortogonae
Progetto Matematica in Rete - Geometria euclidea - La similitudine. La similitudine. Figure simili
 Figure simili Se consideriamo due triangoli equilateri di lato diverso, due quadrati di lato diverso intuitivamente diciamo che hanno la stessa forma. Ma cosa comporta avere la stessa forma? Se osserviamo
Figure simili Se consideriamo due triangoli equilateri di lato diverso, due quadrati di lato diverso intuitivamente diciamo che hanno la stessa forma. Ma cosa comporta avere la stessa forma? Se osserviamo
C6. Quadrilateri - Esercizi
 C6. Quadrilateri - Esercizi DEFINIZIONI E COSTRUZIONI 1) Dato il seguente quadrilatero completa al posto dei puntini. I lati AB e BC sono I lati AB e CD sono I lati AD e sono consecutivi I lati AD e sono
C6. Quadrilateri - Esercizi DEFINIZIONI E COSTRUZIONI 1) Dato il seguente quadrilatero completa al posto dei puntini. I lati AB e BC sono I lati AB e CD sono I lati AD e sono consecutivi I lati AD e sono
Esercitazione 4 - Forze distribuite
 Università degi Studi di ergamo orso di Laurea in Ingegneria essie orso di Eementi di eccanica Esercitazione 4 - Forze distribuite Esercizio n. acoare e reazioni vincoari e e azioni interne per asta di
Università degi Studi di ergamo orso di Laurea in Ingegneria essie orso di Eementi di eccanica Esercitazione 4 - Forze distribuite Esercizio n. acoare e reazioni vincoari e e azioni interne per asta di
Anno 1. Quadrilateri
 Anno 1 Quadrilateri 1 Introduzione In questa lezione impareremo a risolvere i problemi legati all utilizzo dei quadrilateri. Forniremo la definizione di quadrilatero e ne analizzeremo le proprietà e le
Anno 1 Quadrilateri 1 Introduzione In questa lezione impareremo a risolvere i problemi legati all utilizzo dei quadrilateri. Forniremo la definizione di quadrilatero e ne analizzeremo le proprietà e le
1 L'omotetia. 2 Il teorema del rapporto dei perimetri e delle aree di due triangoli simili
 1 L'omotetia Per definire un'omotetia bisogna disegnare una generica figura nel piano (nel nostro caso utilizzeremo un triangolo), un punto (il centro dell'omotetia) e un numero (il rapporto k dell'omotetia).
1 L'omotetia Per definire un'omotetia bisogna disegnare una generica figura nel piano (nel nostro caso utilizzeremo un triangolo), un punto (il centro dell'omotetia) e un numero (il rapporto k dell'omotetia).
LE POTENZE DEI NUMERI
 ARITMETICA LE POTENZE DEI NUMERI PREREQUISITI conoscere e proprietaá dee quattro operazioni svogere cacoi a mente ed in coonna con e quattro operazioni risovere espressioni con e quattro operazioni distinguere
ARITMETICA LE POTENZE DEI NUMERI PREREQUISITI conoscere e proprietaá dee quattro operazioni svogere cacoi a mente ed in coonna con e quattro operazioni risovere espressioni con e quattro operazioni distinguere
Quadrilateri. Il Parallelogramma
 Il Parallelogramma 2. Fai clic su Ic3 e scegli Retta per due punti : disegna la retta a. 3. Fai clic su Ic2 e scegli Nuovo Punto : fai clic fuori dalla retta a 4. Fai clic su Ic4 e scegli Retta parallela
Il Parallelogramma 2. Fai clic su Ic3 e scegli Retta per due punti : disegna la retta a. 3. Fai clic su Ic2 e scegli Nuovo Punto : fai clic fuori dalla retta a 4. Fai clic su Ic4 e scegli Retta parallela
Geometria euclidea. Alessio del Vigna
 Geometria euclidea Alessio del Vigna La geometria euclidea è una teoria fondata su quattro enti primitivi e sulle relazioni che tra essi intercorrono. I quattro enti primitivi in questione sono il punto,
Geometria euclidea Alessio del Vigna La geometria euclidea è una teoria fondata su quattro enti primitivi e sulle relazioni che tra essi intercorrono. I quattro enti primitivi in questione sono il punto,
Proporzioni tra grandezze
 Definizione Due grandezze omogenee A e B (con B 0) e altre due grandezze omogenee C e D (con D 0) si dicono in proporzione quando il rapporto tra le prime due è uguale al rapporto tra la terza e la quarta
Definizione Due grandezze omogenee A e B (con B 0) e altre due grandezze omogenee C e D (con D 0) si dicono in proporzione quando il rapporto tra le prime due è uguale al rapporto tra la terza e la quarta
1. costruzione di un TRIANGOLO ISOSCELE di assegnati lati
 LABORATORIO DI GEOMETRIA COSTRUZIONI DI BASE DI POLIGONI 1. costruzione di un TRIANGOLO ISOSCELE di assegnati lati Si costruisce un segmento AB, base del triangolo, ed un segmento CD, lato obliquo. Si
LABORATORIO DI GEOMETRIA COSTRUZIONI DI BASE DI POLIGONI 1. costruzione di un TRIANGOLO ISOSCELE di assegnati lati Si costruisce un segmento AB, base del triangolo, ed un segmento CD, lato obliquo. Si
In un triangolo altezza mediana bisettrice asse Proprietà di angoli e lati di un triangolo
 In un triangolo si dice altezza relativa a un lato il segmento di perpendicolare al lato condotta dal vertice opposto. Si dice mediana relativa a un lato il segmento che unisce il punto medio del lato
In un triangolo si dice altezza relativa a un lato il segmento di perpendicolare al lato condotta dal vertice opposto. Si dice mediana relativa a un lato il segmento che unisce il punto medio del lato
Due rette si dicono INCIDENTI se hanno esattamente un punto in comune, altrimenti si dicono PARALLELE.
 Riepilogo di Geometria: Assioma A1 Per tutte le coppie di punti P,Q dell insieme S è assegnato un numero reale (=)> 0, che si dice distanza di P da Q e si indica don d(p,q) 1- Se i punti P,Q sono distinti
Riepilogo di Geometria: Assioma A1 Per tutte le coppie di punti P,Q dell insieme S è assegnato un numero reale (=)> 0, che si dice distanza di P da Q e si indica don d(p,q) 1- Se i punti P,Q sono distinti
Costruzione di un triangolo simile a un triangolo dato
 C Costruzione di un triangolo simile a un triangolo dato Disegna un triangolo ABC e un segmento A 0 B 0. Costruisci poi un punto C 0 in modo che il triangolo A 0 B 0 C 0 sia simile ad ABC. Verifica quindi
C Costruzione di un triangolo simile a un triangolo dato Disegna un triangolo ABC e un segmento A 0 B 0. Costruisci poi un punto C 0 in modo che il triangolo A 0 B 0 C 0 sia simile ad ABC. Verifica quindi
LE TRASFORMAZIONI GEOMETRICHE
 LE TRASFORMAZIONI GEOMETRICHE LA SIMMETRIA ASSIALE Definizione: il simmetrico P di un punto P, rispetto alla simmetria assiale di asse r gode delle seguenti proprietà: P e P sono equidistanti da r e il
LE TRASFORMAZIONI GEOMETRICHE LA SIMMETRIA ASSIALE Definizione: il simmetrico P di un punto P, rispetto alla simmetria assiale di asse r gode delle seguenti proprietà: P e P sono equidistanti da r e il
CONOSCENZE 1. gli elementi e le caratteristiche
 GEOMETRIA PREREQUISITI l conoscere le caratteristiche del sistema decimale l conoscere le proprietaá delle quattro operazioni e saper operare con esse l conoscere gli enti fondamentali della geometria
GEOMETRIA PREREQUISITI l conoscere le caratteristiche del sistema decimale l conoscere le proprietaá delle quattro operazioni e saper operare con esse l conoscere gli enti fondamentali della geometria
Due incognite ipertstatiche con cedimento elastico lineare sul vincolo
 Dott. Ing aoo Serafini Cic per tutti gi appunti (AUTOAZIONE TRATTAENTI TERICI ACCIAIO SCIENZA dee COSTRUZIONI ) e-mai per suggerimenti Due incognite ipertstatiche con cedimento eastico ineare su vincoo
Dott. Ing aoo Serafini Cic per tutti gi appunti (AUTOAZIONE TRATTAENTI TERICI ACCIAIO SCIENZA dee COSTRUZIONI ) e-mai per suggerimenti Due incognite ipertstatiche con cedimento eastico ineare su vincoo
Dato un triangolo ABC, è il segmento che partendo dal vertice opposto al lato, incontra il lato stesso formando due angoli retti.
 Anno 2014 1 Sommario Altezze, mediane, bisettrici dei triangoli... 2 Altezze relativa a un vertice... 2 Mediane relative a un lato... 2 Bisettrici relativi a un lato... 2 Rette perpendicolari... 3 Teorema
Anno 2014 1 Sommario Altezze, mediane, bisettrici dei triangoli... 2 Altezze relativa a un vertice... 2 Mediane relative a un lato... 2 Bisettrici relativi a un lato... 2 Rette perpendicolari... 3 Teorema
IL PENDOLO REVERSIBILE DI KATER
 IL PENDOLO REVERSIBILE DI KATER I periodo dee osciazioni de pendoo sempice è dato daa formua: T 0 = π g Questa reazione è vaida per e piccoe osciazioni, quando, cioè, si può assimiare i seno de'angoo massimo
IL PENDOLO REVERSIBILE DI KATER I periodo dee osciazioni de pendoo sempice è dato daa formua: T 0 = π g Questa reazione è vaida per e piccoe osciazioni, quando, cioè, si può assimiare i seno de'angoo massimo
Rette, piani e figure nello spazio
 CAPITOLO Rette, piani e figure neo spazio. LA GEOMETRIA DELLO SPAZIO CON CABRI 3D Cabri 3D eá un software che, consentendo una facie costruzione di soidi, piani e figure deo spazio in genere, permette
CAPITOLO Rette, piani e figure neo spazio. LA GEOMETRIA DELLO SPAZIO CON CABRI 3D Cabri 3D eá un software che, consentendo una facie costruzione di soidi, piani e figure deo spazio in genere, permette
Equivalenza, misura di grandezze e aree
 MATEMATICAperTUTTI Equivalenza, misura di grandezze e aree 1 ESERCIZIO GUIDATO L equivalenza dei poligoni. Sappiamo che per stabilire se due figure sono equivalenti si può vedere se sono equiscomponibili,
MATEMATICAperTUTTI Equivalenza, misura di grandezze e aree 1 ESERCIZIO GUIDATO L equivalenza dei poligoni. Sappiamo che per stabilire se due figure sono equivalenti si può vedere se sono equiscomponibili,
L equivalenza delle superfici piane
 GEOMETRIA EUCLIDEA L equivalenza delle superfici piane Superficie piana Il concetto di superficie piana è un concetto primitivo: i poligoni, i cerchi o in generale regioni di piano delimitate da una linea
GEOMETRIA EUCLIDEA L equivalenza delle superfici piane Superficie piana Il concetto di superficie piana è un concetto primitivo: i poligoni, i cerchi o in generale regioni di piano delimitate da una linea
L equivalenza delle superfici piane
 GEOMETRIA EUCLIDEA L equivalenza delle superfici piane Superficie piana Il concetto di superficie piana è un concetto primitivo: i poligoni, i cerchi o in generale regioni di piano delimitate da una linea
GEOMETRIA EUCLIDEA L equivalenza delle superfici piane Superficie piana Il concetto di superficie piana è un concetto primitivo: i poligoni, i cerchi o in generale regioni di piano delimitate da una linea
I PARALLELOGRAMMI E I TRAPEZI
 I PARALLELOGRAMMI E I TRAPEZI 1. Il parallelogramma ESERCIZI 1 A Disegna un parallelogramma ABCD, la diagonale BD e i segmenti AK e CH, perpendicolari a BD. Dimostra che il quadrilatero AHCK è un parallelogramma.
I PARALLELOGRAMMI E I TRAPEZI 1. Il parallelogramma ESERCIZI 1 A Disegna un parallelogramma ABCD, la diagonale BD e i segmenti AK e CH, perpendicolari a BD. Dimostra che il quadrilatero AHCK è un parallelogramma.
c) Determina per quali valori di k il segmento BC ha misura 2. 3) Ricava l equazione della spezzata rappresentata in figura
 VERIFICHE TERZA C a.s. 2010 2011 1) Sono assegnati i punti A(0; 10) B(8; - 6) C(0; 0). Rappresentali. a) Verifica che il triangolo ABC è isoscele e calcola la sua area b) Tra i punti P che hanno ordinata
VERIFICHE TERZA C a.s. 2010 2011 1) Sono assegnati i punti A(0; 10) B(8; - 6) C(0; 0). Rappresentali. a) Verifica che il triangolo ABC è isoscele e calcola la sua area b) Tra i punti P che hanno ordinata
Le equazioni e le disequazioni lineari
 MATEMATICAperTUTTI Le equazioni e e disequazioni ineari Le equazioni ineari ESERCIZIO SVOLTO Le equazioni. Chiamiamo equazione ad una incognita un uguagianza fra due espressioni agebriche di cui ameno
MATEMATICAperTUTTI Le equazioni e e disequazioni ineari Le equazioni ineari ESERCIZIO SVOLTO Le equazioni. Chiamiamo equazione ad una incognita un uguagianza fra due espressioni agebriche di cui ameno
La statistica descrittiva
 MATEMATICAperTUTTI Dee seguenti indagine statistiche individua a popoazione, i carattere oggetto di studio e e possibii modaità di tae carattere. 1 ESERCIZIO SVOLTO Indagine: utiizzo de tempo ibero da
MATEMATICAperTUTTI Dee seguenti indagine statistiche individua a popoazione, i carattere oggetto di studio e e possibii modaità di tae carattere. 1 ESERCIZIO SVOLTO Indagine: utiizzo de tempo ibero da
1 Congruenza diretta e inversa
 1 Congruenza diretta e inversa PROPRIETÀ. La congruenza tra due figure piane mantiene inalterata la lunghezza dei segmenti e l ampiezza degli angoli; ciò che cambia è la posizione delle figure nel piano.
1 Congruenza diretta e inversa PROPRIETÀ. La congruenza tra due figure piane mantiene inalterata la lunghezza dei segmenti e l ampiezza degli angoli; ciò che cambia è la posizione delle figure nel piano.
Chi ha avuto la sospensione di giudizio, deve aggiungere:
 CLASSE 1A Gli esercizi sono sul quaderno di recupero allegato al libro di testo: Esercizi da 80 a 94 pagina 49 Esercizi da 101 a 105 pagina 52-53 Esercizi da 108 a 118 pagina 52-53 Esercizi da 37 a 61
CLASSE 1A Gli esercizi sono sul quaderno di recupero allegato al libro di testo: Esercizi da 80 a 94 pagina 49 Esercizi da 101 a 105 pagina 52-53 Esercizi da 108 a 118 pagina 52-53 Esercizi da 37 a 61
IL PIANO CARTESIANO. Preparazione. Esercizi
 IN CLASSE IL PIANO CARTESIANO Preparazione Per questi esercizi con GeoGebra dovrai utilizzare i seguenti pulsanti. Leggi le procedure di esecuzione nella zona in alto a destra, accanto alla barra degli
IN CLASSE IL PIANO CARTESIANO Preparazione Per questi esercizi con GeoGebra dovrai utilizzare i seguenti pulsanti. Leggi le procedure di esecuzione nella zona in alto a destra, accanto alla barra degli
Problemi sui punti notevoli di un triangolo
 1 Sia O l ortocentro del triangolo ABC; dimostra che B è l ortocentro del triangolo AOC. 2 Dimostra che in un triangolo rettangolo il circocentro è il punto medio dell ipotenusa. 3 Il baricentro del triangolo
1 Sia O l ortocentro del triangolo ABC; dimostra che B è l ortocentro del triangolo AOC. 2 Dimostra che in un triangolo rettangolo il circocentro è il punto medio dell ipotenusa. 3 Il baricentro del triangolo
Principali Definizioni e Teoremi di Geometria
 Principali Definizioni e Teoremi di Geometria Segmento (definizione) Si dice segmento di estremi A e B l insieme costituito dai punti A e B e da tutti i punti della retta AB compresi tra A e B. Angolo
Principali Definizioni e Teoremi di Geometria Segmento (definizione) Si dice segmento di estremi A e B l insieme costituito dai punti A e B e da tutti i punti della retta AB compresi tra A e B. Angolo
Appunti di Matematica 2 - Geometria euclidea - La similitudine GEOMETRIA EUCLIDEA. La similitudine
 Appunti di Matematica GEOMETRIA EUCLIDEA Se consideriamo due triangoli equilateri di lato diverso, due quadrati di lato diverso intuitivamente diciamo che hanno la stessa forma. Ma cosa comporta avere
Appunti di Matematica GEOMETRIA EUCLIDEA Se consideriamo due triangoli equilateri di lato diverso, due quadrati di lato diverso intuitivamente diciamo che hanno la stessa forma. Ma cosa comporta avere
I teoremi di Euclide e Pitagora
 GEOMETRIA EUCLIDEA Vediamo tre importanti teoremi che riguardano i triangoli rettangoli e che si dimostrano utilizzando l equivalenza delle superfici piane. 44 Primo teorema di Euclide In un triangolo
GEOMETRIA EUCLIDEA Vediamo tre importanti teoremi che riguardano i triangoli rettangoli e che si dimostrano utilizzando l equivalenza delle superfici piane. 44 Primo teorema di Euclide In un triangolo
I quadrati sono 5. Esercizio pagina 198 numero 119 Calcola la misura del perimetro dell'area del trapezio in figura
 Considera il piano cartesiano. Quanti sono i quadrati aventi un vertice in (-1;-1) e tali che uno degli assi coordinati sia asse di simmetria del quadrato stesso? I quadrati sono 5 Esercizio pagina 198
Considera il piano cartesiano. Quanti sono i quadrati aventi un vertice in (-1;-1) e tali che uno degli assi coordinati sia asse di simmetria del quadrato stesso? I quadrati sono 5 Esercizio pagina 198
LA CIRCONFERENZA, I POLIGONI INSCRITTI E CIRCOSCRITTI
 LA CIRCONFERENZA, I POLIGONI INSCRITTI E CIRCOSCRITTI 1. La circonferenza e il cerchio ESERCIZI 1 A Disegna un triangolo ABC di altezza CH relativa ad AB. Fissa un segmento ED minore di CH. Determina il
LA CIRCONFERENZA, I POLIGONI INSCRITTI E CIRCOSCRITTI 1. La circonferenza e il cerchio ESERCIZI 1 A Disegna un triangolo ABC di altezza CH relativa ad AB. Fissa un segmento ED minore di CH. Determina il
Equazioni goniometriche
 Appunti di Matematica Equazioni goniometriche a) Consideriamo un equazione elementare : Equazioni goniometriche elementari sen Le soluzioni saranno: 5 In generale se abbiamo sen con < < avremo: α α Se
Appunti di Matematica Equazioni goniometriche a) Consideriamo un equazione elementare : Equazioni goniometriche elementari sen Le soluzioni saranno: 5 In generale se abbiamo sen con < < avremo: α α Se
Testi verifiche 3 C 3 I a. s. 2008/2009
 Testi verifiche 3 C 3 I a. s. 2008/2009 1) Sono assegnati i punti A(- 1; 3) C(3; 0) M ;1 a) Ricavare le coordinate del simmetrico di A rispetto a M e indicarlo con B. Verificare che il segmento congiungente
Testi verifiche 3 C 3 I a. s. 2008/2009 1) Sono assegnati i punti A(- 1; 3) C(3; 0) M ;1 a) Ricavare le coordinate del simmetrico di A rispetto a M e indicarlo con B. Verificare che il segmento congiungente
Unità 8 Esercizi per il recupero
 LA GEOMETRIA DEL PIANO E LE TRASFORMAZIONI VOLUME Unità 8 Esercizi per il recupero ARGOMENTO: I quadrilateri. Teorema di Talete CONTENUTI: Il trapezio isoscele I parallelogrammi Il piccolo teorema di Talete
LA GEOMETRIA DEL PIANO E LE TRASFORMAZIONI VOLUME Unità 8 Esercizi per il recupero ARGOMENTO: I quadrilateri. Teorema di Talete CONTENUTI: Il trapezio isoscele I parallelogrammi Il piccolo teorema di Talete
Problemi di geometria
 criteri di similitudine sui triangoli 1 Dimostra che le altezze di un triangolo sono inversamente proporzionali ai relativi lati. 2 Dimostra che due triangoli rettangoli sono simili se hanno ordinatamente
criteri di similitudine sui triangoli 1 Dimostra che le altezze di un triangolo sono inversamente proporzionali ai relativi lati. 2 Dimostra che due triangoli rettangoli sono simili se hanno ordinatamente
AREE DEI POLIGONI. b = A h
 AREE DEI POLIGONI 1. RETTANGOLO E un parallelogramma avente quattro angoli retti, i lati opposti uguali e paralleli, le diagonali uguali non perpendicolari che si scambiano vicendevolmente a metà. Def.
AREE DEI POLIGONI 1. RETTANGOLO E un parallelogramma avente quattro angoli retti, i lati opposti uguali e paralleli, le diagonali uguali non perpendicolari che si scambiano vicendevolmente a metà. Def.
esercizi 107 Problemi sulla retta
 esercizi 107 Problemi sulla retta Es. 1 Detto C il punto in cui l asse del segmento di estremi A( 3, 3) e B(1, 5) incontra l asse x, calcolare le coordinate del punto D equidistante da A, B e C. Determinare
esercizi 107 Problemi sulla retta Es. 1 Detto C il punto in cui l asse del segmento di estremi A( 3, 3) e B(1, 5) incontra l asse x, calcolare le coordinate del punto D equidistante da A, B e C. Determinare
CONOSCENZE 1. le proprietaá dei poligoni inscritti. 2. le proprietaá dei quadrilateri inscritti e circoscritti 3. le proprietaá dei poligoni regolari
 GEOMETRIA I POLIGONI INSCRITTI E CIRCOSCRITTI PREREQUISITI l l l l conoscere le proprietaá delle quattro operazioni e operare con esse conoscere gli enti fondamentali della geometria e le loro proprietaá
GEOMETRIA I POLIGONI INSCRITTI E CIRCOSCRITTI PREREQUISITI l l l l conoscere le proprietaá delle quattro operazioni e operare con esse conoscere gli enti fondamentali della geometria e le loro proprietaá
VERIFICA DI GEOMETRIA A
 VERIFICA DI GEOMETRIA A n1 classe IV F data nome e cognome Tre punti allineati A,B,C in modo che AB=2BC Disegna un fascio proprio di rette Due angoli consecutivi e complementari Un poligono convesso Disegna
VERIFICA DI GEOMETRIA A n1 classe IV F data nome e cognome Tre punti allineati A,B,C in modo che AB=2BC Disegna un fascio proprio di rette Due angoli consecutivi e complementari Un poligono convesso Disegna
Costruzione 1 Condurre la perpendicolare ad un retta data, passante per un punto della retta stessa.
 Costruzioni Costruzioni di rette, segmenti ed angoli Costruzione 1 Condurre la perpendicolare ad un retta data, passante per un punto della retta stessa. Costruzione. Consideriamo la retta r ed un punto
Costruzioni Costruzioni di rette, segmenti ed angoli Costruzione 1 Condurre la perpendicolare ad un retta data, passante per un punto della retta stessa. Costruzione. Consideriamo la retta r ed un punto
Lezione 6 Richiami di Geometria Analitica
 1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
Università di Pisa. Esame di SCIENZA DELLE COSTRUZIONI I Corso di Laurea in Ingegneria Civile, Ambientale e Edile
 Università di Pisa Esame di SCIENZA DELLE COSTRUZIONI I Corso di Laurea in Ingegneria Civie, Ambientae e Edie Esame di SCIENZA DELLE COSTRUZIONI - Parte I Corso di Laurea in Ingegneria Aerospaziae Corso
Università di Pisa Esame di SCIENZA DELLE COSTRUZIONI I Corso di Laurea in Ingegneria Civie, Ambientae e Edie Esame di SCIENZA DELLE COSTRUZIONI - Parte I Corso di Laurea in Ingegneria Aerospaziae Corso
Assumendo 1 u = 1 cm, calcola il perimetro e l area del quadrilatero ABCD.
 Esercizio 1a Disegna un piano cartesiano ortogonale ed in esso inserisci i punti che seguono, poi uniscili nell ordine dato: Secondo te che tipo di quadrilatero hai ottenuto? Perché? Quali sono le sue
Esercizio 1a Disegna un piano cartesiano ortogonale ed in esso inserisci i punti che seguono, poi uniscili nell ordine dato: Secondo te che tipo di quadrilatero hai ottenuto? Perché? Quali sono le sue
Cosa puoi dire del quadrilatero ABCD? Come sono i lati, le diagonali, gli angoli?
 Dal parallelogramma al rombo (fase 1 e 2) Fase 1 Disegna due circonferenze concentriche c e c di centro O; disegna su c un punto A e su c un punto B; traccia la retta r passante per i punti A e O, chiama
Dal parallelogramma al rombo (fase 1 e 2) Fase 1 Disegna due circonferenze concentriche c e c di centro O; disegna su c un punto A e su c un punto B; traccia la retta r passante per i punti A e O, chiama
1B GEOMETRIA. Gli elementi fondamentali della geometria. Esercizi supplementari di verifica
 Gli elementi fondamentali della geometria Esercizi supplementari di verifica Esercizio 1 a) V F Si dice linea retta una qualsiasi linea che non ha né un inizio né una fine. b) V F Il punto è una figura
Gli elementi fondamentali della geometria Esercizi supplementari di verifica Esercizio 1 a) V F Si dice linea retta una qualsiasi linea che non ha né un inizio né una fine. b) V F Il punto è una figura
