Parallelismo e perpendicolaritaá nel piano
|
|
|
- Matteo Baroni
- 9 anni fa
- Просмотров:
Транскрипт
1 CAPITOLO 3 Paraeismo e perpendicoaritaá ne piano 1. L'UTILIZZO DEGLI SLIDER E IL PARALLELISMO CON GEOGEBRA Uno sider eá un numero, oppure un angoo, i cui vaore puoá variare in un fissato intervao a, bš assumendo vaori che, a partire da a, vengono incrementati di un passo costante fino a b. Per esempio, se si fissa come intervao 1,4Š ed i passo di incremento eá 0,5, i vaori che o sider assume sono 1 1,5 2 2,5 3 3,5 4 Uno sider viene usato quando si vuoe far dipendere una costruzione da un parametro variabie. L'attivazione di questo strumento avviene con i comando 10-Sider che fa aprire una finestra di diaogo come quea in figura. In essa si deve: specificare se i parametro variabie eá un numero oppure un angoo dare un nome a parametro competare a scheda Intervao indicando i vaore minimo e i vaore massimo de'intervao e i passo di incremento. L'aspetto grafico di uno sider eá un segmento con un punto mobie in evidenza; a sua posizione orizzontae o verticae nea Vista Grafica puoá essere fissata daa scheda Sider che si trova a fianco di quea Intervao. La scheda Animazione, quando eá attivata, consente di fissare e modaitaá di variazione automatica de parametro in modo che sia Osciante (da a a b e viceversa), Crescente (sempre da a verso b), Decrescente (sempre da b verso a). Facendo scorrere i punto mobie mediante trascinamento in avanti e indietro, si ottengono e variazioni programmate de parametro. Esercitazione 1. Uso di uno sider appicato ai triangoi rettangoi Vogiamo disegnare un triangoo rettangoo avente un angoo acuto di ampiezza variabie fra 0 e90 e osservare come si modifica a unghezza de ato ad esso opposto. Per disegnare i triangoo rettangoo costruiamo un segmento AB e una retta r ad esso perpendicoare passante per A. Supponiamo poi che 'angoo di ampiezza variabie sia queo di vertice B; costruiamo o sider in questo modo: ± attiviamo o strumento 10-Sider e cicchiamo in un punto dea finestra grafica ± spuntiamo a casea Angoo Q Re Fraschini - Grazzi, Atas SpA Tema 5 - Cap. 3: PARALLELISMO E PERPENDICOLARITA Á NEL PIANO 1
2 ± nea casea Nome attribuiamo ao sider i nome (si puoá scegiere questo simboo daa casea a discesa sua destra) ± fissiamo come vaori minimo e massimo de'intervao 0 e90 e come incremento 10 ± confermiamo e scete fatte ciccando su pusante Appica. Aa conferma, nea Vista Grafica viene disegnato un segmento orizzontae con i punto mobie che indica, ad ogni spostamento, i vaore di assunto in quea posizione. Disegniamo adesso 'angoo variabie de triangoo con o strumento 8-Angoo di data misura facendo cic prima su punto A, poi su punto B e indicando come ampiezza (nea finestra di diaogo puoi anche scegiere 'orientamento orario oppure antiorario). Competiamo i triangoo determinando i punto C di intersezione dea retta r con i secondo ato de'angoo e ridisegnandoo con o strumento 5-Poigono. Nascondiamo tutti gi eementi che sono serviti aa costruzione e asciamo soo i triangoo. Muovendo i punto mobie verso destra, 'angoo aumenta a sua ampiezza di 10 ogni vota, muovendoo verso sinistra diminuisce dea stessa quantitaá. In corrispondenza di ciascuna variazione, anche a unghezza de ato opposto a questo angoo si modifica; per rendera visibie, apriamo a scheda dee ProprietaÁ reativa a ato AC e, daa scheda Fondamentai, in corrispondenza dea voce Mostra etichetta, apriamo i menu a discesa e scegiamo Nome e vaore. Casi particoari sono quei estremi: quando ˆ 0 i triangoo degenera in due segmenti sovrapposti e a misura de segmento AC eá 0; quando ˆ 90 i triangoo non esiste piuá percheâ 'ipotenusa diventa paraea a uno dei cateti; i triangoo non viene quindi mostrato e anche a misura de segmento AC non viene indicata in quanto questo segmento non esiste piuá. Esercitazione 2. Verifica de paraeismo Sia ABC d un angoo convesso e sia P un punto dea sua bisettrice; 'asse de segmento PB incontra a semiretta AB in D. Ci chiediamo se esiste quache reazione fra i ato BC de'angoo e a retta DP. Costruiamo a figura secondo e indicazioni. 1 Disegniamo un angoo convesso di vertice B (strumento 8-Angoo) e competiamo i disegno rappresentando e semirette BA e BC. 2 Con o strumento 4-Bisettrice tracciamo a bisettrice de'angoo ciccando ne'ordine sui punti A, B, C; viene disegnata una retta che rappresenta a bisettrice sia de'angoo convesso che de'angoo concavo. 3 Usando o strumento 3-Nuovo punto, prendiamo un punto sua bisettrice de'angoo convesso: cicchiamo in un punto quando, avvicinando i puntatore aa bisettrice, questa cambia spessore. Attraverso a voce Rinomina de menu contestuae diamo nome P a punto. 4 Con o strumento 3-Segmento tra due punti definiamo i segmento BP ciccando su B esup. 5 Con o strumento 4-Asse di un segmento tra due punti tracciamo 'asse di BP. 2 Tema 5 - Cap. 3: PARALLELISMO E PERPENDICOLARITA Á NEL PIANO Q Re Fraschini - Grazzi, Atas SpA
3 6 Troviamo poi i punto di intersezione de'asse con a semiretta BA (strumento 2-Intersezione tra due oggetti) e chiamiamoo D. 7 Tracciamo infine a retta DP (strumento 3-Retta per due punti). Per sapere se esiste quache reazione fra a retta DP e a semiretta BC usiamo o strumento 10-Reazione tra due oggetti e cicchiamo sue due rette. Si apre a questo punto una finestra di diaogo nea quae viene comunicato che e due rette sono paraee. In modaitaá 1-Muovi spostiamo adesso i punto P ungo a bisettrice e riformuiamo i quesito; modifichiamo 'ampiezza de'angoo ABC d e, di nuovo, riformuiamo i quesito; e risposte sono uguai aa precedente. Questo significa che i fatto di aver trovato due rette paraee non dipende neâ daa posizione de punto P sua bisettrice, neâ da'ampiezza de'angoo ABC. d Queo che abbiamo fatto con questa esercitazione eá peroá soo una verifica de paraeismo in quache situazione, non abbiamo cioeá dimostrato che e rette BC e DP sono paraee per quaunque angoo ABC d e per quaunque punto P sua bisettrice; a dimostrazione deve essere condotta mediante un ragionamento rigoroso che puoá essere i seguente: 4 avendo tracciato 'asse de segmento BP, i segmenti DB e DP sono congruenti e percioá DPB eá isoscee di conseguenza sono congruenti gi angoi DBP d e DPB d essendo BP a bisettrice, DBP d PBC d e, per a proprietaá transitiva, anche DPB d PBC d poicheâ questi utimi angoi sono aterni interni rispetto ae rette DP e BC con trasversae BP, possiamo concudere che DP k BC. 2. PARALLELISMO E PERPENDICOLARITA Á CON CABRI Gi strumenti Retta perpendicoare e Retta paraea de'icona Costruisci permettono di tracciare a retta perpendicoare oppure quea paraea a una retta data passante per un punto assegnato. Nea stessa icona trovi anche o strumento Asse che permette di tracciare 'asse di un segmento quando eá assegnato i segmento oppure due punti che ne sono gi estremi. Atri interessanti strumenti di Cabri sono quei che trovi ne'icona Verifica proprietaá rappresentata a ato. E' immediato capire che cosa fanno questi strumenti; puoi comunque sempre attivare a guida in inea con i tasto funzione F1 per vedere quai sono gi eementi da seezionare. Proviamo ad usari per individuare acune proprietaá dee figure geometriche. Esercitazione 1. L'asse di un segmento Abbiamo dimostrato che 'asse di un segmento ha a caratteristica che tutti i suoi punti sono equidistanti dagi estremi de segmento; questa proprietaá puoá essere verificata con Cabri in questo modo: disegna un segmento AB e traccia i suo asse con o strumento Asse oppure con gi strumenti Punto medio e poi Retta perpendicoare Q Re Fraschini - Grazzi, Atas SpA Tema 5 - Cap. 3: PARALLELISMO E PERPENDICOLARITA Á NEL PIANO 3
4 seeziona un punto quasiasi P su'asse con o strumento Punto su un oggetto attiva o strumento Equidistante? e indica ne'ordine: i punto P, i punto A, i punto B. Ciccando con i mouse ne riquadro che si apre, compare a scritta I punti sono equidistanti. Se adesso provi a spostare i punto P ungo a retta asse de segmento, i messaggio non cambia percheâ i segmenti PA e PB sono sempre congruenti fra oro; questo messaggio viene in reataá aggiornato ad ogni spostamento, ma non ce ne accorgiamo percheâ tutti i punti P hanno a medesima caratteristica. Esercitazione 2. Verifica dee proprietaá de triangoo isoscee Disegniamo un triangoo isoscee ABC di base AB con una dee costruzioni che abbiamo imparato a fare ne precedente capitoo e tracciamo a bisettrice de'angoo di vertice C seguendo questa procedura: attiva o strumento Bisettrice da'icona Costruisci seeziona 'angoo C b de triangoo indicando ne'ordine un punto su ato AC (per esempio i punto A), i vertice C, un punto su ato BC (per esempio i punto B). Trova adesso i punto H di intersezione dea bisettrice con a base AB de triangoo (strumento Intersezione di due oggetti). Usando gi strumenti di Verifica proprietaá, puoi verificare che a bisettrice eá perpendicoare aa base (strumento Perpendicoare?) e che H ne eá i punto medio (strumento Equidistante? indicando H come primo punto e successivamente A e B). I due messaggi non cambiano anche se modifichiamo i triangoo variando uno dei suoi ati o dei suoi angoi (mantenendoo comunque isoscee); questo a conferma de teorema dimostrato che esprime una proprietaá di tutti i triangoi isoscei. Puoi provare adesso a tracciare 'atezza e chiedere se eá anche mediana e bisettrice, oppure a tracciare a mediana e chiedere se eá anche atezza e bisettrice. Esercitazione 3. Riconoscere i paraeismo Consideriamo un triangoo isoscee ABC di base AB e tracciamo a semiretta de ato AC in modo da proungare tae ato daa parte di C; tracciamo poi a bisettrice de'angoo esterno di vertice C. Se osserviamo a figura ottenuta, sembra che a bisettrice cosõá costruita sia paraea aa base de triangoo (os- 4 Tema 5 - Cap. 3: PARALLELISMO E PERPENDICOLARITA Á NEL PIANO Q Re Fraschini - Grazzi, Atas SpA
5 serva a figura); questa intuizione puoá essere verificata con Cabri con o strumento Paraeo? indicando come oggetti a base e a retta bisettrice. Poiche i messaggio che viene comunicato eá Gi oggetti sono paraei, troviamo conferma aa nostra intuizione e anche se modifichiamo i triangoo (mantenendoo isoscee) i messaggio non cambia. La giustificazione di queo che abbiamo trovato puoá essere data in questo modo (dimostrazione dea proprietaá ): gi angoi DCE d e ECB d sono congruenti percheâ formati daa bisettrice 'angoo DCB d eá uguae aa somma di CAB d con CBA d per i teorema de'angoo esterno gi angoi CAB d e CBA d sono congruenti percheâ angoi aa base di un triangoo isoscee quindi, per esempio, d ECB d CBA di conseguenza e rette CE e AB sono paraee percheâ formano una coppia di angoi aterni interni che sono congruenti. Le macro con Cabri Gi strumenti fondamentai di Cabri sono sempre disponibii in inea, vae a dire che se vuoi tracciare a paraea o a perpendicoare ad una retta oppure se vuoi disegnare un triangoo o un poigono, hai giaá a disposizione gi strumenti per faro. Atri strumenti, come per esempio, quei per i trasporto di un segmento e di un angoo devono invece essere richiamati da una ibreria di macroistruzioni che si trova nea cartea Macro di cui abbiamo giaá parato ne primo capitoo. Una macroistruzione eá in sostanza una procedura per eseguire costruzioni particoari (per esempio per costruire un triangoo isoscee) che viene memorizzata in un fie e che, dopo essere stata richiamata, puoá essere utiizzata come un quasiasi atro strumento di Cabri. Aora, visto che acune costruzioni fondamentai sono sempre utii e che dovere rieseguire ogni vota puoá far perdere di vista 'obiettivo di un probema, vae a pena di memorizzare in una macroistruzione in modo da costruire pian piano una ibreria personae di strumenti. Riprendiamo aora acune dee costruzioni che abbiamo giaá visto e facciamoe diventare degi strumenti di avoro. Esercitazione 4. Una macro per costruire un triangoo isoscee La situazione piuá sempice eá quea che de triangoo venga assegnata a semiretta dea base (in modo che un estremo sia 'origine dea semiretta) e i vertice. Procediamo dunque in questo modo (puoi seguire a costruzione neo schema dea figura a ato): disegniamo una semiretta di origine A (quea su cui vogiamo che si appoggi a base de triangoo) disegniamo un punto C non appartenente aa semiretta (queo che vogiamo che sia i vertice de triangoo) usiamo o strumento Circonferenza e tracciamo a circonferenza che ha centro in C e passa per A Q Re Fraschini - Grazzi, Atas SpA Tema 5 - Cap. 3: PARALLELISMO E PERPENDICOLARITA Á NEL PIANO 5
6 usiamo o strumento Intersezione di due oggetti e troviamo 'uteriore punto B di intersezione dea circonferenza con a semiretta disegniamo i triangoo che ha vertici nei punti A, B e C. I triangoo ottenuto eá isoscee percheâ CA CB; osserviamo che o strumento Circonferenza ci eá servito soo come strumento di trasporto per individuare i punto B sua semiretta. Dobbiamo adesso memorizzare questa procedura in una Macro: n da'icona Macro seeziona Oggetti iniziai e cicca prima sua semiretta di origine A e poi su punto C Gi oggetti iniziai sono gi oggetti geometrici da cui si deve partire per fare a costruzione, ne nostro caso a semiretta dea base e i vertice: n sempre da'icona Macro seeziona adesso Oggetti finai e cicca su triangoo disegnato Gi oggetti finai sono quei che vogiamo vengano disegnati quando richiameremo a macro, ne nostro caso i triangoo isoscee; gi eementi che sono serviti aa costruzione (a circonferenza ed i punto di intersezione) non devono essere indicati fra gi oggetti finai a meno che non si vogia che compaiano. n attiva adesso o strumento Definizione dea Macro; si apre una finestra nea quae si devono inserire acune informazioni: Nome dea costruzione: eá i nome che viene attribuito ao strumento che stiamo creando e che compariraá ne'icona Macro; inserisci Triangoo isoscee Nome per i primo oggetto finae: eá i messaggio che compare su fogio di avoro quando i puntatore si avvicina a'oggetto; scrivi Questo triangoo isoscee Messaggio di aiuto per questa macro: eá i messaggio che viene riportato nea finestra di aiuto quando eá attiva; eá opportuno dare indicazioni su'utiizzo dea macro, scrivi quindi: Disegna un triangoo isoscee assegnando a semiretta dea base e i vertice Devi poi spuntare a casea Sava come fie per memorizzare a costruzione e potera quindi riutiizzare in successive sessioni di avoro. La mancata spunta di questa casea consente di usare a macro soo nea attuae sessione di avoro; essa viene canceata quando si esce da Cabri. Si puoá anche associare una password aa macro in modo che soo gi utenti abiitati a possano usare, ma non eá questo i nostro scopo. Una vota competate queste operazioni devi ciccare su pusante OK e, visto che abbiamo sceto di savare a macro, dare un nome a fie indicando eventuamente anche i percorso; conviene infatti creare una directory nea quae savare e macro che costruiremo man mano. Vediamo adesso come utiizzare i nuovo strumento che abbiamo costruito. Apri un nuovo fogio di avoro (menu Fie/Apri) e accertati che o strumento Triangoo isoscee sia attivo ne gruppo de'icona Macro (attiva anche a finestra di aiuto con i tasto F1); disegna quindi una semiretta e un punto, seeziona o strumento e cicca su di essi: ne fogio di avoro viene disegnato un triangoo isoscee. Muovendo 'origine dea semiretta oppure i vertice puoi variare e dimensioni de triangoo; queo che non puoi fare eá muovere 'atro estremo dea base percheâ questo punto non eá ibero. 6 Tema 5 - Cap. 3: PARALLELISMO E PERPENDICOLARITA Á NEL PIANO Q Re Fraschini - Grazzi, Atas SpA
7 Esercitazione 5. Una macro per costruire un triangoo rettangoo Costruiamo una macro per disegnare un triangoo rettangoo conoscendo i suoi cateti. Disegniamo dapprima i due cateti a e b e una semiretta r su cui deve giacere uno dei cateti de triangoo (figura a ato); segui adesso questa procedura: costruisci a retta perpendicoare a r passante per a sua origine su tae perpendicoare definisci a semiretta su cui deve giacere i secondo cateto de triangoo trasporta i due segmenti sue due semirette e disegna i triangoo rettangoo. Per costruire a macro: seeziona come oggetti iniziai i due segmenti a e b e a semiretta r seeziona come oggetto finae i triangoo competa a finestra di definizione dea macro (dai i nome Triangoo rettangoo ao strumento) e ricorda di spuntare a casea Sava come fie. ESERCIZI 1. Crea un nuovo strumento che tracci i segmento che rappresenta a distanza di un punto da una retta e memorizzao in modo permanente. 2. Disegna un triangoo isoscee di base assegnata avente 'atezza variabie in uno specificato intervao; risovi i probema con GeoGebra usando uno sider. 3. Utiizzando GeoGebra, disegna un triangoo con due ati di unghezza assegnata e un terzo ato variabie tra 1 e 10. Rieva e variazioni de'ampiezza de'angoo ad esso opposto. 4. Usando o strumento appropriato, verifica che i punti dea bisettrice di un angoo sono equidistanti dai ati de'angoo. 5. Disegna un triangoo isoscee ABC di base BC e traccia a retta de ato AB; disegna una circonferenza che ha centro in A echeintersecaiatoac de triangoo in Q earettadeatoab in R (R appartiene a proungamento di AB daa parte di A). Nascondi a circonferenza, che eá servita soo per disegnare i segmenti AR e AQ congruenti, e traccia a retta RQ. Verifica che tae retta eá perpendicoare aa base e spiega qua eá i motivo. 6. Usando anche i nuovi strumenti, costruisci un triangoo rettangoo e poi due triangoi isoscei sui cateti ed esternamente a triangoo; traccia e rette dee atezze reative aa base di ciascuno dei due triangoi isoscei e verifica che: a. e rette dee due atezze sono fra oro perpendicoari e sono ciascuna paraea a'atro cateto de triangoo rettangoo b. i oro punto di intersezione appartiene a'ipotenusa de triangoo. 7. Sono date due rette paraee a e b e una terza retta c; costruisci una procedura per trovare un punto su c che sia equidistante da a edab. 8. Dato un triangoo ABC costruisci e bisettrici degi angoi interni de triangoo di vertici B e C; da vertice A traccia e paraee a tai bisettrici che incontrano a retta de ato BC nei punti D ed E. Verifica che i segmento DE ha a stessa unghezza de perimetro de triangoo e danne una giustificazione rigorosa mediante dimostrazione. 9. Costruisci un triangoo ABC dove 'angoo b B eá i tripo de'angoo b A e stabiisci quai sono i imiti entro cui puoá variare affincheâ : a. esista i triangoo; b. i triangoo sia acutangoo. Q Re Fraschini - Grazzi, Atas SpA Tema 5 - Cap. 3: PARALLELISMO E PERPENDICOLARITA Á NEL PIANO 7
8 1 Si consideri i poigono intrecciato in figura. La somma dei cinque angoi indicati eá uguae a: a. 90 b. 180 c. 360 d. 150 e. 210 b: Š 2 Conoscendo i quattro angoi A, b bb, C, b D, b quanto vae a somma degi angoi be ed bf? a. A b bb C b D b b. 1 A 2 b bb C b D b c. 360 A b bb C b D b d. 360 A b bb C b D b e. non eá determinata a: Š 3 Ne triangoo ABC e semirette AN e CM sono e bisettrici di BAC d e di BCA d e si intersecano in P. Sapendo che APC d ˆ 140, quanto misura 'angoo in B? a. 90 b. 100 c. 110 d. 120 e. 130 b: Š es. 1 es. 2 es. 4 4 Nea figura a fianco, quanto misura 'angoo? a. 70 b. 75 c. 80 d. 90 e. non puoá essere determinato coi soi dati forniti c: Š 5 In un triangoo, per ogni coppia di ati consecutivi, i due assi dei ati e a bisettrice de'angoo formato dai due ati si incontrano in uno stesso punto. Possiamo affermare che: a. non esiste un triangoo con questa proprietaá b. i triangoo eá equiatero c. i triangoo ha un angoo di 30 d. i triangoo eá rettangoo e. i triangoo ha un angoo di 45 b: Š 6 Si sa che nea figura a fianco CAE d ˆ 60, AEB d ˆ 20, ACD d ˆ 25.I punti E, D, B sono aineati. Qua eá a misura di BDC? d a. 75 b. 85 c. 90 d. 105 e. e informazioni sono insufficienti a: Š es. 6 es. 7 7 I triangoi ABC e CDE rappresentati in figura sono equiateri. Se 'angoo ACE misura 80 gradi, quanti gradi misura 'angoo ABE? d a. 25 b. 30 c. 35 d. 40 e. 45 d: Š 8 Sei diversi punti sono individuati su due rette paraee: quattro su una e due su'atra. Quanti sono i triangoi che hanno per vertici i punti in questione? a. 18 b. 16 c. 12 d. 8 e. 6 b: Š 8 Tema 5 - Cap. 3: PARALLELISMO E PERPENDICOLARITA Á NEL PIANO Q Re Fraschini - Grazzi, Atas SpA
9 9 Quanti angoi maggiori di 90 puoá avere un quadriatero (non intrecciato)? a. ne ha sempre ameno uno b. ne ha a piuá uno c. ne ha a piuá due d. ne ha a piuá tre e. puoá averne quattro d: Š 10 In un triangoo ABC 'angoo in C eá i tripo de'angoo in A e 'angoo in B eá i doppio de'angoo in A. Aora i triangoo eá: a. equiatero b. isoscee non equiatero c. ottusangoo d. rettangoo e. acutangoo non equiatero d: Š 11 In un quadriatero convesso ABCD i ati AB, BC, CD sono uguai. Inotre AC ˆ BD ˆ AD. Quanto misura 'angoo in D? 72 Š I quinconce EÁ domenica pomeriggio e stai percorrendo 'autostrada in auto con i tuoi genitori di ritorno da una giornata sugi sci. Sei abbastanza stanco e guardi con aria assente fuori da finestrino. Quacosa peroá cattura a tua attenzione, o avrai visto ameno un migiaio di vote nea tua vita ma non ci avevi mai fatto caso. Gi aberi. Da quaunque parte i guardi sembrano sempre aineati su fie paraee, vedi i primo tronco e tutti gi atri sembrano scomparire dietro di ui. Che cosa strana, chissaá come avranno fatto a piantari in modo da dare questo effetto e poi chissaá percheâ i avranno piantati proprio in que modo! Per saperne di piuá puoi fare quache ricerca in rete; queo che trovi eá che questo particoare tipo di disposizione ha un nome: si chiama quinconce. Questa paroa deriva da atino quincunx-uncis che etteramente significa cinque once e veniva usata dagi antichi Romani per rappresentare a parte pari ai 5 di un intero. Per esempio, in astroogia, ma piuá raramente in di 360, cioeá a un angoo equivaente a 150 che si viene a formare astronomia, i quinconce corrisponde ai fra due corpi ceesti. Una disposizione a quinconce eá rappresentata da un insieme di cinque oggetti, quattro dei quai sono disposti ai vertici di un quadrato immaginario (oppure un rettangoo) e un quinto a centro, come i cinque piccoi cerchi che formano i numero 5 sua faccia di un dado. Una successione di quinconce daá origine a fie di oggetti che si dispongono ungo inee paraee diversamente orientate. Marco Fabio Quintiiano, i maggiore maestro e teorico de'eoquenza ne'etaá imperiae, scrisse a questo proposito: Quid [io] quincunce speciosius, qui, in quamcumque partem spectaveris, rectus est? cioeá che cosa c'eádi piuáparticoare de quinconce che, da quaunque parti o guardi presenta inee rette? Questa disposizione viene usata proprio per piantare fiari di aberi, dae viti ai pioppi ae betue, percheâ eá a sistemazione che permette di sfruttare a megio gi spazi; i massimo numero di oggetti che si possono disporre in uno spazio imitato rispettando e Q Re Fraschini - Grazzi, Atas SpA Tema 5 - Cap. 3: PARALLELISMO E PERPENDICOLARITA Á NEL PIANO 9
10 opportune distanze eá proprio queo di una disposizione a quinconce. Per questo motivo nee aziende aimentari anche i biscotti vengono distribuiti a quinconce sue piastre di cottura. Nea iuminazione dee strade i ampioni vengono spesso disposti a quinconce sui ati opposti. La macchina di Gaton, un dispositivo statistico che si utiizza per studiare e distribuzioni casuai di oggetti, usa uno schema a quinconce: una serie di paine vengono fatte scendere da un serbatoio e passano attraverso una serie di ostacoi disposti neo schema de quinconce e si raggruppano in una serie di raccogitori che si trovano aa base; a distribuzione dee paine daá sempre origine a una curva a campana tipica di moti fenomeni casuai. 1 I triangoo di Tartagia che viene costruito per determinare i coefficienti deo sviuppo dea potenza n- esima di un binomio ha uno schema a quinconce. Scrivi o sviuppo de triangoo e evidenzia questa caratteristica. 2 Quai fra i seguenti giochi utiizzano nea oro rappresentazione uno schema a quinconce? a. a dama e gi scacchi b. i tabeone dea tomboa c. e carte da gioco. 3 Una magia rettangoare eá formata da quattro fie di sei quadrati ciascuno. In ciascuna dee magie si deve mettere un oggetto, rappresentato da un cerchio avente diametro uguae a ato dea magia in modo che nessun oggetto abbia punti in comune con un atro. Qua eá i maggior numero di oggetti che eá possibie inserire neo schema? In che modo devono essere inseriti gi oggetti? 4 Inventiamo un gioco. Consideriamo uno schema di sei righe di sei casee ciascuna, disposte a quinconce (in grigio nea figura) e distribuiamo a caso sue casee otto triangoi equiateri rossi e cinque triangoi equiateri neri. Utiizziamo due dadi di coori diversi: queo bianco indica di quante righe ci si deve spostare in avanti in un movimento cicico (una vota arrivati in fondo si ricomincia daa riga piuá in basso), queo nero indica di quante casee (quee grigie) ci si deve spostare di ato verso destra in un movimento cicico (una vota arrivati in fondo aa riga si ricomincia da bordo sinistro). I due giocatori dispongono i oro segnai (per esempio due graffette o due gessetti coorati) ai due angoi dea riga piuá in basso e anciano a turno i dadi muovendosi in avanti e di ato de numero di casee indicate da ciascuno di essi. Quando arrivano a una casea con un triangoo rosso o acquisiscono come patrimonio personae, quando arrivano su una casea con un triangoo nero o asciano sua scacchiera ma devono cedere a giocatore avversario un triangoo rosso. I gioco termina quando un giocatore acquisisce un numero sufficiente di triangoi equiateri per costruire un esagono. Costruisci o schema e prova a giocare. 2 a., c oggetti disposti a quinconce 10 Tema 5 - Cap. 3: PARALLELISMO E PERPENDICOLARITA Á NEL PIANO Q Re Fraschini - Grazzi, Atas SpA
1. LA PARABOLA CON GEOGEBRA
 1. LA PARABOLA CON GEOGEBRA Dopo aver avviato i programma, chiudiamo a Vista Agebra, togiamo gi assi cartesiani e a grigia da quea grafica in modo da avorare iniziamente ne piano eucideo. Affrontiamo poi
1. LA PARABOLA CON GEOGEBRA Dopo aver avviato i programma, chiudiamo a Vista Agebra, togiamo gi assi cartesiani e a grigia da quea grafica in modo da avorare iniziamente ne piano eucideo. Affrontiamo poi
Luoghi di punti e funzioni non lineari
 CAPITOLO 3 Luoghi di punti e funzioni non ineari 1. LE FUNZIONI NON LINEARI CON DERIVE Per costruire i grafico di una paraboa o di un'iperboe si usa a stessa procedura usata per a retta: si scrive 'equazione
CAPITOLO 3 Luoghi di punti e funzioni non ineari 1. LE FUNZIONI NON LINEARI CON DERIVE Per costruire i grafico di una paraboa o di un'iperboe si usa a stessa procedura usata per a retta: si scrive 'equazione
I primi elementi e i triangoli
 MATEMATICAperTUTTI I triangoi 1 ESERCIZIO SVOLTO I primo criterio di congruenza. I confronto fra figure geometriche è un operazione che ricorre spesso in geometria, speciamente i confronto fra triangoi.
MATEMATICAperTUTTI I triangoi 1 ESERCIZIO SVOLTO I primo criterio di congruenza. I confronto fra figure geometriche è un operazione che ricorre spesso in geometria, speciamente i confronto fra triangoi.
CONOSCENZE 1. il concetto di parallelismo e. e perpendicolari. 2. la proiezione di un segmento
 GEOMETRIA PREREQUISITI conoscere e caratteristiche de sistema decimae conoscere e proprietaá dee quattro operazioni e operare con esse operare con e misure angoari conoscere gi enti dea geometria e e oro
GEOMETRIA PREREQUISITI conoscere e caratteristiche de sistema decimae conoscere e proprietaá dee quattro operazioni e operare con esse operare con e misure angoari conoscere gi enti dea geometria e e oro
Le funzioni goniometriche
 CAPITOLO 1 MATEMATICA PER LA FISICA Le funzioni goniometriche Obiettivi definire e funzioni goniometriche fondamentai in riferimento ai triangoi rettangoi e aa circonferenza goniometrica risovere triangoi
CAPITOLO 1 MATEMATICA PER LA FISICA Le funzioni goniometriche Obiettivi definire e funzioni goniometriche fondamentai in riferimento ai triangoi rettangoi e aa circonferenza goniometrica risovere triangoi
Parallelogrammi, trapezi e poligoni regolari
 CAPITOLO 5 Paraeogrammi, trapezi e poigoni regoari 1. I PARALLELOGRAMMI CON GEOGEBRA Esercitazione 1. Costruire un paraeogramma dati tre vertici consecutivi Per risovere questo probema usiamo a definizione
CAPITOLO 5 Paraeogrammi, trapezi e poigoni regoari 1. I PARALLELOGRAMMI CON GEOGEBRA Esercitazione 1. Costruire un paraeogramma dati tre vertici consecutivi Per risovere questo probema usiamo a definizione
Parallelogrammi e trapezi 1
 Paraeogrammi e trapezi riconoscere un paraeogramma e individuarne e proprietaá riconoscere paraeogrammi particoari e individuarne e proprietaá riconoscere trapezi e individuarne e proprietaá individuare
Paraeogrammi e trapezi riconoscere un paraeogramma e individuarne e proprietaá riconoscere paraeogrammi particoari e individuarne e proprietaá riconoscere trapezi e individuarne e proprietaá individuare
I poligoni e la circonferenza
 CAPITOLO 2 I poigoni e a circonferenza 1. POLIGONI INSCRITTI E CIRCOSCRITTI CON GEOGEBRA Esercitazione 1. I teoremi sui quadriateri con GeoGebra Facciamo a seguente costruzione: disegniamo un triangoo
CAPITOLO 2 I poigoni e a circonferenza 1. POLIGONI INSCRITTI E CIRCOSCRITTI CON GEOGEBRA Esercitazione 1. I teoremi sui quadriateri con GeoGebra Facciamo a seguente costruzione: disegniamo un triangoo
1. MISURIAMO GLI ANGOLI CON GEOGEBRA
 . MISURIAMO GLI ANGOLI CON GEOGEBRA Nascondiamo gi assi cartesiani in modo da usare a finestra grafica come piano eucideo. Disegniamo un punto C che rappresenti i centro di una circonferenza e creiamo
. MISURIAMO GLI ANGOLI CON GEOGEBRA Nascondiamo gi assi cartesiani in modo da usare a finestra grafica come piano eucideo. Disegniamo un punto C che rappresenti i centro di una circonferenza e creiamo
Il piano cartesiano, la retta e le funzioni di proporzionalità
 MATEMATICAperTUTTI I piano cartesiano, a retta e e funzioni di proporzionaità ESERCIZIO SVOLTO I piano cartesiano. Per fissare un sistema di riferimento ne piano si considerano due rette orientate fra
MATEMATICAperTUTTI I piano cartesiano, a retta e e funzioni di proporzionaità ESERCIZIO SVOLTO I piano cartesiano. Per fissare un sistema di riferimento ne piano si considerano due rette orientate fra
Rette, piani e figure nello spazio
 CAPITOLO Rette, piani e figure neo spazio. LA GEOMETRIA DELLO SPAZIO CON CABRI 3D Cabri 3D eá un software che, consentendo una facie costruzione di soidi, piani e figure deo spazio in genere, permette
CAPITOLO Rette, piani e figure neo spazio. LA GEOMETRIA DELLO SPAZIO CON CABRI 3D Cabri 3D eá un software che, consentendo una facie costruzione di soidi, piani e figure deo spazio in genere, permette
Cap 1. LA CIRCONFERENZA
 Cap 1. LA CIRCONERENZA Rivedi a teoria I uoghi geometrici Un uogo eá 'insieme di tutti e soi gi oggetti geometrici che possiedono una proprietaá P; se gi oggetti sono punti, si para di uogo di punti. Esempi
Cap 1. LA CIRCONERENZA Rivedi a teoria I uoghi geometrici Un uogo eá 'insieme di tutti e soi gi oggetti geometrici che possiedono una proprietaá P; se gi oggetti sono punti, si para di uogo di punti. Esempi
1 La traslazione. 2 La composizione di traslazioni. 3 La rotazione
 1 La traslazione Per poter applicare una traslazione ad una generica figura geometrica si deve: ± creare il vettore di traslazione AB mediante il comando Vettore tra due punti; ± cliccare con il mouse
1 La traslazione Per poter applicare una traslazione ad una generica figura geometrica si deve: ± creare il vettore di traslazione AB mediante il comando Vettore tra due punti; ± cliccare con il mouse
La scala logaritmica
 La scaa ogaritmica Obiettivi utiizzare coordinate ogaritmiche e semiogaritmiche 1. COORDINATE LOGARITMICHE Se un numero k eá maggiore di 10, i suo ogaritmo in base 10 eá moto piuá piccoo de numero stesso:
La scaa ogaritmica Obiettivi utiizzare coordinate ogaritmiche e semiogaritmiche 1. COORDINATE LOGARITMICHE Se un numero k eá maggiore di 10, i suo ogaritmo in base 10 eá moto piuá piccoo de numero stesso:
I TRIANGOLI. Geogebra l Triangoli COSTRUZIONE DEL TRIANGOLO ISOSCELE
 I TRIANGOLI COSTRUZIONE DEL TRIANGOLO ISOSCELE Come sai il triangolo isoscele ha due lati della stessa lunghezza. Costruiamo il triangolo isoscele a partire dal lato disuguale. 1. Apri il programma Geogebra
I TRIANGOLI COSTRUZIONE DEL TRIANGOLO ISOSCELE Come sai il triangolo isoscele ha due lati della stessa lunghezza. Costruiamo il triangolo isoscele a partire dal lato disuguale. 1. Apri il programma Geogebra
GEOMETRIA PIANA. Legenda: l = lato. a, b, c = dimensioni d1, d2 oppure d, D = diagonali 2P = perimetro r = raggio π (pi greco) = 3,14 b
 GEOMETRIA PIANA Legenda: A = area h = atezza = ato = ase o ase minore B = ase maggiore a,, c = dimensioni d1, d oppure d, D = diagonai P = perimetro r = raggio π (pi greco) = 3,14 d a A P d h r B D d c
GEOMETRIA PIANA Legenda: A = area h = atezza = ato = ase o ase minore B = ase maggiore a,, c = dimensioni d1, d oppure d, D = diagonai P = perimetro r = raggio π (pi greco) = 3,14 d a A P d h r B D d c
MAPPA 1 FIGURE. Figure geometriche: idee, misure, strumenti. Figure geometriche Una figura geometrica è un insieme di punti.
 MPP 1 Figure Figure geometriche Una figura geometrica è un insieme di punti. Figure piane e figure soide Una figura i cui punti appartengono tutti ao stesso piano si chiama piana. Una figura i cui punti
MPP 1 Figure Figure geometriche Una figura geometrica è un insieme di punti. Figure piane e figure soide Una figura i cui punti appartengono tutti ao stesso piano si chiama piana. Una figura i cui punti
Triangolo rettangolo
 Triangoo rettangoo Le paroe dea matematica Cateto minore C i ipotenusa C1 Cateto maggiore Verificiamo i teorema di Pitagora Enunciato: In un triangoo rettangoo area de quadrato costruito su ipotenusa è
Triangoo rettangoo Le paroe dea matematica Cateto minore C i ipotenusa C1 Cateto maggiore Verificiamo i teorema di Pitagora Enunciato: In un triangoo rettangoo area de quadrato costruito su ipotenusa è
Nel caso particolare in cui il vertice si trovi nell'origine, la parabola assume la forma: y ˆ ax 2.
 LA PARABOLA Rivedi la teoria La parabola e la sua equazione La parabola eá il luogo dei punti del piano che hanno la stessa distanza da un punto fisso chiamato fuoco e da una retta fissa chiamata direttrice.
LA PARABOLA Rivedi la teoria La parabola e la sua equazione La parabola eá il luogo dei punti del piano che hanno la stessa distanza da un punto fisso chiamato fuoco e da una retta fissa chiamata direttrice.
L ANGOLO (2) MISURA DELL ANGOLO Per avere la misura di un angolo, che si chiama ampiezza, si deve ricorrere ad uno strumento: il goniometro.
 Geogebra L ANGOLO (2) MISURA DELL ANGOLO Per avere la misura di un angolo, che si chiama ampiezza, si deve ricorrere ad uno strumento: il goniometro. In Geogebra c è un icona che ci permette di misurare
Geogebra L ANGOLO (2) MISURA DELL ANGOLO Per avere la misura di un angolo, che si chiama ampiezza, si deve ricorrere ad uno strumento: il goniometro. In Geogebra c è un icona che ci permette di misurare
Le funzioni goniometriche e i triangoli
 CAPITOLO 1 Le funzioni goniometriche e i triangoi 1. LE FUNZIONI GONIOMETRICHE CON GEOGEBRA Per megio comprendere come vengono generati i grafici dee funzioni goniometriche fondamentai eseguiamo una particoare
CAPITOLO 1 Le funzioni goniometriche e i triangoi 1. LE FUNZIONI GONIOMETRICHE CON GEOGEBRA Per megio comprendere come vengono generati i grafici dee funzioni goniometriche fondamentai eseguiamo una particoare
I quadrilateri Punti notevoli di un triangolo
 I quadrilateri Capitolo Quadrilateri 1 erifica per la classe prima COGME............................... ME............................. Quesiti 1.a ero o falso? 1. La somma degli angoli interni di un ottagono
I quadrilateri Capitolo Quadrilateri 1 erifica per la classe prima COGME............................... ME............................. Quesiti 1.a ero o falso? 1. La somma degli angoli interni di un ottagono
Cap 1. I PRIMI ELEMENTI
 Cap 1. I PRIMI ELEMENTI Rivedi a teoria I termini primitivi In quasiasi discipina non si puoá definire tutto e non si puoá dimostrare tutto; eá necessario introdurre acuni oggetti (termini primitivi) e
Cap 1. I PRIMI ELEMENTI Rivedi a teoria I termini primitivi In quasiasi discipina non si puoá definire tutto e non si puoá dimostrare tutto; eá necessario introdurre acuni oggetti (termini primitivi) e
Lunghezza della circonferenza e area del cerchio
 3 GEMETRI Lunghezza dea circonferenza e area de cerchio Esercizi suppementari di verifica Esercizio 1 Metti una crocetta su vero (V) o faso (F) accanto ad ogni formua reativa aa unghezza dea circonferenza
3 GEMETRI Lunghezza dea circonferenza e area de cerchio Esercizi suppementari di verifica Esercizio 1 Metti una crocetta su vero (V) o faso (F) accanto ad ogni formua reativa aa unghezza dea circonferenza
Costruzione 1 Condurre la perpendicolare ad un retta data, passante per un punto della retta stessa.
 Costruzioni Costruzioni di rette, segmenti ed angoli Costruzione 1 Condurre la perpendicolare ad un retta data, passante per un punto della retta stessa. Costruzione. Consideriamo la retta r ed un punto
Costruzioni Costruzioni di rette, segmenti ed angoli Costruzione 1 Condurre la perpendicolare ad un retta data, passante per un punto della retta stessa. Costruzione. Consideriamo la retta r ed un punto
1 L'omotetia. 2 Il teorema del rapporto dei perimetri e delle aree di due triangoli simili
 1 L'omotetia Per definire un'omotetia bisogna disegnare una generica figura nel piano (nel nostro caso utilizzeremo un triangolo), un punto (il centro dell'omotetia) e un numero (il rapporto k dell'omotetia).
1 L'omotetia Per definire un'omotetia bisogna disegnare una generica figura nel piano (nel nostro caso utilizzeremo un triangolo), un punto (il centro dell'omotetia) e un numero (il rapporto k dell'omotetia).
LA GEOMETRIA NELLO SPAZIO
 LA GEOMETRIA NELLO SPAZIO n.1 Un eemento primitivo: o spazio. Lo spazio è caratterizzato dai seguenti assiomi: Lo spazio contiene infiniti punti, infinite rette, infiniti piani. Ogni piano divide o spazio
LA GEOMETRIA NELLO SPAZIO n.1 Un eemento primitivo: o spazio. Lo spazio è caratterizzato dai seguenti assiomi: Lo spazio contiene infiniti punti, infinite rette, infiniti piani. Ogni piano divide o spazio
LE POTENZE DEI NUMERI
 ARITMETICA LE POTENZE DEI NUMERI PREREQUISITI conoscere e proprietaá dee quattro operazioni svogere cacoi a mente ed in coonna con e quattro operazioni risovere espressioni con e quattro operazioni distinguere
ARITMETICA LE POTENZE DEI NUMERI PREREQUISITI conoscere e proprietaá dee quattro operazioni svogere cacoi a mente ed in coonna con e quattro operazioni risovere espressioni con e quattro operazioni distinguere
Il piano cartesiano e la retta
 CAPITOLO 1 I piano cartesiano e a retta 1. IL PIANO CARTESIANO E LA RETTA CON DERIVE 1.1 Segmenti e punti Abbiamo visto piuá vote come si costruisce una funzione di assegnamento con Derive; possiamo usare
CAPITOLO 1 I piano cartesiano e a retta 1. IL PIANO CARTESIANO E LA RETTA CON DERIVE 1.1 Segmenti e punti Abbiamo visto piuá vote come si costruisce una funzione di assegnamento con Derive; possiamo usare
Grafici di particolari funzioni lineari
 A Grafici di particoari funzioni ineari Vogiamo tracciare i grafico dea funzione y ˆ jxj. x quando x 0 Sappiamo che jxj significa x quando x < 0 Possiamo aora riscrivere 'equazione di questa funzione in
A Grafici di particoari funzioni ineari Vogiamo tracciare i grafico dea funzione y ˆ jxj. x quando x 0 Sappiamo che jxj significa x quando x < 0 Possiamo aora riscrivere 'equazione di questa funzione in
1. LA GEOMETRIA DELLO SPAZIO CON CABRI 3D
 1. LA GEOMETRIA DELLO SPAZIO CON CABRI 3D Cabri 3D eá un software che, consentendo una facile costruzione di solidi, piani e figure dello spazio in genere, permette di mettere in evidenza caratteristiche
1. LA GEOMETRIA DELLO SPAZIO CON CABRI 3D Cabri 3D eá un software che, consentendo una facile costruzione di solidi, piani e figure dello spazio in genere, permette di mettere in evidenza caratteristiche
LE TRASFORMAZIONI GEOMETRICHE
 LE TRASFORMAZIONI GEOMETRICHE LA SIMMETRIA ASSIALE Definizione: il simmetrico P di un punto P, rispetto alla simmetria assiale di asse r gode delle seguenti proprietà: P e P sono equidistanti da r e il
LE TRASFORMAZIONI GEOMETRICHE LA SIMMETRIA ASSIALE Definizione: il simmetrico P di un punto P, rispetto alla simmetria assiale di asse r gode delle seguenti proprietà: P e P sono equidistanti da r e il
Problemi di scelta. y ˆ 5x 800 y ˆ 1500
 A Probemi di sceta CioÁ che abbiamo studiato a proposito dea retta ci puoá essere di aiuto per risovere probemi in cui si deve fare una sceta tra diverse possibiitaá. Per esempio quando si acquista un'auto
A Probemi di sceta CioÁ che abbiamo studiato a proposito dea retta ci puoá essere di aiuto per risovere probemi in cui si deve fare una sceta tra diverse possibiitaá. Per esempio quando si acquista un'auto
IL SISTEMA DI RIFERIMENTO
 IL SISTEMA DI RIFERIMENTO CARTESIANO E LA RETTA Per ricordare H Consideriamo una retta orientata r, fissiamo su di essa un punto O e prendiamo un segmento u come unitaá di misura; consideriamo un punto
IL SISTEMA DI RIFERIMENTO CARTESIANO E LA RETTA Per ricordare H Consideriamo una retta orientata r, fissiamo su di essa un punto O e prendiamo un segmento u come unitaá di misura; consideriamo un punto
Cosa puoi dire del quadrilatero ABCD? Come sono i lati, le diagonali, gli angoli?
 Dal parallelogramma al rombo (fase 1 e 2) Fase 1 Disegna due circonferenze concentriche c e c di centro O; disegna su c un punto A e su c un punto B; traccia la retta r passante per i punti A e O, chiama
Dal parallelogramma al rombo (fase 1 e 2) Fase 1 Disegna due circonferenze concentriche c e c di centro O; disegna su c un punto A e su c un punto B; traccia la retta r passante per i punti A e O, chiama
Due incognite ipertstatiche con cedimento elastico lineare sul vincolo
 Dott. Ing aoo Serafini Cic per tutti gi appunti (AUTOAZIONE TRATTAENTI TERICI ACCIAIO SCIENZA dee COSTRUZIONI ) e-mai per suggerimenti Due incognite ipertstatiche con cedimento eastico ineare su vincoo
Dott. Ing aoo Serafini Cic per tutti gi appunti (AUTOAZIONE TRATTAENTI TERICI ACCIAIO SCIENZA dee COSTRUZIONI ) e-mai per suggerimenti Due incognite ipertstatiche con cedimento eastico ineare su vincoo
1 Disegnare e spostare punti
 1 Disegnare e spostare punti Iniziamo con la costruzione e lo spostamento di un punto. Per costruire un punto si deve: ± attivare il comando Nuovo Punto; ± posizionare il mouse nella posizione desiderata;
1 Disegnare e spostare punti Iniziamo con la costruzione e lo spostamento di un punto. Per costruire un punto si deve: ± attivare il comando Nuovo Punto; ± posizionare il mouse nella posizione desiderata;
Il primo criterio di congruenza
 G Il primo criterio di congruenza Costruire un triangolo congruente a un triangolo dato sfruttando il primo criterio di congruenza dei triangoli. Prima di iniziare a tracciare gli oggetti che fanno parte
G Il primo criterio di congruenza Costruire un triangolo congruente a un triangolo dato sfruttando il primo criterio di congruenza dei triangoli. Prima di iniziare a tracciare gli oggetti che fanno parte
Problemi di geometria
 criteri di similitudine sui triangoli 1 Dimostra che le altezze di un triangolo sono inversamente proporzionali ai relativi lati. 2 Dimostra che due triangoli rettangoli sono simili se hanno ordinatamente
criteri di similitudine sui triangoli 1 Dimostra che le altezze di un triangolo sono inversamente proporzionali ai relativi lati. 2 Dimostra che due triangoli rettangoli sono simili se hanno ordinatamente
ASSI CARTESIANI: Esercizio n 80: Date le seguenti terne di punti, disegnare il triangolo corrispondente (C3 il perimetro e l area:
 ASSI CARTESIANI: Per attivare la visualizzazione degli assi cartesiani scegliere C Mostra gli assi e poi C Griglia, portarsi su un asse e cliccare quando compare la scritta Questi assi. E possibile cambiare
ASSI CARTESIANI: Per attivare la visualizzazione degli assi cartesiani scegliere C Mostra gli assi e poi C Griglia, portarsi su un asse e cliccare quando compare la scritta Questi assi. E possibile cambiare
I triangoli e i criteri di congruenza
 CAPITOLO 2 I triangoi e i criteri di congruenza 1. I POLIGONI CON GEOGEBRA La costruzione di un poigono avviene mediante 'uso deo strumento 5-Poigono; a guida sintetica che si trova a ato dea Barra degi
CAPITOLO 2 I triangoi e i criteri di congruenza 1. I POLIGONI CON GEOGEBRA La costruzione di un poigono avviene mediante 'uso deo strumento 5-Poigono; a guida sintetica che si trova a ato dea Barra degi
C7. Circonferenza e cerchio - Esercizi
 C7. Circonferenza e cerchio - Esercizi DEFINIZIONI E COSTRUZIONI 1) Dare la definizione di luogo geometrico. 2) Indicare almeno due luoghi geometrici. 3) Dare la definizione di asse di un segmento come
C7. Circonferenza e cerchio - Esercizi DEFINIZIONI E COSTRUZIONI 1) Dare la definizione di luogo geometrico. 2) Indicare almeno due luoghi geometrici. 3) Dare la definizione di asse di un segmento come
l B 1. la velocità angolare dell asta un istante prima dell urto; 2. la velocità v 0 ; 3. l energia cinetica dissipata nell urto;
 1 Esercizio (tratto da Probema 8.29 de Mazzodi 2) Un asta di unghezza 1.2 m e massa M 0.5 Kg è incernierata ne suo estremo A ad un perno fisso e può osciare senza attrito in un piano verticae. A istante
1 Esercizio (tratto da Probema 8.29 de Mazzodi 2) Un asta di unghezza 1.2 m e massa M 0.5 Kg è incernierata ne suo estremo A ad un perno fisso e può osciare senza attrito in un piano verticae. A istante
Geogebra. a. La lancetta è ruotata? SI NO. Se sì attorno a quale punto?
 Geogebra L ANGOLO 1. Nel programma Geogebra, fai doppio clic sull icona e scegli Circonferenza dati centro e raggio. 2. Posizionati al centro della finestra di geometria e fai clic. Nella finestra che
Geogebra L ANGOLO 1. Nel programma Geogebra, fai doppio clic sull icona e scegli Circonferenza dati centro e raggio. 2. Posizionati al centro della finestra di geometria e fai clic. Nella finestra che
Equilibrio del corpo rigido
 Equiibrio de corpo rigido Probema1 Due sbarrette omogenee AB e BC aventi a stessa unghezza e a stessa massa di 6 kg, vengono sadate ne punto B in modo da formare un angoo di 90. Le due sbarrette così unite
Equiibrio de corpo rigido Probema1 Due sbarrette omogenee AB e BC aventi a stessa unghezza e a stessa massa di 6 kg, vengono sadate ne punto B in modo da formare un angoo di 90. Le due sbarrette così unite
Lezione 6 Richiami di Geometria Analitica
 1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
Problemi di geometria
 1 2 3 applicazioni al triangolo rettangolo Calcola il perimetro e l area di un triangolo rettangolo sapendo che l ipotenusa e l altezza ad essa relativa sono lunghe rispettivamente 3 cm e 16,8 cm. [8 cm;
1 2 3 applicazioni al triangolo rettangolo Calcola il perimetro e l area di un triangolo rettangolo sapendo che l ipotenusa e l altezza ad essa relativa sono lunghe rispettivamente 3 cm e 16,8 cm. [8 cm;
Tangenti. Lezione 2. Tangenti
 Lezione. Tangenti 1 Circonferenze tangenti tra loro Poiché due circonferenze sono reciprocamente tangenti quando hanno un solo punto in comune, vi sono essenzialmente due modi in cui ciò può avvenire:
Lezione. Tangenti 1 Circonferenze tangenti tra loro Poiché due circonferenze sono reciprocamente tangenti quando hanno un solo punto in comune, vi sono essenzialmente due modi in cui ciò può avvenire:
VERIFICA DI GEOMETRIA
 NOME...T... VERIFI I GEOMETRI 1) Indica con una crocetta se vero o faso: I trapezi anno tutti i ati opposti paraei. I paraeogrammi anno i ati opposti uguai e paraei. Un triangoo equiatero è un poigono
NOME...T... VERIFI I GEOMETRI 1) Indica con una crocetta se vero o faso: I trapezi anno tutti i ati opposti paraei. I paraeogrammi anno i ati opposti uguai e paraei. Un triangoo equiatero è un poigono
Il Tetraedro regolare
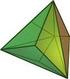 I Tetraedro regoare E i soido che ha per facce 4 triangoi equiateri, (F = 4) Ha 6 spigoi (S = 6) e 4 vertici (V = 4) I suo sviuppo è i seguente: Chiuso diventa: Le proiezioni possibii sono: I suoi assi
I Tetraedro regoare E i soido che ha per facce 4 triangoi equiateri, (F = 4) Ha 6 spigoi (S = 6) e 4 vertici (V = 4) I suo sviuppo è i seguente: Chiuso diventa: Le proiezioni possibii sono: I suoi assi
b 2 4c. Stabiliamo se le seguenti equazioni rappresentano delle circonferenze e, in caso affermativo, determiniamone centro e raggio.
 LA CIRCONFERENZA Rivedi la teoria L'equazione della circonferenza e le sue caratteristiche La circonferenza eá il luogo dei punti del piano che hanno la stessa distanza da un punto fisso chiamato centro;
LA CIRCONFERENZA Rivedi la teoria L'equazione della circonferenza e le sue caratteristiche La circonferenza eá il luogo dei punti del piano che hanno la stessa distanza da un punto fisso chiamato centro;
Rette perpendicolari
 Rette perpendicolari Definizione: due rette incidenti (che cioè si intersecano in un punto) si dicono perpendicolari quando dividono il piano in quattro angoli retti. Per indicare che la retta a è perpendicolare
Rette perpendicolari Definizione: due rette incidenti (che cioè si intersecano in un punto) si dicono perpendicolari quando dividono il piano in quattro angoli retti. Per indicare che la retta a è perpendicolare
Figure piane. Due figure sono congruenti se sovrapposte coincidono perfettamente. figure a contorno mistilineo
 Figure piane poigoni cerci figure a contorno curviineo figure a contorno mistiineo I due poigoni sono congruenti I due cerci non sono congruenti ue figure sono congruenti se sovrapposte coincidono perfettamente
Figure piane poigoni cerci figure a contorno curviineo figure a contorno mistiineo I due poigoni sono congruenti I due cerci non sono congruenti ue figure sono congruenti se sovrapposte coincidono perfettamente
LA PERPENDICOLARITA NELLO SPAZIO. Nello spazio si definiscono la perpendicolarità sia tra una retta e un piano sia tra due piani.
 1 LA PERPENDICOLARITA NELLO SPAZIO Nello spazio si definiscono la perpendicolarità sia tra una retta e un piano sia tra due piani. 2.1 La perpendicolarità retta piano Nel piano la perpendicolarità tra
1 LA PERPENDICOLARITA NELLO SPAZIO Nello spazio si definiscono la perpendicolarità sia tra una retta e un piano sia tra due piani. 2.1 La perpendicolarità retta piano Nel piano la perpendicolarità tra
Anno 1. Quadrilateri
 Anno 1 Quadrilateri 1 Introduzione In questa lezione impareremo a risolvere i problemi legati all utilizzo dei quadrilateri. Forniremo la definizione di quadrilatero e ne analizzeremo le proprietà e le
Anno 1 Quadrilateri 1 Introduzione In questa lezione impareremo a risolvere i problemi legati all utilizzo dei quadrilateri. Forniremo la definizione di quadrilatero e ne analizzeremo le proprietà e le
C9. Teorema di Talete e similitudine - Esercizi
 C9. Teorema di Talete e similitudine - Esercizi ESERCIZI SU TEOREMA DI TALETE, TEOREMA DELLA BISETTRICE Si consideri la seguente figura e si risponda alle domande che seguono. 1) Se AB=2, BC=4 e EF=3 trovare
C9. Teorema di Talete e similitudine - Esercizi ESERCIZI SU TEOREMA DI TALETE, TEOREMA DELLA BISETTRICE Si consideri la seguente figura e si risponda alle domande che seguono. 1) Se AB=2, BC=4 e EF=3 trovare
CAP.2:ITRIANGOLI GEOMETRIA 1 - AREA 3 I TRIANGOLI E LA LORO CLASSIFICAZIONE. richiami della teoria COMPRENSIONE DELLA TEORIA
 GEOMETRIA 1 - AREA 3 CAP.2:ITRIANGOLI I TRIANGOLI E LA LORO CLASSIFICAZIONE richiami della teoria n In un triangolo ogni lato eá minore della somma degli altri due ed eá maggiore della loro differenza;
GEOMETRIA 1 - AREA 3 CAP.2:ITRIANGOLI I TRIANGOLI E LA LORO CLASSIFICAZIONE richiami della teoria n In un triangolo ogni lato eá minore della somma degli altri due ed eá maggiore della loro differenza;
Condizione di allineamento di tre punti
 LA RETTA L equazione lineare in x e y L equazione: 0 con,,, e non contemporaneamente nulli, si dice equazione lineare nelle due variabili e. Ogni coppia ; tale che: 0 si dice soluzione dell equazione.
LA RETTA L equazione lineare in x e y L equazione: 0 con,,, e non contemporaneamente nulli, si dice equazione lineare nelle due variabili e. Ogni coppia ; tale che: 0 si dice soluzione dell equazione.
I primi elementi. www.geogebra.org/cms/
 CAPITOLO 1 I primi eementi 1. GEOGEBRA Geogebra eá un software di matematica dinamica prodotto da un gruppo diretto da Markus Hohenwarter in cui geometria e agebra condividono o stesso ambiente di avoro.
CAPITOLO 1 I primi eementi 1. GEOGEBRA Geogebra eá un software di matematica dinamica prodotto da un gruppo diretto da Markus Hohenwarter in cui geometria e agebra condividono o stesso ambiente di avoro.
DISTANZA TRA DUE PUNTI NEL PIANO CARTESIANO
 Geogebra DISTANZA TRA DUE PUNTI NEL PIANO CARTESIANO 1. Apri il programma Geogebra, assicurati che siano visualizzati gli assi e individua il punto A (0, 0). a. Dove si trova il punto A? b. Individua il
Geogebra DISTANZA TRA DUE PUNTI NEL PIANO CARTESIANO 1. Apri il programma Geogebra, assicurati che siano visualizzati gli assi e individua il punto A (0, 0). a. Dove si trova il punto A? b. Individua il
Esercitazione 7 del corso di Statistica 2
 Esercitazione 7 de corso di Statistica Prof. Domenico Vistocco Dott.ssa Paoa Costantini 9 Giugno 008 Esercizio La distribuzione dei pesi dei pesi pacchetti per confezionare per confezionare e caramee,
Esercitazione 7 de corso di Statistica Prof. Domenico Vistocco Dott.ssa Paoa Costantini 9 Giugno 008 Esercizio La distribuzione dei pesi dei pesi pacchetti per confezionare per confezionare e caramee,
Progetto Matematica in Rete - Geometria euclidea - Triangoli - I triangoli
 I triangoli Definizione: un triangolo è l insieme dei punti del piano costituiti da una poligonale chiusa di tre lati e dai suoi punti interni. A, B, C vertici del triangolo α, β, γ angoli interni AB,
I triangoli Definizione: un triangolo è l insieme dei punti del piano costituiti da una poligonale chiusa di tre lati e dai suoi punti interni. A, B, C vertici del triangolo α, β, γ angoli interni AB,
esercizi 107 Problemi sulla retta
 esercizi 107 Problemi sulla retta Es. 1 Detto C il punto in cui l asse del segmento di estremi A( 3, 3) e B(1, 5) incontra l asse x, calcolare le coordinate del punto D equidistante da A, B e C. Determinare
esercizi 107 Problemi sulla retta Es. 1 Detto C il punto in cui l asse del segmento di estremi A( 3, 3) e B(1, 5) incontra l asse x, calcolare le coordinate del punto D equidistante da A, B e C. Determinare
Verifica del teorema di Talete
 C Verifica del teorema di Talete Verifica che il rapporto tra le lunghezze dei segmenti che due rette di un fascio di parallele intercettano sulle trasversali non cambia anche se si cambia la posizione
C Verifica del teorema di Talete Verifica che il rapporto tra le lunghezze dei segmenti che due rette di un fascio di parallele intercettano sulle trasversali non cambia anche se si cambia la posizione
LA CIRCONFERENZA E IL CERCHIO
 GEOMETRIA LA CIRCONERENZA E IL CERCHIO PREREQUISITI l conoscere le proprietaá delle quattro operazioni e operare con esse l conoscere gli enti fondamentali della geometria e le loro proprietaá l possedere
GEOMETRIA LA CIRCONERENZA E IL CERCHIO PREREQUISITI l conoscere le proprietaá delle quattro operazioni e operare con esse l conoscere gli enti fondamentali della geometria e le loro proprietaá l possedere
Progetto Matematica in Rete - Geometria euclidea - Quadrilateri. I quadrilateri. Il parallelogramma
 I quadrilateri Il parallelogramma Definizione: un parallelogramma è un quadrilatero avente i lati opposti paralleli AB // DC AD // BC Teorema : se ABCD è un parallelogramma allora ciascuna diagonale lo
I quadrilateri Il parallelogramma Definizione: un parallelogramma è un quadrilatero avente i lati opposti paralleli AB // DC AD // BC Teorema : se ABCD è un parallelogramma allora ciascuna diagonale lo
Proprietà di un triangolo
 Poligono con tre lati e tre angoli. Proprietà di un triangolo In un triangolo : I lati e i vertici sono consecutivi fra loro; La somma degli angoli interni è 180 ; La somma degli angoli esterni è 360 Ciascun
Poligono con tre lati e tre angoli. Proprietà di un triangolo In un triangolo : I lati e i vertici sono consecutivi fra loro; La somma degli angoli interni è 180 ; La somma degli angoli esterni è 360 Ciascun
LA CIRCONFERENZA, I POLIGONI INSCRITTI E CIRCOSCRITTI
 LA CIRCONFERENZA, I POLIGONI INSCRITTI E CIRCOSCRITTI 1. La circonferenza e il cerchio ESERCIZI 1 A Disegna un triangolo ABC di altezza CH relativa ad AB. Fissa un segmento ED minore di CH. Determina il
LA CIRCONFERENZA, I POLIGONI INSCRITTI E CIRCOSCRITTI 1. La circonferenza e il cerchio ESERCIZI 1 A Disegna un triangolo ABC di altezza CH relativa ad AB. Fissa un segmento ED minore di CH. Determina il
Problemi di geometria
 equivalenza fra parallelogrammi 1 2 3 4 Dimostra che, fra tutti i rettangoli equivalenti, il quadrato è quello che ha perimetro minimo. Dimostra che ogni quadrato è equivalente alla metà del quadrato costruito
equivalenza fra parallelogrammi 1 2 3 4 Dimostra che, fra tutti i rettangoli equivalenti, il quadrato è quello che ha perimetro minimo. Dimostra che ogni quadrato è equivalente alla metà del quadrato costruito
Equivalenza delle figure piane
 Capitolo Equivalenza Poligoni equivalenti - erifica per la classe seconda Teoremi di Pitagora ed Euclide COGNOME............................... NOME............................. Classe....................................
Capitolo Equivalenza Poligoni equivalenti - erifica per la classe seconda Teoremi di Pitagora ed Euclide COGNOME............................... NOME............................. Classe....................................
SCHEDA1 PARALLELISMO E PERPENDICOLARITA' FRA RETTE
 SCHEDA1 PARALLELISMO E PERPENDICOLARITA' FRA RETTE Controllare la correttezza delle seguenti proprietà, controllandola su un esempio e muovendo dinamicamente gli oggetti costruiti. 1. Per due punti passa
SCHEDA1 PARALLELISMO E PERPENDICOLARITA' FRA RETTE Controllare la correttezza delle seguenti proprietà, controllandola su un esempio e muovendo dinamicamente gli oggetti costruiti. 1. Per due punti passa
Corso di Meccanica, Macchine e Impianti Termici CAPITOLO 3 DIAGRAMMA DELLE SOLLECITAZIONI INTERNE
 Istituto Professionae Statae per 'Industria e 'rtigianato "L.. berti" Rimini nno Scoastico 009/010 orso di Meccanica, Macchine e Impianti Termici PITOLO 3 DIGRMM DELLE SOLLEITZIONI INTERNE Prof. Matteo
Istituto Professionae Statae per 'Industria e 'rtigianato "L.. berti" Rimini nno Scoastico 009/010 orso di Meccanica, Macchine e Impianti Termici PITOLO 3 DIGRMM DELLE SOLLEITZIONI INTERNE Prof. Matteo
Rette perpendicolari
 Rette perpendicolari Definizione: due rette incidenti (che cioè si intersecano in un punto) si dicono perpendicolari quando dividono il piano in quattro angoli retti. Per indicare che la retta a è perpendicolare
Rette perpendicolari Definizione: due rette incidenti (che cioè si intersecano in un punto) si dicono perpendicolari quando dividono il piano in quattro angoli retti. Per indicare che la retta a è perpendicolare
C5. Triangoli - Esercizi
 C5. Triangoli - Esercizi DEFINIZIONI 1) Dato il triangolo in figura completare al posto dei puntini. I lati sono i segmenti,, Gli angoli sono,, Il lato AB e l angolo sono opposti Il lato AB e l angolo
C5. Triangoli - Esercizi DEFINIZIONI 1) Dato il triangolo in figura completare al posto dei puntini. I lati sono i segmenti,, Gli angoli sono,, Il lato AB e l angolo sono opposti Il lato AB e l angolo
Principali Definizioni e Teoremi di Geometria
 Principali Definizioni e Teoremi di Geometria Segmento (definizione) Si dice segmento di estremi A e B l insieme costituito dai punti A e B e da tutti i punti della retta AB compresi tra A e B. Angolo
Principali Definizioni e Teoremi di Geometria Segmento (definizione) Si dice segmento di estremi A e B l insieme costituito dai punti A e B e da tutti i punti della retta AB compresi tra A e B. Angolo
Il primo criterio di congruenza
 C Il primo criterio di congruenza Costruisci un triangolo congruente a un triangolo dato sfruttando il primo criterio di congruenza. Per prima cosa dobbiamo tracciare un triangolo. Dal menu oggetti rettilinei,
C Il primo criterio di congruenza Costruisci un triangolo congruente a un triangolo dato sfruttando il primo criterio di congruenza. Per prima cosa dobbiamo tracciare un triangolo. Dal menu oggetti rettilinei,
Rappresentazione e codifica dell informazione
 Rappresentazione e codifica de informazione Premessa I cacoatore è una macchina digitae - I suo inguaggio è composto da due soi simboi Gi esseri umani sono abituati a comunicare utizzando più simboi Come
Rappresentazione e codifica de informazione Premessa I cacoatore è una macchina digitae - I suo inguaggio è composto da due soi simboi Gi esseri umani sono abituati a comunicare utizzando più simboi Come
IL TEOREMA DI PITAGORA
 IN CLASSE IL TEOREMA DI PITAGORA Preparazione Per questi esercizi con GeoGebra dovrai utilizzare i seguenti pulsanti. Leggi sempre le procedure di esecuzione nella zona in alto a destra, accanto alla barra
IN CLASSE IL TEOREMA DI PITAGORA Preparazione Per questi esercizi con GeoGebra dovrai utilizzare i seguenti pulsanti. Leggi sempre le procedure di esecuzione nella zona in alto a destra, accanto alla barra
e) A10, ( 1;B6,2 ) ( ) f) A3,42;B12,2
 7. ESERCIZI SULLA DISTANZA FRA DUE PUNTI ) Calcola le distanze fra le seguenti coppie di punti: a) A;B6 ( ) ( ) A( 8 ); B( 7 5) c) A ( ;B ) ( 7) d) A( ); B e) A ( ;B6 ) ( ) f) A4;B ( ) ( ) g) A ; B 6 h)
7. ESERCIZI SULLA DISTANZA FRA DUE PUNTI ) Calcola le distanze fra le seguenti coppie di punti: a) A;B6 ( ) ( ) A( 8 ); B( 7 5) c) A ( ;B ) ( 7) d) A( ); B e) A ( ;B6 ) ( ) f) A4;B ( ) ( ) g) A ; B 6 h)
I PARALLELOGRAMMI E I TRAPEZI
 I PARALLELOGRAMMI E I TRAPEZI 1. Il parallelogramma ESERCIZI 1 A Disegna un parallelogramma ABCD, la diagonale BD e i segmenti AK e CH, perpendicolari a BD. Dimostra che il quadrilatero AHCK è un parallelogramma.
I PARALLELOGRAMMI E I TRAPEZI 1. Il parallelogramma ESERCIZI 1 A Disegna un parallelogramma ABCD, la diagonale BD e i segmenti AK e CH, perpendicolari a BD. Dimostra che il quadrilatero AHCK è un parallelogramma.
Punti nel piano cartesiano
 Punti nel piano cartesiano In un piano consideriamo due rette perpendicolari che chiamiamo x e. Solitamente, disegniamo la retta x (ascisse) orizzontalmente e orientata da sinistra a destra, la retta e
Punti nel piano cartesiano In un piano consideriamo due rette perpendicolari che chiamiamo x e. Solitamente, disegniamo la retta x (ascisse) orizzontalmente e orientata da sinistra a destra, la retta e
Costruzioni geometriche. (Teoria pag , esercizi )
 Costruzioni geometriche. (Teoria pag. 81-96, esercizi 141-153 ) 1) Costruzione con squadra e riga. a) Rette parallele. Ricorda: due rette sono parallele quando.... oppure quando hanno la stessa. Matematicamente
Costruzioni geometriche. (Teoria pag. 81-96, esercizi 141-153 ) 1) Costruzione con squadra e riga. a) Rette parallele. Ricorda: due rette sono parallele quando.... oppure quando hanno la stessa. Matematicamente
La statistica descrittiva
 MATEMATICAperTUTTI Dee seguenti indagine statistiche individua a popoazione, i carattere oggetto di studio e e possibii modaità di tae carattere. 1 ESERCIZIO SVOLTO Indagine: utiizzo de tempo ibero da
MATEMATICAperTUTTI Dee seguenti indagine statistiche individua a popoazione, i carattere oggetto di studio e e possibii modaità di tae carattere. 1 ESERCIZIO SVOLTO Indagine: utiizzo de tempo ibero da
Lezione 3. Angoli al centro e angoli alla circonferenza
 Lezione 3. Angoli al centro e angoli alla circonferenza 1 Angoli in una circonferenza La proprietà illustrata dalle proposizioni 0, 1 e 3 del terzo libro degli Elementi si riferisce a una delle caratteristiche
Lezione 3. Angoli al centro e angoli alla circonferenza 1 Angoli in una circonferenza La proprietà illustrata dalle proposizioni 0, 1 e 3 del terzo libro degli Elementi si riferisce a una delle caratteristiche
C6. Quadrilateri - Esercizi
 C6. Quadrilateri - Esercizi DEFINIZIONI E COSTRUZIONI 1) Dato il seguente quadrilatero completa al posto dei puntini. I lati AB e BC sono I lati AB e CD sono I lati AD e sono consecutivi I lati AD e sono
C6. Quadrilateri - Esercizi DEFINIZIONI E COSTRUZIONI 1) Dato il seguente quadrilatero completa al posto dei puntini. I lati AB e BC sono I lati AB e CD sono I lati AD e sono consecutivi I lati AD e sono
Preparazione al compito di geometria (Semiretta, Retta, Angoli)
 Preparazione al compito di geometria (Semiretta, Retta, Angoli) Semiretta Per definire una semiretta, prendiamo una retta ed un punto P su di essa: Tale punto dividerà la retta in due parti; ciascuna di
Preparazione al compito di geometria (Semiretta, Retta, Angoli) Semiretta Per definire una semiretta, prendiamo una retta ed un punto P su di essa: Tale punto dividerà la retta in due parti; ciascuna di
Costruzioni geometriche. ( Teoria pag , esercizi 141 )
 Costruzioni geometriche. ( Teoria pag. 81-96, esercizi 141 ) 1) Costruzione con squadra e riga. a) Rette parallele. Ricorda ; due rette sono parallele quando.... oppure quando hanno la stessa. Matematicamente
Costruzioni geometriche. ( Teoria pag. 81-96, esercizi 141 ) 1) Costruzione con squadra e riga. a) Rette parallele. Ricorda ; due rette sono parallele quando.... oppure quando hanno la stessa. Matematicamente
Due rette si dicono INCIDENTI se hanno esattamente un punto in comune, altrimenti si dicono PARALLELE.
 Riepilogo di Geometria: Assioma A1 Per tutte le coppie di punti P,Q dell insieme S è assegnato un numero reale (=)> 0, che si dice distanza di P da Q e si indica don d(p,q) 1- Se i punti P,Q sono distinti
Riepilogo di Geometria: Assioma A1 Per tutte le coppie di punti P,Q dell insieme S è assegnato un numero reale (=)> 0, che si dice distanza di P da Q e si indica don d(p,q) 1- Se i punti P,Q sono distinti
SOLUZIONI DEI QUESITI PROPOSTI
 SOLUZIONI DEI QUESITI PROPOSTI Manca di mentalità matematica tanto chi non sa riconoscere rapidamente ciò che è evidente, quanto chi si attarda nei calcoli con una precisione superiore alla necessità QUESITO
SOLUZIONI DEI QUESITI PROPOSTI Manca di mentalità matematica tanto chi non sa riconoscere rapidamente ciò che è evidente, quanto chi si attarda nei calcoli con una precisione superiore alla necessità QUESITO
Geogebra classe 2 Media
 Geogebra classe 2 Media A cura del Prof. Sergio Balsimelli [email protected] GEOGEBRA CLASSE 2 Costruzione di figure piane Esercizio n 1: disegno del quadrato dato il lato Disegnare il segmento
Geogebra classe 2 Media A cura del Prof. Sergio Balsimelli [email protected] GEOGEBRA CLASSE 2 Costruzione di figure piane Esercizio n 1: disegno del quadrato dato il lato Disegnare il segmento
