Equilibrio del corpo rigido
|
|
|
- Oreste Santini
- 8 anni fa
- Visualizzazioni
Transcript
1 Equiibrio de corpo rigido Probema1 Due sbarrette omogenee AB e BC aventi a stessa unghezza e a stessa massa di 6 kg, vengono sadate ne punto B in modo da formare un angoo di 90. Le due sbarrette così unite vengono poi appese per i punto B. Ne punto A viene appeso un cubo di auminio. Ad equiibrio raggiunto a sbarretta BC forma un angoo di 60 con a verticae passante per B. Sapendo che a densità de auminio e.7 gcm -3, si cacoi a spigoo de cubo e i moduo dea forza ne punto B. Le forze agenti su sistema formato dae due sbarrette e da cubo di auminio sono: F 1, forza peso dea sbarretta AB. E appicata ne baricentro dea sbarretta AB, ha direzione perpendicoare a suoo ed ha moduo F 1 = mγ g F, forza peso dea sbarretta BC. E appicata ne baricentro dea sbarretta BC, ha direzione normae a suoo ed ha moduo F = mγ g 1
2 F A, forza peso de cubo di auminio. E appicata ne baricentro di tae corpo, è diretta perpendicoarmente a suoo ed ha moduo F A = m A γ g = ρvγ g = ρa 3 γ g ove a è o spigoo de cubo. F B, forza ne punto B. Ha a stessa direzione dee atre tre forze. Le condizioni di equiibrio per i corpo rigido sono F 1 + F + F A + F B = 0 M 1 + M + M A + M B = 0 Sceto i sistema di riferimento rappresentato in figura, e come poo per a vautazione dei momenti torcenti i punto B, se s 1, s, s A e s B sono i vettori posizione dei punti d appicazione dee forze F 1, F, F ga ed F B, rispetto a tae poo, per definizione si ha M 1 = s 1 F 1 M = s F M A = s A F A M B = s B F B I vettori posizione e e forze si trovano tutti ne piano x,y e quindi i momenti torcenti sono diretti perpendicoarmente a tae piano ossia ungo asse z. L equazione vettoriae dei momenti è dunque equivaente ad una soa equazione scaare. Le componenti dei momenti torcenti ungo tae asse possono essere cacoati secondo diverse modaità. Tenendo presente a definizione di prodotto vettoriae, si ha M 1z = F 1 s 1 sin α = mγ g sin α M z = F s sin β = mγ g sin β M Az = F A s A sin α = ρa 3 γ g sin α M Bz = 0 ove è a unghezza dea sbarretta ed α e β sono gi angoi che e sbarrette AB e BC formano con a normae per i punto B. Tai componenti possono essere cacoate anche motipicando i moduo di ogni forza per i reativo braccio e assumendo tae prodotto positivo quando a forza tende a far ruotare i corpo rigido in verso antiorario. In riferimento aa figura 1e, se b 1, b, b A e b B sono i bracci di F 1, F, F A ed F B, si ha M 1z = F 1 b 1 = mγ g sin α M z = F b = mγ g sin β M Az = F A b A = ρa 3 γ g sin α M Bz = F B b B = 0 Infine e componenti dei momenti torcenti possono essere cacoate anche utiizzando espressione cartesiana de prodotto vettoriae tra i vettore posizione de punto d appicazione dea forza rispetto a poo prefissato e a forza stessa. Poiché e componenti dei vettori posizione de punto d appicazione dee forze rispetto a poo prefissato e e forze stesse sono s 1x = sin α s 1y = cos α F 1x = 0 F 1y = mγ g s x = sin β s y = cos β F x = 0 F y = mγ g s Ax = sin α s Ay = cos α F Ax = 0 F Ay = m A γ g s Bx = 0 s By = 0 F Bx = 0 F By = F B
3 e componenti dei momenti ungo asse z risutano M 1z = s 1x F 1y s 1y F 1x = mγ g sin α M z = s x F y s y F x = mγ g M Az = s Ax F Ay s Ay F Ax = m A γ g sin α M Bz = s Bx F By s By F Bx = 0 L equazione vettoriae dei momenti è quindi equivaente a unica equazione scaare mγ g sin α mγ g sin β + ρa3 γ g sin α = 0 sin β daa quae si ricava a 3 = m(sin β sin α) ρ sin α Sostituendo i vaori numerici espressi ne SI si ottiene a 3 = = m 3 ossia a = m = 9.33 cm Le forze hanno tutte a stessa retta d azione e quindi equazione vettoriae dee forze è equivaente aa soa equazione scaare mγ g mγ g ρa 3 γ g + F B = 0 Sostituendo ai simboi dee grandezze fisiche i oro vaori numerici espressi ne SI si ottiene F B = N 3
4 Probema Un asta omogenea avente massa 0.8 kg ha un estremità incernierata ad una parete. A estremità ibera viene fissata una sfera di rame e, per ottenere equiibrio, si deve appicare una forza di 100 N ad ¼ dea unghezza dea sbarra da estremità ibera avente a direzione de campo gravitazionae e verso opposto. Si cacoi i voume dea sfera e i moduo, a direzione ed i verso dea forza esercitata daa cerniera assumendo che a densità de rame sia 8.5 gcm 3 Le forze agenti su asta di estremi A e B e sua sfera di rame fissata in B sono: F a, forza peso de asta. E appicata ne baricentro de asta, ha direzione perpendicoare a suoo ed ha moduo F a = m a γ g F e, forza appicata a asta per avere equiibrio. E appicata ad ¼ da punto B, ha a stessa direzione dea forza peso de asta verso opposto e moduo F e = 100 N F Cu, forza peso dea sfera di rame. E appicata ne baricentro di tae corpo, è diretta perpendicoarmente a suoo ed ha moduo F Cu = m Cu γ g = ρvγ g. F A, forza ne punto A. Ha a stessa direzione dee atre tre forze. Le condizioni di equiibrio per i corpo rigido sono F a + F e + F Cu + F A = 0 M a + M e + M Cu + M A = 0 4
5 Sceto i sistema di riferimento rappresentato in figura e, e come poo per a vautazione dei momenti torcenti i punto A, poiché i vettori posizione dei punti d appicazione dee forze rispetto ad A e e forze stesse giacciono ne piano x,y, i momenti torcenti sono vettori diretti ungo asse z. Se è a unghezza de asta, i bracci dee forze F a, F e, F Cu ed F A sono b a = b e = 3 4 b Cu = b A = 0 e quindi e componenti dei momenti torcenti ungo asse z sono M az = m a γ g M ez = 3 4 F e M Cuz = ρvγ g M Az = 0 L equazione vettoriae dei momenti è quindi equivaente a unica equazione scaare m a γ g F e ρvγ g = 0 da cui si ricava V = 3F e m a γ g 4ργ g Sostituendo i vaori numerici si ottiene V = = m Le forze hanno tutte a stessa retta d azione e quindi equazione vettoriae dee forze è equivaente aa soa equazione scaare m a γ g + F e ρvγ g + F A = 0 ossia da cui F A = 0 F A = 1.11 N Tenendo presente i riferimento sceto, a forza in A ha moduo 1.11 N ed ha a stessa direzione e verso de campo gravitazionae. 5
6 Probema3 Un asta omogenea di massa 3 kg ha un estremità incernierata ad una parete. A estremo ibero è appeso un ciindro cavo di auminio di raggio interno 1.0 cm e raggio esterno.0 cm. Per avere equiibrio viene appicata ad 1 6 dea unghezza de asta da estremità incernierata una forza di 130 N incinata verso estremo ibero e formante un angoo di 60 con asta. Assumendo che a densità de auminio sia.7 gcm 3, si determini atezza de ciindro e i moduo dea forza esercitata daa cerniera. Le forze agenti su sistema di corpi sono: F a, forza peso de asta AB. E appicata ne baricentro de asta, ha direzione perpendicoare a suoo ed ha moduo F a = m a γ g F e, forza appicata aa sbarra per avere equiibrio. E appicata ad 1 6 da punto A, è rivota verso estremo B formando un angoo α = 60 con a sbarra e moduo F e = 130 N F A, forza peso de ciindro cavo di auminio. E appicata ne baricentro di tae corpo, è diretta perpendicoarmente a suoo ed ha moduo F A = m A γ g = ρvγ g. F A, forza esercitata dea cerniera ne punto A.. 6
7 Le condizioni di equiibrio per i corpo rigido sono F a + F e + F A + F A = 0 M a + M e + M A + M A = 0 Sceto i sistema di riferimento rappresentato in figura 3e, e come poo per a vautazione dei momenti torcenti i punto A, indicando con a unghezza de asta, i bracci dee forze F a, F e, F A ed F A sono b a = b e = 1 6 sin α b A = b A = 0 e quindi e componenti dei momenti torcenti ungo asse z sono M az = m a γ g M ez = 1 6 F e sin α M Az = ρvγ g M Az = 0 L equazione vettoriae dei momenti è quindi equivaente aa seguente equazione scaare m a γ g F e sin α ρvγ g = 0 I voume V de ciindro cavo è V = π(r e r i ) h ove r e, r i ed h sono i raggio esterno, queo interno e atezza. Inserendo tae espressione ne equazione dei momenti e risovendo rispetto a atezza de ciindro, si ottiene h = F e sin α 3m s γ g 6πρ(r e r i )γ g e, sostituendo i vaori numerici, espressi ne SI, si ottiene h = 0.16 m L equazione vettoriae dee forze è equivaente ae due seguenti equazioni scaari F Ax + F e cos α = 0 F Ay + F e sin α m a γ g m A γ g = 0 Daa prima si ottiene a componente dea forza esercitata in A diretta ungo asse dee ascisse F Ax = F e cos α = 130 cos 60 = 65 N Risovendo a seconda equazione si ottiene a componente dea forza esercitata daa cerniera diretta ungo asse dee ordinate F Ay = F e sin α + m a γ g + m A γ g = = 79 N I moduo dea forza esercitata daa cerniera è F A = F Ax + F Ay = = 103 N 7
l B 1. la velocità angolare dell asta un istante prima dell urto; 2. la velocità v 0 ; 3. l energia cinetica dissipata nell urto;
 1 Esercizio (tratto da Probema 8.29 de Mazzodi 2) Un asta di unghezza 1.2 m e massa M 0.5 Kg è incernierata ne suo estremo A ad un perno fisso e può osciare senza attrito in un piano verticae. A istante
1 Esercizio (tratto da Probema 8.29 de Mazzodi 2) Un asta di unghezza 1.2 m e massa M 0.5 Kg è incernierata ne suo estremo A ad un perno fisso e può osciare senza attrito in un piano verticae. A istante
Si supponga ora che, con le stesse condizioni iniziali, l urto avvenga elasticamente. Calcolare in questo caso:
 1 Esercizio (tratto da Probema 8.21 de Mazzodi 2) Un asta rigida di sezione trascurabie, unga = 1 m e di massa M = 12 Kg è imperniata ne centro ed è ibera di ruotare in un piano orizzontae xy. Contro un
1 Esercizio (tratto da Probema 8.21 de Mazzodi 2) Un asta rigida di sezione trascurabie, unga = 1 m e di massa M = 12 Kg è imperniata ne centro ed è ibera di ruotare in un piano orizzontae xy. Contro un
ESERCIZI IN PREPARARZIONE ALLA PROVA PER IL SUPERAMENTO DEL DEBITO DI FISICA. CLASSE 1TGC2
 ESERCIZI IN PREPARARZIONE ALLA PROVA PER IL SUPERAMENTO DEL DEBITO DI FISICA. 1) Risovere e seguenti equivaenze CLASSE 1TGC2 1 5 m = mm 6 44 km 2 = m 2 2 34,5 dam 2 = dm 2 7 9 cm 3 = m 3 3 5 cm 2 = m 2
ESERCIZI IN PREPARARZIONE ALLA PROVA PER IL SUPERAMENTO DEL DEBITO DI FISICA. 1) Risovere e seguenti equivaenze CLASSE 1TGC2 1 5 m = mm 6 44 km 2 = m 2 2 34,5 dam 2 = dm 2 7 9 cm 3 = m 3 3 5 cm 2 = m 2
Conservazione dell energia
 mercoledì 15 gennaio 2014 Conservazione dell energia Problema 1. Un corpo inizialmente fermo, scivola su un piano lungo 300 m ed inclinato di 30 rispetto all orizzontale, e, dopo aver raggiunto la base,
mercoledì 15 gennaio 2014 Conservazione dell energia Problema 1. Un corpo inizialmente fermo, scivola su un piano lungo 300 m ed inclinato di 30 rispetto all orizzontale, e, dopo aver raggiunto la base,
Nel Sistema Internazionale l unità di misura dell angolo è il radiante
 Scienze Motorie Grandezze fisiche Il Sistema Internazionale di Unità di Misura 1) Nel Sistema Internazionale il prefisso Giga equivale a a) 10 15 b) 10 12 c) 10 9 d) 10 6 e) 10 3 Nel Sistema Internazionale
Scienze Motorie Grandezze fisiche Il Sistema Internazionale di Unità di Misura 1) Nel Sistema Internazionale il prefisso Giga equivale a a) 10 15 b) 10 12 c) 10 9 d) 10 6 e) 10 3 Nel Sistema Internazionale
IL PENDOLO REVERSIBILE DI KATER
 IL PENDOLO REVERSIBILE DI KATER I periodo dee osciazioni de pendoo sempice è dato daa formua: T 0 = π g Questa reazione è vaida per e piccoe osciazioni, quando, cioè, si può assimiare i seno de'angoo massimo
IL PENDOLO REVERSIBILE DI KATER I periodo dee osciazioni de pendoo sempice è dato daa formua: T 0 = π g Questa reazione è vaida per e piccoe osciazioni, quando, cioè, si può assimiare i seno de'angoo massimo
Esercitazione 4 - Forze distribuite
 Università degi Studi di ergamo orso di Laurea in Ingegneria essie orso di Eementi di eccanica Esercitazione 4 - Forze distribuite Esercizio n. acoare e reazioni vincoari e e azioni interne per asta di
Università degi Studi di ergamo orso di Laurea in Ingegneria essie orso di Eementi di eccanica Esercitazione 4 - Forze distribuite Esercizio n. acoare e reazioni vincoari e e azioni interne per asta di
Due incognite ipertstatiche con cedimento elastico lineare sul vincolo
 Dott. Ing aoo Serafini Cic per tutti gi appunti (AUTOAZIONE TRATTAENTI TERICI ACCIAIO SCIENZA dee COSTRUZIONI ) e-mai per suggerimenti Due incognite ipertstatiche con cedimento eastico ineare su vincoo
Dott. Ing aoo Serafini Cic per tutti gi appunti (AUTOAZIONE TRATTAENTI TERICI ACCIAIO SCIENZA dee COSTRUZIONI ) e-mai per suggerimenti Due incognite ipertstatiche con cedimento eastico ineare su vincoo
Lunghezza della circonferenza e area del cerchio
 3 GEMETRI Lunghezza dea circonferenza e area de cerchio Esercizi suppementari di verifica Esercizio 1 Metti una crocetta su vero (V) o faso (F) accanto ad ogni formua reativa aa unghezza dea circonferenza
3 GEMETRI Lunghezza dea circonferenza e area de cerchio Esercizi suppementari di verifica Esercizio 1 Metti una crocetta su vero (V) o faso (F) accanto ad ogni formua reativa aa unghezza dea circonferenza
Compito scritto di Elettricità e Magnetismo ed Elettromagnetismo 24 Giugno 2004
 Compito scritto di Eettricità e Magnetismo ed Eettromagnetismo 4 Giugno 4 ecupero I (II) esonero di Eettromagnetismo: esercizio C (D) in due ore Prova scritta di Eettricità e Magnetismo: esercizi A e B
Compito scritto di Eettricità e Magnetismo ed Eettromagnetismo 4 Giugno 4 ecupero I (II) esonero di Eettromagnetismo: esercizio C (D) in due ore Prova scritta di Eettricità e Magnetismo: esercizi A e B
L EQUAZIONE DIFFERENZIALE DELLA LINEA ELASTICA
 http://www.itimarconi.ct.it/sezioni/didatticaonine/edie/ostruzioni/linea%0eastic... Pagina di 06/0/006 L EQUAZIONE DIFFERENZIALE DELLA LINEA ELASTIA. BREVI RIHIAMI SULLA TEORIA DELLE TRAVI INFLESSE Si
http://www.itimarconi.ct.it/sezioni/didatticaonine/edie/ostruzioni/linea%0eastic... Pagina di 06/0/006 L EQUAZIONE DIFFERENZIALE DELLA LINEA ELASTIA. BREVI RIHIAMI SULLA TEORIA DELLE TRAVI INFLESSE Si
Il piano cartesiano, la retta e le funzioni di proporzionalità
 MATEMATICAperTUTTI I piano cartesiano, a retta e e funzioni di proporzionaità ESERCIZIO SVOLTO I piano cartesiano. Per fissare un sistema di riferimento ne piano si considerano due rette orientate fra
MATEMATICAperTUTTI I piano cartesiano, a retta e e funzioni di proporzionaità ESERCIZIO SVOLTO I piano cartesiano. Per fissare un sistema di riferimento ne piano si considerano due rette orientate fra
CONOSCENZE 1. il concetto di parallelismo e. e perpendicolari. 2. la proiezione di un segmento
 GEOMETRIA PREREQUISITI conoscere e caratteristiche de sistema decimae conoscere e proprietaá dee quattro operazioni e operare con esse operare con e misure angoari conoscere gi enti dea geometria e e oro
GEOMETRIA PREREQUISITI conoscere e caratteristiche de sistema decimae conoscere e proprietaá dee quattro operazioni e operare con esse operare con e misure angoari conoscere gi enti dea geometria e e oro
RISOLUZIONE DI UN TELAIO CON IL METODO MATRICIALE
 Università degi Studi di Paermo Facotà di Ingegneria Dipartimento di Ingegneria Strutturae e Geotecnica a.a. 5-6 RISOLUZIOE DI U TELAIO CO IL METODO MATRICIALE Si ringrazia Ing. Faio Di Trapani per a coaorazione
Università degi Studi di Paermo Facotà di Ingegneria Dipartimento di Ingegneria Strutturae e Geotecnica a.a. 5-6 RISOLUZIOE DI U TELAIO CO IL METODO MATRICIALE Si ringrazia Ing. Faio Di Trapani per a coaorazione
Esempio di risoluzione di struttura iperstatica col metodo misto. Complemento alla lezione 47/50: Telai a nodi mobili
 Esempio di risouzione di struttura iperstatica co metodo misto ompemento aa ezione 47/50: Teai a nodi mobii La struttura in figura è soggetta ad un cedimento verticae dea cerniera. Tutto i teaio ha sezione
Esempio di risouzione di struttura iperstatica co metodo misto ompemento aa ezione 47/50: Teai a nodi mobii La struttura in figura è soggetta ad un cedimento verticae dea cerniera. Tutto i teaio ha sezione
Un metodo di calcolo per le strutture monodimensionali piane
 www.carosantagata.it n metodo di cacoo per e strutture monodimensionai piane bstract. Si propone un metodo di cacoo per a determinazione dea configurazione di equiibrio dee strutture monodimensionai piane.
www.carosantagata.it n metodo di cacoo per e strutture monodimensionai piane bstract. Si propone un metodo di cacoo per a determinazione dea configurazione di equiibrio dee strutture monodimensionai piane.
Il Tetraedro regolare
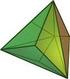 I Tetraedro regoare E i soido che ha per facce 4 triangoi equiateri, (F = 4) Ha 6 spigoi (S = 6) e 4 vertici (V = 4) I suo sviuppo è i seguente: Chiuso diventa: Le proiezioni possibii sono: I suoi assi
I Tetraedro regoare E i soido che ha per facce 4 triangoi equiateri, (F = 4) Ha 6 spigoi (S = 6) e 4 vertici (V = 4) I suo sviuppo è i seguente: Chiuso diventa: Le proiezioni possibii sono: I suoi assi
Lezione 2 Equazioni famose
 Moduo 7 U.D. Lez. Laura Citrini - Matematica de continuo Lezione Equazioni amose Matematica de continuo Moduo 7 - Funzioni di più variabii Unità didattica 4 Equazioni dierenziai Laura Citrini Università
Moduo 7 U.D. Lez. Laura Citrini - Matematica de continuo Lezione Equazioni amose Matematica de continuo Moduo 7 - Funzioni di più variabii Unità didattica 4 Equazioni dierenziai Laura Citrini Università
ESERCIZI SVOLTI SU: GEOMETRIA TRIDIMENSIONALE. 2. Fissato un sistema di riferimento cartesiano dello spazio euclideo O, i, j, k,
 ESERCIZI SVOLTI SU: GEOMETRIA TRIDIMENSIONALE 1. Fissato un sistema di riferimento cartesiano dello spazio euclideo O, i, j, k, determinare un equazione omogenea del piano parallelo al vettore v = i+j,
ESERCIZI SVOLTI SU: GEOMETRIA TRIDIMENSIONALE 1. Fissato un sistema di riferimento cartesiano dello spazio euclideo O, i, j, k, determinare un equazione omogenea del piano parallelo al vettore v = i+j,
Formulario di Geometria Analitica a.a
 Formulario di Geometria Analitica a.a. 2006-2007 Dott. Simone Zuccher 23 dicembre 2006 Nota. Queste pagine potrebbero contenere degli errori: chi li trova è pregato di segnalarli all autore [email protected]).
Formulario di Geometria Analitica a.a. 2006-2007 Dott. Simone Zuccher 23 dicembre 2006 Nota. Queste pagine potrebbero contenere degli errori: chi li trova è pregato di segnalarli all autore [email protected]).
DIDATTICA DI DISEGNO E PROGETTAZIONE DELLE COSTRUZIONI PROF. CARMELO MAJORANA ING. LAURA SGARBOSSA MODULO UNO
 ATTCA SEGNO E PROGETTAZONE ELLE COSTRUZON PROF. CARELO AJORANA NG. LAURA SGARBOSSA OULO UNO L PROBLEA ELLA TRAVE E SANT VENANT (PARTE A OULO PER LO SPECALZZANO oduo N QUESTO OULO: L PROBLEA ELLA TRAVE
ATTCA SEGNO E PROGETTAZONE ELLE COSTRUZON PROF. CARELO AJORANA NG. LAURA SGARBOSSA OULO UNO L PROBLEA ELLA TRAVE E SANT VENANT (PARTE A OULO PER LO SPECALZZANO oduo N QUESTO OULO: L PROBLEA ELLA TRAVE
LA GEOMETRIA NELLO SPAZIO
 LA GEOMETRIA NELLO SPAZIO n.1 Un eemento primitivo: o spazio. Lo spazio è caratterizzato dai seguenti assiomi: Lo spazio contiene infiniti punti, infinite rette, infiniti piani. Ogni piano divide o spazio
LA GEOMETRIA NELLO SPAZIO n.1 Un eemento primitivo: o spazio. Lo spazio è caratterizzato dai seguenti assiomi: Lo spazio contiene infiniti punti, infinite rette, infiniti piani. Ogni piano divide o spazio
Problemi di Fisica. Elettromagnetismo. La Carica Elettrica e la Legge di Coulomb
 Problemi di isica Elettromagnetismo La arica Elettrica e la Legge di oulomb Data la distribuzione di carica rappresentata in figura, calcolare la forza totale che agisce sulla carica Q posta nell origine
Problemi di isica Elettromagnetismo La arica Elettrica e la Legge di oulomb Data la distribuzione di carica rappresentata in figura, calcolare la forza totale che agisce sulla carica Q posta nell origine
Esercizi geometria analitica nello spazio. Corso di Laurea in Informatica. Docente: Andrea Loi. Correzione
 Esercizi geometria analitica nello spazio Corso di Laurea in Informatica Docente: Andrea Loi Correzione 1. Denotiamo con P 1, P 13, P 3, P 1, P, P 3, P i simmetrici di un punto P rispetto ai piani coordinati
Esercizi geometria analitica nello spazio Corso di Laurea in Informatica Docente: Andrea Loi Correzione 1. Denotiamo con P 1, P 13, P 3, P 1, P, P 3, P i simmetrici di un punto P rispetto ai piani coordinati
I grafici derivati e la periodicità
 A I grafici derivati e a periodicità A partire dai grafici dee funzioni goniometriche fondamentai possiamo costruire queo di atre funzioni appicando opportune isometrie. Di seguito vediamo acuni esempi.
A I grafici derivati e a periodicità A partire dai grafici dee funzioni goniometriche fondamentai possiamo costruire queo di atre funzioni appicando opportune isometrie. Di seguito vediamo acuni esempi.
Esercizi di Statica. Esercitazioni di Fisica per ingegneri - A.A
 Esercizio 1 Esercizi di Statica Esercitazioni di Fisica per ingegneri - A.A. 2011-2012 Un punto materiale di massa m = 0.1 kg (vedi FIG.1) è situato all estremità di una sbarretta indeformabile di peso
Esercizio 1 Esercizi di Statica Esercitazioni di Fisica per ingegneri - A.A. 2011-2012 Un punto materiale di massa m = 0.1 kg (vedi FIG.1) è situato all estremità di una sbarretta indeformabile di peso
Dinamica del punto materiale: problemi con gli oscillatori.
 Dinamica del punto materiale: problemi con gli oscillatori. Problema: Una molla ideale di costante elastica k = 300 Nm 1 e lunghezza a riposo l 0 = 1 m pende verticalmente avendo un estremità fissata ad
Dinamica del punto materiale: problemi con gli oscillatori. Problema: Una molla ideale di costante elastica k = 300 Nm 1 e lunghezza a riposo l 0 = 1 m pende verticalmente avendo un estremità fissata ad
Esercizi di Statica - Moti Relativi
 Esercizio 1 Esercizi di Statica - Moti Relativi Esercitazioni di Fisica LA per ingegneri - A.A. 2004-2005 Un punto materiale di massa m = 0.1 kg (vedi sotto a sinistra)é situato all estremitá di una sbarretta
Esercizio 1 Esercizi di Statica - Moti Relativi Esercitazioni di Fisica LA per ingegneri - A.A. 2004-2005 Un punto materiale di massa m = 0.1 kg (vedi sotto a sinistra)é situato all estremitá di una sbarretta
Le equazioni di alcune superfici dello spazio
 A Le equazioni di acune suerfici deo sazio L equazione di una suerficie ciindrica In geometria anaitica si dice suerficie ciindrica una quaunque suerficie ce a come direttrice una curva aartenente ad un
A Le equazioni di acune suerfici deo sazio L equazione di una suerficie ciindrica In geometria anaitica si dice suerficie ciindrica una quaunque suerficie ce a come direttrice una curva aartenente ad un
Prima esercitazione progettuale Progetto di un capannone industriale in acciaio
 Corso di Tecnica dee Costruzioni II Teoria dee Esercitazioni Bozza de 1//11 Prima esercitazione progettuae Progetto di un capannone industriae in acciaio 1 Verifica di stabiità fesso-torsionae dea capriata....
Corso di Tecnica dee Costruzioni II Teoria dee Esercitazioni Bozza de 1//11 Prima esercitazione progettuae Progetto di un capannone industriae in acciaio 1 Verifica di stabiità fesso-torsionae dea capriata....
[3] Un asta omogenea di sezione trascurabile, di massa M = 2.0 kg e lunghezza l = 50 cm, può ruotare senza attrito in un piano verticale x y attorno a
![[3] Un asta omogenea di sezione trascurabile, di massa M = 2.0 kg e lunghezza l = 50 cm, può ruotare senza attrito in un piano verticale x y attorno a [3] Un asta omogenea di sezione trascurabile, di massa M = 2.0 kg e lunghezza l = 50 cm, può ruotare senza attrito in un piano verticale x y attorno a](/thumbs/48/23887254.jpg) [1] Un asta rigida omogenea di lunghezza l = 1.20 m e massa m = 2.5 kg reca ai due estremi due corpi puntiformi di massa pari a 0.2 kg ciascuno. Tale sistema è in rotazione in un piano orizzontale attorno
[1] Un asta rigida omogenea di lunghezza l = 1.20 m e massa m = 2.5 kg reca ai due estremi due corpi puntiformi di massa pari a 0.2 kg ciascuno. Tale sistema è in rotazione in un piano orizzontale attorno
Studio dei vincoli di un solaio
 Studio dei vincoi di un soaio ttraverso gi schemi statici per un determinato soaio, vengono definiti i gradi di vincoo per a vautazioni dee caratteristiche dee soecitazioni, agenti sua struttura. Tai vautazioni
Studio dei vincoi di un soaio ttraverso gi schemi statici per un determinato soaio, vengono definiti i gradi di vincoo per a vautazioni dee caratteristiche dee soecitazioni, agenti sua struttura. Tai vautazioni
Scrittura delle equazioni del moto di un sistema lineare viscoso a più gradi di libertà. Prof. Adolfo Santini - Dinamica delle Strutture 1
 Scrittura dee equazioni de moto di un sistema ineare viscoso a più gradi di ibertà Prof. Adofo Santini - Dinamica dee Strutture 1 Matrice di rigidezza Teoricamente, i coefficienti dea matrice di rigidezza
Scrittura dee equazioni de moto di un sistema ineare viscoso a più gradi di ibertà Prof. Adofo Santini - Dinamica dee Strutture 1 Matrice di rigidezza Teoricamente, i coefficienti dea matrice di rigidezza
Grafici di particolari funzioni lineari
 A Grafici di particoari funzioni ineari Vogiamo tracciare i grafico dea funzione y ˆ jxj. x quando x 0 Sappiamo che jxj significa x quando x < 0 Possiamo aora riscrivere 'equazione di questa funzione in
A Grafici di particoari funzioni ineari Vogiamo tracciare i grafico dea funzione y ˆ jxj. x quando x 0 Sappiamo che jxj significa x quando x < 0 Possiamo aora riscrivere 'equazione di questa funzione in
Equilibrio di un punto materiale (anelli, giunti ecc.)
 Equilibrio di un punto materiale (anelli, giunti ecc.) Per l equilibrio di un punto basta Obiettivo: verificare che Σ F i 0 Determinare le forze trasmesse al nodo da tutti gli elementi concorrenti, e
Equilibrio di un punto materiale (anelli, giunti ecc.) Per l equilibrio di un punto basta Obiettivo: verificare che Σ F i 0 Determinare le forze trasmesse al nodo da tutti gli elementi concorrenti, e
Esercitazione Esame di Stato Secondaria di primo grado. Quesito 1 Piano cartesiano. Quesito 2 Equazioni. Quesito 3 Geometria 3D.
 Esame di stato scuola media Esempio di tema d esame 004 UbiMath - 1 Esercitazione Esame di Stato Secondaria di primo grado Quesito 1 Piano cartesiano Fissando come unità di misura il centimetro (1 cm =
Esame di stato scuola media Esempio di tema d esame 004 UbiMath - 1 Esercitazione Esame di Stato Secondaria di primo grado Quesito 1 Piano cartesiano Fissando come unità di misura il centimetro (1 cm =
Il segno del momento è positivo perché il corpo ruota in senso antiorario.
 MOMENTO DI UNA FORZA E DI UNA COPPIA DI FORZE Esercizi Esempio 1 Calcola il momento della forza con cui si apre una porta, ruotando in verso antiorario, nell'ipotesi che l'intensità della forza applicata
MOMENTO DI UNA FORZA E DI UNA COPPIA DI FORZE Esercizi Esempio 1 Calcola il momento della forza con cui si apre una porta, ruotando in verso antiorario, nell'ipotesi che l'intensità della forza applicata
RELAZIONI e CORRISPONDENZE
 RELAZIONI e CORRISPONDENZE Siano X e Y due insiemi non vuoti si chiama relazione tra X e Y un qualunque sottoinsieme del prodotto cartesiano: X x Y = {(x,y): x X, y Y} L insieme costituito dai primi (secondi)
RELAZIONI e CORRISPONDENZE Siano X e Y due insiemi non vuoti si chiama relazione tra X e Y un qualunque sottoinsieme del prodotto cartesiano: X x Y = {(x,y): x X, y Y} L insieme costituito dai primi (secondi)
ROTAZIONI DEGLI ESTREMI DI UNA TRAVE PRISMATICA APPOGGIATA ALLE ESTREMITÁ E SOGGETTA AD UN CARICO VERTICALE
 M. G. USTO ROTZIONI DEGLI ESTREMI DI UN TRVE PRISMTIC PPOGGIT LLE ESTREMITÁ E SOGGETT D UN CRICO VERTICLE CSO DEI CRICHI TRINGOLRE, UNIFORME E CONCENTRTO mgbstudio.net PGIN INTENZIONLMENTE VUOT SOMMRIO
M. G. USTO ROTZIONI DEGLI ESTREMI DI UN TRVE PRISMTIC PPOGGIT LLE ESTREMITÁ E SOGGETT D UN CRICO VERTICLE CSO DEI CRICHI TRINGOLRE, UNIFORME E CONCENTRTO mgbstudio.net PGIN INTENZIONLMENTE VUOT SOMMRIO
Grandezze scalari e vettoriali
 Grandezze scalari e vettoriali Per caratterizzare completamente una grandezza fisica, a volte è sufficiente dare soltanto un numero (scalare), mentre altre volte questo non è sufficiente. Massa, lunghezza,
Grandezze scalari e vettoriali Per caratterizzare completamente una grandezza fisica, a volte è sufficiente dare soltanto un numero (scalare), mentre altre volte questo non è sufficiente. Massa, lunghezza,
Note di geometria analitica nel piano
 Note di geometria analitica nel piano e-mail: [email protected] Versione provvisoria. Novembre 2015. 1 Indice 1 Punti e vettori spiccati dall origine 3 1.1 Coordinate......................................
Note di geometria analitica nel piano e-mail: [email protected] Versione provvisoria. Novembre 2015. 1 Indice 1 Punti e vettori spiccati dall origine 3 1.1 Coordinate......................................
Corso di Meccanica, Macchine e Impianti Termici CAPITOLO 3 DIAGRAMMA DELLE SOLLECITAZIONI INTERNE
 Istituto Professionae Statae per 'Industria e 'rtigianato "L.. berti" Rimini nno Scoastico 009/010 orso di Meccanica, Macchine e Impianti Termici PITOLO 3 DIGRMM DELLE SOLLEITZIONI INTERNE Prof. Matteo
Istituto Professionae Statae per 'Industria e 'rtigianato "L.. berti" Rimini nno Scoastico 009/010 orso di Meccanica, Macchine e Impianti Termici PITOLO 3 DIGRMM DELLE SOLLEITZIONI INTERNE Prof. Matteo
Grandezze Fisiche, Sistema Internazionale e Calcolo Vettoriale
 Grandezze Fisiche, Sistema Internazionale e Calcolo Vettoriale Soluzioni ai Quiz 1 Il Sistema Internazionale di Unità di Misura Le grandezze fisiche di base sono sei, ognuna delle quali ha una unità di
Grandezze Fisiche, Sistema Internazionale e Calcolo Vettoriale Soluzioni ai Quiz 1 Il Sistema Internazionale di Unità di Misura Le grandezze fisiche di base sono sei, ognuna delle quali ha una unità di
1. MISURIAMO GLI ANGOLI CON GEOGEBRA
 . MISURIAMO GLI ANGOLI CON GEOGEBRA Nascondiamo gi assi cartesiani in modo da usare a finestra grafica come piano eucideo. Disegniamo un punto C che rappresenti i centro di una circonferenza e creiamo
. MISURIAMO GLI ANGOLI CON GEOGEBRA Nascondiamo gi assi cartesiani in modo da usare a finestra grafica come piano eucideo. Disegniamo un punto C che rappresenti i centro di una circonferenza e creiamo
VII ESERCITAZIONE - 29 Novembre 2013
 VII ESERCITAZIONE - 9 Novembre 013 I. MOMENTO DI INERZIA DEL CONO Calcolare il momento di inerzia di un cono omogeneo massiccio, di altezza H, angolo al vertice α e massa M, rispetto al suo asse di simmetria.
VII ESERCITAZIONE - 9 Novembre 013 I. MOMENTO DI INERZIA DEL CONO Calcolare il momento di inerzia di un cono omogeneo massiccio, di altezza H, angolo al vertice α e massa M, rispetto al suo asse di simmetria.
La statistica descrittiva
 MATEMATICAperTUTTI Dee seguenti indagine statistiche individua a popoazione, i carattere oggetto di studio e e possibii modaità di tae carattere. 1 ESERCIZIO SVOLTO Indagine: utiizzo de tempo ibero da
MATEMATICAperTUTTI Dee seguenti indagine statistiche individua a popoazione, i carattere oggetto di studio e e possibii modaità di tae carattere. 1 ESERCIZIO SVOLTO Indagine: utiizzo de tempo ibero da
Figura 1.1. La struttura illustrata in figura risulta essere, dall analisi cinematica, una struttura due volte iperstatica a nodi spostabili.
 TEMI ESAME Esercizio 1 Tema d esame de 1/09/1998 Si consideri a struttura iustrata in figura, con EJ costante. I vaore de azione concentrata F è pari a: Figura 1.1 1 F p 4 La struttura iustrata in figura
TEMI ESAME Esercizio 1 Tema d esame de 1/09/1998 Si consideri a struttura iustrata in figura, con EJ costante. I vaore de azione concentrata F è pari a: Figura 1.1 1 F p 4 La struttura iustrata in figura
Sistemi cristallini 1
 Sistemi cristallini Esercizio Calcolare la densità atomica definita come il rapporto tra il numero di atomi e il volume unitario per ) il litio sapendo che la distanza tra i centri dei primi vicini è R
Sistemi cristallini Esercizio Calcolare la densità atomica definita come il rapporto tra il numero di atomi e il volume unitario per ) il litio sapendo che la distanza tra i centri dei primi vicini è R
CORSO DI LAUREA IN SCIENZE BIOLOGICHE Secondo Compitino di FISICA 15 giugno 2012
 CORSO DI LAUREA IN SCIENZE BIOLOGICHE Secondo Compitino di FISICA 15 giugno 01 1) FLUIDI: Un blocchetto di legno (densità 0,75 g/ cm 3 ) di dimensioni esterne (10x0x5)cm 3 è trattenuto mediante una fune
CORSO DI LAUREA IN SCIENZE BIOLOGICHE Secondo Compitino di FISICA 15 giugno 01 1) FLUIDI: Un blocchetto di legno (densità 0,75 g/ cm 3 ) di dimensioni esterne (10x0x5)cm 3 è trattenuto mediante una fune
Comportamento meccanico dei materiali Unità 4: Cinematica ed equilibrio del corpo rigido
 omportamento meccanico dei materiai Unità 4: inematica ed equiibrio de corpo rigido Definizioni Gradi di ibertà Numero minimo di coordinate con e quai è possibie definire in modo non ambiguo a posizione
omportamento meccanico dei materiai Unità 4: inematica ed equiibrio de corpo rigido Definizioni Gradi di ibertà Numero minimo di coordinate con e quai è possibie definire in modo non ambiguo a posizione
Esercizi e problemi supplementari sulla dinamica dei sistemi di punti materiali
 Esercizi e problemi supplementari sulla dinamica dei sistemi di punti materiali A) Applicazione del teorema dell impulso + conservazione quantità di moto Problema n. 1: Un blocco A di massa m = 4 kg è
Esercizi e problemi supplementari sulla dinamica dei sistemi di punti materiali A) Applicazione del teorema dell impulso + conservazione quantità di moto Problema n. 1: Un blocco A di massa m = 4 kg è
Esercitazioni di Meccanica Razionale
 Esercitazioni di Meccanica Razionale a.a. 2002/2003 Svincolamento statico Maria Grazia Naso [email protected] Dipartimento di Matematica Università degli Studi di Brescia Esercitazioni di Meccanica Razionale
Esercitazioni di Meccanica Razionale a.a. 2002/2003 Svincolamento statico Maria Grazia Naso [email protected] Dipartimento di Matematica Università degli Studi di Brescia Esercitazioni di Meccanica Razionale
Corso di Laurea in Ingegneria Meccanica Anno Accademico 2012/2013 Meccanica Razionale
 orso di Laurea in Ingegneria Meccanica nno ccadeico 2012/2013 Meccanica azionae Noe... N. Matricoa... ncona, 11 gennaio 2013 1. Un punto P di assa si uove senza attrito su una guida verticae. Una oa di
orso di Laurea in Ingegneria Meccanica nno ccadeico 2012/2013 Meccanica azionae Noe... N. Matricoa... ncona, 11 gennaio 2013 1. Un punto P di assa si uove senza attrito su una guida verticae. Una oa di
Fisica dei Materiali A.A Dinamica III. P.A. Tipler, "Invito alla Fisica", volume 1, Zanichelli 2001, 5.2, 5.3, 6.5
 Dinamica III.A. Tipler, "Invito alla isica", volume 1, Zanichelli 2001, 5.2, 5.3, 6.5 A.A. 2003-2004 isica dei Materiali 71 Equilibrio statico di un corpo esteso La statica è quella parte della dinamica
Dinamica III.A. Tipler, "Invito alla isica", volume 1, Zanichelli 2001, 5.2, 5.3, 6.5 A.A. 2003-2004 isica dei Materiali 71 Equilibrio statico di un corpo esteso La statica è quella parte della dinamica
1 Distanza di un punto da una retta (nel piano)
 Esercizi 26/10/2007 1 Distanza di un punto da una retta (nel piano) Sia r = {ax + by + c = 0} una retta. Sia P = (p 1, p 2 ) R 2 un punto che non sta sulla retta r. Vogliamo vedere se si può parlare di
Esercizi 26/10/2007 1 Distanza di un punto da una retta (nel piano) Sia r = {ax + by + c = 0} una retta. Sia P = (p 1, p 2 ) R 2 un punto che non sta sulla retta r. Vogliamo vedere se si può parlare di
ELEMENTI COSTRUTTIVI DI MACCHINE BIOMEDICHE
 ELEMENTI COSTRUTTIVI DI MACCHINE BIOMEDICHE PROBLEMA DELLA LINEA ELASTICA INSTABILITA DELLA TRAVE A CARICO DI PUNTA (PROBLEMA BUCKLING O DI EULERO) A cura di ing. Andrea Spezzaneve Ph.D. Mechanica Engineer
ELEMENTI COSTRUTTIVI DI MACCHINE BIOMEDICHE PROBLEMA DELLA LINEA ELASTICA INSTABILITA DELLA TRAVE A CARICO DI PUNTA (PROBLEMA BUCKLING O DI EULERO) A cura di ing. Andrea Spezzaneve Ph.D. Mechanica Engineer
FISICA per SCIENZE BIOLOGICHE A.A. 2013/2014 1) FLUIDI V= 5 dm3 a= 2 m/s2 aria = g / cm 3 Spinta Archimedea Tensione della fune
 FISICA per SCIENZE BIOLOGICHE A.A. 2013/2014 II Compitino 26 Giugno 2014 1) FLUIDI Un bambino trattiene un palloncino, tramite una sottile fune. Il palloncino ha volume V= 5 dm 3. La sua massa, senza il
FISICA per SCIENZE BIOLOGICHE A.A. 2013/2014 II Compitino 26 Giugno 2014 1) FLUIDI Un bambino trattiene un palloncino, tramite una sottile fune. Il palloncino ha volume V= 5 dm 3. La sua massa, senza il
Sistemi cristallini - Soluzioni degli esercizi
 Sistemi cristallini - Soluzioni degli esercizi Fisica della Materia Condensata Dipartimento di Matematica e Fisica Università degli Studi Roma Tre A.A. 06/07 Sistemi cristallini Esercizio.........................................
Sistemi cristallini - Soluzioni degli esercizi Fisica della Materia Condensata Dipartimento di Matematica e Fisica Università degli Studi Roma Tre A.A. 06/07 Sistemi cristallini Esercizio.........................................
Problemi di dinamica del punto materiale
 Problemi di dinamica del punto materiale 1. Un corpo di massa M = 200 kg viene lanciato con velocità v 0 = 36 km/ora su un piano inclinato di un angolo θ = 30 o rispetto all orizzontale. Nel salire, il
Problemi di dinamica del punto materiale 1. Un corpo di massa M = 200 kg viene lanciato con velocità v 0 = 36 km/ora su un piano inclinato di un angolo θ = 30 o rispetto all orizzontale. Nel salire, il
La scala logaritmica
 La scaa ogaritmica Obiettivi utiizzare coordinate ogaritmiche e semiogaritmiche 1. COORDINATE LOGARITMICHE Se un numero k eá maggiore di 10, i suo ogaritmo in base 10 eá moto piuá piccoo de numero stesso:
La scaa ogaritmica Obiettivi utiizzare coordinate ogaritmiche e semiogaritmiche 1. COORDINATE LOGARITMICHE Se un numero k eá maggiore di 10, i suo ogaritmo in base 10 eá moto piuá piccoo de numero stesso:
1. LA PARABOLA CON GEOGEBRA
 1. LA PARABOLA CON GEOGEBRA Dopo aver avviato i programma, chiudiamo a Vista Agebra, togiamo gi assi cartesiani e a grigia da quea grafica in modo da avorare iniziamente ne piano eucideo. Affrontiamo poi
1. LA PARABOLA CON GEOGEBRA Dopo aver avviato i programma, chiudiamo a Vista Agebra, togiamo gi assi cartesiani e a grigia da quea grafica in modo da avorare iniziamente ne piano eucideo. Affrontiamo poi
approfondimento Cinematica ed energia di rotazione equilibrio statico di un corpo esteso conservazione del momento angolare
 approfondimento Cinematica ed energia di rotazione equilibrio statico di un corpo esteso conservazione del momento angolare Moto di rotazione Rotazione dei corpi rigidi ϑ(t) ω z R asse di rotazione v m
approfondimento Cinematica ed energia di rotazione equilibrio statico di un corpo esteso conservazione del momento angolare Moto di rotazione Rotazione dei corpi rigidi ϑ(t) ω z R asse di rotazione v m
Geometria analitica del piano pag 12 Adolfo Scimone
 Geometria analitica del piano pag 12 Adolfo Scimone Fasci di rette Siano r e r' due rette distinte di equazioni r: ax + by + c r': a' x + b' y + c' Consideriamo la retta combinazione lineare delle due
Geometria analitica del piano pag 12 Adolfo Scimone Fasci di rette Siano r e r' due rette distinte di equazioni r: ax + by + c r': a' x + b' y + c' Consideriamo la retta combinazione lineare delle due
Esercitazione 7 del corso di Statistica 2
 Esercitazione 7 de corso di Statistica Prof. Domenico Vistocco Dott.ssa Paoa Costantini 9 Giugno 008 Esercizio La distribuzione dei pesi dei pesi pacchetti per confezionare per confezionare e caramee,
Esercitazione 7 de corso di Statistica Prof. Domenico Vistocco Dott.ssa Paoa Costantini 9 Giugno 008 Esercizio La distribuzione dei pesi dei pesi pacchetti per confezionare per confezionare e caramee,
Le funzioni goniometriche
 CAPITOLO 1 MATEMATICA PER LA FISICA Le funzioni goniometriche Obiettivi definire e funzioni goniometriche fondamentai in riferimento ai triangoi rettangoi e aa circonferenza goniometrica risovere triangoi
CAPITOLO 1 MATEMATICA PER LA FISICA Le funzioni goniometriche Obiettivi definire e funzioni goniometriche fondamentai in riferimento ai triangoi rettangoi e aa circonferenza goniometrica risovere triangoi
Interazione tra forze verticali e longitudinali: effetti anti 5.5 aggiornato 19-11-2013
 Interazione tra forze verticai e ongitudinai: effetti anti 5.5 aggiornato 19-11-2013 Ne piano frontae si studia interazione tra forze verticai Fz e forze aterai Fy sviuppate a iveo de impronta a terra.
Interazione tra forze verticai e ongitudinai: effetti anti 5.5 aggiornato 19-11-2013 Ne piano frontae si studia interazione tra forze verticai Fz e forze aterai Fy sviuppate a iveo de impronta a terra.
Corso di Idraulica ed Idrologia Forestale
 Corso di Idraulica ed Idrologia Forestale Docente: Prof. Santo Marcello Zimbone Collaboratori: Dott. Giuseppe Bombino - Ing. Demetrio Zema Lezione n. 4: Idrostatica (parte III - equazione globale - legge
Corso di Idraulica ed Idrologia Forestale Docente: Prof. Santo Marcello Zimbone Collaboratori: Dott. Giuseppe Bombino - Ing. Demetrio Zema Lezione n. 4: Idrostatica (parte III - equazione globale - legge
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016
 Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
Esercizi di Algebra Lineare Superfici rigate
 Esercizi di Algebra Lineare Superfici rigate Anna M. Bigatti 29 ottobre 2012 Definizione 1. Una superficie rigata è una superficie tale che per ogni suo punto passa una retta interamente contenuta nella
Esercizi di Algebra Lineare Superfici rigate Anna M. Bigatti 29 ottobre 2012 Definizione 1. Una superficie rigata è una superficie tale che per ogni suo punto passa una retta interamente contenuta nella
TRASFORMAZIONI GEOMETRICHE
 TRASFORMAZIONI GEOMETRICHE Def. Una trasformazione geometrica T tra i punti di un piano è una corrispondenza biunivoca che ad ogni punto P del piano associa uno e un solo punto P' appartenente al piano
TRASFORMAZIONI GEOMETRICHE Def. Una trasformazione geometrica T tra i punti di un piano è una corrispondenza biunivoca che ad ogni punto P del piano associa uno e un solo punto P' appartenente al piano
Università degli studi di Palermo Corso di Laurea in Ingegneria Informatica Docente: Prof.ssa D. Persano Adorno
 Esame di Fisica Generale (per laureandi) 19 giugno 2006 Problema 1: Un blocco di massa m 1 =2 kg ed un blocco di massa m 2 =6 kg sono collegati da una fune leggera tramite una puleggia a forma di disco
Esame di Fisica Generale (per laureandi) 19 giugno 2006 Problema 1: Un blocco di massa m 1 =2 kg ed un blocco di massa m 2 =6 kg sono collegati da una fune leggera tramite una puleggia a forma di disco
Scienza delle Costruzioni II Prova scritta del 13/11/01
 Prova scritta de //0 P γ P γ > M 0 0 costante Appicando i teorema cinematico de anaisi imite, determinare i carico di coasso P s a variare de parametro positivo γ. p / L Comportamento e. p. Von Mises π
Prova scritta de //0 P γ P γ > M 0 0 costante Appicando i teorema cinematico de anaisi imite, determinare i carico di coasso P s a variare de parametro positivo γ. p / L Comportamento e. p. Von Mises π
Esercitazione VI - Leggi della dinamica III
 Esercitazione VI - Leggi della dinamica III Esercizio 1 I corpi 1, 2 e 3 rispettivamente di massa m 1 = 2kg, m 2 = 3kg ed m 3 = 4kg sono collegati come in figura tramite un filo inestensibile. Trascurando
Esercitazione VI - Leggi della dinamica III Esercizio 1 I corpi 1, 2 e 3 rispettivamente di massa m 1 = 2kg, m 2 = 3kg ed m 3 = 4kg sono collegati come in figura tramite un filo inestensibile. Trascurando
Trasformazioni Logaritmiche
 Trasformazioni Logaritmiche Una funzione y = f(x) può essere rappresentata in scala logaritmica ponendo Si noti che y = f(x) diventa ossia Quando mi conviene? X = log α x, Y = log α y. log α (x) = log
Trasformazioni Logaritmiche Una funzione y = f(x) può essere rappresentata in scala logaritmica ponendo Si noti che y = f(x) diventa ossia Quando mi conviene? X = log α x, Y = log α y. log α (x) = log
GEOMETRIA. Studio dei luoghi /relazioni tra due variabili. Studio delle figure (nel piano/spazio) Problemi algebrici sulle figure geometriche
 GEOMETRIA ANALITICA EUCLIDEA Studio dei luoghi /relazioni tra due variabili Studio delle figure (nel piano/spazio) Funzioni elementari Problemi algebrici sulle figure geometriche Grafici al servizio dell
GEOMETRIA ANALITICA EUCLIDEA Studio dei luoghi /relazioni tra due variabili Studio delle figure (nel piano/spazio) Funzioni elementari Problemi algebrici sulle figure geometriche Grafici al servizio dell
SESSIONE SUPPLETIVA QUESTIONARIO QUESITO 1
 www.matefilia.it SESSIONE SUPPLETIVA 015 - QUESTIONARIO x QUESITO 1 Data la funzione integrale ln(t) dt, determinare per quali valori di x il suo grafico 1 incontra la retta di equazione y = x + 1. Calcoliamo
www.matefilia.it SESSIONE SUPPLETIVA 015 - QUESTIONARIO x QUESITO 1 Data la funzione integrale ln(t) dt, determinare per quali valori di x il suo grafico 1 incontra la retta di equazione y = x + 1. Calcoliamo
Luoghi di punti e funzioni non lineari
 CAPITOLO 3 Luoghi di punti e funzioni non ineari 1. LE FUNZIONI NON LINEARI CON DERIVE Per costruire i grafico di una paraboa o di un'iperboe si usa a stessa procedura usata per a retta: si scrive 'equazione
CAPITOLO 3 Luoghi di punti e funzioni non ineari 1. LE FUNZIONI NON LINEARI CON DERIVE Per costruire i grafico di una paraboa o di un'iperboe si usa a stessa procedura usata per a retta: si scrive 'equazione
CORSO DI LAUREA IN SCIENZE BIOLOGICHE Prova scritta di FISICA 30 gennaio 2012
 CORSO DI LAUREA IN SCIENZE BIOLOGICHE Prova scritta di FISICA 30 gennaio 2012 1) Un corpo di massa m = 1 kg e velocità iniziale v = 5 m/s si muove su un piano orizzontale scabro, con coefficiente di attrito
CORSO DI LAUREA IN SCIENZE BIOLOGICHE Prova scritta di FISICA 30 gennaio 2012 1) Un corpo di massa m = 1 kg e velocità iniziale v = 5 m/s si muove su un piano orizzontale scabro, con coefficiente di attrito
C I R C O N F E R E N Z A...
 C I R C O N F E R E N Z A... ESERCITAZIONI SVOLTE 3 Equazione della circonferenza di noto centro C e raggio r... 3 Equazione della circonferenza di centro C passante per un punto A... 3 Equazione della
C I R C O N F E R E N Z A... ESERCITAZIONI SVOLTE 3 Equazione della circonferenza di noto centro C e raggio r... 3 Equazione della circonferenza di centro C passante per un punto A... 3 Equazione della
M p. θ max. P v P. Esercizi di Meccanica (M6) Consegna: giovedì 3 giugno.
 Esercizi di Meccanica (M6) Consegna: giovedì 3 giugno. Problema 1: Si consideri un corpo rigido formato da una sfera omogenea di raggio R e massa M 1 e da una sbarretta omogenea di lunghezza L, massa M
Esercizi di Meccanica (M6) Consegna: giovedì 3 giugno. Problema 1: Si consideri un corpo rigido formato da una sfera omogenea di raggio R e massa M 1 e da una sbarretta omogenea di lunghezza L, massa M
Problemi aggiuntivi sulla Dinamica dei Sistemi di punti materiali: A) Impulso + conservazione quantità di moto
 Problemi aggiuntivi sulla Dinamica dei Sistemi di punti materiali: A) Impulso + conservazione quantità di moto Problema n. 1: Un carro armato, posto in quiete su un piano orizzontale, spara una granata
Problemi aggiuntivi sulla Dinamica dei Sistemi di punti materiali: A) Impulso + conservazione quantità di moto Problema n. 1: Un carro armato, posto in quiete su un piano orizzontale, spara una granata
Esercitazioni di Meccanica Razionale
 Esercitazioni di Meccanica Razionale a.a. 2002/2003 Dinamica dei sistemi materiali Maria Grazia Naso [email protected] Dipartimento di Matematica Università degli Studi di Brescia Esercitazioni di Meccanica
Esercitazioni di Meccanica Razionale a.a. 2002/2003 Dinamica dei sistemi materiali Maria Grazia Naso [email protected] Dipartimento di Matematica Università degli Studi di Brescia Esercitazioni di Meccanica
Formule Utili Analisi Matematica per Informatici a.a
 Formule Utili Analisi Matematica per Informatici a.a. 006-007 Dott. Simone Zuccher dicembre 006 Nota. Queste pagine potrebbero contenere degli errori: chi li trova è pregato di segnalarli all autore [email protected]).
Formule Utili Analisi Matematica per Informatici a.a. 006-007 Dott. Simone Zuccher dicembre 006 Nota. Queste pagine potrebbero contenere degli errori: chi li trova è pregato di segnalarli all autore [email protected]).
Esercizio 1 L/3. mg CM Mg. La sommatoria delle forze e dei momenti deve essere uguale a 0 M A. ω è il verso di rotazione con cui studio il sistema
 Esercizio 1 Una trave omogenea di lunghezza L e di massa M è appoggiata in posizione orizzontale su due fulcri lisci posti alle sue estremità. Una massa m è appoggiata sulla trave ad una distanza L/3 da
Esercizio 1 Una trave omogenea di lunghezza L e di massa M è appoggiata in posizione orizzontale su due fulcri lisci posti alle sue estremità. Una massa m è appoggiata sulla trave ad una distanza L/3 da
Geometria analitica del piano
 Geometria analitica del piano dott.ssa Vita Leonessa Università degli Studi della Basilicata (27 marzo 2008) (Analisi) Matematica 2 CdL in Chimica, Biotecnologie, Scienze Geologiche Rette Fissato un sistema
Geometria analitica del piano dott.ssa Vita Leonessa Università degli Studi della Basilicata (27 marzo 2008) (Analisi) Matematica 2 CdL in Chimica, Biotecnologie, Scienze Geologiche Rette Fissato un sistema
FUNZIONI GONIOMETRICHE
 FUNZIONI GONIOMETRICHE Misura degli angoli Seno, coseno e tangente di un angolo Relazioni fondamentali tra le funzioni goniometriche Angoli notevoli Grafici delle funzioni goniometriche GONIOMETRIA : scienza
FUNZIONI GONIOMETRICHE Misura degli angoli Seno, coseno e tangente di un angolo Relazioni fondamentali tra le funzioni goniometriche Angoli notevoli Grafici delle funzioni goniometriche GONIOMETRIA : scienza
Prova scritta di Meccanica Razionale
 Prova scritta di Meccanica Razionale - 0.07.013 ognome e Nome... N. matricola....d.l.: MLT UTLT IVLT MTLT MELT nno di orso: altro FIL 1 Esercizio 1. Nel riferimento cartesiano ortogonale, si consideri
Prova scritta di Meccanica Razionale - 0.07.013 ognome e Nome... N. matricola....d.l.: MLT UTLT IVLT MTLT MELT nno di orso: altro FIL 1 Esercizio 1. Nel riferimento cartesiano ortogonale, si consideri
determinare le coordinate di P ricordando la relazione che permette di calcolare le coordinate del punto medio di un segmento si
 PROBLEMA Determinare il punto simmetrico di P( ;) rispetto alla retta x y =0 Soluzione Il simmetrico di P rispetto ad una retta r è il punto P che appartiene alla retta passante per P, perpendicolare ad
PROBLEMA Determinare il punto simmetrico di P( ;) rispetto alla retta x y =0 Soluzione Il simmetrico di P rispetto ad una retta r è il punto P che appartiene alla retta passante per P, perpendicolare ad
