Rette, piani e figure nello spazio
|
|
|
- Alessio Rossa
- 8 anni fa
- Просмотров:
Транскрипт
1 CAPITOLO Rette, piani e figure neo spazio. LA GEOMETRIA DELLO SPAZIO CON CABRI 3D Cabri 3D eá un software che, consentendo una facie costruzione di soidi, piani e figure deo spazio in genere, permette di mettere in evidenza caratteristiche e proprietaá dee quai eá difficie rendersi conto con i disegno manuae. La sua struttura eá de tutto simie a quea de'anaogo software che opera ne piano; gi strumenti di disegno e costruzione sono raggruppati nea Barra degi strumenti, suddivisi nei gruppi rappresentati dae icone che puoi vedere di seguito. Puntatore Linee Costruzioni Poigoni regoari Poiedri regoari Punti Superfici Trasformazioni Poiedri Strumenti di misura e cacoatrice A'apertura, Cabri 3D crea in modo automatico una zona di avoro a sfondo bianco (detta anche vista) che contiene un piano detto piano di base, con un sistema di riferimento rappresentato da tre vettori ortogonai. La parte in grigio di questo piano eá a parte visibie (PV) che occorre peroá pensare proungata indefinitamente. Tutte e costruzioni di punti, rette, soidi, vengono sempre poste iniziamente su piano di base (a'interno dea PV o fuori di essa). Come esempio iniziae, costruiamo un paraeepipedo rettangoo e vediamo come operano i principai comandi di gestione dea pagina video. n Per costruire un paraeepipedo rettangoo:. cicca su'icona Poiedri e scegi o strumento Paraeepipedo XYZ 2. cicca in un punto dea PV (primo vertice dea base de paraeepipedo) e sposta i mouse fino a definire a base de paraeepipedo (i puntatore indica i vertice opposto de rettangoo di base; attenzione: non si deve ciccare) Q Re Fraschini - Grazzi, Atas SpA Tema 6 - Cap. : RETTE, PIANI E FIGURE NELLO SPAZIO
2 3. tenendo premuto i tasto Maiuscoo dea tastiera sposta i mouse verso 'ato (o verso i basso) per definire 'atezza de paraeepipedo; 4. quando hai deciso quai devono essere e sue dimensioni, cicca in modo da confermare a costruzione. Le dimensioni e a posizione de paraeepipedo ne piano di base possono essere modificate in modaitaá Puntatore agendo in questo modo: ± per variare e dimensioni: cicca su'utimo punto sceto (queo che eá servito per definire 'atezza) e trascinao fino a raggiungere e nuove dimensioni; ± per variare a posizione: cicca in un punto quasiasi de soido (un vertice o una faccia) e trascinao. Anche quando, durante i trascinamento, i soido esce daa PV, ricorda che non abbandona mai i piano di base. n I punto di vista Quaunque costruzione viene vista "da'esterno" secondo una certa angoazione che puoá essere variata mediante trascinamento de mouse con i tasto destro quando ci si trova in modaitaá Puntatore. Nea figura che segue abbiamo rappresentato acuni soidi (che imparerai a costruire ne corso di questa esercitazione) secondo punti di vista diversi. Come disegnare e spostare punti Un punto si disegna con o strumento Punto de'icona Punti con un cic de mouse su piano di base; tutti i punti, sia che i mouse sia posizionato sua PV o a di fuori di essa, vengono iniziamente disegnati ne piano di base. Per creare un punto a di fuori de piano di base, si deve usare i tasto Maiuscoo e, tenendoo premuto, spostare i mouse nea posizione in cui si vuoe creare i punto. Attenzione a messaggio che identifica ciascun punto de piano di base in fase di creazione: ± se i punto appartiene aa PV i messaggio eá : un nuovo punto (su piano) ± se i punto appartiene a piano di base ma non eá sua PV i messaggio eá : un nuovo punto (neo spazio) La differenza eá sostanziae, in quanto un punto che appartiene aa PV puoá essere spostato soo su piano di base e non puoá uscire da esso, mentre un punto che appartiene a piano di base, ma non aa PV, puoá essere spostato anche in un piano diverso da queo di base. Un punto quasiasi puoá essere spostato: ± ungo i piano stesso con i metodo de trascinamento ± a di fuori de piano cui appartiene trascinando i mouse dopo aver premuto i tasto Maiuscoo (questo comando non ha effetto sui punti dea PV). 2 Tema 6 - Cap. : RETTE, PIANI E FIGURE NELLO SPAZIO Q Re Fraschini - Grazzi, Atas SpA
3 Per imparare ad usare questi comandi, disegna acuni punti su piano di base, sia nea PV che a di fuori di essa, e acuni punti non su piano di base; cambia adesso 'angoo di visuae usando i tasto destro de mouse per verificare a posizione dei punti in reazione a piano di base. Prova poi a spostari cercando di far uscire da piano di base quei che vi appartengono. Come tracciare rette e piani Per tracciare una retta si usa o strumento Retta de'icona Linee andando a seezionare due punti de piano di base; a retta giace dunque su tae piano. Per costruire una retta che non appartiene a piano di base si possono eseguire due differenti costruzioni: n disegnare a retta su piano di base seezionando i due punti in modo che ameno uno di essi non appartenga aa PV e trascinare poi i punto non sua PV a di fuori de piano di base; n disegnare un punto che non appartiene a piano di base e condurre per esso a retta ('atro punto puoá essere sceto su piano di base). Operazioni anaoghe devono essere eseguite per tracciare semirette e segmenti. Per tracciare un piano si usa o strumento Piano de'icona Superfici. Sono possibii diverse costruzioni, ciascuna corrispondente ad una proprietaá diversa dei piani; per ognuna di esse eá comunque necessario aver definito in primo uogo un punto non appartenente a piano di base, chiamiamoo A. n Piano per tre punti: dopo aver seezionato o strumento Piano: ± cicca su A e su atri due punti su piano di base, oppure: ± definisci prima atri due punti otre ad A e cicca poi su ciascuno di essi. n Piano definito da due rette companari: ± disegnare due rette passanti per A ± attivare o strumento Piano e seezionare e due rette. n Piano definito da una retta e un punto: ± disegnare una retta passante per A ± attivare o strumento Piano e seezionare a retta e un punto fuori di essa. In modo anaogo si costruiscono: ± un semipiano (occorre aver definito a retta origine e scegiere poi un punto che non e appartiene); ± un angoo convesso (si seeziona i vertice e atri due punti per definire e semirette che o individuano); ± un triangoo (si seezionano i tre punti che ne sono i vertici). PerpendicoaritaÁ e paraeismo neo spazio L'icona Costruzioni contiene tutti gi strumenti per costruire rette e piani mutuamente perpendicoari oppure paraei. n Con o strumento Perpendicoare si possono costruire: a retta perpendicoare a un piano: ± disegnare i piano e i punto A da quae si vuoe tracciare a perpendicoare ± seezionare o strumento Perpendicoare ± ciccare su punto A e su piano ('ordine puoá anche essere invertito); i piano perpendicoare a una retta: ± disegnare a retta ± seezionare o strumento Perpendicoare ± ciccare sua retta e su punto per i quae deve passare i piano ('ordine puoá anche essere invertito); a retta perpendicoare a un'atra retta: ± disegnare a prima retta ± seezionare o strumento Perpendicoare ± ciccare sua retta e, tenendo premuto i tasto Ctr, ciccare su punto per i quae deve passare a retta. Q Re Fraschini - Grazzi, Atas SpA Tema 6 - Cap. : RETTE, PIANI E FIGURE NELLO SPAZIO 3
4 n Con modaitaá de tutto anaoghe ae precedenti, o strumento Paraeo consente di tracciare: una retta paraea a un'atra retta un piano paraeo a un atro piano. I teorema dee tre perpendicoari Utiizzando gi strumenti che abbiamo descritto, possiamo verificare i teorema dee tre perpendicoari che ricordiamo di seguito: dato un piano e una retta r ad esso perpendicoare che o incontra in P, sia t una retta di non passante per P e sia s a perpendicoare a t passante per P; aora a retta t eá perpendicoare a piano definito da r e da s. Assumiamo come piano i piano di base; esegui e seguenti costruzioni tenendo presente che per attribuire un nome a un oggetto basta ciccare su di esso e digitare i nome da tastiera (per e ettere greche occorre usare i corrispondente codice ASCII preceduto da tasto ALT: per esempio ALT 225 corrisponde a ): ± preso un punto P su, traccia a retta r perpendicoare a piano di base ± traccia una retta su piano di base e indicaa con t ± traccia da P a perpendicoare aa retta t e indicaa con s ± traccia i piano passante per e rette r e s. Per verificare che i piano cosõá costruito eá perpendicoare aa retta t si puoá usare o strumento Misura di un angoo de'icona Strumenti di misura. Seezionando a retta e i piano viene evidenziato che 'angoo eá di 90. Nee figura a ato eá rappresentata 'immagine che si ottiene da questa costruzione; in essa abbiamo modificato i coore dee rette e nascosto acuni oggetti che non servono aa rappresentazione de teorema. Per fare queste operazioni si deve agire con i tasto destro de mouse su ciascun oggetto e scegiere e impostazioni da menu che viene proposto. La costruzione dei poiedri Abbiamo giaá visto come si costruisce un paraeepipedo rettangoo; con modaitaá anaoghe si possono costruire poiedri di ogni genere usando gi strumenti de'icona Poiedri. La cosa da tenere presente eá che ameno uno dei punti che servono per individuare i soido non deve appartenere ao stesso piano degi atri, atrimenti i soido risuta "appiattito" su piano. Diamo di seguito e indicazioni per a costruzione dei principai poiedri. n Un tetraedro eá definito da 4 punti che sono i suoi vertici, tre dei quai appartengono ad uno stesso piano mentre i quarto deve trovarsi su un piano diverso. n Un prisma si puoá costruire se prima si sono disegnati: ± i poigono di base con o strumento Poigono de'icona Superfici oppure con gi strumenti de'icona Poigoni regoari ± un vettore (da'icona Linee) che rappresenta 'atezza de prisma. Dopo aver seezionato o strumento Prisma basta ora indicare i poigono e i vettore. n Anche per costruire una piramide si deve prima disegnare i poigono di base; dopo aver seezionato o strumento Piramide eá sufficiente poi indicare a base e un punto non appartenente a piano di base che ne sia i vertice. 4 Tema 6 - Cap. : RETTE, PIANI E FIGURE NELLO SPAZIO Q Re Fraschini - Grazzi, Atas SpA
5 Uno strumento interessante eá Apri poiedro che consente di aprire e facce de soido ed eventuamente sviuppare su un piano. Nea figura a ato abbiamo costruito un prisma regoare avente per base un pentagono e abbiamo poi appicato ad esso questo strumento; o sviuppo piano puoá essere competato trascinando con i mouse una dee facce. In modo de tutto anaogo si possono costruire i poiedri regoari con gi strumenti de'icona Poiedri regoari. La cosa piuá conveniente eá disegnare un poigono regoare compatibie con i tipo di poiedro (un triangoo equiatero per i tetraedro, 'ottaedro e 'icosaedro, un quadrato per i cubo, un pentagono regoare per i dodecaedro) e poi, dopo aver seezionato 'opportuno strumento, ciccare su poigono che rappresenta una dee facce de poiedro; voendo disegnare i poiedro ne semispazio opposto a queo che viene proposto si deve premere i tasto Ctr. Proviamo a costruire un cubo e 'ottaedro in esso inscritto; per eseguire questa costruzione segui i seguenti passaggi: ± disegna un quadrato su piano di base ± appica o strumento Cubo indicando i quadrato come faccia ± individua i centri di tre facce concorrenti in un vertice mediante 'intersezione dee oro diagonai (o strumento Punto di intersezione si trova ne'icona Punti) ± costruisci i triangoo equiatero che ha per vertici i centri di queste facce; tae triangoo eá una dee facce de'ottaedro ± costruisci 'ottaedro indicando i triangoo come faccia. Di ottaedri che hanno come faccia i triangoo ce ne sono due: per disegnare queo interno a cubo puoá essere necessario usare i tasto Ctr. Nea figura a ato abbiamo reso trasparente i cubo agendo co tasto destro de mouse e scegiendo o stie dea superficie a righe sottii. Le potenziaitaá di questo software sono davvero interessanti e senza dubbio possono faciitare 'apprendimento dee proprietaá dee figure neo spazio. Per acquisire maggiori abiitaá ne suo utiizzo ti consigiamo di eseguire e costruzioni proposte di seguito e di provare 'uso degi strumenti che non abbiamo potuto descrivere; troverai un aiuto ne manuae di utiizzo che trovi in corrispondenza de punto di domanda nea riga dei menu. ESERCIZI. Disegna due rette sghembe che non giacciono su piano di riferimento. Q Re Fraschini - Grazzi, Atas SpA Tema 6 - Cap. : RETTE, PIANI E FIGURE NELLO SPAZIO 5
6 2. Disegna due semipiani che hanno 'origine in comune e a sezione normae de diedro che essi individuano. 3. Disegna una piramide in modo che: a. sia retta a base rettangoare b. sia regoare a base triangoare c. abbia per base un triangoo rettangoo e per atezza un segmento perpendicoare a piano di base e passante per i vertice de'angoo retto de triangoo. 4. Usando i comandi Cono e Ciindro, costruisci un cono e un ciindro retti tenendo presente che: i comando Cono genera a superficie aterae di un cono dati i suo vertice e a circonferenza di base i comando Ciindro genera un ciindro indefinito se eá dato i suo asse di rotazione (se 'asse eá un segmento viene generata a superficie aterae de ciindro). 5. Costruisci gi atri poiedri regoari usando i comandi appropriati. 6. L'ottaedro regoare si puoá anche costruire come poiedro inscritto in un tetraedro regoare considerando i punti medi dei suoi spigoi; prova ad eseguire questa costruzione. 6 Tema 6 - Cap. : RETTE, PIANI E FIGURE NELLO SPAZIO Q Re Fraschini - Grazzi, Atas SpA
7 AB e BC sono due diagonai dee facce di un cubo. Quanto misura 'angoo ABC? d a. 90 b. 20 c. 60 d. 45 e. nessuna dee precedenti risposte eá corretta c: Š 2 Tra i seguenti disegni, individuare tutti quei che rappresentano o sviuppo piano di un cubo. a. b. e c.,, d.,,, e.,,,, d: Š 3 Sia Q un cubo e sia S una sfera che ha centro in uno dei vertici di Q e raggio uguae a ato di Q. I voume de'intersezione tra Q e S eá: a. un ottavo de voume dea sfera b. un quarto de voume dea sfera c. un sesto de voume de cubo d. un quarto de voume de cubo e. metaá de voume de cubo. a: Š 4 Una cassetta di egno, senza coperchio, eá fabbricata con tavoe spesse 2cm. Se e dimensioni esterne dea base (rettangoare) sono 38cm e 44cm e 'atezza esterna eá 47cm, di quanti centimetri cubi eá i voume interno dea cassetta? a. 6200cm 3 b cm 3 c cm 3 d cm 3 e cm 3 a: Š 5 Un paraeepipedo a base quadrata eá inscritto in una sfera. Se i ato di base eá de'atezza, quanto vae 4 i rapporto tra a superficie dea sfera e a superficie totae de paraeepipedo? a. b. 4 c. 2 d. 2 e. dipende da raggio dea sfera a: Š 6 In una vasca a forma di paraeepipedo con base quadrata di ato 40cm viene immessa de'acqua fino a raggiungere un iveo di 30cm. Poi viene competamente immerso nea vasca un cubo pieno di ato 20cm. Qua eá ora i iveo de'acqua? a. 32cm b. 32,5cm c. 35cm d. 40cm e. 50cm c: Š 7 I deposito dea ibreria di Tuio eá una stanza cubica di ato 5m e negi utimi tempi eá diventato troppo piccoo per poter contenere tutte e giacenze di magazzino. PercioÁ Tuio ne ha comprato uno nuovo, sempre di forma cubica, che, sostituito a precedente, gi ha permesso di guadagnare 28m 3 di spazio. Di quanti metri i ato de nuovo deposito eá piuá ungo di queo vecchio? a. m b. 2m c. 3m d. 4m e. 5m b: Š 8 Dato i cubo in figura, con gi spigoi di ato, o si tagi ungo i piano ABC. Qua eá i voume dea parte piuá piccoa cosõá ottenuta? a. 3 b. 4 c. 6 d. 8 Q Re Fraschini - Grazzi, Atas SpA Tema 6 - Cap. : RETTE, PIANI E FIGURE NELLO SPAZIO 7 e. 2 c: Š
8 Questa proposta si ispira direttamente ad uno degi esercizi presentati ne progetto P.I.S.A. Edificio a spirae Ne'architettura moderna, gi edifici hanno spesso forme insoite. La figura che segue mostra un modeo fatto a computer di un "edificio a spirae" e una pianta de piano terra. I punti cardinai mostrano 'orientamento de'edificio. A piano terra de'edificio si trovano 'ingresso principae e uno spazio per i negozi. Sopra a piano terra ci sono 20 piani di appartamenti. La pianta di ciascun piano eá simie aa pianta de piano terra, ma ognuna ha un orientamento eggermente diverso rispetto a piano inferiore. I ciindro contiene i vano de'ascensore e un pianerottoo ad ogni piano. Stima 'atezza totae de'edificio, in metri. Spiega come sei arrivato aa tua risposta. 2 Le figure a ato sono vedute aterai de'edificio a spirae. Da che direzione eá stata presa a veduta aterae? a. Da Nord b. Da Ovest c. Da Est d. Da Sud Da che direzione eá stata presa a veduta aterae 2? a. Da Nord-Ovest b. Da Nord-Est c. Da Sud-Ovest d. Da Sud-Est Ciascun piano di appartamenti presenta una certa "torsione" rispetto a piano terra. L'utimo piano (i ventesimo sopra i piano terra) eá ad angoo retto rispetto a piano terra. I disegno che segue rappresenta i piano terra. Su questo disegno traccia a pianta de decimo piano, mostrando come questo piano eá situato rispetto a piano terra. Ipotizzando un'atezza da 3m a 4m per piano piuá i piano terra di atezza di soito superiore, diciamo 5m, a stima va da 65m a 85m 2 c., d. 3 8 Tema 6 - Cap. : RETTE, PIANI E FIGURE NELLO SPAZIO Q Re Fraschini - Grazzi, Atas SpA
9 right circuar cone to comprise cube net cono circoare retto comporre cubo rete, reticoo ratio sphere surface area rapporto sfera area dea superficie Consider the right circuar cone shown beow. A cross-section of the cone is shown which is perpendicuar to the base, and passes through the center of the base. Find the tota surface area of the cone. 2 The net on the right hand is comprised of three rectanges and two congruent right trianges. Find the voume of the soid formed from this net. ex. 2 3 A cube of back materia is painted bue on a sides, then cut into 26 smaer cubes. How many of the smaer cubes are bue on ony one side? a. 8 b. 2 c. 48 d. 96 e Let A be the ratio of the voume of a sphere to the voume of a cube each of whose face is tangent to the sphere, and et B be the ratio of the surface area of this sphere to the surface area of the cube. Then: a. A B ˆ 6 d. A B ˆ 3 b. A B ˆ c. A B ˆ 2 3 e. A B ˆ 2 ex. 5 5 Three ounces of water are paced into a right circuar cone, as shown. How many more ounces of water must be added to doube the height of the water? p cm 3 3 d. 4 d. 5 2 ounces p 6 2 Q Re Fraschini - Grazzi, Atas SpA Tema 6 - MATH IN ENGLISH 9
Meccanica dei Manipolatori. Corso di Robotica Prof. Davide Brugali Università degli Studi di Bergamo
 Meccanica dei Manipoatori Corso di Robotica Prof. Davide Brugai Università degi Studi di Bergamo Definizione di robot industriae Un robot industriae è un manipoatore mutifunzionae riprogrammabie, comandato
Meccanica dei Manipoatori Corso di Robotica Prof. Davide Brugai Università degi Studi di Bergamo Definizione di robot industriae Un robot industriae è un manipoatore mutifunzionae riprogrammabie, comandato
Le sezioni piane del cubo
 Le sezioni piane del cubo Versione provvisoria 11 dicembre 006 1 Simmetrie del cubo e sezioni speciali Sezioni speciali si presentano in corrispondenza di piani perpendicolari agli assi di simmetria del
Le sezioni piane del cubo Versione provvisoria 11 dicembre 006 1 Simmetrie del cubo e sezioni speciali Sezioni speciali si presentano in corrispondenza di piani perpendicolari agli assi di simmetria del
I primi elementi. www.geogebra.org/cms/
 CAPITOLO 1 I primi eementi 1. GEOGEBRA Geogebra eá un software di matematica dinamica prodotto da un gruppo diretto da Markus Hohenwarter in cui geometria e agebra condividono o stesso ambiente di avoro.
CAPITOLO 1 I primi eementi 1. GEOGEBRA Geogebra eá un software di matematica dinamica prodotto da un gruppo diretto da Markus Hohenwarter in cui geometria e agebra condividono o stesso ambiente di avoro.
descrivere le caratteristiche della sfera utilizzare le formule inerenti. Introduzione
 Anno 4 Sfera 1 Introduzione In questa lezione parleremo di un importante solido di rotazione detto sfera. Ne daremo la definizione, ne studieremo le caratteristiche e le formule a essa inerenti. Al termine
Anno 4 Sfera 1 Introduzione In questa lezione parleremo di un importante solido di rotazione detto sfera. Ne daremo la definizione, ne studieremo le caratteristiche e le formule a essa inerenti. Al termine
L INTERFACCIA GRAFICA DI EXCEL
 Dopo l avvio del foglio elettronico apparirà un interfaccia grafica nella quale verrà aperta una nuova cartella di lavoro alla quale il PC assegnerà automaticamente il nome provvisorio di Cartel1. La cartella
Dopo l avvio del foglio elettronico apparirà un interfaccia grafica nella quale verrà aperta una nuova cartella di lavoro alla quale il PC assegnerà automaticamente il nome provvisorio di Cartel1. La cartella
per immagini guida avanzata Modificare il contenuto del foglio di lavoro Geometra Luigi Amato Guida Avanzata per immagini Excel 2000 1
 Modificare il contenuto del foglio di lavoro Geometra Luigi Amato Guida Avanzata per immagini Excel 2000 1 Selezione delle celle per immagini guida avanzata La cella attiva è la B7 Selezionare una cella
Modificare il contenuto del foglio di lavoro Geometra Luigi Amato Guida Avanzata per immagini Excel 2000 1 Selezione delle celle per immagini guida avanzata La cella attiva è la B7 Selezionare una cella
Percorsi di Matematica on line ESERCIZI DI RECUPERO 3
 Gariea ori Sivia Vivada Rita Martinei Percorsi di Matematica on ine ESERCIZI DI RECUPERO Sommario Numeri Souzioni Spazio e figure 9 Souzioni 9 Reazioni e funzioni Souzioni 6 Misure, dati e previsioni 66
Gariea ori Sivia Vivada Rita Martinei Percorsi di Matematica on ine ESERCIZI DI RECUPERO Sommario Numeri Souzioni Spazio e figure 9 Souzioni 9 Reazioni e funzioni Souzioni 6 Misure, dati e previsioni 66
Uno spazio per lo spazio.
 Uno spazio per lo spazio. Il gruppo di matematica del Laboratorio Franco Conti ha lavorato quest anno nella direzione di ripensare l insegnamento della geometria dello spazio, unendo la riflessione teorica
Uno spazio per lo spazio. Il gruppo di matematica del Laboratorio Franco Conti ha lavorato quest anno nella direzione di ripensare l insegnamento della geometria dello spazio, unendo la riflessione teorica
Grafici di particolari funzioni lineari
 A Grafici di particoari funzioni ineari Vogiamo tracciare i grafico dea funzione y ˆ jxj. x quando x 0 Sappiamo che jxj significa x quando x < 0 Possiamo aora riscrivere 'equazione di questa funzione in
A Grafici di particoari funzioni ineari Vogiamo tracciare i grafico dea funzione y ˆ jxj. x quando x 0 Sappiamo che jxj significa x quando x < 0 Possiamo aora riscrivere 'equazione di questa funzione in
5. Spiegare perché la somma di due lati di un triangolo sferico è maggiore del terzo lato.
 ESERCIZI E PROBLEMI 1. Spiegare perché sulla sfera non ci sono rette parallele e mostrare che per due punti passa una ed una sola retta. Basta ricordare che retta significa circonferenza massima su S,
ESERCIZI E PROBLEMI 1. Spiegare perché sulla sfera non ci sono rette parallele e mostrare che per due punti passa una ed una sola retta. Basta ricordare che retta significa circonferenza massima su S,
Introduzione a GeoGebra
 Introduzione a GeoGebra Nicola Sansonetto Istituto Sanmicheli di Verona 31 Marzo 2016 Nicola Sansonetto (Sanmicheli) Introduzione a GeoGebra 31 Marzo 2016 1 / 14 Piano dell incontro 1 Introduzione 2 Costruzioni
Introduzione a GeoGebra Nicola Sansonetto Istituto Sanmicheli di Verona 31 Marzo 2016 Nicola Sansonetto (Sanmicheli) Introduzione a GeoGebra 31 Marzo 2016 1 / 14 Piano dell incontro 1 Introduzione 2 Costruzioni
Come utilizzare i riferimenti assoluti e relativi in Microsoft Excel
 Come utilizzare i riferimenti assoluti e relativi in Microsoft Excel In un foglio elettronico, le celle sono identificate mediante delle coordinate; in genere, sono utilizzate le lettere per identificare
Come utilizzare i riferimenti assoluti e relativi in Microsoft Excel In un foglio elettronico, le celle sono identificate mediante delle coordinate; in genere, sono utilizzate le lettere per identificare
Capitolo 16: Piano di lavoro speciale
 Capitolo 16: Piano di lavoro speciale Avviate MasterChef dall icona presente sul vostro Desktop. Nota: Se state utilizzando una versione dimostrativa, una volta caricato il programma, un messaggio vi comunicherà
Capitolo 16: Piano di lavoro speciale Avviate MasterChef dall icona presente sul vostro Desktop. Nota: Se state utilizzando una versione dimostrativa, una volta caricato il programma, un messaggio vi comunicherà
COS È UN PRISMA. Due POLIGONI congruenti e paralleli, come basi. È UN POLIEDRO DELIMITATO DA
 PRISMI E PIRAMIDI COS È UN PRISMA È UN POLIEDRO DELIMITATO DA Due POLIGONI congruenti e paralleli, come basi. Tanti PARALLELOGRAMMI quanti sono i lati del poligono di base (come facce laterali). PRISMA
PRISMI E PIRAMIDI COS È UN PRISMA È UN POLIEDRO DELIMITATO DA Due POLIGONI congruenti e paralleli, come basi. Tanti PARALLELOGRAMMI quanti sono i lati del poligono di base (come facce laterali). PRISMA
LA CIRCONFERENZA La circonferenza è il luogo geometrico dei punti equidistanti da un punto C, detto centro.
 Geometria Analitica Le coniche Queste curve si chiamano coniche perché sono ottenute tramite l'intersezione di una superficie conica con un piano. Si possono definire tutte come luoghi geometrici e, di
Geometria Analitica Le coniche Queste curve si chiamano coniche perché sono ottenute tramite l'intersezione di una superficie conica con un piano. Si possono definire tutte come luoghi geometrici e, di
Esercizi sulle affinità - aprile 2009
 Esercizi sulle affinità - aprile 009 Ingegneria meccanica 008/009 Esercizio Sono assegnate nel piano le sei rette r : =, s : =, t : =, r : =, s : =, t : = determinare l affinità che trasforma ordinatamente
Esercizi sulle affinità - aprile 009 Ingegneria meccanica 008/009 Esercizio Sono assegnate nel piano le sei rette r : =, s : =, t : =, r : =, s : =, t : = determinare l affinità che trasforma ordinatamente
ESPERIENZE CON GLI SPECCHI PIANI
 1. Qual è la posizione dell immagine fornita da uno specchio piano? Di che tipo di immagine si tratta? Disponi il cilindro giallo dietro lo specchio, in modo che coincida con l immagine riflessa del cilindro
1. Qual è la posizione dell immagine fornita da uno specchio piano? Di che tipo di immagine si tratta? Disponi il cilindro giallo dietro lo specchio, in modo che coincida con l immagine riflessa del cilindro
Postulati e definizioni di geometria piana
 I cinque postulati di Euclide I postulato Adimandiamo che ce sia concesso, che da qualunque ponto in qualunque ponto si possi condurre una linea retta. Tra due punti qualsiasi è possibile tracciare una
I cinque postulati di Euclide I postulato Adimandiamo che ce sia concesso, che da qualunque ponto in qualunque ponto si possi condurre una linea retta. Tra due punti qualsiasi è possibile tracciare una
PSICOMETRIA. Esercitazione n.1. C.d.L. Comunicazione e Psicologia a.a. 2012/13
 PSICOMETRIA Esercitazione n.1 C.d.L. Comunicazione e Psicologia a.a. 2012/13 ESERCITAZIONE 1: INDICE 1. Informazioni di carattere generale sulle esercitazioni 2. Il foglio di calcolo (Excel) 3. Avviare
PSICOMETRIA Esercitazione n.1 C.d.L. Comunicazione e Psicologia a.a. 2012/13 ESERCITAZIONE 1: INDICE 1. Informazioni di carattere generale sulle esercitazioni 2. Il foglio di calcolo (Excel) 3. Avviare
IL MIO PRIMO IPERTESTO CON POWERPOINT
 IL MIO PRIMO IPERTESTO CON POWERPOINT 1. Realizzare la prima diapositiva 1. Dal menu File fai clic su Nuovo, quindi dalla finestra Nuova Presentazione fai clic su Da modello struttura. 2. Scegli il modello
IL MIO PRIMO IPERTESTO CON POWERPOINT 1. Realizzare la prima diapositiva 1. Dal menu File fai clic su Nuovo, quindi dalla finestra Nuova Presentazione fai clic su Da modello struttura. 2. Scegli il modello
UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria A.A. 2009/10
 UNIVERSITÀ DEGLI STUDI DI PDOV Facoltà di Ingegneria Corso di Disegno Tecnico Industriale per i Corsi di Laurea triennale in Ingegneria Meccanica e in Ingegneria dell Energia Costruzioni geometriche in
UNIVERSITÀ DEGLI STUDI DI PDOV Facoltà di Ingegneria Corso di Disegno Tecnico Industriale per i Corsi di Laurea triennale in Ingegneria Meccanica e in Ingegneria dell Energia Costruzioni geometriche in
TUTORIAL LIBRI IN SIMBOLI
 TUTORIAL LIBRI IN SIMBOLI Questo tutorial guida alla costruzione di un libro in simboli utilizzando il programma ARAWORD e OPENOFFICE DRAW. I programmi devono essere aperti entrambi. Si consiglia di scrivere
TUTORIAL LIBRI IN SIMBOLI Questo tutorial guida alla costruzione di un libro in simboli utilizzando il programma ARAWORD e OPENOFFICE DRAW. I programmi devono essere aperti entrambi. Si consiglia di scrivere
Marziana Monfardini 2004-2005 lezioni di word
 1 2 3 4 5 TABUlAZIONI, RIENTRI, ELENCHI...IN BREVE PER IMPOSTARE UNA TABULAZIONE... Posizionarsi nella riga in cui si vuole inserire una tabulazione. Selezionare il tipo di tabulazione desiderato sul pulsante
1 2 3 4 5 TABUlAZIONI, RIENTRI, ELENCHI...IN BREVE PER IMPOSTARE UNA TABULAZIONE... Posizionarsi nella riga in cui si vuole inserire una tabulazione. Selezionare il tipo di tabulazione desiderato sul pulsante
Si dice parabola il luogo geometrico dei punti del piano, equidistanti da un punto fisso, detto fuoco, e da una retta fissa, detta direttrice.
 LA PARABOLA Definizione: Si dice parabola il luogo geometrico dei punti del piano, equidistanti da un punto fisso, detto fuoco, e da una retta fissa, detta direttrice. Dimostrazione della parabola con
LA PARABOLA Definizione: Si dice parabola il luogo geometrico dei punti del piano, equidistanti da un punto fisso, detto fuoco, e da una retta fissa, detta direttrice. Dimostrazione della parabola con
Video Scrittura (MS Word) Lezione 1 Funzioni di base
 Video Scrittura (MS Word) Lezione 1 Funzioni di base Cos e un programma di Video Scrittura Un programma di Video Scrittura serve per effettuare tutte quelle operazioni che consentono di creare, modificare,
Video Scrittura (MS Word) Lezione 1 Funzioni di base Cos e un programma di Video Scrittura Un programma di Video Scrittura serve per effettuare tutte quelle operazioni che consentono di creare, modificare,
3.5.1 PREPARAZ1ONE I documenti che si possono creare con la stampa unione sono: lettere, messaggi di posta elettronica, o etichette.
 3.5 STAMPA UNIONE Le funzioni della stampa unione (o stampa in serie) permettono di collegare un documento principale con un elenco di nominativi e indirizzi, creando così tanti esemplari uguali nel contenuto,
3.5 STAMPA UNIONE Le funzioni della stampa unione (o stampa in serie) permettono di collegare un documento principale con un elenco di nominativi e indirizzi, creando così tanti esemplari uguali nel contenuto,
Autodesk Map parte I digitalizzazione e importazione dati
 Autodesk Map parte I digitalizzazione e importazione dati Marco Negretti e-mail: [email protected] http://geomatica.como.polimi.it V 5.1 10/10/08 I dati in Autodesk Map I dati vengono memorizzati
Autodesk Map parte I digitalizzazione e importazione dati Marco Negretti e-mail: [email protected] http://geomatica.como.polimi.it V 5.1 10/10/08 I dati in Autodesk Map I dati vengono memorizzati
WINDOWS95. 1. Avviare Windows95. Avviare Windows95 non è un problema: parte. automaticamente all accensione del computer. 2. Barra delle applicazioni
 WINDOWS95 1. Avviare Windows95 Avviare Windows95 non è un problema: parte automaticamente all accensione del computer. 2. Barra delle applicazioni 1 La barra delle applicazioni permette di richiamare le
WINDOWS95 1. Avviare Windows95 Avviare Windows95 non è un problema: parte automaticamente all accensione del computer. 2. Barra delle applicazioni 1 La barra delle applicazioni permette di richiamare le
valore di a: verso l alto (ordinate crescenti) se a>0, verso il basso (ordinate decrescenti) se a<0;
 La parabola è una particolare conica definita come è una curva aperta, nel senso che non può essere contenuta in alcuna superficie finita del piano; è simmetrica rispetto ad una retta, detta ASSE della
La parabola è una particolare conica definita come è una curva aperta, nel senso che non può essere contenuta in alcuna superficie finita del piano; è simmetrica rispetto ad una retta, detta ASSE della
Manuale d uso DropSheep 4 imaio Gestione Pixmania-PRO Ver 1.1
 Manuale d uso DropSheep 4 imaio Gestione Pixmania-PRO Ver 1.1 Release NOTE 1.1 Prima Versione del Manuale INDICE 1-INTRODUZIONE... 4 2- GESTIONE DEL CATALOGO PIXMANIA-PRO SU IMAIO... 5 3-Configurazione
Manuale d uso DropSheep 4 imaio Gestione Pixmania-PRO Ver 1.1 Release NOTE 1.1 Prima Versione del Manuale INDICE 1-INTRODUZIONE... 4 2- GESTIONE DEL CATALOGO PIXMANIA-PRO SU IMAIO... 5 3-Configurazione
Introduzione alle macchine a stati (non definitivo)
 Introduzione alle macchine a stati (non definitivo) - Introduzione Il modo migliore per affrontare un problema di automazione industriale (anche non particolarmente complesso) consiste nel dividerlo in
Introduzione alle macchine a stati (non definitivo) - Introduzione Il modo migliore per affrontare un problema di automazione industriale (anche non particolarmente complesso) consiste nel dividerlo in
Pianificare una riunione
 34 / 2010 Pianificare una riunione con Outlook XP Pianificazione di appuntamenti e riunioni, verifica della disponibilità delle persone, invio di inviti e creazione di ricorrenze In questa edizione: Chi
34 / 2010 Pianificare una riunione con Outlook XP Pianificazione di appuntamenti e riunioni, verifica della disponibilità delle persone, invio di inviti e creazione di ricorrenze In questa edizione: Chi
Prontuario di geometria euclidea nello spazio. Per la scuola secondaria di I grado
 Prontuario di geometria euclidea nello spazio Per la scuola secondaria di I grado N. B. Gli argomenti presentati sono una sintesi di quelli trattati in classe e non sostituiscono ma integrano il libro
Prontuario di geometria euclidea nello spazio Per la scuola secondaria di I grado N. B. Gli argomenti presentati sono una sintesi di quelli trattati in classe e non sostituiscono ma integrano il libro
1/6. Esercizi su Circonferenza/retta e circonferenza/circonferenza. Dimostrazioni. Ipotesi. Tesi. Dimostrazione. Ipotesi. Tesi.
 Dimostrazioni Risoluzione 1) Le circonferenze Γ e Γ' (e Γ'') sono tangenti P appartiene alla retta tangente comune t PA, PB (e PB*) sono tangenti PA = PB (= PB*) Non ha importanza se le due circonferenze
Dimostrazioni Risoluzione 1) Le circonferenze Γ e Γ' (e Γ'') sono tangenti P appartiene alla retta tangente comune t PA, PB (e PB*) sono tangenti PA = PB (= PB*) Non ha importanza se le due circonferenze
Giochi con due specchi. (Laboratorio sulla simmetria rotazionale)
 Giochi con due specchi. (Laboratorio sulla simmetria rotazionale) Prima parte. Abbiamo a disposizione alcune coppie di specchi, dei piccoli oggetti (poligoni, matite, palline), alcuni disegni. Tra due
Giochi con due specchi. (Laboratorio sulla simmetria rotazionale) Prima parte. Abbiamo a disposizione alcune coppie di specchi, dei piccoli oggetti (poligoni, matite, palline), alcuni disegni. Tra due
Modulo1. Ricercare nelle mappe
 Modulo1 Ricercare nelle mappe 1. Trovare latitudine e longitudine di un punto 2. Trovare un punto sapendo latitudine e longitudine N.B. Dal 2014 Google Maps ha una nuova versione Clicca Qui la presentazione
Modulo1 Ricercare nelle mappe 1. Trovare latitudine e longitudine di un punto 2. Trovare un punto sapendo latitudine e longitudine N.B. Dal 2014 Google Maps ha una nuova versione Clicca Qui la presentazione
SOTTOSPAZI E OPERAZIONI IN SPAZI DIVERSI DA R n
 SPAZI E SOTTOSPAZI 1 SOTTOSPAZI E OPERAZIONI IN SPAZI DIVERSI DA R n Spazi di matrici. Spazi di polinomi. Generatori, dipendenza e indipendenza lineare, basi e dimensione. Intersezione e somma di sottospazi,
SPAZI E SOTTOSPAZI 1 SOTTOSPAZI E OPERAZIONI IN SPAZI DIVERSI DA R n Spazi di matrici. Spazi di polinomi. Generatori, dipendenza e indipendenza lineare, basi e dimensione. Intersezione e somma di sottospazi,
Risoluzione di problemi ingegneristici con Excel
 Risoluzione di problemi ingegneristici con Excel Problemi Ingegneristici Calcolare per via numerica le radici di un equazione Trovare l equazione che lega un set di dati ottenuti empiricamente (fitting
Risoluzione di problemi ingegneristici con Excel Problemi Ingegneristici Calcolare per via numerica le radici di un equazione Trovare l equazione che lega un set di dati ottenuti empiricamente (fitting
ORDINE INGEGNERI PROVINCIA DI CATANIA FONDAZIONE ORDINE INGEGNERI PROVINCIA DI CATANIA PROGETTO INGEGNERE ANALISI DEL PROCESSO EDILIZIO
 ORDINE INGEGNERI PROVINCIA DI CATANIA FONDAZIONE ORDINE INGEGNERI PROVINCIA DI CATANIA PROGETTO INGEGNERE ANALISI DEL PROCESSO EDILIZIO SEMINARI DI AVVIO ALLA PROFESSIONE PER GIOVANI INGEGNERI COMMISSIONE
ORDINE INGEGNERI PROVINCIA DI CATANIA FONDAZIONE ORDINE INGEGNERI PROVINCIA DI CATANIA PROGETTO INGEGNERE ANALISI DEL PROCESSO EDILIZIO SEMINARI DI AVVIO ALLA PROFESSIONE PER GIOVANI INGEGNERI COMMISSIONE
Guida per l utente agli organigrammi cross-browser di OrgPublisher
 Guida per l utente agli organigrammi cross-browser di OrgPublisher Sommario Sommario... 3 Visualizzazione di tutorial sugli organigrammi cross-browser pubblicati... 3 Esecuzione di una ricerca in un organigramma
Guida per l utente agli organigrammi cross-browser di OrgPublisher Sommario Sommario... 3 Visualizzazione di tutorial sugli organigrammi cross-browser pubblicati... 3 Esecuzione di una ricerca in un organigramma
BILANCIO DEI VINCOLI ED ANALISI CINEMATICA
 BILANCIO DEI VINCOLI ED ANALISI CINEMATICA ESERCIZIO 1 Data la struttura piana rappresentata in Figura 1, sono richieste: - la classificazione della struttura in base alla condizione di vincolo; - la classificazione
BILANCIO DEI VINCOLI ED ANALISI CINEMATICA ESERCIZIO 1 Data la struttura piana rappresentata in Figura 1, sono richieste: - la classificazione della struttura in base alla condizione di vincolo; - la classificazione
Protocollo dei saperi imprescindibili Ordine di scuola: professionale
 Protocollo dei saperi imprescindibili Ordine di scuola: professionale DISCIPLINA: MATEMATICA RESPONSABILE: CAGNESCHI F. IMPERATORE D. CLASSE: prima servizi commerciali Utilizzare le tecniche e le procedure
Protocollo dei saperi imprescindibili Ordine di scuola: professionale DISCIPLINA: MATEMATICA RESPONSABILE: CAGNESCHI F. IMPERATORE D. CLASSE: prima servizi commerciali Utilizzare le tecniche e le procedure
Quadro riassuntivo di geometria analitica
 Quadro riassuntivo di geometria analitica IL PIANO CARTESIANO (detta ascissa o coordinata x) e y quella dall'asse x (detta ordinata o coordinata y). Le coordinate di un punto P sono: entrambe positive
Quadro riassuntivo di geometria analitica IL PIANO CARTESIANO (detta ascissa o coordinata x) e y quella dall'asse x (detta ordinata o coordinata y). Le coordinate di un punto P sono: entrambe positive
Quick Print. Quick Print. Guida Utente. Copyright 2013 Hyperbolic Software. www.hyperbolicsoftware.com
 Quick Print Quick Print Guida Utente I nomi dei prodotti menzionati in questo manuale sono proprietà delle rispettive società. Copyright 2013 Hyperbolic Software. www.hyperbolicsoftware.com 1 Tabella dei
Quick Print Quick Print Guida Utente I nomi dei prodotti menzionati in questo manuale sono proprietà delle rispettive società. Copyright 2013 Hyperbolic Software. www.hyperbolicsoftware.com 1 Tabella dei
Esercizi sulla conversione tra unità di misura
 Esercizi sulla conversione tra unità di misura Autore: Enrico Campanelli Prima stesura: Settembre 2013 Ultima revisione: Settembre 2013 Per segnalare errori o per osservazioni e suggerimenti di qualsiasi
Esercizi sulla conversione tra unità di misura Autore: Enrico Campanelli Prima stesura: Settembre 2013 Ultima revisione: Settembre 2013 Per segnalare errori o per osservazioni e suggerimenti di qualsiasi
Capitolo 6: Inserimento infissi
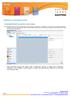 Capitolo 6: Inserimento infissi Avviate MasterChef dall icona presente sul vostro Desktop. Nota: Se state utilizzando una versione dimostrativa, una volta caricato il programma, un messaggio vi comunicherà
Capitolo 6: Inserimento infissi Avviate MasterChef dall icona presente sul vostro Desktop. Nota: Se state utilizzando una versione dimostrativa, una volta caricato il programma, un messaggio vi comunicherà
Capitolo 18 - Progetto DWG Creazione del layout di stampa
 Capitolo 18 - Progetto DWG Creazione del layout di stampa Avviate MasterChef dall icona presente sul vostro Desktop. Nota: Se state utilizzando una versione dimostrativa, una volta caricato il programma,
Capitolo 18 - Progetto DWG Creazione del layout di stampa Avviate MasterChef dall icona presente sul vostro Desktop. Nota: Se state utilizzando una versione dimostrativa, una volta caricato il programma,
Questa è la finestra dei dettagli, è possibile selezionare anche da qui un modello o un pezzo per essere aperto.
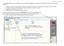 Il sistema CONFELMOD come tutti gli analoghi sistemi per la confezione d abbigliamento, svolge 3 funzioni distinte (anche dal punto di vista del tipo di programma) 1. la gestione di tutti i dati relativi
Il sistema CONFELMOD come tutti gli analoghi sistemi per la confezione d abbigliamento, svolge 3 funzioni distinte (anche dal punto di vista del tipo di programma) 1. la gestione di tutti i dati relativi
Il magnetismo magnetismo magnetite
 Magnetismo Il magnetismo Fenomeno noto fin dall antichità. Il termine magnetismo deriva da Magnesia città dell Asia Minore dove si era notato che un minerale, la magnetite, attirava a sé i corpi ferrosi.
Magnetismo Il magnetismo Fenomeno noto fin dall antichità. Il termine magnetismo deriva da Magnesia città dell Asia Minore dove si era notato che un minerale, la magnetite, attirava a sé i corpi ferrosi.
TRIGONOMETRIA E COORDINATE
 Y Y () X O (Y Y ) - α X (X X ) 200 c TRIGONOMETRI E OORDINTE ngoli e sistemi di misura angolare Funzioni trigonometriche Risoluzione dei triangoli rettangoli Risoluzione dei poligoni Risoluzione dei triangoli
Y Y () X O (Y Y ) - α X (X X ) 200 c TRIGONOMETRI E OORDINTE ngoli e sistemi di misura angolare Funzioni trigonometriche Risoluzione dei triangoli rettangoli Risoluzione dei poligoni Risoluzione dei triangoli
Lezione 19 Esercitazione InDesign
 Lezione 19 Esercitazione InDesign Pasquale Savino ISTI - CNR Utilizzo dei frame 2 Sommario Questa esercitazione è dedicata all uso dei frame Cosa contiene questa esercitazione Uso del tool di selezione
Lezione 19 Esercitazione InDesign Pasquale Savino ISTI - CNR Utilizzo dei frame 2 Sommario Questa esercitazione è dedicata all uso dei frame Cosa contiene questa esercitazione Uso del tool di selezione
CREARE UN GRAFICO CON EXCEL 2007
 CREARE UN GRAFICO CON EXCEL 2007 Ecco come creare un grafico velocemente. Crea la seguente tabella: Seleziona, col tasto sinistro del mouse premuto, dalla casella B3 alla C7; nella Barra dei Menù, sotto
CREARE UN GRAFICO CON EXCEL 2007 Ecco come creare un grafico velocemente. Crea la seguente tabella: Seleziona, col tasto sinistro del mouse premuto, dalla casella B3 alla C7; nella Barra dei Menù, sotto
Procedura operativa per la gestione della funzione di formazione classi prime
 Procedura operativa per la gestione della funzione di formazione classi prime Questa funzione viene fornita allo scopo di effettuare la formazione delle classi prime nel rispetto dei parametri indicati
Procedura operativa per la gestione della funzione di formazione classi prime Questa funzione viene fornita allo scopo di effettuare la formazione delle classi prime nel rispetto dei parametri indicati
10. Quale dei seguenti numeri
 Test d'ingresso di matematica per la secondaria di secondo grado (liceo classico) Il test si basa su alcuni test di ingresso (opportunamente modificati) assegnati al liceo classico e trovati in Rete Nome:
Test d'ingresso di matematica per la secondaria di secondo grado (liceo classico) Il test si basa su alcuni test di ingresso (opportunamente modificati) assegnati al liceo classico e trovati in Rete Nome:
SUPERFICI CONICHE. Rappresentazione di coni e cilindri
 SUPERFICI CONICHE Rappresentazione di coni e cilindri Si definisce CONO la superficie che si ottiene proiettando tutti i punti di una curva, detta DIRETTRICE, da un punto proprio, non appartenente al piano
SUPERFICI CONICHE Rappresentazione di coni e cilindri Si definisce CONO la superficie che si ottiene proiettando tutti i punti di una curva, detta DIRETTRICE, da un punto proprio, non appartenente al piano
OPERAZIONI CHIUSURA E APERTURA Note operative
 OPERAZIONI CHIUSURA E APERTURA Note operative N.B. E importante accertarsi, in caso di multiutenza, che altri operatori non effettuino operazioni contabili mentre ci si appresta a generare le chiusure
OPERAZIONI CHIUSURA E APERTURA Note operative N.B. E importante accertarsi, in caso di multiutenza, che altri operatori non effettuino operazioni contabili mentre ci si appresta a generare le chiusure
Navigazione Tattica. L intercettazione
 Navigazione Tattica I problemi di navigazione tattica si distinguono in: Intercettazione, che riguarda lo studio delle procedure atte a raggiungere nel minor tempo possibile un aeromobile o un qualsiasi
Navigazione Tattica I problemi di navigazione tattica si distinguono in: Intercettazione, che riguarda lo studio delle procedure atte a raggiungere nel minor tempo possibile un aeromobile o un qualsiasi
Manuale di Estimo Vittorio Gallerani, Giacomo Zanni, Davide Viaggi Copyright 2005 The McGraw-Hill Companies srl
 Copyright 2005 The Companies srl Caso 13 Stima della tabella millesimale di proprietà in un condominio di 4 piani con appartamenti e negozi nella periferia di Torino 1. Descrizione del fabbricato... 2
Copyright 2005 The Companies srl Caso 13 Stima della tabella millesimale di proprietà in un condominio di 4 piani con appartamenti e negozi nella periferia di Torino 1. Descrizione del fabbricato... 2
SESSIONE ORDINARIA 2007 CORSO DI ORDINAMENTO SCUOLE ITALIANE ALL ESTERO - AMERICHE
 SESSIONE ORDINARIA 007 CORSO DI ORDINAMENTO SCUOLE ITALIANE ALL ESTERO - AMERICHE PROBLEMA Si consideri la funzione f definita da f ( x) x, il cui grafico è la parabola.. Si trovi il luogo geometrico dei
SESSIONE ORDINARIA 007 CORSO DI ORDINAMENTO SCUOLE ITALIANE ALL ESTERO - AMERICHE PROBLEMA Si consideri la funzione f definita da f ( x) x, il cui grafico è la parabola.. Si trovi il luogo geometrico dei
Utilizzo collegamento remoto
 Utilizzo collegamento remoto Introduzione Il collegamento VPN (virtual private network) consente a PC collegati ad internet ma fisicamente fuori dalla rete interna regionale, di accedere, con le credenziali
Utilizzo collegamento remoto Introduzione Il collegamento VPN (virtual private network) consente a PC collegati ad internet ma fisicamente fuori dalla rete interna regionale, di accedere, con le credenziali
Gestione risorse (Windows)
 Gestione risorse (Windows) Organizzazione dei file Il sistema di memorizzazione è organizzato ad albero secondo una struttura gerarchica DISCO (drive) FILES CARTELLE (directory) FILES SOTTOCARTELLE FILES
Gestione risorse (Windows) Organizzazione dei file Il sistema di memorizzazione è organizzato ad albero secondo una struttura gerarchica DISCO (drive) FILES CARTELLE (directory) FILES SOTTOCARTELLE FILES
Grafici e Pagina web
 Grafici e Pagina web Grafici Un grafico utilizza i valori contenuti in un foglio di lavoro per creare una rappresentazione grafica delle relazioni esistenti tra loro. Quando si crea un grafico ogni riga
Grafici e Pagina web Grafici Un grafico utilizza i valori contenuti in un foglio di lavoro per creare una rappresentazione grafica delle relazioni esistenti tra loro. Quando si crea un grafico ogni riga
Modellazione Poligonale Avanzata
 Informatica Grafica I Modellazione Poligonale Avanzata Il (FFD) inserisce un oggetto in una gabbia (a forma di parallelepipedo o di cilindro). Spostando i vertici della gabbia si deforma il solido in esso
Informatica Grafica I Modellazione Poligonale Avanzata Il (FFD) inserisce un oggetto in una gabbia (a forma di parallelepipedo o di cilindro). Spostando i vertici della gabbia si deforma il solido in esso
Problemi di scelta ESEMPI
 ESEMPI Risolvere i seguenti problemi 1. Una ditta deve effettuare delle spedizioni di un certo tipo di merce. Ha la possibilità di scegliere una o l altra delle due tariffe seguenti: a) 2.500 lire al quintale
ESEMPI Risolvere i seguenti problemi 1. Una ditta deve effettuare delle spedizioni di un certo tipo di merce. Ha la possibilità di scegliere una o l altra delle due tariffe seguenti: a) 2.500 lire al quintale
La parallela tracciata dal punto medio di un lato di un triangolo a uno degli altri due lati incontra il terzo lato nel suo punto medio.
 TEOREMA DI TALETE Piccolo Teorema di Talete Dato un fascio di rette parallele tagliate da due trasversali, a segmenti congruenti su una trasversale corrispondono segmenti congruenti sull altra trasversale.
TEOREMA DI TALETE Piccolo Teorema di Talete Dato un fascio di rette parallele tagliate da due trasversali, a segmenti congruenti su una trasversale corrispondono segmenti congruenti sull altra trasversale.
Le Coordinate Astronomiche
 Le Stelle vanno a scuola Le Coordinate Astronomiche Valentina Alberti Novembre 2003 1 2 INDICE Indice 1 Coordinate astronomiche 3 1.1 Sistema dell orizzonte o sistema altazimutale.......... 3 1.2 Sistema
Le Stelle vanno a scuola Le Coordinate Astronomiche Valentina Alberti Novembre 2003 1 2 INDICE Indice 1 Coordinate astronomiche 3 1.1 Sistema dell orizzonte o sistema altazimutale.......... 3 1.2 Sistema
La disposizione estetica della lettera commerciale
 La disposizione estetica della lettera commerciale Gli elementi costitutivi della lettera commerciale vengono disposti sul foglio secondo stili diversi: ogni a- zienda, infatti, caratterizza la sua immagine
La disposizione estetica della lettera commerciale Gli elementi costitutivi della lettera commerciale vengono disposti sul foglio secondo stili diversi: ogni a- zienda, infatti, caratterizza la sua immagine
nome: classe: data: delle quattro figure sottostanti non risulta in ogni caso congruente a quella sopra?
 Verifica IVPROVA_MAT_Sim_01 nome: classe: data: 1. Osserva la figura. Immaginiamo di spostarla tramite movimenti rigidi: quale delle quattro figure sottostanti non risulta in ogni caso congruente a quella
Verifica IVPROVA_MAT_Sim_01 nome: classe: data: 1. Osserva la figura. Immaginiamo di spostarla tramite movimenti rigidi: quale delle quattro figure sottostanti non risulta in ogni caso congruente a quella
LA PREDISPOSIZIONE DEL BILANCIO IN FORMATO XBRL
 LA PREDISPOSIZIONE DEL BILANCIO IN FORMATO XBRL PREMESSA Dal 2015, le società di capitali devono presentare l'intero bilancio di esercizio (comprensivo di nota integrativa) in formato XBRL, adottando la
LA PREDISPOSIZIONE DEL BILANCIO IN FORMATO XBRL PREMESSA Dal 2015, le società di capitali devono presentare l'intero bilancio di esercizio (comprensivo di nota integrativa) in formato XBRL, adottando la
Modulo 2 Data Base - Modello Relazionale
 Modulo 2 Data Base - Modello Relazionale Università degli Studi di Salerno Corso di Laurea in Scienze della comunicazione Informatica generale Docente: Angela Peduto A.A. 2004/2005 Modello Relazionale
Modulo 2 Data Base - Modello Relazionale Università degli Studi di Salerno Corso di Laurea in Scienze della comunicazione Informatica generale Docente: Angela Peduto A.A. 2004/2005 Modello Relazionale
GEOMETRIA ANALITICA. (*) ax+by+c=0 con a,b,c numeri reali che è detta equazione generale della retta.
 EQUAZIONE DELLA RETTA Teoria in sintesi GEOMETRIA ANALITICA Dati due punti A e B nel piano, essi individuano (univocamente) una retta. La retta è rappresentata da un equazione di primo grado in due variabili:
EQUAZIONE DELLA RETTA Teoria in sintesi GEOMETRIA ANALITICA Dati due punti A e B nel piano, essi individuano (univocamente) una retta. La retta è rappresentata da un equazione di primo grado in due variabili:
1B GEOMETRIA. Gli elementi fondamentali della geometria. Esercizi supplementari di verifica
 Gli elementi fondamentali della geometria Esercizi supplementari di verifica Esercizio 1 a) V F Si dice linea retta una qualsiasi linea che non ha né un inizio né una fine. b) V F Il punto è una figura
Gli elementi fondamentali della geometria Esercizi supplementari di verifica Esercizio 1 a) V F Si dice linea retta una qualsiasi linea che non ha né un inizio né una fine. b) V F Il punto è una figura
ESAME DI STATO. SIMULAZIONE PROVA NAZIONALE Scuola Secondaria di I grado Classe Terza. Prova 3. Anno Scolastico 20. - 20. Classe:... Data:...
 Prova Nazionale di Matematica: Simulazioni - a cura di M. Zarattini Prova ESAME DI STATO Anno Scolastico 0. - 0. SIMULAZIONE PROVA NAZIONALE Scuola Secondaria di I grado Classe Terza Classe:... Data:...
Prova Nazionale di Matematica: Simulazioni - a cura di M. Zarattini Prova ESAME DI STATO Anno Scolastico 0. - 0. SIMULAZIONE PROVA NAZIONALE Scuola Secondaria di I grado Classe Terza Classe:... Data:...
COLLEGIO DEI GEOMETRI E DEI GEOMETRI LAUREATI DELLA PROVINCIA DI NUORO MANUALE UTILIZZO GPS
 COLLEGIO DEI GEOMETRI E DEI GEOMETRI LAUREATI DELLA PROVINCIA DI NUORO MANUALE UTILIZZO GPS ACCENSIONE DEL PALMARE X7 Tenere premuto il tasto I/0, in basso a destra sulla tastiera, ed attendere la comparsa
COLLEGIO DEI GEOMETRI E DEI GEOMETRI LAUREATI DELLA PROVINCIA DI NUORO MANUALE UTILIZZO GPS ACCENSIONE DEL PALMARE X7 Tenere premuto il tasto I/0, in basso a destra sulla tastiera, ed attendere la comparsa
Esercizio Excel Avanzato
 Esercizio Excel Avanzato Bilancio familiare Richianare Excel e predisporre il foglio 1 come in figura: Step operativi Scrittura dei codici delle tipologie di spesa. 1. Posizionarsi sulla cella B3 e scrivere:
Esercizio Excel Avanzato Bilancio familiare Richianare Excel e predisporre il foglio 1 come in figura: Step operativi Scrittura dei codici delle tipologie di spesa. 1. Posizionarsi sulla cella B3 e scrivere:
Quarta Lezione. Il prospettografo. Il vetro è dotato di una griglia che permette al pittore di riportare il punto traguardato su un foglio di carta.
 Quarta Lezione I prospettografo La ezione inizia facendo e prime esperienze pratiche co prospettografo. I prospettografo è uno strumento di uso rinascimentae che aiuta a studiare a geometria dea proiezione
Quarta Lezione I prospettografo La ezione inizia facendo e prime esperienze pratiche co prospettografo. I prospettografo è uno strumento di uso rinascimentae che aiuta a studiare a geometria dea proiezione
SOFTWARE DI NOTAZIONE MUSICALE
 Tux Guitar SOFTWARE DI NOTAZIONE MUSICALE Tux Guitar è un software open source: questo significa che gli sviluppatori interessati possono modificare il programma, estendendone le funzioni. Come dice il
Tux Guitar SOFTWARE DI NOTAZIONE MUSICALE Tux Guitar è un software open source: questo significa che gli sviluppatori interessati possono modificare il programma, estendendone le funzioni. Come dice il
(1) (2) (3) (4) 11 nessuno/a 9 10. (1) (2) (3) (4) X è il minore tra A e B nessuno/a X è sempre uguale ad A X è il maggiore tra A e B
 Compito: Domanda 1 Per l'algoritmo fornito di seguito, qual è il valore assunto dalla variabile contatore quando l'algoritmo termina: Passo 1 Poni il valore di contatore a 1 Passo 2 Ripeti i passi da 3
Compito: Domanda 1 Per l'algoritmo fornito di seguito, qual è il valore assunto dalla variabile contatore quando l'algoritmo termina: Passo 1 Poni il valore di contatore a 1 Passo 2 Ripeti i passi da 3
ELEMENTI DI EUCLIDE, LIBRO VI: Le figure simili e le proporzioni in geometria
 Richiami dal libro VI di Euclide: ELEMENTI DI EUCLIDE, LIBRO VI: Le figure simili e le proporzioni in geometria Definizione I del libro VI: due figure poligonali si dicono simili se hanno angoli uguali
Richiami dal libro VI di Euclide: ELEMENTI DI EUCLIDE, LIBRO VI: Le figure simili e le proporzioni in geometria Definizione I del libro VI: due figure poligonali si dicono simili se hanno angoli uguali
Istruzioni per la tavola d esame n. 1
 Istruzioni per la tavola d esame n. 1 Traduzione in una rappresentazione codificata (proiezioni ortogonali) dell immagine fotografica del plastico oggetto della prima esercitazione di laboratorio di progettazione.
Istruzioni per la tavola d esame n. 1 Traduzione in una rappresentazione codificata (proiezioni ortogonali) dell immagine fotografica del plastico oggetto della prima esercitazione di laboratorio di progettazione.
PROBLEMI DI SCELTA dipendenti da due variabili d azione
 prof. Guida PROBLEMI DI SCELTA dipendenti da due variabili d azione in un problema di programmazione lineare, si ricorda che la funzione obiettivo z=f(x,y)=ax+by+c assume il suo valore massimo (o minimo)
prof. Guida PROBLEMI DI SCELTA dipendenti da due variabili d azione in un problema di programmazione lineare, si ricorda che la funzione obiettivo z=f(x,y)=ax+by+c assume il suo valore massimo (o minimo)
EXCEL. Alfabetizzazione Informatica Prof. GIUSEPPE PATTI
 EXCEL Alfabetizzazione Informatica Prof. GIUSEPPE PATTI Operazioni base Excel è un programma che trasforma il vostro computer in un foglio a quadretti, così come Word lo trasformava in un foglio a righe.
EXCEL Alfabetizzazione Informatica Prof. GIUSEPPE PATTI Operazioni base Excel è un programma che trasforma il vostro computer in un foglio a quadretti, così come Word lo trasformava in un foglio a righe.
ESERCIZI PER LE VACANZE
 ESERCIZI PER LE VACANZE Tutti gli esercizi devono essere svolti sul quaderno. 1. Trova il quoziente di ciascuna frazione senza usare la calcolatrice (ricorda che puoi ridurre le frazioni ai minimi termini
ESERCIZI PER LE VACANZE Tutti gli esercizi devono essere svolti sul quaderno. 1. Trova il quoziente di ciascuna frazione senza usare la calcolatrice (ricorda che puoi ridurre le frazioni ai minimi termini
OBIETTIVI SPECIFICI DI APPRENDIMENTO a. Conoscere l ambiente laboratorio informatico
 classe prima 1. Esplorare l ambiente scuola per individuare la funzione di materiali e oggetti 2. Acquisire procedure per una prima forma di interazione tra l uomo e la macchina APPRENMENTO a. Conoscere
classe prima 1. Esplorare l ambiente scuola per individuare la funzione di materiali e oggetti 2. Acquisire procedure per una prima forma di interazione tra l uomo e la macchina APPRENMENTO a. Conoscere
La codifica. dell informazione
 La codifica dell informazione (continua) Codifica dei numeri Il codice ASCII consente di codificare le cifre decimali da 0 a 9 fornendo in questo modo un metodo per la rappresentazione dei numeri Il numero
La codifica dell informazione (continua) Codifica dei numeri Il codice ASCII consente di codificare le cifre decimali da 0 a 9 fornendo in questo modo un metodo per la rappresentazione dei numeri Il numero
ESERCIZI PER IL RECUPERO DEL DEBITO di FISICA CLASSI PRIME Prof.ssa CAMOZZI FEDERICA
 ESERCIZI PER IL RECUPERO DEL DEBITO di FISICA CLASSI PRIME Prof.ssa CAMOZZI FEDERICA NOTAZIONE ESPONENZIALE 1. Scrivi i seguenti numeri usando la notazione scientifica esponenziale 147 25,42 0,0001 0,00326
ESERCIZI PER IL RECUPERO DEL DEBITO di FISICA CLASSI PRIME Prof.ssa CAMOZZI FEDERICA NOTAZIONE ESPONENZIALE 1. Scrivi i seguenti numeri usando la notazione scientifica esponenziale 147 25,42 0,0001 0,00326
Manuale rapido Zimbra Posta elettronica e agenda
 ZIMBRA Pagina 1 Manuale rapido Zimbra Posta elettronica e agenda Zimbra è una suite di collaborazione, che permette con un solo strumento di poter accedere al proprio account di posta elettronica regionale,
ZIMBRA Pagina 1 Manuale rapido Zimbra Posta elettronica e agenda Zimbra è una suite di collaborazione, che permette con un solo strumento di poter accedere al proprio account di posta elettronica regionale,
testo Saveris Web Access Software Istruzioni per l'uso
 testo Saveris Web Access Software Istruzioni per l'uso 2 1 Indice 1 Indice 1 Indice... 3 2 Descrizione delle prestazioni... 4 2.1. Utilizzo... 4 2.2. Requisiti di sistema... 4 3 Installazione... 5 3.1.
testo Saveris Web Access Software Istruzioni per l'uso 2 1 Indice 1 Indice 1 Indice... 3 2 Descrizione delle prestazioni... 4 2.1. Utilizzo... 4 2.2. Requisiti di sistema... 4 3 Installazione... 5 3.1.
ESERCIZI DEL CORSO DI INFORMATICA
 ESERCIZI DEL CORSO DI INFORMTIC Questa breve raccolta di esercizi vuole mettere in luce alcuni aspetti della prima parte del corso e fornire qualche spunto di riflessione. Il contenuto del materiale seguente
ESERCIZI DEL CORSO DI INFORMTIC Questa breve raccolta di esercizi vuole mettere in luce alcuni aspetti della prima parte del corso e fornire qualche spunto di riflessione. Il contenuto del materiale seguente
CHE COS È UN FOGLIO ELETTRONICO CHE COS È UN FOGLIO ELETTRONICO CHE COS È UN FOGLIO ELETTRONICO. Modulo: Elementi di Informatica
 Facoltà di Medicina Veterinaria Corso di laurea in Tutela e benessere animale CHE COS È UN FOGLIO ELETTRONICO Una tabella che contiene parole e numeri che possono essere elaborati applicando formule matematiche
Facoltà di Medicina Veterinaria Corso di laurea in Tutela e benessere animale CHE COS È UN FOGLIO ELETTRONICO Una tabella che contiene parole e numeri che possono essere elaborati applicando formule matematiche
Note_Batch_Application 04/02/2011
 Note Utente Batch Application Cielonext La Batch Application consente di eseguire lavori sottomessi consentendo agli utenti di procedere con altre operazioni senza dover attendere la conclusione dei suddetti
Note Utente Batch Application Cielonext La Batch Application consente di eseguire lavori sottomessi consentendo agli utenti di procedere con altre operazioni senza dover attendere la conclusione dei suddetti
GUIDA RAPIDA. Versione 2.0; 26.01.2012. Indice
 Indice GUIDA Versione 2.0; 26.01.2012 RAPIDA CD LAB AG, Irisweg 12, CH-3280 Murten, Tel. +41 (0)26 672 37 37, Fax +41 (0)26 672 37 38, www.wincan.com Indice 1 Introduzione 3 2 Avviare WinCan8 4 3 Creare
Indice GUIDA Versione 2.0; 26.01.2012 RAPIDA CD LAB AG, Irisweg 12, CH-3280 Murten, Tel. +41 (0)26 672 37 37, Fax +41 (0)26 672 37 38, www.wincan.com Indice 1 Introduzione 3 2 Avviare WinCan8 4 3 Creare
MINISTERO DELL'ISTRUZIONE, DELL'UNIVERSITÀ, DELLA RICERCA SCUOLE ITALIANE ALL ESTERO
 Sessione Ordinaria in America 4 MINISTERO DELL'ISTRUZIONE, DELL'UNIVERSITÀ, DELLA RICERCA SCUOLE ITALIANE ALL ESTERO (Americhe) ESAMI DI STATO DI LICEO SCIENTIFICO Sessione Ordinaria 4 SECONDA PROVA SCRITTA
Sessione Ordinaria in America 4 MINISTERO DELL'ISTRUZIONE, DELL'UNIVERSITÀ, DELLA RICERCA SCUOLE ITALIANE ALL ESTERO (Americhe) ESAMI DI STATO DI LICEO SCIENTIFICO Sessione Ordinaria 4 SECONDA PROVA SCRITTA
VBA è un linguaggio di scripting derivato da Visual Basic, da cui prende il nome. Come ogni linguaggio ha le sue regole.
 Excel VBA VBA Visual Basic for Application VBA è un linguaggio di scripting derivato da Visual Basic, da cui prende il nome. Come ogni linguaggio ha le sue regole. 2 Prima di iniziare. Che cos è una variabile?
Excel VBA VBA Visual Basic for Application VBA è un linguaggio di scripting derivato da Visual Basic, da cui prende il nome. Come ogni linguaggio ha le sue regole. 2 Prima di iniziare. Che cos è una variabile?
LA SUA PROIEZIONE ORTOGONALE E SEMPRE UGUALE AD ESSA
 PROIEZIONI ORTOGONALI DI FIGURE PIANE Per figura piana si intende una parte di piano delimitata da una linea chiusa. Poiché questo contorno è riconducibile ad un insieme di punti, si può ottenere la proiezione
PROIEZIONI ORTOGONALI DI FIGURE PIANE Per figura piana si intende una parte di piano delimitata da una linea chiusa. Poiché questo contorno è riconducibile ad un insieme di punti, si può ottenere la proiezione
POLITECNICO DI BARI C.d.L. ingegneria CIVILE - AMBIENTALE CORSO DI DISEGNO
 POLITECNICO DI BARI C.d.L. ingegneria CIVILE - AMBIENTALE CORSO DI DISEGNO Geometria descrittiva Le volte Le diapositive costituiscono unicamente una base per lo sviluppo della lezione e, come tali, non
POLITECNICO DI BARI C.d.L. ingegneria CIVILE - AMBIENTALE CORSO DI DISEGNO Geometria descrittiva Le volte Le diapositive costituiscono unicamente una base per lo sviluppo della lezione e, come tali, non
PG5 Starter Training Applicazione File System Daniel Ernst EN02 2012-02-26 Stefano Peracchi IT01 2013-05-20
 PG5 Starter Training Applicazione File System Daniel Ernst EN02 2012-02-26 Stefano Peracchi IT01 2013-05-20 Introduzione Materiale richiesto Notebook o computer Controllore PCD1 E Cavo USB Scheda «Training»
PG5 Starter Training Applicazione File System Daniel Ernst EN02 2012-02-26 Stefano Peracchi IT01 2013-05-20 Introduzione Materiale richiesto Notebook o computer Controllore PCD1 E Cavo USB Scheda «Training»
GeoGebra vers.5 - vista Grafici 3D
 GeoGebra vers.5 - vista Grafici 3D Marzo 2015 (manuale on-line, con aggiunte a cura di L. Tomasi) Questo articolo si riferisce a un componente della interfaccia utente di GeoGebra. Viste Menu Vista Algebra
GeoGebra vers.5 - vista Grafici 3D Marzo 2015 (manuale on-line, con aggiunte a cura di L. Tomasi) Questo articolo si riferisce a un componente della interfaccia utente di GeoGebra. Viste Menu Vista Algebra
