Sistemi lineari. 1. Generalità. a 1 x 1 + a 2 x 2 + a 3 x a n x n = k (matrice completa)
|
|
|
- Annibale Quaranta
- 7 anni fa
- Visualizzazioni
Transcript
1 Sistemi lineari. Generalità La teoria dei sistemi di equaioni lineari costituisce uno dei capitoli molto importanti della matematica pura e applicata. Infatti molte questioni teoriche o tecniche si traducono agevolmente in sistemi di equaioni lineari che si risolvono con la regola di Cramer o col metodo di Gauss. Le difficoltà di risoluione dei sistemi aumentano all aumentare del numero delle equaioni e delle incognite. I sistemi di due equaioni con due incognite si risolvono facilmente applicando uno qualsiasi dei quattro metodi, di sostituione, di confronto, di riduione o di Cramer, che si studiano sin dai primi anni delle scuole medie superiori. La risoluione di un sistema di tre equaioni a tre incognite comincia invece a essere piuttosto laboriosa. Lo studio delle matrici e dei determinanti agevola notevolmente la ricerca delle soluioni di un sistema con più di tre equaioni e tre incognite. Poiché un sistema può essere tale da non ammettere soluioni, sarebbe bene sapere a priori se esso sia di questo tipo. Così, se le soluioni esistono, si può procedere con i calcoli per pervenire al risultato; se non esistono, invece, si rinuncia allo svolgimento delle operaioni. Il problema circa l esistena o meno delle soluioni di un sistema di equaioni lineari viene risolto molto bene dal teorema di ouché Capelli. Prima di enunciare tale teorema si rendono necessarie alcune precisaioni. Un equaione lineare o di primo grado è una relaione del tipo: a a a a n n dove,,,, n si dicono incognite e a, a, a,, a n si dicono coefficienti delle incognite. Mentre le i sono delle variabili, le a i e sono delle costanti, ossia dei numeri reali. Il numero è detto termine noto dell equaione. Se il termine noto è nullo, l equaione si dice omogenea, altrimenti non omogenea. Un insieme di m equaioni lineari a n incognite costituisce un sistema di equaioni lineari. Generalmente un sistema di tale tipo viene rappresentato nel modo seguente: a a... a n a a... ann... am am... amnn n m dove a ij è il coefficiente dell incognita j dell iesima equaione. Se m, il sistema si dice omogeneo; se, invece, almeno uno dei termini i è diverso da ero, il sistema si dice non omogeneo. Si chiama matrice incompleta di un sistema la matrice formata con i coefficienti delle incognite. Si chiama matrice completa di un sistema la matrice formata con i coefficienti delle incognite e con i termini noti. Se si indica con A la prima e con B la seconda, in questo caso, si ha: a a... a a a... a n a a... an A... am am... amn n a a... an B... am am... amn m Sistemi lineari
2 Si chiama soluione di un sistema di m equaioni lineari a n incognite ogni n pla ordinata (m, m,, m n ) di numeri che trasforma ogni equaione del sistema in una identità quando si pone m, m,, n m n. Il sistema si dice compatibile se ammette almeno una soluione, incompatibile nel caso contrario. ESEMPI. Il sistema: soluione:,,. In seguito si vedrà che un tale sistema ammette infinite soluioni.. è compatibile perché ammette la Il sistema: è manifestamente incompatibile. Non esiste, cioè, nessuna terna di numeri che trasformi in identità entrambe le equaioni.. Teorema di ouché Capelli Condiione necessaria e sufficiente affinché un sistema di equaioni lineari ammetta soluioni è che le matrici completa e incompleta abbiano lo stesso rango (o caratteristica). Si omette la dimostraione. Si consideri il sistema del primo esempio del paragrafo precedente. Le due matrici incompleta e completa sono rispettivamente: A e B Si calcoli prima il rango della matrice incompleta. Il rango della matrice A al massimo può essere perché è proprio l ordine massimo dei minori non nulli che da tale matrice possono essere estratti. Si consideri il minore del secondo ordine formato con le prime due colonne. Si ha: Essendo diverso da ero il minore di ordine estratto dalla matrice A, si ha: rang (A) Si calcoli ora il rango della matrice completa B del sistema. Si osservi che il rango della matrice completa non può essere minore di quello della matrice incompleta perché dalla prima può essere estratto lo stesso minore della seconda. Quindi il rango della matrice completa è maggiore o uguale a quello della matrice incompleta del medesimo sistema.in questo caso il rango della matrice B non può essere maggiore di perché da essa non possono essere estratti minori di ordine maggiore di. Infatti essa ha due righe soltanto. Si ha, quindi: rang (B) Essendo: rang (A) rang (B) Sistemi lineari
3 per il teorema di ouché Capelli, il sistema è compatibile. Si applichi ora il teorema di ouché Capelli al secondo sistema del paragrafo precedente. Si ha: A B Poiché la matrice A è formata da due righe uguali, tutti i minori di ordine che da essa possono essere estratti sono nulli. Non essendo A una matrice nulla, i minori del primo ordine non sono tutti nulli. Si ha, perciò: rang (A ) Poiché dalla matrice B si può estrarre un minore del secondo ordine diverso da ero, il suo rango è. Infatti, si ha: Mentre tutti i minori del secondo ordine estratti da A sono nulli, fra quelli estratti da B ve ne è almeno uno che è diverso da ero. Si ha, perciò: rang (B ) Essendo: rang (A ) rang (B ) per il teorema di ouché Capelli, il sistema è incompatibile.. Determinaione delle soluioni di un sistema lineare In questo paragrafo vengono presentati alcuni esempi esplicativi mediante i quali si vuole mettere in risalto l importana del teorema di ouché Capelli per la risoluione dei sistemi lineari. ESEMPI. isolvere il sistema: 8 Il numero delle incognite supera quello delle equaioni. Il sistema può essere indeterminato o impossibile. Cioè: o esistono infinite terne di numeri che verificano il sistema oppure nessuna. Per stabilire a priori quale delle due condiioni sussista, si considerino le due matrici del sistema: A 8 B E facile constatare che il rango della matrice incompleta è. Infatti, preso il minore formato con le prime due colonne, si ha: 9 Sistemi lineari
4 Poiché il rango della matrice completa non può essere maggiore di, si ha: rang (A) rang (B) Il sistema allora è compatibile. Poiché, come si è detto prima, il numero delle incognite supera il rango delle due matrici, il sistema è indeterminato. La differena fra il numero delle incognite e il rango esprime il grado di indeterminaione del sistema. In questo caso il grado di indeterminaione è perché, essendo il numero delle incognite. Si dice che il sistema ammette (infinito alla ) soluioni. Per determinarle si attribuisce a una delle incognite, ad esempio, un valore arbitrario. Posto Z m, il sistema diviene: 8 m m Si trovano così i valori delle incognite e in funione di m. Si risolve ora il sistema con la regola di Cramer: 8 m m 8 m m 8 m 9 8 m m m m m 9 La soluione del sistema è: 8 m m m dove m può assumere un valore arbitrario. Ad esempio: per m si ha la soluione: 8 per m si ha la soluione: per m si ha la soluione: 9 8 per m si ha la soluione: 8 per m si ha la soluione: E possibile ora dare un interpretaione geometrica dei sistemi di due equaioni a tre incognite. Come è noto, un equaione di primo grado a due incognite rappresenta una retta di un piano riferito a un sistema di assi cartesiani ortogonali. Un sistema di due equaioni a due incognite rappresenta l interseione di due rette, ossia un punto del piano.ad esempio, il sistema: a b c a' b' c' Sistemi lineari
5 rappresenta il punto comune alle rette corrispondenti alle due equaioni. Se il determinante della matrice incompleta o dei coefficienti è diverso da ero, il sistema è compatibile e la coppia (, ) di numeri, soluione del sistema, rappresenta le coordinate del punto di interseione delle due rette. La condiione di compatibilità è espressa dalla relaione: a b ab' a' b a' b' Se, invece, tale determinante è nullo, il rango della matrice incompleta è. In tal caso bisogna trovare il rango della matrice completa. Se è uguale a, il sistema è incompatibile. Ciò significa che le due rette sono parallele. Se il rango delle due matrici è, il sistema è indeterminato. Ciò significa che le due rette sono coincidenti. Nello spaio, un equaione lineare a tre incognite rappresenta un piano, mentre un sistema di due equaioni a tre incognite rappresenta l interseione di due piani. Se i due piani si intersecano, tale interseione è una retta e il sistema è compatibile. Le infinite terne che verificano il sistema sono le coordinaste dei punti della retta. E opportuno precisare che un punto nello spaio è individuato da una terna di numeri. Se i due piani sono paralleli, non si intersecano e perciò il sistema è incompatibile. Si consideri allora il sistema: a b c d a' bì c' d' a) Se il rango delle matrici è, il sistema è compatibile e i due piani si intersecano lungo una retta; b) Se il rango delle due matrici è, il sistema è compatibile e i due piani sono coincidenti; c) Se il rango della matrice incompleta è e quello della matrice completa è, il sistema è incompatibile e i due piani risultano paralleli.. 9 Si considerino le matrici del sistema: A B 9 Poiché gli elementi della seconda riga di A sono proporionali ai corrispondenti elementi della prima riga, tutti i minori del secondo ordine sono nulli. Si ha, perciò: rang (A) Il rango della matrice B, invece, è. Infatti, si ha: 8 Quindi: rang (B) 9 Non essendo uguali i due ranghi, il sistema è incompatibile. I due piani sono paralleli.. 8 Il numero delle equaioni supera quello delle incognite. Sistemi lineari
6 Si considerino le matrici del sistema: a eq. O A 8 B Il rango della matrice incompleta è. Infatti, preso il minore formato con le prime due righe, si ha: 8 9 Si calcola ora il determinante della matrice completa: a eq. Fig. 8 a eq. Quindi: rang (A) 8 ( ) (8 ) 8( 8). Poiché è nullo l unico minore del tero ordine che può essere estratto dalla matrice completa, si ha: rang (B) Essendo uguali i due ranghi, il sistema è compatibile. Considerando il sistema formato con le prime due equaioni, cioè quelle corrispondenti al minore del secondo ordine diverso da ero, si ha: 8 La soluione di questo sistema è anche la soluione della tera equaione, che perciò può essere trascurata. Ciò significa che la retta rappresentata dalla tera equaione passa per il punto di interseione delle due rette rappresentate dalle prime due equaioni. Le tre rette appartengono dunque a un medesimo fascio di rette passanti per uno stesso punto. Questa situaione si presenta allorché una delle tre equaioni si ottiene sommando membro a membro le altre due dopo averle moltiplicate rispettivamente per due numeri. In questo caso la tera equaione è uguale alla somma della prima moltiplicata per e della seconda. isolvendo il sistema, si trova:, Si provi ora se anche la tera equaione viene verificata. Si ha: 8 Si può allora dire che un sistema di n equaioni lineari a due incognite è compatibile se i ranghi delle due matrici sono uguali a oppure a. Nel primo caso, il sistema ammette un unica soluione che si trova risolvendo il sistema di due delle equaioni date. Le rette appartengono al medesimo fascio il cui centro è un punto del piano. Nel secondo caso le rette sono tutte coincidenti e il sistema è indeterminato, ossia tutte le coppie di numeri che verificano una delle equaioni date verificano anche tutte le altre. Sistemi lineari
7 Se il rango della matrice incompleta è e quello della matrice completa è, il sistema è incompatibile. Ciò significa che le rette non appartengono a un medesimo fascio.. a eq. a eq. a eq. O Si considerino le matrici del sistema. A Fig. B Si calcolano i minori del secondo ordine che possono essere estratti dalla matrice A. ; ; Poiché almeno uno dei tre minori del secondo ordine è diverso da ero, si ha: rang (A).. 8 Si calcola il determinante della matrice B. Si ha: Si costruiscono le due matrici del sistema: A Quindi: rang (B). Essendo rang (A) rang (B), il sistema è incompatibile. Le tre rette non appartengono al medesimo fascio. Poiché soltanto due dei minori del secondo ordine sono diversi da ero, non tutte le rette si incontrano a due a due. Infatti, la prima e la tera sono parallele. 8 B Si trovano i minori del secondo ordine estratti dalla matrice A. ; ; Tutti i minori del secondo ordine sono diversi da ero. isulta: rang (A) Sistemi lineari
8 a eq. O a eq. a eq. Fig. Si calcola ora il determinante della matrice B. 8 isulta, così: rang (B). Essendo disuguali i ranghi delle due matrici, il sistema è incompatibile. Poiché inoltre i tre minori del secondo ordine della matrice incompleta sono diversi da ero, le tre rette si intersecano a due a due. Individuano cioè un triangolo.. 8 Si costruiscono le due matrici del sistema. Si ha: A Si calcola il determinante della matrice A. isulta: rang (A). B 8 ( ) ( ). Poiché il rango della matrice completa non può essere minore di quello della matrice incoompleta, si ha: rang (B). Il sistema è compatibile. Essendo inoltre nulla la differena fra il numero delle incognite () e il rango (), esiste una terna soltanto che verifica simultanreamente ler tre equaioni del sistema. Cioè, il grado di indeterminaione è ero. Il sistema quindi è determinato. I tre piani passano per uno stesso punto dello spaio. La soluione del sistema rappresenta le coordinate di tale punto. Si risolve il sistema con la formula di Cramer. Il determinante della matrice dei coefficienti delle incognite è già stato calcolato. Si ha, cioè: Δ A Si calcolano ora i determinanti delle matrici che si ottengono sostituendo una delle colonne della matrice incompleta con la colonna dei termini noti. Si ha: Δ ; Δ 9 ; Δ Sistemi lineari
9 Sistemi lineari 9 isulta: Δ Δ 9 Δ Δ Δ Δ. Si costruiscono le due matrici del sistema. Si ha: A B Si può notare subito che le tere righe di entrambe le matrici sono uguali al doppio della prima sommata alla seconda. Tali righe sono dunque combinaioni lineari delle prime due. Ciò significa che tutti i minori del tero ordine sono nulli. Invece i minori del secondo ordine non sono tutti nulli. Infatti, considerando il minore formato con le prime due righe e le prime due colonne, si ha: isulta, così: rang (A) rang (B) Il sistema è compatibile. Il grado di indeterminaione è perché la differena tra il numero delle incognite e il rango è proprio ( ). Si considerano le prime due equaioni ponendo. Si ha: Si trova: 8 Attribuendo a tutti i valori reali, si ottengono le infinite terne ordinate di numeri che verificano il sistema. Poiché il grado di indeterminaione del sistema è, esso ammette soluioni. I piani rappresentati dalle tre equaioni passano tutti per una stessa retta; i tre piani appartengono quindi allo stesso fascio. Le infinite soluioni del sistema rappresentano le coordinate di tutti i punti della retta interseione dei tre piani Si costruiscono le due matrici del sistema. Si ha: 9 A 9 B
10 Si nota subito che entrambe le matrici hanno la tera riga uguale alla somma delle prime due. Ciò significa che tutti i minori del tero ordine sono nulli. Si constata facilmente che risultano nulli anche tuti i minori del secondo ordine. Di conseguena le caratteristiche di entrambe le matrici sono uguali a. Si ha, cioè: rang (A) rang (B) Il sistema è compatibile. Essendo la differena tra il numero delle incognite e il rango, il sistema è indeterminato con grado di indetereminaione. Ciò significa che due equaioni si possono eliminare. Si considera allora solamente la prima equaione; ponendo e h, si ha: h Il risultato del sistema è: h h Attribuendo tutti i possibili valori reali a e h, si trovano leinfinite terne ordinate di numeri che verificano il sistema. Poiché le soluioni sono funioni di due parametri, il sistema ammette una doppia infinità di soluioni, ossia ammette soluioni. I tre piani sono coincidenti Le matrici del sistema sono: A, B 8 Nella prima matrice la quarta riga è uguale alla somma della prima e della tera moltiplicata per. Inoltre la tera riga è uguale alla somma della prima e della seconda moltiplicata per. Ciò significa che sono tutti nulli i minori del quarto e del tero ordine che possono essere estratti da tale matrice. Poiché il minore del secondo ordine:, si ha: rang(a). Nella seconda matrice tutti i minori del quarto ordine sono nulli perché la tera riga è combinaione lineare delle prime due. Infatti essa è uguale alla somma della prima riga e della seconda moltiplicata per. Con la regola di Cramer si sarebbe indotti a concludere che il sistema è indeterminato, essendo nulli tutti i determinanti del quarto ordine. Infatti, si avrebbe ero fratto ero. Ciò sarebbe vero se il sistema fosse compatibile, ossia se le matrici A e B avessero lo stesso rango. Si constata invece che il rango della matrice completa è. Infatti, si ha: 8 Ossia: rang(b). Il sistema è incompatibile, essendo diversi i ranghi dele due matrici. Applicando la regola di Cramer, invece, si sarebbe ottenuto: Sistemi lineari
11 Sistemi lineari e avremmo concluso che il sistema è indeterminato e quindi compatibile. Da ciò si può comprendere l importana del teorema di ouché Capelli.. Le matrici del sistema sono: A B Il rango della matrice completa è. Infatti preso il minore formato con la prima, la seconda e la quarta colonna, si ha: 8) ( Affinché il sistema sia compatibile, dev essere: Sviluppando, si ottiene: 8, 8. Si può concludere allora che: per 8 il sistema è incompatibile; per 8 il sistema è compatibile e ammette un unica soluione.. Determinare il parametro in modo che il sistema: sia compatibile. Dev essere: ; ; ( ) ( ) ( ) ; ; 8 ; ± ±
12 . Sistemi omogenei DEFINIZIONE In simboli, si ha: Sistemi lineari Un sistema lineare di n equaioni ad n incognite si dice omogeneo se sono nulli tutti i termini noti. a a... a n n a a... an n... an an... ann n Se il determinante della matrice dei coefficienti è diverso da ero, il sistema ammette soltanto la soluione banale: n Se il determinante della matrice dei coefficienti è nullo, il sistema ammette la soluione generale: j A ij (j,,, n) (dove i è un qualunque numero compreso fra e n; fattore di proporionalità; A ij complemento algebrico del termine a ij della matrice dei coefficienti). Quanto detto vale soltanto se non sono tutti nulli i complementi algebrici della riga considerata. Infatti, tenuto conto della regola di Laplace e della proprietà 9 dei determinanti, sussistono le seguenti identità: aai aai... a nain aai aai... an Ain... aiai ai Ai... ain Ain... anai anai... ann Ain Si dimostra facilmente che i sistemi lineari omogenei sono sempre compatibili. Considerando le matrici del sistema, si ha: a a... a n a a... a A... an an... a n nn a a... a n a a... an B... an an... ann Poiché l ultima colonna della matrice completa è formata tutta di eri, il rango di questa matrice è sempre uguale a quello della matrice dei coefficienti. Ecco provato che un sistema lineare omogeneo è sempre compatibile. Il sistema è determinato se il rango della matrice dei coefficienti è uguale al numero delle incognite. La soluione è quella banale formata tutta di eri. Il sistema è indeterminato se il rango della matrice dei coefficienti è minore del numero delle incognite. ESEMPI isolvere il sistema:. ()
13 Sistemi lineari Si calcola il determinante della matrice dei coefficienti. Si ha: Essendo diverso da ero il determinante della matrice dei coefficienti, il sistema ammette soltanto la soluione banale:,,.. Si calcola il determinante della matrice dei coefficienti. Si ha: Essendo nullo il determinante della matrice dei coefficienti, il sistema è indeterminato. Si calcolano i complementi algebrici dei termini della prima riga della matrice dei coefficienti. Si ha: A ) ( A A La terna:,, è una soluione del sistema. La soluione generale del sistema è:,, dove è un qualunque numero reale. La soluione generale di un sistema lineare omogeneo viene denominata anche soluione propria o autosoluione del sistema. Le soluioni espresse nella forma vettoriale:, esprimono il fatto che esse formino un sottospaio di di dimensione : è lo spaio generato dal vettore che ne rappresenta una base.
14 Sistemi lineari. t t t Si calcola il determinante della matrice dei coefficienti. Si ha: perché la quarta colonna è uguale alla somma delle prime due. Si calcolano ora i complementi algebrici della prima riga. Si ha: A 9 A 9 A A 9 Una soluione particolare del sistema è: 9, 9,, t 9. La soluione generale del sistema è: 9, 9,, t 9. In forma vettoriale, si può scrivere. t.. 8 Si trasforma la matrice dei coefficienti, in modo da leggerne il rango. 8 Il rango della matrice dei coefficienti del sistema è. Poiché le incognite sono, le soluioni formano un sottospaio di dimensione. Si risolve l equaione.
15 Sistemi lineari Posto: e h, si ha: h. La soluione del sistema è:, h, h. In forma vettoriale, si ha: h,, h.. Il rango della matrice dei coefficienti è. Infatti, si ha: Poiché il numero delle incognite del sistema è lo stesso di quello che denota il rango della matrice dei coefficienti, il sistema è determinato e ammette perciò soltanto la soluione banale:,. TEOEMA Sia AX B un sistema lineare. Se X è una sua soluione particolare e Z una soluione del sistema omogeneo associato AX O, la soluione del sistema dato può essere espressa nella forma X X Z. IPOTESI AX B, AZ O. TESI X X Z. Sommando membro a membro le due espressioni dell ipotesi, si ha: AX AZ B O. Da cui: A(X Z) B. C.V.D.. 9 Una soluione particolare del sistema è rappresentata dalla terna:,. Si consideri il sistema omogeneo associato : Si trasforma la matrice dei coefficienti, in modo da leggerne il rango.
16 Sistemi lineari Il rango della matrice dei coefficienti del sistema è. Poiché le incognite sono, le soluioni formano un sottospaio di dimensione. Posto, si risolve il sistema: Si trova:., La soluione del sistema omogeneo è: Ossia: h La soluione del sistema dato è: X (,, ) (,, ) h(,, ).
SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI
 SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI Appunti presi dalle lezioni del prof. Nedo Checcaglini Liceo Scientifico di Castiglion Fiorentino (Classe 4B) January 17, 005 1 SISTEMI LINEARI Se a ik, b i R,
SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI Appunti presi dalle lezioni del prof. Nedo Checcaglini Liceo Scientifico di Castiglion Fiorentino (Classe 4B) January 17, 005 1 SISTEMI LINEARI Se a ik, b i R,
1. Sistemi di equazioni lineari. 1.1 Considerazioni preliminari
 1. Sistemi di equazioni lineari 1.1 Considerazioni preliminari I sistemi lineari sono sistemi di equazioni di primo grado in più incognite. Molti problemi di matematica e fisica portano alla soluzione
1. Sistemi di equazioni lineari 1.1 Considerazioni preliminari I sistemi lineari sono sistemi di equazioni di primo grado in più incognite. Molti problemi di matematica e fisica portano alla soluzione
Testi di esercizi di preparazione alla I prova in itinere Gli esercizi in elenco sono in gran parte tratti da vecchie prove d esame
 Testi di esercii di preparaione alla I prova in itinere Gli esercii in elenco sono in gran parte tratti da veccie prove d esame Eserciio Al variare di k discutere e ove possibile risolvere il sistema lineare
Testi di esercii di preparaione alla I prova in itinere Gli esercii in elenco sono in gran parte tratti da veccie prove d esame Eserciio Al variare di k discutere e ove possibile risolvere il sistema lineare
Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE. Giovanni Villani
 Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE Giovanni Villani Matrici Definizione 1 Si definisce matrice di tipo m n una funzione che associa
Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE Giovanni Villani Matrici Definizione 1 Si definisce matrice di tipo m n una funzione che associa
UNIVERSITA DEGLI STUDI LA SAPIENZA DI ROMA POLO DI RIETI FACOLTA DI INGEGNERIA CORSO DI LAUREA IN INGEGNERIA DELL AMBIENTE E DEL TERRITORIO
 UNIVERSITA DEGLI STUDI LA SAPIENZA DI ROMA POLO DI RIETI FACOLTA DI INGEGNERIA CORSO DI LAUREA IN INGEGNERIA DELL AMBIENTE E DEL TERRITORIO Geometria III esonero pariale A.A. 6 Cognome Nome Matricola Codice
UNIVERSITA DEGLI STUDI LA SAPIENZA DI ROMA POLO DI RIETI FACOLTA DI INGEGNERIA CORSO DI LAUREA IN INGEGNERIA DELL AMBIENTE E DEL TERRITORIO Geometria III esonero pariale A.A. 6 Cognome Nome Matricola Codice
Equazioni lineari con due o più incognite
 Equazioni lineari con due o più incognite Siano date le uguaglianze: k 0; x + y = 6; 3a + b c = 8. La prima ha un termine incognito rappresentato dal simbolo letterale k; la seconda ha due termini incogniti
Equazioni lineari con due o più incognite Siano date le uguaglianze: k 0; x + y = 6; 3a + b c = 8. La prima ha un termine incognito rappresentato dal simbolo letterale k; la seconda ha due termini incogniti
MATEMATICA. a.a. 2014/ Sistemi di equazioni lineari
 MATEMATICA a.a. 2014/15 8. Sistemi di equazioni lineari SISTEMI LINEARI Si definisce sistema lineare un sistema di p equazioni di primo grado in q incognite. a11x1 + a12 x2 +... + a1 qxq = k1 a21x1 + a22x2
MATEMATICA a.a. 2014/15 8. Sistemi di equazioni lineari SISTEMI LINEARI Si definisce sistema lineare un sistema di p equazioni di primo grado in q incognite. a11x1 + a12 x2 +... + a1 qxq = k1 a21x1 + a22x2
Corso di Matematica e Statistica 3 Algebra delle matrici. Una tabella rettangolare: la matrice. Una tabella rettangolare: la matrice
 Pordenone Corso di Matematica e Statistica 3 Algebra delle UNIVERSITAS STUDIORUM UTINENSIS Giorgio T. Bagni Facoltà di Scienze della Formazione Dipartimento di Matematica e Informatica Università di Udine
Pordenone Corso di Matematica e Statistica 3 Algebra delle UNIVERSITAS STUDIORUM UTINENSIS Giorgio T. Bagni Facoltà di Scienze della Formazione Dipartimento di Matematica e Informatica Università di Udine
Geometria per fisica (L-P), a. a Esercizi svolti. e (2)
 Geometria per fisica (L-P, a a 016-17 - Esercii svolti Eserciio 1 Si considerino i sistemi lineari + + = 1 + = 0 (1 3 + 3 + 13 = 8 5 + 5 9 = 5 + 5 + = 3 e ( + + = 0 + = 0 3 + 3 + 13 = 0 5 + 5 9 = 0 5 +
Geometria per fisica (L-P, a a 016-17 - Esercii svolti Eserciio 1 Si considerino i sistemi lineari + + = 1 + = 0 (1 3 + 3 + 13 = 8 5 + 5 9 = 5 + 5 + = 3 e ( + + = 0 + = 0 3 + 3 + 13 = 0 5 + 5 9 = 0 5 +
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA INDUSTRIALE 27 GENNAIO 2014
 FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA INDUSTRIALE 27 GENNAIO 2014 DOCENTE: MATTEO LONGO Rispondere alle domande di Teoria in modo esauriente e completo. Svolgere il maggior numero di esercizi
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA INDUSTRIALE 27 GENNAIO 2014 DOCENTE: MATTEO LONGO Rispondere alle domande di Teoria in modo esauriente e completo. Svolgere il maggior numero di esercizi
Esercitazione N.2. Sistemi lineari con parametro. di sistemi lineari con parametro. La regola di Cramer Discussione e risoluzione
 Esercitaione N. maro 7 Sistemi lineari con parametro La regola di Cramer Discussione e risoluione di sistemi lineari con parametro sistemi lineari omogenei Rosalba Barattero ESERCIZIO. Sistema di Cramer
Esercitaione N. maro 7 Sistemi lineari con parametro La regola di Cramer Discussione e risoluione di sistemi lineari con parametro sistemi lineari omogenei Rosalba Barattero ESERCIZIO. Sistema di Cramer
Argomento 13 Sistemi lineari
 Sistemi lineari: definizioni Argomento Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto
Sistemi lineari: definizioni Argomento Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto
Il teorema di Rouché-Capelli
 Luciano Battaia Questi appunti (1), ad uso degli studenti del corso di Matematica (A-La) del corso di laurea in Commercio Estero dell Università Ca Foscari di Venezia, campus di Treviso, contengono un
Luciano Battaia Questi appunti (1), ad uso degli studenti del corso di Matematica (A-La) del corso di laurea in Commercio Estero dell Università Ca Foscari di Venezia, campus di Treviso, contengono un
FUNZIONI REALI DI DUE VARIABILI REALI
 FUNZIONI REALI DI DUE VARIABILI REALI DEFINIZIONE VARIABILI Una funione f, associa ad ogni una coppia ordinata di numeri reali,, appartenente ad un sottoinsieme S del piano, uno e un solo numero reale.
FUNZIONI REALI DI DUE VARIABILI REALI DEFINIZIONE VARIABILI Una funione f, associa ad ogni una coppia ordinata di numeri reali,, appartenente ad un sottoinsieme S del piano, uno e un solo numero reale.
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA
 Cognome Nome Matricola FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA Ciarellotto, Esposito, Garuti Prova del 21 settembre 2013 Dire se è vero o falso (giustificare le risposte. Bisogna necessariamente rispondere
Cognome Nome Matricola FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA Ciarellotto, Esposito, Garuti Prova del 21 settembre 2013 Dire se è vero o falso (giustificare le risposte. Bisogna necessariamente rispondere
APPLICAZIONI. Im f = {b B a A tale che f (a) = b}.
 APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
= (cioè le due terne di numeri direttori ( devono essere ) proporzionali). Tale uguaglianza non è verificata, poiché risulta ρ
 Alcuni esercizi sullo spazio euclideo R Nel seguito R indicherà lo spazio euclideo tridimensionale standard, dotato del riferimento cartesiano naturale (pag 56-57 del libro Nota: gli esercizi proposti
Alcuni esercizi sullo spazio euclideo R Nel seguito R indicherà lo spazio euclideo tridimensionale standard, dotato del riferimento cartesiano naturale (pag 56-57 del libro Nota: gli esercizi proposti
PreCorso di Matematica - PCM Corso M-Z
 PreCorso di Matematica - PCM Corso M-Z DOCENTE: M. Auteri Outline Docente: Auteri PreCorso di Matematica 2016 2 Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti
PreCorso di Matematica - PCM Corso M-Z DOCENTE: M. Auteri Outline Docente: Auteri PreCorso di Matematica 2016 2 Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti
Facsimile di prova d esame Esempio di svolgimento
 Geometria analitica 18 marzo 009 Facsimile di prova d esame Esempio di svolgimento 1 Nello spazio, riferito a coordinate cartesiane ortogonali e monometriche x,y,z, è assegnata la retta r di equazioni
Geometria analitica 18 marzo 009 Facsimile di prova d esame Esempio di svolgimento 1 Nello spazio, riferito a coordinate cartesiane ortogonali e monometriche x,y,z, è assegnata la retta r di equazioni
2 Sistemi lineari. Metodo di riduzione a scala.
 Sistemi lineari. Metodo di riduzione a scala. Esercizio.1 Utilizzando il metodo di eliminazione di Gauss, risolvere i seguenti sistemi lineari: 1. 3. x 1 x + 3x 3 = 1 x 1 x x 3 = x 1 + x + 3x 3 = 5 x 1
Sistemi lineari. Metodo di riduzione a scala. Esercizio.1 Utilizzando il metodo di eliminazione di Gauss, risolvere i seguenti sistemi lineari: 1. 3. x 1 x + 3x 3 = 1 x 1 x x 3 = x 1 + x + 3x 3 = 5 x 1
Esercizio 1 Dato il sistema:
 Leione - Esercitaioni di Algebra e Geometria - Anno accademico 9- Eserciio Dato il sistema: R ) ( a) studiare il rango della matrice incompleta del sistema; b) studiare il rango della matrice completa
Leione - Esercitaioni di Algebra e Geometria - Anno accademico 9- Eserciio Dato il sistema: R ) ( a) studiare il rango della matrice incompleta del sistema; b) studiare il rango della matrice completa
Risoluzione di sistemi lineari
 Risoluzione di sistemi lineari Teorema (Rouché-Capelli) Dato il sistema di m equazioni in n incognite Ax = b, con A M at(m, n) b R n x R n [A b] si ha che: matrice dei coefficienti, vettore dei termini
Risoluzione di sistemi lineari Teorema (Rouché-Capelli) Dato il sistema di m equazioni in n incognite Ax = b, con A M at(m, n) b R n x R n [A b] si ha che: matrice dei coefficienti, vettore dei termini
Geometria BAER I canale Foglio esercizi 2
 Geometria BAER I canale Foglio esercizi 2 Esercizio 1. Calcolare il determinante e l inversa (quando esiste) della matrice ( ) cos θ sin θ R θ =, θ [0, 2π] sin θ cos θ Soluzione: Il determinante ( é cos
Geometria BAER I canale Foglio esercizi 2 Esercizio 1. Calcolare il determinante e l inversa (quando esiste) della matrice ( ) cos θ sin θ R θ =, θ [0, 2π] sin θ cos θ Soluzione: Il determinante ( é cos
Le risposte vanno giustificate con chiarezza. 1) Nello spazio vettoriale V delle matrici 2 2 a coefficienti reali, considera le matrici A 1 = , A 4 =
 Università degli Studi di Roma Tor Vergata. Corso di Laurea in Matematica Esame di Geometria 1 con Elementi di Storia Prof. F. Tovena 30 gennaio 2015 Le risposte vanno giustificate con chiarezza. 1 Nello
Università degli Studi di Roma Tor Vergata. Corso di Laurea in Matematica Esame di Geometria 1 con Elementi di Storia Prof. F. Tovena 30 gennaio 2015 Le risposte vanno giustificate con chiarezza. 1 Nello
1 Ampliamento del piano e coordinate omogenee
 1 Ampliamento del piano e coordinate omogenee Vogliamo dare una idea, senza molte pretese, dei concetti che stanno alla base di alcuni calcoli svolti nella classificazione delle coniche. Supponiamo di
1 Ampliamento del piano e coordinate omogenee Vogliamo dare una idea, senza molte pretese, dei concetti che stanno alla base di alcuni calcoli svolti nella classificazione delle coniche. Supponiamo di
Soluzioni del Foglio 2 I sistemi lineari
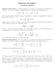 Soluzioni del Foglio 2 I sistemi lineari Soluzione dell esercizio 1 Il sistema assegnato è un sistema di 2 equazioni in 2 incognite non omogeneo Le matrici incompleta e completa associate al sistema sono
Soluzioni del Foglio 2 I sistemi lineari Soluzione dell esercizio 1 Il sistema assegnato è un sistema di 2 equazioni in 2 incognite non omogeneo Le matrici incompleta e completa associate al sistema sono
Appunti su Indipendenza Lineare di Vettori
 Appunti su Indipendenza Lineare di Vettori Claudia Fassino a.a. Queste dispense, relative a una parte del corso di Matematica Computazionale (Laurea in Informatica), rappresentano solo un aiuto per lo
Appunti su Indipendenza Lineare di Vettori Claudia Fassino a.a. Queste dispense, relative a una parte del corso di Matematica Computazionale (Laurea in Informatica), rappresentano solo un aiuto per lo
P z. OP x, OP y, OP z sono le proiezioni ortogonali di v sugli assi x, y, z, per cui: OP x = ( v i) i. k j. P x. OP z = ( v k) k
 Richiami di calcolo vettoriale Consideriamo il vettore libero v = OP. Siano P x, P y, P z le proiezioni ortogonali di P sui tre assi cartesiani. v è la diagonale del parallelepipedo costruito su OP x,
Richiami di calcolo vettoriale Consideriamo il vettore libero v = OP. Siano P x, P y, P z le proiezioni ortogonali di P sui tre assi cartesiani. v è la diagonale del parallelepipedo costruito su OP x,
Federica Gregorio e Cristian Tacelli
 1 Sistemi lineari Federica Gregorio e Cristian Tacelli Un sistema lineare m n (m equazioni in n incognite) è un insieme di equazioni lineari che devono essere soddisfatte contemporaneamente a 11 x 1 +
1 Sistemi lineari Federica Gregorio e Cristian Tacelli Un sistema lineare m n (m equazioni in n incognite) è un insieme di equazioni lineari che devono essere soddisfatte contemporaneamente a 11 x 1 +
La Retta Ogni funzione di primo grado rappresenta, graficamente, una retta. L equazione della retta può essere scritta in due modi
 La Retta Ogni funzione di primo grado rappresenta, graficamente, una retta. L equazione della retta può essere scritta in due modi Forma implicita Forma esplicita a x b y c 0 y m x q a c y x b b Esempio
La Retta Ogni funzione di primo grado rappresenta, graficamente, una retta. L equazione della retta può essere scritta in due modi Forma implicita Forma esplicita a x b y c 0 y m x q a c y x b b Esempio
Università di Modena e Reggio Emilia Facoltà di Scienze MM.FF.NN. PROVA DI ALGEBRA LINEARE (esercitazione del 18 gennaio 2011)
 Università di Modena e Reggio Emilia Facoltà di Scienze MM.FF.NN. PROVA DI ALGEBRA LINEARE (esercitazione del 18 gennaio 2011) ISTRUZIONI PER LO SVOLGIMENTO. Scrivere cognome, nome, numero di matricola
Università di Modena e Reggio Emilia Facoltà di Scienze MM.FF.NN. PROVA DI ALGEBRA LINEARE (esercitazione del 18 gennaio 2011) ISTRUZIONI PER LO SVOLGIMENTO. Scrivere cognome, nome, numero di matricola
Sistemi di equazioni lineari
 Sistemi di equazioni lineari Siano X 1,, X n indeterminate Un equazione lineare (o di primo grado) nelle incognite X 1,, X n a coefficienti nel campo K è della forma a 1 X 1 + + a n X n = b, a i, b K,
Sistemi di equazioni lineari Siano X 1,, X n indeterminate Un equazione lineare (o di primo grado) nelle incognite X 1,, X n a coefficienti nel campo K è della forma a 1 X 1 + + a n X n = b, a i, b K,
Non hanno lo stesso coefficiente angolare e dunque non sono parallele, ma non sono nemmeno perpendicolari in quanto il prodotto dei coeffiecienti
 Università degli Studi Roma Tre Corso di Laurea in Ottica ed Optometria Tutorato di Istituzioni di Matematica - A.A.06/07 Docente: Prof.ssa E. Scoppola Tutore: Gianclaudio Pietrazzini Soluzioni del Tutorato
Università degli Studi Roma Tre Corso di Laurea in Ottica ed Optometria Tutorato di Istituzioni di Matematica - A.A.06/07 Docente: Prof.ssa E. Scoppola Tutore: Gianclaudio Pietrazzini Soluzioni del Tutorato
a.a Esercizi 3. Spazi vettoriali e sottospazi. Soluzioni.
 a.a. 5-6 Esercii. Spai vettoriali e sottospai. Soluioni.. Determinare quali dei seguenti insiemi sono sottospai vettoriali di R, giustificando le risposte: (i ) U = y y + = : }. = (ii ) V = y : y + = }.
a.a. 5-6 Esercii. Spai vettoriali e sottospai. Soluioni.. Determinare quali dei seguenti insiemi sono sottospai vettoriali di R, giustificando le risposte: (i ) U = y y + = : }. = (ii ) V = y : y + = }.
Condizione di allineamento di tre punti
 LA RETTA L equazione lineare in x e y L equazione: 0 con,,, e non contemporaneamente nulli, si dice equazione lineare nelle due variabili e. Ogni coppia ; tale che: 0 si dice soluzione dell equazione.
LA RETTA L equazione lineare in x e y L equazione: 0 con,,, e non contemporaneamente nulli, si dice equazione lineare nelle due variabili e. Ogni coppia ; tale che: 0 si dice soluzione dell equazione.
Registro Lezioni di Algebra lineare del 15 e 16 novembre 2016.
 Registro Lezioni di Algebra lineare del 15 e 16 novembre 2016 Di seguito si riporta il riassunto degli argomenti svolti; i riferimenti sono a parti del Cap8 Elementi di geometria e algebra lineare Par5
Registro Lezioni di Algebra lineare del 15 e 16 novembre 2016 Di seguito si riporta il riassunto degli argomenti svolti; i riferimenti sono a parti del Cap8 Elementi di geometria e algebra lineare Par5
INGEGNERIA EDILE ARCHITETTURA ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA 17 SETTEMBRE 2012
 INGEGNERIA EDILE ARCHITETTURA ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA 7 SETTEMBRE 202 Esercizio. Sia V = R[X] 2 lo spazio vettoriale dei polinomi ax 2 + bx + c nella variabile X di grado al più 2 a coefficienti
INGEGNERIA EDILE ARCHITETTURA ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA 7 SETTEMBRE 202 Esercizio. Sia V = R[X] 2 lo spazio vettoriale dei polinomi ax 2 + bx + c nella variabile X di grado al più 2 a coefficienti
VETTORI E MATRICI. Ing. Nicola Cappuccio 2014 U.F.5 ELEMENTI SCIENTIFICI ED ELETTRONICI APPLICATI AI SISTEMI DI TELECOMUNICAZIONI
 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 I VETTRORI E MATRICI (RICHIAMI) Ad ogni matrice quadrata a coefficienti reali è possibile associare un numero reale, detto determinante, calcolato
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 I VETTRORI E MATRICI (RICHIAMI) Ad ogni matrice quadrata a coefficienti reali è possibile associare un numero reale, detto determinante, calcolato
Capitolo 7 Algebra Lineare. Coordinate cartesiane in uno spazio a 3 dimensioni S 3
 Capitolo 7 7.1 Vettori 7.1.1 - Richiami di geometria analitica Coordinate cartesiane in uno spazio a 3 dimensioni S 3 In S 3 si considerino tre rette perpendicolari, aventi in comune un punto (origine);
Capitolo 7 7.1 Vettori 7.1.1 - Richiami di geometria analitica Coordinate cartesiane in uno spazio a 3 dimensioni S 3 In S 3 si considerino tre rette perpendicolari, aventi in comune un punto (origine);
Esame scritto di Geometria I
 Esame scritto di Geometria I Università degli Studi di Trento Corso di laurea in Fisica A.A. 26/27 Appello di febbraio 27 Esercizio Sia f h : R R l applicazione lineare definita da f h (e ) = 2e + (2 h)e
Esame scritto di Geometria I Università degli Studi di Trento Corso di laurea in Fisica A.A. 26/27 Appello di febbraio 27 Esercizio Sia f h : R R l applicazione lineare definita da f h (e ) = 2e + (2 h)e
MATRICI E SISTEMI LINEARI
 1 Rappresentazione di dati strutturati MATRICI E SISTEMI LINEARI Gli elementi di una matrice, detti coefficienti, possono essere qualsiasi e non devono necessariamente essere omogenei tra loro; di solito
1 Rappresentazione di dati strutturati MATRICI E SISTEMI LINEARI Gli elementi di una matrice, detti coefficienti, possono essere qualsiasi e non devono necessariamente essere omogenei tra loro; di solito
Esercizi sui sistemi di equazioni lineari.
 Esercizi sui sistemi di equazioni lineari Risolvere il sistema di equazioni lineari x y + z 6 x + y z x y z Si tratta di un sistema di tre equazioni lineari nelle tre incognite x, y e z Poichè m n, la
Esercizi sui sistemi di equazioni lineari Risolvere il sistema di equazioni lineari x y + z 6 x + y z x y z Si tratta di un sistema di tre equazioni lineari nelle tre incognite x, y e z Poichè m n, la
Esercizi svolti sulle applicazioni lineari
 Francesco Daddi - dicembre Esercii svolti sulle applicaioni lineari Eserciio. Si consideri la trasformaione lineare T : R R che ha come matrice associata, rispetto alla base β = {,, ) T ;,, ) T ;,, ) T}
Francesco Daddi - dicembre Esercii svolti sulle applicaioni lineari Eserciio. Si consideri la trasformaione lineare T : R R che ha come matrice associata, rispetto alla base β = {,, ) T ;,, ) T ;,, ) T}
Pagine di Algebra lineare. di premessa al testo Pagine di Geometria di Sara Dragotti. Parte terza: SISTEMI LINEARI
 Pagine di Algebra lineare di premessa al testo Pagine di Geometria di Sara Dragotti Parte terza: SISTEMI LINEARI 1. Definizioni Dato un campo K ed m 1 polinomi su K in n indeterminate di grado non superiore
Pagine di Algebra lineare di premessa al testo Pagine di Geometria di Sara Dragotti Parte terza: SISTEMI LINEARI 1. Definizioni Dato un campo K ed m 1 polinomi su K in n indeterminate di grado non superiore
La retta nel piano. Supponiamo che la retta r sia assegnata attraverso un suo punto P 0 (x 0, y 0 ) e un vettore v (l, m) che ne indichi la direzione.
 La retta nel piano Equazioni vettoriale e parametriche di una retta Supponiamo che la retta r sia assegnata attraverso un suo punto P 0 (x 0, y 0 ) e un vettore v (l, m) che ne indichi la direzione. Condizione
La retta nel piano Equazioni vettoriale e parametriche di una retta Supponiamo che la retta r sia assegnata attraverso un suo punto P 0 (x 0, y 0 ) e un vettore v (l, m) che ne indichi la direzione. Condizione
c x esiste un vettore v = y tale che F(v) = u. z In caso di risposta negativa, si determini un vettore che non appartiene a Im(F).
 Avvertena. Si consiglia di leggere attentamente gli svolgimenti dei seguenti esercii e di non limitarsi a cercare di vedere come si fa. Se ci si limita a questo, sena considerare gli aspetti teorici su
Avvertena. Si consiglia di leggere attentamente gli svolgimenti dei seguenti esercii e di non limitarsi a cercare di vedere come si fa. Se ci si limita a questo, sena considerare gli aspetti teorici su
I sistemi lineari di n equazioni in n incognite
 I sistemi lineari I sistemi lineari di n equazioni in n incognite I sistemi lineari di n equazioni in n incognite, sono formati da equazioni di primo grado, in cui le incognite hanno tutte esponente uguale
I sistemi lineari I sistemi lineari di n equazioni in n incognite I sistemi lineari di n equazioni in n incognite, sono formati da equazioni di primo grado, in cui le incognite hanno tutte esponente uguale
Sistemi Lineari. Elisabetta Colombo. Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico
 Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 200-20 2 a di o.0 4 Capelli Rango o Caratterisca : definizioni a di o.0 Un equazione nelle n incognite x,..., x n della forma dove
Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 200-20 2 a di o.0 4 Capelli Rango o Caratterisca : definizioni a di o.0 Un equazione nelle n incognite x,..., x n della forma dove
Geometria analitica: rette e piani
 Geometria analitica: rette e piani parametriche Allineamento nel piano nello spazio Angoli tra rette e distanza 2 2006 Politecnico di Torino 1 Esempio 2 Sia A = (1, 2). Per l interpretazione geometrica
Geometria analitica: rette e piani parametriche Allineamento nel piano nello spazio Angoli tra rette e distanza 2 2006 Politecnico di Torino 1 Esempio 2 Sia A = (1, 2). Per l interpretazione geometrica
1.[25 punti] Risolvere il seguente sistema di equazioni lineari al variare del parametro reale λ: X +Y +Z = 2. X 2Y +λz = 2
![1.[25 punti] Risolvere il seguente sistema di equazioni lineari al variare del parametro reale λ: X +Y +Z = 2. X 2Y +λz = 2 1.[25 punti] Risolvere il seguente sistema di equazioni lineari al variare del parametro reale λ: X +Y +Z = 2. X 2Y +λz = 2](/thumbs/69/60506353.jpg) Università di Modena e Reggio Emilia Facoltà di Scienze MM.FF.NN. PROVA SCRITTA DI GEOMETRIA A del 27 giugno 2011 ISTRUZIONI PER LO SVOLGIMENTO. Scrivere cognome, nome, numero di matricola in alto a destra
Università di Modena e Reggio Emilia Facoltà di Scienze MM.FF.NN. PROVA SCRITTA DI GEOMETRIA A del 27 giugno 2011 ISTRUZIONI PER LO SVOLGIMENTO. Scrivere cognome, nome, numero di matricola in alto a destra
SISTEMI LINEARI. x y + 2t = 0 2x + y + z t = 0 x z t = 0 ; S 3 : ; S 5x 2y z = 1 4x 7y = 3
 SISTEMI LINEARI. Esercizi Esercizio. Verificare se (,, ) è soluzione del sistema x y + z = x + y z = 3. Trovare poi tutte le soluzioni del sistema. Esercizio. Scrivere un sistema lineare di 3 equazioni
SISTEMI LINEARI. Esercizi Esercizio. Verificare se (,, ) è soluzione del sistema x y + z = x + y z = 3. Trovare poi tutte le soluzioni del sistema. Esercizio. Scrivere un sistema lineare di 3 equazioni
Esercizi svolti. risolvere, se possibile, l equazione xa + B = O, essendo x un incognita reale
 Esercizi svolti 1. Matrici e operazioni fra matrici 1.1 Date le matrici 1 2 1 6 A = B = 5 2 9 15 6 risolvere, se possibile, l equazione xa + B = O, essendo x un incognita reale Osservazione iniziale: qualunque
Esercizi svolti 1. Matrici e operazioni fra matrici 1.1 Date le matrici 1 2 1 6 A = B = 5 2 9 15 6 risolvere, se possibile, l equazione xa + B = O, essendo x un incognita reale Osservazione iniziale: qualunque
Analisi Matematica 1 e Matematica 1 Geometria Analitica: Rette
 Analisi Matematica 1 e Matematica 1 Geometria Analitica: Rette Annalisa Amadori e Benedetta Pellacci amadori@uniparthenope.it pellacci@uniparthenope.it Università di Napoli Parthenope Contenuti Nel Piano
Analisi Matematica 1 e Matematica 1 Geometria Analitica: Rette Annalisa Amadori e Benedetta Pellacci amadori@uniparthenope.it pellacci@uniparthenope.it Università di Napoli Parthenope Contenuti Nel Piano
Argomenti trattati nella settimana novembre Il libro cui faccio riferimento, se non specificato altrimenti, è Lang, Algebra lineare
 Argomenti trattati nella settimana 23-27 novembre 2009 Il libro cui faccio riferimento, se non specificato altrimenti, è Lang, Algebra lineare 1 Sistemi lineari; 2 applicazioni lineari; Sistemi lineari;
Argomenti trattati nella settimana 23-27 novembre 2009 Il libro cui faccio riferimento, se non specificato altrimenti, è Lang, Algebra lineare 1 Sistemi lineari; 2 applicazioni lineari; Sistemi lineari;
il determinante che si ottiene da A, sopprimendo la i - esima riga e la j - esima colonna. Si definisce complemento algebrico dell'elemento a ij
 Determinanti Sia data la matrice quadrata a... a n a a n =...... a... a n nn Chiamiamo determinante di il numero det o che ad essa viene associato. det = a a... a... a... a n n n... a nn Un generico elemento
Determinanti Sia data la matrice quadrata a... a n a a n =...... a... a n nn Chiamiamo determinante di il numero det o che ad essa viene associato. det = a a... a... a... a n n n... a nn Un generico elemento
CORSO DI LAUREA IN INGEGNERIA MECCANICA A.A PROVA SCRITTA DI GEOMETRIA DEL Compito A Corso del Prof.
 CORSO DI LAUREA IN INGEGNERIA MECCANICA A.A. 202-203 PROVA SCRITTA DI GEOMETRIA DEL 8-02-3 Compito A Corso del Prof. Manlio BORDONI Esercizio. Sia W il sottospazio vettoriale di R 4 generato dai vettori
CORSO DI LAUREA IN INGEGNERIA MECCANICA A.A. 202-203 PROVA SCRITTA DI GEOMETRIA DEL 8-02-3 Compito A Corso del Prof. Manlio BORDONI Esercizio. Sia W il sottospazio vettoriale di R 4 generato dai vettori
RETTE E PIANI NELLO SPAZIO
 VETTORI E GEOMETRIA ANALITICA 1 RETTE E PIANI NELLO SPAZIO Rette e piani in forma cartesiana e parametrica. Parallelismo e perpendicolarità, posizioni reciproche tra rette e piani, distanze. Esercizio
VETTORI E GEOMETRIA ANALITICA 1 RETTE E PIANI NELLO SPAZIO Rette e piani in forma cartesiana e parametrica. Parallelismo e perpendicolarità, posizioni reciproche tra rette e piani, distanze. Esercizio
Anno Accademico 2015/2016
 Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2015/2016 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2015/2016 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
(V) (FX) L unione di due basi di uno spazio vettoriale è ancora una base dello spazio vettoriale.
 8 gennaio 2009 - PROVA D ESAME - Geometria e Algebra T NOME: MATRICOLA: a=, b=, c= Sostituire ai parametri a, b, c rispettivamente la terzultima, penultima e ultima cifra del proprio numero di matricola
8 gennaio 2009 - PROVA D ESAME - Geometria e Algebra T NOME: MATRICOLA: a=, b=, c= Sostituire ai parametri a, b, c rispettivamente la terzultima, penultima e ultima cifra del proprio numero di matricola
Capitolo 7 Algebra Lineare. Coordinate cartesiane in uno spazio a 3 dimensioni S 3
 Capitolo 7 7.1 Vettori 7.1.1 - Richiami di geometria analitica Coordinate cartesiane in uno spazio a 3 dimensioni S 3 In S 3 si considerino tre rette perpendicolari, aventi in comune un punto (origine);
Capitolo 7 7.1 Vettori 7.1.1 - Richiami di geometria analitica Coordinate cartesiane in uno spazio a 3 dimensioni S 3 In S 3 si considerino tre rette perpendicolari, aventi in comune un punto (origine);
ossia può anche essere localizzato univocamente sul piano complesso con la sua forma polare.
 ALGEBRA COMPLESSA Nel corso dei secoli gli insiemi dei numeri sono andati man mano allargandosi per rispondere all esigenza di dare soluzione a equazioni e problemi sempre nuovi I numeri complessi sono
ALGEBRA COMPLESSA Nel corso dei secoli gli insiemi dei numeri sono andati man mano allargandosi per rispondere all esigenza di dare soluzione a equazioni e problemi sempre nuovi I numeri complessi sono
Coordinate cartesiane e coordinate omogenee
 Coordinate cartesiane e coordinate omogenee Fissiamo nel piano un sistema di riferimento cartesiano ortogonale O, x, y, u. Ad ogni punto P del piano possiamo associare le coordinate cartesiane (x, y),
Coordinate cartesiane e coordinate omogenee Fissiamo nel piano un sistema di riferimento cartesiano ortogonale O, x, y, u. Ad ogni punto P del piano possiamo associare le coordinate cartesiane (x, y),
UNIVERSITA DEGLI STUDI LA SAPIENZA DI ROMA POLO DI RIETI FACOLTA DI INGEGNERIA CORSO DI LAUREA IN INGEGNERIA DELL AMBIENTE E DEL TERRITORIO
 UNIVERSITA DEGLI STUDI LA SAPIENZA DI ROMA POLO DI RIETI FACOLTA DI INGEGNERIA CORSO DI LAUREA IN INGEGNERIA DELL AMBIENTE E DEL TERRITORIO Geometria 9 5 A.A. 5 Cognome Nome Matricola Codice Scrivere in
UNIVERSITA DEGLI STUDI LA SAPIENZA DI ROMA POLO DI RIETI FACOLTA DI INGEGNERIA CORSO DI LAUREA IN INGEGNERIA DELL AMBIENTE E DEL TERRITORIO Geometria 9 5 A.A. 5 Cognome Nome Matricola Codice Scrivere in
Chi non risolve esercizi non impara la matematica.
 5.5 esercizi 9 Per trovare la seconda equazione ragioniamo così: la parte espropriata del primo terreno è x/00, la parte espropriata del secondo è y/00 e in totale sono stati espropriati 000 m, quindi
5.5 esercizi 9 Per trovare la seconda equazione ragioniamo così: la parte espropriata del primo terreno è x/00, la parte espropriata del secondo è y/00 e in totale sono stati espropriati 000 m, quindi
1 Combinazioni lineari e Sottospazi.
 Geometria Lingotto. LeLing6: Sottospai Vettoriali. Ārgomenti svolti: Sottospai vettoriali. Sistemi lineari e combinaioni lineari. Somma e interseioni di sottospai. Sottospai delle righe e colonne di una
Geometria Lingotto. LeLing6: Sottospai Vettoriali. Ārgomenti svolti: Sottospai vettoriali. Sistemi lineari e combinaioni lineari. Somma e interseioni di sottospai. Sottospai delle righe e colonne di una
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA
 UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito B 3/05/005 A. A. 004 005 ) Risolvere il seguente sistema
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito B 3/05/005 A. A. 004 005 ) Risolvere il seguente sistema
LE EQUAZIONI LINEARI LE IDENTITA ( )( ) 5. a Cosa hanno in comune le seguenti uguaglianze? Uguaglianza (1) a
 LE EQUAZIONI LINEARI 1 LE IDENTITA a b = ( a + b)( a b) () 1 a = a + a ( ) ( a + b) = a + ab + b () 3 Cosa hanno in comune le seguenti uguaglianze? Uguaglianza (1) a b = ( a+ b)( a b) È sempre vera qualunque
LE EQUAZIONI LINEARI 1 LE IDENTITA a b = ( a + b)( a b) () 1 a = a + a ( ) ( a + b) = a + ab + b () 3 Cosa hanno in comune le seguenti uguaglianze? Uguaglianza (1) a b = ( a+ b)( a b) È sempre vera qualunque
Esercizi di geometria per Fisica / Fisica e Astrofisica
 Esercizi di geometria per Fisica / Fisica e Astrofisica Foglio 3 - Soluzioni Esercizio. Stabilire se i seguenti sottoinsiemi di R 3 sono sottospazi vettoriali: (a) S = {(x y z) R 3 : x + y + z = }. (b)
Esercizi di geometria per Fisica / Fisica e Astrofisica Foglio 3 - Soluzioni Esercizio. Stabilire se i seguenti sottoinsiemi di R 3 sono sottospazi vettoriali: (a) S = {(x y z) R 3 : x + y + z = }. (b)
EQUAZIONE DELLA RETTA
 EQUAZIONE DELLA RETTA EQUAZIONE DEGLI ASSI L equazione dell asse x è 0. L equazione dell asse y è 0. EQUAZIONE DELLE RETTE PARALLELE AGLI ASSI L equazione di una retta r parallela all asse x è cioè è uguale
EQUAZIONE DELLA RETTA EQUAZIONE DEGLI ASSI L equazione dell asse x è 0. L equazione dell asse y è 0. EQUAZIONE DELLE RETTE PARALLELE AGLI ASSI L equazione di una retta r parallela all asse x è cioè è uguale
12 - Sistemi di Equazioni Lineari
 Università degli Studi di Palermo Facoltà di Economia Dipartimento SEAS Appunti del corso di Matematica - Sistemi di Equazioni Lineari Anno Accademico 5/6 D. Provenzano, M. Tumminello, V. Lacagnina e A.
Università degli Studi di Palermo Facoltà di Economia Dipartimento SEAS Appunti del corso di Matematica - Sistemi di Equazioni Lineari Anno Accademico 5/6 D. Provenzano, M. Tumminello, V. Lacagnina e A.
Esercizi svolti sui sistemi lineari
 Francesco Daddi - www.webalice.it/francesco.daddi Esercizi svolti sui sistemi lineari Esercizio 1. Risolvere il seguente sistema lineare al variare del parametro reale t: tx+(t 1)y + z =1 (t 1)y + tz =1
Francesco Daddi - www.webalice.it/francesco.daddi Esercizi svolti sui sistemi lineari Esercizio 1. Risolvere il seguente sistema lineare al variare del parametro reale t: tx+(t 1)y + z =1 (t 1)y + tz =1
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA
 UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito C 3/5/25 A. A. 24 25 ) Risolvere il seguente sistema
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito C 3/5/25 A. A. 24 25 ) Risolvere il seguente sistema
Sistemi di equazioni lineari
 Sistemi di equazioni lineari A. Bertapelle 25 ottobre 212 Cos è un sistema lineare? Definizione Un sistema di m equazioni lineari (o brevemente sistema lineare) nelle n incognite x 1,..., x n, a coefficienti
Sistemi di equazioni lineari A. Bertapelle 25 ottobre 212 Cos è un sistema lineare? Definizione Un sistema di m equazioni lineari (o brevemente sistema lineare) nelle n incognite x 1,..., x n, a coefficienti
Geometria BAER PRIMO CANALE Foglio esercizi 1
 Geometria BAER PRIMO CANALE Foglio esercizi 1 Esercizio 1. Risolvere le seguenti equazioni lineari nelle variabili indicate trovando una parametrizzazione dell insieme delle soluzioni. a) x + 5y = nelle
Geometria BAER PRIMO CANALE Foglio esercizi 1 Esercizio 1. Risolvere le seguenti equazioni lineari nelle variabili indicate trovando una parametrizzazione dell insieme delle soluzioni. a) x + 5y = nelle
21 - Sistemi di Equazioni Lineari
 Università degli Studi di Palermo Facoltà di Economia Dipartimento di Scienze Economiche, Aziendali e Statistiche Appunti del corso di Matematica - Sistemi di Equazioni Lineari Anno Accademico 5/6 M. Tumminello,
Università degli Studi di Palermo Facoltà di Economia Dipartimento di Scienze Economiche, Aziendali e Statistiche Appunti del corso di Matematica - Sistemi di Equazioni Lineari Anno Accademico 5/6 M. Tumminello,
SUI SISTEMI LINEARI. 1. Richiami.Il metodo di Gauss. Un equazione nelle incognite. si dice lineare o di primo grado se si può ridurre. R.
 SUI SISTEMI LINEARI. Richiami.Il metodo di Gauss Un equaione nelle incognite..., n si dice lineare o di primo grado se si può ridurre alla forma: a a... an n b con a, a... an, b R. I numeri a, a... an
SUI SISTEMI LINEARI. Richiami.Il metodo di Gauss Un equaione nelle incognite..., n si dice lineare o di primo grado se si può ridurre alla forma: a a... an n b con a, a... an, b R. I numeri a, a... an
Sistemi Lineari. Andrea Galasso
 Sistemi Lineari Andrea Galasso Esercizi svolti Teorema. (Rouché-Capelli. Un sistema lineare Ax = b ammette soluzioni se e solo se il rango della matrice dei coefficienti A è uguale al rango della matrice
Sistemi Lineari Andrea Galasso Esercizi svolti Teorema. (Rouché-Capelli. Un sistema lineare Ax = b ammette soluzioni se e solo se il rango della matrice dei coefficienti A è uguale al rango della matrice
1. GRADO DI UN SISTEMA. METODI GENERALI DI RISOLUZIONE
 8 SISTEMI DI GRADO SUPERIORE AL. GRADO DI UN SISTEMA. METODI GENERALI DI RISOLUZIONE Si dice grado di un sistema il prodotto fra i gradi delle sue equaioni. + y ( grado) + y ( grado) sistema di 6 grado
8 SISTEMI DI GRADO SUPERIORE AL. GRADO DI UN SISTEMA. METODI GENERALI DI RISOLUZIONE Si dice grado di un sistema il prodotto fra i gradi delle sue equaioni. + y ( grado) + y ( grado) sistema di 6 grado
Corso di Geometria BIAR, BSIR Esercizi 3: soluzioni
 Corso di Geometria - BIAR, BSIR Esercizi : soluzioni Rango e teorema di Rouché-Capelli Esercizio. Calcolare il rango di ciascuna delle seguenti matrici: ( ) ( ) ( ) A =, A =, A =, A 4 = ( ). a a a Soluzione.
Corso di Geometria - BIAR, BSIR Esercizi : soluzioni Rango e teorema di Rouché-Capelli Esercizio. Calcolare il rango di ciascuna delle seguenti matrici: ( ) ( ) ( ) A =, A =, A =, A 4 = ( ). a a a Soluzione.
0.1 Soluzioni esercitazione IV, del 28/10/2008
 1 0.1 Soluzioni esercitazione IV, del 28/10/2008 Esercizio 0.1.1. Risolvere, usando il teorema di Cramer, i seguenti sistemi lineari 2x + y + z = 0 x + 3z = 1 x y z = 1 kx + y z = 1 x y + 2z = 1 2x + 2y
1 0.1 Soluzioni esercitazione IV, del 28/10/2008 Esercizio 0.1.1. Risolvere, usando il teorema di Cramer, i seguenti sistemi lineari 2x + y + z = 0 x + 3z = 1 x y z = 1 kx + y z = 1 x y + 2z = 1 2x + 2y
Argomento 13 Sistemi lineari
 Sistemi lineari: definizioni Argomento 3 Sistemi lineari I Un equazione nelle n incognite x,,x n della forma c x + + c n x n = b ove c,,c n sono numeri reali (detti coefficienti) eb è un numero reale (detto
Sistemi lineari: definizioni Argomento 3 Sistemi lineari I Un equazione nelle n incognite x,,x n della forma c x + + c n x n = b ove c,,c n sono numeri reali (detti coefficienti) eb è un numero reale (detto
Introduzione soft alla matematica per l economia e la finanza. Marta Cardin, Paola Ferretti, Stefania Funari
 Introduzione soft alla matematica per l economia e la finanza Marta Cardin, Paola Ferretti, Stefania Funari Capitolo Sistemi di equazioni lineari.8 Il Teorema di Cramer Si consideri un generico sistema
Introduzione soft alla matematica per l economia e la finanza Marta Cardin, Paola Ferretti, Stefania Funari Capitolo Sistemi di equazioni lineari.8 Il Teorema di Cramer Si consideri un generico sistema
1. [15 punti] Calcolare il rango della seguente matrice a coefficienti reali: ( 1/2) 1 (1/2)
![1. [15 punti] Calcolare il rango della seguente matrice a coefficienti reali: ( 1/2) 1 (1/2) 1. [15 punti] Calcolare il rango della seguente matrice a coefficienti reali: ( 1/2) 1 (1/2)](/thumbs/101/152415317.jpg) Università di Modena e Reggio Emilia Facoltà di Scienze MM.FF.NN. PROVA DI ALGEBRA LINEARE del 17 febbraio 011 ISTRUZIONI PER LO SVOLGIMENTO. Scrivere cognome, nome, numero di matricola in alto a destra
Università di Modena e Reggio Emilia Facoltà di Scienze MM.FF.NN. PROVA DI ALGEBRA LINEARE del 17 febbraio 011 ISTRUZIONI PER LO SVOLGIMENTO. Scrivere cognome, nome, numero di matricola in alto a destra
Sia Q: R 3 R la forma quadratica Q(X) = X T AX. (a) Determinare gli autovalori di A e le relative molteplicità algebriche e geometriche;
 CORSO DI GEOMETRIA E ALGEBRA 26 febbraio 219 Cognome e Nome: Matricola: = = = = Scrivere in modo LEGGIBILE nome e cognome! = = = = 1. (8 pt) Si consideri la matrice 1 1 A = 1 1 ; sia inoltre X = y R 3.
CORSO DI GEOMETRIA E ALGEBRA 26 febbraio 219 Cognome e Nome: Matricola: = = = = Scrivere in modo LEGGIBILE nome e cognome! = = = = 1. (8 pt) Si consideri la matrice 1 1 A = 1 1 ; sia inoltre X = y R 3.
Esempio. L immagine di f è l insieme dei vettori w = (w 1, w 2 ) R 2 che hanno w 1 = w 2. Quindi:
 Nucleo, immagine e loro proprietà [Abate, 5.2] Data una applicazione lineare f : V W, chiamiamo nucleo di f l insieme N(f) := { v V : f(v) = 0 W } Se S V è un sottoinsieme del dominio, indichiamo con f(s)
Nucleo, immagine e loro proprietà [Abate, 5.2] Data una applicazione lineare f : V W, chiamiamo nucleo di f l insieme N(f) := { v V : f(v) = 0 W } Se S V è un sottoinsieme del dominio, indichiamo con f(s)
Definizione: Due equazioni si dicono equivalenti se ammettono le stesse soluzioni.
 Facoltà di Medicina e Chirurgia Corso Zero di Matematica Gruppi: MC-MF3 / PS-MF3 II Lezione EQUAZIONI E SISTEMI Dr. E. Modica erasmo@galois.it www.galois.it IDENTITÀ ED EQUAZIONI Si consideri un uguaglianza
Facoltà di Medicina e Chirurgia Corso Zero di Matematica Gruppi: MC-MF3 / PS-MF3 II Lezione EQUAZIONI E SISTEMI Dr. E. Modica erasmo@galois.it www.galois.it IDENTITÀ ED EQUAZIONI Si consideri un uguaglianza
Corso di Geometria BIAR, BSIR Esercizi 9: soluzioni
 Corso di Geometria 2010-11 BIAR, BSIR Esercizi 9: soluzioni Esercizio 1. Nello spazio sono dati i punti A = (1, 2, 3), B = (2, 4, 5), C = (1, 1, 4). a) Scrivere equazioni parametriche della retta r 1 passante
Corso di Geometria 2010-11 BIAR, BSIR Esercizi 9: soluzioni Esercizio 1. Nello spazio sono dati i punti A = (1, 2, 3), B = (2, 4, 5), C = (1, 1, 4). a) Scrivere equazioni parametriche della retta r 1 passante
Sistemi lineari. Lorenzo Pareschi. Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara
 Sistemi lineari Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
Sistemi lineari Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
INGEGNERIA EDILE ARCHITETTURA ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA 19 GIUGNO 2012
 INGEGNERIA EDILE ARCHITETTURA ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA 19 GIUGNO 2012 MATTEO LONGO Esercizio 1. Al variare del parametro a R, si consideri l applicazione lineare L a : R R definita dalle
INGEGNERIA EDILE ARCHITETTURA ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA 19 GIUGNO 2012 MATTEO LONGO Esercizio 1. Al variare del parametro a R, si consideri l applicazione lineare L a : R R definita dalle
( ) TEORIA DELLE MATRICI. A. Scimone a.s pag 1
 . Scimone a.s 1997 98 pag 1 TEORI DELLE MTRICI Dato un campo K, definiamo matrice ad elementi in K di tipo (m, n) un insieme di numeri ordinati secondo righe e colonne in una tabella rettangolare del tipo
. Scimone a.s 1997 98 pag 1 TEORI DELLE MTRICI Dato un campo K, definiamo matrice ad elementi in K di tipo (m, n) un insieme di numeri ordinati secondo righe e colonne in una tabella rettangolare del tipo
Si consideri il sistema a coefficienti reali di m equazioni lineari in n incognite
 3 Sistemi lineari 3 Generalità Si consideri il sistema a coefficienti reali di m equazioni lineari in n incognite ovvero, in forma matriciale, a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n x
3 Sistemi lineari 3 Generalità Si consideri il sistema a coefficienti reali di m equazioni lineari in n incognite ovvero, in forma matriciale, a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n x
Soluzioni esercizi complementari
 Soluzioni esercizi complementari Relazioni 1) Quali delle seguenti relazioni sono di equivalenza? x, y R {0} xry x/y Q x, y Z xry x + y è divisibile per 17 x, y Z xry x y X, Y sottoinsiemi di un insieme
Soluzioni esercizi complementari Relazioni 1) Quali delle seguenti relazioni sono di equivalenza? x, y R {0} xry x/y Q x, y Z xry x + y è divisibile per 17 x, y Z xry x y X, Y sottoinsiemi di un insieme
Corso di Geometria, a.a Ing. Informatica e Automatica Esercizi VI: soluzioni
 Corso di Geometria, a.a. 2009-2010 Ing. Informatica e Automatica Esercizi VI: soluzioni 5 novembre 2009 1 Geometria del piano e prodotto scalare Richiami. Il prodotto scalare di due vettori del piano v,
Corso di Geometria, a.a. 2009-2010 Ing. Informatica e Automatica Esercizi VI: soluzioni 5 novembre 2009 1 Geometria del piano e prodotto scalare Richiami. Il prodotto scalare di due vettori del piano v,
Lezione 6 Richiami di Geometria Analitica
 1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
Corso di Geometria Ing. Informatica e Automatica Test 1: soluzioni
 Corso di Geometria Ing. Informatica e Automatica Test : soluzioni k Esercizio Data la matrice A = k dipendente dal parametro k, si consideri il k sistema lineare omogeneo AX =, con X = x x. Determinare
Corso di Geometria Ing. Informatica e Automatica Test : soluzioni k Esercizio Data la matrice A = k dipendente dal parametro k, si consideri il k sistema lineare omogeneo AX =, con X = x x. Determinare
Geometria BAER Canale A-K Esercizi 9
 Geometria BAER 2016-2017 Canale A-K Esercizi 9 Esercizio 1. Si considerino i punti del piano A (1, 1), B (4, 1), C ( 1/2, 2) (a) Si determini se i punti A, B, C sono allineati e, in caso affermativo, si
Geometria BAER 2016-2017 Canale A-K Esercizi 9 Esercizio 1. Si considerino i punti del piano A (1, 1), B (4, 1), C ( 1/2, 2) (a) Si determini se i punti A, B, C sono allineati e, in caso affermativo, si
Matrici triangolari [Abate, 3.2] Lezioni 05 e 06. Determinante di una matrice triangolare [Abate, es. 9.3] Matrici ridotte per righe.
![Matrici triangolari [Abate, 3.2] Lezioni 05 e 06. Determinante di una matrice triangolare [Abate, es. 9.3] Matrici ridotte per righe. Matrici triangolari [Abate, 3.2] Lezioni 05 e 06. Determinante di una matrice triangolare [Abate, es. 9.3] Matrici ridotte per righe.](/thumbs/100/147138366.jpg) Matrici triangolari [Abate, 32] Definizione Una matrice A = a ij ) R m,n si dice triangolare superiore se a ij = 0 per ogni i > j; triangolare inferiore se a ij = 0 per ogni i < j Lezioni 05 e 06 Una matrice
Matrici triangolari [Abate, 32] Definizione Una matrice A = a ij ) R m,n si dice triangolare superiore se a ij = 0 per ogni i > j; triangolare inferiore se a ij = 0 per ogni i < j Lezioni 05 e 06 Una matrice
GEOMETRIA svolgimento di uno scritto del 11 Gennaio 2012
 GEOMETRIA svolgimento di uno scritto del Gennaio ) Trovare una base per lo spazio delle soluzioni del seguente sistema omogeneo: x + y 5z = 3x y + z = x y + 8z =. Il sistema può essere scritto in forma
GEOMETRIA svolgimento di uno scritto del Gennaio ) Trovare una base per lo spazio delle soluzioni del seguente sistema omogeneo: x + y 5z = 3x y + z = x y + 8z =. Il sistema può essere scritto in forma
Sistemi di equazioni lineari da 2 D a 3 D: risoluzione grafica
 Sistemi di equazioni lineari da 2 D a 3 D: risoluzione grafica Questa è una attività che si svolge comunemente in una classe del biennio di scuola superiore.c è però una novità : l estensione dell interpretazione
Sistemi di equazioni lineari da 2 D a 3 D: risoluzione grafica Questa è una attività che si svolge comunemente in una classe del biennio di scuola superiore.c è però una novità : l estensione dell interpretazione
Sistemi lineari - Parte Seconda - Esercizi
 Sistemi lineari - Parte Seconda - Esercizi Terminologia Operazioni elementari sulle righe. Equivalenza per righe. Riduzione a scala per righe. Rango di una matrice. Forma canonica per righe. Eliminazione
Sistemi lineari - Parte Seconda - Esercizi Terminologia Operazioni elementari sulle righe. Equivalenza per righe. Riduzione a scala per righe. Rango di una matrice. Forma canonica per righe. Eliminazione
