ESERCIZI ELEMENTARI DI FLUIDODINAMICA
|
|
|
- Sofia Grande
- 9 anni fa
- Visualizzazioni
Transcript
1 ISTITUZIONI I INGEGNERI EROSPZILE ESERCIZI ELEMENTRI I FLUIOINMIC ESERCIZI ELEMENTRI I FLUIOINMIC RICHIMI INTROUTTII Il fluido viene onsiderato ome un ontinuo, ossia vengono identifiate alune grandezze marosopihe he servono per desrivere il suo omportamento e le sue proprietà. Nel aso ideale di fluido non visoso, queste sono la pressione p, la densità e la veloità. Per questi eserizi, onsidereremo soltanto fluidi ideali non visosi. Portata (in massa) Speifia la massa di fluido he transita nell unità di tempo attraverso la sezione :. nalisi dimensionale: [ML ][LT ][L ] [M][T ] Portata volumetria Speifia il volume di fluido he transita nell unità di tempo attraverso la sezione :. nalisi dimensionale: [LT ][L ] [L ][T ] Conservazione della massa Consideriamo il semplie aso di tubo di flusso on una sezione di entrata E ed una sezione di usita U. La onservazione della massa i impone di eguagliare la portata in E on quella in U: E E E U U U. Ne segue l equazione di ontinuità nel fluido: ost E U Nel aso di fluido inomprimibile, la densità è ostante in ogni punto, e quindi E E U U, e l equazione di ontinuità si srive ost. Conservazione dell energia Consideriamo solo il aso di fluido inomprimibile ( ostante). Per il tubo di flusso da E a U, la onservazione dell energia (meania) onsente di srivere he la variazione di energia inetia, per unità di volume e per unità di tempo, orrisponde al lavoro ompiuto dalle pressioni in E ed in U per unità di tempo, p p, U E E U
2 ISTITUZIONI I INGEGNERI EROSPZILE ESERCIZI ELEMENTRI I FLUIOINMIC da ui risulta he si onserva la somma p : p p. E E U U Ne segue l equazione di Bernoulli nella sua forma più semplie: p ost nalisi dimensionale di Qui: : [ML ][L T ] [MLT ][L ] [F][L ] p è la pressione (nel gergo, questa viene anhe hiamata pressione statia ). è l energia inetia per unità di volume del fluido (ha le dimensioni della pressione, e nel gergo viene hiamata pressione dinamia e spesso indiata on la lettera q); infatti è la massa per unità di volume; è il prodotto salare della veloità su sé stessa,. La ostante ost ha le dimensioni della pressione, e nel gergo viene hiamata pressione totale e indiata ad esempio ome p T. Il teorema di Bernoulli implia he la somma dei due termini in ogni punto onsiderato resta ostante, vale a dire he la osiddetta pressione totale si onserva. Per ui la diminuzione di un termine dovrà essere ompensata dall aumento dell altro. d esempio, nel aso in ui aumentasse la veloità, e quindi la pressione dinamia, avremo una diminuzione di pressione. Per potere trovare il valore della ost dovremmo prima onosere il termine statio e quello dinamio in un punto, ed estendere poi il valore del binomio di Bernoulli a tutto il tubo di flusso (e a tutto il dominio, se i tubi di flusso sono tutti uguali entrando nel dominio). ESERCIZI Eserizio ato un tubo on diametro di ingresso = 6 mm e diametro di usita = 4 mm, sapendo he nel tubo fluise aqua he entra on veloità = 0.5 m/s, determinare la veloità on ui l aqua ese dal tubo. Imponendo la onservazione della massa,, ed espliitando l area della sezione on il rispettivo diametro, 0.5 m/s, si riava: 0.5 m/s 8 m/s.
3 ISTITUZIONI I INGEGNERI EROSPZILE ESERCIZI ELEMENTRI I FLUIOINMIC Eserizio ato un tubo on portata di aqua in ingresso Q = l/s e veloità in ingresso =.6 m/s, sapendo he la veloità in usita è = 0 m/s, si determinino i diametri di ingresso e usita. Trasformiamo la portata volumetria nel Sistema Internazionale (ioè in m /s), sapendo he l = 0.00 m. Si ottiene una portata in ingresso pari a Q = 0.00 m /s = 0.0 m /s. all espressione della portata è possibile riavare il valore del diametro di ingresso. Infatti 4 Q.6 m/s 0.0 m /s, da ui 0.0 m /s e quindi m 4.6 m/s m m. nalogamente si proede per la sezione e si trova: 0.09 m. Eserizio d un ondotto irolare di diametro 0.0 m in ui sorre aria, viene ollegato un tubo di enturi, onsistente in una riduzione loale del ondotto fino ad un diametro di gola di 0.07 m. Il ondotto è p p strumentato on due prese di pressione he misurano le pressioni p = 765 mmhg prima della strizione e p = 75 mmhg nella sezione di gola. eterminare la portata del ondotto. Per determinare la portata i serve onosere il valore della veloità in una delle due sezioni. Sono inognite entrambe le veloità. Possiamo però utilizzare le due equazioni di onservazione a nostra disposizione per hiudere il problema: equazione di ontinuità ed equazione di Bernoulli. Iniziamo quindi on l imporre la onservazione della massa, supponendo il fluido inomprimibile (ipotesi sempre da verifiare a posteriori) e riavando una veloità in funzione dell altra,. Il teorema di Bernoulli si può quindi srivere p p,
4 ISTITUZIONI I INGEGNERI EROSPZILE ESERCIZI ELEMENTRI I FLUIOINMIC ioè p p, da ui si riava ( p p ). Per riavare dobbiamo: alolare il valore delle aree, m, 0.0 m 0.07 m m ; onosere la densità dell aria, per ui assumiamo il valore standard a livello del mare, =.5 kg/m ; esprimere la pressione in unità internazionali (ioè in Pa), usando la onversione: mmhg =. Pa. Risulta: ( p p ) (765 75) mmhg (.) Pa/mmHg 6.04 m/s kg/m Si può quindi alolare la portata, onsiderando ad esempio la sezione : Q Q..5 kg/m 6.04 m/s m 0.88 kg/s Oorre infine verifiare he l ipotesi di inomprimibilità sia effettivamente soddisfatta. Caloliamo il numero di Mah e verifihiamo he sia al di sotto del valore di riferimento standard 0., oltre il quale tipiamente gli effetti di omprimibilità non sono più trasurabili. Il numero di Mah M è dato dal rapporto tra la veloità loale del fluido e la veloità del suono, M = /. La veloità del suono è la veloità on ui un onda sonora si propaga nel fluido onsiderato. Il valore di varia da fluido a fluido (ad esempio, il suono si propaga più veloemente nell aqua he nell aria), e varia on la sua temperatura. La veloità del suono si determina ome RT, in ui è il rapporto p / v tra alore speifio a pressione ostante e alore speifio a volume ostante (nel aso dell aria si assume =.4), R è la ostante universale dei gas per unità di massa (R = 87 J/(kg K)), T è la temperatura assoluta, per ui assumiamo il valore standard a livello del mare, T = 88.6 K. Nel nostro aso risulta quindi RT.4 87 Nm kg K 88.6 K m/s. Il numero di Mah nella sezione vale quindi M 6.04 m/s m/s 0.8. Nota he la verifia è stata fatta proprio nella sezione dove >, e dove quindi il numero di Mah è maggiore. 4
5 ISTITUZIONI I INGEGNERI EROSPZILE ESERCIZI ELEMENTRI I FLUIOINMIC Eserizio 4 Riferendosi al disegno a lato, si onsideri he nella sezione rettangolare, di dimensioni 0 m 0 m, la pressione dinamia sia q = 00 Pa. La sezione è irolare: alolare il diametro sapendo he la veloità è pari a m/s. Il fluido onsiderato è aria in ondizioni standard. Conosendo la pressione dinamia q si può riavare il valore della veloità : q 00 Pa q 44.6 m/s.5 kg/m Imponendo la onservazione della massa si alola l area, m/s 0. m0. m m/s 0.06 m 0.44 m, e quindi si riava il diametro erato, m 0.55 m. Eserizio 5 In figura è illustrata la amera di prova di una galleria del vento. La galleria è dotata di 4 ventole, iasuna on portata di 66.5 kg s -. La amera di prova ha una sezione di.8 m 4 m ed è lunga 4.5 m. La sezione a monte del onvergente è di.8 m 4 m. ssumendo he la pressione nella sezione a monte del onvergente sia pari a quella atmosferia in ondizioni standard, determinare:. la veloità della vena in amera di prova;. la forza agente su iasuna delle quattro pareti della amera di prova, indiandone il verso. Sezione a monte del onvergente 4 x.8 m 4.5 m Camera di prova 4 x.8 m 5
6 ISTITUZIONI I INGEGNERI EROSPZILE ESERCIZI ELEMENTRI I FLUIOINMIC La portata in massa omplessiva dei ventilatori vale Q kgs 9kgs. Le aree delle due sezioni valgono m 5. m, m 5. m. Caloliamo le veloità nelle due sezioni: Q 9 kgs.5 kg/m 5. m Q 9 kgs.5 kg/m 5. m 4.9 ms, 50.0 ms. Conosendo la pressione nel ondotto a monte del onvergente, pari alla pressione atmosferia p a = 05 Pa, aloliamo la pressione totale, p p p 05Pa.5 kg/m (4.9 ms ) T a 05Pa 5 kg ms /m 0450 Pa. Riaviamo quindi la pressione nella amera di prova, p p p p.5 kg/m (50 ms ) T T 0450 Pa 5.5 kg ms /m Pa. Ciasuna delle quattro pareti della amera di prova è sottoposta su una faia alla pressione interna e sull altra faia alla pressione esterna (la pressione atmosferia). L = 4.5 m Per alolare la forza derivante da questo sistema di pressioni appliate alle fae, è neessario alolare la differenza di pressione p tra l interno e l esterno, he risulta p p pa 9999Pa 05Pa 406 Pa. Camera di prova 4 x.8 m Il segno meno india he la pressione risultante è verso l interno. 6
7 ISTITUZIONI I INGEGNERI EROSPZILE ESERCIZI ELEMENTRI I FLUIOINMIC Ciasuna delle pareti è sottoposta a una forza omplessiva pari a p per l area della sua superfiie. Le pareti hanno area inf-sup laterale m 8 m, m 7. m. Le azioni eseritate dalle forze di pressione sulle pareti risultano F F inf-sup laterale p inf-sup laterale 406 Pa 8 m 508 N, p 406 Pa 7. m 404 N, e sono dirette verso l interno. La forza più elevata orrisponde a Finf-sup 508 kgf 580 kgf.580 ton. 9.8 Eserizio 6 Si onsideri un velivolo in volo orizzontale rettilineo uniforme alla quota z = 4060, a ui la densità vale = kg m. Sul profilo dell ala agisono una distribuzione di pressioni sul dorso e una sul ventre, he per sempliità si rionduono a distribuzioni trapezie seondo lo shema grossolano di figura, on: p = 569 Pa, p = 6676 Pa, p = 608 Pa. M M eterminare:. La veloità di volo, nell ipotesi he la pressione nel punto di ristagno sia pari a p. B. Il oeffiiente di pressione p nei punti M a M a metà orda, rispettivamente sul ventre e sul dorso. p p p C. Il diagramma della distribuzione in orda del ario di portanza.. La posizione in orda del punto di appliazione della risultante della portanza. E. Il valore del ario alare Q/S del velivolo, supponendo l ala a pianta rettangolare. p eloità di volo. Sriviamo il bilanio energetio di una orrente inomprimibile (equazione di Bernoulli) lungo la linea di flusso he ondue al punto di ristagno, p pp.ristagno p.ristagno. 7
8 ISTITUZIONI I INGEGNERI EROSPZILE ESERCIZI ELEMENTRI I FLUIOINMIC Qui p, e sono la pressione ambiente, la densità dell aria alla quota onsiderata e la veloità di volo; la veloità p.ristagno è nulla per definizione. Riaviamo la pressione dinamia q della orrente asintotia, sfruttando l ipotesi he la pressione nel punto di ristagno sia pari a p nota: q pp.ristagno p p p Pa 5509 Pa, e quindi la veloità di volo, q 5509 Pa 59 m s 6. ms kg/m. B Coeffiienti di pressione. Caloliamo la pressione nei punti medi rihiesti: pm ( p p ) Pa Pa, pm ( p p ) Pa 696 Pa. Caloliamo quindi i oeffiienti di pressione seondo la definizione, M pm M pm p p Pa 0.89, 5509 Pa p p Pa Pa p p p : C istribuzione in orda della portanza. La portanza è data dalla differenza delle pressioni tra il ventre e il dorso p p dell ala. Nelle ipotesi dello shema grossolano adottato di distribuzioni trapezie in orda, he terminano on lo stesso valore di pressione al bordo di usita, la portanza è ovviamente distribuita in orda in forma triangolare. L ordinata, al bordo di attao, di tale distribuzione di portanza vale p p Pa 979 Pa. Posizione della risultante di portanza. La posizione del punto di appliazione della risultante di portanza è nel barientro della figura del ario. Con una distribuzione di ario triangolare, si trova quindi a / della orda. / 8
9 ISTITUZIONI I INGEGNERI EROSPZILE ESERCIZI ELEMENTRI I FLUIOINMIC E Cario alare. Il ario alare di un velivolo è il peso diviso la superfiie alare, Q/S. Possiamo determinare il peso Q dall equilibrio he deve sussistere on la portanza P, essendo il velivolo in volo orizzontale rettilineo uniforme. La portanza è l integrale, sulla superfiie alare, del ario di portanza dovuto alla differenza di pressioni tra il ventre e il dorso dell ala. bbiamo appena determinato la distribuzione in orda di tale ario, e (nell ipotesi he l ala sia a pianta rettangolare ed in mananza di informazioni più preise) supponiamo he tale distribuzione sia uniforme in apertura. La portanza vale quindi P p p b, mentre la superfiie alare vale S b, dove è la orda del profilo e b l apertura alare. Quindi aloliamo Q S P b ( p p ) 979 Pa 4897 Nm. 9
MOMENTI E CENTRAGGIO DEL VELIVOLO
 x 1 x ISTITUZIONI DI INGEGNERIA AEROSAZIALE OENTI E CENTRAGGIO VELIVOLO OENTI E CENTRAGGIO DEL VELIVOLO er il alolo delle prestazioni in volo orizzontale rettilineo ed uniforme, il velivolo può essere
x 1 x ISTITUZIONI DI INGEGNERIA AEROSAZIALE OENTI E CENTRAGGIO VELIVOLO OENTI E CENTRAGGIO DEL VELIVOLO er il alolo delle prestazioni in volo orizzontale rettilineo ed uniforme, il velivolo può essere
Fisica dei mezzi trasmissivi Prof. G. Macchiarella Prova del 28 Febbraio 2013
 Fisia dei mezzi trasmissivi Prof. G. Mahiarella Prova del 8 Febbraio 013 1 3 4 non srivere nella zona soprastante COGNOME E NOME MTRICO FIRM Eserizio 1 Un generatore, la ui tensione varia nel tempo ome
Fisia dei mezzi trasmissivi Prof. G. Mahiarella Prova del 8 Febbraio 013 1 3 4 non srivere nella zona soprastante COGNOME E NOME MTRICO FIRM Eserizio 1 Un generatore, la ui tensione varia nel tempo ome
Esercizi sulle reti elettriche in corrente continua
 serizi sulle reti elettrihe in orrente ontinua serizio 1: eterminare la P erogata generatore, e la P R assorita resistore R del iruito in figura 4 Ω Ω Ω 15 Ω 5 Ω Ω R Ω 10 Ω Soluzione: P = 150 W P R =.08
serizi sulle reti elettrihe in orrente ontinua serizio 1: eterminare la P erogata generatore, e la P R assorita resistore R del iruito in figura 4 Ω Ω Ω 15 Ω 5 Ω Ω R Ω 10 Ω Soluzione: P = 150 W P R =.08
Politecnico di Torino Laurea a Distanza in Ingegneria Meccanica Corso di Macchine
 ESERCIZI SVOLTI Sono di seguito svolti due eserizi sulle turbine a vapore assiali, aggiuntivi rispetto a quelli svolti durante il tutorato (i ui testi e i risultati numerii sono riportati alla fine del
ESERCIZI SVOLTI Sono di seguito svolti due eserizi sulle turbine a vapore assiali, aggiuntivi rispetto a quelli svolti durante il tutorato (i ui testi e i risultati numerii sono riportati alla fine del
Spin. La hamiltoniana classica di una particella di massa m e carica q in presenza di un potenziale elettromagnetico (Φ, A) si scrive.
 Spin La hamiltoniana lassia di una partiella di massa m e aria q in presenza di un potenziale elettromagnetio Φ, A si srive Sviluppando il quadrato si ha H = H = p q A 2 + qφ p 2 + A 2 2q A p + qφ 2 Se
Spin La hamiltoniana lassia di una partiella di massa m e aria q in presenza di un potenziale elettromagnetio Φ, A si srive Sviluppando il quadrato si ha H = H = p q A 2 + qφ p 2 + A 2 2q A p + qφ 2 Se
Corso di Meccanica del Volo - Mod. Prestazioni - Prof. Coiro / Nicolosi
 ap.9 AUTONOMIE Quando harles indberg effettuò il suo spettaolare volo transatlantio nel 97 ad egli non importavano poi osì tanto i onetto di veloità massima di rateo di salita o di tempo di salita. a osa
ap.9 AUTONOMIE Quando harles indberg effettuò il suo spettaolare volo transatlantio nel 97 ad egli non importavano poi osì tanto i onetto di veloità massima di rateo di salita o di tempo di salita. a osa
ESAME DI AERODINAMICA 11/02/2015
 ESAME DI AERODINAMICA 11/02/2015 In un profilo alare non simmetrico, al diminuire dell angolo di incidenza, la coordinata del centro di pressione: (a) tende verso il bordo di attacco (b) tende verso il
ESAME DI AERODINAMICA 11/02/2015 In un profilo alare non simmetrico, al diminuire dell angolo di incidenza, la coordinata del centro di pressione: (a) tende verso il bordo di attacco (b) tende verso il
TEORIA SUI LIMITI DEFINIZIONE DI LIMITE FINITO DI UNA FUNZIONE PER X CHE TENDE AD UN VALORE FINITO
 TEORIA SUI LIMITI DEFINIZIONE DI LIMITE FINITO DI UNA FUNZIONE PER X CHE TENDE AD UN VALORE FINITO Si die he, per he tende a, la funzione y=f() ha per ite l e si srive: l = l I( ) ESEMPIO DI VERIFICA DI
TEORIA SUI LIMITI DEFINIZIONE DI LIMITE FINITO DI UNA FUNZIONE PER X CHE TENDE AD UN VALORE FINITO Si die he, per he tende a, la funzione y=f() ha per ite l e si srive: l = l I( ) ESEMPIO DI VERIFICA DI
Dimensionamento rete aria compressa. Impianti Industriali
 Dimensionamento rete aria Impianti Industriali 2-2009 1 1 - Tratto di tubazione ogni tratto dell'impianto di distribuzione dell aria è individuato da lettere e numeri che ne definiscono gli estremi. Con
Dimensionamento rete aria Impianti Industriali 2-2009 1 1 - Tratto di tubazione ogni tratto dell'impianto di distribuzione dell aria è individuato da lettere e numeri che ne definiscono gli estremi. Con
Idraulica e Idrologia: Lezione 16 Agenda del giorno
 Idraulica e Idrologia: Lezione 16 Agenda del giorno Conservazione dell energia Applicazioni del teorema di Bernoulli alle correnti rettilinee Tubo di Pitot Efflusso libero da luci: luce di fondo, luce
Idraulica e Idrologia: Lezione 16 Agenda del giorno Conservazione dell energia Applicazioni del teorema di Bernoulli alle correnti rettilinee Tubo di Pitot Efflusso libero da luci: luce di fondo, luce
Statica dei fluidi & Termodinamica: I principio, gas perfetti e trasformazioni, calore
 Statica dei fluidi & Termodinamica: I principio, gas perfetti e trasformazioni, calore Legge di Stevino La pressione in un liquido a densità costante cresce linearmente con la profondità Il principio di
Statica dei fluidi & Termodinamica: I principio, gas perfetti e trasformazioni, calore Legge di Stevino La pressione in un liquido a densità costante cresce linearmente con la profondità Il principio di
Esempio di progetto di un telaio di c.a.
 q q 1 q 5 8 11 13 h q q 1 q 1 4 7 10 1 h 1 3 6 9 L L 1 L 1 L Fig. 1 Shema statio. La struttura intelaiata in.a. riportata in Fig. 1 è ostituita da travi di sez. 80 m x 4 m e pilastri di sezione 30 m x
q q 1 q 5 8 11 13 h q q 1 q 1 4 7 10 1 h 1 3 6 9 L L 1 L 1 L Fig. 1 Shema statio. La struttura intelaiata in.a. riportata in Fig. 1 è ostituita da travi di sez. 80 m x 4 m e pilastri di sezione 30 m x
TEOREMA DEL CAMPIONAMENTO
 1 TEOREMA DEL CAMPIONAMENTO nota per il orso di Teleomuniazioni a ura di F. Benedetto G. Giunta 1. Introduzione Il proesso di ampionamento è di enorme importanza ai fini della realizzazione dei dispositivi
1 TEOREMA DEL CAMPIONAMENTO nota per il orso di Teleomuniazioni a ura di F. Benedetto G. Giunta 1. Introduzione Il proesso di ampionamento è di enorme importanza ai fini della realizzazione dei dispositivi
Moto vario elastico: fenomeno del colpo d ariete
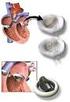 Moto vario elastio: fenomeno del olpo d ariete 1. Desrizione del fenomeno Si onsideri un semplie impianto ostituito da un serbatoio di grande ampiezza in modo tale he in esso il livello di ario rimanga
Moto vario elastio: fenomeno del olpo d ariete 1. Desrizione del fenomeno Si onsideri un semplie impianto ostituito da un serbatoio di grande ampiezza in modo tale he in esso il livello di ario rimanga
PRESSIONE ATMOSFERICA
 PRESSIONE ATMOSFERICA Peso della colonna di aria che ci sovrasta di altezza quindi pari all altezza dell atmosfera p atm = d g h con d densita aria h altezza atmosfera 197 MISURA DELLA PRESSIONE ATMOSFERICA:
PRESSIONE ATMOSFERICA Peso della colonna di aria che ci sovrasta di altezza quindi pari all altezza dell atmosfera p atm = d g h con d densita aria h altezza atmosfera 197 MISURA DELLA PRESSIONE ATMOSFERICA:
Meccanica dei Fluidi. stati di aggregazione della materia: solidi liquidi gas. fluidi assumono la forma del contenitore
 Meccanica dei luidi stati di aggregazione della materia: solidi liquidi gas fluidi assumono la forma del contenitore Caratteristiche di un fluido LUIDO sostanza senza forma propria (assume la forma del
Meccanica dei luidi stati di aggregazione della materia: solidi liquidi gas fluidi assumono la forma del contenitore Caratteristiche di un fluido LUIDO sostanza senza forma propria (assume la forma del
4. Esercitazione 4: Dimensionamento del primo stadio di un compressore assiale
 4. Esercitazione 4: Dimensionamento del primo stadio di un compressore assiale Lo scopo della presente esercitazione è il dimensionamento del primo stadio di un compressore assiale. Con riferimento alla
4. Esercitazione 4: Dimensionamento del primo stadio di un compressore assiale Lo scopo della presente esercitazione è il dimensionamento del primo stadio di un compressore assiale. Con riferimento alla
INTRODUZIONE ALLA TERMODINAMICA. Supponiamo di voler studiare il comportamento di una determinata quantità di gas contenuta
 INTRODUZIONE ALLA TERMODINAMICA Supponiamo di voler studiare il comportamento di una determinata quantità di gas contenuta in un recipiente, ad esempio 5g di ossigeno. Dato l elevato numero di molecole
INTRODUZIONE ALLA TERMODINAMICA Supponiamo di voler studiare il comportamento di una determinata quantità di gas contenuta in un recipiente, ad esempio 5g di ossigeno. Dato l elevato numero di molecole
CORSO DI LAUREA IN SCIENZE BIOLOGICHE Prova di FISICA del 9 novembre 2004
 ORSO DI LURE IN SIENZE IOLOGIHE Prova di FISI del 9 novembre 004 1) Una particella di massa m= 0.5 kg viene lanciata dalla base di un piano inclinato O con velocità iniziale v o = 4 m/s, parallela al piano.
ORSO DI LURE IN SIENZE IOLOGIHE Prova di FISI del 9 novembre 004 1) Una particella di massa m= 0.5 kg viene lanciata dalla base di un piano inclinato O con velocità iniziale v o = 4 m/s, parallela al piano.
Peso della colonna di aria che ci sovrasta di altezza quindi pari all altezza dell atmosfera
 PRESSIONE ATMOSFERICA Peso della colonna di aria che ci sovrasta di altezza quindi pari all altezza dell atmosfera p atm = d g h con d densita aria h altezza atmosfera 1 MISURA DELLA PRESSIONE ATMOSFERICA:
PRESSIONE ATMOSFERICA Peso della colonna di aria che ci sovrasta di altezza quindi pari all altezza dell atmosfera p atm = d g h con d densita aria h altezza atmosfera 1 MISURA DELLA PRESSIONE ATMOSFERICA:
PER ESERCITARSI Parte 2. Esercizi su Corpo rigido, variabili angolari, momenti, fluidi, termodinamica
 PER ESERCITARSI Parte 2 Esercizi su Corpo rigido, variabili angolari, momenti, fluidi, termodinamica ESERCIZIO n.1 Due forze uguali ed opposte sono applicate ad un oggetto lungo rette di azione tra loro
PER ESERCITARSI Parte 2 Esercizi su Corpo rigido, variabili angolari, momenti, fluidi, termodinamica ESERCIZIO n.1 Due forze uguali ed opposte sono applicate ad un oggetto lungo rette di azione tra loro
Protezione Civile - Regione Friuli Venezia Giulia. Protezione Civile - Regione Friuli Venezia Giulia
 1 Principi di idraulica Definizioni MECCANICA DEI FLUIDI È il ramo della fisica che studia le proprietà dei fluidi, cioè liquidi, vapori e gas. Idrostatica Studia i fluidi in quiete Idrodinamica Studia
1 Principi di idraulica Definizioni MECCANICA DEI FLUIDI È il ramo della fisica che studia le proprietà dei fluidi, cioè liquidi, vapori e gas. Idrostatica Studia i fluidi in quiete Idrodinamica Studia
Scambiatori di calore
 Fisia enia G. Grazzini UNIVERSIA DI FIRENZE Sambiatori di alore Con il termine sambiatori di alore indihiamo una apparehiatura in ui si ha trasmissione di alore da un luido ad un altro. In ampo termotenio
Fisia enia G. Grazzini UNIVERSIA DI FIRENZE Sambiatori di alore Con il termine sambiatori di alore indihiamo una apparehiatura in ui si ha trasmissione di alore da un luido ad un altro. In ampo termotenio
TERMODINAMICA E TERMOFLUIDODINAMICA TRASMISSIONE DEL CALORE PER CONVEZIONE
 TERMODINAMICA E TERMOFUIDODINAMICA TRASMISSIONE DE CAORE PER CONVEZIONE h C T Q ( T ) m ( ) ρ = V T V ost T = A T S Trasmissione del alore per onvezione Indie 1. a onvezione termia forzata e naturale 2.
TERMODINAMICA E TERMOFUIDODINAMICA TRASMISSIONE DE CAORE PER CONVEZIONE h C T Q ( T ) m ( ) ρ = V T V ost T = A T S Trasmissione del alore per onvezione Indie 1. a onvezione termia forzata e naturale 2.
DIMENSIONAMENTO DELLA STAZIONE DI SOLLEVAMENTO A SERVIZIO DI UN SOTTOPASSO
 DIMENSIONAMENTO DELLA STAZIONE DI SOLLEVAMENTO A SERVIZIO DI UN SOTTOPASSO Appliazione: Dimensionare l impianto di sollevamento per il sottopasso illustrato alle figure 3.60 e 3.61. Elaborazione delle
DIMENSIONAMENTO DELLA STAZIONE DI SOLLEVAMENTO A SERVIZIO DI UN SOTTOPASSO Appliazione: Dimensionare l impianto di sollevamento per il sottopasso illustrato alle figure 3.60 e 3.61. Elaborazione delle
Stati di aggregazione della materia. Luca Stanco - Fisica 2015/16 Corso di Laurea in Igiene Dentale - Lezione 5
 Fluidi 1 Stati di aggregazione della materia 2 Densità (II) n La densità assoluta è definita dal rapporto tra la massa M di una sostanza omogenea ed il suo volume V: d = M / V n Nel sistema internazionale
Fluidi 1 Stati di aggregazione della materia 2 Densità (II) n La densità assoluta è definita dal rapporto tra la massa M di una sostanza omogenea ed il suo volume V: d = M / V n Nel sistema internazionale
Densita. FLUIDI : liquidi o gas. macroscop.:
 6-SBAC Fisica 1/10 FLUIDI : liquidi o gas macroscop.: microscop.: sostanza che prende la forma del contenitore che la occupa insieme di molecole tenute insieme da deboli forze di coesione (primi vicini)
6-SBAC Fisica 1/10 FLUIDI : liquidi o gas macroscop.: microscop.: sostanza che prende la forma del contenitore che la occupa insieme di molecole tenute insieme da deboli forze di coesione (primi vicini)
CALCOLO DELLA RESISTENZA DI UN PROFILO
 CACOO DEA RESISTENZA DI UN PROFIO A cura di: Andrea Fogante Davide Gambarara Emanuel Gomez Antonio Grande Ivan Josipovic Anwar Koshakji allievi aerospaziali del anno, corso di Fluidodinamica I 1 Prefazione
CACOO DEA RESISTENZA DI UN PROFIO A cura di: Andrea Fogante Davide Gambarara Emanuel Gomez Antonio Grande Ivan Josipovic Anwar Koshakji allievi aerospaziali del anno, corso di Fluidodinamica I 1 Prefazione
Unità Didattica 1. Sistemi di Numerazione
 Unità Didattia Sistemi di Numerazione Sistemi di Numerazione Posizionali Criterio per la rappresentazione di un insieme infinito di numeri mediante un insieme limitato di simoli. Un sistema di numerazione
Unità Didattia Sistemi di Numerazione Sistemi di Numerazione Posizionali Criterio per la rappresentazione di un insieme infinito di numeri mediante un insieme limitato di simoli. Un sistema di numerazione
Sussidi didattici per il corso di PROGETTAZIONE, COSTRUZIONI E IMPIANTI. Prof. Ing. Francesco Zanghì ELEMENTI DI IDRAULICA AGGIORNAMENTO 26/11/2013
 Sussidi didattici per il corso di PROGETTAZIONE, COSTRUZIONI E IMPIANTI Prof. Ing. Francesco Zanghì ELEMENTI DI IDRAULICA AGGIORNAMENTO 26/11/2013 L'idraulica è la scienza che studia l'utilizzazione dei
Sussidi didattici per il corso di PROGETTAZIONE, COSTRUZIONI E IMPIANTI Prof. Ing. Francesco Zanghì ELEMENTI DI IDRAULICA AGGIORNAMENTO 26/11/2013 L'idraulica è la scienza che studia l'utilizzazione dei
Pag. 1. Esercizi sui Diagrammi di Flusso. Stampa di alcuni numeri interi
 Università degli studi di Parma Dipartimento di Ingegneria dell Informazione Informatia a.a. 202/ Stampa di aluni numeri interi Informatia Faoltà di Mediina Veterinaria a.a. 202/ prof. Stefano Cagnoni
Università degli studi di Parma Dipartimento di Ingegneria dell Informazione Informatia a.a. 202/ Stampa di aluni numeri interi Informatia Faoltà di Mediina Veterinaria a.a. 202/ prof. Stefano Cagnoni
Esperienza n 6: COSTANTE di PLANCK
 Laboratorio IV Esperienza n 6: COSTANTE di PLANCK Esperienza n 6: COSTANTE di PLANCK Misura della ostante di Plank Inviando su un fotoatodo fotoni di energia hν, vengono estratti elettroni on una energia
Laboratorio IV Esperienza n 6: COSTANTE di PLANCK Esperienza n 6: COSTANTE di PLANCK Misura della ostante di Plank Inviando su un fotoatodo fotoni di energia hν, vengono estratti elettroni on una energia
IDRAULICA STUDIA I FLUIDI, IL LORO EQUILIBRIO E IL LORO MOVIMENTO
 A - IDRAULICA IDRAULICA STUDIA I FLUIDI, IL LORO EQUILIBRIO E IL LORO MOVIMENTO FLUIDO CORPO MATERIALE CHE, A CAUSA DELLA ELEVATA MOBILITA' DELLE PARTICELLE CHE LO COMPONGONO, PUO' SUBIRE RILEVANTI VARIAZIONI
A - IDRAULICA IDRAULICA STUDIA I FLUIDI, IL LORO EQUILIBRIO E IL LORO MOVIMENTO FLUIDO CORPO MATERIALE CHE, A CAUSA DELLA ELEVATA MOBILITA' DELLE PARTICELLE CHE LO COMPONGONO, PUO' SUBIRE RILEVANTI VARIAZIONI
Dall idrostatica alla idrodinamica. Fisica con Elementi di Matematica 1
 Dall idrostatica alla idrodinamica Fisica con Elementi di Matematica 1 Concetto di Campo Insieme dei valori che una certa grandezza fisica assume in ogni punto di una regione di spazio. Esempio: Consideriamo
Dall idrostatica alla idrodinamica Fisica con Elementi di Matematica 1 Concetto di Campo Insieme dei valori che una certa grandezza fisica assume in ogni punto di una regione di spazio. Esempio: Consideriamo
PROBLEMI E QUESITI DI TERMOLOGIA (SOLUZIONI)
 1 PROBLEMI E QUESITI DI TERMOLOGIA (SOLUZIONI) Qui di seguito viene riportata la risoluzione dei problemi presentati nel file Unità omonimo (enunciati). Si raccomanda di prestare molta attenzione ai ragionamenti
1 PROBLEMI E QUESITI DI TERMOLOGIA (SOLUZIONI) Qui di seguito viene riportata la risoluzione dei problemi presentati nel file Unità omonimo (enunciati). Si raccomanda di prestare molta attenzione ai ragionamenti
Test di autovalutazione
 Test di autovalutazione 0 0 0 0 40 50 0 70 80 90 00 n Il mio punteggio, in entesimi, è n Rispondi a ogni quesito segnando una sola delle 5 alternative. n Confronta le tue risposte on le soluzioni. n Colora,
Test di autovalutazione 0 0 0 0 40 50 0 70 80 90 00 n Il mio punteggio, in entesimi, è n Rispondi a ogni quesito segnando una sola delle 5 alternative. n Confronta le tue risposte on le soluzioni. n Colora,
UNIVERSITÀ DEGLI STUDI DI GENOVA FACOLTÀ DI INGEGNERIA MODULO DIDATTICO N 5
 UNIVERSITÀ DEGLI STUDI DI GENOVA FACOLTÀ DI INGEGNERIA Esercitazioni di Fisica Tecnica Ambientale 1 CORSO DI LAUREA INGEGNERIA CIVILE EDILE E AMBIENTE E TERRITORIO (Dott. Ing. Paolo Cavalletti) MODULO
UNIVERSITÀ DEGLI STUDI DI GENOVA FACOLTÀ DI INGEGNERIA Esercitazioni di Fisica Tecnica Ambientale 1 CORSO DI LAUREA INGEGNERIA CIVILE EDILE E AMBIENTE E TERRITORIO (Dott. Ing. Paolo Cavalletti) MODULO
FISICA per SCIENZE BIOLOGICHE A.A. 2013/2014 1) FLUIDI V= 5 dm3 a= 2 m/s2 aria = g / cm 3 Spinta Archimedea Tensione della fune
 FISICA per SCIENZE BIOLOGICHE A.A. 2013/2014 II Compitino 26 Giugno 2014 1) FLUIDI Un bambino trattiene un palloncino, tramite una sottile fune. Il palloncino ha volume V= 5 dm 3. La sua massa, senza il
FISICA per SCIENZE BIOLOGICHE A.A. 2013/2014 II Compitino 26 Giugno 2014 1) FLUIDI Un bambino trattiene un palloncino, tramite una sottile fune. Il palloncino ha volume V= 5 dm 3. La sua massa, senza il
Prova scritta di Fisica Generale I Corso di studio in Astronomia 16 luglio 2013
 Prova scritta di Fisica Generale I Corso di studio in Astronomia 16 luglio 013 Problema 1 Un cubo di legno di densità ρ = 800 kg/m 3 e lato a = 50 cm è inizialmente in quiete, appoggiato su un piano orizzontale.
Prova scritta di Fisica Generale I Corso di studio in Astronomia 16 luglio 013 Problema 1 Un cubo di legno di densità ρ = 800 kg/m 3 e lato a = 50 cm è inizialmente in quiete, appoggiato su un piano orizzontale.
Fluidi (FMLP: Cap. 11 Meccanica dei fluidi)
 In un fluido Fluidi (FMLP: Cap. 11 Meccanica dei fluidi) le molecole non sono vincolate a posizioni fisse a differenza di quello che avviene nei solidi ed in particolare nei cristalli Il numero di molecole
In un fluido Fluidi (FMLP: Cap. 11 Meccanica dei fluidi) le molecole non sono vincolate a posizioni fisse a differenza di quello che avviene nei solidi ed in particolare nei cristalli Il numero di molecole
Equazioni di secondo grado intere letterali
 Equazioni di seondo grado intere letterali Esempio. k ) x k + )x + k + 0 a k b k + ) k + Disussione. Se k 0 k l equazione si abbassa di grado. Disutiamo il aso a 0 aso in ui l equazione diventa di primo
Equazioni di seondo grado intere letterali Esempio. k ) x k + )x + k + 0 a k b k + ) k + Disussione. Se k 0 k l equazione si abbassa di grado. Disutiamo il aso a 0 aso in ui l equazione diventa di primo
PROFILI DI CORRENTE IN MOTO PERMANENTE
 PROFILI DI CORRENTE IN MOTO PERMANENTE I lassii approi relativi al dimensionamento ed alla verifia delle analizzazioni per fognatura e, più in generale, delle orrenti a pelo libero, muovono dall'ipotesi
PROFILI DI CORRENTE IN MOTO PERMANENTE I lassii approi relativi al dimensionamento ed alla verifia delle analizzazioni per fognatura e, più in generale, delle orrenti a pelo libero, muovono dall'ipotesi
Movimento nei fluidi : prima parte Applicazioni della meccanica dei fluidi
 In questa sezione vi sono argomenti he non fanno normalmente parte di un orso tradizionale di Fisia. Si tratta di una breve esursione nei viini ampi della biologia e della zoologia: appliazioni delle leggi
In questa sezione vi sono argomenti he non fanno normalmente parte di un orso tradizionale di Fisia. Si tratta di una breve esursione nei viini ampi della biologia e della zoologia: appliazioni delle leggi
16 L INTEGRALE INDEFINITO
 9. Integrali immediati 6 L INTEGRALE INDEFINITO Riassumiamo le puntate preedenti: si die INTEGRALE INDEFINITO di una funzione f ( ), la famiglia di tutte e sole quelle funzioni la ui derivata è uguale
9. Integrali immediati 6 L INTEGRALE INDEFINITO Riassumiamo le puntate preedenti: si die INTEGRALE INDEFINITO di una funzione f ( ), la famiglia di tutte e sole quelle funzioni la ui derivata è uguale
Moto Monodimensionale in Condotti. Esercizi
 Moto Monodimensionale in Condotti Fluido Comprimibile Esercizi 2D axisymmetric, ideally contoured nozzle upon startup. http://flowgallery.stanford.edu/research.html Moti Monodimensionali - Applicazioni
Moto Monodimensionale in Condotti Fluido Comprimibile Esercizi 2D axisymmetric, ideally contoured nozzle upon startup. http://flowgallery.stanford.edu/research.html Moti Monodimensionali - Applicazioni
Meccanica dei Fluidi: statica e dinamica
 Meccanica dei Fluidi: statica e dinamica Stati della materia (classificazione assai approssimativa!) Solido: ha una forma propria, poco compressibile, alta densità Liquido: non ha una forma propria, poco
Meccanica dei Fluidi: statica e dinamica Stati della materia (classificazione assai approssimativa!) Solido: ha una forma propria, poco compressibile, alta densità Liquido: non ha una forma propria, poco
La distribuzione delle pressioni all interno di un fluido in quiete, pesante e incomprimibile, è governata da:
 Statica Distribuzione delle pressioni La distribuzione delle pressioni all interno di un fluido in quiete, pesante e incomprimibile, è governata da: z+p/γ= cost LEE DI STEVIN Il valore della costante è
Statica Distribuzione delle pressioni La distribuzione delle pressioni all interno di un fluido in quiete, pesante e incomprimibile, è governata da: z+p/γ= cost LEE DI STEVIN Il valore della costante è
CORSO DI FISICA dispensa n.2 MECCANICA DEI FLUIDI
 CORSO DI FISICA dispensa n.2 MECCANICA DEI FLUIDI Meccanica dei fluidi La meccanica dei fluidi si occupa sia della statica (idrostatica) sia del movimento (idrodinamica) dei fluidi. Per fluidi si intendono
CORSO DI FISICA dispensa n.2 MECCANICA DEI FLUIDI Meccanica dei fluidi La meccanica dei fluidi si occupa sia della statica (idrostatica) sia del movimento (idrodinamica) dei fluidi. Per fluidi si intendono
FISICA. Elaborazione dei dati sperimentali. Autore: prof. Pappalardo Vincenzo docente di Matematica e Fisica
 FISICA Elaborazione dei dati sperimentali Autore: prof. Pappalardo Vincenzo docente di Matematica e Fisica LE GRANDEZZE FISICHE Una grandezza fisica è una quantità che può essere misurata con uno strumento
FISICA Elaborazione dei dati sperimentali Autore: prof. Pappalardo Vincenzo docente di Matematica e Fisica LE GRANDEZZE FISICHE Una grandezza fisica è una quantità che può essere misurata con uno strumento
Sistemi Gassosi. GAS = specie che occupa tutto lo spazio disponibile. VOLUME = spazio occupato si misura in: m 3, L (1L = 1dm 3 )
 Sistemi Gassosi GAS = specie che occupa tutto lo spazio disponibile VOLUME = spazio occupato si misura in: m 3, L (1L = 1dm 3 ) PRESSIONE = forza per unità di superficie Unità di misura: Forza Newton (N)
Sistemi Gassosi GAS = specie che occupa tutto lo spazio disponibile VOLUME = spazio occupato si misura in: m 3, L (1L = 1dm 3 ) PRESSIONE = forza per unità di superficie Unità di misura: Forza Newton (N)
1) Per quale valore minimo della velocità angolare iniziale il cilindro riesce a compiere un giro completo.
 Esame di Fisica per Ingegneria Elettronica e delle Telecomunicazioni (Parte I): 04-02-2016 Problema 1. Un punto materiale si muove nel piano su una guida descritta dall equazione y = sin kx [ = 12m, k
Esame di Fisica per Ingegneria Elettronica e delle Telecomunicazioni (Parte I): 04-02-2016 Problema 1. Un punto materiale si muove nel piano su una guida descritta dall equazione y = sin kx [ = 12m, k
P3 CIRCUITI RISONANTI E AMPLIFICATORI SELETTIVI.
 P CICUITI ISONANTI E AMPIFICATOI SEETTIVI. P. Un iruito C serie è alimentato alla frequenza di risonanza da un generatore a tensione ostante, avente f.e.m. di valore iae E, V. a bobina, di induttanza 4,5
P CICUITI ISONANTI E AMPIFICATOI SEETTIVI. P. Un iruito C serie è alimentato alla frequenza di risonanza da un generatore a tensione ostante, avente f.e.m. di valore iae E, V. a bobina, di induttanza 4,5
Chimica e Tecnologia Farmaceutiche Esercitazioni di Fisica a.a Emanuele Biolcati
 Esercitazione 5 Dr. Monica Casale Chimica e Tecnologia Farmaceutiche Esercitazioni di Fisica a.a. 2010-2011 Emanuele Biolcati Ringraziamenti speciali a Monica Casale per la preparazione delle slides Fluidi
Esercitazione 5 Dr. Monica Casale Chimica e Tecnologia Farmaceutiche Esercitazioni di Fisica a.a. 2010-2011 Emanuele Biolcati Ringraziamenti speciali a Monica Casale per la preparazione delle slides Fluidi
Meccanica dei fluidi. ! definizioni; ! statica dei fluidi (principio di Archimede); ! dinamica dei fluidi (teorema di Bernoulli).
 Meccanica dei fluidi! definizioni;! statica dei fluidi (principio di Archimede);! dinamica dei fluidi (teorema di Bernoulli). [importanti applicazioni in biologia / farmacia : ex. circolazione del sangue]
Meccanica dei fluidi! definizioni;! statica dei fluidi (principio di Archimede);! dinamica dei fluidi (teorema di Bernoulli). [importanti applicazioni in biologia / farmacia : ex. circolazione del sangue]
Lezione 9. Statica dei fluidi
 Lezione 9 Statica dei fluidi Meccanica dei fluidi Un fluido e un corpo che non ha una forma definita, ma che, se e contenuto da un contenitore solido, tende a occupare (riempire) una parte o tutto il volume
Lezione 9 Statica dei fluidi Meccanica dei fluidi Un fluido e un corpo che non ha una forma definita, ma che, se e contenuto da un contenitore solido, tende a occupare (riempire) una parte o tutto il volume
Accoppiatore direzionale
 Aoppiatore direzionale 1 Rete 4 porte 3 4 Un aoppiatore direzionale ideale è un giunzione a 4 bohe on Adattamento alle porte quando sono hiuse sul ario di riferimento (ioè S 11 =S =S 33 =S 44 =) Due oppie
Aoppiatore direzionale 1 Rete 4 porte 3 4 Un aoppiatore direzionale ideale è un giunzione a 4 bohe on Adattamento alle porte quando sono hiuse sul ario di riferimento (ioè S 11 =S =S 33 =S 44 =) Due oppie
15/04/2014. Serway, Jewett Principi di Fisica IV Ed. Capitolo 15
 Serway, Jewett Principi di Fisica IV Ed. Capitolo 15 Un fluido è un insieme di molecole tenute insieme da deboli forze di coesione e da forze esercitate dalla parete del contenitore (possono essere sia
Serway, Jewett Principi di Fisica IV Ed. Capitolo 15 Un fluido è un insieme di molecole tenute insieme da deboli forze di coesione e da forze esercitate dalla parete del contenitore (possono essere sia
Misure di grandezze elettriche fondamentali
 Misure di grandezze elettrihe fondamentali - Misure di grandezze elettrihe fondamentali - ensione e orrente Il iruito elettrio La tensione e la orrente sono le grandezze elettrihe più importanti. A queste
Misure di grandezze elettrihe fondamentali - Misure di grandezze elettrihe fondamentali - ensione e orrente Il iruito elettrio La tensione e la orrente sono le grandezze elettrihe più importanti. A queste
GEOMETRIA ANALITICA 8 LE CONICHE
 GEOMETRIA ANALITICA 8 LE CONICHE Tra tutte le urve, ne esistono quattro partiolari he vengono hiamate onihe perhé sono ottenute tramite l intersezione di una superfiie i-onia on un piano. A seonda della
GEOMETRIA ANALITICA 8 LE CONICHE Tra tutte le urve, ne esistono quattro partiolari he vengono hiamate onihe perhé sono ottenute tramite l intersezione di una superfiie i-onia on un piano. A seonda della
Il prodotto della pressione per il volume di una determinata massa gassosa è direttamente proporzionale alla temperatura assoluta: PV = KT
 ESERCITAZIONE 5 LEGGI DEI GAS Le leggi che governano i rapporti che si stabiliscono tra massa, volume, temperatura e pressione di un gas, sono leggi limite, riferite cioè ad un comportamento ideale, cui
ESERCITAZIONE 5 LEGGI DEI GAS Le leggi che governano i rapporti che si stabiliscono tra massa, volume, temperatura e pressione di un gas, sono leggi limite, riferite cioè ad un comportamento ideale, cui
Corso di MECCANICA DEL VOLO. Prof. F. Nicolosi. Corso di Meccanica del Volo - Mod. Prestazioni - Prof. F. Nicolosi
 Corso di MECCANICA DEL VOLO Modulo Prestazioni CAP 1 Atmosfera e Misura della Velocità Prof. F. Nicolosi 1 ARIA Proprietà del gas: - Pressione - Temperatura - Densità 2 ATMOSFERA DRY ATMOSHERE Atmosfera
Corso di MECCANICA DEL VOLO Modulo Prestazioni CAP 1 Atmosfera e Misura della Velocità Prof. F. Nicolosi 1 ARIA Proprietà del gas: - Pressione - Temperatura - Densità 2 ATMOSFERA DRY ATMOSHERE Atmosfera
Don Bosco 2014/15, Classe 3B - Primo compito in classe di Fisica
 Don Bosco 014/15, Classe B - Primo compito in classe di Fisica 1. Enuncia il Teorema dell Energia Cinetica. Soluzione. Il lavoro della risultante delle forze agenti su un corpo che si sposta lungo una
Don Bosco 014/15, Classe B - Primo compito in classe di Fisica 1. Enuncia il Teorema dell Energia Cinetica. Soluzione. Il lavoro della risultante delle forze agenti su un corpo che si sposta lungo una
Liceo Scientifico Marconi Delpino. Classi 1^ Materia: Fisica
 Liceo Scientifico Marconi Delpino Classi 1^ Materia: Fisica Compiti per le vacanze estive Gli alunni promossi devono svolgere soltanto gli esercizi del libro di testo, gli alunni con sospensione del giudizio
Liceo Scientifico Marconi Delpino Classi 1^ Materia: Fisica Compiti per le vacanze estive Gli alunni promossi devono svolgere soltanto gli esercizi del libro di testo, gli alunni con sospensione del giudizio
Soluzione: In direzione verticale non c è movimento, perciò F N mg = 0. Quindi, in ogni caso, la forza normale è pari a 24.5 N.
 Un oggetto con massa pari a 2500 g è appoggiato su un pavimento orizzontale. Il coefficiente d attrito statico è s = 0.80 e il coefficiente d attrito dinamico è k = 0.60. Determinare la forza d attrito
Un oggetto con massa pari a 2500 g è appoggiato su un pavimento orizzontale. Il coefficiente d attrito statico è s = 0.80 e il coefficiente d attrito dinamico è k = 0.60. Determinare la forza d attrito
Esercitazione VI - Leggi della dinamica III
 Esercitazione VI - Leggi della dinamica III Esercizio 1 I corpi 1, 2 e 3 rispettivamente di massa m 1 = 2kg, m 2 = 3kg ed m 3 = 4kg sono collegati come in figura tramite un filo inestensibile. Trascurando
Esercitazione VI - Leggi della dinamica III Esercizio 1 I corpi 1, 2 e 3 rispettivamente di massa m 1 = 2kg, m 2 = 3kg ed m 3 = 4kg sono collegati come in figura tramite un filo inestensibile. Trascurando
CORSO DI LAUREA IN SCIENZE BIOLOGICHE Secondo Compitino di FISICA 15 giugno 2012
 CORSO DI LAUREA IN SCIENZE BIOLOGICHE Secondo Compitino di FISICA 15 giugno 01 1) FLUIDI: Un blocchetto di legno (densità 0,75 g/ cm 3 ) di dimensioni esterne (10x0x5)cm 3 è trattenuto mediante una fune
CORSO DI LAUREA IN SCIENZE BIOLOGICHE Secondo Compitino di FISICA 15 giugno 01 1) FLUIDI: Un blocchetto di legno (densità 0,75 g/ cm 3 ) di dimensioni esterne (10x0x5)cm 3 è trattenuto mediante una fune
Facoltà di Farmacia - Anno Accademico A 18 febbraio 2010 primo esonero
 Facoltà di Farmacia - Anno Accademico 2009-2010 A 18 febbraio 2010 primo esonero Corso di Laurea: Laurea Specialistica in FARMACIA Nome: Cognome: Matricola Aula: Canale: Docente: Riportare sul presente
Facoltà di Farmacia - Anno Accademico 2009-2010 A 18 febbraio 2010 primo esonero Corso di Laurea: Laurea Specialistica in FARMACIA Nome: Cognome: Matricola Aula: Canale: Docente: Riportare sul presente
Modelli di base per la politica economica
 Modelli di base per la politia eonomia Capitolo Marella Mulino Modelli di base per la politia eonomia Corso di Politia eonomia a.a. 22-23 Modelli di base per la politia eonomia Capitolo Capitolo Modello
Modelli di base per la politia eonomia Capitolo Marella Mulino Modelli di base per la politia eonomia Corso di Politia eonomia a.a. 22-23 Modelli di base per la politia eonomia Capitolo Capitolo Modello
Lezione 2 FORZE AGENTI SU UN CONTINUO (FLUIDO)
 Appunti dei corsi di Idraulica 1 e Idrodinamica 1 Lezione FORZE AGENTI SU UN CONTINUO (FLUIDO) Le molecole che costituiscono la materia esercitano delle forze sulle molecole circostanti che vengono suddivise
Appunti dei corsi di Idraulica 1 e Idrodinamica 1 Lezione FORZE AGENTI SU UN CONTINUO (FLUIDO) Le molecole che costituiscono la materia esercitano delle forze sulle molecole circostanti che vengono suddivise
Geometria figure piane Raccolta di esercizi
 Geometria figure piane Raccolta di esercizi RETTANGOLO 1. Calcola il perimetro e l area di un rettangolo le cui dimensioni misurano rispettivamente 13 cm e 22 cm. [70 cm; 286 cm 2 ] 2. Un rettangolo ha
Geometria figure piane Raccolta di esercizi RETTANGOLO 1. Calcola il perimetro e l area di un rettangolo le cui dimensioni misurano rispettivamente 13 cm e 22 cm. [70 cm; 286 cm 2 ] 2. Un rettangolo ha
Applicando al pistone una forza esterna, si esercita una pressione p ext sul fluido immediatamente sottostante al pistone.
 IL PRINCIPIO DI PASCAL Consideriamo un fluido incomprimibile come in figura contenuto in un cilindro chiuso superiormente da un pistone. Applicando al pistone una forza esterna, si esercita una pressione
IL PRINCIPIO DI PASCAL Consideriamo un fluido incomprimibile come in figura contenuto in un cilindro chiuso superiormente da un pistone. Applicando al pistone una forza esterna, si esercita una pressione
Corso di fisica tecnica ambientale ESERCIZI SULLE ENERGIE RINNOVABILI. Prof. Davide Astiaso Garcia Prof. Marco Cecconi
 Faoltà di rhitettura - Laurea magistrale in rhitettura a ilo unio Corso di fisia tenia ambientale ESERCIZI SULLE ENERGIE RINNOVBILI Prof. Davide stiaso Garia Prof. Maro Ceoni Dimensionamento solare termio
Faoltà di rhitettura - Laurea magistrale in rhitettura a ilo unio Corso di fisia tenia ambientale ESERCIZI SULLE ENERGIE RINNOVBILI Prof. Davide stiaso Garia Prof. Maro Ceoni Dimensionamento solare termio
Esercitazione 8: Aria Umida
 Esercitazione 8: Umida 8.1) Dell aria alla temperatura di 40 C e pressione atmosferica ha una temperatura di bulbo umido di 30 C. Calcolare l umidità assoluta, l umidità relativa e il punto di rugiada
Esercitazione 8: Umida 8.1) Dell aria alla temperatura di 40 C e pressione atmosferica ha una temperatura di bulbo umido di 30 C. Calcolare l umidità assoluta, l umidità relativa e il punto di rugiada
L invarianza della velocità della luce. Dai postulati della teoria della relatività alle equazioni di Lorentz. (2) R
 L inarianza della eloità della lue. Dai postulati della teoria della relatiità alle equazioni di Lorentz. Conferma sperimentale dell inarianza della eloità della lue. Relazioni tra spostamenti e eloità
L inarianza della eloità della lue. Dai postulati della teoria della relatiità alle equazioni di Lorentz. Conferma sperimentale dell inarianza della eloità della lue. Relazioni tra spostamenti e eloità
15/04/2014. Serway, Jewett Principi di Fisica IV Ed. Capitolo 8. Generalizziamo, considerando due particelle interagenti.
 Serway, Jewett Principi di Fisica IV Ed. Capitolo 8 Esempio arciere su una superficie ghiacciata che scocca la freccia: l arciere (60 kg) esercita una forza sulla freccia 0.5 kg (che parte in avanti con
Serway, Jewett Principi di Fisica IV Ed. Capitolo 8 Esempio arciere su una superficie ghiacciata che scocca la freccia: l arciere (60 kg) esercita una forza sulla freccia 0.5 kg (che parte in avanti con
