Modello atomico. di Bohr
|
|
|
- Agata Napoli
- 9 anni fa
- Просмотров:
Транскрипт
1 Modello atomico di Bohr
2 Bohr e lo spettro a righe dell Idrogeno Visto il successo ottenuto nella risoluzione del problema del corpo nero e dell'effetto fotoelettrico, attraverso l'introduzione nel formalismo matematico della costante di Planck e del concetto di fotone, il fisico danese Niels Bohr decise di tentare la stessa strada anche per risolvere il problema degli spettri a righe. Poiché lo spettro a righe è caratteristico di ciascun tipo di atomo era verosimile che esso dipendesse dalla struttura atomica e dunque fosse necessario intervenire modificando il modello di Rutherford.
3 Bohr e lo spettro a righe dell Idrogeno Bohr prese in considerazione l atomo di Idrogeno, il cui spettro è particolarmente semplice (serie di Balmer), ed introdusse alcune ipotesi arbitrarie in modo da far intervenire all'interno della struttura atomica la costante h di Planck e il concetto di fotone.
4 Prima ipotesi di Bohr Esiste uno stato stazionario dell'atomo caratterizzato da particolari orbite circolari lungo le quali gli elettroni si muovono senza emettere radiazioni elettromagnetiche. Gli elettroni che percorrono tali orbite stazionarie possiedono una certa quantità ben definita di energia detta livello energetico dell orbita, data dalla somma dell energia cinetica e potenziale.
5 Prima ipotesi di Bohr L elettrone che si muove su un orbita di raggio r è soggetto alla forza coulombiana del nucleo, pari alla forza centrifuga Eguagliandole si può esplicitare il raggio r e verificare che l elettrone si può muovere su qualsiasi orbita. Il raggio è inversamente proporzionale all energia cinetica dell elettrone
6 Seconda ipotesi di Bohr Tra le infinite orbite possibili sono permesse ed esistono solo quelle che soddisfano la seguente relazione mvr = momento angolare orbitale dell elettrone h/π = costante di Planck standardizzata (o normalizzata) = (accatagliato) n = numero quantico principale = 1,, 3, 4, Viene cioè arbitrariamente introdotta una condizione di quantizzazione del momento angolare orbitale dell elettrone che può assumere solo valori multipli interi di accatagliato. Il momento angolare quantizzato condiziona i valori che possono assumere il raggio delle orbite e l energia totale (livello energetico) dell elettrone. Raggi e livelli energetici risultano pertanto anch essi quantizzati in funzione di n.
7 Raggi e livelli energetici quantizzati Ricavando la velocità dalla relazione di quantizzazione del momento angolare e sostituendola nella relazione del raggio, si ottiene h n r m m e mv e r ossia m e h n r 0
8 Raggi e livelli energetici quantizzati per n = 1 per n = per n = 3 r = 5, m = a o = raggio di Bohr r = 4 a o r = 9 a o etc.
9 Raggi e livelli energetici quantizzati Ovviamente a ogni orbita quantizzata sarà associata una ben precisa Energia Totale (cinetica + potenziale), anch essa quantizzata r e mv U K E E poiché r e mv r e r v m r e E 0 8 1
10 Raggi e livelli energetici quantizzati r e E m e h n r n h me m e h n e E o, come direbbe un prof di scienze,
11 Raggi e livelli energetici quantizzati Anche l energia, come il raggio, cresce con l inverso del quadrato di n
12 Terza ipotesi di Bohr Nel suo condizione di minima energia (stato fondamentale) l elettrone si trova sulla prima orbita. L elettrone può passare ad uno stato eccitato, passando ad un orbita esterna (transizione elettronica o salto quantico) assorbendo solo quantità di energia discrete (quantizzate), pari alla differenza di energia tra il livello di partenza e quello di arrivo
13 Terza ipotesi di Bohr Quando l elettrone si trova in un orbita superiore, l'atomo possiede un surplus di energia che lo rende instabile (eccitato) e l'elettrone è destinato a tornare nell'orbita di partenza riemettendo l energia precedentemente assorbita tramite un fotone la cui energia è appunto pari a E = E E1 = h
14 Le orbite quantizzate giustificano lo spettro a righe Avendo definito l energia di ciascun livello, Bohr è in grado di calcolare il E e, di conseguenza, le frequenze ν dei fotoni emessi nelle varie transizioni di ritorno che risultano perfettamente identiche alle righe spettrali dell Idrogeno L energia emessa durante una transizione da un livello esterno n e ad un livello interno n i è
15 Le orbite quantizzate giustificano lo spettro a righe Calcoliamo il numero d onda 1/λ del fotone me h Formula di Balmer Adesso la Rydberg ha un significato fisico: R 8 me 0 4 h 3 c
16 Atomo di Bohr e serie di Balmer I numeri interi n ed m che nella relazione di Balmer erano empirici, nel modello di Bohr diventano il numero quantico del livello più interno ni ed il numero quantico del livello più esterno ne tra i quali avviene la transizione. La serie di Balmer è dunque prodotta da transizioni di ritorno dell elettrone verso il secondo livello energetico (n = )
17 Le serie dell Idrogeno fuori dal visibile La serie di Lyman (UV) è prodotta da transizioni di ritorno dell elettrone verso il primo livello energetico (n = 1) Le transizioni di ritorno verso livelli superiori al secondo generano invece le serie dell infrarosso (Paschen Bracket, Pfund)
18 Modello atomico di Bohr - Sommerfeld
19 Struttura fine e sottolivelli Il numero quantico principale n descrive i livelli energetici consentiti e assume negli atomi valori interi (da 1 a 7. Non si va oltre i 7 livelli energetici) Con l affinamento delle tecniche spettroscopiche risultò che ciascuna riga spettrale appariva composta da una serie di sottili righe molto ravvicinate (struttura fine dello spettro a righe) a indicare la probabile esistenza di sottolivelli. Come i livelli anche i sottolivelli risultarono quantizzati e la loro descrizione richiese l introduzione di ulteriori numeri quantici
20 Il modello di Bohr-Sommerfeld il numero quantico secondario l Per spiegare la complessità degli spettri, nel 1915 Sommerfeld modificò il modello di Bohr introducendo, accanto a quelle circolari, delle orbite ellittiche, caratterizzate dall avere la stessa energia. Se per un livello energetico l energia è la stessa, il momento angolare L diminuisce con l eccentricità. Occorre un secondo numero quantico. Il numero quantico secondario l quantizza il tipo di orbite permesse per ogni livello energetico; il numero n non rappresenta più la quantizzazione del momento angolare ora indicato da l ma solo il livello di energia.
21 Il modello di Bohr-Sommerfeld Se ora noi ammettiamo che per un certo valore del numero quantico principale n possano esistere, oltre all orbita circolare, anche alcune orbite ellittiche più o meno eccentriche, l elettrone che le percorre, cambiando massa lungo il percorso (perché varia la sua velocità), dovrà cambiare anche contenuto energetico. Pertanto gli elettroni che percorrono l una o l altra orbita avranno energia diversa (ma non di molto), e il passaggio da un orbita all'altra comporterà l apparire di una serie di righe, anche se molto vicine fra loro, e non di una sola. In questo modo veniva spiegato il fatto che una riga dello spettro era in realtà composta da un insieme di altre righe (STRUTTURA FINE).
22 Orbite ellittiche di Sommerfeld Il numero quantico secondario l determina il tipo di orbite permesse per ciascun livello. Le orbite circolari sono presenti in tutti i livelli, mentre le orbite ellittiche solo dal secondo livello in poi. I diversi tipi di orbite ellittiche si differenziano per l eccentricità. Presentano: semiasse maggiore semiasse minore b a n n a l 1 n Gli elettroni che percorrono le orbite ellittiche di Sommersfeld, caratterizzate dal numero quantico azimutale l, hanno momenti angolari che sono multipli di ħ 0 l a n L ( l 1)ħ l = n 1, n,, 1, 0
23 Orbite ellittiche di Sommerfeld il nucleo dell atomo occupa uno dei fuochi l =0 l =1 l = n=1 l=0 l =1 n= l =0 il momento angolare L ( l 1)ħ n=3 il semiasse maggiore è a n n a0 il semiasse minore è b l l 1 a n n
24 Orbite ellittiche di Sommerfeld
25 Orbite ellittiche di Sommerfeld Per un codice che risale agli inizi della spettroscopia a ogni numero l che indica il sottolivello (e che procede dal maggior al minor momento angolare) è associata una lettera l =0 l =1 l = l =3 l =4 l =5 s (sharp = netta) p (principal) d (diffused) f (foundamental) g h n=3 l =,1,0
26 Il modello di Bohr-Sommerfeld numero quantico secondario l per n = 1 l = 0 orbita di tipo s (circolare di Bohr) per n = per n = 3 per n = 4 l = 1 orbita di tipo p (circolare di Bohr) l = 0 orbita di tipo s (ellittica b=1/ a) l = orbita di tipo d (circolare di Bohr) l = 1 orbita di tipo p (ellittica b=/3 a) l = 0 orbita di tipo s (ellittica b=1/3 a) l = 3 orbita di tipo f (circolare di Bohr) l = orbita di tipo d (ellittica b=3/4 a) l = 1 orbita di tipo p (ellittica b=/4 a) l = 0 orbita di tipo s (ellittica b=1/4 a)
27 Effetto Zeeman (scoperto nel 1896) Ulteriore possibilità di alterazione energetica in seno alle varie orbite: quando un gas rarefatto eccitato viene sottoposto a un campo magnetico, alcune sue righe spettrali si scompongono in multipletti di 3, 5 o 7 righe, tanto più separate quanto più intenso è il campo (effetto Zeeman).
28 Effetto Zeeman L effetto evidenzia la presenza di sottolivelli energetici (resi più evidenti dal campo magnetico)
29 Come spiegare l effetto Zeeman Un'orbita elettronica si comporta come una spira percorsa da corrente elettrica e, come previsto da Ampere nel 180, produce un campo magnetico ad essa perpendicolare la cui orientazione può essere prevista con la regola della mano destra. Una stessa orbita, sottoposta a un campo magnetico esterno, può orientare il suo campo magnetico e di conseguenza il suo piano orbitale
30 Numero quantico magnetico m Per spiegare l effetto Zeeman si dovette ammettere che le orbite elettroniche, oltre che essere quantizzate nel momento angolare L, dovevano essere quantizzate anche nell orientazione. Serviva dunque un terzo numero quantico magnetico m m=1 m=0 l = 1 m= 1
31 Numero quantico magnetico m Una stessa orbita, sottoposta ad un campo magnetico esterno, può orientare il suo campo magnetico e di conseguenza il suo piano orbitale solo in alcune direzioni, diversificando il suo contenuto energetico e dando perciò luogo ad ulteriori sottolivelli. Il numero delle direzioni consentite e quindi il numero delle orbite permesse per ciascun tipo (s p d f) viene espresso dal numero quantico magnetico m che può assumere solo i valori interi compresi tra l e + l
32 Numero quantico magnetico m L l( l 1)ħ L ħ l = La sua proiezione lungo un asse parallelo a B vale L 1ħ L 0ħ L 6ħ L ( l 1)ħ L 1ħ L ħ B possibili orientazioni per L quando l = in presenza di un campo magnetico B m =, 1, 0, 1,
33 numero di orbite permesse - l m + l per n = 1 l = 0 orbita di tipo s m = 0 1 orbita di tipo s per n = l = 0 orbita di tipo s m = 0 1 orbita di tipo s l = 1 orbita di tipo p m = orbite di tipo p per n = 3 l = 0 orbita di tipo s m = 0 1 orbita di tipo s l = 1 orbita di tipo p m = orbite di tipo p l = orbita di tipo d m = orbite di tipo d per n = 4 l = 0 orbita di tipo s m = 0 1 orbita di tipo s l = 1 orbita di tipo p m = orbite di tipo p l = orbita di tipo d m = orbite di tipo d l = 3 orbita di tipo f m = orbite di tipo f
34 Numeri quantici riassunto (fino a questo momento) Il numero quantico principale n (introdotto da Bohr nel 1913) definisce il numero dei livelli energetici permessi (non si va oltre 7) Il numero quantico secondario l (introdotto da Sommersfeld nel 1916) definisce il tipo di orbite permesse per ciascun livello (s p d f) Il numero quantico magnetico m l (introdotto da Sommersfeld) definisce il numero di orbite permesse per ciascun tipo (1 s; 3 p; 5 d; 7 f)
35 Limiti del modello di Bohr-Sommerfeld Il modello di Bohr-Sommerfeld rimane invariato anche per atomi con più protoni nel nucleo e quindi con più elettroni in orbita intorno ad esso. L'unica differenza è dovuta al fatto che la maggior attrazione esercitata dal nucleo fa diminuire il diametro di tutte le orbite permesse. Tuttavia, se tutti gli elettroni di un atomo plurielettronico tendessero (come fa l Idrogeno) a stazionare nel primo livello (stato fondamentale), le dimensioni di un atomo (volume occupato dai suoi elettroni) diminuirebbero progressivamente con l aumentare di Z.
36 Limiti del modello di Bohr-Sommerfeld Con la presenza di più elettroni intorno al nucleo non poteva infatti essere trascurata la loro interazione. Se, ad esempio, gli elettroni di un atomo non interagissero reciprocamente, e risentissero solo dell attrazione del nucleo, essi sarebbero tutti equivalenti e tutti si andrebbero a sistemare spontaneamente sul livello a minor contenuto energetico, cioè su quello più vicino al nucleo. L'idea di sistemare tutti gli elettroni di un atomo sull orbita a più basso contenuto energetico fu però immediatamente scartata anche perché contraria ai fatti sperimentali. Lo studio degli spettri atomici mostrava infatti chiaramente che gli elettroni, nello stato fondamentale (cioè a minimo contenuto di energia), erano distribuiti su vari livelli energetici.
37 Stern e Gerlach (19) Volendo verificare l esistenza del numero quantico l, O. Stern e W. Gerlach realizzarono, nel 19, un famoso esperimento. Un fascio di atomi d argento veniva indirizzato su uno schermo, dopo aver attraversato un magnete. Classicamente il fascio si sarebbe distribuito con continuità; invece, secondo il modello quantistico, si pensava di osservare solo macchie ben distanziate, indici di un atomo che poteva orientare la propria orbita solo in direzioni quantizzate. Stern e Gerlach osservarono davvero una distribuzione quantizzata, come in figura
38 apparato di Stern e Gerlach
39 Lo spin La comunità scientifica calcolò che l atomo di argento presenta allo stato fondamentale un numero quantico azimutale l =0 Per spiegare il fenomeno scoperto da Stern e W. Gerlach, due giovani fisici olandesi S.A. Goudsmith e G.E. Uhlenbeck, avanzarono l ipotesi che gli elettroni fossero animati anche da un moto rotatorio su se stessi. L elettrone «viene pensato» come una minuscola trottola rotante intorno al suo asse che presenta pertanto un momento angolare intrinseco (mvr) o spin (vettore S) e un momento magnetico (vettore μ)
40 Lo spin La rotazione di una carica elettrica produce anche un campo magnetico associato all elettrone, il quale si comporta come un minuscolo magnete
41 Lo spin Tuttavia, se esso fosse il risultato della rotazione delle particelle su se stesse, analoga alla rotazione dei pianeti, la velocità di rotazione dovrebbe essere maggiore di quella della luce: tale spiegazione è dunque errata. Inoltre, se si usa un modello in cui le particelle sono puntiformi, cioè non hanno estensione, non è possibile definire un momento di rotazione su se stesse. Lo spin quindi non è legato alla rotazione ed è un fenomeno puramente quantistico; per questo motivo è definito come "momento angolare intrinseco".
42 Lo spin Esperimenti condotti sull atomo di idrogeno dimostrarono che il momento angolare di spin è: S 3 e il modulo del momento magnetico di spin è: s e ħ m ħ anche definito magnetone di Bohr.
43 Il numero quantico di spin Anche il momento angolare di spin è spazialmente quantizzato in quanto può assumere soltanto due orientazioni specificate dal numero quantico di spin m s : Lo spin dell elettrone in valore assoluto è pari a ed è una quantità vettoriale che si determina con la regola della mano destra. B m s m s 1 S 1 3 ħ
44 Principio di esclusione di Pauli (195) (dicevamo) Se tutti gli elettroni di un atomo plurielettronico tendessero (come fa l Idrogeno) a stazionare nel primo livello (stato fondamentale), le dimensioni di un atomo (volume occupato dai suoi elettroni) diminuirebbero progressivamente con l aumentare di Z. In realtà gli elettroni di un atomo plurielettronico si distribuiscono anche sui livelli più esterni, obbedendo al principio di esclusione di Pauli: in uno stesso atomo due elettroni non possono avere gli stessi quattro numeri quantici.
45 Spin antiparalleli Il principio di esclusione spiega in modo semplice la periodicità degli elementi chimici. Quando infatti un livello risulta pieno di elettroni, gli elettroni successivi sono costretti a riempire il livello successivo, dove si trovano orbite dello stesso tipo del precedente, anche se di dimensioni maggiori.
46 Numeri quantici - Riassunto Il numero quantico principale n definisce il numero dei livelli energetici permessi (7) Il numero quantico secondario l definisce il tipo di orbite permesse per ciascun livello (s p d f) Il numero quantico magnetico m definisce il numero di orbite permesse per ciascun tipo (1 s; 3 p; 5 d; 7 f) Il numero quantico di spin m s individua i due elettroni presenti in ogni orbita. Per il principio di Pauli, in ogni orbita possono coesistere al massimo due elettroni i quali si distinguono per avere i vettori spin ad essi associati controversi o, come si usa dire, antiparalleli.
47 Modelli atomici quantomeccanici Il modello di Bohr otteneva risultati buoni e aderenti ai dati sperimentali solamente per lo spettro dell idrogeno, mentre non riusciva a fare previsioni soddisfacenti per gli atomi plurielettronici. Il modello subì una radicale e a tutt oggi definitiva revisione con la nascita della meccanica quantistica e la conseguente introduzione di modelli atomici quantomeccanici.
48 i numeri quantici dopo Schrödinger (196) Per determinare le funzioni che sono soluzioni dell equazione di Schrödinger, si constata che tali funzioni sono caratterizzate dalla presenza di tre parametri che possono assumere solo numeri interi. questi parametri vengono indicato con n, l, m il parametro n è associato al livello energetico fondamentale in cui si trova l elettrone e corrisponde al numero n nel modello di Bohr gli altri due numeri sono associati ai termini angolari presenti nella funzione d onda e il loro valore determina la forma dell orbitale.
49 Fermioni e Bosoni Tutte le particelle possiedono spin e, in base al valore che esso presenta, possono essere classificate in due grandi famiglie. Le particelle con spin semidispari o semintero (1/, 3/, 5/.) obbediscono al principio di esclusione di Pauli e non possono pertanto occupare lo stesso livello energetico (stato quantico), in numero superiore a due. La loro distribuzione energetica è descritta dalla statistica di Fermi- Dirac e sono perciò dette fermioni. Le particelle con spin intero (0, 1,, 3.) NON obbediscono al principio di esclusione di Pauli e possono presentarsi pertanto in numero qualsiasi nello stesso livello energetico (stato quantico). La loro distribuzione energetica è descritta dalla statistica di Bose-Einstein e sono per questo dette bosoni (sono particelle di campo ovvero mediatori di forza)
L atomo di Bohr. Argomenti. Al tempo di Bohr. Spettri atomici 19/03/2010
 Argomenti Spettri atomici Modelli atomici Effetto Zeeman Equazione di Schrödinger L atomo di Bohr Numeri quantici Atomi con più elettroni Al tempo di Bohr Lo spettroscopio è uno strumento utilizzato per
Argomenti Spettri atomici Modelli atomici Effetto Zeeman Equazione di Schrödinger L atomo di Bohr Numeri quantici Atomi con più elettroni Al tempo di Bohr Lo spettroscopio è uno strumento utilizzato per
Capitolo 8 La struttura dell atomo
 Capitolo 8 La struttura dell atomo 1. La doppia natura della luce 2. La «luce» degli atomi 3. L atomo di Bohr 4. La doppia natura dell elettrone 5. L elettrone e la meccanica quantistica 6. L equazione
Capitolo 8 La struttura dell atomo 1. La doppia natura della luce 2. La «luce» degli atomi 3. L atomo di Bohr 4. La doppia natura dell elettrone 5. L elettrone e la meccanica quantistica 6. L equazione
L atomo. Il neutrone ha una massa 1839 volte superiore a quella dell elettrone. 3. Le particelle fondamentali dell atomo
 L atomo 3. Le particelle fondamentali dell atomo Gli atomi sono formati da tre particelle fondamentali: l elettrone con carica negativa; il protone con carica positiva; il neutrone privo di carica. Il
L atomo 3. Le particelle fondamentali dell atomo Gli atomi sono formati da tre particelle fondamentali: l elettrone con carica negativa; il protone con carica positiva; il neutrone privo di carica. Il
La teoria atomica moderna: il modello planetario L ELETTRONE SI MUOVE LUNGO UN ORBITA INTORNO AL NUCLEO
 La teoria atomica moderna: il modello planetario L ELETTRONE SI MUOVE LUNGO UN ORBITA INTORNO AL NUCLEO La luce La LUCE è una forma di energia detta radiazione elettromagnetica che si propaga nello spazio
La teoria atomica moderna: il modello planetario L ELETTRONE SI MUOVE LUNGO UN ORBITA INTORNO AL NUCLEO La luce La LUCE è una forma di energia detta radiazione elettromagnetica che si propaga nello spazio
LE ONDE E I FONDAMENTI DELLA TEORIA QUANTISTICA
 LE ONDE E I FONDAMENTI DELLA TEORIA QUANTISTICA I PROBLEMI DEL MODELLO PLANETARIO F Secondo Rutherford l elettrone si muoverebbe sulla sua orbita in equilibrio tra la forza elettrica di attrazione del
LE ONDE E I FONDAMENTI DELLA TEORIA QUANTISTICA I PROBLEMI DEL MODELLO PLANETARIO F Secondo Rutherford l elettrone si muoverebbe sulla sua orbita in equilibrio tra la forza elettrica di attrazione del
Generalità delle onde elettromagnetiche
 Generalità delle onde elettromagnetiche Ampiezza massima: E max (B max ) Lunghezza d onda: (m) E max (B max ) Periodo: (s) Frequenza: = 1 (s-1 ) Numero d onda: = 1 (m-1 ) = v Velocità della luce nel vuoto
Generalità delle onde elettromagnetiche Ampiezza massima: E max (B max ) Lunghezza d onda: (m) E max (B max ) Periodo: (s) Frequenza: = 1 (s-1 ) Numero d onda: = 1 (m-1 ) = v Velocità della luce nel vuoto
Le Caratteristiche della Luce
 7. L Atomo Le Caratteristiche della Luce Quanti e Fotoni Spettri Atomici e Livelli Energetici L Atomo di Bohr I Modelli dell Atomo - Orbitali atomici - I numeri quantici e gli orbitali atomici - Lo spin
7. L Atomo Le Caratteristiche della Luce Quanti e Fotoni Spettri Atomici e Livelli Energetici L Atomo di Bohr I Modelli dell Atomo - Orbitali atomici - I numeri quantici e gli orbitali atomici - Lo spin
Struttura Elettronica degli Atomi Meccanica quantistica
 Prof. A. Martinelli Struttura Elettronica degli Atomi Meccanica quantistica Dipartimento di Farmacia 1 Il comportamento ondulatorio della materia 2 1 Il comportamento ondulatorio della materia La diffrazione
Prof. A. Martinelli Struttura Elettronica degli Atomi Meccanica quantistica Dipartimento di Farmacia 1 Il comportamento ondulatorio della materia 2 1 Il comportamento ondulatorio della materia La diffrazione
Unità Didattica 3. L atomo di idrogeno
 Diapositiva 1 Unità Didattica 3 L atomo di idrogeno Questa unità contiene informazioni sull atomo di idrogeno, i modelli di Tomson, Ruterford e Bor, l esperimento di Frank-Hertz e infine la formula di
Diapositiva 1 Unità Didattica 3 L atomo di idrogeno Questa unità contiene informazioni sull atomo di idrogeno, i modelli di Tomson, Ruterford e Bor, l esperimento di Frank-Hertz e infine la formula di
GLI ORBITALI ATOMICI
 GLI ORBITALI ATOMICI I numeri quantici Le funzioni d onda Ψ n, soluzioni dell equazione d onda, sono caratterizzate da certe combinazioni di numeri quantici: n, l, m l, m s n = numero quantico principale,
GLI ORBITALI ATOMICI I numeri quantici Le funzioni d onda Ψ n, soluzioni dell equazione d onda, sono caratterizzate da certe combinazioni di numeri quantici: n, l, m l, m s n = numero quantico principale,
GLI ORBITALI ATOMICI
 GLI ORBITALI ATOMICI Orbitali atomici e loro rappresentazione Le funzioni d onda Ψ n che derivano dalla risoluzione dell equazione d onda e descrivono il moto degli elettroni nell atomo si dicono orbitali
GLI ORBITALI ATOMICI Orbitali atomici e loro rappresentazione Le funzioni d onda Ψ n che derivano dalla risoluzione dell equazione d onda e descrivono il moto degli elettroni nell atomo si dicono orbitali
Corso di CHIMICA LEZIONE 2
 Corso di CHIMICA LEZIONE 2 MODELLO ATOMICO DI THOMSON 1904 L atomo è formato da una sfera carica positivamente in cui gli elettroni con carica negativa, distribuiti uniformemente all interno, neutralizzano
Corso di CHIMICA LEZIONE 2 MODELLO ATOMICO DI THOMSON 1904 L atomo è formato da una sfera carica positivamente in cui gli elettroni con carica negativa, distribuiti uniformemente all interno, neutralizzano
CORSO DI LAUREA IN OTTICA E OPTOMETRIA
 CORSO DI LAUREA IN OTTICA E OPTOMETRIA Anno Accademico 007-008 CORSO di FISCA ED APPLICAZIONE DEI LASERS Questionario del Primo appello della Sessione Estiva NOME: COGNOME: MATRICOLA: VOTO: /30 COSTANTI
CORSO DI LAUREA IN OTTICA E OPTOMETRIA Anno Accademico 007-008 CORSO di FISCA ED APPLICAZIONE DEI LASERS Questionario del Primo appello della Sessione Estiva NOME: COGNOME: MATRICOLA: VOTO: /30 COSTANTI
Teoria Atomica di Dalton
 Teoria Atomica di Dalton Il concetto moderno della materia si origina nel 1806 con la teoria atomica di John Dalton: Ogni elementoè composto di atomi. Gli atomi di un dato elemento sono uguali. Gli atomi
Teoria Atomica di Dalton Il concetto moderno della materia si origina nel 1806 con la teoria atomica di John Dalton: Ogni elementoè composto di atomi. Gli atomi di un dato elemento sono uguali. Gli atomi
Bohr e la struttura dell atomo. Lezioni 11-12
 Bohr e la struttura dell atomo Lezioni 11-12 Onde elettromagnetiche Radiazione Elettromagnetica raggi X e raggi > 10 3 Hz
Bohr e la struttura dell atomo Lezioni 11-12 Onde elettromagnetiche Radiazione Elettromagnetica raggi X e raggi > 10 3 Hz
3. Struttura dell atomo
 Di cosa parleremo L organizzazione interna delle particelle che costituiscono gli atomi è stata oggetto di studio per lungo tempo e le ipotesi sulla struttura atomica si sono evolute nel tempo in base
Di cosa parleremo L organizzazione interna delle particelle che costituiscono gli atomi è stata oggetto di studio per lungo tempo e le ipotesi sulla struttura atomica si sono evolute nel tempo in base
MODELLO ATOMICO DI BOHR - ULTERIORI APPROFONDIMENTI
 MODELLO ATOMICO DI BOHR - ULTERIORI APPROFONDIMENTI Se riscaldiamo un qualsiasi elemento chimico ponendolo ad esempio su una fiamma, notiamo che esso emette un colore caratteristico. Ad esempio riscaldando
MODELLO ATOMICO DI BOHR - ULTERIORI APPROFONDIMENTI Se riscaldiamo un qualsiasi elemento chimico ponendolo ad esempio su una fiamma, notiamo che esso emette un colore caratteristico. Ad esempio riscaldando
CONFIGURAZIONE ELETTRONICA. In generale la configurazione elettronica indica come sono posizionati gli elettroni intorno al nucleo di un atomo.
 CONFIGURAZIONE ELETTRONICA In generale la configurazione elettronica indica come sono posizionati gli elettroni intorno al nucleo di un atomo. ORBITA : Zona intorno al nucleo di diversa energia dove ruotano
CONFIGURAZIONE ELETTRONICA In generale la configurazione elettronica indica come sono posizionati gli elettroni intorno al nucleo di un atomo. ORBITA : Zona intorno al nucleo di diversa energia dove ruotano
La Teoria dei Quanti e la Struttura Elettronica degli Atomi. Capitolo 7
 La Teoria dei Quanti e la Struttura Elettronica degli Atomi Capitolo 7 Proprietà delle Onde Lunghezza d onda (λ) E la distanza tra due punti identici su due onde successive. Ampiezza è la distanza verticale
La Teoria dei Quanti e la Struttura Elettronica degli Atomi Capitolo 7 Proprietà delle Onde Lunghezza d onda (λ) E la distanza tra due punti identici su due onde successive. Ampiezza è la distanza verticale
Quarta unità didattica. Disposizione degli elettroni nell atomo
 Quarta unità didattica Disposizione degli elettroni nell atomo Modello atomico di Bohr 1913 L' atomo di Borh consiste in un nucleo di carica positiva al quale ruotano intorno gli elettroni di carica negativa
Quarta unità didattica Disposizione degli elettroni nell atomo Modello atomico di Bohr 1913 L' atomo di Borh consiste in un nucleo di carica positiva al quale ruotano intorno gli elettroni di carica negativa
La teoria del corpo nero
 La teoria del corpo nero Max Planck Primo Levi 2014 Roberto Bedogni INAF Osservatorio Astronomico di Bologna via Ranzani, 1 40127 - Bologna - Italia Tel, 051-2095721 Fax, 051-2095700 http://www.bo.astro.it/~bedogni/primolevi
La teoria del corpo nero Max Planck Primo Levi 2014 Roberto Bedogni INAF Osservatorio Astronomico di Bologna via Ranzani, 1 40127 - Bologna - Italia Tel, 051-2095721 Fax, 051-2095700 http://www.bo.astro.it/~bedogni/primolevi
Particelle Subatomiche
 GLI ATOMI Particelle Subatomiche ELEMENTI I diversi atomi sono caratterizzati da un diverso numero di protoni e neutroni; il numero di elettroni è sempre uguale al numero dei protoni (negli atomi neutri)
GLI ATOMI Particelle Subatomiche ELEMENTI I diversi atomi sono caratterizzati da un diverso numero di protoni e neutroni; il numero di elettroni è sempre uguale al numero dei protoni (negli atomi neutri)
L ATOMO SECONDO LA MECCANICA ONDULATORIA IL DUALISMO ONDA-PARTICELLA. (Plank Einstein)
 L ATOMO SECONDO LA MECCANICA ONDULATORIA IL DUALISMO ONDA-PARTICELLA POSTULATO DI DE BROGLIÈ Se alla luce, che è un fenomeno ondulatorio, sono associate anche le caratteristiche corpuscolari della materia
L ATOMO SECONDO LA MECCANICA ONDULATORIA IL DUALISMO ONDA-PARTICELLA POSTULATO DI DE BROGLIÈ Se alla luce, che è un fenomeno ondulatorio, sono associate anche le caratteristiche corpuscolari della materia
ATOMO. Legge della conservazione della massa Legge delle proporzioni definite Dalton
 Democrito IV secolo A.C. ATOMO Lavoisier Proust Legge della conservazione della massa Legge delle proporzioni definite Dalton (808) Teoria atomica Gay-Lussac volumi di gas reagiscono secondo rapporti interi
Democrito IV secolo A.C. ATOMO Lavoisier Proust Legge della conservazione della massa Legge delle proporzioni definite Dalton (808) Teoria atomica Gay-Lussac volumi di gas reagiscono secondo rapporti interi
Si arrivò a dimostrare l esistenza di una forma elementare della materia (atomo) solo nel 1803 (John Dalton)
 Atomi 16 Si arrivò a dimostrare l esistenza di una forma elementare della materia (atomo) solo nel 1803 (John Dalton) 17 Teoria atomica di Dalton Si basa sui seguenti postulati: 1. La materia è formata
Atomi 16 Si arrivò a dimostrare l esistenza di una forma elementare della materia (atomo) solo nel 1803 (John Dalton) 17 Teoria atomica di Dalton Si basa sui seguenti postulati: 1. La materia è formata
STRUTTURA ATOMICA E CONFIGURAZIONE ELETTRONICA
 pg 1 STRUTTURA ATOMICA E CONFIGURAZIONE ELETTRONICA Per capire il comportamento degli atomi dobbiamo studiare il comportamento dei suoi elettroni L'atomo e le sue particelle NON sono direttamente visibili
pg 1 STRUTTURA ATOMICA E CONFIGURAZIONE ELETTRONICA Per capire il comportamento degli atomi dobbiamo studiare il comportamento dei suoi elettroni L'atomo e le sue particelle NON sono direttamente visibili
Tabella periodica degli elementi
 Tabella periodica degli elementi Perchè ha questa forma? Ovvero, esiste una regola per l ordinamento dei singoli atomi? Le proprietà dei materiali hanno una relazione con la tabella? L applicazione dei
Tabella periodica degli elementi Perchè ha questa forma? Ovvero, esiste una regola per l ordinamento dei singoli atomi? Le proprietà dei materiali hanno una relazione con la tabella? L applicazione dei
1. La forza di Lorentz. Se un fascio catodico è in un campo magnetico:
 Il campo magnetico 1. La forza di Lorentz Se un fascio catodico è in un campo magnetico: La forza di Lorentz Gli elettroni risentono di una forza magnetica anche se non sono in un filo metallico; l'importante
Il campo magnetico 1. La forza di Lorentz Se un fascio catodico è in un campo magnetico: La forza di Lorentz Gli elettroni risentono di una forza magnetica anche se non sono in un filo metallico; l'importante
4. Lo spettro discreto: emissione e assorbimento di luce da parte di atomi stato fondamentale stati eccitati
 4. Lo spettro discreto: emissione e assorbimento di luce da parte di atomi Accanto allo spettro continuo che i corpi emettono in ragione del loro stato termico, si osservano spettri discreti che sono caratteristici
4. Lo spettro discreto: emissione e assorbimento di luce da parte di atomi Accanto allo spettro continuo che i corpi emettono in ragione del loro stato termico, si osservano spettri discreti che sono caratteristici
Lezione n. 19. L equazione. di Schrodinger L atomo. di idrogeno Orbitali atomici. 02/03/2008 Antonino Polimeno 1
 Chimica Fisica - Chimica e Tecnologia Farmaceutiche Lezione n. 19 L equazione di Schrodinger L atomo di idrogeno Orbitali atomici 02/03/2008 Antonino Polimeno 1 Dai modelli primitivi alla meccanica quantistica
Chimica Fisica - Chimica e Tecnologia Farmaceutiche Lezione n. 19 L equazione di Schrodinger L atomo di idrogeno Orbitali atomici 02/03/2008 Antonino Polimeno 1 Dai modelli primitivi alla meccanica quantistica
Misura del momento magnetico dell elettrone
 FACOLTÀ Università degli Studi di Roma Tre DI SCIENZE MATEMATICHE, FISICHE E NATURALI Corso di Laurea in Fisica Misura del momento magnetico dell elettrone Candidato: Andrea Sciandra Matricola 4480 Relatore:
FACOLTÀ Università degli Studi di Roma Tre DI SCIENZE MATEMATICHE, FISICHE E NATURALI Corso di Laurea in Fisica Misura del momento magnetico dell elettrone Candidato: Andrea Sciandra Matricola 4480 Relatore:
La struttura della materia
 La struttura della materia IL CORPO NERO In fisica, i corpi solidi o liquidi emettono radiazioni elettromagnetiche, a qualsiasi temperatura. Il corpo nero, invece, è un oggetto ideale che assorbe tutta
La struttura della materia IL CORPO NERO In fisica, i corpi solidi o liquidi emettono radiazioni elettromagnetiche, a qualsiasi temperatura. Il corpo nero, invece, è un oggetto ideale che assorbe tutta
CHIMICA E SCIENZA E TECNOLOGIA DEI MATERIALI ELETTRICI
 CHIMICA E SCIENZA E TECNOLOGIA DEI MATERIALI ELETTRICI Elettrici I anno - III Quadr. a.acc. 2006/07 Laboratorio: Laboratorio Materiali piano S-1 26/04/2007 Chimica e Scienza e Tecnologia dei Materiali
CHIMICA E SCIENZA E TECNOLOGIA DEI MATERIALI ELETTRICI Elettrici I anno - III Quadr. a.acc. 2006/07 Laboratorio: Laboratorio Materiali piano S-1 26/04/2007 Chimica e Scienza e Tecnologia dei Materiali
Lezioni di Meccanica Quantistica
 Luigi E. Picasso Lezioni di Meccanica Quantistica seconda edizione Edizioni ETS www.edizioniets.com Copyright 2015 EDIZIONI ETS Piazza Carrara, 16-19, I-56126 Pisa [email protected] www.edizioniets.com
Luigi E. Picasso Lezioni di Meccanica Quantistica seconda edizione Edizioni ETS www.edizioniets.com Copyright 2015 EDIZIONI ETS Piazza Carrara, 16-19, I-56126 Pisa [email protected] www.edizioniets.com
I NUMERI QUANTICI NUMERO QUANTICO PRINCIPALE Q P O N M L K
 I NUMERI QUANTICI NUMERO QUANTICO PRINCIPALE Il numero quantico principale n indica il livello energetico e la dimensione degli orbitali. Il numero quantico principale può assumere soltanto i valori interi
I NUMERI QUANTICI NUMERO QUANTICO PRINCIPALE Il numero quantico principale n indica il livello energetico e la dimensione degli orbitali. Il numero quantico principale può assumere soltanto i valori interi
Esp. 4: Spettrofotometro
 Esp. 4: Spettrofotometro Spettrofotometria Reticolo di diffrazione d sinϑ = mλ Schermo Nel nostro esp. Si acquisisce al variare dell angolo l intensità luminosa. Noi riusciamo a misurare solo il primo
Esp. 4: Spettrofotometro Spettrofotometria Reticolo di diffrazione d sinϑ = mλ Schermo Nel nostro esp. Si acquisisce al variare dell angolo l intensità luminosa. Noi riusciamo a misurare solo il primo
Testi Consigliati. I. Bertini, C. Luchinat, F. Mani CHIMICA, Zanichelli. Qualsiasi altro testo che tratti gli argomenti elencati nel programma
 Chimica Generale ed Inorganica Testi Consigliati I. Bertini, C. Luchinat, F. Mani CHIMICA, Zanichelli Chimica Organica Hart-Craine Introduzione alla Chimica Organica Zanichelli. Qualsiasi altro testo che
Chimica Generale ed Inorganica Testi Consigliati I. Bertini, C. Luchinat, F. Mani CHIMICA, Zanichelli Chimica Organica Hart-Craine Introduzione alla Chimica Organica Zanichelli. Qualsiasi altro testo che
Effetto Zeeman anomalo
 Effetto Zeeman anomalo Direzione del campo B esempio: : j=3/2 Direzione del campo B j=1+1/2 = 3/2 s m j =+3/2 m j =+1/2 l m j =-1/2 m j =-3/2 La separazione tra i livelli é diversa l e µ l antiparalleli
Effetto Zeeman anomalo Direzione del campo B esempio: : j=3/2 Direzione del campo B j=1+1/2 = 3/2 s m j =+3/2 m j =+1/2 l m j =-1/2 m j =-3/2 La separazione tra i livelli é diversa l e µ l antiparalleli
LASER. Light Amplification by Stimulated Emission of Radiation. Introduzione. Assorbimento, emissione spontanea, emissione stimolata
 LASER Light Amplification by Stimulated Emission of Radiation Introduzione. Assorbimento, emissione spontanea, emissione stimolata Cenni storici 1900 Max Planck introduce la teoria dei quanti (la versione
LASER Light Amplification by Stimulated Emission of Radiation Introduzione. Assorbimento, emissione spontanea, emissione stimolata Cenni storici 1900 Max Planck introduce la teoria dei quanti (la versione
Fisica atomica. Marcello Borromeo corso di Fisica per Farmacia - Anno Accademico
 Fisica atomica Nel 1905 Einstein sostiene che la luce viaggia in pacchetti di energia, chiamati fotoni Ogni fotone ha energia proporzionale alla propria frequenza E = hν: h = 6.626 10 34 J s è chiamata
Fisica atomica Nel 1905 Einstein sostiene che la luce viaggia in pacchetti di energia, chiamati fotoni Ogni fotone ha energia proporzionale alla propria frequenza E = hν: h = 6.626 10 34 J s è chiamata
Università Primo Levi
 Università Primo Levi Primo Levi 2013 Le forze fondamentali e la fisica dei quanta INAF Osservatorio Astronomico di Bologna via Ranzani, 1 40127 - Bologna - Italia Tel, 051-2095721 Fax, 051-2095700 http://www.bo.astro.it/~bedogni/primolevi
Università Primo Levi Primo Levi 2013 Le forze fondamentali e la fisica dei quanta INAF Osservatorio Astronomico di Bologna via Ranzani, 1 40127 - Bologna - Italia Tel, 051-2095721 Fax, 051-2095700 http://www.bo.astro.it/~bedogni/primolevi
Struttura dell atomo atomo particelle sub-atomiche - protoni positiva - neutroni } nucleoni - elettroni negativa elemento
 Struttura dell atomo L atomo è la più piccola parte dell elemento che conserva le proprietà dell elemento Negli atomi ci sono tre diverse particelle sub-atomiche: - protoni (con carica positiva unitaria)
Struttura dell atomo L atomo è la più piccola parte dell elemento che conserva le proprietà dell elemento Negli atomi ci sono tre diverse particelle sub-atomiche: - protoni (con carica positiva unitaria)
Fenomeni quantistici
 Fenomeni quantistici 1. Radiazione di corpo nero Leggi di Wien e di Stefan-Boltzman Equipartizione dell energia classica Correzione quantistica di Planck 2. Effetto fotoelettrico XIII - 0 Radiazione da
Fenomeni quantistici 1. Radiazione di corpo nero Leggi di Wien e di Stefan-Boltzman Equipartizione dell energia classica Correzione quantistica di Planck 2. Effetto fotoelettrico XIII - 0 Radiazione da
Lo spin dell elettrone
 Lo spin dell elettrone Abbiamo visto che un elettrone che ruota intorno al nucleo possiede un momento angolare orbitale, con il quale è associato anche un momento magnetico. Ci sono evidenze sperimentali
Lo spin dell elettrone Abbiamo visto che un elettrone che ruota intorno al nucleo possiede un momento angolare orbitale, con il quale è associato anche un momento magnetico. Ci sono evidenze sperimentali
TEORIA QUANTISTICA E STRUTTURA ATOMICA
 TEORIA QUANTISTICA E STRUTTURA ATOMICA Gli argomenti di queste lezioni sono trattati nel Capitolo 7 del testo e nei paragrafi 1, e 3 del Capitolo 8. Non ci sono parti da non considerare. La moderna definizione
TEORIA QUANTISTICA E STRUTTURA ATOMICA Gli argomenti di queste lezioni sono trattati nel Capitolo 7 del testo e nei paragrafi 1, e 3 del Capitolo 8. Non ci sono parti da non considerare. La moderna definizione
FISICA QUANTISTICA LIMITI AL MODELLO ATOMICO DI RUTHERFORD. e - Per spiegare la disposizione degli elettroni nell atomo (STRUTTURA ELETTRONICA)
 LIMITI AL MODELLO ATOMICO DI RUTHERFORD e - + nucleo In base alle leggi della FISICA CLASSICA, una particella carica dotata di un movimento circolare libera energia. Di conseguenza, gli elettroni che,
LIMITI AL MODELLO ATOMICO DI RUTHERFORD e - + nucleo In base alle leggi della FISICA CLASSICA, una particella carica dotata di un movimento circolare libera energia. Di conseguenza, gli elettroni che,
Il principio di indeterminazione di Heisenberg
 Il principio di indeterminazione di Heisenberg Il prodotto degli errori nella determinazione contemporanea della quantità di moto (q = mv) e della posizione di un corpo in movimento è almeno uguale a h
Il principio di indeterminazione di Heisenberg Il prodotto degli errori nella determinazione contemporanea della quantità di moto (q = mv) e della posizione di un corpo in movimento è almeno uguale a h
Meccanica quantistica (5)
 Meccanica quantistica (5) 0/7/14 1-MQ-5.doc 0 Oscillatore armonico Se una massa è sottoposta ad una forza di richiamo proporzionale allo spostamento da un posizione di equilibrio F = kx il potenziale (
Meccanica quantistica (5) 0/7/14 1-MQ-5.doc 0 Oscillatore armonico Se una massa è sottoposta ad una forza di richiamo proporzionale allo spostamento da un posizione di equilibrio F = kx il potenziale (
Spettro elettromagnetico
 Spettro elettromagnetico Sorgenti Finestre Tipo Oggetti rilevabili Raggi γ ev Raggi X Lunghezza d onda E hc = hν = = λ 12. 39 λ( A o ) Visibile Infrarosso icro onde Onde-radio Dimensione degli oggetti
Spettro elettromagnetico Sorgenti Finestre Tipo Oggetti rilevabili Raggi γ ev Raggi X Lunghezza d onda E hc = hν = = λ 12. 39 λ( A o ) Visibile Infrarosso icro onde Onde-radio Dimensione degli oggetti
CHIMICA: studio della struttura e delle trasformazioni della materia
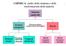 CHIMICA: studio della struttura e delle trasformazioni della materia 1 Materia (materali) Sostanze (omogenee) Processo fisico Miscele Elementi (atomi) Reazioni chimiche Composti (molecole) Miscele omogenee
CHIMICA: studio della struttura e delle trasformazioni della materia 1 Materia (materali) Sostanze (omogenee) Processo fisico Miscele Elementi (atomi) Reazioni chimiche Composti (molecole) Miscele omogenee
Sulla nascita di questo libro. Introduzione 1
 Indice Sulla nascita di questo libro V Introduzione 1 1 Luce e materia 7 Che cos è veramente la luce? 7 Ma qui che cosa oscilla? 9 Che cosa sono la frequenza e la lunghezza d onda della luce? 11 Che cos
Indice Sulla nascita di questo libro V Introduzione 1 1 Luce e materia 7 Che cos è veramente la luce? 7 Ma qui che cosa oscilla? 9 Che cosa sono la frequenza e la lunghezza d onda della luce? 11 Che cos
Interazione luce- atomo
 Interazione luce- atomo Descrizione semiclassica L interazione predominante è quella tra il campo elettrico e le cariche ASSORBIMENTO: Elettrone e protone formano un dipolo che viene messo in oscillazione
Interazione luce- atomo Descrizione semiclassica L interazione predominante è quella tra il campo elettrico e le cariche ASSORBIMENTO: Elettrone e protone formano un dipolo che viene messo in oscillazione
2bis. I modelli atomici
 2bis. I modelli atomici 2.1 Il modello di Thomson 2.2 Il modello di Rutherford; 2.3 Il dualismo particella-onda; 2.4 Il modello di Bohr 2.5 Il modello a orbitali 2.6 Il riempimento degli orbitali e le
2bis. I modelli atomici 2.1 Il modello di Thomson 2.2 Il modello di Rutherford; 2.3 Il dualismo particella-onda; 2.4 Il modello di Bohr 2.5 Il modello a orbitali 2.6 Il riempimento degli orbitali e le
La nascita della fisica moderna. (un racconto di inizio 900)
 La nascita della fisica moderna (un racconto di inizio 900) Sviluppo storico della fisica tra fine 800 e il 1927 Fisica sperimentale fine 800 Fisica teorica fine 800 1900 1905 1911 1913 1916 1924 1925-1927
La nascita della fisica moderna (un racconto di inizio 900) Sviluppo storico della fisica tra fine 800 e il 1927 Fisica sperimentale fine 800 Fisica teorica fine 800 1900 1905 1911 1913 1916 1924 1925-1927
Come sono disposti gli elettroni intorno al nucleo in un atomo?
 Come sono disposti gli elettroni intorno al nucleo in un atomo? La natura ondulatoria della radiazione elettromagnetica e della luce La luce è una radiazione elettromagnetica che si muove nello spazio
Come sono disposti gli elettroni intorno al nucleo in un atomo? La natura ondulatoria della radiazione elettromagnetica e della luce La luce è una radiazione elettromagnetica che si muove nello spazio
n(z) = n(0) e m gz/k B T ; (1)
 Corso di Introduzione alla Fisica Quantistica (f) Prova scritta 4 Luglio 008 - (tre ore a disposizione) [sufficienza con punti 8 circa di cui almeno 4 dagli esercizi nn. 3 e/o 4] [i bonus possono essere
Corso di Introduzione alla Fisica Quantistica (f) Prova scritta 4 Luglio 008 - (tre ore a disposizione) [sufficienza con punti 8 circa di cui almeno 4 dagli esercizi nn. 3 e/o 4] [i bonus possono essere
L energia assorbita dall atomo durante l urto iniziale è la stessa del fotone che sarebbe emesso nel passaggio inverso, e quindi vale: m
 QUESITI 1 Quesito Nell esperimento di Rutherford, una sottile lamina d oro fu bombardata con particelle alfa (positive) emesse da una sorgente radioattiva. Secondo il modello atomico di Thompson le particelle
QUESITI 1 Quesito Nell esperimento di Rutherford, una sottile lamina d oro fu bombardata con particelle alfa (positive) emesse da una sorgente radioattiva. Secondo il modello atomico di Thompson le particelle
LA STRUTTURA DELLE MOLECOLE. Meccanica Quantistica e Orbitali Atomici
 LA STRUTTURA DELLE MOLECOLE Meccanica Quantistica e Orbitali Atomici LE MOLECOLE Le molecole sono i costituenti di tutta la materia e possono essere considerate degli oggetti costruiti con componenti chiamati
LA STRUTTURA DELLE MOLECOLE Meccanica Quantistica e Orbitali Atomici LE MOLECOLE Le molecole sono i costituenti di tutta la materia e possono essere considerate degli oggetti costruiti con componenti chiamati
Elettricità e Fisica Moderna
 Esercizi di fisica per Medicina C.Patrignani, Univ. Genova (rev: 9 Ottobre 2003) 1 Elettricità e Fisica Moderna 1) Una candela emette una potenza di circa 1 W ad una lunghezza d onda media di 5500 Å a)
Esercizi di fisica per Medicina C.Patrignani, Univ. Genova (rev: 9 Ottobre 2003) 1 Elettricità e Fisica Moderna 1) Una candela emette una potenza di circa 1 W ad una lunghezza d onda media di 5500 Å a)
Orbitali nei primi tre livelli
 Orbitali nei primi tre livelli La tavola periodica degli elementi Numeri quantici e tavola Configurazioni elettroniche degli atomi Elenco degli orbitali occupati in un atomo nel suo stato fondamentale
Orbitali nei primi tre livelli La tavola periodica degli elementi Numeri quantici e tavola Configurazioni elettroniche degli atomi Elenco degli orbitali occupati in un atomo nel suo stato fondamentale
Lo Spettro Elettromagnetico
 Spettroscopia 1 Lo Spettro Elettromagnetico Lo spettro elettromagnetico è costituito da un insieme continuo di radiazioni (campi elettrici e magnetici che variano nel tempo, autogenerandosi) che va dai
Spettroscopia 1 Lo Spettro Elettromagnetico Lo spettro elettromagnetico è costituito da un insieme continuo di radiazioni (campi elettrici e magnetici che variano nel tempo, autogenerandosi) che va dai
Spettroscopia. Spettroscopia
 Spettroscopia Spettroscopia IR Spettroscopia NMR Spettrometria di massa 1 Spettroscopia E un insieme di tecniche che permettono di ottenere informazioni sulla struttura di una molecola attraverso l interazione
Spettroscopia Spettroscopia IR Spettroscopia NMR Spettrometria di massa 1 Spettroscopia E un insieme di tecniche che permettono di ottenere informazioni sulla struttura di una molecola attraverso l interazione
Numero atomico Z : numero di protoni presenti nell atomo di quell elemento. Numero di massa A : somma dei protoni e dei neutroni in un atomo
 ATOMI E TAVOLA PERIODICA ATOMO: è il più piccolo costituente di un elemento che ne conservi le proprietà chimiche ELEMENTO: sostanza che non può essere scissa in una sostanza più semplice mediante reazione
ATOMI E TAVOLA PERIODICA ATOMO: è il più piccolo costituente di un elemento che ne conservi le proprietà chimiche ELEMENTO: sostanza che non può essere scissa in una sostanza più semplice mediante reazione
Modelli atomici. Teoria atomica Dalton (1803) La materia non è continua, ma costituita da particelle.
 Modelli atomici Teoria atomica Dalton (1803) La materia non è continua, ma costituita da particelle. Presupposti 1. Legge di Lavoisier della conservazione della massa: in una reazione chimica nulla si
Modelli atomici Teoria atomica Dalton (1803) La materia non è continua, ma costituita da particelle. Presupposti 1. Legge di Lavoisier della conservazione della massa: in una reazione chimica nulla si
Il modello atomico a orbitali
 Il modello atomico a orbitali Il modello atomico di Bohr ha rappresentato un notevole passo avanti nel tentativo di dare spiegaione ai fatti sperimentali. In effetti l idea di utiliare i concetti della
Il modello atomico a orbitali Il modello atomico di Bohr ha rappresentato un notevole passo avanti nel tentativo di dare spiegaione ai fatti sperimentali. In effetti l idea di utiliare i concetti della
2.1 (p. 37) Bohr descrisse un orbitale atomico come una traiettoria circolare seguita dall elettrone. Un orbitale è una
 Capitolo 2 Risposte alle Domande ed esercizi inclusi nel Capitolo 2.1 (p. 37) Bohr descrisse un orbitale atomico come una traiettoria circolare seguita dall elettrone. Un orbitale è una regione di spazio
Capitolo 2 Risposte alle Domande ed esercizi inclusi nel Capitolo 2.1 (p. 37) Bohr descrisse un orbitale atomico come una traiettoria circolare seguita dall elettrone. Un orbitale è una regione di spazio
S P E T T R O S C O P I A. Dispense di Chimica Fisica per Biotecnologie Dr.ssa Rosa Terracciano
 S P E T T R O S C O P I A SPETTROSCOPIA I PARTE Cenni generali di spettroscopia: La radiazione elettromagnetica e i parametri che la caratterizzano Le regioni dello spettro elettromagnetico Interazioni
S P E T T R O S C O P I A SPETTROSCOPIA I PARTE Cenni generali di spettroscopia: La radiazione elettromagnetica e i parametri che la caratterizzano Le regioni dello spettro elettromagnetico Interazioni
Pinzani, Panero, Bagni Sperimentare la chimica Soluzioni degli esercizi Capitolo 9
 Pinzani, Panero, Bagni Sperimentare la chimica Soluzioni degli esercizi Capitolo 9 Esercizio PAG 198 ES 1 PAG 198 ES 2 PAG 198 ES 3 PAG 198 ES 4 PAG 198 ES 5 PAG 198 ES 6 PAG 198 ES 7 PAG 198 ES 8 PAG
Pinzani, Panero, Bagni Sperimentare la chimica Soluzioni degli esercizi Capitolo 9 Esercizio PAG 198 ES 1 PAG 198 ES 2 PAG 198 ES 3 PAG 198 ES 4 PAG 198 ES 5 PAG 198 ES 6 PAG 198 ES 7 PAG 198 ES 8 PAG
I 4 NUMERI QUANTICI. I numeri quantici consentono di definire forma, dimensioni ed energia degli orbitali.
 I 4 NUMERI QUANTICI I numeri quantici consentono di definire forma, dimensioni ed energia degli orbitali. n, numero quantico principale, indica il livello energetico e le dimensioni degli orbitali. Può
I 4 NUMERI QUANTICI I numeri quantici consentono di definire forma, dimensioni ed energia degli orbitali. n, numero quantico principale, indica il livello energetico e le dimensioni degli orbitali. Può
5) Modello atomico di BOHR
 5) Modello atomico di BOHR (pag.92 par.3 - parziale- ) PREMESSA: LIMITI DEL MODELLO DI RUTHERFORD Il modello planetario dell atomo sostenuto da Rutherford si adattava bene a molti dati sperimentali ma
5) Modello atomico di BOHR (pag.92 par.3 - parziale- ) PREMESSA: LIMITI DEL MODELLO DI RUTHERFORD Il modello planetario dell atomo sostenuto da Rutherford si adattava bene a molti dati sperimentali ma
Introduzione al corso di Fisica dei Semiconduttori
 Introduzione al corso di Fisica dei Semiconduttori Mara Bruzzi 8 settembre 016 1 a lezione : dualismo onda-corpuscolo a.l ipotesi di Planck e il corpo nero b.effetto Fotoelettrico c. Primi modelli atomici
Introduzione al corso di Fisica dei Semiconduttori Mara Bruzzi 8 settembre 016 1 a lezione : dualismo onda-corpuscolo a.l ipotesi di Planck e il corpo nero b.effetto Fotoelettrico c. Primi modelli atomici
TECNICHE SPETTROSCOPICHE
 TECNICHE SPETTROSCOPICHE L interazione delle radiazioni elettromagnetiche con la materia e essenzialmente un fenomeno quantico, che dipende sia dalle proprieta della radiazione sia dalla natura della materia
TECNICHE SPETTROSCOPICHE L interazione delle radiazioni elettromagnetiche con la materia e essenzialmente un fenomeno quantico, che dipende sia dalle proprieta della radiazione sia dalla natura della materia
6) Modello atomico a ORBITALI
 6) Modello atomico a ORBITALI PREMESSA: LIMITI DEL MODELLO DI BOHR (pag. 94 par.3) Applicando il concetto di quantizzazione dell E all atomo, Bohr ipotizzò che un atomo potesse esistere solo in determinati
6) Modello atomico a ORBITALI PREMESSA: LIMITI DEL MODELLO DI BOHR (pag. 94 par.3) Applicando il concetto di quantizzazione dell E all atomo, Bohr ipotizzò che un atomo potesse esistere solo in determinati
La struttura elettronica degli atomi
 1 In unità atomiche: a 0 me 0,59A unità di lunghezza e H 7, ev a H=Hartree unità di energia L energia dell atomo di idrogeno nello stato fondamentale espresso in unità atomiche è: 4 0 me 1 e 1 E H 13,
1 In unità atomiche: a 0 me 0,59A unità di lunghezza e H 7, ev a H=Hartree unità di energia L energia dell atomo di idrogeno nello stato fondamentale espresso in unità atomiche è: 4 0 me 1 e 1 E H 13,
FISICA ATOMICA E CHIMICA SPAZIO-DINAMICHE
 FISICA ATOMICA E CHIMICA SPAZIO-DINAMICHE IL MISTERO DELL ATOMO SVELATO I CAMPI COULOMBIANI ATOMICI QUALI APPARENZE DI CAMPI ROTANTI TODESCHINI VECCHIE E NUOVE LEGGI DELL ATOMO TRATTE DALLA SPAZIO- DINAMICA
FISICA ATOMICA E CHIMICA SPAZIO-DINAMICHE IL MISTERO DELL ATOMO SVELATO I CAMPI COULOMBIANI ATOMICI QUALI APPARENZE DI CAMPI ROTANTI TODESCHINI VECCHIE E NUOVE LEGGI DELL ATOMO TRATTE DALLA SPAZIO- DINAMICA
INDICE 1. LA CRISI DELLA FISICA CLASSICA
 INDICE 1. LA CRISI DELLA FISICA CLASSICA 1.1 Modelli atomici... 1 1.2 Il problema delle dimensioni atomiche e del collasso per irraggiamento 4 1.3 Difficoltà connesse con i calori specifici... 7 1.4 L
INDICE 1. LA CRISI DELLA FISICA CLASSICA 1.1 Modelli atomici... 1 1.2 Il problema delle dimensioni atomiche e del collasso per irraggiamento 4 1.3 Difficoltà connesse con i calori specifici... 7 1.4 L
Quadro di Riferimento della II prova di Fisica dell esame di Stato per i Licei Scientifici
 Quadro di Riferimento della II prova di Fisica dell esame di Stato per i Licei Scientifici Il presente documento individua le conoscenze, abilità e competenze che lo studente dovrà aver acquisito al termine
Quadro di Riferimento della II prova di Fisica dell esame di Stato per i Licei Scientifici Il presente documento individua le conoscenze, abilità e competenze che lo studente dovrà aver acquisito al termine
Misura del rapporto carica massa dell elettrone
 Relazione di: Pietro Ghiglio, Tommaso Lorenzon Laboratorio di fisica del Liceo Scientifico L. da Vinci - Gallarate Misura del rapporto carica massa dell elettrone Lezioni di maggio 2015 Lo scopo dell esperienza
Relazione di: Pietro Ghiglio, Tommaso Lorenzon Laboratorio di fisica del Liceo Scientifico L. da Vinci - Gallarate Misura del rapporto carica massa dell elettrone Lezioni di maggio 2015 Lo scopo dell esperienza
Risonanza magnetica nucleare
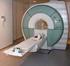 Risonanza magnetica nucleare Università di Firenze Corso di Tecnologie Biomediche Lezione del 31 ottobre 2003 Leonardo Bocchi Principi fisici Premessa Modello classico Visualizzazione semplificata Equazione
Risonanza magnetica nucleare Università di Firenze Corso di Tecnologie Biomediche Lezione del 31 ottobre 2003 Leonardo Bocchi Principi fisici Premessa Modello classico Visualizzazione semplificata Equazione
Chimica e Propedeutica Biochimica
 Chimica e Propedeutica Biochimica Beatrice Vallone Linda Savino Dipartimento di Scienze Biochimiche Sapienza - Università di Roma E-mail: [email protected] CHIMICA: STUDIO DELLA MATERIA: Proprietà
Chimica e Propedeutica Biochimica Beatrice Vallone Linda Savino Dipartimento di Scienze Biochimiche Sapienza - Università di Roma E-mail: [email protected] CHIMICA: STUDIO DELLA MATERIA: Proprietà
