Meccanica quantistica (5)
|
|
|
- Letizia Giuseppe
- 8 anni fa
- Просмотров:
Транскрипт
1 Meccanica quantistica (5) 0/7/14 1-MQ-5.doc 0
2 Oscillatore armonico Se una massa è sottoposta ad una forza di richiamo proporzionale allo spostamento da un posizione di equilibrio F = kx il potenziale ( armonico) F = dv dx ) sarà la parabola (potenziale V ( x) = kx 1 d V ( x) dx La costante k, ( la larghezza della curva La frequenza è ) determina la curvatura e quindi ω = k m 0/7/14 1-MQ-5.doc 1
3 Oscillatore armonico Quantistico Per una massa m sottoposta ad un potenziale armonico l eq. di Schroedinger è: h m d ψ ( x) + dx 1 kx ψ ( x) = Eψ ( x) Dove x è lo spostamento dalla posizione di equilibrio Perché la ψ (x) abbia il comportamento corretto all infinto Lim ψ ( x) = 0 x ± Ovvero gli spostamenti molto grandi sono molto improbabili La soluzione deve allora essere del tipo: H v ( x) e cx Dove H v (y) è un polinomio di grado v ( polinomi di Hermite). (qualsiasi polinomio per x ± va a più lentamente di quanto yx e va a 0) 0/7/14 1-MQ-5.doc
4 Le condizioni poste alla funzione d onda portano a E = ( v + 1 )hω ω = k m v non negativo intero Gli stati sono a intervalli costanti di energia h ω All aumentare dell energia la frequenza ω non cambia 0/7/14 1-MQ-5.doc 3
5 Energia di punto zero E = ( v + 1)hω v non negativo intero L energia dell oscillatore non può mai essere nulla L oscillatore è sempre in moto Viene rispettato il principio di indeterminazione Se fosse fermo: il momento cinetico sarebbe identicamente nullo con varianza nulla lo spostamento sarebbe identicamente nullo e quindi la posizione avrebbe varianza nulla L energia minima: È detta: E = 1 hω Energia di punto zero 0/7/14 1-MQ-5.doc 4
6 Funzione d onda Il numero di nodi è dato dal grado del polinomio I polinomi di grado pari sono simmetrici: H(-x) = H(x) dispari sono antisimmetrici: H(-x) = - H(x) All aumentare dell energia aumenta lo spostamento più probabile 0/7/14 1-MQ-5.doc 5
7 Probabilità La distribuzione di probabilità per l oscillatore classico ha una posizione limite: c è uno spostamento massimo rispettoalla posizione di equilibrio La distribuzione di probabilità per l oscillatore quantstico va a zero all infinito: qualsiasi spostamento è possibile 0/7/14 1-MQ-5.doc 6
8 Equazione di Schrödinger in 3D h ψ ( x, y, z) + Vψ ( x, y, z) = Eψ ( x, y, z) m ( è detto operatore Laplaciano) Dove In coordinate cartesiane ortogonali V = V ( x, y, z) ψ = ψ ( x, y, z) = + + x y z In coordinate polari sferiche: x = r sinθ cosϕ y = r sinθ sinϕ z = r cosθ 0 r 0 θ π 0 ϕ π V = V ( r, θ, ϕ) ψ = ψ ( r, θ, ϕ) 0/7/14 1-MQ-5.doc 7
9 = r + sinθ + r r r sinθ θ θ sin θ ϕ 0/7/14 1-MQ-5.doc 8
10 Moto rotazionale (moto centrale) m v=p Energia cinetica p E = m Grandezza del momento angolare Momento d inerzia: L E = mr I = mr L E = I L = pr Per rappresentare il moto rotazionale è conveniente usare coordinate polari sferiche 0/7/14 1-MQ-5.doc 9
11 Rotazione in 3D Si consideri il moto su una superficie sferica di raggio r Essendo r costante le derivate in r si annullano Il potenziale V è costante è può essere assunto 0 h mr 1 sin θ 1 sinθ + θ θ sin θ ϕ ψ ( θ, ϕ) = Eψ ( θ, ϕ) Tenendo conto che I = mr è il momento d inerzia 1 1 IE sinθ + ψ ( θ, ϕ) = ψ ( θ, ϕ) sinθ θ θ sin θ ϕ h Risolvendo l equazione tenendo conto che ψ ( θ, ϕ) deve essere finita, continua e con derivate continue dappertutto ψ ( 0, θ ) = ψ (π, θ ) ψ '(0, θ ) = ψ '(π, θ ) ψ (ϕ,0) < ψ ( ϕ, π ) < si ha che le soluzioni dipendono da parametri interi: l = 0,1,,...; l ml ; m l = 0, ± 1, ±,... Le autofunzioni sono: m Y l l ( θ, ϕ) Gli autovalori: l ( l +1) 0/7/14 1-MQ-5.doc 10
12 Armoniche sferiche 1 1 le autofunzioni di: sinθ + sinθ θ θ sin θ ϕ ml l sono: Yl ( θ, ϕ) = N Θl ( θ ) Φm ( ϕ) m l m l l = 0,1,,...; = l, l 1, K,.0,...,. l + 1,. l Hanno l superfici nodali 0/7/14 1-MQ-5.doc 11
13 Superfici nodali l m l Funzione N nodi z x /7/14 1-MQ-5.doc 1
14 Momento angolare IE Essendo = l( l + 1) h l( l + 1) E =h l = 0,1,,. I L energia rotazionale è quantizzata dipende solo da l può essere nulla Quindi tutti gli stati rotazionali con lo stesso l hanno la stessa energia Ma L E I = e quindi L = h l( l + 1) Il modulo del momento angolare L, è quantizzato Anche la componente z di L r è quantizzata: L z = m l h 0/7/14 1-MQ-5.doc 13
15 Momento angolare Al variare di m l cambia l orientazione rispetto a z Ci sono l+1 orientazioni 0/7/14 1-MQ-5.doc 14
16 Indeterminazione di L Siccome le componenti x e y di L r possono assumere qualsiasi valore Qualsiasi vettore sulla superficie di un cono è soluzione del moto rotatorio con una data L z Il momento angolare di un sistema quantistico ha modulo definito e orientazione definita solo in parte Si può determinare esattamente una sola componente del momento angolare 0/7/14 1-MQ-5.doc 15
17 Spin Le particelle elementari sono caratterizzate da tre proprietà: Massa, Carica elettrica e Spin Massa: scalare senza segno m Carica elettrica: scalare con segno ± q Spin: vettoriale S r Lo spin si comporta matematicamente come il Momento Angolare: S = h s( s + 1) s = 0,1,,...; Dato che non si hanno condizioni di continuità, s può essere non intero: s =,,,... 3 m s = s, s 1,...,. s + 1,. s S z = m s h Lo spin è determinato dal numero s s è una proprietà intrinseca della particella (non può cambiare) l orientamento (m s ) invece può cambiare 0/7/14 1-MQ-5.doc 16
18 Tutte le particelle elementari si dividono in: Bosoni s = 0,1,, Fermioni s =,,,... 3 m (Kg) q (e) s fotone elettrone / protone / neutrone / I nuclei essendo composti di protoni e neutroni hanno uno spin totale che può essere 0, intero, semi-intero (isotopi diversi hanno spin diverso) 1 1 Quando s = : m s = ± sono possibili solo 1 3 orientazioni, quindi S z = ± h S = h 0/7/14 1-MQ-5.doc 17
19 Momento magnetico di e - Allo spin è associato un dipolo magnetico µ r In un campo magnetico gli elettroni vengono deflessi in modo opposto secondo l orientazione s E un momento magnetico intrinsico della particella Non è legato ad una effettiva rotazione della particella Dal momento magnetico dell elettrone si ricaverrebbe una velocità lineare massima (un punto sull equatore dell elettrone) di 137 volte la velocità della luce!!!!!!! Lo Spin non è descrivibile come una particella carica che ruota su se stessa 0/7/14 1-MQ-5.doc 18
1.3 L effetto tunnel (trattazione semplificata)
 1.3 L effetto tunnel (trattazione semplificata) Se la parete di energia potenziale non ha altezza infinita e E < V, la funzione d onda non va rapidamente a zero all interno della parete stessa. Di conseguenza,
1.3 L effetto tunnel (trattazione semplificata) Se la parete di energia potenziale non ha altezza infinita e E < V, la funzione d onda non va rapidamente a zero all interno della parete stessa. Di conseguenza,
GLI ORBITALI ATOMICI
 GLI ORBITALI ATOMICI Orbitali atomici e loro rappresentazione Le funzioni d onda Ψ n che derivano dalla risoluzione dell equazione d onda e descrivono il moto degli elettroni nell atomo si dicono orbitali
GLI ORBITALI ATOMICI Orbitali atomici e loro rappresentazione Le funzioni d onda Ψ n che derivano dalla risoluzione dell equazione d onda e descrivono il moto degli elettroni nell atomo si dicono orbitali
Lezione n. 19. L equazione. di Schrodinger L atomo. di idrogeno Orbitali atomici. 02/03/2008 Antonino Polimeno 1
 Chimica Fisica - Chimica e Tecnologia Farmaceutiche Lezione n. 19 L equazione di Schrodinger L atomo di idrogeno Orbitali atomici 02/03/2008 Antonino Polimeno 1 Dai modelli primitivi alla meccanica quantistica
Chimica Fisica - Chimica e Tecnologia Farmaceutiche Lezione n. 19 L equazione di Schrodinger L atomo di idrogeno Orbitali atomici 02/03/2008 Antonino Polimeno 1 Dai modelli primitivi alla meccanica quantistica
Comune ordine di riempimento degli orbitali di un atomo
 Comune ordine di riempimento degli orbitali di un atomo Le energie relative sono diverse per differenti elementi ma si possono notare le seguenti caratteristiche: (1) La maggior differenza di energia si
Comune ordine di riempimento degli orbitali di un atomo Le energie relative sono diverse per differenti elementi ma si possono notare le seguenti caratteristiche: (1) La maggior differenza di energia si
Corso di Laurea in Chimica e Tecnologie Chimiche - A.A Chimica Fisica II. Esame scritto del 25 Febbraio P = i.
 1 Corso di Laurea in Chimica e Tecnologie Chimiche - A.A. 212-213 Chimica Fisica II Esame scritto del 25 Febbraio 213 Quesiti d esame: 1. Definire gli operatori componente del momento cinetico P x e del
1 Corso di Laurea in Chimica e Tecnologie Chimiche - A.A. 212-213 Chimica Fisica II Esame scritto del 25 Febbraio 213 Quesiti d esame: 1. Definire gli operatori componente del momento cinetico P x e del
OSCILLATORE ARMONICO SEMPLICE
 OSCILLATORE ARMONICO SEMPLICE Un oscillatore è costituito da una particella che si muove periodicamente attorno ad una posizione di equilibrio. Compiono moti oscillatori: il pendolo, un peso attaccato
OSCILLATORE ARMONICO SEMPLICE Un oscillatore è costituito da una particella che si muove periodicamente attorno ad una posizione di equilibrio. Compiono moti oscillatori: il pendolo, un peso attaccato
L equazione di Schrödinger unidimensionale: soluzione analitica e numerica
 Chapter 3 L equazione di Schrödinger unidimensionale: soluzione analitica e numerica In questo capitolo verrà descritta una metodologia per risolvere sia analiticamente che numericamente l equazione di
Chapter 3 L equazione di Schrödinger unidimensionale: soluzione analitica e numerica In questo capitolo verrà descritta una metodologia per risolvere sia analiticamente che numericamente l equazione di
L ATOMO SECONDO LA MECCANICA ONDULATORIA IL DUALISMO ONDA-PARTICELLA. (Plank Einstein)
 L ATOMO SECONDO LA MECCANICA ONDULATORIA IL DUALISMO ONDA-PARTICELLA POSTULATO DI DE BROGLIÈ Se alla luce, che è un fenomeno ondulatorio, sono associate anche le caratteristiche corpuscolari della materia
L ATOMO SECONDO LA MECCANICA ONDULATORIA IL DUALISMO ONDA-PARTICELLA POSTULATO DI DE BROGLIÈ Se alla luce, che è un fenomeno ondulatorio, sono associate anche le caratteristiche corpuscolari della materia
Esercizi di Fisica Matematica 3, anno , parte di meccanica hamiltoniana e quantistica
 Esercizi di Fisica Matematica 3, anno 014-015, parte di meccanica hamiltoniana e quantistica Dario Bambusi 09.06.015 Abstract Gli esercizi dei compiti saranno varianti dei seguenti esercizi. Nei compiti
Esercizi di Fisica Matematica 3, anno 014-015, parte di meccanica hamiltoniana e quantistica Dario Bambusi 09.06.015 Abstract Gli esercizi dei compiti saranno varianti dei seguenti esercizi. Nei compiti
Spettroscopia. 05/06/14 SPET.doc 0
 Spettroscopia 05/06/14 SPET.doc 0 Spettroscopia Analisi del passaggio di un sistema da uno stato all altro con scambio di fotoni Spettroscopia di assorbimento Spettroscopia di emissione: In entrambi i
Spettroscopia 05/06/14 SPET.doc 0 Spettroscopia Analisi del passaggio di un sistema da uno stato all altro con scambio di fotoni Spettroscopia di assorbimento Spettroscopia di emissione: In entrambi i
Risonanza Magnetica Nucleare
 Risonanza Magnetica Nucleare Il fenomeno della risonanza magnetica nucleare è legato ad una proprietà p di alcuni nuclei quale lo spin. Lo spin è una proprietà fondamentale come la carica e la massa. Protoni,
Risonanza Magnetica Nucleare Il fenomeno della risonanza magnetica nucleare è legato ad una proprietà p di alcuni nuclei quale lo spin. Lo spin è una proprietà fondamentale come la carica e la massa. Protoni,
Esercizi di Fisica Matematica 3, anno
 Esercizi di Fisica Matematica 3, anno 01-013 Dario Bambusi, Andrea Carati 5.06.013 Abstract Tra i seguenti esercizi verranno scelti gli esercizi dell esame di Fisica Matematica 3. 1 Meccanica Hamiltoniana
Esercizi di Fisica Matematica 3, anno 01-013 Dario Bambusi, Andrea Carati 5.06.013 Abstract Tra i seguenti esercizi verranno scelti gli esercizi dell esame di Fisica Matematica 3. 1 Meccanica Hamiltoniana
Momento angolare. Operatori: richiami. Momento angolare classico. z Momento angolare v. Operatore posizione in 3D
 Operatori: richiami Operatore posizione in 3D Non Operatore è permessa, momento in particolare, la riproduzione anche parziale i Per l autorizzazione a riprodurre in parte [ o in tutto la presente Detti
Operatori: richiami Operatore posizione in 3D Non Operatore è permessa, momento in particolare, la riproduzione anche parziale i Per l autorizzazione a riprodurre in parte [ o in tutto la presente Detti
PROBLEMI DI FISICA MODERNA E MECCANICA QUANTISTICA. MECCANICA QUANTISTICA anno accademico
 PROBLEMI DI FISICA MODERNA E MECCANICA QUANTISTICA MECCANICA QUANTISTICA anno accademico 2012-2013 (1) Per un sistema n-dimensionale si scrivano: (a) gli elementi di matrice dell operatore posizione x
PROBLEMI DI FISICA MODERNA E MECCANICA QUANTISTICA MECCANICA QUANTISTICA anno accademico 2012-2013 (1) Per un sistema n-dimensionale si scrivano: (a) gli elementi di matrice dell operatore posizione x
Struttura Elettronica degli Atomi Meccanica quantistica
 Prof. A. Martinelli Struttura Elettronica degli Atomi Meccanica quantistica Dipartimento di Farmacia 1 Il comportamento ondulatorio della materia 2 1 Il comportamento ondulatorio della materia La diffrazione
Prof. A. Martinelli Struttura Elettronica degli Atomi Meccanica quantistica Dipartimento di Farmacia 1 Il comportamento ondulatorio della materia 2 1 Il comportamento ondulatorio della materia La diffrazione
Funzioni di R n a R m e la matrice Jacobiana
 0.1 Funzioni di R n a R m. Politecnico di Torino. Funzioni di R n a R m e la matrice Jacobiana Nota Bene: delle lezioni. Questo materiale non deve essere considerato come sostituto 0.1 Funzioni di R n
0.1 Funzioni di R n a R m. Politecnico di Torino. Funzioni di R n a R m e la matrice Jacobiana Nota Bene: delle lezioni. Questo materiale non deve essere considerato come sostituto 0.1 Funzioni di R n
Dinamica Rotazionale
 Dinamica Rotazionale Richiamo: cinematica rotazionale, velocità e accelerazione angolare Energia cinetica rotazionale: momento d inerzia Equazione del moto rotatorio: momento delle forze Leggi di conservazione
Dinamica Rotazionale Richiamo: cinematica rotazionale, velocità e accelerazione angolare Energia cinetica rotazionale: momento d inerzia Equazione del moto rotatorio: momento delle forze Leggi di conservazione
ATOMI MONOELETTRONICI
 ATOMI MONOELETTRONICI L equazione di Schrödinger per gli atomi contenenti un solo elettrone (atomo di idrogeno, ioni He +, Li 2+ ) può essere risolta in maniera esatta e le soluzioni ottenute permettono
ATOMI MONOELETTRONICI L equazione di Schrödinger per gli atomi contenenti un solo elettrone (atomo di idrogeno, ioni He +, Li 2+ ) può essere risolta in maniera esatta e le soluzioni ottenute permettono
Elettronica II L equazione di Schrödinger p. 2
 Elettronica II L equazione di Schrödinger Valentino Liberali Dipartimento di Tecnologie dell Informazione Università di Milano, 26013 Crema e-mail: [email protected] http://www.dti.unimi.it/ liberali
Elettronica II L equazione di Schrödinger Valentino Liberali Dipartimento di Tecnologie dell Informazione Università di Milano, 26013 Crema e-mail: [email protected] http://www.dti.unimi.it/ liberali
Unità didattica 2. Seconda unità didattica (Fisica) 1. Corso integrato di Matematica e Fisica per il Corso di Farmacia
 Unità didattica 2 Dinamica Leggi di Newton.. 2 Le forze 3 Composizione delle forze 4 Esempio di forza applicata...5 Esempio: il piano inclinato.. 6 Il moto del pendolo.. 7 La forza gravitazionale 9 Lavoro
Unità didattica 2 Dinamica Leggi di Newton.. 2 Le forze 3 Composizione delle forze 4 Esempio di forza applicata...5 Esempio: il piano inclinato.. 6 Il moto del pendolo.. 7 La forza gravitazionale 9 Lavoro
ATOMO. Legge della conservazione della massa Legge delle proporzioni definite Dalton
 Democrito IV secolo A.C. ATOMO Lavoisier Proust Legge della conservazione della massa Legge delle proporzioni definite Dalton (808) Teoria atomica Gay-Lussac volumi di gas reagiscono secondo rapporti interi
Democrito IV secolo A.C. ATOMO Lavoisier Proust Legge della conservazione della massa Legge delle proporzioni definite Dalton (808) Teoria atomica Gay-Lussac volumi di gas reagiscono secondo rapporti interi
Applicazioni delle leggi della meccanica: moto armnico
 Applicazioni delle leggi della meccanica: moto armnico Discutiamo le caratteristiche del moto armonico utilizzando l esempio di una molla di costante k e massa trascurabile a cui è fissato un oggetto di
Applicazioni delle leggi della meccanica: moto armnico Discutiamo le caratteristiche del moto armonico utilizzando l esempio di una molla di costante k e massa trascurabile a cui è fissato un oggetto di
Fisica per scienze ed ingegneria
 Serway, Jewett Fisica per scienze ed ingegneria Capitolo 15 Blocchetto legato ad una molla in moto su un piano orizzontale privo di attrito. Forza elastica di richiamo: F x =-Kx (Legge di Hooke). Per x>0,
Serway, Jewett Fisica per scienze ed ingegneria Capitolo 15 Blocchetto legato ad una molla in moto su un piano orizzontale privo di attrito. Forza elastica di richiamo: F x =-Kx (Legge di Hooke). Per x>0,
Si arrivò a dimostrare l esistenza di una forma elementare della materia (atomo) solo nel 1803 (John Dalton)
 Atomi 16 Si arrivò a dimostrare l esistenza di una forma elementare della materia (atomo) solo nel 1803 (John Dalton) 17 Teoria atomica di Dalton Si basa sui seguenti postulati: 1. La materia è formata
Atomi 16 Si arrivò a dimostrare l esistenza di una forma elementare della materia (atomo) solo nel 1803 (John Dalton) 17 Teoria atomica di Dalton Si basa sui seguenti postulati: 1. La materia è formata
CONDENSATI DI BOSE-EINSTEIN E SUPERFLUIDI
 CONDENSATI DI BOSE-EINSTEIN E SUPERFLUIDI Consideriamo un fluido in una scatola. Questo è un insieme di tanti piccoli costituenti che supponiamo per semplicità essere identici. Dalla meccanica quantistica
CONDENSATI DI BOSE-EINSTEIN E SUPERFLUIDI Consideriamo un fluido in una scatola. Questo è un insieme di tanti piccoli costituenti che supponiamo per semplicità essere identici. Dalla meccanica quantistica
Quesiti dell Indirizzo Tecnologico
 Quesiti dell Indirizzo Tecnologico 1) Sapendo che la massa di Marte é 1/10 della massa della Terra e che il suo raggio é ½ di quello della Terra l accelerazione di gravità su Marte è: a) 1/10 di quella
Quesiti dell Indirizzo Tecnologico 1) Sapendo che la massa di Marte é 1/10 della massa della Terra e che il suo raggio é ½ di quello della Terra l accelerazione di gravità su Marte è: a) 1/10 di quella
Interazione luce- atomo
 Interazione luce- atomo Descrizione semiclassica L interazione predominante è quella tra il campo elettrico e le cariche ASSORBIMENTO: Elettrone e protone formano un dipolo che viene messo in oscillazione
Interazione luce- atomo Descrizione semiclassica L interazione predominante è quella tra il campo elettrico e le cariche ASSORBIMENTO: Elettrone e protone formano un dipolo che viene messo in oscillazione
Fisica Quantistica III Esercizi Natale 2009
 Fisica Quantistica III Esercizi Natale 009 Philip G. Ratcliffe ([email protected]) Dipartimento di Fisica e Matematica Università degli Studi dell Insubria in Como via Valleggio 11, 100 Como
Fisica Quantistica III Esercizi Natale 009 Philip G. Ratcliffe ([email protected]) Dipartimento di Fisica e Matematica Università degli Studi dell Insubria in Como via Valleggio 11, 100 Como
Esercitazioni di Meccanica Razionale
 Esercitazioni di Meccanica Razionale a.a. 2002/2003 Composizione di stati cinetici Maria Grazia Naso [email protected] Dipartimento di Matematica Università degli Studi di Brescia Esercitazioni di Meccanica
Esercitazioni di Meccanica Razionale a.a. 2002/2003 Composizione di stati cinetici Maria Grazia Naso [email protected] Dipartimento di Matematica Università degli Studi di Brescia Esercitazioni di Meccanica
Cinematica in due o più dimensioni
 Cinematica in due o più dimensioni Le grandezze cinematiche fondamentali: posizione, velocità, accelerazione, sono dei vettori nello spazio a due o tre dimensioni, dotati di modulo, direzione, verso. In
Cinematica in due o più dimensioni Le grandezze cinematiche fondamentali: posizione, velocità, accelerazione, sono dei vettori nello spazio a due o tre dimensioni, dotati di modulo, direzione, verso. In
L atomo di idrogeno (1) H T = p2 1 2m 1. + p2 2 2m 2. + V ( r 1 r 2 ) (2) Definiamo le nuove variabili: 1. La massa totale M M = m 1 + m 2 (3)
 L atomo di idrogeno Il problema dell atomo di idrogeno é un problema esattamente risolubili ed i suoi risultati possono essere estesi agli atomi idrogenoidi, in cui solo c é solo un elettrone sottoposto
L atomo di idrogeno Il problema dell atomo di idrogeno é un problema esattamente risolubili ed i suoi risultati possono essere estesi agli atomi idrogenoidi, in cui solo c é solo un elettrone sottoposto
P = r. o + r. O + ω r (1)
 1 5.1-MOTI RELATIVI Parte I 5.1-Moti relativi-cap5 1 5.1-Moti relativi Teorema delle velocità relative Riprendiamo l impostazione tracciata nel paragrafo 2.6 (moti relativi 2-D) e consideriamo un sistema
1 5.1-MOTI RELATIVI Parte I 5.1-Moti relativi-cap5 1 5.1-Moti relativi Teorema delle velocità relative Riprendiamo l impostazione tracciata nel paragrafo 2.6 (moti relativi 2-D) e consideriamo un sistema
approfondimento Cinematica ed energia di rotazione equilibrio statico di un corpo esteso conservazione del momento angolare
 approfondimento Cinematica ed energia di rotazione equilibrio statico di un corpo esteso conservazione del momento angolare Moto di rotazione Rotazione dei corpi rigidi ϑ(t) ω z R asse di rotazione v m
approfondimento Cinematica ed energia di rotazione equilibrio statico di un corpo esteso conservazione del momento angolare Moto di rotazione Rotazione dei corpi rigidi ϑ(t) ω z R asse di rotazione v m
Angolo polare, versori radiale e trasverso
 Angolo polare, versori radiale e trasverso Desideriamo descrivere il moto di un corpo puntiforme che ruota su una circonferenza attorno ad un asse fisso. Nella figura l asse di rotazione coincide con l
Angolo polare, versori radiale e trasverso Desideriamo descrivere il moto di un corpo puntiforme che ruota su una circonferenza attorno ad un asse fisso. Nella figura l asse di rotazione coincide con l
Grandezze angolari. Lineare Angolare Relazione x θ x = rθ. m I I = mr 2 F N N = rf sin θ 1 2 mv2 1
 Grandezze angolari Lineare Angolare Relazione x θ x = rθ v ω v = ωr a α a = αr m I I = mr 2 F N N = rf sin θ 1 2 mv2 1 2 Iω 2 Energia cinetica In forma vettoriale: v = ω r questa collega la velocità angolare
Grandezze angolari Lineare Angolare Relazione x θ x = rθ v ω v = ωr a α a = αr m I I = mr 2 F N N = rf sin θ 1 2 mv2 1 2 Iω 2 Energia cinetica In forma vettoriale: v = ω r questa collega la velocità angolare
Laurea Magistrale di INGEGNERIA ELETTRONICA (LM-29) a.a , I semestre! Programma del corso di FISICA SUPERIORE! Docente: MAURO PAPINUTTO!
 Laurea Magistrale di INGEGNERIA ELETTRONICA (LM-29) a.a. 2013-14, I semestre Programma del corso di FISICA SUPERIORE Docente: MAURO PAPINUTTO Dipartimento di Fisica Phone: +39 06 4991 4376 Universita`
Laurea Magistrale di INGEGNERIA ELETTRONICA (LM-29) a.a. 2013-14, I semestre Programma del corso di FISICA SUPERIORE Docente: MAURO PAPINUTTO Dipartimento di Fisica Phone: +39 06 4991 4376 Universita`
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016
 Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
Indice 3. Note di utilizzo 9. Ringraziamenti 10. Introduzione 11
 Indice Indice 3 Note di utilizzo 9 Ringraziamenti 10 Introduzione 11 Capitolo 1 Grandezze fisiche e schematizzazione dei sistemi materiali 13 1.1 Grandezze fisiche ed operazione di misura 13 1.2 Riferimento
Indice Indice 3 Note di utilizzo 9 Ringraziamenti 10 Introduzione 11 Capitolo 1 Grandezze fisiche e schematizzazione dei sistemi materiali 13 1.1 Grandezze fisiche ed operazione di misura 13 1.2 Riferimento
LA STRUTTURA DELL ATOMO
 Università degli studi di MILANO Facoltà di AGRARIA El. di Chimica e Chimica Fisica Mod. 1 CHIMICA Mod. 2 CHIMICA FISICA Lezione 3 Anno Accademico 2010-2011 Docente: Dimitrios Fessas LA STRUTTURA DELL
Università degli studi di MILANO Facoltà di AGRARIA El. di Chimica e Chimica Fisica Mod. 1 CHIMICA Mod. 2 CHIMICA FISICA Lezione 3 Anno Accademico 2010-2011 Docente: Dimitrios Fessas LA STRUTTURA DELL
Analisi del moto dei proietti
 Moto dei proietti E il moto di particelle che vengono lanciate con velocità iniziale v 0 e sono soggette alla sola accelerazione di gravità g supposta costante. La pallina rossa viene lasciata cadere da
Moto dei proietti E il moto di particelle che vengono lanciate con velocità iniziale v 0 e sono soggette alla sola accelerazione di gravità g supposta costante. La pallina rossa viene lasciata cadere da
Particelle Subatomiche
 GLI ATOMI Particelle Subatomiche ELEMENTI I diversi atomi sono caratterizzati da un diverso numero di protoni e neutroni; il numero di elettroni è sempre uguale al numero dei protoni (negli atomi neutri)
GLI ATOMI Particelle Subatomiche ELEMENTI I diversi atomi sono caratterizzati da un diverso numero di protoni e neutroni; il numero di elettroni è sempre uguale al numero dei protoni (negli atomi neutri)
Modello atomico ad orbitali e numeri quantici
 Modello atomico ad orbitali e numeri quantici Il modello atomico di Bohr permette di scrivere correttamente la configurazione elettronica di un atomo ma ha dei limiti che sono stati superati con l introduzione
Modello atomico ad orbitali e numeri quantici Il modello atomico di Bohr permette di scrivere correttamente la configurazione elettronica di un atomo ma ha dei limiti che sono stati superati con l introduzione
RISOLUZIONE DI PROBLEMI DI FISICA
 RISOUZIONE DI PROBEMI DI FISICA Problema 1 Una massa puntiforme m = 2 kg è soggetta ad una forza centrale con associata energia potenziale radiale U( r) 6 A =, dove A = 2 J m 6. Il momento angolare della
RISOUZIONE DI PROBEMI DI FISICA Problema 1 Una massa puntiforme m = 2 kg è soggetta ad una forza centrale con associata energia potenziale radiale U( r) 6 A =, dove A = 2 J m 6. Il momento angolare della
Generalità delle onde elettromagnetiche
 Generalità delle onde elettromagnetiche Ampiezza massima: E max (B max ) Lunghezza d onda: (m) E max (B max ) Periodo: (s) Frequenza: = 1 (s-1 ) Numero d onda: = 1 (m-1 ) = v Velocità della luce nel vuoto
Generalità delle onde elettromagnetiche Ampiezza massima: E max (B max ) Lunghezza d onda: (m) E max (B max ) Periodo: (s) Frequenza: = 1 (s-1 ) Numero d onda: = 1 (m-1 ) = v Velocità della luce nel vuoto
Lavoro. Esempio. Definizione di lavoro. Lavoro motore e lavoro resistente. Lavoro compiuto da più forze ENERGIA, LAVORO E PRINCIPI DI CONSERVAZIONE
 Lavoro ENERGIA, LAVORO E PRINCIPI DI CONSERVAZIONE Cos è il lavoro? Il lavoro è la grandezza fisica che mette in relazione spostamento e forza. Il lavoro dipende sia dalla direzione della forza sia dalla
Lavoro ENERGIA, LAVORO E PRINCIPI DI CONSERVAZIONE Cos è il lavoro? Il lavoro è la grandezza fisica che mette in relazione spostamento e forza. Il lavoro dipende sia dalla direzione della forza sia dalla
Oscillazioni. Si produce un oscillazione quando un sistema viene perturbato rispetto a una posizione di equilibrio stabile
 Oscillazioni Si produce un oscillazione quando un sistema viene perturbato rispetto a una posizione di equilibrio stabile Caratteristica più evidente del moto oscillatorio è di essere un moto periodico,
Oscillazioni Si produce un oscillazione quando un sistema viene perturbato rispetto a una posizione di equilibrio stabile Caratteristica più evidente del moto oscillatorio è di essere un moto periodico,
Elettronica II Segnali periodici; serie di Fourier; trasformata di Fourier p. 2
 Elettronica II Segnali periodici; serie di Fourier; trasformata di Fourier Valentino Liberali Dipartimento di Tecnologie dell Informazione Università di Milano, 26013 Crema e-mail: [email protected]
Elettronica II Segnali periodici; serie di Fourier; trasformata di Fourier Valentino Liberali Dipartimento di Tecnologie dell Informazione Università di Milano, 26013 Crema e-mail: [email protected]
Lavoisier (1770) Legge della conservazione della massa in una trasf. chimica es. C + O 2 CO 2 Dalton (1808) Teoria atomica
 ATOMO Democrito IV secolo A.C. Lavoisier (1770) Legge della conservazione della massa in una trasf. chimica es. C + O 2 CO 2 Dalton (1808) Teoria atomica E=mc 2 Avogadro (1811) Volumi uguali di gas diversi
ATOMO Democrito IV secolo A.C. Lavoisier (1770) Legge della conservazione della massa in una trasf. chimica es. C + O 2 CO 2 Dalton (1808) Teoria atomica E=mc 2 Avogadro (1811) Volumi uguali di gas diversi
Problemi di Meccanica Quantistica. Capitolo IX. Spin. a cura di Fedele Lizzi, Gennaro Miele e Francesco Nicodemi
 Problemi di Meccanica Quantistica Capitolo IX Spin a cura di Fedele Lizzi, Gennaro Miele e Francesco Nicodemi http://people.na.infn.it/%7epq-qp Problema IX.1 Un sistema consiste di due particelle distinguibili
Problemi di Meccanica Quantistica Capitolo IX Spin a cura di Fedele Lizzi, Gennaro Miele e Francesco Nicodemi http://people.na.infn.it/%7epq-qp Problema IX.1 Un sistema consiste di due particelle distinguibili
Particella in un campo elettromagnetico
 Particella in un campo elettromagnetico Vogliamo descrivere dal punto di vista quantistico una particella carica posta in un campo elettromagnetico. Momento di una particella Dal punto di vista classico
Particella in un campo elettromagnetico Vogliamo descrivere dal punto di vista quantistico una particella carica posta in un campo elettromagnetico. Momento di una particella Dal punto di vista classico
Calcolo vettoriale. Versore: vettore u adimensionale di modulo unitario (rapporto tra un vettore e il suo modulo)
 Grandezze scalari: caratterizzate da un valore numerico in una unità di misura scelta (ex: massa, temperatura, ecc) Grandezze vettoriali: oltre al valore numerico necessitano della definizione di una direzione
Grandezze scalari: caratterizzate da un valore numerico in una unità di misura scelta (ex: massa, temperatura, ecc) Grandezze vettoriali: oltre al valore numerico necessitano della definizione di una direzione
Università dell Aquila - Ingegneria Prova Scritta di Fisica Generale I - 03/07/2015 Nome Cognome N. Matricola CFU
 Università dell Aquila - Ingegneria Prova Scritta di Fisica Generale I - 03/07/2015 Nome Cognome N. Matricola CFU............ Tempo a disposizione (tre esercizi) 2 ore e 30 1 esercizio (esonero) 1 ora
Università dell Aquila - Ingegneria Prova Scritta di Fisica Generale I - 03/07/2015 Nome Cognome N. Matricola CFU............ Tempo a disposizione (tre esercizi) 2 ore e 30 1 esercizio (esonero) 1 ora
Equazioni differenziali
 Equazioni differenziali Antonino Polimeno Università degli Studi di Padova Equazioni differenziali - 1 Un equazione differenziale è un equazione la cui soluzione è costituita da una funzione incognita
Equazioni differenziali Antonino Polimeno Università degli Studi di Padova Equazioni differenziali - 1 Un equazione differenziale è un equazione la cui soluzione è costituita da una funzione incognita
(trascurare la massa delle razze della ruota, e schematizzarla come un anello; momento d inerzia dell anello I A = MR 2 )
 1 Esercizio Una ruota di raggio R e di massa M può rotolare senza strisciare lungo un piano inclinato di un angolo θ 2, ed è collegato tramite un filo inestensibile ad un blocco di massa m, che a sua volta
1 Esercizio Una ruota di raggio R e di massa M può rotolare senza strisciare lungo un piano inclinato di un angolo θ 2, ed è collegato tramite un filo inestensibile ad un blocco di massa m, che a sua volta
F (t)dt = I. Urti tra corpi estesi. Statica
 Analogamente a quanto visto nel caso di urto tra corpi puntiformi la dinamica degli urti tra può essere studiata attraverso i principi di conservazione. Distinguiamo tra situazione iniziale, prima dell
Analogamente a quanto visto nel caso di urto tra corpi puntiformi la dinamica degli urti tra può essere studiata attraverso i principi di conservazione. Distinguiamo tra situazione iniziale, prima dell
CORSO DI LAUREA IN OTTICA E OPTOMETRIA
 CORSO DI LAUREA IN OTTICA E OPTOMETRIA Anno Accademico 007-008 CORSO di FISCA ED APPLICAZIONE DEI LASERS Questionario del Primo appello della Sessione Estiva NOME: COGNOME: MATRICOLA: VOTO: /30 COSTANTI
CORSO DI LAUREA IN OTTICA E OPTOMETRIA Anno Accademico 007-008 CORSO di FISCA ED APPLICAZIONE DEI LASERS Questionario del Primo appello della Sessione Estiva NOME: COGNOME: MATRICOLA: VOTO: /30 COSTANTI
Violazione della Parità
 Violazione della Parità Raffaele Pontrandolfi Corso di Astrosica e Particelle Elementari Motivazione Per spiegare l asimmetria nell universo tra particelle e antiparticelle bisogna trovare dei processi
Violazione della Parità Raffaele Pontrandolfi Corso di Astrosica e Particelle Elementari Motivazione Per spiegare l asimmetria nell universo tra particelle e antiparticelle bisogna trovare dei processi
p V Velocita di propagazione del suono ρ = densita del mezzo k = modulo di compressione
 1 Onde longitudinali o acustiche del tutto in generale si definisce onda acustica qualsiasi onda longitudinale dovuta alla perturbazione longitudinale di un qualsiasi mezzo meccanico nello specifico e
1 Onde longitudinali o acustiche del tutto in generale si definisce onda acustica qualsiasi onda longitudinale dovuta alla perturbazione longitudinale di un qualsiasi mezzo meccanico nello specifico e
GLI ORBITALI ATOMICI
 GLI ORBITALI ATOMICI I numeri quantici Le funzioni d onda Ψ n, soluzioni dell equazione d onda, sono caratterizzate da certe combinazioni di numeri quantici: n, l, m l, m s n = numero quantico principale,
GLI ORBITALI ATOMICI I numeri quantici Le funzioni d onda Ψ n, soluzioni dell equazione d onda, sono caratterizzate da certe combinazioni di numeri quantici: n, l, m l, m s n = numero quantico principale,
Università del Sannio
 Università del Sannio Corso di Fisica 1 Lezione 6 Dinamica del punto materiale II Prof.ssa Stefania Petracca 1 Lavoro, energia cinetica, energie potenziali Le equazioni della dinamica permettono di determinare
Università del Sannio Corso di Fisica 1 Lezione 6 Dinamica del punto materiale II Prof.ssa Stefania Petracca 1 Lavoro, energia cinetica, energie potenziali Le equazioni della dinamica permettono di determinare
Lezione 15 Geometrie lineari di confinamento magnetico
 Lezione 15 Geometrie lineari di confinamento magnetico G. Bosia Universita di Torino G. Bosia Introduzione alla fisica del plasma Lezione 15 1 Disuniformità con gradiente in direzione del campo ( ) Una
Lezione 15 Geometrie lineari di confinamento magnetico G. Bosia Universita di Torino G. Bosia Introduzione alla fisica del plasma Lezione 15 1 Disuniformità con gradiente in direzione del campo ( ) Una
4πε. h m. Eq. di Schrödinger per un atomo di idrogeno:
 Eq. di Schrödinger per un atomo di idrogeno: h m e 1 ψ 4πε r 0 ( r) = Eψ ( r) Questa equazione è esattamente risolubile ed il risultato sono degli orbitali di energia definita E n = m e 1 α 1 1 e mc n
Eq. di Schrödinger per un atomo di idrogeno: h m e 1 ψ 4πε r 0 ( r) = Eψ ( r) Questa equazione è esattamente risolubile ed il risultato sono degli orbitali di energia definita E n = m e 1 α 1 1 e mc n
n(z) = n(0) e m gz/k B T ; (1)
 Corso di Introduzione alla Fisica Quantistica (f) Prova scritta 4 Luglio 008 - (tre ore a disposizione) [sufficienza con punti 8 circa di cui almeno 4 dagli esercizi nn. 3 e/o 4] [i bonus possono essere
Corso di Introduzione alla Fisica Quantistica (f) Prova scritta 4 Luglio 008 - (tre ore a disposizione) [sufficienza con punti 8 circa di cui almeno 4 dagli esercizi nn. 3 e/o 4] [i bonus possono essere
Esercizi di elettrostatica (prima parte)
 Esercizi di elettrostatica (prima parte) Esercizi di elettrostatica: forza di coulomb, campo elettrico. 1. Date tre cariche elettriche puntiformi identiche ( Q ) poste ai vertici di un triangolo equilatero
Esercizi di elettrostatica (prima parte) Esercizi di elettrostatica: forza di coulomb, campo elettrico. 1. Date tre cariche elettriche puntiformi identiche ( Q ) poste ai vertici di un triangolo equilatero
7. Forze elastiche. Nella figura 1 il periodo è T = 2s e corrisponde ad un moto unidimensionale limitato tra i valori x = 0 ed x = 1.
 1 Moti periodici 7. Forze elastiche Un caso particolare di moto accelerato è un moto periodico. In figura 1 è riportato un esempio di moto periodico unidimensionale. Un moto periodico si ripete identicamente
1 Moti periodici 7. Forze elastiche Un caso particolare di moto accelerato è un moto periodico. In figura 1 è riportato un esempio di moto periodico unidimensionale. Un moto periodico si ripete identicamente
Esercitazioni di Meccanica Razionale
 Esercitazioni di Meccanica Razionale a.a. 2002/2003 Cinematica Maria Grazia Naso [email protected] Dipartimento di Matematica Università degli Studi di Brescia Esercitazioni di Meccanica Razionale - a.a.
Esercitazioni di Meccanica Razionale a.a. 2002/2003 Cinematica Maria Grazia Naso [email protected] Dipartimento di Matematica Università degli Studi di Brescia Esercitazioni di Meccanica Razionale - a.a.
CORPO RIGIDO MOMENTO DI UNA FORZA EQUILIBRIO DI UN CORPO RIGIDO CENTRO DI MASSA BARICENTRO
 LEZIONE statica-1 CORPO RIGIDO MOMENTO DI UNA FORZA EQUILIBRIO DI UN CORPO RIGIDO CENTRO DI MASSA BARICENTRO GRANDEZZE SCALARI E VETTORIALI: RICHIAMI DUE SONO LE TIPOLOGIE DI GRANDEZZE ESISTENTI IN FISICA
LEZIONE statica-1 CORPO RIGIDO MOMENTO DI UNA FORZA EQUILIBRIO DI UN CORPO RIGIDO CENTRO DI MASSA BARICENTRO GRANDEZZE SCALARI E VETTORIALI: RICHIAMI DUE SONO LE TIPOLOGIE DI GRANDEZZE ESISTENTI IN FISICA
Struttura elettronica degli atomi. La teoria dei quanti e la meccanica ondulatoria. La moderna descrizione dell atomo
 Struttura elettronica degli atomi La teoria dei quanti e la meccanica ondulatoria La moderna descrizione dell atomo 1 Generalità delle onde elettromagnetiche λ Ampiezza massima: E max (B max ) Lunghezza
Struttura elettronica degli atomi La teoria dei quanti e la meccanica ondulatoria La moderna descrizione dell atomo 1 Generalità delle onde elettromagnetiche λ Ampiezza massima: E max (B max ) Lunghezza
approfondimento Lavoro ed energia
 approfondimento Lavoro ed energia Lavoro compiuto da una forza costante W = F. d = F d cosθ dimensioni [W] = [ML T - ] Unità di misura del lavoro N m (Joule) in MKS dine cm (erg) in cgs N.B. Quando la
approfondimento Lavoro ed energia Lavoro compiuto da una forza costante W = F. d = F d cosθ dimensioni [W] = [ML T - ] Unità di misura del lavoro N m (Joule) in MKS dine cm (erg) in cgs N.B. Quando la
Introduzione e modellistica dei sistemi
 Introduzione e modellistica dei sistemi Modellistica dei sistemi dinamici meccanici Sistemi meccanici in traslazione: elementi base Sistemi in traslazione: equazioni del moto Sistemi in traslazione: rappresentazione
Introduzione e modellistica dei sistemi Modellistica dei sistemi dinamici meccanici Sistemi meccanici in traslazione: elementi base Sistemi in traslazione: equazioni del moto Sistemi in traslazione: rappresentazione
L atomo di Bohr. Argomenti. Al tempo di Bohr. Spettri atomici 19/03/2010
 Argomenti Spettri atomici Modelli atomici Effetto Zeeman Equazione di Schrödinger L atomo di Bohr Numeri quantici Atomi con più elettroni Al tempo di Bohr Lo spettroscopio è uno strumento utilizzato per
Argomenti Spettri atomici Modelli atomici Effetto Zeeman Equazione di Schrödinger L atomo di Bohr Numeri quantici Atomi con più elettroni Al tempo di Bohr Lo spettroscopio è uno strumento utilizzato per
Problemi di Fisica per l ammissione alla Scuola Galileana Problema 1
 Problemi di Fisica per l ammissione alla Scuola Galileana 014-015 Problema 1 Nella regione di spazio interna alla sfera S 1, centrata in O 1 e di raggio R 1, è presente una densità di carica di volume
Problemi di Fisica per l ammissione alla Scuola Galileana 014-015 Problema 1 Nella regione di spazio interna alla sfera S 1, centrata in O 1 e di raggio R 1, è presente una densità di carica di volume
Compito del 14 giugno 2004
 Compito del 14 giugno 004 Un disco omogeneo di raggio R e massa m rotola senza strisciare lungo l asse delle ascisse di un piano verticale. Il centro C del disco è collegato da una molla di costante elastica
Compito del 14 giugno 004 Un disco omogeneo di raggio R e massa m rotola senza strisciare lungo l asse delle ascisse di un piano verticale. Il centro C del disco è collegato da una molla di costante elastica
= E qz = 0. 1 d 3 = N
 Prova scritta d esame di Elettromagnetismo 7 ebbraio 212 Proff.. Lacava,. Ricci, D. Trevese Elettromagnetismo 1 o 12 crediti: esercizi 1, 2, 4 tempo 3 h; Elettromagnetismo 5 crediti: esercizi 3, 4 tempo
Prova scritta d esame di Elettromagnetismo 7 ebbraio 212 Proff.. Lacava,. Ricci, D. Trevese Elettromagnetismo 1 o 12 crediti: esercizi 1, 2, 4 tempo 3 h; Elettromagnetismo 5 crediti: esercizi 3, 4 tempo
Teoria Atomica Moderna. Chimica generale ed Inorganica: Chimica Generale. sorgenti di emissione di luce. E = hν. νλ = c. E = mc 2
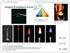 sorgenti di emissione di luce E = hν νλ = c E = mc 2 FIGURA 9-9 Spettro atomico, o a righe, dell elio Spettri Atomici: emissione, assorbimento FIGURA 9-10 La serie di Balmer per gli atomi di idrogeno
sorgenti di emissione di luce E = hν νλ = c E = mc 2 FIGURA 9-9 Spettro atomico, o a righe, dell elio Spettri Atomici: emissione, assorbimento FIGURA 9-10 La serie di Balmer per gli atomi di idrogeno
Introduciamo il sistema di riferimento indicato in figura b) con F 1 = ( f, 0) ed F 2 = (f, 0). Se P = (x, y) la condizione (1) fornisce
 1 L ellisse 1.1 Definizione Consideriamo due punti F 1 ed F 2 e sia 2f la loro distanza. L ellisse è il luogo dei punti P tali che la somma delle distanze PF 1 e PF 2 da F 1 ed F 2 è costante. Se indichiamo
1 L ellisse 1.1 Definizione Consideriamo due punti F 1 ed F 2 e sia 2f la loro distanza. L ellisse è il luogo dei punti P tali che la somma delle distanze PF 1 e PF 2 da F 1 ed F 2 è costante. Se indichiamo
Formulario Meccanica
 Formulario Meccanica Cinematica del punto materiale 1 Cinematica del punto: moto nel piano 3 Dinamica del punto: le leggi di Newton 3 Dinamica del punto: Lavoro, energia, momenti 5 Dinamica del punto:
Formulario Meccanica Cinematica del punto materiale 1 Cinematica del punto: moto nel piano 3 Dinamica del punto: le leggi di Newton 3 Dinamica del punto: Lavoro, energia, momenti 5 Dinamica del punto:
la geometria degli orbitali atomici
 1. Il modello elettronico dell atomo e la geometria degli orbitali atomici 1.1 Introduzione Gli orbitali atomici vengono descritti da funzioni d onda ψ (psi), calcolate per singole particelle ed atomi
1. Il modello elettronico dell atomo e la geometria degli orbitali atomici 1.1 Introduzione Gli orbitali atomici vengono descritti da funzioni d onda ψ (psi), calcolate per singole particelle ed atomi
CAMPI VETTORIALI (Note)
 CAMPI VETTORIALI (Note) Sia v(x,y,z) il vettore che definisce la grandezza fisica del campo: il problema che ci si pone è di caratterizzare il campo vettoriale sia in termini locali, cioè validi punto
CAMPI VETTORIALI (Note) Sia v(x,y,z) il vettore che definisce la grandezza fisica del campo: il problema che ci si pone è di caratterizzare il campo vettoriale sia in termini locali, cioè validi punto
