Analisi e controllo di soluzioni periodiche in sistemi non lineari

Transcript

1 Dottorato di Ricerca in Ingegneria dei Sistemi IX Ciclo Università degli Studi di Bologna Sedi consorziate: Firenze, Padova, Siena Analisi e controllo di soluzioni periodiche in sistemi non lineari Tesi di Dottorato Michele Basso Coordinatore: Prof. Giovanni Marro Tutori: Prof. Roberto Genesio Prof. Alberto Tesi Febbraio 1997

2 Indice 1 Introduzione 1 2 Dinamica dei Sistemi Non Lineari Introduzione Traiettorie Sistemi autonomi Sistemi periodici Soluzioni di regime permanente Soluzioni costanti Soluzioni periodiche Soluzioni quasi-periodiche Soluzioni caotiche Stabilità Strutturale Introduzione Biforcazioni locali Biforcazioni di un equilibrio v

3 vi INDICE Biforcazioni di un ciclo limite Biforcazioni globali Passaggi al caos Analisi delle Soluzioni Periodiche Introduzione Il Sistema Predizione dei cicli limite Stabilità dei cicli limite predetti Analisi delle Biforcazioni dei Cicli Limite Introduzione Modello frequenziale di biforcazioni locali Condizioni analitiche di biforcazione Biforcazioni locali nei sistemi di Lur e Stabilità delle biforcazioni Esempi Rottura di simmetria Biforcazione tangente Neimark-Sacker - Esempio Neimark-Sacker - Esempio Raddoppiamento di periodo - Esempio Raddoppiamento di periodo - Esempio

4 INDICE vii 6 Controllo di Soluzioni Periodiche Introduzione Controllo subarmonico Esempio - Controllo di una biforcazione di Neimark Esempio - Controllo di un laser a CO Stabilizzazione di Sistemi Periodici Forzati Introduzione Formulazione del problema Risultati principali Esempi Pendolo forzato Equazione di Duffing Conclusioni 99 A 101

5 viii INDICE

6 Capitolo 1 Introduzione Negli ultimi anni si è assistito ad un crescente interesse verso i problemi di analisi e di controllo nei sistemi dinamici non lineari. La motivazione che spinge allo studio dei fenomeni di dinamica non lineare deriva sempre più spesso da considerazioni di carattere applicativo, poiché tali sistemi costituiscono efficaci modelli di descrizione di fenomeni complessi in un numero crescente di settori di ricerca. Fra gli obiettivi di maggior importanza nella progettazione di un sistema di controllo si pone, sicuramente, quello di garantire adeguati margini di stabilità nel funzionamento di un dato impianto, compatibilmente con l esigenza di ottenere elevate prestazioni. D altra parte, lavorare in prossimità di regioni critiche per la stabilità del sistema mette spesso in risalto l inadeguatezza dell uso di modelli linearizzati e di tecniche di controllo derivate dalla teoria lineare classica. Di recente, lo studio delle proprietà strutturali dei sistemi dinamici ha consentito di ampliare la conoscenza del loro comportamento in prossimità delle regioni critiche suddette. Ciò ha reso possibile la messa a punto di nuove tecniche di controllo mirate ad ampliare la regione di funzionamento sicuro del sistema, così da renderlo insensibile alla presenza di eventuali disturbi esterni o variazioni parametriche che possano causare effetti indesiderati. 1

7 2 CAPITOLO 1. INTRODUZIONE In questo lavoro viene affrontato lo studio delle soluzioni periodiche di una classe di sistemi dinamici non lineari costituita dall interconnessione, in uno schema in retroazione, di un sistema dinamico lineare scalare e di un blocco non lineare con opportune proprietà. I principali meccanismi di generazione delle biforcazioni, come il raddoppiamento di periodo, la nascita di una soluzione quasi-periodica o la rottura di simmetria, sono stati chiariti assumendo una loro descrizione in termini di perturbazioni subarmoniche rispetto alla frequenza della soluzione periodica non perturbata. Questo tipo di approccio, basato su tecniche di bilanciamento armonico, fornisce una più intuitiva interpretazione dei fenomeni complessi che sono all origine di comportamenti caotici nei sistemi dinamici. Il principale risultato ottenuto consiste nella determinazione in forma chiusa e con ottima approssimazione delle superfici di biforcazione locale nello spazio dei parametri, fornendo così un quadro generale della stabilità strutturale del sistema. L analisi in frequenza ha permesso di mettere a punto efficaci tecniche di controllo con l obiettivo di evitare l insorgere di dinamiche complesse indesiderate in un opportuna regione dello spazio dei parametri. In particolare, avendo fissato come obiettivo prioritario nelle specifiche quello di garantire un controllo a minima energia, è stato introdotto il concetto di controllo subarmonico, basato sul filtraggio nell anello di retroazione delle subarmoniche indesiderate. Tale schema di controllo risulta avere alcune caratteristiche comuni a quello recentemente introdotto sotto il nome di controllo ETDAS (Extended Time Delay Auto-Synchronization) che consiste nell uso di un segnale di controllo generato dalla differenza di una componente dello stato del sistema e dalla stessa variabile ritardata di un tempo pari al periodo dell orbita da stabilizzare. Questo tipo di controllo, utilizzato per la stabilizzazione di orbite periodiche instabili immerse in un attrattore caotico, presenta il vantaggio di non alterare i punti di equilibrio e la soluzione periodica del sistema non controllato, anche se non si conosce ancora una procedura sistematica

8 3 per il progetto. La tesi è organizzata nel modo seguente: nel Capitolo 2 vengono brevemente illustrate le proprietà caratteristiche dei sistemi dinamici non lineari con particolare enfasi sulle soluzioni di regime permanente come i punti di equilibrio e le orbite periodiche. Il Capitolo 3 affronta lo studio della stabilità strutturale di tali sistemi e presenta un analisi dei principali tipi di biforcazione. Il problema della predizione delle soluzioni periodiche e delle loro biforcazioni viene sviluppato nei Capitoli 4 e 5, per una classe di sistemi dinamici in retroazione. Nel Capitoli 6 e 7, infine, vengono proposte nuove tecniche di controllo e di stabilizzazione di soluzioni periodiche in prossimità di biforcazioni locali e all interno di attrattori caotici.

9 4 CAPITOLO 1. INTRODUZIONE

10 Capitolo 2 Dinamica dei Sistemi Non Lineari 2.1 Introduzione In questo capitolo verranno presentati alcuni concetti base e alcune definizioni relative al comportamento asintotico delle soluzioni di sistemi dinamici non lineari a tempo continuo, rappresentabili attraverso sistemi di equazioni differenziali ordinarie del primo ordine [Arn83, Kha92, GH83, Wig90, TS86, Rin93a]. In particolare, verrà introdotto il concetto di soluzione ricorrente e saranno passati in rassegna i principali risultati nell analisi di stabilità di queste soluzioni. Definizione 2.1 Un sistema dinamico tempo continuo di ordine n è definito dall equazione di stato ẋ = f(x, t), x(t 0 ) = x 0 (2.1) dove x(t) IR n è il vettore di stato al tempo t e la funzione f : IR n IR IR n è il campo vettoriale. Spesso, alla (2.1) viene associata l equazione algebrica di uscita y = g(x, t), (2.2) 5

11 6 CAPITOLO 2. DINAMICA DEI SISTEMI NON LINEARI dove y(t) IR p rappresenta il vettore di variabili misurabili nel sistema o, in generale, variabili di specifico interesse e g : IR n IR IR p, è una funzione sufficientemente regolare. Definizione 2.2 Il sistema dinamico (2.1) è lineare se il suo campo vettoriale è una funzione lineare in x, ovvero il sistema può essere espresso nella forma matriciale ẋ = A(t)x, x(t 0 ) = x 0. (2.3) Questa classe di sistemi rappresenta un caso molto particolare di (2.1) e le proprietà che caratterizzano le sue soluzioni, non sono in generale possedute da quelle dei sistemi nonlineari. In particolare, l analisi dei sistemi lineari è basata sul noto principio di sovrapposizione degli effetti, proprietà non valida per la generica classe (2.1) Traiettorie L insieme delle soluzioni o traiettorie del sistema (2.1) viene indicato con φ t (x 0, t 0 ) in modo da evidenziare in modo esplicito la sua dipendenza dalle condizioni iniziali. Sotto opportune ipotesi di regolarità sulla funzione f è possibile dimostrare l esistenza e unicità delle sue soluzioni, fissate le condizioni iniziali (x 0, t 0 ). In particolare, essendo interessati al comportamento asintotico delle soluzioni di un sistema dinamico, si riporta l enunciato del seguente Teorema 2.1 Sia f(x, t) una funzione continua rispetto a t che soddisfi la seguente condizione di Lipschitz in un insieme D IR n f(x, t) f(y, t) L x y f(x 0, t) h (2.4)

12 2.1. INTRODUZIONE 7 x, y D, t t 0. Supponiamo inoltre che ogni soluzione di (2.1) appartenga ad un sottoinsieme compatto di D, t t 0. Allora la (2.1) ammette un unica soluzione sull intervallo [t 0, + ). Dimostrazione: per la dimostrazione si può fare riferimento ad un qualsiasi testo di analisi di sistemi nonlineari (per esempio, [Arn83, Kha92]). Sotto le ipotesi del Teorema 2.1 si possono quindi elencare le seguenti caratteristiche per le traiettorie di un sistema dinamico: Le soluzioni sono definite per ogni istante di tempo t t 0 e sono continue rispetto a x 0 e a variazioni parametriche del campo vettoriale f; t, φ t (, t 0 ) è un diffeomorfismo; t, φ t (x, t 0 ) = φ t (y, t 0 ) se e solo se x = y. L ultima proprietà menzionata, ovvero l unicità, merita alcune osservazioni: i) due traiettorie che partono da stati diversi al tempo t = t 0 non potranno mai intersecarsi dopo il medesimo lasso di tempo; ii) è possibile che un intersezione fra le due traiettorie avvenga ad istanti di tempo diversi. Come vedremo, esistono classi di sistemi per i quali la seconda osservazione non può valere. Questi sistemi sono caratterizzati da una proprietà di invarianza temporale del loro campo vettoriale e rivestono una notevole importanza nello studio della dinamica nonlineare.

13 8 CAPITOLO 2. DINAMICA DEI SISTEMI NON LINEARI Sistemi autonomi Il sistema dinamico (2.1) è autonomo o tempo-invariante se il suo campo vettoriale è indipendente dal tempo. Per i sistemi autonomi si può sempre assumere come istante iniziale t 0 = 0, poiché il campo vettoriale risulta indipendente rispetto alla trasformazione che sposta l origine della variabile temporale. Anche la traiettoria risulta indipendente dall istante iniziale, dipendendo solo dal valore dello stato iniziale x 0 e dal lasso di tempo intercorso t t 0, ovvero φ t (x 0, t 0 ) = φ t t0 (x 0, 0) (2.5) In genere viene assunto come istante iniziale t 0 = 0 e, nel seguito, si indicherà la traiettoria all istante t con il solo termine φ t (x 0 ). L applicazione del Teorema 2.1 ad un sistema autonomo porta a concludere che due traiettorie che si originano da stati iniziali distinti, non possono mai intersecarsi, neanche ad istanti di tempo differenti Sistemi periodici Tra i più comuni sistemi non autonomi sono da annoverare i sistemi periodici, ovvero quei sistemi che posseggono un campo vettoriale descrivibile da una funzione periodica nel tempo di periodo minimo T, tale che f(x, t) = f(x, t + T ), x, t. (2.6) Un sistema periodico può sempre essere trasformato in uno autonomo introducendo lo stato θ =. 2πt/T mod 2π (2.7) e l equazione aggiuntiva θ = 2π/T. (2.8)

14 2.2. SOLUZIONI DI REGIME PERMANENTE 9 L uso della funzione modulo permette inoltre di limitare la variabile θ all intervallo [0, 2π) evitando così che tutte le soluzioni del sistema autonomo risultino non limitate. Il notevole interesse posto nello studio dei sistemi dinamici non autonomi è generalmente limitato proprio al caso dei sistemi periodici. Grazie alla trasformazione (2.7) è possibile classificare il comportamento asintotico delle soluzioni di questi sistemi con lo stesso criterio che verrà utilizzato per le soluzioni dei sistemi autonomi. 2.2 Soluzioni di regime permanente Il comportamento asintotico delle soluzioni di un sistema dinamico non lineare autonomo (o periodico trasformato) può essere classificato, generalizzando il caso lineare, facendo ricorso ai concetti di soluzione ricorrente e di insieme limite. Definizione 2.3 φ t (x 0 ) è una soluzione ricorrente se t > 0, T > 0, ɛ > 0 t > t + T t.c. φ t (x 0 ) φ t (x 0 ) < ɛ Una soluzione ricorrente è sempre una traiettoria limitata. Definizione 2.4 y è un punto limite di ˆx IR n se la traiettoria uscente da ˆx entra ripetutamente in un intorno di y, ovvero: T > 0, ɛ > 0, t > T t.c. φ t (ˆx) y < ɛ. Si definisce insieme limite di ˆx l insieme Ω(ˆx) formato da tutti i punti limite di ˆx. Si possono dimostrare le seguenti proprietà: 1. Ω(ˆx) è un insieme chiuso;

15 10 CAPITOLO 2. DINAMICA DEI SISTEMI NON LINEARI 2. Ω(ˆx) è invariante sulla traiettoria del sistema che passa da ˆx 3. Ω(ˆx) non è vuoto se ˆx è un punto di una traiettoria ricorrente Definizione 2.5 Un insieme limite Ω è un attrattore se esiste un intorno aperto U che lo contiene tale che per ogni z U, allora Ω(z) = Ω. Si definisce bacino di attrazione di un attrattore Ω l insieme B(Ω) = {x IR n t.c. Ω(x) = Ω}. Definizione 2.6 Una varietà k-dimensionale (1 < k < n) è un sottoinsieme di IR n definito dall equazione η(x) = 0, dove η : IR n IR n k è una funzione differenziabile con differenziale continuo. Ai fini dello studio dei sistemi dinamici, sono importanti quelle varietà che possiedono la proprietà di invarianza, ovvero η(x 0 ) = 0 implica η(φ t (x 0 )), t 0, dove φ t (x 0 ) è soluzione del problema (2.1). Viene definita varietà stabile di un insieme limite Ω, quell insieme invariante X tale che per ogni z X, allora Ω(z) = Ω. In base alle definizioni introdotte si possono classificare quattro diversi tipi di soluzioni ricorrenti. Questi risultano caratterizzati da insiemi limite diversi e possono essere significativamente rappresentati anche nel dominio della frequenza. Nei seguenti paragrafi verranno discussi dettagliatamente in ordine crescente di complessità.

16 2.2. SOLUZIONI DI REGIME PERMANENTE Soluzioni costanti Un vettore di stato ˆx IR n è un punto di equilibrio per il sistema (2.1) se la traiettoria che si origina in ˆx all istante t 0 resta costante nel tempo. Pertanto i punti di equilibrio ˆx devono soddisfare l equazione f(x, t) = 0, t t 0. (2.9) L insieme limite di un punto di equilibrio è rappresentato dal punto di equilibrio stesso. Questo insieme è, inoltre, un attrattore se vale la definizione classica di asintotica stabilità alla Lyapunov, ovvero (A) ɛ > 0, t 0, δ = δ(ɛ, t 0 ) > 0 tale che x 0 ˆx < δ implica φ t (x 0 ) ˆx < ɛ t t 0 ; (B) lim t φ t (x 0, t 0 ) = ˆx. Inoltre, come noto, se vale solo la proprietà (A), l equilibrio si definisce semplicemente stabile, mentre se non vale la (A), il punto di equilibrio è instabile. In molti casi, l analisi della stabilità dell equilibrio è riconducibile allo studio della stabilità del sistema linearizzato [ ] f x(t) = x(t), x ˆx x(t) = x(t) ˆx (2.10) che, per i sistemi autonomi, si effettua con la determinazione degli autovalori dello Jacobiano [ ] f e con la conseguente suddivisione dello spazio degli stati nei tre x ˆx sottospazi relativi agli autovalori con parte reale rispettivamente negativa, positiva e nulla. Questi sottospazi risultano essere tangenti in ˆx a tre corrispondenti insiemi invarianti definiti come varietà stabile, instabile e centro del sistema non lineare. Un punto di equilibrio asintoticamente stabile è caratterizzato dalla presenza della sola varietà stabile, mentre la varietà instabile è indice di un equilibrio instabile.

17 12 CAPITOLO 2. DINAMICA DEI SISTEMI NON LINEARI A parte il caso lineare, la presenza di una varietà centro non permette di individuare le caratteristiche di stabilità del sistema originale. In tal caso, l analisi del sistema linearizzato risulta inadeguata ed è necessario utilizzare strumenti più sofisticati come, ad esempio, lo studio della stabilità sulla varietà centrale Soluzioni periodiche Una soluzione periodica di (2.1) è una traiettoria chiusa per cui risulti φ t (x 0, t 0 ) = φ t+t (x 0, t 0 ), t t 0, (2.11) per un valore minimo di T > 0 definito periodo della soluzione. In virtù della unicità delle soluzioni in (2.1), soluzioni periodiche si possono riscontrare solo in sistemi autonomi di ordine non inferiore al secondo, oppure in quelli non autonomi periodici di qualsiasi ordine. Una soluzione periodica viene classificata isolata se non ne esistono altre in un suo intorno. Nel caso di sistemi autonomi, una soluzione isolata viene anche definita ciclo limite. Per i sistemi periodici, tenendo conto della trasformazione (2.7), si può concludere che possono esistere solo soluzioni di periodo multiplo del minimo periodo del sistema. L analisi nel dominio della frequenza, effettuabile attraverso uno sviluppo in serie del segnale periodico, evidenzia uno spettro formato da un infinito numero di componenti a frequenze multiple della frequenza fondamentale ω = 2π/T della soluzione. L insieme limite di una soluzione periodica corrisponde alla curva chiusa percorsa dalla traiettoria in un singolo periodo. Per quanto riguarda le sue caratteristiche di

18 2.2. SOLUZIONI DI REGIME PERMANENTE 13 stabilità, può essere utile ricorrere alla trasformazione che genera il sistema tangente x(t) = f( x(t) + ˆx(t), t) f(ˆx(t), t), x(t) = x(t) ˆx(t). (2.12) la cui stabilità nell origine è legata a quella della soluzione periodica in esame. Infatti, è possibile dimostrare che l orbita descritta da una soluzione periodica del sistema non autonomo (2.1) è un attrattore se e solo se l origine del sistema tangente (2.12) è un punto di equilibrio asintoticamente stabile. Se il sistema (2.1) è invece di tipo autonomo, questa equivalenza non è più valida, si può anzi dimostrare, in quest ultimo caso, che l equilibrio del sistema (2.12) non può mai essere asintoticamente stabile. In entrambi i casi può essere effettuata la linearizzazione del sistema (2.12), ottenendo il sistema lineare T -periodico dipendente da ˆx(t) x(t) = [ ] f x(t) =. A(t) x(t), x(t) = x(t) ˆx(t). (2.13) x ˆx(t) È ben noto che l analisi degli autovalori λ i (t) della matrice periodica A(t) non può fornire alcuna indicazione sulla stabilità dell origine [HC87], nè quindi sulla stabilità locale della soluzione periodica in esame. È possibile, invece, integrare sul periodo T il sistema lineare (2.13), ottenendo il sistema discreto tempo-invariante x ((k + 1)T ) = Φ(T ) x(kt ), (2.14) dove Φ(T ) corrisponde alla matrice di transizione dello stato al tempo T. La stabilità del ciclo può allora essere dedotta dal calcolo degli autovalori m i, i = 1... n, di Φ(T ) definiti come i moltiplicatori caratteristici del sistema in ˆx(t) [HC87]. Escludendo il moltiplicatore m = 1, sempre presente nel caso di sistemi autonomi, la stabilità dell orbita è individuata dalla appartenenza dei restanti moltiplicatori al cerchio unitario del piano complesso. Il motivo della presenza del moltiplicatore

19 14 CAPITOLO 2. DINAMICA DEI SISTEMI NON LINEARI m = 1 in Φ(T ) è intuitivo: i moltiplicatori, infatti, descrivono la dinamica delle perturbazioni sul ciclo ad intervalli fotografati di un periodo, quindi una perturbazione infinitesima che agisce lungo la direzione tangente alla traiettoria rimane costante negli istanti multipli del periodo stesso. Un importante strumento per l analisi delle orbite periodiche nei sistemi continui sono le mappe di Poincaré. Esse permettono, infatti, di sostituire ad un sistema dinamico di ordine n un sistema discreto di ordine n 1 che descrive localmente la dinamica del sistema tangente alla soluzione periodica. Queste mappe vengono determinate numericamente a partire da un sezione trasversale all orbita descritta dalla soluzione periodica in esame e possono essere descritti dal generico sistema discreto x (k+1) = P ( x (k)), (2.15) dove P è una funzione nonlineare e x (k) IR n 1, k = 0, 1,.... La caratteristica fondamentale delle mappe di Poincaré è la proprietà di equivalenza fra l analisi di stabilità di una soluzione periodica del sistema (2.1) e quella relativa all origine del sistema discreto (2.15). In particolare, si può dimostrare che gli n 1 moltiplicatori caratteristici diversi dall unità della soluzione periodica sono uguali agli autovalori dello Jacobiano della mappa P rispetto a x (k). Da un punto di vista prettamente operativo, questa tecnica è applicabile solo numericamente, prevedendo il calcolo della soluzione periodica del sistema (2.1) che permette di giungere tramite l operazione di linearizzazione alle forme (2.13) e (2.14).

20 2.2. SOLUZIONI DI REGIME PERMANENTE Soluzioni quasi-periodiche Un segnale quasi-periodico viene definito come una funzione del tempo esprimibile attraverso una somma numerabile di segnali periodici x(t) = i h i (t), (2.16) dove h i (t) ha periodo T i, tale che esista una base di p frequenze distinte { ˆf1,..., ˆf p } che soddisfi le seguenti proprietà: 1. la base è formata da numeri reali il cui rapporto è irrazionale, ovvero non è possibile trovare una combinazione di interi {k 1,..., k p } tale che k 1 ˆf1 + + k p ˆfp = 0; 2. la base permette di generare i valori di T i, i, cioè esistono {k 1,..., k p } tale che 1/T i = k 1 ˆf1 + + k p ˆfp. In base alla definizione data, lo spettro di tale segnale sarà generalmente costituito da una infinità numerabile di picchi a frequenze multiple di 1/T i, i. È possibile trovare segnali quasi-periodici come soluzioni ricorrenti in sistemi dinamici autonomi e non autonomi di ordine rispettivamente non inferiore al terzo e al secondo. In genere il fenomeno è riscontrabile in quei sistemi dove sono presenti sottosistemi debolmente accoppiati capaci di generare segnali periodici di periodo incommensurabile. A differenza delle soluzioni costanti e di quelle periodiche, l insieme limite corrispondente ad una soluzione quasi-periodica di un sistema autonomo (o di un sistema non autonomo trasformato secondo la (2.7)) non è formato da una traiettoria del sistema. Esso è invece costituito da una varietà p-dimensionale diffeomorfa alla superficie di un p-toro e sulla quale si avvolge la traiettoria senza mai richiudersi.

21 16 CAPITOLO 2. DINAMICA DEI SISTEMI NON LINEARI La stabilità dell attrattore può essere studiata attraverso una generalizzazione del concetto di moltiplicatore caratteristico. È necessario innanzitutto introdurre la matrice di transizione locale dello stato sulla traiettoria φ t (x 0, t 0 ) di (2.1), definita come la matrice n n tempo-variante Φ t (x 0, t 0 ) =. D x0 φ t (x 0, t 0 ), dove D x0 indica la differenziazione rispetto al vettore x 0. Questa operazione permette di calcolare l evoluzione temporale di ogni perturbazione infinitesima x 0 di x 0, cioè x(t) = Φ t (x 0, t 0 ) x 0. (2.17) Si definiscono esponenti di Lyapunov di x 0 gli n valori reali 1 λ i = lim t t ln m i(t), i = 1,..., n, (2.18) dove m i (t), i = 1,..., n rappresentano gli autovalori di Φ t (x 0, t 0 ). In base alla definizione data, gli esponenti di Lyapunov sono invarianti sui punti di una soluzione ricorrente, inoltre essi forniscono il comportamento medio di una perturbazione infinitesima che giace fuori dall insieme limite. In particolare, se q è la dimensione geometrica del suddetto insieme, i primi q esponenti sono nulli, mentre i restanti n q indicano stabilità dell attrattore se sono negativi, non stabilità se qualche esponente risulta positivo. È interessante rianalizzare mediante gli esponenti di Lyapunov le soluzioni ricorrenti di (2.1) descritte fino ad ora: Soluzioni costanti: si può facilmente dimostrare che λ i = Re[ˆλ i ], i = 1,..., n, dove ˆλ i sono gli autovalori del sistema linearizzato in x 0 ; Soluzioni periodiche: se T è il periodo della soluzione, λ i = 1 T ln m i, i = 1,..., n, dove m i sono i moltiplicatori caratteristici del ciclo;

22 2.2. SOLUZIONI DI REGIME PERMANENTE 17 Soluzioni quasi-periodiche: se p è la dimensione della base di frequenze indipendenti, allora λ 1 =... = λ p = 0, mentre i restanti n p esponenti danno l indicazione della stabilità dell attrattore Soluzioni caotiche Un modo universalmente accettato per la definizione di soluzione caotica è basato sulla sua esclusione dalle tre precedenti classi di soluzioni ricorrenti. Viene quindi definita come soluzione caotica, quella soluzione ricorrente che non è possibile classificare come costante, periodica o quasi-periodica. Le caratteristiche salienti di una soluzione caotica possono essere brevemente riassunte nei seguenti punti: Insieme limite: può avere dimensione non intera e/o caratteristiche di complessità comuni agli insiemi di Cantor. Non è quindi una varietà e viene spesso indicato con il termine di strano attrattore. Come per le soluzioni quasi-periodiche, quelle caotiche non possono esistere in sistemi autonomi di ordine inferiore al terzo o in quelli non autonomi di ordine inferiore al secondo; Sensitività alle condizioni iniziali: traiettorie che si originano da condizioni iniziali infinitamente vicine, all interno del bacino di attrazione della soluzione caotica, tendono ad allontanarsi fra loro, pur restando confinate all interno dell attrattore stesso. In pratica, esiste almeno una direzione all interno dell attrattore in cui si può considerare instabile il sistema. Questa caratteristica è riscontrabile nel calcolo degli esponenti di Lyapunov della soluzione caotica: almeno uno degli

23 18 CAPITOLO 2. DINAMICA DEI SISTEMI NON LINEARI n esponenti è positivo, ne esiste sempre uno nullo e i restanti sono negativi. La stabilità dell attrattore è assicurata dalla somma totale degli esponenti che deve risultare negativa. Spettro di frequenza: è caratterizzato dalla presenza di una infinità non numerabile di frequenze (spettro continuo) in cui si possono evidenziare alcune componenti predominanti. Non è distinguibile da spettri di segnali stocastici.

24 Capitolo 3 Stabilità Strutturale 3.1 Introduzione Si consideri la famiglia di sistemi dinamici autonomi ẋ = f(x, p), (3.1) dove x IR n è lo stato del sistema, p IR k è un vettore di parametri e f : IR n IR k IR n è una funzione sufficientemente regolare che rappresenta il campo vettoriale. L obiettivo della teoria della stabilità strutturale è lo studio del comportamento asintotico del sistema (3.1) al variare del suo vettore di parametri p. In particolare, l interesse è posto sulla determinazione di quelle regioni nello spazio dei parametri, all interno delle quali una infinitesima perturbazione parametrica sul sistema non modifica qualitativamente il quadro delle sue traettorie, ma ne provoca solo una deformazione. Per presentare più rigorosamente questo concetto è necessario introdurre alcune definizioni [Arn83, PC89, Rin93b]. 19

25 20 CAPITOLO 3. STABILITÀ STRUTTURALE Definizione 3.1 Due campi vettoriali, f(, p 1 ), f(, p 2 ) : IR n IR n, sono topologicamente equivalenti per la famiglia di sistemi (3.1) se esiste un omeomorfismo h : IR n IR n che trasforma traiettorie di f(, p 1 ) in traiettorie di f(, p 2 ), conservandone il senso di percorrenza rispetto al tempo, cioè t e x, esiste t tale che e, inoltre, se t 2 > t 1 allora t 2 > t 1. h φ p 1 t (x) = φ p 2 h(x), (3.2) t Definizione 3.2 Il sistema (3.1), con p = p 0 P, dove P è un sottoinsieme aperto e connesso di IR k, si definisce strutturalmente stabile se esiste un intorno aperto U P di p 0 tale che, per ogni p U, f(, p 0 ) e f(, p) sono campi vettoriali topologicamente equivalenti. In pratica, la stabilità strutturale di un sistema dinamico assicura che, al variare di un suo parametro all interno di una regione P, si conservino quegli elementi che contraddistinguono il comportamento di regime permanente, cioè i suoi insiemi limite, attrattori, ecc. Questa proprietà, per definizione, non è conservata qualora il sistema appartenga alla frontiera di separazione fra due regioni distinte P 1 e P 2. In questo caso una generica perturbazione sul parametro provoca sempre una alterazione qualitativa della dinamica del sistema che viene indicata con il termine di biforcazione. La superficie di biforcazione, cioè la frontiera di P può essere descritta dall equazione algebrica g(p) = 0, (3.3) dove g : IR k IR q è una funzione sufficientemente regolare e la dimensione q viene

26 3.2. BIFORCAZIONI LOCALI 21 indicata come codimensione della biforcazione. Le biforcazioni più comuni sono ovviamente quelle di codimensione uno e solo queste saranno trattate in questo lavoro. Senza perdita di generalità, possiamo supporre che la superficie (3.3) relativa ad una biforcazione di codimensione uno venga attraversata trasversalmente al variare di un parametro scalare µ tale che p = p 0 + µ p 1, (3.4) dove g(p) = 0 per µ = 0, e p 1 = D p0 g(p 0 ). Definizione 3.3 Una biforcazione è catastrofica quando, in seguito ad una variazione infinitesima dei parametri del sistema, si innesca un transitorio al termine del quale il nuovo funzionamento di regime (se esiste) è macroscopicamente diverso da quello di partenza. 3.2 Biforcazioni locali Il primo meccanismo di biforcazione descritto viene individuato quando, al variare di un parametro del sistema, due insiemi limite, inizialmente distinti, entrano fra loro in collisione. Definizione 3.4 Si definisce supercritica (subcritica) quella biforcazione locale che, in seguito alla collisione, genera un insieme limite stabile (instabile). Una biforcazione locale avviene sempre in concomitanza con la presenza di una singolarità nello Jacobiano associato localmente all insieme limite. Poichè, infatti,

27 22 CAPITOLO 3. STABILITÀ STRUTTURALE quando gli autovalori dello Jacobiano sono distanti dalla frontiera di stabilità, non è possibile alterare qualitativamente la natura della soluzione ricorrente e del suo insieme limite, una biforcazione locale di codimensione uno deve essere necessariamente legata alla presenza di un autovalore reale oppure una coppia di autovalori complessi che giacciono sulla frontiera di stabilità. Un analisi delle più comuni biforcazioni locali è possibile ricorrendo ad una opportuna riduzione dell ordine del sistema. Si può infatti dimostrare che le caratteristiche che contraddistinguono questo tipo di biforcazioni sono determinate esclusivamente dalla dinamica sull insieme invariante corrispondente alla varietà centrale del sistema [Kha92]. Nei prossimi paragrafi verranno classificate le biforcazioni locali di codimensione uno relative, rispettivamente, ai punti di equilibrio e ai cicli limite. I sistemi del primo e del secondo ordine che verranno presentati vengono definiti forme normali e si intendono come già ridotti alle rispettive varietà centrali. Si assume inoltre stabile la dinamica sulla varietà omessa Biforcazioni di un equilibrio Con una opportuna trasformazione di variabili, il sistema ridotto alla varietà centrale assume la forma [Kha92, AW95] dove f 0 (0, 0) = 0 e gli autovalori di f 0(z,0) z ż(t) = f 0 (z(t), µ), z IR o z IR 2 (3.5) hanno parte reale nulla. z=0 Si possono avere le seguenti forme normali del primo e del secondo ordine: 1. Tangente ż = µ ± z 2 (catastrofica) (3.6)

28 3.2. BIFORCAZIONI LOCALI 23 collisione di un equilibrio stabile e di uno instabile con conseguente scomparsa dell equilibrio; 2. Transcritica (scambio di stabilità) ż = µz ± z 2 (3.7) collisione di un equilibrio stabile e di uno instabile con conseguente scambio di stabilità; 3. Forcone (perdita di simmetria) ż = µz z 3 supercritica subcritica (3.8) collisione di un equilibrio instabile (stabile) e di due stabili (instabili) che spariscono alla collisione; 4. Hopf ż 1 = µz 1 + ωz 2 z 1 (z z 2 2) ż 2 = ωz 1 + µz 2 z 2 (z z 2 2) supercritica subcritica (3.9) collisione di un equilibrio instabile (stabile) e di un ciclo limite stabile (instabile) di periodo 2π/ω. (3.6), (3.7) e (3.8) sono forme normali del primo ordine caratterizzate dall autovalore nullo per µ = 0; la (3.9) è una forma normale del secondo ordine che per µ = 0 possiede una coppia di autovalori sull asse immaginario Biforcazioni di un ciclo limite Le biforcazioni dei cicli limite vengono analizzate attraverso le forme normali relative alla loro mappa di Poincaré z k+1 = P 0 (z k, µ), z IR o z IR 2 (3.10)

29 24 CAPITOLO 3. STABILITÀ STRUTTURALE dove P 0 (0, 0) = 0 e gli autovalori dello Jacobiano di P 0 rispetto a z appartengono alla circonferenza complessa unitaria. Si determinano così dei casi del tutto analoghi a quelli riscontrati per i punti di equilibrio: 1. Tangente collisione di un ciclo stabile e di uno instabile con conseguente scomparsa della soluzione periodica (biforcazione catastrofica); 2. Transcritica (scambio di stabilità) collisione di un ciclo stabile e di uno instabile con conseguente scambio di stabilità; 3. Forcone (perdita di simmetria) collisione di un ciclo instabile (stabile) e di due stabili (instabili) che spariscono alla collisione; 4. Hopf secondaria (Neimark-Sacker) collisione di un ciclo instabile (stabile) e di una soluzione quasi-periodica stabile (instabile). Le prime tre biforcazioni possono essere caratterizzate da forme normali del primo ordine con un moltiplicatore m = 1 per µ = 0, mentre l ultima può essere descritta da una forma normale del secondo ordine che per µ = 0 possiede una coppia di moltiplicatori complessi coniugati sulla circonferenza unitaria. A queste forme se ne aggiunge un altra che non trova un analogo per i punti di equlibrio, ed è caratterizzata dal passaggio di un moltiplicatore dal punto 1 : Flip (raddoppiamento di periodo) z k+1 = (1 + µ)z k ± z 3 k supercritica subcritica (3.11)

30 3.3. BIFORCAZIONI GLOBALI 25 collisione di un ciclo instabile (stabile) di periodo T e di uno stabile (instabile) di periodo 2T. 3.3 Biforcazioni globali Le biforcazioni globali sono interpretabili come collisioni fra varietà stabili e instabili di insiemi limite uguali (biforcazioni omocline) oppure varietà stabili e instabili di insiemi limite diversi (biforcazioni eterocline). 3.4 Passaggi al caos Un sistema a comportamento periodico o quasi-periodico può diventare caotico per una variazione dei suoi parametri. Questa transizione è pertanto caratterizzata da delle biforcazioni. Le più frequenti di queste transizioni sono note come passaggi al caos. Sulla base di quanto oggi noto, esse possono essere catalogate in due grandi classi. La prima è nota come cascata di Feigenbaum, è una sequanza di infiniti raddoppiamenti di periodo. La seconda strada verso il caos è concentrata in una sola biforcazione di tipo globale (caos omoclino e caos eteroclino).

31 26 CAPITOLO 3. STABILITA STRUTTURALE

32 Capitolo 4 Analisi delle Soluzioni Periodiche 4.1 Introduzione In questo capitolo verrà affrontato il problema della determinazione di soluzioni periodiche in una ampia classe di sistemi autonomi non lineari. L approccio seguito è basato su tecniche di bilanciamento armonico che permettono di affrontare l analisi del problema nel dominio della frequenza e utilizzano una descrizione di tipo ingresso-uscita della dinamica del sistema. Queste tecniche sono necessariamente di natura approssimata ma presentano l indubbio vantaggio di consentire una predizione a basso costo computazionale di queste soluzioni e della loro dipendenza dai parametri del sistema. Una stima dell errore di approssimazione è comunque possibile insieme a risultati che garantiscano l esistenza dei cicli limite predetti. Esempi che dimostrino l efficacia di questa tecnica verranno presentati nel prossimo capitolo. 27

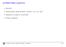
33 28 CAPITOLO 4. ANALISI DELLE SOLUZIONI PERIODICHE u(t) = 0 + j L, L(s) y(t) N z(t) n K ( )< L K (s)< < n 1 ( ) < L 1 (s) x K (t) x 1 (t) Figura 4.1: Diagramma a blocchi del sistema analizzato. 4.2 Il Sistema Si consideri il sistema dinamico non forzato descritto in Figura 4.1, costituito dalla interconnessione in retroazione dei due sottosistemi L e N. Questi blocchi presentano le seguenti caratteristiche: L è un sistema dinamico lineare tempo-invariante singolo-ingresso singolauscita (SISO) (cioè, u, y, z sono segnali scalari) descritto dalla sua funzione di trasferimento razionale L(s); N è un sistema dinamico non lineare singolo-ingresso singola-uscita (SISO) generato da una cascata di blocchi dinamici lineari e di blocchi statici non lineari. Essendo i segnali interni x 1,..., x K, in generale, multivariabili, i blocchi lineari vengono descritti tramite matrici di funzioni di trasferimento razionali L 1 (s),..., L K (s) di ordine opportuno, così come i blocchi non lineari vengono descritti da funzioni vettoriali multivariabili n 1 (x 1 ),..., n K (x K ).

34 4.2. IL SISTEMA 29 Al fine di evidenziare le soluzioni periodiche, l equazione che descrive il sistema di Figura 4.1 può essere scritta mediante gli operatori L e N, nella forma y + LN y = 0 (4.1) trascurando così lo stato iniziale dei blocchi dinamici che contribuisce solo al comportamento transitorio. A parte l interconnessione scalare tra L e N, l altra ipotesi di base che contraddistingue la classe da analizzare viene imposta sulla struttura in cascata del blocco non lineare N in Figura 4.1. Questo blocco deve essere infatti formato da un sistema non lineare esplicito, [GV68] dove cioè è possibile calcolare direttamente l uscita corrispondente a qualsiasi ingresso assegnato. Questa caratteristica, di fatto, esclude la presenza in N di blocchi in retroazione contenenti non linearità. Le classi principali definite per N possono essere rappresentate nel modo seguente, in ordine crescente di complessità: i) K = 1, x 1 IR. La funzione di trasferimento scalare L 1 (s) può essere inglobata in L(s) e solo la non linearità scalare n 1 (x 1 ). = n(y) rappresenta il sistema N. ii) iii) K = 1, x 1 IR p, p > 1. Il minimo comune denominatore della funzione di trasferimento vettoriale L 1 (s) può essere unito a L(s) e la non linearità scalare n 1 (x 1 ) =. n(y, ẏ,...) rappresenta il sistema N. K > 1. Questo caso corrisponde a un sistema dinamico non lineare N in cui le funzioni di trasferimento L 2 (s),..., L k (s) sono dinamiche, cioè, hanno il minimo comune denominatore dipendente da s. La situazione può essere altrimenti facilmente riportata al caso ii). La struttura introdotta presenta realmente una generalità molto ampia. La possibilità di derivarla dalle usuali equazioni di stato è stata considerata in dettaglio in

35 30 CAPITOLO 4. ANALISI DELLE SOLUZIONI PERIODICHE [GT92b, GT92a] per il caso K = 2. In particolare è stato provato che un gran numero di modelli che manifestano dinamiche complesse (Lorenz, Rossler, Chua, etc.) possono essere espressi in questa forma. Alcune ulteriori osservazioni sono necessarie per concludere la descrizione del sistema in oggetto. Nota 4.1 Le non linearità n i rappresentate in Figura 4.1 non sono necessariamente delle funzioni regolari, ma sono ammesse anche funzioni continue a tratti. Inoltre, n i può essere ad un singolo valore (cioè senza memoria) o a più valori. Nel caso i) quando N viene descritto da una non linearità senza memoria n, la struttura di Figura 4.1 prende il nome di sistema di Lur e, solitamente noto nella risoluzione dei classici problemi di stabilità in retroazione [ Sil69, HM68, Vid93]. Nota 4.2 La funzione di trasferimento L(s) e/o L 1 (s),..., L K (s) può anche rappresentare sistemi lineari distribuiti e può essere espressa sia in forma irrazionale sia in forma trascendente. In questo caso, solo la semplice condizione i) può essere chiaramente separata dal caso generale nel sistema non lineare N. Nota 4.3 Lo schema di Figura 4.1 può essere ulteriormente generalizzato per comprendere i segnali forzanti u(t) costanti o sinusoidali, o segnali simili agenti su N. In principio, questo implica leggere modificazioni del metodo sviluppato in questo studio. 4.3 Predizione dei cicli limite Questo paragrafo riassume i maggiori risultati sulla predizione dei cicli limite tramite il bilanciamento armonico [ Sil69, JS87, GV68, HM68, Ath75, Vid93]. I punti di equilibrio e i cicli limite sono soluzioni del sistema di Figura 4.1 quando la

36 4.3. PREDIZIONE DEI CICLI LIMITE 31 variabile di uscita y(t) è rispettivamente costante o periodica. Per ottenere queste soluzioni, esprimiamo un generico segnale periodico di periodo 2π/ω con la serie di Fourier y(t) =. A 0 + A 1 cos ωt + A k cos(kωt + φ k ) A 1 0, ω > 0. (4.2) k=2 È opportuno notare che ogni segnale periodico può essere espresso nella forma (4.2) previa una opportuna traslazione temporale. Ipotizziamo che il segnale y(t) dell equazione (4.2) entri nel sistema non lineare N, e consideriamo il suo segnale di regime periodico in uscita, definito da z(t) ed espresso in serie come { } z(t) = N 0 A 0 + Re N 1 A 1 e jωt + N k A k e jkωt+φ k k=2. (4.3) I termini N k, k = 0, 1,..., rappresentano i guadagni armonici del blocco N e sono rappresentati dalla espressione (normalizzata) dei coefficienti di Fourier N 0 = N 0 (A 0, A 1,..., ω) =. 1 z(t) dωt, 2πA 0 π (4.4) N k = N k (A 0, A 1,..., ω) =. 1 π z(t)e jωkt dωt. πa k π (4.5) Assumiamo inoltre, senza perdita di generalità, che z(t) = 0 per y(t) = 0. Il bilanciamento armonico impone l uguaglianza lungo l anello del sistema delle armoniche di y(t) alle frequenze kω con le armoniche corrispondenti generate dal blocco L pilotato dal segnale z(t) in (4.3). sistema di equazioni algebriche π Ciò conduce alla determinazione del A k + L(jkω)N k A k = 0, k = 0, 1,... (4.6) equivalente all equazione (4.1) e che deve essere risolto rispetto alle incognite A k ed alla frequenza di oscillazione ω. Ovviamente, trattandosi di un sistema di equazioni a dimensione infinita, sarà necessario introdurre un troncamento dopo aver preso in considerazione un

37 32 CAPITOLO 4. ANALISI DELLE SOLUZIONI PERIODICHE opportuno numero di armoniche. Questa operazione è supportata dal fatto che, per i sistemi fisici, la funzione di trasferimento L(s) è sempre un filtro passa-basso il cui modulo diventa trascurabile alle alte frequenze. Per molti sistemi è sufficiente descrivere l uscita con la sola approssimazione di prima armonica y 1 (t) = A + B cos ωt, (4.7) e risolvere il sistema algebrico (4.6) che, per k = 1, 2, si riduce alle due equazioni A + L(0)N 0 A = 0 (4.8) B + L(jω)N 1 B = 0, (4.9) la prima delle quali è reale, mentre la seconda è generalmente complessa. Il procedimento, solitamente noto come metodo della funzione descrittiva, può portare ai seguenti tipi di soluzioni che caratterizzano il comportamento asintotico del sistema: A = Â, B = 0: punti di equilibrio; A = 0, B = ˆB 0, ω = ˆω 0: cicli limite simmetrici; A = Â 0, B = ˆB 0, ω = ˆω 0: cicli limite asimmetrici. Un segnale y 1 (t) nella forma (4.7) in cui Â, ˆB ed ˆω soddisfino la (4.8) e (4.9) viene definito un ciclo limite predetto (PLC). Bisogna sottolineare che la derivazione delle semplici equazioni (4.8) e (4.9) si avvale delle ipotesi principali fatte per il sistema nel paragrafo precedente. In particolare, l interconnessione scalare in retroazione permette la descrizione delle soluzioni periodiche tramite i soli parametri A, B ed ω, mentre la struttura esplicita della non linearità conduce ad un calcolo diretto del segnale stazionario z(t) e quindi, tramite le relazioni (4.4) e (4.5), dei guadagni N 0 e N 1.

38 4.3. PREDIZIONE DEI CICLI LIMITE 33 In riferimento all accuratezza di questa tecnica, i risultati ottenuti sui punti di equilibrio sono esatti, mentre quelli relativi ai cicli limite sono approssimati a causa dell analisi limitata alla prima armonica nella dinamica del sistema. L affidabilità di un PLC si basa su una forte attenuazione (ipotesi di filtraggio [ Sil69, JS87, GV68, Ath75, HM68, Vid93]) delle componenti di frequenza superiore 2ω, 3ω,... lungo l anello di Figura 4.1. In questo senso l indice di distorsione, definito per ogni PLC come la quantità positiva [Ath75, GT92a, GTV93] (Â, ˆB, ˆω) = ỹ 1(t) y 1 (t) 2 y 1 (t) 2 (4.10) può essere un attendibile misura dell errore, dove ỹ 1 (t) è l uscita periodica del sistema ad anello aperto quando y 1 (t) viene immesso in N. La possibilità di quantificare una distorsione sufficientemente piccola può essere connessa alle considerazioni della Nota 4.7 seguente. D altro canto, in presenza di complicate oscillazioni che richiedano una descrizione con un numero superiore di armoniche, il metodo può ancora essere applicato come tecnica numerica (nello stesso contesto vedi [Pic94, MC96]), ma perde la sua tipica efficacia nello spiegare qualitativamente il comportamento asintotico del sistema e non permette una semplice caratterizzazione delle sue proprietà strutturali. Di seguito vengono elencati altri commenti relativi al metodo di bilanciamento armonico appena introdotto. Nota 4.4 Il caso di oscillazioni simmetriche (A = 0) si osserva tipicamente quando tutte le non linearità sono dispari, cioè, tali che n i (x i ) = n i ( x i ). In questo caso, dall equazione (4.4), possiamo imporre N 0 (0, B, ω). = lim A 0 N 0 (A, B, ω). Nota 4.5 Nell importante caso dei sistemi di Lur e, quando il termine N si riduce ad una funzione n ad un singolo valore, risulta facilmente dalla (4.4) e dalla (4.5), con z(t) = n(y 1 (t)), che N 0 e N 1 sono indipendenti da ω e reali. Quindi, la

39 34 CAPITOLO 4. ANALISI DELLE SOLUZIONI PERIODICHE parte immaginaria dell equazione (4.6) diventa semplicemente Im {L(jω)} = 0 (4.11) determinando così la frequenza del ciclo limite a partire da un equazione disaccoppiata che dipende solo dalla parte lineare del sistema. Nota 4.6 La presenza di segnali forzanti u(t), costanti o sinusoidali, agenti sul sistema di Figura 4.1 può essere tenuta in conto, introducendoli opportunamente nel bilanciamento dell equazione (4.6). Nel caso sinusoidale, la frequenza di oscillazione è fissata dai termini forzanti, ma dobbiamo ipotizzare una fase incognita nel termine y 1 (t) dell equazione (4.7), in modo tale che il sistema di equazioni (4.6) abbia sempre tre incognite. I segnali forzanti su N entrano nel calcolo di N 0 e N 1 con le variazioni già evidenziate nel caso sinusoidale. Nota 4.7 A parte il suo positivo utilizzo soprattutto di tipo empirico nel corso degli anni, l esistenza delle soluzioni periodiche derivata dal metodo della funzione descrittiva può essere supportata da argomenti rigorosi. Sotto opportune ipotesi è possibile garantire che il sistema possieda realmente un ciclo limite in un intorno misurabile del PLC [Mee81, GT88, Vid93]. Nota 4.8 per B tendente a zero le soluzioni dell equazione (4.6) generalmente indicano condizioni di biforcazione Hopf del sistema. Infine, si deve ossevare che gli elementi lineari, L(0) ed L(jω), e gli elementi non lineari, N 0 and N 1, nell equazione (4.6) sono funzioni dei parametri del sistema di Figura 4.1. Così anche le soluzioni predette derivanti dalle condizioni di bilanciamento armonico, risultano dipendenti da tali parametri.

40 4.4. STABILITÀ DEI CICLI LIMITE PREDETTI Stabilità dei cicli limite predetti Le soluzioni delle equazioni (4.8) e (4.9) riguardanti i punti di equilibrio e i cicli limite sono state ottenute usando relazioni di stazionaietà tra i blocchi del sistema. In realtà, le possibili condizioni iniziali dei blocchi dinamici sono state trascurate, sottintendendo che dovessero essere concordi con i risultati dell analisi. Per analizzare la stabilità locale delle soluzioni, consideriamo un transitorio generato da piccole perturbazioni su queste soluzioni, in particolare si assume che  viene modificato in  + A(t) per i punti di equilibrio (B = 0); ˆB viene modificato quasi-staticamente in ˆB + B per i cicli limite, nell ipotesi che altre perturbazioni diano vita a moti tendenti a zero. Nel pimo caso si ottiene la conseguente dinamica del sistema, linearizzando ciascuna non linearità nei valori x i0 corrispondenti alla soluzione y = Â. Prendendo in considerazione la struttura di Figura 4.1 si ricava l equazione caratteristica nella forma 1 + L(s)n K(x K0 )L K (s) n 1(x 10 )L 1 (s) = 0 (4.12) dove il termine n i(x i0 ), i = 1,..., K, indica le derivate di n i (x i ) calcolate in x i = x i0. Se escludiamo i casi critici, un criterio lineare standard (per esempio il criterio di Nyquist) applicato all equazione (4.12) permette di determinare le caratteristiche di stabilità locale in qualsiasi punto di equilibrio del sistema. Per i PLC dell espressione (4.7), in base al criterio di Loeb [GV68, Ath75], ipotizziamo che l equazione di bilanciamento armonico (4.9) sia ancora valida per piccole perturbazioni, così che ad un ampiezza modificata ˆB + B corrisponda un oscillazione smorzata di frequenza complessa j ˆω + ( σ + j ω). Inoltre, poiché la dipendenza del termine in continua deriva dall equazione (4.8) nella forma statica

41 36 CAPITOLO 4. ANALISI DELLE SOLUZIONI PERIODICHE semplificata A = A(B, ω), l equazione riguardante la dinamica del PLC diventa 1 + L ( σ + j(ˆω + ω)) N 1 (A( ˆB + B, ˆω + ω), ˆB + B, ˆω + ω j σ) = 0. (4.13) Considerando le variazioni intorno alla soluzione nominale definita da Â, ˆB ed ˆω, il criterio di Loeb richiede che, per la stabilità del PLC, il termine Λ. = σ/ B sia negativo. In altre parole, si prevede che ad una qualsiasi perturbazione che sposti la condizione iniziale del sistema internamente al PLC ( B < 0), corrisponda una uscita crescente nel tempo ( σ > 0), e viceversa per quanto riguarda una perturbazione esterna al PLC. Questa condizione applicata all equazione (4.13) conduce alla formula di stabilità Λ = Im { [ L(j ˆω) dn 1 db (A(B, ω), B, ω) ] ˆB,ˆω } d dω L(jω) N 1 (A( ˆB, ω), ˆB, ˆω) < 0 (4.14) ˆω dove il segno * indica il complesso coniugato e le derivate sono calcolate nel punto nominale. Come per i risultati della predizione del precedente paragrafo, le conclusioni derivate dalle equazioni (4.12) e (4.14) sono esatte per i punti di equilibrio e di natura approssimata per le soluzioni periodiche. L approssimazione è peggiore di quella riguardante l esistenza dei PLC per le ulteriori ipotesi semplificative fatte nell approccio proposto. D altro canto, il criterio di Loeb risulta molto spesso corretto e, nella maggior parte dei casi, quando N 0 e N 1 sono indipendenti dalla frequenza, rappresenta intuitivamente un tipo di estensione del criterio di stabilità di Nyquist. Nota 4.9 Per le non linearità n i continue o derivabili a tratti, le derivate presenti nell espressione (4.12), ed anche nella (4.14) attraverso N 0 e N 1, devono essere sostituite dal limite di opportuni rapporti incrementali. Nota 4.10 Nel caso dei sistemi di Lur e, in cui N 1 è reale ed indipendente dalla frequenza e L(j ˆω) è, di conseguenza, reale, la condizione di stabilità di Loeb