Politecnico di Milano Appunti delle lezioni del corso di Statistica (2L) per gli allievi INF e TEL, AA 2007/2008. Intervalli di confidenza
|
|
|
- Albino Manzo
- 5 anni fa
- Visualizzazioni
Transcript
1 Politecico di Milao Apputi delle lezioi del corso di Statistica L per gli allievi INF e TEL, AA 007/008 Itervalli di cofideza Ileia Epifai 5 maggio 010 Il coteuto di queste dispese è protetto dalle leggi sul copyright e dalle disposizioi dei trattati iterazioali. Il materiale qui coteuto può essere copiato o comuque riprodotto ed utilizzato liberamete dagli studeti, dagli istituti di ricerca, scolastici ed uiversitari affereti ai Miisteri della Pubblica Istruzioe e dell Uiversità e della Ricerca Scietifica e Tecologica per scopi istituzioali, o a fie di lucro. Ogi altro utilizzo o riproduzioe ivi icluse, ma o limitatamete a, le riproduzioi a mezzo stampa, su supporti magetici o su reti di calcolatori i toto o i parte è vietata, se o esplicitamete autorizzata per iscritto, a priori, da parte degli autori. L iformazioe coteuta i queste pagie è riteuta essere accurata alla data della pubblicazioe. Essa è forita per scopi meramete didattici. L iformazioe coteuta i queste pagie è soggetta a cambiameti seza preavviso. L autore o si assume alcua resposabilità per il coteuto di queste pagie ivi icluse, ma o limitatamete a, la correttezza, completezza, applicabilità ed aggiorameto dell iformazioe. I ogi caso o può essere dichiarata coformità all iformazioe coteuta i queste pagie. I ogi caso questa ota di copyright o deve mai essere rimossa e deve essere riportata ache i utilizzi parziali. Copyright 006 Ileia Epifai Prima versioe AA 003/004; Secoda versioe AA 004/005; Terza versioe AA 006/007; Edizioe riveduta e corretta AA 007/008 Gli sperabili migliorameti ella correte edizioe derivao da quelli sicuramete apportati dal Prof. Barchielli e dalla Dott.ssa Salvati alla versioe iglese 1
2 Idice 1 Itervalli di cofideza per media e variaza di popolazioe gaussiaa Itervalli di cofideza per la media Itervalli di cofideza per la variaza Regioe di cofideza simultaea per media e variaza Itervalli di cofideza 10.1 Metodo della quatità pivotale Itervalli di cofideza per gradi campioi 1 4 Dualità fra verifica di ipotesi e stima itervallare Dall itervallo di cofideza al test di ipotesi Dalla teoria delle ipotesi alla regioe di cofideza
3 1 Itervalli di cofideza per media e variaza di popolazioe gaussiaa I questa sezioe affrotiamo il problema della stima itervallare dei parametri media e variaza della popolazioe gaussiaa. Nella Sezioe defiiremo gli itervalli di cofideza i geerale per i parametri icogiti di u modello statistico qualuque. Nel seguito useremo le segueti otazioi per i quatili delle distribuzioi campioarie: z a idicherà il quatile di ordie a 0, 1 della f.d.r. gaussiaa stadard Φ, cioè z a = Φ 1 a; t a sarà il quatile di ordie a della f.d.r. t di Studet co gradi di libertà; ifie χ a sarà il quatile di ordie a della f.d.r. chiquadrato co gradi di libertà. 1.1 Itervalli di cofideza per la media Sia X 1,..., X u campioe casuale estratto dalla popolazioe di desità gaussiaa di parametri µ, σ X 1,..., X i.i.d. Nµ, σ. Suppoiamo che la deviazioe stadard σ sia ota e pari a 0.8. Abbiamo proposto e motivato elle lezioi passate l uso della media campioaria X come stimatore di µ. X è uo stimatore putuale di µ. Ma la ozioe di stima putuale o è completamete soddisfacete per il seguete motivo: qualuque sia il valore di µ, X è variabile aleatoria assolutamete cotiua e quidi P µ,σ X = c = 0, c R, µ R, σ > 0 I particolare è ulla la probabilità che X assuma il vero valore icogito di µ. Ma, possiamo forire i termii probabilistici ua misura dell errore che si commette sostituedo al valore del parametro µ il valore assuto dallo stimatore X per data realizzazioe campioaria. Sia ɛ > 0 tale che 1 P µ,σ ɛ < X µ σ/ < ɛ = 0.95 Assegati e σ, ɛ è uivocamete determiato dall equazioe Φɛ 1 = 0.95 e quidi Φɛ 1 = 0.95 sse Φɛ = sse ɛ = Φ 1 = z A priori, cioè prima di osservare il risultato dell esperimeto, e quidi, idipedetemete dalla realizzazioe campioaria, siamo abbastaza fiduciosi che l errore che commettiamo stimado µ co X è al più pari a 1.96σ/. Se, per esempio, la dimesioe del campioe è 4, questo errore è / 4 = Il grado di fiducia el verificarsi di ciò è misurato i termii di probabilità ed è pari a 95%. La relazioe 1 può essere riscritta come segue: dove P µ,σ T 1 < µ < T = 0.95 T 1 = X z / σ e T = X + z / σ I altri termii, a priori, c è ua possibilità pari a 95% che il valore icogito ma determiistico di µ cada ell itervallo aleatorio T 1, T. Gli estremi T 1, T soo statistiche 3
4 che dipedoo a dal campioe X 1,..., X, b da iformazioi ote sulla f.d.r. del campioe cioè σ e c dal grado di fiducia o livello o coefficiete di cofideza 95%. Ovviamete, essezialmete, T 1 < T. Se poi implemetiamo l esperimeto e osserviamo la realizzazioe campioaria x 1 = 4.87, x = 5.06, x 3 =.8, x 4 = 5.3 allora x = 4.515, t 1 = = e t = = L itervallo aperto t 1, t = 3.785, è detto itervallo di cofideza per il parametro µ di livello Il sigificato del livello di cofideza è il seguete: se ripetiamo l estrazioe di u campioe di dimesioe 4 dalla popolazioe gaussiaa u umero grade di volte e calcoliamo per oguo dei campioi l itervallo x 0.784, x , ci aspettiamo che più o meo il 95% di questi itervalli cotega il valore della vera media µ. Il termie iglese cofidece che abbiamo tradotto come fiducia è usato dopo che l esperimeto è stato effettuato, riservado la parola chace possibilità all itervallo aleatorio prima di osservare l esperimeto campioario. Ifatti quado la realizzazioe campioaria è a ostra disposizioe o ha più seso parlare di possibilità o probabilità: a quel puto, il vero valore della media o cade o o cade ell itervallo umerico trovato e la probabilità coessa a questo eveto sarà zero o uo. I geerale abbiamo la seguete defiizioe. Defiizioe 1.1 Sia x 1,..., x ua realizzazioe del campioe casuale X 1,..., X dalla popolazioe Nµ, σ. Fissato γ 0, 1, se la variaza σ è ota, u itervallo di cofideza per la media µ di livello γ100% è dato da x z 1+γ σ, x + z 1+γ σ Suppoiamo ora che ache la variaza σ sia icogita. Per valutare a priori l errore che commettiamo approssimado µ co X cosideriamo P µ,σ ɛ < X µ/s < ɛ, dove S = S e S è la variaza campioaria e calcoliamo ɛ tale che P µ,σ ɛ < X µ S/ < ɛ = 0.95 Usado il fatto che X µ/s t 1 e che t 1 è ua desità di probabilità simmetrica itoro allo 0, aalogamete al caso di variaza ota, otteiamo che ɛ coicide co il quatile di ordie / della f.d.r. t di studet co 1 gradi di libertà, cioè ɛ = t /. Suppoedo di avere acora u campioe di dimesioe 4: ɛ = t e la relazioe può essere riscritta come X 3.18 S < µ < X S = 0.95 P µ,σ Nell ultima equazioe leggiamo che, prima di osservare le realizzazioi campioarie, è pari a 0.95 la probabilità che l itervallo aleatorio di estremi X 3.18S/ cotega µ. Se poi abbiamo osservato il campioe x 1 = 4.87, x = 5.06, x 3 =.8, x 4 = 5.3 4
5 allora j=1 x j / , s = / e s = Quidi, x 3.18s/ e x s/ , è u itervallo di cofideza per µ di livello 95%. Notate che per calcolare S abbiamo usato la seguete decomposizioe: S = 1 j=1 X j X = j=1 X j 1 X = j=1 X j 1 1 X I geerale Defiizioe 1. Siao x 1,..., x ua realizzazioe del campioe casuale X 1,..., X estratto dalla popolazioe Nµ, σ e x e s le realizzazioi su questo campioe rispettivamete di media e variaza campioarie. Allora 1 + γ s x t 1, x + t γ s è u itervallo di cofideza per µ di livello γ100%, quado la variaza σ è icogita. Osservazioe 1.3 Credo o sia iutile sottolieare che µ è u parametro il cui valore è icogito ma determiistico; quidi, µ X 3.18S/, X S/ è u eveto aleatorio i quato gli estremi dell itervallo soo aleatori e o µ. Osservazioe 1.4 U itervallo di cofideza stima µ tramite u itervallo; la lughezza dell itervallo aleatorio a partire dal quale costruiamo l itervallo di cofideza è u idice della precisioe di questa stima itervallare di µ. 1.1 Se σ è ota, la lughezza dell itervallo di cofideza è L = σ z 1+γ L o è aleatoria perché NON dipede dalla particolare realizzazioe campioaria, ma dipede da σ,, γ. I particolare: Fissati σ e, L è fuzioe crescete di γ. Quidi, l itervallo di cofideza è u compromesso fra precisioe e cofideza: più vogliamo essere sicuri che µ cada i u itervallo, meo precisa sarà la stima itervallare, ossia più lugo sarà l itervallo di cofideza cetrato i x. Fissati σ e γ, L è fuzioe decrescete di. All aumetare di, la variaza di X dimiuisce e quidi è sesato che più preciso cioè più corto sia l itervallo. Fissati γ e, L è fuzioe crescete di σ. Ifatti la variaza di X è fuzioe crescete di σ è quidi quato maggiore è σ, tato più grade è la probabilità che X assuma valori lotai da µ e quidi o è trascurabile la probabilità che l itervallo sia più lugo. 1. Se σ è icogita, la lughezza è: t 1+γ 1 L = S 5
6 Se σ è icogita, L è aleatoria, dipede dalla realizzazioe campioaria tramite S e ha media t 1+γ 1 3/ t 1+γ 1 Γ EL = ES = 1 Γ 1 σ Ifatti, se Y = S 1/σ, allora Y χ 1 e ES = E σ Y = 1 σ E Y 1/ σ = y 1/ σ f 1 χ 1 y dy = Γ 1 Γ = σ 1 Γ Γ 1 f χ y dy = σ 0 1 Γ 1 e y y 1 dy Osservazioe 1.5 La scelta di ua stima itervallare di µ simmetrica ella media campioaria o è del tutto arbitraria. Questa scelta è giustificata dal fatto che le variabili aleatorie da cui siamo partiti, X µ/σ se σ è ota e X µ/s se σ è icogita, hao etrambe desità di probabilità simmetriche itoro allo zero e quidi la loro moda cioè il puto i cui la desità è massima è zero. σ Segue per esempio che l itervallo di cofideza di estremi x z 1+γ/ forisce la stima itervallare più precisa di µ el caso di variaza ota e popolazioe gaussiaa fra tutte le stime itervallari del tipo x + a, x + b e di livello γ100%. Osservazioe 1.6 Se la variaza è icogita, per determiare EL abbiamo dovuto calcolare ES e abbiamo otteuto ES = σ 1 Γ Γ 1 I particolare ES σ =,..., qualuque sia il valore di σ. Per esempio, se = allora ES = σ /π < σ. Pertato, il fatto che S sia uo stimatore o distorto della variaza σ o implica che S sia uo stimatore o distorto della deviazioe stadard σ. Comuque, S è u esempio di stimatore asitoticamete o distorto. Ifatti: lim ES = lim σ 1 Γ Γ 1 = lim σ 1 e = σ Osservazioe 1.7 Effettivamete S sottostima σ. aleatoria costate e quidi VarS > 0. Pertato Ifatti ES = σ, S o è variabile 0 < VarS = ES ES = σ ES da cui otteiamo che ES è strettamete miore di σ. 6
7 1. Itervalli di cofideza per la variaza Se µ è icogita, per costruire u itervallo di cofideza per σ partiamo dalla quatità aleatoria S 1/σ che dipede dal parametro icogito σ di cui cerchiamo ua stima itervallare ma la cui f.d.r. o dipede da essu parametro icogito, ifatti S 1/σ χ 1. Fissato γ 0, 1, dobbiamo determiare a, b tali che 3 P µ,σ a < S 1 σ < b = γ Per a, b abbiamo varie possibilità. Prediamo i cosiderazioe solo le segueti tre che porterao alla costruzioe di tre diversi itervalli di cofideza γ100% per σ. 1. [a = 0] Se a = 0, allora l equazioe 3 si riduce all equazioe S 1 4 P µ,σ < b = γ σ ell uica icogita b; ecessariamete b = χ 1 γ, quatile di ordie γ della f.d.r. χ 1. L Equazioe 4 è equivalete a P µ,σ σ > S 1 χ 1 γ = γ Se abbiamo la realizzazioe campioaria x 1 = 4.87, x = 5.06, x 3 =.8, x 4 = 5.3 e se γ = 0.95, allora s , χ e , , + è u itervallo di cofideza a ua coda superiore upper oe-side cofidece iterval di livello 95%. I geerale, Defiizioe 1.8 Sia γ 0, 1 e sia s il valore assuto da S i corrispodeza della realizzazioe campioaria x 1,..., x di u campioe casuale estratto dalla popolazioe Nµ, σ. Allora s 1 χ, + 1 γ è u itervallo di cofideza a ua coda superiore di livello γ100% per la variaza σ, quado µ è icogita. Ioltre, la statistica S 1/χ 1 γ è detta limite iferiore di cofideza per la variaza.. [b = + ] I questo caso l equazioe 3 diveta 5 P µ,σ a < S 1 σ = γ e abbiamo ua sola icogita a; ecessariamete a = χ 1 1 γ; 5 è equivalete a P µ,σ σ < S 1 χ = γ 1 1 γ 7
8 Se abbiamo osservato x 1 = 4.87, x = 5.06, x 3 =.8, x 4 = 5.3 e γ = 0.95, allora s , χ ; l itervallo 0, , è u itervallo di cofideza a ua coda iferiore lower oe-side cofidece iterval di livello 95%. I geerale, Defiizioe 1.9 Sia γ 0, 1 e sia s il valore assuto da S i corrispodeza della realizzazioe campioaria x 1,..., x di u campioe casuale estratto dalla popolazioe Nµ, σ. Allora s 1 0, 1 γ χ 1 è u itervallo di cofideza a ua coda iferiore di livello γ100% per la variaza σ, quado µ è icogita. Ioltre, la statistica S 1/χ 1 1 γ è detta limite superiore di cofideza per la variaza < a < b < + Risolviamo l equazioe 3 elle icogite a, b i modo tale che la massa rimaete 1 γ sia uiformemete distribuita a siistra e a destra dell itervallo a, b. Necessariamete: a = χ 1 1 γ e b = χ 1 1 γ + γ = χ 1 Co questa scelta di a e b, riscriviamo l equazioe 3 el seguete modo: 6 P µ,σ S 1 < σ < S 1 = γ χ 1 1+γ χ 1 1 γ 1 + γ Defiizioe 1.10 Sia γ 0, 1 e sia s il valore assuto da S i corrispodeza della realizzazioe campioaria x 1,..., x di u campioe casuale estratto dalla f.d.r. Nµ, σ. Allora s 1, χ 1 1+γ s 1 χ 1 1 γ è u itervallo di cofideza bilatero per σ di livello γ100%, quado µ è icogita. Se abbiamo osservato il campioe x 1 = 4.87, x = 5.06, x 3 =.8, x 4 = 5.3 estratto dalla popolazioe Nµ, σ e γ = 0.95, allora χ , χ e , , è u itervallo di cofideza bilatero per σ di livello 95%. 8
9 Osservazioe 1.11 I dati usati erao stati simulati dalla f.d.r. N4.4, 0.8. Alla luce di questa iformazioe che ovviamete i ua vera applicazioe o abbiamo otiamo che l estremo superiore dell itervallo di cofideza bilatero per la variaza o è affidabile. D altro cato, ella scelta degli estremi o abbiamo seguito essu criterio di ottimalità, ma abbiamo solo semplificato il problema, impoedo ua codizioe di simmetria sulle code. Ifie, costruiamo ua stima itervallare per σ el caso di media µ ota. Se µ è ota, stimiamo σ co la statistica S0 j=1 := X j µ che rappreseta ua misura empirica della dispersioe del campioe itoro alla media teorica µ. Vedremo i seguito che S0 è lo stimatore di massima verosimigliaza di σ el caso di media ota. Notate che la variabile aleatoria S0 /σ ha desità χ e pertato, procededo aalogamete al caso di media µ icogita, troviamo i segueti itervalli di cofideza per σ di livello γ100% quado µ è ota: j=1 x j µ χ, + itervallo di cofideza a ua coda superiore; γ j=1 0, x j µ χ itervallo di cofideza a ua coda iferiore; 1 γ j=1 x j µ j=1, x j µ itervallo di cofideza bilatero. χ 1+γ χ 1 γ 1.3 Regioe di cofideza simultaea per media e variaza Usiamo ora i risultati precedeti per costruire ua regioe di cofideza per ua stima simultaea di µ e σ per popolazioi gaussiae. Partiamo dall osservazioe che X µ/σ e S 1/σ soo variabili aleatorie idipedeti. Allora gli eveti e { } X µ A = σ < z 1+ γ = B = X µ z 1+ γ S 1 < σ < S 1 χ 1 1+ γ χ 1 1 γ < σ soo eveti idipedeti. Ioltre, per quato discusso ella costruzioe dell itervallo di cofideza per µ quado σ è ota e per σ quado µ è icogita, abbiamo P µ,σ A = P µ,σ B = γ e quidi P µ,σ X µ z 1+ γ < σ, S 1 < σ < S 1 = χ 1 1+ γ χ 1 1 γ = P µ,σ A B = P µ,σ AP µ,σ B = γ 9
10 Segue che 7 µ, σ R 0, : x µ z 1+ γ < σ, s 1 < σ < s 1 χ 1 1+ γ χ 1 1 γ è ua regioe di cofideza per µ, σ di livello γ100%, per ogi realizzazioe campioaria x 1,..., x di X 1,..., X i.i.d. Nµ, σ tale che la media campioaria e la variaza campioaria hao valore rispettivamete x e s. Se abbiamo osservato x 1 = 4.87, x = 5.06, x 3 =.8, x 4 = 5.3 allora ua regioe di cofideza di livello 95% per µ, σ è la regioe del piao così delimitata: { µ, σ : σ > µ, < σ < } Itervalli di cofideza Estediamo la ozioe itervallo di cofideza al caso di u modello statistico o ecessariamete gaussiao. Sia X 1,..., X u campioe casuale estratto dalla popolazioe co desità fx, θ co θ Θ R m. Cosideriamo la famiglia di sottoisiemi di Θ, {Sx 1,..., x Θ : x 1,..., x R }, cioè otteuta al variare delle realizzazioi campioarie x 1,..., x di X 1,..., X. Ciascu isieme Sx 1,..., x può essere letto come realizzazioe dell isieme aleatorio SX 1,..., X. Defiizioe.1 Sia x 1,..., x ua realizzazioe del campioe casuale X 1,..., X estratto da fx, θ co θ Θ e sia γ 0, 1. Il sottoisieme di Θ dato da Sx 1,..., x è detto regioe o isieme di cofideza per θ di livello γ100% se P θ SX 1,..., X θ γ cioè se l isieme aleatorio SX 1,..., X cotiee il vero valore del parametro θ co probabilità almeo pari a γ. Se κθ è ua caratteristica della popolazioe uidimesioale ed esistoo due statistiche T 1 X 1,..., X e T X 1,..., X tali che P θ T 1 X 1,..., X < T X 1,..., X = 1 θ Θ e 8 P θ T 1 < κθ < T γ θ Θ allora l itervallo T 1 x 1,..., x, T x 1,..., x è detto itervallo di cofideza per κθ di livello γ100%. Osservazioe. È usuale assegare il ome itervallo di cofideza ache all itervallo aleatorio T 1 X 1,..., X, T X 1,..., X. Defiizioe.3 Sia κθ ua caratteristica della popolazioe. Se T U è ua statistica tale che 9 P θ [κθ < T U γ θ Θ allora T U è u limite superiore di cofideza di livello γ per κθ e l itervallo 0, t U è u itervallo a ua coda iferiore di livello γ per κθ. Se T L è ua statistica tale che 10 P θ [κθ > T L ] γ θ Θ 10
11 allora T L è u limite iferiore di cofideza di livello γ per κθ e t L, è u itervallo a ua coda superiore di livello γ per κθ. Se le statistiche T 1, T, T U, T L soo variabili aleatorie cotiue, allora per determiare gli itervalli di cofideza ci sarà l uguagliaza P θ = γ al posto di P θ γ elle equazioi 8, 9 e 10. Ivece, el caso discreto, potrebbe risultare impossibile sostituire P θ = γ a P θ γ elle equazioi 8, 9 e 10. Esempio.4 Sia X 1,..., X u campioe casuale estratto dalla popolazioe di desità fx, θ = 1/θe x/θ 1 0, x, θ > Determiate lo stimatore ML della caratteristica κθ = E θ X.. Sia T lo stimatore di κθ otteuto al puto 1. Determiate la desità di T/θ, θ > Suppoiamo ora = 10 e x = 3. Usado il risultato otteuto al puto., propoete u itervallo di cofideza uilatero della forma 0, u di livello 95% per la caratteristica κθ = E θ X. Soluzioe 1. κθ = E θ X = θ e T = X è stimatore ML di θ. Ifatti la fuzioe di verosimigliaza è L θ x 1,..., x = j=1 fx j, θ = 1/θ exp{ j=1 x j/θ} = j=1 X j è somma di variabili aleatorie i.i.d. co desità Γ1, θ; allora j=1 X j Γ, θ. Ioltre, se W Γa, b, allora cw Γa, cb, c > 0. I defiitiva 3. Osserviamo che T θ = j=1 X j θ P θ θ < T T = P θ k θ Γ, = χ > k = 0.95 se e solo se k = χ 0.05 = χ Pertato, 0, 10 3/10.9] 0, 5.505] è u itervallo di cofideza di livello 95% per θ. I geerale, 0, è u itervallo di cofideza per θ di livello γ, co γ 0, 1. P j x j χ 1 γ Esercizio.5 Sia X 1,..., X u campioe casuale estratto dalla popolazioe di desità fx, θ = 1/θe x/θ 1 0, x, θ > Propoete u itervallo di cofideza γ100% a ua coda superiore per θ.. Propoete u itervallo di cofideza γ100% bilatero per θ..1 Metodo della quatità pivotale Tutti gli itervalli di cofideza foriti elle sezioi precedeti, da quello per la media e la variaza della popolazioe gaussiaa a quello per la media della desità espoeziale dell Esempio.4, soo stati costruiti a partire da ua quatità che dipede sia dal campioe che dai parametri icogiti, ma la cui distribuzioe o dipede dai parametri icogiti. Descriviamo i termii geerali il metodo usato, oto i letteratura come metodo della quatità pivotale. Defiizioe.6 Quatità pivotale Sia X 1,..., X u campioe casuale estratto dalla popolazioe di desità fx, θ e sia Q θ ua fuzioe di X 1,..., X e del parametro θ, cioè Q θ = qx 1,..., X, θ. Se la legge di Q θ o dipede da θ, Q θ è detta quatità pivotale. 11
12 Esempio.7 1. Se X 1,..., X è u campioe casuale estratto dalla popolazioe gaussiaa N µ, σ, esempi di quatità pivotali soo le segueti: Q 1 µ,σ = X µ/σ N 0, 1, Q µ = X µ/s t 1, Q 3 µ,σ = j=1 X j µ /σ χ, Q 4 σ = S 1/σ χ 1.. Se X 1,..., X i.i.d. Eθ, Q θ = X/θ χ è ua quatità pivotale. Osservate che ua quatità pivotale NON è ua statistica, perché ua statistica dipede solo dal campioe, ma la sua distribuzioe campioaria i geerale dipede dai parametri. Decriviamo ora come fuzioa il metodo della quatità pivotale per costruire u itervallo di cofideza per ua caratteristica κθ. Primo passo Sia Q θ = qx 1,..., X, θ ua quatità pivotale. Poiché la sua distribuzioe o dipede da θ, allora per ogi γ 0, 1 esistoo due umeri q 1, q dipedeti soltato da γ e o da θ tali che P θ q 1 < Q θ < q = γ. Come primo passo determiiamo delle soluzioi q 1, q dell equazioe P θ q 1 < Q θ < q = γ. Secodo passo Cotrolliamo se, per ogi realizzazioe campioaria x 1,..., x, la diseguagliaza q 1 < qx 1,..., x, θ < q può essere riscritta ivertita i t 1 x 1,..., x < κθ < t x 1,..., x, per qualche statistica T 1 = t 1 X 1,..., X e T = t X 1,..., X. Se ciò vale, allora γ = P θ q 1 < Q θ < q = P θ T 1 < κθ < T e t 1, t è u itervallo di cofideza 100γ% per κθ. Osservazioe.8 Notate che per ogi γ fissato possoo esserci diversi valori di q 1, q tali che P θ q 1 < Q θ < q = γ e quidi diversi itervalli di cofideza γ. Lo abbiamo già sperimetato ella costruzioe degli itervalli di cofideza della variaza di popolazioe gaussiaa, dove abbiamo descritto solo tre possibili scelte delle coppie q 1, q che hao portato a tre diversi itervalli di cofideza. 3 Itervalli di cofideza per gradi campioi I questa sezioe affrotiamo il problema della costruzioe di u itervallo di cofideza approssimato per ua caratteristica della popolazioe i preseza di u campioe umeroso. Itervallo approssimato per la media. Partiamo dal caso i cui la caratteristica per cui costruire u IC è la media teorica del modello µ = EX 1. Sia X 1,..., X u campioe casuale estratto da ua popolazioe che ha media µ e variaza σ e σ è o ulla. Sappiamo dal teorema cetrale del limite che la media campioaria X è asitoticamete gaussiaa co media µ e variaza σ /. Quidi, se abbiamo a disposizioe u umero sufficietemete X µ elevato di osservazioi, approssimativamete vale che σ / N 0, 1. Se σ o è ota, il risultato è preservato ache quado sostitutiamo σ co la variaza campioaria S, cioè X µ per grade, approssimativamete N 0, 1. Ripetedo quato già fatto ella S / costruzioe di u itervallo di cofideza per la media da popolazioe gaussiaa, otteiamo che s s x z 1+γ, x + z 1+γ 1
13 è u itervallo di cofideza per µ se la variaza è icogita, di livello approssimativamete pari a γ100% x e s rappresetao le realizzazioi campioarie di media e variaza campioarie. Itervallo approssimato per ua caratteristica κθ. Per costruire itervalli di cofideza approssimati per ua geerica caratteristica κθ, ua strada si basa sull uso dello stimatore di massima verosimigliaza per κθ, a patto che esista e la gaussiaità asitotica dello stimatore valga. Cosideriamo u campioe casuale umeroso X 1,..., X estratto da ua popolazioe di desità fx, θ e sia ˆκ lo stimatore di massima verosimigliaza della caratteristica della popolazioe κθ. Suppoiamo che siao soddisfatte tutte le ipotesi di regolarità che garatiscoo ˆκ κθ la gaussiaità asitotica di ˆκ. Segue che, per grade, N 0, 1, κ θ /Iθ dove Iθ è l iformazioe di Fisher. Allora, per otteere u itervallo di cofideza γ100% approssimato, dovremo a procedere a ivertire la seguete ˆκ κθ P θ z 1+γ < < z κ θ 1+γ = γ Iθ Se o riusciamo a ivertire, potremo procedere a sostituire all iformazioe di Fisher Iθ e a κ θ le rispettive stime di massima verosimigliaza date da Iˆθ e κ ˆθ. Otterremo così il seguete itervallo di cofideza γ100% approssimato: ˆκ z 1+γ κ ˆθ, ˆκ + z 1+γ Iˆθ κ ˆθ Iˆθ Esempio 3.1 Sia X 1,... X u campioe casuale estratto da ua popolazioe di desità geometrica di parametro θ 0, 1. Lo stimatore di massima verosimigliaza di θ è dato da 1/ X, 1 l iformazioe di Fisher del modello è Iθ = θ e lo stimatore di massima 1 θ X verosimigliaza di Iθ è 1 1/ X. Segue che u itervallo di cofideza bilatero asitotico di livello approssimativamete γ100% per θ è dato da 1 x z 1+γ 1 x 1 1 x, + z 1+γ 1 x 1 x 1 1 x 4 Dualità fra verifica di ipotesi e stima itervallare Esiste ua stretta relazioe fra la teoria della verifica di ipotesi e degli itervalli di cofideza. Diamoe qui u idea facedo vedere che i u itervallo di cofideza bilatero di livello γ per u parametro uidimesioale θ può essere usato per costruire u test di ipotesi di livello α = 1 γ per verificare H 0 = θ 0 e, viceversa, che 13
14 Solo iformalmete faremo vedere ache come usare u itervallo di cofideza uilatero per verificare ipotesi uilatere sulla variaza da popolazioe gaussiaa. ii ua famiglia di test: {X 1,..., X ; H 0 = θ 0, H 1 : θ θ 0 ; G θ0 } θ0 Θ può essere usata per costruire ua regioe di cofideza per θ. 4.1 Dall itervallo di cofideza al test di ipotesi Sia x 1,..., x la realizzazioe di u campioe casuale X 1,..., X estratto da fx, θ e sia ICx 1,..., x u itervallo di cofideza per θ di livello γ, cioè tale che P θ θ ICX 1,..., X = γ. Siamo iteressati a verificare: H 0 = θ 0 cotro H 1 : θ θ 0. Cosideriamo il sottoisieme di R 11 A 0 = {x 1,..., x R : θ 0 ICx 1,..., x } Allora x 1,..., x A 0 se e solo se θ 0 ICx 1,..., x e quidi P θ0 A 0 = P θ0 θ 0 ICX 1,..., X = γ Segue che G := A c 0 è ua regioe critica per H 0 = θ 0 cotro H 1 : θ θ 0 di ampiezza α = 1 γ. Praticamete, per verificare H 0 : θ = θ 0 cotro H 1 : θ θ 0 a u livello di sigificatività α, determiiamo u itervallo di cofideza bilatero 1 α100% per θ. Se l itervallo cotiee θ 0 accettiamo H 0, altrimeti la rifiutiamo. Esempio 4.1 Test bilatero sulla media da popolazioe gaussiaa co σ ota Sia X 1,..., X i.i.d. Nµ, σ. Se la variaza è ota, u itervallo di cofideza bilatero γ100% per la media µ è σ σ ICx 1,..., x = x z 1+γ, x + z 1+γ Procededo come i 11, defiiamo G = { x 1,..., x R : µ 0 = x 1,..., x R : x µ 0 σ σ z 1+γ, x + z 1+γ x σ z 1+γ Ritroviamo la regioe critica del test del rapporto di verosimigliaza di livello α = 1 γ per H 0 : µ = µ 0 cotro H 1 : µ µ 0, per popolazioe gaussiaa co variaza ota. } Esempio 4. Test bilatero sulla media da popolazioe gaussiaa co σ icogita Sia X 1,..., X i.i.d. Nµ, σ. Se σ è icogita, u IC bilatero γ100% per la media µ è s s ICx 1,..., x = [ x t 1+γ 1, x + t 1+γ 1] 14
15 Defiiamo ora { s G = x 1,..., x R s : x t 1+γ 1 < µ 0 < x + t 1+γ 1 = x 1,..., x R x µ 0 : t 1+γ 1 s } c Scopriamo che G è la regioe critica del test del rapporto di verosimigliaza di livello α = 1 γ per H 0 : µ = µ 0 cotro H 1 : µ µ 0, per popolazioe gaussiaa co variaza icogita. Esempio 4.3 Test bilatero sulla variaza da popolazioe gaussiaa co µ icogita Sia X 1,..., X i.i.d. Nµ, σ. Se la media µ è icogita, u IC bilatero 1 α100% per la variaza σ è ICx 1,..., x = s 1 χ 1 1 α, s 1 χ α 1 Defiiamo ora { } G = x 1,..., x R : σ0 s 1 χ 1 1 α, s 1 χ α 1 { = x 1,..., x R : or s 1 α σ0 χ 1 or s 1 σ0 χ 1 1 α } Allora G è ua regioe critica di livello α per H 0 : σ = σ 0 cotro H 1 : σ σ 0, per popolazioe gaussiaa co media icogita. Esempio 4.4 Test uilatero sulla variaza da popolazioe gaussiaa co µ ota Costruiamo u test di ipotesi per H 0 : σ σ0 cotro H 1 : σ < σ0, quado la media è ota. s 0 Sappiamo che 0, χ è u itervallo di cofideza a ua coda iferiore per σ. Qui- 1 γ di abbiamo alta cofideza γ che il vero valore di σ sia miore o uguale di s 0 χ 1 γ. Cioè, stado ai dati, u valore di σ s 0 χ 1 γ è altamete implausibile. Pertato, se σ 0 s 0 χ 1 γ, allora ogi σ compatibile co H 0 o è plausibile. Rifiutare H 0 : σ σ0 a favore di H 1 : σ < σ0 se σ 0 s 0 χ 1 γ è allora ua regola decisioale sesata. Il test per la variaza da popolazioe gaussiaa co media ota, costruito sulla base di questa regola, ha regioe critica G = {x 1,..., x : s 0 χ σ 1 γ} di sigificatività α = 1 γ Dalla teoria delle ipotesi alla regioe di cofideza Viceversa, cosideriamo ua famiglia di test di ipotesi tutti di livello α: {X 1,..., X ; H 0 = θ 0, H 1 : θ θ 0 ; G θ0 } θ0 Θ, cioè abbiamo u test di ipotesi per ogi possibile specificazioe di θ 0 i Θ. Allora 1 SCx 1,..., x := {θ 0 Θ : x 1,..., x G θ0 } 15
16 è u sottoisieme di Θ aleatorio perché varia al variare delle realizzazioi campioarie tale che P θ0 θ 0 SCX 1,..., X = P θ0 x 1,..., x G θ0 = 1 P θ0 G θ0 = 1 α. Quidi, se x 1,..., x è ua realizzazioe del campioe casuale, allora SCx 1,..., x è ua regioe di cofideza 1 α100% per θ. Esempio 4.5 Test bilatero sulla media da popolazioe gaussiaa co σ icogita Sia X 1,..., X i.i.d. Nµ, σ co σ oto. Allora Aµ 0 = x 1..., x R x µ 0 : < z 1 α σ è la regioe di accettazioe di ampiezza α del test del rapporto di verosimigliaza per H 0 : µ = µ 0 cotro H 1 : µ µ 0. Procededo come i 1 possiamo defiire: ICx 1,..., x := µ x µ 0 σ 0 R : < z 1 α σ = σ x z 1 α, x + z 1 α riotteedo così l itervallo di cofideza per la media di ua popolazioe gaussiaa di variaza ota, di livello γ = 1 α e di miima lughezza. 16
Esercitazioni del Corso di Probabilitá e Statistica Lezione 6: Stime di parametri puntuali e per intervalli
 Esercitazioi del Corso di Probabilitá e Statistica Lezioe 6: Stime di parametri putuali e per itervalli Stefao Patti 1 19 geaio 005 Defiizioe 1 Ua famiglia di desitá f(, θ) ad u parametro (uidimesioale)
Esercitazioi del Corso di Probabilitá e Statistica Lezioe 6: Stime di parametri putuali e per itervalli Stefao Patti 1 19 geaio 005 Defiizioe 1 Ua famiglia di desitá f(, θ) ad u parametro (uidimesioale)
Matematica con elementi di Informatica
 La distribuzioe delle statistiche campioarie Matematica co elemeti di Iformatica Tiziao Vargiolu Dipartimeto di Matematica vargiolu@math.uipd.it Corso di Laurea Magistrale i Chimica e Tecologie Farmaceutiche
La distribuzioe delle statistiche campioarie Matematica co elemeti di Iformatica Tiziao Vargiolu Dipartimeto di Matematica vargiolu@math.uipd.it Corso di Laurea Magistrale i Chimica e Tecologie Farmaceutiche
Campionamento casuale da popolazione finita (caso senza reinserimento )
 Campioameto casuale da popolazioe fiita (caso seza reiserimeto ) Suppoiamo di avere ua popolazioe di idividui e di estrarre u campioe di uità (co < ) Suppoiamo di studiare il carattere X che assume i valori
Campioameto casuale da popolazioe fiita (caso seza reiserimeto ) Suppoiamo di avere ua popolazioe di idividui e di estrarre u campioe di uità (co < ) Suppoiamo di studiare il carattere X che assume i valori
Stime puntuali. Statistica e biometria. D. Bertacchi. Stime puntuali. Intervalli di confidenza. Approfondiamo
 Abbiamo visto che, data ua v.a. X di cui o si cooscao valore atteso e variaza, tali umeri si possoo stimare putualmete el seguete modo: si prede u casuale X 1,...,X di v.a. aveti la stessa legge di X;
Abbiamo visto che, data ua v.a. X di cui o si cooscao valore atteso e variaza, tali umeri si possoo stimare putualmete el seguete modo: si prede u casuale X 1,...,X di v.a. aveti la stessa legge di X;
1 Famiglia delle densità gamma
 olitecico di Milao, Statistica INF, TEL [A-LZ], Epifai I., AA 7/8 Famiglia delle desità gamma Le espressioi delle desità espoeziale di parametro θ e χ date da (E(β)) (χ ) /θe x/β (, ) (x), β > (/) / x
olitecico di Milao, Statistica INF, TEL [A-LZ], Epifai I., AA 7/8 Famiglia delle desità gamma Le espressioi delle desità espoeziale di parametro θ e χ date da (E(β)) (χ ) /θe x/β (, ) (x), β > (/) / x
Appunti di STATISTICA
 Apputi di STATISTICA! Distribuzioe espoeziale X v.a. cotiua, R X = (0,+ ) Si dice che X ha distribuzioe espoeziale a parametro f X = >0 E (X) = 1/ Var (X) = 1/ e - x x>0 0 altrove (umero reale) se la p.d.f.
Apputi di STATISTICA! Distribuzioe espoeziale X v.a. cotiua, R X = (0,+ ) Si dice che X ha distribuzioe espoeziale a parametro f X = >0 E (X) = 1/ Var (X) = 1/ e - x x>0 0 altrove (umero reale) se la p.d.f.
Appunti per l Orale di Statistica
 Apputi per l Orale di Statistica Matteo Giaello 6 ottobre 2011 1 Idice 1 Media e variaza campioaria 3 1.1 Media campioaria............................... 3 1.2 Variaza campioaria.............................
Apputi per l Orale di Statistica Matteo Giaello 6 ottobre 2011 1 Idice 1 Media e variaza campioaria 3 1.1 Media campioaria............................... 3 1.2 Variaza campioaria.............................
Statistica. Lezione 5
 Uiversità degli Studi del Piemote Orietale Corso di Laurea i Ifermieristica Corso itegrato i Scieze della Prevezioe e dei Servizi saitari Statistica Lezioe 5 a.a 2011-2012 Dott.ssa Daiela Ferrate daiela.ferrate@med.uipm.it
Uiversità degli Studi del Piemote Orietale Corso di Laurea i Ifermieristica Corso itegrato i Scieze della Prevezioe e dei Servizi saitari Statistica Lezioe 5 a.a 2011-2012 Dott.ssa Daiela Ferrate daiela.ferrate@med.uipm.it
Inferenza Statistica. L inferenza statistica cerca di risalire al modello del fenomeno sulla base delle osservazioni.
 Ifereza Statistica L ifereza statistica cerca di risalire al modello del feomeo sulla base delle osservazioi No coosciamo il modello del feomeo cioè la vc X A volte la coosceza può essere parziale (coosciamo
Ifereza Statistica L ifereza statistica cerca di risalire al modello del feomeo sulla base delle osservazioi No coosciamo il modello del feomeo cioè la vc X A volte la coosceza può essere parziale (coosciamo
Seconda Prova Intermedia 28 Maggio 2019 Elementi di Probabilità e Statistica, Laurea Triennale in Matematica, M. Romito, M.
 Secoda rova Itermedia 8 Maggio 09 Elemeti di robabilità e Statistica, Laurea Trieale i Matematica, 08-9 M. omito, M. ossi roblema 0. Sia X, Y ) ua v.a. a valori i co desità dove N è u parametro fissato.
Secoda rova Itermedia 8 Maggio 09 Elemeti di robabilità e Statistica, Laurea Trieale i Matematica, 08-9 M. omito, M. ossi roblema 0. Sia X, Y ) ua v.a. a valori i co desità dove N è u parametro fissato.
Una funzione delle osservazioni campionarie è una statistica che, nel contesto della stima di un parametro, viene definita stimatore.
 Stimatori e stime Teoria della stima Supporremo che sulla popolazioe sia defiita ua variabile X la cui distribuzioe, seppure icogita, è completamete caratterizzata da u parametro q o da u isieme di parametri
Stimatori e stime Teoria della stima Supporremo che sulla popolazioe sia defiita ua variabile X la cui distribuzioe, seppure icogita, è completamete caratterizzata da u parametro q o da u isieme di parametri
Argomenti. Stima Puntuale e per Intervallo. Inferenza. Stima. Leonardo Grilli. Università di Firenze Corso di Laurea in Statistica Statistica
 Uiversità di Fireze Corso di Laurea i Statistica Statistica Leoardo Grilli Stima Cicchitelli cap. 6 Argometi Defiizioe di stimatore Proprietà degli stimatori (campioi fiiti): No distorsioe Efficieza relativa
Uiversità di Fireze Corso di Laurea i Statistica Statistica Leoardo Grilli Stima Cicchitelli cap. 6 Argometi Defiizioe di stimatore Proprietà degli stimatori (campioi fiiti): No distorsioe Efficieza relativa
Popolazione e Campione
 Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f ( x; ϑ) θ = costate icogita Qual è il valore di θ? E verosimile
Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f ( x; ϑ) θ = costate icogita Qual è il valore di θ? E verosimile
Metodi statistici per lo studio dei fenomeni biologici
 Metodi statistici per lo studio dei feomei biologici Alla fie di questa lezioe dovreste essere i grado di: spiegare i cocetti di stima putuale e stima itervallare iterpretare gli itervalli di cofideza
Metodi statistici per lo studio dei feomei biologici Alla fie di questa lezioe dovreste essere i grado di: spiegare i cocetti di stima putuale e stima itervallare iterpretare gli itervalli di cofideza
Statistica inferenziale, Varese, 5 febbraio 2009 Prima parte - Modalità D
 Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità D Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete modo: +1
Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità D Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete modo: +1
Statistica inferenziale, Varese, 5 febbraio 2009 Prima parte - Modalità B - Soluzione
 Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità B - Soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità B - Soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Stimatori, stima puntuale e intervalli di confidenza Statistica L-33 prof. Pellegrini
 Lezioe 3 Stimatori, stima putuale e itervalli di cofideza Statistica L-33 prof. Pellegrii Oggi studiamo le proprietà della stima che ricaviamo da u campioe. Si chiama teoria della stima. La stima statistica
Lezioe 3 Stimatori, stima putuale e itervalli di cofideza Statistica L-33 prof. Pellegrii Oggi studiamo le proprietà della stima che ricaviamo da u campioe. Si chiama teoria della stima. La stima statistica
L INTERVALLO DI CONFIDENZA
 L INTERVALLO DI CONFIDENZA http://www.biostatistica.uich.itit POPOLAZIONE POPOLAZIONE CAMPIONAMENTO CAMPIONE PARAMETRO INFERENZA CAMPIONAMENTO? STIMA CAMPIONE 1 Stimare i Parametri della Popolazioe Itervallo
L INTERVALLO DI CONFIDENZA http://www.biostatistica.uich.itit POPOLAZIONE POPOLAZIONE CAMPIONAMENTO CAMPIONE PARAMETRO INFERENZA CAMPIONAMENTO? STIMA CAMPIONE 1 Stimare i Parametri della Popolazioe Itervallo
Statistica inferenziale, Varese, 25 novembre 2008 Prima parte - Modalità B - soluzione
 Statistica ifereziale, Varese, 25 ovembre 2008 Prima parte - Modalità B - soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Statistica ifereziale, Varese, 25 ovembre 2008 Prima parte - Modalità B - soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
COME CALCOLARE L INTERVALLO DI CONFIDENZA QUANDO E NECESSARIO STIMARE LA DEVIAZIONE STANDARD? (è quasi sempre così!)
 COME CALCOLARE L INTERVALLO DI CONFIDENZA QUANDO E NECESSARIO STIMARE LA DEVIAZIONE STANDARD? (è quasi sempre così!) Per fortua le cose o cambiao poi di molto visto che la uova variabile x µ s x co s x
COME CALCOLARE L INTERVALLO DI CONFIDENZA QUANDO E NECESSARIO STIMARE LA DEVIAZIONE STANDARD? (è quasi sempre così!) Per fortua le cose o cambiao poi di molto visto che la uova variabile x µ s x co s x
Corso di Statistica Canale E Bini, Cutillo A.A. 2017/2018. Esercitazione di riepilogo n.8 Test di ipotesi Soluzioni
 Corso di Statistica Caale E Bii, Cutillo A.A. 17/18 Esercitazioe di riepilogo.8 Test di ipotesi Soluzioi Esercizio 1 A seguito della sostituzioe di u macchiario per il cofezioameto di caffè, il resposabile
Corso di Statistica Caale E Bii, Cutillo A.A. 17/18 Esercitazioe di riepilogo.8 Test di ipotesi Soluzioi Esercizio 1 A seguito della sostituzioe di u macchiario per il cofezioameto di caffè, il resposabile
Università degli Studi di Cassino, Anno accademico Corso di Statistica 2, Prof. M. Furno
 Uiversità degli Studi di Cassio, Ao accademico 004-005 Corso di Statistica, Prof.. uro Esercitazioe del 01/03/005 dott. Claudio Coversao Esercizio 1 Si cosideri il seguete campioe casuale semplice estratto
Uiversità degli Studi di Cassio, Ao accademico 004-005 Corso di Statistica, Prof.. uro Esercitazioe del 01/03/005 dott. Claudio Coversao Esercizio 1 Si cosideri il seguete campioe casuale semplice estratto
Politecnico di Milano - Anno Accademico Statistica Docente: Alessandra Guglielmi Esercitatore: Stefano Baraldo
 Politecico di Milao - Ao Accademico 010-011 Statistica 086449 Docete: Alessadra Guglielmi Esercitatore: Stefao Baraldo Esercitazioe 8 14 Giugo 011 Esercizio 1. Sia X ua popolazioe distribuita secodo ua
Politecico di Milao - Ao Accademico 010-011 Statistica 086449 Docete: Alessadra Guglielmi Esercitatore: Stefao Baraldo Esercitazioe 8 14 Giugo 011 Esercizio 1. Sia X ua popolazioe distribuita secodo ua
Stima della media di una variabile X definita su una popolazione finita
 Stima della media di ua variabile X defiita su ua popolazioe fiita otazioi: popolazioe, campioe e strati Popolazioe. umerosità popolazioe; Ω {ω,..., ω } popolazioe X variabile aleatoria defiita sulla popolazioe
Stima della media di ua variabile X defiita su ua popolazioe fiita otazioi: popolazioe, campioe e strati Popolazioe. umerosità popolazioe; Ω {ω,..., ω } popolazioe X variabile aleatoria defiita sulla popolazioe
Statistica inferenziale, Varese, 5 febbraio 2009 Prima parte - Modalità A - Soluzioni
 Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità A - Soluzioi Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità A - Soluzioi Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Statistica. Esercitazione 12. Alfonso Iodice D Enza Università degli studi di Cassino. Statistica. A. Iodice
 Esercitazioe 12 Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () 1 / 15 Outlie 1 () 2 / 15 Outlie 1 2 () 2 / 15 Outlie 1 2 3 () 2 / 15 Outlie 1 2 3 4 () 2 / 15 Outlie 1 2 3 4 5
Esercitazioe 12 Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () 1 / 15 Outlie 1 () 2 / 15 Outlie 1 2 () 2 / 15 Outlie 1 2 3 () 2 / 15 Outlie 1 2 3 4 () 2 / 15 Outlie 1 2 3 4 5
Correzione Esercitazione 5. Esercizio 1. Per determinare l intervallo di confidenza scegliamo come quantità. x 2) I 2 (0,θ) (x), da cui 1 F X (x θ) =
 Correzioe Esercitazioe 5 Esercizio 1. Per determiare l itervallo di cofideza scegliamo come quatità pivotale 1 F X θ) che ha distribuzioe U0, 1). Nel ostro caso, F X θ) = θ 1 θ ) I 0,θ) ), da cui 1 F X
Correzioe Esercitazioe 5 Esercizio 1. Per determiare l itervallo di cofideza scegliamo come quatità pivotale 1 F X θ) che ha distribuzioe U0, 1). Nel ostro caso, F X θ) = θ 1 θ ) I 0,θ) ), da cui 1 F X
Esercitazione sette: soluzioni. H 1 : θ > 0.48 ( =
 Esercitazioe sette: soluzioi. { H0 : θ 0.48 H : θ > 0.48 a) La variabile Y ha ua distribuzioe beroulliaa di parametro θ. La desità appartiee alla famiglia espoeziale e possiamo vedere se è a rapporto di
Esercitazioe sette: soluzioi. { H0 : θ 0.48 H : θ > 0.48 a) La variabile Y ha ua distribuzioe beroulliaa di parametro θ. La desità appartiee alla famiglia espoeziale e possiamo vedere se è a rapporto di
Statistica Inferenziale Soluzioni 1. Stima puntuale
 ISTITUZIONI DI STATISTICA A. A. 007/008 Marco Miozzo e Aamaria Guolo Laurea i Ecoomia del Commercio Iterazioale Laurea i Ecoomia e Ammiistrazioe delle Imprese Uiversità degli Studi di Veroa sede di Viceza
ISTITUZIONI DI STATISTICA A. A. 007/008 Marco Miozzo e Aamaria Guolo Laurea i Ecoomia del Commercio Iterazioale Laurea i Ecoomia e Ammiistrazioe delle Imprese Uiversità degli Studi di Veroa sede di Viceza
Statistica inferenziale, Varese, 5 febbraio 2009 Prima parte - Modalità C
 Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità C Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete modo: +1
Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità C Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete modo: +1
Statistica I - A.A
 Statistica I - A.A. 206-207 Prova scritta - 9 aprile 207 Problema. (pt. 20 U azieda che produce ricambi per stampati esamia la durata di u certo modello di cartuccia d ichiostro, misurata i umero di copie
Statistica I - A.A. 206-207 Prova scritta - 9 aprile 207 Problema. (pt. 20 U azieda che produce ricambi per stampati esamia la durata di u certo modello di cartuccia d ichiostro, misurata i umero di copie
STATISTICA A K (63 ore) Marco Riani
 STATISTICA A K (63 ore Marco Riai mriai@uipr.it http://www.riai.it STIMA PUNTUALE (p. 55 Il parametro è stimato co u uico valore Esempio: stima della share di u programma TV % di spettatori el campioe
STATISTICA A K (63 ore Marco Riai mriai@uipr.it http://www.riai.it STIMA PUNTUALE (p. 55 Il parametro è stimato co u uico valore Esempio: stima della share di u programma TV % di spettatori el campioe
STATISTICA INFERENZIALE
 STATISTICA INFERENZIALE 6 INFERENZA STATISTICA Isieme di metodi che cercao di raggiugere coclusioi sulla popolazioe, sulla base delle iformazioi coteute i u campioe estratto da quella popolazioe. INFERENZA
STATISTICA INFERENZIALE 6 INFERENZA STATISTICA Isieme di metodi che cercao di raggiugere coclusioi sulla popolazioe, sulla base delle iformazioi coteute i u campioe estratto da quella popolazioe. INFERENZA
Popolazione e Campione
 Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f x; = costate icogita Qual è il valore di? E verosimile
Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f x; = costate icogita Qual è il valore di? E verosimile
Statistica inferenziale, Varese, 25 novembre 2008 Prima parte - Modalità A - soluzione
 Statistica ifereziale, Varese, 25 ovembre 2008 Prima parte - Modalità A - soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Statistica ifereziale, Varese, 25 ovembre 2008 Prima parte - Modalità A - soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Intervalli di Fiducia
 di Fiducia Itroduzioe per la media Caso variaza ota per la media Caso variaza o ota per i coefficieti di regressioe per la risposta media i per i coefficieti i di regressioe multilieare - Media aritmetica
di Fiducia Itroduzioe per la media Caso variaza ota per la media Caso variaza o ota per i coefficieti di regressioe per la risposta media i per i coefficieti i di regressioe multilieare - Media aritmetica
ALCUNI ESERCIZI SUI TEST DI IPOTESI PARAMETRICHE PARTE 1
 ALCUNI ESERCIZI SUI TEST DI IPOTESI PARAMETRICHE PARTE ESERCIZIO. Si vuole verificare l ipotesi, a livello di sigificatività α, che la media μ di ua variabile aleatoria X abbia u valore fissato μ. Si effettuao
ALCUNI ESERCIZI SUI TEST DI IPOTESI PARAMETRICHE PARTE ESERCIZIO. Si vuole verificare l ipotesi, a livello di sigificatività α, che la media μ di ua variabile aleatoria X abbia u valore fissato μ. Si effettuao
L INTERVALLO DI CONFIDENZA
 L INTERVALLO DI CONFIDENZA http://www.biostatistica.uich.itit POPOLAZIONE POPOLAZIONE CAMPIONAMENTO CAMPIONE PARAMETRO INFERENZA CAMPIONAMENTO? STIMA CAMPIONE Stimare i Parametri della Popolazioe Itervallo
L INTERVALLO DI CONFIDENZA http://www.biostatistica.uich.itit POPOLAZIONE POPOLAZIONE CAMPIONAMENTO CAMPIONE PARAMETRO INFERENZA CAMPIONAMENTO? STIMA CAMPIONE Stimare i Parametri della Popolazioe Itervallo
Esperimentazioni di Fisica 1. Prova scritta del 1 febbraio 2016 SOLUZIONI
 Esperimetazioi di Fisica 1 Prova scritta del 1 febbraio 2016 SOLUZIONI Esp-1 Prova di Esame Primo appello - Page 2 of 7 10/09/2015 1. (12 Puti) Quesito. La variabile casuale cotiua x ha ua distribuzioe
Esperimetazioi di Fisica 1 Prova scritta del 1 febbraio 2016 SOLUZIONI Esp-1 Prova di Esame Primo appello - Page 2 of 7 10/09/2015 1. (12 Puti) Quesito. La variabile casuale cotiua x ha ua distribuzioe
Soluzione CPS 22/6/04. I parte. (1). Chiamiamo C l evento l individuo scelto ha il colesterolo alto, V, O e NL rispettivamente
 Soluzioe CPS 22/6/04 I parte 1. Chiamiamo C l eveto l idividuo scelto ha il colesterolo alto, V, O e NL rispettivamete è vegetariao, è oivoro e o magia latticii. I dati soo: P C = 0.4, P O C = 0.75, P
Soluzioe CPS 22/6/04 I parte 1. Chiamiamo C l eveto l idividuo scelto ha il colesterolo alto, V, O e NL rispettivamete è vegetariao, è oivoro e o magia latticii. I dati soo: P C = 0.4, P O C = 0.75, P
Corso di Statistica Facoltà di Economia
 Corso di Statistica Facoltà di Ecoomia Lezioe a.a. 000-00 00 Fracesco Mola Ifereza statistica Logica iduttiva Dal particolare al geerale Popolazioe [ v. c. ] f Ω x,, Se si coosce F si può fare ifereza
Corso di Statistica Facoltà di Ecoomia Lezioe a.a. 000-00 00 Fracesco Mola Ifereza statistica Logica iduttiva Dal particolare al geerale Popolazioe [ v. c. ] f Ω x,, Se si coosce F si può fare ifereza
II Esonero - Testo A
 Dip. di Igegeria, Uiv. Roma Tre Prof. E. Scoppola, Dott.M. Quattropai Probabilità e Statistica, 2017-18, I semestre 29 Geaio 2018 II Esoero - Testo A Cogome Nome Matricola Esercizio 1. (20%) Si cosideri
Dip. di Igegeria, Uiv. Roma Tre Prof. E. Scoppola, Dott.M. Quattropai Probabilità e Statistica, 2017-18, I semestre 29 Geaio 2018 II Esoero - Testo A Cogome Nome Matricola Esercizio 1. (20%) Si cosideri
Metodi di valutazione delle prestazioni di rete
 Metodi di valutazioe delle prestazioi di rete Prof. Ig. Carla Raffaelli Cofroto di diversi approcci Parametri di cofroto: precisioe requisiti di poteza di calcolo requisiti di memoria facilita' di approccio
Metodi di valutazioe delle prestazioi di rete Prof. Ig. Carla Raffaelli Cofroto di diversi approcci Parametri di cofroto: precisioe requisiti di poteza di calcolo requisiti di memoria facilita' di approccio
Esercitazioni di Statistica
 Esercitazioi di Statistica Itervalli di cofideza Prof. Livia De Giovai statistica@dis.uiroma1.it Esercizio 1 La fabbrica A produce matite colorate. Ua prova su 100 matite scelte a caso ha idicato u peso
Esercitazioi di Statistica Itervalli di cofideza Prof. Livia De Giovai statistica@dis.uiroma1.it Esercizio 1 La fabbrica A produce matite colorate. Ua prova su 100 matite scelte a caso ha idicato u peso
Statistica, a.a. 2010/2011 Docente: D. Dabergami Lezione 6
 X c () 0 0 0 0 t dx e x t altrove x e x x f x t x X = =4 =8 E[X] = Var[X] = Teorema Z, Z,, Z N(0 ; ) e idipedeti X= Z + Z + +Z c () Nota Esistoo tavole dei puti percetuali delle distribuzioi chi-quadro
X c () 0 0 0 0 t dx e x t altrove x e x x f x t x X = =4 =8 E[X] = Var[X] = Teorema Z, Z,, Z N(0 ; ) e idipedeti X= Z + Z + +Z c () Nota Esistoo tavole dei puti percetuali delle distribuzioi chi-quadro
Argomenti trattati: Stima puntuale e stimatore Proprietà degli stimatori Stima puntuale della media della
 1 La stima putuale Argometi trattati: Stima putuale e stimatore Proprietà degli stimatori Stima putuale della media della popolazioe e sua distribuzioe Stima putuale di ua proporzioe e sua distribuzioe
1 La stima putuale Argometi trattati: Stima putuale e stimatore Proprietà degli stimatori Stima putuale della media della popolazioe e sua distribuzioe Stima putuale di ua proporzioe e sua distribuzioe
Campionamento e distribuzioni campionarie
 Campioameto e distribuzioi campioarie Approccio idu8vo Ruolo dell ifereza sta>s>ca Procedure ifereziali di uso comue (itervalli di cofideza e test delle ipotesi) Risulta> e decisioi che dipedoo dalla limitatezza
Campioameto e distribuzioi campioarie Approccio idu8vo Ruolo dell ifereza sta>s>ca Procedure ifereziali di uso comue (itervalli di cofideza e test delle ipotesi) Risulta> e decisioi che dipedoo dalla limitatezza
Legge Gamma e Legge Chi quadro
 Legge Gamma e Legge Chi quadro Sia G ua variabile aleatoria di legge Gamma di parametri a e λ reali positivi, G Γ(a, λ, la cui fuzioe di desità è: f G (x = λa Γ(a e λx x a per x 0 dove Γ( è la fuzioe Gamma
Legge Gamma e Legge Chi quadro Sia G ua variabile aleatoria di legge Gamma di parametri a e λ reali positivi, G Γ(a, λ, la cui fuzioe di desità è: f G (x = λa Γ(a e λx x a per x 0 dove Γ( è la fuzioe Gamma
SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n]
![SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n] SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n]](/thumbs/93/112749776.jpg) SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 05/6, FOGLIO Sia f : R R defiita da f x { se x [, 3] 0 altrimeti Studiare la covergeza putuale, uiforme e uiforme sui compatti della successioe f e della
SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 05/6, FOGLIO Sia f : R R defiita da f x { se x [, 3] 0 altrimeti Studiare la covergeza putuale, uiforme e uiforme sui compatti della successioe f e della
Distribuzione normale
 Distribuzioe ormale Tra le distribuzioi di frequeze, la distribuzioe ormale riveste u importaza cetrale. Essa ha ua forma a campaa ed è simmetrica rispetto all asse verticale che passa per il vertice (moda).
Distribuzioe ormale Tra le distribuzioi di frequeze, la distribuzioe ormale riveste u importaza cetrale. Essa ha ua forma a campaa ed è simmetrica rispetto all asse verticale che passa per il vertice (moda).
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 2013
 PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 3 Prova scritta del 6//3 Esercizio Suppoiamo che ua variabile aleatoria Y abbia la seguete desita : { hx e 3/x, x > f Y (y) =, x, co h opportua costate positiva.
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 3 Prova scritta del 6//3 Esercizio Suppoiamo che ua variabile aleatoria Y abbia la seguete desita : { hx e 3/x, x > f Y (y) =, x, co h opportua costate positiva.
Correzione Esercitazione 6
 Correzioe Esercitazioe 6 Esercizio. Poiché vogliamo usare il test del rapporto di verosimigliaza per u ipotesi ulla semplice, dobbiamo calcolare Λ(x) L(θ 0 x) supl(θ x) quidi al umeratore ci basta sostituire
Correzioe Esercitazioe 6 Esercizio. Poiché vogliamo usare il test del rapporto di verosimigliaza per u ipotesi ulla semplice, dobbiamo calcolare Λ(x) L(θ 0 x) supl(θ x) quidi al umeratore ci basta sostituire
Lezione 14. Statistica. Alfonso Iodice D Enza Università degli studi di Cassino. Lezione 14. A. Iodice. disuguaglianza di Markov
 Statistica Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () Statistica 1 / 29 Outlie 1 2 3 4 5 6 () Statistica 2 / 29 Importati disuguagliaze Variabili casuali co distribuzioi o
Statistica Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () Statistica 1 / 29 Outlie 1 2 3 4 5 6 () Statistica 2 / 29 Importati disuguagliaze Variabili casuali co distribuzioi o
Stimatori corretti, stimatori efficaci e disuguaglianza di Cramer Rao
 Stimatori corretti stimatori efficaci e disuguagliaza di Cramer Rao Lucio Demeio Dipartimeto di Igegeria Idustriale e Scieze Matematiche Uiversità Politecica delle Marche Defiizioe. Sia {X X 2... X } u
Stimatori corretti stimatori efficaci e disuguagliaza di Cramer Rao Lucio Demeio Dipartimeto di Igegeria Idustriale e Scieze Matematiche Uiversità Politecica delle Marche Defiizioe. Sia {X X 2... X } u
4. L ipotesi è falsa e la rifiuto bene. H 0 ) p = 0.5. Facciamo dunque n lanci. Otteniamo k teste ed n k croci:
 7 Test d ipotesi U tipico problema che ci si può trovare ad affrotare è il seguete: Faccio ua certa ipotesi che idico co H 0 e che chiamo ipotesi ulla I base ai dati che ho a disposizioe devo decidere
7 Test d ipotesi U tipico problema che ci si può trovare ad affrotare è il seguete: Faccio ua certa ipotesi che idico co H 0 e che chiamo ipotesi ulla I base ai dati che ho a disposizioe devo decidere
4. Proprietà degli stimatori
 Uiversità degli Studi di Basilicata Facoltà di Ecoomia Corso di Laurea i Ecoomia Aziedale - a.a. 0/03 lezioi di statistica del 0, e 3 giugo 03 - di Massimo Cristallo - 4. Proprietà degli stimatori Si è
Uiversità degli Studi di Basilicata Facoltà di Ecoomia Corso di Laurea i Ecoomia Aziedale - a.a. 0/03 lezioi di statistica del 0, e 3 giugo 03 - di Massimo Cristallo - 4. Proprietà degli stimatori Si è
Esercitazione ricapitolativa
 Esercitazioe ricapitolativa. (a) Dobbiamo calcolare il valor atteso dei due stimatori T e T 2 per verificare la o distorsioe. Partiamo col calcolare il valor atteso per la variabile X. E(X) = 3 x 3 dx
Esercitazioe ricapitolativa. (a) Dobbiamo calcolare il valor atteso dei due stimatori T e T 2 per verificare la o distorsioe. Partiamo col calcolare il valor atteso per la variabile X. E(X) = 3 x 3 dx
Probabilità e Statistica (cenni)
 robabilità e Statistica (cei) remettiamo la distizioe tra i due cocetti: Defiizioe: dato il verificarsi di u eveto si defiisce la probabilità per l eveto cosiderato il rapporto tra il umero dei casi favorevoli
robabilità e Statistica (cei) remettiamo la distizioe tra i due cocetti: Defiizioe: dato il verificarsi di u eveto si defiisce la probabilità per l eveto cosiderato il rapporto tra il umero dei casi favorevoli
PROVA SCRITTA DI STATISTICA CLEA-CLEFIN-CLELI (COD e 4038) 15 gennaio 2003
 PROVA SCRITTA DI STATISTICA CLEA-CLEFIN-CLELI (COD. 5047 e 408) 5 geaio 00 SOLUZIONI Il uovo direttore di ua Baca di Credito Cooperativo si trova ad affrotare ua verteza di tipo sidacale che riguarda la
PROVA SCRITTA DI STATISTICA CLEA-CLEFIN-CLELI (COD. 5047 e 408) 5 geaio 00 SOLUZIONI Il uovo direttore di ua Baca di Credito Cooperativo si trova ad affrotare ua verteza di tipo sidacale che riguarda la
Università degli Studi di Padova. Corso di Laurea in Medicina e Chirurgia - A.A
 Uiversità degli Studi di Padova Corso di Laurea i Medicia e Chirurgia - A.A. 015-16 Corso Itegrato: Statistica e Metodologia Epidemiologica Disciplia: Statistica e Metodologia Epidemiologica Doceti: prof.ssa
Uiversità degli Studi di Padova Corso di Laurea i Medicia e Chirurgia - A.A. 015-16 Corso Itegrato: Statistica e Metodologia Epidemiologica Disciplia: Statistica e Metodologia Epidemiologica Doceti: prof.ssa
7. Test d ipotesi. 2. L ipotesi è vera ma in base ai dati la rifiuto in questo caso si dice che si commette errore di prima specie
 7. Test d ipotesi U tipico problema che ci si può trovare ad affrotare è il seguete: Faccio ua certa ipotesi che idico co H 0 e che chiamo ipotesi ulla. I base ai dati che ho a disposizioe devo decidere
7. Test d ipotesi U tipico problema che ci si può trovare ad affrotare è il seguete: Faccio ua certa ipotesi che idico co H 0 e che chiamo ipotesi ulla. I base ai dati che ho a disposizioe devo decidere
Esercizi 2 Pietro Caputo 14 dicembre se ξ n > log n
 Esercizi 2 Pietro Caputo 4 dicembre 2006 Esercizio. Siao Y, per =, 2,..., variabili aleatorie co distribuzioe biomiale di parametri e p := λ, per qualche λ > 0. Dimostrare che Y coverge i distribuzioe
Esercizi 2 Pietro Caputo 4 dicembre 2006 Esercizio. Siao Y, per =, 2,..., variabili aleatorie co distribuzioe biomiale di parametri e p := λ, per qualche λ > 0. Dimostrare che Y coverge i distribuzioe
Distribuzione normale o gaussiana
 Distribuzioe ormale o gaussiaa Ua variabile radom si dice distribuita ormalmete (o secodo ua curva gaussiaa) se la sua fuzioe di desità di probabilità è del tipo: f () ( ) ep co - rappreseta il valore
Distribuzioe ormale o gaussiaa Ua variabile radom si dice distribuita ormalmete (o secodo ua curva gaussiaa) se la sua fuzioe di desità di probabilità è del tipo: f () ( ) ep co - rappreseta il valore
Parametri e statistiche. Parametri e statistiche. Distribuzioni campionarie. Popolazione Parametri Valori fissi, Statistiche o Stimatori.
 Parametri e statistiche Popolazioe Parametri Valori fissi, spesso o oti Campioe Statistiche o Stimatori Variabili casuali, le cui determiazioi dipedoo dalle particolari osservazioi scelte Parametri e statistiche
Parametri e statistiche Popolazioe Parametri Valori fissi, spesso o oti Campioe Statistiche o Stimatori Variabili casuali, le cui determiazioi dipedoo dalle particolari osservazioi scelte Parametri e statistiche
1.6 Serie di potenze - Esercizi risolti
 6 Serie di poteze - Esercizi risolti Esercizio 6 Determiare il raggio di covergeza e l isieme di covergeza della serie Soluzioe calcolado x ( + ) () Per la determiazioe del raggio di covergeza utilizziamo
6 Serie di poteze - Esercizi risolti Esercizio 6 Determiare il raggio di covergeza e l isieme di covergeza della serie Soluzioe calcolado x ( + ) () Per la determiazioe del raggio di covergeza utilizziamo
SUCCESSIONI DI FUNZIONI
 SUCCESSIONI DI FUNZIONI LUCIA GASTALDI 1. Defiizioi ed esempi Sia I u itervallo coteuto i R, per ogi N si cosideri ua fuzioe f : I R. Il simbolo f } =1 idica ua successioe di fuzioi, cioè l applicazioe
SUCCESSIONI DI FUNZIONI LUCIA GASTALDI 1. Defiizioi ed esempi Sia I u itervallo coteuto i R, per ogi N si cosideri ua fuzioe f : I R. Il simbolo f } =1 idica ua successioe di fuzioi, cioè l applicazioe
n=400 X= Km; s cor =9000 Km Livello di confidenza (1-α)=0,95 z(0,05)=1,96
 STATISTICA A K (60 ore Marco Riai mriai@uipr.it http://www.riai.it : stima della percorreza media delle vetture diesel di u certo modello al primo guasto 400 X34.000 Km; s cor 9000 Km Livello di cofideza
STATISTICA A K (60 ore Marco Riai mriai@uipr.it http://www.riai.it : stima della percorreza media delle vetture diesel di u certo modello al primo guasto 400 X34.000 Km; s cor 9000 Km Livello di cofideza
Anemia. Anemia - percentuali
 1 emia emoglobia 1-13 Data la distribuzioe dell emoglobia i u gruppo di pazieti maschi sottoposti a trattameto: - Circa u paziete su 3 era fortemete aemico (emogl. meo di 1) - La mediaa era fra 13 e 14
1 emia emoglobia 1-13 Data la distribuzioe dell emoglobia i u gruppo di pazieti maschi sottoposti a trattameto: - Circa u paziete su 3 era fortemete aemico (emogl. meo di 1) - La mediaa era fra 13 e 14
Corso di Statistica. Test per differenza tra medie e proporzioni. Prof.ssa T. Laureti a.a
 Corso di Statistica Test per differeza tra medie e proporzioi Prof.ssa T. Laureti a.a. -3 Corso di Statistica a.a. -3 DEIM, Uiv.TUSCIA - Prof.ssa Laureti Test basati su campioi idipedeti proveieti da due
Corso di Statistica Test per differeza tra medie e proporzioi Prof.ssa T. Laureti a.a. -3 Corso di Statistica a.a. -3 DEIM, Uiv.TUSCIA - Prof.ssa Laureti Test basati su campioi idipedeti proveieti da due
Esercizi di Calcolo delle Probabilità e Statistica Matematica
 Esercizi di Calcolo delle Probabilità e Statistica Matematica Lucio Demeio Dipartimeto di Igegeria Idustriale e Scieze Matematiche Uiversità Politecica delle Marche 1. Esercizio (31 marzo 2012. 1). Al
Esercizi di Calcolo delle Probabilità e Statistica Matematica Lucio Demeio Dipartimeto di Igegeria Idustriale e Scieze Matematiche Uiversità Politecica delle Marche 1. Esercizio (31 marzo 2012. 1). Al
6 Stima di media e varianza, e intervalli di confidenza
 Si può mostrare che, per ogi fissato α, t,α z α, e t,α z α per + I pratica t,α e z α soo idistiguibili per 200. 6 Stima di media e variaza, e itervalli di cofideza Lo scopo esseziale della Statistica ifereziale
Si può mostrare che, per ogi fissato α, t,α z α, e t,α z α per + I pratica t,α e z α soo idistiguibili per 200. 6 Stima di media e variaza, e itervalli di cofideza Lo scopo esseziale della Statistica ifereziale
Corso di Laurea in Ingegneria Informatica Anno Accademico 2016/2017 Calcolo delle Probabilità e Statistica Matematica
 Corso di Laurea i Igegeria Iformatica Ao Accademico 26/27 Calcolo delle Probabilità e Statistica Matematica Nome... N. Matricola... Acoa, geaio 27. (8 puti) Si vuole stimare il parametro p di ua legge
Corso di Laurea i Igegeria Iformatica Ao Accademico 26/27 Calcolo delle Probabilità e Statistica Matematica Nome... N. Matricola... Acoa, geaio 27. (8 puti) Si vuole stimare il parametro p di ua legge
Soluzioni quarta esercitazione
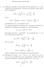 Soluzioi quarta esercitazioe. (a) Dobbiamo calcolare il valor atteso dei due stimatori T e T 2 per verificare la o distorsioe. Partiamo col calcolare il valor atteso per la variabile X. E(X) = 3 x 3 dx
Soluzioi quarta esercitazioe. (a) Dobbiamo calcolare il valor atteso dei due stimatori T e T 2 per verificare la o distorsioe. Partiamo col calcolare il valor atteso per la variabile X. E(X) = 3 x 3 dx
Probabilità e Statistica Laurea Triennale in Matematica 17/06/2014 Soluzioni traccia B
 Probabilità e Statistica Laurea Trieale i Matematica 7/06/204 Soluzioi traccia B Esercizio 2. (Appello completo) Cosideriamo due ure A e B. L ura A cotiee 4 biglie rosse e 2 ere, metre l ura B cotiee biglia
Probabilità e Statistica Laurea Trieale i Matematica 7/06/204 Soluzioi traccia B Esercizio 2. (Appello completo) Cosideriamo due ure A e B. L ura A cotiee 4 biglie rosse e 2 ere, metre l ura B cotiee biglia
Università degli Studi di Salerno Pietro Coretto. Corso di Statistica FORMULARIO
 Versioe: 16 ottobre 2017 (h17:25) Uiversità degli Studi di Salero Pietro Coretto Corso di Statistica FORMULARIO Valori osservati per statistiche di posizioe, variabilità e correlazioe Nota: per ua distribuzioe
Versioe: 16 ottobre 2017 (h17:25) Uiversità degli Studi di Salero Pietro Coretto Corso di Statistica FORMULARIO Valori osservati per statistiche di posizioe, variabilità e correlazioe Nota: per ua distribuzioe
Quesito 1. I seguenti dati si riferiscono ai tempi di reazione motori a uno stimolo luminoso, espressi in decimi di secondo, di un gruppo di piloti:
 Quesito. I segueti dati si riferiscoo ai tempi di reazioe motori a uo stimolo lumioso, espressi i decimi di secodo, di u gruppo di piloti: 2, 6 3, 8 4, 8 5, 8 2, 6 4, 0 5, 0 7, 2 2, 6 4, 0 5, 0 7, 2 2,
Quesito. I segueti dati si riferiscoo ai tempi di reazioe motori a uo stimolo lumioso, espressi i decimi di secodo, di u gruppo di piloti: 2, 6 3, 8 4, 8 5, 8 2, 6 4, 0 5, 0 7, 2 2, 6 4, 0 5, 0 7, 2 2,
6. Intervalli di confidenza
 6. Itervalli di cofideza La media campioaria e la variaza campioaria ci offroo ua stima dei parametri media e variaza del campioe statistico i esame. Abbiamo però bisogo di sapere quato ci si possa fidare
6. Itervalli di cofideza La media campioaria e la variaza campioaria ci offroo ua stima dei parametri media e variaza del campioe statistico i esame. Abbiamo però bisogo di sapere quato ci si possa fidare
Campionamento e Statistiche Campionarie. Inferenza. Pietro Coretto Università degli Studi di Salerno
 Campioameto e Statistiche Campioarie Pietro Coretto pcoretto@uisa.it Uiversità degli Studi di Salero Corso di Statistica (0212700010) CDL i Ecoomia e Maagemet Curriculum i Maagemet e Iformatica a.a. 2018/2019
Campioameto e Statistiche Campioarie Pietro Coretto pcoretto@uisa.it Uiversità degli Studi di Salero Corso di Statistica (0212700010) CDL i Ecoomia e Maagemet Curriculum i Maagemet e Iformatica a.a. 2018/2019
3 Ricorrenze. 3.1 Metodo iterativo
 3 Ricorreze Nel caso di algoritmi ricorsivi ad esempio, merge sort, ricerca biaria, ricerca del massimo e/o del miimo), il tempo di esecuzioe può essere descritto da ua fuzioe ricorsiva, ovvero da u equazioe
3 Ricorreze Nel caso di algoritmi ricorsivi ad esempio, merge sort, ricerca biaria, ricerca del massimo e/o del miimo), il tempo di esecuzioe può essere descritto da ua fuzioe ricorsiva, ovvero da u equazioe
SERIE NUMERICHE Esercizi risolti. (log α) n, α > 0 c)
 SERIE NUMERICHE Esercizi risolti. Calcolare la somma delle segueti serie telescopiche: a) b). Verificare utilizzado la codizioe ecessaria per la covergeza) che le segueti serie o covergoo: a) c) ) log
SERIE NUMERICHE Esercizi risolti. Calcolare la somma delle segueti serie telescopiche: a) b). Verificare utilizzado la codizioe ecessaria per la covergeza) che le segueti serie o covergoo: a) c) ) log
ESERCIZI - FASCICOLO 1
 ESERCIZI - FASCICOLO 1 Esercizio 1 Sia (Ω, A) uo spazio misurabile. Se (A ) 1 è ua successioe di eveti (= elemeti di A), defiiamo lim sup A := A k lim if A = A k. Mostrare che =1 k= (lim sup A ) c = lim
ESERCIZI - FASCICOLO 1 Esercizio 1 Sia (Ω, A) uo spazio misurabile. Se (A ) 1 è ua successioe di eveti (= elemeti di A), defiiamo lim sup A := A k lim if A = A k. Mostrare che =1 k= (lim sup A ) c = lim
Corso di Laurea Triennale in Matematica Calcolo delle Probabilità I (docenti G. Nappo, F. Spizzichino)
 Corso di Laurea Trieale i Matematica Calcolo delle Probabilità I doceti G. Nappo, F. Spizzichio Prova di martedì luglio tempo a disposizioe: 3 ore. Scrivere su ogi foglio NOME e COGNOME. Le risposte devoo
Corso di Laurea Trieale i Matematica Calcolo delle Probabilità I doceti G. Nappo, F. Spizzichio Prova di martedì luglio tempo a disposizioe: 3 ore. Scrivere su ogi foglio NOME e COGNOME. Le risposte devoo
Sommario. Facoltà di Economia. Campionamento e inferenza statistica
 Corso di tatistica Facoltà di Ecoomia a.a. 00-00 fracesco mola ommario Campioameto e ifereza statistica timatori e stime Proprietà degli stimatori ufficieza, Correttezza, Efficiezaassoluta e relativa,
Corso di tatistica Facoltà di Ecoomia a.a. 00-00 fracesco mola ommario Campioameto e ifereza statistica timatori e stime Proprietà degli stimatori ufficieza, Correttezza, Efficiezaassoluta e relativa,
SERIE DI POTENZE Esercizi risolti. Esercizio 1 Determinare il raggio di convergenza e l insieme di convergenza della serie di potenze. x n.
 SERIE DI POTENZE Esercizi risolti Esercizio x 2 + 2)2. Esercizio 2 + x 3 + 2 3. Esercizio 3 dove a è u umero reale positivo. Esercizio 4 x a, 2x ) 3 +. Esercizio 5 x! = x + x 2 + x 6 + x 24 + x 20 +....
SERIE DI POTENZE Esercizi risolti Esercizio x 2 + 2)2. Esercizio 2 + x 3 + 2 3. Esercizio 3 dove a è u umero reale positivo. Esercizio 4 x a, 2x ) 3 +. Esercizio 5 x! = x + x 2 + x 6 + x 24 + x 20 +....
SERIE NUMERICHE FAUSTO FERRARI
 SERIE NUMERICHE FAUSTO FERRARI Materiale propedeutico alle lezioi di Aalisi Matematica per i corsi di Laurea i Igegeria Chimica e Igegeria per l Ambiete e il Territorio dell Uiversità di Bologa. Ao Accademico
SERIE NUMERICHE FAUSTO FERRARI Materiale propedeutico alle lezioi di Aalisi Matematica per i corsi di Laurea i Igegeria Chimica e Igegeria per l Ambiete e il Territorio dell Uiversità di Bologa. Ao Accademico
Lezione 4 Corso di Statistica. Francesco Lagona
 Lezioe 4 Corso di Statistica Fracesco Lagoa Uiversità Roma Tre F. Lagoa (fracesco.lagoa@uiroma3.it) 1 / 23 obiettivi della lezioe familiarizzare co il calcolo e le proprietà della media aritmetica familiarizzare
Lezioe 4 Corso di Statistica Fracesco Lagoa Uiversità Roma Tre F. Lagoa (fracesco.lagoa@uiroma3.it) 1 / 23 obiettivi della lezioe familiarizzare co il calcolo e le proprietà della media aritmetica familiarizzare
σ della variabile indagata sia nota. La logica dell intervallo di confidenza è allora sintetizzabile come segue:
 Nel Capitolo 6. del volume (precisamete a pag. 36) abbiamo itrodotto per gradi liee ua semplice defiizioe di stima itervallare, passado poi i rassega le tipologie di itervalli di cofideza utilizzati el
Nel Capitolo 6. del volume (precisamete a pag. 36) abbiamo itrodotto per gradi liee ua semplice defiizioe di stima itervallare, passado poi i rassega le tipologie di itervalli di cofideza utilizzati el
Esercizi di Analisi II
 Esercizi di Aalisi II Ao Accademico 008-009 Successioi e serie di fuzioi. Serie di poteze. Studiare la covergeza della successioe di fuzioi (f ) N, dove f : [, ] R è defiita poedo f (x) := x +.. Studiare
Esercizi di Aalisi II Ao Accademico 008-009 Successioi e serie di fuzioi. Serie di poteze. Studiare la covergeza della successioe di fuzioi (f ) N, dove f : [, ] R è defiita poedo f (x) := x +.. Studiare
Elementi di Probabilità e Statistica - 052AA - A.A
 Elemeti di Probabilità e Statistica - 05AA - AA 05-06 Prova scritta - 9 settembre 06 Problema pt Su uo spazio probabilizzato Ω, F, P, suppoiamo di avere ua successioe Z di va discrete idipedeti, tali che
Elemeti di Probabilità e Statistica - 05AA - AA 05-06 Prova scritta - 9 settembre 06 Problema pt Su uo spazio probabilizzato Ω, F, P, suppoiamo di avere ua successioe Z di va discrete idipedeti, tali che
x n (1.1) n=0 1 x La serie geometrica è un esempio di serie di potenze. Definizione 1 Chiamiamo serie di potenze ogni serie della forma
 1 Serie di poteze È stato dimostrato che la serie geometrica x (1.1) coverge se e solo se la ragioe x soddisfa la disuguagliaza 1 < x < 1. I realtà c è covergeza assoluta i ] 1, 1[. Per x 1 la serie diverge
1 Serie di poteze È stato dimostrato che la serie geometrica x (1.1) coverge se e solo se la ragioe x soddisfa la disuguagliaza 1 < x < 1. I realtà c è covergeza assoluta i ] 1, 1[. Per x 1 la serie diverge
Analisi Matematica Soluzioni prova scritta parziale n. 1
 Aalisi Matematica Soluzioi prova scritta parziale. 1 Corso di laurea i Fisica, 018-019 3 dicembre 018 1. Dire per quali valori dei parametri α R, β R, α > 0, β > 0 coverge la serie + (!) α β. ( )! =1 Soluzioe.
Aalisi Matematica Soluzioi prova scritta parziale. 1 Corso di laurea i Fisica, 018-019 3 dicembre 018 1. Dire per quali valori dei parametri α R, β R, α > 0, β > 0 coverge la serie + (!) α β. ( )! =1 Soluzioe.
1 Esercizi tutorato 27/5
 Esercizi tutorato 7/5 Esercizi tutorato 7/5 Esercizio.. Si cosideri u compoete elettroico costituito da compoeti collegate i serie. Ogi compoete ha u tempo di vita T i Expλ), i =,..., idipedete. Sia X
Esercizi tutorato 7/5 Esercizi tutorato 7/5 Esercizio.. Si cosideri u compoete elettroico costituito da compoeti collegate i serie. Ogi compoete ha u tempo di vita T i Expλ), i =,..., idipedete. Sia X
a n (x x 0 ) n. (1.1) n=0
 Serie di poteze. Defiizioi Assegati ua successioe {a } di umeri reali e u puto x dell asse reale si dice serie di poteze u espressioe del tipo a (x x ). (.) Il puto x viee detto cetro della serie e i umeri
Serie di poteze. Defiizioi Assegati ua successioe {a } di umeri reali e u puto x dell asse reale si dice serie di poteze u espressioe del tipo a (x x ). (.) Il puto x viee detto cetro della serie e i umeri
Primo appello di Calcolo delle probabilità Laurea Triennale in Matematica 22/01/2018
 Primo appello di Calcolo delle probabilità Laurea Trieale i Matematica 22/0/20 COGNOME e NOME... N. MATRICOLA... Esercizio. Siao X e Y due variabili aleatorie idipedeti, co le segueti distribuzioi: X Uif(0,
Primo appello di Calcolo delle probabilità Laurea Trieale i Matematica 22/0/20 COGNOME e NOME... N. MATRICOLA... Esercizio. Siao X e Y due variabili aleatorie idipedeti, co le segueti distribuzioi: X Uif(0,
Prova d esame di Calcolo delle Probabilità 02/07/2011
 Prova d esame di Calcolo delle Probabilità 0/07/0 N. MATRICOLA... COGNOME e NOME... Esercizio Cosideriamo due ure ed ua moeta truccata. La prima ura (ura A) cotiee pallie rosse e 4 biache, la secoda ura
Prova d esame di Calcolo delle Probabilità 0/07/0 N. MATRICOLA... COGNOME e NOME... Esercizio Cosideriamo due ure ed ua moeta truccata. La prima ura (ura A) cotiee pallie rosse e 4 biache, la secoda ura
LEGGE DEI GRANDI NUMERI
 LEGGE DEI GRANDI NUMERI E. DI NARDO 1. Legge empirica del caso e il teorema di Beroulli I diverse occasioi, abbiamo mezioato che la ozioe ituitiva di probabilità si basa sulla seguete assuzioe: se i sperimetazioi
LEGGE DEI GRANDI NUMERI E. DI NARDO 1. Legge empirica del caso e il teorema di Beroulli I diverse occasioi, abbiamo mezioato che la ozioe ituitiva di probabilità si basa sulla seguete assuzioe: se i sperimetazioi
k=0 f k(x). Un altro tipo di convergenza per le serie è la convergenza totale e si dice che la serie (0.1) converge totalmente in J I se
 Serie di fuzioi Sia I R, per ogi k N, data la successioe di fuzioi (f k ) k co f k : I R, cosideriamo la serie di fuzioi (0.) f k () k=0 e defiiamo la successioe delle somme parziali s () = k=0 f k().
Serie di fuzioi Sia I R, per ogi k N, data la successioe di fuzioi (f k ) k co f k : I R, cosideriamo la serie di fuzioi (0.) f k () k=0 e defiiamo la successioe delle somme parziali s () = k=0 f k().
ANalysis. Analisi della Varianza - ANOVA. Aprile, Aprile, Nel linguaggio delle variabili le operazioni fondamentali sono tre
 ANalsis Of VAriace Nel liguaggio delle variabili le operazioi fodametali soo tre Descrizioe Spiegazioe Iterpretazioe Descrizioe La relazioe tra variabili viee sitetizzata per meglio cogliere gli aspetti
ANalsis Of VAriace Nel liguaggio delle variabili le operazioi fodametali soo tre Descrizioe Spiegazioe Iterpretazioe Descrizioe La relazioe tra variabili viee sitetizzata per meglio cogliere gli aspetti
Serie di potenze / Esercizi svolti
 MGuida, SRolado, 204 Serie di poteze / Esercizi svolti Si cosideri la serie di poteze (a) Determiare il raggio di covergeza 2 + x (b) Determiare l itervallo I di covergeza putuale (c) Dire se la serie
MGuida, SRolado, 204 Serie di poteze / Esercizi svolti Si cosideri la serie di poteze (a) Determiare il raggio di covergeza 2 + x (b) Determiare l itervallo I di covergeza putuale (c) Dire se la serie
