Modelli stocastici a valori discreti
|
|
|
- Ortensia Spina
- 10 anni fa
- Visualizzazioni
Transcript
1 Modelli stocastici a valori discreti Note del corso di CP per la L.M. in Informatica A.Calzolari 1
2 Indice 1 Catene di Markov a tempo discreto Richiami sull indipendenza stocastica per eventi e variabili aleatorie Definizione di catena di Markov Esempio di due successioni di variabili aleatorie relative ad un unico esperimento di cui una Markov e l altra no Passeggiata aleatoria sugli interi Catene di Markov per ricorrenza Legge al tempo e legge al tempo Matrice di transizione in più passi Leggi ad un tempo e leggi congiunte Matrice di transizione in due passi per la catena della rovina del giocatore La catena di nascita e morte e l urna di Ehrenfest Un modello per una fila d attesa Costruzione di una catena data la matrice di transizione e la legge iniziale Rappresentazione grafica di una catena di Markov Stati comunicanti Classi chiuse e classi irriducibili Definizione di transienza e persistenza in termini del tempo di primo ritorno Transienza e persistenza in termini del numero dei ritorni Legge e valor medio del numero dei ritorni in uno stato Transienza e persistenza di uno stato in termini del numero dei passaggi per esso partendo da uno stato qualsiasi Una condizione sufficiente per la transienza Una condizione sufficiente per la persistenza Persistenza e transienza in classi finite Teorema di decomposizione dello spazio degli stati Sistema di equazioni per le probabilità di assorbimento Unicità della soluzione del sistema di equazioni per le probabilità di assorbimento nel caso stati finiti Probabilità di estinzione per la catena di nascita e morte con estremi assorbenti Persistenza o transienza per la catena di nascita e morte irriducibile Tempi medi di assorbimento nella classe degli stati persistenti La catena a due stati: comportamento asintotico delle leggi al tempo n Definizione di misura invariante
3 1.31 Esempi nel caso finito Esistenza e unicità della misura invariante Catene ergodiche Catene regolari La misura invariante per l urna di Ehrenfest Non esistenza della misura invariante per la passeggiata aleatoria simmetrica in Z Misura invariante per le catene di nascita e morte Esempi di catene periodiche Periodo di una catena irriducibile Reversibilità Algoritmo di Metropolis Schema di dimostrazione del teorema di esistenza della misura invariante per catene irriducibili persistenti positive Approssimazione della misura invariante con la distribuzione empirica Esercizi di riepilogo Processo di Poisson Definizione Perdita di memoria Merging e splitting Processo di Poisson non stazionario Distribuzione dei tempi di salto in [, T ] condizionata a N(T)=n13 3 Processi di rinnovo 16 4 Catene di Markov a tempo continuo Definizione Funzione di transizione e tassi di salto Catene di nascita e morte Code markoviane Misura invariante
4 1 Catene di Markov a tempo discreto 1.1 Richiami sull indipendenza stocastica per eventi e variabili aleatorie Dato uno spazio di probabilità (Ω, F, P), due eventi A e B in F sono indipendenti se e solo se P(A B) = P(A)P(B). Allora una condizione sufficiente per l indipendenza è che almeno uno dei due eventi abbia probabilità nulla; la condizione diventa anche necessaria se gli eventi sono incompatibili, ovvero A B =. Se P(B), si definisce la probabilità condizionata di A dato B P(A B) = P(A B) P(B) e A e B sono indipendenti se solo se P(A B) = P(A). Sia {A i, i = 1,..., n} una famiglia di eventi: essi si dicono indipendenti se per ogni k n e per ogni scelta di indici {i 1,..., i k } P ( k ) k A ij = P(A ij ). j=1 L indipendenza implica per ogni k n e per ogni scelta di indici i 1,..., i k j=1 P(A ik A ik 1... A i1 ) = P(A ik ), quando la probabilità condizionata ha senso. Una famiglia numerabile di eventi si dice costituita da eventi indipendenti se ogni sua sottofamiglia finita lo è. Vale la seguente formula (formula del prodotto): se è n 2 P(A 1 A 2... A n ) = P(A n A n 1 A n 2... A 1 )P(A n 1 A n 2... A 1 )... P(A 2 A 1 )P(A 1 ) (se le probabilità condizionate hanno senso). Si userà la seguente notazione: così p.es. P(A B) = P(A, B) P(A 1, A 2, A 3 ) = P(A 3 A 2, A 1 )P(A 2 A 1 )P(A 1 ). 4
5 Si dimostra la formula del prodotto per induzione: per n = 2 è immediata dalla definizione di probabilità condizionata; assunta vera per n, vale per n+1, infatti applicando la formula del prodotto ai due eventi A 1 A 2... A n e A n+1 P(A 1, A 2,..., A n, A n+1 ) = P(A n+1 A n,..., A 1 )P(A n,..., A 1 ) e si conclude applicando l ipotesi induttiva. X 1,..., X m variabili aleatorie reali definite sullo stesso spazio di probabilità (Ω, F, P ) sono indipendenti: nel caso discreto (cioè quando le v.a. assumono una quantità al più numerabile di valori) se e solo se comunque scelti i valori reali x 1,..., x m, P(X 1 = x 1,..., X m = x m ) = m P(X j = x j ); nel caso continuo (cioè quando la funzione di distribuzione è una funzione continua che si ottiene integrando una funzione densità) se e solo se comunque scelti i valori reali x 1,..., x m P(X 1 x 1,..., X m x m ) = j=1 m P(X j x j ). Si può facilmente dimostrare che questo equivale a dire che sono indipendenti nel caso discreto gli eventi della forma {X i = x i } e nel caso continuo gli eventi della forma {X i x i }, al variare comunque di i e x i. Così, p.es., nel caso discreto l indipendenza implica, per ogni k m e per ogni scelta di indici {i 1,..., i k } e di valori {x i1,..., x ik }, j=1 P(X ik = x ik X ik 1 = x ik 1,..., X i1 = x i1 ) = P(X ik = x ik ). Indipendenza di famiglie infinite di variabili: è quando qualsiasi sottofamiglia finita verifica l indipendenza. Variabili aleatorie indipendenti e tutte con la stessa legge di probabilità si dicono indipendenti e identicamente distribuite e questo si abbrevia con i.i.d. Si può dimostrare ([1]) che: Teorema Se le variabili aleatorie reali X 1,..., X m, Y 1,..., Y k sono indipendenti, allora sono indipendenti le variabili aleatorie Φ(X 1,..., X m ) e Ψ(Y 1,..., Y k ) definite tramite le funzioni Φ : R m R l e Ψ : R k R h. 5
6 1.2 Definizione di catena di Markov Sia S un insieme finito o numerabile. Una famiglia (X n ) n di variabili aleatorie a valori in S definite tutte sullo stesso spazio di probabilità è una catena di Markov se qualsiasi sia n (quando le probabilità condizionate hanno senso) P(X n+1 = j X n = i, X n 1 = i n 1,..., X =i ) = P(X n+1 = j X n = i). Interpretazione: la conoscenza del valore di X n può dare informazioni sul valore di X n+1, ma la conoscenza dei valori di (X n 1,..., X ) non dà ulteriori informazioni. Gli elementi di S sono gli stati possibili della catena e si può sempre assumere S Z. Si pone p ij (n) = P(X n+1 = j X n = i). Il parametro n è interpretato come tempo e il numero p ij (n) è detto probabilità di transizione dallo stato i al tempo n allo stato j al tempo successivo, n + 1. Si definiscono catene di Markov omogenee quelle in cui qualsiasi sia n e per ogni i, j p ij (n) = p ij. La matrice (eventualmente infinita) P = (p ij ) (i,j) è detta matrice delle probabilità di transizione della catena (o più brevemente matrice di transizione) e i suoi elementi soddisfano p ij e qualsiasi sia i p ij = 1. j Una matrice i cui elementi soddisfano le precedenti proprietà si dice matrice stocastica. 1.3 Esempio di due successioni di variabili aleatorie relative ad un unico esperimento di cui una Markov e l altra no Si estrae una pallina da un bussolotto contenente N palline, di cui N B sono bianche e N R sono rosse; l estrazione è casuale con reimmissione della pallina estratta e di c palline del colore estratto e d del colore non estratto. a) (X n ) n 1, con X n =risultato della n-ma estrazione non è in generale una catena di Markov. Qui S = {B, R}. Si dimostra p.es. che se c d 6
7 Si ha e P(X 3 = B X 2 = R) P(X 3 = B X 2 = R, X 1 = R). P(X 3 = B X 2 = R) P(X 3 = B X 2 = R, X 1 = R) = N B + 2d N + 2(c + d), = P(X 3 = B, X 2 = R, X 1 = R) + P(X 3 = B, X 2 = R, X 1 = B) P(X 2 = R) 1 ( NB + 2d N R + c N R = P(X 2 = R) N + 2(c + d) N + c + d N + N B + (c + d) N R + d N + 2(c + d) N + c + d N ) B, N dove per calcolare ciascuno dei due addendi del numeratore si è utilizzata la formula del prodotto, p.es. P(X 3 = B, X 2 = R, X 1 = R) = P(X 3 = B X 2 = R, X 1 = R) P(X 2 = R X 1 = R) P(X 1 = R). Poiché P(X 2 = R) coincide con P(X 2 = R X 1 = R)P(X 1 = R) + P(X 2 = R X 1 = B)P(X 1 = B) = N R + c N R N + c + d N + N R + d N B N + c + d N, semplificando si ottiene P(X 3 = B X 2 = R) = (N B + 2d)(N R + c)n R + ( N B + (c + d) ) (N R + d)n B ( )( ). N + 2(c + d) (NR + c)n R + (N R + d)n B Dall uguaglianza P(X 3 = B X 2 = R, X 1 = R) = P(X 3 = B X 2 = R) con semplici passaggi si ottiene ( (N R + c)n ) ( R NB + (c + d) ) (N R + d)n B (N B +2d) 1 =. (N R + c)n R + (N R + d)n B (N R + c)n R + (N R + d)n B Risolvendo si trova che l uguaglianza sussiste solo se c = d. Se fosse per esempio c > d, allora si troverebbe, coerentemente con l intuizione, P(X 3 = B X 2 = R, X 1 = R) < P(X 3 = B X 2 = R). b) (X n ) n 1, con X n =numero di palline bianche nel bussolotto dopo la n-ma estrazione è una catena di Markov non omogenea. Qui S = N ed è immediato dalla definizione che P(X n+1 = j X n = i, X n 1 = i n 1,..., X 1 = i 1 ) = P(X n+1 = j X n = i) e in particolare, qualsiasi sia n, la probabilità di transizione p ij (n) è nulla se i i j i + c, i + d, vale N+n(c+d) quando j = i + c e vale 1 j = i + d. N+n(c+d) quando 7
8 1.4 Passeggiata aleatoria sugli interi Siano ξ 1, ξ 2,..., ξ n,... variabili aleatorie a valori interi sullo stesso spazio di probabilità e i.i.d. di densità f( ) (e quindi f( ) una densità discreta su Z). Sia X una variabile aleatoria sullo stesso spazio di probabilità e a valori in Z indipendente dalle altre (p.es. X una costante in Z). Se si definisce X n+1 = X + ξ 1 + ξ ξ n+1, n allora (X n ) n è una catena di Markov omogenea detta passeggiata aleatoria in Z. Questo è il modello per la posizione di una particella che si muove su Z secondo la regola: inizialmente è in Z distribuita secondo la legge di X e poi se è in i salta in j con probabilità f(j i). Infatti poiché X n+1 = X n + ξ n+1 P(X n+1 = j X n = i) = P(X n + ξ n+1 = j, X n = i) P(X n = i) = P(ξ n+1 = j i X n = i) = P(ξ n+1 = j i X + ξ 1 + ξ ξ n = i) = P(ξ n+1 = j i) = f(j i), dove nella penultima uguaglianza si utilizza il teorema del paragrafo 1 applicato alle variabili ξ n+1 e (X, ξ 1, ξ 2,..., ξ n ) dunque con m = 1, l = 1, k = n + 1, h = 1, Φ(x) = x, Ψ(y 1,..., y k ) = y y k. Analogamente si può calcolare P(X n+1 = j X n = i, X n 1 = i n 1,..., X = i ) = f(j i), dimostrando così che (X n ) n è una catena di Markov con probabilità di transizione p ij = f(j i). Un caso semplice è il seguente: f(1) = p, f( 1) = q, f() = r con r, p, q e r + p + q = 1 e quindi p ij = p, r, q o a seconda che sia j = i + 1, i, i 1 o altro. 1.5 Catene di Markov per ricorrenza Teorema Siano ξ 1, ξ 2,..., ξ n,... variabili aleatorie i.i.d. a valori in un sottoinsieme U dei reali e X variabile aleatoria a valori in S sottoinsieme discreto dei reali, definita sullo stesso spazio di probabilità e indipendente dalle altre. Sia h : S U S. Posto per n X n+1 = h(x n, ξ n+1 ), (X n ) n è una catena di Markov omogenea a valori in S. 8
9 Dimostrazione Per ricorrenza esiste g n+1 : S U... U S tale che X n+1 = g n+1 (X, ξ 1,... ξ n+1 ), dove { g1 (x, y 1 ) = h(x, y 1 ) ) g n+1 (x, y 1,..., y n+1 ) = h (g n (x, y 1,..., y n ), y n+1. Segue che P(X n+1 = j X n = i) = P(h(X n, ξ n+1 ) = j, X n = i) P(X n = i) ( ) = P h(i, ξ n+1 ) = j g n (X, ξ 1,..., ξ n ) = i ( ) ( ) = P h(i, ξ n+1 ) = j = P h(i, ξ 1 ) = j, dove la penultima uguaglianza segue dal teorema del paragrafo 1 applicato alle variabili ξ n+1 e (X, ξ 1,..., ξ n ) dunque con m = 1, l = 1, k = n + 1, h = 1, Φ(x) = h(i, x) e Ψ(y 1,..., y k ) = g n (y 1,..., y k ) e l ultima dal fatto che le variabili ξ 1 e ξ n+1 hanno la stessa legge. Allo stesso modo vale P(X n+1 = j X n = i, X n 1 = i n 1,..., X = i ) ) = P (h(i, ξ n+1 ) = j g n (X, ξ 1,..., ξ n ) = i,..., g 1 (X, ξ 1 ) = i, X = i ( ) = P h(i, ξ 1 ) = j per il teorema del paragrafo 1 applicato in modo opportuno alle variabili ξ n+1 e (X, ξ 1,..., ξ n ). Si è così dimostrato che P(X n+1 = j X n = i) = P(X n+1 = j X n = i, X n 1 = i n 1,..., X = i ) ( ) = P h(i, ξ 1 ) = j, ovvero che il processo ( è una catena ) di Markov omogenea con probabilità di transizione p ij = P h(i, ξ 1 ) = j. La passeggiata aleatoria sugli interi è un esempio di catena per ricorrenza con S = U = Z e h(x, y) = x + y e quindi, come già mostrato, p ij = P(i + ξ 1 = j) = P(ξ 1 = j i) = f(j i). Esercizio 1 Dimostrare che il numero dei successi su n prove bernoulliane è una catena. Soluzione Indicata con S n la v.a. numero dei successi su n prove bernoulliane, n 1, 9
10 vale S n = ξ 1 + ξ ξ n con ξ 1, ξ 2,..., ξ n,... variabili aleatorie i.i.d. definite sullo spazio di Bernoulli così ξ i (ω) = ω i = 1 o con probabilità 1 o 1 p. Dunque, posto S, la successione di variabili aleatorie (S n ) n è una catena di Markov per ricorrenza con S = N, U = {, 1} e h(x, y) = x + y. Le probabilità di transizione sono dunque p ij = p, 1 p o rispettivamente per j = i + 1, i o altro e quindi la matrice di transizione con infinite righe e infinite colonne è 1 p p p p p p P = p p (S n ) n è un caso particolare di passeggiata aleatoria su Z: il valore iniziale S è costante pari a, la densità di salto f( ) è la densità di Bernoulli di parametro p ovvero f(1) = p e f() = 1 p. 1.6 Legge al tempo e legge al tempo 1 Introdotta la notazione π (i) = P(X = i), i S, π è la densità di probabilità di X che induce una misura di probabilità sui sottoinsiemi di S, ovvero la legge di X, detta legge iniziale della catena o legge al tempo. Può esistere i S tale che π (i ) = 1 e quindi π (i) = per qualsiasi i i ; in tal caso la legge iniziale assegna valore 1 ai sottoinsiemi che contengono i e valore agli altri e si chiama delta di Dirac in i. Per la densità al tempo 1 definita da si può ricavare la formula π 1 (j) = P(X 1 = j), j S, π 1 (j) = i S p ij π (i). 1
11 Infatti per la formula delle probabilità totali π 1 (j) = P(X 1 = j) = i S P(X 1 = j X = i)p(x = i). Si può scrivere con notazione matriciale π 1 = π P dove qui e in seguito si intende esteso il concetto di moltiplicazione di due matrici anche a matrici con un numero infinito di righe e/o colonne e i vettori sono pensati come vettori riga, p.es. π = ( π (1) π (2)... π (card(s) ). La densità al tempo 1 induce una misura di probabilità sui sottoinsiemi di S detta legge al tempo 1, che è la legge della variabile X Matrice di transizione in più passi È facile dimostrare che se (X n ) n è una catena di Markov omogenea vale anche per ogni n, r > 1 P(X n+r = j X n = i, X n 1 = i n 1,..., X = i ) = P(X n+r = j X n = i). Nel caso r = 2: P(X n+2 = j X n = i,..., X = i ) coincide con k S P(X n+2 = j, X n+1 = k, X n = i,..., X = i ) P(X n = i,..., X = i ) e, moltiplicando e dividendo il termine generale della serie per P(X n+1 = k, X n = i,..., X = i ), si ottiene P(X n+2 = j X n+1 = k,x n = i,..., X = i ) k S che per la proprietà di Markov coincide con p ik p kj. P(X n+1 = k X n = i,..., X = i ) k S L espressione precedente è l elemento di posto i, j del prodotto righe per colonne di P per sé stessa, cioè di P 2 = P P. 11
12 In modo analogo si calcola P(X n+2 = j X n = i), ottenendo lo stesso risultato. Si indica con p (2) ij l elemento generico di P 2, cioè (P 2 ) ij : dunque esso rappresenta la probabilità di passare dallo stato i allo stato j in 2 passi. Si consideri ora il caso generale: si dimostra per induzione che P(X n+r = j X n = i) = P(X n+r = j X n = i,..., X = i ) = (P r ) ij, assumendolo vero per r 1 e utilizzando l ipotesi di Markov (corrispondente al caso r = 1). Qui con ovvia notazione P r è il prodotto di P per sé stessa r volte. Si ha che P(X n+r = j X n = i,..., X = i ) coincide con k S P(X n+r = j, X n+r 1 = k, X n = i,..., X = i ) P(X n = i,..., X = i ) e quindi moltiplicando e dividendo il termine generale della serie per P(X n+r 1 = k, X n = i,..., X = i ), coincide con P(X n+r = j X n+r 1 = k,x n = i,..., X = i ) k S cioè con P(X n+r 1 = k X n = i,..., X = i ) p kj P(X n+r 1 = k X n = i,..., X = i ). k S Per l ipotesi induttiva l espressione precedente coincide con p kj (P r 1 ) ik = (P r ) ij. k S Dunque P r, la potenza r ma di P, è la matrice di transizione in r passi e il suo generico elemento (P r ) ij si denota con p (r) ij. È facile verificare che si tratta di una matrice stocastica, cioè p (r) ij 1 j S p (r) ij = 1. 12
13 La seconda proprietà segue osservando che p (r) ij = P(X r = j X = i) = j S j S P ( {X r = j} X = i ) = P(X r S X = i) = 1. j S 1.8 Leggi ad un tempo e leggi congiunte Se (X n ) n è una catena allora per ogni n la densità di X n si denota con π n, cioè π n (i) = P(X n = i), i S e la legge di X n si dice legge al tempo n. La densità al tempo n 1 si calcola in termini della densità iniziale e della matrice di transizione in n passi: π n (i) = i S P(X n = i X = i )P(X = i ) = i S p (n) i i π (i ), dove al primo passaggio si è usata la formula delle probabilità totali. Fissati m > 1 e n 1 < n 2 <... < n m, la legge del vettore aleatorio (X n1,..., X nm ) è la legge congiunta ai tempi n 1,..., n m e la sua densità definita da P(X n1 = i 1,..., X nm = i m ), è detta densità congiunta ai tempi n 1,..., n m. i 1, i 2,..., i m S S... S Si calcola la densità congiunta ai tempi n 1,..., n m utilizzando la formula del prodotto del paragrafo 1 applicata agli eventi e la proprietà di Markov: P(X n1 = i 1,..., X nm = i m ) {X n1 = i 1 },..., {X nm = i m } = P(X nm = i m X nm 1 = i m 1 )... P(X n2 = i 2 X n1 = i 1 )P (X n1 = i 1 ) = p (n m n m 1 ) i m 1 i m... p (n 2 n 1 ) i 1 i 2 π n1 (i 1 ) Dunque concludendo si può affermare che, conoscendo la legge iniziale e la matrice di transizione, si calcolano le leggi ad un tempo e tutte le leggi congiunte. 13
14 1.9 Matrice di transizione in due passi per la catena della rovina del giocatore Due giocatori A e B di capitali a e b rispettivamente, scommettono ogni volta 1 euro e ogni volta A vince con probabilità p e quindi B vince con probabilità q = 1 p. Il gioco termina se uno dei due esaurisce il capitale. Se X n è il capitale di A dopo la n-ma scommessa, posto d = a + b, si può scrivere ) X n+1 = (X n + ξ n+1 I {1,...,d 1} (X n ) + X n I {,d} (X n ), n dove I A (x) = 1 se x A e altrimenti e le ξ n, n 1 sono variabili aleatorie tra loro indipendenti che valgono 1 con probabilità p e 1 con probabilità q = 1 p. Posto X a, (X n ) n è una catena di Markov per ricorrenza con: π la delta di Dirac in a, S = {, 1,..., d}, U = { 1, 1} e h(x, y) = (x + y)i {1,...,d 1} (x) + xi {,d} (y). La matrice di transizione è una matrice di ordine d+1 e ha la forma 1... q p... q p P = q p... 1 Se assumiamo d = 4, la matrice P è di ordine 5 e coincide con 1 q p P = q p q p 1 e il suo quadrato è 1 P 2 q qp p 2 = q 2 2qp p 2 q 2 qp p. 1 14
15 Si osservi che per ogni i 4 j= p (2) ij = 1 come deve essere. Così se, per esempio X = a = 2, essendo π (2) = 1 e π (i) = per ogni i 2, vale P(X 2 = ) = p (2) i π (i) = p (2) 2 = q2, i S come ci si aspetta dovendo P(X 2 = ) coincidere con la probabilità di due perdite consecutive. 1.1 La catena di nascita e morte e l urna di Ehrenfest Una catena su S = {, 1,..., d} con matrice di transizione r p q 1 r 1 p 1... P = q 2 r 2 p q d 1 r d 1 p d 1... q d r d dove q i, r i, p i 1 e q i +r i +p i = 1, è chiamata catena di nascita e morte. Il nome deriva dal fatto che questa catena può essere pensata come modello per la consistenza numerica di una popolazione su una scala temporale in cui ad ogni unità di tempo può accadere che un solo individuo generi un nuovo individuo o muoia, dunque le possibili transizioni dallo stato i sono solo in i + 1, i, i 1 e p i (i+1) = p i p i i = r i p i (i 1) = q i e p i j = j i+, i, i 1. Allora p i e q i prendono rispettivamente il nome di probabilità di nascita e probabilità di morte (quando la consistenza della popolazione è i). La rovina del giocatore è una particolare catena di nascita e morte con parametri r = 1 = r d p i = p r i = q i = q, i = 1,..., d 1. 15
16 Un altra catena di nascita e morte è quella di Ehrenfest, la cui matrice di transizione è d 1 d d... 2 d 2 P = d d... d d d È modello per lo scambio di molecole tra due corpi isolati ovvero è modello per la seguente situazione: d palline numerate sono contenute in due urne, un intero tra 1 e d è estratto ripetutamente a caso e la pallina corrispondente è spostata di urna. Fissata un urna, X è il numero di palline inizialmente nell urna e X n, n 1 è il numero di palline nella stessa urna dopo la n-ma estrazione Un modello per una fila d attesa Si considera la catena per ricorrenza seguente { X = X n+1 = max {, X n 1 } + ξ n+1, n dove ξ 1, ξ 2,..., ξ n,... sono i.i.d. a valori in N di densità assegnata f( ). Si può anche scrivere per n ) X n+1 = I [1,+ ) (X n ) (X n 1 + ξ n+1 + I {} (X n )ξ n+1 Chiaramente S = N e p j = f(j) mentre per ogni i 1, usando la definizione di probabilità condizionata e l indipendenza di ξ n+1 da X n, si ottiene p ij = P(X n 1 + ξ n+1 = j X n = i) = P(ξ n+1 = j i + 1) = f(j i + 1). Questo è un modello per una fila d attesa ad uno sportello che in ogni unità di tempo serve un cliente e riceve un numero aleatorio di clienti ogni volta di stessa legge indipendentemente dal passato. Per n 1 la variabile aleatoria X n rappresenta il numero dei clienti in fila alla fine della n-ma unità temporale. 16
17 Esercizio 2 a) Scrivere la matrice di transizione per la catena su S = {, 1, 2} definita da X n+1 = X n + ξ n+1 (modulo 3) dove ξ 1, ξ 2,..., ξ n... sono variabili i.i.d. a valori in S con densità f( ) e indipendenti da X, variabile sullo stesso spazio di probabilità e a valori in S. Per esempio se X (ω) = 1, ξ 1 (ω) = 1, ξ 2 (ω) = 2, ξ 3 (ω) = 1,... sarà X (ω) = 1, X 1 (ω) = 2, X 2 (ω) = 1, X 3 (ω) = 2,.... b) Calcolare π 1 (2) = P(X 1 = 2), nel caso f() =.5, f(1) =.1, f(2) =.4 e π () =.5, π (1) =.5, π (2) =. Soluzione a) La matrice di transizione è di ordine 3 e ha la forma seguente f() f(1) f(2) P = f(2) f() f(1). f(1) f(2) f() Notare che non solo per ogni i {, 1, 2} p ij = j S 2 f(l) = 1, l= ma anche per ogni j {, 1, 2} p ij = i S 2 f(l) = 1. l= Una matrice stocastica tale che gli elementi di ciascuna colonna hanno somma pari a 1 si dice doppiamente stocastica. b) Con i dati assegnati la matrice di transizione è e π 1 (2) = P(X 1 = 2) = P = p i2 π (i) =.5 p p 12 =.25 i= 17
18 1.12 Costruzione di una catena data la matrice di transizione e la legge iniziale È immediato verificare che una v.a. X a valori in N \ {} con densità assegnata (p 1, p 2,..., p N ) si costruisce così: se ξ è una v.a. uniforme in [, 1], posto j 1 a(1) =, a(j) = p k, j > 1 b(1) = p 1, b(j) = k=1 j p k, j > 1 k=1 si definisce X := j 1 j I [a(j),b(j)) (ξ). Siano assegnate una densità di probabilità π e una matrice di transizione P su N \ {}. Siano (ξ n ) n 1 variabili aleatorie i.i.d. uniformi in [, 1] indipendenti da un altra variabile aleatoria X definita sullo stesso spazio di probabilità e con densità π. Posto j 1 a(i, 1) =, a(i, j) = p i k, j > 1 b(i, 1) = p i 1, b(i, j) = h(i, y) = j 1 k=1 j p i k, j > 1 k=1 j I [a(i,j),b(i,j)) (y), si definisca X n+1 := h(x n, ξ n+1 ), n. Allora (X n ) n è una catena di Markov per ricorrenza a valori in N\{} con legge iniziale π e matrice di transizione quella assegnata. Infatti ricordando che per le catene per ricorrenza P(X n+1 = j X n = i) = P(h(i, ξ 1 ) = j), in questo caso dall espressione di h segue che ( P(X n+1 = j X n = i) = P ) ξ 1 [a(i, j), b(i, j)) = p i j, 18
19 dove l ultima uguaglianza segue dal fatto che ξ 1 ha legge uniforme nell intervallo [, 1] e l ampiezza dell intervallo [a(i, j), b(i, j)) è p i j. Questa costruzione suggerisce come simulare una catena di Markov con spazio degli stati finito {1, 2,..., N} e con legge iniziale e matrice di transizione assegnata. Per simulazione di una catena di Markov (X n ) n fino al tempo n si intende la determinazione di una sequenza di n valori (i 1, i 2,..., i n ) {1, 2,..., N} che costituiscano una realizzazione del vettore aleatorio (X 1, X 2,..., X n ), ovvero tali che si abbia per un qualche ω Ω (X 1 (ω), X 2 (ω),..., X n (ω)) = (i 1, i 2,..., i n ). Si assuma inizialmente per semplicità che la legge iniziale sia una delta di Dirac e quindi che sia X = i, dove i è un numero in {1, 2,..., N}. I più noti linguaggi di programmazione hanno in libreria una procedura che genera una variabile aleatoria uniforme in [, 1] e richiamando n volte la stessa procedura si realizza un vettore n-dimensionale le cui componenti sono i.i.d. uniformi in [, 1], ovvero un vettore come (ξ 1, ξ 2,..., ξ n ): in altre parole si genera una sequenza di n numeri che coincidono con (ξ 1 (ω), ξ 2 (ω),..., ξ n (ω)) per un qualche ω Ω. Al primo passo della simulazione si genera X 1 come variabile aleatoria di densità assegnata pari a (p i 1, p i 2,..., p i N), cioè il numero i 1 : N i 1 = X 1 (ω) = j I [a(i,j),b(i,j))(ξ 1 (ω)); j=1 al secondo passo si genera X 2 come variabile aleatoria di densità assegnata pari a (p i1 1, p i1 2,..., p i1 N), cioè il numero i 2 i 2 = X 2 (ω) = N j I [a(i1,j),b(i 1,j))(ξ 2 (ω)); j=1 e si ripete il procedimento fino a generare X n come variabile aleatoria di densità (p in 1 1, p in 1 2,..., p in 1 N), cioè il numero i n i n = X n (ω) = N j I [a(in 1,j),b(i n 1,j))(ξ n (ω)). j=1 Nel caso in cui X non sia deterministico, c è in più il passo iniziale della generazione di X. In tal caso occorre richiamare una volta di più la procedura di simulazione di un uniforme in [, 1] per generare ξ indipendente da (ξ 1, ξ 2,..., ξ n ) e con ξ generare X come variabile aleatoria di densità (π (1), π (2),..., π (N)), cioè il numero i. 19
20 Esercizio 3 Per la catena dell Esercizio 2 calcolare la densità congiunta ai tempi 1 e 2 nel punto 2. Calcolare poi la probabilità che la catena si trovi nello stato 2 dopo 2 passi. Soluzione a) Ricordando che P = e π () = π (1) =.5 e che nell Esercizio 2 si è ottenuto π 1 (2) =.25, si ha per la formula del prodotto P(X 2 =, X 1 = 2) = P(X 2 = X 1 = 2)P(X 1 = 2) = p 2 π 1 (2) =.25. Invece π 2 (2) = P(X 2 = 2) = 2 i= p (2) i2 π (i) = p (2) 2 (.5) + p(2) 12 (.5). Si devono calcolare dunque gli elementi di posto prima riga, terza colonna e seconda riga, terza colonna del quadrato di P. Si trova.41 P 2 =.26 e quindi π 2 (2) = (.5)( ) = Rappresentazione grafica di una catena di Markov Il grafico di una catena di Markov si ottiene segnando un punto per ogni stato della catena, una freccia orientata da un punto ad un altro se la probabilità di transizione in un passo è positiva e il valore della probabilità di transizione accanto alla freccia. Così per esempio La rappresentazione grafica consente di calcolare rapidamente le probabilità di transizione in più passi. Per esempio se la matrice di transizione è.5.5 P =
21 Figura 1: rovina del giocatore Figura 2: random walk modulo 3 con f(i) >, i =, 1, f() + f(1) = 1 e quindi il grafico è per calcolare p (2) 12 = P(X 3 = 2 X 1 = 1) = 3 k=1 p 1kp k2 basta calcolare i cammini lunghi 2 passi che dal punto 1 portano al punto 2; ciascun cammino ha probabilità pari al prodotto dei valori scritti sulle frecce e occorre sommare tutte queste probabilità. Dunque mentre p (2) 12 p (2) 23 = (.5)(.1) + (.5)(.8) =.45, = (.1)(.5) + (.4)(.5) =.25. In modo analogo si procede per esempio nel calcolo di p (3) = p 1l p (2) l1 = l=1 p 1l l=1 k=1 3 p lk p k1 = 3 p 1l p lk p k1, l,k=1 ovvero si sommano le probabilità di tutti i cammini lunghi 3 passi che da 1 riportano in 1 e che hanno ciascuno probabilità pari al prodotto dei valori scritti sulle frecce p (3) 11 = (.5)(.1)(.4) + (.5)(.8)(.4) + (.5)(.5)(.2) =
22 Figura 3: coda con f(i) >, i =, 1, 2, f() + f(1) + f(2) = Stati comunicanti Si dice che uno stato i comunica con lo stato j se c è un cammino finito sul grafico che porta da i a j e si scrive i j. È immediato che questo equivale a chiedere che esista n 1 tale che p (n) ij >. (ricorda che p (1) ij = p ij ). Due stati i e j si dicono comunicanti se esiste n 1 tale che p (n) ij > e esiste m 1 tale che p (m) ij >, ovvero se i j e j i, ovvero se esiste un cammino finito che porta dall uno all altro e viceversa (i due cammini potrebbero avere lunghezze diverse). Si scrive i j. Per esempio nella catena di nascita e morte con q i > e p i > tutti gli stati sono comunicanti. Mentre nella catena della rovina del giocatore tutti gli stati in {1,..., d 1} sono comunicanti, inoltre qualsiasi sia i {1,..., d 1} si ha che i e i d, mentre e d comunicano solo con sé stessi. 22
23 1.15 Classi chiuse e classi irriducibili Un sottoinsieme C di S si dice una classe chiusa di stati se qualsiasi sia i C si ha p ij = 1. j C Questa condizione implica che indicato con C c il complementare di C nessuno stato di C comunica con uno stato di C c : si ha subito dalla definizione che se i C e j C c allora p ij = ; inoltre p (2) ij = h S p ih p hj = h C p ih p hj = poiché per la seconda uguaglianza si usa il fatto che per definizione di classe chiusa se i C si ha p ih = qualsiasi sia h C c e per la terza il fatto che, se j C c, ancora per definizione di classe chiusa p hj = qualsiasi sia h C; allo stesso modo per induzione si prova che p (n) ij = per ogni n > 2. Infatti p (n) ij = h S p ih p (n 1) hj = h C p ih p (n 1) hj =, dove nell ultima uguaglianza si usa l ipotesi induttiva Il viceversa è immediato ovvero: se nessuno stato di C comunica con uno stato in C c, essendo p ij = qualsiasi siano i C e j C c, allora fissato i C si ha cioè C è chiusa. p ij = 1, j C Se C = {i} è chiusa allora lo stato i si dice assorbente. Per esempio nella catena della rovina del giocatore e d sono stati assorbenti. Una classe chiusa si dice irriducibile se tutti i suoi stati sono comunicanti. Se S è l unica classe chiusa irriducibile, allora la catena si dice irriducibile. Nella catena rappresentata dal grafico seguente 23
24 1, 2, 3 sono stati comunicanti, {4, 5, 6, 7} è una classe chiusa non irriducibile, {4, 5} è una classe irriducibile, 7 è uno stato assorbente Definizione di transienza e persistenza in termini del tempo di primo ritorno Si ricordi che p (n) ij indica la probabilità di passare da i a j in n passi. Si introduce il simbolo ρ (n) ij per indicare la probabilità di arrivare in j partendo da i per la prima volta dopo n passi, ovvero ρ (n) ij = P(X n1 +n = j, X n1 +n 1 j,..., X n1 +1 j X n1 = i) qualsiasi sia n 1 (è facile verificare che per la proprietà di Markov la probabilità precedente è indipendente da n 1 ). p (n) ij Naturalmente ρ (1) ij = p (1) ij = p ij, mentre qualsiasi sia n 2 vale ρ (n) ij. Per esempio nel caso della catena con matrice di transizione facilmente si calcola ρ (2) 12 = (.5)(.8) =.4 p(2) P = = (.5)(.8) + (.5)(.1) =.45. La disuguaglianza discende dal considerare che vale la relazione seguente p (n) n 1 ij = ρ (s) ij p(n s) jj + ρ (n) ij. s=1 Si introduce il simbolo ρ ij = n 1 ρ (n) ij per indicare quindi la probabilità di arrivare in j in un numero finito di passi essendo partiti da i. Immediatamente seguono ρ ij ρ (n) ij, qualsiasi sia n 1 e quindi in particolare ρ ij ρ (1) ij = p ij. Se si indica con τ j la variabile aleatoria tempo di primo passaggio per j, ovvero { min{n 1 t.c. X n (ω) = j}, se il minimo esiste τ j (ω) := +, altrimenti 24
25 allora Naturalmente ρ (n) ij = P(τ j = n X = i) e ρ ij = P(τ j < X = i). ρ ij > i j. Si dimostra la condizione necessaria: infatti ρ ij > implica che esiste n 1 tale che ρ (n) ij > e questo a sua volta implica p (n) ij >, essendo ρ (n) ij p (n) ij. Si dimostra la condizione sufficiente: infatti i j implica che esiste n 1 tale che p (n) ij > e poiché p (n) ij = n 1 s=1 ρ(s) ij p(n s) jj + ρ (n) ij, segue che esiste 1 s n tale che ρ (s) ij > e quindi ρ ij >. Si definisce uno stato i persistente (o anche ricorrente) se e transiente se ρ ii = 1 ρ ii < 1, ovvero a parole uno stato è persistente se il tempo di primo ritorno in i partendo da i è finito con probabilità 1; è transiente se la stessa variabile è finita con probabilità minore di 1 e quindi con probabilità positiva partendo da i la catena non vi fa più ritorno. Banalmente ogni stato assorbente è persistente essendo ρ ii p ii = P(X 1 = i X = i) = P(τ i = 1 X = i) = Transienza e persistenza in termini del numero dei ritorni A giustificazione della terminologia introdotta nel precedente paragrafo si dimostra il prossimo teorema. D ora in avanti si userà la notazione P( X = i) = P i ( ). Teorema ρ ii < 1 P i (X n = i inf.nte spesso) = ρ ii = 1 P i (X n = i inf.nte spesso) = 1 25
26 La dimostrazione utilizza il seguente lemma di probabilità elementare. Lemma Se (B k ) k 1, B k F, è una successione crescente di eventi (Ω, F, P), ovvero se qualsiasi sia k 1 vale B k B k+1, allora P( k 1 B k ) = lim k P(B k ). Se (A k ) k 1 è una successione decrescente di eventi (Ω, F, P), ovvero se A k A k+1, allora P( k 1 A k ) = lim k P(A k ). Dimostrazione del lemma Infatti P ( ) ( B k = P {B k \ B k 1 } ) k 1 avendo posto B =. Infine = k 1 (P(B k ) P(B k 1 )) k=1 = lim n k=1 = lim n P(B n). n ( P(Bk ) P(B k 1 ) ) P( k 1 A k ) = 1 P( k 1 A c k ) = 1 lim n P(Ac n) = lim n P(A n) essendo la successione degli eventi complementari (A c k ) k 1 successione crescente di eventi. Dimostrazione del teorema L evento {X n inf.nte spesso} si può riscrivere come intersezione di una successione decrescente di eventi. Più precisamente {X n = i inf.nte spesso } = k 1 A k con A k = {X n1 = i, X n2 = i,..., X nk = i, X s i, s n 1, n 2,..., n k, s < n k } dove l unione disgiunta è estesa a n 1 < n 2 <... < n k, cioè A k è l evento definito a parole dal fatto che la catena visita almeno k volte lo stato i. Dal lemma segue che P i (X n = i inf.nte spesso) = lim k P i(a k ). Inoltre P i (A k ) si può calcolare così: n 1 <n 2 <...<n k 1 P i (X n1 = i, X n2 = i,..., X nk = i, X s i, s n 1, n 2,..., n k, s < n k ) 26
27 e l ultima somma coincide con ρ (n1) ii ρ (n 2 n 1 ) ii... ρ (n k 1 n k 2 ) ii ρ (n k n k 1 ) ii = n 1 <n 2 <...<n k ρ (n1) ii ρ (n 2 n 1 ) ii... ρ (n k 1 n k 2 ) ii n 1 <n 2 <...<n k 1 ρ (nk nk 1) ii n k 1 <n k e, poiché, fissati n 1 < n 2 <... < n k 1, al variare di n k la differenza n k n k 1 varia in N \ {}, allora l espressione precedente è uguale a ρ (n1) ii ρ (n 2 n 1 ) ii... ρ (n k 1 n k 2 ) ii ρ (h) ii = n 1 <n 2 <...<n k 1 = ρ ii ρ (n1) ii ρ (n 2 n 1 ) n 1 <n 2 <...<n k 1 ii... ρ (n k 2 n k 3 ) h=1 ii ρ (n k 1 n k 2 ) ii. Fissando n 1 < n 2 <... < n k 2 e sommando su n k 1 si ottiene ρ 2 ii ρ (n1) ii ρ (n 2 n 1 ) ii... ρ (n k 3 n k 4 ) ii ρ (n k 2 n k 3 ) ii n 1 <n 2 <...<n k 2 e iterando k volte lo stesso procedimento si verifica P i (A k ) = ρ k ii. La dimostrazione si conclude utilizzando il lemma precedente e ricordando che quando a < 1 allora lim k a k = e quando a = 1 allora lim k a k = Legge e valor medio del numero dei ritorni in uno stato In quel che segue si utilizzerà la variabile aleatoria N n (i) che conta il numero delle visite fatte dalla catena allo stato i in n passi. Si ha N n (i) = n I {i} (X k ), k=1 ricordando che I {i} (x) è la funzione indicatrice dell insieme {i} che vale 1 se x {i}, cioè x = i, e altrimenti. La variabile aleatoria definita da N (i) = lim n N n(i) = I {i} (X k ) k=1 27
28 conta il numero totale delle visite della catena allo stato i (attenzione: il limite si intende così: N (i)(ω) = lim n N n (i)(ω) per ogni ω Ω). Osserviamo che, come la variabile aleatoria tempo di primo passaggio τ i, anche N (i) è una variabile estesa, cioè a valori in N {+ }. Si osserva che vale l uguaglianza tra eventi {X n = i inf.nte spesso} = {N (i) = + } e che quindi si può enunciare il teorema precedente così ρ ii < 1 P i (N (i) = + ) = ρ ii = 1 P i (N (i) = + ) = 1. La densità della variabile numero dei ritorni nello stato, ovvero del numero dei passaggi della catena per i quando la sua legge iniziale è la delta di Dirac in i, è dunque determinata nel caso di stati persistenti. Nel caso di stati transienti vale il seguente lemma. Lemma 1 ρ ii, k = i transiente = P i (N (i) = k) =, k = + ρ k ii (1 ρ ii), altrimenti Dimostrazione Il caso k = + è contenuto, come già osservato, nel teorema precedente. Il caso k = deriva dalla definizione di ρ ii. Per il resto si osserva che P i (N (i) k) = ρ k ii; infatti {N (i) k} coincide con l evento A k della dimostrazione del teorema precedente. Quindi P i (N (i) = k) = P i (N (i) k) P i (N (i) k + 1) = ρ k ii(1 ρ ii ), che conclude la dimostrazione. Si vuole calcolare ora il valore medio della variabile di cui si è appena trovata la densità condizionata all evento {X = i}; per ricordare che la catena parte da i si scrive i sotto il simbolo di media. Chiaramente nel caso [ persistente, per definizione di valor medio di variabile aleatoria estesa, E i N (i) ] [ = +. Nel caso transiente invece E i N (i) ] < +, infatti utilizzando la densità di N (i) del lemma precedente si trova E i [ N (i) ] = kρ k ii(1 ρ ii ) = k=1 ρ ii 1 ρ ii < + 28
29 poiché k=1 kρk ii (1 ρ ii) è media della geometrica trasformata di parametro 1 ρ ii (legge del numero dei fallimenti prima del successo in uno schema di Bernoulli di parametro 1 ρ ii ). Si osserva ora che [ [ E i N (i)] = E i lim N n(i) ] = lim E [ i Nn (i) ], n n poiché qui è lecito scambiare il limite con il valore medio (di ciò si tralascia la dimostrazione). Inoltre utilizzando la linearità della media, si ha E i [ Nn (i) ] = n [ E i I{i} (X k ) ]. k=1 e, essendo I {i} (X k ) B(p) con p = P i (X k = i) = p (k) ii, E i [ Nn (i) ] = poiché il valor medio di una binomiale coincide con il suo parametro. Si è [ così mostrato che E i N (i) ] = k=1 p(k) ii. Si può allora enunciare il teorema seguente. n k=1 p (k) ii Teorema i transiente E i [ N (i) ] = k=1 p (k) ii < + La parte necessaria del teorema è immediata e la parte sufficiente segue dal fatto che se i è persistente allora il numero medio dei ritorni è infinito. Naturalmente il teorema si può anche enunciare così: i persistente k=1 p (k) ii = Transienza e persistenza di uno stato in termini del numero dei passaggi per esso partendo da uno stato qualsiasi La densità del numero dei passaggi per i condizionata all evento {X = j} con j i si calcola utilizzando l uguaglianza P j (N (i) k) = ρ ji ρ k 1 ii, 29
30 che si ricava similmente a P i (N (i) k) = P i (A k ) = ρ k ii. Se è i persistente e j i si trova 1 ρ ji, k = P j (N (i) = k) = ρ ji ρ k 1 ii ρ ji ρ k ii = ρ jiρ k 1 ii (1 ρ ii ) =, k 1 ρ ji, k = + mentre se i è transiente 1 ρ ji, k = P j (N (i) = k) = ρ ji ρ k 1 ii (1 ρ ii ), k 1, k = +. In entrambi i casi la densità in k = + si deriva considerando che deve essere P j (N (i) = k) + P j (N (i) = + ) = 1. k= Si noti che nel caso j = i si ritrova la densità del numero dei ritorni nello stato i già precedentemente calcolata. Dalla densità appena calcolata si ricava il valore medio del numero dei passaggi per i condizionata all evento {X = j}, ottenendo: i persistente o transiente e j i = E j [ N (i) ] = [ i persistente e j i = E j N (i) ] = + [ i transiente e j i = E j N (i) ] = ρ ji < + 1 ρ ii dove in particolare l ultima implicazione segue dall uguaglianza k 1 kρ k 1 ii (1 ρ ii ) = 1 1 ρ ii. Tenendo presente anche i risultati del precedente paragrafo, si può riassumere così: se i è persistente quando la catena parte da i vi ritorna infinite volte con probabilità 1, mentre se parte da uno stato diverso da i è possibile che essa non passi mai per i, ma se raggiunge i una volta allora vi passa in media infinite volte; se i è transiente, qualsiasi sia il punto di partenza della catena, il numero di visite a i con probabilità 1 è finito (eventualmente nullo) e anche il numero medio di visite a i è finito (eventualmente nullo). Infine in modo simile al paragrafo precedente si dimostra E j [ N (i) ] = 3 k=1 p (k) ji
31 e quindi da quanto esposto si deriva il teorema seguente. Teorema Qualsiasi sia j S i transiente = k=1 p (k) ji < +. Utilizzando poi il fatto che il termine generico di serie convergente è infinitesimo, si ottiene immediatamente il seguente corollario. Corollario Qualsiasi sia j S i transiente = Esercizio 4 lim k p(k) ji =. Dimostrare che vale l equazione detta di Chapman-Kolmogorov p (n+m) ij = h S p (n) ih p(m) hj e dedurne che, se i comunica con l e l comunica con j, allora i comunica con j. Soluzione p (n+m) ij = h S P(X n+m = j, X n = h X = i) = h S P(X n+m = j, X n = h, X = i). P(X = i) Allora applicando la formula del prodotto, semplificando e usando la proprietà di Markov, si ottiene Infine ricordando p (n+m) ij = h S P(X n+m = j X n = h)p (X n = h X = i). P(X n+m = j X n = h) = p (m) hj, P(X n = h X = i) = p (n) ih, si ottiene l equazione di Chapman-Kolmogorov. Inoltre se i l esiste n > tale che p (n) tale che p (m) lj il > e se l j esiste m > > e poiché per Chapman-Kolmogorov p (n+m) ij = h S p (n) ih p(m) hj p (n) il p (m) lj >, si trova p (n+m) ij > e quindi anche i j. 31
32 1.2 Una condizione sufficiente per la transienza Un criterio utile per verificare il carattere transiente di uno stato è j i, i j = j transiente. Per la dimostrazione si procede così. Posto m = min{n 1 : p (n) ji > }, esistono i 1, i 2,..., i m 1 S e diversi da i e da j tali che P j (A) > se A è l evento definito da A = {X 1 = i 1,..., X m 1 = i m 1, X m = i}; dunque P j (A c ) = 1 P j (A) < 1. Allora se si dimostra che P j ({τ j < } A) =, si ha come conseguenza che ρ jj è minore di 1; infatti ρ jj = P j (τ j < ) = P j ({τ j < } A)+P j ({τ j < } A c ) = P j ({τ j < } A c ) e essendo {τ j < } A c A c vale P j ({τ j < } A c ) P j (A c ). Per dimostrare che P j ({τ j < } A) =, si scrive P j ({τ j < } A) = = k=m+1 k=m+1 P j ({τ j = k} A) P j (τ j = k A)P j (A). Poiché per la proprietà di Markov P j (τ j = k A) = ρ (k m) ij, con il cambio di variabile n = k m, si ottiene p (k m) ij P j ({τ j < } A) n=1 p (n) ij P j(a) e poiché ρ (k m) ij Si conclude osservando che per ipotesi, qualsiasi sia n 1, si ha p (n) ij =. Si fa notare che quando S ha cardinalità finita l implicazione appena dimostrata vale anche nel verso contrario (si veda il paragrafo 22), ma questo non è vero se S è infinito (per un controesempio si veda il paragrafo 27). 32
33 1.21 Una condizione sufficiente per la persistenza Un criterio utile per verificare il carattere persistente di uno stato è i persistente e i j = ρ ji = 1 e j persistente. Per la dimostrazione si procede così. Si comincia con il mostrare che ρ ji = 1. Sia n = min{n 1 t.c. p (n) ij > }, allora esistono i 1, i 2,..., i n 1 j, i tali che posto B = {X 1 = i 1,..., X n 1 = i n 1, X n = j} vale P i (B) >. Poiché i è persistente vale P i ( B {Xn i, qualsiasi sia n n + 1} ) = ; inoltre per la proprietà di Markov è anche vero che P i (B {X n i, n n + 1}) = P i (B) P j (τ i = + ) = P i (B)(1 ρ ji ); dalle due affermazioni segue ρ ji = 1. Si fa poi vedere che vale la condizione k=1 p(k) jj = + sufficiente per la persistenza di j. Sia n 1 1 tale che p (n 1) ji > (n esiste poiché, essendo ρ ji = 1 è vero che j i). k=1 p (k) jj = p (k) jj k=n +1+n 1 h=1 p (h+n +n 1 ) jj. Utilizzando l equazione di Chapman-Kolmogorov, con semplici minorazioni si ottiene k=1 p (k) jj p (n 1) jl p (h) ll p (n ) lj h=1 l S h=1 = p (n 1) ji p (n ) ij p (n 1) ji p (h) ii p (n ) ij k=1 p (h) ii. Poiché, essendo per ipotesi i persistente, si ha che k=1 p(h) ii = +, per confronto si deduce che anche k=1 p(h) jj = +. Come corollario di questo criterio si ottiene: Corollario Sia C S un classe irriducibile, allora tutti gli stati sono persistenti o tutti transienti. 33
34 Si fa notare che, sia per S finito che infinito, l implicazione appena dimostrata vale anche nel verso contrario. Infatti: ρ ji = 1 implica banalmente j i e quindi per l implicazione diretta se j è persistente ρ ij = 1 (dunque i j) e i è persistente Persistenza e transienza in classi finite Si dimostra che se C S è una classe chiusa e finita allora in C esiste almeno uno stato persistente. Si procede per assurdo. Infatti se tutti gli stati in C fossero transienti, fissato uno di essi, j, si avrebbe (da un risultato precedentemente dimostrato), per ogni i in C, lim k p (k) = e quindi i C D altro canto lim k p(k) ji = lim k i C lim k p(k) i C p (k) ji ji =. ji = lim k P j(x k C) = 1, infatti limite e somma si scambiano poiché la somma è su un numero finito di termini e l ultima uguaglianza segue dal fatto che C è una classe chiusa. Due sono le conseguenze importanti. La prima è che tutti gli stati di una classe irriducibile finita sono persistenti (segue mettendo insieme quanto appena detto e il corollario del paragrafo precedente) e quindi se una catena ha spazio degli stati finito ed è irriducibile allora tutti gli stati sono persistenti (segue dal precedente poiché tutto lo spazio degli stati è una particolare classe chiusa). La seconda conseguenza è che nel caso S finito la condizione sufficiente per la transienza è anche necessaria: infatti, se per ogni j con i j vale anche j i, allora i è elemento di una classe irriducibile finita e quindi è persistente. Si ricorda che, come già accennato, nel caso S infinito invece la condizione non è necessaria: esistono classi irriducibili infinite di stati transienti (si veda il paragrafo 27). Da quanto detto segue che quando S è finito per analizzare il carattere degli stati si può procedere così: si individuano subito tutti gli stati transienti, che sono tutti e soli quelli che comunicano con almeno uno stato che non li ricambia, e poi intorno a ciascuno dei rimanenti si costruisce la classe irriducibile (finita) di stati persistenti che lo contiene. Per esempio, si consideri la catena con matrice di transizione P =
35 Gli stati 3 e 2 comunicano con 1, ma 1 non comunica né con 2 né con 3 e quindi gli stati 2 e 3 sono transienti; C 1 = {4, 5, 6} è classe irriducibile di stati persistenti; C 2 = {1} è classe irriducibile formata da un unico stato assorbente Teorema di decomposizione dello spazio degli stati Lo spazio degli stati ammette una decomposizione di questo tipo S = T C 1 C 2... dove T è l insieme degli stati transienti e C n, n = 1, 2,... sono classi disgiunte irriducibili persistenti. Per dimostrarlo si considera i 1 S \ T e si costruisce C 1 come la classe che contiene tutti gli stati con cui comunica i 1 che, grazie al criterio sufficiente per la persistenza, sono tutti persistenti. C 1 è non vuota poiché contiene i 1. C 1 è chiusa poiché se j C 1 allora, per il criterio sufficiente per la persistenza, j è persistente e i 1 j e inoltre se j h per lo stesso criterio j h e per la proprietà transitiva i 1 h. C 1 è irriducibile poiché se j e l sono in C 1 allora i 1 j e i 1 l e usando la proprietà transitiva j l. Scelto uno stato i 2 che non appartiene a C 1 né a T, si costruisce C 2 nello stesso modo e così via. È facile verificare poi che le classi C n, n = 1, 2... sono disgiunte: infatti se per esempio fosse h C 1 C 2, allora ogni elemento di C 1, i, sarebbe tale che h i, ma allora, poiché C 2 è chiuso e h C 2, sarebbe anche i C 2 e quindi C 1 C 2.In modo analogo si prova il viceversa.segue che C 1 = C 2. Dunque: quando la catena parte da uno stato di un qualsiasi C n rimane per sempre in C n visitando infinitamente spesso ogni stato di C n (con probabilità 1); quando la catena parte da uno stato di T e T è numerabile, può rimanere per sempre in T o entrare in qualche C n e rimanere poi lì per sempre visitando ogni suo stato infinitamente spesso; se T ha cardinalità finita, invece, qualsiasi sia la legge iniziale, la catena esce prima o poi da T e non vi rientra più. Più precisamente, posto N (T ) = i T N (i), N (T ) è la variabile aleatoria che conta il numero dei passaggi per T e si dimostra che P(N (T ) = + ) =. Infatti, qualsiasi sia la legge iniziale, per la proprietà di Markov P(N (T ) = + ) = j S P j (N (T ) = + ) π (j) 35
36 e quindi è sufficiente far vedere che, per ogni j S, P j (N (T ) = + ) =. Poiché T ha cardinalità finita, N (T ) = + = esiste i T t.c. N (i) = + cioè e quindi {N (T ) = + } = {N (i) = + } i T P j (N (T ) = + ) P j (N (i) = + ) =, i T dove la disuguaglianza segue dal fatto che in generale la probabilità di un unione di eventi è minore o uguale alla somma delle probabilità dei singoli eventi e l ultima uguaglianza segue dal fatto che P j (N (i) = + ) =, per ogni j S e per ogni i T. Esercizio 5 Studiare il carattere degli stati della matrice di transizione seguente P = Soluzione Gli stati 1, 3, 4 sono transienti: infatti 1 3 ma 3 1, 3 5 ma 5 3, 4 3 ma 3 4. Facilmente si verifica poi che {2, 5, 6} è classe irriducibile, finita e quindi persistente Sistema di equazioni per le probabilità di assorbimento Sia C una classe chiusa di S (si ricordi che C può contenere anche stati transienti). Indicata con τ C la variabile aleatoria che indica il tempo di ingresso della catena in C, ovvero { min{n 1 t.c. X n (ω) C}, se il minimo esiste τ C (ω) = +, altrimenti si definisca λ C i = P i (τ C < + ), i S, 36
37 allora λ C i è la probabilità che partendo da i la catena arrivi in un tempo aleatorio finito in C. Dopo questo istante la catena non potrà più lasciare C essendo la classe chiusa e per questo λ C i si chiama probabilità di assorbimento in C partendo da i. Allora è ovvio che i C = λ C i = 1 e i C chiusa, C C = = λ C i =. Si fa vedere che le quantità λ C i, i T \ C soddisfano un sistema di equazioni lineari in tante incognite e tante equazioni quanto è la cardinalità di T \ C. Fissato i T \ C λ C i = P i (τ C = n), inoltre e Ora, poiché P i (τ C = n) = P i (τ C = n + 1) = n=1 h C, h j T \C, j=1,...,n 1 h C, h j T \C, j=1,...,n = h 1 T \C λ C i = P i (τ C = 1) + con il cambio di variabile n = m + 1 λ C i = P i (τ C = 1) + p ih1 P h1 (τ C = n). p ih1 p h1 h 2... p hn 1 h p ih1 p h1 h 2... p hn h P i (τ C = n), n=2 P i (τ C = m + 1) m=1 e sostituendo a P i (τ C = m + 1) l espressione h 1 T \C p ih 1 P h1 (τ C = m) e a P i (τ C = 1) il suo valore j C p ij, si ottiene qualsiasi sia i T \ C λ C i = j C p ij + m=1 h 1 T \C p ih1 P h1 (τ C = m) e scambiando l ordine delle sommatorie (cosa possibile poiché i termini sono non negativi) λ C i = p ij + p ih1 λ C h 1. j C h 1 T \C 37
38 Si vedrà nel prossimo paragrafo che se T ha cardinalità finita il sistema x i = p ij + p ih1 x h1. j C h 1 T \C ha soluzione unica, che quindi coincide con le probabilità di assorbimento. Si osservi che, grazie al criterio sufficiente per la persistenza, la classe S \ T di tutti gli stati persistenti di una catena (finita e non) è una classe chiusa. In tal caso il sistema soddisfatto dalle probabilità di assorbimento diventa x i = p ij + p ij x j, i T. j T j S\T È immediato verificare che x i = 1 qualsiasi sia i T è una soluzione del sistema, che quindi nel caso finito coincide con la probabilità di assorbimento nella classe degli stati persistenti. Così nel caso T finito, qualsiasi sia la legge iniziale P(τ S\T < + ) = λ S\T j π (j) = π (j) = 1. j S j S Lo stesso risultato si può anche mostrare mettendo insieme il fatto che P(τ S\T < + ) = P(N (T ) < + ), e che nel caso T finito come si è già visto P(N (T ) < + ) = Unicità della soluzione del sistema di equazioni per le probabilità di assorbimento nel caso stati finiti Sia x i, i T \ C una soluzione del sistema x i = h C p ih + h T \C p ih x h ; si dimostra che x i coincide con λ i = P i (τ C < + ). Per questo si sostituisce nell equazione precedente il valore di x h dato dall equazione stessa x i = p ih + p ih p hj + p ih p hj x j h C h T \C j C h T \C j T \C = p ih + p ih p hj + p ih p hj x j, h C j C h S h T \C j T \C dove nella riscrittura del terzo termine si è usato il fatto che se j T \ C e h C allora p hj =. 38
39 Si osserva che, poiché i primi due addendi insieme danno la probabilità di passare da i in C in al più due passi, x i = P i (τ C 2) + j T \C p (2) ij x j. Con analogo procedimento dall equazione precedente si ottiene x i = P i (τ C 3) + p (3) ij x j, e iterando n 1 volte j T \C x i = P i (τ C n) + j T \C p (n) ij x j. Passando al limite per n nel secondo membro e utilizzando il fatto che T, e quindi T \ C, è finito e pertanto si possono scambiare somma e limite, si ottiene x i = lim P i(τ C n) + lim n n p(n) ij x j. j T \C Ora {τ C n} è una successione crescente di eventi, ovvero e inoltre {τ C n} {τ C n + 1}, {τ C n} = {τ C < + }, n=1 così, applicando il lemma di continuità della probabilità per successioni crescenti di eventi del paragrafo 17, lim P i(τ C n) = P i (τ C < + ). n Inoltre si è dimostrato nel paragrafo 19 che qualsiasi sia i S per j transiente lim n p (n) ij = e quindi in definitiva si ottiene come si voleva x i = P i (τ C < + ). 39
40 1.26 Probabilità di estinzione per la catena di nascita e morte con estremi assorbenti In questa sezione si calcola la probabilità di assorbimento in {} per una catena di nascita e morte con e m assorbenti, ovvero r = 1 (quindi p = ) e r m = 1 (e quindi q m = ), e con p i > e q i >, e quindi tutti gli stati intermedi comunicanti e transienti. Ponendo per semplicità di notazione λ C i = λ{} i = λ i, il sistema si scrive λ i = q i λ i 1 + p i λ i+1 + r i λ i, i {1,..., m 1}, dove λ = 1 e λ m =. Sostituendo a r i il valore 1 p i q i, dopo facili passaggi algebrici, si trova per i {1,..., m 1} λ i λ i+1 = q i p i (λ i 1 λ i ) (attenzione: si usa p i > ). Si calcola in modo ricorsivo per i {1,..., m 1} λ i λ i+1 = q iq i 1... q 1 p i p i 1... p 1 (1 λ 1 ) = γ i (1 λ 1 ) avendo posto γ i = q iq i 1... q 1. p i p i 1... p 1 Si noti che posto γ = 1 l uguaglianza λ i λ i+1 = γ i (1 λ 1 ) vale anche per i =, dunque vale per i {,..., m 1}. Allora sommando da a m 1 ambo i membri dell uguaglianza precedente, si ricava λ λ m = m 1 i= γ i (1 λ 1 ) da cui, ricordando che λ = 1 e λ m =, si ottiene 1 λ 1 = 1 m 1 i= γ i (attenzione: si usa q i > ). Sommando ora da j a m 1 ambo i membri dell uguaglianza già utilizzata e ricordando che λ m =, si ricava λ j λ m = λ j = m 1 i=j γ i m 1 i= γ i Si assuma p i = p e q i = q, allora r i = r e si ottiene γ i = ( q p) i e quindi ( q p ) j + ( q p ) j ( q p) m 1. λ j = 1 + ( q p ) ( ) m q p 4
41 e se q = p = 1/2 o anche solo q = p, r λ j = m j m. Così nella rovina del giocatore la probabilità che A perda è λ a = b a + b Persistenza o transienza per la catena di nascita e morte irriducibile Per analizzare il carattere degli stati della catena di nascita e morte a valori in S = N e con p i > e q i > per ogni i S, si osserva che: poiché essa è irriducibile gli stati hanno tutti lo stesso carattere, in particolare il carattere dello stato e inoltre ρ = p + p 1 ρ 1 = r + p P 1 (τ < + ). Pertanto la catena è persistente se e solo se 1 = r + p P 1 (τ < + ) e quindi, ricordando che r + p = 1, se e solo se P 1 (τ < + ) = 1. Per calcolare P 1 (τ < + ) si osserva che {τ < +, X = 1} = {τ < τ m, X = 1}. m=1 Infatti τ (ω) < + implica che esiste M, dipendente da ω, tale che τ (ω) < M; inoltre, poiché, per ω tale che X (ω) = 1, si ha τ m (ω) + 1 τ m+1 (ω), allora, per ω tale che X (ω) = 1, τ m (ω) diverge a + crescendo, e quindi esiste m, dipendente da ω, tale che τ (ω) < M < τ m (ω). Pertanto {τ < +, X = 1} {τ < τ m, X = 1}. m=1 L inclusione inversa è immediata. Dunque, applicando il lemma di continuità della probabilità per successioni crescenti di eventi del paragrafo 17 P 1 (τ < + ) = lim m P 1(τ < τ m ). 41
42 Ma P 1 (τ < τ m ) è pari alla probabilità di assorbimento in partendo da 1 per la catena di nascita e morte su {,..., m} con le stesse p i, r i, q i per i = 1,..., m 1 ma con e m assorbenti. Pertanto, ricordando l espressione di λ j per j = 1 calcolata nel paragrafo precedente, si ha m 1 i=1 P 1 (τ < + ) = lim γ i m m 1 i= γ i Concludendo, la catena è persistente se e solo se Se q i = q, p i = p γ i = +. i= γ i = i= ( = lim 1 m ( q ) i = + p i= se e solo se q p 1 ovvero se e solo se q p. Esempio: p i = i+2 2i+2 e q i = i 2i+2 ; allora q i p i = i i+2 e γ i = 1 ) m 1 i= γ. i (i 2)(i 1)i i (i + 1)(i + 2) = 2 (i + 1)(i + 2) e poiché γ i ha lo stesso comportamento di 1 i 2 transiente. Esercizio 6 < +, la catena è Tre libri sono messi uno sopra l altro a formare una pila. In ogni istante se ne sceglie uno a caso e si mette in cima alla pila lasciando invariata la posizione degli altri due. Assumendo che i libri siano contraddistinti con le lettere A,B,C: descrivere con una catena di Markov il sistema il cui stato è costituito in ogni istante dalla disposizione dei libri nella pila. Soluzione Ci sono tanti stati quante sono le permutazioni della terna(a,b,c), ovvero 3! = 6. Inoltre da ogni stato le transizioni possibili equiprobabili sono 3. Così se per esempio ordiniamo i possibili stati in questo modo: {(A B C), (B A C), (C A B), (A C B), (B C A), (C B A)} la matrice di transizione è la seguente P =
43 La catena è irriducibile poiché tutti gli stati sono comunicanti e, essendo lo spazio di stato finito, tutti gli stati sono persistenti Tempi medi di assorbimento nella classe degli stati persistenti In questa sezione si determina il sistema di equazioni al quale devono soddisfare i valori medi dei tempi di assorbimento nella classe chiusa C di tutti gli stati persistenti, quando l insieme degli stati transienti è finito. In tal caso qualsiasi sia i T vale λ C i = P i(τ C < + ) = 1 e qui si vogliono determinare le equazioni per E i [τ C ], valor medio di τ C condizionato a (X = i). Sia i T allora E i [τ C ] = 1 P i (τ C = 1) + = P i (τ C = 1) + n P i (τ C = n) n=2 (1 + l) P i (τ C = 1 + l) l=1 e essendo P i (τ C = 1 + l) = h T p ihp h (τ C = l), E i [τ C ] = P i (τ C = 1) + P i (τ C = 1 + l) + l p ih P h (τ C = l) l=1 l=1 h T = P i (τ C = n) + l p ih P h (τ C = l). n=1 l=1 h T Dunque, potendo scambiare l ordine delle somme nel secondo addendo, se è i T si ha E i [τ C ] = P i (τ C < + ) + h T = 1 + h T p ih E h [τ C ], p ih l P h (τ C = l) l=1 dove nell ultimo passaggio si è usato P i (τ C < + ) = λ C i = 1. Si può dimostrare che il sistema x i = 1 + h T p ih x h, i T, quando T ha cardinalità finita, in particolare se lo spazio degli stati della catena è finito, ammette un unica soluzione e dunque risolvendolo si ottengono proprio i valori medi desiderati. 43
44 Nel caso della rovina del giocatore con p = q per C = {, m} e T = {1,... m 1} si calcola E i [τ C ] = i(a + b i) e quindi, se il capitale iniziale di A è a, in media affinché il gioco finisca si aspetta un tempo pari ad ab. Continuazione dell Esercizio 6 Quanto tempo in media occorre se la catena è inizialmente nello stato (A,B,C) (dall alto verso il basso) affinché il primo libro dall alto sia quello contraddistinto dalla lettera C? Soluzione Per rispondere si calcola il tempo medio di assorbimento partendo dallo stato 1 nella classe chiusa C = {3, 6} per la catena modificata rendendo assorbenti gli stati 3 e 6. Il grafico della nuova catena è Il sistema da risolvere per calcolare E 1 [τ C ] è: x 1 = x x 2 x 2 = x x 1 x 4 = x x 2 x 5 = x x 1 le cui soluzioni sono x 1 = x 2 = x 4 = x 5 = 3. Pertanto E 1 [τ C ] = 3. 44
45 Esercizio 7 a) Calcolare le probabilità di assorbimento nello stato per la catena con matrice di transizione P = b) Calcolare la probabilità che la catena sia assorbita nello stato se la densità iniziale è quella uniforme. c) Calcolare i tempi medi di assorbimento in {, 3}. Soluzione a) Le probabilità di assorbimento nello stato risolvono { x 1 = x 2 x 2 = 1 4 x x 2 da cui si calcola facilmente λ {} 1 = x 1 = 3 8 e λ{} 2 = x 2 = 1 8. b) Se poi la legge iniziale è uniforme, allora P(τ < + ) = 3 i= λ {} 1 i 4 = = 3 8. c) I tempi medi di assorbimento in C = {, 3} risolvono { x 1 = x 2 x 2 = x x 2 e quindi si calcola E 1 [τ C ] = 13 8, E 2[τ C ] =
46 Esercizio 8 Sia (X n ) n la catena che descrive la seguente passeggiata aleatoria sui vertici di un triangolo, numerati con 1,2,3 procedendo in senso antiorario: ci si muove in senso antiorario con probabilità p e orario con probabilità 1 p e la densità iniziale è π = ( ). Calcolare il valore medio del tempo di primo arrivo nello stato 2. Soluzione Vale la formula Infatti poiché si ha E[τ 2 ] = P(τ 2 = n) = 3 π (i)e i [τ 2 ]. i=1 3 π (i)p i (τ 2 = n) i=1 3 E[τ 2 ] = np(τ 2 = n) = n π (i)p i (τ 2 = n) n=1 n=1 i=1 e scambiando l ordine delle sommatorie E[τ 2 ] = np(τ 2 = n) = n=1 3 π (i) np i (τ 2 = n). i=1 n=1 Si osserva che la stessa formula si sarebbe potuta ottenere anche nel modo che segue. La variabile aleatoria, τ 2, tempo di primo arrivo nello stato 2, si può scrivere così τ 2 = τ 2 I {1} (X ) + τ 2 I {2} (X ) + τ 2 I {3} (X ) e quindi per la linearità della media E[τ 2 ] = 3 E [ τ 2 I {i} (X ) ]. i=1 La densità della variabile τ 2 I {i} (X ) in k 1 si calcola così: P(τ 2 I {i} (X ) = k) = P(τ 2 = k, X = i) = P(τ 2 = k X = i)p(x = i). Pertanto P(τ 2 I {i} (X ) = k) = P i (τ 2 = k)π (i) se k 1 e E[τ 2 I {i} (X )] = k P i (τ 2 = k)π (i) = π (i) k P i (τ 2 = k) = π (i)e i [τ 2 ]. k=1 k=1 46
47 Sostituendo dunque nella formula E[τ 2 ] = 3 i=1 π (i)e i [τ 2 ] i valori della densità iniziale si ottiene E[τ 2 ] = 1 5 E 1[τ 2 ] E 3[τ 2 ]. Un modo per calcolare le medie E 1 [τ 2 ], E 3 [τ 2 ] è quello di pensare che esse sono le stesse per la catena in cui rendiamo assorbente lo stato 2, ovvero per la catena Questa catena ha il vantaggio di avere gli stati 1 e 3 transienti e 2 unica classe persistente. Così si può impostare il sistema { x 1 = 1 + p 13 x 3 = 1 + (1 p)x 3 x 3 = 1 + p 31 x 1 = 1 + p x 1 la cui soluzione (x 1, x 3 ) fornisce E 1 [τ 2 ] e E 3 [τ 2 ]. Si trova E 1 [τ 2 ] = 2 p 1 p + p 2, E 3[τ 2 ] = 1 + p 1 p + p 2 Si noti che se p = 1 p, ovvero nel caso simmetrico, come ci si può aspettare, E 1 [τ 2 ] = E 3 [τ 2 ] e in particolare entrambi i valori sono uguali a 2. In conclusione E[τ 2 ] = 1 2 p 5 1 p + p p 5 1 p + p 2 = 6 + 3p 5(1 p + p 2 ). 47
48 Esercizio 9 Quattro fratelli di età differente giocano a tirarsi la palla: ciascuno la lancia con uguale probabilità a quelli più piccoli di lui, ma il più piccolo di tutti non la lancia affatto e ferma il gioco. a) Descrivere con una catena di Markov il gioco. Quanto tempo in media dura il gioco se ad iniziarlo è il maggiore? b) Arriva un amico e il gioco cambia così: ciascuno lancia la palla a caso al gruppo composto dai fratelli più piccoli e dall amico, tranne il fratello minore e l amico che non lanciano la palla a nessuno e fermano il gioco. Se ad iniziare è il maggiore, con che probabilità il gioco finisce con la palla nelle mani del minore? In media quanto tempo dura questo secondo gioco? Soluzione a) Numerati con {1, 2, 3, 4} i fratelli dal più grande al più piccolo, la catena ha la matrice di transizione seguente il suo grafico è P = e lo spazio degli stati è costituito dagli stati transienti T = {1, 2, 3} e dallo stato assorbente 4, poiché i 4 e 4 i qualsiasi sia i = 1, 2, 3 e 4 comunica solo con sé stesso. Allora la classe C di tutti gli stati 48
49 persistenti coincide con {4} e il sistema di equazioni risolto dai tempi medi di assorbimento in C è x 1 = x x 3 x 2 = x 3 x 3 = 1 La soluzione è x 1 = 11 6, x 2 = 3 2, x 3 = 1 e dunque la risposta è Si sarebbe anche potuto calcolare facilmente in questo caso la densità del tempo di assorbimento τ C trovando P 1 (τ C = 1) = 1 3, P 1(τ C = 2) = = 1 2, P 1(τ C = 3) = 1 6. Il tempo medio si calcolava allora così E 1 [τ C ] = = 11 6 b) Lo spazio degli stati diventa {1, 2, 3, 4, 5} dove come prima i fratelli sono numerati dal più grande al più piccolo e l ultimo stato indica l amico; la matrice di transizione si modifica così il suo grafico è P = e lo spazio degli stati è costituito dagli stati transienti T = {1, 2, 3} e dagli stati assorbenti 4 e 5, poiché i 4 e 4 i qualsiasi sia i = 1, 2, 3 e 4 e 5 comunicano solo con sé stessi. C 1 = {4} e C 2 = {5} sono dunque ora le uniche due classi irriducibili persistenti. In questo caso la classe C di tutti gli stati persistenti coincide con C 1 C 2 = {4, 5}. 49
50 Le probabilità di assorbimento nella classe C 1 = {4} sono la soluzione del sistema x 1 = x x 3 x 2 = x 3 x 3 = 1 2 e quindi x 1 = x 2 = x 3 = 1 2, come era da aspettarsi per ragioni di simmetria. Dunque se ad iniziare è il maggiore, con probabilità 1 2 il gioco finisce con la palla nelle mani del minore. Il sistema di equazioni risolto dai tempi medi di assorbimento in C è x 1 = x x 3 x 2 = x 3 x 3 = 1 la cui soluzione è x 1 = 19 12, x 2 = 4 3, x 3 = 1 e dunque la risposta è Del resto P 1 (τ C = 1) = 1 2, P 1(τ C = 2) = = 5 12, P 1(τ C = 3) = 1 12, e quindi E 1 [τ C ] = = La catena a due stati: comportamento asintotico delle leggi al tempo n Si consideri la catena con S = {, 1} e ( ) 1 p p P = q 1 q con q, p [, 1] e si calcoli la densità al tempo n, π n. Chiaramente basterà calcolare per esempio π n () = P(X n = ). Si ha π n () = P(X n = X n 1 = )π n 1 () + P(X n = X n 1 = 1)π n 1 (1) = (1 p)π n 1 () + qπ n 1 (1) = (1 p)π n 1 () + q(1 π n 1 ()) = (1 p q) π n 1 () + q, 5
51 e ricorsivamente Pertanto, essendo n 1 π n () = (1 p q) n π () + q (1 p q) j. j= n 1 (1 p q) j = j= 1 (1 p q)n, p + q si ottiene π n () = q p + q + (1 p q)n( π () q ) p + q π n (1) = p p + q + (1 p q)n( π (1) p ). p + q Si osserva che, qualsiasi sia la densità iniziale π, se p + q = 1 si ottiene, per ogni n 1, π n () = q e π n (1) = p. Se invece si assume 1 p q < 1, si ha lim n (1 p q) n =, qualsiasi sia la densità iniziale π, e quindi e lim π n() = n lim π n(1) = n q p + q p p + q. Dunque in entrambi i casi si può dire che, qualsiasi sia la densità iniziale π, la legge di questa catena al crescere del tempo si stabilizza. Ci si può chiedere se questo comportamento sia eccezionale. Per ora si noti che posto π () = q p+q e quindi π (1) = p p+q si ha per ogni n 1, π n() = q p+q e quindi p p+q π n (1) =, ovvero, se la legge iniziale coincide con la legge limite, la stessa legge è la legge della catena in ogni tempo. Si osserva che il conto precedente vale anche nel caso in cui uno dei due parametri è in (, 1) e l altro assume uno dei valori estremi dell intervallo. Inoltre la stessa convergenza delle densità ha luogo anche nel caso in cui uno dei due parametri è nullo e l altro è 1; anzi in tal caso si calcola facilmente che, qualsiasi sia la densità iniziale π, vale π n () = q p+q e π n(1) = p p+q per ogni n 1. Invece se entrambi i parametri sono nulli oppure se entrambi sono pari ad 1 allora non c è convergenza della successione delle densità; infatti, se entrambi i parametri sono nulli, la matrice di transizione è la matrice identità e, qualsiasi sia la densità iniziale π, la successione (π n, n ) è costante uguale a π ; se i due parametri sono entrambi uguali ad 1 allora, qualsiasi sia la densità iniziale π, per n pari π n coincide con π, mentre per n dispari π n coincide con (π () π (1)). 51
52 1.3 Definizione di misura invariante Si definisce misura di probabilità invariante o stazionaria per una matrice di transizione P un applicazione v : S [, 1] tale che i) v i = 1 i S ii) se (X n ) n è la catena associata a P con densità iniziale π = v, allora qualsiasi sia n 1 π n = v P n = v. Condizione necessaria e sufficiente affinché v : S [, 1] sia una misura di probabilità invariante è che a) i S v i = 1 b) v P = v. La condizione necessaria è immediata. La condizione sufficiente segue osservando che a) e i) coincidono e b) implica ii): infatti se b) è vera, allora, poiché π n = π n 1 P, assumendo l ipotesi induttiva π n 1 = v si ha 1.31 Esempi nel caso finito π n = v P = v. Data P finita e bistocastica, cioè tale che per ogni i S n p ji = 1 j=1 (n= cardinalità di S) si dimostra che esiste una costante k tale che v i = k per ogni i S è una misura di probabilità invariante. Affinché v sia invariante la costante k deve verificare a) n i=1 k = 1 b) n j=1 k p ji = k per ogni i S. La condizione b) è chiaramente vera essendo n j=1 k p ji = k n j=1 p ji e P bistocastica. La condizione a) fornisce k = 1 n. Dunque una misura invariante per P bistocastica è la misura uniforme. È l unica? 52
53 Come secondo esempio si considera la catena che descrive una passeggiata aleatoria sui vertici di un grafo: la catena ha tanti stati quanti sono i vertici e la probabilità di transizione da uno stato (vertice) è uniforme sugli stati adiacenti (vertici connessi al primo da un arco). Dato per esempio il grafo il grafico della catena associata è il seguente Se k i è il numero dei vertici adiacenti a i S e k = i S k i, allora v tale che v i = k i k è una misura invariante per la catena. Infatti j S k j k p ji = j adiacenti a i k j k 1 k j = k i k, l ultima uguaglianza usa il fatto che solo k i sono gli stati per i quali p ji. È l unica misura invariante? Per la catena di nascita e morte su {, 1,..., m} con gli stati e m assorbenti e q i >, p i > se i = 1,..., m 1, è chiaro che v (1) = (1... ) è invariante, poiché v (1) P = v (1) e m i= v(1) i = 1. Analogamente v (2) = (... 1) è invariante. 53
54 Sia ora il vettore w definito così w i = αv (1) i + (1 α)v (2) i per una qualche costante α (, 1). Allora w è invariante poiché w i per ogni i =,..., m e inoltre a) b) m m w i = α v (1) i + (1 α) i= i= m i= v (2) i = α + (1 α) = 1. w P = α v (1) P + (1 α) v (2) P = αv (1) + (1 α)v (2) = w. La famiglia precedente definisce un infinità di misure invarianti e dal prossimo risultato segue che ogni misura invariante appartiene alla famiglia. Proposizione Se i é transiente e v é invariante vale v i =. Dimostrazione Se v è invariante, per ogni i S v i = π n (i) = j S v j p (n) ji e passando al limite in n in entrambi i membri si ottiene per ogni i S v i = lim v j p (n) n ji = v j lim n p(n) ji = j S j S Lo scambio tra somma e limite è immediato se S è finito ed è lecito in generale poiché si può utilizzare il seguente risultato sulle serie ([1]): le condizioni lim n a nj =, a nj A per ogni n, j, j=1 b j < + implicano lim n j=1 a njb j =. Nel caso in esame: a nj = p (n) ji 1, b j = v j e j=1 b j = Esistenza e unicità della misura invariante Si sono trovate una o più misure invarianti per tre diversi esempi di catene. Ma in generale esiste sempre almeno una misura invariante? Se esiste quando è unica? Teorema(Markov Kakutani) ([1]) Una matrice di transizione su uno spazio finito ammette sempre almeno una misura invariante. Si è già dimostrato nel caso della catena di nascita e morte che ogni combinazione convessa di due misure invarianti è invariante e si vede subito che la dimostrazione non dipende né dalla catena né dalla forma di v (1) e v (2) 54
55 e quindi il risultato vale in generale. Pertanto se esiste più di una misura invariante allora ne esistono infinite. Su S eventualmente infinito sia P irriducibile. Già si è detto che la caratterizzazione degli stati è globale, cioè o sono tutti persistenti o sono tutti transienti, di conseguenza la catena si dice persistente o transiente. Si ricorda che i è persistente se e solo se P i (τ i < + ) = 1, ma se una variabile aleatoria è finita con probabilità 1 questo non implica necessariamente che il suo valore medio sia finito. Nel caso persistente si distinguono così due sottocasi: catena persistente positiva: per ogni i S, E i [τ i ] < +, catena persistente nulla: per ogni i S, E i [τ i ] = +. Anche il carattere della persistenza nel caso irriducibile è globale (vedi [3]). Teorema Ogni catena irriducibile persistente positiva ammette un unica misura invariante data da v i = 1 E i [τ i ], i S. Le catene irriducibili transienti o persistenti nulle non ammettono misura invariante. Si rimanda per un idea della dimostrazione alla fine di queste note e per maggior dettaglio a [3]. Nel caso irriducibile dunque per determinare l esistenza della misura invariante occorre poter stabilire se la media dei tempi di ritorno negli stati è finita e, per il carattere globale della nozioni di persistenza nulla e positiva e transienza, è sufficiente verificarlo per un solo stato. È intuitivo (ma richiederebbe una dimostrazione che qui si omette) il fatto che tutte le catene irriducibili finite sono persistenti positive e quindi hanno un unica misura invariante. Se si calcola la misura invariante allora automaticamente si calcolano anche i tempi medi di ritorno negli stati Catene ergodiche Una matrice di transizione P si dice ergodica se fissato j qualsiasi sia i S lim n p(n) ij = v j per qualche v : S [, 1] tale che j v j = 1. Si può dimostrare che dall ergodicità discende i) fissato j, qualsiasi sia la misura iniziale della catena, lim n π n (j) = v j ii) v è una misura invariante 55
56 iii) v è l unica misura invariante. La dimostrazione si fa vedere ora nel caso finito, quando limiti e somme si scambiano senza problema: i) lim π n(j) = lim n n = i = i i π (i) p (n) ij π (i) lim n p(n) ij π (i)v j = v j π (i) = v j ( La dimostrazione di questo punto nel caso infinito richiede il risultato di i scambio di limite e serie enunciato precedentemente: lim π (i)(p (n) n ij v j) lim π (i) p (n) n ij v j = i i i e p (n) ij v j 2 per ogni n, i. ) π (i) lim n p(n) ij v j = ii) per ogni i S si ha (v P) i = v i poiché v j p ji = j j lim n p(n) kj p ji = lim n j p (n) kj p ji = lim n p(n+1) ki = v i (k è arbitrario fissato) iii) Se w fosse un altra misura invariante, scelta π = w si avrebbe π n (i) = w i per ogni i, n e quindi, dovendo anche essere per il punto precedente lim n π n (i) = v i, seguirebbe, per l unicità del limite, w i = v i per ogni i Catene regolari Nel caso delle catene irriducibili con spazio degli stati finito esiste una condizione necessaria e sufficiente per l ergodicità: la regolarità. Una matrice di transizione su uno spazio di stati finito si dice regolare se esiste n 1 tale che p (n) ij > per ogni i, j. Una condizione sufficiente per la regolarità è che P sia irriducibile e esista h S tale che p hh >. Infatti se m = max{n(i, j), i, j S t.c. p (n(i,j)) ij > } (n(i, j) esiste per l irriducibilità), allora p (2m) ij > per ogni i, j poiché p (2m) ij p (n(i,h)) ih p hh... p hh p (n(h,j)) hj >, dove il prodotto di p hh per se stesso è ripetuto 2m n(i, h) n(h, j) volte. 56
57 Si noti bene che la regolarità è condizione necessaria per l ergodicità solo nel caso in cui la catena sia irriducibile. Come controesempio si tenga presente la catena a due stati con uno dei due parametri nullo e l altro pari ad 1 (vedi sezione 29). Esercizio 1 Sia X n la catena su S = {1, 2, 3} tale che: se lanciando una moneta si ottiene testa allora X = 1, altrimenti X = 2 o X = 3 con uguale probabilità; nei tempi successivi se la catena è in 1 vi rimane, se è in 3 passa in 2, se è in 2 passa in 3 con probabilità 2 3 o rimane in 2. a) Calcolare le eventuali misure invarianti. b) Calcolare lim n p (n) ij per ogni i, j. c) Calcolare lim n π n (i) per ogni i. Soluzione La catena ha matrice di transizione 1 P = e misura iniziale π = ( ) e il suo grafico è a) Pertanto S = C 1 C 2 = {1} {2, 3}, ovvero 1 è stato assorbente e {2, 3} è classe persistente positiva. Esistono pertanto infinite misure invarianti che sono tutte le combinazioni convesse di v (1) = (1 ) e v (2) = ( ). I vettori 1 e ( ) sono infatti le misure invarianti della catena ristretta rispettivamente alle classi {1} e {2, 3}. 57
58 b) È evidente che qualsiasi sia n la matrice di transizione in n passi avrà la forma 1 P (n) = p (n) 22 p (n) 23 p (n) 32 p (n) 33, da cui subito si ricava che lim n p(n) 11 = 1, lim n p(n) 12 =, lim n p(n) 13 =, lim n p(n) 21 =, lim n p(n) 31 =. Per quanto riguarda gli altri elementi, poiché la matrice di transizione ristretta agli stati 2 e 3 è regolare (in quanto irriducibile con p 22 > ) allora è ergodica e si ha per i = 2, 3 c) Infine poiché lim n p(n) i2 = v(2) 2 = 3 5, lim n p(n) i3 = v(2) 3 = 2 5 π n (1) = π n (2) = π n (3) = 3 i=1 3 i=1 3 i=1 π (i) p (n) i1 π (i) p (n) i2 π (i) p (n) i3 = 1 2 p(n) p(n) p(n) 31 = 1 2 = 1 4 p(n) p(n) 32 = 1 4 p(n) p(n) 33, allora lim π n(1) = 1 n 2 lim π n(2) = 1 n 4 ( ) = 3 1 lim π n(3) = 1 n 4 ( ) = 1 5. Esercizio 11 Sia data la matrice di transizione P =
59 Calcolare l unica misura invariante. Soluzione La matrice è irriducibile finita e quindi persistente positiva e con un unica misura invariante soluzione del sistema x 1 + x 2 + x 3 = 1 x 1 + x 2 + x 3 = 1.4 x x x 3 = x 1.4 x x x 3 = x 2.2 x x x 3 = x 3 x i equivalente a 6 x x x 3 = 4 x 1 6 x x 3 = 2 x x 2 6 x 3 = x i. Moltiplicando la seconda equazione per 2 e sottraendole la terza e al tempo stesso moltiplicando la quarta per 2 e sottraendole la terza si ottiene il sistema equivalente x 1 + x 2 + x 3 = 1 8 x x 2 = 12 x 2 16 x 3 = x i dal quale facilmente si ricava x 1 = 3 4 x 2, x 3 = 3 4 x 2 e infine x 2 = 2 5. Assegnata la matrice di transizione Esercizio P = a) calcolare la misura invariante se esiste b) la media del tempo di primo ritorno in 1 c) la media dei tempi di assorbimento in 3. Soluzione a) La decomposizione dello spazio degli stati è S = {1, 2, 3} = T C = {1, 2} {3} ovvero: 1 e 2 sono stati transienti poiché comunicano con 3 che non comunica né con 1 né con 2; 3 è uno stato assorbente. Pertanto l unica misura invariante è v = ( 1), unica soluzione non negativa del sistema xi = 1 x P = x x 1 = x 2 = 59
60 (si ricordi: le misure invarianti valgono sugli stati transienti) b) Poiché 1 è transiente, si ha ρ 11 = P 1 (τ 1 < + ) < 1 ovvero e quindi E 1 [τ 1 ] = +. P 1 (τ 1 = + ) > c) Per calcolare i tempi di assorbimento in 3 si può risolvere il sistema E i [τ 3 ] = 1 + j T p ij E j [τ 3 ], i = 1, 2 che coincide con { E 1 [τ 3 ] = E 2[τ 3 ] E 2 [τ 3 ] = E 2[τ 3 ] che dà E 2 [τ 3 ] = 2 e E 1 [τ 3 ] = 3/2. Altrimenti si può determinare la densità di τ 3, ovvero P i (τ 3 = k) per k 1 corrispondente alla legge iniziale delta di Dirac in i, e calcolare poi E i [τ 3 ] = kp i (τ 3 = k), i = 1, 2. k=1 Per esempio, dal grafico della catena subito si calcola e quindi P 1 (τ 3 = 1) = 3 4, P 1(τ 3 = k) = 1 2 k+1, k 2 E 1 [τ 3 ] = k=2 k 1 2 k+1 = ( E[Z] 1 ) = con Z variabile aleatoria geometrica di parametro 1 2 e quindi E[Z] = 2. Analogamente P 2 (τ 3 = 1) = 1 2, P 2(τ 3 = k) = 1 2 k, k > 1 e quindi Naturalmente E 3 [τ 3 ] = 1. E 2 [τ 3 ] = E[Z] = 2. 6
61 Assegnata la matrice Esercizio P = a) trovare tutte le misure invarianti b) calcolare la probabilità di raggiungere l insieme {1, 4} partendo dallo stato 2. Quanto vale allora la probabilità di raggiungere l insieme {3, 5}? Soluzione a) In questo caso S = {1, 2, 3, 4, 5} = T C 1 C 2 = {2} {1, 4} {3, 5}, ovvero vi sono due classi irriducibili persistenti positive. sistema x 1 + x 2 + x 3 + x 4 + x 5 = 1 Risolvendo il x 1 = 3 4 x x 4 x 2 = x 3 = 1 4 x 5 x 4 = 1 4 x x 4 x 5 = x x 5. si trova x = (2x 4 x 3 x 4 4x 3 ) con 3x 4 + 5x 3 = 1 dove x 3 e x 4 sono lasciate come parametri. Dunque le misure invarianti sono tutti i vettori della forma (2α β α 4β) al variare di α e β in R + tali che 3α + 5β = 1. Si osserva che la prima e la quarta componente della generica misura invariante (2α β α 4β) risolvono un sistema separato dal sistema risolto dalla terza e dalla quinta e precisamente il sistema risolto dalla misura invariante della dinamica su C 1 e la la terza e la quinta componente risolvono il sistema risolto dalla misura invariante della dinamica su C 2. Segue che per β = si ottiene v (1) = ( ) e che (v(1) 1 v (1) 4 ) è la misura invariante della dinamica su C 1 e per α = si ottiene v (2) = ( ) e che (v(2) 3 v (2) 5 ) è la misura invariante della dinamica su C 2. Inoltre, poiché dividendo la soluzione di un sistema omogeneo per la somma delle sue componenti si ottiene una soluzione le cui componenti hanno come somma 1, esiste una costante γ > tale che (2α α) = γ(v (1) 1 v (1) 4 ) e quindi (2α α ) = γv(1). Per lo stesso motivo esiste una costante δ > tale che ( β 4β) = 61
62 δv (2). Così poiché (2α β α 4β) = (2α α ) + ( β 4β) allora γ e δ sono tali che γ(v (1) 1 + v (1) 4 ) + δ(v(2) 3 + v (2) 5 )=1, ovvero, ricordando che v (1) 1 + v (1) 4 = 1 = v (2) 3 + v (2) 5, sono tali che γ = 1 δ. Si è mostrato che ogni misura invariante si esprime come combinazione convessa di v (1) e v (2), cioè v = γv (1) + (1 γ)v (2) con γ [, 1]. Con dimostrazione analoga si prova l affermazione generale per cui: le misure invarianti di una catena a valori in uno spazio finito sono tutte e sole quelle che si ottengono per combinazione convessa a partire dalle misure invarianti della dinamica ristretta alle classi persistenti. b) Si devono calcolare le probabilità di assorbimento λ C 1 2 e λ C 2 2. Per calcolare λ C 1 2 si risolve e si ottiene λ C 1 2 = 2 3. Dal fatto che x = x λ C 2 2 = P 2(τ C2 < + ) = P 2 (τ C2 < τ C1 ) = 1 P 2 (τ C1 < τ C2 ) = 1 λ C 1 2, segue λ C 2 2 = La misura invariante per l urna di Ehrenfest Si ricordano le probabilità di transizione dell urna di Ehrenfest con d biglie: p j = I {1} (j), p dj = I {d 1} (j), p ij = I {i+1} (j) d i + I d {i 1} (j) i d, 1 i d 1. La catena è una catena di nascita e morte irriducibile finita e quindi persistente positiva. Esiste dunque un unica misura invariante che è la soluzione di x + x x d = 1 x = x 1 d d (i 1) i+1 x i = x i 1 d + x i+1 d, 1 i d 1 x d = x d 1 d x i. Scelto x come parametro, si verifica subito che il sistema è equivalente al sistema x + x x d = 1 x 1 = d x ( ) d (d 1)... (d i+1) d x i = i! x = x, 1 i d i x i. 62
63 Per dimostrarlo si osservi che dalla seconda equazione segue che x 1 = d x e sostituendo nella terza per i = 1 il valore di x 1 in termini di x si ottiene ( ) d(d 1) d x 2 = x = x 2 2. Iterando il procedimento dalla terza equazione si ricavano tutti i valori in funzione di x. Infatti l equazione si riscrive anche così e se si assume che valga ( ) d x i 1 = x i 1 = e si ottiene x i = x i+1 = d i + 1 x i d i + 1 i + 1 x i 1, d (d 1)... (d i + 2) (i 1)! ( ) d d (d 1)... (d i + 1) x i = x, i! x i+1 = d d (d 1)... (d i + 1) x d i + 1 d (d 1)... (d i + 2) i + 1 i! i + 1 (i 1)! ( ) d(d i) (d 1)... (d i + 1) d = x = x (i + 1)! i + 1 Per ricavare il valore di x si sostituiscono le espressioni ottenute nella prima equazione ottenendo d ( ) d x i = 1 i= e dalla formula del binomio di Newton si ricava x = 1. Concludendo la 2 d misura invariante è v con v i = 1 ( ) d 2 d i =,..., d i x x ovvero la densità della binomiale di parametri n = d, p =
64 1.36 Non esistenza della misura invariante per la passeggiata aleatoria simmetrica in Z Si può dimostrare che la passeggiata aleatoria su Z in cui sono possibili solo le transizioni sugli stati adiacenti (p ij = I {i 1} (j) q+i {i+1} (j) p) è persistente se e solo se è simmetrica, cioè con stessa probabilità di un passo avanti e uno indietro. Qui si dimostra che la passeggiata aleatoria simmetrica su Z non ammette misura invariante e dunque si conclude che è catena persistente nulla. Nel caso simmetrico p ij = I {i 1} (j) 1 2 +I {i+1}(j) 1 2 e il sistema di equazioni per la misura invariante si riscrive { i Z x i = 1, x i x i = x i x i+1 2, i Z. Dall equazione generale si ricava x i+1 = 2x i x i 1 e quindi x i+1 x i = x i x i 1, i Z, e quindi x i+1 x i = x 1 x. Pertanto per ogni i 1 e quindi i 1 x i x = (x j+1 x j ) = i(x 1 x ) j= x i = i(x 1 x ) + x. Segue che, poiché i Z x i = 1 < +, non può essere x 1 x > altrimenti lim i + x i = + (mentre il termine generico di una serie convergente è infinitesimo); né può essere x 1 x < altrimenti lim i x i =, mentre x i. Dunque x 1 x =, cioè x i = x per ogni i 1. Inoltre dovendo essere i Z x i < + e quindi i 1 x i < +, potrà solo essere x i = x = per ogni i 1. Inoltre per ragioni di simmetria vale anche per ogni i 1 x i = ( i + 1 ) (x x 1 ) + x 1 e quindi x i = per ogni i 1. Dunque il sistema non ammette soluzione poiché quella identicamente nulla non verifica i Z x i = Misura invariante per le catene di nascita e morte L enunciato che si vuole dimostrare è il seguente: una catena di nascita e morte infinita persistente ammette una misura invariante se e solo se, posto γ = 1 γ i = p p 1... p i 1 q 1 q 2... q i, i 1, 64
65 si ha γ i < + i= e la misura invariante si calcola così per ogni i v i = γ i i= γ. i Il sistema per il calcolo della misura invariante è x = x r + x 1 q 1 x i = x i 1 p i 1 + x i r i + x i+1 q i+1, i 1 + i= x i = 1 x i e sostituendo a r i il valore 1 p i q i si ottiene x 1 q 1 x p = x i+1 q i+1 x i p i = x i q i x i 1 p i 1, i 1 + i= x i = 1 x i e quindi da cui x i = p i 1 q i + i= x i = 1 x i. x i q i x i 1 p i 1 =, i 1 + i= x i = 1 x i x i 1 = p i 1 q i p i 2 q i 1 x i 2 =... = γ i x, i 1 Dalla seconda equazione si ottiene il valore di x : x = 1 i= γ. i e dunque contemporaneamente la condizione necessaria e sufficiente e l espressione della misura invariante. Se la catena è irriducibile ma lo spazio è finito S = {, 1,..., m} allora essendo persistente positiva ammette un unica misura invariante che risolve x = x r + x 1 q 1 x i = x i 1 p i 1 + x i r i + x i+1 q i+1, 1 i m 1 x m = x m 1 p m 1 + x m q m + i= x i = 1 x i 65
66 e quindi v i = γ i m i= γ. i Esercizio 14 Si indichi con (X n ) n la catena di Markov che descrive una coda in cui le variabili aleatorie numero dei clienti in arrivo e in partenza in ogni unità temporale sono indipendenti di legge Bernoulli rispettivamente di parametri α = 1 4 e β = 1 2. a) Calcolare le probabilità di transizione della catena. È persistente? Ammette una misura invari- b) La catena è irriducibile? ante unica? c) Dare le condizioni su α e β generici che consentono di rispondere affermativamente alle precedenti domande. Soluzione a) Indicati con A e B rispettivamente gli eventi {arriva un cliente} e {parte un cliente}, per ipotesi A e B sono eventi indipendenti e da ogni stato i diverso da si transita in i + 1 con la probabilità di A B c che è P i (A) P i (B c ) = α (1 β) = 1 8 e in i 1 con la probabilità di Ac B che è P i (A c ) P i (B) = (1 α) β = 3 8 e infine si rimane in i con la probabilità di A B A c B c che è αβ +(1 α)(1 β) = 1 2. Infine da si transita in 1 con probabilità α = 1 4 e si resta in con probabilità 1 α = 3 4. Riassumendo r = 3 4, p = 1 4, e, per ogni i 1, q i = q = 3 8, p i = p = 1 8, r i = r = 1 2. b) La catena è irriducibile poiché per ogni i 1 si ha p i > e q i >. La catena è persistente poiché sappiamo che, se le probabilità di nascita e morte non dipendono dallo stato, condizione sufficiente è che q i p i, i 1. La catena ammette un unica misura invariante poiché la condizione necessaria e sufficiente in generale è i= γ i < + e, se si ha come in questo caso ( ) i p i = p, q i = q, i 1, allora per i 1 vale γ i = p p p q e quindi la serie è convergente se e solo se p q < 1 cioè p < q, come in questo caso. La misura invariante in generale è γ i v i = i= γ i e qui per i 1, e quindi γ i = γ i = i= ( 1 3 ) i ) i 1 = 3( 3 ( 1 ) i = = 2 i=1 66
67 e in conclusione v = 1 ( 1 ) i, 2, v i = i 1. 3 [c)] Se α e β sono in (, 1) allora p i > e q i >, per ogni i 1, e la catena è irriducibile. La condizione per la persistenza è p = α (1 β) (1 α) β = q ovvero α β ovvero probabilità di arrivo minore o uguale alla probabilità di partenza. La condizione per l esistenza della misura invariante è p = α (1 β) < (1 α) β = q, ovvero α < β, ovvero probabilità di arrivo minore della probabilità di partenza. Se è α =, allora si vede subito che la catena non è irriducibile (infatti nessuno stato comunica con i successivi), tutti gli stati positivi sono transienti (per ogni i 1, i comunica con ma non comunica con i) e lo stato è assorbente. Esiste un unica misura invariante che è la delta di Dirac in i =. Se è β = la catena non è irriducibile (nessuno stato comunica con i precedenti), gli stati sono tutti transienti e naturalmente non esiste misura invariante. Esercizio 15 Trovare la misura di probabilità invariante per la catena con grafico Soluzione In questo caso S = {1, 2, 3, 4} = T C = {3} {1, 2, 4} e pertanto la misura invariante sarà della forma v = (v 1 v 2 v 4 ) dove (v 1 v 2 v 4 ) è la misura invariante per la matrice di transizione irriducibile P =
68 ottenuta da quella originaria cancellando la terza riga e la terza colonna. Occorre risolvere dunque x 1 + x 2 + x 3 = x 1 = 3 4 x x 2 x 2 = 1 4 x x x 3 x 3 = 1 4 x x 3 x i. Si trova x = ( ) e dunque v = ( 3 7 la catena originaria ) è l unica misura invariante per Assegnata la matrice Esercizio P = a) calcolare la misura invariante se esiste b) la media del tempo di primo ritorno in 1 Soluzione a) La catena è irriducibile e quindi, poiché finita, anche persistente positiva. Esiste dunque un unica misura invariante che si ottiene risolvendo x 1 + x 2 + x 3 = 1 x 1 = x 3 x 2 = 1 4 x x 2 x 3 = 3 4 x x 2 x i equivalente a x 1 + x 2 + x 3 = x 1 = 2x 2 = x 3 x i da cui x = ( ) è la misura invariante. b) Dal teorema sulle catene irriducibili si sa che la media del tempo di primo ritorno in uno stato è il reciproco del valore della misura invariante nello stato e quindi E 1 [τ 1 ] = 5 2 = 1 v 1. 68
69 Esercizio 17 Calcolare la misura invariante per l urna di Ehrenfest con d = 3 modificata nel modo seguente: la biglia corrispondente al numero estratto viene inserita in una delle due urne scelta a caso e la catena conta le biglie in un urna fissata. Soluzione La matrice di transizione della catena di Ehrenfest modificata con d = 3 è P = Infatti, indicati con A e B rispettivamente gli eventi {il numero estratto corrisponde ad una biglia dell urna fissata} e {l urna estratta è quella fissata}, per ipotesi A e B sono eventi indipendenti condizionatamente al numero di biglie nell urna fissata e per esempio da ogni stato i diverso da e d si transita in i 1 con la probabilità di A B c che è P i (A) P i (B c ) = i 1 d 2 e in i + 1 con la probabilità di A c B che è P i (A c ) P i (B) = d i 1 d 2 e infine si rimane in i con la probabilità di A B A c B c che è 1 2. In modo analogo si calcolano le probabilità di transizione da e da d. Si tratta di una catena di nascita e morte irriducibile e persistente positiva ed è facile calcolare risolvendo il sistema di equazioni corrispondente che l unica misura invariante è ( 1 v = ). 8 Per lo stesso calcolo si possono anche utilizzare le formule generali per la misura invariante di una catena di nascita e morte finita Esempi di catene periodiche Si assuma che la catena di Ehrenfest si trovi nello stato i {, 1,..., d}, allora certamente al tempo successivo si troverà in uno stato diverso, ma potrà tornare in i in un tempo che dista dall attuale un numero pari; sarà impossibile per la catena, invece, essere in i in tempi che sono a distanza dispari dal tempo attuale. Ovvero usando le probabilità di transizione qualsiasi sia i p (2n) ii >, n 1 p (2n+1) ii =, n. La stessa cosa accade per una qualsiasi catena di nascita e morte finita irriducibile a barriere riflettenti (r =, p = 1, r d =, q d = 1) e con r i = qualsiasi sia i = 1,..., d 1. 69
70 La stessa proprietà è verificata dalla matrice di transizione della catena associata al grafo ovvero la potenza P n per n pari ha tutti gli elementi sulla diagonale positivi e per n dispari ha tutti gli elementi sulla diagonale nulli. Si individua subito anche un altra particolarità: + + P 2n+1 = P 2n = dove il segno + indica che l elemento corrispondente è positivo. Dunque se parto da uno stato dispari allora mi trovo in ogni tempo dispari in uno stato pari e in ogni tempo pari in uno stato dispari. È dunque chiaro che pur essendo questa catena irriducibile e quindi, essendo finita, persistente positiva e esistendo un unica misura invariante v, non potrà certo essere qualsiasi sia j lim n p(n) ij = v j. Infatti fissati i e j se il limite esistesse non potrebbe che essere lim n p(n) ij =. Si consideri ora la catena con grafico È facile accorgersi che anche in questo caso c è una regolarità in P. In questo caso qualsiasi sia i p (3n) ii >, n 1 p (h) ii =, h 3n, n 1. 7
71 Così come prima lo spazio degli stati veniva diviso in due classi, i pari e i dispari, che erano, da qualunque stato si partisse ciclicamente rivisitati (periodo 2), anche ora lo spazio viene suddiviso in classi rivisitate ciclicamente e precisamente {1}, {2}, {, 3}: comunque si parta dopo 3 passi ci si ritrova nella classe di appartenenza dello stato iniziale Periodo di una catena irriducibile Nel caso delle catene irriducibili persistenti positive, sia S finito o infinito, l ergodicità è equivalente all aperiodicità. Si definisce periodo di uno stato persistente i in una catena generica (non a priori irriducibile) il numero t i definito come MCD{n : p (n) ii > } (MCD=massimo comun divisore). Vale il seguente teorema. Teorema In una catena irriducibile il periodo è lo stesso per ogni stato (e si chiama periodo della catena). Dimostrazione Si dimostra che fissato i S per qualsiasi k i, t i e t k sono divisori l uno dell altro e da questo seguirà la tesi. Poiché la catena è irriducibile esistono m 1 e n 1 tali che p (m) ik p (m+n) ii > > e p (n) ki >. Dunque e dunque t i è divisore di m + n e inoltre, qualsiasi sia r 1 tale che p (r) kk >, essendo p (m+n+r) ii p (m) ik p(r) kk p(n) ki vale p (m+n+r) ii > e dunque t i è divisore di m + n + r e in conclusione t i è divisore di r e poiché r è qualsiasi (tra le lunghezze dei cammini che portano da k in k), per definizione di MCD, t i t k. La dimostrazione è conclusa poiché l argomento è simmetrico in t i e t k. 71
72 Si definisce aperiodica una catena di periodo 1. Naturalmente una condizione sufficiente per l aperiodicità è che esista uno stato h tale che p hh >. Si osservi che l aperiodicità quando la catena è irriducibile ma non è persistente positiva non è sufficiente per avere l ergodicità : basta ricordare il caso di una catena di nascita e morte con probabilità non nulla di tornare con un passo in uno stato ma senza misura invariante ovvero con i= γ i = +. Come esempio si consideri il caso r > e p i = p q = q i qualsiasi sia i 1. Esercizio 18 Sia (X n ) n una catena di nascita e morte su N con p i = 1 3, i q i = 2 3, i 1. i) La catena è transiente o persistente? ii) Esiste una misura invariante? In caso affermativo calcolarla. iii) La catena è ergodica? Soluzione i) La catena è irriducibile essendo p i > e q i >, per ogni i 1. Si ricorda che la condizione di persistenza per una catena di nascita e morte su N irriducibile è γ i = +, i= dove Qui γ = 1, γ i = q iq i 1... q 1 p i p i 1... p 1, i 1. γ = 1, γ i = ( 2 3) i ( 1 3) i = 2 i i 1 e quindi la serie è divergente e la catena persistente. ii) La misura invariante esiste se e solo se γ i < +, i= 72
73 dove Qui γ = 1, γ i = p p 1... p i 1 q 1 q 2... q i, i 1. ( 1 i γ = 1, γ i = 3) ( 2 i = 3) 1 2 i, i 1. e quindi la serie è convergente come serie geometrica di ragione minore di 1. Dunque esiste la misura invariante ed è v = 1 ( 1 i 2, v i = 2) = 1, i i+1 iii) La catena è ergodica perché è aperiodica: questo si deduce per esempio osservando che p >. 1.4 Reversibilità La proprietà di Markov si conserva rovesciando il tempo, infatti utilizzando la definizione di probabilità condizionata e la formula del prodotto si ottiene P(X n = i X n+1 = j, X n+2 = j 2,..., X n+k = j k ) = P(X n+2 = j 2,..., X n+k = j k X n+1 = j, X n = i)p(x n+1 = j X n = i)p(x n = i) P(X n+2 = j 2,..., X n+k = j k X n+1 = j)p(x n+1 = j) = P(X n+1 = j X n = i)p(x n = i) P(X n+1 = j) = π n(i) p ij π n+1 (j) e allo stesso risultato si perviene calcolando P(X n = i X n+1 = j). Una catena di Markov si dice reversibile quando si verifica che P(X n = i X n+1 = j) = P(X n+1 = i X n = j) cioè quando le probabilità di transizione (in un passo) all indietro coincidono con le probabilità di transizione in avanti, ovvero quando il comportamento statistico della catena rimane lo stesso rovesciando il tempo (si ricordi che le leggi congiunte sono determinate dalle probabilità di transizione e dalla legge iniziale). Si dice che una misura di probabilità v soddisfa l equazione del bilancio dettagliato per una matrice di transizione P se qualsiasi siano i e j v i p ij = v j p ji. 73
74 Se v soddisfa l equazione precedente allora è invariante per P. qualsiasi sia i v l p li = v i p il = v i p il = v i. l S l S l S Infatti Inoltre la catena con matrice di transizione P e legge iniziale v risulta reversibile; infatti per l invarianza π n (i) = v i e π n+1 (j) = v j da cui P(X n = i X n+1 = j) = π n(i) p ij π n+1 (j) = v i p ij v j = v j p ji v j = p ji. Esempi di catene reversibili sono l urna di Ehrenfest, la catena di un grafo e qualsiasi catena di nascita e morte persistente positiva in regime di stazionarietà, ovvero inizializzata con la relativa misura invariante. Infatti si può facilmente verificare l equazione del bilancio dettagliato in ciascun caso: per ( ) l urna di Ehrenfest dobbiamo verificare v i p i(i+1) = v i+1 p (i+1)i con v i = d 1 i 2 d e p i(i+1) = d i d e p (i+1)i = i+1 d ; per la catena di un grafo dobbiamo verificare v i p ij = v j p ji con v i = k i k e p ij se e solo se p ji ; per la catena di nascita e morte persistente positiva dobbiamo verificare v i p i(i+1) = v i+1 p (i+1)i con v i = γ i i= γ, γ i = p p 1...,p i 1 i q 1 q 2...,q i i 1, γ = 1 e p i(i+1) = p i, p (i+1)i = q i Algoritmo di Metropolis Si dimostra ([1]) che, dato uno spazio S finito e assegnata una misura di probabilità v su S diversa dalla uniforme tale che per qualsiasi i valga v i >, si può costruire una matrice stocastica P regolare per la quale v soddisfa l equazione del bilancio dettagliato. Il metodo per costruire P si chiama algoritmo di Metropolis e la sua importanza applicativa è evidente: volendo simulare una variabile aleatoria con legge v basterà simulare una catena di matrice di transizione P e legge iniziale qualsiasi e poi considerarne il valore per n grande. Si sa infatti che la catena è ergodica e quindi, per n grande, π n, la densità al tempo n di X n, approssima v. La matrice P non è unica ma se ne può costruire una per ogni matrice stocastica Q irriducibile e simmetrica di dimensione pari allo spazio S. Fissata Q il generico elemento p ij di P è per i j { q ij se v i v j p ij = v q j ij v i se v i > v j ; e naturalmente p ii = 1 j i Per simulare una catena di Markov con la matrice di transizione P definita nell algoritmo di Metropolis è utile la seguente osservazione, che suggerisce p ij. 74
75 come costruire la catena al passo n + 1 sapendo che al passo n si trova in i. Si assuma che siano k i possibili stati della catena. Sia Y una variabile di densità (q i1 q i2..., q ik ) e sia U una variabile definita sullo stesso spazio di probabilità, uniforme in [, 1] e indipendente da Y. Allora la variabile è tale che qualsiasi sia j X = Y I [, v Y vi ) (U) + i I [ v Y vi,1] (U) P(X = j) = p ij ovvero ha densità (p i1 p i2..., p ik ). Infatti qualsiasi sia j i ( P(X = j) = P Y = j, U < v ) ( Y = P Y = j, U < v ) j v i v ( i = P(Y = j)p U < v ) ( j = q ij P U < v ) j. v i v i Ricordando che per definizione di legge uniforme ( P U < v ) j = v i { 1 se v i v j v j v i se v i > v j, si ottiene il risultato. Così, se j = i, P(X = i) = 1 j i p ij = p ii. Dunque la procedura per simulare il valore al passo (n+1)-mo della catena se al passo n-mo si trova in i, è la seguente: si genera una variabile di densità (q i1 q i2..., q ik ); se si ottiene i si lascia la catena in i; se si ottiene un valore j diverso da i con v j v i si sposta la catena in j; se invece il valore j è tale che v j < v i, si simula una uniforme in [, 1] e se questa è più piccola di v j v i si sposta la catena in j, altrimenti la si lascia in i. Esercizio 19 Sia (X n ) n una catena di Markov su S = {1, 2, 3, 4} con matrice di transizione i) Determinare il carattere degli stati della catena. ii) Calcolare le eventuali misure invarianti. iii) Calcolare lim n π n (i), i S nel caso π (1) + π (3) = 1. 75
76 Soluzione i) Lo spazio degli stati S = {1, 2, 3, 4} si decompone nell unione disgiunta della classe transiente T = {2} e delle due classi irriducibili persistenti positive C 1 = {1, 3} e C 1 = {4}; dunque 2 è l unico stato transiente e 4 è stato assorbente. ii) Le misure invarianti sono tutte e sole le combinazioni convesse delle misure invarianti v (1) e v (2) per la dinamica ristretta rispettivamente a C 1 e C 2, ovvero sono tutte e solo quelle della forma δv (1) +(1 δ)v (2) con δ [, 1]. Inoltre v (1) = (x 1,, x 3, ) dove { x 1 = 1 2 x 1 + x 3 x 3 = 1 2 x 1, da cui v (1) = ( 2 3,, 1 3, ). Infine facilmente si ricava v(2) = (,,, 1). iii) Se π (1)+π (3) = 1, poiché {1, 3} è classe chiusa, qualsiasi sia n vale π n (2) =, π n (4) = e pertanto lim n π n (2) = lim n π n (4) =. Per calcolare lim n π n (1) e lim n π n (3), osserviamo che la catena ristretta a C 1 = {1, 3} ha matrice di transizione regolare e quindi è ergodica; dunque, qualsiasi sia la densità iniziale π che soddisfa π (1) + π (3) = 1, le densità al crescere di n convergono a v (1) 1, v(1) 3, quindi lim n π n(1) = 2 3 Esercizio 2 lim π n(3) = 1 n 3. Si consideri una catena di Markov su N avente matrice di transizione data p i i+1 = p e p i = 1 p dove < p < 1. Determinare l unica misura invariante della catena. Si tratta di una misura di probabilità nota? Determinare il periodo della catena. La catena è ergodica? Soluzione La matrice di transizione della catena è 1 p p p p p p P = p... p
77 e quindi la misura invariante risolve il sistema x = i N (1 p)x i x i = px i 1, i 1 i N x i = 1 x i. Si ricava x = (1 p) i N x i = 1 p e x i = px i 1 = p 2 x i 2 =... = p i x = p i (1 p), i 1. Dunque l unica misura invariante è v i = p i (1 p), i e si tratta della densità di una geometrica trasformata di parametro 1 p, cioè la densità del numero di fallimenti prima del primo successo in uno schema di Bernoulli infinito di parametro 1 p. La catena che è irriducibile è aperiodica come si deduce dal fatto che p >. Dall unicità della misura invariante segue che esiste un unica classe persistente positiva che per l irriducibilità è tutto lo spazio di stato; si sa che una catena irriducibile persistente positiva e aperiodica è ergodica. Un altro procedimento consiste nel dimostrare direttamente che qualsiasi sia i lim n p(n) ij = p j (1 p). e questo segue subito dopo aver calcolato che per qualsiasi siano i, j, per ogni n j + 1 vale p (n) ij = p j (1 p) n j 1 h= ( n j 1 h ) p h (1 p) n j 1 h = p j (1 p). Infatti per arrivare a j in n j +1 passi occorre naturalmente passare per se i j e lo stesso vale se i < j, poiché dall ipotesi n j +1 segue n > j i. Dunque: inizialmente n j 1 passi qualsiasi (per n = j + 1 nessuno), un passo per andare a e i successivi ed ultimi j passi per arrivare in j Schema di dimostrazione del teorema di esistenza della misura invariante per catene irriducibili persistenti positive Si ricorda che v è invariante se e solo se si ha qualsiasi sia j e qualsiasi sia k v j = i S v i p (k) ij. 77
78 Dunque v invariante implica che per ogni n v j = 1 n = i S n v i p (k) ij k=1 i S ( 1 n n k=1 ) p (k) ij v i e usando l uguaglianza E i [N n (j)] = n ottiene v j = E i [N n (j)] v i = n i S i S k=1 p(k) ij (vedi paragrafi 18 e 19) si [ Nn (j) ] E i v i. n Si osserva che la variabile aleatoria N n(j) n = 1 n n k=1 I {j}(x k ) rappresenta la frequenza relativa di visita allo stato j su n tempi. Passando al limite in n nell uguaglianza precedente si ottiene v j = i S lim n E i [ Nn (j) n ] v i, dove il passaggio al limite sotto il segno di serie, ovvio nel caso S finito, è lecito in generale. Si ottiene l esistenza e la forma dell unica misura invariante per catene persistenti posistive usando il fatto che per le catene irriducibili persistenti, qualsiasi sia i vale [ lim E Nn (j) ] i = n n { 1 E j [τ j ], se E j[τ j ] < +, altrimenti (vedi per un idea della dimostrazione il paragrafo successivo e per una dimostrazione completa [3]) Approssimazione della misura invariante con la distribuzione empirica Nel paragrafo precedente [ si ] identifica la misura invariante utilizzando il valore del lim n E Nn (j) i n. Questo valore si può derivare dal risultato seguente: se (X n ) n è catena irriducibile persistente allora qualsiasi sia j con probabilità 1, ovvero a meno di un insieme trascurabile di traiettorie, N n (j) lim = n n { 1 E j [τ j ], se E j[τ j ] < +, altrimenti. 78
79 È intuitivo: il rapporto tra n e il numero dei passaggi per j fino al tempo n è vicino, quando n è grande, alla durata media degli intertempi tra un passaggio e l altro per j. Questo fatto ha la conseguenza applicativa seguente: non potendo calcolare facilmente la misura invariante (p.es. perché è grande il numero degli stati), nel caso persistente positivo, se ne può approssimare il valore in uno stato j con il valore aleatorio, per n grande, della frequenza relativa delle visite a j su n tempi, ovvero con la distribuzione empirica nello stato j. Inoltre controllando se il valore di frequenza relativa dei passaggi per un qualsiasi stato fissato si avvicina a per n grande, si può dedurre la persistenza nulla della catena. Viceversa la frequenza di visita ad uno stato fissato si può approssimare a regime con il valore della misura invariante nello stato. Si dà un idea qui della dimostrazione dell enunciato nel caso in cui la catena parta da j: secondo le notazioni già introdotte, si dimostra che l enunciato vale con probabilità 1 quando la densità iniziale è la delta di Dirac in j. A tale scopo si utilizza la legge forte dei grandi numeri nella formulazione seguente: Legge forte dei grandi numeri Siano X 1, X 2,..., X k,... variabili aleatorie definite sullo stesso spazio di probabilità i.i.d. e di valore medio finito m. Allora con probabilità 1 X 1 + X X k lim k k = m Se X k qualsiasi sia k e E[X k ] = +, allora con probabilità 1 X 1 + X X k lim k k = + Si utilizza il risultato precedente applicato alle variabili seguenti: definite da dove τ 1 j, τ 2 j, τ k j,... τ k j = T k j T k 1 j, k 1 T j =, T k j = min{n 1 t.c. N n (j) = k}, k 1 e quindi τj k è il tempo che intercorre tra la k 1-ma e la k ma visita a j e in particolare τj 1 = T j 1 = τ j. Si osservi che per l ipotesi di persistenza Tj k è finito con probabilità 1. Le variabili aleatorie τj k sono indipendenti e tutte con la stessa legge di τ j e dunque per la legge dei grandi numeri con probabilità 1 τj 1 lim + τ j τ { j k E j [τ j ], se E j [τ j ] < + = k k +, altrimenti. 79
80 Allora, poiché τj 1 + τ j τ j k k con probabilità 1 vale Inoltre è chiaro che Tj k lim k k = = T j 1 + (T j 2 T j 1) (T j k T j k 1 ) = T j k k k, { E j [τ j ], se E j [τ j ] < + T Nn(j) j +, altrimenti n < T Nn(j)+1 j, poiché la scrittura T Nn(j) j indica la variabile tempo dell ultima visita a j prima del tempo n (n incluso), e quindi qualsiasi sia n τ j (altrimenti N n (j) = ) T Nn(j) j N n (j) n N n (j) < T N n(j)+1 j N n (j). Essendo j persistente con probabilità 1 T Nn(j) j lim n N n (j) = lim n lim N n(j) = + n e quindi si può dedurre da quanto sopra che con probabilità 1 { E j [τ j ], se E j [τ j ] < + T Nn(j)+1 j N n (j) = +, altrimenti. Il teorema del confronto per le successioni di variabili reali conclude la dimostrazione Esercizi di riepilogo 1. Sono date due urne e 2d biglie di cui d nere e d bianche. Inizialmente d biglie scelte a caso sono collocate nell urna 1 e le restanti d biglie sono collocate nell urna 2. Ad ogni istante una biglia è scelta a caso da ciascuna delle due urne ed è spostata nell altra urna. Sia X il numero iniziale delle biglie nere nell urna 1 e X n il numero delle biglie nere nell urna 1 al tempo n. Trovare le probabilità di transizione della catena di Markov (X n ) n. 2. Sia P =
81 matrice di transizione su S = {1, 2, 3, 4, 5, 6}. i) Determinare il carattere degli stati. ii) Dimostrare che muovendosi dallo stato 4 con la dinamica descritta da P la probabilità di raggiungere lo stato 6 in un tempo finito è almeno 3 4. iii) Calcolare la probabilità di raggiungere lo stato 1 partendo dallo stato 2 in un tempo finito, ρ 21, e dare un interpretazione probabilistica del numero 1 ρ 21. iv) Calcolare le eventuali misure invarianti della catena. v) Determinare la media del tempo di ritorno nello stato 4. vi) Per la catena con matrice di transizione P e densità iniziale uniforme su {4, 5, 6}, calcolare la probabilità degli eventi A = {X 2 = 4}, B = {X 2 = 4, X 3 = 5} e C = {X 1 = 4, X 11 = 2}. In che modo si potrebbe procedere per calcolare in modo approssimato la probabilità dell evento D = {X 5 = 5}? E quanto vale la probabilità dell evento E = {X 5 = 2}? 3. Calcola la probabilità di raggiungere in un tempo finito lo stato 3 partendo dallo stato 1, per la catena con spazio degli stati S = {1, 2, 3, 4} e con matrice di transizione P = E se la densità iniziale fosse quella uniforme? 4. Un uomo possiede 2 ombrelli e ne prende uno al mattino per andare in ufficio e a sera quando torna, naturalmente se piove e se ce n è uno disponibile. Assumi che ogni volta la probabilità che piova sia p. Indica con (X n ) n 1 la catena di Markov che conta gli ombrelli disponibili prima dell n-mo tragitto (senza distinguere tra tragitti di andata e ritorno). i) Scrivi la matrice di transizione della catena e determina il carattere degli stati. ii) Con che probabilità l uomo non ha ombrelli disponibili prima del secondo, del terzo e del quarto tragitto se si assume che prima del primo tragitto li abbia entrambi disponibili (la legge iniziale, ovvero la legge di X 1, è la delta di Dirac in 2)? 81
82 iii) Dopo quanto tempo in media, se si assume che prima del primo tragitto abbia entrambi gli ombrelli disponibili, l uomo non ha ombrelli disponibili? iv) Calcola le eventuali misure invarianti. Cosa puoi dire sul comportamento di p (n) ij per n grande? v) Come approssimeresti la probabilità con cui l uomo si bagna al 96-mo tragitto? 5. Un apparecchiatura di età j all inizio della giornata si guasta durante la giornata con probabilità p j e in tal caso è sostituita da un apparecchiatura identica ma nuova, che entra in funzione all inizio della giornata successiva. L apparecchiatura è sostituita anche quando è troppo vecchia e si conviene che questo corrisponda all età N (per età di un apparecchiatura si intende qui il numero delle giornate intere (24 ore) in cui l apparecchiatura ha funzionato). Per n, si indica con X n la v.a. che conta l età dell apparecchiatura funzionante all inizio della n + 1-ma giornata. i) Scrivi la matrice di transizione della catena di Markov (X n ) n e determina il carattere degli stati. ii) Se al tempo n = l apparecchiatura è nuova, con che probabilità è nuova al tempo n = 2? iii) Calcola, nell ipotesi del punto precedente, con che probabilità l apparecchiatura installata inizialmente viene utilizzata al massimo, ovvero sostituita per vecchiaia e non per guasto. iv) Calcola le eventuali misure invarianti. Cosa puoi dire sul comportamento di p (n) ij per n grande? v) Ogni quanto tempo in media avviene una sostituzione? 6. È assegnata la catena (X n ) n con matrice di transizione e misura iniziale π (1) = P = i) Studiare il comportamento della legge di X n per n grande. ii) Calcolare in modo approssimato P(X 82 = 3, X 81 = 4) e P(X 6 = 1, X 58 = 3). 82
83 Soluzioni 1. Si vuole calcolare P(X n+1 = j X n = i) per n, i, j S = {, 1,..., d}. Indicati con E e F rispettivamente gli eventi {la biglia scelta a caso dall urna 1 è nera} e {la biglia scelta a caso dall urna 2 è nera}, gli eventi E e F sono indipendenti condizionatamente al sapere il numero delle biglie nere nell urna 1. Inoltre se nell urna 1 ci sono i biglie la probabilità di E è i d i d e quella di F è d. Si calcola P(X n+1 = i + 1 X n = i) = ( d i P(E c F X n = i) = P(E c X n = i)p(f X n = i) = d P(X n+1 = i 1 X n = i) = ( i ) 2. P(E F c X n = i) = P(E X n = i)p(f c X n = i) = d Poiché se j i 1, i, i + 1 si ha P(X n+1 = j X n = i) =, segue P(X n+1 = i X n = i) = 1 (d i)2 d 2 (i)2 2i(d i) = d2 d 2. Dunque si tratta di catena omogenea, catena di nascita e morte con p i = (d i)2, r d 2 i = 2i(d i) e q d 2 i = i2. Si osservi che in particolare p d 2 = 1 e q d = 1, ovvero le barriere sono riflettenti. ) 2 2. i) 1 è stato assorbente, poiché comunica solo con sé stesso; 2 e 3 sono transienti, infatti p.es. 2 1 ma 2 1 e 3 6 ma 6 3; {4,5,6} costituiscono una classe irriducibile finita e dunque costituita da stati persistenti positivi. ii) Si tratta di dimostrare la disuguaglianza ρ Per definizione ρ 46 P 4 (X 1 = 6) + P 4 (X 1 6, X 2 = 6) e, poiché P 4 (X 1 6, X 2 = 6) = P 4 (X 1 = 4, X 2 = 6) + P 4 (X 1 = 5, X 2 = 6), segue ρ 46 p 46 + p 44 p 46 + p 45 p 56 = = 3 4. iii) Poiché 1 è stato assorbente, ρ 21 coincide con la probabilità di assorbimento λ {1} 2 nella classe {1} partendo dallo stato 2. Occorre dunque risolvere il sistema x 1 = x x 2 x 1 = 1 5 x x 2. 83
84 Facilmente si calcola x 1 = λ {1} 2 = 3 5 e x 2 = λ {1} 3 = 1 5. Indicata con C la classe di tutti gli stati persistenti, poiché gli stati transienti sono in numero finito, si ha e quindi 1 = P(τ C < + ) = λ {1} 2 + λ {4,5,6} 2 1 ρ 21 = 1 λ {1} 2 = λ {4,5,6} 2, ovvero a parole 1 ρ 21 è la probabilità di assorbimento nella classe {4, 5, 6} partendo da 2. iv) La catena è finita e quindi le misure invarianti sono tutte e sole le combinazioni convesse delle misure invarianti sulle classi irriducibili. Dunque una qualsiasi misura invariante è della forma v = αv (1) + (1 α)v (2) con α [, 1], dove v (1) = (1 ) e v (2) si calcola risolvendo il sistema x 1 + x 2 + x 3 + x 4 + x 5 + x 6 = 1 Si ottiene v (2) = x i =, i = 2, 3 x 4 = 1 6 x x x 6 x 5 = 1 3 x 4 x 6 = 1 2 x x x 6 x i. ( ) 2 3. v) Poiché 4 è nella classe irriducibile {4, 5, 6} possiamo considerare la dinamica ristretta a questa classe (la classe è chiusa!). È noto che per una catena persistente positiva la media del tempo di primo ritorno in uno stato è il reciproco del valore della misura invariante nello stato. La catena ristretta a {4, 5, 6} è persistente positiva (in quanto irriducibile ) e finita) e la sua misura invariante è (v (2) 4 v (2) 5 v (2) 6 ) = e quindi E 4 [τ 4 ] = 4. ( 1 4 vi) P(A) = π 2 (4) = i S π (i)p (2) i4 = 1 3 (p(2) 44 + p(2) 54 + p(2) 64 ). Per calcolare le probabilità di transizione in più passi occorre calcolare le potenze della matrice P. Per rendere più agevole il conto si osservi che le probabilità di transizione in n passi all interno della classe irriducibile {4, 5, 6}, coincidono con gli elementi della potenza n-ma della sottomatrice ottenuta cancellando prima, seconda e terza 84
85 riga e colonna della matrice P, ovvero della matrice Si ottiene p (2) 44 = 23 72, p(2) 54 = 5 24, p(2) 64 = , da cui P(A) = 432. Inoltre si ha P(B) = p 45 P(A) = P(A) = 1296 e infine P(C) = π 1 (4)p 42 = poiché, essendo la classe {4, 5, 6} chiusa, si ha p 42 =. La probabilità dell evento {X 5 = 5} si può approssimare con il valore in 5 della misura invariante della dinamica ristretta alla classe {4, 5, 6}, cioè 1 12 ; infatti la dinamica ristretta alla classe {4, 5, 6} è ergodica poichè la sua matrice di transizione è regolare essendo verificato il criterio sufficiente (almeno un elemento sulla diagonale positivo). Si noti invece che la probabilità dell evento {X 5 = 2} è esattamente in quanto coincide con i S π (i) p (5) 1 3 (p(5) 42 p(5) 52 p(5) 62.. i2 = ) e per definizione di classe chiusa p(5) i2 =, i = 4, 5, Gli stati 3 e 4 sono assorbenti, mentre gli stati 1 e 2 sono transienti poiché p.es. entrambi comunicano con 3 ma 3 non comunica con essi. Si tratta dunque di calcolare la probabilità di assorbimento in {3} partendo da 1, cioè il valore λ {3} 1 che risolve insieme a λ {3} 2 (probabilità di assorbimento in {3} partendo da 2) il sistema { λ {3} 1 = λ{3} 2 λ {3} 2 = λ{3} 1. Si trova λ {3} 1 = 5 6, λ{3} 2 = 2 3. Se la densità iniziale fosse uniforme, poiché vale l uguaglianza P(τ 3 < + ) = i π (i)ρ i3, tenendo conto del risultato precedente e del fatto che essendo 3, 4 assorbenti le probabilità di raggiungere 3 in tempo finito partendo da 3 e da 4 sono rispettivamente 1 e, si ha che la probabilità richiesta è 1 4 ( ) =
86 4. i) La matrice di transizione è 1 P = q p, q p con q = 1 p. Tutti gli stati sono comunicanti e quindi, poiché lo spazio degli stati è finito, persistenti positivi. ii) Si assume che π 1 (2) = 1 e quindi π 1 (1) = π 1 () =. evidente che la probabilità dell evento { ombrelli disponibili prima del secondo tragitto} è q e infatti in formule Allora è π 2 () = i π 1 (i)p i = p 2 = q. Analogamente per calcolare P( ombrelli disponibili prima del terzo tragitto) si procede così π 3 () = i π 1 (i)p (2) i = p(2) 2 = i p 2i p i =. E infine per calcolare P( ombrelli disponibili prima del quarto tragitto) π 4 () = i = i π 1 (i)p (3) i = q 2 + p 2 q. = p(3) 2 = i p 2i p ij p j = q j j p 2i p (2) i p j p j + p j p 1j p j iii) Rispondere a questo punto equivale a rispondere alla domanda: qual è il tempo medio di assorbimento in partendo da 2 per la catena corrispondente alla matrice di transizione 1 q p, q p ovvero per la dinamica modificata rendendo assorbente lo stato e quindi la classe {} coincidente con la classe di tutti gli stati persistenti (in tal caso infatti 1 e 2 comunicano con ma non comunica con essi e quindi sono transienti). La risposta è quindi x 2 dove x 1, x 2 risolvono il sistema dei tempi medi di assorbimento { x 1 = 1 + px 2 + qx 1 x 2 = 1 + px 1, 86
87 che risolto dà x 1 = 1+p p p 2 e x 2 = 2p p p 2. iv) Poiché la catena è persistente positiva esiste un unica misura invariante che si ottiene risolvendo il sistema v = qv 1 v 1 = qv 1 + pv 2 v 2 = v + pv 1 v + v 1 + v 2 = 1 che risolto dà v = 1 p 3 p e v 1 = v 2 = 1 3 p. La catena soddisfa il criterio sufficiente per la regolarità (essere irriducibile e avere un elemento non nullo sulla diagonale di P) e quindi è ergodica e dunque lim n p (n) ij = v j indipendentemente da i. ( v) P(si bagna al 96 mo tragitto) = P {piove al 96 mo tragitto} ) {X 96 = } = pp(x 96 = ) e questo per l indipendenza tra gli eventi. Inoltre per l ergodicità si approssima P(X 96 = ) con v = 1 p 3 p. 5. i) Lo spazio degli stati è S = {, 1,..., N} e la matrice di transizione è p q... p 1 q 1... P = p 2 q , p N 1... q N con q j = 1 p j. Tutti gli stati sono comunicanti e quindi, poiché lo spazio degli stati è finito, persistenti positivi. ii) Si assume che π () = 1 e quindi π (1) =... = π (N) = e dunque si calcola π 2 () = i π (i)p (2) i = p(2) = i p i p i = p 2 + p 1 q. iii) Indicati con τ e τ N i tempi di primo raggiungimento degli stati e N, rispondere a questo punto equivale a calcolare P (τ N < τ ) e poiché P (τ N < τ ) = P (τ N < τ, X 1 = 1) e l ultimo membro coincide con P (τ N < τ X 1 = 1)P (X 1 = 1) = P 1 (τ N < τ )q, 87
88 occorre calcolare P 1 (τ N < τ ). L ultima probabilità coincide con la probabilità di assorbimento in N partendo da 1 per la catena corrispondente alla matrice di transizione 1... p 1 q 1... P = p 2 q , p N 1... q N ovvero per la dinamica modificata rendendo assorbenti gli stati e N. La risposta è quindi x 1 dove x 1, x 2..., x N 1 risolvono il seguente sistema delle probabilità di assorbimento in N x 1 = q 1 x 2 x 2 = q 2 x x N 1 = q N 1 Risolvendo si ottiene x j = q j q j+1... q N 1 e in particolare x 1 = q 1 q 2... q N 1. iv) Poiché la catena è persistente positiva esiste un unica misura invariante che si ottiene risolvendo il sistema v = p v + p 1 v p N 1 v N 1 + v N v 1 = q v v 2 = q 1 v v N = q N 1 v N 1 v + v 1 + v v N = 1 v A ritroso dalla penultima equazione si ricava v j = N q q 1 q 2...q j 1, per j =,..., N 1 e sostituendo questi valori nell ultima equazione si q calcola v N = q 1 q 2...q N 1 1+q +q q q q 1 q 2...q N 1. Infine sostituendo il valore ottenuto per v N nell espressione del generico v j si trova v j = q q 1 q 2... q j q + q q q q 1 q 2... q N 1, j = 1,..., N, v = q + q q q q 1 q 2... q N 1. La catena soddisfa il criterio sufficiente per la regolarità (essere irriducibile e avere un elemento non nullo sulla diagonale di P) e quindi è ergodica e dunque lim n p (n) ij = v j indipendentemente da i. 88
89 v) Occorre calcolare il tempo medio di ritorno nello stato che in formule è E [τ ]. Si sa che nelle catene persistenti positive questo valore coincide con v 1 e dunque in questo caso con 1 + q + q q q q 1 q 2... q N La catena è irriducibile e quindi il periodo è lo stesso per ogni stato ed è facile verificare che è 2. Inoltre per π tale che π (1) = 1 si ha qualsiasi sia n i) Si ha π 2n+1 (1) = π 2n+1 (3) = π 2n+2 (2) = π 2n+2 (4) =. π 2n+1 (2) = 1 2 π 2n(1) + π 2n (3) = 1 2 π 2n(1) + ( ) 1 π 2n (1) = π 2n(1) e, essendo π 2n (1) = 1 2 π 2n 1(2) qualsiasi sia n 1, si ottiene qualsiasi sia n 1 π 2n+1 (2) = π 2n 1(2). Dunque i valori della densità in i = 2 sui tempi dispari costituiscono una successione per ricorrenza della forma { a m+1 = a m a 1 = 1 2 Pertanto il limite, se esiste, risolve L = 1 1 4L e non può che essere quindi L = 4 5. Si può inoltre verificare che a m per m dispari è monotona crescente e per m pari è monotona decrescente e che entrambe le sottosuccessioni convergono a L = 4 5. Così resta dimostrato che lim n π 2n+1 (2) = 4 5 e di conseguenza lim n π 2n+1 (4) = 1 5. Inoltre poichè π 2n (1) = 1 2 π 2n 1(2) si ricava lim n π 2n (1) = 2 5 e di conseguenza lim n π 2n (3) = 3 5. In definitiva la densità di X n quando n è grande è approssimata se n è dispari da ( ) e se n è pari da ( ). Si può verificare che ( ) e ( ) sono le misure invarianti per la dinamica in due passi ristretta rispettivamente a {2, 4} e {1, 3}. Infatti la dinamica in due passi e multipli di due passi su {2, 4} è data dalla matrice ( 3 ) e il sistema soddisfatto dalla misura invariante è x 1 = 3 4 x 1 + x 2 x 2 = 1 4 x 1 x 1 + x 2 = 1 ; 89
90 mentre la dinamica in due passi e multipli di due passi su {1, 3} è data dalla matrice ( 1 ) e il sistema soddisfatto dalla misura invariante è x 1 = 1 4 x x 2 x 2 = 3 4 x x 2 x 1 + x 2 = 1. ii) 1 2 P(X 82 = 3, X 81 = 4) = π 81 (4)p = P(X 6 = 1, X 58 = 3) = π 58 (3)p ( 31 2) = Processo di Poisson 2.1 Definizione Tra i processi stocastici a tempo continuo a valori in N, ovvero nell insieme delle famiglie di v.a. definite su di uno stesso spazio di probabilità, a valori in N ed indicizzate da un parametro reale continuo non negativo, interpretato come il tempo, si chiamano processi di conteggio quelli che hanno traiettorie uscenti dallo, non decrescenti, costanti a tratti e con salti di ampiezza unitaria. Sia (X k, k 1) una famiglia di v.a. indipendenti (dunque in particolare definite sullo stesso spazio di probabilità) di legge esponenziale di parametro λ. Posto n S := S n := X k, n 1 si costruisce il processo di Poisson (N(t)) t mediante l uguaglianza k=1 N(t) := max(n, S n t). Si deve osservare che dalla definizione segue che N() = e che ogni traiettoria del processo è costante a tratti, non decrescente, continua da destra ed ha salti unitari. Dunque il processo di Poisson è processo di conteggio. Se si immagina che la v.a.x k sia il tempo aleatorio che intercorre tra il k-mo ed il k + 1-mo evento di un determinato flusso di eventi, allora S n rappresenta il tempo aleatorio in cui si verifica l n mo evento e la v.a.n(t) conta il numero degli eventi occorsi fino al tempo t incluso. Dunque la v.a. N(t) può assumere ogni valore naturale e se ne determina facilmente la densità 9
91 di probabilità a partire dall assunzione sulla legge degli intertempi di salto. Fissato k N, per calcolare P(N(t) = k) il punto di partenza sono le due semplici uguaglianze tra eventi e (N(t) = k) = (N(t) k)\(n(t) k + 1) (N(t) k) = (S k t). Infatti insieme forniscono la terza uguaglianza (N(t) = k) = (S k t)\(s k+1 t) ovvero, passando alle probabilità, l uguaglianza P(N(t) = k) = P(S k t) P(S k+1 t). L ultima uguaglianza riduce il calcolo della densità di N(t) alla conoscenza della funzione di ripartizione dei tempi S n, n 1. A questo proposito occorre ricordare i due fatti seguenti noti dai corsi di probabilità elementare. In primo luogo, se X 1, X 2,..., X m sono v.a. indipendenti rispettivamente di legge Γ(α 1, λ), Γ(α 2, λ),..., Γ(α m, λ), allora X 1 + X X m Γ(α 1 + α α m, λ). Da cui ricordando che la legge esponenziale di parametro λ è la legge gamma di parametri (1, λ) e che le leggi gamma con il primo parametro intero prendono il nome di Erlang (così Γ(m, λ) si chiama anche Erlang di parametri (m, λ) e si scrive Erl(m, λ)), segue che se X 1, X 2,..., X m sono v.a. i.i.d. di legge esp(λ), allora X 1 + X X m Erl(m, λ). Inoltre, la funzione di ripartizione di una v.a.z Erl(m, λ) si calcola con procedura ricorsiva integrando per parti la funzione densità corrispondente, x λm (m 1)! xm 1 e λx fino ad ottenere m 1 P(Z t) = 1 i= (λt) i e λt. i! Da quanto detto segue che la legge di S n, tempo di occorrenza dell n mo evento di un processo di Poisson di parametro λ, è una Erlang di parametri (n, λ) e in particolare n 1 P(S n t) = 1 91 i= (λt) i e λt. i!
92 Pertanto, andando a sostituire le corrispondenti espressioni nella formula per il calcolo della densità di N(t), si trova k 1 (λt) i P(N(t) = k) = 1 e λt 1 + i! i= k (λt) i e λt = (λt)k e λt. i! k! In conclusione si è ottenuto che il processo di Poisson al tempo t ha legge di Poisson di parametro λt, ovvero, fissato t, vale N(t) Poiss(λt). Così, ricordando il significato del parametro della legge esponenziale e del parametro della legge Poisson, si vede che il parametro λ del processo di Poisson è al tempo stesso il reciproco del tempo medio di attesa tra un evento e l altro e il numero medio degli eventi che si verificano nell intervallo di tempo unitario. Dunque per esempio se λ cresce allora diminuisce il tempo medio tra un evento e l altro e cresce la frequenza degli eventi. 2.2 Perdita di memoria Per perdita di memoria del processo di Poisson di parametro λ si intende la proprietà per la quale, fissato un qualsiasi tempo t, il tempo che occorre attendere a partire da t affinché si verifichi un evento è v.a. che ha legge esponenziale di parametro λ e che è indipendente dai successivi intertempi del flusso. Fissato t >, si introduce la v.a. γ t definita da i= γ t := S N(t)+1 t e si dimostra che qualsiasi sia x numero reale positivo vale P(γ t x) = 1 e λx. Il punto di partenza per la dimostrazione è l uguaglianza tra eventi (γ t > x) = + n=( Sn t, S n+1 t > x), dalla quale, tenendo conto che gli eventi dell unione sono disgiunti, si ricava passando alle probabilità P(γ t > x) = + n= P ( S n t, S n+1 t > x). Il primo termine della somma, ovvero quello corrispondente all indice n =, coincide con P ( S t, S 1 t > x) = P(S 1 t > x) = P(S 1 > t + x) = P(X 1 > t + x) = e λ(t+x). 92
93 Il termine generico per n 1 si può invece riscrivere così P ( S n t, S n + X n+1 > t + x) e, condizionando al valore di S n Erl(n, λ), così + P ( S n t, S n + X n+1 > t + x S n = y) (n 1)! yn 1 e λy dy. L espressione precedente coincide con t P ( X n+1 > t + x y S n = y) (n 1)! yn 1 e λy dy e ancora, per l ipotesi di indipendenza di X n+1 da X 1, X 2,..., X n e quindi da S n, con t λ n λ n λ n P ( X n+1 > t + x y) (n 1)! yn 1 e λy dy. Infine, poiché X n+1 ha densità esponenziale di parametro λ e t + x y è positivo, l integrale precedente si riscrive In definitiva t e λ(t+x y) P(γ t > x) =e λ(t+x) + n 1 e λ(t+x) + e λ(t+x) + t t λ n (n 1)! yn 1 e λy dy. t e λ(t+x y) e λ(t+x y) n 1 e λ(t+x y) λ n 1 λ n (n 1)! yn 1 e λy dy = λ n (n 1)! yn 1 e λy dy = λ n 1 (n 1)! yn 1 e λy dy. Con il cambio di indice n 1 in m si trasforma la sommatoria in e quindi si conclude m P(γ t > x) = e λ(t+x) + λ m m! ym = e λy t λe λ(t+x y) dy = e λx. Come applicazione di quanto esposto si considera il seguente problema. 93
94 Problema del taxi Una vettura è pronta a svolgere il servizio ad una fermata dei taxi. Si assume che i passeggeri in arrivo alla fermata del taxi seguano un flusso di Poisson e che in media a quella fermata arrivino 2 passeggeri all ora. Le vetture partono solo a pieno carico, ovvero con 4 persone, o 1 minuti dopo l arrivo del primo passeggero. a) Con quale probabilità il primo passeggero aspetta 1 minuti? b) Se altri 2 passeggeri arrivano dopo 8 minuti, con quale probabilità il taxi non parte a pieno carico? Soluzione a) Sia (N(t)) t il processo che conta i passeggeri arrivati dopo il primo, allora, quando il tempo è calcolato in minuti, N(t) Poiss(t/3) e gli intertempi tra un arrivo e l altro sono esponenziali indipendenti di parametro 1/3. Per rispondere alla domanda bisogna calcolare con quale probabilità arrivano non più di 2 clienti nei successivi 1 minuti, ovvero P(N(1) 2) = 2 h= ( 1 3 ) h e 1/3. h! b) Per rispondere alla seconda domanda si utilizza la proprietà di perdita di memoria del Poisson, perché la probabilità richiesta coincide con la probabilità che tra l ottavo ed il decimo minuto non vi siano arrivi. Dunque, indicato con γ 8 il tempo occorrente dopo l ottavo minuto (a partire dall arrivo del primo passeggero) per vedere arrivare un altro passeggero, bisogna calcolare P(γ 8 > 2) e, poiché per la perdita di memoria γ 8 esp(1/3), il risultato è e 2/3. Si può dimostrare che gli incrementi del processo di Poisson di parametro λ su intervalli disgiunti sono v.a. indipendenti e che, ciascun incremento ha legge di Poisson di parametro pari al prodotto del parametro λ per l ampiezza dell intervallo. Qui si fa vedere che P(N(s) = n, N(s + t) N(s) = k) = (λs)n λs (λt)k e e λt. n! k! Questo dimostra al tempo stesso l indipendenza degli incrementi su due intervalli disgiunti adiacenti e l affermazione sulla legge di probabilità di un generico incremento. L uguaglianza tra eventi (N(s) = n, N(s + t) N(s) = k) = (N(s) = n, N(s + t) N(s) k) \ (N(s) = n, N(s + t) N(s) k 1) riduce la dimostrazione a quella della relazione P(N(s) = n, N(s + t) N(s) k) = (λs)n e λs n! 94 k (λt) i e λt. i! i=
95 Ora P(N(s) = n, N(s + t) N(s) k) = P(S n s < S n+1, S n+1 + X n X n+k s + t) = P(S n s, S n + X n+1 > s, S n + X n+1 + Z s + t) ricordando che S n+1 = S n +X n+1 e indicando con Z la v.a.x n , X n+k. Utilizzando due volte la probabilità condizionata, in particolare condizionando la prima volta al valore di S n Erl(n, λ) e la seconda volta al valore di X n+1 esp(λ) e ricordando che le v.a. S n, X n+1 e Z sono indipendenti, si ottiene P(N(s) = n, N(s + t) N(s) k) = s s P(y + X n+1 > s, y + X n+1 + Z > s + t) (n 1)! yn 1 e λy dy = ( + ) P(y + x + Z > s + t)λe λx dx s y λ n λ n (n 1)! yn 1 e λy dy Si noti che nel primo passaggio è y < s e questo insieme alla condizione y + X n+1 > s implica che sia x > s y >. Poiché Z ha legge Erl(k, λ), se s + t y x ovvero x s y + t allora mentre se x < s y + t allora P(y + x + Z > s + t) = P(y + x + Z > s + t) = 1, k 1 i= (λ(s + t y x)) i e λ(s+t y x). i! Sostituendo questi valori nell ultimo integrale si ottiene s s ( s y+t k 1 (λ(s + t y x)) i s y ( + s y+t i= i! ) λ λe λx n y n 1 dx (n 1)! e λy dy ) λ e λ(s+t y x) λe λx n y n 1 dx (n 1)! e λy dy+ espressione che, effettuate nel primo addendo le dovute semplificazioni e calcolato nel secondo addendo l integrale in x, diventa s s ( s y+t k 1 (λ(s + t y x)) i s y i= i! e λ(s y+t) λn y n 1 (n 1)! e λy dy. ) λ e λ(s+t) n y n 1 λ dx (n 1)! dy+ 95
96 Per completare il calcolo del primo addendo è sufficiente scambiare sommatoria ed integrale e quindi integrare prima in x e poi in y. Si ottengono così facilmente le uguaglianze seguenti e λ(s+t) s e λ(s+t) ( k 1 i= λ n s (n 1)! k 1 e λ(s+t) e λ(s+t) (λs) n n! i= λ i+1 s y+t i! s y y n 1 dy = (λt) i+1 λ n (i + 1)! (n 1)! k (λt) i (λs) n i=1 e λ(s) i! n! k (λt) i e λt. i! i= La dimostrazione è conclusa. s ) λ (s + t y x) i n y n 1 dx (n 1)! dy+ λ(s+t) (λs)n + e n! y n 1 λ(s+t) (λs)n dy + e n! Dalla densità della variabile N(t + t) N(t) e dallo sviluppo di Taylor della funzione esponenziale si ricavano immediatamente anche le proprietà seguenti: i) P(N(t + t) N(t) = 1) = λ t + o( t) ii) P(N(t + t) N(t) = ) = 1 λ t + o( t), da cui segue naturalmente = P(N(t + t) N(t) 2) = o( t). Riassumendo: se l intervallo temporale è piccolo, la probabilità che si verifichi un solo evento, a meno di termini trascurabili, è proporzionale all ampiezza dell intervallo temporale secondo il coefficiente λ e il verificarsi di due o più eventi è trascurabile. Di fatto si può anche dimostrare che queste regole del susseguirsi degli eventi, unite al fatto che il numero degli eventi che si verificano su intervalli disgiunti sono variabili indipendenti e al fatto che si iniziano a contare gli eventi al tempo iniziale, ovvero il processo al tempo iniziale vale, sono assiomi, ovvero costituiscono una definizione alternativa per il processo di Poisson (vedi il paragrafo seguente sul processo di Poisson non stazionario). = Problema della multa Parcheggio in sosta vietata 2 volte al giorno lasciando ferma la vettura ogni volta per 1 ora; so che i vigili passano mediamente λ volte in un ora. Come 96
97 stimo la probabilità di prendere una multa? Soluzione Con una certa approssimazione, per il processo che conta il numero dei passaggi dei vigili si possono ritenere soddisfatte le proprietà che caratterizzano il processo di Poisson: si assume dunque che il processo che conta il numero dei passaggi dei vigili con il tempo misurato in ore sia un processo di Poisson di parametro λ. Indicati con t 1 e t 2, t 1 t 2, gli istanti in cui parcheggio, la probabilità di prendere una multa è la probabilità dell evento (N(t 1 + 1) N(t 1 ) 1) (N(t 2 + 1) N(t 2 ) 1) probabilità che coincide con ( ) 1 P (N(t 1 + 1) N(t 1 ) = ) (N(t 2 + 1) N(t 2 ) = ) = 1 P(N(t 1 + 1) N(t 1 ) = )P(N(t 2 + 1) N(t 2 ) = ) = 1 e 2λ dove per la prima uguaglianza si usa il fatto che le v.a. N(t 1 + 1) N(t 1 ) e N(t 2 + 1) N(t 2 ) sono indipendenti e per la seconda che hanno entrambe legge Poiss(λ). 2.3 Merging e splitting Siano (N 1 (t)) t e (N 2 (t)) t due processi di Poisson tra loro indipendenti rispettivamente di parametri λ 1 e λ 2. Ci si domanda se il processo che conta il numero complessivo degli eventi sia ancora un processo di Poisson. La risposta è affermativa e la proprietà va sotto il nome di merging. Definito qualsiasi sia t N(t) := N 1 (t) + N 2 (t), la dimostrazione consiste nell osservare che il processo (N(t)) t è un processo che inizialmente vale, ha gli incrementi indipendenti come somma di v.a. indipendenti e nel dimostrare che (N(t)) t verifica le proprietà i) e ii) del paragrafo precedente. Per la verifica della i) si osserva che vale l uguaglianza tra eventi (N(t + t) N(t) = 1) = (N 1 (t + t) N 1 (t) = 1, N 2 (t + t) N 2 (t) = ) (N 2 (t + t) N 2 (t) = 1, N 1 (t + t) N 1 (t) = ) dove l unione è disgiunta. Quindi passando alle probabilità, tenendo conto dell indipendenza di (N 1 (t)) t e (N 2 (t)) t, si ottiene P(N(t + t) N(t) = 1) = P(N 1 (t + t) N 1 (t) = 1)P(N 2 (t + t) N 2 (t) = )+ P(N 2 (t + t) N 2 (t) = 1)P(N 1 (t + t) N 1 (t) = ). 97
98 Utilizzando allora il fatto che le i) e ii) del paragrafo precedente valgono per (N 1 (t)) t e (N 2 (t)) t, con λ sostituito da λ 1 e λ 2 rispettivamente, e tenendo conto delle semplici regole sugli infinitesimi, si ottiene la relazione voluta con λ 1 + λ 2 al posto di λ. In modo analogo si verifica che il processo (N(t)) t verifica anche la ii) con λ 1 + λ 2 al posto di λ: naturalmente in tal caso si parte dall uguaglianza tra eventi (N(t + t) N(t) = ) = (N 1 (t + t) N 1 (t) =, N 2 (t + t) N 2 (t) = ). Dunque il processo (N(t)) t risulta un processo di Poisson di parametro λ 1 + λ 2. Si osservi che quanto dimostrato implica in particolare che per t > N(t) Poiss ( (λ 1 + λ 2 )t ) e che questo segue anche direttamente dal fatto noto che somma di v.a. di Poisson indipendenti è v.a. di Poisson con parametro la somma dei parametri. Un esempio di applicazione del merging è la soluzione del seguente problema. Problema della scorta Determinare la distribuzione di probabilità del tempo di esaurimento della scorta complessiva di due prodotti di cui si conosce la richiesta media giornaliera, assumendo che i due flussi di richiesta dei prodotti siano indipendenti e modellizzabili ciascuno con un processo di Poisson e assumendo anche che in assenza di un prodotto ci si accontenta dell altro. Un altra domanda interessante nella medesima situazione è la seguente: fissato un prodotto, con quale probabilità si esaurisce prima la scorta di quel prodotto? Soluzione Si indichi con λ i la richiesta media giornaliera del prodotto i = 1, 2.Per quanto appena detto allora, se la consistenza della scorta è n, il tempo di esaurimento è il tempo dell n-mo evento di un Poisson di parametro λ 1 + λ 2 e quindi ha distribuzione Erlang di parametri n e λ 1 + λ 2. Inoltre per calcolare la probabilità che si esaurisca prima la scorta del prodotto 1, si osserva che, assumendo che le singole scorte ammontino a n 1 e n 2 con n 1 +n 2 = n, questo accade se si verificano al più n 2 1 richieste del prodotto 2 (ovvero, almeno n 1 richieste del prodotto 1) entro le prime n 1 = n 1 +n 2 1 richieste. Infatti indicata con R i, i = 1, 2 la v.a. che conta le richieste del prodotto i entro le prime n 1 richieste, si ha banalmente R 2 n 2 1 = R 1 n 1 e R 1 n 1 implica che si esaurisce prima la scorta del prodotto 1. Mentre se R 2 > n 2 1 allora R 2 n 2 e quindi si esaurisce prima la scorta del prodotto 2. Ora, indicata con p 2 la probabilità che una generica richiesta 98
99 sia del flusso 2, si tratta di calcolare la probabilità di al più n 2 1 successi per uno schema di Bernoulli di parametri n 1 = n 1 + n 2 1 e p 2. Dunque la probabilità richiesta coincide con n 2 1 k= ( ) n 1 p k k 2(1 p 2 ) n 1 k. Infine per calcolare il valore p 2 si osservi che dalla proprietà di perdita di memoria applicata ai singoli flussi segue che a partire dal tempo di una qualsiasi richiesta occorre attendere un tempo esponenziale di parametro λ 1 per una nuova richiesta del prodotto 1 e un tempo esponenziale di parametro λ 2 per una nuova richiesta del prodotto 2. Inoltre questi due tempi esponenziali sono indipendenti poiché si è assunto che i flussi lo siano e quindi hanno densità congiunta (pari al prodotto delle densità) e dunque non possono assumere lo stesso valore. Così il valore p 2 deve coincidere con la probabilità che il tempo esponenziale (strettamente) più piccolo sia quello di parametro λ λ 2 ovvero 2 λ 1 +λ 2. In conclusione p 2 = λ 2 λ 1 + λ 2. Per dimostrare l ultima uguaglianza si procede così: indicate con X e Y due v.a. esponenziali rispettivamente di parametri λ 2 e λ 1 P(X < Y ) = P(X < Y Y = y)λ 2 e λ 2y dy = P(X < y Y = y)λ 2 e λ 2y dy = P(X y)λ 2 e λ 2y dy = + + P(X < y)λ 2 e λ 2y dy = (1 e λ 1y )λ 2 e λ 2y dy = λ 2 λ 1 + λ 2. La proprietà del processo di Poisson che va sotto il nome di splitting lavora al contrario della proprietà del merging: da un processo di Poisson si generano due processi di Poisson indipendenti. Si assume che (N(t)) t sia un processo di Poisson di parametro λ e che ogni evento del processo sia etichettato, in modo indipendente dagli altri, come evento di tipo i = 1, 2 con probabilità p i, i = 1, 2, p 1 + p 2 = 1. Allora, indicati con N i (t), i = 1, 2, il numero degli eventi di tipo i verificatisi fino al tempo t, i processi (N 1 (t)) t e (N 2 (t)) t sono processi di Poisson tra loro indipendenti rispettivamente di parametri p 1 λ e p 2 λ. Per dimostrare la proprietà precedente si verifica che, qualsiasi siano t > e k e m naturali, vale P(N 1 (t) = k, N 2 (t) = m) = (p 1λt) k 99 k! e p 1λt (p 2λt) m e p2λt. m!
100 Infatti si calcola P(N 1 (t) = k, N 2 (t) = m) = + P(N 1 (t) = k, N 2 (t) = m N(t) = n)p(n(t) = n) n= e, ricordando che N 1 (t) + N 2 (t) = N(t), risulta evidente che l unico valore possibile per n, indice della somma, è k + m e l espressione precedente coincide con P(N 1 (t) = k, N 2 (t) = m N(t) = k + m)p(n(t) = k + m). Il primo fattore dell espressione precedente per ipotesi si calcola come la probabilità di k successi ciascuno di probabilità p 1 su k + m prove indipendenti, mentre il secondo è il valore k + m della densità di una v.a. con legge Poisson di parametro λt = λ(p 1 + p 2 )t (si ricordi p 1 + p 2 = 1). Quindi si scrive ( ) ( ) k+m k + m λt p k k 1p m 2 (k + m)! e λ(p 1+p 2 )t. Usando il valore del coefficiente binomiale e riscrivendo l esponenziale come e λp 1t e λp 2t si ottiene proprio l espressione voluta e la proprietà di splitting è dimostrata. Si osservi che N 1 () = e per t > N 1 (t) può anche scriversi N(t) i=1 D i, dove le v.a. D 1, D 2,... sono i.i.d. di legge Bernoulli di parametro p 1, indipendenti da (N(t)) t. Un processo (X(t)) t uscente dallo e definito al tempo t > dalla formula X(t) := N(t) dove D 1, D 2,... sono i.i.d. a valori interi positivi indipendenti dal processo (N(t)) t, prende il nome di processo di Poisson composto. Si tratta di un processo a valori in N con traiettorie costanti a tratti e continue a destra, ma non necessariamente con salti unitari e quindi non necessariamente un processo di conteggio. Per esempio si può rappresentare con un processo di questo tipo l ammontare delle richieste di un certo prodotto in un generico istante se si assume che i clienti che cercano il prodotto giungano secondo un flusso di Poisson e ogni cliente chieda un numero aleatorio di pezzi del prodotto indipendente dal numero di pezzi richiesti dagli altri clienti ma di stessa legge (la v.a.d i è il numero di pezzi richiesti dal cliente i-mo). Per il calcolo del valor medio del processo al tempo t si procede così E[X(t)] = + n=1 i=1 D i, E[X(t) N(t) = n]p(n(t) = n). 1
101 Allora sostituendo l espressione di X(t) nella formula, per la linearità della media condizionata, l indipendenza delle v.a. D 1, D 2,... da (N(t)) t, e l uguaglianza in legge delle D 1, D 2,..., l espressione precedente coincide con + n n=1 i=1 + E[D i ]P(N(t) = n) = E[D 1 ] np(n(t) = n) = E[D 1 ]λt. n=1 Si consideri la seguente applicazione della proprietà di splitting. Problema della coda con flusso di ingresso Poisson, infiniti sportelli e tempo di servizio a due valori In un ideale ufficio di servizio il numero degli sportelli è infinito, il flusso di ingresso dei clienti è Poisson di parametro λ e il tempo di servizio di ciascuno sportello è T 1 con probabilità p 1 e T 2 con probabilità p 2 = 1 p 1. Ci si domanda quanti saranno gli sportelli occupati ad un tempo grande fissato. Soluzione Il tempo medio di servizio per ipotesi è pari a T 1 p 1 + T 2 p 2. Indicato con (N i (t)) t, i = 1, 2, il flusso dei clienti ad uno sportello di tipo i (ovvero con tempo di servizio T i ), si sa, per la proprietà di splitting, che si tratta di un flusso di Poisson di parametro λp i e che i due flussi sono indipendenti. Allora, per ogni tempo t maggiore del massimo tra T 1 e T 2, il numero degli sportelli occupati al tempo t sarà uguale al numero dei clienti arrivati ad uno sportello di tipo 1 nell intervallo di tempo (t T 1, t] più il numero dei clienti arrivati ad uno sportello di tipo 2 nell intervallo di tempo (t T 2, t], ovvero sarà pari a (N 1 (t) N 1 (t T 1 )) + (N 2 (t) N 2 (t T 2 )) e le v.a. N 1 (t) N 1 (t T 1 ) e N 2 (t) N 2 (t T 2 ) sono indipendenti con legge di Poisson rispettivamente di parametri λp 1 T 1 e λp 2 T 2. È noto che la somma di v.a. di Poisson indipendenti è ancora Poisson con parametro la somma dei parametri e dunque (N 1 (t) N 1 (t T 1 )) + (N 2 (t) N 2 (t T 2 )) è v.a. di Poisson di parametro λp 1 T 1 + λp 2 T 2 = λ(p 1 T 1 + p 2 T 2 ). Si conclude che per tempi grandi, ovvero maggiori del massimo tra T 1 e T 2, se la legge del tempo di servizio è discreta a due valori, il numero degli sportelli occupati è v.a. di legge Poisson di parametro pari al prodotto del numero medio dei clienti in ingresso nel tempo unitario per il tempo medio di servizio. Di fatto si può dimostrare che l affermazione precedente è vera qualsiasi sia la legge del tempo di servizio degli sportelli purché comune e di media finita. 2.4 Processo di Poisson non stazionario Un processo di Poisson non stazionario (N(t)) t è un processo di conteggio che ha incrementi indipendenti e che verifica le proprietà i) e ii) del paragrafo 2 con al posto della costante λ una funzione t λ(t), ovvero le proprietà i ) P(N(t + t) N(t) = 1) = λ(t) t + o( t) 11
102 e ii ) da cui segue naturalmente P(N(t + t) N(t) = ) = 1 λ(t) t + o( t), P(N(t + t) N(t) 2) = o( t). Si determina qui la legge dell incremento N(s + t) N(s), per s e t generici, ovvero si calcola la probabilità che l incremento assuma un generico valore k, cioè P(N(s + t) N(s) = k). Indicata questa probabilità con p k (s, t), considerando s come costante e t come variabile, poiché in un intervallo t può verificarsi, con probabilità non trascurabile rispetto all ampiezza t, un evento o nessuno e poiché il numero di eventi su intervalli disgiunti costituisce una famiglia di v.a. indipendenti, vale, qualsiasi sia k 1, p k (s, t + t) =p k 1 (s, t) ( λ(s + t) t + o( t) ) + + p k (s, t) ( 1 λ(s + t) t + o( t) ) + o( t). Nel membro di destra dell uguaglianza l ultimo termine o( t) tiene conto della trascurabile probabilità che nell intervallo [s + t, s + t + t) si verifichi più di un evento. L espressione precedente si può riscrivere p k (s, t + t) p k (s, t) t = p k 1 (s, t)λ(s + t) p k (s, t)λ(s + t) + o( t) t e dividendo ambo i membri per t e mandando t a zero, si ottiene, qualsiasi sia k 1, d dt p k(s, t) = p k 1 (s, t)λ(s + t) p k (s, t)λ(s + t). In modo analogo si ricava che d dt p (s, t) = p (s, t)λ(s + t). Risolvendo l ultima equazione con dato iniziale p (s, ) = 1 si ottiene dove p (s, t) = e (M(s+t) M(s)) M(x) := x λ(y) dy e poi procedendo per ricorrenza si calcola, qualsiasi sia k 1, tenendo conto che p k (s, ) =, (M(s+t) M(s)) (M(s + t) M(s))k p k (s, t) = e. k! 12
103 Dunque l incremento sull intervallo (s, s + t] del processo di Poisson non stazionario ha legge di Poisson di parametro M(s+t) M(s). In particolare, scegliendo s =, si ricava che la legge al tempo t del processo di Poisson non stazionario è Poisson di parametro M(t) e dunque M(t) = t λ(y) dy rappresenta il numero medio degli eventi che si verificano fino al tempo t (incluso). Si osserva che se si assume che λ(t) = λ per ogni t > si ritrova la densità degli incrementi del processo di Poisson stazionario. 2.5 Distribuzione dei tempi di salto in [, T ] condizionata a N(T)=n Una importante proprietà dei tempi di salto di un processo di Poisson si enuncia a parole così: condizionatamente al sapere che si verificano n eventi nell intervallo [, T ], i tempi S 1,..., S n sono il riordinamento in senso crescente di n v.a. i.i.d. di legge uniforme in [, T ]. Qui non si dimostra la proprietà ma si calcola soltanto la k-ma marginale di questa distribuzione condizionata, ovvero per 1 k n si calcola la funzione di distribuzione di S k, tempo in cui si verifica il k mo evento, condizionata al sapere che nell intervallo [, T ] si sono verificati n eventi. Per t T, utilizzando tra le altre cose l uguaglianza tra eventi (S k t) = (N(t) k) e l indipendenza delle v.a. N(t) e N(T ) N(t), si calcola P(S k t N(T ) = n) = P(N(t) k N(T ) = n) = P(N(t) k, N(T ) = n) = P(N(T ) = n) n j=k P(N(t) = j, N(T ) N(t) = n j) = P(N(T ) = n) n j=k P(N(t) = j)p(n(t ) N(t) = n j) = P(N(T ) = n) ( n je ( n je j=k λt) λt /j! λ(t t)) λ(t t) /(n j)! ( ) ne λt λt /n! e dopo le dovute semplificazioni si ottiene n P(S k t N(T ) = n) = j=k ( n j ) ( t T ) j ( 1 t ) n j T Quanto ottenuto è coerente con la proprietà enunciata inizialmente, che implica che, condizionatamente all evento (N(T ) = n), la v.a. S k ha la 13
104 legge della k ma v.a. del riordinamento crescente di n v.a. i.i.d. uniformi in [, T ]. Infatti la probabilità che esattamente j tra n v.a. i.i.d. di legge uniforme in [, T ] assumano valore nell intervallo [, t] è ( ) n ( t ) j ( 1 t ) n j j T T e quindi la probabilità che almeno k tra n v.a. i.i.d. di legge uniforme in [, T ] assumano valore nell intervallo [, t] è proprio n ( ) n ( t ) j ( 1 t ) n j. j T T j=k Un applicazione della distribuzione dei tempi di salto condizionata al numero dei salti è la seguente. Problema del costo di attesa Una sequenza di messaggi arriva secondo un flusso di Poisson di parametro λ alla porta di un canale di comunicazione; il canale viene aperto in tempi deterministici multipli di un tempo fissato T. Ciascun messaggio che arriva tra un tempo e l altro rimane conservato in un buffer ad un certo costo fisso per ogni unità temporale. All apertura del canale i messaggi in attesa vengono trasmessi istantaneamente. Qual è il costo medio per la conservazione di tutti i messaggi arrivati tra una trasmissione e la successiva? Soluzione Indicato con (N(t)) t il processo di Poisson che conta i messaggi, il tempo totale di conservazione dei messaggi è la v.a. (T S 1 ) + (T S 2 ) (T S N(T ) ) e dunque, indicato con C il costo fisso per ogni unità temporale per ogni singolo messaggio, il costo totale per la conservazione è C ( T S 1 + T S T S N(T ) ). Dunque essendo C deterministico, condizionando al valore di N(T ) Poiss(λT) si ottiene [ E C ( ) ] T S 1 + T S T S N(T ) = ] CE [T S 1 + T S T S N(T ) = C C + n= + n= [ ] (λt ) n E T S 1 + T S T S n N(T ) = n e λt = n! [ nt E S 1 + S S n N(T ) = n ] (λt ) n e λt. n! 14
105 Per quanto enunciato precedentemente, condizionatamente al fatto che vi siano n arrivi, la somma delle v.a. tempo di arrivo entro il tempo T coincide con la somma di n v.a. uniformi in [, T ]. Dunque, poiché il valor medio condizionato è lineare e il valor medio di una v.a. uniforme in [, T ] è T/2, si ottiene [ ] E S 1 + S S n N(T ) = n = n T 2. Pertanto il valor medio del costo totale risulta C + n=1 n T (λt ) n 2 n! e λt = C λt2 2 + n=1 (λt) n 1 (n 1)! e λt = C λt2 2. Si conclude questa sezione dimostrando che per ogni k n vale la formula E[S k S k 1 N(T ) = n] = T n + 1. Si premettono due enunciati relativi ad una v.a. X non negativa. Se X è discreta vale E[X] = + k=1 P(X k), essendo + + n + + np(x = n) = P(X = n) = P(X = n). n=1 n=1 k=1 Analogamente, se X è continua vale E[X] = + P(X t) dt = + k=1 n=k P(X > t) dt. Analoghe rappresentazioni valgono per il valor medio condizionato di v.a. non negative. Dunque per la linearità della media condizionata, dopo aver notato che per k n e t > T vale P(S k > t N(T ) = n) =, si scrive [ ] E S k S k 1 N(T ) = n = [ ] [ ] E S k N(T ) = n E S k 1 N(T ) = n = + T T ( ) P S k > t N(T ) = n dt ( ) P S k > t N(T ) = n dt + T ( ) P S k 1 > t N(T ) = n dt = ( ) P S k 1 > t N(T ) = n dt = [ P(S k 1 t N(T ) = n) P(S k t N(T ) = n) ] dt. Andando a sostituire le espressioni della distribuzione condizionata precedentemente dimostrata ci si riduce al calcolo di T ( ) n ( t ) k 1 ( 1 t ) n+1 k dt = k 1 T T 1 ( ) n T s k 1 (1 s) n+1 k ds k 1 15
106 che integrato per parti dà il risultato. 3 Processi di rinnovo Si chiamano processi di rinnovo quei processi di conteggio per i quali gli intertempi tra eventi successivi sono v.a. i.i.d. di media finita. Dunque i processi di Poisson sono particolari processi di rinnovo. In un processo di rinnovo gli eventi sono pensati come rinnovi nel senso di nuove inizializzazioni di situazioni che hanno una durata aleatoria indipendente dalle precedenti ma sempre statisticamente la stessa. Ad esempio sono processi di rinnovo quelli che contano le sostituzioni immediate di apparecchiature identiche a tasso di guasto non necessariamente costante e quindi per esempio soggette ad usura. Si ricorda la nozione di tasso di guasto di una distribuzione di v.a. X non negativa continua. Si calcola P(t < X < t + t X > t) = t+ t t f X (x) dx = f X(t) t + o( t) = f X(t) t + o( t), 1 F X (t) 1 F X (t) 1 F X (t) dove la seconda uguaglianza discende dal teorema fondamentale del calcolo integrale. Si definisce tasso di guasto o rischio al tempo t (della distribuzione) di X la quantità f X (t) 1 F X (t). Dalle precedenti uguaglianze segue che f X (t) 1 F X (t) t costituisce, a meno di termine trascurabili rispetto a t, un approssimazione per la probabilità che un apparecchiatura con tempo di vita X e ancora in vita al tempo t, si guasti tra t e t + t. A secondo che il tasso di rischio rimanga costante o no nel tempo l apparecchiatura non è soggetta o è soggetta all usura ed in particolare se il tasso di rischio rimane costante, cresce o decresce nel tempo allora l aspettativa sul tempo di vita dell apparecchiatura in seguito all utilizzo rispettivamente rimane la stessa, peggiora o migliora. Indicato con r(t) il tasso di rischio al tempo t, integrando l uguaglianza si ottiene r(t) = f X(t) 1 F X (t) ln(1 F X (t)) = t r(s) ds 16
107 ovvero 1 F X (t) = e t r(s) ds e da ciò segue che la distribuzione esponenziale è l unica con tasso di rischio costante. Imponendo che valga r(t) = Ct β con C > e β > 1, dalla relazione 1 F X (t) = e t r(s) ds, si ricava F X (t) = t I [,+ ) (1 e Ctβ+1 /(β+1) ). Si tratta della funzione di distribuzione nota con il nome di Weibull di parametri C e β: qualsiasi sia C >, per β > la funzione t r(t) è crescente, per 1 < β < è decrescente, e infine per β = la distribuzione coincide con l esponenziale e quindi t r(t) è costante. Si dimostra facilmente che la distribuzione Γ(α, λ) ha tasso di rischio variabile crescente per α > 1 e decrescente per α < 1, qualsiasi sia λ. Per dare una definizione formale di un processo di rinnovo si può ripetere quella del processo di Poisson sostituendo però alla assunzione che la legge degli intertempi sia esponenziale quella che la media degli intertempi sia finita. Innanzitutto si deve osservare che l ipotesi di media finita garantisce che in un tempo finito il numero dei rinnovi può soltanto essere finito. Infatti, indicata con µ la media degli intertempi, la legge forte dei grandi numeri implica che X X n lim n + n con probabilità 1 e questo implica che lim S n = +. n + S n = lim n + n = µ Da questo segue che se si indica con (N(t)) t il processo di rinnovo e si fissa un tempo t, a meno di un insieme probabilisticamente irrilevante di traiettorie, esiste un indice n abbastanza grande (che dipende dalla traiettoria) tale che è S n > t e quindi, N(t) n 1. In secondo luogo si nota che esattamente come nel caso del processo di Poisson vale l uguaglianza P(N(t) k) = P(S k t) che riduce il calcolo della densità di N(t) alla conoscenza della funzione di ripartizione dei tempi S n, n 1. Il valore medio del processo di rinnovo ad un tempo t fissato, cioè M(t) := E[N(t)] 17
108 si calcola a partire dalla funzione di ripartizione dei tempi S n, n 1 per mezzo della formula M(t) = + k=1 P(S k t) che segue immediatamente dalla formula M(t) = + k=1 P(N(t) k), vera essendo N(t) v.a. non negativa (vedi paragrafo 5 del I capitolo). Nel seguito ci si limita a considerazioni asintotiche sul valore medio del processo di rinnovo ad un tempo t fissato, M(t), e sul valore medio del tempo che occorre attendere a partire da t affinché si verifichi un rinnovo, cioè E[γ t ] dove, come per il processo di Poisson, si definisce γ t := S N(t)+1 t. La funzione t M(t) si chiama funzione di rinnovo e γ t si chiama tempo di vita residua al tempo t, con riferimento all interpretazione degli intertempi dei rinnovi come tempi di guasto di apparecchiature identiche a sostituzione immediata. Si ricordi subito che nel particolare caso del processo di Poisson di parametro λ, poiché vale µ = 1 λ, valgono le uguaglianze M(t) = t µ E[γ t ] = µ, dove in particolare l ultima uguaglianza segue dalla proprietà di perdita di memoria del processo di Poisson. Dunque per il processo di Poisson la funzione di rinnovo è lineare e il tempo medio di vita residuo è costante nel tempo. Per i processi di rinnovo con intertempi di rinnovo non esponenziali la funzione di rinnovo non è lineare ma lo è asintoticamente e il tempo medio di vita residua non è costante ma lo è asintoticamente. Più precisamente si può dimostrare che quando gli intertempi di rinnovo sono v.a. continue con momento secondo finito, ovvero E[X1 2 ] < +, valgono per tempi grandi le due approssimazioni seguenti M(t) t µ + E[X2 1 ] 2µ 2 1 E[γ t ] E[X2 1 ] 2µ. Qui non si dimostra la prima approssimazione, ma si spiega come dalla prima si ricava la seconda e a questo scopo si introduce e si dimostra un lemma interessante di per sé: si tratta dell equazione di Wald che generalizza il risultato relativo al valore medio della somma di un numero aleatorio di termini aleatori indipendenti di stessa legge visto per il processo di Poisson composto. 18
109 Si assuma che D 1, D 2,... siano v.a. i.i.d. non negative di media finita, N sia un v.a. a valori naturali con media finita e infine l evento (N = i) sia indipendente dalle v.a. D i+1, D i+2,... (ciò vale in particolare se la v.a. N è indipendente dalle v.a. D 1, D 2,...), allora [ N ] E D i = E[N]E[D 1 ]. i=1 Per la dimostrazione basta osservare che il primo membro dell uguaglianza coincide con [ + ] E D i I i N i=1 e, potendo scambiare media e serie poiché i termini sono non negativi, coincide con + E[D i I i N ]. i=1 Ora la v.a. D i è indipendente dalla v.a. I i N, essendo l evento (N i) complementare di (N < i) = i 1 k=1 (N = k), indipendente dalla v.a.d i in quanto unione di eventi per ipotesi indipendenti dalla v.a.d i. Inoltre si sa che il valor medio del prodotto di v.a. indipendenti è il prodotto dei valori medi e quindi l espressione precedente coincide con + i=1 E[D i ] E[I i N ]. Si conclude osservando che le v.a. D i hanno tutte media E[D 1 ] e che P(N i) = E[N]. + i=1 Dall equazione di Wald si deriva la relazione tra la funzione di rinnovo e il tempo medio di vita residua. Infatti si scrive E[γ t ] = E [ N(t)+1 i=1 e applicando l equazione di Wald si ottiene ] X i t E[γ t ] = µ ( 1 + M(t) ) t. Si noti l evento ( N(t) + 1 = i ) coincide con l evento ( S i 1 t < S i ) che chiaramente è indipendente dalle v.a. X i+1, X i+2,.... Sostituendo a M(t) nel membro di destra dell ultima uguaglianza la sua approssimazione t µ + E[X2 1 ] 2µ 2 1 si ottiene subito E[γ t ] E[X2 1 ] 2µ 19
110 Ricordando che V ar(x 1 ) = E[X 2 1 ] µ2, l approssimazione si riscrive E[γ t ] ( V ar(x1 ) ) µ µ Si osservi che ( V ar(x1 ) ) µ µ > µ V ar(x 1) µ 2 > 1 V ar(x1 ) > 1. µ Per una generica v.a. Z, di media µ e con varianza finita si può leggere V ar(z) il coefficiente µ, ricordando il significato di media e varianza, come V ar(z) una misura della regolarità della distribuzione e in particolare µ > 1 indica una distribuzione irregolare. Sono irregolari in questo senso per esempio le v.a. con distribuzione Γ(α, λ) per α > 1, qualsiasi sia λ >. Il fatto che per distribuzioni degli intertempi irregolari il tempo medio di vita residua si approssima con un valore che supera la media degli intertempi si ricorda con il nome di paradosso del tempo di attesa: se le partenze ai capolinea sono irregolari arrivando a caso ad una fermata si aspetta in media più del tempo medio tra una partenza e l altra. 4 Catene di Markov a tempo continuo 4.1 Definizione La generalizzazione al tempo continuo del concetto di catena di Markov a tempo discreto e a valori discreti è naturale. Una famiglia di v.a. (X(t)) t a valori in S discreto definite tutte sullo stesso spazio di probabilità è una catena di Markov a tempo continuo se, qualsiasi sia n, qualsiasi siano t, t 1,... t n+1, qualsiasi siano i, j, i,..., i n 1 in S (quando le probabilità condizionate hanno senso) P(X(t n+1 ) = j X(t n ) = i, X(t n 1 ) = i n 1,..., X(t ) = i ) = P(X(t n+1 ) = j X(t n ) = i). Qui si considera il caso omogeneo ovvero quello in cui, fissato t, per ogni s p ij (t) := P(X(t) = j X() = i) = P(X(s + t) = j X(s) = i) e p ij (t) è detto probabilità di transizione da i a j nel tempo t. Vale naturalmente p ij () = I i (j). Si consideri una dinamica stocastica su uno spazio discreto S che segua due regole: in ogni stato i o si rimane per sempre (stato assorbente) o si 11
111 rimane un tempo esponenziale di parametro ν i, indipendentemente dal passato; se lo stato i è non assorbente, quando si lascia lo stato i si salta in un altro stato j i con probabilità p ij, indipendentemente dal passato. Sia (X(t)) t il processo che al tempo t assume per valore lo stato in cui ci si trova al tempo t seguendo questa dinamica, precisando che per stato quando t è un tempo di transizione si intende quello assunto dopo la transizione, cosicché le traiettorie risultano continue a destra. Si può dimostrare, usando l indipendenza tra salti e tempi di permanenza e la perdita di memoria della distribuzione esponenziale, che (X(t)) t è una catena di Markov a tempo continuo omogenea. Viceversa è anche vero il contrario: se un sistema aleatorio si muove in uno spazio di stati discreto, allora affinché valga la proprietà di Markov è necessario che il tempo di permanenza negli stati non assorbenti sia esponenziale. Qui si dà un idea della dimostrazione: la probabilità che il tempo di permanenza nello stato i (non assorbente) superi t coincide con P(X(s) = i, s t X() = i) e questa probabilità, per la continuità da destra delle traiettorie e per la densità dei razionali nei reali, coincide con la probabilità che X(q) = i su tutti i razionali q in [, t] e per il lemma di continuità della probabilità con ( ) lim P X(s) = i, s = kt/n, k =, 1,..., n 1 X() = i. n + Richiedere la proprietà di Markov equivale allora a richiedere che indicata con f(t) la probabilità cercata valga ( n. f(t) = p ii (t/n)) Segue che per ogni α > Infatti f(αt) = lim n + f(αt) = f(t) α. ( ) n lim p ii (αt/n) n + e per ogni α razionale esiste una successione divergente di interi della forma m = n/α da cui ( n ( αm lim p ii (αt/n)) = lim p ii (t/ m)) = f(t) α. n + m + Per α reale qualsiasi si usa la monotonia della funzione f. Fissato t tale che f(t) < 1 (tale t esiste poiché lo stato i non è assorbente), qualsiasi sia s > si scrive come s = αt per qualche α e si riscrive f(αt) = f(t) α come f(s) = e s ln f(t) t 111
112 da cui segue ln f(t) f(s) = e c s posto c := t. Questo ricordando la definizione di f(s) è quello che si voleva dimostrare. Dunque numerati gli elementi di un insieme discreto S, una dinamica di Markov a tempo continuo su S è data se sono dati: una matrice stocastica P, di elemento generico p ij, che assegna le probabilità con cui avvengono i salti con la convenzione p ij = I i (j) quando i è assorbente; i parametri ν i >, i = 1, 2,... delle leggi esponenziali dei tempi di permanenza negli stati, con la convenzione ν i = quando i è assorbente. Si noti che la matrice P, matrice delle probabilità di salto, ha gli elementi sulla diagonale pari a 1 se lo stato è assorbente e pari a altrimenti. Si può dimostrare che muovendosi con questa dinamica, se i parametri ν i, i = 1, 2,... sono limitati, ovvero se esiste ν tale che ν i ν qualsiasi sia i, si compiono solo un numero finito di salti su ogni intervallo di tempo finito (proprietà di non esplosione). In particolare naturalmente i parametri ν i, i = 1, 2,... sono limitati quando S è finito. L esempio più semplice di catena di Markov a tempo continuo è il processo di Poisson di parametro λ: in questo caso S = N, nessuno stato è assorbente, ν i = λ, i = 1, 2,... e la matrice P ha per ogni riga un unico elemento non nullo, p i,i+1 = 1. Infine il processo di Poisson, come ogni processo di rinnovo, ammette su un intervallo di tempo finito solo un numero finito di salti. Viene naturale chiedersi se, dati su di uno stesso spazio di probabilità un processo di Poisson (N(t)) t di parametro λ e una catena di Markov a tempo discreto (Z n ) n, il processo definito con X(t) := Z n, S n t < S n+1, n sia una catena di Markov a tempo continuo (qui S n è come al solito l n-mo tempo di salto del processo di Poisson). Si noti che il processo introdotto si può anche scrivere così: (Z N(t) ) t. La risposta è affermativa. Il punto è che se la matrice di transizione di (Z n ) n ha almeno un elemento della diagonale diverso da 1 e da, ovvero la catena (Z n ) n ha almeno uno stato non assorbente i con probabilità di transizione in se stesso non nulla, i tempi di salto di (X(t)) t sono un sottoinsieme eventualmente proprio dei tempi di salto di (N(t)) t e il tempo di soggiorno in i risulta esponenziale di parametro λ(1 p ii ) (in generale si può dimostrare che somma di un numero aleatorio, con distribuzione geometrica di parametro p di v.a. esponenziali di parametro λ è esponenziale di parametro λp). Va anche notato che ogni catena di Markov a tempo continuo, (X(t)) t, contiene una catena di Markov a tempo discreto, (Z n ) n : posto S := e 112
113 detti S n, n 1 i tempi di salto di (X(t)) t, si pone Z n := X(S n ), n. Naturalmente la matrice dei salti P della catena a tempo continuo coincide con la matrice di transizione P della catena a tempo discreto e dunque per la dinamica discreta gli stati non assorbenti hanno probabilità nulla di tornare dopo un passo in se stessi. 4.2 Funzione di transizione e tassi di salto Data una catena di Markov a tempo continuo in 1, 2,..., in analogia al caso tempo discreto si indica con π t la densità di probabilità al tempo t, ovvero per ogni j π t (j) := P(X(t) = j). Come calcolare π t, t > a partire dalla densità iniziale π e dalla dinamica, ovvero dai parametri dei tempi di permanenza ν i, i = 1, 2,... e dalla matrice delle probabilità di salto P? Dalla formula delle probabilità totali si ricava π t (j) = i 1 p ij (t)π (i) e quindi, introdotta la funzione a valori matriciali t P(t) := ( p ij (t) ) ij, funzione di transizione al tempo t, in analogia al caso discreto, qualsiasi sia t, si può scrivere π t = π P(t) (P() è la matrice identità). Dunque il problema si sposta su come calcolare la funzione di transizione P(t), t a partire dalla dinamica, ovvero dai parametri dei tempi di permanenza ν i, i = 1, 2,... e dalla matrice delle probabilità di salto P. Si può dimostrare che la funzione di transizione soddisfa le seguenti equazioni differenziali P (t) = QP(t) dove Q è così definita P (t) = P(t)Q, q ij = ν i p ij, i j q ii = ν i. Si può osservare che, con le convenzioni adottate sul valore di ν i per i assorbente, nella matrice Q una riga corrispondente ad uno stato assorbente è tutta nulla. Del resto, ricordando che P() è la matrice identità, dalle equazioni si ricava che P () = Q e se i è assorbente, qualsiasi sia t, p ij (t) = I i (j) per 113
114 ogni j e quindi p ij (t) = per ogni j. Le precedenti equazioni (matriciali) sono note rispettivamente con il nome di equazioni all indietro e all avanti di Kolmogorov. Riscrivendole in forma estesa si trova p ij(t) = q ik p kj (t) k p ij(t) = k p ik (t)q kj e si nota che l equazione all indietro lega in un sistema di equazioni differenziali lineare del I ordine gli elementi di colonna della funzione di transizione, mentre viceversa quella all avanti gli elementi di riga. Inoltre per entrambe le equazioni il dato iniziale è noto: nel primo caso p jj () = 1 e p ij () = per i j, nel secondo caso p ii () = 1 e p ij () = per j i. Naturalmente affinché le equazioni enunciate siano utili ai fini del calcolo di P(t), occorre che esse abbiano un unica soluzione: ciò accade per esempio nel caso di parametri ν i limitati e quindi in particolare nel caso a stati finiti. Si dimostra l equazione all indietro, p ij (t) = k q ikp kj (t), nel modo seguente. Se lo stato i è assorbente p ij (t) = qualsiasi sia j e q ik = qualsiasi sia k e quindi l equazione è vera. Se lo stato i non è assorbente, indicato con T 1 il tempo di primo salto della catena di Markov, si scrive p ij (t) = P(T 1 > t, X(t) = j X() = i) + P(T 1 t, X(t) = j X() = i). Per il primo termine si osserva che, condizionatamente a partire da i, T 1 esp(ν i ) e T 1 > t implica X(t) = i e quindi P(T 1 > t, X(t) = j X() = i) = I i (j)p(t 1 > t X() = i) = I i (j)e ν it. Il secondo termine si riscrive condizionando al valore di T 1, avendo indicato con f T1 la densità di T 1 + t P(T 1 t, X(t) = j X() = i, T 1 = s)f T1 (s) ds = P(X(t) = j X() = i, T 1 = s)ν i e ν is ds 114
115 Ma per la formula delle probabilità totali, la formula del prodotto e la proprietà di Markov P(X(t) = j X() = i, T 1 = s) = P(X(t) = j, X(T 1 ) = k X() = i, T 1 = s) = k i P(X(t) = j X(T 1 ) = k, X() = i, T 1 = s)p(x(t 1 ) = k X() = i, T 1 = s) = k i P(X(t) = j X(s) = k)p(x(t 1 ) = k X() = i) k i p kj (t s)p ik k i e quindi l integrale si riscrive t p kj (t s)p ik ν i e νis ds k i e con il cambio di variabile s in t u In conclusione ν i e ν it t p kj (u)p ik e νiu du. k i p ij (t) = I i (j)e ν it + ν i e ν it t p kj (u)p ik e νiu du e la funzione t p ij (t) è derivabile in quanto composizione di funzioni derivabili, con derivata pari a cioè a ν i ( I i (j)e ν iu ν i e ν it t k i ) p kj (u)p ik e νiu du + ν i p kj (t)p ik k i ν i p ij (t) + ν i p kj (t)p ik k i e ricordando la definizione di q ij l equazione è dimostrata. A questo punto dimostrare l equazione all avanti, p ij (t) = k p kj (t)q kj, è più semplice. Si deriva in s la relazione k i p ij (t + s) = k p ik (t)p kj (s) 115
116 (equazione di Chapman Kolmogorov); la derivata esiste poiché è stata già dimostrata l equazione all indietro e derivando si ottiene p ij(t + s) = k p ik (t)p kj (s). Inoltre dall equazione all indietro già dimostrata segue che P () = Q e quindi l ultima uguaglianza in s = è l equazione cercata. Proprio l uguaglianza P () = Q consente di interpretare gli elementi della matrice Q, che non sono sulla diagonale, come tassi di salto: infatti per la formula di Taylor con il resto di Peano, qualsiasi siano i, j con i j p ii (t) = 1 + q ii t + o(t) p ij (t) = q ij t + o(t) e dunque, a meno di termini trascurabili rispetto a t, p ij (t) = q ij t, ovvero q ij t è l approssimazione al I ordine della probabilità che in un intervallo di ampiezza t di tempo si passi da i a j. Si sottolinea che la matrice Q, detta anche matrice dei parametri infinitesimali, non è una matrice stocastica ed in particolare gli elementi non sono necessariamente in [, 1] e la somma degli elementi di riga è nulla. Infatti se i è assorbente si è già detto che la riga corrispondente in Q è tutta nulla, mentre se i è non assorbente q ii = ν i e inoltre q ij = ν i p ij = ν i p ij = ν i j i j i j i dove nell ultima riga si usa j i p ij = 1. Si deve anche notare che dati i parametri infinitesimali, ovvero data Q, la dinamica è assegnata. Infatti si calcolano i parametri dei tempi di soggiorno ν i, i = 1, 2,... e la matrice delle probabilità di salto P nel modo seguente: se la riga i-ma di Q è nulla allora ν i = e la riga i-ma di P ha solo l elemento sulla diagonale non nullo, ovvero i è stato assorbente; altrimenti ν i = j i q ij, p ij = q ij ν i. In conclusione così, come nel caso tempo discreto una dinamica markoviana è individuata dalla matrice di transizione P, nel caso tempo continuo una dinamica markoviana è individuata dalla matrice dei parametri infinitesimali Q. 116
117 4.3 Catene di nascita e morte Le catene di Markov a tempo continuo per le quali q ij i j 1 sono dette catene di nascita e morte. Esse possono assumere valori su (, 1, 2..., d) o (, 1, 2...), ma il salto possibile da ogni stato è solo verso gli stati adiacenti, ovvero da i solo in i + 1 o in i 1. Si pone qualsiasi sia i λ i := q i,i+1, i µ i := q i,i 1, i 1 λ i si chiama tasso di nascita e µ i tasso di morte e si pone anche µ := e se S è finito λ d :=. Segue che valgono le uguaglianze ν i = λ i + µ i, ν = λ e, nel caso S sia finito, ν d = µ d e per le probabilità di salto p i,i+1 = e se S è finito p d,d 1 = 1. λ i λ i + µ i, p i,i 1 = µ i λ i + µ i, p,1 = 1 Si considera la catena a due stati, cioè il caso S = (, 1), e si calcola la funzione di transizione risolvendo le equazioni all indietro: per calcolare gli elementi della prima colonna di P(t) si impostano le equazioni ovvero p (t) = q p (t) + q 1 p 1 (t) p 1(t) = q 11 p 1 (t) + q 1 p (t) p (t) = λp (t) + λp 1 (t) p 1(t) = µp 1 (t) + µp (t), avendo posto per semplicità λ = λ e µ = µ 1. Sottraendo la seconda equazione dalla prima si ottiene ( p (t) p 1 (t) ) ( )( = λ + µ p (t) p 1 (t) ) e quindi, tenendo conto che p () p 1 () = 1, p (t) p 1 (t) = e (λ+µ)t. Sostituendo nella prima equazione l espressione calcolata si ottiene p (t) = λe (λ+µ)t 117
118 e poi integrando con condizione iniziale p () = 1 Infine p (t) = µ λ + µ + λ λ + µ e (λ+µ)t. p 1 (t) = µ λ + µ µ λ + µ e (λ+µ)t. Per evidenti ragioni di simmetria valgono anche p 1 (t) = λ λ + µ λ λ + µ e (λ+µ)t, p 11 (t) = λ λ + µ + µ λ + µ e (λ+µ)t. L analogia con la catena a due stati a tempo discreto è completa se si osserva che vale ) lim P(t) = t + ( µ λ+µ µ λ+µ λ λ+µ λ λ+µ. Per una generale catena di nascita e morte le equazioni all indietro e all avanti si scrivono rispettivamente così ovvero p ij(t) = q i,i 1 p i 1,j (t) + q ii p ij (t) + q i,i+1 p i+1,j (t) p ij(t) = p i,j 1 (t)q j 1,j + p ij (t)q jj + p i,j+1 (t)q j+1,j p ij(t) = µ i p i 1,j (t) (λ i + µ i )p ij (t) + λ i p i+1,j (t) p ij(t) = λ j 1 p i,j 1 (t) (λ j + µ j )p ij (t) + µ j+1 p i,j+1 (t) qualsiasi siano i, j ricordandosi di porre µ 1 = e nel caso S sia finito anche µ d+1 :=. Si chiamano catene di pura nascita le catene di Markov a tempo continuo con µ i = qualsiasi sia i e quindi ν i = λ i e p i,i+1 = 1. Le equazioni di Kolmogorov si scrivono p ij(t) = λ i p ij (t) + λ i p i+1,j (t) p ij(t) = λ j 1 p i,j 1 (t) λ j p ij (t) con le solite convenzioni. Fissati i e t, non essendo ammessi salti all indietro, se è j < i vale p ij (t) = ; dalle equazioni di Kolmogorov si ricava p ii(t) = λ i p ii (t) e dunque, essendo p ii () = 1, segue che p ii (t) = e λ it ; 118
119 per j > i, p ij (t) si calcola ricorsivamente da una delle due equazioni di Kolmogorov. Infatti utilizzando, per esempio, l equazione all avanti t p ij (t) = λ j 1 e λj(t s) p i,j 1 (s) ds. Nel caso in cui il tasso di nascita sia costante, ovvero λ i = λ si ha p i,i+1 (t) = λ p i,i+2 (t) = λ t t p ii (t) = e λt ; t e λ(t s) e λs ds = λe λt ds = λte λt t ( ) 2 λt e λ(t s) λse λs ds = λ 2 e λt s ds = 2 e λt e per induzione ( ) k λt p i,i+k (t) = e λt. k! Una catena di pura nascita con tasso di nascita λ, uscente dallo zero, ovvero con π () = 1, assume valore k al tempo t > con probabilità π t (k) = p k (t) = e infatti è un processo di Poisson. ( λt ) k k! e λt Un esempio di catena di nascita e morte a tempo continuo a valori in N con tassi lineari è costituito dai processi di ramificazione: sono i processi che contano il numero di individui di una popolazione in cui: ogni individuo, dopo un tempo di quiescenza di legge esponenziale di parametro α >, si duplica con probabilità p o muore con probabilità 1 p, indipendentemente dagli altri; nuovi individui si aggiungono alla popolazione seguendo un flusso di Poisson di parametro β indipendente dalle altre variabili aleatorie del processo. Si determinano i parametri dei tempi di permanenza della catena nei singoli stati. Se la popolazione non ha individui, ovvero il processo è nello stato, arriverà un nuovo individuo dopo un tempo σ esp(β) e quindi ν = β. Altrimenti se nella popolazione ci sono i 1 individui (numerati), indicati con τ 1, τ 2,..., τ i i tempi di quiescenza degli individui e indicato con T 1 il tempo di primo salto del processo, varrà T 1 = min(σ, τ 1, τ 2,..., τ i ) 119
120 e T 1 esp(β + i α) (si ricordi: minimo di esponenziali indipendenti è esponenziale con parametro la somma dei parametri) e quindi ν i = β + i α, i 1. Non sono ammessi salti di ampiezza maggiore di 1 dal momento che le v.a. σ, τ 1, τ 2,..., τ i sono v.a. indipendenti con densità e quindi con densità congiunta (si ricordi: v.a. indipendenti hanno come densità congiunta il prodotto delle densità e la differenza di due di esse ha densità). Si calcolano le probabilità di salto. Vale p i,i 1 = P(X(T 1 ) = i 1 X() = i) = P(X(T 1 ) = i 1, T 1 σ X() = i) = P(X(T 1 ) = i 1 T 1 σ, X() = i)p(t 1 σ X() = i). Ora P(X(T 1 ) = i 1 T 1 σ, X() = i) è la probabilità che, coincidendo il tempo di primo salto con la fine del tempo di quiescenza di un individuo, l individuo muoia e quindi Inoltre P(X(T 1 ) = i 1 T 1 σ, X() = i) = 1 p. (T 1 σ) = ( min(τ 1, τ 2,..., τ i ) < σ ) e, poiché le v.a. σ e min(τ 1, τ 2,..., τ i ) sono, condizionatamente a X() = i, indipendenti ed esponenziali rispettivamente di parametro β e iα, allora P ( T 1 σ X() = i ) = iα β + iα (si ricordi: date due esponenziali indipendenti allora, se X esp(λ) e Y esp(µ), si ha Y < X con probabilità µ/(λ + µ)). In definitiva p i,i 1 = iα(1 p) β + iα. Di conseguenza p i,i+1 = 1 p i,i 1 = β + iαp β + iα. I tassi di nascita e morte sono dunque λ i = β + iαp, µ i = iα(1 p). 12
121 4.4 Code markoviane Un altro esempio di catene di nascita e morte sono le code markoviane, ovvero i processi che contano il numero dei clienti all interno di un servizio, sia quelli serviti che quelli in attesa di servizio. Qui si considera soltanto il caso semplificato in cui non vi sia uscita dei clienti se non per fine servizio, corrispondente all idea che la sala di attesa sia infinita, ovvero il buffer sia infinito. Si assume che il flusso di arrivo dei clienti sia un processo di Poisson di parametro λ indipendente dal tempo di servizio ad ogni sportello che si assume sempre esponenziale di parametro µ. Nel caso in cui il numero degli sportelli sia finito, N, la coda si indica con M M N, altrimenti la coda si indica con M M. I salti della catena possono essere solo di ampiezza unitaria, positivi o negativi, dal momento che i tempi esponenziali in gioco sono v.a. indipendenti con densità. I tassi di nascita e morte sono lineari nel caso M M, in particolare λ i = λ, i µ i = iµ, i 1 µ =. Per calcolarli si usino le uguaglianze λ i = ν i p i,i+1 e µ i = ν i p i,i 1 tenendo presente che ν = λ, p 1 = 1 e qualsiasi sia i 1, ν i = iλ + µ (per la regola: il minimo di esponenziali indipendenti ha legge... ) e p i,i+1 = λ/(λ + iµ) e p i,i 1 = iµ/(λ + iµ) (per la regola: la probabilità che di due v.a. la più piccola sia una fissata delle due è... ). Nel caso M M N, i tassi di nascita e morte si calcolano analogamente e sono { iµ, 1 i N λ i = λ, i µ i =, µ =. Nµ, i > N E ovvio che, avendo stabilito una regola di precedenza per i clienti in attesa di servizio (per esempio, first in first out ovvero l ordine di arrivo diventa ordine di servizio), il primo cliente in attesa nel caso infiniti sportelli viene servito subito mentre in questo caso aspetta un tempo esponenziale di parametro N µ (si ricordi la perdita di memoria dell esponenziale). Quanto tempo in media aspetterà il secondo cliente in fila? Si calcola ora la funzione di transizione della coda M M. Indicato con X(t) il processo al tempo t, si osserva che X(t) = Y (t)+z(t), dove Y (t) conta il numero dei clienti presenti al tempo e ancora in servizio al tempo t, mentre Z(t) conta i clienti arrivati in (, t] e ancora in servizio al tempo t. Segue l uguaglianza tra eventi ( ) X(t) = j, X() = i = i j ( ) k= Y (t) = k, Z(t) = j k, X() = i e quindi passando alla probabilità, dopo aver applicato l additività della probabilità al secondo membro, dividendo ambo i membri per P(X() = i) 121
122 si ottiene i j p ij (t) = P ( Y (t) = k, Z(t) = j k X() = i ). k= Applicando poi l indipendenza dei tempi di servizio e di ingresso segue p ij (t) = i j P ( Y (t) = k X() = i ) P(Z(t) = j k X() = i ) k= Per quanto riguarda il primo fattore, poichè un cliente presente al tempo è ancora in servizio al tempo t con probabilità e µt, si ha P ( Y (t) = k X() = i ) ( ) i = e kµt (1 e µt ) i k. k Per quanto riguarda il secondo fattore, indicata con q t la probabilità che un cliente entrato in coda dopo il tempo sia ancora in servizio al tempo t, per la formula delle probabilità totali, se N(t) conta tutti i clienti entrati in coda dopo il tempo iniziale, si ha P ( Z(t) = j k X() = i ) = ( ) n q j k j k t (1 q t ) n j+k P(N(t) = n X() = i) = n j k ( ) n q j k n j+k (λt)n j k t (1 q t ) e λt = n! n j k ( q j k (λt) j k λt(1 qt ) ) n j+k t (j k)! e λt = (n j + k)! q j k t Così in definitiva (λt) j k (j k)! e λq tt k= n j k i j ( ) i p ij (t) = e kµt (1 e µt ) i k (λq tt) j k k (j k)! e λqtt. Inoltre, detto τ tempo di arrivo del generico cliente entrato in coda dopo il tempo iniziale, si può calcolare q t condizionando al valore di τ così q t = + e µ(t s) f τ (s) ds. 122
123 Infatti se τ = s affinchè il cliente resti in coda fino al tempo t il suo servizio deve durare almeno t s e questo avviene con probabilità e µ(t s). Infine, poiché si sa che, condizionatamente al numero di arrivi in [, t] di un Poisson, i tempi di arrivo sono v.a. uniformi in [, t], si riscrive Si osservi che q t = t e µ(t s) 1 t 1 e µt ds =. µt ( λ ) j e λ/µ lim p ij(t) = t + µ j! poiché i termini corrispondenti a k si annullano con e kµt. Dunque riassumendo si è calcolato l elemento generico della funzione di transizione p ij (t) e si è visto che, indipendentemente da i, per tempi grandi approssima la densità di Poisson di parametro λ/µ calcolata in j. Ricordando che per una v.a. esponenziale il valore medio coincide con l inverso del parametro, si può riformulare la frase precedente dicendo che la generica riga della funzione di transizione converge alla densità di Poisson di parametro pari al tasso di ingresso per il valore medio del tempo di servizio. Questo risultato è generale per le code con infiniti sportelli, flusso di ingresso Poisson e tempo di servizio di legge qualsiasi con media finita. In particolare per esempio lo si è dimostrato come applicazione dello splitting nel caso di tempo di servizio a due valori. Si tratta del secondo esempio, dopo quello della catena a due stati, di convergenza della funzione di transizione al divergere del tempo ovvero di ciò che, in analogia con il caso tempo discreto, si definisce comportamento ergodico delle catene di Markov a tempo continuo. 4.5 Misura invariante Data su S una dinamica markoviana a tempo continuo Q, in analogia al caso tempo discreto, una densità di probabilità w su S si dice misura invariante per Q quando se π = w allora vale π t = w qualsiasi sia t >. Quindi, ricordando che π t = π P(t), w è una misura invariante se e solo se w = wp(t), ovvero w è autovettore con autovalore 1 della funzione di transizione in ogni tempo. Si dimostra ora che w = wp(t), t wq =. Per dimostrare la condizione necessaria basta osservare che derivando a destra e a sinistra la relazione w = wp(t) si ottiene = wp (t) che calcolata 123
124 in dà l uguaglianza wq =, essendo P () = Q. Viceversa wq = implica che ( wp(t) ) = qualsiasi sia t e quindi wp(t) = wp() = w. Infatti qualsiasi sia i dall equazione di Kolmogorov all indietro segue w k p ki (t) = w k q kj p ji (t) = p ji (t) w k q kj, k k j j k ma l ipotesi dice che k w kq kj = e quindi k w kp ki (t) =. Esiste un legame tra la misura invariante di una dinamica markoviana a tempo continuo Q e quella della dinamica a tempo discreto in essa contenuta definita dalla matrice delle probabilità di salto P? Per esempio: l esistenza nel caso continuo è legata in qualche modo all esistenza nel caso discreto? E in caso affermativo, le due misure invarianti, w del caso continuo e v del discreto si scrivono una in termini dell altra? Una prima risposta sono le due implicazioni seguenti: wq =, j w j ν j < + = vp = v, v i := w iν i j w jν j, i. v = vp, j v j ν j < + = wq =, w i := v i/ν i j v j/ν j, i. Si ricava qui soltanto la prima delle due implicazioni. L ipotesi implica che qualsiasi sia j w k q kj = w k q kj + w j q jj = k j da cui k w k q kj = w j q jj = w j ν j. k j Ricordando la relazione q kj = ν k p kj vera per k j, si ricava w k ν k p kj = w j ν j, k j ovvero in forma compatta detto v il vettore di componente generica w k ν k si ricava v = vp ovvero v è autovettore di autovalore 1 per la matrice delle probabilità di salto P, che è anche matrice di transizione della catena (Z n ) n. Dividendo il vettore di componente generica w k ν k per la somma delle sue componenti si ottiene una densità invariante per la dinamica a tempo discreto associata a P. 124
125 Dal risultato visto immediatamente segue che nel caso S finito per quanto riguarda esistenza e unicità della misura invariante la dinamica continua Q e la dinamica discreta associata a P si equivalgono. Inoltre per il caso S infinito con parametri ν i, i = 1, 2... limitati se la dinamica discreta associata a P è persistente positiva e quindi ha un unica misura invariante allora anche la dinamica continua Q ammette un unica misura invariante (segue subito ragionando per assurdo dalla prima delle precedenti implicazioni). Riferimenti bibliografici [1] P.Baldi, Calcolo delle probabilità e statistica, Milano : McGraw-Hill, 1992 [2] P.Bremaud, Markov Chains, Gibbs fields, Monte Carlo simulation and queues, New York : Springer, 1999 [3] P.G.Hoel, S.C.Port, C.J.Stone, Introduction to Stochastic Processes, Boston: Houghton Mifflin, c1972 [4] S.M.Ross, Introduction to Probability Models, San Diego [etc.] : Harcourt Academic Press, 2 [5] H.C.Tijms, A First Course in Stochastic Models, Wiley,
5. La teoria astratta della misura.
 5. La teoria astratta della misura. 5.1. σ-algebre. 5.1.1. σ-algebre e loro proprietà. Sia Ω un insieme non vuoto. Indichiamo con P(Ω la famiglia di tutti i sottoinsiemi di Ω. Inoltre, per ogni insieme
5. La teoria astratta della misura. 5.1. σ-algebre. 5.1.1. σ-algebre e loro proprietà. Sia Ω un insieme non vuoto. Indichiamo con P(Ω la famiglia di tutti i sottoinsiemi di Ω. Inoltre, per ogni insieme
19. Inclusioni tra spazi L p.
 19. Inclusioni tra spazi L p. Nel n. 15.1 abbiamo provato (Teorema 15.1.1) che, se la misura µ è finita, allora tra i corispondenti spazi L p (µ) si hanno le seguenti inclusioni: ( ) p, r ]0, + [ : p
19. Inclusioni tra spazi L p. Nel n. 15.1 abbiamo provato (Teorema 15.1.1) che, se la misura µ è finita, allora tra i corispondenti spazi L p (µ) si hanno le seguenti inclusioni: ( ) p, r ]0, + [ : p
1 Serie di Taylor di una funzione
 Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE
 LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
Matematica generale CTF
 Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Per lo svolgimento del corso risulta particolarmente utile considerare l insieme
 1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
10. Insiemi non misurabili secondo Lebesgue.
 10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
CRITERI DI CONVERGENZA PER LE SERIE. lim a n = 0. (1) s n+1 = s n + a n+1. (2) CRITERI PER LE SERIE A TERMINI NON NEGATIVI
 Il criterio più semplice è il seguente. CRITERI DI CONVERGENZA PER LE SERIE Teorema(condizione necessaria per la convergenza). Sia a 0, a 1, a 2,... una successione di numeri reali. Se la serie a k è convergente,
Il criterio più semplice è il seguente. CRITERI DI CONVERGENZA PER LE SERIE Teorema(condizione necessaria per la convergenza). Sia a 0, a 1, a 2,... una successione di numeri reali. Se la serie a k è convergente,
SUCCESSIONI NUMERICHE
 SUCCESSIONI NUMERICHE Definizione: Si chiama successione numerica una funzione definita su IN a valori in IR, cioè una legge che associa ad ogni intero n un numero reale a n. Per abuso di linguaggio, si
SUCCESSIONI NUMERICHE Definizione: Si chiama successione numerica una funzione definita su IN a valori in IR, cioè una legge che associa ad ogni intero n un numero reale a n. Per abuso di linguaggio, si
Parte 2. Determinante e matrice inversa
 Parte. Determinante e matrice inversa A. Savo Appunti del Corso di Geometria 013-14 Indice delle sezioni 1 Determinante di una matrice, 1 Teorema di Cramer (caso particolare), 3 3 Determinante di una matrice
Parte. Determinante e matrice inversa A. Savo Appunti del Corso di Geometria 013-14 Indice delle sezioni 1 Determinante di una matrice, 1 Teorema di Cramer (caso particolare), 3 3 Determinante di una matrice
Proof. Dimostrazione per assurdo. Consideriamo l insieme complementare di P nell insieme
 G Pareschi Principio di induzione Il Principio di Induzione (che dovreste anche avere incontrato nel Corso di Analisi I) consente di dimostrare Proposizioni il cui enunciato è in funzione di un numero
G Pareschi Principio di induzione Il Principio di Induzione (che dovreste anche avere incontrato nel Corso di Analisi I) consente di dimostrare Proposizioni il cui enunciato è in funzione di un numero
u 1 u k che rappresenta formalmente la somma degli infiniti numeri (14.1), ordinati al crescere del loro indice. I numeri u k
 Capitolo 4 Serie numeriche 4. Serie convergenti, divergenti, indeterminate Data una successione di numeri reali si chiama serie ad essa relativa il simbolo u +... + u +... u, u 2,..., u,..., (4.) oppure
Capitolo 4 Serie numeriche 4. Serie convergenti, divergenti, indeterminate Data una successione di numeri reali si chiama serie ad essa relativa il simbolo u +... + u +... u, u 2,..., u,..., (4.) oppure
MATEMATICA DEL DISCRETO elementi di teoria dei grafi. anno acc. 2009/2010
 elementi di teoria dei grafi anno acc. 2009/2010 Grafi semplici Un grafo semplice G è una coppia ordinata (V(G), L(G)), ove V(G) è un insieme finito e non vuoto di elementi detti vertici o nodi di G, mentre
elementi di teoria dei grafi anno acc. 2009/2010 Grafi semplici Un grafo semplice G è una coppia ordinata (V(G), L(G)), ove V(G) è un insieme finito e non vuoto di elementi detti vertici o nodi di G, mentre
1. Distribuzioni campionarie
 Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 3 e 6 giugno 2013 - di Massimo Cristallo - 1. Distribuzioni campionarie
Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 3 e 6 giugno 2013 - di Massimo Cristallo - 1. Distribuzioni campionarie
x u v(p(x, fx) q(u, v)), e poi
 0.1. Skolemizzazione. Ogni enunciato F (o insieme di enunciati Γ) è equisoddisfacibile ad un enunciato universale (o insieme di enunciati universali) in un linguaggio estensione del linguaggio di F (di
0.1. Skolemizzazione. Ogni enunciato F (o insieme di enunciati Γ) è equisoddisfacibile ad un enunciato universale (o insieme di enunciati universali) in un linguaggio estensione del linguaggio di F (di
2.1 Definizione di applicazione lineare. Siano V e W due spazi vettoriali su R. Un applicazione
 Capitolo 2 MATRICI Fra tutte le applicazioni su uno spazio vettoriale interessa esaminare quelle che mantengono la struttura di spazio vettoriale e che, per questo, vengono dette lineari La loro importanza
Capitolo 2 MATRICI Fra tutte le applicazioni su uno spazio vettoriale interessa esaminare quelle che mantengono la struttura di spazio vettoriale e che, per questo, vengono dette lineari La loro importanza
LEZIONE 23. Esempio 23.1.3. Si consideri la matrice (si veda l Esempio 22.2.5) A = 1 2 2 3 3 0
 LEZIONE 23 231 Diagonalizzazione di matrici Abbiamo visto nella precedente lezione che, in generale, non è immediato che, data una matrice A k n,n con k = R, C, esista sempre una base costituita da suoi
LEZIONE 23 231 Diagonalizzazione di matrici Abbiamo visto nella precedente lezione che, in generale, non è immediato che, data una matrice A k n,n con k = R, C, esista sempre una base costituita da suoi
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria).
 Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
Parte 3. Rango e teorema di Rouché-Capelli
 Parte 3. Rango e teorema di Rouché-Capelli A. Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Rango di una matrice, 2 Teorema degli orlati, 3 3 Calcolo con l algoritmo di Gauss, 6 4 Matrici
Parte 3. Rango e teorema di Rouché-Capelli A. Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Rango di una matrice, 2 Teorema degli orlati, 3 3 Calcolo con l algoritmo di Gauss, 6 4 Matrici
1 Applicazioni Lineari tra Spazi Vettoriali
 1 Applicazioni Lineari tra Spazi Vettoriali Definizione 1 (Applicazioni lineari) Si chiama applicazione lineare una applicazione tra uno spazio vettoriale ed uno spazio vettoriale sul campo tale che "!$%!
1 Applicazioni Lineari tra Spazi Vettoriali Definizione 1 (Applicazioni lineari) Si chiama applicazione lineare una applicazione tra uno spazio vettoriale ed uno spazio vettoriale sul campo tale che "!$%!
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI
 CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
SERIE NUMERICHE. prof. Antonio Greco 6-11-2013
 SERIE NUMERICHE prof. Antonio Greco 6--203 Indice Motivazioni........... 3 Definizione........... 3 Errore tipico........... 3 Un osservazione utile...... 3 Condizione necessaria...... 4 Serie armonica.........
SERIE NUMERICHE prof. Antonio Greco 6--203 Indice Motivazioni........... 3 Definizione........... 3 Errore tipico........... 3 Un osservazione utile...... 3 Condizione necessaria...... 4 Serie armonica.........
Analisi dei Dati 12/13 Esercizi proposti 3 soluzioni
 Analisi dei Dati 1/13 Esercizi proposti 3 soluzioni 0.1 Un urna contiene 6 palline rosse e 8 palline nere. Si estraggono simultaneamente due palline. Qual è la probabilità di estrarle entrambe rosse? (6
Analisi dei Dati 1/13 Esercizi proposti 3 soluzioni 0.1 Un urna contiene 6 palline rosse e 8 palline nere. Si estraggono simultaneamente due palline. Qual è la probabilità di estrarle entrambe rosse? (6
Viene lanciata una moneta. Se esce testa vinco 100 euro, se esce croce non vinco niente. Quale è il valore della mia vincita?
 Viene lanciata una moneta. Se esce testa vinco 00 euro, se esce croce non vinco niente. Quale è il valore della mia vincita? Osserviamo che il valore della vincita dipende dal risultato dell esperimento
Viene lanciata una moneta. Se esce testa vinco 00 euro, se esce croce non vinco niente. Quale è il valore della mia vincita? Osserviamo che il valore della vincita dipende dal risultato dell esperimento
Corso di Analisi Matematica Serie numeriche
 Corso di Analisi Matematica Serie numeriche Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 25 1 Definizione e primi esempi 2 Serie a
Corso di Analisi Matematica Serie numeriche Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 25 1 Definizione e primi esempi 2 Serie a
1 Giochi a due, con informazione perfetta e somma zero
 1 Giochi a due, con informazione perfetta e somma zero Nel gioco del Nim, se semplificato all estremo, ci sono due giocatori I, II e una pila di 6 pedine identiche In ogni turno di gioco I rimuove una
1 Giochi a due, con informazione perfetta e somma zero Nel gioco del Nim, se semplificato all estremo, ci sono due giocatori I, II e una pila di 6 pedine identiche In ogni turno di gioco I rimuove una
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI
 APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
Introduzione al MATLAB c Parte 2
 Introduzione al MATLAB c Parte 2 Lucia Gastaldi Dipartimento di Matematica, http://dm.ing.unibs.it/gastaldi/ 18 gennaio 2008 Outline 1 M-file di tipo Script e Function Script Function 2 Costrutti di programmazione
Introduzione al MATLAB c Parte 2 Lucia Gastaldi Dipartimento di Matematica, http://dm.ing.unibs.it/gastaldi/ 18 gennaio 2008 Outline 1 M-file di tipo Script e Function Script Function 2 Costrutti di programmazione
Dimensione di uno Spazio vettoriale
 Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Teoria delle code. Sistemi stazionari: M/M/1 M/M/1/K M/M/S
 Teoria delle code Sistemi stazionari: M/M/1 M/M/1/K M/M/S Fabio Giammarinaro 04/03/2008 Sommario INTRODUZIONE... 3 Formule generali di e... 3 Leggi di Little... 3 Cosa cerchiamo... 3 Legame tra N e le
Teoria delle code Sistemi stazionari: M/M/1 M/M/1/K M/M/S Fabio Giammarinaro 04/03/2008 Sommario INTRODUZIONE... 3 Formule generali di e... 3 Leggi di Little... 3 Cosa cerchiamo... 3 Legame tra N e le
Appunti sulle Catene di Markov
 Appunti sulle Catene di Markov Calcolo delle Probabilità, L.S. in Informatica, A.A. 2006/2007 A.Calzolari 1 Indice 1 Definizioni di base 3 2 Classificazione degli stati 20 3 Misure invarianti e proprietà
Appunti sulle Catene di Markov Calcolo delle Probabilità, L.S. in Informatica, A.A. 2006/2007 A.Calzolari 1 Indice 1 Definizioni di base 3 2 Classificazione degli stati 20 3 Misure invarianti e proprietà
L espressione torna invece sempre vera (quindi la soluzione originale) se cambiamo contemporaneamente il verso: 1 < 0.
 EQUAZIONI E DISEQUAZIONI Le uguaglianze fra espressioni numeriche si chiamano equazioni. Cercare le soluzioni dell equazione vuol dire cercare quelle combinazioni delle lettere che vi compaiono che la
EQUAZIONI E DISEQUAZIONI Le uguaglianze fra espressioni numeriche si chiamano equazioni. Cercare le soluzioni dell equazione vuol dire cercare quelle combinazioni delle lettere che vi compaiono che la
Esercizio 1 Dato il gioco ({1, 2, 3}, v) con v funzione caratteristica tale che:
 Teoria dei Giochi, Trento, 2004/05 c Fioravante Patrone 1 Teoria dei Giochi Corso di laurea specialistica: Decisioni economiche, impresa e responsabilità sociale, A.A. 2004/05 Soluzioni degli esercizi
Teoria dei Giochi, Trento, 2004/05 c Fioravante Patrone 1 Teoria dei Giochi Corso di laurea specialistica: Decisioni economiche, impresa e responsabilità sociale, A.A. 2004/05 Soluzioni degli esercizi
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI
 FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
CONTINUITÀ E DERIVABILITÀ Esercizi proposti. 1. Determinare lim M(sinx) (M(t) denota la mantissa di t)
 CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
Iniziamo con un esercizio sul massimo comun divisore: Esercizio 1. Sia d = G.C.D.(a, b), allora:
 Iniziamo con un esercizio sul massimo comun divisore: Esercizio 1. Sia d = G.C.D.(a, b), allora: G.C.D.( a d, b d ) = 1 Sono state introdotte a lezione due definizioni importanti che ricordiamo: Definizione
Iniziamo con un esercizio sul massimo comun divisore: Esercizio 1. Sia d = G.C.D.(a, b), allora: G.C.D.( a d, b d ) = 1 Sono state introdotte a lezione due definizioni importanti che ricordiamo: Definizione
Capitolo 2. Operazione di limite
 Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
SUCCESSIONI NUMERICHE
 SUCCESSIONI NUMERICHE Una funzione reale di una variabile reale f di dominio A è una legge che ad ogni x A associa un numero reale che denotiamo con f(x). Se A = N, la f è detta successione di numeri reali.
SUCCESSIONI NUMERICHE Una funzione reale di una variabile reale f di dominio A è una legge che ad ogni x A associa un numero reale che denotiamo con f(x). Se A = N, la f è detta successione di numeri reali.
Metodi Computazionali
 Metodi Computazionali Elisabetta Fersini [email protected] A.A. 2009/2010 Catene di Markov Applicazioni: Fisica dinamica dei sistemi Web simulazione del comportamento utente Biologia evoluzione delle
Metodi Computazionali Elisabetta Fersini [email protected] A.A. 2009/2010 Catene di Markov Applicazioni: Fisica dinamica dei sistemi Web simulazione del comportamento utente Biologia evoluzione delle
Kangourou della Matematica 2014 finale nazionale italiana Mirabilandia, 12 maggio 2014
 Kangourou della Matematica 2014 finale nazionale italiana Mirabilandia, 12 maggio 2014 LIVELLO STUDENT K,M N CD BC A S1. (5 punti ) In figura si vede una circonferenza della quale i segmenti AB, BC e CD
Kangourou della Matematica 2014 finale nazionale italiana Mirabilandia, 12 maggio 2014 LIVELLO STUDENT K,M N CD BC A S1. (5 punti ) In figura si vede una circonferenza della quale i segmenti AB, BC e CD
Soluzioni del giornalino n. 16
 Soluzioni del giornalino n. 16 Gruppo Tutor Soluzione del Problema 1 Soluzioni corrette ci sono pervenute da : Gianmarco Chinello, Andrea Conti, Simone Costa, Marco Di Liberto, Simone Di Marino, Valerio
Soluzioni del giornalino n. 16 Gruppo Tutor Soluzione del Problema 1 Soluzioni corrette ci sono pervenute da : Gianmarco Chinello, Andrea Conti, Simone Costa, Marco Di Liberto, Simone Di Marino, Valerio
Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R
 Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Esercizi di Macroeconomia per il corso di Economia Politica
 Esercizi di Macroeconomia per il corso di Economia Politica (Gli esercizi sono suddivisi in base ai capitoli del testo di De Vincenti) CAPITOLO 3. IL MERCATO DEI BENI NEL MODELLO REDDITO-SPESA Esercizio.
Esercizi di Macroeconomia per il corso di Economia Politica (Gli esercizi sono suddivisi in base ai capitoli del testo di De Vincenti) CAPITOLO 3. IL MERCATO DEI BENI NEL MODELLO REDDITO-SPESA Esercizio.
8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica.
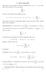 8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica la nuova successione {s n } definita come s 1 = a 1, s 2 = a 1 + a 2, s 3
8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica la nuova successione {s n } definita come s 1 = a 1, s 2 = a 1 + a 2, s 3
Serie numeriche. 1 Definizioni e proprietà elementari
 Serie numeriche Definizioni e proprietà elementari Sia { } una successione, definita per ogni numero naturale n n. Per ogni n n, consideriamo la somma s n degli elementi della successione di posto d s
Serie numeriche Definizioni e proprietà elementari Sia { } una successione, definita per ogni numero naturale n n. Per ogni n n, consideriamo la somma s n degli elementi della successione di posto d s
PROBABILITÀ - SCHEDA N. 2 LE VARIABILI ALEATORIE
 Matematica e statistica: dai dati ai modelli alle scelte www.dima.unige/pls_statistica Responsabili scientifici M.P. Rogantin e E. Sasso (Dipartimento di Matematica Università di Genova) PROBABILITÀ -
Matematica e statistica: dai dati ai modelli alle scelte www.dima.unige/pls_statistica Responsabili scientifici M.P. Rogantin e E. Sasso (Dipartimento di Matematica Università di Genova) PROBABILITÀ -
La Programmazione Lineare
 4 La Programmazione Lineare 4.1 INTERPRETAZIONE GEOMETRICA DI UN PROBLEMA DI PROGRAMMAZIONE LINEARE Esercizio 4.1.1 Fornire una rappresentazione geometrica e risolvere graficamente i seguenti problemi
4 La Programmazione Lineare 4.1 INTERPRETAZIONE GEOMETRICA DI UN PROBLEMA DI PROGRAMMAZIONE LINEARE Esercizio 4.1.1 Fornire una rappresentazione geometrica e risolvere graficamente i seguenti problemi
risulta (x) = 1 se x < 0.
 Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
4. Operazioni elementari per righe e colonne
 4. Operazioni elementari per righe e colonne Sia K un campo, e sia A una matrice m n a elementi in K. Una operazione elementare per righe sulla matrice A è una operazione di uno dei seguenti tre tipi:
4. Operazioni elementari per righe e colonne Sia K un campo, e sia A una matrice m n a elementi in K. Una operazione elementare per righe sulla matrice A è una operazione di uno dei seguenti tre tipi:
EQUAZIONI DIFFERENZIALI. 1. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x 2 log t (d) x = e t x log x (e) y = y2 5y+6
 EQUAZIONI DIFFERENZIALI.. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x log t (d) x = e t x log x (e) y = y 5y+6 (f) y = ty +t t +y (g) y = y (h) xy = y (i) y y y = 0 (j) x = x (k)
EQUAZIONI DIFFERENZIALI.. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x log t (d) x = e t x log x (e) y = y 5y+6 (f) y = ty +t t +y (g) y = y (h) xy = y (i) y y y = 0 (j) x = x (k)
Appunti sulla Macchina di Turing. Macchina di Turing
 Macchina di Turing Una macchina di Turing è costituita dai seguenti elementi (vedi fig. 1): a) una unità di memoria, detta memoria esterna, consistente in un nastro illimitato in entrambi i sensi e suddiviso
Macchina di Turing Una macchina di Turing è costituita dai seguenti elementi (vedi fig. 1): a) una unità di memoria, detta memoria esterna, consistente in un nastro illimitato in entrambi i sensi e suddiviso
Luigi Piroddi [email protected]
 Automazione industriale dispense del corso 10. Reti di Petri: analisi strutturale Luigi Piroddi [email protected] Analisi strutturale Un alternativa all analisi esaustiva basata sul grafo di raggiungibilità,
Automazione industriale dispense del corso 10. Reti di Petri: analisi strutturale Luigi Piroddi [email protected] Analisi strutturale Un alternativa all analisi esaustiva basata sul grafo di raggiungibilità,
Calcolo delle probabilità
 Calcolo delle probabilità Laboratorio di Bioinformatica Corso A aa 2005-2006 Statistica Dai risultati di un esperimento si determinano alcune caratteristiche della popolazione Calcolo delle probabilità
Calcolo delle probabilità Laboratorio di Bioinformatica Corso A aa 2005-2006 Statistica Dai risultati di un esperimento si determinano alcune caratteristiche della popolazione Calcolo delle probabilità
Cosa dobbiamo già conoscere?
 Cosa dobbiamo già conoscere? Insiemistica (operazioni, diagrammi...). Insiemi finiti/numerabili/non numerabili. Perché la probabilità? In molti esperimenti l esito non è noto a priori tuttavia si sa dire
Cosa dobbiamo già conoscere? Insiemistica (operazioni, diagrammi...). Insiemi finiti/numerabili/non numerabili. Perché la probabilità? In molti esperimenti l esito non è noto a priori tuttavia si sa dire
1. PRIME PROPRIETÀ 2
 RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
x 1 + x 2 3x 4 = 0 x1 + x 2 + x 3 = 0 x 1 + x 2 3x 4 = 0.
 Problema. Sia W il sottospazio dello spazio vettoriale R 4 dato da tutte le soluzioni dell equazione x + x 2 + x = 0. (a. Sia U R 4 il sottospazio dato da tutte le soluzioni dell equazione Si determini
Problema. Sia W il sottospazio dello spazio vettoriale R 4 dato da tutte le soluzioni dell equazione x + x 2 + x = 0. (a. Sia U R 4 il sottospazio dato da tutte le soluzioni dell equazione Si determini
1) Si consideri un esperimento che consiste nel lancio di 5 dadi. Lo spazio campionario:
 Esempi di domande risposta multipla (Modulo II) 1) Si consideri un esperimento che consiste nel lancio di 5 dadi. Lo spazio campionario: 1) ha un numero di elementi pari a 5; 2) ha un numero di elementi
Esempi di domande risposta multipla (Modulo II) 1) Si consideri un esperimento che consiste nel lancio di 5 dadi. Lo spazio campionario: 1) ha un numero di elementi pari a 5; 2) ha un numero di elementi
I sistemi di numerazione
 I sistemi di numerazione 01-INFORMAZIONE E SUA RAPPRESENTAZIONE Sia dato un insieme finito di caratteri distinti, che chiameremo alfabeto. Utilizzando anche ripetutamente caratteri di un alfabeto, si possono
I sistemi di numerazione 01-INFORMAZIONE E SUA RAPPRESENTAZIONE Sia dato un insieme finito di caratteri distinti, che chiameremo alfabeto. Utilizzando anche ripetutamente caratteri di un alfabeto, si possono
Esercizi di Calcolo delle Probabilita (I)
 Esercizi di Calcolo delle Probabilita (I) 1. Si supponga di avere un urna con 15 palline di cui 5 rosse, 8 bianche e 2 nere. Immaginando di estrarre due palline con reimmissione, si dica con quale probabilità:
Esercizi di Calcolo delle Probabilita (I) 1. Si supponga di avere un urna con 15 palline di cui 5 rosse, 8 bianche e 2 nere. Immaginando di estrarre due palline con reimmissione, si dica con quale probabilità:
1 Insiemi e terminologia
 1 Insiemi e terminologia Assumeremo come intuitiva la nozione di insieme e ne utilizzeremo il linguaggio come strumento per studiare collezioni di oggetti. Gli Insiemi sono generalmente indicati con le
1 Insiemi e terminologia Assumeremo come intuitiva la nozione di insieme e ne utilizzeremo il linguaggio come strumento per studiare collezioni di oggetti. Gli Insiemi sono generalmente indicati con le
16. Vari modi di convergenza delle successioni di funzioni reali misurabili.
 16. Vari modi di convergenza delle successioni di funzioni reali misurabili. L argomento centrale di questa ultima parte del corso è lo studio in generale della convergenza delle successioni negli spazi
16. Vari modi di convergenza delle successioni di funzioni reali misurabili. L argomento centrale di questa ultima parte del corso è lo studio in generale della convergenza delle successioni negli spazi
Teoria in sintesi 10. Attività di sportello 1, 24 - Attività di sportello 2, 24 - Verifica conclusiva, 25. Teoria in sintesi 26
 Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
Applicazioni lineari
 Applicazioni lineari Esempi di applicazioni lineari Definizione. Se V e W sono spazi vettoriali, una applicazione lineare è una funzione f: V W tale che, per ogni v, w V e per ogni a, b R si abbia f(av
Applicazioni lineari Esempi di applicazioni lineari Definizione. Se V e W sono spazi vettoriali, una applicazione lineare è una funzione f: V W tale che, per ogni v, w V e per ogni a, b R si abbia f(av
4 3 4 = 4 x 10 2 + 3 x 10 1 + 4 x 10 0 aaa 10 2 10 1 10 0
 Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8. Cognome:... Nome:... Matricola:...
 Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8 Cognome:................ Nome:................ Matricola:................ (Dare una dimostrazione esauriente di tutte le
Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8 Cognome:................ Nome:................ Matricola:................ (Dare una dimostrazione esauriente di tutte le
Processi stocastici. variabile casuale: funzione da uno spazio campione S a valori nello spazio E R X(t) : S E. spazio degli stati del processo
 Processi stocastici Processo stocastico: famiglia di variabili casuali {X(t) t T} definite su uno spazio di probabilità indiciate dal parametro t (tempo) X(t) variabile casuale: funzione da uno spazio
Processi stocastici Processo stocastico: famiglia di variabili casuali {X(t) t T} definite su uno spazio di probabilità indiciate dal parametro t (tempo) X(t) variabile casuale: funzione da uno spazio
Capitolo 1 ANALISI COMPLESSA
 Capitolo 1 ANALISI COMPLESSA 1 1.4 Serie in campo complesso 1.4.1 Serie di potenze Una serie di potenze è una serie del tipo a k (z z 0 ) k. Per le serie di potenze in campo complesso valgono teoremi analoghi
Capitolo 1 ANALISI COMPLESSA 1 1.4 Serie in campo complesso 1.4.1 Serie di potenze Una serie di potenze è una serie del tipo a k (z z 0 ) k. Per le serie di potenze in campo complesso valgono teoremi analoghi
E naturale chiedersi alcune cose sulla media campionaria x n
 Supponiamo che un fabbricante stia introducendo un nuovo tipo di batteria per un automobile elettrica. La durata osservata x i delle i-esima batteria è la realizzazione (valore assunto) di una variabile
Supponiamo che un fabbricante stia introducendo un nuovo tipo di batteria per un automobile elettrica. La durata osservata x i delle i-esima batteria è la realizzazione (valore assunto) di una variabile
Corso di Analisi Matematica. Successioni e serie numeriche
 a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Successioni e serie numeriche Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità
a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Successioni e serie numeriche Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità
A i è un aperto in E. i=1
 Proposizione 1. A è aperto se e solo se A c è chiuso. Dimostrazione. = : se x o A c, allora x o A = A o e quindi esiste r > 0 tale che B(x o, r) A; allora x o non può essere di accumulazione per A c. Dunque
Proposizione 1. A è aperto se e solo se A c è chiuso. Dimostrazione. = : se x o A c, allora x o A = A o e quindi esiste r > 0 tale che B(x o, r) A; allora x o non può essere di accumulazione per A c. Dunque
Moto uniforme sul toro bidimensionale
 4/3/06 Luigi Chierchia Moto uniforme sul toro bidimensionale 1. Il toro bidimensionale Denotiamo con R l insieme dei numeri reali e con Z l insieme dei numeri interi (con segno) {..., 2, 1, 0, 1, 2,...};
4/3/06 Luigi Chierchia Moto uniforme sul toro bidimensionale 1. Il toro bidimensionale Denotiamo con R l insieme dei numeri reali e con Z l insieme dei numeri interi (con segno) {..., 2, 1, 0, 1, 2,...};
Calcolo delle Probabilita, INGEGNERIA INFORMATICA, semestre II, laurea (ord. Leonardo.
 Capitolo 1 9 Ottobre 00 Calcolo delle Probabilita, INGEGNERIA INFORMATICA, semestre II, laurea (ord. Leonardo. 000, Milano Esercizio 1.0.1 (svolto in classe [II recupero Ing. Matematica aa.00-0-rivisitato]nel
Capitolo 1 9 Ottobre 00 Calcolo delle Probabilita, INGEGNERIA INFORMATICA, semestre II, laurea (ord. Leonardo. 000, Milano Esercizio 1.0.1 (svolto in classe [II recupero Ing. Matematica aa.00-0-rivisitato]nel
CONCETTO DI LIMITE DI UNA FUNZIONE REALE
 CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
Esercizi su lineare indipendenza e generatori
 Esercizi su lineare indipendenza e generatori Per tutto il seguito, se non specificato esplicitamente K indicherà un campo e V uno spazio vettoriale su K Cose da ricordare Definizione Dei vettori v,,v
Esercizi su lineare indipendenza e generatori Per tutto il seguito, se non specificato esplicitamente K indicherà un campo e V uno spazio vettoriale su K Cose da ricordare Definizione Dei vettori v,,v
CORSO DI CALCOLO DELLE PROBABILITÀ E STATISTICA. Esercizi su eventi, previsioni e probabilità condizionate
 CORSO DI CALCOLO DELLE PROBABILITÀ E STATISTICA Esercizi su eventi, previsioni e probabilità condizionate Nota: Alcuni esercizi sono tradotti, più o meno fedelmente, dal libro A first course in probability
CORSO DI CALCOLO DELLE PROBABILITÀ E STATISTICA Esercizi su eventi, previsioni e probabilità condizionate Nota: Alcuni esercizi sono tradotti, più o meno fedelmente, dal libro A first course in probability
3.1 Successioni. R Definizione (Successione numerica) E Esempio 3.1 CAPITOLO 3
 CAPITOLO 3 Successioni e serie 3. Successioni Un caso particolare di applicazione da un insieme numerico ad un altro insieme numerico è quello delle successioni, che risultano essere definite nell insieme
CAPITOLO 3 Successioni e serie 3. Successioni Un caso particolare di applicazione da un insieme numerico ad un altro insieme numerico è quello delle successioni, che risultano essere definite nell insieme
Parte 6. Applicazioni lineari
 Parte 6 Applicazioni lineari A Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Applicazioni fra insiemi, 2 Applicazioni lineari tra spazi vettoriali, 2 3 Applicazioni lineari da R n a R
Parte 6 Applicazioni lineari A Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Applicazioni fra insiemi, 2 Applicazioni lineari tra spazi vettoriali, 2 3 Applicazioni lineari da R n a R
( x) ( x) 0. Equazioni irrazionali
 Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
f(x) = 1 x. Il dominio di questa funzione è il sottoinsieme proprio di R dato da
 Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
CALCOLO COMBINATORIO
 CALCOLO COMBINATORIO 1 Modi di formare gruppi di k oggetti presi da n dati 11 disposizioni semplici, permutazioni Dati n oggetti distinti a 1,, a n si chiamano disposizioni semplici di questi oggetti,
CALCOLO COMBINATORIO 1 Modi di formare gruppi di k oggetti presi da n dati 11 disposizioni semplici, permutazioni Dati n oggetti distinti a 1,, a n si chiamano disposizioni semplici di questi oggetti,
ESERCIZI DI ALGEBRA LINEARE E GEOMETRIA
 ESERCIZI DI ALGEBRA LINEARE E GEOMETRIA Francesco Bottacin Padova, 24 febbraio 2012 Capitolo 1 Algebra Lineare 1.1 Spazi e sottospazi vettoriali Esercizio 1.1. Sia U il sottospazio di R 4 generato dai
ESERCIZI DI ALGEBRA LINEARE E GEOMETRIA Francesco Bottacin Padova, 24 febbraio 2012 Capitolo 1 Algebra Lineare 1.1 Spazi e sottospazi vettoriali Esercizio 1.1. Sia U il sottospazio di R 4 generato dai
1 Probabilità condizionata
 1 Probabilità condizionata Accade spesso di voler calcolare delle probabilità quando si è in possesso di informazioni parziali sull esito di un esperimento, o di voler calcolare la probabilità di un evento
1 Probabilità condizionata Accade spesso di voler calcolare delle probabilità quando si è in possesso di informazioni parziali sull esito di un esperimento, o di voler calcolare la probabilità di un evento
Schemi delle Lezioni di Matematica Generale. Pierpaolo Montana
 Schemi delle Lezioni di Matematica Generale Pierpaolo Montana A volte i fenomeni economici che ci interessano non variano con continuitá oppure non possono essere osservati con continuitá, ma solo a intervalli
Schemi delle Lezioni di Matematica Generale Pierpaolo Montana A volte i fenomeni economici che ci interessano non variano con continuitá oppure non possono essere osservati con continuitá, ma solo a intervalli
VARIABILI ALEATORIE MULTIPLE E TEOREMI ASSOCIATI. Dopo aver trattato delle distribuzioni di probabilità di una variabile aleatoria, che
 VARIABILI ALATORI MULTIPL TORMI ASSOCIATI Fonti: Cicchitelli Dall Aglio Mood-Grabill. Moduli 6 9 0 del programma. VARIABILI ALATORI DOPPI Dopo aver trattato delle distribuzioni di probabilità di una variabile
VARIABILI ALATORI MULTIPL TORMI ASSOCIATI Fonti: Cicchitelli Dall Aglio Mood-Grabill. Moduli 6 9 0 del programma. VARIABILI ALATORI DOPPI Dopo aver trattato delle distribuzioni di probabilità di una variabile
La variabile casuale Binomiale
 La variabile casuale Binomiale Si costruisce a partire dalla nozione di esperimento casuale Bernoulliano che consiste in un insieme di prove ripetute con le seguenti caratteristiche: i) ad ogni singola
La variabile casuale Binomiale Si costruisce a partire dalla nozione di esperimento casuale Bernoulliano che consiste in un insieme di prove ripetute con le seguenti caratteristiche: i) ad ogni singola
Ottimizazione vincolata
 Ottimizazione vincolata Ricordiamo alcuni risultati provati nella scheda sulla Teoria di Dini per una funzione F : R N+M R M di classe C 1 con (x 0, y 0 ) F 1 (a), a = (a 1,, a M ), punto in cui vale l
Ottimizazione vincolata Ricordiamo alcuni risultati provati nella scheda sulla Teoria di Dini per una funzione F : R N+M R M di classe C 1 con (x 0, y 0 ) F 1 (a), a = (a 1,, a M ), punto in cui vale l
Sono casi particolari di MCF : SPT (cammini minimi) non vi sono vincoli di capacità superiore (solo x ij > 0) (i, j) A : c ij, costo di percorrenza
 Il problema di flusso di costo minimo (MCF) Dati : grafo orientato G = ( N, A ) i N, deficit del nodo i : b i (i, j) A u ij, capacità superiore (max quantità di flusso che può transitare) c ij, costo di
Il problema di flusso di costo minimo (MCF) Dati : grafo orientato G = ( N, A ) i N, deficit del nodo i : b i (i, j) A u ij, capacità superiore (max quantità di flusso che può transitare) c ij, costo di
Il principio di induzione e i numeri naturali.
 Il principio di induzione e i numeri naturali. Il principio di induzione è un potente strumento di dimostrazione, al quale si ricorre ogni volta che si debba dimostrare una proprietà in un numero infinito
Il principio di induzione e i numeri naturali. Il principio di induzione è un potente strumento di dimostrazione, al quale si ricorre ogni volta che si debba dimostrare una proprietà in un numero infinito
Probabilità condizionata: p(a/b) che avvenga A, una volta accaduto B. Evento prodotto: Evento in cui si verifica sia A che B ; p(a&b) = p(a) x p(b/a)
 Probabilità condizionata: p(a/b) che avvenga A, una volta accaduto B Eventi indipendenti: un evento non influenza l altro Eventi disgiunti: il verificarsi di un evento esclude l altro Evento prodotto:
Probabilità condizionata: p(a/b) che avvenga A, una volta accaduto B Eventi indipendenti: un evento non influenza l altro Eventi disgiunti: il verificarsi di un evento esclude l altro Evento prodotto:
Capitolo 4: Ottimizzazione non lineare non vincolata parte II. E. Amaldi DEIB, Politecnico di Milano
 Capitolo 4: Ottimizzazione non lineare non vincolata parte II E. Amaldi DEIB, Politecnico di Milano 4.3 Algoritmi iterativi e convergenza Programma non lineare (PNL): min f(x) s.v. g i (x) 0 1 i m x S
Capitolo 4: Ottimizzazione non lineare non vincolata parte II E. Amaldi DEIB, Politecnico di Milano 4.3 Algoritmi iterativi e convergenza Programma non lineare (PNL): min f(x) s.v. g i (x) 0 1 i m x S
3 GRAFICI DI FUNZIONI
 3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
Sulla monotonia delle funzioni reali di una variabile reale
 Liceo G. B. Vico - Napoli Sulla monotonia delle funzioni reali di una variabile reale Prof. Giuseppe Caputo Premetto due teoremi come prerequisiti necessari per la comprensione di quanto verrà esposto
Liceo G. B. Vico - Napoli Sulla monotonia delle funzioni reali di una variabile reale Prof. Giuseppe Caputo Premetto due teoremi come prerequisiti necessari per la comprensione di quanto verrà esposto
CP110 Probabilità: Esame del 3 giugno 2010. Testo e soluzione
 Dipartimento di Matematica, Roma Tre Pietro Caputo 2009-2010, II semestre 8 luglio, 2010 CP110 Probabilità: Esame del 3 giugno 2010 Testo e soluzione 1. (6 pts 12 monete da 1 euro vengono distribuite tra
Dipartimento di Matematica, Roma Tre Pietro Caputo 2009-2010, II semestre 8 luglio, 2010 CP110 Probabilità: Esame del 3 giugno 2010 Testo e soluzione 1. (6 pts 12 monete da 1 euro vengono distribuite tra
La funzione è continua nel suo dominio perchè y = f(x) è composizione di funzioni continue. Il punto x = 0 è un punto isolato per D f.
 FUNZIONI CONTINUE - ALCUNI ESERCIZI SVOLTI SIMONE ALGHISI 1. Continuità di una funzione Dati un insieme D R, una funzione f : D R e x 0 R, si è detto che f è continua in x 0 se sono soddisfatte le seguenti
FUNZIONI CONTINUE - ALCUNI ESERCIZI SVOLTI SIMONE ALGHISI 1. Continuità di una funzione Dati un insieme D R, una funzione f : D R e x 0 R, si è detto che f è continua in x 0 se sono soddisfatte le seguenti
DOMINI A FATTORIZZAZIONE UNICA
 DOMINI A FATTORIZZAZIONE UNICA CORSO DI ALGEBRA, A.A. 2012-2013 Nel seguito D indicherà sempre un dominio d integrità cioè un anello commutativo con unità privo di divisori dello zero. Indicheremo con
DOMINI A FATTORIZZAZIONE UNICA CORSO DI ALGEBRA, A.A. 2012-2013 Nel seguito D indicherà sempre un dominio d integrità cioè un anello commutativo con unità privo di divisori dello zero. Indicheremo con
Insiemi di livello e limiti in più variabili
 Insiemi di livello e iti in più variabili Insiemi di livello Si consideri una funzione f : A R, con A R n. Un modo per poter studiare il comportamento di una funzione in più variabili potrebbe essere quello
Insiemi di livello e iti in più variabili Insiemi di livello Si consideri una funzione f : A R, con A R n. Un modo per poter studiare il comportamento di una funzione in più variabili potrebbe essere quello
RETI DI TELECOMUNICAZIONE
 RETI DI TELECOMUNICAZIONE SISTEMI M/G/1 e M/D/1 Sistemi M/G/1 Nei sistemi M/G/1: i clienti arrivano secondo un processo di Poisson con parametro λ i tempi di servizio hanno una distribuzione generale della
RETI DI TELECOMUNICAZIONE SISTEMI M/G/1 e M/D/1 Sistemi M/G/1 Nei sistemi M/G/1: i clienti arrivano secondo un processo di Poisson con parametro λ i tempi di servizio hanno una distribuzione generale della
Massimi e minimi vincolati di funzioni in due variabili
 Massimi e minimi vincolati di funzioni in due variabili I risultati principali della teoria dell ottimizzazione, il Teorema di Fermat in due variabili e il Test dell hessiana, si applicano esclusivamente
Massimi e minimi vincolati di funzioni in due variabili I risultati principali della teoria dell ottimizzazione, il Teorema di Fermat in due variabili e il Test dell hessiana, si applicano esclusivamente
Una ricetta per il calcolo dell asintoto obliquo. Se f(x) è asintotica a mx+q allora abbiamo f(x) mx q = o(1), da cui (dividendo per x) + o(1), m =
 Una ricetta per il calcolo dell asintoto obliquo Se f() è asintotica a m+q allora abbiamo f() m q = o(1), da cui (dividendo per ) m = f() q + 1 f() o(1) = + o(1), mentre q = f() m = o(1). Dunque si ha
Una ricetta per il calcolo dell asintoto obliquo Se f() è asintotica a m+q allora abbiamo f() m q = o(1), da cui (dividendo per ) m = f() q + 1 f() o(1) = + o(1), mentre q = f() m = o(1). Dunque si ha
