MATERIALI PIEZOELETTRICI (piezo = pressione)

Transcript

1 MATERIALI PIEZOELETTRICI (piezo = preione) La piezoelettriità è la proprietà manifetata a aluni ritalli i ariari elettriamente e vengono eformati o olleitati meaniamente (effetto piezoelettrio iretto). Vievera, e tali ritalli vengono attraverati a una orrente elettria o epoti a un ampo elettrio, allora manifetano una eformazione (effetto piezoelettrio invero). I materiali piezoelettrii vengono pertanto utilizzati per onvertire energia elettria in energia meania (ome attuatori) e vievera (ome enori).

2 STRUTTURA CRISTALLINA Aluni materiali in natura poieono tale proprietà (quarzo, tormalina). Nei moerni ipoitivi i utilizzano ritalli artifiiali (ale i Rohelle, olfato i litio) e i piezoeramii (titanato i bario, titanato i piombo, PZT) apprima ottopoti a un proeo i polarizzazione (poling) Le proprietà piezoelettrihe ono ovute alla truttura ritallina i tali materiali 1) Prima he il materiale iventi piezoelettrio la ua truttura ritallina è formata a una ella elementare ubia on un atomo entrale i Titanio o Zironio. Data la immetria ella ipoizione atomia, in aenza i olleitazioni la truttura non preenta polarità i arihe elettrihe. ) Sotto l azione i un ampo elettrio o i una olleitazione meania, l atomo entrale i pota al entro auano uno quilibrio nelle arihe, he à origine alla formazione i un ipolo elettrio

3 POLARIZZAZIONE Il proeo i polarizzazione onite nell orientazione ei ipoli elettrii all interno el materiale e i effettua attravero le eguenti fai 1) il materiale viene rialato a una temperatura proima a quella i Curie ) i applia un inteno ampo elettrio in moo a allineare i omini i polarizzazione nel materiale eono la irezione el ampo appliato 3) raffreano il materiale l orientazione ei omini viene bloata e permane anhe opo la rimozione el ampo elettrio. Il riultato el proeo è una polarizzazione reiua on i ipoli orientati nella irezione el ampo elettrio appliato 1) ) 3)

4 VANTAGGI E LIMITI OPERATIVI Caratteritihe ei materiali piezoeramii: elevata effiienza i traformazione elettro meania buona lavorabilità e ampia tipologia i forme ottenibili Le limitazioni al loro utilizzo ono ovute a epolarizzazione invehiamento iterei Le proprietà piezoelettrihe eaono veloemente in preenza i forti ampi elettrii i irezione oppota al ampo polarizzante o alternati, i elevate olleitazioni meanihe e i temperature uperiori alla temperatura i Curie* *temperatura alla quale i verifia una tranizione i fae nella truttura ritallina, a aimmetria a immetria, he etermina la perita elle proprietà piezoelettrihe

5 BUTTERLY LOOP E E E = ampo elettrio oeritivo 1 Appliano un ampo elettrio E nella irezione i polarizzazione il materiale i allunga (ɛ > ) 3 4 Se i inverte il ampo elettrio il materiale apprima i ontrae (ɛ < ), finhé non raggiunge un intenità E uffiiente a far invertire la irezione i polarizzazione el materiale 4 5 Per E < E l atomo entrale i pota alla parte oppota, variano il vero el ipolo, e il materiale riprene a allungari In realtà, i materiali piezoelettrii evienziano omportamenti non lineari e iterei

6 ISTERESI P E E E Per valori elevati el ampo elettrio il legame tra E e P non è lineare e la polarizzazione non i annulla quano viene rimoo il ampo elettrio P r = polarizzazione reiua P = polarizzazione i aturazione Le equazioni he erivono il fenomeno piezoelettrio eprimono l interazione tra le granezze elettrihe e meanihe, e vengono riavate ia alle equazioni i Maxwell he alla meania ei ontinui eformabili

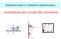
7 EETTO PIEZOELETTRICO DIRETTO E INVERSO Effetto piezoelettrio iretto Si onieri un ilinro i materiale piezoelettrio i lunghezza L e ezione A poto tra ue elettroi in orto. Appliano una forza i ha (σ = /A, = ΔL/L, E = ): L = σ / Y D = σ ove Y moulo elatio i Young in orto [N/m ] otante i eformazione piezoelettria [C/N] D potamento elettrio o enità i aria [C/m ] Effetto piezoelettrio invero Appliano un ampo elettrio E = V/L i ha: L = E D = e E ove e otante i permettività ielettria [C /Nm]

8 PIEZOELASTICITÀ LINEARE 1D Il legame otitutivo 1D in forma iretta e in forma invera riulta = D 1/ Y σ e E σ 1 Y Y / e = E 1 k Y / e 1/ e D la otante i eformazione piezoelettria è reponabile ell aoppiamento elettromeanio e è proporzionale alla apaità el materiale i onvertire energia meania in energia elettria e vievera. Effettuano una prova meania i trazione a iruito aperto non i ha potamento elettrio, per ui D =. In tal ao L e σ = e/ Y E = e/ Y Y = 1 k = Y * k = (1 k ove k = Y / e è il oeffiiente i aoppiamento piezoelettrio ( < k < 1) Y * = Y/(1 k ) è il moulo elatio a iruito aperto Si oervi he Y * > Y e la ifferenza ipene al oeffiiente i aoppiamento k )

9 σ = σ σ σ σ σ σ 3 1 = PIEZOELASTICITÀ LINEARE 3D 3 1 D = D D D 1 3 E = E E E 1 3 Per valori pioli i e E il omportamento elettromeanio i un materiale piezoelettrio i può erivere attravero elle equazioni otitutive lineari, erivate a una funzione energia potenziale ϕ(, E) quaratia nelle variabili e E: matrie i rigiezza elatia (6x6) 1 ϕ(, E) = 1 E h E e E h matrie piezoelettria (3x6) e matrie i permittività a ot (3x3) Il 1 e il 3 termine ono l energia i eformazione elatia e l energia elettria immagazzinate nel materiale ielettrio, mentre il è l energia piezoelettria Le tenioni e lo potamento elettrio ono efinite alle erivate i ϕ(, E): σ ij = D i = ϕ ij ϕ E i U = u u u per ui σ = h T E (6 equazioni) per ui D = h + e E (3 equazioni) 1 3 Φ σ tenioni eformazioni D potamento elettrio E ampo elettrio U potamento Φ potenziale elettrio

10 EQUAZIONI COSTITUTIVE In generale, i materiali piezoelettrii non ono iotropi ma traveralmente iotropi, poihé motrano un omportamento elettromeanio ivero e olleitati nella irezione i polarizzazione (x 3 ) oppure in irezione traverale (x 1, x ). Per ei i ha = Le equazioni otitutive poono riveri anhe nella forma invera in ui = 1 = 1 = (σ + h T E) = σ + T E ( 1) h = h 31 h 31 =h = 31 h 31 h 15 h 15 D = σ + e σ E e = e e e e σ = e + h h T matrie (6x6 immetria) matrie (3x6) i matrie (3x3 iagonale) i eformabilità elatia eformabilità piezoelettria i permittività a σ ot

11 In aenza i forze eterne (σ = ): 31 E = = T 31 E = V /t COSTANTI PIEZOELETTRICHE V t Δ L ΔW V Δ t V = = = = 31 = = L W t t t 3j = rapporto tra la eformazione lungo l ae x j e il ampo elettrio in irezione 3 NB: 31 = 3 < poihé un ampo elettrio poitivo E 3 > inue eformazioni negative (ontrazioni) lungo le irezioni x 1 e x. In onizioni i orto iruito (E = ): σ = LW Q = D3 = LW LW D = σ = LW = Q = rapporto tra la aria elettria Q i orto iruito e la forza appliata lungo x 3 V 1 3 W W L L t

12 EQUAZIONI DI EQUILIBRIO E COMPATIBILITÀ In aenza i forze i volume b i e enità i aria ρ, le equazioni i equilibrio ella tatia e quelle i onervazione ella aria elettria ell elettrotatia rihieono 3 3 σ ij,j = D i,i = (3+1 = 4 equazioni) i, = j 1 = i 1 Inoltre le equazioni i ongruenza e il potenziale elettrio rihieono ij = 1 (ui,j + u j,i ) E i = Φ,i (6+3 = 9 equazioni) Alle equazioni i ampo vanno aggiunte le 9 equazioni el legame otitutivo e affianate le onizioni al ontorno, ia meanihe he elettrihe σ n = u S 1 u = u S D n = q u S D Φ = Φ u S Φ S 1 e S ono le parti omplementari el ontorno S u ui ono aegnate forze e potamenti, mentre u S D e S Φ ono aegnate arihe e potenziale. La aria totale e il fluo i orrente elettria u S Φ valgono Q = Sφ D n A i = Q &

13 APPLICAZIONI in ampo inutriale SONAR e MICROONI L appliazione i una tenione alternata on una erta frequenza fa vibrare il trauttore alla tea frequenza generano one autihe e vievera SENSORI DI DISTANZA e DI LIVELLO Uati anhe ome ontatori nelle atene i montaggio MISURATORI DI LUSSO Sfruttano l effetto Doppler miurano la frequenza i potamento elle one ultraonore riflee alle partielle el liquio. SALDATURA ULTRASONORA Appliano ultrauoni i forte potenza u ue parti in ontatto, ee iniziano a vibrare rialanoi per attrito e foneno. Imballaggi termoplatii, attrezzature biomeiali. PULITORI ULTRASONICI Sfruttano la potenza ultraonora, generano avitazione nel liquio, he aiura la pulitura i uperfii anhe omplee.