2 + 2(seny) 2 per (x, y) (0, 0),
|
|
|
- Ilario Alfieri
- 4 anni fa
- Visualizzazioni
Transcript
1 Analisi II, a.a Soluzioni 1) Sia f la funzione di due variabili definita da xy α (senx) + (seny) per (x, y) (0, 0), 0 in (0, 0) dove α 0 è un parametro reale fissato. Determinare l insieme di definizione di f. Inoltre determinare per quali valori di α la funzione è continua in 0, per quali valori è derivabile in 0, per quali valori è differenziabile in 0. La funzione è definita nell origine e in tutti i punti in cui il denominatore non si annulla. Il denominatore si annulla per (senx) + (seny) = 0 senx = seny = 0 cioè nei punti In conclusione l insieme di definizione è Continuità in 0: utilizziamo la disuguaglianza vera per tutti gli x, e la disuguaglianza x = lπ, y = mπ, l, m Z. {(0, 0)} ( R \ {(lπ, mπ): l, m Z} ). senx x senx c x vera per una qualunque fissata costante c < 1 purché x sia sufficientemente vicino a 0 (ad esempio senx x /π è vera per tutti gli x tali che x π/). Possiamo scrivere allora, per (x, y) vicino all origine, xy α (senx) + (seny) xy α c (x + y ) xy α c (x + y ) 1 c rα e quindi vediamo subito che f 0 quando (x, y) 0 non appena α > 1. Se invece 0 α 1 otteniamo, sui punti del tipo (x, x) f(x, x) = x α 3(senx) che non tende a 0 quando x 0 (infatti tende a 1/3 per α = 1, e tende a + per α < 1). In conclusione f è continua in 0 se e solo se α > 1. Derivabilità in 0: se α > 0, abbiamo f(x, 0) = f(0, y) = 0 per tutti gli x, y vicini a 0, quindi i rapporti incrementali nell origine sono entrambi identicamente nulli e la funzione è derivabile in (0, 0) con D 1 f(0, 0) = D f(0, 0) = 0. Invece quando α = 0 la funzione diventa (per (x, y) (0, 0)) 1 (senx) + (seny) che non può essere derivabile né rispetto a x né rispetto a y (perché?). Differenziabilità in 0: se esiste, il differenziale in 0 deve essere L = df(0, 0) 0 dato che le derivate parziali sono nulle. Si tratta allora di capire quando è vero che f(h, k) f(0, 0) L(h, k) f(h, k) (h,k) 0 (h,k) 0 = 0. Scrivendo esplicitamente l espressione ( = h + k ), vogliamo sapere per quali valori di α si ha (h,k) 0 Come prima, possiamo scrivere subito hk α (senh) + (senk) 1 h + k = 0. hk α (senh) + (senk) 1 h + k 1 c rα 3 1
2 dato che h + k = r. Quindi per α > 3/ il ite è zero e la funzione è differenziabile nell origine. Se invece 0 α 3/, proviamo a fare il ite per punti del tipo (h, h); l espressione precedente diventa h α 1 3(senh) h = h 3(senh) h α 3 ed esattamente come prima vediamo che il ite non è zero se 0 α 3/, quindi la funzione non è differenziabile in 0 per tali valori del parametro. ) (i) Siano f, φ, g : R R tre funzioni, supponiamo che f e g siano differenziabili nell origine 0 con f(0) = g(0), e che si abbia f(x, y) φ(x, y) g(x, y) per tutti gli (x, y). Dimostrare che allora anche φ è differenziabile in 0 e che df(0) = dφ(0) = dg(0). (ii) Siano f, g : R n R due funzioni, f differenziabile nel punto 0 con f(0) = 0, g soltanto continua. Dimostrare che il prodotto f(x)g(x) è differenziabile in 0 e d(fg)(0) = g(0)df(0). (i) Anzitutto la funzione u = g f non è mai negativa e vale zero in 0, cioè ha un minimo in 0. Quindi la funzione u(x, 0) ha un minimo per x = 0 ed essendo u derivabile otteniamo D 1 u(0, 0) = 0 = D 1 g(0) D 1 f(0). Analogamente studiando u(0, y) otteniamo D u(0, 0) = 0 = D g(0) D f(0). Quindi f e g hanno lo stesso gradiente nell origine ed essendo esse differenziabili i loro differenziali coincidono in 0: df(0) = dg(0) = L. Dimostriamo infine che L è anche il differenziale di φ: infatti si ha f(h, k) f(0, 0) L(h, k) φ(h, k) φ(0, 0) L(h, k) g(h, k) g(0, 0) L(h, k) (notare che f(0) = φ(0) = g(0)) e dato che il primo e l ultimo termine tendono a 0 per (h, k) 0, ne segue che anche il termine centrale tende a zero ossia la tesi. (ii) Sia L il differenziale di f nell origine. L esercizio chiede di dimostrare che g(0)l è il differenziale di f g nell origine, ossia che il rapporto (fg)(h, k) (fg)(0, 0) g(0)l(h, k) Riscriviamo il tutto come somma di due termini: (fg)(h, k) g(0) L(h, k) = f(h, k) L(h, k) g(h, k) + Il termine I tende a zero perché g(h, k) g(0) (g è continua) mentre f(h, k) L(h, k) = 0 (h,k) 0 (fg)(h, k) g(0) L(h, k) L(h, k) (g(h, k) g(0)) = I + II. dato che L è il differenziale di f in 0. Nel secondo termine II il fattore g(h, k) g(0) tende a zero dato che g è continua; quindi basta dimostrare che il fattore L(h, k)/ è itato. Ma questo è evidente perché L(h, k) = D h 1f(0) + D k f(0) da cui L(h, k) D 1 f(0) + D f(0) e quindi anche il termine II tende a zero. 3) Siano u, v : R R due funzioni. Possiamo allora definire una funzione f : C C ponendo f(z) = f(x + iy) = u(x, y) + iv(x, y). Dimostrare che se esiste il ite in z 0 = x 0 + iy 0 f f(z) f(z 0 ) (z 0 ) = z z 0 z z 0 allora le due funzioni sono derivabili nel punto (x 0, y 0 ) e devono valere le relazioni di Cauchy-Riemann nel punto (x 0, y 0 ), ossia D 1 u(x 0, y 0 ) = D v(x 0, y 0 ), D u(x 0, y 0 ) = D 1 v(x 0, y 0 ). Il ite non dipende dal modo in cui la variabile z = x + iy tende al punto x 0 + iy 0. Ad esempio possiamo considerare punti del tipo z = x + iy = (x 0 + h) + iy 0, h 0
3 (h reale) e allora otteniamo f f(x 0 + h + iy 0 ) f(x 0 + iy 0 ) f(x 0 + h + iy 0 ) f(x 0 + iy 0 ) (z 0 ) = =. h 0 (x 0 + h) + iy 0 (x 0 + iy 0 ) Dire che questo ite (di numeri complessi!) esiste equivale a dire che esistono i iti sia della parte reale che della parte immaginaria. Allora se prendiamo la parte reale otteniamo (ricordando che f = u + iv) Re f u(x 0 + h, y 0 ) u(x 0, y 0 ) (z 0 ) = D 1 u(x 0, y 0 ) mentre se prendiamo la parte immaginaria otteniamo Im f v(x 0 + h, y 0 ) v(x 0, y 0 ) (z 0 ) = D 1 v(x 0, y 0 ) Ora invece scegliamo di avvicinare la variabile z al punto z 0 nel modo seguente: e stavolta si ha z = x + iy = x 0 + i(y 0 + h), h 0 f f(x 0 + iy 0 + ih) f(x 0 + iy 0 ) f(x 0 + h + iy 0 ) f(x 0 + iy 0 ) (z 0 ) = =. h 0 x 0 + iy 0 (x 0 + iy 0 + ih) h 0 ih Attenzione alla differenza: adesso c è i a denominatore quindi f(x 0 + iy 0 + ih) f(x 0 + iy 0 ) ih Prendendo la parte reale otteniamo = i u(x 0, y 0 + h) u(x 0, y 0 ) h Re f v(x 0, y 0 + h) v(x 0, y 0 ) (z 0 ) = D v(x 0, y 0 ) mentre se prendiamo la parte immaginaria otteniamo Im f u(x 0, y 0 + h) u(x 0, y 0 ) (z 0 ) = D u(x 0, y 0 ) Uguagliando i due risultati otteniamo finalmente e D 1 u(x 0, y 0 ) = Re f (z 0 ) = D v(x 0, y 0 ) D 1 v(x 0, y 0 ) = Im f (z 0 ) = D u(x 0, y 0 ). + v(x 0, y 0 + h) v(x 0, y 0 ) h 4) Una funzione f : R n \ {0} R si dice positivamente omogenea di grado α se per ogni x R n \ {0} e per ogni t > 0 si ha f(tx) = t α f(x). Dimostrare il Teorema di Eulero: sia f differenziabile, allora f è positivamente omogenea di grado α se e solo se x Df(x) = αf(x) per ogni x 0. Sia f positivamente omogenea. Allora derivando l identità f(tx) = t α f(x) rispetto a t otteniamo x 1 D 1 f(tx) + + x n D n f(tx) = αt α 1 f(x) e scegliendo t = 1 otteniamo la tesi. (Notare che questo vale anche per α = 0). Viceversa, supponiamo che valga l identità x Df(x) = αf(x), e consideriamo la funzione φ(t) = f(tx) = t α f(tx) t α per un x 0 fissato. La funzione è chiaramente ben definita e derivabile per t 0, e la sua derivata è φ (t) = αt α 1 f(tx) + t α x Df(tx) ma l identità x Df(x) = αf(x) implica che (tx) Df(tx) = αf(tx) ossia x Df(tx) = t 1 αf(tx), e sostituendo Ne segue che la funzione è costante: φ(t) = φ(1) cioè φ (t) = αt α 1 f(tx) + t α t 1 αf(tx) 0. f(tx) t α = f(x). 3
4 4 5) Determinare, se esiste, a in R tale che sia continua su R la funzione { sen(y sen(x)) e y sen(x) 1 a se y > sen(x) se y sen(x) Gli unici punti nei quali la funzione può non essere continua sono i punti sul grafico della funzione y = sen(x). Dal momento che se (x, y) (x 0, sen(x 0 )) con y sen(x), il ite vale a, non resta che calcolare (x,y) (x 0,sen(x 0)),y>sen(x) Con la sostituzione z = y sen(x), si tratta di calcolare e quindi a = 1. z 0 + sen(z) e z 1 = 1, sen(y sen(x)) e y sen(x) 1. 6) Studiare continuità, derivabilità e differenziabilità in R della funzione { x se y < x 3 y se y x 3 Ragionando come nell esercizio precedente, gli unici problemi si hanno per i punti (x, y) sulla curva y = x 3. Usando la definizione di f, si ha x 0, (x,y) (x 0,x 3 0,y<x3 ) x 3 (x,y) (x 0,x 3 0, 0,y x3 ) e quindi f è continua solo in ( 1, 1), (0, 0) e (1, 1). Per quanto riguarda la derivabilità, è facile verificare che in nessun punto della curva y = x 3 esistono le derivate parziali, e quindi f è derivabile solo fuori da tale curva. Là dove è derivabile, è anche differenziabile (le derivate) parziali sono continue. 7) Dimostrare che sono definite e differenziabili su R le funzioni y x sen(t) t dt, g(x, y) = y x 1 cos(t) dt. La funzione h(t) = sen(t)/t, posta uguale ad 1 nell origine, è continua e quindi integrabile su ogni intervallo di R. Pertanto, f è be definita su R. Per il teorema fondamentale del calcolo, si ha f x (x, y) = h(x), f y (x, y) = h(y). Essendo le derivate parziali continue, f è differenziabile su R. La funzione k(t) = 1 cos(t) non è prolongabile per continuità nell origine, ma, dal momento che ha un andamento asintotico uguale a t 1, è integrabile in senso improprio. La funzione g è pertanto ben definita. Se x e y sono diversi da zero, si ha (per il teorema fondamentale del calcolo integrale), g x (x, y) = cos(x ) 1 x 4, g y (x, y) = cos(y ) 1 y 4. Se, ad esempio, x = 0, e vogliamo calcolare la derivata parziale rispetto ad x in (0, y 0 ), dobbiamo calcolare h 0 h 0 1 cos(s) ds. Usando il teorema di de l Hopital, tale ite vale 1, che esattamente il ite di g x (x, y) per (x, y) tendente a (0, y 0 ). Lo stesso ragionamento essendo ripetibile per ogni altra derivata, si ha che le derivate parziali sono continue su R, e quindi f è differenziabile. 8) Studiare continuità, derivabilità e differenziabilità in R 3 di { x α y β z γ f(x, y, z) = x +y +z (x, y, z) (0, 0, 0) 0 (x, y, z) = (0, 0, 0) s 5 t 5 t 5 α, β, γ > 0.
5 5 Usando il fatto che x x + y + z, e le analoghe per y e z, è facile vedere che f è continua se α + β + γ >. Se α + β + γ =, è sufficiente calcolare il ite sulle rette x = l t, y = m t, z = n t per rendersi conto che dipende dalla retta scelta. Se, poi, α + β + γ <, la funzione è ilitata superiormente in un intorno dell origine, e quindi non ammette ite zero. Essendo α > 0 (così come β e γ), le derivate parziali di f nell origine sono tutte nulle. Per la differenziabilità, si tratta di verificare quando (h,k,l) (0,0,0) h α k β l γ (h + k + l ) 3 ed è facile vedere che ciò accade se e solo se α + β + γ > 3. = 0, 9) Per quali valori del parametro reale α la funzione f(x, y) è continua in R : x log(1+y) (x +arctan y) (x, y) (0, 0) α 0 (x, y) = (0, 0). La funzione f(x, y) per ogni α e continua in R \ {(0, 0)}, inoltre sarà continua nell origine se e solo se : x log(1 + y) (x + arctan = f(0, 0) = 0. y) α Per y vicino a zero si ha log(1 + y) = y + o(y) e arctan(y) = y + o(y) dove o(y) è un quantitativo tale che y 0 o(y)/y = 0. Da ciò segue che: passando a coordinate polari: x log(1 + y) (x + arctan y) α = xy + xo(y) (x + y + o(y )) α = = ρ (cos θ sin θ + o(ρ )/ρ ) (ρ + o(ρ )) α = ρ α (cos θ sin θ + o(ρ )/ρ ) (1 + o(ρ )/ρ ) α = 0 se e solo se α > 0 cioè se α < 1. Per α 0 la continuita era in realtà immediata. 10) Studiare la continuità e la differenziabilità in R di: x y x + y (x, y) (0, 0) 0 (x, y) = (0, 0). La funzione f(x, y) e continua in R \ {(0, 0)}, inoltre sarà continua nell origine se e solo se Passando a coordinate polari si ha: x y x + y = x y x = f(0, 0) = 0. + y ρ 3 (cos θ senθ) ρ cos θ + ρ sin θ = ρ cos θ senθ ρ cos θ + sin θ = 0 indipendentemente da θ. Quindi f è continua in R. Per dimostrare la differenziabilità di f in R \ {(0, 0)}, utilizzeremo il teorema del differenziale totale, che ci permette di dedurre la differenziabilità in un punto a partire dalla continuità in un intorno delle derivate prime di f, che possono essere calcolate facilmente: (x, y) = xy y x (x + y ) y (x, y) = x 4 (x + y ),
6 6 essendo le stesse continue in R \ {(0, 0)}, se ne deduce che f è differenziabile in R \ {(0, 0)}. Per dimostrare la differenziabilità di f nell origine, dobbiamo calcolare le derivate parziali di f nell origine come ite di rapporti incrementali: e verificare che x (0, 0) = y h 0 f(h, 0) f(0, 0) (0, 0) = f(0, h) f(0, 0) h x y x + y = 0. (x + y ) 1 Passando in coordinate polari il precedente ite diventa: = ρ3 (cos θ senθ) ρ 3 cos θ + ρ sin θ = 0 0 == = == = 0, ρ cos θ senθ ρ cos θ + sin θ = 0. Anche quando sin θ = 0, cioè muovendosi lungo i punti dell asse x, si verifica facilmente che il ite è 0. Quindi f risulta differenziabile (e continua) in R.
Esercitazione n 5. 1 Limiti e continuità di funzioni in più variabili. Esercizio 1: Si verifichi che la funzione f definita per ogni (x, y) R 2 da
 Esercitazione n 5 1 Limiti e continuità di funzioni in più variabili Esercizio 1: Si verifici ce la funzione f definita per ogni (, y) R 2 da { 4 y 4 se (, y) (0, 0) f(, y) = 2 +y 2 0 se (, y) = (0, 0)
Esercitazione n 5 1 Limiti e continuità di funzioni in più variabili Esercizio 1: Si verifici ce la funzione f definita per ogni (, y) R 2 da { 4 y 4 se (, y) (0, 0) f(, y) = 2 +y 2 0 se (, y) = (0, 0)
ANALISI B alcuni esercizi proposti
 ANALISI B alcuni esercizi proposti G.P. Leonardi Parte II 1 Limiti e continuità per funzioni di 2 variabili Esercizio 1.1 Calcolare xy log(1 + x ) lim (x,y) (0,0) 2x 2 + 5y 2 Esercizio 1.2 Studiare la
ANALISI B alcuni esercizi proposti G.P. Leonardi Parte II 1 Limiti e continuità per funzioni di 2 variabili Esercizio 1.1 Calcolare xy log(1 + x ) lim (x,y) (0,0) 2x 2 + 5y 2 Esercizio 1.2 Studiare la
Analisi Matematica 2. Continuità, derivabilità e differenziabilità
 Docente: E. G. Casini Università degli Studi dell Insubria DIPATIMENTO DI SCIENZA E ALTA TECNOLOGIA Corso di Studio in Matematica e Fisica Analisi Matematica ichiami di Teoria ed Esercizi con Svolgimento
Docente: E. G. Casini Università degli Studi dell Insubria DIPATIMENTO DI SCIENZA E ALTA TECNOLOGIA Corso di Studio in Matematica e Fisica Analisi Matematica ichiami di Teoria ed Esercizi con Svolgimento
Capitolo 1 ANALISI COMPLESSA
 Capitolo 1 ANALISI COMPLESSA 1 1.2 Funzioni Complesse Una funzione complessa di variabile complessa f : E C, E C è un applicazione ce associa un numero complesso f(z) ad ogni z E, con E sottoinsieme del
Capitolo 1 ANALISI COMPLESSA 1 1.2 Funzioni Complesse Una funzione complessa di variabile complessa f : E C, E C è un applicazione ce associa un numero complesso f(z) ad ogni z E, con E sottoinsieme del
Definizione (Derivata come limite del rapporto incrementale) Se esiste finito (cioè, non + o ) il limite del rapporto incrementale
 Funzione derivabile. La derivata. Dati: f I R funzione; I R intervallo aperto ; x 0 I. Definizione (Derivata come ite del rapporto incrementale) Se esiste finito (cioè, non + o ) il ite del rapporto incrementale
Funzione derivabile. La derivata. Dati: f I R funzione; I R intervallo aperto ; x 0 I. Definizione (Derivata come ite del rapporto incrementale) Se esiste finito (cioè, non + o ) il ite del rapporto incrementale
Analisi Matematica II Corso di Ingegneria Gestionale Compito del f(x, y) = x 2 + y 3 4y. 4 1, y 2 2(1 + }
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del 8-09-07 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito del 8-09-07 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II (Prof. Paolo Marcellini)
 Vero o falso? Analisi Matematica II (Prof. Paolo Marcellini) Università degli Studi di Firenze Corso di laurea in Matematica Esercitazione del 8//205 Michela Eleuteri eleuteri@math.unifi.it web.math.unifi.it/users/eleuteri
Vero o falso? Analisi Matematica II (Prof. Paolo Marcellini) Università degli Studi di Firenze Corso di laurea in Matematica Esercitazione del 8//205 Michela Eleuteri eleuteri@math.unifi.it web.math.unifi.it/users/eleuteri
Le derivate parziali
 Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
1 Limiti di funzioni di più variabili
 1 Limiti di funzioni di più variabili Sia f : D R N R e x 0 un punto di accumulazione per D. Riportiamo alcune utili strategie per verificare se la funzione ammette o non ammette ite finito in x 0. Le
1 Limiti di funzioni di più variabili Sia f : D R N R e x 0 un punto di accumulazione per D. Riportiamo alcune utili strategie per verificare se la funzione ammette o non ammette ite finito in x 0. Le
Analisi II, a.a Soluzioni 5
 Analisi II, a.a. 2017-2018 Soluzioni 5 1) Sia E un sottoinsieme chiuso e limitato di R n e x R n un punto qualunque. Chiamiamo d(x, E) = inf{d(x, y): y E} la distanza di x da E. Dimostrare che esiste un
Analisi II, a.a. 2017-2018 Soluzioni 5 1) Sia E un sottoinsieme chiuso e limitato di R n e x R n un punto qualunque. Chiamiamo d(x, E) = inf{d(x, y): y E} la distanza di x da E. Dimostrare che esiste un
Funzione derivabile. La derivata.
 Funzione derivabile. La derivata. Dati: f I R funzione; I R intervallo aperto ; x 0 I. Definizione (Derivata come limite del rapporto incrementale) Se esiste finito (cioè, non + o ) il limite del rapporto
Funzione derivabile. La derivata. Dati: f I R funzione; I R intervallo aperto ; x 0 I. Definizione (Derivata come limite del rapporto incrementale) Se esiste finito (cioè, non + o ) il limite del rapporto
Analisi Matematica II Corso di Ingegneria Gestionale Compito A del , se (x, y) = (0, 0) ( x e. + y x e (y2 )
 Analisi Matematica II Corso di Ingegneria Gestionale Compito A del -6-9 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito A del -6-9 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
1 Note ed esercizi risolti a ricevimento
 1 Note ed esercizi risolti a ricevimento Nota 1. Il polinomio di Taylor della funzione f x, y) due variabili), del secondo ordine, nel punto x 0, y 0 ), è P 2 x, y) = f x 0, y 0 ) + f x x 0, y 0 ) x x
1 Note ed esercizi risolti a ricevimento Nota 1. Il polinomio di Taylor della funzione f x, y) due variabili), del secondo ordine, nel punto x 0, y 0 ), è P 2 x, y) = f x 0, y 0 ) + f x x 0, y 0 ) x x
Politecnico di Milano Corso di Analisi e Geometria 1. Federico Lastaria
 Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@poi.it Limiti di derivate. Punti angolosi e di cuspide. Ottobre 2012 Indice 1 Limiti della derivata e punti di non
Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@poi.it Limiti di derivate. Punti angolosi e di cuspide. Ottobre 2012 Indice 1 Limiti della derivata e punti di non
Compito di Analisi Matematica, Seconda parte, COGNOME: NOME: MATR.:
 Compito di Analisi Matematica, Seconda parte, gennaio 9 Tema X COGNOME: NOME: MATR.: Esercizio. ( Determinare al variare di β R la soluzione di y (x + y (x + y(x = e x + x tale che y( = β = y (. ( Al variare
Compito di Analisi Matematica, Seconda parte, gennaio 9 Tema X COGNOME: NOME: MATR.: Esercizio. ( Determinare al variare di β R la soluzione di y (x + y (x + y(x = e x + x tale che y( = β = y (. ( Al variare
Analisi II, a.a Soluzioni 4
 Analisi II, a.a. 17-18 Soluzioni 4 1) Consideriamo le curve in forma parametrica in R φ : R R, φ(t) = (cos t, cos(t)), φ : R R, φ(t) = (1 + cos t, sen t) φ :], π/[ R, φ(t) = (sen t, cos t) φ : R R, φ(t)
Analisi II, a.a. 17-18 Soluzioni 4 1) Consideriamo le curve in forma parametrica in R φ : R R, φ(t) = (cos t, cos(t)), φ : R R, φ(t) = (1 + cos t, sen t) φ :], π/[ R, φ(t) = (sen t, cos t) φ : R R, φ(t)
Analisi II, a.a Soluzioni 1. j j + 1 ; ( 1)j
 Analisi II, a.a. 7-8 Soluzioni Calcolare le seguenti distanze e norme: (i d (x, y dove x = {x j } e y = {y j } sono le successioni di l definite da x j = ( j, y j = j/(j + ; (ii d (f, g dove f, g sono
Analisi II, a.a. 7-8 Soluzioni Calcolare le seguenti distanze e norme: (i d (x, y dove x = {x j } e y = {y j } sono le successioni di l definite da x j = ( j, y j = j/(j + ; (ii d (f, g dove f, g sono
Esame di Analisi Matematica 2 18/9/2013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 2012/2013
 Esame di Analisi Matematica 18/9/13 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 1/13 A Esercizio 1. Sia C la regione aperta di R compresa tra le circonferenze di centro l origine e raggi
Esame di Analisi Matematica 18/9/13 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 1/13 A Esercizio 1. Sia C la regione aperta di R compresa tra le circonferenze di centro l origine e raggi
25 IL RAPPORTO INCREMENTALE - DERIVATE
 25 IL RAPPORTO INCREMENTALE - DERIVATE Definizione Sia f una funzione reale di variabile reale. Allora, dati x, y domf con x y, si definisce il rapporto incrementale di f tra x e y come P f (x, y = f(x
25 IL RAPPORTO INCREMENTALE - DERIVATE Definizione Sia f una funzione reale di variabile reale. Allora, dati x, y domf con x y, si definisce il rapporto incrementale di f tra x e y come P f (x, y = f(x
Analisi Matematica II Corso di Ingegneria Gestionale Compito del
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del --9 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle. Esercizio.
Analisi Matematica II Corso di Ingegneria Gestionale Compito del --9 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle. Esercizio.
Scritto di Analisi Vettoriale ( ) proff. F. De Marchis, F. Lanzara, E. Montefusco
 COGNOM, NOM e MATRICOLA: Scritto di Analisi Vettoriale 8..18) proff. F. De Marchis, F. Lanzara,. Montefusco DOCNT: De Marchis Lanzara Montefusco Se ammesso, sosterrò la prova orale: questo appello in un
COGNOM, NOM e MATRICOLA: Scritto di Analisi Vettoriale 8..18) proff. F. De Marchis, F. Lanzara,. Montefusco DOCNT: De Marchis Lanzara Montefusco Se ammesso, sosterrò la prova orale: questo appello in un
Alcuni esercizi: funzioni di due variabili e superfici
 ANALISI MATEMATICA T- (C.d.L. Ing. per l ambiente e il territorio) - COMPL. DI ANALISI MATEMATICA (A-K) (C.d.L. Ing. Civile) A.A.008-009 - Prof. G.Cupini Alcuni esercizi: funzioni di due variabili e superfici
ANALISI MATEMATICA T- (C.d.L. Ing. per l ambiente e il territorio) - COMPL. DI ANALISI MATEMATICA (A-K) (C.d.L. Ing. Civile) A.A.008-009 - Prof. G.Cupini Alcuni esercizi: funzioni di due variabili e superfici
Analisi Matematica 1 Foglio 1 Lunedì 3 ottobre. f(x) = log x 2 6x + 5.
 Analisi Matematica Foglio Lunedì 3 ottobre Esercizio. Trovare il dominio naturale della funzione f data da ( ) f(x) = log x 2 6x + 5. Esercizio 2. Dire quali tra le seguenti funzioni sono iniettive :.
Analisi Matematica Foglio Lunedì 3 ottobre Esercizio. Trovare il dominio naturale della funzione f data da ( ) f(x) = log x 2 6x + 5. Esercizio 2. Dire quali tra le seguenti funzioni sono iniettive :.
Esame di Analisi Matematica 2 24/7/2013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 2012/2013
 Esame di Analisi Matematica 4/7/013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 01/013 A Cognome (in STAMPATELLO):... Nome (in STAMPATELLO):... CFU:... Esercizio 1. Sia f : R R una funzione
Esame di Analisi Matematica 4/7/013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 01/013 A Cognome (in STAMPATELLO):... Nome (in STAMPATELLO):... CFU:... Esercizio 1. Sia f : R R una funzione
Esercitazioni di Matematica
 Università degli Studi di Udine Anno Accademico 009/00 Facoltà di Agraria Corsi di Laurea in VIT e STAL Esercitazioni di Matematica novembre 009 Trovare le soluzioni della seguente disequazione: x + +
Università degli Studi di Udine Anno Accademico 009/00 Facoltà di Agraria Corsi di Laurea in VIT e STAL Esercitazioni di Matematica novembre 009 Trovare le soluzioni della seguente disequazione: x + +
Forme indeterminate e limiti notevoli
 Forme indeterminate e iti notevoli Limiti e continuità Forme indeterminate e iti notevoli Forme indeterminate Teorema di sostituzione Limiti notevoli Altre forme indeterminate 2 2006 Politecnico di Torino
Forme indeterminate e iti notevoli Limiti e continuità Forme indeterminate e iti notevoli Forme indeterminate Teorema di sostituzione Limiti notevoli Altre forme indeterminate 2 2006 Politecnico di Torino
Calcolo differenziale
 ANALISI MATEMATICA T-B (L-Z) (C.d.L. Ing. Gestionale) Università di Bologna - A.A.2008-2009 - Prof. G.Cupini A.A.2008-2009 - Prof. G.Cupini Calcolo differenziale (Grazie agli studenti del corso che comunicheranno
ANALISI MATEMATICA T-B (L-Z) (C.d.L. Ing. Gestionale) Università di Bologna - A.A.2008-2009 - Prof. G.Cupini A.A.2008-2009 - Prof. G.Cupini Calcolo differenziale (Grazie agli studenti del corso che comunicheranno
ANALISI MATEMATICA 1 Area dell Ingegneria dell Informazione. Appello del
 ANALISI MATEMATICA Area dell Ingegneria dell Informazione Appello del 3..7 TEMA Esercizio Calcolare l integrale log(3) 4 dx Svolgimento. Si ha log(3) 4 dx = (ponendo ex = t, per cui dx = dt/t) e = 4 3
ANALISI MATEMATICA Area dell Ingegneria dell Informazione Appello del 3..7 TEMA Esercizio Calcolare l integrale log(3) 4 dx Svolgimento. Si ha log(3) 4 dx = (ponendo ex = t, per cui dx = dt/t) e = 4 3
Esercizi. Misti iniziali. Più variabili. 1. Data la funzione. F (x) = x3 3 + x e t2 dt. se ne studino massimi, minimi, flessi, limiti a ±.
 Esercizi Misti iniziali. Data la funzione se ne studino massimi, minimi, flessi, iti a ±. 2. Provare che Più variabili F x) = 3. Calcolare, se esistono, i seguenti iti a) b) c) d) x,y),) x 2 + y 2 2 x,y),)
Esercizi Misti iniziali. Data la funzione se ne studino massimi, minimi, flessi, iti a ±. 2. Provare che Più variabili F x) = 3. Calcolare, se esistono, i seguenti iti a) b) c) d) x,y),) x 2 + y 2 2 x,y),)
Calcolo integrale. Regole di integrazione
 Calcolo integrale Linearità dell integrale Integrazione per parti Integrazione per sostituzione Integrazione di funzioni razionali 2 2006 Politecnico di Torino Proprietà Siano e funzioni integrabili su
Calcolo integrale Linearità dell integrale Integrazione per parti Integrazione per sostituzione Integrazione di funzioni razionali 2 2006 Politecnico di Torino Proprietà Siano e funzioni integrabili su
ANALISI VETTORIALE COMPITO IN CLASSE DEL 8/11/2013
 ANALISI VETTORIALE COMPITO IN CLASSE DEL 8//3 Premessa (Cfr. gli Appunti di Analisi Vettoriale / del Prof. Troianiello) Nello studio degli integrali impropri il primo approccio all utilizzo del criterio
ANALISI VETTORIALE COMPITO IN CLASSE DEL 8//3 Premessa (Cfr. gli Appunti di Analisi Vettoriale / del Prof. Troianiello) Nello studio degli integrali impropri il primo approccio all utilizzo del criterio
Calcolo I, a.a Secondo esonero
 Calcolo I, a.a. 205 206 Secondo esonero ) 7 punti Determinare i valori di a, b e c (con la condizione che a 0) affinché sia continua e derivabile la funzione ln(a + ) se x > 0, f(x) x e bx c se x 0. Soluzione.
Calcolo I, a.a. 205 206 Secondo esonero ) 7 punti Determinare i valori di a, b e c (con la condizione che a 0) affinché sia continua e derivabile la funzione ln(a + ) se x > 0, f(x) x e bx c se x 0. Soluzione.
Analisi 2 Fisica e Astronomia
 Analisi Fisica e Astronomia Appello scritto del 8 Luglio 0. Soluzione Esercizio 7 pti Sia α > 0 un parametro e consideriamo la curva piana γ : [0, ] R γt = t cos, t sin, se t 0, ], e γ0 = 0, 0. t α t α
Analisi Fisica e Astronomia Appello scritto del 8 Luglio 0. Soluzione Esercizio 7 pti Sia α > 0 un parametro e consideriamo la curva piana γ : [0, ] R γt = t cos, t sin, se t 0, ], e γ0 = 0, 0. t α t α
Funzioni in più variabili
 Funzioni in più variabili Corso di Analisi 1 di Andrea Centomo 7 gennaio 2010 Indichiamo con R n, Z n 1, l insieme delle n-uple ordinate di numeri reali R n 4 {(x 1, x 2,,x n ), x i R, i =1,,n}. Dato X
Funzioni in più variabili Corso di Analisi 1 di Andrea Centomo 7 gennaio 2010 Indichiamo con R n, Z n 1, l insieme delle n-uple ordinate di numeri reali R n 4 {(x 1, x 2,,x n ), x i R, i =1,,n}. Dato X
ESERCIZIO SULLE FUNZIONI DI DUE VARIABILI. g(x, y). x arctan x + y 2.
 Sia f : R R la funzione definita da ESERCIZIO SULLE FUNZIONI DI DUE VARIABILI f, y = + y 4 y + 4, y R e sia g la funzione di due variabili reali definita da g, y = f, y + y.. Determinare il dominio D di
Sia f : R R la funzione definita da ESERCIZIO SULLE FUNZIONI DI DUE VARIABILI f, y = + y 4 y + 4, y R e sia g la funzione di due variabili reali definita da g, y = f, y + y.. Determinare il dominio D di
Corso di Laurea in Ingegneria Elettrica Corso di Analisi Matematica - a.a. 2001/02 Docente: Dott. Alberto Maria BERSANI. xy 2 x 2 + y 4.
 Corso di Laurea in Ingegneria Elettrica Corso di Analisi Matematica - aa 00/0 Docente: Dott Alberto Maria BERSANI ESERCIZI SVOLTI SU LIMITI, CONTINUITÀ, DERIVABILITÀ E DIFFERENZIABILITÀ DI FUNZIONI DI
Corso di Laurea in Ingegneria Elettrica Corso di Analisi Matematica - aa 00/0 Docente: Dott Alberto Maria BERSANI ESERCIZI SVOLTI SU LIMITI, CONTINUITÀ, DERIVABILITÀ E DIFFERENZIABILITÀ DI FUNZIONI DI
Analisi Matematica I modulo Soluzioni prova scritta preliminare n. 2
 Analisi Matematica I modulo Soluzioni prova scritta preinare n 2 Corso di laurea in Matematica, aa 2004-2005 22 dicembre 2004 1 (a) Calcolare il seguente ite A******* ( ) n 2 n 2 + n n 1 n + 2n 2 Soluzione
Analisi Matematica I modulo Soluzioni prova scritta preinare n 2 Corso di laurea in Matematica, aa 2004-2005 22 dicembre 2004 1 (a) Calcolare il seguente ite A******* ( ) n 2 n 2 + n n 1 n + 2n 2 Soluzione
Analisi II, a.a Soluzioni 3
 Analisi II, a.a. 2017-2018 Soluzioni 3 1) Consideriamo la funzione F : R 2 R 2 definita come F (x, y) = (x 2 + y 2, x 2 y 2 ). (i) Calcolare la matrice Jacobiana DF e determinare in quali punti F è localmente
Analisi II, a.a. 2017-2018 Soluzioni 3 1) Consideriamo la funzione F : R 2 R 2 definita come F (x, y) = (x 2 + y 2, x 2 y 2 ). (i) Calcolare la matrice Jacobiana DF e determinare in quali punti F è localmente
AM210 - Analisi Matematica 3: Soluzioni Tutorato 1
 AM210 - Analisi Matematica 3: Soluzioni Tutorato 1 Università degli Studi Roma Tre - Dipartimento di Matematica Docente: Luca Biasco Tutori: Patrizio Caddeo, Davide Ciaccia 19 ottobre 2016 1 Se z = (1
AM210 - Analisi Matematica 3: Soluzioni Tutorato 1 Università degli Studi Roma Tre - Dipartimento di Matematica Docente: Luca Biasco Tutori: Patrizio Caddeo, Davide Ciaccia 19 ottobre 2016 1 Se z = (1
Analisi Matematica II Corso di Ingegneria Gestionale Compito A del f(x, y) = x 2 + 2y 2 x 3 y 3
 Analisi Matematica II Corso di Ingegneria Gestionale Compito A del 7-7-8 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito A del 7-7-8 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito del f(x, y) = sin( x 2 + 2y 2 )
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del 9--9 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo - Le risposte senza giustificazione sono considerate nulle Esercizio
Analisi Matematica II Corso di Ingegneria Gestionale Compito del 9--9 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo - Le risposte senza giustificazione sono considerate nulle Esercizio
CORSO DI ANALISI MATEMATICA 2 SOLUZIONI ESERCIZI PROPOSTI 11/03/2013
 CORSO DI ANALISI MATEMATICA SOLUZIONI ESERCIZI PROPOSTI /0/0 D.BARTOLUCCI, D.GUIDO ESERCIZIO: Sia 0 R e. Il Polinomio di Taylor I A 0 := {f : U f,0 R : U f,0 è un intorno di 0, f è continua in U f,0 },
CORSO DI ANALISI MATEMATICA SOLUZIONI ESERCIZI PROPOSTI /0/0 D.BARTOLUCCI, D.GUIDO ESERCIZIO: Sia 0 R e. Il Polinomio di Taylor I A 0 := {f : U f,0 R : U f,0 è un intorno di 0, f è continua in U f,0 },
COMPLEMENTI DI ANALISI MATEMATICA A.A Primo appello del 5/5/2010
 COMPLEMENTI DI ANALISI MATEMATICA A.A. 29- Primo appello del 5/5/2 Qui trovate le tracce delle soluzioni degli esercizi del compito. Ho tralasciato i calcoli da Analisi (che comunque sono parte della risoluzione),
COMPLEMENTI DI ANALISI MATEMATICA A.A. 29- Primo appello del 5/5/2 Qui trovate le tracce delle soluzioni degli esercizi del compito. Ho tralasciato i calcoli da Analisi (che comunque sono parte della risoluzione),
CORSO DI ANALISI MATEMATICA 2 SOLUZIONI ESERCIZI PROPOSTI 15/04/2013
 CORSO DI ANALISI MATEMATICA SOLUZIONI ESERCIZI PROPOSTI 5/04/03 D.BARTOLUCCI, D.GUIDO. Integrali Impropri Esercizio. (CRITERIO DEL CONFRONTO). Dimostrare che se f : (a, b] R e g(x) : (a, b] R sono integrabili
CORSO DI ANALISI MATEMATICA SOLUZIONI ESERCIZI PROPOSTI 5/04/03 D.BARTOLUCCI, D.GUIDO. Integrali Impropri Esercizio. (CRITERIO DEL CONFRONTO). Dimostrare che se f : (a, b] R e g(x) : (a, b] R sono integrabili
APPELLO C AM1C 19 Gennaio f(x) = log( x + 2) x
 Esercizio 1. Sia data la funzione f(x) = log( x + 2) x (a )Determinarne: insieme di esistenza e di derivabilità, limiti ed eventuali asintoti, eventuali punti angolosi o di cuspide, eventuali massimi e
Esercizio 1. Sia data la funzione f(x) = log( x + 2) x (a )Determinarne: insieme di esistenza e di derivabilità, limiti ed eventuali asintoti, eventuali punti angolosi o di cuspide, eventuali massimi e
D Analisi Matematica 1 (Corso di Laurea in Informatica e Bioinformatica)
 COGNOME NOME Matr. D Firma dello studente Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
COGNOME NOME Matr. D Firma dello studente Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
1.3. Se esistono i limiti sinistro e destro della funzione in un punto, allora esiste anche il limite della funzione nel punto stesso.
 Esercitazione 8 Novembre 018 1. Stabilire quali delle seguenti affermazioni sono vere e quali false. 1.1. Se una funzione f(x) è definita in un intervallo aperto (a, b), ha senso chiedersi se esistono
Esercitazione 8 Novembre 018 1. Stabilire quali delle seguenti affermazioni sono vere e quali false. 1.1. Se una funzione f(x) è definita in un intervallo aperto (a, b), ha senso chiedersi se esistono
Argomento 6: Derivate Esercizi. I Parte - Derivate
 6: Derivate Esercizi I Parte - Derivate E. 6.1 Calcolare le derivate delle seguenti funzioni: 1) log 5 3 + cos ) + 3 + 4 + 3 3) 5 tan 4) ( + 3e ) sin 5) arctan( + 1) 6) log 7) 10) + + 3 8) 3 3 1 + 16 11)
6: Derivate Esercizi I Parte - Derivate E. 6.1 Calcolare le derivate delle seguenti funzioni: 1) log 5 3 + cos ) + 3 + 4 + 3 3) 5 tan 4) ( + 3e ) sin 5) arctan( + 1) 6) log 7) 10) + + 3 8) 3 3 1 + 16 11)
Limite. Se D non è limitato si può fare il limite di f(x) per x che tende
 Appunti sul corso di Complementi di Matematica,mod.Analisi, prof. B.Bacchelli - a.a. 200/20. 05 - Limiti continuità: Riferimenti: R.Adams, Calcolo Differenziale 2. Capitoli 3., 3.2. - Esercizi 3., 3.2.
Appunti sul corso di Complementi di Matematica,mod.Analisi, prof. B.Bacchelli - a.a. 200/20. 05 - Limiti continuità: Riferimenti: R.Adams, Calcolo Differenziale 2. Capitoli 3., 3.2. - Esercizi 3., 3.2.
Analisi Matematica II Corso di Ingegneria Biomedica Compito A del f(x, y) = x 2 + y 2
 Analisi Matematica II Corso di Ingegneria Biomedica Compito A del -7- - È obbligatorio consegnare tutti i fogli, anche quelli della brutta. - Le risposte senza giustificazione sono considerate nulle. Esercizio.
Analisi Matematica II Corso di Ingegneria Biomedica Compito A del -7- - È obbligatorio consegnare tutti i fogli, anche quelli della brutta. - Le risposte senza giustificazione sono considerate nulle. Esercizio.
1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: c) x + 1 d)x sin x.
 Funzioni derivabili Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: a)2x 5 b) x 3 x 4 c) x + 1 d)x sin x. 2) Scrivere l equazione della retta tangente
Funzioni derivabili Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: a)2x 5 b) x 3 x 4 c) x + 1 d)x sin x. 2) Scrivere l equazione della retta tangente
I teoremi della funzione inversa e della funzione implicita
 I teoremi della funzione inversa e della funzione implicita Appunti per il corso di Analisi Matematica 4 G. Mauceri Indice 1 Il teorema della funzione inversa 1 Il teorema della funzione implicita 3 1
I teoremi della funzione inversa e della funzione implicita Appunti per il corso di Analisi Matematica 4 G. Mauceri Indice 1 Il teorema della funzione inversa 1 Il teorema della funzione implicita 3 1
Prima prova in itinere di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2016/2017. Prof. M. Bramanti.
 Prima prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 016/017. Prof. M. Bramanti 1 Tema n 1 4 5 6 Tot. Cognome e nome in stampatello) codice persona
Prima prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 016/017. Prof. M. Bramanti 1 Tema n 1 4 5 6 Tot. Cognome e nome in stampatello) codice persona
Matematica A Corso di Laurea in Chimica. Prova scritta del Tema A
 Matematica A Corso di Laurea in Chimica Prova scritta del 7..6 Tema A P) Data la funzione f(x) = ex+ x determinarne (a) campo di esistenza; (b) zeri e segno; (c) iti agli estremi del campo di esistenza
Matematica A Corso di Laurea in Chimica Prova scritta del 7..6 Tema A P) Data la funzione f(x) = ex+ x determinarne (a) campo di esistenza; (b) zeri e segno; (c) iti agli estremi del campo di esistenza
Analisi Matematica 2. Michele Campiti. Prove scritte di. Ingegneria Industriale a.a
 Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
Corso di Analisi Matematica
 Corso di Laurea in Ingegneria Edile Corso di DERIVATE Lucio Demeio Dipartimento di Ingegneria Industriale e delle Scienze Matematiche Secanti e tangenti Sia f : D R, sia I = [a, b] oppure I = (a, b),
Corso di Laurea in Ingegneria Edile Corso di DERIVATE Lucio Demeio Dipartimento di Ingegneria Industriale e delle Scienze Matematiche Secanti e tangenti Sia f : D R, sia I = [a, b] oppure I = (a, b),
Analisi Matematica II Corso di Ingegneria Gestionale Compito del f(x, y) = e (x3 +x) y
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del 8--7 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito del 8--7 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
TEMI D ESAME DI ANALISI MATEMATICA I
 TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea quadriennale) in Fisica a.a. 003/04 Prova scritta del 3 aprile 003 ] Siano a, c parametri reali. Studiare l esistenza e, in caso affermativo, calcolare
TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea quadriennale) in Fisica a.a. 003/04 Prova scritta del 3 aprile 003 ] Siano a, c parametri reali. Studiare l esistenza e, in caso affermativo, calcolare
Risoluzione del compito n. 4 (Giugno 2014)
 Risoluzione del compito n. 4 Giugno 2014) PROBLEMA 1 Determinate le soluzioni z, w), con z, w C,delsistema { z = w 2 w i Dalla prima equazione ricaviamo 2iz +4i z = w 2. che sostituito nella seconda la
Risoluzione del compito n. 4 Giugno 2014) PROBLEMA 1 Determinate le soluzioni z, w), con z, w C,delsistema { z = w 2 w i Dalla prima equazione ricaviamo 2iz +4i z = w 2. che sostituito nella seconda la
Funzioni di n variabili a valori vettoriali
 Funzioni di n variabili a valori vettoriali Ultimo aggiornamento: 22 maggio 2018 1 Differenziale per funzioni da R n in R k Una funzione F : A R n R k può essere vista come una k-upla di funzioni scalari
Funzioni di n variabili a valori vettoriali Ultimo aggiornamento: 22 maggio 2018 1 Differenziale per funzioni da R n in R k Una funzione F : A R n R k può essere vista come una k-upla di funzioni scalari
Analisi II, a.a Soluzioni 9. dx 1 + y 2 2xy
 Calcolare l integrale γ ω dove Analisi II, a.a. 7-8 Soluzioni 9 ω = + y xy ( + y mentre γ è la curva ( γ(t = e sin t cos t, + cos, t π/. t Non scriviamo neanche la complicata espresssione che si ottiene
Calcolare l integrale γ ω dove Analisi II, a.a. 7-8 Soluzioni 9 ω = + y xy ( + y mentre γ è la curva ( γ(t = e sin t cos t, + cos, t π/. t Non scriviamo neanche la complicata espresssione che si ottiene
Analisi Matematica II Corso di Ingegneria Gestionale Compito del log 1 + x4 +y 2. xy y
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del 9--6 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito del 9--6 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Statistica Matematica e Trattamento Informatico dei Dati. Analisi Matematica 3. Esercizi svolti nelle lezioni. V. Del Prete
 Statistica Matematica e Trattamento Informatico dei Dati A.A.00-0 Analisi Matematica 3 Esercizi svolti nelle lezioni V. Del Prete Numeri complessi Argomenti ed esercizi svolti nelle lezioni 30.09.00 e
Statistica Matematica e Trattamento Informatico dei Dati A.A.00-0 Analisi Matematica 3 Esercizi svolti nelle lezioni V. Del Prete Numeri complessi Argomenti ed esercizi svolti nelle lezioni 30.09.00 e
Analisi Matematica 1+2
 Università degli Studi di Genova Facoltà di Ingegneria - Polo di Savona via Cadorna 7-700 Savona Tel. +39 09 264555 - Fax +39 09 264558 Ingegneria Gestionale Analisi Matematica +2 A.A 998/99 - Prove parziali
Università degli Studi di Genova Facoltà di Ingegneria - Polo di Savona via Cadorna 7-700 Savona Tel. +39 09 264555 - Fax +39 09 264558 Ingegneria Gestionale Analisi Matematica +2 A.A 998/99 - Prove parziali
Analisi Matematica II Corso di Ingegneria Gestionale Compito del (x y) log
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del -6-4 Esercizio. punti Data la funzione { x y log +, fx, y = x +y 4 x, y,, x, y =, i dire in quali punti del dominio è continua; ii dire
Analisi Matematica II Corso di Ingegneria Gestionale Compito del -6-4 Esercizio. punti Data la funzione { x y log +, fx, y = x +y 4 x, y,, x, y =, i dire in quali punti del dominio è continua; ii dire
Analisi Matematica I
 Università degli Studi di Genova Facoltà di Ingegneria - Polo di Savona via Cadorna 7-7 Savona Tel. +39 9 264555 - Fax +39 9 264558 Analisi Matematica I Testi d esame e Prove parziali Analisi Matematica
Università degli Studi di Genova Facoltà di Ingegneria - Polo di Savona via Cadorna 7-7 Savona Tel. +39 9 264555 - Fax +39 9 264558 Analisi Matematica I Testi d esame e Prove parziali Analisi Matematica
Esercitazione di AM120
 Università degli Studi Roma Tre - Corso di Laurea in Matematica Esercitazione di M0.. 07 08 - Esercitatore: Luca Battaglia Soluzioni dell sercitazione 3 4 del 4 Marzo 08 rgomento: Derivate, Massimi e minimi,
Università degli Studi Roma Tre - Corso di Laurea in Matematica Esercitazione di M0.. 07 08 - Esercitatore: Luca Battaglia Soluzioni dell sercitazione 3 4 del 4 Marzo 08 rgomento: Derivate, Massimi e minimi,
Analisi - 10 settembre 2008 Corso di Laurea in Fisica - Fisica ed Astrofisica
 Analisi - 1 settembre 28 Corso di Laurea in Fisica - Fisica ed Astrofisica Chi deve fare lo scritto di Derivate e Integrali (vecchio ordinamento) deve svolgere gli esercizi: 1, 2, 3, 4, 5 Esercizio 1 Data
Analisi - 1 settembre 28 Corso di Laurea in Fisica - Fisica ed Astrofisica Chi deve fare lo scritto di Derivate e Integrali (vecchio ordinamento) deve svolgere gli esercizi: 1, 2, 3, 4, 5 Esercizio 1 Data
Analisi Matematica II Corso di Ingegneria Biomedica Compito del
 Analisi Matematica II Corso di Ingegneria Biomedica Compito del 7-- Esercizio. punti Data la funzione fx, y = log x + y x + y + x y i trovare tutti i punti critici; ii trovare massimo e minimo assoluti
Analisi Matematica II Corso di Ingegneria Biomedica Compito del 7-- Esercizio. punti Data la funzione fx, y = log x + y x + y + x y i trovare tutti i punti critici; ii trovare massimo e minimo assoluti
Analisi Matematica 3 - Soluzioni Tutorato 3
 Analisi Matematica - Soluzioni Tutorato Università degli Studi Roma Tre - Dipartimento di Matematica Docente: Luca Biasco Tutori: Patrizio Caddeo, Jacopo Tenan novembre 017 1. Discutere la continuità e
Analisi Matematica - Soluzioni Tutorato Università degli Studi Roma Tre - Dipartimento di Matematica Docente: Luca Biasco Tutori: Patrizio Caddeo, Jacopo Tenan novembre 017 1. Discutere la continuità e
ANALISI MATEMATICA I, Compito scritto del 5/07/2016 Corso di Laurea in Matematica. COGNOME e NOME... MATR T
 ANALISI MATEMATICA I, Compito scritto del 5/7/6 Corso di Laurea in Matematica COGNOME e NOME... MATR... 3 4 T Nelle risposte devono essere riportati anche i conti principali e le motivazioni principali.
ANALISI MATEMATICA I, Compito scritto del 5/7/6 Corso di Laurea in Matematica COGNOME e NOME... MATR... 3 4 T Nelle risposte devono essere riportati anche i conti principali e le motivazioni principali.
ESERCITAZIONE SUI PUNTI STAZIONARI DI FUNZIONI LIBERE E SULLE FUNZIONI OMOGENEE
 ESERCITAZIONE SUI PUNTI STAZIONARI DI FUNZIONI LIBERE E SULLE FUNZIONI OMOGENEE 1 Funzioni libere I punti stazionari di una funzione libera di più variabili si ottengono risolvendo il sistema di equazioni
ESERCITAZIONE SUI PUNTI STAZIONARI DI FUNZIONI LIBERE E SULLE FUNZIONI OMOGENEE 1 Funzioni libere I punti stazionari di una funzione libera di più variabili si ottengono risolvendo il sistema di equazioni
Compito n. 1 (Gennaio 2013)
 Compito n. 1 (Gennaio 2013) PROBLEMA 1 Determinate le soluzioni (z, w), con z, w C, del sistema z + 2i zw z 6i = 0 z z 2w = 0. Ricavando dalla seconda equazione w = z z/2 e sostituendolo nella prima questa
Compito n. 1 (Gennaio 2013) PROBLEMA 1 Determinate le soluzioni (z, w), con z, w C, del sistema z + 2i zw z 6i = 0 z z 2w = 0. Ricavando dalla seconda equazione w = z z/2 e sostituendolo nella prima questa
Appunti sul corso di Complementi di Matematica mod. Analisi prof. B.Bacchelli - a.a. 2010/2011.
 Appunti sul corso di Complementi di Matematica mod. Analisi prof. B.Baccelli - a.a. 2010/2011. 06 - Derivate, differenziabilità, piano tangente, derivate di ordine superiore. Riferimenti: R.Adams, Calcolo
Appunti sul corso di Complementi di Matematica mod. Analisi prof. B.Baccelli - a.a. 2010/2011. 06 - Derivate, differenziabilità, piano tangente, derivate di ordine superiore. Riferimenti: R.Adams, Calcolo
Corso di Analisi Matematica
 Corso di Laurea in Ingegneria Edile Corso di TEOREMI DEL CALCOLO DIFFERENZIALE Lucio Demeio Dipartimento di Ingegneria Industriale e delle Scienze Matematiche Teorema di Estremi locali Richiamiamo la
Corso di Laurea in Ingegneria Edile Corso di TEOREMI DEL CALCOLO DIFFERENZIALE Lucio Demeio Dipartimento di Ingegneria Industriale e delle Scienze Matematiche Teorema di Estremi locali Richiamiamo la
ANALISI MATEMATICA 1 Area dell Ingegneria dell Informazione
 ANALISI MATEMATICA Area dell Ingegneria dell Informazione Appello del.. TEMA Esercizio. Sia f) = + 3) log + 3), D =] 3, + [. i) Determinare i iti di f agli estremi di D e gli eventuali asintoti; studiarne
ANALISI MATEMATICA Area dell Ingegneria dell Informazione Appello del.. TEMA Esercizio. Sia f) = + 3) log + 3), D =] 3, + [. i) Determinare i iti di f agli estremi di D e gli eventuali asintoti; studiarne
Esame di Analisi Matematica 2 24/9/2013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 2012/2013
 Esame di Analisi Matematica 2 24/9/2013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 2012/2013 Esercizio 1. Sia A il cerchio aperto del piano di centro l origine e raggio 1. Sia f(x, y) una
Esame di Analisi Matematica 2 24/9/2013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 2012/2013 Esercizio 1. Sia A il cerchio aperto del piano di centro l origine e raggio 1. Sia f(x, y) una
Ingegneria civile - ambientale - edile
 Ingegneria civile - ambientale - edile Analisi - Prove scritte dal 7 Prova scritta del 9 giugno 7 Esercizio Determinare i numeri complessi z che risolvono l equazione Esercizio (i) Posto a n = n i z z
Ingegneria civile - ambientale - edile Analisi - Prove scritte dal 7 Prova scritta del 9 giugno 7 Esercizio Determinare i numeri complessi z che risolvono l equazione Esercizio (i) Posto a n = n i z z
Analisi Matematica 3 (Fisica) Prova scritta del 17 febbraio 2012 Un breve svolgimento delle versioni A
 Analisi Matematica 3 (Fisica) Prova scritta del 7 febbraio Un breve svolgimento delle versioni A Vi sarò grato per la segnalazione di eventuali errori. Esercizio. (a) Dimostrare che l equazione () (3 +
Analisi Matematica 3 (Fisica) Prova scritta del 7 febbraio Un breve svolgimento delle versioni A Vi sarò grato per la segnalazione di eventuali errori. Esercizio. (a) Dimostrare che l equazione () (3 +
IL CALCOLO DIFFERENZIALE PER FUNZIONI DI PIÙ VARIABILI
 IL CALCOLO DIFFERENZIALE PER FUNZIONI DI PIÙ VARIABILI 218-19 CLAUDIO BONANNO Richiamiamo le definizioni e le prime principali proprietà delle funzioni differenziabili di più variabili e a valori vettoriali
IL CALCOLO DIFFERENZIALE PER FUNZIONI DI PIÙ VARIABILI 218-19 CLAUDIO BONANNO Richiamiamo le definizioni e le prime principali proprietà delle funzioni differenziabili di più variabili e a valori vettoriali
PROVE SCRITTE DI ANALISI MATEMATICA II (V.O.), ANNO 2002
 PROVE SCRITTE DI ANALISI MATEMATICA II (V.O.), ANNO 22 Prova scritta del 1/1/22 Si esamini la serie di funzioni: 1 log x (e n + n), definita per x IR. Si determini l insieme S in cui tale serie converge,
PROVE SCRITTE DI ANALISI MATEMATICA II (V.O.), ANNO 22 Prova scritta del 1/1/22 Si esamini la serie di funzioni: 1 log x (e n + n), definita per x IR. Si determini l insieme S in cui tale serie converge,
ANALISI MATEMATICA 1 Area dell Ingegneria dell Informazione. Appello del
 ANALISI MATEMATICA Area dell Ingegneria dell Informazione Appello del 9..8 NOTA: lo svolgimento del Tema contiene alcuni commenti di carattere generale. Esercizio Si consideri la funzione TEMA f := log
ANALISI MATEMATICA Area dell Ingegneria dell Informazione Appello del 9..8 NOTA: lo svolgimento del Tema contiene alcuni commenti di carattere generale. Esercizio Si consideri la funzione TEMA f := log
Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 2 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata, Matematica
 DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 2 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 2 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
Integrali Curvilinei
 Integrali Curvilinei Gianluca Gorni 11 gennaio 2006 1 Lunghezza di una curva Definizione 1.1. Una curva N-dimensionale è una funzione definita su un intervallo (compatto, se non specificato altrimenti)
Integrali Curvilinei Gianluca Gorni 11 gennaio 2006 1 Lunghezza di una curva Definizione 1.1. Una curva N-dimensionale è una funzione definita su un intervallo (compatto, se non specificato altrimenti)
Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica 2 del 29 settembre 2012
 Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica del 9 settembre A) Data la funzione f(x, y) = { xy x se (x, y) (, ) se (x, y) = (, ), i) stabilire se risulta continua
Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica del 9 settembre A) Data la funzione f(x, y) = { xy x se (x, y) (, ) se (x, y) = (, ), i) stabilire se risulta continua
Analisi Matematica 3 - Soluzioni Tutorato 2
 Analisi Matematica 3 - Soluzioni Tutorato 2 Università degli Studi Roma Tre - Dipartimento di Matematica Docente: Luca Biasco Tutori: Patrizio Caddeo, Jacopo Tenan 31 ottobre 2017 1. Sia f : R n R una
Analisi Matematica 3 - Soluzioni Tutorato 2 Università degli Studi Roma Tre - Dipartimento di Matematica Docente: Luca Biasco Tutori: Patrizio Caddeo, Jacopo Tenan 31 ottobre 2017 1. Sia f : R n R una
Analisi Matematica 2 (Corso di Laurea in Informatica)
 COGNOME NOME Matr. Firma dello studente A Tempo: 3 ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
COGNOME NOME Matr. Firma dello studente A Tempo: 3 ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
Analisi Matematica II Corso di Ingegneria Gestionale Compito del y 2
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del 15--18 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito del 15--18 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
UNIVERSITÀ DEGLI STUDI DI PERUGIA Facoltà di Scienze MM. FF. e NN.
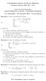 A.A. 213/214 2 Novembre 213 I esercitazione Esercizio 1. Dato il problema di Cauchy ( e y 2 2 1 ) arctan 3y 5 y = 2 sin (1) 2 x 2, 1 + x 2 y() = 1, (b) provare che la soluzione y di (3) è definita in tutto
A.A. 213/214 2 Novembre 213 I esercitazione Esercizio 1. Dato il problema di Cauchy ( e y 2 2 1 ) arctan 3y 5 y = 2 sin (1) 2 x 2, 1 + x 2 y() = 1, (b) provare che la soluzione y di (3) è definita in tutto
Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005
 Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005 Prova orale il: Docente: Determinare, se esistono, il massimo ed il minimo assoluto della funzione
Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005 Prova orale il: Docente: Determinare, se esistono, il massimo ed il minimo assoluto della funzione
Funzioni implicite - Esercizi svolti
 Funzioni implicite - Esercizi svolti Esercizio. È data la funzione di due variabili F (x, y) = y(e y + x) log x. Verificare che esiste un intorno I in R del punto di ascissa x 0 = sul quale è definita
Funzioni implicite - Esercizi svolti Esercizio. È data la funzione di due variabili F (x, y) = y(e y + x) log x. Verificare che esiste un intorno I in R del punto di ascissa x 0 = sul quale è definita
SECONDO TEST DI ANALISI 1 per i CdL in FISICA e MATEMATICA, a.a. 2016/17 assegnato in data lim
 SECONDO TEST DI ANALISI per i CdL in FISICA e MATEMATICA, a.a. 06/7 assegnato in data 5..06. Sia f : R \ {(0, 0)} R 3 la funzione definita da ( ( 4 ) f(x, y) = x + y sin, + arctan(x y), x + y Si calcoli
SECONDO TEST DI ANALISI per i CdL in FISICA e MATEMATICA, a.a. 06/7 assegnato in data 5..06. Sia f : R \ {(0, 0)} R 3 la funzione definita da ( ( 4 ) f(x, y) = x + y sin, + arctan(x y), x + y Si calcoli
Teorema delle Funzioni Implicite
 Teorema delle Funzioni Implicite Sia F una funzione di due variabili definita in un opportuno dominio D di R 2. Consideriamo l equazione F (x, y) = 0, questa avrà come soluzioni coppie di valori (x, y)
Teorema delle Funzioni Implicite Sia F una funzione di due variabili definita in un opportuno dominio D di R 2. Consideriamo l equazione F (x, y) = 0, questa avrà come soluzioni coppie di valori (x, y)
Analisi Matematica II Corso di Ingegneria Gestionale Compito A del f(x, y) = 2x 2 + x 4 + 4y 4., x 2 + y 2 1.
 Analisi Matematica II Corso di Ingegneria Gestionale Compito A del 05-06-08 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito A del 05-06-08 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
1
 1 4 5 6 7 8 Analisi Matematica I (Fisica e Astronomia) TEST n. di Esame Scritto (0/01/015) Università di Padova - Lauree in Fisica ed Astronomia - A.A. 014/15 Cognome-Nome Matr. - IN STAMPATELLO SF /
1 4 5 6 7 8 Analisi Matematica I (Fisica e Astronomia) TEST n. di Esame Scritto (0/01/015) Università di Padova - Lauree in Fisica ed Astronomia - A.A. 014/15 Cognome-Nome Matr. - IN STAMPATELLO SF /
Funzioni derivabili (V. Casarino)
 Funzioni derivabili (V. Casarino) Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in = 0 delle funzioni: a) 5 b) 3 4 c) + 1 d) sin. ) Scrivere l equazione della retta tangente
Funzioni derivabili (V. Casarino) Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in = 0 delle funzioni: a) 5 b) 3 4 c) + 1 d) sin. ) Scrivere l equazione della retta tangente
ANALISI MATEMATICA I MODULO, I e II MODULO, II MODULO CORSO DI LAUREA IN INFORMATICA
 ANALISI MATEMATICA I MODULO, I e II MODULO, II MODULO CORSO DI LAUREA IN INFORMATICA Prova scritta del 6 giugno 2004: soluzioni ESERCIZIO - Data la funzione f) 3 2 4 + 27 + 9 2 ) /3 4 + 27, + 9 si chiede
ANALISI MATEMATICA I MODULO, I e II MODULO, II MODULO CORSO DI LAUREA IN INFORMATICA Prova scritta del 6 giugno 2004: soluzioni ESERCIZIO - Data la funzione f) 3 2 4 + 27 + 9 2 ) /3 4 + 27, + 9 si chiede
1. Funzioni implicite
 1. Funzioni implicite 1.1 Il caso scalare Sia X R 2 e sia f : X R. Una funzione y : (a, b) R si dice definita implicitamente dall equazione f(x, y) = 0 in (a, b) quando: 1. (x, y(x)) X x (a, b); 2. f(x,
1. Funzioni implicite 1.1 Il caso scalare Sia X R 2 e sia f : X R. Una funzione y : (a, b) R si dice definita implicitamente dall equazione f(x, y) = 0 in (a, b) quando: 1. (x, y(x)) X x (a, b); 2. f(x,
Analisi Matematica 2
 Analisi Matematica 2 Differenziabilità per funzioni di due variabili Differenziabilità per funzioni di due variabili CCS Ingegneria Meccanica e Ingegneria Chimica 1 / 26 Differenziabilitá Data la funzione
Analisi Matematica 2 Differenziabilità per funzioni di due variabili Differenziabilità per funzioni di due variabili CCS Ingegneria Meccanica e Ingegneria Chimica 1 / 26 Differenziabilitá Data la funzione
Argomento 6 Derivate
 Argomento 6 Derivate Derivata in un punto Definizione 6. Data una funzione f definita su un intervallo I e 0 incrementale di f in 0 di incremento h = 0 = il rapporto I, si chiama rapporto per = 0 + h =
Argomento 6 Derivate Derivata in un punto Definizione 6. Data una funzione f definita su un intervallo I e 0 incrementale di f in 0 di incremento h = 0 = il rapporto I, si chiama rapporto per = 0 + h =
