1. Cosa si intende dicendo che A e B sono eventi indipendenti.;
|
|
|
- Tiziano Corradini
- 8 anni fa
- Visualizzazioni
Transcript
1 Laurea in Chimica e Tecnologia Farmaceutiche Corso di Matematica e Statistica esercizi di calcolo delle probabilità BASI. Esercizio 1 Siamo alle battute conclusive di una partita al Gioco dell Oca; al giocatore Verde, che sopravanza il giocatore Nero di due caselle, è sufficiente realizzare un 3 per raggiungere la meta. I due giocatori lanciano contemporaneamente un dado (a sei facce): nel caso entrambi raggiungano la meta la partita è considerata patta. Determinare la probabilità che, con un lancio di dadi: 1) il giocatore Verde vinca la partita; 2) il giocatore Nero vinca la partita; 3) la partita finisca in patta; 4) nessuno dei due giocatori raggiunga la meta. Esercizio 2 Siano A, B eventi in uno spazio di eventi Ω. 1. Cosa si intende dicendo che A e B sono eventi indipendenti.; 2. è vero che se A e B sono indipendenti allora anche i loro complementari A e B lo sono? si cerchi di provare in modo rigoroso l affermazione fatta. 3. Da un mazzo di carte napoletane (40 carte in 4 semi diversi) viene estratta una carte; si dica quali coppie fra quelle che si possono costituire fra i seguenti eventi sono indipendenti: A : la carta estratta è un due; B : la carta estratta è una carta di bastoni; C: la carta estratta ha valore minore o uguale a 5; Esercizio 3 Siano A e B eventi in uno spazio di eventi Ω. Cosa si intende dicendo che A e B sono incompatibili? Si dica poi quali fra le seguenti affermazioni sono vere: 1. se A e B sono incompatibili allora p(a) + p(b) 1; 2. se p(a) + p(b) 1 allora A e B sono incompatibili; 3. se A e B sono incompatibili allora A e B sono incompatibili. Esercizio 4 1. Qual è la probabilità che, lanciando tre dadi non truccati la somma dei punti sia minore uguale a sei? 2. Qual è la probabilità che la somma sia 6 sapendo che il primo dado dà 1? Esercizio 5 In un lancio di due dadi a sei facce, si determini la probabilità di ciascuno dei seguenti eventi A: esce almeno un 3; B: esce almeno un 3 sapendo che esce almeno un numero dispari; C: esce almeno un 3 sapendo che esce almeno un numero pari. Esercizio 6 Dei due eventi A, B (di uno stesso spazio Ω) si conosce p(a) 0.75, p(b) 0.6, p(a B) 0.2 (dove, come usuale, B Ω \ B). Si determini: 1. p(a B); 2. p(a B); 3. p(b A).
2 Esercizio 7 La ruota di una roulette contiene i numeri da 1 a 36 (non contiamo lo 0; quindi non si tratta di una vera roulette da casinò). 1. Un giocatore punta un euro sul pari ed un euro sul quadrato costituito dall insieme di numeri {8, 9, 11, 12}; qual è la probabilità che il giocatore vinca qualcosa? 2. Giocando per tre volte di seguito la prima dozzina {1, 2,..., 12}, qual è la probabilità di vincere almeno una volta? PROBABILITÀ CONDIZIONATA. Esercizio 8 Di tre eventi A, B e C (di uno stesso spazio) si conosce Si determini: p(a C) 0.2, p(b C) 0.4, p(a B C) p(a B C); 2. p(a C B); 3. p(a B C). Esercizio 9 Ad una svendita fallimentare il prof. B acquista una partita di 150 lampadine, il 20% delle quali sono fulminate. Sapendo che 100 lampadine sono di colore rosso e 50 giallo, e che la probabilità che una lampadina rossa sia fulminata è il doppio della probabilità che lo sia una lampadina gialla, si dica: 1. qual è la probabilità che una lampadina rossa sia fulminata; 2. qual è la probabilità che una lampadina funzionante sia gialla. Esercizio 10 Durante una seduta spiritica vi è incertezza se lo spirito evocato sia quello di Dante o quello di Petrarca. Alla domanda del medium: Chi sei?, lo spirto risponde: Dante, ovvia!. Sapendo che la probabilità che si tratti di ciascuno dei due sommi letterati è la stessa (cioè 0, 5) e che lo spirito di Dante mente nel 72% dei casi mentre quello di Petrarca mente nel 38% dei casi, si dica qual è la probabilità che lo spirito evocato sia effettivamente quello di Dante. In un altra occasione, alla domanda del medium lo spirto (che si sa essere quello di Dante o quello di Petrarca) risponde con una palese menzogna. Qual è la probabilità che si tratti di Dante? Esercizio 11 Trattate con solfato ferroso due specie di batteri non facilmente distinguibili presentano statisticamente il seguente comportamento: nella specie X diventa azzurro il 30% dei batteri, nella specie Y il 60%. Un trattamento su una cultura mista di batteri X e Y dà come esito l azzurramento del 40% dei batteri. 1. Si dica quale percentuale della coltura è, statisticamente, composta da batteri di specie X. 2. Osservando al microscopio si vede un batterio divenuto azzurro; si dica qual è la probabilità che appartenga alla specie X. Esercizio 12 L arciere Tuk colpisce il centro del bersaglio nel 60% dei casi; l arciere Kuk nel 42%, e l arciere Buk nel 50%. Ad una gara di tiro, ciascuno di loro scaglia una freccia: 1. qual è la probabilità che il bersaglio sia stato centrato almeno una volta? 2. qual è la probabilità che il bersaglio sia stato centrato almeno due volte? 2
3 3. sapendo che il bersaglio è stato centrato, qual è la probabilità che una delle frecce che lo ha colpito sia quella dell arciere Tuk? Esercizio 13 Durante l intera competizione citata nell esercizio precedente Tuk scaglia 10 frecce, Kuk 15 e Buk 20; al termine un paggio raccoglie una freccia finita a terra (cioè: una che non ha centrato il bersaglio). Qual è la probabilità che si tratti di una freccia di Tuk? Raccogliendone due da terra, qual è la probabilità che almeno una sia dell arciere Tuk? TEST DIAGNOSTICI Esercizio 14 In una popolazione di 1200 individui, relativamente ad una malattia M ed un test diagnostico T si rilevano i seguenti dati: T T + M M Si determini: 1) l incidenza della malattia; 2) sensibilità e specificità del test; 3) valore predittivo positivo del test. Esercizio 15 La sensibilità di un test diagnostico è 0.60, la sua specificità Indicando con q l incidenza della malattia, si determini in funzione di q la probabilità che un individuo il cui test è negativo sia sano. Si calcoli poi il valore nel nei casi q 0.10 e q Esercizio 16 Un test diagnostico per una certa malattia ha specificità 0.96 e sensibilità qual è il valore predittivo positivo (cioè la probabilità che risultando il test positivo si abbia la malattia) se l incidenza della malattia è di 2%; 2. quale incidenza dovrebbe avere la stessa malattia affinché il valore predittivo positivo del test superi il 50%? Esercizio 17 Un test diagnostico per una certa malattia M eseguito su un campione di 2000 individui ha dato esito positivo in 200 casi e negativo nei rimanenti. Sapendo che la malattia ha un incidenza del 12% e che la specificità del test è 0.9, si determini la sua sensibilità. IL PROFESSOR B. Esercizio 18 I prof. B tiene reclusa una popolazione di criceti così composta: metà hanno meno di 1, anno, un quarto tra 1 e 2 anni, e il rimanente quarto più di 2 anni. Molti di loro soffrono di depressione: per la precisione: il 18% dei criceti che hanno meno di un anno; il 42% dei criceti che hanno da 1 a 2 anni; il 70% dei criceti che hanno più di 2 anni. Sulla base di questi dati si calcoli: 1. la proabilità che un criceto scelto a caso sia depresso? 2. la probabilità che un criceto non depresso abbia da 1 a 2 anni? 3
4 Esercizio 19 Il criceto Carletto, evaso nottetempo dalla sua gabbia nel laboratorio del prof.b, si imbatte in un sacchetto contenente frutta secca, composto al 24% da anacardi e il rimanente da nocciole. Inoltre, per effetto degli esperimenti del prof. B, un 1/4 dei frutti nel sacchetto sono radioattivi. È noto infine che la percentuale di anacardi radioattivi è del 15%. Qual è la probabilità che, estraendo dal sacchetto un frutto a caso, il criceto Carletto trovi una nocciola non radioattiva? Esercizio 20 Il professor B acquista una scatola contenente 40 funghi neri e 60 funghi rossi, con l intenzione di somministrarli al suo criceto Carletto. Sapendo che (nei criceti) i funghi neri generano allucinazioni con probabilità 0.60 e quelli rossi con probabilità 0.80, e che, inoltre, le allucinazioni generate dai funghi neri conducono Carletto a tentare di mordere il naso del prof. B, calcolare 1. la probabilità che Carletto, ingerito uno dei funghi, abbia le allucinazioni; 2. le probabilità che, sapendo che il nostro criceto ha ingerito uno dei funghi ed è entrato in stato allucinatorio, egli morda il naso del prof. B. 3. la probabilità che, avendo ingerito 5 funghi, Carletto morda almeno una volta il naso al prof.b. Esercizio 21 Il professor B effettua un trattamento musicale sui criceti, diffondendo tra le gabbiette brani scelti da un selezionatore casuale, tra quelli disponibili nella memoria di un ipod da lui sequestrato in un aula universitaria. Sono note le seguenti informazioni: - la probabilità che un brano tra quelli dell ipod piaccia al criceto Carletto è 1/3. - la percentuale dei brani di Frank Zappa che piacciono a Carletto è del 92%; - la probabilità che un brano che piace a Carletto sia di Frank Zappa è sapendo che il numero di brani in memoria è 253, dire quanti sono quelli di Frank Zappa; 2. qual è la probabilità che un brano (selezionato a caso) sia un brano di Frank Zappa che piace al criceto? 3. dire se dopo la selezione consecutiva di tre brani, la probabilità che almeno uno sia un brano di Zappa che piace al criceto è maggiore del 50%. Esercizio 22 Il professor B ha rubato un flacone di un certo siero dallo studio di un collega (tale Jekyll), e lo somministra ai suoi criceti. Durante la notte, il siero agisce sul 40% dei criceti maschi e il 20% dei criceti femmina, trasformando i criceti su cui agisce in sanguinari criceti-hyde. Pochi minuti dopo, ogni criceto-hyde assale un criceto che non ha subito la trasformazione, facendolo a pezzi; al mattino, ogni criceto ritorna normale. Sapendo che i criceti maschi sono il 60% del gruppo si dica 1. qual è la probabilità che, al mattino, il criceto Carletto sia ancora vivo? 2. qual è la probabilità che il criceto Carletto, sapendo che non ha subito la trasformazione notturna, sia una femmina? (non date peso al nome: il prof. B di certe cose non ci ha mai capito molto e, se è per questo, nemmeno il criceto). DADI, CARTE, PALLINE Esercizio 23 Dato un mazzo di carte napoletane (40 carte e quattro semi: bastoni, coppe, danari, spade); una mano consiste in un insieme di 4 carte pescate dal mazzo: 4
5 1. quante sono le mani fatte solo da carte a bastoni? e quante quelle fatte da carte dello stesso seme? 2. qual è la probabilità di avere una mano fatta da carte di semi tutti diversi? 3. quante sono le mani in cui ci sono esattamente due carte a bastoni? 4. pescando 2 carte dal mazzo, qual è la probabilità che siano di semi diversi? Esercizio 24 Un urna A contiene 5 palline bianche e 6 palline rosse; un altra urna B ne contiene 8 rosse e 3 bianche. Un meccanismo casuale sposta una pallina dall urna B all urna A. 1. Qual è la probabilità che (dopo il passaggio) estraendo una pallina dall urna A si trovi una pallina bianca? [usare la legge delle alternative] 2. Dopo il passaggio si estrae a caso una pallina dall urna A; sapendo che questa è bianca, dire qual è la probabilità che la pallina inizialmente trasferita da B ad A sia bianca. Esercizio 25 Dire se lanciando 4 dadi a sei facce non truccati, la probabilità che esca almeno una coppia di valori uguali è superiore o inferiore al 70%. Esercizio 26 Le facce di un dado dodecaedrico (cioè a dodici facce) vengono colorate: 4 di rosso, 3 di bianco, 3 di verde e 2 di nero. Lanciandolo cinque volte di seguito qual è la probabiloità: 1. escano esattamente due facce rosse; 2. escano due facce rosse, due bianche e una nera; 3. escano solo facce rosse e nere. Esercizio 27 Vi sono tre urne ognuna delle quali contiene 12 palline rosse e 18 palline gialle. Viene estratta a caso una pallina da ogni urna. 1. Qual è la probabilità che vengano estratte esattamente 2 palline rosse? 2. qual è la probabilità che vengano estratte tre palline dello stesso colore? Esercizio 28 Una slot-machine è formata da tre ruote, ognuna delle quali contiene otto caselle di cui 2 recano il disegno di una ciliegia e le rimanenti sei i numeri da 1 a 6. Qual è la probabilità che, azionando la leva: 1. escano esattamente due ciliegie; 2. escano tre simboli uguali. I CASSETTI MALEFICI Esercizio 29 In un armadio provvisto di otto cassetti vengono collocate casualmente, una per cassetto, 6 maglie rosse e 2 maglie verdi. 1. Qual è la probabilità di trovare una maglia rossa aprendo un cassetto a caso? 2. Aprendo a caso due cassetti qual è la probabilità di trovare: almeno una maglia rossa, due maglie rosse, due maglie di colori diversi? 5
6 Esercizio 30 Nell armadio a otto cassetti vengono collocate alla rinfusa 14 paia di pantaloni, in due delle quali è stato lasciato un portafoglio. 1. Qual è la probabilità di trovare un paio di pantaloni col portafoglio aprendo un cassetto a caso? 2. Aprendo un cassetto si trovano due paia di pantaloni; qual è la probabilità che ci sia (almeno) un portafoglio? Esercizio 31 Nell armadio a otto cassetti vengono collocate alla rinfusa 12 camicie. 1. Qual è la probabilità di trovare una camicia aprendo un cassetto a caso? 2. Se dopo aver aperto due cassetti non si è trovata alcuna camicia, qual è la probabilità che aprendo il prossimo se ne trovino due? 3. Sapendo che un certo cassetto contiene (almeno) una camicia, qual è la probabilitrà, aprendolo, di trovarne due? Esercizio 32 Un nuovo armadio ha nove cassetti, ma uno - di cui non si conosce la posizione - è stregato, per cui qualsiasi cosa vi si metta dentro essa scompare. Nell armadio vengono riposte 6 camicie, mettendone in ogni cassetto al più una; qual è la probabilità che aprendo un cassetto a caso si trovi una camicia. 6
7 ALCUNE SOLUZIONI Esercizio 1. Ogni giocatore lancia il dado; lo spazio degli eventi è quello naturale delle coppie di numeri da 1 a 6: Ω {(x, y) x, y {1,..., 6}}, dunque Ω 36. Denotiamo con v e con n, rispettivamente, il punteggio realizzato col lancio del dado dal giocatore Verde e quello realizzato dal giocatore Nero. 1. Verde vince la partita se v {3, 4, 5, 6} e n {1, 2, 3, 4}; i casi favorevoli alla vittoria del Verde sono quindi , e la probabilità che Verde vinca è 16/36 4/9. 2. Nero vince la partita se v {1, 2} e n {5, 6}; i casi favorevoli alla vittoria del Nero sono 2 2 4, e la probabilità che Nero vinca è 4/36 1/9. 3. Si ha parità se v {3, 4, 5, 6} e n {5, 6}; i casi favorevoli alla patta sono 4 2 8, e la probabilità che la partita termini in parità è 8/36 2/9. 4. Nessuno giunge alla meta nei casi v {1, 2} e n {1, 2, 3, 4}; il numero di questi casi è 2 4 8, e la probabilità che nessuno vinca è 8/36 2/9. [si osservi che i quattro eventi di cui si è calcolato la probabilità sono a due a due incompatibili e che la loro unione ricopre l intero spazio degli eventi; la somma delle probabilità è, infatti, 4/9 + 1/9 + 2/9 + 2/9 9/9 1.] Esercizio Gli eventi A e B sono indipendenti se p(a B) p(a)p(b). 2. Supponiamo che A e B siano indipendenti e verifichiamo che per i complementari vale l identità p(a B) p(a)p(b) che stabilisce la loro indipendenza. Per farlo, si può ricorrere all identità di De Morgan A B A B, e la formula p(a B) 1 p(a) p(b) + p(a B). Abbiamo, p(a B) p(a B) 1 p(a B) 1 p(a) p(b) + p(a B) 1 p(a) p(b) + p(a)p(b) (1 p(a))(1 p(b)) p(a)p(b). dunque A e B sono indipendenti. 3. Abbiamo, per ovvie considerazioni, E, ancora, p(a) 4/40 1/10, p(b) 10/40 1/4 e p(c) 20/40 1/2. p(a B) 1/40, p(a C) 4/40, p(b C) 5/40. Ora, basta esaminare le varie possibilità. Si trova che p(a B) 1/40 (1/10)(1/4) p(a)p(b) e dunque A e B sono indipendenti. Calcolando allo stesso modo, p(b C) 5/40 1/8 (1/4)(1/2) p(b)p(c) p(a C) 4/40 (1/10)(1/2) p(a)p(c) dunque B e C sono indipendenti, mentre A e C non lo sono. Esercizio 3. Gli eventi A e B sono incompatibili se p(a B) Vero. Infatti, se A e B sono eventi sappiamo che p(a) + p(b) P (A B) p(a B). Se A e B sono incompatibili, p(a B) 0, dunque p(a) + p(b) p(a B) 1. 7
8 2. Falso. Consideriamo, ad esempio, un lancio di un dato a sei facce, e i due eventi: A esce un numero pari, B esce un numero minore a uguale a 2. Allora p(a) + p(b) 1/2 + 1/3 5/6 1, ma A e B non sono incompatibili (infatti p(a B) p(esce 2) 1/6 0). 3. Falso. Ad esempio, ancora nel lancio di un dado a sei facce, consideriamo gli eventi A esce maggiore o uguale a 5, B esce un numero minore a uguale a 2. A e B sono incompatibili mentre, p(a B) p(a B) 1 p(a B) 1 4/6 1/3 0. Dunque, A e B non sono incompatibili. Esercizio I casi possibili sono I casi favorevoli si devono contare; essi sono costituiti dalle seguenti uscite tre 1 due 1 e un 1 due 1 e un 3 due 1 e un 4 un 1 e due 2 un 1 un 2 e un 3 tre 2 1 caso 3 casi 3 casi 3 casi 3 casi 6 casi 1 caso i casi favorevoli (somma 6) sono dunque 20; la probabilità cercata è quindi p Chiaramente, il valore cercato in questo caso è uguale alla probabilità che, lanciando due dadi, la somma dei punti sia uguale a 5. Per questo, i casi favorevoli sono 4 (cioè (1, 4), (2, 3), (3, 2), (4, 1)) su possibili. La probabilità cercata è dunque p Esercizio 5. Per due dadi a sei facce i casi possibili sono : i casi favorevoli all evento A sono 11, quindi p(a) I casi in cui esce almeno un dispari sono 27 (cioè 36 meno quelli in cui escono due pari che sono 3 2 9), quelli con almeno un 3 sono ancora 11 (si osservi che l evento esce almeno un 3 è contenuto nell evento esce almeno un dispari ); la probabilità cercata è quindi p I casi in cui esce almeno un pari sono (come per i dispari) 27; tra questi, quelli dove esce un 3 sono 6; la probabilità cercata è dunque p Esercizio p(a B) p(a) + p(b) p(a B) p(a) + (1 p(b)) p(a B) Osserviamo che p(a B) + p(a B) p(a); quindi p(a B) p(a) p(a B) p(b A) 1 p(b A) 1 p(b A) 1 [p(a) + p(b) p(a B)] 1 ( )
9 Esercizio La probabilità che, per un giro della pallina, esca un numero pari p(p ) , quella che esca un numero di A {8, 9, 11, 12} è p(a) Quindi, la probabilità di vincere qualcosa per un giocatore che punti sul peri e sulla quartina A è p(a P ) p(a) + p(p ) p(a P ) La probabilità di vincere, in un turno, puntando sulla dozzina è p 1 3 (e quella di non vincere è q 1 p 2 3. Gli eventi di diversi turni della roulette sono ovviamente indipendenti; quindi le probabilità che si hanno ad ogni turno si moltiplicano tra loro. Nel caso specifico, la probabilità di non vincere per tre volte di seguito puntando sulla dozzina è: q , e dunque la probabilità di vincere almeno una volta è La probabilità di vincere al primo turno e perdere negli altri è p q 2, e la stessa è per la vincita solo al secondo o solo al terzo turno. Dunque, la probabilità di vincere esattamente una volta è 3(p q 2 ) (si tratta di un caso molto semplice di distribuzione bernoulliana) Esercizio Per definizione di probabilità condizionata e la proprietà distributiva: p(a B C) p((a B) C) p((a C) (B C)) p(c) p(c) p(a C) p(b C) p(a B C) + p(c) p(c) p(c) p(a C) + p(b C) p(a C B) p((a B) C)/p(B) p(a B C)/p(B) 0/p(B) Osserviamo che, poiché p(a C B) p(a B C) 0, si ha p(a C B) p(a C). Quindi p(a B C) p(a C) p(a B C) p(a C) 0.2. p(c) p(c) Esercizio 9. Denotiamo con p(r), p(g), p(f ) la probabiltà che una lampadina presa a caso tra quelle acquistate sia, rispettivamente, rossa, gialla, fulminata. Le informazioni a disposizione sono quindi p(r) , p(g) , p(f ) , e, inoltre, p(f R) 2 p(f G). 1. Ponendo x p(f R), la legge delle alternative si scrive 1 2 p(f ) p(f R)p(R) + p(f G)p(G) x x x da cui si ricava x 6/ Dal punto precedente si ha, anche, p(f G) La probabilità che una lampadina finzuionante sia gialla è p(g F ); per la formula di Bayes: p(g F ) p(f G)p(G) p(f ) 1 p(f G) 1 p(f ) 9 p(g)
10 Esercizio 10. Denotiamo con D e P, rispettivamente gli eventi lo spirito è Dante e lo spirito è Petrarca, e con M l evento lo spirito mente. I dati a nostra disposizione sono quindi - p(d) p(p ) p(m D) 0.72, p(m P ) La prima questione chiede di determinare p(d M) (dove M è l evento complementare a M, ovvero lo spirito dice la varità). Dalla definizione di probabilità condizionata abbiamo: p(d M) p(m D)p(D) (1 p(m D))p(D) (0.28)(0.5) La seconda questione chiede di trovare p(d M). Applicando Bayes p(d M) p(m D)p(D) p(m) (1) e, come si fa spesso, p(m) si calcola mediante la legge delle alternative: p(m) p(m D)p(D) + p(m P )p(p ) (0.72)(0.5) (0.38)(0.5) 0.55 Quindi, da (1) si ricava: p(d M) (0.72)(0.5) Esercizio 11. Denotiamo con X e Y l evento il batterio appartiene alla specie X o, rispettivamente, specie Y, e con A il batterio diventa azzurro. I dati di cui disponiamo si traducono come p(a X) 0.3, p(a Y ) 0.6 e p(a) Nella popolazione sottoposta al trattamento ci sono solo batteri dei due tipi; dunque p(x) + p(y ) 1. Quindi, usando all indietro la formula delle alternative: 0.4 p(a) p(a X)p(X) + p(a Y )p(y ) (0.3)p(X) + (0.6)(1 p(x)) da cui si ricava: p(x) 2/3. Dunque la percentuale di batteri appartenenti alla specie X si può stimare nel 66. 6%. 2. La domanda chiede di calcolare p(x A). Basta applicare la formula dii Bayes: p(x A) p(a X)p(X) p(a) (0.3)(2/3) Esercizio 12. Sia T l evento: la freccia di Tuk centra il bersaglio, K l evento: la freccia di Kuk centra il bersaglio e B l evento: la freccia di Buk centra il bersaglio. Poiché ciascuno lancia una freccia, i tre eventi sono mutuamente indipendenti, e si ha p(t ) 0.6, p(k) 0.42, p(b) ) Si vuol determinare la probabilità p dell evento T K B. Conviene usare il complementare T K B T K B. Poiché anche gli eventi T, K, B sono mutuamente indipendenti si ha p 1 p(t K B) 1 (1 p(t ))(1 p(k))(1 p(b))
11 2) La probabilità p cercata è la somma delle probabilità (per quattro eventi indipendenti); p 0 p(t K B), p 1 p(t K B), p 2 p(t K B), p 3 p(t K B). Poiché le tre frecce determinano eventi indipendenti, si ha: p p p p Quindi, p ) Il bersaglio è stato colpito è l evento C T K B, la cui probabilità, calcolata al punto (1), è p(c) Quel che cerchiamo è la probabilità condizionata p(t C). Poiché l evento T è contenuto nell evento C, non si ha altro che p(t C) p(t C) p(c) p(t ) p(c) Esercizio 13. Cambiando notazione rispetto all esercizio precedente, denotiamo con T, K e B il fatto che la freccia sia stata scagliata, rispettivamente, da Tuk, Kuk e Buk, e con C l evento: la freccia ha centrato il bersaglio. Quindi, i dati del problema forniscono p(t ) 10/45 2/9, p(k) 15/45 3/9, p(b) 20/45 4/9; più i dati del precedente che si traducono con p(c T ) 0.6, p(c K) 0.42, p(c B) 0.5. La formula delle alternative fornisce la probabilità di C: p(c) p(c T )p(t ) + p(c K)p(K) + p(c B)pB) 4/ Quello che cerchiamo è la probabilità p(t C). Applicando la formula di Bayes: p(t C) p(c T )p(t ) p(c) (1 p(c T ))p(t ) 1 p(c) Esercizio Gli individui affetti dalla malattia sono quelli nell insieme M +, e M L incidenza della malattia è dunque 2. Per definizione, la sensibilità del test è e la sua specificità p(m + ) Se p(t + M + ) p(t + M + ) p(m + ) Sp p(t M ) p(t M ) p(m ) 168/ / ; 912/ / Tenendo conto che p(t + ) , il valore predittivo è, per definizione, V p + p(m + T + ) p(t + M + )p(m + ) p(t + )
12 Esercizio 15. Indichiamo, come di consueto, con M + i soggetti affetti dalla malattia, con M quelli non affetti, con T + quelli il cui test risulta positivo e T quelli il cui test risulta negativo. Quindi, l incidenza della malattia è q p(m + ) 0.20, mentre, per definizione, indicando con Sp la specificità del test e con Se la sua sensibilità, Sp p(t M ) e Se p(t + M + ). Vogliamo trovare a probabilità che un individuo il cui test è negativo non sia affetto dalla malattia, cioè p(m T ) p(t )p(t M ) p(m ) Ora, per la formula delle alternative p(t ) Sp 1 q 0.8 p(t ). 1 q p(t ) p(t M )p(m ) + p(t M + )p(m + ) Sp (1 q) + (1 p(t + M + )) q Sp (1 q) + (1 Se) q q Quindi, sostituendo nell uguaglianza precedente, p(m T ) q 1 q q 1 q. Per q 0.10 si ha p(m T ) Per q 0.30 si ha p(m T ) Esercizio Denotiamo con V + il valore predittivo cercato. Per definizione e la formula di Bayes V + p(m + T + ) p(t + M + )p(m + ) p(t +. (2) ) dove p(t + M + ) 0.98 è la sensibilità del test e p(m + ) 0.02 l incidenza della malattia. Per calcolare il denominatore si può usare la formula delle alternative, ricordando che p(t M ) 0.96 è la specificità del test. Si ha p(t + ) p(t + M + )p(m + ) + p(t + M )p(m ) Sostituendo nell equazione (2), che è il valore cercato. p(t + M + )p(m + ) + (1 p(t M ))(1 p(m + )) V / In questo punto l incognita è x p(m + ). Come nel punto precedente, p(t + ) p(t + M + )x + p(t + M )(1 x) 0.98x (1 x) 0.94x Poi, dall equazione (2) e dalle condizioni del testo, 0.5 V + p(t + M + )x p(t + ) Si tratta quindi di risolvere la disequazione 0.98x 0.94x x 0.94x
13 ovvero quindi da cui 0.98x 0.5(0.94x ) 0.47x ( )x 0.02 x % Esercizio 17. Esercizio 18. Esercizio 19. Indicando con p(r) la probabilità che un frutto del sacchetto sia radioattivo, con p(a) la probabilità che sia un anacardo e p(n) che sia una nocciola. I dati del problema si rappresentano quindi con p(r) 1/4 0.25, p(a) 0.24, p(n) 0.76, p(r A) La provbabilità cercata è p(n R). Dalla formula delle alternative, posto x p(r N), 0.25 p(r) p(r A)p(A) + p(r N)p(N) x da cui si ricava x Dunque p(r N) 1 x A questo punto, per definizione di probabilità condizionata, p(n R) p(r N)p(N) Esercizio 20. Fissando le seguenti notazioni per i vari eventi N: fungo nero, R: fungo rosso, A: allucinazioni, i dati del problema si riformulano come p(n) 0.4, p(r) 0.6, p(a N) 0.6, p(a R) Basta applicare la formula delle alternative: p(a) p(a N)p(N) + p(a R)p(R) Osservando che l evento Carletto morde il prof.b coincide con N A, la probabilità cercata è la probabilità condizionata p(n A). Basta quindi applicare la formula di Bayes: p(n A) p(n)p(a N) p(a) ( 76 5 ( Come al punto precedente, la probabilità che un fungo induca a mordere il naso è p(m) (N A) p(a N)p(N) Quindi la probabilità che un fungo non induca a mordere è 1 p(m) La probabilità che, in 5 ingestioni, Carletto mangi solo funghi di questo tipo è ) q ) Pertanto, la probabilità che, mangiando 5 funghi, il criceto abbia le allucinazioni e morda il professore almeno una volta è 1 q
14 Esercizio 21. Denotiamo con Z il brano è di Franz Zappa, con C il brano piace a Carletto. I dati a disposizione si traducono con p(c) 1/3, p(c Z) 0.92, p(z C) Sia x il numero di brani di Zappa; allora la probabilità che un brano selezionato a caso sia di Frank Zappa è x/253. Occorre quindi determinare p(z). Per la formula di Bayes da cui si ricava e quindi x p(z C) p(c Z)p(Z) p(c) 0.92p(Z) 1/3 x 0.6 p(z) p(Z) 2. Qui ci chiede di calcolare p(z C). Dalla definizione di probabilità condizionata si ha da cui p(z C) p(z C) p(z C) pc) p(z C) 1/3 3. La probabilità che un brano casuale sia di Zappa e piaccia al criceto, calcolata al punto 2., è p 0.2. Quindi la probabilità che per tre volte di seguito non sia selezionato un brano del genere è (1 p) 3, e dunque la probabilità che almeno uno lo sia è che è inferiore al 50%. 1 (1 p) 3 1 (0.8) Esercizio Le carte a bastoni sono un insieme di 10 elementi; una mano a bastoni consiste in un suo sottoinsieme di quattro elementi. Il numero di tali sottoinsiemi (e la risposta alla domanda) è: ( ) ! Per la seconda domanda basta ovviamente moltiplicare per quattro: 4 (10 ) Poiché i semi sono tanti quanto le carte di una mano, il numero di mani formate da carte di semi tutti diversi è ciascun Il numero totale di mani possibili è ( ) La probabilità cercata è dunque p 104 ) ( Il numero di coppie di carte a bastoni è ( ) ; quello delle coppie formate da carte degli altri tre semi è ( ) Il numero di mani costituita da una coppia a bastoni ed una coppia di altri semi è dunque Il numero totale di coppie di carte è ( ) Il numero di coppie costituite da carte dello stesso seme è 4 (10 ) 2 180; dunque il numero di coppie di carte di seme diverso è La probabilità di pescare una coppia di carte di seme diverso è dunque p
15 Esercizio 24. Scriviamo R e B per intendere che da B a A è passata una pallina rossa e, rispettivamente, bianca. Quindi p(r) 8/11 e p(b) 3/11. Denotiamo poi con r e b il fatto che dall urna A venga estratta, dopo il passaggio, una pallina di colore rosso o, rispettivamente, di colore bianco. 1. Per la legge delle alternative p(b) p(b B)p(B) + p(b R)p(R) 6 12 p(b) p(r) La domanda chiede di calcolare la probabilità condizionata p(b b). Tenendo conto che p(b B) 6/12 1/2 ed usando la formula di Bayes si trova p(b b) p(b B)p(B) p(b) (1/2)(3/11) 29/ Esercizio 28. La probabilità che, su ciascuna ruota, esca una ciliegia è p Le tre ruote poi sono indipendenti l una dall altra. La risposta al punto 1. è quindi un applicazione della formula per gli eventi bernoulliani: p(2cil) ( ) 3 2 p 2 (1 p) , Lo spazio degli eventi è costituito da 8 3 casi. Di questi quelli in cui i tre simboli sono uguali sono 6 se il simbolo comune non è la ciliegia e se è la ciliegia; quindi i casi favorevoli sono 6 + 8n 14. Pertanto, la probabilità cercata è Il caso di tre simboli diversi è più complicato da analizzare: questo perché la ciliegia ha più probabilità di uscire di uno specifico numero. Mantenendo lo spazio degli eventi quello di tutte le possibili ruotate (quindi Ω 8 3 ), possiamo ripartire l evento A tutti simboli diversi in due casi tra loro incompatibili: A 1 i simboli sono diversi e non c è la ciliegia; A 2 i simboli sono diversi e c è la ciliegia;. A 1 si calcola facilmente, infatti - poiché i numeri sono sei in ogni ruota - è uguale al numero di disposizioni senza ripetizione A 1 D 6, Per calcolare A 2 possiamo calcorae quante sono le coppie ordinate di smboli diversi tra loro e dalla ciliegia, che sono 6 5; poi tener conto che la ciliegia, può uscire in 6 modi; si ha quindi A 2 6 (6 5). Dunque A A 1 + A Pertanto, la probabilità che escano tre simboli diversi è: p(diversi) A Ω Esercizio La probabilità di trovare una maglia rossa aprendo un cassetto a caso è 6/8. 15
16 2. Le possibili scelte per due cassetti sono ( 8 2) 28 e ovviamente c é una sola coppia di cassetti contenenti entrambi una maglia verde. Dunque la probabilità di trovare almeno una maglia rossa aprendo due cassetti a caso è: p Le coppie di cassetti con maglie rosse sono ( 6 2) 15; quindi la probabilità di trovare due maglie rosse aprendo due cassetti a caso è: p La probabilità di trovare due maglie di colori diversi aprendo due cassetti a caso è: p 3 p 1 p
Per poter affrontare il problema abbiamo bisogno di parlare di probabilità (almeno in maniera intuitiva). Analizziamo alcune situazioni concrete.
 Parliamo di probabilità. Supponiamo di avere un sacchetto con dentro una pallina rossa; posso aggiungere tante palline bianche quante voglio, per ogni pallina bianca che aggiungo devo pagare però un prezzo
Parliamo di probabilità. Supponiamo di avere un sacchetto con dentro una pallina rossa; posso aggiungere tante palline bianche quante voglio, per ogni pallina bianca che aggiungo devo pagare però un prezzo
Test sul calcolo della probabilità
 Test sul calcolo della probabilità 2 Test sul calcolo della probabilità Test sul calcolo della probabilità. La probabilità p di un evento E, quando si indica con E il suo complementare, è : a) 0 se E è
Test sul calcolo della probabilità 2 Test sul calcolo della probabilità Test sul calcolo della probabilità. La probabilità p di un evento E, quando si indica con E il suo complementare, è : a) 0 se E è
Analisi dei Dati 12/13 Esercizi proposti 3 soluzioni
 Analisi dei Dati 1/13 Esercizi proposti 3 soluzioni 0.1 Un urna contiene 6 palline rosse e 8 palline nere. Si estraggono simultaneamente due palline. Qual è la probabilità di estrarle entrambe rosse? (6
Analisi dei Dati 1/13 Esercizi proposti 3 soluzioni 0.1 Un urna contiene 6 palline rosse e 8 palline nere. Si estraggono simultaneamente due palline. Qual è la probabilità di estrarle entrambe rosse? (6
Corso di Matematica. Corso di Laurea in Farmacia, Facoltà di Farmacia. Università degli Studi di Pisa. Maria Luisa Chiofalo.
 Corso di Matematica Corso di Laurea in Farmacia, Facoltà di Farmacia Università degli Studi di Pisa Maria Luisa Chiofalo Scheda 18 Esercizi svolti sul calcolo delle probabilità I testi degli esercizi sono
Corso di Matematica Corso di Laurea in Farmacia, Facoltà di Farmacia Università degli Studi di Pisa Maria Luisa Chiofalo Scheda 18 Esercizi svolti sul calcolo delle probabilità I testi degli esercizi sono
Esercizi. Rappresentando le estrazioni con un grafo ad albero, calcolare la probabilità che:
 Esercizi Esercizio 4. Un urna contiene inizialmente 2 palline bianche e 4 palline rosse. Si effettuano due estrazioni con la seguente modalità: se alla prima estrazione esce una pallina bianca, la si rimette
Esercizi Esercizio 4. Un urna contiene inizialmente 2 palline bianche e 4 palline rosse. Si effettuano due estrazioni con la seguente modalità: se alla prima estrazione esce una pallina bianca, la si rimette
Esercizi di Calcolo delle Probabilita (I)
 Esercizi di Calcolo delle Probabilita (I) 1. Si supponga di avere un urna con 15 palline di cui 5 rosse, 8 bianche e 2 nere. Immaginando di estrarre due palline con reimmissione, si dica con quale probabilità:
Esercizi di Calcolo delle Probabilita (I) 1. Si supponga di avere un urna con 15 palline di cui 5 rosse, 8 bianche e 2 nere. Immaginando di estrarre due palline con reimmissione, si dica con quale probabilità:
(concetto classico di probabilità)
 Probabilità matematica (concetto classico di probabilità) Teoria ed esempi Introduzione Il calcolo delle probabilità è la parte della matematica che si occupa di prevedere, sulla base di regole e leggi
Probabilità matematica (concetto classico di probabilità) Teoria ed esempi Introduzione Il calcolo delle probabilità è la parte della matematica che si occupa di prevedere, sulla base di regole e leggi
Calcolo delle probabilità
 Calcolo delle probabilità Laboratorio di Bioinformatica Corso A aa 2005-2006 Statistica Dai risultati di un esperimento si determinano alcune caratteristiche della popolazione Calcolo delle probabilità
Calcolo delle probabilità Laboratorio di Bioinformatica Corso A aa 2005-2006 Statistica Dai risultati di un esperimento si determinano alcune caratteristiche della popolazione Calcolo delle probabilità
Primi esercizi per gli studenti del corso di Statistica ed Elementi di Probabilita
 Primi esercizi per gli studenti del corso di Statistica ed Elementi di Probabilita NOTA 1 Gli esercizi sono presi da compiti degli scorsi appelli, oppure da testi o dispense di colleghi. A questi ultimi
Primi esercizi per gli studenti del corso di Statistica ed Elementi di Probabilita NOTA 1 Gli esercizi sono presi da compiti degli scorsi appelli, oppure da testi o dispense di colleghi. A questi ultimi
Esercizi di Probabilità e Statistica
 Esercizi di Probabilità e Statistica Samuel Rota Bulò 19 marzo 2007 Spazi di probabilità finiti e uniformi Esercizio 1 Un urna contiene due palle nere e una rossa. Una seconda urna ne contiene una bianca
Esercizi di Probabilità e Statistica Samuel Rota Bulò 19 marzo 2007 Spazi di probabilità finiti e uniformi Esercizio 1 Un urna contiene due palle nere e una rossa. Una seconda urna ne contiene una bianca
PROBABILITA CONDIZIONALE
 Riferendoci al lancio di un dado, indichiamo con A l evento esce un punteggio inferiore a 4 A ={1, 2, 3} B l evento esce un punteggio dispari B = {1, 3, 5} Non avendo motivo per ritenere il dado truccato,
Riferendoci al lancio di un dado, indichiamo con A l evento esce un punteggio inferiore a 4 A ={1, 2, 3} B l evento esce un punteggio dispari B = {1, 3, 5} Non avendo motivo per ritenere il dado truccato,
Viene lanciata una moneta. Se esce testa vinco 100 euro, se esce croce non vinco niente. Quale è il valore della mia vincita?
 Viene lanciata una moneta. Se esce testa vinco 00 euro, se esce croce non vinco niente. Quale è il valore della mia vincita? Osserviamo che il valore della vincita dipende dal risultato dell esperimento
Viene lanciata una moneta. Se esce testa vinco 00 euro, se esce croce non vinco niente. Quale è il valore della mia vincita? Osserviamo che il valore della vincita dipende dal risultato dell esperimento
Probabilità discreta
 Probabilità discreta Daniele A. Gewurz 1 Che probabilità c è che succeda...? Una delle applicazioni della combinatoria è nel calcolo di probabilità discrete. Quando abbiamo a che fare con un fenomeno che
Probabilità discreta Daniele A. Gewurz 1 Che probabilità c è che succeda...? Una delle applicazioni della combinatoria è nel calcolo di probabilità discrete. Quando abbiamo a che fare con un fenomeno che
Probabilità Calcolo combinatorio, probabilità elementare, probabilità condizionata, indipendenza, th delle probabilità totali, legge di Bayes
 Sessione Live #3 Settimana dal 7 all 11 marzo 2003 Probabilità Calcolo combinatorio, probabilità elementare, probabilità condizionata, indipendenza, th delle probabilità totali, legge di Bayes Lezioni
Sessione Live #3 Settimana dal 7 all 11 marzo 2003 Probabilità Calcolo combinatorio, probabilità elementare, probabilità condizionata, indipendenza, th delle probabilità totali, legge di Bayes Lezioni
A = { escono 2 teste e due croci (indipendentemente dall ordine) } B = { al primo tiro esce testa }.
 ESERCIZI ELEMENTARI DI CALCOLO DELLE PROBABILITÀ Teorema della somma 1) Giocando alla roulette, calcolare la probabilità che su una estrazione esca: a) Un numero compreso tra 6 e 12 (compresi) oppure maggiore
ESERCIZI ELEMENTARI DI CALCOLO DELLE PROBABILITÀ Teorema della somma 1) Giocando alla roulette, calcolare la probabilità che su una estrazione esca: a) Un numero compreso tra 6 e 12 (compresi) oppure maggiore
CORSO DI CALCOLO DELLE PROBABILITÀ E STATISTICA. Esercizi su eventi, previsioni e probabilità condizionate
 CORSO DI CALCOLO DELLE PROBABILITÀ E STATISTICA Esercizi su eventi, previsioni e probabilità condizionate Nota: Alcuni esercizi sono tradotti, più o meno fedelmente, dal libro A first course in probability
CORSO DI CALCOLO DELLE PROBABILITÀ E STATISTICA Esercizi su eventi, previsioni e probabilità condizionate Nota: Alcuni esercizi sono tradotti, più o meno fedelmente, dal libro A first course in probability
Calcolo delle Probabilità
 Calcolo delle Probabilità Il calcolo delle probabilità studia i modelli matematici delle cosidette situazioni di incertezza. Molte situazioni concrete sono caratterizzate a priori da incertezza su quello
Calcolo delle Probabilità Il calcolo delle probabilità studia i modelli matematici delle cosidette situazioni di incertezza. Molte situazioni concrete sono caratterizzate a priori da incertezza su quello
Probabilità e Statistica Esercitazioni. a.a. 2006/2007
 Probabilità e Statistica Esercitazioni a.a. 2006/2007 C.d.L.: Ingegneria per l Ambiente ed il Territorio, Ingegneria Civile, Ingegneria Gestionale, Ingegneria dell Informazione C.d.L.S.: Ingegneria Civile
Probabilità e Statistica Esercitazioni a.a. 2006/2007 C.d.L.: Ingegneria per l Ambiente ed il Territorio, Ingegneria Civile, Ingegneria Gestionale, Ingegneria dell Informazione C.d.L.S.: Ingegneria Civile
Si considerino gli eventi A = nessuno studente ha superato l esame e B = nessuno studente maschio ha superato l esame. Allora A c B è uguale a:
 TEST DI AUTOVALUTAZIONE - SETTIMANA 2 I diritti d autore sono riservati. Ogni sfruttamento commerciale non autorizzato sarà perseguito. Metodi statistici per la biologia 1 Parte A 1.1 Si considerino gli
TEST DI AUTOVALUTAZIONE - SETTIMANA 2 I diritti d autore sono riservati. Ogni sfruttamento commerciale non autorizzato sarà perseguito. Metodi statistici per la biologia 1 Parte A 1.1 Si considerino gli
Calcolo delle Probabilita, INGEGNERIA INFORMATICA, semestre II, laurea (ord. Leonardo.
 Capitolo 1 9 Ottobre 00 Calcolo delle Probabilita, INGEGNERIA INFORMATICA, semestre II, laurea (ord. Leonardo. 000, Milano Esercizio 1.0.1 (svolto in classe [II recupero Ing. Matematica aa.00-0-rivisitato]nel
Capitolo 1 9 Ottobre 00 Calcolo delle Probabilita, INGEGNERIA INFORMATICA, semestre II, laurea (ord. Leonardo. 000, Milano Esercizio 1.0.1 (svolto in classe [II recupero Ing. Matematica aa.00-0-rivisitato]nel
8. Qual è la probabilità di estrarre da un mazzo di 40 carte napoletane una figura?
 www.matematicamente.it Probabilità 1 Calcolo delle probabilità Cognome e nome: Classe Data 1. Quali affermazioni sono vere? A. Un evento impossibile ha probabilità 1 B. Un vento certo ha probabilità 0
www.matematicamente.it Probabilità 1 Calcolo delle probabilità Cognome e nome: Classe Data 1. Quali affermazioni sono vere? A. Un evento impossibile ha probabilità 1 B. Un vento certo ha probabilità 0
Ulteriori problemi di fisica e matematica
 Facoltà di Medicina e Chirurgia Università degli Studi di Firenze Agosto 2010 Ulteriori problemi di fisica e matematica Giovanni Romano Perché un raggio di luce proveniente dal Sole e fatto passare attraverso
Facoltà di Medicina e Chirurgia Università degli Studi di Firenze Agosto 2010 Ulteriori problemi di fisica e matematica Giovanni Romano Perché un raggio di luce proveniente dal Sole e fatto passare attraverso
Cosa dobbiamo già conoscere?
 Cosa dobbiamo già conoscere? Insiemistica (operazioni, diagrammi...). Insiemi finiti/numerabili/non numerabili. Perché la probabilità? In molti esperimenti l esito non è noto a priori tuttavia si sa dire
Cosa dobbiamo già conoscere? Insiemistica (operazioni, diagrammi...). Insiemi finiti/numerabili/non numerabili. Perché la probabilità? In molti esperimenti l esito non è noto a priori tuttavia si sa dire
1 Probabilità condizionata
 1 Probabilità condizionata Accade spesso di voler calcolare delle probabilità quando si è in possesso di informazioni parziali sull esito di un esperimento, o di voler calcolare la probabilità di un evento
1 Probabilità condizionata Accade spesso di voler calcolare delle probabilità quando si è in possesso di informazioni parziali sull esito di un esperimento, o di voler calcolare la probabilità di un evento
CALCOLO COMBINATORIO
 CALCOLO COMBINATORIO 1 Modi di formare gruppi di k oggetti presi da n dati 11 disposizioni semplici, permutazioni Dati n oggetti distinti a 1,, a n si chiamano disposizioni semplici di questi oggetti,
CALCOLO COMBINATORIO 1 Modi di formare gruppi di k oggetti presi da n dati 11 disposizioni semplici, permutazioni Dati n oggetti distinti a 1,, a n si chiamano disposizioni semplici di questi oggetti,
Statistica e biometria. D. Bertacchi. Variabili aleatorie. V.a. discrete e continue. La densità di una v.a. discreta. Esempi.
 Iniziamo con definizione (capiremo fra poco la sua utilità): DEFINIZIONE DI VARIABILE ALEATORIA Una variabile aleatoria (in breve v.a.) X è funzione che ha come dominio Ω e come codominio R. In formule:
Iniziamo con definizione (capiremo fra poco la sua utilità): DEFINIZIONE DI VARIABILE ALEATORIA Una variabile aleatoria (in breve v.a.) X è funzione che ha come dominio Ω e come codominio R. In formule:
ESERCIZI EVENTI E VARIABILI ALEATORIE
 ESERCIZI EVENTI E VARIABILI ALEATORIE 1) Considera la tabella seguente, che descrive la situazione occupazionale di 63 persone in relazione al titolo di studio. Occupazione SI NO Titolo Licenza media 5%
ESERCIZI EVENTI E VARIABILI ALEATORIE 1) Considera la tabella seguente, che descrive la situazione occupazionale di 63 persone in relazione al titolo di studio. Occupazione SI NO Titolo Licenza media 5%
Esercizi sul calcolo delle probabilità
 Esercizi sul calcolo delle probabilità Svolti e da svolgere (per MAR 13 marzo) Dati due eventi A e B dello spazio campionario Ω. Si sappia che P(A c )=0,3 P(B)=0,4 e P(A B c )=0,5 si determinino le probabilità
Esercizi sul calcolo delle probabilità Svolti e da svolgere (per MAR 13 marzo) Dati due eventi A e B dello spazio campionario Ω. Si sappia che P(A c )=0,3 P(B)=0,4 e P(A B c )=0,5 si determinino le probabilità
PROBABILITA' E VARIABILI CASUALI
 PROBABILITA' E VARIABILI CASUALI ESERCIZIO 1 Due giocatori estraggono due carte a caso da un mazzo di carte napoletane. Calcolare: 1) la probabilità che la prima carta sia una figura oppure una carta di
PROBABILITA' E VARIABILI CASUALI ESERCIZIO 1 Due giocatori estraggono due carte a caso da un mazzo di carte napoletane. Calcolare: 1) la probabilità che la prima carta sia una figura oppure una carta di
ESERCIZI. x + 3 x 2 1. a) y = 4x2 + 3x 2x + 2 ; b) y = 6x2 x 1. (x + 2) 2 c) y =
 ESERCIZI Testi (1) Un urna contiene 20 palline di cui 8 rosse 3 bianche e 9 nere; calcolare la probabilità che: (a) tutte e tre siano rosse; (b) tutte e tre bianche; (c) 2 rosse e una nera; (d) almeno
ESERCIZI Testi (1) Un urna contiene 20 palline di cui 8 rosse 3 bianche e 9 nere; calcolare la probabilità che: (a) tutte e tre siano rosse; (b) tutte e tre bianche; (c) 2 rosse e una nera; (d) almeno
risulta (x) = 1 se x < 0.
 Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Somma logica di eventi
 Somma logica di eventi Da un urna contenente 24 palline numerate si estrae una pallina. Calcolare la probabilità dei seguenti eventi: a) esce un numero divisibile per 5 o superiore a 20, b) esce un numero
Somma logica di eventi Da un urna contenente 24 palline numerate si estrae una pallina. Calcolare la probabilità dei seguenti eventi: a) esce un numero divisibile per 5 o superiore a 20, b) esce un numero
Una sperimentazione. Probabilità. Una previsione. Calcolo delle probabilità. Nonostante ciò, è possibile dire qualcosa.
 Una sperimentazione Probabilità Si sta sperimentando l efficacia di un nuovo farmaco per il morbo di Parkinson. Duemila pazienti partecipano alla sperimentazione: metà di essi vengono trattati con il nuovo
Una sperimentazione Probabilità Si sta sperimentando l efficacia di un nuovo farmaco per il morbo di Parkinson. Duemila pazienti partecipano alla sperimentazione: metà di essi vengono trattati con il nuovo
Esercizi di calcolo combinatorio
 CORSO DI CALCOLO DELLE PROBABILITÀ E STATISTICA Esercizi di calcolo combinatorio Nota: Alcuni esercizi sono tradotti, più o meno fedelmente, dal libro A first course in probability di Sheldon Ross, quinta
CORSO DI CALCOLO DELLE PROBABILITÀ E STATISTICA Esercizi di calcolo combinatorio Nota: Alcuni esercizi sono tradotti, più o meno fedelmente, dal libro A first course in probability di Sheldon Ross, quinta
matematica probabilmente
 IS science centre immaginario scientifico Laboratorio dell'immaginario Scientifico - Trieste tel. 040224424 - fax 040224439 - e-mail: lis@lis.trieste.it - www.immaginarioscientifico.it indice Altezze e
IS science centre immaginario scientifico Laboratorio dell'immaginario Scientifico - Trieste tel. 040224424 - fax 040224439 - e-mail: lis@lis.trieste.it - www.immaginarioscientifico.it indice Altezze e
Probabilità e Statistica Esercitazioni. a.a. 2009/2010. C.d.L.S.: Ingegneria Civile-Architettonico, Ingegneria Civile-Strutturistico.
 Probabilità e Statistica Esercitazioni a.a. 2009/2010 C.d.L.S.: Ingegneria Civile-Architettonico, Ingegneria Civile-Strutturistico Probabilità Ines Campa e Marco Longhi Probabilità e Statistica - Esercitazioni
Probabilità e Statistica Esercitazioni a.a. 2009/2010 C.d.L.S.: Ingegneria Civile-Architettonico, Ingegneria Civile-Strutturistico Probabilità Ines Campa e Marco Longhi Probabilità e Statistica - Esercitazioni
PROBABILITA. Sono esempi di fenomeni la cui realizzazione non è certa a priori e vengono per questo detti eventi aleatori (dal latino alea, dado)
 L esito della prossima estrazione del lotto L esito del lancio di una moneta o di un dado Il sesso di un nascituro, così come il suo peso alla nascita o la sua altezza.. Il tempo di attesa ad uno sportello
L esito della prossima estrazione del lotto L esito del lancio di una moneta o di un dado Il sesso di un nascituro, così come il suo peso alla nascita o la sua altezza.. Il tempo di attesa ad uno sportello
Elementi di calcolo delle probabilità
 Elementi di calcolo delle probabilità Definizione di probabilità A) Qui davanti a me ho un urna contenente 2 palline bianche e 998 nere. Mi metto una benda sugli occhi, scuoto ripetutamente l urna ed estraggo
Elementi di calcolo delle probabilità Definizione di probabilità A) Qui davanti a me ho un urna contenente 2 palline bianche e 998 nere. Mi metto una benda sugli occhi, scuoto ripetutamente l urna ed estraggo
Calcolare la probabilità dei seguenti eventi: P(fare ambo con i numeri 7 ed 17 con le prime due estrazioni):
 ESERCIZIO 1 Il signor Felice sta giocando a tombola nel circolo PASSATEMPO e ha deciso di giocare usando la sola cartella di seguito riportata: 7 17 26 40 74 1 14 50 69 87 13 43 57 62 73 Serie 1, n. 1
ESERCIZIO 1 Il signor Felice sta giocando a tombola nel circolo PASSATEMPO e ha deciso di giocare usando la sola cartella di seguito riportata: 7 17 26 40 74 1 14 50 69 87 13 43 57 62 73 Serie 1, n. 1
( x) ( x) 0. Equazioni irrazionali
 Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
Capitolo 2. Operazione di limite
 Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Corso di ELEMENTI DI STATISTICA Alcuni problemi di probabilità, con soluzioni
 Corso di ELEMENTI DI STATISTICA Alcuni problemi di probabilità, con soluzioni Si tratta di problemi elementari, formulati nel linguaggio ordinario Quindi, per ogni problema la suluzione proposta è sempre
Corso di ELEMENTI DI STATISTICA Alcuni problemi di probabilità, con soluzioni Si tratta di problemi elementari, formulati nel linguaggio ordinario Quindi, per ogni problema la suluzione proposta è sempre
Tabella 7. Dado truccato
 0 ALBERTO SARACCO 4. Compiti a casa 7novembre 200 4.. Ordini di grandezza e calcolo approssimato. Esercizio 4.. Una valigia misura 5cm di larghezza, 70cm di lunghezza e 45cm di altezza. Quante palline
0 ALBERTO SARACCO 4. Compiti a casa 7novembre 200 4.. Ordini di grandezza e calcolo approssimato. Esercizio 4.. Una valigia misura 5cm di larghezza, 70cm di lunghezza e 45cm di altezza. Quante palline
Matematica Applicata. Probabilità e statistica
 Matematica Applicata Probabilità e statistica Fenomeni casuali Fenomeni che si verificano in modi non prevedibili a priori 1. Lancio di una moneta: non sono in grado di prevedere con certezza se il risultato
Matematica Applicata Probabilità e statistica Fenomeni casuali Fenomeni che si verificano in modi non prevedibili a priori 1. Lancio di una moneta: non sono in grado di prevedere con certezza se il risultato
Esercitazione #5 di Statistica. Test ed Intervalli di Confidenza (per una popolazione)
 Esercitazione #5 di Statistica Test ed Intervalli di Confidenza (per una popolazione) Dicembre 00 1 Esercizi 1.1 Test su media (con varianza nota) Esercizio n. 1 Il calore (in calorie per grammo) emesso
Esercitazione #5 di Statistica Test ed Intervalli di Confidenza (per una popolazione) Dicembre 00 1 Esercizi 1.1 Test su media (con varianza nota) Esercizio n. 1 Il calore (in calorie per grammo) emesso
Complemento al corso di Fondamenti di Informatica I corsi di laurea in ingegneria, settore dell informazione Università la Sapienza Consorzio Nettuno
 Rappresentazione di numeri Complemento al corso di Fondamenti di Informatica I corsi di laurea in ingegneria, settore dell informazione Università la Sapienza Consorzio Nettuno Un numero e un entità teorica,
Rappresentazione di numeri Complemento al corso di Fondamenti di Informatica I corsi di laurea in ingegneria, settore dell informazione Università la Sapienza Consorzio Nettuno Un numero e un entità teorica,
MATEMATICA E STATISTICA CORSO B PROF. MARCO ABATE. 23 novembre 2006
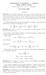 MATEMATICA E STATISTICA CORSO B PROF. MARCO ABATE PRIMO COMPITINO FILA B SOLUZIONI 3 novembre 006. Parte I Esercizio.. Al mercato della frutta i prezzi sono scontati rispetto ai prezzi nei supermercati.
MATEMATICA E STATISTICA CORSO B PROF. MARCO ABATE PRIMO COMPITINO FILA B SOLUZIONI 3 novembre 006. Parte I Esercizio.. Al mercato della frutta i prezzi sono scontati rispetto ai prezzi nei supermercati.
1 Giochi a due, con informazione perfetta e somma zero
 1 Giochi a due, con informazione perfetta e somma zero Nel gioco del Nim, se semplificato all estremo, ci sono due giocatori I, II e una pila di 6 pedine identiche In ogni turno di gioco I rimuove una
1 Giochi a due, con informazione perfetta e somma zero Nel gioco del Nim, se semplificato all estremo, ci sono due giocatori I, II e una pila di 6 pedine identiche In ogni turno di gioco I rimuove una
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Probabilità e statistica
 Indice generale.probabilità ed eventi aleatori....come si può definire una probabilità....eventi equiprobabili....eventi indipendenti, eventi dipendenti....eventi incompatibili....eventi compatibili....probabilità
Indice generale.probabilità ed eventi aleatori....come si può definire una probabilità....eventi equiprobabili....eventi indipendenti, eventi dipendenti....eventi incompatibili....eventi compatibili....probabilità
Ancora sull indipendenza. Se A e B sono indipendenti allora lo sono anche
 Ancora sull indipendenza Se A e B sono indipendenti allora lo sono anche A e B Ā e B Ā e B Sfruttiamo le leggi di De Morgan Leggi di De Morgan A B = Ā B A B = Ā B P (Ā B) = P (A B) = 1 P (A B) = 1 (P (A)
Ancora sull indipendenza Se A e B sono indipendenti allora lo sono anche A e B Ā e B Ā e B Sfruttiamo le leggi di De Morgan Leggi di De Morgan A B = Ā B A B = Ā B P (Ā B) = P (A B) = 1 P (A B) = 1 (P (A)
Capitolo 4 Probabilità
 Levine, Krehbiel, Berenson Statistica II ed. 2006 Apogeo Capitolo 4 Probabilità Insegnamento: Statistica Corso di Laurea Triennale in Economia Facoltà di Economia, Università di Ferrara Docenti: Dott.
Levine, Krehbiel, Berenson Statistica II ed. 2006 Apogeo Capitolo 4 Probabilità Insegnamento: Statistica Corso di Laurea Triennale in Economia Facoltà di Economia, Università di Ferrara Docenti: Dott.
E naturale chiedersi alcune cose sulla media campionaria x n
 Supponiamo che un fabbricante stia introducendo un nuovo tipo di batteria per un automobile elettrica. La durata osservata x i delle i-esima batteria è la realizzazione (valore assunto) di una variabile
Supponiamo che un fabbricante stia introducendo un nuovo tipo di batteria per un automobile elettrica. La durata osservata x i delle i-esima batteria è la realizzazione (valore assunto) di una variabile
1) Si consideri un esperimento che consiste nel lancio di 5 dadi. Lo spazio campionario:
 Esempi di domande risposta multipla (Modulo II) 1) Si consideri un esperimento che consiste nel lancio di 5 dadi. Lo spazio campionario: 1) ha un numero di elementi pari a 5; 2) ha un numero di elementi
Esempi di domande risposta multipla (Modulo II) 1) Si consideri un esperimento che consiste nel lancio di 5 dadi. Lo spazio campionario: 1) ha un numero di elementi pari a 5; 2) ha un numero di elementi
PROBABILITA CONDIZIONALE
 Riferendoci al lancio di un dado, indichiamo con A l evento esce un punteggio inferiore a 4 A ={1, 2, 3} B l evento esce un punteggio dispari B = {1, 3, 5} Non avendo motivo per ritenere il dado truccato,
Riferendoci al lancio di un dado, indichiamo con A l evento esce un punteggio inferiore a 4 A ={1, 2, 3} B l evento esce un punteggio dispari B = {1, 3, 5} Non avendo motivo per ritenere il dado truccato,
Corso di Laurea in Scienze e Tecnologie Biomolecolari. NOME COGNOME N. Matr.
 Corso di Laurea in Scienze e Tecnologie Biomolecolari Matematica e Statistica II Prova di esame del 18/7/2013 NOME COGNOME N. Matr. Rispondere ai punti degli esercizi nel modo più completo possibile, cercando
Corso di Laurea in Scienze e Tecnologie Biomolecolari Matematica e Statistica II Prova di esame del 18/7/2013 NOME COGNOME N. Matr. Rispondere ai punti degli esercizi nel modo più completo possibile, cercando
Siamo così arrivati all aritmetica modulare, ma anche a individuare alcuni aspetti di come funziona l aritmetica del calcolatore come vedremo.
 DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
Matematica e giochi di gruppo
 Matematica e giochi di gruppo Possiamo riempire di contenuti matematici situazioni di piccola sfida personale, situazioni di giochi di società. Di seguito proponiamo attività che affrontano i seguenti
Matematica e giochi di gruppo Possiamo riempire di contenuti matematici situazioni di piccola sfida personale, situazioni di giochi di società. Di seguito proponiamo attività che affrontano i seguenti
Statistica Matematica A - Ing. Meccanica, Aerospaziale I prova in itinere - 19 novembre 2004
 Statistica Matematica A - Ing. Meccanica, Aerospaziale I prova in itinere - 19 novembre 200 Esercizio 1 Tre apparecchiature M 1, M 2 e M 3 in un anno si guastano, in maniera indipendente, con probabilità
Statistica Matematica A - Ing. Meccanica, Aerospaziale I prova in itinere - 19 novembre 200 Esercizio 1 Tre apparecchiature M 1, M 2 e M 3 in un anno si guastano, in maniera indipendente, con probabilità
Corso di Calcolo delle Probabilità e Statistica. Esercizi su variabili aleatorie discrete
 Corso di Calcolo delle Probabilità e Statistica Esercizi su variabili aleatorie discrete Es.1 Da un urna con 10 pallina bianche e 15 palline nere, si eseguono estrazioni con reimbussolamento fino all estrazione
Corso di Calcolo delle Probabilità e Statistica Esercizi su variabili aleatorie discrete Es.1 Da un urna con 10 pallina bianche e 15 palline nere, si eseguono estrazioni con reimbussolamento fino all estrazione
LA STATISTICA si interessa del rilevamento, dell elaborazione e dello studio dei dati; studia ciò che accade o come è fatto un gruppo numeroso di
 STATISTICA LA STATISTICA si interessa del rilevamento, dell elaborazione e dello studio dei dati; studia ciò che accade o come è fatto un gruppo numeroso di oggetti; cerca, attraverso l uso della matematica
STATISTICA LA STATISTICA si interessa del rilevamento, dell elaborazione e dello studio dei dati; studia ciò che accade o come è fatto un gruppo numeroso di oggetti; cerca, attraverso l uso della matematica
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI
 APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
BALDAZZI STYL ART S.p.A. - Via dell artigiano 17-40065 Pianoro (BO) Tel. 051-6516102 - Fax 051-6516142 info@baldazzi.com
 BALDAZZI STYL ART S.p.A. Via dell artigiano 17 40065 Pianoro (BO) Tel. 0516516102 Fax 0516516142 info@baldazzi.com 1.f Regole che governano il gioco All avvio della partita si gioca sempre nei 5 rulli.
BALDAZZI STYL ART S.p.A. Via dell artigiano 17 40065 Pianoro (BO) Tel. 0516516102 Fax 0516516142 info@baldazzi.com 1.f Regole che governano il gioco All avvio della partita si gioca sempre nei 5 rulli.
Corrispondenze e funzioni
 Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
Esercizio 1 Dato il gioco ({1, 2, 3}, v) con v funzione caratteristica tale che:
 Teoria dei Giochi, Trento, 2004/05 c Fioravante Patrone 1 Teoria dei Giochi Corso di laurea specialistica: Decisioni economiche, impresa e responsabilità sociale, A.A. 2004/05 Soluzioni degli esercizi
Teoria dei Giochi, Trento, 2004/05 c Fioravante Patrone 1 Teoria dei Giochi Corso di laurea specialistica: Decisioni economiche, impresa e responsabilità sociale, A.A. 2004/05 Soluzioni degli esercizi
Regole di gioco Roulette Mobile
 Regole di gioco Roulette Mobile European Classic Roulette European Premium Roulette European VIP Roulette Regole di gioco European Classic Roulette Il gioco si svolge esclusivamente nella modalità a solitario,
Regole di gioco Roulette Mobile European Classic Roulette European Premium Roulette European VIP Roulette Regole di gioco European Classic Roulette Il gioco si svolge esclusivamente nella modalità a solitario,
PROBABILITÀ - SCHEDA N. 2 LE VARIABILI ALEATORIE
 Matematica e statistica: dai dati ai modelli alle scelte www.dima.unige/pls_statistica Responsabili scientifici M.P. Rogantin e E. Sasso (Dipartimento di Matematica Università di Genova) PROBABILITÀ -
Matematica e statistica: dai dati ai modelli alle scelte www.dima.unige/pls_statistica Responsabili scientifici M.P. Rogantin e E. Sasso (Dipartimento di Matematica Università di Genova) PROBABILITÀ -
Il confronto fra proporzioni
 L. Boni Il rapporto Un rapporto (ratio), attribuendo un ampio significato al termine, è il risultato della divisione di una certa quantità a per un altra quantità b Il rapporto Spesso, in maniera più specifica,
L. Boni Il rapporto Un rapporto (ratio), attribuendo un ampio significato al termine, è il risultato della divisione di una certa quantità a per un altra quantità b Il rapporto Spesso, in maniera più specifica,
2 CERTAMEN NAZIONALE DI PROBABILITA E STATISTICA FELICE FUSATO Fase di Istituto 15 febbraio 2011
 2 CERTAMEN NAZIONALE DI PROBABILITA E STATISTICA FELICE FUSATO Fase di Istituto 15 febbraio 2011 1) Non sfogliare questo fascicolo finché l insegnante non ti dice di farlo. 2) E ammesso l utilizzo di calcolatrici
2 CERTAMEN NAZIONALE DI PROBABILITA E STATISTICA FELICE FUSATO Fase di Istituto 15 febbraio 2011 1) Non sfogliare questo fascicolo finché l insegnante non ti dice di farlo. 2) E ammesso l utilizzo di calcolatrici
LA MOLTIPLICAZIONE IN CLASSE SECONDA
 LA MOLTIPLICAZIONE IN CLASSE SECONDA Rossana Nencini, 2013 Le fasi del lavoro: 1. Proponiamo ai bambini una situazione reale di moltiplicazione: portiamo a scuola una scatola di biscotti (. ) e diamo la
LA MOLTIPLICAZIONE IN CLASSE SECONDA Rossana Nencini, 2013 Le fasi del lavoro: 1. Proponiamo ai bambini una situazione reale di moltiplicazione: portiamo a scuola una scatola di biscotti (. ) e diamo la
Statistica 1. Esercitazioni. Dott. Luigi Augugliaro 1. Università di Palermo
 Statistica 1 Esercitazioni Dott. 1 1 Dipartimento di Scienze Statistiche e Matematiche S. Vianelli, Università di Palermo ricevimento: lunedì ore 15-17 mercoledì ore 15-17 e-mail: luigi.augugliaro@unipa.it
Statistica 1 Esercitazioni Dott. 1 1 Dipartimento di Scienze Statistiche e Matematiche S. Vianelli, Università di Palermo ricevimento: lunedì ore 15-17 mercoledì ore 15-17 e-mail: luigi.augugliaro@unipa.it
Anteprima Finale Categoria Corsi di Statistica
 1 di 8 08/04/2011 9.01 SiS-Scuola-28-SEZIONE STATISTICA fad TC128STAT Quiz Finale Categoria Corsi di Statistica Tentativo 1 Sei collegato come piero zulli. (Esci) Info Risultati Anteprima Modifica Anteprima
1 di 8 08/04/2011 9.01 SiS-Scuola-28-SEZIONE STATISTICA fad TC128STAT Quiz Finale Categoria Corsi di Statistica Tentativo 1 Sei collegato come piero zulli. (Esci) Info Risultati Anteprima Modifica Anteprima
Calcolo combinatorio
 Probabilità e Statistica Esercitazioni a.a. 2009/2010 C.d.L.S.: Ingegneria Civile-Architettonico, Ingegneria Civile-Strutturistico Calcolo combinatorio Ines Campa e Marco Longhi Probabilità e Statistica
Probabilità e Statistica Esercitazioni a.a. 2009/2010 C.d.L.S.: Ingegneria Civile-Architettonico, Ingegneria Civile-Strutturistico Calcolo combinatorio Ines Campa e Marco Longhi Probabilità e Statistica
STATISTICA MEDICA Prof. Tarcisio Niglio http://www.tarcisio.net tarcisio@mclink.it oppure su Facebook Anno Accademico 2011-2012
 STATISTICA MEDICA Prof. Tarcisio Niglio http://www.tarcisio.net tarcisio@mclink.it oppure su Facebook Anno Accademico 2011-2012 Calcolo delle Probabilità Teoria & Pratica La probabilità di un evento è
STATISTICA MEDICA Prof. Tarcisio Niglio http://www.tarcisio.net tarcisio@mclink.it oppure su Facebook Anno Accademico 2011-2012 Calcolo delle Probabilità Teoria & Pratica La probabilità di un evento è
CORSO DI STATISTICA (parte 1) - ESERCITAZIONE 7
 CORSO DI STATISTICA (parte 1) - ESERCITAZIONE 7 Dott.ssa Antonella Costanzo a.costanzo@unicas.it Incompatibilità ed indipendenza stocastica. Probabilità condizionate, legge della probabilità totale, Teorema
CORSO DI STATISTICA (parte 1) - ESERCITAZIONE 7 Dott.ssa Antonella Costanzo a.costanzo@unicas.it Incompatibilità ed indipendenza stocastica. Probabilità condizionate, legge della probabilità totale, Teorema
Traduzione e adattamento a cura di Gylas per Giochi Rari
 Traduzione e adattamento a cura di Gylas per Giochi Rari Versione 1.0 Luglio 2001 NOTA. La presente traduzione non sostituisce in alcun modo il regolamento originale del gioco; il presente documento è
Traduzione e adattamento a cura di Gylas per Giochi Rari Versione 1.0 Luglio 2001 NOTA. La presente traduzione non sostituisce in alcun modo il regolamento originale del gioco; il presente documento è
1. Distribuzioni campionarie
 Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 3 e 6 giugno 2013 - di Massimo Cristallo - 1. Distribuzioni campionarie
Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 3 e 6 giugno 2013 - di Massimo Cristallo - 1. Distribuzioni campionarie
Dimensione di uno Spazio vettoriale
 Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Soluzione degli esercizi sul moto rettilineo uniformemente accelerato
 Liceo Carducci Volterra - Classe 3 a B Scientifico - Francesco Daddi - 8 novembre 00 Soluzione degli esercizi sul moto rettilineo uniformemente accelerato Esercizio. Un corpo parte da fermo con accelerazione
Liceo Carducci Volterra - Classe 3 a B Scientifico - Francesco Daddi - 8 novembre 00 Soluzione degli esercizi sul moto rettilineo uniformemente accelerato Esercizio. Un corpo parte da fermo con accelerazione
1. Calcolare la probabilità che estratte a caso ed assieme tre carte da un mazzo di 40, fra di esse vi sia un solo asso, di qualunque seme.
 Esercizi difficili sul calcolo delle probabilità. Calcolare la probabilità che estratte a caso ed assieme tre carte da un mazzo di, fra di esse vi sia un solo asso, di qualunque seme. Le parole a caso
Esercizi difficili sul calcolo delle probabilità. Calcolare la probabilità che estratte a caso ed assieme tre carte da un mazzo di, fra di esse vi sia un solo asso, di qualunque seme. Le parole a caso
Esercizi sul moto rettilineo uniformemente accelerato
 Liceo Carducci Volterra - Classe 3 a B Scientifico - Francesco Daddi - 8 novembre 010 Esercizi sul moto rettilineo uniformemente accelerato Esercizio 1. Un corpo parte da fermo con accelerazione pari a
Liceo Carducci Volterra - Classe 3 a B Scientifico - Francesco Daddi - 8 novembre 010 Esercizi sul moto rettilineo uniformemente accelerato Esercizio 1. Un corpo parte da fermo con accelerazione pari a
VINCERE AL BLACKJACK
 VINCERE AL BLACKJACK Il BlackJack è un gioco di abilità e fortuna in cui il banco non può nulla, deve seguire incondizionatamente le regole del gioco. Il giocatore è invece posto continuamente di fronte
VINCERE AL BLACKJACK Il BlackJack è un gioco di abilità e fortuna in cui il banco non può nulla, deve seguire incondizionatamente le regole del gioco. Il giocatore è invece posto continuamente di fronte
Una moderna versione grafica di un antico gioco Dernier con l aggiunta di carte azione che rendono più movimentato e piacevole
 SOLO Una moderna versione grafica di un antico gioco Dernier con l aggiunta di carte azione che rendono più movimentato e piacevole il gioco. Giocatori: da 2 a 10 Eta: da 6 a 106 anni 1 Regole del gioco
SOLO Una moderna versione grafica di un antico gioco Dernier con l aggiunta di carte azione che rendono più movimentato e piacevole il gioco. Giocatori: da 2 a 10 Eta: da 6 a 106 anni 1 Regole del gioco
LANCIAMO UN DADO PER DECIDERE CHI DEVE INIZIARE IL GIOCO. PARTIRA IL NUMERO PIU ALTO
 IL GIOCO DEL CALCIO I bimbi della sezione 5 anni sono molto appassionati al gioco del calcio. Utilizzo questo interesse per costruire e proporre un gioco con i dadi che assomigli ad una partita di calcio.
IL GIOCO DEL CALCIO I bimbi della sezione 5 anni sono molto appassionati al gioco del calcio. Utilizzo questo interesse per costruire e proporre un gioco con i dadi che assomigli ad una partita di calcio.
Percorsi, strategie e geometrie in gioco Complementi e spunti di lavoro Primaria e Secondaria Inferiore
 Percorsi, strategie e geometrie in gioco Complementi e spunti di lavoro Primaria e Secondaria Inferiore In queste note troverete suggerimenti e osservazioni per attività che traggono spunto dal problema
Percorsi, strategie e geometrie in gioco Complementi e spunti di lavoro Primaria e Secondaria Inferiore In queste note troverete suggerimenti e osservazioni per attività che traggono spunto dal problema
= variazione diviso valore iniziale, il tutto moltiplicato per 100. \ Esempio: PIL del 2000 = 500; PIL del 2001 = 520:
 Fig. 10.bis.1 Variazioni percentuali Variazione percentuale di x dalla data zero alla data uno: x1 x 0 %x = 100% x 0 = variazione diviso valore iniziale, il tutto moltiplicato per 100. \ Esempio: PIL del
Fig. 10.bis.1 Variazioni percentuali Variazione percentuale di x dalla data zero alla data uno: x1 x 0 %x = 100% x 0 = variazione diviso valore iniziale, il tutto moltiplicato per 100. \ Esempio: PIL del
Esercizi di Calcolo delle Probabilità (calcolo combinatorio)
 Esercizi di Calcolo delle Probabilità (calcolo combinatorio 1. Lanciamo due dadi regolari. Qual è la probabilità che la somma delle facce rivolte verso l alto sia pari a 7? 1/6 2. Due palline vengono estratte
Esercizi di Calcolo delle Probabilità (calcolo combinatorio 1. Lanciamo due dadi regolari. Qual è la probabilità che la somma delle facce rivolte verso l alto sia pari a 7? 1/6 2. Due palline vengono estratte
SIMULAZIONE TEST INVALSI
 SIMULAZIONE TEST INVALSI STATISTICA E PROBABILITA Nel sacchetto A ci sono 4 palline rosse e 8 nere mentre nel sacchetto B ci sono 4 palline rosse e 6 nere. a. Completa correttamente la seguente frase inserendo
SIMULAZIONE TEST INVALSI STATISTICA E PROBABILITA Nel sacchetto A ci sono 4 palline rosse e 8 nere mentre nel sacchetto B ci sono 4 palline rosse e 6 nere. a. Completa correttamente la seguente frase inserendo
APPUNTI SU PROBLEMI CON CALCOLO PERCENTUALE
 APPUNTI SU PROBLEMI CON CALCOLO PERCENTUALE 1. Proporzionalità diretta e proporzionalità inversa Analizziamo le seguenti formule Peso Lordo = Peso Netto + Tara Ricavo = Utile + Costo Rata = Importo + Interesse
APPUNTI SU PROBLEMI CON CALCOLO PERCENTUALE 1. Proporzionalità diretta e proporzionalità inversa Analizziamo le seguenti formule Peso Lordo = Peso Netto + Tara Ricavo = Utile + Costo Rata = Importo + Interesse
Il principio di induzione e i numeri naturali.
 Il principio di induzione e i numeri naturali. Il principio di induzione è un potente strumento di dimostrazione, al quale si ricorre ogni volta che si debba dimostrare una proprietà in un numero infinito
Il principio di induzione e i numeri naturali. Il principio di induzione è un potente strumento di dimostrazione, al quale si ricorre ogni volta che si debba dimostrare una proprietà in un numero infinito
Tasso di interesse e capitalizzazione
 Tasso di interesse e capitalizzazione Tasso di interesse = i = somma che devo restituire dopo un anno per aver preso a prestito un euro, in aggiunta alla restituzione dell euro iniziale Quindi: prendo
Tasso di interesse e capitalizzazione Tasso di interesse = i = somma che devo restituire dopo un anno per aver preso a prestito un euro, in aggiunta alla restituzione dell euro iniziale Quindi: prendo
Convertitori numerici in Excel
 ISTITUTO DI ISTRUZIONE SUPERIORE G. M. ANGIOY CARBONIA Convertitori numerici in Excel Prof. G. Ciaschetti Come attività di laboratorio, vogliamo realizzare dei convertitori numerici con Microsoft Excel
ISTITUTO DI ISTRUZIONE SUPERIORE G. M. ANGIOY CARBONIA Convertitori numerici in Excel Prof. G. Ciaschetti Come attività di laboratorio, vogliamo realizzare dei convertitori numerici con Microsoft Excel
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE
 LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
Rilevazione degli apprendimenti. Anno Scolastico 2012 2013 PROVA DI MATEMATICA. Scuola primaria. Classe Seconda Fascicolo 1
 Prova di MateMatica - Scuola Primaria - Classe Seconda Rilevazione degli apprendimenti Anno Scolastico 2012 2013 PROVA DI MATEMATICA Scuola primaria Classe Seconda Fascicolo 1 Spazio per l etichetta autoadesiva
Prova di MateMatica - Scuola Primaria - Classe Seconda Rilevazione degli apprendimenti Anno Scolastico 2012 2013 PROVA DI MATEMATICA Scuola primaria Classe Seconda Fascicolo 1 Spazio per l etichetta autoadesiva
1. PRIME PROPRIETÀ 2
 RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
SPECTER OPS. L'obiettivo del giocatore agente è quello che il suo agente completi 3 su 4 missioni obiettivo qualsiasi
 SPECTER OPS REGOLE 2-3 giocatori: 1 agente e 2 cacciatori - Le 4 missioni obiettivo sono conosciute dai giocatori: si lancia il dado e si segnano col relativo gettone sul lato verde sulla plancia e sul
SPECTER OPS REGOLE 2-3 giocatori: 1 agente e 2 cacciatori - Le 4 missioni obiettivo sono conosciute dai giocatori: si lancia il dado e si segnano col relativo gettone sul lato verde sulla plancia e sul
Università di Milano Bicocca. Esercitazione 6 di Matematica per la Finanza. 14 Maggio 2015
 Università di Milano Bicocca Esercitazione 6 di Matematica per la Finanza 14 Maggio 2015 Esercizio 1 Un agente presenta una funzione di utilitá u(x) = ln(1 + 6x). Egli dispone di un progetto incerto che
Università di Milano Bicocca Esercitazione 6 di Matematica per la Finanza 14 Maggio 2015 Esercizio 1 Un agente presenta una funzione di utilitá u(x) = ln(1 + 6x). Egli dispone di un progetto incerto che
STATISTICA E PROBABILITá
 STATISTICA E PROBABILITá Statistica La statistica è una branca della matematica, che descrive un qualsiasi fenomeno basandosi sulla raccolta di informazioni, sottoforma di dati. Questi ultimi risultano
STATISTICA E PROBABILITá Statistica La statistica è una branca della matematica, che descrive un qualsiasi fenomeno basandosi sulla raccolta di informazioni, sottoforma di dati. Questi ultimi risultano
ESERCIZI DI RIEPILOGO 2. 7 jj(addi
 ESERCIZI DI RIEPILOGO 2 ESERCIZIO 1 Da un comune mazzo di 52 carte francesi (13 carte per ognuno dei quattro semi: picche, cuori, fiori e quadri) viene estratta casualmente una carta. Definiti gli eventi:
ESERCIZI DI RIEPILOGO 2 ESERCIZIO 1 Da un comune mazzo di 52 carte francesi (13 carte per ognuno dei quattro semi: picche, cuori, fiori e quadri) viene estratta casualmente una carta. Definiti gli eventi:
Logica Numerica Approfondimento 1. Minimo Comune Multiplo e Massimo Comun Divisore. Il concetto di multiplo e di divisore. Il Minimo Comune Multiplo
 Logica Numerica Approfondimento E. Barbuto Minimo Comune Multiplo e Massimo Comun Divisore Il concetto di multiplo e di divisore Considerato un numero intero n, se esso viene moltiplicato per un numero
Logica Numerica Approfondimento E. Barbuto Minimo Comune Multiplo e Massimo Comun Divisore Il concetto di multiplo e di divisore Considerato un numero intero n, se esso viene moltiplicato per un numero
