Circuiti a Microonde: Introduzione
|
|
|
- Giada Pisani
- 9 anni fa
- Просмотров:
Транскрипт
1 Ciruiti a Miroonde: Introduzione Un iruito a miroonde è un interonnessione di elementi le ui dimensioni fisihe possono essere omparabili on la lunghezza d onda orrispondente alle frequenze operative Tipologie di omponenti: Interonnessioni (non hanno dimensioni nulle ome nei iruiti a ostanti onentrate!) Elementi pseudo-onentrati (simulano il omportamento di omponenti ideali, tenendo però onto delle dimensioni fisihe) Elementi distribuiti (tratti di linee di trasmissione terminati o passanti) Nei iruiti a miroonde non esistono nodi ideali. Quando due o più omponenti sono onnessi tra loro, nel punto di giunzione si rea una disontinuità he produe effetti più o meno evidenti sul omportamento della rete.
2 Disontinuità tra due linee di trasmissione 1 =10 m 2 =10 m Non va bene! Coassiale 1: R 1 =5 m, r 1 =2.17 m Coassiale 2: R 2 =3 m, r 1 =1.3 m Matrie S R R ln 60ln 50 r1 r2 Disontinuità Modello orretto. Perhé?
3 Eitazioni di modi superiori Onda TEM inidente Onda TEM trasmessa Onda TEM Campi E, H trasversi Ampiezza modi superiori Eitati alla disontinuità Nella disontinuità il ampo non può essere trasverso (imposto dalle ondizioni al ontorno) Si generano modi superiori he, non essendo in propagazione, sono in pratia onfinati viino alla disontinuità In pratia è ome se i fosse del ampo elettromagnetio immagazzinato loalmente, he produe un effetto sulla propagazione del modo TEM. Tale effetto può essere rappresentato mediante un iruito equivalente o, più in generale, dalla matrie di satter olloata nella sezione della disontinuità
4 Calolo di S della disontinuità Parametri S ottenuti da un simulatore elettromagnetio dei due oax onnessi alla frequenza di 1 GHz (=50 ): S S , S S m 10 m Disontinuità Porta Porta 2 Rete a miroonde Per ottenere i parametri S della disontinuità bisogna spostare le sezioni di riferimento delle due porte verso l interno di 10 m, ioè: 2 f 10 m 10 m rad 120 S S S exp , S S S exp
5 Dipendenza dalla frequenza -10 Return oss vs. Frequeny DB( S(1,1) ) CoaxStep Frequeny (MHz) e disontinuità sono in generale variabili on la frequenza!
6 Componenti e disontinuità disponibili in MWOffie (eleno parziale)
7 Esempio: rete di adattamento a doppio stub Giunzioni a T 1 2, 0, 1, 0 S1, S1 S2, S2 Open Shema ideale
8 Rappresentazione delle disontinuità PORT P=1 =50 Ohm ID=T3 W=2.2 mm =10 mm MTEE$ ID=T4 ID=T6 W=0.622 mm =79.68 mm MTEE$ ID=T5 ID=T1 W=2.2 mm =5 mm PORT P=2 =50 Ohm ID=T7 W=1.33 mm =32.92 mm ID=T8 W=1.22 mm =8 mm MOPEN$ ID=T2 MOPEN$ ID=T9 MSUB Er= 2.55 H= 0.8 mm T=.035 mm Rho= 1 Tand= 0
9 Confronto 0-10 Ideale Doppio Stub 1 2 IMPED ID=1 R=17 Ohm X=66 Ohm Mirostrip Frequeny (GHz)
10 Metodi di alolo delle disontinuità Rappresentazioni on iruiti equivalenti (parametri alolati on tenihe numerihe e suessiva interpolazione dei risultati) Formule analitihe (asi più semplii) Analisi elettromagnetia (direttamente dalla rappresentazione iruitale) Spesso sono disponibili più rappresentazioni della stessa disontinuità (maggiore preisione=più tempo di alolo)
11 Disontinuità in mirostrisia: Giunzioni Step (2-port) Tee (3-port) S 1 S 2 Cross (4-port) S 2 S3 S 1 S 3 S4 S 1 -S 2 ID=T1 W=1 mm =4 mm MSTEPX$ ID=MS1 Offset=0 mm 1 2 ID=T3 =4 mm ID=T1 W=1 mm =4 mm MTEE$ ID=T ID=T3 =4 mm ID=T1 W=1 mm =4 mm MCROSS$ ID=T2 1 2 ID=T5 W=2.5 mm =5 mm 3 ID=T3 =4 mm ID=T4 =5 mm 4 ID=T4 =5 mm
12 Bend (2-port) S 1 S 1 S 1 S 2 S 2 S 2 ID=T1 =4 mm MBENDA ID=T2 ANG=90 Deg MCURVE ID=T2 ID=T1 ANG=45 Deg =4 mm R=2 mm ID=T1 =4 mm MUBEND$ ID=T4 S=2 mm M=0.5 ID=T3 =4 mm ID=T3 =4 mm ID=T3 =4 mm
13 Terminazioni (1-port) Open end Via hole Radial Stub S 1 S 1 S 1 ID=T1 =4 mm MOPENX$ ID=MO1 ID=T1 =4 mm VIA1P ID=V1 D=1.5 mm H=1 mm T=0.05 mm RHO=1 ID=T1 =4 mm MRSTUB2W ID=T2 Ro=7 mm Theta=50 Deg
14 Componenti pseudo-onentrati Approssimazioni di apaità e induttanze in asata on un tratto di linea, ot sin ot sin Se è molto piolo e Y molto piolo: Y Y Y Y Y X= eq =/Y =/(vy ) eq =. /v Se è molto piolo e molto piolo: B=C eq =/ =/(v ) C eq =/(v. ) ot sin ot sin Y Y Y Y Y
15 Altri omponenti Capaità Interdigitale Spiral Indutors S 1 S 2 ID=T1 =4 mm MICAP$ ID=MI1 W=1 mm S=1 mm G=1 mm =10 mm N=4 WP=1 mm ID=T2 =4 mm ID=T1 W=1 mm =2 mm EPSB=1 TDB=0 TB=0.001 mm RhoB=1 ID=T2 W=1 mm =2 mm
16 Ciruiti a due porte Matrie S per iruiti reiproi e senza perdite: SS * U S S S S E suffiiente speifiare tre numeri reali per definire ompletamente S (ad es. S 11, 11, 22 )
17 Ciruito equivalente di un tratto di linea, 0 e S e 0 Con 0 = ot sin sin ot Y Y ot Y sin Y sin Yot z A z A y C z C y A y A A tan, C Y Y tan, Y A C 2 sin 2 sin
18 Calolo di in, out e G T s S (50) Tutti i oeffiienti di riflessione sono definiti rispetto a 50 in out S S, S in in in 50 s s s s out 50 out out 50 1S s11 s S s s G T s (1 S ) (1 ) 21 2 (1 s ) (1 s ) s s S S 12 21
Circuiti a Microonde: Introduzione
 Circuiti a Microonde: Introduzione Un circuito a microonde è un interconnessione di elementi le cui dimensioni fisiche possono essere comparabili con la lunghezza d onda corrispondente alle frequenze operative
Circuiti a Microonde: Introduzione Un circuito a microonde è un interconnessione di elementi le cui dimensioni fisiche possono essere comparabili con la lunghezza d onda corrispondente alle frequenze operative
Corso di Microonde II
 POLITECNICO DI MILANO Corso di Microonde II Lezione n. 1: Richiami sui circuiti a microonde - 1 - Parametri Concentrati e Distribuiti Quando le dimensioni fisiche dei componenti di un circuito sono molto
POLITECNICO DI MILANO Corso di Microonde II Lezione n. 1: Richiami sui circuiti a microonde - 1 - Parametri Concentrati e Distribuiti Quando le dimensioni fisiche dei componenti di un circuito sono molto
Fisica dei mezzi trasmissivi Prof. G. Macchiarella Prova del 28 Febbraio 2013
 Fisia dei mezzi trasmissivi Prof. G. Mahiarella Prova del 8 Febbraio 013 1 3 4 non srivere nella zona soprastante COGNOME E NOME MTRICO FIRM Eserizio 1 Un generatore, la ui tensione varia nel tempo ome
Fisia dei mezzi trasmissivi Prof. G. Mahiarella Prova del 8 Febbraio 013 1 3 4 non srivere nella zona soprastante COGNOME E NOME MTRICO FIRM Eserizio 1 Un generatore, la ui tensione varia nel tempo ome
Accoppiatore direzionale
 Aoppiatore direzionale 1 Rete 4 porte 3 4 Un aoppiatore direzionale ideale è un giunzione a 4 bohe on Adattamento alle porte quando sono hiuse sul ario di riferimento (ioè S 11 =S =S 33 =S 44 =) Due oppie
Aoppiatore direzionale 1 Rete 4 porte 3 4 Un aoppiatore direzionale ideale è un giunzione a 4 bohe on Adattamento alle porte quando sono hiuse sul ario di riferimento (ioè S 11 =S =S 33 =S 44 =) Due oppie
Report Tecnico. Accoppiatore di Potenza Cilindrico
 Report Tecnico Accoppiatore di Potenza Cilindrico Di seguito è riportata una linea coassiale (quindi in modo TEM) adattata a 50 Ω (lunghezza di 500mm). Il dielettrico interno è aria. 45 mm 104 mm Le due
Report Tecnico Accoppiatore di Potenza Cilindrico Di seguito è riportata una linea coassiale (quindi in modo TEM) adattata a 50 Ω (lunghezza di 500mm). Il dielettrico interno è aria. 45 mm 104 mm Le due
TEOREMA DEL CAMPIONAMENTO
 1 TEOREMA DEL CAMPIONAMENTO nota per il orso di Teleomuniazioni a ura di F. Benedetto G. Giunta 1. Introduzione Il proesso di ampionamento è di enorme importanza ai fini della realizzazione dei dispositivi
1 TEOREMA DEL CAMPIONAMENTO nota per il orso di Teleomuniazioni a ura di F. Benedetto G. Giunta 1. Introduzione Il proesso di ampionamento è di enorme importanza ai fini della realizzazione dei dispositivi
Antenne e Collegamento Radio
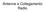 Antenne e Collegamento Radio Trasmissione irradiata Oltre ad essere guidato attraverso le linee di trasmissione, il campo elettromagnetico si può propagare nello spazio (radiazione) Anche la radiazione
Antenne e Collegamento Radio Trasmissione irradiata Oltre ad essere guidato attraverso le linee di trasmissione, il campo elettromagnetico si può propagare nello spazio (radiazione) Anche la radiazione
Unità Didattica 1. Sistemi di Numerazione
 Unità Didattia Sistemi di Numerazione Sistemi di Numerazione Posizionali Criterio per la rappresentazione di un insieme infinito di numeri mediante un insieme limitato di simoli. Un sistema di numerazione
Unità Didattia Sistemi di Numerazione Sistemi di Numerazione Posizionali Criterio per la rappresentazione di un insieme infinito di numeri mediante un insieme limitato di simoli. Un sistema di numerazione
MOMENTI E CENTRAGGIO DEL VELIVOLO
 x 1 x ISTITUZIONI DI INGEGNERIA AEROSAZIALE OENTI E CENTRAGGIO VELIVOLO OENTI E CENTRAGGIO DEL VELIVOLO er il alolo delle prestazioni in volo orizzontale rettilineo ed uniforme, il velivolo può essere
x 1 x ISTITUZIONI DI INGEGNERIA AEROSAZIALE OENTI E CENTRAGGIO VELIVOLO OENTI E CENTRAGGIO DEL VELIVOLO er il alolo delle prestazioni in volo orizzontale rettilineo ed uniforme, il velivolo può essere
Capitolo 14. Il progetto di circuiti a microonde assistito da CAD
 Capitolo 14 Il progetto di circuiti a microonde assistito da CAD 14.1 Introduzione Il progetto di un circuito a microonde segue le stesse linee sia che si tratti di una rete di adattamento, di un filtro,
Capitolo 14 Il progetto di circuiti a microonde assistito da CAD 14.1 Introduzione Il progetto di un circuito a microonde segue le stesse linee sia che si tratti di una rete di adattamento, di un filtro,
TEORIA SUI LIMITI DEFINIZIONE DI LIMITE FINITO DI UNA FUNZIONE PER X CHE TENDE AD UN VALORE FINITO
 TEORIA SUI LIMITI DEFINIZIONE DI LIMITE FINITO DI UNA FUNZIONE PER X CHE TENDE AD UN VALORE FINITO Si die he, per he tende a, la funzione y=f() ha per ite l e si srive: l = l I( ) ESEMPIO DI VERIFICA DI
TEORIA SUI LIMITI DEFINIZIONE DI LIMITE FINITO DI UNA FUNZIONE PER X CHE TENDE AD UN VALORE FINITO Si die he, per he tende a, la funzione y=f() ha per ite l e si srive: l = l I( ) ESEMPIO DI VERIFICA DI
ESEMPI DI PIASTRE SOTTILI PIANE E CURVE. Corso di Meccanica delle Strutture- ing. Elena Benvenuti
 PIASTRE ESEMPI DI PIASTRE SOTTILI PIANE E CURVE Corso di Meania delle Strutture- ing. Elena Benvenuti Elementi di piastra Disuteremo solo EF piastra (plate) volti a modellare solo il omportamento flessionale
PIASTRE ESEMPI DI PIASTRE SOTTILI PIANE E CURVE Corso di Meania delle Strutture- ing. Elena Benvenuti Elementi di piastra Disuteremo solo EF piastra (plate) volti a modellare solo il omportamento flessionale
Esempio di progetto di un telaio di c.a.
 q q 1 q 5 8 11 13 h q q 1 q 1 4 7 10 1 h 1 3 6 9 L L 1 L 1 L Fig. 1 Shema statio. La struttura intelaiata in.a. riportata in Fig. 1 è ostituita da travi di sez. 80 m x 4 m e pilastri di sezione 30 m x
q q 1 q 5 8 11 13 h q q 1 q 1 4 7 10 1 h 1 3 6 9 L L 1 L 1 L Fig. 1 Shema statio. La struttura intelaiata in.a. riportata in Fig. 1 è ostituita da travi di sez. 80 m x 4 m e pilastri di sezione 30 m x
Appendice 1 MODI DI PROPAGAZIONE IN CAVI COASSIALI. b/a. Lunghezza d'onda critica in cavi coassiali per alcuni modi di propagazione ( e r =1 ).
 Appendice 1 MODI DI PROPAGAZIONE IN CAVI COASSIALI I cavi coassiali oltre al modo di propagazione TEM consentono la propagazione anche con modi tipici delle guide d'onda. Due distinti gruppi di modi sono
Appendice 1 MODI DI PROPAGAZIONE IN CAVI COASSIALI I cavi coassiali oltre al modo di propagazione TEM consentono la propagazione anche con modi tipici delle guide d'onda. Due distinti gruppi di modi sono
Moto vario elastico: fenomeno del colpo d ariete
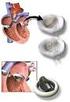 Moto vario elastio: fenomeno del olpo d ariete 1. Desrizione del fenomeno Si onsideri un semplie impianto ostituito da un serbatoio di grande ampiezza in modo tale he in esso il livello di ario rimanga
Moto vario elastio: fenomeno del olpo d ariete 1. Desrizione del fenomeno Si onsideri un semplie impianto ostituito da un serbatoio di grande ampiezza in modo tale he in esso il livello di ario rimanga
Pag. 1. Esercizi sui Diagrammi di Flusso. Stampa di alcuni numeri interi
 Università degli studi di Parma Dipartimento di Ingegneria dell Informazione Informatia a.a. 202/ Stampa di aluni numeri interi Informatia Faoltà di Mediina Veterinaria a.a. 202/ prof. Stefano Cagnoni
Università degli studi di Parma Dipartimento di Ingegneria dell Informazione Informatia a.a. 202/ Stampa di aluni numeri interi Informatia Faoltà di Mediina Veterinaria a.a. 202/ prof. Stefano Cagnoni
SISTEMI ELETTRONICI A RF (A.A )
 SISTEMI ELETTRONICI A RF (A.A. 2016-2017) Docenti: Ing. Pasquale Tommasino Prof. Stefano Pisa Orario Lezioni - Lunedì 12.00-14.00 AULA 6 -Martedì 10:00-12.00 AULA 6 - Mercoledì 12.00-14.00 AULA 6 LABORATORIO
SISTEMI ELETTRONICI A RF (A.A. 2016-2017) Docenti: Ing. Pasquale Tommasino Prof. Stefano Pisa Orario Lezioni - Lunedì 12.00-14.00 AULA 6 -Martedì 10:00-12.00 AULA 6 - Mercoledì 12.00-14.00 AULA 6 LABORATORIO
Lezione 15. Stabilità di sistemi retroazionati. F. Previdi - Automatica - Lez. 15 1
 ezione 15. Stabilità di sistemi retroazionati F. Previdi Automatia ez. 15 1 Shema 1. Stabilità di sistemi retroazionati 2. Stabilità & inertezza 3. Margine di guadagno 4. Margine di fase 5. Criterio di
ezione 15. Stabilità di sistemi retroazionati F. Previdi Automatia ez. 15 1 Shema 1. Stabilità di sistemi retroazionati 2. Stabilità & inertezza 3. Margine di guadagno 4. Margine di fase 5. Criterio di
Progetto di Microonde. Accoppiatore di tipo rat-race. Relazione a cura di Caracciolo Etienne, Piccoli Riccardo, Gabriele Porro
 Progetto di Microonde Accoppiatore di tipo rat-race Relazione a cura di Caracciolo Etienne, Piccoli Riccardo, Gabriele Porro 09/02/2009 Richieste del progetto Si vuole analizzare con MWOffice il comportamento
Progetto di Microonde Accoppiatore di tipo rat-race Relazione a cura di Caracciolo Etienne, Piccoli Riccardo, Gabriele Porro 09/02/2009 Richieste del progetto Si vuole analizzare con MWOffice il comportamento
Misure su linee di trasmissione
 Appendice A A-1 A-2 APPENDICE A. Misure su linee di trasmissione 1) Misurare, in trasmissione o in riflessione, la lunghezza elettrica TL della linea. 2) Dal valore di TL e dalla lunghezza geometrica calcolare
Appendice A A-1 A-2 APPENDICE A. Misure su linee di trasmissione 1) Misurare, in trasmissione o in riflessione, la lunghezza elettrica TL della linea. 2) Dal valore di TL e dalla lunghezza geometrica calcolare
Caratterizzazione in laboratorio di componentistiche a microonde
 Caratterizzazione in laboratorio di componentistiche a microonde Dott.ssa Paola Battaglia Dott. Cristian Franceschet Università degli Studi di Milano Dipartimento di Fisica Cosa trattiamo oggi Caratterizzazione
Caratterizzazione in laboratorio di componentistiche a microonde Dott.ssa Paola Battaglia Dott. Cristian Franceschet Università degli Studi di Milano Dipartimento di Fisica Cosa trattiamo oggi Caratterizzazione
Spin. La hamiltoniana classica di una particella di massa m e carica q in presenza di un potenziale elettromagnetico (Φ, A) si scrive.
 Spin La hamiltoniana lassia di una partiella di massa m e aria q in presenza di un potenziale elettromagnetio Φ, A si srive Sviluppando il quadrato si ha H = H = p q A 2 + qφ p 2 + A 2 2q A p + qφ 2 Se
Spin La hamiltoniana lassia di una partiella di massa m e aria q in presenza di un potenziale elettromagnetio Φ, A si srive Sviluppando il quadrato si ha H = H = p q A 2 + qφ p 2 + A 2 2q A p + qφ 2 Se
Corso di Fondamenti di Telecomunicazioni
 Fondamenti di TLC - Prof. G. Shemra Corso di Fondamenti di Teleomuniazioni 8 MODULAZIONI DIGITALI Prof. Giovanni Shemra 1 Fondamenti di TLC - Prof. G. Shemra Struttura della lezione Modulazioni digitali
Fondamenti di TLC - Prof. G. Shemra Corso di Fondamenti di Teleomuniazioni 8 MODULAZIONI DIGITALI Prof. Giovanni Shemra 1 Fondamenti di TLC - Prof. G. Shemra Struttura della lezione Modulazioni digitali
CAMPIONAMENTO E RICOSTRUZIONE DI SEGNALI. 1 Fondamenti Segnali e Trasmissione
 CAMPIONAMENTO E RICOSTRUZIONE DI SEGNALI Fondamenti Segnali e Trasmissione Numerizzazione dei segnali Nei moderni sistemi di memorizzazione e trasmissione i segnali in ingresso sono di tipo numerio, normalmente
CAMPIONAMENTO E RICOSTRUZIONE DI SEGNALI Fondamenti Segnali e Trasmissione Numerizzazione dei segnali Nei moderni sistemi di memorizzazione e trasmissione i segnali in ingresso sono di tipo numerio, normalmente
Esperienza n 6: COSTANTE di PLANCK
 Laboratorio IV Esperienza n 6: COSTANTE di PLANCK Esperienza n 6: COSTANTE di PLANCK Misura della ostante di Plank Inviando su un fotoatodo fotoni di energia hν, vengono estratti elettroni on una energia
Laboratorio IV Esperienza n 6: COSTANTE di PLANCK Esperienza n 6: COSTANTE di PLANCK Misura della ostante di Plank Inviando su un fotoatodo fotoni di energia hν, vengono estratti elettroni on una energia
MISURE DI RESISTENZA CON IL METODO DI CONFRONTO DELLE CADUTE DI TENSIONE
 MISUR DI RSISTNZA CON IL MTODO DI CONFRONTO DLL CADUT DI TNSION 1. Premessa Oggigiorno esistono strumenti ompatti e semplii da utilizzare per la misura di resistenza: gli ohmetri (parte integrante dei
MISUR DI RSISTNZA CON IL MTODO DI CONFRONTO DLL CADUT DI TNSION 1. Premessa Oggigiorno esistono strumenti ompatti e semplii da utilizzare per la misura di resistenza: gli ohmetri (parte integrante dei
Campi Elettromagnetici e Circuiti I Adattatori d impedenza
 Facoltà di Ingegneria Università degli studi di Pavia Corso di aurea Triennale in Ingegneria Elettronica e Informatica Campi Elettromagnetici e Circuiti I Adattatori d impedenza Campi Elettromagnetici
Facoltà di Ingegneria Università degli studi di Pavia Corso di aurea Triennale in Ingegneria Elettronica e Informatica Campi Elettromagnetici e Circuiti I Adattatori d impedenza Campi Elettromagnetici
GEOMETRIA ANALITICA 8 LE CONICHE
 GEOMETRIA ANALITICA 8 LE CONICHE Tra tutte le urve, ne esistono quattro partiolari he vengono hiamate onihe perhé sono ottenute tramite l intersezione di una superfiie i-onia on un piano. A seonda della
GEOMETRIA ANALITICA 8 LE CONICHE Tra tutte le urve, ne esistono quattro partiolari he vengono hiamate onihe perhé sono ottenute tramite l intersezione di una superfiie i-onia on un piano. A seonda della
simmetria sferica. L intensità (potenza per unità di superficie) a distanza L vale allora I = P / 4π L
 Fisia Generale Modulo di Fisia II A.A. -5 seritaione OND LTTROMAGNTICH Gb. Si onsideri un onda elettromagnetia piana sinusoidale he si propaga nel vuoto nella direione positiva dell asse x. La lunghea
Fisia Generale Modulo di Fisia II A.A. -5 seritaione OND LTTROMAGNTICH Gb. Si onsideri un onda elettromagnetia piana sinusoidale he si propaga nel vuoto nella direione positiva dell asse x. La lunghea
Linee di trasmissione
 Linee di trasmissione Finora esperienza con circuiti a costanti concentrate. E un approssimazione, valida solo per lunghezze d onda dei segnali grandi rispetto alle dimensioni del circuito. Esempio Sinusoidale
Linee di trasmissione Finora esperienza con circuiti a costanti concentrate. E un approssimazione, valida solo per lunghezze d onda dei segnali grandi rispetto alle dimensioni del circuito. Esempio Sinusoidale
Si vuole progettare un filtro passabanda in microstriscia con le seguenti specifiche:
 Si vuole progettare un filtro passabanda in microstriscia con le seguenti specifiche: Tipologia di filtro: equiripple Numero di poli: 5 Massimo ripple in banda: 0.5 db Frequenza centrale: 2.45 Ghz Banda
Si vuole progettare un filtro passabanda in microstriscia con le seguenti specifiche: Tipologia di filtro: equiripple Numero di poli: 5 Massimo ripple in banda: 0.5 db Frequenza centrale: 2.45 Ghz Banda
1. Calcolo del Momento di plasticizzazione per una sezione tubolare in acciaio.
 1. Calolo del Momento di plastiizzazione per una sezione tubolare in aiaio. La sezione presa in onsiderazione è la seguente: Shema di riferimento per il alolo del momento di plastiizzazione della sezione
1. Calolo del Momento di plastiizzazione per una sezione tubolare in aiaio. La sezione presa in onsiderazione è la seguente: Shema di riferimento per il alolo del momento di plastiizzazione della sezione
Lezione. Progetto di Strutture
 Lezione Progetto di Strutture PROGETTO DEGLI ELEMENTI RESISTENTI DI STRUTTURE INTELAIATE IN C.A. TRAVI Strutture intelaiate Limitazioni per travi Geometria Definizione: Il rapporto tra larghezza e altezza
Lezione Progetto di Strutture PROGETTO DEGLI ELEMENTI RESISTENTI DI STRUTTURE INTELAIATE IN C.A. TRAVI Strutture intelaiate Limitazioni per travi Geometria Definizione: Il rapporto tra larghezza e altezza
Mezzi non omogenei. Corso di Microonde I A.A. 2004/2005
 Mezzi non omogenei Nelle microonde si usano spesso mezzi trasmissivi non omogenei; Lo studio di questi mezzi viene ricondotto al caso equivalente TEM mediante la definizione di opportuni parametri caratteristici;
Mezzi non omogenei Nelle microonde si usano spesso mezzi trasmissivi non omogenei; Lo studio di questi mezzi viene ricondotto al caso equivalente TEM mediante la definizione di opportuni parametri caratteristici;
P3 CIRCUITI RISONANTI E AMPLIFICATORI SELETTIVI.
 P CICUITI ISONANTI E AMPIFICATOI SEETTIVI. P. Un iruito C serie è alimentato alla frequenza di risonanza da un generatore a tensione ostante, avente f.e.m. di valore iae E, V. a bobina, di induttanza 4,5
P CICUITI ISONANTI E AMPIFICATOI SEETTIVI. P. Un iruito C serie è alimentato alla frequenza di risonanza da un generatore a tensione ostante, avente f.e.m. di valore iae E, V. a bobina, di induttanza 4,5
1. Circuito equivalente di un trasformatore trifase
 . Circuito equivalente di un trasformatore trifase Poiché la rete magnetica rappresentativa del nucleo dei trasformatori trifase a due avvolgimenti (per colonna) può essere rappresentata come indipendente
. Circuito equivalente di un trasformatore trifase Poiché la rete magnetica rappresentativa del nucleo dei trasformatori trifase a due avvolgimenti (per colonna) può essere rappresentata come indipendente
ESERCIZIO PRELIMINARE
 ESERCIZIO PRELIMINARE Prima di cominciare le misure, svolgere quanto indicato sotto e poi verificare con il docente le conclusioni. Sulla carta di Smith, la misura di un componente concentrato ha l andamento
ESERCIZIO PRELIMINARE Prima di cominciare le misure, svolgere quanto indicato sotto e poi verificare con il docente le conclusioni. Sulla carta di Smith, la misura di un componente concentrato ha l andamento
Misure di grandezze elettriche fondamentali
 Misure di grandezze elettrihe fondamentali - Misure di grandezze elettrihe fondamentali - ensione e orrente Il iruito elettrio La tensione e la orrente sono le grandezze elettrihe più importanti. A queste
Misure di grandezze elettrihe fondamentali - Misure di grandezze elettrihe fondamentali - ensione e orrente Il iruito elettrio La tensione e la orrente sono le grandezze elettrihe più importanti. A queste
Dispersione modale. Dispersione modale
 Dispersione modale Se determiniamo l allargamento dell impulso per unità di lunghezza della fibra otteniamo l indice di dispersione modale σ ns m km A causa dell allargamento dell impulso la banda di frequenza
Dispersione modale Se determiniamo l allargamento dell impulso per unità di lunghezza della fibra otteniamo l indice di dispersione modale σ ns m km A causa dell allargamento dell impulso la banda di frequenza
Esercizio no.1 soluzione a pag.3
 Edutenia.it Modulazioni digitali eserizi risolti 1 Eserizio no.1 soluzione a pag.3 Quanti bit sono neessari per trasmettere 3 simboli e quale è la veloità di modulazione e la veloità di trasmissione se
Edutenia.it Modulazioni digitali eserizi risolti 1 Eserizio no.1 soluzione a pag.3 Quanti bit sono neessari per trasmettere 3 simboli e quale è la veloità di modulazione e la veloità di trasmissione se
Esercitazione 8 : LINEE DI TRASMISSIONE
 Esercitazione 8 : LINEE DI TRASMISSIONE Specifiche Scopo di questa esercitazione è verificare il comportamento di spezzoni di linea in diverse condizioni di pilotaggio e di terminazione. L'esecuzione delle
Esercitazione 8 : LINEE DI TRASMISSIONE Specifiche Scopo di questa esercitazione è verificare il comportamento di spezzoni di linea in diverse condizioni di pilotaggio e di terminazione. L'esecuzione delle
Antenne per Stazioni Radio Base: Antenne per UMTS
 Antenne per Stazioni Radio Base: Antenne per UMTS Docente: Filiberto Bilotti Sommario Antenne per stazioni radio base di sistemi UMTS concetto di dipolo a larga banda concetto di dipolo parassita per aumentare
Antenne per Stazioni Radio Base: Antenne per UMTS Docente: Filiberto Bilotti Sommario Antenne per stazioni radio base di sistemi UMTS concetto di dipolo a larga banda concetto di dipolo parassita per aumentare
1.5 Calcolo di erenziale vettoriale Derivata ordinaria Gradiente Esempio n. 3 - Gradiente di 1
 Indice 1 ANALISI VETTORIALE 1 1.1 Scalari e vettori......................... 1 1.1.1 Vettore unitario (versore)............... 2 1.2 Algebra dei vettori....................... 3 1.2.1 Somma di due vettori.................
Indice 1 ANALISI VETTORIALE 1 1.1 Scalari e vettori......................... 1 1.1.1 Vettore unitario (versore)............... 2 1.2 Algebra dei vettori....................... 3 1.2.1 Somma di due vettori.................
TRASFORMATA DI HILBERT
 TRASFORMATA DI ILBERT La Trasformata di ilbert è una partiolare rappresentazione he, ontrariamente ad altre trasformate (Fourier, Laplae, Z, ) non realizza un ambiamento del dominio di definizione. In
TRASFORMATA DI ILBERT La Trasformata di ilbert è una partiolare rappresentazione he, ontrariamente ad altre trasformate (Fourier, Laplae, Z, ) non realizza un ambiamento del dominio di definizione. In
Analisi di segnali campionati
 Analisi nel dominio della frequenza Analisi di segnali ampionati - 1 Analisi di segnali ampionati 1 Analisi dei segnali nel dominio della frequenza I prinipali metodi di analisi dei segnali di misura possono
Analisi nel dominio della frequenza Analisi di segnali ampionati - 1 Analisi di segnali ampionati 1 Analisi dei segnali nel dominio della frequenza I prinipali metodi di analisi dei segnali di misura possono
RELAZIONE GEOTECNICA GENERALE E DELLE FONDAZIONI
 Studio Assoiato di Ingegneria IDG Comune di Collegno Provinia di Torino RELAZIONE GEOTECNICA GENERALE E DELLE FONDAZIONI OGGETTO: Relazione geotenia relativa al progetto Cimitero Comunale Ampliamento EST
Studio Assoiato di Ingegneria IDG Comune di Collegno Provinia di Torino RELAZIONE GEOTECNICA GENERALE E DELLE FONDAZIONI OGGETTO: Relazione geotenia relativa al progetto Cimitero Comunale Ampliamento EST
CORSO OPERATORI RADIO IN EMERGENZA
 ARI Associazione Radioamatori italiani Sezione di Belluno CORSO OPERATORI RADIO IN EMERGENZA - 1 - Presentazione Scopo del corso Le comunicazioni radio L informazione nella gestione delle emergenze La
ARI Associazione Radioamatori italiani Sezione di Belluno CORSO OPERATORI RADIO IN EMERGENZA - 1 - Presentazione Scopo del corso Le comunicazioni radio L informazione nella gestione delle emergenze La
Confronto fra i sistemi di modulazione AM, DSB e SSB
 ngelo rotopapa - IK0VVG Conronto ra i sistemi di modulazione M, B e B 1. Introduzione Chi si oupa di autoostruzione avrà siuramente notato he aluni progetti sono relativi a operanti in banda laterale unia
ngelo rotopapa - IK0VVG Conronto ra i sistemi di modulazione M, B e B 1. Introduzione Chi si oupa di autoostruzione avrà siuramente notato he aluni progetti sono relativi a operanti in banda laterale unia
CAPITOLO 15 CAPACITÀ PORTANTE DELLE FONDAZIONI SUPERFICIALI
 CAPITOLO 15 La fondazione è uella parte della struttura he trasmette il ario dell opera al terreno sottostante. La superfiie di ontatto tra la base della fondazione e il terreno è detta piano di posa.
CAPITOLO 15 La fondazione è uella parte della struttura he trasmette il ario dell opera al terreno sottostante. La superfiie di ontatto tra la base della fondazione e il terreno è detta piano di posa.
Prof. Giuseppe Lanzo
 CORSO DI LAUREA SPECIALISTICA QUIQUEALE I ARCHITETTURA UE Laboratorio di Costruzioni Modulo di GEOTECICA E FODAZIOI Prof. Giuseppe Lanzo Dipartimento di Ingegneria Strutturale e Geotenia Via A. Gramsi
CORSO DI LAUREA SPECIALISTICA QUIQUEALE I ARCHITETTURA UE Laboratorio di Costruzioni Modulo di GEOTECICA E FODAZIOI Prof. Giuseppe Lanzo Dipartimento di Ingegneria Strutturale e Geotenia Via A. Gramsi
16 L INTEGRALE INDEFINITO
 9. Integrali immediati 6 L INTEGRALE INDEFINITO Riassumiamo le puntate preedenti: si die INTEGRALE INDEFINITO di una funzione f ( ), la famiglia di tutte e sole quelle funzioni la ui derivata è uguale
9. Integrali immediati 6 L INTEGRALE INDEFINITO Riassumiamo le puntate preedenti: si die INTEGRALE INDEFINITO di una funzione f ( ), la famiglia di tutte e sole quelle funzioni la ui derivata è uguale
!!!"! ARTECO MOTION TECH SpA - Via Mengolina, 22 48018 Faenza (RA) Italy Tel. +39 0546 645777 Fax +39 0546 645750 [email protected] - www.arteco-cnc.
 !!!"! #$% &'() (*+,$---'() *))) # Copyright Arteco Motion Tech S.p.A. 2003 Le informazioni contenute in questo manuale sono di proprietà della Arteco Motion Tech SpA e non possono essere riprodotte né
!!!"! #$% &'() (*+,$---'() *))) # Copyright Arteco Motion Tech S.p.A. 2003 Le informazioni contenute in questo manuale sono di proprietà della Arteco Motion Tech SpA e non possono essere riprodotte né
Compito di Elettrotecnica, Ing. Gestionale, Pisa, 5 Giugno vista dai morsetti 1-2 del bipolo in figura (A da tabella)
 Compito di Elettrotecnica, Ing. Gestionale, Pisa, 5 Giugno 214 Allievo... 1) Calcolare la R eq vista dai morsetti 1-2 del bipolo in figura (A da tabella) 2) Calcolare la E th (tensione di Thevenin) ai
Compito di Elettrotecnica, Ing. Gestionale, Pisa, 5 Giugno 214 Allievo... 1) Calcolare la R eq vista dai morsetti 1-2 del bipolo in figura (A da tabella) 2) Calcolare la E th (tensione di Thevenin) ai
FFT (FAST FOURIER TRANSFORM ALGORITHM) ALGORITMI VELOCI per la TRASFORMATA DISCRETA DI FOURIER. Slide 1
 FFT (FAST FOURIER TRANSFORM ALGORITHM ALGORITMI VELOCI per la TRASFORMATA DISCRETA DI FOURIER Slide Introduzione / Gli algoritmi noti ome Fast Fourier Transorm hanno rivoluzionato l'analisi di segnali
FFT (FAST FOURIER TRANSFORM ALGORITHM ALGORITMI VELOCI per la TRASFORMATA DISCRETA DI FOURIER Slide Introduzione / Gli algoritmi noti ome Fast Fourier Transorm hanno rivoluzionato l'analisi di segnali
CBM a.s. 2012/2013 PROBLEMA DELLE SCORTE
 CBM a.s. 212/213 PROBLEMA DELLE SCORTE Chiamiamo SCORTA ogni riserva di materiali presente all interno del sistema produttivo in attesa di essere sottoposto ad un proesso di trasformazione o di distribuzione.
CBM a.s. 212/213 PROBLEMA DELLE SCORTE Chiamiamo SCORTA ogni riserva di materiali presente all interno del sistema produttivo in attesa di essere sottoposto ad un proesso di trasformazione o di distribuzione.
Il fido e i finanziamenti bancari
 Modulo 7 Il fido e i finanziamenti anari 65 I destinatari del Modulo sono gli studenti he, dopo aver analizzato e appreso le aratteristihe fondamentali dell attività delle aziende di redito, le loro funzioni
Modulo 7 Il fido e i finanziamenti anari 65 I destinatari del Modulo sono gli studenti he, dopo aver analizzato e appreso le aratteristihe fondamentali dell attività delle aziende di redito, le loro funzioni
Politecnico di Torino Laurea a Distanza in Ingegneria Meccanica Corso di Macchine
 ESERCIZI SVOLTI Sono di seguito svolti due eserizi sulle turbine a vapore assiali, aggiuntivi rispetto a quelli svolti durante il tutorato (i ui testi e i risultati numerii sono riportati alla fine del
ESERCIZI SVOLTI Sono di seguito svolti due eserizi sulle turbine a vapore assiali, aggiuntivi rispetto a quelli svolti durante il tutorato (i ui testi e i risultati numerii sono riportati alla fine del
Reti di Calcolatori a.a
 Analogico e digitale 2 Corso di laurea in Informatica Reti di Calcolatori a.a. 2007-2008 Prof. Roberto De Prisco Capitolo 3 Dati e segnali Per essere trasmessi i dati devono essere trasformati in segnali
Analogico e digitale 2 Corso di laurea in Informatica Reti di Calcolatori a.a. 2007-2008 Prof. Roberto De Prisco Capitolo 3 Dati e segnali Per essere trasmessi i dati devono essere trasformati in segnali
MISURE SU CAVI COASSIALI
 MISURE SU CAVI COASSIALI Carlo Vignali I4VIL 05 RIDUZIONE DEL VSWR Il valore del VSWR del carico viene osservato di valore ridotto quando è misurato all'ingresso di una linea con attenuazione Allo stesso
MISURE SU CAVI COASSIALI Carlo Vignali I4VIL 05 RIDUZIONE DEL VSWR Il valore del VSWR del carico viene osservato di valore ridotto quando è misurato all'ingresso di una linea con attenuazione Allo stesso
Esempio di antenna a telaio, con spire rettangolari e circolari.
 ANTENNE A TELAIO LA QUAD di Giovanni G. Turco, ik0ziz Questo tipo di antenna fu realizzata da Clarence J. Moore, ingegnere, ed adottata per la prima volta a Quito, in Equator, oltre sessant anni fa, quando
ANTENNE A TELAIO LA QUAD di Giovanni G. Turco, ik0ziz Questo tipo di antenna fu realizzata da Clarence J. Moore, ingegnere, ed adottata per la prima volta a Quito, in Equator, oltre sessant anni fa, quando
Equazioni di secondo grado intere letterali
 Equazioni di seondo grado intere letterali Esempio. k ) x k + )x + k + 0 a k b k + ) k + Disussione. Se k 0 k l equazione si abbassa di grado. Disutiamo il aso a 0 aso in ui l equazione diventa di primo
Equazioni di seondo grado intere letterali Esempio. k ) x k + )x + k + 0 a k b k + ) k + Disussione. Se k 0 k l equazione si abbassa di grado. Disutiamo il aso a 0 aso in ui l equazione diventa di primo
PROGETTAZIONE COMPOSTE DI STRUTTURE ACCIAIO-CALCESTRUZZOALCESTRUZZO
 Comune di Napoli Corso di Aggiornamento su Nuovi Criteri e Norme per la Progettazione in Zona Sismia PROGETTAZIONE DI STRUTTURE COMPOSTE ACCIAIO-CALCESTRUZZOALCESTRUZZO - SECONDA PARTE - Pro. Emidio NIGRO
Comune di Napoli Corso di Aggiornamento su Nuovi Criteri e Norme per la Progettazione in Zona Sismia PROGETTAZIONE DI STRUTTURE COMPOSTE ACCIAIO-CALCESTRUZZOALCESTRUZZO - SECONDA PARTE - Pro. Emidio NIGRO
Corso di Fondamenti di Telecomunicazioni
 Corso di Fondamenti di Teleomuniazioni 8 MODULAZIONI DIGITALI Prof. Giovanni Shemra Fondamenti di TLC - Prof. G. Shemra Struttura della lezione Modulazioni digitali inarie ( ) Modulazione ASK Modulazione
Corso di Fondamenti di Teleomuniazioni 8 MODULAZIONI DIGITALI Prof. Giovanni Shemra Fondamenti di TLC - Prof. G. Shemra Struttura della lezione Modulazioni digitali inarie ( ) Modulazione ASK Modulazione
MATEMATICA CORSO A COMPITINO DI RECUPERO (Tema 1) 13 Febbraio 2014
 MATEMATICA CORSO A COMPITINO DI RECUPERO (Tema 1) 13 Febbraio 2014 Soluzioni 1. In un sahetto i sono 7 palline olorate: 2 rosse, 3 verdi e 2 gialle. Si fanno 4 estrazioni on rimessa. a) Calola la probabilità
MATEMATICA CORSO A COMPITINO DI RECUPERO (Tema 1) 13 Febbraio 2014 Soluzioni 1. In un sahetto i sono 7 palline olorate: 2 rosse, 3 verdi e 2 gialle. Si fanno 4 estrazioni on rimessa. a) Calola la probabilità
Il comportamento di un amplificatore ideale, ad esempio di tensione, è descritto dalla relazione lineare V out = A V in (3.1)
 Capitolo 3 Amplificazione 3.1 Circuiti attivi Gli elementi circuitali considerati sino ad ora, sia lineari (resistenze, capacità, induttanze e generatori indipendenti), sia non lineari (diodi), sono detti
Capitolo 3 Amplificazione 3.1 Circuiti attivi Gli elementi circuitali considerati sino ad ora, sia lineari (resistenze, capacità, induttanze e generatori indipendenti), sia non lineari (diodi), sono detti
Turbomacchine Radiali -Compressori Centrifughi -Turbine Centripete
 Turbomahine Radiali -Compressori Centrifughi -Turbine Centripete Testi di Riferimento Cumpsty, N.A. Compressor Aerodynamis, ISBN 0-470-334-5 Japikse, D. Centrifugal Compressor Design and Performane, ISBN
Turbomahine Radiali -Compressori Centrifughi -Turbine Centripete Testi di Riferimento Cumpsty, N.A. Compressor Aerodynamis, ISBN 0-470-334-5 Japikse, D. Centrifugal Compressor Design and Performane, ISBN
Corso di Fondamenti di Telecomunicazioni
 Corso di Fondameni di Teleomuniazioni 6 - SEGNALI IN BANDA ASSANTE E MODULAZIONI rof. Mario Barbera [pare 4] 1 Modulazioni digiali binarie Il segnale m() sia un segnale digiale in banda base, rappresenao
Corso di Fondameni di Teleomuniazioni 6 - SEGNALI IN BANDA ASSANTE E MODULAZIONI rof. Mario Barbera [pare 4] 1 Modulazioni digiali binarie Il segnale m() sia un segnale digiale in banda base, rappresenao
