Appunti di lezione ( 2 parte) Mario Bossa
|
|
|
- Florindo Mauro
- 9 anni fa
- Visualizzazioni
Transcript
1 Appunti di lezione ( 2 parte) Mario Bossa Metodo M.O.L.C.A.O. per sistemi di elettroni π Una delle applicazioni più importanti del metodo M.O.L.C.A.O è stata quella che ha permesso lo studio sistematico della struttura elettronica delle molecole contenenti sistemi di elettroni π. Queste molecole sono planari e sono caratterizzate da uno scheletro di legami σ che tengono insieme principalmente atomi di carbonio, idrogeno, azoto e ossigeno. Tali legami impegnano, se supponiamo che il piano molecolare sia il piano xy, gli orbitali atomici 2s, 2px e 2py di carbonio, azoto e ossigeno e gli orbitali 1s dell'idrogeno, possiamo anche supporre che gli orbitali 2s, 2px e 2py di ciascun atomo siano combinati fra loro per formare ibridi sp 2.Resta, pertanto, per ogni atomo di carbonio, azoto ed ossigeno, un orbitale 2pz che può essere combinato linearmente con gli orbitali 2pz degli altri atomi formando orbitali molecolari che hanno tutti la caratteristica di cambiare segno sotto l'operazione di riflessione rispetto al piano molecolare ( che è sicuramente un piano di simmetria per le molecole planari ); per analogia con quanto si ha per le molecole lineari, si dice che questi orbitali molecolari sono di tipo π e si parla di sistemi di elettroni π. Si classificano anche gli orbitali atomici 2s, 2px, 2py e 1s dell'idrogeno come orbitali σ e l'orbitale 2pz come orbitale π: la motivazione per tale differenziazione risiede nel fatto che, per il diverso comportamento sotto l'operazione di riflessione rispetto al piano molecolare gli orbitali che abbiamo chiamato σ non si possono mescolare con i π. La molecola più semplice che possiede un sistema di elettroni π è l'etilene. In Fig. 1 è mostrato lo scheletro della molecola che comprende i nuclei degli atomi con gli elettroni interni e i legami σ, insieme al sistema di riferimento adottato. Per quanto detto circa il diverso comportamento degli orbitali π e σ sotto l'operazione di riflessione rispetto al piano molecolare, possiamo in buona approssimazione, trattare separatamente i due tipi di elettroni e costruire orbitali molecolari formati solo da orbitali atomici π, così facendo abbiamo applicato quella che si chiama separazione σ π. In altre parole tratteremo solo gli elettroni π e diremo che questi si muovono in un campo di potenziale generato dallo scheletro σ descritto prima. Per la molecola dell'etilene costruiremo, quindi, gli orbitali molecolari π formando combinazioni lineari degli orbitali atomici 2pz degli atomi di carbonio 1 e 2, orbitali che chiameremo z 1 e z 2. Il procedimento matematico è perfettamente analogo a quello seguito per la trattazione della molecola H 2, anche qui abbiamo due atomi ognuno dei quali mette a disposizione un solo orbitale atomico. L'unica differenza consiste nel fatto che per la molecola H 2 l'orbitale atomico è lo 1s, mentre per il sistema π è il 2pz. Gli orbitali molecolari avranno la forma: ψ = c 1 z 1 c 2 z 2 e, se calcoliamo il valore minimo dell'energia rispetto ai coefficienti c 1 e c 2, troveremo due orbitali molecolari (non normalizzati ): ψ = z 1 z 2 e ψ = z 1 z 2.Le energie corrispondenti a questi due orbitali molecolari saranno, con le notazioni e le approssimazioni introdotte per il calcolo della molecola H 2 : E = H 11 H 12 e E_ = H 11 H 12 Per gli integrali H 11 e H 12 si possono usare le notazioni introdotte da Hückel: H 11 = α e H 12 = β. α è sostanzialmente il valore dell'energia che possiede un elettrone quando si trova in un orbitale 2pz del carbonio con gli altri orbitali di valenza del carbonio ibridizzati sp 2. Tale valore viene solitamente preso come lo zero nella scala delle energie. La Fig 2 riporta il diagramma delle energie degli orbitali molecolari π dell'etilene. ( β ha un valore negativo). Vediamo ora come l'uso delle proprietà di simmetria dell'etilene ci possa aiutare per il calcolo degli orbitali molecolari. Osserviamo innanzituto che gli elementi di simmetria presenti in questa molecola, sono: l'identità E, gli assi C 2 coincidenti con gli assi x,y, z, i piani coordinati σ xy, σ xz, σ yx
2 e il centro di inversione i. Notiamo pure che le operazioni che possiamo effettuare rispetto a questi elementi di simmetria, in particolare le tre riflessioni e le tre rotazioni, non sono fra loro equivalenti e quindi non possono essere raggruppate in una stessa classe. L'insieme di queste otto operazioni di simmetria costituisce il gruppo D 2h. Se studiamo il comportamento degli orbitali z 1 e z 2 sotto le diverse operazioni del gruppo, vediamo che questi due orbitali sono trasformati l'uno nell'altro per effetto di qualcuna delle operazioni di simmetria. Come sappiamo, ciò significa che queste due funzioni sono base per una rappresentazione bidimensionale del gruppo. E', però, possibile formare due loro combinazioni lineari ognuna delle quali è da sola base per una rappresentazione monodimensionale, e qundi irriducibile, del gruppo. Le due combinazioni sono (normalizzate): 1/ 2 ( z 1 z 2 ) e 1/ 2 ( z 1 z 2 ).Le rappresentazioni indotte da queste due combinazioni sono indicate in Tab 1 Tab 1 Gruppo D 2h E C 2 (z) C 2 (x) C 2 (y) i ơ xy ơ xz ơ yz A u 1/ 2 (z 1 z 2 ) B 2g 1/ 2 ( z 1 z 2 ) Notiamo quindi che, con l'aiuto della simmetria, abbiamo trovato le combinazioni lineari degli orbitali z 1 e z 2 che costituiscono gli orbitali molecolari legante e antilegante, ricavati precedentemente con la risoluzione del sistema di equazioni lineari omogenee e del deteminante secolare collegato. Vediamo, quindi, che la simmetria della molecola dell'etilene, determina da sola la forma degli orbitali molecolari nell'approssimazione L.C.A.O. L'energia degli orbitali molecolari la otterremo, poi, calcolando l'integrale: ψ H ψ dv con ψ = 1/ 2 ( z 1 z 2 ) oppure 1/ 2 ( z 1 z 2 ) ed applicando, nel calcolo di questi integrali, le approssimazioni di Hückel. Non sempre, però, la simmetria determina da sola la forma degli orbitali molecolari, ci permette comunque di semplificare il trattamento matematico, poichè, se costruiamo combiazioni lineari adattate per simmetria ( S.A.L.C. ), cioè funzioni basi per rappresentazioni irriducibili del gruppo di simmetria, sappiamo che possiamo combinare fra loro solo quelle che sono basi per la stessa rappresentazione. Un primo esempio lo troviamo nell'anione allile.( La Fig. 3 ne mostra lo scheletro degli atomi di carbonio). L'anione allile contiene quattro elettroni nel sistema π. Le operazioni di simmetria sono: l'identità E, l'asse C 2 coincidente con l'asse y nel sistema di riferimento di Fig. 3, il piano molecolare σ xy e l'altro piano σ yz. Il gruppo è il C 2v. Gli orbitali atomici che formeranno gli orbitali molecolari π sono i 2pz dei tre atomi di carbonio e li chiameremo z 1, z 2, z 3. Vediamo che tutte le operazioni di simmetria del gruppo trasformano l'orbitale z 1 sempre in se stesso o meno se stesso e, quindi, è da solo base per rappresentare il gruppo. Le funzioni z 2 e z 3, invece, si trasformano l'una nell'altra e sono quindi base per una rappresentazione bidimensionale. Possiamo, però, formare due loro combiazioni lineari che, da sole, sono base per una rappresentazione del gruppo. Queste combinazioni sono (normalizzate): 1/ 2(z 2 z 3 ) e 1 / 2 (z 2 z 3 ). In Tab 2 sono riportate le rappresentazioni (irriducibili ) indotte dagli orbitali atomici π dell'allile. Tab 2 gruppo C 2v E C 2 σ xy σ yz B 2 z B 2 1/ 2 (z 2 z 3 ) A 2 1/ 2 (z 2 z 3 )
3 Si vede, quindi, che la combinazione 1 / 2 (z 2 z 3 ) è la sola funzione per la rappresentazione A 2 e quindi non si può mescolare con nessun altro orbitale atomico. Essa costituisce, pertanto, uno dei tre orbitali molecolari π del nostro sistema. I due orbitali base per la rappresentazione B 2 si possono, invece, combinare tra loro e formeranno gli altri due orbitali π del sistema. Per calcolare le energie dei due orbitali molecolari di simmetria B 2 dobbiamo risolvere il determinante secolare: Haa E Saa Hba E Sba Hab E Sab Hbb E Sbb = 0 Dove gli elementi di matrice sono calcolati sulla base delle funzioni φ a = z 1 e φ b = 1/ 2 (z 2 z 3 ). Per calcolare questi elementi di matrice, una volta che li abbiamo sviluppati in termini di integrali tra orbitali atomici, possiamo usare le approssimazuioni di Hückel: H ii = α = 0 ; H ij = β se l'atomo i è legato all'atomo j ; H ij = 0 negli altri casi. Sij = δij cioè uguale uno se i =j, uguale zero se i j. Con queste approssimazioni, il determinante diviene: E 2 β 2 β = 0 E Da cui: E = 2 β e E = 2β L'energia della funzione 1/ 2 (z 2 z 3 ) calcolata con le stesse approssimazioni è uguale ad α cioè zero. Possiamo, quindi. costruire il diagramma delle energie degli orbitali molecolari per l'anione allile, che è mosttrato in Fig. 4. Nella Fig. 4 sono anche riportati, accanto ad ogni livello energetico, i segni che hanno i coefficienti degli orbitali atomici nei rispettivi orbitali molecolari. Si evidenzia, così, il fatto che, all'aumentare dell'energia, corrisponde un aumento del numero di piani nodali perpendicolari al piano molecolare, (ricordiamo che tutti questi orbitali, di simmetria π, possiedono un piano nodale coincidente col piano molecolare). Vediamo che l'orbitale 1b 2 non ha piani nodali perpendicolari, l'orbitale 1a 2, ne ha uno e l'orbitale 2b 2 ne ha due. Questa regola ci permetterà di ordinare in ordine crescente le energie degli orbitali molecolari anche per le molecole che tratteremo in seguito, per le quali non faremo il calcolo esplicito dell'energia. Trattiamo, adesso, la molecola del butadiene. In Fig. 5 è riportato lo scheletro σ di questa molecola nella configurazione trans, insieme al sistema di riferimento scelto. Le operazioni di simmetria per questa molecola sono: l'identità E, la rotazione intorno all'asse C 2, coincidente con l'asse z nel nostro sistema di riferimento, l'inversione i e la riflessione rispetto al piano σ xy, che è il piano molecolare e che si chiama σ h. L'insieme di queste operazioni costituisce il gruppo C 2h. Gli orbitali atomici che saranno interessati alla formazione degli orbitali molecolari π, sono i quattro orbitali 2pz degli atomi di carbonio, che chiameremo z 1, z 2, z 3, z 4. Dobbiamo vedere come questi orbitali si trasformano sotto le operazioni di simmetria del gruppo C 2h. Notiamo che gli orbitali z 1 e z 4 si trasformano sempre tra di loro per effetto di tutte le operazioni del gruppo e, quindi, insieme, sono base per una rappresentazione bidimesionale del gruppo, è, però, possibile formare due loro combinazioni lineari che, da sole, sono base per una rappresentazione monodimensionale e quindi irriducibile. Queste combinazioni sono (non normalizzate ): ( z 1 z 4 ) e ( z 1 z 4 ). Lo stesso discorso vale per la coppia di orbitali z 2 e z 3 e per le loro cobinazioni ( z 2 z 3 ) e ( z 2 z 3 ). La Tab.3 riassume il comportamento di queste quattro combinazioni lineari sotto le operazioni del gruppo:
4 Tab. 3 gruppo C 2h E C 2 i σ A u ( z 1 z 4 ) A u ( z 2 z 3 ) B g ( z 1 z 4 ) B g ( z 2 z 3 ) Dai risultati riportati in Tab. 2, si vede che due degli orbitali molecolari π potranno essere formati combinando fra loro le due funzioni base per la rappresentazione A u e avranno la forma: c a ( z 1 z 4 ) c b ( z 2 z 3 ) e, rispettivamente c c ( z 1 z 4 ) c d ( z 2 z 3 ) con c a, c b, c c, c d tutti di segno positivo. Analogamente gli altri due orbitali molecolari, si otterranno dal mescolamento delle due funzioni base per la rappresentazione B g.i segni dei coefficienti degli orbitali atomici in questi quattro orbitali molecolari saranno, pertanto, come riportato in Fig. 6.La Fig. 6 mostra i livelli dell'energia degli orbitali molecolari nell'ordine che si può ricavare tenendo conto del numero dei piani nodali perpendicolari al piano molecolare. Valori numerici delle energie e coefficienti degli orbitali atomici possono essere ricavati, per ognuna delle due rappresentazioni irriducibili, dalla risoluzione dei due sistemi di equazioni lineari omogenei e dei rispettivi determinanti secolari, facendo uso, per esmpio, delle approssimazioni di Hückel. Molecole cicliche con sistemi di elettroni π Una importante classe di molecole che si può trattare molto covenientemente con l'aiuto delle proprietà di simmetria, è quella delle molecole cicliche con sistemi di elettroni π. Queste molecole hanno la formula generica (CH)n e si possono considerare formate da un anello di n atomi di carbonio disposti ai vertici di un poligono regolare di n lati. Ogni atomo di carbonio è legato con legame σ ad un atomo di idrogeno verso l'esterno del poligono e forma due altri legami σ con altri due atomi di carbonio; gli rimane, pertanto, un orbitale 2pz perpendicolare al piano molecoare ( che assumiamo essere il piano xy ) che verrà combinato con tutti gli altri orbitali 2pz degli altri atomi di carbonio, per formare gli orbitali molecolari π. La simmetria di queste molecole è sufficientemente alta da determinare i coefficienti degli orbitali atomici nei vari orbitali molecolari. Qui ci limiteremo ad una loro descrizione sommaria sulla base dei piani nodali perpendicolari al piano molecolare, dal numero dei quali, come abbiamo visto, possiamo ordinare le energie in ordine crescente. Le molecole di questa classe che tratteremo saranno il benzene con un anello esagonale di sei atomi di carbonio e sei eletroni π e l'anione del ciclopentadienile con un anello pentagonale di cinque atomi di carbonio e sei elettroni π. Fig 7. Le operazioni di simmetria del benzene sono: l'identità E,le operazioni che derivano dall'asse C 6, che sono 2C 6, 2C 3 e C 2, tre rotazioni intorno ai tre assi C 2 ' che passano per due vertici opposti dell'esagono, tre rotazioni intorno ai tre assi C 2 " che passano per il centro di due lati opposti dell'esagono, l'inversione i, le operazioni che derivano dalla presenza dell'asse improprio S 6 che sono 2S 6 e 2S 3, la riflessione rispetto al piano molecolare σ h, le tre riflessioni rispetto ai tre piani σ v ognuno dei quali contiene l'asse C 6 e uno degli assi C 2 ', le tre riflessioni rispetto ai tre piani σ d, ognuno dei quali contiene l'asse C 6 e uno degli assi C 2 ". L'insieme di queste 24 operazioni costituisce il gruppo D 6h.Gli orbitali atomici che useremo per formare gli orbitali molecolari, sono i sei orbitali 2pz dei sei atomi di carbonio, che chiameremo z 1, z 2, z 3,z 4, z 5, z 6. Questi orbitali sono trasformati uno nell'altro per effetto delle operazioni del gruppo e sono, quindi, base per una rappresentazione esadimensionale del gruppo. I caratteri di questa rappresentazione si possono facilmente ricavare guardando quanti orbitali atomici restano al loro posto o cambiano segno in seguito all'esecuzione di una operazione di simmetria. Essi sono riportati in Tab. 4
5 Tab. 4 gruppod 6h E 2C 6 2C 3 C 2 3C 2 ' 3C 2 " i 2S 6 2 S 3 σ h 3σ v 3σ d (z 1 z 2 z 3 z 4 z 5 z 6 ) Le regole della teoria dei gruppi, ci fanno conoscere che, dai sei orbitali atomici z 1, z 2, z 3,z 4, z 5, z 6 è possibile formare sei combinazioni lineari basi per rappresentazioni irriducibili del gruppo. In particolare, una combinazione è base per la rappresentazione A 2u, due combinazioni sono base per la E 1g altre due per la E 2u e la sesta per la B 1g. Le stesse regole ci dicono anche quali sono queste combinazioni, che non sono altro che gli orbitali molecolri π del benzene. Come si vede essi sono stati ricavati direttamente dalle proprietà di simmetria del sistema. Le energie si possono ricavare calcolando l'integrale: Φ H Φ dv, in cui Φ è uno degli orbitali molecolari. In Fig. 8 è riportato, in modo solo qualitativo, il diagramma delle energie degli orbitali molecolari del benzene, è riportato anche lo schema dei piani nodali perpendicolari al piano molecolare, il numero dei quali ci ha permesso di ordinare gli orbitali molecolari in ordine crescente di energia. Ricordiamo che due orbitali molecolari che sono basi per una rappresentazione irriducibile bidimensionale del gruppo. sono necessariamente degeneri. Passiamo all'anione del ciclopentadienile, le operazioni di simmetria sono quelle proprie di un pentagono regolare: l'identità E, le operazioni derivanti dall'asse C 5 e cioè 2C 5 e 2C 5 2, le cinque rotazioni derivanti dalla presenza dei cinque assi C 2 sul piano molecolare e passanti per un vertice del pentagono e per il centro del lato opposto, la riflessione rispetto al piano molecolare σ h, le rotazioni improprie derivanti dalla presenza dell'asse improprio S 5, e, cioè, 2S 5 e 2S 5 3, le cinque riflessioni rispetto ai cinque piani σ v ognuno dei quali contiene l'asse C 5 e uno dei C 2.L'insieme di queste 20 operazioni di simmetria costituisce il gruppo D 5h.Gli orbitali atomici che useremo per formare gli orbitali molecolari sono i cinque orbitali 2pz dei cinque atomi di carbonio che chiameremo: z 1, z 2, z 3, z 4, e z 5. Le operazioni del gruppo trasformano questi cinque orbitali l'uno nell'altro, essi sono pertanto base per una rappresentazione pentadimensionale del gruppo. I caratteri di questa rappresentazione si possono facilmente ricavare guardando quanti orbitali atomici restano al loro posto o cambiano segno in seguito all'esecuzione di una operazione di simmetria. Essi sono riportati in Tab. 5. Tab. 5 guppod 5h E 2C 5 2 2C 5 5C 2 σ h 2S 5 2S 5 3 z 1,z 2,z 3,z 4,z σ v Le regole della teoria dei gruppi, ci fanno conoscere che, dai cinque orbitali atomici z 1, z 2, z 3,z 4, z 5 è possibile formare cinque combinazioni lineari basi per rappresentazioni irriducibili del gruppo. In particolare, una combinazione è base per la rappresentazione A 2 ", due combinazioni sono base per la rappresentazione E 1 " e altre due per la rappresentazione E 2 ". Le stesse regole ci dicono anche quali sono queste combinazioni, che non sono altro che gli orbitali molecolri π dell'anione ciclopentadienile. Come si vede essi sono stati ricavati direttamente dalle proprietà di simmetria del sistema. Le energie si possono ricavare calcolando l'integrale: Φ H Φ dv, in cui Φ è uno degli orbitali molecolari. In Fig. 9 è riportato, in modo solo qualitativo, il diagramma delle energie degli orbitali molecolari dell'anione ciclopentadienile, è riportato anche lo schema dei piani nodali perpendicolari al piano molecolare, il numero dei quali ci ha permesso di ordinare gli orbitali molecolari in ordine crescente di energia. Ricordiamo, ancora, che due orbitali molecolari che sono basi per una rappresentazione irriducibile bidimensionale del gruppo. sono necessariamente degeneri. Vediamo ora come si possono applicare i risultati ottenuti per i sistemi ciclici con elettroni π, in
6 particolare l'anione ciclopentadienile, allo studio degli orbitali molecolari di composti di coordinazione come il ferrrocene in cui due anioni ciclopentadienilici sono coordinati a sandwich con uno ione Fe 2. Se assumiamo per i due anelli pentagonali la conformazione sfalsata, le operazioni di simmetria sono: l'identità E, le operazioni derivanti dall'asse C 5, cioè 2C 5 e 2C 5 2, le cinque rotazioni intorno agli assi C 2 perpendicolari al C 5 e passanti per il ferro, l'inversione i, le operazioni derivanti dalla presenza dell'asse improprio S 10, che è coincidente con l'asse C 5 e che sono 2S 10 e 2S 10 3, le cinque riflessioni rispetto ai cinque piani σ v che contengono l'asse C 5 e bisecano due assi C 2. L'insieme di queste 20 operazioni di simmetria costituisce il gruppo D 5d. Dobbiamo vedere quali sono le rappresentazioni irriducibili di questo gruppo indotte dagli orbitali atomici che vogliamo usare come base per il calcolo degli orbitali molecolari. Gli orbitali che useremo sono: gli orbitali 2pz degli atomi di carbonio dei ciclopentadienili e gli orbitali di valenza del ferro cioè i 3d, i 4s e i 4p. Possiamo, in realtà, prendere come base da una parte gli orbitali del ferro e, dall'altra, gli orbitali molecolari già trovati per il sistema π del ciclopentadienile. Vediamo, così, che, se combiniamo due orbitali molecolari, della stessa rappresentazione irriducibile, dei due anelli, otteniamo due funzioni combinazioni dei 10 orbitali 2pz degli atomi di carbonio, che sono basi per due rappresentazioni irriducibili del gruppo D 5d, delle quali una è simmetrica rispetto all'inversione e l'altra è antisimmetrica. Così dall'orbitale a 2 " del ciclopentadienile avremo un orbitale a 1g ed un orbitale a 2u, dai due orbitali e 1 ne avremo due e 1g e due e 1u, dai due orbitali e 2 ne avremo due e 2g e due e 2u. I nove orbitali di valenza del ferro sono base per le seguenti rappresentazioni irriducibili: i cinque orbitali 3d sono base per le rappresentazioni a 1g, e 1g ed e 2g, l'orbitale 4s è base per la a 1g e i tre orbitali 4p sono base per le rappresentazioni a 2u ed e 2u. A questo punto, tenendo conto che si possono combinare tra loro solo funzioni che sono basi per la stessa rappresentazione irriducibile, è possibile ricavare il diagramma delle energie degli orbitali molecolari del ferrocene. Questo diagramma è riportato alla pag. 702 del libro Chimica Inorganica di J. E, Huheey, E. A. Keiter e R.L. Keiter e può essere consultato colà dagli studenti. Notiamo in particolare che i 18 elettroni del ferrrocene vanno a riempire i primi 9 orbitali molecolari, fino all'orbitale a 1g che è sostanzialmente l'orbitale 3dz 2 del ferro. Questi nove orbitali sono tutti leganti o non leganti e ciò spiega la stabilità del ferrocene, inoltre i primi orbitali vuoti, che sono i due e 1g ( dxz e dyz del ferro ) sono anche loro poco antileganti e quest rende conto dell'esistenza di complessi sandwich sia con numero di elettroni inferiore a 18 che con numero superiore, come ben chiarito nel testo sopra citato.
7 y H H C 2 C 1 x H H Fig. 1: Struttura della molecola di etilene nel sistema di riferimento E αβ α = 0 2β αβ Fig. 2: diagramma dell energia degli orbitali molecolari π dell etilene
8 y C1 x C3 C 2 Fig 3: struttura dello ione allile nel sistema di riferimento. 2β 2b 2 α = 0 1a 2 0 2β 1b 2 Fig. 4: diagramma dell energia degli orbitali molecolari π dello ione allile
9 y C 1 C 3 C 2 x C 4 Fig 5: struttura della molecola di butadiene nel sistema di riferimento E 2b g 2a u α= 0 1b g 1a u Fig 6: diagramma dell energia degli orbitali molecolari π del butadiene
10 y x x y Fig. 7: anelli del benzene e del cilopentadienile nel sistema di riferimento E α=0 a 2u e 1g e 2u b 1g E α=0 a 2u e 1g e 2u b 1g Fig. 8: diagramma dell energia degli orbitali molecolari π del benzene
11 E e 2 α=0 e 1 a 2 Fig 9: diagramma dell energia degli orbitali molecolari π del ciclopentadienile
Esercizio 1. CF 2 CS 2 CCl 4 ClF 3
 Esercizio 1 Determinare in base al metodo del legame di valenza la forma delle seguenti molecole, tenendo conto delle repulsioni coulombiane tra le coppie elettroniche di valenza CF 2 CS 2 CCl 4 ClF 3
Esercizio 1 Determinare in base al metodo del legame di valenza la forma delle seguenti molecole, tenendo conto delle repulsioni coulombiane tra le coppie elettroniche di valenza CF 2 CS 2 CCl 4 ClF 3
Appunti delle lezioni di Chimica Inorganica II Mario Bossa
 Appunti delle lezioni di Chimica Inorganica II Mario Bossa Metodo M.O. L.C.A.O. Sappiamo che l'equazione di Schrödinger, che schematicamente scriviamo: Hψ = Eψ, dove H è l'operatore dell'energia (nel nostro
Appunti delle lezioni di Chimica Inorganica II Mario Bossa Metodo M.O. L.C.A.O. Sappiamo che l'equazione di Schrödinger, che schematicamente scriviamo: Hψ = Eψ, dove H è l'operatore dell'energia (nel nostro
Lezione n. 22. Molecole poliatomiche Metodo VSEPR Orbitali ibridi Coniugazione π. 02/03/2008 Antonino Polimeno 1
 Chimica Fisica - Chimica e Tecnologia Farmaceutiche Lezione n. 22 Molecole poliatomiche Metodo VSEPR Orbitali ibridi Coniugazione π 02/03/2008 Antonino Polimeno 1 Molecole poliatomiche (1) - Siamo ora
Chimica Fisica - Chimica e Tecnologia Farmaceutiche Lezione n. 22 Molecole poliatomiche Metodo VSEPR Orbitali ibridi Coniugazione π 02/03/2008 Antonino Polimeno 1 Molecole poliatomiche (1) - Siamo ora
IBRIDAZIONE e GEOMETRIA MOLECOLARE
 IBRIDAZIONE e GEOMETRIA MOLECOLARE Esempio: struttura della molecola del metano CH 4 1s 2s 2p Configurazione elettronica del C Per esempio il carbonio può utilizzare la configurazione in cui un elettrone
IBRIDAZIONE e GEOMETRIA MOLECOLARE Esempio: struttura della molecola del metano CH 4 1s 2s 2p Configurazione elettronica del C Per esempio il carbonio può utilizzare la configurazione in cui un elettrone
Teoria dell Orbitale Molecolare
 Teoria dell Orbitale Molecolare Un orbitale molecolare è il risultato della combinazione lineare degli orbitali atomici appartenenti agli atomi che costituiscono la molecola; questi orbitali molecolari
Teoria dell Orbitale Molecolare Un orbitale molecolare è il risultato della combinazione lineare degli orbitali atomici appartenenti agli atomi che costituiscono la molecola; questi orbitali molecolari
Aromaticità Un composto si definisce aromatico se possiede un anello di elettroni chiuso.
 Aromaticità Un composto si definisce aromatico se possiede un anello di elettroni chiuso. E anche detto aromatico, quando tramite i seguenti criteri soddisfa la regola di ückel: 1. I composti aromatici
Aromaticità Un composto si definisce aromatico se possiede un anello di elettroni chiuso. E anche detto aromatico, quando tramite i seguenti criteri soddisfa la regola di ückel: 1. I composti aromatici
un legame covalente due legami covalenti? tre legami covalenti due legami covalenti un legame covalente
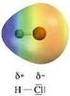 e C N un legame covalente due legami covalenti? tre legami covalenti O F Ne 1s 2s 2p due legami covalenti un legame covalente C 1s 2s 2p ibridazione quattro legami covalenti Cariche Formali Usando le strutture
e C N un legame covalente due legami covalenti? tre legami covalenti O F Ne 1s 2s 2p due legami covalenti un legame covalente C 1s 2s 2p ibridazione quattro legami covalenti Cariche Formali Usando le strutture
IL LEGAME SIGMA σ E IL LEGAME PI- GRECO π
 IL LEGAME SIGMA σ E IL LEGAME PI- GRECO π La teoria di Lewis considera gli elettroni di valenza degli atomi che formano legami,ma prescinde totalmente dal fatto che tali elettroni sono descritti da orbitali
IL LEGAME SIGMA σ E IL LEGAME PI- GRECO π La teoria di Lewis considera gli elettroni di valenza degli atomi che formano legami,ma prescinde totalmente dal fatto che tali elettroni sono descritti da orbitali
La struttura di ioni e molecole
 La struttura di ioni e molecole Inizialmente: consideriamo atomi che non danno espansione dell ottetto e non ci interessiamo della geometria delle molecole Alcune regole per individuare la posizione degli
La struttura di ioni e molecole Inizialmente: consideriamo atomi che non danno espansione dell ottetto e non ci interessiamo della geometria delle molecole Alcune regole per individuare la posizione degli
I. Foglio di esercizi su vettori linearmente dipendenti e linearmente indipendenti. , v 2 = α v 1 + β v 2 + γ v 3. α v 1 + β v 2 + γ v 3 = 0. + γ.
 ESERCIZI SVOLTI DI ALGEBRA LINEARE (Sono svolti alcune degli esercizi proposti nei fogli di esercizi su vettori linearmente dipendenti e vettori linearmente indipendenti e su sistemi lineari ) I. Foglio
ESERCIZI SVOLTI DI ALGEBRA LINEARE (Sono svolti alcune degli esercizi proposti nei fogli di esercizi su vettori linearmente dipendenti e vettori linearmente indipendenti e su sistemi lineari ) I. Foglio
Lezione 3. Legame Chimico. Teoria degli Orbitali Molecolari
 Lezione 3 Legame Chimico Teoria degli Orbitali Molecolari 1 Perchè si formano i legami? Un diagramma di energia mostra che un legame fra due atomi si forma se l energia del sistema diminuisce quando i
Lezione 3 Legame Chimico Teoria degli Orbitali Molecolari 1 Perchè si formano i legami? Un diagramma di energia mostra che un legame fra due atomi si forma se l energia del sistema diminuisce quando i
Teoria degli orbitali ibridi
 Legami σ e π Teoria degli orbitali ibridi FORMAZIONE DEI LEGAMI CHIMICI COVALENTI L orbitale della molecola H 2 ha simmetria cilindrica intorno all asse internucleare H-H LEGAME SIGMA Gli orbitali molecolari
Legami σ e π Teoria degli orbitali ibridi FORMAZIONE DEI LEGAMI CHIMICI COVALENTI L orbitale della molecola H 2 ha simmetria cilindrica intorno all asse internucleare H-H LEGAME SIGMA Gli orbitali molecolari
Corso di Chimica Inorganica II (A-L) Laurea Triennale in Chimica (L-27) PROPRIETA DI TRASFORMAZIONE DEGLI ORBITALI ATOMICI
 Corso di Chimica Inorganica II (A-L) Laurea Triennale in Chimica (L-27) Dr. Andrea G. Marrani PROPRIETA DI TRASFORMAZIONE DEGLI ORBITALI ATOMICI Le funzioni d onda per l elettrone nell atomo di H sono
Corso di Chimica Inorganica II (A-L) Laurea Triennale in Chimica (L-27) Dr. Andrea G. Marrani PROPRIETA DI TRASFORMAZIONE DEGLI ORBITALI ATOMICI Le funzioni d onda per l elettrone nell atomo di H sono
Metodi basati sulla meccanica quantistica
 Metodi basati sulla meccanica quantistica La descrizione più corretta della struttura elettronica delle molecole, come quella degli atomi, è basata sulla meccanica quantistica. Esistono due principali
Metodi basati sulla meccanica quantistica La descrizione più corretta della struttura elettronica delle molecole, come quella degli atomi, è basata sulla meccanica quantistica. Esistono due principali
Il legame chimico II: la geometria molecolare e l ibridizzazione degli orbitali atomici. Capitolo 10
 Il legame chimico II: la geometria molecolare e l ibridizzazione degli orbitali atomici Capitolo 10 Legame tra un derivato del Buckyball e il sito dell HIV-Protease Repulsione delle coppie di elettroni
Il legame chimico II: la geometria molecolare e l ibridizzazione degli orbitali atomici Capitolo 10 Legame tra un derivato del Buckyball e il sito dell HIV-Protease Repulsione delle coppie di elettroni
Valitutti, Falasca, Tifi, Gentile. Chimica. concetti e modelli.blu
 Valitutti, Falasca, Tifi, Gentile Chimica concetti e modelli.blu 2 Capitolo 14 Le nuove teorie di legame 3 Sommario 1. I limiti della teoria di Lewis 2. Il legame chimico secondo la meccanica quantistica
Valitutti, Falasca, Tifi, Gentile Chimica concetti e modelli.blu 2 Capitolo 14 Le nuove teorie di legame 3 Sommario 1. I limiti della teoria di Lewis 2. Il legame chimico secondo la meccanica quantistica
LA STRUTTURA DELLE MOLECOLE. Le Molecole Poliatomiche
 LA STRUTTURA DELLE MOLECOLE Le Molecole Poliatomiche LE MOLECOLE POLIATOMICE Le molecole poliatomiche sono quelle molecole che sono composte da più di due atomi e contengono nella maggior parte dei casi
LA STRUTTURA DELLE MOLECOLE Le Molecole Poliatomiche LE MOLECOLE POLIATOMICE Le molecole poliatomiche sono quelle molecole che sono composte da più di due atomi e contengono nella maggior parte dei casi
CORSO DI LAUREA IN BIOTECNOLOGIE CHIMICA ORGANICA. - Brown, Poon, INTRODUZIONE ALLA CHIMICA ORGANICA, EdiSES
 CORSO DI LAUREA IN BIOTECNOLOGIE CHIMICA ORGANICA TESTI: - John McMurry, CHIMICA ORGANICA, PICCIN - Brown, Poon, INTRODUZIONE ALLA CHIMICA ORGANICA, EdiSES - Janice Gorzynski Smith, FONDAMENTI DI CHIMICA
CORSO DI LAUREA IN BIOTECNOLOGIE CHIMICA ORGANICA TESTI: - John McMurry, CHIMICA ORGANICA, PICCIN - Brown, Poon, INTRODUZIONE ALLA CHIMICA ORGANICA, EdiSES - Janice Gorzynski Smith, FONDAMENTI DI CHIMICA
Nell'atomo l'energia dell'elettrone varia per quantità discrete (quanti).
 4. ORBITALI ATOMICI Energia degli orbitali atomici Nell'atomo l'energia dell'elettrone varia per quantità discrete (quanti). Il diagramma energetico dell'atomo di idrogeno: i livelli (individuati da n)
4. ORBITALI ATOMICI Energia degli orbitali atomici Nell'atomo l'energia dell'elettrone varia per quantità discrete (quanti). Il diagramma energetico dell'atomo di idrogeno: i livelli (individuati da n)
06/03/2012. Elementi in chimica organica
 CORSO DI LAUREA IN BIOINFORMATICA CHIMICA ORGANICA E DELLE MACROMOLECOLE BIOLOGICHE MICHAEL ASSFALG Lezione: 6 CFU = 48 ORE Lun 14:30-16:30, 16:30, Mer 8:30-10:30 PROVA FINALE: SCRITTO (+ ORALE) TESTI:
CORSO DI LAUREA IN BIOINFORMATICA CHIMICA ORGANICA E DELLE MACROMOLECOLE BIOLOGICHE MICHAEL ASSFALG Lezione: 6 CFU = 48 ORE Lun 14:30-16:30, 16:30, Mer 8:30-10:30 PROVA FINALE: SCRITTO (+ ORALE) TESTI:
Teorie del legame chimico. Teorie del legame chimico
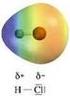 Teorie del legame chimico Le teorie proposte per la trattazione del legame chimico si prefiggono i seguenti scopi: 1. Prevedere la formazione di un legame tra due elementi 2. Predire la lunghezza del legame
Teorie del legame chimico Le teorie proposte per la trattazione del legame chimico si prefiggono i seguenti scopi: 1. Prevedere la formazione di un legame tra due elementi 2. Predire la lunghezza del legame
Zolfo (Z = 16) Conf. Elettronica 1s 2 2s 2 2p 6 3s 2 3p 4 Conf. Elettronica esterna 3s 2 3p 4
 TAVOLA PERIODICA DEGLI ELEMENTI Gli elementi sono ordinati nella tavola periodica secondo numero atomico crescente ed in base alle loro proprietà chimico-fisiche che seguono un andamento periodico. Gli
TAVOLA PERIODICA DEGLI ELEMENTI Gli elementi sono ordinati nella tavola periodica secondo numero atomico crescente ed in base alle loro proprietà chimico-fisiche che seguono un andamento periodico. Gli
LA STRUTTURA DELLE MOLECOLE. Orbitali molecolari e legame chimico
 LA STRUTTURA DELLE MOLECOLE Orbitali molecolari e legame chimico GLI ORBITALI MOLECOLARI Quando degli atomi collidono tra di loro i loro nuclei ed elettroni vengono a trovarsi in prossimità influenzandosi
LA STRUTTURA DELLE MOLECOLE Orbitali molecolari e legame chimico GLI ORBITALI MOLECOLARI Quando degli atomi collidono tra di loro i loro nuclei ed elettroni vengono a trovarsi in prossimità influenzandosi
Elementi di Chimica Organica
 CORSO DI LAUREA IN BIOINFORMATICA Elementi di Chimica Organica Mariapina D Onofrio ([email protected]) Orario ricevimento: mar e giov 11:30-13:30 Corso: 6 CFU = 48 ORE Lezioni: Mar 8:30-10:30,
CORSO DI LAUREA IN BIOINFORMATICA Elementi di Chimica Organica Mariapina D Onofrio ([email protected]) Orario ricevimento: mar e giov 11:30-13:30 Corso: 6 CFU = 48 ORE Lezioni: Mar 8:30-10:30,
Prodotto scalare, ortogonalitá e basi ortonormali
 CAPITOLO 0 Prodotto scalare, ortogonalitá e basi ortonormali Esercizio 0.. Dati i seguenti vettori di R si calcoli il prodotto scalare (v i,v j per i,j =,,...,6: v = (6,3 v = (,0 v 3 = (, v 4 = (,0 v 5
CAPITOLO 0 Prodotto scalare, ortogonalitá e basi ortonormali Esercizio 0.. Dati i seguenti vettori di R si calcoli il prodotto scalare (v i,v j per i,j =,,...,6: v = (6,3 v = (,0 v 3 = (, v 4 = (,0 v 5
IL LEGAME COVALENTE SECONDO LA MECCANICA ONDULATORIA L
 IL LEGAME COVALENTE SECONDO LA MECCANICA ONDULATORIA L elettrone è dissolto in una nube di carica, ovvero il concetto di orbitale sostituisce il di Lewis LEGAME DI VALENZA (VB) Sviluppo quantomeccanico
IL LEGAME COVALENTE SECONDO LA MECCANICA ONDULATORIA L elettrone è dissolto in una nube di carica, ovvero il concetto di orbitale sostituisce il di Lewis LEGAME DI VALENZA (VB) Sviluppo quantomeccanico
Appunti sui Codici di Reed Muller. Giovanni Barbarino
 Appunti sui Codici di Reed Muller Giovanni Barbarino Capitolo 1 Codici di Reed-Muller I codici di Reed-Muller sono codici lineari su F q legati alle valutazioni dei polinomi sullo spazio affine. Per semplicità
Appunti sui Codici di Reed Muller Giovanni Barbarino Capitolo 1 Codici di Reed-Muller I codici di Reed-Muller sono codici lineari su F q legati alle valutazioni dei polinomi sullo spazio affine. Per semplicità
Corso di Geometria BIAR, BSIR Esercizi 10: soluzioni
 Corso di Geometria 2010-11 BIAR, BSIR Esercizi 10: soluzioni 1 Geometria dello spazio Esercizio 1. Dato il punto P 0 = ( 1, 0, 1) e il piano π : x + y + z 2 = 0, determinare: a) Le equazioni parametriche
Corso di Geometria 2010-11 BIAR, BSIR Esercizi 10: soluzioni 1 Geometria dello spazio Esercizio 1. Dato il punto P 0 = ( 1, 0, 1) e il piano π : x + y + z 2 = 0, determinare: a) Le equazioni parametriche
GEOMETRIA MOLECOLARE
 GEOMETRIA MOLECOLARE Ibridazione La teoria VSEPR 1 Ibridazione e geometria molecolare Teoria di Lewis e VB vista finora non sono in grado di descrivere correttamente la geometria di molte molecole anche
GEOMETRIA MOLECOLARE Ibridazione La teoria VSEPR 1 Ibridazione e geometria molecolare Teoria di Lewis e VB vista finora non sono in grado di descrivere correttamente la geometria di molte molecole anche
Fissiamo nello spazio un sistema di riferimento cartesiano ortogonale O, x, y, z, u.
 Fissiamo nello spazio un sistema di riferimento cartesiano ortogonale O, x, y, z, u. Definizione Una quadriche è il luogo dei punti, propri o impropri, reali o immaginari, che con le loro coordinate omogenee
Fissiamo nello spazio un sistema di riferimento cartesiano ortogonale O, x, y, z, u. Definizione Una quadriche è il luogo dei punti, propri o impropri, reali o immaginari, che con le loro coordinate omogenee
CONFIGURAZIONE ELETTRONICA. In generale la configurazione elettronica indica come sono posizionati gli elettroni intorno al nucleo di un atomo.
 CONFIGURAZIONE ELETTRONICA In generale la configurazione elettronica indica come sono posizionati gli elettroni intorno al nucleo di un atomo. ORBITA : Zona intorno al nucleo di diversa energia dove ruotano
CONFIGURAZIONE ELETTRONICA In generale la configurazione elettronica indica come sono posizionati gli elettroni intorno al nucleo di un atomo. ORBITA : Zona intorno al nucleo di diversa energia dove ruotano
Unità Didattica N 9 : La parabola
 0 Matematica Liceo \ Unità Didattica N 9 La parabola Unità Didattica N 9 : La parabola ) La parabola ad asse verticale ) La parabola ad asse orizzontale 5) Intersezione di una parabola con una retta 6)
0 Matematica Liceo \ Unità Didattica N 9 La parabola Unità Didattica N 9 : La parabola ) La parabola ad asse verticale ) La parabola ad asse orizzontale 5) Intersezione di una parabola con una retta 6)
La retta nel piano cartesiano
 La retta nel piano cartesiano Se proviamo a disporre, sul piano cartesiano, una retta vediamo che le sue possibili posizioni sono sei: a) Coincidente con l asse delle y; b) Coincidente con l asse delle
La retta nel piano cartesiano Se proviamo a disporre, sul piano cartesiano, una retta vediamo che le sue possibili posizioni sono sei: a) Coincidente con l asse delle y; b) Coincidente con l asse delle
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
GLI ORBITALI ATOMICI
 GLI ORBITALI ATOMICI Orbitali atomici e loro rappresentazione Le funzioni d onda Ψ n che derivano dalla risoluzione dell equazione d onda e descrivono il moto degli elettroni nell atomo si dicono orbitali
GLI ORBITALI ATOMICI Orbitali atomici e loro rappresentazione Le funzioni d onda Ψ n che derivano dalla risoluzione dell equazione d onda e descrivono il moto degli elettroni nell atomo si dicono orbitali
x 1 Fig.1 Il punto P = P =
 Geometria di R 2 In questo paragrafo discutiamo le proprietà geometriche elementari del piano Per avere a disposizione delle coordinate nel piano, fissiamo un punto, che chiamiamo l origine Scegliamo poi
Geometria di R 2 In questo paragrafo discutiamo le proprietà geometriche elementari del piano Per avere a disposizione delle coordinate nel piano, fissiamo un punto, che chiamiamo l origine Scegliamo poi
1 Ampliamento del piano e coordinate omogenee
 1 Ampliamento del piano e coordinate omogenee Vogliamo dare una idea, senza molte pretese, dei concetti che stanno alla base di alcuni calcoli svolti nella classificazione delle coniche. Supponiamo di
1 Ampliamento del piano e coordinate omogenee Vogliamo dare una idea, senza molte pretese, dei concetti che stanno alla base di alcuni calcoli svolti nella classificazione delle coniche. Supponiamo di
L Atomo e le Molecole
 L Atomo e le Molecole L atomo L'atomo, la particella che come un mattone costituisce tutta la materia, non è un corpicciolo semplice. Esso è a sua volta composto da particelle elementari piccolissime:
L Atomo e le Molecole L atomo L'atomo, la particella che come un mattone costituisce tutta la materia, non è un corpicciolo semplice. Esso è a sua volta composto da particelle elementari piccolissime:
La circonferenza nel piano cartesiano
 6 La circonferenza nel piano cartesiano onsideriamo la circonferenza in figura in cui il centro è ; e il raggio 5 r : se indichiamo con P ; un punto della circonferenza avremo, per definizione, che la
6 La circonferenza nel piano cartesiano onsideriamo la circonferenza in figura in cui il centro è ; e il raggio 5 r : se indichiamo con P ; un punto della circonferenza avremo, per definizione, che la
MATEMATICA PRIMO COMPITINO SOLUZIONE DI ALCUNI ESERCIZI PRIMA PARTE. Esercizio 1. (Testo B) Determina, motivando la risposta, se la funzione f : R R
 ANNO ACCADEMICO 25 6 SCIENZE GEOLOGICHE E SCIENZE NATURALI E AMBIENTALI MATEMATICA PRIMO COMPITINO SOLUZIONE DI ALCUNI ESERCIZI PROFF MARCO ABATE E MARGHERITA LELLI-CHIESA PRIMA PARTE Esercizio (Testo
ANNO ACCADEMICO 25 6 SCIENZE GEOLOGICHE E SCIENZE NATURALI E AMBIENTALI MATEMATICA PRIMO COMPITINO SOLUZIONE DI ALCUNI ESERCIZI PROFF MARCO ABATE E MARGHERITA LELLI-CHIESA PRIMA PARTE Esercizio (Testo
1) Bilanciare la seguente reazione redox con il metodo ionico-elettronico Ag (s) + H + (aq) + NO 3
 A ) Soluzioni Esercizi I esonero del 29/11/2005 1) Bilanciare la seguente reazione redox con il metodo ionicoelettronico Ag (s) + + (aq) + N 3 (aq) Ag + (aq) + N 2 (g) + 2 (l) Calcolare quanti grammi di
A ) Soluzioni Esercizi I esonero del 29/11/2005 1) Bilanciare la seguente reazione redox con il metodo ionicoelettronico Ag (s) + + (aq) + N 3 (aq) Ag + (aq) + N 2 (g) + 2 (l) Calcolare quanti grammi di
Fissiamo nel piano un sistema di riferimento cartesiano ortogonale O, x, y, u.
 Fissiamo nel piano un sistema di riferimento cartesiano ortogonale O, x, y, u. Definizione Una conica è il luogo dei punti, propri o impropri, reali o immaginari, che con le loro coordinate omogenee (x,
Fissiamo nel piano un sistema di riferimento cartesiano ortogonale O, x, y, u. Definizione Una conica è il luogo dei punti, propri o impropri, reali o immaginari, che con le loro coordinate omogenee (x,
UNITÀ DIDATTICA 5 LA RETTA
 UNITÀ DIDATTICA 5 LA RETTA 5.1 - La retta Equazione generica della retta Dalle considerazioni emerse nel precedente capitolo abbiamo compreso come una funzione possa essere rappresentata da un insieme
UNITÀ DIDATTICA 5 LA RETTA 5.1 - La retta Equazione generica della retta Dalle considerazioni emerse nel precedente capitolo abbiamo compreso come una funzione possa essere rappresentata da un insieme
Corso di Chimica Inorganica II (A-L) Laurea Triennale in Chimica (L-27) GRUPPO: insieme di elementi correlati dalle seguenti regole:
 APPUNTI DI TEORIA DEI GRUPPI Corso di Chimica Inorganica II (A-L) Laurea Triennale in Chimica (L-27) Dr. Andrea G. Marrani DEFINIZIONI GRUPPO: insieme di elementi correlati dalle seguenti regole: 1) PRODOTTO
APPUNTI DI TEORIA DEI GRUPPI Corso di Chimica Inorganica II (A-L) Laurea Triennale in Chimica (L-27) Dr. Andrea G. Marrani DEFINIZIONI GRUPPO: insieme di elementi correlati dalle seguenti regole: 1) PRODOTTO
Rappresentazione matriciale del Gruppo puntuale di simmetria C3v (ammoniaca)
 Rappresentazione matriciale del Gruppo puntuale di simmetria C3v (ammoniaca) La prima cosa da fare è scegliere una BASE. Per l ammoniaca sceglieremo gli orbitali s di valenza dell azoto e degli atomi di
Rappresentazione matriciale del Gruppo puntuale di simmetria C3v (ammoniaca) La prima cosa da fare è scegliere una BASE. Per l ammoniaca sceglieremo gli orbitali s di valenza dell azoto e degli atomi di
CHIMICA: studio della struttura e delle trasformazioni della materia
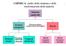 CHIMICA: studio della struttura e delle trasformazioni della materia 1 Materia (materali) Sostanze (omogenee) Processo fisico Miscele Elementi (atomi) Reazioni chimiche Composti (molecole) Miscele omogenee
CHIMICA: studio della struttura e delle trasformazioni della materia 1 Materia (materali) Sostanze (omogenee) Processo fisico Miscele Elementi (atomi) Reazioni chimiche Composti (molecole) Miscele omogenee
Esercitazioni di Meccanica Quantistica I
 Esercitazioni di Meccanica Quantistica I Sistema a due stati Consideriamo come esempio di sistema a due stati l ammoniaca. La struttura del composto è tetraedrico : alla sommità di una piramide con base
Esercitazioni di Meccanica Quantistica I Sistema a due stati Consideriamo come esempio di sistema a due stati l ammoniaca. La struttura del composto è tetraedrico : alla sommità di una piramide con base
Problema n.1 Bilanciare la seguente reazione redox utilizzando il metodo ionico elettronico: I - (aq) + NO 3
 Problema n.1 Bilanciare la seguente reazione redox utilizzando il metodo ionico elettronico: I (aq) + 3 (aq) + + (aq) I 2(s) + (g) + 2 (l). Calcolare i grammi di I 2 (s) che si ottengono se si formano
Problema n.1 Bilanciare la seguente reazione redox utilizzando il metodo ionico elettronico: I (aq) + 3 (aq) + + (aq) I 2(s) + (g) + 2 (l). Calcolare i grammi di I 2 (s) che si ottengono se si formano
Geometria Analitica Domande e Risposte
 Geometria Analitica Domande e Risposte A. Il Piano Cartesiano. Qual è la formula della distanza tra due punti nel piano cartesiano? Per calcolare la formula della distanza tra due punti nel piano cartesiano
Geometria Analitica Domande e Risposte A. Il Piano Cartesiano. Qual è la formula della distanza tra due punti nel piano cartesiano? Per calcolare la formula della distanza tra due punti nel piano cartesiano
La chimica della vita: i composti organici. CARBOIDRATI LIPIDI PROTEINE ACIDI NUCLEICI (DNA, RNA)
 La chimica della vita: i composti organici. CARBOIDRATI LIPIDI PROTEINE ACIDI NUCLEICI (DNA, RNA) IL CARBONIO E un non metallo, appartiene al IV gruppo ed al II periodo. Possiede 4 elettroni esterni per
La chimica della vita: i composti organici. CARBOIDRATI LIPIDI PROTEINE ACIDI NUCLEICI (DNA, RNA) IL CARBONIO E un non metallo, appartiene al IV gruppo ed al II periodo. Possiede 4 elettroni esterni per
Legame covalente Puro Polare Legame dativo o di coordinazione Legame ionico Legame metallico
 I LEGAMI CHIMICI Legami atomici o forti Legami molecolari o deboli Legame covalente Puro Polare Legame dativo o di coordinazione Legame ionico Legame metallico Legame dipolo-dipolo Legame idrogeno Legame
I LEGAMI CHIMICI Legami atomici o forti Legami molecolari o deboli Legame covalente Puro Polare Legame dativo o di coordinazione Legame ionico Legame metallico Legame dipolo-dipolo Legame idrogeno Legame
2 HCl. H 2 + Cl 2 ATOMI E MOLECOLE. Ipotesi di Dalton
 Ipotesi di Dalton ATOMI E MOLECOLE 1.! Un elemento è formato da particelle indivisibili chiamate atomi. 2.! Gli atomi di uno specifico elemento hanno proprietà identiche. 3.! Gli atomi si combinano secondo
Ipotesi di Dalton ATOMI E MOLECOLE 1.! Un elemento è formato da particelle indivisibili chiamate atomi. 2.! Gli atomi di uno specifico elemento hanno proprietà identiche. 3.! Gli atomi si combinano secondo
Le reazioni di ossido-riduzione
 Le reazioni di ossido-riduzione Si dicono reazioni di ossidazione e di riduzione (o ossido-riduzione) quelle reazioni che avvengono con cambiamento del numero di elettroni che una specie chimica coinvolge
Le reazioni di ossido-riduzione Si dicono reazioni di ossidazione e di riduzione (o ossido-riduzione) quelle reazioni che avvengono con cambiamento del numero di elettroni che una specie chimica coinvolge
Argomenti Capitolo 1 Richiami
 Argomenti Capitolo 1 Richiami L insieme dei numeri reali R si rappresenta geometricamente con l insieme dei punti di una retta orientata su cui sia stato fissato un punto 0 e un segmento unitario. L insieme
Argomenti Capitolo 1 Richiami L insieme dei numeri reali R si rappresenta geometricamente con l insieme dei punti di una retta orientata su cui sia stato fissato un punto 0 e un segmento unitario. L insieme
Introduzione alla Simmetria Molecolare
 Scuola di Ingegneria Industriale e dell Informazione Insegnamento di Chimica Generale 083424 - CCS CHI e MAT Introduzione alla Simmetria Molecolare Prof. Dipartimento CMIC Giulio Natta http://iscamap.chem.polimi.it/citterio/it/education/general-chemistry-lessons/
Scuola di Ingegneria Industriale e dell Informazione Insegnamento di Chimica Generale 083424 - CCS CHI e MAT Introduzione alla Simmetria Molecolare Prof. Dipartimento CMIC Giulio Natta http://iscamap.chem.polimi.it/citterio/it/education/general-chemistry-lessons/
CHIMICA ORGANICA = STUDIO DEI COMPOSTI DEL CARBONIO. energia superiore. energia inferiore. orbitale s
 CIMICA ORGANICA = STUDIO DEI COMPOSTI DEL CARBONIO C elemento del secondo periodo della tavola periodica; numero atomico = 6 configurazione elettronica del C 2p 2s 1s energia superiore energia inferiore
CIMICA ORGANICA = STUDIO DEI COMPOSTI DEL CARBONIO C elemento del secondo periodo della tavola periodica; numero atomico = 6 configurazione elettronica del C 2p 2s 1s energia superiore energia inferiore
Riassumiamo le proprietà dei numeri reali da noi utilizzate nel corso di Geometria.
 Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Cos è un trasformazione chimica?
 Chimica Lezione 1 Cos è un trasformazione chimica? Una reazione chimica è una trasformazione della materia che avviene senza variazioni misurabili di massa, in cui uno o più reagenti iniziali modificano
Chimica Lezione 1 Cos è un trasformazione chimica? Una reazione chimica è una trasformazione della materia che avviene senza variazioni misurabili di massa, in cui uno o più reagenti iniziali modificano
0.1 Spazi Euclidei in generale
 0.1. SPAZI EUCLIDEI IN GENERALE 1 0.1 Spazi Euclidei in generale Sia V uno spazio vettoriale definito su R. Diremo, estendendo una definizione data in precedenza, che V è uno spazio vettoriale euclideo
0.1. SPAZI EUCLIDEI IN GENERALE 1 0.1 Spazi Euclidei in generale Sia V uno spazio vettoriale definito su R. Diremo, estendendo una definizione data in precedenza, che V è uno spazio vettoriale euclideo
ax 1 + bx 2 + c = 0, r : 2x 1 3x 2 + 1 = 0.
 . Rette in R ; circonferenze. In questo paragrafo studiamo le rette e le circonferenze in R. Ci sono due modi per descrivere una retta in R : mediante una equazione cartesiana oppure mediante una equazione
. Rette in R ; circonferenze. In questo paragrafo studiamo le rette e le circonferenze in R. Ci sono due modi per descrivere una retta in R : mediante una equazione cartesiana oppure mediante una equazione
Prodotto scalare e ortogonalità
 Prodotto scalare e ortogonalità 12 Novembre 1 Il prodotto scalare 1.1 Definizione Possiamo estendere la definizione di prodotto scalare, già data per i vettori del piano, ai vettori dello spazio. Siano
Prodotto scalare e ortogonalità 12 Novembre 1 Il prodotto scalare 1.1 Definizione Possiamo estendere la definizione di prodotto scalare, già data per i vettori del piano, ai vettori dello spazio. Siano
La struttura di Lewis
 La struttura di Lewis Scritto dal Prof. Lombardo Per disegnare la struttura delle molecole uno dei sistemi che preferisco è il metodo di Lewis. Spesso però vedo che gli studenti hanno notevoli difficoltà,
La struttura di Lewis Scritto dal Prof. Lombardo Per disegnare la struttura delle molecole uno dei sistemi che preferisco è il metodo di Lewis. Spesso però vedo che gli studenti hanno notevoli difficoltà,
ATOMO. Legge della conservazione della massa Legge delle proporzioni definite Dalton
 Democrito IV secolo A.C. ATOMO Lavoisier Proust Legge della conservazione della massa Legge delle proporzioni definite Dalton (808) Teoria atomica Gay-Lussac volumi di gas reagiscono secondo rapporti interi
Democrito IV secolo A.C. ATOMO Lavoisier Proust Legge della conservazione della massa Legge delle proporzioni definite Dalton (808) Teoria atomica Gay-Lussac volumi di gas reagiscono secondo rapporti interi
Parte 12b. Riduzione a forma canonica
 Parte 2b. Riduzione a forma canonica A. Savo Appunti del Corso di Geometria 202-3 Indice delle sezioni. Coniche, 2. Esempio di riduzione, 4 3. Teoremi fondamentali, 6 4. Come determinare l equazione canonica,
Parte 2b. Riduzione a forma canonica A. Savo Appunti del Corso di Geometria 202-3 Indice delle sezioni. Coniche, 2. Esempio di riduzione, 4 3. Teoremi fondamentali, 6 4. Come determinare l equazione canonica,
Prodotto scalare e prodotto vettoriale. Elisabetta Colombo
 Corso di Approfondimenti di Matematica Biotecnologie, Anno Accademico 2010-2011, http://users.mat.unimi.it/users/colombo/programmabio.html Vettori Vettori 1 2 3 4 di di Ricordiamo il in R n Dati a = (a
Corso di Approfondimenti di Matematica Biotecnologie, Anno Accademico 2010-2011, http://users.mat.unimi.it/users/colombo/programmabio.html Vettori Vettori 1 2 3 4 di di Ricordiamo il in R n Dati a = (a
ATOMI E MOLECOLE. Tutte le varie forme di materia esistenti sono costituite da sostanze semplici (elementi) e da sostanze composte (composti).
 1 ATOMI E MOLECOLE Tutte le varie forme di materia esistenti sono costituite da sostanze semplici (elementi) e da sostanze composte (composti). Un elemento (es. il mercurio) è una sostanza che non può
1 ATOMI E MOLECOLE Tutte le varie forme di materia esistenti sono costituite da sostanze semplici (elementi) e da sostanze composte (composti). Un elemento (es. il mercurio) è una sostanza che non può
Lezione 6 Richiami di Geometria Analitica
 1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
Francesco Zumbo
 La retta - Teorema di Talete - Equazione della retta: passante per due punti, implicita, esplicita - Parallele e Perpendicolari - Fascio Propio e improprio - Intersezione tra rette Francesco Zumbo www.francescozumbo.it
La retta - Teorema di Talete - Equazione della retta: passante per due punti, implicita, esplicita - Parallele e Perpendicolari - Fascio Propio e improprio - Intersezione tra rette Francesco Zumbo www.francescozumbo.it
I NUMERI QUANTICI. per l = orbitale: s p d f
 I NUMERI QUANTICI I numeri quantici sono quattro. I primi tre servono a indicare e a distinguere i diversi orbitali. Il quarto numero descrive una proprietà tipica dell elettrone. Esaminiamo in dettaglio
I NUMERI QUANTICI I numeri quantici sono quattro. I primi tre servono a indicare e a distinguere i diversi orbitali. Il quarto numero descrive una proprietà tipica dell elettrone. Esaminiamo in dettaglio
Fasci di Coniche. Salvino Giuffrida. 2. Determinare e studiare il fascio Φ delle coniche che passano per A (1, 0) con tangente
 1 Fasci di Coniche Salvino Giuffrida 1. Determinare e studiare il fascio Φ delle coniche che passano per O = (0, 0), con tangente l asse y, e per i punti (1, 0), (1, ). Determinare vertice e asse della
1 Fasci di Coniche Salvino Giuffrida 1. Determinare e studiare il fascio Φ delle coniche che passano per O = (0, 0), con tangente l asse y, e per i punti (1, 0), (1, ). Determinare vertice e asse della
La teoria atomica moderna: il modello planetario L ELETTRONE SI MUOVE LUNGO UN ORBITA INTORNO AL NUCLEO
 La teoria atomica moderna: il modello planetario L ELETTRONE SI MUOVE LUNGO UN ORBITA INTORNO AL NUCLEO La luce La LUCE è una forma di energia detta radiazione elettromagnetica che si propaga nello spazio
La teoria atomica moderna: il modello planetario L ELETTRONE SI MUOVE LUNGO UN ORBITA INTORNO AL NUCLEO La luce La LUCE è una forma di energia detta radiazione elettromagnetica che si propaga nello spazio
SEMICONDUTTORI BANDE DI ENERGIA
 SEMICONDUTTORI BANDE DI ENERGIA Si dice banda di energia un insieme di livelli energetici posseduti dagli elettroni. Si dice banda di valenza l'insieme degli elettroni che hanno un livello energetico basso,
SEMICONDUTTORI BANDE DI ENERGIA Si dice banda di energia un insieme di livelli energetici posseduti dagli elettroni. Si dice banda di valenza l'insieme degli elettroni che hanno un livello energetico basso,
1.1 Coordinate sulla retta e nel piano; rette nel piano
 1 Sistemi lineari 11 Coordinate sulla retta e nel piano; rette nel piano Coordinate sulla retta Scelti su una retta un primo punto O (origine) ed un diverso secondo punto U (unita ), l identificazione
1 Sistemi lineari 11 Coordinate sulla retta e nel piano; rette nel piano Coordinate sulla retta Scelti su una retta un primo punto O (origine) ed un diverso secondo punto U (unita ), l identificazione
Condizione di allineamento di tre punti
 LA RETTA L equazione lineare in x e y L equazione: 0 con,,, e non contemporaneamente nulli, si dice equazione lineare nelle due variabili e. Ogni coppia ; tale che: 0 si dice soluzione dell equazione.
LA RETTA L equazione lineare in x e y L equazione: 0 con,,, e non contemporaneamente nulli, si dice equazione lineare nelle due variabili e. Ogni coppia ; tale che: 0 si dice soluzione dell equazione.
NUMERI COMPLESSI Esercizi svolti. d) (1 i) 3. b) (1 + i)(1 i)(1 + 3 i) c) 1 i 1
 Calcolare le seguenti potenze di i: NUMERI COMPLESSI Esercizi svolti a) i b) i 7 c) i d) i e) i f) i 9 Semplificare le seguenti espressioni: a) i) i i) b) + i) i) + ) 0 i c) i) i) i) d) i) Verificare che
Calcolare le seguenti potenze di i: NUMERI COMPLESSI Esercizi svolti a) i b) i 7 c) i d) i e) i f) i 9 Semplificare le seguenti espressioni: a) i) i i) b) + i) i) + ) 0 i c) i) i) i) d) i) Verificare che
Coordiante omogenee e proiezioni
 CAPITOLO 15 Coordiante omogenee e proiezioni Esercizio 15.1. Utilizzando le coordinate omogenee, determinare l equazione della retta r passante per i punti A(2,) e B( 1,0) e della retta s passante per
CAPITOLO 15 Coordiante omogenee e proiezioni Esercizio 15.1. Utilizzando le coordinate omogenee, determinare l equazione della retta r passante per i punti A(2,) e B( 1,0) e della retta s passante per
Problemi con discussione grafica
 Problemi con discussione grafica Un problema con discussione grafica consiste nel determinare le intersezioni tra un fascio di rette (proprio o improprio) e una particolare funzione che viene assegnata
Problemi con discussione grafica Un problema con discussione grafica consiste nel determinare le intersezioni tra un fascio di rette (proprio o improprio) e una particolare funzione che viene assegnata
I LEGAMI CHIMICI. Configurazione elettronica stabile: è quella in cui tutti i livelli energetici dell atomo sono pieni di elettroni
 I LEGAMI CIMICI In natura sono pochi gli elementi che presentano atomi allo stato libero. Gli unici elementi che sono costituiti da atomi isolati si chiamano gas nobili o inerti, formano il gruppo VIII
I LEGAMI CIMICI In natura sono pochi gli elementi che presentano atomi allo stato libero. Gli unici elementi che sono costituiti da atomi isolati si chiamano gas nobili o inerti, formano il gruppo VIII
TEORIA DEL LEGAME DI VALENZA (VB) e GEOMETRIA MOLECOLARE (teoria VSEPR)
 TEORIA DEL LEGAME DI VALENZA (VB) e GEOMETRIA MOLECOLARE (teoria VSEPR) Metodi basati sulla meccanica quantistica: VB e MO La descrizione più corretta e quantitativa della struttura elettronica delle molecole,
TEORIA DEL LEGAME DI VALENZA (VB) e GEOMETRIA MOLECOLARE (teoria VSEPR) Metodi basati sulla meccanica quantistica: VB e MO La descrizione più corretta e quantitativa della struttura elettronica delle molecole,
Le derivate parziali
 Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
Dipendenza e indipendenza lineare
 Dipendenza e indipendenza lineare Luciano Battaia Questi appunti () ad uso degli studenti del corso di Matematica (A-La) del corso di laurea in Commercio Estero dell Università Ca Foscari di Venezia campus
Dipendenza e indipendenza lineare Luciano Battaia Questi appunti () ad uso degli studenti del corso di Matematica (A-La) del corso di laurea in Commercio Estero dell Università Ca Foscari di Venezia campus
Soluzioni dello scritto di Analisi Matematica II - 10/07/09. C.L. in Matematica e Matematica per le Applicazioni
 Soluzioni dello scritto di Analisi Matematica II - /7/9 C.L. in Matematica e Matematica per le Applicazioni Proff. K. Payne, C. Tarsi, M. Calanchi Esercizio. a La funzione f è limitata e essendo lim fx
Soluzioni dello scritto di Analisi Matematica II - /7/9 C.L. in Matematica e Matematica per le Applicazioni Proff. K. Payne, C. Tarsi, M. Calanchi Esercizio. a La funzione f è limitata e essendo lim fx
Sviluppi e derivate delle funzioni elementari
 Sviluppi e derivate delle funzioni elementari In queste pagine dimostriamo gli sviluppi del prim ordine e le formule di derivazioni delle principali funzioni elementari. Utilizzeremo le uguaglianze lim
Sviluppi e derivate delle funzioni elementari In queste pagine dimostriamo gli sviluppi del prim ordine e le formule di derivazioni delle principali funzioni elementari. Utilizzeremo le uguaglianze lim
METODO DEI MINIMI QUADRATI
 METODO DEI MINIMI QUADRATI Torniamo al problema della crescita della radice di mais in funzione del contenuto di saccarosio nel terreno di coltura. Ripetendo varie volte l esperimento con diverse quantità
METODO DEI MINIMI QUADRATI Torniamo al problema della crescita della radice di mais in funzione del contenuto di saccarosio nel terreno di coltura. Ripetendo varie volte l esperimento con diverse quantità
Dispense CHIMICA GENERALE E ORGANICA (STAL) 2012/13 Prof. P. Carloni GLI ATOMI
 GLI ATOMI L'atomo e le particelle che lo compongono, il nucleo e gli elettroni, numero atomico e numero di massa, isotopi, la struttura dell'atomo, gli orbitali s, p e d, la configurazione fondamentale
GLI ATOMI L'atomo e le particelle che lo compongono, il nucleo e gli elettroni, numero atomico e numero di massa, isotopi, la struttura dell'atomo, gli orbitali s, p e d, la configurazione fondamentale
Precorso di Matematica
 Precorso di Matematica Lezione 3 Andrea Susa OPERATORE DI PRODOTTO Π 2 1 Operatore di prodotto Π Consideriamo un insieme numerico ={ =1, }. Definiamo prodotto degli elementi in, = Esempio: ={ =1, =2, =3,
Precorso di Matematica Lezione 3 Andrea Susa OPERATORE DI PRODOTTO Π 2 1 Operatore di prodotto Π Consideriamo un insieme numerico ={ =1, }. Definiamo prodotto degli elementi in, = Esempio: ={ =1, =2, =3,
Geometria BATR-BCVR Esercizi 9
 Geometria BATR-BCVR 2015-16 Esercizi 9 Esercizio 1. Per ognuna delle matrici A i si trovi una matrice ortogonale M i tale che Mi ta im sia diagonale. ( ) 1 1 2 3 2 A 1 = A 2 1 2 = 1 1 0 2 0 1 Esercizio
Geometria BATR-BCVR 2015-16 Esercizi 9 Esercizio 1. Per ognuna delle matrici A i si trovi una matrice ortogonale M i tale che Mi ta im sia diagonale. ( ) 1 1 2 3 2 A 1 = A 2 1 2 = 1 1 0 2 0 1 Esercizio
Lezione 7: Il Teorema di Rouché-Capelli
 Lezione 7: Il Teorema di Rouché-Capelli In questa lezione vogliamo rivisitare i sistemi lineari e dare alcuni risultati che ci permettono di determinare dato un sistema lineare se ammette soluzioni e da
Lezione 7: Il Teorema di Rouché-Capelli In questa lezione vogliamo rivisitare i sistemi lineari e dare alcuni risultati che ci permettono di determinare dato un sistema lineare se ammette soluzioni e da
EQUAZIONI CARTESIANE DELLA CIRCONFERENZA
 EQUAZIONI CARTESIANE DELLA CIRCONFERENZA G. MEZZETTI Definizione. Siano dati un punto C e un numero r R, r 0; si dice circonferenza di centro C e raggio r l insieme di quei punti del piano la cui distanza
EQUAZIONI CARTESIANE DELLA CIRCONFERENZA G. MEZZETTI Definizione. Siano dati un punto C e un numero r R, r 0; si dice circonferenza di centro C e raggio r l insieme di quei punti del piano la cui distanza
