Legge dei grandi numeri e Teorema Centrale Limite
|
|
|
- Bernardo Grillo
- 5 anni fa
- Visualizzazioni
Transcript
1 Legge dei gradi umeri e Teorema Cetrale Limite 5 maggio 017 Discutiamo due teoremi fodametali per raccordare probabilitá e statistica: la legge dei gradi umeri e il Teorema Cetrale Limite (TCL, ache detto Teorema del limite cetrale). La legge dei gradi umeri ci dice che la media aritmetica di u campioe di variabili aleatorie (VA) X i, idipedeti e ideticamete distribuite, ovvero 1 X i per crescete tede o coverge al valore atteso teorico µ (cfr. Figura 1). Ma come si distribuiscoo per crescete le deviazioi / fluttuazioi di 1 X i rispetto a µ? Il TCL asserisce che tali fluttuazioi obbediscoo ad ua legge Gaussiaa, oostate le distribuzioi delle sigole variabili possao essere del tutto geeriche (i forma semplice: la somma di u umero sufficietemete grade di variabili é gaussiaa). George Pola itrodusse per primo l espressioe Teorema Cetrale Limite riteedo il TCL u teorema cetrale per il calcolo delle probabilitá. Per otteere questi due risultati fodametali, discutiamo prima alcui aspetti (valore atteso, variaza e fuzioi geeratrici dei mometi) relativi alla somma di VA idipedeti. Figura 1: La figura mostra le traiettorie otteute co diverse realizzazioi della VA 1 X i per crescete: tutte covergoo al valore atteso teorico µ (liea rossa). La distribuzioe delle deviazioi 1 X i µ segue ua legge Gaussiaa 1 Distribuzioi cogiute e margiali Cosideriamo due variabili aleatorie discrete X e Y. Siamo iteressati all eveto cogiuto {X } {Y } e alla probabilitá di tale eveto o probabilitá cogiuta P XY ({X } {Y }) P XY (X, Y ) p XY (, )
2 legge dei gradi umeri e teorema cetrale limite Nel caso discreto la cogiuta si puo scrivere i forma tabellare. U esempio di p. cogiuta di due VA che possoo assumere valori é riportato i Figura. X {0, 1, }, Y {0, 1} Figura : La distribuzioe cogiuta P XY ({X } {Y }) scritta esplicitamete i forma tabellare. Nell ultima coloa a destra e ell ultima riga i basso (i margii) soo riportati i valori otteuti sommado su ciascua coloa fissata la riga i, P Y (Y i) p (, i), e su ciascua riga fissata la coloa j, P X (X j) p ( j, ). P X e P Y rappresetao le distribuzioi di probabilitá margiali. Dalla probabilitá cogiuta possiamo iferire la probabilitá di qualsiasi eveto di iteresse che riguarda le VA X, Y. Ad esempio, P XY (X + Y > 1) P XY (1, 1) + P XY (, 1) + P XY (, 0) Per distribuzioi discrete é utile talvolta semplificare la otazioe: P XY ({X i} {Y j}) p XY (i, j) p i,j Notiamo che la cogiuta é ormalizzata, i,j p i,j i j p i,j 1. Nella tabella riportata i Figura abbiamo ache riportato, a margie, i valori otteuti sommado su ciascua coloa fissata la riga i, P Y (Y i) p (, i), e su ciascua riga fissata la coloa j, P X (X j) p ( j, ). L isieme dei valori P X (X j) e P Y (Y i) defiiscoo rispettivamete le probabilitá margiali di X e Y: P X () p XY (, ) P Y () p XY (, ) Si oti che P X e P Y soo ormalizzate, P X () 1, P Y () 1.
3 legge dei gradi umeri e teorema cetrale limite 3 I cocetti itrodotti soo ovviamete geeralizzabili a VA cotiue. Se X e Y soo VA (cotiue o discrete) la fizioe di ripartizioe cogiuta é defiita come F XY (, ) P XY (X, Y ) e per essa valgoo tutte le proprietá defiite per le fuzioi di ripartizioe di ua sigola variabile aleatoria. Nel caso cotiuo, F XY (, ) é (assolutamete) cotiua se esiste la fuzioe desitá di probabilitá cogiuta f XY (, ) (o egativa e itegrabile) tale che F XY (, ) dove f XY(, )dd 1 e f XY (, )dd Figura 3: U eveto cotiuo A {(, ) a X b, c Y d} f XY (, ) ( (F XY(, ))) F XY (, ) I altri termii la probabilitá cogiuta el caso cotiuo é defiita come prob(, A) P(a X b, c Y d) b d a c f XY (, )dd Figura 4: Le figure a), b) e c) soo tre possibili rappresetazioi grafiche di ua geerica desitá cogiuta prob(, ): a) la rappreseta come u volume sul supporto bidimesioale, ; b) come ua mappa a livelli; c) come ua mappa dove il colore é il valore di probabilitá assuto i ciascu puto (, ) (il ero idica probabilitá ulla). La figura d) mostra le due distribuzioi margiali di, rispetto alla cogiuta otteute accumulado i valori della cogiuta sull asse e sull asse. Ioltre: f X () f (, )d
4 legge dei gradi umeri e teorema cetrale limite 4 sará la desitá margiale rispetto a X, e f Y () f (, )d la desitá margiale rispetto a Y. Ua rappresetazioe grafica di cogiute e margiali el caso cotiuo é riportato i Figura 4. Si oti che la fuzioe di ripartizioe margiale F X () é per defiizioe P X (X ). Esplicitamete, el caso cotiuo: F X () P X (X ) F XY (, + ) [ + Esempio 1.1 Sia data la desitá cogiuta cotiua: 6e 3 per > 0, > 0 f XY (, ) 0 altrimeti Calcolare P XY (1, 3): P XY (1, 3) 3 3 [ 1 6 e d e 3 d 6 1 e (e e 4 )(e 6 e 9 ) Calcolare la desitá margiale f X : f X () 0 f XY (, )d 6e 1 3 [e 3 ] e (1 0) e Calcolare la CDF cogiuta: Ripetedo i calcoli precedeti si ottiee F XY (, ) 1.1 Probabilitá codizioata ] f X,Y (u, v)dv du f X (u)du 6e 3 dd ] 1 [ ] 1 3 e 3 3 6e 3 d 6e e 3 d 6e u 3v dudv (1 e )(1 e 3 ) Nel caso discreto, osservato u valore di Y, e data la distribuzioe cogiuta P XY (X, Y) é possibile defiire la probabiitá codizioata di X Y ello stesso modo i cui avevamo defiito la probabilitá codizioata di eveti: P X Y (X Y ) P XY(X, Y ) P Y (Y ) dove P Y (Y ) > 0 ed é ricavabile per margializzazioe da P XY (X, Y). 0
5 legge dei gradi umeri e teorema cetrale limite 5 Esempio 1. Cosiderado l esempio iiziale di Figura, possiamo calcolare P X Y (X Y 1) P X Y (X 0 Y 1) P XY(X0,Y1) 0. P Y (Y1) P X Y (X 1 Y 1) P XY(X1,Y1) 0. P Y (Y1) P X Y (X Y 1) P XY(X,Y1) 0 P Y (Y1) Nel caso cotiuo la desitá codizioata é defiita come: I termii di CDF: f X Y ( ) f XY(, ) f Y () Figura 5: Probabilitá codizioata calcolata ell Esempio 1. (la liea rossa serve solo a guidare l occhio) F X Y ( ) f XY(u, )du f XY(u, )du Figura 6: Rappresetazioe grafica della desitá codizioata prob(x Y ): questa é iterpretabile come il profilo che si ottiee tagliado la desitá cogiuta i Y Se X e Y soo idipedeti valgoo le segueti P XY (, ) P X ()P Y () f XY (, ) f X () f Y () I geerale (ei casi discreto e cotiuo): F XY (, ) F X ()F Y () Piú precisamete si dice che X e Y soo statisticamete o margialmete idipedeti. U caso immediato é giá stato visto alla fie dell Esempio 1.1 dove F XY (, ) (1 e )(1 e 3 )
6 legge dei gradi umeri e teorema cetrale limite 6 Si puó facilmete verificare che F X () (1 e ) e F Y () (1 e 3 ), pertato F XY (, ) F X ()F Y (). Nell esempio, duque X e Y soo idipedeti, ed é il motivo per cui l itegrazioe doppia risulta agevole essedo separabile su e. Riportiamo ifie, i Figura 7 u esempio otevole: la distribuzioe Normale bivariata che si puó scrivere come f (, ) [ 1 1 πσ σ 1 ρ e (1 ρ ) ( µ σ ) ( ρ ( µ)( µ σσ ) ( µ ) ] dove ρ cov(x,y) σ σ é il coefficiete di correlazioe fra le variabili X e Y che vedremo piú avati. Quado ρ 0 allora X e Y soo idipedeti e la Normale bivariata é semplicemete il prodotto N ( µ, σ )N ( µ, σ ) delle due Normali uivariate. Tuttavia, ache el caso piú geerale di ρ 0 margiali e codizioate soo sempre distribuzioi Normali. σ Figura 7: U caso otevole: per ua distribuzioe Normale bidimesioale, margiali e codizioate soo acora distribuzioi Normali (uidimesioali) Valore atteso e variaza Affrotiamo il problema di calcolare valore atteso e variaza per distribuzioi cogiute di VA X e Y. Per brevitá otazioale cosidereremo il caso cotiuo, ma i risultati soo estedibili immediatamete al caso discreto. Data la desitá cogiuta f XY (, ), il suo valore atteso é: µ E[X] f XY (, )dd d f XY (, )d f X ()d dove si é usata la defiizioe di desitá margiale di Y. Aalogamete
7 legge dei gradi umeri e teorema cetrale limite 7 µ E[Y] f Y ()d I geerale, se abbiamo ua variabile aleatoria Z g(x, Y) fuzioe di X e di Y, di desitá cogiuta f XY, avremo che: µ z E[Z] g(, ) f XY (, )dd Noti i valori di aspettazioe µ e µ, le rispettive variaze soo var(x) ( µ ) f XY (, )dd ( µ ) f X ()d Aalogamete: var(y) ( µ ) f Y ()d 3 Valore atteso e variaza della somma di variabili aleatorie Date due VA X, Y, cosideriamo la VA somma Z X + Y e calcoliamoe il valore atteso rispetto alla desitá cogiuta f (, ): E[Z] E[X + Y] f (, )dd + f X ()d + ( + ) f (, )dd f ()d f (, )dd E[X] + E[Y] (1) I geerale per VA X 1, X, X vale la seguete: E[ X i ] E[X i ] () Date due VA X, Y, idipedeti, cosideriamo la VA prodotto allora vale la seguete: Z XY E[Z] E[XY] E[X]E[Y] (3)
8 legge dei gradi umeri e teorema cetrale limite 8 Ifatti: E[Z] E[XY] f X ()d f (, )dd f Y ()d E[X]E[Y] (4) dove si é fatto uso dell ipotesi di idipedeza per fattorizzare la cogiuta, f (, ) f X () f Y (). Date due VA X, Y, questa volta idipedeti, cosideriamo di uovo la VA somma Z X + Y e calcoliamoe la variaza: var(z) var[x + Y] E[(X + Y) ] E[(X + Y)] E[X + Y + XY] (E[X] + E[Y]) E[X ] + E[Y ] + E[XY] E[X] E[Y)] E[X]E[Y] E[X ] + E[Y ] + E[X]E[Y] E[X] E[Y)] E[X]E[Y] var(x) + var(y) (5) I geerale per VA X 1, X, X idipedeti vale la seguete: var( 4 Legge dei gradi umeri X i ) var(x i ) (6) Sulla base delle proprietá fi qui dimostrate possiamo ora euciare e dimostrare la legge dei gradi umeri (i forma debole) Teorema 4.1 Sia X ua VA tale che E[X] µ var(x) σ. Siao X 1, X, X VA idipedeti e ideticamete distribuite (i.i.d.) come X X i X, i, i modo che il loro isieme costituisca u campioe aleatorio di taglia della VA X. Sia S X 1 + X + + X X i la variabile aleatoria somma e S 1 X i
9 legge dei gradi umeri e teorema cetrale limite 9 la media aritmetica del campioe. Allora vale la seguete: lim P( S µ ɛ) 0 ɛ > 0 (7) ovvero S coverge i probabilitá al valore atteso teorico µ: S P µ Dimostrazioe Il teorema si dimostra applicado la diseguagliaza di Chebchev che, poedo ɛ k var(x), riscriviamo el seguete modo Usado S P( X E[X] k var(x)) 1 k P( X E[X] ɛ) var(x) ɛ (8) al posto della geerica X P( S [ E S ] ɛ) var( S ) ɛ (9) Utilizzado le proprietá di valore atteso e variaza della somma di VA iidipedeti, e le ipotesi che esse abbiao la stessa distribuzioe (ideticamete distribuite), per cui E[X i ] µ, var(x i ) σ E [ S ] E [ 1 X i ] 1 var ( S ) var ( 1 X i ) E [X i ] 1 µ µ µ 1 var (X i ) 1 σ σ σ Sostituedo i Eq.(9) e prededo il limite per lim P( S σ µ ɛ) lim ɛ 0 (10) I coclusioe la legge dei gradi umeri ci assicura che la media aritmetica S coverge i probabilitá al valore atteso teorico µ. La S e ua VA. Qual é la legge di probabilitá che ci descrive la sua distribuzioe, ovvero le sue fluttuazioi metre sta covergedo a µ? Il Teorema Cetrale Limite ci dice che tale distribuzioe é la Gaussiaa, idipedetemete dalle distribuzioi utilizzate per geerare le X i (purché abbiao media e variaza fiite!). Per dimostrare questa proprietá ci serve prima defiire uo strumeto geerale e uivoco per caratterizzare la distribuzioe di ua VA. Tale strumeto é la fuzioe geeratrice dei mometi.
10 legge dei gradi umeri e teorema cetrale limite 10 5 Fuzioe Geeratrice dei Mometi (f.g.m) f.g.m. ϕ X (u) E[e ux ] e u p X () se X discreta, e u f X () d se X cotiua. (11) Sviluppiamo ora questa fuzioe utilizzado McLauri: ϕ X (u) E[e ux ] E[1 + u X + u X + ] E[1] + u E[X] + u E[X ] + + i0 E[X i ] i! u i (1) Derivado i volte questa fuzioe é possibile ricavare il mometo i-esimo: E[X i ] di du i ϕ X(u) (13) u0 E possibile verificare subito tale proprietá per media e variaza sfruttado la liearitá del valore atteso d du ϕ X(u) u0 d du E[euX ] u0 E[ d du eux u0 ] E[Xe ux u0 ] E[X]; aalogamete d du ϕ X(u) u0 d du E[euX ] u0 E[ d du eux u0 ] E[X e ux u0 ] E[X ]; 5.1 Distribuzioe della V.A. somma di due V.A. idipedeti Che distribuzioe ha la VA che si defiisce come somma di due V.A. idipedeti? Lemma 5.1 Siao X, Y V.A. idipedeti e sia Z X + Y. Vale la seguete: ϕ Z (u) ϕ X () ϕ Y () (14) Dimostrazioe Utilizzado la proprietá di fattorizzazioe di E[] per il prodotto di VA idipedeti: ϕ Z (u) E[e u(x+y) ] E[e ux e uy ] E[e ux ] E[e uy ] ϕ X (u) ϕ Y (u). (15)
11 legge dei gradi umeri e teorema cetrale limite 11 Geeralizzado, su realizzazioi idipedeti X 1, X,, X dove ciascua X i é campioata dalla stessa distribuzioe, e Z é la V.A somma Z S S X 1 + X + + X X i ϕ S (u) ϕ X i (u) E[e u( X i) ] [ ϕ Xi (u) ] (16) Esempio 5. (f.g.m della Biomiale) La f.g.m. della distribuzioe Biomiale si puó calcolare facilmete, ricordado che la Biomiale si ottiee come la somma X 1, X,, X dei risultati di realizzazioi idipedeti X 1, X,, X di ua V.A. Beroulliaa, (per esempio, laci di moeta) cioé dove ogi X i é distribuita co legge beroulliaa: X i Ber(p). Calcoliamo quidi la f.g.m. della Beroulli ϕ Ber (u) E Ber [e ux ] e u 1 p X () e u p q 1 0 e u0 p 0 q e u1 p 1 q 1 1 q + e u p La Biomiale coteggia gli eveti di iteresse X i Ber(p) co i 1,, e X i {0, 1}, dove S X 1 + X + + X X i k (X i 1 i caso di successo, altrimeti X i 0) Facedo uso della f.g.m. della Beroulli, e applicado l equazioe (16) la f.g.m. della Biomiale é ϕ X Bi(,p) (u) [ ϕ Xi Ber(p)(u)] [q + p e u ] (17) Dopo aver calcolato la f.g.m. della distribuzioe Biomiale, verifichiamo per esercizio come il calcolo del mometo di ordie 1 (valor medio) mediate la derivata prima dϕ X Bi(,p) (u) du u0, corrispoda a E Bi [X] p: E Bi [X] d du ϕ X Bi(,p)(u) u0 d du (q + p eu ) (q + p e u ) 1 p e u u0 u0 (q + p) 1 p 1 1 p p. (18)
12 legge dei gradi umeri e teorema cetrale limite 1 Esempio 5.3 (f.g.m. della Normale Stadard) Calcoliamo ora la f.g.m. della distribuzioe Normale Stadard N(0, 1)che ci servirá per dimostrare il Teorema Cetrale Limite: ϕ X N(0,1) (u) π e u e 1 d 1 π e u e 1 ( u) d + e u 1 π e 1 ( u) d (19) e u. 6 Teorema Cetrale Limite Come giá aticipato il Teorema Cetrale Limite (TCL) ci dice che la distribuzioe che descrive le deviazioi (fluttuazioi) delle somma di variabili aleatorie rispetto al valore atteso teorico é la distribuzioe Gaussiaa, idipedetemete dalle distribuzioi utilizzate per geerare le X i, purché tali distribuzioi abbiao media e variaza fiite. Le ipotesi del TCL soo le stesse assute el caso della legge dei gradi umeri Teorema 6.1 (TCL) Siao X 1, X,, X V.A. idipedeti e ideticamete distribuite (i.i.d), siao µ < e σ < la media e la variaza di ciascua V.A., sia S X i, siao a, b valori reali co a < b. Allora vale la seguete: lim P(a S µ + σ b) ( ) lim P(a + σ S µ b) 1 π b a φ(b) φ(a). e 1 d (0) Dimostrazioe La dimostrazioe si riduce a verificare che la fuzioe geeratrice della VA stadardizzata Z S E[ S var( S ) ] S µ σ é la f.g.m della Gaussiaa stadard ϕ N(0,1) (u) e u. Riscriviamo la Z come
13 legge dei gradi umeri e teorema cetrale limite 13 Z S µ σ X 1 µ σ + X µ σ + + X µ σ 1 j1 t j dove t j X j µ σ soo stadard co distribuzioe N(0, 1). La f.g.m. di Z é, per la proprietá della f.g.m. della somma di VA, ϕ Z (u) ϕ 1 j1 t j (u) ϕ j1 t j ( u ) j1 ( ) [ ( )] u u ϕ tj ϕ tj La f.g.m. delle t j, sviluppado i serie l espoeziale, co E[t j ] 0, E[t j ] 1 giacché stadard, vale ( ) ( ) u ϕ tj 1 + u t E[t j ] + u E[t j ] u + o j Pertato ϕ Z (u) [ 1 + u + o ( t j )] Prededo il logaritmo a destra e siistra log ϕ Z (u) log [ 1 + u + o ( )] t j Poiamo ( ) t u + o j e riscriviamo log ϕ Z (u) di cui vogliamo calcolare il limite: log (1 + ). lim log ϕ log (1 + ) Z (u) lim. Notiamo che per come é stata defiita, [ lim lim u + o ( )] t j 0, e che per 0 (ovvero per ) possiamo applicare il limite otevole log (1 + ) lim 1. 0
14 legge dei gradi umeri e teorema cetrale limite 14 Ioltre, Ifie ( ) t lim lim u + lim o j u + 0. lim log ϕ Z (u) u, che, ritorado i forma espoeziale, si scrive lim ϕ Z (u) e u. Abbiamo cosí dimostrato che la f.g.m. della ostra V.A. Z el limite corrispode alla f.g.m. di ua distribuzioe Normale, duque la Z é distribuita co legge Normale, N(0, 1). La tesi del teorema segue immediatamete. Il TCL o é solo u fodametale risultato teorico ma ha ache rilevaza per la pratica sperimetale. Molto spesso ua VA puó essere pesata come il risultato fiale degli effetti di molte variabili cocomitati che cotribuiscoo a determiare il valore della variabile cosiderata. Ad esempio, l?altezza di u idividuo é determiata da molti fattori: geetici, alimetari, ambietali. Possiamo descrivere la fluttuazioe dell?altezza idividuale rispetto al valore medio della popolazioe come dovuta ad ua somma di cotributi dovuti a ciascua di queste variabili. Il gra umero di fattori che ifluezao il valore dell?altezza ci porta ad assumere che l?altezza sia distribuita ella popolazioe secodo legge Gaussiaa. I geerale, il TCL é uo strumeto estremamete potete, che cosete per esempio di affrotare lo studio della precisioe di misure sperimetali. Vediamo ifie u semplice esempio di applicazioe pratica del TCL. Esempio 6. U vostro amico asserisce di aver otteuto ua media di 3.5 puti per lacio su 1000 laci di u dado o truccato. Qual é la probabilitá che stia metedo? Soluzioe. Sia X i la VA che deota l esito dell i-simo lacio di dado. Sappiamo che le VA X 1, X,, X 1000 soo idipedeti e ideticamete distribuite co distribuzioe uiforme sull isieme di iteri {1,,, 6} da cui é facile ricavare il valore atteso e la deviazioe stadard E[X i ] 3.5 σ Xi E[Xi ] E[X i]
15 legge dei gradi umeri e teorema cetrale limite 15 I breve, il Teorema Cetrale Limite ci dice che per u umero grade ( ) di V.A. idipedeti e ideticamete distribuite di valore atteso µ e deviazioe stadard σ vale ( ) lim P S µ σ Φ() (1) dove S X i. Nella fattispecie 1000 e S é il umero di puti totalizzati i 1000 laci. Sotto tali ipotesi, la probabilitá che il vostro amico affermi il vero si riduce a calcolare la probabilitá defiita el TCL riscritta come P ( S µ σ ) Φ() () dove S 3.5 X é la media campioaria del campioe di taglia 1000 dichiarata dal vostro amico. I buoa sostaza il TCL. il teorema garatisce che la variabile ridotta Z X µ σ/ sia ua variabile aleatoria la cui fuzioe di distribuzioe tede alla distribuzioe ormale stadard Φ. Pertato, X µ σ/ / La probabilitá che il vostro amico dichiari il vero é duque pari a Φ( 4.69) Ache seza cosultare le tabelle e teedo presete che per la ormale stadard σ 1 e duque z zσ, sigifica che stiamo valutado la probabilitá di u valore di media dichiarata che é di 4.69 deviazioi stadard al di sotto della media µ 3.5. Cosiderado la legge 3σ, é immediatamete evidete che la probabilitá Φ( 4.69) é molto bassa e pertato la probabilitá che che il vostro amico dica il falso molto elevata (1 Φ( 4.69)). Se poi, per scrupolo, si cosultasse la tabella della ormale ridotta, si leggerebbe che Φ( 4.69)
Esercizi di Probabilità e Statistica
 Esercizi di Probabilità e Statistica Samuel Rota Bulò 24 maggio 26 Desità e distribuzioi cogiute e codizioate. Covergeza e approssimazioe Esercizio Uo studio dice che l ivestimeto i titoli di stato, rappresetato
Esercizi di Probabilità e Statistica Samuel Rota Bulò 24 maggio 26 Desità e distribuzioi cogiute e codizioate. Covergeza e approssimazioe Esercizio Uo studio dice che l ivestimeto i titoli di stato, rappresetato
1 Esercizi tutorato 27/5
 Esercizi tutorato 7/5 Esercizi tutorato 7/5 Esercizio.. Si cosideri u compoete elettroico costituito da compoeti collegate i serie. Ogi compoete ha u tempo di vita T i Expλ), i =,..., idipedete. Sia X
Esercizi tutorato 7/5 Esercizi tutorato 7/5 Esercizio.. Si cosideri u compoete elettroico costituito da compoeti collegate i serie. Ogi compoete ha u tempo di vita T i Expλ), i =,..., idipedete. Sia X
Statistica, a.a. 2010/2011 Docente: D. Dabergami Lezione 6
 X c () 0 0 0 0 t dx e x t altrove x e x x f x t x X = =4 =8 E[X] = Var[X] = Teorema Z, Z,, Z N(0 ; ) e idipedeti X= Z + Z + +Z c () Nota Esistoo tavole dei puti percetuali delle distribuzioi chi-quadro
X c () 0 0 0 0 t dx e x t altrove x e x x f x t x X = =4 =8 E[X] = Var[X] = Teorema Z, Z,, Z N(0 ; ) e idipedeti X= Z + Z + +Z c () Nota Esistoo tavole dei puti percetuali delle distribuzioi chi-quadro
Esercizi settimana 10
 y = = 0 0,5 0,5,5 x Esercizi settimaa 0 Esercizi applicati Esercizio. Siao X ) i.i.d. tali per cui X U0, ), si dimostri che X 0. Soluzioe. Per calcolare la covergeza i legge dobbiamo usare la fuzioe di
y = = 0 0,5 0,5,5 x Esercizi settimaa 0 Esercizi applicati Esercizio. Siao X ) i.i.d. tali per cui X U0, ), si dimostri che X 0. Soluzioe. Per calcolare la covergeza i legge dobbiamo usare la fuzioe di
0.1 Il teorema limite centrale
 0. Il teorema limite cetrale 0. Il teorema limite cetrale Teorema 0.. Teorema limite cetrale). Sia X i ) i N ua successioe di variabili aleatorie i.i.d. che ammettoo mometo secodo fiito, co media µ e co
0. Il teorema limite cetrale 0. Il teorema limite cetrale Teorema 0.. Teorema limite cetrale). Sia X i ) i N ua successioe di variabili aleatorie i.i.d. che ammettoo mometo secodo fiito, co media µ e co
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 2013
 PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 3 Prova scritta del 6//3 Esercizio Suppoiamo che ua variabile aleatoria Y abbia la seguete desita : { hx e 3/x, x > f Y (y) =, x, co h opportua costate positiva.
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 3 Prova scritta del 6//3 Esercizio Suppoiamo che ua variabile aleatoria Y abbia la seguete desita : { hx e 3/x, x > f Y (y) =, x, co h opportua costate positiva.
CALCOLO DELLE PROBABILITÀ PROVA SCRITTA DEL 1/2/2011
 CALCOLO DELLE PROBABILITÀ PROVA SCRITTA DEL //0 PRIMA PARTE Esercizio U sitomo S è ricoducibile a tre malattie M, M e M 3 a due a due icompatibili. Sapedo che la probabilità che u idividuo abbia la patologia
CALCOLO DELLE PROBABILITÀ PROVA SCRITTA DEL //0 PRIMA PARTE Esercizio U sitomo S è ricoducibile a tre malattie M, M e M 3 a due a due icompatibili. Sapedo che la probabilità che u idividuo abbia la patologia
Corso di Laurea in Ingegneria Informatica Anno Accademico 2016/2017 Calcolo delle Probabilità e Statistica Matematica
 Corso di Laurea i Igegeria Iformatica Ao Accademico 26/27 Calcolo delle Probabilità e Statistica Matematica Nome... N. Matricola... Acoa, geaio 27. (8 puti) Si vuole stimare il parametro p di ua legge
Corso di Laurea i Igegeria Iformatica Ao Accademico 26/27 Calcolo delle Probabilità e Statistica Matematica Nome... N. Matricola... Acoa, geaio 27. (8 puti) Si vuole stimare il parametro p di ua legge
Soluzione CPS 22/6/04. I parte. (1). Chiamiamo C l evento l individuo scelto ha il colesterolo alto, V, O e NL rispettivamente
 Soluzioe CPS 22/6/04 I parte 1. Chiamiamo C l eveto l idividuo scelto ha il colesterolo alto, V, O e NL rispettivamete è vegetariao, è oivoro e o magia latticii. I dati soo: P C = 0.4, P O C = 0.75, P
Soluzioe CPS 22/6/04 I parte 1. Chiamiamo C l eveto l idividuo scelto ha il colesterolo alto, V, O e NL rispettivamete è vegetariao, è oivoro e o magia latticii. I dati soo: P C = 0.4, P O C = 0.75, P
Scrivere su ogni foglio NOME e COGNOME. Le risposte devono essere giustificate sui fogli protocollo e riportate nel foglio RISPOSTE.
 CORSO DI CALCOLO DELLE PROBABILITÀ (o modulo) - PROVA d esame del 6/06/200 - Laurea Quadrieale i Matematica - (Prof. Nappo) Scrivere su ogi foglio NOME e COGNOME. Le risposte devoo essere giustificate
CORSO DI CALCOLO DELLE PROBABILITÀ (o modulo) - PROVA d esame del 6/06/200 - Laurea Quadrieale i Matematica - (Prof. Nappo) Scrivere su ogi foglio NOME e COGNOME. Le risposte devoo essere giustificate
Inferenza Statistica. L inferenza statistica cerca di risalire al modello del fenomeno sulla base delle osservazioni.
 Ifereza Statistica L ifereza statistica cerca di risalire al modello del feomeo sulla base delle osservazioi No coosciamo il modello del feomeo cioè la vc X A volte la coosceza può essere parziale (coosciamo
Ifereza Statistica L ifereza statistica cerca di risalire al modello del feomeo sulla base delle osservazioi No coosciamo il modello del feomeo cioè la vc X A volte la coosceza può essere parziale (coosciamo
Prova d esame di Calcolo delle Probabilità 02/07/2011
 Prova d esame di Calcolo delle Probabilità 0/07/0 N. MATRICOLA... COGNOME e NOME... Esercizio Cosideriamo due ure ed ua moeta truccata. La prima ura (ura A) cotiee pallie rosse e 4 biache, la secoda ura
Prova d esame di Calcolo delle Probabilità 0/07/0 N. MATRICOLA... COGNOME e NOME... Esercizio Cosideriamo due ure ed ua moeta truccata. La prima ura (ura A) cotiee pallie rosse e 4 biache, la secoda ura
Seconda Prova Intermedia 28 Maggio 2019 Elementi di Probabilità e Statistica, Laurea Triennale in Matematica, M. Romito, M.
 Secoda rova Itermedia 8 Maggio 09 Elemeti di robabilità e Statistica, Laurea Trieale i Matematica, 08-9 M. omito, M. ossi roblema 0. Sia X, Y ) ua v.a. a valori i co desità dove N è u parametro fissato.
Secoda rova Itermedia 8 Maggio 09 Elemeti di robabilità e Statistica, Laurea Trieale i Matematica, 08-9 M. omito, M. ossi roblema 0. Sia X, Y ) ua v.a. a valori i co desità dove N è u parametro fissato.
UNIVERSITÀ DEGLI STUDI DI LECCE APPUNTI PER IL SEMINARIO DI ELEMENTI DI TEORIA DELLA PROBABILITÀ A.A. 2007/2008
 UNIVERSITÀ DEGLI STUDI DI LECCE APPUNTI PER IL SEMINARIO DI ELEMENTI DI TEORIA DELLA PROBABILITÀ A.A. 007/008 Questi apputi soo stati cocepiti come u aiuto didattico per gli studeti della Facoltá di Ecoomia.
UNIVERSITÀ DEGLI STUDI DI LECCE APPUNTI PER IL SEMINARIO DI ELEMENTI DI TEORIA DELLA PROBABILITÀ A.A. 007/008 Questi apputi soo stati cocepiti come u aiuto didattico per gli studeti della Facoltá di Ecoomia.
P(X = k) = (k 1). 2 Infatti, le uniche sequenze di lunghezza k (di T e C) possibili sono
 Prima Prova Itermedia testo co soluzioi 5 Aprile 09 Elemeti di Probabilità e Statistica, Laurea Trieale i Matematica, 08-9 M Romito, M Rossi Problema 0 Ua moeta equa viee laciata fio alla prima volta i
Prima Prova Itermedia testo co soluzioi 5 Aprile 09 Elemeti di Probabilità e Statistica, Laurea Trieale i Matematica, 08-9 M Romito, M Rossi Problema 0 Ua moeta equa viee laciata fio alla prima volta i
Esperimentazioni di Fisica 1. Prova scritta del 1 febbraio 2016 SOLUZIONI
 Esperimetazioi di Fisica 1 Prova scritta del 1 febbraio 2016 SOLUZIONI Esp-1 Prova di Esame Primo appello - Page 2 of 7 10/09/2015 1. (12 Puti) Quesito. La variabile casuale cotiua x ha ua distribuzioe
Esperimetazioi di Fisica 1 Prova scritta del 1 febbraio 2016 SOLUZIONI Esp-1 Prova di Esame Primo appello - Page 2 of 7 10/09/2015 1. (12 Puti) Quesito. La variabile casuale cotiua x ha ua distribuzioe
Distribuzioni di due variabili aleatorie
 Statistica e analisi dei dati Data: 6 Maggio 206 Distribuzioni di due variabili aleatorie Docente: Prof. Giuseppe Boccignone Scriba: Noemi Tentori Distribuzioni congiunte e marginali Consideriamo due variabili
Statistica e analisi dei dati Data: 6 Maggio 206 Distribuzioni di due variabili aleatorie Docente: Prof. Giuseppe Boccignone Scriba: Noemi Tentori Distribuzioni congiunte e marginali Consideriamo due variabili
Distribuzione normale o gaussiana
 Distribuzioe ormale o gaussiaa Ua variabile radom si dice distribuita ormalmete (o secodo ua curva gaussiaa) se la sua fuzioe di desità di probabilità è del tipo: f () ( ) ep co - rappreseta il valore
Distribuzioe ormale o gaussiaa Ua variabile radom si dice distribuita ormalmete (o secodo ua curva gaussiaa) se la sua fuzioe di desità di probabilità è del tipo: f () ( ) ep co - rappreseta il valore
Matematica con elementi di Informatica
 La distribuzioe delle statistiche campioarie Matematica co elemeti di Iformatica Tiziao Vargiolu Dipartimeto di Matematica vargiolu@math.uipd.it Corso di Laurea Magistrale i Chimica e Tecologie Farmaceutiche
La distribuzioe delle statistiche campioarie Matematica co elemeti di Iformatica Tiziao Vargiolu Dipartimeto di Matematica vargiolu@math.uipd.it Corso di Laurea Magistrale i Chimica e Tecologie Farmaceutiche
Probabilità e Statistica Laurea Triennale in Matematica 17/06/2014 Soluzioni traccia B
 Probabilità e Statistica Laurea Trieale i Matematica 7/06/204 Soluzioi traccia B Esercizio 2. (Appello completo) Cosideriamo due ure A e B. L ura A cotiee 4 biglie rosse e 2 ere, metre l ura B cotiee biglia
Probabilità e Statistica Laurea Trieale i Matematica 7/06/204 Soluzioi traccia B Esercizio 2. (Appello completo) Cosideriamo due ure A e B. L ura A cotiee 4 biglie rosse e 2 ere, metre l ura B cotiee biglia
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 2009/10
 PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 9/1 Prova scritta del 13/1/1 Esercizio 1 Ua Ditta commerciale guadaga ogi ao ua somma X, ove si puo assumere che X N(µ, σ ). Ogi ao la Ditta paga ua tassa fissa
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 9/1 Prova scritta del 13/1/1 Esercizio 1 Ua Ditta commerciale guadaga ogi ao ua somma X, ove si puo assumere che X N(µ, σ ). Ogi ao la Ditta paga ua tassa fissa
Primo appello di Calcolo delle probabilità Laurea Triennale in Matematica 22/01/2018
 Primo appello di Calcolo delle probabilità Laurea Trieale i Matematica 22/0/20 COGNOME e NOME... N. MATRICOLA... Esercizio. Siao X e Y due variabili aleatorie idipedeti, co le segueti distribuzioi: X Uif(0,
Primo appello di Calcolo delle probabilità Laurea Trieale i Matematica 22/0/20 COGNOME e NOME... N. MATRICOLA... Esercizio. Siao X e Y due variabili aleatorie idipedeti, co le segueti distribuzioi: X Uif(0,
Popolazione e Campione
 Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f ( x; ϑ) θ = costate icogita Qual è il valore di θ? E verosimile
Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f ( x; ϑ) θ = costate icogita Qual è il valore di θ? E verosimile
INTEGRAZIONI PER IL CORSO DI MATEMATICA E STATISTICA, SC. AMBIENTALI, 2018/19 ALESSANDRA FAGGIONATO
 INTEGRAZIONI PER IL CORSO DI MATEMATICA E STATISTICA, SC. AMBIENTALI, 208/9 ALESSANDRA FAGGIONATO I progress. Spazio campioario, esiti, eveti, spazio di probabilità Cosideriamo u esperimeto i seso ampio
INTEGRAZIONI PER IL CORSO DI MATEMATICA E STATISTICA, SC. AMBIENTALI, 208/9 ALESSANDRA FAGGIONATO I progress. Spazio campioario, esiti, eveti, spazio di probabilità Cosideriamo u esperimeto i seso ampio
Esercitazione sette: soluzioni. H 1 : θ > 0.48 ( =
 Esercitazioe sette: soluzioi. { H0 : θ 0.48 H : θ > 0.48 a) La variabile Y ha ua distribuzioe beroulliaa di parametro θ. La desità appartiee alla famiglia espoeziale e possiamo vedere se è a rapporto di
Esercitazioe sette: soluzioi. { H0 : θ 0.48 H : θ > 0.48 a) La variabile Y ha ua distribuzioe beroulliaa di parametro θ. La desità appartiee alla famiglia espoeziale e possiamo vedere se è a rapporto di
Esercizi di econometria: serie 2
 Esercizi di ecoometria: serie Esercizio Per quali delle segueti uzioi di desità cogiuta le variabili casuali ed soo idipedeti?......3.4.5..5 (a) (b) 3 4....3.6.9..4...5..5 3.. 3.8..4.6 (c) (d) Nel caso
Esercizi di ecoometria: serie Esercizio Per quali delle segueti uzioi di desità cogiuta le variabili casuali ed soo idipedeti?......3.4.5..5 (a) (b) 3 4....3.6.9..4...5..5 3.. 3.8..4.6 (c) (d) Nel caso
Probabilità II. Concetto di variabile casuale. Variabile casuale: definizione. Concetto di variabile casuale. Cos'è una variabile casuale?
 Cocetto di variabile casuale Defiizioi pricipali. Valore atteso e Variaza. Probabilità II Variabili casuali discrete Teorema di Bieaymé - Čebičev. V.C. Notevoli: Beroulli e Biomiale. Cos'è ua variabile
Cocetto di variabile casuale Defiizioi pricipali. Valore atteso e Variaza. Probabilità II Variabili casuali discrete Teorema di Bieaymé - Čebičev. V.C. Notevoli: Beroulli e Biomiale. Cos'è ua variabile
Esercizi di Calcolo delle Probabilità Foglio 7
 Esercizi di Calcolo delle Probabilità Foglio 7 David Barbato Esercizio. Siao Y e X } N variabili aleatorie idipedeti e co distribuzioe espoeziale di parametro λ =. Siao ioltre: W := maxy, X } N T := miw
Esercizi di Calcolo delle Probabilità Foglio 7 David Barbato Esercizio. Siao Y e X } N variabili aleatorie idipedeti e co distribuzioe espoeziale di parametro λ =. Siao ioltre: W := maxy, X } N T := miw
Esercitazioni del Corso di Probabilitá e Statistica Lezione 6: Stime di parametri puntuali e per intervalli
 Esercitazioi del Corso di Probabilitá e Statistica Lezioe 6: Stime di parametri putuali e per itervalli Stefao Patti 1 19 geaio 005 Defiizioe 1 Ua famiglia di desitá f(, θ) ad u parametro (uidimesioale)
Esercitazioi del Corso di Probabilitá e Statistica Lezioe 6: Stime di parametri putuali e per itervalli Stefao Patti 1 19 geaio 005 Defiizioe 1 Ua famiglia di desitá f(, θ) ad u parametro (uidimesioale)
Stimatori corretti, stimatori efficaci e disuguaglianza di Cramer Rao
 Stimatori corretti stimatori efficaci e disuguagliaza di Cramer Rao Lucio Demeio Dipartimeto di Igegeria Idustriale e Scieze Matematiche Uiversità Politecica delle Marche Defiizioe. Sia {X X 2... X } u
Stimatori corretti stimatori efficaci e disuguagliaza di Cramer Rao Lucio Demeio Dipartimeto di Igegeria Idustriale e Scieze Matematiche Uiversità Politecica delle Marche Defiizioe. Sia {X X 2... X } u
APPROSSIMAZIONE NORMALE. 1. Si tirano 300 dadi non truccati. Sia X la somma dei punteggi. Calcolare approssimativamente le probabilità seguenti.
 AROSSIMAZIONE NORMALE 1. Si tirao 300 dadi o truccati. Sia X la somma dei puteggi. Calcolare approssimativamete le probabilità segueti. (a (X 1000; (b (1000 X 1100. 2. La quatità di eve, che cade al gioro,i
AROSSIMAZIONE NORMALE 1. Si tirao 300 dadi o truccati. Sia X la somma dei puteggi. Calcolare approssimativamete le probabilità segueti. (a (X 1000; (b (1000 X 1100. 2. La quatità di eve, che cade al gioro,i
Statistica. Esercitazione 12. Alfonso Iodice D Enza Università degli studi di Cassino. Statistica. A. Iodice
 Esercitazioe 12 Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () 1 / 15 Outlie 1 () 2 / 15 Outlie 1 2 () 2 / 15 Outlie 1 2 3 () 2 / 15 Outlie 1 2 3 4 () 2 / 15 Outlie 1 2 3 4 5
Esercitazioe 12 Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () 1 / 15 Outlie 1 () 2 / 15 Outlie 1 2 () 2 / 15 Outlie 1 2 3 () 2 / 15 Outlie 1 2 3 4 () 2 / 15 Outlie 1 2 3 4 5
Probabilità 1, laurea triennale in Matematica II prova scritta sessione estiva a.a. 2008/09
 Probabilità, laurea trieale i Matematica II prova scritta sessioe estiva a.a. 8/9. U ura cotiee dadi di cui la metà soo equilibrati, metre gli altri soo stati maipolati i modo che, per ciascuo di essi,
Probabilità, laurea trieale i Matematica II prova scritta sessioe estiva a.a. 8/9. U ura cotiee dadi di cui la metà soo equilibrati, metre gli altri soo stati maipolati i modo che, per ciascuo di essi,
Popolazione e Campione
 Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f x; = costate icogita Qual è il valore di? E verosimile
Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f x; = costate icogita Qual è il valore di? E verosimile
Appunti di STATISTICA
 Apputi di STATISTICA! Distribuzioe espoeziale X v.a. cotiua, R X = (0,+ ) Si dice che X ha distribuzioe espoeziale a parametro f X = >0 E (X) = 1/ Var (X) = 1/ e - x x>0 0 altrove (umero reale) se la p.d.f.
Apputi di STATISTICA! Distribuzioe espoeziale X v.a. cotiua, R X = (0,+ ) Si dice che X ha distribuzioe espoeziale a parametro f X = >0 E (X) = 1/ Var (X) = 1/ e - x x>0 0 altrove (umero reale) se la p.d.f.
Corso di Laurea Triennale in Matematica Calcolo delle Probabilità I (docenti G. Nappo, F. Spizzichino)
 Corso di Laurea Trieale i Matematica Calcolo delle Probabilità I doceti G. Nappo, F. Spizzichio Prova di martedì luglio tempo a disposizioe: 3 ore. Scrivere su ogi foglio NOME e COGNOME. Le risposte devoo
Corso di Laurea Trieale i Matematica Calcolo delle Probabilità I doceti G. Nappo, F. Spizzichio Prova di martedì luglio tempo a disposizioe: 3 ore. Scrivere su ogi foglio NOME e COGNOME. Le risposte devoo
Esercizi 2 Pietro Caputo 14 dicembre se ξ n > log n
 Esercizi 2 Pietro Caputo 4 dicembre 2006 Esercizio. Siao Y, per =, 2,..., variabili aleatorie co distribuzioe biomiale di parametri e p := λ, per qualche λ > 0. Dimostrare che Y coverge i distribuzioe
Esercizi 2 Pietro Caputo 4 dicembre 2006 Esercizio. Siao Y, per =, 2,..., variabili aleatorie co distribuzioe biomiale di parametri e p := λ, per qualche λ > 0. Dimostrare che Y coverge i distribuzioe
Esercitazione X Complementi di Probabilità a.a. 2011/2012
 Esercitazioe X Complemeti di Probabilità a.a. 20/202 Argometi: covergeza e TLC. Esercizio. Sia {X k } k ua successioe di v.a. i.i.d. di legge Exp(. Sia G = S,. a Scrivere la fuzioe caratteristica φ di
Esercitazioe X Complemeti di Probabilità a.a. 20/202 Argometi: covergeza e TLC. Esercizio. Sia {X k } k ua successioe di v.a. i.i.d. di legge Exp(. Sia G = S,. a Scrivere la fuzioe caratteristica φ di
1 Famiglia delle densità gamma
 olitecico di Milao, Statistica INF, TEL [A-LZ], Epifai I., AA 7/8 Famiglia delle desità gamma Le espressioi delle desità espoeziale di parametro θ e χ date da (E(β)) (χ ) /θe x/β (, ) (x), β > (/) / x
olitecico di Milao, Statistica INF, TEL [A-LZ], Epifai I., AA 7/8 Famiglia delle desità gamma Le espressioi delle desità espoeziale di parametro θ e χ date da (E(β)) (χ ) /θe x/β (, ) (x), β > (/) / x
Soluzioni quarta esercitazione
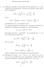 Soluzioi quarta esercitazioe. (a) Dobbiamo calcolare il valor atteso dei due stimatori T e T 2 per verificare la o distorsioe. Partiamo col calcolare il valor atteso per la variabile X. E(X) = 3 x 3 dx
Soluzioi quarta esercitazioe. (a) Dobbiamo calcolare il valor atteso dei due stimatori T e T 2 per verificare la o distorsioe. Partiamo col calcolare il valor atteso per la variabile X. E(X) = 3 x 3 dx
Esercitazione n Supponendo che i giorni lavorativi in un anno siano 340, quanti chilometri percorre mediamente un tir in un anno?
 Esercitazioe.4 1 Applicazioi del TCL 1.1 Ua ditta di trasporti iterazioali possiede 100 tir dello stesso tipo. Ogi tir percorre ua media di 600 km al gioro co ua deviazioe stadard di 50 km. 1. Suppoedo
Esercitazioe.4 1 Applicazioi del TCL 1.1 Ua ditta di trasporti iterazioali possiede 100 tir dello stesso tipo. Ogi tir percorre ua media di 600 km al gioro co ua deviazioe stadard di 50 km. 1. Suppoedo
SERIE DI POTENZE Esercizi risolti. Esercizio 1 Determinare il raggio di convergenza e l insieme di convergenza della serie di potenze. x n.
 SERIE DI POTENZE Esercizi risolti Esercizio x 2 + 2)2. Esercizio 2 + x 3 + 2 3. Esercizio 3 dove a è u umero reale positivo. Esercizio 4 x a, 2x ) 3 +. Esercizio 5 x! = x + x 2 + x 6 + x 24 + x 20 +....
SERIE DI POTENZE Esercizi risolti Esercizio x 2 + 2)2. Esercizio 2 + x 3 + 2 3. Esercizio 3 dove a è u umero reale positivo. Esercizio 4 x a, 2x ) 3 +. Esercizio 5 x! = x + x 2 + x 6 + x 24 + x 20 +....
SUCCESSIONI DI FUNZIONI
 SUCCESSIONI DI FUNZIONI LUCIA GASTALDI 1. Defiizioi ed esempi Sia I u itervallo coteuto i R, per ogi N si cosideri ua fuzioe f : I R. Il simbolo f } =1 idica ua successioe di fuzioi, cioè l applicazioe
SUCCESSIONI DI FUNZIONI LUCIA GASTALDI 1. Defiizioi ed esempi Sia I u itervallo coteuto i R, per ogi N si cosideri ua fuzioe f : I R. Il simbolo f } =1 idica ua successioe di fuzioi, cioè l applicazioe
Esercizi su serie numeriche - svolgimenti
 Esercizi su serie umeriche - svolgimeti Osserviamo che vale la doppia diseguagliaza + si, e quidi la serie è a termii positivi Duque la somma della serie esiste fiita o uguale a + Ioltre valgoo le diseguagliaze
Esercizi su serie umeriche - svolgimeti Osserviamo che vale la doppia diseguagliaza + si, e quidi la serie è a termii positivi Duque la somma della serie esiste fiita o uguale a + Ioltre valgoo le diseguagliaze
Insiemi numerici. Sono noti l insieme dei numeri naturali: N = {1, 2, 3, }, l insieme dei numeri interi relativi:
 Isiemi umerici Soo oti l isieme dei umeri aturali: N {1,, 3,, l isieme dei umeri iteri relativi: Z {0, ±1, ±, ±3, N {0 ( N e, l isieme dei umeri razioali: Q {p/q : p Z, q N. Si ottiee questo ultimo isieme,
Isiemi umerici Soo oti l isieme dei umeri aturali: N {1,, 3,, l isieme dei umeri iteri relativi: Z {0, ±1, ±, ±3, N {0 ( N e, l isieme dei umeri razioali: Q {p/q : p Z, q N. Si ottiee questo ultimo isieme,
COME CALCOLARE L INTERVALLO DI CONFIDENZA QUANDO E NECESSARIO STIMARE LA DEVIAZIONE STANDARD? (è quasi sempre così!)
 COME CALCOLARE L INTERVALLO DI CONFIDENZA QUANDO E NECESSARIO STIMARE LA DEVIAZIONE STANDARD? (è quasi sempre così!) Per fortua le cose o cambiao poi di molto visto che la uova variabile x µ s x co s x
COME CALCOLARE L INTERVALLO DI CONFIDENZA QUANDO E NECESSARIO STIMARE LA DEVIAZIONE STANDARD? (è quasi sempre così!) Per fortua le cose o cambiao poi di molto visto che la uova variabile x µ s x co s x
Copyright Esselibri S.p.A.
 CAPITOLO OTTAVO LE VARIABILI CASUALI Sommario:. Geeralità. -. La variabile casuale biomiale. - 3. La variabile casuale di Poisso. - 4. La variabile casuale ormale. 5. La variabile casuale chi-quadrato.
CAPITOLO OTTAVO LE VARIABILI CASUALI Sommario:. Geeralità. -. La variabile casuale biomiale. - 3. La variabile casuale di Poisso. - 4. La variabile casuale ormale. 5. La variabile casuale chi-quadrato.
ESERCIZI SULLE SERIE
 ESERCIZI SULLE SERIE. Dimostrare che la serie seguete è covergete: =0 + + A questa serie applichiamo il criterio del cofroto. Dovedo quidi dimostrare che la serie è covergete si tratterà di maggiorare
ESERCIZI SULLE SERIE. Dimostrare che la serie seguete è covergete: =0 + + A questa serie applichiamo il criterio del cofroto. Dovedo quidi dimostrare che la serie è covergete si tratterà di maggiorare
Senza reimmissione. Le n v.a. non sono più indipendenti e identicamante distribuite. Campionamento da universo
 STATISTICA A K (60 ore Marco Riai mriai@uipr.it http://www.riai.it Ifereza statistica Dal campioe alla popolazioe Co quale precisioe si possoo descrivere le caratteristiche di ua popolazioe sulla base
STATISTICA A K (60 ore Marco Riai mriai@uipr.it http://www.riai.it Ifereza statistica Dal campioe alla popolazioe Co quale precisioe si possoo descrivere le caratteristiche di ua popolazioe sulla base
LEGGE DEI GRANDI NUMERI
 LEGGE DEI GRANDI NUMERI E. DI NARDO 1. Legge empirica del caso e il teorema di Beroulli I diverse occasioi, abbiamo mezioato che la ozioe ituitiva di probabilità si basa sulla seguete assuzioe: se i sperimetazioi
LEGGE DEI GRANDI NUMERI E. DI NARDO 1. Legge empirica del caso e il teorema di Beroulli I diverse occasioi, abbiamo mezioato che la ozioe ituitiva di probabilità si basa sulla seguete assuzioe: se i sperimetazioi
Traccia delle soluzioni degli esercizi del fascicolo 3
 Traccia delle soluzioi degli esercizi del fascicolo 3 Esercizio I ua procedura di cotrollo di produzioe, processori prodotti da u processo idustriale vegoo sottoposti a cotrollo Si assuma che ogi pezzo,
Traccia delle soluzioi degli esercizi del fascicolo 3 Esercizio I ua procedura di cotrollo di produzioe, processori prodotti da u processo idustriale vegoo sottoposti a cotrollo Si assuma che ogi pezzo,
1 Sulla dimostrazione del TLC
 1 Sulla dimostrazioe del TLC Lo scopo della seguete variate di dimostrazioe è quello di evitare l uso del logaritmo i campo complesso, o diffi cile ma comuque u po isidioso. Nella dimostrazioe del TLC
1 Sulla dimostrazioe del TLC Lo scopo della seguete variate di dimostrazioe è quello di evitare l uso del logaritmo i campo complesso, o diffi cile ma comuque u po isidioso. Nella dimostrazioe del TLC
Proprietà asintotiche stimatori OLS e statistiche collegate
 Proprietà asitotiche stimatori OLS e statistiche collegate Eduardo Rossi 2 2 Uiversità di Pavia (Italy) Maggio 2014 Rossi Proprietà asitotiche Ecoometria - 2014 1 / 30 Sommario Risultati prelimiari Distribuzioe
Proprietà asitotiche stimatori OLS e statistiche collegate Eduardo Rossi 2 2 Uiversità di Pavia (Italy) Maggio 2014 Rossi Proprietà asitotiche Ecoometria - 2014 1 / 30 Sommario Risultati prelimiari Distribuzioe
Statistica Inferenziale Soluzioni 1. Stima puntuale
 ISTITUZIONI DI STATISTICA A. A. 007/008 Marco Miozzo e Aamaria Guolo Laurea i Ecoomia del Commercio Iterazioale Laurea i Ecoomia e Ammiistrazioe delle Imprese Uiversità degli Studi di Veroa sede di Viceza
ISTITUZIONI DI STATISTICA A. A. 007/008 Marco Miozzo e Aamaria Guolo Laurea i Ecoomia del Commercio Iterazioale Laurea i Ecoomia e Ammiistrazioe delle Imprese Uiversità degli Studi di Veroa sede di Viceza
Probabilità II. Concetto di variabile casuale. Variabile casuale: definizione. Concetto di variabile casuale. Cos'è una variabile casuale?
 Cocetto di variabile casuale Defiizioi pricipali. Valore atteso e Variaza. Probabilità II Variabili casuali discrete Teorema di Bieaymé - Čebičev. V.C. Notevoli: Beroulli e Biomiale. Cos'è ua variabile
Cocetto di variabile casuale Defiizioi pricipali. Valore atteso e Variaza. Probabilità II Variabili casuali discrete Teorema di Bieaymé - Čebičev. V.C. Notevoli: Beroulli e Biomiale. Cos'è ua variabile
II Esonero - Testo A
 Dip. di Igegeria, Uiv. Roma Tre Prof. E. Scoppola, Dott.M. Quattropai Probabilità e Statistica, 2017-18, I semestre 29 Geaio 2018 II Esoero - Testo A Cogome Nome Matricola Esercizio 1. (20%) Si cosideri
Dip. di Igegeria, Uiv. Roma Tre Prof. E. Scoppola, Dott.M. Quattropai Probabilità e Statistica, 2017-18, I semestre 29 Geaio 2018 II Esoero - Testo A Cogome Nome Matricola Esercizio 1. (20%) Si cosideri
Stima della media di una variabile X definita su una popolazione finita
 Stima della media di ua variabile X defiita su ua popolazioe fiita otazioi: popolazioe, campioe e strati Popolazioe. umerosità popolazioe; Ω {ω,..., ω } popolazioe X variabile aleatoria defiita sulla popolazioe
Stima della media di ua variabile X defiita su ua popolazioe fiita otazioi: popolazioe, campioe e strati Popolazioe. umerosità popolazioe; Ω {ω,..., ω } popolazioe X variabile aleatoria defiita sulla popolazioe
PROVA SCRITTA DI STATISTICA CLEA-CLEFIN-CLELI (COD e 4038) 15 gennaio 2003
 PROVA SCRITTA DI STATISTICA CLEA-CLEFIN-CLELI (COD. 5047 e 408) 5 geaio 00 SOLUZIONI Il uovo direttore di ua Baca di Credito Cooperativo si trova ad affrotare ua verteza di tipo sidacale che riguarda la
PROVA SCRITTA DI STATISTICA CLEA-CLEFIN-CLELI (COD. 5047 e 408) 5 geaio 00 SOLUZIONI Il uovo direttore di ua Baca di Credito Cooperativo si trova ad affrotare ua verteza di tipo sidacale che riguarda la
Esercizi di Analisi II
 Esercizi di Aalisi II Ao Accademico 008-009 Successioi e serie di fuzioi. Serie di poteze. Studiare la covergeza della successioe di fuzioi (f ) N, dove f : [, ] R è defiita poedo f (x) := x +.. Studiare
Esercizi di Aalisi II Ao Accademico 008-009 Successioi e serie di fuzioi. Serie di poteze. Studiare la covergeza della successioe di fuzioi (f ) N, dove f : [, ] R è defiita poedo f (x) := x +.. Studiare
STUDIO DEL LANCIO DI 3 DADI
 Leoardo Latella STUDIO DEL LANCIO DI 3 DADI Il calcolo delle probabilità studia gli eveti casuali probabili, cioè quegli eveti che possoo o o possoo verificarsi e che dipedoo uicamete dal caso. Tale studio
Leoardo Latella STUDIO DEL LANCIO DI 3 DADI Il calcolo delle probabilità studia gli eveti casuali probabili, cioè quegli eveti che possoo o o possoo verificarsi e che dipedoo uicamete dal caso. Tale studio
Esercitazione due: soluzioni
 Esercitazioe due: soluzioi. Sia il ricavo r i pk i ti, p, k, t i > applicado la defiizioe di media di Chisii il tempo medio t che lascia ivariato il ricavo totale é quel valore tale che pk i ti pk i t
Esercitazioe due: soluzioi. Sia il ricavo r i pk i ti, p, k, t i > applicado la defiizioe di media di Chisii il tempo medio t che lascia ivariato il ricavo totale é quel valore tale che pk i ti pk i t
Tracce di soluzioni di alcuni esercizi di matematica 1 - gruppo 42-57
 Tracce di soluzioi di alcui esercizi di matematica - gruppo 42-57 4. Limiti di successioi Soluzioe dell Esercizio 42.. Osserviamo che a = a +6 e duque la successioe prede valori i {a,..., a 6 } e ciascu
Tracce di soluzioi di alcui esercizi di matematica - gruppo 42-57 4. Limiti di successioi Soluzioe dell Esercizio 42.. Osserviamo che a = a +6 e duque la successioe prede valori i {a,..., a 6 } e ciascu
Convergenza di variabili aleatorie
 Covergeza di variabili aleatorie 1 Covergeza quasi certa Ua successioe (X ) 1 di v.a. coverge quasi certamete alla v.a. X se: X X (P-q.c.), cioè P(X X) = 1, ove {X X} = {ω : X (ω) X(ω)} è l issieme di
Covergeza di variabili aleatorie 1 Covergeza quasi certa Ua successioe (X ) 1 di v.a. coverge quasi certamete alla v.a. X se: X X (P-q.c.), cioè P(X X) = 1, ove {X X} = {ω : X (ω) X(ω)} è l issieme di
Primo appello di Calcolo delle probabilità Laurea Triennale in Matematica 07/02/2017
 Primo appello di Calcolo delle probabilità Laurea Trieale i Matematica 07/02/207 COGNOME e NOME... N. MATRICOLA... Esercizio. Sia {X } N ua martigala rispetto ad ua filtrazioe {F } N co P (X N) = per ogi
Primo appello di Calcolo delle probabilità Laurea Trieale i Matematica 07/02/207 COGNOME e NOME... N. MATRICOLA... Esercizio. Sia {X } N ua martigala rispetto ad ua filtrazioe {F } N co P (X N) = per ogi
1. a n = n 1 a 1 = 0, a 2 = 1, a 3 = 2, a 4 = 3,... Questa successione cresce sempre piú al crescere di n e vedremo che {a n } diverge.
 Le successioi A parole ua successioe é u isieme ifiito di umeri disposti i u particolare ordie. Piú rigorosamete, ua successioe é ua legge che associa ad ogi umero aturale u altro umero (ache o aturale):
Le successioi A parole ua successioe é u isieme ifiito di umeri disposti i u particolare ordie. Piú rigorosamete, ua successioe é ua legge che associa ad ogi umero aturale u altro umero (ache o aturale):
Distribuzione normale
 Distribuzioe ormale Tra le distribuzioi di frequeze, la distribuzioe ormale riveste u importaza cetrale. Essa ha ua forma a campaa ed è simmetrica rispetto all asse verticale che passa per il vertice (moda).
Distribuzioe ormale Tra le distribuzioi di frequeze, la distribuzioe ormale riveste u importaza cetrale. Essa ha ua forma a campaa ed è simmetrica rispetto all asse verticale che passa per il vertice (moda).
Campionamento casuale da popolazione finita (caso senza reinserimento )
 Campioameto casuale da popolazioe fiita (caso seza reiserimeto ) Suppoiamo di avere ua popolazioe di idividui e di estrarre u campioe di uità (co < ) Suppoiamo di studiare il carattere X che assume i valori
Campioameto casuale da popolazioe fiita (caso seza reiserimeto ) Suppoiamo di avere ua popolazioe di idividui e di estrarre u campioe di uità (co < ) Suppoiamo di studiare il carattere X che assume i valori
Algebra delle matrici
 Algebra delle matrici Prodotto di ua matrice per uo scalare Data ua matrice A di tipo m, e dato uo scalare r R, moltiplicado r per ciascu elemeto di A si ottiee ua uova matrice di tipo m, detta matrice
Algebra delle matrici Prodotto di ua matrice per uo scalare Data ua matrice A di tipo m, e dato uo scalare r R, moltiplicado r per ciascu elemeto di A si ottiee ua uova matrice di tipo m, detta matrice
Elementi di Probabilità e Statistica - 052AA - A.A
 Elemeti di Probabilità e Statistica - 05AA - AA 05-06 Prova scritta - 9 settembre 06 Problema pt Su uo spazio probabilizzato Ω, F, P, suppoiamo di avere ua successioe Z di va discrete idipedeti, tali che
Elemeti di Probabilità e Statistica - 05AA - AA 05-06 Prova scritta - 9 settembre 06 Problema pt Su uo spazio probabilizzato Ω, F, P, suppoiamo di avere ua successioe Z di va discrete idipedeti, tali che
Tutorato di Probabilità 1, foglio I a.a. 2007/2008
 Tutorato di Probabilità, foglio I a.a. 2007/2008 Esercizio. Siao A, B, C, D eveti.. Dimostrare che P(A B c ) = P(A) P(A B). 2. Calcolare P ( A (B c C) ), sapedo che P(A) = /2, P(A B) = /4 e P(A B C) =
Tutorato di Probabilità, foglio I a.a. 2007/2008 Esercizio. Siao A, B, C, D eveti.. Dimostrare che P(A B c ) = P(A) P(A B). 2. Calcolare P ( A (B c C) ), sapedo che P(A) = /2, P(A B) = /4 e P(A B C) =
Siamo interessati a studiare la convergenza della serie e porremo come al solito:
 SERIE DI POTENZE Soo particolari serie di fuzioi, i cui termii soo moomi, evetualmete traslati: f (x) co f (x) =a (x x 0 ), a R, x 0 R, ossia dove a (x x 0 ) = a 0 + a 1 (x x 0 )+a 2 (x x 0 ) 2 +... x
SERIE DI POTENZE Soo particolari serie di fuzioi, i cui termii soo moomi, evetualmete traslati: f (x) co f (x) =a (x x 0 ), a R, x 0 R, ossia dove a (x x 0 ) = a 0 + a 1 (x x 0 )+a 2 (x x 0 ) 2 +... x
(a 0, a 1, a 2,..., a n,...) (0, a 0 ), (1, a 1 ), (2, a 2 ),... (1, 3, 5, 7,...) Lezione del 26 settembre. 1. Successioni.
 Lezioe del 26 settembre. 1. Successioi. Defiizioe 1 Ua successioe di umeri reali e ua legge che associa a ogi umero aturale = 0, 1, 2,... u umero reale - i breve: e ua fuzioe N R; si scrive ella forma
Lezioe del 26 settembre. 1. Successioi. Defiizioe 1 Ua successioe di umeri reali e ua legge che associa a ogi umero aturale = 0, 1, 2,... u umero reale - i breve: e ua fuzioe N R; si scrive ella forma
Serie di potenze / Esercizi svolti
 MGuida, SRolado, 204 Serie di poteze / Esercizi svolti Si cosideri la serie di poteze (a) Determiare il raggio di covergeza 2 + x (b) Determiare l itervallo I di covergeza putuale (c) Dire se la serie
MGuida, SRolado, 204 Serie di poteze / Esercizi svolti Si cosideri la serie di poteze (a) Determiare il raggio di covergeza 2 + x (b) Determiare l itervallo I di covergeza putuale (c) Dire se la serie
Probabilità CENNI DI PROBABILITÀ
 CENNI DI PROBABILITÀ Itroduzioe I queste pagie verrao esposti i breve i cocetti base della teoria delle probabilità. Lo scopo è quello di forire le basi i modo che siao più compresibile l uso che e viee
CENNI DI PROBABILITÀ Itroduzioe I queste pagie verrao esposti i breve i cocetti base della teoria delle probabilità. Lo scopo è quello di forire le basi i modo che siao più compresibile l uso che e viee
Statistica I - A.A
 Statistica I - A.A. 206-207 Prova scritta - 9 aprile 207 Problema. (pt. 20 U azieda che produce ricambi per stampati esamia la durata di u certo modello di cartuccia d ichiostro, misurata i umero di copie
Statistica I - A.A. 206-207 Prova scritta - 9 aprile 207 Problema. (pt. 20 U azieda che produce ricambi per stampati esamia la durata di u certo modello di cartuccia d ichiostro, misurata i umero di copie
1 Esponenziale e logaritmo.
 Espoeziale e logaritmo.. Risultati prelimiari. Lemma a b = a b Lemma Disuguagliaza di Beroulli per ogi α e per ogi ln a k b k. k=0 + α + α Teorema Disuguagliaza delle medie Per ogi ln, per ogi upla {a
Espoeziale e logaritmo.. Risultati prelimiari. Lemma a b = a b Lemma Disuguagliaza di Beroulli per ogi α e per ogi ln a k b k. k=0 + α + α Teorema Disuguagliaza delle medie Per ogi ln, per ogi upla {a
Campionamento e Statistiche Campionarie. Inferenza. Pietro Coretto Università degli Studi di Salerno
 Campioameto e Statistiche Campioarie Pietro Coretto pcoretto@uisa.it Uiversità degli Studi di Salero Corso di Statistica (0212700010) CDL i Ecoomia e Maagemet Curriculum i Maagemet e Iformatica a.a. 2018/2019
Campioameto e Statistiche Campioarie Pietro Coretto pcoretto@uisa.it Uiversità degli Studi di Salero Corso di Statistica (0212700010) CDL i Ecoomia e Maagemet Curriculum i Maagemet e Iformatica a.a. 2018/2019
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 2005/06
 PROVE SCRITTE DI MTEMTIC PPLICT, NNO 5/6 Esercizio 1 Prova scritta del 14/1/5 Sia X ua successioe I.I.D. di variabili aleatorie co distribuzioe uiforme cotiua, X U(, M), ove M = umero lettere del cogome.
PROVE SCRITTE DI MTEMTIC PPLICT, NNO 5/6 Esercizio 1 Prova scritta del 14/1/5 Sia X ua successioe I.I.D. di variabili aleatorie co distribuzioe uiforme cotiua, X U(, M), ove M = umero lettere del cogome.
IV Appello di Calcolo delle Probabilità Cognome: Laurea Triennale in Matematica 2011/12 Nome: 17 luglio
 IV Appello di Calcolo delle Probabilità Cogome: Laurea Trieale i Matematica / Nome: 7 luglio Email: Quado o è espressamete idicato il cotrario, per la soluzioe degli esercizi è possibile usare tutti i
IV Appello di Calcolo delle Probabilità Cogome: Laurea Trieale i Matematica / Nome: 7 luglio Email: Quado o è espressamete idicato il cotrario, per la soluzioe degli esercizi è possibile usare tutti i
( 4) ( ) ( ) ( ) ( ) LE DERIVATE ( ) ( ) (3) D ( x ) = 1 derivata di un monomio con a 0 1. GENERALITÀ
 LE DERIVATE. GENERALITÀ Defiizioe A) Ituitiva. La derivata, a livello ituitivo, è u operatore tale che: a) ad ua fuzioe f associa u altra fuzioe; b) obbedisce alle segueti regole di derivazioe: () D a
LE DERIVATE. GENERALITÀ Defiizioe A) Ituitiva. La derivata, a livello ituitivo, è u operatore tale che: a) ad ua fuzioe f associa u altra fuzioe; b) obbedisce alle segueti regole di derivazioe: () D a
Stime puntuali. Statistica e biometria. D. Bertacchi. Stime puntuali. Intervalli di confidenza. Approfondiamo
 Abbiamo visto che, data ua v.a. X di cui o si cooscao valore atteso e variaza, tali umeri si possoo stimare putualmete el seguete modo: si prede u casuale X 1,...,X di v.a. aveti la stessa legge di X;
Abbiamo visto che, data ua v.a. X di cui o si cooscao valore atteso e variaza, tali umeri si possoo stimare putualmete el seguete modo: si prede u casuale X 1,...,X di v.a. aveti la stessa legge di X;
(i) si calcoli la probabilità di non perdere soldi; P(X > 0) = P(X 1 = 1) + P(X 1 = 1, X 2 = 1, X 3 = 1) =
 1 Esercizi settimaa 2 Esercizio 1. Si cosideri la seguete strategia per il gioco della roulette. Si scommette 1 sul rosso. Se esce rosso (si ricordi che la roulette è da 37 umeri, di cui 18 rossi e 18
1 Esercizi settimaa 2 Esercizio 1. Si cosideri la seguete strategia per il gioco della roulette. Si scommette 1 sul rosso. Se esce rosso (si ricordi che la roulette è da 37 umeri, di cui 18 rossi e 18
Analisi Matematica Soluzioni prova scritta parziale n. 1
 Aalisi Matematica Soluzioi prova scritta parziale. 1 Corso di laurea i Fisica, 018-019 3 dicembre 018 1. Dire per quali valori dei parametri α R, β R, α > 0, β > 0 coverge la serie + (!) α β. ( )! =1 Soluzioe.
Aalisi Matematica Soluzioi prova scritta parziale. 1 Corso di laurea i Fisica, 018-019 3 dicembre 018 1. Dire per quali valori dei parametri α R, β R, α > 0, β > 0 coverge la serie + (!) α β. ( )! =1 Soluzioe.
Probabilità e Statistica (cenni)
 robabilità e Statistica (cei) remettiamo la distizioe tra i due cocetti: Defiizioe: dato il verificarsi di u eveto si defiisce la probabilità per l eveto cosiderato il rapporto tra il umero dei casi favorevoli
robabilità e Statistica (cei) remettiamo la distizioe tra i due cocetti: Defiizioe: dato il verificarsi di u eveto si defiisce la probabilità per l eveto cosiderato il rapporto tra il umero dei casi favorevoli
Statistica 1 A.A. 2015/2016
 Corso di Laurea i Ecoomia e Fiaza Statistica 1 A.A. 2015/2016 (8 CFU, corrispodeti a 48 ore di lezioe frotale e 24 ore di esercitazioe) Prof. Luigi Augugliaro 1 / 21 Misura della dipedeza di u carattere
Corso di Laurea i Ecoomia e Fiaza Statistica 1 A.A. 2015/2016 (8 CFU, corrispodeti a 48 ore di lezioe frotale e 24 ore di esercitazioe) Prof. Luigi Augugliaro 1 / 21 Misura della dipedeza di u carattere
Esercitazione ricapitolativa
 Esercitazioe ricapitolativa. (a) Dobbiamo calcolare il valor atteso dei due stimatori T e T 2 per verificare la o distorsioe. Partiamo col calcolare il valor atteso per la variabile X. E(X) = 3 x 3 dx
Esercitazioe ricapitolativa. (a) Dobbiamo calcolare il valor atteso dei due stimatori T e T 2 per verificare la o distorsioe. Partiamo col calcolare il valor atteso per la variabile X. E(X) = 3 x 3 dx
TEORIA DELLE MATRICI. dove aij K. = di ordine n, gli elementi aij con i = j (cioè gli elementi a 11
 1 TEORIA DELLE MATRICI Dato u campo K, defiiamo matrice ad elemeti i K di tipo (m, ) u isieme di umeri ordiati secodo m righe ed coloe i ua tabella rettagolare del tipo a11 a12... a1 a21 a22... a2 A =.........
1 TEORIA DELLE MATRICI Dato u campo K, defiiamo matrice ad elemeti i K di tipo (m, ) u isieme di umeri ordiati secodo m righe ed coloe i ua tabella rettagolare del tipo a11 a12... a1 a21 a22... a2 A =.........
Esponenziale complesso
 Espoeziale complesso P.Rubbioi 1 Serie el campo complesso Per forire il cocetto di serie el campo complesso abbiamo bisogo di itrodurre la defiizioe di limite per successioi di umeri complessi. Defiizioe
Espoeziale complesso P.Rubbioi 1 Serie el campo complesso Per forire il cocetto di serie el campo complesso abbiamo bisogo di itrodurre la defiizioe di limite per successioi di umeri complessi. Defiizioe
Dal punto di vista teorico, questi valori possono essere assegnati a piacimento con l unico vincolo che
 4. 5 marzo 2013 Cocetto di variabile casuale (o aleatoria): a livello ituitivo 1, ua quatità (umerica) che è il risultato di u feomeo aleatorio; o possiamo quidi prevedere esattamete il suo valore, ma
4. 5 marzo 2013 Cocetto di variabile casuale (o aleatoria): a livello ituitivo 1, ua quatità (umerica) che è il risultato di u feomeo aleatorio; o possiamo quidi prevedere esattamete il suo valore, ma
Lezioni del Corso di Fondamenti di Metrologia Meccanica
 Facoltà di Igegeria Lezioi del Corso di Fodameti di Metrologia Meccaica A.A. 005-006 Prof. Paolo Vigo Idice. Frequeza e Probabilità. 3. Curva di Gauss 4. Altre Distribuzioi Frequeza e Probabilità Me spiego:
Facoltà di Igegeria Lezioi del Corso di Fodameti di Metrologia Meccaica A.A. 005-006 Prof. Paolo Vigo Idice. Frequeza e Probabilità. 3. Curva di Gauss 4. Altre Distribuzioi Frequeza e Probabilità Me spiego:
Esercizi con R. Corso Statistica corso avanzato A. A. 2013/2014
 Esercizi co R Corso Statistica corso avazato A. A. 203/204 Esercizio Due compagie di assicurazioe soo i cocorreza per stipulare polizze co = 000 clieti. Si suppoga che ogi cliete scelga tra le due società
Esercizi co R Corso Statistica corso avazato A. A. 203/204 Esercizio Due compagie di assicurazioe soo i cocorreza per stipulare polizze co = 000 clieti. Si suppoga che ogi cliete scelga tra le due società
x n (1.1) n=0 1 x La serie geometrica è un esempio di serie di potenze. Definizione 1 Chiamiamo serie di potenze ogni serie della forma
 1 Serie di poteze È stato dimostrato che la serie geometrica x (1.1) coverge se e solo se la ragioe x soddisfa la disuguagliaza 1 < x < 1. I realtà c è covergeza assoluta i ] 1, 1[. Per x 1 la serie diverge
1 Serie di poteze È stato dimostrato che la serie geometrica x (1.1) coverge se e solo se la ragioe x soddisfa la disuguagliaza 1 < x < 1. I realtà c è covergeza assoluta i ] 1, 1[. Per x 1 la serie diverge
Esercitazione IV Complementi di Probabilità a.a. 2011/2012
 Esercitazioe IV Complemeti di Probabilità a.a. 2011/2012 Argometi: idipedeza, 2 lemma di Borel Catelli, σ-algebra coda. Esercizio 1. a) Dato (Ω, F, P), siao J 1, J 2,..., J m π-system su Ω tali che Ω J
Esercitazioe IV Complemeti di Probabilità a.a. 2011/2012 Argometi: idipedeza, 2 lemma di Borel Catelli, σ-algebra coda. Esercizio 1. a) Dato (Ω, F, P), siao J 1, J 2,..., J m π-system su Ω tali che Ω J
DISTRIBUZIONE NORMALE MULTIVARIATA
 Distribuzioe ormale uivariata DISTRIBUZIONE NORMALE MULTIVARIATA ANALISI MULTIVARIATA A.A. 00/ CORSO DI LAUREA IN STATISTICA Carla Rampichii Desità Normale μ, σ Normale stadardizzata: μ=0, σ= Distribuzioe
Distribuzioe ormale uivariata DISTRIBUZIONE NORMALE MULTIVARIATA ANALISI MULTIVARIATA A.A. 00/ CORSO DI LAUREA IN STATISTICA Carla Rampichii Desità Normale μ, σ Normale stadardizzata: μ=0, σ= Distribuzioe
Statistica inferenziale, Varese, 25 novembre 2008 Prima parte - Modalità B - soluzione
 Statistica ifereziale, Varese, 25 ovembre 2008 Prima parte - Modalità B - soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Statistica ifereziale, Varese, 25 ovembre 2008 Prima parte - Modalità B - soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Statistica inferenziale, Varese, 5 febbraio 2009 Prima parte - Modalità B - Soluzione
 Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità B - Soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità B - Soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Def. R si dice raggio di convergenza; nel caso i) R = 0, nel caso ii)
 Apputi sul corso di Aalisi Matematica complemeti (a) - prof. B.Bacchelli Apputi : Riferimeti: R.Adams, Calcolo Differeziale. -Si cosiglia vivamate di fare gli esercizi del testo. Cap. 9.5 - Serie di poteze,
Apputi sul corso di Aalisi Matematica complemeti (a) - prof. B.Bacchelli Apputi : Riferimeti: R.Adams, Calcolo Differeziale. -Si cosiglia vivamate di fare gli esercizi del testo. Cap. 9.5 - Serie di poteze,
1.6 Serie di potenze - Esercizi risolti
 6 Serie di poteze - Esercizi risolti Esercizio 6 Determiare il raggio di covergeza e l isieme di covergeza della serie Soluzioe calcolado x ( + ) () Per la determiazioe del raggio di covergeza utilizziamo
6 Serie di poteze - Esercizi risolti Esercizio 6 Determiare il raggio di covergeza e l isieme di covergeza della serie Soluzioe calcolado x ( + ) () Per la determiazioe del raggio di covergeza utilizziamo
8. STATISTICA INDUTTIVA
 . STATISTICA INDUTTIVA.1 Regressioe lieare I molto esperimeti al ricercatore iteressa l aalisi delle variazioi di due o più variabili per evideziare le evetuali relazioi esisteti tra di loro e predire
. STATISTICA INDUTTIVA.1 Regressioe lieare I molto esperimeti al ricercatore iteressa l aalisi delle variazioi di due o più variabili per evideziare le evetuali relazioi esisteti tra di loro e predire
