Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 24 giugno 2011 Tema A
|
|
|
- Gianpaolo Barbato
- 4 anni fa
- Visualizzazioni
Transcript
1 Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 24 giugno 20 Tema A Tempo a disposizione: 2 ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio va iniziato all inizio di una pagina. Vanno consegnati solo questo foglio e la bella. Non saranno accettate risposte non giustificate. SOLUZIONI Esercizio. Si considerino il punto A(,0,2) e il piano π di equazione x 3y 2z +4 = 0. a) Si trovi la retta r perpendicolare a π e passante per A. La direzione di r è data da v r = n π, dove n π = (, 3, 2) è un vettore normale a π. Pertanto le equazioni parametriche di r sono x = +t r : y = 3t z = 2 2t b) Si dimostri che r è parallela alla retta s : { 2x+z 5 = 0 3x+y 3z +3 = 0 La direzione di s è data da v s = n n 2, dove n = (2,0,) e n 2 = ( 3,, 3) sono i vettori normali ai piani che compaiono nelle equazioni cartesiane di s. Si trova che v s = (,3,2) = v r e quindi r ed s sono parallele. c) Si determini il piano contenente r ed s. Il piano cercato è quello contenente s e passante per A. Consideriamo quindi il fascio dei piani contenenti s, ossia λ(2x+z 5)+µ( 3x+y 3z +3) = 0, e imponiamo il passaggio per A(,0,2). Otteniamo λ = 6µ e quindi l equazione del piano cercato è 5x y +9z 33 = 0.
2 d) Si calcoli la distanza AB, dove B è il punto d intersezione tra π e r. Non c è bisogno di calcolare le coordinate del punto B, poiché la distanza tra A e B coincide con la distanza tra A e il piano π; pertanto essa è data da AB = x A 3y A 2z A +4 ( 3)2 +5 = 4. Esercizio 2. Sia dove a è un parametro reale. A = 3 a a a 0 4 a) Verificare che è un autovalore di A. A I 3 = 0 3 a a a 0 3 e osserviamo che la prima e la terza riga sono uguali per cui il determinante di A I 3 è 0. Da questo deduciamo che è autovalore di A. b) Determinare il polinomio caratteristico di A e fattorizzarlo. λ 3 A λi 3 = 0 4 λ quindi il polinomio caratteristico di A è λ 3 P(λ) = 0 4 λ λ 3 = λ 0 λ (C 3 C ) λ 3 = (λ ) 0 4 λ 3 = (λ ) 0 a λ a sommando la terza colonna alla prima 0 0 = ( λ)(a λ)(4 λ). 2
3 c) Determinare per quali valori del parametro a la matrice A è diagonalizzabile. Gli autovalori di A sono λ =, λ 2 = 4 e λ 3 = a. Se a è diverso da e 4 allora la matrice A è automaticamente diagonalizzabile perché i suoi autovalori sono semplici. Per a =, l autovalore 4 è semplice (quindi regolare) e l autovalore è doppio. 3 A = 0 4 e 0 3 A I 3 = La matrice 2 2 in alto a sinistra è di determinante 0 quindi A I 3 e di caratteristica almeno 2 (per altro sappiamo che non è 3). Segue che l autovalore λ = ha molteplicità geometrica 3 2 = e quindi non è regolare. Per a = 4, l autovalore è semplice (quindi regolare) e l autovalore 4 è doppio. 3 A = e 3 3 A 4I 3 = La matrice 2 2 in basso a destra ha determinante 4 e quindi l autovalore λ 2 = 4 di nuovo non è regolare e la matrice quindi non è diagonalizzabile. In conclusione la matrice A è diagonalizzabile per tutti e soli i valori di a diversi da e 4. d) Determinare gli autovettori di A per a = 2. giàtrovatogliautovaloridiasitrattasolodirisolvereitresistemiomogenei (si ricorda che una volta trovato gli autovettori conviene verificare che Av = λv). Esercizio 3. Si calcoli I = D x 2 (+y) 2 dxdy, dove D è il triangolo di vertici A(,0), B(0,2) e C(,0). Poiché D è simmetrico rispetto all asse y e l integranda è pari rispetto ad x, l integrale richiesto è dato da 2 x 2 dxdy, dove E (+y) 2 E = {(x,y) R 2 0 x, 0 y 2 2x} 3
4 è la parte di D contenuta nel primo quadrante. Calcoliamo quindi x 2 ( 2 2x ) E (+y) dxdy = x (+y) dy dx = 2 0 ( = x 2 ) dx = 0 3 2x 3 0 = ( x ) dx 43 2x 0 = ln3. x 2 [ +y x 2 3 2x dx ] y=2 2x y=0 dx Pertanto I = ln3. Esercizio 4. Si consideri la funzione f(x,y) = x + y2 x 3 4ln(y +). a) Si trovi il campo di esistenza D di f. È facile vedere che D = {(x,y) R 2 x 3,y > }. b) Si mostri che A(4,) è un punto critico di f. Basta calcolare le derivate parziali di f, f x = y 2 (x 3) 2, f y = 2y x 3 4 y +, e mostrare che le coordinate di A le annullano entrambe. c) Si mostri che A(4,) è l unico punto critico di f. In questo caso bisogna risolvere il sistema y 2 (x 3) = 0 2 2y x 3 4 y + = 0 everificarechenonhaaltresoluzioni. Convienericavarex 3dallasecondaequazione e sostituirlo nella prima; si ottiene un equazione di secondo grado in y le cui soluzioni sono y = e y = 3. Quest ultima non è accettabile (si ricordi come è fatto il campo di esistenza D) e quindi l unico punto critico di f è A(4,). d) Si determinino gli estremi relativi di f (in D). Dobbiamo ora studiare la natura dell unico punto critico A. Le derivate seconde di f sono f xx = 2y2 (x 3) 3, f xy = 2y (x 3) 2, f yy = 2 x (y +) 2. 4
5 La matrice hessiana di f in A, Hf(4,) = ( ) 2 2, 2 3 è definita positiva e quindi A è un punto di minimo relativo. e) Si trovino gli estremi assoluti di f (in D). Dobbiamo capire se A è un punto di minimo assoluto. Ciò non è possibile, perché f(x,0) = x e quindi lim x f(x,0) =. 5
6
7 Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 24 giugno 20 Tema B Tempo a disposizione: 2 ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio va iniziato all inizio di una pagina. Vanno consegnati solo questo foglio e la bella. Non saranno accettate risposte non giustificate. SOLUZIONI Esercizio. Si considerino il punto A(,0,2) e il piano π di equazione x 2y 2z +4 = 0. a) Si trovi la retta r perpendicolare a π e passante per A. La direzione di r è data da v r = n π, dove n π = (, 2, 2) è un vettore normale a π. Pertanto le equazioni parametriche di r sono x = +t r : y = 2t z = 2 2t b) Si dimostri che r è parallela alla retta s : { 2x+z 5 = 0 2x+y 2z +3 = 0 La direzione di s è data da v s = n n 2, dove n = (2,0,) e n 2 = ( 2,, 2) sono i vettori normali ai piani che compaiono nelle equazioni cartesiane di s. Si trova che v s = (,2,2) = v r e quindi r ed s sono parallele. c) Si determini il piano contenente r ed s. Il piano cercato è quello contenente s e passante per A. Consideriamo quindi il fascio dei piani contenenti s, ossia λ(2x+z 5)+µ( 2x+y 2z +3) = 0, e imponiamo il passaggio per A(,0,2). Otteniamo λ = 3µ e quindi l equazione del piano cercato è 8x y +5z 8 = 0.
8 d) Si calcoli la distanza AB, dove B è il punto d intersezione tra π e r. Non c è bisogno di calcolare le coordinate del punto B, poiché la distanza tra A e B coincide con la distanza tra A e il piano π; pertanto essa è data da AB = x A 2y A 2z A +4 ( 2)2 +5 = 9. Esercizio 2. Sia dove a è un parametro reale. A = a a a 0 2 a) Verificare che è un autovalore di A. A I 3 = 0 a a a 0 e osserviamo che la prima e la terza riga sono uguali per cui il determinante di A I 3 è 0. Da questo deduciamo che è autovalore di A. b) Determinare il polinomio caratteristico di A e fattorizzarlo. λ A λi 3 = 0 2 λ quindi il polinomio caratteristico di A è λ P(λ) = 0 2 λ λ = λ 0 λ (C 3 C ) λ = (λ ) 0 2 λ = (λ ) 0 a λ a sommando la terza colonna alla prima 0 0 = ( λ)(a λ)(2 λ). 2
9 c) Determinare per quali valori del parametro a la matrice A è diagonalizzabile. Gli autovalori di A sono λ =, λ 2 = 2 e λ 3 = a. Se a è diverso da e 2 allora la matrice A è automaticamente diagonalizzabile perché i suoi autovalori sono semplici. Per a =, l autovalore 2 è semplice (quindi regolare) e l autovalore è doppio. A = 0 2 e 0 A I 3 = La matrice 2 2 in alto a sinistra è di determinante 0 quindi A I 3 e di caratteristica almeno 2 (per altro sappiamo che non è 3). Segue che l autovalore λ = ha molteplicità geometrica 3 2 = e quindi non è regolare. Per a = 2, l autovalore è semplice (quindi regolare) e l autovalore 2 è doppio. A = e A 2I 3 = La matrice 2 2 in basso a destra ha determinante 2 e quindi l autovalore λ 2 = 2 di nuovo non è regolare e la matrice quindi non è diagonalizzabile. In conclusione la matrice A è diagonalizzabile per tutti e soli i valori di a diversi da e 2. d) Determinare gli autovettori di A per a = 2. giàtrovatogliautovaloridiasitrattasolodirisolvereitresistemiomogenei (si ricorda che una volta trovato gli autovettori conviene verificare che Av = λv). Esercizio 3. Si calcoli I = D x 2 (+y) 2 dxdy, dove D è il triangolo di vertici A(,0), B(0,5) e C(,0). Poiché D è simmetrico rispetto all asse y e l integranda è pari rispetto ad x, l integrale richiesto è dato da 2 x 2 dxdy, dove E (+y) 2 E = {(x,y) R 2 0 x, 0 y 5 5x} 3
10 è la parte di D contenuta nel primo quadrante. Calcoliamo quindi x 2 ( 5 5x ) E (+y) dxdy = x (+y) dy dx = 2 0 ( = x 2 ) dx = 0 6 5x 3 0 = ( x ) dx 256 5x = ln6. Pertanto I = ln6. x 2 [ +y x 2 6 5x dx ] y=5 5x y=0 dx Esercizio 4. Si consideri la funzione f(x,y) = x 2+ y2 x 4 4ln(y +). a) Si trovi il campo di esistenza D di f. È facile vedere che D = {(x,y) R 2 x 4,y > }. b) Si mostri che A(5,) è un punto critico di f. Basta calcolare le derivate parziali di f, f x = y 2 (x 4) 2, f y = 2y x 4 4 y +, e mostrare che le coordinate di A le annullano entrambe. c) Si mostri che A(5,) è l unico punto critico di f. In questo caso bisogna risolvere il sistema y 2 (x 4) = 0 2 2y x 4 4 y + = 0 everificarechenonhaaltresoluzioni. Convienericavarex 4dallasecondaequazione e sostituirlo nella prima; si ottiene un equazione di secondo grado in y le cui soluzioni sono y = e y = 3. Quest ultima non è accettabile (si ricordi come è fatto il campo di esistenza D) e quindi l unico punto critico di f è A(5,). d) Si determinino gli estremi relativi di f (in D). Dobbiamo ora studiare la natura dell unico punto critico A. Le derivate seconde di f sono f xx = 2y2 (x 4) 3, f xy = 2y (x 4) 2, f yy = 2 x (y +) 2. 4
11 La matrice hessiana di f in A, Hf(5,) = ( ) 2 2, 2 3 è definita positiva e quindi A è un punto di minimo relativo. e) Si trovino gli estremi assoluti di f (in D). Dobbiamo capire se A è un punto di minimo assoluto. Ciò non è possibile, perché f(x,0) = x 2 e quindi lim x f(x,0) =. 5
12
13 Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 24 giugno 20 Tema C Tempo a disposizione: 2 ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio va iniziato all inizio di una pagina. Vanno consegnati solo questo foglio e la bella. Non saranno accettate risposte non giustificate. SOLUZIONI Esercizio. Si considerino il punto A(,0,2) e il piano π di equazione x+y 2z +4 = 0. a) Si trovi la retta r perpendicolare a π e passante per A. La direzione di r è data da v r = n π, dove n π = (,, 2) è un vettore normale a π. Pertanto le equazioni parametriche di r sono x = +t r : y = t z = 2 2t b) Si dimostri che r è parallela alla retta s : { 2x+z 5 = 0 x+y +z +3 = 0 La direzione di s è data da v s = n n 2, dove n = (2,0,) e n 2 = (,,) sono i vettori normali ai piani che compaiono nelle equazioni cartesiane di s. Si trova che v s = (,,2) = v r e quindi r ed s sono parallele. c) Si determini il piano contenente r ed s. Il piano cercato è quello contenente s e passante per A. Consideriamo quindi il fascio dei piani contenenti s, ossia λ(2x+z 5)+µ(x+y +z +3) = 0, e imponiamo il passaggio per A(,0,2). Otteniamo λ = 6µ e quindi l equazione del piano cercato è 3x+y +7z 27 = 0.
14 d) Si calcoli la distanza AB, dove B è il punto d intersezione tra π e r. Non c è bisogno di calcolare le coordinate del punto B, poiché la distanza tra A e B coincide con la distanza tra A e il piano π; pertanto essa è data da AB = x A +y A 2z A = 6. Esercizio 2. Sia dove a è un parametro reale. A = 2 a a a 0 a) Verificare che è un autovalore di A. A I 3 = 0 2 a a a 0 2 e osserviamo che la prima e la terza riga sono uguali per cui il determinante di A I 3 è 0. Da questo deduciamo che è autovalore di A. b) Determinare il polinomio caratteristico di A e fattorizzarlo. A λi 3 = λ 2 0 λ quindi il polinomio caratteristico di A è λ 2 P(λ) = 0 λ λ 2 = λ 0 λ (C 3 C ) λ 2 = (λ ) 0 λ 2 = (λ ) 0 a λ a sommando la terza colonna alla prima 0 0 = ( λ)(a λ)( λ). 2
15 c) Determinare per quali valori del parametro a la matrice A è diagonalizzabile. Gli autovalori di A sono λ =, λ 2 = e λ 3 = a. Se a è diverso da e allora la matrice A è automaticamente diagonalizzabile perché i suoi autovalori sono semplici. Per a =, l autovalore è semplice (quindi regolare) e l autovalore è doppio. 2 A = 0 e 0 2 A I 3 = 0 0 La matrice 2 2 in alto a sinistra è di determinante 0 quindi A I 3 e di caratteristica almeno 2 (per altro sappiamo che non è 3). Segue che l autovalore λ = ha molteplicità geometrica 3 2 = e quindi non è regolare. Per a =, l autovalore è semplice (quindi regolare) e l autovalore è doppio. 2 A = 0 e 2 2 A+I 3 = La matrice 2 2 in basso a destra ha determinante e quindi l autovalore λ 2 = di nuovo non è regolare e la matrice quindi non è diagonalizzabile. In conclusione la matrice A è diagonalizzabile per tutti e soli i valori di a diversi da e. d) Determinare gli autovettori di A per a = 2. giàtrovatogliautovaloridiasitrattasolodirisolvereitresistemiomogenei (si ricorda che una volta trovato gli autovettori conviene verificare che Av = λv). Esercizio 3. Si calcoli I = D x 2 (+y) 2 dxdy, dove D è il triangolo di vertici A(,0), B(0,3) e C(,0). Poiché D è simmetrico rispetto all asse y e l integranda è pari rispetto ad x, l integrale richiesto è dato da 2 x 2 dxdy, dove E (+y) 2 E = {(x,y) R 2 0 x, 0 y 3 3x} 3
16 è la parte di D contenuta nel primo quadrante. Calcoliamo quindi x 2 ( 3 3x ) E (+y) dxdy = x (+y) dy dx = 2 0 ( = x 2 ) dx = 0 4 3x 3 0 = ( x ) dx 9 4 3x = ln4. Pertanto I = ln4 = 64 ln x 2 [ +y x 2 4 3x dx ] y=3 3x y=0 dx Esercizio 4. Si consideri la funzione f(x,y) = x++ y2 x 4ln(y +). a) Si trovi il campo di esistenza D di f. È facile vedere che D = {(x,y) R 2 x,y > }. b) Si mostri che A(2,) è un punto critico di f. Basta calcolare le derivate parziali di f, f x = y 2 (x ) 2, f y = 2y x 4 y +, e mostrare che le coordinate di A le annullano entrambe. c) Si mostri che A(2,) è l unico punto critico di f. In questo caso bisogna risolvere il sistema y 2 (x ) = 0 2 2y x 4 y + = 0 everificarechenonhaaltresoluzioni. Convienericavarex dallasecondaequazione e sostituirlo nella prima; si ottiene un equazione di secondo grado in y le cui soluzioni sono y = e y = 3. Quest ultima non è accettabile (si ricordi come è fatto il campo di esistenza D) e quindi l unico punto critico di f è A(2,). d) Si determinino gli estremi relativi di f (in D). Dobbiamo ora studiare la natura dell unico punto critico A. Le derivate seconde di f sono f xx = 2y2 (x ) 3, f xy = 2y (x ) 2, f yy = 2 x + 4 (y +) 2. 4
17 La matrice hessiana di f in A, Hf(2,) = ( ) 2 2, 2 3 è definita positiva e quindi A è un punto di minimo relativo. e) Si trovino gli estremi assoluti di f (in D). Dobbiamo capire se A è un punto di minimo assoluto. Ciò non è possibile, perché f(x,0) = x+ e quindi lim x f(x,0) =. 5
18
19 Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 24 giugno 20 Tema D Tempo a disposizione: 2 ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio va iniziato all inizio di una pagina. Vanno consegnati solo questo foglio e la bella. Non saranno accettate risposte non giustificate. SOLUZIONI Esercizio. Si considerino il punto A(,0,2) e il piano π di equazione x+2y 2z +4 = 0. a) Si trovi la retta r perpendicolare a π e passante per A. La direzione di r è data da v r = n π, dove n π = (,2, 2) è un vettore normale a π. Pertanto le equazioni parametriche di r sono x = +t r : y = 2t z = 2 2t b) Si dimostri che r è parallela alla retta s : { 2x+z 5 = 0 2x+y +2z +3 = 0 La direzione di s è data da v s = n n 2, dove n = (2,0,) e n 2 = (2,,2) sono i vettori normali ai piani che compaiono nelle equazioni cartesiane di s. Si trova che v s = (, 2,2) = v r e quindi r ed s sono parallele. c) Si determini il piano contenente r ed s. Il piano cercato è quello contenente s e passante per A. Consideriamo quindi il fascio dei piani contenenti s, ossia λ(2x+z 5)+µ(2x+y +2z +3) = 0, e imponiamo il passaggio per A(,0,2). Otteniamo λ = 9µ e quindi l equazione del piano cercato è 20x+y +z 42 = 0.
20 d) Si calcoli la distanza AB, dove B è il punto d intersezione tra π e r. Non c è bisogno di calcolare le coordinate del punto B, poiché la distanza tra A e B coincide con la distanza tra A e il piano π; pertanto essa è data da AB = x A +2y A 2z A = 9. Esercizio 2. Sia dove a è un parametro reale. A = 2 a a a 0 3 a) Verificare che è un autovalore di A. A I 3 = 0 2 a a a 0 2 e osserviamo che la prima e la terza riga sono uguali per cui il determinante di A I 3 è 0. Da questo deduciamo che è autovalore di A. b) Determinare il polinomio caratteristico di A e fattorizzarlo. λ 2 A λi 3 = 0 3 λ quindi il polinomio caratteristico di A è λ 2 P(λ) = 0 3 λ λ 2 = λ 0 λ (C 3 C ) λ 2 = (λ ) 0 3 λ 2 = (λ ) 0 a λ a sommando la terza colonna alla prima 0 0 = ( λ)(a λ)(3 λ). 2
21 c) Determinare per quali valori del parametro a la matrice A è diagonalizzabile. Gli autovalori di A sono λ =, λ 2 = 3 e λ 3 = a. Se a è diverso da e 3 allora la matrice A è automaticamente diagonalizzabile perché i suoi autovalori sono semplici. Per a =, l autovalore 3 è semplice (quindi regolare) e l autovalore è doppio. 2 A = 0 3 e 0 2 A I 3 = La matrice 2 2 in alto a sinistra è di determinante 0 quindi A I 3 e di caratteristica almeno 2 (per altro sappiamo che non è 3). Segue che l autovalore λ = ha molteplicità geometrica 3 2 = e quindi non è regolare. Per a = 3, l autovalore è semplice (quindi regolare) e l autovalore 3 è doppio. 2 A = e 2 2 A 3I 3 = La matrice 2 2 in basso a destra ha determinante 3 e quindi l autovalore λ 2 = 3 di nuovo non è regolare e la matrice quindi non è diagonalizzabile. In conclusione la matrice A è diagonalizzabile per tutti e soli i valori di a diversi da e 3. d) Determinare gli autovettori di A per a = 2. giàtrovatogliautovaloridiasitrattasolodirisolvereitresistemiomogenei (si ricorda che una volta trovato gli autovettori conviene verificare che Av = λv). Esercizio 3. Si calcoli I = D x 2 (+y) 2 dxdy, dove D è il triangolo di vertici A(,0), B(0,4) e C(,0). Poiché D è simmetrico rispetto all asse y e l integranda è pari rispetto ad x, l integrale richiesto è dato da 2 x 2 dxdy, dove E (+y) 2 E = {(x,y) R 2 0 x, 0 y 4 4x} 3
22 è la parte di D contenuta nel primo quadrante. Calcoliamo quindi x 2 ( 4 4x ) E (+y) dxdy = x (+y) dy dx = 2 0 ( = x 2 ) dx = 0 5 4x 3 0 = ( x ) dx 65 4x = ln5. Pertanto I = ln5. x 2 [ +y x 2 5 4x dx ] y=4 4x y=0 dx Esercizio 4. Si consideri la funzione f(x,y) = x+3+ y2 x+ 4ln(y +). a) Si trovi il campo di esistenza D di f. È facile vedere che D = {(x,y) R 2 x,y > }. b) Si mostri che A(0,) è un punto critico di f. Basta calcolare le derivate parziali di f, f x = y 2 (x+) 2, f y = 2y x+ 4 y +, e mostrare che le coordinate di A le annullano entrambe. c) Si mostri che A(0,) è l unico punto critico di f. In questo caso bisogna risolvere il sistema y 2 (x+) = 0 2 2y x+ 4 y + = 0 everificarechenonhaaltresoluzioni. Convienericavarex+dallasecondaequazione e sostituirlo nella prima; si ottiene un equazione di secondo grado in y le cui soluzioni sono y = e y = 3. Quest ultima non è accettabile (si ricordi come è fatto il campo di esistenza D) e quindi l unico punto critico di f è A(0,). d) Si determinino gli estremi relativi di f (in D). Dobbiamo ora studiare la natura dell unico punto critico A. Le derivate seconde di f sono f xx = 2y2 (x+) 3, f xy = 2y (x+) 2, f yy = 2 x+ + 4 (y +) 2. 4
23 La matrice hessiana di f in A, Hf(0,) = ( ) 2 2, 2 3 è definita positiva e quindi A è un punto di minimo relativo. e) Si trovino gli estremi assoluti di f (in D). Dobbiamo capire se A è un punto di minimo assoluto. Ciò non è possibile, perché f(x,0) = x+3 e quindi lim x f(x,0) =.
Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 18 febbraio 2010 Tema A
 Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 18 febbraio 21 Tema A Tempo a disposizione: 2 ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio va iniziato all inizio
Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 18 febbraio 21 Tema A Tempo a disposizione: 2 ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio va iniziato all inizio
Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 30 agosto 2011 Tema A
 Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) agosto Tema A Tempo a disposizione: ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio va iniziato all inizio di una pagina.
Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) agosto Tema A Tempo a disposizione: ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio va iniziato all inizio di una pagina.
Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 2 settembre 2008 Tema A
 Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti 2 settembre 28 Tema A Tempo a disposizione: 2 ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio va iniziato all inizio
Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti 2 settembre 28 Tema A Tempo a disposizione: 2 ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio va iniziato all inizio
Università degli Studi di Bergamo Corso integrato di Analisi 1 (Geometria e Algebra Lineare) 29 aprile 2011 Tema A
 Università degli Studi di Bergamo Corso integrato di Analisi 1 (Geometria e Algebra Lineare) 9 aprile 011 Tema A Tempo a disposizione: ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio
Università degli Studi di Bergamo Corso integrato di Analisi 1 (Geometria e Algebra Lineare) 9 aprile 011 Tema A Tempo a disposizione: ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio
Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 3 settembre 2009 Tema A
 Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 3 settembre 29 Tema A Tempo a disposizione: 2 ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio va iniziato all inizio
Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 3 settembre 29 Tema A Tempo a disposizione: 2 ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio va iniziato all inizio
Matematica II per Edili (5 cfu). Soluzioni. 12 Giugno 2006
 Matematica II per Edili ( cfu). Soluzioni. Giugno 6 Nome Matricola L esame dura ore. Il nome e il numero di matricola vanno scritti su ogni foglio. Non è consentito l uso di calcolatrici, libri, appunti
Matematica II per Edili ( cfu). Soluzioni. Giugno 6 Nome Matricola L esame dura ore. Il nome e il numero di matricola vanno scritti su ogni foglio. Non è consentito l uso di calcolatrici, libri, appunti
Si deve verificare (sulla brutta copia) che (1 i 3)z dà lo stesso risultato usando l espressione del testo e la soluzione trovata.
 Università degli Studi di Bergamo Corso integrato di Analisi 1 (Geometria e Algebra Lineare 18 febbraio 1 Tema A Tempo a disposizione: ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio
Università degli Studi di Bergamo Corso integrato di Analisi 1 (Geometria e Algebra Lineare 18 febbraio 1 Tema A Tempo a disposizione: ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio
Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 16 Luglio 2008 Tema A
 Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 16 Luglio 008 Tema A Tempo a disposizione: ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio va iniziato all inizio di
Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 16 Luglio 008 Tema A Tempo a disposizione: ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio va iniziato all inizio di
Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 5 luglio 2013 Tema A
 Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 5 luglio 2013 Tema A Tempo a disposizione: 1 ora e mezza. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio va iniziato all
Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 5 luglio 2013 Tema A Tempo a disposizione: 1 ora e mezza. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio va iniziato all
Es. 1 Es. 2 Es. 3 Es. 4 Totale. Analisi e Geometria 2 Docente: 12 settembre 2013
 Es. 1 Es. 2 Es. 3 Es. 4 Totale Analisi e Geometria 2 Docente: 12 settembre 213 Cognome: Nome: Matricola: Ogni risposta dev essere giustificata. Gli esercizi vanno svolti su questi fogli, nello spazio sotto
Es. 1 Es. 2 Es. 3 Es. 4 Totale Analisi e Geometria 2 Docente: 12 settembre 213 Cognome: Nome: Matricola: Ogni risposta dev essere giustificata. Gli esercizi vanno svolti su questi fogli, nello spazio sotto
Università degli Studi di Bergamo Scuola di Ingegneria Corso di Geometria e Algebra Lineare Appello 5 settembre 2018 Parte B Tema B1
 Università degli Studi di Bergamo Scuola di Ingegneria Corso di Geometria e Algebra Lineare Appello 5 settembre 08 Parte B Tema B Tempo a disposizione: due ore. Calcolatrici, libri e appunti non sono ammessi.
Università degli Studi di Bergamo Scuola di Ingegneria Corso di Geometria e Algebra Lineare Appello 5 settembre 08 Parte B Tema B Tempo a disposizione: due ore. Calcolatrici, libri e appunti non sono ammessi.
Università degli Studi di Bergamo Corso integrato di Analisi 1 (Geometria e Algebra Lineare) 3 settembre 2009 Tema A
 Università degli Studi di Bergamo Corso integrato di Analisi (Geometria e Algebra Lineare) settembre 009 Tema A Tempo a disposizione: ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio
Università degli Studi di Bergamo Corso integrato di Analisi (Geometria e Algebra Lineare) settembre 009 Tema A Tempo a disposizione: ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio
Università degli Studi di Bergamo Modulo di Geometria e Algebra Lineare (vecchio programma) 19 giugno 2013 Tema A
 Università degli Studi di Bergamo Modulo di Geometria e Algebra Lineare (vecchio programma) 9 giugno 203 Tema A Tempo a disposizione: 2 ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio
Università degli Studi di Bergamo Modulo di Geometria e Algebra Lineare (vecchio programma) 9 giugno 203 Tema A Tempo a disposizione: 2 ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio
Università degli Studi di Bergamo Corso integrato di Analisi 1 (Geometria e Algebra Lineare) 24 giugno 2009 Tema A. Parte comune
 Università degli Studi di Bergamo Corso integrato di Analisi 1 (Geometria e Algebra Lineare) 4 giugno 009 Tema A Tempo a disposizione: ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio
Università degli Studi di Bergamo Corso integrato di Analisi 1 (Geometria e Algebra Lineare) 4 giugno 009 Tema A Tempo a disposizione: ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio
Università degli Studi di Bergamo Scuola di Ingegneria Corso di Geometria e Algebra Lineare Appello 19 gennaio 2018 Parte B Tema B1
 Università degli Studi di Bergamo Scuola di Ingegneria Corso di Geometria e Algebra Lineare Appello 19 gennaio 18 Parte B Tema B1 Tempo a disposizione: due ore. Calcolatrici, libri e appunti non sono ammessi.
Università degli Studi di Bergamo Scuola di Ingegneria Corso di Geometria e Algebra Lineare Appello 19 gennaio 18 Parte B Tema B1 Tempo a disposizione: due ore. Calcolatrici, libri e appunti non sono ammessi.
Università degli Studi di Bergamo Modulo di Geometria e Algebra Lineare (vecchio programma) 2 settembre 2013 Tema A
 Università degli Studi di Bergamo Modulo di Geometria e Algebra Lineare (vecchio programma) settembre 013 Tema A Tempo a disposizione: ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio
Università degli Studi di Bergamo Modulo di Geometria e Algebra Lineare (vecchio programma) settembre 013 Tema A Tempo a disposizione: ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio
Università degli Studi di Bergamo Modulo di Geometria e Algebra Lineare (nuovo programma) 2 settembre 2013 Tema A
 Università degli Studi di Bergamo Modulo di Geometria e Algebra Lineare (nuovo programma) settembre 013 Tema A Tempo a disposizione: ore e mezza Calcolatrici, libri e appunti non sono ammessi Ogni esercizio
Università degli Studi di Bergamo Modulo di Geometria e Algebra Lineare (nuovo programma) settembre 013 Tema A Tempo a disposizione: ore e mezza Calcolatrici, libri e appunti non sono ammessi Ogni esercizio
Università degli Studi di Bergamo Modulo di Geometria e Algebra Lineare (nuovo programma) 28 aprile 2014 Tema A
 Università degli Studi di Bergamo Modulo di Geometria e Algebra Lineare (nuovo programma 8 aprile 04 Tema A Tempo a disposizione: ore e mezza. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio
Università degli Studi di Bergamo Modulo di Geometria e Algebra Lineare (nuovo programma 8 aprile 04 Tema A Tempo a disposizione: ore e mezza. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio
Università degli Studi di Bergamo Facoltà di Ingegneria. Matematica II Ingegneria Edile. Appello del 10 settembre 2007 AC = (2, 2, 2),
 Università degli Studi di Bergamo Facoltà di Ingegneria Matematica II Ingegneria Edile Appello del 1 settembre 7 Cognome e Nome Matr. 1.1. Si considerino nello spaio tridimensionale R 3 i tre punti A (3,
Università degli Studi di Bergamo Facoltà di Ingegneria Matematica II Ingegneria Edile Appello del 1 settembre 7 Cognome e Nome Matr. 1.1. Si considerino nello spaio tridimensionale R 3 i tre punti A (3,
Esame scritto di Geometria I
 Esame scritto di Geometria I Università degli Studi di Trento Corso di laurea in Fisica A.A. 26/27 Appello di febbraio 27 Esercizio Sia f h : R R l applicazione lineare definita da f h (e ) = 2e + (2 h)e
Esame scritto di Geometria I Università degli Studi di Trento Corso di laurea in Fisica A.A. 26/27 Appello di febbraio 27 Esercizio Sia f h : R R l applicazione lineare definita da f h (e ) = 2e + (2 h)e
Non saranno accettate risposte non giustificate.
 Università degli Studi di Bergamo Corso integrato di Analisi (Geometria e Algebra Lineare) 3 giugno Tema A Tempo a disposizione: ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio va iniziato
Università degli Studi di Bergamo Corso integrato di Analisi (Geometria e Algebra Lineare) 3 giugno Tema A Tempo a disposizione: ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio va iniziato
Università degli Studi di Bergamo Modulo di Geometria e Algebra Lineare (vecchio programma) 24 gennaio 2013 Tema A
 Università degli Studi di Bergamo Modulo di Geometria e Algebra Lineare (vecchio programma) 24 gennaio 23 Tema A Tempo a disposizione: 2 ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio
Università degli Studi di Bergamo Modulo di Geometria e Algebra Lineare (vecchio programma) 24 gennaio 23 Tema A Tempo a disposizione: 2 ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio
Geometria e algebra lineare 7/2/2018 Corso di laurea in Ing. Elett. Tel., Ing. Inf. Org. e Informatica Correzione
 Geometria e algebra lineare 7//08 Corso di laurea in Ing. Elett. Tel., Ing. Inf. Org. e Informatica Correzione A Esercizio A Siano r la retta passante per i punti A = (0,, 0) e B = (,, ) ed s la retta
Geometria e algebra lineare 7//08 Corso di laurea in Ing. Elett. Tel., Ing. Inf. Org. e Informatica Correzione A Esercizio A Siano r la retta passante per i punti A = (0,, 0) e B = (,, ) ed s la retta
Università degli Studi di Bergamo Scuola di Ingegneria Corso di Geometria e Algebra Lineare Appello 4 luglio 2016 Parte B Tema B1
 Università degli Studi di Bergamo Scuola di Ingegneria Corso di Geometria e Algebra Lineare Appello luglio 6 Parte B Tema B Tempo a disposizione: due ore. Calcolatrici, libri e appunti non sono ammessi.
Università degli Studi di Bergamo Scuola di Ingegneria Corso di Geometria e Algebra Lineare Appello luglio 6 Parte B Tema B Tempo a disposizione: due ore. Calcolatrici, libri e appunti non sono ammessi.
Corso di Laurea in Scienza dei Materiali PROVA SCRITTA DI GEOMETRIA DEL 27/09/2016 SOLUZIONE DEGLI ESERCIZI PROPOSTI
 Corso di Laurea in Scienza dei Materiali PROVA SCRITTA DI GEOMETRIA DEL 7/9/6 SOLUZIONE DEGLI ESERCIZI PROPOSTI Esercizio. Si consideri la quadrica affine C d equazione cartesiana xy + yz z + 4x =. ()
Corso di Laurea in Scienza dei Materiali PROVA SCRITTA DI GEOMETRIA DEL 7/9/6 SOLUZIONE DEGLI ESERCIZI PROPOSTI Esercizio. Si consideri la quadrica affine C d equazione cartesiana xy + yz z + 4x =. ()
Algebra lineare Geometria 1 15 luglio 2009
 Algebra lineare Geometria 1 15 luglio 2009 Esercizio 1. Nello spazio vettoriale reale R 3 [x] si considerino l insieme A k = {1 + x, k + (1 k)x 2, 1 + (k 1)x 2 + x 3 }, il vettore v k = k + kx x 3 e la
Algebra lineare Geometria 1 15 luglio 2009 Esercizio 1. Nello spazio vettoriale reale R 3 [x] si considerino l insieme A k = {1 + x, k + (1 k)x 2, 1 + (k 1)x 2 + x 3 }, il vettore v k = k + kx x 3 e la
Osservazioni generali
 Osservazioni generali Innanzitutto Non si può dividere per. Per i numeri complessi Quando si risolve z 3 = az con a dato, ricordarsi di stare attento per che cosa si divide. Infatti non si può dividere
Osservazioni generali Innanzitutto Non si può dividere per. Per i numeri complessi Quando si risolve z 3 = az con a dato, ricordarsi di stare attento per che cosa si divide. Infatti non si può dividere
LAUREA IN INGEGNERIA CIVILE Corso di Matematica 2 II a prova di accertamento Padova Docenti: Chiarellotto - Cantarini TEMA n.
 LAUREA IN INGEGNERIA CIVILE Corso di Matematica II a prova di accertamento Padova 10-1-07 Docenti: Chiarellotto - Cantarini TEMA n.1 PARTE 1. Quesiti preliminari Stabilire se le seguenti affermazioni sono
LAUREA IN INGEGNERIA CIVILE Corso di Matematica II a prova di accertamento Padova 10-1-07 Docenti: Chiarellotto - Cantarini TEMA n.1 PARTE 1. Quesiti preliminari Stabilire se le seguenti affermazioni sono
11 settembre Soluzione esame di geometria - Ingegneria gestionale - a.a COGNOME... NOME... N. MATRICOLA...
 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura 3 ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura 3 ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
Es. 1 Es. 2 Es. 3 Es. 4 Totale. Analisi e Geometria 2 Docente: 13 febbraio 2014
 Es. 1 Es. 2 Es. 3 Es. 4 Totale Analisi e Geometria 2 Docente: 13 febbraio 214 Cognome: Nome: Matricola: Ogni risposta dev essere giustificata. Gli esercizi vanno svolti su questi fogli, nello spazio sotto
Es. 1 Es. 2 Es. 3 Es. 4 Totale Analisi e Geometria 2 Docente: 13 febbraio 214 Cognome: Nome: Matricola: Ogni risposta dev essere giustificata. Gli esercizi vanno svolti su questi fogli, nello spazio sotto
Università di Pisa. Corso di Laurea in Ingegneria Meccanica Geometria e Algebra Lineare
 Università di Pisa Corso di Laurea in Ingegneria Meccanica Geometria e Algebra Lineare Cognome e Nome: Corso di studi: Anno di iscrizione: Numero di matricola: Scritto n. 1 del 16 Esercizio 1. Si studi
Università di Pisa Corso di Laurea in Ingegneria Meccanica Geometria e Algebra Lineare Cognome e Nome: Corso di studi: Anno di iscrizione: Numero di matricola: Scritto n. 1 del 16 Esercizio 1. Si studi
Corso di Laurea in Ingegneria Informatica (Cp-I e J-Pr) - Ingegneria Elettronica (Cp-I e J-Pr) - Ingegneria REA
 Corso di Laurea in Ingegneria Informatica (Cp-I e J-Pr) - Ingegneria Elettronica (Cp-I e J-Pr) - Ingegneria REA Prova scritta di Algebra lineare e Geometria- 0 Febbraio 019 Durata della prova: tre ore.
Corso di Laurea in Ingegneria Informatica (Cp-I e J-Pr) - Ingegneria Elettronica (Cp-I e J-Pr) - Ingegneria REA Prova scritta di Algebra lineare e Geometria- 0 Febbraio 019 Durata della prova: tre ore.
13 gennaio Soluzione esame di geometria - Ingegneria gestionale - a.a COGNOME... NOME... N. MATRICOLA...
 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica GE110 - Geometria 1 a.a Prova scritta del TESTO E SOLUZIONI
 UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica GE0 - Geometria a.a. 07-08 Prova scritta del 7-7-08 TESTO E SOLUZIONI Svolgere tutti gli esercizi.. Per R considerare il sistema lineare X
UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica GE0 - Geometria a.a. 07-08 Prova scritta del 7-7-08 TESTO E SOLUZIONI Svolgere tutti gli esercizi.. Per R considerare il sistema lineare X
Esercizi di ripasso: geometria e algebra lineare.
 Esercizi di ripasso: geometria e algebra lineare. Esercizio. Sia r la retta passante per i punti A(2,, 3) e B(,, 2) in R 3. a. Scrivere l equazione cartesiana del piano Π passante per A e perpendicolare
Esercizi di ripasso: geometria e algebra lineare. Esercizio. Sia r la retta passante per i punti A(2,, 3) e B(,, 2) in R 3. a. Scrivere l equazione cartesiana del piano Π passante per A e perpendicolare
10 luglio Soluzione esame di geometria - Ingegneria gestionale - a.a COGNOME... NOME... N. MATRICOLA...
 10 luglio 014 - Soluzione esame di geometria - Ingegneria gestionale - a.a. 01-014 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI
10 luglio 014 - Soluzione esame di geometria - Ingegneria gestionale - a.a. 01-014 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI
Geometria BATR-BCVR Esercizi 9
 Geometria BATR-BCVR 2015-16 Esercizi 9 Esercizio 1. Per ognuna delle matrici A i si trovi una matrice ortogonale M i tale che Mi ta im sia diagonale. ( ) 1 1 2 3 2 A 1 = A 2 1 2 = 1 1 0 2 0 1 Esercizio
Geometria BATR-BCVR 2015-16 Esercizi 9 Esercizio 1. Per ognuna delle matrici A i si trovi una matrice ortogonale M i tale che Mi ta im sia diagonale. ( ) 1 1 2 3 2 A 1 = A 2 1 2 = 1 1 0 2 0 1 Esercizio
11 luglio Soluzione esame di geometria - Ing. gestionale - a.a COGNOME... NOME... N. MATRICOLA... ISTRUZIONI
 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
Corso di Geometria, a.a Ing. Informatica e Automatica Esercizi VII: soluzioni
 Corso di Geometria, a.a. 2009-2010 Ing. Informatica e Automatica Esercizi VII: soluzioni 12 novembre 2009 1 Geometria dello spazio Esercizio 1 Dato il punto P 0 = ( 1, 0, 1) e il piano π : x + y + z 2
Corso di Geometria, a.a. 2009-2010 Ing. Informatica e Automatica Esercizi VII: soluzioni 12 novembre 2009 1 Geometria dello spazio Esercizio 1 Dato il punto P 0 = ( 1, 0, 1) e il piano π : x + y + z 2
Secondo Compitino di Matematica II per Edili (5 cfu). Soluzioni. 7 Giugno 2006
 Secondo Compitino di Matematica II per Edili (5 cfu). Soluzioni. 7 Giugno 6 Nome Matricola L esame dura ore. Non è consentito l uso di calcolatrici, libri, appunti o altro. Lo svolgimento degli esercizi
Secondo Compitino di Matematica II per Edili (5 cfu). Soluzioni. 7 Giugno 6 Nome Matricola L esame dura ore. Non è consentito l uso di calcolatrici, libri, appunti o altro. Lo svolgimento degli esercizi
Geometria BAER Canale I Esercizi 11
 Geometria BAER Canale I Esercizi 11 Esercizio 1. Data la retta x = t r : y = t z = 1 si trovi il punto A di r tale che l angolo di r con il vettore AO sia π/2, e il punto B di r tale che l angolo di r
Geometria BAER Canale I Esercizi 11 Esercizio 1. Data la retta x = t r : y = t z = 1 si trovi il punto A di r tale che l angolo di r con il vettore AO sia π/2, e il punto B di r tale che l angolo di r
Corso di Laurea in Ingegneria Informatica (J-Pr) e Ingegneria Elettronica (J-Pr)
 Corso di Laurea in Ingegneria Informatica (J-Pr e Ingegneria Elettronica (J-Pr Prova scritta di Algebra lineare e Geometria- 2 Luglio 218 Durata della prova: tre ore. È vietato uscire dall aula prima di
Corso di Laurea in Ingegneria Informatica (J-Pr e Ingegneria Elettronica (J-Pr Prova scritta di Algebra lineare e Geometria- 2 Luglio 218 Durata della prova: tre ore. È vietato uscire dall aula prima di
Università degli Studi di Bergamo Modulo di Geometria e Algebra Lineare (vecchio programma) 5 luglio 2013 Tema A
 Università degli Studi di Bergamo Modulo di Geometria e Algebra Lineare (vecchio programma) 5 luglio 2013 Tema A Tempo a disposizione: 2 ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio
Università degli Studi di Bergamo Modulo di Geometria e Algebra Lineare (vecchio programma) 5 luglio 2013 Tema A Tempo a disposizione: 2 ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio
Esercizi Enti lineari nel piano e nello spazio
 Esercizi Enti lineari nel piano e nello spazio 010 01 (1) Sia Π R il piano di equazione x + y = 0 e sia f : R R la riflessione rispetto al piano Π (f invia un vettore v = (x y z) nel vettore f((x y x))
Esercizi Enti lineari nel piano e nello spazio 010 01 (1) Sia Π R il piano di equazione x + y = 0 e sia f : R R la riflessione rispetto al piano Π (f invia un vettore v = (x y z) nel vettore f((x y x))
Esercizi Riepilogativi Svolti
 Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA Edile-Architettura e dell Edilizia SPAZI EUCLIDEI. TRASFORMAZIONI. ORIENTAZIONI. FORMULE DI GEOMETRIA IN R. Docente:
Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA Edile-Architettura e dell Edilizia SPAZI EUCLIDEI. TRASFORMAZIONI. ORIENTAZIONI. FORMULE DI GEOMETRIA IN R. Docente:
Università di Pisa. Corso di Laurea in Ingegneria Meccanica Geometria e Algebra Lineare
 Università di Pisa Corso di Laurea in Ingegneria Meccanica Geometria e Algebra Lineare Cognome e Nome: Corso di studi: Anno di iscrizione: Numero di matricola: Scritto n. 1 del 016 Esercizio 1. Si studi
Università di Pisa Corso di Laurea in Ingegneria Meccanica Geometria e Algebra Lineare Cognome e Nome: Corso di studi: Anno di iscrizione: Numero di matricola: Scritto n. 1 del 016 Esercizio 1. Si studi
Università degli Studi di Bergamo Corso integrato di Analisi 1 (Geometria e Algebra Lineare) 26 gennaio 2011 Tema A
 Università degli Studi di Bergamo Corso integrato di Analisi (Geometria e Algebra Lineare) 6 gennaio Tema A Tempo a disposizione: ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio va
Università degli Studi di Bergamo Corso integrato di Analisi (Geometria e Algebra Lineare) 6 gennaio Tema A Tempo a disposizione: ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio va
Corso di Laurea in Scienza dei Materiali PROVA SCRITTA DI GEOMETRIA DEL 12/07/2016 SOLUZIONE DEGLI ESERCIZI PROPOSTI
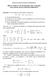 Corso di Laurea in Scienza dei Materiali PROVA SCRITTA DI GEOMETRIA DEL 12/07/2016 SOLUZIONE DEGLI ESERCIZI PROPOSTI Esercizio 1 Si consideri la conica affine d equazione 9x 2 + 6y 2 4xy 6x + 8y = 1 (1)
Corso di Laurea in Scienza dei Materiali PROVA SCRITTA DI GEOMETRIA DEL 12/07/2016 SOLUZIONE DEGLI ESERCIZI PROPOSTI Esercizio 1 Si consideri la conica affine d equazione 9x 2 + 6y 2 4xy 6x + 8y = 1 (1)
Corso di Geometria Ing. Informatica e Automatica Test 1: soluzioni
 Corso di Geometria Ing. Informatica e Automatica Test : soluzioni k Esercizio Data la matrice A = k dipendente dal parametro k, si consideri il k sistema lineare omogeneo AX =, con X = x x. Determinare
Corso di Geometria Ing. Informatica e Automatica Test : soluzioni k Esercizio Data la matrice A = k dipendente dal parametro k, si consideri il k sistema lineare omogeneo AX =, con X = x x. Determinare
Università degli Studi di Bergamo Modulo di Geometria e Algebra Lineare (vecchio programma) 2 luglio 2014 Tema A
 Università degli Studi di Bergamo Modulo di Geometria e Algebra Lineare (vecchio programma) 2 luglio 24 Tema A Tempo a disposizione: 2 ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio
Università degli Studi di Bergamo Modulo di Geometria e Algebra Lineare (vecchio programma) 2 luglio 24 Tema A Tempo a disposizione: 2 ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio
Geometria e algebra lineare 20/6/2017 Corso di laurea in Ing. Elett. Tel., Ing. Inf. Org. e Informatica Correzione. x 2y = 0
 Geometria e algebra lineare 20/6/2017 Corso di laurea in Ing. Elett. Tel., Ing. Inf. Org. e Informatica Correzione A Esercizio 1A Siano r la retta di equazioni { x + y 2z = 1 e P il punto di coordinate
Geometria e algebra lineare 20/6/2017 Corso di laurea in Ing. Elett. Tel., Ing. Inf. Org. e Informatica Correzione A Esercizio 1A Siano r la retta di equazioni { x + y 2z = 1 e P il punto di coordinate
20 gennaio Soluzione esame di geometria - 12 crediti Ingegneria gestionale - a.a COGNOME... NOME... N. MATRICOLA...
 0 gennaio 010 - Soluzione esame di geometria - 1 crediti Ingegneria gestionale - a.a. 009-010 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore.
0 gennaio 010 - Soluzione esame di geometria - 1 crediti Ingegneria gestionale - a.a. 009-010 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore.
Prova scritta di Geometria 1 Docente: Giovanni Cerulli Irelli 20 Gennaio 2017
 Prova scritta di Geometria Docente: Giovanni Cerulli Irelli Gennaio 7 Esercizio. Si considerino i seguenti tre punti dello spazio euclideo: P :=, Q :=, R :=.. Dimostrare che P, Q ed R non sono collineari.
Prova scritta di Geometria Docente: Giovanni Cerulli Irelli Gennaio 7 Esercizio. Si considerino i seguenti tre punti dello spazio euclideo: P :=, Q :=, R :=.. Dimostrare che P, Q ed R non sono collineari.
Geometria A. Università degli Studi di Trento Corso di laurea in Matematica A.A. 2017/ Febbraio 2018 Appello di Febbraio
 Geometria A Università degli Studi di Trento Corso di laurea in Matematica A.A. 27/28 Febbraio 28 Appello di Febbraio Il tempo per la prova è di 3 ore. Durante la prova non è permesso l uso di appunti
Geometria A Università degli Studi di Trento Corso di laurea in Matematica A.A. 27/28 Febbraio 28 Appello di Febbraio Il tempo per la prova è di 3 ore. Durante la prova non è permesso l uso di appunti
15 luglio Soluzione esame di geometria - Ing. gestionale - a.a COGNOME... NOME... N. MATRICOLA... ISTRUZIONI
 15 luglio 01 - Soluzione esame di geometria - Ing. gestionale - a.a. 01-01 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono
15 luglio 01 - Soluzione esame di geometria - Ing. gestionale - a.a. 01-01 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono
LAUREA IN INGEGNERIA CIVILE ED AMBIENTE-TERRITORIO Corso di Matematica 2 Padova TEMA n.1
 LAUREA IN INGEGNERIA CIVILE ED AMBIENTE-TERRITORIO Corso di Matematica Padova -8-8 TEMA n.1 PARTE 1. Quesiti preliminari Stabilire se le seguenti affermazioni sono vere o false giustificando brevemente
LAUREA IN INGEGNERIA CIVILE ED AMBIENTE-TERRITORIO Corso di Matematica Padova -8-8 TEMA n.1 PARTE 1. Quesiti preliminari Stabilire se le seguenti affermazioni sono vere o false giustificando brevemente
ANALISI MATEMATICA I MODULO, I e II MODULO, II MODULO CORSO DI LAUREA IN INFORMATICA
 ANALISI MATEMATICA I MODULO, I e II MODULO, II MODULO CORSO DI LAUREA IN INFORMATICA Prova scritta del 6 giugno 2004: soluzioni ESERCIZIO - Data la funzione f) 3 2 4 + 27 + 9 2 ) /3 4 + 27, + 9 si chiede
ANALISI MATEMATICA I MODULO, I e II MODULO, II MODULO CORSO DI LAUREA IN INFORMATICA Prova scritta del 6 giugno 2004: soluzioni ESERCIZIO - Data la funzione f) 3 2 4 + 27 + 9 2 ) /3 4 + 27, + 9 si chiede
Prova scritta di Geometria 1 Docente: Giovanni Cerulli Irelli 15 Febbraio 2017
 Prova scritta di Geometria Docente: Giovanni Cerulli Irelli 5 Febbraio 7 Esercizio. Si considerino i due sottospazi π e π di R dati dalle seguenti equazioni: π : x y + z = ; π : x + y z =.. Trovare una
Prova scritta di Geometria Docente: Giovanni Cerulli Irelli 5 Febbraio 7 Esercizio. Si considerino i due sottospazi π e π di R dati dalle seguenti equazioni: π : x y + z = ; π : x + y z =.. Trovare una
Corso di Geometria, a.a Ing. Informatica e Automatica Esercizi VI: soluzioni
 Corso di Geometria, a.a. 2009-2010 Ing. Informatica e Automatica Esercizi VI: soluzioni 5 novembre 2009 1 Geometria del piano e prodotto scalare Richiami. Il prodotto scalare di due vettori del piano v,
Corso di Geometria, a.a. 2009-2010 Ing. Informatica e Automatica Esercizi VI: soluzioni 5 novembre 2009 1 Geometria del piano e prodotto scalare Richiami. Il prodotto scalare di due vettori del piano v,
T.(a) T.(b) Es.1 Es.2 Es.3 Es.4 Totale. Cognome: Nome: Matricola:
 T.(a) T.(b) Es.1 Es.2 Es.3 Es.4 Totale Analisi e Geometria 1 Primo Appello 4 Febbraio 2019 Docente: Numero di iscrizione: Cognome: Nome: Matricola: Istruzioni: Tutte le risposte devono essere motivate.
T.(a) T.(b) Es.1 Es.2 Es.3 Es.4 Totale Analisi e Geometria 1 Primo Appello 4 Febbraio 2019 Docente: Numero di iscrizione: Cognome: Nome: Matricola: Istruzioni: Tutte le risposte devono essere motivate.
14 febbraio Soluzione esame di geometria - 12 crediti Ingegneria gestionale - a.a COGNOME... NOME... N. MATRICOLA...
 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
(2) Dato il vettore w = (1, 1, 1), calcolare T (w). (3) Determinare la matrice A associata a T rispetto alla base canonica.
 1. Applicazioni lineari Esercizio 1.1. Sia T : R 2 R 3 l applicazione lineare definita sulla base canonica di R 2 nel seguente modo: T (e 1 ) = (1, 2, 1), T (e 2 ) = (1, 0, 1). a) Esplicitare T (x, y).
1. Applicazioni lineari Esercizio 1.1. Sia T : R 2 R 3 l applicazione lineare definita sulla base canonica di R 2 nel seguente modo: T (e 1 ) = (1, 2, 1), T (e 2 ) = (1, 0, 1). a) Esplicitare T (x, y).
21 settembre Soluzione esame di geometria - Ingegneria gestionale - a.a COGNOME... NOME... N. MATRICOLA...
 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
Esercizi per Geometria II Geometria euclidea e proiettiva
 Esercizi per Geometria II Geometria euclidea e proiettiva Filippo F. Favale 10 aprile 01 Esercizio 1 Sia E 3 lo spazio euclideo tridimensionale dotato di un riferimento cartesiano ortonormale di coordinate
Esercizi per Geometria II Geometria euclidea e proiettiva Filippo F. Favale 10 aprile 01 Esercizio 1 Sia E 3 lo spazio euclideo tridimensionale dotato di un riferimento cartesiano ortonormale di coordinate
Prova scritta del 18/12/2008, tema A
 1 È Data la funzione: fx) e x x 3x + 3) Prova scritta del 18/1/8, tema A Determinarne: a) dominio, limiti significativi, asintoti; b) derivata prima, crescenza, punti di massimo e di minimo; c) derivata
1 È Data la funzione: fx) e x x 3x + 3) Prova scritta del 18/1/8, tema A Determinarne: a) dominio, limiti significativi, asintoti; b) derivata prima, crescenza, punti di massimo e di minimo; c) derivata
Politecnico di Milano Ingegneria Industriale e dell Informazione Analisi e Geometria 2 Primo Appello 13 Luglio 2017
 Politecnico di Milano Ingegneria Industriale e dell Informazione Analisi e Geometria Primo Appello 13 Luglio 017 Cognome: Nome: Matricola: Es.1: 11 punti Es.: 6 punti Es.3: 7 punti Es.: 8 punti Totale
Politecnico di Milano Ingegneria Industriale e dell Informazione Analisi e Geometria Primo Appello 13 Luglio 017 Cognome: Nome: Matricola: Es.1: 11 punti Es.: 6 punti Es.3: 7 punti Es.: 8 punti Totale
Geometria BAER Canale A-K Esercizi 9
 Geometria BAER 2016-2017 Canale A-K Esercizi 9 Esercizio 1. Si considerino i punti del piano A (1, 1), B (4, 1), C ( 1/2, 2) (a) Si determini se i punti A, B, C sono allineati e, in caso affermativo, si
Geometria BAER 2016-2017 Canale A-K Esercizi 9 Esercizio 1. Si considerino i punti del piano A (1, 1), B (4, 1), C ( 1/2, 2) (a) Si determini se i punti A, B, C sono allineati e, in caso affermativo, si
18 gennaio Soluzione esame di geometria - 12 crediti Ingegneria gestionale - a.a COGNOME... NOME... N. MATRICOLA...
 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
Analisi Matematica II Corso di Ingegneria Gestionale Compito del xy + 2x + 2y + 2xy + 2x + 2y + sin
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del 9--8 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito del 9--8 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
LICEO SCIENTIFICO SESSIONE STRAORDINARIA 2016 QUESTIONARIO QUESITO 1. lim. = lim cos(x) = 1 2 QUESITO 2
 www.matefilia.it LICEO SCIENTIFICO SESSIONE STRAORDINARIA 6 QUESTIONARIO QUESITO Calcolare il limite: sen(cos(x) ) lim x ln (cos (x)) Ricordiamo che, se f(x) tende a zero, risulta: senf(x)~f(x) ed ln (
www.matefilia.it LICEO SCIENTIFICO SESSIONE STRAORDINARIA 6 QUESTIONARIO QUESITO Calcolare il limite: sen(cos(x) ) lim x ln (cos (x)) Ricordiamo che, se f(x) tende a zero, risulta: senf(x)~f(x) ed ln (
ESAMI E ESERCITAZIONI A.A. 2010/11. Calcolare la lunghezza del grafico di f. Suggerimento: ricordare che, se h(u) è una funzione continua e.
 ESAMI E ESERCITAZIONI AA 2010/11 ANDREA RATTO Sommario In questo file presentiamo esercitazioni ed esami relativi al Corso Integrato di Matematica per Scienze dell Architettura 1 Esercitazione del 2 Maggio
ESAMI E ESERCITAZIONI AA 2010/11 ANDREA RATTO Sommario In questo file presentiamo esercitazioni ed esami relativi al Corso Integrato di Matematica per Scienze dell Architettura 1 Esercitazione del 2 Maggio
Politecnico di Milano Ingegneria Industriale Analisi e Geometria 2 Secondo compito in itinere 30 Giugno 2016
 Politecnico di Milano Ingegneria Industriale Analisi e Geometria Secondo compito in itinere Giugno 6 Cognome: Nome: Matricola: Es.: 9 punti Es.: 9 punti Es.: 6 punti Es.4: 9 punti Totale. Si consideri
Politecnico di Milano Ingegneria Industriale Analisi e Geometria Secondo compito in itinere Giugno 6 Cognome: Nome: Matricola: Es.: 9 punti Es.: 9 punti Es.: 6 punti Es.4: 9 punti Totale. Si consideri
Corso di Geometria BIAR, BSIR Esercizi 10: soluzioni
 Corso di Geometria 2010-11 BIAR, BSIR Esercizi 10: soluzioni 1 Geometria dello spazio Esercizio 1. Dato il punto P 0 = ( 1, 0, 1) e il piano π : x + y + z 2 = 0, determinare: a) Le equazioni parametriche
Corso di Geometria 2010-11 BIAR, BSIR Esercizi 10: soluzioni 1 Geometria dello spazio Esercizio 1. Dato il punto P 0 = ( 1, 0, 1) e il piano π : x + y + z 2 = 0, determinare: a) Le equazioni parametriche
CORSO DI FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA - LAUREA IN INGEGNERIA MECCANICA Padova II prova parziale TEMA n.1
 CORSO DI FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA - LAUREA IN INGEGNERIA MECCANICA Padova 15-06-2010 II prova parziale TEMA n.1 Parte 1. Quesiti preliminari. Stabilire se le seguenti affermazioni sono
CORSO DI FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA - LAUREA IN INGEGNERIA MECCANICA Padova 15-06-2010 II prova parziale TEMA n.1 Parte 1. Quesiti preliminari. Stabilire se le seguenti affermazioni sono
Politecnico di Milano Ingegneria Chimica, dei Materiali e delle Nanotecnologie Analisi Matematica 1 e Geometria Primo Appello 6 Febbraio 2018
 Politecnico di Milano Ingegneria Chimica, dei Materiali e delle Nanotecnologie Analisi Matematica e Geometria Primo Appello 6 Febbraio 208 Cognome: Nome: Matricola: Prima Parte. Stabilire se le successioni
Politecnico di Milano Ingegneria Chimica, dei Materiali e delle Nanotecnologie Analisi Matematica e Geometria Primo Appello 6 Febbraio 208 Cognome: Nome: Matricola: Prima Parte. Stabilire se le successioni
24 luglio Soluzione esame di geometria - Ing. gestionale - a.a COGNOME... NOME... N. MATRICOLA... ISTRUZIONI
 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
5 dicembre Soluzione esame di geometria - Ing. gestionale - a.a COGNOME... NOME... N. MATRICOLA... ISTRUZIONI
 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
13 gennaio Soluzione esame di geometria - Ing. gestionale - a.a COGNOME... NOME... N. MATRICOLA... ISTRUZIONI
 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura 3 ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura 3 ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
Per le risposte utilizza gli spazi predisposti. Quando richiesto, il procedimento va esposto brevemente, ma in maniera comprensibile.
 COGNOME............................... NOME..................................... Punti ottenuti Esame di geometria Scrivi cognome e nome negli spazi predisposti in ciascuno dei tre fogli. Per ogni domanda
COGNOME............................... NOME..................................... Punti ottenuti Esame di geometria Scrivi cognome e nome negli spazi predisposti in ciascuno dei tre fogli. Per ogni domanda
1 settembre Soluzione esame di geometria - 12 crediti Ingegneria gestionale - a.a COGNOME... NOME... N. MATRICOLA...
 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
Corso di Laurea in Matematica - Esame di Geometria UNO. Prova scritta del 22 gennaio 2015
 Corso di Laurea in Matematica - Esame di Geometria UNO Prova scritta del 22 gennaio 2015 Cognome Nome Numero di matricola Corso (A o B) Voto ATTENZIONE. Riportare lo svolgimento completo degli esercizi.
Corso di Laurea in Matematica - Esame di Geometria UNO Prova scritta del 22 gennaio 2015 Cognome Nome Numero di matricola Corso (A o B) Voto ATTENZIONE. Riportare lo svolgimento completo degli esercizi.
Prova scritta di Geometria 18/01/2016, Soluzioni Ing. Meccanica a.a
 Prova scritta di Geometria 8//26, Soluzioni Ing. Meccanica a.a. 25-6 Esercizio È data la conica γ : 3x2 2xy + 3y 2 + 8x + 3 =. a) Verificare che la conica è un ellisse e determinarne la forma canonica.
Prova scritta di Geometria 8//26, Soluzioni Ing. Meccanica a.a. 25-6 Esercizio È data la conica γ : 3x2 2xy + 3y 2 + 8x + 3 =. a) Verificare che la conica è un ellisse e determinarne la forma canonica.
10 aprile Soluzione esame di geometria - Ing. gestionale - a.a COGNOME... NOME... N. MATRICOLA... ISTRUZIONI
 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
Geometria BAER Canale A-K Esercizi 8
 Geometria BAER Canale A-K Esercizi 8 Esercizio. Si consideri il sottospazio U = L v =, v, v 3 =. (a) Si trovino le equazioni cartesiane ed una base ortonormale di U. (b) Si trovi una base ortonormale di
Geometria BAER Canale A-K Esercizi 8 Esercizio. Si consideri il sottospazio U = L v =, v, v 3 =. (a) Si trovino le equazioni cartesiane ed una base ortonormale di U. (b) Si trovi una base ortonormale di
CORSO DI LAUREA IN INGEGNERIA MECCANICA A.A PROVA SCRITTA DI GEOMETRIA DEL Compito A Corso del Prof.
 CORSO DI LAUREA IN INGEGNERIA MECCANICA A.A. 202-203 PROVA SCRITTA DI GEOMETRIA DEL 8-02-3 Compito A Corso del Prof. Manlio BORDONI Esercizio. Sia W il sottospazio vettoriale di R 4 generato dai vettori
CORSO DI LAUREA IN INGEGNERIA MECCANICA A.A. 202-203 PROVA SCRITTA DI GEOMETRIA DEL 8-02-3 Compito A Corso del Prof. Manlio BORDONI Esercizio. Sia W il sottospazio vettoriale di R 4 generato dai vettori
Soluzioni verifica di Matematica 5 a E Liceo Scientifico - 17/10/2013
 Istituto Superiore XXV aprile Pontedera - Prof Francesco Daddi Soluzioni verifica di Matematica 5 a E Liceo Scientifico - 7/0/03 Esercizio Si consideri la funzione e x+ se x < f(x) = 0 se x = x x x se
Istituto Superiore XXV aprile Pontedera - Prof Francesco Daddi Soluzioni verifica di Matematica 5 a E Liceo Scientifico - 7/0/03 Esercizio Si consideri la funzione e x+ se x < f(x) = 0 se x = x x x se
1 Esercizi di ripasso 4
 Esercizi di ripasso 4. Determinare k in modo che il piano kx + 2y 6z + = 0 sia parallelo al piano x + y z + = 0. Soluzione. La condizione di parallelismo richiede che ( ) k 2 6 rg = Ne segue che k = e
Esercizi di ripasso 4. Determinare k in modo che il piano kx + 2y 6z + = 0 sia parallelo al piano x + y z + = 0. Soluzione. La condizione di parallelismo richiede che ( ) k 2 6 rg = Ne segue che k = e
6 dicembre Soluzione esame di geometria - Ing. gestionale - a.a COGNOME... NOME... N. MATRICOLA... ISTRUZIONI
 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
Tutorato di GE110. Universitá degli Studi Roma Tre - Corso di Laurea in Matematica
 Universitá degli Studi Roma Tre - Corso di Laurea in Matematica Tutorato di GE110 AA 2013-2014 - Docente: Prof Angelo Felice Lopez Tutori: Dario Giannini e Giulia Salustri Soluzioni Tutorato 7 24 Aprile
Universitá degli Studi Roma Tre - Corso di Laurea in Matematica Tutorato di GE110 AA 2013-2014 - Docente: Prof Angelo Felice Lopez Tutori: Dario Giannini e Giulia Salustri Soluzioni Tutorato 7 24 Aprile
SOLUZIONI (PROVA DELL 11 FEBBRAIO 2019) Due rette sghembe sono simultaneamente parallele a infiniti piani. [ V ]
![SOLUZIONI (PROVA DELL 11 FEBBRAIO 2019) Due rette sghembe sono simultaneamente parallele a infiniti piani. [ V ] SOLUZIONI (PROVA DELL 11 FEBBRAIO 2019) Due rette sghembe sono simultaneamente parallele a infiniti piani. [ V ]](/thumbs/103/159439756.jpg) SOLUZIONI (PROVA DELL FEBBRAIO 209) Il rango per righe può superare di il rango per colonne [ F ] In R 6 possono esistere 7 generatori di un sottospazio [ V ] {( + 2k, 2 k, 0), (,, 0), (0, 0, )} è una
SOLUZIONI (PROVA DELL FEBBRAIO 209) Il rango per righe può superare di il rango per colonne [ F ] In R 6 possono esistere 7 generatori di un sottospazio [ V ] {( + 2k, 2 k, 0), (,, 0), (0, 0, )} è una
3 settembre Soluzione esame di geometria - Ing. gestionale - a.a COGNOME... NOME... N. MATRICOLA... ISTRUZIONI
 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA
 CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA FOGLIO DI ESERCIZI # 7 GEOMETRIA 2005/06 Ricordiamo le seguenti formule: L Area di un parallelogramma in R 2, di lati u = (u 1, u 2 ), v = (v 1, v 2 ) è:
CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA FOGLIO DI ESERCIZI # 7 GEOMETRIA 2005/06 Ricordiamo le seguenti formule: L Area di un parallelogramma in R 2, di lati u = (u 1, u 2 ), v = (v 1, v 2 ) è:
Esercitazione n 6. Esercizio 1: Determinare i punti di massimo e minimo relativo delle seguenti funzioni: (b)f(x, y) = 4y 4 16x 2 y + x
 Esercitazione n 6 1 Massimi e minimi di funzioni di più variabili Esercizio 1: Determinare i punti di massimo e minimo relativo delle seguenti funzioni: (a)f(x, y) = x 3 + y 3 + xy (b)f(x, y) = 4y 4 16x
Esercitazione n 6 1 Massimi e minimi di funzioni di più variabili Esercizio 1: Determinare i punti di massimo e minimo relativo delle seguenti funzioni: (a)f(x, y) = x 3 + y 3 + xy (b)f(x, y) = 4y 4 16x
GEOMETRIA svolgimento di uno scritto del 11 Gennaio 2012
 GEOMETRIA svolgimento di uno scritto del Gennaio ) Trovare una base per lo spazio delle soluzioni del seguente sistema omogeneo: x + y 5z = 3x y + z = x y + 8z =. Il sistema può essere scritto in forma
GEOMETRIA svolgimento di uno scritto del Gennaio ) Trovare una base per lo spazio delle soluzioni del seguente sistema omogeneo: x + y 5z = 3x y + z = x y + 8z =. Il sistema può essere scritto in forma
10 dicembre Soluzione esame di geometria - Ingegneria gestionale - a.a COGNOME... NOME... N. MATRICOLA...
 10 dicembre 003 - Soluzione esame di geometria - Ingegneria gestionale - a.a. 003-004 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura 3 ore. ISTRUZIONI
10 dicembre 003 - Soluzione esame di geometria - Ingegneria gestionale - a.a. 003-004 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura 3 ore. ISTRUZIONI
Soluzione facsimile 1 d esame di geometria - Ingegneria gestionale - a.a ISTRUZIONI
 Soluzione facsimile 1 d esame di geometria - Ingegneria gestionale - a.a. 003-004 COGNOME......................................... NOME......................................... N. MATRICOLA................
Soluzione facsimile 1 d esame di geometria - Ingegneria gestionale - a.a. 003-004 COGNOME......................................... NOME......................................... N. MATRICOLA................
Esercizio 2 SI NO Determinare l equazione cartesiana del piano passante per il punto P 0 = (2, 3, 1) e contenente
 GENNAIO 2014 A Calcolare gli autovalori della matrice ( 2 ) 2 1 3 Determinare l equazione cartesiana del piano passante per il punto P 0 = (2, 3, 1) e contenente i due vettori u = (1, 2, 2) e v = (5, 3,
GENNAIO 2014 A Calcolare gli autovalori della matrice ( 2 ) 2 1 3 Determinare l equazione cartesiana del piano passante per il punto P 0 = (2, 3, 1) e contenente i due vettori u = (1, 2, 2) e v = (5, 3,
Corso di Geometria BIAR, BSIR Esercizi 9: soluzioni
 Corso di Geometria 2010-11 BIAR, BSIR Esercizi 9: soluzioni Esercizio 1. Nello spazio sono dati i punti A = (1, 2, 3), B = (2, 4, 5), C = (1, 1, 4). a) Scrivere equazioni parametriche della retta r 1 passante
Corso di Geometria 2010-11 BIAR, BSIR Esercizi 9: soluzioni Esercizio 1. Nello spazio sono dati i punti A = (1, 2, 3), B = (2, 4, 5), C = (1, 1, 4). a) Scrivere equazioni parametriche della retta r 1 passante
