Operazioni sulle immagini. Multimedia

Transcript

1 Operazioni sulle immagini

2 Semplificazione: toni di grigio Per semplificare la trattazione del problema lavoreremo solo su immagini a toni di grigio. Le medesime operazioni descritte per tali immagini si estendono alle immagini RGB operando separatamente sui tre canali (piani) R, G e B e trattando ciascuno di essi come una immagine a toni di grigio indipendente dagli altri canali (soluzione non sempre apprezzata in ambito della ricerca).

3 L istogramma I pixel di una immagine sono una popolazione sulla quale possiamo calcolare tutte le quantità statistiche descrittive che si usano normalmente: Media, mediana, varianza, deviazione standard, quartili, percentili... Particolarmente importante è la conoscenza della distribuzione delle frequenze dei toni di grigio: l istogramma.

4 Istogramma Per ogni livello di grigio, riporta il numero di pixel di quel colore. Per una immagine I[m,n] si ha H(k)= numero di pixel di valore k E la somma di tutti gli H è esattamente mxn L istogramma è utile a comprendere in maniera immediata le caratteristiche dell immagine.

5 Istogramma 5

6 Immagini diverse potrebbero avere istogrammi simili! L istogramma non tiene conto della distribuzione spaziale 6 dei pixel!

7 Immagine chiara: istogramma più denso a destra 7

8 Immagine scura: istogramma più denso a sinistra 8

9 Immagine sottoesposta 9

10 Immagine sovraesposta 10

11 Operazioni sulle immagini 11

12 Operazioni sulle immagini Sono operazioni alterano i valori dei pixel di una immagine. L immagine finale apparirà differente da quella iniziale. Questi operatori lavorano sia su immagini a colori che su immagini a toni di grigio. 12

13 Operazione su una immagine Le elaborazioni nel dominio spaziale possono essere espresse come: g ( x, y) = T[ f ( x, y)] essendo f l immagine di ingresso alla elaborazione, g quella di uscita e T un operatore su f definito in un intorno di (x,y). 13

14 Tipi di operazioni La dimensione dell intorno di (x,y) definisce il carattere della elaborazione: puntuale (l intorno coincide con il pixel stesso); locale (per esempio una piccola regione quadrata centrata sul pixel); globale (l intorno coincide con l intera f). 14

15 Operatori puntuali 15

16 Operatori puntuali Si dice operatore puntuale, un operatore che preso in input il valore di un pixel ne restituisce uno cambiato che dipende esclusivamente dal valore del pixel in ingresso. 16

17 Tipiche operazioni puntuali: aggiunta o sottrazione di una costante a tutti i pixel (per compensare sotto o sovraesposizioni); inversione della scala dei grigi (negativo); espansione del contrasto; modifica (equalizzazione o specifica) dell'istogramma; presentazione in falsi colori. 17

18 Operatori puntuali Un operatore puntuale può essere rappresentato da una funzione che preso in input un valore x lo modifica in un valore y=f(x) con x,y appartenenti allo stesso campo di definizione (es. entrambi tra 0 e 255). Poiché un operatore puntuale dipende solo dal valore del pixel esso è completamente descritto da una tabella come quella che segue: IN OUT f(0) f(1) f(2) f(3) f(4) f(5) f(6) f(7) 18

19 Questa è universalmente l interfaccia che tutti i programmi commerciali di immagini offrono per la visualizzazione e gestione delle operazioni puntuali OUT f(x) 8 7 X X X 6 X 5 X 4 X 3 X X 2 X x IN

20 LUT Questo tipo di grafico si chiama look-up tables (LUT). 20

21 In Photoshop: aggiusta curve 21

22 Negativo E la più semplice operazione puntuale. Consiste nell associare al valore x del pixel il valore 255-x 22

23 Negativo Come cambia la curva? 23

24 Negativo Cosa cambia nell istogramma? 24

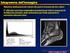
25 Esempio (a) Mammografia digitale (b) Negativo dell immagine ottenuta usando la trasformazione negativo

26 Incupimento dell immagine Come devo modificare la mia curva? 26

27 Incupimento dell immagine Cosa è cambiato nell istogramma? 27

28 Schiarimento dell immagine Come devo modificare la curva? 28

29 Schiarimento dell immagine Come è cambiato l istogramma? 29

30 Trasformazione logaritmica Si tratta di una trasformazione che consente di comprimere la gamma dinamica, permettendo la memorizzazione o la visualizzazione, con una scala dei grigi usuale, di immagini caratterizzate da escursioni di intensità molto ampie. Può essere espressa come: s = clog( 1+ r Dove c è una costante positiva che serve a normalizzare il risultato tra 0 e 255. ) 30

31 31

32 Trasformazione logaritmica 32

33 Trasformazione di potenza La trasformazione di potenza può essere espressa come: γ s = cr dove c e γ sono costanti positive. La costante c è scelta di volta in volta in modo da normalizzare i valori di s nell intervallo [0, 255]. Come vedremo, per valori di γ minori di 1 la trasformazione ha effetti analoghi alla trasformazione logaritmica (espansione della dinamica per bassi valori di r, compressione della dinamica per alti valori di r), mentre per valori di γ maggiori di 1 la trasformazione ha esattamente gli effetti opposti. 33

34 LUT al variare di gamma 34

35 35

36 Esempi Originale Gamma=3 Gamma=10 36 Gamma=17

37 37

38 38

39 Applicazione di gamma alla resa dei monitor Su un monitor CRT (con γ= 2.5) si può applicare una correzione pre-processando l input con la corrispondente funzione inversa: s = r 1/2.5 = r

40 40

41 Binarizzazione Produce una immagine che ha solo due livelli: nero e bianco. Si ottiene scegliendo una soglia T e mettendo a nero tutti i pixel il cui valore è minore a T e a bianco tutti gli altri. 41

42 Binarizzazione Come si agisce sulla curva? 42

43 Binarizzazione Come cambia l istogramma? 43

44 Variazioni di contrasto Aumentare il contrasto, significa rendere più evidenti le differenze di colore. Ciò si ottiene andando a cambiare il valore di un pixel con un altro che sia più scuro o più chiaro. 44

45 Aumento del contrasto 45

46 Aumento del contrasto Come si deve cambiare la curva? 46

47 47

48 Aumento del contrasto Cosa cambia nell istogramma? 48

49 Contrast Enhancement

50 Altro esempio 50

51 Diminuizione di contrasto 52

52 Diminuizione del contrasto Come cambio la curva? 53

53 Diminuizione del contrasto Come cambia l istogramma? 54

54 Curve non monotone È possibile fare delle variazioni alle curve in modo che questa diventi non monotona. Un esempio è la solarizzazione 55

55 Curve non monotone Ecco come si deve cambiare la curva: 56

56 Curve non monotone Ecco come è cambiato l istogramma: 57

57 Espansione del contrasto (contrast stretching) Serve per aumentare la dinamica di un immagine il cui istogramma è concentrato su un intervallo limitato dei valori possibili. Si ottiene spostando (con appositi algoritmi) i valori di un bin dell istogramma verso un altro bin non utilizzato. L istogramma apparirà in maniera differente, tipo pettine. Ciò è fatto per mettere in risalto che i bin mancanti sono stati distribuiti lungo altri livelli. 58

58 Contrast stretching Immagine originale Immagine corretta Toni non usati

59 Aritmetica sulle immagini Operando aritmeticamente può accadere che un pixel abbia: a) Un valore negativo; b) Un valore maggiore del massimo (tipicamente 255); c) Un valore non intero (facilmente risolubile con una approssimazione o un troncamento); 60

60 Normalizzazione I problemi a) e b) della precedente slide si chiamano problemi di range. Due le soluzioni più comuni: Settare a 0 (nero) i valori negativi e a 255 (bianco) i valori maggiori di 255. Ri-normalizzare il range trasformando ciascun valore secondo la equazione: v nuovo = 255 * (v vecchio min osservato ) (max osservato min osservato ) 61

61 Equalizzazione Si parla di immagine equalizzata quando il contributo di ogni differente tonalità di grigio è pressappoco eguale. Si parla anche di istogramma uniforme o appiattito. L equalizzazione si ottiene usando appositi algoritmi Attenzione non sempre la equalizzazione migliora l immagine! 62

62 Immagine equalizzata

63 Immagine equalizzata 64

64 65

65 Algoritmo di Equalizzazione Se r k è un livello di grigio e n k il numero di pixel nell immagine MxN di quel livello di grigio, si può definire Se facciamo il plot di r k versus p r (r k ) quello che si ottiene è l istogramma dell immagine. 66

66 Algoritmo di Equalizzazione I nuovi valori di grigio dell istogramma sono così definiti: 67

67 Algoritmo di Equalizzazione: Esempio Sia data una immagine a 3 bit (L=8) con 64x64 pixel (MN=4096) con la seguente distribuzione di intensità: 68

68 Algoritmo di Equalizzazione: Esempio Applicando la formula si ha: Arrotondando: 69

69 Algoritmo di Equalizzazione: Esempio 70

70 Algoritmo di Equalizzazione: Esempio 71

71 Equalizzazione: un esempio

72 Equalizzazione dell Istogramma Come si può notare, l istogramma della immagine equalizzata non è piatto. D altro canto, l uniformità della p s (s) è stata verificata solo nel caso continuo, e non nel caso discreto. Tuttavia, i livelli di grigio dell immagine equalizzata spaziano su tutta la dinamica possibile (anche se alcuni livelli possono non essere presenti), ed in particolare raggiungono sempre il bianco. Al conseguente incremento del contrasto si possono aggiungere effetti sgradevoli quali lo sgranamento dell immagine, la comparsa di false regioni, ecc., soprattutto quando il contrasto dell immagine originale è molto basso. L apparenza dell immagine può essere migliorata anche con altre tecniche di modifica del contrasto, ma l equalizzazione dell istogramma ha il vantaggio di essere completamente automatica.

73 Bit-plane Un immagine con una profondità colore di N bit può essere rappresentata da N piani di bit (bit-planes), ciascuno dei quali può essere vista come una singola immagine binaria. In particolare si può indurre un ordine che varia dal Most Significant Bit (MSB) fino al Least Significant Bit (LSB). 91

74 Bit-plane 92

75 Bit-planes Most Significant bit (MSB) Least Significant bit (LSB) 93

76 Bit-planes 94

77 Bit-planes: Osservazioni I piani di bit più significativi contengono informazioni sulla struttura dell immagine, mentre quelli via via meno significativi forniscono i dettagli sempre più piccoli. Si noti che solo i piani dal 7 al 3 contengono dati significativi dal punto di vista visuale. Il rumore delle immagini e gli errori di acquisizione sono più evidenti nei piani bassi. 95

78 Bit-planes 96

79 Bit-plane 97

80 Esempio: Questo genere di scomposizione è molto utile per eliminare tutti i valori compresi in un certo range. Ad esempio, se si vogliono eliminare tutti i grigi compresi tra 32 e 64, è necessario porre a 0 il quinto bit, e quindi tutto il piano 5. 98

81 Bit-plane 99

82 100

83 Operatori locali 101

84 Operazioni locali Il valore d uscita di ogni pixel dipende da un limitato intorno del corrispondente punto in input. Sono usati per migliorare la qualità delle immagini o per estrarre delle informazioni dall immagine. Si possono pensare come filtraggi dell immagine. Un filtraggio è ottenuto facendo la convoluzione tra l immagine ed una matrice. 102

85 Operatori Lineari Un operatore F : V W si dice LINEARE se per ogni coppia di vettori v 1 e v 2 in V e per ogni coppia di scalari a,b si ha che: F(a v 1 + b v 2 ) = a F(v 1 ) + b F(v 2 ) Conseguenza: se conosco una base di V ed il comportamento dell operatore F su ogni elemento di tale base, posso calcolare il comportamento di F su ogni elemento di V. 103

86 Esempi Sia F l operatore da R 3 a R 3 che trasforma ogni vettore (x,y,z) in (x/2, y/3, z/4). Esso è lineare ed è completamente descritto una volta che si descrive il suo comportamento su ogni elemento della base canonica: F((1,0,0)) = (1/2, 0, 0); F((0,1,0)) = (0, 1/3, 0); F((0,0,1)) = (0, 0, 1/4). L operatore puntuale negativo NON E LINEARE perché F((x,y,z)) = (255-x, 255-y, 255-z); È diverso da x*f((1,0,0))+y* F((0,1,0)) z* F((0,0,1)) = x*(255-1, 0, 0)+y* (0, 255-1, 0)+z*(0, 0, 255-1) = x*(255-1)+y* (255-1)+z*(255-1) 104

87 NON invariante per traslazione L esempio nella slide precedente ha un comportamento che non è lo stesso su tutti gli elementi della base canonica di R N. Infatti: il comportamento varia da elemento ad elemento a seconda della posizione all interno della immagine. Questo è un operatore NON invariante per traslazioni! Per descrivere questi operatori, dobbiamo conoscere il suo comportamento su ciascun impulso in ciascuna locazione delle immagini! Attenzione: questi operatori non sono cattivi ma solo difficili da studiare 105

88 Operatori invarianti per traslazione Un operatore si dice invariante per traslazione (shift invariant) quando il suo comportamento sulle immagini impulsive è sempre il medesimo indipendentemente dalla posizione in cui si trova il pixel. Tutti gli operatori puntuali sono invarianti per traslazione (anche se non sono lineari). 106

89 Riassumendo: Se F è lineare per descriverlo basta conoscere il comportamento su tutte le immagini impulsive Se F è shift invariant si comporta allo stesso modo su tutti gli impulsi, indipendentemente dalla loro posizione Se F è sia lineare che shift invariant per descriverlo basta conoscere come si comporta su un solo impulso. La risposta all impulso o point spread function di F è la carta di indentità di tale operatore. 107

90 Ad un operatore lineare e shift invariante corrisponde una maschera ma vale anche il viceversa: ad una maschera corrisponde un simile operatore ESEMPIO Si consideri l operazione che preso un impulso: lo trasforma in: Tale risposta all impulso o PSF definisce completamente un operatore lineare e invariante per traslazioni F. Spesso un operatore su una immagine prende il nome di filtro. La matrice che descrive la risposta all impulso si chiama anche kernel o maschera dell operatore. Essa è detta anche maschera di convoluzione di F per ragioni che vedremo tra breve. 108

91 prima dopo 109

92 Kernel finiti o infiniti e complessità La grandezza del kernel può variare fino ad essere infinita Per ragioni pratiche, però, si usano solo kernel con dimensioni finite. Le dimensioni del kernel influenzano la complessità della operazione di filtraggio. Tale complessità dipende ovviamente anche dal numero dei pixel di una immagine. 110

93 Perché filtri convolutivi? I filtri lineari e invarianti per traslazione vengono chiamati anche filtri convolutivi. Dobbiamo studiare la operazione di convoluzione per capire meglio come un filtro può essere calcolato. Inoltre la convoluzione è un fenomeno estremamente importante per ogni tipo di signal processing e per la descrizione di numerosi eventi fisici. 111

94 Convoluzione: proprietà Per indicare l operazione di convoluzione si usa la notazione h = f g La convoluzione è commutativa f g = g f La convoluzione è associativa (f g) h = f (g h) 112

95 g f 113

96 Nel caso finito (1) Se il kernel f ha dimensioni kxh la formula va riscritta nella seguente maniera h k 2 = k / 1 h / 2 1 m, n = * i 2 j= h / 2 ( f ) i, j gm+ i, n+ j a b c d e f g h i Se gli indici del kernel sono disposti in modo da avere il punto di coordinate (0,0) nella posizione centrale. 114

97 Nel caso finito (2) h Se il kernel f ha dimensioni kxh la formula va riscritta nella seguente maniera k, h = m, n fi, j * i= 1, j= 1 g m+ ( i k + k / 2 ), n+ ( j h+ h / 2 Se gli indici del kernel sono disposti partendo da 1 fino ad arrivare ad h o k. ) a b c d e f g h i 115

98 Esempio

99 Esempio

100 Esempio

101 Esempio

102 Convoluzione e filtraggio Applicare un filtro lineare e shift invariante ad una immagine è equivalente a calcolare la convoluzione del kernel del filtro con l immagine. 120

103 Nell implementazione Un problema è quello dei bordi: come fare la convoluzione e il filtraggio ai bordi? POSSIBILI SOLUZIONI: a) Filtrare solo le zone centrali dell immagine b) Supporre che tutto intorno all immagine ci sia 0 c) Assumere una topologia toroidale : quando si sfora a destra si rientra a sinistra, quando si sfora in basso di rientra in alto e viceversa; d) Aggiungere una riga all inizio uguale alle riga precedente, una riga alla fine uguale all ultima riga, una colonna all inizio uguale alla colonna iniziale, e una colonna alla fine uguale alla colonna finale. 121

104 a) Filtrare solo le zone centrali dell immagine input Le aree in grigio non verranno calcolate output

105 b) Supporre che tutto intorno all immagine di input ci sia lo 0 input output

106 c) Riempire le righe e le colonne aggiunte in maniera toroidale input output

107 d) Riempire le righe e le colonne aggiunte con i valori più vicini input output

108 Estrazione di contorni 126

109 Caratteristiche di immagini In Visione Computazionale il termine feature di immagini si può riferire a due entità possibili: Una proprietà globale di un immagine o una regione (es. il livello di grigio medio, la distribuzione di colore,...); Una parte dell immagine con alcune proprietà speciali (es. una linea, un ellisse,...) Le caratteristiche o proprietà di cui devono godere tali features, per poter essere utilizzate in maniera robusta dipendono dal contesto applicativo

110 Feature Tipicamente le feature hanno una dimensione molto ridotta rispetto ai dati di origine (ad esempio da un immagine di alcuni MB si potrebbero voler estrarre solo poche decine di valori). Sono generalmente (ma non necessariamente) costituite da una serie di dati numerici, rappresentabile come un vettore multidimensionale. Esempi di finalità specifiche che la fase di feature extraction si può prefiggere (per esempio per migliorare il successivo riconoscimento): Riduzione del rumore e di altre informazioni non utili Estrazione di dati invarianti per determinate trasformazioni (es. rotazione e scala) Normalizzazione dei dati per renderli maggiormente confrontabili

111 Feature globali Le feature globali (per immagini non opportunamente segmentate) sono inefficaci se l oggetto cercato non è separato dal background L orientazione corrente è utilizzare feature locali che in genere dipendono sia dalla forma che dalla texture degli oggetti presenti nella scena

112 Feature locali Un passo importante dell elaborazione visiva consiste nell identificare feature locali che siano utili ad interpretare l immagine. Le feature locali sono parti dell immagine facilmente rilevabili, che possono corrispondere o meno a parti della scena. Ci occuperemo nell ordine di Edge.

113 Edge Detection L estrazione dei contorni (edge) è sicuramente uno degli argomenti che hanno ricevuto più attenzione nella letteratura sull image processing. Il contorno di un oggetto rappresenta infatti la separazione tra l oggetto e lo sfondo o tra l oggetto ed altri oggetti, per cui la sua estrazione è molto spesso il primo passo verso l individuazione dell oggetto.

114 Edge su Lena

115 Origine degli edge surface normal discontinuity depth discontinuity surface color discontinuity illumination discontinuity

116 Edge Detection Un edge si presenta in una immagine come il confine tra due regioni caratterizzate da proprietà dei livelli di grigio in qualche modo distinguibili. Ipotizziamo inizialmente che le regioni in questione siano sufficientemente omogenee, di modo che la determinazione della transizione tra le due regioni sia possibile sulla sola base della discontinuità dei valori di grigio. Le prime tecniche di edge detection che analizziamo sono basate sull applicazione di un operatore locale di derivata.

117 Edge Detection: Teoria Consideriamo il comportamento delle derivate in corrispondenza a particolari andamenti del livello di grigio f(x): andamento costante (segmento piatto nel caso 1-D) e discontinuità, sia a gradino che a rampa, che possono modellare punti isolati, linee ed edge in una immagine. Le derivate di una funzione digitale possono essere definite in termini delle differenze tra i valori assunti dalla funzione in punti vicini. Qualunque sia il modo con cui si utilizzano queste differenze, devono essere soddisfatti i seguenti requisiti. La derivata prima deve essere nulla nelle zone piatte non nulla in presenza di una discontinuità non nulla lungo una rampa

118 Estrazione dei contorni Gli operatori locali ci aiutano ad estrarre i contorni da una immagine. I contorni sono definiti come delle discontinuità locali della luminanza. Gli edge detector forniscono immagini in cui sono preservate le variazioni di luminanza ed eliminate tutte le altre informazioni. 136

119 Esempi di lato in 1D 137

120 Edge in pratica

121 Direzione del gradiente

122 Edge detector basati sulla derivata prima Se ho un segnale monodimensionale e calcolo la derivata prima, scopro che i lati sono i corrispondenza dei massimi della derivata. Quindi i filtri devono calcolare la derivata in direzione x quella in direzione y e poi combinarle insieme. 140

123 Filtri basati sul gradiente L implementazione di queste equazioni può essere effettuata usando le seguenti maschere 2x2 dette anche operatori di Roberts: I valori assoluti delle risposte delle due maschere vengono sommati per determinare f. Più comune è tuttavia l impiego di maschere 3x3, che rendono più semplici le operazioni di filtraggio:

124 Operatori di Roberts: Esempi

125 Filtri basati sul Gradiente Gli operatori di gradiente sicuramente più diffusi, in grado di effettuare simultaneamente la differenziazione lungo una direzione e una media spaziale lungo la direzione ortogonale, che riduce la sensibilità al rumore, sono: Prewitt Sobel

126 Kernel notevoli: lati orizzontali Ne esistono molti, ne presentiamo due: X-Prewitt 144

127 Sobel x 145

128 Prewitt x 146

129 Dopo l applicazione di X-Prewitt e un passo di equalizzazione Dopo l applicazione di x-sobel e un passo di equalizzazione

130 Kernel notevoli: lati verticali La situazione è identica al caso dei lati orizzontali, i filtri sono solo ruotati di 90 gradi. 148

131 Sobel y 149

132 Prewitt y 150

133 Dopo l applicazione di Y-Prewitt e un passo di equalizzazione Dopo l applicazione di y-sobel e un passo di equalizzazione

134 Migliori risultati Si ottengono con algoritmi più sofisticati (non lineari) per il calcolo della grandezza del gradiente (somma del quadrato della risposta di un edge finder orizzontale e del quadrato della risposta di un edge finder verticale) Si ottengono con strategie più intelligenti (algoritmo di Canny, algoritmi fuzzy, tecniche di backtracking eccetera) 152

135 Edge detector basati sulla derivata seconda Se ho un segnale monodimensionale e calcolo la derivata seconda, scopro che in corrispondenza del lato essa passa per lo zero. 153

136 Kernel notevoli: Laplaciano Il filtro più diffuso per calcolare la derivata seconda è detto Laplaciano, ed è definito dalla maschera: 154

137 Laplaciano 155

138 Laplaciano 156

139 Zero-crossing Dopo aver applicato l operatore Laplaciano è necessario che si verifichi la condizione di Zero-crossing. Cioè, deve sempre accadere che rispetto al punto in questione ci sia nel suo intorno un valore positivo e un valore negativo. 157

140 Filtri di sharpening Sono filtri il cui scopo è quello di incrementare la nitidezza di una immagine aumentando il contrasto locale. Questa è una operazione opposta allo sfocamento. Per ottenere tale effetto si può adottare una maschera che, derivata dal Laplaciano, rinforza i lati presenti nell immagine. Purtroppo essa rinforza anche il rumore presente nella immagine! 158

141 Filtro di sharpening 159

142 Unsharp mask: un algoritmo non lineare L uso del kernel derivato dal Laplaciano per fare edge enhancing ha un difetto: esso viene applicato SEMPRE a tutti i pixel dell immagine. Come conseguenza esso accentua i dettagli anche nelle zone omogene mettendo in evidenza i difetti ed il rumore. Sono stati proposti vari algoritmi per evitare questo fenomeno. La famiglia di algoritmi chiamata unsharp mask è la più famosa usata per questo scopo. Noi non vedremo i dettagli di questo algoritmo. 160

143 Edge Detection in pratica

144 Ancora Noise Gli operatori di gradiente risultano quindi poco efficaci in presenza di rumore. Per esempio, applicando gli operatori di Sobel ad una versione rumorosa dell immagine di test si ottiene: Il problema può essere alleviato estendendo l area di calcolo del gradiente, il che consente una migliore azione di media (Farlo per esercizio). Più in generale, possono essere presi in considerazione degli operatori composti, nei quali una operazione di smoothing per la riduzione del rumore è compiuta prima dell operazione di differenziazione.

145 Operatore DroG Un esempio molto noto di operatore di gradiente composto è la Derivata della Gaussiana (DroG), nel quale l operazione di smoothing utilizza una funzione gaussiana. La gaussiana è una funzione a simmetria rotazionale la cui equazione nel caso 2-D continuo è la seguente: h( x, y) = e 2 x + y 2 2σ 2 = e 2 r 2σ 2 Il valore di σ determina l apertura della Gaussiana (ovvero la deviazione standard ossia ossia il valore di r per il quale h si riduce a 1/ e del massimo), che aumenta al crescere di σ.

146 Operatore DroG In figura una funzione gaussiana in cui h è rappresentata, per diversi valori di σ, al variare di r, quindi in un piano passante per il suo asse di simmetria. Dalla risposta impulsiva è possibile ricavare i coefficienti del relativo kernel di convoluzione attraverso un opportuno campionamento della funzione continua, a partire dalla origine, che rappresenta il punto di applicazione della maschera. Nel caso della gaussiana il ruolo di σ è determinante nella definizione dei pesi della maschera: se l apertura è maggiore, l azione di filtraggio può riguardare un intorno più ampio del punto centrale. A tal fine, σ è normalmente espresso in pixel.

147 Gaussiana con Kernel 3x3, 5x5 (sigma = 0.5) Per quanto riguarda l operatore DroG, le risposte impulsive lungo le due direzioni, che lo caratterizzano completamente, si possono determinare effettuando la convoluzione delle due componenti del gradiente, nella formulazione preferita, con la maschera precedente che caratterizza la gaussiana.

148 Operatore DroG In alternativa, si può procedere al calcolo delle derivate della gaussiana rispetto a x e a y, che rappresentano le componenti dell operatore DroG nel caso continuo: h x = 2 x + y 2 2σ 2 x + y 2σ 2 2 x y 2 σ 2 e Le corrispondenti maschere si possono ottenere campionando le due funzioni. Per esempio, per la componente lungo x si ha la seguente situazione, sempre nell ipotesi σ = 0.5: h y = σ 2 e

149 Operatore DroG

150 Operatori basati sul Laplaciano La determinazione degli zero crossing della derivata seconda della f(x,y) localizza con precisione i contorni dell immagine, mentre il segno della derivata seconda permette di stabilire l appartenenza di un pixel al versante scuro o al versante chiaro di un contorno. Un modo molto comune di effettuare le operazioni di derivata seconda di una f(x,y) in un punto è quello di calcolare il laplaciano in quel punto. Ricordiamo che data una funzione f(x,y), il laplaciano di f in (x,y) è definito come: L( x, y) = 2 f = 2 f 2 x + 2 f 2 y

151 OPERATORE LAPLACIANO Con la traslazione di un pixel in orizzontale, ottenuta sostituendo j con j-1 si calcola il valore approssimato del laplaciano nel punto (i,j) definito da: 2 f 2 = f ( i, j + 1) 2 f ( i, j) + f ( i, j 1) x operando in modo analogo per la componente verticale si ottiene: 2 f 2 = f ( i + 1, j) 2 f ( i, j) + f ( i 1, j) y Queste approssimazioni conducono alle corrispondenti maschere di convoluzione orizzontale e verticale: 1 h R = [ 1 2 1] h C = 2 1 Dalla combinazione delle componenti orizzontali e verticali si ottiene una singola maschera di convoluzione del laplaciano: h( i, j) = =

152 Operatori basati sul Laplaciano Il modo più semplice di approssimare il laplaciano nel caso discreto consiste nel calcolo delle differenze delle derivate prime lungo i due assi: L(x,y)=[f(x,y)-f(x-1,y)]-[f(x+1,y)-f(x,y)]+[f(x,y)-f(x,y-1)]-[f(x,y+1)- f(x,y)] Pertanto L(x,y)=4 f(x,y)-f(x-1,y)-f(x+1,y)-f(x,y -1)- f(x,y+1) Il Laplaciano si può quindi implementare come un filtro la cui risposta impulsiva è:

153 Operatori basati sul Laplaciano La versione normalizzata prevede un fattore moltiplicativo pari a ¼ Una versione (normalizzate) del laplaciano riferito agli 8-vicini, quindi con le differenze delle derivate prime mediate su tre righe e tre colonne, è: In questo caso il fattore moltiplicativo è pari a 1/8. Il laplaciano è eccessivamente sensibile al rumore (in quanto operatore di derivata seconda) ed è incapace di rilevare la direzione del contorno (in quanto entità scalare). Per tali motivi, il laplaciano è raramente usato da solo per l edge detection.

154 Laplacian of Gaussian Di Marr e Hildreth è stata l idea di utilizzare il laplaciano in connessione con un filtro di smoothing, ancora una volta una gaussiana, realizzando un operatore detto Laplaciano della Gaussiana o LoG (in figura una sezione trasversale ottenuta per σ=1) + = = = ), ( σ σ σ σ σ r r y x e r h e e y x h

155 LoG in 2D Si tratta quindi di una funzione a simmetria circolare, con ZC per r=±σ Si può dimostrare che il valor medio della funzione è 0, e lo stesso avviene per il risultato della sua convoluzione con una immagine. La tipica forma a sombrero indica inoltre che la convoluzione dell operatore LoG con una immagine provoca un blurring (di entità proporzionale a σ) dell immagine stessa, e quindi ha un effetto positivo in termini di riduzione del rumore.

156 LoG Il vantaggio principale offerto dall operatore LoG resta comunque quello legato alla presenza degli ZC. All immagine in alto a sinistra viene applicato l operatore LoG, con il risultato mostrato in alto a destra come immagine di intensità, nella quale i neri rappresentano i valori più negativi, i bianchi i valori più positivi. Dopo la binarizzazione: valori negativi a 0 e i valori positivi a 1 (in basso a sinistra). Gli ZC, cioè i confini tra zone nere e bianche nell immagine binaria, sono ora facilmente individuabili (in basso a destra)

157 Laplaciano e Zero Crossing

158 Edge Linking

159 Metodo di Canny Un approccio analitico è stato invece seguito da J. Canny, che ha studiato in dettaglio il comportamento dell operatore gradiente applicato ad un contorno rumoroso. Il modello di bordo considerato è un fronte ripido monodimensionale b(x) cui è aggiunto rumore Gaussiano bianco. Si assume che l individuazione del bordo sia realizzata tramite una convoluzione con un filtro f(x) avente risposta impulsiva h(x) antisimmetrica e nulla al di fuori di un intervallo [-W,W]. Un bordo è individuato da un massimo locale della convoluzione tra l immagine ed il filtro. Il filtro è scelto sulla base di tre criteri di efficacia definiti da Canny.

160 Criteri di Canny Buona capacità di individuazione: l operatore ha una bassa probabilità di non individuare un bordo reale (elevata sensibilità falsi negativi) ed una bassa probabilità di individuare falsi bordi (elevata specificità falsi positivi) Buona capacità di localizzazione: i punti evidenziati dall operatore dovrebbero essere quanto più vicini possibile al centro del bordo reale Unicità della risposta: l operatore dovrebbe fornire una sola risposta in corrispondenza di un bordo reale

161 Canny edge detector Immagine Input (Lena)

162 Canny edge detector Norma del gradiente

163 Canny edge detector thresholding

164 Canny edge detector Thinning (non-maximum suppression)

165 Canny Step 1 Calcolo Gradiente (Drog): magnitudo e direzione Step 2 Eliminazione dei punti il cui valore del gradiente non è superiore ai valori dei vicini (interpolazione lineare) nella direzione del gradiente Step 3 Sogliatura con Isteresi mediante 2 soglie T1 e T2 Step 4 Edge linking per legare gli strong edge individuati con eventuali weak edge adiacenti

166 Canny Primo Step L Individuazione (detection) dell edge, si realizza attraverso la massimizzazione del rapporto segnale-rumore (delle ampiezze) del gradiente. L espressione adoperata per il rapporto s/r è: dove h E è l ampiezza del gradino mentre σ n è la deviazione standard del rumore.

167 Canny Step 2 I punti riconosciuti come di edge dovrebbero essere il più possibile vicini al centro dell edge effettivo. A tal fine è definito un fattore di localizzazione (h è la derivata di h):

168 Canny Step 3 Per quanto riguarda l unicità della risposta dell operatore la distanza x m tra due picchi del gradiente, in presenza solo di rumore, è supposta uguale ad una frazione k della larghezza W dell operatore: x m =kw Canny ha combinato i tre criteri, cercando il massimo del prodotto S(h)L(h) soggetto al vincolo espresso dalla condizione di cui sopra

169 Canny - Discussioni Anche se la complessità della formulazione impedisce la determinazione di una soluzione analitica, è possibile procedere alla ricerca del massimo con metodi numerici. La figura mostra i profili di diversi valori della risposta impulsiva del filtro di Canny al crescere di x m. Si può notare come per grandi valori di x m l operatore di Canny è ben approssimato dall operatore DroG. In effetti, il filtro adoperato nelle implementazioni del metodo di Canny è proprio di questo tipo.

170 Canny: Non-Maximum Suppression L'immagine di risposta all'operatore, se vista come una superfice 3D, è caratterizzata da valli (valleys) e rilievi. Le curve di massimo dei rilievi, le creste, sono detti ridges. Per ottenere una risposta univoca dall'edge detector è necessario un algoritmo che sopprima tutti i responsi multipli, ovvero i pixel che sono caratterizzati da valori alti di risposta all'operatore ma che non sono massimi locali per esso. La non-maximum suppression si ottiene cercando i pixel che sono di massimo per la magnitudo lungo la direzione del gradiente. Si tengono solo i ridges sopprimendo tutti gli altri punti che non sono all'altezza massima locale.

171 Non-maximum suppression Si verifica l esistenza di un massimo locale lungo la direzione del gradiente. Ciò richiede l interpolazione dei pixel mancanti (pixel p ed r in figura)

172 Canny: Thresholding La qualità dei risultati ottenibili con il metodo di Canny, superiore a quella di tutti gli altri operatori di gradiente, si giustifica con il fatto che il metodo utilizza due soglie, una per la individuazione degli edge più netti, l altra per l individuazione degli edge più deboli. Questi ultimi sono però presi in considerazione solo se risultano connessi ad edge netti. Ruolo fondamentale nell'algoritmo di Canny gioca anche la scelta di sostituire il tradizionale approccio di sogliatura (thresholding) a soglia singola con una tecnica a doppia soglia detta histeresys thresholding.

173 Canny: Thresholding La doppia sogliatura (Histeresys thresholding) viene operata dopo l'applicazione della non-maximum suppression. Si fissano due soglie T1 e T2 con T1>T2 Tutti i punti di valore maggiore di T1 sono di edge; Tutti i punti di valore compreso fra T1 e T2 sono detti weak edges. Un weak edge diventa edge solo se è contiguo ad un edge.

174 Canny Diminuisce pertanto l influenza del rumore, ed aumenta la probabilità di rivelare veri edge deboli. In tutti i metodi di edge detection basati sul gradiente, occorre confrontare il risultato dell operazione di derivazione in ogni punto dell immagine con uno (o più) valori di soglia, per determinare se si tratta di un punto di edge. Il valore di soglia determina direttamente la sensibilità dell edge detector. Per immagini non rumorose, la soglia può essere scelta in modo che le discontinuità di ampiezza, anche relative a zone a basso contrasto, siano interpretate come edge. Nelle immagini rumorose la scelta del valore di soglia è molto più critica, diventando un elemento di tradeoff tra la possibilità di rivelare falsi contorni (indotti dal rumore) e la possibilità di mancare contorni veri (relativi a piccoli dettagli).

175 Edge Linking Individuato il punto di edge si costruisce la tangente alla curva (normale al gradiente in quel punto) e si usa questa informazione per predire il successivo punto (in questo caso r o s) (Forsyth & Ponce)

176 Canny Integrando la fase di thresholding con quella di linking il metodo ne guadagna in robustezza e versatilità.

177 Canny Step 1 Calcolo Gradiente (Drog): magnitudo e direzione Step 2 Eliminazione dei punti il cui valore del gradiente non è superiore ai valori dei vicini (interpolazione lineare) nella direzione del gradiente Step 3 Sogliatura con Isteresi mediante 2 soglie T1 e T2 Step 4 Edge linking per legare gli strong edge individuati con eventuali weak edge adiacenti

178 Impatto del parametro σ (Gaussian kernel size) Input Canny con σ=1 Canny con σ=2 La scelta di σ impatta sulla detection dei relativi edge come segue: Alti valori di σ permettono di trovare edge a scale più grandi Piccoli valori di σ permettono di scovare I dettagli più fini

179 Esempi