Facoltà di Matematica, Fisica e Scienze Naturali Corso di Laurea in Scienze dell informazione sede di Cesena. Tesi di Laurea
|
|
|
- Achille Vacca
- 5 anni fa
- Visualizzazioni
Transcript
1 UNIVERSITÀ DEGLI STUDI DI BOLOGNA Facoltà di Matematica, Fisica e Scienze Naturali Corso di Laurea in Scienze dell informazione sede di Cesena Tesi di Laurea Rilevazione di segnali tramite trasformata KLT nel progetto SETI Relatori: prof. Enzo Gandolfi dott. Orlati Andrea Presentata da: Pierpaolo Pari Anno accademico 22-23
2 Sommario Se dal profondo del cosmo giungessero a noi segnali intelligenti con gli attuali metodi di analisi solo una piccola tipologia di questi segnali potrebbero essere riconosciuti. La KLT per la rilevazione di segnali è un utilizzo pionieristico nella radioastronomia e nell ambito del progetto SETI. I
3 II
4 Ringraziamenti Desidero ringraziare l Osservatorio Radioastronomico del CNR di Medicina per avermi permesso l utilizzo degli strumenti di calcolo per lo svolgimento di questa tesi, un ringraziamento a tutti i componenti team SETI ITALIA, in particolare all Ing. Stelio Montebugnoli per la sua costante presenza durante tutto lo sviluppo di questa tesi e al Dott. Andrea Orlati per la disponibilità e i suggerimenti. Un doveroso ringraziamento al Dott. Claudio Maccone(Alenia Spazio) per aver gettato le prime luci sull argomento. In ultimo ma non per questo di meno importanza ringrazio mio padre per i suoi consigli, mia madre per aver sopportato quest ultimo periodo di tesi e i miei fratelli che mi hanno sempre appoggiato. Grazie. III
5 IV
6 Indice Sommario Ringraziamenti I III 1 Introduzione Onde Radio e Progetto S.E.T.I Lasituazioneattuale LaTesi Rilevazione di Segnali e Trasformata di Fourier SeriediFourier Latrasformata FFT RilevamentodiSegnali L autocorrelazione Trasformata KLT L approcciointuitivo Lateoria:casocontinuo Ilcasodiscreto AnalisidiSegnali L eigen-spectrum L algoritmo V
7 4 Gli autovalori Introduzionealproblema La soluzione del problema MetododellePotenze IlmetododiJacobi Il metodo di Lanczos La piattaforma Glistrumenti Ilsistema PENTEK MCJ Schedadicontrollo Il Software Ilclient Server PPC KLT Server Itempi Test SoftwarediSimulazione Testevalutazioni Conclusioni Conclusioni Sviluppi Futuri Basi... I.2 Trasformazioni di similitudine I.3 MatriceSingolare... II Bibliografia... 3 VI
8 VII Alla mia Famiglia...
9 VIII
10 Capitolo 1 Introduzione 1
11 1 Introduzione 1.1 Onde Radio e Progetto S.E.T.I Le onde radio sono una particolare sottoclasse della famiglia delle Onde Elettromagnetiche (vedi 1.1) che sono classificate in base alla loro frequenza o lunghezza d onda. Le onde comprese fra i 4-7nm sono appartenenti alla fascia del visibile, quelle fra i.7µ 1mm appartengono alla fascia degli infrarossi, le onde fra 1mm 1m appartengono quelle delle microonde mentre quelle onde superiori a 1m appartengono alla fascia delle onde radio. A partire dal 1895, anno in cui Guglielmo Marconi lanciò il primo segnale radio della Storia, sono state inviate nello spazio onde elettromagnetiche a varie frequenze e le cui potenze sono aumentate con l aumentare della tecnologia. All inizio erano solo segnali radio ma poi si aggiunsero trasmissioni TV, impulsi laser e tanti altri. Questi segnali sono tutt ora in espansione radiale dal nostro pianeta propagandosi in un raggio di 6 o 7 anni luce nel cosmo. Queste emissioni radio causano notevoli problemi agli Figura 1.1. Spettro Elettromagnetico 2
12 1.1 Onde Radio e Progetto S.E.T.I astronomi e a tutti coloro che usano sistemi di acquisizione radio: il problema di cui stiamo parlando è quello delle interferenze. Esempi di questo tipo di interferenze sono tutti quei servizi in radio-frequenza quali i palloni aerostatici usati in meteorologia, le trasmissioni satellitari,... Oltre alle interferenze di provenienza terrestre naturalmente si aggiunge la radiazione di fondo generata dal big bang, più nota come rumore di fondo(cmb 1 ). Il progetto SETI(acronimo di Search for Extra Terrestrial Intelligence) nasce nel 1959 ad opera di due fisici Cocconi e Morrison i quali misero in evidenza il potenziale rappresentato dall uso delle radioonde per la comunicazione interstellare. Qualche mese più tardi Frank Drake puntava il suo telescopio Tatel, 26 metri di diametro sintonizzato sulla frequenza di 1.42 GHz, verso le stelle Tau Ceti ed Epsilon Eridani: le due più vicine alla terra, fra quelle di tipo solare e con probabili pianeti. Anche se tale esperimento non ha portato fino ad ora alla ricezione di 1 Cosmic Microwave Background Figura 1.2. Finestra delle microonde 3
13 1 Introduzione segnali di risposta, questo evento fu di fatto l inizio della moderna era SETI. Supportato dalla famosa equazione di Drake, N = R f p n e f l f i f t L, che vuole enumerare le civiltà nella nostra galassia, il progetto in questione si propone di analizzare e rilevare eventuali segnali provenienti da radio-sorgenti di origine intelligente. I fattori della precedente equazione hanno il seguente significato: R è il numero di stelle di tipo solare che nascono ogni anno, f p frazione di queste stelle che possiede un sistema planetario, n e numero medio di pianeti di tali sistemi che si trovano nella zona di abitabilità della stella, f l frazione di di questi pianeti su cui la vita è presente se pur in modo primitivo, f i quantità di pianeti su cui la vita si è evoluta fino a sviluppare l intelligenza, f t frazione di mondi intelligenti padroni di una tecnologia osservabile dalla terra infine L che indica la durata media in anni di tali civiltà. La frequenza 1.42GHz(corrispondente ad una lunghezza d onda di 21cm) fu scelta poichè corrisponde all emissione spontanea di radiazione da parte degli atomi di idrogeno neutro interstellare. Tale elemento è quello più diffuso nell universo ed una eventuale razza aliena, tecnologicamente avanzata, conoscerebbe sicuramente la sua frequenza di emissione. Questa particolare frequenza ha il vantaggio di trovarsi in una regione dello spettro radio particolarmente adatto per rivelare deboli segnali artificiali di provenienza extraterrestre. In tale regione infatti, detta finestra delle microonde, il rumore di fondo della galassia e l assorbimento dovuto all atmosfera terrestre sono entrambi ai loro minimi assoluti. La 1.2 evidenzia la finestra delle microonde: la fascia verticale scura al centro dell immagine, si mostra che 1.42Ghz ricadono proprio nell intervallo della finestra in questione [1GHz,11GHz]. Come si può notare la ricerca di segnali si concentra su precise frequenze, in particolare l analisi SETI punta alla rilevazione di segnali monocromatici. Il Seti Institute coordina le attività mondiali nella ricerca di segnali extraterrestri, in Italia tale ricerca è effettuata 4
14 1.1 Onde Radio e Progetto S.E.T.I per mezzo di uno spettrometro 2 molto potente collegato all antenna che analizza i segnali ricevuti mentre si stanno svolgendo le normali attività radioastronomiche. Figura 1.3. Parabola dell Osservatorio Radioastronomico di Medicina(Bo) Lo sforzo che attualmente i ricercatori e ingegneri stanno facendo si sta muovendo nella costruzione di Super-radiotelescopi che avranno sensibilità sempre maggiori. Questi nuovi strumenti permetteranno una scansione dell intera volta celeste a tutto cielo cioè forniranno un immagine radio dell intero cielo. Un esempio di questi nuovi strumenti è il progetto SKA 3. Tale progetto mira alla costruzione di un array di parabole di dimensioni ridotte ricoprenti un area di un chilometro quadrato e che avrà una sensibilità mai raggiunta sino ad ora. Altri progetti sono in fase di analisi come ad esempio la costruzione del telescopio Allen, insomma dal punto di vista ingegneristico il mondo radioastronomico è in fermento. Ma cosa si può dire circa la parte software e matematica di analisi dei segnali? L analisi dei segnali viene eseguita tramite l utilizzo di Trasformate veloci che giocano un ruolo sempre 2 serendip IV:uno spettrometro che elabora fino a 24 milioni di canali in una banda larga 15MHz 3 Square Kilometer Array 5
15 1 Introduzione più importante non solo nella radioastronomia ma anche in ambiti sonar, radar, filtraggio dei segnali,... La trasformata di Fourier è una fra le trasformate più usate, e dal punto di vista della complessità computazionale un efficiente algoritmo che calcola questa trasformata è la FFT 4. Per analizzare segnali di cui si conosce la natura(in particolare se si sa che il segnale è periodico) tale algoritmo è senz altro molto adatto, ma se non conoscessimo la provenienza di tale segnale cosa potremmo ancora affermare riguardo l efficienza della trasformata di Fourier? Ad esempio su segnali non periodici, cioè quei segnali che non possono essere generati come somma di sinusoidi, tale algoritmo risulta ancora il miglior approccio? Bisogna tenere presente però che questa non è l unica tecnica di analisi di segnali ma ne esistono molte altre, ad esempio la Walsh Transform, la Hadamard Transform(HD), la Discrete Cosine Transform(DCT),la Haar Transform,la Slant Transform, la trasformata Wavelet(WT). E stata trascurata volutamente un ultima trasformata scoperta nel 1946: la trasformata KLT nome derivante dai due scienziati Kari Karhunen e Maurice Loève. La KLT ha un costo computazionale molto elevato e questo è il motivo per cui fino pochi anni fa i campi di applicazione di tale trasformata erano pochi o addirittura nulli. Da alcuni anni a questa parte però l incremento della potenza di calcolo da parte degli elaboratori ha reso possibile la soluzione di operazioni complesse come la KLT. L ambito in cui oggi con tale trasformata si sta ottenendo i risultati più brillanti è quello di compressione di immagini. Ulteriori studi di applicazione della trasformata sono rivolti all estrazione di caratteristiche da un oggetto in esame in modo da poterlo classificare e quindi riconoscere(pattern recognition). Negli esempi appena citati non si hanno vincoli sul tempo, una volta memorizzata l informazione da elaborare non importa quanto tempo sia 4 FFT: Fast Fourier Transform 6
16 1.2 La situazione attuale impiegato nel calcolo della trasformata. Una situazione diametralmente opposta è quella si hanno vincoli temporali e quindi l analisi che si sta eseguendo deve dare una risposta quasi istantaneamente (real time). In quest ultimo caso ricade il campo della radioastronomia che effettua osservazioni radio di fenomeni che possono variare nel tempo. Uno dei motivi per cui fino ad oggi la KLT non è stata applicata in modo approfondito nel campo radioastronomico è proprio questo: non si aveva una risposta istantanea al problema. 1.2 La situazione attuale Ci sono vari problemi da risolvere nel campo della radioastronomia, uno dei quali è quello delle interferenze radio dovute, come già detto, a quegli apparecchi che trasmettono in radiofrequenza. Un altro problema è quello di estrarre dai dati ricevuti il maggior numero di informazioni possibili e questo si ripercuote sulla scelta del metodo di analisi da adottare. L utilizzo della trasformata di Fourier permette un analisi molto accurata di segnali periodici, non si potrebbe dire altrettanto se venisse meno questa condizione. Supponiamo che i dati in analisi provengano da una sorgente che è noto emettere segnali sinusoidali, in questo caso l utilizzo della trasformata di Fourier risulta essere ottimale poichè lo spettro 5 risultante da tale analisi evidenzierà un picco in corrispondenza della frequenza di emissione della sorgente. Inoltre se il rapporto segnale rumore (S/N) è minore di 1, ciò vuol dire che il rumore domina il segnale, si può effettuare una sorta di integrazione ovvero sommare spettri consecutivi con conseguente abbassamento del livello del rumore e innalzamento del segnale. Questo procedimento è comunemente adottato e lo si ottiene tenendo presente che in spettri consecutivi dal 5 rappresenta in che quantità le varie frequenze compaiono nei dati in analisi 7
17 1 Introduzione punto di vista statistico il rumore si distribuisce in maniera randomatica(casuale) mentre il contributo della sorgente rimane sulla frequenza in esame contribuendo nell esaltazione del segnale. Cambiamo ora situazione, si supponga di non sapere nulla circa l informazione da analizzare. Si può prendere come esempio l ambiente marino, recenti studi stanno cercando di analizzare e capire il metodo di comunicazione dei delfini, si è oramai certi che questi mammiferi adoperano una tecnica di comunicazione assai complessa basata su fischi emessi dalle cavità nasali. Fino ad ora tali ricerche si sono basate sull analisi di spettri di Fourier, ma i segnali emessi da questi mammiferi sono tutt altro che monocromatici. La KLT costituirebbe uno strumento di analisi innovativo e potrebbe rilevare caratteristiche che la trasformata di Fourier non rileva. 1.3 La Tesi Punto base su cui poggia questa tesi è il frutto di una ricerca condotta dal ricercatore Robert S.Dixon che, in un paper da lui pubblicato[.1] nel 1993 durante il Third Decennial US-USSR Conference on SETI, affermò l efficacia dell utilizzo della KLT nell analisi di segnali complessi. A questa scoperta seguì uno studio portato avanti dal matematico italiano Claudio Maccone il quale confermò l utilizzo della KLT in questo ambito ma ancora di più affermò la KLT essere la miglior trasformata per comunicazioni con navicelle interstellari[.2]. Con questa tesi si vuole applicare la KLT per la rilevazione di segnali nell ambito del progetto SETI e quindi in campo radioastronomico. Il Capitolo 2 espone la teoria di Fourier e mostra come fare rilevazione di segnali, il capitolo 3 introduce la teoria della KLT mentre nel Capitolo 4 si espone il problema degli autovalori e si accennerà l algoritmo adottato. Il capitolo 5 descrive la macchina parallela 8
18 1.3 LaTesi e il software implementato, il capitolo 6 mostra i test infine nel capitolo 7 le conclusioni e gli sviluppi futuri. 9
19 1 Introduzione 1
20 Capitolo 2 Rilevazione di Segnali e Trasformata di Fourier 11
21 2 Rilevazione di Segnali e Trasformata di Fourier 2.1 Serie di Fourier Tutti i segnali periodici possono essere espressi come combinazione lineare di funzioni base ortogonali. Queste funzioni base,secondo Fourier, sono definite in modo preciso(matematicamente) come sinusoidi. I coefficienti nell espansione della serie sono calcolati usando equazioni integrali. Supponiamo che le funzioni base siano espresse in termini della variabile indipendente t e rappresentate dalla variabile φ k (t) perk =..., 1,,1,2,... Sia x(t) il segnale e X(k) il k-esimo coefficiente. Allora il segnale x(t) può essere decomposto in termini delle funzioni base φ k (t) come x(t) = X(k)φ k (t). (2.1) k= Se la eq. (2.1) descrive x(t) pertuttiivaloridit allora descrive x(t) anche per specifici valori di t. Supponiamo infatti che questi valori siano nt dove T è fissato a priori e n =..., 1,,1,2,... Definiamo x(n) eφ k (n) comex(t) eφ k (t),rispettivamente, valutate per t = nt.la (2.1) diventa allora x(n) = k= X(k)φ k (n). (2.2) Ora supponiamo che solo N dei coefficienti nella (2.2) siano non zero allora possiamo riscrivere l espansione come segue x(n) = N 1 k= Se poi definiamo Φ come la matrice definita da 12 X(k)φ k (n). (2.3)
22 2.1 Serie di Fourier Φ = φ () φ 1 () φ N 1 () φ (1) φ 1 (1) φ N 1 (1)... φ (N 1) φ 1 (N 1) φ N 1 (N 1) (2.4) eseponiamox =[X(),X(1),X(2),...,X(N 1)] T la eq. (2.3) può essere riscritta in modo compatto come allora x = ΦX (2.5) I coefficienti X(k) scalano i valori di Φ e causano una completa descrizione di x. Poichè le funzioni base contenute nella matrice(di trasformazione) Φ sono ben definite, le componenti X costituiscono il dominio della trasformata rappresentante x. La trasformazione del dominio di rappresentazione di x è particolarmente utile nell elaborazione digitale del segnale. Se x(),x(1),x(2),... è una sequenza di dati allora può essere trasformata in un altro dominio di rappresentazione dalla sequenza X(),X(1),X(2),... che è molto utile per evidenziare le caratteristiche frequenziali. In quest ultimo caso si parla più propriamente di Analisi spettrale 1 che corrisponde proprio all analisi dei coefficienti X(k), della serie di Fourier del segnale x(t), e che costituiscono lo spettro. Tale spettro può essere il risultato dell analisi di vibrazioni strutturali, sonar, segnale vocale, sistemi di controllo, o telecomunicazioni; il primo passo quindi è quello di trasformare l energia fisica in dati digitali interpretabili mediante calcolatore, questo processo è effettuato mediante un trasduttore. 1 Spectral Analysis 13
23 2 Rilevazione di Segnali e Trasformata di Fourier 2.2 La trasformata L operazione di trasformazione da un dominio ad un altro, ovvero passare dai dati da analizzare x(t) ai coefficienti della serie di Fourier X(k), è ottenuto mediante l operatore di trasformata di Fourier che denoteremo con F. Supponiamo che il segnale x(t), nel dominio temporale, sia di tipo periodico di periodo P allora la serie di Fourier a coefficienti reali è data dalla x(t) = a 2 + k=1 [ a k cos 2πkt P + b k sin 2πkt P ] (2.6) dove k =,1,2,... è il numero di cicli in P s, quindi k/p èla frequenza in Hz e gli a,a 1,a 2,... sono i coefficienti della serie di Fourier. Da questa è possibile ottenere la serie con coefficienti complessi utilizzando le seguenti identità cos θ = 1 2 (ejθ + e jθ ) (2.7) sin θ = 1 2j (ejθ e jθ ) (2.8) e infatti ponendo θ = 2πkt P e sostituendo la (2.7) e la (2.8) nella (2.6) si ottiene tramite alcuni passaggi algebrici la seguente x(t) = a [ ( a k e jθ + e jθ) j b ( k e jθ e jθ)] dove k=1 = a 2 + = k= k=1 [ 1 2 (a k jb k )e jθ + 1 ] 2 (a k + jb k )e jθ 1[ ] a k jsign(k)b k e jθ 2 sign(k) = { +1, k 1, k < 14 (2.9) (2.1)
24 2.3 FFT ] quindi ponendo X(k) = 2[ 1 a k jsign(k)b k si può riscrivere la (2.9) come x(t) = X(k)e j2πkt P (2.11) k= abbiamo appena riscritto x(t) come combinazione lineare di funzioni sinusoidali e con coefficienti complessi. La formula che permette di calcolare i coefficienti è facilmente deducibile dall ultima equazione e risulta X(k) = 1 P P/2 P/2 x(t)e j2πkt P dt (2.12) Poichè stiamo parlando di sistemi digitali risulta più conveniente discretizzare la (2.12) ottenendo X(k) = 1 N N t= x(t)e j2πkt P (2.13) In conclusione l operatore F(trasformata di Fourier) applicato al segnale da analizzare è così definito F [ x(t) ] = X(k) = 1 N N t= x(t)e j2πkt P (2.14) Analogamente esiste l operatore inverso permette di ricostruire il segnale x(t) dai coefficienti X(k) x(t) =F 1[ X(k) ] = 1 N N k= X(k)e j2πkt P (2.15) 2.3 FFT Algoritmi veloci di trasformazione riducono il numero di calcoli richiesti per determinare i coefficienti X(k). Per ottenere questi 15
25 2 Rilevazione di Segnali e Trasformata di Fourier coefficienti si potrebbe stabilire una matrice di equazioni invertendo la (2.5) X = Φ 1 x (2.16) tuttavia questo modo di procedere non è molto efficiente poiché richiede N 2 moltiplicazioni e N 2 addizioni. Un metodo più efficiente è quello di utilizzare le trasformate veloci che permettono di ridurre il numero di calcoli in modo significativo. Uno di questi algoritmi è la FFT che permette il calcolo della serie di Fourier con un costo computazionale pari a O(nlogn), tale algoritmo richiede però che il numero di punti n sia una potenza di 2. Come già accennato esistono altre trasformate oltre a Fourier ad esempio la WHT in cui le basi 2 sono composte dagli unici valori +1,-1. Le funzioni base della trasformata Haar sono composte da soli valori +1,,-1. In quest ottica la trasformata KLT, pur essendo la migliore sotto vari punti di vista, presenta delle difficoltà poichè le basi sono estratte direttamente dal segnale che si sta analizzando e quindi non possono essere pre-calcolate(eccetto che per limitati casi). Le serie di Fourier sono usate per decomporre segnali periodici in somma di sinusoidi di appropriate ampiezze. Queste sinusoidi di ampiezza arbitraria sono proprio le funzioni base per questa trasformata. Se un segnale è periodico con periodo di P secondi allora le frequenze sinusoidali nella serie di Fourier saranno 1/P,2/P,3/P,...Hz in questa maniera la rappresentazione di segnali come somme di sinusoidi di frequenza conosciuta risulta essere una tecnica di analisi molto utile. Per capire meglio tutto quanto appena descritto si osservi la figura (2.1) che presenta un segnale composto da una sinusoide alla frequenza di 17Hz campionata a 512Hz. Il grafico rappresentante lo spettro del segnale evidenzierà un picco relativo alla linea in corrispondenza di 17Hz. Occorre fare alcune precisazioni; la prima è che, come abbiamo precedentemente detto, i coefficienti X(k) 2 si veda l appendice per una definizione di base 16
26 2.3 FFT 2 1 Amplitude Time Amplitude Frequency Figura 2.1. In alto il segnale x(t), in basso lo spettro X(k) sono complessi per cui nel grafico dello spettro è stato applicato il modulo. Una seconda osservazione riguarda il fatto che nel grafico compaiono due linee causate dalla simmetria dello spettro. Nella figura (2.2) è stato aggiunto un ulteriore segnale con frequenza 13Hz e ampiezza 1 4 della sinusoide precedente. Come si può notare dallo spettro ci sono le due righe corrispondenti ai due segnali presenti nel frame-dati analizzato. Nell ambito della radioastronomia i segnali da analizzare provengono dal cosmo per cui contengono rumore che deriva da molteplici fattori fra i quali quelli terrestri come le interferenze e quelli extra-terrestri come la radiazione cosmica di fondo. Allo scopo di evidenziare l influenza del rumore sullo spettro di Fourier, come simulazione, si è preso il segnale sinusoidale iniziale e lo si è immerso nel rumore 3 (noise), la figura (2.3) mostra il segnale e il suo spettro. Risulta ora chiaro che all aumentare del rumore diventa sempre 3 in questo caso il rumore è considerato come un processo randomatico uniforme 17
27 2 Rilevazione di Segnali e Trasformata di Fourier Amplitude Time Amplitude Frequency Figura 2.2. In alto il segnale x(t) in basso lo spettro X(k) Amplitude Time 5 4 Amplitude Frequency Figura 2.3. In alto il segnale x(t) in basso lo spettro X(k) più difficile discernere una frequenza importante (nel caso in 18
28 2.4 RilevamentodiSegnali esame 17Hz) dal rumore di fondo. Per spiegare meglio nella figura (2.3) è stata posta una linea orizzontale che serve come livello di soglia;cioè tutti quei coefficienti X(k) che oltrepassano, in modulo, la soglia sono considerati frequenze importanti per la serie di Fourier.Questo esempio mostra come un frame-dati x(t), che nel dominio del tempo apparentemente non presenta alcuna informazione, mostra invece una componente sinusoidale nel dominio delle frequenze(figura 2.3 in basso). 2.4 Rilevamento di Segnali Il rilevamento di segnali(signal Detection) è quel processo mediante il quale un software in modo automatico determina se nel frame-dati 4 analizzato è presente un segnale. Per ottenere tale risultato procedere con la FFT è un passo quasi obbligatorio.il comune metodo di rilevamento si può riassumere in tre passi fondamentali come segue: 1. Si suppone che il segnale che ci si aspetta di rilevare sia periodico. 2. Si usa la Trasformata di Fourier per calcolare lo spettro del segnale utilizzando un elevato numero di canali(frequenze). 3. Si fa un controllo sull ampiezza di ciascun canale e se si oltrepassa una certa soglia si ha una rilevazione di segnale. Da un punto di vista filosofico i passi appena descritti traducono quanto segue: 1. Calcola le ampiezze delle componenti X(k) per ogni frequenza. 4 si veda la definizione 2 del capitolo 3 19
29 2 Rilevazione di Segnali e Trasformata di Fourier 2. Controlla se un segnale è presente o no in ciascuna di queste frequenze. 3. Se è presente un tale segnale restituisci la frequenza e l ampiezza relativa. Il punto cruciale del procedimento è il punto numero 2: Controlla se un segnale è presente o no...,è importante notare che una semplice risposta del tipo Si/No sarebbe sufficiente ai fini di un software di rilevamento. Non importa conoscere l ampiezza di ogni componente 5 dello spettro poichè ancora non si sa se un segnale è presente nel frame-dati. Se questa semplice risposta potesse essere risolta direttamente senza calcolare lo spettro si avrebbe un notevole guadagno in termini di calcolo. Una volta poi stabilito che un segnale è presente allora lo si può analizzare in maniera più precisa con vari tipi di trasformate. Tutto il metodo di rilevazione sarebbe molto più efficiente se trasformato nella risposta alla domanda basilare(db): C è un segnale nei dati acquisiti?. Naturalmente si potrebbe obbiettare che per segnali periodici la FFT sia la miglior trasformata(ottimizzata) e quindi non ci siano alternative. Occorre però fare un paio di importanti osservazioni: 1. Il calcolo della FFT restituisce le ampiezze di ogni canale. 2. Il segnale proveniente dal cosmo potrebbe essere non periodico. Tutto ciò può essere ottimizzato in maniera molto elegante cambiando radicalmente il punto di vista dell analisi dei segnali. 5 da ora in poi ogni elemento X(k) sarà chiamato canale o bin 2
30 2.5 L autocorrelazione 2.5 L autocorrelazione Nell elaborazione digitale delle informazioni la correlazione assume un importanza rilevante infatti questo operatore permette di misurare la somiglianza fra due vettori. Se si esegue una correlazione di un vettore con se stesso allora si sta eseguendo un autocorrelazione. Per poter applicare la KLT occorre fare una precisazione e cioè si suppone da qui in avanti che il frame-dati sarà stazionario in senso lato. Questo tipo di segnali hanno le seguenti caratteristiche: 1. E{f(n)} = µ costante. 2. E{f(n) f(n + k)} = R(k) cioè l autocorrelazione dipende solo dalla distanza dei campioni. 3. C(k) =E{(f(n) µ) (f(n+k) µ)} = R(k) µ 2 covarianza Come si vedra più avanti si assume che il frame-dati abbia media eciò rende R C. Nel caso di segnali casuali l autocorrelazione si può definire nel seguente modo: Definizione 1 Si definisce autocorrelazione il valore atteso del prodotto di due campioni del segnale x(t) R rispettivamente ai tempi t 1 e t 2 : R x (t 1,t 2 )=E { } x t1 x t2 = a bf xt1,x t2 (a,b) da db. (2.17) che, nel caso discreto, sostituendo la variabile t con n e gli integrali con sommatorie di opportuni indici, diventa R x (n 1,n 2 )=E { x n1 x n2 } = T a= T a bf xn1,x n2 (a,b). (2.18) Quest ultima si può anche riscrivere ponendo m = n 1 n 2 come segue R x [n 2,m] =E[x n2 +m x n 2 ]. (2.19) 21 b=
31 2 Rilevazione di Segnali e Trasformata di Fourier Il caso stazionaro in senso lato ci permette di dare un importante affermazione: sia l autocorrelazione che il valor medio sono indipendenti da n. In altri termini è possibile riscrivere la (2.19) in funzione del parametro m come segue R X [m] =E[x n+m x n]. (2.2) calcolata per m =..N. Si può inoltre utilizzare la simmetria per dimezzare i calcoli poichè R X [m] =R X [ m]. (2.21) In ultima analisi osserviamo che nel caso continuo si considera un supporto illimitato per l integrazione(lo si nota dagli indici degli integrali della 2.17) mentre nella realtà ci troviamo ad avere un supporto limitato(nel nostro caso T) dobbiamo quindi fare uso di uno stimatore per l autocorrelazione che è dato dalla seguente R X [m] = 1 N N m n= x n x n+m. (2.22) Per illustrare meglio l importanza della autocorrelazione nell estrazione dei segnali immersi nel rumore si osservi la figura 2.4 dove è presente un frame-dati con solo rumore. Si può notare che la massima verosimiglianza la si ha solo in corrispondenza dello -shift(energia) e cioè per m= nella equazione Questo lo si spiega perchè il rumore, essendo un processo casuale, ottiene la massima verosimiglianza solo con se stesso e con nessun altra versione shiftata. Dalla figura infatti si vede come l autocorrelazione concentra l energia del rumore a metà grafico(-shift) dove compare la riga. Se nel frame-dati ci fosse un segnale alterato da rumore (si veda la figura 2.5), la parte relativa al rumore verrebbe per gran parte concentrata nello -shift pulendo il segnale quanto più possibile, si nota infatti che nell autocorrelazione la componente sinusoidale viene esaltata. 22
32 2.5 L autocorrelazione Frequency Time 8 6 Frequency Time Figura 2.4. Correlazione del rumore 2 1 Amplitude Time 2 15 Amplitude Time Figura 2.5. Correlazione di un segnale rumoroso 23
33 2 Rilevazione di Segnali e Trasformata di Fourier 24
34 Capitolo 3 Trasformata KLT 25
35 3 Trasformata KLT 3.1 L approccio intuitivo La Karhunen-Loève Transform (KLT) è un argomento che spazia molti campi della scienza contemporanea: principalmente il signal processing ma anche statistica e matematica, fisica e astrofisica, e ora relatività e viaggi spaziali. Nei prossimi anni nuove tecniche di calcolo parallelo permetteranno un ulteriore incremento delle prestazioni nella ricerca di autovalori e autovettori di matrici simmetriche in modo tale che anche altri campi come la realtà virtuale, la biologia possano trarre vantaggi dalla KLT. Per capire perchè, in certi contesti, la KLT è migliore rispetto la FFT ci si può riferire ad un analogia meccanica. Si consideri un oggetto, per esempio un libro, e un sistema di riferimento composto dai tre assi cartesiani dello spazio. Per la meccanica classica tutte le proprieta del libro relative alla dinamica di rotazione possono essere descritte mediante una matrice simmetrica 3x3 chiamata matrice d inerzia e i cui elementi sono in generale non zero. Gestire una matrice i cui elementi sono non zero è chiaramente più complicato che gestire una matrice in cui gli unici elementi non zero sono sulla diagonale principale. Quindi quello che ci si può domandare è se esiste una qualsiasi trasformazione che cambia la matrice di inerzia in una matrice diagonale. La meccanica classica aiuta in questo passo dimostrando che esiste un solo sistema di orientamento privilegiato rispetto al libro. Il sistema di cui stiamo parlando èformatoda quegli assi paralleli ai lati dell oggetto in analisi, in questo caso il libro; tali assi sono proprio gli autovettori 1. In altre parole ciascun oggetto possiede un proprio sistema privilegiato che descrive nel modo migliore la sua dinamica rotazionale. Si possono in definitiva calcolare sempre gli autovettori rispetto un generico sistema di riferimento per mezzo di una procedura matematica 1 eigen-vector 26
36 3.2 La teoria: caso continuo di ricerca degli autovettori di una matrice quadrata. Ora torniamo all elaborazione dei segnali, aggiungendo una componente casuale ad un segnale deterministico si ottiene un segnale rumoroso, anche chiamato noisy signal. Come già precedentemente accennato l autocorrelazione è una buona tecnica per estrarre il segnale dal rumore, se infine consideriamo proprio l autocorrelazione come il libro del precedente esempio, allora si può cercare gli autovettori della matrice di autocorrelazione per trovare la più semplice rappresentazione dei dati. Questa è l idea chiave della KLT. 3.2 La teoria: caso continuo Consideriamo un processo stocastico X(t) su un intervallo finito t T,è possibile separare la componente probabilistica dal suo comportamento nel tempo? La risposta è si e lo strumento matematico per fare ciòè la KLT. L espansione KLT del processo X(t) che si vuole èdatoda X(t) = Z n φ n (t) (3.1) n=1 dove gli Z n sono le variabili casuali e le φ n (t) costituiscono la dipendenza temporale.vediamo ora come si può ottenere tale decomposizione. Le funzioni φ n (t) sono gli autovettori ottenuti dalla soluzione dell equazione integrale del eigen-problem seguente: T E { X(t 1 )X(t 2 ) } φ n (t 2 )dt 2 = λ n φ n (t 1 ) (3.2) dove E { X(t 1 )X(t 2 ) } è l autocorrelazione del processo X(t) che èdatada { } E X(t 1 )X(t 2 ) = dx 1 x 1 x 2 f (x1,x2)dx X(t1 )X(t 2 ) 2 27
37 3 Trasformata KLT e ricordando che il valor medio èdatoda E{X(t)} = xf X(t) (x)dx (3.3) Per il calcolo del equazione 3.2 si suppone che l autocorrelazione sia funzione di t 1 e t 2 inoltre si presuppone che E { X(t) } =. L equazione integrale 3.2 rappresenta l eigen-problem 2 dove l operatore ha un nucleo simmetrico. Questo rende l operatore autoaggiunto e come conseguenza gli autovalori sono reali e gli autovettori sono ortogonali fra loro. Possiamo anche esprimere l ortogonalità nei seguenti termini T {, for m n, φ m (t)φ n (t)dt = δ mn = (3.4) 1, for m = n Riguardo ai set di autovettori si può dire che sono completi e quindi le φ n (t) formano una base ortonormale nello spazio L 2 (,T ) 3. Se l espansione (3.1) è moltiplicata da una delle φ m (t) e integrata sul tempo allora grazie all ortonormalità degli autovettori si puo giungere alla seguente forma per i coefficienti Z m Z m = T X(t)φ m (t)dt (3.5) Ora possiamo mostrare che anche i coefficienti Z n sono ortogonali dal punto di vista dell autocorrelazione, infatti E { { } T T } Z m Z n = E X(t 1 )φ m (t 1 )dt 1 X(t 2 )φ n (t 2 )dt 2 = T T dt 1 φ m (t 1 ) dt 2 φ n (t 2 )E { X(t 1 )X(t 2 ) } T = λ n dt 1 φ m (t 1 )φ n (t 1 )=λ n δ nm. (3.6) 2 si veda l apposito capitolo sul problema degli autovalori 3 spazio delle funzioni ad energia finita definite nell intervallo [,T] 28
38 3.2 La teoria: caso continuo cioè E{Z m Z n } = λ n δ nm. (3.7) Ora possiamo dimostrare che il valor medio di Z n è zero { T E{Z n } = E = = T T =. } X(t)φ n (t)dt E{X(t)}φ n (t)dt φ n (t)dt Un altra proprietà che possiedono i coefficienti Z n riguardano la varianza,σ 2 Z n,cheè uguale all autovalore associato, come si dimostra nella seguente formula σ 2 Z n = E{Z 2 n} E 2 {Z n } = E{Z 2 n} =E{Z n Z n } = λ n δ nn = λ n. (3.8) dalla quale che la deviazione standard di ciascun Z n attorno alla media, zero, è uguale a ± λ n. Si può ora ottenere l autocorrelazione e la varianza in termini dell espansione delle autofunzioni(autovettori).l autocorrelazione diventa allora { E{X(t 1 )X(t 2 )} = E = = = m=1 m=1 n=1 m=1 n=1 Z m φ m (t 1 ) n=1 } Z n φ n (t 2 ) E { } Z m Z n φm (t 1 )φ n (t 2 ) λ n δ mn φ m (t 1 )φ n (t 2 ) λ n φ n (t 1 )φ n (t 2 ) (3.9) n=1 29
39 3 Trasformata KLT Ricordando che X(t) ha media zero,e utilizzando la (3.9) avendo posto t 1 = t 2 = t, possiamo scrivere la seguente σ 2 X(t) = E{X(t)X(t)} E 2 {X(t)} = λ n φ 2 n(t) = n=1 λ n φ 2 n(t). (3.1) n=1 Si arriva così a stabilire la seguente identità cheè di importanza fondamentale per il resto della comprensione dell analisi KLT: T σ2 X(t) dt = n=1 λ n (3.11) Quest ultima formula stabilisce il fatto che l energia totale è uguale alla sommatoria degli autovalori.occorre notare a questo punto che è consuetudine ordinare tali autovalori in ordine decrescente λ 1 >λ 2 >...>λ n >. dove λ 1 è detto autovalore dominante.da queste ultime considerazioni poi si ottiene la convergenza dell equazione (3.1) infatti, poichè i coefficienti Z n sono random con media e varianza λ n, e richiedendo che sia soddisfatto il seguente limite lim λ n =. n si ottiene che i coefficienti casuali Z n per n crescente diventano coefficienti a varianza tendente a zero e poichè hanno media zero ciò comporta che nella condizione al limite n essi diventano deterministici di valore zero. Quanto appena detto lo si può rappresentare bene con la figura (3.1). 3
40 3.3 Il caso discreto 2 Standard Deviation dei coefficienti Z n λ n 1.5 Z n Coefficient.5 1 λ n Time(n ) Figura Il caso discreto Varianza dei coefficienti Z n E buona norma procedere con l analisi matematica partendo dal caso continuo poichè è il miglior modo per dimostrare proprietà che altrimenti sarebbero di difficile comprensione, ma il passo successivo è quello di utilizzare quanto detto nell ambito discreto poichè sarà quello in cui tale trasformata verrà utilizzata. Come precedentemente descritto supponendo di avere una matrice di autocorrelazione, che chiameremo A, vogliamo trovare un set di vettori che la descrivono in modo ottimale. A questo punto occorre dare in maniera rigorosa alcune definizioni Definizione 2 Indichiamo con il termine frame-dati(samples, campioni), gli N dati ottenuti per mezzo di una conversione ADC, che in questo ambito derivano da osservazioni radioastronomiche eseguite per mezzo di apparati di ricezione. x R N (3.12) 31
41 3 Trasformata KLT Poiché abbiamo appena affermato che il frame è di tipo N dimensionale si ha come conseguenza che la matrice di autocorrelazione 4 AèdiordineN A R NxN (3.13) Possiamo ora riscrivere l equazione (3.2) del caso continuo, che nel caso discreto diventa Av = λv (3.14) dove λ è l autovalore e v è l autovettore 5. È possibile stabilire l equazione che lega la correlazione agli autovalori come segue NA(,) = N 1 i= λ i (3.15) dove con A(,) è rappresentata l energia del segnale. Definizione 3 Data una matrice di ordine N è possibile estrarre un insieme di N autovalori e un insieme di N autovettori. Ogni autovettore ha associato un autovalore, definiamo come eigenpair la coppia di questi due elementi dove (v i,λ i ) v i è l autovettore o asse privileggiato λ i è l autovalore che indica l energia associata all autovettore. La matrice A ha N assi privilegiati che sono gli autovettori, si puó quindi pensare di decomporre il frame-dati ricevuto come 4 si veda il paragrafo 3.6 la definizione 5 per una definizione formale si veda l apposito capitolo sugli autovalori 32
42 3.3 Il caso discreto somma di autovettori pesati dai valori di un opportuno vettore p. Ció si traduce con la riformulazione dell equazione (3.1) del caso continuo come segue: x = V p (3.16) dove v () v 1 () v N 1 () v (1) v 1 (1) v N 1 (1) V = (3.17) v (N 1) v 1 (N 1) v N 1 (N 1) cioè V contiene gli autovettori disposti per colonna. Mentre p =[p 1,p 2,...,p N ]. (3.18) Per meglio evidenziare l analogia caso discreto caso continuo si è riscritto la formula nei due casi X(t) = Z n φ n (t) vedi equazione (3.1) x(t) = n=1 N 1 V i (t)p i vedi equazione (3.16) (3.19) i= dove i pesi p i sono ottenuti, per analogia con la (3.5), dalla seguente equazione p i = N 1 k= V T i (k)x(k) (3.2) In altre parole i pesi sono ottenuti mediante la proiezione del frame-dati sulla matrice di trasformazione data dagli autovettori. Poichè la ricostruzione del segnale non è importante per il caso in discussione in questa tesi, si trascureranno tali dettagli. È bene precisare che la rilevazione del segnale che ci si appresta ad implementare non è una KLT completa ma è una KLT-troncata poichè non verrà fatta la parte di ricostruzione del segnale. 33
43 3 Trasformata KLT 3.4 Analisi di Segnali Supponiamo di avere una funzione f L(,2π) 6 che rappresenta una sinusoide con frequenza w allora possiamo dimostrare che una decomposizione KLT di tale funzione in eigen-pair come descritto precedentemente restituisce due autovettori uguali alla funzione f(t). Analogamente i due autovalori sono uguali, mentre i restanti autovalori sono nulli. Supponiamo che la funzione f(t) sia somma di diverse sinusoidi, in questo caso non si può piùdire che f(t) è un autovettore. Possiamo però notare che le sinusoidi costituenti f(t) sono gli autovettori. Ora estendiamo il concetto e supponiamo nuovamente che la funzione f(t) sia somma di diverse sinusoidi. In questa situazione la relazione fra KLT e Fourier diventa evidente in effetti in questo caso la decomposizione KLT estrae le medesime basi(autovettori) di quelle che usa la trasformata di Fourier. Possiamo continuare ad estendere l esempio generalizzando ancora di più ecioè facendo cadere la supposizione di periodicità della funzione f(t), le basi che la KLT genera in questa circostanza non sono più sinusoidi ed infatti in questo caso diventa evidente l efficienza di questa trasformata. Tutto cio si può sintetizzare dicendo che la KLT può estrarre basi ortogonali non periodiche, a differenza della serie di Fourier dove le basi sono fissate(periodiche) a priori. Un ulteriore proprietà che rende questa trasformata così interessante riguarda la compressione. Considerando la funzione f possiamo dire che esistono infinite serie che la decompongono in somma pesata di vettori: la serie di Fourier e la KLT sono due esempi di tali espansioni 7. Supponiamo ora che si voglia approssimare la funzione f utilizzando solo i primi k termini di un espansione qualsiasi. Ebbene la KLT è quella serie che a parità di termini 6 rappresenta lo spazio delle funzioni periodiche di 2π etaliche 2π f(x) 2 dx < + 7 con il termine serie o espansione si intende il medesimo concetto 34
44 3.4 Analisi di Segnali utilizzati restituisce la miglior approssimazione f alla funzione f originale. Quest ultima affermazione è stata sfruttata in letteratura come un mezzo di compressione dati[.3]. Si mostra ora l analisi di un segnale sinusoidale rappresentato dalla funzione f(t) definita come segue f(t) =f(t)+n(t), (3.21) dove con n(t) si intende il rumore bianco 8 o gaussiano, mentre f(t) è la funzione sinusoidale precedentemente citata ad inizio paragrafo. Allo scopo di rendere più chiaro il comportamento della KLT all aumentare del rumore si è analizzato il segnale f con delle simulazioni con diversi rapporti segnale rumore segnale puro,assenza di rumore (Fig. 3.2); 2. segnale e rumore, SNR=1.623 (Fig. 3.3); 3. segnale e rumore, SNR=1.694 (Fig. 3.4); 4. segnale e rumore, SNR=1.124 (Fig. 3.5); 5. segnale e rumore, SNR=1.73 (Fig. 3.6). Come si può vedere in tutte le figure sono presenti 4 riquadri che raffigurano rispettivamente partendo dall alto * il segnale f(t) nel dominio temporale; * la trasformata di Fourier di f(t); * la trasformata di Fourier dell autovettore relativo all autovalore dominante; 8 si intende un rumore la cui varianza rimane costante al variare della frequenza,diversamente avremmo rumore colorato 9 rapporto segnale rumore(snr o rapporto S/N): indica in che quantitàilsegnale è alterato dalla componente casuale dovuta al rumore. 35
45 3 Trasformata KLT 2 S/N ratio=3 Amplitude Time 1 Amplitude Frequency FFT 1 Amplitude x 14 Frequency KLT Energy 1 5 EigenValue 1 15 Figura 3.2. caso 1 Amplitude Amplitude Amplitude S/N ratio= Time Frequency FFT Frequency KLT Energy 5 5 EigenValue 1 15 Figura 3.3. caso 2 36
46 3.4 Analisi di Segnali S/N ratio= Amplitude 1 5 Time Amplitude Amplitude Frequency FFT Frequency KLT Energy 5 5 EigenValue 1 15 Figura 3.4. caso 3 2 S/N ratio= Amplitude 2 5 Time Amplitude Frequency FFT Amplitude x 14 Frequency KLT Energy EigenValue 1 15 Figura 3.5. caso 4 37
47 3 Trasformata KLT S/N ratio= Amplitude 2 5 Time Amplitude Frequency FFT decomposition 1 Amplitude.5 Energy x 14 Frequency KLT decomposition EigenValue 1 15 Figura 3.6. caso 5 * il grafico degli autovalori calcolati tramite la KLT. Nella figura 3.2 viene analizzato il segnale f(t) in cui non è stato aggiunto rumore cioè con n(t)=, si veda il 1 riquadro. Chiaramente la FFT evidenzia una componente relativamente alla frequenza della sinusoide f(t), che in questo caso è a 34Hz. Come precedentemente descritto in questa situazione KLT e Fourier hanno lo stesso identico comportamento ed infatti ci si può convincere di questo confrontando il 2 eil3 riquadro. Il quarto riquadro mostra la distribuzione dell energia che in questo caso è contenuta nella quasi interamente nei primi due autovalori, ciò spiega il perchè siè visualizzata la FFT di uno dei due autovalori dominanti. Continuando nell analisi si è aggiunto una certa quantità di rumore al segnale f(t), cioè n(t) nell eq. (3.21), si veda la fig Naturalmente nella trasformata di Fourier compaiono le componenti relative al rumore immesso ed ènormale un tale comportamento; confrontando i due spettri nelle 38
48 3.5 L eigen-spectrum due trasformate, riquadro nr.2 e riquadro nr.3, notiamo però che nella KLT il rumore non è apparso, o per lo meno il suo contributo è molto meno importante. Per valutare la performance della KLT quindi si è aumentato in maniera progressiva il livello di rumore diminuendo così il rapporto S/N. I grafici sono molto eloquenti e si farà solo un paio di osservazioni sull ultimo grafico. Nella fig. 3.6 si è nella condizione estrema in cui, facendo una ricerca del massimo valore in ogni canale(o bin o coefficiente) della FFT, non si può più dire con certezza che è presente una componente sinusoidale nella funzione f(t). Se però guardiamo lo spettro dell autovettore relativo all autovalore dominante allora si può dare una risposta immediata e sicura. Questo ci permette di dire che la trasformata KLT si comporta esattamente come la serie di Fourier, nel caso di un segnale sinusoidale, separa le componenti in frequenza evidenziando, nello spettro dell autovettore dominante, solo la frequenza della sinusoide con rapporto S/N maggiore e nessun altra componente. Analizzando gli spettri dei successivi autovettori verranno isolate componenti con rapporti S/N via via decrescenti. Si noti il comportamento dello spettro degli autovalori(riquadro 4 di ogni grafico) che da qui in avanti chiameremo empheigen-spectrum. 3.5 L eigen-spectrum Definizione 4 Sia λ il vettore avente come componenti gli autovalori λ 1,λ 2,...,λ N definiamo l eigen-spectrum il grafico dell andamento di tali valori ordinati in maniera decrescente. Nei precedenti grafici si può notare che nel primo caso(si veda fig. 3.2) l eigen-spectrum evidenzia un andamento a gradino, cioè le prime due componenti(autovalori dominanti) relative ai due autovettori hanno la quasi totalità dell energia associata, mentre i restanti decadono a zero molto velocemente. Nell esempio in 39
49 3 Trasformata KLT questione il supporto della funzione era N=15 per cui l eigenspectrum non evidenzia un andamento a gradino ideale, situazione che si sarebbe ottenuta se avessimo considerato il limite per N. Andando ad analizzare i quadri del grafico in fig. 3.3 si nota che l inserimento di una piccola quantità dirumorehainfluenzato leggermente l eigen-spectrum e precisamente l energia non èpiù concentrata esclusivamente sui primi due autovalori ma una piccola quantità siè spostata verso il terzo e quarto autovalore. Se la fig. 3.3 e la fig. 3.4 non sono molto esplicative da questo punto di vista, si osservino le restanti fig.3.5 e fig.3.6 dove l energia rappresentata dall eigen-spectrum è letteralmente spalmata su tutti gli autovalori. Questa situazione permette di fare una considerazione: nel caso in cui il rapporto segnale rumore è grande abbastanza noteremo che il grafico dell energia presenta un gradino che permette di eseguire la rilevazione di segnale. Infatti in questa situazione è facile determinare un valore 1 (detto soglia) che permette di stabilire se nel frame-dati è presente un segnale. Si è accennato al rapporto segnale rumore abbastanza grande più avanti nel paragrafo specificheremo meglio cosa significa. Per la rilevazione di segnali si cerca di stabilire una soglia da applicare all eigen-spectrum del frame-dati in analisi. Per spiegare meglio questo metodo si osservi la fig. 3.7 dove si mette a confronto lo spettro di potenza del frame-dati di cui si vuole sapere se è presente un segnale con l eigen-spectrum. Nel primo riquadro è raffigurato lo spettro di potenza del frame in analisi, nel secondo riquadro si è fatto un ordinamento decrescente del quadro 1 relativamente alle ampiezze delle frequenze, per meglio evidenziare l analogia fra l andamento degli autovalori e l ordinamento decrescente delle frequenze del secondo riquadro si è creato un terzo riquadro(riquadro in basso della fig. 3.7) dove si è tracciato il grafico di entrambi gli andamenti. Questo modo 1 in gergo tecnico è detto thresold 4
50 3.5 L eigen-spectrum 2 15 S/N ratio= Energy Amplitude Amplitude Frequency FFT FFT Sorted Freq. 1.5 Segnale Rumore KLT Energy FFT sorted Frequency Thresold EigenValue Figura 3.7. Comparazione spettri di confrontare le due tecniche permette di asserire che in questa situazione FFT e KLT si assomigliano molto. A questo punto diventa cruciale la scelta del valore soglia, thresold che deve stabilire se è presente un segnale o meno. Nell esempio in questione la linea che demarca l andamento a gradino dall andamento più uniforme nel grafico è molto netta e ciò permette di dare una risposta con un buon margine di errore: il frame-dati contiene un segnale. Questa, purtroppo, è una situazione didattica in cui non ci si trova quasi mai nell ambito della radio astronomia dove, per raggiungere radio sorgenti sempre più lontane dalla terra, ci si spinge sempre al limite del rilevamento dei dati. Per capire la KLT considereremo inizialmente il caso didattico. Ora il problema è il come stabilire il valore soglia e questo può essere risolto, come citato da R.Dixon, tramite le seguenti misure M KLT = 2Max(λ) NA(,) (3.22) 41
51 3 Trasformata KLT M FFT = Max(E i) Ei (3.23) dove con N si intende il numero di punti nel frame-dati, con A(,) si intende l energia nell autocorrelazione 11,conMax(λ) si intende il massimo autovalore, con E i invece si intende l energia nel i-esimo canale o frequency-bin. Questi due parametri varianoinunintervallodaa1indicandorispettivamente(nessun segnale), 1(segnale puro). Ora diventa possibile dare un peso quantitativo all affermazione grande abbastanza riguardo al rapporto segnale rumore. Infatti il rapporto segnale rumore è legato direttamente all eq. (3.22) e all eq. (3.23) cioè tanto più è grande il rapporto segnale rumore tanto maggiore è la sensibilitá di queste equazioni alla presenza del rumore. 3.6 L algoritmo La rilevazione dei segnali fatta nel modo classico è un analisi dello spettro derivante dal calcolo della FFT, in ciascun canale ottenuto si esegue una ricerca di quei valori che eventualmente eccedono una prefissata soglia e se tali valori esistono allora si può affermare che un segnale è presente nel frame-dati in analisi. Come già detto però si può cambiare totalmente modo di procedere nella rilevazione dei segnali, infatti è possibile ragionare in termini di energia di un determinato segnale piuttosto che in termini di ampiezza ad una determinata frequenza. Questo ci porta subito ad una considerazione: ci si focalizza solo su un parametro, detto appunto energia, che permette di eseguire il processo di rilevamento. Per illustrare meglio questo nuovo modo di approccio per la rilevazione del segnale si osservino i blocchi della fig Qui di seguito viene spiegato il loro significato. 11 si veda più avanticomeè costruita la matrice di autocorrelazione 42
52 3.6 L algoritmo 1. Questo blocco riguarda la conversione dei dati ottenuti dall osservazione radioastronomica, la conversione è a 12bit alla frequenza di 13.3MS/s(ciò significa che ogni secondo si hanno 13.3 milioni di punti che descrivono il segnale analogico in ingresso). In input a questo blocco si ha un segnale analogico mentre l output restituisce il segnale tempo-discreto x(n). 2. Il secondo blocco ha come input il frame-dati x ad N componenti e ne calcola l autocorrelazione come precedentemente descritto nel capitolo 2. L output restituito è un vettore a 2*N-1 componenti con simmetria centrata sull elemento N Dal vettore di autocorrelazione si passa al calcolo della matrice di autocorrelazione che ha una struttura molto particolare: la matrice è simmetrica e gli elementi su ciascuna diagonale sono costanti. Questo tipo di matrice è comunemente chiamata matrice di Toeplitz. Si dà qui di seguito un Figura 3.8. Diagramma a blocchi del procedimento 43
53 3 Trasformata KLT esempio con N=5: CORR vector = [edcbabcde] a b c d e b a b c d A = c b a b c d c b a b, e d c b a dove l energia calcolata dallo stimatore dell autocorrelazione è identificata dalla lettera a in CORR vector. 4. Il blocco Lanczos factorization serve per ridurre la matrice A (di ordine N), in modo tale che il calcolo dei suoi autovalori risulti di minor complessità computazionale. In effetti l output di questo blocco è una matrice quadrata(tridiagonale) di ordine k con k N. 5. Quest ultimo blocco estrae gli autovalori dalla matrice tridiagonale appena sopra citata a tal fine si usa un algoritmo conosciuto come rotazioni di Givens. L output finale è una matrice diagonale di ordine k contenente i k maggiori autovalori approssimati della matrice A(autocorrelazione). Avendo quindi ottenuto gli autovalori e autovettori si può passare ad eseguire una valutazione energetica e frequenziale del segnale in analisi. Il prossimo capitolo spiegherà inmodoapprofondito come ottenere gli autovalori e autovettori calcolati dall insieme dei blocchi 4 e 5. 44
54 Capitolo 4 Gli autovalori 45
55 4 Gli autovalori 4.1 Introduzione al problema Il problema della ricerca degli autovalori e autovettori interessa vari campi di applicazionedallo studio dellastabilità di strutture, ai problemi di statistica, dai problemi di fisica(stati dell energia) alla propagazione dei segnali. Il calcolo degli autovalori èun problema di tipo non-lineare e quindi per la loro risoluzione si potrebbero usare le tecniche per risolvere i sistemi non-lineari. Il calcolo della KLT richiede appunto la soluzione di un problema di questo tipo infatti come già citato in precedenza quello che si vuole ottenere è un sistema di assi privilegiati che descrivano il fenomeno in analisi nella maniera migliore possibile. Questo si traduce nel calcolo degli autovettori/autovalori della matrice di autocorrelazione del frame-dati in analisi. Occorre però notare che nel capitolo precedente si utilizzava solo il primo autovalore per avere una stima da confrontare con la soglia di rilevamento. Questo modo di procedere ha portato alla ricerca di algoritmi di estrazione di pochi, più grandi, autovalori piuttosto che all estrazione di tutti gli autovalori di una matrice. In tal senso la ricerca ha condotto all utilizzo del algoritmo generale di Arnoldi che, per matrici simmetriche come in questo caso, diventa quello di Lanczos. Questo algoritmo ha permesso l abbattimento dei tempi di calcolo in maniera considerevole(come si vedra più avanti) permettendo al tempo stesso quindi di aumentare il numero di punti N del frame-dati. 4.2 La soluzione del problema Si da la definizione formale del problema come segue tenendo presente che per matrici simmetriche gli autovalori sono reali Definizione 5 Si chiama autovalore di A uno scalare λ R per 46
56 4.3 Metodo delle Potenze il quale esiste un autovettore x R N non nullo tale che Ax = λx (4.1) inoltre possiamo anche dire che se esiste una matrice P non singolare 1 tale che: P 1 AP = diag[λ 1,λ 2,...,λ n ] : D (4.2) allora la matrice A è detta diagonalizzabile. Le colonne di P sono gli autovettori di A e i corrispondenti autovalori sono i λ i della matrice diagonale D. 4.3 Metodo delle Potenze Per spiegare il metodo adottato nello sviluppo di questa tesi occorre presentare l algoritmo base che mostra in maniera più chiara i concetti. Si tratta di un metodo iterativo che è adatto per approssimare l autovalore di modulo massimo e il relativo autovettore. Supponiamo che una matrice qualsiasi A R NxN sia diagonalizzabile, cioè che esista X 1 AX = diag(λ 1,...,λ N )conx = [x 1,...,x N ] allora dato q () R N il metodo delle potenze produce le successioni q (k) come segue: for k =1,2,... z (k) = Aq (k 1) q (k) = z(k) z (k) 2 λ (k) =[q (k) ] T Aq(k) end Poichè q () R N si può scrivere q () = a 1 x 1 + a 2 x a n x n supponendo poi che a 1 1 e tenendo presente che per A k si ha 1 si veda l appendice per la definizione di matrice singolare 47
57 4 Gli autovalori che gli autovalori sono elevati della rispettiva potenza k allora otteniamo ( N ) A k q () = a 1 λ k a j (λ j ) kxj 1 x 1 + (4.3) a 1 λ 1 Poichè siha λ j λ 1 < 1perj 2 allora la direzione di q (k) tende a quella di x 1.Concludendo a parole, il metodo delle potenze consiste in una modifica iterativa delle componenti del vettore di partenza q in modo da convergere all autovettore dominante 2 ottenendo anche il relativo autovalore. Va fatta attenzione che in questo caso l indice k indica l iterazione non la k-esima componente. La convergenza è chiaro che dipende dal rapporto fra l autovalore dominante λ 1 e λ 2. A questo punto però si può fare un osservazione: questo metodo calcola un solo autovalore/autovettore per volta, la convergenza può essere estremamente lenta o addirittura non convergere affatto. Occorre quindi un algoritmo che calcoli più autovalori(parametrizzabili come numero) e che abbia una buona convergenza. j=2 4.4 Il metodo di Jacobi Il metodo di Jacobi, molto popolare per matrici di piccole dimensioni, approssima tutti gli autovalori di una matrice simmetrica utilizzando trasformazioni ortogonali di tipo rotazione. Ad ogni iterazione viene annullato un elemento fuori della diagonale principale. Il principio del metodo è il seguente A k = G T k A k 1 G k (4.4) dove G k è una matrice di rotazione di angolo θ che definisce i seguenti scalari c =cosθ, s =sinθ. Per la costruzione della 2 si ricorda che autovettore dominante è quello riferito all autovalore di modulo massimo 48
58 4.5 Il metodo di Lanczos matrice A k allora devono essere calcolate le seguenti operazioni: a (k) ij a (k) pj a (k) qj a (k) pq a (k) pp a (k 1) qq = a (k 1) ij, per i p,q; j p,q = ca (k 1) pj sa (k 1) qj, per j p,q = sa (k 1) pj = cs(a (k 1) pp = c 2 a (k 1) pp = s 2 a (k 1) pp + ca (k 1) qj per j p,q a (k 1) qq )+(c 2 s 2 )a (k 1) pq + s 2 a (k 1) qq + c 2 a (k 1) qq 2csa (k 1) pq +2csa (k 1) pq. Poichè fra un iterazione ed un altra alcuni elementi che erano stati annullati possono ridiventare non nulli quindi tale metodo è del tipo a a terminazione non finita. Per questo motivo esistono vari criteri per la scelta dell elemento da annullare fra i quali il criterio classico che elimina l elemento di modulo massimo e il metodo con soglia. Il metodo di jacobi peròè molto lento su matrici di grandi dimensioni e approssima tutti gli autovalori cosa che, in questa tesi, non è di alcuna utilità. 4.5 Il metodo di Lanczos L algorimto di Lanczos risponde proprio a questa esigenza, buona convergenza e ricerca di un numero di autovalori parametrizzabile. Questo metodo permette di ottenere una fattorizzazione della matrice A. Con il termine fattorizzazione si intende la decomposizione della matrice A come si può vedere dalla fig. 4.1 dove è mostrato il risultato dell algoritmo di Lanczos, la matrice V contiene i k autovettori disposti per colonna mentre una importante proprietà della matrice tridiagonale H è che i suoi autovalori sono una buona approssimazione di quelli della matrice A. 49
59 4 Gli autovalori Figura 4.1. Fattorizzazione tramite Lanczos Sia A T = A R NxN indichiamo con λ i (A) l i-esimo autovalore più grande di A allora si ha λ N (A) λ N 1... λ 2 (A) λ 1 (A). Per un noto teorema di Rayleigth si ha che gli autovalori di una matrice simmetrica sono i punti stazionari della funzione che mappa x x T Ax/x T x con x inoltre essi soddisfano il seguente teorema: Teorema 1 (Courant-Fischer Minimax Theorem) Se A R NxN è simmetrica, allora per k=1...n. λ k (A) = max dim(s)=k y T Ay min y S y T y (4.5) dove con S si intende il sottospazio invariante di dimensione k.senza addentrarci troppo nella teoria, poichè è molto vasta, possiamo dire che il metodo di Lanczos genera una successione di vettori ortonormali che costituisce il sottospazio invariante S appena sopra citato. Se nel teorema di Courant-Fischer assumiamo che i vettori y 5
60 4.5 Il metodo di Lanczos siano unitari allora noteremo come il numeratore è una trasformazione di similarità su uno spazio 1-dimensionale. A questo punto si può descrivere brevemente l iterazione Lanczos r = q 1 ; β =1;q =;j = while(β j ) q j+1 = r j /β j ; j = j +1;α j = q T j Aq j; r j =(A α j I)q j β j 1 q j 1 ; β j = r j 2 end Il caso più fortunato che si può incontrare è quello in cui si ottiene, dopo N passi, β N =eciò sta ad indicare che si ha un spazio invariante di dimensione N dove le basi sono date dai q j. Ponendo poi Q = [q 1,q 2,...,q n ] α 1 β 1... β 1 α T = β n 1... β n 1 α n (4.6) si è ottenuto la tridiagonalizzazione di A ei vettori colonna q i costituiscono la matrice Q, notiamo ulteriormente che T = Q T AQ (4.7) premoltiplicando a sinistra, e ricordando che per matrici ortogonali si ha che Q T Q = I, otteniamo AQ = QT (4.8) È importante notare che l algoritmo di Lanczos soffre di grandi problemi di stabilità numerica quando β j causando la non 51
61 4 Gli autovalori ortogonalità delle basi del sottospazio invariante. Questo problema diventa tanto più evidente quando la dimensione di S diventa grande. Nel nostro caso,poichè la dimensione del sottospazio invariante che cerchiamo è molto piccola(rispetto al numero di punti N del frame-dati), si è calcolata la completa ri-ortogonalità delle basi ottenute. È utile notare la somiglianza fra l equazione (4.8) e la fattorizzazione mostrata in figura (4.1) in effetti questa situazione e proprio quella in cui abbiamo trovato esattamente un sottospazio invariante ma nella realtà questa situazione èmolto rara. A questo punto si può riscrivere la fattorizzazione in modo più completo come segue AV = VH+ fe T k (4.9) dove V R NxK, V T = I k, H R kxk tridiagonale simmetrica e f R N con = V T f. L ultimo termine dell eq. 4.9 è direttamente correlato alla distanza rispetto un sottospazio invariante. Questa fattorizzazione è ottenuta dal seguente algoritmo Input (A,v ) Output (V k,h k,f k ) begin v 1 v 1 / v 1 w Av; α 1 = v1 T w H 1 =(α 1 ); V 1 =(v 1 ); f 1 w v 1 α 1 for j=1,...,k-1 β j = f ; v j+1 f/β j ( ) Hj V j+1 =(V j,v j+1 ); H j β j e t j h Av j+1 h Vj T z; H =(H j,h) f z V j+1 h; end 52
62 Capitolo 5 La piattaforma 53
63 5 Lapiattaforma 5.1 Gli strumenti Lo sviluppo di tecnologie sempre più miniaturizzate e potenti ha reso possibile la disponibilità sul mercato di strumenti che integrano varie unità di calcolo. Si sta parlando di calcolatori paralleli ovvero quei calcolatori formati da diverse unità diin- put/ouput(i/o) ma soprattutto dotati di più di un processore. L osservatorio radioastronomico del C.N.R di Medicina, nel gennaio 21 ha acquistato uno strumento per il calcolo parallelo come si può vedere dalla figura 5.1. Questo super-computer, Figura 5.1. Elaboratore parallelo costruito dalla azienda americana Mercury, è uno strumento modulare poichè ha la possibilità di alloggiare al suo interno fino a 9 elementi. 54
64 5.2 Ilsistema 5.2 Il sistema Il sistema utilizzato per lo sviluppo della KLT ècompostoda un bus VME e da un insieme di 9 slot per l alloggiamento dei vari sottosistemi di calcolo. Nell ordine, partendo dal lato sinistro del modulo parallelo(vedi fig. 5.1), sono presenti le seguenti componenti: 1. Il processore che gestisce tutto il sistema modulare(host), quindi anche il sistema operativo. 2. Il convertitore analogico-digitale PENTEK. 3. La scheda MCJ6 su cui alloggiano due processori(ce=computer element) di tipo Risc. 4. La scheda di controllo del bus del sistema. 5.3 PENTEK Il convertitore analogico/digitale riceve i dati attraverso il cavo che è connesso agli apparati di ricezione come la parabola o la Croce del Nord. Questa scheda ADC converte i segnali di tipo analogico in dati digitali che sono trattabili numericamente tramite software. Questo componente può campionare i segnali ad una frequenza compresa fra e 2Mhz e poichè la banda da analizzare è di pochi 6MHz si è settato la frequenza di campionamento a 13.3Mhz coerentemente con il teorema di campionamento. 5.4 MCJ6 La MCJ6 denominata anche PPC74 è composta da due CE ciascuno dei quali consiste di un processore a 4Mhz MPC74 55
65 5 Lapiattaforma ad architettura RISC con un unità vettoriale di tipo ALTIVEC (denominata anche Velocity Engine). Queste schede possono essere aggiunte facilmente al un sistema in modo da formare cluster di elaboratori anche dell ordine di centinaia di nodi. Come si può Figura 5.2. Struttura della scheda vedere dalla fig. 5.2 ciascun CE MPC74 ha a sua disposizione una memoria RAM, da 64MB, una cache di primo livello da 32kb e una cache L2 da 2MB. Nella figura l unità denominata ASIC è un chip che gestisce in modo ottimale il transito dei dati fra varie schede di questo tipo attraverso il bus VME. Chiaramente in ambito parallelo diversi processi possono comunicare con altri processi in esecuzione su diversi processori di diverso tipo. La gestione di una tal tipologia di programmazione è basata su ICS(Interprocessor Comunication System). ICS fornisce un interfaccia standard per la comunicazione di processi che eseguono su processori diversi in cluster di computer eterogenei. In effetti gli oggetti interessati da ICS sono 1. CE: unità logica capace di eseguire processi, ciascuno di questi elementi è identificato da un numero univoco(ceid 1 ). 1 acronimo di Computer Element IDentification 56
66 5.4 MCJ6 2. HOST: è l unico componente a poter caricare il sistema operativo in modo autonomo, esso gestisce servizi di input e output standard, servizi per dischi, servizi d errore. L HOST è l unico ad avere un filesystem e quindi è indispensabile, è inoltre compito di questo componente inizializzare il primo CE. 3. Clusters: Un cluster è un gruppo di CE che condivide un database. Questo database, residente su un CE, contiene le traccie per permettere ad un qualsiasi CE di comunicare con un altro per mezzo di ICS. 4. Processi: sono programmi indipendenti che possono competere per l utilizzo di risorse di sistema come CPU, memoria, controllori DMA e cosi via. ICS supporta la creazione e il lancio di processi in modo remoto. 5. SMB: è l oggetto primario di utilizzo basato su ICS. Un SMB 2 è un buffer di memoria che può essere acceduto da più di un processo attraverso diversi CE. Queste particolari locazioni di memoria sono gestite attraverso puntatori, detti anche SMB handler. Per capire meglio come funziona un ambiente parallelo di questo tipo si elencano qui di seguito i passi occorrenti per rendere attivo il cluster: 1. l accensione della macchina, vedi fig. 5.1, comporta l avvio dell HOST che, nella nostra configurazione, è caratterizzata da una macchina SPARC sistema operativo UNIX; 2. dalla linea di comando del sistema operativo UNIX si lanciano i comandi di inizializzazione: initmcs e sysmc; 2 acronimo di Shared Memory Buffer 57
67 5 Lapiattaforma 3. il comando sysmc serve per inizializzare i CE e per descrivere la topologia del cluster che sarà poi memorizzata in un database adeguato; 4. il comando runmc serve per eseguire i processi sui CE, in particolare runmc carica l imagine del file oggetto relativo al processo su un particolare CE. Il file oggetto è generato da un apposito programma di compilazione chiamato ccmc. La fig. 5.3 mostra in maniera schematica, ma molto chiara, quali Figura 5.3. Comunicazioni fra HOST e CE sono i componenti lanciati durante l inizializzazione di ogni CE e quali sono quelli lanciati durante il ciclo di attività diunce. Per fornire accesso a dispositivi di memorizzazione come dischi, 58
68 5.5 Scheda di controllo i processi devono sfruttare l HOST poichè è l unico ad avere un filesystem. Questo tipo di accesso è ottenuto tramite l utilizzo di due tipo di processi: il console server el OSM server. Laconsole server fornisce al CE una console attraverso la quale i messaggi del CE-kernel 3 raggiungono lo sviluppatore, si noti che esiste un unico processo di questo tipo. L OMS server fornisce ai processi, in esecuzione su un CE, servizi di standard input/output e accesso ai dischi, in questo caso ad ogni processo su CE viene associato un OSM sull HOST. Ad esempio quando funzioni come printf,fread e write vengono richiamate su un CE di tipo Mercury, il kernel richiede all OSM relativo di completare la richiesta sull HOST. 5.5 Scheda di controllo Questa scheda mostra sulla facciata una serie di led che specificano lo stato del bus in tempo reale. In particolare sono presenti led relativi al bus dati e al bus indirizzi. Questi insieme ad altri led servono per monitorare l utilizzo del bus VME. 5.6 Il Software Il software sviluppato per il problema del rilevamento di segnali tramite KLT trae vantaggio dalla potente macchina parallela che, nell osservatorio di radioastronomia, è battezzata MEDALT1. Il progetto è stato sviluppato in ambiente UNIX per quanto riguarda il lato server mentre il lato client è stato sviluppato in ambiente Windows, va precisato l implementazione del client è stata effettuata avendo cura di non vincolarsi a tale sistema operativo, infatti è possibile eseguire la ricompilazione con modifiche 3 insieme di processi che costituiscono il nucleo del sistema operativo 59
69 5 Lapiattaforma Figura 5.4. Moduli software implementati minime al sorgente. Non si può dire altrettanto del lato server poichè un uso appropriato della potenza di calcolo dell ALTIVEC costringe ad utilizzare funzioni proprietarie basate sulla libreria SAL 4. Per avere una visione generale del progetto si osservi la fig I moduli presenti in figura sono: 1. Client: è l interfaccia grafica che visualizza i dati analizzati. 4 acronimo di Scientific algorithm library 6
70 5.6 Il Software 2. Server1: è il server con il quale si stabilisce le connessioni per il lancio dei task KLT. 3. Server2: è il processo che modifica i flag per la terminazione dei task KLT. 4. Server PPC: è il modulo che distribuisce i dati campionati ai task KLT. 5. KLT: sono i processi che indefinitamente eseguono la trasformata KLT Il client Questo modulo costituisce il front-end grafico per l utilizzo della KLT. Non ci sono molti parametri da settare infatti gli unici bottoni presenti sul pannello sono quelli relativi al numero di punti del frame-dati che si vuole analizzare, il numero di autovalori/autovettori che si vuole calcolare e il numero di processori che si vuole adoperare. C e inoltre un ulteriore checkbox che permette, in modo automatico quando si ferma l analisi, di memorizzare il frame-dati in un file con indice progressivo e con estensione ON oppure OFF. Il formato di memorizzazione di questi file è quello ASCII. Quando si è lanciata l elaborazione nel area grande dello schermo compare il grafico dei risultati in tempo reale, proprio per questo motivo ci si è appoggiati su una libreria grafica come OpenGL per la sua efficienza Server1 Una volta premuto il tasto di avvio(start) nell interfaccia client, i parametri settati vengono trasferiti via TCP/IP al processo server1 che esegue i seguenti passi: 61
71 5 Lapiattaforma Figura 5.5. Interfaccia grafica OPENGL del client 1. Passa i parametri al modulo PPC che avvia il campionamento dei dati. 2. Entra in ciclo infinito e aspetta i risultati delle KLT. 3. Se ci sono risultati dai task KLT li spedisce al client PPC Questo modulo come già detto assolve il compito di campionare i dati e metterli a disposizione per la elaborazione KLT vera e propria. Prima però di fare questo lancia i processi KLT i quali restano in attesa di dati da elaborare. Il ciclo principale del modulo PPC è composto dai seguenti passi: 1. ParamFromGCC: è la procedura che si incarica di ottenere 62
72 5.6 Il Software i parametri dal server GCC; 2. RIOJ-Init: inizializza il chip RINOJ presente sulla MCJ6 per il trasferimento dei dati dal convertitore al buffer; 3. CreateTransfer: prepara le strutture dati per inizializzare il DMA; 4. BootKLT: lancia i task KLT; 5. Acquisition: ciclo infinito di acquisizione tramite DMA; 6. DownKLT: distrugge tutte le strutture dati precedentemente inizializzate per il DMA e per il chip RINOJ. Poiché il calcolo della trasformata KLT richiede un tempo di calcolo che è maggiore di quello necessario per il campionamento da un frame all altro, non è stato necessario fare uso del doublebuffering KLT Questi sono i processi che eseguono letteralmente il calcolo della KLT applicando il metodo di Lanczos. Il numero di processi KLT che si può lanciare dipende strettamente dal numero di processori a disposizione. Il sistema implementato è stato pensato in maniera da rilevare eventuali nuovi processori per permettere una certa scalabilità del software. In modo totalmente automatico il task una volta processato il frame-dati pone il risultato in un buffer condiviso, setta un flag ricomincia con un nuovo ciclo di elaborazione. A questo punto si attiva il processo server1 che, rilevando il flag appena attivato dal task KLT, estrae il risultato e lo spedisce attraverso il TCP/IP al client. 63
73 5 Lapiattaforma Server2 Quest ultimo modulo serve per interrompere l intera sessione di calcoli in atto. Anche questo modulo accetta connessione via TCP/IP con il lato client, mentre dialoga con i restanti moduli attraverso flag,semafori e segnali. 5.7 I tempi Come detto in precedenza l analisi dei dati provenienti da strumenti radioastronomici dovrebbe essere fatta in real-time. Per quanto riguarda la serie di Fourier esistono metodi veloci come la FFT e hardware realizzati specificamente allo scopo di calcolare questa trasformata che eseguono milioni di operazioni al secondo. Per quanto riguarda la KLT, purtroppo, fin ora non è stato inventato nessun algoritmo veloce ne tanto meno hardware di calcolo dedicato. Ci si è quindi concentrati sull ottimizzazione del codice, sfruttando la particolare struttura della matrice di Toeplitz, la cache, la contiguit`dei dati in memoria(striding). La matrice di Toeplitz è stata sfruttata osservando che il prodotto della matrice A per il vettore generico x può essere ottimizzato notando che questo corrisponde ad una convoluzione del vettore di correlazione con il vettore x. Inoltre la convoluzione corrisponde ad una moltiplicazione nel dominio di Fourier, quindi si è utilizzata tale trasformata per abbattere i calcoli. Un ulteriore ottimizzazione la si è ottenuta posizionando il codice in sequenze più idonee dal punto di vista dello sfruttamento della cache. In ultima analisi si è cercato il più possibile di memorizzare vettori in aree di memoria contigue poichè in tal modo l utilizzo dell unità ALTIVEC risulta più efficiente.la tab. 5.6 mette in evidenza il tempo impiegato per calcolare gli autovalori di un frame-dati con N=124 a seconda del metodo utilizzato. La tab. 5.7 mette in evidenza la velocità di calcolo degli autovalori con 64
74 5.7 Itempi Metodo 3 Autovalori 1 Autovalori 8 Autovalori µsec µsec µsec Jacobi sec. Lanczos Classico Figura 5.6. Tabella dei tempi in microsecondi (µsec) Nr.Punti Autocorrelazione IRL Totale Tempi µsec µsec µsec µsec Figura 5.7. Tabella dei tempi in microsecondi (µsec) il metodo ottimizzato di Lanczos(IRL), si tenga presente che per N=496 si ha una matrice di autocorrelazione di ben 16 milioni di punti. Nella tabella la quarta colonna riportante il Totale Tempi è comprensiva dei calcoli della correlazione, di fattorizzazione di Lanczos, di estrazione autovalori e di un ulteriore modulo di integrazione degli autovettori. 65
75 5 Lapiattaforma 66
76 Capitolo 6 Test 67
77 6 Test 6.1 Software di Simulazione Allo scopo di capire l efficacia della formula di rilevazione proposta da Dixon e presentata nel capitolo 4(vedi eq. 3.22) si è reso necessario lo sviluppo di un software di simulazione tramite il quale sono stati effettuati diversi test che hanno permesso una miglior comprensione del comportamento degli autovalori e degli autovettori. L interfaccia grafica sviluppata si compone essenzialmente di tre parti: o una sezione di impostazioni dei parametri dei segnali posta sul lato destro dell interfaccia; o una sezione che visualizza lo spettro di Fourier del frame-dati posta nella parte superiore; o una sezione che visualizza lo spettro di Fourier degli autovettori situata nella area centrale dell interfaccia. Tramite la sezione impostazioni è possibile determinare le caratteristiche di 3 segnali indipendenti. I parametri che si possono modificare sono l ampiezza, la frequenza, la modulazione (in ampiezza e/o frequenza) e il numero di autovalori da calcolare. Questi segnali sono sommati assieme in modo da generare un unico segnale; inoltre sempre attraverso la sezione impostazioni è possibile impostare la quantità di noise da aggiungere. Il pulsante RUN fa partire il calcolo del simulatore che genera il frame risultante dalla somma dei segnali e dal rumore, tale frame èpoi usato per il calcolo della FFT e della KLT. Il risultato della simulazione è il grafico della FFT del frame generato, visualizzato nella parte superiore dell interfaccia, e il tracciato dello spettro degli autovettori calcolati dalla KLT, che sono visualizzati nell area grande del programma. 68
78 6.2 Test e valutazioni 6.2 Test e valutazioni Dopo aver spiegato il metodo proposto da Dixon per la rilevazione dei segnali, si è giunti alla fase dei test in situazioni reali. Nei precedenti capitoli si è discusso il rilevamento di segnali in situazioni di tipo didattico cioè quando il rapporto segnale rumore è maggiore di 1(il rumore aggiunto non modifica il segnale in modo sostanziale). Si ricorda la formula per calcolare l even- Figura 6.1. Eigenspectrum multipli tuale presenza di segnale M KLT = 2Max(λ) NA(,) (6.1) dove λ è l autovalore massimo, N sono il numero di punti del frame-dati, A(,) è l energia dell autocorrelazione. Per il rilevamento di segnali, prima si procede con il calcolo della formula 69
79 6 Test 6.1 con un frame-dati rumoroso(nessun segnale presente), in seguito si usa la stessa formula con un frame-dati di cui si vuole conoscere l eventuale presenza di segnali. I due valori trovati e messi a confronto danno la risposta: se M KLT (segnale) >M KLT (rumore) allolra rilevazione. A questo punto occorre utilizzare il simulatore descritto nel paragrafo 6.1 facendo alcuni test in casi dove il rapporto segnale rumore è buono e in altri dove tale rapporto èpiù scarso. Nella Figura 6.2. Analisi autovettori figura 6.2 si è generato un segnale sinusoidale leggermente alterato da rumore bianco. In alto nella figura è rappresentato lo spettro di Fourier del frame-dati mentre in basso nell area grande sono rappresentati gli spettri dei primi 15 autovettori a partire 7
80 6.2 Test e valutazioni dal dominante raffigurato più in basso. Come si può notare in tutti i singoli spettri compare una riga nella posizione in corrispondenza della frequenza della sinusoide in analisi. La figura 6.3 Figura 6.3. Particolare dell area FFT rappresenta l area FFT ingrandita, evidentemente in questa situazione è ben evidente la componente sinusoidale presente circa a 125Hz. Se si immerge ulteriormente il segnale sinusoidale nel Figura 6.4. Analisi autovettori: con rumore 71
81 6 Test rumore(vedi fig. 6.4), gli spettri di alcuni autovettori meno importanti non evidenziano più la riga relativa alla frequenza della sinusoide in analisi. Possiamo notare però che lo spettro dell autovettore dominante rimane ancora coerente con la frequenza della sinusoide. In questo caso, in cui lo spettro di Fourier del frame-dati riesce ancora a evidenziare la presenza di un segnale, il metodo illustrato dalla formula 6.1 è ancora valido. Vogliamo però analizzare cosa succede quando il segnale è immerso nel rumore cioè quando dallo spettro di Fourier non si può piùdirese è presente un qualsiasi tipo di segnale diverso dal rumore. Allo scopo si osservi la fig. 6.5, dallo spettro di Fourier(in alto nella Figura 6.5. Analisi autovettori: segnale rumoroso figura) non si può direcheè presente un segnale, in questo caso l autovettore dominante non presenta più la riga nella posizione della frequenza corretta. Nella figura 6.6 è illustrato lo spettro 72
82 6.2 Test e valutazioni Figura 6.6. Particolare ingrandito dell Area FFT di Fourier per mostrare che la componente sinusoidale non è più evidente rispetto alla componente casuale del rumore. Tutto ciò è riassumibile come segue, quando nello spettro di Fourier il picco massimo è relativo alla frequenza del segnale in analisi la formula 6.1 restituisce un valore utile per il rilevamento(condizione in cui il rapporto segnale su rumore è buono: maggiore di uno). Se invece nello spettro di Fourier non èpiù possibile distinguere il segnale dal rumore, l autovettore dominante non mantiene più la riga sulla frequenza corretta. In quest ultima condizione la formula 6.1 non èpiù utile ai fini della rilevazione. I primi esperimenti con questa formula hanno evidenziato il comportamento appena citato. La fig. 6.1 riporta sull asse delle ascisse il tempo e su quello delle ordinate 2 autovalori più grandi in ordine decrescente partendo dall alto(il primo autovalore in alto è quello relativo all autovettore dominante). I vari tracciati sono ottenuti calcolando la KLT su un frame-dati, proveniente dalla parabola, ai vari istanti di tempo T. In altre parole la T-esima osservazione contenuta nel frame-dati relativa all istante T genera,tramite il calcolo KLT, un eigen-spectrum che è impilato come evidenzia l ellisse nella figura. I vari autovalori di diverse osservazioni sono poi collegati tramite linee in modo da evidenziare l andamento in funzione del tempo. Occorre precisare quanto segue: o i dati acquisiti nel tracciato di fig. 6.1 sono dati reali con S/N<1(sorgente non forte); 73
83 6 Test o nella prima metà temporale del tracciato della figura, il dispositivo di acquisizione(la parabola) era off-source cioè non puntava sulla sorgente; o nella seconda metà temporale il dispositivo è stato messo on-source, cioè puntato sulla radiosorgente. Questo tipo di tracciato ha evidenziato che l autovalore dominante 1, passando da on-source a off-source, nonè influenzato infatti mantiene un andamento regolare quelli che cambiano sono alcuni degli autovalori successivi. In situazioni con segnale debole(come nella maggioranza dei casi in radioastronomia) è evidente che, con questo metodo basato sulla variabilità dell autovalore dominante, non è possibile fare un qualsiasi tipo di rilevamento di segnali. Questo comportamento inatteso ha costretto la ricerca di un nuovo metodo mirato all aumento della sensibilità nelle situazioni di basso rapporto segnale rumore. Per ovviare al problema della sensibilità siè notato che lo spettro di Fourier di qualcuno dei primi autovettori(non è chiaro quali), non necessariamente il primo, contiene l informazione sulla frequenza relativa al segnale in analisi. Per questo motivo ai fini della rilevazione dei segnali è stato modificato il metodo: o si calcolano i primi p autovettori e di ciascuno si calcola lo spettro; o si calcola la media di ciascun canale dei p spettri, producendo un unico spettro di Fourier; o si è integrato rispetto al tempo. Quando si lancia il programma, ad ogni istante di tempo, il secondo punto appena citato produce uno spettro(medie); i vari 1 autovalore dominate è quello massimo, mentre l autovettore dominante è quello associato all autovalore massimo 74
84 6.2 Test e valutazioni spettri ottenuti in istanti di tempo successivi sono a loro volta mediati(integrazione). L integrazione permette di evidenziare i segnali e di annullare il rumore questo poichè un segnale da un contributo su frequenze fisse mentre il rumore, proprio a causa della sua natura casuale, non da contributo su particolari frequenze ma tende ad annullarsi. La figura 6.7 rappresenta il risultato del metodo modificato analizzando frame-dati senza segnali. La prima osservazione fatta, fig. 6.7, è ottenuta puntando la parabola su una parte del cosmo dove non sono presenti radiosorgenti, per questo si dice osservazione off-source. I parametri settati per questa osservazione erano N=248 punti, 2 processori, 6 autovalori, tempo di integrazione 18 secondi. In modo analogo è stata fatta una seconda analisi, vedi figura 6.8, con un Figura 6.7. elaborazione KLT senza segnale 75
85 6 Test Figura 6.8. elaborazione KLT con segnale segnale immerso nel rumore a -52.6db m 2 con gli stessi parametri impostati come nell esempio precedente. Questa osservazione invece, fig. 6.8, corrisponde a quella fatta puntando la parabola sulla radio-sorgente e per questo si dice on-source. La tecnica on/off source apporta i seguenti vantaggi: o eliminare la forma della banda; o eliminare interferenze; o evidenziare segnali di interesse; L eliminazionedelle interferenzeterrestri è ottenuto tenendo presente che l interferenza rimane presente sia nello stato on-source 2 db m =1log 1 P otenza Media in W att
25 - Funzioni di più Variabili Introduzione
 Università degli Studi di Palermo Facoltà di Economia CdS Statistica per l Analisi dei Dati Appunti del corso di Matematica 25 - Funzioni di più Variabili Introduzione Anno Accademico 2013/2014 M. Tumminello
Università degli Studi di Palermo Facoltà di Economia CdS Statistica per l Analisi dei Dati Appunti del corso di Matematica 25 - Funzioni di più Variabili Introduzione Anno Accademico 2013/2014 M. Tumminello
SCHEDA DIDATTICA N 7
 FACOLTA DI INGEGNERIA CORSO DI LAUREA IN INGEGNERIA CIVILE CORSO DI IDROLOGIA PROF. PASQUALE VERSACE SCHEDA DIDATTICA N 7 LA DISTRIBUZIONE NORMALE A.A. 01-13 La distribuzione NORMALE Uno dei più importanti
FACOLTA DI INGEGNERIA CORSO DI LAUREA IN INGEGNERIA CIVILE CORSO DI IDROLOGIA PROF. PASQUALE VERSACE SCHEDA DIDATTICA N 7 LA DISTRIBUZIONE NORMALE A.A. 01-13 La distribuzione NORMALE Uno dei più importanti
Prof. Carlo Rossi DEIS - Università di Bologna Tel:
 Prof. Carlo Rossi DEIS - Università di Bologna Tel: 051 2093020 email: carlo.rossi@unibo.it Sistemi Tempo-Discreti In questi sistemi i segnali hanno come base l insieme dei numeri interi: sono sequenze
Prof. Carlo Rossi DEIS - Università di Bologna Tel: 051 2093020 email: carlo.rossi@unibo.it Sistemi Tempo-Discreti In questi sistemi i segnali hanno come base l insieme dei numeri interi: sono sequenze
scoprirono che tutti i calcoli della FT potevano essere velocizzate di un fattore N/ln(N), ove N è la quantità dei numeri da calcolare; e
 IL KLT Premessa Supponiamo che dallo Spazio ci giungono segnali alieni, come ci giungerebbero? in banda stretta o in banda larga? Ovvio che, se i segnali fossero emessi in banda larga, noi non potremmo
IL KLT Premessa Supponiamo che dallo Spazio ci giungono segnali alieni, come ci giungerebbero? in banda stretta o in banda larga? Ovvio che, se i segnali fossero emessi in banda larga, noi non potremmo
In realtà i segnali con i quali dobbiamo confrontarci più frequentemente sono limitati nel tempo
 Segnali trattati sino ad ora: continui, durata infinita,.. Su essi sono stati sviluppati strumenti per analizzare output di circuiti e caratteristiche del segnale: Risposta all impulso, prodotto di convoluzione,
Segnali trattati sino ad ora: continui, durata infinita,.. Su essi sono stati sviluppati strumenti per analizzare output di circuiti e caratteristiche del segnale: Risposta all impulso, prodotto di convoluzione,
Officine Orbitali, primo livello di espansione civile nello spazio INAF-IRA, Bologna maggio 2018
 OFFICINE ORBITALI - Primo livello di espansione civile nello spazio" Ricerca della vita intelligente: pianeti extraterrestri e SETI STELIO MONTEBUGNOLI, IRA / INAF Tutti gli elementi che formarono l uomo
OFFICINE ORBITALI - Primo livello di espansione civile nello spazio" Ricerca della vita intelligente: pianeti extraterrestri e SETI STELIO MONTEBUGNOLI, IRA / INAF Tutti gli elementi che formarono l uomo
UNIVERSITÀ DI PISA Corso di Laurea in Scienze Motorie. Tecnologie e strumentazione biomedica. Accenni sulla Trasformata di Fourier.
 UNIVERSITÀ DI PISA Corso di Laurea in Scienze Motorie Tecnologie e strumentazione biomedica Accenni sulla Trasformata di Fourier Alberto Macerata Dipartimento di Ingegneria dell Informazione Fourier (1768-183)
UNIVERSITÀ DI PISA Corso di Laurea in Scienze Motorie Tecnologie e strumentazione biomedica Accenni sulla Trasformata di Fourier Alberto Macerata Dipartimento di Ingegneria dell Informazione Fourier (1768-183)
Trasformata discreta di Fourier diunasequenzafinita: algoritmifft
 diunasequenzafinita: algoritmifft La TDF di una sequenza finita può essere calcolata utilizzando algoritmi, computazionalmente efficienti, quali gli algoritmi Fast Fourier Transform (FFT). L efficienza
diunasequenzafinita: algoritmifft La TDF di una sequenza finita può essere calcolata utilizzando algoritmi, computazionalmente efficienti, quali gli algoritmi Fast Fourier Transform (FFT). L efficienza
La Retta Ogni funzione di primo grado rappresenta, graficamente, una retta. L equazione della retta può essere scritta in due modi
 La Retta Ogni funzione di primo grado rappresenta, graficamente, una retta. L equazione della retta può essere scritta in due modi Forma implicita Forma esplicita a x b y c 0 y m x q a c y x b b Esempio
La Retta Ogni funzione di primo grado rappresenta, graficamente, una retta. L equazione della retta può essere scritta in due modi Forma implicita Forma esplicita a x b y c 0 y m x q a c y x b b Esempio
1 Calcolo approssimato della serie di Fourier
 1 Calcolo approssimato della serie di Fourier Come è noto, se f(x) è una funzione periodica di periodo L di classe C 1 e si definisce, per ogni intero, F = 1 L allora, se è un intero pari, f (x) L/2 L/2
1 Calcolo approssimato della serie di Fourier Come è noto, se f(x) è una funzione periodica di periodo L di classe C 1 e si definisce, per ogni intero, F = 1 L allora, se è un intero pari, f (x) L/2 L/2
Analisi Matematica 3/Analisi 4 - SOLUZIONI (20/01/2016)
 Corso di Laurea in Matematica Docente: Claudia Anedda Analisi Matematica 3/Analisi 4 - SOLUZIONI (//6) ) i) Dopo averla classificata, risolvere l equazione differenziale tẋ x = t cos(t), t >. ii) Scrivere
Corso di Laurea in Matematica Docente: Claudia Anedda Analisi Matematica 3/Analisi 4 - SOLUZIONI (//6) ) i) Dopo averla classificata, risolvere l equazione differenziale tẋ x = t cos(t), t >. ii) Scrivere
Ripasso segnali e processi casuali. Trasmissione dell Informazione
 Ripasso segnali e processi casuali 1 Breve ripasso di segnali e trasformate Dato un segnale s(t), la sua densità spettrale si calcola come dove S(f) è la trasformata di Fourier. L energia di un segnale
Ripasso segnali e processi casuali 1 Breve ripasso di segnali e trasformate Dato un segnale s(t), la sua densità spettrale si calcola come dove S(f) è la trasformata di Fourier. L energia di un segnale
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA CHIMICA E DEI MATERIALI 27 GIUGNO 2016
 FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA CHIMICA E DEI MATERIALI 7 GIUGNO 06 MATTEO LONGO Ogni versione del compito contiene solo due tra i quattro esercizi 6-7-8-9. Esercizio. Considerare
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA CHIMICA E DEI MATERIALI 7 GIUGNO 06 MATTEO LONGO Ogni versione del compito contiene solo due tra i quattro esercizi 6-7-8-9. Esercizio. Considerare
Note sulle Catene di Markov
 Note sulle Catene di Markov ELAUT Prof. Giuseppe C. Calafiore Sommario Queste note contengono un estratto schematico ridotto di parte del materiale relativo alle Catene di Markov a tempo continuo e a tempo
Note sulle Catene di Markov ELAUT Prof. Giuseppe C. Calafiore Sommario Queste note contengono un estratto schematico ridotto di parte del materiale relativo alle Catene di Markov a tempo continuo e a tempo
Calcolo numerico per utilizzare i residui di udito
 Calcolo numerico per utilizzare i residui di udito Andrea Trucco, Ph.D. Dipartimento Ingegneria Biofisica ed Elettronica DIBE - Università di Genova trucco@ieee.org 1 Segnale audio Variazione della pressione
Calcolo numerico per utilizzare i residui di udito Andrea Trucco, Ph.D. Dipartimento Ingegneria Biofisica ed Elettronica DIBE - Università di Genova trucco@ieee.org 1 Segnale audio Variazione della pressione
Note per il corso di Geometria Corso di laurea in Ing. Edile/Architettura. 4 Sistemi lineari. Metodo di eliminazione di Gauss Jordan
 Note per il corso di Geometria 2006-07 Corso di laurea in Ing. Edile/Architettura Sistemi lineari. Metodo di eliminazione di Gauss Jordan.1 Operazioni elementari Abbiamo visto che un sistema di m equazioni
Note per il corso di Geometria 2006-07 Corso di laurea in Ing. Edile/Architettura Sistemi lineari. Metodo di eliminazione di Gauss Jordan.1 Operazioni elementari Abbiamo visto che un sistema di m equazioni
4 Autovettori e autovalori
 4 Autovettori e autovalori 41 Cambiamenti di base Sia V uno spazio vettoriale tale che dim V n Si è visto in sezione 12 che uno spazio vettoriale ammette basi distinte, ma tutte con la medesima cardinalità
4 Autovettori e autovalori 41 Cambiamenti di base Sia V uno spazio vettoriale tale che dim V n Si è visto in sezione 12 che uno spazio vettoriale ammette basi distinte, ma tutte con la medesima cardinalità
CAPITOLO 2: Algoritmo Fast Fourier Transform (FFT)
 CAPITOLO : Algoritmo Fast Fourier Transform () L algoritmo (Fast Fourier Transform) è decisamente uno dei più utilizzati all interno dell elaborazione dei segnali digitali. Il suo scopo è quello di calcolare
CAPITOLO : Algoritmo Fast Fourier Transform () L algoritmo (Fast Fourier Transform) è decisamente uno dei più utilizzati all interno dell elaborazione dei segnali digitali. Il suo scopo è quello di calcolare
Distribuzioni di probabilità nel continuo
 Distribuzioni di probabilità nel continuo Prof.ssa Fabbri Francesca Classe 5C Variabili casuali continue Introduzione: Una Variabile Casuale o Aleatoria è una grandezza che, nel corso di un esperimento
Distribuzioni di probabilità nel continuo Prof.ssa Fabbri Francesca Classe 5C Variabili casuali continue Introduzione: Una Variabile Casuale o Aleatoria è una grandezza che, nel corso di un esperimento
ANALISI DI FOURIER. Segnali a Tempo Discreto:
 ANALISI DI FOURIER Segnali a Tempo Discreto: - - Sequenza periodica - Taratura degli assi frequenziali - TDF di una sequenza finita - Campionamento in Frequenza Serie discreta di Fourier Consideriamo una
ANALISI DI FOURIER Segnali a Tempo Discreto: - - Sequenza periodica - Taratura degli assi frequenziali - TDF di una sequenza finita - Campionamento in Frequenza Serie discreta di Fourier Consideriamo una
CONTROLLI AUTOMATICI LS Ingegneria Informatica. Analisi modale
 CONTROLLI AUTOMATICI LS Ingegneria Informatica Analisi modale Prof. Claudio Melchiorri DEIS-Università di Bologna Tel. 5 9334 e-mail: claudio.melchiorri@unibo.it http://www-lar.deis.unibo.it/~cmelchiorri
CONTROLLI AUTOMATICI LS Ingegneria Informatica Analisi modale Prof. Claudio Melchiorri DEIS-Università di Bologna Tel. 5 9334 e-mail: claudio.melchiorri@unibo.it http://www-lar.deis.unibo.it/~cmelchiorri
Sequenze (Sistemi) di Variabili Aleatorie Se consideriamo un numero di variabili aleatorie, generalmente dipendenti si parla equivalentemente di:
 Teoria dei Fenomeni Aleatori AA 01/13 Sequenze (Sistemi) di Variabili Aleatorie Se consideriamo un numero di variabili aleatorie, generalmente dipendenti si parla equivalentemente di: N-pla o Sequenza
Teoria dei Fenomeni Aleatori AA 01/13 Sequenze (Sistemi) di Variabili Aleatorie Se consideriamo un numero di variabili aleatorie, generalmente dipendenti si parla equivalentemente di: N-pla o Sequenza
RICHIAMI SU PROCESSI ALEATORI E DENSITÀ SPETTRALE DI POTENZA
 RICHIAMI SU PROCESSI ALEATORI E DENSITÀ SPETTRALE DI POTENZA Paolo Bestagini Ph.D. Student bestagini@elet.polimi.it http://home.deib.polimi.it/bestagini Sommario 2 Segnali deterministici Continui Discreti
RICHIAMI SU PROCESSI ALEATORI E DENSITÀ SPETTRALE DI POTENZA Paolo Bestagini Ph.D. Student bestagini@elet.polimi.it http://home.deib.polimi.it/bestagini Sommario 2 Segnali deterministici Continui Discreti
Risposta in vibrazioni libere di un sistema lineare viscoso a più gradi di libertà. Prof. Adolfo Santini - Dinamica delle Strutture 1
 Risposta in vibrazioni libere di un sistema lineare viscoso a più gradi di libertà Prof. Adolfo Santini - Dinamica delle Strutture 1 Vibrazioni libere non smorzate 1/6 Le equazioni del moto di un sistema
Risposta in vibrazioni libere di un sistema lineare viscoso a più gradi di libertà Prof. Adolfo Santini - Dinamica delle Strutture 1 Vibrazioni libere non smorzate 1/6 Le equazioni del moto di un sistema
INTERPOLAZIONI CON SPLINE
 INTERPOLAZIONI CON SPLINE Assegnati gli n +1valori che la funzione f assume nei nodi x i, si costruisce un interpolazione polinomiale a tratti. In ognuno degli intervalli [x i 1,x i ] il polinomio interpolatore
INTERPOLAZIONI CON SPLINE Assegnati gli n +1valori che la funzione f assume nei nodi x i, si costruisce un interpolazione polinomiale a tratti. In ognuno degli intervalli [x i 1,x i ] il polinomio interpolatore
La Trasformata di Fourier
 La Trasformata di Fourier Preliminari: Spazi di Hilbert Da Wikipedia In matematica uno spazio di Hilbert è uno spazio vettoriale che generalizza la nozione di spazio euclideo. Gli spazi di Hilbert sono
La Trasformata di Fourier Preliminari: Spazi di Hilbert Da Wikipedia In matematica uno spazio di Hilbert è uno spazio vettoriale che generalizza la nozione di spazio euclideo. Gli spazi di Hilbert sono
Analisi delle corrispondenze
 Capitolo 11 Analisi delle corrispondenze L obiettivo dell analisi delle corrispondenze, i cui primi sviluppi risalgono alla metà degli anni 60 in Francia ad opera di JP Benzécri e la sua equipe, è quello
Capitolo 11 Analisi delle corrispondenze L obiettivo dell analisi delle corrispondenze, i cui primi sviluppi risalgono alla metà degli anni 60 in Francia ad opera di JP Benzécri e la sua equipe, è quello
Capitolo 5 Variabili aleatorie discrete notevoli Insegnamento: Statistica Applicata Corso di Laurea in "Scienze e Tecnologie Alimentari"
 Levine, Krehbiel, Berenson Statistica Capitolo 5 Variabili aleatorie discrete notevoli Insegnamento: Statistica Applicata Corso di Laurea in "Scienze e Tecnologie Alimentari" Unità Integrata Organizzativa
Levine, Krehbiel, Berenson Statistica Capitolo 5 Variabili aleatorie discrete notevoli Insegnamento: Statistica Applicata Corso di Laurea in "Scienze e Tecnologie Alimentari" Unità Integrata Organizzativa
Materiale didattico per il corso di Statistica I Quarta esercitazione SOLUZIONI
 Materiale didattico per il corso di Statistica I Quarta esercitazione SOLUZIONI Claudia Furlan 1 Anno Accademico 2006-2007 1 Ringrazio Carlo Gaetan, Nicola Sartori e Aldo Solari per il materiale, aggiunte
Materiale didattico per il corso di Statistica I Quarta esercitazione SOLUZIONI Claudia Furlan 1 Anno Accademico 2006-2007 1 Ringrazio Carlo Gaetan, Nicola Sartori e Aldo Solari per il materiale, aggiunte
APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof. F.Podestà, a.a
 APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof FPodestà, aa 003-004 Sia V uno spazio vettoriale e sia f : V V una applicazione lineare una tale applicazione da uno spazio vettoriale in se stesso è chiamata
APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof FPodestà, aa 003-004 Sia V uno spazio vettoriale e sia f : V V una applicazione lineare una tale applicazione da uno spazio vettoriale in se stesso è chiamata
II Università degli Studi di Roma
 Versione preliminare gennaio TOR VERGATA II Università degli Studi di Roma Dispense di Geometria. Capitolo 3. 7. Coniche in R. Nel Capitolo I abbiamo visto che gli insiemi di punti P lineare di primo grado
Versione preliminare gennaio TOR VERGATA II Università degli Studi di Roma Dispense di Geometria. Capitolo 3. 7. Coniche in R. Nel Capitolo I abbiamo visto che gli insiemi di punti P lineare di primo grado
La trasformazione di camera
 La trasformazione di camera 1 Introduzione Per rappresentare un oggetto tridimensionale nello spazio (scena) in un piano bidimensionale (spazio delle immagini, quale il monitor o un foglio) è necessario
La trasformazione di camera 1 Introduzione Per rappresentare un oggetto tridimensionale nello spazio (scena) in un piano bidimensionale (spazio delle immagini, quale il monitor o un foglio) è necessario
SEGNALI STAZIONARI: ANALISI SPETTRALE
 SEGNALI STAZIONARI: ANALISI SPETTRALE Analisi spettrale: rappresentazione delle componenti in frequenza di un segnale (ampiezza vs. frequenza). Fornisce maggiori dettagli rispetto all analisi temporale
SEGNALI STAZIONARI: ANALISI SPETTRALE Analisi spettrale: rappresentazione delle componenti in frequenza di un segnale (ampiezza vs. frequenza). Fornisce maggiori dettagli rispetto all analisi temporale
PROCESSI CASUALI 1 Fondamenti di segnf a o lin d e a t m ra e s n mtii s T si L o C ne
 PROCESSI CASUALI Fondamenti di segnali Fondamenti e trasmissione TLC Segnali deterministici Un segnale (t) si dice deterministico se è una funzione nota di t, cioè se ad un qualsiasi istante di tempo t
PROCESSI CASUALI Fondamenti di segnali Fondamenti e trasmissione TLC Segnali deterministici Un segnale (t) si dice deterministico se è una funzione nota di t, cioè se ad un qualsiasi istante di tempo t
Matematica Lezione 22
 Università di Cagliari Corso di Laurea in Farmacia Matematica Lezione 22 Sonia Cannas 14/12/2018 Indici di posizione Indici di posizione Gli indici di posizione, detti anche misure di tendenza centrale,
Università di Cagliari Corso di Laurea in Farmacia Matematica Lezione 22 Sonia Cannas 14/12/2018 Indici di posizione Indici di posizione Gli indici di posizione, detti anche misure di tendenza centrale,
Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Processi casuali A.A Alberto Perotti, Roberto Garello
 Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Processi casuali A.A. 2006-07 Alberto Perotti, Roberto Garello DELEN-DAUIN Processi casuali Sono modelli probabilistici
Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Processi casuali A.A. 2006-07 Alberto Perotti, Roberto Garello DELEN-DAUIN Processi casuali Sono modelli probabilistici
Analisi armonica su dati campionati
 Sistemi di misura digitali Analisi armonica su dati campionati - 1 Analisi armonica su dati campionati 1 - Troncamento del segnale Distorsione di leakage L analisi di Fourier è un metodo ben noto per ottenere
Sistemi di misura digitali Analisi armonica su dati campionati - 1 Analisi armonica su dati campionati 1 - Troncamento del segnale Distorsione di leakage L analisi di Fourier è un metodo ben noto per ottenere
Progetto dei Sistemi di Controllo Digitali. Docente: Prof. Francesco Amato
 Progetto dei Sistemi di Controllo Digitali Docente: Prof. Francesco Amato 1 Schema di un sistema di controllo digitale Controllore digitale r e A/D e* u* D/A u y Processo Sistema a empo-continuo Sistema
Progetto dei Sistemi di Controllo Digitali Docente: Prof. Francesco Amato 1 Schema di un sistema di controllo digitale Controllore digitale r e A/D e* u* D/A u y Processo Sistema a empo-continuo Sistema
2. Analisi in frequenza di segnali
 2.1 Serie di Fourier 2. Analisi in frequenza di segnali Secondo il teorema di Fourier, una funzione periodica y(t) è sviluppabile in una serie costituita da un termine costante A 0 e da una somma di infinite
2.1 Serie di Fourier 2. Analisi in frequenza di segnali Secondo il teorema di Fourier, una funzione periodica y(t) è sviluppabile in una serie costituita da un termine costante A 0 e da una somma di infinite
Il tema proposto può essere risolto seguendo due ipotesi:
 Per la trattazione delle tecniche TDM, PM e Trasmissione dati si rimanda alle schede 41, 42, 43, 44, 45, 46, 47 e 48 del libro Le Telecomunicazioni del Prof. F. Dell Aquila. Il tema proposto può essere
Per la trattazione delle tecniche TDM, PM e Trasmissione dati si rimanda alle schede 41, 42, 43, 44, 45, 46, 47 e 48 del libro Le Telecomunicazioni del Prof. F. Dell Aquila. Il tema proposto può essere
IL CRITERIO DELLA MASSIMA VEROSIMIGLIANZA
 Metodi per l Analisi dei Dati Sperimentali AA009/010 IL CRITERIO DELLA MASSIMA VEROSIMIGLIANZA Sommario Massima Verosimiglianza Introduzione La Massima Verosimiglianza Esempio 1: una sola misura sperimentale
Metodi per l Analisi dei Dati Sperimentali AA009/010 IL CRITERIO DELLA MASSIMA VEROSIMIGLIANZA Sommario Massima Verosimiglianza Introduzione La Massima Verosimiglianza Esempio 1: una sola misura sperimentale
Maria Prandini Dipartimento di Elettronica e Informazione Politecnico di Milano
 Note relative a test di bianchezza rimozione delle componenti deterministiche da una serie temporale a supporto del Progetto di Identificazione dei Modelli e Analisi dei Dati Maria Prandini Dipartimento
Note relative a test di bianchezza rimozione delle componenti deterministiche da una serie temporale a supporto del Progetto di Identificazione dei Modelli e Analisi dei Dati Maria Prandini Dipartimento
Rango di una matrice e teorema di Rouché-Capelli
 Rango di una matrice e teorema di Rouché-Capelli Sappiamo che a una matrice m n, A, è associata l applicazione lineare L A : R n R m, L A (X) = AX, X R n. Definizione 1. Lo spazio nullo di A, N (A), è
Rango di una matrice e teorema di Rouché-Capelli Sappiamo che a una matrice m n, A, è associata l applicazione lineare L A : R n R m, L A (X) = AX, X R n. Definizione 1. Lo spazio nullo di A, N (A), è
Sequenze (Sistemi) di Variabili Aleatorie Se consideriamo un numero di variabili aleatorie, generalmente dipendenti si parla equivalentemente di:
 Teoria dei Fenomeni Aleatori AA 01/13 Sequenze (Sistemi) di Variabili Aleatorie Se consideriamo un numero di variabili aleatorie, generalmente dipendenti si parla equivalentemente di: N-pla o Sequenza
Teoria dei Fenomeni Aleatori AA 01/13 Sequenze (Sistemi) di Variabili Aleatorie Se consideriamo un numero di variabili aleatorie, generalmente dipendenti si parla equivalentemente di: N-pla o Sequenza
Laboratorio di Elaborazione di Immagini. Esercitazione 2: TRASFORMATA DI FOURIER
 Laboratorio di Elaborazione di Immagini Esercitazione 2: TRASFORMATA DI FOURIER Serie di Fourier Fourier ebbe la brillante idea di rappresentare funzioni continue e periodiche come una sommatoria di funzioni
Laboratorio di Elaborazione di Immagini Esercitazione 2: TRASFORMATA DI FOURIER Serie di Fourier Fourier ebbe la brillante idea di rappresentare funzioni continue e periodiche come una sommatoria di funzioni
Cos è una wavelet? Applicazioni della trasformata wavelet. Analisi multirisoluzione
 Cos è una wavelet? Applicazioni della trasformata wavelet Analisi multirisoluzione Tre tecniche: Piramidi di immagine Trasformata di Haar Codifica per sottobande Il numero totale di pixel nel caso di una
Cos è una wavelet? Applicazioni della trasformata wavelet Analisi multirisoluzione Tre tecniche: Piramidi di immagine Trasformata di Haar Codifica per sottobande Il numero totale di pixel nel caso di una
TEORIA DEI SISTEMI ANALISI DEI SISTEMI LTI
 TEORIA DEI SISTEMI Laurea Specialistica in Ingegneria Meccatronica Laurea Specialistica in Ingegneria Gestionale Indirizzo Gestione Industriale TEORIA DEI SISTEMI ANALISI DEI SISTEMI LTI Ing. Cristian
TEORIA DEI SISTEMI Laurea Specialistica in Ingegneria Meccatronica Laurea Specialistica in Ingegneria Gestionale Indirizzo Gestione Industriale TEORIA DEI SISTEMI ANALISI DEI SISTEMI LTI Ing. Cristian
CANALE STAZIONARIO CANALE TEMPO INVARIANTE
 CANALE STAZIONARIO Si parla di un Canale Stazionario quando i fenomeni che avvengono possono essere modellati da processi casuali e le proprietà statistiche di tali processi sono indipendenti dal tempo.
CANALE STAZIONARIO Si parla di un Canale Stazionario quando i fenomeni che avvengono possono essere modellati da processi casuali e le proprietà statistiche di tali processi sono indipendenti dal tempo.
PROBABILITÀ - SCHEDA N. 3 VARIABILI ALEATORIE CONTINUE E SIMULAZIONE
 PROBABILITÀ - SCHEDA N. 3 VARIABILI ALEATORIE CONTINUE E SIMULAZIONE (da un idea di M. Impedovo Variabili aleatorie continue e simulazione Progetto Alice n. 15, ) 1. La simulazione Nelle schede precedenti
PROBABILITÀ - SCHEDA N. 3 VARIABILI ALEATORIE CONTINUE E SIMULAZIONE (da un idea di M. Impedovo Variabili aleatorie continue e simulazione Progetto Alice n. 15, ) 1. La simulazione Nelle schede precedenti
ANALISI DI FOURIER. Segnali tempo continui:
 ANALISI DI FOURIER Segnali tempo continui: Segnali aperiodici Introduzione alla Trasformata Continua di - Derivazione intuitiva della TCF a partire dallo Sviluppo in Serie di - Spettro di ampiezza e fase
ANALISI DI FOURIER Segnali tempo continui: Segnali aperiodici Introduzione alla Trasformata Continua di - Derivazione intuitiva della TCF a partire dallo Sviluppo in Serie di - Spettro di ampiezza e fase
Introduciamo il sistema di riferimento indicato in figura b) con F 1 = ( f, 0) ed F 2 = (f, 0). Se P = (x, y) la condizione (1) fornisce
 1 L ellisse 1.1 Definizione Consideriamo due punti F 1 ed F 2 e sia 2f la loro distanza. L ellisse è il luogo dei punti P tali che la somma delle distanze PF 1 e PF 2 da F 1 ed F 2 è costante. Se indichiamo
1 L ellisse 1.1 Definizione Consideriamo due punti F 1 ed F 2 e sia 2f la loro distanza. L ellisse è il luogo dei punti P tali che la somma delle distanze PF 1 e PF 2 da F 1 ed F 2 è costante. Se indichiamo
FONDAMENTI DI INFORMATICA
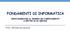 FONDAMENTI DI INFORMATICA CENNI ELEMENTARI AL TEOREMA DEL CAMPIONAMENTO E SPETTRO DI UN SEGNALE Prof. Alfredo Accattatis Fondamenti di Informatica - Alfredo Accattatis 2 Vi ricordate la slide introdotta
FONDAMENTI DI INFORMATICA CENNI ELEMENTARI AL TEOREMA DEL CAMPIONAMENTO E SPETTRO DI UN SEGNALE Prof. Alfredo Accattatis Fondamenti di Informatica - Alfredo Accattatis 2 Vi ricordate la slide introdotta
01CXGBN Trasmissione numerica. parte 6: calcolo delle probabilità I
 01CXGBN Trasmissione numerica parte 6: calcolo delle probabilità I 1 Probabilità di errore BER e SER Per rappresentare la bontà di un sistema di trasmissione numerica in termini di probabilità di errore
01CXGBN Trasmissione numerica parte 6: calcolo delle probabilità I 1 Probabilità di errore BER e SER Per rappresentare la bontà di un sistema di trasmissione numerica in termini di probabilità di errore
1 Successioni di funzioni
 Analisi Matematica 2 Successioni di funzioni CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 6 SERIE DI POTENZE Supponiamo di associare ad ogni n N (rispettivamente ad ogni n p, per qualche
Analisi Matematica 2 Successioni di funzioni CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 6 SERIE DI POTENZE Supponiamo di associare ad ogni n N (rispettivamente ad ogni n p, per qualche
PROBLEMI DI FISICA MODERNA E MECCANICA QUANTISTICA. FISICA MODERNA anno accademico
 PROBLEMI DI FISICA MODERNA E MECCANICA QUANTISTICA FISICA MODERNA anno accademico 007-008 () Sia dato un sistema che può trovarsi in tre stati esclusivi,, 3, e si supponga che esso si trovi nello stato
PROBLEMI DI FISICA MODERNA E MECCANICA QUANTISTICA FISICA MODERNA anno accademico 007-008 () Sia dato un sistema che può trovarsi in tre stati esclusivi,, 3, e si supponga che esso si trovi nello stato
ax 1 + bx 2 + c = 0, r : 2x 1 3x = 0.
 . Rette in R ; circonferenze. In questo paragrafo studiamo le rette e le circonferenze in R. Ci sono due modi per descrivere una retta in R : mediante una equazione cartesiana oppure mediante una equazione
. Rette in R ; circonferenze. In questo paragrafo studiamo le rette e le circonferenze in R. Ci sono due modi per descrivere una retta in R : mediante una equazione cartesiana oppure mediante una equazione
Esercitazione ENS su processi casuali (13 e 14 Maggio 2008)
 Esercitazione ES su processi casuali ( e 4 Maggio 2008) D. Donno Esercizio : Calcolo di autovalori e autovettori Si consideri un processo x n somma di un segnale e un disturbo: x n = Ae π 2 n + w n, n
Esercitazione ES su processi casuali ( e 4 Maggio 2008) D. Donno Esercizio : Calcolo di autovalori e autovettori Si consideri un processo x n somma di un segnale e un disturbo: x n = Ae π 2 n + w n, n
Analisi delle corrispondenze
 Analisi delle corrispondenze Obiettivo: analisi delle relazioni tra le modalità di due (o più) caratteri qualitativi Individuazione della struttura dell associazione interna a una tabella di contingenza
Analisi delle corrispondenze Obiettivo: analisi delle relazioni tra le modalità di due (o più) caratteri qualitativi Individuazione della struttura dell associazione interna a una tabella di contingenza
RICHIAMI DI CALCOLO DELLE PROBABILITÀ
 UNIVERSITA DEL SALENTO INGEGNERIA CIVILE RICHIAMI DI CALCOLO DELLE PROBABILITÀ ing. Marianovella LEONE INTRODUZIONE Per misurare la sicurezza di una struttura, ovvero la sua affidabilità, esistono due
UNIVERSITA DEL SALENTO INGEGNERIA CIVILE RICHIAMI DI CALCOLO DELLE PROBABILITÀ ing. Marianovella LEONE INTRODUZIONE Per misurare la sicurezza di una struttura, ovvero la sua affidabilità, esistono due
Elettronica II Segnali periodici; serie di Fourier; trasformata di Fourier p. 2
 Elettronica II Segnali periodici; serie di Fourier; trasformata di Fourier Valentino Liberali Dipartimento di Tecnologie dell Informazione Università di Milano, 26013 Crema e-mail: liberali@dti.unimi.it
Elettronica II Segnali periodici; serie di Fourier; trasformata di Fourier Valentino Liberali Dipartimento di Tecnologie dell Informazione Università di Milano, 26013 Crema e-mail: liberali@dti.unimi.it
1 Schemi alle differenze finite per funzioni di una variabile
 Introduzione In questa dispensa vengono forniti alcuni elementi di base per la soluzione di equazioni alle derivate parziali che governano problemi al contorno. A questo scopo si introducono, in forma
Introduzione In questa dispensa vengono forniti alcuni elementi di base per la soluzione di equazioni alle derivate parziali che governano problemi al contorno. A questo scopo si introducono, in forma
ONDE STAZIONARIE : DESCRIZIONE MATEMATICA
 ONDE STAZIONARIE : DESCRIZIONE MATEMATICA In questi appunti tratterò della descrizione matematica di un onda stazionaria, cioè di come rappresentare un onda stazionaria attraverso un equazione matematica.
ONDE STAZIONARIE : DESCRIZIONE MATEMATICA In questi appunti tratterò della descrizione matematica di un onda stazionaria, cioè di come rappresentare un onda stazionaria attraverso un equazione matematica.
BLAND-ALTMAN PLOT. + X 2i 2 la differenza ( d ) tra le due misure per ognuno degli n campioni; d i. X i. = X 1i. X 2i
 BLAND-ALTMAN PLOT Il metodo di J. M. Bland e D. G. Altman è finalizzato alla verifica se due tecniche di misura sono comparabili. Resta da comprendere cosa si intenda con il termine metodi comparabili
BLAND-ALTMAN PLOT Il metodo di J. M. Bland e D. G. Altman è finalizzato alla verifica se due tecniche di misura sono comparabili. Resta da comprendere cosa si intenda con il termine metodi comparabili
5.2 Sistemi ONC in L 2
 5.2 Sistemi ONC in L 2 Passiamo ora a considerare alcuni esempi di spazi L 2 e di relativi sistemi ONC al loro interno. Le funzioni trigonometriche Il sistema delle funzioni esponenziali { e ikx 2π },
5.2 Sistemi ONC in L 2 Passiamo ora a considerare alcuni esempi di spazi L 2 e di relativi sistemi ONC al loro interno. Le funzioni trigonometriche Il sistema delle funzioni esponenziali { e ikx 2π },
Pulse Amplitude Modulation (PAM) 2 Scelta delle risposte impulsive dei filtri in trasmissione e ricezione
 Pulse Amplitude Modulation (PAM 1 Definizione La trasmissione di una sequenza di numeri {a k } mediante un onda PAM consiste nel generare, a partire dalla sequenza {a k } il segnale a tempo continuo u(t
Pulse Amplitude Modulation (PAM 1 Definizione La trasmissione di una sequenza di numeri {a k } mediante un onda PAM consiste nel generare, a partire dalla sequenza {a k } il segnale a tempo continuo u(t
11 luglio Soluzione esame di geometria - Ing. gestionale - a.a COGNOME... NOME... N. MATRICOLA... ISTRUZIONI
 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
ATTENZIONE: : giustificate le vostre argomentazioni! Geometria Canale 3. Lettere J-PE (Prof P. Piazza) Esame scritto del 12/02/2014. Compito A.
 Geometria Canale. Lettere J-PE (Prof P. Piazza) Esame scritto del 12/02/2014. Compito A. Nome e Cognome: Numero di Matricola: Esercizio Punti totali Punteggio 1 7 2 6 6 4 6+1 5 6+2 Totale 1+ ATTENZIONE:
Geometria Canale. Lettere J-PE (Prof P. Piazza) Esame scritto del 12/02/2014. Compito A. Nome e Cognome: Numero di Matricola: Esercizio Punti totali Punteggio 1 7 2 6 6 4 6+1 5 6+2 Totale 1+ ATTENZIONE:
ossia può anche essere localizzato univocamente sul piano complesso con la sua forma polare.
 ALGEBRA COMPLESSA Nel corso dei secoli gli insiemi dei numeri sono andati man mano allargandosi per rispondere all esigenza di dare soluzione a equazioni e problemi sempre nuovi I numeri complessi sono
ALGEBRA COMPLESSA Nel corso dei secoli gli insiemi dei numeri sono andati man mano allargandosi per rispondere all esigenza di dare soluzione a equazioni e problemi sempre nuovi I numeri complessi sono
Sistemi lineari. Lorenzo Pareschi. Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara
 Sistemi lineari Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
Sistemi lineari Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI
 CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
Trasformata wavelet. 1 Introduzione. 2 Filtri wavelet di Daubechies
 Trasformata wavelet Introduzione L pari della trasforamta di Fourier veloce (FFT), la trasformata wavelet discreta (DWT) è un operazione veloce e lineare che opera su un vettore di dati di lunghezza pari
Trasformata wavelet Introduzione L pari della trasforamta di Fourier veloce (FFT), la trasformata wavelet discreta (DWT) è un operazione veloce e lineare che opera su un vettore di dati di lunghezza pari
Capitolo 2. Cenni di geometria analitica nel piano
 Capitolo Cenni di geometria analitica nel piano 1 Il piano cartesiano Il piano cartesiano è una rappresentazione grafica del prodotto cartesiano R = R R La rappresentazione grafica è possibile se si crea
Capitolo Cenni di geometria analitica nel piano 1 Il piano cartesiano Il piano cartesiano è una rappresentazione grafica del prodotto cartesiano R = R R La rappresentazione grafica è possibile se si crea
Segnali (processi) aleatori (casuali)
 Segnali (processi) aleatori (casuali) Definizione di processo aleatorio Descrizione statistica di un processo aleatorio Media, potenza, varianza Autocorrelazione e autocovarianza Filtraggio di un processo
Segnali (processi) aleatori (casuali) Definizione di processo aleatorio Descrizione statistica di un processo aleatorio Media, potenza, varianza Autocorrelazione e autocovarianza Filtraggio di un processo
Conversione analogico-digitale
 Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Campionamento e quantizzazione A.A. 2004-05 Alberto Perotti DELEN-DAUIN Conversione analogico-digitale L elaborazione
Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Campionamento e quantizzazione A.A. 2004-05 Alberto Perotti DELEN-DAUIN Conversione analogico-digitale L elaborazione
Soluzione. (a) L insieme F 1 e linearmente indipendente; gli insiemi F 2 ed F 3 sono linearmente
 1. Insiemi di generatori, lineare indipendenza, basi, dimensione. Consideriamo nello spazio vettoriale R 3 i seguenti vettori: v 1 = (0, 1, ), v = (1, 1, 1), v 3 = (, 1, 0), v 4 = (3, 3, ). Siano poi F
1. Insiemi di generatori, lineare indipendenza, basi, dimensione. Consideriamo nello spazio vettoriale R 3 i seguenti vettori: v 1 = (0, 1, ), v = (1, 1, 1), v 3 = (, 1, 0), v 4 = (3, 3, ). Siano poi F
0 < x 3. A1 1 [7 punti] Determinare le eventuali soluzioni del seguente sistema di congruenze: x 2 mod 5 2x 1 mod 3. x 21 mod 7
![0 < x 3. A1 1 [7 punti] Determinare le eventuali soluzioni del seguente sistema di congruenze: x 2 mod 5 2x 1 mod 3. x 21 mod 7 0 < x 3. A1 1 [7 punti] Determinare le eventuali soluzioni del seguente sistema di congruenze: x 2 mod 5 2x 1 mod 3. x 21 mod 7](/thumbs/96/126857371.jpg) Dipartimento di Matematica e Informatica Anno Accademico 017-018 Corso di Laurea in Informatica L-31 Prova scritta di Matematica Discreta 1 CFU 5 Settembre 018 A1 1 [7 punti] Determinare le eventuali soluzioni
Dipartimento di Matematica e Informatica Anno Accademico 017-018 Corso di Laurea in Informatica L-31 Prova scritta di Matematica Discreta 1 CFU 5 Settembre 018 A1 1 [7 punti] Determinare le eventuali soluzioni
Kernel Methods. Corso di Intelligenza Artificiale, a.a Prof. Francesco Trovò
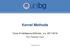 Kernel Methods Corso di Intelligenza Artificiale, a.a. 2017-2018 Prof. Francesco Trovò 14/05/2018 Kernel Methods Definizione di Kernel Costruzione di Kernel Support Vector Machines Problema primale e duale
Kernel Methods Corso di Intelligenza Artificiale, a.a. 2017-2018 Prof. Francesco Trovò 14/05/2018 Kernel Methods Definizione di Kernel Costruzione di Kernel Support Vector Machines Problema primale e duale
Laboratorio di Fisica Moderna Cosmologia
 Laboratorio di Fisica Moderna Cosmologia Programma di oggi Da dove vengono le mappe di CMB Le mappe di CMB del satellite Planck Estrazione dello spettro di potenza Localizzazione del primo picco Misura
Laboratorio di Fisica Moderna Cosmologia Programma di oggi Da dove vengono le mappe di CMB Le mappe di CMB del satellite Planck Estrazione dello spettro di potenza Localizzazione del primo picco Misura
Teoria dei segnali terza edizione
 Capitolo 9 Segnali aleatori a tempo continuo e a tempo discreto SOLUZIONI DEGLI ESERCIZI Soluzione dell esercizio 9.3 Si osservi innanzitutto che, essendo il processo () t Gaussiano, anche il processo
Capitolo 9 Segnali aleatori a tempo continuo e a tempo discreto SOLUZIONI DEGLI ESERCIZI Soluzione dell esercizio 9.3 Si osservi innanzitutto che, essendo il processo () t Gaussiano, anche il processo
Questa viene trasmessa sul canale (wireless o wired). In questo corso, modellizzeremo il canale di trasmissione come un canale Gaussiano bianco
 Canale di trasmissione Dati una costellazione M un labeling binario e è possibile associare alle sequenze binarie di informazione u da trasmettere una forma d onda s(t). Questa viene trasmessa sul canale
Canale di trasmissione Dati una costellazione M un labeling binario e è possibile associare alle sequenze binarie di informazione u da trasmettere una forma d onda s(t). Questa viene trasmessa sul canale
Analisi Matematica 2. Michele Campiti. Prove scritte di. Ingegneria Industriale a.a
 Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
Esercizi sulle coniche (prof.ssa C. Carrara)
 Esercizi sulle coniche prof.ssa C. Carrara Alcune parti di un esercizio possono ritrovarsi in un altro esercizio, insieme a parti diverse. È un occasione per affrontarle da un altra angolazione.. Determinare
Esercizi sulle coniche prof.ssa C. Carrara Alcune parti di un esercizio possono ritrovarsi in un altro esercizio, insieme a parti diverse. È un occasione per affrontarle da un altra angolazione.. Determinare
12 gennaio Commenti esame di geometria - Ing. gestionale - a.a
 Questo documento riporta commenti, approfondimenti o metodi di soluzione alternativi per alcuni esercizi dell esame Ovviamente alcuni esercizi potevano essere risolti utilizzando metodi ancora diversi
Questo documento riporta commenti, approfondimenti o metodi di soluzione alternativi per alcuni esercizi dell esame Ovviamente alcuni esercizi potevano essere risolti utilizzando metodi ancora diversi
Statistica. Lezione : 18, 19. Variabili casuali
 Corsi di Laurea: a.a. 2017-18 Diritto per le Imprese e le istituzioni Scienze dell Amministrazione e Consulenza del Lavoro sienze Internazionali dello Sviluppo e della Cooperazione Statistica Variabili
Corsi di Laurea: a.a. 2017-18 Diritto per le Imprese e le istituzioni Scienze dell Amministrazione e Consulenza del Lavoro sienze Internazionali dello Sviluppo e della Cooperazione Statistica Variabili
Matematica per l Economia, a.a Integrazione al libro di testo
 Matematica per l Economia, a.a. 2016 2017 Integrazione al libro di testo Gianluca Amato 20 dicembre 2016 1 Note ed errata corrige Sezione 2.3, definizione di dominio. La definizione di dominio data dal
Matematica per l Economia, a.a. 2016 2017 Integrazione al libro di testo Gianluca Amato 20 dicembre 2016 1 Note ed errata corrige Sezione 2.3, definizione di dominio. La definizione di dominio data dal
Analisi Matematica 1 e Matematica 1 Geometria Analitica: Rette
 Analisi Matematica 1 e Matematica 1 Geometria Analitica: Rette Annalisa Amadori e Benedetta Pellacci amadori@uniparthenope.it pellacci@uniparthenope.it Università di Napoli Parthenope Contenuti Nel Piano
Analisi Matematica 1 e Matematica 1 Geometria Analitica: Rette Annalisa Amadori e Benedetta Pellacci amadori@uniparthenope.it pellacci@uniparthenope.it Università di Napoli Parthenope Contenuti Nel Piano
Riassumiamo le proprietà dei numeri reali da noi utilizzate nel corso di Geometria.
 Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Campionamento e quantizzazione
 Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Campionamento e quantizzazione A.A. 2008-09 Alberto Perotti DELEN-DAUIN Conversione analogico-digitale L elaborazione
Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Campionamento e quantizzazione A.A. 2008-09 Alberto Perotti DELEN-DAUIN Conversione analogico-digitale L elaborazione
CALCOLO DELL ERRORE E VALUTAZIONE DI UN METODO ANALITICO
 CALCOLO DELL ERRORE E VALUTAZIONE DI UN METODO ANALITICO In chimica analitica un settore importante riguarda il calcolo dell errore e la valutazione della significatività di una misura. Generalmente nell
CALCOLO DELL ERRORE E VALUTAZIONE DI UN METODO ANALITICO In chimica analitica un settore importante riguarda il calcolo dell errore e la valutazione della significatività di una misura. Generalmente nell
TRASFORMATE DI LAPLACE
 FONDAMENTI DI CONTROLLI AUTOMATICI Ingegneria Meccanica http://web.ing.unimo.it/~lbiagiotti/fondamenticontrolli1415.html TRASFORMATE DI LAPLACE Ing. e-mail: luigi.biagiotti@unimore.it http://www.dii.unimore.it/~lbiagiotti
FONDAMENTI DI CONTROLLI AUTOMATICI Ingegneria Meccanica http://web.ing.unimo.it/~lbiagiotti/fondamenticontrolli1415.html TRASFORMATE DI LAPLACE Ing. e-mail: luigi.biagiotti@unimore.it http://www.dii.unimore.it/~lbiagiotti
assuma valori in un determinato intervallo è data dall integrale della sua densità ( = )=
 VARIABILI ALEATORIE CONTINUE Esistono parecchi fenomeni reali per la cui descrizione le variabili aleatorie discrete non sono adatte. Per esempio è necessaria una variabile aleatoria continua ovvero una
VARIABILI ALEATORIE CONTINUE Esistono parecchi fenomeni reali per la cui descrizione le variabili aleatorie discrete non sono adatte. Per esempio è necessaria una variabile aleatoria continua ovvero una
Capitolo 3 Matrici. Marco Robutti. Facoltà di ingegneria Università degli studi di Pavia. Anno accademico
 Capitolo 3 Matrici Marco Robutti Facoltà di ingegneria Università degli studi di Pavia Anno accademico 2017-2018 Tutorato di geometria e algebra lineare Definizione (Matrice) Una matrice A M R (k, n) è
Capitolo 3 Matrici Marco Robutti Facoltà di ingegneria Università degli studi di Pavia Anno accademico 2017-2018 Tutorato di geometria e algebra lineare Definizione (Matrice) Una matrice A M R (k, n) è
Parte 1: tipi primitivi e istruzioni C
 Parte 1: tipi primitivi e istruzioni C Esercizio 1 Scrivere un programma che stampa la somma di una sequenza di N numeri inseriti dall utente. Esercizio 2 Scrivere un programma che stampa la somma di una
Parte 1: tipi primitivi e istruzioni C Esercizio 1 Scrivere un programma che stampa la somma di una sequenza di N numeri inseriti dall utente. Esercizio 2 Scrivere un programma che stampa la somma di una
Serie di Fourier. Tra queste funzioni definiamo un prodotto scalare nel seguente modo: date f, g V poniamo f (x) g (x) dx. f (x) [g (x) + h (x)] dx
![Serie di Fourier. Tra queste funzioni definiamo un prodotto scalare nel seguente modo: date f, g V poniamo f (x) g (x) dx. f (x) [g (x) + h (x)] dx Serie di Fourier. Tra queste funzioni definiamo un prodotto scalare nel seguente modo: date f, g V poniamo f (x) g (x) dx. f (x) [g (x) + h (x)] dx](/thumbs/96/128133073.jpg) Serie di Fourier Indichiamo con V l insieme delle funzioni f : R R che siano periodiche di periodo π, si abbia cioè f ( + π) = f (), e che risultino integrabili nell intervallo [, π]. Tra queste funzioni
Serie di Fourier Indichiamo con V l insieme delle funzioni f : R R che siano periodiche di periodo π, si abbia cioè f ( + π) = f (), e che risultino integrabili nell intervallo [, π]. Tra queste funzioni
