SISTEMI INSTABILI. U(t) k
|
|
|
- Michelangelo Falcone
- 5 anni fa
- Visualizzazioni
Transcript
1 14/ DECADIMENTO DI SISTEMI INSTABILI 09/10 1 SISTEMI INSTABILI Esistono stati, detti instabili, che, pur non essendo stazionari, presentano tuttavia caratteristiche di stabilità tali per cui si trasformano lentamente o rapidamente (rispetto alla scala di tempi considerata) nella sovrapposizione dello stato instabile iniziale e di altri termini, ciascuno dei quali è identificabile come stato dei prodotti di un tipo di decadimento del sistema nello stato instabile, cioè (1) u i U(t) a(t) u i + dp f k,p (t) u k,p. k Vedremo in seguito come può essere caratterizzato lo stato u i affinché possa essere considerato uno stato instabile e non un generico stato non stazionario. Nota Per un dato sistema instabile, i tipi di decadimento possono essere in generale più d uno. Esempi di situazioni di questo genere sono i decadimenti alfa e beta dei nuclei radioattivi e le trasformazioni che subiscono le particelle elementari (tranne le poche perfettamente stabili). Grandezza canale Lo stato instabile iniziale e gli stati dei prodotti di decadimento di ciascun tipo contengono particelle diverse o considerate diverse in questa descrizione e appartengono pertanto a sottospazi ortogonali dello spazio di Hilbert in cui tutti sono descritti. Esiste quindi una grandezza fisica K, che possiamo chiamare grandezza canale, rappresentata da un operatore autoaggiunto ˆK i cui autovalori k distinguono tra lo stato instabile (diciamo k = i) e i prodotti di decadimento di ciascun tipo (l indice k che compare nella (1)). Ad esempio, nel caso di un nucleo instabile N che presenta radioattività alfa, oltre al canale iniziale N (k = i) è presente il canale di decadimento N + α (k = 1), dove N è il nucleo residuo.
2 14/ DECADIMENTO DI SISTEMI INSTABILI 09/10 Probabilità dinamica di non decadimento Se u i è lo stato instabile iniziale e U(t) è l operatore di evoluzione temporale, U(t) u i è lo stato al tempo t. La componente di U(t) u i sullo stato iniziale u i () u i U(t) u i = a(t) si dice ampiezza di non decadimento e il suo modulo quadrato (3) P (t) = u i U(t) u i = a(t), che diremo probabilità dinamica di non decadimento, rappresenta la probabilità di ritrovare lo stato u i in un accertamento effettuato al tempo t. Misurazione della probabilità dinamica di non decadimento Qualora si voglia effettuare una determinazione sperimentale della probabilità dinamica di non decadimento P (t), occorre, per ogni t di interesse, costruire un apposito ensemble E t costituito da N(0) sistemi tutti nello stato u i e, lasciato trascorrere il tempo t, accertare quale frazione (4) dei membri dell ensemble E t sia nello stato u i N(t) N(0) = P (t) (ad esempio rivelando se sono presenti o meno prodotti di decadimento). Non è possibile utilizzare il medesimo ensemble per determinare P (t) a due o più tempi, poiché un accertamento a un dato tempo altera l evoluzione ai tempi successivi. FIGURE Il procedimento può essere illustrato dalla figura seguente. E 1 t 1 E t E 3 t 3 E 4 t 4 E 5 t 5
3 E 1 14/ DECADIMENTO DI SISTEMI INSTABILI t 1 09/10 3 E Probabilità operativa di non decadimento E 3 Di fatto la determinazione sperimentale della legge N(t) non avviene di regola accertando al tempo t quanti sistemi siano non decaduti E 4 t e ripetendo l accertamento su nuovi ensemble per diversi valori di t. t 3 t 4 Si accerta invece su ogni sistema di un unico ensemble di N(0) sistemi nello stato u i al tempo 0, E 5 ripetutamente con un periodo τ sufficientemente t 5 piccolo, se il sistema sia decaduto o no fino a che viene finalmente trovato decaduto e scartato dall ensemble. A ogni determinazione (tranne l ultima) il sistema viene ridotto di nuovo allo stato u i. Il procedimento può essere illustrato dalla figura seguente. E t 1 t t 3 t 4 t 5 Allora e quindi N(τ) = P (τ) N(0), N(τ) = P (τ) N(τ), N((n + 1) τ) = P (τ) N(nτ) 0 E1,0 0 E,0 0 Ei 0 N((n + 1)τ) N(nτ) τ = P (τ) 1 τ N(nτ), da cui, fingendo che il tempo t = nτ sia continuo, (5) dn(t) dt = γ N(t), avendo posto (6) γ = 1 P (τ) τ Intendendo che N(t) abbia il significato descritto qui, definiamo la probabilità operativa di non decadimento P (t) = N(t)/N(0) per la quale, come segue dalla (5), risulta (7) P (t) = exp( γ t).
4 14/ DECADIMENTO DI SISTEMI INSTABILI 09/10 4 Significato fisico della legge di decadimento esponenziale La legge di decadimento esponenziale espressa dalla (7) ha un significato fisico notevole. La legge di evoluzione (5) per N(t), equivalente alla legge esponenziale, può essere riscritta (8) dn(t) = ( N(t + dt) N(t) ) = γ N(t) dt. Poiché dn(t) è il numero di sistemi che decadono nell intervallo di tempo (t, t + dt) e N(t) è il numero di sistemi instabili ancora presenti al tempo t, la relazione (8) dice che il numero di sistemi che decadono nell intervallo di tempo (t, t + dt) è proporzionale, oltre che a dt, al numero di sistemi presenti al tempo t. Questo comportamento viene spesso descritto dicendo che il sistema instabile candidato al decadimento non ha memoria del tempo al quale è stato in origine creato. La perdita di memoria è evidentemente dovuta alla riduzione a u i che avviene a ogni tempo t = nτ. La probabilità Q(t, t + dt) che il sistema decada nell intervallo di tempo (t, t + dt) si ottiene dividendo per N(0) il numero di sistemi dato dalla (8) che decadono in tale intervallo ed è quindi data da Q(t, t + dt) = γ P (t) dt. Il valore medio del tempo di sopravvivenza o vita media t è pertanto t = t Q(t, t + dt) = γ 0 0 dt t exp( γ t) = 1 γ Nota Se N(t) e N(t + dt), anziché essere definiti operativamente come descritto, sono dati dalla (4) in termini della probabilità dinamica di non decadimento P (t), l interpretazione di dn(t) = ( N(t + dt) N(t) ) come il numero di sistemi che decadono tra t e t + dt non vale. L evoluzione temporale descritta dalla (1) porta sempre a una sovrapposizione dello stato non decaduto e degli stati decaduti e mai all uno o all altro di questi stati. Il sistema instabile può essere dichiarato non decaduto o decaduto a un certo tempo solo eseguendo un accertamento a tale tempo. Il numero di sistemi che decadono tra t e t + dt è definito solo se viene eseguito l accertamento sia a t che a t + dt, ma allora N(t + dt) N(0) P (t + dt) poiché N(t + dt) = N(0) P (t + dt) è il numero di sistemi non decaduti al tempo t + dt solo se non vengono fatti accertamenti ai tempi precedenti, compreso t.
5 14/ DECADIMENTO DI SISTEMI INSTABILI 09/10 5 Caratterizzazione dei sistemi instabili Avendo eliminato il moto del centro di massa, sia Ĥ l operatore hamiltoniano del sistema, con spettro continuo da E thr a + ed eventuali autovalori discreti E n < E thr. Siano E, s gli autostati dello spettro continuo normalizzati rispetto a E, cioè Ĥ E, s = E E, s, E, s E, s = δ(e E ) δ ss. Scrivendo lo stato instabile come (9) u i = la sua distribuzione in energia è s E thr de s c s(e) E, s, E, s ui = cs (E). s La condizione di normalizzazione di u i è u i u i = e l ampiezza di non decadimento risulta u i U(t) u i = de c s (E) = 1 E s thr de c s (E) exp ( i ) E s thr ħ E t.
6 14/ DECADIMENTO DI SISTEMI INSTABILI 09/10 6 Funzione di Lorentz La funzione lorentziana è una campana centrata in E i, normalizzata in modo che sia L(E) = π 1 Ẽ (E E i ) + Ẽ + de L(E) = 1. L integrale non converge, + de (E E i ) L(E) ma Ẽ può ugualmente essere interpretato come larghezza della lorentziana. Assunzione Assumiamo che u i sia uno stato instabile quando la sua distribuzione in energia sia, con buona approssimazione, una lorentziana, cioè (10) cs (E) = L(E). s Ovviamente, poiché c s (E) è priva di significato per E E thr, s dobbiamo anche assumere che L(E) sia trascurabile per tali valori di E, cioè in concreto che sia Ẽ E i E thr. La caratterizzazione degli stati instabili mediante le (9) e (10) può essere giustificata nel modo seguente. Se u i fosse stabile, la sua distribuzione in energia sarebbe δ(e E i ). Non essendo stabile, ma con proprietà che lo rendono assimilabile a uno stato stabile, è naturale assumere che la sua distribuzione in energia sia una campana di larghezza non nulla. Perché tale campana sia proprio lorentziana è difficile da spiegare con mezzi elementari. Tuttavia le conseguenze di tale assunzione, come vedremo, la rendono estremamente plausibile. Il valore centrale E i ha il significato di energia approssimata dello stato u i e la larghezza Ẽ ha il significato di larghezza in energia di u i.
7 14/ DECADIMENTO DI SISTEMI INSTABILI 09/10 7 Conseguenze dell assunzione Ammesso che sia Ẽ E i E thr, il limite inferiore dell integrale di normalizzazione può, con buona approssimazione, essere portato a e u i risulta normalizzato. Sotto la medesima condizione, l ampiezza di non decadimento può essere scritta, con buona approssimazione, u i U(t) u i = + de L(E) exp ( i ) ħ E t ( ) ( = exp Ẽ ħ t exp i ) ħ E i t. La probabilità dinamica di non decadimento risulta quindi, con buona approssimazione, ( (11) P (t) = exp Ẽ ) ħ t = exp ( γ t), avendo posto Ẽ ħ = γ. Dunque una distribuzione in energia lorentziana, estesa inferiormente fino a, implica che P (t) sia una funzione esponenziale (decrescente) del tempo. Il parametro 1 γ può essere interpretato come il tempo di vita t caratteristico dello stato instabile. Vale quindi la relazione (1) Ẽ t = ħ, secondo la quale tanto più a lungo vive lo stato instabile, tanto più stretta deve essere la sua distribuzione in energia e viceversa.
8 14/ DECADIMENTO DI SISTEMI INSTABILI 09/10 8 In realtà si può dimostrare che P (t) non può essere esattamente esponenziale, come d altra parte non è affatto necessario che sia. Tuttavia la legge (13) P (t) = exp ( γ t) vale, con buona approssimazione, in un dominio temporale molto grande che si estende da una frazione molto piccola f a un multiplo molto grande M di Nelle condizioni concrete di applicazione della definizione di probabilità operativa di non decadimento l intervallo τ tra due successivi accertamenti del decadimento o non decadimento è grande rispetto a f 1 γ e piccolo rispetto a 1 γ. 1 γ. Poiché f 1 γ τ 1 γ risulta γ = 1 P (τ) τ 1 exp( γτ) τ γτ τ = γ. Il parametro dinamico γ può quindi essere determinato operativamente. Nota L appartenenza di τ al dominio di esponenzialità di P (t) si traduce nella sostanziale indipendenza di γ dal valore di τ. Se τ assumesse valori inferiori a f 1 γ, il valore di γ dipenderebbe criticamente da τ. Nota Poiché γ = γ, per i tempi t ai quali vale la (13), cioè tali che f 1 γ < t < M 1 γ, si ha P (t) = P (t). Tuttavia P (t) resta esponenziale a tutti i tempi, mentre per t > M 1 γ la probabilità dinamica P (t) devia significativamente dalla legge esponenziale.
9 14/ DECADIMENTO DI SISTEMI INSTABILI 09/10 9 DECADIMENTI PROVOCATI DA UNA PERTURBAZIONE Esistono situazioni in cui l operatore hamiltoniano totale del sistema Ĥ si può scomporre in due termini (14) Ĥ = Ĥ0 + Ĥ1 tali che Ĥ0 è compatibile con l operatore canale ˆK e Ĥ1 è tale da poter essere trattato come una perturbazione. Se non fosse presente Ĥ1 (o se anche Ĥ1 commutasse con ˆK) il decadimento non avrebbe luogo. Un esempio tipico è il decadimento beta del neutrone o di un nucleo. Ci proponiamo di sviluppare una teoria per calcolare, in questo tipo di situazioni, le probabilità dinamiche di decadimento e non decadimento. Autostati di Ĥ 0 e ˆK Siano k gli autovalori discreti di ˆK (che numerano convenzionalmente i canali). Gli autostati simultanei di Ĥ 0 e ˆK sono individuati, oltre che da k, da indici continui (la cui struttura dipende da k) che indichiamo complessivamente con p, cioè ˆK u k,p = k u k,p, Ĥ 0 u k,p = Ek,p 0 u k,p, u k,p u k,p = δ kk δ(p p ). Se trascuriamo l interazione tra i prodotti di decadimento eventualmente presente in Ĥ0, per ogni k, p è il momento lineare dello stato instabile iniziale o il complesso dei momenti lineari dei prodotti di decadimento; inoltre, per ognuno dei prodotti di decadimento, (15) u p (x) = 1 ( ) i (πħ) exp 3/ ħ p x. Se si elimina il moto del centro di massa (ovvero si suppone fermo il sistema instabile iniziale) p sparisce nel canale dello stato instabile iniziale k = i e diventa nel canale k i, nel quale il numero dei prodotti di decadimento è n k, p [k] = {p 1,..., p nk } con la condizione p p nk = 0 (per la conservazione del momento lineare totale contenuta negli elementi di matrice di Ĥ 1 ), Possiamo scegliere come momenti lineari indipendenti nel canale k p [k] = {p 1,..., p nk 1}. Per alleggerire la notazione, quando non siano possibili confusioni tra i canali, indicheremo semplicemente con p il complesso dei momenti lineari indipendenti in ciascun canale.
10 14/ DECADIMENTO DI SISTEMI INSTABILI 09/10 10 Energie imperturbate L espressione relativistica dell energia di una particella libera di massa a riposo m e momento p è E 0 = c m c + p ; se la massa a riposo è nulla E 0 diventa E 0 = c p ; se la massa a riposo non è nulla e p m c FIGURE si può usare per E 0 l espressione non relativistica E 1 E 0 = m c + 1 m p. Poiché le somma delle energie a riposo dei prodotti di decadimento è sempre inferiore E all energia a riposo del sistema instabile iniziale (la differenza fornisce l energia t di movimento dei prodotti di decadimento), le energie a riposo devono essere ritenute anche se si usa l espressionenon relativistica. E 3 Avendo eliminato il moto del centro di massa, l energia imperturbata E 4 E 0 i nel canale iniziale k = i è semplicemente l energia a riposo m i c. L energia imperturbata nel canale k i è E 5 t 1 t 3 t 4 t 5 n k n k n k n k 1 Ek,p 0 = jm jc + jt j(p j) = jm jc + jt j(p ( j) + T nk (p1 + + p nk 1) ), dove, secondo i casi, T (p ) = cp o 1 m p o c m c + p m c. Nell ultimo termine in Ek,p 0 intervengono gli angoli tra i vettori p 1,..., p nk 1. n k E Il valore minimo Ek,0 0 = jm jc dell energia imperturbata Ek,p 0 t 1 t t 3 t 4 t 5 nel canale k 1 è detto energia di soglia del canale k. Le energie di soglia dei diversi possibili canali di decadimento devono essere tutte inferiori all energia imperturbata del sistema instabile iniziale. 0 E 0 1,0 E 0,0 E 0 i
11 14/ DECADIMENTO DI SISTEMI INSTABILI 09/10 11 Probabilità di un particolare decadimento Al fine di mantenere semplici le scritture consideriamo dapprima il caso del decadimento in un canale a 3 corpi. I momenti lineari indipendenti nel canale di decadimento sono (16) p = {p 1, p }. La probabilità di transizione perturbativa dallo stato instabile iniziale agli stati del canale considerato individuati dagli indici p entro il dominio dp risulta (17) P ip,dp (t) = π ħ dp 1dp p Ĥ1 i δħ/t (E 0 p E 0 i ) t Poiché la funzione δ ħ/t (Ep 0 E 0 i ) seleziona le transizioni per le quali l energia imperturbata è praticamente conservata, si ottiene un risultato significativo solo integrando sulle energie Ep 0 Ep 0 1 p. Posto (18) q = {Ω p1, Ω p, p 1 }, p = {q, p }, e introdotta la variabile (19) E 0 = E 0 q,p, invertendo (in funzione di q) la relazione tra E 0 e p otteniamo (0) p = p (q, E 0 ). Allora l elemento di volume dp 1 dp si può riscrivere (1) dp 1 dp 1 = dq dp p = dq de 0 p E 0 p (q, E 0 ), dq = dω p1 dω p dp 1 p 1. Integrando l espressione (17) nell energia Ep 0 = Eq,p 0 = E 0 otteniamo () P iq,dq (t) = π ħ dq de 0 p E 0 p (q, E 0 ) p Ĥ1 δħ/t i (E 0 E 0 i ) t.
12 14/ DECADIMENTO DI SISTEMI INSTABILI 09/10 1 La funzione δ ħ/t (E 0 E 0 i ) presenta un picco in E0 = E 0 i di larghezza ħ/t. Per t sufficientemente grande, i rimanenti fattori dell integrando sono di regola funzioni di E 0 praticamente costanti su un intervallo di larghezza ħ/t attorno a E 0 i. Possiamo pertanto approssimarli con il loro valore in E 0 i e portarli fuori dall integrale. Se inoltre la differenza tra E 0 i e il valore di soglia E 0 0 è grande rispetto a ħ/t possiamo portare il limite inferiore di integrazione fino a. Poiché + dx δ a (x) = 1, si ha allora la probabilità di decadimento per unità di tempo (3) P iq,dq = π [ ] ħ dq p E 0 p (q, E 0 i ) p Ĥ1 0. E 0 =E 0 E 0 =E 0 i i Nota Le ultime approssimazioni fatte corrispondono evidentemente a sostituire δ ħ/t (E 0 E 0 i ) con δ(e0 E 0 i ) Nel caso generale del decadimento in un canale a n corpi in modo analogo si ottiene l espressione della probabilità di decadimento per unità di tempo (4) P iq,dq = π [ ] ħ dq pn 1 E 0 p n 1(q, E 0 i ) p Ĥ1 0, E 0 =E 0 E 0 =E 0 i i dove ora q = {Ω p1,..., Ω pn 1, p 1,..., p n }, dq = dω p1... dω pn 1 dp 1... dp n p 1... p n.
13 14/ DECADIMENTO DI SISTEMI INSTABILI 09/10 13 Espressione alternativa della probabilità di un particolare decadimento Supponiamo che gli stati di decadimento siano normalizzabili e quindi caratterizzati da un complesso di indici discreti n. La probabilità di transizione perturbativa agli stati di decadimento appartenenti al set f è P if (t) = π ħ ( f) n n Ĥ1 δħ/t i (En 0 E 0 i ) t. Consideriamo un piccolo intervallo energetico de 0 f attorno a un valore E 0 f. Sia ϱ f (E 0 f ) de 0 f = numero di stati di decadimento f in de 0 f. Allora, intendendo che f non contenga specificazioni relative all energia imperturbata e assumendo che per n f si possa porre n,e 0 H 1 f i = f,e 0 H 1 f i, si può scrivere ( f,e 0 n de0 f ) n [ ] = ϱ f (E 0 f ) de 0 f [ ]. Integrando nell energia imperturbata E 0 f si ottiene P if (t) = π ħ def 0 ϱ f (Ef 0 ) f,e 0 f H 1 i δħ/t (E 0 f E 0 i ) t. Con lo stesso tipo di approssimazioni già usate si ottiene in definitiva la probabilità di transizione per unità di tempo (5) P if = π ħ ϱ f (E 0 i ) f,e 0 H 1 i. i L espressione della probabilità di transizione in questa forma si designa di solito come regola d oro di Fermi. La quantità ϱ f (E 0 f ) si dice densità di stati finali.
14 14/ DECADIMENTO DI SISTEMI INSTABILI 09/10 14 Calcolo della densità di stati finali Per rendere normalizzabili gli autostati di H 0 imponiamo condizioni al contorno di periodicità in un volume cubico V = L 3. Gli autostati normalizzati di H 0 sono allora (per ciascun prodotto di decadimento) u (V p ) (x) = 1 ( ) i exp V ħ p x, p = πħ L n. Il volume occupato da uno stato nello spazio dei momenti è ( ) 3 πħ = (πħ)3 L V e quindi il numero di stati entro un volume d 3 p è V (πħ) 3 d3 p. Nel caso del decadimento in un canale con n prodotti di decadimento e n 1 momenti indipendenti, il numero di stati con le specificazioni p 1, d 3 p 1..., p n 1, d 3 p n 1 è ( ) n 1 ( ) n 1 V (πħ) 3 d 3 p 1... d 3 V p n 1 = (πħ) 3 dq p n 1 E 0 p n 1 de 0 }{{} ϱ q,dq (E 0 ) La quantità indicata è la densità di stati finali da inserire nella (5). Confronto Apparentemente l espressione (5) differisce dalla (4) per il fattore ( ) n 1 V (πħ) 3. Ma tale fattore è compensato dalla diversa normalizzazione degli stati finali negli elementi di matrice dell interazione. Infatti nella (5) gli stati finali sono (per ogni momento indipendente) u p (V ) (x) = 1 ( ) i exp V ħ p x, mentre nella (4) sono u p (x) = 1 (πħ) 3/ exp ( i ħ p x ).
15 14/ DECADIMENTO DI SISTEMI INSTABILI 09/10 15 Probabilità totale di decadimento La probabilità totale di decadimento per unità di tempo si ottiene integrando l espressione (4) in dq e sommando sui canali; risulta (6) P if = π ħ ( i) k dq p nk 1 E 0 k E 0 k =E0 i p n k 1(q, Ei 0 ) k,p Ĥ1 i E 0 k =E0 i. Condizioni di validità Per l applicazione della teoria perturbativa Possiamo assumere come ragionevole criterio che la probabilità di transizione sia molto minore di 1, cioè (a) P if t 1. Per le approssimazioni successive Sia D la quantità più piccola tra 1) l intervallo energetico attorno a E 0 k = E 0 i nel quale i fattori dipendenti da E 0 k non hanno variazioni apprezzabili, ) la distanza di E 0 i dalla soglia di E 0 k. Allora deve essere (b) ħ t D. ( Le condizioni (a) t 1 ) ( ) ħ e (b) P D t sono di regola compatibili, cioè esiste un dominio temporale (di solito molto ampio) ( nel quale sono entrambe soddisfatte P 1 ħ ). D Relazione con la legge esponenziale In conclusione le probabilità dinamiche di decadimento P if (t) e di non decadimento P (t) sono espresse in termini di P if data dalla (6) da P if (t) = P if t = 1 exp( P if t), P (t) = 1 P if t = exp( P if t), } per tempi tali che ħ D t 1 P if La quantità P if è da identificare con la quantità γ che caratterizza la probabiltà dinamica di non decadimento nel dominio di esponenzialità.
16 14/ DECADIMENTO DI SISTEMI INSTABILI 09/10 16 DECADIMENTO BETA DI UN NUCLEO Un nucleo instabile N decade (unico canale) in un nucleo residuo N, un elettrone e e un opportuno neutrino ν. Ci proponiamo di valutare la forma dello spettro di emissione dell elettrone prescindendo dal valore assoluto della probabilità di decadimento. Eliminando il moto del baricentro, cioè supponendo il nucleo instabile inziale fermo, per la conservazione del momento linere totale, sarà p e + p ν + p N = 0. Assunta nulla la massa del neutrino, le energie imperturbate in termini dei momenti lineari sono date da E 0 i = E0 N = m N c nel canale iniziale, Ee 0 = c m ec + p e, Eν 0 = c p ν, EN 0 = m N c + 1 p N m N nel canale di decadimento. Con riferimento alle formule particolarizzate per il caso di un decadimento a tre corpi, identifichiamo i prodotti di decadimento 1,, 3 con 1 = e, = ν, 3 = N. Allora q = {Ω pe, Ω pν, p e }, p = p ν, (7) E 0 = E 0 q,p ν = c m ec + p e + c p ν + m N c + 1 m N p ν = p ν (q, E 0 ). p N }{{}, = (p e + p ν ) Conviene introdurre l energia = m N c m N c che rappresenta l energia fornita dalla transizione nucleare, con il che la condizione E 0 = E 0 i si scrive (8) = c m ec + p e + c p ν + 1 p N m N cioè si suddivide nelle energie di e e di ν e nell energia 1 p N m di rinculo di N. N
17 14/ DECADIMENTO DI SISTEMI INSTABILI 09/10 17 Dimostreremo che l energia di rinculo di N è sempre trascurabile rispetto alle energie di e e di ν. Le equazioni (7) e (8) diventano allora (9) E 0 = Eq,p 0 ν = c m ec + p e + c p ν + m N c, (30) = c m ec + p e + c p ν. Dalla (9) otteniamo e quindi Dalla (30) otteniamo inoltre p ν = 1 c (E0 c m ec + p e m N c ) p ν E 0 = 1 c p ν = 1 c ( c m ec + p e). La probabilità di transizione per unità di tempo risulta P NN e ν; p e,ω ν,dp e,dω e,dω ν = π ħc 3 p e Ovviamente possiamo sempre sostituire ( c m ec + p e dω e dω ν dω e dω eν dω e dϕ eν d cos ϑ eν. ) pe,pν Ĥ1 N dp e dω e dω ν. Ee 0+E0 ν = Per evidenti motivi di simmetria, l unica dipendenza effettiva dagli angoli di p e e p ν è quella dall angolo tra p e e p ν. Possiamo quindi integrare in dω e dϕ eν, ottenendo P NN e ν; p e,ω ν,dp e,dω e,dω ν = 8π π ħc 3 p e ( c m ec + p e ) pe,pν Ĥ1 N dp e d cos ϑ eν. Ee 0+E0 ν = Il calcolo dell elemento di matrice nucleare pe,p ν Ĥ1 N richiederebbe la conoscenza delle funzioni d onda interne dei nuclei N e N Tuttavia, poiché la dipendenza da p ( e dell elemento di matrice di Ĥ1 è verosimilmente poco pronunciata, il fattore cosiddetto cinematico p e c m ec + pe) dà in pratica lo spettro di pe. La correzione più importante a tale risultato proviene dall interazione coulombiana tra N e e nel canale di decadimento, della quale non abbiamo tenuto conto. Un ulteriore correzione potrebbe provenire da un eventuale massa non nulla del neutrino, che abbiamo assunto essere zero (anche se si potrebbe facilmente ripetere il conto con m ν 0). La figura che segue dà lo spettro di p e nei due casi m ν = 0 e m ν 0. I limiti sperimentali rendono impossibile la rivelazione dell eventuale massa del neutrino per questa via.
18 14/ DECADIMENTO DI SISTEMI INSTABILI 09/10 17 Energia di rinculo del nucleo residuo L energia di rinculo di N è massima in funzione dell angolo tra p e e p ν quando questi sono collineari. Inoltre, al variare dei moduli p e e p ν, essa è massima quando tutta l energia va a e che è dotato di massa piuttosto che a ν che ne è privo. 1 Dunque p N m è massimo rispetto a E0 e + Eν 0 quando p ν = 0; N allora, per la conservazione del momento lineare, p N = p e. Nella situazione descritta, la condizione (8) diventa (31) = c m ec + p e + 1 m N p e dove il primo termine è l energia E 0 e = E 0 e + E 0 ν e il secondo termine è l energia di rinculo di N. Posto l equazione (31) si scrive ( ) pe m m e c = x, e m = q, N m e c = δ, (3) δ = 1 + x + 1 q x. È sempre e, nei casi concreti, q 1 δ 30. La soluzione dell equazione (3) al primo ordine in q è x = (δ 1)(1 δ q), da cui, sempre al primo ordine in q, 1 q x 1 + x = δ 1 δ q. In conclusione 1 m N Ee 0 + Eν 0 p N δ 1 δ q 1.
VALORI E DISTRIBUZIONI DI VALORI DI UNA GRANDEZZA GENERICA
 3/7 GENERALIZZAZIONI E SVILUPPI 09/10 1 VALORI E DISTRIBUZIONI DI VALORI DI UNA GRANDEZZA GENERICA Forma unificata dei risultati già ottenuti I risultati ottenuti nei fascicoli 3/3, 3/5 e 3/6 sulle grandezze
3/7 GENERALIZZAZIONI E SVILUPPI 09/10 1 VALORI E DISTRIBUZIONI DI VALORI DI UNA GRANDEZZA GENERICA Forma unificata dei risultati già ottenuti I risultati ottenuti nei fascicoli 3/3, 3/5 e 3/6 sulle grandezze
Metodo variazionale e applicazione all atomo di elio
 Metodo variazionale e applicazione all atomo di elio Descrizione del metodo Il metodo detto variazionale è un metodo approssimato che si usa per ottenere una stima dell energia dello stato fondamentale
Metodo variazionale e applicazione all atomo di elio Descrizione del metodo Il metodo detto variazionale è un metodo approssimato che si usa per ottenere una stima dell energia dello stato fondamentale
H = H 0 + V. { V ti t t f 0 altrove
 Esercizio 1 (Regola d oro di Fermi Determinare la probabilità di transizione per unità di tempo da uno stato a ad uno stato b al primo ordine perturbativo di un sistema per cui si suppone di aver risolto
Esercizio 1 (Regola d oro di Fermi Determinare la probabilità di transizione per unità di tempo da uno stato a ad uno stato b al primo ordine perturbativo di un sistema per cui si suppone di aver risolto
Effetto Stark (1) H 0 nlm > = E n nlm > (4) Ricordiamo che. E n = me4 2 h 2 n 2 = E 1
 Effetto Stark Studiamo l equazione di Schrödinger per l atomo di idrogeno in presenza di un campo elettrico costante e diretto lungo l asse z, E = E k. La hamiltoniana di Schrödinger per l atomo di idrogeno
Effetto Stark Studiamo l equazione di Schrödinger per l atomo di idrogeno in presenza di un campo elettrico costante e diretto lungo l asse z, E = E k. La hamiltoniana di Schrödinger per l atomo di idrogeno
 DIFFUSIONE DA UN BERSAGLIO DI MASSA FINITA bozza 0/ DIFFUSIONE DA UN BERSAGLIO DI MASSA FINITA L esperimento Un fascio composto di un grande numero di particelle proiettile di tipo incide su un bersaglio
DIFFUSIONE DA UN BERSAGLIO DI MASSA FINITA bozza 0/ DIFFUSIONE DA UN BERSAGLIO DI MASSA FINITA L esperimento Un fascio composto di un grande numero di particelle proiettile di tipo incide su un bersaglio
Stati Coerenti. Definizione di stato coerente Consideriamo un oscillatore 1-dimensionale descritto dalla hamiltoniana. p = i d.
 1 Stati Coerenti Definizione di stato coerente Consideriamo un oscillatore 1-dimensionale descritto dalla hamiltoniana H = 1 m p + 1 m ω x (1) Per semplicitá introduciamo gli operatori autoaggiunti adimensionali
1 Stati Coerenti Definizione di stato coerente Consideriamo un oscillatore 1-dimensionale descritto dalla hamiltoniana H = 1 m p + 1 m ω x (1) Per semplicitá introduciamo gli operatori autoaggiunti adimensionali
MECCANICA QUANTISTICA. Corso di laurea in fisica PROGRAMMA DEL CORSO E PROGRAMMA D ESAME. Anno accademico 2011/2012
 MECCANICA QUANTISTICA Corso di laurea in fisica PROGRAMMA DEL CORSO E PROGRAMMA D ESAME Anno accademico 2011/2012 Argomenti facenti parte del programma d esame. Argomenti facenti parte del programma d
MECCANICA QUANTISTICA Corso di laurea in fisica PROGRAMMA DEL CORSO E PROGRAMMA D ESAME Anno accademico 2011/2012 Argomenti facenti parte del programma d esame. Argomenti facenti parte del programma d
Introduzione alla Fisica Moderna - a.a
 Introduzione alla Fisica Moderna - a.a. 2016-17 18/12/2017 Nome Cognome Matricola: 1) Si consideri il sistema dinamico nonlineare ẋ = y x 2, ẏ = x + y 2, Si determinino i punti di equilibrio, si caratterizzi
Introduzione alla Fisica Moderna - a.a. 2016-17 18/12/2017 Nome Cognome Matricola: 1) Si consideri il sistema dinamico nonlineare ẋ = y x 2, ẏ = x + y 2, Si determinino i punti di equilibrio, si caratterizzi
PROBLEMA A DUE CORPI: STATI DEL CONTINUO
 Capitolo 10 PROBLEMA A DUE CORPI: STATI DEL CONTINUO Riprendiamo l equazione di Schrödinger per il sistema di due particelle interagenti con l intento di cercare la classe di soluzioni che descrivono stati
Capitolo 10 PROBLEMA A DUE CORPI: STATI DEL CONTINUO Riprendiamo l equazione di Schrödinger per il sistema di due particelle interagenti con l intento di cercare la classe di soluzioni che descrivono stati
Capitolo 6 : Decadimenti, Risonanze, Modello di Yukawa, Interazioni tra Particelle
 Capitolo 6 : Decadimenti, Risonanze, Modello di Yukawa, Interazioni tra Particelle Corso di Fisica Nucleare e Subnucleare I Professor Carlo Dionisi A.A. 2004-2005 1 Legge di decadimento Decadimento di
Capitolo 6 : Decadimenti, Risonanze, Modello di Yukawa, Interazioni tra Particelle Corso di Fisica Nucleare e Subnucleare I Professor Carlo Dionisi A.A. 2004-2005 1 Legge di decadimento Decadimento di
L equazione di Schrödinger
 1 Forma dell equazione L equazione di Schrödinger Postulato - ψ r, t 0 ) definisce completamente lo stato dinamico del sistema al tempo t 0. L equazione che regola l evoluzione di ψ r, t) deve essere:
1 Forma dell equazione L equazione di Schrödinger Postulato - ψ r, t 0 ) definisce completamente lo stato dinamico del sistema al tempo t 0. L equazione che regola l evoluzione di ψ r, t) deve essere:
20 giugno La sezione d urto invariante impolarizzata per il processo (1) è
 20 giugno 2002 e (p 1 ) + e + (p 2 ) γ(k) + Z 0 (q) (1) (i tetra-impulsi delle particelle sono indicati in parentesi). 1. Si scrivano i diagrammi di Feynman rilevanti per il processo, e si scriva l espressione
20 giugno 2002 e (p 1 ) + e + (p 2 ) γ(k) + Z 0 (q) (1) (i tetra-impulsi delle particelle sono indicati in parentesi). 1. Si scrivano i diagrammi di Feynman rilevanti per il processo, e si scriva l espressione
Esercitazioni di Meccanica Quantistica I
 Esercitazioni di Meccanica Quantistica I Sistema a due stati Consideriamo come esempio di sistema a due stati l ammoniaca. La struttura del composto è tetraedrico : alla sommità di una piramide con base
Esercitazioni di Meccanica Quantistica I Sistema a due stati Consideriamo come esempio di sistema a due stati l ammoniaca. La struttura del composto è tetraedrico : alla sommità di una piramide con base
I POSTULATI DELLA MECCANICA QUANTISTICA
 68 I POSTULATI DELLA MECCANICA QUANTISTICA Si intende per postulato una assunzione da accettarsi a priori e non contraddetta dall esperienza. I postulati trovano la loro unica giustificazione nella loro
68 I POSTULATI DELLA MECCANICA QUANTISTICA Si intende per postulato una assunzione da accettarsi a priori e non contraddetta dall esperienza. I postulati trovano la loro unica giustificazione nella loro
Effetto Compton. Nicola Cabibbo 27 Novembre 2000
 Effetto Compton Nicola Cabibbo 27 Novembre 2000 In questa nota consideriano il processo Compton di diffusione di un fotone su un elettrone,γ + e γ + e. La nota integra la trattazione che si trova in Mandl
Effetto Compton Nicola Cabibbo 27 Novembre 2000 In questa nota consideriano il processo Compton di diffusione di un fotone su un elettrone,γ + e γ + e. La nota integra la trattazione che si trova in Mandl
ed infine le interazioni nucleari forte e debole? dove E rappresenta l energia cinetica della particella α, e K è: K = e2 2Z
 Introduzione 1. Stima il valore delle energie dei fotoni necessarie per risolvere distanze atomiche, e poi nucleari. 2. Per quali ragioni fisiche le interazioni fondamentali sono state storicamente identificate
Introduzione 1. Stima il valore delle energie dei fotoni necessarie per risolvere distanze atomiche, e poi nucleari. 2. Per quali ragioni fisiche le interazioni fondamentali sono state storicamente identificate
PROBLEMI DI FISICA MODERNA E MECCANICA QUANTISTICA. FISICA MODERNA anno accademico
 PROBLEMI DI FISICA MODERNA E MECCANICA QUANTISTICA FISICA MODERNA anno accademico 007-008 () Sia dato un sistema che può trovarsi in tre stati esclusivi,, 3, e si supponga che esso si trovi nello stato
PROBLEMI DI FISICA MODERNA E MECCANICA QUANTISTICA FISICA MODERNA anno accademico 007-008 () Sia dato un sistema che può trovarsi in tre stati esclusivi,, 3, e si supponga che esso si trovi nello stato
NOTE SU VARIABILI AZIONE ANGOLO E TEORIA PERTURBATIVA. Armando Bazzani Dipartimento di Fisica e Astranomia - Meccanica Analitica
 NOTE SU VARIABILI AZIONE ANGOLO E TEORIA PERTURBATIVA Armando Bazzani Dipartimento di Fisica e Astranomia - Meccanica Analitica 9 Ottobre 13 Consideriamo un sistema dinamico unidimensionale con Hamiltoniana
NOTE SU VARIABILI AZIONE ANGOLO E TEORIA PERTURBATIVA Armando Bazzani Dipartimento di Fisica e Astranomia - Meccanica Analitica 9 Ottobre 13 Consideriamo un sistema dinamico unidimensionale con Hamiltoniana
PROPRIETÀ GENERALI. L equazione di Schrödinger, per una particella che si muove in un campo di forze corrispondente all energia potenziale V (x, t),
 1/3 STUDIO PRELIMINARE DELL EQUAZIONE DI SCHRÖDINGER 10/11 1 PROPRIETÀ GENERALI L equazione di Schrödinger, per una particella che si muove in un campo di forze corrispondente all energia potenziale V
1/3 STUDIO PRELIMINARE DELL EQUAZIONE DI SCHRÖDINGER 10/11 1 PROPRIETÀ GENERALI L equazione di Schrödinger, per una particella che si muove in un campo di forze corrispondente all energia potenziale V
4. MODELLO DI EINSTEIN
 4. MODELLO DI EISTEI Einstein fu il primo ad elaborare un modello per la descrizione dell interazione radiazione-materia (molecole) tenendo conto della quantizzazione delle energie molecolari e della radiazione.
4. MODELLO DI EISTEI Einstein fu il primo ad elaborare un modello per la descrizione dell interazione radiazione-materia (molecole) tenendo conto della quantizzazione delle energie molecolari e della radiazione.
Figura 7.1: Ipotesi di Heisenberg
 Capitolo 7 Isospin nei nuclei Nel 9 Heisenberg scrisse tre articoli sulla forza nucleare, trattando neutrone e protone come due stati della stessa particella, il nucleone, distinti dal valore assunto da
Capitolo 7 Isospin nei nuclei Nel 9 Heisenberg scrisse tre articoli sulla forza nucleare, trattando neutrone e protone come due stati della stessa particella, il nucleone, distinti dal valore assunto da
DISTRIBUZIONI SINGOLARI E FUNZIONE DENSITÀ
 2/3 DISTRIBUZIONI SINGOLARI E "FUNZIONE" DELTA DI DIRAC 0/ DISTRIBUZIONI SINGOLARI E FUNZIONE DENSITÀ Consideriamo una distribuzione continua di una data quantità Q ad esempio la carica elettrica o la
2/3 DISTRIBUZIONI SINGOLARI E "FUNZIONE" DELTA DI DIRAC 0/ DISTRIBUZIONI SINGOLARI E FUNZIONE DENSITÀ Consideriamo una distribuzione continua di una data quantità Q ad esempio la carica elettrica o la
L atomo di idrogeno (1) H T = p2 1 2m 1. + p2 2 2m 2. + V ( r 1 r 2 ) (2) Definiamo le nuove variabili: 1. La massa totale M M = m 1 + m 2 (3)
 L atomo di idrogeno Il problema dell atomo di idrogeno é un problema esattamente risolubili ed i suoi risultati possono essere estesi agli atomi idrogenoidi, in cui solo c é solo un elettrone sottoposto
L atomo di idrogeno Il problema dell atomo di idrogeno é un problema esattamente risolubili ed i suoi risultati possono essere estesi agli atomi idrogenoidi, in cui solo c é solo un elettrone sottoposto
Funzione d onda dello stato fondamentale (trascurando l interazione elettrone-elettrone)
 -e -e +2e ATOMO DI ELIO. Considero il nucleo fisso (sistema di riferimento del centro di massa, circa coincidente col nucleo). I due elettroni vanno trattati come indistinguibili. -e -e +2e SENZA il termine
-e -e +2e ATOMO DI ELIO. Considero il nucleo fisso (sistema di riferimento del centro di massa, circa coincidente col nucleo). I due elettroni vanno trattati come indistinguibili. -e -e +2e SENZA il termine
Corso di Modelli Matematici in Biologia Esame del 6 Luglio 2016
 Corso di Modelli Matematici in Biologia Esame del 6 Luglio 206 Scrivere chiaramente in testa all elaborato: Nome, Cognome, numero di matricola. Risolvere tutti gli esercizi. Tempo a disposizione: DUE ORE.
Corso di Modelli Matematici in Biologia Esame del 6 Luglio 206 Scrivere chiaramente in testa all elaborato: Nome, Cognome, numero di matricola. Risolvere tutti gli esercizi. Tempo a disposizione: DUE ORE.
Effetto Zeeman. p q c A) 2. i h ψ t. = Hψ (2)
 Effetto Zeeman Effetto Zeeman normale La hamiltoniana di una particella in presenza di un campo elettromagnetico, descritto dal potenziale vettore A e dal potenziale scalare Φ é H = 2M e l euazione di
Effetto Zeeman Effetto Zeeman normale La hamiltoniana di una particella in presenza di un campo elettromagnetico, descritto dal potenziale vettore A e dal potenziale scalare Φ é H = 2M e l euazione di
OPERAZIONI SU SPAZI DI HILBERT. Nel seguito introdurremo i concetti di prodotto diretto e somma diretta di due spazi di Hilbert.
 2/7 OPERAZIONI SU SPAZI DI HILBERT 11/12 1 OPERAZIONI SU SPAZI DI HILBERT Dati due spazi di Hilbert H (1) e H (2) si possono definire su di essi operazioni il cui risultato è un nuovo spazio di Hilbert
2/7 OPERAZIONI SU SPAZI DI HILBERT 11/12 1 OPERAZIONI SU SPAZI DI HILBERT Dati due spazi di Hilbert H (1) e H (2) si possono definire su di essi operazioni il cui risultato è un nuovo spazio di Hilbert
Esercizi di Fisica Matematica 3, anno , parte di meccanica hamiltoniana e quantistica
 Esercizi di Fisica Matematica 3, anno 014-015, parte di meccanica hamiltoniana e quantistica Dario Bambusi 09.06.015 Abstract Gli esercizi dei compiti saranno varianti dei seguenti esercizi. Nei compiti
Esercizi di Fisica Matematica 3, anno 014-015, parte di meccanica hamiltoniana e quantistica Dario Bambusi 09.06.015 Abstract Gli esercizi dei compiti saranno varianti dei seguenti esercizi. Nei compiti
R è definita infine dall insieme delle curve percorse da ogni singolo punto della corda.
 1. Problema della corda vibrante Si consideri una corda monodimensionale, di sezione nulla avente densità per unità di lunghezza ρ e modulo elastico lineare E. Una corda reale approssima quella ideale
1. Problema della corda vibrante Si consideri una corda monodimensionale, di sezione nulla avente densità per unità di lunghezza ρ e modulo elastico lineare E. Una corda reale approssima quella ideale
TEORIA DEI SISTEMI SISTEMI LINEARI
 TEORIA DEI SISTEMI Laurea Specialistica in Ingegneria Meccatronica Laurea Specialistica in Ingegneria Gestionale Indirizzo Gestione Industriale TEORIA DEI SISTEMI SISTEMI LINEARI Ing. Cristian Secchi Tel.
TEORIA DEI SISTEMI Laurea Specialistica in Ingegneria Meccatronica Laurea Specialistica in Ingegneria Gestionale Indirizzo Gestione Industriale TEORIA DEI SISTEMI SISTEMI LINEARI Ing. Cristian Secchi Tel.
Esperimenti computazionali con Mathematica: la trasformata di Fourier
 Matematica Open Source http://www.extrabyte.info Quaderni di Analisi Matematica 06 Esperimenti computazionali con Mathematica: la trasformata di Fourier Marcello Colozzo 3 0 5 5 0 Ω LA TRASFORMATA DI FOURIER
Matematica Open Source http://www.extrabyte.info Quaderni di Analisi Matematica 06 Esperimenti computazionali con Mathematica: la trasformata di Fourier Marcello Colozzo 3 0 5 5 0 Ω LA TRASFORMATA DI FOURIER
Corso di Laurea in Informatica Calcolo delle Probabilità e Statistica (269AA) A.A. 2016/17 - Prima prova in itinere
 Corso di Laurea in Informatica Calcolo delle Probabilità e Statistica 69AA) A.A. 06/7 - Prima prova in itinere 07-0-03 La durata della prova è di tre ore. Le risposte devono essere adeguatamente giustificate.
Corso di Laurea in Informatica Calcolo delle Probabilità e Statistica 69AA) A.A. 06/7 - Prima prova in itinere 07-0-03 La durata della prova è di tre ore. Le risposte devono essere adeguatamente giustificate.
Metalli come gas di elettroni liberi
 Metalli come gas di elettroni liberi I metalli sono caratterizzati da elevata conducibilità elettrica e termica. La conducibilità elettrica in particolare (o il suo inverso, la resistività) è una delle
Metalli come gas di elettroni liberi I metalli sono caratterizzati da elevata conducibilità elettrica e termica. La conducibilità elettrica in particolare (o il suo inverso, la resistività) è una delle
sulla massa invariante Consideriamo i due processi per la produzione di antiprotoni
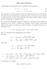 sulla massa invariante Consideriamo i due processi per la produzione di antiprotoni e + + e p + p, (1) p + p p + p + p + p. (2) Per entrambi si calcoli l energia cinetica di soglia del processo sia nel
sulla massa invariante Consideriamo i due processi per la produzione di antiprotoni e + + e p + p, (1) p + p p + p + p + p. (2) Per entrambi si calcoli l energia cinetica di soglia del processo sia nel
8π c 3 ν2. dx x 2 /(e x 1) fotoni/m 2 /sec,
 Corso di Introduzione alla Fisica Quantistica (f) Prova scritta 8 Giugno 7 - (tre ore a disposizione) Soluzione 1.) Una stazione radio trasmette emettendo una potenza di un kilowatt alla frequenza di 9
Corso di Introduzione alla Fisica Quantistica (f) Prova scritta 8 Giugno 7 - (tre ore a disposizione) Soluzione 1.) Una stazione radio trasmette emettendo una potenza di un kilowatt alla frequenza di 9
Capitolo 6. Variabili casuali continue. 6.1 La densità di probabilità
 Capitolo 6 Variabili casuali continue Le definizioni di probabilità che abbiamo finora usato sono adatte solo per una variabile casuale che possa assumere solo valori discreti; vediamo innanzi tutto come
Capitolo 6 Variabili casuali continue Le definizioni di probabilità che abbiamo finora usato sono adatte solo per una variabile casuale che possa assumere solo valori discreti; vediamo innanzi tutto come
L analisi dei dati. Primi elementi. EEE- Cosmic Box proff.: M.Cottino, P.Porta
 L analisi dei dati Primi elementi Metodo dei minimi quadrati Negli esperimenti spesso si misurano parecchie volte due diverse variabili fisiche per investigare la relazione matematica tra le due variabili.
L analisi dei dati Primi elementi Metodo dei minimi quadrati Negli esperimenti spesso si misurano parecchie volte due diverse variabili fisiche per investigare la relazione matematica tra le due variabili.
Prova Scritta di di Meccanica Analitica
 Prova Scritta di di Meccanica Analitica 7 gennaio 015 Problema 1 Un punto di massa unitaria si muove sull asse x soggetto al potenziale V (x) = x e x a) Determinare le posizioni di equilibrio e la loro
Prova Scritta di di Meccanica Analitica 7 gennaio 015 Problema 1 Un punto di massa unitaria si muove sull asse x soggetto al potenziale V (x) = x e x a) Determinare le posizioni di equilibrio e la loro
Compito di MD 13 febbraio 2014
 Compito di MD 13 febbraio 2014 IMPORTANTE: Non si possono consultare libri e appunti. Non si possono usare calcolatrici, computer o altri dispositivi elettronici. Non si può scrivere con il lapis. Motivare
Compito di MD 13 febbraio 2014 IMPORTANTE: Non si possono consultare libri e appunti. Non si possono usare calcolatrici, computer o altri dispositivi elettronici. Non si può scrivere con il lapis. Motivare
Note sull algoritmo di Gauss
 Note sull algoritmo di Gauss 29 settembre 2009 Generalità Un sistema lineare di m equazioni in n incognite x,..., x n è un espressione del tipo: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n
Note sull algoritmo di Gauss 29 settembre 2009 Generalità Un sistema lineare di m equazioni in n incognite x,..., x n è un espressione del tipo: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n
Dom. 1 Dom 2 Es. 1 Es. 2 Es. 3 Es. 4 Totale. Cognome: Nome: Matricola:
 Dom. 1 Dom Es. 1 Es. Es. 3 Es. 4 Totale Analisi e Geometria 1 Primo appello 16 febbraio 016 Docente: Politecnico di Milano Scuola di Ingegneria Industriale e dell Informazione Cognome: Nome: Matricola:
Dom. 1 Dom Es. 1 Es. Es. 3 Es. 4 Totale Analisi e Geometria 1 Primo appello 16 febbraio 016 Docente: Politecnico di Milano Scuola di Ingegneria Industriale e dell Informazione Cognome: Nome: Matricola:
Equazioni di Eulero del corpo rigido.
 Equazioni di Eulero del corpo rigido. In questa nota vogliamo scrivere e studiare le equazioni del moto di un corpo rigido libero, sottoposto alla sola forza di gravità. Ci occuperemo in particolare delle
Equazioni di Eulero del corpo rigido. In questa nota vogliamo scrivere e studiare le equazioni del moto di un corpo rigido libero, sottoposto alla sola forza di gravità. Ci occuperemo in particolare delle
RETI DI TELECOMUNICAZIONE
 RETI DI TELECOMUNICAZIONE PROCESSI DI POISSON Definizione Un processo stocastico che assume valori interi non negativi si dice essere un processo di Poisson con frequenza λ se 1. A(t) è un prosesso di
RETI DI TELECOMUNICAZIONE PROCESSI DI POISSON Definizione Un processo stocastico che assume valori interi non negativi si dice essere un processo di Poisson con frequenza λ se 1. A(t) è un prosesso di
Geometria delle masse
 Geometria delle masse BA. Baricentri Per la trattazione riguardante i baricentri non ci è più sufficiente considerare i corpi come insiemi di punti geometrici, ma abbiamo bisogno di introdurre una nuova
Geometria delle masse BA. Baricentri Per la trattazione riguardante i baricentri non ci è più sufficiente considerare i corpi come insiemi di punti geometrici, ma abbiamo bisogno di introdurre una nuova
OSCILLATORE ARMONICO UNIDIMENSIONALE. Consideriamo una particella sottoposta a una forza armonica di costante mω 2.
 4/7 OSCILLATORE ARMONICO 09/10 1 OSCILLATORE ARMONICO UNIDIMENSIONALE Lo spazio di Hilbert e l operatore hamiltoniano Consideriamo una particella sottoposta a una forza armonica di costante mω 2. Nello
4/7 OSCILLATORE ARMONICO 09/10 1 OSCILLATORE ARMONICO UNIDIMENSIONALE Lo spazio di Hilbert e l operatore hamiltoniano Consideriamo una particella sottoposta a una forza armonica di costante mω 2. Nello
Conteggi e sezione d urto
 Capitolo 1 Conteggi e sezione d urto Consideriamo la reazione a due corpi: a + X b + Y (1.1) che comprende come caso particolare lo scattering elastico. La sezione d urto differenziale per la reazione
Capitolo 1 Conteggi e sezione d urto Consideriamo la reazione a due corpi: a + X b + Y (1.1) che comprende come caso particolare lo scattering elastico. La sezione d urto differenziale per la reazione
Prova Scritta di di Meccanica Analitica. 4 Luglio ) Si consideri un punto materiale di massa m soggetto al potenziale.
 Prova Scritta di di Meccanica Analitica 4 Luglio 7 Problema ) Si consideri un punto materiale di massa m soggetto al potenziale V x) ax 4 determinare la dipendenza del periodo dall energia. ) Si scriva
Prova Scritta di di Meccanica Analitica 4 Luglio 7 Problema ) Si consideri un punto materiale di massa m soggetto al potenziale V x) ax 4 determinare la dipendenza del periodo dall energia. ) Si scriva
Teoria delle Perturbazioni (aspetti elementari)
 Teoria delle Perturbazioni (aspetti elementari) Corso MMMQ UNIMI (G. Gaeta, a.a. 2018/19) 3 Novembre 2018 Questa breve dispensa discute gli aspetti più elementari della teoria delle perturbazioni in Meccanica
Teoria delle Perturbazioni (aspetti elementari) Corso MMMQ UNIMI (G. Gaeta, a.a. 2018/19) 3 Novembre 2018 Questa breve dispensa discute gli aspetti più elementari della teoria delle perturbazioni in Meccanica
Fisica Quantistica III Esercizi Natale 2009
 Fisica Quantistica III Esercizi Natale 009 Philip G. Ratcliffe (philip.ratcliffe@uninsubria.it) Dipartimento di Fisica e Matematica Università degli Studi dell Insubria in Como via Valleggio 11, 100 Como
Fisica Quantistica III Esercizi Natale 009 Philip G. Ratcliffe (philip.ratcliffe@uninsubria.it) Dipartimento di Fisica e Matematica Università degli Studi dell Insubria in Como via Valleggio 11, 100 Como
Prova Scritta di di Meccanica Analitica. 7 Giugno 2017
 Prova Scritta di di Meccanica Analitica 7 Giugno 217 Problema 1 1) Si consideri un pendolo di massa m e lunghezza l il cui punto di aggancio si muove di moto uniformente accelerato lungo l asse orizzontale
Prova Scritta di di Meccanica Analitica 7 Giugno 217 Problema 1 1) Si consideri un pendolo di massa m e lunghezza l il cui punto di aggancio si muove di moto uniformente accelerato lungo l asse orizzontale
Meccanica. 5. Moti Relativi. Domenico Galli. Dipartimento di Fisica e Astronomia
 Meccanica 5. Moti Relativi http://campus.cib.unibo.it/2423/ Domenico Galli Dipartimento di Fisica e Astronomia 22 febbraio 2017 Traccia 1. Cambiamento del Sistema di Riferimento 2. Trasformazione del Vettore
Meccanica 5. Moti Relativi http://campus.cib.unibo.it/2423/ Domenico Galli Dipartimento di Fisica e Astronomia 22 febbraio 2017 Traccia 1. Cambiamento del Sistema di Riferimento 2. Trasformazione del Vettore
FM210 - Fisica Matematica I
 FM10 - Fisica Matematica I Seconda Prova di Esonero [13-01-01] Soluzioni Problema 1 1. Il moto si svolge in un campo di forze centrale in assenza di attrito. Pertanto si avranno due integrali primi del
FM10 - Fisica Matematica I Seconda Prova di Esonero [13-01-01] Soluzioni Problema 1 1. Il moto si svolge in un campo di forze centrale in assenza di attrito. Pertanto si avranno due integrali primi del
Se la funzione è analiticamente invertibile, estratto q, si può ricavare x = x(q).
 La tecnica Monte Carlo Il metodo Monte Carlo è basato sulla scelta di eventi fisici con una probabilità di accadimento nota a priori. sia p(x) la distribuzione di probabilità con la quale si manifesta
La tecnica Monte Carlo Il metodo Monte Carlo è basato sulla scelta di eventi fisici con una probabilità di accadimento nota a priori. sia p(x) la distribuzione di probabilità con la quale si manifesta
SOLUZIONE DELL EQUAZIONE DI FOURIER PER PER PIASTRA SOTTILE CON SORGENTE TERMICA IN MOTO UNIFORME
 SOLUZIONE DELL EUAZIONE DI FOURIER PER PER PIASTRA SOTTILE CON SORGENTE TERMICA IN MOTO UNIFORME Luca Ghezzi May 2 Abstract L equazione del calore di Fourier è risolta analiticamente nel caso di un mezzo
SOLUZIONE DELL EUAZIONE DI FOURIER PER PER PIASTRA SOTTILE CON SORGENTE TERMICA IN MOTO UNIFORME Luca Ghezzi May 2 Abstract L equazione del calore di Fourier è risolta analiticamente nel caso di un mezzo
PROBLEMI DI FISICA MODERNA E MECCANICA QUANTISTICA. SECONDA PARTE anno accademico
 PROBLEMI DI FISICA MODERNA E MECCANICA QUANTISTICA SECONDA PARTE anno accademico 2016-2017 (1) Per un sistema meccanico n-dimensionale scrivere: (a) gli elementi di matrice dello operatore posizione x
PROBLEMI DI FISICA MODERNA E MECCANICA QUANTISTICA SECONDA PARTE anno accademico 2016-2017 (1) Per un sistema meccanico n-dimensionale scrivere: (a) gli elementi di matrice dello operatore posizione x
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI
 CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
Analisi nel dominio del tempo delle rappresentazioni in variabili di stato
 4 Analisi nel dominio del tempo delle rappresentazioni in variabili di stato Versione del 21 marzo 2019 In questo capitolo 1 si affronta lo studio, nel dominio del tempo, dei modelli di sistemi lineari,
4 Analisi nel dominio del tempo delle rappresentazioni in variabili di stato Versione del 21 marzo 2019 In questo capitolo 1 si affronta lo studio, nel dominio del tempo, dei modelli di sistemi lineari,
11/3 IRRIDUCIBILITÀ NELLO SPAZIO DI HILBERT 10/11 1 IRRIDUCIBILITÀ
 11/3 IRRIDUCIBILITÀ NELLO SPAZIO DI HILBERT 10/11 1 IRRIDUCIBILITÀ Sistemi irriducibili di operatori in uno spazio di Hilbert Un insieme o sistema di operatori {A, B,...} in uno spazio di Hilbert H si
11/3 IRRIDUCIBILITÀ NELLO SPAZIO DI HILBERT 10/11 1 IRRIDUCIBILITÀ Sistemi irriducibili di operatori in uno spazio di Hilbert Un insieme o sistema di operatori {A, B,...} in uno spazio di Hilbert H si
PRIMA PARTE anno accademico
 PROBLEMI DI FISICA MODERNA E MECCANICA QUANTISTICA PRIMA PARTE anno accademico 017-018 (1) Si consideri una particella che può colpire uno schermo in cui sono praticate tre fenditure, indicate dai ket
PROBLEMI DI FISICA MODERNA E MECCANICA QUANTISTICA PRIMA PARTE anno accademico 017-018 (1) Si consideri una particella che può colpire uno schermo in cui sono praticate tre fenditure, indicate dai ket
la forma esplicita delle correzioni
 la forma esplicita delle correzioni al leading order (ma nei programmi di fit le correzioni si spingono, a seconda dei casi, ad ordini superiori) e per m H >m W le correzioni dipendenti dal flavour sono
la forma esplicita delle correzioni al leading order (ma nei programmi di fit le correzioni si spingono, a seconda dei casi, ad ordini superiori) e per m H >m W le correzioni dipendenti dal flavour sono
11/1 PRINCIPI GENERALI DELLA MECCANICA QUANTISTICA 08/09 1 STATI E GRANDEZZE
 11/1 PRINCIPI GENERALI DELLA MECCANICA QUANTISTICA 08/09 1 STATI E GRANDEZZE Principio S: stati di un sistema fisico A ogni sistema fisico S è associato un opportuno spazio di Hilbert H S. Se il sistema
11/1 PRINCIPI GENERALI DELLA MECCANICA QUANTISTICA 08/09 1 STATI E GRANDEZZE Principio S: stati di un sistema fisico A ogni sistema fisico S è associato un opportuno spazio di Hilbert H S. Se il sistema
La struttura elettronica degli atomi
 1 In unità atomiche: a 0 me 0,59A unità di lunghezza e H 7, ev a H=Hartree unità di energia L energia dell atomo di idrogeno nello stato fondamentale espresso in unità atomiche è: 4 0 me 1 e 1 E H 13,
1 In unità atomiche: a 0 me 0,59A unità di lunghezza e H 7, ev a H=Hartree unità di energia L energia dell atomo di idrogeno nello stato fondamentale espresso in unità atomiche è: 4 0 me 1 e 1 E H 13,
Esercizio 1 Risolvere l equazione di Schrödinger per una particella unidimensionale in presenza di un potenziale periodico:
 Esercizio 1 Risolvere l equazione di Schrödinger per una particella unidimensionale in presenza di un potenziale periodico: H P + V (x, V (x + L V (x. (1 m Hψ Eψ. ( Soluzione. In rappresentazione {X }
Esercizio 1 Risolvere l equazione di Schrödinger per una particella unidimensionale in presenza di un potenziale periodico: H P + V (x, V (x + L V (x. (1 m Hψ Eψ. ( Soluzione. In rappresentazione {X }
Equazioni differenziali. f(x, u, u,...,u (n) )=0,
 Lezione Equazioni differenziali Un equazione differenziale è una relazione del tipo f(x, u, u,...,u (n) )=, che tiene conto del valori di una funzione (incognita) u e delle sue derivate fino ad un certo
Lezione Equazioni differenziali Un equazione differenziale è una relazione del tipo f(x, u, u,...,u (n) )=, che tiene conto del valori di una funzione (incognita) u e delle sue derivate fino ad un certo
FM210 - Fisica Matematica I
 FM21 - Fisica Matematica I Seconda Prova Scritta [16-2-212] Soluzioni Problema 1 1. Chiamiamo A la matrice del sistema e cerchiamo anzitutto gli autovalori della matrice: l equazione secolare è (λ + 2β)λ
FM21 - Fisica Matematica I Seconda Prova Scritta [16-2-212] Soluzioni Problema 1 1. Chiamiamo A la matrice del sistema e cerchiamo anzitutto gli autovalori della matrice: l equazione secolare è (λ + 2β)λ
; r 0 2 m = l 2 (s 2 θ + c 2 θ) = l 2
 1 Calcolo del momento d inerzia Esercizio I.1 Pendolo semplice Si faccia riferimento alla Figura 1, dove è rappresentato un pendolo semplice; si utilizzeranno diversi sistemi di riferimento: il primo,
1 Calcolo del momento d inerzia Esercizio I.1 Pendolo semplice Si faccia riferimento alla Figura 1, dove è rappresentato un pendolo semplice; si utilizzeranno diversi sistemi di riferimento: il primo,
Eccitazioni nucleari. Capitolo Spettro rotazionale
 Capitolo 1 Eccitazioni nucleari 1.1 Spettro rotazionale Consideriamo un nucleo pari pari, con spin zero, che abbia però una deformazione permanente. Supponiamo inoltre che il nucleo goda di una simmetria
Capitolo 1 Eccitazioni nucleari 1.1 Spettro rotazionale Consideriamo un nucleo pari pari, con spin zero, che abbia però una deformazione permanente. Supponiamo inoltre che il nucleo goda di una simmetria
Eccitazioni nucleari
 1 Spettro rotazionale Lezione 28 Eccitazioni nucleari Consideriamo un nucleo pari pari, con spin zero, che abbia però una deformazione permanente. Supponiamo inoltre che il nucleo goda di una simmetria
1 Spettro rotazionale Lezione 28 Eccitazioni nucleari Consideriamo un nucleo pari pari, con spin zero, che abbia però una deformazione permanente. Supponiamo inoltre che il nucleo goda di una simmetria
Richiami di Meccanica Classica
 Richiami di Meccanica Classica Corso di Fisica Matematica 3 (seconda parte), a.a. 2016/17 G. Gaeta 18/4/2017 Questa dispensa, che va vista in connessione a quella sul principio variazionale e la formulazione
Richiami di Meccanica Classica Corso di Fisica Matematica 3 (seconda parte), a.a. 2016/17 G. Gaeta 18/4/2017 Questa dispensa, che va vista in connessione a quella sul principio variazionale e la formulazione
DEDUZIONE DEL TEOREMA DELL'ENERGIA CINETICA DELL EQUAZIONE SIMBOLICA DELLA DINAMICA
 DEDUZIONE DEL TEOREMA DELL'ENERGIA CINETICA DELL EQUAZIONE SIMBOLICA DELLA DINAMICA Sia dato un sistema con vincoli lisci, bilaterali e FISSI. Ricaviamo, dall equazione simbolica della dinamica, il teorema
DEDUZIONE DEL TEOREMA DELL'ENERGIA CINETICA DELL EQUAZIONE SIMBOLICA DELLA DINAMICA Sia dato un sistema con vincoli lisci, bilaterali e FISSI. Ricaviamo, dall equazione simbolica della dinamica, il teorema
La radiazione elettromagnetica nucleare deve avere una lunghezza d onda dell ordine delle dimensioni del nucleo, e pertanto: c A 1/ 3
 Emissione gamma La radiazione γ è l emissione spontanea di quanti da parte del nucleo. Emettendo fotoni il nucleo passa da uno stato eccitato ed uno stato meno eccitato. Vi possono essere transizioni radiative
Emissione gamma La radiazione γ è l emissione spontanea di quanti da parte del nucleo. Emettendo fotoni il nucleo passa da uno stato eccitato ed uno stato meno eccitato. Vi possono essere transizioni radiative
8.1 Problema della diffusione in meccanica quantistica
 8.1 Problema della diffusione in meccanica quantistica Prima di procedere oltre nello studio dell interazione puntuale, in questo paragrafo vogliamo dare un breve cenno alle nozioni di base della teoria
8.1 Problema della diffusione in meccanica quantistica Prima di procedere oltre nello studio dell interazione puntuale, in questo paragrafo vogliamo dare un breve cenno alle nozioni di base della teoria
FM210 / MA - Terzo scritto ( ), con l > 0. Il vincolo può supporsi ideale. Oltre alle forze di reazione vincolare, il punto è soggetto a
 FM10 / MA - Terzo scritto (9-9-017) Esercizio 1. Un punto materiale P di massa m è vincolato a muoversi senza attrito sulla superficie di equazione z = l log x +y, con l > 0. Il vincolo può l supporsi
FM10 / MA - Terzo scritto (9-9-017) Esercizio 1. Un punto materiale P di massa m è vincolato a muoversi senza attrito sulla superficie di equazione z = l log x +y, con l > 0. Il vincolo può l supporsi
Unità 3 Segnali a potenza media finita e conversione A/D
 Teoria dei segnali Unità 3 e conversione A/D e conversione A/D Rappresentazione in frequenza Segnali periodici Conversione A/D 005 Politecnico di Torino Obiettivi Introdurre gli strumenti per l analisi
Teoria dei segnali Unità 3 e conversione A/D e conversione A/D Rappresentazione in frequenza Segnali periodici Conversione A/D 005 Politecnico di Torino Obiettivi Introdurre gli strumenti per l analisi
Sistemi lineari. Lorenzo Pareschi. Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara
 Sistemi lineari Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
Sistemi lineari Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
UNIVERSITÀ DI ROMA TOR VERGATA. Analisi Matematica II per Ingegneria Prof. C. Sinestrari. (c) e5 e 4 e (2x 3y) dx + (1 + x)dx +
 UNIVERSITÀ DI ROMA TOR VERGATA Analisi Matematica II per Ingegneria Prof. C. Sinestrari Risposte (sintetiche) agli esercizi del 5.XI.7. Gli integrali richiesti valgono: (a) + ( e ) (b) (c) e5 e e + (d)
UNIVERSITÀ DI ROMA TOR VERGATA Analisi Matematica II per Ingegneria Prof. C. Sinestrari Risposte (sintetiche) agli esercizi del 5.XI.7. Gli integrali richiesti valgono: (a) + ( e ) (b) (c) e5 e e + (d)
Compitino 1 di Meccanica Quantistica I
 Compitino di Meccanica Quantistica I Facoltà di Scienze, M.F.N., Università degli Studi di Pisa, 5 dicembre 00 (A.A. 0/) (Tempo a disposizione: 3 ore ) Problema. Un sistema a due stati è caratterizzato
Compitino di Meccanica Quantistica I Facoltà di Scienze, M.F.N., Università degli Studi di Pisa, 5 dicembre 00 (A.A. 0/) (Tempo a disposizione: 3 ore ) Problema. Un sistema a due stati è caratterizzato
Soluzioni. Foglio 1. Rette e piani. n x + c = 0. (1)
 Soluzioni Foglio 1. Rette e piani. Esercizio 1. Se n è la normale al piano, sia c = n x 0. Dimostriamo prima che se x π, allora x soddisfa Si ha Sostituendo dentro (1) si ottiene n x + c = 0. (1) x = x
Soluzioni Foglio 1. Rette e piani. Esercizio 1. Se n è la normale al piano, sia c = n x 0. Dimostriamo prima che se x π, allora x soddisfa Si ha Sostituendo dentro (1) si ottiene n x + c = 0. (1) x = x
Minimi quadrati vincolati e test F
 Minimi quadrati vincolati e test F Impostazione del problema Spesso, i modelli econometrici che stimiamo hanno dei parametri che sono passibili di interpretazione diretta nella teoria economica. Consideriamo
Minimi quadrati vincolati e test F Impostazione del problema Spesso, i modelli econometrici che stimiamo hanno dei parametri che sono passibili di interpretazione diretta nella teoria economica. Consideriamo
Università di Pisa - Corso di Laurea in Fisica Meccanica Classica a.a. 2015/ Prova Scritta del 22/07/2016
 Università di Pisa - Corso di Laurea in Fisica Meccanica Classica a.a. 2015/2016 - Prova Scritta del 22/07/2016 ISTRUZIONI: LEGGERE ATTENTAMENTE Può essere svolta la prima parte (A1 e A2 oppure la seconda
Università di Pisa - Corso di Laurea in Fisica Meccanica Classica a.a. 2015/2016 - Prova Scritta del 22/07/2016 ISTRUZIONI: LEGGERE ATTENTAMENTE Può essere svolta la prima parte (A1 e A2 oppure la seconda
PNI 2005 QUESITO 1
 www.matefilia.it PNI 2005 QUESITO 1 Consideriamo il lato AB del decagono regolare inscritto nella circonferenza e indichiamo con AC la bisettrice dell angolo alla base A. Essendo l angolo in O di 36 (360
www.matefilia.it PNI 2005 QUESITO 1 Consideriamo il lato AB del decagono regolare inscritto nella circonferenza e indichiamo con AC la bisettrice dell angolo alla base A. Essendo l angolo in O di 36 (360
CALCOLO NUMERICO. Francesca Mazzia. Calcolo degli autovalori. Dipartimento Interuniversitario di Matematica. Università di Bari
 CALCOLO NUMERICO Francesca Mazzia Dipartimento Interuniversitario di Matematica Università di Bari Calcolo degli autovalori 1 Calcolo degli autovalori Gli autovalore e gli autovettore di una matrice quadrata
CALCOLO NUMERICO Francesca Mazzia Dipartimento Interuniversitario di Matematica Università di Bari Calcolo degli autovalori 1 Calcolo degli autovalori Gli autovalore e gli autovettore di una matrice quadrata
Corso di Laurea in Informatica Calcolo delle Probabilità e Statistica (269AA) A.A. 2016/17 - Prima prova in itinere
 Corso di Laurea in Informatica Calcolo delle Probabilità e Statistica (69AA) A.A. 016/17 - Prima prova in itinere 017-01-13 La durata della prova è di tre ore. Le risposte devono essere adeguatamente giustificate.
Corso di Laurea in Informatica Calcolo delle Probabilità e Statistica (69AA) A.A. 016/17 - Prima prova in itinere 017-01-13 La durata della prova è di tre ore. Le risposte devono essere adeguatamente giustificate.
m p 6, j m 1 2 m e 3, j m 1 2 5, m 2 82, N w
 Teoria della carica elettrica e calcolo del valore teorico Questa relazione è stata ricavata senza porre alcuna ipotesi restrittiva e dunque risulta di validità universale, applicabile in ogni circostanza
Teoria della carica elettrica e calcolo del valore teorico Questa relazione è stata ricavata senza porre alcuna ipotesi restrittiva e dunque risulta di validità universale, applicabile in ogni circostanza
I conteggi in fisica. Appendice D. D.1 Urti di particelle
 Appendice D I conteggi in fisica Il conteggio di eventi è un importante modalità di indagine delle leggi che governano alcuni fenomeni fisici. In un esperimento di conteggio si raccolgono e analizzano
Appendice D I conteggi in fisica Il conteggio di eventi è un importante modalità di indagine delle leggi che governano alcuni fenomeni fisici. In un esperimento di conteggio si raccolgono e analizzano
λ : autovalore di ĵ 2, H λ : corrispondente autospazio di ĵ 2.
 6/ TEORIA GENERALE DEL MOMENTO ANGOLARE 9/ TEORIA GENERALE DEL MOMENTO ANGOLARE In un qualsiasi spazio di Hilbert H, siano ĵ x ĵ, ĵ y ĵ 2 e ĵ z ĵ 3 tre operatori autoaggiunti con il significato di componenti
6/ TEORIA GENERALE DEL MOMENTO ANGOLARE 9/ TEORIA GENERALE DEL MOMENTO ANGOLARE In un qualsiasi spazio di Hilbert H, siano ĵ x ĵ, ĵ y ĵ 2 e ĵ z ĵ 3 tre operatori autoaggiunti con il significato di componenti
' $ Teoria del traffico & % 1
 Teoria del traffico Andamento della distribuzione di Poisson P(k) = (λt)k k! e λt 1 k=0 k=1 k=2 k=3 0.8 0.6 P(k) 0.4 0.2 0 0 1 2 3 4 5 λt Proprietá La sovrapposizione di h processi di Poisson aventi frequenze
Teoria del traffico Andamento della distribuzione di Poisson P(k) = (λt)k k! e λt 1 k=0 k=1 k=2 k=3 0.8 0.6 P(k) 0.4 0.2 0 0 1 2 3 4 5 λt Proprietá La sovrapposizione di h processi di Poisson aventi frequenze
Raggiungibilità e controllabilità
 Capitolo. TEORIA DEI SISTEMI 4. Raggiungibilità e controllabilità Raggiungibilità. Il problema della raggiungibilità consiste nel determinare l insieme di stati raggiungibili a partire da un dato stato
Capitolo. TEORIA DEI SISTEMI 4. Raggiungibilità e controllabilità Raggiungibilità. Il problema della raggiungibilità consiste nel determinare l insieme di stati raggiungibili a partire da un dato stato
2.3 Percorso residuo (range)
 Figure 13: Determinazione del range a partire da una curva di trasmissione (I èil numero di particelle tramesse per unità di tempo in funzione delle spessore t essendo I 0 il numero di particelle entranti)
Figure 13: Determinazione del range a partire da una curva di trasmissione (I èil numero di particelle tramesse per unità di tempo in funzione delle spessore t essendo I 0 il numero di particelle entranti)
15/04/2014. Serway, Jewett Principi di Fisica IV Ed. Capitolo 8. Generalizziamo, considerando due particelle interagenti.
 Serway, Jewett Principi di Fisica IV Ed. Capitolo 8 Esempio arciere su una superficie ghiacciata che scocca la freccia: l arciere (60 kg) esercita una forza sulla freccia 0.5 kg (che parte in avanti con
Serway, Jewett Principi di Fisica IV Ed. Capitolo 8 Esempio arciere su una superficie ghiacciata che scocca la freccia: l arciere (60 kg) esercita una forza sulla freccia 0.5 kg (che parte in avanti con
Capitolo 3 Modelli nucleari collettivi: il modello a goccia di liquido
 Capitolo 3 Modelli nucleari collettivi: il modello a goccia di liquido 3.1 Introduzione Già nel 1911 Rutherford, per spiegare i risultati del suo esperimento di diffusione di particelle α da nuclei pesanti
Capitolo 3 Modelli nucleari collettivi: il modello a goccia di liquido 3.1 Introduzione Già nel 1911 Rutherford, per spiegare i risultati del suo esperimento di diffusione di particelle α da nuclei pesanti
ARGOMENTO: Cenni di Fisica del Nucleo
 UNIVERSITA DEGLI STUDI DI GENOVA C.L. TECNICHE DIAGNOSTICHE RADIOLOGICHE CORSO INTEGRATO: MISURE ELETTRICHE ED ELETTRONICHE MATERIA: FISICA APPLICATA 2 (2 anno 1 sem) ARGOMENTO: Cenni di Fisica del Nucleo
UNIVERSITA DEGLI STUDI DI GENOVA C.L. TECNICHE DIAGNOSTICHE RADIOLOGICHE CORSO INTEGRATO: MISURE ELETTRICHE ED ELETTRONICHE MATERIA: FISICA APPLICATA 2 (2 anno 1 sem) ARGOMENTO: Cenni di Fisica del Nucleo
Origine fisica di equazioni alle derivate parziali
 Origine fisica di equazioni alle derivate parziali Equazione del calore Dato un corpo nello spazio, rappresentato con un sottoinsieme A di 3, indichiamo con u(, y, z, t) la temperatura del corpo nel punto(,
Origine fisica di equazioni alle derivate parziali Equazione del calore Dato un corpo nello spazio, rappresentato con un sottoinsieme A di 3, indichiamo con u(, y, z, t) la temperatura del corpo nel punto(,
rettilinei ", che mettono in evidenza una dipendenza del tipo :
 Livelli neutronici teorici nel nucleo atomico Se riportiamo su assi cartesiani l energia per strato sperimentale, N, in funzione del numero di neutroni presenti nei nuclei, otteniamo una curva che mette
Livelli neutronici teorici nel nucleo atomico Se riportiamo su assi cartesiani l energia per strato sperimentale, N, in funzione del numero di neutroni presenti nei nuclei, otteniamo una curva che mette
Problemi di topologia metrica.
 Problemi di topologia metrica. 1.) Sia X un insieme, munito di una distanza d : X X R +. Siano x 1 ;x ;x 3 ;x 4 quattro punti qualsiasi di X. Verificare che: d (x 1 ; x 4 ) d (x 1 ; x ) + d (x ; x 3 )
Problemi di topologia metrica. 1.) Sia X un insieme, munito di una distanza d : X X R +. Siano x 1 ;x ;x 3 ;x 4 quattro punti qualsiasi di X. Verificare che: d (x 1 ; x 4 ) d (x 1 ; x ) + d (x ; x 3 )
Due osservazioni sulla diffusione dei raggi corpuscolari. come fenomeno di diffrazione. G. Wentzel a Lipsia
 Due osservazioni sulla diffusione dei raggi corpuscolari 1 come fenomeno di diffrazione. G. Wentzel a Lipsia (ricevuto il 19 novembre 196) 1. Nel caso limite della meccanica classica il quadrato dell ampiezza
Due osservazioni sulla diffusione dei raggi corpuscolari 1 come fenomeno di diffrazione. G. Wentzel a Lipsia (ricevuto il 19 novembre 196) 1. Nel caso limite della meccanica classica il quadrato dell ampiezza
Analisi Matematica III 16 Gennaio (x 1) 2 + y2
 Analisi Matematica III 6 Gennaio 7. ( punti) Calcolare il seguente integrale triplo ( e z + y(x ) + dove = {(x, y, z) R 3 : (x ) + y 4 + z }. y + (x ) + y 4 + z ) dxdz, Il dominio di integrazione è un
Analisi Matematica III 6 Gennaio 7. ( punti) Calcolare il seguente integrale triplo ( e z + y(x ) + dove = {(x, y, z) R 3 : (x ) + y 4 + z }. y + (x ) + y 4 + z ) dxdz, Il dominio di integrazione è un
