Teoria dei Sistemi - A.A. 2003/2004
|
|
|
- Eugenia Ippolito
- 5 anni fa
- Visualizzazioni
Transcript
1 ANAISI ODAE DEI SISTEI INEARI A TEPO CONTINUO Dr. Crisian Scchi ARSconrol ab Univrsià di odna Rggio Emilia Il movimno di un sisma TI & ( A( + Bu( y( C( + Du( Formula di agrang ( A A( τ + Bu( τ dτ A I + A + A n n + + A +! n! Crisian Scchi Conrollo di Sismi Roboici Analisi odal -- Crisian Scchi Pag.
2 Analisi odal Il rmin A ha un ruolo crucial sia pr la drminazion dl movimno libro ch di qullo forzao obiivo dll analisi modal pr un sisma linar mpo invarian (TI è qullo di scoprir qual è da cosa dipnd l andamno dl rmin A, Un analisi accuraa dlla sruura di al rmin pora una conoscnza profonda dll dinamich inrinsch dl sisma di com ali dinamich si combinano nlla risposa libra nlla risposa forzaa Crisian Scchi Conrollo di Sismi Roboici Analisi odal -- 3 I modi dl sisma Si considri il sisma auonomo &( A( Il cui sao inizial sia ( Il movimno (libro dl sisma è dao da: A ( funzioni lmnari dl mpo ch compaiono all inrno dlla maric A prndono il nom di modi dl sisma in sam. Crisian Scchi Conrollo di Sismi Roboici Analisi odal -- 4 Crisian Scchi Pag.
3 Forma canonica di Jordan I modi di un sisma possono ssr facilmn vidnziai rami un cambio di bas nllo spazio dgli sai ch rasformi la maric A nlla corrispondn forma canonica di Jordan. Sia A una maric di sao n n di un sisma TI siano λ,, λ h gli auovalori disini di A siano r,, r h l loro rispiv molplicià algbrich. Il polinomio cararisico può cioè ssr dcomposo scrio com: Esis smpr una maric quadraa di dimnsion n non singolar T ch pora la maric A nlla sua forma canonica di Jordan T A T AT Crisian Scchi Analisi odal -- 5 Forma canonica di Jordan a forma canonica di Jordan dlla maric A è: J J A T AT J h ad ogni auovalor disino λ i corrispond un blocco di Jordan di dimnsion r i : dim J ir i i,,h Crisian Scchi Analisi odal -- 6 Crisian Scchi Pag. 3
4 Forma canonica di Jordan Ogni blocco di Jordan è una maric diagonal a blocchi d è formao da q i miniblocchi di Jordan: ognuno di quali ha dimnsion i ν i,j : Crisian Scchi Analisi odal -- 7 Procdura pr drminar la maric T Si drminano i q i auovori disini associai all auovalor λ i risolvndo: ( λ I A, j, K, q i v i, j i Nl caso in cui si abbia q i <r i è ncssario procdr, pr ogni auovori v i,j, alla drminazion dlla corrispondn cana v i,j (k di auovori gnralizzai k,,ν i,j. Tali can si drminano risolvndo iraivamn al sisma: Crisian Scchi ( ( ( λ ii A v i, j v i, j v i (3 ( ( λii A vi, j vi, j ( ν i, j ( ν i, j ( λ ii A vi, j vi, j (, j Analisi odal -- 8 Crisian Scchi Pag. 4
5 Procdura pr drminar la maric T a maric T ha com colonn l can di auovori gnralizzai T [ v ( i, j, v ( i, j, K, v ( ν i, i, j j ] Crisian Scchi Analisi odal -- 9 Proprià dll sponnzial di maric sponnzial di maric god dll sguni uili proprià: Sia T una maric non singolar; allora: sponnzial di una maric diagonal a blocchi è una maric diagonal a blocchi in cui ciascun blocco è l sponnzial dl blocco dlla maric di parnza: Crisian Scchi Analisi odal -- Crisian Scchi Pag. 5
6 Crisian Scchi Pag. 6 ovimno libro di sismi TI ovimno libro di sismi TI Dao il sisma auonomo ( ( A & la rasformazion: pr cui la maric di sao nll nuov coordina è in forma di Jordan ( ( A T Analisi odal -- Crisian Scchi pr cui la maric di sao nll nuov coordina è in forma di Jordan, abbiamo ch il movimno libro ( è dao da: ( T T A A ovimno libro di sismi TI ovimno libro di sismi TI Siccom è in forma canonica di Jordan J J J J quindi, pr calcolar il movimno libro, è sufficin sapr calcolar l sponnzial dl gnrico miniblocco di Jordan di dimnsion ν λ ( T T T T J J h h Analisi odal -- Crisian Scchi N I J + λ λ λ λ λ λ
7 Crisian Scchi Pag. 7 a maric N, ch ha ui gli lmni nulli rann qulli nlla sopradiagonal ch valgono, è una maric nilpon di ordin ν ovimno libro di sismi TI ovimno libro di sismi TI ν N N ν dim sponnzial di un miniblocco di Jordan si calcola com: N N I N I J I λ λ λ + ( ν λ λ n n n n N N Analisi odal -- 3 Crisian Scchi!! n n N n N n ! (! ν ν λ ν N N N I ovimno libro di sismi TI ovimno libro di sismi TI! (! ( 3!! 3 ν ν ν ν! (! ( ( J ν ν λ Analisi odal -- 4 Crisian Scchi
8 ovimno libro di sismi TI All sprssion quasi diagonal ch cararizza la forma canonica di Jordan, si giung smpr, anch nl caso vi siano auovalori complssi coniugai. In quso caso, prò, i blocchi dlla forma di Jordan conngono di rmini complssi, prano, il loro uilizzo risula molo poco inuiivo nll analisi di sismi TI dl loro movimno. Pr ovviar quso inconvnin, nl caso di auovalori complssi coniugai, si applica una rasformazion nllo spazio dgli sai ch pora la maric in forma di Jordan ad avr sulla diagonal principal di blocchi rali di dimnsion. Si considri, ad smpio, una maric A di dimnsion 6 cararizzaa da una coppia di auovalori complssi coniugai λ, σ±jω di molplicià 3. Siano v, v, v 3 gli auovori associai a un auovalor v *, v *,v 3* gli auovori complssi coniugai associai al suo complsso coniugao. Crisian Scchi Analisi odal -- 5 ovimno libro di sismi TI Applicando la rasformazion di coordina: * * * T T [ v v v v v ] Si oin la forma di Jordan dlla maric A: 3 v3 Si ongono cioè du blocchi di Jordan ciascuno cosiuio da un solo miniblocco di dimnsion 3 Crisian Scchi Analisi odal -- 6 Crisian Scchi Pag. 8
9 ovimno libro di sismi TI Si indichi con v i,r v i,i rispivamn la par ral la par complssa dll auovor complsso i-simo (i,,3. Uilizzando la sgun rasformazion di coordina: ~ [ v v v v v v ] T ~ ~ T, R, I, R, I 3, R 3, I ~ ~ è possibil rasformar la maric A nll T sgun forma canonica ral di Jordan: Crisian Scchi Analisi odal -- 7 ovimno libro di sismi TI In al modo è possibil sprimr il movimno libro di sismi TI com combinazion linar di soli rmini rali. Infai: occorr prò dar una formula pr l sponnzial dlla maric E possibil mosrar ch, nll smpio considrao: Crisian Scchi Analisi odal -- 8 Crisian Scchi Pag. 9
10 odi di un sisma funzioni dl mpo ch compaiono ch compaiono nlla maric J i sono di modi dl sisma rlaivi all auovalor associao a J i funzioni dl mpo ch compaiono nll marici Ji, i,, h, cioè nlla maric sono d modi dl sisma. Crisian Scchi Analisi odal -- 9 Combinazion di modi di un sisma Il movimno libro può prano ssr dcomposo in h soomovimni libri: Crisian Scchi Analisi odal -- Crisian Scchi Pag.
11 Combinazion di modi di un sisma Il movimno di un sisma libro è la combinazion linar di modi dl sisma. I cofficini con cui i modi sono combinai sono dai da: o sao inizial a maric T ( T ( o sudio dll andamno di modi di un sisma ci consn di lgar il ipo di andamno dl movimno libro agli auovalori dlla maric di sao. E prano possibil bl cararizzar il movimno libro lb dl sisma dal smplic sudio dgli auovalori dlla maric di sao dlla loro molplicià. Crisian Scchi Analisi odal -- Analisi modal Auovalori rali disini Nl caso in cui gli auovalori dlla maric di sao siano ui rali disini, ncssariamn la forma di Jordan è una maric diagonal: a maric di ransizion dllo sao è, quindi: Crisian Scchi Analisi odal -- Crisian Scchi Pag.
12 Analisi modal Auovalori rali disini I modi dl sisma sono dai dall sguni funzioni: λ.5 λ λ. 5 Crisian Scchi Analisi odal -- 3 Analisi modal Auovalori complssi disini Nl caso in cui gli auovalori dlla maric di sao siano complssi coniugai disini, dl ipo λ i σ i ± ω i la maric di ransizion dllo sao: I modi dl sisma sono dai dall sguni funzioni: Crisian Scchi Analisi odal -- 4 Crisian Scchi Pag.
13 Analisi modal Auovalori complssi disini σ cos(ω dov λ,.5 ± j Crisian Scchi Conrollo di Sismi Roboici Analisi odal -- 5 Analisi modal Auovalori complssi disini σ cos(ω dov λ, ± j Crisian Scchi Conrollo di Sismi Roboici Analisi odal -- 6 Crisian Scchi Pag. 3
14 Analisi modal Auovalori complssi disini σ cos(ω dov λ, -.5 ±j Crisian Scchi Conrollo di Sismi Roboici Analisi odal -- 7 Analisi modal Auovalori rali mulipli Nl caso di auovalori mulipli, la maric di ransizion dllo sao è daa da: dov: Crisian Scchi Analisi odal -- 8 Crisian Scchi Pag. 4
15 Analisi modal Auovalori rali mulipli In quso caso i modi dl sisma sono: Crisian Scchi Analisi odal -- 9 Analisi modal Auovalori rali mulipli Si considri, ad smpio, il sisma in forma di Jordan con auovalor λ di molplicià : Il movimno libro dl sisma è dao da: Analizziamo i du modi dl sisma: Crisian Scchi Analisi odal -- 3 Crisian Scchi Pag. 5
16 Analisi modal Auovalori rali mulipli Auovalor doppio λ modi m m Auovalor doppio λ-.5 modi m m Crisian Scchi Conrollo di Sismi Roboici Analisi odal -- 3 Analisi modal Auovalori complssi mulipli Analogamn al caso di auovalori complssi coniugai mulipli, i modi associai agli auovalori complssi coniugai mulipli dl ipo σ ± jω sono: Dov ν è la dimnsion dl miniblocco di Jordan associao alla coppia di auovalori complssi coniugai. Crisian Scchi Analisi odal -- 3 Crisian Scchi Pag. 6
17 Analisi modal Auovalori complssi mulipli Considriamo un sisma con una coppia di auovalori complssi coniugai σ ± jω doppia. I modi rlaivi alla coppia sono Analizziamo l andamno dlla coppia di modi m ( m 3 (. andamno dll alra coppia di modi è analogo. Crisian Scchi Analisi odal Analisi modal Auovalori complssi mulipli Auovalor doppio λ-.5 ± j modi m m 3 Auovalor doppio λ±j modi m m 3 Crisian Scchi Conrollo di Sismi Roboici Analisi odal Crisian Scchi Pag. 7
18 Analisi modal In un gnrico sisma TI possono ssr prsni ui i ipi di auovalori analizzai finora. Prano, il movimno libro dl sisma è dao, in gnral, dalla combinazion linar di ui i ipi di modi visi finora. Crisian Scchi Analisi odal Carar di convrgnza di modi Considriamo un sisma TI. Dirmo ch un modo m(, dfinio pr è: convrgn s: limiao, ma non convrgn s sis un numro ral << al ch 8 si abbia: non limiao (o divrgn s: Crisian Scchi Analisi odal Crisian Scchi Pag. 8
19 Carar di convrgnza di modi Dall analisi modal faa, sgu la sgun: Proposizion: I modi dl sisma sono: convrgni s solo s ui gli auovalori di A hanno par ral ngaiva limiai s solo s gli auovalori di A hanno par ral ngaiva o nulla qulli a par ral nulla sono associai a miniblocchi di Jordan di dimnsion non limiai s almno un auovalor di A è a par ral posiiva oppur a par ral nulla ma associao a un miniblocco di Jordan di dimnsion maggior di. Crisian Scchi Analisi odal Considrazioni I modi sono una proprià inrinsca dl sisma Il loro andamno può ssr ddoo da una smplic analisi dgli auovalori dlla maric di sao Dai modi dl sisma dipnd sia l andamno dl movimno libro ch il ransiorio dl movimno forzao Nl caso di sismi SISO rapprsnai da funzioni di rasfrimno i poli sono un sooinsim dgli auovalori dl sisma, prano, il ipo di ransiorio dlla risposa può ssr ddoo dalla posizion dalla molplicià di poli Crisian Scchi Analisi odal Crisian Scchi Pag. 9
20 Esmpio Dao il sisma: A C Calcolar l uscia libra dl sisma a parir dallo sao inizial Crisian Scchi Analisi odal Esmpio uscia libra è daa da: Pr por calcolar l sponnzial di maric, poro la maric di sao nlla forma canonica di Jordan. Gli auovalori dlla maric di sao sono l soluzioni di: Crisian Scchi Analisi odal -- 4 Crisian Scchi Pag.
21 Esmpio Gli auovori corrispondni a λ si drminano risolvndo: ( λ I A v v Si ongono du auovori linarmn indipndni: v v Crisian Scchi Analisi odal -- 4 Esmpio Gli auovori corrispondni a λ - si drminano risolvndo: ( λ I A v v Si oin un auovalor: v 3 Crisian Scchi Analisi odal -- 4 Crisian Scchi Pag.
22 Esmpio T [ v v ] v3.5.5 T.5.5 Facndo il cambio di variabil: T marici A C vngono rasforma in: Crisian Scchi Analisi odal Esmpio A T AT Forma canonica di Jordan di A C CT [ ] Il movimno libro dl sisma è dao da: A A ( T( T T T Crisian Scchi Analisi odal Crisian Scchi Pag.
23 Esmpio Uilizzando i dai dl problma: Crisian Scchi Analisi odal Esmpio E quindi l uscia libra val: Crisian Scchi Analisi odal Crisian Scchi Pag. 3
24 Conclusioni analisi modal consn di ricavar l dinamich fondamnali di un sisma TI da una smplic analisi dgli auovalori a forma canonica di Jordan consn di calcolar agvolmn quali sono i modi di un sisma Parndo dalla conoscnza di modi dl sisma è possibil capir qual sarà il ransiorio di un movimno oppur il movimno libro Crisian Scchi Conrollo di Sismi Roboici Analisi odal ANAISI ODAE DEI SISTEI INEARI A TEPO CONTINUO Dr. Crisian Scchi ARSconrol ab Univrsià di odna Rggio Emilia Crisian Scchi Pag. 4
25 Esmpio Si considri un sisma massa-molla-smorzaor u k m b y Crisian Scchi Analisi odal Esmpio Scglindo com variabili di sao pr dscrivr il sisma la posizion dlla massa ( la sua vlocià (, il sisma è dscrio da: Crisian Scchi Analisi odal -- 5 Crisian Scchi Pag. 5
Autovalori complessi e coniugati
Auovalori complssi coniugai Noazioni A A α ω ω α λ λ λ α + jω, λ α jω, maric ad lmni rali α + jω, maric diagonal ad lmni complssi α jω L du marici A A hanno gli sssi auovalori λ, λ. aa una gnrica maric
Circuiti dinamici. Introduzione. (versione del ) Circuiti resistivi e circuiti dinamici
ircuii dinamici nroduzion www.di.ing.unibo.i/prs/masri/didaica.m (vrsion dl --3) ircuii rsisivi circuii dinamici ircuii rsisivi: circuii formai solo da componni rsisivi l quazioni dl circuio cosiuiscono
Lezione 6. Stabilità e matrice A nei sistemi LTI. F.Previdi - Fondamenti di Automatica - Lez. 6
Lzion 6. Sabilià maric A ni imi LTI F.Prvidi - Fondamni di Auomaica - Lz. 6 Schma dlla lzion A. Sudio dlla maric pr. Tormi ulla abilià di imi LTI. Rgion di ainoica abilià. Criri di abilià baai ulla maric
Determinare il dominio di una funzione
Drminar il dominio di una funzion CHE COSA SONO LE FUNZON. Una funzion = f( è una rlazion ch lga du grandzz (variabili: la variabil vin chiamaa variabil indipndn, mnr la variabil dipndn. Pr smpio la rlazion
Facoltà di Economia. Equazioni differenziali Lineari ed Applicazioni Economiche
Facolà di Economia Equazioni diffrnziali Linari d Applicazioni Economich prof. EQUAZIONI DIFFERENZIALI LINEARI APPLICAZIONI ECONOMICHE EQUAZIONI DIFFERENZIALI DEL PRIMO ORDINE LINEARI Quso ipo di quazioni
Richiami su numeri complessi
Richiami su numri complssi Insim C di numri complssi E' l'insim dll coppi ordina di numri rali = Z R j Z I ; Z R, Z I R Z = Z R, Z I j Δ = (0,1) unià immaginaria Si noi ch C conin R; in paricolar linsim
Compito di Matematica sul problema di Cauchy e sulle equazioni differenziali ordinarie del 2º ordine. [1]
![Compito di Matematica sul problema di Cauchy e sulle equazioni differenziali ordinarie del 2º ordine. [1]](/thumbs/88/115203540.jpg "Compito di Matematica sul problema di Cauchy e sulle equazioni differenziali ordinarie del 2º ordine. [1]")
Compio di Mamaica sul problma di Cauch sull quazioni diffrnziali ordinari dl º ordin [] Esrcizio Spigar la formulazion, il significao com si procd alla risoluzion dl problma di Cauch pr EDO dl º ordin
Corso di Analisi: Algebra di Base. 3^ Lezione
Corso di Analisi: Algbra di Bas ^ Lzion Disquazioni algbrich. Disquazioni di. Disquazioni di. Disquazioni faoriali. Disquazioni biquadraich. Disquazioni binomi. Disquazioni fra. Sismi di disquazioni. Allgao
INGEGNERIA CIVILE E AMBIENTALE ESERCITAZIONI DI ANALISI C SETTIMANA 7 DEFINIZIONE: FUNZIONE DIFFERENZIABILE IN UN PUNTO.
DEFINIZIONE: FUNZIONE DIFFERENZIABILE IN UN PUNTO Sia A un apro di : sis un vor ab, al ch,, f A Prso, A si dic ch f è diffrnziabil in,, 0, 0 0 0 f f a b 0 si pon df, a, b f Si dimosra ch a, b,, quindi
Esercizi sulla CONVOLUZIONE INTRODUZIONE. x(t)y( τ - t)dt. x(τ - t)y(t)dt
INTRODUZIONE Si ricorda ch la convoluzion ra du sgnali x() y(), rali o complssi, indicaa simbolicamn com: C xy () = x() * y() è daa indiffrnmn dall du sprssioni: Esrcizi sulla CONVOLUZIONE C xy () = C
Serie di Fourier a tempo continuo. La rappresentazione dei segnali nel dominio della frequenza. Jean Baptiste Joseph Fourier (1768 1830 )
Sri di Fourir a mpo coninuo La rapprsnazion di sgnali nl dominio dlla frqunza Jan Bapis Josph Fourir (768 83 ) Fourir sviluppò la oria mamaica dl calor uilizzando funzioni rigonomrich (sni cosni), ch noi
Modi dominanti. L evoluzione libera del sistema lineare. x(k + 1) = Ax(k) a partire dalla condizione iniziale x(0) = x 0 è:
Capitolo. INTRODUZIONE. L voluzion libra dl sistma linar Modi dominanti ẋ(t) = Ax(t), x(k + ) = Ax(k) a partir dalla condizion inizial x() = x è: x(t) = At x, x(k) = A k x Al tndr di t [di k all infinito,
Analisi Matematica 3 (Fisica e Astronomia) Esercizi sulle equazioni differenziali ordinarie lineari
Analisi Mamaica Fisica Asronomia Esrcizi sull quazioni diffrnziali ordinari linari Risolvr i sguni problmi sull quazioni diffrnziali linari a Risolvr x y y in du modi Vi sono soluzioni dfini su uo R? b
Lezione 15 (BAG cap. 14) Le aspettative: nozioni di base
Lzion 5 (BAG cap. 4) L aspaiv: nozioni di bas Corso di Macroconomia Prof. Guido Ascari, Univrsià di Pavia Il asso di inrss in rmini di mona è do asso di inrss nominal Il asso di inrss in rmini di bni è
Integrale di sin t/t e varianti
Ingral di sin / variani Annalisa Massaccsi dicmbr Ingral di sin / In rifrimno all s. 7 dl VII gruppo di srcizi, com già viso ad srciazion, vogliamo dimosrar ch sin / d R. Ossrvazion. Ossrviamo innanziuo
La Trasformata di Laplace. Pierre-Simon Laplace
a Traformaa di aplac Pirr-Simon aplac 749-827 a Traformaa di Eulro onhard Eulr Eulro 707-783 Dfinizion Si dfinic raformaa di aplac dlla funzion f la funzion F coì dfinia: Dov σjωσj2πf. 0 F { f } f d Dfinizion
Università Carlo Cattaneo Ingegneria gestionale Analisi matematica a.a. 2017/2018 PRIMITIVE E INTEGRALI DEFINITI
Univrsià Carlo Caano Inggnria gsional nalisi mamaia aa 7/8 PRIMITIVE E INTEGRLI DEFINITI ESERCIZI CON SOLUZIONE Calolar i sguni ingrali indfinii: ) d ; ) d ; ) d ; ) os sin d ; 6 ) d SOLUZIONI ) La funzion
Appendice Analisi in frequenza dei segnali
Appndic Analisi in rqunza di sgnali - Appndic Analisi in rqunza di sgnali - Sgnali priodici Sviluppo in sri di Fourir Un sgnal è priodico nl mpo quando si rip ogni scondi. Si vda, com smpio, il sgnal in
Segnali e sistemi nel dominio della frequenza
oria di sgnali Sgnali sismi nl dominio dlla rqunza EORIA DEI SEGNALI LAUREA IN INGEGNERIA DELL INORMAZIONE Sommario Sgnali mpo coninuo priodici Sri di ourir Sgnali mpo coninuo apriodici rasormaa di ourir
PROVA SCRITTA DI FONDAMENTI DI AUTOMATICA A.A. 2004/ gennaio 2005 TESTO E SOLUZIONE
PROVA SCRITTA DI FONDAMENTI DI AUTOMATICA A.A. 24/25 2 gnnaio 25 TESTO E SOLUZIONE Esrcizio In rifrimnto allo schma a blocchi in figura. s3 r y 2 s2 s y K Domanda.. Dtrminar una ralizzazion in quazioni
Il ruolo delle aspettative in economia
Capiolo XV. Il ruolo dll aspaiv in conomia . Tassi di inrss nominali rali Il asso di inrss in rmini di mona è chiamao asso di inrss nominal. Il asso di inrss sprsso in rmini di bni è chiamao asso di inrss
Analisi dei Sistemi. Soluzione del compito del 26 Giugno ÿ(t) + (t 2 1)y(t) = 6u(t T ). 2 x1 (t) 0 1
Analisi di Sistmi Soluzion dl compito dl 26 Giugno 23 Esrcizio. Pr i du sistmi dscritti dai modlli sgunti, individuar l proprità strutturali ch li carattrizzano: linar o non linar, stazionario o tmpovariant,
Massa M. dt Il modello dinamico del sistema nel dominio del tempo continuo è espresso dal secondo principio della dinamica: j.
EEI E: AA E ZATE VI Un carrllo di massa è riidamn collao ad uno smorzaor iscoso, ralizzao rami un pison c si muo un cildro connn dl liquido cararizzao dal coffic di iscosià, c produc l ffo di una forza
ESERCITAZIONE N 12 SIMULAZIONE DI UN SISTEMA DI ATTESA M/M/1
ESERCITAZIONE N 12 SIMULAZIONE DI UN SISTEMA DI ATTESA M/M/1 Toria dll cod La oria dll cod comprnd lo sudio mamaico dll cod o sismi d'asa. La formazion dll lin di asa è un fnomno comun ch si vrifica ogni
Blanchard, Macroeconomia, Il Mulino 2009 Capitolo VIII. Il tasso naturale di disoccupazione e la curva di Phillips. Capitolo VIII.
Capiolo VIII. Il asso naral di disoccpazion la crva di Phillips Capiolo VIII. Il asso naral di disoccpazion la crva di Phillips Capiolo VIII. Il asso naral di disoccpazion la crva di Phillips 1. Inflazion,
Corso di Macroeconomia
Corso di Macroconomia LE ASPETTATIVE: NOZIONI DI BASE. Tassi di inrss nominali rali Il asso di inrss in rmini di mona è chiamao asso di inrss nominal. Il asso di inrss sprsso in rmini di bni è chiamao
Modello di Einstein. Stato eccitato. Stato fondamentale
Modllo di Einsin Il modllo di Einsin dscriv in manira fnomnoloica d a livllo microscopico i procssi di l inrazion ra la r..m. maria ch porano ai fnomni di assorbimno d mission radiaiva. Il sisma modllo
Università Carlo Cattaneo Ingegneria gestionale Analisi matematica a.a. 2017/2018 FUNZIONI INTEGRALI
Univrsià Carlo Caano Inggnria gsional Analisi mamaica aa 7/8 FUNZIONI INTEGRALI ESERCIZI CON SOLUZIONE 6 ) Daa la funzion F d a) calcolar F, F ', '' F ; b) scrivr l quazion dlla ra angn nl puno ; c) scrivr
Lemma 2. Se U V é un sottospazio vettoriale di V allora 0 U.
APPUNTI d ESERCIZI PER CASA di GEOMETRIA pr il Corso di Laura in Chimica, Facoltà di Scinz MM.FF.NN., UNICAL (Dott.ssa Galati C.) Rnd, 3 April 2 Sottospazi di uno spazio vttorial, sistmi di gnratori, basi
Aspettative. In questa lezione: Discutiamo di previsioni sulle variabili future, e di aspettative. Definiamo tassi di interesse nominale e reale.
Aspaiv In qusa lzion: Discuiamo di prvisioni sull variabili fuur, di aspaiv. Dfiniamo assi di inrss nominal ral. Ridfiniamo lo schma IS-LM con inflazion. 198 Imporanza dll Aspaiv L dcisioni rlaiv a consumo
Appunti di Statistica
Appunti di Statistica Appunti dall lzioni Nicola Vanllo 27 dicmbr 2018 2 Capitolo 1 Variabili Alatori Discrt 1.1 Variabil alatoria di Brnoulli Una variabil alatoria di Brnoulli, può assumr du valori, dnominati
SVOLGIMENTO. 2 λ = b S
RELAZIONE Dimnsionar sol d anima dl longhron d il rivsimno dl bordo di aacco, in una szion disan 4 m dalla mzzria, pr un ala monolonghron di un vlivolo avn l sguni cararisich: - pso oal W 4700 N - suprfici
Laurea triennale in BIOLOGIA A. A
Laura rinnal in BIOLOGIA A. A. 3-4 4 CHIMICA Vn 8 novmbr 3 Lzioni di Chimica Fisica Cinica chimica: razioni paralll razioni conscuiv Effo dlla mpraura sulla cosan di vlocià Prof. Anonio Toffoli Chimica
[ ] [ ] [ ] [ ] lim. x 1 3 R. lim. lim. lim. lim. lim. lim 5 R. lim. Calcola i seguenti limiti risolvendo le eventuali forme di indeterminazione
![[ ] [ ] [ ] [ ] lim. x 1 3 R. lim. lim. lim. lim. lim. lim 5 R. lim. Calcola i seguenti limiti risolvendo le eventuali forme di indeterminazione](/thumbs/92/110333272.jpg "[ ] [ ] [ ] [ ] lim. x 1 3 R. lim. lim. lim. lim. lim. lim 5 R. lim. Calcola i seguenti limiti risolvendo le eventuali forme di indeterminazione")
Educnica.i Calcolo di ii Calcola i sguni ii risolvndo l vnuali form di indrminazion Esrcizio no. Esrcizio no. Soluzion a pag.8 Soluzion a pag.8 [ ] Esrcizio no. Esrcizio no. Esrcizio no. lg Esrcizio no.6
Esercizi per il corso Matematica clea
Esrcizi pr il corso Mamaica cla Danil Rilli anno accadmico 8/9 Lzion : Ingrali Esrcizi svoli. Provar, usando il cambio di variabil ch:. Dimosrar ch. Ingrando pr pari dimosrar ch + = + = 6 sin(π) = π Svolgimno.
Oscillazioni e onde. Oscillatore armonico. x( t) e sostituendo nell equazione originale si ha. dx dt. x cos infatti. Periodo del moto armonico T
No il k:\scuola\corsi\corso isica\ond\oscillaori aronico sorzao orzaodoc Crao il 5// 87 Dinsion il: 86 b ndra Zucchini Elaborao il 5// all or 885, salao il 5// 87 sapao il 5// 88 Wb: hp://digilandrioli/prozucchini
Innanzitutto, dalla descrizione data nel testo dell esercizio possiamo scrivere:
Corso di conomia Poliica II (HZ) /0/202 Soluzion srcizio Innanziuo, dalla dscrizion daa nl so dll srcizio possiamo scrivr: i * 0,06, 5. a) Sappiamo ch il asso di apprzzamno/dprzzamno dlla mona nazional
TEORIA DEI SISTEMI ANALISI MODALE
TEORIA DEI SISTEMI Laurea Specialistica in Ingegneria Meccatronica Laurea Specialistica in Ingegneria Gestionale Indirizzo Gestione Industriale TEORIA DEI SISTEMI ANALISI MODALE Ing. Cristian Secchi Tel.
Sistemi lineari a tempo continuo. Un sistema lineare analogico, in generale tempo variante, caratterizzato da una risposta
Capiolo V SISTEMI LIERI CO IGRESSI LETORI Sisi linari a po coninuo V. - Cararizzazion nl doinio dl po. Un sisa linar analogico, in gnral po arian, cararizzao da una risposa ipulsia daa da h (, ) rasfora
Lezione 3. Movimento ed Equilibrio. F. Previdi - Fondamenti di Automatica - Lez. 3 1
Lio 3. Movimo d Eqilibrio F. Prvidi - Fodami di Aomaica - L. 3 Schma dlla lio. Movimo dllo sao dll scia (gral). (Movimo di) Eqilibrio (gral) 3. Sismi LTI 4. Eqilibrio di sismi LTI 5. Movimo di sismi LTI
SISTEMI A TEMPO DISCRETO. x t + = f x( t ),u( t ) = Ax( t ) + Bu( t ), x( t ) = x R y(t) = η x(t),u(t) = Cx(t) + Du(t)
Assumiamo la variabile emporale discrea; sia f lineare. Si consideri la seguene rappresenazione implicia: 1 x f x,u Ax Bu, x x R y η x,u Cx Du n 1 1 Rappresenazioni equivaleni Si consideri la rasformazione:
Esercizi sullo studio di funzione
Esrcizi sullo studio di funzion Prima part Pr potr dscrivr una curva, data la sua quazion cartsiana splicita f () occorr procdr scondo l ordin sgunt: 1) Dtrminar l insim di sistnza dlla f () ) Dtrminar
Modelli e Metodi Matematici della Fisica. Scritto 1/A
Modlli Mtodi Matmatici dlla Fisica. Scritto 1/A Csi/Prsilla A.A. 007 08 Nom Cognom Il voto dllo scritto sostituisc gli sonri 1 problma voto 1 4 5 6 7 total voto in trntsimi Rgolamnto: 1) Tutti gli srcizi,
Phillips (1958): Correlazione negativa stabile tra variazione percentuale dei salari monetari e il tasso di disoccupazione (Dati UK, )
INFLAZIONE E DISOCCUAZIONE: INTRODUZIONE hillips (958): Corrlazion ngaiva sabil ra variazion prcnal di salari monari il asso di disoccpazion (Dai UK, 86-957) Samlson Solow (960): confrmano il rislao di
Nota Come sinonimo di funzione lineare spesso si usano i termini operatore lineare o applicazione lineare o trasformazione lineare
Funioni Linari tra Spai Vttoriali D. Siano V V du spai vttoriali sia : V V. è dtta FUNZIONE LINEARE s: v, v V, k R si ha : v v v additività v kv k omognità v Oppur con l unica proprità: v v v v Nota Com
METODO DI NEWTON Esempio di non convergenza
METODO DI NEWTON S F(x) è C 2 si sa ch (x R k ) F(x+h) = F(x) + F(x) t h + 1/2 h t H(x)h +o( h 3 ) d una stima possibil dl punto di minimo è data da x# = x - H(x) -1 F(x) dov H(x) è la matric hssiana in
TEORIA DEI SISTEMI ANALISI DEI SISTEMI LTI
TEORIA DEI SISTEMI Laurea Specialistica in Ingegneria Meccatronica Laurea Specialistica in Ingegneria Gestionale Indirizzo Gestione Industriale TEORIA DEI SISTEMI ANALISI DEI SISTEMI LTI Ing. Cristian
Istogrammi ad intervalli
Istogrammi ad intrvalli Abbiamo visto com costruir un istogramma pr rapprsntar un insim di misur dlla stssa granda isica. S la snsibilità dllo strumnto di misura è alta, è probabil ch tra gli N valori
LABORATORIO DI FISICA INGEGNERIA "La Sapienza"
ABOATOO D FSA NGEGNEA "a Sapinza" Prof. A. Sciubba APPOSSMAZONE NEAE o sudio di un qualsiasi sisma fisico richid una prima fas di modllizzazion nlla qual si crca di schmaizzar il fnomno in sudio in rmini
Chimica Fisica Industriale Modulo A
Chimica Fisica Indusrial Modulo Prof. Savrio Sani Diparimno di Scinz Chimich Via Marzolo Padova 49 8759 savrio.sani@unipd.i Ricvimno: ui i giorni pr appunamno Savrio Sani -Scinz Chimich - Principi di Cinica
Numeri complessi - svolgimento degli esercizi
Numri complssi - svolgimnto dgli srcizi ) Qusto srcizio richid di calcolar la potnza n-sima (n 45) di un numro complsso. Scriviamo z nlla forma sponnzial z ρ iθ dov ) ( ) ρ ( + θ π 6 dato ch sin θ cos
[ ] ( ) ( ) ( e ) jωn. [ ] [ [ n. [ n] = T [ ] [ ] [ ] [ ]
![[ ] ( ) ( ) ( e ) jωn. [ ] [ [ n. [ n] = T [ ] [ ] [ ] [ ]](/thumbs/70/62246785.jpg "[ ] ( ) ( ) ( e ) jωn. [ ] [ [ n. [ n] = T [ ] [ ] [ ] [ ]")
Sistmi Linari Tmpo Invarianti (LTI) a Tmpo Discrto Dfiniamo il sistma tramit una trasformaion T []. La proprità di linarità implica ch [ α 1x1[ n] + α2x2[ n ] α1t x1[ n] + α2t x La proprità di tmpo invariana
Diagonalizzazione delle forme quadratiche
Diagonaliaion dll form uadraich Illusrrmo ora du modi pr diagonaliar una forma uadraica (o uivalnmn una forma bilinar Modo dl complamno dl uadrao Quso modo consis in una succssion di passaggi algbrici
Progetto di cinghie trapezoidali
Progo i cinghi rapzoiali L cinghi rapzoiali sono uilizza rqunmn pr la rasmission i ponza Vanaggi Basso coso Smplicià i insallazion Capacià i assorbir vibrazioni orsionali picchi i coppia Svanaggi Mancanza
0.1. CIRCONFERENZA 1. La 0.1.1, espressa mediante la formula per la distanza tra due punti, diviene:
0.1. CIRCONFERENZA 1 0.1 Circonfrnza Considriamo una circonfrnza di cntro P 0 (x 0, y 0 ) raggio r, cioè il luogo di punti dl piano P (x, y) pr i quali si vrifica la rlazion: 0.1.1. P 0 P = r. La 0.1.1,
Equazioni differenziali ordinarie
4/11/015 Equazioni diffrnziali ordinari Equazioni diffrnziali ordinari Equazioni diffrnziali dl 1 ordin a variabili sparabili, Equazioni diffrnziali linari dl 1 ordin Equazioni diffrnziali dl 1 ordin non
Capitolo 8. La curva di Phillips, il tasso naturale di disoccupazione e l inflazione
Capiolo 8. La curva di Phillips, il asso naural di disoccupazion l inflazion 1. Inflazion, inflazion asa disoccupazion Inflazion disoccupazion ngli Sai Unii, 1900-1960. = (1931 1939) Duran il priodo 1900-1960,
Macroeconomia. Laura Vici. laura.vici@unibo.it. www.lauravici.com/macroeconomia LEZIONE 22. Rimini, 19 novembre 2014
Macroconomia Laura Vici laura.vici@unibo.i www.lauravici.com/macroconomia LEZIONE 22 Rimini, 19 novmbr 2014 Macroconomia 362 I mrcai finanziari in conomia apra Dao ch l acquiso o la vndia di aivià finanziari
La valutazione finanziaria
STUDIO BERETTA DOTTTARELLI TTARELLI DOTTORI COMMERCIALISTI ASSOCIATI Srgio Bra La valuazion finanziaria Prmssa Il valor dl capial conomico vin simao considrando i flussi di cassa prodoi in fuuro dall imprsa
Esercizio 1 Approssimare il seguente integrale con la formula di Gauss a tre nodi (n=2)
Esrcizi su intgrazion numrica sistmi linari Approssimar il sgunt intgral con la formula di Gauss a tr nodi (n) x cos xdx Si considri il sistma Applicando il mtodo di Eulro implicito con h π /( ω), quanto
EQUAZIONI DIFFERENZIALI. Saper integrare equazioni differenziali del primo ordine lineari e a variabili separabili.
EQUAZIONI DIFFERENZIALI OBIETTIVI MINIMI Sapr riconoscr classificar l quazioni diffrnziali. Sapr intgrar quazioni diffrnziali dl primo ordin linari a variabili sparabili. Sapr intgrar quazioni diffrnziali
Funzioni lineari e affini. Funzioni lineari e affini /2
Funzioni linari aini In du variabili l unzioni linari sono dl tipo a b l unzioni aini sono dl tipo a b c Il graico di una unzion linar è un piano passant pr l origin il graico di una unzion ain è un piano.
PROPORZIONI. Cosa possiamo dire di esse? Che la superficie della figura A sta alla superficie della figura B come 4 sta a 6.
Corso di laura: BIOLOGIA Tutor: Floris Marta PRECORSI DI MATEMATICA PROPORZIONI Ossrvar l sgunti figur: Cosa possiamo dir di ss? Ch la suprfici dlla figura A sta alla suprfici dlla figura B com sta a 6.
Nozioni di base sulle coniche (ellisse (x^2/a^2)+(y^2/b^2)=1, iperbole(x^2/a^2)-(y^2/b^2)=1, parabola e circonferenza):
Nozioni di bas sull conich (lliss (x^2/a^2)+(y^2/b^2)=1, iprbol(x^2/a^2)-(y^2/b^2)=1, parabola circonfrnza): Dlta =0, significa un solo punto di intrszion tra fascio di rtt conica Dlta >=0, significa 2
Introduzione alla Trasformata di Fourier
Corso di Laura Magisral in Chimica A.A. 3-4 Sproscopi Magnich Inroduzion alla Trasformaa di Fourir La Trasformaa di Fourir è usaa in moli divrsi campi: dalla analisi di sgnali lrici, alla analisi dll immagini
Correnti di linea e tensioni concatenate
Sismi Trifas Sismi rifas l rasporo la disribuzion di nrgia lrica avvngono in prvalnza pr mzzo di lin rifas Un sisma rifas è alimnao mdian gnraori a r rminali rapprsnabili mdian rn di gnraori sinusoidali
Lezione 21 (BAG cap. 19) Regimi di cambio. Corso di Macroeconomia Prof. Guido Ascari, Università di Pavia
Lzion 21 (BAG cap. 19) Rgimi di cambio Corso di Macroconomia Prof. Guido Ascari, Univrsià di Pavia Il capiolo si occupa Aggiusamno nl mdio priodo d ffi di una svaluazion Crisi dl asso di cambio Tasso di
Formule generali di carica e scarica dei condensatori in un circuito RC
Formul gnrali di aria saria di ondnsaori in un iruio A ura di ugnio Amirano onnuo dll ariolo:. Inroduzion........ 2 2. aria saria di un ondnsaor..... 2 3. Formula gnral pr nsioni fiss..... 4 4. Formula
Soluzione degli esercizi del Capitolo 3
Soluzione degli esercizi del Capiolo Soluzione dell Esercizio. Ricordando dal Paragrafo A.6 dell Appendice A che è facile oenere ẋ () d d ( (e A e A x + Ae (e A A x + ( A e A( ) x + Ax () + Bu () d ( e
Esercizio 3. Determinare la dimensione, la codimensione, una base, equazioni cartesiane, equazioni parametriche ed un complemento per U R 3, dove
Sapinza Univrsità di Roma Corso di laura in Inggnria Enrgtica Gomtria - A.A. 2015-2016 Foglio n.10 Somma intrszion di sottospazi vttoriali prof. Cigliola Esrcizio 1. Sono dati i vttori v 1 = ( 1, 0, 0),
Figura 1. supporre inoltre che il disco sia soggetto ad una coppia frenante di tipo viscoso Γ
DIMOSTRAZIONE DEL PERCHÉ AD UN UOVO CRUDO APPOGGIATO SU UN TAVOLO NON SI RIESCE AD IMPRIMERE UNA RAPIDA ROTA- ZIONE ASSIALE (COSA INVECE POSSIBILE PER UN UOVO SODO). Com è noo, s a un uovo soo appoggiao
Induzione magnetica. Capitolo. 1. Autoinduzione
Capiolo nduzion magnica B. Auoinduzion La forza lromoric indoa rapprsna il lavoro pr unià di carica svolo dall forz ch gnrano la corrn indoa. Essa è lgaa alla variazion dl flusso magnico F concanao al
I criteri di resistenza (o teorie della rottura) definiscono un legame tra lo stato tensionale e la sua pericolosità.
6-0 6- I critri di rsistnza (o tori dlla rottura) dfiniscono un lgam tra lo stato tnsional la sua pricolosità. Ogni stato tnsional può ssr rapprsntato da una funzion scalar dll tnsioni principali ch può
Criteri basati sullo stato di deformazione!massima deformazione normale (Poncelet-de St. Venant-Grashof)
Critri dirttamnt basati sullo stato di tnsion!massima tnsion normal (Ranin-Lamé-Navir)!Massima tnsion tangnzial (Trsca-Gust)!Curva dlla rsistnza intrinsca (Coulomb-Mohr)!Massima tnsion tangnzial ottadral
Fondamenti di Automatica Test di autovalutazione. può anche essere rappresentato come
Fondameni di Auomaica Tes di auovaluazione PARTE A A. Il numero complesso [a] 2 j2 3 [b] 2 3 j2 [c] 8 3 j [d] 2 + j2 3 /6 4e jπ può anche essere rappresenao come A2. L argomeno, espresso in radiani, del
Esercizi sullo studio di funzione
Esrcizi sullo studio di funzion Trza part Com visto nll parti prcdnti pr potr dscrivr una curva data la sua quazion cartsiana splicita f () occorr procdr scondo l ordin sgunt: ) Dtrminar l insim di sistnza
CONTROLLO DI SISTEMI ROBOTICI ANALISI MODALE
CONTROLLO DI SISTEMI ROBOTICI Laurea Specialistica in Ingegneria Meccatronica CONTROLLO DI SISTEMI ROBOTICI ANALISI MODALE Ing. Cristian Secchi Tel. 0522 522235 e-mail: secchi.cristian@unimore.it http://www.dismi.unimo.it/members/csecchi
ANALISI MATEMATICA II Sapienza Università di Roma - Laurea in Ingegneria Informatica Esame del 15 settembre Soluzioni compito 1
ANALISI MATEMATICA II Sapinza Univrsità di Roma - Laura in Inggnria Informatica Esam dl 15 sttmbr 016 - Soluzioni compito 1 E 1 Calcolar il sgunt intgral di funzion di variabil ral con i mtodi dlla variabil
Modello AD-AS. Mercato del lavoro. Mercato dei beni. Mercati finanziari
Modllo AD-AS Mrcao dl lavoro Equilibrio di mdio priodo su Mrcao di bni Mrcai finanziari.b. A un dao asso di disoccupazion corrispond un dao livllo dlla produzion (assumndo funzion di produzion =): U u
E stato dimostrato sperimentalmente che la rapidità con cui una famiglia di nuclei radioattivi decade dipende da una legge di natura statistica.
5. La lgg dl dcadino radioaivo Il nuro di nucli naurali arificiali oggi conosciui sono circa 700 di cui solo circa 70 sono qulli sabili. I nucli insabili ndono a rasforarsi sponanan in alr spci nuclari
Forma canonica di Jordan
Capitolo INTRODUZIONE Forma canonica di Jordan Siano λ i, per i =,, h, gli autovalori distinti della matrice A e siano r i i corrispondenti gradi di molteplicità all interno del polinomio caratteristico:
Applicazioni dell integrazione matematica
Applicazioni dll intgrazion matmatica calcolo dlla biodisponibilità di un farmaco Prof. Carlo Albrini Indic Indic 1 Elnco dll figur 1 1 Prliminari 1 Intrprtazion matmatica dl problma 3 Elnco dll figur
FUNZIONI. Dominio: il dominio di una funzione è l insieme delle x in cui una funzione è definita.
FUNZIONI Dominio: il dominio di una funzion è l insim dll in cui una funzion è dfinita. Funzioni Fratt: una funzion si dic fratta quando compar la al dnominator Pr calcolar il dominio di una funzion fratta
Fondamenti di Automatica Test di autovalutazione n.1 (test di ingresso) può anche essere rappresentato come
Fondameni di Auomaica Tes di auovaluazione n. (es di ingresso). Il numero complesso [a] 2 j2 3 [b] 2 3 j2 [c] 8 3 j [d] 2 + j2 3 /6 4e jπ può anche essere rappresenao come 2. L argomeno, espresso in radiani,
CONTROLLO DI SISTEMI ROBOTICI Laurea Specialistica in Ingegneria Meccatronica
CONTROLLO DI SISTEMI ROBOTICI Laurea Specialistica in Ingegneria Meccatronica CONTROLLO DI SISTEMI ROBOTICI ANALISI DEI SISTEMI LTI Ing. Tel. 0522 522235 e-mail: secchi.cristian@unimore.it http://www.dismi.unimo.it/members/csecchi
Risoluzione dei problemi
Risoluzion di problmi a) f rapprsnta un fascio di funzioni omografich, al variar dl paramtro a in R, s si vrifica la condizion: a$ (- a) +! 0 " a!! S a!! il grafico rapprsnta iprboli quilatr di asintoti
INDICE 1. 1 Triangolazione di matrici Teorema di Cayley-Hamilton Matrici nilpotenti Forma canonica delle matrici 3 3.
INDICE Torma di Cayly-Hamilton, forma canonica triangolazioni. Vrsion dl Maggio Argomnti sclti sulla triangolazion di matrici, il torma di Cayly-Hamilton sulla forma canonica dll matrici 3 3 pr i corsi
I APPELLO (& II ESONERO) DI SEGNALI E SISTEMI 05 giugno 2017
I PPELLO (& II ESONERO) DI SEGNLI E SISTEMI 05 giugno 017 Esrcizio 1. [+ punti] SOLO PER CHI SOSTIENE L PROV COMPLET Si considri il modllo ingrsso/uscita LTI causal dscritto dalla sgunt quazion diffrnzial:
SOLUZIONE PROBLEMA 1 SOLUZIONE PROBLEMA 1 1
SOLUZIONE PROBLEMA 1 1 SOLUZIONE PROBLEMA 1 1. Studiamo la funzion q ( = at, ssndo a b costanti rali con a >. Il dominio dlla funzion è tutto R la funzion è ovunqu continua. Il grafico dlla funzion non
= l. x 0. In realtà può aversi una casistica più amplia potendo sia x che f ( x) tendere ad un elemento dell insieme
LIMITI DI FUNZINI. CNCETT DI LIMITE Esula dallo scopo di qusto libro la trattazion dlla toria sui iti. Tuttavia, pnsando di far cosa gradita allo studnt, ch dv possdr qusta nozion com background, ritniamo
RUMORE TERMICO - SOLUZIONI
UMOE EMICO - SOLUZIONI Nl circuio in i. è una rsisnza rumorosa alla mpraura assolua L è un induanza. Si uol drminar il alor quadraico mdio dlla corrn i ch scorr all inrno dll induor. Da un puno di isa
Esercitazione 2. Francesca Apollonio Dipartimento Ingegneria Elettronica
srcitaion Francsca pollonio Dipartimnto Inggnria lttronica -mail: () t cos( ω t ϕ) ampia pulsaion Vttori complssi Data una granda scalar (t) variabil cosinusoidalmnt nl tmpo fas i può sprimr (t) com sgu:
Distribuzione gaussiana
Appunti di Misur Elttric Distribuion gaussiana Funion dnsità di probabilità di Gauss... Calcolo dlla distribuion cumulativa pr una variabil di Gauss... Funion dnsità di probabilità congiunta...6 Funion
Analisi Matematica I Soluzioni tutorato 8
Corso di laura in Fisica - Anno Accadmico 7/8 Analisi Matmatica I Soluzioni tutorato 8 A cura di David Macra Esrcizio (i) abbiamo ch R( i) I( i), quindi inoltr,dividndo pr il modulo i (R( i)) + (I( i))
I sensori di spostamento
I snsori di sposamno Mol grandzz (prssion, mpraura, forza, acclrazion, c.) vngono rasforma in uno sposamno, prima di ssr convri in un sgnal lrico. 1 I ponziomri i p p i o i p I ponziomri sono snsori di
P.M. Azzoni, Strumenti e misure per l ingegneria meccanica - copyright 2006, Hoepli, Milano.
Capiolo 4 No sull amplificaor oprazional 7 4. NOTE ULL AMPLIFICATORE OPERAZIONALE 4. LIMITI FIICI DELL AMPLIFICATORE OPERAZIONALE Il comporamno dll amplificaor a circuio chiuso, dscrio ni capioli prcdni,
I criteri di resistenza (o teorie della rottura) definiscono un legame tra lo stato tensionale e la sua pericolosità.
6-0 6- I critri di rsistnza (o tori dlla rottura) dfiniscono un lgam tra lo stato tnsional la sua pricolosità. Ogni stato tnsional può ssr rapprsntato da una funzion scalar dll tnsioni principali ch può
x 1 = t + 2s x 2 = s x 4 = 0
Sapinza Univrsità di Roma Corso di laura in Inggnria Enrgtica Gomtria - A.A. 2015-2016 prof. Cigliola Foglio n.10 Somma intrszion di sottospazi vttoriali Esrcizio 1. Sono dati i vttori v 1 = ( 1, 0, 0),
PROPORZIONI. Cosa possiamo dire di esse? Che la superficie della figura A sta alla superficie della figura B come 4 sta a 6.
Corso di laura: BIOLOGIA Tutor: Floris Marta PRECORSI DI MATEMATICA PROPORZIONI Ossrvar l sgunti figur: Cosa possiamo dir di ss? Ch la suprfici dlla figura A sta alla suprfici dlla figura B com sta a 6.
Sollecitazioni semplici La torsione
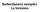Sollciazioni smlici La orsion Considrazioni inroduiv Un lmno sruural è soggo a sollciazion di orsion quando su di sso agiscono du momni uguali d oosi giacni su un iano rndicolar al suo ass longiudinal