Capitolo VI. I regimi sinusoidali
|
|
|
- Tito Landi
- 5 anni fa
- Visualizzazioni
Transcript
1 Capitolo VI I regimi sinusoidali Siamo dunque alla ricerca di una tecnica che ci consenta di semplificar e le operazioni sulle grandezze sinusoidali. Osser viamo che nelle equazioni relative alla LKC ed alla LKT intervengono essenzialmente le seguenti operazioni: a) moltiplicazione per una costante, come nella caratteristica di un resistore. b) somma, come nella somma dei vari termini in una equazione. c) derivata, come nelle caratteristiche di induttori e condensatori. Immaginiamo ora di trovare un insieme di grandezze, che chiamer emo insieme delle "A" - mentre chiameremo "a" l'insieme delle funzioni sinusoidali di pulsazione - e supponiamo che esista una corrispondenza biu - nivoca che metta in relazione ogni elemento di a con uno di "A". Supponiamo anche che tale corrispondenza conservi le operazioni che abbiamo in precedenza elencato; con questa affermazione intendiamo che se il
2 160 Luciano De Menna Corso di Elettrotecnica risultato di una determinata operazione - per esempio la somma - fatta su elementi di "a" è un certo elemento c, cioè: a + b = c, e se il risultato della operazione corrispondente - simbolo - fatta sugli elementi corrispondenti di "A" è C : A B = C, allora risulta anche che C è l elemento associato a c nella cor rispondenza in esame. Dunque, se esiste un tale insieme "A" ed una tale applicazione, e se operare su "A" risulta più agevole che operare su "a", si potrà in ogni caso trasformare tutte le grandezze di "a" nelle corrispondenti di "A", operare su queste e, una volta ottenuto il risultato, ritornar e in "a" mediante l'applicazione inversa. Orbene, facciamo vedere che l insieme di tutte le funzioni complesse di variabile reale del tipo Ae j( t+ ) è un possibile candidato insieme "A". Infatti, dato che ogni elemento di "a" del tipo a(t) = A M sen ( t + ) dipende da tre parametri, e precisamente A M, ed, e che lo stesso accade per ogni elemento di "A" (perché A = Ae j( t+ ) ), è evidente che tra gli insiemi "a" e "A" descritti esiste una corrispondenza biunivoca se ad ogni valore A M facciamo corrispondere un opportuno valore A. Naturalmente la scelta più immediata sarebbe di porre A = A M. Per motivi che saranno chiari in seguito, si preferisce porre A = A M / 2, cioè pari al valore efficace della corrispondente grandezza sinusoidale invece che al suo valore massimo. Notiamo che, per la formula di Eulero, Ae j t + = A cos t+ + j A sen t+, si può affermare che l'applicazione introdotta fa corri-
3 Luciano De Menna Corso di Elettrotecnica 161 spondere ad ogni elemento di "A" un elemento di "a" che, a meno del fattore 2, coincide con il coefficiente della parte immaginaria di A. Che una tale applicazione conservi le operazioni che abbiamo elencato in precedenza, è cosa semplice da dimostrare. Per quanto riguarda la somma e la moltiplicazione per una costante, il fatto è di per sé evidente. Per quel che riguarda l'operazione di derivazione, notiamo che: d dt Aej t + = j Ae j t + = = j A cos t+ - A M sen t+. Anche in questo caso, quindi, il coefficiente della derivata è, sempre a meno del fattore 2, uguale alla derivata dell'elemento di partenza, a(t) = A M sen ( t + ). È facile verificare, invece, che l'operazione di prodotto, come è usualmente definita nei due insiemi in esame, non viene conservata dall'applicazione introdotta. Si ha infatti: Ae j t + Be j t + = AB e j 2 t + + = = AB cos 2 t j sen 2 t + +. Il coefficiente dell'immaginario dell'espressione trovata non coincide con il prodotto delle due funzioni sinusoidali cor rispondenti. In conclusione in regime sinusoidale si può così operare: in primo luogo si trasformano tutte le grandezze - tensioni e correnti che variano con legge sinusoidale - nelle corrispondenti funzioni complesse del tipo Ae j( t+ ) ; d'ora in poi useremo il termine fasori per tali grandezze e conserveremo il simbolo A per indicarle. Successivamente si scrivono le equazioni che rappresentano le condizioni imposte dalla LKC e dalla LKT, tenendo conto delle caratteristiche dei singoli bipoli -
4 162 Luciano De Menna Corso di Elettrotecnica espresse in termini di fasori - e ricordando che ogni operazione di derivazione equivale ad una moltiplicazione per j. Così facendo le equazioni differenziali si trasfor mano in equazioni algebriche ed è, dunque, semplice risolverle, ricavando i fasori rappresentativi delle grandezze incognite. A questo punto si può ritornare alle funzioni sinusoidali e determinare le grandezze incognite nel dominio del tempo. Proviamo ad applicare questo metodo al circuito RL serie già risolto in precedenza. L'equazione all'unica maglia presente si scrive E = RI + j L I, da cui si ricava immediatamente: I = E R + j L. (VI.2) Il modulo del numero complesso rappresentativo della corrente è, dunque, il rapporto tra i moduli I = E R 2 + L 2, e la sua fase è la differenza tra le fasi del numeratore e del denominatore: = arctg L R. (VI.1) Il che è in perfetto accordo, se si tiene conto della relazione tra valor massimo e valor efficace di una funzione sinusoidale, con i risultati già trovati. Come si vede, la tecnica che abbiamo costruito semplifica notevolmente tutte le operazioni. In pratica, per un circuito in regime sinusoidale, basterà scrivere direttamente le equazioni relative alla LKC ed alla LKT in termini di fasori, esprimendo anche le caratteristiche dei bipoli presenti nella rete come relazioni tra fasori. In particolare, per il resistore, v=ri si trasforma in:
5 Luciano De Menna Corso di Elettrotecnica 163 per l'induttore, v=ldi/dt si trasforma in: per il condensatore, i C dv/dt si trasforma in: Il rapporto tra i due fasori rappresentativi della tensione e della corrente prende il nome di impedenza e verrà indicato d'ora in poi con il simbolo Z : L'impedenza Z è dunque un numero complesso; la sua parte reale conserva il nome di resistenza, mentre il coefficiente della parte immaginaria è detto reattanza. Si noti che, coer entemente alle definizioni date, si può affermare che l'impedenza caratteristica di un induttore è pari a jx=j L e che la sua r eattanza è X= L, positiva per definizione. Un condensatore invece presenterà una impedenza -jx=-j/ C, ed una re a t t a n z a X=1/ C. Infine chiameremo ammettenza Y l'inverso di una impedenza. In questo caso: Anche l'ammettenza è dunque un numero complesso la cui parte reale è una conduttanza mentre il coefficiente dell'immaginario prende il nome di suscettanza. Come tutti i numeri complessi, anche l'impedenza e l'ammettenza possono essere rappresentate in forma polare, Si ha, quindi: Y = 1 R + j X = V = R I ; V = j L I ; I = j C V. Z = R + j X. R - j X. (VI.4) R 2 + X 2 R 2 + X 2 Z = Z e j ; Y = Y e - j, (VI.3)
6 164 Luciano De Menna Corso di Elettrotecnica La corrente i(t) è dunque sfasata di un angolo - rispetto alla tensione e(t), dove è l'angolo di fase dell'impedenza. Osserviamo che, nella equazione (VI.1), sia il fasore rappresentativo della tensione, a primo membro, che il fasore rappresentativo della corrente, presente a secondo membro, contengono come fattore il termine e j t ; tale fattore è dunque inessenziale e può essere eliminato. È evidente che ciò si verifica in ogni equazione scritta in termini fasoriali. In pratica questa scelta equivale a utilizzare, come grandezze simboliche rappresentative delle funzioni sinusoidali, numeri complessi del tipo Ee j e non funzioni complesse del tipo Ee j( t+ ). Il fattore e j t è comune a tutti i termini. Sarebbe giusto riservare simboli diversi per le grandezze Ee j( t+ ) ed Ee j, ma in pratica si è soliti utilizzare lo stesso simbolo per le due grandezze, dato che il contesto, in generale, chiarisce l'oggetto del discorso. Il senso di questa scelta sarà ancora più chiaro quando si i n t ro d u r rà una rappresentazione grafica dei fasori. Questa lunga introduzione al metodo simbolico può sembrare un po' eccessiva, data la semplicità dell'argomento. Essa ha un unico scopo: mettere bene in evidenza che l'insieme delle "a" e quello delle "A" sono due insiemi completamente distinti, ognuno dei quali può essere usato per rappresentare l'altro. Non è lecito però mescolare elementi dei due insiemi; non è lecito, per esempio, sommare una funzione sinusoidale a = a(t) ed un fasore rappresentativo A = A e j( t+ )! Esercizi I = Eej t + Z e j = E Z ej t + -. Per l'esercizio proposto precedentemente, le equazioni
7 Luciano De Menna Corso di Elettrotecnica 165 alle maglie forniscono: E = v L + v R ; v L = v c. Mentre l'equazione ad uno dei due nodi è: i = i c + i L. Con facili passaggi si ricava l'unica equazione: E RCL = d2 i L dt RC di L dt + i L CL. L'altro esercizio proposto richiede di calcolare le reattanze di alcuni bipoli assegnati. Notare il ruolo giocato dalla frequenza angolare: al suo aumentare la reattanza dell'induttore aumenta mentre quella del condensatore diminuisce in valore assoluto. Il circuito RLC con forzamento sinusoidale Proviamo ad applicare il metodo dei fasori per calcolare la soluzione di regime in un caso più complesso: il circuito RLC serie con forzamento costante. La soluzione dell'omogenea associata è già nota; limitiamoci quindi a calcolare la soluzione a regime con il metodo dei fasori. L'equazione alla maglia è: E = RI + j LI - j 1 C I. (VI.5) Si ricava immediatamente: I = E R + j L - j 1 C. (VI.6) Da cui: V c = - j 1 C I = - j 1 C E R + j L - j 1 C. (VI.7)
8 166 Luciano De Menna Corso di Elettrotecnica Ricordando che - j = e - j 2, la VI.7 può anche essere scritta: V c = 1 C dove è la fase iniziale del generatore di f.e.m. e, =arctg è l'angolo di sfasamento tra la tensione del generatore e la corrente: In conclusione abbiamo: E e j t R 2 + L - 1 C 2, (VI.8) L - 1 C R, (VI.9) i(t) = I M sen t+ - = 2Isen t+ -. (VI.10) v cp (t) = 2 V c sen t +. (VI.11) Dove V c = 1 C E R 2 + L C, (VI.12) e: = (VI.13) Aggiungendo questa soluzione di regime all'integrale generale della omogenea associata, si ottiene l'integrale generale della equazione completa. Anche in questo caso abbiamo i tre regimi caratteristici del circuito RLC, sopracritico, critico e subcritico: v c (t) = k 1 e 1t +k 2 e 2t + 2V c sen t +. (VI.14) v c (t) = k 1 e t +k 2 te t + 2V c sen t +. (VI.15)
9 Luciano De Menna Corso di Elettrotecnica 167 v c (t) = ke t sen t+ + 2V c sen t+. (VI.16) Nelle immagini a lato sono mostrati alcuni tipici andamenti. Naturalmente, per determinare la soluzione del particolare problema in esame, occorre imporre le condizioni iniziali e deter minare le costanti di integrazione. Per il caso subcritico, per esempio, con facili passaggi si ha: V 0 = ksen - 2 V c cos -, (VI.17) I 0C = k sen + k cos + 2 V c sen -. Dalle (VI.17) si ricavano i valori di k e. Si osservi ancora una volta che le condizioni iniziali vanno imposte all' integrale generale dell'equazione completa, e non a quello dell'omogenea associata, anche se, e questo può indurre in errore, le costanti da determinare sono tutte contenute in quest'ultimo. Le formulazioni (VI.14),(VI.15) e (VI.16) della soluzione sono tutte del tipo termine transitorio + termine di regime ; come abbiamo visto non è questo l'unico punto di vista dal quale guardare a tali espressioni. Infatti, dalla (VI.17) si vede che le costanti k e non dipendono soltanto dalle condizioni iniziali, ma anche dal forzamento e(t), attraverso ed E, che è contenuto in V c (vedi la VI.12). Si può quindi guardare alla soluzione (VI.16) immaginando di separare il termine che dipende esclusivamente dalle particolari condizioni iniziali da quello che dipende dal forzamento e che sarebbe nullo in sua assenza. Ma, a differenza del caso discusso nel capitolo V, questa volta una tale separazione non è immediata. Che essa sia sempre possibile, in condizioni di linearità, lo assicura, però, il principio di sovrapposizione degli ef fetti. Infatti, possiamo immagi-
10 168 Luciano De Menna Corso di Elettrotecnica nare che la dinamica del circuito sia in realtà determinata dalla sovrapposizione di due fenomeni: l'evoluzione libera del circuito, dovuta alle assegnate condizioni iniziali, e la dinamica con cui il forzamento, partendo da condizioni iniziali tutte nulle, porta il circuito al suo regime. I due diversi punti di vista sono graficamente mostrati nelle due ultime immagini a lato, per il caso in esame. L'evoluzione libera si sviluppa indipendentemente dal forzamento ed è destinata comunque ad estinguersi per la presenza di una causa dissipativa e di una energia disponibile limitata. Il generatore, invece, disponendo di energia illimitata, potrà imporre alla lunga il suo regime. Queste considerazioni portano, ancora una volta, alla conclusione che bisogna aspettarsi che, per particolari condizioni iniziali che assicurano la completa compatibilità tra regime voluto dal forzamento e "tendenza spontanea" del circuito, il fenomeno transitorio non abbia luogo ed il regime si stabilisca istantaneamente. Dalla VI.16 si vede che ciò effettivamente si verifica, nel nostro caso, per k=0. Perché ciò accada le condizioni iniziali debbono essere: V 0 = 2 V c cos -, I 0C = - 2 V c sen -. (VI.18) Si noti che la frequenza di oscillazione a regime è, naturalmente, quella imposta dal forzamento, diversa, in generale, da quella 0 = 1 LC alla quale il circuito è in grado di oscillare in evoluzione libera, in assenza di una causa dissipatrice (R=0). C'è da attendersi un comportamento singolare, e quindi interessante, quando tali frequenze coincidono!
11 Luciano De Menna Corso di Elettrotecnica 169 Esercizi Per il circuito mostrato, scrivere l'equazione risolvente in ter mini della incognita v c. È utile prendere dimestichezza con il passaggio dall'insieme delle grandezze sinusoidali a quello dei fasori, come è indicato negli esercizi proposti a lato.
12 170 Luciano De Menna Corso di Elettrotecnica Fasori e vettori rappresentativi Come abbiamo visto, in regime sinusoidale è possibile caratterizzare ogni bipolo attraverso la sua impedenza: un numero complesso con una parte reale, che continueremo a chiamare resistenza, ed una parte immaginaria il cui coefficiente prende il nome di reattanza. L'impedenza è il rapporto tra il fasore rappresentativo della tensione ai morsetti del bipolo e quello rappresentativo della corrente che lo attraversa. Se sul bipolo si è assunta una convenzione dell'utilizzatore, la resistenza è necessariamente positiva, almeno per i componenti fin qui introdotti. Analogamente è possibile caratterizzar e lo stesso bipolo attraverso la sua ammettenza: il rapporto tra fasore rappresentativo della corrente e fasore rappresentativo della tensione. La parte reale dell'ammettenza prende il nome di conduttanza e, con una convenzione dell'utilizzatore, è definita positiva; il coefficiente della parte immaginaria prende il nome di suscettanza e può essere positivo o negativo. Resistenze e reattanze si misurano in ohm, mentre conduttanze e suscettanze si misurano in siemens. Introduciamo una rappresentazione grafica dei fasori che ci sarà di grande utilità nel seguito. Consideriamo il piano complesso {Re ( A ), Im ( A )} e seguiamo in esso il punto rappresentativo della funzione Ae j t durante lo scorrere del tempo. All'istante 0 tale punto è sull'asse reale ad una distanza pari al modulo A del numero complesso. Negli istanti successivi il punto rappresentativo, essendo il modulo di A costante, si muove lungo una circonferenza di raggio pari ad A con una velocità angolare. Il fasore A può dunque essere rappresentato con un vettore rotante che ha un estremo nell'origine delle coordinate e l'altr o nel punto sulla circonferenza. Se rappresentia-
13 Luciano De Menna Corso di Elettrotecnica 171 mo tutte le grandezze sinusoidali del nostro circuito sullo stesso piano, essendo esse tutte caratterizzate dalla stessa frequenza, i vettori rappresentativi ruoteranno tutti con la stessa velocità angolare, e si conserveranno, quindi, tra loro gli stessi sfasamenti che si presentavano all'istante 0. Se siamo dunque interessati esclusivamente alle relazioni in modulo e fase tra i vari fasori basta prendere in considerazione il diagramma vettoriale rappresentativo all'istante 0, o ad un qualsiasi altro istante t. Tutte le operazioni necessarie nel campo complesso per la soluzione di una rete hanno le loro corrispondenti operazioni grafiche nel piano complesso; per esempio, è immediato rendersi conto che l'operazione di somma di due fasori corrisponde, nel diagramma vettoriale rappresentativo alla consueta somma di vettori (regola del parallelogramma). L'operazione di derivazione corrisponde a ruotare il vettore rappresentativo di /2 in verso antiorario (anticipo) oltre che a moltiplicare il suo modulo per. Si noti che mentre il fasore Ae j( t + ) corrisponde ad un vettore rotante con velocità angolare, il fasore Ae j corrisponde al vettore fermo alla sua posizione all'i - stante 0. In generale è consentito utilizzare lo stesso simbolo A per tutte queste grandezze, non potendo ciò generare alcuna confusione. Il diagramma vettoriale del circuito RLC serie è molto semplice da costruire. Si parte dall'assegnare il vettore rappresentativo della corrente I. La somma della caduta di tensione resistiva R I, in fase con la corrente, di quella induttiva j L I, sfasata di 90 in anticipo, e di quella capacitiva -1/j C I, sfasata di 90 in ritardo, fornisce il vettore rappresentativo della tensione E del generatore. È immediato, a questo punto, determinare graficamen-
14 172 Luciano De Menna Corso di Elettrotecnica te lo sfasamento fra tensione e corrente. Nel caso rappresentato nella prima immagine a lato si è supposto che il modulo della caduta induttiva sia magg i o re del modulo della caduta capacit iva. Naturalmente se accade l'inverso il diagramma prende la forma rappresentata nella successiva immagine. Nel primo caso la corrente è sfasata in ritardo rispetto alla tensione (carico prevalentemente induttivo, > 0); nel secondo caso, in anticipo (carico prevalentemente capacitivo, < 0). Osserviamo che nel caso particolare in cui L = 1/ C il diagramma vettoriale assume la caratteristica forma descritta nella prima immagine della pagina seguente. In pratica le cadute induttive e capacitive si compensano mutuamente con il risultato che al generatore il carico appare puramente resistivo; l'impedenza complessiva si riduce alla sola resistenza ed ha quindi solo parte
15 Luciano De Menna Corso di Elettrotecnica 173 reale. È questo il fenomeno della risonanza che esamineremo in dettaglio in uno dei prossimi paragrafi. Per ora limitiamoci a riepilogare il comportamento dei tr e bipoli introdotti in regime sinusoidale, induttore, c o n d e n s a t o re e re s i s t o re, mostrandone le re l a z i o n i caratteristiche nelle diverse formulazioni. Bipolo induttore: Bipolo condensatore: Bipolo resistore:
16 174 Luciano De Menna Corso di Elettrotecnica Insieme agli andamenti di tensione e corrente nei tre casi è stato riportato anche l'andamento del prodotto v(t)i(t). P er definizione tale prodotto rappre s e n t a, istante per istante, la potenza assorbita dal bipolo - convenzione dell'utilizzatore. Si noti che solo per il resistore tale potenza è sempre positiva; per l'induttore e per il condensatore, invece, la potenza è positiva in un semiperiodo - pari ad un quarto del periodo di tensione e corrente - e negativa nel successivo. Ma questo argomento merita una trattazione a parte. Potenza nei regimi sinusoidali Affrontiamo il problema dal punto di vista generale. La potenza istantanea assorbita da un qualsiasi bipolo sottoposto alla tensione v(t) e percorso dalla corrente i(t) è, per definizione, p(t) = v(t) i(t). Nel caso particolare di un regime sinusoidale si ha: p t = v t i t = 2 V sen t 2 I sen t - = (VI.19) = V I cos + sen 2 t - - 2, In altri termini, la potenza in regime sinusoidale è la somma di un termine costante, pari al prodotto del valore efficace della tensione per il valor e efficace della corrente per il coseno dell'angolo tra i due fasori, più un termine oscillante di frequenza 2. Dato che il termine oscillante ha valor medio nullo, il valore medio della potenza istantanea è pari al termine costante VIcos : P = 1 T 0 T v t i t dt = V I cos. (VI.20) Ciò giustifica anche la nostra scelta di utilizzare il valore efficace anziché il valore massimo quale modulo del
17 Luciano De Menna Corso di Elettrotecnica 175 fasore rappresentativo di tensioni e correnti. In particolare, con questa scelta, se si dà all'operatore prodotto scalare tra due vettori l'usuale significato di prodotto dei moduli dei vettori per il coseno dell'angolo che essi formano, si può affermare che in regime sinusoidale la potenza media è pari al prodotto scalare del vettore rappresentativo della tensione per quello rappresentativo della corrente: P = V I = V I cos. La potenza media viene anche detta potenza attiva. In effetti il valore della potenza media consente di calcolare agevolmente la quantità di energia, trasferita in un determinato intervallo di tempo t-t 0, come il pr odotto della potenza media per l'intervallo stesso (si presume, naturalmente che l'intervallo t-t 0 contenga molti periodi T). Ci aspettiamo dunque che per la potenza media valga, così come per l'energia, un teorema di conservazione: la potenza attiva fornita dai generatori deve essere eguale a quella utilizzata dagli utilizzatori. Proprietà delle reti in regime sinusoidale (VI.21) Come abbiamo visto, a condizione di trasformare tutte le grandezze sinusoidali nei corrispondenti fasori, si può operare in regime sinusoidale alla stessa maniera in cui si è operato in regime continuo. Ai concetti di resistenza e di conduttanza dei bipoli si sostituiscono quelli di impedenza ed ammettenza. Tali grandezze, a differenza delle precedenti, sono espresse da numeri complessi, e ciò naturalmente comporterà inizialmente qualche lieve complicazione. Per superarle basta ricordar e le principali operazioni sui numeri complessi, nella loro forma cartesiana:
18 176 Luciano De Menna Corso di Elettrotecnica a + jb + c + jd = a + c + j b + d, a + jb c + jd = ac - bd + j bc + ad, a + jb c + jd = a + jb c - jd c 2 + d 2 = ac + bd + j bc - ad c 2 + d 2 ; ed in quella polare: A e j = A B e j B ej -. Così, per esempio, serie e parallelo di due bipoli portano alle stesse formule utilizzate in continua. Serie: Parallelo: a + jb = A e j, con A = a 2 + b 2 e tg = b a, A e j B e j = A Be j +, Z = Z 1 + Z 2, Y = Y 1 Y 2 Y 1 + Y 2. Z = Z 1 Z 2 Z 1 + Z 2, Y = Y 1 + Y 2. In generale potremo affermar e che tutte le proprietà ed i teoremi sulle reti, dimostrati in regime continuo sulla base delle leggi di Kirchhoff, hanno un loro equivalente in regime sinusoidale in termini di fasori. Fanno eccezione i teoremi di non amplificazione; ripercorrendo i passi della dimostrazione a suo tempo sviluppata, non sarà difficile evidenziarne il motivo. Il teorema di Tellegen, merita una discussione più a p p rofondita. Naturalmente tale teorema è valido istante per istante: k v t i t = 0, (VI.22)
19 Luciano De Menna Corso di Elettrotecnica 177 in quanto le tensioni e le correnti ad ogni istante soddisfano le leggi di Kirchhoff. La (VI.22) è l'espressione di un teorema di conservazione delle potenze istantanee che avremmo potuto dedurre anche da semplici considerazioni sulla conservazione dell'energia. Ma dato che il sistema dei fasori rappresentativi delle tensioni sui lati e quello rappresentativo delle correnti nei rami soddisfano anche essi alle leggi di Kirchhoff, si può certamente affermare che anche la somma di tutti i pr odotti V I, estesa all'intera rete deve essere identicamente nulla. Con facili passaggi si può sviluppare il generico termine, ma il risultato non è particolarmente significativo. Più interessante è invece il caso in cui al posto dei fasori rappresentativi delle correnti si utilizzano i rispettivi coniugati. È evidente infatti che anche tali coniugati - in cui, si ricorderà, cambia solo il segno della parte immaginaria - debbono sottostare alla prima legge di Kirchhoff. Si avrà dunque: k V k I k = V k e j t+ k I k e -j t+ k- k =0.(VI.23) k Lo sviluppo del generico termine della sommatoria fornisce: V k I k = V k I k cos k + j sen k. (VI.24) Tale grandezza viene detta potenza complessa; la sua par te reale coincide con la potenza media o attiva. La (V.23) esprime un teorema di conservazione per le potenze complesse: in una rete in regime sinusoidale la somma delle potenze complesse fornite dai generatori deve essere uguale alla somma delle potenze complesse assorbite dagli utilizzatori. D'altra parte l'annullarsi di un numero complesso implica l'annullarsi della sua parte reale e di quella immaginaria. L'annullamento della somma delle parti reali delle potenze complesse
20 178 Luciano De Menna Corso di Elettrotecnica fornisce di nuovo il teorema di conservazione delle potenze attive che avevamo già dedotto in base a semplici considerazioni energetiche. L'annullamento della par te immaginaria, invece, introduce la conservazione di un'altra grandezza, rappresentata per ogni bipolo da VI sen. A tale grandezza, che ha evidentemente le dimensioni di una potenza, si dà il nome di potenza reattiva, e si usa per essa il simbolo Q. In un resistore, la potenza reattiva assorbita è evidentemente nulla, mentre diversa da zero è la potenza attiva che è pari a VI, dato che cos = 1. Per l'induttore ed il condensator e, invece, la potenza attiva assorbita è nulla, cos = 0, mentre la potenza reattiva è rispettivamente pari a VI ed a -VI. Una potenza reattiva non nulla in una rete è indubbiamente indice della presenza di energie immagazzinate associate al campo elettrico o al campo magnetico; per ogni induttore presente nella rete si avrà, infatti: Q L = VI = L I 2 = 1 2 L I M 2 = W BM. (VI.25) mentre per ogni condensatore: Q c = - VI = - C V 2 = = C V M 2 = - W EM. (VI.26) La potenza reattiva totale è dunque proporzionale, secondo il fattore, alla differenza tra i valori massimi dell'energia associata al campo magnetico e di quella associata al campo elettrico nella rete. Ma questa relazione non è particolarmente utile. Infine va ricor dato che al prodotto VI viene dato il nome di potenza apparente. Si noti che tra le tre potenze, attiva P a, reattiva Q ed apparente P, sussiste la relazione: P = P a 2 + Q 2. (VI.27)
21 Luciano De Menna Corso di Elettrotecnica 179 Tale relazione può utilmente essere rappresentata graficamente in un cosiddetto triangolo delle potenze. Il fatto che la potenza reattiva sia una grandezza che si conser va può essere di grande utilità nella risoluzione delle reti. Si consideri per esempio il caso di due carichi in parallelo di cui siano note le potenze attive e reattive assorbite da ognuno di essi; si può affermare che il complesso dei due carichi è equivalente ad un unico carico che assorbe una potenza attiva e reattiva che sono la somma algebrica (la potenza reattiva può essere negativa!) delle rispettive potenze dei singoli carichi. A riprova del fatto che questo non è un risultato banale, si osservi che la stessa affermazione non può essere fatta per le potenze apparenti, come è facile verificare con i semplici calcoli mostrati nella successiva immagine a lato. Esercizi Per il cir cuito proposto in precedenza l'equazione risolvente è: con: d 2 v c dt + 1 dv c 2 R e C dt + v c LC = 1 R 0 C de dt, R e = R R 0 R + R 0. Si noti che R e è il parallelo tra le due resistenze R ed R 0. Per la rete nella successiva immagine si calcolino le potenze attive, reattive ed apparenti assorbite dai singoli bipoli e quelle erogate dal generatore e si verifichino i teoremi di conservazione. Si risolva la rete mostrata nell'ultima immagine.
22 180 Luciano De Menna Corso di Elettrotecnica Il circuito risonante Abbiamo visto che in un circuito RLC serie, alimentato da un generatore di for za elettromotrice sinusoidale di frequenza angolare, si può verificare la condizione per cui la caduta capacitiva compensa perfettamente la caduta induttiva ed il circuito appare al generatore come puramente ohmico. Per assegnati valori di L e C, ciò accade per una frequenza del generatore pari ad 0, 0 = 1 LC, (VI.28) che è proprio la frequenza alla quale il cir cuito, in assenza di cause dissipative (R = 0), è in grado di oscillare liberamente. Siamo dunque nella già menzionata condizione di risonanza tra la fr equenza del forzamento e quella propria del sistema. Un circuito di tal genere è detto anche circuito risonante. Del tutto equivalente è il caso del circuito RLC parallelo, a volte detto anche antirisonante. In esso la corrente erogata dal generatore, che è somma delle tre correnti rispettivamente nell'induttore, nel resistore e nel condensatore, si riduce ad essere uguale alla sola corrente nel resistore perché le altre due si compensano perfettamente, essendo eguali ed opposte. Mentre nel circuito serie, in assenza della resistenza R, l'impedenza risultante è nulla, nel circuito parallelo, sempr e in assenza di resistenza (questa volta R = ), l'impedenza risultante è infinita. Si noti che nel circuito antirisonante senza perdite, cioè per R = 0, pur essendo la corrente totale fornita dal generatore identicamente nulla, non sono nulle le correnti nell'induttore e nel condensatore, che si calcolano agevolmente come rapporto tra tensione applicata e relativa impedenza. Per comprendere il fenomeno della risonanza bisogna
23 Luciano De Menna Corso di Elettrotecnica 181 tener presente che implicitamente si è assunto che la rete sia a regime; il che vuol dire che si suppone vi sia stato un transitorio - in tempi lontani di cui sembra non essere rimasto traccia - che ha portato all'attuale situazione di r egime. Durante il transitorio il generatore ha fornito al complesso dei due elementi con memoria presenti nella rete una cer ta quantità di energia; d'altra par te, dato che l'energia immagazzinata nel condensatore è proporzionale al quadrato della tensione su di esso e quella nell'induttore è proporzionale al quadrato della corrente che lo attraversa, è evidente che se tensione e corrente non sono in fase, ma in quadratura, come nel nostro caso, accadrà che quando l'energia associata al campo elettrico (condensatore) è massima, quella associata al campo magnetico (induttore) è nulla e viceversa. Se poi in particolare tali energie massime sono eguali, una volta raggiunto il regime si assisterà ad un periodico scambio di energia tra campo elettrico e campo magnetico che vede completamente estraneo il generatore; esso dovrà solo occuparsi di fornire la potenza dissipata nel resistore. Il fenomeno della risonanza, caratteristico di qualsiasi sistema che abbia la capacità di oscillare su frequenze proprie, è molto importante anche dal punto di vista applicativo, specialmente nel campo dei circ u i t i. Esaminiamolo dunque in maggior dettaglio. Supponiamo che, nel circuito risonante serie, il generator e di tensione sia a frequenza variabile; si possa cioè variare a piacimento tra 0 ed la frequenza della tensione che esso eroga. Riportiamo in un diagramma la cur va del modulo della corrente I in funzione della frequenza; evidentemente tale diagramma è anche il diagramma dell'inverso del modulo della impedenza. Per
24 182 Luciano De Menna Corso di Elettrotecnica = 0, I = 0 perché il condensatore a tale "frequenza" presenta una impedenza infinita; analogamente per che va all'infinito la corrente è nulla, questa volta per merito dell'induttore. Per = 0 il modulo della corrente ha un massimo pari ad E/R, così come mostrato nel diagramma a lato, dove è riportato l'andamento di I normalizzato al suo valore massimo E/R. Nello stesso diagramma è rappresentata la fase della impedenza al variare di. Come era prevedibile, per frequenze inferiori a quella di risonanza il circuito si comporta globalmente come un carico prevalentemente capacitivo: l'impedenza offerta dal condensatore prevale. Per frequenze invece superiori a quella di risonanza, il carico è prevalentemente induttivo. Alla frequenza di risonanza, come abbiamo visto, il carico si comporta come se fosse puramente resistivo. La curva di cui al diagramma precedente è, in effetti, la rappresentazione della funzione: f = R R 2 + L - 1. (VI.29) 2 C La curva che descrive la funzione f( ) prende il nome di curva di risonanza ed il parametro Q quello di fatto - re di qualità o di merito del circuito. All'aumentare del fattore di qualità del circuito, la curva di risonanza diventa sempre più ripida nell'intor- Con qualche semplice passaggio, avendo posto Q = 0L R = 1 0RC, (VI.30) si ottiene anche: f = 1. (VI.31) 1 + Q
25 Luciano De Menna Corso di Elettrotecnica 183 no della frequenza di risonanza 0. Le motivazioni di tale terminologia si compr endono facilmente se si considera la seguente situazione. Si immagini che la tensione del generatore non sia sinu - soidale ma semplicemente periodica. Come si è visto, una tale tensione può essere scomposta in una somma di infiniti termini sinusoidali di frequenza diversa (le armoniche della serie di Fourier). Vediamo il circuito come un doppio bipolo che abbia in ingresso il generatore a frequenza variabile e dal quale si prelevi in uscita la tensione sul resistore R. Evidentemente, per la sovrapponibilità degli effetti, anche la tensione in uscita può essere vista come somma delle risposte alle singole armoniche. D'altra parte ogni ar monica della tensione in ingr esso vede una diversa impedenza del circuito a causa della diversa frequenza. Se ne conclude che le ampiezze delle armoniche con frequenze vicine a quella di risonanza risulteranno amplificate rispetto alle altre. Per questo motivo si dice che il circuito si è comportato come un filtro, lasciando "passare" di preferenza un determinato intervallo di frequenze (banda), e attenuando le altre. Così, per esempio, se in ingresso abbiamo una onda quadra, il cui sviluppo in serie di Fourier abbiamo già visto, in uscita avremo un andamento temporale che sarà tanto più vicino ad una sinusoide quanto più alto è il fattore di qualità (curva di risonanza più ripida!). Se la fr equenza di risonanza del circuito è pari a quella della fondamentale armonica dell'onda quadra, in uscita si avrà una sinusoide a quella frequenza; essa sarà leggermente deformata per la presenza delle armoniche di ordine superiore che, seppur attenuate, sono sempre presenti. Ma se la frequenza di risonanza del circuito è uguale a quella della succesiva armonica (di frequenza tripla di quella fondamentale, nel nostro
26 184 Luciano De Menna Corso di Elettrotecnica caso) ecco che in uscita comparirà la terza armonica. Coerentemente con tutto ciò, se il circuito è sintonizza - to sulla seconda armonica - se cioè la sua frequenza di risonanza è pari al doppio di quella della fondamentale dell'ingresso - in uscita si avrà un segnale nullo. Lo sviluppo in serie di Fourier dell'onda quadra, infatti, non prevede armoniche pari! Le applicazioni che sfruttano il fenomeno della risonanza nelle reti elettriche sono numerosissime e tutte di importanza eccezionale; a titolo di puro esempio citiamo quello del circuito di sintonia di un apparecchio radiofonico o televisivo: quando ruotiamo la manopola della sintonia di un ricevitore possiamo immaginare di non fare altro che modificare la capacità di un circuito risonante, variando quindi la sua frequenza di risonanza, in modo tale da selezionare l'opportuna banda che desideriamo filtrare. È interessante notare che l'introduzione del concetto di potenza media ci consente di dare una interpretazione del fattore di qualità di un circuito risonante in termini di energie in gioco. Alla risonanza infatti l'energia totale immagazzinata nel condensatore e nell'induttore è pari a: W t = 1 2 Li2 t + Cv 2 t = 1 2 L I 2 M sen C V 2 M sen 2 t + t + = L I 2 M sen C I M 2 2 cos2 t = 1 0 C 2 L I 2 M sen L I 2 M cos 2 t = 1 2 L I 2 M. t + (VI.32) t + Essa è dunque costante ed uguale all'energia massima immagazzinata nell'induttore (o nel condensatore ). D'altra parte l'energia dissipata nel resistore in un
27 Luciano De Menna Corso di Elettrotecnica 185 periodo è pari a R I 2 T per cui si ha: Q = 0L R = 0LI 2 T RI 2 T = 2 LI2 RI 2 T. (VI.33) Se ne deduce dunque: energia immagazzinata Q = 2 energia dissipata in un periodo. (VI.34) Esercizi Le potenze richieste, nell'esercizio proposto in precedenza sono: P a = 5 W; Q c = 10 VAr; Q L = - 5 VAr. Per l'esercizio successivo ci limitiamo a mostrare alcuni passi della soluzione.
28 186 Luciano De Menna Corso di Elettrotecnica La stessa soluzione può anche essere ottenuta applicando la regola del partitore di cor rente. Ancora un esercizio sulla verifica della conservazione delle potenze nella prima immagine in colonna. Nei due esercizi successivi si chiede il calcolo delle impedenze equivalenti dei bipoli mostrati. Infine l'ultimo esercizio richiede la soluzione della rete con il metodo dei fasori.
29 Luciano De Menna Corso di Elettrotecnica 187 Gli n-poli e gli N-bipoli in regime sinusoidale La teoria degli n-poli e degli N-bipoli in regime sinusoidale si sviluppa in maniera del tutto analoga a quanto fatto per gli stessi dispositivi in corrente continua. Così avremo una matrice delle impedenze ed una matrice delle ammettenze del tutto analoghe a quelle delle resistenze e delle conduttanze introdotte per il regime continuo. Gli elementi delle matrici avranno definizioni analoghe a quelle già introdotte per i corrispondenti parametri in continua; l'unica differenza sarà nel fatto che si dovrà operare con fasori e numeri complessi piuttosto che con numeri reali. Le pr oprietà dei parametri Y o Z sono le stesse già dimostrate per i parametri G ed R, salvo quelle per la dimostrazione delle quali si è fatto uso del teorema di non amplificazione delle tensioni o delle correnti che, come abbiamo più volte rilevato, non sono validi se non in regime continuo. Per i doppi bipoli, in particolare, abbiamo le due rappresentazioni, della matrice delle impedenze, e delle ammettenze, V 1 = Z 11 I 1 + Z 12 I 2 V 2 = Z 21 I 1 + Z 22 I 2, (VI.35) I 1 = Y 11 V 1 + Y 12 V 2 I 2 = Y 21 V 1 + Y 22 V 2. (VI.36) Nei regimi dinamici ha senso introdurre un particolare doppio bipolo, che non ha il suo equivalente in c.c.: l'accoppiamento magnetico mutuo tra due circuiti. Vediamo di cosa si tratta. Abbiamo già visto che un induttore altro non è che un avvolgimento di un certo numero di spire su di un supporto che, in generale, ha anche il compito di amplifi-
30 188 Luciano De Menna Corso di Elettrotecnica care il fenomeno sul quale il sistema fonda le sue proprietà: il campo magnetico prodotto dalla corrente che circola nell'avvolgimento. I due estremi dell'avvolgimento costituiscono i morsetti del bipolo. Supponiamo che il campo magnetico prodotto dalla corrente in un avvolgimento si estenda anche in una regione di spazio in cui è presente un altro avvolgimento. Avremo, in tal caso, un sistema a quattro morsetti, e quindi un doppio bipolo. Sarebbe facile dimostrar e in base alle leggi fondamentali del campo elettromagnetico che le relazioni caratteristiche di un tale doppio bipolo sono, in condizioni abbastanza generali: v 1 = L di 1 1 dt + M di 2 12 dt v 2 = M 21 di 1 dt + L 2 di 2 dt, (VI.37) dove i coefficienti M 12 ed M 21 prendono il nome di coefficienti di mutua induzione, e, per contrasto, quelli L 1 ed L 2, rispettivamente, di coefficienti di auto induzione primaria e secondaria. A differenza dei coefficienti di autoinduzione, i coefficienti di mutua induzione possono essere sia negativi che positivi. Per una introduzione del doppio bipolo mutuo accoppiamento, che metta meglio in risalto il ruolo svolto dal campo magnetico, si consiglia di legger e l'appendice A4. Un sistema di questo genere si presenta dunque intrinsecamente come un doppio bipolo e sarà schematizzato con il simbolo di cui alle immagini a lato, dove i due puntini neri stanno ad indicare che, se si sceglie come verso positivo per le correnti quello entrante nel morsetto contrassegnato con il punto, e si adotta una convenzione dell'utilizzatore, allora il segno di M è quello
31 Luciano De Menna Corso di Elettrotecnica 189 fornito. La semplice applicazione del teorema di reciprocità induce a richiedere che: M 12 = M 21. Infatti M 21 di 1 /dt non è nient'altro che la tensione prodotta al secondario per la presenza della corrente i 1 al primario, e, viceversa, M 12 di 2 /dt la tensione prodotta al primario per la presenza della corrente i 2 al secondario. D'altra parte allo stesso risultato si giunge anche in base a considerazioni energetiche, che ci aiuteranno a fare ulteriori passi nella comprensione del comportamento di un tale doppio bipolo. Infatti la potenza istantanea assorbita (convenzioni dell'utilizzatore ad entrambe le porte) dal doppio bipolo è: p = v 1 i 1 + v 2 i 2 = L 1 i di 1 1 dt + M 12i di 2 1 dt + + M 21 i di 1 2 dt + L 2i di 2 2 dt Quindi l'energia assorbita dw in un intervallo infinitesimo di tempo dt è:. (VI.38) dw = p dt = 1 2 L 1di M 12 i 1 di M 21 i 2 di L 2di 2 2. (VI.39) D'altra parte la variazione infinitesima di energia deve essere un dif ferenziale esatto: solo in tal caso infatti la variazione finita di energia che si ottiene integrando quella infinitesima tra due "punti" (i 1 -,i 2 - ) ed (i 1 +,i 2 + ) del piano delle correnti [i 1,i 2 ], sarà indipendente dal "percorso", cioè dal modo in cui si è andati dalla condizione in cui le correnti erano (i 1 -,i 2 - ) a quella in cui esse erano (i 1 +,i 2 + ) - vedi l'immagine a lato. Perché ciò sia vero occorre che M 12 =M 21 =M e, in tal caso, dw è il differenziale esatto della funzione W:
32 190 Luciano De Menna Corso di Elettrotecnica W = 1 2 L 1i Mi 1 i L 2i 2 2. (VI.40) La VI.40 è l'espressione della ener gia magnetica immagazzinata in un accoppiamento mutuo. Essa ci consente ulteriori deduzioni; infatti, l' energia magnetica immagazzinata deve, evidentemente, essere definita positiva. Tale sarà dunque anche il rapporto tra l'energia immagazzinata ed il quadrato della corrente alla porta primaria W i = L 1 + M i i1 2 L i i = 2 1 = 1 2 L 1 + M x L 2 x. (VI.41) dove si è detto x il rapporto tra le due correnti. La parabola che la VI.41 descrive nel piano[x,w] è rappresentata nella immagine a lato. È evidente che, solo nel caso in cui la parabola non interseca l'asse delle x, non esisterà alcuna coppia di valori delle correnti per cui l'energia immagazzinata è negativa - il che corrisponde al fatto che l'equazione, che si ottiene annullando la VI.41, ha radici complesse. Questa condizione si verifica quando: M L 1 L 2. (VI La condizione limite M 2 =L 1 L 2 si dice di accoppiamento perfetto; infatti se tale condizione è verificata, esiste una coppia di valori di i 1 ed i 2 per i quali risulta W = 0. Ma dato che per annullare l'energia magnetica associata ad un campo magnetico bisogna necessariamente annullare lo stesso campo magnetico in ogni punto dello spazio, l'affermazione precedente equivale alla seguente: se l'accoppiamento è perfetto, è possibile annullar e completamente il campo prodotto dalla corrente in uno dei due circuiti, facendo circolare nel-
33 Luciano De Menna Corso di Elettrotecnica 191 l'altro una opportuna corrente. E ciò giustifica evidentemente il fatto che tale condizione si dica di accoppiamento perfetto. Al coefficiente k, k = M, (VI.43) L 1 L 2 viene dato il nome di coefficiente di accoppiamento; esso varia tra -1 ed 1. Esercizi Le impedenze dei due bipoli assegnati precedentemente sono, nel primo caso, Z e = j 90, e nel secondo caso, Z e = 10 + j 5. Per l'esercizio successivo diamo il valore della corrente: i t = 2 sen 1000 t + 4 ma. Per risolvere la rete, naturalmente, si sarà utilizzato la sovrapposizione degli effetti considerando i due generatori separatamente; ciò è necessario in quanto i generatori hanno frequenza diversa - uno dei generatori ha frequenza nulla -. Si noti che la rete è in risonanza rispetto alla componente sinusoidale e quindi la corrente da essa prodotta è in fase con la tensione. La componente continua della tensione non produce una corrispondente corrente per la presenza del condensatore che non consente il passaggio di una corrente continua. Si noti che la tensione sul condensatore (convenzione dell'utilizzatore), però, ha una componente continua: v c t = ,1 sen 1000 t - 4. V Quando i generatori presenti invece hanno la stessa frequenza non è necessario utilizzare la sovrapposizione degli effetti, come nel caso dell'esercizio seguente.
34 Luciano De Menna Corso di Elettrotecnica 192 L'accoppiamento mutuo in regime sinusoidale In particolare, se il doppio bipolo accoppiamento mutuo è in regime sinusoidale, si potrà fare uso del simbolismo vettoriale e parlare di impedenza propria o autoimpedenza ed impedenza mutua. Le equazioni saranno: V 1 = Z 11 I 1 + Z 12 I 2 = j L 1 I 1 + j M I 2 (VI.44) V 2 = Z 21 I 1 + Z 22 I 2 = j M I 1 + j L 2 I 2. Il doppio bipolo accoppiamento magnetico in regime sinusoidale è dunque caratterizzato globalmente dai valori delle tre impedenze Z11, Z22 ed Zm, corrispondenti ai tre parametri indipendenti che lo individuano L 1, L 2 ed M. È possibile, però, costruire un circuito equivalente del doppio bipolo in esame, nel quale la dipendenza da tre parametri indipendenti è messa in particolar e evidenza. Cominciamo dal caso dell'accoppiamento perfetto; sarà allora M 2 = L 1 L 2 e quindi L 1 /M = M/L 2. A tale quantità daremo il nome di rap - porto di trasformazione e lo indicheremo con il simbolo a. Consideriamo ora le equazioni (VI.44) e riscriviamole mettendo in evidenza nella prima equazione il fattore j L 1 e nella seconda j M. Si ottiene: V 1 = I j L 1 + M I 1 L 2 = I 1 + I 2 1 a V 2 j M = I 1 + L 2 M I 2 = I 1 + I (VI.45) 2 a. Dividendo membro a membro le due ultime equazioni si ottiene ancora: V 1 = a. (VI.46) V 2 Mentre dalla prima delle (VI.45) si ha:
35 193 Luciano De Menna Corso di Elettrotecnica I 1 = - I 2 a + Le due equazioni (VI.46) e (VI.47), essendo equivalenti alle equazioni (VI.44), descrivono anche esse il doppio bipolo accoppiamento magnetico perfetto. Nella ipotesi che L 1 sia molto grande, al limite per L 1 che tende all'infinito, si ha: V 1 V 2 = a, V 1 j L 1. (VI.47) I 1 I 2 = - 1 a. (VI.48) Le equazioni (VI.48) definiscono un doppio bipolo ideale che chiameremo trasformatore ideale e che rappresenteremo con il simbolo mostrato nell'immagine a lato; esso è ideale in quanto descrive un doppio bipolo accoppiamento magnetico perfetto solo nel limite in cui l'induttanza primaria di tale accoppiamento vada all'infinito. Il trasformatore ideale è caratterizzato da un solo parametro: il suo rapporto di trasformazione a. Se ora ritorniamo alle equazioni (VI.46) e (VI.47), che descrivono il doppio bipolo accoppiamento perfetto, vediamo che mentre la prima di esse afferma che le tensioni sono nello stesso rapporto che avrebbero in un trasfor matore ideale, la seconda ci dice che la corrente al primario può essere vista come somma di una corrente, che è la stessa che si avrebbe in un trasformatore ideale, più la corrente che circola nell'induttanza L 1 quando essa è sottoposta alla tensione primaria. In altri termini le stesse equazioni (VI.46) e (VI.47) caratterizzano anche un circuito del tipo mostrato nelle immagini a lato, e quindi tale circuito è equivalente all'accoppiamento magnetico perfetto. Il caso dell'accoppiamento non perfetto si risolve ora con grande semplicità. Supponiamo, infatti, di scomporre le due induttanze L 1 ed L 2 in due parti L 1 ' ed L 2 ', e L 1 " ed L 2 " tali che L 1 " L 2 " = M 2 :
36 Luciano De Menna Corso di Elettrotecnica 194 Evidentemente, le tre equazioni (VI.49) definiscono i quattro parametri L con un grado di libertà in quanto le equazioni che li determinano sono solo tre. Esistono dunque infinite scelte possibili per la scomposizione descritta; per ottenerne una basterà fissare ad arbitrio uno dei parametri ed ottenere gli altri dalle (VI.49). Introduciamo ora le posizioni fatte nelle equazioni (VI.44): V 1 = j V 2 = j L 1 ' L 2 ' ' L 1 ' L 2 + L 1 " = L 1, + L 2 " = L 2, L 1 " L 2 " = M 2. I 1 + j L 1 " I 1 + j M I 2, I 2 + j M I 1 + j L 2 " I 2. (VI.49) (VI.50) È evidente che i termini in par entesi, per come li abbiamo costruiti, descrivono un accoppiamento perfetto. Per ottenere il circuito equivalente di un accoppiamento non perfetto, basterà aggiungere, a quello di un accoppiamento perfetto, le due cadute di tensione j L ' e j L ' 1 I 1 2 I 2 rispettivamente al primario ed al secondario, così come mostrato nella seconda immagine a lato. Naturalmente, data l'arbitrarietà della scelta di cui alla (VI.49), si possono costruire infiniti circuiti equivalenti dell'accoppiamento dato; in particolare sono possibili le due scelte L' 1 = 0 oppure L' 2 = 0: in questo secondo caso il circuito equivalente che ne risulta è quello mostrato in figura. Si noti che se i morsetti secondari di un doppio bipolo trasformatore ideale sono chiusi su di una impedenza Z, il rapporto tra tensione e corrente al primario è dato da:
37 195 Luciano De Menna Corso di Elettrotecnica V 1 I 1 = - a 2 V 2 I 2 = a 2 Z. (VI.51) Cioè il primario vede una impedenza a 2 volte più grande di quella su cui è chiuso il secondario. Questa osservazione fornisce un metodo generale per eliminare gli accoppiamenti mutui presenti in un circuito e ricondurre la rete ad una equivalente cosí come mostrato nelle immagini a lato. L'accoppiamento mutuo, e a maggior ragione il trasformatore ideale, sono, evidentemente, trasparenti per le potenze attive; infatti in tali doppi bipoli non sono presenti elementi dissipativi e quindi la potenza attiva alla por ta primaria è eguale ed opposta a quella alla porta secondaria - si ricordi che si è assunta una convenzione dell'utilizzatore ad entrambe le porte - di modo che la potenza attiva totale assorbita dal doppio bipolo è identicamente nulla. Mentre però il trasformatore ideale è trasparente anche per le potenze reattive - ed in generale per qualsiasi tipo di potenza - l'accoppiamento mutuo invece assorbe una certa potenza reattiva; si dimostri che tale potenza può essere messa nella forma: Q = L 1 I V 1 2. M 2 L 2 (VI.52) Esercizi Per il primo esercizio a lato, proposto in precedenza, diamo la corrente i 1, per verificare i risultati ottenuti: i 1 t = 100 sen 100t - 4. Si provi a risolvere la stessa rete applicando la sovrapposizione degli effetti. Nell'esercizio successivo si propone la soluzione con il metodo delle correnti di maglia o dei potenziali ai nodi.
38 196 Luciano De Menna Corso di Elettrotecnica Il trasformatore Il nome "trasformatore ideale" dato al doppio bipolo introdotto per costruire il circuito equivalente di un accoppiamento mutuo, deriva dal fatto che "trasformator e" viene detto un dispositivo, di larghissimo uso nelle pratiche applicazioni, del quale il trasformatore ideale è, appunto, una idealizzazione. Si tratta di un accoppiamento mutuo realizzato con due avvolgimenti, che, con accorgimenti tecnici sui quali non è possibile ora soffermarsi, vengono fatti interagire in maniera molto stretta (coefficiente di accoppiamento in modulo prossimo ad 1!). La relazione (VI.46) stabilisce che in tali condizioni le tensioni primarie e secondarie sono nel rapporto a, mentre, trascurando la corrente derivata dalla induttanza L 1 del circuito equivalente, la (VI.47) afferma che le correnti primarie e secondarie sono nel rapporto - 1/a. Sarebbe facile dimostrare che tale rapporto di trasformazione altro non è che, con buona approssimazione, il rapporto tra il numero delle spire dell'avvolgimento primario e quello dell'avvolgimento secondario. Un tale dispositivo, dunque, consente con grande semplicità di ridurre o elevare una tensione, aumentando o riducendo nel contempo la corrente; da ciò il suo nome. Si noti che tutto ciò accade, almeno nel caso teorico che stiamo qui esaminando, senza nessuna dissipazione di potenza attiva. Il trasformatore dunque consente di adattare la tensione alla particolare applicazione. Ma c'è di più e, per comprenderlo, bisogna sviluppare qualche considerazione elementare sul problema della produzione e della distribuzione dell'energia elettrica. Motivi di sicurezza degli operatori, e ragioni di ordine economico, consigliano l'uso di tensioni relativamente basse per la distribuzione capillare dell'energia elettri-
39 Luciano De Menna Corso di Elettrotecnica 197 ca. È abbastanza intuitivo infatti comprendere che il danno prodotto sugli organismi viventi, a parità di condizioni, è tanto maggiore quanto maggiore è la tensione. Inoltre gli "isolamenti", sempre necessari in un dispositivo elettrico, diventano sempre più costosi e delicati quando la tensione cresce. Nell'Europa continentale, come è noto, il valore efficace della tensione alla distribuzione è di 220 V. D'altra parte il trasporto dell'energia elettrica, dal punto di produzione a quello di utilizzo, avviene mediante conduttori che, naturalmente, non essendo perfetti, presentano una certa resistenza. In una situazione schematica di un generatore G ad una distanza L dal carico che assorbe una corrente I con un determinato cos, sotto una tensione V, la potenza dissipata lungo la linea è: P d = 2 L S I2, (VI.53) dove è la resistività del materiale di cui i conduttori di linea sono fatti ed S la loro sezione. Tale potenza dipende soltanto dal quadrato del valore efficace della corrente richiesta dal carico! È evidente che se a monte dell'utilizzatore disponessimo un trasformatore riduttor e di tensione in modo da mantenere bassa la tensione sul carico ma da elevare quella sulla linea di trasporto, potremmo nel contempo ridurre la corrente di linea - vedi le VI.48 - e quindi le perdite su di essa. Se si pensa ai chilometri e chilometri di linee di trasmissione elettrica che caratterizzano il panorama di un qualsiasi paese sviluppato, si comprende la convenienza del trasportare l'energia elettrica, sulle grandi tratte, ad alta tensione e relativamente bassa corrente. Si potrebbe pensare di produrre l'energia elettrica direttamente a tale tensione elevata. Ma anche questo non è conveniente economicamente perché, come si è
40 198 Luciano De Menna Corso di Elettrotecnica detto, la complicazione ed il costo di un qualsiasi dispositivo elettrico - e quindi anche di un generatore - cresce notevolmente al crescere della tensione. Ciò porta al classico schema, rappresentato a lato, che prevede un trasformatore elevatore di tensione a valle dei generatori ed a monte della linea, ed un trasformatore riduttore a monte del carico. Naturalmente le cose sono in realtà molto più complesse ed articolate di quanto queste semplici considerazioni possano far credere; si pensi, per esempio, al semplice fatto che supporre un trasformatore privo di perdite è chiaramente una idealizzazione, non foss'altro perché gli avvolgimenti di cui esso è costituito presentano necessariamente una certa resistenza e quindi introducono una dissipazione aggiuntiva. Queste ed altre problematiche sono oggetto di studio di altre discipline che si occupano in modo specifico delle macchine elettriche e degli impianti elettrici; a noi basta qui aver evidenziato, in linea di principio, il fondamentale ruolo svolto nella tecnica dal dispositivo "trasformatore".
41 Luciano De Menna Corso di Elettrotecnica 199 Il problema del rifasamento nelle reti elettriche. La necessità di lunghe linee di trasmissione dell'energia elettrica che collegano i luoghi della generazione con quelli della utilizzazione e la presenza di una inevitabile dissipazione in linea dovuta alla resistenza dei conduttori, ha anche altre inter essanti conseguenze che cercher emo ora di illustrare in maniera molto elementare. Consideriamo un carico che sotto una determinata tensione V, assorbe una potenza attiva P ed una potenza reattiva Q. Supponiamo ancora che la fase della impedenza equivalente del carico, =arctg(q/p), sia positiva (carico induttivo), come in realtà si verifica nella maggioranza dei carichi industriali. Il diagramma fasoriale cor rispondente alla situazione descritta è rappresentato a lato. Nella successiva figura è rappresentata anche una diversa condizione di funzionamento in cui la stessa potenza attiva P è assorbita con una differente potenza reattiva Q'. La potenza attiva è la stessa nei due casi perché la componente Icos del fasore rap - presentativo della corrente, la sola che entra a determinare la potenza attiva, non è variata. Il fatto è ancora più chiaro se si considera il triangolo delle potenze nei due casi considerati, così come mostrato in figura. È evidente però che, nei due casi, è diverso il modulo della corrente I, e quindi diverse sono le potenze dissipate lungo la linea che che collega il carico ai generatori che lo alimentano. Tali potenze, infatti, sono proporzionali al quadrato del modulo della corrente secondo un fattore R che rappresenta, appunto, la resistenza equivalente della linea. Queste perdite potrebbero, dunque, essere ridotte se si disponesse in parallelo al carico un secondo carico, puramente reattivo - nelle nostr e ipotesi, capacitivo - in grado di assorbire una
42 200 Luciano De Menna Corso di Elettrotecnica potenza reattiva pari a - (Q - Q'); ciò senza variare in alcun modo la potenza attiva assorbita dal carico stesso. In tali condizioni il carico si dirà rifasato da cos a cos '. In pratica con il rifasamento si evita che l'energia immagazzinata nel carico, che, come è noto, oscilla tra un punto di massimo ed uno di nullo, venga continuamente trasferita lungo la linea, avanti ed indietro, con le conseguenti perdite; l'aver disposto un "serbatoio di energia" in controfase in prossimità del carico - è questa appunto la funzione che svolgono i condensatori posti in parallelo al carico - consente che tale scambio di energia avvenga tra il "serbatoio" ed il carico e non tra i generatori ed il carico stesso. Gli Enti produttori di energia elettrica, interessati a questo risparmio di energia, cercano di favorire l'uso di tale tecnica adottando opportune politiche contrattuali e tariffarie. In pratica l'energia utilizzata viene fatturata a prezzi diversi a seconda del cos, quando esso scende al di sotto di un certo valore. In Italia tale valor e è cos = 0,9. In conclusione il problema del rifasamento si riduce al calcolo della capacità del banco di condensatori da dispor re in parallelo al carico per ottenere il voluto rifasamento. Tale banco dovrà assorbire la potenza reattiva: Q c = - (Q-Q') = - P(tan -tan '). Si avrà, quindi: da cui: Q c = - V2 X c = - CV 2, C = P tg - tg ' (VI.54) V 2, (VI.55) dove è l'angolo di fase del carico non rifasato e ' quello che si vuole ottenere dopo il rifasamento.
43 Luciano De Menna Corso di Elettrotecnica 201 Esercizi La corrente che circola nel condensatore centrale, della rete assegnata in precedenza, è nulla. Il circuito ha, infatti, un grafo a ponte - di cui si è già parlato in regime continuo - con i lati del ponte che verificano la condizione di equilibrio: jx L2 -jx C4 = R 1 R 3. Allo stesso risultato si può arrivare rapidamente applicando il teorema del generatore equivalente di tensione ai morsetti del condensatore centrale. L'ultimo esercizio richiede di applicare il teorema del generatore equivalente di corrente ai morsetti A e B della r ete mostrata.
44 202 Luciano De Menna Corso di Elettrotecnica Bipoli e strumenti di misura in regime dinamico Anche i bipoli introdotti in regime dinamico, nella loro concreta realizzazione, si discostano in alcuni aspetti dalla loro idealizzazione, che fin qui abbiamo preso in considerazione. Abbiamo già visto che un condensatore può essere realizzato con una semplice struttura piana di due armature conduttrici con un isolante (dielettrico) interposto. Se S è l'area delle armature, d la distanza tra le stesse, ed la costante dielettrica del mezzo interposto, la capacità del condensatore è: C = S d. (VI.56) Cominciamo con l'osservare che l'unità di misura farad è in realtà molto grande; è facile verificare, per esempio, che per ottenere una capacità di un farad con un condensatore ad armature piane separate da uno spazio vuoto - o con aria - di un decimo di millimetro, occorrerebbe una superficie delle armature di dieci milioni di metri quadri. Per questo motivo sono molto usati, come unità di misura delle capacità, i sottomultipli del farad: millifarad, microfarad, nanofarad e picofarad. Come per i resistori, il valore della capacità del condensatore non è l'unico parametro che caratterizza il componente. Tra gli altri parametri importanti ricordiamo la tolleranza, il margine di incer tezza, cioè, con cui il valore della capacità è dato, e la tensione di lavo - ro che è la tensione per la quale lo spessore di isolante è stato progettato; tensioni maggiori mettono a rischio l'integrità del componente. A caratterizzare ulteriormente il componente, intervengono a volte, le modalità di costruzione dello stesso; alcuni condensatori, per esempio, detti polarizzati, hanno le polarità dei loro morsetti fissate a priori, nel senso che uno dei morset-
Fasori e vettori rappresentativi
 170 Luciano De Menna Corso di Elettrotecnica Fasori e vettori rappresentativi Come abbiamo visto, in regime sinusoidale è possibile caratterizzare ogni bipolo attraverso la sua impedenza: un numero complesso
170 Luciano De Menna Corso di Elettrotecnica Fasori e vettori rappresentativi Come abbiamo visto, in regime sinusoidale è possibile caratterizzare ogni bipolo attraverso la sua impedenza: un numero complesso
182 Luciano De Menna Corso di Elettrotecnica
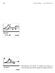 182 Luciano De Menna Corso di Elettrotecnica All'aumentare del fattore di qualità del circuito, la curva di risonanza diventa sempre più ripida nell'intor- Luciano De Menna Corso di Elettrotecnica 183
182 Luciano De Menna Corso di Elettrotecnica All'aumentare del fattore di qualità del circuito, la curva di risonanza diventa sempre più ripida nell'intor- Luciano De Menna Corso di Elettrotecnica 183
Capitolo VI. I regimi sinusoidali
 Capitolo VI I regimi sinusoidali Siamo dunque alla ricerca di una tecnica che ci consenta di semplificare le operazioni sulle grandezze sinusoidali. Osserviamo che nelle equazioni relative alla LKC ed
Capitolo VI I regimi sinusoidali Siamo dunque alla ricerca di una tecnica che ci consenta di semplificare le operazioni sulle grandezze sinusoidali. Osserviamo che nelle equazioni relative alla LKC ed
Lezione 14. Vettori rotanti. RL con forzamento sinusoidale. e( t) = E M. i( t) = ke R L t + I M. e(t) E = RI + jω LI. E ( ) 2 ; η arctg ω L
 ezione 4 ( A) A Vettori rotanti ( A) Piano di Gauss A = Ae j( ωt+α ) = Acos( ωt + α ) + jasen( ωt + α ) Prima di procedere oltre, facciamo vedere perché il termine fasori. a parte reale ed il coefficiente
ezione 4 ( A) A Vettori rotanti ( A) Piano di Gauss A = Ae j( ωt+α ) = Acos( ωt + α ) + jasen( ωt + α ) Prima di procedere oltre, facciamo vedere perché il termine fasori. a parte reale ed il coefficiente
Luciano De Menna Corso di Elettrotecnica 183
 Luciano De Menna Corso di Elettrotecnica 183 Le motivazioni di tale terminologia si comprendono facilmente se si considera la seguente situazione. Si immagini che la tensione del generatore non sia sinusoidale
Luciano De Menna Corso di Elettrotecnica 183 Le motivazioni di tale terminologia si comprendono facilmente se si considera la seguente situazione. Si immagini che la tensione del generatore non sia sinusoidale
Potenza in regime sinusoidale
 26 Con riferimento alla convenzione dell utilizzatore, la potenza istantanea p(t) assorbita da un bipolo è sempre definita come prodotto tra tensione v(t) e corrente i(t): p(t) = v(t) i(t) Considerando
26 Con riferimento alla convenzione dell utilizzatore, la potenza istantanea p(t) assorbita da un bipolo è sempre definita come prodotto tra tensione v(t) e corrente i(t): p(t) = v(t) i(t) Considerando
LEZIONE DI ELETTRONICA
 LEZIONE DI ELETTRONICA Analisi dei circuiti lineari in regime sinusoidale 2 MODULO : Analisi dei circuiti lineari in regime sinusoidale PREMESSA L analisi dei sistemi elettrici lineari, in regime sinusoidale,
LEZIONE DI ELETTRONICA Analisi dei circuiti lineari in regime sinusoidale 2 MODULO : Analisi dei circuiti lineari in regime sinusoidale PREMESSA L analisi dei sistemi elettrici lineari, in regime sinusoidale,
Lezione 16. Il circuito risonante. Il circuito risonante. Fasori. Fasori. Al variare dei parametri L, R e C. Al variare dei parametri L, R e C
 ezione 6 l circuito risonante = + jω j = + jω j Al variare dei parametri, e ω = Fasori Abbiamo visto che in un circuito serie, alimentato da un generatore di forza elettromotrice sinusoidale di frequenza
ezione 6 l circuito risonante = + jω j = + jω j Al variare dei parametri, e ω = Fasori Abbiamo visto che in un circuito serie, alimentato da un generatore di forza elettromotrice sinusoidale di frequenza
Capitolo VIII Dinamica dei circuiti di ordine superior e
 Capitolo VIII Dinamica dei circuiti di ordine superior e Nei capitoli precedenti abbiamo già esaminato, partendo da alcuni classici esempi, gli aspetti salienti della soluzione di una rete elettrica in
Capitolo VIII Dinamica dei circuiti di ordine superior e Nei capitoli precedenti abbiamo già esaminato, partendo da alcuni classici esempi, gli aspetti salienti della soluzione di una rete elettrica in
CIRCUITI IN REGIME SINUSOIDALE
 CIRCUITI IN REGIME SINUSOIDALE CIRCUITO PURAMENTE OHMICO Esaminiamo il comportamento dei circuiti in regime sinusoidale iniziando da un circuito puramente ohmico. Si consideri (figura 1) un circuito costituito
CIRCUITI IN REGIME SINUSOIDALE CIRCUITO PURAMENTE OHMICO Esaminiamo il comportamento dei circuiti in regime sinusoidale iniziando da un circuito puramente ohmico. Si consideri (figura 1) un circuito costituito
Lezione 17. Accoppiamento mutuo. Accoppiamento mutuo. isolante N 1 spire. conduttore. N 2 spire. sezione S , M 21 ) , L 11 , M 12.
 Lezione 7 Nei regimi namici ha senso introdurre un particolare doppio bipolo, che non ha il suo equivalente in c.c.: laccoppiamento magnetico mutuo tra due circuiti. Veamo cosa si tratta. Abbiamo già visto
Lezione 7 Nei regimi namici ha senso introdurre un particolare doppio bipolo, che non ha il suo equivalente in c.c.: laccoppiamento magnetico mutuo tra due circuiti. Veamo cosa si tratta. Abbiamo già visto
per la matrice R, e: I 1 = G 11 V 1 + G 12 V 2, I 2 = G 21 V 1 + G 22 V 2,
 100 Luciano De Menna Corso di Elettrotecnica Il caso N = 2 è particolarmente interessante tanto da meritare un nome speciale: doppio bipolo I parametri indipendenti saranno tre: R 11, R 22 ed R 12 =R 21
100 Luciano De Menna Corso di Elettrotecnica Il caso N = 2 è particolarmente interessante tanto da meritare un nome speciale: doppio bipolo I parametri indipendenti saranno tre: R 11, R 22 ed R 12 =R 21
RISONANZA. Fig.1 Circuito RLC serie
 RISONANZA Risonanza serie Sia dato il circuito di fig. costituito da tre bipoli R, L, C collegati in serie, alimentati da un generatore sinusoidale a frequenza variabile. Fig. Circuito RLC serie L impedenza
RISONANZA Risonanza serie Sia dato il circuito di fig. costituito da tre bipoli R, L, C collegati in serie, alimentati da un generatore sinusoidale a frequenza variabile. Fig. Circuito RLC serie L impedenza
UNIVERSITA DEGLI STUDI DI NAPOLI FEDERICO II
 Mod. 2 UNIVERSITA DEGLI STUDI DI NAPOLI FEDERICO II REGISTRO DEGLI INCARICHI DIDATTICI conferiti ai sensi del Regolamento per il conferimento di incarichi didattici e per la determinazione della retribuzione
Mod. 2 UNIVERSITA DEGLI STUDI DI NAPOLI FEDERICO II REGISTRO DEGLI INCARICHI DIDATTICI conferiti ai sensi del Regolamento per il conferimento di incarichi didattici e per la determinazione della retribuzione
Indice. XI Prefazione. 1 Capitolo 1 METODO CIRCUITALE: COMPONENTI E LEGGI DI KIRCHHOFF Modello circuitale dei fenomeni elettromagnetici
 XI Prefazione 1 Capitolo 1 METODO CIRCUITALE: COMPONENTI E LEGGI DI KIRCHHOFF 1 1.1 Modello circuitale dei fenomeni elettromagnetici 1.1.1 Modello a parametri concentrati, p. 1-1.1.2 Modello a parametri
XI Prefazione 1 Capitolo 1 METODO CIRCUITALE: COMPONENTI E LEGGI DI KIRCHHOFF 1 1.1 Modello circuitale dei fenomeni elettromagnetici 1.1.1 Modello a parametri concentrati, p. 1-1.1.2 Modello a parametri
I bipoli in regime dinamico: bipoli attivi.
 Luciano De Menna Corso di Elettrotecnica 145 I bipoli in regime dinamico: bipoli attivi. I circuiti in regime dinamico che abbiamo fino ad ora studiato contenevano esclusivamente bipoli passivi. La dinamica
Luciano De Menna Corso di Elettrotecnica 145 I bipoli in regime dinamico: bipoli attivi. I circuiti in regime dinamico che abbiamo fino ad ora studiato contenevano esclusivamente bipoli passivi. La dinamica
Insegnamento Introduzione ai circuiti. Argomento: Introduzione al corso e sua organizzazione. Note:
 data 20 settembre 2017 data 22 settembre 2017 data 27 settembre 2017 data 29 settembre 2017 Introduzione al corso e sua organizzazione didattica, sussidi didattici. Interazione elettromagnetica, sistemi
data 20 settembre 2017 data 22 settembre 2017 data 27 settembre 2017 data 29 settembre 2017 Introduzione al corso e sua organizzazione didattica, sussidi didattici. Interazione elettromagnetica, sistemi
Lezione 13. Circuito R L C in evoluzione forzata. Circuito R L C in evoluzione forzata. ( t) = k 1 ( ) + E. Es. II.4, II.5, II.6. + v L.
 ezione 13 Circuito C in evoluzione forzata E i C v + v C + = E v v C C dv C dt + v C + C d 2 v C dt 2 = di dt = E d 2 v C dt 2 + i = C dv C dt dv C dt v = i + v C C = E C Passiamo ora ad esaminare il caso
ezione 13 Circuito C in evoluzione forzata E i C v + v C + = E v v C C dv C dt + v C + C d 2 v C dt 2 = di dt = E d 2 v C dt 2 + i = C dv C dt dv C dt v = i + v C C = E C Passiamo ora ad esaminare il caso
9.8 Con la LKT si scrive l equazione seguente: di (1) dt La costante di tempo èτ
 9.8 Con la LKT si scrive l equazione seguente: di L Ri cos( t) () dt La costante di tempo èτ L / R ms / 5s ; la soluzione della () è 5t i( t) Ke Acos(t θ ) () Sia A θ il fasore corrispondente alla risposta
9.8 Con la LKT si scrive l equazione seguente: di L Ri cos( t) () dt La costante di tempo èτ L / R ms / 5s ; la soluzione della () è 5t i( t) Ke Acos(t θ ) () Sia A θ il fasore corrispondente alla risposta
Esercizi aggiuntivi Unità A2
 Esercizi aggiuntivi Unità A2 Esercizi svolti Esercizio 1 A2 ircuiti in corrente alternata monofase 1 Un circuito serie, con 60 Ω e 30 mh, è alimentato con tensione V 50 V e assorbe la corrente 0,4 A. alcolare:
Esercizi aggiuntivi Unità A2 Esercizi svolti Esercizio 1 A2 ircuiti in corrente alternata monofase 1 Un circuito serie, con 60 Ω e 30 mh, è alimentato con tensione V 50 V e assorbe la corrente 0,4 A. alcolare:
1. RELAZIONI TENSIONE-CORRENTE NEL DOMINIO DEL TEMPO. i(t) = v(t) / R = V M / R sen ωt i(t) = I M sen ωt I(t) = I M e jωt
 1. RELAZIONI TENSIONE-CORRENTE NEL DOMINIO DEL TEMPO i(t) Tensione applicata : v(t) v(t) = V M sen ωt V(t) = V M e jωt : vettore ruotante che genera la sinusoide RESISTORE i(t) = v(t) / R = V M / R sen
1. RELAZIONI TENSIONE-CORRENTE NEL DOMINIO DEL TEMPO i(t) Tensione applicata : v(t) v(t) = V M sen ωt V(t) = V M e jωt : vettore ruotante che genera la sinusoide RESISTORE i(t) = v(t) / R = V M / R sen
Capitolo VII I sistemi trifasi
 Capitolo VII I sistemi trifasi Nell'introdurre il regime sinusoidale abbiamo accennato a come sia, in linea di principio, molto semplice i m m a g i n a re un generatore di tensione sinusoidale costruito
Capitolo VII I sistemi trifasi Nell'introdurre il regime sinusoidale abbiamo accennato a come sia, in linea di principio, molto semplice i m m a g i n a re un generatore di tensione sinusoidale costruito
Elettrotecnica - Ing. Biomedica Ing. Elettronica Informatica e Telecomunicazioni (V. O.) A.A. 2013/14 Prova n luglio 2014.
 ognome Nome Matricola Firma Parti svolte: E E E D Esercizio I I R 6 R 5 D 6 G 0 g Supponendo noti i parametri dei componenti e la matrice di conduttanza del tripolo, illustrare il procedimento di risoluzione
ognome Nome Matricola Firma Parti svolte: E E E D Esercizio I I R 6 R 5 D 6 G 0 g Supponendo noti i parametri dei componenti e la matrice di conduttanza del tripolo, illustrare il procedimento di risoluzione
università DEGLI STUDI DI NAPOLI FEDERICO II
 università DEGLI STUDI DI NAPOLI FEDERICO II Facoltà di Ingegneria Registro delle Lezioni dell insegnamento di: Introduzione ai Circuiti Corso di Laurea in Ingegneria dell'automazione Corso di Laurea in
università DEGLI STUDI DI NAPOLI FEDERICO II Facoltà di Ingegneria Registro delle Lezioni dell insegnamento di: Introduzione ai Circuiti Corso di Laurea in Ingegneria dell'automazione Corso di Laurea in
ELETTROTECNICA (10 CFU) CS INGEGNERIA MATEMATICA I
 ELETTROTECNICA (10 CFU) CS INGEGNERIA MATEMATICA I prova in itinere 1 Novembre 008 SOLUZIONE - 1 - D1. (punti 8 ) Rispondere alle seguenti domande: punto per ogni risposta corretta, - 0.5 per ogni risposta
ELETTROTECNICA (10 CFU) CS INGEGNERIA MATEMATICA I prova in itinere 1 Novembre 008 SOLUZIONE - 1 - D1. (punti 8 ) Rispondere alle seguenti domande: punto per ogni risposta corretta, - 0.5 per ogni risposta
. Il modulo è I R = = A. La potenza media è 1 VR 2
 0.4 La corrente nel resistore vale 0. l modulo è A. La potenza media è 0 W 0.7 l circuito simbolico è mostrato di seguito. La potenza viene dissipata solo nel resistore. 0, 4 - La corrente è 4 4 0, 0,
0.4 La corrente nel resistore vale 0. l modulo è A. La potenza media è 0 W 0.7 l circuito simbolico è mostrato di seguito. La potenza viene dissipata solo nel resistore. 0, 4 - La corrente è 4 4 0, 0,
( ) ( t) Lezione 15. Teorema di Tellegen. Potenza in regime sinusoidale ( ) ( ) = 0. i k P = V I
 ezion5 Anche in regime sinusoidale, naturalmente, il prodotto vi della tensione ai morsetti di un bipolo e della corrente che lo attraversa rappresenta, istante per istante, la potenza assorbita dal bipolo
ezion5 Anche in regime sinusoidale, naturalmente, il prodotto vi della tensione ai morsetti di un bipolo e della corrente che lo attraversa rappresenta, istante per istante, la potenza assorbita dal bipolo
Capitolo 1 (ultimo aggiornamento 04/05/04) 1.1 Rappresentazione della grandezza a(t) funzione sinusoidale del tempo
 Capitolo 1 (ultimo aggiornamento 04/05/04) 1.1 Rappresentazione della grandezza a(t) funzione sinusoidale del tempo A M valore massimo Am valore medio Fig.1.1 a t A M sin t valore medio in un semiperiodo
Capitolo 1 (ultimo aggiornamento 04/05/04) 1.1 Rappresentazione della grandezza a(t) funzione sinusoidale del tempo A M valore massimo Am valore medio Fig.1.1 a t A M sin t valore medio in un semiperiodo
Note sui circuiti a corrente alternata
 Note sui circuiti a corrente alternata Versione provvisoria. Novembre 018 1 Per commenti o segnalazioni di errori scrivere, per favore, a: maurosaita@tiscalinet.it Indice 1 Corrente alternata 1.1 Circuito
Note sui circuiti a corrente alternata Versione provvisoria. Novembre 018 1 Per commenti o segnalazioni di errori scrivere, per favore, a: maurosaita@tiscalinet.it Indice 1 Corrente alternata 1.1 Circuito
Componenti di un circuito elettrico in regime sinusoidale
 omponenti di un circuito elettrico in regime sinusoidale omponenti di un circuito elettrico in regime sinusoidale Introduzione: a corrente elettrica, nel suo passaggio all interno di un conduttore, produce
omponenti di un circuito elettrico in regime sinusoidale omponenti di un circuito elettrico in regime sinusoidale Introduzione: a corrente elettrica, nel suo passaggio all interno di un conduttore, produce
Elettrotecnica. 13 Doppi bipoli di ordine uno
 Elettrotecnica 13 Doppi bipoli di ordine uno 1 Doppi bipoli ideali di ordine uno governati da due semplici equazioni funzionali F 1 [v 1 (t),v (t),i 1 (t),i (t)]=0 F [v 1 (t),v (t),i 1 (t),i (t)]=0 contenti
Elettrotecnica 13 Doppi bipoli di ordine uno 1 Doppi bipoli ideali di ordine uno governati da due semplici equazioni funzionali F 1 [v 1 (t),v (t),i 1 (t),i (t)]=0 F [v 1 (t),v (t),i 1 (t),i (t)]=0 contenti
Luciano De Menna Corso di Elettrotecnica 153
 Luciano De Menna Corso di Elettrotecnica 153 Per le funzione periodiche si può dimostrare una importante proprietà che prende il nome di sviluppo in serie di Fourier. ale proprietà consente di porre una
Luciano De Menna Corso di Elettrotecnica 153 Per le funzione periodiche si può dimostrare una importante proprietà che prende il nome di sviluppo in serie di Fourier. ale proprietà consente di porre una
124 Luciano De Menna Corso di Elettrotecnica. I circuiti RC ed RL
 124 Luciano De Menna Corso di Elettrotecnica I circuiti RC ed RL Se nella rete sono presenti anche resistori, le cose si complicano. Consideriamo il caso della serie di un condensatore e di un resistore.
124 Luciano De Menna Corso di Elettrotecnica I circuiti RC ed RL Se nella rete sono presenti anche resistori, le cose si complicano. Consideriamo il caso della serie di un condensatore e di un resistore.
UNIVERSITA DEGLI STUDI DI BERGAMO Facoltà di Ingegneria
 UNIVERSITA DEGLI STUDI DI BERGAMO Facoltà di Ingegneria Corso di Elettrotecnica A.A. 2001/2002 Prova scritta del 4 settembre 1999 Esercizio n 1 Data la rete in figura, determinare tutte le correnti (4
UNIVERSITA DEGLI STUDI DI BERGAMO Facoltà di Ingegneria Corso di Elettrotecnica A.A. 2001/2002 Prova scritta del 4 settembre 1999 Esercizio n 1 Data la rete in figura, determinare tutte le correnti (4
Impedenze ed Ammettenze 1/5
 Impedenze ed Ammettenze 1/5 V=Z I. Rappresentazione alternativa I=Y V Z ed Y sono numeri complessi Bipolo di impedenza Z = R+ j X Resistenza Reattanza Conduttanza 1 Y = = G+ jb Z Suscettanza Lezione 2
Impedenze ed Ammettenze 1/5 V=Z I. Rappresentazione alternativa I=Y V Z ed Y sono numeri complessi Bipolo di impedenza Z = R+ j X Resistenza Reattanza Conduttanza 1 Y = = G+ jb Z Suscettanza Lezione 2
I SEGNALI SINUSOIDALI
 I SEGNALI SINUSOIDALI I segnali sinusoidali sono i segnali più importanti nello studio dell elettronica e dell elettrotecnica. La forma d onda sinusoidale è una funzione matematica indispensabile per interpretare
I SEGNALI SINUSOIDALI I segnali sinusoidali sono i segnali più importanti nello studio dell elettronica e dell elettrotecnica. La forma d onda sinusoidale è una funzione matematica indispensabile per interpretare
Principi di ingegneria elettrica. Reti in regime sinusoidale. Lezione 13 a. Impedenza Ammettenza
 Principi di ingegneria elettrica Lezione 3 a Reti in regime sinusoidale mpedenza Ammettenza Legge di Ohm simbolica n un circuito lineare comprendente anche elementi dinamici (induttori e condensatori)
Principi di ingegneria elettrica Lezione 3 a Reti in regime sinusoidale mpedenza Ammettenza Legge di Ohm simbolica n un circuito lineare comprendente anche elementi dinamici (induttori e condensatori)
. Il modulo è I R = = A. La potenza media è 1 VR 2
 0.4 La corrente nel resistore vale 0. l modulo è A. La potenza media è P 0 W 0.7 l circuito simbolico è mostrato di seguito. La potenza viene dissipata solo nel resistore. 0, 4 - La corrente è 4 4 0, 0,
0.4 La corrente nel resistore vale 0. l modulo è A. La potenza media è P 0 W 0.7 l circuito simbolico è mostrato di seguito. La potenza viene dissipata solo nel resistore. 0, 4 - La corrente è 4 4 0, 0,
TRASFORMATA DI LAPLACE
 TRASFORMATA DI LAPLACE La Trasformata di Laplace è un operatore funzionale che stabilisce una corrispondenza biunivoca tra una funzione di variabile reale (tempo t), definita per t, e una funzione di variabile
TRASFORMATA DI LAPLACE La Trasformata di Laplace è un operatore funzionale che stabilisce una corrispondenza biunivoca tra una funzione di variabile reale (tempo t), definita per t, e una funzione di variabile
università DEGLI STUDI DI NAPOLI FEDERICO II
 università DEGLI STUDI DI NAPOLI FEDERICO II Facoltà o Scuola di INGEGNERIA Registro delle Lezioni del Corso di Introduzione ai Circuiti C.d.L. in Ingegneria dell'automazione e D.d.L. in Ingegneria informatica
università DEGLI STUDI DI NAPOLI FEDERICO II Facoltà o Scuola di INGEGNERIA Registro delle Lezioni del Corso di Introduzione ai Circuiti C.d.L. in Ingegneria dell'automazione e D.d.L. in Ingegneria informatica
Grande rilevanza hanno in elettronica i segnali sinusoidali. Un. segnale sinusoidale è un segnale che varia nel tempo con una legge
 I segnali sinusoidali Grande rilevanza hanno in elettronica i segnali sinusoidali. Un segnale sinusoidale è un segnale che varia nel tempo con una legge del seguente tipo u = U sen( ω t+ ϕ ) Figura A andamento
I segnali sinusoidali Grande rilevanza hanno in elettronica i segnali sinusoidali. Un segnale sinusoidale è un segnale che varia nel tempo con una legge del seguente tipo u = U sen( ω t+ ϕ ) Figura A andamento
a.a. 2017/2018 Stefano Bifaretti Vincenzo Bonaiuto Dipartimento di Ingegneria Industriale
 a.a. 2017/2018 Stefano Bifaretti Vincenzo Bonaiuto Dipartimento di Ingegneria Industriale Le macchine in c.a. impiegate negli azionamenti industriali sono caratterizzate da un circuito elettrico di statore
a.a. 2017/2018 Stefano Bifaretti Vincenzo Bonaiuto Dipartimento di Ingegneria Industriale Le macchine in c.a. impiegate negli azionamenti industriali sono caratterizzate da un circuito elettrico di statore
Transitori del secondo ordine
 Università di Ferrara Corso di Teoria dei circuiti Transitori del secondo ordine Si consideri il circuito in figura e si supponga che all istante la corrente della serie e la tensione sul condensatore
Università di Ferrara Corso di Teoria dei circuiti Transitori del secondo ordine Si consideri il circuito in figura e si supponga che all istante la corrente della serie e la tensione sul condensatore
università DEGLI STUDI DI NAPOLI FEDERICO II
 università DEGLI STUDI DI NAPOLI FEDERICO II Facoltà o Scuola di INGEGNERIA Registro delle Lezioni del Corso di Introduzione ai Circuiti C.d.L. in Ingegneria dell'automazione e D.d.L. in Ingegneria informatica
università DEGLI STUDI DI NAPOLI FEDERICO II Facoltà o Scuola di INGEGNERIA Registro delle Lezioni del Corso di Introduzione ai Circuiti C.d.L. in Ingegneria dell'automazione e D.d.L. in Ingegneria informatica
ˆ b, si usa la convenzione di prendere. come verso positivo quello antiorario e come verso negativo quello orario.
 Capitolo 4 Le rotazioni 4.1 Richiami di teoria E' opportuno ricordare che, dato un angolo orientato ao ˆ b, si usa la convenzione di prendere come verso positivo quello antiorario e come verso negativo
Capitolo 4 Le rotazioni 4.1 Richiami di teoria E' opportuno ricordare che, dato un angolo orientato ao ˆ b, si usa la convenzione di prendere come verso positivo quello antiorario e come verso negativo
Introduzione ai circuiti
 università DEGLI STUDI DI NAPOLI FEDERICO II Facoltà di Ingegneria Registro delle Lezioni dell insegnamento di Introduzione ai circuiti Corso di laurea in Ingegneria delle Telecomunicazioni Dettate dal
università DEGLI STUDI DI NAPOLI FEDERICO II Facoltà di Ingegneria Registro delle Lezioni dell insegnamento di Introduzione ai circuiti Corso di laurea in Ingegneria delle Telecomunicazioni Dettate dal
Esercitazioni di Elettrotecnica
 Esercitazioni di Elettrotecnica a cura dell Ing ntonio Maffucci Parte II: ircuiti in regime sinusoidale /3 Esercitazioni di Elettrotecnica /3 Maffucci ESEIZIONE N7: Fasori ed impedenze ESEIZIO 7 Esprimere
Esercitazioni di Elettrotecnica a cura dell Ing ntonio Maffucci Parte II: ircuiti in regime sinusoidale /3 Esercitazioni di Elettrotecnica /3 Maffucci ESEIZIONE N7: Fasori ed impedenze ESEIZIO 7 Esprimere
Elettrotecnica - A.A Prova n. 2 3 febbraio 2011
 Cognome Nome Matricola Firma 1 Parti svolte: E1 E2 D Esercizio 1 Supponendo noti i valori delle resistenze, della tensione V G1 e dei parametri di trasferimento dei generatori dipendenti, illustrare il
Cognome Nome Matricola Firma 1 Parti svolte: E1 E2 D Esercizio 1 Supponendo noti i valori delle resistenze, della tensione V G1 e dei parametri di trasferimento dei generatori dipendenti, illustrare il
Metodo dei potenziali ai nodi
 Luciano De Menna Corso di Elettrotecnica 45 Metodo dei potenziali ai nodi Esiste un modo per ridurre ulteriormente il numero delle incognite. Esso consiste nello scegliere come incognite del problema invece
Luciano De Menna Corso di Elettrotecnica 45 Metodo dei potenziali ai nodi Esiste un modo per ridurre ulteriormente il numero delle incognite. Esso consiste nello scegliere come incognite del problema invece
Lez.23 Accoppiamento mutuo. Università di Napoli Federico II, CdL Ing. Meccanica, A.A , Elettrotecnica. Lezione 23 Pagina 1
 Lez.3 Accoppiamento mutuo Università di Napoli Federico, CdL ng. Meccanica, A.A. 07-08, Elettrotecnica. Lezione 3 Pagina Doppio bipolo Trasformatore deale È un doppio bipolo caratterizzato da un solo parametro
Lez.3 Accoppiamento mutuo Università di Napoli Federico, CdL ng. Meccanica, A.A. 07-08, Elettrotecnica. Lezione 3 Pagina Doppio bipolo Trasformatore deale È un doppio bipolo caratterizzato da un solo parametro
UNIVERSITA DEGLI STUDI DI NAPOLI FEDERICO II
 Mod. 1 UNIVERSITA DEGLI STUDI DI NAPOLI FEDERICO II REGISTRO DELLE LEZIONI Anno accademico 2016-2017 Insegnamento: Introduzione ai circuiti Prof. Massimiliano de Magistris DIPARTIMENTO di Ingegneria Elettrica
Mod. 1 UNIVERSITA DEGLI STUDI DI NAPOLI FEDERICO II REGISTRO DELLE LEZIONI Anno accademico 2016-2017 Insegnamento: Introduzione ai circuiti Prof. Massimiliano de Magistris DIPARTIMENTO di Ingegneria Elettrica
Luciano De Menna Corso di Elettrotecnica 233. I segnali impulsivi
 Luciano De Menna Corso di Elettrotecnica 233 I segnali impulsivi Un metodo completamente diverso di affrontare il problema della dinamica nei circuiti lineari è quello basato sulla convoluzione di risposte
Luciano De Menna Corso di Elettrotecnica 233 I segnali impulsivi Un metodo completamente diverso di affrontare il problema della dinamica nei circuiti lineari è quello basato sulla convoluzione di risposte
valore v u = v i / 2 V u /V i = 1/ 2
 I Filtri Il filtro è un circuito che ricevendo in ingresso segnali di frequenze diverse è in grado di trasferire in uscita solo i segnali delle frequenze volute, in pratica seleziona le frequenze che si
I Filtri Il filtro è un circuito che ricevendo in ingresso segnali di frequenze diverse è in grado di trasferire in uscita solo i segnali delle frequenze volute, in pratica seleziona le frequenze che si
TEST DI ELETTROTECNICA - 2
 Zeno Martini (admin) TEST DI ELETTROTECNICA - 2 10 September 2012 Potenza ed energia 1 La potenza elettrica in continua è data da: A - Il rapporto tra la tensione ai capi di un bipolo e l'intensità di
Zeno Martini (admin) TEST DI ELETTROTECNICA - 2 10 September 2012 Potenza ed energia 1 La potenza elettrica in continua è data da: A - Il rapporto tra la tensione ai capi di un bipolo e l'intensità di
Come visto precedentemente l equazione integro differenziale rappresentativa dell equilibrio elettrico di un circuito RLC è la seguente: 1 = (1)
 Transitori Analisi nel dominio del tempo Ricordiamo che si definisce transitorio il periodo di tempo che intercorre nel passaggio, di un sistema, da uno stato energetico ad un altro, non è comunque sempre
Transitori Analisi nel dominio del tempo Ricordiamo che si definisce transitorio il periodo di tempo che intercorre nel passaggio, di un sistema, da uno stato energetico ad un altro, non è comunque sempre
Lez.16 Il metodo simbolico. Università di Napoli Federico II, CdL Ing. Meccanica, A.A , Elettrotecnica. Lezione 16 Pagina 1
 Lez.16 Il metodo simbolico Università di Napoli Federico II, CdL Ing. Meccanica, A.A. 2017-2018, Elettrotecnica. Lezione 16 Pagina 1 Regime sinusoidale Stato di funzionamento di un circuito in cui tutte
Lez.16 Il metodo simbolico Università di Napoli Federico II, CdL Ing. Meccanica, A.A. 2017-2018, Elettrotecnica. Lezione 16 Pagina 1 Regime sinusoidale Stato di funzionamento di un circuito in cui tutte
I j e jarctag. ovvero. ESERCIZIO 7.1: Determinare le espressioni temporali sinusoidali relative alle grandezze rappresentate dai seguenti fasori.
 EEO 7.: Determinare le espressioni temporali sinusoidali relative alle grandezze rappresentate dai seguenti fasori. 0 8e 3+ 4 ( 5 isulta necessario applicare le trasformazioni fra espressione polare ed
EEO 7.: Determinare le espressioni temporali sinusoidali relative alle grandezze rappresentate dai seguenti fasori. 0 8e 3+ 4 ( 5 isulta necessario applicare le trasformazioni fra espressione polare ed
Complementi di Analisi per Informatica *** Capitolo 2. Numeri Complessi. e Circuiti Elettrici
 Complementi di Analisi per nformatica *** Capitolo 2 Numeri Complessi e Circuiti Elettrici Sergio Benenti Prima versione settembre 2013 Revisione settembre 2017? ndice 21 Circuito elettrico elementare
Complementi di Analisi per nformatica *** Capitolo 2 Numeri Complessi e Circuiti Elettrici Sergio Benenti Prima versione settembre 2013 Revisione settembre 2017? ndice 21 Circuito elettrico elementare
cos( ωt + ϕ)= Re v t = V o e jωt cos ωt + ϕ vt ()=V o e jϕ che è un numero complesso costante, di modulo V O ed e jωt = cos ωt + j sinωt
 . METODO SIMBOLIO, O METODO DEI FASORI..Introduzione Questo metodo applicato a reti lineari permanenti consente di determinare la soluzione in regime sinusoidale solamente per quanto attiene il regime
. METODO SIMBOLIO, O METODO DEI FASORI..Introduzione Questo metodo applicato a reti lineari permanenti consente di determinare la soluzione in regime sinusoidale solamente per quanto attiene il regime
Elettrotecnica - A.A Prova n gennaio 2012
 ognome Nome Matricola Firma 1 Parti svolte: E1 E2 D Esercizio 1 V G1 1 2 3 I G6 ri 2 4 7 8 E D Supponendo noti i valori delle resistenze, della tensione V G1, della corrente I G6 e del parametro di trasferimento
ognome Nome Matricola Firma 1 Parti svolte: E1 E2 D Esercizio 1 V G1 1 2 3 I G6 ri 2 4 7 8 E D Supponendo noti i valori delle resistenze, della tensione V G1, della corrente I G6 e del parametro di trasferimento
EdmondDantes. 19 July 2010
 EdmondDantes RISONANZA SERIE 19 July 2010 Introduzione Il fenomeno della risonanza può manifestarsi solo in circuiti che presentano proprietà induttive-capacitive In un circuito esclusivamente ohmico-induttivo
EdmondDantes RISONANZA SERIE 19 July 2010 Introduzione Il fenomeno della risonanza può manifestarsi solo in circuiti che presentano proprietà induttive-capacitive In un circuito esclusivamente ohmico-induttivo
Il trasformatore Principio di funzionamento
 Il trasformatore Principio di funzionamento Il trasformatore è una macchina elettrica statica reversibile, che funziona sul principio della mutua induzione. È formato da un nucleo in lamierino ferromagnetico
Il trasformatore Principio di funzionamento Il trasformatore è una macchina elettrica statica reversibile, che funziona sul principio della mutua induzione. È formato da un nucleo in lamierino ferromagnetico
Università degli Studi di Napoli Federico II
 Università degli Studi di Napoli Federico II Facoltà di Ingegneria Registro delle lezioni del corso di Elettrotecnica per allievi Meccanici dettate da Luigi Verolino, professore ordinario nell Anno Accademico
Università degli Studi di Napoli Federico II Facoltà di Ingegneria Registro delle lezioni del corso di Elettrotecnica per allievi Meccanici dettate da Luigi Verolino, professore ordinario nell Anno Accademico
Corso di Principi di ingegneria elettrica I
 Anno Accad. 2008/2009, II anno: Corso di Laurea in Ingegneria Elettrica Nuovo Ordinamento Corso di Principi di ingegneria elettrica I (prof. G. Rubinacci) Diario delle Lezioni Materiale didattico di riferimento:
Anno Accad. 2008/2009, II anno: Corso di Laurea in Ingegneria Elettrica Nuovo Ordinamento Corso di Principi di ingegneria elettrica I (prof. G. Rubinacci) Diario delle Lezioni Materiale didattico di riferimento:
Tipo 1 - Compiti A01 A04 A07 A10 A13 A16 A19 A22 A25 A28 A31. Esercizio 1. Esercizio 2
 Tipo - Compiti A0 A0 A07 A0 A A6 A9 A A5 A8 A Esercizio Esempio di risoluzione. Scelto come riferimento il nodo C, le incognite sono le tensioni di nodo V A e V D. (La tensione V B = V 6 è nota.). Il sistema
Tipo - Compiti A0 A0 A07 A0 A A6 A9 A A5 A8 A Esercizio Esempio di risoluzione. Scelto come riferimento il nodo C, le incognite sono le tensioni di nodo V A e V D. (La tensione V B = V 6 è nota.). Il sistema
Elettrotecnica - Ing. Aerospaziale, Ing. Meccanica A.A. 2014/15 - Prova n. 2-2 luglio 2015
 ognome Nome Matricola Firma Parti svolte: E E D Esercizio I G 4 gv E 5 D 6 Supponendo noti i parametri dei componenti, illustrare il procedimento di risoluzione del circuito rappresentato in figura con
ognome Nome Matricola Firma Parti svolte: E E D Esercizio I G 4 gv E 5 D 6 Supponendo noti i parametri dei componenti, illustrare il procedimento di risoluzione del circuito rappresentato in figura con
Oscillazioni libere e risonanza di un circuito RLC-serie (Trattazione analitica del circuito RLC-serie)
 III a Esperienza del Laboratorio di Fisica Generale II Oscillazioni libere e risonanza di un circuito LC-serie (Trattazione analitica del circuito LC-serie) Con questa breve nota si vuole fornire la trattazione
III a Esperienza del Laboratorio di Fisica Generale II Oscillazioni libere e risonanza di un circuito LC-serie (Trattazione analitica del circuito LC-serie) Con questa breve nota si vuole fornire la trattazione
 . Applicando la KT al percorso chiuso evidenziato si ricava v v v v4 n Applicando la KC al nodo si ricava: i i i4 i n i i : n i v v v v 4 : n i 4 v v i i.7 Dalla relazione tra le correnti del trasformatore
. Applicando la KT al percorso chiuso evidenziato si ricava v v v v4 n Applicando la KC al nodo si ricava: i i i4 i n i i : n i v v v v 4 : n i 4 v v i i.7 Dalla relazione tra le correnti del trasformatore
Lezione 1 Definizione di circuito, delle grandezze circuitali e classificazione dei bipoli. Lezione n.1
 Lezione n.1 Definizione di circuito, delle grandezze circuitali e classificazione dei bipoli 1. Definizione di circuito elettrico 2. Bipolo e relazione caratteristica di un bipolo 3. Corrente elettrica
Lezione n.1 Definizione di circuito, delle grandezze circuitali e classificazione dei bipoli 1. Definizione di circuito elettrico 2. Bipolo e relazione caratteristica di un bipolo 3. Corrente elettrica
Energia accumulata in un condensatore
 Energia accumulata in un condensatore In base alla seconda legge di Kirchhoff istante per istante avremo Sappiamo che potenza istantanea fornita dal generatore Sostituendo nella eq. diff. e integrando
Energia accumulata in un condensatore In base alla seconda legge di Kirchhoff istante per istante avremo Sappiamo che potenza istantanea fornita dal generatore Sostituendo nella eq. diff. e integrando
Appunti di Elettronica I Lezione 3 Risoluzione dei circuiti elettrici; serie e parallelo di bipoli
 Appunti di Elettronica I Lezione 3 Risoluzione dei circuiti elettrici; serie e parallelo di bipoli Valentino Liberali Dipartimento di Tecnologie dell Informazione Università di Milano, 2603 Crema email:
Appunti di Elettronica I Lezione 3 Risoluzione dei circuiti elettrici; serie e parallelo di bipoli Valentino Liberali Dipartimento di Tecnologie dell Informazione Università di Milano, 2603 Crema email:
ossia può anche essere localizzato univocamente sul piano complesso con la sua forma polare.
 ALGEBRA COMPLESSA Nel corso dei secoli gli insiemi dei numeri sono andati man mano allargandosi per rispondere all esigenza di dare soluzione a equazioni e problemi sempre nuovi I numeri complessi sono
ALGEBRA COMPLESSA Nel corso dei secoli gli insiemi dei numeri sono andati man mano allargandosi per rispondere all esigenza di dare soluzione a equazioni e problemi sempre nuovi I numeri complessi sono
Esercizi sulle reti elettriche in corrente alternata (parte 1)
 Esercizi sulle reti elettriche in corrente alternata (parte ) Esercizio : alcolare l andamento nel tempo delle correnti i, i 2 e i 3 del circuito in figura e verificare il bilancio delle potenze attive
Esercizi sulle reti elettriche in corrente alternata (parte ) Esercizio : alcolare l andamento nel tempo delle correnti i, i 2 e i 3 del circuito in figura e verificare il bilancio delle potenze attive
Liberamente tratto da Prima Legge di Ohm
 Liberamente tratto da www.openfisica.com Prima Legge di Ohm Agli estremi di due componenti elettrici di un circuito (che si possono chiamare conduttore X ed Y) è applicata una differenza di potenziale
Liberamente tratto da www.openfisica.com Prima Legge di Ohm Agli estremi di due componenti elettrici di un circuito (che si possono chiamare conduttore X ed Y) è applicata una differenza di potenziale
Elettronica I Leggi di Kirchhoff; risoluzione dei circuiti elettrici in continua; serie e parallelo
 Elettronica I Leggi di Kirchhoff; risoluzione dei circuiti elettrici in continua; serie e parallelo Valentino Liberali Dipartimento di Tecnologie dell Informazione Università di Milano, 603 Crema email:
Elettronica I Leggi di Kirchhoff; risoluzione dei circuiti elettrici in continua; serie e parallelo Valentino Liberali Dipartimento di Tecnologie dell Informazione Università di Milano, 603 Crema email:
UNIVERSITÀ DEGLI STUDI DI PAVIA Laurea in Ingegneria Elettronica e Informatica
 22.0.206 Problema Con riferimento al circuito in figura, nel quale entrambi gli interruttori si aprono all istante t = 0, determinare l espressione di i(t) (per ogni istante di tempo t) e rappresentarne
22.0.206 Problema Con riferimento al circuito in figura, nel quale entrambi gli interruttori si aprono all istante t = 0, determinare l espressione di i(t) (per ogni istante di tempo t) e rappresentarne
Il modello circuitale. Università di Napoli Federico II, CdL Ing. Meccanica, A.A , Elettrotecnica. Lezione 6 Pagina 1
 Lez.6 Il modello circuitale Università di Napoli Federico II, CdL Ing. Meccanica, A.A. 2017-2018, Elettrotecnica. Lezione 6 Pagina 1 Legge di Kirchhoff Legge di Kirchhoff delle correnti per gli insiemi
Lez.6 Il modello circuitale Università di Napoli Federico II, CdL Ing. Meccanica, A.A. 2017-2018, Elettrotecnica. Lezione 6 Pagina 1 Legge di Kirchhoff Legge di Kirchhoff delle correnti per gli insiemi
Consideriamo ora circuiti in cui siano presenti più componenti. Circuito ohmico-induttivo R-L con resistenza e reattanza in serie.
 Circuiti RC ed RL Consideriamo ora circuiti in cui siano presenti più componenti. Circuito ohmico-induttivo R-L con resistenza e reattanza in serie. Figura A In figura vi è lo schema riferito ad un generatore
Circuiti RC ed RL Consideriamo ora circuiti in cui siano presenti più componenti. Circuito ohmico-induttivo R-L con resistenza e reattanza in serie. Figura A In figura vi è lo schema riferito ad un generatore
Trasformatore reale monofase
 Macchine elettriche parte Trasformatore reale monofase ei paragrafi precedenti si è ricavato il circuito equivalente del trasformatore ideale, si è anche visto che la corrente di primario (corrente di
Macchine elettriche parte Trasformatore reale monofase ei paragrafi precedenti si è ricavato il circuito equivalente del trasformatore ideale, si è anche visto che la corrente di primario (corrente di
CIRCUITI IN REGIME SINUSOIDALE
 IUITI IN EGIME SINUSOIDALE 9.1. Nel circuito della figura il voltaggio alternato è V = V 0 cost con = 314 rad/s, V 0 = 311 V, L = 0.9 H, = 6.96 F. Se il fattore di potenza del circuito è pari a 0.98, la
IUITI IN EGIME SINUSOIDALE 9.1. Nel circuito della figura il voltaggio alternato è V = V 0 cost con = 314 rad/s, V 0 = 311 V, L = 0.9 H, = 6.96 F. Se il fattore di potenza del circuito è pari a 0.98, la
 Trasformatore monofase Da un punto di vista di trasformazioni di energia, si tratta di una macchina elettrica in grado di trasformare energia elettrica in altra energia elettrica. Il suo funzionamento
Trasformatore monofase Da un punto di vista di trasformazioni di energia, si tratta di una macchina elettrica in grado di trasformare energia elettrica in altra energia elettrica. Il suo funzionamento
L INDUZIONE ELETTROMAGNETICA. V Scientifico Prof.ssa Delfino M. G.
 L INDUZIONE ELETTROMAGNETICA V Scientifico Prof.ssa Delfino M. G. INDUZIONE E ONDE ELETTROMAGNETICHE 1. Il flusso del vettore B 2. La legge di Faraday-Neumann-Lenz 3. Induttanza e autoinduzione 4. I circuiti
L INDUZIONE ELETTROMAGNETICA V Scientifico Prof.ssa Delfino M. G. INDUZIONE E ONDE ELETTROMAGNETICHE 1. Il flusso del vettore B 2. La legge di Faraday-Neumann-Lenz 3. Induttanza e autoinduzione 4. I circuiti
CORRENTI ALTERNATE. Dopo che la spira è ruotata di in certo angolo in un tempo t si ha
 1 easy matematica CORRENI ALERNAE Consideriamo una bobina ruotante, con velocità angolare ω costante all'interno di un campo magnetico uniforme B. Gli estremi della spira sono collegati a due anelli chiamati
1 easy matematica CORRENI ALERNAE Consideriamo una bobina ruotante, con velocità angolare ω costante all'interno di un campo magnetico uniforme B. Gli estremi della spira sono collegati a due anelli chiamati
TRASFORMATORE. Struttura generale dei trasformatori
 TRASFORMATORE Il trasformatore è una macchina elettrica statica(priva di parti in movimento), trasforma l energia elettrica che riceve dalla rete di alimentazione ancora in energia elettrica data al carico,
TRASFORMATORE Il trasformatore è una macchina elettrica statica(priva di parti in movimento), trasforma l energia elettrica che riceve dalla rete di alimentazione ancora in energia elettrica data al carico,
TRASFORMATE DI LAPLACE
 CONTROLLI AUTOMATICI Ingegneria Gestionale http://www.automazione.ingre.unimore.it/pages/corsi/controlliautomaticigestionale.htm TRASFORMATE DI LAPLACE Ing. Federica Grossi Tel. 059 2056333 e-mail: federica.grossi@unimore.it
CONTROLLI AUTOMATICI Ingegneria Gestionale http://www.automazione.ingre.unimore.it/pages/corsi/controlliautomaticigestionale.htm TRASFORMATE DI LAPLACE Ing. Federica Grossi Tel. 059 2056333 e-mail: federica.grossi@unimore.it
Corso di Sistemi Prof. Aniello Celentano anno scolastico 2015/2016 ITIS G. Ferraris (NA)
 I Numeri complessi I numeri complessi sono costituiti da una coppia di numeri reali (a,b). Il numero reale a è la parte reale, mentre b è la parte immaginaria. La parte immaginaria è sempre accompagnata
I Numeri complessi I numeri complessi sono costituiti da una coppia di numeri reali (a,b). Il numero reale a è la parte reale, mentre b è la parte immaginaria. La parte immaginaria è sempre accompagnata
Corso di LABORATORIO DI ELETTROMAGNETISMO E CIRCUITI A.A. 2013/2014 Prof. A. Di Domenico. Bibliografia dettagliata degli argomenti svolti a lezione
 Corso di LABORATORIO DI ELETTROMAGNETISMO E CIRCUITI A.A. 2013/2014 Prof. A. Di Domenico Bibliografia dettagliata degli argomenti svolti a lezione MS : C. Mencuccini, V. Silvestrini, Fisica II, ed. Liguori
Corso di LABORATORIO DI ELETTROMAGNETISMO E CIRCUITI A.A. 2013/2014 Prof. A. Di Domenico Bibliografia dettagliata degli argomenti svolti a lezione MS : C. Mencuccini, V. Silvestrini, Fisica II, ed. Liguori
Università degli studi di Bergamo Facoltà di Ingegneria Corso di Elettrotecnica A.A /2002 Mancini Fabio mtr: 30739
 Università degli studi di Bergamo Facoltà di Ingegneria Corso di Elettrotecnica A.A.. 2001/2002 Mancini Fabio mtr: 30739 1 Es. 4 Prova scritta del 04 luglio 1996. Determinare la corrente funzione del tempo
Università degli studi di Bergamo Facoltà di Ingegneria Corso di Elettrotecnica A.A.. 2001/2002 Mancini Fabio mtr: 30739 1 Es. 4 Prova scritta del 04 luglio 1996. Determinare la corrente funzione del tempo
Corso di Elettrotecnica 1 - Cod N Diploma Universitario Teledidattico in Ingegneria Informatica ed Automatica Polo Tecnologico di Alessandria
 Schede di Elettrotecnica orso di Elettrotecnica - od. 900 N Diploma Universitario Teledidattico in ngegneria nformatica ed utomatica olo Tecnologico di lessandria cura di uca FES Scheda N 0 ircuiti in
Schede di Elettrotecnica orso di Elettrotecnica - od. 900 N Diploma Universitario Teledidattico in ngegneria nformatica ed utomatica olo Tecnologico di lessandria cura di uca FES Scheda N 0 ircuiti in
Onde. Antonio Pierro. Per consigli, suggerimenti, eventuali errori o altro potete scrivere una a antonio.pierro[at]gmail.com
![Onde. Antonio Pierro. Per consigli, suggerimenti, eventuali errori o altro potete scrivere una a antonio.pierro[at]gmail.com Onde. Antonio Pierro. Per consigli, suggerimenti, eventuali errori o altro potete scrivere una a antonio.pierro[at]gmail.com](/thumbs/67/56787927.jpg) Onde Video Introduzione Onde trasversali e onde longitudinali. Lunghezza d'onda e frequenza. Interferenza fra onde. Battimenti. Moto armonico smorzato e forzato Antonio Pierro Per consigli, suggerimenti,
Onde Video Introduzione Onde trasversali e onde longitudinali. Lunghezza d'onda e frequenza. Interferenza fra onde. Battimenti. Moto armonico smorzato e forzato Antonio Pierro Per consigli, suggerimenti,
UNIVERSITÀ DEGLISTUDIDIPAVIA Laurea in Ingegneria Elettronica e Informatica
 7.09.0 Problema L interruttore indicato nel circuito in figura commuta nell istante t 0 dalla posizione AA alla posizione BB. Determinare le espressioni delle tensioni v (t) ev (t) per ogni istante di
7.09.0 Problema L interruttore indicato nel circuito in figura commuta nell istante t 0 dalla posizione AA alla posizione BB. Determinare le espressioni delle tensioni v (t) ev (t) per ogni istante di
Equazioni differenziali lineari a coefficienti costanti
 Equazioni differenziali lineari a coefficienti costanti Generalità Il modello matematico di un qualsiasi sistema fisico in regime variabile conduce alla scrittura di una o più equazioni differenziali.
Equazioni differenziali lineari a coefficienti costanti Generalità Il modello matematico di un qualsiasi sistema fisico in regime variabile conduce alla scrittura di una o più equazioni differenziali.
RETI IN REGIME SINUSOIDALE #1
 Roronoa Lillo (lillo) RETI IN REGIME SINUSOIDALE #1 6 November 2012 Introduzione Una domanda, che, chi è alle prime esperienze di studi elettrotecnici, si pone, è l'utilità della corrente o della tensione
Roronoa Lillo (lillo) RETI IN REGIME SINUSOIDALE #1 6 November 2012 Introduzione Una domanda, che, chi è alle prime esperienze di studi elettrotecnici, si pone, è l'utilità della corrente o della tensione
68 Luciano De Menna Corso di Elettrotecnica. Metodi sistematici per la risoluzione delle reti
 68 Luciano De Menna Corso di Elettrotecnica Metodi sistematici per la risoluzione delle reti La scrittura delle equazioni risolventi per una rete di bipoli attivi e passivi può essere resa automatica e
68 Luciano De Menna Corso di Elettrotecnica Metodi sistematici per la risoluzione delle reti La scrittura delle equazioni risolventi per una rete di bipoli attivi e passivi può essere resa automatica e
CIRCUITI IN ALTERNATA
 CIRCUITI IN ALTERNATA I primi impianti di illuminazione pubblica sorti fra fine 700 e inizio 800 erano in corrente continua. La limitazione principale dell uso di questi impianti era la breve distanza
CIRCUITI IN ALTERNATA I primi impianti di illuminazione pubblica sorti fra fine 700 e inizio 800 erano in corrente continua. La limitazione principale dell uso di questi impianti era la breve distanza
Analisi in regime sinusoidale (parte II)
 Appunti di lettrotecnica Analisi in regime sinusoidale (parte ) Analisi di circuiti elementari in regime sinusoidale... ntroduzione... esistore a terminali... nduttore a terminali...3 ondensatore a terminali...5
Appunti di lettrotecnica Analisi in regime sinusoidale (parte ) Analisi di circuiti elementari in regime sinusoidale... ntroduzione... esistore a terminali... nduttore a terminali...3 ondensatore a terminali...5
INDUZIONE E AUTOINDUZIONE
 E possibile avere un effetto analogo anche in un singolo circuito Un circuito percorso da una corrente variabile può indurre una f.e.m., e quindi una corrente indotta su se stesso, in questo caso il fenomeno
E possibile avere un effetto analogo anche in un singolo circuito Un circuito percorso da una corrente variabile può indurre una f.e.m., e quindi una corrente indotta su se stesso, in questo caso il fenomeno
Appendice Il trasformatore monofase
 Appendice l trasformatore monofase - Appendice l trasformatore monofase - Principio di funzionamento Schema generale l trasformatore è un dispositivo costituito da un nucleo in materiale ferromagnetico
Appendice l trasformatore monofase - Appendice l trasformatore monofase - Principio di funzionamento Schema generale l trasformatore è un dispositivo costituito da un nucleo in materiale ferromagnetico
Esercizi sulle reti elettriche in corrente alternata (parte 2)
 Esercizi sulle reti elettriche in corrente alternata (parte 2) Esercizio 7: Verificare il bilancio delle potenze. Nota. l ramo costituito dal generatore di corrente in serie al resistore ha come caratteristica
Esercizi sulle reti elettriche in corrente alternata (parte 2) Esercizio 7: Verificare il bilancio delle potenze. Nota. l ramo costituito dal generatore di corrente in serie al resistore ha come caratteristica
