Lezione 13. Circuito R L C in evoluzione forzata. Circuito R L C in evoluzione forzata. ( t) = k 1 ( ) + E. Es. II.4, II.5, II.6. + v L.
|
|
|
- Fabiola Maggio
- 5 anni fa
- Visualizzazioni
Transcript
1 ezione 13 Circuito C in evoluzione forzata E i C v + v C + = E v v C C dv C dt + v C + C d 2 v C dt 2 = di dt = E d 2 v C dt 2 + i = C dv C dt dv C dt v = i + v C C = E C Passiamo ora ad esaminare il caso del circuito C serie in presenza di un forzamento costante. È facile ricavare l'equazione nella incognita v C. Anche in questo caso essendo l'integrale generale della omogenea associata già noto, occorrerà determinare soltanto la soluzione particolare. Essendo il forzamento costante, è possibile utilizzare la stessa tecnica usata per l'equazione del primo ordine: si assume che la soluzione particolare sia una costante e si ricava immediatamente che v Cp = E 0. Si noti che in questo modo si è automaticamente scelto come soluzione particolare quella di regime. Utilizzeremo questa tecnica in seguito anche quando il forzamento non è più costante nel tempo; naturalmente la soluzione di regime non potrà essere costante ma dovrà ricalcare l'andamento del forzamento. E i C d v v C Circuito C in evoluzione forzata 2 v C dt 2 + v Cr = E dv C dt + v C C = E C Come nel caso dell'evoluzione libera avremo i tre casi possibili: aperiodico, o smorzato, o sopracritico - critico e oscillatorio, o subcritico. Evidentemente, le costanti k 1, k 2, k e ϕ sono da determinarsi utilizzando le condizioni iniziali. v C v C v C ( t) = k 1 e α1t + k 2 e α2t + E ( t) = k 1 e αt + k 2 te αt + E ( t) = ke αt sen βt +φ ( ) + E Es. II.4, II.5, II.6
2 e(t) Generatori non costanti t Fino a questo punto abbiamo preso in considerazione esclusivamente generatori di tensione e di corrente costanti. Essendo ora il nostro modello in grado di descrivere anche regimi dinamici, possiamo prendere in considerazione anche generatori di tensione e di corrente variabili nel tempo. Si tratterà sempre di generatori ideali nel senso che si assume che l'andamento nel tempo della grandezza erogata non dipenda in alcun modo dalle condizioni in cui il generatore lavora. Generatori ideali di tensione a forma d'onda della tensione non dipende dalla corrente! Generatori ideali di corrente a forma d'onda della corrente non dipende dalla tensione!
3 Generatori ideali di corrente a forma d'onda della corrente non dipende dalla tensione ai morsetti! In un primo momento limiteremo la nostra attenzione ai generatori in grado di fornire forme d'onda periodiche, ed in particolare sinusoidali. I motivi per questa scelta sono diversi e proveremo ad illustrarne alcuni brevemente più avanti. Generatori periodici Forma d'onda Per ora ricordiamo qualche definizione che ci sarà necessaria nel seguito. Una variazione temporale che si ripeta identicamente dopo un certo intervallo di tempo viene detta periodica; l'intervallo viene detto periodo della grandezza periodica. Nel periodo la funzione periodica a(t) assumerà un massimo che indicheremo con il simbolo A M. Generatori non costanti Valor medio diverso da zero Definiremo ancora, per a(t), il valore medio in un periodo. In generale il valor medio di una funzione periodica non è nullo: l'area sottesa dalla funzione nella sua parte positiva non è eguale alla corrispondente area della sua parte negativa. A m = 1 a(t) dt 0 0
4 Generatori non costanti a condizione di valor medio nullo individua una particolare classe di funzioni periodiche. Valor medio nullo A m = 1 0 a(t) d Generatori non costanti Per esse potrà essere utile a volte definire il valor medio in un semiperiodo. Valor medio in mezzo periodo diverso da zero /2 A m(/2) = /2 2 a(t) dt 0 0 Generatori non costanti Valore efficace Più interessante è in questi casi il valore efficace definito come la radice quadrata del valore quadratico medio. A = 1 a 2 (t) dt 0
5 Generatori sinusoidali Particolari funzioni periodiche a valor medio nullo sono le ben note funzioni sinusoidali e cosinusoidali: a(t) ω = 2π a( t) = A M sen( ωt +ϕ) t a(t) Generatori sinusoidali ω = 2π a( t) = A M sen( ωt +ϕ) È facile verificare che il valore efficace di una grandezza sinusoidale è pari al suo valor massimo diviso la radice di 2 e che il suo valor medio in un semiperiodo è pari al valor massimo moltiplicato per 2/π. 'argomento della funzione sinusoidale viene detto fase istantanea della funzione stessa mentre ϕ prende il nome di fase iniziale. A m = 0 A m(/2) = 2 A M π t A = A M 2 Perchè generatori sinusoidali? Serie di Fourier a t A 0 = J. B. Fourier ( ) + B n cos( ωt +ϕ) ( ) = A 0 + A n sen( ωt +ϕ) n=1 0 a( t)dt n=1 ω = 2π/ Per le funzione periodiche si può dimostrare un importante proprietà che prende il nome di sviluppo in serie di Fourier. ale proprietà consente di porre una qualsiasi funzione periodica a(t) come somma di infiniti termini del tipo A n sin(nωt) ed B n cos(nωt), con n intero ed ω = 2π/ = frequenza angolare, o spesso, per brevità, solo frequenza. In realtà si preferisce conservare al termine frequenza il significato di inverso del periodo per cui f=1/=ω/2π; da cui il nome di frequenza angolare per ω. Dalla formula dello sviluppo di Fourier si può facilmente calcolare che Il coefficiente A 0 è il valore medio della grandezza periodica.
6 Perchè generatori sinusoidali? E che i coefficienti A n e B n sono, rispettivamente, le medie pesate secondo le funzioni seno e coseno della funzione periodica da sviluppare. Serie di Fourier ω = 2π/ a t + B n cos( ωt +ϕ) ( ) = A 0 + A n sen( ωt +ϕ) n=1 n=1 A n = 2 0 a( t)sennωt dt B n = 2 0 a( t)cosnωt dt Serie di Fourier Un esempio ( ) = 4 π a t Onda quadra n=0 sen ( 2n +1)ωt 2n +1 Per la funzione rettangolare mostrata in figura, per esempio, lo sviluppo in serie è quello mostrato, come si può verificare con una semplice simulazione. Se siamo in regime lineare, se cioè è valido il principio di sovrapposizione degli effetti, una volta noto il comportamento di un sistema quando in esso tutte le grandezze variano con legge sinusoidale, è possibile ricavare il comportamento del sistema, utilizzando appunto la sovrapposizione degli effetti, in condizioni di variabilità temporale diverse. Fourier e( t) = dφ dt I generatori ω α S Φ( t) = BS cosα α = ωt B e( t) = BSωsenωt = E M senωt Un altro motivo che ci spinge a focalizzare la nostra attenzione sui generatori ideali di tipo sinusoidale, altrettanto importante, è, potremmo dire, di carattere essenzialmente pratico. Infatti sarebbe facile far vedere, utilizzando la legge di Faraday-Neumann, che il modo più naturale, in linea di principio, per costruire un generatore di f.e.m. è quello di far ruotare una spira conduttrice in un campo magnetico. Se il campo è uniforme, e la velocità angolare di rotazione della spira è costante, la forza elettromotrice che ne scaturisce è di forma d'onda sinusoidale. Naturalmente, le cose sono molto più complesse di quanto una descrizione così sintetica possa far immaginare; ma, al fondo, è questo uno dei principali motivi per cui la produzione della energia elettrica si realizza in regime sinusoidale.
7 i con forzamento sinusoidale e( t) = E M sen( ωt + η) di dt + i = e t ( ) i( t) = ke t + i r ( t) Consideriamo, per esempio, il circuito serie che abbiamo già preso in considerazione, e supponiamo che esso sia alimentato da un generatore di tensione sinusoidale e(t)= E M sen (ωt + η). È necessario assumere una fase iniziale η 0 in quanto l origine dei tempi è già stata fissata quando si è assunto che l'interruttore viene chiuso a t=0. È facile scrivere l equazione che esprime la K all'unica maglia presente. e(t) i r ( t) =? Es. III.1 i con forzamento sinusoidale e(t) e( t) = E M sen( ωt + η) i t ( ) di dt + i = e t ω I M sen ωt + η ϕ + π 2 + I M sen ωt + η ϕ ( ) = ( ) = ke t + i r ( t) i r = I M sen( ωt + η ϕ) E M sen ( ωt + η ) a soluzione dell omogenea - t/ associata sarà ancora del tipo ke, ma non possiamo più supporre che la soluzione particolare sia costante, in quanto il forzamento non è costante. Possiamo, però, utilizzare lo stesso modo di ragionare che ci ha portato a trovare la soluzione particolare quando il generatore di tensione era costante. In fondo nel caso del forzamento costante abbiamo cercato una soluzione particolare che avesse le stesse caratteristiche del forzamento, e cioè costante. Nel caso del forzamento sinusoidale possiamo cercare una soluzione particolare che sia dello stesso tipo, cioè sinusoidale. con forzamento sinusoidale Ben note formule trigonometriche (FOMUA DE ANGOO AGGIUNO) ci permettono di scrivere relazioni i i( t) = ke t + i r ( t) i r = I M sen( ωt + η ϕ) e(t) ω I sen ωt + η ϕ + π M 2 + I M sen ωt + η ϕ ( ) = A M sen( ωt + α ) + B M sen( ωt + β ) = C M sen( ωt + γ ) E M sen ( ωt + η )
8 con forzamento sinusoidale che ci consentono i ω I M sen ωt + η ϕ + π I M sen( ωt + η ϕ) = e(t) = E M sen ( ωt + η ) ( ) + B M sen( ωt + β ) = C M sen( ωt + γ ) ( ) A M sen ωt + α C M 2 = A M 2 + B M 2 + 2A M B M cos α β A γ = arctg M senα + B M senβ A M cosα + B M cosβ con forzamento sinusoidale di ottenere agevolmente la soluzione. ω I M sen ωt + η ϕ + π 2 + I M sen ωt + η ϕ ( ) + B M sen( ωt + β ) = C M sen( ωt + γ ) A M sen ωt + α C 2 M = A 2 M + B 2 M + 2A M B M cos( α β ) A γ = arctg M senα + B M senβ A M cosα + B M cosβ I M = E M ϕ = arctg ω ( ) ω ( ) == E M i sen ( ωt + η ) e(t) i con forzamento sinusoidale e(t) ( ) = E M sen( ωt + η) e t ( ) di dt + i = e t I M = i( t) = ke t + I M sen( ωt + η ϕ) i( 0) = k + I M sen( η ϕ) = I 0 E M ϕ = arctg ω ( ) ω Es. III.1 A questo punto si determina il valore della costante di integrazione imponendo la condizione iniziale. a soluzione trovata è ancora una volta somma di un termine che tende a zero ed un termine che, invece, si ripete periodicamente senza mai scomparire: la soluzione a regime permanente. A questo punto ci appare logico interpretare anche il regime stazionario, da cui abbiamo preso le mosse, come un regime permanente in cui i generatori, stazionari appunto, abbiano preso il sopravvento, e si sia persa traccia di un termine transitorio ormai estintosi nel tempo. esta il fatto che il calcolo della soluzione permanente in regime sinusoidale è più complicato sul piano operativo.
9 Corrispondenza biunivoca a(t) A Devono essere conservate alcune operazioni Siamo dunque alla ricerca di una tecnica che ci consenta di semplificare le operazioni sulle grandezze sinusoidali. Osserviamo che nelle equazioni relative alla KC ed alla K intervengono essenzialmente le seguenti operazioni: a) moltiplicazione per una costante, come nella caratteristica di un resistore, b) somma, come nella somma dei vari termini in una equazione, c) derivata, come nelle caratteristiche di induttori e condensatori. Immaginiamo ora di trovare un insieme di grandezze, che chiameremo insieme delle Ᾱ - mentre chiameremo "a" l'insieme delle funzioni sinusoidali di pulsazione ω - e supponiamo che esista una corrispondenza biunivoca che metta in relazione ogni elemento di a con uno di Ᾱ. Supponiamo anche che tale corrispondenza conservi le operazioni che abbiamo in precedenza elencato. Moltiplicazione per una costante Somma Derivazione a(t) A a + b = c A B = C Con questa affermazione intendiamo che se il risultato di una determinata operazione - per esempio la somma - fatta su elementi di "a" è un certo elemento c, allora il risultato della operazione corrispondente - simbolo - fatta sugli elementi corrispondenti di Ᾱ fornisce proprio l elemento di Ᾱ associato a c. Dunque, se esiste un tale insieme ed una tale applicazione, e se operare su Ᾱ risulta più agevole che operare su "a", si potrà in ogni caso trasformare tutte le grandezze di "a" nelle corrispondenti di Ᾱ, operare su queste e, una volta ottenuto il risultato, ritornare in "a" mediante l'applicazione inversa.
10 a(t) A A M ;ω; α A ;ω; α Orbene, facciamo vedere che l insieme di tutte le j(ωt+α) funzioni complesse di variabile reale del tipo Ae è un possibile candidato insieme Ᾱ. Infatti, dato che ogni elemento di "a" del tipo a(t) = A M sen (ωt + α) dipende da tre parametri, e precisamente A M, ω ed α, e che lo stesso accade per j(ωt+α) ogni elemento di Ᾱ (perché Ᾱ = Ae ), è evidente che tra gli insiemi "a" e Ᾱ descritti esiste una corrispondenza biunivoca se ad ogni valore A M facciamo corrispondere un opportuno valore A. Naturalmente la scelta più immediata sarebbe di porre A = A M. Per motivi che saranno chiari in seguito, si preferisce porre A = A M / 2, cioè pari al valore efficace della corrispondente grandezza sinusoidale invece che al suo valore massimo. a(t) A A ;ω; α Notiamo che, per la formula di Eulero, si può affermare che l'applicazione introdotta fa corrispondere ad ogni elemento di Ᾱ un elemento di "a" che, a meno del fattore 2, coincide con il coefficiente della parte immaginaria di Ᾱ. Che una tale applicazione conservi le operazioni che abbiamo elencato in precedenza, è cosa semplice da dimostrare. A = Ae j( ωt+α ) A = Ae j( ωt+α ) = Acos( ωt + α ) + jasen( ωt + α ) Per quanto riguarda la moltiplicazione per una costante, il fatto è di per sé evidente. A = Ae j( ωt+α ) = Acos( ωt + α ) + jasen( ωt + α ) Moltiplicazione per una costante A = Ae j( ωt+α ) = Acos( ωt + α ) + jasen( ωt + α )
11 Come pure per la somma. A = Ae j( ωt+α ) = Acos( ωt + α ) + jasen( ωt + α ) Somma a(t) + B(t) = A M sen( ωt + α ) + B M sen( ωt + β ) Ae j( ωt+α ) + Be j( ωt+β ) = Acos( ωt + α ) + Bcos( ωt + β ) + + j( Asen( ωt + α ) + Bsen( ωt + β )) Ma anche per quel che riguarda l'operazione di derivazione la corrispondenza si mantiene. A = Ae j( ωt+α ) = Acos( ωt + α ) + jasen( ωt + α ) Derivazione d dt A M sen(ωt + α ) = ω A M cos ωt + α ( ) d dt Ae j ωt+α ( ) = ω Asen ωt + α ( ) + jω Acos ωt + α ( ) A = Ae j( ωt+α ) = Acos( ωt + α ) + jasen( ωt + α ) a moltiplicazione tra due grandezze del tipo a(t) non si conserva! Ae j( ωt+α ) Be j( ωt+β ) = Acos( ωt + α )Bcos( ωt + β ) + Asen( ωt + α )Bsen ωt + β j Acos( ωt + α )Bsen ωt + α ( ) + ( ) + Bcos( ωt + α )Asen( ωt + α ) Notiamo che, invece, la moltiplicazione tra due elementi di Ᾱ, non si conserva. In conclusione in regime sinusoidale si può così operare: in primo luogo si trasformano tutte le grandezze - tensioni e correnti che variano con legge sinusoidale - nelle corrispondenti j(ωt+α) funzioni complesse del tipo Ae ; d'ora in poi useremo il termine fasori per tali grandezze e conserveremo il simbolo Ᾱ per indicarle.
12 In conclusione A = Ae j( ωt+α ) = Acos( ωt + α ) + jasen( ωt + α ) Dalle grandezze sinusoidali si passa ai fasori Si opera nel dominio dei fasori Si ritorna alle grandezze sinusoidali A + a( t) Successivamente si scrivono le equazioni che rappresentano le condizioni imposte dalla KC e dalla K, tenendo conto delle caratteristiche dei singoli bipoli - espresse in termini di fasori - e ricordando che ogni operazione di derivazione equivale ad una moltiplicazione per jω. Così facendo le equazioni differenziali si trasformano in equazioni algebriche ed è, dunque, semplice risolverle, ricavando i fasori rappresentativi delle grandezze incognite. A questo punto si può ritornare alle funzioni sinusoidali e determinare le grandezze incognite nel dominio del tempo. Val a pena di osservare che non ha senso compiere operazioni che coinvolgano elementi di a e di Ᾱ. iepilogo della ezione a soluzione particolare o di regime e l'integrale completo;. Circuito C con gen. costante ; Circuito C con gen. costante ; Generatori variabili; Forme d onda periodiche; Perché il regime sinusoidale? Il circuito con un generatore sinusoidale; Metodo simbolico
Luciano De Menna Corso di Elettrotecnica 153
 Luciano De Menna Corso di Elettrotecnica 153 Per le funzione periodiche si può dimostrare una importante proprietà che prende il nome di sviluppo in serie di Fourier. ale proprietà consente di porre una
Luciano De Menna Corso di Elettrotecnica 153 Per le funzione periodiche si può dimostrare una importante proprietà che prende il nome di sviluppo in serie di Fourier. ale proprietà consente di porre una
I bipoli in regime dinamico: bipoli attivi.
 Luciano De Menna Corso di Elettrotecnica 145 I bipoli in regime dinamico: bipoli attivi. I circuiti in regime dinamico che abbiamo fino ad ora studiato contenevano esclusivamente bipoli passivi. La dinamica
Luciano De Menna Corso di Elettrotecnica 145 I bipoli in regime dinamico: bipoli attivi. I circuiti in regime dinamico che abbiamo fino ad ora studiato contenevano esclusivamente bipoli passivi. La dinamica
Lezione 14. Vettori rotanti. RL con forzamento sinusoidale. e( t) = E M. i( t) = ke R L t + I M. e(t) E = RI + jω LI. E ( ) 2 ; η arctg ω L
 ezione 4 ( A) A Vettori rotanti ( A) Piano di Gauss A = Ae j( ωt+α ) = Acos( ωt + α ) + jasen( ωt + α ) Prima di procedere oltre, facciamo vedere perché il termine fasori. a parte reale ed il coefficiente
ezione 4 ( A) A Vettori rotanti ( A) Piano di Gauss A = Ae j( ωt+α ) = Acos( ωt + α ) + jasen( ωt + α ) Prima di procedere oltre, facciamo vedere perché il termine fasori. a parte reale ed il coefficiente
Capitolo VIII Dinamica dei circuiti di ordine superior e
 Capitolo VIII Dinamica dei circuiti di ordine superior e Nei capitoli precedenti abbiamo già esaminato, partendo da alcuni classici esempi, gli aspetti salienti della soluzione di una rete elettrica in
Capitolo VIII Dinamica dei circuiti di ordine superior e Nei capitoli precedenti abbiamo già esaminato, partendo da alcuni classici esempi, gli aspetti salienti della soluzione di una rete elettrica in
Lez.16 Il metodo simbolico. Università di Napoli Federico II, CdL Ing. Meccanica, A.A , Elettrotecnica. Lezione 16 Pagina 1
 Lez.16 Il metodo simbolico Università di Napoli Federico II, CdL Ing. Meccanica, A.A. 2017-2018, Elettrotecnica. Lezione 16 Pagina 1 Regime sinusoidale Stato di funzionamento di un circuito in cui tutte
Lez.16 Il metodo simbolico Università di Napoli Federico II, CdL Ing. Meccanica, A.A. 2017-2018, Elettrotecnica. Lezione 16 Pagina 1 Regime sinusoidale Stato di funzionamento di un circuito in cui tutte
Capitolo VI. I regimi sinusoidali
 Capitolo VI I regimi sinusoidali Siamo dunque alla ricerca di una tecnica che ci consenta di semplificare le operazioni sulle grandezze sinusoidali. Osserviamo che nelle equazioni relative alla LKC ed
Capitolo VI I regimi sinusoidali Siamo dunque alla ricerca di una tecnica che ci consenta di semplificare le operazioni sulle grandezze sinusoidali. Osserviamo che nelle equazioni relative alla LKC ed
( ) ( t) Lezione 15. Teorema di Tellegen. Potenza in regime sinusoidale ( ) ( ) = 0. i k P = V I
 ezion5 Anche in regime sinusoidale, naturalmente, il prodotto vi della tensione ai morsetti di un bipolo e della corrente che lo attraversa rappresenta, istante per istante, la potenza assorbita dal bipolo
ezion5 Anche in regime sinusoidale, naturalmente, il prodotto vi della tensione ai morsetti di un bipolo e della corrente che lo attraversa rappresenta, istante per istante, la potenza assorbita dal bipolo
Lez.21 Circuiti dinamici di ordine due. 1. Università di Napoli Federico II, CdL Ing. Meccanica, A.A , Elettrotecnica. Lezione 21 Pagina 1
 Lez.21 Circuiti dinamici di ordine due. 1 Università di Napoli Federico II, CdL Ing. Meccanica, A.A. 2017-2018, Elettrotecnica. Lezione 21 Pagina 1 Circuito RLC serie All istante t=0 inseriamo il generatore
Lez.21 Circuiti dinamici di ordine due. 1 Università di Napoli Federico II, CdL Ing. Meccanica, A.A. 2017-2018, Elettrotecnica. Lezione 21 Pagina 1 Circuito RLC serie All istante t=0 inseriamo il generatore
La corrente alternata
 La corrente alternata Corrente continua e corrente alternata Le correnti continue sono dovute ad un generatore i cui poli hanno sempre lo stesso segno e pertanto esse percorrono un circuito sempre nello
La corrente alternata Corrente continua e corrente alternata Le correnti continue sono dovute ad un generatore i cui poli hanno sempre lo stesso segno e pertanto esse percorrono un circuito sempre nello
Transitori del secondo ordine
 Università di Ferrara Corso di Teoria dei circuiti Transitori del secondo ordine Si consideri il circuito in figura e si supponga che all istante la corrente della serie e la tensione sul condensatore
Università di Ferrara Corso di Teoria dei circuiti Transitori del secondo ordine Si consideri il circuito in figura e si supponga che all istante la corrente della serie e la tensione sul condensatore
Onde. Antonio Pierro. Per consigli, suggerimenti, eventuali errori o altro potete scrivere una a antonio.pierro[at]gmail.com
![Onde. Antonio Pierro. Per consigli, suggerimenti, eventuali errori o altro potete scrivere una a antonio.pierro[at]gmail.com Onde. Antonio Pierro. Per consigli, suggerimenti, eventuali errori o altro potete scrivere una a antonio.pierro[at]gmail.com](/thumbs/67/56787927.jpg) Onde Video Introduzione Onde trasversali e onde longitudinali. Lunghezza d'onda e frequenza. Interferenza fra onde. Battimenti. Moto armonico smorzato e forzato Antonio Pierro Per consigli, suggerimenti,
Onde Video Introduzione Onde trasversali e onde longitudinali. Lunghezza d'onda e frequenza. Interferenza fra onde. Battimenti. Moto armonico smorzato e forzato Antonio Pierro Per consigli, suggerimenti,
cos( ωt + ϕ)= Re v t = V o e jωt cos ωt + ϕ vt ()=V o e jϕ che è un numero complesso costante, di modulo V O ed e jωt = cos ωt + j sinωt
 . METODO SIMBOLIO, O METODO DEI FASORI..Introduzione Questo metodo applicato a reti lineari permanenti consente di determinare la soluzione in regime sinusoidale solamente per quanto attiene il regime
. METODO SIMBOLIO, O METODO DEI FASORI..Introduzione Questo metodo applicato a reti lineari permanenti consente di determinare la soluzione in regime sinusoidale solamente per quanto attiene il regime
9.8 Con la LKT si scrive l equazione seguente: di (1) dt La costante di tempo èτ
 9.8 Con la LKT si scrive l equazione seguente: di L Ri cos( t) () dt La costante di tempo èτ L / R ms / 5s ; la soluzione della () è 5t i( t) Ke Acos(t θ ) () Sia A θ il fasore corrispondente alla risposta
9.8 Con la LKT si scrive l equazione seguente: di L Ri cos( t) () dt La costante di tempo èτ L / R ms / 5s ; la soluzione della () è 5t i( t) Ke Acos(t θ ) () Sia A θ il fasore corrispondente alla risposta
INTERPRETAZIONE CINEMATICA DELLA DERIVATA
 INTERPRETAZIONE CINEMATICA DELLA DERIVATA Consideriamo un punto mobile sopra una qualsiasi linea Fissiamo su tale linea un punto O, come origine degli archi, e un verso di percorrenza come verso positivo;
INTERPRETAZIONE CINEMATICA DELLA DERIVATA Consideriamo un punto mobile sopra una qualsiasi linea Fissiamo su tale linea un punto O, come origine degli archi, e un verso di percorrenza come verso positivo;
Luciano De Menna Corso di Elettrotecnica 233. I segnali impulsivi
 Luciano De Menna Corso di Elettrotecnica 233 I segnali impulsivi Un metodo completamente diverso di affrontare il problema della dinamica nei circuiti lineari è quello basato sulla convoluzione di risposte
Luciano De Menna Corso di Elettrotecnica 233 I segnali impulsivi Un metodo completamente diverso di affrontare il problema della dinamica nei circuiti lineari è quello basato sulla convoluzione di risposte
Complementi di Analisi per Informatica *** Capitolo 2. Numeri Complessi. e Circuiti Elettrici
 Complementi di Analisi per nformatica *** Capitolo 2 Numeri Complessi e Circuiti Elettrici Sergio Benenti Prima versione settembre 2013 Revisione settembre 2017? ndice 21 Circuito elettrico elementare
Complementi di Analisi per nformatica *** Capitolo 2 Numeri Complessi e Circuiti Elettrici Sergio Benenti Prima versione settembre 2013 Revisione settembre 2017? ndice 21 Circuito elettrico elementare
Scopi del corso. lezione 1 2
 lezione 1 1 Scopi del corso Lo studente saprà analizzare circuiti elettrici dinamici per determinare il loro comportamento nel dominio del tempo e per ricavare le proprietà essenziali nel dominio della
lezione 1 1 Scopi del corso Lo studente saprà analizzare circuiti elettrici dinamici per determinare il loro comportamento nel dominio del tempo e per ricavare le proprietà essenziali nel dominio della
TRASFORMATA DI LAPLACE
 TRASFORMATA DI LAPLACE La Trasformata di Laplace è un operatore funzionale che stabilisce una corrispondenza biunivoca tra una funzione di variabile reale (tempo t), definita per t, e una funzione di variabile
TRASFORMATA DI LAPLACE La Trasformata di Laplace è un operatore funzionale che stabilisce una corrispondenza biunivoca tra una funzione di variabile reale (tempo t), definita per t, e una funzione di variabile
Oscillazioni libere e risonanza di un circuito RLC-serie (Trattazione analitica del circuito RLC-serie)
 III a Esperienza del Laboratorio di Fisica Generale II Oscillazioni libere e risonanza di un circuito LC-serie (Trattazione analitica del circuito LC-serie) Con questa breve nota si vuole fornire la trattazione
III a Esperienza del Laboratorio di Fisica Generale II Oscillazioni libere e risonanza di un circuito LC-serie (Trattazione analitica del circuito LC-serie) Con questa breve nota si vuole fornire la trattazione
Capitolo Trasformata di Laplace
 Capitolo Trasformata di Laplace. Segnali lo studio dei sistemi. Trasformata di Laplace.3 Antitrasformata di Laplace.4 Antitrasformata di Laplace: metodo delle frazioni parziali . SEGNALI PER LO STUDIO
Capitolo Trasformata di Laplace. Segnali lo studio dei sistemi. Trasformata di Laplace.3 Antitrasformata di Laplace.4 Antitrasformata di Laplace: metodo delle frazioni parziali . SEGNALI PER LO STUDIO
Esercizi: circuiti dinamici con generatori costanti
 ezione Esercizi: circuiti dinamici con generatori costanti ezione n. Esercizi: circuiti dinamici con generatori costanti. Esercizi con circuiti del I ordine in transitorio con generatori costanti. ircuiti..
ezione Esercizi: circuiti dinamici con generatori costanti ezione n. Esercizi: circuiti dinamici con generatori costanti. Esercizi con circuiti del I ordine in transitorio con generatori costanti. ircuiti..
124 Luciano De Menna Corso di Elettrotecnica. I circuiti RC ed RL
 124 Luciano De Menna Corso di Elettrotecnica I circuiti RC ed RL Se nella rete sono presenti anche resistori, le cose si complicano. Consideriamo il caso della serie di un condensatore e di un resistore.
124 Luciano De Menna Corso di Elettrotecnica I circuiti RC ed RL Se nella rete sono presenti anche resistori, le cose si complicano. Consideriamo il caso della serie di un condensatore e di un resistore.
Equazioni differenziali lineari a coefficienti costanti
 Equazioni differenziali lineari a coefficienti costanti Generalità Il modello matematico di un qualsiasi sistema fisico in regime variabile conduce alla scrittura di una o più equazioni differenziali.
Equazioni differenziali lineari a coefficienti costanti Generalità Il modello matematico di un qualsiasi sistema fisico in regime variabile conduce alla scrittura di una o più equazioni differenziali.
CORRENTI ALTERNATE. Dopo che la spira è ruotata di in certo angolo in un tempo t si ha
 1 easy matematica CORRENI ALERNAE Consideriamo una bobina ruotante, con velocità angolare ω costante all'interno di un campo magnetico uniforme B. Gli estremi della spira sono collegati a due anelli chiamati
1 easy matematica CORRENI ALERNAE Consideriamo una bobina ruotante, con velocità angolare ω costante all'interno di un campo magnetico uniforme B. Gli estremi della spira sono collegati a due anelli chiamati
Note sui circuiti a corrente alternata
 Note sui circuiti a corrente alternata Versione provvisoria. Novembre 018 1 Per commenti o segnalazioni di errori scrivere, per favore, a: maurosaita@tiscalinet.it Indice 1 Corrente alternata 1.1 Circuito
Note sui circuiti a corrente alternata Versione provvisoria. Novembre 018 1 Per commenti o segnalazioni di errori scrivere, per favore, a: maurosaita@tiscalinet.it Indice 1 Corrente alternata 1.1 Circuito
Potenza in regime sinusoidale
 26 Con riferimento alla convenzione dell utilizzatore, la potenza istantanea p(t) assorbita da un bipolo è sempre definita come prodotto tra tensione v(t) e corrente i(t): p(t) = v(t) i(t) Considerando
26 Con riferimento alla convenzione dell utilizzatore, la potenza istantanea p(t) assorbita da un bipolo è sempre definita come prodotto tra tensione v(t) e corrente i(t): p(t) = v(t) i(t) Considerando
determinare una soluzione y(t) dell equazione completa e, quindi dedurne tutte le y(t) soluzioni dell equazione.
 ANALISI VETTORIALE Soluzione esercizi 4 febbraio 2011 10.1. Esercizio. Assegnata l equazione lineare omogenea di primo ordine y + a y = 0 determinare le soluzioni di tale equazione in corrispondenza ai
ANALISI VETTORIALE Soluzione esercizi 4 febbraio 2011 10.1. Esercizio. Assegnata l equazione lineare omogenea di primo ordine y + a y = 0 determinare le soluzioni di tale equazione in corrispondenza ai
Equazioni differenziali
 Equazioni differenziali Generalità sulle equazioni differenziali ordinarie del primo ordine Si chiama equazione differenziale ordinaria[ ] del primo ordine un equazione nella quale compare y = y e la sua
Equazioni differenziali Generalità sulle equazioni differenziali ordinarie del primo ordine Si chiama equazione differenziale ordinaria[ ] del primo ordine un equazione nella quale compare y = y e la sua
ˆ b, si usa la convenzione di prendere. come verso positivo quello antiorario e come verso negativo quello orario.
 Capitolo 4 Le rotazioni 4.1 Richiami di teoria E' opportuno ricordare che, dato un angolo orientato ao ˆ b, si usa la convenzione di prendere come verso positivo quello antiorario e come verso negativo
Capitolo 4 Le rotazioni 4.1 Richiami di teoria E' opportuno ricordare che, dato un angolo orientato ao ˆ b, si usa la convenzione di prendere come verso positivo quello antiorario e come verso negativo
UNIVERSITA DEGLI STUDI DI BERGAMO Facoltà di Ingegneria
 UNIVERSITA DEGLI STUDI DI BERGAMO Facoltà di Ingegneria Corso di Elettrotecnica A.A. 2001/2002 Prova scritta del 4 settembre 1999 Esercizio n 1 Data la rete in figura, determinare tutte le correnti (4
UNIVERSITA DEGLI STUDI DI BERGAMO Facoltà di Ingegneria Corso di Elettrotecnica A.A. 2001/2002 Prova scritta del 4 settembre 1999 Esercizio n 1 Data la rete in figura, determinare tutte le correnti (4
. Il modulo è I R = = A. La potenza media è 1 VR 2
 0.4 La corrente nel resistore vale 0. l modulo è A. La potenza media è 0 W 0.7 l circuito simbolico è mostrato di seguito. La potenza viene dissipata solo nel resistore. 0, 4 - La corrente è 4 4 0, 0,
0.4 La corrente nel resistore vale 0. l modulo è A. La potenza media è 0 W 0.7 l circuito simbolico è mostrato di seguito. La potenza viene dissipata solo nel resistore. 0, 4 - La corrente è 4 4 0, 0,
ELETTROTECNICA (10 CFU) CS INGEGNERIA MATEMATICA I
 ELETTROTECNICA (10 CFU) CS INGEGNERIA MATEMATICA I prova in itinere 1 Novembre 008 SOLUZIONE - 1 - D1. (punti 8 ) Rispondere alle seguenti domande: punto per ogni risposta corretta, - 0.5 per ogni risposta
ELETTROTECNICA (10 CFU) CS INGEGNERIA MATEMATICA I prova in itinere 1 Novembre 008 SOLUZIONE - 1 - D1. (punti 8 ) Rispondere alle seguenti domande: punto per ogni risposta corretta, - 0.5 per ogni risposta
per la matrice R, e: I 1 = G 11 V 1 + G 12 V 2, I 2 = G 21 V 1 + G 22 V 2,
 100 Luciano De Menna Corso di Elettrotecnica Il caso N = 2 è particolarmente interessante tanto da meritare un nome speciale: doppio bipolo I parametri indipendenti saranno tre: R 11, R 22 ed R 12 =R 21
100 Luciano De Menna Corso di Elettrotecnica Il caso N = 2 è particolarmente interessante tanto da meritare un nome speciale: doppio bipolo I parametri indipendenti saranno tre: R 11, R 22 ed R 12 =R 21
Come visto precedentemente l equazione integro differenziale rappresentativa dell equilibrio elettrico di un circuito RLC è la seguente: 1 = (1)
 Transitori Analisi nel dominio del tempo Ricordiamo che si definisce transitorio il periodo di tempo che intercorre nel passaggio, di un sistema, da uno stato energetico ad un altro, non è comunque sempre
Transitori Analisi nel dominio del tempo Ricordiamo che si definisce transitorio il periodo di tempo che intercorre nel passaggio, di un sistema, da uno stato energetico ad un altro, non è comunque sempre
Oscillazioni LC Applicando la legge di Faraday: ma Φ B. in direzione I. ovvero. La soluzione di questa equazone e:
 Oscillazioni Applicando la legge di Faraday: E d l d ma Φ B con d l in direzione d E dl ovvero ovvero d + q / n base alla nostra scelta di polarizzazione di pero', si ha' che: dq Segue che: A d d q Allora,
Oscillazioni Applicando la legge di Faraday: E d l d ma Φ B con d l in direzione d E dl ovvero ovvero d + q / n base alla nostra scelta di polarizzazione di pero', si ha' che: dq Segue che: A d d q Allora,
Esercitazioni di Elettrotecnica
 Esercitazioni di Elettrotecnica a cura dell Ing ntonio Maffucci Parte II: ircuiti in regime sinusoidale /3 Esercitazioni di Elettrotecnica /3 Maffucci ESEIZIONE N7: Fasori ed impedenze ESEIZIO 7 Esprimere
Esercitazioni di Elettrotecnica a cura dell Ing ntonio Maffucci Parte II: ircuiti in regime sinusoidale /3 Esercitazioni di Elettrotecnica /3 Maffucci ESEIZIONE N7: Fasori ed impedenze ESEIZIO 7 Esprimere
Grande rilevanza hanno in elettronica i segnali sinusoidali. Un. segnale sinusoidale è un segnale che varia nel tempo con una legge
 I segnali sinusoidali Grande rilevanza hanno in elettronica i segnali sinusoidali. Un segnale sinusoidale è un segnale che varia nel tempo con una legge del seguente tipo u = U sen( ω t+ ϕ ) Figura A andamento
I segnali sinusoidali Grande rilevanza hanno in elettronica i segnali sinusoidali. Un segnale sinusoidale è un segnale che varia nel tempo con una legge del seguente tipo u = U sen( ω t+ ϕ ) Figura A andamento
. Il modulo è I R = = A. La potenza media è 1 VR 2
 0.4 La corrente nel resistore vale 0. l modulo è A. La potenza media è P 0 W 0.7 l circuito simbolico è mostrato di seguito. La potenza viene dissipata solo nel resistore. 0, 4 - La corrente è 4 4 0, 0,
0.4 La corrente nel resistore vale 0. l modulo è A. La potenza media è P 0 W 0.7 l circuito simbolico è mostrato di seguito. La potenza viene dissipata solo nel resistore. 0, 4 - La corrente è 4 4 0, 0,
Prova scritta di Elettrotecnica professor Luigi Verolino
 Prova scritta di Elettrotecnica professor Luigi Verolino Cognome Matricola Nome Data La rete mostrata in figura, a riposo per t
Prova scritta di Elettrotecnica professor Luigi Verolino Cognome Matricola Nome Data La rete mostrata in figura, a riposo per t
I j e jarctag. ovvero. ESERCIZIO 7.1: Determinare le espressioni temporali sinusoidali relative alle grandezze rappresentate dai seguenti fasori.
 EEO 7.: Determinare le espressioni temporali sinusoidali relative alle grandezze rappresentate dai seguenti fasori. 0 8e 3+ 4 ( 5 isulta necessario applicare le trasformazioni fra espressione polare ed
EEO 7.: Determinare le espressioni temporali sinusoidali relative alle grandezze rappresentate dai seguenti fasori. 0 8e 3+ 4 ( 5 isulta necessario applicare le trasformazioni fra espressione polare ed
Calcolo degli integrali indefiniti
 Appendice B Calcolo degli integrali indefiniti Se f è una funzione continua nell intervallo X, la totalità delle sue primitive prende il nome di integrale indefinito della funzione f, o del differenziale
Appendice B Calcolo degli integrali indefiniti Se f è una funzione continua nell intervallo X, la totalità delle sue primitive prende il nome di integrale indefinito della funzione f, o del differenziale
Esercizi sulle reti elettriche in corrente alternata (parte 1)
 Esercizi sulle reti elettriche in corrente alternata (parte ) Esercizio : alcolare l andamento nel tempo delle correnti i, i 2 e i 3 del circuito in figura e verificare il bilancio delle potenze attive
Esercizi sulle reti elettriche in corrente alternata (parte ) Esercizio : alcolare l andamento nel tempo delle correnti i, i 2 e i 3 del circuito in figura e verificare il bilancio delle potenze attive
7. Forze elastiche. Nella figura 1 il periodo è T = 2s e corrisponde ad un moto unidimensionale limitato tra i valori x = 0 ed x = 1.
 1 Moti periodici 7. Forze elastiche Un caso particolare di moto accelerato è un moto periodico. In figura 1 è riportato un esempio di moto periodico unidimensionale. Un moto periodico si ripete identicamente
1 Moti periodici 7. Forze elastiche Un caso particolare di moto accelerato è un moto periodico. In figura 1 è riportato un esempio di moto periodico unidimensionale. Un moto periodico si ripete identicamente
1 Primitive e integrali indefiniti
 Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 2 CALCOLO INTEGRALE Primitive e integrali indefiniti. Definizione di primitiva e di integrale indefinito Data una funzione
Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 2 CALCOLO INTEGRALE Primitive e integrali indefiniti. Definizione di primitiva e di integrale indefinito Data una funzione
Analisi in regime sinusoidale (parte II)
 Appunti di lettrotecnica Analisi in regime sinusoidale (parte ) Analisi di circuiti elementari in regime sinusoidale... ntroduzione... esistore a terminali... nduttore a terminali...3 ondensatore a terminali...5
Appunti di lettrotecnica Analisi in regime sinusoidale (parte ) Analisi di circuiti elementari in regime sinusoidale... ntroduzione... esistore a terminali... nduttore a terminali...3 ondensatore a terminali...5
La risposta numerica deve essere scritta nell apposito riquadro e giustificata accludendo i calcoli relativi.
 Corso di Laurea in Matematica Seconda prova in itinere di Fisica (Prof. E. Santovetti) 13 gennaio 016 Nome: La risposta numerica deve essere scritta nell apposito riquadro e giustificata accludendo i calcoli
Corso di Laurea in Matematica Seconda prova in itinere di Fisica (Prof. E. Santovetti) 13 gennaio 016 Nome: La risposta numerica deve essere scritta nell apposito riquadro e giustificata accludendo i calcoli
Reti nel dominio delle frequenze. Lezione 10 2
 Lezione 10 1 Reti nel dominio delle frequenze Lezione 10 2 Introduzione Lezione 10 3 Cosa c è nell Unità 3 In questa sezione si affronteranno Introduzione all Unità Trasformate di Laplace Reti nel dominio
Lezione 10 1 Reti nel dominio delle frequenze Lezione 10 2 Introduzione Lezione 10 3 Cosa c è nell Unità 3 In questa sezione si affronteranno Introduzione all Unità Trasformate di Laplace Reti nel dominio
Elettronica II Segnali periodici; serie di Fourier; trasformata di Fourier p. 2
 Elettronica II Segnali periodici; serie di Fourier; trasformata di Fourier Valentino Liberali Dipartimento di Tecnologie dell Informazione Università di Milano, 26013 Crema e-mail: liberali@dti.unimi.it
Elettronica II Segnali periodici; serie di Fourier; trasformata di Fourier Valentino Liberali Dipartimento di Tecnologie dell Informazione Università di Milano, 26013 Crema e-mail: liberali@dti.unimi.it
UNIVERSITÀ DEGLI STUDI DEL SANNIO
 UNIVERSITÀ DEGI STUDI DE SANNIO ORSI DI AUREA IN ING. ENERGETIA, INFORMATIA E TEEOMUNIAZIONI D Prova scritta di Elettrotecnica Teoria dei ircuiti 26/01/2006 Proff. D. Davino e. Visone ognome: Nome: Matr.
UNIVERSITÀ DEGI STUDI DE SANNIO ORSI DI AUREA IN ING. ENERGETIA, INFORMATIA E TEEOMUNIAZIONI D Prova scritta di Elettrotecnica Teoria dei ircuiti 26/01/2006 Proff. D. Davino e. Visone ognome: Nome: Matr.
Correnti alternate. L di. dt 1 C. Equazione integro-differenziale a coefficienti costanti equivalente a. Idt + RI = dt = d I 1 R 1.
 Correnti alternate In condizioni quasi stazionarie (tempo impiegato dai segnali elettromagnetici per attraversare il circuito, piccolo rispetto alle variazioni di densita di carica e corrente) un circuito
Correnti alternate In condizioni quasi stazionarie (tempo impiegato dai segnali elettromagnetici per attraversare il circuito, piccolo rispetto alle variazioni di densita di carica e corrente) un circuito
06. Analisi Armonica. Controlli Automatici. Prof. Cesare Fantuzzi Ing. Cristian Secchi Ing. Federica Ferraguti
 Controlli Automatici 6. Analisi Armonica Prof. Cesare Fantuzzi Ing. Cristian Secchi Ing. Federica Ferraguti ARSControl - DISMI - Università di Modena e Reggio Emilia E-mail: {nome.cognome}@unimore.it http://www.arscontrol.org/teaching
Controlli Automatici 6. Analisi Armonica Prof. Cesare Fantuzzi Ing. Cristian Secchi Ing. Federica Ferraguti ARSControl - DISMI - Università di Modena e Reggio Emilia E-mail: {nome.cognome}@unimore.it http://www.arscontrol.org/teaching
Esercizi sulle reti elettriche in corrente alternata (parte 2)
 Esercizi sulle reti elettriche in corrente alternata (parte 2) Esercizio 7: Verificare il bilancio delle potenze. Nota. l ramo costituito dal generatore di corrente in serie al resistore ha come caratteristica
Esercizi sulle reti elettriche in corrente alternata (parte 2) Esercizio 7: Verificare il bilancio delle potenze. Nota. l ramo costituito dal generatore di corrente in serie al resistore ha come caratteristica
11.1. Esercizio. Dato il numero complesso z = 2 + i 2, calcolare z, z, scrivere la rappresentazione trigonometrica di z, calcolare z 8.
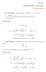 ANALISI Soluzione esercizi gennaio 0.. Esercizio. Dato il numero complesso z = + i, calcolare z, z, scrivere la rappresentazione trigonometrica di z, calcolare z 8. z = i ( ) + ( ) =, π z = arg(z) = 4
ANALISI Soluzione esercizi gennaio 0.. Esercizio. Dato il numero complesso z = + i, calcolare z, z, scrivere la rappresentazione trigonometrica di z, calcolare z 8. z = i ( ) + ( ) =, π z = arg(z) = 4
CORSO DI LAUREA in Fisica, aa 2017/18 (canale Pb-Z)
 CORSO DI LAUREA in Fisica, aa 2017/18 (canale Pb-Z) Equazioni lineari del II ordine a coefficienti costanti: questo è un richiamo dei risultati con altri esempi svolti. Il testo di riferimento è Bramanti
CORSO DI LAUREA in Fisica, aa 2017/18 (canale Pb-Z) Equazioni lineari del II ordine a coefficienti costanti: questo è un richiamo dei risultati con altri esempi svolti. Il testo di riferimento è Bramanti
Risposta temporale: esempi
 ...4 Risposta temporale: esempi Esempio. Calcolare la risposta al gradino unitario del seguente sistema: x(t) = u(t) s + 5 (s + )(s + ) y(t) Il calcolo della trasformata del segnale di uscita è immediato:
...4 Risposta temporale: esempi Esempio. Calcolare la risposta al gradino unitario del seguente sistema: x(t) = u(t) s + 5 (s + )(s + ) y(t) Il calcolo della trasformata del segnale di uscita è immediato:
Circuiti Elettrici Lineari Sinusoidi e fasori
 Facoltà di Ingegneria Uniersità degli studi di Paia Corso di Laurea Triennale in Ingegneria Elettronica e Informatica Circuiti Elettrici Lineari Sinusoidi e fasori Circuiti Elettrici Lineari a.a. 08/9
Facoltà di Ingegneria Uniersità degli studi di Paia Corso di Laurea Triennale in Ingegneria Elettronica e Informatica Circuiti Elettrici Lineari Sinusoidi e fasori Circuiti Elettrici Lineari a.a. 08/9
Segnali e trasformate
 Segnali e trasformate - Corso di Laurea in Ingegneria Meccanica Segnali e trasformate DEIS-Università di Bologna Tel. 5 2932 Email: crossi@deis.unibo.it URL: www-lar.deis.unibo.it/~crossi Segnali e trasformate
Segnali e trasformate - Corso di Laurea in Ingegneria Meccanica Segnali e trasformate DEIS-Università di Bologna Tel. 5 2932 Email: crossi@deis.unibo.it URL: www-lar.deis.unibo.it/~crossi Segnali e trasformate
Esame Scritto Fisica Generale T-B/T-2
 Esame Scritto Fisica Generale T-B/T- (CdL Ingegneria Civile e Informatica [A-K] Prof. M. Sioli II Appello A.A. 013-01 - 9/01/01 Soluzioni Esercizi Ex. 1 Sulla superficie della Terra, in condizioni di bel
Esame Scritto Fisica Generale T-B/T- (CdL Ingegneria Civile e Informatica [A-K] Prof. M. Sioli II Appello A.A. 013-01 - 9/01/01 Soluzioni Esercizi Ex. 1 Sulla superficie della Terra, in condizioni di bel
Capitolo VII I sistemi trifasi
 Capitolo VII I sistemi trifasi Nell'introdurre il regime sinusoidale abbiamo accennato a come sia, in linea di principio, molto semplice i m m a g i n a re un generatore di tensione sinusoidale costruito
Capitolo VII I sistemi trifasi Nell'introdurre il regime sinusoidale abbiamo accennato a come sia, in linea di principio, molto semplice i m m a g i n a re un generatore di tensione sinusoidale costruito
Energia accumulata in un condensatore
 Energia accumulata in un condensatore In base alla seconda legge di Kirchhoff istante per istante avremo Sappiamo che potenza istantanea fornita dal generatore Sostituendo nella eq. diff. e integrando
Energia accumulata in un condensatore In base alla seconda legge di Kirchhoff istante per istante avremo Sappiamo che potenza istantanea fornita dal generatore Sostituendo nella eq. diff. e integrando
Cenni sulla Serie di Fourier
 Cenni sulla Serie di Fourier Note per le lezioni del corso di Controlli Automatici Prof.ssa Maria Elena Valcher 1 Serie di Fourier Osserviamo preliminarmente che la somma di segnali periodici non è necessariamente
Cenni sulla Serie di Fourier Note per le lezioni del corso di Controlli Automatici Prof.ssa Maria Elena Valcher 1 Serie di Fourier Osserviamo preliminarmente che la somma di segnali periodici non è necessariamente
Applicazioni delle derivate alla Fisica
 Liceo Scientifico Statale S. Cannizzaro Applicazioni delle derivate alla Fisica erasmo@galois.it Indice 1 Intensità di corrente elettrica 1 2 Tensione e corrente ai capi di un condensatore 2 3 Forza elettromotrice
Liceo Scientifico Statale S. Cannizzaro Applicazioni delle derivate alla Fisica erasmo@galois.it Indice 1 Intensità di corrente elettrica 1 2 Tensione e corrente ai capi di un condensatore 2 3 Forza elettromotrice
Esercitazione 05: Trasformata di Laplace e funzione di trasferimento
 Esercitazione 05: Trasformata di Laplace e funzione di trasferimento 28 marzo 208 (3h) Fondamenti di Automatica Prof. M. Farina Responsabile delle esercitazioni: Enrico Terzi Queste dispense sono state
Esercitazione 05: Trasformata di Laplace e funzione di trasferimento 28 marzo 208 (3h) Fondamenti di Automatica Prof. M. Farina Responsabile delle esercitazioni: Enrico Terzi Queste dispense sono state
UNIVERSITÀ DEGLISTUDIDIPAVIA Laurea in Ingegneria Elettronica e Informatica
 7.09.0 Problema L interruttore indicato nel circuito in figura commuta nell istante t 0 dalla posizione AA alla posizione BB. Determinare le espressioni delle tensioni v (t) ev (t) per ogni istante di
7.09.0 Problema L interruttore indicato nel circuito in figura commuta nell istante t 0 dalla posizione AA alla posizione BB. Determinare le espressioni delle tensioni v (t) ev (t) per ogni istante di
Università degli studi di Bergamo Facoltà di Ingegneria Corso di Elettrotecnica A.A /2002 Mancini Fabio mtr: 30739
 Università degli studi di Bergamo Facoltà di Ingegneria Corso di Elettrotecnica A.A.. 2001/2002 Mancini Fabio mtr: 30739 1 Es. 4 Prova scritta del 04 luglio 1996. Determinare la corrente funzione del tempo
Università degli studi di Bergamo Facoltà di Ingegneria Corso di Elettrotecnica A.A.. 2001/2002 Mancini Fabio mtr: 30739 1 Es. 4 Prova scritta del 04 luglio 1996. Determinare la corrente funzione del tempo
Capitolo 1 (ultimo aggiornamento 04/05/04) 1.1 Rappresentazione della grandezza a(t) funzione sinusoidale del tempo
 Capitolo 1 (ultimo aggiornamento 04/05/04) 1.1 Rappresentazione della grandezza a(t) funzione sinusoidale del tempo A M valore massimo Am valore medio Fig.1.1 a t A M sin t valore medio in un semiperiodo
Capitolo 1 (ultimo aggiornamento 04/05/04) 1.1 Rappresentazione della grandezza a(t) funzione sinusoidale del tempo A M valore massimo Am valore medio Fig.1.1 a t A M sin t valore medio in un semiperiodo
Lez.22 Circuiti dinamici di ordine due. 2. Università di Napoli Federico II, CdL Ing. Meccanica, A.A , Elettrotecnica. Lezione 22 Pagina 1
 Lez.22 Circuiti dinamici di ordine due. 2 Università di Napoli Federico II, CdL Ing. Meccanica, A.A. 2017-2018, Elettrotecnica. Lezione 22 Pagina 1 Equazioni di stato L analisi dei circuiti dinamici tramite
Lez.22 Circuiti dinamici di ordine due. 2 Università di Napoli Federico II, CdL Ing. Meccanica, A.A. 2017-2018, Elettrotecnica. Lezione 22 Pagina 1 Equazioni di stato L analisi dei circuiti dinamici tramite
TRASFORMATE DI LAPLACE
 CONTROLLI AUTOMATICI Ingegneria Gestionale http://www.automazione.ingre.unimore.it/pages/corsi/controlliautomaticigestionale.htm TRASFORMATE DI LAPLACE Ing. Federica Grossi Tel. 059 2056333 e-mail: federica.grossi@unimore.it
CONTROLLI AUTOMATICI Ingegneria Gestionale http://www.automazione.ingre.unimore.it/pages/corsi/controlliautomaticigestionale.htm TRASFORMATE DI LAPLACE Ing. Federica Grossi Tel. 059 2056333 e-mail: federica.grossi@unimore.it
Derivazione Numerica
 Derivazione Numerica I metodi alle differenze finite sono basati sull approssimazione numerica di derivate parziali. Per questo consideriamo come problema iniziale quello di approssimare le derivate di
Derivazione Numerica I metodi alle differenze finite sono basati sull approssimazione numerica di derivate parziali. Per questo consideriamo come problema iniziale quello di approssimare le derivate di
Transitori nelle reti ad una costante di tempo. Lezione 6 1
 Transitori nelle reti ad una costante di tempo Lezione 6 1 Circuito con amplificatore Calcolare v(t) vt () = v(0 ), t< 0 [ ] t τ vt () = v(0 ) V e + V, t> 0 + Continuità della tensione sul condensatore
Transitori nelle reti ad una costante di tempo Lezione 6 1 Circuito con amplificatore Calcolare v(t) vt () = v(0 ), t< 0 [ ] t τ vt () = v(0 ) V e + V, t> 0 + Continuità della tensione sul condensatore
3. (Da Medicina e Odontoiatria 2012) Determinare quale delle seguenti funzioni soddisfa la relazione f(-x) = -f(x), per ogni numero reale x.
 QUESITI 1 TRIGONOMETRIA 1. (Da Veterinaria 2014) Calcolare il valore dell espressione: cosπ + cos2π + cos3π + cos4π + + cos10π [gli angoli sono misurati in radianti] a) -10 b) -1 c) 0 d) 1 e) 10 2. (Da
QUESITI 1 TRIGONOMETRIA 1. (Da Veterinaria 2014) Calcolare il valore dell espressione: cosπ + cos2π + cos3π + cos4π + + cos10π [gli angoli sono misurati in radianti] a) -10 b) -1 c) 0 d) 1 e) 10 2. (Da
Ingegneria Elettrica Politecnico di Torino. Luca Carlone. ControlliAutomaticiI LEZIONE IV
 Ingegneria Elettrica Politecnico di Torino Luca Carlone ControlliAutomaticiI LEZIONE IV Sommario LEZIONE IV Importanza dello studio di segnali sinusoidali nell ingegneria Sistemi lineari con ingressi sinusoidali
Ingegneria Elettrica Politecnico di Torino Luca Carlone ControlliAutomaticiI LEZIONE IV Sommario LEZIONE IV Importanza dello studio di segnali sinusoidali nell ingegneria Sistemi lineari con ingressi sinusoidali
Fasori e vettori rappresentativi
 170 Luciano De Menna Corso di Elettrotecnica Fasori e vettori rappresentativi Come abbiamo visto, in regime sinusoidale è possibile caratterizzare ogni bipolo attraverso la sua impedenza: un numero complesso
170 Luciano De Menna Corso di Elettrotecnica Fasori e vettori rappresentativi Come abbiamo visto, in regime sinusoidale è possibile caratterizzare ogni bipolo attraverso la sua impedenza: un numero complesso
TRASFORMATE DI LAPLACE
 FONDAMENTI DI CONTROLLI AUTOMATICI Ingegneria Meccanica http://web.ing.unimo.it/~lbiagiotti/fondamenticontrolli1415.html TRASFORMATE DI LAPLACE Ing. e-mail: luigi.biagiotti@unimore.it http://www.dii.unimore.it/~lbiagiotti
FONDAMENTI DI CONTROLLI AUTOMATICI Ingegneria Meccanica http://web.ing.unimo.it/~lbiagiotti/fondamenticontrolli1415.html TRASFORMATE DI LAPLACE Ing. e-mail: luigi.biagiotti@unimore.it http://www.dii.unimore.it/~lbiagiotti
Fisica Generale T2 - Prof. Mauro Villa CdL in Ingegneria Elettronica e Telecomunicazioni 11 Gennaio 2018 Scritto - Onde
 Fisica Generale T - Prof. Mauro Villa CdL in Ingegneria Elettronica e Telecomunicazioni 11 Gennaio 018 Scritto - Onde Esercizi: 1) Un onda armonica viaggia lungo una corda, lunga L = 3.7 m e di massa m
Fisica Generale T - Prof. Mauro Villa CdL in Ingegneria Elettronica e Telecomunicazioni 11 Gennaio 018 Scritto - Onde Esercizi: 1) Un onda armonica viaggia lungo una corda, lunga L = 3.7 m e di massa m
9. Appunti ELETTROTECNICA CIRCUITI CON MEMORIA
 9. Appunti ELETTROTECNICA CIRCUITI CON MEMORIA Vengono detti circuiti con memoria quelli in cui è presente almeno un componente la cui legge costitutiva lega la tensione e la corrente attraverso una equazione
9. Appunti ELETTROTECNICA CIRCUITI CON MEMORIA Vengono detti circuiti con memoria quelli in cui è presente almeno un componente la cui legge costitutiva lega la tensione e la corrente attraverso una equazione
Matematica e Statistica
 Matematica e Statistica Prova d Esame (26/07/2010) Università di Verona - Laurea in Biotecnologie - A.A. 2009/10 1 Matematica e Statistica Prova d Esame di MATEMATICA (26/07/2010) Università di Verona
Matematica e Statistica Prova d Esame (26/07/2010) Università di Verona - Laurea in Biotecnologie - A.A. 2009/10 1 Matematica e Statistica Prova d Esame di MATEMATICA (26/07/2010) Università di Verona
CIRCUITI IN REGIME SINUSOIDALE
 CIRCUITI IN REGIME SINUSOIDALE CIRCUITO PURAMENTE OHMICO Esaminiamo il comportamento dei circuiti in regime sinusoidale iniziando da un circuito puramente ohmico. Si consideri (figura 1) un circuito costituito
CIRCUITI IN REGIME SINUSOIDALE CIRCUITO PURAMENTE OHMICO Esaminiamo il comportamento dei circuiti in regime sinusoidale iniziando da un circuito puramente ohmico. Si consideri (figura 1) un circuito costituito
Transitori del primo ordine
 Università di Ferrara Corso di Teoria dei Circuiti Transitori del primo ordine Si consideri il circuito in figura, composto da un generatore ideale di tensione V, una resistenza R ed una capacità C. I
Università di Ferrara Corso di Teoria dei Circuiti Transitori del primo ordine Si consideri il circuito in figura, composto da un generatore ideale di tensione V, una resistenza R ed una capacità C. I
Equazioni differenziali
 4 Equazioni differenziali Determinare le primitive di una funzione f(x) significa risolvere y (x) = f(x) dove l incognita è la funzione y(x). Questa equazione è un semplice esempio di equazione differenziale.
4 Equazioni differenziali Determinare le primitive di una funzione f(x) significa risolvere y (x) = f(x) dove l incognita è la funzione y(x). Questa equazione è un semplice esempio di equazione differenziale.
Equazioni differenziali Problema di Cauchy
 Equazioni differenziali Problema di Cauch Primo esempio - Risolvere l equazione '( ) = g( ) con g( ) :[ a, b] R continua Teor. fondamentale del calcolo integrale ( ) = + g ( t )dt Primo esempio - Osserviamo
Equazioni differenziali Problema di Cauch Primo esempio - Risolvere l equazione '( ) = g( ) con g( ) :[ a, b] R continua Teor. fondamentale del calcolo integrale ( ) = + g ( t )dt Primo esempio - Osserviamo
La funzione di risposta armonica
 Funzione di risposta armonica - Corso di Laurea in Ingegneria Meccanica Controlli Automatici L La funzione di risposta armonica DEIS-Università di Bologna Tel. 5 2932 Email: crossi@deis.unibo.it URL: www-lar.deis.unibo.it/~crossi
Funzione di risposta armonica - Corso di Laurea in Ingegneria Meccanica Controlli Automatici L La funzione di risposta armonica DEIS-Università di Bologna Tel. 5 2932 Email: crossi@deis.unibo.it URL: www-lar.deis.unibo.it/~crossi
LISTA DELLE DOMANDE D'ESAME FISICA GENERALE 2 A/A
 PRIMA PARTE: Elettrostatica LISTA DELLE DOMANDE D'ESAME FISICA GENERALE 2 A/A 2017-2018 Proff. P. Monaco e F. Longo 1. Cos'e' la quantizzazione della carica elettrica? 2. Cosa stabilisce il principio di
PRIMA PARTE: Elettrostatica LISTA DELLE DOMANDE D'ESAME FISICA GENERALE 2 A/A 2017-2018 Proff. P. Monaco e F. Longo 1. Cos'e' la quantizzazione della carica elettrica? 2. Cosa stabilisce il principio di
Il contenuto di questo file e di completa proprieta del Politecnico di Torino. Lezione 3 1
 Il contenuto di questo file e di completa proprieta del Politecnico di Torino. Lezione 3 1 Calcolo simbolico Lezione 3 2 Effetti di fulminazione 1/4 Modello di fulminazione elettrica Rete nel dominio del
Il contenuto di questo file e di completa proprieta del Politecnico di Torino. Lezione 3 1 Calcolo simbolico Lezione 3 2 Effetti di fulminazione 1/4 Modello di fulminazione elettrica Rete nel dominio del
Quick calculus Capitolo 1 Il problema della tangente
 Quick calculus Capitolo 1 Il problema della tangente Introduzione Ricavare una retta tangente ad una curva di secondo grado come un circonferenza o una parabola, è un problema che si risolve facilmente.
Quick calculus Capitolo 1 Il problema della tangente Introduzione Ricavare una retta tangente ad una curva di secondo grado come un circonferenza o una parabola, è un problema che si risolve facilmente.
 . Applicando la KT al percorso chiuso evidenziato si ricava v v v v4 n Applicando la KC al nodo si ricava: i i i4 i n i i : n i v v v v 4 : n i 4 v v i i.7 Dalla relazione tra le correnti del trasformatore
. Applicando la KT al percorso chiuso evidenziato si ricava v v v v4 n Applicando la KC al nodo si ricava: i i i4 i n i i : n i v v v v 4 : n i 4 v v i i.7 Dalla relazione tra le correnti del trasformatore
Equazioni differenziali del 2 ordine Prof. Ettore Limoli. Sommario. Equazione differenziale omogenea a coefficienti costanti
 Equazioni differenziali del 2 ordine Prof. Ettore Limoli Sommario Equazione differenziale omogenea a coefficienti costanti... 1 Equazione omogenea di esempio... 2 Equazione differenziale non omogenea a
Equazioni differenziali del 2 ordine Prof. Ettore Limoli Sommario Equazione differenziale omogenea a coefficienti costanti... 1 Equazione omogenea di esempio... 2 Equazione differenziale non omogenea a
Elettrotecnica - Ing. Biomedica Ing. Elettronica Informatica e Telecomunicazioni (V. O.) A.A. 2013/14 Prova n luglio 2014.
 ognome Nome Matricola Firma Parti svolte: E E E D Esercizio I I R 6 R 5 D 6 G 0 g Supponendo noti i parametri dei componenti e la matrice di conduttanza del tripolo, illustrare il procedimento di risoluzione
ognome Nome Matricola Firma Parti svolte: E E E D Esercizio I I R 6 R 5 D 6 G 0 g Supponendo noti i parametri dei componenti e la matrice di conduttanza del tripolo, illustrare il procedimento di risoluzione
ANALISI ARMONICA FUNZIONE DI RISPOSTA ARMONICA
 ANALISI ARMONICA I procedimenti per la soluzione delle equazioni differenziali lineari e tempoinvarianti, basati in particolare sulla trasformazione di Laplace, hanno come obiettivo la deduzione della
ANALISI ARMONICA I procedimenti per la soluzione delle equazioni differenziali lineari e tempoinvarianti, basati in particolare sulla trasformazione di Laplace, hanno come obiettivo la deduzione della
Esperienza 12: oscillatore. forzato e risonanza. Laboratorio di Fisica 1 A. Baraldi, M. Riccò. Università di Parma. a.a. 2011/2012. Copyright M.
 Esperienza 1: oscillatore Università di Parma forzato e risonanza a.a. 11/1 Laboratorio di Fisica 1 A. Baraldi, M. Riccò Copyright M.Solzi Oscillazioni libere smorzate a.a. 11/1 1: Oscillatore forzato
Esperienza 1: oscillatore Università di Parma forzato e risonanza a.a. 11/1 Laboratorio di Fisica 1 A. Baraldi, M. Riccò Copyright M.Solzi Oscillazioni libere smorzate a.a. 11/1 1: Oscillatore forzato
Capitolo X. La trasformata di Laplace
 Capitolo X La trasformata di Laplace La soluzione delle reti in regime dinamico può essere ricercata anche con un altro metodo che si basa sulle notevoli proprietà di una trasformazione, detta di Laplace.
Capitolo X La trasformata di Laplace La soluzione delle reti in regime dinamico può essere ricercata anche con un altro metodo che si basa sulle notevoli proprietà di una trasformazione, detta di Laplace.
Equazioni differenziali ordinarie (ODE) lineari del secondo ordine a coefficienti costanti
 Equazioni differenziali ordinarie (ODE) lineari del secondo ordine a coefficienti costanti Fulvio Bisi Corso di Analisi Matematica A (ca) Università di Pavia Facoltà di Ingegneria 1 ODE lineari del secondo
Equazioni differenziali ordinarie (ODE) lineari del secondo ordine a coefficienti costanti Fulvio Bisi Corso di Analisi Matematica A (ca) Università di Pavia Facoltà di Ingegneria 1 ODE lineari del secondo
Le Derivate. Appunti delle lezioni di matematica di A. Pisani Liceo Classico Dante Alighieri
 Le Derivate Appunti delle lezioni di matematica di A. Pisani Liceo Classico Dante Alighieri Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato durante
Le Derivate Appunti delle lezioni di matematica di A. Pisani Liceo Classico Dante Alighieri Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato durante
SEGNALI E SISTEMI Proff. L. Finesso, M. Pavon e S. Pinzoni (a.a ) Homework assignment #2 Testo e Soluzione
 SEGNALI E SISTEMI Proff. L. Finesso, M. Pavon e S. Pinzoni (a.a. 00-005) Homework assignment # Testo e Soluzione Esercizio Si consideri l equazione differenziale ordinaria, lineare a coefficienti costanti
SEGNALI E SISTEMI Proff. L. Finesso, M. Pavon e S. Pinzoni (a.a. 00-005) Homework assignment # Testo e Soluzione Esercizio Si consideri l equazione differenziale ordinaria, lineare a coefficienti costanti
PROVA SCRITTA DI ELETTROTECNICA, 20 febbraio 2018 CdS Ing. Meccanica canali (A-L) e (M-Z) Docenti: C. Petrarca F. Villone
 PROVA SCRITTA DI ELETTROTECNICA, 20 febbraio 208 CdS Ing. Meccanica canali (A-L) e (M-Z) Docenti: C. Petrarca F. Villone COMPITO B Esercizio: La rete di Fig. è a regime sinusoidale per t < 0. Determinare
PROVA SCRITTA DI ELETTROTECNICA, 20 febbraio 208 CdS Ing. Meccanica canali (A-L) e (M-Z) Docenti: C. Petrarca F. Villone COMPITO B Esercizio: La rete di Fig. è a regime sinusoidale per t < 0. Determinare
Contenuti dell unità + C A0 L
 1 ontenuti dell unità Questa unità considera problemi di transitorio in reti: 1) contenenti un solo elemento reattivo (1 condensatore oppure 1 induttore) a) alimentate da generatori costanti in presenza
1 ontenuti dell unità Questa unità considera problemi di transitorio in reti: 1) contenenti un solo elemento reattivo (1 condensatore oppure 1 induttore) a) alimentate da generatori costanti in presenza
Principi di ingegneria elettrica. Reti in regime sinusoidale. Lezione 13 a. Impedenza Ammettenza
 Principi di ingegneria elettrica Lezione 3 a Reti in regime sinusoidale mpedenza Ammettenza Legge di Ohm simbolica n un circuito lineare comprendente anche elementi dinamici (induttori e condensatori)
Principi di ingegneria elettrica Lezione 3 a Reti in regime sinusoidale mpedenza Ammettenza Legge di Ohm simbolica n un circuito lineare comprendente anche elementi dinamici (induttori e condensatori)
Soluzione di circuiti RC ed RL del primo ordine
 Principi di ingegneria elettrica Lezione 11 a parte 2 Soluzione di circuiti RC ed RL del primo ordine Metodo sistematico Costante di tempo Rappresentazione del transitorio Metodo sistematico per ricavare
Principi di ingegneria elettrica Lezione 11 a parte 2 Soluzione di circuiti RC ed RL del primo ordine Metodo sistematico Costante di tempo Rappresentazione del transitorio Metodo sistematico per ricavare
1. conoscere la terminologia e le proprietà dei logaritmi e saperne utilizzare le regole di calcolo
 Quinto modulo: Funzioni Obiettivi. conoscere la terminologia e le proprietà dei logaritmi e saperne utilizzare le regole di calcolo. saper operare con le funzioni esponenziale e logaritmo per risolvere
Quinto modulo: Funzioni Obiettivi. conoscere la terminologia e le proprietà dei logaritmi e saperne utilizzare le regole di calcolo. saper operare con le funzioni esponenziale e logaritmo per risolvere
Esercizi di Fisica LB: Induzione Elettromagnetica
 Esercizi di Fisica LB: Induzione Elettromagnetica Esercizio 1 Esercitazioni di Fisica LB per ingegneri - A.A. 23-24 Una sbarra conduttrice di lunghezza l è fissata ad un estremo ed è fatta ruotare con
Esercizi di Fisica LB: Induzione Elettromagnetica Esercizio 1 Esercitazioni di Fisica LB per ingegneri - A.A. 23-24 Una sbarra conduttrice di lunghezza l è fissata ad un estremo ed è fatta ruotare con
