Quantità di moto. F tavola ragazzo
|
|
|
- Marianna Carboni
- 4 anni fa
- Visualizzazioni
Transcript
1 Quanttà d moto Consderamo un ragazzo su uno skateboard mentre cade. La forza peso gestsce l moto erso l basso durante la caduta, Lungo la drezone orzzontale aremo nece che: Mentre l ragazzo cade spnge n aant lo skateboard Lo skateboard per la terza legge d Newton reagsce con una spnta uguale ed opposta sul ragazzo. N La forza rsultante sul pano orzzontale del sstema ragazzo-skateboard è nulla F taola ragazzo Come s spega l moto orzzontale? F ragazzo taola Sa l ragazzo che lo skateboard acqustano energa cnetca che però non può essere spegato con una arazone d energa potenzale gratazonale. Per comprendere questo tpo d moto bsogna ntrodurre una nuoa grandezza fsca: La QUANTITÀ DI MOTO p L ragazzo L taola
2 Quanttà d moto(1) p Nuoa grandezza : la quanttà d moto Ø La quanttà d moto d un corpo d massa m è un ettore par al prodotto della ettore eloctà moltplcato per la massa del corpo stesso p = m Ø La quanttà d moto ha stessa drezone e erso del ettore eloctà Ø Questa grandezza racchude n sé sa le propretà d moto del corpo (tramte la eloctà ) che d resstenza alla modfca d tale moto (tramte la massa m). Ø La quanttà d moto ha un sgnfcato pù generale della massa o della eloctà prese sngolarmente, e dstngue tra corp d masse derse che s muoono con stessa eloctà. Ø Le dmenson della quanttà d moto sono [M][L][T] -1 e l untà d msura è kg m/s Ø La quanttà d moto d un corpo spesso è chamata momento del corpo Ø Se l corpo s muoe n una drezone qualsas dello spazo, p s può descrere medante le sue tre component lungo x,y e z: p = p x î + p y ĵ + p z ˆk doe: p x = m x # " p y = m y # $ # p z = m z
3 Quanttà d moto(2) La quanttà d moto permette d defnre la seconda legge d Newton n una forma generalzzata. La forma che abbamo sto : F = m a ale nfatt solo nel caso n cu m rmanga costante. Rformulando questa legge medante la quanttà d moto, s ncludono anche cas un cu m ara. Legge d Newton generalzzata: La arazone della quanttà d moto d un corpo nell untà d tempo (coè la derata temporale della quanttà d moto) è proporzonale alla rsultante delle forze ad esso applcata ed ha la stessa drezone F = d p Forma generalzzata della 2 legge d Newton La quanttà d moto d una partcella ara se su d essa è applcata una forza rsultante non nulla Se la rsultante delle forze agent su corpo è nulla la quanttà d moto del corpo rmane costante (s consera): Se: F = 0 d p = 0 p = costante
4 Quanttà d moto(3) Naturalmente se m è costante la forma pù generale della seconda legge d Newton s rduce alla ben nota equazone ΣF=ma F = d p = d ( m ) = dm + m d = m d = m a 0 F = m a Ø Il concetto d quanttà d moto è partcolarmente mportante quando applcato ad un sstema costtuto da pù corp Ø S edrà nfatt che se la forza totale agente sul sstema è nulla la quanttà d moto del sstema s consera. Ma come s applca l concetto d quanttà d moto ad un sstema costtuto da due o pù partcelle? Descrzone de sstem d partcelle n termn d forze applcate
5 Sstem d punt materal -Forze nterne ed esterne P F j F = j F j P j F j Ø Consderamo un sstema d punt materal, nteragent tra loro e con l resto dell unerso. Ø In generale su cascun punto agranno forze eserctate dagl altr punt materal costtuent l sstema I Se F E sono forze nterne ed F sono le forze esterne agent sul sstema La forza agente sul sngolo punto j e data dalla rsultante d tutte le forze agent: F j = I F + nj n k F E k Somma d tutte le forze nterne agent sulla partcella j-sma Somma d tutte le forze esterne agent sulla partcella j-sma Ø Per le forze nterne ale l prncpo d azone e reazone: per ogn forza nterna esste un altra forza nterna tale che a coppe s annullno.
6 Sstem d punt materal -Forze nterne ed esterne F j = + F nj Ø Se s consdera la rsultante d tutte le forze agent su tutt punt d un sstema: j Ø Le forze nterne s annullano a coppe qund: n F j = La rsultante delle forze agent su un sstema è par alla rsultante delle sole forze esterne k F k E F = F I + F E Somma d tutte le forze INTERNE agent sul sstema F = F E TOT F I = 0 Somma d tutte le forze INTERNE agent sul sstema Un sstema per l quale la rsultante delle forze esterne agent su d esso è nulla s dce ISOLATO F E = 0 Sstema solato Un sstema che non scamba massa con l esterno s dce CHIUSO
7 Quanttà d moto d un sstema solato In un sstema solato, costtuto da due o pù partcelle la quanttà d moto totale P del sstema s consera: Dmostrazone: Consderamo un sstema costtuto da due partcelle d massa m 1 ed m 2 che nteragscono tra d loro. L nterazone tra due corp aene medante una coppa d forze F e F 21 ugual ed opposte : F E = 0 F 12 = F 21 P = p F 21 + F 12 = 0 = Costante 12 Per l secondo prncpo della dnamca questa relazone s può rscrere: m 1 a1 + m 2 a2 = 0 m 1 d 1 + m 2 d 2 = 0
8 Quanttà d moto d un sstema solato (2) Se la massa delle due partcelle rmane costante nel tempo s può trasformare la somma d derate n una derata della somma: m 1 d 1 + m 2 Ma: Qund : S ha che: d( m 1 ) 1 d( m m 2 2 ) + d m 2 ( ) 2 P = d ( p 1 + p 2 ) = 0 = d P = 0 d( m m 2 ) 2 = 0 = quanttà d moto totale del sstema solato In un sstema solato la quanttà d moto totale del sstema s consera d 2 = 0 m m 2 2 = p 1 + p 2 = P F E = 0 d P = 0 P = costante
9 Esempo dell arcere Un arcere d massa m A = 60kg è fermo su un blocco d ghacco ( assenza d attrto) e tra una frecca d massa m F = 0.50 kg orzzontalmente a 50m/s. L arcere comncerà a muoers mmedatamente dopo l lanco? Se sì, con quale eloctà? Questo eserczo può essere solto solo utlzzando la conserazone della quanttà d moto del sstema ARCIERE-FRECCIA Il sstema n realtà non è solato n quanto sa sulla frecca che sull arcere agsce la forza gratazonale e la normale. Queste forze però sono perpendcolar al moto del sstema. Non esstono qund forze esterne che agscono lungo l asse orzzontale e possamo consderare l sstema solato lungo tale drezone. La quanttà d moto totale del sstema P x lungo la drezone orzzontale (data dalla somma della quanttà d moto dell arcere p Ax con la quanttà d moto della frecca p Fx ) s dee conserare: P = p Ax + p Fx = m A Ax + m F Fx = costante Poché prma del lanco la quanttà d moto del sstema era nulla anche dopo l lanco essa dorà rsultare nulla, qund, dopo l lanco l arcere s dorà muoere n modo da compensare con la sua quanttà d moto la quanttà d moto della frecca: m A A + m F F = 0 P x = m A A + m F F = m A Af + m F Ff = costante m A Af + m F Ff = 0 Af = m F m A Ff = 0.42m s
10 URTI ED IMPULSO- Introduzone Ø Gl urt sono eent comun nella ta quotdana.. Esemp: Una racchetta da tenns che colpsce una pallna, due palle da blardo che s scontrano, un martello che batte sul chodo, un proettle che s confcca n un pezzo d legno Ø L urto è assocato sempre ad un nterazone fra corp conolt molto pù olenta d qualsas forza esterna agente al momento dell urto stesso Ø Nella descrzone dell urto (nell arco d tempo racchuso nel bree nterallo dell urto stesso) s possono qund gnorare gl effett d tutte le forze esterne e focalzzars solo sulle ntense forze d nterazone che danno ta all eento Ø Le forze d nterazone responsabl dell urto partono da un alore nullo (stante prma dell urto) ad un alore molto grande n un tempo molto bree (dell ordne de mcrosecond) per po rtornare a zero. Ø S ntroduce una nuoa grandezza n grado d tener conto dell ntenstà della forza d nterazone ed l tempo durante l quale essa agsce => IMPULSO
11 Impulso e quanttà d moto Abbamo sto che se su una partcella agsce una forza rsultante sua quanttà d moto ara. F tot = d p d p = F tot F tot non nulla la Varazone nfntesma d p nell nterallo nfntesmo d tempo Integrando entramb membr s ottene la arazone della quanttà d moto nell nterallo d tempo Δt=t f -t : d p = F tot f L ntegrale della forza rspetto al tempo è defnto IMPULSO DELLA FORZA I = t f t d p = p f p = Δ p F tot = Δ p L mpulso è l ettore che rappresenta la arazone della quanttà d moto aenuta nell nterallo d tempo Δt. Quando la forza applcata è costante (nel tempo) l mpulso è dato semplcemente dal prodotto della forza per l nterallo d tempo n cu essa è applcata Se F tot =costante I = F tot Δt = Δ p = t f t F tot Impulso della forza F tot I
12 Forze mpulse ed urt Approssmazone dell Impulso: Ø In molte stuazon s può assumere che una delle forze agent su una partcella agsca per un bree nterallo d tempo, ma che n tale nterallo sa molto pù ntensa delle altre. Ø In questa approssmazone s può trascurare l contrbuto all mpulso da parte delle altre forze agent e la arazone d quanttà d moto della partcella sarà determnata dall mpulso della sola forza domnante. Ø Negl urt tra partcelle s assume che la mutua nterazone tra le partcelle nell urto sa molto pù ntensa d tutte le forze esterne. Ø L urto può essere douto ad un contatto fsco tra due corp (aldo solo a lello macroscopco) o ad un nterazone molto ntensa che non preede l contatto fsco ( urto a lello mcroscopco) Ø Quando due partcelle d massa m 1 ed m 2 s urtano (consderamo queste due partcelle come un sstema solato), la loro quanttà d moto totale s consera nfatt: se Δ p 1 e Δ p 2 sono le arazon dell mpulso delle due partcelle durante l urto: Δ p f doe 1 = F 21 Δ p f 2 = F 12 F 12 = F21 Δp 1 = Δp2 Δp p1f p 1 + p 2f p 2 = Δp2 = 0 P P = f = cost % % + p 2 $ #" % % p1 f p f $#" p1 = + 2 % % P Pf La quanttà d moto totale del sstema costtuto dalle due partcelle s consera
13 Urt Abbamo appena sto che negl urt s consera la quanttà d moto del sstema, n generale però NON s consera l energa cnetca. Propro n funzone del comportamento dell energa cnetca gl urt engono dfferenzat n tre categore: Ø Urt elastc ne qual s consera anche l energa cnetca del sstema ΔT=0 Ø Urt anelastc ne qual NON s consera l energa cnetca del sstema ΔT 0 Ø Urt perfettamente anelastc ne qual NON s consera l energa cnetca del sstema (ΔT 0) ed corp dopo l urto rsultano unt l uno all altro e s comportano come un sngolo corpo d massa m 1 +m 2 DA RICORDARE: Mentre la quanttà d moto s consera n tutt tp d urt, l energa cnetca s consera solo negl urt elastc
14 Urt elastc (non c è dsspazone d energa cnetca) Consderamo due partcelle d massa m 1 ed m 2, che s muoono lungo una retta con eloctà nzal 1 e 2, urtano ed escono dall urto con eloctà fnal 1f e 2f Nell urto elastco s conserano sa la quanttà d moto totale del sstema che l energa cnetca. algono qund le relazon: Conserazone della quanttà d moto Conserazone dell energa cnetca m1 1 + m 2 2 = m 1 1f + m 2 2f 1 2 m m 2 = m 1 1 f m f da cu s può rcaare che: 1 + 1f = 2f + 2 Ed anche: " 1f = m m 1 2 $ # m 1 + m 2 % " ' 2m & $ # m 1 + m 2 % ' 2 2f = & 2m 1 # " m 1 + m 2 $ & + m m % # " m 1 + m 2 $ & 2 % NB: le eloctà possono essere poste negate o nulle
15 Dmostrazone per Urto frontale: m1 1 + m 2 2 = m 1 1f + m 2 2f 1 2 m m 2 = m 1 1 f m f Sosttuendo * n s ottene: m 1 m 1 m 1 * ( 1 1f ) = m 2 ( 2 2 f ) ( 2 ) 2 = m f ( f 1 ) 1f + 1 1f ( ) ( ) = m ( )( ) f 2 2 f m 2 ( 2 )( 2f + ) = m ( 1 1f )( ) ( f ) = ( 1f + ) 2 2 f f 2f = 1 + 1f 2 Sosttuendo l espressone per 2f nell equazone della conserazone della quanttà d moto s ottene la eloctà fnale della prma partcella n funzone delle masse delle due partcelle, della sua eloctà nzale e della eloctà nzale della seconda partcella m m 2 2 = m 1 1f + m 2 1f + m 2 1 m 2 2 ( m 1 + m 2 ) 1f = m 2 m 1 ( ) 1 + 2m 2 2 1f = m m 1 2 m 1 + m 2 Con un dscorso analogo s troa la eloctà fnale della seconda partcella: 2f = m m 2 1 ( ) ( ) 2m ( m 1 + m 2 ) 2 ( ) ( m 1 + m 2 ) 2m ( m 1 + m 2 ) 1
16 Urt elastc- qualche caso partcolare " 1f = m m % " 1 2 $ # m 1 + m ' + 2m % 2 1 $ 2 & # m 1 + m ' 2m $ 2 2f = 1 # 2 & " m 1 + m & + m m # 2 % " m 1 + m 2 $ & 2 % Ø Se m 1 =m 2 Ø Se la partcella 2 è nzalmente n quete Ø Se m 1 >>m 2 e 1f = = 0 1f 1 2f 2 1 2f = 1 In un urto frontale tra due partcelle ugual queste s scambano la eloctà 2 = 0 " 1f = m m % 1 2 $ # m 1 + m ' 1 2 & 2m $ 2f = 1 # " m 1 + m & 1 2 % Se una massa molto pesante urta una massa leggera nzalmente ferma, la pallna molto pù pesante prosegue pressochè ndsturbata l suo moto mentre la massa pù pccola rmbalza con eloctà doppa rspetto a quella nzale della partcella pesante Ø Se m 2 >>m 1 e 2 = 0 1f 1 2f 0 Se una massa molto leggera urta una massa molto pesante nzalmente ferma, la pallna leggera nerte la sua drezone mantenendo costante la sua eloctà mentre quella pesante rmane ferma
17 Urto perfettamente anelastco Consderamo due partcelle d massa m 1 ed m 2, che s muoono lungo una retta con eloctà nzal 1 e 2 Dopo un urto perfettamente anelastco tra le due partcelle esse rsultano fuse nseme e s muoono con una stessa eloctà fnale La quanttà totale del sstema s consera: f P = costante p 1 + p 2 = p f m m 2 2 = ( m 1 + m ) 2 f f = m m 2 2 m 1 + m 2 Conoscendo le eloctà nzal delle due partcelle è possble calcolare la eloctà fnale comune
18 Sstema d punt In generale, per determnare completamente l moto d un sstema costtuto da n punt materal, s dee rsolere un sstema d 3n equazon. Abbamo nfatt che: Il moto del sstema errà descrtto da n equazon ettoral (una per cascun punto): m j a j = F j con j=1,n Ed ognuna d queste equazon ettoral può essere rscrtta come tre equazon lungo x,y,z: m j a jx = F jx m j a jy = F jy m j a jz = F jz j = 1,n Defnamo allora per cascun punto -smo le seguent grandezze: Poszone: r eloctà Accelerazone: a = F m quanttà d moto Momento Angolare: L = r m energa cnetca p = m T = 1 2m 2 Per l sstema complesso d punt defnamo noltre: Quanttà d moto totale del sstema P = p = m Momento angolare totale del sstema L = = r m Energa cnetca totale del sstema L 2 T = = 1 2m T
19 Sstema d punt La quanttà d moto è uno strumento molto utle non solo per analzzare gl urt, ma anche per studare l moto traslatoro d oggett estes (coè con dmenson defnte) Fnora abbamo sempre applcato l approssmazone degl oggett a partcelle puntform che qund fossero soggette solo a mot traslator. I corp nella realtà possono essere sottopost sa a mot traslator che a mot rotator (anche n contemporanea) Descrere l moto d un corpo esteso o d un sstema d punt può qund rsultare molto complcato dato che ogn punto del corpo s muoe n manera dfferente dagl altr seguendo traettore dfferent Consderamo per esempo una mazza da baseball che ene lancata roteando n ara. Benché l moto sa complcato e dfferente per cascuna parte della mazza esste un punto della mazza che s muoe come se n esso fosse contenuta tutta la massa della mazza e come se tutte le forze esterne agssero su tale punto => moto parabolco
20 Centro d massa d un sstema S defnsce CENTRO DI MASSA d un corpo o d un sstema d corpo l punto che s muoe come se tutta la massa fosse contenuta n esso e come se tutte le forze esterne agssero su d esso Dal punto d sta matematco: S defnsce Centro d Massa d un sstema d punt materal l punto geometrco la cu poszone è ndduata dal raggo ettore r cm che dentfca la poszone meda pesata n funzone delle masse: r = cm m r = m 1 m r 1 +m 2 r2 +m 3 r3 +m 4 r m n rn m 1 +m 2 +m 3 +m m n NB: Pù un punto del sstema ha massa grande pù sposta erso d se l centro d massa
21 doe r cm = r r cm m r = m 1 m = x Centro d Massa r 1 +m 2 r2 +m 3 r3 +m 4 r m n rn m 1 +m 2 +m 3 +m m n ˆ + y ˆj + z kˆ = x cm î + y cm ĵ + z cm ˆk R cm Centro d massa d due partcelle d massa m 1 ed m 2 poste entrambe sull asse x m x x = = m1x1 + cm m m 1+ m m 2 2 x 2 Se m 2 > m 1, x cm s troerà pù cno alla poszone x 2
22 Centro d massa Esempo: Centro d massa d tre partcelle d massa m 1 ed m 2 ed m 3 come mostrate n fgura. r cm = m r = m 1 m r 1 +m 2 r2 +m 3 r3 m 1 +m 2 +m 3 r 1 x1 = d y1 = 0 m1 = 2m x2 = d + b r2 y2 = 0 m2 = m r 3 x3 = d + b y3 = h m3 = 4m x cm = m 1 x 1 + m 2 x 2 + m 3 x 3 m 1 + m 2 + m 3 = 2md + m(d +b) + 4m(d +b) 2m + m + 4m = 7md + 5mb 7m = d b y cm = m 1 y 1 + m 2 y 2 + m 3 y 3 m 1 + m 2 + m 3 = mh 7m r cm = x cm î + y cm ĵ = d b î bĵ = 4 7 h
23 Consderamo un sstema costtuto da n punt materal. Assumendo che la massa totale del sstema rmanga costante possamo determnare la eloctà del centro d massa derando rspetto al tempo l ettore poszone del CM: Moto d un sstema d partcelle cm = d r cm M = Rcordando la defnzone d quanttà d moto totale del sstema: possamo screre: = m d r m = 1 m M m cm = 1 M La quanttà d moto totale del sstema è par al prodotto della massa totale del sstema per la eloctà del suo centro d massa=> coè è uguale alla quanttà d moto d una partcella d massa M che s muoe con eloctà P P = M cm Veloctà del centro d massa Quanttà d moto totale del sstema P = p = m cm
24 Moto d un sstema d partcelle (2) Analogamente a quanto fatto per la eloctà s può rcaare l accelerazone del centro d massa: a cm = d cm = d m Se l sstema d rfermento è nerzale per ogn punto -smo ale l secondo prncpo della dnamca: nt m a = F + m m a = F nt + F E = 1 M m a F E Rcordando che la somma d tuttele forze nterne è nulla: m a = F E = F E a cm = F E M F E = M a cm Teorema del centro d massa: Ø l centro d massa s muoe come un punto materale n cu sa concentrata tutta la massa del sstema ed a cu sa applcata la rsultante delle forze esterne, oppure Ø la rsultante delle forze esterne agent sul sstema d partcelle è uguale alla massa totale del sstema moltplcata per l accelerazone del centro d massa
25 Moto d un sstema d partcelle (3) r cm cm a cm sono dat dalle mede pesate sulle masse de ettor poszone eloctà ed accelerazone de sngol punt e fornscono nformazon sulle propretà mede del moto. Rcordando le defnzon d eloctà del centro d massa e d quanttà d moto totale del sstema: F E = M a cm = M d cm = dm cm P = M cm s ottene che: F E = d P la rsultante delle forze esterne è par alla derata della quanttà d moto totale del sstema Ø Il centro d massa è qund una quanttà matematca, che gode d noteol propretà: 1) Il moto del CM è determnato dalle sole forze esterne F E = M a cm = d P 2) La eloctà del CM è par alla quanttà d moto totale dsa la massa totale del sstema cm = P M 3) a cm = F E Il CM rappresenta l moto globale dell nseme d punt materal. M
26 Accenno a corp rgd ed al moto rotazonale Quando s consderano de corp estes ( una ruota, un dsco, un pattnatore )che ruotano ntorno ad un asse non è possble assmlarl ad un punto materale poché ogn loro punto ruoterà con eloctà e drezon derse Modello d corpo rgdo: S consdera l corpo esteso assmlable ad un nseme d partcelle la cu mutua dstanza rmane costante nel tempo ( l corpo non s deforma ) => è solo un approssmazone n quanto nella realtà la maggor parte de corp sono deformabl. Con l modello d corpo rgdo la trattazone delle rotazon è molto semplfcata Forte analoga tra le grandezze che descrono mot traslazonal e quelle che descrono mot rotazonal: mot traslazonal mot rotazonal Poszone (coord. Cartesane x,y) Poszone (coord. Polar r,θ) Veloctà lneare Accelerazone lneare a Forza rsultante F Veloctà angolare Accelerazone angolare α Momento della forza rsultante Μ
27 Coordnate Polar- eloctà angolare accelerazone angolare Consderamo un dsco che ruota ntorno ad un asse fsso passante per l punto O e perpendcolare alla fgura. Il punto P ene rappresentato dalle sue coordnate polar (r,θ) Durante la rotazone l punto P s sposta d un arco s = rθ Da cu s ottene la poszone angolare θ: L angolo sta a mot rotazonal come la poszone x sta al moto traslazonale In analoga con quanto sto per lo spostamento lneare Δx, s può defnre lo spostamento angolare Δθ : quando l punto P s sposta da una poszone A ad una B con una rotazone lo spostamento angolare è dato da: La eloctà angolare meda ω meda con cu aene questo spostamento è data da: E la θ = s r ω meda = Δθ Δt Δθ = θ B θ A = θ f θ [ω] = [rad][t ] 1 doe l radante è admensonale s ottene facendo l lmte per Δtè0 Δθ ω lm Δt 0 Δt = dθ NB : ω> 0 quando P ruota n senso antoraro (θ crescente)
28 Coordnate Polar- eloctà angolare accelerazone angolare (2) Se la eloctà angolare ara da un alore ω ad un alore ω f nell nterallo Δt l corpo è soggetto ad un accelerazone angolare α. L accelerazone angolare meda e l accelerazone stantanea sono date rspettamente da: α meda Δω Δt ed Δω α lm Δt 0 Δt = dω [α] = [rad][t ] 2 NB : α> 0 quando P ruota n senso antoraro con ω crescente o quando P ruota n senso oraro con ω decrescente Tutt punt d un corpo rgdo ruotando ntorno ad un asse, n un dato nterallo d tempo, spazzeranno lo stesso angolo θ, con la stessa eloctà angolare ω, e la stessa accelerazone angolare α. I mot rotator d un corpo rgdo ntorno ad un asse possono essere completamente caratterzzat medante le tre grandezze θ,ω,α In realtà w ed α sono de ettor n quanto deono portare l nformazone rguardo la drezone dell asse d rotazone ed l erso d rotazone. S defnsce ettore eloctà angolare ω l ettore aente come modulo ω, come drezone la drezone dell asse d rotazone e erso defnto dalla regola della mano destra S defnsce ettore accelerazone angolare l ettore aente come modulo α, come drezone la drezone dell asse d rotazone e erso concorde con ω se ω è crescente o dscorde se ω è decrescente α
29 Momento d una forza Abbamo sto che, per l moto traslatoro, la forza rsultante agente su un corpo è par alla derata temporale della quanttà d moto : F = d p Per procedere con lo studo dnamco de mot rotazonal è necessaro troare un equalente rotazonale delle forze e della quanttà d moto, n modo da poter esprmere un enuncato analogo al 2 prncpo nel caso n cu l moto sa una rotazone. Consderamo d oler aprre una porta. Applchamo a tal scopo 4 forze d uguale ntenstà ma con drezon e punt d applcazone ders La forza F 2 non aprrà la porta F 1 F 3 La forza F 3 aprrà la porta La forza F 4 aprrà la porta ma meno Cardne F 2 F 4 faclmente d F 3 Porta La forza F 1 aprrà la porta ma con dffcoltà L esperenza c dce che la capactà d aprre la porta dpende: 1. Dall ntenstà della forza applcata 2. Dalla dstanza d applcazone della forza dall asse d rotazone (FULCRO 3. Dall angolo d applcazone tra la porta e la forza
30 Momento d una forza(2) S possono rassumere le tre osserazon ntroducendo una nuoa grandezza che rappresenta l analogo rotazonale della forza: IL MOMENTO DELLA FORZA (ndcato con la lettera M o τ) Prendendo n consderazone l precedente esempo della porta: Il momento della forza F 3 sarà scuramente maggore del momento della forza F 4 o della forza F 1. Il momento della forza F 2 sarà nece nullo Cardne (Fulcro) Porta In generale: Dato un corpo rgdo mpernato su un asse, quando su questo corpo s applca una forza F e la retta d azone della forza non passa per l perno l corpo tende a ruotare ntorno all asse. F 1 F 2 F 3 F 4 Il momento della forza M descre la tendenza della forza a far ruotare l corpo ntorno all asse che fa da perno
31 Momento d una forza(3) Il momento M della forza F è defnto come l prodotto ettorale tra l ettore poszone (defnto dal punto n cu è applcata la forza rspetto alla stessa orgne, detto polo) e la forza stessa. O A Momento della forza M = r F M r è perpendcolare al pano determnato da (punto d applcazone rspetto ad O) ed. doe F M = rf snφ = Fb b = r snφ = bracco della forza b = r snφ è l bracco della forza, e corrsponde alla dstanza dell asse d rotazone dalla retta su cu gace F. Il momento della forza sarà nullo se la forza ene applcata lungo la drezone del ettore poszone, coè della retta congungente l punto d azone della forza all asse d rotazone NB: Il momento d una forza descre la capactà della forza stessa d mettere un corpo n rotazone rspetto ad un punto. M r φ F P φ
32 Ø Consderamo una partcella d massa m posta nella poszone con una quanttà d moto (che forma con un angolo φ) e che s muoe Ø S defnsce ettore momento angolare l prodotto ettorale tra e : L = r p = r m Momento Angolare(1) Ø Il momento angolare è l analogo rotazonale della quanttà d moto NB: l prodotto r snθ è la componente d nella drezone perpendcolare a, coè r snφ = r. Analogamente l prodotto p snθ è la componente d nella drezone ortogonale ad : p sn φ = p. p r L r p L = rpsnϕ r p p r L = L = pr = rp = rm L al pano def. da r e p contrbusce al momento angolare solo la componente della eloctà perpendcolare al raggo ettore. r
33 Momento angolare(2) Se φ = 0, π, coè se e sono parallel l momento angolare Questo corrsponde al caso n cu l moto è traslatoro lneare, passante per l orgne Se φ = π/2, coè se e sono perpendcolar l momento angolare L è massmo ed Nel caso d moto crcolare, con centro nell orgne s ha: E qund: r L = rpsnφ = mrsnφ p = 0 r p L = rm = = ωr L = mr 2 ω Inoltre l ettore L è dretto come l asse d rotazone. S può ntrodurre la notazone ettorale: Momento L = mr 2 ω angolare n un moto crcolare poché la eloctà angolare è assocata ad una rotazone ntorno ad un asse fsso, essa ene defnta come un ettore che ha per modulo l alore ω, per drezone la drezone dell asse d rotazone e per erso quello della regola della mano destra L L
34 Relazone tra momento angolare e momento d una forza Defnt l momento d una forza ed l momento angolare possamo rcaare l analogo rotazonale del secondo prncpo della dnamca Consderamo l momento angolare d un corpo rspetto ad un punto posto a dstanza r dal corpo stesso, ed andamo a studarne la arazone nel tempo: d L = d r p ( ) = d r p + r d p = "#$ m + r F F 0 M M = d L S troa qund che: Il momento rsultante delle forze agent su una partcella è par alla derata temporale del momento angolare della partcella. F = d p M = d L
35 Forze central Ø S defnsce forza centrale una forza agente n ogn punto dello spazo la cu drezone passa sempre attraerso un punto fsso, detto centro della forza. Ø Se l centro concde con l orgne d un sstema d rfermento la forza centrale è dretta parallelamente al raggo ettore. Ø Esemp d forze central sono la forza gratazonale e la forza d Coulomb, drette sempre come la congungente l corpo d proa con la sorgente del campo. r F Ø poché nel caso d forze central è parallelo ad, s ha che l momento della forza è nullo: M = r Fc Ø Il momento angolare dee qund essere costante: Coè: per un corpo sottoposto all azone d una forza centrale l momento angolare è una quanttà conserata. NB:Poché L s consera ( e qund non ara la sua drezone) la traettora d una partcella sottoposta alle sole forze central gace su un pano ( che dee rmanere narato n quanto perpendcolare al momento angolare) = 0 M dl = 0 L = costate
36 I flud La matera può presentars n tre stat: Soldo, lqudo e gassoso: Ø Un soldo ha una forma ed un olume ed è ncomprmble Ø Un lqudo ha un olume defnto, non ha una forma propra ed è ncomprmble Ø Le propretà de lqud e de sold dpendono dal loro struttura mcroscopca, oero dal legame tra le molecole. Ø Un gas non ha né olume ne forma defnt ed è comprmble Ø Queste defnzon sono n realtà un artfco, pù n generale lo stato n cu s presenta la matera ene determnato n funzone del tempo necessaro a quella matera per cambare la sua forma sotto l azone d una forza esterna Ø Una sostanza che non è dotata d forma propra è detta fludo. I flud assumono la forma del recpente che l contene. Ø I flud sono un nseme d molecole sstemate casualmente legate da debol forze d coesone e forze eserctate da paret del contentore Ø Sono flud : le sostanze lqude - che hanno olume defnto ed una superfce lmte le sostanze gassose - che non hanno un olume defnto e tendono ad occupare tutto l olume a dsposzone. Dal punto d sta meccanco un fludo s può pensare composto da element nfntesm d massa dm = ρ dv, che scorrono tra loro n una qualunque drezone. Ø Un fludo può essere descrtto da tre parametr denstà, pressone e flusso
37 Denstà Ø Con flud non ha molto senso parlare d massa, ma puttosto d denstà ( o massa olumca). Se consderamo un elemento d olume ΔV d un fludo ntorno ad un certo punto e msuramo la sua massa Δm la denstà è data dal rapporto: Δm ρ = Denstà La denstà d un corpo (o fludo) è una grandezza scalare ed è par alla massa per l untà d olume. Ø L untà d msura della denstà è l kg/m 3 ρ = Ø La denstà d un fludo ara ( anche se debolmente) con la temperatura poché al arare della temperatura ara l olume. Ø La denstà de lqud ρ = M/V è molto maggore d quella de gas (d crca un fattore 10 3 ) m V ΔV Doe m e V sono massa e olume d un campone d fludo Ø Dal punto d sta meccanco un fludo s può pensare composto da element nfntesm d massa dm = ρ dv, che scorrono tra loro n una qualunque drezone.
38 Tabella denstà
Urti. Abbiamo appena visto che negli urti si conserva la quantità di moto del sistema, in generale però NON si conserva l energia cinetica.
 Urt Abbao appena sto che negl urt s consera la quanttà d oto del sstea, n generale però NON s consera l energa cnetca. Propro n funzone del coportaento dell energa cnetca gl urt engono dfferenzat n tre
Urt Abbao appena sto che negl urt s consera la quanttà d oto del sstea, n generale però NON s consera l energa cnetca. Propro n funzone del coportaento dell energa cnetca gl urt engono dfferenzat n tre
Energia e Lavoro. In pratica, si determina la dipendenza dallo spazio invece che dal tempo
 Energa e Lavoro Fnora abbamo descrtto l moto de corp (puntform) usando le legg d Newton, tramte le forze; abbamo scrtto l equazone del moto, determnato spostamento e veloctà n funzone del tempo. E possble
Energa e Lavoro Fnora abbamo descrtto l moto de corp (puntform) usando le legg d Newton, tramte le forze; abbamo scrtto l equazone del moto, determnato spostamento e veloctà n funzone del tempo. E possble
urto v 2f v 2i e forza impulsiva F r F dt = i t
 7. Urt Sstem a due partcelle Defnzone d urto elastco, urto anelastco e mpulso L urto è un nterazone fra corp che avvene n un ntervallo d tempo normalmente molto breve, al termne del quale le quanttà d
7. Urt Sstem a due partcelle Defnzone d urto elastco, urto anelastco e mpulso L urto è un nterazone fra corp che avvene n un ntervallo d tempo normalmente molto breve, al termne del quale le quanttà d
UNIVERSITÀ DEGLI STUDI DI TERAMO
 UIVERSITÀ DEGLI STUDI DI TERAMO CORSO DI LAUREA I TUTELA E BEESSERE AIMALE Corso d : FISICA MEDICA A.A. 015 /016 Docente: Dott. Chucch Rccardo mal:rchucch@unte.t Medcna Veternara: CFU 5 (corso ntegrato
UIVERSITÀ DEGLI STUDI DI TERAMO CORSO DI LAUREA I TUTELA E BEESSERE AIMALE Corso d : FISICA MEDICA A.A. 015 /016 Docente: Dott. Chucch Rccardo mal:rchucch@unte.t Medcna Veternara: CFU 5 (corso ntegrato
Lezione mecc n.14 pag 1
 Lezone mecc n.4 pag Argoment d questa lezone: Urt ra due corp Legg d conserazone negl urt ra due corp Urt stantane e orze mpulse Urt elastc ed anelastc Prm cenn a sstem d pù partcelle (energa d rotazone
Lezone mecc n.4 pag Argoment d questa lezone: Urt ra due corp Legg d conserazone negl urt ra due corp Urt stantane e orze mpulse Urt elastc ed anelastc Prm cenn a sstem d pù partcelle (energa d rotazone
L = L E k 2 ENERGIA CINETICA DI ROTAZIONE. Espressione generica dell energia cinetica di rotazione: 1 ω
 NRGIA CINTICA DI ROTAZION k m R ) ( k R m R m spressone generca dell energa cnetca d rotazone: I k Se la rotazone aene ntorno ad un asse prncpale d nerza, allora: I L da cu: I L k NRGIA CINTICA DI ROTOTRASLAZION
NRGIA CINTICA DI ROTAZION k m R ) ( k R m R m spressone generca dell energa cnetca d rotazone: I k Se la rotazone aene ntorno ad un asse prncpale d nerza, allora: I L da cu: I L k NRGIA CINTICA DI ROTOTRASLAZION
Sistemi di punti materiali -Forze interne ed esterne
 Sste d punt ateral -orze nterne ed esterne P P Consderao un sstea d n punt ateral, nteragent tra loro e con l resto dell unerso. In generale sul punto agranno orze eserctate dagl altr n- punt ateral I
Sste d punt ateral -orze nterne ed esterne P P Consderao un sstea d n punt ateral, nteragent tra loro e con l resto dell unerso. In generale sul punto agranno orze eserctate dagl altr n- punt ateral I
Appunti di Dinamica dei Sistemi Materiali
 Appunt d Dnamca de Sstem ateral Cnematca Rotazonale Scopo d questa parte è quello d presentare le legg del moto crcolare unformemente accelerato e d approfondre la conoscenza del moto crcolare del punto.
Appunt d Dnamca de Sstem ateral Cnematca Rotazonale Scopo d questa parte è quello d presentare le legg del moto crcolare unformemente accelerato e d approfondre la conoscenza del moto crcolare del punto.
6.1- Sistemi punti, forze interne ed esterne
 1 CAP 6 - SISTEMI DI PUNTI MATERIALI Parte I 1 Cap 6 - Sstem d punt materal Cap 6 - Sstem d punt materal Il punto materale è un astrazone alla quale poch cas s possono assmlare. La maggor parte degl oggett
1 CAP 6 - SISTEMI DI PUNTI MATERIALI Parte I 1 Cap 6 - Sstem d punt materal Cap 6 - Sstem d punt materal Il punto materale è un astrazone alla quale poch cas s possono assmlare. La maggor parte degl oggett
F E risultante t delle forze esterne agenti su P i. F forza esercitata t sul generico punto P ij del sistema da P : forza interna al sistema
 DINAMICA DEI SISTEMI Sstema costtuto da N punt materal P 1, P 2,, P N F E rsultante t delle forze esterne agent su P F E F forza eserctata t sul generco punto P j del sstema da P : forza nterna al sstema
DINAMICA DEI SISTEMI Sstema costtuto da N punt materal P 1, P 2,, P N F E rsultante t delle forze esterne agent su P F E F forza eserctata t sul generco punto P j del sstema da P : forza nterna al sstema
Meccanica Dinamica dei sistemi
 Meccanca 7-8 Dnamca de sstem 5 W Dnamca de sstem d unt materal Laoro er un sstema d unt materal er la artcella -esma: O r m F dw n dr F ds T dw F dr F W F dr W + W n n m, m, W W + W E m d Laoro totale
Meccanca 7-8 Dnamca de sstem 5 W Dnamca de sstem d unt materal Laoro er un sstema d unt materal er la artcella -esma: O r m F dw n dr F ds T dw F dr F W F dr W + W n n m, m, W W + W E m d Laoro totale
Centro di massa. Coppia di forze. Condizioni di equilibrio. Statica Fisica Sc.Tecn. Natura. P.Montagna Aprile pag.1
 L EQUILIBRIO LEQU L Corpo rgdo Centro d massa Equlbro Coppa d forze Momento d una forza Condzon d equlbro Leve pag.1 Corpo esteso so e corpo rgdo Punto materale: corpo senza dmenson (approx.deale) Corpo
L EQUILIBRIO LEQU L Corpo rgdo Centro d massa Equlbro Coppa d forze Momento d una forza Condzon d equlbro Leve pag.1 Corpo esteso so e corpo rgdo Punto materale: corpo senza dmenson (approx.deale) Corpo
Sistemi punti, forze interne ed esterne
 Ncola GglettoA.A. 2017/18 3 6.2- IL CENTRO DI MASSA Parte I 1 Cap 6 - Sstem d punt materal Cap 6 - Sstem d punt materal Il punto materale è un astrazone alla quale poch cas s possono assmlare. La maggor
Ncola GglettoA.A. 2017/18 3 6.2- IL CENTRO DI MASSA Parte I 1 Cap 6 - Sstem d punt materal Cap 6 - Sstem d punt materal Il punto materale è un astrazone alla quale poch cas s possono assmlare. La maggor
QUANTITA DI MOTO LEGGE DI CONSERVAZIONE DELLA QUANTITA DI MOTO. Kg m/s. p tot. = p 1. + p 2
 QUANTITA DI MOTO r p = r mv Kg m/s LEGGE DI CONSERVAZIONE DELLA QUANTITA DI MOTO La quanttà d moto totale n un sstema solato s conserva, coè rmane costante nel tempo p tot = p 1 + p 2 = m 1 v 1 + m 2 v
QUANTITA DI MOTO r p = r mv Kg m/s LEGGE DI CONSERVAZIONE DELLA QUANTITA DI MOTO La quanttà d moto totale n un sstema solato s conserva, coè rmane costante nel tempo p tot = p 1 + p 2 = m 1 v 1 + m 2 v
Dinamica del corpo rigido
 Anna Nobl 1 Defnzone e grad d lbertà S consder un corpo d massa totale M formato da N partcelle cascuna d massa m, = 1,..., N. Il corpo s dce rgdo se le dstanze mutue tra tutte le partcelle che lo compongono
Anna Nobl 1 Defnzone e grad d lbertà S consder un corpo d massa totale M formato da N partcelle cascuna d massa m, = 1,..., N. Il corpo s dce rgdo se le dstanze mutue tra tutte le partcelle che lo compongono
Dinamica dei sistemi particellari
 Dnamca de sstem partcellar Marco Favrett Aprl 11, 2010 1 Cnematca Sa dato un sstema d rfermento nerzale (O, e ), = 1, 2, 3 e consderamo un sstema d punt materal (sstema partcellare) S = {(OP, m )}, = 1,,
Dnamca de sstem partcellar Marco Favrett Aprl 11, 2010 1 Cnematca Sa dato un sstema d rfermento nerzale (O, e ), = 1, 2, 3 e consderamo un sstema d punt materal (sstema partcellare) S = {(OP, m )}, = 1,,
NATURA ATOMICA DELLA MATERIA
 NATURA ATOMICA DLLA MATRIA Un qualunque fludo è costtuto da un gran numero d partcelle (sa sngol atom che molecole) n un contnuo moto dsordnato defnto agtaone termca. Questo fenomeno sta alla base de cosddett
NATURA ATOMICA DLLA MATRIA Un qualunque fludo è costtuto da un gran numero d partcelle (sa sngol atom che molecole) n un contnuo moto dsordnato defnto agtaone termca. Questo fenomeno sta alla base de cosddett
Il lavoro L svolto da una forza costante è il prodotto scalare della forza per lo spostamento del punto di applicazione della forza medesima
 avoro ed Energa F s Fs cos θ F// s F 0 0 se: s 0 θ 90 Il lavoro svolto da una orza costante è l prodotto scalare della orza per lo spostamento del punto d applcazone della orza medesma [] [M T - ] N m
avoro ed Energa F s Fs cos θ F// s F 0 0 se: s 0 θ 90 Il lavoro svolto da una orza costante è l prodotto scalare della orza per lo spostamento del punto d applcazone della orza medesma [] [M T - ] N m
Soluzione del compito di Fisica febbraio 2012 (Udine)
 del compto d Fsca febbrao (Udne) Elettrodnamca È data una spra quadrata d lato L e resstenza R, ed un flo percorso da corrente lungo z (ved fgura). Dcamo a e b le dstanze del lato parallelo pù vcno e pù
del compto d Fsca febbrao (Udne) Elettrodnamca È data una spra quadrata d lato L e resstenza R, ed un flo percorso da corrente lungo z (ved fgura). Dcamo a e b le dstanze del lato parallelo pù vcno e pù
Lavoro ed Energia. Scorciatoia: concetto di energia/lavoro. devo conoscere nel dettaglio la traiettoria: molto complicato!!!
 avoro ed Energa esempo: corpo soggetto a orza varable con la poszone [orza d gravtà, orza della molla] oppure traettora complcata utlzzando la sola legge d Newton F ma non posso calcolare la veloctà del
avoro ed Energa esempo: corpo soggetto a orza varable con la poszone [orza d gravtà, orza della molla] oppure traettora complcata utlzzando la sola legge d Newton F ma non posso calcolare la veloctà del
Lez. 10 Forze d attrito e lavoro
 4/03/015 Lez. 10 Forze d attrto e lavoro Pro. 1 Dott., PhD Dpartmento Scenze Fsche Unverstà d Napol Federco II Compl. Unv. Monte S.Angelo Va Cnta, I-8016, Napol mettver@na.nn.t +39-081-676137 1 4/03/015
4/03/015 Lez. 10 Forze d attrto e lavoro Pro. 1 Dott., PhD Dpartmento Scenze Fsche Unverstà d Napol Federco II Compl. Unv. Monte S.Angelo Va Cnta, I-8016, Napol mettver@na.nn.t +39-081-676137 1 4/03/015
FISICA per SCIENZE BIOLOGICHE, A.A. 2005/2006 Prova scritta del 21 Giugno 2006
 FISICA per SCIENZE BIOLOGICHE, A.A. 5/6 Prova scrtta del Gugno 6 ) Un corpo d massa m = 5 g scvola lungo un pano nclnato lsco d altezza h = m e nclnazone θ=3 rspetto all orzzontale. Il corpo parte da ermo
FISICA per SCIENZE BIOLOGICHE, A.A. 5/6 Prova scrtta del Gugno 6 ) Un corpo d massa m = 5 g scvola lungo un pano nclnato lsco d altezza h = m e nclnazone θ=3 rspetto all orzzontale. Il corpo parte da ermo
Meccanica Dinamica del corpo rigido
 Meccanca 8-9 6 Fora peso sul corpo rgdo Corpo sottoposto alla fora peso: Su ogn elemento nfntesmo d massa dm agsce la fora Rsultante delle fore: F peso V g dm Momento rsultante (polo ): M V Energa potenale:
Meccanca 8-9 6 Fora peso sul corpo rgdo Corpo sottoposto alla fora peso: Su ogn elemento nfntesmo d massa dm agsce la fora Rsultante delle fore: F peso V g dm Momento rsultante (polo ): M V Energa potenale:
Sistemi di punti materiali
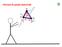 Sste d punt ateral F P F F,3 F P 3, 3 F P3 Sstea d n punt ateral n 3 j con:,,...... r, r,... r... r n,,...... n a, a,... a... a n n p,, p,... p...... p n n, Sstea d n punt ateral 3 F E F I j I F j j n
Sste d punt ateral F P F F,3 F P 3, 3 F P3 Sstea d n punt ateral n 3 j con:,,...... r, r,... r... r n,,...... n a, a,... a... a n n p,, p,... p...... p n n, Sstea d n punt ateral 3 F E F I j I F j j n
PROVA SCRITTA DI MECCANICA RAZIONALE (13 gennaio 2017) (Prof. A. Muracchini)
 PRV SCRITT DI ECCNIC RZINLE (13 gennao 017) (Prof.. uracchn) Il sstema rappresentato n fgura è costtuto da: a) una lamna pesante, omogenea a forma d trangolo soscele (massa m, base l, altezza h) vncolata
PRV SCRITT DI ECCNIC RZINLE (13 gennao 017) (Prof.. uracchn) Il sstema rappresentato n fgura è costtuto da: a) una lamna pesante, omogenea a forma d trangolo soscele (massa m, base l, altezza h) vncolata
F = 0 L = 0 se: s = 0 = 90 [L] = [ML 2 T -2 ] F // 1J = 10 7 erg
![F = 0 L = 0 se: s = 0 = 90 [L] = [ML 2 T -2 ] F // 1J = 10 7 erg F = 0 L = 0 se: s = 0 = 90 [L] = [ML 2 T -2 ] F // 1J = 10 7 erg](/thumbs/96/128573130.jpg) ) Un corpo d massa 5 kg è posto su un pano nclnato d 0. Una orza orzzontale d 00 N a rsalre l corpo lungo l pano nclnato con un accelerazone d 0.5 m/s. Qual è l coecente d attrto ra l corpo e l pano nclnato?
) Un corpo d massa 5 kg è posto su un pano nclnato d 0. Una orza orzzontale d 00 N a rsalre l corpo lungo l pano nclnato con un accelerazone d 0.5 m/s. Qual è l coecente d attrto ra l corpo e l pano nclnato?
Si dice corpo rigido un oggetto ideale che mantiene la stessa forma e le stesse dimensioni qualunque sia la sollecitazione cui lo si sottopone.
 Captolo 7 I corp estes 1. I movment d un corpo rgdo Che cosa s ntende per corpo esteso? Con l termne d corpo esteso c s rfersce ad oggett per qual non è lecto adoperare l approssmazone d partcella, coè
Captolo 7 I corp estes 1. I movment d un corpo rgdo Che cosa s ntende per corpo esteso? Con l termne d corpo esteso c s rfersce ad oggett per qual non è lecto adoperare l approssmazone d partcella, coè
Unità Didattica N 5. Impulso e quantità di moto
 Imnpulso e quanttà d moto - - Impulso e quanttà d moto ) Sstema solato : orze nterne ed esterne...pag. 2 2) Impulso e quanttà d moto...pag. 3 3) Teorema d conservazone della quanttà d moto...pag. 6 4)
Imnpulso e quanttà d moto - - Impulso e quanttà d moto ) Sstema solato : orze nterne ed esterne...pag. 2 2) Impulso e quanttà d moto...pag. 3 3) Teorema d conservazone della quanttà d moto...pag. 6 4)
l energia è la capacità di compiere un lavoro
 Energa cnetca e teorema delle orze e m energa cnetca teorema delle orze e l energa è la capactà d compere un laoro m m m d d m Fd d m ma F d a Un montacarch ha una potenza d x0 4 W quanto tempo mpega a
Energa cnetca e teorema delle orze e m energa cnetca teorema delle orze e l energa è la capactà d compere un laoro m m m d d m Fd d m ma F d a Un montacarch ha una potenza d x0 4 W quanto tempo mpega a
l energia è la capacità di compiere un lavoro
 Energa cnetca e teorema delle orze e K m energa cnetca K teorema delle orze e l energa è la capactà d compere un laoro m m m d d m Fd d m ma F d a Calcola l'energa cnetca d una automoble d 900 kg che agga
Energa cnetca e teorema delle orze e K m energa cnetca K teorema delle orze e l energa è la capactà d compere un laoro m m m d d m Fd d m ma F d a Calcola l'energa cnetca d una automoble d 900 kg che agga
Meccanica Dinamica del corpo rigido
 Meccanca 08-09 Dnamca del corpo rgdo 7 ω L Equaon del moto: Momento angolare: Energa cnetca: Sstem corpo rgdo E F K dp dt L L + L ω M otaone d un corpo rgdo L ω Momento d nera: r dm V dl dt r m L L ω L
Meccanca 08-09 Dnamca del corpo rgdo 7 ω L Equaon del moto: Momento angolare: Energa cnetca: Sstem corpo rgdo E F K dp dt L L + L ω M otaone d un corpo rgdo L ω Momento d nera: r dm V dl dt r m L L ω L
L energia cinetica. ( x)
 energa cnetca x x F ( x) dx K m energa cnetca K teorema delle orze e l energa è la capactà d compere un laoro m m m d d m Fd d m ma F d a Energa cnetca e teorema delle orze e Calcola l'energa cnetca d
energa cnetca x x F ( x) dx K m energa cnetca K teorema delle orze e l energa è la capactà d compere un laoro m m m d d m Fd d m ma F d a Energa cnetca e teorema delle orze e Calcola l'energa cnetca d
CORSO DI LAUREA IN SCIENZE BIOLOGICHE APPELLO di FISICA, 16 Giugno 2017
 CORSO DI LAUREA IN SCIENZE BIOLOGICHE APPELLO d FISICA, 6 Gugno 07 ) Un corpo d massa m 00 g è messo n moto, con eloctà 0 5 m/s, su un pano orzzontale scabro, con coecente d attrto dnamco µ 0. e lunghezza
CORSO DI LAUREA IN SCIENZE BIOLOGICHE APPELLO d FISICA, 6 Gugno 07 ) Un corpo d massa m 00 g è messo n moto, con eloctà 0 5 m/s, su un pano orzzontale scabro, con coecente d attrto dnamco µ 0. e lunghezza
1. MOTIVAZIONI DELLA RELATIVITA' GENERALE
 . MOTIVAZIONI DELLA RELATIVITA' GENERALE I mot che hanno spnto Ensten a formulare una nuoa teora che ncludesse la meccanca classca e la relattà specale come lmt, per camp gratazonal "debol" e eloctà
. MOTIVAZIONI DELLA RELATIVITA' GENERALE I mot che hanno spnto Ensten a formulare una nuoa teora che ncludesse la meccanca classca e la relattà specale come lmt, per camp gratazonal "debol" e eloctà
l energia è la capacità di compiere un lavoro
 Energa cnetca e teorema delle orze e K m energa cnetca K teorema delle orze e l energa è la capactà d compere un laoro m m m d d m Fd d m ma F d a Un montacarch ha una potenza d x0 4 W quanto tempo mpega
Energa cnetca e teorema delle orze e K m energa cnetca K teorema delle orze e l energa è la capactà d compere un laoro m m m d d m Fd d m ma F d a Un montacarch ha una potenza d x0 4 W quanto tempo mpega
Esercitazione sulle Basi di di Definizione
 Eserctazone sulle as d d Defnzone ESERIZIO Un bpolo ressto (dodo) ha la seguente equazone: = k [ 0 + 00] con k 0 nella quale ed sono descrtt dalla conenzone degl utlzzator come n fgura. Stablre se l bpolo
Eserctazone sulle as d d Defnzone ESERIZIO Un bpolo ressto (dodo) ha la seguente equazone: = k [ 0 + 00] con k 0 nella quale ed sono descrtt dalla conenzone degl utlzzator come n fgura. Stablre se l bpolo
Integrazione numerica dell equazione del moto per un sistema lineare viscoso a un grado di libertà. Prof. Adolfo Santini - Dinamica delle Strutture 1
 Integrazone numerca dell equazone del moto per un sstema lneare vscoso a un grado d lbertà Prof. Adolfo Santn - Dnamca delle Strutture 1 Introduzone 1/2 L equazone del moto d un sstema vscoso a un grado
Integrazone numerca dell equazone del moto per un sstema lneare vscoso a un grado d lbertà Prof. Adolfo Santn - Dnamca delle Strutture 1 Introduzone 1/2 L equazone del moto d un sstema vscoso a un grado
Sistema arciere-arco
 Sistema arciere-arco Consideriamo un ragazzo su uno sateboard mentre cade. Oltre alla forza peso che gestisce il moto verso il basso durante la caduta, nella direzione orizzontale al terreno avremo che
Sistema arciere-arco Consideriamo un ragazzo su uno sateboard mentre cade. Oltre alla forza peso che gestisce il moto verso il basso durante la caduta, nella direzione orizzontale al terreno avremo che
PROBLEMA 1. Soluzione. β = 64
 PROBLEMA alcolare l nclnazone β, rspetto al pano stradale, che deve avere un motocclsta per percorrere, alla veloctà v = 50 km/h, una curva pana d raggo r = 4 m ( Fg. ). Fg. Schema delle condzon d equlbro
PROBLEMA alcolare l nclnazone β, rspetto al pano stradale, che deve avere un motocclsta per percorrere, alla veloctà v = 50 km/h, una curva pana d raggo r = 4 m ( Fg. ). Fg. Schema delle condzon d equlbro
Teoria cinetica dei gas
 Teora cnetca de gas Fsca de gas n Termodnamca Grandezze macroscopche P, V, T tutte conseguenza del moto delle partcelle Pressone: Urt contro paret Volume: Assenza d legam tra le partcelle Temperatura:
Teora cnetca de gas Fsca de gas n Termodnamca Grandezze macroscopche P, V, T tutte conseguenza del moto delle partcelle Pressone: Urt contro paret Volume: Assenza d legam tra le partcelle Temperatura:
ELEMENTI DI MECCANICA. 3 Meccanica del corpo rigido
 ELEMENT D MECCANCA 3 Meccanca del corpo rgdo Govann Buccoler Unverstà del Salento, Dpartmento Matematca e Fsca e-mal: govann.buccoler@unsalento.t 1 Sstem d punt Fnora abbamo consderato sstem format da
ELEMENT D MECCANCA 3 Meccanca del corpo rgdo Govann Buccoler Unverstà del Salento, Dpartmento Matematca e Fsca e-mal: govann.buccoler@unsalento.t 1 Sstem d punt Fnora abbamo consderato sstem format da
Dinamica dei sistemi di punti materiali. Dott.ssa Elisabetta Bissaldi
 Dnamca de sstem d punt materal Dott.ssa Elsabetta Bssald Elsabetta Bssald (Poltecnco d Bar) A.A. 2018-2019 2 Sstem d punt materal Sno ad ora s è studato l moto d un sngolo punto materale. Nella dnamca
Dnamca de sstem d punt materal Dott.ssa Elsabetta Bssald Elsabetta Bssald (Poltecnco d Bar) A.A. 2018-2019 2 Sstem d punt materal Sno ad ora s è studato l moto d un sngolo punto materale. Nella dnamca
! A! B = Scalare. !! A B = Vettore. I vettori sono quantità più complicate degli scalari
 Moltplcazone d vettor I vettor sono quanttà pù complcate degl scalar la somma d due scalar è una semplce operazone algebrca ( es: s +3 s 5 s senza ambgutà) la somma d due vettor non è la semplce somma
Moltplcazone d vettor I vettor sono quanttà pù complcate degl scalar la somma d due scalar è una semplce operazone algebrca ( es: s +3 s 5 s senza ambgutà) la somma d due vettor non è la semplce somma
l energia è la capacità di compiere un lavoro
 Energa cnetca e teorema delle orze e K energa cnetca K teorema delle orze e l energa è la capactà d compere un laoro m d d m Fd d m ma F d a Calcolare l laoro computo dal motore d un'auto che ha massa
Energa cnetca e teorema delle orze e K energa cnetca K teorema delle orze e l energa è la capactà d compere un laoro m d d m Fd d m ma F d a Calcolare l laoro computo dal motore d un'auto che ha massa
Determinazione del momento d inerzia di una massa puntiforme
 Determnazone del momento d nerza d una massa puntorme Materale utlzzato Set d accessor per mot rotator Sensore d rotazone Portamasse e masse agguntve Statvo con base Blanca elettronca Calbro nteracca GLX
Determnazone del momento d nerza d una massa puntorme Materale utlzzato Set d accessor per mot rotator Sensore d rotazone Portamasse e masse agguntve Statvo con base Blanca elettronca Calbro nteracca GLX
Dilatazione termica di solidi e liquidi:
 Dlatazone termca d sold e lqud: temperatura aumenta corp s dlatano; es.: bnaro de tren Dlatazone lneare: sbarra spazo tra d loro L L 0 α pù e lunga, pù s dlata coeffcente d dlatazone lneare es: α Fe 12
Dlatazone termca d sold e lqud: temperatura aumenta corp s dlatano; es.: bnaro de tren Dlatazone lneare: sbarra spazo tra d loro L L 0 α pù e lunga, pù s dlata coeffcente d dlatazone lneare es: α Fe 12
ω 0 =, abbiamo L = 1 H. LC 8.1 Per t il condensatore si comporta come un circuito aperto pertanto la corrente tende a zero: la R
 8. Per t l condensatore s comporta come un crcuto aperto pertanto la corrente tende a zero: la funzone non può essere la (c). caando α e ω 0 s ottengono seguent alor: α 5 0 e ω 0 0. Essendo α > ω 0 l crcuto
8. Per t l condensatore s comporta come un crcuto aperto pertanto la corrente tende a zero: la funzone non può essere la (c). caando α e ω 0 s ottengono seguent alor: α 5 0 e ω 0 0. Essendo α > ω 0 l crcuto
Rotazione rispetto ad asse fisso Asse z : asse di rotazione
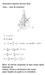 Rotaone rspetto ad asse fsso Asse : asse d rotaone 1 1 1 Ek= ω = ω= ω om. d nera: propreta d ogn corpo rgdo Dpende da: massa, forma e dmenson del corpo asse rspetto al quale lo s consdera Asta omogenea:
Rotaone rspetto ad asse fsso Asse : asse d rotaone 1 1 1 Ek= ω = ω= ω om. d nera: propreta d ogn corpo rgdo Dpende da: massa, forma e dmenson del corpo asse rspetto al quale lo s consdera Asta omogenea:
IV - Conservazione della quantità di moto; sistemi a più corpi ed urti
 IV - Conserazone della quanttà d oto; sste a pù corp ed urt Per una partcella s defnsce quanttà d oto la grandezza: p. La seconda legge della dnaca, nella sua fora pù generale, s scre: F dp dt doe F è
IV - Conserazone della quanttà d oto; sste a pù corp ed urt Per una partcella s defnsce quanttà d oto la grandezza: p. La seconda legge della dnaca, nella sua fora pù generale, s scre: F dp dt doe F è
Circuiti elettrici in regime stazionario
 rcut elettrc n regme stazonaro omponent www.de.ng.unbo.t/pers/mastr/ddattca.htm (ersone del 3-9-0) Bpol resst Equazon caratterstca d un bpolo ressto f, 0 L equazone d un bpolo ressto defnsce una cura nel
rcut elettrc n regme stazonaro omponent www.de.ng.unbo.t/pers/mastr/ddattca.htm (ersone del 3-9-0) Bpol resst Equazon caratterstca d un bpolo ressto f, 0 L equazone d un bpolo ressto defnsce una cura nel
Gas ideale (perfetto):
 Gas deale (perfetto): non esste n realtà drogeno e elo assomglano d pù a un gas deale - le molecole sono puntform; - nteragscono tra loro e con le paret del recpente medante urt perfettamente elastc (ovvero
Gas deale (perfetto): non esste n realtà drogeno e elo assomglano d pù a un gas deale - le molecole sono puntform; - nteragscono tra loro e con le paret del recpente medante urt perfettamente elastc (ovvero
( F) Anello frenato Dati. M=2 kg massa dell anello R=2 m raggio dell anello rad ω= 10 (negativo perchè in senso orario) velocità iniziale dell'anello
 Anello renato Dat M= kg massa dell anello R= m raggo dell anello rad = 10 (negatvo perchè n senso oraro) veloctà nale dell'anello s = 0 veloctà nale dell'anello F= 10 ˆ 5ˆj ora applcata al dsco r = O=+
Anello renato Dat M= kg massa dell anello R= m raggo dell anello rad = 10 (negatvo perchè n senso oraro) veloctà nale dell'anello s = 0 veloctà nale dell'anello F= 10 ˆ 5ˆj ora applcata al dsco r = O=+
Gas ideale (perfetto):
 C.d.L. Scenze e ecnologe grare,.. 2015/2016, Fsca Gas deale (perfetto): non esste n realtà drogeno e elo assomglano d pù a un gas deale - le molecole sono puntform; - nteragscono tra loro e con le paret
C.d.L. Scenze e ecnologe grare,.. 2015/2016, Fsca Gas deale (perfetto): non esste n realtà drogeno e elo assomglano d pù a un gas deale - le molecole sono puntform; - nteragscono tra loro e con le paret
PROVA SCRITTA DI MECCANICA RAZIONALE (15 gennaio 2016) ( C.d.L. Ing. Energetica - Prof. A. Muracchini)
 PRV SRITT DI MENI RZINLE (15 gennao 2016) (.d.l. Ing. Energetca - Prof.. Muracchn) Il sstema n fgura, moble n un pano vertcale, è costtuto d un asta omogenea (massa m, lunghezza 2l) l cu estremo è vncolato
PRV SRITT DI MENI RZINLE (15 gennao 2016) (.d.l. Ing. Energetca - Prof.. Muracchn) Il sstema n fgura, moble n un pano vertcale, è costtuto d un asta omogenea (massa m, lunghezza 2l) l cu estremo è vncolato
Teoremi dei circuiti
 Teorem de crcut www.de.ng.unbo.t/pers/mastr/ddattca.htm (ersone del --04) Teorema d Tellegen potes: Crcuto con n nod e l lat ers d rfermento scelt per tutt lat secondo la conenzone dell utlzzatore {,...,
Teorem de crcut www.de.ng.unbo.t/pers/mastr/ddattca.htm (ersone del --04) Teorema d Tellegen potes: Crcuto con n nod e l lat ers d rfermento scelt per tutt lat secondo la conenzone dell utlzzatore {,...,
FISICA GENERALE LB INGEGNERIA ALIMENTARE, per L AMBIENTE ed Il TERRITORIO E CHIMICA. Esercizi in preparazione del secondo parziale
 FISIC GENERLE L INGEGNERI LIMENTRE, per L MIENTE ed Il TERRITORIO E CHIMIC Teora: Esercz n preparazone del secondo parzale 1. Enuncare e commentare le legg d mpere-maxwell.. Enuncare e commentare le legg
FISIC GENERLE L INGEGNERI LIMENTRE, per L MIENTE ed Il TERRITORIO E CHIMIC Teora: Esercz n preparazone del secondo parzale 1. Enuncare e commentare le legg d mpere-maxwell.. Enuncare e commentare le legg
DINAMICA DEI SISTEMI DI PUNTI MATERIALI. Dott.ssa Silvia Rainò
 DIAMICA DI SISTMI DI PUTI MATRIALI Dott.ssa Slva Ranò Sste d punt ateral Sstea costtuto da punt ateral P, P,, P F rsultante delle forze esterne agent su P F j forza eserctata sul generco punto P del sstea
DIAMICA DI SISTMI DI PUTI MATRIALI Dott.ssa Slva Ranò Sste d punt ateral Sstea costtuto da punt ateral P, P,, P F rsultante delle forze esterne agent su P F j forza eserctata sul generco punto P del sstea
Fisica Generale LA N.1 Prova Scritta del 12 Febbraio 2018 Prof. Nicola Semprini Cesari
 Fsca Generale A N. Prova Scrtta del Febbrao 8 Prof. Ncola Semprn Cesar Meccanca: quest ) Al tempo t= una carrozza ferrovara comnca a muovers d moto rettlneo unformemente accelerato (a). Al tempo t=t, da
Fsca Generale A N. Prova Scrtta del Febbrao 8 Prof. Ncola Semprn Cesar Meccanca: quest ) Al tempo t= una carrozza ferrovara comnca a muovers d moto rettlneo unformemente accelerato (a). Al tempo t=t, da
Teorema di Thévenin-Norton
 87 Teorema d Téenn-Norton E detto ance teorema d rappresentazone del bpolo, consente nfatt d rappresentare una rete lneare a due morsett (A, B) con: un generatore d tensone ed un resstore sere (Téenn)
87 Teorema d Téenn-Norton E detto ance teorema d rappresentazone del bpolo, consente nfatt d rappresentare una rete lneare a due morsett (A, B) con: un generatore d tensone ed un resstore sere (Téenn)
Statistica di Bose-Einstein
 Statstca d Bose-Ensten Esstono sstem compost d partcelle dentche e ndstngubl che non sono soggette al prncpo d esclusone. In quest sstem non esste un lmte al numero d partcelle che possono essere osptate
Statstca d Bose-Ensten Esstono sstem compost d partcelle dentche e ndstngubl che non sono soggette al prncpo d esclusone. In quest sstem non esste un lmte al numero d partcelle che possono essere osptate
Corso di Laurea in Medicina e Chirurgia Prova scritta di Fisica del 22/2/2016: MED 3-4
 Corso d Laurea n Medcna e Chrurga Prova scrtta d Fsca del 22/2/206: MED 3-4 Nome: Cognome: N. matrcola: * Segnare con una x la rsposta corretta, svolgere problem ne fogl allegat scrvendo le formule utlzzate
Corso d Laurea n Medcna e Chrurga Prova scrtta d Fsca del 22/2/206: MED 3-4 Nome: Cognome: N. matrcola: * Segnare con una x la rsposta corretta, svolgere problem ne fogl allegat scrvendo le formule utlzzate
Elasticità nei mezzi continui
 Elastctà ne mezz contnu l tensore degl sforz o tensore d stress, σ j Consderamo un cubo d dmenson untare n un mezzo elastco deformato. l cubo è deformato dalle forze eserctate sulle sue facce dal resto
Elastctà ne mezz contnu l tensore degl sforz o tensore d stress, σ j Consderamo un cubo d dmenson untare n un mezzo elastco deformato. l cubo è deformato dalle forze eserctate sulle sue facce dal resto
links utili:
 dspensa d Govann Bachelet Meccanca de Sstem, maggo 2003 lnks utl: http://scenceworld.wolfram.com/physcs/angularmomentum.html http://hyperphyscs.phy-astr.gsu.edu/hbase/necon.html Momento della quanttà d
dspensa d Govann Bachelet Meccanca de Sstem, maggo 2003 lnks utl: http://scenceworld.wolfram.com/physcs/angularmomentum.html http://hyperphyscs.phy-astr.gsu.edu/hbase/necon.html Momento della quanttà d
lim Flusso Elettrico lim E ΔA
 Flusso lettrco Nel caso pù generale l campo elettrco può varare sa n ntenstà che drezone e verso. La defnzone d flusso data n precedenza vale solo se l elemento d superfce A è suffcentemente pccolo da
Flusso lettrco Nel caso pù generale l campo elettrco può varare sa n ntenstà che drezone e verso. La defnzone d flusso data n precedenza vale solo se l elemento d superfce A è suffcentemente pccolo da
Intorduzione alla teoria delle Catene di Markov
 Intorduzone alla teora delle Catene d Markov Mchele Ganfelce a.a. 2014/2015 Defnzone 1 Sa ( Ω, F, {F n } n 0, P uno spazo d probabltà fltrato. Una successone d v.a. {ξ n } n 0 defnta su ( Ω, F, {F n }
Intorduzone alla teora delle Catene d Markov Mchele Ganfelce a.a. 2014/2015 Defnzone 1 Sa ( Ω, F, {F n } n 0, P uno spazo d probabltà fltrato. Una successone d v.a. {ξ n } n 0 defnta su ( Ω, F, {F n }
2.1 Parabola nella forma canonica
 5 Clc per tutt gl appunt (AUTOMAZIONE TRATTAMENTI TERMICI ACCIAIO SCIENZA delle COSTRUZIONI ) e-mal per suggerment. Paraola nella forma canonca Studamo con metod general la conca nella espressone canonca
5 Clc per tutt gl appunt (AUTOMAZIONE TRATTAMENTI TERMICI ACCIAIO SCIENZA delle COSTRUZIONI ) e-mal per suggerment. Paraola nella forma canonca Studamo con metod general la conca nella espressone canonca
1) Un blocchetto di massa M = 300 g scende senza attrito lungo un piano inclinato di lunghezza L = 90 cm che forma un angolo
 ENERGA ) Un blocchetto d massa M 00 g scende senza attrto lungo un pano nclnato d lunghezza L 90 cm che orma un angolo α 0 con l orzzontale e a a nre su una molla d costante elastca k 5 N/m. Determnare
ENERGA ) Un blocchetto d massa M 00 g scende senza attrto lungo un pano nclnato d lunghezza L 90 cm che orma un angolo α 0 con l orzzontale e a a nre su una molla d costante elastca k 5 N/m. Determnare
Molla e legge di Hooke
 Molla e legge d Hooke Consderamo un corpo d massa m poggato su una superce prva d attrto ed attaccato all estremtà lbera d una molla e consderamo che la poszone d equlbro (F0) sa n 0 Ø Se la molla vene
Molla e legge d Hooke Consderamo un corpo d massa m poggato su una superce prva d attrto ed attaccato all estremtà lbera d una molla e consderamo che la poszone d equlbro (F0) sa n 0 Ø Se la molla vene
RIPARTIZIONE DELLE FORZE SISMICHE ORIZZONTALI
 RIPARTIZIONE DELLE FORZE SISMICHE ORIZZONTALI (Modellazone approssmata alla rnter) Le strutture degl edfc sottopost alle forze ssmche sono organsm spazal pù o meno compless, l cu comportamento va analzzato
RIPARTIZIONE DELLE FORZE SISMICHE ORIZZONTALI (Modellazone approssmata alla rnter) Le strutture degl edfc sottopost alle forze ssmche sono organsm spazal pù o meno compless, l cu comportamento va analzzato
Università degli Studi di Torino D.E.I.A.F.A. Forze conservative. Forze conservative (1)
 Unverstà degl Stud d Torno D.E.I.A..A. orze conservatve Unverstà degl Stud d Torno D.E.I.A..A. orze conservatve () Una orza s dce conservatva se l lavoro da essa computo su un corpo che s muove tra due
Unverstà degl Stud d Torno D.E.I.A..A. orze conservatve Unverstà degl Stud d Torno D.E.I.A..A. orze conservatve () Una orza s dce conservatva se l lavoro da essa computo su un corpo che s muove tra due
Gas ideale (perfetto):
 Gas deale (erfetto): non esste n realtà drogeno e elo assomglano d ù a un gas deale - le molecole sono untform; - nteragscono tra loro e con le aret del recente medante urt erfettamente elastc (ovvero
Gas deale (erfetto): non esste n realtà drogeno e elo assomglano d ù a un gas deale - le molecole sono untform; - nteragscono tra loro e con le aret del recente medante urt erfettamente elastc (ovvero
PROPRIETÀ DEL CAMPO ELETTROSTATICO. G. Pugliese 1
 PROPRIETÀ DEL CMPO ELETTROSTTICO G. Puglese 1 Campo elettrostatco & elettrco F = 0 E S parla d forza elettrostatca uando sa le carche che generano l campo (elettrostatco) che 0 sono fsse e costant Quando
PROPRIETÀ DEL CMPO ELETTROSTTICO G. Puglese 1 Campo elettrostatco & elettrco F = 0 E S parla d forza elettrostatca uando sa le carche che generano l campo (elettrostatco) che 0 sono fsse e costant Quando
Significato delle EQUAZIONI COSTITUTIVE dei tessuti viventi
 Per flud n movmento occorre consderare l campo delle veloctà. Inun sstema cartesano Oxyz l campo è descrtto dal vettore v(x,y,z) che defnsce le component della veloctà del fludo n ogn punto x,y,z : v (x,y,z)
Per flud n movmento occorre consderare l campo delle veloctà. Inun sstema cartesano Oxyz l campo è descrtto dal vettore v(x,y,z) che defnsce le component della veloctà del fludo n ogn punto x,y,z : v (x,y,z)
Università Politecnica delle Marche, Facoltà di Agraria. C.d.L. Scienze Forestali e Ambientali, A.A. 2010/2011, Fisica. Diagramma di fase:
 Dagramma d fase: Cambament d stato dell acqua: Spazo tra bnar de tren - per far s che la la dlatazone ndotta dalle temperature estve possa avvenre lungo l'asse del bnaro stesso Dlatazone termca d sold
Dagramma d fase: Cambament d stato dell acqua: Spazo tra bnar de tren - per far s che la la dlatazone ndotta dalle temperature estve possa avvenre lungo l'asse del bnaro stesso Dlatazone termca d sold
PICCOLE OSCILLAZIONI ATTORNO ALLA POSIZIONE DI EQUILIBRIO
 PICCOLE OSCILLAZIONI ATTORNO ALLA POSIZIONE DI EQUILIBRIO Stabltà e Teorema d Drclet Defnzone S dce ce la confgurazone C 0 d un sstema è n una poszone d equlbro stable se, portando l sstema n una confgurazone
PICCOLE OSCILLAZIONI ATTORNO ALLA POSIZIONE DI EQUILIBRIO Stabltà e Teorema d Drclet Defnzone S dce ce la confgurazone C 0 d un sstema è n una poszone d equlbro stable se, portando l sstema n una confgurazone
FISICA per SCIENZE BIOLOGICHE, A.A. 2014/2015 Prova scritta del 24 Febbraio 2015
 FISICA per SCIENZE BIOLOGICHE, A.A. 04/05 Prova scrtta del 4 Febbrao 05 ) Un corpo d massa m = 300 g scvola lungo un pano nclnato lsco d altezza h = 3m e nclnazone θ=30 0 rspetto all orzzontale. Il corpo
FISICA per SCIENZE BIOLOGICHE, A.A. 04/05 Prova scrtta del 4 Febbrao 05 ) Un corpo d massa m = 300 g scvola lungo un pano nclnato lsco d altezza h = 3m e nclnazone θ=30 0 rspetto all orzzontale. Il corpo
FISICA. Lezione n. 6 (2 ore) Gianluca Colò Dipartimento di Fisica sede Via Celoria 16, Milano
 Unverstà degl Stud d Mlano Facoltà d Scenze Matematche Fsche e Natural Cors d aurea n: Informatca ed Informatca per le Telecomuncazon Anno accademco 010/11, aurea Trennale, Edzone durna FISICA ezone n.
Unverstà degl Stud d Mlano Facoltà d Scenze Matematche Fsche e Natural Cors d aurea n: Informatca ed Informatca per le Telecomuncazon Anno accademco 010/11, aurea Trennale, Edzone durna FISICA ezone n.
La corrente vale metà del valore finale quando 0,2(1 e ) = 0, 1; risolvendo l equazione si
 7.6 La corrente nzale è edentemente nulla. on l nterruttore chuso la costante d tempo è τ = L/ = 1/200 s. Il alore fnale è ( ) = 20/100 = 0,2 A. on l espressone (7.13b) a pag. 235 del lbro s ottene 200t
7.6 La corrente nzale è edentemente nulla. on l nterruttore chuso la costante d tempo è τ = L/ = 1/200 s. Il alore fnale è ( ) = 20/100 = 0,2 A. on l espressone (7.13b) a pag. 235 del lbro s ottene 200t
Ci sono solo forze interne se il sistema scelto e costituito dalla pallina e dal pupazzetto. In questo caso si conserva la quantità di moto per cui:
 Una pallna d plastlna da 500 g vene lancata alla veloctà d 3 m/s contro un pupazzetto, nzalmente ermo. Se la plastlna s attacca al pupazzetto e successvamente s muovono d m/s, quale è la massa del pupazzetto?
Una pallna d plastlna da 500 g vene lancata alla veloctà d 3 m/s contro un pupazzetto, nzalmente ermo. Se la plastlna s attacca al pupazzetto e successvamente s muovono d m/s, quale è la massa del pupazzetto?
Teoremi dei circuiti
 Teorem de crcut www.de.ng.unbo.t/pers/mastr/ddattca.htm (ersone del 0-0-03) Teorema d Tellegen Ipotes: Crcuto con n nod e l lat ers d rfermento scelt per tutt lat secondo la conenzone dell utlzzatore {,...,
Teorem de crcut www.de.ng.unbo.t/pers/mastr/ddattca.htm (ersone del 0-0-03) Teorema d Tellegen Ipotes: Crcuto con n nod e l lat ers d rfermento scelt per tutt lat secondo la conenzone dell utlzzatore {,...,
3 = 3 Ω. quindi se v g = 24 V, i = 1,89 A Dobbiamo studiare tre circuiti; in tutti e tre i casi si ottiene un partitore di corrente.
 5. Per la propretà d lneartà la tensone può essere espressa come = k g, doe g è la corrente del generatore. Utlzzando dat n Fgura a abbamo - = k 6, qund k = - ½. In Fgura b la corrente del generatore è
5. Per la propretà d lneartà la tensone può essere espressa come = k g, doe g è la corrente del generatore. Utlzzando dat n Fgura a abbamo - = k 6, qund k = - ½. In Fgura b la corrente del generatore è
Elementi di strutturistica cristallina I
 Chmca fsca superore Modulo 1 Element d strutturstca crstallna I Sergo Brutt Impacchettamento compatto n 2D Esstono 2 dfferent mod d arrangare n un pano 2D crconferenze dentche n modo da tassellare n modo
Chmca fsca superore Modulo 1 Element d strutturstca crstallna I Sergo Brutt Impacchettamento compatto n 2D Esstono 2 dfferent mod d arrangare n un pano 2D crconferenze dentche n modo da tassellare n modo
Soluzioni 3.1. n(n 1) (n k + 1) z n k! k + 1 n k. lim k
 (1) La sere bnomale è B n (z) = k=0 Con l metodo del rapporto s ottene R = lm k Soluzon 3.1 n(n 1) (n k + 1) z n k! c k c k+1 = lm k k + 1 n k lm k c k z k. k=0 1 + 1 k 1 n k = 1 (2) La multfunzone f(z)
(1) La sere bnomale è B n (z) = k=0 Con l metodo del rapporto s ottene R = lm k Soluzon 3.1 n(n 1) (n k + 1) z n k! c k c k+1 = lm k k + 1 n k lm k c k z k. k=0 1 + 1 k 1 n k = 1 (2) La multfunzone f(z)
Lezione 16 - Corrente e resistenza
 Lezone 16 - Corrente e resstenza Inzamo ora lo studo degl effett delle carche n movmento In presenza d carche n movmento s parla d corrente elettrca quando esste un trasporto netto d carca elettrca Esemp
Lezone 16 - Corrente e resstenza Inzamo ora lo studo degl effett delle carche n movmento In presenza d carche n movmento s parla d corrente elettrca quando esste un trasporto netto d carca elettrca Esemp
Campo elettrico. F E q. Qq k r. r q r
 Campo elettrco In passato s potzzava che le nterazon (lumnose, elettrche) potessero vaggare a veloctà nfnta, per cu due carche poste ad una certa dstanza avrebbero dovuto stantaneamente rsentre d una forza
Campo elettrco In passato s potzzava che le nterazon (lumnose, elettrche) potessero vaggare a veloctà nfnta, per cu due carche poste ad una certa dstanza avrebbero dovuto stantaneamente rsentre d una forza
Corpi rigidi (prima parte)
 Corp rgd (prma parte) Corp rgd Un corpo rgdo è un corpo n cu le dstane tra le vare par che lo compongono rmangono costan3. r CM d CM È un po parcolare d sstema d N parcelle. Valgono ancora le legg dp dt
Corp rgd (prma parte) Corp rgd Un corpo rgdo è un corpo n cu le dstane tra le vare par che lo compongono rmangono costan3. r CM d CM È un po parcolare d sstema d N parcelle. Valgono ancora le legg dp dt
Fisica. Architettura
 Fsca Facoltà d Ingegnera, Archtettura e delle Scenze otore Lezone 9 aprle 03 Archtettura (corso magstrale a cclo unco qunquennale) Prof. Lanzalone Gaetano CORPO RIGIDO Il corpo rgdo È un partcolare sstema
Fsca Facoltà d Ingegnera, Archtettura e delle Scenze otore Lezone 9 aprle 03 Archtettura (corso magstrale a cclo unco qunquennale) Prof. Lanzalone Gaetano CORPO RIGIDO Il corpo rgdo È un partcolare sstema
AA Insegnamento di BIOMECCANICA. Pietro Picerno, PhD. Programma del corso
 AA 2012-2013 UNIVERSITA DEGLI STUDI DI ROMA TOR VERGATA FACOLTA DI MEDICINA E CHIRURGIA LAUREA TRIENNALE IN SCIENZE MOTORIE Insegnamento d BIOMECCANICA Petro, PhD Programma del corso MODULO 1: Introduzone
AA 2012-2013 UNIVERSITA DEGLI STUDI DI ROMA TOR VERGATA FACOLTA DI MEDICINA E CHIRURGIA LAUREA TRIENNALE IN SCIENZE MOTORIE Insegnamento d BIOMECCANICA Petro, PhD Programma del corso MODULO 1: Introduzone
F est. I int. I est. ,L int. costante. Kcm
 Urt Sere, anztutto, rleare alcune caratterstche coun agl urt. Gl urt sono olto bre ed e dunque dcle tener conto esplctaente delle orze che nterengono nell urto. Se ne rcaa norazone a partre dalle propreta
Urt Sere, anztutto, rleare alcune caratterstche coun agl urt. Gl urt sono olto bre ed e dunque dcle tener conto esplctaente delle orze che nterengono nell urto. Se ne rcaa norazone a partre dalle propreta
Secondo Principio della Termodinamica
 Secondo Prncpo della ermodnamca Problema: n che modo s puo pedere se un processo è spontaneo e quale è la drezone d un processo spontaneo Notamo: Il I prncpo della D stablsce che un sstema puo modfcare
Secondo Prncpo della ermodnamca Problema: n che modo s puo pedere se un processo è spontaneo e quale è la drezone d un processo spontaneo Notamo: Il I prncpo della D stablsce che un sstema puo modfcare
1 Le equazioni per le variabili macroscopiche: i momenti dell equazione di Boltzmann
 FISICA DEI FLUIDI Lezone 5-5 Maggo 202 Le equazon per le varabl macroscopche: moment dell equazone d Boltzmann Teorema H a parte, non è facle estrarre altre consderazon general sulla funzone denstà d probabltà
FISICA DEI FLUIDI Lezone 5-5 Maggo 202 Le equazon per le varabl macroscopche: moment dell equazone d Boltzmann Teorema H a parte, non è facle estrarre altre consderazon general sulla funzone denstà d probabltà
La teoria cinetica dei gas
 La teora cnetca de gas Gas: un numero grandssmo gandssmodmolecole n moto caotco. Interazone tra molecole solo n caso d urto. Calcolando la pressone come dovuta all urto d tutte le molecole con le paret
La teora cnetca de gas Gas: un numero grandssmo gandssmodmolecole n moto caotco. Interazone tra molecole solo n caso d urto. Calcolando la pressone come dovuta all urto d tutte le molecole con le paret
Campo magnetico e forza di Lorentz (II)
 Campo magnetco e forza d Lorentz (II) Moto d partcelle carche n un campo magnetco Legg elementar d Laplace Prncpo d equvalenza d Ampere Moto d una partcella carca n un campo magnetco dp dt F q v qv d v
Campo magnetco e forza d Lorentz (II) Moto d partcelle carche n un campo magnetco Legg elementar d Laplace Prncpo d equvalenza d Ampere Moto d una partcella carca n un campo magnetco dp dt F q v qv d v
12. Dinamica dei sistemi
 1. Dnamca de sstem 1. Sstem d punt e seconda legge della dnamca In cnematca s èntrodotto l concetto d sstema d punt materal; se ne è studato l atto d moto ponendo partcolare attenzone su sstem rgd. Quando
1. Dnamca de sstem 1. Sstem d punt e seconda legge della dnamca In cnematca s èntrodotto l concetto d sstema d punt materal; se ne è studato l atto d moto ponendo partcolare attenzone su sstem rgd. Quando
INTRODUZIONE ALL ESPERIENZA 4: STUDIO DELLA POLARIZZAZIONE MEDIANTE LAMINE DI RITARDO
 INTODUZION ALL SPINZA 4: STUDIO DLLA POLAIZZAZION DIANT LAIN DI ITADO Un utle rappresentazone su come agscono le lamne su fasc coerent è ottenuta utlzzando vettor e le matrc d Jones. Vettore d Jones e
INTODUZION ALL SPINZA 4: STUDIO DLLA POLAIZZAZION DIANT LAIN DI ITADO Un utle rappresentazone su come agscono le lamne su fasc coerent è ottenuta utlzzando vettor e le matrc d Jones. Vettore d Jones e
Circuiti elettrici in regime stazionario
 Crcut elettrc n regme stazonaro Component www.de.ng.unbo.t/pers/mastr/ddattca.htm (ersone del 0-0-00) Bpol resst Equazon caratterstca d un bpolo ressto f, 0 L equazone d un bpolo ressto defnsce una cura
Crcut elettrc n regme stazonaro Component www.de.ng.unbo.t/pers/mastr/ddattca.htm (ersone del 0-0-00) Bpol resst Equazon caratterstca d un bpolo ressto f, 0 L equazone d un bpolo ressto defnsce una cura
Forze di massa gravitazionali inerziali elettromagnetiche. attraverso una superficie. sollecitazioni
 Unverstà d Roma La Sapenza Tecnologa de Process Produttv Resstenza de materal Forze d massa gravtazonal nerzal elettromagnetche d contatto fra sold fra sold e lqud fra sold e gas attraverso una superfce
Unverstà d Roma La Sapenza Tecnologa de Process Produttv Resstenza de materal Forze d massa gravtazonal nerzal elettromagnetche d contatto fra sold fra sold e lqud fra sold e gas attraverso una superfce
Equilibrio e stabilità di sistemi dinamici. Stabilità dell equilibrio di sistemi dinamici non lineari per linearizzazione
 Equlbro e stabltà d sstem dnamc Stabltà dell equlbro d sstem dnamc non lnear per lnearzzazone Stabltà dell equlbro d sstem dnamc non lnear per lnearzzazone Stabltà dell equlbro d sstem NL TC Crter d stabltà
Equlbro e stabltà d sstem dnamc Stabltà dell equlbro d sstem dnamc non lnear per lnearzzazone Stabltà dell equlbro d sstem dnamc non lnear per lnearzzazone Stabltà dell equlbro d sstem NL TC Crter d stabltà
Studio delle oscillazioni del pendolo semplice e misura dell accelerazione di gravita g.
 Studo delle oscllazon del pendolo semplce e msura dell accelerazone d ravta. Introduzone fsca Un pendolo semplce e costtuto da un flo d lunhezza L nestensble e d massa trascurable a cu e appesa un corpo
Studo delle oscllazon del pendolo semplce e msura dell accelerazone d ravta. Introduzone fsca Un pendolo semplce e costtuto da un flo d lunhezza L nestensble e d massa trascurable a cu e appesa un corpo
INDICE. Scaricabile su: Derivate TEORIA. Derivata in un punto. Significato geometrico della derivata
 P r o f Gu d of r a n c n Anteprma Anteprma Anteprma www l e z o n j md o c o m Scarcable su: ttp://lezonjmdocom/ INDICE TEORIA Dervata n un punto Sgnfcato geometrco della dervata Funzone dervata e dervate
P r o f Gu d of r a n c n Anteprma Anteprma Anteprma www l e z o n j md o c o m Scarcable su: ttp://lezonjmdocom/ INDICE TEORIA Dervata n un punto Sgnfcato geometrco della dervata Funzone dervata e dervate
