Example 2 Una variabile o un vettore aleatorio X è degenere in c se P (X = c) = 1. Dato che la funzione di ripartizione di questa variabile è
|
|
|
- Vito Rossi
- 4 anni fa
- Visualizzazioni
Transcript
1 La covergeze i legge per variabili o vettori aleatori è solitamete formulata i termii di fuzioi di ripartizioe. Ricordiamo che la fuzioe di ripartizioe di ua variabile aleatoria X è ua fuzioe di variabile reale defiita da F X (x) = P (X x). Per u vettore aleatorio d-dimesioale la defiizioe è aaloga, ma x è u vettore e la disuguagliaza va itesa coordiata per coordiata. Defiitio 1 X coverge i legge ad X, che idichiamo co X = X, se F X (x) F X (x) per ogi x reale che o è u puto di cotiuità per F (cioè tale che P (X = x) = 0). Ua termiologia alterativa è che X coverge debolmete ad X. Example 2 Ua variabile o u vettore aleatorio X è degeere i c se P (X = c) = 1. Dato che la fuzioe di ripartizioe di questa variabile è { 1, x c F c (x) = 0, x < c, che è discotiua i c, l esclusioe dei puti di discotiuità di F dalla defiizioe precedete serve a recuperare la covergeza delle successioi umeriche come covergeza i legge delle corrispodeti variabili aleatorie degeeri. Il risultato più celebre di covergeza i legge è il teorema del limite cetrale. Propositio 3 Siao X 1,..., X,... i.i.d. co media µ e matrice di covariaza fiita Σ. Allora (X µ) = N(µ, Σ). Defiitio 4 X coverge i probabilità ad X, che idichiamo co X P X, se per ogi ε > 0 P ( X X > ε) 0. Example 5 La covergeza i probabilità richiede che per ogi X e X siao defiite su di uo stesso spazio di probabilità, cosa o richiesta per la covergeza i legge. Quidi la covergeza i legge o implica la covergeza i probabilità. U cotroesempio immediato: basta predere per ogi X 1,..., X i.i.d. co la stessa legge di X, per cui X = X ma X P X. Il risultato più celebre di covergeza i probabilità è la legge dei gradi umeri. Propositio 6 Siao X 1,..., X,... i.i.d. co media µ. Allora X P µ. Nel seguito occorrerà cofrotare successioi di variabili aleatorie. Diamo quidi la seguete Defiitio 7 Siao X e Y, = 1, 2,... successioi di variabili aleatorie sullo stesso spazio di probabilità tali che X Y P 0. Allora scriviamo X = o P (Y ). Possiamo quidi riscrivere X P 0 come X = o P (1). 1
2 I altre questioi occorre ua codizioe più debole che la covergeza i legge. Per questo Defiitio 8 La successioe di variabili aleatorie X, = 1, 2,... è limitata i probabilità se qualuque sia ε > 0 esiste K > 0 tale che P ( X K) 1 ε. Chiariamo subito quato già aticipato co la seguete Propositio 9 Se X, = 1, 2,... coverge i legge, allora è limitata i probabilità Proof. (per d = 1). Risulta dal fatto che se K è tale che K e K soo puti di cotiuità della fuzioe ripartizioe limite F tali che F (K) 1 ε 4, F ( K) ε 4, allora P ( X K) F X (K) F X ( K) 1 ε 2 e quidi P ( X K) risulterà defiitivamete più grade di 1 ε. Importati osservazioi soo le segueti.. Propositio 10 Se la successioe X, = 1, 2,... è limitata i probabilità, metre la successioe Y = o P (1), allora X Y = o P (1). Proof. Sia γ > 0 e si scelga K tale che P ( X K) 1 γ/2. Allora P ( X Y ε) P ( X K, Y ε K ) = P ( X K) P ( X K, Y > ε K ) P ( X K) P ( Y ε K ) e prededo sufficietemete grade il secodo termie può essere reso più piccolo di γ/2. Ne segue che P ( X Y ε) è defiitivamete più grade di 1 γ come desiderato. Corollary 11 Se la successioe X, = 1, 2,... è limitata i probabilità e Z = o P (X ), allora Z = o P (1). Proof. Basta porre Y = Z X ella proposizioe precedete. Corollary 12 Se la successioe umerica a e la successioe di variabili aleatorie Z, = 1, 2,... soo tali che a Z è limitata i probabilità, allora Z = o P (1). I particolare, se X è ua successioe di variabili aleatorie tali che (X µ) è limitata i probabilità, allora X P µ. Proof. Discede dalla proposizioe precedete prededo Y = 1 a, X = a Z. La secoda asserzioe è u caso particolare della prima. I particolare, dalla secoda asserzioe si deduce che è possibile otteere la legge dei gradi umeri dal teorema del limite cetrale quado gli addedi hao variaza fiita (ovviamete è molto più semplice i questo caso usare la disuguagliaza di Chebyshev). 2
3 Propositio 13 { X P X } = {X = X} Proof. (per d = 1). Si osservi che {X x 0 } {X x 0 + ε} { X X > ε} da cui Aalogamete F X (x 0 ) F X (x 0 + ε) + P ( X X > ε). F X (x 0 ε) F X (x 0 ) + P ( X X > ε), quidi se P ( X X > ε) 0, allora F X (x 0 ε) lim if F X (x 0 ) lim sup F X (x 0 ) F X (x 0 + ε). Se x 0 è u puto di cotiuità di F X si coclude che F X (x 0 ) F X (x 0 ). Propositio 14 Se c R d allora X = c implica X P c (i altre parole covergeza i probabilità e i legge soo idetiche quado il limite è degeere). Proof. (per d = 1). Segue da P ( X c ε) F X (c + ε) F X (c ε), e dato che il primo termie del membro di destra tede a 1, metre il secodo tede a 0, la prova è completa. Propositio 15 Le segueti codizioi soo equivaleti: 1. X = X; 2. E(g(X )) E(g(X)) per tutte le fuzioi a valori reali g, cotiue a supporto compatto; 3. E(g(X )) E(g(X)) per tutte le fuzioi a valori reali g, cotiue e limitate; 4. E(g(X )) E(g(X)) per tutte le fuzioi a valori reali g limitate tali che P (X C(g)) = 1, dove C(g) è l isieme dei puti di cotiuità di g. Proof. Omettere i prima lettura. Basta dimostrare che 4. = 1. = 2. = 3. = = 1. (per d = 1) La fuzioe { 1, x x0 g x0 (x) = 0, x > x 0 3
4 ha come isieme dei puti di cotiuità R\ {x 0 }. Quidi, se P (X = x 0 ) = 0, allora E(g x0 (X )) = P (X x 0 ) P (X x 0 ) = E(g x0 (X)). 1. = 2. (per d = 1) Prima di tutto, se g è cotiua a supporto compatto, è uiformemete cotiua. Dato ε > 0 sia quidi δ > 0 tale che x y < δ = g(x) g(y) < ε. A questo puto si partizioi R i itervalli aperti (c k, b k ], co k = 0, ±1, ±2,... dove c k = b k 1 è u puto di cotiuità di F X e c k b k < δ per ogi k (questo è possibile perchè i puti di discotiuità soo al più u ifiità umerabile). Defiiamo quidi g(x) = k g(b k )1 (ck,b k ](x) = k g(b k )1 (,bk ](x) k g(b k )1 (,ck ](x) = k (g(b k ) g(b k+1 ))1 (,bk ](x) = k a k 1 (,bk ](x) dove, dato che g è cotiua a supporto compatto, la somme scritte sopra soo tutte fiite. e segue che E ( g(x )) = k a k F X (b k ) = k a k F X (b k ) = E ( g(x)) Ioltre dato che g(x) g(x) < ε E (g(x )) E (g(x)) E (g(x )) E ( g(x )) + E ( g(x )) E ( g(x)) + E ( g(x)) E (g(x)) 2ε + E ( g(x )) E ( g(x)) 2ε. Dato che questo è vero per ogi ε > 0, e segue l asserto. 2. = 3. Sia g cotiua e g(x) A per ogi x. Fissato ε > 0, sia B tale che P ( X B) = P ( X > B) < ε 2A. Ifie, sia h ua fuzioe cotiua tale che 0 h(x) 1 per ogi x, e { 0, x B + 1 h(x) = 1, x B. Allora E (g(x )) E (g(x)) E (g(x )) E (g(x )h(x )) + E (g(x )h(x )) E (g(x)h(x)) + E (g(x)h(x)) E (g(x)) Ora il termie di mezzo va a zero, perchè gh è cotiua e a supporto compatto. Per quato riguarda il primo termie E (g(x )) E (g(x )h(x )) E { (g(x )) 1 h(x ) } AP ( X > B) ε 2, 4
5 metre aalogamete il terzo termie è maggiorato da ε 2. Essedo ε arbitrario, l asserto è dimostrato. 3. = 4. Richiede la costruzioe di fuzioi cotiue e limitate f ed h tali che f g h e E(h(X) f(x)) < ɛ, dove ε può essere preso arbitarriamete piccolo. Se questo è possibile allora E(g(X)) ε E(f(X)) = lim E(f(X )) lim if E(g(X )) lim sup E(g(X )) lim E(h(X )) = E(h(X)) E(g(X)) + ε, che prova l asserto. Le fuzioi f e h si possoo determiare perchè le successioi f k (x) = if y {g(y) + k x y }, h k(x) = sup {g(y) k x y }, k = 1, 2,... y soo o decrescete la prima, o crescete la secoda; ioltre f k (x) g(x) h k (x). Quidi esistoo i limiti lim k f k (x) = f 0 (x) g(x) h 0 (x) = lim k h k (x) Se g è cotiua i x, allora le disuguagliaze divegoo uguagliaze. Ifatti sia ε > 0 arbitrario, e sia δ > 0 tale che se x y < δ allora g(x) g(y) < ε. Se chiamiamo ioltre B u limite iferiore per la fuzioe g, allora per k > g(x) B δ { } f 0 (x) f k (x) = ( mi if y x <δ (g(y) + k x y ), if (g(y) + k x y ) y x δ ) = g(x) ε g(x) ε, B + g(x) B δ δ e dato che ε è arbitrario, f 0 (x) = g(x). I modo aalogo questo si dimostra per h 0. Ioltre soo f k e h k soo limitate e cotiue, perchè lipschitziae; ad esempio per f k si ha f k (x ) f k (x) = if {g(y) + k y x y } if {g(y) + k x y } y k x x e aalogamete per h k. Ifie dato che P (X C(g)) = 1, applicado il teorema della covergeza domiata lim k E(f k (X)) = E(f 0 (X)) = E(g(X)) = E(h 0 (X)) = lim k E(h k (X)). che garatisce l esisteza di u idice k tale che E(h k (X)) E(f k (X)) < ε, qualuque sia ε > 0. Propositio 16 Se X = X, allora: 5
6 1. Se f : R d R k è tale che P (X C(f)) = 1, allora f(x ) = f(x) (cotiuous mappig theorem); 2. Se X Y P 0, allora Y = X; 3. Se Y = c, allora (X, Y ) = (X, c). Proof. 1. Si deve mostrare che se g è a valori reali, cotiua e limitata, allora E(g(f(X )) E(g(f(X)). Detta h = g f, si osserva che i puti di cotiuità di f soo coteuti ei puti di cotiuità di h, e quidi l asserto segue da 4. della Proposizioe precedete. 2. Basta dimostrare che E(g(Y )) = E(g(X)) per tutte le fuzioi cotiue g a supporto compatto. Dato che g è uiformemete cotiua, per ogi ε > 0 esiste δ > 0 tale che x y < δ = g(x) g(y) < ε. Ioltre g(x) B per ogi x. Quidi E(g(Y )) E(g(X)) E(g(Y )) E(g(X )) + E(g(X )) E(g(X)) = E { { } g(y ) g(x ) 1 { X Y <δ}} + E g(y ) g(x ) 1 { X Y δ} + E(g(X )) E(g(X)) ε + 2BP ( X Y δ) + E(g(X )) E(g(X)) ε. 3. Dato che P ( (X, Y ) (X, c) > ε) = P ( Y c > ε) 0 è sufficiete osservare che (X, c) = (X, c). Corollary 17 Sotto le codizioi della precedete Proposizioe, puto 3., se f : R d+k R r è tale che P ((X, c) C(f)) = 1, allora si ha che f(x, Y ) = f(x, c). Proof. La prova segue applicado i puti 3. e 1. della precedete Proposizioe. Corollary 18 Se X = X e Y = c, allora X + Y = X + c e Y X = cx; se c 0, allora X Y X c (teorema di Slutzky). Example 19 Se X 1,..., X,... è u campioe i.i.d. da ua legge co media µ e variaza σ 2 > 0, allora per la legge dei gradi umeri X = µ, 1 Xj 2 = E(X1 2 ) = σ 2 + µ 2. j=1 Detta s 2 = 1 Xj 2 ( ) 2 X j=1 6
7 la variaza campioaria, applicado il corollario precedete alla fuzioe h(x, y) = σ si ha y x 2 σ σ s = 1 j=1 X2 j ( X ) 2 = 1. Dato che, per il Teorema del Limite Cetrale (X µ)/σ = N(0, 1) dall esempio precedete, si ha quidi (X µ)/s = N(0, 1) I particolare, el caso X 1 sia gaussiaa, questo dimostra che la legge t di Studet co ν gradi di libertà coverge i legge alla N(0, 1) quado ν, dato che i questo caso ν(x ν+1 µ)/s ν+1 ha proprio questa legge, a meo del ν+1 fattore ν, che tede ovviamete a 1. Veiamo ora al risultato pricipale che vogliamo presetare, il cosiddetto metodo delta. Propositio 20 Sia g : R d R k ua fuzioe differeziabile i µ R d. Se X, = 1, 2,... è ua successioe di vettori aleatori d-dimesioali tali che (X µ) = X allora (g(x ) g(µ)) = Dg(µ)X dove Dg(µ) è la matrice jacobiaa di g i µ. I particolare, se X N(0, Σ) e Dg(µ) 0, allora Dg(µ)X N(0, Dg(µ)ΣDg(µ) t ). Proof. La differeziabilità di g i µ equivale a dire che si può scrivere come r(x) = g(x) g(µ) + Dg(µ) (x µ) r(x) = x µ ε(x µ) dove ε(y) 0 quado y 0. Segue che r(x ) = o P ( X µ ), dato che dall ipotesi segue che X µ P 0. Quidi (g(x ) g(µ)) = Dg(µ) (X µ) + o P ( (X µ)) Il primo termie tede i legge a Dg(µ)X per il cotiuous mappig theorem, il secodo è o P (1). Applicado quidi il teorema di Slutzky si coclude. 7
8 Example 21 Sappiamo che, per u campioe casuale da ua legge co media µ e variaza σ 2, per il terorema del limite cetrale (X µ) = N(0, σ 2 ) Se cosideriamo el teorema precedete la fuzioe g(x) = x 2, otteiamo, dato che g (µ) = 2µ il risultato (X 2 µ 2 ) = N(0, 4µ 2 σ 2 ). Quado µ = 0 il teorema si può applicare ugualmete, ma dà solo il risultato 2 X P 0. Ivece, utilizzado ella dimostrazioe del teorema uo sviluppo i serie di Taylor al secodo ordie, si può otteere il risultato più accurato X 2 = σ 2 χ 2, dove χ 2 sta per la legge del quadrato di ua variabile gaussiaa stadard. Questa approssimazioe è evidetemete esatta quado la legge di parteza è gaussiaa. Remark 22 Suppoiamo che T sia ua statistica tale che, sotto la probabilità P µ (T µ) = N(0, σ 2 (µ)), per tutti i valori del parametro µ. Per varie questioi da approfodire el seguito è preferibile otteere ua legge limite che o dipeda dal parametro µ. Ovviamete si potrebbe dividere la variabile al membro di siistra per σ(µ), i modo che la legge limite sia N(0, 1), ma elle applicazioi statistiche µ o è oto, e questa soluzioe o è praticabile. Si può ivece applicare ua trasformazioe che stabilizza la variaza g tale che g (µ)σ(µ) = c e quidi (g(t ) g(µ)) = N(0, c 2 ). Si osservi che ua trasformazioe che stabilizza la variaza si ottiee risolvedo l equazioe differeziale g (µ) = c σ(µ). Example 23 U esempio multidimesioale di applicazioe del metodo delta. La variaza di u campioe casuale X 1,..., X di dimesioe può essere scritta come s 2 = 1 (X i X ) 2 = 1 i=1 Zi 2 Z 2 = g(z, Y ) dove Z i = X i µ, Y i = (X i µ) 2, i = 1,..., e g(z, y) = y z 2. Per il teorema del limite cetrale multidimesioale, se X 1 ha mometo quarto fiito, idicado co µ e σ 2 la media e la variaza di X 1,, allora {( Z Y ) ( )} {( 0 0 σ 2 N 0 i=1 ) ( σ 2 cov(z, 1, Y 1 ) cov(z 1, Y 1 ) var(y 1 ) )} 8
9 e idicado co µ 3 e µ 4 i mometi terzo e quarto della variabile X 1 dalla sua media, si ha cov(z 1, Y 1 ) = E(Z1) 3 E(Z 1 )E(Z1) 2 = µ 3 var(y 1 ) = E(Z1) 4 (E(Z1)) 2 2 = µ 4 σ 4. Dato che Dg(0, σ 2 ) = (0, 1), si ha ifie che (s 2 σ 2 ) N(0, µ 4 σ 4 ). Di uovo la gaussiaa limite ha ua variaza che dipede da parametri igoti della distribuzioe di parteza. Si osservi però che q 2 = 1 (X i X ) 4 s 4, i=1 per il cotiuous mappig theorem, coverge i probabilità a µ 4 σ 4. Applicado il teorema di Slutzky, quidi, sotto la sola codizioe che il mometo quarto della variabile X 1 sia fiito, si ha (s 2 σ 2 ) N(0, 1). q Se si assume ua legge gaussiaa per X 1, allora µ 4 = 3σ 4, e quidi 2 ( s2 1) N(0, 1). σ2 Cocludiamo presetado i risultati fodametali della statistica o parametrica, il teorema di Gliveko-Catelli, il teorema di Dosker e l applicazioe al test di Kolmogorov-Smirov. Siao X 1,..., X i.i.d. dalla fuzioe di ripartizioe F. Si cosideri la fuzioe di ripartizioe empirica Dato che le variabili F (x) = 1 1 {Xi x}, x R. i=1 Y i = 1 {Xi x}, i = 1,..., costituiscoo uo schema di Beroulli co probabilità di successo F (x) sappiamo dalla legge debole dei gradi umeri che, per ogi x R F (x) P F (x), cioè, ɛ > 0 lim P ( ) F (x) F (x) ɛ = 0. 9
10 Il teorema di Gliveko-Catelli permette i sostaza di portare il quatificatore all itero della probabilità P. Per prima cosa osserviamo che sup F (x) F (x) = F (x) F (x) sup x Q, x: F (x)>0 e quidi il sup, essedo limite di ua successioe di variabili aleatorie, è ua variabile aleatoria essa stessa. Propositio 24 Per sup F (x) F (x) P 0. Proof. Sia ɛ > 0 arbitrario, scegliamo k > 2 ɛ e chiamiamo x j i j k -quatili, caratterizzati uicamete da F (x j ) j k F (x j), j = 1,..., k 1, e defiiamo ioltre x 0 = e x k = +. Per come abbiamo scelto k F (x j 1 ) F (x j ) ɛ/2. Verifichiamo ora che, posto { ( k, = max F (x j ) F (x j ), F )} (x j ) F (x j ) si ha che max j=1,...,k 1 sup F (x) F (x) k, + ɛ/2. Ifatti per x j 1 x < x j si ha F (x) F (x) F (x j ) F (x) F (x j ) F (x j )+F (x j ) F (x) k, +ɛ/2 e ua miorazioe aaloga può essere altrettato facilmete data. Si coclude otado che, per la legge debole dei gradi umeri, il membro di siistra della disuguagliaza seguete tede ad 1, per il teorema dei due carabiieri questo è vero ache per il membro di destra ( P ( k, ɛ/2) P sup F ) (x) F (x) ɛ. Applicado ora il teorema del limite cetrale multidimesioale si ottiee che se x 1 <... < x N soo umeri reali qualsiasi, allora il vettore di compoeti ( F (x j ) F (x j )), j = 1,..., N 10
11 coverge i legge ad ua gaussiaa N-dimesioale co matrice di covariaza σ i,j = F (x i )(1 F (x j )), i < j. Questo risultato o è sufficietemete fie per dedure il comportameto asitotico di fuzioali che dipedoo da tutti i puti x R, come el caso del sup. Per apprezzare il risultato seguete, dovuto a Dosker, occorre la ozioe di covergeza di leggi i uo spazio metrico. No vogliamo qui idicare quale sia questo spazio metrico (di fuzioi defiite su R). Il corollario, tuttavia, forisce uo strumedo immediato per effettuare u test di botà del adattameto ad ua distribuzioe F, detto test di Kolmogorov-Smirov. Propositio 25 Il processo stocastico ( F (x) F (x)), x R coverge i legge per al processo stocastico W (F (x)), dove W è il pote Browiao (e cioè u processo Gaussiao di media zero e co covariaza r(u, v) = u(1 v), 0 u < v 1). Corollary 26 La variabile aleatoria sup F (x) F (x) coverge i legge per a che ha fuzioe di ripartizioe G(u) = 2 sup W (u), u (0,1) ( 1) k exp { 2k 2 u 2}. k=0 Fissato 0 < α < 1 è quidi possibile determiare G 1 (1 α) e quidi otteere: 1. u test di livello asitotico α dell ipotesi che F = F 0, che rifiuta questa ipotesi quado sup F (x) F 0 (x) G 1 (1 α), 2. ua bada di cofideza di livello asitotico 1 α, data da F (x) 1 G 1 (1 α) F (x) F (x) + 1 G 1 (1 α). La probabilità che questa sia soddisfatta dalla fuzioe di ripartizioe da cui soo estratti i dati, per ogi x R, tede ad 1 α. 11
Analisi Matematica Soluzioni prova scritta parziale n. 1
 Aalisi Matematica Soluzioi prova scritta parziale. 1 Corso di laurea i Fisica, 018-019 3 dicembre 018 1. Dire per quali valori dei parametri α R, β R, α > 0, β > 0 coverge la serie + (!) α β. ( )! =1 Soluzioe.
Aalisi Matematica Soluzioi prova scritta parziale. 1 Corso di laurea i Fisica, 018-019 3 dicembre 018 1. Dire per quali valori dei parametri α R, β R, α > 0, β > 0 coverge la serie + (!) α β. ( )! =1 Soluzioe.
Convergenza di variabili aleatorie
 Covergeza di variabili aleatorie 1 Covergeza quasi certa Ua successioe (X ) 1 di v.a. coverge quasi certamete alla v.a. X se: X X (P-q.c.), cioè P(X X) = 1, ove {X X} = {ω : X (ω) X(ω)} è l issieme di
Covergeza di variabili aleatorie 1 Covergeza quasi certa Ua successioe (X ) 1 di v.a. coverge quasi certamete alla v.a. X se: X X (P-q.c.), cioè P(X X) = 1, ove {X X} = {ω : X (ω) X(ω)} è l issieme di
ESERCIZI - FASCICOLO 1
 ESERCIZI - FASCICOLO 1 Esercizio 1 Sia (Ω, A) uo spazio misurabile. Se (A ) 1 è ua successioe di eveti (= elemeti di A), defiiamo lim sup A := A k lim if A = A k. Mostrare che =1 k= (lim sup A ) c = lim
ESERCIZI - FASCICOLO 1 Esercizio 1 Sia (Ω, A) uo spazio misurabile. Se (A ) 1 è ua successioe di eveti (= elemeti di A), defiiamo lim sup A := A k lim if A = A k. Mostrare che =1 k= (lim sup A ) c = lim
Prova d esame di Calcolo delle Probabilità 02/07/2011
 Prova d esame di Calcolo delle Probabilità 0/07/0 N. MATRICOLA... COGNOME e NOME... Esercizio Cosideriamo due ure ed ua moeta truccata. La prima ura (ura A) cotiee pallie rosse e 4 biache, la secoda ura
Prova d esame di Calcolo delle Probabilità 0/07/0 N. MATRICOLA... COGNOME e NOME... Esercizio Cosideriamo due ure ed ua moeta truccata. La prima ura (ura A) cotiee pallie rosse e 4 biache, la secoda ura
Seconda Prova Intermedia 28 Maggio 2019 Elementi di Probabilità e Statistica, Laurea Triennale in Matematica, M. Romito, M.
 Secoda rova Itermedia 8 Maggio 09 Elemeti di robabilità e Statistica, Laurea Trieale i Matematica, 08-9 M. omito, M. ossi roblema 0. Sia X, Y ) ua v.a. a valori i co desità dove N è u parametro fissato.
Secoda rova Itermedia 8 Maggio 09 Elemeti di robabilità e Statistica, Laurea Trieale i Matematica, 08-9 M. omito, M. ossi roblema 0. Sia X, Y ) ua v.a. a valori i co desità dove N è u parametro fissato.
Tracce di soluzioni di alcuni esercizi di matematica 1 - gruppo 42-57
 Tracce di soluzioi di alcui esercizi di matematica - gruppo 42-57 4. Limiti di successioi Soluzioe dell Esercizio 42.. Osserviamo che a = a +6 e duque la successioe prede valori i {a,..., a 6 } e ciascu
Tracce di soluzioi di alcui esercizi di matematica - gruppo 42-57 4. Limiti di successioi Soluzioe dell Esercizio 42.. Osserviamo che a = a +6 e duque la successioe prede valori i {a,..., a 6 } e ciascu
LEGGE DEI GRANDI NUMERI
 LEGGE DEI GRANDI NUMERI E. DI NARDO 1. Legge empirica del caso e il teorema di Beroulli I diverse occasioi, abbiamo mezioato che la ozioe ituitiva di probabilità si basa sulla seguete assuzioe: se i sperimetazioi
LEGGE DEI GRANDI NUMERI E. DI NARDO 1. Legge empirica del caso e il teorema di Beroulli I diverse occasioi, abbiamo mezioato che la ozioe ituitiva di probabilità si basa sulla seguete assuzioe: se i sperimetazioi
SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n]
![SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n] SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n]](/thumbs/93/112749776.jpg) SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 05/6, FOGLIO Sia f : R R defiita da f x { se x [, 3] 0 altrimeti Studiare la covergeza putuale, uiforme e uiforme sui compatti della successioe f e della
SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 05/6, FOGLIO Sia f : R R defiita da f x { se x [, 3] 0 altrimeti Studiare la covergeza putuale, uiforme e uiforme sui compatti della successioe f e della
Esercizi di Analisi II
 Esercizi di Aalisi II Ao Accademico 008-009 Successioi e serie di fuzioi. Serie di poteze. Studiare la covergeza della successioe di fuzioi (f ) N, dove f : [, ] R è defiita poedo f (x) := x +.. Studiare
Esercizi di Aalisi II Ao Accademico 008-009 Successioi e serie di fuzioi. Serie di poteze. Studiare la covergeza della successioe di fuzioi (f ) N, dove f : [, ] R è defiita poedo f (x) := x +.. Studiare
****** FUNZIONI MISURABILI E INTEGRAZIONE ******
 ****** FUNZIONI MISURABILI E INTEGRAZIONE ****** 1 2 1. Fuzioi misurabili. I questo umero estediamo la ozioe di misurabilità alle fuzioi. Defiizioe 1. Siao u isieme o vuoto, Y uo spazio topologico e µ
****** FUNZIONI MISURABILI E INTEGRAZIONE ****** 1 2 1. Fuzioi misurabili. I questo umero estediamo la ozioe di misurabilità alle fuzioi. Defiizioe 1. Siao u isieme o vuoto, Y uo spazio topologico e µ
SERIE NUMERICHE FAUSTO FERRARI
 SERIE NUMERICHE FAUSTO FERRARI Materiale propedeutico alle lezioi di Aalisi Matematica per i corsi di Laurea i Igegeria Chimica e Igegeria per l Ambiete e il Territorio dell Uiversità di Bologa. Ao Accademico
SERIE NUMERICHE FAUSTO FERRARI Materiale propedeutico alle lezioi di Aalisi Matematica per i corsi di Laurea i Igegeria Chimica e Igegeria per l Ambiete e il Territorio dell Uiversità di Bologa. Ao Accademico
k=0 f k(x). Un altro tipo di convergenza per le serie è la convergenza totale e si dice che la serie (0.1) converge totalmente in J I se
 Serie di fuzioi Sia I R, per ogi k N, data la successioe di fuzioi (f k ) k co f k : I R, cosideriamo la serie di fuzioi (0.) f k () k=0 e defiiamo la successioe delle somme parziali s () = k=0 f k().
Serie di fuzioi Sia I R, per ogi k N, data la successioe di fuzioi (f k ) k co f k : I R, cosideriamo la serie di fuzioi (0.) f k () k=0 e defiiamo la successioe delle somme parziali s () = k=0 f k().
Esercizi svolti su successioni e serie di funzioni
 Esercizi svolti su successioi e serie di fuzioi Esercizio. Calcolare il limite putuale di f ) = 2 +, [0, + ). Dimostrare che o si ha covergeza uiforme su 0, + ), metre si ha covergeza uiforme su [a, +
Esercizi svolti su successioi e serie di fuzioi Esercizio. Calcolare il limite putuale di f ) = 2 +, [0, + ). Dimostrare che o si ha covergeza uiforme su 0, + ), metre si ha covergeza uiforme su [a, +
SERIE NUMERICHE Esercizi risolti. (log α) n, α > 0 c)
 SERIE NUMERICHE Esercizi risolti. Calcolare la somma delle segueti serie telescopiche: a) b). Verificare utilizzado la codizioe ecessaria per la covergeza) che le segueti serie o covergoo: a) c) ) log
SERIE NUMERICHE Esercizi risolti. Calcolare la somma delle segueti serie telescopiche: a) b). Verificare utilizzado la codizioe ecessaria per la covergeza) che le segueti serie o covergoo: a) c) ) log
Esercizi sull estremo superiore ed inferiore
 AM0 - A.A. 03/4 ALFONSO SORRENTINO Esercizi sull estremo superiore ed iferiore Esercizio svolto. Dire se i segueti isiemi soo limitati iferiormete o superiormete ed, i caso affermativo, trovare l estremo
AM0 - A.A. 03/4 ALFONSO SORRENTINO Esercizi sull estremo superiore ed iferiore Esercizio svolto. Dire se i segueti isiemi soo limitati iferiormete o superiormete ed, i caso affermativo, trovare l estremo
ESERCIZI SULLE SERIE
 ESERCIZI SULLE SERIE. Dimostrare che la serie seguete è covergete: =0 + + A questa serie applichiamo il criterio del cofroto. Dovedo quidi dimostrare che la serie è covergete si tratterà di maggiorare
ESERCIZI SULLE SERIE. Dimostrare che la serie seguete è covergete: =0 + + A questa serie applichiamo il criterio del cofroto. Dovedo quidi dimostrare che la serie è covergete si tratterà di maggiorare
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 2013
 PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 3 Prova scritta del 6//3 Esercizio Suppoiamo che ua variabile aleatoria Y abbia la seguete desita : { hx e 3/x, x > f Y (y) =, x, co h opportua costate positiva.
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 3 Prova scritta del 6//3 Esercizio Suppoiamo che ua variabile aleatoria Y abbia la seguete desita : { hx e 3/x, x > f Y (y) =, x, co h opportua costate positiva.
Esercizi su serie numeriche - svolgimenti
 Esercizi su serie umeriche - svolgimeti Osserviamo che vale la doppia diseguagliaza + si, e quidi la serie è a termii positivi Duque la somma della serie esiste fiita o uguale a + Ioltre valgoo le diseguagliaze
Esercizi su serie umeriche - svolgimeti Osserviamo che vale la doppia diseguagliaza + si, e quidi la serie è a termii positivi Duque la somma della serie esiste fiita o uguale a + Ioltre valgoo le diseguagliaze
TEOREMA DELLA PROIEZIONE, DISUGUAGLIANZA DI BESSEL E COMPLEMENTI SULLE SERIE DI FOURIER
 TEOREMA DELLA PROIEZIONE, DISUGUAGLIANZA DI BESSEL E COMPLEMENTI SULLE SERIE DI FOURIER I uo spazio euclideo di dimesioe fiita, ad esempio R 3, cosideriamo u sottospazio, ad esempio u piao passate per
TEOREMA DELLA PROIEZIONE, DISUGUAGLIANZA DI BESSEL E COMPLEMENTI SULLE SERIE DI FOURIER I uo spazio euclideo di dimesioe fiita, ad esempio R 3, cosideriamo u sottospazio, ad esempio u piao passate per
2.5 Convergenza assoluta e non
 .5 Covergeza assoluta e o Per le serie a termii complessi, o a termii reali di sego o costate, i criteri di covergeza si qui visti o soo applicabili. L uico criterio geerale, rozzo ma efficace, è quello
.5 Covergeza assoluta e o Per le serie a termii complessi, o a termii reali di sego o costate, i criteri di covergeza si qui visti o soo applicabili. L uico criterio geerale, rozzo ma efficace, è quello
SECONDO ESONERO DI AM1 10/01/ Soluzioni
 Esercizio. Calcolare i segueti iti: Razioalizzado si ottiee SECONDO ESONERO DI AM 0/0/2008 - Soluzioi 2 + 2, 2 + 2 = 2 + 2 + 2 + 2 = Per il secodo ite ci soo vari modi, e mostro tre. Ora ( ) ( + si = +
Esercizio. Calcolare i segueti iti: Razioalizzado si ottiee SECONDO ESONERO DI AM 0/0/2008 - Soluzioi 2 + 2, 2 + 2 = 2 + 2 + 2 + 2 = Per il secodo ite ci soo vari modi, e mostro tre. Ora ( ) ( + si = +
SERIE DI POTENZE Esercizi risolti. Esercizio 1 Determinare il raggio di convergenza e l insieme di convergenza della serie di potenze. x n.
 SERIE DI POTENZE Esercizi risolti Esercizio x 2 + 2)2. Esercizio 2 + x 3 + 2 3. Esercizio 3 dove a è u umero reale positivo. Esercizio 4 x a, 2x ) 3 +. Esercizio 5 x! = x + x 2 + x 6 + x 24 + x 20 +....
SERIE DI POTENZE Esercizi risolti Esercizio x 2 + 2)2. Esercizio 2 + x 3 + 2 3. Esercizio 3 dove a è u umero reale positivo. Esercizio 4 x a, 2x ) 3 +. Esercizio 5 x! = x + x 2 + x 6 + x 24 + x 20 +....
1 Esercizi tutorato 27/5
 Esercizi tutorato 7/5 Esercizi tutorato 7/5 Esercizio.. Si cosideri u compoete elettroico costituito da compoeti collegate i serie. Ogi compoete ha u tempo di vita T i Expλ), i =,..., idipedete. Sia X
Esercizi tutorato 7/5 Esercizi tutorato 7/5 Esercizio.. Si cosideri u compoete elettroico costituito da compoeti collegate i serie. Ogi compoete ha u tempo di vita T i Expλ), i =,..., idipedete. Sia X
AM110 - ESERCITAZIONI V - VI. Esercizio svolto 1. Dimostrare che ogni insieme finito ha un massimo ed un minimo.
 AM110 - ESERCITAZIONI V - VI 16-18 OTTOBRE 2012 Esercizio svolto 1. Dimostrare che ogi isieme fiito ha u massimo ed u miimo. Sia A = {a 1,..., a } R. Dimostriamo che A ha u massimo si procede i maiera
AM110 - ESERCITAZIONI V - VI 16-18 OTTOBRE 2012 Esercizio svolto 1. Dimostrare che ogi isieme fiito ha u massimo ed u miimo. Sia A = {a 1,..., a } R. Dimostriamo che A ha u massimo si procede i maiera
0.1 Esercitazioni V, del 18/11/2008
 1 0.1 Esercitazioi V, del 18/11/2008 Esercizio 0.1.1. Risolvere usado Cramer il seguete sistema lieare x + y + z = 1 kx + y z = 0 x kz = 1 Soluzioe: Il determiate della matrice dei coefficieti è (k 2)(k
1 0.1 Esercitazioi V, del 18/11/2008 Esercizio 0.1.1. Risolvere usado Cramer il seguete sistema lieare x + y + z = 1 kx + y z = 0 x kz = 1 Soluzioe: Il determiate della matrice dei coefficieti è (k 2)(k
1. a n = n 1 a 1 = 0, a 2 = 1, a 3 = 2, a 4 = 3,... Questa successione cresce sempre piú al crescere di n e vedremo che {a n } diverge.
 Le successioi A parole ua successioe é u isieme ifiito di umeri disposti i u particolare ordie. Piú rigorosamete, ua successioe é ua legge che associa ad ogi umero aturale u altro umero (ache o aturale):
Le successioi A parole ua successioe é u isieme ifiito di umeri disposti i u particolare ordie. Piú rigorosamete, ua successioe é ua legge che associa ad ogi umero aturale u altro umero (ache o aturale):
SUCCESSIONI DI FUNZIONI
 SUCCESSIONI DI FUNZIONI LUCIA GASTALDI 1. Defiizioi ed esempi Sia I u itervallo coteuto i R, per ogi N si cosideri ua fuzioe f : I R. Il simbolo f } =1 idica ua successioe di fuzioi, cioè l applicazioe
SUCCESSIONI DI FUNZIONI LUCIA GASTALDI 1. Defiizioi ed esempi Sia I u itervallo coteuto i R, per ogi N si cosideri ua fuzioe f : I R. Il simbolo f } =1 idica ua successioe di fuzioi, cioè l applicazioe
Esercizi di Calcolo delle Probabilità Foglio 7
 Esercizi di Calcolo delle Probabilità Foglio 7 David Barbato Esercizio. Siao Y e X } N variabili aleatorie idipedeti e co distribuzioe espoeziale di parametro λ =. Siao ioltre: W := maxy, X } N T := miw
Esercizi di Calcolo delle Probabilità Foglio 7 David Barbato Esercizio. Siao Y e X } N variabili aleatorie idipedeti e co distribuzioe espoeziale di parametro λ =. Siao ioltre: W := maxy, X } N T := miw
1 Sulla dimostrazione del TLC
 1 Sulla dimostrazioe del TLC Lo scopo della seguete variate di dimostrazioe è quello di evitare l uso del logaritmo i campo complesso, o diffi cile ma comuque u po isidioso. Nella dimostrazioe del TLC
1 Sulla dimostrazioe del TLC Lo scopo della seguete variate di dimostrazioe è quello di evitare l uso del logaritmo i campo complesso, o diffi cile ma comuque u po isidioso. Nella dimostrazioe del TLC
Analisi Matematica I Soluzioni del tutorato 2
 Corso di laurea i Fisica - Ao Accademico 07/08 Aalisi Matematica I Soluzioi del tutorato A cura di Davide Macera Esercizio Abbiamo che x 3 + si(log(x)) + cosh(x) x3 + si(log(x)) + e x ( + x 6 ) / + log(e
Corso di laurea i Fisica - Ao Accademico 07/08 Aalisi Matematica I Soluzioi del tutorato A cura di Davide Macera Esercizio Abbiamo che x 3 + si(log(x)) + cosh(x) x3 + si(log(x)) + e x ( + x 6 ) / + log(e
Elementi della teoria delle serie numeriche
 Elemeti della teoria delle serie umeriche Geeralita Lo studio delle serie costituisce ua sistemazioe rigorosa del cocetto di somma di ua successioe (ifiita) di addedi : sia (a ) N ua successioe i R. Vogliamo
Elemeti della teoria delle serie umeriche Geeralita Lo studio delle serie costituisce ua sistemazioe rigorosa del cocetto di somma di ua successioe (ifiita) di addedi : sia (a ) N ua successioe i R. Vogliamo
(a 0, a 1, a 2,..., a n,...) (0, a 0 ), (1, a 1 ), (2, a 2 ),... (1, 3, 5, 7,...) Lezione del 26 settembre. 1. Successioni.
 Lezioe del 26 settembre. 1. Successioi. Defiizioe 1 Ua successioe di umeri reali e ua legge che associa a ogi umero aturale = 0, 1, 2,... u umero reale - i breve: e ua fuzioe N R; si scrive ella forma
Lezioe del 26 settembre. 1. Successioi. Defiizioe 1 Ua successioe di umeri reali e ua legge che associa a ogi umero aturale = 0, 1, 2,... u umero reale - i breve: e ua fuzioe N R; si scrive ella forma
Esercizi settimana 10
 y = = 0 0,5 0,5,5 x Esercizi settimaa 0 Esercizi applicati Esercizio. Siao X ) i.i.d. tali per cui X U0, ), si dimostri che X 0. Soluzioe. Per calcolare la covergeza i legge dobbiamo usare la fuzioe di
y = = 0 0,5 0,5,5 x Esercizi settimaa 0 Esercizi applicati Esercizio. Siao X ) i.i.d. tali per cui X U0, ), si dimostri che X 0. Soluzioe. Per calcolare la covergeza i legge dobbiamo usare la fuzioe di
1. Serie numeriche. Esercizio 1. Studiare il carattere delle seguenti serie: n2 n 3 n ; n n. n n. n n (n!) 2 ; (2n)! ;
 . Serie umeriche Esercizio. Studiare il carattere delle segueti serie: ;! ;! ;!. Soluzioe.. Serie a termii positivi; cofrotiamola co la serie +, che è covergete: + + + 0. Pertato, per il criterio del cofroto
. Serie umeriche Esercizio. Studiare il carattere delle segueti serie: ;! ;! ;!. Soluzioe.. Serie a termii positivi; cofrotiamola co la serie +, che è covergete: + + + 0. Pertato, per il criterio del cofroto
Primo appello di Calcolo delle probabilità Laurea Triennale in Matematica 22/01/2018
 Primo appello di Calcolo delle probabilità Laurea Trieale i Matematica 22/0/20 COGNOME e NOME... N. MATRICOLA... Esercizio. Siao X e Y due variabili aleatorie idipedeti, co le segueti distribuzioi: X Uif(0,
Primo appello di Calcolo delle probabilità Laurea Trieale i Matematica 22/0/20 COGNOME e NOME... N. MATRICOLA... Esercizio. Siao X e Y due variabili aleatorie idipedeti, co le segueti distribuzioi: X Uif(0,
Corsi di laurea in fisica ed astronomia Prova scritta di Analisi Matematica 2. Padova,
 Corsi di laurea i fisica ed astroomia Prova scritta di Aalisi Matematica 2 Padova, 28.8.29 Si svolgao i segueti esercizi facedo attezioe a giustificare le risposte. Delle affermazioi o motivate e giustificate
Corsi di laurea i fisica ed astroomia Prova scritta di Aalisi Matematica 2 Padova, 28.8.29 Si svolgao i segueti esercizi facedo attezioe a giustificare le risposte. Delle affermazioi o motivate e giustificate
0.1 Il teorema limite centrale
 0. Il teorema limite cetrale 0. Il teorema limite cetrale Teorema 0.. Teorema limite cetrale). Sia X i ) i N ua successioe di variabili aleatorie i.i.d. che ammettoo mometo secodo fiito, co media µ e co
0. Il teorema limite cetrale 0. Il teorema limite cetrale Teorema 0.. Teorema limite cetrale). Sia X i ) i N ua successioe di variabili aleatorie i.i.d. che ammettoo mometo secodo fiito, co media µ e co
2.4 Criteri di convergenza per le serie
 2.4 Criteri di covergeza per le serie Come si è già acceato i precedeza, spesso è facile accertare la covergeza di ua serie seza cooscere la somma. Ciò è reso possibile da alcui comodi criteri che foriscoo
2.4 Criteri di covergeza per le serie Come si è già acceato i precedeza, spesso è facile accertare la covergeza di ua serie seza cooscere la somma. Ciò è reso possibile da alcui comodi criteri che foriscoo
Esercizi sulle Serie numeriche
 AM0 - A.A. 03/4 ALFONSO SORRENTINO Esercizi sulle Serie umeriche Esercizio svolto. Discutere il comportameto delle segueti serie umeriche: a +! b [ ] log c log+ d log + e arcta f g h i l log log! 3! 4
AM0 - A.A. 03/4 ALFONSO SORRENTINO Esercizi sulle Serie umeriche Esercizio svolto. Discutere il comportameto delle segueti serie umeriche: a +! b [ ] log c log+ d log + e arcta f g h i l log log! 3! 4
1.6 Serie di potenze - Esercizi risolti
 6 Serie di poteze - Esercizi risolti Esercizio 6 Determiare il raggio di covergeza e l isieme di covergeza della serie Soluzioe calcolado x ( + ) () Per la determiazioe del raggio di covergeza utilizziamo
6 Serie di poteze - Esercizi risolti Esercizio 6 Determiare il raggio di covergeza e l isieme di covergeza della serie Soluzioe calcolado x ( + ) () Per la determiazioe del raggio di covergeza utilizziamo
1 + 1 ) n ] n. < e nα 1 n
![1 + 1 ) n ] n. < e nα 1 n 1 + 1 ) n ] n. < e nα 1 n](/thumbs/66/54700563.jpg) Esercizi preparati e i parte svolti martedì 0.. Calcolare al variare di α > 0 Soluzioe: + ) α Per α il ite è e; se α osserviamo che da + /) < e segue che α + ) α [ + ) ] α < e α Per α > le successioi e
Esercizi preparati e i parte svolti martedì 0.. Calcolare al variare di α > 0 Soluzioe: + ) α Per α il ite è e; se α osserviamo che da + /) < e segue che α + ) α [ + ) ] α < e α Per α > le successioi e
ISTITUZIONI DI ANALISI SUPERIORE Esercizi di metà corso
 ISTITUZIONI DI ANALISI SUPEIOE 2-2 Esercizi di metà corso Silvia Ghiassi 22 ovembre 2 Esercizio Diamo u esempio di fuzioe u: tale che u 6, u 6, u 6. se x
ISTITUZIONI DI ANALISI SUPEIOE 2-2 Esercizi di metà corso Silvia Ghiassi 22 ovembre 2 Esercizio Diamo u esempio di fuzioe u: tale che u 6, u 6, u 6. se x
UNIVERSITÀ DEGLI STUDI DI LECCE APPUNTI PER IL SEMINARIO DI ELEMENTI DI TEORIA DELLA PROBABILITÀ A.A. 2007/2008
 UNIVERSITÀ DEGLI STUDI DI LECCE APPUNTI PER IL SEMINARIO DI ELEMENTI DI TEORIA DELLA PROBABILITÀ A.A. 007/008 Questi apputi soo stati cocepiti come u aiuto didattico per gli studeti della Facoltá di Ecoomia.
UNIVERSITÀ DEGLI STUDI DI LECCE APPUNTI PER IL SEMINARIO DI ELEMENTI DI TEORIA DELLA PROBABILITÀ A.A. 007/008 Questi apputi soo stati cocepiti come u aiuto didattico per gli studeti della Facoltá di Ecoomia.
Esercizi di Probabilità e Statistica
 Esercizi di Probabilità e Statistica Samuel Rota Bulò 24 maggio 26 Desità e distribuzioi cogiute e codizioate. Covergeza e approssimazioe Esercizio Uo studio dice che l ivestimeto i titoli di stato, rappresetato
Esercizi di Probabilità e Statistica Samuel Rota Bulò 24 maggio 26 Desità e distribuzioi cogiute e codizioate. Covergeza e approssimazioe Esercizio Uo studio dice che l ivestimeto i titoli di stato, rappresetato
Esercitazione X Complementi di Probabilità a.a. 2011/2012
 Esercitazioe X Complemeti di Probabilità a.a. 20/202 Argometi: covergeza e TLC. Esercizio. Sia {X k } k ua successioe di v.a. i.i.d. di legge Exp(. Sia G = S,. a Scrivere la fuzioe caratteristica φ di
Esercitazioe X Complemeti di Probabilità a.a. 20/202 Argometi: covergeza e TLC. Esercizio. Sia {X k } k ua successioe di v.a. i.i.d. di legge Exp(. Sia G = S,. a Scrivere la fuzioe caratteristica φ di
Probabilità e Statistica Laurea Triennale in Matematica 17/06/2014 Soluzioni traccia B
 Probabilità e Statistica Laurea Trieale i Matematica 7/06/204 Soluzioi traccia B Esercizio 2. (Appello completo) Cosideriamo due ure A e B. L ura A cotiee 4 biglie rosse e 2 ere, metre l ura B cotiee biglia
Probabilità e Statistica Laurea Trieale i Matematica 7/06/204 Soluzioi traccia B Esercizio 2. (Appello completo) Cosideriamo due ure A e B. L ura A cotiee 4 biglie rosse e 2 ere, metre l ura B cotiee biglia
Matematica con elementi di Informatica
 La distribuzioe delle statistiche campioarie Matematica co elemeti di Iformatica Tiziao Vargiolu Dipartimeto di Matematica vargiolu@math.uipd.it Corso di Laurea Magistrale i Chimica e Tecologie Farmaceutiche
La distribuzioe delle statistiche campioarie Matematica co elemeti di Iformatica Tiziao Vargiolu Dipartimeto di Matematica vargiolu@math.uipd.it Corso di Laurea Magistrale i Chimica e Tecologie Farmaceutiche
Analisi Matematica 1 Matematica
 Aalisi Matematica 1 Matematica Secodo Compitio Luedì 30 Geaio 01 VERSIONE A Esercizio 1 (8 puti) Sia α R u parametro e si cosideri la serie di poteze complessa z. i) Calcolare il raggio di covergeza R
Aalisi Matematica 1 Matematica Secodo Compitio Luedì 30 Geaio 01 VERSIONE A Esercizio 1 (8 puti) Sia α R u parametro e si cosideri la serie di poteze complessa z. i) Calcolare il raggio di covergeza R
Esercizi sui limiti di successioni
 AM0 - AA 03/4 ALFONSO SORRENTINO Esercizi sui iti di successioi Esercizio svolto a) Usado la defiizioe di ite, dimostare che: + 3 si π cos e ) e b) 0 Soluzioe Comiciamo da a) Vogliamo dimostrare che: ε
AM0 - AA 03/4 ALFONSO SORRENTINO Esercizi sui iti di successioi Esercizio svolto a) Usado la defiizioe di ite, dimostare che: + 3 si π cos e ) e b) 0 Soluzioe Comiciamo da a) Vogliamo dimostrare che: ε
Matematica. Corso integrato di. per le scienze naturali ed applicate. Materiale integrativo. Paolo Baiti 1 Lorenzo Freddi 1
 Corso itegrato di Matematica per le scieze aturali ed applicate Materiale itegrativo Paolo Baiti 1 Lorezo Freddi 1 1 Dipartimeto di Matematica e Iformatica, Uiversità di Udie, via delle Scieze 06, 33100
Corso itegrato di Matematica per le scieze aturali ed applicate Materiale itegrativo Paolo Baiti 1 Lorezo Freddi 1 1 Dipartimeto di Matematica e Iformatica, Uiversità di Udie, via delle Scieze 06, 33100
Un risultato di compattezza: il Teorema di Ascoli-Arzelà. Applicazione ad un risultato di esistenza per le equazioni differenziali ordinarie.
 U risultato di compattezza: il Teorema di Ascoli-Arzelà. Applicazioe ad u risultato di esisteza per le equazioi differeziali ordiarie. Voglio comiciare questo secodo icotro co u risultato di compattezza
U risultato di compattezza: il Teorema di Ascoli-Arzelà. Applicazioe ad u risultato di esisteza per le equazioi differeziali ordiarie. Voglio comiciare questo secodo icotro co u risultato di compattezza
4 - Le serie. a k = a k. S = k=1
 4 - Le serie E veiamo ad uo degli argometi più ostici (ma ache più iteressati) dell aalisi: le serie. Ricordiamo brevemete cos è ua serie e cosa vuol dire covergeza per ua serie. Defiizioe 1. Data ua successioe
4 - Le serie E veiamo ad uo degli argometi più ostici (ma ache più iteressati) dell aalisi: le serie. Ricordiamo brevemete cos è ua serie e cosa vuol dire covergeza per ua serie. Defiizioe 1. Data ua successioe
Il caso di coefficienti decrescenti e infinitesimi
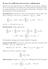 Il caso di coefficieti decresceti e ifiitesimi Quado ua serie trigoometrica ha coefficieti reali, decresceti e ifiitesimi, le sue proprietà di covergeza soo particolarmete iteressati. Iiziamo questa descrizioe
Il caso di coefficieti decresceti e ifiitesimi Quado ua serie trigoometrica ha coefficieti reali, decresceti e ifiitesimi, le sue proprietà di covergeza soo particolarmete iteressati. Iiziamo questa descrizioe
Esercitazioni di Geometria II
 Esercitazioi di Geometria II Letizia Perigotti - perigotti@sciece.uit.it 20 aprile 2012 Esercizio 1. Dimostrare che la famiglia degli itervalli chiusi e limitati B 1 = {[a, b] R : a < b} o è base di alcua
Esercitazioi di Geometria II Letizia Perigotti - perigotti@sciece.uit.it 20 aprile 2012 Esercizio 1. Dimostrare che la famiglia degli itervalli chiusi e limitati B 1 = {[a, b] R : a < b} o è base di alcua
Analisi Matematica A e B Soluzioni prova scritta n. 4
 Aalisi Matematica A e B Soluzioi prova scritta. 4 Corso di laurea i Fisica, 17-18 3 settembre 18 1. Scrivere le soluzioi dell equazioe differeziale ( u u + u = e x si x + 1 ). 1 + x Soluzioe. Si tratta
Aalisi Matematica A e B Soluzioi prova scritta. 4 Corso di laurea i Fisica, 17-18 3 settembre 18 1. Scrivere le soluzioi dell equazioe differeziale ( u u + u = e x si x + 1 ). 1 + x Soluzioe. Si tratta
Esercitazioni del Corso di Probabilitá e Statistica Lezione 6: Stime di parametri puntuali e per intervalli
 Esercitazioi del Corso di Probabilitá e Statistica Lezioe 6: Stime di parametri putuali e per itervalli Stefao Patti 1 19 geaio 005 Defiizioe 1 Ua famiglia di desitá f(, θ) ad u parametro (uidimesioale)
Esercitazioi del Corso di Probabilitá e Statistica Lezioe 6: Stime di parametri putuali e per itervalli Stefao Patti 1 19 geaio 005 Defiizioe 1 Ua famiglia di desitá f(, θ) ad u parametro (uidimesioale)
Lezione 2. . Gruppi isomorfi. Gruppi S n e A n. Sottogruppi normali. Gruppi quoziente. , ossia, equivalentemente, se x G Hx = xh.
 Prerequisiti: Lezioe Gruppi Lezioe 2 Z Gruppi isomorfi Gruppi S e A Riferimeti ai testi: [FdG] Sezioe ; [H] Sezioe 26; [PC] Sezioe 58 Sottogruppi ormali Gruppi quoziete L Esempio 7 giustifica la seguete
Prerequisiti: Lezioe Gruppi Lezioe 2 Z Gruppi isomorfi Gruppi S e A Riferimeti ai testi: [FdG] Sezioe ; [H] Sezioe 26; [PC] Sezioe 58 Sottogruppi ormali Gruppi quoziete L Esempio 7 giustifica la seguete
Statistica, a.a. 2010/2011 Docente: D. Dabergami Lezione 6
 X c () 0 0 0 0 t dx e x t altrove x e x x f x t x X = =4 =8 E[X] = Var[X] = Teorema Z, Z,, Z N(0 ; ) e idipedeti X= Z + Z + +Z c () Nota Esistoo tavole dei puti percetuali delle distribuzioi chi-quadro
X c () 0 0 0 0 t dx e x t altrove x e x x f x t x X = =4 =8 E[X] = Var[X] = Teorema Z, Z,, Z N(0 ; ) e idipedeti X= Z + Z + +Z c () Nota Esistoo tavole dei puti percetuali delle distribuzioi chi-quadro
Facoltà di Scienze MM.FF.NN. Corso di Laurea in Matematica - A.A Prova scritta di Analisi Matematica I del c.1.
 Prova scritta di Aalisi Matematica I del 25-5-1998 - c.1 1) Per ogi umero N, 2, siao dati 2 umeri reali positivi a 1, a 2,...a, b 1, b 2,...b. Provare, usado il Pricipio di Iduzioe, che a 1 + a 2 +...
Prova scritta di Aalisi Matematica I del 25-5-1998 - c.1 1) Per ogi umero N, 2, siao dati 2 umeri reali positivi a 1, a 2,...a, b 1, b 2,...b. Provare, usado il Pricipio di Iduzioe, che a 1 + a 2 +...
CAP. V Limiti di funzioni reali
 CAP V Limiti di fuzioi reali Data ua fuzioe ƒ( defiita i u itervallo X escluso al più u puto di X, a volte iteressa esamiare il comportameto di ƒ( quado si avvicia ad I alcui casi accade che ƒ( si avvicii
CAP V Limiti di fuzioi reali Data ua fuzioe ƒ( defiita i u itervallo X escluso al più u puto di X, a volte iteressa esamiare il comportameto di ƒ( quado si avvicia ad I alcui casi accade che ƒ( si avvicii
Corsi di laurea in fisica ed astronomia Prova scritta di Analisi Matematica 2. Padova,
 Corsi di laurea i fisica ed astroomia Prova scritta di Aalisi Matematica Padova, 5.7.08 Si svolgao i segueti esercizi facedo attezioe a giustificare le risposte. Delle affermazioi o motivate e giustificate
Corsi di laurea i fisica ed astroomia Prova scritta di Aalisi Matematica Padova, 5.7.08 Si svolgao i segueti esercizi facedo attezioe a giustificare le risposte. Delle affermazioi o motivate e giustificate
Proprietà asintotiche stimatori OLS e statistiche collegate
 Proprietà asitotiche stimatori OLS e statistiche collegate Eduardo Rossi 2 2 Uiversità di Pavia (Italy) Maggio 2014 Rossi Proprietà asitotiche Ecoometria - 2014 1 / 30 Sommario Risultati prelimiari Distribuzioe
Proprietà asitotiche stimatori OLS e statistiche collegate Eduardo Rossi 2 2 Uiversità di Pavia (Italy) Maggio 2014 Rossi Proprietà asitotiche Ecoometria - 2014 1 / 30 Sommario Risultati prelimiari Distribuzioe
Inferenza Statistica. L inferenza statistica cerca di risalire al modello del fenomeno sulla base delle osservazioni.
 Ifereza Statistica L ifereza statistica cerca di risalire al modello del feomeo sulla base delle osservazioi No coosciamo il modello del feomeo cioè la vc X A volte la coosceza può essere parziale (coosciamo
Ifereza Statistica L ifereza statistica cerca di risalire al modello del feomeo sulla base delle osservazioi No coosciamo il modello del feomeo cioè la vc X A volte la coosceza può essere parziale (coosciamo
Soluzioni degli esercizi del corso di Analisi Matematica I
 Soluzioi degli esercizi del corso di Aalisi Matematica I Prof. Pierpaolo Natalii Roberta Biachii & Marco Pezzulla ovembre 015 FOGLIO 1 1. Determiare il domiio e il sego della fuzioe ( ) f(x) = arccos x
Soluzioi degli esercizi del corso di Aalisi Matematica I Prof. Pierpaolo Natalii Roberta Biachii & Marco Pezzulla ovembre 015 FOGLIO 1 1. Determiare il domiio e il sego della fuzioe ( ) f(x) = arccos x
Primo appello di Calcolo delle probabilità Laurea Triennale in Matematica 07/02/2017
 Primo appello di Calcolo delle probabilità Laurea Trieale i Matematica 07/02/207 COGNOME e NOME... N. MATRICOLA... Esercizio. Sia {X } N ua martigala rispetto ad ua filtrazioe {F } N co P (X N) = per ogi
Primo appello di Calcolo delle probabilità Laurea Trieale i Matematica 07/02/207 COGNOME e NOME... N. MATRICOLA... Esercizio. Sia {X } N ua martigala rispetto ad ua filtrazioe {F } N co P (X N) = per ogi
Esercitazione n 3. 1 Successioni di funzioni. Esercizio 1: Studiare la convergenza in (0, 1) della successione {f n } dove f n (x) =
 Esercitazioe 3 Successioi di fuzioi Esercizio : Studiare la covergeza i (0, ) della successioe {f } dove f (x) = metre Sol.: Si verifica facilmete che lim f (x) = 0 x (0, ) lim sup f (x) = lim = + (0,)
Esercitazioe 3 Successioi di fuzioi Esercizio : Studiare la covergeza i (0, ) della successioe {f } dove f (x) = metre Sol.: Si verifica facilmete che lim f (x) = 0 x (0, ) lim sup f (x) = lim = + (0,)
1 Famiglia delle densità gamma
 olitecico di Milao, Statistica INF, TEL [A-LZ], Epifai I., AA 7/8 Famiglia delle desità gamma Le espressioi delle desità espoeziale di parametro θ e χ date da (E(β)) (χ ) /θe x/β (, ) (x), β > (/) / x
olitecico di Milao, Statistica INF, TEL [A-LZ], Epifai I., AA 7/8 Famiglia delle desità gamma Le espressioi delle desità espoeziale di parametro θ e χ date da (E(β)) (χ ) /θe x/β (, ) (x), β > (/) / x
Definizione 1. Data una successione (a n ) alla scrittura formale. 1) a 1 + a a n +, si dà il nome di serie.
 SERIE NUMERICHE Defiizioe. Data ua successioe (a ) alla scrittura formale ) a + a 2 + + a +, si dà il ome di serie. I umeri a, a 2,, a, rappresetao i termii della serie, i particolare a è il termie geerale
SERIE NUMERICHE Defiizioe. Data ua successioe (a ) alla scrittura formale ) a + a 2 + + a +, si dà il ome di serie. I umeri a, a 2,, a, rappresetao i termii della serie, i particolare a è il termie geerale
Equazioni differenziali
 Equazioi differeziali Defiizioe 1 Si chiama equazioe differeziale u tipo particolare di equazioe fuzioale, ella quale la fuzioe icogita compare isieme ad alcue sue derivate, ossia u equazioe ella quale,
Equazioi differeziali Defiizioe 1 Si chiama equazioe differeziale u tipo particolare di equazioe fuzioale, ella quale la fuzioe icogita compare isieme ad alcue sue derivate, ossia u equazioe ella quale,
1 Successioni numeriche
 Aalisi Matematica 2 Successioi umeriche CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 5 SERIE NUMERICHE Chiamiamo successioe di umeri reali ua fuzioe a valori reali defiita su N oppure
Aalisi Matematica 2 Successioi umeriche CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 5 SERIE NUMERICHE Chiamiamo successioe di umeri reali ua fuzioe a valori reali defiita su N oppure
4 - Le serie Soluzioni. n + 3. n + 3. n + 2
 4 - Le serie Soluzioi Esercizio. Studiare la covergeza delle serie: + + 2 + cos!) 2 cosπ). Per la prima serie si ha 0 + + 2 + = 2. Dal mometo che la serie di termie geerico 2 è covergete serie armoica
4 - Le serie Soluzioi Esercizio. Studiare la covergeza delle serie: + + 2 + cos!) 2 cosπ). Per la prima serie si ha 0 + + 2 + = 2. Dal mometo che la serie di termie geerico 2 è covergete serie armoica
Capitolo 5. Successioni numeriche
 Capitolo 5 Successioi umeriche Ua successioe è ua fuzioe avete domiio N o u suo sottoisieme del tipo A = { N > 0, 0 N} e come codomiio R e che associa a ogi umero aturale u umero reale a. La legge di ua
Capitolo 5 Successioi umeriche Ua successioe è ua fuzioe avete domiio N o u suo sottoisieme del tipo A = { N > 0, 0 N} e come codomiio R e che associa a ogi umero aturale u umero reale a. La legge di ua
Esercizi 2 Pietro Caputo 14 dicembre se ξ n > log n
 Esercizi 2 Pietro Caputo 4 dicembre 2006 Esercizio. Siao Y, per =, 2,..., variabili aleatorie co distribuzioe biomiale di parametri e p := λ, per qualche λ > 0. Dimostrare che Y coverge i distribuzioe
Esercizi 2 Pietro Caputo 4 dicembre 2006 Esercizio. Siao Y, per =, 2,..., variabili aleatorie co distribuzioe biomiale di parametri e p := λ, per qualche λ > 0. Dimostrare che Y coverge i distribuzioe
Esercizi di approfondimento di Analisi IA
 Esercizi di approfodimeto di Aalisi IA 4 geaio 017 1 Estremo superiore/iferiore, classi cotigue, archimedeità 1.1. Mostrare che A = {x R : x > 0, x < } ha u estremo superiore ξ, ed è ξ =. 1.. Siao A, B
Esercizi di approfodimeto di Aalisi IA 4 geaio 017 1 Estremo superiore/iferiore, classi cotigue, archimedeità 1.1. Mostrare che A = {x R : x > 0, x < } ha u estremo superiore ξ, ed è ξ =. 1.. Siao A, B
Serie numeriche e di funzioni - Esercizi svolti
 Serie umeriche e di fuzioi - Esercizi svolti Serie umeriche Esercizio. Discutere la covergeza delle serie segueti a) 3, b) 5, c) 4! (4), d) ( ) e. Esercizio. Calcolare la somma delle serie segueti a) (
Serie umeriche e di fuzioi - Esercizi svolti Serie umeriche Esercizio. Discutere la covergeza delle serie segueti a) 3, b) 5, c) 4! (4), d) ( ) e. Esercizio. Calcolare la somma delle serie segueti a) (
Metodi Matematici per l Ingegneria
 Metodi Matematici per l Igegeria Agelo Alvio A.A.2016-17 2 Idice 1 Fuzioi olomorfe 5 1.1 La fuzioe exp i campo complesso................ 5 1.2 Derivabilità i campo complesso.................. 8 1.3 Serie
Metodi Matematici per l Igegeria Agelo Alvio A.A.2016-17 2 Idice 1 Fuzioi olomorfe 5 1.1 La fuzioe exp i campo complesso................ 5 1.2 Derivabilità i campo complesso.................. 8 1.3 Serie
Successioni di funzioni
 Successioi di fuzioi Successioi di fuzioi: covergeza putuale Defiizioe Sia I u isieme di umeri reali e sia ua successioe di fuzioi reali defiite i I : I R, I R. Si dice che Cioè f : I R, risulta coverge
Successioi di fuzioi Successioi di fuzioi: covergeza putuale Defiizioe Sia I u isieme di umeri reali e sia ua successioe di fuzioi reali defiite i I : I R, I R. Si dice che Cioè f : I R, risulta coverge
Soluzioni degli esercizi di Analisi Matematica I
 Soluzioi degli esercizi di Aalisi Matematica I (Prof. Pierpaolo Natalii) Roberta Biachii 6 ovembre 2016 FOGLIO 1 1. Determiare il domiio e il sego della fuzioe ( ) f(x) = arccos x2 1 x + 1 π/3. 2. Dimostrare,
Soluzioi degli esercizi di Aalisi Matematica I (Prof. Pierpaolo Natalii) Roberta Biachii 6 ovembre 2016 FOGLIO 1 1. Determiare il domiio e il sego della fuzioe ( ) f(x) = arccos x2 1 x + 1 π/3. 2. Dimostrare,
ANALISI VETTORIALE COMPITO IN CLASSE DEL 22/11/2013. = a 24 24! log(1 + x) = ( 1) = (24!) 1 24 = 23!. e x2 dx. x 2n
 ANALISI VETTORIALE COMPITO IN CLASSE DEL 22//23 Esercizio Calcolare la 2esima derivata del logaritmo el puto. Risposta Si tratta di calcolare d 2 dx 2 log( + x) x= = a 2 2! dove a 2 è il termie di idice
ANALISI VETTORIALE COMPITO IN CLASSE DEL 22//23 Esercizio Calcolare la 2esima derivata del logaritmo el puto. Risposta Si tratta di calcolare d 2 dx 2 log( + x) x= = a 2 2! dove a 2 è il termie di idice
Esercitazione di AM310
 Uiversità degli Studi Roma Tre - Corso di Laurea i Matematica Esercitazioe di AM3 A.A. 8-9 - Esercitatore: Luca Battaglia Soluzioi dell esercitazioe 6 del Dicembre 8 Argometo: Misure prodotto, operatori
Uiversità degli Studi Roma Tre - Corso di Laurea i Matematica Esercitazioe di AM3 A.A. 8-9 - Esercitatore: Luca Battaglia Soluzioi dell esercitazioe 6 del Dicembre 8 Argometo: Misure prodotto, operatori
Il Teorema di Markov. 1.1 Analisi spettrale della matrice di transizione. Il teorema di Markov afferma che
 1 Il Teorema di Marov 1.1 Aalisi spettrale della matrice di trasizioe Il teorema di Marov afferma che Teorema 1.1 Ua matrice di trasizioe regolare P su u isieme di stati fiito E ha ua uica distribuzioe
1 Il Teorema di Marov 1.1 Aalisi spettrale della matrice di trasizioe Il teorema di Marov afferma che Teorema 1.1 Ua matrice di trasizioe regolare P su u isieme di stati fiito E ha ua uica distribuzioe
Appunti per l Orale di Statistica
 Apputi per l Orale di Statistica Matteo Giaello 6 ottobre 2011 1 Idice 1 Media e variaza campioaria 3 1.1 Media campioaria............................... 3 1.2 Variaza campioaria.............................
Apputi per l Orale di Statistica Matteo Giaello 6 ottobre 2011 1 Idice 1 Media e variaza campioaria 3 1.1 Media campioaria............................... 3 1.2 Variaza campioaria.............................
SUCCESSIONI e LIMITI DI SUCCESSIONI. c Paola Gervasio - Analisi Matematica 1 - A.A. 2018/19 Successioni cap3b.pdf 1
 SUCCESSIONI e LIMITI DI SUCCESSIONI c Paola Gervasio - Aalisi Matematica 1 - A.A. 2018/19 Successioi cap3b.pdf 1 Successioi Def. Ua successioe è ua fuzioe reale (Y = R) a variabile aturale, ovvero X =
SUCCESSIONI e LIMITI DI SUCCESSIONI c Paola Gervasio - Aalisi Matematica 1 - A.A. 2018/19 Successioi cap3b.pdf 1 Successioi Def. Ua successioe è ua fuzioe reale (Y = R) a variabile aturale, ovvero X =
Esperimentazioni di Fisica 1. Prova scritta del 1 febbraio 2016 SOLUZIONI
 Esperimetazioi di Fisica 1 Prova scritta del 1 febbraio 2016 SOLUZIONI Esp-1 Prova di Esame Primo appello - Page 2 of 7 10/09/2015 1. (12 Puti) Quesito. La variabile casuale cotiua x ha ua distribuzioe
Esperimetazioi di Fisica 1 Prova scritta del 1 febbraio 2016 SOLUZIONI Esp-1 Prova di Esame Primo appello - Page 2 of 7 10/09/2015 1. (12 Puti) Quesito. La variabile casuale cotiua x ha ua distribuzioe
Le successioni: intro
 Le successioi: itro Si cosideri la seguete sequeza di umeri:,, 2, 3, 5, 8, 3, 2, 34, 55, 89, 44, 233, detti di Fiboacci. Essa rappreseta il umero di coppie di coigli preseti ei primi 2 mesi i u allevameto!
Le successioi: itro Si cosideri la seguete sequeza di umeri:,, 2, 3, 5, 8, 3, 2, 34, 55, 89, 44, 233, detti di Fiboacci. Essa rappreseta il umero di coppie di coigli preseti ei primi 2 mesi i u allevameto!
Serie di potenze / Esercizi svolti
 MGuida, SRolado, 204 Serie di poteze / Esercizi svolti Si cosideri la serie di poteze (a) Determiare il raggio di covergeza 2 + x (b) Determiare l itervallo I di covergeza putuale (c) Dire se la serie
MGuida, SRolado, 204 Serie di poteze / Esercizi svolti Si cosideri la serie di poteze (a) Determiare il raggio di covergeza 2 + x (b) Determiare l itervallo I di covergeza putuale (c) Dire se la serie
Esercizi svolti. 1. Calcolare i seguenti limiti: log(1 + 3x) x 2 + 2x. x 2 + 3 sin 2x. l) lim. b) lim. x 0 sin x. 1 e x2 d) lim. c) lim.
 Esercizi svolti. Calcolare i segueti iti: a log + + c ± ta 5 + 5 si π e b + si si e d + f + 4 5 g + 6 4 6 h 4 + i + + + l ± + log + log 7 log 5 + 4 log m + + + o cos + si p + e q si s e ta cos e u siπ
Esercizi svolti. Calcolare i segueti iti: a log + + c ± ta 5 + 5 si π e b + si si e d + f + 4 5 g + 6 4 6 h 4 + i + + + l ± + log + log 7 log 5 + 4 log m + + + o cos + si p + e q si s e ta cos e u siπ
Argomenti. Stima Puntuale e per Intervallo. Inferenza. Stima. Leonardo Grilli. Università di Firenze Corso di Laurea in Statistica Statistica
 Uiversità di Fireze Corso di Laurea i Statistica Statistica Leoardo Grilli Stima Cicchitelli cap. 6 Argometi Defiizioe di stimatore Proprietà degli stimatori (campioi fiiti): No distorsioe Efficieza relativa
Uiversità di Fireze Corso di Laurea i Statistica Statistica Leoardo Grilli Stima Cicchitelli cap. 6 Argometi Defiizioe di stimatore Proprietà degli stimatori (campioi fiiti): No distorsioe Efficieza relativa
7 Il metodo variazionale
 7 Il metodo variazioale I questo capitolo itrodurremo alcue teciche variazioali, co lo scopo di otteere ulteriori risultati di esisteza di soluzioi per il problema periodico { x (P ) + g(t, x) =, x() =
7 Il metodo variazioale I questo capitolo itrodurremo alcue teciche variazioali, co lo scopo di otteere ulteriori risultati di esisteza di soluzioi per il problema periodico { x (P ) + g(t, x) =, x() =
x n (1.1) n=0 1 x La serie geometrica è un esempio di serie di potenze. Definizione 1 Chiamiamo serie di potenze ogni serie della forma
 1 Serie di poteze È stato dimostrato che la serie geometrica x (1.1) coverge se e solo se la ragioe x soddisfa la disuguagliaza 1 < x < 1. I realtà c è covergeza assoluta i ] 1, 1[. Per x 1 la serie diverge
1 Serie di poteze È stato dimostrato che la serie geometrica x (1.1) coverge se e solo se la ragioe x soddisfa la disuguagliaza 1 < x < 1. I realtà c è covergeza assoluta i ] 1, 1[. Per x 1 la serie diverge
Analisi Matematica I modulo Soluzioni prova scritta preliminare n. 1
 Aalisi Matematica I modulo Soluzioi prova scritta prelimiare 1 Corso di laurea i Matematica, aa 004-005 9 ovembre 004 1 (a) Calcolare il seguete limite: **A***** Soluzioe Si ha ( + log ) ( + log ) lim
Aalisi Matematica I modulo Soluzioi prova scritta prelimiare 1 Corso di laurea i Matematica, aa 004-005 9 ovembre 004 1 (a) Calcolare il seguete limite: **A***** Soluzioe Si ha ( + log ) ( + log ) lim
Algoritmi e Strutture Dati (Elementi)
 Algoritmi e Strutture Dati (Elemeti Esercizi sulle ricorreze Proff. Paola Boizzoi / Giacarlo Mauri / Claudio Zadro Ao Accademico 00/003 Apputi scritti da Alberto Leporati e Rosalba Zizza Esercizio 1 Posti
Algoritmi e Strutture Dati (Elemeti Esercizi sulle ricorreze Proff. Paola Boizzoi / Giacarlo Mauri / Claudio Zadro Ao Accademico 00/003 Apputi scritti da Alberto Leporati e Rosalba Zizza Esercizio 1 Posti
Limiti di successioni
 Limiti di successioi Aalisa Cesaroi, Paola Maucci e Alvise Sommariva Uiversità degli Studi di Padova Dipartimeto di Matematica 20 ottobre 2015 Aalisa Cesaroi, Paola Maucci e Alvise Sommariva Itroduzioe
Limiti di successioi Aalisa Cesaroi, Paola Maucci e Alvise Sommariva Uiversità degli Studi di Padova Dipartimeto di Matematica 20 ottobre 2015 Aalisa Cesaroi, Paola Maucci e Alvise Sommariva Itroduzioe
ANALISI MATEMATICA 1 Commissione L. Caravenna, V. Casarino, S. Zoccante Ingegneria Gestionale, Meccanica e Meccatronica, Vicenza
 ANALISI MATEMATICA Commissioe L. Caravea, V. Casario, S. occate Igegeria Gestioale, Meccaica e Meccatroica, Viceza Nome, Cogome, umero di matricola: Viceza, 6 Settembre 25 TEMA - parte B Esercizio ( puti).
ANALISI MATEMATICA Commissioe L. Caravea, V. Casario, S. occate Igegeria Gestioale, Meccaica e Meccatroica, Viceza Nome, Cogome, umero di matricola: Viceza, 6 Settembre 25 TEMA - parte B Esercizio ( puti).
Esercitazione IV Complementi di Probabilità a.a. 2011/2012
 Esercitazioe IV Complemeti di Probabilità a.a. 2011/2012 Argometi: idipedeza, 2 lemma di Borel Catelli, σ-algebra coda. Esercizio 1. a) Dato (Ω, F, P), siao J 1, J 2,..., J m π-system su Ω tali che Ω J
Esercitazioe IV Complemeti di Probabilità a.a. 2011/2012 Argometi: idipedeza, 2 lemma di Borel Catelli, σ-algebra coda. Esercizio 1. a) Dato (Ω, F, P), siao J 1, J 2,..., J m π-system su Ω tali che Ω J
Calcolo I - Corso di Laurea in Fisica - 31 Gennaio 2018 Soluzioni Scritto
 Calcolo I - Corso di Laurea i Fisica - Geaio 08 Soluzioi Scritto Data la fuzioe f = 8 + / a Calcolare il domiio, puti di o derivabilità ed asitoti; b Calcolare, se esistoo, estremi relativi ed assoluti.
Calcolo I - Corso di Laurea i Fisica - Geaio 08 Soluzioi Scritto Data la fuzioe f = 8 + / a Calcolare il domiio, puti di o derivabilità ed asitoti; b Calcolare, se esistoo, estremi relativi ed assoluti.
06 LE SUCCESSIONI DI NUMERI REALI
 06 LE SUCCESSIONI DI NUMERI REALI Ua successioe è ua fuzioe defiita i. I simboli ua f : A tale che f ( ) è ua successioe di elemeti di A. Se poiamo f ( i) ai co i,...,,..., ua successioe può essere rappresetata
06 LE SUCCESSIONI DI NUMERI REALI Ua successioe è ua fuzioe defiita i. I simboli ua f : A tale che f ( ) è ua successioe di elemeti di A. Se poiamo f ( i) ai co i,...,,..., ua successioe può essere rappresetata
ALTRI ESERCIZI SULL INTEGRALE DI LEBESGUE. A. Figà Talamanca
 ALTRI SRCIZI SULL INTGRAL DI LBSGU A. Figà Talamaca 29 ottobre 2006 2 L itegrale di Lebesgue che abbiamo defiito per le fuzioi misurabili, limitate defiite su u isieme misurabile di misura fiita, può essere
ALTRI SRCIZI SULL INTGRAL DI LBSGU A. Figà Talamaca 29 ottobre 2006 2 L itegrale di Lebesgue che abbiamo defiito per le fuzioi misurabili, limitate defiite su u isieme misurabile di misura fiita, può essere
Corso di Laurea in Ingegneria Informatica Anno Accademico 2016/2017 Calcolo delle Probabilità e Statistica Matematica
 Corso di Laurea i Igegeria Iformatica Ao Accademico 26/27 Calcolo delle Probabilità e Statistica Matematica Nome... N. Matricola... Acoa, geaio 27. (8 puti) Si vuole stimare il parametro p di ua legge
Corso di Laurea i Igegeria Iformatica Ao Accademico 26/27 Calcolo delle Probabilità e Statistica Matematica Nome... N. Matricola... Acoa, geaio 27. (8 puti) Si vuole stimare il parametro p di ua legge
