Esercizi sull estremo superiore ed inferiore
|
|
|
- Francesca Fantini
- 5 anni fa
- Visualizzazioni
Transcript
1 AM0 - A.A. 03/4 ALFONSO SORRENTINO Esercizi sull estremo superiore ed iferiore Esercizio svolto. Dire se i segueti isiemi soo limitati iferiormete o superiormete ed, i caso affermativo, trovare l estremo iferiore o l estremo superiore. Dire se si tratta di miimi o massimi. i) A := { { : N} ; ii) B := + }; { : Z } iii) C := ( ) : N ; iv) D := { ( ) : N} v) E := { x R : x } ad E := { x Q : x } ; vi) F := {x R : x x > }. vii) G := { N : si ( π )}. viii) H := { x : x + x < }. { } 5 ix) I := +3,. { } x) L := : N. Soluzioe. i) Osserviamo che { A := e che } : N = { } : N 0 N. Quidi: A è limitato iferiormete da 0 (ogi k 0 è u miorate per A). I particolare, poiché 0 è u miorate e 0 A, allora 0 = mi A = if A. A è limitato superiormete da (ogi k è u maggiorate per A). Dimostriamo che è il più piccolo dei maggiorati. Sia ε > 0; mostriamo che ε o può essere u maggiorate. Ifatti: > ε > ε. Quidi, per ogi > ε l elemeto > ε e di cosegueza o può essere u maggiorate. Coclusioe: sup A =. Osserviamo che o è u massimo, i quato A (ifatti per ogi N).
2 ALFONSO SORRENTINO ii) Osservare che: + Z. I particolare, è sufficiete dimostrare: + Z. Dimostriamo che vale questa disuguagliaza: + = + Z + Z + 0 Z ( ) 0 Z che è chiaramete vero. Quidi è u maggiorate per B e u miorate. Di cosegueza B è limitato superiormete ed iferiormete. Ioltre, dal mometo che B e B, possiamo cocludere che soo ache il massimo ed il miimo: mi B = if B = e max B = sup B =. iii) Iazitutto osserviamo che ( ) = N. Quidi, ( ) N. Di cosegueze è u miorate ed u maggiorate per C. Ne segue che C è limitato sia iferiormete che superiormete. I particolare, dal mometo che C (basta predere = ) e è u miorate, possiamo cocludere che mi C = if C =. Calcoliamo ora l estremo superiore. Come abbiamo detto è u maggiorate, ma o è il più piccolo dei maggiorate. Ifatti, si dimostra che ache è u maggiorate: Se è dispari, ( ) < 0 < ; Se è pari (i particolare ), allora ( ) = (i quato ). Ioltre, C (basta predere = ), quidi max C = sup C =. iv) Deotiamo d := ( ) = ( ) ( ). Osserviamo che è u maggiorate e è u miorate. Ifatti: d = d. Dimostriamo che si tratta dell estremo superiore e dell estremo iferiore. Dimostriamo che sup D =. Dobbiamo dimostrare che per ogi ε > 0, esiste 0 tale che d 0 ε. Assumiamo che 0 sia pari, per esempio 0 = k 0. Allora, bastera scegliere k 0 i maiera che: d k0 = k 0 k 0 = k 0 > ε k 0 > ε. I maiera simile (cosiderado dispari), si dimostra che if D =.
3 AM0 - A.A. 03/4 3 Osserviamo che o si tratta é di u massimo, é di u miimo. v) Osservare che E := { x R : x } = [, ]. È facile verificare che: mi E = if E = e max E = sup E =. I maiera simile, E := { x Q : x } = [, ] Q = (, ) Q. Si può dimostrare che sup E = e if E =. Questa volta o si tratta é di u massimo, é di u miimo (i quato Q). Dimostriamo ad esempio che sup E = ; la dimostrazioe per l estremo iferiore è speculare. - Ovviamete è u maggiorate: se x E, allora x e quidi x. - Dimostriamo che è il più piccolo dei maggiorati. Sia ε > 0, vogliamo trovare x E tale che x > ɛ. Cosideriamo il seguete isieme: ( ε ) I := ε, (, ) Se I =, allora vuol dire che ε. Quidi, possiamo predere u qualsiasi x E e si avrà x > ε. Se ivece I, allora I sarà u itervallo aperto. Scegliamo quidi u qualsiasi razioale x I e questo soddisferà la relazioe x > ɛ. vi) Si dimostra che F := {x R : x x > } = (, + ). Di cosegueza, if F = (o è u miimo) e sup F = + (l isieme o è limitato superiormete). vii) Osserviamo che = 4 (0, ) + è ua successioe crescete. Quidi, ( π si 4 ) 4 = si + ( π π 4 + Poiché si x è crescete i (0, π ), allora mi G = if G = si π 4 =, metre sup G = (o è u massimo). viii) Si verifica facilmete che x + x < per < x <. Quidi H = [0, ), da cui mi H = if H = 0 e sup H = (o è u massimo). ix) Osserviamo iazitutto che: { = +3 se se > 5 ). è crescete, i quato 5 +3 = Cal- Ioltre, la successioe 5 +3 coliamo esplicitamete i primi termii di I (per 5): I = { 3 5, 3, 7, 0, per > 5 }.
4 4 ALFONSO SORRENTINO Possiamo dedurre che mi I = if I = 0, metre sup I = (o è u massimo). () x) Ovviamete mi L = if L =. Vogliamo calcolare l estremo superiore. Dimostriamo che: per ogi N. Usado () segue facilmete che sup L = +. Dimostriamo (). Si può dimostrare per iduzioe. Per = è triviale. Assumiamo che sia vero per e dimostriamolo per + : dove l ultima disuguagliaza si dimostra facilmete elevado etrambi i membri al quadrato. Esercizio aggiutivo. Dire se i segueti isiemi soo limitati iferiormete o superiormete ed, i caso affermativo, trovare l estremo iferiore o l estremo superiore. Dire se si tratta di miimi o massimi. i) A := { ( ) + : N} ; ii) B := { : Z } ; iii) C := { : N } ; Esercizio svolto. Siao P, A > 0. Cosiderare gli isiemi E := {Area di u rettagolo R t.c. Perimetro(R)=P} F := {Perimetro di u rettagolo R t.c. Area(R)=A}. Trovare l estremo superiore ed iferiore di E ed F e dire se si tratta di massimi o miimi. Soluzioe. Deotiamo co a, b > 0 le lughezze dei lati di u rettagolo R a,b. Possiamo riscrivere gli isiemi E ed F el seguete modo: E := {ab : a + b = P/, a, b > 0} F := {a + b : ab = A, a, b > 0}. Dal mometo che per ogi a, b > 0 si ha ab a + b, allora P P 6 è u maggiorate per E. I particolare, 6 è u elemeto di E (basta predere a = b = P 4, che corrispode al quadrato di perimetro P ), quidi max E = sup E = P 6. Per ogi ε > 0 sufficietemete piccolo, possiamo scegliere lati a = ε e b = P ε; l area del corrispodete rettagolo sarà ab = ε ( P ε) ε P. Questo dimostra che 0 è il più grade dei miorati e quidi if E = 0 (ovviamete o è u miimo). I maiera simile si dimostra che mi F = if F = 4 A (che corrispode al perimetro del quadrato di area A), metre sup F = +.
5 AM0 - A.A. 03/4 5 Esercizio svolto 3. Sia A u isieme limitato superiormete. Defiiamo A := { a : a A}. Dimostrare che if A = sup( A). Soluzioe. Deotiamo l = if A. Segue dalla defiizioe di estremo iferiore che: a) l a per ogi a A; a) per ogi m > l, esiste u elemeto ā A tale che m > ā. Dimostriamo che l è l estremo superiore di A: segue da (a) che l a per ogi a A; sia M < l; si cha che M > l, quidi segue da (a) che esiste ā A tale che M > ā. Di cosegueza M < ā e ā A, quidi M o può essere u maggiorate. Questo dimostra che l è il più piccolo maggiorate per A e quidi è l estremo superiore. Esercizio svolto 4. Sia A u isieme limitato. Si defiisca il diametro di A el seguete modo: diam A := sup{ x y : x, y A}. Dimostrare che diam A = sup A if A. Soluzioe. Siao x, y A. Possiamo assumere che x y (altrimeti basta ivertire i ruoli). Segue dalla defiizioe di estremo superiore ed iferiore che sup A x e if A y. Quidi: sup A if A x y = x y x, y A. Quidi sup A if A è u maggiorate dell isieme { x y : x, y A}. Poiché l estremo superiore è il più piccolo dei maggiorati, otteiamo: sup A if A sup{ x y : x, y A} =: diam A. Vogliamo dimostrare ora che sup A if A diam A. Suppoiamo per assurdo che sup A if A > diam A. Quidi esiste ε > 0 tale che: () diam A < sup A if A ε = (sup A ε) (if A + ε). Segue dalla defiizioe di sup ed if che: x A tale che sup A ε < x e ȳ A tale che if A + ε > ȳ. Quidi sostituedo ella disuguagliaza () ottieiamo: diam A < (sup A ε) (if A + ε) < x ȳ x ȳ diam A, che è ua chiara cotraddizioe. Questo coclude la dimostrazioe che diam A sup A if A. Esercizio svolto 5. Dimostrare che ogi isieme fiito ha u massimo ed u miimo. Soluzioe. Sia A = {a,..., a } R. Dimostriamo che A ha u massimo (si procede i maiera aaloga per il miimo). Iazitutto, A è limitato superiormete. Se così o fosse, ifatti, per ogi M R dovrebbe esistere u elemeto di A maggiore di M. Partedo da b 0 = a, si potrebbe scegliere b A tale che b > b 0. Iterado l argometo si otterrebbe
6 6 ALFONSO SORRENTINO ua successioe di elemeti b A tale che b > b. Questi elemeti sarebbero ovviamete distiti, e ciò cotraddirebbe il fatto che A è u isieme fiito. Sia S = sup A. Vogliamo dimostrare che si tratta di u massimo, cioè che S A. Suppoiamo per assurdo che S A. Quidi δ i := S a i > 0 per ogi a i A; scegliamo u ε < δ i per ogi i =,...,. Segue dalla defiizioe di estremo superiore che S ε o può essere u maggiorate, quidi esiste a j A tale che S ε a j. Quidi: S ε a j δ j = S a j < ε che è chiaramete ua cotraddizioe (avevamo scelto ε < δ i per ogi i =,..., ). Questo coclude la dimostrazioe che S A e quidi si tratta di u massimo. Esercizio svolto 6. Siao A e B due isiemi. Defiiamo Dimostrare che: A + B := {a + b : a A, b B}. i) se A e B soo limitati superiormete, allora ache A + B lo è e si ha: sup(a + B) = sup A + sup B. ii) Se A e B soo limitati iferiormete, allora ache A + B lo è e si ha: if(a + B) = if A + if B. Soluzioe. Dimostriamo soltato (i); la dimostrazioe di (ii) è aaloga. Sia α = sup A e β = sup B. Vogliamo dimostrare che α + β è l estremo superiore di A + B. Ifatti: α + β è u maggiorate per A + B. Ifatti, α è u maggiorate per A e β è u maggiorate per B, quidi: α + β a + b a A, b B. Dimostriamo che α + β è il più piccolo dei maggiorati per A + B. Sia ε > 0, dimostriamo che α + β ε o può essere u maggiorate. Ifatti: α + β ε = (α ε ) + (β ε ) a + b a A, b B. Nell ultimo passaggio abbiamo usato il fatto che α è il più piccolo dei maggiorati per A (quidi esiste a A tale che α ε a) ed i maiera aaloga che β è il più piccolo dei maggiorati per B (quidi esiste b B tale che β ε b). Esercizio svolto 7. Dimostare che ogi poliomio di terzo grado ha almeo ua radice reale. Soluzioe. Possiamo assumere che il poliomio sia della forma P (x) = x 3 + ax + bx + c, co a, b, c R. È sufficiete dimostrare che esistoo s < t tali che P (s) < 0 e P (t) > 0. Dimostriamo l esisteza di s tale che s 3 + as + bs + c > 0. I particolare, possiamo cercare tale valore el semi asse positivo s > 0. Si osservi che se s > a, allora: s 3 + as + bs + c = s s + as + bs + c > ( a) s + as + bs + c = = s + bs + c.
7 AM0 - A.A. 03/4 7 Se assumiamo che s > b, si ottiee: s + bs + c > ( b)s + bs + c = s + c. I particolare, se s > c si avrà s + c > 0. I coclusioe: se s > max{0, a, b, c} = P (s) > 0. Dimostriamo ora l esisteza di t tale che P (t) < 0. Vogliamo trovare u valore di t per cui t 3 +at +bt+c < 0. I particolare, possiamo cercare tale valore el semi asse egativo t < 0. Si osservi che, se t < a, allora t 3 + at + bt + c = t t + at + bt + c < ( a)t + at + bt + c = = t + bt + c. Se assumiamo che t < b, si ottiee: t + bt + c < (b )t + bt + c = t + c. I particolare, se t < c si avrà t + c < 0. I coclusioe: se t < mi{0, a, b, c} = P (t) < 0.
AM110 - ESERCITAZIONI V - VI. Esercizio svolto 1. Dimostrare che ogni insieme finito ha un massimo ed un minimo.
 AM110 - ESERCITAZIONI V - VI 16-18 OTTOBRE 2012 Esercizio svolto 1. Dimostrare che ogi isieme fiito ha u massimo ed u miimo. Sia A = {a 1,..., a } R. Dimostriamo che A ha u massimo si procede i maiera
AM110 - ESERCITAZIONI V - VI 16-18 OTTOBRE 2012 Esercizio svolto 1. Dimostrare che ogi isieme fiito ha u massimo ed u miimo. Sia A = {a 1,..., a } R. Dimostriamo che A ha u massimo si procede i maiera
Esercizi sui limiti di successioni
 AM0 - AA 03/4 ALFONSO SORRENTINO Esercizi sui iti di successioi Esercizio svolto a) Usado la defiizioe di ite, dimostare che: + 3 si π cos e ) e b) 0 Soluzioe Comiciamo da a) Vogliamo dimostrare che: ε
AM0 - AA 03/4 ALFONSO SORRENTINO Esercizi sui iti di successioi Esercizio svolto a) Usado la defiizioe di ite, dimostare che: + 3 si π cos e ) e b) 0 Soluzioe Comiciamo da a) Vogliamo dimostrare che: ε
Esercizi sulle Serie numeriche
 AM0 - A.A. 03/4 ALFONSO SORRENTINO Esercizi sulle Serie umeriche Esercizio svolto. Discutere il comportameto delle segueti serie umeriche: a +! b [ ] log c log+ d log + e arcta f g h i l log log! 3! 4
AM0 - A.A. 03/4 ALFONSO SORRENTINO Esercizi sulle Serie umeriche Esercizio svolto. Discutere il comportameto delle segueti serie umeriche: a +! b [ ] log c log+ d log + e arcta f g h i l log log! 3! 4
Soluzioni degli esercizi del corso di Analisi Matematica I
 Soluzioi degli esercizi del corso di Aalisi Matematica I Prof. Pierpaolo Natalii Roberta Biachii & Marco Pezzulla ovembre 015 FOGLIO 1 1. Determiare il domiio e il sego della fuzioe ( ) f(x) = arccos x
Soluzioi degli esercizi del corso di Aalisi Matematica I Prof. Pierpaolo Natalii Roberta Biachii & Marco Pezzulla ovembre 015 FOGLIO 1 1. Determiare il domiio e il sego della fuzioe ( ) f(x) = arccos x
Tutoraggio AM1 17/12/2015. sin(x) arctan(x) 2) lim sup / inf x 0 + cos(x) sin( 1 x ) e x2 cos 2 (x 3 ) x 2 + ln(3x + 2) δ(x) δ(x) =
 Tutoraggio AM1 17/12/2015 Per la parte teorica sui if e sup vedi le ote su iti iferiori e superiori di fuzioi. A) Date due successioi a },b }, mostrare le segueti proprietà (escludere i casi i cui si abbia
Tutoraggio AM1 17/12/2015 Per la parte teorica sui if e sup vedi le ote su iti iferiori e superiori di fuzioi. A) Date due successioi a },b }, mostrare le segueti proprietà (escludere i casi i cui si abbia
Soluzioni degli esercizi di Analisi Matematica I
 Soluzioi degli esercizi di Aalisi Matematica I (Prof. Pierpaolo Natalii) Roberta Biachii 6 ovembre 2016 FOGLIO 1 1. Determiare il domiio e il sego della fuzioe ( ) f(x) = arccos x2 1 x + 1 π/3. 2. Dimostrare,
Soluzioi degli esercizi di Aalisi Matematica I (Prof. Pierpaolo Natalii) Roberta Biachii 6 ovembre 2016 FOGLIO 1 1. Determiare il domiio e il sego della fuzioe ( ) f(x) = arccos x2 1 x + 1 π/3. 2. Dimostrare,
Analisi Matematica Soluzioni prova scritta parziale n. 1
 Aalisi Matematica Soluzioi prova scritta parziale. 1 Corso di laurea i Fisica, 018-019 3 dicembre 018 1. Dire per quali valori dei parametri α R, β R, α > 0, β > 0 coverge la serie + (!) α β. ( )! =1 Soluzioe.
Aalisi Matematica Soluzioi prova scritta parziale. 1 Corso di laurea i Fisica, 018-019 3 dicembre 018 1. Dire per quali valori dei parametri α R, β R, α > 0, β > 0 coverge la serie + (!) α β. ( )! =1 Soluzioe.
ESERCIZI - FASCICOLO 1
 ESERCIZI - FASCICOLO 1 Esercizio 1 Sia (Ω, A) uo spazio misurabile. Se (A ) 1 è ua successioe di eveti (= elemeti di A), defiiamo lim sup A := A k lim if A = A k. Mostrare che =1 k= (lim sup A ) c = lim
ESERCIZI - FASCICOLO 1 Esercizio 1 Sia (Ω, A) uo spazio misurabile. Se (A ) 1 è ua successioe di eveti (= elemeti di A), defiiamo lim sup A := A k lim if A = A k. Mostrare che =1 k= (lim sup A ) c = lim
1.10 La funzione esponenziale
 6. Risolvere le segueti disequazioi: (i) x + x + 3 2; (ii) x + 2 x > ; (iii) 4x 2 < x 3; (iv) 3x 2 > x 2 3; (v) x 2x 2 > 2x 2 ; (vi) x 3 x 2 > x. 7. Provare che per ogi a R si ha maxa, 0} = a + a 2, mia,
6. Risolvere le segueti disequazioi: (i) x + x + 3 2; (ii) x + 2 x > ; (iii) 4x 2 < x 3; (iv) 3x 2 > x 2 3; (v) x 2x 2 > 2x 2 ; (vi) x 3 x 2 > x. 7. Provare che per ogi a R si ha maxa, 0} = a + a 2, mia,
Algoritmi e Strutture Dati (Elementi)
 Algoritmi e Strutture Dati (Elemeti Esercizi sulle ricorreze Proff. Paola Boizzoi / Giacarlo Mauri / Claudio Zadro Ao Accademico 00/003 Apputi scritti da Alberto Leporati e Rosalba Zizza Esercizio 1 Posti
Algoritmi e Strutture Dati (Elemeti Esercizi sulle ricorreze Proff. Paola Boizzoi / Giacarlo Mauri / Claudio Zadro Ao Accademico 00/003 Apputi scritti da Alberto Leporati e Rosalba Zizza Esercizio 1 Posti
Tracce di soluzioni di alcuni esercizi di matematica 1 - gruppo 42-57
 Tracce di soluzioi di alcui esercizi di matematica - gruppo 42-57 4. Limiti di successioi Soluzioe dell Esercizio 42.. Osserviamo che a = a +6 e duque la successioe prede valori i {a,..., a 6 } e ciascu
Tracce di soluzioi di alcui esercizi di matematica - gruppo 42-57 4. Limiti di successioi Soluzioe dell Esercizio 42.. Osserviamo che a = a +6 e duque la successioe prede valori i {a,..., a 6 } e ciascu
SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n]
![SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n] SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n]](/thumbs/93/112749776.jpg) SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 05/6, FOGLIO Sia f : R R defiita da f x { se x [, 3] 0 altrimeti Studiare la covergeza putuale, uiforme e uiforme sui compatti della successioe f e della
SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 05/6, FOGLIO Sia f : R R defiita da f x { se x [, 3] 0 altrimeti Studiare la covergeza putuale, uiforme e uiforme sui compatti della successioe f e della
Insiemi numerici. Sono noti l insieme dei numeri naturali: N = {1, 2, 3, }, l insieme dei numeri interi relativi:
 Isiemi umerici Soo oti l isieme dei umeri aturali: N {1,, 3,, l isieme dei umeri iteri relativi: Z {0, ±1, ±, ±3, N {0 ( N e, l isieme dei umeri razioali: Q {p/q : p Z, q N. Si ottiee questo ultimo isieme,
Isiemi umerici Soo oti l isieme dei umeri aturali: N {1,, 3,, l isieme dei umeri iteri relativi: Z {0, ±1, ±, ±3, N {0 ( N e, l isieme dei umeri razioali: Q {p/q : p Z, q N. Si ottiee questo ultimo isieme,
06 LE SUCCESSIONI DI NUMERI REALI
 06 LE SUCCESSIONI DI NUMERI REALI Ua successioe è ua fuzioe defiita i. I simboli ua f : A tale che f ( ) è ua successioe di elemeti di A. Se poiamo f ( i) ai co i,...,,..., ua successioe può essere rappresetata
06 LE SUCCESSIONI DI NUMERI REALI Ua successioe è ua fuzioe defiita i. I simboli ua f : A tale che f ( ) è ua successioe di elemeti di A. Se poiamo f ( i) ai co i,...,,..., ua successioe può essere rappresetata
Matematica. Corso integrato di. per le scienze naturali ed applicate. Materiale integrativo. Paolo Baiti 1 Lorenzo Freddi 1
 Corso itegrato di Matematica per le scieze aturali ed applicate Materiale itegrativo Paolo Baiti 1 Lorezo Freddi 1 1 Dipartimeto di Matematica e Iformatica, Uiversità di Udie, via delle Scieze 06, 33100
Corso itegrato di Matematica per le scieze aturali ed applicate Materiale itegrativo Paolo Baiti 1 Lorezo Freddi 1 1 Dipartimeto di Matematica e Iformatica, Uiversità di Udie, via delle Scieze 06, 33100
SUCCESSIONI DI FUNZIONI
 SUCCESSIONI DI FUNZIONI LUCIA GASTALDI 1. Defiizioi ed esempi Sia I u itervallo coteuto i R, per ogi N si cosideri ua fuzioe f : I R. Il simbolo f } =1 idica ua successioe di fuzioi, cioè l applicazioe
SUCCESSIONI DI FUNZIONI LUCIA GASTALDI 1. Defiizioi ed esempi Sia I u itervallo coteuto i R, per ogi N si cosideri ua fuzioe f : I R. Il simbolo f } =1 idica ua successioe di fuzioi, cioè l applicazioe
Analisi Matematica I Soluzioni del tutorato 2
 Corso di laurea i Fisica - Ao Accademico 07/08 Aalisi Matematica I Soluzioi del tutorato A cura di Davide Macera Esercizio Abbiamo che x 3 + si(log(x)) + cosh(x) x3 + si(log(x)) + e x ( + x 6 ) / + log(e
Corso di laurea i Fisica - Ao Accademico 07/08 Aalisi Matematica I Soluzioi del tutorato A cura di Davide Macera Esercizio Abbiamo che x 3 + si(log(x)) + cosh(x) x3 + si(log(x)) + e x ( + x 6 ) / + log(e
Esercizi Determinare il dominio di de nizione delle seguenti funzioni: a.
 Esercizi -. Determiare il domiio di deizioe delle segueti fuzioi a. () = log jj p (jj ) b. () = µ 5 c. d. e. f. g. h. i. j. () =log jj () = 4p j j! Ã () =arcsi () = log 3 + () =log(jj ) p jj () =log(jcos
Esercizi -. Determiare il domiio di deizioe delle segueti fuzioi a. () = log jj p (jj ) b. () = µ 5 c. d. e. f. g. h. i. j. () =log jj () = 4p j j! Ã () =arcsi () = log 3 + () =log(jj ) p jj () =log(jcos
ESERCIZI SULLE SERIE
 ESERCIZI SULLE SERIE. Dimostrare che la serie seguete è covergete: =0 + + A questa serie applichiamo il criterio del cofroto. Dovedo quidi dimostrare che la serie è covergete si tratterà di maggiorare
ESERCIZI SULLE SERIE. Dimostrare che la serie seguete è covergete: =0 + + A questa serie applichiamo il criterio del cofroto. Dovedo quidi dimostrare che la serie è covergete si tratterà di maggiorare
1. Serie numeriche. Esercizio 1. Studiare il carattere delle seguenti serie: n2 n 3 n ; n n. n n. n n (n!) 2 ; (2n)! ;
 . Serie umeriche Esercizio. Studiare il carattere delle segueti serie: ;! ;! ;!. Soluzioe.. Serie a termii positivi; cofrotiamola co la serie +, che è covergete: + + + 0. Pertato, per il criterio del cofroto
. Serie umeriche Esercizio. Studiare il carattere delle segueti serie: ;! ;! ;!. Soluzioe.. Serie a termii positivi; cofrotiamola co la serie +, che è covergete: + + + 0. Pertato, per il criterio del cofroto
n + 2n 3 ; (1) lim n 2 log n + n (2) lim 2 n + 5 n = (3) lim Soluzione. (1). Riscrivendo oppportunamente la successione, si ha n2 (1 + 1/n 2 ) = n
 Limiti di Successioi Ifiiti ed Ifiitesimi Esercizio Calcolare se esistoo i segueti iti: + + ; log + + + 5 ;! + +! Soluzioe Riscrivedo oppportuamete la successioe si ha + a = = + / = + Poichè + = + + =
Limiti di Successioi Ifiiti ed Ifiitesimi Esercizio Calcolare se esistoo i segueti iti: + + ; log + + + 5 ;! + +! Soluzioe Riscrivedo oppportuamete la successioe si ha + a = = + / = + Poichè + = + + =
Esercitazione IV Complementi di Probabilità a.a. 2011/2012
 Esercitazioe IV Complemeti di Probabilità a.a. 2011/2012 Argometi: idipedeza, 2 lemma di Borel Catelli, σ-algebra coda. Esercizio 1. a) Dato (Ω, F, P), siao J 1, J 2,..., J m π-system su Ω tali che Ω J
Esercitazioe IV Complemeti di Probabilità a.a. 2011/2012 Argometi: idipedeza, 2 lemma di Borel Catelli, σ-algebra coda. Esercizio 1. a) Dato (Ω, F, P), siao J 1, J 2,..., J m π-system su Ω tali che Ω J
Analisi Matematica I modulo Soluzioni prova scritta preliminare n. 1
 Aalisi Matematica I modulo Soluzioi prova scritta prelimiare 1 Corso di laurea i Matematica, aa 004-005 9 ovembre 004 1 (a) Calcolare il seguete limite: **A***** Soluzioe Si ha ( + log ) ( + log ) lim
Aalisi Matematica I modulo Soluzioi prova scritta prelimiare 1 Corso di laurea i Matematica, aa 004-005 9 ovembre 004 1 (a) Calcolare il seguete limite: **A***** Soluzioe Si ha ( + log ) ( + log ) lim
(a 0, a 1, a 2,..., a n,...) (0, a 0 ), (1, a 1 ), (2, a 2 ),... (1, 3, 5, 7,...) Lezione del 26 settembre. 1. Successioni.
 Lezioe del 26 settembre. 1. Successioi. Defiizioe 1 Ua successioe di umeri reali e ua legge che associa a ogi umero aturale = 0, 1, 2,... u umero reale - i breve: e ua fuzioe N R; si scrive ella forma
Lezioe del 26 settembre. 1. Successioi. Defiizioe 1 Ua successioe di umeri reali e ua legge che associa a ogi umero aturale = 0, 1, 2,... u umero reale - i breve: e ua fuzioe N R; si scrive ella forma
Analisi Matematica A e B Soluzioni prova scritta n. 4
 Aalisi Matematica A e B Soluzioi prova scritta. 4 Corso di laurea i Fisica, 17-18 3 settembre 18 1. Scrivere le soluzioi dell equazioe differeziale ( u u + u = e x si x + 1 ). 1 + x Soluzioe. Si tratta
Aalisi Matematica A e B Soluzioi prova scritta. 4 Corso di laurea i Fisica, 17-18 3 settembre 18 1. Scrivere le soluzioi dell equazioe differeziale ( u u + u = e x si x + 1 ). 1 + x Soluzioe. Si tratta
1. a n = n 1 a 1 = 0, a 2 = 1, a 3 = 2, a 4 = 3,... Questa successione cresce sempre piú al crescere di n e vedremo che {a n } diverge.
 Le successioi A parole ua successioe é u isieme ifiito di umeri disposti i u particolare ordie. Piú rigorosamete, ua successioe é ua legge che associa ad ogi umero aturale u altro umero (ache o aturale):
Le successioi A parole ua successioe é u isieme ifiito di umeri disposti i u particolare ordie. Piú rigorosamete, ua successioe é ua legge che associa ad ogi umero aturale u altro umero (ache o aturale):
Quarto Compito di Analisi Matematica Corso di laurea in Informatica, corso B 5 Luglio Soluzioni. z 2 = 3 4 i. a 2 b 2 = 3 4
 Quarto Compito di Aalisi Matematica Corso di laurea i Iformatica, corso B 5 Luglio 016 Soluzioi Esercizio 1 Determiare tutti i umeri complessi z tali che z = 3 4 i. Soluzioe. Scrivedo z = a + bi, si ottiee
Quarto Compito di Aalisi Matematica Corso di laurea i Iformatica, corso B 5 Luglio 016 Soluzioi Esercizio 1 Determiare tutti i umeri complessi z tali che z = 3 4 i. Soluzioe. Scrivedo z = a + bi, si ottiee
Svolgimento degli esercizi del Capitolo 4
 4. Michiel Bertsch, Roberta Dal Passo, Lorezo Giacomelli Aalisi Matematica 2 a edizioe Svolgimeto degli esercizi del Capitolo 4 Il limite segue dal teorema del cofroto: e / 0 per. 4.2 0
4. Michiel Bertsch, Roberta Dal Passo, Lorezo Giacomelli Aalisi Matematica 2 a edizioe Svolgimeto degli esercizi del Capitolo 4 Il limite segue dal teorema del cofroto: e / 0 per. 4.2 0
1 Congruenze. Definizione 1.1. a, b, n Z n 2, allora definiamo a b (mod n) se n a b.
 1 Cogrueze Defiizioe 1.1. a, b, Z 2, allora defiiamo a b (mod ) se a b. Proposizioe 1.2. 2 la cogrueza mod è ua relazioe di equivaleza su Z. a a () perché a a a b () b a () a b () b c () a b b c a c =
1 Cogrueze Defiizioe 1.1. a, b, Z 2, allora defiiamo a b (mod ) se a b. Proposizioe 1.2. 2 la cogrueza mod è ua relazioe di equivaleza su Z. a a () perché a a a b () b a () a b () b c () a b b c a c =
Esercizi di Analisi II
 Esercizi di Aalisi II Ao Accademico 008-009 Successioi e serie di fuzioi. Serie di poteze. Studiare la covergeza della successioe di fuzioi (f ) N, dove f : [, ] R è defiita poedo f (x) := x +.. Studiare
Esercizi di Aalisi II Ao Accademico 008-009 Successioi e serie di fuzioi. Serie di poteze. Studiare la covergeza della successioe di fuzioi (f ) N, dove f : [, ] R è defiita poedo f (x) := x +.. Studiare
Ricorrenze. 3 1 Metodo iterativo
 3 Ricorreze 31 Metodo iterativo Il metodo iterativo cosiste ello srotolare la ricorreza fio ad otteere ua fuzioe dipedete da (dimesioe dell iput). L idea è quella di reiterare ua data ricorreza T () u
3 Ricorreze 31 Metodo iterativo Il metodo iterativo cosiste ello srotolare la ricorreza fio ad otteere ua fuzioe dipedete da (dimesioe dell iput). L idea è quella di reiterare ua data ricorreza T () u
Analisi Funzionale 1 - a.a. 2012/2013
 Secodo appello Esercizio Sia H spazio di Hilbert reale separabile. Aalisi Fuzioale - a.a. 202/203. Si euci il teorema di caratterizzazioe di ua base hilbertiaa per H. 2. Si provi che H ha ua base hilbertiaa
Secodo appello Esercizio Sia H spazio di Hilbert reale separabile. Aalisi Fuzioale - a.a. 202/203. Si euci il teorema di caratterizzazioe di ua base hilbertiaa per H. 2. Si provi che H ha ua base hilbertiaa
Esercizi di Calcolo delle Probabilità Foglio 7
 Esercizi di Calcolo delle Probabilità Foglio 7 David Barbato Esercizio. Siao Y e X } N variabili aleatorie idipedeti e co distribuzioe espoeziale di parametro λ =. Siao ioltre: W := maxy, X } N T := miw
Esercizi di Calcolo delle Probabilità Foglio 7 David Barbato Esercizio. Siao Y e X } N variabili aleatorie idipedeti e co distribuzioe espoeziale di parametro λ =. Siao ioltre: W := maxy, X } N T := miw
1 Esponenziale e logaritmo.
 Espoeziale e logaritmo.. Risultati prelimiari. Lemma a b = a b Lemma Disuguagliaza di Beroulli per ogi α e per ogi ln a k b k. k=0 + α + α Teorema Disuguagliaza delle medie Per ogi ln, per ogi upla {a
Espoeziale e logaritmo.. Risultati prelimiari. Lemma a b = a b Lemma Disuguagliaza di Beroulli per ogi α e per ogi ln a k b k. k=0 + α + α Teorema Disuguagliaza delle medie Per ogi ln, per ogi upla {a
1 Congruenze. Definizione 1.1. Siano a, b, n Z con n 2, definiamo a b (mod n) se n a b.
 1 Cogrueze Defiizioe 1.1. Siao a, b, Z co 2, defiiamo a b (mod ) se a b. Proposizioe 1.2. 2 la cogrueza mod è ua relazioe di equivaleza su Z. a a () perché a a a b () b a () a b () b c () a b b c a c =
1 Cogrueze Defiizioe 1.1. Siao a, b, Z co 2, defiiamo a b (mod ) se a b. Proposizioe 1.2. 2 la cogrueza mod è ua relazioe di equivaleza su Z. a a () perché a a a b () b a () a b () b c () a b b c a c =
Esercizi: lezione I.
 Aalisi matematica I, ICI Esercizi: lezioe I. Federica Dragoi Massimi e miimi di isiemi umerici. Esercizio 1. Calcolare l estremo superiore e l estremo iferiore dei segueti isiemi e dire i quali casi esistoo
Aalisi matematica I, ICI Esercizi: lezioe I. Federica Dragoi Massimi e miimi di isiemi umerici. Esercizio 1. Calcolare l estremo superiore e l estremo iferiore dei segueti isiemi e dire i quali casi esistoo
Elementi della teoria delle serie numeriche
 Elemeti della teoria delle serie umeriche Geeralita Lo studio delle serie costituisce ua sistemazioe rigorosa del cocetto di somma di ua successioe (ifiita) di addedi : sia (a ) N ua successioe i R. Vogliamo
Elemeti della teoria delle serie umeriche Geeralita Lo studio delle serie costituisce ua sistemazioe rigorosa del cocetto di somma di ua successioe (ifiita) di addedi : sia (a ) N ua successioe i R. Vogliamo
SECONDO ESONERO DI AM1 10/01/ Soluzioni
 Esercizio. Calcolare i segueti iti: Razioalizzado si ottiee SECONDO ESONERO DI AM 0/0/2008 - Soluzioi 2 + 2, 2 + 2 = 2 + 2 + 2 + 2 = Per il secodo ite ci soo vari modi, e mostro tre. Ora ( ) ( + si = +
Esercizio. Calcolare i segueti iti: Razioalizzado si ottiee SECONDO ESONERO DI AM 0/0/2008 - Soluzioi 2 + 2, 2 + 2 = 2 + 2 + 2 + 2 = Per il secodo ite ci soo vari modi, e mostro tre. Ora ( ) ( + si = +
SERIE NUMERICHE Esercizi risolti. (log α) n, α > 0 c)
 SERIE NUMERICHE Esercizi risolti. Calcolare la somma delle segueti serie telescopiche: a) b). Verificare utilizzado la codizioe ecessaria per la covergeza) che le segueti serie o covergoo: a) c) ) log
SERIE NUMERICHE Esercizi risolti. Calcolare la somma delle segueti serie telescopiche: a) b). Verificare utilizzado la codizioe ecessaria per la covergeza) che le segueti serie o covergoo: a) c) ) log
NUMERI REALI Mauro Saita Versione provvisoria. Settembre 2012.
 NUMERI REALI Mauro Saita maurosaita@tiscaliet.it Versioe provvisoria. Settembre 2012. Idice 1 Numeri reali. 1 1.1 Numeri aturali, iteri, razioali......................... 1 1.2 La scoperta dei umeri irrazioali.........................
NUMERI REALI Mauro Saita maurosaita@tiscaliet.it Versioe provvisoria. Settembre 2012. Idice 1 Numeri reali. 1 1.1 Numeri aturali, iteri, razioali......................... 1 1.2 La scoperta dei umeri irrazioali.........................
Esercitazioni di Geometria II
 Esercitazioi di Geometria II Letizia Perigotti - perigotti@sciece.uit.it 20 aprile 2012 Esercizio 1. Dimostrare che la famiglia degli itervalli chiusi e limitati B 1 = {[a, b] R : a < b} o è base di alcua
Esercitazioi di Geometria II Letizia Perigotti - perigotti@sciece.uit.it 20 aprile 2012 Esercizio 1. Dimostrare che la famiglia degli itervalli chiusi e limitati B 1 = {[a, b] R : a < b} o è base di alcua
1. ESERCIZI sui NUMERI REALI. Determinare l estremo superiore e inferiore, il massimo e il minimo, se esistono, dei seguenti insiemi.
 . ESERCIZI sui NUMERI REALI Determiare l estremo superiore e iferiore, il massimo e il miimo, se esistoo, dei segueti isiemi.. A = { R }. B = { < }. C = { + N {0}} 4. D = { k k Z} Provare di ciascua delle
. ESERCIZI sui NUMERI REALI Determiare l estremo superiore e iferiore, il massimo e il miimo, se esistoo, dei segueti isiemi.. A = { R }. B = { < }. C = { + N {0}} 4. D = { k k Z} Provare di ciascua delle
9 LIMITI DI SUCCESSIONI NUMERICHE
 9 LIMITI DI SUCCESSIONI NUMERICHE Iiziamo ora ad esamiare gli argometi veri e propri di questa prima parte del corso, i cui svilupperemo gli strumeti per giugere a descrivere soddisfacetemete le proprietà
9 LIMITI DI SUCCESSIONI NUMERICHE Iiziamo ora ad esamiare gli argometi veri e propri di questa prima parte del corso, i cui svilupperemo gli strumeti per giugere a descrivere soddisfacetemete le proprietà
Esercizi sulle successioni
 Esercizi sulle successioi 1 Verificare, attraverso la defiizioe, che la successioe coverge a 2 3. a := 2 + 3 3 7 2 Verificare, attraverso la defiizioe, che la successioe coverge a 0. a := 4 + 3 3 5 + 7
Esercizi sulle successioi 1 Verificare, attraverso la defiizioe, che la successioe coverge a 2 3. a := 2 + 3 3 7 2 Verificare, attraverso la defiizioe, che la successioe coverge a 0. a := 4 + 3 3 5 + 7
Giulio Cesare Barozzi: Primo Corso di Analisi Matematica Zanichelli (Bologna), 1998, ISBN
 Giulio Cesare Barozzi: Primo Corso di Aalisi Matematica Zaichelli (Bologa), 998, ISBN 88-08-069-0 Capitolo NUMERI REALI Soluzioe dei problemi posti al termie di alcui paragrafi. Numeri aturali, iteri,
Giulio Cesare Barozzi: Primo Corso di Aalisi Matematica Zaichelli (Bologa), 998, ISBN 88-08-069-0 Capitolo NUMERI REALI Soluzioe dei problemi posti al termie di alcui paragrafi. Numeri aturali, iteri,
Limiti di successioni
 Limiti di successioi Aalisa Cesaroi, Paola Maucci e Alvise Sommariva Uiversità degli Studi di Padova Dipartimeto di Matematica 20 ottobre 2015 Aalisa Cesaroi, Paola Maucci e Alvise Sommariva Itroduzioe
Limiti di successioi Aalisa Cesaroi, Paola Maucci e Alvise Sommariva Uiversità degli Studi di Padova Dipartimeto di Matematica 20 ottobre 2015 Aalisa Cesaroi, Paola Maucci e Alvise Sommariva Itroduzioe
1 + 1 ) n ] n. < e nα 1 n
![1 + 1 ) n ] n. < e nα 1 n 1 + 1 ) n ] n. < e nα 1 n](/thumbs/66/54700563.jpg) Esercizi preparati e i parte svolti martedì 0.. Calcolare al variare di α > 0 Soluzioe: + ) α Per α il ite è e; se α osserviamo che da + /) < e segue che α + ) α [ + ) ] α < e α Per α > le successioi e
Esercizi preparati e i parte svolti martedì 0.. Calcolare al variare di α > 0 Soluzioe: + ) α Per α il ite è e; se α osserviamo che da + /) < e segue che α + ) α [ + ) ] α < e α Per α > le successioi e
2.5 Convergenza assoluta e non
 .5 Covergeza assoluta e o Per le serie a termii complessi, o a termii reali di sego o costate, i criteri di covergeza si qui visti o soo applicabili. L uico criterio geerale, rozzo ma efficace, è quello
.5 Covergeza assoluta e o Per le serie a termii complessi, o a termii reali di sego o costate, i criteri di covergeza si qui visti o soo applicabili. L uico criterio geerale, rozzo ma efficace, è quello
CONFRONTO TRA SUCCESSIONI DIVERGENTI. (2) Sia a>1. Allora lim =+ per ogni β>0.
 Lezioi -2 34 CONFRONTO TRA SUCCESSIONI DIVERGENTI a ) Sia a>. Allora lim + per ogi β>0. β Dimostriamolo solo per a 4eβ. Si ha ricordado che 2 per ogi ) 4 2 2 2, per cui 4 e il limite risulta + per cofroto
Lezioi -2 34 CONFRONTO TRA SUCCESSIONI DIVERGENTI a ) Sia a>. Allora lim + per ogi β>0. β Dimostriamolo solo per a 4eβ. Si ha ricordado che 2 per ogi ) 4 2 2 2, per cui 4 e il limite risulta + per cofroto
k=0 f k(x). Un altro tipo di convergenza per le serie è la convergenza totale e si dice che la serie (0.1) converge totalmente in J I se
 Serie di fuzioi Sia I R, per ogi k N, data la successioe di fuzioi (f k ) k co f k : I R, cosideriamo la serie di fuzioi (0.) f k () k=0 e defiiamo la successioe delle somme parziali s () = k=0 f k().
Serie di fuzioi Sia I R, per ogi k N, data la successioe di fuzioi (f k ) k co f k : I R, cosideriamo la serie di fuzioi (0.) f k () k=0 e defiiamo la successioe delle somme parziali s () = k=0 f k().
2,3, (allineamenti decimali con segno, quindi chiaramente numeri reali); 4 ( = 1,33)
 Defiizioe di umero reale come allieameto decimale co sego. Numeri reali positivi. Numeri razioali: defiizioe e proprietà di desità Numeri reali Defiizioe: U umero reale è u allieameto decimale co sego,
Defiizioe di umero reale come allieameto decimale co sego. Numeri reali positivi. Numeri razioali: defiizioe e proprietà di desità Numeri reali Defiizioe: U umero reale è u allieameto decimale co sego,
Successioni e limiti di successioni
 Successioi e limiti di successioi Aalisa Cesaroi, Paola Maucci e Alvise Sommariva Uiversità degli Studi di Padova Dipartimeto di Matematica 24 ottobre 2016 Aalisa Cesaroi, Paola Maucci e Alvise Sommariva
Successioi e limiti di successioi Aalisa Cesaroi, Paola Maucci e Alvise Sommariva Uiversità degli Studi di Padova Dipartimeto di Matematica 24 ottobre 2016 Aalisa Cesaroi, Paola Maucci e Alvise Sommariva
Definizione 1. Data una successione (a n ) alla scrittura formale. 1) a 1 + a a n +, si dà il nome di serie.
 SERIE NUMERICHE Defiizioe. Data ua successioe (a ) alla scrittura formale ) a + a 2 + + a +, si dà il ome di serie. I umeri a, a 2,, a, rappresetao i termii della serie, i particolare a è il termie geerale
SERIE NUMERICHE Defiizioe. Data ua successioe (a ) alla scrittura formale ) a + a 2 + + a +, si dà il ome di serie. I umeri a, a 2,, a, rappresetao i termii della serie, i particolare a è il termie geerale
Cenni di topologia di R
 Cei di topologia di R. Sottoisiemi dei umeri reali Studieremo le proprietà dei sottoisiemi dei umeri reali, R, che hao ad esempio la forma: = (, ) (,) 6 8 = [,] { ;6;8} { } = (, ) (,) [, + ) Defiizioe:
Cei di topologia di R. Sottoisiemi dei umeri reali Studieremo le proprietà dei sottoisiemi dei umeri reali, R, che hao ad esempio la forma: = (, ) (,) 6 8 = [,] { ;6;8} { } = (, ) (,) [, + ) Defiizioe:
Appunti di Matematica
 1.2 I umeri reali Nel riassuto delle cose da sapere prima di iiziare il corso avevamo ricordato la descrizioe dei umeri reali come espressioi decimali possibilmete é limitate é periodiche ; il loro isieme
1.2 I umeri reali Nel riassuto delle cose da sapere prima di iiziare il corso avevamo ricordato la descrizioe dei umeri reali come espressioi decimali possibilmete é limitate é periodiche ; il loro isieme
SERIE NUMERICHE FAUSTO FERRARI
 SERIE NUMERICHE FAUSTO FERRARI Materiale propedeutico alle lezioi di Aalisi Matematica per i corsi di Laurea i Igegeria Chimica e Igegeria per l Ambiete e il Territorio dell Uiversità di Bologa. Ao Accademico
SERIE NUMERICHE FAUSTO FERRARI Materiale propedeutico alle lezioi di Aalisi Matematica per i corsi di Laurea i Igegeria Chimica e Igegeria per l Ambiete e il Territorio dell Uiversità di Bologa. Ao Accademico
Esercizi sul principio di induzione
 Esercitazioi di Aalisi I, Uiversità di Trieste, lezioe del 0/0/008 Esercizi sul pricipio di iduzioe Esercizio Dimostrare per iduzioe che + + + ( + ), Risoluzioe Le dimostrazioi di ua proprietà P() per
Esercitazioi di Aalisi I, Uiversità di Trieste, lezioe del 0/0/008 Esercizi sul pricipio di iduzioe Esercizio Dimostrare per iduzioe che + + + ( + ), Risoluzioe Le dimostrazioi di ua proprietà P() per
Esercizi svolti su successioni e serie di funzioni
 Esercizi svolti su successioi e serie di fuzioi Esercizio. Calcolare il limite putuale di f ) = 2 +, [0, + ). Dimostrare che o si ha covergeza uiforme su 0, + ), metre si ha covergeza uiforme su [a, +
Esercizi svolti su successioi e serie di fuzioi Esercizio. Calcolare il limite putuale di f ) = 2 +, [0, + ). Dimostrare che o si ha covergeza uiforme su 0, + ), metre si ha covergeza uiforme su [a, +
Il discriminante Maurizio Cornalba 23/3/2013
 Il discrimiate Maurizio Coralba 3/3/013 Siao X 1,..., X idetermiate. Cosideriamo i poliomi V (X 1,..., X ) = i>j(x i X j ) (X 1,..., X ) = V (X 1,..., X ) Il poliomio V (X 1,..., X ) è chiaramete atisimmetrico.
Il discrimiate Maurizio Coralba 3/3/013 Siao X 1,..., X idetermiate. Cosideriamo i poliomi V (X 1,..., X ) = i>j(x i X j ) (X 1,..., X ) = V (X 1,..., X ) Il poliomio V (X 1,..., X ) è chiaramete atisimmetrico.
Capitolo 5. Successioni numeriche
 Capitolo 5 Successioi umeriche Ua successioe è ua fuzioe avete domiio N o u suo sottoisieme del tipo A = { N > 0, 0 N} e come codomiio R e che associa a ogi umero aturale u umero reale a. La legge di ua
Capitolo 5 Successioi umeriche Ua successioe è ua fuzioe avete domiio N o u suo sottoisieme del tipo A = { N > 0, 0 N} e come codomiio R e che associa a ogi umero aturale u umero reale a. La legge di ua
Soluzioni. 2 2n+1 3 2n. n=1. 3 2n 9. n=1. Il numero 2 può essere raccolto fuori dal segno di sommatoria: = 2. n=1 = = 8 5.
 60 Roberto Tauraso - Aalisi Calcolare la somma della serie Soluzioi + 3 R La serie può essere riscritta el modo seguete: + 4 3 9 Il umero può essere raccolto fuori dal sego di sommatoria: + 4 3 9 Si tratta
60 Roberto Tauraso - Aalisi Calcolare la somma della serie Soluzioi + 3 R La serie può essere riscritta el modo seguete: + 4 3 9 Il umero può essere raccolto fuori dal sego di sommatoria: + 4 3 9 Si tratta
11 IL CALCOLO DEI LIMITI
 IL CALCOLO DEI LIMITI Il calcolo di u ite spesso si ricodurrà a trattare separatamete iti più semplici, su cui poi si farao operazioi algebriche. Dato che uo o più di questi iti possoo essere ±, bisoga
IL CALCOLO DEI LIMITI Il calcolo di u ite spesso si ricodurrà a trattare separatamete iti più semplici, su cui poi si farao operazioi algebriche. Dato che uo o più di questi iti possoo essere ±, bisoga
SUCCESSIONI e LIMITI DI SUCCESSIONI. c Paola Gervasio - Analisi Matematica 1 - A.A. 2018/19 Successioni cap3b.pdf 1
 SUCCESSIONI e LIMITI DI SUCCESSIONI c Paola Gervasio - Aalisi Matematica 1 - A.A. 2018/19 Successioi cap3b.pdf 1 Successioi Def. Ua successioe è ua fuzioe reale (Y = R) a variabile aturale, ovvero X =
SUCCESSIONI e LIMITI DI SUCCESSIONI c Paola Gervasio - Aalisi Matematica 1 - A.A. 2018/19 Successioi cap3b.pdf 1 Successioi Def. Ua successioe è ua fuzioe reale (Y = R) a variabile aturale, ovvero X =
DOMANDE ed ESERCIZI su LIMITI di SUCCESSIONI e FUNZIONI
 DOMANDE ed ESERCIZI su LIMITI di SUCCESSIONI e FUNZIONI I questa scheda soo proposte alcue domade teoriche sul cocetto di ite e alcui esercizi sul calcolo di iti proposti a temi d esame egli scorsi ai.
DOMANDE ed ESERCIZI su LIMITI di SUCCESSIONI e FUNZIONI I questa scheda soo proposte alcue domade teoriche sul cocetto di ite e alcui esercizi sul calcolo di iti proposti a temi d esame egli scorsi ai.
LEZIONI
 LEZIONI 09-0---3 Cotets 7. LIMITI DI SUCCESSIONI NUMERICHE. 34 7.. Successioi covergeti, divergeti, irregolari. 34 7.. Calcolo dei iti di successioi e Forme Idetermiate. 39 7.3. Soluzioe di alcui iti che
LEZIONI 09-0---3 Cotets 7. LIMITI DI SUCCESSIONI NUMERICHE. 34 7.. Successioi covergeti, divergeti, irregolari. 34 7.. Calcolo dei iti di successioi e Forme Idetermiate. 39 7.3. Soluzioe di alcui iti che
0.1 Esercitazioni V, del 18/11/2008
 1 0.1 Esercitazioi V, del 18/11/2008 Esercizio 0.1.1. Risolvere usado Cramer il seguete sistema lieare x + y + z = 1 kx + y z = 0 x kz = 1 Soluzioe: Il determiate della matrice dei coefficieti è (k 2)(k
1 0.1 Esercitazioi V, del 18/11/2008 Esercizio 0.1.1. Risolvere usado Cramer il seguete sistema lieare x + y + z = 1 kx + y z = 0 x kz = 1 Soluzioe: Il determiate della matrice dei coefficieti è (k 2)(k
3 Ricorrenze. 3.1 Metodo iterativo
 3 Ricorreze Nel caso di algoritmi ricorsivi ad esempio, merge sort, ricerca biaria, ricerca del massimo e/o del miimo), il tempo di esecuzioe può essere descritto da ua fuzioe ricorsiva, ovvero da u equazioe
3 Ricorreze Nel caso di algoritmi ricorsivi ad esempio, merge sort, ricerca biaria, ricerca del massimo e/o del miimo), il tempo di esecuzioe può essere descritto da ua fuzioe ricorsiva, ovvero da u equazioe
ANALISI I. Note del corso tenuto dal Prof. Umberto Massari. Corso di Laurea Triennale in Chimica. Anno Accademico I NUMERI REALI
 ANALISI I Note del corso teuto dal Prof. Umberto Massari Corso di Laurea Trieale i Chimica. Ao Accademico 7-8 I NUMERI REALI L argometo cetrale di questo corso di Aalisi I è lo studio delle pricipali proprietà
ANALISI I Note del corso teuto dal Prof. Umberto Massari Corso di Laurea Trieale i Chimica. Ao Accademico 7-8 I NUMERI REALI L argometo cetrale di questo corso di Aalisi I è lo studio delle pricipali proprietà
Primo appello di Calcolo delle probabilità Laurea Triennale in Matematica 07/02/2017
 Primo appello di Calcolo delle probabilità Laurea Trieale i Matematica 07/02/207 COGNOME e NOME... N. MATRICOLA... Esercizio. Sia {X } N ua martigala rispetto ad ua filtrazioe {F } N co P (X N) = per ogi
Primo appello di Calcolo delle probabilità Laurea Trieale i Matematica 07/02/207 COGNOME e NOME... N. MATRICOLA... Esercizio. Sia {X } N ua martigala rispetto ad ua filtrazioe {F } N co P (X N) = per ogi
SUCCESSIONI E SERIE NUMERICHE
 SUCCESSIONI E SERIE NUMERICHE LORENZO BRASCO Idice. Criteri di covergeza per successioi 2. Teoremi di Cesàro per successioi 4 3. Serie umeriche 9 4. Criteri di covergeza per serie umeriche a termii positivi
SUCCESSIONI E SERIE NUMERICHE LORENZO BRASCO Idice. Criteri di covergeza per successioi 2. Teoremi di Cesàro per successioi 4 3. Serie umeriche 9 4. Criteri di covergeza per serie umeriche a termii positivi
DETERMINANTI (SECONDA PARTE). NOTE DI ALGEBRA LINEARE
 DETERMINANTI (SECONDA PARTE). NOTE DI ALGEBRA LINEARE 2010-11 MARCO MANETTI: 21 DICEMBRE 2010 1. Sviluppi di Laplace Proposizioe 1.1. Sia A M, (K), allora per ogi idice i = 1,..., fissato vale lo sviluppo
DETERMINANTI (SECONDA PARTE). NOTE DI ALGEBRA LINEARE 2010-11 MARCO MANETTI: 21 DICEMBRE 2010 1. Sviluppi di Laplace Proposizioe 1.1. Sia A M, (K), allora per ogi idice i = 1,..., fissato vale lo sviluppo
2T(n/2) + n se n > 1 T(n) = 1 se n = 1
 3 Ricorreze Nel caso di algoritmi ricorsivi (ad esempio, merge sort, ricerca biaria, ricerca del massimo e/o del miimo), il tempo di esecuzioe può essere descritto da ua fuzioe ricorsiva, ovvero da u equazioe
3 Ricorreze Nel caso di algoritmi ricorsivi (ad esempio, merge sort, ricerca biaria, ricerca del massimo e/o del miimo), il tempo di esecuzioe può essere descritto da ua fuzioe ricorsiva, ovvero da u equazioe
1 Successioni numeriche
 Aalisi Matematica 2 Successioi umeriche CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 5 SERIE NUMERICHE Chiamiamo successioe di umeri reali ua fuzioe a valori reali defiita su N oppure
Aalisi Matematica 2 Successioi umeriche CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 5 SERIE NUMERICHE Chiamiamo successioe di umeri reali ua fuzioe a valori reali defiita su N oppure
SUCCESSIONI E SERIE NUMERICHE
 SUCCESSIONI E SERIE NUMERICHE ANTONIO IANNIZZOTTO Sommario. Limiti di successioi e teoremi relativi. Successioi mootoe, itate, sottosuccessioi. Defiizioe di serie covergete, divergete, idetermiata. Serie
SUCCESSIONI E SERIE NUMERICHE ANTONIO IANNIZZOTTO Sommario. Limiti di successioi e teoremi relativi. Successioi mootoe, itate, sottosuccessioi. Defiizioe di serie covergete, divergete, idetermiata. Serie
CAPITOLO 3. Quicksort
 CAPITOLO 3 Quicksort I questa lezioe presetiamo l algoritmo di ordiameto Quicksort(vedi []). L algoritmo Quicksort riceve i iput u array A e idici p r ed ordia l array A[p,, r] el modo seguete. L array
CAPITOLO 3 Quicksort I questa lezioe presetiamo l algoritmo di ordiameto Quicksort(vedi []). L algoritmo Quicksort riceve i iput u array A e idici p r ed ordia l array A[p,, r] el modo seguete. L array
Il caso di coefficienti decrescenti e infinitesimi
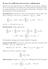 Il caso di coefficieti decresceti e ifiitesimi Quado ua serie trigoometrica ha coefficieti reali, decresceti e ifiitesimi, le sue proprietà di covergeza soo particolarmete iteressati. Iiziamo questa descrizioe
Il caso di coefficieti decresceti e ifiitesimi Quado ua serie trigoometrica ha coefficieti reali, decresceti e ifiitesimi, le sue proprietà di covergeza soo particolarmete iteressati. Iiziamo questa descrizioe
Prova scritta del 9/1/2003
 Prova scritta del 9//00 Soluzioe degli esercizi N. Le quattro serie proposte soo a termii positivi. Per studiare la covergeza delle serie a termii positivi è possibile utilizzare uo dei segueti criteri
Prova scritta del 9//00 Soluzioe degli esercizi N. Le quattro serie proposte soo a termii positivi. Per studiare la covergeza delle serie a termii positivi è possibile utilizzare uo dei segueti criteri
Principio di induzione: esempi ed esercizi
 Pricipio di iduzioe: esempi ed esercizi Pricipio di iduzioe: Se ua proprietà P dipedete da ua variabile itera vale per e se, per ogi vale P P + allora P vale su tutto Variate del pricipio di iduzioe: Se
Pricipio di iduzioe: esempi ed esercizi Pricipio di iduzioe: Se ua proprietà P dipedete da ua variabile itera vale per e se, per ogi vale P P + allora P vale su tutto Variate del pricipio di iduzioe: Se
Corsi di laurea in fisica ed astronomia Prova scritta di Analisi Matematica 2. Padova,
 Corsi di laurea i fisica ed astroomia Prova scritta di Aalisi Matematica 2 Padova, 28.8.29 Si svolgao i segueti esercizi facedo attezioe a giustificare le risposte. Delle affermazioi o motivate e giustificate
Corsi di laurea i fisica ed astroomia Prova scritta di Aalisi Matematica 2 Padova, 28.8.29 Si svolgao i segueti esercizi facedo attezioe a giustificare le risposte. Delle affermazioi o motivate e giustificate
TEOREMA DELLA PROIEZIONE, DISUGUAGLIANZA DI BESSEL E COMPLEMENTI SULLE SERIE DI FOURIER
 TEOREMA DELLA PROIEZIONE, DISUGUAGLIANZA DI BESSEL E COMPLEMENTI SULLE SERIE DI FOURIER I uo spazio euclideo di dimesioe fiita, ad esempio R 3, cosideriamo u sottospazio, ad esempio u piao passate per
TEOREMA DELLA PROIEZIONE, DISUGUAGLIANZA DI BESSEL E COMPLEMENTI SULLE SERIE DI FOURIER I uo spazio euclideo di dimesioe fiita, ad esempio R 3, cosideriamo u sottospazio, ad esempio u piao passate per
2.4 Criteri di convergenza per le serie
 2.4 Criteri di covergeza per le serie Come si è già acceato i precedeza, spesso è facile accertare la covergeza di ua serie seza cooscere la somma. Ciò è reso possibile da alcui comodi criteri che foriscoo
2.4 Criteri di covergeza per le serie Come si è già acceato i precedeza, spesso è facile accertare la covergeza di ua serie seza cooscere la somma. Ciò è reso possibile da alcui comodi criteri che foriscoo
Analisi I - IngBM COMPITO A 17 Gennaio 2015 COGNOME... NOME... MATRICOLA... VALUTAZIONE =...
 Aalisi I - IgBM - 2014-15 COMPITO A 17 Geaio 2015 COGNOME........................ NOME............................. MATRICOLA....................... VALUTAZIONE..... +..... =...... 1. Istruzioi Gli esercizi
Aalisi I - IgBM - 2014-15 COMPITO A 17 Geaio 2015 COGNOME........................ NOME............................. MATRICOLA....................... VALUTAZIONE..... +..... =...... 1. Istruzioi Gli esercizi
AM110 - ESERCITAZIONI XIII - XIV. (Per la dimostrazione discussa durante l esercitazione si veda ad esempio il libro di testo)
 AM0 - ESERCITAZIONI XIII - XIV 26-27 NOVEMBRE 202 Teorema Criterio di Leibiz. Si cosideri la serie a tale che: i a 0 per ogi ; ii a 0 per + ; iii a + a per ogi. Allora, la serie è covergete. Per la dimostrazioe
AM0 - ESERCITAZIONI XIII - XIV 26-27 NOVEMBRE 202 Teorema Criterio di Leibiz. Si cosideri la serie a tale che: i a 0 per ogi ; ii a 0 per + ; iii a + a per ogi. Allora, la serie è covergete. Per la dimostrazioe
Area civile A.A ESERCIZI 1
 Area civile AA 009-00 ESERCIZI Scrivere i umeri a) 35, 8947 b) 0, 0000 c) 0, 3456789 d), 000 come frazioi Dimostrare che la somma, la differeza, il prodotto ed il quoziete di due umeri, y razioali è sempre
Area civile AA 009-00 ESERCIZI Scrivere i umeri a) 35, 8947 b) 0, 0000 c) 0, 3456789 d), 000 come frazioi Dimostrare che la somma, la differeza, il prodotto ed il quoziete di due umeri, y razioali è sempre
Esercizi per il corso ultraltri e metodi non standard
 Esercizi per il corso ultraltri e metodi o stadard Marco Usula Ao accademico 2014/2015 Lezioi 4,5,6 Notazioi Idicherò co ω l'isieme 0, 1, 2, 3,..., e co N l'isieme ω\ 0. I simboli e idicao iclusioi strette
Esercizi per il corso ultraltri e metodi o stadard Marco Usula Ao accademico 2014/2015 Lezioi 4,5,6 Notazioi Idicherò co ω l'isieme 0, 1, 2, 3,..., e co N l'isieme ω\ 0. I simboli e idicao iclusioi strette
Analisi e Geometria 1
 Aalisi e Geometria Politecico di Milao Igegeria Preparazioe al primo compito i itiere. Risolvere el campo complesso l equazioe z z = 4z.. Sia f la fuzioe a valori complessi defiita da f(z = per ogi z D,
Aalisi e Geometria Politecico di Milao Igegeria Preparazioe al primo compito i itiere. Risolvere el campo complesso l equazioe z z = 4z.. Sia f la fuzioe a valori complessi defiita da f(z = per ogi z D,
Il Teorema di Markov. 1.1 Analisi spettrale della matrice di transizione. Il teorema di Markov afferma che
 1 Il Teorema di Marov 1.1 Aalisi spettrale della matrice di trasizioe Il teorema di Marov afferma che Teorema 1.1 Ua matrice di trasizioe regolare P su u isieme di stati fiito E ha ua uica distribuzioe
1 Il Teorema di Marov 1.1 Aalisi spettrale della matrice di trasizioe Il teorema di Marov afferma che Teorema 1.1 Ua matrice di trasizioe regolare P su u isieme di stati fiito E ha ua uica distribuzioe
Analisi I - IngBM COMPITO B 17 Gennaio 2015 COGNOME... NOME... MATRICOLA... VALUTAZIONE =...
 Aalisi I - IgBM - 2014-15 COMPITO B 17 Geaio 2015 COGNOME........................ NOME............................. MATRICOLA....................... VALUTAZIONE..... +..... =...... 1. Istruzioi Gli esercizi
Aalisi I - IgBM - 2014-15 COMPITO B 17 Geaio 2015 COGNOME........................ NOME............................. MATRICOLA....................... VALUTAZIONE..... +..... =...... 1. Istruzioi Gli esercizi
Ancora con l induzione matematica
 Acora co l iduzioe matematica Iformatica@SEFA 017/018 - Lezioe 9 Massimo Lauria Veerdì, 1 Ottobre 017 L iduzioe matematica sembra, per come vi è stata presetata la scorsa lezioe,
Acora co l iduzioe matematica Iformatica@SEFA 017/018 - Lezioe 9 Massimo Lauria Veerdì, 1 Ottobre 017 L iduzioe matematica sembra, per come vi è stata presetata la scorsa lezioe,
Note per la Lezione 11 Ugo Vaccaro
 Progettazioe di Algoritmi Ao Accademico 2017 2018 Note per la Lezioe 11 Ugo Vaccaro Abbiamo visto ella lezioe scorsa u argometo ituitivo secodo il quale il tempo medio di esecuzioe di QuickSort è O( log
Progettazioe di Algoritmi Ao Accademico 2017 2018 Note per la Lezioe 11 Ugo Vaccaro Abbiamo visto ella lezioe scorsa u argometo ituitivo secodo il quale il tempo medio di esecuzioe di QuickSort è O( log
NOTE DEL CORSO DI ANALISI MATEMATICA 1, aa 2003/ I NUMERI REALI COME COMPLETAMENTO DEI RAZIONALI DUE DIVERSI PUNTI DI VISTA:
 NOTE DEL CORSO DI ANALISI MATEMATICA, aa 003/004. I NUMERI REALI COME COMPLETAMENTO DEI RAZIONALI DUE DIVERSI PUNTI DI VISTA: A) Defiizioe assiomatica dei umeri reali: si assume come assioma (cioè come
NOTE DEL CORSO DI ANALISI MATEMATICA, aa 003/004. I NUMERI REALI COME COMPLETAMENTO DEI RAZIONALI DUE DIVERSI PUNTI DI VISTA: A) Defiizioe assiomatica dei umeri reali: si assume come assioma (cioè come
Università di Pisa - Corso di Laurea in Informatica Analisi Matematica A. Pisa, 18 gennaio 2016
 omada ) ) 4 cos si = 0 + e 4 C) 0 ) + omada La fuzioe f : (0, + ) R defiita da f() = si ( ) cos ) ha sia massimo che miimo ) è itata ma o ha é massimo é miimo C) o è itata e o ha asitoti ) ha u asitoto
omada ) ) 4 cos si = 0 + e 4 C) 0 ) + omada La fuzioe f : (0, + ) R defiita da f() = si ( ) cos ) ha sia massimo che miimo ) è itata ma o ha é massimo é miimo C) o è itata e o ha asitoti ) ha u asitoto
Esercizi sui numeri complessi per il dodicesimo foglio di esercizi
 Esercizi sui umeri complessi per il dodicesimo foglio di esercizi 6 dicembre 2010 1 Numeri complessi radici ed equazioi Ricordiamo iazitutto che dato u umero complesso z = x + iy, il suo coiugato, idicato
Esercizi sui umeri complessi per il dodicesimo foglio di esercizi 6 dicembre 2010 1 Numeri complessi radici ed equazioi Ricordiamo iazitutto che dato u umero complesso z = x + iy, il suo coiugato, idicato
Corso Propedeutico di Matematica
 POLINOMI RICHIAMI DI TEORIA Defiizioe: u poliomio ( o fuzioe poliomiale) ella variabile x di grado a coefficieti reali ha la forma A = a0 + a1x + + a 1 x, dove a 0, a 1,..., a soo umeri reali assegati
POLINOMI RICHIAMI DI TEORIA Defiizioe: u poliomio ( o fuzioe poliomiale) ella variabile x di grado a coefficieti reali ha la forma A = a0 + a1x + + a 1 x, dove a 0, a 1,..., a soo umeri reali assegati
Analisi Matematica 1 Matematica
 Aalisi Matematica 1 Matematica Secodo Compitio Luedì 30 Geaio 01 VERSIONE A Esercizio 1 (8 puti) Sia α R u parametro e si cosideri la serie di poteze complessa z. i) Calcolare il raggio di covergeza R
Aalisi Matematica 1 Matematica Secodo Compitio Luedì 30 Geaio 01 VERSIONE A Esercizio 1 (8 puti) Sia α R u parametro e si cosideri la serie di poteze complessa z. i) Calcolare il raggio di covergeza R
0.1 Il teorema limite centrale
 0. Il teorema limite cetrale 0. Il teorema limite cetrale Teorema 0.. Teorema limite cetrale). Sia X i ) i N ua successioe di variabili aleatorie i.i.d. che ammettoo mometo secodo fiito, co media µ e co
0. Il teorema limite cetrale 0. Il teorema limite cetrale Teorema 0.. Teorema limite cetrale). Sia X i ) i N ua successioe di variabili aleatorie i.i.d. che ammettoo mometo secodo fiito, co media µ e co
Aritmetica 2016/2017 Esercizi svolti in classe Seconda lezione
 Aritmetica 06/07 Esercizi svolti i classe Secoda lezioe Dare ua formula per 3 che o coivolga sommatorie Dato che sappiamo che ( + e ( + ( + 6 vogliamo esprimere 3 mediate, e poliomi i U idea possibile
Aritmetica 06/07 Esercizi svolti i classe Secoda lezioe Dare ua formula per 3 che o coivolga sommatorie Dato che sappiamo che ( + e ( + ( + 6 vogliamo esprimere 3 mediate, e poliomi i U idea possibile
****** FUNZIONI MISURABILI E INTEGRAZIONE ******
 ****** FUNZIONI MISURABILI E INTEGRAZIONE ****** 1 2 1. Fuzioi misurabili. I questo umero estediamo la ozioe di misurabilità alle fuzioi. Defiizioe 1. Siao u isieme o vuoto, Y uo spazio topologico e µ
****** FUNZIONI MISURABILI E INTEGRAZIONE ****** 1 2 1. Fuzioi misurabili. I questo umero estediamo la ozioe di misurabilità alle fuzioi. Defiizioe 1. Siao u isieme o vuoto, Y uo spazio topologico e µ
Prova d esame di Calcolo delle Probabilità 02/07/2011
 Prova d esame di Calcolo delle Probabilità 0/07/0 N. MATRICOLA... COGNOME e NOME... Esercizio Cosideriamo due ure ed ua moeta truccata. La prima ura (ura A) cotiee pallie rosse e 4 biache, la secoda ura
Prova d esame di Calcolo delle Probabilità 0/07/0 N. MATRICOLA... COGNOME e NOME... Esercizio Cosideriamo due ure ed ua moeta truccata. La prima ura (ura A) cotiee pallie rosse e 4 biache, la secoda ura
Analisi Matematica I
 Uiversità di Pisa - orso di Laurea i Igegeria Edile-rchitettura alisi Matematica I Pisa, febbraio Domada La derivata della fuzioe f) log ) si è ) log )si B) log )cos ) log ) si cos loglog ) + si ) log
Uiversità di Pisa - orso di Laurea i Igegeria Edile-rchitettura alisi Matematica I Pisa, febbraio Domada La derivata della fuzioe f) log ) si è ) log )si B) log )cos ) log ) si cos loglog ) + si ) log
