LA TEORIA DELLE MATRICI
|
|
|
- Adriana Cosentino
- 4 anni fa
- Visualizzazioni
Transcript
1 LA TEORIA DELLE MATRICI Il concetto di matrice (dal latino matrix o mater) fu introdotto da James Joseph Silvester (84-97) in An essay on canonical forms (Londra, 85) per indicare una disposizione rettangolare di numeri alla quale si potessero, nel caso quadrato, associare quantità numeriche dette determinanti. A parte alcuni prodromi risalenti a vari autori, quali Gabriel Cramer (750, Genova), Pierre Simon Laplace e Alexandre Théophile Vandermonde (770), Etienne Bezout (779), la teoria dei determinanti è nata in una Memoria di Cauchy del 82 ed in un contemporaneo lavoro, meno perfetto, di Jacques Binet ( ). Augustin Louis Cauchy ( , ingegnere militare e Professore all Ecole Polytechnique di Parigi) riprende il termine di determinante da Carl Friedrich Gauss (che non diede effettivamente contributi alla teoria), sviluppandone di fatto l intera teoria. La notazione a due indici attuale è dovuta al matematico tedesco Leopold Kronecker (823-89) mentre la nozione di rango (o caratteristica) di una matrice è merito del tedesco Ferdinand Georg Frobenius (849-97). A partire dal 858, in una serie di lavori, Arthur Cayley (82-895), matematico ed avvocato inglese, professore di Algebra a Cambridge ed autore di più di mille Memorie, ha iniziato ad operare con le matrici definendo per esse le operazioni di addizione e moltiplicazione, costruendo, in tal modo, le basi del moderno calcolo matriciale. La teoria delle matrici, dunque, sviluppata in stretta connessione con la teoria dei vettori, ha trovato notevoli applicazioni in molte branche, sia della Matematica che della Fisica.. Generalità Siano dati mn numeri reali a ij (non necessariamente tutti nulli). Definizione.. Si definisce matrice ad m righe ed n colonne o brevemente matrice di ordine mn, e la si indica, per comodità, con una lettera maiuscola dell alfabeto, una m-upla ordinata di n-uple ordinate. Da un punto di vista più intuitivo si può definire una matrice come un insieme A di mn elementi disposti come segue: a... a i... an A ai... aii... a in am... ami... a mn Generalmente si è soliti indicare, per comodità, una matrice anche in modo compatto, ovvero attraverso la seguente notazione: A a ij per i=, 2,..., m e j=, 2,..., n Ogni elemento a ij della matrice A è dotato di due indici, i e j, il primo dei quali denota il numero d ordine dell orizzontale a cui l elemento appartiene ed il secondo il numero d ordine della verticale. Le orizzontali si chiamano righe della matrice e le verticali colonne; si definisce linea indifferentemente un orizzontale od una verticale. L elemento a ij, pertanto, appartiene alla riga i-esima e alla colonna j-esima. A volte occorre indicare esplicitamente, in basso a destra della lettera che denota la matrice, il numero m delle righe ed n delle colonne da cui è composta; in tal caso si scrive A m n al posto di A.
2 Esempi ) 2 A 3 5 A3 2 è una matrice 32 (m=3 ed n=2) 7 9 2) 7 4 A A33 è una matrice 33 (m=3 ed n=3) Definizione.2. Una matrice A di ordine mn si dice rettangolare se in essa il numero delle righe è diverso da quello delle colonne. Nel caso in cui sia m=n, allora la matrice A si dice quadrata di ordine n (o m) con elementi. Una siffatta matrice si indica brevemente come segue: con i=j=, 2,..., n A a ij 2 2 n = m e gli elementi a,..., aii,..., ann formano la diagonale principale di A, mentre gli elementi an,,..., ai, n i,..., a n costituiscono la sua diagonale secondaria. In particolare se m=n= la matrice è quadrata ed in questo caso la diagonale principale e quella secondaria coincidono con l unico elemento a. Esempi ) A è una matrice rettangolare 23 (m=2 ed n=3) 3 4 2) A 2 è una matrice quadrata 22 (n=m=2) 3 2 In tal caso gli elementi 2, 2 formano la diagonale principale mentre gli elementi, 3 quella secondaria. A 2 è una matrice quadrata con m=n=. 3) A ( a ) In questo esempio la diagonale principale e quella secondaria coincidono con il solo elemento 2 della matrice A. Definizione.3. Una matrice quadrata D si dice diagonale se in essa sono nulli tutti gli elementi al di fuori di quelli che si trovano sulla diagonale principale. Esempio D 0 0 è una matrice diagonale Definizione.4. Una matrice quadrata A di ordine n si dice triangolare superiore se sono nulli tutti gli elementi al di sotto della diagonale principale e triangolare inferiore se sono nulli tutti gli elementi al di sopra della diagonale principale. 2
3 Esempi 0 0 ) A 3 0 è una matrice triangolare inferiore ) A è una matrice triangolare superiore Osservazione Una matrice diagonale è una matrice triangolare sia superiore che inferiore. Definizione.5. Data una qualunque matrice A di ordine mn si definisce trasposta di A, e la si indica con matrice di ordine nm ottenuta da A scambiando le righe con le colonne. Esempi t ) A A t 2) A 2 7 A t A, la Definizione.6. Una matrice A di ordine mn si dice simmetrica se Esempio 2 3 A 2 2 è una matrice simmetrica A t. A Definizione.7. Una matrice quadrata del tipo se i= j In ij con ij per i, j=, 2,..., n 0 se i j si chiama matrice identica o unitaria di ordine n. In altre parole una matrice identica è una matrice diagonale in cui tutti gli elementi della diagonale principale sono uguali ad uno. Esempio 0 0 I3 0 0 è la matrice identità di ordine 3 (diagonale con gli elementi unitari) 0 0 3
4 Definizione.8. Siano m ed n. Fissato un elemento qualsiasi a ij della matrice A di ordine mn si definisce minore complementare di a ij, e lo si indica con m ij, la matrice, di ordine (m)(n), che si ottiene da A cancellando tutti gli elementi della i-esima riga e j-esima colonna. Esempi ) A 3 5 m2 è il minore complementare di a ) A 3 5 m2 è il minore complementare di a DETERMINANTI Scopo del presente paragrafo è di introdurre un numero reale associato ad una matrice quadrata A, denominato determinante di A ed indicato con deta oppure con A. Poiché siffatto numero riveste notevole interesse in molti argomenti occorre impararne il suo calcolo. Sia A una matrice quadrata di ordine n. Definizione 2.. A a Se n=, cioè Esempi A 2 deta 2 2 ) 2) A 5 deta 5 5 Definizione 2.2. a Se n=2, cioè A a, il determinante di A è dato da: a 2 a 2 22 deta a a, allora il determinante di A è dato da: a a2 deta a a a a a a Esempi ) A deta ( ) ) 2 2 A deta ) 2 2 A deta ( 2) ) 4 4 A deta
5 Definizione 2.3. a a a Se n=3, cioè A a a a a a a a a a , allora il determinante di A è dato da: deta a a a a a a a a a a a a a a a a a a a a a a a a Un metodo pratico, però, che consente di calcolare il determinante solo di una matrice del terzo ordine, è fornito dalla seguente regola di Sarrus: data una matrice A di ordine tre, si consideri la tabella ottenuta da A aggiungendo ad essa, a destra, nell ordine, le sue prime due colonne, cioè: a a a a a a a a a a a3 a32 a33 a3 a32 Si ottiene, quindi, il determinante di A eseguendo la somma dei prodotti degli elementi delle diagonali principali, aa 22a33 a2 a23a3 a3, a2, a32, e sottraendo ad essa la somma dei prodotti degli elementi delle diagonali secondarie, a3a 22a3 a32a 23a a33a 2a2. Esempi ) Data la matrice 3 5 A Per poter calcolare il determinante di A in modo piuttosto agevole, occorre applicare la regola di Sarrus, scrivendo, in primo luogo, la seguente tabella mnemonica: da cui segue che: deta ( ) ( ) ) A deta (0 60 0) Osservazione Le definizioni precedenti forniscono anche metodi pratici per il calcolo del determinante di una matrice quadrata A di ordine n=,2,3. Si analizzerà di seguito, invece, un criterio generale che consente di calcolare il determinante di una matrice quadrata A di ordine qualsiasi n 2. A tal fine, però, occorre premettere la seguente: Definizione 2.4. Data una matrice A di ordine mn, si definisce minore di ordine mi, estratto da A, il determinante ottenuto dalla matrice cancellando i righe e j colonne in modo che sia mi=nj. Ne segue, in particolare, che ogni elemento di una qualunque matrice rappresenta un minore del primo ordine. 5
6 Esempi ) Se A, allora i minori di ordine tre estraibili da A sono: , 2 4, 2 3, ) Se A , allora i minori di ordine tre estraibili da A sono: , 2 2 6, 2 4 6, mentre alcuni minori di ordine due estraibili da A sono, ad esempio: ,,,,, e così via. Definizione 2.5. Sia a ij un elemento qualsiasi di una matrice quadrata A di ordine n 2. Si chiama complemento algebrico di a ij, e si indica con c ij, il determinante del minore complementare di a ij preso con il segno positivo o negativo a seconda che la somma degli indici, ovvero i+j, sia rispettivamente pari o dispari. Esempi 3 ) Se A 2 4, allora: 2 c 4 4 è il complemento algebrico di a c è il complemento algebrico di a2 2 e così via ) Se A allora: 2 6 c 5 è il complemento algebrico di a 6 c è il complemento algebrico di a c3 2 e via dicendo. è il complemento algebrico di a3 2 6
7 Osservazione La definizione generale di determinante di ordine n viene data per ricorrenza, ovvero in funzione di quella di determinante di ordine quelli di ordine direttamente. n ; i determinanti di ordine 7 n si ottengono in funzione di n 2 e così via, fino a quelli di ordine almeno tre che si sanno calcolare Definizione 2.6. (definizione generale di determinante) Data una matrice quadrata A di ordine, si chiama determinante di A quel numero, che si indica con deta oppure con A, formato dalla somma dei prodotti degli elementi di una linea (riga o colonna) qualsiasi, ovvero scelta a piacere, della matrice per i rispettivi complementi algebrici. n 2 Dalla precedente definizione, però, può sorgere il dubbio che il calcolo di un determinante dipenda dalla particolare linea scelta. Si dimostra, quindi, a tal riguardo, il seguente: Teorema (di Laplace): se A è una matrice quadrata di ordine n, allora il valore numerico del deta è sempre il medesimo a prescindere dalla linea scelta per il suo calcolo. Esempi ) Calcolare il determinante associato alla seguente matrice 3 2 A secondo gli elementi della prima riga (è consigliabile, in fase preliminare, eseguire tale calcolo utilizzando anche la regola di Sarrus, in modo tale da poter verificare che il risultato ottenuto è il medesimo, ovvero 4). Si ha: deta 3c 2c c Osserviamo ora che, se si calcola il determinante secondo gli elementi di un altra riga o colonna, ad esempio la seconda colonna, si ottiene, in accordo con il teorema di Laplace, sempre il medesimo risultato: deta 2c2 4c22 7c ) Calcolare deta, essendo A Per economia di calcolo conviene, in questo caso, fissare la riga o la colonna nella quale figuri il maggior numero possibile di elementi nulli. Se, ad esempio, si fissa la prima riga si ha: deta Lo studente provi, per esercizio, a calcolare il determinante della stessa matrice fissando, ad esempio, la terza riga oppure la prima colonna; potrà verificare, quindi, che, variando la linea di
8 partenza, il valore del determinante non muta. Naturalmente si può calcolare suddetto determinante fissando un altra riga, ad esempio, la quarta; risulta evidente, però, che, in alcuni casi, il procedimento è di gran lunga più laborioso. 3. OPERAZIONI CON LE MATRICI Siano A e B due matrici di tipo mk ed hn rispettivamente. Definizione 3.. A e B si dicono sommabili (sottraibili) se m=h e k=n. Se A e B sono sommabili (sottraibili), ovvero entrambe di tipo mn, allora risulta: A B a b a b ij ij ij ij Esempi ) A 3 2, B Poiché A e B sono entrambe di ordine 33, sono sommabili e sottraibili; risulta allora: A B A B ) A 3 3, B Poiché A e B sono sommabili (sottraibili), in quanto entrambe di ordine 32, si ha: A B= A B= ) A 0, B Poiché A e B sono di ordine rispettivamente 33 e 23, le due matrici non sono sommabili (sottraibili). Osservazioni Comunque data A= A m n e considerata la matrice O= O mn, risulta: () AO= O A A 8
9 Esempi 2 3 ) A La matrice nulla, associata ad A, di ordine tre, è data da: O Essendo A ed O sommabili, è facile verificare, sfruttando la definizione 4.., che la () è soddisfatta ) A 0 3 In questo caso la matrice nulla associata ad A è di ordine 23, ovvero della forma: O Dunque la () è verificata. Se A è la matrice ottenuta da A cambiando segno a tutti i suoi elementi si ha: A A = A A O (2) Esempi ) A 4 A Utilizzando ora la definizione 4.., si verifica banalmente la (2) ) A 2 A La verifica della (2) è lasciata, per esercizio, allo studente. Osservazione Nell insieme M di tutte le matrici, l operazione di addizione tra matrici (+) è un operazione parziale in quanto non sempre eseguibile: matrici di egual tipo, infatti, sono sommabili, a differenza di matrici di diverso tipo che non sono (e non potrebbero essere) sommabili (posto a posto). Quanto fino ad ora affermato si può riassumere nel seguente: M m, n Teorema: sia l insieme di tutte le matrici; l insieme si può ripartire nell insieme di tutte le matrici di egual tipo, ovvero a due a due sommabili; inoltre ciascuna di queste classi M m, n, corredate con l addizione tra matrici, costituisce quello che in algebra si chiama gruppo commutativo. 9
10 Tale teorema, dunque, può essere schematizzato nel seguente diagramma: M M 2, 3 2, 2 = M2, Mn M n n M m, n Si cercherà ora di introdurre una seconda operazione parziale su (parziale in quanto non sempre definita), precisamente il prodotto (righe per colonne) tra due matrici. Seppur la definizione risulta essere complessa e macchinosa e non si giustifica con l intuito, sicuramente, insieme a tutta la teoria che la circonda, è di grande utilità per le applicazioni. Siano A e B due matrici di tipo rispettivamente mk ed hn. Definizione 3.2. A e B si dicono conformabili o moltiplicabili se il numero k delle colonne di A eguaglia il numero h delle righe di B. Tale definizione può essere schematizzata come segue: A B mk hn Esempio Siano k=h A, B moltiplicabili x... A a a a X x... i... n, i... x n rispettivamente una matrice riga n ed una matrice colonna n. Allora A è moltiplicabile per X. Definizione 3.3. (definizione particolare) Si definisce prodotto di A per X la matrice data da: AX ax... ai xi... anxn (prodotto dell unica riga di A per l unica colonna di B). Si può definire anche, ma in modo totalmente differente, il prodotto XA (cfr. Esempio 3). 0
11 Esempio 2 Siano a A c b d e B ' ' ' A è moltiplicabile per B mentre B non è moltiplicabile per A. Definizione 4.4. (definizione particolare) Nel caso riportato nell Esempio 2, il prodotto righe per colonne di A per B si definisce ponendo: A B = a b ' a b ' a b ' c d ' c d ' c d ' = AB Si noti che ogni elemento della matrice prodotto non è altro che il prodotto di una riga di A per la corrispondente colonna di B. Osservazione Se A e B sono due matrici di ordine rispettivamente mk ed hn con k=h, allora il prodotto AB è una matrice opportuna ma di ordine mn, ovvero risulta: A B m k k = h h n m n Esempio 3 Con riferimento all Esempio si ha: x xa... xai... xa n XA x i a... ai... an xia... xiai... xia n x n xna... xnai... xna n Definizione 3.5. (definizione generale) Se A e B sono matrici di ordine rispettivamente mk ed hn con k=h allora il prodotto AB è una matrice S di ordine m n della forma: AB S s ij con i=, 2,..., m e j=, 2,..., n
12 dove l elemento s ij è il prodotto della riga i-esima di A per la colonna j-esima di B. In formule si ha: b j... n s a... a... a b a b... a b... a b a b ij i ii in ij i j ii ij in nj ip pj p... b nj Osservazione Talvolta risulta possibile interpretare la Definizione 3.5 anche nel seguente modo: date A e B si evidenziano le righe di A e le colonne di B ponendo A... A A i, B B... B j... Bn... A m dove: A a... a... a,..., A a... a... a,..., A a... a... a i k i i ii ik m m mi mk b b j b n B b j,..., B b j jj,..., Bn b jn b b k kj b kn Ne segue che: A A B... A B j... A Bn AB A i... i j... i B B A B A B A j Bn ib n A Am B... Am B j... A m mb n Esempi ) A 3 0, B Poiché A ha ordine 32 e B ha ordine 24, il prodotto AB è eseguibile (il numero delle colonne di A è uguale al numero delle righe di B, cioè A e B sono conformabili). La matrice prodotto avrà, pertanto, ordine 34, precisamente: s s2 s3 s4 S AB s2 s22 s23 s24 s3 s32 s33 s 34 2
13 dove: 2 s ; s ; s ; s ; 0 2 s ; s ; s ; s ; 0 2 s ; s ; s ; s Dunque: S AB ) A , B A e B sono conformabili e la matrice prodotto avrà, pertanto, ordine 34 (3 è il numero delle righe di A e 4 è il numero delle colonne di B). Dunque si ha: S AB Osservazione Si può dimostrare che, indipendentemente dalle matrici A, B, C e dal numero, il prodotto tra matrici gode delle seguenti proprietà: det AB detadetb (proprietà che ha molteplici applicazioni) Teorema (di Binet): det A deta (se A è una matrice quadrata) orda associativa: ABC ABC distributiva: AB C AB AC (a destra); A B C AC BC (a sinistra) sotto le ipotesi che tutte le operazioni indicate nelle formule precedenti siano eseguibili. In generale, però, il prodotto tra matrici non è commutativo: se si considerano, infatti, due matrici, B k, n, allora AB è sempre possibile (A e B sono conformabili) mentre BA è possibile Am k e 3
14 solo se m n. Tuttavia anche se esistono entrambi i prodotti, ovvero AB e BA, non è detto che questi siano eguali. Esempio 2 A4 5 6, B 3 AB AB BA BA A 3, B3 AB BA 33 Osservazione Nell esempio precedente, pur essendo stato possibile eseguire entrambi i prodotti AB e BA, perché il numero delle righe e delle colonne di A erano uguali, rispettivamente, al numero delle colonne e delle righe di B, si sono ottenuti prodotti ben diversi tra loro. Dunque, in generale, si ha: - ; - AB O non implica necessariamente A O oppure B O; - AB AC oppure BA CA non implicano necessariamente B C. Esempi 2 ) A, B Risulta: AB BA ) AB A O oppure B O (le matrici A e B non sono infatti nulle) ) AB, AC ma è evidente che risulta B C. AB BA Definizione 3.6. Data una matrice quadrata A di ordine n si definisce matrice inversa di A, e la si indica con A, una matrice quadrata di ordine n tale che AA I ed A A I. La matrice inversa può essere determinata attraverso due metodi: il primo, teorico, e che verrà illustrato in questa sede, che conduce ad una formula, ed il secondo, pratico, e che verrà tralasciato in quanto ritenuto di minore importanza per le applicazioni economico-statistiche, che porta, invece, alla determinazione della A attraverso un calcolo ben preciso. Il primo metodo, quindi, si basa sul seguente: Teorema: data una matrice quadrata A di ordine n, esiste A se e solo se risulta deta 0 4
15 Osservazioni Applicando il teorema di Binet alla relazione fondamentale della matrice inversa si ha: deti = det AA detadeta da cui segue: deta deta = relazione che consente di calcolare il determinante della matrice inversa. Se A è una matrice con deta 0, allora esiste sempre una seconda matrice B tale che: AB 0 Due matrici siffatte, cioè due matrici A e B con A0, B 0 ma dello zero. Se A e B sono due matrici divisori dello zero, allora dal teorema di Binet risulta: det AB detadetb 0 AB 0, si dicono matrici divisori Infatti essendo A0, B 0, la condizione detb 0 implicherebbe l esistenza di risulterebbe AB B 0 e quindi A 0 mentre, per ipotesi, è A 0. B per cui Verrà ora illustrato in dettaglio il primo metodo, ovvero quello teorico, per il calcolo dell inversa di una data matrice, metodo questo che, come già detto, conduce ad una formula che non verrà dimostrata in questa sede. Occorre, in primo luogo, determinare la matrice dei complementi algebrici per poi applicare la seguente relazione: t * (3) A A det A Esempi 0 0 ) A 2 0 Osserviamo in primo luogo che deta 0, cioè la matrice data ammette inversa. Calcoliamo allora A utilizzando la (3). La matrice dei complementi algebrici associata ad A è data da: 0 0 * t * A 0 A Dalla (3) segue che: A ) A È facile verificare che deta 0. Pertanto A ammette l inversa. Risulta: A * A * 5
16 * t * A A 0 2 A ) A Si noti che, essendo deta 2 0, esiste A. Si ha: * t * A A A
17 ESERCIZI PROPOSTI A) Calcolare, se possibile, A+B, AB, AB, BA e ca, dove A,B e c sono dati, degli esercizi )-8), dopo aver analizzato gli esempi a)-g): a) A2 2, B2 2, c Sommando e sottraendo termine a termine risulta rispettivamente: A B, A B Svolgendo il prodotto righe per colonne si ha: AB BA Moltiplicando ciascun elemento della matrice A per il numero c assegnato si ottiene: ca A b) A , B , c Si ha: A B 6 2 3, A B AB BA ca 3A c) A2 3, B2 3, c Risulta: A B, A B AB non è possibile perché il numero delle colonne di A è diverso dal numero delle righe di B. BA non è possibile per il ragionamento precedente. 7
18 3 2 ca A d) A3 0 2, B 3 2, c Si ha: A B 3, A B AB BA ca 2 A Osservazione La somma e la differenza si possono effettuare solo nel caso di matrici aventi lo stesso ordine (il medesimo numero di righe e di colonne): non è possibile, infatti, sommare o sottrarre, ad esempio, una matrice di ordine 23 ed una di ordine 33; analogamente, come già osservato, è possibile calcolare il prodotto tra due matrici solo se il numero delle colonne della prima matrice è uguale al numero delle righe della seconda matrice, precisamente A(m,k) e B(k,n) sono moltiplicabili e la matrice prodotto è S(m,n); il prodotto tra matrici, in generale, non è commutativo, ossia è ABBA, com è facile verificare dagli esempi precedenti e) A , B , c A B ed A B non sono possibili per quanto asserito nella precedente osservazione AB è la matrice nulla BA non è possibile 8
19 0 3 2 ca A f) A2 3, B , c ed A B non sono possibili AB A B BA ca 6A g) A3 4 3, B 42, c A B e A B non sono possibili AB non è possibile ca A è la matrice nulla BA ) R: 3 A, B, c A B, A B, AB, BA, ca
20 ) A 0 2, B 0 2 5, c R: A B 0 0 4, A B 0 4 6, AB BA , ca ) A, B 3, c R: A+B, AB, BA non sono possibili; AB, ca ) A, B, c R: A B, A B, AB, , BA ca
21 ) A, B 0 2 3, c R: AB, A B non sono possibili; AB, BA 5 9, ca A ) A , B, c R: AB, A B, BA non sono possibili; AB 20 48, ca ) A 3, B 3, c R: AB, A B, AB non sono possibili; BA 3 5, ca ) A 2, B 0, c R: AB, A B, BA non sono possibili; AB, ca B) Scrivere la trasposta delle seguenti matrici )-6) dopo aver analizzato gli esempi a)-d): 7 a) A 4 5 Come già accennato in precedenza la trasposta di una matrice si ottiene scambiando tra di loro le righe e le colonne; si ha, quindi: 2
22 t 4 A b) A Risulta: 2 t A Osservazione Nell esempio b) risulta ovvero la matrice A è simmetrica c) A 0 3 Si ottiene: 2 0 t A d) A D La trasposta della matrice diagonale D è la matrice, anch essa diagonale, data da: t D t A A Osservazione Ogni matrice diagonale è simmetrica; nel caso in cui la matrice A sia quadrata di ordine n, allora la sua trasposta risulterà ancora una matrice quadrata di ordine n; se, invece, A è una matrice rettangolare di ordine mn allora la sua trasposta sarà ancora una matrice rettangolare di ordine, però, nm. ) 2) 2 A A 2 3 t A t A
23 3) 4) 5) 6) A A D A t 2 A t 2 4 A t D t A C) Calcolare i determinanti delle matrici )-30) dopo aver osservato quanto riportato nei seguenti esempi a)-d) 2 2 a) A 3 Applicando la definizione data sui determinanti del secondo ordine si ha: 2 2 deta b) A Applicando la regola di Sarrus si ha: deta c) A Il determinante richiesto si può calcolare con la regola di Sarrus, come fatto nel precedente esempio, oppure con la regola di Laplace, cioè sviluppando il determinante rispetto agli elementi di una riga o di una colonna. Se si considerano, ad esempio, gli elementi della seconda riga, si ha: 23
24 deta 0 c2 0c22 c23 c2 c Dunque, per il calcolo dei determinanti del terzo ordine, risulta possibile utilizzare entrambi i metodi di cui agli esempi b) e c) d) A Applicando la regola di Laplace, cioè sviluppando il determinante, ad esempio, secondo gli elementi della prima colonna, si ha: deta c 5c2 4c3 3c4 c 5c2 4c3 3c I precedenti determinanti di ordine tre, a loro volta, possono essere calcolati applicando nuovamente la regola di Laplace, sviluppando ciascuno di essi secondo, ad esempio, gli elementi della prima riga. Risulta quindi: deta Osservazione Si sarebbe pervenuti allo stesso risultato se si fossero calcolati i determinanti del terzo ordine con la regola di Sarrus. 24
25 Osservazione Tutti i determinanti di ordine n 5 si risolvono sempre con la regola di Laplace. ) 2) 3) 4) 5) 6) 7) 8) 9) 0) ) 2) 3) 4) 5) 3 A A A A A 3 7 A A 4 A A 4 A A A A A A [ deta 9 ] [ [ [ deta 5] deta 8] deta ] [ deta 29 ] [ deta 37 ] [ deta 34] [ deta 7] [ deta 9] [ deta 3 ] [ deta ] [ deta 2] [ deta 26] [ deta 4] [ deta 7] 25
26 6) 7) 8) 9) 20) 2) 22) 23) 24) 25) 3 5 A A A A A A A A A A [ deta 87 ] [ [ [ deta 4] deta 0] deta 70] [ deta 65] [ deta ] [ deta 0] [ deta 24] [ deta 24] [ deta 5] 26
27 26) 27) 28) 29) 30) A A A A A [ deta 38] [ deta 256] [ deta 0] [ deta 885 ] [ deta 52] D) Calcolare la matrice dei complementi algebrici riportata negli esercizi )-2) dopo aver analizzato gli esempi a)-f): 2 5 c c2 a) A 3 c2 c22 Si ha: * c c2 A c2 c22 dove i c, complementi algebrici relativi agli elementi a ij, sono il risultato del prodotto tra il ij determinante, ottenuto da A cancellando la riga i-esima e la colonna j-esima, e i j. Pertanto risulta: c = 3 [cancellando la prima riga e la prima colonna si ottiene il 3 3, moltiplicato 2 per ] c2 [cancellando la prima riga e la seconda colonna si ottiene il, moltiplicato per 2 3 ] 27
28 c2 5 c22 2 [cancellando la seconda riga e la prima colonna si ottiene il per 2 3 ] [cancellando la seconda riga e la seconda colonna si ottiene il per ] Quindi alla fine risulta: * 3 A b) A 3 5 Procedendo come nel precedente esempio si ha: [cancellando la prima riga e la prima colonna si ha il c 5 c2 3 2 poi moltiplicato per ] [cancellando la prima riga e la seconda colonna si ha il 2 3 poi moltiplicato per ] c2 0 0 [cancellando la seconda riga e la prima colonna si ha il poi moltiplicato per ] , moltiplicato 0 0, moltiplicato che va che va che va c [cancellando la seconda riga e la seconda colonna si ha il che va poi moltiplicato per ] Dunque: * 5 3 A 0 0 c) A Anche per le matrici di ordine n 3 si può applicare la regola analizzata nel caso n 2, chiaramente con le opportune variazioni. Pertanto si ha: c c2 c3 * A c2 c22 c23 c3 c32 c 33 Restano da calcolare i c ij, complementi algebrici degli elementi a ij. Quindi si ha: c (il determinante 22 è stato ottenuto cancellando la prima riga e la prima colonna di A) c (il determinante 22 è stato ottenuto cancellando la prima riga e la seconda colonna di A) 28
29 c (il determinante 22 è stato ottenuto cancellando la prima riga e la terza colonna di A) c (il determinante 22 è stato ottenuto cancellando la seconda riga e la prima colonna di A) 22 4 c (il determinante 22 è stato ottenuto cancellando la seconda riga e la seconda colonna di A) c23 0 (il determinante 22 è stato ottenuto cancellando la seconda riga e la terza colonna di A) c (il determinante 22 è stato ottenuto cancellando la terza riga e la prima colonna di A) 32 5 c (il determinante 22 è stato ottenuto cancellando la terza riga e la seconda colonna di A) c (il determinante 22 è stato ottenuto cancellando la terza riga e la terza colonna di A) Dunque la matrice cercata è: * A d) A Calcoliamo, in primo luogo, come fatto nei precedenti esempi, i complementi algebrici relativi agli elementi della matrice data. Risulta allora: 0 2 c 00 ; 0 c c c c ; ; ; ; 2 29
30 c c ; 0 3 0; 3 c ; c Dunque si ha: 0 2 * A e) A Procedendo in maniera più rapida di quanto non sia stato fatto in precedenza si ha: c 2 ; c2 6 5 ; c3 6 ; c ; c ; c ; c3 ; c ; c Dunque: 2 6 * A f) A Si ha: c c c c ; ; ; c ; ; c ;
31 23 0 c c ; 24 0 c ; 0 3 ; c c ; c ; c ; ; c ; c ; 44 0 c Dunque: * 3 0 A ) 2) 3) 4) 5) 6) 7) A A 2 A A 3 5 A A A * 3 4 A * 2 A 2 * 3 2 A 3 * 5 A 3 * 0 9 A * A A *
32 8) 9) 3 A A ) D ) 2) A A A * A * * D * A * A E) Calcolare, con il metodo teorico, l inversa delle matrici riportate negli esercizi )-2) dopo aver analizzato i seguenti esempi a)-h): 3 a) A 2 4 Risulta necessario calcolare, in primo luogo, il determinante di A per poter affermare che la matrice data ammette o meno l inversa. Si ha: Quindi, essendo rispettata la condizione necessaria e sufficiente, esiste l inversa di A. Occorre ora calcolare la matrice dei complementi algebrici; si ha: c 4 ; c2 2 ; c2 ; c22 3 Ne segue che: * * t A A Dunque: 2 t * A A det A b) A
33 Si ha: Quindi A ammette inversa. Si calcolano i complementi algebrici relativi agli elementi di A: c 2 ; c2 0 ; ; da cui: * 2 0 t * 2 A A 0 Dunque: 2 A c) A Risulta: 0 c 2 c Come già visto nell esempio d) in D) i complementi algebrici relativi agli elementi di A sono i seguenti: c ; c2 0 ; c3 2 ; c2 ; c22 ; c23 2; c3 0; c32 0 ; c33 Quindi: * t * A 2 A Dunque: 0 0 A Si osservi che in questo esempio A A * t 3 2 d) A Si ha:
34 Dunque la nostra matrice A non ha inversa. 3 2 e) A Risulta: I complementi algebrici sono: ; ; ; ; ; ; ; ; da cui segue: * * t A A Dunque: 4 3 A f) A Innanzitutto bisogna calcolare il determinante di A utilizzando la regola di Laplace. Si ha, sviluppando, ad esempio, rispetto alla seconda riga: c c 2 0 c 3 c 2 4 c c23 5 c3 3 c32 c33 3 Poiché deta 5 0, la matrice data ha l inversa. Si calcolino ora i complementi algebrici relativi agli elementi di A. Si ha: c ; c2 3 ; c3 3; c4 0 ; c2 ; c22 6 ; c23 4 ; c24 5; c3 2; c32 3; 3 c33 2; c34 5; c4 7 ; c42 3; c43 7 ; c44 5 Dunque si ottiene: * t * A A da cui: 34
35 A g) D Risulta evidente che il determinante di una qualunque matrice diagonale è uguale al prodotto degli elementi della sua diagonale principale. Ne segue, pertanto: detd 6 0 Si verifica immediatamente, poi, che i complementi algebrici degli elementi nulli sono uguali a zero da cui si ottiene: ; ; Quindi: * * t D D Dunque: D h) A Come di consueto si calcola, in primo luogo, il determinante della matrice data: 0 c 2 c c33 3 Pertanto A ammette l inversa. I complementi algebrici relativi agli elementi di A sono: c 5; c2 2 ; c3 6 ; c2 2 ; c22 2 ; c23 ; c3 ; c32 ; c33 3 Quindi si ha: * 2 2 * t A A Dunque: 35
36 A Verifica: ) (in generale ) AA ) AA I 3 AA I n I (in generale ) A A I 3 A A I n A A 0 3 = I Le verifiche degli esempi precedentemente riportati sono lasciate per esercizio allo studente. 3 ) 2) 3) 4) 5) A A A 3 0 A A 0 A A A A A 3 2 = 2 0 = = = = 0 36
37 6) 7) 8) 9) 0) ) 2) 2 2 A A A A A A A A A A A A A A = = = = = = =
= elemento che compare nella seconda riga e quinta colonna = -4 In generale una matrice A di m righe e n colonne si denota con
 Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti su m righe e n colonne. I numeri che compaiono nella tabella si dicono elementi della matrice. La loro individuazione
Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti su m righe e n colonne. I numeri che compaiono nella tabella si dicono elementi della matrice. La loro individuazione
determinante della sottomatrice ottenuta da A cancellando la i-esima riga e la j-esima colonna
 Data una matrice quadrata A di ordine n si definisce minore complementare m ij dell elemento generico a ij della matrice A il determinante della sottomatrice ottenuta da A cancellando la i-esima riga e
Data una matrice quadrata A di ordine n si definisce minore complementare m ij dell elemento generico a ij della matrice A il determinante della sottomatrice ottenuta da A cancellando la i-esima riga e
Argomento 12 Matrici
 Argomento 2 Matrici 2 Vettori di R n eoperazioni I Vettore di R n : x =(x i ) i=n =(x i ) n i=,conx i R componenti di x I R n = spazio dei vettori reali a n componenti = spazio vettoriale reale n-dimensionale
Argomento 2 Matrici 2 Vettori di R n eoperazioni I Vettore di R n : x =(x i ) i=n =(x i ) n i=,conx i R componenti di x I R n = spazio dei vettori reali a n componenti = spazio vettoriale reale n-dimensionale
Elementi di Algebra Matriciale. (richiami)
 Elementi di Algebra Matriciale Definizione di matrice (richiami) Matrice quadrata, diagonale, identità, triangolare, simmetrica Matrice trasposta Principali operazioni su matrici e vettori: somma, sottrazione,
Elementi di Algebra Matriciale Definizione di matrice (richiami) Matrice quadrata, diagonale, identità, triangolare, simmetrica Matrice trasposta Principali operazioni su matrici e vettori: somma, sottrazione,
LEZIONE i i 3
 LEZIONE 5 51 Determinanti In questo lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 5 51 Determinanti In questo lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
Operazioni tra matrici. Moltiplicazione per uno Scalare Moltiplicare ogni elemento della matrice per lo scalare. Sia c = 3
 Operazioni tra matrici Definizione di matrice a ij è un elemento di A a ij è detto l elemento ij-esimo di A Moltiplicazione per uno Scalare Moltiplicare ogni elemento della matrice per lo scalare. Sia
Operazioni tra matrici Definizione di matrice a ij è un elemento di A a ij è detto l elemento ij-esimo di A Moltiplicazione per uno Scalare Moltiplicare ogni elemento della matrice per lo scalare. Sia
Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE. Giovanni Villani
 Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE Giovanni Villani Matrici Definizione 1 Si definisce matrice di tipo m n una funzione che associa
Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE Giovanni Villani Matrici Definizione 1 Si definisce matrice di tipo m n una funzione che associa
LEZIONE i 0 3 Le sottomatrici 2 2 di A sono. 1 2 i i 3. Invece (
 LEZIONE 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
( ) TEORIA DELLE MATRICI. A. Scimone a.s pag 1
 . Scimone a.s 1997 98 pag 1 TEORI DELLE MTRICI Dato un campo K, definiamo matrice ad elementi in K di tipo (m, n) un insieme di numeri ordinati secondo righe e colonne in una tabella rettangolare del tipo
. Scimone a.s 1997 98 pag 1 TEORI DELLE MTRICI Dato un campo K, definiamo matrice ad elementi in K di tipo (m, n) un insieme di numeri ordinati secondo righe e colonne in una tabella rettangolare del tipo
MATRICI e DETERMINANTI. Prof.ssa Maddalena Dominijanni
 MATRICI e DETERMINANTI Le matrici non sono altro che tabelle di elementi ordinati per righe e colonne. Se m = n la matrice si dice quadrata Matrice quadrata di ordine 3 Matrice rettangolare di tipo 2 3
MATRICI e DETERMINANTI Le matrici non sono altro che tabelle di elementi ordinati per righe e colonne. Se m = n la matrice si dice quadrata Matrice quadrata di ordine 3 Matrice rettangolare di tipo 2 3
MATRICI. Matrici Una matrice A con n-righe e m-colonne, ad elementi reali, è una tabella con la seguente forma: a 2 m. a n m) i j R, 1 i n, 1 j m.
 MATRICI Matrici Una matrice A con n-righe e m-colonne, ad elementi reali, è una tabella con la seguente forma: 11 a 12 a 1 3 a 1m A=(a a 21 a 2 3 a 2m con a a n1 a n2 a n 3 a nm i j R, 1 i n, 1 j m. per
MATRICI Matrici Una matrice A con n-righe e m-colonne, ad elementi reali, è una tabella con la seguente forma: 11 a 12 a 1 3 a 1m A=(a a 21 a 2 3 a 2m con a a n1 a n2 a n 3 a nm i j R, 1 i n, 1 j m. per
MATRICI E SISTEMI LINEARI
 MATRICI E SISTEMI LINEARI - PARTE I - Felice Iavernaro Dipartimento di Matematica Università di Bari 27 Febbraio 2006 Felice Iavernaro (Univ. Bari) Matrici e Sistemi lineari 27/02/2006 1 / 1 Definizione
MATRICI E SISTEMI LINEARI - PARTE I - Felice Iavernaro Dipartimento di Matematica Università di Bari 27 Febbraio 2006 Felice Iavernaro (Univ. Bari) Matrici e Sistemi lineari 27/02/2006 1 / 1 Definizione
LEZIONE 4. Le sottomatrici 2 2 di A sono. Invece ( 1 3 non è sottomatrice di A.
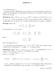 LEZIONE 4 4 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 4 4 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
Matrici. Prof. Walter Pugliese
 Matrici Prof. Walter Pugliese Le matrici Una matrice è un insieme di numeri reali organizzati in righe e colonne. Se n è il numero delle righe e m e il numero delle colonne si dice che la matrice è di
Matrici Prof. Walter Pugliese Le matrici Una matrice è un insieme di numeri reali organizzati in righe e colonne. Se n è il numero delle righe e m e il numero delle colonne si dice che la matrice è di
VETTORI E MATRICI. Ing. Nicola Cappuccio 2014 U.F.5 ELEMENTI SCIENTIFICI ED ELETTRONICI APPLICATI AI SISTEMI DI TELECOMUNICAZIONI
 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 I VETTRORI E MATRICI (RICHIAMI) Ad ogni matrice quadrata a coefficienti reali è possibile associare un numero reale, detto determinante, calcolato
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 I VETTRORI E MATRICI (RICHIAMI) Ad ogni matrice quadrata a coefficienti reali è possibile associare un numero reale, detto determinante, calcolato
MATRICI E SISTEMI LINEARI
 1 Rappresentazione di dati strutturati MATRICI E SISTEMI LINEARI Gli elementi di una matrice, detti coefficienti, possono essere qualsiasi e non devono necessariamente essere omogenei tra loro; di solito
1 Rappresentazione di dati strutturati MATRICI E SISTEMI LINEARI Gli elementi di una matrice, detti coefficienti, possono essere qualsiasi e non devono necessariamente essere omogenei tra loro; di solito
CAPITOLO II MATRICI E DETERMINANTI
 CAPITOLO II MATRICI E DETERMINANTI PARTE STORICA Il concetto di matrice (dal latino matrix o mater) fu introdotto da James Joseph Silvester (84-9) in An essay on canonical forms (Londra, 85) per indicare
CAPITOLO II MATRICI E DETERMINANTI PARTE STORICA Il concetto di matrice (dal latino matrix o mater) fu introdotto da James Joseph Silvester (84-9) in An essay on canonical forms (Londra, 85) per indicare
Introduzione all algebra delle matrici. Appunti a cura di Lara Ercoli
 Introduzione all algebra delle matrici ppunti a cura di Lara Ercoli Indice Definizioni 3. Matrici particolari............................ 4 2 Operazioni con le matrici 8 2. Somma di matrici.............................
Introduzione all algebra delle matrici ppunti a cura di Lara Ercoli Indice Definizioni 3. Matrici particolari............................ 4 2 Operazioni con le matrici 8 2. Somma di matrici.............................
il determinante che si ottiene da A, sopprimendo la i - esima riga e la j - esima colonna. Si definisce complemento algebrico dell'elemento a ij
 Determinanti Sia data la matrice quadrata a... a n a a n =...... a... a n nn Chiamiamo determinante di il numero det o che ad essa viene associato. det = a a... a... a... a n n n... a nn Un generico elemento
Determinanti Sia data la matrice quadrata a... a n a a n =...... a... a n nn Chiamiamo determinante di il numero det o che ad essa viene associato. det = a a... a... a... a n n n... a nn Un generico elemento
PreCorso di Matematica - PCM Corso M-Z
 PreCorso di Matematica - PCM Corso M-Z DOCENTE: M. Auteri Outline Docente: Auteri PreCorso di Matematica 2016 2 Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti
PreCorso di Matematica - PCM Corso M-Z DOCENTE: M. Auteri Outline Docente: Auteri PreCorso di Matematica 2016 2 Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti
Corso di Matematica e Statistica 3 Algebra delle matrici. Una tabella rettangolare: la matrice. Una tabella rettangolare: la matrice
 Pordenone Corso di Matematica e Statistica 3 Algebra delle UNIVERSITAS STUDIORUM UTINENSIS Giorgio T. Bagni Facoltà di Scienze della Formazione Dipartimento di Matematica e Informatica Università di Udine
Pordenone Corso di Matematica e Statistica 3 Algebra delle UNIVERSITAS STUDIORUM UTINENSIS Giorgio T. Bagni Facoltà di Scienze della Formazione Dipartimento di Matematica e Informatica Università di Udine
APPLICAZIONI. Im f = {b B a A tale che f (a) = b}.
 APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
MATRICI E VETTORI APPROFONDIMENTO PER IL CORSO DI LABORATORIO DI INFORMATICA SARA POLTRONIERI
 MATRICI E VETTORI APPROFONDIMENTO PER IL CORSO DI LABORATORIO DI INFORMATICA SARA POLTRONIERI LE MATRICI DEFINIZIONE: Una matrice è un insieme di numeri disposti su righe e colonne. 1 3 7 M = 2 5 1 M è
MATRICI E VETTORI APPROFONDIMENTO PER IL CORSO DI LABORATORIO DI INFORMATICA SARA POLTRONIERI LE MATRICI DEFINIZIONE: Una matrice è un insieme di numeri disposti su righe e colonne. 1 3 7 M = 2 5 1 M è
Lezione Determinanti
 Lezione 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
Lezione 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
APPUNTI DI ALGEBRA LINEARE
 APPUNTI DI ALGEBRA LINEARE. Definizione Si dice spazio vettoriale (sul campo dei numeri reali R) un insieme V per il quale siano definite l operazione interna di somma (che ad ogni coppia di vettori e
APPUNTI DI ALGEBRA LINEARE. Definizione Si dice spazio vettoriale (sul campo dei numeri reali R) un insieme V per il quale siano definite l operazione interna di somma (che ad ogni coppia di vettori e
Il prodotto tra matrici non è commutativo. Nelle notazioni precedenti, ponendo n = p e m = q si hanno:
 L anello delle matrici Esempio. Siano A = [ ] 0 1 3 0 2 1, B = 1 2 0 0 1 2 3 4, 1 0 calcolare AB e BA. Osservazioni Siano A Mat m,n (K) e B Mat p,q (K). Il prodotto AB è definito se n = p. Si ha AB Mat
L anello delle matrici Esempio. Siano A = [ ] 0 1 3 0 2 1, B = 1 2 0 0 1 2 3 4, 1 0 calcolare AB e BA. Osservazioni Siano A Mat m,n (K) e B Mat p,q (K). Il prodotto AB è definito se n = p. Si ha AB Mat
Appunti su Indipendenza Lineare di Vettori
 Appunti su Indipendenza Lineare di Vettori Claudia Fassino a.a. Queste dispense, relative a una parte del corso di Matematica Computazionale (Laurea in Informatica), rappresentano solo un aiuto per lo
Appunti su Indipendenza Lineare di Vettori Claudia Fassino a.a. Queste dispense, relative a una parte del corso di Matematica Computazionale (Laurea in Informatica), rappresentano solo un aiuto per lo
Esercitazioni di Algebra e Geometria
 Esercitazioni di Algebra e Geometria Anno Accademico 2011 2012 Dott.ssa Elisa Pelizzari e-mail elisa.peli@libero.it Esercitazioni: lunedì 14.30 16.30 venerdì 14.30 16.30 Ricevimento studenti: venerdì 13.00
Esercitazioni di Algebra e Geometria Anno Accademico 2011 2012 Dott.ssa Elisa Pelizzari e-mail elisa.peli@libero.it Esercitazioni: lunedì 14.30 16.30 venerdì 14.30 16.30 Ricevimento studenti: venerdì 13.00
4. Richiami: sistemi lineari e matrici
 4 Richiami: sistemi lineari e matrici Vettori 4a Combinazioni lineari Indichiamo con R n l insieme delle n-uple ordinate di elementi di R, { } R n := x = (x 1, x 2,, x n ) x i R, i = 1,,n Si dice che x
4 Richiami: sistemi lineari e matrici Vettori 4a Combinazioni lineari Indichiamo con R n l insieme delle n-uple ordinate di elementi di R, { } R n := x = (x 1, x 2,, x n ) x i R, i = 1,,n Si dice che x
Si noti che la matrice trasposta A ha lo stesso determinante. Questa proprietà è generale;
 Ottavio Serra Matrici e determinanti In questa nota estenderemo a matrici quadrate di ordine n qualsiasi il concetto di determinante introdotto nelle scuole secondarie per matrici di ordine 2 come tecnica
Ottavio Serra Matrici e determinanti In questa nota estenderemo a matrici quadrate di ordine n qualsiasi il concetto di determinante introdotto nelle scuole secondarie per matrici di ordine 2 come tecnica
Determinante. Elisabetta Colombo. Determinante. Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico ,
 Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2011-2012, 1 n=2 2 3 con le 4 n=2 n=2 con le Ad ogni matrice quadrata A = (a ij ) j=1...n i=1...n di ordine n si può associare
Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2011-2012, 1 n=2 2 3 con le 4 n=2 n=2 con le Ad ogni matrice quadrata A = (a ij ) j=1...n i=1...n di ordine n si può associare
Matrici e sistemi. Geometria. Matrici e operazioni tra matrici. Operazioni elementari e riduzione Sistemi lineari Matrici invertibili Determinante
 Geometria Matrici e sistemi Operazioni elementari e riduzione Sistemi lineari Matrici invertibili Determinante 2 2006 Politecnico di Torino 1 Matrici e sistemi Matrici: definizione e notazioni Somma e
Geometria Matrici e sistemi Operazioni elementari e riduzione Sistemi lineari Matrici invertibili Determinante 2 2006 Politecnico di Torino 1 Matrici e sistemi Matrici: definizione e notazioni Somma e
Geometria BAER I canale Foglio esercizi 2
 Geometria BAER I canale Foglio esercizi Esercizio. ( ) Data la matrice, determinare tutte le matrici X Mat( ) tali che AX = 0 e tutte le matrici Y Mat( ) tali che Y 0. ( ) ( ) ( ) x y x + z y + w Soluzione:
Geometria BAER I canale Foglio esercizi Esercizio. ( ) Data la matrice, determinare tutte le matrici X Mat( ) tali che AX = 0 e tutte le matrici Y Mat( ) tali che Y 0. ( ) ( ) ( ) x y x + z y + w Soluzione:
Capitolo 3 Matrici. Marco Robutti. Facoltà di ingegneria Università degli studi di Pavia. Anno accademico
 Capitolo 3 Matrici Marco Robutti Facoltà di ingegneria Università degli studi di Pavia Anno accademico 2017-2018 Tutorato di geometria e algebra lineare Definizione (Matrice) Una matrice A M R (k, n) è
Capitolo 3 Matrici Marco Robutti Facoltà di ingegneria Università degli studi di Pavia Anno accademico 2017-2018 Tutorato di geometria e algebra lineare Definizione (Matrice) Una matrice A M R (k, n) è
Vettori e matrici. Lorenzo Pareschi. Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara
 Vettori e matrici Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utentiunifeit/lorenzopareschi/ lorenzopareschi@unifeit Lorenzo Pareschi Univ Ferrara
Vettori e matrici Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utentiunifeit/lorenzopareschi/ lorenzopareschi@unifeit Lorenzo Pareschi Univ Ferrara
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA
 UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito C 3/5/25 A. A. 24 25 ) Risolvere il seguente sistema
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito C 3/5/25 A. A. 24 25 ) Risolvere il seguente sistema
G. Parmeggiani, 17/5/2018 Algebra Lineare, a.a. 2017/2018, numero di MATRICOLA PARI
 G Parmeggiani, 17/5/2018 Algebra Lineare, aa 2017/2018, Scuola di Scienze - Corsi di laurea: Studenti: Statistica per l economia e l impresa Statistica per le tecnologie e le scienze numero di MATRICOLA
G Parmeggiani, 17/5/2018 Algebra Lineare, aa 2017/2018, Scuola di Scienze - Corsi di laurea: Studenti: Statistica per l economia e l impresa Statistica per le tecnologie e le scienze numero di MATRICOLA
Introduzione soft alla matematica per l economia e la finanza. Marta Cardin, Paola Ferretti, Stefania Funari
 Introduzione soft alla matematica per l economia e la finanza Marta Cardin, Paola Ferretti, Stefania Funari Capitolo Sistemi di equazioni lineari.8 Il Teorema di Cramer Si consideri un generico sistema
Introduzione soft alla matematica per l economia e la finanza Marta Cardin, Paola Ferretti, Stefania Funari Capitolo Sistemi di equazioni lineari.8 Il Teorema di Cramer Si consideri un generico sistema
MATRICI E OPERAZIONI
 MATRICI E SISTEMI MATRICI E OPERAZIONI Matrici, somma e prodotto (definizioni, esempi, non commutatività del prodotto, legge di annullamento del prodotto Potenze e inverse di matrici quadrate (definizioni
MATRICI E SISTEMI MATRICI E OPERAZIONI Matrici, somma e prodotto (definizioni, esempi, non commutatività del prodotto, legge di annullamento del prodotto Potenze e inverse di matrici quadrate (definizioni
ALGEBRA LINEARE PARTE II
 DIEM sez. Matematica Finanziaria Marina Resta Università degli studi di Genova Dicembre 005 Indice PREMESSA INVERSA DI UNA MATRICE DETERMINANTE. DETERMINANTE DI MATRICI ELEMENTARI................. MATRICI
DIEM sez. Matematica Finanziaria Marina Resta Università degli studi di Genova Dicembre 005 Indice PREMESSA INVERSA DI UNA MATRICE DETERMINANTE. DETERMINANTE DI MATRICI ELEMENTARI................. MATRICI
A titolo di esempio proponiamo la risoluzione del sistema sia con il metodo della matrice inversa sia con il metodo di Cramer.
 ) Trovare le soluzioni del seguente sistema lineare: x+ y+ z = 3x y + z = 0 x + 5y 4z = 5 Osserviamo in primo luogo che il sistema dato è un sistema quadrato di tre equazioni in tre incognite, precisamente
) Trovare le soluzioni del seguente sistema lineare: x+ y+ z = 3x y + z = 0 x + 5y 4z = 5 Osserviamo in primo luogo che il sistema dato è un sistema quadrato di tre equazioni in tre incognite, precisamente
Definizione. In algebra lineare, una matrice è una tabella ordinata di elementi.
 Matrici Definizione In algebra lineare, una matrice è una tabella ordinata di elementi. Algebra lineare Branca della matematica che si occupa dello studio di : vettori, spazi vettoriali, trasformazioni
Matrici Definizione In algebra lineare, una matrice è una tabella ordinata di elementi. Algebra lineare Branca della matematica che si occupa dello studio di : vettori, spazi vettoriali, trasformazioni
, è Det(A) = a 11 a 22 a 12 a 21. ( il determinante della matrice che si ottiene da A. la 1 a riga e la 2 a colonna di A
 G Parmeggiani, 2/12/2013 Algebra Lineare 1 A, corso di laurea SGI, aa 2013/2014 Nota 4: Calcolo di determinanti Sia A una matrice quadrata di ordine n Il determinante di A è un numero che dipende da A
G Parmeggiani, 2/12/2013 Algebra Lineare 1 A, corso di laurea SGI, aa 2013/2014 Nota 4: Calcolo di determinanti Sia A una matrice quadrata di ordine n Il determinante di A è un numero che dipende da A
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA
 UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito B 3/05/005 A. A. 004 005 ) Risolvere il seguente sistema
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito B 3/05/005 A. A. 004 005 ) Risolvere il seguente sistema
A =, c d. d = ad cb. c d A =
 Geometria e Algebra (II), 271112 1 Definizione D ora innanzi, al posto di dire matrice quadrata di tipo n n o matrice quadrata n n diremo matrice quadrata di ordine n o in breve matrice di ordine n Il
Geometria e Algebra (II), 271112 1 Definizione D ora innanzi, al posto di dire matrice quadrata di tipo n n o matrice quadrata n n diremo matrice quadrata di ordine n o in breve matrice di ordine n Il
x n i sima pos. x, y = x T y = x i y i R. i=1
 1 Elementi di Algebra Lineare In questo capitolo introduttivo al corso di Calcolo Numerico per la laurea triennale in Informatica, saranno presentate una serie di definizioni e proprietà di matrici e dei
1 Elementi di Algebra Lineare In questo capitolo introduttivo al corso di Calcolo Numerico per la laurea triennale in Informatica, saranno presentate una serie di definizioni e proprietà di matrici e dei
Esercitazione di Matematica su matrici e sistemi lineari
 Esercitazione di Matematica su matrici e sistemi lineari Notazioni: deta, A T =trasposta di A, A 1 =inversa di A. 1. Si considerino le matrici A, B, C, D denite da 1 0 5 1 A = 0, B = 0 0, C = 0 1 0 6 1
Esercitazione di Matematica su matrici e sistemi lineari Notazioni: deta, A T =trasposta di A, A 1 =inversa di A. 1. Si considerino le matrici A, B, C, D denite da 1 0 5 1 A = 0, B = 0 0, C = 0 1 0 6 1
Algebra lineare. Laboratorio di programmazione e calcolo CdL in Chimica. Pierluigi Amodio
 Algebra lineare Laboratorio di programmazione e calcolo CdL in Chimica Pierluigi Amodio Dipartimento di Matematica Università di Bari pierluigi.amodio@uniba.it http://dm.uniba.it/ amodio A.A. 2016/17 P.
Algebra lineare Laboratorio di programmazione e calcolo CdL in Chimica Pierluigi Amodio Dipartimento di Matematica Università di Bari pierluigi.amodio@uniba.it http://dm.uniba.it/ amodio A.A. 2016/17 P.
Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari
 Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari Antonio Lanteri e Cristina Turrini UNIMI - 2016/2017 Antonio Lanteri e Cristina Turrini (UNIMI - 2016/2017 Elementi di Algebra Lineare
Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari Antonio Lanteri e Cristina Turrini UNIMI - 2016/2017 Antonio Lanteri e Cristina Turrini (UNIMI - 2016/2017 Elementi di Algebra Lineare
Elementi di Algebra Lineare Il determinante
 Elementi di Algebra Lineare Cristina Turrini UNIMI - 2015/2016 Cristina Turrini (UNIMI - 2015/2016) Elementi di Algebra Lineare 1 / 17 index 1 2 Sottomatrici e minori Cristina Turrini (UNIMI - 2015/2016)
Elementi di Algebra Lineare Cristina Turrini UNIMI - 2015/2016 Cristina Turrini (UNIMI - 2015/2016) Elementi di Algebra Lineare 1 / 17 index 1 2 Sottomatrici e minori Cristina Turrini (UNIMI - 2015/2016)
Il determinante. Calcolo del determinante di matrici particolari. matrici di ordine 2: sia. a11 a A = allora
 Calcolo del determinante di matrici particolari matrici di ordine 2: sia allora Esempio. [ ] a11 a A = 12, a 21 a 22 det A = a 11 a 22 a 21 a 12. Calcolare il determinante di [ ] 1 2 A =. 3 4 matrici di
Calcolo del determinante di matrici particolari matrici di ordine 2: sia allora Esempio. [ ] a11 a A = 12, a 21 a 22 det A = a 11 a 22 a 21 a 12. Calcolare il determinante di [ ] 1 2 A =. 3 4 matrici di
Matematica II
 Matematica II 29..0. Somma di due matrici. Siano m ed n due interi positivi fissati. Date due matrici A, B R m n di tipo m n, sommando a ciascun elemento di A il corrispondente elemento di B, si ottiene
Matematica II 29..0. Somma di due matrici. Siano m ed n due interi positivi fissati. Date due matrici A, B R m n di tipo m n, sommando a ciascun elemento di A il corrispondente elemento di B, si ottiene
Le matrici. Sia K un campo con elemento neutro dell addizione 0 ed elemento neutro della moltiplicazione 1.
 Le matrici Sia K un campo con elemento neutro dell addizione 0 ed elemento neutro della moltiplicazione 1. Siano m, n N\{0}. Una matrice m n a coefficienti in K è una tabella di m n elementi di K disposti
Le matrici Sia K un campo con elemento neutro dell addizione 0 ed elemento neutro della moltiplicazione 1. Siano m, n N\{0}. Una matrice m n a coefficienti in K è una tabella di m n elementi di K disposti
08 - Matrici, Determinante e Rango
 Università degli Studi di Palermo Facoltà di Economia CdS Sviluppo Economico e Cooperazione Internazionale Appunti del corso di Matematica 08 - Matrici, Determinante e Rango Anno Accademico 2013/2014 D.
Università degli Studi di Palermo Facoltà di Economia CdS Sviluppo Economico e Cooperazione Internazionale Appunti del corso di Matematica 08 - Matrici, Determinante e Rango Anno Accademico 2013/2014 D.
Richiami di algebra delle matrici a valori reali
 Richiami di algebra delle matrici a valori reali Vettore v n = v 1 v 2. v n Vettore trasposto v n = (v 1, v 2,..., v n ) v n = (v 1, v 2,..., v n ) A. Pollice - Statistica Multivariata Vettore nullo o
Richiami di algebra delle matrici a valori reali Vettore v n = v 1 v 2. v n Vettore trasposto v n = (v 1, v 2,..., v n ) v n = (v 1, v 2,..., v n ) A. Pollice - Statistica Multivariata Vettore nullo o
UNIVERSITA DEGLI STUDI LA SAPIENZA DI ROMA POLO DI RIETI FACOLTA DI INGEGNERIA CORSO DI LAUREA IN INGEGNERIA DELL AMBIENTE E DEL TERRITORIO
 UNIVERSITA DEGLI STUDI LA SAPIENZA DI ROMA POLO DI RIETI FACOLTA DI INGEGNERIA CORSO DI LAUREA IN INGEGNERIA DELL AMBIENTE E DEL TERRITORIO Geometria 9 5 A.A. 5 Cognome Nome Matricola Codice Scrivere in
UNIVERSITA DEGLI STUDI LA SAPIENZA DI ROMA POLO DI RIETI FACOLTA DI INGEGNERIA CORSO DI LAUREA IN INGEGNERIA DELL AMBIENTE E DEL TERRITORIO Geometria 9 5 A.A. 5 Cognome Nome Matricola Codice Scrivere in
Piccola rassegna di Algebra delle Matrici
 Piccola rassegna di Algebra delle Matrici 1 Introduzione Questa nota va intesa semplicemente come un brevissimo sommario di alcuni concetti relativi alle Matrici, che dovete utilizzare nell ambito dello
Piccola rassegna di Algebra delle Matrici 1 Introduzione Questa nota va intesa semplicemente come un brevissimo sommario di alcuni concetti relativi alle Matrici, che dovete utilizzare nell ambito dello
Geometria BIAR Esercizi 2
 Geometria BIAR 0- Esercizi Esercizio. a Si consideri il generico vettore v b R c (a) Si trovi un vettore riga x (x, y, z) tale che x v a (b) Si trovi un vettore riga x (x, y, z) tale che x v kb (c) Si
Geometria BIAR 0- Esercizi Esercizio. a Si consideri il generico vettore v b R c (a) Si trovi un vettore riga x (x, y, z) tale che x v a (b) Si trovi un vettore riga x (x, y, z) tale che x v kb (c) Si
Terminiamo gli esercizi dell ultima lezione. (LUCIDI) Calcolare, se possibile, AC, CA, CH e HC. (LUCIDI)
 Terminiamo gli esercizi dell ultima lezione. (LUCIDI) Esempi Calcolare, se possibile, AC, CA, CH e HC. (LUCIDI) Osservazioni per le matrici quadrate a) Data A M n (K) è possibile definire ricorsivamente
Terminiamo gli esercizi dell ultima lezione. (LUCIDI) Esempi Calcolare, se possibile, AC, CA, CH e HC. (LUCIDI) Osservazioni per le matrici quadrate a) Data A M n (K) è possibile definire ricorsivamente
SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI
 SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI Appunti presi dalle lezioni del prof. Nedo Checcaglini Liceo Scientifico di Castiglion Fiorentino (Classe 4B) January 17, 005 1 SISTEMI LINEARI Se a ik, b i R,
SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI Appunti presi dalle lezioni del prof. Nedo Checcaglini Liceo Scientifico di Castiglion Fiorentino (Classe 4B) January 17, 005 1 SISTEMI LINEARI Se a ik, b i R,
Geometria BAER I canale Foglio esercizi 2
 Geometria BAER I canale Foglio esercizi 2 Esercizio 1. Calcolare il determinante e l inversa (quando esiste) della matrice ( ) cos θ sin θ R θ =, θ [0, 2π] sin θ cos θ Soluzione: Il determinante ( é cos
Geometria BAER I canale Foglio esercizi 2 Esercizio 1. Calcolare il determinante e l inversa (quando esiste) della matrice ( ) cos θ sin θ R θ =, θ [0, 2π] sin θ cos θ Soluzione: Il determinante ( é cos
Lezione 4 - Esercitazioni di Algebra e Geometria - Anno accademico
 Trasformazioni elementari sulle matrici Data una matrice A K m,n definiamo su A le seguenti tre trasformazioni elementari: T : scambiare tra loro due righe (o due colonne) di A; T : sommare ad una riga
Trasformazioni elementari sulle matrici Data una matrice A K m,n definiamo su A le seguenti tre trasformazioni elementari: T : scambiare tra loro due righe (o due colonne) di A; T : sommare ad una riga
Richiami di Algebra Lineare
 Richiami di Algebra Lineare Fabrizio Silvestri December 14, 010 Matrice Sia R il campo dei numeri reali. Si indica con R m n l insieme delle matrici ad elementi reali con m righe ed n colonne. Se A R n
Richiami di Algebra Lineare Fabrizio Silvestri December 14, 010 Matrice Sia R il campo dei numeri reali. Si indica con R m n l insieme delle matrici ad elementi reali con m righe ed n colonne. Se A R n
TEMPUS PECUNIA EST COLLANA DI MATEMATICA PER LE SCIENZE ECONOMICHE FINANZIARIE E AZIENDALI
 TEMPUS PECUNIA EST COLLANA DI MATEMATICA PER LE SCIENZE ECONOMICHE FINANZIARIE E AZIENDALI 2 Direttore Beatrice VENTURI Università degli Studi di Cagliari Comitato scientifico Umberto NERI University of
TEMPUS PECUNIA EST COLLANA DI MATEMATICA PER LE SCIENZE ECONOMICHE FINANZIARIE E AZIENDALI 2 Direttore Beatrice VENTURI Università degli Studi di Cagliari Comitato scientifico Umberto NERI University of
Sistemi II. Sistemi II. Elisabetta Colombo
 Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2011-2012, http://users.mat.unimi.it/users/colombo/programmabio.html 1 2 3 con R.C.+ o 1.10 Rango massimo e determinante con R.C.+
Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2011-2012, http://users.mat.unimi.it/users/colombo/programmabio.html 1 2 3 con R.C.+ o 1.10 Rango massimo e determinante con R.C.+
Determinante, autovalori e autovettori
 Determinante, autovalori e autovettori Lorenzo Pareschi Dipartimento di Matematica, Universitá di Ferrara http://wwwlorenzopareschicom lorenzopareschi@unifeit Lorenzo Pareschi (Univ Ferrara) Determinante,
Determinante, autovalori e autovettori Lorenzo Pareschi Dipartimento di Matematica, Universitá di Ferrara http://wwwlorenzopareschicom lorenzopareschi@unifeit Lorenzo Pareschi (Univ Ferrara) Determinante,
Matrici quadrate particolari
 Matrici quadrate particolari Sia A Mn(K) una matrice quadrata. Gli elementi (a 1,1, a 2,2,, a n,n ) costituiscono la diagonale principale di A. Gli elementi (a 1,n, a 2,n-1,, a n-1,2, a n,1 ) costituiscono
Matrici quadrate particolari Sia A Mn(K) una matrice quadrata. Gli elementi (a 1,1, a 2,2,, a n,n ) costituiscono la diagonale principale di A. Gli elementi (a 1,n, a 2,n-1,, a n-1,2, a n,1 ) costituiscono
1.1 Matrici a coefficienti in R. Vi sono alcuni casi particolari che vale la pena evidenziare:
 Lezione Matrici a coefficienti in R Definizione Siano m, n Z numeri interi positivi Una matrice m n acoefficientiinrèuninsiemedimn numeri reali disposti su m righe ed n colonne circondata da parentesi
Lezione Matrici a coefficienti in R Definizione Siano m, n Z numeri interi positivi Una matrice m n acoefficientiinrèuninsiemedimn numeri reali disposti su m righe ed n colonne circondata da parentesi
I determinanti. a11 a A = 12 a 21 a 22
 I determinanti. Queste note, basate sugli appunti delle lezioni, riepilogano rapidamente la definizione e le proprietà del determinante. Vengono inoltre illustrati i metodi di calcolo e alcune dimostrazioni.
I determinanti. Queste note, basate sugli appunti delle lezioni, riepilogano rapidamente la definizione e le proprietà del determinante. Vengono inoltre illustrati i metodi di calcolo e alcune dimostrazioni.
Metodi Matematici per l Economia anno 2017/2018 Gruppo B
 Metodi Matematici per l Economia anno 2017/2018 Gruppo B Docente: Giacomo Dimarco Dipartimento di Matematica e Informatica Università di Ferrara https://sites.google.com/a/unife.it/giacomo-dimarco-home-page/
Metodi Matematici per l Economia anno 2017/2018 Gruppo B Docente: Giacomo Dimarco Dipartimento di Matematica e Informatica Università di Ferrara https://sites.google.com/a/unife.it/giacomo-dimarco-home-page/
DETERMINANTE DI MATRICI QUADRATE
 DETERMINANTE DI MATRICI QUADRATE Definizioni e Proprietà 12 Novembre 2015 Pietro Pennestrì pennestri1694905@studentiuniroma1it Università di Roma Sapienza SOMMARIO 1 Introduzione 11 Cenni Storici 12 Definizione
DETERMINANTE DI MATRICI QUADRATE Definizioni e Proprietà 12 Novembre 2015 Pietro Pennestrì pennestri1694905@studentiuniroma1it Università di Roma Sapienza SOMMARIO 1 Introduzione 11 Cenni Storici 12 Definizione
Lezione 11. Somma di matrici Prodotto di una matrice per uno scalare Prodotto di matrici Determinante Sistemi lineari in forma matriciale
 Lezione Somma di matrici Prodotto di una matrice per uno scalare Prodotto di matrici Determinante Sistemi lineari in forma matriciale Matrici. Somma Date due matrici n x m, A = A ij e B = B ij, con i =,,,
Lezione Somma di matrici Prodotto di una matrice per uno scalare Prodotto di matrici Determinante Sistemi lineari in forma matriciale Matrici. Somma Date due matrici n x m, A = A ij e B = B ij, con i =,,,
a.a MATEMATICA GENERALE: SISTEMI LINEARI E MATRICI
 aa 2012-2013 MATEMATICA GENERALE: SISTEMI LINEARI E MATRICI 1 Sistemi di equazioni lineari Definizione 11 i Un equazione lineare nelle indeterminate (o incognite X 1,, X 1 m a coefficienti interi (o razionali,
aa 2012-2013 MATEMATICA GENERALE: SISTEMI LINEARI E MATRICI 1 Sistemi di equazioni lineari Definizione 11 i Un equazione lineare nelle indeterminate (o incognite X 1,, X 1 m a coefficienti interi (o razionali,
Sistemi di equazioni lineari
 Sistemi di equazioni lineari Siano X 1,, X n indeterminate Un equazione lineare (o di primo grado) nelle incognite X 1,, X n a coefficienti nel campo K è della forma a 1 X 1 + + a n X n = b, a i, b K,
Sistemi di equazioni lineari Siano X 1,, X n indeterminate Un equazione lineare (o di primo grado) nelle incognite X 1,, X n a coefficienti nel campo K è della forma a 1 X 1 + + a n X n = b, a i, b K,
1 Introduzione alle matrici quadrate 2 2 a coefficienti in R.
 1 Introduzione alle matrici quadrate 2 2 a coefficienti in R Per introdurre il concetto di matrice, a 2 righe e 2 colonne, iniziamo col considerare griglie o tabelle di numeri Gli elementi della griglia,
1 Introduzione alle matrici quadrate 2 2 a coefficienti in R Per introdurre il concetto di matrice, a 2 righe e 2 colonne, iniziamo col considerare griglie o tabelle di numeri Gli elementi della griglia,
Matematica II,
 Matematica II,.05.04 Diamo qui la nozione di determinante di una matrice quadrata, le sue prime proprieta, e ne deriviamo una caratterizzazione delle matrici non singolari e una formula per l inversa di
Matematica II,.05.04 Diamo qui la nozione di determinante di una matrice quadrata, le sue prime proprieta, e ne deriviamo una caratterizzazione delle matrici non singolari e una formula per l inversa di
Corso di Geometria BIAR, BSIR Esercizi 2: soluzioni
 Corso di Geometria 2- BIAR, BSIR Esercizi 2: soluzioni Esercizio Calcolare il determinante della matrice 2 3 : 3 2 a) con lo sviluppo lungo la prima riga, b) con lo sviluppo lungo la terza colonna, c)
Corso di Geometria 2- BIAR, BSIR Esercizi 2: soluzioni Esercizio Calcolare il determinante della matrice 2 3 : 3 2 a) con lo sviluppo lungo la prima riga, b) con lo sviluppo lungo la terza colonna, c)
Sui determinanti e l indipendenza lineare di vettori
 Sui determinanti e l indipendenza lineare di vettori 1 Si dice che m vettori v 1, v 2,,v m di R n sono linearmente indipendenti, se una loro combinazione lineare può dare il vettore nullo solo se i coefficienti
Sui determinanti e l indipendenza lineare di vettori 1 Si dice che m vettori v 1, v 2,,v m di R n sono linearmente indipendenti, se una loro combinazione lineare può dare il vettore nullo solo se i coefficienti
Algebra delle matrici
 Algebra delle matrici Metodo di Gauss-Jordan per l inversione di una matrice. Nella lezione scorsa abbiamo visto che un modo per determinare l eventuale inversa di una matrice quadrata A consiste nel risolvere
Algebra delle matrici Metodo di Gauss-Jordan per l inversione di una matrice. Nella lezione scorsa abbiamo visto che un modo per determinare l eventuale inversa di una matrice quadrata A consiste nel risolvere
Applicazioni eliminazione di Gauss
 Applicazioni eliminazione di Gauss. Premessa Nel seguito supporremo sempre di applicare il metodo di eliminazione di Gauss allo scopo di trasformare la matrice del sistema Ax = b in una matrice triangolare
Applicazioni eliminazione di Gauss. Premessa Nel seguito supporremo sempre di applicare il metodo di eliminazione di Gauss allo scopo di trasformare la matrice del sistema Ax = b in una matrice triangolare
0.1 Soluzioni esercitazione IV, del 28/10/2008
 1 0.1 Soluzioni esercitazione IV, del 28/10/2008 Esercizio 0.1.1. Risolvere, usando il teorema di Cramer, i seguenti sistemi lineari 2x + y + z = 0 x + 3z = 1 x y z = 1 kx + y z = 1 x y + 2z = 1 2x + 2y
1 0.1 Soluzioni esercitazione IV, del 28/10/2008 Esercizio 0.1.1. Risolvere, usando il teorema di Cramer, i seguenti sistemi lineari 2x + y + z = 0 x + 3z = 1 x y z = 1 kx + y z = 1 x y + 2z = 1 2x + 2y
COGNOME E NOME MATRICOLA FIRMA. METODI MATEMATICI PER L INGEGNERIA DELL INFORMAZIONE (Comunicazioni Elettronica a.a.
 ..................................................................................................................... COGNOME E NOME MATRICOLA FIRMA METODI MATEMATICI PER L INGEGNERIA DELL INFORMAZIONE
..................................................................................................................... COGNOME E NOME MATRICOLA FIRMA METODI MATEMATICI PER L INGEGNERIA DELL INFORMAZIONE
Capitolo 3. Determinante e rango Permutazioni
 Capitolo 3 Determinante e rango 303 Permutazioni Ricordiamo innanzitutto che, dato un insieme, l insieme S () delle applicazioni biunivoche da in sè stesso, può essere munito di una operazione, indicata
Capitolo 3 Determinante e rango 303 Permutazioni Ricordiamo innanzitutto che, dato un insieme, l insieme S () delle applicazioni biunivoche da in sè stesso, può essere munito di una operazione, indicata
Note per il corso di Geometria e algebra lineare 2009-10 Corso di laurea in Ing. Elettronica e delle Telecomunicazioni
 Note per il corso di Geometria e algebra lineare 009-0 Corso di laurea in Ing. Elettronica e delle Telecomunicazioni Spazi di n-uple e matrici. I prodotti cartesiani RR R e RRR R 3, costituiti dalle coppie
Note per il corso di Geometria e algebra lineare 009-0 Corso di laurea in Ing. Elettronica e delle Telecomunicazioni Spazi di n-uple e matrici. I prodotti cartesiani RR R e RRR R 3, costituiti dalle coppie
MATEMATICA. a.a. 2014/ Sistemi di equazioni lineari
 MATEMATICA a.a. 2014/15 8. Sistemi di equazioni lineari SISTEMI LINEARI Si definisce sistema lineare un sistema di p equazioni di primo grado in q incognite. a11x1 + a12 x2 +... + a1 qxq = k1 a21x1 + a22x2
MATEMATICA a.a. 2014/15 8. Sistemi di equazioni lineari SISTEMI LINEARI Si definisce sistema lineare un sistema di p equazioni di primo grado in q incognite. a11x1 + a12 x2 +... + a1 qxq = k1 a21x1 + a22x2
Giuseppe Accascina. Note del corso di Geometria e Algebra
 Giuseppe Accascina Note del corso di Geometria e Algebra Corso di Laurea Specialistica in Ingegneria Gestionale Anno Accademico 27-28 ii Istruzioni per l uso Faremo spesso riferimento a ciò che è stato
Giuseppe Accascina Note del corso di Geometria e Algebra Corso di Laurea Specialistica in Ingegneria Gestionale Anno Accademico 27-28 ii Istruzioni per l uso Faremo spesso riferimento a ciò che è stato
1. Proprietà della somma di matrici. 1. (A + B) + C = A + (B + C) qualunque. 2. A + B = B + A qualunque siano le matrici
 Matrici R. Notari 1 1. Proprietà della somma di matrici 1. (A + B) + C = A + (B + C) qualunque siano le matrici A, B, C Mat(m, n; K). 2. A + B = B + A qualunque siano le matrici A, B Mat(m, n; K). 3. Sia
Matrici R. Notari 1 1. Proprietà della somma di matrici 1. (A + B) + C = A + (B + C) qualunque siano le matrici A, B, C Mat(m, n; K). 2. A + B = B + A qualunque siano le matrici A, B Mat(m, n; K). 3. Sia
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI
 CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
VETTORI E MATRICI. De nizione 1 Chiamiamo vettore x una n-pla ordinata di numeri reali. x 1 x 2. x n
 VETTORI E MATRICI De nizione 1 Chiamiamo vettore x una n-pla ordinata di numeri reali x 1 x. x n 5 L insieme di tutti i vettori con n componenti reali si indica con R n :I numeri reali si possono pensare
VETTORI E MATRICI De nizione 1 Chiamiamo vettore x una n-pla ordinata di numeri reali x 1 x. x n 5 L insieme di tutti i vettori con n componenti reali si indica con R n :I numeri reali si possono pensare
3. Elementi di Algebra Lineare.
 CALCOLO NUMERICO Francesca Mazzia Dipartimento Interuniversitario di Matematica Università di Bari 3. Elementi di Algebra Lineare. 1 Sistemi lineari Sia A IR m n, x IR n di n Ax = b è un vettore di m componenti.
CALCOLO NUMERICO Francesca Mazzia Dipartimento Interuniversitario di Matematica Università di Bari 3. Elementi di Algebra Lineare. 1 Sistemi lineari Sia A IR m n, x IR n di n Ax = b è un vettore di m componenti.
Riassumiamo le proprietà dei numeri reali da noi utilizzate nel corso di Geometria.
 Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Def. 1. Si chiamano operazioni elementari sulle righe di A le tre seguenti operazioni:
 Facoltà di Scienze Statistiche, Algebra Lineare 1 A, G.Parmeggiani LEZIONE 5 Operazioni elementari sulle righe di una matrice Sia A una matrice m n. Def. 1. Si chiamano operazioni elementari sulle righe
Facoltà di Scienze Statistiche, Algebra Lineare 1 A, G.Parmeggiani LEZIONE 5 Operazioni elementari sulle righe di una matrice Sia A una matrice m n. Def. 1. Si chiamano operazioni elementari sulle righe
Anno 4 Matrice inversa
 Anno 4 Matrice inversa 1 Introduzione In questa lezione parleremo della matrice inversa di una matrice quadrata: definizione metodo per individuarla Al termine della lezione sarai in grado di: descrivere
Anno 4 Matrice inversa 1 Introduzione In questa lezione parleremo della matrice inversa di una matrice quadrata: definizione metodo per individuarla Al termine della lezione sarai in grado di: descrivere
Esercitazioni di Algebra e Geometria
 Esercitazioni di Algebra e Geometria Anno Accademico 2010 2011 Dott.ssa Elisa Pelizzari e-mail elisa.peli@libero.it Esercitazioni: lunedì 14.30 16.30 venerdì 14.30 16.30 Ricevimento studenti: venerdì 13.30
Esercitazioni di Algebra e Geometria Anno Accademico 2010 2011 Dott.ssa Elisa Pelizzari e-mail elisa.peli@libero.it Esercitazioni: lunedì 14.30 16.30 venerdì 14.30 16.30 Ricevimento studenti: venerdì 13.30
LeLing12: Ancora sui determinanti.
 LeLing2: Ancora sui determinanti. Ārgomenti svolti: Sviluppi di Laplace. Prodotto vettoriale e generalizzazioni. Rango e determinante: i minori. Il polinomio caratteristico. Ēsercizi consigliati: Geoling
LeLing2: Ancora sui determinanti. Ārgomenti svolti: Sviluppi di Laplace. Prodotto vettoriale e generalizzazioni. Rango e determinante: i minori. Il polinomio caratteristico. Ēsercizi consigliati: Geoling
Giuseppe Accascina. Note del corso di Geometria e Algebra
 Giuseppe Accascina Note del corso di Geometria e Algebra Corso di Laurea Specialistica in Ingegneria Gestionale Anno Accademico 26-27 ii Istruzioni per l uso Faremo spesso riferimento a ciò che è stato
Giuseppe Accascina Note del corso di Geometria e Algebra Corso di Laurea Specialistica in Ingegneria Gestionale Anno Accademico 26-27 ii Istruzioni per l uso Faremo spesso riferimento a ciò che è stato
Riassumiamo le proprietà dei numeri reali da noi utilizzate nel corso di Geometria.
 Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
