Focometria Relazione sperimentale
|
|
|
- Angelo Micheli
- 9 anni fa
- Visualizzazioni
Transcript
1 1 Relazione sperimentale Lo scopo di questa esperienza è quello di ottenere la distanza focale di lenti convergenti e divergenti mediante differenti approcci di misura. Inizialmente considereremo le lenti in approssimazione di lenti sottili, successivamente invece in approssimazione di lenti spesse. Richiami di ottica Le leggi di ottica in approssimazione di lenti sottili che verranno utilizzate per i vari metodi di misura: dove p è la distanza tra la lente e l oggetto, q è la distanza tra la lente e l immagine e f è la focale della lente. dove l è l altezza reale dell oggetto, l' è l altezza dell immagine dell oggetto prodotta sullo schermo e G è l ingrandimento laterale. dove D e la distanza tra oggetto e schermo e L e la distanza tra le due posizioni in cui la lente fornisce un immagine nitida sullo schermo. I metodi di misura della distanza focale utilizzati sono i seguenti: I. Metodo delle distanze coniugate. Si determini il valore della distanza focale della lente ponendo la stessa a una distanza p dalla nostra fenditura (ovvero l oggetto) e si sposti quindi lo schermo lungo il binario finché non sia possibile mettere a fuoco la fenditura. Misurando la distanza tra la lente e lo schermo, ovvero q, tramite la legge (1), si ricava la distanza focale f. II. Metodo dell ingrandimento. Si fissi la distanza p tra l oggetto e la lente e si sposti lo schermo fino al raggiungimento della messa a fuoco. Si proceda all acquisizione delle altezze delle fenditura reale e della fenditura immagine, denotandole rispettivamente con l e l' e da ciò si calcoli l ingrandimento laterale G tramite (2) e successivamente la distanza focale f tramite (3). III. Metodo di Bessel. Si fissi la distanza D tra schermo e fenditura e si misurino le due posizioni in cui si vede in maniera nitida l immagine della fenditura sullo schermo. Si è quindi in grado di ottenere il valore della focale semplicemente sfruttando la (4), dove L è la distanza tra le due posizioni menzionate poc anzi. I primi tre metodi descritti richiedono la misura della distanza tra la fenditura (o lo schermo) e il centro della lente, dato ben definito se la lente è sottile, ovvero se lo spessore è trascurabile (2) (3) (4) (1) Pagina 1 di 6
2 2 rispetto ai suoi raggi di curvatura. Le lenti che verranno utilizzate in questo esperimento sono invece lenti spesse e quindi imprecisione è evidentemente non trascurabile. Il metodo di Bessel elimina però gran parte dell incertezza sul valore di f, in quanto vengono utilizzate nel conteggio solo quantità differenziali. Bisogna tuttavia avere l accortezza di mantenere una distanza tra l oggetto e lo schermo maggiore o al più uguale a 4f, come risulta evidente dal determinante del polinomio di secondo grado dell equazione Lenti sottili e lenti spesse L esperienza di laboratorio avverrà principalmente in approssimazione di lenti sottili, in quanto lo spessore è molto inferiore rispetto al raggio di curvatura; tuttavia questa semplificazione sarà assunta a solo scopo di rapida verifica della correttezza dell acquisizione dati, a cui dovrà seguire necessariamente una rielaborazione dei dati raccolti in chiave di lenti spesse. Al fine di poter effettuare questi ultimi calcoli dovremo essere a conoscenza delle posizioni dei piani principali della lente che stiamo analizzando, grandezze dipendenti dai. Le posizioni dei piani principali π1 e π2 rispetto ai vertici delle lenti si trovano con le seguenti leggi: (5) (6) dove s è lo spessore della lente, r1 e r2 sono i raggi di curvatura della lente e n è l indice di rifrazione del vetro di cui è fatta la lente. Si noti che le posizioni dei due piani principali sono riferite a due distinti sistemi di riferimento. Le posizioni dei piani focali rispetto ai piani principali sono date da: (7) (8) Utilizzando i dati raccolti con il metodo di Bessel, tramite il metodo iterativo sotto esposto è possibile trovare la distanze focali f delle lenti : Dove ε è la distanza che intercorre tra i piani principali, data da: E n è data dalla relazione(8) invertita, tale che n risulti essere: Pagina 2 di 6
3 3 Per far ciò è stato implementato un algoritmo che, simulando questa iterazione, invia in output i risultati della convergenza dello stesso. Apparato sperimentale L apparato sperimentale è composto da: una lente convergente piano-convessa; una lente divergente piano-concava; supporti mobili per le lenti e lo schermo; una sorgente di luce bianca sul cui vetro anteriore è stilizzata una figura simmetrica, da proiettare sullo schermo; uno schermo per raccogliere l immagine; un binario dotato di scala millimetrata; campioni di aste allungabili; un calibro; uno sferometro, atto alla stima del raggio di curvatura delle lenti. Lo sferometro è essenzialmente costituito da un sostegno o treppiede sul centro del quale può ruotare una vite micrometrica. Le punte del treppiede sono poste ai vertici di un triangolo equilatero giacente su un piano perpendicolare alla direzione di avanzamento della vite, ma i piedini dello strumento a nostra disposizione non sono perfettamente perpendicolari al piano di appoggio, quindi viene a mancare il presupposto che sono poste ai vertici di un triangolo equilatero. Questo causerà una scarsa precisione delle misure che andremo ad effettuare. Sensibilità degli strumenti: Misure effettuate col calibro: cm; Misure effettuate con la scala millimetrica: 0,05 cm; Misure effettuate con lo sferometro: 0,005 cm. Procedimento sperimentale La prima misura richiesta è quella delle distanze reciproche tra la fenditura, la lente e lo schermo; a questo proposito si è scelta l accortezza di utilizzare la scala millimetrata sul binario su cui sono montati i supporti,al fine di evitare eventuali scomode nonché imprecise misurazioni acquisite con un metro esterno. Tuttavia, pur essendo comoda per effettuare le misurazioni, essa non esprime le distanze effettive tra gli oggetti da analizzare,bensì quelle tra le basi dei rispettivi supporti. E stato quindi preso un campione di un asta allungabile rigida, misurata con il calibro la sua lunghezza e posta successivamente tra fenditura-lente, lente-schermo e fenditura-schermo. La lettura sul binario millimetrato delle misure unita alla conoscenza dell effettiva distanza degli oggetti fornisce il fattore di conversione tra le due. Si procede quindi a misurare la distanza focale della lente convergente (utilizzando i tre metodi descritti prima). Una volta terminata questa procedura,si accoppia (accostando il lato piano delle rispettive lenti) la lente convergente di focale Pagina 3 di 6
4 4 appena calcolata con la lente divergente,ottenendo così una lente spessa di distanza focale complessiva (5) Dove fc è la distanza focale della lente convergente, fd quella della lente divergente e D l eventuale distanza tra le lenti ( se le due lenti sono poste a contatto, come nel nostro caso, D risulta nullo). Dato che a questo punto la lente equivalente ottenuta è notevolmente spessa, si è ritenuto ragionevole utilizzare solamente il metodo di Bessel, unico tra tutti ad essere indipendente dalle posizioni effettive dei centri di curvatura delle lenti;da ciò, sfruttando il valore della focale della lente convergente precedentemente calcolato, invertendo la legge (5) si ottiene il valore della focale fd della lente divergente. Per applicare il metodo iterativo necessario per l approssimazione di lente spessa è necessario calcolare il raggio di curvatura delle lenti tramite lo sferometro. A tale scopo si stabilisce prima di tutto il valore dello zero dello sferometro, posizionandolo su una superficie piatta (ad es. sul banco di lavoro) e leggendo sulla scala il valore corrispondente;una volta fatto ciò, se lo sferometro risulta ben funzionante si procede con la misura mediante il calibro delle distanze l tra i tre piedi dello sferometro stesso e, sempre a partire dal valore letto sulla scala dello strumento (rappresentativo del dislivello tra l altezza del piede centrale con i tre piedi laterali) si ricava il raggio di curvatura della lente, tramite dalla seguente relazione: Lente convergente approssimazione di lente sottile Metodo delle distanze coniugate p (cm) σp (cm) q (cm) σq (cm) f (cm) σf (cm) 8,52 90,76 7,79 0,06 9,12 51,16 7,74 0,05 8,42 110,86 7,82 0,06 9,44 50,16 7,94 0,05 11,42 22,91 7,62 10,65 23,71 7,48 valore medio: f = 7,68+-0,02 cm OSS: di seguito dove non specificato tutte le misure sono da intendersi in centimetri Metodo dell ingrandimento l σ l l' σ l' p σ p G σ G f σ f 1,044 1,044 1,044 6,224 14,688 2,334 9,12 8,42 11,42 5,96 14,06 2,23 0,001 7,8 7,86 7,88 0,06 0,05 Valore medio: f = 7,85± cm Pagina 4 di 6
5 5 Metodo di Bessel D σ D L σ L f σ f 3 42,55 7, ,2 7, ,5 7, ,1 7, ,35 7, ,45 7, ,58 7,36 Valore medio: f = 7,42±0,02 cm Lente divergente approssimazione di lente sottile Metodo di Bessel D σ D L σ L ,9 23,3 82,2 61,2 22,9 Valore medio: 15,51±0,01 cm 15,59 15,45 15,78 15,5 15,52 0,02 0,02 Valore medio della distanza focale della sola lente divergente: fd =-14,22± cm Lente convergente lente spessa I dati relativi allo sferometro sono riportati di seguito (zero della scala, distanza l tra i piedi),uniti ai dati relativi alla lente convergente, quali spessore, altezza h della faccia convessa, raggio r di curvatura: zero σ zero l σ l s σ s h σ h r σ r 0,005 3,623 1,1 0,571 0,005 3,54 Inserendo questi dati nel algoritmo iterativo e tenendo presente la caratteristica di pianoconvessità della lente ( r1=r e r2= ) si ottengono i seguenti valori: D L r1 r2 s f n 42,55 3,54 1,1 7, ,2 3,54 1,1 7, ,5 3,54 1,1 7, ,1 3,54 1,1 7, ,35 3,54 1,1 7, ,45 3,54 1,1 7, , , , , , , , , , , , , Pagina 5 di 6
6 6 83,58 3,54 1,1 7, , , Da cui i valore medi sono: fc = 7,48987 cm n =1, cm = 0, cm Lente divergente lente spessa Riportiamo quindi I risultati relativi alla lente divergente,dove s rappresenta lo spessore della lente, h l altezza della faccia concava e r il raggio di curvatura: s σ s h σ h r σ r 0,510 0,005 0,279 0,005 5,83 0,13 Considerando infine il sistema come costituito dall accoppiamento della lente convergente e della lente divergente è possibile calcolare sua distanza focale sfruttando sempre l algoritmo iterativo. La distanza focale fd della lente divergente può così essere calcolata tramite la (5), in cui D rappresenta la distanza tra i piani principali relativi alle facce piane delle due lenti a contatto: dove sc e sd rappresentano rispettivamente gli spessori della lente convergente e di quella divergente e n è l indice di rifrazione del vetro, ipotizzata uguale per le due lenti. Da ciò si ottiene che la distanza focale della lente divergente vale: ottenendo quindi i seguenti risultati D L r1 r2 s n 60,9 3,54-5,38 1,61 15, ,3 3,54-5,38 1,61 15, ,2 3,54-5,38 1,61 15, ,2 3,54-5,38 1,61 15, ,9 3,54-5,38 1,61 15,5623 1, , , , , , , , ,1661 0, Da cui i valore medi sono: = 15,61967 cm n = 1,139797cm = 0, cm e fd = - 11,6763 cm Conclusioni In definitiva, risulta evidente che il metodo più efficace per misurare le distanze focali delle lenti e dei sistemi di lenti sia il metodo di Bessel poiché, in quanto differenziale, risente nettamente di meno degli errori di posizionamento assoluto dei componenti sul banco ottico; è sufficiente un accurata misura di spostamento per ottenere la focale con una discreta precisione. Pagina 6 di 6
1 S/f. M = A t = A + CT = 1 S f
 Ot Una lente sottile con focale f 50 mm è utilizzata per proiettare su di uno schermo l immagine di un oggetto posto a 5 m. SI determini la posizione T dello schermo e l ingrandimento che si ottiene La
Ot Una lente sottile con focale f 50 mm è utilizzata per proiettare su di uno schermo l immagine di un oggetto posto a 5 m. SI determini la posizione T dello schermo e l ingrandimento che si ottiene La
Esperienza n 1: LENTI
 NOZIONI TEORICHE DI BASE: Approssimazione di Gauss Diottro sferico Lenti sottili Sistema di lenti Distribuzione gaussiana Propagazione degli errori Test di Student Esperienza n : LENTI Lente sottile convergente
NOZIONI TEORICHE DI BASE: Approssimazione di Gauss Diottro sferico Lenti sottili Sistema di lenti Distribuzione gaussiana Propagazione degli errori Test di Student Esperienza n : LENTI Lente sottile convergente
MISURA DELLA DISTANZA FOCALE DI UNA LENTE CONVERGENTE
 MISURA DELLA DISTANZA FOCALE DI UNA LENTE CONVERGENTE La distanza focale f di una lente convergente sottile è data dalla formula: da cui 1 f = 1 p + 1 q f = pq p + q dove p e q sono, rispettivamente, le
MISURA DELLA DISTANZA FOCALE DI UNA LENTE CONVERGENTE La distanza focale f di una lente convergente sottile è data dalla formula: da cui 1 f = 1 p + 1 q f = pq p + q dove p e q sono, rispettivamente, le
d >> λ rettilinea raggio luminoso riflessione rifrazione
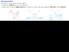 Ottica geometrica Proprietà più macroscopiche della luce d >> λ Propagazione rettilinea della luce (no diffrazione) Fondamentale concetto di raggio luminoso il cui percorso è determinato dalle leggi della
Ottica geometrica Proprietà più macroscopiche della luce d >> λ Propagazione rettilinea della luce (no diffrazione) Fondamentale concetto di raggio luminoso il cui percorso è determinato dalle leggi della
Esercizi di Ottica. Università di Cagliari Laurea Triennale in Biologia Corso di Fisica
 Università di Cagliari Laurea Triennale in Biologia Corso di Fisica Esercizi di Ottica 1. Un fascio di luce di lunghezza λ passa attraverso una fenditura rettangolare di larghezza a. La sua immagine viene
Università di Cagliari Laurea Triennale in Biologia Corso di Fisica Esercizi di Ottica 1. Un fascio di luce di lunghezza λ passa attraverso una fenditura rettangolare di larghezza a. La sua immagine viene
I esonero di Ottica Geometria a.a compito A
 I esonero di Ottica Geometria a.a. 2016-17 compito A Un onda elettromagnetica piana con frequenza 5x10 12 Hz entra con incidenza normale in un mezzo spesso 10 Km. Sapendo che la luce impiega un tempo t=50
I esonero di Ottica Geometria a.a. 2016-17 compito A Un onda elettromagnetica piana con frequenza 5x10 12 Hz entra con incidenza normale in un mezzo spesso 10 Km. Sapendo che la luce impiega un tempo t=50
o i Π = Π La forma generale è: n1/o + nu/i = n1/f1 = nu/f2 dove nu = indice di rifrazione dell ultimo mezzo Pertanto f1/f2 = n1/nu 1
 Richiami di ottica geometrica: Sistema diottrico: successione di mezzi omogenei, diversamente rifrangenti, in genere delimitati da superfici sferiche Centrato: i centri di curvatura giacciono sull asse
Richiami di ottica geometrica: Sistema diottrico: successione di mezzi omogenei, diversamente rifrangenti, in genere delimitati da superfici sferiche Centrato: i centri di curvatura giacciono sull asse
Misure della lunghezza focale di una lente
 Padova, Gennaio 2004 Misure della lunghezza focale di una lente Cognome... Nome... Matricola... Cognome... Nome... Matricola... Cognome... Nome... Matricola... Indicare il numero identificativo e le caratteristiche
Padova, Gennaio 2004 Misure della lunghezza focale di una lente Cognome... Nome... Matricola... Cognome... Nome... Matricola... Cognome... Nome... Matricola... Indicare il numero identificativo e le caratteristiche
SPECCHI. Dalla posizione dell'immagine non emergono raggi luminosi; essa si trova sull'immaginario prolungamento dei raggi di luce riflessa.
 SPECCHI SPECCHI PIANI Per specchio si intende un dispositivo la cui superficie è in grado di riflettere immagini di oggetti posti davanti a essa. Uno specchio è piano se la superficie riflettente è piana.
SPECCHI SPECCHI PIANI Per specchio si intende un dispositivo la cui superficie è in grado di riflettere immagini di oggetti posti davanti a essa. Uno specchio è piano se la superficie riflettente è piana.
Misure di fenomeni di aberrazione di una lente
 Padova, gennaio 00 Misure di fenomeni di aberrazione di una lente Indicare il numero identificativo e le caratteristiche geometriche della lente utilizzata: Lente num. =... Spessore =... Spigolo =... Indice
Padova, gennaio 00 Misure di fenomeni di aberrazione di una lente Indicare il numero identificativo e le caratteristiche geometriche della lente utilizzata: Lente num. =... Spessore =... Spigolo =... Indice
Guida alle esperienze di laboratorio
 LABORATORIO III Corso di Laurea in Fisica (Orientamento Generale) Guida alle esperienze di laboratorio Anno accademico 2008 09 (October 2, 2011) La descrizione di ogni esperienza è pensata come una scheda
LABORATORIO III Corso di Laurea in Fisica (Orientamento Generale) Guida alle esperienze di laboratorio Anno accademico 2008 09 (October 2, 2011) La descrizione di ogni esperienza è pensata come una scheda
Esperimento sull ottica
 Esperimento sull ottica Gruppo: Valentina Sotgiu, Irene Sini, Giorgia Canetto, Federica Pitzalis, Federica Schirru, Jessica Atzeni, Martina Putzu, Veronica, Orgiu e Deborah Pilleri. Teoria di riferimento:
Esperimento sull ottica Gruppo: Valentina Sotgiu, Irene Sini, Giorgia Canetto, Federica Pitzalis, Federica Schirru, Jessica Atzeni, Martina Putzu, Veronica, Orgiu e Deborah Pilleri. Teoria di riferimento:
Lezione 7 Specchi Sferici Concavi, Convessi e Piani
 Lezione 7 Specchi Sferici Concavi, Convessi e Piani 1/13 Per determinare l immagine prodotta da uno specchio è necessario applicare la legge della riflessione di Snell Angolo di incidenza (misurato rispetto
Lezione 7 Specchi Sferici Concavi, Convessi e Piani 1/13 Per determinare l immagine prodotta da uno specchio è necessario applicare la legge della riflessione di Snell Angolo di incidenza (misurato rispetto
Microscopia (specchi, lenti, ecc.) Principio generale per cui si creano le immagini nel nostro occhio:
 Microscopia (specchi, lenti, ecc.) Principio generale per cui si creano le immagini nel nostro occhio: Specchi piani O e un oggetto (= sorgente di luce), nel caso piu semplice e puntiforme Immagine virtuale
Microscopia (specchi, lenti, ecc.) Principio generale per cui si creano le immagini nel nostro occhio: Specchi piani O e un oggetto (= sorgente di luce), nel caso piu semplice e puntiforme Immagine virtuale
ESPERIMENTO SULL OTTICA. L ottica geometrica può essere considerata un metodo per la costruzione di immagini date
 ESPERIMENTO SULL OTTICA Introduzione L ottica geometrica può essere considerata un metodo per la costruzione di immagini date da sistemi ottici quali lenti e specchi. Essa costituisce una teoria approssimata,
ESPERIMENTO SULL OTTICA Introduzione L ottica geometrica può essere considerata un metodo per la costruzione di immagini date da sistemi ottici quali lenti e specchi. Essa costituisce una teoria approssimata,
Effetto convergente di uno specchio concavo: osservazione. Dimostrare la riflessione di raggi paralleli su uno specchio concavo
 ESPERIENZA 7 Effetto convergente di uno specchio concavo: osservazione 1. Argomenti Dimostrare la riflessione di raggi paralleli su uno specchio concavo 2. Montaggio Fig. 1 3. Note al montaggio 3.1 Fissare
ESPERIENZA 7 Effetto convergente di uno specchio concavo: osservazione 1. Argomenti Dimostrare la riflessione di raggi paralleli su uno specchio concavo 2. Montaggio Fig. 1 3. Note al montaggio 3.1 Fissare
ESPERIENZA 8 Effetto divergente di uno specchio convesso: osservazione
 ESPERIENZA 8 Effetto divergente di uno specchio convesso: osservazione 1. Argomenti Osservare la riflessione di raggi paralleli su uno specchio convesso 2. Montaggio Fig.1. 3. Note al montaggio 3.1 Fissare
ESPERIENZA 8 Effetto divergente di uno specchio convesso: osservazione 1. Argomenti Osservare la riflessione di raggi paralleli su uno specchio convesso 2. Montaggio Fig.1. 3. Note al montaggio 3.1 Fissare
Fisica II - CdL Chimica. Formazione immagini Superfici rifrangenti Lenti sottili Strumenti ottici
 Formazione immagini Superfici rifrangenti Lenti sottili Strumenti ottici Ottica geometrica In ottica geometrica si analizza la formazione di immagini assumendo che la luce si propaghi in modo rettilineo
Formazione immagini Superfici rifrangenti Lenti sottili Strumenti ottici Ottica geometrica In ottica geometrica si analizza la formazione di immagini assumendo che la luce si propaghi in modo rettilineo
Fisica II - CdL Chimica. Formazione immagini Superfici rifrangenti Lenti sottili Strumenti ottici
 Formazione immagini Superfici rifrangenti Lenti sottili Strumenti ottici Ottica geometrica In ottica geometrica si analizza la formazione di immagini assumendo che la luce si propaghi in modo rettilineo
Formazione immagini Superfici rifrangenti Lenti sottili Strumenti ottici Ottica geometrica In ottica geometrica si analizza la formazione di immagini assumendo che la luce si propaghi in modo rettilineo
1 LENTE SPESSA Calcoliamo la matrice dei raggi di una lente spessa, ovvero di una lente in cui non sia possibile trascurare la propagazione interna tr
 1 LENTE SPESSA Calcoliamo la matrice dei raggi di una lente spessa, ovvero di una lente in cui non sia possibile trascurare la propagazione interna tra le due rifrazioni. In analogia al caso di lente sottile,
1 LENTE SPESSA Calcoliamo la matrice dei raggi di una lente spessa, ovvero di una lente in cui non sia possibile trascurare la propagazione interna tra le due rifrazioni. In analogia al caso di lente sottile,
5 Lenti e Specchi. Formazione immagini Specchi Superfici rifrangenti Lenti sottili Lenti spessi Punti cardinali
 Laboratorio di didattica della Fisica (III modulo): Metodologie di insegnamento del Laboratorio di Ottica Formazione immagini Specchi Superfici rifrangenti Lenti sottili Lenti spessi Punti cardinali 5
Laboratorio di didattica della Fisica (III modulo): Metodologie di insegnamento del Laboratorio di Ottica Formazione immagini Specchi Superfici rifrangenti Lenti sottili Lenti spessi Punti cardinali 5
OTTICA GEOMETRICA. Ovvero la retta perpendicolare alla superficie riflettente. Figura 1. Figura 2
 OTTICA GEOMETRICA L ottica geometrica si occupa di tutta quella branca della fisica che ha a che fare con lenti, specchi, vetri e cose simili. Viene chiamata geometrica in quanto non interessa la natura
OTTICA GEOMETRICA L ottica geometrica si occupa di tutta quella branca della fisica che ha a che fare con lenti, specchi, vetri e cose simili. Viene chiamata geometrica in quanto non interessa la natura
ONDE ELETTROMAGNETICE OTTICA LEZIONE 33
 ONDE ELETTROMAGNETICE OTTICA LEZIONE 33 L'Ottica Geometrica è la più antica branca dell'ottica: essa studia i fenomeni ottici assumendo che la luce si propaghi mediante raggi rettilinei. Dal punto di vista
ONDE ELETTROMAGNETICE OTTICA LEZIONE 33 L'Ottica Geometrica è la più antica branca dell'ottica: essa studia i fenomeni ottici assumendo che la luce si propaghi mediante raggi rettilinei. Dal punto di vista
Ottica (1/2) Ottica geometrica Lezione 17, 3/12/2018, JW ,
 Ottica (1/2) Ottica geometrica Lezione 17, 3/12/2018, JW 19.1-19.2, 19.5-19.7 1 1. Fronti d'onda e raggi Se lasciamo cadere un sasso in una pozza, dal punto di impatto partono onde circolari. Le circonferenze
Ottica (1/2) Ottica geometrica Lezione 17, 3/12/2018, JW 19.1-19.2, 19.5-19.7 1 1. Fronti d'onda e raggi Se lasciamo cadere un sasso in una pozza, dal punto di impatto partono onde circolari. Le circonferenze
ESPERIMENTO 6: OTTICA GEOMETRICA E DIFFRAZIONE
 ESPERIMENTO 6: OTTICA GEOMETRICA E DIFFRAZIONE Scopo dell esperimento: studiare l ottica geometrica e i fenomeni di diffrazione MATERIALE A DISPOSIZIONE: 1 banco ottico 1 blocco di plexiglass 2 lenti con
ESPERIMENTO 6: OTTICA GEOMETRICA E DIFFRAZIONE Scopo dell esperimento: studiare l ottica geometrica e i fenomeni di diffrazione MATERIALE A DISPOSIZIONE: 1 banco ottico 1 blocco di plexiglass 2 lenti con
a.a. 2005/2006 Laurea Specialistica in Fisica Corso di Fisica Medica 1 Ottica 28/2/2006
 a.a. 2005/2006 Laurea Specialistica in Fisica Corso di Fisica Medica 1 Ottica 28/2/2006 Leggi dell ottica 1. Il raggio incidente, il raggio riflesso e il raggio rifratto giacciono sullo stesso piano 2.
a.a. 2005/2006 Laurea Specialistica in Fisica Corso di Fisica Medica 1 Ottica 28/2/2006 Leggi dell ottica 1. Il raggio incidente, il raggio riflesso e il raggio rifratto giacciono sullo stesso piano 2.
Esercizi di Fisica LB - Ottica
 Esercizi di Fisica LB - Ottica Esercitazioni di Fisica LB per ingegneri - A.A. 2003-2004 Esercizio Un sistema ottico centrato è costituito (da sinistra a destra) da una lente sottile biconcava (l indice
Esercizi di Fisica LB - Ottica Esercitazioni di Fisica LB per ingegneri - A.A. 2003-2004 Esercizio Un sistema ottico centrato è costituito (da sinistra a destra) da una lente sottile biconcava (l indice
Ottica geometrica. Propagazione per raggi luminosi (pennello di luce molto sottile)
 Ottica geometrica Propagazione per raggi luminosi (pennello di luce molto sottile) All interno di un mezzo omogeneo la propagazione e rettilinea: i raggi luminosi sono pertanto rappresentati da tratti
Ottica geometrica Propagazione per raggi luminosi (pennello di luce molto sottile) All interno di un mezzo omogeneo la propagazione e rettilinea: i raggi luminosi sono pertanto rappresentati da tratti
GLI SPECCHI SPECCHI SFERICI (CONCAVI E CONVESSI) E PIANI
 GLI SPECCHI SPECCHI SFERICI (CONCAVI E CONVESSI) E PIANI Specchi sferici In approssimazione parassiale l equazione dei punti coniugati in uno specchio sferico è l: posizione oggetto (S nella figura) l
GLI SPECCHI SPECCHI SFERICI (CONCAVI E CONVESSI) E PIANI Specchi sferici In approssimazione parassiale l equazione dei punti coniugati in uno specchio sferico è l: posizione oggetto (S nella figura) l
Risposte ai quesiti D E H D
 Perugia, dic. 2009/gen. 2010 Risposte ai quesiti 1. Dati i quadrati CD e C D, come in figura, provare che la perpendicolare uscente da alla retta DD passa per il punto medio del segmento quale che sia
Perugia, dic. 2009/gen. 2010 Risposte ai quesiti 1. Dati i quadrati CD e C D, come in figura, provare che la perpendicolare uscente da alla retta DD passa per il punto medio del segmento quale che sia
RIFLESSIONE. Riflessione - 1/17
 RIFLESSIONE Sommario Leggi della riflessione... 2 Specchi piani... 3 Specchi sferici... 6 Lunghezza focale di specchi sferici... 9 Immagine generata da specchi sferici... 11 Ingrandimento generato da specchi
RIFLESSIONE Sommario Leggi della riflessione... 2 Specchi piani... 3 Specchi sferici... 6 Lunghezza focale di specchi sferici... 9 Immagine generata da specchi sferici... 11 Ingrandimento generato da specchi
MISURA DI LUNGHEZZE D ONDA CON UNO SPETTROSCOPIO A RETICOLO DI DIFFRAZIONE
 MISURA DI LUNGHEZZE D ONDA CON UNO SPETTROSCOPIO A RETICOLO DI DIFFRAZIONE Il reticolo di diffrazione può essere utilizzato per determinare la lunghezza d onda di una radiazione monocromatica. Detto d
MISURA DI LUNGHEZZE D ONDA CON UNO SPETTROSCOPIO A RETICOLO DI DIFFRAZIONE Il reticolo di diffrazione può essere utilizzato per determinare la lunghezza d onda di una radiazione monocromatica. Detto d
Lenti. Capitolo Lenti sottili
 Capitolo 3 Lenti 3. Lenti sottili Indichiamo con il termine lente un sistema ottico costituito da materiale trasparente e omogeneo limitato da due superfici che possono essere entrambe sferiche oppure
Capitolo 3 Lenti 3. Lenti sottili Indichiamo con il termine lente un sistema ottico costituito da materiale trasparente e omogeneo limitato da due superfici che possono essere entrambe sferiche oppure
Corso di Laurea in Scienza dei Materiali Laboratorio di Fisica II ESPERIENZA OTT1. Ottica geometrica e polarizzazione
 Scopo dell'esperienza: Corso di Laurea in Scienza dei Materiali Laboratorio di Fisica II ESPERIENZA OTT Ottica geometrica e polarizzazione. Misura della distanza focale di una lente sottile; 2. misura
Scopo dell'esperienza: Corso di Laurea in Scienza dei Materiali Laboratorio di Fisica II ESPERIENZA OTT Ottica geometrica e polarizzazione. Misura della distanza focale di una lente sottile; 2. misura
5 Fondamenti di Ottica
 Laboratorio 2B A.A. 2012/2013 5 Fondamenti di Ottica Formazione immagini Superfici rifrangenti Lenti sottili Lenti spessi Punti cardinali Ottica geometrica In ottica geometrica si analizza la formazione
Laboratorio 2B A.A. 2012/2013 5 Fondamenti di Ottica Formazione immagini Superfici rifrangenti Lenti sottili Lenti spessi Punti cardinali Ottica geometrica In ottica geometrica si analizza la formazione
LABORATORIO DI FISICA I
 UNIVERSITA DEGLI STUDI DI PALERMO CORSO DI LAUREA IN SCIENZE FISICHE A.A. 2018/2019 13 Dicembre 2018 LABORATORIO DI FISICA I RELAZIONE TERZA ESPERIENZA DI LABORATORIO GRUPPO 1 Nigrelli Giulia Valenti Giuseppe
UNIVERSITA DEGLI STUDI DI PALERMO CORSO DI LAUREA IN SCIENZE FISICHE A.A. 2018/2019 13 Dicembre 2018 LABORATORIO DI FISICA I RELAZIONE TERZA ESPERIENZA DI LABORATORIO GRUPPO 1 Nigrelli Giulia Valenti Giuseppe
GLI ERRORI DI MISURA
 Revisione del 26/10/15 ISTITUTO TECNICO INDUSTRIALE V.E.MARZOTTO Valdagno (VI) Corso di Fisica prof. Nardon GLI ERRORI DI MISURA Richiami di teoria Caratteristiche degli strumenti di misura Portata: massimo
Revisione del 26/10/15 ISTITUTO TECNICO INDUSTRIALE V.E.MARZOTTO Valdagno (VI) Corso di Fisica prof. Nardon GLI ERRORI DI MISURA Richiami di teoria Caratteristiche degli strumenti di misura Portata: massimo
Lenti sottili. Lenti convergenti e divergenti
 Lenti sottili Lente: oggetto trasparente con due superfici rifrangenti luce rifrange entrando la lente e rifrange di nuovo uscendo Le due superfici sono approssimativamente sferiche con raggi r " e r #
Lenti sottili Lente: oggetto trasparente con due superfici rifrangenti luce rifrange entrando la lente e rifrange di nuovo uscendo Le due superfici sono approssimativamente sferiche con raggi r " e r #
IIS Moro Dipartimento di matematica e fisica
 IIS Moro Dipartimento di matematica e fisica Obiettivi minimi per le classi prime - Fisica Poiché la disciplina Fisica è parte dell Asse Scientifico Tecnologico, essa concorre, attraverso lo studio dei
IIS Moro Dipartimento di matematica e fisica Obiettivi minimi per le classi prime - Fisica Poiché la disciplina Fisica è parte dell Asse Scientifico Tecnologico, essa concorre, attraverso lo studio dei
Lezione 12. Sistemi di Lenti. TRE Università degli Studi ROMA. Laboratorio di Calcolo per l Ottica 1/9
 Lezione 12 Sistemi di Lenti 1/9 Ingrandimento angolare Abbiamo visto che quando si pone un oggetto tra il fuoco e il centro di una lente semplice, l immagine risulta Virtuale e Ingrandita. L ingrandimento
Lezione 12 Sistemi di Lenti 1/9 Ingrandimento angolare Abbiamo visto che quando si pone un oggetto tra il fuoco e il centro di una lente semplice, l immagine risulta Virtuale e Ingrandita. L ingrandimento
I Esonero di Elementi di Ottica del 13/06/2011
 I Esonero di Elementi di Ottica del 13/06/2011 1) L onda elettromagnetica piana sinusoidale di frequenza f= 100 khz emessa da un sottomarino in superficie, si propaga orizzontalmente sia nell aria che
I Esonero di Elementi di Ottica del 13/06/2011 1) L onda elettromagnetica piana sinusoidale di frequenza f= 100 khz emessa da un sottomarino in superficie, si propaga orizzontalmente sia nell aria che
Sismica a Rifrazione: fondamenti. Sismica rifrazione - Michele Pipan
 Sismica a Rifrazione: fondamenti 1 Sismica a Rifrazione: fondamenti Onde P ed S (2) Velocita delle Onde P: Velocita delle Onde S : Definiamo poi il rapporto di Poisson σ come 2 λ Sismica a Rifrazione:
Sismica a Rifrazione: fondamenti 1 Sismica a Rifrazione: fondamenti Onde P ed S (2) Velocita delle Onde P: Velocita delle Onde S : Definiamo poi il rapporto di Poisson σ come 2 λ Sismica a Rifrazione:
Dati sperimentali Nella serie di 10 misurazioni di tempo effettuate, si sono ottenuti i seguenti valori espressi in secondi:
 ESPERIMENTO DI LABORATORIO DI FISICA MISURE DI TEMPO Obiettivo L obiettivo dell esperimento, oltre che familiarizzare con le misure di tempo, è quello di rivelare gli errori casuali, elaborare statisticamente
ESPERIMENTO DI LABORATORIO DI FISICA MISURE DI TEMPO Obiettivo L obiettivo dell esperimento, oltre che familiarizzare con le misure di tempo, è quello di rivelare gli errori casuali, elaborare statisticamente
MISURE DI MASSA E VOLUME
 MISURE DI MASSA E VOLUME QUALI STRUMENTI SI UTILIZZANO PER MISURARE MASSA E VOLUME? STRUMENTO DI MISURA: Bilancia digitale Grandezza da misurare MASSA Unità di misura della massa grammi Caratteristiche
MISURE DI MASSA E VOLUME QUALI STRUMENTI SI UTILIZZANO PER MISURARE MASSA E VOLUME? STRUMENTO DI MISURA: Bilancia digitale Grandezza da misurare MASSA Unità di misura della massa grammi Caratteristiche
I raggi luminosi. Per secoli si sono contrapposti due modelli della luce. il modello ondulatorio (Christiaan Huygens)
 I raggi luminosi Per secoli si sono contrapposti due modelli della luce il modello corpuscolare (Newton) * la luce è un flusso di particelle microscopiche il modello ondulatorio (Christiaan Huygens) *
I raggi luminosi Per secoli si sono contrapposti due modelli della luce il modello corpuscolare (Newton) * la luce è un flusso di particelle microscopiche il modello ondulatorio (Christiaan Huygens) *
Corso di Laurea in Astronomia. Laurea Triennale DISPENSE DI ESPERIMENTAZIONI DI FISICA 2
 Corso di Laurea in Astronomia Laurea Triennale DISPENSE DI ESPERIMENTAZIONI DI FISICA A.A. 01-013 Indice 1 Introduzione 5 1.1 Indice di rifrazione.............................. 5 1. Riflessione e rifrazione............................
Corso di Laurea in Astronomia Laurea Triennale DISPENSE DI ESPERIMENTAZIONI DI FISICA A.A. 01-013 Indice 1 Introduzione 5 1.1 Indice di rifrazione.............................. 5 1. Riflessione e rifrazione............................
PROGRAMMA di FISICA Classe 2^ I a.s. 2013/14 Docente: Marcella Cotroneo
 PROGRAMMA di FISICA Classe 2^ I a.s. 2013/14 Docente: Marcella Cotroneo RIPASSO di alcune parti del programma svolto l anno scolastico precedente La misura delle grandezze fisiche e la notazione scientifica
PROGRAMMA di FISICA Classe 2^ I a.s. 2013/14 Docente: Marcella Cotroneo RIPASSO di alcune parti del programma svolto l anno scolastico precedente La misura delle grandezze fisiche e la notazione scientifica
La luce Pagina 1 di 12. I raggi di luce
 La luce Pagina di I raggi di luce L ottica è quella parte della fisica che studia la propagazione della luce e la sua interazione con i corpi materiali. L esperienza comune ci consente di affermare che
La luce Pagina di I raggi di luce L ottica è quella parte della fisica che studia la propagazione della luce e la sua interazione con i corpi materiali. L esperienza comune ci consente di affermare che
Interferenza da doppia fenditura
 Corso di Fisica per Scienze Biologiche A.A. 2016-17 Esperienza di laboratorio: OTTICA - ESPERIMENTO DI YOUNG Interferenza da doppia fenditura Nomi degli studenti:......... Data:... Introduzione L'obiettivo
Corso di Fisica per Scienze Biologiche A.A. 2016-17 Esperienza di laboratorio: OTTICA - ESPERIMENTO DI YOUNG Interferenza da doppia fenditura Nomi degli studenti:......... Data:... Introduzione L'obiettivo
Esercizi Ottica: la rifrazione
 Esercizi Ottica: la rifrazione " = = = "# "# 1) Scrivere la legge di snell tra due superfici di indice di rifrazione n1 (mezzo dove parte l onda) e n2 (mezzo dove l onda arriva). Se l indice di rifrazione
Esercizi Ottica: la rifrazione " = = = "# "# 1) Scrivere la legge di snell tra due superfici di indice di rifrazione n1 (mezzo dove parte l onda) e n2 (mezzo dove l onda arriva). Se l indice di rifrazione
Palmer (Micrometro) Profondimetro Sferometro Sonar Telemetro (ottico e laser)
 Misurazioni delle lunghezze La lunghezza è una grandezza fisica estensiva che si misura in modo diretto, per lunghezze comprese nell intervallo che va da 0.01 mm circa fino a un massimo di 10 m circa;
Misurazioni delle lunghezze La lunghezza è una grandezza fisica estensiva che si misura in modo diretto, per lunghezze comprese nell intervallo che va da 0.01 mm circa fino a un massimo di 10 m circa;
RIFLESSIONE TOTALE, DIOTTRO
 RIFLESSIONE TOTALE, DIOTTRO 11.1. In un parallelepipedo di quarzo (n q = 1.553) è scavato un cilindro di raggio R = 10 cm ripieno di acetone (n a = 1.358). Un fascio uniforme di luce di sezione LxL = 20x20
RIFLESSIONE TOTALE, DIOTTRO 11.1. In un parallelepipedo di quarzo (n q = 1.553) è scavato un cilindro di raggio R = 10 cm ripieno di acetone (n a = 1.358). Un fascio uniforme di luce di sezione LxL = 20x20
L errore percentuale di una misura è l errore relativo moltiplicato per 100 ed espresso in percentuale. Si indica con e p e risulta: e ( e 100)%
 UNITÀ L ELBORZIONE DEI DTI IN FISIC 1. Gli errori di misura.. Errori di sensibilità, errori casuali, errori sistematici. 3. La stima dell errore. 4. La media, la semidispersione e lo scarto quadratico
UNITÀ L ELBORZIONE DEI DTI IN FISIC 1. Gli errori di misura.. Errori di sensibilità, errori casuali, errori sistematici. 3. La stima dell errore. 4. La media, la semidispersione e lo scarto quadratico
Laboratorio di Ottica, Spettroscopia, Astrofisica
 Università degli Studi di Palermo Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea in Fisica Progetto Lauree Scientifiche Laboratorio di Ottica, Spettroscopia, Astrofisica Antonio Maggio
Università degli Studi di Palermo Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea in Fisica Progetto Lauree Scientifiche Laboratorio di Ottica, Spettroscopia, Astrofisica Antonio Maggio
1. Misura di lunghezze. Dr. Paola Romano - Università del Sannio
 1. Misura di lunghezze Misure di lunghezze:calibro (1) Il calibro a nonio o ventesimale è costituito da un'asta graduata (6) con un'estremità piegata a becco e da un corsoio (3), recante anch'esso un becco.
1. Misura di lunghezze Misure di lunghezze:calibro (1) Il calibro a nonio o ventesimale è costituito da un'asta graduata (6) con un'estremità piegata a becco e da un corsoio (3), recante anch'esso un becco.
Equilibrio statico sul piano inclinato
 Esperienza 3 Equilibrio statico sul piano inclinato Obiettivi - Comprendere la differenza tra grandezze vettoriali e grandezze scalari attraverso lo studio delle condizioni di equilibrio statico di un
Esperienza 3 Equilibrio statico sul piano inclinato Obiettivi - Comprendere la differenza tra grandezze vettoriali e grandezze scalari attraverso lo studio delle condizioni di equilibrio statico di un
RELAZIONE DELL ESPERIENZA DI LABORATORIO N.3
 RELAZIONE DELL ESPERIENZA DI LABORATORIO N.3 Gruppo 11: Bilardello Naima, Calvaruso Paolo, Daidone Fabio, Marino Martino, Mortillaro Vincenzo, Napoli Leonardo Titolo: Misura del periodo di un oscillatore
RELAZIONE DELL ESPERIENZA DI LABORATORIO N.3 Gruppo 11: Bilardello Naima, Calvaruso Paolo, Daidone Fabio, Marino Martino, Mortillaro Vincenzo, Napoli Leonardo Titolo: Misura del periodo di un oscillatore
Effetto Faraday. Relazione sperimentale
 1 Apparato Sperimentale Relazione sperimentale Al fine3 della realizzazione dell esperienza, sono necessari i seguenti strumenti di lavoro: una lampada di luce al sodio, scelta pressoché monocromatica
1 Apparato Sperimentale Relazione sperimentale Al fine3 della realizzazione dell esperienza, sono necessari i seguenti strumenti di lavoro: una lampada di luce al sodio, scelta pressoché monocromatica
Spettrometro a reticolo e a prisma
 Spettrometro a reticolo e a prisma Marilena Teri, Valerio Toso & Ettore Zaffaroni (gruppo Lu4) 1 Introduzione 1.1 Introduzione ai feomeni in esame Quando la luce viene fatta incidere normalmente alla superficie
Spettrometro a reticolo e a prisma Marilena Teri, Valerio Toso & Ettore Zaffaroni (gruppo Lu4) 1 Introduzione 1.1 Introduzione ai feomeni in esame Quando la luce viene fatta incidere normalmente alla superficie
Compiti per le vacanze Per non dimenticare le cose studiate e imparare qualche cosa di nuovo!!
 a.s. 2014/2015 classe1 C Compiti per le vacanze Per non dimenticare le cose studiate e imparare qualche cosa di nuovo!! Prof.ssa F. BARBIN FISICA (lavori per tutti): Testo: S.Fabbri M.Masini, Phoenomena
a.s. 2014/2015 classe1 C Compiti per le vacanze Per non dimenticare le cose studiate e imparare qualche cosa di nuovo!! Prof.ssa F. BARBIN FISICA (lavori per tutti): Testo: S.Fabbri M.Masini, Phoenomena
S± S [cm 2 ] h± h [cm] 79±3 12,7±0,2 201±5 5,0±0,2 314±6 3,2±0,2 452±8 2,2±0,2
![S± S [cm 2 ] h± h [cm] 79±3 12,7±0,2 201±5 5,0±0,2 314±6 3,2±0,2 452±8 2,2±0,2 S± S [cm 2 ] h± h [cm] 79±3 12,7±0,2 201±5 5,0±0,2 314±6 3,2±0,2 452±8 2,2±0,2](/thumbs/71/64598992.jpg) SOLUZIONI VERIFICA A CLASSI I^L I^F- I^D TESTO Supponiamo di avere svolto il seguente esperimento: si sono presi 4 cilindri di vetro di diametro diverso e si è versato in ciascuno di essi SEMPRE 1 LITRO
SOLUZIONI VERIFICA A CLASSI I^L I^F- I^D TESTO Supponiamo di avere svolto il seguente esperimento: si sono presi 4 cilindri di vetro di diametro diverso e si è versato in ciascuno di essi SEMPRE 1 LITRO
Misura del campo magnetico di un magnete permanente
 1 Relazione sperimentale Abbiamo misurato il campo magnetico nel traferro di un magnete permanente a C mediante il metodo di misura di Felici. Per la misure elettriche di precisione si è ricorso all uso
1 Relazione sperimentale Abbiamo misurato il campo magnetico nel traferro di un magnete permanente a C mediante il metodo di misura di Felici. Per la misure elettriche di precisione si è ricorso all uso
LENTI SOTTILI. Le lenti sottili sono gli strumenti ottici più importanti tra quelli più semplici.
 LENTI SOTTILI Chiamiamo lente un qualsiasi corpo trasparente limitato da due superfici curve o da una superficie piana ed una curva, in grado di trasmettere un fascio di luce focalizzandolo in modo da
LENTI SOTTILI Chiamiamo lente un qualsiasi corpo trasparente limitato da due superfici curve o da una superficie piana ed una curva, in grado di trasmettere un fascio di luce focalizzandolo in modo da
ANNO SCOLASTICO CLASSE II E DISCIPLINA: FISICA DOCENTE: Romio Silvana A. PROGRAMMA
 ANNO SCOLASTICO 2014-2015 CLASSE II E DISCIPLINA: FISICA DOCENTE: Romio Silvana A. PROGRAMMA LE FORZE: Ripasso degli argomenti della classe I: Grandezze scalari e vettoriali, concetto di forza, peso e
ANNO SCOLASTICO 2014-2015 CLASSE II E DISCIPLINA: FISICA DOCENTE: Romio Silvana A. PROGRAMMA LE FORZE: Ripasso degli argomenti della classe I: Grandezze scalari e vettoriali, concetto di forza, peso e
Lezione 22 - Ottica geometrica
 Lezione 22 - Ottica geometrica E possibile, in certe condizioni particolari, prescindere dal carattere ondulatorio della radiazione luminosa e descrivere la propagazione della luce usando linee rette e
Lezione 22 - Ottica geometrica E possibile, in certe condizioni particolari, prescindere dal carattere ondulatorio della radiazione luminosa e descrivere la propagazione della luce usando linee rette e
(a) che relazione sussiste fra A e x? (b) come si modificherebbe tale relazione se il cartoncino non fosse parallelo allo schermo?
 ESERCIZI DI OTTICA PROPAGAZIONE RETTILINEA E OMBRE 1. Una donna che ha gli occhi ad altezza di 1,55m da terra è a distanza di 10m da un albero alto 25m. Sotto quale angolo visuale lo vede? 2. In una stanza
ESERCIZI DI OTTICA PROPAGAZIONE RETTILINEA E OMBRE 1. Una donna che ha gli occhi ad altezza di 1,55m da terra è a distanza di 10m da un albero alto 25m. Sotto quale angolo visuale lo vede? 2. In una stanza
RELAZIONE DELL ESPERIENZA DI LABORATORIO N.2
 RELAZIONE DELL ESPERIENZA DI LABORATORIO N. Gruppo 11: Titolo: taratura di un bilancia Finalità: Bilardello Naima, Calvaruso Paolo, Daidone Fabio, Marino Martino, Mortillaro Vincenzo, Napoli Leonardo -
RELAZIONE DELL ESPERIENZA DI LABORATORIO N. Gruppo 11: Titolo: taratura di un bilancia Finalità: Bilardello Naima, Calvaruso Paolo, Daidone Fabio, Marino Martino, Mortillaro Vincenzo, Napoli Leonardo -
OTTICA DELLA VISIONE. Disegno schematico dell occhio umano
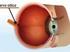 OTTICA DELLA VISIONE Disegno schematico dell occhio umano OTTICA DELLA VISIONE Parametri fisici Raggio di curvatura (cm) Cornea 0.8 Anteriore del cristallino Posteriore del cristallino.0 0.6 Indice di
OTTICA DELLA VISIONE Disegno schematico dell occhio umano OTTICA DELLA VISIONE Parametri fisici Raggio di curvatura (cm) Cornea 0.8 Anteriore del cristallino Posteriore del cristallino.0 0.6 Indice di
ESERCIZI DI OTTICA GEOMETRICA
 ESERCIZI DI OTTICA GEOMETRICA Prima di ogni argomento sono raccolte alcune formule utili, e non banali, per lo svolgimento degli esercizi. Si presuppongono lo studio e la comprensione teorica delle stesse.
ESERCIZI DI OTTICA GEOMETRICA Prima di ogni argomento sono raccolte alcune formule utili, e non banali, per lo svolgimento degli esercizi. Si presuppongono lo studio e la comprensione teorica delle stesse.
I vertici e i lati di ogni poligono vengono detti rispettivamente vertici e spigoli del poliedro.
 1 I poliedri diagonale DEFINIZIONE. Un poliedro è la parte di spazio delimitata da poligoni posti su piani diversi in modo tale che ogni lato sia comune a due di essi. I poligoni che delimitano il poliedro
1 I poliedri diagonale DEFINIZIONE. Un poliedro è la parte di spazio delimitata da poligoni posti su piani diversi in modo tale che ogni lato sia comune a due di essi. I poligoni che delimitano il poliedro
1 p. 1 q 1 R. altrimenti se il mezzo circostante ha un indice di rifrazione n 0. , al posto di n si deve usare
 2 Lenti Le lenti sono costituite da un mezzo rifrangente, di indice di rifrazione n, omogeneo, delimitato da superfici sferiche nel caso in cui il mezzo circostante é l aria: l equazione delle lenti é
2 Lenti Le lenti sono costituite da un mezzo rifrangente, di indice di rifrazione n, omogeneo, delimitato da superfici sferiche nel caso in cui il mezzo circostante é l aria: l equazione delle lenti é
Capitolo 2 Le misure delle grandezze fisiche
 Capitolo 2 Le misure delle grandezze fisiche Gli strumenti di misura Gli errori di misura Il risultato di una misura Errore relativo ed errore percentuale Propagazione degli errori Rappresentazione di
Capitolo 2 Le misure delle grandezze fisiche Gli strumenti di misura Gli errori di misura Il risultato di una misura Errore relativo ed errore percentuale Propagazione degli errori Rappresentazione di
ACUITÀ VISIVA, DIOTTRIE E LENTI CORRETTIVE: TUTTO CIÒ CHE NON SERVE SAPERE PER GUARIRE LA VISTA
 ACUITÀ VISIVA, DIOTTRIE E LENTI CORRETTIVE: TUTTO CIÒ CHE NON SERVE SAPERE PER GUARIRE LA VISTA Ci proponiamo in questo articolo di gettare luce su tre argomenti sempre molto confusi e malcompresi: l acuità
ACUITÀ VISIVA, DIOTTRIE E LENTI CORRETTIVE: TUTTO CIÒ CHE NON SERVE SAPERE PER GUARIRE LA VISTA Ci proponiamo in questo articolo di gettare luce su tre argomenti sempre molto confusi e malcompresi: l acuità
La distribuzione delle frequenze. T 10 (s)
 1 La distribuzione delle frequenze Si vuole misurare il periodo di oscillazione di un pendolo costituito da una sferetta metallica agganciata a un filo (fig. 1). A Figura 1 B Ricordiamo che il periodo
1 La distribuzione delle frequenze Si vuole misurare il periodo di oscillazione di un pendolo costituito da una sferetta metallica agganciata a un filo (fig. 1). A Figura 1 B Ricordiamo che il periodo
-
 STAZIONE TOTALE E costituita dal sistema basetta-base, che viene fissato sulla testa rettificata del treppiede di supporto, dall alidada, un dispositivo a U che si innesta sulla base tramite un perno (attorno
STAZIONE TOTALE E costituita dal sistema basetta-base, che viene fissato sulla testa rettificata del treppiede di supporto, dall alidada, un dispositivo a U che si innesta sulla base tramite un perno (attorno
RELAZIONE DI LABORATORIO DI FISICA ANNO ACCADEMICO
 RELAZIONE DI LABORATORIO DI FISICA ANNO ACCADEMICO 018/019 Esperienza di laboratorio n 19/11/18 Taratura di una bilancia dinamometrica. GRUPPO N 1 Componenti del gruppo: Cirincione Salvatore Pio Vulcanico
RELAZIONE DI LABORATORIO DI FISICA ANNO ACCADEMICO 018/019 Esperienza di laboratorio n 19/11/18 Taratura di una bilancia dinamometrica. GRUPPO N 1 Componenti del gruppo: Cirincione Salvatore Pio Vulcanico
1 Guida alle relazioni di laboratorio
 1 Guida alle relazioni di laboratorio Un aspetto basilare dell attività di laboratorio è quello di imparare a registrare accuratamente tutti i dati sperimentali, così come sono stati misurati, in modo
1 Guida alle relazioni di laboratorio Un aspetto basilare dell attività di laboratorio è quello di imparare a registrare accuratamente tutti i dati sperimentali, così come sono stati misurati, in modo
Problema ( ) = 0,!
 Domanda. Problema ( = sen! x ( è! Poiché la funzione seno è periodica di periodo π, il periodo di g x! = 4. Studio di f. La funzione è pari, quindi il grafico è simmetrico rispetto all asse y. È sufficiente
Domanda. Problema ( = sen! x ( è! Poiché la funzione seno è periodica di periodo π, il periodo di g x! = 4. Studio di f. La funzione è pari, quindi il grafico è simmetrico rispetto all asse y. È sufficiente
Unità di misura di lunghezza usate in astronomia
 Unità di misura di lunghezza usate in astronomia In astronomia si usano unità di lunghezza un po diverse da quelle che abbiamo finora utilizzato; ciò è dovuto alle enormi distanze che separano gli oggetti
Unità di misura di lunghezza usate in astronomia In astronomia si usano unità di lunghezza un po diverse da quelle che abbiamo finora utilizzato; ciò è dovuto alle enormi distanze che separano gli oggetti
