Analisi Matematica II
|
|
|
- Rosa Brunelli
- 6 anni fa
- Visualizzazioni
Transcript
1 2 Analisi Matematica II 2.1. Prova assegnata il 29 febbraio 1984 corso di laurea in Fisica. 1. Rappresentare graficamente l insieme di definizione della funzione reale di due variabili reali (4x f(x,y)= 2 + y 2 16)(x y+ x ) 64 4x 2 y 2 2. Dire quali dei seguenti limiti esistono: Giustificare le risposte. e x3y 1 y 3 1 lim (x,y) (0,0) x 2 + y 2, lim (x,y) (1,1) x 1 lim (x 6 + y 6 x 2 y 3 ). (x,y) 3. Sia g la funzione reale di due variabili reali definita dalla legge g(x, y) = x arctang 1 x 2 y
2 2 Analisi Matematica II a) Dire qual è l insieme di definizione di g. b) Dire se esiste il limite lim g(x, y). (x,y) Giustificare la risposta. c) Provare che esiste una ed una sola funzione f : R 2 R continua in R 2 e coincidente con g in ogni punto dell insieme di definizione di g. d) Provare che f è parzialmente derivabile rispetto ad x in ogni punto di R 2 ecalcolaref x. e) Calcolare, in tutti i punti in cui esiste, la derivata parziale f y. f) Dire se f è parzialmente differenziabile in (0, 0). Giustificare la risposta Prova assegnata il 8 giugno 1984 corso di laurea in Fisica. 1. Sia } f n la successione di funzioni reali f n (x) = log nx + 1 nx 2 x [0, + [, n N. + 1 a) Verificare che la successione } f n converge in [0, + [ e che la convergenza non è uniforme. b ) SiaY un sottoinsieme non vuoto dell intervallo aperto ]0, + [.Dimostrare che la condizione inf Y > 0 è sufficiente affinchè la successione } f n converga uniformemente in Y. c) Dire se tale condizione è anche necessaria. Giustificare la risposta. 2. Sia γ il grafico della restrizione della funzione cos x all intervallo [0, 2π]. Calcolare l integrale curvilineo esteso alla curva γ, orientata nel verso delle ascisse crescenti, della forma differenziale x 4 + y 4 + 2xy(xy 1) (x 2 + y 2 ) 2 dx + x2 y 2 (x 2 + y 2 ) 2 dy. 3. Calcolare il seguente integrale triplo ( ) xy 2 + z2 dxdydz, T x essendo T l insieme T = (x,y,z) R 3 :0 z xy, x 4 x 2 y 2 + z 2 4x 4, 1 x 2 }.
3 Analisi Matematica II Prova assegnata il 29 giugno 1984 corso di laurea in Fisica. 1. Determinare il carattere della serie ( ) n=1 ( 1) n sen 1 n Denotata, per ogni n N, cont n la somma parziale n sima della serie ( ), determinare, al variare di x in ] 1, + [, il carattere della serie di potenze ( ) n=1 T n x n. Dimostrare che la serie ( ) èdivergentea+ per x = 1. Dimostrare che la serie ( ) è oscillante per x< Calcolare il seguente integrale doppio 1 (x 2 + y 2 ) 2 dxdy, essendo D l insieme D D = (x, y) R 2 : x 0,y 0,x 2 + y 2 1 3x 2 y 2 2 } Prova assegnata il 19 luglio 1984 corso di laurea in Fisica. 1. Sia ϕ la soluzione del problema di Cauchy y + 9y + 20y = e 3x sen e x y(log π) = y (log π) = 0 i) Dimostrare che la funzione ϕ è decrescente nel punto x = log π. ii) Esprimere ϕ(x) mediante le funzioni elementari. 2. Sia f la funzione reale di due variabili reali definita in R 2 mediante la posizione f(x,y)= x 2 y 2 + 3xy + 2y (x, y) R 2. a) Determinare gli eventuali punti di estremo relativo per la funzione f.
4 4 Analisi Matematica II b) Calcolare il massimo ed il minimo assoluti della restrizione di f all insieme T = (x, y) R 2 : y x 2,x y 2}. c) Determinare gli eventuali punti di estremo per la funzione f sotto la condizione 3x 2 y + 2xy 3xy 2 2y 2 = Prova assegnata il 29 ottobre 1984 corso di laurea in Fisica. 1. Calcolare un valore approssimato a meno di 10 3 dell integrale 1 0 sen x x dx. 2. Determinare gli eventuali punti di massimo e di minimo relativo della funzione reale di due variabili reali cosh ( x 2 y 3 (x + y 2) ). 3. Calcolare il seguente integrale doppio x x 2 + y 2 dxdy, essendo D l insieme D D = (x, y) R 2 : x 0,y 2 x 2, 2 9 x2 + y 2 1 } Prova assegnata il 19 novembre 1984 corso di laurea in Fisica. 1. Sia T l insieme T = (x,y,z) R 3 : z 0, 1 4x 2 + y 2 + z 2 4 }. a) Verificare che T è misurabile.
5 Analisi Matematica II 5 b ) Calcolare T z 1 dxdydz. 2. Determinare gli eventuali punti di estremo relativo e quelli di estremo assoluto per la funzione reale di due variabili reali ( ) 1 cosh [(x 2 y 2 )(x 2 1)] Dire, giustificando le risposte, quali dei seguenti limiti esistono e xy 1 lim (x,y) (0,0) x 2 + y 2, lim (x 2 + y + 1), (x,y) lim (x 4 + y 2 sen ( 4(x 1) 2 + 9y 2) 2 + 1), lim (x,y) (x,y) (1,0) (x 1) 2 + y Prova assegnata il 11 dicembre 1984 corso di laurea in Fisica. 1. Sia g la funzione di due variabili reali definita mediante la posizione g(x, y) = x 2 1 arctang x y a) Dire qual è l insieme di definizione di g. b) Dire se esiste il limite lim g(x, y). (x,y) Giustificare la risposta. c) Denotato con G l insieme di definizione di g, calcolare al variare di (x 0,y 0 ) in R 2 \ G, il limite lim g(x, y). (x,y) (x 0,y 0 ) d) Provare che esiste una funzione f : R 2 R continua in R 2 etaleche f(x,y)= g(x, y) per ogni (x, y) G. Provare altresì che tale funzione è unica. e) Provare che f è parzialmente derivabile rispetto a x in ogni punto di R 2 e calcolare f x. f) Calcolare, in tutti i punti in cui esiste, la derivata f y. h) Dire se f è differenziabile in (0, 0). Giustificare la risposta.
6 6 Analisi Matematica II 2.8. Prova assegnata il 13 febbraio 1985 corso di laurea in Fisica. 1. Sia γ la curva di equazioni parametriche x = 1 t y = e 2t z = 1/t 2e tu 1 u du t [1, 2]. Dimostrare che γ è regolare e calcolarne la lunghezza. 2. Calcolare il seguente integrale doppio y x dxdy, essendo D l insieme D D = (x, y) R 2 : y 2 x y,9(x 2 + y 2 ) 4 }. 3. Dire se il simbolo con T y x dxdy T = (x, y) R 2 : y 2 x y } ha significato numerico e, in caso affermativo, dirne il valore. 4. Scrivere l equazione differenziale lineare il cui integrale generale in ]0, + [ è y(x) = c 1 e x + c 2 e x + c 3 cos 2x + c 4 sen 2x + log x, dove c 1,c 2,c 3,c 4 sono costanti arbitrarie. Determinare, poi, i valori del parametro a, a R, per i quali esistono integrali y 1 (x) di tale equazione verificanti le condizioni y (v) 1 (1) = a 2,y 1 (1) = 0,y 1 (1) = a.
7 Analisi Matematica II Prova assegnata il 9 luglio 1985 corso di laurea in Matematica. 1. Provare che la successione di funzioni ( ) } 1 cos x n 2 x [ π,π] è convergente, ma non uniformemente convergente. Determinare un sottointervallo di [ π,π] incuisihaconvergenzauniforme. 2. Calcolare il seguente integrale triplo xdxdydz, essendo T l insieme di R 3 definito dalle limitazioni y (x 1) 2 y (x + 1) 2 y 0 x 1 0 z sen x 2 y T Prova assegnata il 19 novembre 1985 corso di laurea in Matematica. 1. Sia a n } una successione di numeri positivi tale che Studiare il carattere delle due serie lim n na n = l>0. n=1 a n, n=1 (a 1 + a 2 + +a n )x 2n,x R. 2. Data la forma differenziale lineare ( ( ) log(x + y) + x ) x + y dx + x + k x + y dy k R determinare k in modo che la forma differenziale ( ) sia esatta ed in tal caso determinarne la primitiva F(x, y) tale che F(0, 1) = 0.
8 8 Analisi Matematica II Prova assegnata il 10 dicembre 1985 corso di laurea in Matematica. 1. Determinare il massimo ed il minimo assoluti della funzione (y log x)(y log x 2 ) definita nell insieme (x, y) R 2 :1 x e, 0 y 1 }. 2. Integrare l equazione differenziale essendo k un parametro reale. y y + 2y = e kx (x + sen kx) Prova assegnata il 13 febbraio 1986 corso di laurea in Matematica. 1. Integrare l equazione differenziale y = y x + ( 2 sen y x + cos y ). x 2. Determinare gli eventuali punti di massimo e di minimo relativo della funzione reale di due variabili reali 2 x2 +2y 2 2x. 3. Integrare per serie la funzione x 2 2 x2 x [0, 1] Prova assegnata il 14 marzo 1986 corso di laurea in Matematica. 1. Calcolare il seguente integrale doppio ydxdy, D
9 Analisi Matematica II 9 essendo D l insieme D = (x, y) R 2 :1 xy 2, 2 (x 2)y 1 }. 2. Determinare gli eventuali punti di massimo e di minimo relativo della funzione reale di due variabili reali y 2 (y 2 + x 2 2x). Determinarne, inoltre, gli eventuali punti di massimo e minimo assoluto Prova assegnata il 9 giugno 1986 corso di laurea in Matematica. 1. Studiare il carattere delle seguenti serie numeriche ( ) ( ) ( ) n n n n Calcolare il seguente integrale doppio 2x 3 y D 4x 2 + 9y 2 dxdy, essendo D l insieme D = (x, y) R 2 :1 4x 2 + 9y 2 9 }. 3. Sia D l insieme di definizione della funzione reale di due variabili reali f(x,y)= log(y + 4) + (x + y) 2 4y. Sia C la chiusura di D esiar la retta di equazione 3x 4y + 4 = 0. i) Disegnare gli insiemi D e C. ii) Provare che nell insieme C esistono punti di minima (risp. massima) distanza dalla retta r. Determinare tali punti. iii) Dire se nell insieme D esistono punti di minima (risp. massima) distanza dalla retta r. Giustificare la risposta.
10 10 Analisi Matematica II Prova assegnata il 10 giugno 1986 corsi di laurea in Ingegneria elettrotecnica, elettronica e meccanica. 1. Determinare il campo di esistenza e gli eventuali punti di massimo e minimo relativi ed assoluti della funzione 3 [ log cos 2 y+log sen2 x ] cos 2 1 y. 2. Calcolare il seguente integrale doppio x log(x 2 + 4y 2 ) y 2 dxdy, essendo D l insieme D D = (x, y) R 2 :1 x 2 + 4y 2 4y }. 3. Determinare lo sviluppo in serie di Fourier della funzione f(x)prolungamento periodico di periodo 2π della funzione x cos x, x [ π,π[ Prova assegnata il 30 giugno 1986 corso di laurea in Matematica. 1. Denotata con f la funzione definita nell aperto A = (x, y) R 2 : (y x 2 ) 2 > 0 } mediante la posizione ( ) f(x,y) = e 1 (y x 2 ) 2, i) dire, giustificando la risposta, se esiste il limite lim f(x,y) ; (x,y) ii) verificare che in ogni punto di A risulta f x (x, y) + 2f y (x, y) = 0;
11 Analisi Matematica II 11 iii) sia v(x,y) la restrizione di f all aperto B = (x, y) R 2 : y<0 }. Determinare la funzione u : B R in modo che la forma differenziale ( ) u(x,y)dx + v(x,y)dy sia esatta in B echerisulti lim u(x, y) = x x R ; y iv) calcolare l integrale curvilineo della forma differenziale ( ) esteso al segmento che ha per estremi i punti della parabola y x = 0di ascissa rispettivamente x = 1ex = 2, orientato nel verso delle ascisse crescenti. 2. Sia C = (x, y) R 2 :4x y 2 5 }. a) Dimostrare che l insieme C è compatto. b) Calcolare il massimo ed il minimo assoluti della funzione (y x 2 ) 2 in C. c) Sia h(x, y) la restrizionedella funzione f definita in ( ) all insiemea C. Verificare che h è limitata. Calcolare sup h einfh, precisando se si tratta di massimo ovvero di minimo. d) Provare che lim f(x,y) (x,y) (x 0,y 0 ) esiste finito per ogni (x 0,y 0 ) R 2. e) Provare che esiste una ed una sola funzione g : R 2 R continua in R 2 e tale da risultare g(x, y) = f(x,y) per ogni (x, y) A. f) Provare che la funzione g è differenziabile nel punto (0, 0) Prova assegnata il 21 luglio 1986 corso di laurea in Matematica. 1. Date le due serie di funzioni n=1 x n2 n 2 2 n2 1 e e xn n n=1 x R,
12 12 Analisi Matematica II dire per quali x esse convergono e per quali convergono uniformemente. Calcolare la funzione somma della seconda serie. 2. Sia data la funzione x y f(x,y)= arctang 1 xy a) Si determini l insieme di definizione E della f esiprovichee èuninsieme aperto. L insieme E è connesso? Si determini la frontiera E di E. b ) Sidicasef èdotataine di estremi finiti, precisando se si tratta di massimo e minimo. c) Si determini l insieme B di tutti i punti P 0 (x 0,y 0 ) E per cui esiste finito il limite seguente lim f(x,y). (x,y) (x 0,y 0 ) Si provi che l insieme B E è aperto connesso. Considerato l insieme E ( E \ B) si dica se esso èchiusooapertooppurenè chiuso nè aperto. E ( E \ B) è internamente connesso? d) Si definisca una nuova funzione g : B E R ponendo f(x,y) se (x, y) E g(x, y) = lim f(u,v) se (x, y) B (u,v) (x,y) Si provi che g è continua in B E ed è ivi dotata di massimo. e) È possibile prolungare g a tutto R 2 in modo che, detta h la funzione prolungamento, h risulti continua in R 2? f) Dire in quali punti di R 2 esistono le derivate g x, g y ed in quali non esistono. 3. Si consideri l equazione differenziale lineare omogenea xy (2x + 2)y + (x + 2)y = 0 x R. i) Trovare due funzioni reali y 1, y 2 definite in tutto R, che siano ivi soluzioni linearmente indipendenti dell equazione data. Provare che il loro determinante wronskiano è diverso da zero se e solo se x 0. Quest ultimo fatto contrasta con quanto studiato sul valore del determinante wronskiano di n soluzioni di certe equazioni differenziali lineari di ordine n?
13 Analisi Matematica II 13 ii) Posto per a 1,a 2,b 1,b 2 R z 1 (x) = a 1 y 1 (x) + a 2 y 2 (x), z 2 (x) = b 1 y 1 (x) + b 2 y 2 (x) x R, provare che il determinante wronskiano di z 1 e z 2 si annulla per x = 0. Si dimostri, inoltre, che z 1 e z 2 sono linearmente indipendenti in R se e solo se il loro determinante wronskiano si annulla solo per x = Prova assegnata il 5 settembre 1986 corsi di laurea in Ingegneria elettrotecnica, elettronica e meccanica. 1. Calcolare il volume del solido di R 3 definito dalle limitazioni x 2 + y 2 x 0 x 2 + y 2 2x 0 y x z 2 x 2 y Determinare le soluzioni y(x) dell equazione differenziale 4y + y 5y = cos x e x tali che y(0) = 0e lim y(x) = 0. x + 3. Integrare per serie la funzione arctang(sen x), x [0, π 4 ] Prova assegnata il 14 ottobre 1986 corsi di laurea in Ingegneria elettrotecnica, elettronica e meccanica. 1. Determinare il massimo ed il minimo della funzione 8y x 2 y 2
14 14 Analisi Matematica II sotto la condizione 6(y 4) 2 x 2 y = Calcolare la lunghezza della curva di equazioni parametriche x(t) = 1 2π/t 2 t sen t + sen tu + cos tu du [ π/t u π 3π/(2t) t sen tu + cos tu 6, π ] 2 y(t) = du u π/(2t) 3. Calcolare il seguente integrale triplo arccos(3x 2 + 2y 2 ) dxdydz, T 2 3x 2 + 2y 2 essendo T l insieme T = (x,y,z) R 3 : 1 2 3x2 + 2y 2 1, 2 y x,z 2 3x 2 2y 2 0 } Prova assegnata il 29 ottobre 1986 corso di laurea in Matematica. 1. Determinare gli eventuali punti di estremo relativo e quelli di estremo assoluto per la funzione reale di due variabili reali (y x 3 ) y 3 x. 2. Date le serie numeriche (a) a 1 + a 2 + +a n + (b) b 1 + b 2 + +b n + la prima a termini non negativi, si supponga che esistano λ<1ek N tali da aversi a n+k λa n + b n, n N. Dimostrare che condizione sufficiente affinchè laserie(a) sia convergente è che le somme parziali della serie (b) siano limitate superiormente.
15 Analisi Matematica II 15 Provare, inoltre, che condizione necessaria affinchè la serie(a) sia divergente èchelaserie(b) siadivergentea+. Che cosa si può direseλ = 1? 3. Calcolare il seguente integrale triplo x arctang(x 2 + 4y 2 )dxdydz, essendo T l insieme T T = (x,y,z) R 3 : x 2 + 4y 2 z 2 1 } Prova assegnata il 19 novembre 1986 corso di laurea in Matematica. 1. Calcolare il seguente integrale doppio x + y 1 (x 2 + y 2 ) 2 dxdy, essendo D l insieme D D = (x, y) R 2 : 1 4 x2 + y 2 1 }. 2. Dimostrare che se le serie numeriche a n n=1 e b n n=1 sono convergenti, allora anche la serie n=1 (a n + b n ) èconvergente.è vero il viceversa? Sia } c n una successione di numeri positivi. Utilizzando il risultato precedente provare che se c n+2 lim = h<1, n + c n
16 16 Analisi Matematica II allora la serie c 1 + c 2 + +c n + èconvergente. 3. Data la funzione f(x,y)= x y 3 (x 3 y), dire, giustificando le risposte a) se esiste il limite lim f(x,y) ; (x,y) b) in quali punti (x, y) esistono le derivate parziali f x e f y ; c) se f è differenziabile nel punto ( 2, 2); d) se f è differenziabile nel punto (0, 0) Prova assegnata il 25 novembre 1986 corsi di laurea in Ingegneria elettrotecnica, elettronica e meccanica. 1. Calcolare il seguente integrale doppio D x 2 y 2 x 2 + y 2 dxdy, essendo D l insieme D = (x, y) R 2 :1 xy 2,x 3 y 3x }. 2. Considerata la funzione f(x,y) = y x x 2 y 2 i) dire se esiste il limite lim f(x,y) ; (x,y) ii) trovare i punti in cui esistono le derivate parziali f x e f y.
17 Analisi Matematica II Data la serie di funzioni ( ) n=1 [ log nx + 1 log n ] (n + 1)x + 1 n + 1 provare che ( ) converge in ]0, + [ ma non uniformemente. Provare che ( ) converge uniformemente in [1, + [ Prova assegnata il 28 novembre 1986 corsi di laurea in Ingegneria elettrotecnica, elettronica e meccanica. 1. Integrare l equazione differenziale ( ) y y x = 2 x y. Il problema di Cauchy relativo alla ( ) e di punto iniziale (1, 0) ha soluzione unica? 2. Calcolare l integrale superficiale Σ dσ 1 + x 2 + y 2, essendo Σ la porzione del paraboloide iperbolico z = xy che si proietta sul piano xy nell insieme D definito dalle limitazioni x 2 + y 2 2x 0 x 2 + y 2 4x Data la funzione f(x,y) = 1 cos x cos y a) trovare il campo di esistenza di f(x,y); b) esiste lim (x,y) f(x,y)?
18 18 Analisi Matematica II Prova assegnata il 10 dicembre 1986 corso di laurea in Matematica. 1. Calcolare il seguente integrale triplo [e z2 ] x 2 + y 2 + z sen(1 x 2 y 2 ) 2 dxdydz, essendo T l insieme T T = (x,y,z) R 3 : x 2 + y 2 z 1 }. 2. Sia M la famiglia di tutti i sottoinsiemi numerabili dell intervallo [0, 1]. Sia fn } una successione di funzioni reali definite in [0, 1]. Dimostrare che condizione necessaria e sufficiente affinchè f n } converga uniformemente in [0, 1] èche f n } converga uniformemente in ogni insieme M M. 3. Trovare una funzione ϕ : ], 0[ R che sia soluzione nell intervallo ], 0[ del problema di Cauchy y = e y x y( 1) = 0 + y x Dimostrare, inoltre, che tale soluzione è unica Prova assegnata il 12 dicembre 1986 corsi di laurea in Ingegneria elettrotecnica, elettronica e meccanica. 1. Data la funzione di due variabili reali definita nell insieme f(x,y) = xy(4x 2 + y 2 1) D = (x, y) R 2 :0 x y }, i) provare che essa non è dotata di massimo assoluto; ii) provare che è dotata di minimo assoluto e determinarlo. 2. Si consideri la funzione di due variabili reali g(x, y) = log(49 y 2 ),
19 Analisi Matematica II 19 a) verificare che la curva γ di equazioni parametriche x = cos t + t sen t y = sen t t cos t t [0, 2π] ha il sostegno contenuto nel campo di esistenza della funzione g(x, y); b) calcolare l integrale curvilineo della forma differenziale lineare esteso alla curva γ definita in a). 3. Data l equazione differenziale log(49 y 2 )dy ( ) y = λx y + 1 x + 3y + 2, i) determinare senza integrare l equazione differenziale il valore di λ tale che il diagramma di una qualunque soluzione relativa a tale valore abbia nel punto di ascissa 1 come tangente la retta di equazione x 6y + 5 = 0; ii) integrare l equazione differenziale ( ) ponendoλ = Prova assegnata il 12 febbraio 1987 corso di laurea in Matematica. 1. Data la serie di funzioni ( ) n=0 e n2 cos n 2 x, a) provare che essa converge uniformemente in R; b) provare che la funzione somma della serie ( ) è derivabile in R; c) provare che la funzione somma della serie ( ) è di classe C in R. 2. Sia Γ l insieme dei punti (x, y) R 2 tali che 2x 2 + y 2 + 8xy y + 8 = 0. i) Determinare i punti P 0 (x 0,y 0 ) Γ per i quali esiste un intorno U di P 0 tale che U Γ è il grafico di una funzione della variabile x. ii) Determinare gli eventuali punti x 0 R che sono di estremo relativo per qualche funzione y = f(x) il cui grafico è contenuto in Γ.
20 20 Analisi Matematica II 3. Sia f(x,y) una funzione reale di due variabili reali continua nell insieme (x, y) R 2 :0<x 2 + y 2 1 }. Posto per ogni r ]0, 1[ C r = (x, y) R 2 : r 2 x 2 + y 2 1 }, si supponga che il limite lim f (x, y) dxdy r 0 C r esista finito. È vero che f è integrabile nel cerchio (x, y) R 2 : x 2 + y 2 1 }? Giustificare la risposta Prova assegnata il 20 febbraio 1987 corsi di laurea in Ingegneria elettrotecnica, elettronica e meccanica. 1. Determinare gli eventuali punti di massimo e di minimo relativo della funzione reale di due variabili reali (x + y) 2 cos xy. 2. Calcolare l integrale curvilineo x + 2y (x + y) 2 dx + y (x + y) 2 dy, γ essendo γ la curva x = t + cos 2 t y = 1 + sen 2 t t [ π 2, π ] 2 3. Sia C l insieme dei punti (x, y) R 2 tali che e x+y x + y 1 = 0.
21 Analisi Matematica II 21 Determinare i punti P 0 (x 0,y 0 ) C per i quali esiste un intorno U di P 0 tale che U C è il grafico di una funzione della variabile x. Determinare, inoltre, i punti x 0 R che sono di estremo relativo per qualche funzione y = ϕ(x)il cui grafico è contenuto in C Prova assegnata il 16 marzo 1987 corso di laurea in Matematica. 1. Sia C n = (x, y) R 2 : x 0,y 0,x 1/n + y 1/n = 1 }, n N. Verificare che C n è una curva generalmente regolare, semplice e trovare le coordinate di quel punto P n C n che determina su C n due archi di eguale lunghezza. Sia L n la lunghezza di C n. Provare che L n 2eche (Usare la diseguaglianza 1 + a 2 1+ a ) 2. Calcolare il seguente integrale doppio xy (x 2 + y 2 ) 3 e 1 x 2 +y 2 dxdy, essendo D l insieme D lim L n = 2. n + D = (x, y) R 2 : x 1,y 1,x 2 + y 2 4 }. 3. Siano A e B due sottoinsiemi chiusi non vuoti di R 2.Dimostrareche,seA, B sono entrambi limitati, allora esistono a A e b B tali che d(a, b) = d(a, B). Che cosa si può direse a) entrambi gli insiemi A, B sono non limitati? b) almeno uno dei due insiemi A, B è limitato? Prova assegnata il 20 marzo 1987 corsi di laurea in Ingegneria elettrotecnica, elettronica e meccanica. 1. Calcolare il seguente integrale doppio xy (x 2 + 4y 2 ) 3/2 log(x2 + 4y 2 )dxdy, D
22 22 Analisi Matematica II essendo D l insieme 2. Data la funzione D = (x, y) R 2 : x 2 + 4y 2 4,x 1,y 1 2}. ϕ(x) = e 2x + sen x + 2cosx + x 3 x ], + [, determinare due equazioni differenziali lineari del terzo ordine di cui ϕ(x) sia soluzione. Trovare gli integrali generali delle equazioni differenziali così determinate. 3. Considerata la funzione g(x) = x 3 x [ π,π[, dire se il prolungamento periodico di periodo 2π a ], + [ di g(x) è sviluppabile in serie di Fourier e determinare tale sviluppo Prova assegnata il 9 giugno 1987 corso di laurea in Matematica. 1. Dimostrare che al variare del parametro positivo λ la successione di funzioni } nx n 2 x 2 + λ èconvergentein], + [ ma non è ivi uniformemente convergente. 2. Integrare la seguente equazione differenziale y 3y + 2y = sen 2 (2x). 3. Determinare gli eventuali punti di massimo e di minimo relativo della funzione reale di due variabili reali e (x2 +y 2 4)(4x 2 +y 2 16). 4. Calcolare il seguente integrale doppio sen x y dxdy, essendo D l insieme D D = (x, y) R 2 :0 x π 2, 0 y π 2 }.
23 Analisi Matematica II Prova assegnata il 19 giugno 1987 corsi di laurea in Ingegneria elettrotecnica, elettronica e meccanica. 1. Determinare gli eventuali punti di massimo e di minimo relativo della funzione reale di due variabili reali (x + y) y x 2 e (x+y) y x2. 2. Data la curva di equazioni parametriche e t x = t + log(1 + t 2 ) y = t2 2 + t log(t2 + 1) 2t + arctang t t [4, 5] a) provare [ che ] il sostegno di γ è il grafico di una funzione f(x) crescente in x(4), x(5) ; b) determinarela misuradel rettangoloide relativoad f(x) di base l intervallo [ x(4), x(5) ]. (Non è richiesta la determinazione esplicita di f(x)) 3. Sviluppare in serie di Fourier la funzione e x [x] ; [x] denota la parte intera contenuta in x Prova assegnata il 30 giugno 1987 corso di laurea in Matematica. 1. Risolvere il problema di Cauchy y = y x + xy2 sen x y( π 2 ) = 4 π precisando il più ampio intervallo aperto dove è definita la soluzione. 2. Calcolare il seguente integrale triplo e x2 +y 2 e z zdxdydz, T
24 24 Analisi Matematica II essendo T l insieme T = (x,y,z) R 3 : x 2 + y 2 z 1 }. 3. Determinare gli eventuali punti di massimo e di minimo relativo della funzione reale di due variabili reali (y x 2 )(y 4x 2 )(y 1) Prova assegnata il 14 luglio 1987 corso di laurea in Fisica. 1. Calcolare il seguente integrale triplo ( ) x z 3 2 sen 4 + y2 dxdydz, essendo T l insieme T T = (x,y,z) R 3 : x2 4 + y2 + z 2 1 }. 2. Sia ϕ una funzione reale, definita e continua in [0,π] etaledaaversi ϕ(x) = π 0 sen(x + t)ϕ(t) dt + x x [0,π]. a) Dimostrare che ϕ è derivabile in [0,π]. b ) Dimostrare che ϕ è indefinitamente derivabile in [0,π]. c) Dimostrare che ϕ è unica ed esprimerla mediante le funzioni elementari. (Si determini una equazione differenziale lineare di cui ϕ è soluzione) 3. Dimostrare che la forma differenziale è esatta nell aperto 2x 3 x 2 2xy y (x 2 y) 2 dx + x2 + x + y (x 2 y) 2 dy A = (x, y) R 2 : x 2 y>0 }. Determinare le primitive di tale forma differenziale.
25 Analisi Matematica II Prova assegnata il 15 settembre 1987 corsi di laurea in Ingegneria elettrotecnica, elettronica e meccanica. 1. Determinare gli eventuali punti di massimo e di minimo relativo della funzione reale di due variabili reali e (x2 xy )(x 2 y 2) (x 2 xy ) 3 (y 2 x 2 ) Calcolare il seguente integrale triplo z 3 (z 2 x 2 + y 2 dxdydz, ) 3/2 essendo T l insieme 3. Sia T T = (x,y,z) R 3 :1 z 2 x 2 + y 2 4,x 1,y 0, 1 z 2 }. k=0 a k una serie numerica assolutamente convergente. Posto per ogni k intero non negativo A k = provare che i) la serie a k k 4 k 2 + 1, δ k tale che cos(kδ k ) = sen(kδ k ) = 1 k 2 k 4 k k k 4 k ( ) k=0 A k cos k(t δ k ), e le serie ottenute derivando termine a termine la ( ) rispettivamente una volta e due volte sono totalmente convergenti; ii) detta u(t) la somma della serie ( ), u(t) è soluzione dell equazione differenziale u + u + u = k=0 a k cos kt.
26 26 Analisi Matematica II Prova assegnata il 22 settembre 1987 corso di laurea in Matematica. 1. Risolvere il problema di Cauchy y = x x y 1 1 (x 2 + 1) 2 y y(0) = 2 precisando l intervallo di definizione della soluzione. 2. Calcolare la lunghezza della curva avente rappresentazione parametrica t x = u 2 + 2sen 2 udu 0 y =, t [1, 2]. 2sent 3. Determinare il massimo ed il minimo assoluti della funzione e y2 xy+1 definita nell insieme (x, y) R 2 : x 2, y 2,x 2 + y 2 1 } Prova assegnata il 28 ottobre 1987 corsi di laurea in Ingegneria elettrotecnica, elettronica e meccanica. 1. Determinare il massimo ed il minimo assoluti della funzione ( f(x,y)= y + y ) [y y 1 ] (x 1) 2 definita nell insieme intersezione tra il campo di esistenza della f ed il cerchio (x, y) R 2 : (x 1) 2 + y 2 1 }. 2. Calcolare il volume del solido di R 3 definito dalle limitazioni y x 2 2z 0 y + x 2 z 0 y 0 1 z 0
27 Analisi Matematica II Determinare la soluzione y(x) dell equazione differenziale y = (x + 3) y + 4 definita in ], + [ etalechey(x) = 4 se e solo se 4 x Prova assegnata il 29 ottobre 1987 corso di laurea in Matematica. 1. Calcolare il seguente integrale triplo (x 2 + y 2 + z) dxdydz, essendo T l insieme T T = (x,y,z) R 3 : x 2 + y 2 + z 2 2,x 2 + y 2 z 2,z 0 }. 2. Integrare l equazione differenziale y + y = 2cos(x π 4 ). 3. Determinare il massimo ed il minimo assoluti della funzione ( f(x,y)= x + x ) x 1 (2x x 2 y 2 ) definita nell insieme intersezione tra il cerchio (x, y) R 2 : x 2 + y 2 1 } e il campo di esistenza della f(x,y) Prova assegnata il 19 novembre 1987 corso di laurea in Matematica. 1. Determinare il massimo ed il minimo assoluti della funzione (x 2 y 2 )(y x 2 )
28 28 Analisi Matematica II definita nell insieme (x, y) R 2 : x 2 + y 1,y 0 }. 2. Calcolare il seguente integrale curvilineo Q (γ) xy 2 dx + e y cos xdy P dove γ è l arco di curva avente rappresentazione parametrica x = t y = cos t, t [0, π 2 ]. 3. Risolvere il seguente problema di Cauchy y = xy + x 4 y y(1) = 1 precisando il più ampio intervallo dove è definita la soluzione Prova assegnata il 4 dicembre 1987 corsi di laurea in Ingegneria elettrotecnica, elettronica e meccanica. 1. Provare che la forma differenziale ( ) x ( ) x 2 + y 2 x 1 (x 1) 2 + y 2 dx + ( y x 2 + y 2 ) y (x 1) 2 + y 2 dy è esatta in R 2 \ (0, 0), (1, 0) }. Determinare la primitiva F(x, y) di ( ) tale che F(2, 0) = Risolvere il seguente problema di Cauchy y 7y + 14y 8y = log x y(1) = y (1) = y (1) = 0 Dire se è possibile integrare per serie gli eventuali integrali non elementarmente calcolabili.
29 Analisi Matematica II Sia C 1( [0, 1] ) ; la posizione N (x) = max [0,1] x (t), x C 1( [0, 1] ) definisce una norma in C 1( [0, 1] )? Sia A = x C 1( [0, 1] ) tali che x(0) = 0 }. La N (x) definisce una norma in A? In tal caso provare che A è completo con la norma N (x) Prova assegnata il 10 dicembre 1987 corso di laurea in Matematica. 1. Determinare gli eventuali punti di massimo e di minimo relativo della funzione reale di due variabili reali (x 2 y 2 )(x 2 + 4y 2 4). 2. Sia f la funzione di due variabili reali definita in tutto R 2 mediante la posizione f(x,y)= 2 1 x 2 y 2 se xy 0 0 se xy = 0 a) Dire se esiste il limite lim f(x,y). (x,y) Giustificare la risposta. b) Verificare che le derivate parziali f x, f y esistono in ogni punto di R 2. c) Dire se f è differenziabile in (0, 0). Giustificare la risposta. 3. Sia ϕ una funzione reale di una variabile reale continua in ], + [. Posto, per ogni n N ed ogni x ], + [, ϕ n (x) = ϕ ( x + 1 n), dimostrare che condizione sufficiente affinchè la successione di funzioni ϕ n } converga uniformemente in ], + [ è che ϕ sia iviuniformementecontinua. Dimostrare inoltre che, se ϕ è monotona, la predetta condizione è anche necessaria.
30 30 Analisi Matematica II Provaassegnatail 8 febbraio 1988 corsi di laurea in Ingegneria elettrotecnica, elettronica e meccanica. 1. Calcolare la lunghezza della curva semplice il cui sostegno èl intersezionetra il piano di equazione x 2y = 0 e il diagramma della funzione f(x,y)= xy + x + y definita nell insieme (x, y) R 2 : xy 1,(x 1) 2 + (y 1) 2 2 }. 2. Risolvere il seguente problema di Cauchy y 3 x y + 1 x 2 y = 1 y(1) = y (1) = 0 3. Determinare gli eventuali punti di massimo e di minimo relativo della funzione reale di due variabili reali 1 ( ) log 2 x + log 2 y + 2 log x log y + log log 2 x + log 2 y + 2 log x log y Prova assegnata il 11 febbraio 1988 corso di laurea in Fisica. 1. Determinare il campo di esistenza ed il massimo ed il minimo assoluti della funzione ( ) arcsen log 2 x + log 2 y + 2 log x log y. 2. Calcolare il volume del cilindroide avente per base il dominio (x, y) R 2 :0 x 1 1 2, 0 y x 2} e relativo alla funzione f(x,y) = y 3. Trovare per quali valori di λ R,λ ±1, esiste una soluzione dell equazione differenziale y + y = cos λx + sen λx soddisfacente le condizioni y(0) = y(π) = 0.
31 Analisi Matematica II Prova assegnata il 10 marzo 1988 corso di laurea in Fisica. 1. Calcolare il seguente integrale triplo x 2 + y 2 + z 2 dxdydz, T essendo T l insieme intersezione tra le due sfere chiuse che hanno centro nei punti (0, 0, 1 2 ) e (0, 0, 1) rispettivamente e passanti per l origine. 2. Integrare l equazione differenziale y (iv) + y = 2senh3x cosh x. 3. Data la successione di funzioni (1 sen x) n } x [0, 2π], determinare l insieme di convergenza e gli intervalli in cui c è convergenza uniforme Prova assegnata il 25 marzo 1988 corsi di laurea in Ingegneria elettrotecnica, elettronica e meccanica. 1. Calcolare, usando gli sviluppi in serie di potenze, la derivata sesta in 0 della funzione x 4 + (1 + x 2 )e x2 1 + x 2 2. Calcolare il seguente integrale doppio essendo D l insieme D x y x 2 + y 2 dxdy, D = (x, y) R 2 : x 2 + 2y 2 2,x 2 + 2y 2 + 4y 0 }. 3. Verificare che esiste un intorno U di (0, 0) in cui l equazione 2x + y + arctang y = 0 definisce implicitamente una funzione y = ϕ(x). Studiare la funzione ϕ(x).
32 32 Analisi Matematica II Prova assegnata il 8 giugno 1988 corsi di laurea in Ingegneria elettrotecnica, elettronica e meccanica. 1. Calcolare il seguente integrale doppio 1 dxdy, D x 2 + y 2 1 essendo D l insieme D = (x, y) R 2 : x 2 + y 2 2 }. 2. Sia f(x,y) la funzione definita in (x, y) R 2 : x 1, y 1 } mediante la legge 0 se x <y f(x,y)= 2x 3 3x 2 y + y se x y. a) Provare che essa èdotatadimassimoediminimo. b) Determinare il massimo ed il minimo. 3. Si consideri il problema di Cauchy ( ) y = 2y y 2 y(0) = y 0, y 0 R i) per quali valori di y 0 il problema ( ) ammette una sola soluzione locale; ii) per quali valori di y 0 il problema ( ) ammette soluzioni definite in ], + [ Prova assegnata il 7 luglio 1988 corsi di laurea in Ingegneria elettrotecnica, elettronica e meccanica. 1. Calcolare il volume del solido di R 3 definito dalle limitazioni x 0 y π z 7 4 π ( 2 x 2 + cos 4 z + sen 2 z cos 2 z + 1) y 2 sen 2 z
33 Analisi Matematica II Determinare, se esistono, il massimo ed il minimo assoluti della funzione f(x,y) = y 2 0 x 2 + t dt. 3. Data l equazione differenziale ( ) y = x ( ) λ y2 y x 2 1 x R,λ R. a) Provare che la retta y = mx (m 0) è tangente ai grafici delle soluzioni di ( ) seλ = m2 +1 m. 2 b) Determinare le soluzioni di ( ) di cui al punto a) per m = Prova assegnata il 5 settembre 1988 corso di laurea in Ingegneria civile. 1. Per ogni n N risolvere il problema di Cauchy (P n ) y = x 2 y n 1 n 2 y(0) = 1 n 2 Detta y n (x) la soluzione di (P n ), calcolare min y n (x) e lim y n(x). ],+ [ n + Verificare che lim n + ( ) min y n (x) ],+ [ ( = min ],+ [ lim y n(x) n + ). 2. Studiare la convergenza semplice, uniforme e calcolare la somma della serie n=0 e nx.
34 34 Analisi Matematica II 3. Determinare il massimo ed il minimo assoluti della funzione log(x 2 y 2 + 2) definita nell insieme (x, y) R 2 : x y2 1 }. 4. Calcolare il seguente integrale doppio ϕ(α, β) = dove α, βsono parametri reali e T αx e βy dxdy T = (x, y) R 2 : x 1, y 1 }. Studiare il campo di esistenza e la derivabilità della funzione ϕ(α, β) Prova assegnata il 15 settembre 1988 corsi di laurea in Ingegneria elettrotecnica, elettronica e meccanica. 1. Calcolare il seguente integrale doppio 4x 3 y dxdy, 16x 2 + y 2 essendo D l insieme D D = (x, y) R 2 :16x 2 + y 2 16, 0 y 4 3 x, x 2 }. 2. Determinare gli eventuali punti di estremo relativo della funzione log x 2 2x +log y 2 2y +log(x 2 + y 2 2x 2y + 3) [ 2 (x 2 2x)(y 2 2y)(x 2 + y 2 2x 2y + 3)]. 3. Studiare la convergenza puntuale ed uniforme della serie di funzioni n=1 x (1 + x) n x> 1.
35 Analisi Matematica II Prova assegnata il 8 ottobre 1988 corso di laurea in Ingegneria civile. 1. Determinare gli eventuali punti di estremo relativo e quelli di estremo assoluto per la funzione reale di due variabili reali e y x. 2. Studiare la serie n=1 n 3 x n. 3. Dire se la funzione di due variabili reali x 2 y f(x,y)= x 2 + y 2 per x 2 + y per x 2 + y 2 = 0 è continua e se ammette derivate parziali prime. 4. Sia y : ]0, 1[ R una soluzione dell equazione differenziale y = f(x,y) con f C 0 (R 2 ), f limitata. Provare che y è limitata. 5. Calcolare il seguente integrale doppio essendo D l insieme D x 2 + y 2 dxdy, D = (x, y) R 2 : (x 1) 2 + y 2 1 }.
36 36 Analisi Matematica II Prova assegnata il 27 ottobre 1988 corsi di laurea in Ingegneria elettrotecnica, elettronica e meccanica. 1. Considerata la forma differenziale lineare (α) x + qy rx + sy x 2 dx + + y2 x 2 + y 2 dy q, r, s R, dire per quali valori di q, r, s (α)è esatta in R 2 \ (0, 0) } ed in tal caso determinarne le primitive. 2. Calcolare il seguente integrale triplo ydxdydz, T essendo T l insieme T = (x,y,z) R 3 :0 x 1,z+ x y 1, 0 z }. 3. Determinare il massimo ed il minimo assoluti della funzione f(x,y)= y 1 e xt t dt definita nell insieme (x, y) R 2 :1 x 2, 1 y 2 } Prova assegnata il 5 dicembre 1988 corsi di laurea in Ingegneria elettrotecnica, elettronica e meccanica. 1. Calcolare il seguente integrale triplo log(x 2 + 1)dxdydz, essendo T l insieme T T = (x,y,z) R 3 :0 x 1,x 4 z 2 + y 2 x 4 0 }.
37 Analisi Matematica II Determinare gli eventuali punti di massimo e di minimo relativo della funzione reale di due variabili reali x 2 y 3 (1 x y). 3. Posto F(x) = 1 provare che F(x) C 1 (]0, + [). 0 (x + y) 2/3 cos(x + y)dy, Prova assegnata il 10 febbraio 1989 corsi di laurea in Ingegneria elettrotecnica, elettronica e meccanica. 1. Calcolare il seguente integrale doppio dxdy T λ x 2 + y 2 essendo T λ = (x, y) R 2 :4 x 2 + y 2 4x,1 x λ, y 0 }. 2. Calcolare la lunghezza dell arco di curva γ di equazioni parametriche x = t 2 y = 1 t 2 log τ log 2 1 t 2. τ + 8 dτ Data la funzione f(x,y)= y x 2 1 sen y, 2 provare che esiste un intorno V di (0, 0) tale che (x, y) R 2 : f(x,y)= 0 } V è il grafico di una funzione ϕ(x). Studiare la funzione ϕ(x) in 0.
38 38 Analisi Matematica II Prova assegnata il 29 marzo 1989 corsi di laurea in Ingegneria elettrotecnica, elettronica e meccanica. 1. Data la superficie Σ di equazioni parametriche x = (R cos v)cos u y = (R cos v)sen u (u, v) [ π,π] [ π,π], z = sen v provare che Σ non èregolareperr = 1. Per R = 2 calcolare il seguente integrale superficiale (x + y + z) dσ. Σ 2. Determinare gli eventuali punti di massimo e di minimo relativo della funzione reale di due variabili reali e sen( x + y ) sen( x y ). 3. Sia T una applicazione di uno spazio metrico (S, d) in sè. Posto U(x) = T(T(x)), x S, provare che se U è una contrazione in S ed x è il suo punto unito si ha i) T ha al più un punto unito; ii) T(x ) è un punto unito per U; iii) T(x ) = x Prova assegnata il 2 giugno 1989 corsi di laurea in Ingegneria elettrotecnica, elettronica e meccanica. 1. Determinare la funzione u(x, y) definita nel semipiano delle y positive di classe C 1 tale che x u x + y u y = 2u u(x, 1) = e x 2. Calcolare il seguente integrale triplo xyz 1 + (xy) 2 dxdydz, T
39 Analisi Matematica II 39 essendo T l insieme T = (x,y,z) R 3 : z xy z 2,x y 2x, 1 z 2 }. y (si può utilizzare il cambiamento di variabili xy = u, x = v) 3. Verificare che la forma differenziale [ ] sen(xy) + xy cos(xy) dx + x 2 cos(xy) dy è esatta. Risolvere il seguente problema di Cauchy y sen(xy) + xy cos(xy) = x 2 cos(xy) y(1) = Prova assegnata il 5 giugno 1989 corso di laurea in Ingegneria civile (A L). 1. Detta ϕ la curva semplice di classe C 1 che ha per sostegno il diagramma D f della funzione x 1 f(x) = 0 cos 2 t 1 dt 0 x π 4, determinarne la lunghezza l ϕ. Determinare, poi, una curva rettificabile ψ, che ha per sostegno D f e lunghezza l ψ = 2l ϕ. 2. Calcolare il seguente integrale curvilineo y x2 + y 2 γ (x 2 y 2 ) 2 dx + x x2 + y 2 (x 2 y 2 ) 2 dy, essendo γ la curva di equazioni parametriche x = log t y = 1 + log 2 t e t e Determinare le eventuali soluzioni dell equazione differenziale y + α 2 y = sen x che soddisfano la condizione y(0) = y(π) = 0. α R
40 40 Analisi Matematica II Prova assegnata il 12 giugno 1989 corso di laurea in fisica. 1. Calcolare il seguente integrale doppio D 2 x 2 4y 2 4 x 2 4y 2 dxdy, essendo D l insieme D = (x, y) R 2 : x 2 + y 2 2,x 2 + (2y 1) 2 1 }. 2. Data la funzione definita nell insieme provare che f(x,y)= 1 x log x 2 + y 2 x A = (x, y) R 2 : x 0 }, sup f =+, min f = 0. A A, 3. Studiare la convergenza della serie n=1 x n cos y al variare di x e y con x>0e0 y π. 4. Dimostrare che esiste l integrale improprio ecalcolarlo. + 0 e t dt
41 Analisi Matematica II Prova assegnata il 30 giugno 1989 corso di laurea in Ingegneria civile. 1. Considerato l insieme K = (x, y) R 2 :0 x 1,y 2 x }, provare che 0 < K sen(e x/2 + cos y) e x/2 + cos y dx dy < Determinare gli eventuali punti di massimo e di minimo relativo della funzione reale di due variabili reali ( ) ( x +1)log(2+y 1 2 ) 1 + ( x +1) log(2 + y 2 ). 3. Calcolare il seguente integrale doppio D arctang x y (x 2 + y 2 dxdy, ) 3/2 essendo D l insieme D = (x, y) R 2 : x 2 + y 2 1,x+ y 1,y x } Prova assegnata il 3 luglio 1989 corsi di laurea in Ingegneria elettrotecnica, elettronica e meccanica. 1. Integrare l equazione differenziale di Bernoulli y + y cos x Calcolare il seguente integrale doppio e 2senx x 3 1 y3 = 0. D e (x2 +2y 2 ) e x 2 +2y 2 1 dxdy,
42 42 Analisi Matematica II essendo D l insieme D = (x, y) R 2 : x 2 + 2y 2 1 }. 3. Data la funzione f(x)= e x x [ π,π[, determinare lo sviluppo in serie di Fourier del prolungamento periodico a ], + [ di periodo 2π di f(x). Utilizzare il risultato ottenuto per calcolare la somma della serie n= n Prova assegnata il 3 luglio 1989 corso di laurea in fisica. 1. Calcolare il volume dell insieme T dei punti (x,y,z) dello spazio le cui coordinate soddisfano le relazioni x 2 a 2 + y2 b 2 + z2 c 2 1, x ( 2 a c 2 ) + dove a, b, c sono costanti positive con c>1. y 2 b 2 ( 1 1 c 2 ) + z 2 0, z 0, 2. Determinare gli eventuali punti di massimo e di minimo relativo della funzione reale di due variabili reali (y x 2 )(x 2 y2 4 1). 3. Integrare l equazione differenziale y y 2y + 2y = xe x.
43 Analisi Matematica II Prova assegnata il 25 settembre 1989 corso di laurea in fisica. 1. Determinare i punti di massimo e di minimo assoluti della funzione x cos y x 2 nell insieme (x, y) R 2 :0 x 1, 0 y π/2 }. 2. Stabilire se le serie n=1 1 + sen 2 n 1 + n 2, n=1 ( ) e n, cosh n sono convergenti, divergenti oppure oscillanti. 3. Dimostrare che la forma differenziale lineare y x log ydx + xy x 1 dy n=1 ( 1) n n è, nell aperto A = (x, y) R 2 : x > 0, y > 0 }, un differenziale esatto e determinarne la primitiva che si annulla nel punto (3, 2). 4. Provare che, per ogni λ R, la funzione non ha limite per (x, y). f(x,y)= x 2 λ 2 y Prova assegnata il 11 ottobre 1989 corso di laurea in Ingegneria civile. 1. Calcolare il seguente integrale curvilineo y(4y 2 x 2 ) (x 2 + 4y 2 ) 2 dx + x(x2 4y 2 ) (x 2 + 4y 2 ) 2 dy ϕ essendo ϕ la curva di equazioni parametriche x = cos t y = sen t t [0,π]. 2. Risolvere il seguente problema di Cauchy y + k 2 y = kx + cos kx y(0) = y (0) = 0
44 44 Analisi Matematica II essendo k un parametro reale. 3. Studiare la uniforme convergenza in ]0, + [ della successione di funzioni } sen nx n 2 x Prova assegnata il 13 ottobre 1989 corsi di laurea in Ingegneria elettrotecnica, elettronica e meccanica. 1. Provare, utilizzando gli sviluppi in serie di Fourier, che per x [0,π] valgono le seguenti uguaglianze x( x + π) = π 2 6 n=1 cos 2nx n 2 = 8 π n=1 sen ( (2n 1)x ) (2n 1) 3 Le suddette uguaglianze valgono per x = 100? 2. Calcolare il seguente integrale superficiale z 2 dσ, Σ essendo Σ la porzione del paraboloide z = 4 x 2 y 2 la cui proiezione sul piano z = 0 èl insieme (x, y) R 2 :1 x 2 + y 2 4 }. 3. Determinare in ]0, + [ l integrale generale dell equazione differenziale y 2 x + 1 x y + x + 2 x y = x2 e 2x, sapendo che l equazione omogenea associata ha soluzioni del tipo x α e x,α R.
45 Analisi Matematica II Prova assegnata il 24 ottobre 1989 corso di laurea in fisica. 1. Calcolare l area della porzione S della superficie conica di equazione: x 2 + y 2 = (1 z) 2, che è contenuta nel solido: 2x 2 + 2y 2 3x + 1 0, 0 z Denotato con λ un parametro che può assumere qualunque valore reale, determinare le eventuali soluzioni y(x) dell equazione differenziale: soddisfacenti le condizioni: y + λy = sen x, y(x) y(0) = 0, lim x + x = Studiare la continuità della funzione: arctang(y/x) per x>0,y R π + arctang(y/x) per x<0,y 0 v(x,y) = π + arctang(y/x) per x<0,y<0 π/2 per x = 0,y>0 π/2 per x = 0,y<0 4. Dimostrare che la serie di funzioni: (1 x 2 ) + x 2 (1 x 2 ) + x 4 (1 x 2 ) + +x 2n (1 x 2 ) + è convergente nell intervallo chiuso [ 1, 1], ma non è ivi uniformemente convergente.
46 46 Analisi Matematica II Prova assegnata il 20 novembre 1989 corso di laurea in Ingegneria civile (A L). 1. Calcolare il seguente integrale triplo 1 x(3 + sen x) dxdydz, essendo T l insieme T T = (x,y,z) R 3 : π 4 x π 3,y2 + 3z 2 2 x }. 2. Determinare gli eventuali punti di massimo e di minimo relativo della funzione reale di due variabili reali x + 2 (x 3y ). 3. Dire, giustificando la risposta, se la funzione ècontinuaelimitata. f(x)= n=1 arctang n 2 x n 4 x 4 x R Prova assegnata il 20 novembre 1989 corso di laurea in fisica. 1. Calcolare la lunghezza della curva del semispazio z 0, ottenuta secando il cono di equazione: x 2 + y 2 = (1 z) 2 con il piano y = z. 2. Determinare gli eventuali punti di massimo e di minimo relativo della funzione reale di due variabili reali x 2 y 2 (x + y 1). 3. Verificare che risulta: lim log y (x,y) (x 0,y 0 ) x = + se x0 = 0,y 0 0 se x 0 > 0,y 0 = 0
47 Analisi Matematica II 47 Esiste il limite al tendere di (x, y) al punto (0, 0)? 4. Dimostrare che la serie di funzioni n=1 1 (sen x)n n2 converge su R a una funzione di classe C Prova assegnata il 30 novembre 1989 corsi di laurea in Ingegneria elettrotecnica, elettronica e meccanica. 1. Data la serie di funzioni (σ ) n=1 cos n x n provare che i) (σ ) è uniformemente convergente in ogni compatto contenuto in ]0, π 2 ]; ii) (σ ) non è uniformemente convergente in ]0, π 2 ]. Calcolare la somma della serie (σ ) in [ π 4, π 2 ] facendo uso del teorema di derivazione per serie. 2. Determinare, se esistono, il massimo ed il minimo assoluti della funzione 1 x + 1 y definita nell insieme (x, y) R 2 : x>0,y>0,x 2 + y 2 x 2 y 2 = 0 }., 3. Determinare la funzione ϕ(x) C 2 (]0,π[) tale che la funzione ϕ(x) sen x sia soluzione del problema di Cauchy y + cos x sen x y 1 sen 2 x y = 0 y( π 2 ) = 0, y ( π 2 ) = 1
48 48 Analisi Matematica II Prova assegnata il 11 dicembre 1989 corso di laurea in Fisica. 1. Sia P 0 = (x 0,y 0 ) un punto del piano e K un insieme piano non vuoto. Provare che se K è chiuso e limitato, allora esiste il massimo dell insieme numerico dist (P0,P), P = (x, y) K }, dove dist (P 0,P)= (x x 0 ) 2 + (y y 0 ) Calcolare il seguente integrale doppio xy y dxdy, D essendo D l insieme D = (x, y) R 2 : x 2 + y 2 1,x 2 + y 2 2x 0 }. 3. Determinare il massimo ed il minimo assoluti della funzione xy y + 3 x 2 3 x definita nell insieme (x, y) R 2 :0 x 1, 3 x y 0 }. 4. Risolvere il seguente problema di Cauchy (x 2 + 1)y + xy = x e x sen x y(0) = 2
49 Analisi Matematica II Prova assegnata il 4 febbraio 1990 corsi di laurea in Ingegneria elettrotecnica, elettronica e meccanica. 1. i) Determinare una funzione ϕ(x) di classe C 1( ]0, + [ ) tale che la forma differenziale ( ) ( ) (x 3 + y 3 )ϕ(x) dx + xy 2 ϕ(x) dy sia esatta in ]0, + [ ]0, + [. Scrivere una primitiva della forma differenziale così ottenuta. ii) Risolvere il problema di Cauchy y = x3 + y 3 xy 2 y(1) = 1 2. Posto, per k R \ 0 y(t) = 1 k t 0 e x2 sen ( k(t x) ) dx, calcolare, verificando che sono soddisfatte le ipotesi del teorema di derivazione sotto il segno di integrale, le derivate prima e seconda della funzione y(t). 3. Integrare, per k R \ 0, l equazione differenziale y + k 2 y = e x Prova assegnata il 6 febbraio 1990 corsi di laurea in Ingegneria elettrotecnica, elettronica e meccanica. 1. Calcolare l integrale superficiale z dσ, 1 + x 2 + y 2 Σ essendo Σ la superficie regolare avente per sostegno l insieme (x,y,z) R 3 : x 2 + y 2 = 2z, 0 z 1 }.
50 50 Analisi Matematica II 2. Data l equazione differenziale ( ) y 4y + λy = e x (λ R) determinare, se esistono, i valori di λ tali che ( ) ammette soluzioni verificanti le condizioni y(x) y(0) = 0, lim x + xe 3x = Provare che la successione di funzioni nx 2 log nx + 1 } nx è uniformemente convergente in [1, 2] Prova assegnata il 12 febbraio 1990 corso di laurea in Ingegneria civile (A L). 1. Studiare la serie n=0 x n log(3n 2 + 2) x R. 2. Determinare gli eventuali punti di massimo e di minimo relativo della funzione reale di due variabili reali (3x 2 y 2 )(2 x 2 y 2 ). 3. Calcolare la lunghezza della curva ϕ di equazioni parametriche x = t 2 π/2 t [0, π y = sen 2 2 ]. u + sen udu t
51 Analisi Matematica II Prova assegnata il 15 febbraio 1990 corso di laurea in Fisica. 1. Sia u(x, y) una funzione reale continua nel semicerchio B + (1) = (x, y) R 2 : x 2 + y 2 < 1,y 0 }, nulla nei punti di B + (1) che stanno sull asse delle x. Provare che la funzione f(x,y) definita nel cerchio B(1) = (x, y) R 2 : x 2 + y 2 < 1 } dalla legge f(x,y) = u(x, y) se (x, y) B + (1) u(x, y) se (x, y) B(1) \ B + (1) è continua in B(1). 2. Trovare gli eventuali punti di massimo o di minimo relativi della funzione x 2 y f(x,y) = x 2 + x se xy > 0 + 4y2 x(y + 1) se xy 0 3. Denotate con (x, y) le coordinate cartesiane del generico punto del piano, riferito ad un sistema cartesiano ortogonale, e con (ϱ, ϑ) le coordinate polari nel sistema polare associato, siano C i (i = 1, 2, 3) le seguenti curve C 1 = (ϱ, ϑ) : ϱ = 2(1 + cos ϑ), ϑ [ 0, 3 4 π]}, C 2 = (x, y) : x = 1 2, 0 y 2 1 }, C 3 = (x, y) :1 2 x 4,y= 0 } e D il dominio piano racchiuso dalla curva C 1 C 2 C 3. Calcolare l area di D e la lunghezza della sua frontiera.
52 52 Analisi Matematica II Prova assegnata il 12 marzo 1990 corso di laurea in Ingegneria civile (A L). 1. Determinare gli eventuali punti di massimo e di minimo relativo della funzione reale di due variabili reali (1 x) 2 xy Calcolare il seguente integrale curvilineo ϕ 4y 2 x 2 (x 2 + 4y 2 ) 2 dx 8xy (x 2 + 4y 2 ) 2 dy essendo ϕ la curva di equazioni parametriche 2 x = 1 + t( 2 1) y = 2 4 t 0 t Detto A l insieme (x, y) R 2 :0 x 1, 0 y 1 } e B un suo sottoinsieme misurabile secondo Lebesgue di misura m(b) = 1, provare che la chiusura di B èugualeada Prova assegnata il 15 marzo 1990 corso di laurea in Fisica. 1. Provare che la forma differenziale cos x cosh ydx + sen x senh ydy è esatta in R 2 e calcolarne l integrale curvilineo esteso alla semicirconferenza γ situata nel semipiano y 0, di centro nell origine e raggio π/2, nel verso da A = (π/2, 0) a B = ( π/2, 0). 2. Provare che la funzione definita in R 2 \ (0, 0) } dalla legge f(x,y) = 3 xy x 4 + y 4
53 Analisi Matematica II 53 è positivamente omogenea di grado 2/3. Verificare la validità dell identità di Eulero per la restrizione di f(x,y)al piano privato degli assi coordinati. 3. Calcolare il seguente integrale triplo x 2 + y 2 + z 2 dxdydz, essendo T l insieme T T = (x,y,z) R 3 : x 2 + y 2 + z 2 z 0,x 2 + y 2 z 2, 0 z 1 }. 4. Integrare l equazione differenziale y + y = x y Prova assegnata il 21 marzo 1990 corsi di laurea in Ingegneria elettrotecnica, elettronica e meccanica. 1. Calcolare il seguente integrale triplo e xyz x 2 ydxdydz, essendo T l insieme T T = (x,y,z) R 3 :1 xyz 2,x 2 2x + 2 y x 2 + 2x + 1 }. 2. Data la forma differenziale lineare (2xy y 2 y)dx + (2xy x 2 x) dy, determinare una funzione ϕ(t) di classe C 1, non identicamente nulla, tale che la forma differenziale lineare ϕ(x + y)(2xy y 2 y) } dx + ϕ(x + y)(2xy x 2 x) } dy
54 54 Analisi Matematica II sia chiusa nell insieme (x, y) R 2 : x>0,y>0 }. 3. Data la funzione f(x)= x 2 + x x [ 1, 1[ determinare lo sviluppo in serie di Fourier del prolungamento periodico a ], + [ di periodo 2 di f(x) Prova assegnata il 6 giugno 1990 corso di laurea in Ingegneria elettronica (A L). 1. Calcolare 1 0 senx 2 dx x con un errore minore di Dire per quali valori di λ R il problema di Cauchy ammette un unica soluzione locale. 3. Calcolare il seguente integrale doppio D y = 1 y 2 y(0) = λ 1 4 x 2 4y 2 dxdy, essendo D l insieme D = (x, y) R 2 :4 x 2 4y 2 0 }.
Facoltà di Scienze MM.FF.NN. Corso di Laurea in Matematica - A.A Prova scritta di Analisi Matematica II del
 Prova scritta di nalisi Matematica II del 12-06-2001. C1 1) Studiare la convergenza semplice, uniforme e totale della serie di funzioni seguente ( 1) [ n 2 ] n x 1 + n 2 x. n=0 2) Data la funzione (x 2
Prova scritta di nalisi Matematica II del 12-06-2001. C1 1) Studiare la convergenza semplice, uniforme e totale della serie di funzioni seguente ( 1) [ n 2 ] n x 1 + n 2 x. n=0 2) Data la funzione (x 2
Facoltà di Scienze MM.FF.NN. Corso di Laurea in Matematica - A.A Prova scritta di Analisi Matematica II del c.1.
 Prova scritta di Analisi Matematica II del 14-07-1999 - c.1 1) Sia (d n ) una successione di numeri reali tali che inf d n > 0. Studiare il carattere della serie + n=1 al variare del parametro reale positivo
Prova scritta di Analisi Matematica II del 14-07-1999 - c.1 1) Sia (d n ) una successione di numeri reali tali che inf d n > 0. Studiare il carattere della serie + n=1 al variare del parametro reale positivo
Ingegneria Elettronica Prova scritta di Analisi Matematica II del giorno ( 3) n x n n + 1
 Prova scritta di Analisi Matematica II del giorno 31-01-2007 1) Studiare la serie di potenze ( 3) n x n n + 1 2) Determinare i punti di estremo relativo ed assoluto della funzione seguente f(x, y) = x
Prova scritta di Analisi Matematica II del giorno 31-01-2007 1) Studiare la serie di potenze ( 3) n x n n + 1 2) Determinare i punti di estremo relativo ed assoluto della funzione seguente f(x, y) = x
Facoltà di Ingegneria Prova scritta di Analisi Matematica II. Lecce, y y x = x3 y 4. y(1) = 1.
 Lecce, 10.4.2003 1. Risolvere il seguente problema di Cauchy: y y x = x3 y 4 y(1) = 1. 2. Determinare gli estremi della funzione f(x, y) = x 2 y 2 nell insieme } E = {(x, y) R 2 : (x 1) 2 + y2 4 1, y 0.
Lecce, 10.4.2003 1. Risolvere il seguente problema di Cauchy: y y x = x3 y 4 y(1) = 1. 2. Determinare gli estremi della funzione f(x, y) = x 2 y 2 nell insieme } E = {(x, y) R 2 : (x 1) 2 + y2 4 1, y 0.
PROVE SCRITTE DI ANALISI MATEMATICA II (V.O.), ANNO 2002
 PROVE SCRITTE DI ANALISI MATEMATICA II (V.O.), ANNO 22 Prova scritta del 1/1/22 Si esamini la serie di funzioni: 1 log x (e n + n), definita per x IR. Si determini l insieme S in cui tale serie converge,
PROVE SCRITTE DI ANALISI MATEMATICA II (V.O.), ANNO 22 Prova scritta del 1/1/22 Si esamini la serie di funzioni: 1 log x (e n + n), definita per x IR. Si determini l insieme S in cui tale serie converge,
Analisi Matematica 2. Michele Campiti. Prove scritte di. Ingegneria Industriale a.a
 Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
Esonero di Analisi Matematica II (A)
 Esonero di Analisi Matematica II (A) Ingegneria Edile, 8 aprile 3. Studiare la convergenza del seguente integrale improprio: + x log 3 x (x ) 3 dx.. Studiare la convergenza puntuale ed uniforme della seguente
Esonero di Analisi Matematica II (A) Ingegneria Edile, 8 aprile 3. Studiare la convergenza del seguente integrale improprio: + x log 3 x (x ) 3 dx.. Studiare la convergenza puntuale ed uniforme della seguente
Facoltà di Scienze MM.FF.NN. Corso di Laurea in Matematica - A.A Prova scritta di Analisi Matematica I del c.
 Prova scritta di Analisi Matematica I del 22-5-2 - c. ) Provare che 3 3è irrazionale. 2) Provare che il grafico di f(x) =(x ) + 2 sin[(x ) ]:R \{} R ammette la retta di equazione x = come asintoto verticale.
Prova scritta di Analisi Matematica I del 22-5-2 - c. ) Provare che 3 3è irrazionale. 2) Provare che il grafico di f(x) =(x ) + 2 sin[(x ) ]:R \{} R ammette la retta di equazione x = come asintoto verticale.
sen n x( tan xn n n=1
 8 Gennaio 2016 Nome (in stampatello): 1) (8 punti) Discutere la convergenza della serie di funzioni al variare di x in [ 1, 1]. n x( tan xn n ) xn sen n 2) (7 punti) Provare che la forma differenziale
8 Gennaio 2016 Nome (in stampatello): 1) (8 punti) Discutere la convergenza della serie di funzioni al variare di x in [ 1, 1]. n x( tan xn n ) xn sen n 2) (7 punti) Provare che la forma differenziale
ANALISI MATEMATICA II PROVA DI TEORIA (23/6/2009)
 ANALISI MATEMATICA II PROVA DI TEORIA (23/6/2009) 1. Sia S = { } (x, y, z) : x 2 + y 2 = 4, 0 z 3 + x. Scrivere le equazioni parametriche di una superficie regolare che abbia S come sostegno. 2. Enunciare
ANALISI MATEMATICA II PROVA DI TEORIA (23/6/2009) 1. Sia S = { } (x, y, z) : x 2 + y 2 = 4, 0 z 3 + x. Scrivere le equazioni parametriche di una superficie regolare che abbia S come sostegno. 2. Enunciare
Contents. 1. Funzioni di più variabili.
 RACCOLTA DI ESERCIZI PER IL CORSO DI ANALISI MATEMATICA II A.A. 03/04 CORSI DI LAUREA IN INGEGNERIA DELL EDILIZIA, INGEGNERIA EDILE-ARCHITETTURA PROF. D. BARTOLUCCI Contents. Funzioni di più variabili..
RACCOLTA DI ESERCIZI PER IL CORSO DI ANALISI MATEMATICA II A.A. 03/04 CORSI DI LAUREA IN INGEGNERIA DELL EDILIZIA, INGEGNERIA EDILE-ARCHITETTURA PROF. D. BARTOLUCCI Contents. Funzioni di più variabili..
Prima Prova Scritta 18/03/1997
 Prima Prova Scritta 18/03/1997 1 + x y6 f(x, y) = x 6 + y 6, (x, y) (0, 0) k, (x, y) = (0, 0) A 2 Determinare, per k R, l insieme di continuità di f. B 2 Determinare, per k R, l insieme di differenziabilità
Prima Prova Scritta 18/03/1997 1 + x y6 f(x, y) = x 6 + y 6, (x, y) (0, 0) k, (x, y) = (0, 0) A 2 Determinare, per k R, l insieme di continuità di f. B 2 Determinare, per k R, l insieme di differenziabilità
Corso di Laurea in Ingegneria Edile Prova scritta dell esame di Analisi Matematica I (M-Z).C
 Analisi Matematica I (M-Z).C1 08-0-1997 1) Data la funzione h(x) = x log(x + 1 + x + x + ) + log(1 + ) determinarne il dominio D. Provare poi che h(x) > 0 x D ]0, + [, h(x) = 0 x = 0. ) Utilizzando i risultati
Analisi Matematica I (M-Z).C1 08-0-1997 1) Data la funzione h(x) = x log(x + 1 + x + x + ) + log(1 + ) determinarne il dominio D. Provare poi che h(x) > 0 x D ]0, + [, h(x) = 0 x = 0. ) Utilizzando i risultati
Esercizi. Misti iniziali. Più variabili. 1. Data la funzione. F (x) = x3 3 + x e t2 dt. se ne studino massimi, minimi, flessi, limiti a ±.
 Esercizi Misti iniziali. Data la funzione se ne studino massimi, minimi, flessi, iti a ±. 2. Provare che Più variabili F x) = 3. Calcolare, se esistono, i seguenti iti a) b) c) d) x,y),) x 2 + y 2 2 x,y),)
Esercizi Misti iniziali. Data la funzione se ne studino massimi, minimi, flessi, iti a ±. 2. Provare che Più variabili F x) = 3. Calcolare, se esistono, i seguenti iti a) b) c) d) x,y),) x 2 + y 2 2 x,y),)
Quesito 1. f(x, y) = xy log (x 2 + y 2 ) Quesito 2. Quesito 3. y = 2y3 +x 3. xy 2 y(1) = 1. Quesito 4
 Corso di laurea in Ing. Meccanica, a.a. 2002/2003 Prova scritta di Analisi Matematica 2 del 7 gennaio 2003 Determinare gli eventuali estremi relativi della funzione f(x, y) = xy log (x 2 + y 2 ) Calcolare
Corso di laurea in Ing. Meccanica, a.a. 2002/2003 Prova scritta di Analisi Matematica 2 del 7 gennaio 2003 Determinare gli eventuali estremi relativi della funzione f(x, y) = xy log (x 2 + y 2 ) Calcolare
Esame di Analisi Matematica 2 24/9/2013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 2012/2013
 Esame di Analisi Matematica 2 24/9/2013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 2012/2013 Esercizio 1. Sia A il cerchio aperto del piano di centro l origine e raggio 1. Sia f(x, y) una
Esame di Analisi Matematica 2 24/9/2013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 2012/2013 Esercizio 1. Sia A il cerchio aperto del piano di centro l origine e raggio 1. Sia f(x, y) una
ESERCIZI DI ANALISI MATEMATICA Università di Firenze - Facoltà di Ingegneria Corso di Laurea in Ingegneria Meccanica M Z Prof. M.
 ESERCIZI DI ANALISI MATEMATICA Università di Firenze - Facoltà di Ingegneria Corso di Laurea in Ingegneria Meccanica M Z Prof. M.Patrizia Pera Parte 2 Funzioni reali di più variabili 1. Stabilire se i
ESERCIZI DI ANALISI MATEMATICA Università di Firenze - Facoltà di Ingegneria Corso di Laurea in Ingegneria Meccanica M Z Prof. M.Patrizia Pera Parte 2 Funzioni reali di più variabili 1. Stabilire se i
Prove d Esame A.A. 2012/2013
 Complementi di Analisi Polo di Savona Complementi di Analisi Matematica Prove d Esame A.A. 2012/2013 1- PrCam.TEX [] Complementi di Analisi Polo di Savona Prima Prova parziale 23/11/2011 Prima Prova parziale
Complementi di Analisi Polo di Savona Complementi di Analisi Matematica Prove d Esame A.A. 2012/2013 1- PrCam.TEX [] Complementi di Analisi Polo di Savona Prima Prova parziale 23/11/2011 Prima Prova parziale
a) 1 n b) n cos(nx) n 2 + x 2, c) nx n2 x nx 2 (su IR), 1 + nx x x 2 e) n + x 2, f) nx (come sopra), n sin x g) 2n2 x 2 1 n 2 x + n,
 1. Determinare, ove esista, il limite puntuale delle seguenti successioni di funzioni, e stabilire se esse convergono uniformemente sugli insiemi indicati alla fine della riga. 1 n 1 + n2 x 2, b) n cos(nx)
1. Determinare, ove esista, il limite puntuale delle seguenti successioni di funzioni, e stabilire se esse convergono uniformemente sugli insiemi indicati alla fine della riga. 1 n 1 + n2 x 2, b) n cos(nx)
DIARIO DELLE LEZIONI DI ANALISI MATEMATICA II Corso di laurea in Ingegneria Clinica Canale PZ A.A. 2017/2018 Codocente: Dott. Salvatore Fragapane
 DIARIO DELLE LEZIONI DI ANALISI MATEMATICA II Corso di laurea in Ingegneria Clinica Canale PZ A.A. 07/08 Codocente: Dott. Salvatore Fragapane Lezione - 09/03/08, dalle 6.00 alle 8.00 in aula 6 Es. Studiare
DIARIO DELLE LEZIONI DI ANALISI MATEMATICA II Corso di laurea in Ingegneria Clinica Canale PZ A.A. 07/08 Codocente: Dott. Salvatore Fragapane Lezione - 09/03/08, dalle 6.00 alle 8.00 in aula 6 Es. Studiare
Prima prova di verifica in itinere di ANALISI MATEMATICA II. 12 Marzo 2008 Compito A. 1 (punti 3)
 anno accademico 007-008 Prima prova di verifica in itinere di ANALISI MATEMATICA II Marzo 008 Compito A (punti ) y = x + xy + y x. (punti 4) y + y x = ln x x y. (punti ) y = y + y ln y. 4 (punti 6) Determinare
anno accademico 007-008 Prima prova di verifica in itinere di ANALISI MATEMATICA II Marzo 008 Compito A (punti ) y = x + xy + y x. (punti 4) y + y x = ln x x y. (punti ) y = y + y ln y. 4 (punti 6) Determinare
1) Studiare la natura dei seguenti integrali impropri: 2x2 1. x dx (c) e x + 1. log x. n n + 1 n (a) n=1. (b) n + log n n 2n 2 1.
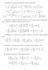 ) Studiare la natura dei seguenti integrali impropri: 0 x 3 dx (b) + 2x2 2 x 2 + 2 dx (c) e x + 0 e x dx (g) (d) + 0 + 0 x( + x) dx x sin x x 2 dx (h) (e) 0 + log x x 2 dx (f) 2 log x dx x + log( + x 2
) Studiare la natura dei seguenti integrali impropri: 0 x 3 dx (b) + 2x2 2 x 2 + 2 dx (c) e x + 0 e x dx (g) (d) + 0 + 0 x( + x) dx x sin x x 2 dx (h) (e) 0 + log x x 2 dx (f) 2 log x dx x + log( + x 2
ELIO CABIB. Esami di Analisi 2
 ELIO CABIB Esami di Analisi ELIO CABIB cabib@uniud.it professore di Analisi Matematica Università di Udine Esami di Analisi Indice Appelli 997-98 3//998..................................... 6//998.....................................
ELIO CABIB Esami di Analisi ELIO CABIB cabib@uniud.it professore di Analisi Matematica Università di Udine Esami di Analisi Indice Appelli 997-98 3//998..................................... 6//998.....................................
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016
 Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
COMPLEMENTI DI ANALISI MATEMATICA II. Prova scritta del 20 gennaio 2014
 Prova scritta del 2 gennaio 214 Studiare la convergenza puntuale e uniforme della serie di potenze n=1 n x 2n 2n + e n. Valutare poi la misurabilità e l integrabilità secondo Lebesgue della funzione somma
Prova scritta del 2 gennaio 214 Studiare la convergenza puntuale e uniforme della serie di potenze n=1 n x 2n 2n + e n. Valutare poi la misurabilità e l integrabilità secondo Lebesgue della funzione somma
D : 0 E : arctan 2 1 F : 2 arctan 1. 3y + 3y y = 0 y(0) = 3 y (0) = 0.
 Analisi Matematica B 31 marzo 003 Compito 1 1. L integrale 1 x arctan( 1 x ) dx vale Risp.: A : arctan 1 1 B : C : arctan 1 3 D : 0 E : arctan 1 F : arctan 1 + arctan 1. Sia ỹ(x) la soluzione del problema
Analisi Matematica B 31 marzo 003 Compito 1 1. L integrale 1 x arctan( 1 x ) dx vale Risp.: A : arctan 1 1 B : C : arctan 1 3 D : 0 E : arctan 1 F : arctan 1 + arctan 1. Sia ỹ(x) la soluzione del problema
Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006. Matematica 2 (Analisi)
 Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006 Matematica 2 (Analisi) Nome:................................. N. matr.:.................................
Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006 Matematica 2 (Analisi) Nome:................................. N. matr.:.................................
Esercizi di Analisi Matematica II assegnati nell A.A. 2011/12. Corsi di laurea in Ingegneria Elettronica ed Informatica
 Esercizi di Analisi Matematica II assegnati nell A.A. 2011/12 Corsi di laurea in Ingegneria Elettronica ed Informatica 1) Rappresentare nel piano xy i campi di esistenza delle seguenti funzioni: a) xy
Esercizi di Analisi Matematica II assegnati nell A.A. 2011/12 Corsi di laurea in Ingegneria Elettronica ed Informatica 1) Rappresentare nel piano xy i campi di esistenza delle seguenti funzioni: a) xy
x(y + z)dx dy dz y(x 2 + y 2 + z 2 )dx dy dz y 2 zdx dy dz Esempio di insieme non misurabile secondo Lebesgue.
 /3/23 Calcolare dove x(y + z)dx dy dz = {(x, y, z) R 3 : x, y, z, x + y + z }. Calcolare y(x 2 + y 2 + z 2 )dx dy dz dove = {(x, y, z) R 3 : x 2 + y 2 + z 2 z, x 2 + y 2 + z 2 3zx y }. Calcolare dove y
/3/23 Calcolare dove x(y + z)dx dy dz = {(x, y, z) R 3 : x, y, z, x + y + z }. Calcolare y(x 2 + y 2 + z 2 )dx dy dz dove = {(x, y, z) R 3 : x 2 + y 2 + z 2 z, x 2 + y 2 + z 2 3zx y }. Calcolare dove y
Analisi Matematica 3
 Testi delle prove d esame del corso di Analisi Matematica 3 presso la Facoltà di Ingegneria Bruno Rubino L Aquila, 2006 Indice 1 Curve 3 2 Superfici 4 3 Teorema di Gauss-Green e formula dell area 4 4 Campi
Testi delle prove d esame del corso di Analisi Matematica 3 presso la Facoltà di Ingegneria Bruno Rubino L Aquila, 2006 Indice 1 Curve 3 2 Superfici 4 3 Teorema di Gauss-Green e formula dell area 4 4 Campi
Corso di laurea in Scienze Biologiche Compito di Istituzioni di Matematiche assegnato il 16 giugno 1999
 assegnato il 16 giugno 1999 16 2 x+7 x 2 + 3x 4 + (2x + 1)2 2 Scrivere l equazione della circonferenza passante per i punti A = (0, 2), B = (0, 10) e tangente alla retta r di equazione x 8 = 0 3 Sia f
assegnato il 16 giugno 1999 16 2 x+7 x 2 + 3x 4 + (2x + 1)2 2 Scrivere l equazione della circonferenza passante per i punti A = (0, 2), B = (0, 10) e tangente alla retta r di equazione x 8 = 0 3 Sia f
Compiti d Esame A.A. 2005/2006
 Compiti d Esame A.A. 25/26 UNIVERSITÀ DEGLI STUDI DI PERUGIA A.A. 25/26 I Esercitazione 21 Aprile 26 { y = xy ln(xy) si chiede di dimostrare che: y(1) = 1, (a) ammette un unica soluzione massimale y =
Compiti d Esame A.A. 25/26 UNIVERSITÀ DEGLI STUDI DI PERUGIA A.A. 25/26 I Esercitazione 21 Aprile 26 { y = xy ln(xy) si chiede di dimostrare che: y(1) = 1, (a) ammette un unica soluzione massimale y =
Analisi Matematica III
 Università di Pisa - Corso di Laurea in Ingegneria Civile dell ambiente e territorio Analisi Matematica III Pisa, 1 giugno 4 (Cognome (Nome (Numero di matricola Esercizio 1 Si consideri la successione
Università di Pisa - Corso di Laurea in Ingegneria Civile dell ambiente e territorio Analisi Matematica III Pisa, 1 giugno 4 (Cognome (Nome (Numero di matricola Esercizio 1 Si consideri la successione
Analisi Matematica 2 Quaderno degli esercizi settimanali. Roberto Monti. Fisica e Astronomia Anno Accademico
 Analisi Matematica 2 Quaderno degli esercizi settimanali Roberto Monti Fisica e Astronomia Anno Accademico 2018-19 Indice Introduzione 5 Settimana 1. Serie numeriche I 7 Settimana 2. Serie numeriche II
Analisi Matematica 2 Quaderno degli esercizi settimanali Roberto Monti Fisica e Astronomia Anno Accademico 2018-19 Indice Introduzione 5 Settimana 1. Serie numeriche I 7 Settimana 2. Serie numeriche II
ARGOMENTI MATEMATICA PER L INGEGNERIA
 ARGOMENTI DI MATEMATICA PER L INGEGNERIA VOLUME 2 Esercizi proposti Quando non diversamente precisato, nel seguito si intenderà( sempre che nel piano sia stato introdotto un sistema cartesiano ortogonale
ARGOMENTI DI MATEMATICA PER L INGEGNERIA VOLUME 2 Esercizi proposti Quando non diversamente precisato, nel seguito si intenderà( sempre che nel piano sia stato introdotto un sistema cartesiano ortogonale
Anno accademico
 Scuola Normale Superiore Ammissione al 4 anno della Classe di Scienze Prova di Analisi per l ammissione alla Laurea Specialistica in Fisica applicata, Informatica, Matematica, Scienze fisiche, Tecnologie
Scuola Normale Superiore Ammissione al 4 anno della Classe di Scienze Prova di Analisi per l ammissione alla Laurea Specialistica in Fisica applicata, Informatica, Matematica, Scienze fisiche, Tecnologie
ESERCIZI DI ANALISI MATEMATICA Università di Firenze - Facoltà di Ingegneria Corso di Laurea in Ingegneria Meccanica M Z Prof. M.
 ESERCIZI DI ANALISI MATEMATICA Università di Firenze - Facoltà di Ingegneria Corso di Laurea in Ingegneria Meccanica M Z Prof. M.Patrizia Pera Insiemi e numeri reali Parte -a. Risolvere le seguenti disequazioni:
ESERCIZI DI ANALISI MATEMATICA Università di Firenze - Facoltà di Ingegneria Corso di Laurea in Ingegneria Meccanica M Z Prof. M.Patrizia Pera Insiemi e numeri reali Parte -a. Risolvere le seguenti disequazioni:
Cognome Nome Matricola Codice ESEMPIO 1
 Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Definizione di derivata di una funzione in un punto. Sia A R N ; sia a A; sia f : A R M ; sia f differenziabile in a; allora la derivata di f in a è...
Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Definizione di derivata di una funzione in un punto. Sia A R N ; sia a A; sia f : A R M ; sia f differenziabile in a; allora la derivata di f in a è...
Analisi Matematica II. Prove Parziali A.A. 1992/2017
 Complementi di Analisi Polo di Savona Analisi Matematica II Complementi di Analisi Matematica Prove Parziali A.A. 1992/2017 1- PrPzCa.TEX [] Complementi di Analisi Polo di Savona Prima Prova Parziale 92/93
Complementi di Analisi Polo di Savona Analisi Matematica II Complementi di Analisi Matematica Prove Parziali A.A. 1992/2017 1- PrPzCa.TEX [] Complementi di Analisi Polo di Savona Prima Prova Parziale 92/93
COMPLEMENTI DI ANALISI MATEMATICA II. Prova scritta del 20 gennaio 2014
 Prova scritta del 20 gennaio 2014 Studiare la convergenza puntuale e uniforme della serie di potenze n x 2n 2n + e n. Valutare poi la misurabilità e l integrabilità secondo Lebesgue della funzione somma
Prova scritta del 20 gennaio 2014 Studiare la convergenza puntuale e uniforme della serie di potenze n x 2n 2n + e n. Valutare poi la misurabilità e l integrabilità secondo Lebesgue della funzione somma
PROVA SCRITTA DI ANALISI MATEMATICA 2 Corso di laurea in Matematica 4 Luglio Risoluzione a cura di N. Fusco & G. Floridia
 PROVA SCRITTA DI ANALISI MATEMATICA Corso di laurea in Matematica 4 Luglio 6 Risoluzione a cura di N Fusco & G Floridia Discutere la convergenza puntuale, assoluta, uniforme e totale della serie di funzioni
PROVA SCRITTA DI ANALISI MATEMATICA Corso di laurea in Matematica 4 Luglio 6 Risoluzione a cura di N Fusco & G Floridia Discutere la convergenza puntuale, assoluta, uniforme e totale della serie di funzioni
ESERCIZI DI ANALISI MATEMATICA II. sin(tv) v. f(v) dv = (1 + t) (e 1/t + 1)
 ESERCIZI DI ANALISI MATEMATICA II Equazioni differenziali ED 1 Stabilire se l equazione integrale f(t) 1/2 0 sin(tv) v f(v) dv = (1 + t) (e 1/t + 1) ammette una soluzione nello spazio C([0, 1/2]). (Suggerimento:
ESERCIZI DI ANALISI MATEMATICA II Equazioni differenziali ED 1 Stabilire se l equazione integrale f(t) 1/2 0 sin(tv) v f(v) dv = (1 + t) (e 1/t + 1) ammette una soluzione nello spazio C([0, 1/2]). (Suggerimento:
Recupero 1 compitino di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2016/2017. Prof. M. Bramanti.
 Recupero 1 compitino di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 16/17. Prof. M. Bramanti 1 Tema n 1 3 4 6 Tot. Cognome e nome in stampatello codice persona o n di
Recupero 1 compitino di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 16/17. Prof. M. Bramanti 1 Tema n 1 3 4 6 Tot. Cognome e nome in stampatello codice persona o n di
1. Riconoscere la natura delle coniche rappresentate dalle seguenti equazioni e disegnarle:
 Università degli Studi della Basilicata Corsi di Laurea in Chimica / Scienze Geologiche Matematica II A. A. 204-205 (dott.ssa Vita Leonessa) Esercizi proposti n. 3: Funzioni a due variabili. Riconoscere
Università degli Studi della Basilicata Corsi di Laurea in Chimica / Scienze Geologiche Matematica II A. A. 204-205 (dott.ssa Vita Leonessa) Esercizi proposti n. 3: Funzioni a due variabili. Riconoscere
1 Limiti e continuità
 Calcolo infinitesimale e differenziale Gli esercizi indicati con l asterisco (*) sono più impegnativi. Limiti e continuità Si ricorda che per una funzione di più variabili, la definizione di continuità
Calcolo infinitesimale e differenziale Gli esercizi indicati con l asterisco (*) sono più impegnativi. Limiti e continuità Si ricorda che per una funzione di più variabili, la definizione di continuità
Esercizi di Analisi 2. Nicola Fusco (Dipartimento di Matematica e Applicazioni, Università Federico II, Napoli) 1. Successioni e Serie di Funzioni
 Esercizi di Analisi 2 Nicola Fusco (Dipartimento di Matematica e Applicazioni, Università Federico II, Napoli) 1. Successioni e Serie di Funzioni 1.1 Al variare di α IR studiare la convergenza della serie
Esercizi di Analisi 2 Nicola Fusco (Dipartimento di Matematica e Applicazioni, Università Federico II, Napoli) 1. Successioni e Serie di Funzioni 1.1 Al variare di α IR studiare la convergenza della serie
Analisi Matematica 3 (Fisica), , M. Peloso e L. Vesely Prova scritta del 14 luglio 2009 Breve svolgimento (con alcuni conti omessi)
 Analisi Matematica 3 Fisica, 8-9, M. Peloso e L. Vesely Prova scritta del 4 luglio 9 Breve svolgimento con alcuni conti omessi. a Dimostrare che l insieme G = { x, y R : x + x + log y = ye x} coincide
Analisi Matematica 3 Fisica, 8-9, M. Peloso e L. Vesely Prova scritta del 4 luglio 9 Breve svolgimento con alcuni conti omessi. a Dimostrare che l insieme G = { x, y R : x + x + log y = ye x} coincide
Recupero 1 compitino di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2017/2018. Prof. M. Bramanti.
 Recupero compitino di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 7/8. Prof. M. Bramanti Tema n 3 4 5 6 Tot. Cognome e nome in stampatello codice persona o n di matricola
Recupero compitino di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 7/8. Prof. M. Bramanti Tema n 3 4 5 6 Tot. Cognome e nome in stampatello codice persona o n di matricola
Soluzione dei problemi assegnati
 ANALISI MATEMATICA 3 Soluzione dei problemi assegnati anno accademico 2018/19 prof. Antonio Greco http://people.unica.it/antoniogreco Dipartimento di Matematica e Informatica Università di Cagliari 23-5-2019
ANALISI MATEMATICA 3 Soluzione dei problemi assegnati anno accademico 2018/19 prof. Antonio Greco http://people.unica.it/antoniogreco Dipartimento di Matematica e Informatica Università di Cagliari 23-5-2019
CODICE= Compiti di Analisi Matematica II per il Corso di Laurea in Ingegneria Edile A.A , Appelli 1, 2, 3 e 4
 Compiti di Analisi Matematica II per il Corso di Laurea in Ingegneria Edile A.A. 00-0, Appelli,, 3 e 4 Cognome: Nome: Matricola: CODICE = 33877 A B C D E 3 4 5 6 7 8 9 CODICE=33877 PARTE A. Lo sviluppo
Compiti di Analisi Matematica II per il Corso di Laurea in Ingegneria Edile A.A. 00-0, Appelli,, 3 e 4 Cognome: Nome: Matricola: CODICE = 33877 A B C D E 3 4 5 6 7 8 9 CODICE=33877 PARTE A. Lo sviluppo
Esame di Analisi Matematica 2 24/7/2013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 2012/2013
 Esame di Analisi Matematica 4/7/013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 01/013 A Cognome (in STAMPATELLO):... Nome (in STAMPATELLO):... CFU:... Esercizio 1. Sia f : R R una funzione
Esame di Analisi Matematica 4/7/013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 01/013 A Cognome (in STAMPATELLO):... Nome (in STAMPATELLO):... CFU:... Esercizio 1. Sia f : R R una funzione
Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica 2 del 19/06/2010 A
 Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica del 9/6/ A ) ata la funzione f(x, y) x y log( + x + y ), a) stabilire dove risulta derivabile parzialmente nel suo
Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica del 9/6/ A ) ata la funzione f(x, y) x y log( + x + y ), a) stabilire dove risulta derivabile parzialmente nel suo
ANALISI MATEMATICA 1. (Ingegneria Industriale, corsi A e B) Esempi di prove scritte
 ANALISI MATEMATICA 1 (Ingegneria Industriale, corsi A e B) Esempi di prove scritte Rispondere ai quesiti a risposta multipla Qi, risolvere gli esercizi Ei, enunciare le definizioni Di e svolgere le dimostrazioni
ANALISI MATEMATICA 1 (Ingegneria Industriale, corsi A e B) Esempi di prove scritte Rispondere ai quesiti a risposta multipla Qi, risolvere gli esercizi Ei, enunciare le definizioni Di e svolgere le dimostrazioni
Risoluzione del compito n. 2 (Febbraio 2018/2)
 Risoluzione del compito n. 2 (Febbraio 218/2) PROBLEMA 1 Sia esiano Φ(t) (cost, sen t, t 2 ), f(x, y, z) z, g(x, y, z) t 2π ( y + x, y x, x 2 ). z a) Dite se Φ è una curva regolare; scrivete un equazione
Risoluzione del compito n. 2 (Febbraio 218/2) PROBLEMA 1 Sia esiano Φ(t) (cost, sen t, t 2 ), f(x, y, z) z, g(x, y, z) t 2π ( y + x, y x, x 2 ). z a) Dite se Φ è una curva regolare; scrivete un equazione
Corso di Laurea in Ingegneria Gestionale - Sede di Fermo Anno Accademico 2009/2010 Matematica 2 Esercizi d esame
 Corso di Laurea in Ingegneria Gestionale - ede di Fermo Anno Accademico 2009/2010 Matematica 2 Esercizi d esame Nome... N. Matricola... Fermo, gg/mm/aaaa 1. tabilire l ordine di ciascuna delle seguenti
Corso di Laurea in Ingegneria Gestionale - ede di Fermo Anno Accademico 2009/2010 Matematica 2 Esercizi d esame Nome... N. Matricola... Fermo, gg/mm/aaaa 1. tabilire l ordine di ciascuna delle seguenti
Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005
 Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005 Prova orale il: Docente: Determinare, se esistono, il massimo ed il minimo assoluto della funzione
Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005 Prova orale il: Docente: Determinare, se esistono, il massimo ed il minimo assoluto della funzione
Cognome Nome Matricola Codice ESEMPIO 1
 Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Definizione di forma differenziale chiusa. Sia A R N ; sia A aperto; sia ω = N i=1 ω i dx i una forma differenziale su A; sia ω di classe C 1 ; si dice
Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Definizione di forma differenziale chiusa. Sia A R N ; sia A aperto; sia ω = N i=1 ω i dx i una forma differenziale su A; sia ω di classe C 1 ; si dice
Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica 2 del 29 settembre 2012
 Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica del 9 settembre A) Data la funzione f(x, y) = { xy x se (x, y) (, ) se (x, y) = (, ), i) stabilire se risulta continua
Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica del 9 settembre A) Data la funzione f(x, y) = { xy x se (x, y) (, ) se (x, y) = (, ), i) stabilire se risulta continua
ANALISI MATEMATICA 1-11/02/2019 Corso di Laurea in Ingegneria Meccanica. Primo Appello - Test 1
 ANALISI MATEMATICA - /2/29 Corso di Laurea in Ingegneria Meccanica Il candidato deve riportare nella griglia le risposte che ritiene corrette. Al termine della prova il candidato deve riconsegnare questo
ANALISI MATEMATICA - /2/29 Corso di Laurea in Ingegneria Meccanica Il candidato deve riportare nella griglia le risposte che ritiene corrette. Al termine della prova il candidato deve riconsegnare questo
Analisi 2 Fisica e Astronomia
 Analisi Fisica e Astronomia Appello scritto del 8 Luglio 0. Soluzione Esercizio 7 pti Sia α > 0 un parametro e consideriamo la curva piana γ : [0, ] R γt = t cos, t sin, se t 0, ], e γ0 = 0, 0. t α t α
Analisi Fisica e Astronomia Appello scritto del 8 Luglio 0. Soluzione Esercizio 7 pti Sia α > 0 un parametro e consideriamo la curva piana γ : [0, ] R γt = t cos, t sin, se t 0, ], e γ0 = 0, 0. t α t α
Gli argomenti denotati con un asterisco tra parentesi (e solo quelli) sono stati dimostrati.
 Corso di laurea: Fisica ed Astronomia Programma di Analisi Matematica 2 a.a. 2016/17 Docente: Fabio Paronetto Gli argomenti denotati con un asterisco tra parentesi (e solo quelli) sono stati dimostrati.
Corso di laurea: Fisica ed Astronomia Programma di Analisi Matematica 2 a.a. 2016/17 Docente: Fabio Paronetto Gli argomenti denotati con un asterisco tra parentesi (e solo quelli) sono stati dimostrati.
Corso di laurea in Scienze Biologiche Compito di Istituzioni di Matematiche assegnato il 12 giugno 2000
 assegnato il 1 giugno 1 Risolvere il sistema di disequazioni ( ) 1 x 1 3 9 3 log (13 x) > 3 x 9 x 4 + 1 < Scrivere le equazioni delle circonferenze che passano per il punto A = (, ) e sono tangenti alle
assegnato il 1 giugno 1 Risolvere il sistema di disequazioni ( ) 1 x 1 3 9 3 log (13 x) > 3 x 9 x 4 + 1 < Scrivere le equazioni delle circonferenze che passano per il punto A = (, ) e sono tangenti alle
Scritto d esame di Matematica I
 Capitolo 2: Scritti d esame 139 Pisa, 19 Gennaio 2005 x 1 + (x + 1) log x (x 1)(2x 2). 2. Studiare la convergenza dei seguenti integrali impropri 1 dx e 2x 1, 0 dx e 2x 1, e, nel caso in cui convergano,
Capitolo 2: Scritti d esame 139 Pisa, 19 Gennaio 2005 x 1 + (x + 1) log x (x 1)(2x 2). 2. Studiare la convergenza dei seguenti integrali impropri 1 dx e 2x 1, 0 dx e 2x 1, e, nel caso in cui convergano,
x + 1 2x], g(x) = x x + 2, h(x) = ln(x 1 2x 2 4x).
![x + 1 2x], g(x) = x x + 2, h(x) = ln(x 1 2x 2 4x). x + 1 2x], g(x) = x x + 2, h(x) = ln(x 1 2x 2 4x).](/thumbs/102/153351382.jpg) Funzioni Esercizio Siano f, g due funzioni definite da fx) = x x 2, gx) = ln x Trovare l insieme di definizione di f e g 2 Determinare le funzioni composte f g e g f, precisandone insieme di definizione
Funzioni Esercizio Siano f, g due funzioni definite da fx) = x x 2, gx) = ln x Trovare l insieme di definizione di f e g 2 Determinare le funzioni composte f g e g f, precisandone insieme di definizione
Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1
 Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1 22 luglio 2016 Scrivere subito nome e cognome e matricola sul foglio risposte e preparare il libretto sul banco per il controllo.
Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1 22 luglio 2016 Scrivere subito nome e cognome e matricola sul foglio risposte e preparare il libretto sul banco per il controllo.
COMPLEMENTI DI ANALISI MATEMATICA DI BASE. Prova scritta del 26 gennaio 2005
 Prova scritta del 26 gennaio 2005 Esercizio 1. Posto B = x R 2 : x 2 2}, sia f n } una successione di funzioni (misurabili e) integrabili in B tali che f n f q.o. in B e, per ogni n N, f n (x) 2 x 3 per
Prova scritta del 26 gennaio 2005 Esercizio 1. Posto B = x R 2 : x 2 2}, sia f n } una successione di funzioni (misurabili e) integrabili in B tali che f n f q.o. in B e, per ogni n N, f n (x) 2 x 3 per
Analisi Matematica I
 Università degli Studi di Genova Facoltà di Ingegneria - Polo di Savona via Cadorna 7-7 Savona Tel. +39 9 264555 - Fax +39 9 264558 Analisi Matematica I Testi d esame e Prove parziali Analisi Matematica
Università degli Studi di Genova Facoltà di Ingegneria - Polo di Savona via Cadorna 7-7 Savona Tel. +39 9 264555 - Fax +39 9 264558 Analisi Matematica I Testi d esame e Prove parziali Analisi Matematica
Analisi Matematica 3 prof. Antonio Greco
 Analisi Matematica 3 prof. Antonio Greco Alcune domande da rivolgere agli studenti in sede d esame ( ) 18 giugno 2018 Equazioni differenziali 1. Spiegare che cosa si intende per equazione differenziale
Analisi Matematica 3 prof. Antonio Greco Alcune domande da rivolgere agli studenti in sede d esame ( ) 18 giugno 2018 Equazioni differenziali 1. Spiegare che cosa si intende per equazione differenziale
Gli argomenti denotati con un asterisco tra parentesi (e solo quelli) sono stati dimostrati.
 Corso di laurea: Fisica ed Astronomia Programma di Analisi Matematica 2 a.a. 2017/18 Docente: Fabio Paronetto Gli argomenti denotati con un asterisco tra parentesi (e solo quelli) sono stati dimostrati.
Corso di laurea: Fisica ed Astronomia Programma di Analisi Matematica 2 a.a. 2017/18 Docente: Fabio Paronetto Gli argomenti denotati con un asterisco tra parentesi (e solo quelli) sono stati dimostrati.
DIARIO DELLE LEZIONI DI ANALISI MATEMATICA II Corso di laurea in Ingegneria Gestionale Canale PZ Secondo codocente: Dott. Salvatore Fragapane
 DIARIO DELLE LEZIONI DI ANALISI MATEMATICA II Corso di laurea in Ingegneria Gestionale Canale PZ Secondo codocente: Dott. Salvatore Fragapane Lezione 1-04/10/2016 - Serie Numeriche (1): definizione e successione
DIARIO DELLE LEZIONI DI ANALISI MATEMATICA II Corso di laurea in Ingegneria Gestionale Canale PZ Secondo codocente: Dott. Salvatore Fragapane Lezione 1-04/10/2016 - Serie Numeriche (1): definizione e successione
Compito di Analisi Matematica 1 per Ingegneria Elettronica a delle Telecomunicazioni COGNOME: NOME: MATR.: 1. x n
 Compito di Analisi Matematica 1 per Ingegneria Elettronica a delle Telecomunicazioni 17 gennaio 2017 COGNOME: NOME: MATR.: Esercizio 1. Sia f : R R definita da f(x) = 1 4 x x + 1 2. a) Disegnare grafico
Compito di Analisi Matematica 1 per Ingegneria Elettronica a delle Telecomunicazioni 17 gennaio 2017 COGNOME: NOME: MATR.: Esercizio 1. Sia f : R R definita da f(x) = 1 4 x x + 1 2. a) Disegnare grafico
9/11/2010 (I prova in itinere): solo test a risposta multipla
 9/11/2010 (I prova in itinere): solo test a risposta multipla 23/12/2010 (II prova in itinere, II parte) Esercizio 1. Posto Σ = {(x, y, z) R 3 x 2 + y 2 + z 2 = 4, z 1}, si chiede di calcolare il flusso
9/11/2010 (I prova in itinere): solo test a risposta multipla 23/12/2010 (II prova in itinere, II parte) Esercizio 1. Posto Σ = {(x, y, z) R 3 x 2 + y 2 + z 2 = 4, z 1}, si chiede di calcolare il flusso
UNIVERSITÀ DEGLI STUDI DI PERUGIA Corso di Analisi Matematica III - 9 CFU C.d.S. Triennale in Matematica A.A. 2016/2017 I Esercitazione 12 Aprile 2017
 C.d.S. Triennale in Matematica A.A. 2016/2017 I Esercitazione 12 Aprile 2017 Esercizio 1. Data la successione di funzioni f n t = en1+t4 + e nt2 n 3 + e, t R, n1+t2 a determinare l insieme di convergenza
C.d.S. Triennale in Matematica A.A. 2016/2017 I Esercitazione 12 Aprile 2017 Esercizio 1. Data la successione di funzioni f n t = en1+t4 + e nt2 n 3 + e, t R, n1+t2 a determinare l insieme di convergenza
1) Calcolare, se esiste, il limite seguente. 1 cos x + log(1 + x) lim 1) 2) Dire per quali numeri reali x converge la serie. ( 1) n ( e 1 n 1.
 Prova scritta di Analisi Matematica I del giorno 05-1-009 Appello riservato a studenti fuori corso o ripetenti 1) Calcolare, se esiste, il ite seguente 1 cos x + log(1 + x) x 0+ x(e x 1) ) Dire per quali
Prova scritta di Analisi Matematica I del giorno 05-1-009 Appello riservato a studenti fuori corso o ripetenti 1) Calcolare, se esiste, il ite seguente 1 cos x + log(1 + x) x 0+ x(e x 1) ) Dire per quali
Analisi I Ingegneria Chimica e Aerospaziale 1 o compitino
 1 o compitino 1 febbraio 215 1 Si consideri la funzione f : R R definita da { f) = 2 log se se = a) Si dimostri che f è continua e derivabile su tutto R b) Si dica se f ammette derivata seconda in ogni
1 o compitino 1 febbraio 215 1 Si consideri la funzione f : R R definita da { f) = 2 log se se = a) Si dimostri che f è continua e derivabile su tutto R b) Si dica se f ammette derivata seconda in ogni
Scritto d esame di Analisi Matematica II
 Capitolo 2: Scritti d esame 145 Pisa, 1 Gennaio 2005 e gli insiemi f(x, y) = x 2 x 2 y + y, A = {(x, y) R 2 : x 2 + y 2 6, x 0, y 0}, B = {(x, y) R 2 : x 0, y 0}. (a) massimo e minimo di f(x, y) in A,
Capitolo 2: Scritti d esame 145 Pisa, 1 Gennaio 2005 e gli insiemi f(x, y) = x 2 x 2 y + y, A = {(x, y) R 2 : x 2 + y 2 6, x 0, y 0}, B = {(x, y) R 2 : x 0, y 0}. (a) massimo e minimo di f(x, y) in A,
Provetta scritta di Calcolo I Corsi di laurea in Fisica - Scienza e Tecnologia dei Materiali Prova scritta del 7/12/2005 Fila A
 Provetta scritta di Calcolo I Prova scritta del 7/2/25 Fila A ) Calcolare i limiti 3 x 3 x 4 ; b) lim sin(2x) + x2 x( cos(3x)) c) lim + 5 x 7 x 4 x 2 + x. 2) Determinare il massimo di x 3 (2 + x 4 ) 3/2,
Provetta scritta di Calcolo I Prova scritta del 7/2/25 Fila A ) Calcolare i limiti 3 x 3 x 4 ; b) lim sin(2x) + x2 x( cos(3x)) c) lim + 5 x 7 x 4 x 2 + x. 2) Determinare il massimo di x 3 (2 + x 4 ) 3/2,
f(x, y, z) = xye z (x, y, z) R 3 : x > 0, y > 0, z 1 < x 2 + y 2 < z } 0 < z < 2 x < 1 y < 1
 ANALISI MATEMATICA II Corso di Laurea in Fisica quadriennale Traccia di soluzione della prova scritta del 2 gennaio 24 Durata della prova scritta: 2 ore. Lo studente può svolgere fino a 3 esercizi tra
ANALISI MATEMATICA II Corso di Laurea in Fisica quadriennale Traccia di soluzione della prova scritta del 2 gennaio 24 Durata della prova scritta: 2 ore. Lo studente può svolgere fino a 3 esercizi tra
Esercitazioni di Matematica
 Università degli Studi di Udine Anno Accademico 009/00 Facoltà di Agraria Corsi di Laurea in VIT e STAL Esercitazioni di Matematica novembre 009 Trovare le soluzioni della seguente disequazione: x + +
Università degli Studi di Udine Anno Accademico 009/00 Facoltà di Agraria Corsi di Laurea in VIT e STAL Esercitazioni di Matematica novembre 009 Trovare le soluzioni della seguente disequazione: x + +
Analisi Matematica 2
 Analisi Matematica 2 Differenziabilità per funzioni di due variabili Differenziabilità per funzioni di due variabili CCS Ingegneria Meccanica e Ingegneria Chimica 1 / 26 Differenziabilitá Data la funzione
Analisi Matematica 2 Differenziabilità per funzioni di due variabili Differenziabilità per funzioni di due variabili CCS Ingegneria Meccanica e Ingegneria Chimica 1 / 26 Differenziabilitá Data la funzione
COMPLEMENTI DI ANALISI MATEMATICA A.A Primo appello del 5/5/2010
 COMPLEMENTI DI ANALISI MATEMATICA A.A. 29- Primo appello del 5/5/2 Qui trovate le tracce delle soluzioni degli esercizi del compito. Ho tralasciato i calcoli da Analisi (che comunque sono parte della risoluzione),
COMPLEMENTI DI ANALISI MATEMATICA A.A. 29- Primo appello del 5/5/2 Qui trovate le tracce delle soluzioni degli esercizi del compito. Ho tralasciato i calcoli da Analisi (che comunque sono parte della risoluzione),
Esercizi sull integrazione II
 ANALISI MATEMATICA T-2 (C.d.L. Ing. per l ambiente e il territorio) - COMPL. DI ANALISI MATEMATICA (A-K) (C.d.L. Ing. Civile) A.A.28-29 - Prof. G.Cupini Esercizi sull integrazione II (Grazie agli studenti
ANALISI MATEMATICA T-2 (C.d.L. Ing. per l ambiente e il territorio) - COMPL. DI ANALISI MATEMATICA (A-K) (C.d.L. Ing. Civile) A.A.28-29 - Prof. G.Cupini Esercizi sull integrazione II (Grazie agli studenti
Scritto d esame di Analisi Matematica I
 Capitolo 2: Scritti d esame 07 Pisa, 8 Gennaio 999. Studiare il comportamento della serie al variare del parametro α > /2. ( ) n n sin α n 2α 2. Sia ( ) f(x) = log + sin3 x. 2 (a) Determinare la derivata
Capitolo 2: Scritti d esame 07 Pisa, 8 Gennaio 999. Studiare il comportamento della serie al variare del parametro α > /2. ( ) n n sin α n 2α 2. Sia ( ) f(x) = log + sin3 x. 2 (a) Determinare la derivata
Gli argomenti denotati con un asterisco tra parentesi (e solo quelli) sono stati dimostrati.
 Corso di laurea: Fisica ed Astronomia Programma di Analisi Matematica 2 a.a. 2018/19 Docente: Fabio Paronetto Gli argomenti denotati con un asterisco tra parentesi (e solo quelli) sono stati dimostrati.
Corso di laurea: Fisica ed Astronomia Programma di Analisi Matematica 2 a.a. 2018/19 Docente: Fabio Paronetto Gli argomenti denotati con un asterisco tra parentesi (e solo quelli) sono stati dimostrati.
Analisi Matematica III
 Università di Pisa - Corso di Laurea in Ingegneria Civile dell ambiente e territorio Analisi Matematica III Pisa, 7 gennaio 00 (Cognome) (Nome) (Numero di matricola) Esercizio Si consideri la successione
Università di Pisa - Corso di Laurea in Ingegneria Civile dell ambiente e territorio Analisi Matematica III Pisa, 7 gennaio 00 (Cognome) (Nome) (Numero di matricola) Esercizio Si consideri la successione
Foglio n. 19. Massimi e minimi vincolati
 Foglio n. 19 Massimi e minimi vincolati 1) Calcolare massimo e minimo della funzione x 2 +3y 2 xy y nel quadrato Q = {(x, y) R 2 : x 1, y 1}. 2) Calcolare massimo e minimo della funzione x+y 6z sulla superficie
Foglio n. 19 Massimi e minimi vincolati 1) Calcolare massimo e minimo della funzione x 2 +3y 2 xy y nel quadrato Q = {(x, y) R 2 : x 1, y 1}. 2) Calcolare massimo e minimo della funzione x+y 6z sulla superficie
ANALISI MATEMATICA 3. esercizi assegnati per la prova scritta del 31 gennaio 2011
 esercizi assegnati per la prova scritta del 31 gennaio 2011 Esercizio 1. Per x > 0 e n N si ponga f n (x) = ln ( n 5 x ) a) Provare l integrabilità delle funzioni f n in (0, + ). 3 + n 4 x 2. b) Studiare
esercizi assegnati per la prova scritta del 31 gennaio 2011 Esercizio 1. Per x > 0 e n N si ponga f n (x) = ln ( n 5 x ) a) Provare l integrabilità delle funzioni f n in (0, + ). 3 + n 4 x 2. b) Studiare
Tutorato di Complementi di Analisi Matematica e Statistica Parte di Analisi 6 e 10 aprile 2017
 Tutorato di Complementi di Analisi Matematica e Statistica Parte di Analisi 6 e 10 aprile 2017 Esercizi: serie di potenze e serie di Taylor 1 Date le serie di potenze a.) n=2 ln(n) n 3 (x 5)n b.) n=2 ln(n)
Tutorato di Complementi di Analisi Matematica e Statistica Parte di Analisi 6 e 10 aprile 2017 Esercizi: serie di potenze e serie di Taylor 1 Date le serie di potenze a.) n=2 ln(n) n 3 (x 5)n b.) n=2 ln(n)
Estremi. 5. Determinare le dimensioni di una scatola rettangolare di volume v assegnato, che abbia la superficie minima.
 Estremi 1. Determinare gli estremi relativi di f(x, y) = e x (x 1)(y 1) + (y 1).. Determinare gli estremi relativi di f(x, y) = y (y + 1) cos x. 3. Determinare gli estremi relativi di f(x, y) = xye x +y..
Estremi 1. Determinare gli estremi relativi di f(x, y) = e x (x 1)(y 1) + (y 1).. Determinare gli estremi relativi di f(x, y) = y (y + 1) cos x. 3. Determinare gli estremi relativi di f(x, y) = xye x +y..
Complementi di Analisi Matematica. Foglio di esercizi n.11 16/05/2017 (Aggiornamento del 22/5/2017)
 Complementi di Analisi Matematica Foglio di esercizi n11 16/05/2017 (Aggiornamento del 22/5/2017) Esercizi su serie di funzioni Esercizio 1 Definita g k (x) = e kx2, provare che g k : R R converge puntualmente
Complementi di Analisi Matematica Foglio di esercizi n11 16/05/2017 (Aggiornamento del 22/5/2017) Esercizi su serie di funzioni Esercizio 1 Definita g k (x) = e kx2, provare che g k : R R converge puntualmente
1 Analisi mat. I - Esercizi del 13/10/99
 Analisi mat. I - Esercizi del //99 ES. Delle seguenti funzioni determinare: il dominio l immagine gli eventuali asintoti l insieme dove sono continue e quali siano estendibili per continuita. Determinare
Analisi mat. I - Esercizi del //99 ES. Delle seguenti funzioni determinare: il dominio l immagine gli eventuali asintoti l insieme dove sono continue e quali siano estendibili per continuita. Determinare
PROVE SCRITTE DI ANALISI MATEMATICA II(N.O.), ANNO 2006/07
 PROV SCRITT DI ANALISI MATMATICA II(N.O.), ANNO 6/7 Prova scritta del 5//6 Si determini l insieme di convergenza della serie di funzioni n= n( + sin x) n limitatamente all intervallo x π, e si specifichi
PROV SCRITT DI ANALISI MATMATICA II(N.O.), ANNO 6/7 Prova scritta del 5//6 Si determini l insieme di convergenza della serie di funzioni n= n( + sin x) n limitatamente all intervallo x π, e si specifichi
Teoria della misura Esercizi. 1. Teoremi di convergenza sotto il segno di integrale. n 1 + n 2 x 2. f n (x) =
 Teoria della misura 215-215 Esercizi 1. Teoremi di convergenza sotto il segno di integrale Esercizio 1. Calcolare il Per ogni intero positivo n sia f n : R + R la funzione definita da n 1 + n 2 x 2. lim
Teoria della misura 215-215 Esercizi 1. Teoremi di convergenza sotto il segno di integrale Esercizio 1. Calcolare il Per ogni intero positivo n sia f n : R + R la funzione definita da n 1 + n 2 x 2. lim
Analisi 4 - SOLUZIONI (15/07/2015)
 Corso di Laurea in Matematica Analisi 4 - SOLUZIONI (5/7/5) Docente: Claudia Anedda ) Calcolare l area della superficie totale della regione di spazio limitata, interna al paraboloide di equazione x +y
Corso di Laurea in Matematica Analisi 4 - SOLUZIONI (5/7/5) Docente: Claudia Anedda ) Calcolare l area della superficie totale della regione di spazio limitata, interna al paraboloide di equazione x +y
Analisi Matematica 3 (Fisica) Prova scritta del 27 gennaio 2012 Uno svolgimento
 Analisi Matematica 3 (Fisica) Prova scritta del 27 gennaio 22 Uno svolgimento Prima di tutto, eccovi alcuni commenti che potrebbero aiutarvi a svolgere meglio le prove scritte. Ad ogni domanda del testo
Analisi Matematica 3 (Fisica) Prova scritta del 27 gennaio 22 Uno svolgimento Prima di tutto, eccovi alcuni commenti che potrebbero aiutarvi a svolgere meglio le prove scritte. Ad ogni domanda del testo
Analisi Matematica 2. Michele Campiti. Prove scritte di. Ingegneria Industriale a.a
 Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 2009 2010 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi
Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 2009 2010 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi
ANALISI MATEMATICA 4. Prova scritta del 24 gennaio 2013
 Prova scritta del 24 gennaio 2013 Esercizio 1. Sia Ω R 3 un insieme misurabile secondo Lebesgue e di misura finita. Sia {f n } n N una successione di funzioni f n : Ω R misurabili e tali che 1) f n (x)
Prova scritta del 24 gennaio 2013 Esercizio 1. Sia Ω R 3 un insieme misurabile secondo Lebesgue e di misura finita. Sia {f n } n N una successione di funzioni f n : Ω R misurabili e tali che 1) f n (x)
