y = y(x) d n y dx n 1.1 dx dy 1.2 y = f( y x ), y + p(x)y = q(x) y(x) =Ce x dx1 p(x 1 ),
|
|
|
- Ottavio Sartori
- 5 anni fa
- Visualizzazioni
Transcript
1 I : I x y = y(x) x y y = dy dx,y = d2 y dx,,y (n) = 2 n F (x, y, y,,y (n) )=0 n d n y dx n : y (n) = f(x, y, y,,y (n ) ) : n n : : y = y(x). y = dy = X(x) Y (y), dx dx dy X(x) :x Y (y) :y y dȳ Y (ȳ) = x d xx( x)+c ( ).2 y = f( y x ), f(t) :t u = y x u y = ux y = u x + u.3 ( ) y + p(x)y =0 p(x) :x y(x) =Ce x dx p(x ), C.4 ( ) y + p(x)y = q(x) p(x),q(x) :x
2 I : 2 y(x) =C(x)e x dx p(x ) C(x) ( ) x x dx y(x) =(C 0 + dx q(x )e 2 p( x 2 ) )e x dx p(x ), C 0.5 P (x, y)dx + Q(x, y)dy =0 P (x, y) + Q(x, y) dy dx =0 P (x, y),q(x, y) :x, y P y = Q x = P (x, y) Φ y dy =0 x, y Φ x dφ = Φ x dx + Φ y Φ Φ(x, y) = x Φ(x, y) =C, x 0 dx P (x,y)+ y C y 0 dy Q(x 0,y ), = Q(x, y) Φ(x, y) x 0,y 0 M(x, y) ( ) (MP) y = (MQ) x MPdx+ MQdy =0.6 (i) y + p(x)y = q(x)y n, (n :, 0) y n u = y n (ii) y + P (x)+q(x)y + R(x)y 2 =0 y y = u + y (iii) ( ) p = y x y = xy + f(y ) dp df (p) (x + dx dp )=0
3 I : 3 dp =0 y = Cx + f(c), dx C : { x + f (p) =0 y = xp + f(p) p
4 I : 4 2 P n (x) =,P n (x),,p (x),p 0 (x) Q(x) n L[y(x)] = P j (x) dj dx j y(x) =y(n) (x)+p n (x)y (n ) (x)+ +P (x)y (x)+p 0 (x)y(x) =Q(x) j=0 y = y(x) n C y (x) + + C n y n (x) = 0 C = = C n = 0 n y (x),,y n (x) y (x) y 2 (x) y n (x) y W (x) = det W, W = (x) y 2 (x) y n (x) y (n ) (x) y (n ) 2 (x) y n (n ) (x) W (x) W (x) 0 {y,,y n } 2. Q(x) =0 Q(x) 0 y(x) =y (x) ( L[y ]=Q ) y(x) =y 0 (x) ( L[y 0 ]=0) y(x) =y (x)+y 0 (x) ( L[y 0 + y ]=Q ) y (x) y 2 (x) C y (x)+c 2 y 2 (x) n ( ) (y,,y n ) n j= C j y j (x) 2.2 P n (x) =,P n (x),,p (x),p 0 (x) ( ) I y = e λx L[e λx ] = f(λ)e λx =0 f(λ) = n P j λ j =0 ( ) λ f(λ) = n j= (λ λ j )=0 j=0
5 I : 5 (a) e λjx, j =,,n e θ = cos θ + i sin θ λ j = λ R + iλ I e λrx cos λ I x e λrx sin λ I x (b) λ = λ j k e λjx, xe λjx, x 2 e λjx,,x k e λjx, λ j = λ R + iλ I k e λrx cos λ I x, xe λrx cos λ I x,, x k cos λ I x e λrx sin λ I x, xe λrx sin λ I x,, x k sin λ I x II * Q(x) =e αx α y = Ce αx C α y = Cxe αx C α m y = Cx m e αx C * Q(x) y y (x),,y n (x) n y(x) =C (x)y (x) + + C n (x)y n (x) W W C (x). C n (x) C n(x) = 0. 0 Q(x) W = det W 0 C j (x) C j(x) = x dx Q(x ) W (x) +C0 j (* x ) ( ) ( ) y (x) y 2 (x) y W = y (x) y 2 (x) W = 2 (x) y 2 (x) W (x) y (x) y (x) C (x) = Q(x)y 2(x) C 2 (x) =Q(x)y 2(x) C 0 C0 2 x y(x) =y (x){ dx Q(x ) y 2(x ) x W (x ) + C0 } + y 2 (x){ dx Q(x ) y (x ) W (x ) + C0 2}
6 I : y = y(x) D = d dx f(d)y(x) =Q(x) f(t) t d2 y 3 dy dx 2 dx +2y =(D2 3D +2)y =(D 2)(D )y Q(x) f(d) f(d) f(d)[ Q(x)] = Q(x) f(d) f(d) Q(x) f(d)y 0(x) =0 y 0 x D Q(x) = dx Q(x ) x xn xn x2 D n Q(x) = dxn dxn dxn 2 dx Q(x ) x Q(x) =eαx dx e αx Q(x ) D α Q(x) =eαx (D α) n D n [e αx Q(x)] f(d) eαx = f(α) eαx (f(α) 0) (D α) n eαx = n! xn e αx f(d) = g(d) (D α), g(d) : degree of g(d) is less than d dα α Q(x) ( k ) Q(x) = D α α D α Q(x) = α k ( D α )j Q(x) j=0
7 I : 7 3 N t x = x (t),x 2 = x 2 (t),,x N = x N (t) d dt x (t) = ẋ (t) =a x (t)+a 2 x 2 (t)+ + a N x N (t)+b (t) d dt x 2(t) = ẋ 2 (t) =a 2 x (t)+a 22 x 2 (t)+ + a 2N x N (t)+b 2 (t) d dt x N(t) = ẋ N (t) =a N x (t)+a N2 x 2 (t)+ + a NN x N (t)+b N (t) b (t),,b N (t) N d dt x(t) = x(t) =A x(t)+ b(t), a a 2 a N x (t) a 2 a 22 a 2N x 2 (t) A =., x(t) =, b(t) = a N a N2 a NN x N (t) b (t) b 2 (t). b N (t) 3. b = 0 x 0 N x(t) =e At x 0, e At = n=0 t n n! An ( ẋ = ax(t) x(t) =e at x 0 ) N N N N x j (t) C N x(t) = C j x j (t) =Φ(t) C, Φ(t) = [ x, x 2,, x N ], C C 2 = j=. Phi(t) Case : A N λ j j =,,N N v j, j =,,N A v j = λ j v j N C N x j (t) =e At v j = e λ jt v j
8 I : 8 Case 2 : A n λ (A λi) v = 0 (A λi) v 2 = v, (A λi) 2 v 2 = 0 (A λi) v 3 = v 2, (A λi) 3 v 3 = 0 (A λi) v n = v n, (A λi) n v n = 0 n x = e At v = e λt e (A λi)t v = e λt v [ x 2 = e At v 2 = e λt e (A λi)t v 2 = e λt I + t ]! (A λi) v 2 = e λt [ v 2 + t v ] [ x 3 = e At v 3 = e λt e (A λi)t v 3 = e λt I + t! x n = e At v n = [ e λt e (A λi)t v n = = e λt (A λi)+t2(a λi)2 2! ] v 3 = e λt [ ] v n + t v n + t2 2! v n tn n! v ] v 3 + t v 2 + t2 2! v 3.2 x = A x + b(t) Φ(t) N x(t) = C j (t) x j (t) =Φ(t) C(t), Φ(t) = [ x, x 2,, x N ], C(t) = j= C (t) C 2 (t). C N (t) x = Φ C +Φ C C =Φ b t = t 0 x = x(t 0 ) t x(t) = G(t, t ) b(t )+ x(t 0 ) t 0 G(t, t ) = Φ(t)Φ (t )=e A(t t ) 3.3
9 I : 9 4 y = y(x) 2 y + q(x)y + r(x)y =0 ( ) (*) q(x) = n=0 q n (x a) n r(x) = n=0 r n (x a) n x = a x = a y = c n (x a) n n=0 c n (n ) k (k+2)(k+)c k+2 + {(m+2)(m+)c m+2 +q k m (m+)c m+ +r k m c m }, k =0,, 2, m=0 c 0 c. Legendre x =0 ( x 2 )y 2xy + n(n +)y =0 2 x = a (*) q(x) = n=0 q n (x a) n r(x) = n=0 r n (x a) n q(x) r(x) (*) x = a y + x a q(x)y + r(x)y =0 (x a) 2 y =(x a) ρ k n=0 c n (x a) n f(ρ + k)c k = (m + ρ)(m + ρ ) + q k m (m + ρ)+r k m }c m, k =0,, 2, m=0 f(ρ) ρ(ρ ) + q 0 ρ + r 0 c m m =0 f(ρ) =0
10 I : 0 c 0 m =, 2, 3, f(ρ + m)c m =(c 0,c,,c m ) f(ρ + m) 0 c m ρ f(ρ) =0 2 ρ ρ 2 () ρ ρ 2 ρ ρ 2 (2) ρ ρ 2 ρ. Bessel x =0 y x y +( ν2 )y =0 x2
6y y = p 2z = q² : q² = 4z 6z = 8c + 6c = a 9 = 8n : 4n = m : m = y + y² = m + 3m = q : 9 = a a = n 7n = z ( 3n) = p + p = q² + q² = b b² = 5 + z =
 Verifica n 1 Alunno Data 6y y = p 2z = q² : q² = 4z 6z = 8c + 6c = a 9 = 8n : 4n = m : m = y + y² = m + 3m = q : 9 = a a = n 7n = z ( 3n) = p + p = q² + q² = b b² = 5 + z = m a = n b = 10b³ : 7b = pq pq
Verifica n 1 Alunno Data 6y y = p 2z = q² : q² = 4z 6z = 8c + 6c = a 9 = 8n : 4n = m : m = y + y² = m + 3m = q : 9 = a a = n 7n = z ( 3n) = p + p = q² + q² = b b² = 5 + z = m a = n b = 10b³ : 7b = pq pq
EQUAZIONI DIFFERENZIALI
 EQUAZIONI DIFFERENZIALI 1 Primo ordine - variabili separabili Sia dato il problema di Cauchy seguente: { y = a(x)b(y) Si proceda come segue y(x 0 ) = y 0 (1) Si calcolino le radici dell equazione b(y)
EQUAZIONI DIFFERENZIALI 1 Primo ordine - variabili separabili Sia dato il problema di Cauchy seguente: { y = a(x)b(y) Si proceda come segue y(x 0 ) = y 0 (1) Si calcolino le radici dell equazione b(y)
Analisi 4 - SOLUZIONI (compito del 29/09/2011)
 Corso di laurea in Matematica Analisi 4 - SOLUZIONI compito del 9/09/0 Docente: Claudia Anedda Calcolare, tramite uno sviluppo in serie noto, la radice quinta di e la radice cubica di 9 Utilizzando la
Corso di laurea in Matematica Analisi 4 - SOLUZIONI compito del 9/09/0 Docente: Claudia Anedda Calcolare, tramite uno sviluppo in serie noto, la radice quinta di e la radice cubica di 9 Utilizzando la
Sistemi differenziali 2 2: esercizi svolti. 1 Sistemi lineari Stabilità nei sistemi lineari
 Sistemi differenziali : esercizi svolti 1 Sistemi lineari Stabilità nei sistemi lineari 14 1 Sistemi differenziali : esercizi svolti 1 Sistemi lineari Gli esercizi contrassegnati con il simbolo * presentano
Sistemi differenziali : esercizi svolti 1 Sistemi lineari Stabilità nei sistemi lineari 14 1 Sistemi differenziali : esercizi svolti 1 Sistemi lineari Gli esercizi contrassegnati con il simbolo * presentano
Analisi Matematica 2. Michele Campiti. Prove scritte di. Ingegneria Industriale a.a
 Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
I appello - 24 Marzo 2006
 Facoltà di Ingegneria - Corso di Laurea in Ing. Energetica e Gestionale A.A.2005/2006 I appello - 24 Marzo 2006 Risolvere gli esercizi motivando tutte le risposte. I.) Studiare la convergenza puntuale,
Facoltà di Ingegneria - Corso di Laurea in Ing. Energetica e Gestionale A.A.2005/2006 I appello - 24 Marzo 2006 Risolvere gli esercizi motivando tutte le risposte. I.) Studiare la convergenza puntuale,
Funzioni di più variabili
 Funzioni di più variabili Dr. Daniele Toffoli Dipartimento di Scienze Chimiche e Farmaceutiche, UniTS Dr. Daniele Toffoli (DSCF, UniTS) Concetti di calcolo 1 / 48 Outline 1 Generalità e rappresentazioni
Funzioni di più variabili Dr. Daniele Toffoli Dipartimento di Scienze Chimiche e Farmaceutiche, UniTS Dr. Daniele Toffoli (DSCF, UniTS) Concetti di calcolo 1 / 48 Outline 1 Generalità e rappresentazioni
Calcolo integrale. Regole di integrazione
 Calcolo integrale Linearità dell integrale Integrazione per parti Integrazione per sostituzione Integrazione di funzioni razionali 2 2006 Politecnico di Torino Proprietà Siano e funzioni integrabili su
Calcolo integrale Linearità dell integrale Integrazione per parti Integrazione per sostituzione Integrazione di funzioni razionali 2 2006 Politecnico di Torino Proprietà Siano e funzioni integrabili su
AM210/ : Tracce delle lezioni- Settimana XII
 AM21/214-15: Tracce delle lezioni- Settimana XII SPAZI METRICI ED IL TEOREMA DELLE CONTRAZIONI Spazi metrici completi, spazi di Banach Una successione x n in uno spazio metrico (X, d) si dice di Cauchy
AM21/214-15: Tracce delle lezioni- Settimana XII SPAZI METRICI ED IL TEOREMA DELLE CONTRAZIONI Spazi metrici completi, spazi di Banach Una successione x n in uno spazio metrico (X, d) si dice di Cauchy
Esonero di Analisi Matematica II (A)
 Esonero di Analisi Matematica II (A) Ingegneria Edile, 8 aprile 3. Studiare la convergenza del seguente integrale improprio: + x log 3 x (x ) 3 dx.. Studiare la convergenza puntuale ed uniforme della seguente
Esonero di Analisi Matematica II (A) Ingegneria Edile, 8 aprile 3. Studiare la convergenza del seguente integrale improprio: + x log 3 x (x ) 3 dx.. Studiare la convergenza puntuale ed uniforme della seguente
5. Distribuzioni. Corso di Simulazione. Anno accademico 2009/10
 Anno accademico 2009/10 Spazio di probabilità Ω spazio campione F 2 Ω spazio degli eventi: (i) Ω F (ii) A F = Ω \ A F (iii) A, B F = A B F P: F [0, 1] funzione di probabilità: (i) P(A) 0 (ii) P(Ω) = 1
Anno accademico 2009/10 Spazio di probabilità Ω spazio campione F 2 Ω spazio degli eventi: (i) Ω F (ii) A F = Ω \ A F (iii) A, B F = A B F P: F [0, 1] funzione di probabilità: (i) P(A) 0 (ii) P(Ω) = 1
Compiti d Esame A.A. 2005/2006
 Compiti d Esame A.A. 25/26 UNIVERSITÀ DEGLI STUDI DI PERUGIA A.A. 25/26 I Esercitazione 21 Aprile 26 { y = xy ln(xy) si chiede di dimostrare che: y(1) = 1, (a) ammette un unica soluzione massimale y =
Compiti d Esame A.A. 25/26 UNIVERSITÀ DEGLI STUDI DI PERUGIA A.A. 25/26 I Esercitazione 21 Aprile 26 { y = xy ln(xy) si chiede di dimostrare che: y(1) = 1, (a) ammette un unica soluzione massimale y =
I PROVA SCRITTA DI ANALISI MATEMATICA A Ing. [Informatica, Telecomunicazioni](L-Z)
 I PROVA SCRITTA DI ANALISI MATEMATICA A Ing. [Informatica, Telecomunicazioni](L-Z)](/thumbs/75/72088693.jpg) I PROVA SCRITTA DI ANALISI MATEMATICA A Ing. [Informatica, Telecomunicazioni](L-Z) (Alberto PARMEGGIANI) A.A. 1999/2000: 22 Ottobre 1999 (1) COGNOME e NOME (Stampatello): MATRICOLA: N.B. Ogni risposta
I PROVA SCRITTA DI ANALISI MATEMATICA A Ing. [Informatica, Telecomunicazioni](L-Z) (Alberto PARMEGGIANI) A.A. 1999/2000: 22 Ottobre 1999 (1) COGNOME e NOME (Stampatello): MATRICOLA: N.B. Ogni risposta
Prima prova di verifica in itinere di ANALISI MATEMATICA II. 12 Marzo 2008 Compito A. 1 (punti 3)
 anno accademico 007-008 Prima prova di verifica in itinere di ANALISI MATEMATICA II Marzo 008 Compito A (punti ) y = x + xy + y x. (punti 4) y + y x = ln x x y. (punti ) y = y + y ln y. 4 (punti 6) Determinare
anno accademico 007-008 Prima prova di verifica in itinere di ANALISI MATEMATICA II Marzo 008 Compito A (punti ) y = x + xy + y x. (punti 4) y + y x = ln x x y. (punti ) y = y + y ln y. 4 (punti 6) Determinare
Equazioni differenziali ordinarie
 Equazioni differenziali ordinarie Indice Sistemi di equazioni differenziali del primo ordine 3 Soluzioni per serie di ODE del secondo ordine 0. Soluzione intorno a punti regolari: tecnica di Frobenius...........
Equazioni differenziali ordinarie Indice Sistemi di equazioni differenziali del primo ordine 3 Soluzioni per serie di ODE del secondo ordine 0. Soluzione intorno a punti regolari: tecnica di Frobenius...........
f df(p 0 ) lim = 0 f(x, y) dxdy =
 CORSO I LAUREA IN INGEGNERIA EILE - UNIVERSIÀ LA SAPIENZA, ROMA CORSO I ANALISI MAEMAICA 2 (LEERE M - Z) - a. a. 2007/ 08 FORMULARIO SINEICO I ANALISI MAEMAICA 2 Coordinate polari x = ρ cos(θ) y = ρ sin(θ),
CORSO I LAUREA IN INGEGNERIA EILE - UNIVERSIÀ LA SAPIENZA, ROMA CORSO I ANALISI MAEMAICA 2 (LEERE M - Z) - a. a. 2007/ 08 FORMULARIO SINEICO I ANALISI MAEMAICA 2 Coordinate polari x = ρ cos(θ) y = ρ sin(θ),
Registro delle esercitazioni Analisi Matematica 2 (corso del prof. M. Vignati) corso di laurea triennale in FISICA L.
 Registro delle esercitazioni Analisi Matematica 2 (corso del prof. M. Vignati) corso di laurea triennale in FISICA L. Vesely, 26 27 7/3/27 [2 ore: n.,2] Funzioni primitive ( integrali indefiniti ) Ripasso:
Registro delle esercitazioni Analisi Matematica 2 (corso del prof. M. Vignati) corso di laurea triennale in FISICA L. Vesely, 26 27 7/3/27 [2 ore: n.,2] Funzioni primitive ( integrali indefiniti ) Ripasso:
3. Distribuzioni. Corso di Simulazione. Anno accademico 2006/07
 Anno accademico 2006/07 Spazio di probabilità Ω spazio campione F 2 Ω spazio degli eventi: (i) Ω F (ii) A F = Ω \ A F (iii) A, B F = A B F P: F [0, 1] funzione di probabilità: (i) P(A) 0 (ii) P(Ω) = 1
Anno accademico 2006/07 Spazio di probabilità Ω spazio campione F 2 Ω spazio degli eventi: (i) Ω F (ii) A F = Ω \ A F (iii) A, B F = A B F P: F [0, 1] funzione di probabilità: (i) P(A) 0 (ii) P(Ω) = 1
Derivate. Def. Sia f una funzione reale di variabile reale. Allora, dati x, y domf con x y, si definisce il rapporto incrementale di f tra x e y come
 Lezioni 21-22 72 Derivate Def. Sia f una funzione reale di variabile reale. Allora, dati x, y domf con x y, si definisce il rapporto incrementale di f tra x e y come P f (x, y) = f(x) f(y). x y OSSERVAZIONI:
Lezioni 21-22 72 Derivate Def. Sia f una funzione reale di variabile reale. Allora, dati x, y domf con x y, si definisce il rapporto incrementale di f tra x e y come P f (x, y) = f(x) f(y). x y OSSERVAZIONI:
Risposta La curva r è regolare a tratti per via di quanto succede della sua rappresentazione parametrica nel punto t = 1: pur riuscendo
 ANALISI VETTORIALE OMPITO PER LE VAANZE DI FINE D ANNO Esercizio Sia r(t) la curva regolare a tratti x = t, y = t, t [, ] e x = t, y = t, t [, ]. alcolare la lunghezza di r, calcolare, dove esistono, i
ANALISI VETTORIALE OMPITO PER LE VAANZE DI FINE D ANNO Esercizio Sia r(t) la curva regolare a tratti x = t, y = t, t [, ] e x = t, y = t, t [, ]. alcolare la lunghezza di r, calcolare, dove esistono, i
1 x 2 y 2 dxdy D. 3 (1 ρ2 ) 3/2 = 1 3. = π 12.
 INGEGNERIA CIVILE - AMBIENTE E TERRITORIO ANALISI MATEMATICA II SOLUZIONI DELLA PROVA SCRITTA DEL 19-6-15 ESERCIZIO 1 Calcolare 1 x y dxdy D dove D è il dominio piano delimitato dalla curva x + y = x e
INGEGNERIA CIVILE - AMBIENTE E TERRITORIO ANALISI MATEMATICA II SOLUZIONI DELLA PROVA SCRITTA DEL 19-6-15 ESERCIZIO 1 Calcolare 1 x y dxdy D dove D è il dominio piano delimitato dalla curva x + y = x e
CP110 Probabilità: Esonero 2
 Dipartimento di Matematica, Roma Tre Pietro Caputo 22-3, II semestre 23 maggio, 23 CP Probabilità: Esonero 2 Cognome Nome Matricola Firma Nota:. L unica cosa che si puo usare durante l esame è una penna
Dipartimento di Matematica, Roma Tre Pietro Caputo 22-3, II semestre 23 maggio, 23 CP Probabilità: Esonero 2 Cognome Nome Matricola Firma Nota:. L unica cosa che si puo usare durante l esame è una penna
Alcuni esercizi risolti da esami di anni passati
 Alcuni esercizi risolti da esami di anni passati Andrea Braides ( x. Calcolare, se esiste, il limite lim (x,y (, x + y log + y + x 3 y. x + y Dato che log( + s = s + o(s per s, abbiamo lim (x,y (, ( x
Alcuni esercizi risolti da esami di anni passati Andrea Braides ( x. Calcolare, se esiste, il limite lim (x,y (, x + y log + y + x 3 y. x + y Dato che log( + s = s + o(s per s, abbiamo lim (x,y (, ( x
1 Limiti di funzioni di più variabili
 1 Limiti di funzioni di più variabili Sia f : D R N R e x 0 un punto di accumulazione per D. Riportiamo alcune utili strategie per verificare se la funzione ammette o non ammette ite finito in x 0. Le
1 Limiti di funzioni di più variabili Sia f : D R N R e x 0 un punto di accumulazione per D. Riportiamo alcune utili strategie per verificare se la funzione ammette o non ammette ite finito in x 0. Le
Analisi Matematica II
 2 Analisi Matematica II 2.1. Prova assegnata il 29 febbraio 1984 corso di laurea in Fisica. 1. Rappresentare graficamente l insieme di definizione della funzione reale di due variabili reali (4x f(x,y)=
2 Analisi Matematica II 2.1. Prova assegnata il 29 febbraio 1984 corso di laurea in Fisica. 1. Rappresentare graficamente l insieme di definizione della funzione reale di due variabili reali (4x f(x,y)=
COMPLEMENTI DI ANALISI MATEMATICA A.A Primo appello del 5/5/2010
 COMPLEMENTI DI ANALISI MATEMATICA A.A. 29- Primo appello del 5/5/2 Qui trovate le tracce delle soluzioni degli esercizi del compito. Ho tralasciato i calcoli da Analisi (che comunque sono parte della risoluzione),
COMPLEMENTI DI ANALISI MATEMATICA A.A. 29- Primo appello del 5/5/2 Qui trovate le tracce delle soluzioni degli esercizi del compito. Ho tralasciato i calcoli da Analisi (che comunque sono parte della risoluzione),
Corso di Laurea in Ingegneria Informatica Anno Accademico 2013/2014 Calcolo delle Probabilità e Statistica Matematica
 Corso di Laurea in Ingegneria Informatica Anno Accademico 13/14 Calcolo delle Probabilità e Statistica Matematica Nome... N. Matricola... Ancona, 13 gennaio 14 1. In una data università, le studentesse
Corso di Laurea in Ingegneria Informatica Anno Accademico 13/14 Calcolo delle Probabilità e Statistica Matematica Nome... N. Matricola... Ancona, 13 gennaio 14 1. In una data università, le studentesse
SISTEMI DI EQUAZIONI DIFFERENZIALI- ESERCIZI SVOLTI
 SISTEMI DI EQUAZIONI DIFFERENZIALI- ESERCIZI SVOLTI Generalità sui sistemi Sia xt, yt la soluzione del problema di Cauchy Posto vt = e xtyt, calcolare v x = 3x x = y = x y = 0 Sia x = 3x y y = x + y Scrivere
SISTEMI DI EQUAZIONI DIFFERENZIALI- ESERCIZI SVOLTI Generalità sui sistemi Sia xt, yt la soluzione del problema di Cauchy Posto vt = e xtyt, calcolare v x = 3x x = y = x y = 0 Sia x = 3x y y = x + y Scrivere
AM2: Tracce delle lezioni- IX Settimana INSIEMI DI LIVELLO, MINIMI VINCOLATI PRINCIPIO DEI MOLTIPLICATORI DI LAGRANGE
 AM2: Tracce delle lezioni- IX Settimana INSIEMI DI LIVELLO, MINIMI VINCOLATI PRINCIPIO DEI MOLTIPLICATORI DI LAGRANGE Sia g C 1 R 2 ), c R. L insieme γ = γ c := {x, y) R 2 : gx, y) = c} si chiama insieme
AM2: Tracce delle lezioni- IX Settimana INSIEMI DI LIVELLO, MINIMI VINCOLATI PRINCIPIO DEI MOLTIPLICATORI DI LAGRANGE Sia g C 1 R 2 ), c R. L insieme γ = γ c := {x, y) R 2 : gx, y) = c} si chiama insieme
Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica 2 del 29 settembre 2012
 Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica del 9 settembre A) Data la funzione f(x, y) = { xy x se (x, y) (, ) se (x, y) = (, ), i) stabilire se risulta continua
Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica del 9 settembre A) Data la funzione f(x, y) = { xy x se (x, y) (, ) se (x, y) = (, ), i) stabilire se risulta continua
Analisi Matematica II (2/2/2015)
 Analisi Matematica II (//5) Risposte non giustificate non verranno considerate. Consegnare solo la bella copia. Scrivere anche sul retro del foglio. Cognome: Nome: Matricola, Crediti: 3 4 5 TOTALE Versione
Analisi Matematica II (//5) Risposte non giustificate non verranno considerate. Consegnare solo la bella copia. Scrivere anche sul retro del foglio. Cognome: Nome: Matricola, Crediti: 3 4 5 TOTALE Versione
Analisi Matematica III (Fisica e Astronomia) TEST n. 3 di Esame Scritto (08-10/01/2019) Università di Padova - Lauree in Fisica ed Astronomia - A.A. 2
 Analisi Matematica III (Fisica e Astronomia) TEST n. 3 di Esame Scritto (08-0/0/09) Università di Padova - Lauree in Fisica ed Astronomia - A.A. 08/9 Tempo di consegna: tre ore.. (a) Quali superfici di
Analisi Matematica III (Fisica e Astronomia) TEST n. 3 di Esame Scritto (08-0/0/09) Università di Padova - Lauree in Fisica ed Astronomia - A.A. 08/9 Tempo di consegna: tre ore.. (a) Quali superfici di
Matematica - Prova d esame (25/06/2004)
 Matematica - Prova d esame (/6/4) Università di Verona - Laurea in Biotecnologie AI - A.A. /4. (a) Disegnare sul piano di Gauss i numeri z = i e w = i, e scriverne la forma trigonometrica. Calcolare z
Matematica - Prova d esame (/6/4) Università di Verona - Laurea in Biotecnologie AI - A.A. /4. (a) Disegnare sul piano di Gauss i numeri z = i e w = i, e scriverne la forma trigonometrica. Calcolare z
Fondamenti di Analisi Matematica 2 - a.a. 2016/2017 Primo appello
 Fondamenti di Analisi Matematica 2 - a.a. 216/217 Primo appello Esercizi senza svolgimento - Tema 1 Ω = { x, y, z) R 3 : 4x 2 + y 2 + z 2 1, z }. x = ρ/2) sen ϕ cos ϑ, 1. y = ρ sen ϕ sen ϑ, ρ [, 1], ϕ
Fondamenti di Analisi Matematica 2 - a.a. 216/217 Primo appello Esercizi senza svolgimento - Tema 1 Ω = { x, y, z) R 3 : 4x 2 + y 2 + z 2 1, z }. x = ρ/2) sen ϕ cos ϑ, 1. y = ρ sen ϕ sen ϑ, ρ [, 1], ϕ
Esercizi di Calcolo delle Probabilità
 Esercizi di Calcolo delle Probabilità M. Pratelli e M. Romito Gli esercizi che seguono sono stati proposti nel corso Probabilità dell Università di Pisa negli a.a. 2012-13 e 2013-14 (M. Romito) e 2014-15
Esercizi di Calcolo delle Probabilità M. Pratelli e M. Romito Gli esercizi che seguono sono stati proposti nel corso Probabilità dell Università di Pisa negli a.a. 2012-13 e 2013-14 (M. Romito) e 2014-15
Equazioni differenziali a variabili separabili e lineari del primo ordine. Esercizi.
 Equazioni differenziali a variabili separabili e lineari del primo ordine. Esercizi. Mauro Saita Versione provvisoria. Dicembre 204 Per commenti o segnalazioni di errori scrivere, per favore, a: maurosaita@tiscalinet.it
Equazioni differenziali a variabili separabili e lineari del primo ordine. Esercizi. Mauro Saita Versione provvisoria. Dicembre 204 Per commenti o segnalazioni di errori scrivere, per favore, a: maurosaita@tiscalinet.it
X (o equivalentemente rispetto a X n ) è la
 Esercizi di Calcolo delle Probabilità della 5 a settimana (Corso di Laurea in Matematica, Università degli Studi di Padova). Esercizio 1. Siano (X n ) n i.i.d. di Bernoulli di parametro p e definiamo per
Esercizi di Calcolo delle Probabilità della 5 a settimana (Corso di Laurea in Matematica, Università degli Studi di Padova). Esercizio 1. Siano (X n ) n i.i.d. di Bernoulli di parametro p e definiamo per
4.5 Equazioni differenziali lineari del secondo ordine non omogenee 159
 4.5 Equazioni differenziali lineari del secondo ordine non omogenee 159 Una volta stabilito che per ogni funzione continua f l equazione (4.23) è risolubile, ci interessa determinarne l integrale generale.
4.5 Equazioni differenziali lineari del secondo ordine non omogenee 159 Una volta stabilito che per ogni funzione continua f l equazione (4.23) è risolubile, ci interessa determinarne l integrale generale.
EQUAZIONI DIFFERENZIALI Esercizi con soluzione
 EQUAZIONI DIFFERENZIALI Esercizi con soluzione 1. Calcolare l integrale generale delle seguenti equazioni differenziali lineari del primo ordine: (a) y 2y = 1 (b) y + y = e x (c) y 2y = x 2 + x (d) 3y
EQUAZIONI DIFFERENZIALI Esercizi con soluzione 1. Calcolare l integrale generale delle seguenti equazioni differenziali lineari del primo ordine: (a) y 2y = 1 (b) y + y = e x (c) y 2y = x 2 + x (d) 3y
ANALISI MATEMATICA T-2 (C.d.L. Ing. per l ambiente e il territorio) A.A Prof. G.Cupini
 ANALISI MATEMATICA T-2 (C.d.L. Ing. per l ambiente e il territorio) A.A.2009-2010 - Prof. G.Cupini Equazioni differenziali ordinarie del primo ordine (lineari, a variabili separabili, di Bernoulli) ed
ANALISI MATEMATICA T-2 (C.d.L. Ing. per l ambiente e il territorio) A.A.2009-2010 - Prof. G.Cupini Equazioni differenziali ordinarie del primo ordine (lineari, a variabili separabili, di Bernoulli) ed
x(y 2 + 2z 2 ) dxdydz, (1 y 2 z 2 ) 2 (y 2 + 2z 2 ) dydz, 1 ( x(y 2 + 2z 2 ) dydz) dx, 1 x r 3 dr) (
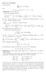 Esame del 5//9. Determinare dove Svolgimento. Due modi diversi. (i) Per fili: l integrale diventa D y z Ω x(y + z ) dxdydz, Ω = {(x, y, z) R 3 ; y + z + x, x }. x(y + z ) dx) dydz = D ( y z ) (y + z )
Esame del 5//9. Determinare dove Svolgimento. Due modi diversi. (i) Per fili: l integrale diventa D y z Ω x(y + z ) dxdydz, Ω = {(x, y, z) R 3 ; y + z + x, x }. x(y + z ) dx) dydz = D ( y z ) (y + z )
Analisi Matematica III a.a. 1999/00
 Versione: 2 luglio 2 Università degli Studi di Pisa Corso di laurea in Ingegneria Elettrica Testi e soluzioni degli scritti d esame di Analisi Matematica III a.a. 999/ docente: Giovanni Alberti Giovanni
Versione: 2 luglio 2 Università degli Studi di Pisa Corso di laurea in Ingegneria Elettrica Testi e soluzioni degli scritti d esame di Analisi Matematica III a.a. 999/ docente: Giovanni Alberti Giovanni
Analisi Vettoriale A.A Soluzioni del Foglio 4
 Analisi Vettoriale A.A. 26-27 - Soluzioni del Foglio 4 Esercizio 4.1. Sia Σ la superficie cartesiana z = 1 x y, (x, y) = {x 2 + y 2 1}, determinare in ogni punto di Σ il versore normale diretto nel verso
Analisi Vettoriale A.A. 26-27 - Soluzioni del Foglio 4 Esercizio 4.1. Sia Σ la superficie cartesiana z = 1 x y, (x, y) = {x 2 + y 2 1}, determinare in ogni punto di Σ il versore normale diretto nel verso
PROVE SCRITTE DI ANALISI MATEMATICA II (V.O.), ANNO 2002
 PROVE SCRITTE DI ANALISI MATEMATICA II (V.O.), ANNO 22 Prova scritta del 1/1/22 Si esamini la serie di funzioni: 1 log x (e n + n), definita per x IR. Si determini l insieme S in cui tale serie converge,
PROVE SCRITTE DI ANALISI MATEMATICA II (V.O.), ANNO 22 Prova scritta del 1/1/22 Si esamini la serie di funzioni: 1 log x (e n + n), definita per x IR. Si determini l insieme S in cui tale serie converge,
Ingegneria Elettronica Prova scritta di Analisi Matematica II del giorno ( 3) n x n n + 1
 Prova scritta di Analisi Matematica II del giorno 31-01-2007 1) Studiare la serie di potenze ( 3) n x n n + 1 2) Determinare i punti di estremo relativo ed assoluto della funzione seguente f(x, y) = x
Prova scritta di Analisi Matematica II del giorno 31-01-2007 1) Studiare la serie di potenze ( 3) n x n n + 1 2) Determinare i punti di estremo relativo ed assoluto della funzione seguente f(x, y) = x
ESERCIZI SULLE EQUAZIONI DIFFERENZIALI
 ESERCIZI SULLE EQUAZIONI DIFFERENZIALI 1. Generalità 1.1. Verifica delle soluzioni. Verificare se le funzioni date sono soluzioni delle equazioni differenziali. xy = 2y, y = 5x 2. y = x 2 + y 2, y = 1
ESERCIZI SULLE EQUAZIONI DIFFERENZIALI 1. Generalità 1.1. Verifica delle soluzioni. Verificare se le funzioni date sono soluzioni delle equazioni differenziali. xy = 2y, y = 5x 2. y = x 2 + y 2, y = 1
1 Equazioni differenziali
 1 Equazioni differenziali Iniziamo adesso lo studio di alcuni tipi di equazioni differenziali. Questo argomento è uno dei più importanti, se non il più importante dal punto di vista applicativo. Basti
1 Equazioni differenziali Iniziamo adesso lo studio di alcuni tipi di equazioni differenziali. Questo argomento è uno dei più importanti, se non il più importante dal punto di vista applicativo. Basti
Riassunto delle Esercitazioni di Analisi Matematica II
 Riassuto delle Esercitazioi di Aalisi Matematica II C.d.L. i Matematica e Matematica per le Applicazioi - A. A. 2006-2007 Prof. Kevi R. Paye e Dott. Libor Vesely 1 Serie Numeriche - Mer. 28 marzo - due
Riassuto delle Esercitazioi di Aalisi Matematica II C.d.L. i Matematica e Matematica per le Applicazioi - A. A. 2006-2007 Prof. Kevi R. Paye e Dott. Libor Vesely 1 Serie Numeriche - Mer. 28 marzo - due
9.2 Il problema di Cauchy per le equazioni differenziali del primo ordine
 9.2 Il problema di Cauchy per le equazioni differenziali del primo ordine 349 y = f(y, x), (9.23) allora la sostituzione z = y conduce all equazione del primo ordine z = f(z, x) nell incognita z = z(x).
9.2 Il problema di Cauchy per le equazioni differenziali del primo ordine 349 y = f(y, x), (9.23) allora la sostituzione z = y conduce all equazione del primo ordine z = f(z, x) nell incognita z = z(x).
TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea (quadriennale) in Fisica a.a. 2002/03
 I seguenti quesiti ed il relativo svolgimento sono coperti dal diritto d autore, pertanto essi non possono essere sfruttati a fini commerciali o di pubblicazione editoriale senza autorizzazione esplicita
I seguenti quesiti ed il relativo svolgimento sono coperti dal diritto d autore, pertanto essi non possono essere sfruttati a fini commerciali o di pubblicazione editoriale senza autorizzazione esplicita
es.1 es.2 es.3 es.4 es.5 somma Analisi Matematica 2: Primo Parziale, , Versione A Cognome e nome:...matricola:...
 es. es. es. es.4 es.5 somma 5 4 8 8 5 Analisi Matematica : Primo Parziale,.4.7, Versione A Cognome e nome:....................................matricola:.......... Calcolare la lunghezza della curva di
es. es. es. es.4 es.5 somma 5 4 8 8 5 Analisi Matematica : Primo Parziale,.4.7, Versione A Cognome e nome:....................................matricola:.......... Calcolare la lunghezza della curva di
LEZIONI DI ANALISI MATEMATICA I. Equazioni Differenziali Ordinarie. Sergio Lancelotti
 LEZIONI DI ANALISI MATEMATICA I Equazioni Differenziali Ordinarie Sergio Lancelotti Anno Accademico 2006-2007 2 Equazioni differenziali ordinarie 1 Equazioni differenziali ordinarie di ordine n.................
LEZIONI DI ANALISI MATEMATICA I Equazioni Differenziali Ordinarie Sergio Lancelotti Anno Accademico 2006-2007 2 Equazioni differenziali ordinarie 1 Equazioni differenziali ordinarie di ordine n.................
Capitolo 9. Equazioni differenziali del primo ordine
 Capitolo 9 Equazioni differenziali del primo ordine Una O.D.E. (acronimo inglese di Ordinary differential equation, ovvero Equazione differenziale ordinaria) è un equazione funzionale 1 in cui compare
Capitolo 9 Equazioni differenziali del primo ordine Una O.D.E. (acronimo inglese di Ordinary differential equation, ovvero Equazione differenziale ordinaria) è un equazione funzionale 1 in cui compare
Es. 1 Es. 2 Es. 3 Totale
 Es. 1 Es. 2 Es. 3 Totale Analisi e geometria 2 Seconda Prova in Itinere Docente: 29 giugno 21 Cognome: Nome: Matricola: Ogni risposta deve essere giustificata. Gli esercizi vanno svolti su questi fogli,
Es. 1 Es. 2 Es. 3 Totale Analisi e geometria 2 Seconda Prova in Itinere Docente: 29 giugno 21 Cognome: Nome: Matricola: Ogni risposta deve essere giustificata. Gli esercizi vanno svolti su questi fogli,
Esercizi di preparazione alla PFB
 Esercizi di preparazione alla PFB A.A. 22/23 A cura di Sara Lamboglia, Gianluca Lauteri, Maria Chiara Timpone. Esercizi di Analisi Matematica, Algebra e Geometria. Parte : Analisi Matematica. Esercizio..
Esercizi di preparazione alla PFB A.A. 22/23 A cura di Sara Lamboglia, Gianluca Lauteri, Maria Chiara Timpone. Esercizi di Analisi Matematica, Algebra e Geometria. Parte : Analisi Matematica. Esercizio..
dove A = arctan ( y y(1) = 1.
 A.A. 27/28 I Esercitazione 5 maggio 28 Esercizio. Data la successione di problemi di Cauchy y n = x 2n+ arctan y n (P n ) y n () =, (a) dimostrare che per ogni n N (P n ) ammette un unica soluzione massimale
A.A. 27/28 I Esercitazione 5 maggio 28 Esercizio. Data la successione di problemi di Cauchy y n = x 2n+ arctan y n (P n ) y n () =, (a) dimostrare che per ogni n N (P n ) ammette un unica soluzione massimale
FM1 - Equazioni differenziali e meccanica
 Corso di laurea in Matematica - Anno Accademico 2006/2007 FM1 - Equazioni differenziali e meccanica Prima prova d esonero (03-04-2006) CORREZIONE Esercizio 1. Lo spettro Σ(A) della matrice A si trova risolvendo
Corso di laurea in Matematica - Anno Accademico 2006/2007 FM1 - Equazioni differenziali e meccanica Prima prova d esonero (03-04-2006) CORREZIONE Esercizio 1. Lo spettro Σ(A) della matrice A si trova risolvendo
3 Introduzione al problema semi-lineare
 3 Introduzione al problema semi-lineare 3.1 Il problema periodico Studiamo il problema (P ) { x + g(t, x) =, x() = x(t ), x () = x (T ), dove g : [, T ] R R è una funzione continua. Consideriamo lo spazio
3 Introduzione al problema semi-lineare 3.1 Il problema periodico Studiamo il problema (P ) { x + g(t, x) =, x() = x(t ), x () = x (T ), dove g : [, T ] R R è una funzione continua. Consideriamo lo spazio
 Analisi Matematica III (Fisica e Astronomia) TEST n. 1 di Esame Scritto (13-14/1/018) Università di Padova - Lauree in Fisica ed Astronomia - A.A. 018/19 Tempo di consegna: tre ore. (1) 1. Nel piano cartesiano
Analisi Matematica III (Fisica e Astronomia) TEST n. 1 di Esame Scritto (13-14/1/018) Università di Padova - Lauree in Fisica ed Astronomia - A.A. 018/19 Tempo di consegna: tre ore. (1) 1. Nel piano cartesiano
ALLEGATO A ELENCO TARGHE OPERATORI DI MERCATO DT 476 CW - DK 013 RD AL 538 LF DT 530 XJ- DL DW 553 RR - EP 638 PX
 ALLEGATO A ELENCO TARGHE OPERATORI DI MERCATO AA 739 YZ DS 491 VV AG 347 WT DS 523 AX AJ 058 TA DT 476 CW - DK 013 RD AL 538 LF DT 530 XJ- DL 69313 AY 093 DM DV 530 RR BB 984 HD DW 553 RR - EP 638 PX BC
ALLEGATO A ELENCO TARGHE OPERATORI DI MERCATO AA 739 YZ DS 491 VV AG 347 WT DS 523 AX AJ 058 TA DT 476 CW - DK 013 RD AL 538 LF DT 530 XJ- DL 69313 AY 093 DM DV 530 RR BB 984 HD DW 553 RR - EP 638 PX BC
25 IL RAPPORTO INCREMENTALE - DERIVATE
 25 IL RAPPORTO INCREMENTALE - DERIVATE Definizione Sia f una funzione reale di variabile reale. Allora, dati x, y domf con x y, si definisce il rapporto incrementale di f tra x e y come P f (x, y = f(x
25 IL RAPPORTO INCREMENTALE - DERIVATE Definizione Sia f una funzione reale di variabile reale. Allora, dati x, y domf con x y, si definisce il rapporto incrementale di f tra x e y come P f (x, y = f(x
Esercizi su formula di Itô
 Esercizi su formula di Itô 1. Scrivere il differenziale stocastico dei seguenti processi: (i) X t = B t (ii) X t = t + e B t (iii) X t = B 3 t 3tB t (iv) X t = 1 + t + e B t (v) X t = [B 1 (t)] + [B (t)]
Esercizi su formula di Itô 1. Scrivere il differenziale stocastico dei seguenti processi: (i) X t = B t (ii) X t = t + e B t (iii) X t = B 3 t 3tB t (iv) X t = 1 + t + e B t (v) X t = [B 1 (t)] + [B (t)]
Foglio n. 19. Massimi e minimi vincolati
 Foglio n. 19 Massimi e minimi vincolati 1) Calcolare massimo e minimo della funzione x 2 +3y 2 xy y nel quadrato Q = {(x, y) R 2 : x 1, y 1}. 2) Calcolare massimo e minimo della funzione x+y 6z sulla superficie
Foglio n. 19 Massimi e minimi vincolati 1) Calcolare massimo e minimo della funzione x 2 +3y 2 xy y nel quadrato Q = {(x, y) R 2 : x 1, y 1}. 2) Calcolare massimo e minimo della funzione x+y 6z sulla superficie
Sulle equazioni differenziali ordinarie a variabili separabili
 Sulle equazioni differenziali ordinarie a variabili separabili Paolo Bonicatto - Luca Lussardi 9 aprile 2008 Indice Introduzione 2 Metodo classico 2 3 Forme differenziali lineari 4 4 Formalizzazione del
Sulle equazioni differenziali ordinarie a variabili separabili Paolo Bonicatto - Luca Lussardi 9 aprile 2008 Indice Introduzione 2 Metodo classico 2 3 Forme differenziali lineari 4 4 Formalizzazione del
CORSO DI LAUREA IN INGEGNERIA ELETTRONICA Prof. A. Avantaggiati (prova scritta di ANALISI MATEMATICA II - 17 gennaio 2000) vecchio ordinamento COGNOME
 CORSO DI LAUREA IN INGEGNERIA ELETTRONICA Prof. A. Avantaggiati (prova scritta di ANALISI MATEMATICA II - 17 gennaio 2000) vecchio ordinamento COGNOME... NOME... Data l'equazione differenziale y 000 +2y
CORSO DI LAUREA IN INGEGNERIA ELETTRONICA Prof. A. Avantaggiati (prova scritta di ANALISI MATEMATICA II - 17 gennaio 2000) vecchio ordinamento COGNOME... NOME... Data l'equazione differenziale y 000 +2y
Analisi Matematica 3
 Testi delle prove d esame del corso di Analisi Matematica 3 presso la Facoltà di Ingegneria Bruno Rubino L Aquila, 2006 Indice 1 Curve 3 2 Superfici 4 3 Teorema di Gauss-Green e formula dell area 4 4 Campi
Testi delle prove d esame del corso di Analisi Matematica 3 presso la Facoltà di Ingegneria Bruno Rubino L Aquila, 2006 Indice 1 Curve 3 2 Superfici 4 3 Teorema di Gauss-Green e formula dell area 4 4 Campi
7.6. Distribuzione Esponenziale. Un n.a. continuo X con densità di probabilità
 7.6 Distribuzione Esponenziale. 111 7.6. Distribuzione Esponenziale. Un n.a. continuo X con densità di probabilità { λe λx se x, (76) f(x) = se x
7.6 Distribuzione Esponenziale. 111 7.6. Distribuzione Esponenziale. Un n.a. continuo X con densità di probabilità { λe λx se x, (76) f(x) = se x
Analisi Matematica 2: Secondo Parziale, , Versione A. Cognome e nome:...matricola:...
 Analisi Matematica : Secondo Parziale, 1.6.17, Versione A Cognome e nome:....................................matricola:......... es.1 es. es.3 es. es.5 es.6 es.7 somma 5cr. 6 6 6 6 6 - - 3 9cr. 5 5 5 5
Analisi Matematica : Secondo Parziale, 1.6.17, Versione A Cognome e nome:....................................matricola:......... es.1 es. es.3 es. es.5 es.6 es.7 somma 5cr. 6 6 6 6 6 - - 3 9cr. 5 5 5 5
Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005
 Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005 Prova orale il: Docente: Determinare, se esistono, il massimo ed il minimo assoluto della funzione
Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005 Prova orale il: Docente: Determinare, se esistono, il massimo ed il minimo assoluto della funzione
Analisi Matematica 2. Continuità, derivabilità e differenziabilità
 Docente: E. G. Casini Università degli Studi dell Insubria DIPATIMENTO DI SCIENZA E ALTA TECNOLOGIA Corso di Studio in Matematica e Fisica Analisi Matematica ichiami di Teoria ed Esercizi con Svolgimento
Docente: E. G. Casini Università degli Studi dell Insubria DIPATIMENTO DI SCIENZA E ALTA TECNOLOGIA Corso di Studio in Matematica e Fisica Analisi Matematica ichiami di Teoria ed Esercizi con Svolgimento
ANALISI MATEMATICA 1 ANALISI MATEMATICA A CORSI DI LAUREA TRIENNALE IN FISICA E MATEMATICA
 ANALISI MATEMATICA ANALISI MATEMATICA A CORSI DI LAUREA TRIENNALE IN FISICA E MATEMATICA 8-9 Queste note hanno il solo scopo di essere un promemoria di quanto svolto a lezione. Le indicazioni dei capitoli
ANALISI MATEMATICA ANALISI MATEMATICA A CORSI DI LAUREA TRIENNALE IN FISICA E MATEMATICA 8-9 Queste note hanno il solo scopo di essere un promemoria di quanto svolto a lezione. Le indicazioni dei capitoli
x(y + z)dx dy dz y(x 2 + y 2 + z 2 )dx dy dz y 2 zdx dy dz Esempio di insieme non misurabile secondo Lebesgue.
 /3/23 Calcolare dove x(y + z)dx dy dz = {(x, y, z) R 3 : x, y, z, x + y + z }. Calcolare y(x 2 + y 2 + z 2 )dx dy dz dove = {(x, y, z) R 3 : x 2 + y 2 + z 2 z, x 2 + y 2 + z 2 3zx y }. Calcolare dove y
/3/23 Calcolare dove x(y + z)dx dy dz = {(x, y, z) R 3 : x, y, z, x + y + z }. Calcolare y(x 2 + y 2 + z 2 )dx dy dz dove = {(x, y, z) R 3 : x 2 + y 2 + z 2 z, x 2 + y 2 + z 2 3zx y }. Calcolare dove y
L indice differenziale di una DAE
 L indice differenziale di una DAE (Metodi Matematici e Calcolo per Ingegneria) Enrico Bertolazzi DIMS Università di Trento anno accademico 2007/2008 L indice differenziale di una DAE 1 / 26 Outline 1 2
L indice differenziale di una DAE (Metodi Matematici e Calcolo per Ingegneria) Enrico Bertolazzi DIMS Università di Trento anno accademico 2007/2008 L indice differenziale di una DAE 1 / 26 Outline 1 2
Università di Bari - Dipartimento di Economia - Prova scritta di Matematica per l Economia L-Z- 19 Dicembre Traccia A
 Università di Bari - Dipartimento di Economia - Prova scritta di Matematica per l Economia L-Z- 9 Dicembre 06 - Traccia A Cognome e nome................................ Numero di matricola............
Università di Bari - Dipartimento di Economia - Prova scritta di Matematica per l Economia L-Z- 9 Dicembre 06 - Traccia A Cognome e nome................................ Numero di matricola............
Es. 1 Es. 2 Es. 3 Totale
 Es. 1 Es. 2 Es. 3 Totale Analisi e geometria 2 Seconda Prova in Itinere Docente: 2 7 212 Cognome: Nome: Matricola: Ogni risposta dev essere giustificata. Gli esercizi vanno svolti su questi fogli, nello
Es. 1 Es. 2 Es. 3 Totale Analisi e geometria 2 Seconda Prova in Itinere Docente: 2 7 212 Cognome: Nome: Matricola: Ogni risposta dev essere giustificata. Gli esercizi vanno svolti su questi fogli, nello
12. I teoremi del calcolo differenziale, II
 2. I teoremi del calcolo differenziale, II 2.a Il teorema di invertibilità locale Sia f : Ω R n R n una applicazione. Se f è lineare, f(x) = Ax, A M n,n (R), l invertibilità di f, i.e. la risolubilità
2. I teoremi del calcolo differenziale, II 2.a Il teorema di invertibilità locale Sia f : Ω R n R n una applicazione. Se f è lineare, f(x) = Ax, A M n,n (R), l invertibilità di f, i.e. la risolubilità
Politecnico di Milano Ingegneria Industriale Analisi e Geometria 2 Secondo compito in itinere 30 Giugno 2016
 Politecnico di Milano Ingegneria Industriale Analisi e Geometria Secondo compito in itinere Giugno 6 Cognome: Nome: Matricola: Es.: 9 punti Es.: 9 punti Es.: 6 punti Es.4: 9 punti Totale. Si consideri
Politecnico di Milano Ingegneria Industriale Analisi e Geometria Secondo compito in itinere Giugno 6 Cognome: Nome: Matricola: Es.: 9 punti Es.: 9 punti Es.: 6 punti Es.4: 9 punti Totale. Si consideri
Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica 2 del 19/06/2010 A
 Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica del 9/6/ A ) ata la funzione f(x, y) x y log( + x + y ), a) stabilire dove risulta derivabile parzialmente nel suo
Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica del 9/6/ A ) ata la funzione f(x, y) x y log( + x + y ), a) stabilire dove risulta derivabile parzialmente nel suo
Analisi 4 - SOLUZIONI (17/01/2013)
 Corso di Laurea in Matematica Analisi 4 - SOLUZIONI 7//23 Docente: Claudia Anedda Utilizzando uno sviluppo in serie noto, scrivere lo sviluppo in serie di MacLaurin della funzione fx = 32 + x, specificando
Corso di Laurea in Matematica Analisi 4 - SOLUZIONI 7//23 Docente: Claudia Anedda Utilizzando uno sviluppo in serie noto, scrivere lo sviluppo in serie di MacLaurin della funzione fx = 32 + x, specificando
2.1 Osservazioni sull esercitazione del
 ¾ ½¾º¼ º¾¼½ Queste note (attualmente, e probabilmente per un bel po ) sono altamente provvisorie e (molto probabilmente) non prive di errori. 2.1 Osservazioni sull esercitazione del 5.3.214 2.1.1 Equazione
¾ ½¾º¼ º¾¼½ Queste note (attualmente, e probabilmente per un bel po ) sono altamente provvisorie e (molto probabilmente) non prive di errori. 2.1 Osservazioni sull esercitazione del 5.3.214 2.1.1 Equazione
Università di Pisa - Corso di Laurea in Informatica Analisi Matematica A. Pisa, 3 settembre 2018
 Università di Pisa - orso di Laurea in Informatica nalisi Matematica Pisa, settembre 208 ( cos x sin se x 0 Domanda Sia f : R R definita da f(x = x 0 se x = 0. non esiste la derivata di f in x = 0 f (0
Università di Pisa - orso di Laurea in Informatica nalisi Matematica Pisa, settembre 208 ( cos x sin se x 0 Domanda Sia f : R R definita da f(x = x 0 se x = 0. non esiste la derivata di f in x = 0 f (0
Istituzioni di Matematica II 5 Luglio 2010
 Istituzioni di Matematica II 5 Luglio 010 1. Classificare, al variare del parametro α R, la forma quadratica (1 + α )x + 4xy + αy.. i) Si determinino tutti i punti critici della seguente funzione f(x,
Istituzioni di Matematica II 5 Luglio 010 1. Classificare, al variare del parametro α R, la forma quadratica (1 + α )x + 4xy + αy.. i) Si determinino tutti i punti critici della seguente funzione f(x,
si ha La lunghezza L si calcola per ciascun tratto L = (2t)2 + (3t 2 ) dt+ 2 (3t2 ) 2 + (2t) 2 dt = 4t2 + 9t 4 dt = t
 ANALISI VETTORIALE Soluzione esercizi 1 gennaio 211 6.1. Esercizio. Sia Γ la curva regolare a tratti di rappresentazione parametrica x = t 2, y = t, t [, 1] e x = t, y = t 2, t [1, 2] calcolare la lunghezza,
ANALISI VETTORIALE Soluzione esercizi 1 gennaio 211 6.1. Esercizio. Sia Γ la curva regolare a tratti di rappresentazione parametrica x = t 2, y = t, t [, 1] e x = t, y = t 2, t [1, 2] calcolare la lunghezza,
Analisi Matematica 2: Scritto Generale, , Versione A. Cognome e nome:...matricola:...
 Analisi Matematica : Scritto Generale, 7.9.16, Versione A Cognome e nome:....................................matricola:......... es.1 es. es.3 es.4 es.5 es.6/7 somma 5cr. 6 6 6 6 6 3 9cr. 5 5 5 5 5 /3
Analisi Matematica : Scritto Generale, 7.9.16, Versione A Cognome e nome:....................................matricola:......... es.1 es. es.3 es.4 es.5 es.6/7 somma 5cr. 6 6 6 6 6 3 9cr. 5 5 5 5 5 /3
FM210 - Fisica Matematica I
 FM21 - Fisica Matematica I Seconda Prova Scritta [16-2-212] Soluzioni Problema 1 1. Chiamiamo A la matrice del sistema e cerchiamo anzitutto gli autovalori della matrice: l equazione secolare è (λ + 2β)λ
FM21 - Fisica Matematica I Seconda Prova Scritta [16-2-212] Soluzioni Problema 1 1. Chiamiamo A la matrice del sistema e cerchiamo anzitutto gli autovalori della matrice: l equazione secolare è (λ + 2β)λ
CP110 Probabilità: Esame del 6 giugno Testo e soluzione
 Dipartimento di Matematica, Roma Tre Pietro Caputo 21-11, II semestre 6 giugno, 211 CP11 Probabilità: Esame del 6 giugno 211 Testo e soluzione 1. (6 pts) Ci sono 6 palline, di cui nere e rosse. Ciascuna,
Dipartimento di Matematica, Roma Tre Pietro Caputo 21-11, II semestre 6 giugno, 211 CP11 Probabilità: Esame del 6 giugno 211 Testo e soluzione 1. (6 pts) Ci sono 6 palline, di cui nere e rosse. Ciascuna,
Forma canonica di Jordan
 Capitolo INTRODUZIONE Forma canonica di Jordan Siano λ i, per i =,, h, gli autovalori distinti della matrice A e siano r i i corrispondenti gradi di molteplicità all interno del polinomio caratteristico:
Capitolo INTRODUZIONE Forma canonica di Jordan Siano λ i, per i =,, h, gli autovalori distinti della matrice A e siano r i i corrispondenti gradi di molteplicità all interno del polinomio caratteristico:
Prove d Esame A.A. 2012/2013
 Complementi di Analisi Polo di Savona Complementi di Analisi Matematica Prove d Esame A.A. 2012/2013 1- PrCam.TEX [] Complementi di Analisi Polo di Savona Prima Prova parziale 23/11/2011 Prima Prova parziale
Complementi di Analisi Polo di Savona Complementi di Analisi Matematica Prove d Esame A.A. 2012/2013 1- PrCam.TEX [] Complementi di Analisi Polo di Savona Prima Prova parziale 23/11/2011 Prima Prova parziale
0.5 setgray0 0.5 setgray1 Integrazione indefinita di funzioni trascendenti
 Esercizi di riepilogo e complemento 3 0.5 setgray0 0.5 setgray Integrazione indefinita di funzioni trascendenti Indicheremo con R(x,x,...,x n ) una funzione razionale dipendente dalle variabili x,x,...,x
Esercizi di riepilogo e complemento 3 0.5 setgray0 0.5 setgray Integrazione indefinita di funzioni trascendenti Indicheremo con R(x,x,...,x n ) una funzione razionale dipendente dalle variabili x,x,...,x
φ X (t) = mentre nel caso continuo, indicando con f(x) la densità di X, si ha e itx f(x) dx + e itx e itx f(x)dx. f(x)dx = e itx +
 10.1 Funzione caratteristica 11 10.1. Funzione caratteristica La funzione caratteristica è uno strumento teorico utile sotto diversi aspetti per studiare la distribuzione di probabilità di numeri aleatori
10.1 Funzione caratteristica 11 10.1. Funzione caratteristica La funzione caratteristica è uno strumento teorico utile sotto diversi aspetti per studiare la distribuzione di probabilità di numeri aleatori
Analisi Matematica II Politecnico di Milano Ingegneria Industriale
 Analisi Matematica II Politecnico di Milano Ingegneria Industriale Autovalutazione #. Sia P l insieme di tutti i parallelepipedi che giacciono nel primo ottante con tre facce sui piani coordinati e un
Analisi Matematica II Politecnico di Milano Ingegneria Industriale Autovalutazione #. Sia P l insieme di tutti i parallelepipedi che giacciono nel primo ottante con tre facce sui piani coordinati e un
Modellistica e Gestione dei Sistemi Ambientali
 Università degli Studi di Siena Facoltà di Ingegneria Modellistica e Gestione dei Sistemi Ambientali Dispense sull analisi di stabilità di sistemi dinamici Prof.ssa Chiara Mocenni A. A. 2009/2010 ... Negli
Università degli Studi di Siena Facoltà di Ingegneria Modellistica e Gestione dei Sistemi Ambientali Dispense sull analisi di stabilità di sistemi dinamici Prof.ssa Chiara Mocenni A. A. 2009/2010 ... Negli
Test in Itinere di Analisi Matematica
 4 Prove d Esame di Analisi Matematica Versione 2006 Pisa, 5 Novembre 2002 La funzione f(x) = x da R in R è surgettiva Per ogni x 0 si ha che x 1 = x 1 La funzione f(x) = x da [0, + [ in [0, + [ è iniettiva
4 Prove d Esame di Analisi Matematica Versione 2006 Pisa, 5 Novembre 2002 La funzione f(x) = x da R in R è surgettiva Per ogni x 0 si ha che x 1 = x 1 La funzione f(x) = x da [0, + [ in [0, + [ è iniettiva
Ingegneria Tessile, Biella Analisi II
 Ingegneria Tessile, Biella Analisi II Esercizi svolti In questo file sono contenute le soluzioni degli esercizi sui campi vettoriali (cf foglio 5 di esercizi) Attenzione: in alcuni esercizi il calcolo
Ingegneria Tessile, Biella Analisi II Esercizi svolti In questo file sono contenute le soluzioni degli esercizi sui campi vettoriali (cf foglio 5 di esercizi) Attenzione: in alcuni esercizi il calcolo
Analisi Matematica II - Ingegneria Meccanica/Energetica - 29 Gennaio 2018
 nalisi Matematica II - Ingegneria Meccanica/Energetica - 29 Gennaio 218 1) ia data la funzione f(x, y, z) = (x 2 + y 2 1) 2 + 8 a) tudiare l esistenza di massimi e minimi assoluti della funzione f nella
nalisi Matematica II - Ingegneria Meccanica/Energetica - 29 Gennaio 218 1) ia data la funzione f(x, y, z) = (x 2 + y 2 1) 2 + 8 a) tudiare l esistenza di massimi e minimi assoluti della funzione f nella
ANALISI MATEMATICA. Prova scritta del 20/12/ FILA 1
 ANALISI MATEMATICA CORSO C - CdL INFORMATICA Prova scritta del 0//004 - FILA ESERCIZIO Studiare la funzione f(x) log x log x determinando in particolare a) campo di esistenza ed eventuali asintoti; b)
ANALISI MATEMATICA CORSO C - CdL INFORMATICA Prova scritta del 0//004 - FILA ESERCIZIO Studiare la funzione f(x) log x log x determinando in particolare a) campo di esistenza ed eventuali asintoti; b)
= 0, y(x, t) < M, e ove 0 < x < L. Poniamo y = X(x) T (t) d 2 X dx 2 = 1. d 2 T dt 2 = κ2 ; v 2 T. dt 2 + v2 κ 2 T = 0.
 Modi normali Una corda di lunghezza è tesa tra i punti x = e x =.All istante t = essa ha una configurazione data da f(x) con < x < ed è rilasciata con velocità nulla. Trovare lo spostamento della corda
Modi normali Una corda di lunghezza è tesa tra i punti x = e x =.All istante t = essa ha una configurazione data da f(x) con < x < ed è rilasciata con velocità nulla. Trovare lo spostamento della corda
