Sistemi differenziali 2 2: esercizi svolti. 1 Sistemi lineari Stabilità nei sistemi lineari
|
|
|
- Giulio Biondi
- 7 anni fa
- Visualizzazioni
Transcript
1 Sistemi differenziali : esercizi svolti 1 Sistemi lineari Stabilità nei sistemi lineari 14 1
2 Sistemi differenziali : esercizi svolti 1 Sistemi lineari Gli esercizi contrassegnati con il simbolo * presentano un grado di difficoltà maggiore Esercizio 1 Determinare l integrale generale dei seguenti sistemi lineari: { x [{ + x y = 0 x(t = c1 e t + c e 3t a y 4x + y = 0 y(t = c 1 e t c e 3t, c 1, c R { x [{ = x + y x(t = c1 e 3t + c e t ] b c 1, c R y = 4x y y(t = c 1 e 3t 4c e t, [ ( 3 4 (c1 c X + c + c te t ] = AX, con X(t = 1 1 (c 1 + c te t, c 1, c R 1 d X = AX, con 4 [ ( ] c X(t = 1 cos t + c sin t e 3t, c (c 1 + c cos t + (c 1 c sin t 1, c R 1 t e X = AX + B(t, con, B(t = 1 1 [ ( c1 e t + c e 3t X(t = t 11 ] 9 c 1 e t + c e 3t 3 t +, c 7 1, c R 9 ( 1 e f X 3t = AX + B(t, con, B(t = 1 0 X(t = c 1e t + c e 3t + 1 t e 3t, c 1, c R c 1 e t + c e 3t + 1 t e3t 0 1 sin t g X = AX + B(t, con, B(t = [ ( c1 cos t + c sin t 1 X(t = cos t + 1 t sin t ] c 1 sin t + c cos t + 1 t cos t, c 1, c R ] Svolgimento a Consideriamo il sistema lineare omogeneo a coefficienti costanti { x + x y = 0 y 4x + y = 0 Scritto in forma esplicita (o normale diventa { x = x + y y = 4x y
3 Sistemi lineari 3 e in forma matriciale è X = AX, dove la matrice dei coefficienti è Calcoliamo gli autovalori di A Si ha che det(a λi = 1 λ λ = (λ Quindi gli autovalori di A sono λ 1 = 1 con molteplicità m 1 = 1 e λ = 3 con molteplicità m = 1 Determiniamo gli autovettori associati a λ 1 e λ Cominiciamo con λ 1 Risolviamo il sistema lineare (A Iv = 0 Posto v = (x, y si ottiene y = x Quindi si ha v = (x, x, x R Sia quindi v 1 = (1, uno di questi autovettori Cerchiamo un autovettore associato a λ = 3 Risolviamo il sistema lineare (A + 3Iv = 0 Posto v = (x, y si ottiene y = x Quindi si ha v = (x, x, x R Sia quindi v = (1, uno di questi autovettori L integrale generale è X(t = c 1 v 1 e t + c v e 3t = ( c1 e t + c e 3t c 1 e t c e 3t, c 1, c R In modo alternativo ma equivalente, si può dire che l integrale generale è dato da X(t = c 1 X 1 (t + c X (t, c 1, c R, dove X 1, X sono le due soluzioni linearmente indipendenti X 1 (t = v 1 e t, X (t = v e 3t b Consideriamo il sistema lineare omogeneo a coefficienti costanti { x = x + y y = 4x y Scritto in forma matriciale è X = AX, dove la matrice dei coefficienti è Calcoliamo gli autovalori di A Si ha che det(a λi = λ λ = λ λ 6
4 4 Sistemi differenziali : esercizi svolti Quindi gli autovalori di A sono λ 1 = 3 con molteplicità m 1 = 1 e λ = con molteplicità m = 1 Determiniamo gli autovettori associati a λ 1 e λ Cominiciamo con λ 1 Risolviamo il sistema lineare (A 3Iv = 0 Posto v = (x, y si ottiene y = x Quindi si ha v = (x, x, x R Sia quindi v 1 = (1, 1 uno di questi autovettori Cerchiamo un autovettore associato a λ = Risolviamo il sistema lineare (A + Iv = 0 Posto v = (x, y si ottiene y = 4x Quindi si ha v = (x, 4x, x R Sia quindi v = (1, 4 uno di questi autovettori L integrale generale è ( c1 e 3t + c X(t = c 1 v 1 e 3t + c v e t e t =, c 1, c R c 1 e 3t 4c e t In modo alternativo ma equivalente, si può dire che l integrale generale è dato da X(t = c 1 X 1 (t + c X (t, c 1, c R, dove X 1, X sono le due soluzioni linearmente indipendenti X 1 (t = v 1 e 3t, X (t = v e t c Consideriamo il sistema lineare omogeneo a coefficienti costanti X = AX, dove Calcoliamo gli autovalori di A Si ha che det(a λi = 3 λ λ = λ λ + 1 Quindi gli autovalori di A sono λ 1 = 1 con molteplicità m 1 = Determiniamo gli autovettori associati a λ 1 Risolviamo il sistema lineare (A Iv = 0 Posto v = (x, y si ottiene y = x Quindi si ha v = (x, x, x R Ne segue che la molteplicità geometrica dell autovalore λ 1 è 1 autovettori Sia v 1 = (1, uno di questi Determiniamo ora un autovettore generalizzato associato a λ 1 Risolviamo il sistema lineare (A Iv = v 1 Posto v = (x, y si ottiene x = y + 1 Quindi gli autovettori generalizzati sono della forma v = (y + 1, y, y R Sia quindi v = (1, 0 uno di questi autovettori
5 Sistemi lineari 5 L integrale generale è ( c1 e t + c X(t = c 1 v 1 e t + c (tv 1 + v e t te t =, c 1, c R c 1 e t + c te t In modo alternativo ma equivalente, si può dire che l integrale generale è dato da X(t = c 1 X 1 (t + c X (t, c 1, c R, dove X 1, X sono le due soluzioni linearmente indipendenti X 1 (t = v 1 e t, X (t = (tv 1 + v e t d Consideriamo il sistema lineare omogeneo a coefficienti costanti X = AX, dove 1 4 Calcoliamo gli autovalori di A Si ha che det(a λi = λ 1 4 λ = λ 6λ + 10 Quindi gli autovalori di A sono complessi coniugati λ 1, = 3 ± i Determiniamo un autovettore associato a λ 1 = 3+i Risolviamo il sistema lineare (A (3+iIw = 0 Posto w = (x, y si ottiene y = (1 + ix Quindi si ha w = (x, (1 + ix, x C Scegliamo ad esempio w = (1, (1 + i Consideriamo la funzione Z(t = w e λ1t 1 = e 3t (cos t + i sin t = 1 + i [( ( ] cos t sin t = + i e 3t cos t + sin t cos t sin t L integrale generale è ( X(t = c 1 Re (Z(t + c Im (Z(t = al variare di c 1, c R c 1 cos t + c sin t (c 1 + c cos t + (c 1 c sin t e 3t, e Consideriamo il sistema lineare non omogeneo a coefficienti costanti X = AX + B(t, dove 1 t, B(t = 1 1 L integrale generale del sistema lineare non omogeneo X = AX +B è dato da X = X o + X p, dove X o è l integrale generale del sistema omogeneo associato X = AX e X p è un integrale particolare del sistema lineare non omogeneo X = AX + B
6 6 Sistemi differenziali : esercizi svolti Calcoliamo inizialmente X o Calcoliamo gli autovalori di A Si ha che det(a λi = 1 λ 1 λ = λ λ 3 Quindi gli autovalori di A sono λ 1 = 1 con molteplicità m 1 = 1 e λ = 3 con molteplicità m = 1 Determiniamo gli autovettori associati a λ 1 e λ Cominiciamo con λ 1 Risolviamo il sistema lineare (A + Iv = 0 Posto v = (x, y si ottiene y = x Quindi si ha v = (x, x, x R Sia quindi v 1 = (1, 1 uno di questi autovettori Cerchiamo un autovettore associato a λ = 3 Risolviamo il sistema lineare (A 3Iv = 0 Posto v = (x, y si ottiene y = x Quindi si ha v = (x, x, x R Sia quindi v = (1, 1 uno di questi autovettori L integrale generale del sistema omogeneo associato è X o (t = c 1 v 1 e t + c v e 3t = ( c1 e t + c e 3t c 1 e t + c e 3t, c 1, c R t Calcoliamo ora X p Il termine noto B del sistema non omogeneo è B(t = = 1 t e 1 0t Quindi le sue componenti sono il prodotto di un polinomio di primo grado e di un polinomio costante per la funzione esponenziale e 0t Poichè 0 non è un autovalore della matrice A, un integrale particolare del sistema non omogeneo è della forma X p (t = at + b e 0t = ct + d at + b, ct + d dove a, b, c, d R Imponiamo che X p risolva il sistema non omogeneo Si ha che X p = AX p + B(t a = c { a = (a + c + 1t + b + d c = (a + ct + b + d + 1 a = 1 3 b = 11 9 c = 3 d = 7 9 (a + c + 1t + b + d (a + ct + b + d + 1 a + c + 1 = 0 a = b + d a + c = 0 c = b + d + 1
7 Sistemi lineari 7 Quindi un integrale particolare è X p (t = ( 1 3 t t L integrale generale del sistema non omogeneo è ( c1 e t + c e 3t X(t = X o (t + X p (t = t 11 9 c 1 e t + c e 3t 3 t +, c 7 1, c R 9 f Consideriamo il sistema lineare non omogeneo a coefficienti costanti X = AX + B(t, dove 1, B(t = 1 ( e 3t L integrale generale del sistema lineare non omogeneo X = AX +B è dato da X = X o + X p, dove X o è l integrale generale del sistema omogeneo associato X = AX e X p è un integrale particolare del sistema lineare non omogeneo X = AX + B Calcoliamo inizialmente X o Calcoliamo gli autovalori di A Si ha che det(a λi = 1 λ 1 λ = λ λ 3 Quindi gli autovalori di A sono λ 1 = 1 con molteplicità m 1 = 1 e λ = 3 con molteplicità m = 1 Determiniamo gli autovettori associati a λ 1 e λ Cominiciamo con λ 1 Risolviamo il sistema lineare (A + Iv = 0 Posto v = (x, y si ottiene y = x Quindi si ha v = (x, x, x R Sia quindi v 1 = (1, 1 uno di questi autovettori Cerchiamo un autovettore associato a λ = 3 Risolviamo il sistema lineare (A 3Iv = 0 Posto v = (x, y si ottiene y = x Quindi si ha v = (x, x, x R Sia quindi v = (1, 1 uno di questi autovettori L integrale generale del sistema omogeneo associato è ( c1 e t + c X o (t = c 1 v 1 e t + c v e 3t e 3t =, c 1, c R c 1 e t + c e 3t ( e 3t Calcoliamo ora X p Il termine noto B del sistema non omogeneo è B(t = = 0 1 e 0 3t Quindi le sue componenti sono il prodotto di due polinomi costanti per la funzione esponenziale e 3t Poichè 3 è un autovalore della matrice A con molteplicità algebrica 1, un integrale particolare del sistema non omogeneo è della forma at + b X p (t = e 3t, ct + d 0
8 8 Sistemi differenziali : esercizi svolti dove a, b, c, d R Imponiamo che X p risolva il sistema non omogeneo Si ha che X p = AX p + B(t 3at + 3b + a e 3t = 3ct + 3d + c { 3at + 3b + a = (a + ct + b + d + 1 Scelto ad esempio b = 1 4 3ct + 3d + c = (a + ct + b + d + 1 a = 1 b R c = 1 d = b 1 4 si ha che un integrale particolare è ( 1 X p (t = t t ( (a + ct + b + d + 1 (a + ct + b + d 3a = a + c 3b + a = b + d 3c = a + c 3d + c = b + d L integrale generale del sistema non omogeneo è X(t = X o (t + X p (t = c 1e t + c e 3t + 1 t e 3t, c 1, c R c 1 e t + c e 3t + 1 t e3t e 3t g Consideriamo il sistema lineare non omogeneo a coefficienti costanti X = AX + B(t, dove 0 1, B(t = 1 0 sin t 0 L integrale generale del sistema lineare non omogeneo X = AX +B è dato da X = X o + X p, dove X o è l integrale generale del sistema omogeneo associato X = AX e X p è un integrale particolare del sistema lineare non omogeneo X = AX + B Calcoliamo inizialmente X o Calcoliamo gli autovalori di A Si ha che det(a λi = λ 1 1 λ = λ + 1 Quindi gli autovalori di A sono complessi coniugati λ 1, = ±i Determiniamo un autovettore associato a λ 1 = i Risolviamo il sistema lineare (A iiw = 0 Posto w = (x, y si ottiene y = ix Quindi si ha w = (x, ix, x C Scegliamo ad esempio w = (1, i Consideriamo la funzione Z(t = w e λ 1t = 1 e 0t cos t sin t (cos t + i sin t = + i i sin t cos t
9 Sistemi lineari 9 L integrale generale del sistema omogeneo associato è c1 cos t + c X o (t = c 1 Re (Z(t + c Im (Z(t = sin t, c c 1 sin t + c cos t 1, c R Calcoliamo ora X p Il termine noto B del sistema non omogeneo è [ ] sin t B(t = = e 0t 0 1 cos t + sin t Quindi le sue componenti sono il prodotto della funzione esponenziale e 0t per delle combinazioni lineari delle funzioni cos t e sin t, in cui i coefficienti sono polinomi costanti Poichè 0 ± 1i = ±i sono autovalori della matrice A con molteplicità algebrica 1, un integrale particolare del sistema non omogeneo è della forma [ ] X p (t = e 0t at + b et + f at + b et + f cos t + sin t = cos t + sin t, ct + d gt + h ct + d gt + h dove a, b, c, d, e, f, g, h R Imponiamo che X p risolva il sistema non omogeneo Si ha che X p = AX p + B(t et + f + a at b + e ct + d gt + h + 1 cos t + sin t = cos t + sin t gt + h + c ct d + g at b et f e = c f + a = d et + f + a = ct + d g = a gt + h + c = at b h + c = b at b + e = gt + h + 1 b + e = h + 1 ct d + g = et f c = e d + g = f a, f, h R b = h 1 c = e = 1 d = f + a g = a Scelto ad esempio a = f = h = 0 si ha che un integrale particolare è ( 1 ( 1 X p (t = 1 t cos t + t sin t 0 L integrale generale del sistema non omogeneo è ( c1 cos t + c sin t 1 X(t = X o (t+x p (t = X(t = cos t + 1 t sin t c 1 sin t + c cos t + 1 t cos t, c 1, c R
10 10 Sistemi differenziali : esercizi svolti Esercizio Determinare la soluzione dei seguenti problemi di Cauchy: X = AX [ ( 1 1 te t ] a 0 X(t = X(0 =, (t + 1e t b c X = AX 1 X(0 =, 0 X = AX 1 X(0 =, 1 [ 3 X(t = 1 3 ( e t + e 5t ] e t e 5t [ ( 3 1 e t ] X(t = 1 1 e t d { X = AX + B X(0 = 0, ( 1 e t, B = 4 1 e t [ ( 3 5 e3t 3 5 e t + 5 te t X(t = 3 5 e3t 3 5 e t 8 5 te t ] Svolgimento a Determiniamo gli autovalori di A Si ha quindi che det (A λi = 1 λ λ = (λ Quindi gli autovalori di A sono λ = con molteplicità algebrica Determiniamo gli autovettori associati a λ Risolviamo il sistema lineare (A Iv = 0 Si ha x + y = 0 = v = (x, x, x R Sia quindi v 1 = (1, 1 uno di questi autovettori Cerchiamo un autovettore generalizzato associato a λ Risolviamo il sistema lineare (A Iv = v 1 Si ha x + y = 1 = v = (x, x + 1, x R Sia quindi v = (0, 1 uno di questi autovettori L integrale generale è X(t = c 1 v 1 e t + c (tv 1 + v e t = ( c 1 e t + c te t (c 1 + c e t + c te t, c 1, c R
11 Sistemi lineari 11 0 Imponendo la condizione iniziale X(0 = si ottiene c 1 1 = 0 e c = 1 Quindi la soluzione del problema di Cauchy è ( te t X(t = (t + 1e t b Determiniamo gli autovalori di A Si ha quindi che det (A λi = λ 3 3 λ = (λ 9 Quindi gli autovalori di A sono λ 1 = 1 con molteplicità m 1 = 1 e λ = 5 con molteplicità m = 1 Determiniamo gli autovettori associati a λ 1 e λ Cominiciamo con λ 1 Risolviamo il sistema lineare (A + Iv = 0 Posto v = (x, y si ottiene y = x Quindi si ha v = (x, x, x R Sia quindi v 1 = (1, 1 uno di questi autovettori Cerchiamo un autovettore associato a λ = 5 Risolviamo il sistema lineare (A 5Iv = 0 Posto v = (x, y si ottiene y = x Quindi si ha v = (x, x, x R Sia quindi v = (1, 1 uno di questi autovettori L integrale generale è ( c1 e t + c X(t = c 1 v 1 e t + c v e 5t e 5t =, c 1, c R c 1 e t c e 5t 1 Imponendo la condizione iniziale X(0 = si ottiene c 0 1 = c = 1 Quindi la soluzione del problema di Cauchy è X(t = 1 ( e t + e 5t e t e 5t c Determiniamo gli autovalori di A Si ha quindi che det (A λi = 3 λ λ = (λ + Quindi gli autovalori di A sono λ = con molteplicità algebrica Determiniamo gli autovettori associati a λ Risolviamo il sistema lineare (A + Iv = 0 Si ha x + y = 0 = v = (x, x, x R Sia quindi v 1 = (1, 1 uno di questi autovettori
12 1 Sistemi differenziali : esercizi svolti Cerchiamo un autovettore generalizzato associato a λ Risolviamo il sistema lineare (A + Iv = v 1 Si ha x + y = 1 = v = (x, x 1, x R Sia quindi v = (0, 1 uno di questi autovettori L integrale generale è ( c X(t = c 1 v 1 e t + c (tv 1 + v e t 1 e t + c te t =, c 1, c R (c 1 + c e t c te t 1 Imponendo la condizione iniziale X(0 = si ottiene c 1 1 = 1 e c = 0 Quindi la soluzione del problema di Cauchy è ( e t X(t = e t d L integrale generale del sistema lineare non omogeneo X = AX +B è dato da X = X o + X p, dove X o è l integrale generale del sistema omogeneo associato X = AX e X p è un integrale particolare del sistema lineare non omogeneo X = AX + B Calcoliamo inizialmente X o Determiniamo gli autovalori di A Si ha quindi che det (A λi = λ λ = λ λ 6 Quindi gli autovalori di A sono λ 1 = 3 e λ = Quindi A è diagonalizzabile Determiniamo gli autovettori associati a λ 1 e λ Cominiciamo con λ 1 Risolviamo il sistema lineare (A 3Iv = 0 Si ha x + y = 0 = v = (x, x, x R Sia quindi v 1 = (1, 1 uno di questi autovettori Cerchiamo un autovettore associato a λ = Risolviamo il sistema lineare (A + Iv = 0 Si ha 4x + y = 0 = v = (x, 4x, x R Sia quindi v = (1, 4 uno di questi autovettori L integrale generale X o del sistema lineare omogeneo X = AX è dato da ( c1 e 3t + c X o (t = c 1 v 1 e 3t + c v e t e t =, c 1, c R c 1 e 3t 4c e t
13 Sistemi lineari 13 e t ( Calcoliamo ora X p Il termine noto B del sistema non omogeneo è B(t = e t 1 = e 1 t Quindi le sue componenti sono il prodotto di un polinomio costante per la funzione esponenziale e t Poichè è un autovalore della matrice A con molteplicità algebrica 1, un integrale particolare del sistema non omogeneo è della forma X p (t = at + b e t, ct + d dove a, b, c, d R Imponiamo che X p risolva il sistema non omogeneo Si ha che X p = AX p +B(t at b + a e t = ct d + c { at b + a = (a + ct + b + d + 1 ct d + c = (4a ct + 4b d 1 a = 5 b R c = 8 5 d = 4b 3 5 (a + ct + b + d + 1 e t (4a ct + 4b d 1 Scelto ad esempio b = 0 si ha che un integrale particolare è X p (t = ( 5 t 8 5 t 3 5 e t L integrale generale del sistema non omogeneo è c 1 e 3t + c e t + 5 t X(t = X o (t + X p (t = c 1 e 3t 4c e t 8 5 t a = a + c b + a = b + d + 1 c = 4a c d + c = 4b d 1 e t, c 1, c R Imponendo la condizione iniziale X(0 = 0 si ottiene c 1 = 3 5 e c = 3 5 Quindi la soluzione del problema di Cauchy è 3 5 e3t + 5 t 3 5 e t X(t = 3 5 e3t 8 5 t e t
14 14 Sistemi differenziali : esercizi svolti Stabilità nei sistemi lineari Gli esercizi contrassegnati con il simbolo * presentano un grado di difficoltà maggiore Esercizio 1 Discutere la stabilità della soluzione nulla dei seguenti sistemi lineari al variare del parametro a X α = X, α α R [Instabile per ogni α R] b dx 4 1 dt = x, α R 0 α α < 0 : α = 0 : α > 0 : x = 0 è asintoticamente stabile, x = 0 è stabile non asintoticamente, x = 0 è instabile c { x = αx + y y = 16x αy, α R α < 4 : α = 4 : α > 4 : (x, y = 0 è stabile non asintoticamente, (x, y = 0 è instabile, (x, y = 0 è instabile d { x = (3 αx + y α R y = (3 α x + (α 4y, α < 3, : (x, y = 0 è instabile, α = 3 : (x, y = 0 è stabile non asintoticamente, α > 3 : (x, y = 0 è asintoticamente stabile Svolgimento a Consideriamo il sistema lineare omogeneo acoefficienti costanti X α = X, α R α La matrice dei coefficienti è α α Determiniamo gli autovalori di A Si ha quindi che det (A λi = λ α α λ = ( λ α Quindi gli autovalori di A sono λ 1, = ±α + Si ha che λ 1, 0 { α + 0 α + 0 { α α Quindi la soluzione X = 0 è instabile per ogni α R = α R
15 Stabilità nei sistemi lineari 15 b Consideriamo il sistema lineare omogeneo a coefficienti costanti dx 4 1 dt = x, α R 0 α La matrice dei coefficienti è α Determiniamo gli autovalori di A Poichè la matrice è triangolare (superiore, i suoi autovalori sono gli elementi della diagonale principale Quindi gli autovalori della matrice A sono 4 e α Ne segue che α < 0 = x = 0 è asintoticamente stabile, α = 0 = x = 0 è stabile ma non asintoticamente, α > 0 = x = 0 è instabile c Consideriamo il sistema lineare omogeneo a coefficienti costanti { x = αx + y α R y = 16x αy, La matrice dei coefficienti è α 1 16 α Quindi gli autovalori di A sono le soluzioni (complesse dell equazione det(a λi = 0, cioè α λ 1 16 α λ = (α λ( α λ + 16 = λ α + 16 = 0 Le soluzioni sono Ne segue che ±i 16 α se α < 4 λ 1, = 0 se α = 4 ± α 16 se α > 4 α < 4 = la soluzione nulla è stabile ma non asintoticamente, α = 4 = la soluzione nulla è instabile, α > 4 = la soluzione nulla è instabile d Consideriamo il sistema lineare omogeneo a coefficienti costanti { x = (3 αx + y α R y = (3 α x + (α 4y,
16 16 Sistemi differenziali : esercizi svolti La matrice dei coefficienti è 3 α 1 (3 α α 4 Per studiare la stabilità della soluzione nulla calcoliamo gli autovalori di A Si ha che det (A λi = 3 α λ 1 (3 α α 4 λ = (3 α λ(α 4 λ+(3 α = λ +λ+α 3 Ne segue che det (A λi = 0 λ + λ + α 3 = 0 λ 1, = 1 ± 13 4α Se α > 13 4, allora λ 1, = 1 ± i 4α 13 Quindi gli autovalori di A hanno parte reale negativa Ne segue che X = 0 è asintoticamente stabile Se α = 13 4, allora λ 1, = 1 Quindi l unico autovalore di A ha parte reale negativa Ne segue che X = 0 è asintoticamente stabile Se α < 13 4, allora λ 1, = 1± 13 4α R Si ha che λ 1 = α < 0 mentre λ = α < α < 1 α > 3 Poichè per α = 3 si ottiene λ = 0, si ha che se 3 < α < 13 4, allora gli autovalori di A sono negativi e quindi X = 0 è asintoticamente stabile Se α = 3, un autovalore è negativo e l altro è nullo, quindi X = 0 è stabile ma non asintoticamente Se α < 3, un autovalore è negativo e l altro è positivo, quindi X = 0 è instabile ma non completamente instabile Ricapitolando si ha che α < 3 = X = 0 è instabile, α = 3 = X = 0 è stabile ma non asintoticamente, α > 3 = X = 0 è asintoticamente stabile
Sistemi differenziali: esercizi svolti. 1 Sistemi lineari 2 2... 2 2 Sistemi lineari 3 3... 10
 Sistemi differenziali: esercizi svolti Sistemi lineari 2 2 2 2 Sistemi lineari 3 3 2 Sistemi differenziali: esercizi svolti Sistemi lineari 2 2 Gli esercizi contrassegnati con il simbolo * presentano un
Sistemi differenziali: esercizi svolti Sistemi lineari 2 2 2 2 Sistemi lineari 3 3 2 Sistemi differenziali: esercizi svolti Sistemi lineari 2 2 Gli esercizi contrassegnati con il simbolo * presentano un
SISTEMI DI EQUAZIONI DIFFERENZIALI- ESERCIZI SVOLTI
 SISTEMI DI EQUAZIONI DIFFERENZIALI- ESERCIZI SVOLTI Generalità sui sistemi Sia xt, yt la soluzione del problema di Cauchy Posto vt = e xtyt, calcolare v x = 3x x = y = x y = 0 Sia x = 3x y y = x + y Scrivere
SISTEMI DI EQUAZIONI DIFFERENZIALI- ESERCIZI SVOLTI Generalità sui sistemi Sia xt, yt la soluzione del problema di Cauchy Posto vt = e xtyt, calcolare v x = 3x x = y = x y = 0 Sia x = 3x y y = x + y Scrivere
Compito di Analisi Matematica II del 28 giugno 2006 ore 11
 Compito di Analisi Matematica II del 28 giugno 26 ore Esercizio. ( punti) Calcolare il flusso del campo vettoriale F (,, z) = (z, z 2, z 2 ) } uscente dalla frontiera di D = (,, z) R 3 : 2 + z 2, z,. Svolgimento
Compito di Analisi Matematica II del 28 giugno 26 ore Esercizio. ( punti) Calcolare il flusso del campo vettoriale F (,, z) = (z, z 2, z 2 ) } uscente dalla frontiera di D = (,, z) R 3 : 2 + z 2, z,. Svolgimento
Compito di Matematica I A.A.2008/09 - C.d.L. in Chimica 16 Novembre 2009 Prof. Elena Comparini
 A.A.2008/09 - C.d.L. in Chimica 6 Novembre 2009 Prof. Elena Comparini f(x) = x x 2 x +, Esercizio 2. Data la funzione dell esercizio precedente, calcolare l area della regione di piano compresa tra il
A.A.2008/09 - C.d.L. in Chimica 6 Novembre 2009 Prof. Elena Comparini f(x) = x x 2 x +, Esercizio 2. Data la funzione dell esercizio precedente, calcolare l area della regione di piano compresa tra il
Traiettorie nello spazio degli stati
 . Traiettorie nello spazio degli stati Per mostrare i tipici andamenti delle traiettorie nello spazio degli stati in funzione della posizione dei poli del sistema si farà riferimento ad un esempio: un
. Traiettorie nello spazio degli stati Per mostrare i tipici andamenti delle traiettorie nello spazio degli stati in funzione della posizione dei poli del sistema si farà riferimento ad un esempio: un
Esercizio Determinare l integrale generale delle seguenti equazioni differenziali lineari del primo ordine: (i) y = 3y cos(x);
 134 Capitolo 4. Equazioni differenziali ordinarie del problema di Cauchy (4.28) bisogna risolvere il sistema lineare (nelle incognite c 1,..., c n )) c 1 y 1 (x 0 ) +... + c n y n (x 0 ) = y 0, c 1 y 1
134 Capitolo 4. Equazioni differenziali ordinarie del problema di Cauchy (4.28) bisogna risolvere il sistema lineare (nelle incognite c 1,..., c n )) c 1 y 1 (x 0 ) +... + c n y n (x 0 ) = y 0, c 1 y 1
Equazioni differenziali
 Equazioni differenziali In un equazione differenziale l incognita da trovare è una funzione, di cui è data, dall equazione, una relazione con le sue derivate (fino ad un certo ordine) e la variabile libera:
Equazioni differenziali In un equazione differenziale l incognita da trovare è una funzione, di cui è data, dall equazione, una relazione con le sue derivate (fino ad un certo ordine) e la variabile libera:
- ciascun autovalore di T ha molteplicità geometrica uguale alla moltplicitaà algebrica.
 Lezioni del 14.05 e 17.05 In queste lezioni si sono svolti i seguenti argomenti. Ripresa del teorema generale che fornisce condizioni che implicano la diagonalizzabilità, indebolimento delle ipotesi, e
Lezioni del 14.05 e 17.05 In queste lezioni si sono svolti i seguenti argomenti. Ripresa del teorema generale che fornisce condizioni che implicano la diagonalizzabilità, indebolimento delle ipotesi, e
PROVE D'ESAME DI MATEMATICA DISCRETA A.A. 2010/2011
 PROVE D'ESAME DI MATEMATICA DISCRETA A.A. 200/20 07/06/20 () In R 3 [t], lo spazio vettoriale dei polinomi nella variabile t di grado al piú 3, sia u = t 2 5t + 6 e w = t 3 + t 2 t. (a) Determinare una
PROVE D'ESAME DI MATEMATICA DISCRETA A.A. 200/20 07/06/20 () In R 3 [t], lo spazio vettoriale dei polinomi nella variabile t di grado al piú 3, sia u = t 2 5t + 6 e w = t 3 + t 2 t. (a) Determinare una
Esercizi di teoria dei sistemi
 Esercizi di teoria dei sistemi Controlli Automatici LS (Prof. C. Melchiorri) Esercizio Dato il sistema lineare tempo continuo: ẋ(t) 2 y(t) x(t) x(t) + u(t) a) Determinare l evoluzione libera dello stato
Esercizi di teoria dei sistemi Controlli Automatici LS (Prof. C. Melchiorri) Esercizio Dato il sistema lineare tempo continuo: ẋ(t) 2 y(t) x(t) x(t) + u(t) a) Determinare l evoluzione libera dello stato
Politecnico di Milano Ingegneria Industriale Analisi e Geometria 2
 Politecnico di Milano Ingegneria Industriale Analisi e Geometria Preparazione al primo compito in itinere. (a) Mostrare che l insieme B = {b, b, b 3 }, formato dai vettori b = (,, ), b = (,, ) e b 3 =
Politecnico di Milano Ingegneria Industriale Analisi e Geometria Preparazione al primo compito in itinere. (a) Mostrare che l insieme B = {b, b, b 3 }, formato dai vettori b = (,, ), b = (,, ) e b 3 =
Esercizi di ripasso: geometria e algebra lineare.
 Esercizi di ripasso: geometria e algebra lineare. Esercizio. Sia r la retta passante per i punti A(2,, 3) e B(,, 2) in R 3. a. Scrivere l equazione cartesiana del piano Π passante per A e perpendicolare
Esercizi di ripasso: geometria e algebra lineare. Esercizio. Sia r la retta passante per i punti A(2,, 3) e B(,, 2) in R 3. a. Scrivere l equazione cartesiana del piano Π passante per A e perpendicolare
Università Carlo Cattaneo Ingegneria gestionale Analisi matematica a.a. 2016/2017 EQUAZIONI DIFFERENZIALI 2
 Università Carlo Cattaneo Ingegneria gestionale Analisi matematica a.a. 2016/2017 EQUAZIONI DIFFERENZIALI 2 ESERCIZI CON SOLUZIONE 1. Risolvere il seguente problema di Cauchy: 1 2 1 2 L equazione differenziale
Università Carlo Cattaneo Ingegneria gestionale Analisi matematica a.a. 2016/2017 EQUAZIONI DIFFERENZIALI 2 ESERCIZI CON SOLUZIONE 1. Risolvere il seguente problema di Cauchy: 1 2 1 2 L equazione differenziale
Analisi Matematica II - INGEGNERIA Gestionale - B 20 luglio 2017 Cognome: Nome: Matricola:
 Analisi Matematica II - INGEGNERIA Gestionale - B luglio 7 Cognome: Nome: Matricola: IMPORTANTE: Giustificare tutte le affermazioni e riportare i calcoli essenziali Esercizio [8 punti] Data la matrice
Analisi Matematica II - INGEGNERIA Gestionale - B luglio 7 Cognome: Nome: Matricola: IMPORTANTE: Giustificare tutte le affermazioni e riportare i calcoli essenziali Esercizio [8 punti] Data la matrice
AM2: Tracce delle lezioni- Settimana 12 SISTEMI DI EQUAZIONI DIFFERENZIALI LINEARI
 AM2: Tracce delle lezioni- Settimana 12 SISTEMI DI EQUAZIONI DIFFERENZIALI LINEARI Sia A = (a ij ), i, j = 1,..., n matrice n n. Le soluzioni del sistema differenziale lineare di n equazioni nelle n incognite
AM2: Tracce delle lezioni- Settimana 12 SISTEMI DI EQUAZIONI DIFFERENZIALI LINEARI Sia A = (a ij ), i, j = 1,..., n matrice n n. Le soluzioni del sistema differenziale lineare di n equazioni nelle n incognite
Elementi di Algebra Lineare. Spazio Vettoriale (lineare)
 Elementi di Algebra Lineare Spazio Vettoriale (lineare) Uno spazio vettoriale su un corpo F è una quadrupla (X, F, +, ) costituita da: un insieme di elementi X, detti vettori, un corpo F, i cui elementi
Elementi di Algebra Lineare Spazio Vettoriale (lineare) Uno spazio vettoriale su un corpo F è una quadrupla (X, F, +, ) costituita da: un insieme di elementi X, detti vettori, un corpo F, i cui elementi
Endomorfismi e matrici simmetriche
 CAPITOLO Endomorfismi e matrici simmetriche Esercizio.. [Esercizio 5) cap. 9 del testo Geometria e algebra lineare di Manara, Perotti, Scapellato] Calcolare una base ortonormale di R 3 formata da autovettori
CAPITOLO Endomorfismi e matrici simmetriche Esercizio.. [Esercizio 5) cap. 9 del testo Geometria e algebra lineare di Manara, Perotti, Scapellato] Calcolare una base ortonormale di R 3 formata da autovettori
CORSO DI LAUREA IN INGEGNERIA.
 CORSO DI LAUREA IN INGEGNERIA. FOGLIO DI ESERCIZI 9 GEOMETRIA E ALGEBRA LINEARE 2012/13 Esercizio 9.1 (8.40). Sia T : R 2 R 3 l applicazione definita da T(x,y) = (2x,x y,2y), e siano B = {(1,0), (1,1)
CORSO DI LAUREA IN INGEGNERIA. FOGLIO DI ESERCIZI 9 GEOMETRIA E ALGEBRA LINEARE 2012/13 Esercizio 9.1 (8.40). Sia T : R 2 R 3 l applicazione definita da T(x,y) = (2x,x y,2y), e siano B = {(1,0), (1,1)
Matrice esponenziale e sistemi differenziali lineari a coefficienti costanti
 Matrice esponenziale e sistemi differenziali lineari a coefficienti costanti Matrice esponenziale Sia A R n,n una matrice quadrata n n Per definire l esponenziale di A, prendiamo spunto dall identità e
Matrice esponenziale e sistemi differenziali lineari a coefficienti costanti Matrice esponenziale Sia A R n,n una matrice quadrata n n Per definire l esponenziale di A, prendiamo spunto dall identità e
Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006. Matematica 2 (Analisi)
 Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006 Matematica 2 (Analisi) Nome:................................. N. matr.:.................................
Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006 Matematica 2 (Analisi) Nome:................................. N. matr.:.................................
Traiettorie nello spazio degli stati
 Capitolo. INTRODUZIONE. Traiettorie nello spazio degli stati Per mostrare i tipici andamenti delle traiettorie nello spazio degli stati in funzione della posizione dei poli del sistema si farà riferimento
Capitolo. INTRODUZIONE. Traiettorie nello spazio degli stati Per mostrare i tipici andamenti delle traiettorie nello spazio degli stati in funzione della posizione dei poli del sistema si farà riferimento
ESERCIZI SUI SISTEMI LINEARI
 ESERCIZI SUI SISTEMI LINEARI Consideriamo ora il sistema lineare omogeneo a coefficienti costanti associato alla matrice A M n n, cioè SLO Vale il seguente = A. Teorema. Sia v R n \ } e sia λ C. Condizione
ESERCIZI SUI SISTEMI LINEARI Consideriamo ora il sistema lineare omogeneo a coefficienti costanti associato alla matrice A M n n, cioè SLO Vale il seguente = A. Teorema. Sia v R n \ } e sia λ C. Condizione
UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica GE110 - Geometria 1 a.a Prova scritta del TESTO E SOLUZIONI
 UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica GE0 - Geometria a.a. 07-08 Prova scritta del 7-7-08 TESTO E SOLUZIONI Svolgere tutti gli esercizi.. Per R considerare il sistema lineare X
UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica GE0 - Geometria a.a. 07-08 Prova scritta del 7-7-08 TESTO E SOLUZIONI Svolgere tutti gli esercizi.. Per R considerare il sistema lineare X
Algebra lineare Geometria 1 15 luglio 2009
 Algebra lineare Geometria 1 15 luglio 2009 Esercizio 1. Nello spazio vettoriale reale R 3 [x] si considerino l insieme A k = {1 + x, k + (1 k)x 2, 1 + (k 1)x 2 + x 3 }, il vettore v k = k + kx x 3 e la
Algebra lineare Geometria 1 15 luglio 2009 Esercizio 1. Nello spazio vettoriale reale R 3 [x] si considerino l insieme A k = {1 + x, k + (1 k)x 2, 1 + (k 1)x 2 + x 3 }, il vettore v k = k + kx x 3 e la
ANALISI MATEMATICA T-2 (C.d.L. Ing. per l ambiente e il territorio) A.A Prof. G.Cupini
 ANALISI MATEMATICA T-2 (C.d.L. Ing. per l ambiente e il territorio) A.A.2009-2010 - Prof. G.Cupini Equazioni differenziali ordinarie del primo ordine (lineari, a variabili separabili, di Bernoulli) ed
ANALISI MATEMATICA T-2 (C.d.L. Ing. per l ambiente e il territorio) A.A.2009-2010 - Prof. G.Cupini Equazioni differenziali ordinarie del primo ordine (lineari, a variabili separabili, di Bernoulli) ed
Forma canonica di Jordan
 Capitolo INTRODUZIONE Forma canonica di Jordan Siano λ i, per i =,, h, gli autovalori distinti della matrice A e siano r i i corrispondenti gradi di molteplicità all interno del polinomio caratteristico:
Capitolo INTRODUZIONE Forma canonica di Jordan Siano λ i, per i =,, h, gli autovalori distinti della matrice A e siano r i i corrispondenti gradi di molteplicità all interno del polinomio caratteristico:
Soluzione della seconda prova intermedia di Algebra lineare del 17 maggio Esercizio 1
 Soluzione della seconda prova intermedia di Algebra lineare del 17 maggio 2012 Esercizio 1 (a) Si calcola il polinomio caratteristico λ 2 1 p(λ) = det k 1 2k λ k 1 2 2 λ usando lo sviluppo di Laplace secondo
Soluzione della seconda prova intermedia di Algebra lineare del 17 maggio 2012 Esercizio 1 (a) Si calcola il polinomio caratteristico λ 2 1 p(λ) = det k 1 2k λ k 1 2 2 λ usando lo sviluppo di Laplace secondo
Es.1 Es.2 Es.3 Es.4 Totale. Analisi e Geometria 2 Docente: 15 Luglio 2013
 Es.1 Es.2 Es.3 Es.4 Totale Analisi e Geometria 2 Docente: 15 Luglio 213 Cognome: Nome: Matricola: Ogni risposta dev essere giustificata. Gli esercizi vanno svolti su questi fogli, nello spazio sotto il
Es.1 Es.2 Es.3 Es.4 Totale Analisi e Geometria 2 Docente: 15 Luglio 213 Cognome: Nome: Matricola: Ogni risposta dev essere giustificata. Gli esercizi vanno svolti su questi fogli, nello spazio sotto il
Istituzioni di Matematica II 3 luglio 2014
 Istituzioni di Matematica II 3 luglio 14 1. i Si dica se la matrice é diagonalizzabile. A = 1 1 1 ii Si studi il carattere della forma quadratica q(, y, z = + y + z Soluzioni. i La matrice é simmetrica
Istituzioni di Matematica II 3 luglio 14 1. i Si dica se la matrice é diagonalizzabile. A = 1 1 1 ii Si studi il carattere della forma quadratica q(, y, z = + y + z Soluzioni. i La matrice é simmetrica
Fondamenti di Matematica del discreto
 Fondamenti di Matematica del discreto M1 - Insiemi numerici 12 gennaio 2013 - Laurea on line Esercizio 1. Dire, motivando la risposta, quali delle seguenti equazione diofantee ammettono soluzioni e risolvere
Fondamenti di Matematica del discreto M1 - Insiemi numerici 12 gennaio 2013 - Laurea on line Esercizio 1. Dire, motivando la risposta, quali delle seguenti equazione diofantee ammettono soluzioni e risolvere
Equazioni differenziali lineari di ordine n
 Equazioni differenziali lineari di ordine n Si tratta di equazioni del tipo u (n) (t) + a 1 (t)u (n 1) (t) +... + a n 1 (t)u (t) + a n (t)u(t) = f(t), t I, (1) con n intero 2 ed I R intervallo reale, in
Equazioni differenziali lineari di ordine n Si tratta di equazioni del tipo u (n) (t) + a 1 (t)u (n 1) (t) +... + a n 1 (t)u (t) + a n (t)u(t) = f(t), t I, (1) con n intero 2 ed I R intervallo reale, in
AUTOVALORI, AUTOVETTORI, AUTOSPAZI
 AUTOVALORI, AUTOVETTORI, AUTOSPAZI. Esercizi Esercizio. Sia f : R 3 R 3 l endomorfismo definito da f(x, y, z) = (x+y, y +z, x+z). Calcolare gli autovalori ed una base per ogni autospazio di f. Dire se
AUTOVALORI, AUTOVETTORI, AUTOSPAZI. Esercizi Esercizio. Sia f : R 3 R 3 l endomorfismo definito da f(x, y, z) = (x+y, y +z, x+z). Calcolare gli autovalori ed una base per ogni autospazio di f. Dire se
FM1 - Equazioni differenziali e meccanica
 Corso di laurea in Matematica - Anno Accademico 2006/2007 FM1 - Equazioni differenziali e meccanica Prima prova d esonero (03-04-2006) CORREZIONE Esercizio 1. Lo spettro Σ(A) della matrice A si trova risolvendo
Corso di laurea in Matematica - Anno Accademico 2006/2007 FM1 - Equazioni differenziali e meccanica Prima prova d esonero (03-04-2006) CORREZIONE Esercizio 1. Lo spettro Σ(A) della matrice A si trova risolvendo
Applicazioni lineari e diagonalizzazione
 Autovalori e autovettori Matrici associate a applicazioni lineari Endomorfismi semplici e matrici diagonalizzabili Prodotti scalari e Teorema Spettrale nel caso generale 2 2006 Politecnico di Torino 1
Autovalori e autovettori Matrici associate a applicazioni lineari Endomorfismi semplici e matrici diagonalizzabili Prodotti scalari e Teorema Spettrale nel caso generale 2 2006 Politecnico di Torino 1
Es.1 Es.2 Es.3 Es.4 Es.5 Totale Analisi e Geometria 2 Docente: 15 Luglio 2013
 Es.1 Es.2 Es.3 Es.4 Es.5 Totale 4+4+2 5 2 5+2 4+4 32 Analisi e Geometria 2 Docente: 15 Luglio 213 Cognome: Nome: Matricola: Ogni risposta dev essere giustificata. Gli esercizi vanno svolti su questi fogli,
Es.1 Es.2 Es.3 Es.4 Es.5 Totale 4+4+2 5 2 5+2 4+4 32 Analisi e Geometria 2 Docente: 15 Luglio 213 Cognome: Nome: Matricola: Ogni risposta dev essere giustificata. Gli esercizi vanno svolti su questi fogli,
ESERCIZI SULLE EQUAZIONI DIFFERENZIALI
 ESERCIZI SULLE EQUAZIONI DIFFERENZIALI 1. Generalità 1.1. Verifica delle soluzioni. Verificare se le funzioni date sono soluzioni delle equazioni differenziali. xy = 2y, y = 5x 2. y = x 2 + y 2, y = 1
ESERCIZI SULLE EQUAZIONI DIFFERENZIALI 1. Generalità 1.1. Verifica delle soluzioni. Verificare se le funzioni date sono soluzioni delle equazioni differenziali. xy = 2y, y = 5x 2. y = x 2 + y 2, y = 1
MOVIMENTO DEI SISTEMI LINEARI
 MOVIMENTO DEI SISTEMI LINEARI I sistemi continui x& = Ax + Bu Formula di Lagrange 3 3 e At = I + At + A t + A t! 3! Nei sistemi lineari, quindi x( t) = x ( t) + x ( t) l Inoltre x l (t) e x f (t) sono
MOVIMENTO DEI SISTEMI LINEARI I sistemi continui x& = Ax + Bu Formula di Lagrange 3 3 e At = I + At + A t + A t! 3! Nei sistemi lineari, quindi x( t) = x ( t) + x ( t) l Inoltre x l (t) e x f (t) sono
Istituzioni di Matematica II 5 Luglio 2010
 Istituzioni di Matematica II 5 Luglio 010 1. Classificare, al variare del parametro α R, la forma quadratica (1 + α )x + 4xy + αy.. i) Si determinino tutti i punti critici della seguente funzione f(x,
Istituzioni di Matematica II 5 Luglio 010 1. Classificare, al variare del parametro α R, la forma quadratica (1 + α )x + 4xy + αy.. i) Si determinino tutti i punti critici della seguente funzione f(x,
CORSO DI LAUREA in Fisica, aa 2017/18 (canale Pb-Z)
 CORSO DI LAUREA in Fisica, aa 2017/18 (canale Pb-Z) Equazioni lineari del II ordine a coefficienti costanti: questo è un richiamo dei risultati con altri esempi svolti. Il testo di riferimento è Bramanti
CORSO DI LAUREA in Fisica, aa 2017/18 (canale Pb-Z) Equazioni lineari del II ordine a coefficienti costanti: questo è un richiamo dei risultati con altri esempi svolti. Il testo di riferimento è Bramanti
Università degli Studi di Bergamo Facoltà di Ingegneria. Matematica II Ingegneria Edile. Appello del 10 settembre 2007 AC = (2, 2, 2),
 Università degli Studi di Bergamo Facoltà di Ingegneria Matematica II Ingegneria Edile Appello del 1 settembre 7 Cognome e Nome Matr. 1.1. Si considerino nello spaio tridimensionale R 3 i tre punti A (3,
Università degli Studi di Bergamo Facoltà di Ingegneria Matematica II Ingegneria Edile Appello del 1 settembre 7 Cognome e Nome Matr. 1.1. Si considerino nello spaio tridimensionale R 3 i tre punti A (3,
Equazioni differenziali del 2 ordine Prof. Ettore Limoli. Sommario. Equazione differenziale omogenea a coefficienti costanti
 Equazioni differenziali del 2 ordine Prof. Ettore Limoli Sommario Equazione differenziale omogenea a coefficienti costanti... 1 Equazione omogenea di esempio... 2 Equazione differenziale non omogenea a
Equazioni differenziali del 2 ordine Prof. Ettore Limoli Sommario Equazione differenziale omogenea a coefficienti costanti... 1 Equazione omogenea di esempio... 2 Equazione differenziale non omogenea a
k 2 m 1 u 2 Figura 1 z 1 β m 1 ż 1 + β m 1 ż m 2 z 2 β m 2 ẋ = A x + B u y = C x + D u
 Esercizio Si consideri il sistema meccanico riportato in Figura, dove m e m sono le masse dei carrelli, z e z sono le rispettive posizioni, k e k sono i coefficienti elastici delle molle, e β è un coefficiente
Esercizio Si consideri il sistema meccanico riportato in Figura, dove m e m sono le masse dei carrelli, z e z sono le rispettive posizioni, k e k sono i coefficienti elastici delle molle, e β è un coefficiente
Autovalori e autovettori
 Autovalori e autovettori Definizione 1 (per endomorfismi). Sia V uno spazio vettoriale su di un campo K e f : V V un suo endomorfismo. Si dice autovettore per f ogni vettore x 0 tale che f(x) = λx, per
Autovalori e autovettori Definizione 1 (per endomorfismi). Sia V uno spazio vettoriale su di un campo K e f : V V un suo endomorfismo. Si dice autovettore per f ogni vettore x 0 tale che f(x) = λx, per
11.1. Esercizio. Dato il numero complesso z = 2 + i 2, calcolare z, z, scrivere la rappresentazione trigonometrica di z, calcolare z 8.
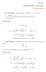 ANALISI Soluzione esercizi gennaio 0.. Esercizio. Dato il numero complesso z = + i, calcolare z, z, scrivere la rappresentazione trigonometrica di z, calcolare z 8. z = i ( ) + ( ) =, π z = arg(z) = 4
ANALISI Soluzione esercizi gennaio 0.. Esercizio. Dato il numero complesso z = + i, calcolare z, z, scrivere la rappresentazione trigonometrica di z, calcolare z 8. z = i ( ) + ( ) =, π z = arg(z) = 4
Alcuni esercizi sulle equazioni di erenziali
 Alcuni esercizi sulle equazioni di erenziali Calcolo dell integrale generale Per ciascuna delle seguenti equazioni di erenziali calcolare l insieme di tutte le possibili soluzioni. SUGGERIMENTO: Ricordatevi
Alcuni esercizi sulle equazioni di erenziali Calcolo dell integrale generale Per ciascuna delle seguenti equazioni di erenziali calcolare l insieme di tutte le possibili soluzioni. SUGGERIMENTO: Ricordatevi
Equazioni differenziali
 4 Equazioni differenziali Determinare le primitive di una funzione f(x) significa risolvere y (x) = f(x) dove l incognita è la funzione y(x). Questa equazione è un semplice esempio di equazione differenziale.
4 Equazioni differenziali Determinare le primitive di una funzione f(x) significa risolvere y (x) = f(x) dove l incognita è la funzione y(x). Questa equazione è un semplice esempio di equazione differenziale.
Prova scritta di Geometria 1 Docente: Giovanni Cerulli Irelli 20 Gennaio 2017
 Prova scritta di Geometria Docente: Giovanni Cerulli Irelli Gennaio 7 Esercizio. Si considerino i seguenti tre punti dello spazio euclideo: P :=, Q :=, R :=.. Dimostrare che P, Q ed R non sono collineari.
Prova scritta di Geometria Docente: Giovanni Cerulli Irelli Gennaio 7 Esercizio. Si considerino i seguenti tre punti dello spazio euclideo: P :=, Q :=, R :=.. Dimostrare che P, Q ed R non sono collineari.
Corso di Laurea in Matematica - Esame di Geometria 1. Prova scritta del 7 settembre 2015
 Corso di Laurea in Matematica - Esame di Geometria 1 Prova scritta del 7 settembre 215 Cognome Nome Numero di matricola Voto ATTENZIONE. Riportare lo svolgimento completo degli esercizi. corretti, non
Corso di Laurea in Matematica - Esame di Geometria 1 Prova scritta del 7 settembre 215 Cognome Nome Numero di matricola Voto ATTENZIONE. Riportare lo svolgimento completo degli esercizi. corretti, non
Esercizio di modellistica a tempo discreto
 Esercizio di modellistica a tempo discreto Si consideri un corso di laurea triennale, e si indichi con k =,, 2,... l anno accademico dall attivazione del corso. Si indichi con x i (k) il numero di studenti
Esercizio di modellistica a tempo discreto Si consideri un corso di laurea triennale, e si indichi con k =,, 2,... l anno accademico dall attivazione del corso. Si indichi con x i (k) il numero di studenti
Compiti di geometria & algebra lineare. Anno: 2004
 Compiti di geometria & algebra lineare Anno: 24 Anno: 24 2 Primo compitino di Geometria e Algebra 7 novembre 23 totale tempo a disposizione : 3 minuti Esercizio. [8pt.] Si risolva nel campo complesso l
Compiti di geometria & algebra lineare Anno: 24 Anno: 24 2 Primo compitino di Geometria e Algebra 7 novembre 23 totale tempo a disposizione : 3 minuti Esercizio. [8pt.] Si risolva nel campo complesso l
Esercizi di GEOMETRIA I - Algebra Lineare B = , calcolare A A t A + I
 Esercizi di GEOMETRIA I - Algebra Lineare. Tra le seguenti matrici, eseguire tutti i prodotti possibili: 2 ( ) A = 0 3 4 B = 2 0 0 2 D = ( 0 ) E = ( ) 4 4 2 C = 2 0 5 F = 4 2 6 2. Data la matrice A = 0
Esercizi di GEOMETRIA I - Algebra Lineare. Tra le seguenti matrici, eseguire tutti i prodotti possibili: 2 ( ) A = 0 3 4 B = 2 0 0 2 D = ( 0 ) E = ( ) 4 4 2 C = 2 0 5 F = 4 2 6 2. Data la matrice A = 0
Tempo a disposizione. 120 minuti. 1 Sia dato l endomorfismo f : R 3 R 3 la cui matrice rispetto alla base canonica di R 3 è.
 Dipartimento di Matematica e Informatica Anno Accademico 2015-2016 Corso di Laurea in Informatica (L-31) Prova in itinere di Matematica Discreta (12 CFU) 13 Giugno 2016 B2 Tempo a disposizione. 120 minuti
Dipartimento di Matematica e Informatica Anno Accademico 2015-2016 Corso di Laurea in Informatica (L-31) Prova in itinere di Matematica Discreta (12 CFU) 13 Giugno 2016 B2 Tempo a disposizione. 120 minuti
ANALISI MATEMATICA II 8 Febbraio 2010 ore 11:00 Versione A. Analisi II 7,5 cr. Analisi D Analisi II V.O. es. 1,2,3 es. 2,4,5 es 2,4,5.
 ANALISI MAEMAICA II 8 Feraio ore : Versione A Nome, Cognome: Docente: Corso di Laurea: Matricola Analisi II 7,5 cr. Analisi D Analisi II V.O. es.,,3 es.,4,5 es,4,5 Codice corso 9ACI ESERCIZIO Dato il sistema
ANALISI MAEMAICA II 8 Feraio ore : Versione A Nome, Cognome: Docente: Corso di Laurea: Matricola Analisi II 7,5 cr. Analisi D Analisi II V.O. es.,,3 es.,4,5 es,4,5 Codice corso 9ACI ESERCIZIO Dato il sistema
5 Un applicazione: le matrici di rotazione
 5 Un applicazione: le matrici di rotazione 51 Rotazioni nel piano di un angolo ϑ Si vuole considerare il caso della rotazione nel piano di un vettore di R di un angolo ϑ assegnato Chiaramente si tratta
5 Un applicazione: le matrici di rotazione 51 Rotazioni nel piano di un angolo ϑ Si vuole considerare il caso della rotazione nel piano di un vettore di R di un angolo ϑ assegnato Chiaramente si tratta
Esame di GEOMETRIA (Appello del 30 gennaio 2018)
 Esame di GEOMETRIA (Appello del 3 gennaio 28) Cognome: Nome: Nr.matricola: Corso di laurea: Esercizio. Siano dati i sottospazi di R 4 : W = L, 4, 5 2 2. Scrivere equazioni cartesiane per W. {, U : x +
Esame di GEOMETRIA (Appello del 3 gennaio 28) Cognome: Nome: Nr.matricola: Corso di laurea: Esercizio. Siano dati i sottospazi di R 4 : W = L, 4, 5 2 2. Scrivere equazioni cartesiane per W. {, U : x +
Esercizi Applicazioni Lineari
 Esercizi Applicazioni Lineari (1) Sia f : R 4 R 2 l applicazione lineare definita dalla legge f(x, y, z, t) = (x + y + z, y + z + t). (a) Determinare il nucleo di f, l immagine di f, una loro base e le
Esercizi Applicazioni Lineari (1) Sia f : R 4 R 2 l applicazione lineare definita dalla legge f(x, y, z, t) = (x + y + z, y + z + t). (a) Determinare il nucleo di f, l immagine di f, una loro base e le
=. Il vettore non è della forma λ, dunque non è un. 2. Il vettore 8 2 non è della forma λ 1
 a.a. 2005-2006 Esercizi. Autovalori e autovettori. Soluzioni. Sia A = e sia x =. Dire se x è autovettore di A. Se si dire per quale 8 autovalore. Sol. Si ha =. Il vettore non è della forma λ dunque 8 29
a.a. 2005-2006 Esercizi. Autovalori e autovettori. Soluzioni. Sia A = e sia x =. Dire se x è autovettore di A. Se si dire per quale 8 autovalore. Sol. Si ha =. Il vettore non è della forma λ dunque 8 29
appunti per il corso di Analisi Matematica I corso di laurea in Ingegneria Gestionale, a.a autore: Giovanni Alberti
 appunti per il corso di Analisi Matematica I corso di laurea in Ingegneria Gestionale, a.a. 2013-14 autore: Giovanni Alberti Equazioni differenziali [versione: 22-12-2013] Richiamo delle nozioni fondamentali
appunti per il corso di Analisi Matematica I corso di laurea in Ingegneria Gestionale, a.a. 2013-14 autore: Giovanni Alberti Equazioni differenziali [versione: 22-12-2013] Richiamo delle nozioni fondamentali
appunti per il corso di Analisi Matematica I corso di laurea in Ingegneria Gestionale, a.a autore: Giovanni Alberti
 appunti per il corso di Analisi Matematica I corso di laurea in Ingegneria Gestionale, a.a. 2014-15 autore: Giovanni Alberti Equazioni differenziali [versione: 2 gennaio 2015] Richiamo delle nozioni fondamentali
appunti per il corso di Analisi Matematica I corso di laurea in Ingegneria Gestionale, a.a. 2014-15 autore: Giovanni Alberti Equazioni differenziali [versione: 2 gennaio 2015] Richiamo delle nozioni fondamentali
Università di Pisa. Corso di Laurea in Ingegneria Meccanica Geometria e Algebra Lineare
 Università di Pisa Corso di Laurea in Ingegneria Meccanica Geometria e Algebra Lineare Cognome e Nome: Corso di studi: Anno di iscrizione: Numero di matricola: Scritto n. 1 del 16 Esercizio 1. Si studi
Università di Pisa Corso di Laurea in Ingegneria Meccanica Geometria e Algebra Lineare Cognome e Nome: Corso di studi: Anno di iscrizione: Numero di matricola: Scritto n. 1 del 16 Esercizio 1. Si studi
Equazioni differenziali lineari del secondo ordine a coefficienti costanti
 Equazioni differenziali lineari del secondo ordine a coefficienti costanti 0.1 Introduzione Una equazione differenziale del secondo ordine è una relazione del tipo F (t, y(t), y (t), y (t)) = 0 (1) Definizione
Equazioni differenziali lineari del secondo ordine a coefficienti costanti 0.1 Introduzione Una equazione differenziale del secondo ordine è una relazione del tipo F (t, y(t), y (t), y (t)) = 0 (1) Definizione
Algebra lineare. {ax 2 + bx + c R 2 [x] : 2a + 3b = 1} a b c d. M(2, 2) : a + c + d = 2. a b. c d
![Algebra lineare. {ax 2 + bx + c R 2 [x] : 2a + 3b = 1} a b c d. M(2, 2) : a + c + d = 2. a b. c d Algebra lineare. {ax 2 + bx + c R 2 [x] : 2a + 3b = 1} a b c d. M(2, 2) : a + c + d = 2. a b. c d](/thumbs/104/162200055.jpg) Algebra lineare 1. Riconoscere se il seguente insieme costituisce uno spazio vettoriale. In caso affermativo trovarne la dimensione e una base. (R n [x] denota lo spazio dei polinomi nell indeterminata
Algebra lineare 1. Riconoscere se il seguente insieme costituisce uno spazio vettoriale. In caso affermativo trovarne la dimensione e una base. (R n [x] denota lo spazio dei polinomi nell indeterminata
Applicazioni lineari e diagonalizzazione
 Applicazioni lineari e diagonalizzazione Autospazi Autovettori e indipendenza lineare Diagonalizzabilità e autovalori 2 2006 Politecnico di Torino 1 Esempio (1/6) Utilizzando un esempio già studiato, cerchiamo
Applicazioni lineari e diagonalizzazione Autospazi Autovettori e indipendenza lineare Diagonalizzabilità e autovalori 2 2006 Politecnico di Torino 1 Esempio (1/6) Utilizzando un esempio già studiato, cerchiamo
Esercizio 1 Dato il sistema:
 Leione - Esercitaioni di Algebra e Geometria - Anno accademico 9- Eserciio Dato il sistema: R ) ( a) studiare il rango della matrice incompleta del sistema; b) studiare il rango della matrice completa
Leione - Esercitaioni di Algebra e Geometria - Anno accademico 9- Eserciio Dato il sistema: R ) ( a) studiare il rango della matrice incompleta del sistema; b) studiare il rango della matrice completa
EQUAZIONI DIFFERENZIALI
 EQUAZIONI DIFFERENZIALI 1 Primo ordine - variabili separabili Sia dato il problema di Cauchy seguente: { y = a(x)b(y) Si proceda come segue y(x 0 ) = y 0 (1) Si calcolino le radici dell equazione b(y)
EQUAZIONI DIFFERENZIALI 1 Primo ordine - variabili separabili Sia dato il problema di Cauchy seguente: { y = a(x)b(y) Si proceda come segue y(x 0 ) = y 0 (1) Si calcolino le radici dell equazione b(y)
ESAMI DI MATEMATICA DISCRETA 2009/2010
 ESAMI DI MATEMATICA DISCRETA 2009/2010 09/06/2009 (1) In R 4 si considerino il sottospazio vettoriale W k = Span{(2, 1, 0, 1), (1, 1, 1, 1), (k, 1, 0, 1)} e il sottospazio vettoriale U dato da tutti i
ESAMI DI MATEMATICA DISCRETA 2009/2010 09/06/2009 (1) In R 4 si considerino il sottospazio vettoriale W k = Span{(2, 1, 0, 1), (1, 1, 1, 1), (k, 1, 0, 1)} e il sottospazio vettoriale U dato da tutti i
Politecnico di Milano Ingegneria Chimica, dei Materiali e delle Nanotecnologie Analisi Matematica 1 e Geometria Primo Appello 6 Febbraio 2018
 Politecnico di Milano Ingegneria Chimica, dei Materiali e delle Nanotecnologie Analisi Matematica e Geometria Primo Appello 6 Febbraio 208 Cognome: Nome: Matricola: Prima Parte. Stabilire se le successioni
Politecnico di Milano Ingegneria Chimica, dei Materiali e delle Nanotecnologie Analisi Matematica e Geometria Primo Appello 6 Febbraio 208 Cognome: Nome: Matricola: Prima Parte. Stabilire se le successioni
LUISS Laurea specialistica in Economia e Finanza Anno Accademico 2009/2010. Esame scritto del 25/02/2010
 LUISS Laurea specialistica in Economia e Finanza Anno Accademico 29/2 Corso di Metodi Matematici per la Finanza Pro Fausto Gozzi, Dr Davide Vergni Esame scritto del 25/2/2 Sia dato lo spazio vettoriale
LUISS Laurea specialistica in Economia e Finanza Anno Accademico 29/2 Corso di Metodi Matematici per la Finanza Pro Fausto Gozzi, Dr Davide Vergni Esame scritto del 25/2/2 Sia dato lo spazio vettoriale
SISTEMI LINEARI E STAZIONARI A TEMPO CONTINUO
 SISTEMI LINEARI E STAZIONARI A TEMPO CONTINUO Movimento ed equilibrio Stabilità Illustrazioni dal Testo di Riferimento per gentile concessione degli Autori MOVIMENTO ED EQUILIBRIO Sistema lineare e stazionario
SISTEMI LINEARI E STAZIONARI A TEMPO CONTINUO Movimento ed equilibrio Stabilità Illustrazioni dal Testo di Riferimento per gentile concessione degli Autori MOVIMENTO ED EQUILIBRIO Sistema lineare e stazionario
Università di Pisa. Corso di Laurea in Ingegneria Meccanica Geometria e Algebra Lineare
 Università di Pisa Corso di Laurea in Ingegneria Meccanica Geometria e Algebra Lineare Cognome e Nome: Corso di studi: Anno di iscrizione: Numero di matricola: Scritto n. 1 del 016 Esercizio 1. Si studi
Università di Pisa Corso di Laurea in Ingegneria Meccanica Geometria e Algebra Lineare Cognome e Nome: Corso di studi: Anno di iscrizione: Numero di matricola: Scritto n. 1 del 016 Esercizio 1. Si studi
Equazioni differenziali
 4 Equazioni differenziali Determinare le primitive di una funzione f(x) significa risolvere y (x) = f(x) dove l incognita è la funzione y(x). Questa equazione è un semplice esempio di equazione differenziale.
4 Equazioni differenziali Determinare le primitive di una funzione f(x) significa risolvere y (x) = f(x) dove l incognita è la funzione y(x). Questa equazione è un semplice esempio di equazione differenziale.
Es. 1 Es. 2 Es. 3 Es. 4 Es. 5 Totale
 Es. 1 Es. 2 Es. Es. 4 Es. 5 Totale Analisi e geometria 2 rimo Appello Docente: 17 luglio 29 Cognome: Nome: Matricola: Tutte le risposte devono essere motivate. Gli esercizi vanno svolti su questi fogli,
Es. 1 Es. 2 Es. Es. 4 Es. 5 Totale Analisi e geometria 2 rimo Appello Docente: 17 luglio 29 Cognome: Nome: Matricola: Tutte le risposte devono essere motivate. Gli esercizi vanno svolti su questi fogli,
Applicazioni lineari e diagonalizzazione. Esercizi svolti
 . Applicazioni lineari Esercizi svolti. Si consideri l applicazione f : K -> K definita da f(x,y) = x + y e si stabilisca se è lineare. Non è lineare. Possibile verifica: f(,) = 4; f(,4) = 6; quindi f(,4)
. Applicazioni lineari Esercizi svolti. Si consideri l applicazione f : K -> K definita da f(x,y) = x + y e si stabilisca se è lineare. Non è lineare. Possibile verifica: f(,) = 4; f(,4) = 6; quindi f(,4)
Matrici diagonalizzabili
 Capitolo INTRODUZIONE 2 Matrici diagonalizzabili Se una matrice A ha n autovalori λ i reali distinti, allora ha anche n autovettori v i reali linearimente indipendenti tra di loro: Av i = λ i v i, i {,
Capitolo INTRODUZIONE 2 Matrici diagonalizzabili Se una matrice A ha n autovalori λ i reali distinti, allora ha anche n autovettori v i reali linearimente indipendenti tra di loro: Av i = λ i v i, i {,
3. Elementi di Algebra Lineare.
 CALCOLO NUMERICO Francesca Mazzia Dipartimento Interuniversitario di Matematica Università di Bari 3. Elementi di Algebra Lineare. 1 Sistemi lineari Sia A IR m n, x IR n di n Ax = b è un vettore di m componenti.
CALCOLO NUMERICO Francesca Mazzia Dipartimento Interuniversitario di Matematica Università di Bari 3. Elementi di Algebra Lineare. 1 Sistemi lineari Sia A IR m n, x IR n di n Ax = b è un vettore di m componenti.
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA INDUSTRIALE 27 GENNAIO 2014
 FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA INDUSTRIALE 27 GENNAIO 2014 DOCENTE: MATTEO LONGO Rispondere alle domande di Teoria in modo esauriente e completo. Svolgere il maggior numero di esercizi
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA INDUSTRIALE 27 GENNAIO 2014 DOCENTE: MATTEO LONGO Rispondere alle domande di Teoria in modo esauriente e completo. Svolgere il maggior numero di esercizi
Equazioni differenziali Corso di Laurea in Scienze Biologiche Istituzioni di Matematiche A.A. 2007-2008. Dott.ssa G. Bellomonte
 Equazioni differenziali Corso di Laurea in Scienze Biologiche Istituzioni di Matematiche A.A. 2007-2008 Dott.ssa G. Bellomonte Indice 1 Introduzione 2 2 Equazioni differenziali lineari del primo ordine
Equazioni differenziali Corso di Laurea in Scienze Biologiche Istituzioni di Matematiche A.A. 2007-2008 Dott.ssa G. Bellomonte Indice 1 Introduzione 2 2 Equazioni differenziali lineari del primo ordine
EQUAZIONI DIFFERENZIALI Esercizi svolti. y = xy. y(2) = 1.
 EQUAZIONI DIFFERENZIALI Esercizi svolti 1. Determinare la soluzione dell equazione differenziale (x 2 + 1)y + y 2 =. y + x tan y = 2. Risolvere il problema di Cauchy y() = 1 2 π. 3. Risolvere il problema
EQUAZIONI DIFFERENZIALI Esercizi svolti 1. Determinare la soluzione dell equazione differenziale (x 2 + 1)y + y 2 =. y + x tan y = 2. Risolvere il problema di Cauchy y() = 1 2 π. 3. Risolvere il problema
Soluzione. (a) L insieme F 1 e linearmente indipendente; gli insiemi F 2 ed F 3 sono linearmente
 1. Insiemi di generatori, lineare indipendenza, basi, dimensione. Consideriamo nello spazio vettoriale R 3 i seguenti vettori: v 1 = (0, 1, ), v = (1, 1, 1), v 3 = (, 1, 0), v 4 = (3, 3, ). Siano poi F
1. Insiemi di generatori, lineare indipendenza, basi, dimensione. Consideriamo nello spazio vettoriale R 3 i seguenti vettori: v 1 = (0, 1, ), v = (1, 1, 1), v 3 = (, 1, 0), v 4 = (3, 3, ). Siano poi F
Istituzioni di Matematica I. Esercizi su sistemi lineari. & % x + y " #z = "1 & '#x " y+ z =1
 Istituzioni di Matematica I Esercizi su sistemi lineari Esempio. Dire per quali valori di λ R il sistema x " y+ z = 2 % x + y " z = " x " y+ z = ha una sola soluzione, per quali nessuna, per quali infinite
Istituzioni di Matematica I Esercizi su sistemi lineari Esempio. Dire per quali valori di λ R il sistema x " y+ z = 2 % x + y " z = " x " y+ z = ha una sola soluzione, per quali nessuna, per quali infinite
7. Equazioni differenziali
 18 Sezione 7. Equazioni differenziali 7. Equazioni differenziali [versione: 25/5/2012] Richiamo delle nozioni fondamentali In un equazione differenziale l incognita da determinare è una funzione (e non
18 Sezione 7. Equazioni differenziali 7. Equazioni differenziali [versione: 25/5/2012] Richiamo delle nozioni fondamentali In un equazione differenziale l incognita da determinare è una funzione (e non
Algebra Lineare Corso di Ingegneria Biomedica Compito del
 Algebra Lineare Corso di Ingegneria Biomedica Compito del -- - È obbligatorio consegnare tutti i fogli, anche il testo del compito e i fogli di brutta. - Le risposte senza giustificazione sono considerate
Algebra Lineare Corso di Ingegneria Biomedica Compito del -- - È obbligatorio consegnare tutti i fogli, anche il testo del compito e i fogli di brutta. - Le risposte senza giustificazione sono considerate
LAUREA IN INGEGNERIA CIVILE Corso di Matematica 2 II a prova di accertamento Padova Docenti: Chiarellotto - Cantarini TEMA n.
 LAUREA IN INGEGNERIA CIVILE Corso di Matematica II a prova di accertamento Padova 10-1-07 Docenti: Chiarellotto - Cantarini TEMA n.1 PARTE 1. Quesiti preliminari Stabilire se le seguenti affermazioni sono
LAUREA IN INGEGNERIA CIVILE Corso di Matematica II a prova di accertamento Padova 10-1-07 Docenti: Chiarellotto - Cantarini TEMA n.1 PARTE 1. Quesiti preliminari Stabilire se le seguenti affermazioni sono
CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA
 CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA II PROVA DI ACCERTAMENTO, FILA B GEOMETRIA 19/06/008 Esercizio 0.1. Si consideri il seguente endomorfismo di R 4 T (x, y, z, w) = (x + y z + w, y z, x +
CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA II PROVA DI ACCERTAMENTO, FILA B GEOMETRIA 19/06/008 Esercizio 0.1. Si consideri il seguente endomorfismo di R 4 T (x, y, z, w) = (x + y z + w, y z, x +
ANALISI MATEMATICA I MODULO, I e II MODULO, II MODULO CORSO DI LAUREA IN INFORMATICA
 ANALISI MATEMATICA I MODULO, I e II MODULO, II MODULO CORSO DI LAUREA IN INFORMATICA Prova scritta del 6 giugno 2004: soluzioni ESERCIZIO - Data la funzione f) 3 2 4 + 27 + 9 2 ) /3 4 + 27, + 9 si chiede
ANALISI MATEMATICA I MODULO, I e II MODULO, II MODULO CORSO DI LAUREA IN INFORMATICA Prova scritta del 6 giugno 2004: soluzioni ESERCIZIO - Data la funzione f) 3 2 4 + 27 + 9 2 ) /3 4 + 27, + 9 si chiede
ANALISI MATEMATICA II 6 luglio 2010 Versione A
 ANALISI MATEMATICA II 6 luglio 2 Versione A Nome Cognome: Matricola Codice corso Docente: Corso di Laurea: Analisi II 75 cr. Analisi D Analisi II V.O. Analisi C es. 23 es. 245 es 24 es. es. 3 pinti b c
ANALISI MATEMATICA II 6 luglio 2 Versione A Nome Cognome: Matricola Codice corso Docente: Corso di Laurea: Analisi II 75 cr. Analisi D Analisi II V.O. Analisi C es. 23 es. 245 es 24 es. es. 3 pinti b c
FM210 - Fisica Matematica 1. Esercizio 1. Si consideri il sistema di equazioni differenziali lineari
 TUTORATO 1 (5-03-2019) FM210 - Fisica Matematica 1 sercizio 1. Si consideri il sistema di equazioni differenziali lineari ( ) ẋ = Ax, x R 2 3 2, A = 6 1 1. Si calcolino gli autovalori e gli autovettori.
TUTORATO 1 (5-03-2019) FM210 - Fisica Matematica 1 sercizio 1. Si consideri il sistema di equazioni differenziali lineari ( ) ẋ = Ax, x R 2 3 2, A = 6 1 1. Si calcolino gli autovalori e gli autovettori.
CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA
 CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA II PROVA DI ACCERTAMENTO, FILA A GEOMETRIA 19/06/008 Esercizio 0.1. Si consideri il seguente endomorfismo di R 4 T (x, y, z, w) = ( x + y + z + w, y + z,
CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA II PROVA DI ACCERTAMENTO, FILA A GEOMETRIA 19/06/008 Esercizio 0.1. Si consideri il seguente endomorfismo di R 4 T (x, y, z, w) = ( x + y + z + w, y + z,
Risolvere i problemi di Cauchy o trovare l integrale generale delle seguenti equazioni differenziali del II ordine lineari a coefficienti costanti:
 Risolvere i problemi di Cauchy o trovare l integrale generale delle seguenti equazioni differenziali del II ordine lineari a coefficienti costanti: 1. y 5y + 6y = 0 y(0) = 0 y (0) = 1 2. y 6y + 9y = 0
Risolvere i problemi di Cauchy o trovare l integrale generale delle seguenti equazioni differenziali del II ordine lineari a coefficienti costanti: 1. y 5y + 6y = 0 y(0) = 0 y (0) = 1 2. y 6y + 9y = 0
Equazioni lineari secondo ordine a coefficienti continui. (Soluzione generale omogenea associata) + (Soluzione particolare).
 Equazioni differenziali Equazioni lineari secondo ordine a coefficienti continui Si tratta di equazioni del tipo y + a(ty + b(ty = f(t, t I. La soluzione generale è della forma (Soluzione generale omogenea
Equazioni differenziali Equazioni lineari secondo ordine a coefficienti continui Si tratta di equazioni del tipo y + a(ty + b(ty = f(t, t I. La soluzione generale è della forma (Soluzione generale omogenea
Sistemi di equazioni differenziali
 Capitolo 5 Sistemi di equazioni differenziali Molti problemi sono governati non da una singola equazione differenziale, ma da un sistema di più equazioni. Ad esempio questo succede se si vuole descrivere
Capitolo 5 Sistemi di equazioni differenziali Molti problemi sono governati non da una singola equazione differenziale, ma da un sistema di più equazioni. Ad esempio questo succede se si vuole descrivere
Il modello preda predatore. Modellistica Ambientale, 2013/14 Dinamiche di Crescita: 2 popo
 Modellistica Ambientale, 2013/14 Dinamiche di Crescita: 2 popolazioni Il modello preda predatore Interazione di due popolazioni: il modello Preda-Predatore Il modello Preda-Predatore è stato sviluppato
Modellistica Ambientale, 2013/14 Dinamiche di Crescita: 2 popolazioni Il modello preda predatore Interazione di due popolazioni: il modello Preda-Predatore Il modello Preda-Predatore è stato sviluppato
Scrivere il numero della risposta sopra alla corrispondente domanda. (voti: 2,0,-1, min=14 sulle prime 10) , C = [3 2 2], D =
![Scrivere il numero della risposta sopra alla corrispondente domanda. (voti: 2,0,-1, min=14 sulle prime 10) , C = [3 2 2], D = Scrivere il numero della risposta sopra alla corrispondente domanda. (voti: 2,0,-1, min=14 sulle prime 10) , C = [3 2 2], D =](/thumbs/67/56407198.jpg) n. 101 cognome nome corso di laurea Analisi e Simulazione di Sistemi Dinamici 18/11/2003 Risposte Domande 1 2 3 4 5 6 7 8 9 10 N. matricola Scrivere il numero della risposta sopra alla corrispondente domanda.
n. 101 cognome nome corso di laurea Analisi e Simulazione di Sistemi Dinamici 18/11/2003 Risposte Domande 1 2 3 4 5 6 7 8 9 10 N. matricola Scrivere il numero della risposta sopra alla corrispondente domanda.
Università degli Studi Roma Tre - Corso di Laurea in Matematica Tutorato di Geometria 1
 Università degli Studi Roma Tre - Corso di Laurea in Matematica Tutorato di Geometria 1 A.A. 28-29 - Docente: Prof. E. Sernesi Tutori: Andrea Abbate e Matteo Acclavio Soluzioni del tutorato numero 1 14
Università degli Studi Roma Tre - Corso di Laurea in Matematica Tutorato di Geometria 1 A.A. 28-29 - Docente: Prof. E. Sernesi Tutori: Andrea Abbate e Matteo Acclavio Soluzioni del tutorato numero 1 14
Capitolo 8 Forme quadratiche e loro applicazioni Esercizi svolti Tutorato di geometria e algebra lineare. Marco Robutti
 Capitolo 8 Forme quadratiche e loro applicazioni Esercizi svolti Tutorato di geometria e algebra lineare Marco Robutti 5 Ottobre 2017 1 Introduzione Gli esercizi di questo capitolo riguardano i seguenti
Capitolo 8 Forme quadratiche e loro applicazioni Esercizi svolti Tutorato di geometria e algebra lineare Marco Robutti 5 Ottobre 2017 1 Introduzione Gli esercizi di questo capitolo riguardano i seguenti
Capitolo Diagonalizzazione e Triangolazione. Esercizio Diagonalizzare la matrice A =
 Capitolo 8 8 Diagonalizzazione e Triangolazione Esercizio 8 Diagonalizzare la matrice A = 3 3 Svolgimento Il polinomio caratteristico della matrice è dato da ( + t) p A (t) = ( + t) = (t + 3) (t 3) 3 3
Capitolo 8 8 Diagonalizzazione e Triangolazione Esercizio 8 Diagonalizzare la matrice A = 3 3 Svolgimento Il polinomio caratteristico della matrice è dato da ( + t) p A (t) = ( + t) = (t + 3) (t 3) 3 3
Esercitazione 6 - Soluzione
 Anno Accademico 28-29 Corso di Algebra Lineare e Calcolo Numerico per Ingegneria Meccanica Esercitazione 6 - Soluzione Immagine, nucleo. Teorema di Rouché-Capelli. Esercizio Sia L : R 3 R 3 l applicazione
Anno Accademico 28-29 Corso di Algebra Lineare e Calcolo Numerico per Ingegneria Meccanica Esercitazione 6 - Soluzione Immagine, nucleo. Teorema di Rouché-Capelli. Esercizio Sia L : R 3 R 3 l applicazione
Sistemi lineari. Sia A R m n, x R n Ax = b è un vettore di m componenti. a m,1 x 1 + a m,2 x a m,n x n = b m
 1 Sistemi lineari. Sia A R m n, x R n Ax = b è un vettore di m componenti. Numero di operazioni per calcolare b: m n moltiplicazioni m (n 1) addizioni. a 1,1 x 1 + a 1,2 x 2 +... + a 1,n x n = b 1 a 2,1
1 Sistemi lineari. Sia A R m n, x R n Ax = b è un vettore di m componenti. Numero di operazioni per calcolare b: m n moltiplicazioni m (n 1) addizioni. a 1,1 x 1 + a 1,2 x 2 +... + a 1,n x n = b 1 a 2,1
1. Equazioni differenziali del primo ordine. Si chiamano equazioni differenziali del primo ordine tutte quelle che si possono ricondurre alla forma
 appunti per il corso di Analisi Matematica I corso di laurea in Ingegneria Gestionale, a.a. 2015-16 autore: Giovanni Alberti Equazioni differenziali [versione: 20 dicembre 2015] Richiamo delle nozioni
appunti per il corso di Analisi Matematica I corso di laurea in Ingegneria Gestionale, a.a. 2015-16 autore: Giovanni Alberti Equazioni differenziali [versione: 20 dicembre 2015] Richiamo delle nozioni
