Analisi Matematica II (2/2/2015)
|
|
|
- Vittore Fantoni
- 5 anni fa
- Visualizzazioni
Transcript
1 Analisi Matematica II (//5) Risposte non giustificate non verranno considerate. Consegnare solo la bella copia. Scrivere anche sul retro del foglio. Cognome: Nome: Matricola, Crediti: TOTALE Versione A Esercizio A. [punti 6] Data l equazione g(x,y) = xcosy ysin x =, (a) verificare che essa definisce implicitamente y = f(x) nell intorno di (π, π ), (b) determinare il polinomio di Taylor di ordine in x = π della funzione f, (c) calcolare lim x π f(x) π/ (x π).
2 Esercizio A. [punti 6] Calcolare il seguente integrale x ylog(x +y ) dxdy, dove D = (x,y) R : x +y,y }. D Esercizio A3. [punti 6] Sia ω la forma differenziale ( y ) ( ω(x,y) = (x ) +y +3y +xy dx+ x (x ) +y +x +6xy ) dy. (a) Verificare che ω è esatta in A = (x,y) R : x > }, e determinarne una primitiva (o funzione potenziale). (b) Calcolare + B ω, dove B = (x,y) R : x x y x x }. Analisi Matematica II (//5). Cognome e Nome, Matricola:
3 Esercizio A4. [punti 6] Data la serie n= (x ) n n 5 (+nx ) (a) determinare gli insiemi di convergenza puntuale (o semplice) e assoluta, (b) determinare il generico intervallo di convergenza uniforme della serie. Esercizio A5. [punti 6] Risolvere il problema di Cauchy y = Ay A =, y =. y() = y 3 Analisi Matematica II (//5). Cognome e Nome, Matricola:
4 Analisi Matematica II (//5) Esercizio A. [punti 6] Data l equazione g(x, y) = x cos y y sin x =, (a) verificare che essa definisce implicitamente y = f(x) nell intorno di (π, π ), (b) determinare il polinomio di Taylor di ordine in x = π della funzione f, (c) calcolare lim x π f(x) π/ (x π). Osserviamo che g(π, π) = e g x(x, y) = cos y y sin(x), g y (x, y) = x sin y sin x, e quindi g x (π, π) =, g y(π, π ) = π. Per il teorema del Dini, g(x, y) = definisce, in un intorno di (π, π), un unica funzione y = f(x), che risulta essere di classe C. Inoltre, g(x, f(x)) =, per ogni x in un intorno di x = π, per cui derivando rispetto ad x si ottiene e sostituendo x = π, f(π) = π, si ottiene Osserviamo che Derivando ( ) di nuovo, si ottiene = g x (x, f(x)) + g y (x, f(x))f (x) (*) = πf (π) f (π) =. g xx (x, y) = y cos(x) = g xx (π, π ) = π, g xy (x, y) = sin y sin(x) = g xy (π, π ) =, g yy (x, y) = x cos y = g yy (π, π ) =. = g xx (x, f(x)) + g xy (x, y)f (x) + g yy (x, f(x))f (x) + g y (x, f(x))f (x) e sostituendo x = π, f(π) = π, f (π) =, si ottiene Ma allora il polinomio richiesto è = π πf () f () =. T (x) = π (x π). Infine, il limite è f(x) π/ lim = lim (x π) ( + o()) = x π (x π) x π (x π).
5 Esercizio A. [punti 6] Calcolare il seguente integrale x y log(x + y ) dxdy, D dove D = (x, y) R : x + y, y }. Posto, per ogni a (, ), D a := (x, y) R : a x + y, y }, si ha x y log(x + y ) dxdy = lim x y log(x + y ) dxdy D a + D a (a) = lim ϱ 3 cos ϑ sin ϑ log ϱ dϱdϑ a + (b) = 4 lim a + Dϱϑ a π/ = lim a + [ sin ϑ [ cos ϑ sin ϑ 4 ϱ4 log ϱ ] 6 ϱ4 ] π/ a dϑ ( 4 a4 log a + ) 4 a4 = 8, dove in (a) si è posto D a ϱϑ = (ϱ, ϑ) R : a ϱ, ϑ [, π]}, e in (b) si sono usate la simmetria del dominio, la parità della funzione, e il risultato ϱ 3 log ϱ dϱ = 4 ϱ4 log ϱ 4 ϱ3 dϱ = 4 ϱ4 log ϱ 6 ϱ4. Esercizio A3. [punti 6] Sia ω la forma differenziale ( y ) ( ω(x, y) = (x ) + y + x ) 3y + xy dx + (x ) + y + x + 6xy dy. (a) Verificare che ω è esatta in A = (x, y) R : x > }, e determinarne una primitiva (o funzione potenziale). (b) Calcolare + B ω, dove B = (x, y) R : x x y x x }. Posto ω(x, y) = f dx + g dy, si ha g x = f y = (x ) y ((x ) +y ) + x + 6y, per cui ω è chiusa in R \ (, )}, e quindi in A, che è semplicemente connesso, e quindi ω è esatta in A. Una funzione potenziale U di ω in A deve soddisfare U = x U = y y + 3y + xy (x ) +y x + x + 6xy. (x ) +y Dalla seconda equazione segue che U(x, y) = ( x +x +6xy ) dy = d ( y (x ) +y +( x ) + y x ) x y + 3xy = arctg ( y x ) + x y + 3xy y + ϕ(x), e derivando rispetto ad x, + xy + (x ) +y 3y + ϕ (x) = U = y + 3y + xy ϕ (x) =, per cui una funzione potenziale in x (x ) +y A è data da ( y ) U(x, y) = arctg + x y + 3xy. x Osserviamo ora che ω non è esatta in un intorno di B, perché somma di una forma ω = (3y + xy) dx+(x y +6xy) dy, che è esatta, e di ω = dx+ x dy, che non lo è, per cui, per (x ) +y (x ) +y calcolare l integrale, usiamo l invarianza omotopica del medesimo. Sia γ(t) = ( + cos t, sin t), t [, π], per cui ω = ω + B + B = ω γ = π ( sin t cos t) dt = π.
6 Esercizio A4. [punti 6] Data la serie n= (x ) n n 5 ( + nx ) (a) determinare gli insiemi di convergenza puntuale (o semplice) e assoluta, (b) determinare il generico intervallo di convergenza uniforme della serie. Osserviamo che, per il criterio della radice, n x lim n n n ( + nx ) = lim x = x < x (, 3). n n n ( + nx ) Inoltre, per x =, si ha ( ) n n=, che converge assolutamente, mentre, per x = 3, si ha n (+n) n=, che converge assolutamente. Quindi la serie converge assolutamente in [, 3], e n (+9n) non converge altrove. Per determinare se la serie converge uniformemente, usiamo il criterio di Weierstrass di convergenza totale, e calcoliamo, M n := sup x [,3] (x ) n n (+nx ). Poiché n n= M n converge, la serie data converge uniformemente in [, 3]. Esercizio A5. [punti 6] Risolvere il problema di Cauchy y = Ay A =, y =. y() = y 3 Cerchiamo gli autovalori di A: λ det(a λi) = 3 λ λ λ 3 + 6λ λ + 8 = ( λ) 3 =, da cui si ottiene la soluzione λ = (tripla). Autovettori per λ = : x = (A I) v = x x + x x 3 =, x + x = x 3 x + x =, x 3 =. Poiché c è un solo autovettore indipendente [due condizioni lineari significa che dim ker(a I) = 3 = ], occorre cercare gli autovettori generalizzati: x = (A I) v = x x + x =, x 3 e quindi scegliamo v 3 = e ker(a I), per cui v = (A I) v 3 = e + e + e 3, e v = (A I) v = e e. Da y = c v + c v + c 3 v 3 si ricava = y () = c c c = = y () = c + c + c 3 c = = y 3 () = c c 3 =.
7 La soluzione del problema di Cauchy è quindi: cioè y(t) = e At y = c e At v + c e At v + c 3 e At v 3 = c e t v + c e t( I + (A I)t ) ( v + c 3 e t I + (A I)t + (A I) t ( = c + c t + c ) 3 t e t v + (c + c 3 t)e t v + c 3 e t v 3 = ( + t + t )e t + ( + t)e t + e t, y (t) = ( t + t )e t y (t) = ( + t t )e t y 3 (t) = ( + t)e t. ) v 3
8 Analisi Matematica II (6//5) Risposte non giustificate non verranno considerate. Consegnare solo la bella copia. Scrivere anche sul retro del foglio. Cognome: Nome: Matricola, Crediti: TOTALE Versione A Esercizio A. [punti 6] Data la seguente funzione f(x,y) = x +4y x +y (a) determinarne i punti stazionari e la loro natura, (b) determinare massimo e minimo di f in D = (x,y) R : x +4y 4}.
9 Esercizio A. [punti 6] Calcolare il seguente integrale x 4 dxdydz, dopo aver disegnato l insieme D = (x,y,z) R 3 : x +z, y x z }. D Esercizio A3. [punti 6] Calcolare S F ndσ, dove S è la superficie laterale del cilindro T = (x,y,z) R 3 : x +z,y [,]}, orientata nel verso della normale esterna n e a T, e ) F(x,y,z) = (x+ x5 5 +z ı (x 4 y +z ) j z k. Analisi Matematica II (6//5). Cognome e Nome, Matricola:
10 Esercizio A4. [punti 6] Data la successione f n (x) := n log(xn + n ), x [,+ ), (a) determinare l insieme di convergenza puntuale e f(x) := lim n f n (x), (b) verificare se f n converge uniformemente in [,+ ). Esercizio A5. [punti 6] Determinare la soluzione generale dell equazione differenziale y y = +e t. Analisi Matematica II (6//5). Cognome e Nome, Matricola:
11 Analisi Matematica II (6//5) Esercizio A. [punti 6] Data la seguente funzione f(x, y) = x + 4y x + y (a) determinarne i punti stazionari e la loro natura, (b) determinare massimo e minimo di f in D = (x, y) R : x + 4y 4}. (a) I punti stazionari sono soluzioni di x f x (x, y) = x x = +4y f y (x, y) = 4y + y = x +4y x = y = x = y = che fornisce i punti P ± = (±, ), mentre in P = (, ) non esiste f. Poiché 4y f xx (x, y) = (x +4y ) 3/ f xy (x, y) = 4xy (x +4y ) 3/ 4x f yy (x, y) = + (x +4y ) 3/ si ha det H f (±, ) = 6 = 6 <, e concludiamo che (±, ) sono punti di sella. (b) Poiché D è chiuso e limitato e f è continua su D, il teorema di Weierstrass ci assicura che f ha massimo e minimo su D. Come conseguenza del teorema di Fermat, cerchiamo i punti di massimo e minimo in tre insiemi: (b) tra i punti stazionari interni a D. In questo caso, P ± D o sono punti di sella, e li possiamo escludere. (b) tra i punti interni a D in cui non esiste almeno una delle derivate parziali prime di f. In questo caso, P D o. (b3) tra i punti di frontiera di D. Determiniamo, allora, i punti di massimo e minimo di f FD. Usiamo il metodo dei moltiplicatori di Lagrange per studiare f FD, e ci accontentiamo di trovare i punti stazionari della Lagrangiana [tra questi ci saranno anche i punti di massimo e minimo di f FD ]. Introduciamo la funzione di vincolo g(x, y) = x + 4y 4, e determiniamo dapprima i punti non regolari per il vincolo, cioè le soluzioni del sistema g x (x, y) = x = g y (x, y) = 8y = g(x, y) = x + 4y 4 =, che non ha soluzione. Introduciamo ora la Lagrangiana L(x, y, λ) = f(x, y) + λg(x, y), e cerchiamo i punti stazionari di L, cioè le soluzioni del sistema x L x (x, y, λ) = x x + xλ = ( x + (λ ) x + 4y ) +4y x = +4y ( L y (x, y, λ) = 4y y + y + 8yλ = x +4y + (4λ + ) x + 4y ) x = +4y L λ (x, y, λ) = x + 4y 4 =,
12 che equivale a x = y = x + 4y 4 = x = + (4λ + ) x + 4y = y = ± + (λ ) x + 4y = + (4λ + ) x + 4y = x + 4y 4 =. + (λ ) x + 4y = y = x = ± Il primo sistema è assurdo, il secondo e il terzo forniscono i punti Q ± = (±, ), e R ± = (, ±), mentre dal quarto [sottraendo la seconda equazione alla prima moltiplicata per ], si ottiene x + 4y = x + 4y 4 =, che è assurdo. In alternativa, e più rapidamente, possiamo ottenere i punti stazionari vincolati se parametrizziamo FD ponendo x = cos ϑ, y = sin ϑ, ϑ [, π], e otteniamo g(ϑ) := f( cos ϑ, sin ϑ) = cos ϑ + sin ϑ = 3 sin ϑ, ϑ [, π]. Poiché g (ϑ) = 6 sin ϑ cos ϑ = ϑ = k π, k Z, otteniamo di nuovo i punti Q ± = (±, ), e R ± = (, ±). (b4) Calcolando il valore di f su tutti i punti trovati, otteniamo f(p ) =, f(q ± ) =, f(r ± ) = 3. Quindi min D f = e max D f = 3. Esercizio A. dopo aver disegnato l insieme [punti 6] Calcolare il seguente integrale x 4 dxdydz, D D = (x, y, z) R 3 : x + z, y x z }. In coordinate cilindriche x = ϱ cos ϑ, y = y, z = ϱ sin ϑ, l insieme diventa D ϱϑy = (ϱ, ϑ, y) R 3 : ϑ [, π], y ϱ, ϱ [, ]}. Quindi D x 4 dxdydz = ϱ 5 cos 4 ϑ dϱdϑdy = D ϱϑy [ (a) 3 = 8 ϑ + 4 sin ϑ + ] π 3 sin 4ϑ = 3π 4 [ ϱ 6 6 ϱ8 8 ] = π 3, π dove in (a) si è usata l identità trigonometrica cos 4 ϑ = ( +cos ϑ 3 + cos ϑ + cos 4ϑ. 8 8 cos 4 ϑ dϑ ϱ ϱ 5 dϱ dy ϱ 5 ( ϱ ) log ϱ dϱ ) = 4 + cos ϑ+ 4 ( +cos 4ϑ ) =
13 Esercizio A3. [punti 6] Calcolare S F n dσ, dove S è la superficie laterale del cilindro T = (x, y, z) R 3 : x + z, y [, ]}, orientata nel verso della normale esterna n e a T, e F (x, y, z) = (x + x5 5 + z ) ı (x 4 y + z ) j z k. Siano S = (x, y, z) R 3 : x +z, y = }, S = (x, y, z) R 3 : x +z, y = }, per cui T = S S S. Una parametrizzazione di S è Φ (x, z) = (x,, z), ı j k (x, z) A := (x, z) R : x + z }, il cui vettore normale è Φ x Φ z = = j, che è esterno a T, mentre una parametrizzazione di S è Φ (x, z) = (x,, z), (x, z) A, il cui vettore normale è Φ x Φ z = j, che è interno a T. Dal teorema della divergenza si ha div F dxdydz = F n e dσ + F ne dσ + F ne dσ, T S S dove n e è il versore normale esterno rispetto a T. Poiché div F = + x 4 x 4 =, si ha F n e dσ = div F F ne dσ F ne dσ S T S S = vol(t ) F Φ Φ x Φ z dxdz + F Φ Φ x Φ z dxdz A A = 3π ( x 4 + z ) dxdz + (x 4 + z ) dxdz (a) = 3π + 3 A π [ (b) ϱ 6 = 3π ] ϱ 4 cos 4 ϑ ϱdϱdϑ [ 3 8 ϑ + 4 sin(ϑ) + ] π 3 sin(4ϑ) A S = 3π + 3π 8 = 8 π, dove in (a) si è usato il cambio di coordinate x = ϱ cos ϑ, z = ϱ sin ϑ, e in (b) l identità trigonometrica cos 4 ϑ = cos(ϑ) + 8 cos(4ϑ). Esercizio A4. [punti 6] Data la successione f n (x) := n log(xn + n ), x [, + ), (a) determinare l insieme di convergenza puntuale e f(x) := lim n f n (x), (b) verificare se f n converge uniformemente in [, + ). Osserviamo che f(x) := lim n f n (x) = log, x [, ], log x, x >, e quindi la successione converge per ogni x [, + ). Poiché f n (x) log = n log(xn + n ) n log(n ) = ( x n )n + ) è positiva e crescente in [, ], e f n (x) log x = n log(xn + n ) n log(xn ) = ( n x )n + ) è positiva e decrescente in [, + ), si ha sup f n (x) f(x) = max sup f n (x) log, sup f n (x) log x } = x [,+ ) x [,] x [,+ ) n per cui f n f in [, + ). log,
14 Esercizio A5. [punti 6] Determinare la soluzione generale dell equazione differenziale y y = + e t. Risolviamo dapprima l equazione omogenea associata. L equazione caratteristica λ = ha radici λ = ±. Quindi, y om (t) = a e t + a e t. Allora la soluzione y del problema di Cauchy ausiliario y y = y() =, y () =, è data da y (t) = et e t = sinh t. Quindi, una soluzione particolare dell equazione non omogenea è data da y p (t) = t e t s t + e ds s e t (a) = e t z dz z + e t e s t ds = et + es e t t e s t ds e s e t + dz [ z + = et z log z + ] e t e s + e s ds = e t( e t log(e t + ) + log ) e t( log(e t + ) log ), e t [ log z + ] e t dove in (a) si è usata la sostituzione z = e s, nel primo integrale, e z = e s, nel secondo. Allora la soluzione generale è data da y gen (t) = a e t + a e t te t + (e t e t ) log(e t + ).
15 Analisi Matematica II (/7/5) Risposte non giustificate non verranno considerate. Consegnare solo la bella copia. Scrivere anche sul retro del foglio. Cognome: Nome: Matricola, Crediti: TOTALE Versione A Esercizio A. [punti 6] Data la funzione xy x + y 4 (a) determinarne i punti stazionari e la loro natura, (b) determinare massimo e minimo di f in D = (x, y) R : x + y }.
16 Esercizio A. [punti 6] Siano γ(t) = ( + cos t, sin t), t [, 3π], e ω la forma differenziale ω(x, y) = x + y + x x + y dx + x y + y 3 + y x + y (a) Verificare che ω è esatta in D = R \ (, )}, e determinarne una primitiva (o potenziale). (b) Calcolare γ ω. dy. Esercizio A3. [punti 6] Sia S la superficie laterale della porzione di sfera T = (x, y, z) R 3 : x + y + z 4, z }, orientata nel verso della normale esterna n e a T. Calcolare S F n e dσ, dove F (x, y, z) = y ı + z j + x k. Analisi Matematica II (/7/5). Cognome e Nome, Matricola:
17 Esercizio A4. [punti 6] Data la serie n= n n n! ( x + (a) determinare gli insiemi di convergenza puntuale (o semplice) e assoluta, (b) determinare il generico intervallo di convergenza uniforme della serie. x ) n Esercizio A5. [punti 6] Risolvere il problema di Cauchy y 4y + 4y = e t y() =, y () =. Analisi Matematica II (/7/5). Cognome e Nome, Matricola:
18 Analisi Matematica II (/7/5) Esercizio A. [punti 6] Data la funzione xy x + y 4 (a) determinarne i punti stazionari e la loro natura, (b) determinare massimo e minimo di f in D = (x, y) R : x + y }. (a) I punti stazionari sono soluzioni di fx (x, y) = y(x y +4) (x +y 4) = f y (x, y) = x(x y 4) (x +y 4) = che, sotto la condizione x + y 4, equivale a y = y = x y + 4 = x = x y 4 = x = x y + 4 = x y 4 = che forniscono i punti P = (, ), P ± = (±, ), Q ± = (, ±), di cui solo il primo soddisfa la condizione x + y 4. Poiché f xx (x, y) = xy(x 3y +) (x +y 4) 3 f xy (x, y) = x4 6x y +y 4 6 (x +y 4) 3 f yy (x, y) = xy( 3x +y +) (x +y 4) 3 si ha det H f (, ) = 4 = <, e concludiamo che (, ) è un punto di sella. 6 4 (b) Poiché D è chiuso e limitato e f è continua su D, il teorema di Weierstrass ci assicura che f ha massimo e minimo su D. Come conseguenza del teorema di Fermat, cerchiamo i punti di massimo e minimo in tre insiemi: (b) tra i punti stazionari interni a D. In questo caso, P D o è un punto di sella, e lo escludiamo. (b) tra i punti interni a D in cui non esiste almeno una delle derivate parziali prime di f. In questo caso non ci sono. (b3) tra i punti di frontiera di D. Determiniamo, allora, i punti di massimo e minimo di f FD. Usiamo il metodo dei moltiplicatori di Lagrange per studiare f FD, e ci accontentiamo di trovare i punti stazionari della Lagrangiana [tra questi ci saranno anche i punti di massimo e minimo di f FD ]. Introduciamo la funzione di vincolo g(x, y) = x + y, e determiniamo dapprima i punti non regolari per il vincolo, cioè le soluzioni del sistema g x (x, y) = x = g y (x, y) = y = g(x, y) = x + y =, che non ha soluzione. Introduciamo ora la Lagrangiana L(x, y, λ) = f(x, y) + λg(x, y), e cerchiamo i punti stazionari di L, cioè le soluzioni del sistema L x (x, y, λ) = y(x y +4) + xλ = (x +y 4) L y (x, y, λ) = x(x y 4) + yλ = (x +y 4) L λ (x, y, λ) = x + y =,
19 che implica, moltiplicando la prima equazione per y, la seconda per x, e sommando, x (x y 4)+y (x y +4) = (x +y 4) x y = x + y = x + y =, che fornisce i quattro punti R ±± = (±, ± ). In alternativa, e più rapidamente, possiamo ottenere i punti stazionari vincolati se parametrizziamo FD ponendo x = cos ϑ, y = sin ϑ, ϑ [, π], e otteniamo g(ϑ) := f(cos ϑ, sin ϑ) = 3 sin ϑ cos ϑ = 6 sin ϑ, ϑ [, π]. Poiché g (ϑ) = 6 cos ϑ = ϑ = π 4 + k π, k Z, otteniamo di nuovo i punti R ±±. (b4) Calcolando il valore di f su tutti i punti trovati, otteniamo f(r ++ ) = f(r ) = 6, f(r + ) = f(r + ) = 6. Quindi min D f = 6 e max D f = 6. Esercizio A. [punti 6] Siano γ(t) = ( + cos t, sin t), t [, 3π], e ω la forma differenziale ω(x, y) = x + y + x x + y dx + x y + y 3 + y x + y (a) Verificare che ω è esatta in D = R \ (, )}, e determinarne una primitiva (o potenziale). (b) Calcolare γ ω. Osserviamo che ω(x, y) = f dx + g dy = ( ) ( ) + x x +y dx + y + y x +y dy, per cui g = f = 4xy, e quindi ω è chiusa in D, che non è semplicemente connesso. Se esiste x y (x +y ) una funzione potenziale U in D, allora deve soddisfare U = + x U = y + y x x +y y. x +y Dalla prima equazione segue che U(x, y) = ( ) + x x +y dx = x+log(x +y )+ϕ(y), e derivando y rispetto ad y, + ϕ (y) = U y = y + ϕ (y) = y = ϕ(y) = y, per cui una x +y y x +y funzione potenziale è data da U(x, y) = log(x + y ) + x + y in D, e ω è ivi esatta. Allora ω = U(γ(3π)) U(γ()) = U(, ) U(3, ) = 4 log 3. γ dy. Esercizio A3. [punti 6] Sia S la superficie laterale della porzione di sfera T = (x, y, z) R 3 : x + y + z 4, z }, orientata nel verso della normale esterna n e a T. Calcolare S F n e dσ, dove F (x, y, z) = y ı + z j + x k. Siano S = (x, y, z) R 3 : x + y 4, z = }, S = (x, y, z) R 3 : x + y 4, z = }, per cui T = S S S. Una parametrizzazione di S è Φ (x, y) = (x, y, ), ı j k (x, y) A := (x, y) R : x + y 4}, il cui vettore normale è Φ x Φ y = = k, che è interno a T. Una parametrizzazione di S è Φ (x, y) = (x, y, 3), (x, y) A := (x, y)
20 ı j k R : x + y 3}, il cui vettore normale è Φ x Φ y = = k, che è esterno a T. Dal teorema della divergenza si ha div F dxdydz = F n e dσ + F ne dσ + F ne dσ, T S S dove n e è il versore normale esterno rispetto a T. Poiché div F =, si ha F n e dσ = F ne dσ F ne dσ S S S = F Φ Φ x Φ y dxdy F Φ Φ x Φ y dxdy A A = x dxdy x dxdy A A (c) = (d) = π ϱ cos ϑ ϱ dϱdϑ [ ϑ + ] π [ ϱ 4 4 sin(ϑ) 4 π 3 ] = 7π 3 4, S ϱ cos ϑ ϱ dϱdϑ dove in (c) si è usato il cambio di coordinate x = ϱ cos ϑ, y = ϱ sin ϑ, e in (d) l identità trigonometrica cos ϑ = + cos(ϑ). Esercizio A4. [punti 6] Data la serie n= n n n! ( x + (a) determinare gli insiemi di convergenza puntuale (o semplice) e assoluta, (b) determinare il generico intervallo di convergenza uniforme della serie. Osserviamo che, per il criterio del rapporto, (n + ) n+ lim n! x + (n+) n = lim ( + ) n x +, x <, n+ = e, x = n (n + )! n n x n n x, +, x >, dove si è usato il fatto che x+ < x <. Quindi la serie converge assolutamente in x (, ), e non converge altrove. Per determinare se la serie converge uniformemente, usiamo il criterio di Weierstrass di convergenza totale, e calcoliamo, per ogni a < b <, M n := sup nn x [a,b] n! ( x + ) n n n ( = sup x n! x [a,b] x + x x ) n ( ) ) n = max f n (a), f n (b) } f n (a) + f n (b), dove in ( ) si è usato il fatto che g(x) := x+ è decrescente in (, ] e crescente in x [, ), per cui sup x [a,b] g(x) = maxg(a), g(b)} <. Poiché sia n= f n(a) che n= f n(b) convergono (per quanto visto sopra), n= M n converge, e la serie data converge uniformemente in [a, b] (per il criterio di Weierstrass), per ogni a < b <.
21 Esercizio A5. [punti 6] Risolvere il problema di Cauchy y 4y + 4y = e t y() =, y () =. Risolviamo dapprima l equazione omogenea associata. L equazione caratteristica λ 4λ + 4 = ha radice λ = (doppia). Quindi, y om (t) = a e t + a te t. Cerchiamo una soluzione particolare, dell equazione non omogenea, della forma y p (t) = at e t. Allora y p(t) = a(t+t )e t, y p(t) = a(+4t+t )e t, per cui a(+8t+4t 8t 8t +4t )e t = e t, e quindi a =. Quindi y gen(t) = a e t + a te t + t e t. Dalle condizioni iniziali otteniamo = y gen () = a = y gen() = a e t + a ( + t)e t + (t + t )e t t= = a + a cioè a =, a =. Allora y Cauchy (t) = e t te t + t e t, t R.
22 Analisi Matematica II (/7/5) Risposte non giustificate non verranno considerate. Consegnare solo la bella copia. Scrivere anche sul retro del foglio. Cognome: Nome: Matricola, Crediti: TOTALE Versione A Esercizio A. [punti 6] Data l equazione g(x, y) = e xy 3x y =, (a) verificare che essa definisce implicitamente y = f(x) nell intorno di (, ), (b) determinare il polinomio di Taylor di ordine in x = della funzione f.
23 Esercizio A. [punti 6] Calcolare il seguente integrale yz dxdydz D dove D = (x, y, z) R 3 : x + 8y z x 8y, x, y }. Esercizio A3. [punti 6] Sia ω la forma differenziale ( x ) ( ω(x, y) = + xy dx + y x (x + y ) ) dy. y x (a) Verificare che ω è esatta in D = (x, y) R : y > x }, e determinarne una primitiva (o potenziale). (b) Calcolare ω, dove γ(t) = (t, t), t [, ]. γ Analisi Matematica II (/7/5). Cognome e Nome, Matricola:
24 Esercizio A4. [punti 6] Data la successione f n (x) := (n x ) (n x ) + 3, x R, (a) determinare l insieme di convergenza puntuale e f(x) := lim n f n (x); (b) verificare se f n converge uniformemente in R; (c) determinare il generico intervallo di convergenza uniforme. Esercizio A5. [punti 6] Risolvere il problema di Cauchy y 3 = Ay A =, y =. y() = y Analisi Matematica II (/7/5). Cognome e Nome, Matricola:
25 Analisi Matematica II (/7/5) Esercizio A. [punti 6] Data l equazione g(x, y) = e xy 3x y =, (a) verificare che essa definisce implicitamente y = f(x) nell intorno di (, ), (b) determinare il polinomio di Taylor di ordine in x = della funzione f. Osserviamo che g(, ) = e g x (x, y) = ye xy 3, g y (x, y) = xe xy, e quindi g x (, ) = 3, g y (, ) =. Per il teorema del Dini, g(x, y) = definisce, in un intorno di (, ), un unica funzione y = f(x), che risulta essere di classe C. Inoltre, g(x, f(x)) =, per ogni x in un intorno di x =, per cui derivando rispetto ad x si ottiene e sostituendo x =, f() =, si ottiene Osserviamo che Derivando ( ) di nuovo, si ottiene = g x (x, f(x)) + g y (x, f(x))f (x) (*) = 3 f () f () = 3. g xx (x, y) = y e xy = g xx (, ) =, g xy (x, y) = (xy + )e xy = g xy (, ) =, g yy (x, y) = x e xy = g yy (, ) =. = g xx (x, f(x)) + g xy (x, y)f (x) + g yy (x, f(x))f (x) + g y (x, f(x))f (x) e sostituendo x =, f() =, f () = 3, si ottiene Ma allora il polinomio richiesto è = 6 f () f () = 6. T (x) = 3x 3x. Esercizio A. [punti 6] Calcolare il seguente integrale yz dxdydz D dove D = (x, y, z) R 3 : x + 8y z x 8y, x, y }. Il solido D è la parte, compresa nell ottante x, y, z }, dell intersezione dell interno della falda positiva del cono ellittico z = x + 8y con l interno dell ellissoide x + 8y + z =. Usando il metodo di integrazione per fili, è necessario determinare la proiezione A di D sul piano z =. Poiché x + 8y = x 8y t = x +8y t = t x +8y = t =, si ha che A = (x, y) R : 4x +6y, x, y }. Allora D yz dxdydz = = = 64 A A ( x 8y ) y z dz dxdy = x +8y y( 4x 6y ) dxdy (a) = [ ϱ 3 [ cos ϑ ] π/ 3 ϱ5 5 ] = 48, π/ A [ ] x 8y y z dxdy x +8y 4 ϱ sin ϑ( ϱ ) 8 ϱdϱdϑ
26 dove in (a) si è usato il cambiamento di variabili x = ϱ cos ϑ, y = ϱ sin ϑ. 4 Alternativamente, usando il cambio di variabili x = ϱ cos ϑ, y = 8 ϱ sin ϑ, z = z, l insieme D diventa D ϱϑz = (ϱ, ϑ, z) R 3 : ϱ z ϱ, cos ϑ, sin ϑ } = (ϱ, ϑ, z) R 3 : ϱ z ϱ, ϑ [, π], ϱ [, ]}, e quindi D yz dxdydz = = 8 = 6 D ϱϑz π/ 8 ϱ sin ϑz 4 ϱ dϱdϑdz / sin ϑ dϑ / ϱ ( ϱ ϱ ( ϱ ) dϱ = 6 ϱ [ ϱ 3 ) z dz dϱ 3 ϱ5 5 ] / = 48. Esercizio A3. [punti 6] Sia ω la forma differenziale ( x ) ( ω(x, y) = + xy dx + y x (x + y ) ) dy. y x (a) Verificare che ω è esatta in D = (x, y) R : y > x }, e determinarne una primitiva (o potenziale). (b) Calcolare ω, dove γ(t) = (t, t), t [, ]. γ Posto ω(x, y) = f dx + g dy, si ha g = f = x x, per cui ω è chiusa x y (y x ) 3/ in D, che è semplicemente connesso, e quindi ω è esatta in D. Una funzione potenziale U deve soddisfare U = x x y x + xy U = y (x + y ) Dalla prima equazione segue che U(x, y) = ( x y x + xy) dx = x y y x + ϕ(y), e derivando rispetto ad y, x y x + ϕ (y) = U y = (x + y ) y x ϕ (y) = y x y = ϕ(y) = 6 y3, per cui una funzione potenziale è data da U(x, y) = x y + 6 y3 y x. Allora γ ω = U(γ()) U(γ()) = U(, ) U(, ) = 3. Esercizio A4. [punti 6] Data la successione f n (x) := (n x ) (n x ) + 3, x R, (a) determinare l insieme di convergenza puntuale e f(x) := lim n f n (x); (b) verificare se f n converge uniformemente in R; (c) determinare il generico intervallo di convergenza uniforme. Osserviamo che f(x) := lim n f n (x) =, e quindi la successione converge per ogni x R. Poiché f n(x) = 8x(x n ) x [ n, ] [n, + ), si ha sup ((n x ) +3) x R f n (x) 3 f(x) = sup = f x R (n x ) +3 n(±n) =, per cui f n f in R. Inoltre, per ogni a >, e n > a, f f n è crescente e positiva in [, a], per cui sup x [ a,a] f n (x) f(x) = f n (a), e quindi f n f in [ a, a], per ogni a >.
27 Esercizio A5. [punti 6] Risolvere il problema di Cauchy y 3 = Ay A =, y =. y() = y Cerchiamo gli autovalori di A: 3 λ det(a λi) = λ λ + 4λ + 4) = (λ + ) 3 =, da cui si ottiene la soluzione λ = (tripla). Autovettori per λ = : x = (A + I) v = x x + x =. x 3 Poiché ci sono solo autovettori indipendenti [una condizione lineare significa che dim ker(a + I) = 3 = ], occorre cercare gli autovettori generalizzati: x = (A + I) v = x v, x 3 e quindi scegliamo v 3 = e, e v = (A + I) v 3 = e + e + e 3, e possiamo prendere v = e e. Da y = c v + c v + c 3 v 3 si ricava = y () = c c c = = y () = c + c + c 3 c = = y 3 () = c c 3 =. La soluzione del problema di Cauchy è quindi: y(t) = e At y = c e At v + c e At v + c 3 e At v 3 = c e t v + c e t v + c 3 e t( I + (A + I)t ) v 3 = c e t v + (c + c 3 t)e t v + c 3 e t v 3 = e t + ( + t)e t + e t, cioè y (t) = ( t)e t y (t) = ( + t)e t y 3 (t) = ( + t)e t.
28 Analisi Matematica II (7/9/5) Risposte non giustificate non verranno considerate. Consegnare solo la bella copia. Scrivere anche sul retro del foglio. Cognome: Nome: Matricola, Crediti: TOTALE Versione A Esercizio A. [punti 6] Data la seguente funzione f(x, y) = x y + y (a) determinarne i punti stazionari e la loro natura, (b) determinare massimo e minimo di f in D = (x, y) R : x + y, x }.
29 Esercizio A. [punti 6] Calcolare il seguente integrale y x + y dxdy, dove D = (x, y) R : x + y, x + (y ) }. D Esercizio A3. [punti 6] Calcolare S F n dσ, dove S è la superficie laterale del paraboloide orientata nel verso della normale esterna, e T = (x, y, z) R 3 : x + y z 4}, F (x, y, z) = (y + ) ı z x + ȷ + x x + y + k. Analisi Matematica II (7/9/5). Cognome e Nome, Matricola:
30 Esercizio A4. [punti 6] Data la successione f n (x) := nx e /(n x), x (, + ), (a) determinare l insieme di convergenza puntuale e f(x) := lim n f n (x), (b) verificare se f n converge uniformemente in (, + ); (c) determinare il generico intervallo di convergenza uniforme. Esercizio A5. [punti 6] Risolvere il problema di Cauchy y 3 = Ay A =, y =. y() = y 3 Analisi Matematica II (7/9/5). Cognome e Nome, Matricola:
31 Analisi Matematica II (7/9/5) Esercizio A. [punti 6] Data la seguente funzione f(x, y) = x y + y (a) determinarne i punti stazionari e la loro natura, (b) determinare massimo e minimo di f in D = (x, y) R : x + y, x }. (a) I punti stazionari sono soluzioni di f x (x, y) = x = f y (x, y) = y + = che fornisce il punto P = (, ). Poiché det H f(, ) = = 4 <, concludiamo che (, ) è di sella. (b) Poiché D è chiuso e limitato e f è continua su D, il teorema di Weierstrass ci assicura che f ha massimo e minimo su D. Come conseguenza del teorema di Fermat, cerchiamo i punti di massimo e minimo in tre insiemi: (b) tra i punti stazionari interni a D. In questo caso, P D o. (b) tra i punti interni a D in cui non esiste almeno una delle derivate parziali prime di f. In questo caso non ci sono. (b3) tra i punti di frontiera di D. Determiniamo, allora, i punti di massimo e minimo di f FD. Osserviamo che FD è costituita di un arco di circonferenza C = (x, y) R : x + y =, x > }, e un segmento di retta S = (, y) R : y [, ]}. Usiamo il metodo dei moltiplicatori di Lagrange per studiare f C, e ci accontentiamo di trovare i punti stazionari della Lagrangiana [tra questi ci saranno anche i punti di massimo e minimo di f C ]. Introduciamo la funzione di vincolo g(x, y) = x + y, x >, e determiniamo dapprima i punti non regolari per il vincolo, cioè le soluzioni del sistema g x (x, y) = x = g y (x, y) = y = g(x, y) = x + y =, x >, che non ha soluzione. Introduciamo ora la Lagrangiana L(x, y, λ) = f(x, y) + λg(x, y), e cerchiamo i punti stazionari di L, cioè le soluzioni del sistema L x (x, y, λ) = x + xλ = L y (x, y, λ) = y + + yλ = L λ (x, y, λ) = x + y =, x >, x = y =, x >, λ = y = 4 x = 5, x >, 6 cioè il punto P = ( 5 4, 4 ). Per quanto riguarda f S, si ha h(y) := f(, y) = y y, y [, ], ed essendo h (y) = y, segue dal teorema di Fermat, che bisogna considerare anche i punti P ± = (, ±), e P 3 = (, ). (b4) Calcolando il valore di f su tutti i punti trovati, otteniamo f(p + ) =, f(p ) =, f(p ) = 9 8, f(p 3) = 4. Quindi min D f = e max D f = 9 8.
32 Esercizio A. [punti 6] Calcolare il seguente integrale y x + y dxdy, D dove D = (x, y) R : x + y, x + (y ) }. Si ha D y x + y dxdy (a) = ϱ 3 sin ϑ dϱdϑ = D ϱ,ϑ = 5π/6 π/6 5π/6 5π/6 π/6 [ ] sin ϑ sin ϑ 4 ϱ4 dϑ = 4 ( sin ϑ sin ϑ 5π/6 π/6 = 4 ( cos ϑ) sin ϑ dϑ + [ ] 5π/6 cos ϑ π/6 4 π/6 3/ (b) 3 = 4 ( t ) dt 3/ 4 = 4 [t 3 t3 + ] 3/ 3 5 t5 3/ 4 = 3, 5 ) ϱ 3 dϱ dϑ sin ϑ(6 sin 4 ϑ ) dϑ dove in (a) si è usato il cambio di variabile x = ϱ cos ϑ, y = ϱ sin ϑ, per cui D ϱϑ = (ϱ, ϑ) R : ϱ sin ϑ, ϑ [ π, 5π ]}, e in (b) il cambio di variabili t = cos ϑ = dt = sin ϑ dϑ. 6 6 Esercizio A3. [punti 6] Calcolare S F n dσ, dove S è la superficie laterale del paraboloide orientata nel verso della normale esterna, e T = (x, y, z) R 3 : x + y z 4}, F (x, y, z) = (y + ) ı z x + j + x x + y + k. Sia S = (x, y, z) R 3 : x + y 4, z = 4}, per cui T = S S. Una parametrizzazione di S è Φ(x, y) = (x, y, 4), (x, y) A := (x, y) R : x + y 4}, il cui vettore normale è Φ x Φ y = k, che è esterno a T. Dal teorema della divergenza si ha div F dxdydz = F n e dσ + F ne dσ, T dove n e è il versore normale esterno rispetto a T. Poiché div F =, si ha F n e dσ = F ne dσ = F Φ Φ x Φ y dxdy S S = (b) = π A x x + y + ( ϱ ϱ ϱ + A S dxdy (a) = ) dϱ = π π [ ϱ S ϱ 3 ϱ + cos ϑ dϱdϑ log(ϱ + ) ] = π + π log 5, dove in (a) si è usato il cambio di coordinate x = ϱ cos ϑ, y = ϱ sin ϑ, e in (b) il risultato π cos ϑ dϑ = π ( + cos(ϑ)) dϑ = π.
33 Esercizio A4. [punti 6] Data la successione f n (x) := x) nx e /(n, x (, + ), (a) determinare l insieme di convergenza puntuale e f(x) := lim n f n (x), (b) verificare se f n converge uniformemente in (, + ); (c) determinare il generico intervallo di convergenza uniforme. Osserviamo che f(x) := lim n f n (x) =, e quindi la successione converge per ogni x (, + ). Poiché f n(x) = n x e /(n x ) x (, ), si ha n 3 x 4 n sup x (,+ ) f n (x) f(x) = e, per cui f n f in (, + ). Inoltre, per ogni a >, e n >, f a n è decrescente in [a, + ), per cui sup x [a,+ ) f n (x) f(x) = f n (a), e quindi f n f in [a, + ), per ogni a >. Esercizio A5. [punti 6] Risolvere il problema di Cauchy y 3 = Ay A =, y =. y() = y 3 Cerchiamo gli autovalori di A: 3 λ det(a λi) = λ 3 λ = λ(3 λ) + λ + (3 λ) + (3 λ) = λ 3 + 6λ λ + 8 = ( λ) 3 =, da cui si ottiene la soluzione λ = (tripla). Autovettori per λ = : x = (A I) v = x x + x x 3 =. x 3 Poiché ci sono solo autovettori indipendenti [una condizione lineare significa che dim ker(a I) = 3 = ], occorre cercare gli autovettori generalizzati: x = (A I) v = x v, x 3 e quindi scegliamo v 3 = e, e v = (A I) v 3 = e e e 3, e possiamo prendere v = e e. Da y = c v + c v + c 3 v 3 si ricava = y () = c + c c = = y () = c c + c 3 c = = y 3 () = c c 3 =. La soluzione del problema di Cauchy è quindi: cioè y(t) = e At y = c e At v + c e At v + c 3 e At v 3 = c e t v + c e t v + c 3 e t( I + (A I)t ) v 3 = c e t v + (c + c 3 t)e t v + c 3 e t v 3 = e t + (t )e t + e t, y (t) = ( + t)e t y (t) = ( t)e t y 3 (t) = ( t)e t.
34 Analisi Matematica II (4/9/5) Risposte non giustificate non verranno considerate. Consegnare solo la bella copia. Scrivere anche sul retro del foglio. Cognome: Nome: Matricola, Crediti: TOTALE Versione A Esercizio A. [punti 6] Data l equazione g(x,y) = xe y +ye x =, (a) verificare che essa definisce implicitamente y = f(x) nell intorno di (, ), (b) determinare il polinomio di Taylor di ordine in x = della funzione f.
35 Esercizio A. [punti 6] Sia data la forma differenziale ( x ) ( ω(x,y) = (x +y ) 4/3 +3y +xy dx+ y (x +y ) 4/3 +x +6xy ) dy. (a) Verificare che ω è esatta in D = R \(,)}, e determinarne una primitiva (o potenziale). (b) Calcolare γ ω, dove γ(t) = (e t cost,e t sint), t [,π]. Esercizio A3. [punti 6] Calcolare F ndσ, dove S è la superficie laterale del cono S T = (x,y,z) R 3 : z x +y,z [,]}, orientata nel verso della normale esterna n e, e F(x,y,z) = xy ı y3 3 j+log(x +y ) k. Analisi Matematica II (4/9/5). Cognome e Nome, Matricola:
36 Esercizio A4. [punti 6] Data la serie n= ) n, (x ( )n 5 (a) determinare gli insiemi di convergenza puntuale (o semplice) e assoluta, (b) determinare il generico intervallo di convergenza uniforme della serie. Esercizio A5. [punti 6] Risolvere il problema di Cauchy y +6y +9y = 8cos3t y() = 4 3, y () =, y () = 6. Analisi Matematica II (4/9/5). Cognome e Nome, Matricola:
37 Analisi Matematica II (4/9/5) Esercizio A. [punti 6] Data l equazione g(x,y) = xe y +ye x =, (a) verificare che essa definisce implicitamente y = f(x) nell intorno di (, ), (b) determinare il polinomio di Taylor di ordine in x = della funzione f. Osserviamo che g(,) = e g x (x,y) = e y +ye x, g y (x,y) = xe y +e x, e quindi g x (,) =, g y (,) =. Per il teorema del Dini, g(x,y) = definisce, in un intorno di (,), un unica funzione y = f(x), che risulta essere di classe C. Inoltre, g(x,f(x)) =, per ogni x in un intorno di x =, per cui derivando rispetto ad x si ottiene e sostituendo x =, f() =, si ottiene Osserviamo che Derivando ( ) di nuovo, si ottiene = g x (x,f(x))+g y (x,f(x))f (x) (*) = +f () f () =. g xx (x,y) = ye x = g xx (,) =, g xy (x,y) = e x +e y = g xy (,) =, g yy (x,y) = xe y = g yy (,) =. = g xx (x,f(x))+g xy (x,y)f (x)+g yy (x,f(x))f (x) +g y (x,f(x))f (x) e sostituendo x =, f() =, f () =, si ottiene = 4+f () f () = 4. Ma allora il polinomio richiesto è T (x) = x+x. Esercizio A. [punti 6] Sia data la forma differenziale ( x ) ( ω(x,y) = (x +y ) 4/3 +3y +xy dx+ y (x +y ) 4/3 +x +6xy ) dy. (a) Verificare che ω è esatta in D = R \(,)}, e determinarne una primitiva (o potenziale). (b) Calcolare γ ω, dove γ(t) = (e t cost,e t sint), t [,π]. Posto ω(x,y) = f dx+gdy, si ha g = f 8xy = x + 6y, per cui ω x y 3(x +y ) 7/3 è chiusa in D, che non è semplicemente connesso. Se esiste una funzione potenziale U in D, allora deve soddisfare U = x +3y +xy x (x +y ) 4/3 U = y y 3(x +y ) 4/3 +x +6xy
38 Dalla prima equazione segue che U(x,y) = ( x y +ϕ(y), e derivando rispetto ad y, 6xy ϕ (y) =, per cui una funzione potenziale è data da x +3y +xy ) 3 dx = (x +y ) 4/3 y 3(x +y ) 4/3 +6xy +x +ϕ (y) = U 3 U(x,y) = (x +y ) /3 +3xy +x y. Allora γ ω = U(γ(π)) U(γ()) = U(e π,) U(,) = 3 ( e4π/3 ). y = +3xy + (x +y ) /3 y +x + 3(x +y ) 4/3 Esercizio A3. [punti 6] Calcolare F ndσ, dove S è la superficie laterale del cono S T = (x,y,z) R 3 : z x +y,z [,]}, orientata nel verso della normale esterna n e, e F(x,y,z) = xy ı y3 3 j+log(x +y ) k. Siano S = (x,y,z) R 3 : x +y,z = }, S = (x,y,z) R 3 : x +y 4,z = }, per cui T = S S S. Una parametrizzazione di S è Φ (x,y) = (x,y,), (x,y) A := (x,y) R : x +y }, il cui vettore normale è Φ x Φ y = ı j k = k, che è interno a T, mentre una parametrizzazione di S è Φ (x,y) = (x,y,), (x,y) A := (x,y) R : x +y 4}, il cui vettore normale è Φ x Φ y = k, che è esterno a T. Dal teorema della divergenza si ha divf dxdydz = F n e dσ+ F ne dσ + F ne dσ, T S S S dove n e è il versore normale esterno rispetto a T. Poiché divf = y y =, si ha F n e dσ = F ne dσ F ne dσ S S S = F Φ Φ x Φ y dxdy F Φ Φ x Φ y dxdy A A = log(x +y )dxdy log(x +y )dxdy A A ( π π ) (a) = lim log( ) d dϑ log( ) d dϑ a + a a ( [ (b) = lim π log ] [ π log ] ) = 3π 8πlog, a + a dove in (a) si è usato il cambio di coordinate x = cosϑ, y = sinϑ, e in (b) il risultato log d = log 4. a Esercizio A4. [punti 6] Data la serie n= ) n, (x ( )n 5 (a) determinare gli insiemi di convergenza puntuale (o semplice) e assoluta, (b) determinare il generico intervallo di convergenza uniforme della serie.
39 Osserviamo che la serie data è somma di due serie di potenze n= (x ( )n 5 ) n = k= ( x 5 ) k + k= ( x+ 5) k, equindi converge assolutamente seentrambelofanno, cioèse x < 5 x+ < x 5 ( 4, 4), e non converge, se almeno una delle due non converge, cioè se x 5 5 (, 4 5 ] [4,+ ). 5 Infine la serie data converge uniformemente in [ 4 + δ, 4 δ], per ogni δ >, per un noto 5 5 teorema. Oppure, usiamo il criterio di Weierstrass di convergenza totale, e calcoliamo, per ogni δ >, M n := sup x 4 x ( ) n n 5 δ = ( δ) n. Poiché 5 n= M n converge, la serie data converge uniformemente in [ 4 +δ, 4 δ], per ogni δ >. 5 5 Esercizio A5. [punti 6] Risolvere il problema di Cauchy y +6y +9y = 8cos3t y() = 4 3, y () =, y () = 6. Risolviamo dapprima l equazione omogenea associata. L equazione caratteristica λ 3 +6λ +9λ = ha radici λ =, λ = 3 (doppia). Quindi, y om (t) = a +a e 3t +a 3 te 3t. Cerchiamounasoluzioneparticolare,dell equazionenonomogenea,dellaformay p (t) = acos3t+ bsin3t. Allora y p(t) = 3asin3t+3bcos3t, y p(t) = 9acos3t 9bsin3t, y p (t) = 7asin3t 7bcos3t, per cui 54acos3t 54bsin3t = 8cos3t, e quindi a =, b =. Quindi 3 y gen (t) = a +a e 3t +a 3 te 3t cos3t. 3 Dalle condizioni iniziali otteniamo 4 = y 3 gen() = a +a 3 = y gen () = 3a e 3t +a 3 ( 3t)e 3t +sin3t t= = 3a +a 3 6 = y gen() = 9a e 3t +3a 3 (3t )e 3t +3cos3t t= = 9a 6a 3 +3 cioè a =, a =, a 3 3 =. Allora y Cauchy (t) = 3 e3t te 3t cos3t, t R. 3
Analisi Matematica II (3/2/2016)
 Analisi Matematica II (3//6) Risposte non giustificate non verranno considerate. Consegnare solo la bella copia. Scrivere anche sul retro del foglio. Cognome: Nome: Matricola, Crediti: 3 4 5 TOTALE Versione
Analisi Matematica II (3//6) Risposte non giustificate non verranno considerate. Consegnare solo la bella copia. Scrivere anche sul retro del foglio. Cognome: Nome: Matricola, Crediti: 3 4 5 TOTALE Versione
Analisi Matematica 3 (Fisica), , M. Peloso e L. Vesely Prova scritta del 14 luglio 2009 Breve svolgimento (con alcuni conti omessi)
 Analisi Matematica 3 Fisica, 8-9, M. Peloso e L. Vesely Prova scritta del 4 luglio 9 Breve svolgimento con alcuni conti omessi. a Dimostrare che l insieme G = { x, y R : x + x + log y = ye x} coincide
Analisi Matematica 3 Fisica, 8-9, M. Peloso e L. Vesely Prova scritta del 4 luglio 9 Breve svolgimento con alcuni conti omessi. a Dimostrare che l insieme G = { x, y R : x + x + log y = ye x} coincide
Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica 2 del 19/06/2010 A
 Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica del 9/6/ A ) ata la funzione f(x, y) x y log( + x + y ), a) stabilire dove risulta derivabile parzialmente nel suo
Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica del 9/6/ A ) ata la funzione f(x, y) x y log( + x + y ), a) stabilire dove risulta derivabile parzialmente nel suo
Analisi Matematica III
 Università di Pisa - Corso di Laurea in Ingegneria Civile dell ambiente e territorio Analisi Matematica III Pisa, 1 giugno 4 (Cognome (Nome (Numero di matricola Esercizio 1 Si consideri la successione
Università di Pisa - Corso di Laurea in Ingegneria Civile dell ambiente e territorio Analisi Matematica III Pisa, 1 giugno 4 (Cognome (Nome (Numero di matricola Esercizio 1 Si consideri la successione
ANALISI MATEMATICA 2 - INGEGNERIA MECCANICA ED ENERGETICA A.A PROVA SCRITTA DEL 28/1/19
 ANALISI MATEMATICA - INGEGNERIA MECCANICA E ENERGETICA A.A. 8-9 PROVA SCRITTA EL 8//9 Scrivere nome cognome e numero di matricola in stampatello su tutti i fogli da consegnare. Consegnare solo la bella
ANALISI MATEMATICA - INGEGNERIA MECCANICA E ENERGETICA A.A. 8-9 PROVA SCRITTA EL 8//9 Scrivere nome cognome e numero di matricola in stampatello su tutti i fogli da consegnare. Consegnare solo la bella
1 x 2 y 2 dxdy D. 3 (1 ρ2 ) 3/2 = 1 3. = π 12.
 INGEGNERIA CIVILE - AMBIENTE E TERRITORIO ANALISI MATEMATICA II SOLUZIONI DELLA PROVA SCRITTA DEL 19-6-15 ESERCIZIO 1 Calcolare 1 x y dxdy D dove D è il dominio piano delimitato dalla curva x + y = x e
INGEGNERIA CIVILE - AMBIENTE E TERRITORIO ANALISI MATEMATICA II SOLUZIONI DELLA PROVA SCRITTA DEL 19-6-15 ESERCIZIO 1 Calcolare 1 x y dxdy D dove D è il dominio piano delimitato dalla curva x + y = x e
Analisi Matematica III
 Università di Pisa - Corso di Laurea in Ingegneria Civile dell ambiente e territorio Analisi Matematica III Pisa, 7 gennaio 00 (Cognome) (Nome) (Numero di matricola) Esercizio Si consideri la successione
Università di Pisa - Corso di Laurea in Ingegneria Civile dell ambiente e territorio Analisi Matematica III Pisa, 7 gennaio 00 (Cognome) (Nome) (Numero di matricola) Esercizio Si consideri la successione
Analisi Matematica II - Ingegneria Meccanica/Energetica - 29 Gennaio 2018
 nalisi Matematica II - Ingegneria Meccanica/Energetica - 29 Gennaio 218 1) ia data la funzione f(x, y, z) = (x 2 + y 2 1) 2 + 8 a) tudiare l esistenza di massimi e minimi assoluti della funzione f nella
nalisi Matematica II - Ingegneria Meccanica/Energetica - 29 Gennaio 218 1) ia data la funzione f(x, y, z) = (x 2 + y 2 1) 2 + 8 a) tudiare l esistenza di massimi e minimi assoluti della funzione f nella
Esonero di Analisi Matematica II (A)
 Esonero di Analisi Matematica II (A) Ingegneria Edile, 8 aprile 3. Studiare la convergenza del seguente integrale improprio: + x log 3 x (x ) 3 dx.. Studiare la convergenza puntuale ed uniforme della seguente
Esonero di Analisi Matematica II (A) Ingegneria Edile, 8 aprile 3. Studiare la convergenza del seguente integrale improprio: + x log 3 x (x ) 3 dx.. Studiare la convergenza puntuale ed uniforme della seguente
Analisi Matematica 2. Michele Campiti. Prove scritte di. Ingegneria Industriale a.a
 Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
Alcuni esercizi risolti da esami di anni passati
 Alcuni esercizi risolti da esami di anni passati Andrea Braides ( x. Calcolare, se esiste, il limite lim (x,y (, x + y log + y + x 3 y. x + y Dato che log( + s = s + o(s per s, abbiamo lim (x,y (, ( x
Alcuni esercizi risolti da esami di anni passati Andrea Braides ( x. Calcolare, se esiste, il limite lim (x,y (, x + y log + y + x 3 y. x + y Dato che log( + s = s + o(s per s, abbiamo lim (x,y (, ( x
Prima prova di verifica in itinere di ANALISI MATEMATICA II. 12 Marzo 2008 Compito A. 1 (punti 3)
 anno accademico 007-008 Prima prova di verifica in itinere di ANALISI MATEMATICA II Marzo 008 Compito A (punti ) y = x + xy + y x. (punti 4) y + y x = ln x x y. (punti ) y = y + y ln y. 4 (punti 6) Determinare
anno accademico 007-008 Prima prova di verifica in itinere di ANALISI MATEMATICA II Marzo 008 Compito A (punti ) y = x + xy + y x. (punti 4) y + y x = ln x x y. (punti ) y = y + y ln y. 4 (punti 6) Determinare
Analisi Matematica II Corso di Ingegneria Gestionale Compito A del , se (x, y) = (0, 0) ( x e. + y x e (y2 )
 Analisi Matematica II Corso di Ingegneria Gestionale Compito A del -6-9 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito A del -6-9 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito del A
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del -7-5 - A Esercizio ( punti Data la funzione f(x, y = x + y + 4xy 8x 4y + 4 i trovare tutti i punti critici e, se possibile, caratterizzarli
Analisi Matematica II Corso di Ingegneria Gestionale Compito del -7-5 - A Esercizio ( punti Data la funzione f(x, y = x + y + 4xy 8x 4y + 4 i trovare tutti i punti critici e, se possibile, caratterizzarli
Analisi Matematica II Corso di Ingegneria Gestionale Compito del f(x, y) = (x 2 2y 2 ) e x y
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del 8--5 - È obbligatorio consegnare tutti i fogli anche la brutta e il testo - Le risposte senza giustificazione sono considerate nulle Esercizio
Analisi Matematica II Corso di Ingegneria Gestionale Compito del 8--5 - È obbligatorio consegnare tutti i fogli anche la brutta e il testo - Le risposte senza giustificazione sono considerate nulle Esercizio
1 x 2 y 2 dxdy D. 3 (1 ρ2 ) 3/2 = 1 3. = π 12.
 INGEGNERIA CIVILE - AMBIENTE E TERRITORIO ANALISI MATEMATICA II SOLUZIONI DELLA PROVA SCRITTA DEL 19-6-15 ESERCIZIO 1 Calcolare 1 x y dxdy D dove D è il dominio piano delimitato dalla curva x + y x e dalle
INGEGNERIA CIVILE - AMBIENTE E TERRITORIO ANALISI MATEMATICA II SOLUZIONI DELLA PROVA SCRITTA DEL 19-6-15 ESERCIZIO 1 Calcolare 1 x y dxdy D dove D è il dominio piano delimitato dalla curva x + y x e dalle
Soluzione della prova scritta di Analisi Matematica II del 15 Aprile 2009 (Ingegneria Edile e Architettura)
 Soluzione della prova scritta di Analisi Matematica II del 5 Aprile 009 Ingegneria Edile e Architettura x. Calcolare J = ds essendo γ la curva ottenuta intersecando γ + y il cilindro di equazione x + y
Soluzione della prova scritta di Analisi Matematica II del 5 Aprile 009 Ingegneria Edile e Architettura x. Calcolare J = ds essendo γ la curva ottenuta intersecando γ + y il cilindro di equazione x + y
sen n x( tan xn n n=1
 8 Gennaio 2016 Nome (in stampatello): 1) (8 punti) Discutere la convergenza della serie di funzioni al variare di x in [ 1, 1]. n x( tan xn n ) xn sen n 2) (7 punti) Provare che la forma differenziale
8 Gennaio 2016 Nome (in stampatello): 1) (8 punti) Discutere la convergenza della serie di funzioni al variare di x in [ 1, 1]. n x( tan xn n ) xn sen n 2) (7 punti) Provare che la forma differenziale
Analisi Matematica II Corso di Ingegneria Biomedica Compito A del f(x, y) = x 2 + y 2
 Analisi Matematica II Corso di Ingegneria Biomedica Compito A del -7- - È obbligatorio consegnare tutti i fogli, anche quelli della brutta. - Le risposte senza giustificazione sono considerate nulle. Esercizio.
Analisi Matematica II Corso di Ingegneria Biomedica Compito A del -7- - È obbligatorio consegnare tutti i fogli, anche quelli della brutta. - Le risposte senza giustificazione sono considerate nulle. Esercizio.
Analisi Matematica 2 - a.a. 2009/2010
 Secondo appello Esercizio 1 Analisi Matematica - aa /1 Sia Γ = (x,y,z) R : x 4 + y 4 z 4 = 1, x + y + z = } 1 Provare che esistono due funzioni y = g(x) e z = h(x) definite in un intorno U di x = 1, tali
Secondo appello Esercizio 1 Analisi Matematica - aa /1 Sia Γ = (x,y,z) R : x 4 + y 4 z 4 = 1, x + y + z = } 1 Provare che esistono due funzioni y = g(x) e z = h(x) definite in un intorno U di x = 1, tali
Esame di Analisi Matematica 2 24/9/2013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 2012/2013
 Esame di Analisi Matematica 2 24/9/2013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 2012/2013 Esercizio 1. Sia A il cerchio aperto del piano di centro l origine e raggio 1. Sia f(x, y) una
Esame di Analisi Matematica 2 24/9/2013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 2012/2013 Esercizio 1. Sia A il cerchio aperto del piano di centro l origine e raggio 1. Sia f(x, y) una
COMPLEMENTI DI ANALISI MATEMATICA A.A Primo appello del 5/5/2010
 COMPLEMENTI DI ANALISI MATEMATICA A.A. 29- Primo appello del 5/5/2 Qui trovate le tracce delle soluzioni degli esercizi del compito. Ho tralasciato i calcoli da Analisi (che comunque sono parte della risoluzione),
COMPLEMENTI DI ANALISI MATEMATICA A.A. 29- Primo appello del 5/5/2 Qui trovate le tracce delle soluzioni degli esercizi del compito. Ho tralasciato i calcoli da Analisi (che comunque sono parte della risoluzione),
Facoltà di Scienze MM.FF.NN. Corso di Laurea in Matematica - A.A Prova scritta di Analisi Matematica II del c.1.
 Prova scritta di Analisi Matematica II del 14-07-1999 - c.1 1) Sia (d n ) una successione di numeri reali tali che inf d n > 0. Studiare il carattere della serie + n=1 al variare del parametro reale positivo
Prova scritta di Analisi Matematica II del 14-07-1999 - c.1 1) Sia (d n ) una successione di numeri reali tali che inf d n > 0. Studiare il carattere della serie + n=1 al variare del parametro reale positivo
Esempi di esercizi d esame A.A. 2006/07 Analisi Matematica 2 Ingegneria Elettronica Proff. G. Vergara Caffarelli e L. Giacomelli
 Esempi di esercizi d esame A.A. 6/7 Analisi Matematica Ingegneria Elettronica Proff. G. Vergara Caffarelli e L. Giacomelli versione preliminare, si prega di segnalare eventuali errori *) Determinare e
Esempi di esercizi d esame A.A. 6/7 Analisi Matematica Ingegneria Elettronica Proff. G. Vergara Caffarelli e L. Giacomelli versione preliminare, si prega di segnalare eventuali errori *) Determinare e
Analisi 4 - SOLUZIONI (compito del 29/09/2011)
 Corso di laurea in Matematica Analisi 4 - SOLUZIONI compito del 9/09/0 Docente: Claudia Anedda Calcolare, tramite uno sviluppo in serie noto, la radice quinta di e la radice cubica di 9 Utilizzando la
Corso di laurea in Matematica Analisi 4 - SOLUZIONI compito del 9/09/0 Docente: Claudia Anedda Calcolare, tramite uno sviluppo in serie noto, la radice quinta di e la radice cubica di 9 Utilizzando la
Facoltà di Scienze MM.FF.NN. Corso di Laurea in Matematica - A.A Prova scritta di Analisi Matematica II del
 Prova scritta di nalisi Matematica II del 12-06-2001. C1 1) Studiare la convergenza semplice, uniforme e totale della serie di funzioni seguente ( 1) [ n 2 ] n x 1 + n 2 x. n=0 2) Data la funzione (x 2
Prova scritta di nalisi Matematica II del 12-06-2001. C1 1) Studiare la convergenza semplice, uniforme e totale della serie di funzioni seguente ( 1) [ n 2 ] n x 1 + n 2 x. n=0 2) Data la funzione (x 2
Compito di Analisi Matematica II del 28 giugno 2006 ore 11
 Compito di Analisi Matematica II del 28 giugno 26 ore Esercizio. ( punti) Calcolare il flusso del campo vettoriale F (,, z) = (z, z 2, z 2 ) } uscente dalla frontiera di D = (,, z) R 3 : 2 + z 2, z,. Svolgimento
Compito di Analisi Matematica II del 28 giugno 26 ore Esercizio. ( punti) Calcolare il flusso del campo vettoriale F (,, z) = (z, z 2, z 2 ) } uscente dalla frontiera di D = (,, z) R 3 : 2 + z 2, z,. Svolgimento
Analisi Matematica II Corso di Ingegneria Gestionale Compito del f(x, y) = tan(2x 2 + 3y 2 )
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del 7-9- - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo - Le risposte senza giustificazione sono considerate nulle Esercizio
Analisi Matematica II Corso di Ingegneria Gestionale Compito del 7-9- - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo - Le risposte senza giustificazione sono considerate nulle Esercizio
Soluzioni degli esercizi proposti nella sessione estiva Terni Perugia. F NdS. div F = 2 div F dxdydz = 2volume (V ) = 36π.
 Soluzioni degli esercizi proposti nella sessione estiva 2-2 Terni Perugia ) Sia F = (2x, y, z) e V il volume delimitato dalle superfici: la semisfera S := z = 9 x 2 y 2 ed il disco S 2 di equazione z =,
Soluzioni degli esercizi proposti nella sessione estiva 2-2 Terni Perugia ) Sia F = (2x, y, z) e V il volume delimitato dalle superfici: la semisfera S := z = 9 x 2 y 2 ed il disco S 2 di equazione z =,
Analisi Matematica 2: Secondo Parziale, , Versione A. Cognome e nome:...matricola:...
 Analisi Matematica : Secondo Parziale, 6.6.7, Versione A Cognome e nome:....................................matricola:......... es. es. es.3 es.4 es.5 es.6 es.7 somma 5cr. 6 6 6 6 6 - - 3 9cr. 5 5 5 5
Analisi Matematica : Secondo Parziale, 6.6.7, Versione A Cognome e nome:....................................matricola:......... es. es. es.3 es.4 es.5 es.6 es.7 somma 5cr. 6 6 6 6 6 - - 3 9cr. 5 5 5 5
Esercizi sull integrazione II
 ANALISI MATEMATICA T-2 (C.d.L. Ing. per l ambiente e il territorio) - COMPL. DI ANALISI MATEMATICA (A-K) (C.d.L. Ing. Civile) A.A.28-29 - Prof. G.Cupini Esercizi sull integrazione II (Grazie agli studenti
ANALISI MATEMATICA T-2 (C.d.L. Ing. per l ambiente e il territorio) - COMPL. DI ANALISI MATEMATICA (A-K) (C.d.L. Ing. Civile) A.A.28-29 - Prof. G.Cupini Esercizi sull integrazione II (Grazie agli studenti
es.1 es.2 es.3 es.4 es.5 somma Analisi Matematica 2: Secondo Parziale, , Versione A Cognome e nome:...matricola:...
 es.1 es. es.3 es. es.5 somma 6 6 6 6 6 3 Analisi Matematica : Secondo Parziale, 3.5.16, Versione A Cognome e nome:....................................matricola:......... 1. Dimostrare che la forma differenziale
es.1 es. es.3 es. es.5 somma 6 6 6 6 6 3 Analisi Matematica : Secondo Parziale, 3.5.16, Versione A Cognome e nome:....................................matricola:......... 1. Dimostrare che la forma differenziale
Politecnico di Milano Ingegneria Industriale Analisi e Geometria 2 Secondo compito in itinere 30 Giugno 2016
 Politecnico di Milano Ingegneria Industriale Analisi e Geometria Secondo compito in itinere Giugno 6 Cognome: Nome: Matricola: Es.: 9 punti Es.: 9 punti Es.: 6 punti Es.4: 9 punti Totale. Si consideri
Politecnico di Milano Ingegneria Industriale Analisi e Geometria Secondo compito in itinere Giugno 6 Cognome: Nome: Matricola: Es.: 9 punti Es.: 9 punti Es.: 6 punti Es.4: 9 punti Totale. Si consideri
Prove scritte dell esame di Analisi Matematica II a.a. 2015/2016
 Prove scritte dell esame di Analisi Matematica II a.a. 5/6 C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 6 giugno 6. Determinare massimi e minimi
Prove scritte dell esame di Analisi Matematica II a.a. 5/6 C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 6 giugno 6. Determinare massimi e minimi
Analisi Matematica II - INGEGNERIA Gestionale - B 20 luglio 2017 Cognome: Nome: Matricola:
 Analisi Matematica II - INGEGNERIA Gestionale - B luglio 7 Cognome: Nome: Matricola: IMPORTANTE: Giustificare tutte le affermazioni e riportare i calcoli essenziali Esercizio [8 punti] Data la matrice
Analisi Matematica II - INGEGNERIA Gestionale - B luglio 7 Cognome: Nome: Matricola: IMPORTANTE: Giustificare tutte le affermazioni e riportare i calcoli essenziali Esercizio [8 punti] Data la matrice
Analisi Matematica II Corso di Ingegneria Gestionale Compito del f(x, y) = sin( x 2 + 2y 2 )
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del 9--9 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo - Le risposte senza giustificazione sono considerate nulle Esercizio
Analisi Matematica II Corso di Ingegneria Gestionale Compito del 9--9 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo - Le risposte senza giustificazione sono considerate nulle Esercizio
Quesito 1. f(x, y) = xy log (x 2 + y 2 ) Quesito 2. Quesito 3. y = 2y3 +x 3. xy 2 y(1) = 1. Quesito 4
 Corso di laurea in Ing. Meccanica, a.a. 2002/2003 Prova scritta di Analisi Matematica 2 del 7 gennaio 2003 Determinare gli eventuali estremi relativi della funzione f(x, y) = xy log (x 2 + y 2 ) Calcolare
Corso di laurea in Ing. Meccanica, a.a. 2002/2003 Prova scritta di Analisi Matematica 2 del 7 gennaio 2003 Determinare gli eventuali estremi relativi della funzione f(x, y) = xy log (x 2 + y 2 ) Calcolare
ANALISI MATEMATICA 3
 ANALISI MATEMATICA 3 Corso di laurea triennale in Fisica, F480 Prova scritta del 8//003 prof. Marco Vignati ] Sia dato il problema di Cauchy xy + y = 0 i) Determinarne la soluzione locale. y () = 3 ii)
ANALISI MATEMATICA 3 Corso di laurea triennale in Fisica, F480 Prova scritta del 8//003 prof. Marco Vignati ] Sia dato il problema di Cauchy xy + y = 0 i) Determinarne la soluzione locale. y () = 3 ii)
Ingegneria Elettronica Prova scritta di Analisi Matematica II del giorno ( 3) n x n n + 1
 Prova scritta di Analisi Matematica II del giorno 31-01-2007 1) Studiare la serie di potenze ( 3) n x n n + 1 2) Determinare i punti di estremo relativo ed assoluto della funzione seguente f(x, y) = x
Prova scritta di Analisi Matematica II del giorno 31-01-2007 1) Studiare la serie di potenze ( 3) n x n n + 1 2) Determinare i punti di estremo relativo ed assoluto della funzione seguente f(x, y) = x
Estremi vincolati, Teorema del Dini.
 Estremi vincolati, Teorema del Dini. 1. Da un cartone di 1m si deve ricavare una scatola rettangolare senza coperchio. Trovare il massimo volume possibile della scatola.. Trovare gli estremi assoluti di
Estremi vincolati, Teorema del Dini. 1. Da un cartone di 1m si deve ricavare una scatola rettangolare senza coperchio. Trovare il massimo volume possibile della scatola.. Trovare gli estremi assoluti di
Analisi Matematica II Corso di Ingegneria Gestionale Compito del f(x, y) = e (x3 +x) y
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del 8--7 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito del 8--7 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica 2 (Corso di Laurea in Informatica)
 COGNOME NOME Matr. Firma dello studente A Tempo: 3 ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
COGNOME NOME Matr. Firma dello studente A Tempo: 3 ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
(1) Determinare l integrale generale dell equazione
 FONDAMENTI DI ANALISI MATEMATICA (9 cfu Commissione F. Albertini, V. Casarino, M. Motta Ingegneria Gestionale, Meccanica e Meccatronica, Vicenza Vicenza, 3 settembre 8 Quarto appello Avvertenza: Nella
FONDAMENTI DI ANALISI MATEMATICA (9 cfu Commissione F. Albertini, V. Casarino, M. Motta Ingegneria Gestionale, Meccanica e Meccatronica, Vicenza Vicenza, 3 settembre 8 Quarto appello Avvertenza: Nella
Analisi 4 - SOLUZIONI (17/01/2013)
 Corso di Laurea in Matematica Analisi 4 - SOLUZIONI 7//23 Docente: Claudia Anedda Utilizzando uno sviluppo in serie noto, scrivere lo sviluppo in serie di MacLaurin della funzione fx = 32 + x, specificando
Corso di Laurea in Matematica Analisi 4 - SOLUZIONI 7//23 Docente: Claudia Anedda Utilizzando uno sviluppo in serie noto, scrivere lo sviluppo in serie di MacLaurin della funzione fx = 32 + x, specificando
Analisi Matematica II Corso di Ingegneria Gestionale Compito A del f(x, y) = 2 x 2 y 2 x y 2 + x y
 Analisi Matematica II Corso di Ingegneria Gestionale Compito A del -7- - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo - Le risposte senza giustificazione sono considerate nulle Esercizio
Analisi Matematica II Corso di Ingegneria Gestionale Compito A del -7- - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo - Le risposte senza giustificazione sono considerate nulle Esercizio
Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 18 febbraio 2010 Tema A
 Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 18 febbraio 21 Tema A Tempo a disposizione: 2 ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio va iniziato all inizio
Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 18 febbraio 21 Tema A Tempo a disposizione: 2 ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio va iniziato all inizio
Analisi Matematica II Corso di Ingegneria Gestionale Compito del xy + 2x + 2y + 2xy + 2x + 2y + sin
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del 9--8 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito del 9--8 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica 3 (Fisica), , M. Peloso e L. Vesely Secondo compitino ( ) Svolgimento della Versione B
 Analisi Matematica (Fisica), 2008-2009, M. Peloso e L. Vesely Secondo compitino (20.01.2009) Svolgimento della Versione B 1. (a) Dimostrare che l insieme G = { (x, y) R 2 : x 2 e 2y e 2y + (x 1)e x y =
Analisi Matematica (Fisica), 2008-2009, M. Peloso e L. Vesely Secondo compitino (20.01.2009) Svolgimento della Versione B 1. (a) Dimostrare che l insieme G = { (x, y) R 2 : x 2 e 2y e 2y + (x 1)e x y =
Estremi vincolati, Teorema del Dini.
 Estremi vincolati, Teorema del Dini. 1. Da un cartone di 1m si deve ricavare una scatola rettangolare senza coperchio. Trovare il massimo volume possibile della scatola.. Trovare gli estremi assoluti di
Estremi vincolati, Teorema del Dini. 1. Da un cartone di 1m si deve ricavare una scatola rettangolare senza coperchio. Trovare il massimo volume possibile della scatola.. Trovare gli estremi assoluti di
Esonero AM220, 2019, con Soluzioni
 Esonero AM22, 29, con oluzioni Ogni risposta va accuratamente motivata. Non si possono usare: libri, appunti, congegni elettronici, etc.. ia := { (x, y, z) R 3, tali che x 2 + y 2 4, z = x 2 + y 2 }. ia
Esonero AM22, 29, con oluzioni Ogni risposta va accuratamente motivata. Non si possono usare: libri, appunti, congegni elettronici, etc.. ia := { (x, y, z) R 3, tali che x 2 + y 2 4, z = x 2 + y 2 }. ia
DIARIO DELLE LEZIONI DI ANALISI MATEMATICA II Corso di laurea in Ingegneria Clinica Canale PZ A.A. 2017/2018 Codocente: Dott. Salvatore Fragapane
 DIARIO DELLE LEZIONI DI ANALISI MATEMATICA II Corso di laurea in Ingegneria Clinica Canale PZ A.A. 07/08 Codocente: Dott. Salvatore Fragapane Lezione - 09/03/08, dalle 6.00 alle 8.00 in aula 6 Es. Studiare
DIARIO DELLE LEZIONI DI ANALISI MATEMATICA II Corso di laurea in Ingegneria Clinica Canale PZ A.A. 07/08 Codocente: Dott. Salvatore Fragapane Lezione - 09/03/08, dalle 6.00 alle 8.00 in aula 6 Es. Studiare
INGEGNERIA MECCANICA - CANALE L-Z ANALISI MATEMATICA II SOLUZIONI DELLA PROVA SCRITTA DEL COMPITO A. ( 1) k 2k + 1 e(2k+1)(x+y),
 1 INGEGNERIA MECCANICA - CANALE L-Z ANALISI MATEMATICA II SOLUZIONI DELLA PROVA SCRITTA DEL 1-6-16 - COMPITO A ESERCIZIO 1 Studiare la convergenza assoluta, puntuale e totale della serie k + 1 e(k+1)(x+y),
1 INGEGNERIA MECCANICA - CANALE L-Z ANALISI MATEMATICA II SOLUZIONI DELLA PROVA SCRITTA DEL 1-6-16 - COMPITO A ESERCIZIO 1 Studiare la convergenza assoluta, puntuale e totale della serie k + 1 e(k+1)(x+y),
Facoltà di Ingegneria Prova scritta di Analisi Matematica II. Lecce, y y x = x3 y 4. y(1) = 1.
 Lecce, 10.4.2003 1. Risolvere il seguente problema di Cauchy: y y x = x3 y 4 y(1) = 1. 2. Determinare gli estremi della funzione f(x, y) = x 2 y 2 nell insieme } E = {(x, y) R 2 : (x 1) 2 + y2 4 1, y 0.
Lecce, 10.4.2003 1. Risolvere il seguente problema di Cauchy: y y x = x3 y 4 y(1) = 1. 2. Determinare gli estremi della funzione f(x, y) = x 2 y 2 nell insieme } E = {(x, y) R 2 : (x 1) 2 + y2 4 1, y 0.
A Analisi Matematica 2 (Corso di Laurea in Informatica) Simulazione compito d esame
 COGNOME NOME Matr. Firma dello studente A Analisi Matematica (Corso di Laurea in Informatica) Simulazione compito Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni
COGNOME NOME Matr. Firma dello studente A Analisi Matematica (Corso di Laurea in Informatica) Simulazione compito Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni
2. Discutere la convergenza puntuale e la convergenza uniforme della serie di Fourier di f(x);
 ANALISI MATEMATICA II Prova di esame del 6 Giugno 1 ore 11, Cognome e Nome (in stampatello): Corso di Laurea: Matricola: Docente: Versione A Avvertenza. Gli studenti immatricolati nell A.A. 1/11 (codice
ANALISI MATEMATICA II Prova di esame del 6 Giugno 1 ore 11, Cognome e Nome (in stampatello): Corso di Laurea: Matricola: Docente: Versione A Avvertenza. Gli studenti immatricolati nell A.A. 1/11 (codice
Analisi Matematica 2: Scritto Generale, Cognome e nome:...matricola:...
 Analisi Matematica 2: Scritto Generale, 21.02.2017 Cognome e nome:....................................matricola:......... es.1 es.2 es.3 es.4 es.5 es.6 es.7 somma 5cr. 6 6 6 6 6 - - 30 6/9cr. 5 5 5 5 5
Analisi Matematica 2: Scritto Generale, 21.02.2017 Cognome e nome:....................................matricola:......... es.1 es.2 es.3 es.4 es.5 es.6 es.7 somma 5cr. 6 6 6 6 6 - - 30 6/9cr. 5 5 5 5 5
Prove scritte dell esame di Analisi Matematica II a.a. 2016/2017
 Prove scritte dell esame di Analisi Matematica II a.a. 6/7 C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 5 giugno 7. Assegnati ( l insieme E {(x,
Prove scritte dell esame di Analisi Matematica II a.a. 6/7 C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 5 giugno 7. Assegnati ( l insieme E {(x,
Es. 1 Es. 2 Es. 3 Es. 4 Totale
 Es. Es. Es. Es. 4 Totale Analisi e Geometria Seconda prova in itinere Docente: luglio Cognome: Nome: Matricola: Ogni risposta dev essere giustificata. Gli esercizi vanno svolti su questi fogli, nello spazio
Es. Es. Es. Es. 4 Totale Analisi e Geometria Seconda prova in itinere Docente: luglio Cognome: Nome: Matricola: Ogni risposta dev essere giustificata. Gli esercizi vanno svolti su questi fogli, nello spazio
Analisi Matematica II 14 Giugno 2019
 Analisi Matematica II 14 Giugno 2019 Cognome: Nome: Matricola: 1. (10 punti) Si determinino i sottoinsiemi del piano in cui valgano, rispettivamente, continuità, derivabilità e differenziabilità della
Analisi Matematica II 14 Giugno 2019 Cognome: Nome: Matricola: 1. (10 punti) Si determinino i sottoinsiemi del piano in cui valgano, rispettivamente, continuità, derivabilità e differenziabilità della
Recupero 1 compitino di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2016/2017. Prof. M. Bramanti.
 Recupero 1 compitino di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 16/17. Prof. M. Bramanti 1 Tema n 1 3 4 6 Tot. Cognome e nome in stampatello codice persona o n di
Recupero 1 compitino di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 16/17. Prof. M. Bramanti 1 Tema n 1 3 4 6 Tot. Cognome e nome in stampatello codice persona o n di
Analisi Matematica II Integrali curvilinei (svolgimenti) 1 t 9t dt (a) = dt t 1 t 2 = 1 2. x dx (b) log y 1. dy.
 Analisi Matematica II Integrali curvilinei svolgimenti Svolgimento esercizio Si ha, successivamente, t t, t, t 9t 4 + 4t t 9t + 4, l t dt t 9t + 4 dt a 8 dove in a si è usata la sostituzione 9t + 4 8t
Analisi Matematica II Integrali curvilinei svolgimenti Svolgimento esercizio Si ha, successivamente, t t, t, t 9t 4 + 4t t 9t + 4, l t dt t 9t + 4 dt a 8 dove in a si è usata la sostituzione 9t + 4 8t
Analisi Matematica II Politecnico di Milano Ingegneria Industriale
 Analisi Matematica II Politecnico di Milano Ingegneria Industriale Autovalutazione #5. Sia f : R R la funzione definita da f(x, y) x + x + y + x + y (x, y) R. (a) Determinare il segno di f. (b) Calcolare
Analisi Matematica II Politecnico di Milano Ingegneria Industriale Autovalutazione #5. Sia f : R R la funzione definita da f(x, y) x + x + y + x + y (x, y) R. (a) Determinare il segno di f. (b) Calcolare
Prove scritte dell esame di Analisi Matematica II a.a. 2011/2012
 Prove scritte dell esame di Analisi Matematica II a.a. / C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 7 giugno. ( punti) Disegnare l insieme E (x,
Prove scritte dell esame di Analisi Matematica II a.a. / C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 7 giugno. ( punti) Disegnare l insieme E (x,
calcolare il lavoro di E lungo il segmento da A = ( 1, 1, 1) a B = (1, 1, 1), calcolare rot ( E ), determinare un potenziale U(x, y, z) per E.
 ANALISI VETTORIALE Soluzione esonero.1. Esercizio. Assegnato il campo E (x, y, z) = x(y + z ), y(x + z ), z(x + y ) } 1111 calcolare il lavoro di E lungo il segmento da A = ( 1, 1, 1) a B = (1, 1, 1),
ANALISI VETTORIALE Soluzione esonero.1. Esercizio. Assegnato il campo E (x, y, z) = x(y + z ), y(x + z ), z(x + y ) } 1111 calcolare il lavoro di E lungo il segmento da A = ( 1, 1, 1) a B = (1, 1, 1),
Analisi Matematica 2 - a.a. 2009/2010
 Quarto appello Esercizio Analisi Matematica 2 - a.a. 29/2 Sia Γ = { (,y,z) R 3 : 2 + y 2 = z 2, y 2 + (z 2) 2 = }.. Provare che tutti i punti di Γ sono regolari. 2. Determinare lo spazio tangente a Γ nel
Quarto appello Esercizio Analisi Matematica 2 - a.a. 29/2 Sia Γ = { (,y,z) R 3 : 2 + y 2 = z 2, y 2 + (z 2) 2 = }.. Provare che tutti i punti di Γ sono regolari. 2. Determinare lo spazio tangente a Γ nel
Istituzioni di Matematica II 5 Luglio 2010
 Istituzioni di Matematica II 5 Luglio 010 1. Classificare, al variare del parametro α R, la forma quadratica (1 + α )x + 4xy + αy.. i) Si determinino tutti i punti critici della seguente funzione f(x,
Istituzioni di Matematica II 5 Luglio 010 1. Classificare, al variare del parametro α R, la forma quadratica (1 + α )x + 4xy + αy.. i) Si determinino tutti i punti critici della seguente funzione f(x,
k [ e x] k ke kx = lim ke kx = lim + + ke kδ =
![k [ e x] k ke kx = lim ke kx = lim + + ke kδ = k [ e x] k ke kx = lim ke kx = lim + + ke kδ =](/thumbs/98/135198238.jpg) F. De Marchis F. Lanzara. Montefusco Se ammesso, sosterrò la prova orale: in questo appello in un appello successivo Istruzioni: tutti i ragionamenti devono essere adeguatamente motivati! sercizio 1. i.
F. De Marchis F. Lanzara. Montefusco Se ammesso, sosterrò la prova orale: in questo appello in un appello successivo Istruzioni: tutti i ragionamenti devono essere adeguatamente motivati! sercizio 1. i.
Analisi Matematica II Corso di Ingegneria Gestionale Compito A del f(x, y) = x 2 + 2y 2 x 3 y 3
 Analisi Matematica II Corso di Ingegneria Gestionale Compito A del 7-7-8 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito A del 7-7-8 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito del
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del --9 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle. Esercizio.
Analisi Matematica II Corso di Ingegneria Gestionale Compito del --9 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle. Esercizio.
x 2 y 2 z 2 (b) Detta z = z(x, y) la funzione definita dall equazione f(x, y, z) = 1 intorno al punto (1, 1, 0), calcolare z
 Analisi Matematica II, Anno Accademico 4-5 Ingegneria Edile, Civile, Ambientale Paolo Acquistapace, Laura Cremaschi, Vincenzo M. Tortorelli giugno 5 - primo appello - gruppo A, prima parte (un ora) N.
Analisi Matematica II, Anno Accademico 4-5 Ingegneria Edile, Civile, Ambientale Paolo Acquistapace, Laura Cremaschi, Vincenzo M. Tortorelli giugno 5 - primo appello - gruppo A, prima parte (un ora) N.
f(x, y, z) = xye z (x, y, z) R 3 : x > 0, y > 0, z 1 < x 2 + y 2 < z } 0 < z < 2 x < 1 y < 1
 ANALISI MATEMATICA II Corso di Laurea in Fisica quadriennale Traccia di soluzione della prova scritta del 2 gennaio 24 Durata della prova scritta: 2 ore. Lo studente può svolgere fino a 3 esercizi tra
ANALISI MATEMATICA II Corso di Laurea in Fisica quadriennale Traccia di soluzione della prova scritta del 2 gennaio 24 Durata della prova scritta: 2 ore. Lo studente può svolgere fino a 3 esercizi tra
(a) è chiuso; (b) il punto (1, 1/e) è punto di accumulazione di A; (c) è convesso.
 Cognome Nome Matricola Laurea Civ Amb Gest Inf Eln Tlc Mec Non scrivere qui 1 3 4 5 6 Università degli Studi di Parma Dipartimento di Ingegneria e Architettura Esame di Analisi Matematica Soluzioni AA
Cognome Nome Matricola Laurea Civ Amb Gest Inf Eln Tlc Mec Non scrivere qui 1 3 4 5 6 Università degli Studi di Parma Dipartimento di Ingegneria e Architettura Esame di Analisi Matematica Soluzioni AA
1) Studiare la natura dei seguenti integrali impropri: 2x2 1. x dx (c) e x + 1. log x. n n + 1 n (a) n=1. (b) n + log n n 2n 2 1.
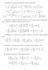 ) Studiare la natura dei seguenti integrali impropri: 0 x 3 dx (b) + 2x2 2 x 2 + 2 dx (c) e x + 0 e x dx (g) (d) + 0 + 0 x( + x) dx x sin x x 2 dx (h) (e) 0 + log x x 2 dx (f) 2 log x dx x + log( + x 2
) Studiare la natura dei seguenti integrali impropri: 0 x 3 dx (b) + 2x2 2 x 2 + 2 dx (c) e x + 0 e x dx (g) (d) + 0 + 0 x( + x) dx x sin x x 2 dx (h) (e) 0 + log x x 2 dx (f) 2 log x dx x + log( + x 2
Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica 2 del 29 settembre 2012
 Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica del 9 settembre A) Data la funzione f(x, y) = { xy x se (x, y) (, ) se (x, y) = (, ), i) stabilire se risulta continua
Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica del 9 settembre A) Data la funzione f(x, y) = { xy x se (x, y) (, ) se (x, y) = (, ), i) stabilire se risulta continua
Analisi Matematica 2 5 febbraio Risposte. (Giusta = 3, non data = 0, sbagliata = 1) Versione Es. 1 Es. 2 Es. 3 Es. 4 Es. 5 Es. 6 Es.
 Analisi Matematica 2 5 febbraio 2013 Nome, Cognome, Matricola: Cognome del Docente: Risposte. (Giusta = 3, non data = 0, sbagliata = 1) Versione Es. 1 Es. 2 Es. 3 Es. 4 Es. 5 Es. 6 Es. 7 1 Esercizio 1.
Analisi Matematica 2 5 febbraio 2013 Nome, Cognome, Matricola: Cognome del Docente: Risposte. (Giusta = 3, non data = 0, sbagliata = 1) Versione Es. 1 Es. 2 Es. 3 Es. 4 Es. 5 Es. 6 Es. 7 1 Esercizio 1.
Recupero 1 compitino di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2017/2018. Prof. M. Bramanti.
 Recupero compitino di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 7/8. Prof. M. Bramanti Tema n 3 4 5 6 Tot. Cognome e nome in stampatello codice persona o n di matricola
Recupero compitino di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 7/8. Prof. M. Bramanti Tema n 3 4 5 6 Tot. Cognome e nome in stampatello codice persona o n di matricola
Analisi Matematica II Corso di Ingegneria Biomedica Compito del
 Analisi Matematica II Corso di Ingegneria Biomedica Compito del 7-- Esercizio. punti Data la funzione fx, y = log x + y x + y + x y i trovare tutti i punti critici; ii trovare massimo e minimo assoluti
Analisi Matematica II Corso di Ingegneria Biomedica Compito del 7-- Esercizio. punti Data la funzione fx, y = log x + y x + y + x y i trovare tutti i punti critici; ii trovare massimo e minimo assoluti
Analisi Matematica 3 (Fisica) Prova scritta del 27 gennaio 2012 Uno svolgimento
 Analisi Matematica 3 (Fisica) Prova scritta del 27 gennaio 22 Uno svolgimento Prima di tutto, eccovi alcuni commenti che potrebbero aiutarvi a svolgere meglio le prove scritte. Ad ogni domanda del testo
Analisi Matematica 3 (Fisica) Prova scritta del 27 gennaio 22 Uno svolgimento Prima di tutto, eccovi alcuni commenti che potrebbero aiutarvi a svolgere meglio le prove scritte. Ad ogni domanda del testo
Analisi Matematica II Corso di Ingegneria Biomedica Compito del
 Analisi Matematica II Corso di Ingegneria Biomedica Compito del -6- - È obbligatorio consegnare tutti i fogli, anche quelli della brutta. - Le risposte senza giustificazione sono considerate nulle. Esercizio.
Analisi Matematica II Corso di Ingegneria Biomedica Compito del -6- - È obbligatorio consegnare tutti i fogli, anche quelli della brutta. - Le risposte senza giustificazione sono considerate nulle. Esercizio.
TEMA 1. F (x, y) = e xy + x + y.
 FONDAMENTI DI ANALII MATEMATICA 2 Commissione F. Albertini, V. Casarino, M. Motta Ingegneria Gestionale, Meccanica e Meccatronica, Vicenza Vicenza, 23 gennaio 217 Primo appello Avvertenza: Nella prima
FONDAMENTI DI ANALII MATEMATICA 2 Commissione F. Albertini, V. Casarino, M. Motta Ingegneria Gestionale, Meccanica e Meccatronica, Vicenza Vicenza, 23 gennaio 217 Primo appello Avvertenza: Nella prima
Esercizi. Misti iniziali. Più variabili. 1. Data la funzione. F (x) = x3 3 + x e t2 dt. se ne studino massimi, minimi, flessi, limiti a ±.
 Esercizi Misti iniziali. Data la funzione se ne studino massimi, minimi, flessi, iti a ±. 2. Provare che Più variabili F x) = 3. Calcolare, se esistono, i seguenti iti a) b) c) d) x,y),) x 2 + y 2 2 x,y),)
Esercizi Misti iniziali. Data la funzione se ne studino massimi, minimi, flessi, iti a ±. 2. Provare che Più variabili F x) = 3. Calcolare, se esistono, i seguenti iti a) b) c) d) x,y),) x 2 + y 2 2 x,y),)
DERIVATE SUCCESSIVE E MATRICE HESSIANA
 FUNZIONI DI DUE VARIABILI 1 DERIVATE SUCCESSIVE E MATRICE HESSIANA Derivate parziali seconde e matrice hessiana. Sviluppo di Taylor del secondo ordine. Punti stazionari. Punti di massimo o minimo (locale
FUNZIONI DI DUE VARIABILI 1 DERIVATE SUCCESSIVE E MATRICE HESSIANA Derivate parziali seconde e matrice hessiana. Sviluppo di Taylor del secondo ordine. Punti stazionari. Punti di massimo o minimo (locale
Scritto Generale del Corso di Analisi Matematica Calcolare la soluzione generale dell equazione differenziale. y (7) + y (6) + y + y = 0.
 del Corso di Analisi Matematica 4 1 y (7) + y (6) + y + y = 0.. Discutere la convergenza puntuale e uniforme della serie di Fourier della funzione f(x) = x ( T < x T ) di periodo T. In particolare, calcolare
del Corso di Analisi Matematica 4 1 y (7) + y (6) + y + y = 0.. Discutere la convergenza puntuale e uniforme della serie di Fourier della funzione f(x) = x ( T < x T ) di periodo T. In particolare, calcolare
ARGOMENTI MATEMATICA PER L INGEGNERIA
 ARGOMENTI DI MATEMATICA PER L INGEGNERIA VOLUME 2 Esercizi proposti Quando non diversamente precisato, nel seguito si intenderà( sempre che nel piano sia stato introdotto un sistema cartesiano ortogonale
ARGOMENTI DI MATEMATICA PER L INGEGNERIA VOLUME 2 Esercizi proposti Quando non diversamente precisato, nel seguito si intenderà( sempre che nel piano sia stato introdotto un sistema cartesiano ortogonale
ANALISI MATEMATICA II 6 luglio 2010 Versione A
 ANALISI MATEMATICA II 6 luglio 2 Versione A Nome Cognome: Matricola Codice corso Docente: Corso di Laurea: Analisi II 75 cr. Analisi D Analisi II V.O. Analisi C es. 23 es. 245 es 24 es. es. 3 pinti b c
ANALISI MATEMATICA II 6 luglio 2 Versione A Nome Cognome: Matricola Codice corso Docente: Corso di Laurea: Analisi II 75 cr. Analisi D Analisi II V.O. Analisi C es. 23 es. 245 es 24 es. es. 3 pinti b c
Scritto di Analisi Vettoriale ( ) proff. F. De Marchis, F. Lanzara, E. Montefusco
 COGNOM, NOM e MATRICOLA: Scritto di Analisi Vettoriale 8..18) proff. F. De Marchis, F. Lanzara,. Montefusco DOCNT: De Marchis Lanzara Montefusco Se ammesso, sosterrò la prova orale: questo appello in un
COGNOM, NOM e MATRICOLA: Scritto di Analisi Vettoriale 8..18) proff. F. De Marchis, F. Lanzara,. Montefusco DOCNT: De Marchis Lanzara Montefusco Se ammesso, sosterrò la prova orale: questo appello in un
Modulo di Matematica
 Università degli Studi di Udine Anno Accademico /3 Corso di Laurea in Biotecnologie Modulo di Matematica Esame del 9//3 N.B.: scrivere nome, cognome e numero di matricola su ogni foglio consegnato. Tempo
Università degli Studi di Udine Anno Accademico /3 Corso di Laurea in Biotecnologie Modulo di Matematica Esame del 9//3 N.B.: scrivere nome, cognome e numero di matricola su ogni foglio consegnato. Tempo
Es. 1 Es. 2 Es. 3 Es. 4 Es. 5 Totale
 Es. 1 Es. 2 Es. Es. 4 Es. 5 Totale Analisi e geometria 2 rimo Appello Docente: 17 luglio 29 Cognome: Nome: Matricola: Tutte le risposte devono essere motivate. Gli esercizi vanno svolti su questi fogli,
Es. 1 Es. 2 Es. Es. 4 Es. 5 Totale Analisi e geometria 2 rimo Appello Docente: 17 luglio 29 Cognome: Nome: Matricola: Tutte le risposte devono essere motivate. Gli esercizi vanno svolti su questi fogli,
Analisi Matematica 2. Ottimizzazione in due variabili. Ottimizzazione in due variabili 1 / 31
 Analisi Matematica 2 Ottimizzazione in due variabili Ottimizzazione in due variabili 1 / 31 Ottimizzazione. Figure: Massimi e minimi relativi (o locali), Massimi e minimi assoluti (o globali) Ottimizzazione
Analisi Matematica 2 Ottimizzazione in due variabili Ottimizzazione in due variabili 1 / 31 Ottimizzazione. Figure: Massimi e minimi relativi (o locali), Massimi e minimi assoluti (o globali) Ottimizzazione
Analisi Matematica II Corso di Ingegneria Gestionale Compito del f(x, y) = log 1 + (x y 2 ) x 2.
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del 7-7-6 - È obbligatorio consegnare tutti i fogli, anche la brutta. - Le risposte senza giustificazione sono considerate nulle. Esercizio.
Analisi Matematica II Corso di Ingegneria Gestionale Compito del 7-7-6 - È obbligatorio consegnare tutti i fogli, anche la brutta. - Le risposte senza giustificazione sono considerate nulle. Esercizio.
Politecnico di Milano Ingegneria Industriale e dell Informazione Analisi e Geometria 2 Primo Appello 13 Luglio 2017
 Politecnico di Milano Ingegneria Industriale e dell Informazione Analisi e Geometria Primo Appello 13 Luglio 017 Cognome: Nome: Matricola: Es.1: 11 punti Es.: 6 punti Es.3: 7 punti Es.: 8 punti Totale
Politecnico di Milano Ingegneria Industriale e dell Informazione Analisi e Geometria Primo Appello 13 Luglio 017 Cognome: Nome: Matricola: Es.1: 11 punti Es.: 6 punti Es.3: 7 punti Es.: 8 punti Totale
Analisi Matematica II Corso di Ingegneria Gestionale Compito del log 1 + x4 +y 2. xy y
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del 9--6 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito del 9--6 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica 2: Secondo Parziale, , Versione A. Cognome e nome:...matricola:...
 Analisi Matematica : Secondo Parziale, 1.6.17, Versione A Cognome e nome:....................................matricola:......... es.1 es. es.3 es. es.5 es.6 es.7 somma 5cr. 6 6 6 6 6 - - 3 9cr. 5 5 5 5
Analisi Matematica : Secondo Parziale, 1.6.17, Versione A Cognome e nome:....................................matricola:......... es.1 es. es.3 es. es.5 es.6 es.7 somma 5cr. 6 6 6 6 6 - - 3 9cr. 5 5 5 5
Analisi Matematica II Corso di Ingegneria Gestionale Compito del f(x, y) = log(1 + x 2 y) lim x 2 x
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del -7-14 Esercizio 1. (14 punti) Data la funzione = log(1 + x y) i) determinare il dominio e studiare l esistenza del ite (x,y) (,) x x ii)
Analisi Matematica II Corso di Ingegneria Gestionale Compito del -7-14 Esercizio 1. (14 punti) Data la funzione = log(1 + x y) i) determinare il dominio e studiare l esistenza del ite (x,y) (,) x x ii)
Fondamenti di Analisi Matematica 2 - a.a. 2016/2017 Primo appello
 Fondamenti di Analisi Matematica 2 - a.a. 216/217 Primo appello Esercizi senza svolgimento - Tema 1 Ω = { x, y, z) R 3 : 4x 2 + y 2 + z 2 1, z }. x = ρ/2) sen ϕ cos ϑ, 1. y = ρ sen ϕ sen ϑ, ρ [, 1], ϕ
Fondamenti di Analisi Matematica 2 - a.a. 216/217 Primo appello Esercizi senza svolgimento - Tema 1 Ω = { x, y, z) R 3 : 4x 2 + y 2 + z 2 1, z }. x = ρ/2) sen ϕ cos ϑ, 1. y = ρ sen ϕ sen ϑ, ρ [, 1], ϕ
PROVA SCRITTA DI ANALISI MATEMATICA 2 Corso di laurea in Matematica 4 Luglio Risoluzione a cura di N. Fusco & G. Floridia
 PROVA SCRITTA DI ANALISI MATEMATICA Corso di laurea in Matematica 4 Luglio 6 Risoluzione a cura di N Fusco & G Floridia Discutere la convergenza puntuale, assoluta, uniforme e totale della serie di funzioni
PROVA SCRITTA DI ANALISI MATEMATICA Corso di laurea in Matematica 4 Luglio 6 Risoluzione a cura di N Fusco & G Floridia Discutere la convergenza puntuale, assoluta, uniforme e totale della serie di funzioni
Analisi Matematica 2. Michele Campiti. Prove scritte di. Ingegneria Industriale a.a
 Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 2009 2010 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi
Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 2009 2010 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi
ESAMI E ESERCITAZIONI A.A. 2010/11. Calcolare la lunghezza del grafico di f. Suggerimento: ricordare che, se h(u) è una funzione continua e.
 ESAMI E ESERCITAZIONI AA 2010/11 ANDREA RATTO Sommario In questo file presentiamo esercitazioni ed esami relativi al Corso Integrato di Matematica per Scienze dell Architettura 1 Esercitazione del 2 Maggio
ESAMI E ESERCITAZIONI AA 2010/11 ANDREA RATTO Sommario In questo file presentiamo esercitazioni ed esami relativi al Corso Integrato di Matematica per Scienze dell Architettura 1 Esercitazione del 2 Maggio
exp(x 2 ) 1 (1 + x 2 ) 2/5 1
 Esame di Matematica II Corso di Laurea Triennale in Scienza dei Materiali Esame di Complementi di Matematica Corso di Laurea Triennale in Scienze e Tecnologie Chimiche 18 Luglio 6 Motivare le soluzioni.
Esame di Matematica II Corso di Laurea Triennale in Scienza dei Materiali Esame di Complementi di Matematica Corso di Laurea Triennale in Scienze e Tecnologie Chimiche 18 Luglio 6 Motivare le soluzioni.
Analisi Matematica II Corso di Ingegneria Gestionale Compito A del x 2 + y 2 sin x 2 + y 2. 2y x x 2 + y 2 dxdy
 Analisi Matematica II Corso di Ingegneria Gestionale Compito A del 4--9 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito A del 4--9 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
