L indice differenziale di una DAE
|
|
|
- Fulvio Cecchini
- 4 anni fa
- Visualizzazioni
Transcript
1 L indice differenziale di una DAE (Metodi Matematici e Calcolo per Ingegneria) Enrico Bertolazzi DIMS Università di Trento anno accademico 2007/2008 L indice differenziale di una DAE 1 / 26 Outline 1 2 L indice Differenziale di una DAE 3 L indice differenziale di una DAE 2 / 26
2 Riduzione del sistema al primo ordine Conviene trasformare il sistema (DAE.1) (DAE.2) dal secondo ordine al primo ponendo p(t) = q(t): q = p M(q)ṗ + Φ q (q, t) T λ = Q(q, p) Φ(q, t) = 0 che possiamo riscrivere come (DAE semi esplicita di indice 3) ẋ = g(x, y, t) ẏ = f(x, y, λ, t) 0 = h(x, t) dove g(x, y, t) = y, h(x, t) = Φ(x, t) e f(x, y, λ, t) = M(x) 1 [ Q(x, y) Φ q (x, t) T λ ] L indice differenziale di una DAE 3 / 26 DAE Lineari Prima di imbarcarci nello studio delle DAE generali conviene vedere cosa succede nei casi semplici ad esempio quando le equazioni sono lineari. Consideriamo ad esempio la seguente DAE lineare Fx (t) + Gx(t) = h(t) dove se F è non singolare otteniamo di nuovo un ODE (Ordinary Differential Equation). Dovremo mettere delle condizioni su F e G altrimenti ci troveremo in casi patologici (ad esempio F = G = 0). L indice differenziale di una DAE 4 / 26
3 Se ad esempio F = ( ) 1 0, G = 0 0 ( ) questo ponendo x(t) = (x(t), y(t)) T corrisponde alla singola equazione differenziale che come soluzione x (t) = y(t) x(t) = t 0 g(z) dz, y(t) = g(t) dove g(t) è una funzione arbitraria che soddisfa le condizioni iniziali. Serve quindi una condizione per avere esistenza e unicità almeno nel caso lineare. L indice differenziale di una DAE 5 / 26 Definizione La coppia di matrici (A, B) sono un Pencil Regolare se esiste un λ R tale che Teorema (Kroneker) det (λa + B) 0 Se (A, B) sono un Pencil Regolare allora esistono due matrici U e V non singolari tali che ( ) ( ) I 0 C 0 UAV = UBV = 0 N 0 I Le matrici N e C sono nella forma normale di Jordan e N ha autovalori tutti nulli. Ovviamente i blocchi corrispondenti nelle matrici partizionate hanno le stesse dimensioni. L indice differenziale di una DAE 6 / 26
4 Di fatto le matrici N e C hanno la seguente forma J 1 0 J 1 0 N =... C =... 0 J d1 0 J d 2 ed i blocchi J k e J k hanno la forma 0 1 J k = J k = λ k λ k inoltre la matrice N è nilpotente cioè esiste un p > 0 finito tale che N p 1 0 e N p = 0. Questo fatto verrà sfruttano per definite l indice di Kroneker. Osservazione Per come è definita si ha sempre p 2. L indice differenziale di una DAE 7 / 26 Torniamo ora alla DAE lineare Fx (t) + Gx(t) = h(t) Se (F, G) è un pencil regolare allora usando U e V che mi portano il pencil alla forma normale otteniamo UFVV 1 x (t) + UGVV 1 x(t) = Uh(t) ponendo (u(t); v(t)) = V 1 x(t) ed (a(t); b(t)) = U 1 h(t) possiamo scrivere ( ) ( I 0 u ) ( ) ( ) ( ) (t) C 0 u(t) a(t) 0 N v + = (t) 0 I v(t) b(t) o meglio u (t) + Cu(t) = a(t) Nv (t) + v(t) = b(t) L indice differenziale di una DAE 8 / 26
5 Soluzione di u (t) + Cu(t) = a(t) L equazione differenziale u (t) + Cu(t) = a(t) ha formalmente la seguente soluzione tramite la matrice esponenziale dove u(t) = exp ( Ct ) u(0) + t 0 exp ( C(s t) ) a(s)ds exp A = I + A A A k! Ak + L indice differenziale di una DAE 9 / 26 Soluzione di Nv (t) + v(t) = b(t) L equazione differenziale Nv (t) + v(t) = b(t) è ancora una DAE ma la matrice N è nilpotente, possiamo allora considerare le sue derivate v(t) = b(t) Nv (t) = b(t) N d dt (b(t) Nv (t)) = b(t) Nb (t) + N 2 v (t). = n 1 ( 1) k N k b (k) (t) ( 1) n N n v (n) (t) k=0 L indice differenziale di una DAE 10 / 26
6 Sfruttando il fatto che N è nilpotente per n = q abbiamo N q = 0 e quindi v(t) = q 1 ( 1) k N k b (k) (t) k=0 Di fatto abbiamo dovuto fare q 1 derivate per eliminare la dipendenza circolare di v(t) con le sue derivate. In questo modo abbiamo calcolato la soluzione v(t). Se facciamo una ulteriore derivata otteniamo una equazione differenziale ordinaria. v (t) = f(t) = q ( 1) k N k b (k) (t) k=1 Di fatto q è il numero minimo di derivate della DAE (o parte della stessa) che devo fare per trasformare la DAE in una ODE. Questo numero prende il nome di Indice di Kroneker. Generalizzando questa idea al caso non lineare otterremo l indice differenzale della DAE. L indice differenziale di una DAE 11 / 26 Soluzione generale Ricordando che x(t) = V(u(t); v(t)) otteniamo è ancora una DAE ma la matrice N è nilpotente, possiamo allora considerare le sue derivate x(t) = V exp ( Ct ) u(0) + t 0 exp ( C(s t) ) a(s)ds d 1 ( 1) k N k b (k) (t) k=0 Inoltre la condizione iniziale di v(0) è determinata e non si può fissare liberamente: v(0) = d 1 ( 1) k N k b (k) (0) k=0 questo implica a sua volta che non posso fissare x(0) liberamente. L indice differenziale di una DAE 12 / 26
7 L indice Differenziale di una DAE L indice Differenziale di una DAE Consideriamo la seguente generica DAE f(x (t), x(t), t) = 0 in generale f(x (t), x(t), t) è singolare e quindi non è possibile ricavare x (t) e ottenere una ODE. Se consideriamo però il le seguenti derivate successive 0 = d dt f(x (t), x(t), t) = f x (t) + f x (t) + f t 0 = d2 dt 2 f(x (t), x(t), t). 0 = dq dt q f(x (t), x(t), t) potremmo trovare una selezione di righe che permetto di ricavare x (t) come funzione di x(t) e t. L indice differenziale di una DAE 13 / 26 L indice Differenziale di una DAE L indice Differenziale di una DAE Ad esempio se consideriamo la seguente DAE x(t) = sin(t) x (t) + y(t) = 0 una prima derivata x (t) = cos(t) x (t) + y (t) = 0 permette di ricavare y (t) = x (t). Una seconda derivata x (t) = sin(t) x (t) + y (t) = 0 permette di ricavare x (t) = sin(t) e quindi y (t) = sin(t). L indice differenziale di una DAE 14 / 26
8 L indice Differenziale di una DAE L indice Differenziale di una DAE Definizione (Indice differenziale) Data una DAE f(x (t), x(t), t) = 0 diremo che ha indice differenziale q se il seguente sistema di derivate d dt f(x (t), x(t), t) = 0 d 2 dt 2 f(x (t), x(t), t) = 0 d q dt q f(x (t), x(t), t) = 0 è il più piccolo sistema che permette di ricavare x (t) in funzione di x(t) e t.. L indice differenziale di una DAE 15 / 26 Una DAE in generale si scrive come dove f(x, x, t) = 0 f(x, x, t) = A(x, x, t) è matrice singolare. Conviene considerare però delle classi di DAE in una forma meno generale ma utile nelle applicazioni. Ad esempio A(x, t)x = g(x, t) dove A(x, t) è matrice singolare. Esistono però in letteratura delle forme particolari semi-esplicite per le DAE di indice 0, 1, 2 e 3. L indice differenziale di una DAE 16 / 26
9 DAE di indice 0 e 1 Una DAE di indice 0 per definizione è una ODE, una DAE di indice 1 in forma semi esplicita è la seguente x = f(x, y, t) 0 = g(x, y, t) dove x(t) R n, y(t) R m, f C 1 (R n+m+1,r n ) e g C 1 (R n+m+1,r m ). Inoltre g deve essere regolare cioè g y (x, y, t) = g(x, y, t) è matrice non singolare. In questo caso applicando il teorema della funzione implicita (vedi prossimo lucido) possiamo determinare y in funzione di x e quindi ottenere una ODE: x (t) = f(x(t), y(x(t), t), t) L indice differenziale di una DAE 17 / 26 Teorema della funzione implicita Teorema Sia A R n+m aperto e f C 1 (A,R m ) sia inoltre 1 (x 0, y 0 ) A; 2 f(x 0, y 0 ) = 0; 3 f(x 0,y 0 ) non singolare. Allora esistono due aperti U R n e V R m e una funzione φ : U V tali che y 0 = φ(x 0 ); f(x, y) = 0 e solo se y = φ(x) (per x U e y V); φ C 1 (U, V) e vale φ(x) ( ) 1 f(x, φ(x)) f(x, φ(x)) = L indice differenziale di una DAE 18 / 26
10 DAE di indice 2 (1/3) Una DAE di indice 1 di fatto è una ODE con dei parametri da determinare implicitamente, ben diversa è la natura della DAE di indice 2 x = f(x, y, t) 0 = g(x, t) dove x(t) R n, y(t) R m, f C 1 (R n+m+1,r n ) e g C 1 (R n+1,r m ). Inoltre g(x, t) f(x, y, t) è matrice non singolare. In questo caso non possiamo applicare il teorema della funzione implicita per determinare y in funzione di x. L indice differenziale di una DAE 19 / 26 DAE di indice 2 (2/3) Per verificare l indice deriviamo una prima volta il vincolo dg(x(t), t) dt = g(x(t), t) x (t) + g(x(t), t) t e da questo otteniamo il nuovo vincolo (nascosto) = 0 h(x, y, t) = 0 dove h(x, y, t) = Otteniamo cosi la nuova DAE g(x, t) f(x, y, t) + x = f(x, y, t) g(x, t) t 0 = h(x, y, t) L indice differenziale di una DAE 20 / 26
11 DAE di indice 2 (3/3) Avendo derivato una volta il vincolo questa DAE dovrebbe essere di indice 1 per verificarlo deve essere x = f(x, y, t) 0 = h(x, y, t) h(x, y, t) = g(x, t) f(x, y, t) non singolare L indice differenziale di una DAE 21 / 26 DAE di indice 3 (1/3) Una DAE di indice 3 semi esplicita prende la forma x = f(x, y, z, t) y = g(x, y, t) 0 = h(y, t) dove x(t) R n y(t) R m z(t) R p f C 1 (R n+m+p+1,r n ) g C 1 (R n+m+1,r m ) h C 1 (R m+1,r n ) L indice differenziale di una DAE 22 / 26
12 DAE di indice 3 (2/3) Per verificare l indice deriviamo una prima volta il vincolo dh(y(t), t) dt = h(y(t), t) y (t) + h(y(t), t) t e da questo otteniamo il nuovo vincolo (nascosto) a(x, y, t) = 0 = 0 dove a(x, y, t) = Otteniamo cosi la nuova DAE h(y, t) g(x, y, t) + x = f(x, y, z, t) h(y, t) t y = g(x, y, t) 0 = a(x, y, t) L indice differenziale di una DAE 23 / 26 DAE di indice 3 (3/3) La DAE ( ) x y = ( ) f(x, y, z, t) g(x, y, t) 0 = a(x, y, t) è di indice 2 se a(x, y, t) f(x, y, z, t) z + a(x, y, t) g(x, y, t) z è non singolare, cioè h(y, t) g(x, y, t) f(x, y, z, t) z è non singolare. L indice differenziale di una DAE 24 / 26
13 DAE di indice µ (nella forma di Hessemberg) La DAE x 1 = f 1(x 1, x 2,..., x µ, t) x 2 = f 2(x 1, x 2,..., x µ 1, t). x k = f k(x k 1, x k,..., x µ 1, t) k = 3,..., µ 1. 0 = f µ (x µ 1, t) dove se f µ µ 1 f µ 1 µ 2 f 2 1 f 1 µ è non singolare allora la DAE ha indice µ. L indice differenziale di una DAE 25 / 26 Bibliografia J. García de Jalón and E. Bayo, Kinematic and Dynamic Simulation of Multibody Systems. The Real-Time Challenge Springer-Verlag, New-York, L indice differenziale di una DAE 26 / 26
Approssimazione Numerica delle DAE
 Approssimazione Numerica delle DAE (Modellistica e Simulazione dei Sistemi Meccanici) Enrico Bertolazzi DIMS Università di Trento anno accademico 2006/2007 Approssimazione Numerica delle DAE 1 / 72 Outline
Approssimazione Numerica delle DAE (Modellistica e Simulazione dei Sistemi Meccanici) Enrico Bertolazzi DIMS Università di Trento anno accademico 2006/2007 Approssimazione Numerica delle DAE 1 / 72 Outline
Approssimazione Numerica delle DAE
 Approssimazione Numerica delle DAE (Modellistica e Simulazione dei Sistemi Meccanici) Enrico Bertolazzi DIMS Università di Trento anno accademico 2006/2007 Approssimazione Numerica delle DAE 1 / 72 Outline
Approssimazione Numerica delle DAE (Modellistica e Simulazione dei Sistemi Meccanici) Enrico Bertolazzi DIMS Università di Trento anno accademico 2006/2007 Approssimazione Numerica delle DAE 1 / 72 Outline
Approssimazione Numerica delle DAE
 Approssimazione Numerica delle DAE (Metodi Matematici e Calcolo per Ingegneria) Enrico Bertolazzi DIMS Università di Trento anno accademico 2008/2009 Approssimazione Numerica delle DAE 1 / 88 Outline 1
Approssimazione Numerica delle DAE (Metodi Matematici e Calcolo per Ingegneria) Enrico Bertolazzi DIMS Università di Trento anno accademico 2008/2009 Approssimazione Numerica delle DAE 1 / 88 Outline 1
Approssimazione Numerica delle DAE
 Approssimazione Numerica delle DAE (Metodi Matematici e Calcolo per Ingegneria) Enrico Bertolazzi DIMS Università di Trento anno accademico 2008/2009 Approssimazione Numerica delle DAE 1 / 88 Outline 1
Approssimazione Numerica delle DAE (Metodi Matematici e Calcolo per Ingegneria) Enrico Bertolazzi DIMS Università di Trento anno accademico 2008/2009 Approssimazione Numerica delle DAE 1 / 88 Outline 1
Il metodo del partizionamento delle coordinate
 Il metodo del partizionamento delle coordinate (Metodi Matematici e Calcolo per Ingegneria) Enrico Bertolazzi DIMS Università di Trento anno accademico 2007/2008 Il metodo del partizionamento delle coordinate
Il metodo del partizionamento delle coordinate (Metodi Matematici e Calcolo per Ingegneria) Enrico Bertolazzi DIMS Università di Trento anno accademico 2007/2008 Il metodo del partizionamento delle coordinate
Il metodo del partizionamento delle coordinate
 Il metodo del partizionamento delle coordinate (Metodi Matematici e Calcolo per Ingegneria) Enrico Bertolazzi DIMS Università di Trento anno accademico 2007/2008 Il metodo del partizionamento delle coordinate
Il metodo del partizionamento delle coordinate (Metodi Matematici e Calcolo per Ingegneria) Enrico Bertolazzi DIMS Università di Trento anno accademico 2007/2008 Il metodo del partizionamento delle coordinate
Outline. 1 Origine delle DAE. 2 L indice di Kroneker. 3 Un esempio semplice. 4 DAE in forma semi-esplicita
 Outline Approssimazione Numerica delle DAE (Modellistica e Simulazione dei Sistemi Meccanici) Enrico Bertolazzi DIMS Università di Trento anno accademico 2006/2007 1 2 3 4 5 6 Approssimazione Numerica
Outline Approssimazione Numerica delle DAE (Modellistica e Simulazione dei Sistemi Meccanici) Enrico Bertolazzi DIMS Università di Trento anno accademico 2006/2007 1 2 3 4 5 6 Approssimazione Numerica
Outline. Alcuni esempi di soluzione Numerica delle DAE. Un esempio semplice. x(t) = sin(t) U = V = ed N = y(t) = cos(t)
 Outline Alcuni esempi di soluzione Numerica delle DAE (Metodi Matematici e Calcolo per Ingegneria) 1 Enrico Bertolazzi DIMS Università di Trento 2 anno accademico 2007/2008 Alcuni esempi di soluzione Numerica
Outline Alcuni esempi di soluzione Numerica delle DAE (Metodi Matematici e Calcolo per Ingegneria) 1 Enrico Bertolazzi DIMS Università di Trento 2 anno accademico 2007/2008 Alcuni esempi di soluzione Numerica
Sistemi di equazioni differenziali
 Capitolo 5 Sistemi di equazioni differenziali Molti problemi sono governati non da una singola equazione differenziale, ma da un sistema di più equazioni. Ad esempio questo succede se si vuole descrivere
Capitolo 5 Sistemi di equazioni differenziali Molti problemi sono governati non da una singola equazione differenziale, ma da un sistema di più equazioni. Ad esempio questo succede se si vuole descrivere
Outline. 1 Teorema dei moltiplicatori di Lagrange. 2 Uso pratico dei moltiplicatori di Lagrange. 3 Derivazione alternativa dei moltiplicatori
 Outline Minimi Vincolati (Metodi Matematici e Calcolo per Ingegneria) Enrico Bertolazzi DIMS Università di Trento anno accademico 2006/2007 1 2 3 Derivazione alternativa dei moltiplicatori 4 Minimi Vincolati
Outline Minimi Vincolati (Metodi Matematici e Calcolo per Ingegneria) Enrico Bertolazzi DIMS Università di Trento anno accademico 2006/2007 1 2 3 Derivazione alternativa dei moltiplicatori 4 Minimi Vincolati
La trasformata di Laplace
 La trasformata di Laplace (Metodi Matematici e Calcolo per Ingegneria) Enrico Bertolazzi DIMS Università di Trento anno accademico 2008/2009 (aggiornata al 21/09/2008) La trasformata di Laplace 1 / 31
La trasformata di Laplace (Metodi Matematici e Calcolo per Ingegneria) Enrico Bertolazzi DIMS Università di Trento anno accademico 2008/2009 (aggiornata al 21/09/2008) La trasformata di Laplace 1 / 31
La trasformata di Laplace
 La trasformata di Laplace (Metodi Matematici e Calcolo per Ingegneria) Enrico Bertolazzi DIMS Universitá di Trento anno accademico 2005/2006 La trasformata di Laplace 1 / 34 Outline 1 La trasformata di
La trasformata di Laplace (Metodi Matematici e Calcolo per Ingegneria) Enrico Bertolazzi DIMS Universitá di Trento anno accademico 2005/2006 La trasformata di Laplace 1 / 34 Outline 1 La trasformata di
SISTEMI DI EQUAZIONI DIFFERENZIALI- ESERCIZI SVOLTI
 SISTEMI DI EQUAZIONI DIFFERENZIALI- ESERCIZI SVOLTI Generalità sui sistemi Sia xt, yt la soluzione del problema di Cauchy Posto vt = e xtyt, calcolare v x = 3x x = y = x y = 0 Sia x = 3x y y = x + y Scrivere
SISTEMI DI EQUAZIONI DIFFERENZIALI- ESERCIZI SVOLTI Generalità sui sistemi Sia xt, yt la soluzione del problema di Cauchy Posto vt = e xtyt, calcolare v x = 3x x = y = x y = 0 Sia x = 3x y y = x + y Scrivere
1 Punti di equilibrio e stabilità: definizioni
 ASPETTI QUALITATIVI DELLA TEORIA DELLE EQUAZIONI DIFFERENZIALI (Schema del contenuto delle lezioni e riferimenti bibliografici) Testi [HS] M. Hirsch and S. Smale Differential Equations, Dynamical Systems
ASPETTI QUALITATIVI DELLA TEORIA DELLE EQUAZIONI DIFFERENZIALI (Schema del contenuto delle lezioni e riferimenti bibliografici) Testi [HS] M. Hirsch and S. Smale Differential Equations, Dynamical Systems
Matematica con elementi di Informatica
 Equazioni differenziali Matematica con elementi di Informatica Tiziano Vargiolu Dipartimento di Matematica vargiolu@math.unipd.it Corso di Laurea Magistrale in Chimica e Tecnologie Farmaceutiche. () Equazioni
Equazioni differenziali Matematica con elementi di Informatica Tiziano Vargiolu Dipartimento di Matematica vargiolu@math.unipd.it Corso di Laurea Magistrale in Chimica e Tecnologie Farmaceutiche. () Equazioni
Sistemi di equazioni differenziali lineari
 Sistemi di equazioni differenziali lineari Corso di Modellistica Ambientale a.a. 2010/2011 Ricordiamo che per un sistema della forma dx/dt = A x + B y dy/dt = C x + D y si considera la tabella dei coefficienti
Sistemi di equazioni differenziali lineari Corso di Modellistica Ambientale a.a. 2010/2011 Ricordiamo che per un sistema della forma dx/dt = A x + B y dy/dt = C x + D y si considera la tabella dei coefficienti
Equazioni differenziali lineari del secondo ordine a coefficienti costanti
 Equazioni differenziali lineari del secondo ordine a coefficienti costanti 0.1 Introduzione Una equazione differenziale del secondo ordine è una relazione del tipo F (t, y(t), y (t), y (t)) = 0 (1) Definizione
Equazioni differenziali lineari del secondo ordine a coefficienti costanti 0.1 Introduzione Una equazione differenziale del secondo ordine è una relazione del tipo F (t, y(t), y (t), y (t)) = 0 (1) Definizione
appunti per il corso di Analisi Matematica I corso di laurea in Ingegneria Gestionale, a.a autore: Giovanni Alberti
 appunti per il corso di Analisi Matematica I corso di laurea in Ingegneria Gestionale, a.a. 2013-14 autore: Giovanni Alberti Equazioni differenziali [versione: 22-12-2013] Richiamo delle nozioni fondamentali
appunti per il corso di Analisi Matematica I corso di laurea in Ingegneria Gestionale, a.a. 2013-14 autore: Giovanni Alberti Equazioni differenziali [versione: 22-12-2013] Richiamo delle nozioni fondamentali
1.1 L equazione di Newton
 ½ ÊÁ ÀÁ ÅÁ Ç Queste note (attualmente, e probabilmente per un bel po sono altamente provvisorie e (molto probabilmente non prive di errori. 1.1 L equazione di Newton L equazione di Newton F = ma per un
½ ÊÁ ÀÁ ÅÁ Ç Queste note (attualmente, e probabilmente per un bel po sono altamente provvisorie e (molto probabilmente non prive di errori. 1.1 L equazione di Newton L equazione di Newton F = ma per un
Esercitazione n 6. Esercizio 1: Determinare i punti di massimo e minimo relativo delle seguenti funzioni: (b)f(x, y) = 4y 4 16x 2 y + x
 Esercitazione n 6 1 Massimi e minimi di funzioni di più variabili Esercizio 1: Determinare i punti di massimo e minimo relativo delle seguenti funzioni: (a)f(x, y) = x 3 + y 3 + xy (b)f(x, y) = 4y 4 16x
Esercitazione n 6 1 Massimi e minimi di funzioni di più variabili Esercizio 1: Determinare i punti di massimo e minimo relativo delle seguenti funzioni: (a)f(x, y) = x 3 + y 3 + xy (b)f(x, y) = 4y 4 16x
appunti per il corso di Analisi Matematica I corso di laurea in Ingegneria Gestionale, a.a autore: Giovanni Alberti
 appunti per il corso di Analisi Matematica I corso di laurea in Ingegneria Gestionale, a.a. 2014-15 autore: Giovanni Alberti Equazioni differenziali [versione: 2 gennaio 2015] Richiamo delle nozioni fondamentali
appunti per il corso di Analisi Matematica I corso di laurea in Ingegneria Gestionale, a.a. 2014-15 autore: Giovanni Alberti Equazioni differenziali [versione: 2 gennaio 2015] Richiamo delle nozioni fondamentali
Analisi Matematica 2. Ottimizzazione in due variabili. Ottimizzazione in due variabili 1 / 31
 Analisi Matematica 2 Ottimizzazione in due variabili Ottimizzazione in due variabili 1 / 31 Ottimizzazione. Figure: Massimi e minimi relativi (o locali), Massimi e minimi assoluti (o globali) Ottimizzazione
Analisi Matematica 2 Ottimizzazione in due variabili Ottimizzazione in due variabili 1 / 31 Ottimizzazione. Figure: Massimi e minimi relativi (o locali), Massimi e minimi assoluti (o globali) Ottimizzazione
FM210 - Fisica Matematica I
 FM21 - Fisica Matematica I Seconda Prova Scritta [16-2-212] Soluzioni Problema 1 1. Chiamiamo A la matrice del sistema e cerchiamo anzitutto gli autovalori della matrice: l equazione secolare è (λ + 2β)λ
FM21 - Fisica Matematica I Seconda Prova Scritta [16-2-212] Soluzioni Problema 1 1. Chiamiamo A la matrice del sistema e cerchiamo anzitutto gli autovalori della matrice: l equazione secolare è (λ + 2β)λ
Sistemi Dinamici Corso di Laurea in Matematica Prova parziale del ẋ = y y 2 + 2x
 Sistemi Dinamici Corso di Laurea in Matematica Prova parziale del --08 Esercizio. 0 punti Studiare al variare del parametro µ R con µ, la stabilità dell origine per il sistema ẋ = µy + y x 3 x 5 ẏ = x
Sistemi Dinamici Corso di Laurea in Matematica Prova parziale del --08 Esercizio. 0 punti Studiare al variare del parametro µ R con µ, la stabilità dell origine per il sistema ẋ = µy + y x 3 x 5 ẏ = x
FM1 - Equazioni differenziali e meccanica. Il metodo di variazione delle costanti (Livia Corsi)
 Corso di laurea in Matematica - Anno Accademico 009/010 FM1 - Equazioni differenziali e meccanica Il metodo di variazione delle costanti (Livia Corsi Il metodo di variazione delle costanti è una tecnica
Corso di laurea in Matematica - Anno Accademico 009/010 FM1 - Equazioni differenziali e meccanica Il metodo di variazione delle costanti (Livia Corsi Il metodo di variazione delle costanti è una tecnica
minimo, massimo, né massimo né minimo (2p.).
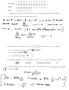 COGNOME: NOME: MATR.: Ingegneria Aerospaziale. Analisi Matematica 2. Compito del 8 giugno 2019 - PARTE A 1. Si scriva l enunciato del teorema di Schwartz (2p.) 2. Consideriamo la serie di Fourier f(t)
COGNOME: NOME: MATR.: Ingegneria Aerospaziale. Analisi Matematica 2. Compito del 8 giugno 2019 - PARTE A 1. Si scriva l enunciato del teorema di Schwartz (2p.) 2. Consideriamo la serie di Fourier f(t)
Matrici e sistemi. Sistemi lineari. Invertibilità Matrici elementari Criteri di invertibilità Sistemi quadrati e Teorema di Cramer
 Sistemi lineari Invertibilità Matrici elementari Criteri di invertibilità Sistemi quadrati e Teorema di Cramer 2 2006 Politecnico di Torino 1 Prodotto tra matrici quadrate Date comunque A e B matrici quadrate
Sistemi lineari Invertibilità Matrici elementari Criteri di invertibilità Sistemi quadrati e Teorema di Cramer 2 2006 Politecnico di Torino 1 Prodotto tra matrici quadrate Date comunque A e B matrici quadrate
1. Equazioni differenziali del primo ordine. Si chiamano equazioni differenziali del primo ordine tutte quelle che si possono ricondurre alla forma
 appunti per il corso di Analisi Matematica I corso di laurea in Ingegneria Gestionale, a.a. 2015-16 autore: Giovanni Alberti Equazioni differenziali [versione: 20 dicembre 2015] Richiamo delle nozioni
appunti per il corso di Analisi Matematica I corso di laurea in Ingegneria Gestionale, a.a. 2015-16 autore: Giovanni Alberti Equazioni differenziali [versione: 20 dicembre 2015] Richiamo delle nozioni
CORSO DI LAUREA in Fisica, aa 2017/18 (canale Pb-Z)
 CORSO DI LAUREA in Fisica, aa 2017/18 (canale Pb-Z) Equazioni lineari del II ordine a coefficienti costanti: questo è un richiamo dei risultati con altri esempi svolti. Il testo di riferimento è Bramanti
CORSO DI LAUREA in Fisica, aa 2017/18 (canale Pb-Z) Equazioni lineari del II ordine a coefficienti costanti: questo è un richiamo dei risultati con altri esempi svolti. Il testo di riferimento è Bramanti
Outline. 1 La trasformata di Laplace. 2 Proprietá della Trasformata. 3 Calcolo di alcune trasformate. 4 Altre proprietá della trasformata di Laplace
 Outline 1 La trasformata di Laplace La trasformata di Laplace (Metodi Matematici e Calcolo per Ingegneria) Enrico Bertolazzi DIMS Universitá di rento anno accademico 25/26 2 Proprietá della rasformata
Outline 1 La trasformata di Laplace La trasformata di Laplace (Metodi Matematici e Calcolo per Ingegneria) Enrico Bertolazzi DIMS Universitá di rento anno accademico 25/26 2 Proprietá della rasformata
Analisi Matematica II Corso di Ingegneria Gestionale Compito del
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del 30-0-08 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito del 30-0-08 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
1.9 Massimi e minimi vincolati
 .9 Massimi e minimi vincolati Sia K un compatto di R N e sia f : K R una funzione continua. Per il teorema di Weierstrass, f assume massimo e minimo su K. Come determinarli? Se K ha punti interni e f è
.9 Massimi e minimi vincolati Sia K un compatto di R N e sia f : K R una funzione continua. Per il teorema di Weierstrass, f assume massimo e minimo su K. Come determinarli? Se K ha punti interni e f è
Sistemi differenziali 2 2: esercizi svolti. 1 Sistemi lineari Stabilità nei sistemi lineari
 Sistemi differenziali : esercizi svolti 1 Sistemi lineari Stabilità nei sistemi lineari 14 1 Sistemi differenziali : esercizi svolti 1 Sistemi lineari Gli esercizi contrassegnati con il simbolo * presentano
Sistemi differenziali : esercizi svolti 1 Sistemi lineari Stabilità nei sistemi lineari 14 1 Sistemi differenziali : esercizi svolti 1 Sistemi lineari Gli esercizi contrassegnati con il simbolo * presentano
Osservazioni sulle funzioni composte
 Osservazioni sulle funzioni composte ) 30 dicembre 2009 Scopo di questo articolo è di trattare alcuni problemi legati alla derivabilità delle funzioni composte nel caso di funzioni di R n in R m Non si
Osservazioni sulle funzioni composte ) 30 dicembre 2009 Scopo di questo articolo è di trattare alcuni problemi legati alla derivabilità delle funzioni composte nel caso di funzioni di R n in R m Non si
7. Equazioni differenziali
 18 Sezione 7. Equazioni differenziali 7. Equazioni differenziali [versione: 25/5/2012] Richiamo delle nozioni fondamentali In un equazione differenziale l incognita da determinare è una funzione (e non
18 Sezione 7. Equazioni differenziali 7. Equazioni differenziali [versione: 25/5/2012] Richiamo delle nozioni fondamentali In un equazione differenziale l incognita da determinare è una funzione (e non
FM1 - Equazioni differenziali e meccanica
 Corso di laurea in Matematica - Anno Accademico 2006/2007 FM1 - Equazioni differenziali e meccanica Prima prova d esonero (03-04-2006) CORREZIONE Esercizio 1. Lo spettro Σ(A) della matrice A si trova risolvendo
Corso di laurea in Matematica - Anno Accademico 2006/2007 FM1 - Equazioni differenziali e meccanica Prima prova d esonero (03-04-2006) CORREZIONE Esercizio 1. Lo spettro Σ(A) della matrice A si trova risolvendo
Alcune nozioni di calcolo differenziale
 Alcune nozioni di calcolo differenziale G. Mastroeni, M. Pappalardo 1 Limiti per funzioni di piu variabili Supporremo noti i principali concetti algebrici e topologici relativi alla struttura dello spazio
Alcune nozioni di calcolo differenziale G. Mastroeni, M. Pappalardo 1 Limiti per funzioni di piu variabili Supporremo noti i principali concetti algebrici e topologici relativi alla struttura dello spazio
Analisi Matematica 2: Esercizi su Equazioni Ordinarie
 Analisi Matematica 2: Esercizi su Equazioni Ordinarie Vladimir Georgiev Dipartimento di Matematica L.Tonelli, Università di Pisa, Largo Bruno Pontecorvo 5, I-56127, Pisa, Italy. E-mail: georgiev@dm.unipi.it
Analisi Matematica 2: Esercizi su Equazioni Ordinarie Vladimir Georgiev Dipartimento di Matematica L.Tonelli, Università di Pisa, Largo Bruno Pontecorvo 5, I-56127, Pisa, Italy. E-mail: georgiev@dm.unipi.it
Equazioni Differenziali
 Università degli Studi di Udine Anno Accademico 2012/2013 Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea in Matematica Equazioni Differenziali Appello del 5 febbraio 2013 N.B.: scrivere
Università degli Studi di Udine Anno Accademico 2012/2013 Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea in Matematica Equazioni Differenziali Appello del 5 febbraio 2013 N.B.: scrivere
7.5 Il caso vincolato: preliminari
 7.5 Il caso vincolato: preliari Consideriamo ora il problema vincolato 3, che qui riscriviamo: fx gx 0 hx = 0, 13 con g : IR n IR p e h : IR n IR m, m n. Ricordiamo che F = {x IR n : gx 0, hx = 0}, denota
7.5 Il caso vincolato: preliari Consideriamo ora il problema vincolato 3, che qui riscriviamo: fx gx 0 hx = 0, 13 con g : IR n IR p e h : IR n IR m, m n. Ricordiamo che F = {x IR n : gx 0, hx = 0}, denota
Massimi e minimi vincolati
 Massimi e minimi vincolati Data una funzione G C 1 (D), dove D è un aperto di R 2, sappiamo bene dove andare a cercare gli eventuali punti di massimo e minimo relativi. Una condizione necessaria affinché
Massimi e minimi vincolati Data una funzione G C 1 (D), dove D è un aperto di R 2, sappiamo bene dove andare a cercare gli eventuali punti di massimo e minimo relativi. Una condizione necessaria affinché
Punti di equilibrio: sistemi tempo continui
 Capitolo 3 ANALISI DELLA STABILITÀ 31 Punti di equilibrio: sistemi tempo continui Si consideri il seguente sistema tempo continuo: ẋ(t) A x(t) + B u(t) y(t) C x(t) + D u(t) I punti di equilibrio x 0 del
Capitolo 3 ANALISI DELLA STABILITÀ 31 Punti di equilibrio: sistemi tempo continui Si consideri il seguente sistema tempo continuo: ẋ(t) A x(t) + B u(t) y(t) C x(t) + D u(t) I punti di equilibrio x 0 del
1. Esercizi Geometria File n. 6: Diagonalizzazione, triangolarizzazione, teorema di Cayley-Hamilton, forma normale di Jordan.
 1 Esercizi Geometria 2 2017-18 File n 6: Diagonalizzazione, triangolarizzazione, teorema di Cayley-Hamilton, forma normale di Jordan ( ) cos θ sin θ Es 11 Sia θ [0, 2π) e sia A θ = (attenzione: non è la
1 Esercizi Geometria 2 2017-18 File n 6: Diagonalizzazione, triangolarizzazione, teorema di Cayley-Hamilton, forma normale di Jordan ( ) cos θ sin θ Es 11 Sia θ [0, 2π) e sia A θ = (attenzione: non è la
Condizioni di Karush-Kuhn-Tucker e Programmazione Lineare
 Condizioni di Karush-Kuhn-Tucker e Programmazione Lineare A. Agnetis 1 Richiami su condizioni di Karush-Kuhn-Tucker e convessità Si consideri il problema di ottimizzazione vincolata: min f(x) (1) x X R
Condizioni di Karush-Kuhn-Tucker e Programmazione Lineare A. Agnetis 1 Richiami su condizioni di Karush-Kuhn-Tucker e convessità Si consideri il problema di ottimizzazione vincolata: min f(x) (1) x X R
Capitolo 6. Sistemi lineari di equazioni differenziali. 1
 Capitolo 6 Sistemi lineari di equazioni differenziali L integrale generale In questo capitolo utilizzeremo la forma canonica di Jordan per studiare alcuni tipi di equazioni differenziali Un sistema lineare
Capitolo 6 Sistemi lineari di equazioni differenziali L integrale generale In questo capitolo utilizzeremo la forma canonica di Jordan per studiare alcuni tipi di equazioni differenziali Un sistema lineare
Allora esistono δ > 0 e σ > 0 tali che. f(x, y) = 0; (2) la funzione ϕ : ]x 0 δ, x 0 + δ [ R, y = ϕ(x), è derivabile e.
![Allora esistono δ > 0 e σ > 0 tali che. f(x, y) = 0; (2) la funzione ϕ : ]x 0 δ, x 0 + δ [ R, y = ϕ(x), è derivabile e. Allora esistono δ > 0 e σ > 0 tali che. f(x, y) = 0; (2) la funzione ϕ : ]x 0 δ, x 0 + δ [ R, y = ϕ(x), è derivabile e.](/thumbs/96/129204172.jpg) 16 42 Funzioni implicite Il seguente teorema fornisce una condizione sufficiente affinché, data un equazione della forma f(x, ) = 0, sia possibile determinare come funzione della x Teo 11 (Teorema della
16 42 Funzioni implicite Il seguente teorema fornisce una condizione sufficiente affinché, data un equazione della forma f(x, ) = 0, sia possibile determinare come funzione della x Teo 11 (Teorema della
COGNOME: NOME: MATR.: 1. Si consideri la serie di Fourier data da n 2
 COGNOME: NOME: MATR.: Ingegneria Aerospaziale. Analisi Matematica 2. Compito del 16 febbraio 2019 - PARTE A 1. Si consideri la serie di Fourier data da n 2 sin(2nt). Diamo per buono che esiste il limite
COGNOME: NOME: MATR.: Ingegneria Aerospaziale. Analisi Matematica 2. Compito del 16 febbraio 2019 - PARTE A 1. Si consideri la serie di Fourier data da n 2 sin(2nt). Diamo per buono che esiste il limite
Esercizio 1, 6 punti [ ] Sapendo che una grandezza P(t) è caratterizzata dalle seguenti proprietà:
![Esercizio 1, 6 punti [ ] Sapendo che una grandezza P(t) è caratterizzata dalle seguenti proprietà: Esercizio 1, 6 punti [ ] Sapendo che una grandezza P(t) è caratterizzata dalle seguenti proprietà:](/thumbs/103/158017970.jpg) Modellistica Ambientale/Modelli Matematici Ambientali - A.A. 2014/2015 Quinta prova scritta, Appello estivo 23 Settembre 2015 Parte comune a Modellistica Ambientale e Modelli Matematici Ambientali Schema
Modellistica Ambientale/Modelli Matematici Ambientali - A.A. 2014/2015 Quinta prova scritta, Appello estivo 23 Settembre 2015 Parte comune a Modellistica Ambientale e Modelli Matematici Ambientali Schema
Soluzione della prova scritta di Analisi Matematica II del 15 Aprile 2009 (Ingegneria Edile e Architettura)
 Soluzione della prova scritta di Analisi Matematica II del 5 Aprile 009 Ingegneria Edile e Architettura x. Calcolare J = ds essendo γ la curva ottenuta intersecando γ + y il cilindro di equazione x + y
Soluzione della prova scritta di Analisi Matematica II del 5 Aprile 009 Ingegneria Edile e Architettura x. Calcolare J = ds essendo γ la curva ottenuta intersecando γ + y il cilindro di equazione x + y
Metodi per la risoluzione di sistemi lineari
 Metodi per la risoluzione di sistemi lineari Sistemi di equazioni lineari. Rango di matrici Come è noto (vedi [] sez.0.8), ad ogni matrice quadrata A è associato un numero reale det(a) detto determinante
Metodi per la risoluzione di sistemi lineari Sistemi di equazioni lineari. Rango di matrici Come è noto (vedi [] sez.0.8), ad ogni matrice quadrata A è associato un numero reale det(a) detto determinante
Equazioni differenziali. f(x, u, u,...,u (n) )=0,
 Lezione Equazioni differenziali Un equazione differenziale è una relazione del tipo f(x, u, u,...,u (n) )=, che tiene conto del valori di una funzione (incognita) u e delle sue derivate fino ad un certo
Lezione Equazioni differenziali Un equazione differenziale è una relazione del tipo f(x, u, u,...,u (n) )=, che tiene conto del valori di una funzione (incognita) u e delle sue derivate fino ad un certo
Massimi e minimi vincolati
 Massimi e minimi vincolati Vedremo tra breve un metodo per studiare il problema di trovare il minimo e il massimo di una funzione su di un sottoinsieme dello spazio ambiente che non sia un aperto. Abbiamo
Massimi e minimi vincolati Vedremo tra breve un metodo per studiare il problema di trovare il minimo e il massimo di una funzione su di un sottoinsieme dello spazio ambiente che non sia un aperto. Abbiamo
Modellazione e controllo Ca1 (a,b,c) Ca2 (d,e,f,g) Mec(a,c,d,e,g)
 Modellazione e controllo Ca1 (a,b,c) Ca (d,e,f,g) Mec(a,c,d,e,g) 13 Luglio 011 a) Una corpo di massa M e soggetto a una forza di richiamo elastica F el = K(x)x, una forza di attrito F att = hẋ e una forza
Modellazione e controllo Ca1 (a,b,c) Ca (d,e,f,g) Mec(a,c,d,e,g) 13 Luglio 011 a) Una corpo di massa M e soggetto a una forza di richiamo elastica F el = K(x)x, una forza di attrito F att = hẋ e una forza
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI
 CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
FM210 - Fisica Matematica I
 Corso di laurea in Matematica - Anno Accademico 22/3 FM2 - Fisica Matematica I Appello Scritto [6-9-23] SOLUZIONI Esercizio Il sistema è della forma ẋ = Ax + b con A = b =. Cerchiamo gli autovalori della
Corso di laurea in Matematica - Anno Accademico 22/3 FM2 - Fisica Matematica I Appello Scritto [6-9-23] SOLUZIONI Esercizio Il sistema è della forma ẋ = Ax + b con A = b =. Cerchiamo gli autovalori della
Analisi Matematica 3 (Fisica) Prova scritta del 17 febbraio 2012 Un breve svolgimento delle versioni A
 Analisi Matematica 3 (Fisica) Prova scritta del 7 febbraio Un breve svolgimento delle versioni A Vi sarò grato per la segnalazione di eventuali errori. Esercizio. (a) Dimostrare che l equazione () (3 +
Analisi Matematica 3 (Fisica) Prova scritta del 7 febbraio Un breve svolgimento delle versioni A Vi sarò grato per la segnalazione di eventuali errori. Esercizio. (a) Dimostrare che l equazione () (3 +
AUTOMATICA I (Ingegneria Biomedica - Allievi da L a Z) Appello dell 8 luglio 2008: testo e soluzione
 AUTOMATICA I (Ingegneria Biomedica - Allievi da L a Z) Appello dell 8 luglio 8: testo e soluzione Prof. Maria Prandini 1. Si consideri il sistema con ingresso u ed uscita y descritto dalle seguenti equazioni:
AUTOMATICA I (Ingegneria Biomedica - Allievi da L a Z) Appello dell 8 luglio 8: testo e soluzione Prof. Maria Prandini 1. Si consideri il sistema con ingresso u ed uscita y descritto dalle seguenti equazioni:
Equazioni separabili. Un esempio importante
 Equazioni separabili. Un esempio importante Esempio La soluzione generale dell equazione y = αy, α R (1) è data da y(x) = Ke αx, K R (2) C è un unica soluzione costante: y = 0: cioè y(x) = 0 per ogni x.
Equazioni separabili. Un esempio importante Esempio La soluzione generale dell equazione y = αy, α R (1) è data da y(x) = Ke αx, K R (2) C è un unica soluzione costante: y = 0: cioè y(x) = 0 per ogni x.
Equazioni differenziali
 Equazioni differenziali Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Equazioni differenziali Analisi Matematica 1 1 / 30 Formulazione del problema In generale
Equazioni differenziali Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Equazioni differenziali Analisi Matematica 1 1 / 30 Formulazione del problema In generale
Serie di Fourier. (Metodi Matematici e Calcolo per Ingegneria) Enrico Bertolazzi. DIMS Università di Trento. anno accademico 2008/2009
 Serie di Fourier (Metodi Matematici e Calcolo per Ingegneria) Enrico Bertolazzi DIMS Università di Trento anno accademico 8/9 Serie di Fourier 1 / 48 Jean Baptiste Joseph Fourier (1768 183) Serie di Fourier
Serie di Fourier (Metodi Matematici e Calcolo per Ingegneria) Enrico Bertolazzi DIMS Università di Trento anno accademico 8/9 Serie di Fourier 1 / 48 Jean Baptiste Joseph Fourier (1768 183) Serie di Fourier
Metodi per la risoluzione di sistemi lineari
 Metodi per la risoluzione di sistemi lineari 1 Sistemi di equazioni lineari 1.1 Determinante di matrici quadrate Ad ogni matrice quadrata A è associato un numero reale det(a) detto determinante della matrice
Metodi per la risoluzione di sistemi lineari 1 Sistemi di equazioni lineari 1.1 Determinante di matrici quadrate Ad ogni matrice quadrata A è associato un numero reale det(a) detto determinante della matrice
Analisi Matematica II, Anno Accademico Ingegneria Edile, Civile, Ambientale Paolo Acquistapace, Laura Cremaschi, Vincenzo M.
 Analisi Matematica II, Anno Accademico 14-15. Ingegneria Edile, Civile, Ambientale Paolo Acquistapace, Laura Cremaschi, Vincenzo M. Tortorelli TEST iniziale sugli argomenti dei corsi di matematica del
Analisi Matematica II, Anno Accademico 14-15. Ingegneria Edile, Civile, Ambientale Paolo Acquistapace, Laura Cremaschi, Vincenzo M. Tortorelli TEST iniziale sugli argomenti dei corsi di matematica del
Esercizi sulle equazioni differenziali
 Esercizi sulle equazioni differenziali Equazioni differenziali lineari del primo ordine. () u (t) = t [t + u(t)]; () u(t) sin t + u (t) = cos t u (t) sin t; (3) u(t) = + t u (t) + ; Risolvere i seguenti
Esercizi sulle equazioni differenziali Equazioni differenziali lineari del primo ordine. () u (t) = t [t + u(t)]; () u(t) sin t + u (t) = cos t u (t) sin t; (3) u(t) = + t u (t) + ; Risolvere i seguenti
Inversione della trasformata di Laplace
 Inversione della trasformata di Laplace (Metodi Matematici e Calcolo per Ingegneria) Enrico Bertolazzi DIMS Università di Trento anno accademico 2008/2009 Inversione della trasformata di Laplace 1 / 28
Inversione della trasformata di Laplace (Metodi Matematici e Calcolo per Ingegneria) Enrico Bertolazzi DIMS Università di Trento anno accademico 2008/2009 Inversione della trasformata di Laplace 1 / 28
Operazioni elementari sui sistemi di erenziali
 Capitolo 3 Operazioni elementari sui sistemi di erenziali 3.1 Derivate lungo le soluzioni Uno strumento fondamentale nello studio delle proprietà di un sistema differenziale è la derivata di opportune
Capitolo 3 Operazioni elementari sui sistemi di erenziali 3.1 Derivate lungo le soluzioni Uno strumento fondamentale nello studio delle proprietà di un sistema differenziale è la derivata di opportune
Soluzione della Prova Scritta di Analisi Matematica III - 28/02/02. C.L. in Matematica e Matematica per le Applicazioni. Prof. Kevin R.
 Soluzione della Prova Scritta di Analisi Matematica III - 28/2/2 C.L. in Matematica e Matematica per le Applicazioni Prof. Kevin R. Payne Esercizio 1. 1a. Teorema: (di ini) Sia Φ : A R n R R dove A è aperto.
Soluzione della Prova Scritta di Analisi Matematica III - 28/2/2 C.L. in Matematica e Matematica per le Applicazioni Prof. Kevin R. Payne Esercizio 1. 1a. Teorema: (di ini) Sia Φ : A R n R R dove A è aperto.
Equazioni di Stato: soluzione tramite la matrice esponenziale
 Equazioni di Stato: soluzione tramite la matrice esponenziale A. Laudani November 15, 016 Un po di Sistemi Consideriamo il problema di Cauchy legato allo stato della nostra rete elettrica {Ẋ(t) = A X(t)
Equazioni di Stato: soluzione tramite la matrice esponenziale A. Laudani November 15, 016 Un po di Sistemi Consideriamo il problema di Cauchy legato allo stato della nostra rete elettrica {Ẋ(t) = A X(t)
Metodo del Gradiente Coniugato. Enrico Bertolazzi
 1 Metodo del Gradiente Coniugato Enrico Bertolazzi 2 Problema: data matrice A SPD SPD=simmetrica e definita positiva) Trovare la soluzione del sistema lineare Ax = b E equivalente a trovare il minimo della
1 Metodo del Gradiente Coniugato Enrico Bertolazzi 2 Problema: data matrice A SPD SPD=simmetrica e definita positiva) Trovare la soluzione del sistema lineare Ax = b E equivalente a trovare il minimo della
Introduzione ai sistemi dinamici
 Introduzione ai sistemi dinamici Prof. G. Ferrari Trecate, Prof. D.M. Raimondo Dipartimento di Ingegneria Industriale e dell Informazione (DIII) Università degli Studi di Pavia Fondamenti di Automatica
Introduzione ai sistemi dinamici Prof. G. Ferrari Trecate, Prof. D.M. Raimondo Dipartimento di Ingegneria Industriale e dell Informazione (DIII) Università degli Studi di Pavia Fondamenti di Automatica
2.1 Osservazioni sull esercitazione del
 ¾ ½¾º¼ º¾¼½ Queste note (attualmente, e probabilmente per un bel po ) sono altamente provvisorie e (molto probabilmente) non prive di errori. 2.1 Osservazioni sull esercitazione del 5.3.214 2.1.1 Equazione
¾ ½¾º¼ º¾¼½ Queste note (attualmente, e probabilmente per un bel po ) sono altamente provvisorie e (molto probabilmente) non prive di errori. 2.1 Osservazioni sull esercitazione del 5.3.214 2.1.1 Equazione
4.1 Introduzione. In questo capitolo consideriamo l equazione differenziale. ẋ = f(t, x) (1) x 1 (t) x n (t) f n (t, x 1,...
 TEORIA QUALITATIVA DELLE EQUAZIONI DIFFERENZIALI 4.1 Introduzione. In questo capitolo consideriamo l equazione differenziale dove e ẋ = f(t, x) (1) x 1 (t) x =., x n (t) f 1 (t, x 1,..., x n ) f(t, x)
TEORIA QUALITATIVA DELLE EQUAZIONI DIFFERENZIALI 4.1 Introduzione. In questo capitolo consideriamo l equazione differenziale dove e ẋ = f(t, x) (1) x 1 (t) x =., x n (t) f 1 (t, x 1,..., x n ) f(t, x)
Esame di Fisica Matematica 2, a.a (8/7/2014)
 Esame di Fisica Matematica 2, a.a. 23-24 (8/7/24) Tempo a disposizione: DUE ORE. Svolgere tutti gli esercizi, che hanno lo stesso nel determinare il voto finale. Scrivere chiaramente e a stampatello nome,
Esame di Fisica Matematica 2, a.a. 23-24 (8/7/24) Tempo a disposizione: DUE ORE. Svolgere tutti gli esercizi, che hanno lo stesso nel determinare il voto finale. Scrivere chiaramente e a stampatello nome,
Equazioni differenziali
 Equazioni differenziali Samuele MONGODI - 14/08/01 Un equazione differenziale è un equazione che coinvolge una funzione reale u : R R, le sue derivate e la variabile indipendente (u = u(t)). Esempi 1.
Equazioni differenziali Samuele MONGODI - 14/08/01 Un equazione differenziale è un equazione che coinvolge una funzione reale u : R R, le sue derivate e la variabile indipendente (u = u(t)). Esempi 1.
Analisi Matematica 3/Analisi 4 - SOLUZIONI (20/01/2016)
 Corso di Laurea in Matematica Docente: Claudia Anedda Analisi Matematica 3/Analisi 4 - SOLUZIONI (//6) ) i) Dopo averla classificata, risolvere l equazione differenziale tẋ x = t cos(t), t >. ii) Scrivere
Corso di Laurea in Matematica Docente: Claudia Anedda Analisi Matematica 3/Analisi 4 - SOLUZIONI (//6) ) i) Dopo averla classificata, risolvere l equazione differenziale tẋ x = t cos(t), t >. ii) Scrivere
Esistenza ed unicità per equazioni differenziali
 Esistenza ed unicità per equazioni differenziali Per concludere queste lezioni sulle equazioni differenziali vogliamo dimostrare il teorema esistenza ed unicità per il problema di Cauchy. Faremo la dimostrazione
Esistenza ed unicità per equazioni differenziali Per concludere queste lezioni sulle equazioni differenziali vogliamo dimostrare il teorema esistenza ed unicità per il problema di Cauchy. Faremo la dimostrazione
FONDAMENTI DI AUTOMATICA (Ingegneria Biomedica) Appello del 16 febbraio 2010: testo e soluzione. y = x 1
 FONDAMENTI DI AUTOMATICA (Ingegneria Biomedica) Appello del 16 febbraio 21: testo e soluzione Prof. Maria Prandini 1. Si consideri il sistema descritto dalle seguenti equazioni: ẋ 1 = x 2 2 + x 1 ẋ 2 =
FONDAMENTI DI AUTOMATICA (Ingegneria Biomedica) Appello del 16 febbraio 21: testo e soluzione Prof. Maria Prandini 1. Si consideri il sistema descritto dalle seguenti equazioni: ẋ 1 = x 2 2 + x 1 ẋ 2 =
La miglior approssimazione esiste se le funzioni descrivono un chiuso
 NON SMOOTH Funzione non C 1 tipico esempio massimo numero finito funzioni Φ(x) = max { f i (x), i I, f i C 1 } e anche massimo(sup) puntuale Φ(x) = sup { f t (x), t I, f t C 1 } Esempi a) Max numero finito
NON SMOOTH Funzione non C 1 tipico esempio massimo numero finito funzioni Φ(x) = max { f i (x), i I, f i C 1 } e anche massimo(sup) puntuale Φ(x) = sup { f t (x), t I, f t C 1 } Esempi a) Max numero finito
Cognome: Nome: Matricola: a. Si enunci e dimostri il teorema della media integrale per funzioni continue. (5 punti)
 Analisi e Geometria Seconda Prova 3 gennaio 207 Docente: Politecnico di Milano Scuola di Ingegneria Industriale e dell Informazione Cognome: Nome: Matricola: a. Si enunci e dimostri il teorema della media
Analisi e Geometria Seconda Prova 3 gennaio 207 Docente: Politecnico di Milano Scuola di Ingegneria Industriale e dell Informazione Cognome: Nome: Matricola: a. Si enunci e dimostri il teorema della media
AUTOMATICA I (Ingegneria Biomedica - Allievi da L a Z) Appello del 20 luglio 2006: testo e soluzione
 AUTOMATICA I (Ingegneria Biomedica - Allievi da L a Z) Appello del 2 luglio 26: testo e soluzione Prof. Maria Prandini 1. Si consideri il sistema lineare con ingresso u ed uscita y descritto dalle seguenti
AUTOMATICA I (Ingegneria Biomedica - Allievi da L a Z) Appello del 2 luglio 26: testo e soluzione Prof. Maria Prandini 1. Si consideri il sistema lineare con ingresso u ed uscita y descritto dalle seguenti
Equazioni differenziali II. Elisabetta Colombo
 Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2011-2012, http://users.mat.unimi.it/users/colombo/programmabio.html Eq. diff.ii Eq. diff.ii 1 2 I differenziali Esercizio Quali
Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2011-2012, http://users.mat.unimi.it/users/colombo/programmabio.html Eq. diff.ii Eq. diff.ii 1 2 I differenziali Esercizio Quali
Definizione di Sistema Dinamico
 Capitolo 1. INTRODUZIONE 1.1 Definizione di Sistema Dinamico Esistono vari tipi di sistemi dinamici: tempo continui, tempo discreti, lineari, non lineari, a variabili concentrate, a variabili distribuite,
Capitolo 1. INTRODUZIONE 1.1 Definizione di Sistema Dinamico Esistono vari tipi di sistemi dinamici: tempo continui, tempo discreti, lineari, non lineari, a variabili concentrate, a variabili distribuite,
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA CHIMICA E DEI MATERIALI 27 GIUGNO 2016
 FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA CHIMICA E DEI MATERIALI 7 GIUGNO 06 MATTEO LONGO Ogni versione del compito contiene solo due tra i quattro esercizi 6-7-8-9. Esercizio. Considerare
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA CHIMICA E DEI MATERIALI 7 GIUGNO 06 MATTEO LONGO Ogni versione del compito contiene solo due tra i quattro esercizi 6-7-8-9. Esercizio. Considerare
COMPITO A: soluzione
 PROVA SCRITTA DI FONDAMENTI DI AUTOMATICA (PRIMA PARTE) A.A. 2005/2006 9 novembre 2005 nome e cognome: numero di matricola: Note: Scrivere le risposte negli spazi appositi. Non consegnare fogli aggiuntivi.
PROVA SCRITTA DI FONDAMENTI DI AUTOMATICA (PRIMA PARTE) A.A. 2005/2006 9 novembre 2005 nome e cognome: numero di matricola: Note: Scrivere le risposte negli spazi appositi. Non consegnare fogli aggiuntivi.
DIFFERENZIAZIONE. Sia f una funzione reale di variabile reale con dominio un intervallo. Se f è derivabile in un punto x 0, allora: f(x) f(x 0 ) lim
 DIFFERENZIAZIONE 1 Regola della catena Sia f una funzione reale di variabile reale con dominio un intervallo. Se f è derivabile in un punto x 0, allora: f(x) f(x 0 ) lim = f (x 0 ). x x 0 x x 0 Questa
DIFFERENZIAZIONE 1 Regola della catena Sia f una funzione reale di variabile reale con dominio un intervallo. Se f è derivabile in un punto x 0, allora: f(x) f(x 0 ) lim = f (x 0 ). x x 0 x x 0 Questa
Geometria affine e proiettiva
 Geometria affine e proiettiva Laura Facchini 7 aprile 20 Esercizio. Sia E 4 il 4-spazio euclideo numerico dotato del riferimento cartesiano standard di coordinate (x, y, z, w. Siano P (0, 0,,, P (, 2,,,
Geometria affine e proiettiva Laura Facchini 7 aprile 20 Esercizio. Sia E 4 il 4-spazio euclideo numerico dotato del riferimento cartesiano standard di coordinate (x, y, z, w. Siano P (0, 0,,, P (, 2,,,
Analisi Matematica II Corso di Ingegneria Gestionale Compito del f(x, y) = sin( x 2 + 2y 2 )
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del 9--9 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo - Le risposte senza giustificazione sono considerate nulle Esercizio
Analisi Matematica II Corso di Ingegneria Gestionale Compito del 9--9 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo - Le risposte senza giustificazione sono considerate nulle Esercizio
Rette e piani nello spazio
 Rette e piani nello spazio Equazioni parametriche di una retta in R 3 : x(t) = x 0 + at r(t) : y(t) = y 0 + bt t R, parametro z(t) = z 0 + ct ovvero r(t) : X(t) = P 0 + vt, t R}, dove: P 0 = (x 0, y 0,
Rette e piani nello spazio Equazioni parametriche di una retta in R 3 : x(t) = x 0 + at r(t) : y(t) = y 0 + bt t R, parametro z(t) = z 0 + ct ovvero r(t) : X(t) = P 0 + vt, t R}, dove: P 0 = (x 0, y 0,
Esprimendo il vettore (u, v) in coordinate polari (u = r cos θ, v = r sin θ), si ha. = u2 v 0 0 u 0 v
 Università di Milano - Bicocca Corso di laurea di primo livello in Scienze statistiche ed economiche Corso di laurea di primo livello in Statistica e gestione delle informazioni Matematica II rova scritta
Università di Milano - Bicocca Corso di laurea di primo livello in Scienze statistiche ed economiche Corso di laurea di primo livello in Statistica e gestione delle informazioni Matematica II rova scritta
4.5 Metodo del gradiente
 4.5 Metodo del gradiente Si cerca un punto stazionario di f : R n R con f C 1. Metodo del gradiente con ricerca 1-D esatta: Scegliere x 0, porre k := 0 Iterazione: d k := f(x k ) Determinare α k > 0 tale
4.5 Metodo del gradiente Si cerca un punto stazionario di f : R n R con f C 1. Metodo del gradiente con ricerca 1-D esatta: Scegliere x 0, porre k := 0 Iterazione: d k := f(x k ) Determinare α k > 0 tale
Introduzione alle equazioni differenziali attraverso esempi. 20 Novembre 2018
 Introduzione alle equazioni differenziali attraverso esempi 20 Novembre 2018 Indice: Equazioni separabili. Esistenza e unicità locale della soluzione di un Problemi di Cauchy. Equazioni differenziali lineari
Introduzione alle equazioni differenziali attraverso esempi 20 Novembre 2018 Indice: Equazioni separabili. Esistenza e unicità locale della soluzione di un Problemi di Cauchy. Equazioni differenziali lineari
2.1 Esponenziale di matrici
 ¾ ½ º¼ º¾¼½ Queste note (attualmente e probabilmente per un bel po sono altamente provvisorie e (molto probabilmente non prive di errori Esponenziale di matrici Esercizio : Data la matrice λ A λ calcolare
¾ ½ º¼ º¾¼½ Queste note (attualmente e probabilmente per un bel po sono altamente provvisorie e (molto probabilmente non prive di errori Esponenziale di matrici Esercizio : Data la matrice λ A λ calcolare
Equazioni differenziali II. Elisabetta Colombo
 Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2014-2015, http://users.mat.unimi.it/users/colombo/programmabio.html Eq. diff.ii Eq. diff.ii 1 2 I differenziali I Esercizio Quali
Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2014-2015, http://users.mat.unimi.it/users/colombo/programmabio.html Eq. diff.ii Eq. diff.ii 1 2 I differenziali I Esercizio Quali
Esercizi su curvatura e torsione.
 Esercizi su curvatura e torsione. e-mail: maurosaita@tiscalinet.it Versione provvisoria, gennaio 016. 1 Indice 1 Curvatura e torsione 1.1 Curve parametrizzate alla lunghezza d arco................... 1.
Esercizi su curvatura e torsione. e-mail: maurosaita@tiscalinet.it Versione provvisoria, gennaio 016. 1 Indice 1 Curvatura e torsione 1.1 Curve parametrizzate alla lunghezza d arco................... 1.
Esame di Fisica Matematica 2, a.a (8/9/2014)
 Esame di Fisica Matematica 2, a.a. 213-214 (8/9/214) Tempo a disposizione: DUE ORE. Svolgere tutti gli esercizi, che hanno lo stesso nel determinare il voto finale. Scrivere chiaramente e a stampatello
Esame di Fisica Matematica 2, a.a. 213-214 (8/9/214) Tempo a disposizione: DUE ORE. Svolgere tutti gli esercizi, che hanno lo stesso nel determinare il voto finale. Scrivere chiaramente e a stampatello
Fondamenti di Analisi Matematica 2 - a.a. 2016/2017 Primo appello
 Fondamenti di Analisi Matematica 2 - a.a. 216/217 Primo appello Esercizi senza svolgimento - Tema 1 Ω = { x, y, z) R 3 : 4x 2 + y 2 + z 2 1, z }. x = ρ/2) sen ϕ cos ϑ, 1. y = ρ sen ϕ sen ϑ, ρ [, 1], ϕ
Fondamenti di Analisi Matematica 2 - a.a. 216/217 Primo appello Esercizi senza svolgimento - Tema 1 Ω = { x, y, z) R 3 : 4x 2 + y 2 + z 2 1, z }. x = ρ/2) sen ϕ cos ϑ, 1. y = ρ sen ϕ sen ϑ, ρ [, 1], ϕ
A Analisi Matematica 2 (Corso di Laurea in Informatica) Simulazione compito d esame
 COGNOME NOME Matr. Firma dello studente A Analisi Matematica (Corso di Laurea in Informatica) Simulazione compito Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni
COGNOME NOME Matr. Firma dello studente A Analisi Matematica (Corso di Laurea in Informatica) Simulazione compito Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni
Esame di Complementi di Matematica Corso di Laurea Triennale in Scienza dei Materiali 1 Febbraio 2007
 Esame di Complementi di Matematica Corso di Laurea Triennale in Scienza dei Materiali 1 Febbraio 27 Motivare le soluzioni. Risposte prive di spiegazioni non saranno considerate valide. Risolvere almeno
Esame di Complementi di Matematica Corso di Laurea Triennale in Scienza dei Materiali 1 Febbraio 27 Motivare le soluzioni. Risposte prive di spiegazioni non saranno considerate valide. Risolvere almeno
Aritmetica 2009/10 Compitino 1/12/2009. (a) Contare gli elementi nilpotenti di A. (b) Contare gli elementi zero-divisori di A.
 Aritmetica 2009/10 Compitino 1/12/2009 1. Sia A = Z2[x]/(x 5 + x 4 + 1). (a) Contare gli elementi nilpotenti di A. (b) Contare gli elementi zero-divisori di A. Possibile risoluzione: Il polinomio f(x)
Aritmetica 2009/10 Compitino 1/12/2009 1. Sia A = Z2[x]/(x 5 + x 4 + 1). (a) Contare gli elementi nilpotenti di A. (b) Contare gli elementi zero-divisori di A. Possibile risoluzione: Il polinomio f(x)
26 - Funzioni di più Variabili Limiti e Derivate
 Università degli Studi di Palermo Facoltà di Economia CdS Statistica per l Analisi dei Dati Appunti del corso di Matematica 26 - Funzioni di più Variabili Limiti e Derivate Anno Accademico 2013/2014 M.
Università degli Studi di Palermo Facoltà di Economia CdS Statistica per l Analisi dei Dati Appunti del corso di Matematica 26 - Funzioni di più Variabili Limiti e Derivate Anno Accademico 2013/2014 M.
