AM : Tracce delle lezioni- VI Settimana
|
|
|
- Angelo Fabbri
- 4 anni fa
- Visualizzazioni
Transcript
1 AM : Tracce delle lezioni- VI Settimana DIFFERENZIABILITÁ E MATRICE JACOBIANA Siano E, F due spazi normati, O aperto in E, f : O F, x O. Si dice che f é differenziabile in x se L L(E, F ) : f(x + h) = f(x) + Lh + ( h ) ( ) (per definizione, (h) F h E h 0 0). Tale L, se esiste é unica. Infatti: (L 1 L )(h) = ( h ) t(l 1 L )(h) = (L 1 L )(th) = ( t ) (L 1 L )(h) = (1) (L 1 L )(h) = 0 h. La trasformazione L in ( ) si chiama differenziale di f in x e si indica df(x). Proprietá delle funzioni differenziabili. Sia f differenziabile in x. Allora i) f é continua in x. Segue dalla continuitá di h df(x)h. ii) Per ogni h E, esiste la derivata direzionale, ovvero il vettore di F cosí definito f(x + th) f(x) (x) := lim = df(x)h h t 0 t (valore di df(x) lungo l incremento h) giacché Se E = R n ed e j é base canonica, scriveremo f(x+th) f(x) t (x) := f(x + te j ) f(x) (x) = lim x j e j t 0 t = df(x)h + (1). = df(x)e j e se inoltre F = R, x j (che si scrive anche f xj, j f, D j f,...) é un numero e si chiama derivata parziale di f fatta rispetto alla j-esima variabile. Quando F = R, il differenziale in x, df(x), é forma lineare su E e, se é anche E = R n, ( f(x) := (x),..., ) (x) x 1 x n si chiama gradiente di f in x, ed é il vettore che rappresenta df(x) nella base e j : df(x)h = df(x)( h j e j ) = h j df(x)e j = x j (x)h i =< f(x), h >= h (x) Se E = R n, F = R m, la matrice rappresentativa di df(x) nelle basi canoniche e j, ê i, j = 1,..., n, i = 1,..., m, é la matrice Jacobiana J f (x): df(x)(h) = J f (x)h h R n 1
2 Se m = 1, J f (x) é il vettore (riga) f(x). Se m > 1, f differenziabile in x 0 f(x 0+h) [ f(x 0 )+df(x 0 )h] h h 0 0 f i(x 0 +h) [ f i (x 0 )+<df(x 0 )h,ê i >] h h 0 0 i f i sono differenziabili con ( ) i i = df i (x 0 )e j =< df(x 0 )e j, ê i > e quindi J f (x 0 ) = x j x j ij ovvero, J f (x 0 ) é la matrice che ha per righe i vettori f i (x 0 ) e per colonne i vettori x j (x) che sono i vettori tangenti alle curve coordinate x j f(x 1,..., x j,..., x n ): n=1: Cammini differenziabili. Date γ i : (a, b) R, i = 1,..., m. γ := m i=1 γ i ê i é cammino in R m. Siccome una funzione lineare L : R R m é completamente determinata dal suo valore in 1 : L(t) = L(t1) = tl(1), il cammino (o traiettoria ) γ risulta differenziabile in t (a, b) se ovvero esiste v = m i=1 v i ê i tale che γ(t + τ) = γ(t) + τv + (τ) i = 1,..., m γ i (t) := lim τ 0 γ i (t + τ) γ i (t) τ γ(t) Il vettore γ(t) := v é il vettore tangente (e, se γ(t) = 0,, é il versore γ(t) tangente ) al cammino γ in γ(t); γ(t) é la velocitá con cui il punto che percorre il cammino γ passa per γ(t). I cammini (o traiettorie ) dotati di vettore tangente si chiamano differenziabili. DUE ESEMPI (i) γ(t) = (cos t, sin t), t [0, π) (equazione parametrica della circonferenza unitaria) é cammino differenziabile con γ(t) = ( sin t, cos t). Notiamo che < γ(t), γ(t) > 0 e quindi, come si vede subito, γ(t), applicato in γ(t), é il versore) alla circonferenza nel punto γ(t). (ii) (cos φ cos θ, cos φ sin θ, sin φ), θ [0, π), φ [ π, π] é rappresentazione parametrica di S = {(x, y, z) R 3 : x + y + z = 1}, sfera unitaria in R 3 : ogni punto della sfera, a parte i poli, sta esattamente su di un meridiano (di longitudine θ 0 ) e su di un parallelo (di latitudine φ 0 ) di equazione parametrica rispettivamente (cos φ cos θ 0, cos φ sin θ 0, sin φ) e (cos φ 0 cos θ, cos φ 0 sin θ, sin φ 0 ). I vettori tangenti a tali curve ( sin φ 0 cos θ 0, sin φ 0 sin θ 0, cos φ 0 ), ( cos φ 0 sin θ 0, cos φ 0 cos θ 0, 0), generano il piano tangente alla sfera nel punto (cos φ 0 cos θ 0, cos φ 0 sin θ 0, sin φ 0 ). = v i
3 DERIVATE PARZIALI E DIFFERENZIABILITÁ Definizione. Sia O aperto in R n. f C 1 (O, R) se le sue derivate parziali esistono e sono continue in O; f = (f 1,..., f m ) é di classe C 1 (O) sse lo sono le f i. Proposizione 1. Sia f C 1 (O, R m ). Allora f é differenziabile. Prova. Basta mostrarlo per funzioni scalari. Per semplicitá, lo dimostriamo per funzioni di due variabili. Da f x, f y continue segue ɛ > 0 δ = δ ɛ > 0 : (w) x x (v) + y (w) y (v) ɛ w, v B δ(u) O d Applicando il Teorema Fondamentale del Calcolo a f(τ, y + t) = (τ, y + t) dτ x d e a f(x, τ) = (x, τ) otteniamo dτ y [ ] f(x + s, y + t) f(x, y) (x, y)s + (x, y)t x y = f(x + s, y + t) f(x, y + t) (x, y)s + f(x, y + t) f(x, y) (x, y)t x y x+s [ ] y+t [ ] (τ, y + t) (x, y) dτ x x + (x, τ) (x, y) dτ y y x ɛ ( s + t ) se s + t δ ɛ ESEMPI E CONTROESEMPI (i) f(x, y) = xy x +y, se x + y 0, f(0, 0) = 0 é di classe C 1 (R \ (0, 0)) ed ha anche derivate parziali, nulle, in (0, 0). Ma non esiste per alcun h e h i, i = 1,, perché t f(tx, ty) non é continua in t = 0 (a meno che non sia xy = 0). In particolare, f non é continua in zero: una funzione puó avere derivate parziali in un punto senza essere continua in quel punto. (ii) f(x, y) = x y x 4 +y, f(0, 0) = 0. Siccome f(x, 0) = 0 x, é f x (x, 0) = 0 x. Allo stesso modo, f y (0, y) = 0 y. In particolare, f ha derivate parziali, nulle, in (0, 0). Poi, se x + y > 0, é f(tx,ty) x = y x t t x 4 +y t 0 e quindi anche nell origine esistono le derivate in tutte y le direzioni, ma non sono tutte nulle (come dovrebbero essere se la funzione fosse differenziabile). Siccome f(x, x ) 1, vediamo che y 3
4 una funzione puó essere derivabile, in un punto, lungo tutte le direzioni senza essere continua in quel punto. (iii) f(x, y) = x3 y x 6 +y, se x + y 0, f(0, 0) = 0 é di classe C 1 (R \ (0, 0)) ed ha derivate parziali, nulle, anche in (0, 0). Inoltre, in (0, 0), f é derivabile in tutte le direzioni: (0, 0) = lim f(tx,ty) = h t t tx lim 3 y = 0. Tuttavia f non é continua in (0, 0), perché f(x, x 3 ) 1. Dunque t t 4 x 6 +y una funzione puó avere derivate nulle lungo tutte le direzioni in un punto senza essere differenziabile in quel punto. (iv) f(x, y) = x3 y x +y se x + y 0, f(0, 0) = 0 x 6 +y ha derivata nulla in tutte le direzioni, ed é anche continua, in (0, 0), ma non é differenziabile in (0, 0), perché non va a zero al tendere f(x,y) f(0,0) x +y = x3 y x 6 +y di x + y a zero (vale infatti 1 lungo la cubica y = x3 ). Dunque una funzione continua puó avere derivate nulle in tutte le direzioni in un punto senza essere differenziabile in quel punto. CONSIDERAZIONI GEOMETRICHE Sia f C 1 (O, R), (0, 0) O R, f(0, 0) = 0. Allora, se (x, y) O, f(x, y) = f x (0, 0)x + f y (0, 0)y + ( x + y ) Ovvero, a meno di un errore di ordine superiore al primo, i valori di f, vicino all origine, sono quelli della funzione lineare z = df(0, 0)(x, y) = f x (0, 0)x + f y (0, 0)y ( ) In linguaggio geometrico: il grafico di df(0, 0), ovvero il piano per l origine in R 3, T f (0, 0) := {(x, y, f x (0, 0)x + f y (0, 0)y)} é il piano tangente al grafico di f nel punto (0, 0, f(0, 0)) = (0, 0, 0). Tale piano interseca i piani coordinati Oxz, Oyz, lungo le rette di equazione z = f x (0, 0)x, z = f y (0, 0)y, rette tangenti ai grafici di z = f(x, 0), z = f(0, y) restrizioni della z = f(x, y) rispettivamente ad Ox, Oy. I vettori tangenti a tali due curve, dati da (1, 0, f x (0, 0), (0, 1, f y (0, 0)y), generano lo spazio tangente 4
5 T f (0, 0) = {(x, y, f x (0, 0)x + f y (0, 0)y)} = {x(1, 0, f x (0, 0) + y(0, 1, f y (0, 0)) : x, y R} Notiamo che il generico vettore (x, y, f x (0, 0)x + f y (0, 0)y) in T f (0, 0) é il vettore tangente alla curva t (tx, ty, f(tx, ty)) (giacente nel piano generato dall asse Oz e dalla retta (tx, ty, 0) ed intersezione del grafico di f con tale piano). Dunque, i vettori del piano tangente sono vettori tangenti al grafico di f. Il piano T f si puó anche descrivere come il piano dei vettori ortogonali al vettore ( f x, f y, 1) = (1, 0, f x (0, 0) (0, 1, f y (0, 0)) che é vettore normale al grafico. Piú in generale, se f C 1 (O, R), x 0 O R n, l iperpiano in R n+1 T f (x 0 ) := {(x, f(x 0 )+ < f(x 0 ), x x 0 >) : x R n } passante per (x 0, f(x 0 )) e parallelo all iperpiano per l origine z =< f(x 0 ), h > (grafico di df(x 0 )) é il piano tangente al grafico di f, G f, in (x 0, f(x 0 )). L equazione del piano tangente é quindi z = f(x 0 )+ < f(x 0 ), x x 0 > Sezionando G f e T f (x 0 ) con il piano z = f(x 0 ) e proiettando tali sezioni sul piano z = 0, otteniamo la superfice di livello Σ := {x : f(x) = f(x 0 )} e la corrispondente retta tangente in x 0, data appunto da < f(x 0 ), x x 0 >= 0, retta per x 0 e ortogonale a f(x 0 ). Infine, f é direzione di massima pendenza del grafico di f in (x, f(x)): d f(x + th) =< f(x + th), h > e sup < f(x), h >= f(x) dt h =1 Se n=k m, X = X(t 1,..., t k ) = (X 1 (t 1,..., t k ),..., X m (t 1,..., t k )) parametrizza una k superfice in R m. Le curve su tale superfice, date da t X(t, t,..., t k ),..., t X(t 1,..., t) determinano k vettori tangenti alla k-superfice, le k colonne di J X, che indichiamo X t j = ( X 1 t j,..., Xm t j ). 5
6 REGOLA DELLA CATENA (derivazione di funzioni composte) Siano E, F, G spazi normati. Sia x E e siano B r (x) g B ρ (g(x)) F, B ρ (g(x)) f G Se g é differenziabile in x e f é differenziabile in g(x), allora f g é differenziabile in x e d(f g)(x) = df(g(x)) dg(x) e J f g (x) = J f (g(x)) J g (x) Prova. Sia h E, k(h) := g(x + h) g(x) = dg(x)h + (h), cosicché k(h) dg(x)h + ( h ) c h se h δ. Siccome f é differenziabile in g(x), si ha che f(g(x + h)) = f(g(x) + k(h)) = f(g(x)) + df(g(x))k + ω(k) = = f(g(x)) + [df(g(x)) dg(x)]h + (h) perché ω(k) ɛ k cɛ h se h << 1. L affermazione sulle matrici Jacobiane segue dal fatto che se L L(R n, R m ), U L(R m, R p ), la matrice rappresentativa del prodotto di composizione U L é il prodotto delle matrici rappresentative R n L R m U R p A U L = A U A L ESEMPIO DI DERIVAZIONE DI FUNZIONI COMPOSTE Derivazione lungo un cammino differenziabile Siano γ : (a, b) R n, f : R n R di classe C 1. Allora d dt f(γ(t)) = n (γ(t)) dγ j (t) = < f(γ(t)), γ(t) > x j dt É una conseguenza della regola della catena e del fatto che J f (x) = f (matrice riga) mentre J γ = γ (matrice colonna). 6
7 COMPLEMENTI 1. Matrice rappresentativa del prodotto di composizione. Se indichiamo con A L, A U e A U L le matrici rappresentative di L L(R n, R m ), di U L(R m, R p ) e di U L L(R n, R p ), allora A U L = A U A L (prodotto di matrici) Siano e j, j = 1,..., n, ê i, i = 1,..., m, ě l, l = 1,..., p basi in R n, R m, R p. Siano Le j = m i=1 (Le j ) i ê i, Uê i = p l=1 (Uê i) l ě l. Allora A U = ( (Uê i ) l ) i=1,...,m, l=1,...,p A L = ( (Le j ) i ),...,n, i=1,...,m A U L Ma (U L)e j = U ( m i=1 (Le j ) i ê i ) = e quindi m (Le j ) i Uê i = i=1 [ m (Le j ) i i=1 = ( ((U L)e j ) l ),...,n; l=1,...,p ] p (Uê i ) l ě l = l=1 m ((U L)e j ) l = (Le j ) i (Uê i ) l i=1 [ p m ] (Le j ) i (Uê i ) l ě l l=1 i=1 ovvero ((U L)e j ) l é l elemento di posto lj della matrice prodotto A U A L.. Il gradiente in coordinate polari.. Data f C 1 (R, R), scriviamo f in coordinate polari: g(ρ, θ) := f(ρ cos θ, ρ sin θ). Allora, g ρ = f x (ρ cos θ, ρ sin θ) cos θ + f y (ρ cos θ, ρ sin θ) sin θ g θ = f x (ρ cos θ, ρ sin θ)ρ sin θ + f y (ρ cos θ, ρ sin θ)ρ cos θ f x (ρ cos θ, ρ sin θ) = g ρ cos θ 1 ρ g θ sin θ f y (ρ cos θ, ρ sin θ) = g ρ sin θ + 1 ρ g θ cos θ f (ρ cos θ, ρ sin θ) = g ρ(ρ, θ) + 1 ρ g θ(ρ, θ) 7
8 COMPLEMENTI E ESERCIZI 1. Provare il Teorema di Heine-Cantor usando il Teorema di Weierstrass. ɛ > 0, x K, ω(f, x, δ) := sup{ρ(f(x ), f(x )) : x, x K B δ (x)} δ ɛ (x) := sup{δ > 0 : ω(f, x, δ) < ɛ} La funzione x δ ɛ (x) é inferiormente semicontinua, perché, se δ < δ ɛ (x), si ha y K, d(y, x) < δ ɛ (x) δ B δ (y) B δɛ(x)(x) ω(f, y, δ) ɛ δ ɛ (y) δ Per Weierstrass, esiste x K tale che δ ɛ (x) δ ɛ (x) x K. Dunque d(x, y) < δ ɛ (x) ρ(f(x), f(y)) ɛ. Provare il Teorema di Heine-Cantor usando il Teorema del ricoprimento finito. ɛ > 0, x K δ ɛ (x) x, x B δɛ(x)(x) ρ(f(x ), f(x )) < ɛ K compatto x j K, j = 1,..., p : K p d(x, y) < δ ɛ, x B δɛ(x j ) d(y, x j ) < δ ɛ + δ ɛ(x j ) 3. Tutte le norme in R n sono tra di loro equivalenti B δɛ(x j ) (x j ). Se δ ɛ := min j δ ɛ (x j ), < δ ɛ (x j ) ρ(f(x), f(y)) < ɛ Sia una norma su R n. Indichiamo con. la norma euclidea in R n. Proviamo che C c > 0 : c x x C x x E. Da x = n x j e j segue 1 x x j e j x j e j 1 = e j 1 x = C x In particolare, ció assicura che x é funzione continua in R n (munito della norma ) e quindi é dotata di minimo sul compatto { x = 1}, ovvero esiste x, con x = 1 tale che: x x se x = 1 e quindi x x x x 0 e quindi x x x = c x x. 4. Provare che, se f C(A, R) é localmente costante in A (cioé x A, B r (x) : f é costante in B r (x) A ) ed A é connesso, allora f é costante in A. 8
9 5. Def.: f C(E, R m ) é Lip loc (E) se x E, B r(x) (x) tale che f Lip(B r(x) (x)). Provare che f Lip loc (K), K compatto f Lip(K) Se no, x j, y j K : f(x j ) f(y j ) x j y j 1 +. Passando eventualmente a sottosuccessioni, possiamo supporre che x j j x K, y j j y K. Siccome f é limitata, necessariamente x j y j 0 e quindi x = y. Ma x j, y j B r(x) (x) per j grande e f Lip(B r(x) (x)), contraddizione. 6. Provare con un esempio che non é vero in generale che da ogni ricoprimento aperto si puó estrarre un sottoricoprimento numerabile. Sia X = l dotato della metrica x := sup n x(n). Sia E = N = {α : N {0, 1}. Questo insieme é non numerabile. Siccome α β l α β = 1, la famiglia (non numerabile) di aperti disgiunti B 1 (α)) é un ricoprimento di E e, chiaramente, cessa di essere tale non appena si lasci da parte anche un solo B 1 (α)). 7. Mostrare, con un esempio, che non é vero in generale che ogni successione limitata in uno spazio normato ammette una estratta convergente. Sia E = l dotato della norma α = ( α(j) ) 1. Siano e j (i) := δ ij. Allora e n e m = se n m e quindi e n non ha estratte convergenti, dato che nessuna sua sottosuccessione é di Cauchy (una successione x n in uno spazio metrico é di Cauchy se per ogni ɛ > 0 esiste n ɛ tale che x n x m ɛ se n, m n ɛ ; ovviamente ogni successione convergente é di Cauchy). 8. A connesso per archi A connesso. Siano O i, i = 1, aperti tali che A = (A O 1 ) (A O ) con A O i per i = 1,. Sia γ cammino continuo in A, con γ(0) O 1, γ(1) O. Siccome, per continuitá, γ(t) O 1 se t é vicino a t = 0, l intervallo I := {t [0, 1] : γ(τ) O 1 τ [0, t)} é un intervallo non vuoto e t := sup I < 1. Siccome, sempre per continuitá, γ(t) / O 1, si ha che γ(t) O e quindi, per continuitá, γ(t) O per t < t vicino a t. Dunque A O 1 O e cioé A é connesso. NOTA. Il viceversa é vero se A é aperto, ma non é vero in generale. 9
10 9 Sia f : A R m uniformemente continua in A X. Allora esiste f : A R continua e tale che f(x) = f(x) x A. Prova. Caso m = 1. Fissato ɛ > 0, sia δ ɛ tale che d(x, y) f(x) f(y) ɛ. Dato x A, esistono x k A tali che x k k x. In particolare, x k é di Cauchy, cioé d(x h, x k ) δ ɛ per h, k grandi. Quindi, per uniforme continuitá, f(x k ) f(x h ) ɛ e quindi f(x h ) é di Cauchy e quindi converge a qualche y. Notiamo che tale y dipende solo da x e non dalla approssimante x k. Infatti, se x k x e quindi, come sopra, f(x k) y per qualche y, si ha y y y f(x k ) + f(x k ) f(x k) + f(x k y k 0 e quindi y = y. Dunque f(x) := lim k f(x k ) é ben definita su A. Resta da provare che f é continua. Ma questo si vede subito: x n x, y n y f(x) f(y) f(x) f(x n ) + f(x n ) f(y n ) + f(y n ) f(y) ɛ+ f(x n ) f(y n ) se n é abbastanza grande. Siccome poi, se d(x, y) δ ɛ, risulta d(x n, y n ) 3δ se n é grande, si ha che f(x n ) f(y n ) ɛ se n é grande. In conclusione, f(x) f(y) 3ɛ. Se m > 1, l argomento precedente assicura che ogni componente ha una estensione continua a A e quindi f si prolunga a tutto A. 10. Sia f : E R. f si dice localmente costante in E se x E, B r (x) tale che f é costante in B r (x) E Notiamo che una funzione siffatta é necessariamente continua in E. 11. f localmente costante in E connesso per archi f é costante in E. Prova. Sia, per ogni x E, B r(x) (x) tale che f sia costante in B r(x) (x). Siano x, y E e sia γ cammino da x a y. Notiamo che (f γ)([0, 1]) é un intervallo, perché f γ é continua. Estraendo da {B r(x) (x) : x γ([0, 1])}, ricoprimento aperto del compatto γ([0, 1]), un sottoricoprimento finito, deduciamo che (f γ)([0, 1]) é un insieme finito di punti, che, trattandosi di un intervallo, deve ridursi a un punto. 1. Sia γ : [a, b] R n curva parametrica in R n e ϕ : [α, β] [a, b] biiezione. Allora γ(ϕ(τ)) : τ [α, β] é riparametrizzazione della curva (o cammino ) γ. Ovviamente le immagini ( sostegno delle curve γ e γ) γ([a, b]) e γ([α, β]) coincidono: le due curve descrivono (percorrono..) in modo diverso lo stesso insieme di R n. Mostrare che, se γ é cammino differenziabile e ϕ é derivabile, con ϕ(τ) > 0 τ, allora γ e γ hanno lo stesso versore tangente in ogni punto. 10
AM2: Tracce delle lezioni- IX Settimana INSIEMI DI LIVELLO, MINIMI VINCOLATI PRINCIPIO DEI MOLTIPLICATORI DI LAGRANGE
 AM2: Tracce delle lezioni- IX Settimana INSIEMI DI LIVELLO, MINIMI VINCOLATI PRINCIPIO DEI MOLTIPLICATORI DI LAGRANGE Sia g C 1 R 2 ), c R. L insieme γ = γ c := {x, y) R 2 : gx, y) = c} si chiama insieme
AM2: Tracce delle lezioni- IX Settimana INSIEMI DI LIVELLO, MINIMI VINCOLATI PRINCIPIO DEI MOLTIPLICATORI DI LAGRANGE Sia g C 1 R 2 ), c R. L insieme γ = γ c := {x, y) R 2 : gx, y) = c} si chiama insieme
AM : Tracce delle lezioni- II Settimana
 AM2 2010-11: Tracce delle lezioni- II Settimana SPAZI METRICI Sia X un insieme. Una d : X X : [0, + ) tale che (i) 0 d(u, v), u, v R n d(u, v) = 0 u = v (positivitá) (ii) d(u, v) = d(v, u) u, v R n (simmetria)
AM2 2010-11: Tracce delle lezioni- II Settimana SPAZI METRICI Sia X un insieme. Una d : X X : [0, + ) tale che (i) 0 d(u, v), u, v R n d(u, v) = 0 u = v (positivitá) (ii) d(u, v) = d(v, u) u, v R n (simmetria)
AM : Tracce delle lezioni- II Settimana
 AM210 2012-13: Tracce delle lezioni- II Settimana SPAZI METRICI Sia X un insieme. Una d : X X : [0, + ) tale che (i) 0 d(u, v), u, v R n d(u, v) = 0 u = v (positivitá) (ii) d(u, v) = d(v, u) u, v R n (simmetria)
AM210 2012-13: Tracce delle lezioni- II Settimana SPAZI METRICI Sia X un insieme. Una d : X X : [0, + ) tale che (i) 0 d(u, v), u, v R n d(u, v) = 0 u = v (positivitá) (ii) d(u, v) = d(v, u) u, v R n (simmetria)
Alcune nozioni di calcolo differenziale
 Alcune nozioni di calcolo differenziale G. Mastroeni, M. Pappalardo 1 Limiti per funzioni di piu variabili Supporremo noti i principali concetti algebrici e topologici relativi alla struttura dello spazio
Alcune nozioni di calcolo differenziale G. Mastroeni, M. Pappalardo 1 Limiti per funzioni di piu variabili Supporremo noti i principali concetti algebrici e topologici relativi alla struttura dello spazio
Le derivate parziali
 Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
1. Richiami. v = x 2 + y 2.
 Gli elementi del prodotto cartesiano 1. Richiami R 2 = x, y R} sono detti vettori. Ogni vettore v è una coppia ordinata ed i numeri reali x e y sono detti le componenti di v. In particolare si denota con
Gli elementi del prodotto cartesiano 1. Richiami R 2 = x, y R} sono detti vettori. Ogni vettore v è una coppia ordinata ed i numeri reali x e y sono detti le componenti di v. In particolare si denota con
IL CALCOLO DIFFERENZIALE PER FUNZIONI DI PIÙ VARIABILI
 IL CALCOLO DIFFERENZIALE PER FUNZIONI DI PIÙ VARIABILI 218-19 CLAUDIO BONANNO Richiamiamo le definizioni e le prime principali proprietà delle funzioni differenziabili di più variabili e a valori vettoriali
IL CALCOLO DIFFERENZIALE PER FUNZIONI DI PIÙ VARIABILI 218-19 CLAUDIO BONANNO Richiamiamo le definizioni e le prime principali proprietà delle funzioni differenziabili di più variabili e a valori vettoriali
COMPATTEZZA. i) X è compatto, cioè ogni ricoprimento aperto ammette un sottoricoprimento finito.
 1 COMPATTEZZA Sia X un sottoinsieme di R. Una famiglia A di sottoinsiemi aperti di R si dice ricoprimento aperto di X se X A, cioè se X è contenuto nell unione degli elementi di A. Una sottofamiglia di
1 COMPATTEZZA Sia X un sottoinsieme di R. Una famiglia A di sottoinsiemi aperti di R si dice ricoprimento aperto di X se X A, cioè se X è contenuto nell unione degli elementi di A. Una sottofamiglia di
0.1 Arco di curva regolare
 .1. ARCO DI CURVA REGOLARE 1.1 Arco di curva regolare Se RC(O, i, j, k ) è un riferimento cartesiano fissato per lo spazio euclideo E, e se v (t) = x(t) i + y(t) j + z(t) k è una funzione a valori vettoriali
.1. ARCO DI CURVA REGOLARE 1.1 Arco di curva regolare Se RC(O, i, j, k ) è un riferimento cartesiano fissato per lo spazio euclideo E, e se v (t) = x(t) i + y(t) j + z(t) k è una funzione a valori vettoriali
Corso di Matematica 3 o A.A. 2016/2017 Argomenti delle lezioni
 Corso di Matematica 3 o A.A. 2016/2017 Argomenti delle lezioni 1 lezione. Martedí 27 settembre. 2 ore. Richiami sulle applicazioni lineari tra spazi vettoriali di dimensione finita. Il teorema di rappresentazione.
Corso di Matematica 3 o A.A. 2016/2017 Argomenti delle lezioni 1 lezione. Martedí 27 settembre. 2 ore. Richiami sulle applicazioni lineari tra spazi vettoriali di dimensione finita. Il teorema di rappresentazione.
1. Richiami. v = x 2 + y 2.
 Gli elementi del prodotto cartesiano 1 Richiami R 2 = x, y R} sono detti vettori Ogni vettore v è una coppia ordinata ed i numeri reali x e y sono detti le componenti di v In particolare si denota con
Gli elementi del prodotto cartesiano 1 Richiami R 2 = x, y R} sono detti vettori Ogni vettore v è una coppia ordinata ed i numeri reali x e y sono detti le componenti di v In particolare si denota con
AM2: Tracce delle lezioni- X Settimana
 AM: Tracce delle lezioni- X Settimana EQUAZIONI DIFFERENZIALI ORDINARIE Equazioni differenziali lineari del I ordine Date le funzioni a(x), b(x) continue in (a, b) determinare, se esistono, le funzioni
AM: Tracce delle lezioni- X Settimana EQUAZIONI DIFFERENZIALI ORDINARIE Equazioni differenziali lineari del I ordine Date le funzioni a(x), b(x) continue in (a, b) determinare, se esistono, le funzioni
Definizione 1.1. Dato un insieme non vuoto X, si dice distanza una funzione d : X X R tale che
 1 Spazi metrici Definizione 1.1. Dato un insieme non vuoto X, si dice distanza una funzione d : X X R tale che 1) d(x, y) 0, x, y X; d(x, y) = 0 x = y, ) d(x, y) = d(y, x), x, y X, 3) d(x, z) d(x, y) +
1 Spazi metrici Definizione 1.1. Dato un insieme non vuoto X, si dice distanza una funzione d : X X R tale che 1) d(x, y) 0, x, y X; d(x, y) = 0 x = y, ) d(x, y) = d(y, x), x, y X, 3) d(x, z) d(x, y) +
Analisi 2 Fisica e Astronomia
 Analisi Fisica e Astronomia Appello scritto del 8 Luglio 0. Soluzione Esercizio 7 pti Sia α > 0 un parametro e consideriamo la curva piana γ : [0, ] R γt = t cos, t sin, se t 0, ], e γ0 = 0, 0. t α t α
Analisi Fisica e Astronomia Appello scritto del 8 Luglio 0. Soluzione Esercizio 7 pti Sia α > 0 un parametro e consideriamo la curva piana γ : [0, ] R γt = t cos, t sin, se t 0, ], e γ0 = 0, 0. t α t α
Gli argomenti denotati con un asterisco tra parentesi (e solo quelli) sono stati dimostrati.
 Corso di laurea: Fisica ed Astronomia Programma di Analisi Matematica 2 a.a. 2016/17 Docente: Fabio Paronetto Gli argomenti denotati con un asterisco tra parentesi (e solo quelli) sono stati dimostrati.
Corso di laurea: Fisica ed Astronomia Programma di Analisi Matematica 2 a.a. 2016/17 Docente: Fabio Paronetto Gli argomenti denotati con un asterisco tra parentesi (e solo quelli) sono stati dimostrati.
1. Mar. 17/1/06 2 ore Presentazione del corso. Libro di testo e altri testi consigliati. Alcune informazioni
 Università degli Studi di Firenze Anno Accademico 2005/2006 Ingegneria per l Ambiente e il Territorio Corso di Analisi Matematica 2 (IAT) Docente: Francesca Bucci Periodo: II periodo (16 gennaio 2006 17
Università degli Studi di Firenze Anno Accademico 2005/2006 Ingegneria per l Ambiente e il Territorio Corso di Analisi Matematica 2 (IAT) Docente: Francesca Bucci Periodo: II periodo (16 gennaio 2006 17
Gli argomenti denotati con un asterisco tra parentesi (e solo quelli) sono stati dimostrati.
 Corso di laurea: Fisica ed Astronomia Programma di Analisi Matematica 2 a.a. 2017/18 Docente: Fabio Paronetto Gli argomenti denotati con un asterisco tra parentesi (e solo quelli) sono stati dimostrati.
Corso di laurea: Fisica ed Astronomia Programma di Analisi Matematica 2 a.a. 2017/18 Docente: Fabio Paronetto Gli argomenti denotati con un asterisco tra parentesi (e solo quelli) sono stati dimostrati.
Analisi Matematica 2. Continuità, derivabilità e differenziabilità
 Docente: E. G. Casini Università degli Studi dell Insubria DIPATIMENTO DI SCIENZA E ALTA TECNOLOGIA Corso di Studio in Matematica e Fisica Analisi Matematica ichiami di Teoria ed Esercizi con Svolgimento
Docente: E. G. Casini Università degli Studi dell Insubria DIPATIMENTO DI SCIENZA E ALTA TECNOLOGIA Corso di Studio in Matematica e Fisica Analisi Matematica ichiami di Teoria ed Esercizi con Svolgimento
Esercizi del Corso di Istituzioni di Analisi Superiore, I modulo
 sercizi del Corso di Istituzioni di Analisi Superiore, I modulo 1. sercizi su massimo e minimo limite 1. lim inf a n lim sup a n 2. Se a n b n per ogni n N, allora lim inf a n lim inf b n. Vale anche lim
sercizi del Corso di Istituzioni di Analisi Superiore, I modulo 1. sercizi su massimo e minimo limite 1. lim inf a n lim sup a n 2. Se a n b n per ogni n N, allora lim inf a n lim inf b n. Vale anche lim
Corso di laurea: Ingegneria aerospaziale e meccanica Programma di Fondamenti di Analisi Matematica II a.a. 2015/16 Docente: Fabio Paronetto
 Corso di laurea: Ingegneria aerospaziale e meccanica Programma di Fondamenti di Analisi Matematica II a.a. 2015/16 Docente: Fabio Paronetto Gli argomenti denotati con un asterisco tra parentesi (e solo
Corso di laurea: Ingegneria aerospaziale e meccanica Programma di Fondamenti di Analisi Matematica II a.a. 2015/16 Docente: Fabio Paronetto Gli argomenti denotati con un asterisco tra parentesi (e solo
AM210/ : Tracce delle lezioni- Settimana XII
 AM21/214-15: Tracce delle lezioni- Settimana XII SPAZI METRICI ED IL TEOREMA DELLE CONTRAZIONI Spazi metrici completi, spazi di Banach Una successione x n in uno spazio metrico (X, d) si dice di Cauchy
AM21/214-15: Tracce delle lezioni- Settimana XII SPAZI METRICI ED IL TEOREMA DELLE CONTRAZIONI Spazi metrici completi, spazi di Banach Una successione x n in uno spazio metrico (X, d) si dice di Cauchy
Corso di laurea: Ingegneria aerospaziale e meccanica Programma di Fondamenti di Analisi Matematica II a.a. 2013/14 Docente: Fabio Paronetto
 Corso di laurea: Ingegneria aerospaziale e meccanica Programma di Fondamenti di Analisi Matematica II a.a. 2013/14 Docente: Fabio Paronetto Gli argomenti denotati con un asterisco tra parentesi (e solo
Corso di laurea: Ingegneria aerospaziale e meccanica Programma di Fondamenti di Analisi Matematica II a.a. 2013/14 Docente: Fabio Paronetto Gli argomenti denotati con un asterisco tra parentesi (e solo
Gli argomenti denotati con un asterisco tra parentesi (e solo quelli) sono stati dimostrati.
 Corso di laurea: Fisica ed Astronomia Programma di Analisi Matematica 2 a.a. 2018/19 Docente: Fabio Paronetto Gli argomenti denotati con un asterisco tra parentesi (e solo quelli) sono stati dimostrati.
Corso di laurea: Fisica ed Astronomia Programma di Analisi Matematica 2 a.a. 2018/19 Docente: Fabio Paronetto Gli argomenti denotati con un asterisco tra parentesi (e solo quelli) sono stati dimostrati.
Analisi Matematica 2
 Analisi Matematica 2 Differenziabilità per funzioni di due variabili Differenziabilità per funzioni di due variabili CCS Ingegneria Meccanica e Ingegneria Chimica 1 / 26 Differenziabilitá Data la funzione
Analisi Matematica 2 Differenziabilità per funzioni di due variabili Differenziabilità per funzioni di due variabili CCS Ingegneria Meccanica e Ingegneria Chimica 1 / 26 Differenziabilitá Data la funzione
Esame di Analisi Matematica 2 24/7/2013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 2012/2013
 Esame di Analisi Matematica 4/7/013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 01/013 A Cognome (in STAMPATELLO):... Nome (in STAMPATELLO):... CFU:... Esercizio 1. Sia f : R R una funzione
Esame di Analisi Matematica 4/7/013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 01/013 A Cognome (in STAMPATELLO):... Nome (in STAMPATELLO):... CFU:... Esercizio 1. Sia f : R R una funzione
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016
 Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
26 - Funzioni di più Variabili Limiti e Derivate
 Università degli Studi di Palermo Facoltà di Economia CdS Statistica per l Analisi dei Dati Appunti del corso di Matematica 26 - Funzioni di più Variabili Limiti e Derivate Anno Accademico 2013/2014 M.
Università degli Studi di Palermo Facoltà di Economia CdS Statistica per l Analisi dei Dati Appunti del corso di Matematica 26 - Funzioni di più Variabili Limiti e Derivate Anno Accademico 2013/2014 M.
Si dimostri che la (*) possiede un unica soluzione (u n ) limitata.
 Scuola Normale Superiore, ammissione al IV anno del corso ordinario Prova scritta di Analisi Matematica per Fisica, Informatica, Matematica 26 Agosto 2 Esercizio. Siano (a n ) e (b n ) successioni di numeri
Scuola Normale Superiore, ammissione al IV anno del corso ordinario Prova scritta di Analisi Matematica per Fisica, Informatica, Matematica 26 Agosto 2 Esercizio. Siano (a n ) e (b n ) successioni di numeri
Corso di laurea: Ingegneria aerospaziale e meccanica Programma di Fondamenti di Analisi Matematica II a.a. 2012/13 Docente: Fabio Paronetto
 Corso di laurea: Ingegneria aerospaziale e meccanica Programma di Fondamenti di Analisi Matematica II a.a. 2012/13 Docente: Fabio Paronetto Gli argomenti denotati con un asterisco tra parentesi (e solo
Corso di laurea: Ingegneria aerospaziale e meccanica Programma di Fondamenti di Analisi Matematica II a.a. 2012/13 Docente: Fabio Paronetto Gli argomenti denotati con un asterisco tra parentesi (e solo
2 + 2(seny) 2 per (x, y) (0, 0),
 Analisi II, a.a. 017-018 Soluzioni 1) Sia f la funzione di due variabili definita da xy α (senx) + (seny) per (x, y) (0, 0), 0 in (0, 0) dove α 0 è un parametro reale fissato. Determinare l insieme di
Analisi II, a.a. 017-018 Soluzioni 1) Sia f la funzione di due variabili definita da xy α (senx) + (seny) per (x, y) (0, 0), 0 in (0, 0) dove α 0 è un parametro reale fissato. Determinare l insieme di
Facoltà di Scienze MM.FF.NN. Corso di Laurea in Matematica - A.A Prova scritta di Analisi Matematica II del
 Prova scritta di nalisi Matematica II del 12-06-2001. C1 1) Studiare la convergenza semplice, uniforme e totale della serie di funzioni seguente ( 1) [ n 2 ] n x 1 + n 2 x. n=0 2) Data la funzione (x 2
Prova scritta di nalisi Matematica II del 12-06-2001. C1 1) Studiare la convergenza semplice, uniforme e totale della serie di funzioni seguente ( 1) [ n 2 ] n x 1 + n 2 x. n=0 2) Data la funzione (x 2
I teoremi della funzione inversa e della funzione implicita
 I teoremi della funzione inversa e della funzione implicita Appunti per il corso di Analisi Matematica 4 G. Mauceri Indice 1 Il teorema della funzione inversa 1 Il teorema della funzione implicita 3 1
I teoremi della funzione inversa e della funzione implicita Appunti per il corso di Analisi Matematica 4 G. Mauceri Indice 1 Il teorema della funzione inversa 1 Il teorema della funzione implicita 3 1
Funzioni di n variabili a valori vettoriali
 Funzioni di n variabili a valori vettoriali Ultimo aggiornamento: 22 maggio 2018 1 Differenziale per funzioni da R n in R k Una funzione F : A R n R k può essere vista come una k-upla di funzioni scalari
Funzioni di n variabili a valori vettoriali Ultimo aggiornamento: 22 maggio 2018 1 Differenziale per funzioni da R n in R k Una funzione F : A R n R k può essere vista come una k-upla di funzioni scalari
Tutorato di Complementi di Analisi Matematica e Statistica Parte di Analisi 6 e 10 aprile 2017
 Tutorato di Complementi di Analisi Matematica e Statistica Parte di Analisi 6 e 10 aprile 2017 Esercizi: serie di potenze e serie di Taylor 1 Date le serie di potenze a.) n=2 ln(n) n 3 (x 5)n b.) n=2 ln(n)
Tutorato di Complementi di Analisi Matematica e Statistica Parte di Analisi 6 e 10 aprile 2017 Esercizi: serie di potenze e serie di Taylor 1 Date le serie di potenze a.) n=2 ln(n) n 3 (x 5)n b.) n=2 ln(n)
ANALISI B alcuni esercizi proposti
 ANALISI B alcuni esercizi proposti G.P. Leonardi Parte II 1 Limiti e continuità per funzioni di 2 variabili Esercizio 1.1 Calcolare xy log(1 + x ) lim (x,y) (0,0) 2x 2 + 5y 2 Esercizio 1.2 Studiare la
ANALISI B alcuni esercizi proposti G.P. Leonardi Parte II 1 Limiti e continuità per funzioni di 2 variabili Esercizio 1.1 Calcolare xy log(1 + x ) lim (x,y) (0,0) 2x 2 + 5y 2 Esercizio 1.2 Studiare la
ARGOMENTI MATEMATICA PER L INGEGNERIA
 ARGOMENTI DI MATEMATICA PER L INGEGNERIA VOLUME 2 Esercizi proposti Quando non diversamente precisato, nel seguito si intenderà( sempre che nel piano sia stato introdotto un sistema cartesiano ortogonale
ARGOMENTI DI MATEMATICA PER L INGEGNERIA VOLUME 2 Esercizi proposti Quando non diversamente precisato, nel seguito si intenderà( sempre che nel piano sia stato introdotto un sistema cartesiano ortogonale
Richiami di Analisi II
 Richiami di Analisi II Kevin R. Payne Appunti per il Corso Analisi Matematica III CdL in Matematica e Matematica per le Applicazioni Università degli Studi di Milano settembre 2004 In questi appunti vogliamo
Richiami di Analisi II Kevin R. Payne Appunti per il Corso Analisi Matematica III CdL in Matematica e Matematica per le Applicazioni Università degli Studi di Milano settembre 2004 In questi appunti vogliamo
Geometria iperbolica - Primo foglio Andrea Petracci
 Geometria iperbolica - Primo foglio Andrea Petracci Esercizio 1. Teorema (Hopf-Rinow). Se M è una varietà riemanniana connessa, allora le seguenti affermazioni sono equivalenti: (1) M è completa con la
Geometria iperbolica - Primo foglio Andrea Petracci Esercizio 1. Teorema (Hopf-Rinow). Se M è una varietà riemanniana connessa, allora le seguenti affermazioni sono equivalenti: (1) M è completa con la
ESERCIZI DI ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 2006/2007
 ESERCIZI I ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 006/007 1 FUNZIONI IN UE VARIABILI (I parte) Insiemi di definizione eterminare gli insiemi di definizione delle seguenti funzioni in due
ESERCIZI I ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 006/007 1 FUNZIONI IN UE VARIABILI (I parte) Insiemi di definizione eterminare gli insiemi di definizione delle seguenti funzioni in due
Esercizi. Misti iniziali. Più variabili. 1. Data la funzione. F (x) = x3 3 + x e t2 dt. se ne studino massimi, minimi, flessi, limiti a ±.
 Esercizi Misti iniziali. Data la funzione se ne studino massimi, minimi, flessi, iti a ±. 2. Provare che Più variabili F x) = 3. Calcolare, se esistono, i seguenti iti a) b) c) d) x,y),) x 2 + y 2 2 x,y),)
Esercizi Misti iniziali. Data la funzione se ne studino massimi, minimi, flessi, iti a ±. 2. Provare che Più variabili F x) = 3. Calcolare, se esistono, i seguenti iti a) b) c) d) x,y),) x 2 + y 2 2 x,y),)
SPAZI METRICI COMPLETI
 Capitolo 1 SPAZI METRICI COMPLETI Sia dato uno spazio metrico (X, d). Definizione 1.1 Una successione {x n } si dice successione di Cauchy se ε > 0 n 0 n, m n 0 = d(x n x m ) < ε (1.1) Esercizio 1.1 Dimostrare
Capitolo 1 SPAZI METRICI COMPLETI Sia dato uno spazio metrico (X, d). Definizione 1.1 Una successione {x n } si dice successione di Cauchy se ε > 0 n 0 n, m n 0 = d(x n x m ) < ε (1.1) Esercizio 1.1 Dimostrare
Curve. Riccarda Rossi. Analisi Matematica B. Università di Brescia. Riccarda Rossi (Università di Brescia) Curve Analisi Matematica B 1 / 66
 Curve Riccarda Rossi Università di Brescia Analisi Matematica B Riccarda Rossi (Università di Brescia) Curve Analisi Matematica B 1 / 66 Introduzione Le curve sono particolari campi vettoriali Le vedremo
Curve Riccarda Rossi Università di Brescia Analisi Matematica B Riccarda Rossi (Università di Brescia) Curve Analisi Matematica B 1 / 66 Introduzione Le curve sono particolari campi vettoriali Le vedremo
Complementi di Analisi Matematica. Foglio di esercizi n.6 16/3/2018 (Aggiornamento del 6/4/2018)
 Complementi di Analisi Matematica. Foglio di esercizi n.6 16/3/2018 (Aggiornamento del 6/4/2018) Esercizio 1 Si consideri l insieme Esercizi sulla funzione implicita e superfici Z = {(x, y) R 2 2y xe y
Complementi di Analisi Matematica. Foglio di esercizi n.6 16/3/2018 (Aggiornamento del 6/4/2018) Esercizio 1 Si consideri l insieme Esercizi sulla funzione implicita e superfici Z = {(x, y) R 2 2y xe y
SPAZI TOPOLOGICI COMPATTI Note informali dalle lezioni
 SPAZI TOPOLOGICI COMPATTI Note informali dalle lezioni Sia X un insieme. Un ricoprimento di X è una famiglia U = {U j } j J di sottoinsiemi di X tali che X = j J U j. Un ricoprimento U = {U j } j J si
SPAZI TOPOLOGICI COMPATTI Note informali dalle lezioni Sia X un insieme. Un ricoprimento di X è una famiglia U = {U j } j J di sottoinsiemi di X tali che X = j J U j. Un ricoprimento U = {U j } j J si
Generalizzazioni del Teorema di Weierstrass
 Capitolo 2 Generalizzazioni del Teorema di Weierstrass Il principale riferimento bibliografico per questa lezione è il testo di Checcucci, Tognoli, Vesentini [1]. Introduzione Supponiamo che X = R n. È
Capitolo 2 Generalizzazioni del Teorema di Weierstrass Il principale riferimento bibliografico per questa lezione è il testo di Checcucci, Tognoli, Vesentini [1]. Introduzione Supponiamo che X = R n. È
PROGRAMMA DI ANALISI MATEMATICA 2 Corsi di Laurea in Ing. Informatica (Prof. Ravaglia) Anno Accademico 2015/16
 PROGRAMMA DI ANALISI MATEMATICA 2 Corsi di Laurea in Ing. Informatica (Prof. Ravaglia) Anno Accademico 2015/16 Simboli: I= introduzione intuitiva, D = definizione, T = teorema C = criterio deduttivo, d
PROGRAMMA DI ANALISI MATEMATICA 2 Corsi di Laurea in Ing. Informatica (Prof. Ravaglia) Anno Accademico 2015/16 Simboli: I= introduzione intuitiva, D = definizione, T = teorema C = criterio deduttivo, d
Soluzione della Prova Scritta di Analisi Matematica III - 28/02/02. C.L. in Matematica e Matematica per le Applicazioni. Prof. Kevin R.
 Soluzione della Prova Scritta di Analisi Matematica III - 28/2/2 C.L. in Matematica e Matematica per le Applicazioni Prof. Kevin R. Payne Esercizio 1. 1a. Teorema: (di ini) Sia Φ : A R n R R dove A è aperto.
Soluzione della Prova Scritta di Analisi Matematica III - 28/2/2 C.L. in Matematica e Matematica per le Applicazioni Prof. Kevin R. Payne Esercizio 1. 1a. Teorema: (di ini) Sia Φ : A R n R R dove A è aperto.
AM5 2008: Tracce delle lezioni- 4
 AM5 008: Tracce delle lezioni- 4 L e gli spazi di HILBERT f := f = < f, f > ove < f, g > := fg dµ, f, g L é un prodotto scalare (ovvero una forma bilineare simmetrica positiva) in L. Notiamo che la diseguaglianza
AM5 008: Tracce delle lezioni- 4 L e gli spazi di HILBERT f := f = < f, f > ove < f, g > := fg dµ, f, g L é un prodotto scalare (ovvero una forma bilineare simmetrica positiva) in L. Notiamo che la diseguaglianza
Anno accademico
 Scuola Normale Superiore Ammissione al 4 anno della Classe di Scienze Prova di Analisi per l ammissione alla Laurea Specialistica in Fisica applicata, Informatica, Matematica, Scienze fisiche, Tecnologie
Scuola Normale Superiore Ammissione al 4 anno della Classe di Scienze Prova di Analisi per l ammissione alla Laurea Specialistica in Fisica applicata, Informatica, Matematica, Scienze fisiche, Tecnologie
Appunti sul corso di Complementi di Matematica mod. Analisi prof. B.Bacchelli - a.a. 2010/2011.
 Appunti sul corso di Complementi di Matematica mod. Analisi prof. B.Baccelli - a.a. 2010/2011. 06 - Derivate, differenziabilità, piano tangente, derivate di ordine superiore. Riferimenti: R.Adams, Calcolo
Appunti sul corso di Complementi di Matematica mod. Analisi prof. B.Baccelli - a.a. 2010/2011. 06 - Derivate, differenziabilità, piano tangente, derivate di ordine superiore. Riferimenti: R.Adams, Calcolo
Analisi Matematica II
 Analisi Matematica II Limiti e continuità in R N Claudio Saccon 1 1 Dipartimento di Matematica, Via F. Buonarroti 1/C,56127 PISA email: claudio.sacconchiocciolaunipi.it sito web: http://pagine.dm.unipi.it/csblog1
Analisi Matematica II Limiti e continuità in R N Claudio Saccon 1 1 Dipartimento di Matematica, Via F. Buonarroti 1/C,56127 PISA email: claudio.sacconchiocciolaunipi.it sito web: http://pagine.dm.unipi.it/csblog1
Risoluzione del compito n. 5 (Luglio 2018/2)
 Risoluzione del compito n. 5 (Luglio 2018/2) PROBLEMA 1 Considerate il luogo di zeri S = {(x, y, z) R 3 : z 4+ x 2 + y 2 =0, 2x y + z =0}. a) Giustificando la risposta, dite se S è una curva liscia. b)
Risoluzione del compito n. 5 (Luglio 2018/2) PROBLEMA 1 Considerate il luogo di zeri S = {(x, y, z) R 3 : z 4+ x 2 + y 2 =0, 2x y + z =0}. a) Giustificando la risposta, dite se S è una curva liscia. b)
Esame scritto di Geometria 2
 Esame scritto di Geometria Università degli Studi di Trento Corso di laurea in Matematica A.A. 013/014 Settembre 014 Esercizio 1 Sia P 3 lo spazio proiettivo reale tridimensionale dotato del riferimento
Esame scritto di Geometria Università degli Studi di Trento Corso di laurea in Matematica A.A. 013/014 Settembre 014 Esercizio 1 Sia P 3 lo spazio proiettivo reale tridimensionale dotato del riferimento
1 Limiti di funzioni di più variabili
 1 Limiti di funzioni di più variabili Sia f : D R N R e x 0 un punto di accumulazione per D. Riportiamo alcune utili strategie per verificare se la funzione ammette o non ammette ite finito in x 0. Le
1 Limiti di funzioni di più variabili Sia f : D R N R e x 0 un punto di accumulazione per D. Riportiamo alcune utili strategie per verificare se la funzione ammette o non ammette ite finito in x 0. Le
Analisi Matematica II - INGEGNERIA Gestionale - B 20 luglio 2017 Cognome: Nome: Matricola:
 Analisi Matematica II - INGEGNERIA Gestionale - B luglio 7 Cognome: Nome: Matricola: IMPORTANTE: Giustificare tutte le affermazioni e riportare i calcoli essenziali Esercizio [8 punti] Data la matrice
Analisi Matematica II - INGEGNERIA Gestionale - B luglio 7 Cognome: Nome: Matricola: IMPORTANTE: Giustificare tutte le affermazioni e riportare i calcoli essenziali Esercizio [8 punti] Data la matrice
Analisi a più variabili: Integrazione sulle curve e superfici, forme differenziali
 Analisi a più variabili: Integrazione sulle curve e superfici, forme differenziali 1 Definizione (Parametrizzazione di T): T R n, una sua parametrizzazione è una coppia φ, con = a, b intervallo di R e
Analisi a più variabili: Integrazione sulle curve e superfici, forme differenziali 1 Definizione (Parametrizzazione di T): T R n, una sua parametrizzazione è una coppia φ, con = a, b intervallo di R e
Funzione derivabile. La derivata.
 Funzione derivabile. La derivata. Dati: f I R funzione; I R intervallo aperto ; x 0 I. Definizione (Derivata come limite del rapporto incrementale) Se esiste finito (cioè, non + o ) il limite del rapporto
Funzione derivabile. La derivata. Dati: f I R funzione; I R intervallo aperto ; x 0 I. Definizione (Derivata come limite del rapporto incrementale) Se esiste finito (cioè, non + o ) il limite del rapporto
Funzioni a valori vettoriali Differenziabilità e regola della catena
 e regola della catena Analisi Matematica A Secondo modulo Corso di Laurea in Matematica Università di Trento 4 aprile 2019 o: le curve o: F : R 2 R 2 Sia E R n. Una funzione a valori vettoriali f : E R
e regola della catena Analisi Matematica A Secondo modulo Corso di Laurea in Matematica Università di Trento 4 aprile 2019 o: le curve o: F : R 2 R 2 Sia E R n. Una funzione a valori vettoriali f : E R
1 Curve. Indice 1. Curve 2. Limiti
 Alcune Note di Calcolo Differenziale ed Integrale Multidimensionale per il corso di Analisi Matematica II a.a. 2011-12 A. Visintin Facoltà di Ingegneria di Trento Premessa. Questo scritto raccoglie alcune
Alcune Note di Calcolo Differenziale ed Integrale Multidimensionale per il corso di Analisi Matematica II a.a. 2011-12 A. Visintin Facoltà di Ingegneria di Trento Premessa. Questo scritto raccoglie alcune
TOPOLOGIA - APPUNTI SETTIMANA 2/12/2013-5/11/2013
 TOPOLOGIA - APPUNTI SETTIMANA 2/12/2013-5/11/2013 KIERAN G. O GRADY - 9 DICEMBRE 2013 1. Connessione Se X è uno spazio topologico connesso per archi vale il Teorema dei valori intermedi : dati una f :
TOPOLOGIA - APPUNTI SETTIMANA 2/12/2013-5/11/2013 KIERAN G. O GRADY - 9 DICEMBRE 2013 1. Connessione Se X è uno spazio topologico connesso per archi vale il Teorema dei valori intermedi : dati una f :
AM5: Tracce delle lezioni- V Settimana
 AM5: Tracce delle lezioni- V Settimana Sia µ misura su X, p. SPAZI L p L p = L p (X, µ) : = {f : X [, + ] f é misurabile e Siccome t + s p ( ) p s p + t p s, t R, é 2 2 f, g L p f + g L p X f p dµ < }
AM5: Tracce delle lezioni- V Settimana Sia µ misura su X, p. SPAZI L p L p = L p (X, µ) : = {f : X [, + ] f é misurabile e Siccome t + s p ( ) p s p + t p s, t R, é 2 2 f, g L p f + g L p X f p dµ < }
ANALISI MATEMATICA II PROVA DI TEORIA (23/6/2009)
 ANALISI MATEMATICA II PROVA DI TEORIA (23/6/2009) 1. Sia S = { } (x, y, z) : x 2 + y 2 = 4, 0 z 3 + x. Scrivere le equazioni parametriche di una superficie regolare che abbia S come sostegno. 2. Enunciare
ANALISI MATEMATICA II PROVA DI TEORIA (23/6/2009) 1. Sia S = { } (x, y, z) : x 2 + y 2 = 4, 0 z 3 + x. Scrivere le equazioni parametriche di una superficie regolare che abbia S come sostegno. 2. Enunciare
ANALISI MATEMATICA T-B xx Maggio 2019 (tempo 90 minuti)
 ESERCIZIO 1 La lunghezza della curva γ(t) = (e t, 2t, e t ), t [0, 1] è γ F d s =, con F (x, y, z) = (xy 4 z 2, 2x 2 y 3 z 2, x 2 y 4 z) ESERCIZIO 2 Sia x = x(t) la soluzione del problema di Cauchy t 2
ESERCIZIO 1 La lunghezza della curva γ(t) = (e t, 2t, e t ), t [0, 1] è γ F d s =, con F (x, y, z) = (xy 4 z 2, 2x 2 y 3 z 2, x 2 y 4 z) ESERCIZIO 2 Sia x = x(t) la soluzione del problema di Cauchy t 2
Funzioni implicite e teorema del Dini
 Funzioni implicite e teorema del Dini Il succo dell argomento può essere presentato così. Sia f una funzione a valori reali, definita in un aperto G del piano euclideo R 2 e sufficientemente buona; consideriamo
Funzioni implicite e teorema del Dini Il succo dell argomento può essere presentato così. Sia f una funzione a valori reali, definita in un aperto G del piano euclideo R 2 e sufficientemente buona; consideriamo
Esercitazione di Analisi Matematica I Esercizi e soluzioni 19/04/2013 TOPOLOGIA
 Esercitazione di Analisi Matematica I Esercizi e soluzioni 9/04/203 TOPOLOGIA Mostrare che uno spazio infinito con la metrica discreta non può essere compatto Soluzione: Per la metrica discreta d : X X
Esercitazione di Analisi Matematica I Esercizi e soluzioni 9/04/203 TOPOLOGIA Mostrare che uno spazio infinito con la metrica discreta non può essere compatto Soluzione: Per la metrica discreta d : X X
Esame scritto di Geometria 2
 Esame scritto di Geometria 2 UNIVERSITÀ DEGLI STUDI DI TRENTO CORSO DI LAUREA IN MATEMATICA A.A. 2014/2015 Settembre 2015 Esercizio 1 Sia E 4 lo spazio euclideo a quattro dimensioni con un sistema di coordinate
Esame scritto di Geometria 2 UNIVERSITÀ DEGLI STUDI DI TRENTO CORSO DI LAUREA IN MATEMATICA A.A. 2014/2015 Settembre 2015 Esercizio 1 Sia E 4 lo spazio euclideo a quattro dimensioni con un sistema di coordinate
Analisi Matematica T-2 Ingegneria Edile Ravenna 2013/14
 Analisi Matematica T-2 Ingegneria Edile Ravenna 2013/14 Maria Manfredini, Daniele Morbidelli Informazioni pratiche: Libro di riferimento: Bramanti, Pagani, Salsa, MATEMATICA, Seconda edizione, Zanichelli
Analisi Matematica T-2 Ingegneria Edile Ravenna 2013/14 Maria Manfredini, Daniele Morbidelli Informazioni pratiche: Libro di riferimento: Bramanti, Pagani, Salsa, MATEMATICA, Seconda edizione, Zanichelli
Analisi Matematica II, Anno Accademico Ingegneria Cvile Ambientale Edile
 Analisi Matematica II, Anno Accademico 2015-2016 Ingegneria Cvile Ambientale Edile FOGLIO DI ESERCIZI 6, dall 11 Novembre al 20 Novembre 2015 Calcolo Differenziale 1 Altri esercizi ed esempi sull argomento
Analisi Matematica II, Anno Accademico 2015-2016 Ingegneria Cvile Ambientale Edile FOGLIO DI ESERCIZI 6, dall 11 Novembre al 20 Novembre 2015 Calcolo Differenziale 1 Altri esercizi ed esempi sull argomento
Esonero di Analisi Matematica II (A)
 Esonero di Analisi Matematica II (A) Ingegneria Edile, 8 aprile 3. Studiare la convergenza del seguente integrale improprio: + x log 3 x (x ) 3 dx.. Studiare la convergenza puntuale ed uniforme della seguente
Esonero di Analisi Matematica II (A) Ingegneria Edile, 8 aprile 3. Studiare la convergenza del seguente integrale improprio: + x log 3 x (x ) 3 dx.. Studiare la convergenza puntuale ed uniforme della seguente
Esercizi per il corso di Analisi 6.
 Esercizi per il corso di Analisi 6. 1. Si verifichi che uno spazio normato (X, ) è uno spazio vettoriale topologico con la topologia indotta dalla norma. Si verifichi poi che la norma è una funzione continua
Esercizi per il corso di Analisi 6. 1. Si verifichi che uno spazio normato (X, ) è uno spazio vettoriale topologico con la topologia indotta dalla norma. Si verifichi poi che la norma è una funzione continua
Cognome Nome Matricola Codice ESEMPIO 1
 Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Definizione di forma differenziale chiusa. Sia A R N ; sia A aperto; sia ω = N i=1 ω i dx i una forma differenziale su A; sia ω di classe C 1 ; si dice
Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Definizione di forma differenziale chiusa. Sia A R N ; sia A aperto; sia ω = N i=1 ω i dx i una forma differenziale su A; sia ω di classe C 1 ; si dice
Istituzioni di Matematiche Modulo A (ST)
 Istituzioni di Matematiche Modulo A (ST V II foglio di esercizi ESERCIZIO. Nei seguenti sistemi lineari, discutere l insieme delle soluzioni al variare del parametro t, o dei parametri t e τ, in R. 5 x
Istituzioni di Matematiche Modulo A (ST V II foglio di esercizi ESERCIZIO. Nei seguenti sistemi lineari, discutere l insieme delle soluzioni al variare del parametro t, o dei parametri t e τ, in R. 5 x
Analisi II. Foglio di esercizi n.2 10/10/2017 (Aggiornamento del 17/10/2017)
 Analisi II Foglio di esercizi n 10/10/017 (Aggiornamento del 17/10/017) Esercizi su massimi e minimi liberi con studi aggiuntivi 1 Siano K R n compatto e Ω R n un aperto contenente K Si consideri f C 1
Analisi II Foglio di esercizi n 10/10/017 (Aggiornamento del 17/10/017) Esercizi su massimi e minimi liberi con studi aggiuntivi 1 Siano K R n compatto e Ω R n un aperto contenente K Si consideri f C 1
CAMPI VETTORIALI. 1. Introduzione Definizione 1.1. Sia A R N un aperto non vuoto, un campo vettoriale su A è una funzione F : A R N.
 CAMPI VETTORIALI Indice. Introduzione 2. Lavoro di un campo vettoriale 2 3. Campi vettoriali conservativi 3 4. Campi irrotazionali 6 5. Esercizi 9. Introduzione Definizione.. Sia A R N un aperto non vuoto,
CAMPI VETTORIALI Indice. Introduzione 2. Lavoro di un campo vettoriale 2 3. Campi vettoriali conservativi 3 4. Campi irrotazionali 6 5. Esercizi 9. Introduzione Definizione.. Sia A R N un aperto non vuoto,
Integrali Curvilinei
 Integrali Curvilinei Gianluca Gorni 11 gennaio 2006 1 Lunghezza di una curva Definizione 1.1. Una curva N-dimensionale è una funzione definita su un intervallo (compatto, se non specificato altrimenti)
Integrali Curvilinei Gianluca Gorni 11 gennaio 2006 1 Lunghezza di una curva Definizione 1.1. Una curva N-dimensionale è una funzione definita su un intervallo (compatto, se non specificato altrimenti)
SPAZI TOPOLOGICI. La nozione di spazio topologico è più generale di quella di spazio metrizzabile.
 SPAZI TOPOLOGICI La nozione di spazio topologico è più generale di quella di spazio metrizzabile. Definizione 1 Uno spazio topologico (X, τ) è una coppia costituita da un insieme X e da una famiglia τ
SPAZI TOPOLOGICI La nozione di spazio topologico è più generale di quella di spazio metrizzabile. Definizione 1 Uno spazio topologico (X, τ) è una coppia costituita da un insieme X e da una famiglia τ
PROVA SCRITTA ANALISI II
 PROA SCRITTA ANALISI II Esercizio. Discutere la convergenza puntuale e la convergenza uniforme in (, + ) e in (, + ) della successione di funzioni (2 punti). f n (x) = e x arctan x n Soluzione. Per avere
PROA SCRITTA ANALISI II Esercizio. Discutere la convergenza puntuale e la convergenza uniforme in (, + ) e in (, + ) della successione di funzioni (2 punti). f n (x) = e x arctan x n Soluzione. Per avere
Analisi Matematica II, Anno Accademico Ingegneria Edile e Architettura Vincenzo M. Tortorelli FOGLIO DI ESERCIZI n.
 Analisi Matematica II, Anno Accademico 17-18. Ingegneria Edile e Architettura Vincenzo M. Tortorelli FOGLIO DI ESERCIZI n. CAMMINI ESERCIZIO 1 Un cammino soddisfa le relazioni y = x z, z = y + x 3, essendo
Analisi Matematica II, Anno Accademico 17-18. Ingegneria Edile e Architettura Vincenzo M. Tortorelli FOGLIO DI ESERCIZI n. CAMMINI ESERCIZIO 1 Un cammino soddisfa le relazioni y = x z, z = y + x 3, essendo
Cognome Nome Matricola Codice ESEMPIO 1
 Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Teorema sulla condizione affinchè φ(t) = e λt sia una soluzione di un equazione differenziale lineare d ordine n a coefficienti costanti. Siano a 1, a
Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Teorema sulla condizione affinchè φ(t) = e λt sia una soluzione di un equazione differenziale lineare d ordine n a coefficienti costanti. Siano a 1, a
Analisi 2. Roberto Monti. Appunti del Corso - Versione 5 Ottobre 2012
 Analisi 2 Roberto Monti Appunti del Corso - Versione 5 Ottobre 212 Indice Capitolo 1. Programma 5 Capitolo 2. Convergenza uniforme 7 1. Convergenza uniforme e continuità 7 2. Criterio di Abel Dirichlet
Analisi 2 Roberto Monti Appunti del Corso - Versione 5 Ottobre 212 Indice Capitolo 1. Programma 5 Capitolo 2. Convergenza uniforme 7 1. Convergenza uniforme e continuità 7 2. Criterio di Abel Dirichlet
Analisi Matematica 2 Quaderno degli esercizi settimanali. Roberto Monti. Fisica e Astronomia Anno Accademico
 Analisi Matematica 2 Quaderno degli esercizi settimanali Roberto Monti Fisica e Astronomia Anno Accademico 2018-19 Indice Introduzione 5 Settimana 1. Serie numeriche I 7 Settimana 2. Serie numeriche II
Analisi Matematica 2 Quaderno degli esercizi settimanali Roberto Monti Fisica e Astronomia Anno Accademico 2018-19 Indice Introduzione 5 Settimana 1. Serie numeriche I 7 Settimana 2. Serie numeriche II
Massimi e minimi vincolati
 Massimi e minimi vincolati Sia f una funzione differenziabile, definita su un aperto A di R N. Se K è un sottoinsieme chiuso e limitato di A, per il teorema di Weierstrass f assume massimo e minimo su
Massimi e minimi vincolati Sia f una funzione differenziabile, definita su un aperto A di R N. Se K è un sottoinsieme chiuso e limitato di A, per il teorema di Weierstrass f assume massimo e minimo su
Esempio di grafico di una funzione reale di due variabili reali
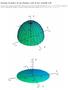 Esempio di grafico di una funzione reale di due variabili reali In questo lucido è rappresentato il grafico della funzione reale di due variabili reali definita da: f(x, y) = 1 x y, in particolare in alto
Esempio di grafico di una funzione reale di due variabili reali In questo lucido è rappresentato il grafico della funzione reale di due variabili reali definita da: f(x, y) = 1 x y, in particolare in alto
10. Calcolo Differenziale, II
 0 alcolo Differenziale, II 0a Differenziale e matrice jacobiana 0 Definizione Sia A R n, n, aperto e f : A R n R m, f = (f, f 2,, f m ), m f si dice differenziabile in x 0 A se esiste una applicazione
0 alcolo Differenziale, II 0a Differenziale e matrice jacobiana 0 Definizione Sia A R n, n, aperto e f : A R n R m, f = (f, f 2,, f m ), m f si dice differenziabile in x 0 A se esiste una applicazione
Analisi Matematica T-2 Ingegneria Edile Ravenna 2014/15
 Analisi Matematica T- Ingegneria Edile Ravenna 014/15 Maria Manfredini, Daniele Morbidelli Informazioni pratiche: Libro di riferimento: Bramanti, Pagani, Salsa, Analisi MAtematica, Seconda edizione, Zanichelli
Analisi Matematica T- Ingegneria Edile Ravenna 014/15 Maria Manfredini, Daniele Morbidelli Informazioni pratiche: Libro di riferimento: Bramanti, Pagani, Salsa, Analisi MAtematica, Seconda edizione, Zanichelli
Analisi Matematica II Corso di Ingegneria Gestionale Compito del (x y) log
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del -6-4 Esercizio. punti Data la funzione { x y log +, fx, y = x +y 4 x, y,, x, y =, i dire in quali punti del dominio è continua; ii dire
Analisi Matematica II Corso di Ingegneria Gestionale Compito del -6-4 Esercizio. punti Data la funzione { x y log +, fx, y = x +y 4 x, y,, x, y =, i dire in quali punti del dominio è continua; ii dire
Analisi Matematica II (Prof. Paolo Marcellini)
 Vero o falso? Analisi Matematica II (Prof. Paolo Marcellini) Università degli Studi di Firenze Corso di laurea in Matematica Esercitazione del 8//205 Michela Eleuteri eleuteri@math.unifi.it web.math.unifi.it/users/eleuteri
Vero o falso? Analisi Matematica II (Prof. Paolo Marcellini) Università degli Studi di Firenze Corso di laurea in Matematica Esercitazione del 8//205 Michela Eleuteri eleuteri@math.unifi.it web.math.unifi.it/users/eleuteri
Funzioni in più variabili
 Funzioni in più variabili Corso di Analisi 1 di Andrea Centomo 7 gennaio 2010 Indichiamo con R n, Z n 1, l insieme delle n-uple ordinate di numeri reali R n 4 {(x 1, x 2,,x n ), x i R, i =1,,n}. Dato X
Funzioni in più variabili Corso di Analisi 1 di Andrea Centomo 7 gennaio 2010 Indichiamo con R n, Z n 1, l insieme delle n-uple ordinate di numeri reali R n 4 {(x 1, x 2,,x n ), x i R, i =1,,n}. Dato X
Esame di Complementi di Matematica (STC) e Parziale di Matematica II (SMat). 3 Maggio Soluzioni
 Esame di Complementi di Matematica (STC) e Parziale di Matematica II (SMat). 3 Maggio 2006. Soluzioni In questo documento sono contenuti gli svolgimenti del tema d esame del 05/06/2006. Alcuni esercizi
Esame di Complementi di Matematica (STC) e Parziale di Matematica II (SMat). 3 Maggio 2006. Soluzioni In questo documento sono contenuti gli svolgimenti del tema d esame del 05/06/2006. Alcuni esercizi
PROVA SCRITTA DI GEOMETRIA 2 MATEMATICA, 20/09/2011
 PROVA SCRITTA DI GEOMETRIA 2 MATEMATICA, 20/09/2011 In questo elenco, la presenza di esercizi relativi ai singoli argomenti non è correlata alla loro rilevanza, né alla ricorrenza nella prova scritta.
PROVA SCRITTA DI GEOMETRIA 2 MATEMATICA, 20/09/2011 In questo elenco, la presenza di esercizi relativi ai singoli argomenti non è correlata alla loro rilevanza, né alla ricorrenza nella prova scritta.
ERRATA CORRIGE e AGGIUNTE: Traccia delle lezioni del corso di Analisi Matematica 2, A.A. 2017/18, aggiornata il 27 gennaio 2018
 1 ERRATA CORRIGE e AGGIUNTE: Traccia delle lezioni del corso di Analisi Matematica 2, A.A. 2017/18, aggiornata il 27 gennaio 2018 p. 5, riga 1: sostituire E E F F p. 5, riga 3: sostituire E E in E F F
1 ERRATA CORRIGE e AGGIUNTE: Traccia delle lezioni del corso di Analisi Matematica 2, A.A. 2017/18, aggiornata il 27 gennaio 2018 p. 5, riga 1: sostituire E E F F p. 5, riga 3: sostituire E E in E F F
AM310- IV Settimana 2012
 AM310- IV Settimana 2012 L 2 e gli spazi di HILBERT f 2 2 := f 2 = < f, f > ove < f, g > := fg dµ, f, g L 2 é un prodotto scalare (ovvero una forma bilineare simmetrica positiva) in L 2. Notiamo che la
AM310- IV Settimana 2012 L 2 e gli spazi di HILBERT f 2 2 := f 2 = < f, f > ove < f, g > := fg dµ, f, g L 2 é un prodotto scalare (ovvero una forma bilineare simmetrica positiva) in L 2. Notiamo che la
Funzioni vettoriali di variabile scalare
 Capitolo 11 Funzioni vettoriali di variabile scalare 11.1 Curve in R n Abbiamo visto (capitolo 2) come la posizione di un punto in uno spazio R n sia individuata mediante le n coordinate di quel punto.
Capitolo 11 Funzioni vettoriali di variabile scalare 11.1 Curve in R n Abbiamo visto (capitolo 2) come la posizione di un punto in uno spazio R n sia individuata mediante le n coordinate di quel punto.
Funzioni di R n a R m e la matrice Jacobiana
 0.1 Funzioni di R n a R m. Politecnico di Torino. Funzioni di R n a R m e la matrice Jacobiana Nota Bene: delle lezioni. Questo materiale non deve essere considerato come sostituto 0.1 Funzioni di R n
0.1 Funzioni di R n a R m. Politecnico di Torino. Funzioni di R n a R m e la matrice Jacobiana Nota Bene: delle lezioni. Questo materiale non deve essere considerato come sostituto 0.1 Funzioni di R n
Il teorema di Ascoli-Arzelà
 Il teorema di Ascoli-Arzelà Alcuni risultati sugli spazi metrici Spazi metrici (e topologici) compatti Richiamiamo le definizioni di compattezza negli spazi metrici. Sia (X, d) una spazio metrico e sia
Il teorema di Ascoli-Arzelà Alcuni risultati sugli spazi metrici Spazi metrici (e topologici) compatti Richiamiamo le definizioni di compattezza negli spazi metrici. Sia (X, d) una spazio metrico e sia
Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 18 febbraio 2010 Tema A
 Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 18 febbraio 21 Tema A Tempo a disposizione: 2 ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio va iniziato all inizio
Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 18 febbraio 21 Tema A Tempo a disposizione: 2 ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio va iniziato all inizio
DIARIO DELLE LEZIONI DI ANALISI MATEMATICA II Corso di laurea in Ingegneria Gestionale Canale PZ Secondo codocente: Dott. Salvatore Fragapane
 DIARIO DELLE LEZIONI DI ANALISI MATEMATICA II Corso di laurea in Ingegneria Gestionale Canale PZ Secondo codocente: Dott. Salvatore Fragapane Lezione 1-04/10/2016 - Serie Numeriche (1): definizione e successione
DIARIO DELLE LEZIONI DI ANALISI MATEMATICA II Corso di laurea in Ingegneria Gestionale Canale PZ Secondo codocente: Dott. Salvatore Fragapane Lezione 1-04/10/2016 - Serie Numeriche (1): definizione e successione
Dimostrazione. Indichiamo con α e β (finiti o infiniti) gli estremi dell intervallo I. Poniamo
 C.6 Funzioni continue Pag. 114 Dimostrazione del Corollario 4.25 Corollario 4.25 Sia f continua in un intervallo I. Supponiamo che f ammetta, per x tendente a ciascuno degli estremi dell intervallo, iti
C.6 Funzioni continue Pag. 114 Dimostrazione del Corollario 4.25 Corollario 4.25 Sia f continua in un intervallo I. Supponiamo che f ammetta, per x tendente a ciascuno degli estremi dell intervallo, iti
Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006. Matematica 2 (Analisi)
 Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006 Matematica 2 (Analisi) Nome:................................. N. matr.:.................................
Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006 Matematica 2 (Analisi) Nome:................................. N. matr.:.................................
