Istituzioni di Matematiche Modulo A (ST)
|
|
|
- Martina Antonini
- 4 anni fa
- Visualizzazioni
Transcript
1 Istituzioni di Matematiche Modulo A (ST V II foglio di esercizi ESERCIZIO. Nei seguenti sistemi lineari, discutere l insieme delle soluzioni al variare del parametro t, o dei parametri t e τ, in R. 5 x + y = t tx 4y = 4 x ty = t x y = 0 x + y = t x t y = t x + y + z = τ y + tz = τ x + y + ( τz = t + τ 4 6 x + y + tz = 0 y + tz = 0 tx + z = 0 { x + ty z = tx + y + z = x + y + z = τ τy + tz = x + ( τy + z = t SOLUZIONE. Le matrici incompleta e completa sono rispettivamente A t = t 4, B t = t t 4 4 t t t Si ha det B t = + 4 t t t, che si può decomporre come + 4 t t t = 4(t + t (t + = (t + (4 t. Quindi det B t = 0 se e solo se t {,, }. Per t {,, }, si ha dunque rk B t =, mentre comunque si ha rk A t, in quanto il rango di una matrice è sempre minore o uguale al minimo tra il numero di righe e di colonne (nel caso di A t tale minimo è (aggiungo che in generale si ha sempre che il rango della completa è o uguale al rango della incompleta oppure uguale al rango della incompleta +, quindi se t {,, } avremo necessariamente rk A t =. In conclusione, se t {,, } allora per il teorema di Rouché-Capelli il sistema non ha soluzioni. Dobbiamo analizzare i casi t {,, }. Osservo che det ( t 4 = 4 t, quindi se t {,, }, abbiamo rk A t, e poiché rk A t, otteniamo rk A t =. D altro canto, se t {,, } abbiamo det B t = 0 e quindi rk B t. Ma comunque rk A t rk B t e quindi, per t {,, } si ha = rk A t rk B t da cui segue che tutti i segni sono uguaglianze. Quindi per t {,, } si ha rk A t = rk B t = : il sistema ha un unica soluzione, in quanto il numero di incognite è.
2 Si tratta di un sistema omogeneo (e quindi ammette sempre soluzioni, quindi basta considerare la matrice incompleta A t = t 0 t t 0 Si ha det A t = t. Quindi det A t = 0 se e solo se t {, }. Per t {, }, si ha dunque rk A t =, per il teorema di Rouché-Capelli il sistema ha un unica soluzione, che necessariamente è la soluzione nulla (x = y = z = 0. Dobbiamo analizzare i casi t {, }. Osservo che det =, quindi se t {, }, abbiamo rk A t, e poiché rk A t, otteniamo ( 0 rk A t = : il sistema ha per soluzioni una varietà linerare (un sottopazio in questo caso di dimensione (una retta. Il problema è simile al problema. Le matrici incompleta e completa sono rispettivamente A t =, B t = 0 t t t t Si ha det B t = t + t, che si può decomporre come t + t = t(t. Quindi det B t = 0 se e solo se t {, 0, }. Per t {, 0, }, si ha dunque rk B t =, mentre comunque si ha rk A t. Quindi, se t {, 0, } allora per il teorema di Rouché-Capelli il sistema non ha soluzioni. Dobbiamo analizzare i casi t {, 0, }. Osservo che det = 4 =, quindi se t {, 0, }, abbiamo rk A t, e poiché ( rk A t, otteniamo rk A t =. D altro canto, se t {, 0, } abbiamo det B t = 0 e quindi rk B t. Ma comunque rk A t rk B t e quindi, per t {, 0, } si ha = rk A t rk B t da cui segue che tutti i segni sono uguaglianze. Quindi per t {, 0, } si ha rk A t = rk B t = : il sistema ha un unica soluzione. 4 Le matrici incompleta e completa sono rispettivamente A t = ( t t, B t = ( t t Si ha rk A t rk B t. Calcoliamo quindi il rango di A t. Ora in A t c è una sottomatrice quadrata di ordine con determinante non nullo, ad esempio (, quindi rk A t per ogni t. Consideriamo adesso i minori di ordine : ( t det = t t, det ( t = t +, det ( = + t t risulta quindi che se t, esiste un minore non nullo di ordine di A t, e quindi per t si ha rk A t =, in quanto già sappiamo che rk A t. Per t il sistema ha soluzioni in quanto si ha rk A t = rk B t = e l insieme delle soluzioni è una varietà lineare di dimensione (una retta. Resta da analizzare il caso t =. In questo caso i tre minori di ordine di A sono nulli e quindi rk A =.
3 ( ( Calcoliamo il rango di B : B =. Si ha det = =, quindi rk B, da cui risulta = rk A < rk B =, e il sistema non ha soluzioni. 5 Le matrici incompleta e completa sono rispettivamente A t,τ = 0 t τ, B t,τ = τ 0 t τ τ t + τ Si ha det A t,τ = τ + t. Quindi det A t,τ = 0 se e solo se τ = t. Per τ t, si ha dunque rk A t,τ =, mentre comunque si ha rk B t,τ, in quanto il rango di una matrice è sempre minore o uguale al minimo tra il numero di righe e di colonne (nel caso di B t,τ tale minimo è. In conclusione, se τ t si ha = rk A t,τ rk B t,τ e quindi rk A t,τ = rk B t,τ = : per il teorema di Rouché-Capelli il sistema ha un unica soluzione. Dobbiamo analizzare i casi τ = t. Osservo che det =, quindi rk A t,τ e se τ = t, allora rk A t,τ = poiché rk A t,τ. ( 0 vediamo adesso come risulta la matrice completa nei casi τ = t: B t,t = t 0 t t t t Vista la forma di B t,t, proviamo a metterla in forma a scalini: B t,t 0 t t t 0 t t t 0 t t t dove ho utilizzato operazioni elementari definite per ogni t. Quindi si ha rk B t,t = se t 0, rk B 0,0 =. In conclusione, nei casi τ = t si hanno soluzioni solo se t = 0, In questo caso l insieme delle soluzioni è una varietà lineare di dimensione (una retta. 6 Il problema è simile al problema 5. Le matrici incompleta e completa sono rispettivamente A t,τ = 0 τ t, B t,τ = τ 0 τ t τ τ t Si ha det A t,τ = tτ. Quindi det A t,τ = 0 se e solo se t = 0 oppure τ = 0. Per tτ 0, si ha dunque rk A t,τ =, mentre comunque si ha rk B t,τ, in quanto il rango di una matrice è sempre minore o uguale al minimo tra il numero di righe e di colonne (nel caso di B t,τ tale minimo è. In conclusione, se tτ 0 si ha = rk A t,τ rk B t,τ e quindi rk A t,τ = rk B t,τ = : per il teorema di Rouché-Capelli il sistema ha un unica soluzione. Dobbiamo analizzare i casi tτ = 0. Consideriamo il caso t = 0: A 0,τ = 0 τ 0, B 0,τ = τ 0 τ 0 τ τ
4 4 ( Osservo che det 0 τ = τ, quindi se τ 0, si ha rk A 0,τ =. Ora det τ 0 τ = τ, τ quindi sempre per τ 0 si ha rk B 0,τ = e il sistema non ha soluzioni. Nel caso τ = 0 si ha A 0,0 = 0 0 0, B 0,0 = e il sistema non ha soluzioni, come si vede direttamente dalla seconda equazione. Consideriamo infine il caso τ = 0. Qui assumiamo t 0, in quanto il caso t = τ = 0 lo abbiamo già considerato. Abbiamo A t,0 = 0 0 t, B t,0 = t t Si ha B t,0 0 0 t t quindi, si ha rk A t,0 = per ogni t 0, rk B t,0 = se t {0, }, rk B 0,0 =, rk B,0 =. In conclusione, nel caso τ = 0 con t 0 si hanno soluzioni se e solo se t =. In questo caso l insieme delle soluzioni è una varietà lineare di dimensione (una retta. ESERCIZIO. Siano S ed S gli insiemi delle soluzioni dei sistemi lineari Σ e Σ rispettivamente. Dire, nei seguenti esempi, in quali casi S = S. ( S = + t 0, t R S = 0 + t 0, t R ( S = 0 + t, t R S = + t 4, t R 0 ( S = 0 + α + β 0, α, β R S = + α 4 + β, α, β R 0 (4 S = 0 + α + β 0, α, β R S = 0 + α 4, α R SOLUZIONE.
5 5 Ricordo che ad esempio S = t R, vuol dire che S ha equazioni parametriche + t x = + t x = x = + t 0, al variare di t R. Allo stesso modo, S = 0 + α α, β R, vuol dire che S ha equazioni parametriche al variare di α, β in R. + β x = + α + β x = α x = + α + β 0, ( Un modo di procedere è il seguente: i punti di S sono del tipo al variare di t in R, i punti di S sono del tipo P t = Q t = + t + t + t t al variare di t in R. Per verificare se S = S, dobbiamo verificare se ogni punto di S è in S e viceversa. Fissato dunque t R dobbiamo verificare se P t S. La domanda che dobbiamo porci è la seguente: esiste s R tale che P t = Q s? (è essenziale l uso di un parametro diverso da t!. Dobbiamo risolvere + s s = dove t è fissato ed s è l incognita. Si ottiene il sistema + t + t { + s = + t s = + t, { s = + t s = + t
6 6 quindi s = (t +. Viceversa, fissato un punto Q t in S, esiste s R tale che Q t = P s? Qui si tratta di risolvere { + s = + t { s = t + s = t s = t quindi s = t. In conclusione S = S. Potremmo ( però risolvere il problema in modo geometrico: ( S è la retta dello spazio passante per il punto P = e parallela al vettore v = 0 ; S è la retta. È chiaro che le due rette sono e parallela al vettore w = ( 0 ( dello spazio passante per il punto 0 parallele, in quanto w = v. Per concludere basta verificare ad esempio se P appartiene ad S. Esiste t R tale che P = Q t? Si tratta di risolvere che ha per soluzione t =. = + t t ( ( In questo caso abbiamo due rette, e sono parallele poiché 4 non esiste alcun t R per cui = 0 + t t + t Si tratta quindi di due rette parallele distinte: in particolare S S. ( Fissiamo a, b R e vediamo se esistono a, b R tali che Otteniamo il sistema in a, b : + a + b a + a + b = 4a + b a + b a + 4a + b + a + b + a = + a + b = + a = + a + b ( è il doppio di. Tuttavia che ha matrice completa B = 4 + a + b + a 0 + a + b ( Ora si ha det 0 = quindi il rango della incompleta è. D altro canto si ha det B = 0, quindi rk B = e il sistema ha soluzione (e la soluzione è unica. Questo è sufficiente per dire che S = S (eventualmente si può scambiare il ruolo degli a, b, a, b, fissando questa volta a e b, e considerando a e b incognite: di nuovo si trova un sistema in cui rango della completa e della incompleta sono uguali a.
7 7 (4 In questo caso S è un piano, mentre S è una retta: in particolare S S (osservo che la retta S è parallela al piano S ma non sta sul piano. Riassumendo, si trovano le seguenti risposte: Sì. No. Sì. 4 No. ( ESERCIZIO. Data la matrice A =, determinare 4 ( l insieme delle matrici B tali che AB = 0; ( l insieme delle matrici B tali che AB = A. SOLUZIONE. Poniamo ( La condizione AB = 0 diventa: dunque otteniamo il sistema ( ( a b = 0, 4 c d ( a b B = c d ( a + c b + d = a + 4c b + 4d a + c = 0 b + d = 0 a + 4c = 0 b + 4d = 0 ( nelle incognite a, b, c, d. Si tratta di un sistema omogeneo di matrice incompleta Quindi il rango è e possiamo parametrizzare lo spazio delle soluzioni considerando parametri c e d: a b c d al variare di α, β in R. Le matrici richieste sono: = α = β = α = β ( α β α β α, β R.
8 8 ( La condizione AB = A diventa: ( ( a b = 4 c d dunque otteniamo il sistema ( 4, a + c = b + d = a + 4c = b + 4d = 4 ( a + c b + d = a + 4c b + 4d nelle incognite a, b, c, d. Si tratta di un sistema lineare di matrice completa ( 4 Quindi il rango della matrice completa e della matrice incompleta è e possiamo parametrizzare lo spazio delle soluzioni considerando parametri c e d: a = α b = β c d = α = β al variare di α, β in R. Le matrici richieste sono: ( α β α β α, β R. Volendo si possono anche descrivere nel seguente modo: ( ( 0 α β + 0 α β α, β R. ESERCIZIO 4. Determinare una terna di vettori (u, u, u dello spazio R in modo che u sia parallelo a, u sia parallelo a, u sia ortogonale ad u e u e tali che u = u = u =. ( ( SOLUZIONE. ( 0 Cerco un vettore ortogonale ad u ed u. Posso prendere v = u u = 7. A questo punto basta normalizzare, scegliendo in ciascun caso un vettore parallelo a quello dato e di lunghezza. Ad esempio, essendo ( = ( 9 =, = 7, ( 0 7 = 5
9 9 possiamo prendere u = (, u = 7 (, u = ( ESERCIZIO 5. Determinare i vettori u dello spazio R che formano un angolo di ( π ( u = e u = e tali che u =. SOLUZIONE. Poniamo u = ( a b c. Ricordo che il coseno dell angolo ϑ tra due vettori non nulli v e w è cos ϑ = v w v w con i vettori dove con v w ho indicato il prodotto scalare di v e w. Essendo cos π =, dobbiamo quindi imporre a + b c Risolviamo prima il sistema u u u u =, u u u u =, u =. =, a + b + c { a + b c = a + b + c = =, a + b + c = che ha matrice completa ( ( / 0 0 / / (al posto della prima riga ho messo la seconda meno la prima. Dalla prima equazione ricavo a = c, e quindi anche b = c. A questo punto a + b + c = diventa 4c c + 5 c + c =, c 65 c =, c 65 c = 0, da cui segue c = , c = I vettori richiesti sono ( , ( ESERCIZIO 6. Si consideri il sistema lineare (w x + 0y = w + Σ w : (w y + (w 7z = w + (8 + wx 0y + 5z = w
10 0 al variare di w in R. Sia S w la varietà delle soluzioni di Σ w. (a Per quali valori di w, S w è vuota? (b Per quali valori di w, S w è costituita da un punto? (c Per quali valori di w, S w è una varietà di dimensione? (d Per i valori di cui in (c, determinare equazioni parametriche di S w. SOLUZIONE. (a, (b, (c Scriviamo in forma compatta Σ w : A w x = b w, dove w 0 0 A w = 0 w w 7, b w = w + w +, 8 + w 0 5 w e quindi la matrice completa è w 0 0 w + B w = 0 w w 7 w w 0 5 w La matrice incompleta è quadrata, quindi calcoliamo il suo determinante. Sviluppiamo secondo una riga o una colonna che contenga possibilmente degli zeri. Sviluppiamo secondo la terza colonna: si ha ( ( w 0 w 0 det A w = (w 7 det + 5 det 8 + w 0 0 w = (w 7( 0(w 0(w (w (w = 5w 50w = 5(w 0w + 6 Quindi det A w = 0 se e solo se w 0w + 6 = 0, se e solo se w =, 8. Pertanto per w, 8 si ha rk A w =, da cui segue anche rk B w = (in quanto si ha sempre rk A w rk B w, visto che min{, 4} =. Possiamo già concludere, per il Teorema di Rouché-Capelli, che per w, 8 il sistema ha un unica soluzione. ( 0 0 Nei casi w =, 8 si ha rk A w = poiché ad esempio det 0 5 = 50 0, (e questo significa che rk A w e già sappiamo che il rango non è, poiché il determinante è nullo (volendo, si possono calcolare direttamente det A e det A 8, e verificare se in entrambi i casi fa zero: in questo modo ci si accorge di un eventuale errore nel precedente calcolo di det A w. Sia w =. Allora la matrice completa diventa B = Vista la forma di B, conviene ridurre B a scalini: B := C
11 In questo modo otteniamo subito sia il rango della completa (che non conoscevamo, sia il rango della incompleta (che conoscevamo. La matrice C ha tre righe non nulle, quindi il rango di C, che coincide con il rango di B è. Invece il rango di A coincide con il rango della matrice costituita dalle prime tre colonne di C. Questa matrice ha due righe non nulle, e quindi ha rango. In particolare S è vuota (faccio notare che C è in forma a scalini, anche se il primo termine non nullo di ogni riga non nulla non è necessariamente uguale ad. L importante è che la forma della matrice sia a scalini! Di solito ci si riconduce ad avere l in quella posizione perchè poi risulta più semplice dare le equazioni parametriche dell insieme delle soluzioni quando questo è non vuoto, ma non è necessario. Osservo che, come al solito, una volta ridotto il sistema in forma a scalini, si può stabilire se il sistema ha soluzioni direttamente dalla matrice C, senza utilizzare il Teorema di Rouché-Capelli: nel nostro caso dalla terza riga di C si deduce subito che Σ non ha soluzioni. Un metodo alternativo consiste nel calcolare i minori di ordine di B, e verificare se almeno uno è non nullo. Si ha ma det A = 0, det = det = quindi rk B =. Poiché abbiamo già calcolato rk A =, per il Teorema di Rouché-Capelli si conclude che per w = non ci sono soluzioni (essendo rka = = rk B. Sia w = 8. La matrice completa diventa Già abbiamo dimostrato che rk A 8 =. B 8 = Anche in questo caso riduciamo B 8 in forma a scalini: B := D Si conclude che sia il rango di D, sia il rango della matrice costituita dalle prime colonne di D hanno rango, quindi rk A 8 = rk B 8 =. Per il Teorema di Rouché-Capelli Σ 8 ha soluzioni (in quanto rk A 8 = rk B 8 e inoltre S 8 è una varietà lineare di dimensione (una retta, in quanto il numero delle incognite è, ed il rango completa = rango incompleta =. Un metodo alternativo consiste nel considerare i minori di ordine di B 8 (che sono quattro: se almeno uno di questi è non nullo, allora il rango di B 8 è, altrimenti, se tutti sono nulli, è <. Si ha det A 8 = det 0 6 = 0, det =
12 4 0 6 det 0 9 = 0, det 6 9 = Si trova quindi sempre 0, e pertanto si ottiene rk B 8. Tuttavia abbiamo = rk A 8 rk B 8, quindi rk A 8 = rk B 8 =. Per il Teorema di Rouché-Capelli S 8 è una varietà lineare di dimensione (una retta, in quanto il numero delle incognite è, ed il rango completa = rango incompleta =. (d Si tratta di determinare equazioni parametriche di S 8. Consideriamo allora la matrice completa, e riduciamola in forma a scalini: B , possiamo porre z = t, e ottenere 6y = 9 t, da cui y = 9 6 6t, e infine da 4x + 0y = 6, x = y = (9 t = 5 t. Quindi S 8 ha equazioni parametriche al variare di t in R. x = 7 5 t y = t z = t Se avessimo voluto ottenere una forma a scalini di B 8 in cui il primo termine non nullo in ciascuna riga è, avremmo ottenuto ad esempio B 8 = , quindi posto z = t, avremmo ottenuto equazioni parametriche x = 7 5 t y = t z = t al variare di t in R.
Esercizi di Matematica di Base Scienze biologiche e Scienze e Tecnologie dell Ambiente
 Esercizi di Matematica di Base Scienze biologiche e Scienze e Tecnologie dell Ambiente Dati i vettori di R (i) Calcolare il prodotto scalare v w, (ii) Stabilire se v e w sono ortogonali, (ii) Stabilire
Esercizi di Matematica di Base Scienze biologiche e Scienze e Tecnologie dell Ambiente Dati i vettori di R (i) Calcolare il prodotto scalare v w, (ii) Stabilire se v e w sono ortogonali, (ii) Stabilire
Istituzioni di Matematiche, Sistemi lineari. corso di laurea in Scienze Geologiche. Mauro Costantini
 Istituzioni di Matematiche, Sistemi lineari corso di laurea in Scienze Geologiche. Mauro Costantini 1 2 3 Il nostro obiettivo è studiare sistemi lineari di m equazioni in n incognite x 1,..., x n : a 11
Istituzioni di Matematiche, Sistemi lineari corso di laurea in Scienze Geologiche. Mauro Costantini 1 2 3 Il nostro obiettivo è studiare sistemi lineari di m equazioni in n incognite x 1,..., x n : a 11
Corso di Geometria BIAR, BSIR Esercizi 4: soluzioni
 Corso di Geometria - BIAR, BSIR Esercizi : soluzioni Esercizio. Sono dati i seguenti sistemi lineari omogenei nelle incognite x, y, z: { x + y z = x + y z = x + y z = S : x y + z =, S :, S 3 : x 3y =,
Corso di Geometria - BIAR, BSIR Esercizi : soluzioni Esercizio. Sono dati i seguenti sistemi lineari omogenei nelle incognite x, y, z: { x + y z = x + y z = x + y z = S : x y + z =, S :, S 3 : x 3y =,
12 gennaio Commenti esame di geometria - Ing. gestionale - a.a
 Questo documento riporta commenti, approfondimenti o metodi di soluzione alternativi per alcuni esercizi dell esame Ovviamente alcuni esercizi potevano essere risolti utilizzando metodi ancora diversi
Questo documento riporta commenti, approfondimenti o metodi di soluzione alternativi per alcuni esercizi dell esame Ovviamente alcuni esercizi potevano essere risolti utilizzando metodi ancora diversi
Prodotto scalare e ortogonalità
 Prodotto scalare e ortogonalità 12 Novembre 1 Il prodotto scalare 1.1 Definizione Possiamo estendere la definizione di prodotto scalare, già data per i vettori del piano, ai vettori dello spazio. Siano
Prodotto scalare e ortogonalità 12 Novembre 1 Il prodotto scalare 1.1 Definizione Possiamo estendere la definizione di prodotto scalare, già data per i vettori del piano, ai vettori dello spazio. Siano
Risoluzione di sistemi lineari
 Risoluzione di sistemi lineari Teorema (Rouché-Capelli) Dato il sistema di m equazioni in n incognite Ax = b, con A M at(m, n) b R n x R n [A b] si ha che: matrice dei coefficienti, vettore dei termini
Risoluzione di sistemi lineari Teorema (Rouché-Capelli) Dato il sistema di m equazioni in n incognite Ax = b, con A M at(m, n) b R n x R n [A b] si ha che: matrice dei coefficienti, vettore dei termini
Rango di una matrice e teorema di Rouché-Capelli
 Rango di una matrice e teorema di Rouché-Capelli Sappiamo che a una matrice m n, A, è associata l applicazione lineare L A : R n R m, L A (X) = AX, X R n. Definizione 1. Lo spazio nullo di A, N (A), è
Rango di una matrice e teorema di Rouché-Capelli Sappiamo che a una matrice m n, A, è associata l applicazione lineare L A : R n R m, L A (X) = AX, X R n. Definizione 1. Lo spazio nullo di A, N (A), è
Istituzioni di Matematiche Modulo B (SG)
 Istituzioni di Matematiche Modulo B (SG) II foglio di esercizi ESERCIZIO 1. Per ciascuna funzione f(, ) calcolare le derivate parziali f (, ) e f (, ) e determinare il relativo dominio di definizione.
Istituzioni di Matematiche Modulo B (SG) II foglio di esercizi ESERCIZIO 1. Per ciascuna funzione f(, ) calcolare le derivate parziali f (, ) e f (, ) e determinare il relativo dominio di definizione.
A titolo di esempio proponiamo la risoluzione del sistema sia con il metodo della matrice inversa sia con il metodo di Cramer.
 ) Trovare le soluzioni del seguente sistema lineare: x+ y+ z = 3x y + z = 0 x + 5y 4z = 5 Osserviamo in primo luogo che il sistema dato è un sistema quadrato di tre equazioni in tre incognite, precisamente
) Trovare le soluzioni del seguente sistema lineare: x+ y+ z = 3x y + z = 0 x + 5y 4z = 5 Osserviamo in primo luogo che il sistema dato è un sistema quadrato di tre equazioni in tre incognite, precisamente
Corso di Geometria BIAR, BSIR Esercizi 3: soluzioni
 Corso di Geometria - BIAR, BSIR Esercizi : soluzioni Rango e teorema di Rouché-Capelli Esercizio. Calcolare il rango di ciascuna delle seguenti matrici: ( ) ( ) ( ) A =, A =, A =, A 4 = ( ). a a a Soluzione.
Corso di Geometria - BIAR, BSIR Esercizi : soluzioni Rango e teorema di Rouché-Capelli Esercizio. Calcolare il rango di ciascuna delle seguenti matrici: ( ) ( ) ( ) A =, A =, A =, A 4 = ( ). a a a Soluzione.
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA
 UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito C 3/5/25 A. A. 24 25 ) Risolvere il seguente sistema
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito C 3/5/25 A. A. 24 25 ) Risolvere il seguente sistema
0.1 Soluzioni esercitazione IV, del 28/10/2008
 1 0.1 Soluzioni esercitazione IV, del 28/10/2008 Esercizio 0.1.1. Risolvere, usando il teorema di Cramer, i seguenti sistemi lineari 2x + y + z = 0 x + 3z = 1 x y z = 1 kx + y z = 1 x y + 2z = 1 2x + 2y
1 0.1 Soluzioni esercitazione IV, del 28/10/2008 Esercizio 0.1.1. Risolvere, usando il teorema di Cramer, i seguenti sistemi lineari 2x + y + z = 0 x + 3z = 1 x y z = 1 kx + y z = 1 x y + 2z = 1 2x + 2y
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA
 UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito B 3/05/005 A. A. 004 005 ) Risolvere il seguente sistema
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito B 3/05/005 A. A. 004 005 ) Risolvere il seguente sistema
8 novembre Soluzione esame di geometria - 12 crediti Ingegneria gestionale - a.a COGNOME... NOME... N. MATRICOLA...
 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica GE110 - Geometria 1 a.a Prova scritta del TESTO E SOLUZIONI
 UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica GE0 - Geometria a.a. 07-08 Prova scritta del 7-7-08 TESTO E SOLUZIONI Svolgere tutti gli esercizi.. Per R considerare il sistema lineare X
UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica GE0 - Geometria a.a. 07-08 Prova scritta del 7-7-08 TESTO E SOLUZIONI Svolgere tutti gli esercizi.. Per R considerare il sistema lineare X
Soluzioni del Foglio 2 I sistemi lineari
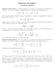 Soluzioni del Foglio 2 I sistemi lineari Soluzione dell esercizio 1 Il sistema assegnato è un sistema di 2 equazioni in 2 incognite non omogeneo Le matrici incompleta e completa associate al sistema sono
Soluzioni del Foglio 2 I sistemi lineari Soluzione dell esercizio 1 Il sistema assegnato è un sistema di 2 equazioni in 2 incognite non omogeneo Le matrici incompleta e completa associate al sistema sono
Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 30 agosto 2011 Tema A
 Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) agosto Tema A Tempo a disposizione: ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio va iniziato all inizio di una pagina.
Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) agosto Tema A Tempo a disposizione: ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio va iniziato all inizio di una pagina.
= (cioè le due terne di numeri direttori ( devono essere ) proporzionali). Tale uguaglianza non è verificata, poiché risulta ρ
 Alcuni esercizi sullo spazio euclideo R Nel seguito R indicherà lo spazio euclideo tridimensionale standard, dotato del riferimento cartesiano naturale (pag 56-57 del libro Nota: gli esercizi proposti
Alcuni esercizi sullo spazio euclideo R Nel seguito R indicherà lo spazio euclideo tridimensionale standard, dotato del riferimento cartesiano naturale (pag 56-57 del libro Nota: gli esercizi proposti
Esercizi per Geometria II Geometria euclidea e proiettiva
 Esercizi per Geometria II Geometria euclidea e proiettiva Filippo F. Favale 10 aprile 01 Esercizio 1 Sia E 3 lo spazio euclideo tridimensionale dotato di un riferimento cartesiano ortonormale di coordinate
Esercizi per Geometria II Geometria euclidea e proiettiva Filippo F. Favale 10 aprile 01 Esercizio 1 Sia E 3 lo spazio euclideo tridimensionale dotato di un riferimento cartesiano ortonormale di coordinate
P z. OP x, OP y, OP z sono le proiezioni ortogonali di v sugli assi x, y, z, per cui: OP x = ( v i) i. k j. P x. OP z = ( v k) k
 Richiami di calcolo vettoriale Consideriamo il vettore libero v = OP. Siano P x, P y, P z le proiezioni ortogonali di P sui tre assi cartesiani. v è la diagonale del parallelepipedo costruito su OP x,
Richiami di calcolo vettoriale Consideriamo il vettore libero v = OP. Siano P x, P y, P z le proiezioni ortogonali di P sui tre assi cartesiani. v è la diagonale del parallelepipedo costruito su OP x,
Esercizi sui sistemi di equazioni lineari.
 Esercizi sui sistemi di equazioni lineari Risolvere il sistema di equazioni lineari x y + z 6 x + y z x y z Si tratta di un sistema di tre equazioni lineari nelle tre incognite x, y e z Poichè m n, la
Esercizi sui sistemi di equazioni lineari Risolvere il sistema di equazioni lineari x y + z 6 x + y z x y z Si tratta di un sistema di tre equazioni lineari nelle tre incognite x, y e z Poichè m n, la
1 Risoluzione di sistemi lineari con l uso dei determinanti
 2006 Trapani Dispensa di Geometria, 1 Risoluzione di sistemi lineari con l uso dei determinanti Sia A una matrice n n con det(a) 0 consideriamo il sistema lineare AX = b abbiamo n = numero di righe di
2006 Trapani Dispensa di Geometria, 1 Risoluzione di sistemi lineari con l uso dei determinanti Sia A una matrice n n con det(a) 0 consideriamo il sistema lineare AX = b abbiamo n = numero di righe di
Geometria BAER I canale Foglio esercizi 2
 Geometria BAER I canale Foglio esercizi 2 Esercizio 1. Calcolare il determinante e l inversa (quando esiste) della matrice ( ) cos θ sin θ R θ =, θ [0, 2π] sin θ cos θ Soluzione: Il determinante ( é cos
Geometria BAER I canale Foglio esercizi 2 Esercizio 1. Calcolare il determinante e l inversa (quando esiste) della matrice ( ) cos θ sin θ R θ =, θ [0, 2π] sin θ cos θ Soluzione: Il determinante ( é cos
I. Foglio di esercizi su vettori linearmente dipendenti e linearmente indipendenti. , v 2 = α v 1 + β v 2 + γ v 3. α v 1 + β v 2 + γ v 3 = 0. + γ.
 ESERCIZI SVOLTI DI ALGEBRA LINEARE (Sono svolti alcune degli esercizi proposti nei fogli di esercizi su vettori linearmente dipendenti e vettori linearmente indipendenti e su sistemi lineari ) I. Foglio
ESERCIZI SVOLTI DI ALGEBRA LINEARE (Sono svolti alcune degli esercizi proposti nei fogli di esercizi su vettori linearmente dipendenti e vettori linearmente indipendenti e su sistemi lineari ) I. Foglio
Università degli Studi di Bergamo Corso integrato di Analisi 1 (Geometria e Algebra Lineare) 3 settembre 2009 Tema A
 Università degli Studi di Bergamo Corso integrato di Analisi (Geometria e Algebra Lineare) settembre 009 Tema A Tempo a disposizione: ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio
Università degli Studi di Bergamo Corso integrato di Analisi (Geometria e Algebra Lineare) settembre 009 Tema A Tempo a disposizione: ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio
ESERCIZI PROPOSTI. det A = = per cui il sistema si può risolvere applicando le formule di Cramer, cioè: dove: = =
 ESERCIZI PROPOSTI Risolvere i seguenti sistemi lineari )-0), utilizzando, dove possibile, sia il metodo di Cramer sia quello della matrice inversa, dopo aver analizzato gli esempi a)-d): 2x + + 4z 5 a)
ESERCIZI PROPOSTI Risolvere i seguenti sistemi lineari )-0), utilizzando, dove possibile, sia il metodo di Cramer sia quello della matrice inversa, dopo aver analizzato gli esempi a)-d): 2x + + 4z 5 a)
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI
 CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
Note sui sistemi lineari
 Note sui sistemi lineari Sia K un campo e siano m e n due numeri interi positivi. Sia A M(m n, K) e sia b K m. Consideriamo il sistema lineare Ax = b nell incognita x K n (o, se preferite, nelle incognite
Note sui sistemi lineari Sia K un campo e siano m e n due numeri interi positivi. Sia A M(m n, K) e sia b K m. Consideriamo il sistema lineare Ax = b nell incognita x K n (o, se preferite, nelle incognite
Soluzioni. Foglio 1. Rette e piani. n x + c = 0. (1)
 Soluzioni Foglio 1. Rette e piani. Esercizio 1. Se n è la normale al piano, sia c = n x 0. Dimostriamo prima che se x π, allora x soddisfa Si ha Sostituendo dentro (1) si ottiene n x + c = 0. (1) x = x
Soluzioni Foglio 1. Rette e piani. Esercizio 1. Se n è la normale al piano, sia c = n x 0. Dimostriamo prima che se x π, allora x soddisfa Si ha Sostituendo dentro (1) si ottiene n x + c = 0. (1) x = x
(V) (FX) L unione di due basi di uno spazio vettoriale è ancora una base dello spazio vettoriale.
 8 gennaio 2009 - PROVA D ESAME - Geometria e Algebra T NOME: MATRICOLA: a=, b=, c= Sostituire ai parametri a, b, c rispettivamente la terzultima, penultima e ultima cifra del proprio numero di matricola
8 gennaio 2009 - PROVA D ESAME - Geometria e Algebra T NOME: MATRICOLA: a=, b=, c= Sostituire ai parametri a, b, c rispettivamente la terzultima, penultima e ultima cifra del proprio numero di matricola
RETTE E PIANI. ove h R. Determinare i valori di h per cui (1) r h e α sono incidenti ed, in tal caso, determinare l angolo ϑ h da essi formato;
 RETTE E PIANI Esercizi Esercizio 1. Nello spazio con riferimento cartesiano ortogonale Oxyz si considerino la retta r h ed il piano α rispettivamente di equazioni x = 1 + t r h : y = 1 t α : x + y + z
RETTE E PIANI Esercizi Esercizio 1. Nello spazio con riferimento cartesiano ortogonale Oxyz si considerino la retta r h ed il piano α rispettivamente di equazioni x = 1 + t r h : y = 1 t α : x + y + z
Esercitazione 6 - Soluzione
 Anno Accademico 28-29 Corso di Algebra Lineare e Calcolo Numerico per Ingegneria Meccanica Esercitazione 6 - Soluzione Immagine, nucleo. Teorema di Rouché-Capelli. Esercizio Sia L : R 3 R 3 l applicazione
Anno Accademico 28-29 Corso di Algebra Lineare e Calcolo Numerico per Ingegneria Meccanica Esercitazione 6 - Soluzione Immagine, nucleo. Teorema di Rouché-Capelli. Esercizio Sia L : R 3 R 3 l applicazione
Ingegneria Gestionale - Corso di Analisi II e Algebra anno accademico 2008/2009
 Ingegneria Gestionale - Corso di Analisi II e Algebra anno accademico 28/29 Dire se le seguenti proposizioni sono vere o false: ESERCITAZIONE. Proposizione Vera Falsa f : R R 4 rk(f f : R 4 R rk(f f :
Ingegneria Gestionale - Corso di Analisi II e Algebra anno accademico 28/29 Dire se le seguenti proposizioni sono vere o false: ESERCITAZIONE. Proposizione Vera Falsa f : R R 4 rk(f f : R 4 R rk(f f :
Sistemi II. Sistemi II. Elisabetta Colombo
 Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2011-2012, http://users.mat.unimi.it/users/colombo/programmabio.html 1 2 3 con R.C.+ o 1.10 Rango massimo e determinante con R.C.+
Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2011-2012, http://users.mat.unimi.it/users/colombo/programmabio.html 1 2 3 con R.C.+ o 1.10 Rango massimo e determinante con R.C.+
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA INDUSTRIALE 27 GENNAIO 2014
 FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA INDUSTRIALE 27 GENNAIO 2014 DOCENTE: MATTEO LONGO Rispondere alle domande di Teoria in modo esauriente e completo. Svolgere il maggior numero di esercizi
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA INDUSTRIALE 27 GENNAIO 2014 DOCENTE: MATTEO LONGO Rispondere alle domande di Teoria in modo esauriente e completo. Svolgere il maggior numero di esercizi
10 aprile Soluzione esame di geometria - Ing. gestionale - a.a COGNOME... NOME... N. MATRICOLA... ISTRUZIONI
 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
Testi di esercizi di preparazione alla I prova in itinere Gli esercizi in elenco sono in gran parte tratti da vecchie prove d esame
 Testi di esercii di preparaione alla I prova in itinere Gli esercii in elenco sono in gran parte tratti da veccie prove d esame Eserciio Al variare di k discutere e ove possibile risolvere il sistema lineare
Testi di esercii di preparaione alla I prova in itinere Gli esercii in elenco sono in gran parte tratti da veccie prove d esame Eserciio Al variare di k discutere e ove possibile risolvere il sistema lineare
Algebra Lineare. a.a Gruppo A-H. Prof. P. Piazza Soluzioni compito pomeridiano del 20/12/2004
 Algebra Lineare. a.a. 2004-05. Gruppo A-H. Prof. P. Piazza Soluzioni compito pomeridiano del 20/12/2004 Esercizio 1. Consideriamo una retta r dello spazio affine. Diremo che le equazioni cartesiane di
Algebra Lineare. a.a. 2004-05. Gruppo A-H. Prof. P. Piazza Soluzioni compito pomeridiano del 20/12/2004 Esercizio 1. Consideriamo una retta r dello spazio affine. Diremo che le equazioni cartesiane di
AUTOVALORI, AUTOVETTORI, AUTOSPAZI
 AUTOVALORI, AUTOVETTORI, AUTOSPAZI. Esercizi Esercizio. Sia f : R 3 R 3 l endomorfismo definito da f(x, y, z) = (x+y, y +z, x+z). Calcolare gli autovalori ed una base per ogni autospazio di f. Dire se
AUTOVALORI, AUTOVETTORI, AUTOSPAZI. Esercizi Esercizio. Sia f : R 3 R 3 l endomorfismo definito da f(x, y, z) = (x+y, y +z, x+z). Calcolare gli autovalori ed una base per ogni autospazio di f. Dire se
INGEGNERIA EDILE ARCHITETTURA ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA 25 FEBBRAIO a a. A a = 1 a 0
 INGEGNERIA EDILE ARCHITETTURA ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA 5 FEBBRAIO 013 Esercizio 1. Al variare del parametro a R, si consideri la matrice A a = 1 a 0 a 1 0. 1 1 a (1) Si discuta al variare
INGEGNERIA EDILE ARCHITETTURA ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA 5 FEBBRAIO 013 Esercizio 1. Al variare del parametro a R, si consideri la matrice A a = 1 a 0 a 1 0. 1 1 a (1) Si discuta al variare
Argomento 13 Sistemi lineari
 Sistemi lineari: definizioni Argomento Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto
Sistemi lineari: definizioni Argomento Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto
Non hanno lo stesso coefficiente angolare e dunque non sono parallele, ma non sono nemmeno perpendicolari in quanto il prodotto dei coeffiecienti
 Università degli Studi Roma Tre Corso di Laurea in Ottica ed Optometria Tutorato di Istituzioni di Matematica - A.A.06/07 Docente: Prof.ssa E. Scoppola Tutore: Gianclaudio Pietrazzini Soluzioni del Tutorato
Università degli Studi Roma Tre Corso di Laurea in Ottica ed Optometria Tutorato di Istituzioni di Matematica - A.A.06/07 Docente: Prof.ssa E. Scoppola Tutore: Gianclaudio Pietrazzini Soluzioni del Tutorato
Esercizi di Algebra Lineare - Foglio 5
 Esercizi di Algebra Lineare - Foglio 5 Soluzioni Esercizio alcolare i determinanti delle seguenti matrici: 3 (a) A = 3 A (b) = A (c) = i i A 3 i i Soluzione (a) alcoliamo il determinante con il metodo
Esercizi di Algebra Lineare - Foglio 5 Soluzioni Esercizio alcolare i determinanti delle seguenti matrici: 3 (a) A = 3 A (b) = A (c) = i i A 3 i i Soluzione (a) alcoliamo il determinante con il metodo
14 febbraio Soluzione esame di geometria - 12 crediti Ingegneria gestionale - a.a COGNOME... NOME... N. MATRICOLA...
 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
CORSO DI LAUREA IN INGEGNERIA DELLE TELECOMUNICAZIONI
 CORSO DI LAUREA IN INGEGNERIA DELLE TELECOMUNICAZIONI FOGLIO DI ESERCIZI # 4 GEOMETRIA E ALGEBRA LINEARE 009/0 Esercizio 4. (Esercizio 7.3). Calcolare l inversa delle matrici (invertibili) [ ] 3 A = B
CORSO DI LAUREA IN INGEGNERIA DELLE TELECOMUNICAZIONI FOGLIO DI ESERCIZI # 4 GEOMETRIA E ALGEBRA LINEARE 009/0 Esercizio 4. (Esercizio 7.3). Calcolare l inversa delle matrici (invertibili) [ ] 3 A = B
1.[25 punti] Risolvere il seguente sistema di equazioni lineari al variare del parametro reale λ: X +Y +Z = 2. X 2Y +λz = 2
![1.[25 punti] Risolvere il seguente sistema di equazioni lineari al variare del parametro reale λ: X +Y +Z = 2. X 2Y +λz = 2 1.[25 punti] Risolvere il seguente sistema di equazioni lineari al variare del parametro reale λ: X +Y +Z = 2. X 2Y +λz = 2](/thumbs/69/60506353.jpg) Università di Modena e Reggio Emilia Facoltà di Scienze MM.FF.NN. PROVA SCRITTA DI GEOMETRIA A del 27 giugno 2011 ISTRUZIONI PER LO SVOLGIMENTO. Scrivere cognome, nome, numero di matricola in alto a destra
Università di Modena e Reggio Emilia Facoltà di Scienze MM.FF.NN. PROVA SCRITTA DI GEOMETRIA A del 27 giugno 2011 ISTRUZIONI PER LO SVOLGIMENTO. Scrivere cognome, nome, numero di matricola in alto a destra
Coordinate cartesiane e coordinate omogenee
 Coordinate cartesiane e coordinate omogenee Fissiamo nel piano un sistema di riferimento cartesiano ortogonale O, x, y, u. Ad ogni punto P del piano possiamo associare le coordinate cartesiane (x, y),
Coordinate cartesiane e coordinate omogenee Fissiamo nel piano un sistema di riferimento cartesiano ortogonale O, x, y, u. Ad ogni punto P del piano possiamo associare le coordinate cartesiane (x, y),
SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI
 SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI Appunti presi dalle lezioni del prof. Nedo Checcaglini Liceo Scientifico di Castiglion Fiorentino (Classe 4B) January 17, 005 1 SISTEMI LINEARI Se a ik, b i R,
SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI Appunti presi dalle lezioni del prof. Nedo Checcaglini Liceo Scientifico di Castiglion Fiorentino (Classe 4B) January 17, 005 1 SISTEMI LINEARI Se a ik, b i R,
Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 3 settembre 2009 Tema A
 Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 3 settembre 29 Tema A Tempo a disposizione: 2 ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio va iniziato all inizio
Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 3 settembre 29 Tema A Tempo a disposizione: 2 ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio va iniziato all inizio
11 settembre Soluzione esame di geometria - Ingegneria gestionale - a.a COGNOME... NOME... N. MATRICOLA...
 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura 3 ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura 3 ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
Università degli Studi di Bergamo Modulo di Geometria e Algebra Lineare (vecchio programma) 2 settembre 2013 Tema A
 Università degli Studi di Bergamo Modulo di Geometria e Algebra Lineare (vecchio programma) settembre 013 Tema A Tempo a disposizione: ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio
Università degli Studi di Bergamo Modulo di Geometria e Algebra Lineare (vecchio programma) settembre 013 Tema A Tempo a disposizione: ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio
r 2 r 2 2r 1 r 4 r 4 r 1
 SPAZI R n 1. Esercizi Esercizio 1. Stabilire quali dei seguenti sottoinsiemi sono sottospazi: V 1 = {(x, y, z) R 3 /x = y = z} V = {(x, y, z) R 3 /x = 4} V 3 = {(x, y, z) R 3 /z = x } V 4 = {(x, y, z)
SPAZI R n 1. Esercizi Esercizio 1. Stabilire quali dei seguenti sottoinsiemi sono sottospazi: V 1 = {(x, y, z) R 3 /x = y = z} V = {(x, y, z) R 3 /x = 4} V 3 = {(x, y, z) R 3 /z = x } V 4 = {(x, y, z)
Lezione 7: Il Teorema di Rouché-Capelli
 Lezione 7: Il Teorema di Rouché-Capelli In questa lezione vogliamo rivisitare i sistemi lineari e dare alcuni risultati che ci permettono di determinare dato un sistema lineare se ammette soluzioni e da
Lezione 7: Il Teorema di Rouché-Capelli In questa lezione vogliamo rivisitare i sistemi lineari e dare alcuni risultati che ci permettono di determinare dato un sistema lineare se ammette soluzioni e da
Soluzioni esercizi complementari
 Soluzioni esercizi complementari Relazioni 1) Quali delle seguenti relazioni sono di equivalenza? x, y R {0} xry x/y Q x, y Z xry x + y è divisibile per 17 x, y Z xry x y X, Y sottoinsiemi di un insieme
Soluzioni esercizi complementari Relazioni 1) Quali delle seguenti relazioni sono di equivalenza? x, y R {0} xry x/y Q x, y Z xry x + y è divisibile per 17 x, y Z xry x y X, Y sottoinsiemi di un insieme
1 Equazioni parametriche e cartesiane di sottospazi affini di R n
 2 Trapani Dispensa di Geometria, Equazioni parametriche e cartesiane di sottospazi affini di R n Un sottospazio affine Σ di R n e il traslato di un sottospazio vettoriale. Cioe esiste un sottospazio vettoriale
2 Trapani Dispensa di Geometria, Equazioni parametriche e cartesiane di sottospazi affini di R n Un sottospazio affine Σ di R n e il traslato di un sottospazio vettoriale. Cioe esiste un sottospazio vettoriale
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
ESERCIZI sui VETTORI
 ESERCIZI sui VETTORI 1. Calcolare la somma di v 1 (2, 3) e v 2 (1, 4). 2. Calcolare la somma di v 1 (1, 5, 4) e v 2 (6, 8, 2). 3. Calcolare il prodotto di α = 2 e v 1 (1, 4). 4. Calcolare il prodotto di
ESERCIZI sui VETTORI 1. Calcolare la somma di v 1 (2, 3) e v 2 (1, 4). 2. Calcolare la somma di v 1 (1, 5, 4) e v 2 (6, 8, 2). 3. Calcolare il prodotto di α = 2 e v 1 (1, 4). 4. Calcolare il prodotto di
Sistemi Lineari. Andrea Galasso
 Sistemi Lineari Andrea Galasso Esercizi svolti Teorema. (Rouché-Capelli. Un sistema lineare Ax = b ammette soluzioni se e solo se il rango della matrice dei coefficienti A è uguale al rango della matrice
Sistemi Lineari Andrea Galasso Esercizi svolti Teorema. (Rouché-Capelli. Un sistema lineare Ax = b ammette soluzioni se e solo se il rango della matrice dei coefficienti A è uguale al rango della matrice
0.1 Soluzioni Esercitazione III, del 21/10/2008
 1 0.1 Soluzioni Esercitazione III, del 21/10/2008 Esercizio 0.1.1. Risolvere il sistema lineare x + y + z = 1 2x + 3y + 2z = 0 x + 2y z = 0 Il determinante della matrice incompleta è 2 e quindi il sistema
1 0.1 Soluzioni Esercitazione III, del 21/10/2008 Esercizio 0.1.1. Risolvere il sistema lineare x + y + z = 1 2x + 3y + 2z = 0 x + 2y z = 0 Il determinante della matrice incompleta è 2 e quindi il sistema
12 dicembre Soluzione esame di geometria - Ing. gestionale - a.a COGNOME... NOME... N. MATRICOLA... ISTRUZIONI
 1 dicembre 005 - Soluzione esame di geometria - Ing. gestionale - a.a. 005-006 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti
1 dicembre 005 - Soluzione esame di geometria - Ing. gestionale - a.a. 005-006 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti
Compito di Geometria e Algebra per Ing. Informatica ed Elettronica
 Compito di Geometria e Algebra per Ing Informatica ed Elettronica 17-02-2015 1) Sia f : R 4 R 3 la funzione lineare definita da f((x, y, z, t)) = ( x + y 2z + kt, x + y + t, 2x + y + z) (x, y, z, t) R
Compito di Geometria e Algebra per Ing Informatica ed Elettronica 17-02-2015 1) Sia f : R 4 R 3 la funzione lineare definita da f((x, y, z, t)) = ( x + y 2z + kt, x + y + t, 2x + y + z) (x, y, z, t) R
Federica Gregorio e Cristian Tacelli
 1 Sistemi lineari Federica Gregorio e Cristian Tacelli Un sistema lineare m n (m equazioni in n incognite) è un insieme di equazioni lineari che devono essere soddisfatte contemporaneamente a 11 x 1 +
1 Sistemi lineari Federica Gregorio e Cristian Tacelli Un sistema lineare m n (m equazioni in n incognite) è un insieme di equazioni lineari che devono essere soddisfatte contemporaneamente a 11 x 1 +
Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE. Giovanni Villani
 Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE Giovanni Villani Matrici Definizione 1 Si definisce matrice di tipo m n una funzione che associa
Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE Giovanni Villani Matrici Definizione 1 Si definisce matrice di tipo m n una funzione che associa
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA
 Cognome Nome Matricola FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA Ciarellotto, Esposito, Garuti Prova del 21 settembre 2013 Dire se è vero o falso (giustificare le risposte. Bisogna necessariamente rispondere
Cognome Nome Matricola FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA Ciarellotto, Esposito, Garuti Prova del 21 settembre 2013 Dire se è vero o falso (giustificare le risposte. Bisogna necessariamente rispondere
1 Rette nel piano ordinario. Rette e piani nello spazio ordinario
 1 Rette nel piano ordinario. Rette e piani nello spazio ordinario 1.1 Vettori applicati Nel seguito denotiamo con P l insieme dei punti del piano ordinario, e con S l insieme dei punti dello spazio ordinario.
1 Rette nel piano ordinario. Rette e piani nello spazio ordinario 1.1 Vettori applicati Nel seguito denotiamo con P l insieme dei punti del piano ordinario, e con S l insieme dei punti dello spazio ordinario.
UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica GE110 - Geometria 1 a.a Prova scritta del TESTO E SOLUZIONI
 UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica GE110 - Geometria 1 a.a. 014-01 Prova scritta del 1-6-01 TESTO E SOLUZIONI Avvertenze: A. Per il recupero del primo esonero svolgere gli esercizi
UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica GE110 - Geometria 1 a.a. 014-01 Prova scritta del 1-6-01 TESTO E SOLUZIONI Avvertenze: A. Per il recupero del primo esonero svolgere gli esercizi
Esercizi svolti sui sistemi lineari
 Francesco Daddi - www.webalice.it/francesco.daddi Esercizi svolti sui sistemi lineari Esercizio 1. Risolvere il seguente sistema lineare al variare del parametro reale t: tx+(t 1)y + z =1 (t 1)y + tz =1
Francesco Daddi - www.webalice.it/francesco.daddi Esercizi svolti sui sistemi lineari Esercizio 1. Risolvere il seguente sistema lineare al variare del parametro reale t: tx+(t 1)y + z =1 (t 1)y + tz =1
Esercizi di ripasso: geometria e algebra lineare.
 Esercizi di ripasso: geometria e algebra lineare. Esercizio. Sia r la retta passante per i punti A(2,, 3) e B(,, 2) in R 3. a. Scrivere l equazione cartesiana del piano Π passante per A e perpendicolare
Esercizi di ripasso: geometria e algebra lineare. Esercizio. Sia r la retta passante per i punti A(2,, 3) e B(,, 2) in R 3. a. Scrivere l equazione cartesiana del piano Π passante per A e perpendicolare
a + 2b + c 3d = 0, a + c d = 0 c d
 SPAZI VETTORIALI 1. Esercizi Esercizio 1. Stabilire quali dei seguenti sottoinsiemi sono sottospazi: V 1 = {(x, y, z) R 3 /x = y = z} V = {(x, y, z) R 3 /x = 4} V 3 = {(x, y, z) R 3 /z = x } V 4 = {(x,
SPAZI VETTORIALI 1. Esercizi Esercizio 1. Stabilire quali dei seguenti sottoinsiemi sono sottospazi: V 1 = {(x, y, z) R 3 /x = y = z} V = {(x, y, z) R 3 /x = 4} V 3 = {(x, y, z) R 3 /z = x } V 4 = {(x,
8 gennaio Soluzione esame di geometria - 12 crediti Ingegneria gestionale - a.a COGNOME... NOME... N. MATRICOLA...
 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
11 giugno Soluzione esame di geometria - 12 crediti Ingegneria gestionale - a.a COGNOME... NOME... N. MATRICOLA...
 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
VETTORI. 1. Si dimostri con un esempio che il prodotto vettoriale non è associativo. u = u u
 VETTORI 1. Si dimostri con un esempio che il prodotto vettoriale non è associativo. Consideriamo i vettori i (1,0,0), j (0,1,0) i ( j j)= i o= o ( i j) j = k j= j k= i il prodotto vettoriale non è associativo
VETTORI 1. Si dimostri con un esempio che il prodotto vettoriale non è associativo. Consideriamo i vettori i (1,0,0), j (0,1,0) i ( j j)= i o= o ( i j) j = k j= j k= i il prodotto vettoriale non è associativo
Esame scritto di Geometria I
 Esame scritto di Geometria I Università degli Studi di Trento Corso di laurea in Fisica A.A. 26/27 Appello di febbraio 27 Esercizio Sia f h : R R l applicazione lineare definita da f h (e ) = 2e + (2 h)e
Esame scritto di Geometria I Università degli Studi di Trento Corso di laurea in Fisica A.A. 26/27 Appello di febbraio 27 Esercizio Sia f h : R R l applicazione lineare definita da f h (e ) = 2e + (2 h)e
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA CHIMICA E DEI MATERIALI 8 LUGLIO 2015
 FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA CHIMICA E DEI MATERIALI 8 LUGLIO 2015 MATTEO LONGO Svolgere entrambe le parti (Teoria ed Esercizi Si richiede la sufficienza su entrambe le parti 1
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA CHIMICA E DEI MATERIALI 8 LUGLIO 2015 MATTEO LONGO Svolgere entrambe le parti (Teoria ed Esercizi Si richiede la sufficienza su entrambe le parti 1
Corso di Geometria, a.a Ing. Informatica e Automatica Esercizi VI: soluzioni
 Corso di Geometria, a.a. 2009-2010 Ing. Informatica e Automatica Esercizi VI: soluzioni 5 novembre 2009 1 Geometria del piano e prodotto scalare Richiami. Il prodotto scalare di due vettori del piano v,
Corso di Geometria, a.a. 2009-2010 Ing. Informatica e Automatica Esercizi VI: soluzioni 5 novembre 2009 1 Geometria del piano e prodotto scalare Richiami. Il prodotto scalare di due vettori del piano v,
Nome:. Data:. 1. Discutere la natura della conica di equazione
 Nome:. Data:. ISTRUZIONI. Riportare le soluzioni in bella copia negli spazi appositi sotto ciascun esercizio, usare eventualmente anche il retro del foglio. Non aggiungere altri fogli. La soluzione deve
Nome:. Data:. ISTRUZIONI. Riportare le soluzioni in bella copia negli spazi appositi sotto ciascun esercizio, usare eventualmente anche il retro del foglio. Non aggiungere altri fogli. La soluzione deve
8 luglio Soluzione esame di geometria - 12 crediti Ingegneria gestionale - a.a COGNOME... NOME... N. MATRICOLA...
 8 luglio 015 - Soluzione esame di geometria - 1 crediti Ingegneria gestionale - a.a. 014-015 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore.
8 luglio 015 - Soluzione esame di geometria - 1 crediti Ingegneria gestionale - a.a. 014-015 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore.
VETTORI NELLO SPAZIO ORDINARIO ,
 VETTORI E GEOMETRIA ANALITICA 1 VETTORI NELLO SPAZIO ORDINARIO Vettori ordinari ed operazioni. Dipendenza ed indipendenza lineare, basi. Prodotto scalare, proiezioni, angoli. Prodotto vettoriale e prodotto
VETTORI E GEOMETRIA ANALITICA 1 VETTORI NELLO SPAZIO ORDINARIO Vettori ordinari ed operazioni. Dipendenza ed indipendenza lineare, basi. Prodotto scalare, proiezioni, angoli. Prodotto vettoriale e prodotto
Note sull algoritmo di Gauss
 Note sull algoritmo di Gauss 29 settembre 2009 Generalità Un sistema lineare di m equazioni in n incognite x,..., x n è un espressione del tipo: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n
Note sull algoritmo di Gauss 29 settembre 2009 Generalità Un sistema lineare di m equazioni in n incognite x,..., x n è un espressione del tipo: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n
Fondamenti di Matematica del discreto
 Fondamenti di Matematica del discreto M1 - Insiemi numerici 25 gennaio 2013 - Laurea on line Esercizio 1. Dire, motivando la risposta, se è possibile scrivere 3 come combinazione lineare di 507 e 2010,
Fondamenti di Matematica del discreto M1 - Insiemi numerici 25 gennaio 2013 - Laurea on line Esercizio 1. Dire, motivando la risposta, se è possibile scrivere 3 come combinazione lineare di 507 e 2010,
LAUREA IN INGEGNERIA CIVILE ED AMBIENTE-TERRITORIO Corso di Matematica 2 Padova TEMA n.1
 LAUREA IN INGEGNERIA CIVILE ED AMBIENTE-TERRITORIO Corso di Matematica Padova -8-8 TEMA n.1 PARTE 1. Quesiti preliminari Stabilire se le seguenti affermazioni sono vere o false giustificando brevemente
LAUREA IN INGEGNERIA CIVILE ED AMBIENTE-TERRITORIO Corso di Matematica Padova -8-8 TEMA n.1 PARTE 1. Quesiti preliminari Stabilire se le seguenti affermazioni sono vere o false giustificando brevemente
UNIVERSITA DEGLI STUDI LA SAPIENZA DI ROMA POLO DI RIETI FACOLTA DI INGEGNERIA CORSO DI LAUREA IN INGEGNERIA DELL AMBIENTE E DEL TERRITORIO
 UNIVERSITA DEGLI STUDI LA SAPIENZA DI ROMA POLO DI RIETI FACOLTA DI INGEGNERIA CORSO DI LAUREA IN INGEGNERIA DELL AMBIENTE E DEL TERRITORIO Geometria 9 5 A.A. 5 Cognome Nome Matricola Codice Scrivere in
UNIVERSITA DEGLI STUDI LA SAPIENZA DI ROMA POLO DI RIETI FACOLTA DI INGEGNERIA CORSO DI LAUREA IN INGEGNERIA DELL AMBIENTE E DEL TERRITORIO Geometria 9 5 A.A. 5 Cognome Nome Matricola Codice Scrivere in
F x 1 = x 1 + x 2. 2x 1 x 2 Determinare la matrice C associata a F rispetto alla base canonica (equivalentemente,
 Corso di Laurea in Fisica. Geometria 1. a.a. 2006-07. Gruppo B. Prof. P. Piazza Esonero del 1/12/06 con soluzione Esercizio. Spazio vettoriale R 2 con base canonica fissata e coordinate associate (x 1,
Corso di Laurea in Fisica. Geometria 1. a.a. 2006-07. Gruppo B. Prof. P. Piazza Esonero del 1/12/06 con soluzione Esercizio. Spazio vettoriale R 2 con base canonica fissata e coordinate associate (x 1,
INGEGNERIA EDILE ARCHITETTURA ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA 17 SETTEMBRE 2012
 INGEGNERIA EDILE ARCHITETTURA ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA 7 SETTEMBRE 202 Esercizio. Sia V = R[X] 2 lo spazio vettoriale dei polinomi ax 2 + bx + c nella variabile X di grado al più 2 a coefficienti
INGEGNERIA EDILE ARCHITETTURA ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA 7 SETTEMBRE 202 Esercizio. Sia V = R[X] 2 lo spazio vettoriale dei polinomi ax 2 + bx + c nella variabile X di grado al più 2 a coefficienti
Esercizi 10. David Barbato
 Esercizi 10 29\05\2017 David Barbato Breve riepilogo di teoria Consideriamo il sistema lineare: a 1,1 x 1 +... + a 1,n x n = b 1...... a k,1 x 1 +... + a k,n x n = b k se il sistema ammette soluzione allora
Esercizi 10 29\05\2017 David Barbato Breve riepilogo di teoria Consideriamo il sistema lineare: a 1,1 x 1 +... + a 1,n x n = b 1...... a k,1 x 1 +... + a k,n x n = b k se il sistema ammette soluzione allora
ESEMPIO DI SISTEMA LINEARE CON SOLUZIONE. Esercizio Si consideri il sistema di equazioni lineari dipendente da un parametro λ R:
 ESEMPIO DI SISTEMA LINEARE CON SOLUZIONE Esercizio Si consideri il sistema di equazioni lineari dipendente da un parametro λ R: x 1 + x = 0 6x 1 + (λ + )x + x 3 + x 4 = 1 x 1 4x + (λ + 1)x 3 + 6x 4 = 3
ESEMPIO DI SISTEMA LINEARE CON SOLUZIONE Esercizio Si consideri il sistema di equazioni lineari dipendente da un parametro λ R: x 1 + x = 0 6x 1 + (λ + )x + x 3 + x 4 = 1 x 1 4x + (λ + 1)x 3 + 6x 4 = 3
Spazi vettoriali euclidei.
 Spazi vettoriali euclidei Prodotto scalare, lunghezza e ortogonalità in R n Consideriamo lo spazio vettoriale R n = { =,,, n R}, n con la somma fra vettori e il prodotto di un vettore per uno scalare definiti
Spazi vettoriali euclidei Prodotto scalare, lunghezza e ortogonalità in R n Consideriamo lo spazio vettoriale R n = { =,,, n R}, n con la somma fra vettori e il prodotto di un vettore per uno scalare definiti
Corso di Geometria BIAR, BSIR Esercizi 10: soluzioni
 Corso di Geometria 2010-11 BIAR, BSIR Esercizi 10: soluzioni 1 Geometria dello spazio Esercizio 1. Dato il punto P 0 = ( 1, 0, 1) e il piano π : x + y + z 2 = 0, determinare: a) Le equazioni parametriche
Corso di Geometria 2010-11 BIAR, BSIR Esercizi 10: soluzioni 1 Geometria dello spazio Esercizio 1. Dato il punto P 0 = ( 1, 0, 1) e il piano π : x + y + z 2 = 0, determinare: a) Le equazioni parametriche
Geometria analitica: rette e piani
 Geometria analitica: rette e piani parametriche Allineamento nel piano nello spazio Angoli tra rette e distanza 2 2006 Politecnico di Torino 1 Esempio 2 Sia A = (1, 2). Per l interpretazione geometrica
Geometria analitica: rette e piani parametriche Allineamento nel piano nello spazio Angoli tra rette e distanza 2 2006 Politecnico di Torino 1 Esempio 2 Sia A = (1, 2). Per l interpretazione geometrica
SISTEMI LINEARI. x y + 2t = 0 2x + y + z t = 0 x z t = 0 ; S 3 : ; S 5x 2y z = 1 4x 7y = 3
 SISTEMI LINEARI. Esercizi Esercizio. Verificare se (,, ) è soluzione del sistema x y + z = x + y z = 3. Trovare poi tutte le soluzioni del sistema. Esercizio. Scrivere un sistema lineare di 3 equazioni
SISTEMI LINEARI. Esercizi Esercizio. Verificare se (,, ) è soluzione del sistema x y + z = x + y z = 3. Trovare poi tutte le soluzioni del sistema. Esercizio. Scrivere un sistema lineare di 3 equazioni
Algebra lineare Geometria 1 11 luglio 2008
 Algebra lineare Geometria 1 11 luglio 2008 Esercizio 1. Si considerino la funzione: { R f : 3 R 3 (α, β, γ) ( 2β α γ, (k 1)β + (1 k)γ α, 3β + (k 2)γ ) dove k è un parametro reale, e il sottospazio U =
Algebra lineare Geometria 1 11 luglio 2008 Esercizio 1. Si considerino la funzione: { R f : 3 R 3 (α, β, γ) ( 2β α γ, (k 1)β + (1 k)γ α, 3β + (k 2)γ ) dove k è un parametro reale, e il sottospazio U =
5 febbraio Soluzione esame di geometria - 12 crediti Ingegneria gestionale - a.a COGNOME... NOME... N. MATRICOLA...
 5 febbraio 015 - Soluzione esame di geometria - 1 crediti Ingegneria gestionale - a.a. 014-15 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore.
5 febbraio 015 - Soluzione esame di geometria - 1 crediti Ingegneria gestionale - a.a. 014-15 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore.
21 settembre Soluzione esame di geometria - Ingegneria gestionale - a.a COGNOME... NOME... N. MATRICOLA...
 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
INGEGNERIA EDILE ARCHITETTURA ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA 19 GIUGNO 2012
 INGEGNERIA EDILE ARCHITETTURA ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA 19 GIUGNO 2012 MATTEO LONGO Esercizio 1. Al variare del parametro a R, si consideri l applicazione lineare L a : R R definita dalle
INGEGNERIA EDILE ARCHITETTURA ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA 19 GIUGNO 2012 MATTEO LONGO Esercizio 1. Al variare del parametro a R, si consideri l applicazione lineare L a : R R definita dalle
Rette e piani nello spazio
 Rette e piani nello spazio Equazioni parametriche di una retta in R 3 : x(t) = x 0 + at r(t) : y(t) = y 0 + bt t R, parametro z(t) = z 0 + ct ovvero r(t) : X(t) = P 0 + vt, t R}, dove: P 0 = (x 0, y 0,
Rette e piani nello spazio Equazioni parametriche di una retta in R 3 : x(t) = x 0 + at r(t) : y(t) = y 0 + bt t R, parametro z(t) = z 0 + ct ovvero r(t) : X(t) = P 0 + vt, t R}, dove: P 0 = (x 0, y 0,
17 luglio Soluzione esame di geometria - 12 crediti Ingegneria gestionale - a.a ISTRUZIONI
 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
Università degli Studi di Bergamo Modulo di Geometria e Algebra Lineare (nuovo programma) 2 settembre 2013 Tema A
 Università degli Studi di Bergamo Modulo di Geometria e Algebra Lineare (nuovo programma) settembre 013 Tema A Tempo a disposizione: ore e mezza Calcolatrici, libri e appunti non sono ammessi Ogni esercizio
Università degli Studi di Bergamo Modulo di Geometria e Algebra Lineare (nuovo programma) settembre 013 Tema A Tempo a disposizione: ore e mezza Calcolatrici, libri e appunti non sono ammessi Ogni esercizio
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA CHIMICA E DEI MATERIALI 8 SETTEMBRE 2015 VERSIONE A
 FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA CHIMICA E DEI MATERIALI 8 SETTEMBRE 015 VERSIONE A DOCENTE: MATTEO LONGO 1. Domande. Esercizi Esercizio 1 (8 punti). Al variare del parametro a R, considerare
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA CHIMICA E DEI MATERIALI 8 SETTEMBRE 015 VERSIONE A DOCENTE: MATTEO LONGO 1. Domande. Esercizi Esercizio 1 (8 punti). Al variare del parametro a R, considerare
