UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA
|
|
|
- Dorotea Di Carlo
- 4 anni fa
- Visualizzazioni
Transcript
1 UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito B 3/05/005 A. A ) Risolvere il seguente sistema lineare: x+ y 3z 5 x + y 4 x + y z 3 con il metodo della matrice inversa e verificare che la soluzione trovata è esatta risolvendo lo stesso sistema con il metodo di Cramer. Osserviamo in primo luogo che il sistema dato è un sistema quadrato di tre equazioni in tre incognite, precisamente x, y e z, ovvero di ordine 3 3. Tenendo conto che nella seconda equazione manca l incognita z, la matrice dei coefficienti associata al sistema è la seguente: 3 A mentre la colonna dei termini noti è data da: 5 N Metodo della matrice inversa Poiché è ben noto che una matrice quadrata ammette l inversa se e solo se il suo determinante è diverso da zero, dobbiamo innanzitutto verificare l esistenza o meno dell inversa di A. Calcoliamone, pertanto, il suo determinante: 3 Dunque: det A A, inversa di A det A
2 Calcoliamo ora l inversa di A utilizzando, ad esempio, il metodo dei complementi algebrici, ovvero la relazione: * t ( A ) A det A Dobbiamo quindi scrivere, in primo luogo, la matrice dei complementi algebrici A * : A A A3 * A A A A 3 A3 A3 A 33 Risulta allora: 0 0 A + ; A + ; A + 0; A 5; A ; A ; A + + 3; A 3 ; A da cui segue: * * t A 5 4 ( A ) Pertanto: * t A ( A ) det A Dunque: 5 3 A Poiché sappiamo che un sistema lineare può scriversi, in forma compatta, come AX N (A è la matrice dei coefficienti del sistema dato, X è il vettore colonna costituito dalle incognite del sistema, N è la colonna dei termini noti del sistema), moltiplicando a sinistra ambo i membri di tale equazione per A, otteniamo: A AX A N IX A N X A N
3 da cui, sostituendo i valori di X, di A e di N, nell equazione X 3 (A ) 3 3N 3, segue: x y z 0 3 e, moltiplicando al secondo membro le righe di A per le colonne di N, otteniamo una matrice di ordine 3, precisamente: x x 6 y y + z z 5 Dunque la soluzione del nostro sistema, con il metodo della matrice inversa, è data dalla terna: ( xyz,, ) ( 6,, 5) Metodo di Cramer Poiché ci troviamo di fronte ad un sistema quadrato ed abbiamo verificato già in precedenza che il determinante della matrice dei coefficienti del sistema è diverso da zero, essendo det A, possiamo affermare che è soddisfatta la condizione necessaria e sufficiente imposta dal Teorema di Cramer (condizione necessaria e sufficiente affinché un sistema quadrato ammetta soluzioni è che il determinante della matrice dei coefficienti del sistema sia diverso da zero). Dunque, sempre per il Teorema di Cramer, il sistema dato ammette una ed una sola soluzione data da: y x z ( xyz,, ),, dove: det A ; x è il determinante della matrice ottenuta da A sostituendo la colonna dei coefficienti dell incognita x con la colonna N dei termini noti; y è il determinante della matrice ottenuta da A sostituendo la colonna dei coefficienti dell incognita y con la colonna N dei termini noti; z è il determinante della matrice ottenuta da A sostituendo la colonna dei coefficienti dell incognita z con la colonna N dei termini noti
4 Poiché: risulta: N y z A ed 3 5 N x x N z y x y N z 4 3 da cui, applicando la regola di Cramer per il calcolo delle soluzioni, otteniamo: y 6 5 x z ( xyz,, ),,,, ( 6,, 5) Dunque la soluzione del nostro sistema, con il metodo di Cramer, è data dalla terna: ( xyz,, ) ( 6,, 5) che è esattamente la stessa trovata precedentemente con il metodo della matrice inversa. ) Risolvere il seguente sistema lineare: 3x+ y z 5 x + y 8z 3 4x + y z La matrice dei coefficienti associata al sistema è: 3 A 8 4
5 da cui segue: 3 det A det A 0 4 Poiché il determinante della matrice dei coefficienti associata al sistema è nullo, dobbiamo verificare se il sistema ammette o meno soluzioni utilizzando il Teorema di Rouché-Capelli, ovvero calcolando i ranghi delle due matrici, quella incompleta e quella completa. Consideriamo, in primo luogo, la matrice incompleta, ovvero quella dei coefficienti del sistema. Osserviamo subito che: 0 r(a) 3 Inoltre, essendo det A 0, risulta necessariamente r(a) 3, da cui: 0 r(a) ed essendo A diversa dalla matrice nulla, segue anche che r(a) 0. Dunque: 0 < r(a) Verifichiamo ora se risulta r(a). Consideriamo, pertanto, un minore del secondo ordine estratto dalla matrice A diverso da zero: 3 M 3 0 r(a) Scriviamo ora la matrice completa, aggiungendo alla matrice A (dei coefficienti del sistema) la colonna dei termini noti: 3 5 ( AN) < r(a N) 3 4 A N Per il calcolo del rango della matrice completa utilizziamo, per comodità, il Teorema di Kronecker. Consideriamo, a tal proposito, un minore del secondo ordine diverso da zero, ad esempio proprio M, ed i suoi due minori orlati. Risulta: det A 0 e Quindi, poiché tutti i minori orlati del terzo ordine sono nulli, segue che r(a N). È dunque soddisfatta la condizione necessaria e sufficiente del Teorema di Rouchè- Capelli, essendo r(a) r(a N).
6 n r 3 Il sistema dato ammette, pertanto, soluzioni (n 3 è il numero delle incognite del sistema, r è il rango delle due matrici), che dipenderanno da n r parametri. Per determinare tali soluzioni scriviamo ora un sistema equivalente al dato, costituito proprio da quelle equazioni i cui coefficienti delle incognite sono stati considerati per trovare un minore del secondo ordine non nullo, ovvero M ; dobbiamo poi tenere ben in mente il fatto che, nel calcolo del minore M di ordine, sono stati tralasciati i coefficienti dell incognita z, che diventerà, quindi, il nostro parametro. In virtù delle precedenti osservazioni possiamo quindi considerare il seguente sistema: 3x+ y z 5 con z t R x + y 8z 3 che può essere scritto anche nel modo seguente: 3x+ y 5+ t x + y 3 + 8t che si può risolvere con Cramer, essendo il determinante della matrice dei coefficienti del sistema, rappresentato proprio da M, diverso da zero. Pertanto: 5+ t 3+ 8t 5+ t 38t 6t 8 x x 3t t y 3+ 8t 39+ 4t 5 t t + 34 y t+ 7 Al variare di t in R, quindi, otteniamo le seguenti soluzioni del sistema: xyz,, 3t 4,t + 7, t ( ) ( ) 3) Determinare, se esiste, l inversa della seguente matrice utilizzando il metodo della matrice identità: 3 7 A 0 3 4
7 Iniziamo con il vedere se esiste o meno la matrice inversa di A calcolando il suo determinante. Risulta pertanto: 3 7 det A Affianchiamo ora alla matrice data, di ordine 3 3, la matrice identità dello stesso ordine: [ A I3] A I 3 Effettuiamo ora le operazioni elementari sulle righe, o sulle colonne, di [A I 3 ] in modo tale da ottenere, alla fine, una matrice della forma [I 3 B], dove la matrice B sarà proprio l inversa A di A: [ A I3] R R 3+ R R R R3 R R 3 0 R R R+ R R3 R3 3R R R+ R R R R R 9 7 R3 R I 3 A A
8 Dunque risulta: A ) Individuare se i seguenti vettori sono linearmente dipendenti o indipendenti: v ( 0,0,), v (,0,), v 3 (,,0) Primo metodo Sfruttiamo la definizione di lineare dipendenza o indipendenza di vettori. Scriviamo una combinazione lineare dei tre vettori e la eguagliamo al vettore nullo, precisamente: (*) kv + kv + kv dove i k i (i,, 3) sono degli scalari ovvero dei numeri reali. Poniamo ora nella (*), al posto dei vettori, le terne assegnate: k( 0,0,) + k (,0,) + k3(,,0) ( 0,0,0) Moltiplichiamo ciascuna componente del vettore per il corrispondente scalare: ( 0,0, k) + ( k,0, k) + ( k3, k3,0) ( 0,0,0) Sommiamo ora componente per componente: ( 0 + k + k3, k3, k+ k + 0) ( 0,0,0) cioè: ( k + k3, k3, k+ k) ( 0,0,0) Affinché l equazione sopra scritta sia soddisfatta, i due membri devono essere uguali, ovvero i due vettori (quello che figura al primo membro e quello che figura al secondo membro) devono avere uguali le componenti che si trovano nella medesima posizione, precisamente deve risultare: k + k3 0 k 0 3 k + k 0 Resta quindi da risolvere il sistema sopra riportato, ovvero determinare i valori delle incognite k i (i,, 3), osservando che se sono tutti nulli allora i vettori assegnati sono linearmente indipendenti, mentre se ne esiste uno diverso da zero allora siamo nel caso della lineare dipendenza dei vettori.
9 Osserviamo, in primo luogo, che si tratta di un sistema quadrato di tre equazioni in tre incognite. Dalla seconda equazione otteniamo: k 3 0 Sostituiamo tale valore, ad esempio, nella prima equazione: k 0 Sostituiamo i valori fino ad ora trovati nella terza equazione: k 0 Abbiamo così ottenuto: k 0 k 0 k 3 0 Dunque il sistema ammette solo la soluzione nulla data dalla terna: (k, k, k 3 ) (0, 0, 0) Poiché gli scalari, soluzione del nostro sistema, sono tutti nulli i tre vettori assegnati risultano essere linearmente indipendenti. Secondo metodo Sfruttiamo la nozione di rango. Consideriamo la matrice costituita dai quattro vettori riga assegnati: 0 0 A Determiniamo il rango di A, sapendo che due o più vettori sono linearmente indipendenti se il rango della matrice ad essi associata è massimo. Risulta, pertanto: 0 < r(a) 3 Applichiamo Kronecker e consideriamo il seguente minore di ordine diverso da zero: 0 M 0 r ( A) Calcoliamo adesso l unico minore orlato di M : Dunque, poiché tale minore è diverso da zero risulta r(a) 3, cioè il rango di A è massimo. I vettori sono pertanto linearmente indipendenti.
10 5) Determinare il rango della seguente matrice utilizzando il metodo di Kronecker: 3 A Iniziamo con l osservare che la matrice A è rettangolare di ordine m n 3 4, per cui risulta: 0 r(a) min{m, n} min{3, 4} 3 Poiché, inoltre, la matrice A non è la matrice nulla segue che r(a) 0. Dunque: 0 < r(a) 3 Consideriamo ora un minore del secondo ordine diverso da zero. Sia esso, ad esempio: 3 M r( A) 5 Calcoliamoci ora i minori orlati di M, osservando che se sono tutti nulli allora è r(a), mentre se ne esiste almeno uno non nullo è r(a) 3. Allora otteniamo: Poiché abbiamo trovato che tutti i minori orlati di M del terzo ordine sono uguali a zero possiamo affermare che: r(a)
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA
 UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito C 3/5/25 A. A. 24 25 ) Risolvere il seguente sistema
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito C 3/5/25 A. A. 24 25 ) Risolvere il seguente sistema
A titolo di esempio proponiamo la risoluzione del sistema sia con il metodo della matrice inversa sia con il metodo di Cramer.
 ) Trovare le soluzioni del seguente sistema lineare: x+ y+ z = 3x y + z = 0 x + 5y 4z = 5 Osserviamo in primo luogo che il sistema dato è un sistema quadrato di tre equazioni in tre incognite, precisamente
) Trovare le soluzioni del seguente sistema lineare: x+ y+ z = 3x y + z = 0 x + 5y 4z = 5 Osserviamo in primo luogo che il sistema dato è un sistema quadrato di tre equazioni in tre incognite, precisamente
ESERCIZI PROPOSTI. det A = = per cui il sistema si può risolvere applicando le formule di Cramer, cioè: dove: = =
 ESERCIZI PROPOSTI Risolvere i seguenti sistemi lineari )-0), utilizzando, dove possibile, sia il metodo di Cramer sia quello della matrice inversa, dopo aver analizzato gli esempi a)-d): 2x + + 4z 5 a)
ESERCIZI PROPOSTI Risolvere i seguenti sistemi lineari )-0), utilizzando, dove possibile, sia il metodo di Cramer sia quello della matrice inversa, dopo aver analizzato gli esempi a)-d): 2x + + 4z 5 a)
Soluzioni del Foglio 2 I sistemi lineari
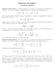 Soluzioni del Foglio 2 I sistemi lineari Soluzione dell esercizio 1 Il sistema assegnato è un sistema di 2 equazioni in 2 incognite non omogeneo Le matrici incompleta e completa associate al sistema sono
Soluzioni del Foglio 2 I sistemi lineari Soluzione dell esercizio 1 Il sistema assegnato è un sistema di 2 equazioni in 2 incognite non omogeneo Le matrici incompleta e completa associate al sistema sono
Esercizi sui sistemi di equazioni lineari.
 Esercizi sui sistemi di equazioni lineari Risolvere il sistema di equazioni lineari x y + z 6 x + y z x y z Si tratta di un sistema di tre equazioni lineari nelle tre incognite x, y e z Poichè m n, la
Esercizi sui sistemi di equazioni lineari Risolvere il sistema di equazioni lineari x y + z 6 x + y z x y z Si tratta di un sistema di tre equazioni lineari nelle tre incognite x, y e z Poichè m n, la
Corso di Geometria BIAR, BSIR Esercizi 3: soluzioni
 Corso di Geometria - BIAR, BSIR Esercizi : soluzioni Rango e teorema di Rouché-Capelli Esercizio. Calcolare il rango di ciascuna delle seguenti matrici: ( ) ( ) ( ) A =, A =, A =, A 4 = ( ). a a a Soluzione.
Corso di Geometria - BIAR, BSIR Esercizi : soluzioni Rango e teorema di Rouché-Capelli Esercizio. Calcolare il rango di ciascuna delle seguenti matrici: ( ) ( ) ( ) A =, A =, A =, A 4 = ( ). a a a Soluzione.
I sistemi lineari di n equazioni in n incognite
 I sistemi lineari I sistemi lineari di n equazioni in n incognite I sistemi lineari di n equazioni in n incognite, sono formati da equazioni di primo grado, in cui le incognite hanno tutte esponente uguale
I sistemi lineari I sistemi lineari di n equazioni in n incognite I sistemi lineari di n equazioni in n incognite, sono formati da equazioni di primo grado, in cui le incognite hanno tutte esponente uguale
SISTEMI LINEARI. x y + 2t = 0 2x + y + z t = 0 x z t = 0 ; S 3 : ; S 5x 2y z = 1 4x 7y = 3
 SISTEMI LINEARI. Esercizi Esercizio. Verificare se (,, ) è soluzione del sistema x y + z = x + y z = 3. Trovare poi tutte le soluzioni del sistema. Esercizio. Scrivere un sistema lineare di 3 equazioni
SISTEMI LINEARI. Esercizi Esercizio. Verificare se (,, ) è soluzione del sistema x y + z = x + y z = 3. Trovare poi tutte le soluzioni del sistema. Esercizio. Scrivere un sistema lineare di 3 equazioni
I. Foglio di esercizi su vettori linearmente dipendenti e linearmente indipendenti. , v 2 = α v 1 + β v 2 + γ v 3. α v 1 + β v 2 + γ v 3 = 0. + γ.
 ESERCIZI SVOLTI DI ALGEBRA LINEARE (Sono svolti alcune degli esercizi proposti nei fogli di esercizi su vettori linearmente dipendenti e vettori linearmente indipendenti e su sistemi lineari ) I. Foglio
ESERCIZI SVOLTI DI ALGEBRA LINEARE (Sono svolti alcune degli esercizi proposti nei fogli di esercizi su vettori linearmente dipendenti e vettori linearmente indipendenti e su sistemi lineari ) I. Foglio
Istituzioni di Matematica I. Esercizi su sistemi lineari. & % x + y " #z = "1 & '#x " y+ z =1
 Istituzioni di Matematica I Esercizi su sistemi lineari Esempio. Dire per quali valori di λ R il sistema x " y+ z = 2 % x + y " z = " x " y+ z = ha una sola soluzione, per quali nessuna, per quali infinite
Istituzioni di Matematica I Esercizi su sistemi lineari Esempio. Dire per quali valori di λ R il sistema x " y+ z = 2 % x + y " z = " x " y+ z = ha una sola soluzione, per quali nessuna, per quali infinite
0.1 Soluzioni Esercitazione III, del 21/10/2008
 1 0.1 Soluzioni Esercitazione III, del 21/10/2008 Esercizio 0.1.1. Risolvere il sistema lineare x + y + z = 1 2x + 3y + 2z = 0 x + 2y z = 0 Il determinante della matrice incompleta è 2 e quindi il sistema
1 0.1 Soluzioni Esercitazione III, del 21/10/2008 Esercizio 0.1.1. Risolvere il sistema lineare x + y + z = 1 2x + 3y + 2z = 0 x + 2y z = 0 Il determinante della matrice incompleta è 2 e quindi il sistema
Introduzione soft alla matematica per l economia e la finanza. Marta Cardin, Paola Ferretti, Stefania Funari
 Introduzione soft alla matematica per l economia e la finanza Marta Cardin, Paola Ferretti, Stefania Funari Capitolo Sistemi di equazioni lineari.8 Il Teorema di Cramer Si consideri un generico sistema
Introduzione soft alla matematica per l economia e la finanza Marta Cardin, Paola Ferretti, Stefania Funari Capitolo Sistemi di equazioni lineari.8 Il Teorema di Cramer Si consideri un generico sistema
MATEMATICA. a.a. 2014/ Sistemi di equazioni lineari
 MATEMATICA a.a. 2014/15 8. Sistemi di equazioni lineari SISTEMI LINEARI Si definisce sistema lineare un sistema di p equazioni di primo grado in q incognite. a11x1 + a12 x2 +... + a1 qxq = k1 a21x1 + a22x2
MATEMATICA a.a. 2014/15 8. Sistemi di equazioni lineari SISTEMI LINEARI Si definisce sistema lineare un sistema di p equazioni di primo grado in q incognite. a11x1 + a12 x2 +... + a1 qxq = k1 a21x1 + a22x2
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI
 CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
Geometria BAER I canale Foglio esercizi 2
 Geometria BAER I canale Foglio esercizi 2 Esercizio 1. Calcolare il determinante e l inversa (quando esiste) della matrice ( ) cos θ sin θ R θ =, θ [0, 2π] sin θ cos θ Soluzione: Il determinante ( é cos
Geometria BAER I canale Foglio esercizi 2 Esercizio 1. Calcolare il determinante e l inversa (quando esiste) della matrice ( ) cos θ sin θ R θ =, θ [0, 2π] sin θ cos θ Soluzione: Il determinante ( é cos
0.1 Soluzioni esercitazione IV, del 28/10/2008
 1 0.1 Soluzioni esercitazione IV, del 28/10/2008 Esercizio 0.1.1. Risolvere, usando il teorema di Cramer, i seguenti sistemi lineari 2x + y + z = 0 x + 3z = 1 x y z = 1 kx + y z = 1 x y + 2z = 1 2x + 2y
1 0.1 Soluzioni esercitazione IV, del 28/10/2008 Esercizio 0.1.1. Risolvere, usando il teorema di Cramer, i seguenti sistemi lineari 2x + y + z = 0 x + 3z = 1 x y z = 1 kx + y z = 1 x y + 2z = 1 2x + 2y
SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI
 SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI Appunti presi dalle lezioni del prof. Nedo Checcaglini Liceo Scientifico di Castiglion Fiorentino (Classe 4B) January 17, 005 1 SISTEMI LINEARI Se a ik, b i R,
SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI Appunti presi dalle lezioni del prof. Nedo Checcaglini Liceo Scientifico di Castiglion Fiorentino (Classe 4B) January 17, 005 1 SISTEMI LINEARI Se a ik, b i R,
Sistemi Lineari. Andrea Galasso
 Sistemi Lineari Andrea Galasso Esercizi svolti Teorema. (Rouché-Capelli. Un sistema lineare Ax = b ammette soluzioni se e solo se il rango della matrice dei coefficienti A è uguale al rango della matrice
Sistemi Lineari Andrea Galasso Esercizi svolti Teorema. (Rouché-Capelli. Un sistema lineare Ax = b ammette soluzioni se e solo se il rango della matrice dei coefficienti A è uguale al rango della matrice
Federica Gregorio e Cristian Tacelli
 1 Sistemi lineari Federica Gregorio e Cristian Tacelli Un sistema lineare m n (m equazioni in n incognite) è un insieme di equazioni lineari che devono essere soddisfatte contemporaneamente a 11 x 1 +
1 Sistemi lineari Federica Gregorio e Cristian Tacelli Un sistema lineare m n (m equazioni in n incognite) è un insieme di equazioni lineari che devono essere soddisfatte contemporaneamente a 11 x 1 +
PROBLEMA. Costruire matrici quadrate contenute. Fare i determinanti delle matrici quadrate contenute in A
 A = PROBLEMA 0 1 2 7 2 5 3 0 (2 4) Costruire matrici quadrate contenute in A (possibili solo matrici quadrate 2 2 e 1 1) Fare i determinanti delle matrici quadrate contenute in A Questo porta al concetto
A = PROBLEMA 0 1 2 7 2 5 3 0 (2 4) Costruire matrici quadrate contenute in A (possibili solo matrici quadrate 2 2 e 1 1) Fare i determinanti delle matrici quadrate contenute in A Questo porta al concetto
Il teorema di Rouché-Capelli
 Luciano Battaia Questi appunti (1), ad uso degli studenti del corso di Matematica (A-La) del corso di laurea in Commercio Estero dell Università Ca Foscari di Venezia, campus di Treviso, contengono un
Luciano Battaia Questi appunti (1), ad uso degli studenti del corso di Matematica (A-La) del corso di laurea in Commercio Estero dell Università Ca Foscari di Venezia, campus di Treviso, contengono un
Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE. Giovanni Villani
 Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE Giovanni Villani Matrici Definizione 1 Si definisce matrice di tipo m n una funzione che associa
Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE Giovanni Villani Matrici Definizione 1 Si definisce matrice di tipo m n una funzione che associa
UNIVERSITA DEGLI STUDI LA SAPIENZA DI ROMA POLO DI RIETI FACOLTA DI INGEGNERIA CORSO DI LAUREA IN INGEGNERIA DELL AMBIENTE E DEL TERRITORIO
 UNIVERSITA DEGLI STUDI LA SAPIENZA DI ROMA POLO DI RIETI FACOLTA DI INGEGNERIA CORSO DI LAUREA IN INGEGNERIA DELL AMBIENTE E DEL TERRITORIO Geometria 9 5 A.A. 5 Cognome Nome Matricola Codice Scrivere in
UNIVERSITA DEGLI STUDI LA SAPIENZA DI ROMA POLO DI RIETI FACOLTA DI INGEGNERIA CORSO DI LAUREA IN INGEGNERIA DELL AMBIENTE E DEL TERRITORIO Geometria 9 5 A.A. 5 Cognome Nome Matricola Codice Scrivere in
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA
 UNIVERITÀ DEGLI TUDI DI TERAMO FACOLTÀ DI CIENZE POLITICHE CORO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED AICURATIVA I Parziale - Compito B 5/4/5 A. A. 4 5 ) Risolvere la seguente disequazione razionale
UNIVERITÀ DEGLI TUDI DI TERAMO FACOLTÀ DI CIENZE POLITICHE CORO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED AICURATIVA I Parziale - Compito B 5/4/5 A. A. 4 5 ) Risolvere la seguente disequazione razionale
il determinante che si ottiene da A, sopprimendo la i - esima riga e la j - esima colonna. Si definisce complemento algebrico dell'elemento a ij
 Determinanti Sia data la matrice quadrata a... a n a a n =...... a... a n nn Chiamiamo determinante di il numero det o che ad essa viene associato. det = a a... a... a... a n n n... a nn Un generico elemento
Determinanti Sia data la matrice quadrata a... a n a a n =...... a... a n nn Chiamiamo determinante di il numero det o che ad essa viene associato. det = a a... a... a... a n n n... a nn Un generico elemento
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA
 UNIVERITÀ DEGLI TUDI DI TERAMO FACOLTÀ DI CIENZE POLITICHE CORO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED AICURATIVA I Parziale - Compito C 5//5 A. A. 5 ) Risolvere la seguente disequazione razionale
UNIVERITÀ DEGLI TUDI DI TERAMO FACOLTÀ DI CIENZE POLITICHE CORO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED AICURATIVA I Parziale - Compito C 5//5 A. A. 5 ) Risolvere la seguente disequazione razionale
1. Sistemi di equazioni lineari. 1.1 Considerazioni preliminari
 1. Sistemi di equazioni lineari 1.1 Considerazioni preliminari I sistemi lineari sono sistemi di equazioni di primo grado in più incognite. Molti problemi di matematica e fisica portano alla soluzione
1. Sistemi di equazioni lineari 1.1 Considerazioni preliminari I sistemi lineari sono sistemi di equazioni di primo grado in più incognite. Molti problemi di matematica e fisica portano alla soluzione
Istituzioni di Matematiche Modulo A (ST)
 Istituzioni di Matematiche Modulo A (ST V II foglio di esercizi ESERCIZIO. Nei seguenti sistemi lineari, discutere l insieme delle soluzioni al variare del parametro t, o dei parametri t e τ, in R. 5 x
Istituzioni di Matematiche Modulo A (ST V II foglio di esercizi ESERCIZIO. Nei seguenti sistemi lineari, discutere l insieme delle soluzioni al variare del parametro t, o dei parametri t e τ, in R. 5 x
Risoluzione di sistemi lineari
 Risoluzione di sistemi lineari Teorema (Rouché-Capelli) Dato il sistema di m equazioni in n incognite Ax = b, con A M at(m, n) b R n x R n [A b] si ha che: matrice dei coefficienti, vettore dei termini
Risoluzione di sistemi lineari Teorema (Rouché-Capelli) Dato il sistema di m equazioni in n incognite Ax = b, con A M at(m, n) b R n x R n [A b] si ha che: matrice dei coefficienti, vettore dei termini
Note sull algoritmo di Gauss
 Note sull algoritmo di Gauss 29 settembre 2009 Generalità Un sistema lineare di m equazioni in n incognite x,..., x n è un espressione del tipo: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n
Note sull algoritmo di Gauss 29 settembre 2009 Generalità Un sistema lineare di m equazioni in n incognite x,..., x n è un espressione del tipo: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n
Sistemi II. Sistemi II. Elisabetta Colombo
 Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2011-2012, http://users.mat.unimi.it/users/colombo/programmabio.html 1 2 3 con R.C.+ o 1.10 Rango massimo e determinante con R.C.+
Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2011-2012, http://users.mat.unimi.it/users/colombo/programmabio.html 1 2 3 con R.C.+ o 1.10 Rango massimo e determinante con R.C.+
Lezione 10: Teorema di Rouchè-Capelli e la classificazione dei sistemi lineari
 Lezione 10: Teorema di Rouchè-Capelli e la classificazione dei sistemi lineari In questa lezione ci dedicheremo a studiare a fondo quali proprietà della matrice dei coefficienti di un sistema (e della
Lezione 10: Teorema di Rouchè-Capelli e la classificazione dei sistemi lineari In questa lezione ci dedicheremo a studiare a fondo quali proprietà della matrice dei coefficienti di un sistema (e della
1. [15 punti] Calcolare il rango della seguente matrice a coefficienti reali: ( 1/2) 1 (1/2)
![1. [15 punti] Calcolare il rango della seguente matrice a coefficienti reali: ( 1/2) 1 (1/2) 1. [15 punti] Calcolare il rango della seguente matrice a coefficienti reali: ( 1/2) 1 (1/2)](/thumbs/101/152415317.jpg) Università di Modena e Reggio Emilia Facoltà di Scienze MM.FF.NN. PROVA DI ALGEBRA LINEARE del 17 febbraio 011 ISTRUZIONI PER LO SVOLGIMENTO. Scrivere cognome, nome, numero di matricola in alto a destra
Università di Modena e Reggio Emilia Facoltà di Scienze MM.FF.NN. PROVA DI ALGEBRA LINEARE del 17 febbraio 011 ISTRUZIONI PER LO SVOLGIMENTO. Scrivere cognome, nome, numero di matricola in alto a destra
Geometria BAER I canale Foglio esercizi 2
 Geometria BAER I canale Foglio esercizi Esercizio. ( ) Data la matrice, determinare tutte le matrici X Mat( ) tali che AX = 0 e tutte le matrici Y Mat( ) tali che Y 0. ( ) ( ) ( ) x y x + z y + w Soluzione:
Geometria BAER I canale Foglio esercizi Esercizio. ( ) Data la matrice, determinare tutte le matrici X Mat( ) tali che AX = 0 e tutte le matrici Y Mat( ) tali che Y 0. ( ) ( ) ( ) x y x + z y + w Soluzione:
CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA
 CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA FOGLIO DI ESERCIZI GEOMETRIA 009/0 Esercizio. (7.9). Si consideri il sistema di equazioni lineari: x + y + z = x + y + z = x + y + 3z = a) Si dica per quali
CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA FOGLIO DI ESERCIZI GEOMETRIA 009/0 Esercizio. (7.9). Si consideri il sistema di equazioni lineari: x + y + z = x + y + z = x + y + 3z = a) Si dica per quali
Riassumiamo le proprietà dei numeri reali da noi utilizzate nel corso di Geometria.
 Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA
 UNIVERITÀ DEGLI TUDI DI TERAMO FACOLTÀ DI CIENZE POLITICHE CORO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED AICURATIVA I Parziale - Compito A 5/4/5 A. A. 4 5 ) Risolvere la seguente disequazione razionale
UNIVERITÀ DEGLI TUDI DI TERAMO FACOLTÀ DI CIENZE POLITICHE CORO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED AICURATIVA I Parziale - Compito A 5/4/5 A. A. 4 5 ) Risolvere la seguente disequazione razionale
SISTEMI LINEARI. x 2y 2z = 0. Svolgimento. Procediamo con operazioni elementari di riga sulla matrice del primo sistema: 1 1 1 3 1 2 R 2 R 2 3R 0 4 5.
 SISTEMI LINEARI Esercizi Esercizio. Risolvere, se possibile, i seguenti sistemi: x y z = 0 x + y + z = 3x + y + z = 0 x y = 4x + z = 0, x y z = 0. Svolgimento. Procediamo con operazioni elementari di riga
SISTEMI LINEARI Esercizi Esercizio. Risolvere, se possibile, i seguenti sistemi: x y z = 0 x + y + z = 3x + y + z = 0 x y = 4x + z = 0, x y z = 0. Svolgimento. Procediamo con operazioni elementari di riga
2x 5y +4z = 3 x 2y + z =5 x 4y +6z = A =
 Esercizio 1. Risolvere il sistema lineare 2x 5y +4z = x 2y + z =5 x 4y +6z =10 (1) Soluz. La matrice dei coefficienti è 1 4 6, calcoliamone il rango. Il determinante di A è (applico la regola di Sarrus):
Esercizio 1. Risolvere il sistema lineare 2x 5y +4z = x 2y + z =5 x 4y +6z =10 (1) Soluz. La matrice dei coefficienti è 1 4 6, calcoliamone il rango. Il determinante di A è (applico la regola di Sarrus):
Esercitazione 6 - Soluzione
 Anno Accademico 28-29 Corso di Algebra Lineare e Calcolo Numerico per Ingegneria Meccanica Esercitazione 6 - Soluzione Immagine, nucleo. Teorema di Rouché-Capelli. Esercizio Sia L : R 3 R 3 l applicazione
Anno Accademico 28-29 Corso di Algebra Lineare e Calcolo Numerico per Ingegneria Meccanica Esercitazione 6 - Soluzione Immagine, nucleo. Teorema di Rouché-Capelli. Esercizio Sia L : R 3 R 3 l applicazione
A.A CORSO DI ALGEBRA 1. PROFF. P. PIAZZA, E. SPINELLI. SOLUZIONE ESERCIZI FOGLIO 5.
 A.A. 2015-2016. CORSO DI ALGEBRA 1. PROFF. P. PIAZZA, E. SPINELLI. SOLUZIONE ESERCIZI FOGLIO 5. Esercizio 5.1. Determinare le ultime tre cifre di n = 13 1625. (Suggerimento. Sfruttare il Teorema di Eulero-Fermat)
A.A. 2015-2016. CORSO DI ALGEBRA 1. PROFF. P. PIAZZA, E. SPINELLI. SOLUZIONE ESERCIZI FOGLIO 5. Esercizio 5.1. Determinare le ultime tre cifre di n = 13 1625. (Suggerimento. Sfruttare il Teorema di Eulero-Fermat)
Metodi per la risoluzione di sistemi lineari
 Metodi per la risoluzione di sistemi lineari Sistemi di equazioni lineari. Rango di matrici Come è noto (vedi [] sez.0.8), ad ogni matrice quadrata A è associato un numero reale det(a) detto determinante
Metodi per la risoluzione di sistemi lineari Sistemi di equazioni lineari. Rango di matrici Come è noto (vedi [] sez.0.8), ad ogni matrice quadrata A è associato un numero reale det(a) detto determinante
ESEMPIO DI SISTEMA LINEARE CON SOLUZIONE. Esercizio Si consideri il sistema di equazioni lineari dipendente da un parametro λ R:
 ESEMPIO DI SISTEMA LINEARE CON SOLUZIONE Esercizio Si consideri il sistema di equazioni lineari dipendente da un parametro λ R: x 1 + x = 0 6x 1 + (λ + )x + x 3 + x 4 = 1 x 1 4x + (λ + 1)x 3 + 6x 4 = 3
ESEMPIO DI SISTEMA LINEARE CON SOLUZIONE Esercizio Si consideri il sistema di equazioni lineari dipendente da un parametro λ R: x 1 + x = 0 6x 1 + (λ + )x + x 3 + x 4 = 1 x 1 4x + (λ + 1)x 3 + 6x 4 = 3
Registro Lezioni di Algebra lineare del 15 e 16 novembre 2016.
 Registro Lezioni di Algebra lineare del 15 e 16 novembre 2016 Di seguito si riporta il riassunto degli argomenti svolti; i riferimenti sono a parti del Cap8 Elementi di geometria e algebra lineare Par5
Registro Lezioni di Algebra lineare del 15 e 16 novembre 2016 Di seguito si riporta il riassunto degli argomenti svolti; i riferimenti sono a parti del Cap8 Elementi di geometria e algebra lineare Par5
Un sistema di equazioni lineari ( o brevemente un sistema lineare) di m equazioni in n incognite, si presenta nella forma:
 SISTEMI LINEARI Un sistema di equazioni lineari ( o brevemente un sistema lineare) di m equazioni in n incognite, si presenta nella forma: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n x n =
SISTEMI LINEARI Un sistema di equazioni lineari ( o brevemente un sistema lineare) di m equazioni in n incognite, si presenta nella forma: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n x n =
1 Risoluzione di sistemi lineari con l uso dei determinanti
 2006 Trapani Dispensa di Geometria, 1 Risoluzione di sistemi lineari con l uso dei determinanti Sia A una matrice n n con det(a) 0 consideriamo il sistema lineare AX = b abbiamo n = numero di righe di
2006 Trapani Dispensa di Geometria, 1 Risoluzione di sistemi lineari con l uso dei determinanti Sia A una matrice n n con det(a) 0 consideriamo il sistema lineare AX = b abbiamo n = numero di righe di
CORSO DI LAUREA IN INGEGNERIA. k R 1 2k 3 0. Il rango di una matrice A corrisponde al massimo ordine di una sottomatrice quadrata di A con deteminante
 CORSO DI LAUREA IN INGEGNERIA. FOGLIO DI ESERCIZI 6 GEOMETRIA E ALGEBRA LINEARE 00/ Esercizio 6. (6.3). Calcolare il rango della seguente matrice A, utilizzando il calcolo del determinante. k + 0 A = k
CORSO DI LAUREA IN INGEGNERIA. FOGLIO DI ESERCIZI 6 GEOMETRIA E ALGEBRA LINEARE 00/ Esercizio 6. (6.3). Calcolare il rango della seguente matrice A, utilizzando il calcolo del determinante. k + 0 A = k
CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA
 CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA FOGLIO DI ESERCIZI 4 GEOMETRIA 2008/09 Esercizio 4.1 (5.10). Dati i vettori di R 3 : v 1 (1, 1, 2), v 2 (2, 4, 6), v 3 ( 1, 2, 5), v 4 (1, 1, 10) determinare
CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA FOGLIO DI ESERCIZI 4 GEOMETRIA 2008/09 Esercizio 4.1 (5.10). Dati i vettori di R 3 : v 1 (1, 1, 2), v 2 (2, 4, 6), v 3 ( 1, 2, 5), v 4 (1, 1, 10) determinare
Metodi per la risoluzione di sistemi lineari
 Metodi per la risoluzione di sistemi lineari 1 Sistemi di equazioni lineari 1.1 Determinante di matrici quadrate Ad ogni matrice quadrata A è associato un numero reale det(a) detto determinante della matrice
Metodi per la risoluzione di sistemi lineari 1 Sistemi di equazioni lineari 1.1 Determinante di matrici quadrate Ad ogni matrice quadrata A è associato un numero reale det(a) detto determinante della matrice
Argomento 13 Sistemi lineari
 Sistemi lineari: definizioni Argomento Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto
Sistemi lineari: definizioni Argomento Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto
r 2 r 2 2r 1 r 4 r 4 r 1
 SPAZI R n 1. Esercizi Esercizio 1. Stabilire quali dei seguenti sottoinsiemi sono sottospazi: V 1 = {(x, y, z) R 3 /x = y = z} V = {(x, y, z) R 3 /x = 4} V 3 = {(x, y, z) R 3 /z = x } V 4 = {(x, y, z)
SPAZI R n 1. Esercizi Esercizio 1. Stabilire quali dei seguenti sottoinsiemi sono sottospazi: V 1 = {(x, y, z) R 3 /x = y = z} V = {(x, y, z) R 3 /x = 4} V 3 = {(x, y, z) R 3 /z = x } V 4 = {(x, y, z)
Ax = b ; b = b 1 b 2. a 11 a 12 a 1n a 21 a 22 a 2n. b m. a m1 a m2 a mn
 SISTEMI LINERI Consideriamo il seguente sistema di m equazioni lineare nelle n incognite,,, n : a + a + + a n n = b >< a + a + + a n n = b = >: a m + a m + + a mn n = b m tale sistema può essere scritto
SISTEMI LINERI Consideriamo il seguente sistema di m equazioni lineare nelle n incognite,,, n : a + a + + a n n = b >< a + a + + a n n = b = >: a m + a m + + a mn n = b m tale sistema può essere scritto
1 Esercizi 13. 3x + λy + 2z = 0 (1 λ)x + 5y + 3z = 0 3x + 2y + z = 0
 1 Esercizi 13 1. Discutere le soluzioni del sistema seguente al variare del parametro λ R. 3x + λy + 2z 0 (1 λ)x + 5y + 3z 0 3x + 2y + z 0 Soluzione. Si tratta di un SLO 3 3 e sappiamo che tale sistema
1 Esercizi 13 1. Discutere le soluzioni del sistema seguente al variare del parametro λ R. 3x + λy + 2z 0 (1 λ)x + 5y + 3z 0 3x + 2y + z 0 Soluzione. Si tratta di un SLO 3 3 e sappiamo che tale sistema
CORSI DI LAUREA IN MATEMATICA E FISICA
 CORSI DI LAUREA IN MATEMATICA E FISICA FOGLIO DI ESERCIZI # 6 GEOMETRIA 1 Esercizio 6.1 (Esercizio 5.1). Scrivere un vettore w R 3 linearmente dipendente dal vettore v ( 1, 9, 0). Per esempio il vettore
CORSI DI LAUREA IN MATEMATICA E FISICA FOGLIO DI ESERCIZI # 6 GEOMETRIA 1 Esercizio 6.1 (Esercizio 5.1). Scrivere un vettore w R 3 linearmente dipendente dal vettore v ( 1, 9, 0). Per esempio il vettore
Geometria BAER I canale Foglio esercizi 3
 Geometria BAER I canale Foglio esercizi 3 Esercizio. Discutere le soluzioni del seguente sistema lineare nelle incognite,, z al variare del parametro k. 3 + kz = k k + 3z = k k + z = Soluzione: Il determinante
Geometria BAER I canale Foglio esercizi 3 Esercizio. Discutere le soluzioni del seguente sistema lineare nelle incognite,, z al variare del parametro k. 3 + kz = k k + 3z = k k + z = Soluzione: Il determinante
Riassumiamo le proprietà dei numeri reali da noi utilizzate nel corso di Geometria.
 Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
SISTEMI LINEARI MATRICI E SISTEMI 1
 MATRICI E SISTEMI SISTEMI LINEARI Sistemi lineari e forma matriciale (definizioni e risoluzione). Teorema di Rouché-Capelli. Sistemi lineari parametrici. Esercizio Risolvere il sistema omogeneo la cui
MATRICI E SISTEMI SISTEMI LINEARI Sistemi lineari e forma matriciale (definizioni e risoluzione). Teorema di Rouché-Capelli. Sistemi lineari parametrici. Esercizio Risolvere il sistema omogeneo la cui
Dipendenza e indipendenza lineare (senza il concetto di rango)
 CAPITOLO 5 Dipendenza e indipendenza lineare (senza il concetto di rango) Esercizio 5.1. Scrivere un vettore w R 3 linearmente dipendente dal vettore v ( 1, 9, 0). Esercizio 5.2. Stabilire se i vettori
CAPITOLO 5 Dipendenza e indipendenza lineare (senza il concetto di rango) Esercizio 5.1. Scrivere un vettore w R 3 linearmente dipendente dal vettore v ( 1, 9, 0). Esercizio 5.2. Stabilire se i vettori
ESERCIZI DI ALGEBRA LINEARE E COMPLEMENTI DI GEOMETRIA
 ESERCIZI DI ALGEBRA LINEARE E COMPLEMENTI DI GEOMETRIA Foglio Esempio. Determinare le soluzioni del sistema lineare Ax = B, in cui 4 A = 6 6, B = Sol. Consideriamo la matrice aumentata C = 4 6 6 6 5 e
ESERCIZI DI ALGEBRA LINEARE E COMPLEMENTI DI GEOMETRIA Foglio Esempio. Determinare le soluzioni del sistema lineare Ax = B, in cui 4 A = 6 6, B = Sol. Consideriamo la matrice aumentata C = 4 6 6 6 5 e
SISTEMI LINEARI, METODO DI GAUSS
 SISTEMI LINEARI, METODO DI GAUSS Abbiamo visto che un sistema di m equazioni lineari in n incognite si può rappresentare in forma matriciale come A x = b dove: A è la matrice di tipo (m, n) dei coefficienti
SISTEMI LINEARI, METODO DI GAUSS Abbiamo visto che un sistema di m equazioni lineari in n incognite si può rappresentare in forma matriciale come A x = b dove: A è la matrice di tipo (m, n) dei coefficienti
Ingegneria Gestionale - Corso di Analisi II e Algebra anno accademico 2008/2009
 Ingegneria Gestionale - Corso di Analisi II e Algebra anno accademico 28/29 Dire se le seguenti proposizioni sono vere o false: ESERCITAZIONE. Proposizione Vera Falsa f : R R 4 rk(f f : R 4 R rk(f f :
Ingegneria Gestionale - Corso di Analisi II e Algebra anno accademico 28/29 Dire se le seguenti proposizioni sono vere o false: ESERCITAZIONE. Proposizione Vera Falsa f : R R 4 rk(f f : R 4 R rk(f f :
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof. Fabio Perroni. 3. Sistemi di equazioni lineari
 Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 3 Sistemi di equazioni lineari Siano m, n N \ {}, sia K un campo Definizione a) Un sistema
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 3 Sistemi di equazioni lineari Siano m, n N \ {}, sia K un campo Definizione a) Un sistema
Esercizi di geometria per Fisica / Fisica e Astrofisica
 Esercizi di geometria per Fisica / Fisica e Astrofisica Foglio 3 - Soluzioni Esercizio. Stabilire se i seguenti sottoinsiemi di R 3 sono sottospazi vettoriali: (a) S = {(x y z) R 3 : x + y + z = }. (b)
Esercizi di geometria per Fisica / Fisica e Astrofisica Foglio 3 - Soluzioni Esercizio. Stabilire se i seguenti sottoinsiemi di R 3 sono sottospazi vettoriali: (a) S = {(x y z) R 3 : x + y + z = }. (b)
UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica GE110 - Geometria 1 a.a Prova scritta del TESTO E SOLUZIONI
 UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica GE110 - Geometria 1 a.a. 014-01 Prova scritta del 1-6-01 TESTO E SOLUZIONI Avvertenze: A. Per il recupero del primo esonero svolgere gli esercizi
UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica GE110 - Geometria 1 a.a. 014-01 Prova scritta del 1-6-01 TESTO E SOLUZIONI Avvertenze: A. Per il recupero del primo esonero svolgere gli esercizi
Manlio Bordoni. APPUNTI SULLA RAPPRESENTAZIONE DEI SOTTOSPAZI VETTORIALI DI R n I MODO. v 11. v n1
 Manlio Bordoni APPUNTI SULLA RAPPRESENTAZIONE DEI SOTTOSPAZI VETTORIALI DI R n I MODO Sia dato un insieme di generatori v v =,, v k = v n di W : questo vuol dire che ogni vettore w W si scrive come combinazione
Manlio Bordoni APPUNTI SULLA RAPPRESENTAZIONE DEI SOTTOSPAZI VETTORIALI DI R n I MODO Sia dato un insieme di generatori v v =,, v k = v n di W : questo vuol dire che ogni vettore w W si scrive come combinazione
Università degli Studi di Bergamo Modulo di Geometria e Algebra Lineare (vecchio programma) 2 settembre 2013 Tema A
 Università degli Studi di Bergamo Modulo di Geometria e Algebra Lineare (vecchio programma) settembre 013 Tema A Tempo a disposizione: ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio
Università degli Studi di Bergamo Modulo di Geometria e Algebra Lineare (vecchio programma) settembre 013 Tema A Tempo a disposizione: ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio
ESERCIZI SULLE MATRICI
 ESERCIZI SULLE MATRICI Consideriamo il sistema lineare a, x + a, x + + a,n x n = b a, x + a, x + + a,n x n = b a m, x + a m, x + + a m,n x n = b m di m equazioni in n incognite che ha a, a,n A = a m, a
ESERCIZI SULLE MATRICI Consideriamo il sistema lineare a, x + a, x + + a,n x n = b a, x + a, x + + a,n x n = b a m, x + a m, x + + a m,n x n = b m di m equazioni in n incognite che ha a, a,n A = a m, a
AUTOVALORI, AUTOVETTORI, AUTOSPAZI
 AUTOVALORI, AUTOVETTORI, AUTOSPAZI. Esercizi Esercizio. Sia f : R 3 R 3 l endomorfismo definito da f(x, y, z) = (x+y, y +z, x+z). Calcolare gli autovalori ed una base per ogni autospazio di f. Dire se
AUTOVALORI, AUTOVETTORI, AUTOSPAZI. Esercizi Esercizio. Sia f : R 3 R 3 l endomorfismo definito da f(x, y, z) = (x+y, y +z, x+z). Calcolare gli autovalori ed una base per ogni autospazio di f. Dire se
Analisi dei dati corso integrato - Algebra lineare, e a b c 0. le soluzioni del sistema lineare omogeneo x d e f 2. a b c.
 Analisi dei dati corso integrato - Algebra lineare 4.3.8 e 5.3.8-1 1. Nella lezione precedente abbiamo definito lo spazio nullo e lo spazio delle colonne di una matrice; ora definiamo lo spazio delle righe
Analisi dei dati corso integrato - Algebra lineare 4.3.8 e 5.3.8-1 1. Nella lezione precedente abbiamo definito lo spazio nullo e lo spazio delle colonne di una matrice; ora definiamo lo spazio delle righe
Esercitazione N.2. Sistemi lineari con parametro. di sistemi lineari con parametro. La regola di Cramer Discussione e risoluzione
 Esercitaione N. maro 7 Sistemi lineari con parametro La regola di Cramer Discussione e risoluione di sistemi lineari con parametro sistemi lineari omogenei Rosalba Barattero ESERCIZIO. Sistema di Cramer
Esercitaione N. maro 7 Sistemi lineari con parametro La regola di Cramer Discussione e risoluione di sistemi lineari con parametro sistemi lineari omogenei Rosalba Barattero ESERCIZIO. Sistema di Cramer
Note sui sistemi lineari per il Corso di Geometria per Chimica, Facoltà di Scienze MM.FF.NN., UNICAL (Dott.ssa Galati C.) Rende, 4 Maggio 2010
 Note sui sistemi lineari per il Corso di Geometria per Chimica, Facoltà di Scienze MM.FF.NN., UNICAL (Dott.ssa Galati C.) Rende, 4 Maggio 21 Sistemi lineari. Un sistema lineare di n 1 equazioni in m incognite
Note sui sistemi lineari per il Corso di Geometria per Chimica, Facoltà di Scienze MM.FF.NN., UNICAL (Dott.ssa Galati C.) Rende, 4 Maggio 21 Sistemi lineari. Un sistema lineare di n 1 equazioni in m incognite
Esercizi svolti. risolvere, se possibile, l equazione xa + B = O, essendo x un incognita reale
 Esercizi svolti 1. Matrici e operazioni fra matrici 1.1 Date le matrici 1 2 1 6 A = B = 5 2 9 15 6 risolvere, se possibile, l equazione xa + B = O, essendo x un incognita reale Osservazione iniziale: qualunque
Esercizi svolti 1. Matrici e operazioni fra matrici 1.1 Date le matrici 1 2 1 6 A = B = 5 2 9 15 6 risolvere, se possibile, l equazione xa + B = O, essendo x un incognita reale Osservazione iniziale: qualunque
Appunti su Indipendenza Lineare di Vettori
 Appunti su Indipendenza Lineare di Vettori Claudia Fassino a.a. Queste dispense, relative a una parte del corso di Matematica Computazionale (Laurea in Informatica), rappresentano solo un aiuto per lo
Appunti su Indipendenza Lineare di Vettori Claudia Fassino a.a. Queste dispense, relative a una parte del corso di Matematica Computazionale (Laurea in Informatica), rappresentano solo un aiuto per lo
Si consideri il sistema a coefficienti reali di m equazioni lineari in n incognite
 3 Sistemi lineari 3 Generalità Si consideri il sistema a coefficienti reali di m equazioni lineari in n incognite ovvero, in forma matriciale, a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n x
3 Sistemi lineari 3 Generalità Si consideri il sistema a coefficienti reali di m equazioni lineari in n incognite ovvero, in forma matriciale, a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n x
Sistemi lineari. Lorenzo Pareschi. Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara
 Sistemi lineari Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
Sistemi lineari Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
0.1 Condizione sufficiente di diagonalizzabilità
 0.1. CONDIZIONE SUFFICIENTE DI DIAGONALIZZABILITÀ 1 0.1 Condizione sufficiente di diagonalizzabilità È naturale porsi il problema di sapere se ogni matrice sia o meno diagonalizzabile. Abbiamo due potenziali
0.1. CONDIZIONE SUFFICIENTE DI DIAGONALIZZABILITÀ 1 0.1 Condizione sufficiente di diagonalizzabilità È naturale porsi il problema di sapere se ogni matrice sia o meno diagonalizzabile. Abbiamo due potenziali
A =, c d. d = ad cb. c d A =
 Geometria e Algebra (II), 271112 1 Definizione D ora innanzi, al posto di dire matrice quadrata di tipo n n o matrice quadrata n n diremo matrice quadrata di ordine n o in breve matrice di ordine n Il
Geometria e Algebra (II), 271112 1 Definizione D ora innanzi, al posto di dire matrice quadrata di tipo n n o matrice quadrata n n diremo matrice quadrata di ordine n o in breve matrice di ordine n Il
0.1 Complemento diretto
 1 0.1 Complemento diretto Dato U V, un complemento diretto di U é un sottospazio W V tale che U W = {0} U + W = V cioé la somma di U con il suo complemento diretto é diretta, e dá tutto lo spazio vettoriale
1 0.1 Complemento diretto Dato U V, un complemento diretto di U é un sottospazio W V tale che U W = {0} U + W = V cioé la somma di U con il suo complemento diretto é diretta, e dá tutto lo spazio vettoriale
8 novembre Soluzione esame di geometria - 12 crediti Ingegneria gestionale - a.a COGNOME... NOME... N. MATRICOLA...
 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
Esempio. L immagine di f è l insieme dei vettori w = (w 1, w 2 ) R 2 che hanno w 1 = w 2. Quindi:
 Nucleo, immagine e loro proprietà [Abate, 5.2] Data una applicazione lineare f : V W, chiamiamo nucleo di f l insieme N(f) := { v V : f(v) = 0 W } Se S V è un sottoinsieme del dominio, indichiamo con f(s)
Nucleo, immagine e loro proprietà [Abate, 5.2] Data una applicazione lineare f : V W, chiamiamo nucleo di f l insieme N(f) := { v V : f(v) = 0 W } Se S V è un sottoinsieme del dominio, indichiamo con f(s)
1 Equazioni parametriche e cartesiane di sottospazi affini di R n
 2 Trapani Dispensa di Geometria, Equazioni parametriche e cartesiane di sottospazi affini di R n Un sottospazio affine Σ di R n e il traslato di un sottospazio vettoriale. Cioe esiste un sottospazio vettoriale
2 Trapani Dispensa di Geometria, Equazioni parametriche e cartesiane di sottospazi affini di R n Un sottospazio affine Σ di R n e il traslato di un sottospazio vettoriale. Cioe esiste un sottospazio vettoriale
Corso di Geometria BIAR, BSIR Esercizi 4: soluzioni
 Corso di Geometria - BIAR, BSIR Esercizi : soluzioni Esercizio. Sono dati i seguenti sistemi lineari omogenei nelle incognite x, y, z: { x + y z = x + y z = x + y z = S : x y + z =, S :, S 3 : x 3y =,
Corso di Geometria - BIAR, BSIR Esercizi : soluzioni Esercizio. Sono dati i seguenti sistemi lineari omogenei nelle incognite x, y, z: { x + y z = x + y z = x + y z = S : x y + z =, S :, S 3 : x 3y =,
Esercizi di Matematica di Base Scienze biologiche e Scienze e Tecnologie dell Ambiente
 Esercizi di Matematica di Base Scienze biologiche e Scienze e Tecnologie dell Ambiente Dati i vettori di R (i) Calcolare il prodotto scalare v w, (ii) Stabilire se v e w sono ortogonali, (ii) Stabilire
Esercizi di Matematica di Base Scienze biologiche e Scienze e Tecnologie dell Ambiente Dati i vettori di R (i) Calcolare il prodotto scalare v w, (ii) Stabilire se v e w sono ortogonali, (ii) Stabilire
Algebra lineare Geometria 1 11 luglio 2008
 Algebra lineare Geometria 1 11 luglio 2008 Esercizio 1. Si considerino la funzione: { R f : 3 R 3 (α, β, γ) ( 2β α γ, (k 1)β + (1 k)γ α, 3β + (k 2)γ ) dove k è un parametro reale, e il sottospazio U =
Algebra lineare Geometria 1 11 luglio 2008 Esercizio 1. Si considerino la funzione: { R f : 3 R 3 (α, β, γ) ( 2β α γ, (k 1)β + (1 k)γ α, 3β + (k 2)γ ) dove k è un parametro reale, e il sottospazio U =
= (cioè le due terne di numeri direttori ( devono essere ) proporzionali). Tale uguaglianza non è verificata, poiché risulta ρ
 Alcuni esercizi sullo spazio euclideo R Nel seguito R indicherà lo spazio euclideo tridimensionale standard, dotato del riferimento cartesiano naturale (pag 56-57 del libro Nota: gli esercizi proposti
Alcuni esercizi sullo spazio euclideo R Nel seguito R indicherà lo spazio euclideo tridimensionale standard, dotato del riferimento cartesiano naturale (pag 56-57 del libro Nota: gli esercizi proposti
Applicazioni eliminazione di Gauss
 Applicazioni eliminazione di Gauss. Premessa Nel seguito supporremo sempre di applicare il metodo di eliminazione di Gauss allo scopo di trasformare la matrice del sistema Ax = b in una matrice triangolare
Applicazioni eliminazione di Gauss. Premessa Nel seguito supporremo sempre di applicare il metodo di eliminazione di Gauss allo scopo di trasformare la matrice del sistema Ax = b in una matrice triangolare
Capitolo 5 Applicazioni lineari Esercizi svolti Tutorato di geometria e algebra lineare. Marco Robutti
 Capitolo 5 Applicazioni lineari Esercizi svolti Tutorato di geometria e algebra lineare Marco Robutti 5 Ottobre 27 Introduzione Gli esercizi di questo capitolo riguardano i seguenti argomenti: Data un
Capitolo 5 Applicazioni lineari Esercizi svolti Tutorato di geometria e algebra lineare Marco Robutti 5 Ottobre 27 Introduzione Gli esercizi di questo capitolo riguardano i seguenti argomenti: Data un
PreCorso di Matematica - PCM Corso M-Z
 PreCorso di Matematica - PCM Corso M-Z DOCENTE: M. Auteri Outline Docente: Auteri PreCorso di Matematica 2016 2 Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti
PreCorso di Matematica - PCM Corso M-Z DOCENTE: M. Auteri Outline Docente: Auteri PreCorso di Matematica 2016 2 Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof. Fabio Perroni. 5. Rango
 Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 5 Rango Definizione 1 Sia A M m,n (K) una matrice m n a coefficienti nel campo K Il rango
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 5 Rango Definizione 1 Sia A M m,n (K) una matrice m n a coefficienti nel campo K Il rango
Compito di MD A.A. 2013/14 4 Settembre 2014
 Compito di MD A.A. 3/4 4 Settembre 4 IMPORTANTE: Non si possono consultare libri e appunti. Non si possono usare calcolatrici, computer o altri dispositivi elettronici. Non saranno valutate risposte prive
Compito di MD A.A. 3/4 4 Settembre 4 IMPORTANTE: Non si possono consultare libri e appunti. Non si possono usare calcolatrici, computer o altri dispositivi elettronici. Non saranno valutate risposte prive
Note per le esercitazioni di Geometria 1 a.a. 2007/08 A. Lotta. Metodi per il calcolo del rango di una matrice
 Note per le esercitazioni di Geometria 1 a.a. 2007/08 A. Lotta Versione del 21/12/07 Metodi per il calcolo del rango di una matrice Sia A M m,n (K). Denotiamo con A (i) la riga i-ma di A, i {1,..., m}.
Note per le esercitazioni di Geometria 1 a.a. 2007/08 A. Lotta Versione del 21/12/07 Metodi per il calcolo del rango di una matrice Sia A M m,n (K). Denotiamo con A (i) la riga i-ma di A, i {1,..., m}.
CORSI DI LAUREA IN MATEMATICA E FISICA. Esercizio 1.1. Risolvere graficamente e algebricamente i seguenti sistemi di due equazioni in due incognite:
 CORS D LAUREA N MATEMATCA E FSCA FOGLO D ESERCZ # 1 GEOMETRA 1 Esercizio 1.1. Risolvere graficamente e algebricamente i seguenti sistemi di due equazioni in due incognite: 2x + y = 4 x 2y = 6 x + 3y =
CORS D LAUREA N MATEMATCA E FSCA FOGLO D ESERCZ # 1 GEOMETRA 1 Esercizio 1.1. Risolvere graficamente e algebricamente i seguenti sistemi di due equazioni in due incognite: 2x + y = 4 x 2y = 6 x + 3y =
ALGEBRA LINEARE PARTE III
 DIEM sez Matematica Finanziaria Università degli studi di Genova Dicembre 200 Indice PREMESSA 2 GENERALITA 2 RAPPRESENTAZIONE DI UN SISTEMA LINEARE IN FORMA MATRI- CIALE 2 3 SOLUZIONE DI SISTEMI LINEARI
DIEM sez Matematica Finanziaria Università degli studi di Genova Dicembre 200 Indice PREMESSA 2 GENERALITA 2 RAPPRESENTAZIONE DI UN SISTEMA LINEARE IN FORMA MATRI- CIALE 2 3 SOLUZIONE DI SISTEMI LINEARI
APPLICAZIONI. Im f = {b B a A tale che f (a) = b}.
 APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica GE110 - Geometria 1 a.a Prova scritta del TESTO E SOLUZIONI
 UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica GE0 - Geometria a.a. 07-08 Prova scritta del 7-7-08 TESTO E SOLUZIONI Svolgere tutti gli esercizi.. Per R considerare il sistema lineare X
UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica GE0 - Geometria a.a. 07-08 Prova scritta del 7-7-08 TESTO E SOLUZIONI Svolgere tutti gli esercizi.. Per R considerare il sistema lineare X
1 Caratteristica di una matrice
 Università Bergamo Primo anno Ingegneria Geometria e Algebra Lineare Anno accademico 207208 Domande su: Caratteristica una matrice; sottospazi vettoriali, basi e mensione; sistemi lineari. Caratteristica
Università Bergamo Primo anno Ingegneria Geometria e Algebra Lineare Anno accademico 207208 Domande su: Caratteristica una matrice; sottospazi vettoriali, basi e mensione; sistemi lineari. Caratteristica
Matematica (proff. Archetti e Pellizzari) Corso di laurea COMES 3 settembre 2012
 Matematica (proff. Archetti e Pellizzari) Corso di laurea COMES A settembre 01 Scarso credito è attribuito a risposte frammentarie e non adeguatamente motivate (1) Rispondete ai seguenti quesiti teorici.
Matematica (proff. Archetti e Pellizzari) Corso di laurea COMES A settembre 01 Scarso credito è attribuito a risposte frammentarie e non adeguatamente motivate (1) Rispondete ai seguenti quesiti teorici.
La riduzione a gradini e i sistemi lineari (senza il concetto di rango)
 CAPITOLO 4 La riduzione a gradini e i sistemi lineari (senza il concetto di rango) Esercizio 4.1. Risolvere il seguente sistema non omogeneo: 2x+4y +4z = 4 x z = 1 x+3y +4z = 3 Esercizio 4.2. Risolvere
CAPITOLO 4 La riduzione a gradini e i sistemi lineari (senza il concetto di rango) Esercizio 4.1. Risolvere il seguente sistema non omogeneo: 2x+4y +4z = 4 x z = 1 x+3y +4z = 3 Esercizio 4.2. Risolvere
Pagine di Algebra lineare. di premessa al testo Pagine di Geometria di Sara Dragotti. Parte terza: SISTEMI LINEARI
 Pagine di Algebra lineare di premessa al testo Pagine di Geometria di Sara Dragotti Parte terza: SISTEMI LINEARI 1. Definizioni Dato un campo K ed m 1 polinomi su K in n indeterminate di grado non superiore
Pagine di Algebra lineare di premessa al testo Pagine di Geometria di Sara Dragotti Parte terza: SISTEMI LINEARI 1. Definizioni Dato un campo K ed m 1 polinomi su K in n indeterminate di grado non superiore
e non ci possono chiaramente essere minori di ordine più grande per cui il rango per minori è 2. Rango per pivot: Svolgiamo la riduzione
 18 ottobre 2011 1. Per le matrici seguenti calcolare il rango per minori, il rango per pivot, il rango per righe ed il rango per colonne. Verificare che si ottiene sempre lo stesso numero. Determinare
18 ottobre 2011 1. Per le matrici seguenti calcolare il rango per minori, il rango per pivot, il rango per righe ed il rango per colonne. Verificare che si ottiene sempre lo stesso numero. Determinare
