Introduzione soft alla matematica per l economia e la finanza. Marta Cardin, Paola Ferretti, Stefania Funari
|
|
|
- Elvira Pasini
- 6 anni fa
- Visualizzazioni
Transcript
1 Introduzione soft alla matematica per l economia e la finanza Marta Cardin, Paola Ferretti, Stefania Funari
2 Capitolo Sistemi di equazioni lineari.8 Il Teorema di Cramer Si consideri un generico sistema di n equazioni lineari in n incognite a x + a x a n x n = b a x + a x a n x n = b =... a n x + a n x a nn x n = b n che, scritto in forma matriciale, ammette la formulazione Ax = b, dove x è il vettore delle incognite, b il vettore dei termini noti e A è la matrice n n dei coefficienti del sistema. Nel paragrafo.5 abbiamo risolto un sistema di due equazioni lineari in due incognite fecendo riferimento alla matrice inversa A della matrice dei coefficienti A. La procedura utilizzata può essere generalizzata al caso in cui n non è necessariamente uguale a due: il teorema di Cramer presenta una condizione che caratterizza l esistenza e l unicità della soluzione del sistema Ax = b. Teorema di Cramer Sia A una matrice di ordine n. Il sistema Ax = b ammette per ogni b IR n un unica soluzione se e solo se la matrice A ha determinante A 0. In tal caso la soluzione x ha componenti x i (i =,..., n con x i = D i A dove D i è il determinante della matrice ottenuta da A sostituendo la colonna i-esima con il vettore b dei termini noti a a... b... a n a a... b... a n D i = det a n a n... b n... a nn 8
3 Dimostrazione Supponiamo che la matrice A abbia determinante A 0: allora esiste la matrice inversa A e la soluzione del sistema x è data da x = A b. Infatti se si premoltiplica Ax = b per A si ottiene A Ax = A b, da cui, sviluppando il primo membro, utilizzando la proprietà associativa dell operazione di moltiplicazione fra matrici ed il fatto che I n x = x, si ha cioè A (Ax = (A Ax = I n x = x x = A b. Quindi, se la matrice dei coefficienti A è invertibile, il sistema ammette un unica soluzione e questa è data da x = A b. Poichè A A... A n A = A A... A n A A n A n... A nn segue che cioè b A + b A b n A n x = b A + b A b n A n A. b A n + b A n b n A nn x i = A (b A i + b A i b n A ni. L espressione tra parentesi rappresenta il determinante della matrice a a... b... a n a a... b... a n a n a n... b n... a nn ottenuta da A sostituendo il vettore b alla colonna i. Viceversa, se il sistema Ax = b ammette una ed una sola soluzione, qualunque sia il vettore b, nel caso particolare in cui b = 0, risolvere il sistema significa determinare quel vettore x tale che Ax = 0. 9
4 Per ipotesi la soluzione x è unica: quindi x = 0. In altre parole, 0 è l unico vettore x tale che x a c + x a c + + x n a c n = 0. Ma allora le colonne di A sono linearmente indipendenti e quindi, ricordando una delle proprietà del determinante, A 0. Un sistema di equazioni lineari si dice sistema di Cramer se la matrice dei coefficienti A è una matrice quadrata di ordine n (il numero di equazioni è uguale al numero n delle incognite con determinante diverso da zero (quindi A invertibile. Esempio Si consideri il sistema Ax = b con A = 0, b = 0 Poichè det(a = 0, la matrice è invertibile e la soluzione (unica del sistema è data da ( 5 x = det 0 =, ( x = det ( x = det = 0, =. La soluzione del sistema così come proposta nell enuncito del teorema permette di ottenere in un modo equivalente la soluzione x = A b..9 Il rango di una matrice Nel paragrafo precedente abbiamo affrontato lo studio delle soluzioni di un sistema di n equazioni in n incognite e abbiamo riconosciuto che il calcolo del determinante A della matrice dei coefficienti A e la verifica che A sia diverso da zero garantiscono l esistenza e l unicità della soluzione. Due questioni rimangono però aperte. La prima riguarda il caso in cui il determinante A sia uguale zero; la seconda è relativa al caso in cui il numero di equazioni non sia necessariamente eguale al numero di incognite. Il concetto di rango di una matrice che andremo a definire ci aiuterà ad affrontare e a dare risposta a queste due questioni. Come abbiamo visto, inoltre, il calcolo del determinante di una matrice dà informazioni relativamente alla possibile dipendenza lineare dei vettori riga e colonna che costituiscono la 0
5 matrice. Infatti per poter riconoscere in modo semplice se n vettori di IR n sono linearmente dipendenti o meno si calcola il determinante della matrice A ottenuta scrivendo i vettori come righe o colonne: se tale determinante è nullo, i vettori sono linearmente dipendenti, altrimenti sono linearmente indipendenti. Chiaramente, il problema di riconoscere se m vettori di IR n sono linearmente dipendenti o meno non può essere affrontato facendo riferimento al calcolo del determinante della matrice associata A (di dimensione m n se i vettori sono scritti come vettori riga, di dimensione n m se i vettori sono scritti come vettori colonna ma, come vedremo suggerito dall esempio che segue, facendo riferimento a sottomatrici quadrate che possono essere definite a partire dalla matrice A e al calcolo del loro determinante. Siano v = 0 v = Evidentemente i vettori v e v sono linearmente indipendenti. Se consideriamo le possibili sottomatrici di ordine estraibili dalla matrice A A = si ottengono le matrici B = ( 0 0 B = ( B = ( 0 0 ottenute cancellando, rispettivamente, la terza, la seconda, la prima riga. Essendo quadrate, è possibile calcolare il loro determinante, ottenendo i valori det(b = 0, det(b =, det(b = 0. Il determinante non nullo della matrice B suggerisce che i due vettori non possono essere proporzionali: la presenza, quindi, di una sottomatrice di ordine con determinante non nullo fa intuire che i due vettori siano linearmente indipendenti. La procedura qui seguita può essere generalizzata al caso di m vettori di IR n : si individueranno le sottomatrici quadrate estraibili dalla matrice A e verrà studiato il loro determinante. Nel caso di una matrice x4, ad esempio, è possibile individuare sottomatrici quadrate di ordine,, e per tali sottomatrici è possibile calcolare il determinante. La definizione di rango o caratteristica di una matrice fa riferimento al calcolo dei determinanti delle possibili sottomatrici quadrate. Il rango di una matrice A, indicato con il simbolo r(a, corrisponde al massimo ordine di una matrice quadrata estraibile da A con determinante non nullo.
6 In altri termini, il rango di A è r se esiste una sottomatrice di ordine r con determinante diverso da zero e tutte le possibili sottomatrici quadrate di ordine maggiore hanno determinante uguale a zero. Ad esempio dire che r(a = se A è una matrice 4, significa affermare che esiste almeno una sottomatrice quadrata di ordine con determinante non nullo e tutte le sottomatrici di ordine hanno determinante uguale a zero. Esempio Sia A = Poichè A è una matrice di dimensione x4, la massima dimensione di una sua sottomatrice quadrata è. Pertanto r(a. Si noti che in generale r(a min{m, n} se la matrice A è una matrice mxn. Per verificare se la caratteristica di A sia è necessario calcolare i determinanti di tutte le possibili sottomatrici x A =, A = 0, 6 6 A = 5 0 6, A 4 = Poichè det(a = 48 è possibile affermare che la caratteristica di A è. Si osservi che nel caso in cui tutte le matrici A, A, A, A 4 avessero avuto determinante nullo sarebbe stato necessario analizzare le sottomatrici di ordine e calcolare il loro determinante. Nel caso in cui si fosse trovata una matrice di ordine con determinante non nullo si sarebbe potuto concludere che la caratteristica di A è. Diversamente (cioè tutte la matrici di ordine hanno determinante nullo, si sarebbe affermato che la caratteristica di A è, poichè la matrice A è non nulla. Si ottiene il seguente teorema, particolarmente interessante ai fini dello studio della dipendenza o indipendenza lineare di m vettori di IR n. Il rango r(a è il massimo numero di righe (colonne linearmente indipendenti di A. In altre parole, se r(a = r allora in A vi sono al massimo r righe linearmente indipendenti; inoltre r è anche uguale al massimo numero di colonne linearmente indipendenti di A.
7 Esempio Sia Il rango r(a è poichè A = ( det 0 ( 4 0. = 0. Ciò è equivalente ad affermare che i due vettori riga v = ( 4 v = ( 0 sono linearmente indipendenti, come pure i due vettori colonna ( ( w = w =. 0 Esempio Se poichè det(a = 0 allora r(a. r(a =. I tre vettori riga A = 4 0 Con riferimento all esempio precedente, si ottiene v = ( 4 v = ( 0 v = ( sono linearmente dipendenti, come pure i vettori colonna w = w = 0 w =.0 Il Teorema di Rouchè-Capelli Si consideri un generico sistema di m equazioni lineari in n incognite a x + a x a n x n = b a x + a x a n x n = b =... a m x + a m x a mn x n = b m che può essere scritto nella forma matriciale Ax = b, dove x denota il vettore delle incognite, b il vettore dei termini noti e A è la matrice m n dei coefficienti del sistema. Per poter riconoscere se un sistema di questo tipo ammette soluzione è possibile fare riferimento al concetto di rango definito nel paragrafo precedente. Il teorema che segue caratterizza l esistenza delle soluzioni di un sistema, nel senso che presenta una condizione necessaria e sufficiente affinchè un sistema ammetta soluzione. 4
8 Sia (A b la matrice m (n + ottenuta affiancando alla matrice A il vettore b a a... a n b a a... a n b a m a m... a mn b m Teorema di Rouchè-Capelli Il sistema lineare Ax = b di m equazioni in n incognite ammette soluzione se e solo se r(a = r(a b. Dimostrazione Supponiamo sia verificata la condizione r(a = r = r(a b. Poichè r(a = r esistono r colonne linearmente indipendenti della matrice A, indichiamole con c, c,..., c r, tali per cui ogni altra colonna della matrice A risulta combinazione lineare dei vettori c, c,..., c r. Inoltre r = r(a b e quindi essendo r il massimo numero di colonne linearmente indipendenti di (A b, il vettore b deve necessariamente essere combinazione lineare delle colonne c, c,..., c r di A. Dunque il sistema ammette soluzione. Supponiamo viceversa che il sistema ammetta soluzione ovvero che il vettore b risulti combinazione lineare delle colonne c, c,..., c r della matrice A. Se r = r(a consideriamo il rango della matrice (A b; sicuramente r(a b r. Se fosse r(a b > r dovrebbero esistere r + colonne di (A b linearmente indipendenti; fra questi vettori deve comparire il vettore b. Ma ciò risulta assurdo perchè ogni colonna della matrice A si scrive come combinazione lineare delle colonne c, c,..., c r e quindi anche b è combinazione delle colonne c, c,..., c r. Da ciò segue che necessariamente r(a b = r. 4
I sistemi lineari di n equazioni in n incognite
 I sistemi lineari I sistemi lineari di n equazioni in n incognite I sistemi lineari di n equazioni in n incognite, sono formati da equazioni di primo grado, in cui le incognite hanno tutte esponente uguale
I sistemi lineari I sistemi lineari di n equazioni in n incognite I sistemi lineari di n equazioni in n incognite, sono formati da equazioni di primo grado, in cui le incognite hanno tutte esponente uguale
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI
 CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
Sistemi Lineari. Andrea Galasso
 Sistemi Lineari Andrea Galasso Esercizi svolti Teorema. (Rouché-Capelli. Un sistema lineare Ax = b ammette soluzioni se e solo se il rango della matrice dei coefficienti A è uguale al rango della matrice
Sistemi Lineari Andrea Galasso Esercizi svolti Teorema. (Rouché-Capelli. Un sistema lineare Ax = b ammette soluzioni se e solo se il rango della matrice dei coefficienti A è uguale al rango della matrice
A titolo di esempio proponiamo la risoluzione del sistema sia con il metodo della matrice inversa sia con il metodo di Cramer.
 ) Trovare le soluzioni del seguente sistema lineare: x+ y+ z = 3x y + z = 0 x + 5y 4z = 5 Osserviamo in primo luogo che il sistema dato è un sistema quadrato di tre equazioni in tre incognite, precisamente
) Trovare le soluzioni del seguente sistema lineare: x+ y+ z = 3x y + z = 0 x + 5y 4z = 5 Osserviamo in primo luogo che il sistema dato è un sistema quadrato di tre equazioni in tre incognite, precisamente
QUADERNI DI DIDATTICA
 Department of Applied Mathematics, University of Venice QUADERNI DI DIDATTICA Marta Cardin Paola Ferretti Stefania Funari Introduzione soft alla matematica per l economia e la finanza: I SISTEMI LINEARI
Department of Applied Mathematics, University of Venice QUADERNI DI DIDATTICA Marta Cardin Paola Ferretti Stefania Funari Introduzione soft alla matematica per l economia e la finanza: I SISTEMI LINEARI
PreCorso di Matematica - PCM Corso M-Z
 PreCorso di Matematica - PCM Corso M-Z DOCENTE: M. Auteri Outline Docente: Auteri PreCorso di Matematica 2016 2 Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti
PreCorso di Matematica - PCM Corso M-Z DOCENTE: M. Auteri Outline Docente: Auteri PreCorso di Matematica 2016 2 Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti
Corso di Geometria BIAR, BSIR Esercizi 3: soluzioni
 Corso di Geometria - BIAR, BSIR Esercizi : soluzioni Rango e teorema di Rouché-Capelli Esercizio. Calcolare il rango di ciascuna delle seguenti matrici: ( ) ( ) ( ) A =, A =, A =, A 4 = ( ). a a a Soluzione.
Corso di Geometria - BIAR, BSIR Esercizi : soluzioni Rango e teorema di Rouché-Capelli Esercizio. Calcolare il rango di ciascuna delle seguenti matrici: ( ) ( ) ( ) A =, A =, A =, A 4 = ( ). a a a Soluzione.
Il teorema di Rouché-Capelli
 Luciano Battaia Questi appunti (1), ad uso degli studenti del corso di Matematica (A-La) del corso di laurea in Commercio Estero dell Università Ca Foscari di Venezia, campus di Treviso, contengono un
Luciano Battaia Questi appunti (1), ad uso degli studenti del corso di Matematica (A-La) del corso di laurea in Commercio Estero dell Università Ca Foscari di Venezia, campus di Treviso, contengono un
MATEMATICA. a.a. 2014/ Sistemi di equazioni lineari
 MATEMATICA a.a. 2014/15 8. Sistemi di equazioni lineari SISTEMI LINEARI Si definisce sistema lineare un sistema di p equazioni di primo grado in q incognite. a11x1 + a12 x2 +... + a1 qxq = k1 a21x1 + a22x2
MATEMATICA a.a. 2014/15 8. Sistemi di equazioni lineari SISTEMI LINEARI Si definisce sistema lineare un sistema di p equazioni di primo grado in q incognite. a11x1 + a12 x2 +... + a1 qxq = k1 a21x1 + a22x2
SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI
 SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI Appunti presi dalle lezioni del prof. Nedo Checcaglini Liceo Scientifico di Castiglion Fiorentino (Classe 4B) January 17, 005 1 SISTEMI LINEARI Se a ik, b i R,
SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI Appunti presi dalle lezioni del prof. Nedo Checcaglini Liceo Scientifico di Castiglion Fiorentino (Classe 4B) January 17, 005 1 SISTEMI LINEARI Se a ik, b i R,
ALGEBRA LINEARE PARTE III
 DIEM sez Matematica Finanziaria Università degli studi di Genova Dicembre 200 Indice PREMESSA 2 GENERALITA 2 RAPPRESENTAZIONE DI UN SISTEMA LINEARE IN FORMA MATRI- CIALE 2 3 SOLUZIONE DI SISTEMI LINEARI
DIEM sez Matematica Finanziaria Università degli studi di Genova Dicembre 200 Indice PREMESSA 2 GENERALITA 2 RAPPRESENTAZIONE DI UN SISTEMA LINEARE IN FORMA MATRI- CIALE 2 3 SOLUZIONE DI SISTEMI LINEARI
Si consideri il sistema a coefficienti reali di m equazioni lineari in n incognite
 3 Sistemi lineari 3 Generalità Si consideri il sistema a coefficienti reali di m equazioni lineari in n incognite ovvero, in forma matriciale, a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n x
3 Sistemi lineari 3 Generalità Si consideri il sistema a coefficienti reali di m equazioni lineari in n incognite ovvero, in forma matriciale, a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n x
Metodi per la risoluzione di sistemi lineari
 Metodi per la risoluzione di sistemi lineari Sistemi di equazioni lineari. Rango di matrici Come è noto (vedi [] sez.0.8), ad ogni matrice quadrata A è associato un numero reale det(a) detto determinante
Metodi per la risoluzione di sistemi lineari Sistemi di equazioni lineari. Rango di matrici Come è noto (vedi [] sez.0.8), ad ogni matrice quadrata A è associato un numero reale det(a) detto determinante
Appunti su Indipendenza Lineare di Vettori
 Appunti su Indipendenza Lineare di Vettori Claudia Fassino a.a. Queste dispense, relative a una parte del corso di Matematica Computazionale (Laurea in Informatica), rappresentano solo un aiuto per lo
Appunti su Indipendenza Lineare di Vettori Claudia Fassino a.a. Queste dispense, relative a una parte del corso di Matematica Computazionale (Laurea in Informatica), rappresentano solo un aiuto per lo
Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE. Giovanni Villani
 Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE Giovanni Villani Matrici Definizione 1 Si definisce matrice di tipo m n una funzione che associa
Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE Giovanni Villani Matrici Definizione 1 Si definisce matrice di tipo m n una funzione che associa
Sistemi II. Sistemi II. Elisabetta Colombo
 Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2011-2012, http://users.mat.unimi.it/users/colombo/programmabio.html 1 2 3 con R.C.+ o 1.10 Rango massimo e determinante con R.C.+
Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2011-2012, http://users.mat.unimi.it/users/colombo/programmabio.html 1 2 3 con R.C.+ o 1.10 Rango massimo e determinante con R.C.+
Sistemi d equazioni lineari
 Introduzione Introduzione Sia dato il seguente sistema d equazioni: S S S S Come si risolve un sistema... come si risolve? Lezione 25.wpd 08/01/2011 XXV - 1 Lezione 25.wpd 08/01/2011 XXV - 2 Introduzione
Introduzione Introduzione Sia dato il seguente sistema d equazioni: S S S S Come si risolve un sistema... come si risolve? Lezione 25.wpd 08/01/2011 XXV - 1 Lezione 25.wpd 08/01/2011 XXV - 2 Introduzione
Istituzioni di Matematica I. Esercizi su sistemi lineari. & % x + y " #z = "1 & '#x " y+ z =1
 Istituzioni di Matematica I Esercizi su sistemi lineari Esempio. Dire per quali valori di λ R il sistema x " y+ z = 2 % x + y " z = " x " y+ z = ha una sola soluzione, per quali nessuna, per quali infinite
Istituzioni di Matematica I Esercizi su sistemi lineari Esempio. Dire per quali valori di λ R il sistema x " y+ z = 2 % x + y " z = " x " y+ z = ha una sola soluzione, per quali nessuna, per quali infinite
Riassumiamo le proprietà dei numeri reali da noi utilizzate nel corso di Geometria.
 Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
SISTEMI LINEARI. x y + 2t = 0 2x + y + z t = 0 x z t = 0 ; S 3 : ; S 5x 2y z = 1 4x 7y = 3
 SISTEMI LINEARI. Esercizi Esercizio. Verificare se (,, ) è soluzione del sistema x y + z = x + y z = 3. Trovare poi tutte le soluzioni del sistema. Esercizio. Scrivere un sistema lineare di 3 equazioni
SISTEMI LINEARI. Esercizi Esercizio. Verificare se (,, ) è soluzione del sistema x y + z = x + y z = 3. Trovare poi tutte le soluzioni del sistema. Esercizio. Scrivere un sistema lineare di 3 equazioni
Metodi per la risoluzione di sistemi lineari
 Metodi per la risoluzione di sistemi lineari 1 Sistemi di equazioni lineari 1.1 Determinante di matrici quadrate Ad ogni matrice quadrata A è associato un numero reale det(a) detto determinante della matrice
Metodi per la risoluzione di sistemi lineari 1 Sistemi di equazioni lineari 1.1 Determinante di matrici quadrate Ad ogni matrice quadrata A è associato un numero reale det(a) detto determinante della matrice
VETTORI E MATRICI. Ing. Nicola Cappuccio 2014 U.F.5 ELEMENTI SCIENTIFICI ED ELETTRONICI APPLICATI AI SISTEMI DI TELECOMUNICAZIONI
 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 I VETTRORI E MATRICI (RICHIAMI) Ad ogni matrice quadrata a coefficienti reali è possibile associare un numero reale, detto determinante, calcolato
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 I VETTRORI E MATRICI (RICHIAMI) Ad ogni matrice quadrata a coefficienti reali è possibile associare un numero reale, detto determinante, calcolato
1. Sistemi di equazioni lineari. 1.1 Considerazioni preliminari
 1. Sistemi di equazioni lineari 1.1 Considerazioni preliminari I sistemi lineari sono sistemi di equazioni di primo grado in più incognite. Molti problemi di matematica e fisica portano alla soluzione
1. Sistemi di equazioni lineari 1.1 Considerazioni preliminari I sistemi lineari sono sistemi di equazioni di primo grado in più incognite. Molti problemi di matematica e fisica portano alla soluzione
Registro Lezioni di Algebra lineare del 15 e 16 novembre 2016.
 Registro Lezioni di Algebra lineare del 15 e 16 novembre 2016 Di seguito si riporta il riassunto degli argomenti svolti; i riferimenti sono a parti del Cap8 Elementi di geometria e algebra lineare Par5
Registro Lezioni di Algebra lineare del 15 e 16 novembre 2016 Di seguito si riporta il riassunto degli argomenti svolti; i riferimenti sono a parti del Cap8 Elementi di geometria e algebra lineare Par5
Corso di Geometria BIAR, BSIR Esercizi 2: soluzioni
 Corso di Geometria 2- BIAR, BSIR Esercizi 2: soluzioni Esercizio Calcolare il determinante della matrice 2 3 : 3 2 a) con lo sviluppo lungo la prima riga, b) con lo sviluppo lungo la terza colonna, c)
Corso di Geometria 2- BIAR, BSIR Esercizi 2: soluzioni Esercizio Calcolare il determinante della matrice 2 3 : 3 2 a) con lo sviluppo lungo la prima riga, b) con lo sviluppo lungo la terza colonna, c)
Esercitazione 6 - Soluzione
 Anno Accademico 28-29 Corso di Algebra Lineare e Calcolo Numerico per Ingegneria Meccanica Esercitazione 6 - Soluzione Immagine, nucleo. Teorema di Rouché-Capelli. Esercizio Sia L : R 3 R 3 l applicazione
Anno Accademico 28-29 Corso di Algebra Lineare e Calcolo Numerico per Ingegneria Meccanica Esercitazione 6 - Soluzione Immagine, nucleo. Teorema di Rouché-Capelli. Esercizio Sia L : R 3 R 3 l applicazione
Riassumiamo le proprietà dei numeri reali da noi utilizzate nel corso di Geometria.
 Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
PROBLEMA. Costruire matrici quadrate contenute. Fare i determinanti delle matrici quadrate contenute in A
 A = PROBLEMA 0 1 2 7 2 5 3 0 (2 4) Costruire matrici quadrate contenute in A (possibili solo matrici quadrate 2 2 e 1 1) Fare i determinanti delle matrici quadrate contenute in A Questo porta al concetto
A = PROBLEMA 0 1 2 7 2 5 3 0 (2 4) Costruire matrici quadrate contenute in A (possibili solo matrici quadrate 2 2 e 1 1) Fare i determinanti delle matrici quadrate contenute in A Questo porta al concetto
ESERCIZI SULLE MATRICI
 ESERCIZI SULLE MATRICI Consideriamo il sistema lineare a, x + a, x + + a,n x n = b a, x + a, x + + a,n x n = b a m, x + a m, x + + a m,n x n = b m di m equazioni in n incognite che ha a, a,n A = a m, a
ESERCIZI SULLE MATRICI Consideriamo il sistema lineare a, x + a, x + + a,n x n = b a, x + a, x + + a,n x n = b a m, x + a m, x + + a m,n x n = b m di m equazioni in n incognite che ha a, a,n A = a m, a
MATRICI E SISTEMI LINEARI
 1 Rappresentazione di dati strutturati MATRICI E SISTEMI LINEARI Gli elementi di una matrice, detti coefficienti, possono essere qualsiasi e non devono necessariamente essere omogenei tra loro; di solito
1 Rappresentazione di dati strutturati MATRICI E SISTEMI LINEARI Gli elementi di una matrice, detti coefficienti, possono essere qualsiasi e non devono necessariamente essere omogenei tra loro; di solito
il determinante che si ottiene da A, sopprimendo la i - esima riga e la j - esima colonna. Si definisce complemento algebrico dell'elemento a ij
 Determinanti Sia data la matrice quadrata a... a n a a n =...... a... a n nn Chiamiamo determinante di il numero det o che ad essa viene associato. det = a a... a... a... a n n n... a nn Un generico elemento
Determinanti Sia data la matrice quadrata a... a n a a n =...... a... a n nn Chiamiamo determinante di il numero det o che ad essa viene associato. det = a a... a... a... a n n n... a nn Un generico elemento
MATRICI E SISTEMI LINEARI
 MATRICI E SISTEMI LINEARI - PARTE I - Felice Iavernaro Dipartimento di Matematica Università di Bari 27 Febbraio 2006 Felice Iavernaro (Univ. Bari) Matrici e Sistemi lineari 27/02/2006 1 / 1 Definizione
MATRICI E SISTEMI LINEARI - PARTE I - Felice Iavernaro Dipartimento di Matematica Università di Bari 27 Febbraio 2006 Felice Iavernaro (Univ. Bari) Matrici e Sistemi lineari 27/02/2006 1 / 1 Definizione
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof. Fabio Perroni. 5. Rango
 Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 5 Rango Definizione 1 Sia A M m,n (K) una matrice m n a coefficienti nel campo K Il rango
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 5 Rango Definizione 1 Sia A M m,n (K) una matrice m n a coefficienti nel campo K Il rango
Geometria BIAR Esercizi 2
 Geometria BIAR 0- Esercizi Esercizio. a Si consideri il generico vettore v b R c (a) Si trovi un vettore riga x (x, y, z) tale che x v a (b) Si trovi un vettore riga x (x, y, z) tale che x v kb (c) Si
Geometria BIAR 0- Esercizi Esercizio. a Si consideri il generico vettore v b R c (a) Si trovi un vettore riga x (x, y, z) tale che x v a (b) Si trovi un vettore riga x (x, y, z) tale che x v kb (c) Si
Esercizi svolti. risolvere, se possibile, l equazione xa + B = O, essendo x un incognita reale
 Esercizi svolti 1. Matrici e operazioni fra matrici 1.1 Date le matrici 1 2 1 6 A = B = 5 2 9 15 6 risolvere, se possibile, l equazione xa + B = O, essendo x un incognita reale Osservazione iniziale: qualunque
Esercizi svolti 1. Matrici e operazioni fra matrici 1.1 Date le matrici 1 2 1 6 A = B = 5 2 9 15 6 risolvere, se possibile, l equazione xa + B = O, essendo x un incognita reale Osservazione iniziale: qualunque
Sistemi di equazioni lineari
 Sistemi di equazioni lineari Siano X 1,, X n indeterminate Un equazione lineare (o di primo grado) nelle incognite X 1,, X n a coefficienti nel campo K è della forma a 1 X 1 + + a n X n = b, a i, b K,
Sistemi di equazioni lineari Siano X 1,, X n indeterminate Un equazione lineare (o di primo grado) nelle incognite X 1,, X n a coefficienti nel campo K è della forma a 1 X 1 + + a n X n = b, a i, b K,
Argomento 13 Sistemi lineari
 Sistemi lineari: definizioni Argomento Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto
Sistemi lineari: definizioni Argomento Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto
I. Foglio di esercizi su vettori linearmente dipendenti e linearmente indipendenti. , v 2 = α v 1 + β v 2 + γ v 3. α v 1 + β v 2 + γ v 3 = 0. + γ.
 ESERCIZI SVOLTI DI ALGEBRA LINEARE (Sono svolti alcune degli esercizi proposti nei fogli di esercizi su vettori linearmente dipendenti e vettori linearmente indipendenti e su sistemi lineari ) I. Foglio
ESERCIZI SVOLTI DI ALGEBRA LINEARE (Sono svolti alcune degli esercizi proposti nei fogli di esercizi su vettori linearmente dipendenti e vettori linearmente indipendenti e su sistemi lineari ) I. Foglio
Geometria BAER I canale Foglio esercizi 3
 Geometria BAER I canale Foglio esercizi 3 Esercizio. Discutere le soluzioni del seguente sistema lineare nelle incognite,, z al variare del parametro k. 3 + kz = k k + 3z = k k + z = Soluzione: Il determinante
Geometria BAER I canale Foglio esercizi 3 Esercizio. Discutere le soluzioni del seguente sistema lineare nelle incognite,, z al variare del parametro k. 3 + kz = k k + 3z = k k + z = Soluzione: Il determinante
0.1 Condizione sufficiente di diagonalizzabilità
 0.1. CONDIZIONE SUFFICIENTE DI DIAGONALIZZABILITÀ 1 0.1 Condizione sufficiente di diagonalizzabilità È naturale porsi il problema di sapere se ogni matrice sia o meno diagonalizzabile. Abbiamo due potenziali
0.1. CONDIZIONE SUFFICIENTE DI DIAGONALIZZABILITÀ 1 0.1 Condizione sufficiente di diagonalizzabilità È naturale porsi il problema di sapere se ogni matrice sia o meno diagonalizzabile. Abbiamo due potenziali
Sui determinanti e l indipendenza lineare di vettori
 Sui determinanti e l indipendenza lineare di vettori 1 Si dice che m vettori v 1, v 2,,v m di R n sono linearmente indipendenti, se una loro combinazione lineare può dare il vettore nullo solo se i coefficienti
Sui determinanti e l indipendenza lineare di vettori 1 Si dice che m vettori v 1, v 2,,v m di R n sono linearmente indipendenti, se una loro combinazione lineare può dare il vettore nullo solo se i coefficienti
Esercizi di Matematica di Base Scienze biologiche e Scienze e Tecnologie dell Ambiente
 Esercizi di Matematica di Base Scienze biologiche e Scienze e Tecnologie dell Ambiente Dati i vettori di R (i) Calcolare il prodotto scalare v w, (ii) Stabilire se v e w sono ortogonali, (ii) Stabilire
Esercizi di Matematica di Base Scienze biologiche e Scienze e Tecnologie dell Ambiente Dati i vettori di R (i) Calcolare il prodotto scalare v w, (ii) Stabilire se v e w sono ortogonali, (ii) Stabilire
SISTEMI LINEARI MATRICI E SISTEMI 1
 MATRICI E SISTEMI SISTEMI LINEARI Sistemi lineari e forma matriciale (definizioni e risoluzione). Teorema di Rouché-Capelli. Sistemi lineari parametrici. Esercizio Risolvere il sistema omogeneo la cui
MATRICI E SISTEMI SISTEMI LINEARI Sistemi lineari e forma matriciale (definizioni e risoluzione). Teorema di Rouché-Capelli. Sistemi lineari parametrici. Esercizio Risolvere il sistema omogeneo la cui
Ax = b ; b = b 1 b 2. a 11 a 12 a 1n a 21 a 22 a 2n. b m. a m1 a m2 a mn
 SISTEMI LINERI Consideriamo il seguente sistema di m equazioni lineare nelle n incognite,,, n : a + a + + a n n = b >< a + a + + a n n = b = >: a m + a m + + a mn n = b m tale sistema può essere scritto
SISTEMI LINERI Consideriamo il seguente sistema di m equazioni lineare nelle n incognite,,, n : a + a + + a n n = b >< a + a + + a n n = b = >: a m + a m + + a mn n = b m tale sistema può essere scritto
Note per le esercitazioni di Geometria 1 a.a. 2007/08 A. Lotta. Metodi per il calcolo del rango di una matrice
 Note per le esercitazioni di Geometria 1 a.a. 2007/08 A. Lotta Versione del 21/12/07 Metodi per il calcolo del rango di una matrice Sia A M m,n (K). Denotiamo con A (i) la riga i-ma di A, i {1,..., m}.
Note per le esercitazioni di Geometria 1 a.a. 2007/08 A. Lotta Versione del 21/12/07 Metodi per il calcolo del rango di una matrice Sia A M m,n (K). Denotiamo con A (i) la riga i-ma di A, i {1,..., m}.
Risoluzione di sistemi lineari
 Risoluzione di sistemi lineari Teorema (Rouché-Capelli) Dato il sistema di m equazioni in n incognite Ax = b, con A M at(m, n) b R n x R n [A b] si ha che: matrice dei coefficienti, vettore dei termini
Risoluzione di sistemi lineari Teorema (Rouché-Capelli) Dato il sistema di m equazioni in n incognite Ax = b, con A M at(m, n) b R n x R n [A b] si ha che: matrice dei coefficienti, vettore dei termini
Manlio Bordoni. APPUNTI SULLA RAPPRESENTAZIONE DEI SOTTOSPAZI VETTORIALI DI R n I MODO. v 11. v n1
 Manlio Bordoni APPUNTI SULLA RAPPRESENTAZIONE DEI SOTTOSPAZI VETTORIALI DI R n I MODO Sia dato un insieme di generatori v v =,, v k = v n di W : questo vuol dire che ogni vettore w W si scrive come combinazione
Manlio Bordoni APPUNTI SULLA RAPPRESENTAZIONE DEI SOTTOSPAZI VETTORIALI DI R n I MODO Sia dato un insieme di generatori v v =,, v k = v n di W : questo vuol dire che ogni vettore w W si scrive come combinazione
MATRICI E VETTORI APPROFONDIMENTO PER IL CORSO DI LABORATORIO DI INFORMATICA SARA POLTRONIERI
 MATRICI E VETTORI APPROFONDIMENTO PER IL CORSO DI LABORATORIO DI INFORMATICA SARA POLTRONIERI LE MATRICI DEFINIZIONE: Una matrice è un insieme di numeri disposti su righe e colonne. 1 3 7 M = 2 5 1 M è
MATRICI E VETTORI APPROFONDIMENTO PER IL CORSO DI LABORATORIO DI INFORMATICA SARA POLTRONIERI LE MATRICI DEFINIZIONE: Una matrice è un insieme di numeri disposti su righe e colonne. 1 3 7 M = 2 5 1 M è
Un sistema di equazioni lineari ( o brevemente un sistema lineare) di m equazioni in n incognite, si presenta nella forma:
 SISTEMI LINEARI Un sistema di equazioni lineari ( o brevemente un sistema lineare) di m equazioni in n incognite, si presenta nella forma: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n x n =
SISTEMI LINEARI Un sistema di equazioni lineari ( o brevemente un sistema lineare) di m equazioni in n incognite, si presenta nella forma: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n x n =
Rango di una matrice e teorema di Rouché-Capelli
 Rango di una matrice e teorema di Rouché-Capelli Sappiamo che a una matrice m n, A, è associata l applicazione lineare L A : R n R m, L A (X) = AX, X R n. Definizione 1. Lo spazio nullo di A, N (A), è
Rango di una matrice e teorema di Rouché-Capelli Sappiamo che a una matrice m n, A, è associata l applicazione lineare L A : R n R m, L A (X) = AX, X R n. Definizione 1. Lo spazio nullo di A, N (A), è
Integrazione di equazioni differenziali lineari. Il metodo di Cauchy
 1 EQUAZIONI DIFFERENZIALI LINEARI OMOGENEE Integrazione di equazioni differenziali lineari. Il metodo di Cauchy Marcello Colozzo 1 Equazioni differenziali lineari omogenee Sia data l equazione differenziale
1 EQUAZIONI DIFFERENZIALI LINEARI OMOGENEE Integrazione di equazioni differenziali lineari. Il metodo di Cauchy Marcello Colozzo 1 Equazioni differenziali lineari omogenee Sia data l equazione differenziale
Algebra lineare. Laboratorio di programmazione e calcolo CdL in Chimica. Pierluigi Amodio
 Algebra lineare Laboratorio di programmazione e calcolo CdL in Chimica Pierluigi Amodio Dipartimento di Matematica Università di Bari pierluigi.amodio@uniba.it http://dm.uniba.it/ amodio A.A. 2016/17 P.
Algebra lineare Laboratorio di programmazione e calcolo CdL in Chimica Pierluigi Amodio Dipartimento di Matematica Università di Bari pierluigi.amodio@uniba.it http://dm.uniba.it/ amodio A.A. 2016/17 P.
Esercizi di Algebra Lineare Determinanti
 Esercizi di Algebra Lineare Determinanti Anna M. Bigatti 3-6 dicembre 2012 Calcolo del determinante Proposizione 1. Alcune proprietà dei determinanti: (a) Il determinante del prodotto è il prodotto dei
Esercizi di Algebra Lineare Determinanti Anna M. Bigatti 3-6 dicembre 2012 Calcolo del determinante Proposizione 1. Alcune proprietà dei determinanti: (a) Il determinante del prodotto è il prodotto dei
CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA
 CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA FOGLIO DI ESERCIZI GEOMETRIA 009/0 Esercizio. (7.9). Si consideri il sistema di equazioni lineari: x + y + z = x + y + z = x + y + 3z = a) Si dica per quali
CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA FOGLIO DI ESERCIZI GEOMETRIA 009/0 Esercizio. (7.9). Si consideri il sistema di equazioni lineari: x + y + z = x + y + z = x + y + 3z = a) Si dica per quali
Corso di Analisi Numerica
 con pivoting Corso di Laurea in Ingegneria Informatica Corso di Analisi Numerica 6 - METODI DIRETTI PER I SISTEMI LINEARI Lucio Demeio Dipartimento di Scienze Matematiche con pivoting 1 Introduzione algebrica
con pivoting Corso di Laurea in Ingegneria Informatica Corso di Analisi Numerica 6 - METODI DIRETTI PER I SISTEMI LINEARI Lucio Demeio Dipartimento di Scienze Matematiche con pivoting 1 Introduzione algebrica
Elementi di Algebra Lineare
 Elementi di Algebra Lineare Corso di Calcolo Numerico, a.a. 2009/2010 Francesca Mazzia Dipartimento di Matematica Università di Bari 13 Marzo 2006 Francesca Mazzia (Univ. Bari) Elementi di Algebra Lineare
Elementi di Algebra Lineare Corso di Calcolo Numerico, a.a. 2009/2010 Francesca Mazzia Dipartimento di Matematica Università di Bari 13 Marzo 2006 Francesca Mazzia (Univ. Bari) Elementi di Algebra Lineare
Soluzioni del Foglio 2 I sistemi lineari
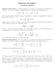 Soluzioni del Foglio 2 I sistemi lineari Soluzione dell esercizio 1 Il sistema assegnato è un sistema di 2 equazioni in 2 incognite non omogeneo Le matrici incompleta e completa associate al sistema sono
Soluzioni del Foglio 2 I sistemi lineari Soluzione dell esercizio 1 Il sistema assegnato è un sistema di 2 equazioni in 2 incognite non omogeneo Le matrici incompleta e completa associate al sistema sono
Note per il corso di Geometria Corso di laurea in Ing. Edile/Architettura. 4 Sistemi lineari. Metodo di eliminazione di Gauss Jordan
 Note per il corso di Geometria 2006-07 Corso di laurea in Ing. Edile/Architettura Sistemi lineari. Metodo di eliminazione di Gauss Jordan.1 Operazioni elementari Abbiamo visto che un sistema di m equazioni
Note per il corso di Geometria 2006-07 Corso di laurea in Ing. Edile/Architettura Sistemi lineari. Metodo di eliminazione di Gauss Jordan.1 Operazioni elementari Abbiamo visto che un sistema di m equazioni
Algebra delle matrici
 Algebra delle matrici Metodo di Gauss-Jordan per l inversione di una matrice. Nella lezione scorsa abbiamo visto che un modo per determinare l eventuale inversa di una matrice quadrata A consiste nel risolvere
Algebra delle matrici Metodo di Gauss-Jordan per l inversione di una matrice. Nella lezione scorsa abbiamo visto che un modo per determinare l eventuale inversa di una matrice quadrata A consiste nel risolvere
LEZIONE Equazioni matriciali. Negli Esempi e si sono studiati più sistemi diversi AX 1 = B 1, AX 2 = R m,n, B = (b i,h ) 1 i m
 LEZIONE 4 41 Equazioni matriciali Negli Esempi 336 e 337 si sono studiati più sistemi diversi AX 1 = B 1, AX 2 = B 2,, AX p = B p aventi la stessa matrice incompleta A Tale tipo di problema si presenta
LEZIONE 4 41 Equazioni matriciali Negli Esempi 336 e 337 si sono studiati più sistemi diversi AX 1 = B 1, AX 2 = B 2,, AX p = B p aventi la stessa matrice incompleta A Tale tipo di problema si presenta
3. Elementi di Algebra Lineare.
 CALCOLO NUMERICO Francesca Mazzia Dipartimento Interuniversitario di Matematica Università di Bari 3. Elementi di Algebra Lineare. 1 Sistemi lineari Sia A IR m n, x IR n di n Ax = b è un vettore di m componenti.
CALCOLO NUMERICO Francesca Mazzia Dipartimento Interuniversitario di Matematica Università di Bari 3. Elementi di Algebra Lineare. 1 Sistemi lineari Sia A IR m n, x IR n di n Ax = b è un vettore di m componenti.
Sviluppando ancora per colonna sulla prima colonna della prima matrice e sulla seconda della seconda matrice si ottiene:
 M. CARAMIA, S. GIORDANI, F. GUERRIERO, R. MUSMANNO, D. PACCIARELLI RICERCA OPERATIVA Isedi Esercizi proposti nel Cap. 5 - Soluzioni Esercizio 5. - La norma Euclidea di è 9 6 5 - Il versore corrispondente
M. CARAMIA, S. GIORDANI, F. GUERRIERO, R. MUSMANNO, D. PACCIARELLI RICERCA OPERATIVA Isedi Esercizi proposti nel Cap. 5 - Soluzioni Esercizio 5. - La norma Euclidea di è 9 6 5 - Il versore corrispondente
ossia può anche essere localizzato univocamente sul piano complesso con la sua forma polare.
 ALGEBRA COMPLESSA Nel corso dei secoli gli insiemi dei numeri sono andati man mano allargandosi per rispondere all esigenza di dare soluzione a equazioni e problemi sempre nuovi I numeri complessi sono
ALGEBRA COMPLESSA Nel corso dei secoli gli insiemi dei numeri sono andati man mano allargandosi per rispondere all esigenza di dare soluzione a equazioni e problemi sempre nuovi I numeri complessi sono
Lezione 10: Teorema di Rouchè-Capelli e la classificazione dei sistemi lineari
 Lezione 10: Teorema di Rouchè-Capelli e la classificazione dei sistemi lineari In questa lezione ci dedicheremo a studiare a fondo quali proprietà della matrice dei coefficienti di un sistema (e della
Lezione 10: Teorema di Rouchè-Capelli e la classificazione dei sistemi lineari In questa lezione ci dedicheremo a studiare a fondo quali proprietà della matrice dei coefficienti di un sistema (e della
LEZIONE i i 3
 LEZIONE 5 51 Determinanti In questo lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 5 51 Determinanti In questo lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari
 Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari Antonio Lanteri e Cristina Turrini UNIMI - 2016/2017 Antonio Lanteri e Cristina Turrini (UNIMI - 2016/2017 Elementi di Algebra Lineare
Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari Antonio Lanteri e Cristina Turrini UNIMI - 2016/2017 Antonio Lanteri e Cristina Turrini (UNIMI - 2016/2017 Elementi di Algebra Lineare
APPLICAZIONI. Im f = {b B a A tale che f (a) = b}.
 APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
SISTEMI LINEARI, METODO DI GAUSS
 SISTEMI LINEARI, METODO DI GAUSS Abbiamo visto che un sistema di m equazioni lineari in n incognite si può rappresentare in forma matriciale come A x = b dove: A è la matrice di tipo (m, n) dei coefficienti
SISTEMI LINEARI, METODO DI GAUSS Abbiamo visto che un sistema di m equazioni lineari in n incognite si può rappresentare in forma matriciale come A x = b dove: A è la matrice di tipo (m, n) dei coefficienti
Determinanti. Definizione ed esempi. Definizione ed esempi. Proprietà dei determinanti Rango di matrici
 Introduzione S S S Rango di matrici Si dice sottomatrice d'una matrice data la matrice ottenuta selezionando un certo numero di righe e di colonne della matrice iniziale. Lezione 24.wpd 08/01/2011 XXIV
Introduzione S S S Rango di matrici Si dice sottomatrice d'una matrice data la matrice ottenuta selezionando un certo numero di righe e di colonne della matrice iniziale. Lezione 24.wpd 08/01/2011 XXIV
LeLing12: Ancora sui determinanti.
 LeLing2: Ancora sui determinanti. Ārgomenti svolti: Sviluppi di Laplace. Prodotto vettoriale e generalizzazioni. Rango e determinante: i minori. Il polinomio caratteristico. Ēsercizi consigliati: Geoling
LeLing2: Ancora sui determinanti. Ārgomenti svolti: Sviluppi di Laplace. Prodotto vettoriale e generalizzazioni. Rango e determinante: i minori. Il polinomio caratteristico. Ēsercizi consigliati: Geoling
Elementi di Algebra Matriciale. (richiami)
 Elementi di Algebra Matriciale Definizione di matrice (richiami) Matrice quadrata, diagonale, identità, triangolare, simmetrica Matrice trasposta Principali operazioni su matrici e vettori: somma, sottrazione,
Elementi di Algebra Matriciale Definizione di matrice (richiami) Matrice quadrata, diagonale, identità, triangolare, simmetrica Matrice trasposta Principali operazioni su matrici e vettori: somma, sottrazione,
Ingegneria Gestionale - Corso di Analisi II e Algebra anno accademico 2008/2009
 Ingegneria Gestionale - Corso di Analisi II e Algebra anno accademico 28/29 Dire se le seguenti proposizioni sono vere o false: ESERCITAZIONE. Proposizione Vera Falsa f : R R 4 rk(f f : R 4 R rk(f f :
Ingegneria Gestionale - Corso di Analisi II e Algebra anno accademico 28/29 Dire se le seguenti proposizioni sono vere o false: ESERCITAZIONE. Proposizione Vera Falsa f : R R 4 rk(f f : R 4 R rk(f f :
Richiami di Algebra Lineare
 Appendice A Richiami di Algebra Lineare In questo capitolo sono presentati alcuni concetti di algebra lineare L algebra lineare è quella branca della matematica che si occupa dello studio di vettori, spazi
Appendice A Richiami di Algebra Lineare In questo capitolo sono presentati alcuni concetti di algebra lineare L algebra lineare è quella branca della matematica che si occupa dello studio di vettori, spazi
0.1 Forme quadratiche
 0.1. FORME QUADRATICHE 1 0.1 Forme quadratiche In questa sezione possiamo applicare il Teorema degli Assi Principali per giustificare alcune fatti che sono stati utilizzati nella riduzione a forma canonica
0.1. FORME QUADRATICHE 1 0.1 Forme quadratiche In questa sezione possiamo applicare il Teorema degli Assi Principali per giustificare alcune fatti che sono stati utilizzati nella riduzione a forma canonica
LEZIONE i 0 3 Le sottomatrici 2 2 di A sono. 1 2 i i 3. Invece (
 LEZIONE 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
Note sui sistemi lineari
 Note sui sistemi lineari Sia K un campo e siano m e n due numeri interi positivi. Sia A M(m n, K) e sia b K m. Consideriamo il sistema lineare Ax = b nell incognita x K n (o, se preferite, nelle incognite
Note sui sistemi lineari Sia K un campo e siano m e n due numeri interi positivi. Sia A M(m n, K) e sia b K m. Consideriamo il sistema lineare Ax = b nell incognita x K n (o, se preferite, nelle incognite
AUTOVALORI, AUTOVETTORI, AUTOSPAZI
 AUTOVALORI, AUTOVETTORI, AUTOSPAZI. Esercizi Esercizio. Sia f : R 3 R 3 l endomorfismo definito da f(x, y, z) = (x+y, y +z, x+z). Calcolare gli autovalori ed una base per ogni autospazio di f. Dire se
AUTOVALORI, AUTOVETTORI, AUTOSPAZI. Esercizi Esercizio. Sia f : R 3 R 3 l endomorfismo definito da f(x, y, z) = (x+y, y +z, x+z). Calcolare gli autovalori ed una base per ogni autospazio di f. Dire se
Inversa di una matrice
 Geometria Lingotto. LeLing: La matrice inversa. Ārgomenti svolti: Inversa di una matrice. Unicita e calcolo della inversa. La inversa di una matrice. Il gruppo delle matrici invertibili. Ēsercizi consigliati:
Geometria Lingotto. LeLing: La matrice inversa. Ārgomenti svolti: Inversa di una matrice. Unicita e calcolo della inversa. La inversa di una matrice. Il gruppo delle matrici invertibili. Ēsercizi consigliati:
Matematica II, aa
 Matematica II, aa 2011-2012 Il corso si e svolto su cinque temi principali: sistemi lineari, algebra delle matrici, determinati, spazio vettoriale R n, spazio euclideo R n ; per ogni tema descrivo gli
Matematica II, aa 2011-2012 Il corso si e svolto su cinque temi principali: sistemi lineari, algebra delle matrici, determinati, spazio vettoriale R n, spazio euclideo R n ; per ogni tema descrivo gli
Si noti che la matrice trasposta A ha lo stesso determinante. Questa proprietà è generale;
 Ottavio Serra Matrici e determinanti In questa nota estenderemo a matrici quadrate di ordine n qualsiasi il concetto di determinante introdotto nelle scuole secondarie per matrici di ordine 2 come tecnica
Ottavio Serra Matrici e determinanti In questa nota estenderemo a matrici quadrate di ordine n qualsiasi il concetto di determinante introdotto nelle scuole secondarie per matrici di ordine 2 come tecnica
21 - Sistemi di Equazioni Lineari
 Università degli Studi di Palermo Facoltà di Economia Dipartimento di Scienze Economiche, Aziendali e Statistiche Appunti del corso di Matematica - Sistemi di Equazioni Lineari Anno Accademico 5/6 M. Tumminello,
Università degli Studi di Palermo Facoltà di Economia Dipartimento di Scienze Economiche, Aziendali e Statistiche Appunti del corso di Matematica - Sistemi di Equazioni Lineari Anno Accademico 5/6 M. Tumminello,
VETTORI E MATRICI. De nizione 1 Chiamiamo vettore x una n-pla ordinata di numeri reali. x 1 x 2. x n
 VETTORI E MATRICI De nizione 1 Chiamiamo vettore x una n-pla ordinata di numeri reali x 1 x. x n 5 L insieme di tutti i vettori con n componenti reali si indica con R n :I numeri reali si possono pensare
VETTORI E MATRICI De nizione 1 Chiamiamo vettore x una n-pla ordinata di numeri reali x 1 x. x n 5 L insieme di tutti i vettori con n componenti reali si indica con R n :I numeri reali si possono pensare
CORSO DI GEOMETRIA DETERMINANTE A.A. 2018/2019 PROF. VALENTINA BEORCHIA
 CORSO DI GEOMETRIA DETERMINANTE AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Definizione induttiva di determinante 1 2 Caratterizzazione delle matrici quadrate di rango massimo 5 3 Regole di Laplace 6
CORSO DI GEOMETRIA DETERMINANTE AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Definizione induttiva di determinante 1 2 Caratterizzazione delle matrici quadrate di rango massimo 5 3 Regole di Laplace 6
4 Autovettori e autovalori
 4 Autovettori e autovalori 41 Cambiamenti di base Sia V uno spazio vettoriale tale che dim V n Si è visto in sezione 12 che uno spazio vettoriale ammette basi distinte, ma tutte con la medesima cardinalità
4 Autovettori e autovalori 41 Cambiamenti di base Sia V uno spazio vettoriale tale che dim V n Si è visto in sezione 12 che uno spazio vettoriale ammette basi distinte, ma tutte con la medesima cardinalità
Richiami di Algebra Lineare
 Richiami di Algebra Lineare Fabrizio Silvestri December 14, 010 Matrice Sia R il campo dei numeri reali. Si indica con R m n l insieme delle matrici ad elementi reali con m righe ed n colonne. Se A R n
Richiami di Algebra Lineare Fabrizio Silvestri December 14, 010 Matrice Sia R il campo dei numeri reali. Si indica con R m n l insieme delle matrici ad elementi reali con m righe ed n colonne. Se A R n
Fondamenti di Matematica del discreto
 Fondamenti di Matematica del discreto M1 - Insiemi numerici 25 gennaio 2013 - Laurea on line Esercizio 1. Dire, motivando la risposta, se è possibile scrivere 3 come combinazione lineare di 507 e 2010,
Fondamenti di Matematica del discreto M1 - Insiemi numerici 25 gennaio 2013 - Laurea on line Esercizio 1. Dire, motivando la risposta, se è possibile scrivere 3 come combinazione lineare di 507 e 2010,
Applicazioni eliminazione di Gauss
 Applicazioni eliminazione di Gauss. Premessa Nel seguito supporremo sempre di applicare il metodo di eliminazione di Gauss allo scopo di trasformare la matrice del sistema Ax = b in una matrice triangolare
Applicazioni eliminazione di Gauss. Premessa Nel seguito supporremo sempre di applicare il metodo di eliminazione di Gauss allo scopo di trasformare la matrice del sistema Ax = b in una matrice triangolare
Corso di Geometria BIAR, BSIR Esercizi 4: soluzioni
 Corso di Geometria - BIAR, BSIR Esercizi : soluzioni Esercizio. Sono dati i seguenti sistemi lineari omogenei nelle incognite x, y, z: { x + y z = x + y z = x + y z = S : x y + z =, S :, S 3 : x 3y =,
Corso di Geometria - BIAR, BSIR Esercizi : soluzioni Esercizio. Sono dati i seguenti sistemi lineari omogenei nelle incognite x, y, z: { x + y z = x + y z = x + y z = S : x y + z =, S :, S 3 : x 3y =,
Esercizi di Geometria Spazi vettoriali e sottospazi - indipendenza lineare
 Esercizi di Geometria Spazi vettoriali e sottospazi - indipendenza lineare 1. Quali dei seguenti sottoinsiemi sono sottospazi di R 3? Motivare la risposta. (a) {(x, y, 1) x, y R} (b) {(0, y, 0) y R} (c)
Esercizi di Geometria Spazi vettoriali e sottospazi - indipendenza lineare 1. Quali dei seguenti sottoinsiemi sono sottospazi di R 3? Motivare la risposta. (a) {(x, y, 1) x, y R} (b) {(0, y, 0) y R} (c)
GEOMETRIA I Prima Prova Intermedia 3 Novembre 2017
 Corso di Laurea in Fisica GEOMETRIA I Prima Prova Intermedia Novembre 017 Cognome: Nome: Matricola: PARTE 1 Test a risposta multipla Una ed una sola delle quattro affermazioni è corretta. Indicarla con
Corso di Laurea in Fisica GEOMETRIA I Prima Prova Intermedia Novembre 017 Cognome: Nome: Matricola: PARTE 1 Test a risposta multipla Una ed una sola delle quattro affermazioni è corretta. Indicarla con
LEZIONE 3. a + b + 2c + e = 1 b + d + g = 0 3b + f + 3g = 2. a b c d e f g
 LEZIONE 3 3.. Matrici fortemente ridotte per righe. Nella precedente lezione abbiamo introdotto la nozione di soluzione di un sistema di equazioni lineari. In questa lezione ci poniamo il problema di descrivere
LEZIONE 3 3.. Matrici fortemente ridotte per righe. Nella precedente lezione abbiamo introdotto la nozione di soluzione di un sistema di equazioni lineari. In questa lezione ci poniamo il problema di descrivere
La retta nel piano. Supponiamo che la retta r sia assegnata attraverso un suo punto P 0 (x 0, y 0 ) e un vettore v (l, m) che ne indichi la direzione.
 La retta nel piano Equazioni vettoriale e parametriche di una retta Supponiamo che la retta r sia assegnata attraverso un suo punto P 0 (x 0, y 0 ) e un vettore v (l, m) che ne indichi la direzione. Condizione
La retta nel piano Equazioni vettoriale e parametriche di una retta Supponiamo che la retta r sia assegnata attraverso un suo punto P 0 (x 0, y 0 ) e un vettore v (l, m) che ne indichi la direzione. Condizione
Dipendenza e indipendenza lineare
 Dipendenza e indipendenza lineare Luciano Battaia Questi appunti () ad uso degli studenti del corso di Matematica (A-La) del corso di laurea in Commercio Estero dell Università Ca Foscari di Venezia campus
Dipendenza e indipendenza lineare Luciano Battaia Questi appunti () ad uso degli studenti del corso di Matematica (A-La) del corso di laurea in Commercio Estero dell Università Ca Foscari di Venezia campus
Metodi Matematici per l Economia anno 2017/2018 Gruppo B
 Metodi Matematici per l Economia anno 2017/2018 Gruppo B Docente: Giacomo Dimarco Dipartimento di Matematica e Informatica Università di Ferrara https://sites.google.com/a/unife.it/giacomo-dimarco-home-page/
Metodi Matematici per l Economia anno 2017/2018 Gruppo B Docente: Giacomo Dimarco Dipartimento di Matematica e Informatica Università di Ferrara https://sites.google.com/a/unife.it/giacomo-dimarco-home-page/
Sistemi Lineari. Elisabetta Colombo. Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico
 Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 200-20 2 a di o.0 4 Capelli Rango o Caratterisca : definizioni a di o.0 Un equazione nelle n incognite x,..., x n della forma dove
Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 200-20 2 a di o.0 4 Capelli Rango o Caratterisca : definizioni a di o.0 Un equazione nelle n incognite x,..., x n della forma dove
Anno Accademico 2016/2017
 Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2016/2017 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2016/2017 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
Equivalentemente, le colonne di A sono linearmente indipendenti se e solo se
 Lezioni di Algebra Lineare. Versione novembre 2008 VI. Il determinante Il determinante det A di una matrice A, reale e quadrata, è un numero reale associato ad A. Dunque det è una funzione dall insieme
Lezioni di Algebra Lineare. Versione novembre 2008 VI. Il determinante Il determinante det A di una matrice A, reale e quadrata, è un numero reale associato ad A. Dunque det è una funzione dall insieme
