Esempio. L immagine di f è l insieme dei vettori w = (w 1, w 2 ) R 2 che hanno w 1 = w 2. Quindi:
|
|
|
- Maddalena Rizzi
- 4 anni fa
- Visualizzazioni
Transcript
1 Nucleo, immagine e loro proprietà [Abate, 5.2] Data una applicazione lineare f : V W, chiamiamo nucleo di f l insieme N(f) := { v V : f(v) = 0 W } Se S V è un sottoinsieme del dominio, indichiamo con f(s) il sottoinsieme di W dei vettori che sono immagine di (almeno) un vettore di S: Lezione 15 f(s) := { w W : v S tale che w = f(v) }. In particolare l insieme Im(f) = f(v) è detto immagine di f. Esercizi C. Carrara: 7. Rango: Rouché-Capelli, dimensione e basi di spazi vettoriali. 8. Applicazioni lineari. Sia f : R 2 R 2 l applicazione f(x, y) := (x + y, x + y). Il nucleo di f è l insieme delle coppie (x, y) che risolvono l equazione x + y = 0. Quindi: N(f) = { (t, t) : t R } = L ( (1, 1) ) L immagine di f è l insieme dei vettori w = (w 1, w 2 ) R 2 che hanno w 1 = w 2. Quindi: Im(f) = { (t, t) : t R } = L ( (1, 1) ) 1 / 23 Teorema (Proprietà di nucleo e immagine) Sia f : V W una applicazione lineare. Allora: 1. N(f) è un sottospazio di V; 2. se S V è un sottospazio, allora anche f(s) W è un sottospazio; (f trasforma sottospazi in sottospazi; in particolare f(v) è un sottospazio di W) 3. se I è un insieme di generatori di S, allora f(i) è un insieme di generatori di f(s). (f trasforma insiemi di generatori in insiemi di generatori) Dimostrazione punto 1. Siano a 1, a 2 R e v 1, v 2 N(f), ovvero v 1 e v 2 sono vettori di V che soddisfano f(v 1 ) = f(v 2 ) = 0 W. Dalla linearità di f segue che: f(a 1 v 1 + a 2 v 2 ) = a 1 f(v 1 ) + a 2 f(v 2 ) = a 1 0 W + a 2 0 W = 0 W, ovvero a 1 v 1 + a 2 v 2 N(f). Per il criterio c) di sottospazio, N(f) è un sottospazio di V. Teorema (Proprietà di nucleo e immagine) Sia f : V W una applicazione lineare. Allora: 1. N(f) è un sottospazio di V; 2. se S V è un sottospazio, allora anche f(s) W è un sottospazio; (f trasforma sottospazi in sottospazi; in particolare f(v) è un sottospazio di W) 3. se I è un insieme di generatori di S, allora f(i) è un insieme di generatori di f(s). (f trasforma insiemi di generatori in insiemi di generatori) Dimostrazione punto 2. Sia S V un sottospazio, w 1, w 2 f(s) e a 1, a 2 R. Per definizione esistono v 1, v 2 S tali che w 1 = f(v 1 ) w 2 = f(v 2 ) Dalla linearità di f segue che w := a 1 w 1 + a 2 w 2 = a 1 f(v 1 ) + a 2 f(v 2 ) = f(a 1 v 1 + a 2 v 2 ). Siccome S è per ipotesi un sottospazio, allora v = a 1 v 1 + a 2 v 2 S, e quindi w = f(v) appartiene f(s) (w è immagine tramite f di un vettore di S). Per il criterio c) di sottospazio, f(s) è un sottospazio di W. 2 / 23 3 / 23
2 Teorema (Proprietà di nucleo e immagine) Sia f : V W una applicazione lineare. Allora: 1. N(f) è un sottospazio di V; 2. se S V è un sottospazio, allora anche f(s) W è un sottospazio; (f trasforma sottospazi in sottospazi; in particolare f(v) è un sottospazio di W) 3. se I è un insieme di generatori di S, allora f(i) è un insieme di generatori di f(s). (f trasforma insiemi di generatori in insiemi di generatori) Dimostrazione punto 3. Siano v 1, v 2,..., v n dei generatori di S. Per costruzione, per ogni w f(s) esiste v S tale che f(v) = w. Possiamo scrivere v come combinazione lineare dei generatori di S: v = a 1 v 1 + a 2 v a n v n, con a 1,..., a n R. Dalla linearità di f ricaviamo w = f(v) = f(a 1 v 1 + a 2 v a n v n ) = a 1 f(v 1 ) + a 2 f(v 2 ) a n f(v n ). Siccome questo vale per ogni w f(s), i vettori f(v 1 ),..., f(v n ) formano un insieme di generatori di f(s). 4 / 23 Osserviamo che per definizione f : V W è suriettiva se e solo se Im(f) = W. Proposizione Una applicazione lineare f : V W è iniettiva se e solo se N(f) = {0 V }. Dimostrazione. Ricordiamo che f è iniettiva se f(v) = f(v ) se e solo se v = v. Se N(f) contiene un vettore v non nullo, allora f(v) = 0 W = f(0 V ) ed f non è iniettiva. Viceversa se N(f) = {0 V }, allora il vettore f(v) f(v ) = f(v v ) è nullo se e solo se v v = 0 V, ovvero v = v. Questo prova l iniettività di f. L applicazione f : R 2 R, f(x, y) = x + y non è inettiva. Infatti il nucleo contiene vettori non nulli, come il vettore (1, 1). 5 / 23 Proposizione Sia f : V W applicazione lineare iniettiva. Se I = {v 1, v 2,..., v n è un insieme di vettori di V linearmente indipendenti, allora f(i) = { f(v 1 ), f(v 2 ),..., f(v n ) } è un insieme di vettori di W linearmente indipendenti. (una applicazione lineare iniettiva trasforma insiemi liberi in insiemi liberi) Dimostrazione. Indichiamo con w i l immagine del vettore v i (per ogni 1 i n): w i = f(v i ) Una immediata conseguenza delle proposizioni precedenti è: Corollario Se f : V W applicazione lineare iniettiva e B = (v 1, v 2,..., v n ) è una base di V, allora f(b) = ( f(v 1 ), f(v 2 ),..., f(v n ) ) è una base di Im(f) W. (una applicazione lineare iniettiva trasforma basi di V in basi di f(v)) Per assurdo, assumiamo che a 1 w 1 + a 2 w a n w n = 0 W coefficienti non tutti nulli. Dalla linearità di f segue: per qualche scelta di In particolare, se V è finitamente generato ed f : V W è una applicazione lineare iniettiva, allora: f(a 1 v a n v n ) = a 1 f(v 1 ) a n f(v n ) = a 1 w a n w n = 0 W, cioè a 1 v a n v n N(f). Siccome N(f) = {0 V } (f è iniettiva), segue che dim Im(f) = dim(v) Se V {0 V }, questa è una conseguenza del precedente corollario. Se V = {0 V } (quindi, non esiste una base di V), allora Im(f) = {0 W } e l uguaglianza diventa un banale 0 = 0. a 1 v a n v n = 0 V contraddicendo l ipotesi che I fosse un insieme libero. 6 / 23 7 / 23
3 Teorema della dimensione [Abate, Teorema 5.7] Se V è finitamente generato ed f : V W è una applicazione lineare, allora: dim N(f) + dim Im(f) = dim(v). Teorema della dimensione [Abate, Teorema 5.7] Se V è finitamente generato ed f : V W è una applicazione lineare, allora: dim N(f) + dim Im(f) = dim(v). Dimostrazione (1a parte). Se N(f) = {0 V }, la dimostrazione è banale: dim N(f) = 0 e, poiché f è iniettiva, per quanto detto in precedenza dim Im(f) = dim(v). Supponiamo che N(f) {0 V }. Indichiamo con n la dimensione di V, k la dimensione di N(f) e sia (v 1,..., v k ) una base di N(f). Usando il metodo del completamento ad una base, possiamo completare tale insieme ad una base (v 1,..., v k, v k+1,..., v n ) di V. Osserviamo che f si annulla sui primi k vettori di base, e w 1 = f(v k+1 ) w 2 = f(v k+2 )... w n k = f(v n ) sono generatori di Im(f). Facciamo ora vedere che sono linearmente indipendenti, da cui segue che sono una base di Im(f), e quindi la tesi dim Im(f) = n k = dim(v) dim N(f). Dimostrazione (2a parte). Dalla linearità di f segue che a 1 w 1 + a 2 w a n k w n k = f(a 1 v k+1 + a 2 v k a n k v n ) per ogni a 1,..., a n R. La precedente combinazione lineare è nulla se e solo se l argomento di f è un vettore del nucleo. Poiché (v 1,..., v k ) è una base di N(f) questo vuol dire che esistono b 1,..., b k R tali che a 1 v k+1 + a 2 v k a n k v n = b 1 v 1 + b 2 v b k v k. Siccome i vettori v 1,..., v n sono linearmente indipendenti, la precedente uguaglianza si può verificare solo se tutti i coefficienti sono nulli: a 1 = a 2 =... = a n k = b 1 = b 2 =... = b k = 0 Questo prova in particolare che i vettori w 1,..., w n k sono linearmente indipendenti. 8 / 23 9 / 23 Corollari Sia f : V W una applicazione lineare fra due spazi finitamente generati. Allora: 1. f suriettiva = dim(v) dim(w) ; 2. f iniettiva = dim(v) dim(w) ; 3. f biunivoca = dim(v) = dim(w). Dimostrazione. 1. Se f è suriettiva (quindi Im(f) = W), dal teorema della dimensione segue che dim(v) = dim N(f) + dim(w) dim(w) 2. Se f è iniettiva (quindi N(f) = 0), dal teorema della dimensione segue che dim(v) = dim Im(f) dim(w) (l ultima disuguaglianza segue dal fatto che Im(f) W è un sottospazio) 3. Se f è sia iniettiva che suriettiva, chiaramente dim(v) = dim(w). Applicazioni e sistemi lineari Sia A = (a ij ) R k,n ed L A : R n R k l applicazione associata, data da L A (x) := Ax x = t (x 1,..., x n ) R n Un vettore B = t (b 1,..., b k ) R k è nell immagine di L A x R n tale che Ax = B ( ) Quindi: B Im(L A ) il sistema di matrice completa (A B) è compatibile. La soluzione generale di ( ) è data dall insieme di tutti i vettori di R n che hanno per immagine la colonna dei termini noti B. Il nucleo di L A è l insieme dei vettori x che hanno per immagine il vettore nullo: Ax = 0 Sia (e 1,..., e n ) la base canonica di R n (i cui vettori scriviamo qui in colonna). Poiché L A (e i ) = t (a 1i, a 2i,..., a ki ) è la i-esima colonna di A, e una applicazione lineare trasforma generatori in generatori: 10 / 23 L immagine di L A è generata dalle colonne della matrice A. 11 / 23
4 Esercizi Esercizio (C. Carrara, es. 8.8) Sia L A : R 2 R 3 l applicazione lineare associata alla matrice 1 1 A = Rango di una matrice [Abate, 5.2] Definizione Chiamiamo rango per colonne di una matrice A la dimensione dello spazio generato dalle colonne di A, indicata con ρ colonne (A) ; chiamiamo rango per righe di una matrice A la dimensione dello spazio generato dalle righe di A, indicata con ρ righe (A). a) Determinare, se esiste, una base di nucleo e immagine di L A. b) Stabilire se t ( 3, 2, 1) Im(L A ). Quindi: ρ colonne (A) = dim Im(L A ) ρ righe (A) = ρ colonne ( t A) Esercizio (Esame del 30/01/2012) Si consideri l applicazione lineare f : R 3 R 3 data da: f(x 1, x 2, x 3 ) := ( x 1 + x 2, x 1 + x 3, x 2 x 3 ) a) Determinare una base, se esiste, del nucleo di f. b) Determinare una base, se esiste, dell immagine di f. c) Il vettore v = ( 3, 3, 3) è nel nucleo di f e/o nell immagine. Teorema [Abate, prop. 5.11(2)] Il rango per righe è uguale al rango per colonne: ρ righe (A) = ρ colonne (A) per ogni A R k,n. Tale numero sarà chiamato rango di A ed indicato con ρ(a). 12 / / 23 Dimostrazione (ρ righe (A) = ρ colonne (A) A R k,n ). Sia A ottenuta da A con la riduzione per righe. Le righe non nulle di A, siano esse r, formano una base per lo spazio generato dalle righe di A. Quindi: ρ righe (A) = r. Il sistema omogeneo Ax = 0 è equivalente ad A x = 0. La dimensione dello spazio delle soluzioni, ovvero del nucleo di L A, è data dal numero di incognite libere: dim N(L A ) = n r Osservazione: possiamo determinare il rango di una matrice riducendola per righe e contando le righe non nulle della matrice ridotta ottenuta. Esercizio Determinare il rango della matrice: A = ( n parametri liberi = n incognite n pivot = n r ). Per il teorema della dimensione: dim N(L A ) + dim Im(L A ) = dim(r n ) = n. Quindi ρ colonne (A) = dim Im(L A ) = n dim N(L A ) = n (n r) = r = ρ righe (A). Corollario Lo spazio delle soluzioni del sistema omogeneo Ax = 0 ha dimensione n ρ(a). Soluzione (per riduzione). Riducendo A si ottiene: A R 2 R 2 R 1 R 3 R 3 2R 1 R 4 R 4 R 1 Quindi ρ(a) = ρ(a ) = R 3 R 3 R 2 A = / / 23
5 Proprietà del rango Osservazioni. Se A è ridotta per righe, ρ(a) è dato dal numero di righe non nulle di A. Se A R k,n è triangolare superiore completa, allora ρ(a) = min(k, n). Proposizione Se A R k,n, allora ρ(a) min(k, n). Se ρ(a) = min(k, n) diciamo che A ha rango massimo. Dimostrazione. Le righe di A generano un sottospazio di R n, la cui dimensione ρ righe (A) è al più n; le colonne di A generano un sottospazio di R k, la cui dimensione ρ colonne (A) è al più k. Da ρ(a) = ρ righe (A) = ρ colonne (A) segue la tesi. 16 / 23 Definizione [Abate, 9.4] Sia A R k,n. Un minore di ordine p di A è una matrice quadrata M di tipo p p ottenuta da A eliminando k p righe e n p colonne. Un orlato di M è un minore di A di ordine p + 1 contenente M [ ] 0 7 A = M = = M = = M è un minore di ordine 2 di A. M è un minore di ordine 3 nonché un orlato di M. Enunciamo senza dimostrazione: Teorema degli orlati [Abate, teorema 9.13] Una matrice ha rango p se e solo se esiste un minore di ordine p il cui determinante è non nullo, e tutti i suoi orlati hanno determinante nullo. 17 / 23 Esercizio Determinare il rango della matrice Soluzione (con il teorema degli orlati) il minore evidenziato ha determinante diverso da zero e tutti i suoi orlati hanno determinante nullo. Per il teorema degli orlati, si ha quindi ρ(a) = 2. Soluzioni di un sistema in forma vettoriale Proposizione [Abate, teorema 5.1] Data una soluzione u di un sistema compatibile Ax = B, ( ) ogni altra soluzione di ( ) si può ottenere sommando ad u una soluzione del sistema omogeneo associato: Ax = 0. ( ) Dimostrazione. Sia v un altra soluzione di ( ). Dalla proprietà distributiva del prodotto righe per colonne segue che A(v u) = Av Au = B B = 0 ovvero v u risolve ( ). Viceversa, se w risolve ( ), cioè Aw = 0, allora detto v = u + w si ha Av = Au + Aw = B + 0 = B 18 / 23 cioè v è soluzione di ( ). 19 / 23
6 Corollario La soluzione generale di un sistema compatibile di matrice completa (A B) R m,n+1 si può sempre scrivere nella forma dove: k = n ρ(a), v 0 è una soluzione particolare del sistema, x = v 0 + t 1 v 1 + t 2 v t k v k }{{} soluzione generale sistema omogeneo associato (v 1,..., v k ) è una base dello spazio delle soluzioni del sistema omogeneo Ax = 0, t 1, t 2,..., t k sono parametri reali. La soluzione generale dell equazione (ossia y = 2x + 6) è data da: { x = t y = 2t + 6 2x + y = 6 ovvero x = v 0 + t v 1 [ ] [ ] [ ] x 0 1 = + t y 6 2 Esercizio (esame del 04/07/2011) Si consideri il seguente sistema lineare dipendente da un parametro λ R: 3x 1 + λx 3 = 0 x 1 + (λ 3)x 2 + x 3 = 0 λx 1 + 3x 3 = 0 a) dire per quali valori di λ il sistema ammette infinite soluzioni; b) per i valori di λ trovati al punto a), scrivere una base per lo spazio delle soluzioni. Soluzione. a) Calcoliamo il determinante della matrice dei coefficienti (con sviluppo di Laplace rispetto alla 2a colonna): 3 0 λ 3 0 λ A = 1 λ 3 1 = (λ 3) 1 λ 3 1 = (λ 3)(9 λ 2 ) λ 0 3 λ 0 3 Le soluzioni sono infinite se e solo se A = 0, ovvero λ = ±3. 20 / / 23 b1) Sia W λ lo spazio delle soluzioni. Per λ = 3 il sistema diventa: 3x 1 + 3x 3 = 0 x 1 + x 3 = 0 = (x 1, x 2, x 3 ) = (t 1, t 2, t 1 ) t 1, t 2 R 3x 1 + 3x 3 = 0 Due generatori v 1, v 2 di W 3 si ottengono scegliendo (t 1, t 2 ) = (1, 0) e (t 1, t 2 ) = (0, 1): v 1 = (1, 0, 1) v 2 = (0, 1, 0) I due vettori sono linearmente indipendenti (verificare), quindi formano una base. b2) Per λ = 3 il sistema diventa: 3x 1 3x 3 = 0 x 1 6x 2 + x 3 = 0 3x 1 + 3x 3 = 0 La soluzione generale è E 2 E E 1 E 3 E 3 +E 1 (x 1, x 2, x 3 ) = (t, 1 t, t) t R. 3 3x 1 3x 3 = 0 2x 1 6x 2 = 0 0 = 0 Teorema di Rouché-Capelli [Abate, cor. 5.9] Un sistema di matrice completa (A B) R m,n+1 è compatibile se e solo se ρ(a B) = ρ(a). Dimostrazione. Ricordiamo che un sistema di matrice completa (A B) è compatibile se e solo se il vettore colonna B appartiene all immagine dell applicazione L A : Ax = B è compatibile B Im(L A ) Due casi: B Im(L A ) (sistema compatibile): se B è combinazione lineare delle colonne di A, le colonne di A e quelle di (A B) generano lo stesso sottospazio di R m e ρ(a B) = ρ(a). B / Im(L A ) (sistema incompatibile): se B non è combinazione lineare delle colonne di A, lo spazio generato dalle colonne di (A B) ha dimensione maggiore dello spazio generato dalle colonne di A, e ρ(a B) > ρ(a). Una base di W 3 è data da una qualsiasi soluzione non nulla, ad esempio scegliendo t = 3 si ottiene il vettore (3, 1, 3). 22 / 23 Osservazione: si ha sempre ρ(a) ρ(a B) ρ(a) + 1 (poiché la matrice (A B) si ottiene da A aggiungendo una colonna). 23 / 23
Esempi. In R 2, le coppia (2, 5) è combinazione lineare dei vettori (0, 1) e (1, 1). Infatti:
 Combinazioni lineari [Abate, 4.2] Sia V uno spazio vettoriale e v 1, v 2,..., v n dei vettori di V. Diremo che un vettore w V è combinazione lineare dei vettori v 1,..., v n se esistono a 1, a 2,..., a
Combinazioni lineari [Abate, 4.2] Sia V uno spazio vettoriale e v 1, v 2,..., v n dei vettori di V. Diremo che un vettore w V è combinazione lineare dei vettori v 1,..., v n se esistono a 1, a 2,..., a
ESEMPIO DI SISTEMA LINEARE CON SOLUZIONE. Esercizio Si consideri il sistema di equazioni lineari dipendente da un parametro λ R:
 ESEMPIO DI SISTEMA LINEARE CON SOLUZIONE Esercizio Si consideri il sistema di equazioni lineari dipendente da un parametro λ R: x 1 + x = 0 6x 1 + (λ + )x + x 3 + x 4 = 1 x 1 4x + (λ + 1)x 3 + 6x 4 = 3
ESEMPIO DI SISTEMA LINEARE CON SOLUZIONE Esercizio Si consideri il sistema di equazioni lineari dipendente da un parametro λ R: x 1 + x = 0 6x 1 + (λ + )x + x 3 + x 4 = 1 x 1 4x + (λ + 1)x 3 + 6x 4 = 3
APPLICAZIONI LINEARI
 APPLICAZIONI LINEARI Esercizi Esercizio Date le seguenti applicazioni lineari f : R 2 R 3 definita da fx y = x 2y x + y x + y; 2 g : R 3 R 2 definita da gx y z = x + y x y; 3 h : Rx] 2 R 2 definita da
APPLICAZIONI LINEARI Esercizi Esercizio Date le seguenti applicazioni lineari f : R 2 R 3 definita da fx y = x 2y x + y x + y; 2 g : R 3 R 2 definita da gx y z = x + y x y; 3 h : Rx] 2 R 2 definita da
Rango di una matrice e teorema di Rouché-Capelli
 Rango di una matrice e teorema di Rouché-Capelli Sappiamo che a una matrice m n, A, è associata l applicazione lineare L A : R n R m, L A (X) = AX, X R n. Definizione 1. Lo spazio nullo di A, N (A), è
Rango di una matrice e teorema di Rouché-Capelli Sappiamo che a una matrice m n, A, è associata l applicazione lineare L A : R n R m, L A (X) = AX, X R n. Definizione 1. Lo spazio nullo di A, N (A), è
1. [15 punti] Calcolare il rango della seguente matrice a coefficienti reali: ( 1/2) 1 (1/2)
![1. [15 punti] Calcolare il rango della seguente matrice a coefficienti reali: ( 1/2) 1 (1/2) 1. [15 punti] Calcolare il rango della seguente matrice a coefficienti reali: ( 1/2) 1 (1/2)](/thumbs/101/152415317.jpg) Università di Modena e Reggio Emilia Facoltà di Scienze MM.FF.NN. PROVA DI ALGEBRA LINEARE del 17 febbraio 011 ISTRUZIONI PER LO SVOLGIMENTO. Scrivere cognome, nome, numero di matricola in alto a destra
Università di Modena e Reggio Emilia Facoltà di Scienze MM.FF.NN. PROVA DI ALGEBRA LINEARE del 17 febbraio 011 ISTRUZIONI PER LO SVOLGIMENTO. Scrivere cognome, nome, numero di matricola in alto a destra
Note sui sistemi lineari per il Corso di Geometria per Chimica, Facoltà di Scienze MM.FF.NN., UNICAL (Dott.ssa Galati C.) Rende, 4 Maggio 2010
 Note sui sistemi lineari per il Corso di Geometria per Chimica, Facoltà di Scienze MM.FF.NN., UNICAL (Dott.ssa Galati C.) Rende, 4 Maggio 21 Sistemi lineari. Un sistema lineare di n 1 equazioni in m incognite
Note sui sistemi lineari per il Corso di Geometria per Chimica, Facoltà di Scienze MM.FF.NN., UNICAL (Dott.ssa Galati C.) Rende, 4 Maggio 21 Sistemi lineari. Un sistema lineare di n 1 equazioni in m incognite
Esercitazione 6 - Soluzione
 Anno Accademico 28-29 Corso di Algebra Lineare e Calcolo Numerico per Ingegneria Meccanica Esercitazione 6 - Soluzione Immagine, nucleo. Teorema di Rouché-Capelli. Esercizio Sia L : R 3 R 3 l applicazione
Anno Accademico 28-29 Corso di Algebra Lineare e Calcolo Numerico per Ingegneria Meccanica Esercitazione 6 - Soluzione Immagine, nucleo. Teorema di Rouché-Capelli. Esercizio Sia L : R 3 R 3 l applicazione
APPLICAZIONI. Im f = {b B a A tale che f (a) = b}.
 APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
Federica Gregorio e Cristian Tacelli
 1 Sistemi lineari Federica Gregorio e Cristian Tacelli Un sistema lineare m n (m equazioni in n incognite) è un insieme di equazioni lineari che devono essere soddisfatte contemporaneamente a 11 x 1 +
1 Sistemi lineari Federica Gregorio e Cristian Tacelli Un sistema lineare m n (m equazioni in n incognite) è un insieme di equazioni lineari che devono essere soddisfatte contemporaneamente a 11 x 1 +
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof. Fabio Perroni. 5. Rango
 Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 5 Rango Definizione 1 Sia A M m,n (K) una matrice m n a coefficienti nel campo K Il rango
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 5 Rango Definizione 1 Sia A M m,n (K) una matrice m n a coefficienti nel campo K Il rango
Nozioni e notazioni: concetti primitivi di insieme, elemento ed appartenenza.
 Geometria I lezione del 30 settembre 2013 Presentazione del corso. Nozioni e notazioni: concetti primitivi di insieme, elemento ed appartenenza. Insiemi numerici: i numeri naturali, gli interi, i numeri
Geometria I lezione del 30 settembre 2013 Presentazione del corso. Nozioni e notazioni: concetti primitivi di insieme, elemento ed appartenenza. Insiemi numerici: i numeri naturali, gli interi, i numeri
Corso di Geometria BIAR, BSIR Esercizi 4: soluzioni
 Corso di Geometria - BIAR, BSIR Esercizi : soluzioni Esercizio. Sono dati i seguenti sistemi lineari omogenei nelle incognite x, y, z: { x + y z = x + y z = x + y z = S : x y + z =, S :, S 3 : x 3y =,
Corso di Geometria - BIAR, BSIR Esercizi : soluzioni Esercizio. Sono dati i seguenti sistemi lineari omogenei nelle incognite x, y, z: { x + y z = x + y z = x + y z = S : x y + z =, S :, S 3 : x 3y =,
0.1 Complemento diretto
 1 0.1 Complemento diretto Dato U V, un complemento diretto di U é un sottospazio W V tale che U W = {0} U + W = V cioé la somma di U con il suo complemento diretto é diretta, e dá tutto lo spazio vettoriale
1 0.1 Complemento diretto Dato U V, un complemento diretto di U é un sottospazio W V tale che U W = {0} U + W = V cioé la somma di U con il suo complemento diretto é diretta, e dá tutto lo spazio vettoriale
Matrici triangolari [Abate, 3.2] Lezioni 05 e 06. Determinante di una matrice triangolare [Abate, es. 9.3] Matrici ridotte per righe.
![Matrici triangolari [Abate, 3.2] Lezioni 05 e 06. Determinante di una matrice triangolare [Abate, es. 9.3] Matrici ridotte per righe. Matrici triangolari [Abate, 3.2] Lezioni 05 e 06. Determinante di una matrice triangolare [Abate, es. 9.3] Matrici ridotte per righe.](/thumbs/100/147138366.jpg) Matrici triangolari [Abate, 32] Definizione Una matrice A = a ij ) R m,n si dice triangolare superiore se a ij = 0 per ogni i > j; triangolare inferiore se a ij = 0 per ogni i < j Lezioni 05 e 06 Una matrice
Matrici triangolari [Abate, 32] Definizione Una matrice A = a ij ) R m,n si dice triangolare superiore se a ij = 0 per ogni i > j; triangolare inferiore se a ij = 0 per ogni i < j Lezioni 05 e 06 Una matrice
Prima prova in itinere di Geometria (Corso di laurea in Fisica, Canali A-C e D-O) Prof. Barucci e Piccinni 29 novembre 2011
 Prima prova in itinere di Geometria (Corso di laurea in Fisica, Canali A-C e D-O) Prof Barucci e Piccinni 29 novembre 2011 a Scrivere subito canale, cognome e nome b Utilizzare questi fogli per le risposte
Prima prova in itinere di Geometria (Corso di laurea in Fisica, Canali A-C e D-O) Prof Barucci e Piccinni 29 novembre 2011 a Scrivere subito canale, cognome e nome b Utilizzare questi fogli per le risposte
Definizione. Sia f : V V un endomorfismo e λ R. Se esiste v V non nullo tale che
 Autovalori ed autovettori [Abate, 131] Sia f : V V un endomorfismo e λ R Se esiste v V non nullo tale che f(v) = λv, diremo che λ è un autovalore di f e che v è un autovettore di f associato a λ Lezioni
Autovalori ed autovettori [Abate, 131] Sia f : V V un endomorfismo e λ R Se esiste v V non nullo tale che f(v) = λv, diremo che λ è un autovalore di f e che v è un autovettore di f associato a λ Lezioni
Elementi di Algebra Lineare Applicazioni lineari
 Elementi di Algebra Lineare Applicazioni lineari Cristina Turrini UNIMI - 2016/2017 Cristina Turrini (UNIMI - 2016/2017) Elementi di Algebra Lineare 1 / 50 index Applicazioni lineari 1 Applicazioni lineari
Elementi di Algebra Lineare Applicazioni lineari Cristina Turrini UNIMI - 2016/2017 Cristina Turrini (UNIMI - 2016/2017) Elementi di Algebra Lineare 1 / 50 index Applicazioni lineari 1 Applicazioni lineari
r 2 r 2 2r 1 r 4 r 4 r 1
 SPAZI R n 1. Esercizi Esercizio 1. Stabilire quali dei seguenti sottoinsiemi sono sottospazi: V 1 = {(x, y, z) R 3 /x = y = z} V = {(x, y, z) R 3 /x = 4} V 3 = {(x, y, z) R 3 /z = x } V 4 = {(x, y, z)
SPAZI R n 1. Esercizi Esercizio 1. Stabilire quali dei seguenti sottoinsiemi sono sottospazi: V 1 = {(x, y, z) R 3 /x = y = z} V = {(x, y, z) R 3 /x = 4} V 3 = {(x, y, z) R 3 /z = x } V 4 = {(x, y, z)
Applicazioni lineari tra spazi euclidei. Cambi di base.
 pplicazioni lineari tra spazi euclidei. Cambi di base. Esercizio. Data la seguente applicazione lineare f : R R : f(x, y, z) = (x z, x + y, y + z), scrivere la matrice B, rappresentativa di f rispetto
pplicazioni lineari tra spazi euclidei. Cambi di base. Esercizio. Data la seguente applicazione lineare f : R R : f(x, y, z) = (x z, x + y, y + z), scrivere la matrice B, rappresentativa di f rispetto
1 Indipendenza lineare e scrittura unica
 Geometria Lingotto. LeLing7: Indipendenza lineare, basi e dimensione. Ārgomenti svolti: Indipendenza lineare e scrittura unica. Basi e dimensione. Coordinate. Ēsercizi consigliati: Geoling. Indipendenza
Geometria Lingotto. LeLing7: Indipendenza lineare, basi e dimensione. Ārgomenti svolti: Indipendenza lineare e scrittura unica. Basi e dimensione. Coordinate. Ēsercizi consigliati: Geoling. Indipendenza
APPLICAZIONI LINEARI O OMOMORFISMI
 42 APPLICAZIONI LINEARI O OMOMORFISMI Definizione 9 Dati due spazi vettoriali U e V sullo stesso campo K, una applicazione f : U V è detta lineare o omomorfismo se soddisfa le seguenti due condizioni:
42 APPLICAZIONI LINEARI O OMOMORFISMI Definizione 9 Dati due spazi vettoriali U e V sullo stesso campo K, una applicazione f : U V è detta lineare o omomorfismo se soddisfa le seguenti due condizioni:
Matematica discreta 1 [145016]
![Matematica discreta 1 [145016] Matematica discreta 1 [145016]](/thumbs/94/119285443.jpg) Facoltà di Scienze Matematiche, Fisiche e Naturali anno accademico 2008/09 Registro dell'attività didattica Matematica discreta 1 [145016] Attività didattica: Attività didattica [codice] Corso di studio
Facoltà di Scienze Matematiche, Fisiche e Naturali anno accademico 2008/09 Registro dell'attività didattica Matematica discreta 1 [145016] Attività didattica: Attività didattica [codice] Corso di studio
Analisi dei dati corso integrato - Algebra lineare, e a b c 0. le soluzioni del sistema lineare omogeneo x d e f 2. a b c.
 Analisi dei dati corso integrato - Algebra lineare 4.3.8 e 5.3.8-1 1. Nella lezione precedente abbiamo definito lo spazio nullo e lo spazio delle colonne di una matrice; ora definiamo lo spazio delle righe
Analisi dei dati corso integrato - Algebra lineare 4.3.8 e 5.3.8-1 1. Nella lezione precedente abbiamo definito lo spazio nullo e lo spazio delle colonne di una matrice; ora definiamo lo spazio delle righe
Esercizi di Geometria Spazi vettoriali e sottospazi - indipendenza lineare
 Esercizi di Geometria Spazi vettoriali e sottospazi - indipendenza lineare 1. Quali dei seguenti sottoinsiemi sono sottospazi di R 3? Motivare la risposta. (a) {(x, y, 1) x, y R} (b) {(0, y, 0) y R} (c)
Esercizi di Geometria Spazi vettoriali e sottospazi - indipendenza lineare 1. Quali dei seguenti sottoinsiemi sono sottospazi di R 3? Motivare la risposta. (a) {(x, y, 1) x, y R} (b) {(0, y, 0) y R} (c)
Note per le esercitazioni di Geometria 1 a.a. 2007/08 A. Lotta. Metodi per il calcolo del rango di una matrice
 Note per le esercitazioni di Geometria 1 a.a. 2007/08 A. Lotta Versione del 21/12/07 Metodi per il calcolo del rango di una matrice Sia A M m,n (K). Denotiamo con A (i) la riga i-ma di A, i {1,..., m}.
Note per le esercitazioni di Geometria 1 a.a. 2007/08 A. Lotta Versione del 21/12/07 Metodi per il calcolo del rango di una matrice Sia A M m,n (K). Denotiamo con A (i) la riga i-ma di A, i {1,..., m}.
Elementi di Algebra Lineare Applicazioni lineari
 Elementi di Algebra Lineare Applicazioni lineari Cristina Turrini UNIMI - 2015/2016 Cristina Turrini (UNIMI - 2015/2016) Elementi di Algebra Lineare 1 / 18 index Applicazioni lineari 1 Applicazioni lineari
Elementi di Algebra Lineare Applicazioni lineari Cristina Turrini UNIMI - 2015/2016 Cristina Turrini (UNIMI - 2015/2016) Elementi di Algebra Lineare 1 / 18 index Applicazioni lineari 1 Applicazioni lineari
Lezione 10: Teorema di Rouchè-Capelli e la classificazione dei sistemi lineari
 Lezione 10: Teorema di Rouchè-Capelli e la classificazione dei sistemi lineari In questa lezione ci dedicheremo a studiare a fondo quali proprietà della matrice dei coefficienti di un sistema (e della
Lezione 10: Teorema di Rouchè-Capelli e la classificazione dei sistemi lineari In questa lezione ci dedicheremo a studiare a fondo quali proprietà della matrice dei coefficienti di un sistema (e della
Registro Lezioni di Algebra lineare del 15 e 16 novembre 2016.
 Registro Lezioni di Algebra lineare del 15 e 16 novembre 2016 Di seguito si riporta il riassunto degli argomenti svolti; i riferimenti sono a parti del Cap8 Elementi di geometria e algebra lineare Par5
Registro Lezioni di Algebra lineare del 15 e 16 novembre 2016 Di seguito si riporta il riassunto degli argomenti svolti; i riferimenti sono a parti del Cap8 Elementi di geometria e algebra lineare Par5
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI
 CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
Anno Accademico 2017/2018
 Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2017/2018 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2017/2018 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
ESERCIZI DI MATEMATICA DISCRETA ANNO 2006/2007
 ESERCIZI DI MATEMATICA DISCRETA ANNO 6/7 //7 () Ridurre la seguente matrice ad una a scala ridotta utilizzando il metodo di Gauss-Jordan. Soluzione. () Determinare quante e quali sono le matrici a scala
ESERCIZI DI MATEMATICA DISCRETA ANNO 6/7 //7 () Ridurre la seguente matrice ad una a scala ridotta utilizzando il metodo di Gauss-Jordan. Soluzione. () Determinare quante e quali sono le matrici a scala
1. Sistemi di equazioni lineari. 1.1 Considerazioni preliminari
 1. Sistemi di equazioni lineari 1.1 Considerazioni preliminari I sistemi lineari sono sistemi di equazioni di primo grado in più incognite. Molti problemi di matematica e fisica portano alla soluzione
1. Sistemi di equazioni lineari 1.1 Considerazioni preliminari I sistemi lineari sono sistemi di equazioni di primo grado in più incognite. Molti problemi di matematica e fisica portano alla soluzione
Esercizi di geometria per Fisica / Fisica e Astrofisica
 Esercizi di geometria per Fisica / Fisica e Astrofisica Foglio 3 - Soluzioni Esercizio. Stabilire se i seguenti sottoinsiemi di R 3 sono sottospazi vettoriali: (a) S = {(x y z) R 3 : x + y + z = }. (b)
Esercizi di geometria per Fisica / Fisica e Astrofisica Foglio 3 - Soluzioni Esercizio. Stabilire se i seguenti sottoinsiemi di R 3 sono sottospazi vettoriali: (a) S = {(x y z) R 3 : x + y + z = }. (b)
CORSO DI GEOMETRIA APPLICAZIONI LINEARI E MATRICI A.A. 2018/2019 PROF. VALENTINA BEORCHIA
 CORSO DI GEOMETRIA APPLICAZIONI LINEARI E MATRICI AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Matrici associate a un applicazione lineare 1 2 Cambiamenti di base 4 3 Diagonalizzazione 6 1 MATRICI ASSOCIATE
CORSO DI GEOMETRIA APPLICAZIONI LINEARI E MATRICI AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Matrici associate a un applicazione lineare 1 2 Cambiamenti di base 4 3 Diagonalizzazione 6 1 MATRICI ASSOCIATE
SOTTOSPAZI E OPERAZIONI IN SPAZI DIVERSI DA R n
 SPAZI E SOTTOSPAZI 1 SOTTOSPAZI E OPERAZIONI IN SPAZI DIVERSI DA R n Spazi di matrici. Spazi di polinomi. Generatori, dipendenza e indipendenza lineare, basi e dimensione. Intersezione e somma di sottospazi,
SPAZI E SOTTOSPAZI 1 SOTTOSPAZI E OPERAZIONI IN SPAZI DIVERSI DA R n Spazi di matrici. Spazi di polinomi. Generatori, dipendenza e indipendenza lineare, basi e dimensione. Intersezione e somma di sottospazi,
Algebra lineare. {ax 2 + bx + c R 2 [x] : 2a + 3b = 1} a b c d. M(2, 2) : a + c + d = 2. a b. c d
![Algebra lineare. {ax 2 + bx + c R 2 [x] : 2a + 3b = 1} a b c d. M(2, 2) : a + c + d = 2. a b. c d Algebra lineare. {ax 2 + bx + c R 2 [x] : 2a + 3b = 1} a b c d. M(2, 2) : a + c + d = 2. a b. c d](/thumbs/104/162200055.jpg) Algebra lineare 1. Riconoscere se il seguente insieme costituisce uno spazio vettoriale. In caso affermativo trovarne la dimensione e una base. (R n [x] denota lo spazio dei polinomi nell indeterminata
Algebra lineare 1. Riconoscere se il seguente insieme costituisce uno spazio vettoriale. In caso affermativo trovarne la dimensione e una base. (R n [x] denota lo spazio dei polinomi nell indeterminata
CORSO DI ALGEBRA (M-Z) Prof. A. Venezia
 CORSO DI ALGEBRA (M-Z) Prof. A. Venezia 2018-19 Complementi ed Esercizi APPLICAZIONI LINEARI Siano V e V spazi vettoriali sul campo K. Una applicazione L: V V si dice lineare se: 1 AL. L(v+w) = L(v) +
CORSO DI ALGEBRA (M-Z) Prof. A. Venezia 2018-19 Complementi ed Esercizi APPLICAZIONI LINEARI Siano V e V spazi vettoriali sul campo K. Una applicazione L: V V si dice lineare se: 1 AL. L(v+w) = L(v) +
a + 2b + c 3d = 0, a + c d = 0 c d
 SPAZI VETTORIALI 1. Esercizi Esercizio 1. Stabilire quali dei seguenti sottoinsiemi sono sottospazi: V 1 = {(x, y, z) R 3 /x = y = z} V = {(x, y, z) R 3 /x = 4} V 3 = {(x, y, z) R 3 /z = x } V 4 = {(x,
SPAZI VETTORIALI 1. Esercizi Esercizio 1. Stabilire quali dei seguenti sottoinsiemi sono sottospazi: V 1 = {(x, y, z) R 3 /x = y = z} V = {(x, y, z) R 3 /x = 4} V 3 = {(x, y, z) R 3 /z = x } V 4 = {(x,
Anno Accademico 2015/2016
 Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2015/2016 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2015/2016 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
Manlio Bordoni. APPUNTI SULLA RAPPRESENTAZIONE DEI SOTTOSPAZI VETTORIALI DI R n I MODO. v 11. v n1
 Manlio Bordoni APPUNTI SULLA RAPPRESENTAZIONE DEI SOTTOSPAZI VETTORIALI DI R n I MODO Sia dato un insieme di generatori v v =,, v k = v n di W : questo vuol dire che ogni vettore w W si scrive come combinazione
Manlio Bordoni APPUNTI SULLA RAPPRESENTAZIONE DEI SOTTOSPAZI VETTORIALI DI R n I MODO Sia dato un insieme di generatori v v =,, v k = v n di W : questo vuol dire che ogni vettore w W si scrive come combinazione
GEOMETRIA 1 terza parte
 GEOMETRIA 1 terza parte Cristina Turrini C. di L. in Fisica - 2014/2015 Cristina Turrini (C. di L. in Fisica - 2014/2015) GEOMETRIA 1 1 / 32 index Applicazioni lineari 1 Applicazioni lineari 2 Nucleo e
GEOMETRIA 1 terza parte Cristina Turrini C. di L. in Fisica - 2014/2015 Cristina Turrini (C. di L. in Fisica - 2014/2015) GEOMETRIA 1 1 / 32 index Applicazioni lineari 1 Applicazioni lineari 2 Nucleo e
Corso di Geometria BIAR, BSIR Esercizi 3: soluzioni
 Corso di Geometria - BIAR, BSIR Esercizi : soluzioni Rango e teorema di Rouché-Capelli Esercizio. Calcolare il rango di ciascuna delle seguenti matrici: ( ) ( ) ( ) A =, A =, A =, A 4 = ( ). a a a Soluzione.
Corso di Geometria - BIAR, BSIR Esercizi : soluzioni Rango e teorema di Rouché-Capelli Esercizio. Calcolare il rango di ciascuna delle seguenti matrici: ( ) ( ) ( ) A =, A =, A =, A 4 = ( ). a a a Soluzione.
Anno Accademico 2016/2017
 Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2016/2017 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2016/2017 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
2. Determinare le dimensioni dei seguenti sottospazi W ed esibirne due basi basi diverse, quando è possibile:
 aa 5-6 Esercizi 5 Basi dimensione e coordinate Soluzioni Apostol: Sezione 5 Esercizi 6a 7 8 9 Determinare le dimensioni dei seguenti sottospazi W ed esibirne due basi basi diverse quando è possibile: i
aa 5-6 Esercizi 5 Basi dimensione e coordinate Soluzioni Apostol: Sezione 5 Esercizi 6a 7 8 9 Determinare le dimensioni dei seguenti sottospazi W ed esibirne due basi basi diverse quando è possibile: i
Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE. Giovanni Villani
 Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE Giovanni Villani Matrici Definizione 1 Si definisce matrice di tipo m n una funzione che associa
Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE Giovanni Villani Matrici Definizione 1 Si definisce matrice di tipo m n una funzione che associa
Lezione 4: Base e dimensione
 Lezione 4: Base e dimensione 1 Base: definizione ed esempi Come la parola stessa suggerisce, il concetto di base di uno spazio vettoriale e fondamentale e racchiude tutte le informazioni necessarie a ricostruire
Lezione 4: Base e dimensione 1 Base: definizione ed esempi Come la parola stessa suggerisce, il concetto di base di uno spazio vettoriale e fondamentale e racchiude tutte le informazioni necessarie a ricostruire
Dim. Usare la chiusura rispetto al prodotto esterno (vedi appunti lezione o libri di testo).
 ESERCIZI PER CASA di GEOMETRIA per il Corso di Laurea di Scienze dei Materiali, Facoltà di Scienze MM.FF.NN., UNICAL (Dott.ssa Galati C.) Rende, 28 maggio 29 Sottospazi di uno spazio vettoriale, sistemi
ESERCIZI PER CASA di GEOMETRIA per il Corso di Laurea di Scienze dei Materiali, Facoltà di Scienze MM.FF.NN., UNICAL (Dott.ssa Galati C.) Rende, 28 maggio 29 Sottospazi di uno spazio vettoriale, sistemi
NOTE DI ALGEBRA LINEARE v = a 1 v a n v n, w = b 1 v b n v n
 NOTE DI ALGEBRA LINEARE 2- MM 9 NOVEMBRE 2 Combinazioni lineari e generatori Sia K un campo e V uno spazio vettoriale su K Siano v,, v n vettori in V Definizione Un vettore v V si dice combinazione lineare
NOTE DI ALGEBRA LINEARE 2- MM 9 NOVEMBRE 2 Combinazioni lineari e generatori Sia K un campo e V uno spazio vettoriale su K Siano v,, v n vettori in V Definizione Un vettore v V si dice combinazione lineare
Metodi per la risoluzione di sistemi lineari
 Metodi per la risoluzione di sistemi lineari Sistemi di equazioni lineari. Rango di matrici Come è noto (vedi [] sez.0.8), ad ogni matrice quadrata A è associato un numero reale det(a) detto determinante
Metodi per la risoluzione di sistemi lineari Sistemi di equazioni lineari. Rango di matrici Come è noto (vedi [] sez.0.8), ad ogni matrice quadrata A è associato un numero reale det(a) detto determinante
Metodi per la risoluzione di sistemi lineari
 Metodi per la risoluzione di sistemi lineari 1 Sistemi di equazioni lineari 1.1 Determinante di matrici quadrate Ad ogni matrice quadrata A è associato un numero reale det(a) detto determinante della matrice
Metodi per la risoluzione di sistemi lineari 1 Sistemi di equazioni lineari 1.1 Determinante di matrici quadrate Ad ogni matrice quadrata A è associato un numero reale det(a) detto determinante della matrice
Esercizi di MATEMATICA PER RCHITETTURA prima parte: Algebra Lineare e Geometria
 Esercizi di MATEMATICA PER RCHITETTURA prima parte: Algebra Lineare e Geometria Avvertenze In quanto segue tutti i vettori hanno il medesimo punto d origine O l origine dello spazio cartesiano. Possiamo
Esercizi di MATEMATICA PER RCHITETTURA prima parte: Algebra Lineare e Geometria Avvertenze In quanto segue tutti i vettori hanno il medesimo punto d origine O l origine dello spazio cartesiano. Possiamo
GE110 - Geometria 1. Prova in Itinere 2 27 Maggio 2010
 GE110 - Geometria 1 Prova in Itinere 2 27 Maggio 2010 COGNOME e NOME : Problema 1: Problema 2: Problema 3: 1 2 Problema 1. Nello spazio affine reale A 5 R si fissi il riferimento affine canonico, e siano
GE110 - Geometria 1 Prova in Itinere 2 27 Maggio 2010 COGNOME e NOME : Problema 1: Problema 2: Problema 3: 1 2 Problema 1. Nello spazio affine reale A 5 R si fissi il riferimento affine canonico, e siano
Sistemi Lineari. Rango di una matrice. Lezione 21, Algebra Lineare,
 Lezione 21, Algebra Lineare, 15.11.2017 Sistemi Lineari Rango di una matrice Esempio principale, I Considerata una matrice, ci poniamo il problema di determinare il massimo numero di colonne linearmente
Lezione 21, Algebra Lineare, 15.11.2017 Sistemi Lineari Rango di una matrice Esempio principale, I Considerata una matrice, ci poniamo il problema di determinare il massimo numero di colonne linearmente
ESAME DI GEOMETRIA. 6 febbraio 2002 CORREZIONE QUIZ
 ESAME DI GEOMETRIA 6 febbraio CORREZIONE QUIZ. La parte reale di ( + i) 9 è positiva. QUIZ Si può procedere in due modi. Un primo modo è osservare che ( + i) =i, dunque ( + i) 9 =(+i)(i) 4 = 4 ( + i) :
ESAME DI GEOMETRIA 6 febbraio CORREZIONE QUIZ. La parte reale di ( + i) 9 è positiva. QUIZ Si può procedere in due modi. Un primo modo è osservare che ( + i) =i, dunque ( + i) 9 =(+i)(i) 4 = 4 ( + i) :
Spazi Vettoriali ed Applicazioni Lineari
 Spazi Vettoriali ed Applicazioni Lineari 1. Sottospazi Definizione. Sia V uno spazio vettoriale sul corpo C. Un sottoinsieme non vuoto W di V è un sottospazio vettoriale di V se è chiuso rispetto alla
Spazi Vettoriali ed Applicazioni Lineari 1. Sottospazi Definizione. Sia V uno spazio vettoriale sul corpo C. Un sottoinsieme non vuoto W di V è un sottospazio vettoriale di V se è chiuso rispetto alla
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof. Fabio Perroni. 3. Sistemi di equazioni lineari
 Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 3 Sistemi di equazioni lineari Siano m, n N \ {}, sia K un campo Definizione a) Un sistema
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 3 Sistemi di equazioni lineari Siano m, n N \ {}, sia K un campo Definizione a) Un sistema
Esercizi svolti. delle matrici
 Esercizi svolti. astratti. Si dica se l insieme delle coppie reali (x, y) soddisfacenti alla relazione x + y è un sottospazio vettoriale di R La risposta è sì, perchè l unica coppia reale che soddisfa
Esercizi svolti. astratti. Si dica se l insieme delle coppie reali (x, y) soddisfacenti alla relazione x + y è un sottospazio vettoriale di R La risposta è sì, perchè l unica coppia reale che soddisfa
Sistemi di equazioni lineari
 Sistemi di equazioni lineari Siano X 1,, X n indeterminate Un equazione lineare (o di primo grado) nelle incognite X 1,, X n a coefficienti nel campo K è della forma a 1 X 1 + + a n X n = b, a i, b K,
Sistemi di equazioni lineari Siano X 1,, X n indeterminate Un equazione lineare (o di primo grado) nelle incognite X 1,, X n a coefficienti nel campo K è della forma a 1 X 1 + + a n X n = b, a i, b K,
APPLICAZIONI LINEARI
 APPLICAZIONI LINEARI Fra le applicazioni definite tra spazi vettoriali sono particolarmente significative quelle che conservano le operazioni, dette applicazioni lineari. Definizione Siano V, W due k-s.v.
APPLICAZIONI LINEARI Fra le applicazioni definite tra spazi vettoriali sono particolarmente significative quelle che conservano le operazioni, dette applicazioni lineari. Definizione Siano V, W due k-s.v.
CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA
 CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA FOGLIO DI ESERCIZI 4 GEOMETRIA 2008/09 Esercizio 4.1 (5.10). Dati i vettori di R 3 : v 1 (1, 1, 2), v 2 (2, 4, 6), v 3 ( 1, 2, 5), v 4 (1, 1, 10) determinare
CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA FOGLIO DI ESERCIZI 4 GEOMETRIA 2008/09 Esercizio 4.1 (5.10). Dati i vettori di R 3 : v 1 (1, 1, 2), v 2 (2, 4, 6), v 3 ( 1, 2, 5), v 4 (1, 1, 10) determinare
APPLICAZIONI LINEARI
 APPLICAZIONI LINEARI 1 APPLICAZIONI LINEARI Applicazioni lineari tra spazi R n spazi di matrici spazi di polinomi e matrice associata rispetto ad una coppia di basi Endomorismi e matrice associata rispetto
APPLICAZIONI LINEARI 1 APPLICAZIONI LINEARI Applicazioni lineari tra spazi R n spazi di matrici spazi di polinomi e matrice associata rispetto ad una coppia di basi Endomorismi e matrice associata rispetto
CAPITOLO IV RISOLUZIONE DEI SISTEMI LINEARI COL METODO DEI DETERMINANTI
 CAPITOLO IV RISOLUZIONE DEI SISTEMI LINEARI COL METODO DEI DETERMINANTI 1. REGOLA DI CRAMER Sia S un sistema lineare di n ( 2) equazioni in n incognite su un campo K : a 11 x 1 + a 12 x 2 + + a 1n x n
CAPITOLO IV RISOLUZIONE DEI SISTEMI LINEARI COL METODO DEI DETERMINANTI 1. REGOLA DI CRAMER Sia S un sistema lineare di n ( 2) equazioni in n incognite su un campo K : a 11 x 1 + a 12 x 2 + + a 1n x n
UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica GE110 - Geometria 1 a.a Prova scritta del TESTO E SOLUZIONI
 UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica GE110 - Geometria 1 a.a. 014-01 Prova scritta del 1-6-01 TESTO E SOLUZIONI Avvertenze: A. Per il recupero del primo esonero svolgere gli esercizi
UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica GE110 - Geometria 1 a.a. 014-01 Prova scritta del 1-6-01 TESTO E SOLUZIONI Avvertenze: A. Per il recupero del primo esonero svolgere gli esercizi
Geometria BAER A.A. Canale I Foglio esercizi 4
 Geometria BAER A.A. Canale I Foglio esercizi 4 Esercizio. Si trovino basi degli spazi delle soluzioni dei seguenti sistemi lineari Soluzione: Sol(S ) = L[ x + 3x x 3 + 5x 4 = S : x + 3x x 3 + x 4 = S x
Geometria BAER A.A. Canale I Foglio esercizi 4 Esercizio. Si trovino basi degli spazi delle soluzioni dei seguenti sistemi lineari Soluzione: Sol(S ) = L[ x + 3x x 3 + 5x 4 = S : x + 3x x 3 + x 4 = S x
CORSO DI MATEMATICA II Prof. Paolo Papi ESERCIZI. 1). Stabilire quali dei seguenti sottoinsiemi di V sono sottospazi vettoriali. (a) V = R 3.
 CORSO DI MATEMATICA II Prof Paolo Papi ESERCIZI ) Stabilire quali dei seguenti sottoinsiemi di V sono sottospazi vettoriali (a) V = R 3 () W = {(x,,x 3 ) x,x 3 R} (2) W 2 = {(x,,x 3 ) x,x 3 R} (3) W 3
CORSO DI MATEMATICA II Prof Paolo Papi ESERCIZI ) Stabilire quali dei seguenti sottoinsiemi di V sono sottospazi vettoriali (a) V = R 3 () W = {(x,,x 3 ) x,x 3 R} (2) W 2 = {(x,,x 3 ) x,x 3 R} (3) W 3
3. Elementi di Algebra Lineare.
 CALCOLO NUMERICO Francesca Mazzia Dipartimento Interuniversitario di Matematica Università di Bari 3. Elementi di Algebra Lineare. 1 Sistemi lineari Sia A IR m n, x IR n di n Ax = b è un vettore di m componenti.
CALCOLO NUMERICO Francesca Mazzia Dipartimento Interuniversitario di Matematica Università di Bari 3. Elementi di Algebra Lineare. 1 Sistemi lineari Sia A IR m n, x IR n di n Ax = b è un vettore di m componenti.
LEZIONE 12. v = α 1 v α n v n =
 LEZIONE 12 12.1. Combinazioni lineari. Definizione 12.1.1. Sia V uno spazio vettoriale su k = R, C e v 1,..., v n V vettori fissati. Un vettore v V si dice combinazione lineare di v 1,..., v n se esistono
LEZIONE 12 12.1. Combinazioni lineari. Definizione 12.1.1. Sia V uno spazio vettoriale su k = R, C e v 1,..., v n V vettori fissati. Un vettore v V si dice combinazione lineare di v 1,..., v n se esistono
Registro dell insegnamento
 Registro dell insegnamento Anno accademico 2016/17 Prof. Settore inquadramento Gabriele Vezzosi MAT-03 Scuola di Ingegneria Dipartimento DIMAI U. Dini Insegnamento Geometria Moduli Settore insegnamento
Registro dell insegnamento Anno accademico 2016/17 Prof. Settore inquadramento Gabriele Vezzosi MAT-03 Scuola di Ingegneria Dipartimento DIMAI U. Dini Insegnamento Geometria Moduli Settore insegnamento
4. Richiami: sistemi lineari e matrici
 4 Richiami: sistemi lineari e matrici Vettori 4a Combinazioni lineari Indichiamo con R n l insieme delle n-uple ordinate di elementi di R, { } R n := x = (x 1, x 2,, x n ) x i R, i = 1,,n Si dice che x
4 Richiami: sistemi lineari e matrici Vettori 4a Combinazioni lineari Indichiamo con R n l insieme delle n-uple ordinate di elementi di R, { } R n := x = (x 1, x 2,, x n ) x i R, i = 1,,n Si dice che x
Sistemi lineari 1 / 12
 Sistemi lineari 1 / 12 Sistemi lineari 2 / 12 Ricordiamo che cosa è un sistema lineare con m equazioni in n incognite (m,n N, m,n 1): a 11 x 1 + +a 1n x n = b 1 a 21 x 1 + +a 2n x n = b 2, (1).. a m1 x
Sistemi lineari 1 / 12 Sistemi lineari 2 / 12 Ricordiamo che cosa è un sistema lineare con m equazioni in n incognite (m,n N, m,n 1): a 11 x 1 + +a 1n x n = b 1 a 21 x 1 + +a 2n x n = b 2, (1).. a m1 x
Soluzione degli esercizi di algebra lineare (del 26 ottobre 2018)
 Soluzione degli esercizi di algebra lineare (del 26 ottobre 28) Esercizio. Siano V un K-spazio vettoriale con base B = (v,..., v n ) e W un K-spazio vettoriale con base C = (w,..., w m ), e sia f : V W
Soluzione degli esercizi di algebra lineare (del 26 ottobre 28) Esercizio. Siano V un K-spazio vettoriale con base B = (v,..., v n ) e W un K-spazio vettoriale con base C = (w,..., w m ), e sia f : V W
Matematica per Chimica, Chimica Industriale e Scienze dei Materiali Primo appello 7/02/2012 Tema A
 Matematica per Chimica, Chimica Industriale e Scienze dei Materiali Primo appello 7/02/202 Tema A NOME:..................................................... COGNOME:.....................................................
Matematica per Chimica, Chimica Industriale e Scienze dei Materiali Primo appello 7/02/202 Tema A NOME:..................................................... COGNOME:.....................................................
Università di Modena e Reggio Emilia Facoltà di Scienze MM.FF.NN. PROVA DI ALGEBRA LINEARE (esercitazione del 18 gennaio 2011)
 Università di Modena e Reggio Emilia Facoltà di Scienze MM.FF.NN. PROVA DI ALGEBRA LINEARE (esercitazione del 18 gennaio 2011) ISTRUZIONI PER LO SVOLGIMENTO. Scrivere cognome, nome, numero di matricola
Università di Modena e Reggio Emilia Facoltà di Scienze MM.FF.NN. PROVA DI ALGEBRA LINEARE (esercitazione del 18 gennaio 2011) ISTRUZIONI PER LO SVOLGIMENTO. Scrivere cognome, nome, numero di matricola
Insiemi di generatori, dipendenza lineare e basi
 Insiemi di generatori, dipendenza lineare e basi July 4, 2015 1 Insiemi di generatori Nel seguito V è uno spazio vettoriale sul campo K. Definizione. Una combinazione lineare di vettori v 1, v 2,..., v
Insiemi di generatori, dipendenza lineare e basi July 4, 2015 1 Insiemi di generatori Nel seguito V è uno spazio vettoriale sul campo K. Definizione. Una combinazione lineare di vettori v 1, v 2,..., v
Elementi di Algebra Lineare
 Elementi di Algebra Lineare Corso di Calcolo Numerico, a.a. 2009/2010 Francesca Mazzia Dipartimento di Matematica Università di Bari 13 Marzo 2006 Francesca Mazzia (Univ. Bari) Elementi di Algebra Lineare
Elementi di Algebra Lineare Corso di Calcolo Numerico, a.a. 2009/2010 Francesca Mazzia Dipartimento di Matematica Università di Bari 13 Marzo 2006 Francesca Mazzia (Univ. Bari) Elementi di Algebra Lineare
Geometria Prova scritta, appello unico, sessione autunnale Corso di laurea in fisica A.A 2017/2018 Canali A C, e L Pa
 Geometria Prova scritta, appello unico, sessione autunnale Corso di laurea in fisica A.A 27/28 Canali A C, e L Pa Durata: 2 ore e 3 minuti Simone Diverio Alessandro D Andrea Paolo Piccinni 7 settembre
Geometria Prova scritta, appello unico, sessione autunnale Corso di laurea in fisica A.A 27/28 Canali A C, e L Pa Durata: 2 ore e 3 minuti Simone Diverio Alessandro D Andrea Paolo Piccinni 7 settembre
Equivalentemente, le colonne di A sono linearmente indipendenti se e solo se
 Lezioni di Algebra Lineare. Versione novembre 2008 VI. Il determinante Il determinante det A di una matrice A, reale e quadrata, è un numero reale associato ad A. Dunque det è una funzione dall insieme
Lezioni di Algebra Lineare. Versione novembre 2008 VI. Il determinante Il determinante det A di una matrice A, reale e quadrata, è un numero reale associato ad A. Dunque det è una funzione dall insieme
Si consideri il sistema a coefficienti reali di m equazioni lineari in n incognite
 3 Sistemi lineari 3 Generalità Si consideri il sistema a coefficienti reali di m equazioni lineari in n incognite ovvero, in forma matriciale, a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n x
3 Sistemi lineari 3 Generalità Si consideri il sistema a coefficienti reali di m equazioni lineari in n incognite ovvero, in forma matriciale, a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n x
Per le risposte utilizza gli spazi predisposti. Quando richiesto, il procedimento va esposto brevemente, ma in maniera comprensibile.
 COGNOME............................... NOME..................................... Punti ottenuti Esame di geometria Scrivi cognome e nome negli spazi predisposti in ciascuno dei tre fogli. Per ogni domanda
COGNOME............................... NOME..................................... Punti ottenuti Esame di geometria Scrivi cognome e nome negli spazi predisposti in ciascuno dei tre fogli. Per ogni domanda
REGISTRO DELLE LEZIONI
 UNIVERSITA DEGLI STUDI DI GENOVA FACOLTA DI SCIENZE MATEMATICHE, FISICHE E NATURALI REGISTRO DELLE LEZIONI del Corso UFFICIALE di GEOMETRIA B tenute dal prof. Domenico AREZZO nell anno accademico 2006/2007
UNIVERSITA DEGLI STUDI DI GENOVA FACOLTA DI SCIENZE MATEMATICHE, FISICHE E NATURALI REGISTRO DELLE LEZIONI del Corso UFFICIALE di GEOMETRIA B tenute dal prof. Domenico AREZZO nell anno accademico 2006/2007
I. Foglio di esercizi su vettori linearmente dipendenti e linearmente indipendenti. , v 2 = α v 1 + β v 2 + γ v 3. α v 1 + β v 2 + γ v 3 = 0. + γ.
 ESERCIZI SVOLTI DI ALGEBRA LINEARE (Sono svolti alcune degli esercizi proposti nei fogli di esercizi su vettori linearmente dipendenti e vettori linearmente indipendenti e su sistemi lineari ) I. Foglio
ESERCIZI SVOLTI DI ALGEBRA LINEARE (Sono svolti alcune degli esercizi proposti nei fogli di esercizi su vettori linearmente dipendenti e vettori linearmente indipendenti e su sistemi lineari ) I. Foglio
Risoluzione di sistemi lineari
 Risoluzione di sistemi lineari Teorema (Rouché-Capelli) Dato il sistema di m equazioni in n incognite Ax = b, con A M at(m, n) b R n x R n [A b] si ha che: matrice dei coefficienti, vettore dei termini
Risoluzione di sistemi lineari Teorema (Rouché-Capelli) Dato il sistema di m equazioni in n incognite Ax = b, con A M at(m, n) b R n x R n [A b] si ha che: matrice dei coefficienti, vettore dei termini
Soluzioni primi compitini - Geometria 1
 Soluzioni primi compitini - Geometria Caterina Vernieri Ottobre 7 Le soluzioni proposte non sono state riviste dai professori Soluzioni Primi Compitini - G I compitino 7//3 Esercizio Al variare di α R
Soluzioni primi compitini - Geometria Caterina Vernieri Ottobre 7 Le soluzioni proposte non sono state riviste dai professori Soluzioni Primi Compitini - G I compitino 7//3 Esercizio Al variare di α R
MATEMATICA. a.a. 2014/ Sistemi di equazioni lineari
 MATEMATICA a.a. 2014/15 8. Sistemi di equazioni lineari SISTEMI LINEARI Si definisce sistema lineare un sistema di p equazioni di primo grado in q incognite. a11x1 + a12 x2 +... + a1 qxq = k1 a21x1 + a22x2
MATEMATICA a.a. 2014/15 8. Sistemi di equazioni lineari SISTEMI LINEARI Si definisce sistema lineare un sistema di p equazioni di primo grado in q incognite. a11x1 + a12 x2 +... + a1 qxq = k1 a21x1 + a22x2
Esercizi su applicazioni lineari. Per tutto il seguito, se non specificato esplicitamente K indicherà un campo e V,W,U spazi vettoriali su K.
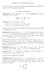 Esercizi su applicazioni lineari Per tutto il seguito, se non specificato esplicitamente K indicherà un campo e V,W,U spazi vettoriali su K. 1. Cose da ricordare Definizione 1.1. Una funzione f : V W si
Esercizi su applicazioni lineari Per tutto il seguito, se non specificato esplicitamente K indicherà un campo e V,W,U spazi vettoriali su K. 1. Cose da ricordare Definizione 1.1. Una funzione f : V W si
Esercizi 9 Rango di una matrice, sistemi lineari
 Esercizi 9 Rango di una matrice, sistemi lineari Quesiti a risposta multipla 0 3 ) Sia A a. Il rango di A è uguale a se e solo se 0 3 a a b a 0 c a k 0 0 ) Sia A, con k numero reale. Allora il rango della
Esercizi 9 Rango di una matrice, sistemi lineari Quesiti a risposta multipla 0 3 ) Sia A a. Il rango di A è uguale a se e solo se 0 3 a a b a 0 c a k 0 0 ) Sia A, con k numero reale. Allora il rango della
Sistemi II. Sistemi II. Elisabetta Colombo
 Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2011-2012, http://users.mat.unimi.it/users/colombo/programmabio.html 1 2 3 con R.C.+ o 1.10 Rango massimo e determinante con R.C.+
Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2011-2012, http://users.mat.unimi.it/users/colombo/programmabio.html 1 2 3 con R.C.+ o 1.10 Rango massimo e determinante con R.C.+
Parte 5. Sottospazi. A. Savo Appunti del Corso di Geometria
 Parte 5. Sottospazi A. Savo Appunti del Corso di Geometria 03-4 Indice delle sezioni Sottospazi di R n, Equazioni di un sottospazio di R n, 3 3 Sottospazio intersezione, 6 4 Sottospazio somma, 8 5 Formula
Parte 5. Sottospazi A. Savo Appunti del Corso di Geometria 03-4 Indice delle sezioni Sottospazi di R n, Equazioni di un sottospazio di R n, 3 3 Sottospazio intersezione, 6 4 Sottospazio somma, 8 5 Formula
1 o ESONERO DI ALGEBRA (Studenti di Informatica canale D Andrea) 10 Novembre 2014 Soluzione
 1 o ESONERO DI ALGEBRA (Studenti di Informatica canale D Andrea) 10 Novembre 2014 Soluzione 1. Scrivere la matrice associata all applicazione lineare T : R 3 R 4 definita da T (x, y, z) (2x + y z, 3y +
1 o ESONERO DI ALGEBRA (Studenti di Informatica canale D Andrea) 10 Novembre 2014 Soluzione 1. Scrivere la matrice associata all applicazione lineare T : R 3 R 4 definita da T (x, y, z) (2x + y z, 3y +
Pagine di Algebra lineare. di premessa al testo Pagine di Geometria di Sara Dragotti. Parte terza: SISTEMI LINEARI
 Pagine di Algebra lineare di premessa al testo Pagine di Geometria di Sara Dragotti Parte terza: SISTEMI LINEARI 1. Definizioni Dato un campo K ed m 1 polinomi su K in n indeterminate di grado non superiore
Pagine di Algebra lineare di premessa al testo Pagine di Geometria di Sara Dragotti Parte terza: SISTEMI LINEARI 1. Definizioni Dato un campo K ed m 1 polinomi su K in n indeterminate di grado non superiore
Esercizi di Geometria
 UNIVERSITÀ DEGLI STUDI DI TRENTO FACOLTÀ DI INGEGNERIA Marco Andreatta Luca Migliorini Gianluca Occhetta Davide Panizzolo Lorenza Tonetto Marina Avitabile Esercizi di Geometria Luglio 2000 2 1. Programma
UNIVERSITÀ DEGLI STUDI DI TRENTO FACOLTÀ DI INGEGNERIA Marco Andreatta Luca Migliorini Gianluca Occhetta Davide Panizzolo Lorenza Tonetto Marina Avitabile Esercizi di Geometria Luglio 2000 2 1. Programma
CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA
 CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA FOGLIO DI ESERCIZI GEOMETRIA 009/0 Esercizio. (7.9). Si consideri il sistema di equazioni lineari: x + y + z = x + y + z = x + y + 3z = a) Si dica per quali
CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA FOGLIO DI ESERCIZI GEOMETRIA 009/0 Esercizio. (7.9). Si consideri il sistema di equazioni lineari: x + y + z = x + y + z = x + y + 3z = a) Si dica per quali
Capitolo VI SISTEMI LINEARI
 Capitolo VI SISTEMI LINEARI 1 Concetti fondamentali 11 Definizione Un equazione in n incognite x 1,, x n a coefficienti in R si dice lineare se è della forma: a 1 x 1 + + a n x n = b con a i R e b R Una
Capitolo VI SISTEMI LINEARI 1 Concetti fondamentali 11 Definizione Un equazione in n incognite x 1,, x n a coefficienti in R si dice lineare se è della forma: a 1 x 1 + + a n x n = b con a i R e b R Una
DIARIO DEL CORSO DI MATHEMATICS FOR DATA SCIENCE TRENTO, A.A. 2018/19 DOCENTI: ANDREA CARANTI, SIMONE UGOLINI
 DIARIO DEL CORSO DI MATHEMATICS FOR DATA SCIENCE TRENTO, A.A. 2018/19 DOCENTI: ANDREA CARANTI, SIMONE UGOLINI Nota. La descrizione di lezioni non ancora svolte si deve intendere come una previsione/pianificazione.
DIARIO DEL CORSO DI MATHEMATICS FOR DATA SCIENCE TRENTO, A.A. 2018/19 DOCENTI: ANDREA CARANTI, SIMONE UGOLINI Nota. La descrizione di lezioni non ancora svolte si deve intendere come una previsione/pianificazione.
dipendenti. Cosa possiamo dire sulla dimensione di V?
 Esercizi Esercizi. In uno spazio vettoriale V ci sono tre vettori v, v 2, v linearmente indipendenti. Cosa possiamo dire sulla dimensione di V? 2. In uno spazio vettoriale V ci sono tre vettori v, v 2,
Esercizi Esercizi. In uno spazio vettoriale V ci sono tre vettori v, v 2, v linearmente indipendenti. Cosa possiamo dire sulla dimensione di V? 2. In uno spazio vettoriale V ci sono tre vettori v, v 2,
e non ci possono chiaramente essere minori di ordine più grande per cui il rango per minori è 2. Rango per pivot: Svolgiamo la riduzione
 18 ottobre 2011 1. Per le matrici seguenti calcolare il rango per minori, il rango per pivot, il rango per righe ed il rango per colonne. Verificare che si ottiene sempre lo stesso numero. Determinare
18 ottobre 2011 1. Per le matrici seguenti calcolare il rango per minori, il rango per pivot, il rango per righe ed il rango per colonne. Verificare che si ottiene sempre lo stesso numero. Determinare
Ingegneria Gestionale - Corso di Analisi II e Algebra anno accademico 2008/2009
 Ingegneria Gestionale - Corso di Analisi II e Algebra anno accademico 28/29 Dire se le seguenti proposizioni sono vere o false: ESERCITAZIONE. Proposizione Vera Falsa f : R R 4 rk(f f : R 4 R rk(f f :
Ingegneria Gestionale - Corso di Analisi II e Algebra anno accademico 28/29 Dire se le seguenti proposizioni sono vere o false: ESERCITAZIONE. Proposizione Vera Falsa f : R R 4 rk(f f : R 4 R rk(f f :
Fondamenti di ALGEBRA LINEARE E GEOMETRIA
 Fondamenti di ALGEBRA LINEARE E GEOMETRIA Corso di laurea in Ingegneria Gestionale 2011-2012 Michel Lavrauw Dipartimento di Tecnica e Gestione dei Sistemi Industriali Università di Padova Lezione 19 Capitolo
Fondamenti di ALGEBRA LINEARE E GEOMETRIA Corso di laurea in Ingegneria Gestionale 2011-2012 Michel Lavrauw Dipartimento di Tecnica e Gestione dei Sistemi Industriali Università di Padova Lezione 19 Capitolo
1 Esercizi 13. 3x + λy + 2z = 0 (1 λ)x + 5y + 3z = 0 3x + 2y + z = 0
 1 Esercizi 13 1. Discutere le soluzioni del sistema seguente al variare del parametro λ R. 3x + λy + 2z 0 (1 λ)x + 5y + 3z 0 3x + 2y + z 0 Soluzione. Si tratta di un SLO 3 3 e sappiamo che tale sistema
1 Esercizi 13 1. Discutere le soluzioni del sistema seguente al variare del parametro λ R. 3x + λy + 2z 0 (1 λ)x + 5y + 3z 0 3x + 2y + z 0 Soluzione. Si tratta di un SLO 3 3 e sappiamo che tale sistema
