SISTEMI LINEARI. x 2y 2z = 0. Svolgimento. Procediamo con operazioni elementari di riga sulla matrice del primo sistema: R 2 R 2 3R
|
|
|
- Lamberto Santini
- 7 anni fa
- Visualizzazioni
Transcript
1 SISTEMI LINEARI Esercizi Esercizio. Risolvere, se possibile, i seguenti sistemi: x y z = 0 x + y + z = 3x + y + z = 0 x y = 4x + z = 0, x y z = 0. Svolgimento. Procediamo con operazioni elementari di riga sulla matrice del primo sistema: 3 R R 3R R 3 R 3 4R R 3 R 3 R Quindi il primo sistema è equivalente a { x y z = 0 4y + 5z = 0, da cui si ricava y = 5/4z e, di conseguenza, x = y + z = z 5/4z = /4z. In particolare l insieme delle soluzioni del primo sistema è V := { ( a, 5a, 4a) a R } = L((, 5, 4)). Procediamo con operazioni elementari di riga sulla matrice completa del secondo sistema: 0 0 R R +R R 3 R 3 +R Typeset by AMS-TEX
2 SISTEMI LINEARI Quindi il secondo sistema è equivalente a x + y + z = z = y z =, da cui si ricava z = e, di conseguenza, y = z = 3, x = y + z = z 4z. In particolare il secondo sistema ha come unica soluzione ( 4, 3, ). Esercizio. Discutere e risolvere, se possibile, i seguenti sistemi al variare di h, k R. x y z = 0 x + y + z = 3x + y + z = 0 x y = 4x + hz = 0, hx y z = k. Svolgimento. Procediamo con operazioni elementari di riga sulla matrice incompleta A h del primo sistema: A h := 3 R R 3R R 3 R 3 4R 4 0 h 4 0 h h + 4 R 3 R 3 R h Risulta ϱ(a ) = e ϱ(a h ) = 3 per h. Quindi se h = il sistema ha soluzioni che formano uno spazio vettoriale poiché il sistema è omogeneo, mentre se h il sistema ha come unica soluzione quella banale. Si noti che se h = il sistema coincide con il primo dei sistemi del esercizio, perciò il suo insieme delle soluzioni è. V := { ( a, 5a, 4a) a R } = L((, 5, 4)). Procediamo ora con operazioni elementari di riga sulla matrice completa del secondo sistema. Definiamo A h := 0, B k :=. h k Allora: (A h B k ) = 0 R R +R 0 0 R 3 R 3 +R h k h k 0 0. h 0 0 k + 4
3 Quindi il secondo sistema è equivalente a x + y + z = z = y z =. SISTEMI LINEARI 3 Risulta ϱ(a ) = ϱ(a B 4 ) =, = ϱ(a ) ϱ(a B k ) = 3 per k 4 ed infine ϱ(a h ) ϱ(a h B k ) = 3 per h. Dal teorema di Rouché Capelli ricaviamo allora le seguenti conseguenze. Se h il sistema ammette un unica soluzione. Precisamente ((k + 4)/(h ), + (k + 4)/(h ), ). Se h = ma k 4 il sistema non ammette soluzione. Infine se h =, k = 4 il sistema ammette un insieme di soluzioni della forma V := { (x, + x, ) x R 3 } = (0,, ) + L((,, 0)). Esercizio 3. Risolvere, se possibile, i sistemi 0 0 x, x, x, x, = 3 3 0, 3 x 3, x 3, 5 ( ) x, x, x,3 0 0 x, x, x,3 3 = ( ). Svolgimento. Procediamo con operazioni elementari di riga sulla matrice completa del primo sistema: R R +R R 3 R 3 R R 3 R 3 +3R Quindi, indicando con x, x, x 3 le righe di X R 3,, il primo sistema è equivalente a x x 3 = (8, 3) x x 3 = (3, 0) x 3 = (6, 4),.
4 4 SISTEMI LINEARI da cui si ricava x = (0, 5) e x = ( 9, 4). In particolare il primo sistema ha come unica soluzione la matrice X := Prima di tutto ci riconduciamo alla forma AX = B mediante trasposizione. Il secondo sistema è equivalente a 3 0 x, x, x, x, = x,3 x,3 5 Procediamo ora con operazioni elementari di riga sulla matrice completa del sistema cosí ottenuto: R R R R 3 R 3 R Quindi, indicando con x, x, x 3 le colonne di X R,3, il secondo sistema è equivalente a x + x 3 = ( 4, ) x + x 3 = (3, 0) x 3 = (9, ), da cui si ricava x = (3, 3) e x = ( 6, ). In particolare il primo sistema ha come unica soluzione la matrice X := ( ) Esercizio 4. Determinare la soluzione generale ed una base per lo spazio delle soluzioni del sistema x + y + 3z + t = 0 x + y + z + t = 0 3y + 5z + t = 0 x + y + z = 0.
5 SISTEMI LINEARI 5 Svolgimento. Procediamo con operazioni elementari sulle righe della matrice del sistema: 3 3 R R +R R 4 R R R 3 R 3 R R 4 R 4 +R Quindi il sistema è equivalente a { x + y + 3z + t = 0 3y + 5z + t = 0. Dalla seconda equazione si ricava y = 5z/3 t/3 e, sostituendo nella prima, x = z/3 + t/3. Quindi la soluzione generale è V := {(a + b, 5a b, 3a, 3b) a, b R } = L((, 5, 3, 0), (,, 0, 3)). Esercizio 5. Siano date le due equazioni 3x y + z = 0 e x y 3z = 0. () Aggiungere una terza equazione in modo da ottenere un sistema con la sola soluzione nulla. () Aggiungere una terza equazione in modo da ottenere un sistema con infinite soluzioni. È possibile ottenere soluzioni? Svolgimento. Consideriamo il sistema 3x y + z = 0 x y 3z = 0 ax + by + cz = d. Le matrici incompleta e completa del sistema sono A := 3 3, (A B) := a b c a b c d
6 6 SISTEMI LINEARI Per il teorema di Rouché Capelli il sistema di cui sopra ammette un unica soluzione se e solo ϱ(a) = 3. Per esempio a = b = 0, c = e d arbitrario. Invece, affiché il sistema abbia infinite soluzioni è necessario e sufficiente che ϱ(a B) = ϱ(a) < 3. Quindi basta scegliere una combinazione lineare delle due prime equazioni: per esempio la loro somma, cioè a = 4, b =, c =, d = 0. Poiché le prime due equazioni sono comunque linearmente indipendenti ϱ(a), perciò la dimensione dello spazio delle soluzioni è 3 ϱ(a) : in particolare non è possibile determinare a, b, c, d in modo tale che il sistema abbia soluzioni. Esercizio 6. Scrivere un sistema AX = B avente come insieme delle soluzioni V := (, 0,, ) + L((0, 0, 0, )). Svolgimento. Poiché V non è un sottospazio di R 4 dobbiamo considerare sistemi non omogenei. Per come è definito V il corrispondente sistema omogeneo deve avere come spazio delle soluzioni L((0, 0, 0, )). Infine per il teorema di Rouché Capelli il rango della matrice incompleta A del sistema deve essere 4 dim(l((0, 0, 0, ))) = 3. Per esempio sia A := (ma potremmo scegliere qualsiasi altra matrice A d ordine m 4 e di rango 3 tale che A t (, 0, 0, 0) = (0, 0, 0, 0)). Sappiamo poi che (, 0,, ) deve essere soluzione particolare, quindi deve essere B = = 0 Concludiamo che un sistema avente V come spazio delle soluzioni è x + y + z = 0 y + z = z =..
7 Quiz. Sia SISTEMI LINEARI 7 Quiz A := 0 5. h h h Quale delle seguenti affermazioni è vera? a) ϱ(a) = 3. b) Per h = il sistema AX = 0 ha soluzioni. c) t A = A per ogni h R. d) A è invertibile per h =. Svolgimento. L affermazione a) è falsa. Infatti le prime due righe di A sono linearmente indipendenti, ma A = 4h + 5h 0h + h, dunque ϱ(a) = per ogni h R. L affermazione b) è vera. Infatti per quanto visto sopra, ϱ(a) = per h = (in effetti, per ogni h R). In particolare lo spazio delle soluzioni del sistema AX = 0 ha dimensione 3 ϱ(a) = per il teorema di Rouché Capelli. L affermazione c) è falsa. Infatti è noto che una matrice quadrata è invertibile se e solo se il suo rango è massimo rispetto al suo ordine. Quindi A è invertibile se e solo se ϱ(a) = 3, mentre abbiamo visto sopra che ϱ(a) = per ogni h R. L affermazione d) è falsa. Si veda la risposta a c). Quiz. Siano date A := ( ) 0 Quale delle seguenti affermazioni è vera? B := ( ) a) Non esiste nessuna matrice X tale che AX = B. b) Esiste una matrice X tale che BA = X. c) ϱ(a + B) = ϱ(a) + ϱ(b). d) (BA)X = 0 non è risolubile in R 3,n. Svolgimento. L affermazione a) è falsa. Infatti AX = B ha soluzione se e solo se ϱ(a) = ϱ(a B) per il teorema di Rouché Capelli. D altra parte ϱ(a) =, dunque necessariamente ϱ(a B) =. L affermazione b) è vera. Infatti equivale ad affermare che si può fare il prodotto BA, il che è vero per l ordine delle matrici. Risulta X = BA = ( ) ( ) = 0 ( )
8 8 SISTEMI LINEARI L affermazione c) è falsa. Infatti l affermazione è priva di senso in quanto le matrici A e B non possono essere sommate avendo diverso numero di colonne. L affermazione d) è falsa. Infatti un sistema omogeneo ha sempre almeno la soluzione banale. Si noti che essendo ϱ(ba) = (come visto sopra) esistono sempre soluzioni non banali. Quiz 3. Si consideri il sistema AX = 0 ove X R 3 ed A := Quale delle seguenti affermazioni è vera? ( ) a) Il sistema non è risolubile. b) Una base del suo spazio delle soluzioni è ((, 0, ), (0,, 0)). c) Ha 3 soluzioni. d) Ha solo la soluzione banale. Svolgimento. L affermazione a) è falsa. Infatti un sistema omogeneo ha sempre almeno la soluzione banale. L affermazione b) è vera. Infatti (, 0, ) e (0,, 0) sono linearmente indipendenti e si verifica, per sostituzione diretta, che sono anche soluzioni di AX = 0. D altra parte la dimensione dello spazio delle soluzioni di AX = 0 è 3 ϱ(a) = per il teorema di Rouché Capelli. L affermazione c) è falsa. Infatti abbiamo visto nel corso della risposta precedente che la dimensione del suo spazio delle soluzioni è. L affermazione d) è falsa. Si proceda come nella risposta precedente. Quiz 4. Siano A := 4 0 0, B := Quale delle seguenti affermazioni è vera? a) AX = B è equivalente ad XA = B. b) AX = B ha come soluzione un unica terna di numeri reali. c) AX = B ha infinite soluzioni. d) Nessuna delle affermazioni precedenti è corretta. Svolgimento. L affermazione a) è falsa. Infatti non è difficile risolvere il sistema AX = B in quanto A è già ridotta per righe. Indicando con x, x, x 3 le righe della matrice X si deve avere x + 4x + x 3 = (0, 0, ) x 3 = (0,, 0) 5x = (,, )
9 SISTEMI LINEARI 9 quindi dalla seconda e terza equazione x = (0, 0, /5) e x 3 = (/, /, /): sostituendo nella prima equazione x = ( x x 3 )/4 = ( /4, 0, 3/0), cioè X = 0 0 /5 /4 0 3/0. / / / Se AX = B fosse equivalente a XA = B si dovrebbe avere = 0 0 /5 /4 0 3/ , / / / ma, come è facile vedere, l elemento di indici, della matrice prodotto è. L affermazione b) è falsa. Infatti la soluzione di un sistema AX = B con A R m,n, B R m,q deve essere X R n,q. Nel nostro caso X R 3,3. L affermazione c) è falsa. Infatti, come si è visto nel corso della risposta ad a), il sistema AX = B ha un unica soluzione. Per esclusione la risposta a d) è vera. Quiz 5. Sia dato il sistema lineare AX = B con B matrice non nulla. Quale delle seguenti affermazioni è vera? a) l insieme delle sue soluzioni è uno spazio vettoriale. b) Tra le sue soluzioni vi è certamente quella banale. c) Per A e B opportune, il sistema ha soluzioni. d) Tutte le affermazioni precedenti sono vere. Svolgimento. L affermazione a) è falsa. Infatti se l insieme delle soluzioni fosse uno spazio vettoriale anche la matrice nulla 0 sarebbe soluzione. Ma A0 = 0 B per ipotesi. L affermazione b) è falsa. Si proceda come nella risposta ad a). L affermazione c) è vera. Basta trovare un esempio: si prendano allora A = , B := Allora il sistema AX = B ha per soluzione V := { (, y, z) R 3 } = (, 0, 0) + L(e, e 3 ). L affermazione d) è falsa. Quiz 6. Siano A, B R 4,4 ed assumiamo che A sia ridotta per righe. Quale delle seguenti affermazioni è vera? a) Se A ha due righe nulle, AX = B ha soluzioni. b) Se A non ha righe nulle, AX = B ha soluzione. c) Se B ha una riga nulla, AX = B non ha soluzioni. d) Il numero di incognite libere di AX = B coincide con ϱ(a) ϱ(b).
10 0 SISTEMI LINEARI Svolgimento. L affermazione a) è falsa. Infatti l esistenza o meno di soluzioni dipende dall eguaglianza o meno delle quantità ϱ(a) e ϱ(a B). Quindi se A ha due righe nulle allora ϱ(a) : ma potrebbe essere ϱ(a B) 3. L affermazione b) è vera. Infatti se A non ha righe nulle allora A ha rango massimo, quindi, essendo quadrata, è invertibile: in particolare X := A B è l unica soluzione di AX = B. L affermazione c) è falsa. Infatti se A non ha righe nulle allora ϱ(a) = 4 e, come si è visto nel caso della risposta a b), AX = B ammette soluzione. L affermazione d) è falsa. Infatti assumiamo ϱ(a) = 4. Abbiamo visto nella risposta a b) che, in questo caso, AX = B ha un unica soluzione qualsiasi sia il rango di B. Quindi in questo caso il numero delle incognite libere di AX = B è sempre 0 che, in generale non coincide con ϱ(a) ϱ(b).
SISTEMI LINEARI MATRICI E SISTEMI 1
 MATRICI E SISTEMI SISTEMI LINEARI Sistemi lineari e forma matriciale (definizioni e risoluzione). Teorema di Rouché-Capelli. Sistemi lineari parametrici. Esercizio Risolvere il sistema omogeneo la cui
MATRICI E SISTEMI SISTEMI LINEARI Sistemi lineari e forma matriciale (definizioni e risoluzione). Teorema di Rouché-Capelli. Sistemi lineari parametrici. Esercizio Risolvere il sistema omogeneo la cui
SISTEMI LINEARI. x y + 2t = 0 2x + y + z t = 0 x z t = 0 ; S 3 : ; S 5x 2y z = 1 4x 7y = 3
 SISTEMI LINEARI. Esercizi Esercizio. Verificare se (,, ) è soluzione del sistema x y + z = x + y z = 3. Trovare poi tutte le soluzioni del sistema. Esercizio. Scrivere un sistema lineare di 3 equazioni
SISTEMI LINEARI. Esercizi Esercizio. Verificare se (,, ) è soluzione del sistema x y + z = x + y z = 3. Trovare poi tutte le soluzioni del sistema. Esercizio. Scrivere un sistema lineare di 3 equazioni
SPAZI VETTORIALI. Esercizi Esercizio 1. Sia V := R 3. Stabilire quale dei seguenti sottoinsiemi di V sono suoi sottospazi:
 SPAZI VETTORIALI Esercizi Esercizio. Sia V := R 3. Stabilire quale dei seguenti sottoinsiemi di V sono suoi sottospazi: V := { (a, a, a) V a R }, V 2 := { (a, b, a) V a, b R }, V 3 := { (a, 2a, a + b)
SPAZI VETTORIALI Esercizi Esercizio. Sia V := R 3. Stabilire quale dei seguenti sottoinsiemi di V sono suoi sottospazi: V := { (a, a, a) V a R }, V 2 := { (a, b, a) V a, b R }, V 3 := { (a, 2a, a + b)
Federica Gregorio e Cristian Tacelli
 1 Sistemi lineari Federica Gregorio e Cristian Tacelli Un sistema lineare m n (m equazioni in n incognite) è un insieme di equazioni lineari che devono essere soddisfatte contemporaneamente a 11 x 1 +
1 Sistemi lineari Federica Gregorio e Cristian Tacelli Un sistema lineare m n (m equazioni in n incognite) è un insieme di equazioni lineari che devono essere soddisfatte contemporaneamente a 11 x 1 +
Note sui sistemi lineari
 Note sui sistemi lineari Sia K un campo e siano m e n due numeri interi positivi. Sia A M(m n, K) e sia b K m. Consideriamo il sistema lineare Ax = b nell incognita x K n (o, se preferite, nelle incognite
Note sui sistemi lineari Sia K un campo e siano m e n due numeri interi positivi. Sia A M(m n, K) e sia b K m. Consideriamo il sistema lineare Ax = b nell incognita x K n (o, se preferite, nelle incognite
LEZIONE 3. Typeset by AMS-TEX
 LEZIONE 3 3 Risoluzione di sistemi Supponiamo che AX = B sia un sistema di equazioni lineari Ad esso associamo la sua matrice completa (A B Per la Proposizione 236 sappiamo di poter trasformare, con operazioni
LEZIONE 3 3 Risoluzione di sistemi Supponiamo che AX = B sia un sistema di equazioni lineari Ad esso associamo la sua matrice completa (A B Per la Proposizione 236 sappiamo di poter trasformare, con operazioni
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA
 UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito C 3/5/25 A. A. 24 25 ) Risolvere il seguente sistema
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito C 3/5/25 A. A. 24 25 ) Risolvere il seguente sistema
Esercitazione 6 - Soluzione
 Anno Accademico 28-29 Corso di Algebra Lineare e Calcolo Numerico per Ingegneria Meccanica Esercitazione 6 - Soluzione Immagine, nucleo. Teorema di Rouché-Capelli. Esercizio Sia L : R 3 R 3 l applicazione
Anno Accademico 28-29 Corso di Algebra Lineare e Calcolo Numerico per Ingegneria Meccanica Esercitazione 6 - Soluzione Immagine, nucleo. Teorema di Rouché-Capelli. Esercizio Sia L : R 3 R 3 l applicazione
ESAME DI GEOMETRIA. 6 febbraio 2002 CORREZIONE QUIZ
 ESAME DI GEOMETRIA 6 febbraio CORREZIONE QUIZ. La parte reale di ( + i) 9 è positiva. QUIZ Si può procedere in due modi. Un primo modo è osservare che ( + i) =i, dunque ( + i) 9 =(+i)(i) 4 = 4 ( + i) :
ESAME DI GEOMETRIA 6 febbraio CORREZIONE QUIZ. La parte reale di ( + i) 9 è positiva. QUIZ Si può procedere in due modi. Un primo modo è osservare che ( + i) =i, dunque ( + i) 9 =(+i)(i) 4 = 4 ( + i) :
Corso di Geometria BIAR, BSIR Esercizi 3: soluzioni
 Corso di Geometria - BIAR, BSIR Esercizi : soluzioni Rango e teorema di Rouché-Capelli Esercizio. Calcolare il rango di ciascuna delle seguenti matrici: ( ) ( ) ( ) A =, A =, A =, A 4 = ( ). a a a Soluzione.
Corso di Geometria - BIAR, BSIR Esercizi : soluzioni Rango e teorema di Rouché-Capelli Esercizio. Calcolare il rango di ciascuna delle seguenti matrici: ( ) ( ) ( ) A =, A =, A =, A 4 = ( ). a a a Soluzione.
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA
 UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito B 3/05/005 A. A. 004 005 ) Risolvere il seguente sistema
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito B 3/05/005 A. A. 004 005 ) Risolvere il seguente sistema
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI
 CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
Sistemi lineari - Parte Seconda - Esercizi
 Sistemi lineari - Parte Seconda - Esercizi Terminologia Operazioni elementari sulle righe. Equivalenza per righe. Riduzione a scala per righe. Rango di una matrice. Forma canonica per righe. Eliminazione
Sistemi lineari - Parte Seconda - Esercizi Terminologia Operazioni elementari sulle righe. Equivalenza per righe. Riduzione a scala per righe. Rango di una matrice. Forma canonica per righe. Eliminazione
Note per le esercitazioni di Geometria 1 a.a. 2007/08 A. Lotta. Metodi per il calcolo del rango di una matrice
 Note per le esercitazioni di Geometria 1 a.a. 2007/08 A. Lotta Versione del 21/12/07 Metodi per il calcolo del rango di una matrice Sia A M m,n (K). Denotiamo con A (i) la riga i-ma di A, i {1,..., m}.
Note per le esercitazioni di Geometria 1 a.a. 2007/08 A. Lotta Versione del 21/12/07 Metodi per il calcolo del rango di una matrice Sia A M m,n (K). Denotiamo con A (i) la riga i-ma di A, i {1,..., m}.
Registro Lezioni di Algebra lineare del 15 e 16 novembre 2016.
 Registro Lezioni di Algebra lineare del 15 e 16 novembre 2016 Di seguito si riporta il riassunto degli argomenti svolti; i riferimenti sono a parti del Cap8 Elementi di geometria e algebra lineare Par5
Registro Lezioni di Algebra lineare del 15 e 16 novembre 2016 Di seguito si riporta il riassunto degli argomenti svolti; i riferimenti sono a parti del Cap8 Elementi di geometria e algebra lineare Par5
CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA
 CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA FOGLIO DI ESERCIZI 4 GEOMETRIA 2008/09 Esercizio 4.1 (5.10). Dati i vettori di R 3 : v 1 (1, 1, 2), v 2 (2, 4, 6), v 3 ( 1, 2, 5), v 4 (1, 1, 10) determinare
CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA FOGLIO DI ESERCIZI 4 GEOMETRIA 2008/09 Esercizio 4.1 (5.10). Dati i vettori di R 3 : v 1 (1, 1, 2), v 2 (2, 4, 6), v 3 ( 1, 2, 5), v 4 (1, 1, 10) determinare
A titolo di esempio proponiamo la risoluzione del sistema sia con il metodo della matrice inversa sia con il metodo di Cramer.
 ) Trovare le soluzioni del seguente sistema lineare: x+ y+ z = 3x y + z = 0 x + 5y 4z = 5 Osserviamo in primo luogo che il sistema dato è un sistema quadrato di tre equazioni in tre incognite, precisamente
) Trovare le soluzioni del seguente sistema lineare: x+ y+ z = 3x y + z = 0 x + 5y 4z = 5 Osserviamo in primo luogo che il sistema dato è un sistema quadrato di tre equazioni in tre incognite, precisamente
Prima prova in itinere di Geometria (Corso di laurea in Fisica, Canali A-C e D-O) Prof. Barucci e Piccinni 29 novembre 2011
 Prima prova in itinere di Geometria (Corso di laurea in Fisica, Canali A-C e D-O) Prof Barucci e Piccinni 29 novembre 2011 a Scrivere subito canale, cognome e nome b Utilizzare questi fogli per le risposte
Prima prova in itinere di Geometria (Corso di laurea in Fisica, Canali A-C e D-O) Prof Barucci e Piccinni 29 novembre 2011 a Scrivere subito canale, cognome e nome b Utilizzare questi fogli per le risposte
r 2 r 2 2r 1 r 4 r 4 r 1
 SPAZI R n 1. Esercizi Esercizio 1. Stabilire quali dei seguenti sottoinsiemi sono sottospazi: V 1 = {(x, y, z) R 3 /x = y = z} V = {(x, y, z) R 3 /x = 4} V 3 = {(x, y, z) R 3 /z = x } V 4 = {(x, y, z)
SPAZI R n 1. Esercizi Esercizio 1. Stabilire quali dei seguenti sottoinsiemi sono sottospazi: V 1 = {(x, y, z) R 3 /x = y = z} V = {(x, y, z) R 3 /x = 4} V 3 = {(x, y, z) R 3 /z = x } V 4 = {(x, y, z)
Applicazioni lineari e diagonalizzazione. Esercizi svolti
 . Applicazioni lineari Esercizi svolti. Si consideri l applicazione f : K -> K definita da f(x,y) = x + y e si stabilisca se è lineare. Non è lineare. Possibile verifica: f(,) = 4; f(,4) = 6; quindi f(,4)
. Applicazioni lineari Esercizi svolti. Si consideri l applicazione f : K -> K definita da f(x,y) = x + y e si stabilisca se è lineare. Non è lineare. Possibile verifica: f(,) = 4; f(,4) = 6; quindi f(,4)
I sistemi lineari di n equazioni in n incognite
 I sistemi lineari I sistemi lineari di n equazioni in n incognite I sistemi lineari di n equazioni in n incognite, sono formati da equazioni di primo grado, in cui le incognite hanno tutte esponente uguale
I sistemi lineari I sistemi lineari di n equazioni in n incognite I sistemi lineari di n equazioni in n incognite, sono formati da equazioni di primo grado, in cui le incognite hanno tutte esponente uguale
0.1 Complemento diretto
 1 0.1 Complemento diretto Dato U V, un complemento diretto di U é un sottospazio W V tale che U W = {0} U + W = V cioé la somma di U con il suo complemento diretto é diretta, e dá tutto lo spazio vettoriale
1 0.1 Complemento diretto Dato U V, un complemento diretto di U é un sottospazio W V tale che U W = {0} U + W = V cioé la somma di U con il suo complemento diretto é diretta, e dá tutto lo spazio vettoriale
CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA
 CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA FOGLIO DI ESERCIZI GEOMETRIA 009/0 Esercizio. (7.9). Si consideri il sistema di equazioni lineari: x + y + z = x + y + z = x + y + 3z = a) Si dica per quali
CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA FOGLIO DI ESERCIZI GEOMETRIA 009/0 Esercizio. (7.9). Si consideri il sistema di equazioni lineari: x + y + z = x + y + z = x + y + 3z = a) Si dica per quali
CORSI DI LAUREA IN MATEMATICA E FISICA
 CORSI DI LAUREA IN MATEMATICA E FISICA FOGLIO DI ESERCIZI # 6 GEOMETRIA 1 Esercizio 6.1 (Esercizio 5.1). Scrivere un vettore w R 3 linearmente dipendente dal vettore v ( 1, 9, 0). Per esempio il vettore
CORSI DI LAUREA IN MATEMATICA E FISICA FOGLIO DI ESERCIZI # 6 GEOMETRIA 1 Esercizio 6.1 (Esercizio 5.1). Scrivere un vettore w R 3 linearmente dipendente dal vettore v ( 1, 9, 0). Per esempio il vettore
Esercizio 1 Trovare, se esistono, le soluzioni del sistema lineare. y + 3z = 3 x y + z = 0. { x + y = 1
 Esercizio 1 Trovare, se esistono, le soluzioni del lineare y + 3z = 3 x y + z = 0 x + y = 1 0 1 3 3 1 1 1 0 1 1 1 0 = 0 1 3 3 = 1 1 0 1 1 1 0 1 = 1 1 1 0 0 1 3 3 0 1 1 = Il di partenza è quindi equivalente
Esercizio 1 Trovare, se esistono, le soluzioni del lineare y + 3z = 3 x y + z = 0 x + y = 1 0 1 3 3 1 1 1 0 1 1 1 0 = 0 1 3 3 = 1 1 0 1 1 1 0 1 = 1 1 1 0 0 1 3 3 0 1 1 = Il di partenza è quindi equivalente
Geometria BAER I canale Foglio esercizi 3
 Geometria BAER I canale Foglio esercizi 3 Esercizio. Discutere le soluzioni del seguente sistema lineare nelle incognite,, z al variare del parametro k. 3 + kz = k k + 3z = k k + z = Soluzione: Il determinante
Geometria BAER I canale Foglio esercizi 3 Esercizio. Discutere le soluzioni del seguente sistema lineare nelle incognite,, z al variare del parametro k. 3 + kz = k k + 3z = k k + z = Soluzione: Il determinante
Esercizi svolti sui sistemi lineari
 Francesco Daddi - www.webalice.it/francesco.daddi Esercizi svolti sui sistemi lineari Esercizio 1. Risolvere il seguente sistema lineare al variare del parametro reale t: tx+(t 1)y + z =1 (t 1)y + tz =1
Francesco Daddi - www.webalice.it/francesco.daddi Esercizi svolti sui sistemi lineari Esercizio 1. Risolvere il seguente sistema lineare al variare del parametro reale t: tx+(t 1)y + z =1 (t 1)y + tz =1
Soluzioni del Foglio 2 I sistemi lineari
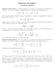 Soluzioni del Foglio 2 I sistemi lineari Soluzione dell esercizio 1 Il sistema assegnato è un sistema di 2 equazioni in 2 incognite non omogeneo Le matrici incompleta e completa associate al sistema sono
Soluzioni del Foglio 2 I sistemi lineari Soluzione dell esercizio 1 Il sistema assegnato è un sistema di 2 equazioni in 2 incognite non omogeneo Le matrici incompleta e completa associate al sistema sono
a + 2b + c 3d = 0, a + c d = 0 c d
 SPAZI VETTORIALI 1. Esercizi Esercizio 1. Stabilire quali dei seguenti sottoinsiemi sono sottospazi: V 1 = {(x, y, z) R 3 /x = y = z} V = {(x, y, z) R 3 /x = 4} V 3 = {(x, y, z) R 3 /z = x } V 4 = {(x,
SPAZI VETTORIALI 1. Esercizi Esercizio 1. Stabilire quali dei seguenti sottoinsiemi sono sottospazi: V 1 = {(x, y, z) R 3 /x = y = z} V = {(x, y, z) R 3 /x = 4} V 3 = {(x, y, z) R 3 /z = x } V 4 = {(x,
La riduzione a gradini e i sistemi lineari (senza il concetto di rango)
 CAPITOLO 4 La riduzione a gradini e i sistemi lineari (senza il concetto di rango) Esercizio 4.1. Risolvere il seguente sistema non omogeneo: 2x+4y +4z = 4 x z = 1 x+3y +4z = 3 Esercizio 4.2. Risolvere
CAPITOLO 4 La riduzione a gradini e i sistemi lineari (senza il concetto di rango) Esercizio 4.1. Risolvere il seguente sistema non omogeneo: 2x+4y +4z = 4 x z = 1 x+3y +4z = 3 Esercizio 4.2. Risolvere
SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI
 SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI Appunti presi dalle lezioni del prof. Nedo Checcaglini Liceo Scientifico di Castiglion Fiorentino (Classe 4B) January 17, 005 1 SISTEMI LINEARI Se a ik, b i R,
SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI Appunti presi dalle lezioni del prof. Nedo Checcaglini Liceo Scientifico di Castiglion Fiorentino (Classe 4B) January 17, 005 1 SISTEMI LINEARI Se a ik, b i R,
Corso di Geometria BIAR, BSIR Esercizi 4: soluzioni
 Corso di Geometria - BIAR, BSIR Esercizi : soluzioni Esercizio. Sono dati i seguenti sistemi lineari omogenei nelle incognite x, y, z: { x + y z = x + y z = x + y z = S : x y + z =, S :, S 3 : x 3y =,
Corso di Geometria - BIAR, BSIR Esercizi : soluzioni Esercizio. Sono dati i seguenti sistemi lineari omogenei nelle incognite x, y, z: { x + y z = x + y z = x + y z = S : x y + z =, S :, S 3 : x 3y =,
APPLICAZIONI LINEARI
 APPLICAZIONI LINEARI Esercizi Esercizio Date le seguenti applicazioni lineari f : R 2 R 3 definita da fx y = x 2y x + y x + y; 2 g : R 3 R 2 definita da gx y z = x + y x y; 3 h : Rx] 2 R 2 definita da
APPLICAZIONI LINEARI Esercizi Esercizio Date le seguenti applicazioni lineari f : R 2 R 3 definita da fx y = x 2y x + y x + y; 2 g : R 3 R 2 definita da gx y z = x + y x y; 3 h : Rx] 2 R 2 definita da
Ax = b ; b = b 1 b 2. a 11 a 12 a 1n a 21 a 22 a 2n. b m. a m1 a m2 a mn
 SISTEMI LINERI Consideriamo il seguente sistema di m equazioni lineare nelle n incognite,,, n : a + a + + a n n = b >< a + a + + a n n = b = >: a m + a m + + a mn n = b m tale sistema può essere scritto
SISTEMI LINERI Consideriamo il seguente sistema di m equazioni lineare nelle n incognite,,, n : a + a + + a n n = b >< a + a + + a n n = b = >: a m + a m + + a mn n = b m tale sistema può essere scritto
SOTTOSPAZI E OPERAZIONI IN SPAZI DIVERSI DA R n
 SPAZI E SOTTOSPAZI 1 SOTTOSPAZI E OPERAZIONI IN SPAZI DIVERSI DA R n Spazi di matrici. Spazi di polinomi. Generatori, dipendenza e indipendenza lineare, basi e dimensione. Intersezione e somma di sottospazi,
SPAZI E SOTTOSPAZI 1 SOTTOSPAZI E OPERAZIONI IN SPAZI DIVERSI DA R n Spazi di matrici. Spazi di polinomi. Generatori, dipendenza e indipendenza lineare, basi e dimensione. Intersezione e somma di sottospazi,
Appunti su Indipendenza Lineare di Vettori
 Appunti su Indipendenza Lineare di Vettori Claudia Fassino a.a. Queste dispense, relative a una parte del corso di Matematica Computazionale (Laurea in Informatica), rappresentano solo un aiuto per lo
Appunti su Indipendenza Lineare di Vettori Claudia Fassino a.a. Queste dispense, relative a una parte del corso di Matematica Computazionale (Laurea in Informatica), rappresentano solo un aiuto per lo
Argomenti trattati nella settimana novembre Il libro cui faccio riferimento, se non specificato altrimenti, è Lang, Algebra lineare
 Argomenti trattati nella settimana 23-27 novembre 2009 Il libro cui faccio riferimento, se non specificato altrimenti, è Lang, Algebra lineare 1 Sistemi lineari; 2 applicazioni lineari; Sistemi lineari;
Argomenti trattati nella settimana 23-27 novembre 2009 Il libro cui faccio riferimento, se non specificato altrimenti, è Lang, Algebra lineare 1 Sistemi lineari; 2 applicazioni lineari; Sistemi lineari;
Pagine di Algebra lineare. di premessa al testo Pagine di Geometria di Sara Dragotti. Parte terza: SISTEMI LINEARI
 Pagine di Algebra lineare di premessa al testo Pagine di Geometria di Sara Dragotti Parte terza: SISTEMI LINEARI 1. Definizioni Dato un campo K ed m 1 polinomi su K in n indeterminate di grado non superiore
Pagine di Algebra lineare di premessa al testo Pagine di Geometria di Sara Dragotti Parte terza: SISTEMI LINEARI 1. Definizioni Dato un campo K ed m 1 polinomi su K in n indeterminate di grado non superiore
1 Equazioni parametriche e cartesiane di sottospazi affini di R n
 2 Trapani Dispensa di Geometria, Equazioni parametriche e cartesiane di sottospazi affini di R n Un sottospazio affine Σ di R n e il traslato di un sottospazio vettoriale. Cioe esiste un sottospazio vettoriale
2 Trapani Dispensa di Geometria, Equazioni parametriche e cartesiane di sottospazi affini di R n Un sottospazio affine Σ di R n e il traslato di un sottospazio vettoriale. Cioe esiste un sottospazio vettoriale
Esercizi sui sistemi di equazioni lineari.
 Esercizi sui sistemi di equazioni lineari Risolvere il sistema di equazioni lineari x y + z 6 x + y z x y z Si tratta di un sistema di tre equazioni lineari nelle tre incognite x, y e z Poichè m n, la
Esercizi sui sistemi di equazioni lineari Risolvere il sistema di equazioni lineari x y + z 6 x + y z x y z Si tratta di un sistema di tre equazioni lineari nelle tre incognite x, y e z Poichè m n, la
Esempio. L immagine di f è l insieme dei vettori w = (w 1, w 2 ) R 2 che hanno w 1 = w 2. Quindi:
 Nucleo, immagine e loro proprietà [Abate, 5.2] Data una applicazione lineare f : V W, chiamiamo nucleo di f l insieme N(f) := { v V : f(v) = 0 W } Se S V è un sottoinsieme del dominio, indichiamo con f(s)
Nucleo, immagine e loro proprietà [Abate, 5.2] Data una applicazione lineare f : V W, chiamiamo nucleo di f l insieme N(f) := { v V : f(v) = 0 W } Se S V è un sottoinsieme del dominio, indichiamo con f(s)
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA
 Cognome Nome Matricola FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA Ciarellotto, Esposito, Garuti Prova del 21 settembre 2013 Dire se è vero o falso (giustificare le risposte. Bisogna necessariamente rispondere
Cognome Nome Matricola FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA Ciarellotto, Esposito, Garuti Prova del 21 settembre 2013 Dire se è vero o falso (giustificare le risposte. Bisogna necessariamente rispondere
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof. Fabio Perroni. 5. Rango
 Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 5 Rango Definizione 1 Sia A M m,n (K) una matrice m n a coefficienti nel campo K Il rango
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 5 Rango Definizione 1 Sia A M m,n (K) una matrice m n a coefficienti nel campo K Il rango
0.1 Soluzioni esercitazione IV, del 28/10/2008
 1 0.1 Soluzioni esercitazione IV, del 28/10/2008 Esercizio 0.1.1. Risolvere, usando il teorema di Cramer, i seguenti sistemi lineari 2x + y + z = 0 x + 3z = 1 x y z = 1 kx + y z = 1 x y + 2z = 1 2x + 2y
1 0.1 Soluzioni esercitazione IV, del 28/10/2008 Esercizio 0.1.1. Risolvere, usando il teorema di Cramer, i seguenti sistemi lineari 2x + y + z = 0 x + 3z = 1 x y z = 1 kx + y z = 1 x y + 2z = 1 2x + 2y
Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari
 Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari Antonio Lanteri e Cristina Turrini UNIMI - 2016/2017 Antonio Lanteri e Cristina Turrini (UNIMI - 2016/2017 Elementi di Algebra Lineare
Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari Antonio Lanteri e Cristina Turrini UNIMI - 2016/2017 Antonio Lanteri e Cristina Turrini (UNIMI - 2016/2017 Elementi di Algebra Lineare
Esercizi svolti. risolvere, se possibile, l equazione xa + B = O, essendo x un incognita reale
 Esercizi svolti 1. Matrici e operazioni fra matrici 1.1 Date le matrici 1 2 1 6 A = B = 5 2 9 15 6 risolvere, se possibile, l equazione xa + B = O, essendo x un incognita reale Osservazione iniziale: qualunque
Esercizi svolti 1. Matrici e operazioni fra matrici 1.1 Date le matrici 1 2 1 6 A = B = 5 2 9 15 6 risolvere, se possibile, l equazione xa + B = O, essendo x un incognita reale Osservazione iniziale: qualunque
Sistemi Lineari. Rango di una matrice. Lezione 21, Algebra Lineare,
 Lezione 21, Algebra Lineare, 15.11.2017 Sistemi Lineari Rango di una matrice Esempio principale, I Considerata una matrice, ci poniamo il problema di determinare il massimo numero di colonne linearmente
Lezione 21, Algebra Lineare, 15.11.2017 Sistemi Lineari Rango di una matrice Esempio principale, I Considerata una matrice, ci poniamo il problema di determinare il massimo numero di colonne linearmente
Risoluzione di sistemi lineari
 Risoluzione di sistemi lineari Teorema (Rouché-Capelli) Dato il sistema di m equazioni in n incognite Ax = b, con A M at(m, n) b R n x R n [A b] si ha che: matrice dei coefficienti, vettore dei termini
Risoluzione di sistemi lineari Teorema (Rouché-Capelli) Dato il sistema di m equazioni in n incognite Ax = b, con A M at(m, n) b R n x R n [A b] si ha che: matrice dei coefficienti, vettore dei termini
Sistemi lineari 1 / 12
 Sistemi lineari 1 / 12 Sistemi lineari 2 / 12 Ricordiamo che cosa è un sistema lineare con m equazioni in n incognite (m,n N, m,n 1): a 11 x 1 + +a 1n x n = b 1 a 21 x 1 + +a 2n x n = b 2, (1).. a m1 x
Sistemi lineari 1 / 12 Sistemi lineari 2 / 12 Ricordiamo che cosa è un sistema lineare con m equazioni in n incognite (m,n N, m,n 1): a 11 x 1 + +a 1n x n = b 1 a 21 x 1 + +a 2n x n = b 2, (1).. a m1 x
Esercizi svolti. delle matrici
 Esercizi svolti. astratti. Si dica se l insieme delle coppie reali (x, y) soddisfacenti alla relazione x + y è un sottospazio vettoriale di R La risposta è sì, perchè l unica coppia reale che soddisfa
Esercizi svolti. astratti. Si dica se l insieme delle coppie reali (x, y) soddisfacenti alla relazione x + y è un sottospazio vettoriale di R La risposta è sì, perchè l unica coppia reale che soddisfa
0.1 Soluzioni Esercitazione III, del 21/10/2008
 1 0.1 Soluzioni Esercitazione III, del 21/10/2008 Esercizio 0.1.1. Risolvere il sistema lineare x + y + z = 1 2x + 3y + 2z = 0 x + 2y z = 0 Il determinante della matrice incompleta è 2 e quindi il sistema
1 0.1 Soluzioni Esercitazione III, del 21/10/2008 Esercizio 0.1.1. Risolvere il sistema lineare x + y + z = 1 2x + 3y + 2z = 0 x + 2y z = 0 Il determinante della matrice incompleta è 2 e quindi il sistema
Sistemi II. Sistemi II. Elisabetta Colombo
 Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2011-2012, http://users.mat.unimi.it/users/colombo/programmabio.html 1 2 3 con R.C.+ o 1.10 Rango massimo e determinante con R.C.+
Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2011-2012, http://users.mat.unimi.it/users/colombo/programmabio.html 1 2 3 con R.C.+ o 1.10 Rango massimo e determinante con R.C.+
Ingegneria Gestionale - Corso di Analisi II e Algebra anno accademico 2008/2009
 Ingegneria Gestionale - Corso di Analisi II e Algebra anno accademico 28/29 Dire se le seguenti proposizioni sono vere o false: ESERCITAZIONE. Proposizione Vera Falsa f : R R 4 rk(f f : R 4 R rk(f f :
Ingegneria Gestionale - Corso di Analisi II e Algebra anno accademico 28/29 Dire se le seguenti proposizioni sono vere o false: ESERCITAZIONE. Proposizione Vera Falsa f : R R 4 rk(f f : R 4 R rk(f f :
1 Esercizi 13. 3x + λy + 2z = 0 (1 λ)x + 5y + 3z = 0 3x + 2y + z = 0
 1 Esercizi 13 1. Discutere le soluzioni del sistema seguente al variare del parametro λ R. 3x + λy + 2z 0 (1 λ)x + 5y + 3z 0 3x + 2y + z 0 Soluzione. Si tratta di un SLO 3 3 e sappiamo che tale sistema
1 Esercizi 13 1. Discutere le soluzioni del sistema seguente al variare del parametro λ R. 3x + λy + 2z 0 (1 λ)x + 5y + 3z 0 3x + 2y + z 0 Soluzione. Si tratta di un SLO 3 3 e sappiamo che tale sistema
Note per il corso di Geometria Corso di laurea in Ing. Edile/Architettura. 4 Sistemi lineari. Metodo di eliminazione di Gauss Jordan
 Note per il corso di Geometria 2006-07 Corso di laurea in Ing. Edile/Architettura Sistemi lineari. Metodo di eliminazione di Gauss Jordan.1 Operazioni elementari Abbiamo visto che un sistema di m equazioni
Note per il corso di Geometria 2006-07 Corso di laurea in Ing. Edile/Architettura Sistemi lineari. Metodo di eliminazione di Gauss Jordan.1 Operazioni elementari Abbiamo visto che un sistema di m equazioni
Lezione 10: Teorema di Rouchè-Capelli e la classificazione dei sistemi lineari
 Lezione 10: Teorema di Rouchè-Capelli e la classificazione dei sistemi lineari In questa lezione ci dedicheremo a studiare a fondo quali proprietà della matrice dei coefficienti di un sistema (e della
Lezione 10: Teorema di Rouchè-Capelli e la classificazione dei sistemi lineari In questa lezione ci dedicheremo a studiare a fondo quali proprietà della matrice dei coefficienti di un sistema (e della
2 Sistemi lineari. Metodo di riduzione a scala.
 Sistemi lineari. Metodo di riduzione a scala. Esercizio.1 Utilizzando il metodo di eliminazione di Gauss, risolvere i seguenti sistemi lineari: 1. 3. x 1 x + 3x 3 = 1 x 1 x x 3 = x 1 + x + 3x 3 = 5 x 1
Sistemi lineari. Metodo di riduzione a scala. Esercizio.1 Utilizzando il metodo di eliminazione di Gauss, risolvere i seguenti sistemi lineari: 1. 3. x 1 x + 3x 3 = 1 x 1 x x 3 = x 1 + x + 3x 3 = 5 x 1
Istituzioni di Matematiche Modulo A (ST)
 Istituzioni di Matematiche Modulo A (ST V II foglio di esercizi ESERCIZIO. Nei seguenti sistemi lineari, discutere l insieme delle soluzioni al variare del parametro t, o dei parametri t e τ, in R. 5 x
Istituzioni di Matematiche Modulo A (ST V II foglio di esercizi ESERCIZIO. Nei seguenti sistemi lineari, discutere l insieme delle soluzioni al variare del parametro t, o dei parametri t e τ, in R. 5 x
Si consideri il sistema a coefficienti reali di m equazioni lineari in n incognite
 3 Sistemi lineari 3 Generalità Si consideri il sistema a coefficienti reali di m equazioni lineari in n incognite ovvero, in forma matriciale, a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n x
3 Sistemi lineari 3 Generalità Si consideri il sistema a coefficienti reali di m equazioni lineari in n incognite ovvero, in forma matriciale, a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n x
Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE. Giovanni Villani
 Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE Giovanni Villani Matrici Definizione 1 Si definisce matrice di tipo m n una funzione che associa
Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE Giovanni Villani Matrici Definizione 1 Si definisce matrice di tipo m n una funzione che associa
Argomento 13 Sistemi lineari
 Sistemi lineari: definizioni Argomento Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto
Sistemi lineari: definizioni Argomento Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto
CORSI DI LAUREA IN MATEMATICA E FISICA. Esercizio 1.1. Risolvere graficamente e algebricamente i seguenti sistemi di due equazioni in due incognite:
 CORS D LAUREA N MATEMATCA E FSCA FOGLO D ESERCZ # 1 GEOMETRA 1 Esercizio 1.1. Risolvere graficamente e algebricamente i seguenti sistemi di due equazioni in due incognite: 2x + y = 4 x 2y = 6 x + 3y =
CORS D LAUREA N MATEMATCA E FSCA FOGLO D ESERCZ # 1 GEOMETRA 1 Esercizio 1.1. Risolvere graficamente e algebricamente i seguenti sistemi di due equazioni in due incognite: 2x + y = 4 x 2y = 6 x + 3y =
Sistemi Lineari. Elisabetta Colombo. Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico
 Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 200-20 2 a di o.0 4 Capelli Rango o Caratterisca : definizioni a di o.0 Un equazione nelle n incognite x,..., x n della forma dove
Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 200-20 2 a di o.0 4 Capelli Rango o Caratterisca : definizioni a di o.0 Un equazione nelle n incognite x,..., x n della forma dove
LEZIONE 5. AX = 0 m,1.
 LEZIONE 5 5 isoluzione di sistemi Supponiamo che AX = B sia un sistema di equazioni lineari Ad esso associamo la sua matrice completa (A B Per quanto visto nella precedente lezione, sappiamo di poter trasformare,
LEZIONE 5 5 isoluzione di sistemi Supponiamo che AX = B sia un sistema di equazioni lineari Ad esso associamo la sua matrice completa (A B Per quanto visto nella precedente lezione, sappiamo di poter trasformare,
Sistemi lineari. Lorenzo Pareschi. Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara
 Sistemi lineari Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
Sistemi lineari Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
Geometria per Fisica e Astrofisica
 Geometria per Fisica e Astrofisica Soluzione esercizi - Foglio 3 Esercizio. Risolvere i seguenti sistemi lineari al variare dei parametri reali α β e k < < (a) x + y z = αx + αy + βz = x + y z = β. (b)
Geometria per Fisica e Astrofisica Soluzione esercizi - Foglio 3 Esercizio. Risolvere i seguenti sistemi lineari al variare dei parametri reali α β e k < < (a) x + y z = αx + αy + βz = x + y z = β. (b)
Note sull algoritmo di Gauss
 Note sull algoritmo di Gauss 29 settembre 2009 Generalità Un sistema lineare di m equazioni in n incognite x,..., x n è un espressione del tipo: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n
Note sull algoritmo di Gauss 29 settembre 2009 Generalità Un sistema lineare di m equazioni in n incognite x,..., x n è un espressione del tipo: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n
Università di Modena e Reggio Emilia Facoltà di Scienze MM.FF.NN. PROVA DI ALGEBRA LINEARE (esercitazione del 18 gennaio 2011)
 Università di Modena e Reggio Emilia Facoltà di Scienze MM.FF.NN. PROVA DI ALGEBRA LINEARE (esercitazione del 18 gennaio 2011) ISTRUZIONI PER LO SVOLGIMENTO. Scrivere cognome, nome, numero di matricola
Università di Modena e Reggio Emilia Facoltà di Scienze MM.FF.NN. PROVA DI ALGEBRA LINEARE (esercitazione del 18 gennaio 2011) ISTRUZIONI PER LO SVOLGIMENTO. Scrivere cognome, nome, numero di matricola
Algebra delle matrici
 Algebra delle matrici Metodo di Gauss-Jordan per l inversione di una matrice. Nella lezione scorsa abbiamo visto che un modo per determinare l eventuale inversa di una matrice quadrata A consiste nel risolvere
Algebra delle matrici Metodo di Gauss-Jordan per l inversione di una matrice. Nella lezione scorsa abbiamo visto che un modo per determinare l eventuale inversa di una matrice quadrata A consiste nel risolvere
DIAGONALIZZAZIONE. M(f) =
 DIAGONALIZZAZIONE Esercizi Esercizio 1. Sia f End(R 3 ) associato alla matrice M(f) = 0 1 2 0. 2 (1) Determinare gli autovalori di f e le relative molteplicità. (2) Determinare gli autospazi di f e trovare,
DIAGONALIZZAZIONE Esercizi Esercizio 1. Sia f End(R 3 ) associato alla matrice M(f) = 0 1 2 0. 2 (1) Determinare gli autovalori di f e le relative molteplicità. (2) Determinare gli autospazi di f e trovare,
Rango di una matrice e teorema di Rouché-Capelli
 Rango di una matrice e teorema di Rouché-Capelli Sappiamo che a una matrice m n, A, è associata l applicazione lineare L A : R n R m, L A (X) = AX, X R n. Definizione 1. Lo spazio nullo di A, N (A), è
Rango di una matrice e teorema di Rouché-Capelli Sappiamo che a una matrice m n, A, è associata l applicazione lineare L A : R n R m, L A (X) = AX, X R n. Definizione 1. Lo spazio nullo di A, N (A), è
APPLICAZIONI. Im f = {b B a A tale che f (a) = b}.
 APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
Prima di risolverli, è necessario prevedere se ci saranno soluzioni e, eventualmente, quante saranno.
 Sistemi lineari Prima di risolverli, è necessario prevedere se ci saranno soluzioni e, eventualmente, quante saranno. La discussione di un sistema si imposta in questo modo: 1 studiare il rango della matrice
Sistemi lineari Prima di risolverli, è necessario prevedere se ci saranno soluzioni e, eventualmente, quante saranno. La discussione di un sistema si imposta in questo modo: 1 studiare il rango della matrice
Sistemi di equazioni lineari
 Sistemi di equazioni lineari Siano X 1,, X n indeterminate Un equazione lineare (o di primo grado) nelle incognite X 1,, X n a coefficienti nel campo K è della forma a 1 X 1 + + a n X n = b, a i, b K,
Sistemi di equazioni lineari Siano X 1,, X n indeterminate Un equazione lineare (o di primo grado) nelle incognite X 1,, X n a coefficienti nel campo K è della forma a 1 X 1 + + a n X n = b, a i, b K,
Manlio Bordoni. APPUNTI SULLA RAPPRESENTAZIONE DEI SOTTOSPAZI VETTORIALI DI R n I MODO. v 11. v n1
 Manlio Bordoni APPUNTI SULLA RAPPRESENTAZIONE DEI SOTTOSPAZI VETTORIALI DI R n I MODO Sia dato un insieme di generatori v v =,, v k = v n di W : questo vuol dire che ogni vettore w W si scrive come combinazione
Manlio Bordoni APPUNTI SULLA RAPPRESENTAZIONE DEI SOTTOSPAZI VETTORIALI DI R n I MODO Sia dato un insieme di generatori v v =,, v k = v n di W : questo vuol dire che ogni vettore w W si scrive come combinazione
Anno Accademico 2015/2016
 Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2015/2016 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2015/2016 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
ESERCIZI sui VETTORI
 ESERCIZI sui VETTORI 1. Calcolare la somma di v 1 (2, 3) e v 2 (1, 4). 2. Calcolare la somma di v 1 (1, 5, 4) e v 2 (6, 8, 2). 3. Calcolare il prodotto di α = 2 e v 1 (1, 4). 4. Calcolare il prodotto di
ESERCIZI sui VETTORI 1. Calcolare la somma di v 1 (2, 3) e v 2 (1, 4). 2. Calcolare la somma di v 1 (1, 5, 4) e v 2 (6, 8, 2). 3. Calcolare il prodotto di α = 2 e v 1 (1, 4). 4. Calcolare il prodotto di
Riassumiamo le proprietà dei numeri reali da noi utilizzate nel corso di Geometria.
 Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
24 giugno Soluzione esame di geometria - 12 crediti Ingegneria gestionale - a.a COGNOME... NOME... N. MATRICOLA...
 4 giugno 010 - Soluzione esame di geometria - 1 crediti Ingegneria gestionale - a.a. 009-010 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore.
4 giugno 010 - Soluzione esame di geometria - 1 crediti Ingegneria gestionale - a.a. 009-010 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore.
UNIVERSITA DEGLI STUDI LA SAPIENZA DI ROMA POLO DI RIETI FACOLTA DI INGEGNERIA CORSO DI LAUREA IN INGEGNERIA DELL AMBIENTE E DEL TERRITORIO
 UNIVERSITA DEGLI STUDI LA SAPIENZA DI ROMA POLO DI RIETI FACOLTA DI INGEGNERIA CORSO DI LAUREA IN INGEGNERIA DELL AMBIENTE E DEL TERRITORIO Geometria 9 5 A.A. 5 Cognome Nome Matricola Codice Scrivere in
UNIVERSITA DEGLI STUDI LA SAPIENZA DI ROMA POLO DI RIETI FACOLTA DI INGEGNERIA CORSO DI LAUREA IN INGEGNERIA DELL AMBIENTE E DEL TERRITORIO Geometria 9 5 A.A. 5 Cognome Nome Matricola Codice Scrivere in
LEZIONE Equazioni matriciali. Negli Esempi e si sono studiati più sistemi diversi AX 1 = B 1, AX 2 = R m,n, B = (b i,h ) 1 i m
 LEZIONE 4 41 Equazioni matriciali Negli Esempi 336 e 337 si sono studiati più sistemi diversi AX 1 = B 1, AX 2 = B 2,, AX p = B p aventi la stessa matrice incompleta A Tale tipo di problema si presenta
LEZIONE 4 41 Equazioni matriciali Negli Esempi 336 e 337 si sono studiati più sistemi diversi AX 1 = B 1, AX 2 = B 2,, AX p = B p aventi la stessa matrice incompleta A Tale tipo di problema si presenta
Istituzioni di Matematiche sesta parte
 Istituzioni di Matematiche sesta parte anno acc. 2013/2014 Univ. Studi di Milano D.Bambusi, C.Turrini (Univ. Studi di Milano Istituzioni di Matematiche 1 / 27 index Matrici e operazioni tra matrici 1 Matrici
Istituzioni di Matematiche sesta parte anno acc. 2013/2014 Univ. Studi di Milano D.Bambusi, C.Turrini (Univ. Studi di Milano Istituzioni di Matematiche 1 / 27 index Matrici e operazioni tra matrici 1 Matrici
1 Rette nel piano ordinario. Rette e piani nello spazio ordinario
 1 Rette nel piano ordinario. Rette e piani nello spazio ordinario 1.1 Vettori applicati Nel seguito denotiamo con P l insieme dei punti del piano ordinario, e con S l insieme dei punti dello spazio ordinario.
1 Rette nel piano ordinario. Rette e piani nello spazio ordinario 1.1 Vettori applicati Nel seguito denotiamo con P l insieme dei punti del piano ordinario, e con S l insieme dei punti dello spazio ordinario.
Argomento 13 Sistemi lineari
 Sistemi lineari: definizioni Argomento 3 Sistemi lineari I Un equazione nelle n incognite x,,x n della forma c x + + c n x n = b ove c,,c n sono numeri reali (detti coefficienti) eb è un numero reale (detto
Sistemi lineari: definizioni Argomento 3 Sistemi lineari I Un equazione nelle n incognite x,,x n della forma c x + + c n x n = b ove c,,c n sono numeri reali (detti coefficienti) eb è un numero reale (detto
ESEMPIO DI SISTEMA LINEARE CON SOLUZIONE. Esercizio Si consideri il sistema di equazioni lineari dipendente da un parametro λ R:
 ESEMPIO DI SISTEMA LINEARE CON SOLUZIONE Esercizio Si consideri il sistema di equazioni lineari dipendente da un parametro λ R: x 1 + x = 0 6x 1 + (λ + )x + x 3 + x 4 = 1 x 1 4x + (λ + 1)x 3 + 6x 4 = 3
ESEMPIO DI SISTEMA LINEARE CON SOLUZIONE Esercizio Si consideri il sistema di equazioni lineari dipendente da un parametro λ R: x 1 + x = 0 6x 1 + (λ + )x + x 3 + x 4 = 1 x 1 4x + (λ + 1)x 3 + 6x 4 = 3
ENDOMORFISMI. ove B := (v 1,v 2,v 3 ). (1) Determinare gli autovalori di f e le relative molteplicità algebriche e geometriche.
 ENDOMORFISMI Esercizi Esercizio 1 Siano v 1 := T (1, 1, 1, 0), v 2 := T (0, 1, 2, 1), v 3 := T (0, 0, 1, 1) Consideriamo V := L(v 1,v 2,v 3 ) R 4 e sia f End R (V ) associato alla matrice A := MB B (f)
ENDOMORFISMI Esercizi Esercizio 1 Siano v 1 := T (1, 1, 1, 0), v 2 := T (0, 1, 2, 1), v 3 := T (0, 0, 1, 1) Consideriamo V := L(v 1,v 2,v 3 ) R 4 e sia f End R (V ) associato alla matrice A := MB B (f)
Esercizi di geometria per Fisica / Fisica e Astrofisica
 Esercizi di geometria per Fisica / Fisica e Astrofisica Foglio 3 - Soluzioni Esercizio. Stabilire se i seguenti sottoinsiemi di R 3 sono sottospazi vettoriali: (a) S = {(x y z) R 3 : x + y + z = }. (b)
Esercizi di geometria per Fisica / Fisica e Astrofisica Foglio 3 - Soluzioni Esercizio. Stabilire se i seguenti sottoinsiemi di R 3 sono sottospazi vettoriali: (a) S = {(x y z) R 3 : x + y + z = }. (b)
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof. Fabio Perroni. 3. Sistemi di equazioni lineari
 Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 3 Sistemi di equazioni lineari Siano m, n N \ {}, sia K un campo Definizione a) Un sistema
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 3 Sistemi di equazioni lineari Siano m, n N \ {}, sia K un campo Definizione a) Un sistema
Le risposte vanno giustificate con chiarezza. 1) Nello spazio vettoriale V delle matrici 2 2 a coefficienti reali, considera le matrici A 1 = , A 4 =
 Università degli Studi di Roma Tor Vergata. Corso di Laurea in Matematica Esame di Geometria 1 con Elementi di Storia Prof. F. Tovena 30 gennaio 2015 Le risposte vanno giustificate con chiarezza. 1 Nello
Università degli Studi di Roma Tor Vergata. Corso di Laurea in Matematica Esame di Geometria 1 con Elementi di Storia Prof. F. Tovena 30 gennaio 2015 Le risposte vanno giustificate con chiarezza. 1 Nello
1. Un sistema di m equazioni lineari in n incognite x 1,... x n aventi tutte termine noto nullo A =...
 Algebra/ Algebra Lineare, 230207 1 Un sistema di m equazioni lineari in n incognite x 1, x n aventi tutte termine noto nullo a i1 x 1 + a i2 x 2 + + a in x n = 0, i = 1,, m si dice omogeneo; ponendo x
Algebra/ Algebra Lineare, 230207 1 Un sistema di m equazioni lineari in n incognite x 1, x n aventi tutte termine noto nullo a i1 x 1 + a i2 x 2 + + a in x n = 0, i = 1,, m si dice omogeneo; ponendo x
SPAZI VETTORIALI CON PRODOTTO SCALARE A =
 SPAZI VETTORIALI CON PRODOTTO SCALARE Esercizi Esercizio. Nello spazio euclideo standard (R 2,, ) sia data la matrice 2 3 A = 3 2 () Determinare una base rispetto alla quale A sia la matrice di un endomorfismo
SPAZI VETTORIALI CON PRODOTTO SCALARE Esercizi Esercizio. Nello spazio euclideo standard (R 2,, ) sia data la matrice 2 3 A = 3 2 () Determinare una base rispetto alla quale A sia la matrice di un endomorfismo
(V) (FX) L unione di due basi di uno spazio vettoriale è ancora una base dello spazio vettoriale.
 8 gennaio 2009 - PROVA D ESAME - Geometria e Algebra T NOME: MATRICOLA: a=, b=, c= Sostituire ai parametri a, b, c rispettivamente la terzultima, penultima e ultima cifra del proprio numero di matricola
8 gennaio 2009 - PROVA D ESAME - Geometria e Algebra T NOME: MATRICOLA: a=, b=, c= Sostituire ai parametri a, b, c rispettivamente la terzultima, penultima e ultima cifra del proprio numero di matricola
Dipendenza e indipendenza lineare (senza il concetto di rango)
 CAPITOLO 5 Dipendenza e indipendenza lineare (senza il concetto di rango) Esercizio 5.1. Scrivere un vettore w R 3 linearmente dipendente dal vettore v ( 1, 9, 0). Esercizio 5.2. Stabilire se i vettori
CAPITOLO 5 Dipendenza e indipendenza lineare (senza il concetto di rango) Esercizio 5.1. Scrivere un vettore w R 3 linearmente dipendente dal vettore v ( 1, 9, 0). Esercizio 5.2. Stabilire se i vettori
8 novembre Soluzione esame di geometria - 12 crediti Ingegneria gestionale - a.a COGNOME... NOME... N. MATRICOLA...
 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
1.[25 punti] Risolvere il seguente sistema di equazioni lineari al variare del parametro reale λ: X +Y +Z = 2. X 2Y +λz = 2
![1.[25 punti] Risolvere il seguente sistema di equazioni lineari al variare del parametro reale λ: X +Y +Z = 2. X 2Y +λz = 2 1.[25 punti] Risolvere il seguente sistema di equazioni lineari al variare del parametro reale λ: X +Y +Z = 2. X 2Y +λz = 2](/thumbs/69/60506353.jpg) Università di Modena e Reggio Emilia Facoltà di Scienze MM.FF.NN. PROVA SCRITTA DI GEOMETRIA A del 27 giugno 2011 ISTRUZIONI PER LO SVOLGIMENTO. Scrivere cognome, nome, numero di matricola in alto a destra
Università di Modena e Reggio Emilia Facoltà di Scienze MM.FF.NN. PROVA SCRITTA DI GEOMETRIA A del 27 giugno 2011 ISTRUZIONI PER LO SVOLGIMENTO. Scrivere cognome, nome, numero di matricola in alto a destra
Esame di GEOMETRIA 27 giugno ore 11
 Esame di GEOMETRIA 27 giugno 2011 - ore 11 Istruzioni: Scrivere cognome, nome, matricola in STAMPATELLO negli appositi spazi. Per ogni quiz nella prima parte, indicare l affermazione giudicata corretta
Esame di GEOMETRIA 27 giugno 2011 - ore 11 Istruzioni: Scrivere cognome, nome, matricola in STAMPATELLO negli appositi spazi. Per ogni quiz nella prima parte, indicare l affermazione giudicata corretta
Metodi per la risoluzione di sistemi lineari
 Metodi per la risoluzione di sistemi lineari Sistemi di equazioni lineari. Rango di matrici Come è noto (vedi [] sez.0.8), ad ogni matrice quadrata A è associato un numero reale det(a) detto determinante
Metodi per la risoluzione di sistemi lineari Sistemi di equazioni lineari. Rango di matrici Come è noto (vedi [] sez.0.8), ad ogni matrice quadrata A è associato un numero reale det(a) detto determinante
Introduzione soft alla matematica per l economia e la finanza. Marta Cardin, Paola Ferretti, Stefania Funari
 Introduzione soft alla matematica per l economia e la finanza Marta Cardin, Paola Ferretti, Stefania Funari Capitolo Sistemi di equazioni lineari.8 Il Teorema di Cramer Si consideri un generico sistema
Introduzione soft alla matematica per l economia e la finanza Marta Cardin, Paola Ferretti, Stefania Funari Capitolo Sistemi di equazioni lineari.8 Il Teorema di Cramer Si consideri un generico sistema
