1. Richiami. v = x 2 + y 2.
|
|
|
- Alberta Magnani
- 6 anni fa
- Visualizzazioni
Transcript
1 Gli elementi del prodotto cartesiano 1 Richiami R 2 = x, y R} sono detti vettori Ogni vettore v è una coppia ordinata ed i numeri reali x e y sono detti le componenti di v In particolare si denota con 0 = (0, 0) il vettore nullo In R 2 sono definite le seguenti operazioni che lo rendono uno spazio vettoriale euclideo (1) La somma di due vettori v 1 = (x 1, y 1 ) e v 1 = (x 1, y 1 ) è il vettore v 1 + v 2 = (x 1 + x 2, y 1 + y 2 ) (2) La moltiplicazione di un vettore v = per uno scalare λ R è il vettore λv = (λx, λy) (3) La norma di un vettore v = è il numero La norma soddisfa le seguenti proprietà v 0 v = 0 v = 0 λv = λ v v = x 2 + y 2 v + w v + w (disuguaglianza triangolare) per ogni v, w R 2 e λ R (4) Il prodotto scalare di due vettori v 1 = (x 1, y 1 ) e v 2 = (x 2, y 2 ) è il numero v 1 v 2 = x 1 x 2 + y 1 y 2 Il prodotto scalare soddisfa le seguenti proprietà v 1 v 2 = v 2 v 1 v 1 (λv 2 ) = λ(v 1 v 2 ) v 1 (v 2 + v 3 ) = (v 1 v 2 ) + (v 1 v 3 ) v 1 v 1 = v 1 2 v 1 v 2 v 1 v 2 (disuguaglianza di Schwarz) per ogni v 1, v 2, v 3 R 2 e λ R Nel piano euclideo, in cui sono stati scelti un origine O ed un sistema di assi cartesiani, ogni vettore v è rappresentato geometricamente da segmento orientato il cui primo estremo è l origine O Il secondo estremo del vettore individua univocamente un punto P del piano di modo che la coppia ordinata indica sia le componenti del vettore v = sia le coordinate del punto P = In particolare il vettore nullo 0 individua l origine O Viceversa due punti del piano, P 1 = (x 1, y 1 ) e P 2 = (x 2, y 2 ), individuano un vettore il cui primo estremo è P 1 e il secondo estremo è P 2 Tale vettore, denotato P 2 P 1, ha componenti P 2 P 1 = (x 2 x 1, y 2 y 1 ) Infine, dato un punto P 1 = (x 1, y 1 ) ed un vettore v = (h, k), il secondo estremo del vettore v, il cui primo estremo è in P 1, individua un punto, denotato con P 1 + v, le cui coordinate sono P 1 + v = (x 1 + h, y 1 + k) Quanto visto si estende naturalmente al prodotto cartesiano di n copie di R R n = v = (x 1,, x n ) x 1 R,, x n R} 1
2 2 2 Elementi di topologia La distanza (euclidea) tra due punti del piano, P 0 = (x 0, y 0 ) e P 1 = (x 1, y 1 ), è definita come e si ha (1) (2) Dato P 0 = (x 0, y 0 ) R 2 e δ > 0 l insieme P 1 P 0 = (x 1 x 0 ) 2 + (y 1 y 0 ) 2 x 1 x 0 P 1 P 0 y 1 y 0 P 1 P 0 B(P 0, δ) = P R 2 P 1 P 0 < δ} = R 2 (x 1 x 0 ) 2 + (y 1 y 0 ) 2 < δ 2} è detto palla o intorno (aperto) di centro P 0 e raggio δ In particolare P 0 B(P 0, δ) per ogni δ > 0 Le seguenti definizioni esprimono le proprietà di vicinanza di un punto ad un insieme Sia A R 2 un insieme Def 1 Un punto P 0 R 2 è interno ad A se esiste δ > 0 tale che B(P 0, δ) A, in altre parole se δ > 0 tale che P R 2 e P P 0 < δ si ha P A L insieme dei punti interni di A si chiama parte interna e si denota con A Poiché un punto interno appartiene necessariamente ad A, si ha A A L insieme A è detto aperto se tutti i suoi punti sono interni ad A, cioè, se A= A Def 2 Un punto P 0 R 2 è di accumulazione per A se per ogni δ > 0 si ha (B(P 0, δ) \ P 0 }) A, in altre parole se δ > 0 P A tale che 0 < P P 0 < δ L insieme A è detto chiuso se tutti i punti di accumulazione di A appartengono ad A Si può dimostrare che A è aperto se e solo se il suo complementare CA è chiuso Def 3 L insieme A è limitato se esiste M > 0 tale che A B(O; M) dove O è l origine, cioè se P O M P A o equivalentemente x 2 + y 2 M 2 A Le definizioni date si estendono a R n in modo naturale
3 3 Funzioni continue Una funzione f : A R n R m è una legge che assegna ad ogni punto P A uno ed un solo elemento Q = f(p ) R m L insieme A è detto dominio ed R m codominio Il sottoinsieme del codominio f(p ) R m P A} è detto immagine di f Se m = 1, f è detta funzione scalare, se m > 1 f è detta vettoriale, infine se n = m, f è detta campo In generale, si hanno n-variabili indipendenti P = (x 1,, x n ) R n e m-variabili dipendenti Q = (f 1 (P ),, f m (P )) R m, di modo che la funzione Q = f(p ) si può scrivere come f : y 1 = f 1 (x 1,, x n ) y m = f m (x 1,, x n ) Le m funzioni scalari f 1 : A R,, f m : A R sono le componenti della funzione f, hanno tutte lo stesso dominio A R n e lo stesso codominio R Una funzione scalare (di due variabili indipendenti) è una funzione z = f con dominio A R 2 e codominio R L equazione z = f definisce un insieme di R 3 (x, y, z) R 3 A, z = f} chiamato grafico della funzione Dato c R l equazione f = c definisce un insieme di R 2 A c = R 2 A, f = c}, chiamato insieme (o linea) di livello di f di quota c Una curva (nel piano) è una funzione γ(t) = (x(t), y(t)) con dominio A R e codominio R 2 Le funzioni x(t) e x(t) sono dette componenti della curva e sono funzioni scalari con dominio A R e codominio R La curva γ si denota spesso con x(t) γ : t A y(t) L immagine di γ γ(a) = R 2 t A } è detta traccia o traiettoria della curva Un campo (bidimensionale) è una funzione F = (u, v) con dominio A R 2 e codominio R 2 Le funzioni u e v sono dette componenti del campo e sono funzioni scalari con dominio A R 2 e codominio R La definizione di funzione continua è la naturale estensione di quella data per funzioni di una variabile Def 4 Sia f : A R n R m una funzione Dato P 0 A, f è continua in P 0 se ɛ > 0 δ > 0 tale che se P A e P P 0 < δ allora f(p ) f(p 0 ) < ɛ La funzione f è continua in B A se f è continua in tutti i punti di B, f è detta continua se è continua sul suo dominio Equivalentemente f è continua in P 0 se per ogni ɛ > 0 esiste δ > 0 tale che P A B(P 0, δ) implica f(p ) B(f(P 0 ), ɛ) Se z = f è una funzione scalare con dominio A R 2, f è continua in (x 0, y 0 ) A se ɛ > 0 δ > 0 tale che A e (x x 0 ) 2 + (y y 0 ) 2 < δ implica f f(x 0, y 0 ) < ɛ Una classe particolare di funzioni continue sono le funzioni infinitesime 3
4 4 Def 5 Una funzione ω : A R n R m è infinitesima (in zero) se 0 A, ω(0) = 0 ed ω è continua in A In altre parole se ɛ > 0, δ > 0 tale che se v A e v < δ allora ω(v) < ɛ In particolare, una funzione f è continua in P 0 se e solo se f(p ) = f(p 0 ) + ω(p P 0 ), dove ω è infinitesima La continuità delle funzioni vettoriale può essere ricondotto allo studio della continuità di funzioni scalari poiché vale il risultato seguente Teo 1 Una funzione f : A R n R m, f(p ) = (f 1 (P ),, f m (P )) è continua in P 0 A se e solo se tutte le sue componenti f 1 : A R,, f m : A R sono continue in P 0 In particolare, una curva γ : x(t) y(t) è continua se e solo se sono continue le funzioni x(t) e y(t) ed un campo F = (u, v) è continuo se e solo se sono continue le funzioni u e v La proposizione seguente mostra la continuità di alcune funzioni elementari Prop 1 Le seguenti funzioni scalari con dominio R 2 sono continue π 1 = x proiezione sull asse x π 2 = y proiezione sull asse y f a = x + y f m = xy In molti casi la continuità di una funzione scalare è conseguenza del seguente teorema, della continuità delle funzioni scalari di una variabile e della precedente proposizione Teo 2 (Continuità della funzione composta) Siano f : A R n R m e g : B R m R p funzioni continue tali che per ogni P A, f(p ) B Allora la funzione composta g(f(p )), definita da A in R p, è continua Il precedente teorema vale anche localmente Q 0 = f(p 0 ), allora g(f(p )) è continua in P 0 Se f(p ) è continua in P 0 e g(q) è continua in Esempio 1 La funzione f = x y è continua sul suo dominio A = R 2 y 0 } Infatti poiché π 2 = y e φ(t) = 1 t sono continue rispettivamente in R2 e R\0}, essendo π 2 (A) R\0}, la funzione g = φ(π 2 ) = 1 y è continua in A; la funzione vettoriale G = (x, 1 y ) è continua in A poiché le sue componenti π 1 = x e g = 1 y sono continue in A; poiché G e f m = xy sono continue rispettivamente in A e R 2, essendo G(A) R 2, la funzione f = f m (π 1 (x), g) = f m (G) è continua in A Si dimostra facilmente, come conseguenza dei due precedenti risultati che somma, differenza, prodotto e rapporto di funzioni scalari continue sono funzioni continue sul loro dominio naturale
5 31 Proprietà delle funzioni continue scalari I seguenti due teoremi valgono solo per funzioni scalari, poiché solo R è un insieme ordinato Teo 3 (Teorema di Weierstrass) Sia f : A R 2 R una funzione continua con A chiuso e limitato, allora esistono P 1 A e P 2 A tali che f(p 1 ) f(p ) f(p 2 ) P A I valori f(p 1 ) = min P A f(p ) e f(p 2 ) = max P A f(p ) sono detti, rispettivamente, minimo e massimo assoluto di f su A La condizione che A sia chiuso e limitato non si può eliminare Esempio 2 La funzione f = x 2 + y 2 con R 2 è continua e sup (x,y) R 2 f = +, poiché lim x + f(x, x) = + Quindi f non ammette massimo assoluto in R 2 1 La funzione f = con A = R 2 x 2 + y 2 < 1 } è continua e sup 1 x 2 y 2 (x,y) R 2 f = +, poiché lim x 1 f(x, 0) = + Quindi f non ammette massimo assoluto in A La definizione che segue estende a R 2 il concetto di intervallo Def 6 Un insieme A R 2 è connesso per archi se, per ogni P 0, P 1 A, esiste una curva γ continua x = x(t) γ : t [0, 1] y = y(t) tale che P 0 = (x(0), y(0)), P 1 = (x(1), y(1)) e (x(t), y(t)) A per ogni t [0, 1], cioè esiste una curva continua γ di estremi γ(0) = P 1 e γ(1) = P 2, la cui traccia è contenuta tutta in A Teo 4 (Teorema dei valori intermedi) Sia f : A R n R una funzione continua con A connesso per archi Dato c R tale che inf P A f(p )} < c < sup P A f(p )}, allora esiste P 0 A per cui f(p 0 ) = c Sia z = f continua con dominio A connesso per archi, allora il teorema dei valori intermedi assicura che se inf f < c < sup f, l equazione f = c ammette almeno una soluzione (x 0, y 0 ) A Ovviamente se c < inf f o c > sup f l equazione f = c non ha soluzioni Se c = inf f, rispettivamente c = sup f, l equazione f = ha soluzione solo se f ammette minimo assoluto, risp massimo assoluto In particolare, se f è continua ed A è connesso per archi, chiuso e limitato, l immagine di f è un intervallo chiuso f(a) = [min f(p ), min f(p )] P A P A La condizione che A sia connesso per archi non può eliminare Esempio 3 Sia f = 1 xy con A = R 2 xy 0 } La funzione è continua, inf (x,y) A f = e sup (x,y) A f = + poiché Tuttavia l equazione 1 xy lim f(x, x) = + lim x 0 = 0 non ha soluzioni f(x, x) = x 0 5
6 6 4 Funzioni differenziabili Trattiamo prima il caso di funzioni scalari di due variabili Ricordiamo che un piano in R 3 passante per il punto P 0 = (x 0, y 0, z 0 ) è l insieme dei punti P = (x, y, z) che soddisfano l equazione a(x x 0 ) + b(y y 0 ) + c(z z 0 ) = 0 in forma vettoriale ˆn ( P P 0 ) = 0, dove ˆn = (a, b, c) 0 è il vettore normale al piano scegliere c = 1 e l equazione diventa z = z 0 + a(x x 0 ) + b(y y 0 ) Per tali piani la corrispondente equazione parametrica è x = x 0 + h y = y 0 + k z = z 0 + a h + b k Se il piano non è parallelo all asse z, si può h, k R, o, in forma vettoriale, P = P 0 + ˆv h + ŵ k P = (x, y, z) dove ˆv = (1, 0, a) e ŵ = (0, 1, b) sono i vettori direzionali Il piano è, quindi, generato dalla retta P = P 0 + ˆv h, intersezione del piano con il piano parallelo al piano xz, e la retta P = P 0 + ŵ k, intersezione del piano con il piano parallelo al piano yz (entrambe le rette passano per P 0 ) La definizione di funzione differenziabile traduce l idea geometrica di funzione il cui grafico ammette piano tangente Def 7 Sia z = f una funzione scalare con dominio A R 2 Dato (x 0, y 0 ) A punto interno di A, f è differenziabile in (x 0, y 0 ) se esiste un vettore (a, b) R 2 tale che f = f(x 0, y 0 ) + a(x x 0 ) + b(y y 0 ) + (x x 0 ) 2 + (y y 0 ) 2 ω(x x 0, y y 0 ) con ω infinitesima In tal caso si pone (x 0, y 0 ) = a derivata parziale di f rispetto a x (x 0, y 0 ) = b derivata parziale di f rispetto a y ( f(x 0, y 0 ) = (x 0, y 0 ), ) (x 0, y 0 ) gradiente di f Il piano in R 3 di equazione z = f(x 0, y 0 ) + (x 0, y 0 )(x x 0 ) + (x 0, y 0 )(y y 0 ) si chiama piano tangente al grafico di f nel punto (x 0, y 0, f(x 0, y 0 )) R 3 differenziabile in ogni punto di A, si dice che f è differenziabile Se A è aperto ed f è Il piano tangente passa per il punto P 0 = (x 0, y 0, f(x 0, y 0 )) = (P 0, f(p 0 )) con vettore normale ˆn = ( (x 0, y 0 ), (x 0, y 0 ), 1) e vettori direzionali (1, 0, a) e (1, 0, b) Dalle definizione di funzione differenziabile si ha che [ ] f f(x 0, y 0 ) + (x 0, y 0 )(x x 0 ) + (x 0, y 0 )(y y 0 ) ω(x x 0, y y 0 ) = (x 0, y 0 ) (x x0 ) 2 + (y y 0 ) 2 0 = (x 0, y 0 ) Il modulo del numeratore è la distanza (nello spazio) tra il punto (x, y, f) sul grafico della funzione ed il corrispondente punto (x, y, f(x 0, y 0 ) + (x 0, y 0 )(x x 0 ) + (x 0, y 0 )(y y 0 )) sul piano
7 tangente, mentre il denominatore è la distanza (nel piano) tra e (x 0, y 0 ) La condizione che ω sia infinitesima implica che il rapporto tra tali distanze è arbitrariamente piccolo se e (x 0, y 0 ) sono sufficientemente vicini La differenziabilità implica che in un intorno di (x 0, y 0 ) la funzione f è approssimabile con il polinomio P = f(x 0, y 0 ) + (x 0, y 0 )(x x 0 ) + (x 0, y 0 )(y y 0 ) (di grado al più uno) ed il resto R = f P = (x x 0 ) 2 + (y y 0 ) 2 ω(x x 0, y y 0 ) va a zero più velocemente di (x x 0 ) 2 + (y y 0 ) 2 Posto P 0 = (x 0, y 0 ) e P =, la definizione di funzione differenziabile diviene f(p ) = f(p 0 ) + f(p 0 ) (P P 0 ) + P P 0 ω(p P 0 ) oppure posto h = x x 0 e k = y y 0 f = f(x 0, y 0 )+ (x 0, y 0 )(x x 0 )+ (x 0, y 0 )(y y 0 )+ (x x 0 ) 2 + (y y 0 ) 2 ω(x x 0, y y 0 ) La differenziabilità implica la continuità Teo 5 (Condizione necessaria per la differenziabilità I) Sia f : A R 2 R una funzione differenziabile in P 0 = (x 0, y 0 ) A, allora f è continua in (x 0, y 0 ) Il seguente teorema dà una condizione necessaria per la differenziabilità e fornisce un modo per calcolare le derivate parziali Teo 6 (Condizione necessaria per la differenziabilità II) Sia f : A R 2 differenziabile in (x 0, y 0 ) A, allora esistono finiti (3) (4) f(x, y 0 ) f(x 0, y 0 ) lim = x x 0 x x 0 (x 0, y 0 ) f(x 0, y) f(x 0, y 0 ) lim = y y 0 y y 0 (x 0, y 0 ) 7 R una funzione Le condizioni date sono solo necessarie Se esistono finiti i limiti (3) e (4), si dice che f è derivabile in (x 0, y 0 ) Inoltre l esistenza del limite (3) finito equivale al fatto che f(x, y 0 ), pensata come funzione della sola x, mentre y = y 0 è costante, è derivabile in x 0 (nel senso della funzioni di una variabile) e vale (x 0, y 0 ) = df(x, y 0), dx x=x0 dove df dx x=x0 denota la derivata ordinaria calcolata in x 0 Analogamente l esistenza del limite (4) finito equivale al fatto che f(x 0, y), pensata come funzione della sola y, mentre x = x 0 è costante, è derivabile e vale (x 0, y 0 ) = df(x, y 0) dy y=x0 I teoremi sulle funzioni derivabili di una variabile implicano che somma, differenza, prodotto e rapporto di funzioni (di due variabili) derivabili è derivabile Il seguente esempio mostra come la derivabilità sia solo una condizione necessaria Esempio 4 La funzione f : R 2 R f = xy x 2 + y 2 (0, 0) 0 = (0, 0)
8 8 non è continua in (0, 0) e, quindi, non è differenziabile in (0, 0) Tuttavia f è derivabile in (0, 0) e vale (0, 0) = 0 (0, 0) = 0 Proviamo che f non è continua Supponiamo, per assurdo, che sia continua in (0, 0) e consideriamo la curva x(t) = t γ : t R y(t) = t Poiché x(t) = t ed y(t) = t sono continue in t = 0 e (x(0), y(0)) = (0, 0), per il Teorema 2 la funzione composta t 2 f(x(t), y(t)) = t 2 + t 2 = 1 t t = 0 dovrebbe essere continua in 0, il che è assurdo D altra parte f(x, 0) f(0, 0) lim x 0 x lim y 0 per cui f è derivabile in (0, 0) f(0, y) f(0, 0) y x 0 = lim x 0 (x 2 + 0)x = 0 0 y = lim y 0 (0 + y 2 )y = 0, Il seguente teorema dà un altra condizione necessaria che contiene la precedente come caso particolare Teo 7 (Condizione necessaria per la differenziabilità III) Sia f : A R 2 differenziabile in P 0 = (x 0, y 0 ) A Per ogni vettore v = (v 1, v 2 ) R 2 esiste finito f(x 0 + tv 1, y 0 + tv 2 ) f(x 0, y 0 ) (5) lim = t 0 t (x 0, y 0 )v 1 + (x 0, y 0 )v 2 = f(p 0 ) v R una funzione Anche in questo caso le condizioni sono solo necessarie Se esiste finito il limite (5) si pone v (x f(x 0 + tv 1, y 0 + tv 2 ) f(x 0, y 0 ) f(p 0 + tv) f(p 0 ) 0, y 0 ) = lim = lim t 0 t t 0 t e si chiama derivata direzionale lungo il vettore v = (v 1, v 2 ) nel punto (x 0, y 0 ) In particolare, v (x 0, y 0 ) = (x 0, y 0 ) se v = (1, 0) v (x 0, y 0 ) = (x 0, y 0 ) se v = (0, 1), per cui il teorema 6 è un caso particolare del teorema 7 Il seguente esempio mostra che l esistenza di tutte le derivate direzionali sia solo una condizione necessaria Esempio 5 La funzione f : R 2 R x 2 y f = x 2 + y 2 (0, 0) 0 = (0, 0) ammette derivate direzionali lungo ogni vettore v = (v 1, v 2 ) R 2 in (0, 0) v1 2v 2 (0, 0) = v v (v 1, v 2 ) (0, 0) v2, 2 0 (v 1, v 2 ) = (0, 0)
9 ma non è differenziabile in (0, 0) Infatti, dato v = (v 1, v 2 ) (0, 0) f(tv 1, tv 2 ) f(0, 0) (tv 1 ) 2 tv 2 lim = lim t 0 t t 0 ((tv 1 ) 2 + (tv 1 ) 2 ) t = v2 1 v 2 v1 2 + v2 2 In particolare si ha che (0, 0) = 0 (se v = (1, 0)) e (0, 0) = 0 (se v = (0, 1)) Tuttavia f non è differenziabile in (0, 0) Infatti, se lo fosse, l equazione (5) implicherebbe v (0, 0) = 0 per ogni v Il seguente teorema dà una condizione sufficiente per la differenziabilità, espressa in termini di continuità delle derivate parziali Teo 8 Sia f : A R 2 R con A aperto Se sono soddisfatte le seguenti tre condizioni (1) f è derivabile in ogni punto A, (2) la funzione è continua in A, (3) la funzione è continua in A, allora f è differenziabile in A Una funzione f che soddisfa le tre condizioni del teorema si dice che è di classe C 1 in A e si scrive f C 1 (A) Dalle proprietà delle funzioni continue e derivabili segue che somma, differenza, prodotto e rapporto di funzioni di classe C 1 è derivabile e, quindi, differenziabile Esempio 6 Sia f : R 2 R la funzione f = x 2 + y 2 = P O 2 (distanza al quadrato di P dall origine O) poiché f è derivabile e le derivate parziali = 2x e = 2y R2 sono funzioni continue, f è di classe C 1 (R 2 ) e, quindi, è differenziabile In particolare, dato un punto P 0 = (x 0, y 0 ) R 2 il gradiente vale f(x 0, y 0 ) = 2(x 0, y 0 ) in forma vettoriale f(p 0 ) = 2(P 0 O) e la differenziabilità assicura l esistenza del piano tangente al grafico di f nel punto (x 0, y 0, x y2 0 ) di equazione z = x y x 0 (x x 0 ) + 2y 0 (y y 0 ) = 2x 0 x + 2y 0 y (x y 2 0) e la derivata direzionale lungo ogni vettore v = (v 1, v 2 ) R 2 in P 0 v (x 0, y 0 ) = 2x 0 v 1 + 2y 0 v 2 in forma vettoriale v (P 0) = 2(P 0 O) v La definizione si estende naturalmente a funzioni scalari f : A R n R in modo ovvio: il gradiente ( f)(p 0 ) è un vettore di R n le cui n componenti sono le derivate parziali ( ( f)(p 0 ) = (P 0 ),, ) (P 0 ) 1 n Anaologamente per funzioni vettoriali si ha la seguente definizione Def 8 Una funzione f : A R n R m, f(p ) = (f 1 (P ),, f m (P )) è differenziabile in P 0 A se esiste una matrice m n, denotata J f (P 0 ), tale che f(p ) = f(p 0 ) + J f (P 0 ) (P P 0 ) + P P 0 ω(p P 0 ) dove ω è infinitesima La matrice J f (P 0 ) è detta la matrice jacobiana di f in P 0 Analogamente, se A è aperto si dice che f è differenziabile se f è differenziabile in ogni punto di A [risp di classe C 1 (A)] 9
10 10 Nella precedente equazione i vettori sono pensati come vettori colonna e J f (P 0 ) (P P 0 ) è la moltiplicazione della matrice J f (P 0 ) per il vettore colonna P P 0 Nel caso di un campo F = (u, v) in R 2 la definizione diventa ( u v ) = ( u(x0, y 0 ) v(x 0, y 0 ) ) + ( a b c d ) ( ) x x0 + ( (x x y y 0 ) 2 + (y y 0 ) 2 ω1 (x x 0, y y 0 ) 0 ω 2 (x x 0, y y 0 ) Il problema della differenziabilità di una funzione a valori vettoriali si riduce a quello di studiare la differenziabilità delle sue componenti Teo 9 Una funzione f : A R n R m, f(p ) = (f 1 (P ),, f m (P )) è differenziabile in P 0 A se e solo se tutte le componenti f 1 : A R,, f m : A R sono differenziabili in P 0 La matrice jacobiana è data da J f (P 0 ) = f 1(P 0 ) f m (P 0 ) = 1 1 n (P 0 ) 1 (P 0 ) m 1 (P 0 ) m n (P 0 ) In particolare f è di classe C 1 (A) se tutte le sue componenti f 1,, f m sono di classe C 1 (A) Si noti che, se f è una funzione scalare per cui m = 1, si ha J f = f In particolare una curva x(t) γ : t A y(t) è differenziabile se e solo se le componenti x(t) e y(t) sono derivabili (nel senso ordinario di funzioni di una variabile) e la matrice jacobiana di γ (pensata come vettore riga) γ (t) = (x (t), y (t)) t A, si chiama vettore tangente (o vettore velocità) dove x (t) e y (t) sono le derivate ordinarie Analogamente un campo Φ = (u, v) è differenziabile se e solo se sono differenziabili le funzioni u e v La matrice jacobiana è una matrice 2 2 data da J Φ = ( u v ) = ( u v u v ) Il seguente teorema assicura che la composizione di due funzioni di differenziabili è differenziabile Teo 10 (Derivazione in catena) Sia f : A R 2 R una funzione differenziabile in A aperto (1) Sia ϕ : ]a, b[ R R una funzione derivabile tale che f ]a, b[ per ogni A La funzione composta g = ϕ(f) con dominio A e codominio R è differenziabile e vale g = ϕ (f) g = ϕ (f) cioè g(p ) = ϕ per ogni P = A (2) Sia γ una curva γ : x(t) y(t) t ]a, b[ (f(p )) f(p ) differenziabile tale che (x(t), y(t)) A per ogni t ]a, b[ La funzione composta ψ(t) = f(γ(t)) = f(x(t), y(t)) con dominio ]a, b[ e codominio R è derivabile e vale (6) ψ (t) = (x(t), y(t)) x (t) + (x(t), y(t)) y (t) = f(γ(t)) γ (t) per ogni t ]a, b[ )
11 11 (3) Sia Φ :  R2 R 2 Φ( x, ŷ) = (x( x, ŷ), y( x, ŷ)) un campo differenziabile nell aperto  tale che Φ( x, ŷ) A per ogni ( x, ŷ)  La funzione composta f( x, ŷ) = f(φ( x, ŷ)) = f(x( x, ŷ), y( x, ŷ)) con dominio  e codominio R è differenziabile e vale f ( x, ŷ) = (x( x, ŷ), y( x, ŷ)) x f ( x, ŷ) = in forma vettoriale (x( x, ŷ), y( x, ŷ)) ŷ f( x, ŷ) = f(φ( x, ŷ)) J Φ ( x, ŷ) ( x, ŷ) + ( x, ŷ) + (x( x, ŷ), y( x, ŷ)) ( x, ŷ) x (x( x, ŷ), y( x, ŷ)) ( x, ŷ) ŷ per ogni ( x, ŷ)  dove f(φ( x, ŷ)) J Φ( x, ŷ) è la moltiplicazione (riga per colonna) di un vettore riga f per la matrice jacobiana J Φ I tre casi di derivazione in catena enunciati sono conseguenza del seguente teorema Date due funzioni f : A R n R m e g : B R m R p con f(a) B Se f è differenziabile in P 0 A e g è differenziabile in Q 0 = f(p 0 ) B, la funzione composta h(p ) = g(f(p )) con dominio A e codominio R p è differenziabile in P 0 e vale J h (P 0 ) = J g (Q 0 ) J f (P 0 ), dove la moltiplicazione è quella righe per colonne tra la matrice p m J g (Q 0 ) ed la matrice m n J f (P 0 ) Esempio 7 Sia g = x 2 + y 2 = P 0 con dominio R 2 Poiché la funzione f = x 2 + y 2 è differenziabile in R 2 con f = (2x, 2y) = 2(P O) e la funzione ϕ(t) = t è derivabile in ]0, + [ con φ (t) = 1 2, per il teorema di derivazione in catena g è differenziabile in A = t R 2 x 2 + y 2 0 } e vale g x = g y = x 2 + y 2 cioè ( g)(p ) = P 0 P 0 x 2 + y 2 Nell origine g non è derivabile poiché non esistono le derivate parziali in (0, 0): infatti le funzioni g(x, 0) = x e g(0, y) = y non sono derivabili in 0 1 Analogamente, la funzione h = = 1 = con dominio R 2 x 2 + y 2 0 } è x 2 +y 2 differenziabile e, poiché ( t 1 2 ) = 1 2( t) 3, vale P 0 ( h)(p ) = P 0 P 0 3 = 1 P 0 P 0 2 P 0 Esempio 8 Sia γ(t) = (x 0 + v 1 t, y 0 + v 2 t) = P 0 + vt, t R, la retta passante per P 0 = (x 0, y 0 ) con direzione v = (v 1, v 2 ) La curva è differenziabile e γ (t) = (v 1, v 2 ) = v per ogni t R Se f : A R 2 R è differenziabile in P 0 A, allora la funzione composta ψ(t) = f(x 0 + v 1 t, y 0 + v 2 t) è derivabile in 0 e l equazione (6) con t = 0 dà che, ovviamente, coincide con (5) ψ (0) = f(x 0 + v 1 t, y 0 + v 2 t) t=0 = f(p 0 ) v
12 12 Esempio 9 Sia Φ : R 2 R 2 il campo Φ( x, ŷ) = (a x + bŷ, c x + dŷ) dove a, b, c, d R Essendo x( x, ŷ) = a x + bŷ ed y( x, ŷ) = c x + dŷ funzioni di classe C 1 (R 2 ), allora Φ C 1 (R 2 ) e ( ) a b J Φ ( x, ŷ) = ( x, ŷ) R c d 2 Se ad bc 0, un teorema dell algebra lineare assicura che Φ è bigettiva e definisce una trasformazione di coordinate nel piano x = a x + bŷ vecchie: nuove: ( x, ŷ) y = c x + dŷ e, con questa notazione, J Φ ( x, ŷ) = ( bx bx by by ) ( a b = c d Sia f : A R 2 R differenziabile in A aperto, la funzione composta (7) f( x, ŷ) = f(a x + bŷ, c x + dŷ) = f ha dominio  = ( x, ŷ) R2 (a x + bŷ, c x + dŷ) A}, che risulta aperto La regola di derivazione in catena mostra che f( x, ŷ) è differenziabile e f x f ŷ ( x, ŷ) = ( x, ŷ) = x ŷ ( x, ŷ) + ( x, ŷ) + x ŷ ) ( x, ŷ) = ( x, ŷ) = a + c b + d dove e indicano le derivate parziali rispetto alla prima e seconda variabile di f, pensata come funzione delle variabili vecchie, mentre f b bx e f b by indicano le derivate parziali rispetto alla prima e seconda variabile di f, pensata come funzione delle variabili nuove ( x, ŷ) (come suggerisce l equazione (7)) Tuttavia è utile usare due simboli diversi per f, funzione delle vecchie variabili, ed f, funzione delle nuove variabili, per evitare confusione notazionale, come mostra il seguente esempio Siano a = 1, b = 0, c = 1 e d = 1, allora x = x y = x + ŷ ŷ ma f x = + f ŷ = Il concetto di derivate di ordine successivo si definisce in modo ricorsivo Def 9 Sia f : A R 2 R una funzione scalare con A aperto tale che esistano le derivate parziali e in A Se tali derivate sono a loro volte derivabili in A, queste quattro derivate seconde si denotano con o, come matrice 2 2, 2 f 2 = ( ) 2 f = ( ) H f = ( 2 f 2 f = ( 2 f 2 2 f ) = 2 ( ) 2 f 2 f 2 ),
13 detta matrice hessiana di f Se, inoltre, tutte e quattro le derivate seconde sono continue, si dice che f è una funzione di classe C 2 e si scrive f C 2 (A) Il seguente risultato mostra che per le funzioni di classe C 2 la matrice hessiana è simmetrica Teo 11 (Teorema di Schwarz) Sia f : A R 2 R con A aperto ed f C 2 (A), allora 2 f = 2 f A Il seguente teorema motiva l introduzione della matrice hessiana Teo 12 (Formula di Taylor di ordine 2) Sia f : A R 2 R con A aperto ed f C 2 (A) Dato P 0 = (x 0, y 0 ) A, per ogni A f = f(x 0, y 0 ) + (x 0, y 0 )(x x 0 ) + (x 0, y 0 )(y y 0 ) + dove ω è infinitesima ( x x 0 y y 0 ) H f (x 0, y 0 ) ( x x 0 y y 0 ) + [(x x 0 ) 2 + (y y 0 ) 2 ] ω(x x 0, y y 0 ) La quantità Q(x x 0, y y 0 ) = ( x x 0 y y 0 ) H f (x 0, y 0 ) ( x x 0 ) è la forma quadratica y y 0 associata alla matrice hessiana ed è esplicitamente da Q(x x 0, y y 0 ) = 2 f 2 (x 0, y 0 ) (x x 0 ) f (x 0, y 0 ) (x x 0 )(y y 0 ) + 2 f 2 (x 0, y 0 ) (y y 0 ) 2 41 Proprietà delle funzioni scalari differenziabili La seguente proposizione fornisce un interpretazione geometrica del gradiente Prop 2 Sia f : A R 2 R, f differenziabile in P 0 A e f(p 0 ) 0 (1) Dato n R 2 con n = 1, sia θ l angolo compreso tra le semirette orientate individuate dai vettori n e f(p 0 ), allora v (P 0) = f(p 0 ) cos θ In particolare, v è massima se n ha la stessa direzione e verso di f(p 0), è nulla se n è perpendicolare a f(p 0 ) e minima se n ha la stessa direzione e verso opposto di f(p 0 ) (2) Sia A c l insieme di livello di quota c = f(p 0 ) Data una curva γ A c = R 2 A, f = f(x 0, y 0 ) } P 0 A c γ : x(t) y(t) t < 1 differenziabile tale che γ(t) A c per ogni t < 1 e γ(0) = P 0, allora f(p 0 ) γ (0) = 0 In particolare la retta tangente all insieme di livello A c nel punto P 0 = (x 0, y 0 ) ha equazione (x 0, y 0 )(x x 0 ) + (x 0, y 0 )(x x 0 ) = 0 in forma vettoriale f(p 0 ) (P P 0 ) = 0 Poiché f(p 0 ) > 0, il vettore f(p 0 ) individua la direzione di massima crescita per f e risulta perpendicolare all insieme di livello di f passante per il punto P 0 13
14 14 Esempio 10 Sia f = x 2 + y 2 = P 0 2 e P 0 = (x 0, y 0 ) (0, 0) L insieme di livello A c = R 2 x 2 + y 2 = x } y2 0 di quota c = x y0 2 è una circonferenza di raggio c Ricordando che f(p 0 ) = 2(x 0, y 0 ) = 2(P 0 O) (0, 0), la funzione ha la massima crescita nella direzione e verso del vettore P 0 0, applicato in P 0, e la retta tangente in P 0 ad A c ha equazione 2x 0 (x x 0 ) + 2y 0 (y y 0 ) = 0 cioè (P P 0 ) (P 0 O) = 0 In (0, 0) il gradiente è nullo e l insieme di livello di quota 0 si riduce ad un punto Il seguente teorema caratterizza le funzioni che hanno gradiente nullo in tutti i punti di A Prop 3 Sia f : A R 2 R con A aperto e connesso per archi Se f differenziabile in A e = 0 A in forma vettoriale f = 0, = 0 allora f è una funzione costante, cioè esiste c R tale che f = c per ogni A La condizione che A sia connesso per archi non si può eliminare affinché la tesi sia vera Esempio 11 Sia A = R 2 x 0, y R } e f : A R 1 se x < 0 f = 2 se x > 0 La funzione f ha gradiente nullo, ma non è costante La seguente proposizione dà una condizione necessaria per l esistenza di estremi relativi Prop 4 (condizione necessaria del prim ordine per estremi relativi) Sia f : A R 2 R, f differenziabile in P 0 = (x 0, y 0 ) A Se esiste δ > 0 tale che allora f f(x 0, y 0 ) A B((x 0, y 0 ), δ) [rispettivamente f f(x 0, y 0 ) A B((x 0, y 0 ), δ)] (x 0, y 0 ) = 0 (x 0, y 0 ) = 0 in forma vettoriale f(x 0, y 0 ) = 0 Il valore f(x 0, y 0 ) è detto minimo [risp massimo] relativo di f in A e (x 0, y 0 ) punto di minimo [risp massimo] relativo La condizione data è solo necessaria Se (x 0, y 0 ) = 0 e (x 0, y 0 ) = 0, (x 0, y 0 ) è detto un punto critico per f in A Esempio 12 La funzione f = y 2 x 2 ha come punti critici solo l origine (0, 0) f(0, 0) = 0 e f > 0 = f(0, 0) f < 0 = f(0, 0) se y > x se y < x, Tuttavia, per cui f cambia segno in ogni palla di centro (0, 0) e, quindi, (0, 0) non è un punto di estremo relativo La seguente proposizione dà una condizione sufficiente affinchè un punto critico sia di estremo relativo A tal fine sia det H f = 2 f 2 2 f 2 2 f 2 f il determinante della matrice hessiana
15 Prop 5 (condizione sufficiente del second ordine per estremi relativi) Data f : A R 2 R con A aperto ed f C 2 (A), sia (x 0, y 0 ) A un punto critico di f (1) Se det H f (x 0, y 0 ) > 0 e 2 f (x 2 0, y 0 ) > 0, allora (x 0, y 0 ) è un punto di minimo relativo di f (2) Se det H f (x 0, y 0 ) > 0 e 2 f (x 2 0, y 0 ) < 0, allora (x 0, y 0 ) è un punto di massimo relativo di f (3) Se det H f (x 0, y 0 ) < 0, (x 0, y 0 ) non è né un punto di massimo né un punto di minimo relativo di f (si dice che (x 0, y 0 ) è un punto di sella di f) Il teorema di Schwarz assicura che 2 f (x 0, y 0 ) = 2 f (x 0, y 0 ) Se det H f (x 0, y 0 ) > 0, allora 2 [ f 2 (x 0, y 0 ) 2 f 2 ] 2 2 (x f 0, y 0 ) > (x 0, y 0 ) 0 per cui 2 f (x 2 0, y 0 ) e 2 f (x 2 0, y 0 ) hanno lo stesso segno e sono entrambe non nulle Se det H f (x 0, y 0 ) = 0, le condizioni del second ordine non permettono di stabilire se un punto critico sia un punto di estremo relativo o meno Esempio 13 Le funzioni f = x 4 + y 4 e g = x 4 y 4 sono di classe C 1 (R 2 ), hanno come unico punto critico l origine (0, 0) e come matrice hessiana nell origine la matrice nulla ( ) 0 0 H f (0, 0) = H g (0, 0) = 0 0 Tuttavia, (0, 0) è un punto di minimo assoluto per f poiché x 4 + y 4 0 e (0, 0) è un punto di sella per g poiché g(x, 0) = x 4 ha un minimo assoluto in x = 0 e g(0, y) = y 4 ha un massimo assoluto in y = 0 Esempio 14 (retta dei minimi quadrati) Siano (x 1, y 1 ),, (x n, y n ) n coppie di punti in R 2 tali che x i x j per almeno una coppia di indici i j Data una retta y = ax + b, non parallela all asse delle ordinate, l errore quadratico associato alla retta è n E(a, b) = (ax i + b y i ) 2 La retta dei minimi quadrati è definita come la retta y = a 0 x + b 0 che minimizza tale errore i=1 15 Per calcolare i punti critici, siano x i = x i x ŷ i = y i y Tenuto conto che n i=1 x i = 0 e n i=1 ŷi = 0, E(a, b) = x = 1 n y = 1 n n i=1 x i n y i i=1 n (a x i ŷ i ) 2 + n(ax + b y) 2 Ne segue che i punti critici di E(a, b) sono le soluzioni del sistema E(a, b) n = 2 (a x i ŷ i ) x i + 2n(ax + b y)x = 0 a i=1 E(a, b) = 2n(ax + b y) = 0 b i=1
16 16 Poiché n i=1 x2 i > 0, si ricava che l unico punto critico è n i=1 a 0 = x iŷ i n i=1 x i 2 b 0 = y a 0 x Calcoliamo la matrice hessiana in (a 0, b 0 ) ( 1 n H f (a 0, b 0 ) = 2n n i=1 x2 i + x2 x x 1 Poiché n i=1 x2 i > 0, det H f (a 0, b 0 ) > 0 e gli elementi sulla diagonale principale sono strettamente positivi Ne segue che (a 0, b 0 ) è un punto di minimo relativo Si vede che in effetti è un punto di minimo assoluto osservando che E(a, b) E(a, b 0 ) E(a 0, b 0 ) (la prima disuguaglianza è ovvia, la seconda segue osservando che il grafico di E(a, b 0 ) in funzione di a è una parabola con la concavità rivolta verso l alto e vertice (a 0, E(a 0, b 0 )) In conclusione La retta dei minimi quadrati è data da e l errore quadratico è E(a 0, b 0 ) = n y = 1 ) n n i=1 (x i x)(y i y) ( x 2 i x ) 2 (x x) + y 1 n n i=1 1 n n i=1 (x i x) 2 1 n n i=1 (y i y) 2 ( 1 n n i=1 (x i x) 2 1 n n i=1 (x i x) (y i y) ) 2 I teoremi dati si estendono in modo naturale al caso di funzioni scalari di n variabili In particolare, la condizione sufficiente del second ordine risulta la seguente Ricordiamo che, poiché la matrice hessiana H f (x 0, y 0 ) è una matrice n n simmetrica per il teorema di Schwarz, un teorema dell algebra lineare assicura che è diagonalizzabile e gli autovalori sono le soluzioni reali del polinomio di grado n dove I è la matrice identità n n det (H f (x 0, y 0 ) λi) = 0, Teo 13 Se f : A R n R con A aperto ed f C 2 (A), un punto critico (x 0, y 0 ) A è di minimo [risp massimo] relativo se la matrice hessiana ha tutti gli autovalori strettamente positivi [risp strettamente negativi]
Le derivate parziali
 Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
Alcune nozioni di calcolo differenziale
 Alcune nozioni di calcolo differenziale G. Mastroeni, M. Pappalardo 1 Limiti per funzioni di piu variabili Supporremo noti i principali concetti algebrici e topologici relativi alla struttura dello spazio
Alcune nozioni di calcolo differenziale G. Mastroeni, M. Pappalardo 1 Limiti per funzioni di piu variabili Supporremo noti i principali concetti algebrici e topologici relativi alla struttura dello spazio
variabili. se i limiti esistono e si chiamano rispettivamente derivata parziale rispetto ad x e rispetto ad y.
 Funzioni di più variabili Derivate parziali Qui saranno considerate soltanto funzioni di due variabili, ma non c è nessuna difficoltà ad estendere le nuove nozioni a funzioni di n ( > variabili ( Definizione:
Funzioni di più variabili Derivate parziali Qui saranno considerate soltanto funzioni di due variabili, ma non c è nessuna difficoltà ad estendere le nuove nozioni a funzioni di n ( > variabili ( Definizione:
Appunti sul corso di Complementi di Matematica mod. Analisi prof. B.Bacchelli - a.a. 2010/2011.
 Appunti sul corso di Complementi di Matematica mod. Analisi prof. B.Baccelli - a.a. 2010/2011. 06 - Derivate, differenziabilità, piano tangente, derivate di ordine superiore. Riferimenti: R.Adams, Calcolo
Appunti sul corso di Complementi di Matematica mod. Analisi prof. B.Baccelli - a.a. 2010/2011. 06 - Derivate, differenziabilità, piano tangente, derivate di ordine superiore. Riferimenti: R.Adams, Calcolo
ANALISI B alcuni esercizi proposti
 ANALISI B alcuni esercizi proposti G.P. Leonardi Parte II 1 Limiti e continuità per funzioni di 2 variabili Esercizio 1.1 Calcolare xy log(1 + x ) lim (x,y) (0,0) 2x 2 + 5y 2 Esercizio 1.2 Studiare la
ANALISI B alcuni esercizi proposti G.P. Leonardi Parte II 1 Limiti e continuità per funzioni di 2 variabili Esercizio 1.1 Calcolare xy log(1 + x ) lim (x,y) (0,0) 2x 2 + 5y 2 Esercizio 1.2 Studiare la
Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006. Matematica 2 (Analisi)
 Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006 Matematica 2 (Analisi) Nome:................................. N. matr.:.................................
Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006 Matematica 2 (Analisi) Nome:................................. N. matr.:.................................
Massimi e minimi relativi in R n
 Massimi e minimi relativi in R n Si consideri una funzione f : A R, con A R n, e sia x A un punto interno ad A. Definizione: si dice che x è un punto di massimo relativo per f se B(x, r) A tale che f(y)
Massimi e minimi relativi in R n Si consideri una funzione f : A R, con A R n, e sia x A un punto interno ad A. Definizione: si dice che x è un punto di massimo relativo per f se B(x, r) A tale che f(y)
Esercitazione n 6. Esercizio 1: Determinare i punti di massimo e minimo relativo delle seguenti funzioni: (b)f(x, y) = 4y 4 16x 2 y + x
 Esercitazione n 6 1 Massimi e minimi di funzioni di più variabili Esercizio 1: Determinare i punti di massimo e minimo relativo delle seguenti funzioni: (a)f(x, y) = x 3 + y 3 + xy (b)f(x, y) = 4y 4 16x
Esercitazione n 6 1 Massimi e minimi di funzioni di più variabili Esercizio 1: Determinare i punti di massimo e minimo relativo delle seguenti funzioni: (a)f(x, y) = x 3 + y 3 + xy (b)f(x, y) = 4y 4 16x
Richiami sugli insiemi numerici
 Richiami sugli insiemi numerici denota l insieme vuoto cioè l insieme privo di elementi. N = {1, 2, 3,...} denota l insieme dei numeri naturali. Z = {..., 2, 1, 0, 1, 2,...} denota l insieme dei numeri
Richiami sugli insiemi numerici denota l insieme vuoto cioè l insieme privo di elementi. N = {1, 2, 3,...} denota l insieme dei numeri naturali. Z = {..., 2, 1, 0, 1, 2,...} denota l insieme dei numeri
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
I teoremi della funzione inversa e della funzione implicita
 I teoremi della funzione inversa e della funzione implicita Appunti per il corso di Analisi Matematica 4 G. Mauceri Indice 1 Il teorema della funzione inversa 1 Il teorema della funzione implicita 3 1
I teoremi della funzione inversa e della funzione implicita Appunti per il corso di Analisi Matematica 4 G. Mauceri Indice 1 Il teorema della funzione inversa 1 Il teorema della funzione implicita 3 1
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016
 Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
Funzioni reali di 2 variabili reali
 Funzioni reali di 2 variabili reali Sono funzioni del tipo: f :domf R 2 R Ad ogni punto P =(x, y) di un sottoinsieme dom f P =(x, y) f (P )=f (x, y) di R 2 associano un numero reale f (P )=f (x, y). Se
Funzioni reali di 2 variabili reali Sono funzioni del tipo: f :domf R 2 R Ad ogni punto P =(x, y) di un sottoinsieme dom f P =(x, y) f (P )=f (x, y) di R 2 associano un numero reale f (P )=f (x, y). Se
R. Capone Analisi Matematica Calcolo Differenziale Funzioni di due variabili
 Richiami teorici Sia una funzione di due variabili definita in un insieme A e sia un punto interno ad A. Se R è un dominio regolare di centro e di dimensioni e la funzione della sola variabile x, risulta
Richiami teorici Sia una funzione di due variabili definita in un insieme A e sia un punto interno ad A. Se R è un dominio regolare di centro e di dimensioni e la funzione della sola variabile x, risulta
Appunti sul corso di Complementi di Matematica (modulo Analisi)
 Appunti sul corso di Complementi di Matematica (modulo Analisi) prof. B.Bacchelli. 04 - Vettori topologia in R n : Riferimenti: R.Adams, Calcolo Differenziale 2. Cap. 1.2: In R n : vettori, somma, prodotto
Appunti sul corso di Complementi di Matematica (modulo Analisi) prof. B.Bacchelli. 04 - Vettori topologia in R n : Riferimenti: R.Adams, Calcolo Differenziale 2. Cap. 1.2: In R n : vettori, somma, prodotto
x 1 Fig.1 Il punto P = P =
 Geometria di R 2 In questo paragrafo discutiamo le proprietà geometriche elementari del piano Per avere a disposizione delle coordinate nel piano, fissiamo un punto, che chiamiamo l origine Scegliamo poi
Geometria di R 2 In questo paragrafo discutiamo le proprietà geometriche elementari del piano Per avere a disposizione delle coordinate nel piano, fissiamo un punto, che chiamiamo l origine Scegliamo poi
Analisi Matematica II
 Analisi Matematica II Limiti e continuità in R N Claudio Saccon 1 1 Dipartimento di Matematica, Via F. Buonarroti 1/C,56127 PISA email: claudio.sacconchiocciolaunipi.it sito web: http://pagine.dm.unipi.it/csblog1
Analisi Matematica II Limiti e continuità in R N Claudio Saccon 1 1 Dipartimento di Matematica, Via F. Buonarroti 1/C,56127 PISA email: claudio.sacconchiocciolaunipi.it sito web: http://pagine.dm.unipi.it/csblog1
Riferimenti: R.Adams, Calcolo Differenziale 2. Capitoli 3.4, 3.9. Esercizi 3.4, 3.9.
 Appunti sul corso di Complementi di Matematica - mod Analisi prof. B.Baccelli 200/ 07 - Funzioni vettoriali, derivata della funzione composta, formula di Taylor. Riferimenti: R.Adams, Calcolo Differenziale
Appunti sul corso di Complementi di Matematica - mod Analisi prof. B.Baccelli 200/ 07 - Funzioni vettoriali, derivata della funzione composta, formula di Taylor. Riferimenti: R.Adams, Calcolo Differenziale
Richiami di algebra delle matrici a valori reali
 Richiami di algebra delle matrici a valori reali Vettore v n = v 1 v 2. v n Vettore trasposto v n = (v 1, v 2,..., v n ) v n = (v 1, v 2,..., v n ) A. Pollice - Statistica Multivariata Vettore nullo o
Richiami di algebra delle matrici a valori reali Vettore v n = v 1 v 2. v n Vettore trasposto v n = (v 1, v 2,..., v n ) v n = (v 1, v 2,..., v n ) A. Pollice - Statistica Multivariata Vettore nullo o
Polinomio di Taylor del secondo ordine per funzioni di due variabili
 Esercitazioni del 15 aprile 2013 Polinomio di Taylor del secondo ordine per funzioni di due variabili Sia f : A R 2 R una funzione di classe C 2. Fissato un p unto (x 0, y 0 A consideriamo il seguente
Esercitazioni del 15 aprile 2013 Polinomio di Taylor del secondo ordine per funzioni di due variabili Sia f : A R 2 R una funzione di classe C 2. Fissato un p unto (x 0, y 0 A consideriamo il seguente
Funzioni di più variabili a valori vettoriali n t m
 Funzioni di più variabili a valori vettoriali n t m Definizione f(x 1, x 2,...x n )=[f 1 (x 1, x 2,...x n ), f 2 (x 1, x 2,...x n ),...f m (x 1, x 2,...x n )] Funzione definita n d m Dove: n = dominio
Funzioni di più variabili a valori vettoriali n t m Definizione f(x 1, x 2,...x n )=[f 1 (x 1, x 2,...x n ), f 2 (x 1, x 2,...x n ),...f m (x 1, x 2,...x n )] Funzione definita n d m Dove: n = dominio
Rette e piani nello spazio Federico Lastaria, Analisi e Geometria 1. Politecnico di Milano Corso di Analisi e Geometria 1
 ette e piani nello spazio Federico Lastaria, Analisi e Geometria 1 Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it ette e piani nello spazio. 9 Gennaio
ette e piani nello spazio Federico Lastaria, Analisi e Geometria 1 Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it ette e piani nello spazio. 9 Gennaio
Estremi. 5. Determinare le dimensioni di una scatola rettangolare di volume v assegnato, che abbia la superficie minima.
 Estremi 1. Determinare gli estremi relativi di f(x, y) = e x (x 1)(y 1) + (y 1).. Determinare gli estremi relativi di f(x, y) = y (y + 1) cos x. 3. Determinare gli estremi relativi di f(x, y) = xye x +y..
Estremi 1. Determinare gli estremi relativi di f(x, y) = e x (x 1)(y 1) + (y 1).. Determinare gli estremi relativi di f(x, y) = y (y + 1) cos x. 3. Determinare gli estremi relativi di f(x, y) = xye x +y..
1. Funzioni implicite
 1. Funzioni implicite 1.1 Il caso scalare Sia X R 2 e sia f : X R. Una funzione y : (a, b) R si dice definita implicitamente dall equazione f(x, y) = 0 in (a, b) quando: 1. (x, y(x)) X x (a, b); 2. f(x,
1. Funzioni implicite 1.1 Il caso scalare Sia X R 2 e sia f : X R. Una funzione y : (a, b) R si dice definita implicitamente dall equazione f(x, y) = 0 in (a, b) quando: 1. (x, y(x)) X x (a, b); 2. f(x,
Teorema delle Funzioni Implicite
 Teorema delle Funzioni Implicite Sia F una funzione di due variabili definita in un opportuno dominio D di R 2. Consideriamo l equazione F (x, y) = 0, questa avrà come soluzioni coppie di valori (x, y)
Teorema delle Funzioni Implicite Sia F una funzione di due variabili definita in un opportuno dominio D di R 2. Consideriamo l equazione F (x, y) = 0, questa avrà come soluzioni coppie di valori (x, y)
4.11 Massimi e minimi relativi per funzioni di più variabili
 5. Determinare, al variare del parametro a R, la natura delle seguenti forme quadratiche: (i) Φ(x, y, z) = x 2 + 2axy + y 2 + 2axz + z 2, (ii) Φ(x, y, z, t) = 2x 2 + ay 2 z 2 t 2 + 2xz + 4yt + 2azt. 4.11
5. Determinare, al variare del parametro a R, la natura delle seguenti forme quadratiche: (i) Φ(x, y, z) = x 2 + 2axy + y 2 + 2axz + z 2, (ii) Φ(x, y, z, t) = 2x 2 + ay 2 z 2 t 2 + 2xz + 4yt + 2azt. 4.11
a) Il denominatore dev essere diverso da zero. Studiamo il trinomio x 2 5x + 6. Si ha: x 1,2 = 5 ± se x ], 2[ ]3, + [;
![a) Il denominatore dev essere diverso da zero. Studiamo il trinomio x 2 5x + 6. Si ha: x 1,2 = 5 ± se x ], 2[ ]3, + [; a) Il denominatore dev essere diverso da zero. Studiamo il trinomio x 2 5x + 6. Si ha: x 1,2 = 5 ± se x ], 2[ ]3, + [;](/thumbs/69/60588320.jpg) ESERCIZIO - Data la funzione f (x) + x2 2x x 2 5x + 6, si chiede di: a) calcolare il dominio di f ; (2 punti) b) studiare la positività e le intersezioni con gli assi; (3 punti) c) stabilire se f ha asintoti
ESERCIZIO - Data la funzione f (x) + x2 2x x 2 5x + 6, si chiede di: a) calcolare il dominio di f ; (2 punti) b) studiare la positività e le intersezioni con gli assi; (3 punti) c) stabilire se f ha asintoti
Massimi e minimi assoluti vincolati: esercizi svolti
 Massimi e minimi assoluti vincolati: esercizi svolti Gli esercizi contrassegnati con il simbolo * presentano un grado di difficoltà maggiore. Esercizio 1. Determinare i punti di massimo e minimo assoluti
Massimi e minimi assoluti vincolati: esercizi svolti Gli esercizi contrassegnati con il simbolo * presentano un grado di difficoltà maggiore. Esercizio 1. Determinare i punti di massimo e minimo assoluti
Estremi liberi. (H x, x) x 2 (1) F (x) =
 Estremi liberi Allo scopo di ottenere delle condizioni sufficienti affinchè un punto stazionario sia un estremante, premettiamo alcuni risultati riguardanti le proprietà delle forme quadratiche. Sia H
Estremi liberi Allo scopo di ottenere delle condizioni sufficienti affinchè un punto stazionario sia un estremante, premettiamo alcuni risultati riguardanti le proprietà delle forme quadratiche. Sia H
Funzioni derivabili (V. Casarino)
 Funzioni derivabili (V. Casarino) Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in = 0 delle funzioni: a) 5 b) 3 4 c) + 1 d) sin. ) Scrivere l equazione della retta tangente
Funzioni derivabili (V. Casarino) Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in = 0 delle funzioni: a) 5 b) 3 4 c) + 1 d) sin. ) Scrivere l equazione della retta tangente
Similitudine (ortogonale) e congruenza (ortogonale) di matrici.
 Lezione del 4 giugno. Il riferimento principale di questa lezione e costituito da parti di: 2 Forme bilineari, quadratiche e matrici simmetriche associate, 3 Congruenza di matrici simmetriche, 5 Forme
Lezione del 4 giugno. Il riferimento principale di questa lezione e costituito da parti di: 2 Forme bilineari, quadratiche e matrici simmetriche associate, 3 Congruenza di matrici simmetriche, 5 Forme
GEOMETRIA PIANA. 1) sia verificata l uguaglianza di segmenti AC = CB (ossia C è punto medio del segmento AB);
 VETTORI E GEOMETRIA ANALITICA 1 GEOMETRIA PIANA Segmenti e distanza tra punti. Rette in forma cartesiana e parametrica. Posizioni reciproche di due rette, parallelismo e perpendicolarità. Angoli e distanze.
VETTORI E GEOMETRIA ANALITICA 1 GEOMETRIA PIANA Segmenti e distanza tra punti. Rette in forma cartesiana e parametrica. Posizioni reciproche di due rette, parallelismo e perpendicolarità. Angoli e distanze.
Rette e piani nello spazio
 Rette e piani nello spazio Equazioni parametriche di una retta in R 3 : x(t) = x 0 + at r(t) : y(t) = y 0 + bt t R, parametro z(t) = z 0 + ct ovvero r(t) : X(t) = P 0 + vt, t R}, dove: P 0 = (x 0, y 0,
Rette e piani nello spazio Equazioni parametriche di una retta in R 3 : x(t) = x 0 + at r(t) : y(t) = y 0 + bt t R, parametro z(t) = z 0 + ct ovvero r(t) : X(t) = P 0 + vt, t R}, dove: P 0 = (x 0, y 0,
Corso di Geometria BIAR, BSIR Esercizi 10: soluzioni
 Corso di Geometria 2010-11 BIAR, BSIR Esercizi 10: soluzioni 1 Geometria dello spazio Esercizio 1. Dato il punto P 0 = ( 1, 0, 1) e il piano π : x + y + z 2 = 0, determinare: a) Le equazioni parametriche
Corso di Geometria 2010-11 BIAR, BSIR Esercizi 10: soluzioni 1 Geometria dello spazio Esercizio 1. Dato il punto P 0 = ( 1, 0, 1) e il piano π : x + y + z 2 = 0, determinare: a) Le equazioni parametriche
Massimi e minimi vincolati
 Massimi e minimi vincolati Vedremo tra breve un metodo per studiare il problema di trovare il minimo e il massimo di una funzione su di un sottoinsieme dello spazio ambiente che non sia un aperto. Abbiamo
Massimi e minimi vincolati Vedremo tra breve un metodo per studiare il problema di trovare il minimo e il massimo di una funzione su di un sottoinsieme dello spazio ambiente che non sia un aperto. Abbiamo
Punti di massimo o di minimo per funzioni di n variabili reali
 Punti di massimo o di minimo per funzioni di n variabili reali Dati f : A R n R ed X 0 A, X 0 si dice : punto di minimo assoluto se X A, f ( x ) f ( X 0 ) punto di massimo assoluto se X A, f ( x ) f (
Punti di massimo o di minimo per funzioni di n variabili reali Dati f : A R n R ed X 0 A, X 0 si dice : punto di minimo assoluto se X A, f ( x ) f ( X 0 ) punto di massimo assoluto se X A, f ( x ) f (
Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 18 febbraio 2010 Tema A
 Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 18 febbraio 21 Tema A Tempo a disposizione: 2 ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio va iniziato all inizio
Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 18 febbraio 21 Tema A Tempo a disposizione: 2 ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio va iniziato all inizio
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA
 Cognome Nome Matricola FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA Ciarellotto, Esposito, Garuti Prova del 21 settembre 2013 Dire se è vero o falso (giustificare le risposte. Bisogna necessariamente rispondere
Cognome Nome Matricola FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA Ciarellotto, Esposito, Garuti Prova del 21 settembre 2013 Dire se è vero o falso (giustificare le risposte. Bisogna necessariamente rispondere
Dipartimento di Matematica Corso di laurea in Matematica Compiti di Geometria II assegnati da dicembre 2000 a dicembre 2003
 Dipartimento di Matematica Corso di laurea in Matematica Compiti di Geometria assegnati da dicembre 2000 a dicembre 2003 11/12/2000 n R 4 sono assegnati i punti A(3, 0, 1, 0), B(0, 0, 1, 0), C(2, 1, 0,
Dipartimento di Matematica Corso di laurea in Matematica Compiti di Geometria assegnati da dicembre 2000 a dicembre 2003 11/12/2000 n R 4 sono assegnati i punti A(3, 0, 1, 0), B(0, 0, 1, 0), C(2, 1, 0,
0.1 Arco di curva regolare
 .1. ARCO DI CURVA REGOLARE 1.1 Arco di curva regolare Se RC(O, i, j, k ) è un riferimento cartesiano fissato per lo spazio euclideo E, e se v (t) = x(t) i + y(t) j + z(t) k è una funzione a valori vettoriali
.1. ARCO DI CURVA REGOLARE 1.1 Arco di curva regolare Se RC(O, i, j, k ) è un riferimento cartesiano fissato per lo spazio euclideo E, e se v (t) = x(t) i + y(t) j + z(t) k è una funzione a valori vettoriali
Soluzioni agli Esercizi di Geometria e Algebra per Ingegneria Aerospaziale (nuovo ordinamento)
 Soluzioni agli Esercizi di Geometria e Algebra per Ingegneria Aerospaziale (nuovo ordinamento) Relazioni 1) Quali delle seguenti relazioni sono di equivalenza? x, y R {0} xry x/y Q x, y Z xry x + y è divisibile
Soluzioni agli Esercizi di Geometria e Algebra per Ingegneria Aerospaziale (nuovo ordinamento) Relazioni 1) Quali delle seguenti relazioni sono di equivalenza? x, y R {0} xry x/y Q x, y Z xry x + y è divisibile
3. Vettori, Spazi Vettoriali e Matrici
 3. Vettori, Spazi Vettoriali e Matrici Vettori e Spazi Vettoriali Operazioni tra vettori Basi Trasformazioni ed Operatori Operazioni tra Matrici Autovalori ed autovettori Forme quadratiche, quadriche e
3. Vettori, Spazi Vettoriali e Matrici Vettori e Spazi Vettoriali Operazioni tra vettori Basi Trasformazioni ed Operatori Operazioni tra Matrici Autovalori ed autovettori Forme quadratiche, quadriche e
Appunti sul corso di Complementi di Matematica mod.analisi prof. B.Bacchelli a.a. 2010/2011
 Appunti sul corso di Complementi di Matematica mod.analisi prof. B.Bacchelli a.a. 2010/2011 08- Estremi: Riferimenti: R.Adams, Calcolo Differenziale 2. Capitoli 4.1. Esercizi 4.1 Estremi liberi: punti
Appunti sul corso di Complementi di Matematica mod.analisi prof. B.Bacchelli a.a. 2010/2011 08- Estremi: Riferimenti: R.Adams, Calcolo Differenziale 2. Capitoli 4.1. Esercizi 4.1 Estremi liberi: punti
Politecnico di Torino Facoltà di Architettura. Raccolta di esercizi proposti nelle prove scritte
 Politecnico di Torino Facoltà di Architettura Raccolta di esercizi proposti nelle prove scritte relativi a: algebra lineare, vettori e geometria analitica Esercizio. Determinare, al variare del parametro
Politecnico di Torino Facoltà di Architettura Raccolta di esercizi proposti nelle prove scritte relativi a: algebra lineare, vettori e geometria analitica Esercizio. Determinare, al variare del parametro
Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile
 Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 41 1 Derivata
Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 41 1 Derivata
Università di Trieste Facoltà d Ingegneria. Esercitazioni per la preparazione della prova scritta di Matematica 3 Dott.
 Università di Trieste Facoltà d Ingegneria. Esercitazioni per la preparazione della prova scritta di Matematica 3 Dott. Franco Obersnel Lezione : struttura di IR n, prodotto scalare, distanza e topologia.
Università di Trieste Facoltà d Ingegneria. Esercitazioni per la preparazione della prova scritta di Matematica 3 Dott. Franco Obersnel Lezione : struttura di IR n, prodotto scalare, distanza e topologia.
1 Rette e piani in R 3
 POLITECNICO DI MILANO. FACOLTÀ DI INGEGNERIA INDUSTRIALE. Analisi e Geometria 1. Sez. D - G. Docenti: Federico G. Lastaria, Mauro Saita, Nadir Zanchetta,. 1 1 Rette e piani in R 3 Una retta parametrizzata
POLITECNICO DI MILANO. FACOLTÀ DI INGEGNERIA INDUSTRIALE. Analisi e Geometria 1. Sez. D - G. Docenti: Federico G. Lastaria, Mauro Saita, Nadir Zanchetta,. 1 1 Rette e piani in R 3 Una retta parametrizzata
1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: c) x + 1 d)x sin x.
 Funzioni derivabili Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: a)2x 5 b) x 3 x 4 c) x + 1 d)x sin x. 2) Scrivere l equazione della retta tangente
Funzioni derivabili Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: a)2x 5 b) x 3 x 4 c) x + 1 d)x sin x. 2) Scrivere l equazione della retta tangente
Laurea in Informatica Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile
 Laurea in Informatica Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile Docente: Anna Valeria Germinario Università di Bari A.V.Germinario (Università di Bari) Analisi Matematica
Laurea in Informatica Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile Docente: Anna Valeria Germinario Università di Bari A.V.Germinario (Università di Bari) Analisi Matematica
Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler)
 Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler) Studio di una funzione Funzioni crescenti e decrescenti Una funzione f è crescente nell intervallo (a, b) se
Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler) Studio di una funzione Funzioni crescenti e decrescenti Una funzione f è crescente nell intervallo (a, b) se
CORSO DI LAUREA in Ingegneria Informatica (Vecchio Ordinamento)
 CORSO D LAUREA in ngegneria nformatica (Vecchio Ordinamento) Prova scritta di Geometria assegnata il 19/3/2002 Sia f : R 3 R 4 l applicazione lineare la cui matrice associata rispetto alle basi canoniche
CORSO D LAUREA in ngegneria nformatica (Vecchio Ordinamento) Prova scritta di Geometria assegnata il 19/3/2002 Sia f : R 3 R 4 l applicazione lineare la cui matrice associata rispetto alle basi canoniche
Esercitazione di Analisi Matematica II
 Esercitazione di Analisi Matematica II Barbara Balossi 06/04/2017 Esercizi di ripasso Esercizio 1 Sia data l applicazione lineare f : R 3 R 3 definita come f(x, y, z) = ( 2x + y z, x 2y + z, x y). a) Calcolare
Esercitazione di Analisi Matematica II Barbara Balossi 06/04/2017 Esercizi di ripasso Esercizio 1 Sia data l applicazione lineare f : R 3 R 3 definita come f(x, y, z) = ( 2x + y z, x 2y + z, x y). a) Calcolare
Università degli Studi di Palermo Facoltà di Economia. Dipartimento di Scienze Economiche, Aziendali e Statistiche. Appunti del corso di Matematica
 Università degli Studi di Palermo Facoltà di Economia Dipartimento di Scienze Economiche, Aziendali e Statistiche Appunti del corso di Matematica 03 - I Numeri Reali Anno Accademico 2015/2016 M. Tumminello,
Università degli Studi di Palermo Facoltà di Economia Dipartimento di Scienze Economiche, Aziendali e Statistiche Appunti del corso di Matematica 03 - I Numeri Reali Anno Accademico 2015/2016 M. Tumminello,
Spazi vettoriali euclidei.
 Spazi vettoriali euclidei Prodotto scalare, lunghezza e ortogonalità in R n Consideriamo lo spazio vettoriale R n = { =,,, n R}, n con la somma fra vettori e il prodotto di un vettore per uno scalare definiti
Spazi vettoriali euclidei Prodotto scalare, lunghezza e ortogonalità in R n Consideriamo lo spazio vettoriale R n = { =,,, n R}, n con la somma fra vettori e il prodotto di un vettore per uno scalare definiti
SPAZI EUCLIDEI, APPLICAZIONI SIMMETRICHE, FORME QUADRATICHE
 SPAZI EUCLIDEI, APPLICAZIONI SIMMETRICHE, FORME QUADRATICHE. Esercizi Esercizio. In R calcolare il modulo dei vettori,, ),,, ) ed il loro angolo. Esercizio. Calcolare una base ortonormale del sottospazio
SPAZI EUCLIDEI, APPLICAZIONI SIMMETRICHE, FORME QUADRATICHE. Esercizi Esercizio. In R calcolare il modulo dei vettori,, ),,, ) ed il loro angolo. Esercizio. Calcolare una base ortonormale del sottospazio
Topologia, continuità, limiti in R n
 Topologia, continuità, limiti in R n Ultimo aggiornamento: 18 febbraio 2017 1. Preliminari Prima di iniziare lo studio delle funzioni di più variabili, in generale funzioni di k variabili e a valori in
Topologia, continuità, limiti in R n Ultimo aggiornamento: 18 febbraio 2017 1. Preliminari Prima di iniziare lo studio delle funzioni di più variabili, in generale funzioni di k variabili e a valori in
Corso di Laurea in Ingegneria Gestionale - Sede di Fermo Anno Accademico 2009/2010 Matematica 2 Esercizi d esame
 Corso di Laurea in Ingegneria Gestionale - ede di Fermo Anno Accademico 2009/2010 Matematica 2 Esercizi d esame Nome... N. Matricola... Fermo, gg/mm/aaaa 1. tabilire l ordine di ciascuna delle seguenti
Corso di Laurea in Ingegneria Gestionale - ede di Fermo Anno Accademico 2009/2010 Matematica 2 Esercizi d esame Nome... N. Matricola... Fermo, gg/mm/aaaa 1. tabilire l ordine di ciascuna delle seguenti
Geometria e Topologia I (U1-4) 2006-mag-10 61
 Geometria e Topologia I (U1-4) 2006-mag-10 61 (15.9) Teorema. Consideriamo il piano affine. Se A A 2 (K) è un punto e r una retta che non passa per A, allora esiste unica la retta per A che non interseca
Geometria e Topologia I (U1-4) 2006-mag-10 61 (15.9) Teorema. Consideriamo il piano affine. Se A A 2 (K) è un punto e r una retta che non passa per A, allora esiste unica la retta per A che non interseca
Prodotto scalare. Piani nello spazio Federico Lastaria, Analisi e Geometria 1. Politecnico di Milano Corso di Analisi e Geometria 1
 Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it Prodotto scalare in R n. Piani nello spazio. 19 Dicembre 2016 Indice 1 Prodotto scalare nello spazio 2
Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it Prodotto scalare in R n. Piani nello spazio. 19 Dicembre 2016 Indice 1 Prodotto scalare nello spazio 2
Fissiamo nel piano un sistema di riferimento cartesiano ortogonale O, x, y, u.
 Fissiamo nel piano un sistema di riferimento cartesiano ortogonale O, x, y, u. Definizione Una conica è il luogo dei punti, propri o impropri, reali o immaginari, che con le loro coordinate omogenee (x,
Fissiamo nel piano un sistema di riferimento cartesiano ortogonale O, x, y, u. Definizione Una conica è il luogo dei punti, propri o impropri, reali o immaginari, che con le loro coordinate omogenee (x,
ORDINAMENTO 2007 SESSIONE STRAORDINARIA - QUESITI QUESITO 1
 www.matefilia.it ORDINAMENTO 2007 SESSIONE STRAORDINARIA - QUESITI QUESITO 1 Si determini il campo di esistenza della funzione y = (x 2 3x) 1 x 4. Ricordiamo che il campo di esistenza di una funzione del
www.matefilia.it ORDINAMENTO 2007 SESSIONE STRAORDINARIA - QUESITI QUESITO 1 Si determini il campo di esistenza della funzione y = (x 2 3x) 1 x 4. Ricordiamo che il campo di esistenza di una funzione del
Argomenti Capitolo 1 Richiami
 Argomenti Capitolo 1 Richiami L insieme dei numeri reali R si rappresenta geometricamente con l insieme dei punti di una retta orientata su cui sia stato fissato un punto 0 e un segmento unitario. L insieme
Argomenti Capitolo 1 Richiami L insieme dei numeri reali R si rappresenta geometricamente con l insieme dei punti di una retta orientata su cui sia stato fissato un punto 0 e un segmento unitario. L insieme
Esercizi geometria analitica nello spazio. Corso di Laurea in Informatica. Docente: Andrea Loi. Correzione
 Esercizi geometria analitica nello spazio Corso di Laurea in Informatica Docente: Andrea Loi Correzione 1. Denotiamo con P 1, P 13, P 3, P 1, P, P 3, P i simmetrici di un punto P rispetto ai piani coordinati
Esercizi geometria analitica nello spazio Corso di Laurea in Informatica Docente: Andrea Loi Correzione 1. Denotiamo con P 1, P 13, P 3, P 1, P, P 3, P i simmetrici di un punto P rispetto ai piani coordinati
Esempio di grafico di una funzione reale di due variabili reali
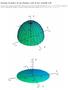 Esempio di grafico di una funzione reale di due variabili reali In questo lucido è rappresentato il grafico della funzione reale di due variabili reali definita da: f(x, y) = 1 x y, in particolare in alto
Esempio di grafico di una funzione reale di due variabili reali In questo lucido è rappresentato il grafico della funzione reale di due variabili reali definita da: f(x, y) = 1 x y, in particolare in alto
Ricordiamo brevemente come possono essere rappresentate le rette nel piano: 1) mediante un'equazione cartesiana. = ( p 1
 Introduzione Nella computer grafica, gli oggetti geometrici sono definiti a partire da un certo numero di elementi di base chiamati primitive grafiche Possono essere punti, rette e segmenti, curve, superfici
Introduzione Nella computer grafica, gli oggetti geometrici sono definiti a partire da un certo numero di elementi di base chiamati primitive grafiche Possono essere punti, rette e segmenti, curve, superfici
Analisi Matematica II Corso di Ingegneria Gestionale Compito del f(x, y) = e (x3 +x) y
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del 8--7 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito del 8--7 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II - INGEGNERIA Gestionale - B 20 luglio 2017 Cognome: Nome: Matricola:
 Analisi Matematica II - INGEGNERIA Gestionale - B luglio 7 Cognome: Nome: Matricola: IMPORTANTE: Giustificare tutte le affermazioni e riportare i calcoli essenziali Esercizio [8 punti] Data la matrice
Analisi Matematica II - INGEGNERIA Gestionale - B luglio 7 Cognome: Nome: Matricola: IMPORTANTE: Giustificare tutte le affermazioni e riportare i calcoli essenziali Esercizio [8 punti] Data la matrice
Note sulle funzioni convesse/concave
 Note sulle funzioni convesse/concave 4th December 2008 1 Definizioni e proprietà delle funzioni convesse/concave. Definizione 1.1 Un insieme A IR n è detto convesso se per ogni x 1 e x 2 punti di A, il
Note sulle funzioni convesse/concave 4th December 2008 1 Definizioni e proprietà delle funzioni convesse/concave. Definizione 1.1 Un insieme A IR n è detto convesso se per ogni x 1 e x 2 punti di A, il
RELAZIONI e CORRISPONDENZE
 RELAZIONI e CORRISPONDENZE Siano X e Y due insiemi non vuoti si chiama relazione tra X e Y un qualunque sottoinsieme del prodotto cartesiano: X x Y = {(x,y): x X, y Y} L insieme costituito dai primi (secondi)
RELAZIONI e CORRISPONDENZE Siano X e Y due insiemi non vuoti si chiama relazione tra X e Y un qualunque sottoinsieme del prodotto cartesiano: X x Y = {(x,y): x X, y Y} L insieme costituito dai primi (secondi)
DIARIO DELLE LEZIONI DI ANALISI MATEMATICA II Corso di laurea in Ingegneria Gestionale Canale PZ Secondo codocente: Dott. Salvatore Fragapane
 DIARIO DELLE LEZIONI DI ANALISI MATEMATICA II Corso di laurea in Ingegneria Gestionale Canale PZ Secondo codocente: Dott. Salvatore Fragapane Lezione 1-04/10/2016 - Serie Numeriche (1): definizione e successione
DIARIO DELLE LEZIONI DI ANALISI MATEMATICA II Corso di laurea in Ingegneria Gestionale Canale PZ Secondo codocente: Dott. Salvatore Fragapane Lezione 1-04/10/2016 - Serie Numeriche (1): definizione e successione
Analisi Matematica II. Esercizi per le vacanze pasquali
 Analisi Matematica II Esercizi per le vacanze pasquali Corso di laurea in Ingegneria Meccanica. A.A. 2008-2009. Esercizio 1. Stabilire se la funzione reale f di due variabili reali, definita come sin(
Analisi Matematica II Esercizi per le vacanze pasquali Corso di laurea in Ingegneria Meccanica. A.A. 2008-2009. Esercizio 1. Stabilire se la funzione reale f di due variabili reali, definita come sin(
ax 1 + bx 2 + c = 0, r : 2x 1 3x 2 + 1 = 0.
 . Rette in R ; circonferenze. In questo paragrafo studiamo le rette e le circonferenze in R. Ci sono due modi per descrivere una retta in R : mediante una equazione cartesiana oppure mediante una equazione
. Rette in R ; circonferenze. In questo paragrafo studiamo le rette e le circonferenze in R. Ci sono due modi per descrivere una retta in R : mediante una equazione cartesiana oppure mediante una equazione
Tutorato di Complementi di Analisi Matematica e Statistica Parte di Analisi 6 e 10 aprile 2017
 Tutorato di Complementi di Analisi Matematica e Statistica Parte di Analisi 6 e 10 aprile 2017 Esercizi: serie di potenze e serie di Taylor 1 Date le serie di potenze a.) n=2 ln(n) n 3 (x 5)n b.) n=2 ln(n)
Tutorato di Complementi di Analisi Matematica e Statistica Parte di Analisi 6 e 10 aprile 2017 Esercizi: serie di potenze e serie di Taylor 1 Date le serie di potenze a.) n=2 ln(n) n 3 (x 5)n b.) n=2 ln(n)
DERIVATA DI UNA FUNZIONE REALE. In quanto segue denoteremo con I un intervallo di IR e con f una funzione di I in IR.
 DERIVATA DI UNA FUNZIONE REALE 1. Definizioni. In quanto segue denoteremo con I un intervallo di IR e con f una funzione di I in IR. DEFINIZIONE 1. Sia x 0 un elemento di I. Per ogni x (I \ {x 0 }) consideriamo
DERIVATA DI UNA FUNZIONE REALE 1. Definizioni. In quanto segue denoteremo con I un intervallo di IR e con f una funzione di I in IR. DEFINIZIONE 1. Sia x 0 un elemento di I. Per ogni x (I \ {x 0 }) consideriamo
25 IL RAPPORTO INCREMENTALE - DERIVATE
 25 IL RAPPORTO INCREMENTALE - DERIVATE Definizione Sia f una funzione reale di variabile reale. Allora, dati x, y domf con x y, si definisce il rapporto incrementale di f tra x e y come P f (x, y = f(x
25 IL RAPPORTO INCREMENTALE - DERIVATE Definizione Sia f una funzione reale di variabile reale. Allora, dati x, y domf con x y, si definisce il rapporto incrementale di f tra x e y come P f (x, y = f(x
Autovalori e autovettori, matrici simmetriche e forme quadratiche (cenni) (prof. M. Salvetti)
 Autovalori e autovettori, matrici simmetriche e forme quadratiche (cenni) (prof. M. Salvetti) April 14, 2011 (alcune note non complete sugli argomenti trattati: eventuali completamenti saranno aggiunti)
Autovalori e autovettori, matrici simmetriche e forme quadratiche (cenni) (prof. M. Salvetti) April 14, 2011 (alcune note non complete sugli argomenti trattati: eventuali completamenti saranno aggiunti)
ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classi 5A-5B PROGRAMMA DI MATEMATICA
 ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classi 5A-5B PROGRAMMA DI MATEMATICA PRIMA PARTE Intervallo limitato di numeri reali Dati due numeri reali a e b, con a
ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classi 5A-5B PROGRAMMA DI MATEMATICA PRIMA PARTE Intervallo limitato di numeri reali Dati due numeri reali a e b, con a
Programmazione Non Lineare
 Capitolo 1 Programmazione Non Lineare 1.1 Introduzione Un problema di ottimizzazione viene definito come la minimizzazione o la massimizzazione di una funzione a valori reali su un insieme specificato.
Capitolo 1 Programmazione Non Lineare 1.1 Introduzione Un problema di ottimizzazione viene definito come la minimizzazione o la massimizzazione di una funzione a valori reali su un insieme specificato.
CALENDARIO BOREALE 1 EUROPA 2015 QUESITO 1
 www.matefilia.it Indirizzi: LI0, EA0 SCIENTIFICO; LI0 - SCIENTIFICO - OPZIONE SCIENZE APPLICATE CALENDARIO BOREALE EUROPA 05 QUESITO La funzione f(x) è continua per x [ 4; 4] il suo grafico è la spezzata
www.matefilia.it Indirizzi: LI0, EA0 SCIENTIFICO; LI0 - SCIENTIFICO - OPZIONE SCIENZE APPLICATE CALENDARIO BOREALE EUROPA 05 QUESITO La funzione f(x) è continua per x [ 4; 4] il suo grafico è la spezzata
Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler)
 Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler) Studio di una funzione Funzioni crescenti e decrescenti Una funzione f é crescente nell intervallo (a, b) se
Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler) Studio di una funzione Funzioni crescenti e decrescenti Una funzione f é crescente nell intervallo (a, b) se
(P x) (P y) = x P t (P y) = x (P t P )y = x y.
 Matrici ortogonali Se P è una matrice reale n n, allora (P x) y x (P t y) per ogni x,y R n (colonne) Dim (P x) y (P x) t y (x t P t )y x t (P t y) x (P t y), CVD Ulteriori caratterizzazioni delle matrici
Matrici ortogonali Se P è una matrice reale n n, allora (P x) y x (P t y) per ogni x,y R n (colonne) Dim (P x) y (P x) t y (x t P t )y x t (P t y) x (P t y), CVD Ulteriori caratterizzazioni delle matrici
A Analisi Matematica 2 (Corso di Laurea in Informatica) Simulazione compito d esame
 COGNOME NOME Matr. Firma dello studente A Analisi Matematica (Corso di Laurea in Informatica) Simulazione compito Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni
COGNOME NOME Matr. Firma dello studente A Analisi Matematica (Corso di Laurea in Informatica) Simulazione compito Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni
Università degli Studi di Palermo Facoltà di Economia. CdS Sviluppo Economico e Cooperazione Internazionale. Appunti del corso di Matematica
 Università degli Studi di Palermo Facoltà di Economia CdS Sviluppo Economico e Cooperazione Internazionale Appunti del corso di Matematica 02 - I Numeri Reali Anno Accademico 2013/2014 D. Provenzano, M.
Università degli Studi di Palermo Facoltà di Economia CdS Sviluppo Economico e Cooperazione Internazionale Appunti del corso di Matematica 02 - I Numeri Reali Anno Accademico 2013/2014 D. Provenzano, M.
ESERCITAZIONE SUI PUNTI STAZIONARI DI FUNZIONI LIBERE E SULLE FUNZIONI OMOGENEE
 ESERCITAZIONE SUI PUNTI STAZIONARI DI FUNZIONI LIBERE E SULLE FUNZIONI OMOGENEE 1 Funzioni libere I punti stazionari di una funzione libera di più variabili si ottengono risolvendo il sistema di equazioni
ESERCITAZIONE SUI PUNTI STAZIONARI DI FUNZIONI LIBERE E SULLE FUNZIONI OMOGENEE 1 Funzioni libere I punti stazionari di una funzione libera di più variabili si ottengono risolvendo il sistema di equazioni
IL TEOREMA DEGLI ZERI Una dimostrazione di Ezio Fornero
 IL TEOREMA DEGLI ZERI Una dimostrazione di Ezio Fornero Il teorema degli zeri è fondamentale per determinare se una funzione continua in un intervallo chiuso [ a ; b ] si annulla in almeno un punto interno
IL TEOREMA DEGLI ZERI Una dimostrazione di Ezio Fornero Il teorema degli zeri è fondamentale per determinare se una funzione continua in un intervallo chiuso [ a ; b ] si annulla in almeno un punto interno
Ottimizzazione libera
 Capitolo 1 Ottimizzazione libera Sia f una funzione a valori reali definita sull intervallo E R n. Diciamo che f ha in a E un massimo relativo se B r (a) : x E B r (a), f(x) f(a) In particolare ci occuperemo
Capitolo 1 Ottimizzazione libera Sia f una funzione a valori reali definita sull intervallo E R n. Diciamo che f ha in a E un massimo relativo se B r (a) : x E B r (a), f(x) f(a) In particolare ci occuperemo
Domande da 6 punti. Prima parte del programma
 Domande da 6 punti Prima parte del programma Domanda. Dare la definizione di arco di curva continua, di sostegno di una curva, di curva chiusa, di curva semplice e di curva piana fornendo qualche esempio.
Domande da 6 punti Prima parte del programma Domanda. Dare la definizione di arco di curva continua, di sostegno di una curva, di curva chiusa, di curva semplice e di curva piana fornendo qualche esempio.
Fissiamo nello spazio un sistema di riferimento cartesiano ortogonale O, x, y, z, u.
 Fissiamo nello spazio un sistema di riferimento cartesiano ortogonale O, x, y, z, u. Definizione Una quadriche è il luogo dei punti, propri o impropri, reali o immaginari, che con le loro coordinate omogenee
Fissiamo nello spazio un sistema di riferimento cartesiano ortogonale O, x, y, z, u. Definizione Una quadriche è il luogo dei punti, propri o impropri, reali o immaginari, che con le loro coordinate omogenee
Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005
 Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005 Prova orale il: Docente: Determinare, se esistono, il massimo ed il minimo assoluto della funzione
Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005 Prova orale il: Docente: Determinare, se esistono, il massimo ed il minimo assoluto della funzione
Derivate. Rette per uno e per due punti. Rette per uno e per due punti
 Introduzione Rette per uno e per due punti Rette per uno e per due punti Rette secanti e tangenti Derivata d una funzione in un punto successive Derivabilità a destra e a sinistra Rette per uno e per due
Introduzione Rette per uno e per due punti Rette per uno e per due punti Rette secanti e tangenti Derivata d una funzione in un punto successive Derivabilità a destra e a sinistra Rette per uno e per due
ESERCIZI DI ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 2006/2007
 ESERCIZI I ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 006/007 1 FUNZIONI IN UE VARIABILI (I parte) Insiemi di definizione eterminare gli insiemi di definizione delle seguenti funzioni in due
ESERCIZI I ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 006/007 1 FUNZIONI IN UE VARIABILI (I parte) Insiemi di definizione eterminare gli insiemi di definizione delle seguenti funzioni in due
Analisi Matematica 1 e Matematica 1 Geometria Analitica: Rette
 Analisi Matematica 1 e Matematica 1 Geometria Analitica: Rette Annalisa Amadori e Benedetta Pellacci amadori@uniparthenope.it pellacci@uniparthenope.it Università di Napoli Parthenope Contenuti Nel Piano
Analisi Matematica 1 e Matematica 1 Geometria Analitica: Rette Annalisa Amadori e Benedetta Pellacci amadori@uniparthenope.it pellacci@uniparthenope.it Università di Napoli Parthenope Contenuti Nel Piano
SPAZI TOPOLOGICI. La nozione di spazio topologico è più generale di quella di spazio metrizzabile.
 SPAZI TOPOLOGICI La nozione di spazio topologico è più generale di quella di spazio metrizzabile. Definizione 1 Uno spazio topologico (X, τ) è una coppia costituita da un insieme X e da una famiglia τ
SPAZI TOPOLOGICI La nozione di spazio topologico è più generale di quella di spazio metrizzabile. Definizione 1 Uno spazio topologico (X, τ) è una coppia costituita da un insieme X e da una famiglia τ
Mauro Sassetti. Calcolo differenziale ed integrale. per funzioni di due variabili reali.
 Mauro Sassetti Calcolo differenziale ed integrale per funzioni di due variabili reali. Breve esposizione dei principali risultati. Parte prima : Calcolo differenziale 1. Generalità 1.1 L insieme R come
Mauro Sassetti Calcolo differenziale ed integrale per funzioni di due variabili reali. Breve esposizione dei principali risultati. Parte prima : Calcolo differenziale 1. Generalità 1.1 L insieme R come
Prima parte: DOMINIO E INSIEMI DI LIVELLO
 FUNZIONI DI DUE VARIABILI 1 Prima parte: DOMINIO E INSIEMI DI LIVELLO Domini e disequazioni in due variabili. Insiemi di livello. Elementi di topologia insiemi aperti, chiusi, limitati, convessi, connessi
FUNZIONI DI DUE VARIABILI 1 Prima parte: DOMINIO E INSIEMI DI LIVELLO Domini e disequazioni in due variabili. Insiemi di livello. Elementi di topologia insiemi aperti, chiusi, limitati, convessi, connessi
1 Curve. Indice 1. Curve 2. Limiti
 Alcune Note di Calcolo Differenziale ed Integrale Multidimensionale per il corso di Analisi Matematica II a.a. 2011-12 A. Visintin Facoltà di Ingegneria di Trento Premessa. Questo scritto raccoglie alcune
Alcune Note di Calcolo Differenziale ed Integrale Multidimensionale per il corso di Analisi Matematica II a.a. 2011-12 A. Visintin Facoltà di Ingegneria di Trento Premessa. Questo scritto raccoglie alcune
Curve n d. f(x, y)=l. x,yda,b
 Curve n d Linee di livello: curva che si ottiene sezionando il grafico di una funzione n d con dei piani del tipo z=k, e quindi paralleli al piano xy e perpendicolari all asse z. Matematicamente si ottengono
Curve n d Linee di livello: curva che si ottiene sezionando il grafico di una funzione n d con dei piani del tipo z=k, e quindi paralleli al piano xy e perpendicolari all asse z. Matematicamente si ottengono
Funzioni vettoriali di variabile scalare
 Capitolo 11 Funzioni vettoriali di variabile scalare 11.1 Curve in R n Abbiamo visto (capitolo 2) come la posizione di un punto in uno spazio R n sia individuata mediante le n coordinate di quel punto.
Capitolo 11 Funzioni vettoriali di variabile scalare 11.1 Curve in R n Abbiamo visto (capitolo 2) come la posizione di un punto in uno spazio R n sia individuata mediante le n coordinate di quel punto.
Alcuni esercizi: funzioni di due variabili e superfici
 ANALISI MATEMATICA T- (C.d.L. Ing. per l ambiente e il territorio) - COMPL. DI ANALISI MATEMATICA (A-K) (C.d.L. Ing. Civile) A.A.008-009 - Prof. G.Cupini Alcuni esercizi: funzioni di due variabili e superfici
ANALISI MATEMATICA T- (C.d.L. Ing. per l ambiente e il territorio) - COMPL. DI ANALISI MATEMATICA (A-K) (C.d.L. Ing. Civile) A.A.008-009 - Prof. G.Cupini Alcuni esercizi: funzioni di due variabili e superfici
REGISTRO DELLE ESERCITAZIONI
 UNIVERSITA DEGLI STUDI DI GENOVA FACOLTA DI SCIENZE MATEMATICHE, FISICHE E NATURALI REGISTRO DELLE ESERCITAZIONI del Corso UFFICIALE di GEOMETRIA A tenute dal prof. Domenico AREZZO nell anno accademico
UNIVERSITA DEGLI STUDI DI GENOVA FACOLTA DI SCIENZE MATEMATICHE, FISICHE E NATURALI REGISTRO DELLE ESERCITAZIONI del Corso UFFICIALE di GEOMETRIA A tenute dal prof. Domenico AREZZO nell anno accademico
