Complessità computazionale
|
|
|
- Biaggio Elia
- 8 anni fa
- Visualizzazioni
Transcript
1 1
2 Introduzione alla complessità computazionale Un problema spesso può essere risolto utilizzando algoritmi diversi Come scegliere il migliore? La bontà o efficienza di un algoritmo si misura in base alla quantità minima di risorse sufficienti per il calcolo: Il tempo richiesto per eseguire le azioni elementari Lo spazio necessario per memorizzare e manipolare i dati La risorsa di maggior interesse è il tempo 2
3 Misurare il tempo di calcolo Non è significativo misurare il tempo di calcolo di un algoritmo in base al numero di secondi richiesti per l esecuzione su un elaboratore di un programma che lo descriva Infatti, tale tempo dipende da: i dati di ingresso il linguaggio in cui è scritto il programma la qualità della traduzione in sequenze di bit la velocità dell elaboratore Una buona misura dell efficienza di un algoritmo deve prescindere dal calcolatore utilizzato Occorre una misura astratta che tenga conto del metodo di risoluzione con cui l algoritmo effettua la computazione 3
4 Misurare il tempo di calcolo La complessità dei problemi da risolvere dipende dalla dimensione dei dati in ingresso Il tempo di calcolo si può quindi esprimere come: il numero complessivo di operazioni elementari in funzione della dimensione n dei dati in ingresso Le operazioni elementari sono quelle: aritmetiche logiche di confronto di assegnamento Solitamente, il numero di operazioni considerate è valutato nel caso peggiore, ossia nel caso di dati in ingresso più sfavorevoli tra tutti quelli di dimensione n 4
5 Calcolo dell efficienza: un esempio Trovare l elemento minimo in un insieme di n numeri {x 1,x 2,,x n } Soluzione: 1. considero x 1 come candidato ad essere il minimo 2. confronto il candidato con tutti gli altri elementi e se trovo un elemento più piccolo lo faccio diventare il nuovo candidato 3. al termine dei confronti, il candidato corrente è sicuramente il minimo Complessivamente sono stati eseguiti n confronti L efficienza dell algoritmo è quindi direttamente proporzionale alla dimensione dell input 5
6 Calcolo dell efficienza: un altro esempio Ordinare in ordine crescente un insieme di n numeri {x 1,x 2,,x n } Soluzione: 1. per i = 1,2,,n ripeti le seguenti operazioni: 2. trova l elemento minimo nel sottoinsieme {x i,x i+1,,x n } 3. scambialo con x i Per n volte bisogna trovare il minimo su insiemi sempre più piccoli Si eseguono n + (n-1) + (n-2) n 2 operazioni 6
7 Efficienza degli algoritmi L efficienza di un algoritmo si può esprimere mediante una funzione f(n) della variabile n: esprime il numero di operazioni compiute per un problema di dimensione n rappresenta la complessità computazionale dell algoritmo Se A e B sono due algoritmi che risolvono lo stesso problema e se f A (n) e f B (n) esprimono la complessità dei due algoritmi allora: A è migliore di B se, al crescere di n, risulta f A (n) f B (n) 7
8 Efficienza degli algoritmi: esempio Supponiamo di avere due algoritmi diversi per ordinare n numeri interi Il primo algoritmo riesce ad ordinare gli n numeri con n 2 istruzioni Il secondo con n * log n istruzioni Supponiamo che l esecuzione di un istruzione avvenga in un sec (10-6 sec) Tempo di esecuzione: n=10 n=10000 n=10 6 n 2 op. n*log n op. 0,1 msec 100 sec (1,5 min) 10 6 sec ( 12 gg.) 23 sec 92 msec 13,8 sec 8
9 Quali fattori influenzano il tempo di esecuzione? L algoritmo scelto per risolvere il problema La dimensione dell input La velocità della macchina Cerchiamo un modello di calcolo per la complessità temporale che tenga conto di Algoritmo Dimensione dell input 9
10 Dipendenza dalla tecnologia Il miglioramento della tecnologia non riduce significativamente il tempo di esecuzione di alcune importanti classi di algoritmi: Algoritmi di Ricerca (n operazioni) Algoritmi di Ordinamento (n 2 operazioni) Algoritmi Decisionali (2 n operazioni) Esempio: Complessità Tecnologia attuale 100 volte più veloce 1000 volte più veloce n N 1 N 1 * 100 N 1 * 1000 n 2 N 2 N 2 * 10 N 2 * 31,6 2 n N 3 N 3 + 6,64 N 3 + 9,97 10 N = numero dati gestiti in un lasso di tempo t (dipendente dalla complessità) Ad es.: 2 N operazioni (op.) nel tempo t. Con tecnologia 100 volte più veloce 2 N op. in t/100, quindi 2 N *100 op. nel tempo t, 2 N *2 6,64 = 2 N+6,64 op. nel tempo t.
11 Il modello di costo Per giungere a un modello di costo è necessario definire: Dimensione dell input Istruzione di costo unitario (passo base) Calcolo della complessità in numero di passi base Complessità Nel caso migliore Nel caso medio Nel caso peggiore Complessità di programmi strutturati Complessità asintotica 11
12 Dimensione dell input A seconda del problema, per dimensione dell input si indicano cose diverse: La grandezza di un numero (es: problemi di calcolo) Quanti elementi sono in ingresso (es: ordinamento) Quanti bit compongono un numero Indipendentemente dal tipo di dati, indichiamo con n la dimensione dell input 12
13 Operazione di costo unitario È un operazione la cui esecuzione non dipende dai valori e dai tipi delle variabili Assegnamento e operazioni aritmetiche di base Accesso ad un elemento qualsiasi di un vettore residente in memoria centrale Valutazione di un espressione booleana qualunque Istruzioni di input/output In seguito, si indicherà un operazione di costo unitario con il termine passo base 13
14 Modello semplificato Il costo del test di una condizione booleana composta di più condizioni booleane semplici è sempre minore o uguale a K volte il costo del test di una condizione semplice, dove K è una opportuna costante numerica, quindi, semplificando, consideriamo comunque un costo unitario Lo stesso vale per le operazioni aritmetiche composte Non si considerano, in questa sede, operazioni di accesso ai file Un modello più sofisticato dovrebbe inoltre: differenziare tra aritmetica intera e reale (floating point) tenere conto di come il compilatore traduce le istruzioni di alto livello (compilatori ottimizzanti) considerare l architettura di una specifica macchina 14
15 Calcolo della complessità in numero di passi base i = 0; while(i < n) i = i+1; Assegnamento esterno al ciclo: i=0; Ciclo while: si compone di un test (i<n) e di un corpo costituito da un operazione di assegnamento (i=i+1) Quindi: Assegnamento esterno: 1 Numero di test: n+1 Assegnamenti interni: 1*n Numero totale di passi base: 2*n+2 15
16 Calcolo della complessità in numero di passi base (2) i = 0; while(i < n){ i = i+1; j = j*3 + 42; } Il corpo del ciclo si compone di 2 passi base: Assegnamento esterno: 1 Numero di test: n+1 Assegnamenti interni: 2*n Numero totale di passi base: 3*n+2 16
17 Calcolo della complessità in numero di passi base (3) i = 0; while(i < 2*n){ i = i+1; j = j* ; } Il test viene eseguito 2*n+1 volte e il corpo è costituito da due passi base: Assegnamento esterno: 1 Numero di test: 2*n+1 Assegnamenti interni: 2*(2*n) Numero totale di passi base: 6*n+2 17
18 Cicli annidati i=0; while(i<n){ for(j=0; j<n; j++){... System.out.println("Ciao!");... } i=i+1; } Assegnamento esterno 1+ Test while: n+1+ Cicli while: n*( Assegnamento iniziale for: 1+ Controlli ciclo for: n+1+ Incrementi ciclo for: n+ Scritture: n+ Assegnamento: 1) Totale passi base 2+4*n+3*n 2 n+1 test un ciclo for per ogni while una scrittura per ogni for un assegnamento per ogni while 18
19 Il costo può dipendere dal valore dei dati in ingresso! Attenzione: esprimere la complessità in funzione dei dati in ingresso! i = 0; while(i*i < n) i = i+1; Quanti test vengono eseguiti? Quante volte viene eseguito il ciclo? 19
20 Il costo può dipendere dal valore dei dati in ingresso! Supponiamo n=9: i=0 i 2 =0 <9? sì i=1 i 2 =1 <9? sì i=2 i 2 =4 <9? sì i=3 i 2 =9 <9? no fine ciclo i = 0; while(i*i < n) i = i+1; Il ciclo viene eseguito 3 = 9 volte, eseguendo 4 = 9+1 test La complessità in passi base di questo blocco è dunque: 1 + ( n+1) + n = 2 + 2* n (con arrotondamento all intero superiore) 20
21 Dipendenza del costo dal valore dei dati in ingresso Due tipici esempi sono dati da: 1. if(condizione){ corpo istruzioni } 2. if(condizione) { corpo1 } else { corpo2 } Nel caso 1) il costo è dato dal costo di un test più: Il costo di esecuzione del corpo istruzioni se la condizione è vera Nessun costo aggiuntivo se la condizione è falsa Nel caso 2) il costo è dato dal costo di un test più: Il costo di esecuzione del corpo1 se la condizione è vera Il costo di esecuzione del corpo2 se la condizione è falsa 21
22 Dipendenza del costo dal valore dei dati in ingresso for(i=0; i<n; i++){ if(condizione){ /* if annidato */ <corpo1> } else{ <corpo2> } } Anche in un caso di questo tipo il costo del ciclo dipende non solo dalla dimensione dei dati, ma anche dal loro valore: All interno di ogni ciclo il costo del blocco <if else> può variare a seconda del valore assunto dalla condizione 22
23 Complessità nei casi migliore, peggiore e medio Supponiamo di avere il seguente vettore A contenente 14 elementi: A = {3, -2, 0, 7, 5, 4, 0, 6, -3, -1, 9, 12, 20, 5} La dimensione dell input è la lunghezza dell array (n=14 nell esempio) Cerchiamo l elemento "6" con un algoritmo di ricerca lineare: i = 0; while(i<14 && A[i]!= 6) i = i+1; Il cui costo corrisponde a: 1 assegnamento + 8 test + 7 cicli = 16 passi base 23
24 Complessità nei casi migliore, peggiore e medio A = {3, -2, 0, 7, 5, 4, 0, 6, -3, -1, 9, 12, 20, 5} Se avessimo cercato l elemento "13"? Poiché tale elemento non è presente nel vettore, avremmo dovuto scorrere interamente il vettore con una complessità: 1 + (n+1) + n = 2 + 2*n passi base (30 passi nell esempio) 24
25 Ricerca di un elemento in un vettore Per il problema della ricerca in un vettore non ordinato, bisogna distinguere 2 casi: Si sa che l elemento cercato è presente nel vettore Non si sa se l elemento cercato sia presente nel vettore 25
26 Prima situazione (elemento presente) Si possono distinguere 3 casi: Caso migliore: l elemento cercato è in prima posizione. Il costo effettivo dell algoritmo è 2 Caso peggiore: l elemento cercato è in ultima posizione. Il costo effettivo è 2*n Caso medio: consideriamo un ipotesi di distribuzione uniforme, ovvero che i valori siano disposti casualmente nel vettore Poiché i valori sono distribuiti uniformemente, la probabilità di trovare l elemento cercato in posizione i nel vettore (di dimensione n) è: Pr(i) = 1/n 26
27 Prima situazione (elemento presente) C(i) = i 27
28 Seconda situazione (non si sa se elemento sia presente) In questa situazione non si può assegnare un valore di probabilità come nel caso precedente Quindi, in questa situazione: Caso migliore: è la presenza dell elemento nel vettore Caso peggiore: è l assenza. Implica il costo di scansione dell intero vettore Caso medio: si può ricavare, se si dispone di una stima della probabilità di presenza, con una somma pesata del caso medio della prima situazione e del caso di assenza 28
29 Complessità nei casi migliore, peggiore e medio Già dai due casi visti nell algoritmo di ricerca sequenziale, si può capire che il concetto di «caso peggiore», «caso migliore» e «caso medio» può dipendere da: Problema ed algoritmo Valori dei dati Nel seguito, salvo diversa indicazione, verrà considerata la complessità nel caso peggiore 29
30 Programmi strutturati Nel calcolo della complessità di un programma strutturato si deve: Calcolare la complessità di ogni procedura/funzione/metodo Per ogni chiamata a procedura/funzione/metodo, aggiungere la complessità della/o stessa/o al costo globale del programma 30
31 Complessità di programmi strutturati public static void main(string[] args) { Scanner scanner=new Scanner(System.in); System.out.println("Quante stelle per riga? "); int n=scanner.nextint(); System.out.println("Quante righe di stelle? "); int m=scanner.nextint(); for(int j=0; j<m; j++) stars(n); } public static void stars(int ns) { System.out.println(); for(int i=0; i<ns; i++) System.out.print('*'); } 31
32 Complessità dell esempio (1) public static void stars(int ns) { System.out.println(); for(int i=0; i<ns; i++) System.out.print('*'); } Complessità di stars: 1 istruzione di output 1 assegnamento ns+1 confronti e ns incrementi ns cicli 1 istruzione di output per ogni iterazione Complessità totale: 3 + 3*ns 32
33 Complessità dell esempio (2) public static void main(string[] args) { Scanner scanner=new Scanner(System.in); System.out.println("Quante stelle per riga? "); int n=scanner.nextint(); System.out.println("Quante righe di stelle? "); int m=scanner.nextint(); for(int j=0; j<m; j++) stars(n); } Complessità del main: 4 istruzione di input/output 1 assegnamento m+1 confronti e m incrementi m cicli 1 chiamata di metodo per ogni iterazione Complessità totale: m m + m*(3 + 3*n) = 6 + 5*m + 3*m*n 33
34 Complessità dell esempio (3) Note: Se in un algoritmo la dimensione dell input è definita da più parametri, come nell esempio precedente, bisogna tenere conto di tutti Il costo di esecuzione di una procedura o funzione (metodo) può dipendere dai parametri che vengono forniti in ingresso Una stessa procedura/funzione/metodo può essere chiamata, all interno del programma principale, con dati diversi (input di dimensione diversa) 34
35 Altro esempio public static void main(string[] args) { Scanner scanner=new Scanner(System.in); System.out.println("Quante righe di stelle? "); int m=scanner.nextint(); for(int j=1; j<=m; j++) stars(j); } 35
36 Altro esempio public static void main(string[] args) { Scanner scanner=new Scanner(System.in); System.out.println("Quante potenze vuoi stampare? "); int n=scanner.nextint(); System.out.println("Base delle potenze? "); int b=scanner.nextint(); for(int exp=0; exp<n; exp++) potenza(b, exp); } public static int potenza(int base, int exp) { int ris=1; for(int i=0; i<exp; i++) ris*=base; return ris; } 36
37 Complessità dell esempio (1) public static int potenza(int base, int exp) { int ris=1; for(int i=0; i<exp; i++) ris*=base; return ris; } Complessità della funzione potenza: 3 + 3*exp 37
38 Complessità dell esempio (2) public static void main(string[] args) { Scanner scanner=new Scanner(System.in); System.out.println("Quante potenze vuoi stampare? "); int n=scanner.nextint(); System.out.println("Base delle potenze? "); int b=scanner.nextint(); for(int exp=0; exp<n; exp++) potenza(b, exp); } Complessità del main: main: 6 + 2*n + 1ª chiamata: 3 + 3*0 + 2ª chiamata: 3 + 3*1 + jª chiamata: 3 + 3*(j-1) + nª chiamata: 3 + 3*(n-1) Totale: 6 + 2*n + n 1 j= j = 6 + 7*n/2 + 3*n 2 /2 38
39 Complessità asintotica Supponiamo di avere, per uno stesso problema, sette algoritmi diversi con diversa complessità. Supponiamo che un passo base venga eseguito in un microsecondo (10-6 sec) Tempi di esecuzione (in secondi) dei sette algoritmi per diversi valori di n Complessità n=10 n=100 n=1000 n=10 6 n 3* * n+5 2*n n 2 n 2 +n 15* sec 2*10-5 2*10-4 2* sec sec 10 6 ( 12 gg.) sec 10 6 ( 12 gg.) n 3 2 n sec 10 5 ( 1 g) ( 300 secoli) *10 14 secoli 3* secoli 3* secoli 39
40 Osservazioni Per piccole dimensioni dell input, osserviamo che tutti gli algoritmi hanno tempi di risposta non significativamente differenti L algoritmo di complessità esponenziale ha tempi di risposta ben diversi da quelli degli altri algoritmi (migliaia di miliardi di secoli contro secondi, ecc.) Per grandi dimensioni dell input (n=10 6 ), i sette algoritmi di partizionano nettamente in cinque classi in base ai tempi di risposta: Algoritmo n frazioni di secondo Algoritmo n+5, 2*n secondi Algoritmo n 2, n 2 +n giorni Algoritmo n 3 secoli Algoritmo 2 n miliardi di secoli 40
41 Gli «O grandi» È un criterio matematico per partizionare gli algoritmi in classi di complessità Si dice che una funzione f(n) è di ordine g(n) e si scrive: f(n) = O(g(n)) se esiste una costante numerica C positiva tale che valga, salvo al più per un numero finito di valori di n, la seguente condizione: f(n) C g(n) Se g(n) non è identicamente nulla (fatto assolutamente certo nell esecuzione di un algoritmo), la condizione precedente può essere espressa come: f(n) / g(n) C ovvero la funzione f(n)/g(n) è limitata 41
42 Gli «O grandi» Esempi 2*n+5 = O(n) poiché 2*n+5 7*n per ogni n 2*n+5 = O(n 2 ) poiché 2*n+5 n 2 per n 4 2*n+5 = O(2 n ) poiché 2*n+5 2 n per n 4 Esempi inversi: n = O(2*n+5)? sì n 2 = O(n)? no, n 2 /n = n, non limitata e n = O(n)? no, e n /n n 2 /n = n, non limitata 42
43 Ordinamento fra gli «O grandi» È possibile definire un criterio di ordinamento fra gli «O grandi» f(n) è più piccola di (di ordine inferiore a) g(n) se valgono le due condizioni seguenti: f(n) = O(g(n)) g(n) non è O(f(n)) Esempi: n è di ordine inferiore a 2n +5 (e quindi a n) (2n +5)/ n = 2 n + 5/ n 2 n + 5 che non è limitata n è di ordine inferiore a e n n = O(e n ), e n non è O(n) 43
44 Complessità asintotica Si dice che f(n) ha complessità asintotica g(n) se valgono le seguenti condizioni: f(n) = O(g(n)) g(n) è la più piccola di tutte le funzioni che soddisfano la prima condizione Esempi: 2n +5 complessità asintotica n (lineare) 3n 2 +5n complessità asintotica n 2 (quadratica) 4*2 n complessità asintotica 2 n (esponenziale di base 2) 3n + 2 n + 5 n complessità asintotica 5 n (esponenziale di base 5) 2 n + 5n + n! + 5 n complessità asintotica n n n (fattoriale) 44
45 Dalla complessità in passi base alla complessità asintotica numero passi base 3n + 2 complessità asintotica n 2n 2 + 2n + 2 n n n 4 + 2m + 2m*n m*n In pratica, la complessità asintotica è definita dal blocco di complessità maggiore Non contano le costanti, né additive, né moltiplicative
46 Esempi 7*3 n ha complessità 3 n (7 è costante moltiplicativa) n 2 +5 ha complessità n 2 (5 è costante additiva) nella funzione di complessità 4 + 2m + 2m*n domina il termine «quadratico» m*n Osservazioni: Le ipotesi semplificative del modello di costo introdotto e il metodo di calcolo della complessità asintotica sono ipotesi molto forti. Si pensi, ad esempio, ad un algoritmo di complessità asintotica n 2 che abbia costo, espresso in numero di passi base, 7n 2 + 2n + 3 Nel nostro modello trascuriamo le costanti e i termini di ordine inferiore ma, nelle applicazioni reali, è ben diverso che un algoritmo termini in un giorno oppure in più di una settimana!!! Basti pensare ad operazioni bancarie, ad analisi ospedaliere, ad esperimenti fisici automatizzati, ecc. 46
47 Algebra degli «O grandi» In precedenza, abbiamo visto due esempi di calcolo della complessità in numero di passi base per programmi a blocchi Definiamo ora, tramite l algebra degli «O grandi», un criterio per il calcolo della complessità asintotica di un programma strutturato In un programma strutturato a blocchi si possono presentare due situazioni: blocchi in sequenza blocchi annidati 47
48 Blocchi in sequenza i=0; while(i<n) { stampastelle(i); i=i+1; } for(i=0; i<2*n; i++) numero = scanner.nextint(); Sia g 1 (n) la complessità del primo blocco e g 2 (n) la complessità del secondo. La complessità globale è: O(g 1 (n)+g 2 (n)) = O(max{g 1 (n),g 2 (n)}) La complessità di un blocco costituito da più blocchi in sequenza è quella del blocco di complessità maggiore 48
49 Blocchi annidati for(i=0; i<n; i++) j = scanner.nextint(); System.out.print(j*j); do{ n = scanner.nextint(); j=j+1; }while(j<=n); } Sia g 1 (n) la complessità del blocco esterno e g 2 (n) la complessità del blocco interno. La complessità globale è: O(g 1 (n)*g 2 (n)) = O(g 1 (n))* O(g 2 (n)) La complessità di un blocco costituito da più blocchi annidati è data dal prodotto delle complessità dei blocchi componenti 49
50 Utilità dell algebra degli «O grandi» Con il concetto di «O grande» e le due operazioni definite dall algebra degli «O grandi» si può calcolare la complessità di qualsiasi algoritmo strutturato senza conoscerne preventivamente la complessità in passi base Esempio: ricerca lineare in un vettore public boolean cercaelemento(int[] V, int n, int el){ for(int i=0; i<n; i++) if(v[i]==el) return true; return false; } Complessità di cercaelemento: Caso peggiore: 2 + 3n Asintotica: n 50
51 Prodotto di matrici float A[]=new float[n][m], B[]=new float[m][p], C[]=new float[n][p]; for(int i=0; i<n; i++) for(int j=0; j<p; j++){ C[i][j]=0; for(int k=0; k<m; k++) C[i][j] += A[i][k]*B[k][j]; } Complessità asintotica del programma: N*M*P 51
Bontà dei dati in ingresso
 COMPLESSITÀ COMPUTAZIONALE DEGLI ALGORITMI Fondamenti di Informatica a.a.2006/07 Prof. V.L. Plantamura Dott.ssa A. Angelini Il costo puo' dipendere dal valore dei dati in ingresso Un tipico esempio è dato
COMPLESSITÀ COMPUTAZIONALE DEGLI ALGORITMI Fondamenti di Informatica a.a.2006/07 Prof. V.L. Plantamura Dott.ssa A. Angelini Il costo puo' dipendere dal valore dei dati in ingresso Un tipico esempio è dato
Algebra di Boole: Concetti di base. Fondamenti di Informatica - D. Talia - UNICAL 1. Fondamenti di Informatica
 Fondamenti di Informatica Algebra di Boole: Concetti di base Fondamenti di Informatica - D. Talia - UNICAL 1 Algebra di Boole E un algebra basata su tre operazioni logiche OR AND NOT Ed operandi che possono
Fondamenti di Informatica Algebra di Boole: Concetti di base Fondamenti di Informatica - D. Talia - UNICAL 1 Algebra di Boole E un algebra basata su tre operazioni logiche OR AND NOT Ed operandi che possono
Complessità Computazionale
 Complessità Computazionale Analisi Algoritmi e pseudocodice Cosa significa analizzare un algoritmo Modello di calcolo Analisi del caso peggiore e del caso medio Esempio di algoritmo in pseudocodice INSERTION
Complessità Computazionale Analisi Algoritmi e pseudocodice Cosa significa analizzare un algoritmo Modello di calcolo Analisi del caso peggiore e del caso medio Esempio di algoritmo in pseudocodice INSERTION
Introduzione al MATLAB c Parte 2
 Introduzione al MATLAB c Parte 2 Lucia Gastaldi Dipartimento di Matematica, http://dm.ing.unibs.it/gastaldi/ 18 gennaio 2008 Outline 1 M-file di tipo Script e Function Script Function 2 Costrutti di programmazione
Introduzione al MATLAB c Parte 2 Lucia Gastaldi Dipartimento di Matematica, http://dm.ing.unibs.it/gastaldi/ 18 gennaio 2008 Outline 1 M-file di tipo Script e Function Script Function 2 Costrutti di programmazione
10 - Programmare con gli Array
 10 - Programmare con gli Array Programmazione e analisi di dati Modulo A: Programmazione in Java Paolo Milazzo Dipartimento di Informatica, Università di Pisa http://www.di.unipi.it/ milazzo milazzo di.unipi.it
10 - Programmare con gli Array Programmazione e analisi di dati Modulo A: Programmazione in Java Paolo Milazzo Dipartimento di Informatica, Università di Pisa http://www.di.unipi.it/ milazzo milazzo di.unipi.it
Tipi primitivi. Ad esempio, il codice seguente dichiara una variabile di tipo intero, le assegna il valore 5 e stampa a schermo il suo contenuto:
 Tipi primitivi Il linguaggio Java offre alcuni tipi di dato primitivi Una variabile di tipo primitivo può essere utilizzata direttamente. Non è un riferimento e non ha senso tentare di istanziarla mediante
Tipi primitivi Il linguaggio Java offre alcuni tipi di dato primitivi Una variabile di tipo primitivo può essere utilizzata direttamente. Non è un riferimento e non ha senso tentare di istanziarla mediante
Algoritmo. I dati su cui opera un'istruzione sono forniti all'algoritmo dall'esterno oppure sono il risultato di istruzioni eseguite precedentemente.
 Algoritmo Formalmente, per algoritmo si intende una successione finita di passi o istruzioni che definiscono le operazioni da eseguire su dei dati (=istanza del problema): in generale un algoritmo è definito
Algoritmo Formalmente, per algoritmo si intende una successione finita di passi o istruzioni che definiscono le operazioni da eseguire su dei dati (=istanza del problema): in generale un algoritmo è definito
Programmazione dinamica
 Capitolo 6 Programmazione dinamica 6.4 Il problema della distanza di edit tra due stringhe x e y chiede di calcolare il minimo numero di operazioni su singoli caratteri (inserimento, cancellazione e sostituzione)
Capitolo 6 Programmazione dinamica 6.4 Il problema della distanza di edit tra due stringhe x e y chiede di calcolare il minimo numero di operazioni su singoli caratteri (inserimento, cancellazione e sostituzione)
Informatica 3. Informatica 3. LEZIONE 10: Introduzione agli algoritmi e alle strutture dati. Lezione 10 - Modulo 1. Importanza delle strutture dati
 Informatica 3 Informatica 3 LEZIONE 10: Introduzione agli algoritmi e alle strutture dati Modulo 1: Perchè studiare algoritmi e strutture dati Modulo 2: Definizioni di base Lezione 10 - Modulo 1 Perchè
Informatica 3 Informatica 3 LEZIONE 10: Introduzione agli algoritmi e alle strutture dati Modulo 1: Perchè studiare algoritmi e strutture dati Modulo 2: Definizioni di base Lezione 10 - Modulo 1 Perchè
Algoritmi di Ricerca. Esempi di programmi Java
 Fondamenti di Informatica Algoritmi di Ricerca Esempi di programmi Java Fondamenti di Informatica - D. Talia - UNICAL 1 Ricerca in una sequenza di elementi Data una sequenza di elementi, occorre verificare
Fondamenti di Informatica Algoritmi di Ricerca Esempi di programmi Java Fondamenti di Informatica - D. Talia - UNICAL 1 Ricerca in una sequenza di elementi Data una sequenza di elementi, occorre verificare
Matematica generale CTF
 Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Corso di Matematica per la Chimica
 Dott.ssa Maria Carmela De Bonis a.a. 203-4 I sistemi lineari Generalità sui sistemi lineari Molti problemi dell ingegneria, della fisica, della chimica, dell informatica e dell economia, si modellizzano
Dott.ssa Maria Carmela De Bonis a.a. 203-4 I sistemi lineari Generalità sui sistemi lineari Molti problemi dell ingegneria, della fisica, della chimica, dell informatica e dell economia, si modellizzano
3 CENNI DI TEORIA DELLA COMPLESSITA COMPUTAZIONALE. E. Amaldi Fondamenti di R.O. Politecnico di Milano 1
 3 CENNI DI TEORIA DELLA COMPLESSITA COMPUTAZIONALE E. Amaldi Fondamenti di R.O. Politecnico di Milano 1 Scopo: Stimare l onere computazionale per risolvere problemi di ottimizzazione e di altra natura
3 CENNI DI TEORIA DELLA COMPLESSITA COMPUTAZIONALE E. Amaldi Fondamenti di R.O. Politecnico di Milano 1 Scopo: Stimare l onere computazionale per risolvere problemi di ottimizzazione e di altra natura
Sommario. Definizione di informatica. Definizione di un calcolatore come esecutore. Gli algoritmi.
 Algoritmi 1 Sommario Definizione di informatica. Definizione di un calcolatore come esecutore. Gli algoritmi. 2 Informatica Nome Informatica=informazione+automatica. Definizione Scienza che si occupa dell
Algoritmi 1 Sommario Definizione di informatica. Definizione di un calcolatore come esecutore. Gli algoritmi. 2 Informatica Nome Informatica=informazione+automatica. Definizione Scienza che si occupa dell
La selezione binaria
 Andrea Marin Università Ca Foscari Venezia Laurea in Informatica Corso di Programmazione part-time a.a. 2011/2012 Introduzione L esecuzione di tutte le istruzioni in sequenza può non è sufficiente per
Andrea Marin Università Ca Foscari Venezia Laurea in Informatica Corso di Programmazione part-time a.a. 2011/2012 Introduzione L esecuzione di tutte le istruzioni in sequenza può non è sufficiente per
Corso di Laurea in Ingegneria Gestionale Esame di Informatica a.a. 2010-11 13 settembre 2011
 Cognome Nome Matricola Postazione PC Corso di Laurea in Ingegneria Gestionale Esame di Informatica a.a. 2010-11 13 settembre 2011 Testo Il database di un videonoleggio è costituito da due vettori paralleli.
Cognome Nome Matricola Postazione PC Corso di Laurea in Ingegneria Gestionale Esame di Informatica a.a. 2010-11 13 settembre 2011 Testo Il database di un videonoleggio è costituito da due vettori paralleli.
INTRODUZIONE AGLI ALGORITMI INTRODUZIONE AGLI ALGORITMI INTRODUZIONE AGLI ALGORITMI INTRODUZIONE AGLI ALGORITMI
 INTRODUZIONE AGLI ALGORITMI Prima di riuscire a scrivere un programma, abbiamo bisogno di conoscere un metodo risolutivo, cioè un metodo che a partire dai dati di ingresso fornisce i risultati attesi.
INTRODUZIONE AGLI ALGORITMI Prima di riuscire a scrivere un programma, abbiamo bisogno di conoscere un metodo risolutivo, cioè un metodo che a partire dai dati di ingresso fornisce i risultati attesi.
COMPLESSITÀ COMPUTAZIONALE
 COMPLESSITÀ COMPUTAZIONALE COSA SI INTENDE PER COMPLESSITÀ? La Complessità Temporale, Spaziale, di Input/Output e di Trasmissione COMPLESSITÀ TEMPORALE Ininfluenza della velocità della macchina per molte
COMPLESSITÀ COMPUTAZIONALE COSA SI INTENDE PER COMPLESSITÀ? La Complessità Temporale, Spaziale, di Input/Output e di Trasmissione COMPLESSITÀ TEMPORALE Ininfluenza della velocità della macchina per molte
Università di Torino Facoltà di Scienze MFN Corso di Studi in Informatica. Programmazione I - corso B a.a. 2009-10. prof.
 Università di Torino Facoltà di Scienze MFN Corso di Studi in Informatica Programmazione I - corso B a.a. 009-10 prof. Viviana Bono Blocco 9 Metodi statici: passaggio parametri, variabili locali, record
Università di Torino Facoltà di Scienze MFN Corso di Studi in Informatica Programmazione I - corso B a.a. 009-10 prof. Viviana Bono Blocco 9 Metodi statici: passaggio parametri, variabili locali, record
Progetto Lauree Scientifiche Liceo Classico L.Ariosto, Ferrara Dipartimento di Matematica Università di Ferrara 24 Gennaio 2012
 Progetto Lauree Scientifiche Liceo Classico L.Ariosto, Ferrara Dipartimento di Matematica Università di Ferrara 24 Gennaio 2012 Concetti importanti da (ri)vedere Programmazione imperativa Strutture di
Progetto Lauree Scientifiche Liceo Classico L.Ariosto, Ferrara Dipartimento di Matematica Università di Ferrara 24 Gennaio 2012 Concetti importanti da (ri)vedere Programmazione imperativa Strutture di
Prestazioni CPU Corso di Calcolatori Elettronici A 2007/2008 Sito Web:http://prometeo.ing.unibs.it/quarella Prof. G. Quarella prof@quarella.
 Prestazioni CPU Corso di Calcolatori Elettronici A 2007/2008 Sito Web:http://prometeo.ing.unibs.it/quarella Prof. G. Quarella prof@quarella.net Prestazioni Si valutano in maniera diversa a seconda dell
Prestazioni CPU Corso di Calcolatori Elettronici A 2007/2008 Sito Web:http://prometeo.ing.unibs.it/quarella Prof. G. Quarella prof@quarella.net Prestazioni Si valutano in maniera diversa a seconda dell
Descrizione di un algoritmo
 Descrizione di un algoritmo Un algoritmo descrive due tipi fondamentali di oper: calcoli ottenibili tramite le oper primitive su tipi di dato (valutazione di espressioni) che consistono nella modifica
Descrizione di un algoritmo Un algoritmo descrive due tipi fondamentali di oper: calcoli ottenibili tramite le oper primitive su tipi di dato (valutazione di espressioni) che consistono nella modifica
Nascita di Java. Che cos e Java? Caratteristiche di Java. Java: linguaggio a oggetti
 Nascita di Java L uscita di Java, verso la metà degli anni novanta, fu accolta con molto entusiasmo dalla comunità dei programmatori e dei provider di servizi internet perché permetteva agli utenti del
Nascita di Java L uscita di Java, verso la metà degli anni novanta, fu accolta con molto entusiasmo dalla comunità dei programmatori e dei provider di servizi internet perché permetteva agli utenti del
Capitolo 18. Complessità
 Capitolo 18 Complessità Complessità computazionale Cosa si intende per complessità? È l impiego, in termini di impegno di risorse, dell intero sistema di calcolo necessario per la risoluzione di un particolare
Capitolo 18 Complessità Complessità computazionale Cosa si intende per complessità? È l impiego, in termini di impegno di risorse, dell intero sistema di calcolo necessario per la risoluzione di un particolare
Siamo così arrivati all aritmetica modulare, ma anche a individuare alcuni aspetti di come funziona l aritmetica del calcolatore come vedremo.
 DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
Le variabili. Olga Scotti
 Le variabili Olga Scotti Cos è una variabile Le variabili, in un linguaggio di programmazione, sono dei contenitori. Possono essere riempiti con un valore che poi può essere riletto oppure sostituito.
Le variabili Olga Scotti Cos è una variabile Le variabili, in un linguaggio di programmazione, sono dei contenitori. Possono essere riempiti con un valore che poi può essere riletto oppure sostituito.
Esercitazione Informatica I AA 2012-2013. Nicola Paoletti
 Esercitazione Informatica I AA 2012-2013 Nicola Paoletti 4 Gigno 2013 2 Conversioni Effettuare le seguenti conversioni, tenendo conto del numero di bit con cui si rappresenta il numero da convertire/convertito.
Esercitazione Informatica I AA 2012-2013 Nicola Paoletti 4 Gigno 2013 2 Conversioni Effettuare le seguenti conversioni, tenendo conto del numero di bit con cui si rappresenta il numero da convertire/convertito.
Processo di risoluzione di un problema ingegneristico. Processo di risoluzione di un problema ingegneristico
 Processo di risoluzione di un problema ingegneristico 1. Capire l essenza del problema. 2. Raccogliere le informazioni disponibili. Alcune potrebbero essere disponibili in un secondo momento. 3. Determinare
Processo di risoluzione di un problema ingegneristico 1. Capire l essenza del problema. 2. Raccogliere le informazioni disponibili. Alcune potrebbero essere disponibili in un secondo momento. 3. Determinare
Funzioni in C. Violetta Lonati
 Università degli studi di Milano Dipartimento di Scienze dell Informazione Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica Funzioni - in breve: Funzioni Definizione di funzioni
Università degli studi di Milano Dipartimento di Scienze dell Informazione Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica Funzioni - in breve: Funzioni Definizione di funzioni
3 - Variabili. Programmazione e analisi di dati Modulo A: Programmazione in Java. Paolo Milazzo
 3 - Variabili Programmazione e analisi di dati Modulo A: Programmazione in Java Paolo Milazzo Dipartimento di Informatica, Università di Pisa http://www.di.unipi.it/ milazzo milazzo di.unipi.it Corso di
3 - Variabili Programmazione e analisi di dati Modulo A: Programmazione in Java Paolo Milazzo Dipartimento di Informatica, Università di Pisa http://www.di.unipi.it/ milazzo milazzo di.unipi.it Corso di
Valutazione delle Prestazioni
 Valutazione delle Prestazioni Sia data una macchina X, definiamo: 1 PrestazioneX = --------------------------- Tempo di esecuzione X La prestazione aumenta con il diminuire del tempo di esecuzione (e diminuisce
Valutazione delle Prestazioni Sia data una macchina X, definiamo: 1 PrestazioneX = --------------------------- Tempo di esecuzione X La prestazione aumenta con il diminuire del tempo di esecuzione (e diminuisce
3. La sintassi di Java
 pag.9 3. La sintassi di Java 3.1 I tipi di dati statici In Java, come in Pascal, esistono tipi di dati statici predefiniti e sono i seguenti: byte 8 bit da -128 a 127 short 16 bit coincide con l integer
pag.9 3. La sintassi di Java 3.1 I tipi di dati statici In Java, come in Pascal, esistono tipi di dati statici predefiniti e sono i seguenti: byte 8 bit da -128 a 127 short 16 bit coincide con l integer
Calcolatori Elettronici A a.a. 2008/2009
 Calcolatori Elettronici A a.a. 2008/2009 PRESTAZIONI DEL CALCOLATORE Massimiliano Giacomin Due dimensioni Tempo di risposta (o tempo di esecuzione): il tempo totale impiegato per eseguire un task (include
Calcolatori Elettronici A a.a. 2008/2009 PRESTAZIONI DEL CALCOLATORE Massimiliano Giacomin Due dimensioni Tempo di risposta (o tempo di esecuzione): il tempo totale impiegato per eseguire un task (include
Valutazione delle Prestazioni. Valutazione delle Prestazioni. Architetture dei Calcolatori (Lettere. Tempo di risposta e throughput
 Valutazione delle Prestazioni Architetture dei Calcolatori (Lettere A-I) Valutazione delle Prestazioni Prof. Francesco Lo Presti Misura/valutazione di un insieme di parametri quantitativi per caratterizzare
Valutazione delle Prestazioni Architetture dei Calcolatori (Lettere A-I) Valutazione delle Prestazioni Prof. Francesco Lo Presti Misura/valutazione di un insieme di parametri quantitativi per caratterizzare
Esempi di algoritmi. Lezione III
 Esempi di algoritmi Lezione III Scopo della lezione Implementare da zero algoritmi di media complessità. Verificare la correttezza di un algoritmo eseguendolo a mano. Imparare a valutare le prestazioni
Esempi di algoritmi Lezione III Scopo della lezione Implementare da zero algoritmi di media complessità. Verificare la correttezza di un algoritmo eseguendolo a mano. Imparare a valutare le prestazioni
Appunti di Sistemi Elettronici
 Prof.ssa Maria Rosa Malizia 1 LA PROGRAMMAZIONE La programmazione costituisce una parte fondamentale dell informatica. Infatti solo attraverso di essa si apprende la logica che ci permette di comunicare
Prof.ssa Maria Rosa Malizia 1 LA PROGRAMMAZIONE La programmazione costituisce una parte fondamentale dell informatica. Infatti solo attraverso di essa si apprende la logica che ci permette di comunicare
Sistemi Informativi Territoriali. Map Algebra
 Paolo Mogorovich Sistemi Informativi Territoriali Appunti dalle lezioni Map Algebra Cod.735 - Vers.E57 1 Definizione di Map Algebra 2 Operatori locali 3 Operatori zonali 4 Operatori focali 5 Operatori
Paolo Mogorovich Sistemi Informativi Territoriali Appunti dalle lezioni Map Algebra Cod.735 - Vers.E57 1 Definizione di Map Algebra 2 Operatori locali 3 Operatori zonali 4 Operatori focali 5 Operatori
Ottimizzazione Multi Obiettivo
 Ottimizzazione Multi Obiettivo 1 Ottimizzazione Multi Obiettivo I problemi affrontati fino ad ora erano caratterizzati da una unica (e ben definita) funzione obiettivo. I problemi di ottimizzazione reali
Ottimizzazione Multi Obiettivo 1 Ottimizzazione Multi Obiettivo I problemi affrontati fino ad ora erano caratterizzati da una unica (e ben definita) funzione obiettivo. I problemi di ottimizzazione reali
Lezione 8. La macchina universale
 Lezione 8 Algoritmi La macchina universale Un elaboratore o computer è una macchina digitale, elettronica, automatica capace di effettuare trasformazioni o elaborazioni su i dati digitale= l informazione
Lezione 8 Algoritmi La macchina universale Un elaboratore o computer è una macchina digitale, elettronica, automatica capace di effettuare trasformazioni o elaborazioni su i dati digitale= l informazione
Obiettivi dell Analisi Numerica. Avviso. Risoluzione numerica di un modello. Analisi Numerica e Calcolo Scientifico
 M. Annunziato, DIPMAT Università di Salerno - Queste note non sono esaustive ai fini del corso p. 3/43 M. Annunziato, DIPMAT Università di Salerno - Queste note non sono esaustive ai fini del corso p.
M. Annunziato, DIPMAT Università di Salerno - Queste note non sono esaustive ai fini del corso p. 3/43 M. Annunziato, DIPMAT Università di Salerno - Queste note non sono esaustive ai fini del corso p.
2. Leggi finanziarie di capitalizzazione
 2. Leggi finanziarie di capitalizzazione Si chiama legge finanziaria di capitalizzazione una funzione atta a definire il montante M(t accumulato al tempo generico t da un capitale C: M(t = F(C, t C t M
2. Leggi finanziarie di capitalizzazione Si chiama legge finanziaria di capitalizzazione una funzione atta a definire il montante M(t accumulato al tempo generico t da un capitale C: M(t = F(C, t C t M
Fasi di creazione di un programma
 Fasi di creazione di un programma 1. Studio Preliminare 2. Analisi del Sistema 6. Manutenzione e Test 3. Progettazione 5. Implementazione 4. Sviluppo 41 Sviluppo di programmi Per la costruzione di un programma
Fasi di creazione di un programma 1. Studio Preliminare 2. Analisi del Sistema 6. Manutenzione e Test 3. Progettazione 5. Implementazione 4. Sviluppo 41 Sviluppo di programmi Per la costruzione di un programma
Esercizi per il corso di Algoritmi, anno accademico 2014/15
 1 Esercizi per il corso di Algoritmi, anno accademico 2014/15 Esercizi sulle Notazioni Asintotiche 1. Esercizio: Provare le seguenti relazioni, esibendo opportune costanti c 1,c 2 ed n 0. Si assuma per
1 Esercizi per il corso di Algoritmi, anno accademico 2014/15 Esercizi sulle Notazioni Asintotiche 1. Esercizio: Provare le seguenti relazioni, esibendo opportune costanti c 1,c 2 ed n 0. Si assuma per
Calcolatori: Algebra Booleana e Reti Logiche
 Calcolatori: Algebra Booleana e Reti Logiche 1 Algebra Booleana e Variabili Logiche I fondamenti dell Algebra Booleana (o Algebra di Boole) furono delineati dal matematico George Boole, in un lavoro pubblicato
Calcolatori: Algebra Booleana e Reti Logiche 1 Algebra Booleana e Variabili Logiche I fondamenti dell Algebra Booleana (o Algebra di Boole) furono delineati dal matematico George Boole, in un lavoro pubblicato
Studente (Cognome Nome): Corso di Informatica Corso di Laurea in Ingegneria Gestionale a.a. 2006-07 Secondo Compitino 21 Dicembre 2006
 Studente (Cognome Nome): Matricola: Corso di Informatica Corso di Laurea in Ingegneria Gestionale a.a. 2006-07 Secondo Compitino 21 Dicembre 2006 Si noti che le soluzioni ai quesiti saranno considerate
Studente (Cognome Nome): Matricola: Corso di Informatica Corso di Laurea in Ingegneria Gestionale a.a. 2006-07 Secondo Compitino 21 Dicembre 2006 Si noti che le soluzioni ai quesiti saranno considerate
PROBLEMA DELLA RICERCA DI UN ELEMENTO IN UN ARRAY E ALGORITMI RISOLUTIVI
 PROBLEMA DELLA RICERCA DI UN ELEMENTO IN UN ARRAY E ALGORITMI RISOLUTIVI PROBLEMA DELLA RICERCA in termini generali: Dati in input un insieme S di elementi (numeri, caratteri, stringhe, ) e un elemento
PROBLEMA DELLA RICERCA DI UN ELEMENTO IN UN ARRAY E ALGORITMI RISOLUTIVI PROBLEMA DELLA RICERCA in termini generali: Dati in input un insieme S di elementi (numeri, caratteri, stringhe, ) e un elemento
AA 2006-07 LA RICORSIONE
 PROGRAMMAZIONE AA 2006-07 LA RICORSIONE AA 2006-07 Prof.ssa A. Lanza - DIB 1/18 LA RICORSIONE Il concetto di ricorsione nasce dalla matematica Una funzione matematica è definita ricorsivamente quando nella
PROGRAMMAZIONE AA 2006-07 LA RICORSIONE AA 2006-07 Prof.ssa A. Lanza - DIB 1/18 LA RICORSIONE Il concetto di ricorsione nasce dalla matematica Una funzione matematica è definita ricorsivamente quando nella
4 3 4 = 4 x 10 2 + 3 x 10 1 + 4 x 10 0 aaa 10 2 10 1 10 0
 Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Dimensione di uno Spazio vettoriale
 Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Richiesta pagina PHP (es: index.php)
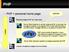 PHP PHP = personal home page SERVER Richiesta pagina PHP (es: index.php) Server Web (Apache) in ascolto sulla porta 80, si accorge che la pagina richiesta è una pagina PHP in base all'estensione o con
PHP PHP = personal home page SERVER Richiesta pagina PHP (es: index.php) Server Web (Apache) in ascolto sulla porta 80, si accorge che la pagina richiesta è una pagina PHP in base all'estensione o con
Realizzazione di Politiche di Gestione delle Risorse: i Semafori Privati
 Realizzazione di Politiche di Gestione delle Risorse: i Semafori Privati Condizione di sincronizzazione Qualora si voglia realizzare una determinata politica di gestione delle risorse,la decisione se ad
Realizzazione di Politiche di Gestione delle Risorse: i Semafori Privati Condizione di sincronizzazione Qualora si voglia realizzare una determinata politica di gestione delle risorse,la decisione se ad
Informatica. Rappresentazione dei numeri Numerazione binaria
 Informatica Rappresentazione dei numeri Numerazione binaria Sistemi di numerazione Non posizionali: numerazione romana Posizionali: viene associato un peso a ciascuna posizione all interno della rappresentazione
Informatica Rappresentazione dei numeri Numerazione binaria Sistemi di numerazione Non posizionali: numerazione romana Posizionali: viene associato un peso a ciascuna posizione all interno della rappresentazione
GESTIONE INFORMATICA DEI DATI AZIENDALI
 GESTIONE INFORMATICA DEI DATI AZIENDALI Alberto ZANONI Centro Vito Volterra Università Tor Vergata Via Columbia 2, 00133 Roma, Italy zanoni@volterra.uniroma2.it Rudimenti di programmazione Programming
GESTIONE INFORMATICA DEI DATI AZIENDALI Alberto ZANONI Centro Vito Volterra Università Tor Vergata Via Columbia 2, 00133 Roma, Italy zanoni@volterra.uniroma2.it Rudimenti di programmazione Programming
Concetto di Funzione e Procedura METODI in Java
 Fondamenti di Informatica Concetto di Funzione e Procedura METODI in Java Fondamenti di Informatica - D. Talia - UNICAL 1 Metodi e Sottoprogrammi Mentre in Java tramite le classi e gli oggetti è possibile
Fondamenti di Informatica Concetto di Funzione e Procedura METODI in Java Fondamenti di Informatica - D. Talia - UNICAL 1 Metodi e Sottoprogrammi Mentre in Java tramite le classi e gli oggetti è possibile
Nozione di algoritmo. Gabriella Trucco
 Nozione di algoritmo Gabriella Trucco Programmazione Attività con cui si predispone l'elaboratore ad eseguire un particolare insieme di azioni su particolari informazioni (dati), allo scopo di risolvere
Nozione di algoritmo Gabriella Trucco Programmazione Attività con cui si predispone l'elaboratore ad eseguire un particolare insieme di azioni su particolari informazioni (dati), allo scopo di risolvere
Esercizi Capitolo 2 - Analisi di Algoritmi
 Esercizi Capitolo - Analisi di Algoritmi Alberto Montresor 19 Agosto, 014 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente, è possibile saltare
Esercizi Capitolo - Analisi di Algoritmi Alberto Montresor 19 Agosto, 014 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente, è possibile saltare
RAPPRESENTAZIONE GRAFICA DEGLI ALGORITMI
 RAPPRESENTAZIONE GRAFICA DEGLI ALGORITMI Diagramma di flusso L algoritmo può essere rappresentato in vari modi, grafici o testuali. Uno dei metodi grafici più usati e conosciuti è il cosiddetto diagramma
RAPPRESENTAZIONE GRAFICA DEGLI ALGORITMI Diagramma di flusso L algoritmo può essere rappresentato in vari modi, grafici o testuali. Uno dei metodi grafici più usati e conosciuti è il cosiddetto diagramma
Programmazione I - Laboratorio
 Programmazione I - Laboratorio Esercitazione 2 - Funzioni Gianluca Mezzetti 1 Paolo Milazzo 2 1. Dipartimento di Informatica, Università di Pisa http://www.di.unipi.it/ mezzetti mezzetti di.unipi.it 2.
Programmazione I - Laboratorio Esercitazione 2 - Funzioni Gianluca Mezzetti 1 Paolo Milazzo 2 1. Dipartimento di Informatica, Università di Pisa http://www.di.unipi.it/ mezzetti mezzetti di.unipi.it 2.
Correttezza. Corso di Laurea Ingegneria Informatica Fondamenti di Informatica 1. Dispensa 10. A. Miola Novembre 2007
 Corso di Laurea Ingegneria Informatica Fondamenti di Informatica 1 Dispensa 10 Correttezza A. Miola Novembre 2007 http://www.dia.uniroma3.it/~java/fondinf1/ Correttezza 1 Contenuti Introduzione alla correttezza
Corso di Laurea Ingegneria Informatica Fondamenti di Informatica 1 Dispensa 10 Correttezza A. Miola Novembre 2007 http://www.dia.uniroma3.it/~java/fondinf1/ Correttezza 1 Contenuti Introduzione alla correttezza
Realizzazione di una classe con un associazione
 Realizzazione di una classe con un associazione Nel realizzare una classe che è coinvolta in un associazione, ci dobbiamo chiedere se la classe ha responsabilità sull associazione. Diciamo che una classe
Realizzazione di una classe con un associazione Nel realizzare una classe che è coinvolta in un associazione, ci dobbiamo chiedere se la classe ha responsabilità sull associazione. Diciamo che una classe
Capitolo 4: Ottimizzazione non lineare non vincolata parte II. E. Amaldi DEIB, Politecnico di Milano
 Capitolo 4: Ottimizzazione non lineare non vincolata parte II E. Amaldi DEIB, Politecnico di Milano 4.3 Algoritmi iterativi e convergenza Programma non lineare (PNL): min f(x) s.v. g i (x) 0 1 i m x S
Capitolo 4: Ottimizzazione non lineare non vincolata parte II E. Amaldi DEIB, Politecnico di Milano 4.3 Algoritmi iterativi e convergenza Programma non lineare (PNL): min f(x) s.v. g i (x) 0 1 i m x S
e-dva - eni-depth Velocity Analysis
 Lo scopo dell Analisi di Velocità di Migrazione (MVA) è quello di ottenere un modello della velocità nel sottosuolo che abbia dei tempi di riflessione compatibili con quelli osservati nei dati. Ciò significa
Lo scopo dell Analisi di Velocità di Migrazione (MVA) è quello di ottenere un modello della velocità nel sottosuolo che abbia dei tempi di riflessione compatibili con quelli osservati nei dati. Ciò significa
Anno 3. Funzioni: dominio, codominio e campo di esistenza
 Anno 3 Funzioni: dominio, codominio e campo di esistenza 1 Introduzione In questa lezione parleremo delle funzioni. Ne daremo una definizione e impareremo a studiarne il dominio in relazione alle diverse
Anno 3 Funzioni: dominio, codominio e campo di esistenza 1 Introduzione In questa lezione parleremo delle funzioni. Ne daremo una definizione e impareremo a studiarne il dominio in relazione alle diverse
Esercizi su. Funzioni
 Esercizi su Funzioni ๒ Varie Tracce extra Sul sito del corso ๓ Esercizi funz_max.cc funz_fattoriale.cc ๔ Documentazione Il codice va documentato (commentato) Leggibilità Riduzione degli errori Manutenibilità
Esercizi su Funzioni ๒ Varie Tracce extra Sul sito del corso ๓ Esercizi funz_max.cc funz_fattoriale.cc ๔ Documentazione Il codice va documentato (commentato) Leggibilità Riduzione degli errori Manutenibilità
Slide Cerbara parte1 5. Le distribuzioni teoriche
 Slide Cerbara parte1 5 Le distribuzioni teoriche I fenomeni biologici, demografici, sociali ed economici, che sono il principale oggetto della statistica, non sono retti da leggi matematiche. Però dalle
Slide Cerbara parte1 5 Le distribuzioni teoriche I fenomeni biologici, demografici, sociali ed economici, che sono il principale oggetto della statistica, non sono retti da leggi matematiche. Però dalle
Più processori uguale più velocità?
 Più processori uguale più velocità? e un processore impiega per eseguire un programma un tempo T, un sistema formato da P processori dello stesso tipo esegue lo stesso programma in un tempo TP T / P? In
Più processori uguale più velocità? e un processore impiega per eseguire un programma un tempo T, un sistema formato da P processori dello stesso tipo esegue lo stesso programma in un tempo TP T / P? In
Problem solving elementare su dati vettoriali
 Problem solving elementare su dati vettoriali Introduzione Verifiche su sequenze di dati Selezione o ricerca di dati 2 2006 Politecnico di Torino 1 Introduzione (1/2) I problemi di verifica consistono
Problem solving elementare su dati vettoriali Introduzione Verifiche su sequenze di dati Selezione o ricerca di dati 2 2006 Politecnico di Torino 1 Introduzione (1/2) I problemi di verifica consistono
4.1 Modelli di calcolo analisi asintotica e ricorrenze
 4 Esercizi Prima Parte 4.1 Modelli di calcolo analisi asintotica e ricorrenze Esercizio 4 1 Rispondere alle seguenti domande: 1. Come misuriamo l efficienza di un algoritmo?. Quali sono gli algoritmi più
4 Esercizi Prima Parte 4.1 Modelli di calcolo analisi asintotica e ricorrenze Esercizio 4 1 Rispondere alle seguenti domande: 1. Come misuriamo l efficienza di un algoritmo?. Quali sono gli algoritmi più
SOMMARIO Coda (queue): QUEUE. QUEUE : specifica QUEUE
 SOMMARIO Coda (queue): Specifica: interfaccia. Implementazione: Strutture indicizzate (array): Array di dimensione variabile. Array circolari. Strutture collegate (nodi). Prestazioni. Strutture Software
SOMMARIO Coda (queue): Specifica: interfaccia. Implementazione: Strutture indicizzate (array): Array di dimensione variabile. Array circolari. Strutture collegate (nodi). Prestazioni. Strutture Software
Corso di Laurea Ingegneria Informatica Fondamenti di Informatica 2
 Corso di Laurea Ingegneria Informatica Fondamenti di Informatica 2 Dispensa 10 Strutture collegate - 2 A. Miola Febbraio 2008 http://www.dia.uniroma3.it/~java/fondinf2/ Strutture collegate - 2 1 Contenuti!Strutture
Corso di Laurea Ingegneria Informatica Fondamenti di Informatica 2 Dispensa 10 Strutture collegate - 2 A. Miola Febbraio 2008 http://www.dia.uniroma3.it/~java/fondinf2/ Strutture collegate - 2 1 Contenuti!Strutture
dall argomento argomento della malloc()
 Allocazione dinamica Quando? Tutte le volte in cui i dati possono crescere in modo non prevedibile staticamente a tempo di sviluppo Un array con dimensione i fissata a compile-time non è sufficiente È
Allocazione dinamica Quando? Tutte le volte in cui i dati possono crescere in modo non prevedibile staticamente a tempo di sviluppo Un array con dimensione i fissata a compile-time non è sufficiente È
Analisi di scenario File Nr. 10
 1 Analisi di scenario File Nr. 10 Giorgio Calcagnini Università di Urbino Dip. Economia, Società, Politica giorgio.calcagnini@uniurb.it http://www.econ.uniurb.it/calcagnini/ http://www.econ.uniurb.it/calcagnini/forecasting.html
1 Analisi di scenario File Nr. 10 Giorgio Calcagnini Università di Urbino Dip. Economia, Società, Politica giorgio.calcagnini@uniurb.it http://www.econ.uniurb.it/calcagnini/ http://www.econ.uniurb.it/calcagnini/forecasting.html
Arduino: Programmazione
 Programmazione formalmente ispirata al linguaggio C da cui deriva. I programmi in ARDUINO sono chiamati Sketch. Un programma è una serie di istruzioni che vengono lette dall alto verso il basso e convertite
Programmazione formalmente ispirata al linguaggio C da cui deriva. I programmi in ARDUINO sono chiamati Sketch. Un programma è una serie di istruzioni che vengono lette dall alto verso il basso e convertite
Esercizi Capitolo 6 - Alberi binari di ricerca
 Esercizi Capitolo 6 - Alberi binari di ricerca Alberto Montresor 23 settembre 200 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente, è possibile
Esercizi Capitolo 6 - Alberi binari di ricerca Alberto Montresor 23 settembre 200 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente, è possibile
Proof. Dimostrazione per assurdo. Consideriamo l insieme complementare di P nell insieme
 G Pareschi Principio di induzione Il Principio di Induzione (che dovreste anche avere incontrato nel Corso di Analisi I) consente di dimostrare Proposizioni il cui enunciato è in funzione di un numero
G Pareschi Principio di induzione Il Principio di Induzione (che dovreste anche avere incontrato nel Corso di Analisi I) consente di dimostrare Proposizioni il cui enunciato è in funzione di un numero
E naturale chiedersi alcune cose sulla media campionaria x n
 Supponiamo che un fabbricante stia introducendo un nuovo tipo di batteria per un automobile elettrica. La durata osservata x i delle i-esima batteria è la realizzazione (valore assunto) di una variabile
Supponiamo che un fabbricante stia introducendo un nuovo tipo di batteria per un automobile elettrica. La durata osservata x i delle i-esima batteria è la realizzazione (valore assunto) di una variabile
Il concetto di valore medio in generale
 Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Corso di Informatica Generale (C. L. Economia e Commercio) Ing. Valerio Lacagnina Rappresentazione in virgola mobile
 Problemi connessi all utilizzo di un numero di bit limitato Abbiamo visto quali sono i vantaggi dell utilizzo della rappresentazione in complemento alla base: corrispondenza biunivoca fra rappresentazione
Problemi connessi all utilizzo di un numero di bit limitato Abbiamo visto quali sono i vantaggi dell utilizzo della rappresentazione in complemento alla base: corrispondenza biunivoca fra rappresentazione
Capitolo 6: Modelli di calcolo per linguaggi imperativi e funzionali
 Capitolo 6: Modelli di calcolo per linguaggi imperativi e funzionali 1 Modelli imperativi: le RAM (Random Access Machine) I modelli di calcolo imperativi sono direttamente collegati al modello Von Neumann,
Capitolo 6: Modelli di calcolo per linguaggi imperativi e funzionali 1 Modelli imperativi: le RAM (Random Access Machine) I modelli di calcolo imperativi sono direttamente collegati al modello Von Neumann,
Architettura hardware
 Architettura dell elaboratore Architettura hardware la parte che si può prendere a calci Sistema composto da un numero elevato di componenti, in cui ogni componente svolge una sua funzione elaborazione
Architettura dell elaboratore Architettura hardware la parte che si può prendere a calci Sistema composto da un numero elevato di componenti, in cui ogni componente svolge una sua funzione elaborazione
Vettori Algoritmi elementari di ordinamento
 Dipartimento di Informatica e Sistemistica Antonio Ruberti Sapienza Università di Roma Vettori Algoritmi elementari di ordinamento Corso di Fondamenti di Informatica Laurea in Ingegneria Informatica (Canale
Dipartimento di Informatica e Sistemistica Antonio Ruberti Sapienza Università di Roma Vettori Algoritmi elementari di ordinamento Corso di Fondamenti di Informatica Laurea in Ingegneria Informatica (Canale
Come ragiona il computer. Problemi e algoritmi
 Come ragiona il computer Problemi e algoritmi Il problema Abbiamo un problema quando ci poniamo un obiettivo da raggiungere e per raggiungerlo dobbiamo mettere a punto una strategia Problema Strategia
Come ragiona il computer Problemi e algoritmi Il problema Abbiamo un problema quando ci poniamo un obiettivo da raggiungere e per raggiungerlo dobbiamo mettere a punto una strategia Problema Strategia
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI
 APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
+ / operatori di confronto (espressioni logiche/predicati) / + 5 3 9 = > < Pseudo codice. Pseudo codice
 Pseudo codice Pseudo codice Paolo Bison Fondamenti di Informatica A.A. 2006/07 Università di Padova linguaggio testuale mix di linguaggio naturale ed elementi linguistici con sintassi ben definita e semantica
Pseudo codice Pseudo codice Paolo Bison Fondamenti di Informatica A.A. 2006/07 Università di Padova linguaggio testuale mix di linguaggio naturale ed elementi linguistici con sintassi ben definita e semantica
La gestione dell input/output da tastiera La gestione dell input/output da file La gestione delle eccezioni
 La gestione dell input/output da tastiera La gestione dell input/output da file La gestione delle eccezioni Autore: Prof. Agostino Sorbara ITIS "M. M. Milano" Autore: Prof. Agostino Sorbara ITIS "M. M.
La gestione dell input/output da tastiera La gestione dell input/output da file La gestione delle eccezioni Autore: Prof. Agostino Sorbara ITIS "M. M. Milano" Autore: Prof. Agostino Sorbara ITIS "M. M.
Dall Algoritmo al Programma. Prof. Francesco Accarino IIS Altiero Spinelli Sesto San Giovanni
 Dall Algoritmo al Programma Prof. Francesco Accarino IIS Altiero Spinelli Sesto San Giovanni IL PROGRAMMA Gli algoritmi sono modelli di descrizione astratti e per controllarne il funzionamento devono essere
Dall Algoritmo al Programma Prof. Francesco Accarino IIS Altiero Spinelli Sesto San Giovanni IL PROGRAMMA Gli algoritmi sono modelli di descrizione astratti e per controllarne il funzionamento devono essere
OTTAVA ESPERIENZA DI LABORATORIO. L elaborazione dei files in C
 CORSO DI LABORATORIO DI INFORMATICA CORSO DI LAUREA IN SDM ANNO ACCADEMICO 2011-2012 Docente: R. Sparvoli Esercitazioni: R. Sparvoli, F. Palma OTTAVA ESPERIENZA DI LABORATORIO L elaborazione dei files
CORSO DI LABORATORIO DI INFORMATICA CORSO DI LAUREA IN SDM ANNO ACCADEMICO 2011-2012 Docente: R. Sparvoli Esercitazioni: R. Sparvoli, F. Palma OTTAVA ESPERIENZA DI LABORATORIO L elaborazione dei files
Introduzione ai tipi di dato astratti: applicazione alle liste
 Universitàdegli Studi di L Aquila Facoltàdi Scienze M.F.N. Corso di Laurea in Informatica Corso di Laboratorio di Algoritmi e Strutture Dati A.A. 2005/2006 Introduzione ai tipi di dato astratti: applicazione
Universitàdegli Studi di L Aquila Facoltàdi Scienze M.F.N. Corso di Laurea in Informatica Corso di Laboratorio di Algoritmi e Strutture Dati A.A. 2005/2006 Introduzione ai tipi di dato astratti: applicazione
Corso di Informatica Corso di Laurea in Ingegneria Gestionale a.a. 2005-06 Secondo Compitino 17 Dicembre 2005
 Studente (Cognome Nome): Matricola: Corso di Informatica Corso di Laurea in Ingegneria Gestionale a.a. 2005-06 Secondo Compitino 17 Dicembre 2005 Si noti che le soluzioni ai quesiti saranno considerate
Studente (Cognome Nome): Matricola: Corso di Informatica Corso di Laurea in Ingegneria Gestionale a.a. 2005-06 Secondo Compitino 17 Dicembre 2005 Si noti che le soluzioni ai quesiti saranno considerate
Sistemi Operativi mod. B. Sistemi Operativi mod. B A B C A B C P 1 2 0 0 P 1 1 2 2 3 3 2 P 2 3 0 2 P 2 6 0 0 P 3 2 1 1 P 3 0 1 1 < P 1, >
 Algoritmo del banchiere Permette di gestire istanze multiple di una risorsa (a differenza dell algoritmo con grafo di allocazione risorse). Ciascun processo deve dichiarare a priori il massimo impiego
Algoritmo del banchiere Permette di gestire istanze multiple di una risorsa (a differenza dell algoritmo con grafo di allocazione risorse). Ciascun processo deve dichiarare a priori il massimo impiego
LA STATISTICA si interessa del rilevamento, dell elaborazione e dello studio dei dati; studia ciò che accade o come è fatto un gruppo numeroso di
 STATISTICA LA STATISTICA si interessa del rilevamento, dell elaborazione e dello studio dei dati; studia ciò che accade o come è fatto un gruppo numeroso di oggetti; cerca, attraverso l uso della matematica
STATISTICA LA STATISTICA si interessa del rilevamento, dell elaborazione e dello studio dei dati; studia ciò che accade o come è fatto un gruppo numeroso di oggetti; cerca, attraverso l uso della matematica
Programmazione in Java (I modulo) Lezione 3: Prime nozioni
 Programmazione in Java (I modulo) Lezione 3: Prime nozioni La volta scorsa Abbiamo avuto un primo assaggio! Abbiamo visto come usare l editor per scrivere un programma Java. Abbiamo analizzato riga per
Programmazione in Java (I modulo) Lezione 3: Prime nozioni La volta scorsa Abbiamo avuto un primo assaggio! Abbiamo visto come usare l editor per scrivere un programma Java. Abbiamo analizzato riga per
SISTEMI DI NUMERAZIONE E CODICI
 SISTEMI DI NUMERAZIONE E CODICI Il Sistema di Numerazione Decimale Il sistema decimale o sistema di numerazione a base dieci usa dieci cifre, dette cifre decimali, da O a 9. Il sistema decimale è un sistema
SISTEMI DI NUMERAZIONE E CODICI Il Sistema di Numerazione Decimale Il sistema decimale o sistema di numerazione a base dieci usa dieci cifre, dette cifre decimali, da O a 9. Il sistema decimale è un sistema
Appunti di informatica. Lezione 2 anno accademico 2015-2016 Mario Verdicchio
 Appunti di informatica Lezione 2 anno accademico 2015-2016 Mario Verdicchio Sistema binario e logica C è un legame tra i numeri binari (0,1) e la logica, ossia la disciplina che si occupa del ragionamento
Appunti di informatica Lezione 2 anno accademico 2015-2016 Mario Verdicchio Sistema binario e logica C è un legame tra i numeri binari (0,1) e la logica, ossia la disciplina che si occupa del ragionamento
Variabili e tipi di dato
 Variabili e tipi di dato Tutte le variabili devono essere dichiarate, specificandone il tipo La dichiarazione deve precedere l uso Il tipo è un concetto astratto che esprime: L allocazione di spazio per
Variabili e tipi di dato Tutte le variabili devono essere dichiarate, specificandone il tipo La dichiarazione deve precedere l uso Il tipo è un concetto astratto che esprime: L allocazione di spazio per
risulta (x) = 1 se x < 0.
 Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
I PROBLEMI ALGEBRICI
 I PROBLEMI ALGEBRICI La risoluzione di problemi è una delle attività fondamentali della matematica. Una grande quantità di problemi è risolubile mediante un modello algebrico costituito da equazioni e
I PROBLEMI ALGEBRICI La risoluzione di problemi è una delle attività fondamentali della matematica. Una grande quantità di problemi è risolubile mediante un modello algebrico costituito da equazioni e
Automazione Industriale (scheduling+mms) scheduling+mms. adacher@dia.uniroma3.it
 Automazione Industriale (scheduling+mms) scheduling+mms adacher@dia.uniroma3.it Introduzione Sistemi e Modelli Lo studio e l analisi di sistemi tramite una rappresentazione astratta o una sua formalizzazione
Automazione Industriale (scheduling+mms) scheduling+mms adacher@dia.uniroma3.it Introduzione Sistemi e Modelli Lo studio e l analisi di sistemi tramite una rappresentazione astratta o una sua formalizzazione
Esercizi per il corso di Algoritmi e Strutture Dati
 1 Esercizi per il corso di Algoritmi e Strutture Dati Esercizi sulla Tecnica Divide et Impera N.B. Tutti gli algoritmi vanno scritti in pseudocodice (non in Java, né in C++, etc. ). Di tutti gli algoritmi
1 Esercizi per il corso di Algoritmi e Strutture Dati Esercizi sulla Tecnica Divide et Impera N.B. Tutti gli algoritmi vanno scritti in pseudocodice (non in Java, né in C++, etc. ). Di tutti gli algoritmi
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE
 LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
