in natura Dalla sequenza di Fibonacci al numero Aureo: le meraviglie della matematica trovano vita nelle mirabili forme naturali
|
|
|
- Cristina Di Mauro
- 8 anni fa
- Visualizzazioni
Transcript
1 Numeri magici in natura Dalla sequenza di Fibonacci al numero Aureo: le meraviglie della matematica trovano vita nelle mirabili forme naturali Sabrina Mugnos Galileo Galilei davvero non sbagliò quando, quasi quattro secoli or sono, nella sua celebre opera Il Saggiatore (1623) scrisse: «la filosofia è scritta in questo grandissimo libro che continuamente ci sta aperto innanzi a gli occhi ma non si può intendere se prima non si impara a intender la lingua, e conoscer i caratteri, né quali è scritto. Egli è scritto in lingua matematica, e i caratteri son triangoli, cerchi, ed altre figure geometriche, senza i quali mezzi è impossibile a intenderne umanamente parola; senza questi è un aggirarsi vanamente per un oscuro labirinto». In effetti è evidente che l universo si esprima in un linguaggio squisitamente matematico attraverso leggi fisiche alle quali soggiacciono i fenomeni naturali che osserviamo (sebbene molte dinamiche rimangano ancora oscure), sebbene le forme della natura siano ben lungi dall assomigliare a figure geometriche perfette. Eppure dietro al senso di bellezza ed armonia che sanno suscitare, a ciò che è esteticamente sublime, inatteso e talvolta spiritualmente mistico si celano ancora eleganti e misteriose leggi matematiche e geometriche. sulle piccole palline candide che punteggiavano il mio piumino nero, ho potuto scorgere la loro forma: erano perfetti e meravigliosi cristalli di ghiaccio. Quel rigido giorno di febbraio piovevano cristalli dal cielo a milioni, a miliardi, e gli occhi di chiunque potevano cogliere la loro bellezza. I miei l hanno fatto. Si dice che nessuno di essi sia uguale all altro; e anche se la statistica potrebbe porre un prudente veto su tale affermazione, resta il fatto che è pressochè impossibile scorgerne di uguali, sebbene possano essere raggruppati in categorie di forme. Non esiste artista che potrebbe partorire dalla sua mente geometrie più belle e suggestive, eppure la loro genesi segue rigidi schemi matematici; l estroso architetto che li assembla è qualche ammasso informe di nubi, destreggiandosi su sottili equilibri di temperatura e umidità dell aria. Alcune delle sublimi forme che esibiscono i fiocchi di neve. Cristalli di ghiaccio e spirali: meraviglie di natura Qualche anno fa mi trovavo a sciare in Valle d Aosta. Era una giornata grigia e talmente fredda che neanche il cielo pareva sentirsela di aprirsi per far cadere la neve. In compenso piovevano fitti ma minuscoli granelli bianchi che, sospinti come piccoli proiettili dalla discesa sugli sci, martoriavano il volto come spilli. Spesso siamo così distratti e assorti nei nostri pensieri che non prestiamo attenzione a ciò che ci circonda (per inciso credo che sia proprio questa la principale virtù che abbiamo perduto nel corso della nostra evoluzione). Tuttavia quel giorno, durante il percorso sulla seggiovia, nell istante in cui il mio sguardo si è soffermato 12 Scienza e Conoscenza - n. 41, luglio/agosto/settembre 2012
2 Numeri magici in natura I segreti di questo straordinario mondo della matemagica, che esibisce vere e proprie opere d arte, sono sbalorditive sequenze numeriche, come si accorse più di otto secoli fa un grande matematico toscano di nome Leonardo Pisano, meglio noto come Fibonacci Galeotta è la preziosa molecola dell acqua, che nella sua fase ghiacciata si sbizzarrisce in inaspettati capolavori artistici e non solo quando piove dal cielo, ma anche quando si dispone su superfici fredde come i parabrezza delle auto, per esempio. Per qualche buona ragione essa non si distribuisce uniformemente come un sottile manto lattiginoso, ma forma una giungla surreale di minuscole felci frastagliate. Ma, a quanto pare, gli spigoli non sono le uniche vanità di madre natura, che si diletta anche con sinuose curve come le spirali. La più affascinante la troviamo dentro le nostre cellule ed è il Codice Genetico, il motore della vita come la conosciamo, ma se ne trovano di sublimi espressioni pressochè ovunque. Il Nautilo, per esempio, è un mollusco marino superstite dell antichissima era Paleozoica, scampato alla più colossale estinzione di massa di tutti i tempi allorchè oltre il 90% delle specie capitolarono per cause ancora non chiare. Questo curioso organismo costruisce la sua dimora calcarea secondo quella che in matematica viene chiamata Spirale Logaritmica. Le spirali sono curve piane che girano intorno ad un punto centrale spostandosi sempre più all esterno via via che si procede. Quelle in cui la distanza tra una spira e la successiva è costante si chiamano Spirali di Archimede, e ne sono ottimi esempi conchiglie altrettanto vetuste come le ammoniti, per esempio, purtroppo non abbastanza fortunate da aver resistito alla crisi Permiana e giunte a noi solo sottoforma di fossili. Quando invece la distanza tra le spire aumenta in maniera esponenziale raddoppiando le dimensioni in un intervallo determinato, la spirale si chiama logaritmica, e abbiamo forme come il Nautilo. Sulla sinistra è visibile la conchiglia del Nautilus (organismo tuttora esistente) strutturata secondo una spirale logaritmica. Alla sua forma si contrappone la spirale di Archimede utilizzata dalle Ammoniti (in alto sulla destra) purtroppo estinte alla fine del periodo Paleozoico. - Scienza e Conoscenza 13
3 Numeri magici in natura Phi esprime una relazione geometrica considerata talmente preziosa da essere definita sezione aurea o numero aureo e da aver ispirato pensatori di tutte le discipline più di qualunque altro numero nella storia della matematica Tale curva fu chiamata anche equiangola dal matematico e filosofo Cartesio nel 1638 perché, tracciando una linea dritta dal polo a un suo punto qualsiasi, questa la intercetta formando sempre lo stesso angolo. E ancora la natura sfrutta tale proprietà. Il falco pellegrino, per esempio, avendo un apparato visivo che guarda lateralmente, seguendo tale spirale, può tenere la testa dritta (e non doverla ruotare di continuo in un senso e nell altro) non perdendo di vista la preda e massimizzando la velocità durante l attacco in picchiata di caccia. Questa forma partorita dalla natura, peraltro scelta per svariati altri oggetti come le galassie, gli uragani ecc., è talmente armonica e ipnotica dall aver ispirato opere d arte come quella dell americano Frank Lloyd Wright, che ha progettato il museo Guggenheim di New York secondo la sua struttura. Ma già il grande Leonardo da Vinci ne restò ammaliato, immortalandola nell opera Leda e il Cigno nei capelli raccolti, e ancora sottoforma di vortici in un impressionante serie di schizzi catastrofici ispirati al Diluvio. E lo stesso dio indù Shiva, danzante, ha in mano questa conchiglia come simbolo della Creazione. Altri gusci come quelli delle chiocciole sia di mare che di terra, invece, esibiscono spirali più anguste che si attorcigliano nello spazio come quelle strette scale da arredamento che portano nelle mansarde. Sempre per tale forma hanno optato molte piante per disporre i loro semi. Le squame delle pigne dell abete, per esempio, sono disposte secondo spirali intrecciate, così come i gustosi semi che punteggiano il capolino di un girasole. La sequenza di Fibonacci I segreti di questo straordinario mondo della matemagica, che esibisce vere e proprie opere d arte, sono sbalorditive sequenze numeriche, come si accorse più di otto secoli fa un grande matematico toscano di nome Leonardo Pisano, meglio noto come Fibonacci. Partendo dalla proliferazione di una coppia di conigli, egli si rese conto che la popolazione delle coppie cresceva secondo la seguente progressione numerica (che ovviamente prese il suo nome): 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, ecc. dove ogni numero a partire dal terzo è la somma dei due precedenti. E il mondo naturale è stracolmo di tali numeri che utilizza per disporre le proprie configurazioni. Facciamo qualche esempio cominciando dal regno floreale e proprio dalla ben nota margherita di campo, che spesso interroghiamo per dissipare i nostri tormenti sentimentali con la domanda: M ama o non m ama?. La maggior parte di questi fiori ha 13, 21 o 34 petali, e a proposito del dilemma amoroso, quando la beccate con i numeri dispari e cominciate col m ama l esito sarà affermativo; quindi vi conviene sempre cominciare con questa domanda! Poi ci sono i gigli che hanno 3 petali, i ranuncoli 5, i delphinia 8, i tageti 13, gli astri 21 e i girasoli che oscillano tra 34, 55, 89 o 144. Se vi cimentate nel conteggio considerate che qualche petalo potrebbe essere caduto, oppure la corolla potrebbe essere doppia (ma sempre multipla dei numeri di Fibonacci) come conseguenza delle tecniche agricole di lavorazione. Le immagini mostrano l intreccio di spirali che assemblano i semi di girasole nel suo capolino. 14 Scienza e Conoscenza - n. 41, luglio/agosto/settembre 2012 scienza41_gatta.indd 14 16/07/12 09:58
4 Anche la corolla della rosa è collegata al rapporto aureo. Gli angoli che definiscono le posizioni dei petali (in frazioni di angolo giro) sono la parte decimale di semplici multipli di phi Nel girasole i semi sono disposti lungo spirali il cui numero dipende di solito dalle sue dimensioni. Nel caso più comune ci sono 34 spirali avvolte in senso orario o antiorario, e 55 avvolte nel senso opposto. Ma sono stati osservati girasoli con rapporti del numero di spirali 89/55, 144/89 e perfino 233/144. Anche gli alberi non sono immuni da tali configurazioni. Le squame della pigna dell abete sono disposte in due famiglie di spirali intrecciate, e ogni famiglia contiene un numero di Fibonacci di squame. E che dire dei frutti? La maggior parte degli ananas presenta sulla superficie 5, 8, 13 o 21 spirali via via più ripide di squame esagonali. Phi, il Numero Aureo Ma c è di più. Oltre un millennio prima che Fibonacci facesse balzare fuori dal cilindro la sua magica sequenza numerica, i primi grandi pensatori erano in piena crisi filosofica per le anomale caratteristiche di alcuni numeri che, per questo, vennero definiti irrazionali. Senza entrare troppo nel dettaglio che esulerebbe dal nostro scopo, diciamo solo che questi utlimi non possono essere il quoziente di due numeri interi (in pratica non scaturiscono da una frazione e, quindi, tramite essa non si possono esprimere); ma, soprattutto, la loro rappresentazione decimale non termina mai e non è periodica. In sostanza sono numeri interminabili, incommensurabili o infiniti, e nel loro esserlo riescono pure a non ripetersi! Il pi greco (π), pari al rapporto tra la circonferenza e il diametro di un cerchio qualsiasi per un valore che parte da 3,14159, è il più noto di questi numeri anche al grande pubblico. Meno famoso ma ancora più affascinante, invece, è phi (φ), corrispondente ad un anonimo 1, Eppure, esprime una relazione geometrica considerata talmente preziosa da essere definita sezione aurea o numero aureo, e da aver ispirato pensatori di tutte le discipline più di qualunque altro numero nella storia della matematica. Il suo potere, poi, si è rafforzato quando nel diciassettesimo secolo l astronomo polacco Giovanni Keplero si accorse del suo legame con la sequenza di Fibonacci: procedendo, infatti, lungo i numeri della sua successione, si trova che il rapporto tra un termine e il suo precedente oscilla (risultando ora in eccesso ora in difetto) intorno a un numero al quale si avvicina sempre di più. E quel numero è proprio Phi, il Rapporto Aureo. Quindi la misteriosa sequenza numerica racchiude qualcosa di ancora più strabiliante che la natura sfrutta di continuo con grande disinvoltura. - Scienza e Conoscenza 15 scienza41_gatta.indd 15 16/07/12 09:58
5 Numeri magici in natura La matematica sembra essere dotata di una dimensione estetica che comunica direttamente all animo umano tramite la semplice contemplazione delle forme che cesella Per esempio, a causa del fenomeno scientifico noto come fillotassi (disposizione delle foglie) le piante tendono a disporre i loro tronchi e il loro fogliame secondo schemi regolari per cercare di massimizzare l esposizione alla luce, alla pioggia e all aria. E tali schemi seguono moti rotatori in quanto evitano che la pianta ombreggi le proprie fronde le une con le altre (vale anche per i frutti come le pigne o i semi; ecco perché la disposizione spiraliforme di questi ultimi come abbiamo visto in precedenza). Qualche esempio? I tigli collocano le proprie foglie da due parti opposte corrispondenti a un mezzo giro intorno al fusto (quoziente di fillotassi ½); il rovo, il faggio e il nocciolo dispongono il passaggio da una foglia all altra con un terzo di giro (quoziente di fillotassi 1/3); il melo, alcune querce e l albicocco 2/5 di giro, il pero e il salice piangente 3/8 ecc. Le foglie, insomma, si succedono tutte lungo una stretta spirale chiamata vegetativa scandita dai numeri di Fibonacci, avanzando lungo una circonferenza secondo un angolo costante (noto come Angolo di Divergenza) prossimo a 137,5 e ancora legato al Rapporto Aureo! Infatti l angolo maggiore risultante dalla divisione dell angolo giro secondo il Rapporto Aureo misura 360 / φ, ovvero 222,5. Quindi l angolo minore in cui l angolo giro è diviso è ,5 cioè 137,5 : l Angolo Aureo. A livello ottico l impressione che questa disposizione genera è quella di due spirali di senso opposto che si avvitano l un l altra così come esibisce il capolino del girasole, le spire delle pigne, e tanti altri organismi ancora. Anche la corolla della rosa è collegata al rapporto aureo. Gli angoli che definiscono le posizioni dei petali (in frazioni di angolo giro) sono la parte decimale di semplici multipli di phi. Il primo petalo è a un 0,618esimo (la parte decimale di 1 x phi) di giro dal petalo 0; il secondo è a un 0,236esimo (la parte decimale di 2 x phi) dal petalo 1 e così via. Ma perché accade tutto ciò? Qualche secolo fa l astronomo polacco Keplero si convinse che si trattava di pura efficienza: se posti secondo la cadenza degli Angoli Aurei i germogli risultano più fitti e utilizzano lo spazio nel modo migliore. D altro canto se l Angolo di Divergenza avesse un ampiezza di qualsiasi altro prodotto razionale dell angolo giro, le foglie si allineerebbero o in modo da lasciare inutilizzata una grande quantità di spazio tra l una e l altra, o sovrapponendosi ostacolandosi a vicenda. Naturalmente è solo un ipotesi, anche perché è giusto sottolineare che più che di regole si tratta di tendenze prevalenti, le cui eccezioni potrebbero invalidare ogni congettura. Idem varrebbe per l ingegno del Nautilo: poiché con l età la creatura dal corpo molle cresce, diventa troppo grande per la camera e amplia la casa secernendo nuovo materiale per la costruzione. Ma mentre la conchiglia si allunga, il raggio aumenta in proporzione, cosicchè la forma del guscio resta immutata. In tal modo questo inconsapevole e geniale architetto della natura, pur ampliandola, trascorre tutta la vita nella stessa dimora in costante equilibrio. In altri casi è una questione di avido sfruttamento degli spazi, come dimostra la forma esagonale dei nidi d api, in assoluto la configurazione più efficiente per stipare cerchi in un piano. E a questo punto sembra che cotanta efficienza valga anche per il mondo inorganico; avendo, infatti, la maggior parte dei cristalli di neve sei punte, essi tendono a incastrarsi egregiamente ottimizzando lo spazio vuoto e agevolando la trasformazione del vapor acqueo in neve. Le figure geometriche auree Ma Aureo non è solo un numero o un angolo, bensì anche alcune figure geometriche. Il Rettangolo Aureo, per esempio, si ottiene quando i suoi lati, maggiore e minore, stanno in rapporto con φ, e accade che è l unico che consente, togliendo un quadrato corrispondente alla sua area, di ottenere un rettangolo simile al primo. Così facendo, tracciando due diagonali che si intersecano in ciascuna coppia di rettangoli padre e figlio, si trova che tutte passano per un punto, in modo che una serie di rettangoli aurei sempre più piccoli converga nel suo intorno senza mai raggiungerlo (il matematico Clifford Pickover lo chiamò l Occhio di Dio ). E se si congiungono i punti in cui questo vortice di quadrati divide i lati secondo il Rapporto Aureo, si ottiene la famosa spirale logaritmica che si avvolge intorno all Occhio. Idem vale per il Triangolo Aureo, un triangolo in cui il rapporto di lunghezza tra i lati uguali e la base è pari a φ. Anche in questo caso continuando a bisecare gli angoli alla base si forma un vortice di triangoli sempre più piccoli i cui vertici, collegati, danno una curva logaritmica. Il legame di phi esiste anche nell ambito di figure 16 Scienza e Conoscenza - n. 41, luglio/agosto/settembre 2012
6 Numeri magici in natura Il grafico illustra la relazione tra il Rettangolo Aureo e la Spirale Logaritmica. Stando i lati maggiore e minore del Rettangolo in rapporto con φ, togliendo un quadrato corrispondente all area del primo si può ottenere un rettangolo simile. Così facendo tracciando due diagonali che si intersecano in ciascuna coppia di rettangoli padre e figlio, si trova che tutte passano per un punto, in modo che una serie di rettangoli aurei sempre più piccoli converga nel suo intorno senza mai raggiungerlo (il matematico Clifford Pickover lo chiamò l Occhio di Dio ). E se si congiungono i punti in cui questo vortice di quadrati divide i lati secondo il Rapporto Aureo, si ottiene la famosa spirale logaritmica che si avvolge intorno all occhio. piane come il Pentagramma, ottenuto collegando tramite diagonali tutti i vertici di un Pentagono. Quest ultimo è la comune stella a cinque punte ognuna costituita da un triangolo isoscele dove il rapporto della lunghezza di uno dei lati con la base è uguale alla Sezione Aurea. Se continuiamo all infinito a inscrivere il Pentagramma all interno del Pentagono, si può dimostrate che ogni segmento è minore del precedente di un fattore esattamente uguale al Rapporto Aureo, e che la diagonale e il lato del Pentagono sono incommensurabili, ovvero che il rapporto delle loro lunghezze non può essere espresso come rapporto di numeri interi. Anche i poliedri regolari (quelli che possono essere inscritti in una sfera, ovvero i solidi platonici tetraedro, cubo, ottaedro, il dodecaedro, l icosaedro) sono legati al Rapporto Aureo, essendo le facce costituite da figure piane; in particolare l icosaedro (con 20 facce triangolari) e il dodecaedro (con dodici facce pentagonali). Nel primo i dodici vertici si possono dividere in tre gruppi di quattro, e i vertici di ciascuna tetrade si possono collocare in cima agli angoli di un Rettangolo Iscrivendo un Pentagramma (la comune stella a cinque punte) all interno di un Pentagono, si può dimostrate che ogni segmento è minore del precedente di un fattore esattamente uguale al Rapporto Aureo, e che la diagonale e il lato del Pentagono sono incommensurabili, ovvero che il rapporto delle loro lunghezze non può essere espresso come rapporto di numeri interi. - Scienza e Conoscenza 17
7 Numeri magici in natura Aureo. In egual modo i centri delle dodici facce pentagonali del dodecaedro si possono raggruppare quattro a quattro, e ciascuno di questi gruppi corrisponde ai vertici di un Rettangolo Aureo. Matematica, storia e arte È indubbio che il senso estetico umano provi un senso di piacere nell ammirare forme che possiedono certe simmetrie, ovvero emanano una sorta di armonia inducendo un estasi quasi mistica. E così nel Rinascimento il Rapporto Aureo sconfinò oltre il mondo matematico per approdare in quello dell arte e dello studio dei fenomeni naturali. Sebbene molti siano convinti che tale proporzione sia stata incorporata già in strutture antichissime come la Grande Piramide di Giza, il Serapeo del Tempio di Seti I o il Partenone di Atene, non sembrano esistere prove scientifiche inattaccabili a suffragio di tale tesi. Di certo, però, sappiamo che il teologo e matematico toscano Luca Pacioli nel 1509 pubblicò a Venezia un trattato in tre volumi sulle proprietà del Rapporto Aureo chiamato Compendio de Divina Proportione ufficializzandone l esistenza anche al mondo dei non matematici. Quindi è probabile che, da allora, numerosi artisti abbiamo provato a sfruttarne la sua efficacia visiva, e anche acustica, nelle loro opere. Ma anche in questo caso l affermazione rimane ambigua, perché spesso si riscontrano parametri figurativi che più che altro si avvicinano a questo numero, come per esempio le dimensioni del quadro di Salvador Dalì Il Sacramento dell Ultima Cena del 1955, grande all incirca 268 x 167 cm, peraltro abbellita di un enorme dodecaedro che fluttua sopra la tavola e la circonda. Poi ci sono opere come la splendida tela de La Madonna di Ognissanti del pittore e architetto Giotto di Bondone, dove molti studi affermano che le figure centrali (rappresentate dalla Madonna e il Bambino) siano inscrivibili in Rettangoli Aurei, così come la Madonna di Rucellai (di Duccio di Buoninsegna) e la Madonna di Trinità di Cimabue, che però sono molto precedenti alla data ufficiale di diffusione del Rapporto Aureo al di fuori del mondo matematico, essendo state dipinte tra il 1200 e il La matematica, insomma, sembra essere dotata di una dimensione estetica che comunica direttamente all animo umano tramite la semplice contemplazione delle forme che cesella. Ma in fondo è una consapevolezza, magari inconscia, che già possediamo; non rimaniamo, forse, estasiati da fiori di vario colore o pietre pregiate al punto che le doniamo per esprimere i nostri sentimenti e le nostre emozioni? Quale gesto d amore può essere più struggente del sacrificio di una rosa rossa o della luce immortale di un gioiello? Ma ciò dischiude tutta un altra serie di domande: questa umanità che trasuda dai numeri è stata fatta per essere contemplata da noi oppure ha un esistenza indipendente? Dio è un matematico? Un geniale architetto? E perché profondere tanti sforzi estetici per cesellare parti di un mondo di cui spesso neppure ci accorgiamo? Letture Keith Devlin I Numeri Magici di Fibonacci L avventurosa scoperta che cambiò la storia della matematica Rizzoli, 2012 Alfred S. Posamentier, Ingmar Lehmann I (favolosi) Numeri di Fibonacci Emmebi, 2011 Mario Livio La Sezione Aurea Storia di un numero e di un mistero che dura da tremila anni BUR, 2007 Cercalo in libreria o su - Letture consigliate Scritto da Sabrina Mugnos Geologa, ha studiato e visitato decine di vulcani in giro per il mondo attraverso esplorazioni avventurose e talvolta estreme. Si occupa da tanti anni anche di astrobiologia e di Archeoastronomia. Il suoi libri, I maya e il 2012, Catastrofi Naturali, Vulcani, L universo che pensa, (Macro Edizioni), stanno riscuotendo un grande successo in Italia e in diversi paesi stranieri. Impegnata in corsi, seminari e convegni a respiro internazionale, è spesso ospite di trasmissioni televisive e radiofoniche. Per maggiori informazioni: 18 Scienza e Conoscenza - n. 41, luglio/agosto/settembre 2012
8 Geometria frattale Broccoli, fegato, mercati finanziari, universo: la struttura similare del mondo Sabrina Mugnos Vi siete mai soffermati, anche solo un istante, a riflettere sulle forme naturali del mondo che ci circonda? Sono montagne, vallate, canyon, fiumi, oceani e mari, caverne, alberi, rocce, nubi e animali di ogni genere. Ma qual è la loro esatta geometria? E se volessimo misurarli? Idem vale per i moti turbolenti dell aria (ovvero la dinamica del clima, delle perturbazioni atmosferiche, ecc.), delle acque in generale (oceaniche, fluviali, lacustri, sotterranee), e di tutti i fenomeni elettromagnetici (fulmini, aurore, propagazione del campo geomagnetico e dell elettricità ecc.). Le curve patologiche Fin dai tempi antichi ci siamo arrangiati con gli schemi e le figure messe a disposizione dalla geometria euclidea, ma la consapevolezza dei limiti di tale approssimazione non è mai venuta meno, e l occasione di affrontarli arrivò nel 1875 quando il matematico Karl Weierstrass scoprì una curva priva di tangente in ogni suo punto, ovvero, in gergo, non derivabile e, quindi, priva di una descrizione analitica. L impeccabile raziocinio del regno matematico astratto, quindi, cominciò a vacillare, e lo scompiglio totale sopraggiunse quando il matematico russo Georg Cantor (la cui ossessione nel risolvere i problemi dell infinito lo portò a impazzire e trascorrere internato buona parte della sua vita) inventò la Teoria degli insiemi (una delle colonne portanti della matematica moderna) dimostrando, nel 1877, uno strabiliante teorema (l infinito numero di punti su una retta monodimensionale è uguale al numero di punti all interno di un qualsiasi cubo tridimensionale). A quel punto uscirono dall ombra altri oggetti stravaganti e inconsueti che indignarono l ortodossia matematica facendo urlare alle mostruosità, a stranezze ripugnanti e deformi o, per usare le parole di Charles Hermite, suscitando «... la paura e l orrore della trista piaga delle funzioni senza derivata...». Una di queste prime curve dette anche patologiche (sia per i folli paradossi che racchiudono che come gioco di parole dall inglese path, percorso), fu inventata dal matematico Giuseppe Peano, ed è in grado di girare in modo così complesso da toccare ogni punto in un piano, così da reiterarsi potenzialmente all infinito, rimanendo però circoscritta a un area limitata. Avete già colto il paradosso? Un linea che serpeggia all infinito ma dentro una spazio definito. La curva di Peano reitera infinitamente se stessa fino a ricoprire un quadrato. Si racconta l aneddoto che a Spinetta di Cuneo, fino a non molto tempo fa sul balcone della casa di Peano fosse ammirabile una piastrellatura simile a quella rappresentata dalla sua curva, poi smantellata dall ignara, attuale inquilina. - Scienza e Conoscenza 19
9 Geometria frattale Nel tentativo di diradare l oscurità dentro alla quale erano piombati gli studiosi, il matematico svedese Helge von Koch, nel 1904, creò un altra di quelle fastidiose curve continue prive di punti di tangenza che prese il suo nome. Cominciò a costruirla partendo da un triangolo equilatero dividendo ogni lato in tre segmenti uguali e collocando nel mezzo un altro triangolo equilatero più piccolo di un terzo, e poi ripetè ancora e ancora la stessa operazione. Stesso controsenso della curva di Peano, a ogni operazione la lunghezza del perimetro della curva aumentava di un fattore 4/3 crescendo indefinitamente, sebbene le La struttura similare Nell indagare questo affascinante mondo astratto gli studiosi si accorsero di un altra caratteristica importante di tali bizzarre curve, chiamata autosimilitudine, secondo la quale ogni loro più piccola parte riproduce, in scala ridotta, la forma dell intero disegno; in pratica troviamo un ordine (la reiterazione di uno stesso motivo) soggiacente a un irregolarità (la forma generale). E notarono altresì che gran parte degli oggetti del mondo naturale sembrano seguire questa regola. Facciamo un meraviglioso esempio? Avete mai notato Una rappresentazione della Curva di Koch, che molto ricorda la forma del fiocco di neve ma anche i confini frastagliati di molti oggetti come una linea costiera. dimensioni dell area del poligono rimanevano limitate a 8/5 dell area del triangolo di partenza. Nel mondo della geometria euclidea gli oggetti hanno un numero di dimensioni espresso da un valore intero: i punti non hanno dimensione, le line rette ne hanno una, le figure piane due e i solidi tre. Tuttavia le forme anomale di cui stiamo parlando cambiano dimensione e in modo irregolare tra l una e le due dimensioni (come la saetta, per esempio, che spostandosi nello spazio oscilla tra 1 e 2 dimensioni); come sciogliere il dilemma? dal verduraio o al supermercato, nel periodo invernale, che ammassati insieme ad altri ortaggi spiccano elaborate sculture? Si tratta della varietà di broccolo verdognolo (chiamato romano o cimoso) che esibisce la parte centrale come un insieme di piccoli torrioni in stile barocco assemblati nella forma di una spirale. Farlo a pezzi e divorarlo è altrettanto sacrilego che sfoderare una coltellata su una tela di Leonardo! La sua bellezza incanta, e, a uno sguardo appena un poco più attento, si nota che l infiorescenza del grosso cavolo è costruita con tanti micro cavoletti assemblati Il broccolo romano o cimoso è forse il più sublime esempio di oggetto frattale nel quale spicca ben visibile la struttura autosimilare. Ogni più piccola parte della sua infiorescenza riproduce il motivo generale. 20 Scienza e Conoscenza - n. 41, luglio/agosto/settembre 2012
10 Geometria frattale con struttura spiraliforme. Un altro bell esempio è la felce, dove ogni fronda presenta una grande somiglianza con l intera pianta; ma sono svariate le forme naturali che rivelano innumerevoli sequenze di motivi sempre uguali o molto simili che si ripetono all in- La felce è un altro splendido esempio di autosimilarità, dove ogni fronda riproduce la forma dell intera pianta. finito variando solo la scala. Non sono solo il regno animale a vegetale a esibire tanto estro. I fenomeni geologici che modellano la superficie terrestre, per esempio, sanno ricamare motivi a dir poco stupefacenti (vedi immagini). Una serie di immagini satellitari di alvei e bacini fluviali mostra la loro complessità, che può essere affrontata quantitativamente solo tramite la geometria frattale. - Scienza e Conoscenza 21 scienza41_gatta.indd 21 16/07/12 09:58
11 Geometria frattale Lassù non troviamo semplici punti sparpagliati nel vuoto, ma centinaia di milioni di assembramenti di stelle (le galassie) organizzati in grumi, ammassi singoli, doppi, tripli, regolari, irregolari ecc. ricamati in estrosi arabeschi con tentacoli filamentosi e separati da giganteschi vuoti a forma di celle di alveare, bolle, e chissà che altro; visione ben distante dalle pacate e uniformi pianure disegnate dalla Legge di Hubble Matematica e geometria frattale I paradossi matematici sembravano avere un corrispettivo nel mondo naturale, dove a quel punto era il caso di trasferirsi per risolvere l arcano; ed è quello che fece il matematico franco-polacco Benoit Mandelbrot che nel 1975, dopo aver battezzato tali bizzarri oggetti come frattali (dal latino fractus, frammentare), affrontò il rompicapo domandandosi quanto fosse lunga la costa della Gran Bretagna (che ricalca una situazione reale della Curva di Koch). Per compiere una tale misura molto dipende dallo strumento che si utilizza. Più la sua scala è grande (per esempio una rilevazione satellitare) più particolari vengono trascurati. Quindi per considerare ogni irregolarità dovremmo compiere un lavoro titanico recandoci in loco e utilizzando un metro a mano! Ma anche in questo caso le sinuosità ancora più piccole ci sfuggirebbero. In altre parole ogni volta che si riducono le dimensioni dello strumento di misura, la lunghezza del soggetto aumenta indefinitamente. Tuttavia, dato un oggetto di un certo numero di dimensioni, e verificando quanti oggetti simili ma più piccoli occorrano per formarlo, si può constatare che vi è una relazione tra il numero di oggetti prodotti (n), il fattore di riduzione (f), e la mono o bi dimensionalità o Dimensione Frattale (D), espressa secondo la semplice formula: Koch è partito da una figura geometrica, ma questa volta togliendo in modo ripetitivo porzioni di essa: si parte da un quadrato e lo si divide in nove quadrati uguali e si elimina quello centrale lasciando un bordo di otto quadrati il cui lato è 1/3 del lato originale. Quindi si compie la stessa proceduta con gli otto quadrati più piccoli e così via all infinito, fino ad ottenere otto copie di se stesso ognuna larga 1/3. Applicando lo stesso meccanismo, ma usando come partenza un triangolo equilatero, la figura che si ottiene è chiamata Gerla o Triangolo di Sierpiski, ed è composta da tre copie di se stessa ognuna delle quali costituita da un triangolo di lato pari a metà del lato del triangolo di partenza. Quest ultima configurazione trova spesso riscontro nel mondo naturale, per esempio come ornamentazione sulla conchiglia di diverse specie di molluschi che vivono negli oceani. Più che un vezzo di madre natura si tratta però di una sorta di elegante schema della dinamica chimica dei pigmenti che vengono depositati sulla parte che si sviluppa. La superficie della Conchiglia Oliva Porphyria è ricamata secondo gli stessi schemi creati matematicamente da Sierpiski. n = (1/f) D dove D = - log n / log f Quindi la Dimensione Frattale di un sistema del genere mette in relazione il numero di elementi costituenti e le loro dimensioni, permettendoci di farne una misura quantitativa. Un altro modello teorico è scaturito dal Tappeto di Sierpinski, inventato dall omonimo matematico polacco all inizio del secolo scorso. Anch egli come 22 Scienza e Conoscenza - n. 41, luglio/agosto/settembre 2012
12 Geometria frattale Sulle tre dimensioni, invece, si è cimentato il matematico austriaco Karl Menger prendendo un cubo pieno di massa, lato e densità unitari, dividendo ogni faccia in nove quadrati uguali e praticando tre aperture che attraversino il solido al centro di ciascuna delle sue facce. Quindi ha ripetuto la procedura per i restanti venti cubetti, ottenendo una struttura che racchiude lo stesso volume, ma con una massa diminuita di un fattore pari a 20/27, ovvero di densità minore di quella di partenza. Una rappresentazione della Spugna di Menger, un esperimento frattale che utilizza le tre dimensioni. Il concetto di frattale ha colto un aspetto intimo ed essenziale della natura che precedentemente era stato trascurato, ovvero che persino i suoi tratti più casuali possiedono simmetrie nascoste. Ciò significa che simmetria e caos sono due facce della stessa medaglia: la forma complessiva (che apparentemente sembra caotica) riflette la prima, e i particolari intricati il secondo. Quindi, fenomeni che esibiscono strutture bizzarre e inattese diventano possibili da studiare quantitativamente a grandezze visivamente inaccessibili, grazie all anello di congiunzione tra la scala micro e macro rappresentato dall autosimilarità. Naturalmente i frattali ottenuti matematicamente (deterministici) sono perfetti, ovvero l autosimilarità si conserva impeccabilmente fino a scale infinitesime. Nei casi reali, invece, ovvero nei fenomeni naturali o negli organismi animali e vegetali, la reiterazione introduce via via un errore statistico, ovvero le strutture non si ripetono sempre e rigorosamente immutate ma esibiscono piccole variazioni (ma è proprio questo il bello di madre natura)! L utilizzo della matematica frattale si è rivelato utilissimo in molti campi come, per esempio, in quello della medicina. Nel corpo umano e animale, infatti, svariati organi presentano tale struttura. Uno è il fegato, suddiviso in diversi lobi ognuno irrorato da una diversa ramificazione della Vena Porta. Se, poniamo il caso, qui si dovesse scatenare un tumore, si può isolare solo il lobo malato e asportarlo senza danneggiare tutto il resto, perché utilizzando gli strumenti di calcolo della geometria frattale a partire dalla versione ridotta della Vena Porta si può risalire alla sua versione complessiva e intervenire in modo mirato. Altro settore che si presta a tale studio è il mercato azionario, perché se si disegna il grafico dell andamento delle sue quotazioni nei mesi, si ottiene una curva irregolare con molti alti e bassi che mantiene l andamento anche quando la si frammenta per osservare il trend settimanale, giornaliero, orario o addirittura in tempo reale. Quindi individuando un oggetto o sistema come frattale, ovvero adottando l autosimilarità come legge della sua struttura, si può vedere matematicamente anche laddove la scala ci impedirebbe di farlo. Universo frattale Balzando dai cavoli alle stelle anche i cieli si rivelano piuttosto inquieti. Il nostro Sistema Solare, per esempio, è si governato da leggi matematiche che ne definiscono la sua struttura (la legge di Gravitazione Universale di Newton, le leggi di Keplero che regolano le orbite planetarie ecc.), tuttavia è anche soggetto al caos nella forma dell imprevedibilità orbitale di milioni e milioni di corpi minuti che interagiscono tra loro rendendosi impredicibili, nonché nella dinamica di titanici vortici atmosferici come la Grande Macchia Rossa su Giove (che potrebbe inglobare almeno un paio di Terre), quella Scura su Nettuno, e le insolite formazioni nuvolose cesellate da venti a 1800 km/h su Saturno. O ancora delle caotiche formazioni geologiche che tormentano le superficie dei pianeti o dei satelliti, soprattutto quelli privi di atmosfera. Ovviamente tutto ciò vale anche per le complesse dinamiche delle stelle, di ammassi di stelle nonché dei moti turbolenti che avvengono nelle nebulose sparpagliate per la galassia e, in ultima analisi, di tutta - Scienza e Conoscenza 23
13 Geometria frattale Potrebbe il cosmo esprimersi in una forma frattale dalla trama di un fiore fino a quella degli spazi siderali? Può essere possibile che all occhio di un osservatore esterno, magari il fantomatico Creatore, non siamo che una delle tante matrioske? la materia che la compone. Ma aumentando ancora lo zoom, dal momento che l universo è formato da miliardi di galassie, viene spontaneo domandarsi fino a che scala si spinge il gioco a incastri dell autosimilarità. Potrebbe, cioè, il cosmo esprimersi in una forma frattale dalla trama di un fiore fino a quella degli spazi siderali? Può essere possibile che, all occhio di un osservatore esterno, magari il fantomatico Creatore, non siamo che una delle tante matrioske? All inizio del secolo scorso, grazie alla sua celeberrima Teoria della Relatività Generale, Albert Einstein, suo malgrado, aveva rivelato al mondo che l universo era tutt altro che statico, bensì in espansione, sebbene da uomo del suo tempo cercò di rinnegarlo in tutti i modi anche contro le evidenze matematiche che lui stesso aveva partorito (gesto che poi riconobbe come il suo più grande abbaglio). Ma fu solo nel 1929 che si ebbe la prova che le sue equazioni non mentivano, quando l astronomo americano Edwin Hubble, fotografando diverse regioni di cielo, si accorse che, ovunque si guardasse, le galassie si allontanavano rapidamente da noi, e tanto più velocemente quanto più erano lontane. E, addirittura, oggi abbiamo scoperto che tale moto sta accelerando sempre più, sospinto da una forma di materia ed energia che non conosciamo e non rileviamo. In realtà è il tessuto cosmico a dilatarsi e le galassie, essendo come le uvette incastonate in un pudding in lievitazione, si allontanano reciprocamente distribuendosi in modo uniforme e isotropo (ovvero si vedono in ugual quantità in qualunque direzione si guardi). Tuttavia quando gli studiosi cominciarono a compilare le prime mappe della distribuzione galattica, si resero conto che è raro trovare una galassia a vagare sola soletta nel vuoto siderale, perché nel suo disegno il cosmo le ha disposte in gruppo. Per esempio, la nostra Via Lattea appartiene al Gruppo Locale delle Galassie composto da una ventina di elementi e di cui fa parte anche la famosa galassia di Andromeda, distante da noi circa 2 milioni di anni luce. L ammasso nostro vicino di casa che ospita centinaia di galassie, invece, è quello che si proietta nella costellazione della Vergine, ed è il centro di un sistema molto più grande chiamato Superammasso Locale. Comprensibilmente tali evidenze si rivelarono una spina nel fianco del modello cosmologico standard e, già al tempo, molti studiosi si affrettarono a metterci una toppa invocando la presenza di nubi di polveri oscure come causa del panorama frastagliato osservato, quindi solo apparente. Ma i dati sperimentali diventavano sempre più schiaccianti, e già nel 1977 Benoit Mandelbrot non aveva dubbi sul disegno frattale del cosmo, esprimendone la convinzione nel suo libro Les Objets fractals, dove ne diede anche la prima descrizione matematica specificando che solamente se l osservatore si trova situato su un punto della struttura frattale riesce a vedere che la distribuzione della materia segue il suo schema, diminuendo di densità verso l esterno. Se, invece, si trova in un vuoto ampio può rilevare la diminuzione di densità frattale solo a scale molto più grandi della dimensione del vuoto stesso. Ne consegue che l asimmetria tra osservatori posti su punti della struttura e osservatori dispersi casualmente nello spazio è di particolare importanza, perché un punto scelto a caso potrebbe trovarsi, con buona probabilità, in un vuoto indefinitamente grande e un osservatore in questa situazione non arriverebbe a conoscere quasi nulla dell universo. La sua convinzione fu sposata dallo studioso italiano Luciano Pietronero che, negli anni Ottanta, dimostrò, tramite studi di fisica statistica, che almeno a livello locale l universo presentava una struttura frattale con l autosimilarità che si manifestava a partire da 0,1 fino a 100 Mpc (Megaparsec, equivale a un milione di parsec, dove quest ultimo equivale a 3,26 anni luce) implicando una diminuzione di densità della materia all aumentare del volume considerato, ovvero al crescere della scala, secondo una legge di potenza. E nel gennaio del 1999 la prestigiosa rivista «Nature» ne diede conferma, pur dichiarando che le opinioni erano ancora divergenti relativamente alle scale più ampie. Pochi mesi dopo (agosto 1999) alla notizia fece eco anche la testata «New Scientist», ospitando l acceso confronto tra il noto cosmologo Ofer Lahav e il giovane astronomo Sylos Labini (dello staff di Pietronero) relativamente alla scala alla quale si spinge la frattalità del cosmo prima di trasformarsi in uniformità. Era evidente che l ultima parola doveva metterla la 24 Scienza e Conoscenza - n. 41, luglio/agosto/settembre 2012
14 Geometria frattale L immagine riproduce parte della mappatura in 3D della distribuzione delle galassie effettuata dal progetto (SDSS). La Terra deve considerarsi al centro, e ogni punto rappresenta una galassia con un contenuto medio di stelle di 100 milioni. La colorazione delle galassie dipende dall età delle stelle che contengono; quelle rosse sono le più vecchie e anche le più ammassate. Il circolo bianco esterno rappresenta il raggio di indagine di 2 miliardi di anni luce. I due cunei scuri di lato rappresentano un vuoto nella mappatura a causa delle polveri oscure che oscurano la nostra visuale in quella direzione. Credit: M. Blanton and the Sloan Digital Sky Survey. tecnologia, permettendoci di avere visioni sempre più lontane e dettagliate della distribuzione galattica. E ciò arrivò col progetto Sloan Digital Sky Survey (SDSS), uno dei più importanti e ambiziosi della storia dell astronomia, che in otto anni di lavoro (dal 2000 al 2008, ma una terza fase si concluderà nel 2014) ottenne una mappa tridimensionale contenente più di galassie e quasar disposti innegabilmente in modo frattale. Il dibattito sulla distanza fino alla quale si spinge la struttura frattale prima di trasformarsi in una monotona uniformità (sempre che davvero ciò accada) è ancora acceso, e di nuovo la chiave di volta per dare una risposta rimane nelle mani della tecnologia. Resta, tuttavia, il fatto che lassù non troviamo semplici punti sparpagliati nel vuoto, ma centinaia di milioni di assembramenti di stelle (le galassie) organizzati in grumi, ammassi singoli, doppi, tripli, regolari, irregolari ecc. ricamati in estrosi arabeschi con tentacoli filamentosi e separati da giganteschi vuoti a forma di celle di alveare, bolle, e chissà che altro; visione ben distante dalle pacate e uniformi pianure disegnate dalla Legge di Hubble. La scienza, dunque, stoicamente e caparbiamente, ancora si avventura nell arte, e si spinge a ritroso ai primordi della formazione dell universo, quando la gravità e il mondo dell infinitamente piccolo della meccanica quantistica si contendevano l appalto della sua geometria. E ipotizza che furono fluttuazioni iniziali di densità a creare l alternanza di galassie e vuoti che osserviamo. Ma da qui a comprendere perché una disposizione tanto peculiare, cioè frattale, beh, la strada è ancora lunga, e percorrerla significherà anche scoprire il significato dell armonica forma di un fiore, una conchiglia o quell anonimo ma straordinario broccolo che rende i verdurai dei mercanti d arte. Letture Benoit Mandelbrot Nel mondo dei frattali Di Renzo Editore, 2001 Giuseppe Arcidiacono Spazio Iperspazi Frattali Il magico mondo della geometria Di Renzo Editore, 2009 Tutti i libri di Sabrina Mugnos possono essere richiesti in libreria oppure su - Letture consigliate - Scienza e Conoscenza 25
La spirale iperbolica: Fu descritta per la prima volta da Pierre Varignon (1654-1722). L equazione, espressa in coordinate polari, è del tipo:
 Esistono delle forme geometriche che sono in grado, per complessi fattori psicologici non del tutto chiariti, di comunicarci un senso d equilibrio, di gradimento e di benessere. Tra queste analizzeremo
Esistono delle forme geometriche che sono in grado, per complessi fattori psicologici non del tutto chiariti, di comunicarci un senso d equilibrio, di gradimento e di benessere. Tra queste analizzeremo
LA GRAFICA E LA GEOMETRIA OPERATIVA
 LA GRAFICA E LA GEOMETRIA OPERATIVA La geometria operativa, contrariamente a quella descrittiva basata sulle regole per la rappresentazione delle forme geometriche, prende in considerazione lo spazio racchiuso
LA GRAFICA E LA GEOMETRIA OPERATIVA La geometria operativa, contrariamente a quella descrittiva basata sulle regole per la rappresentazione delle forme geometriche, prende in considerazione lo spazio racchiuso
ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE P.N.I. 2004
 ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
All interno dei colori primari e secondari, abbiamo tre coppie di colori detti COMPLEMENTARI.
 Teoria del colore La teoria dei colori Gli oggetti e gli ambienti che ci circondano sono in gran parte colorati. Ciò dipende dal fatto che la luce si diffonde attraverso onde di diversa lunghezza: ad ogni
Teoria del colore La teoria dei colori Gli oggetti e gli ambienti che ci circondano sono in gran parte colorati. Ciò dipende dal fatto che la luce si diffonde attraverso onde di diversa lunghezza: ad ogni
ESERCITAZIONE OSSERVARE UN ALBERO
 L esercizio richiesto consiste nella scelta di un albero e il suo monitoraggio/racconto al fine di sviluppare l osservazione attenta come mezzo per la conoscenza del materiale vegetale. L esercitazione
L esercizio richiesto consiste nella scelta di un albero e il suo monitoraggio/racconto al fine di sviluppare l osservazione attenta come mezzo per la conoscenza del materiale vegetale. L esercitazione
Capitolo 2. Operazione di limite
 Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Sezione Aurea: una guida per gli artisti La bellezza delle proporzioni per pittori, fotografi e grafici
 Sezione Aurea: una guida per gli artisti La bellezza delle proporzioni per pittori, fotografi e grafici C'è un rapporto matematico che si trova comunemente in natura, il rapporto di 1-1,618 cui sono stati
Sezione Aurea: una guida per gli artisti La bellezza delle proporzioni per pittori, fotografi e grafici C'è un rapporto matematico che si trova comunemente in natura, il rapporto di 1-1,618 cui sono stati
LA LEGGE DI GRAVITAZIONE UNIVERSALE
 GRAVIMETRIA LA LEGGE DI GRAVITAZIONE UNIVERSALE r La legge di gravitazione universale, formulata da Isaac Newton nel 1666 e pubblicata nel 1684, afferma che l'attrazione gravitazionale tra due corpi è
GRAVIMETRIA LA LEGGE DI GRAVITAZIONE UNIVERSALE r La legge di gravitazione universale, formulata da Isaac Newton nel 1666 e pubblicata nel 1684, afferma che l'attrazione gravitazionale tra due corpi è
Il concetto di valore medio in generale
 Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
La distribuzione Normale. La distribuzione Normale
 La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
LA GEOMETRIA NELLE PIASTRELLE
 LA GEOMETRIA NELLE PIASTRELLE Supponiamo di dover pavimentare delle superfici molto estese e vogliamo evitare le classiche composizioni quadrate, rettangolari o a spina di pesce, per rendere meno banale
LA GEOMETRIA NELLE PIASTRELLE Supponiamo di dover pavimentare delle superfici molto estese e vogliamo evitare le classiche composizioni quadrate, rettangolari o a spina di pesce, per rendere meno banale
INTEGRALI DEFINITI. Tale superficie viene detta trapezoide e la misura della sua area si ottiene utilizzando il calcolo di un integrale definito.
 INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
Proposta di soluzione della prova di matematica Liceo scientifico di Ordinamento - 2014
 Proposta di soluzione della prova di matematica Liceo scientifico di Ordinamento - 14 Problema 1 Punto a) Osserviamo che g (x) = f(x) e pertanto g () = f() = in quanto Γ è tangente all asse delle ascisse,
Proposta di soluzione della prova di matematica Liceo scientifico di Ordinamento - 14 Problema 1 Punto a) Osserviamo che g (x) = f(x) e pertanto g () = f() = in quanto Γ è tangente all asse delle ascisse,
Corso di Laurea in Scienze della Formazione Primaria Università di Genova MATEMATICA Il
 Lezione 5:10 Marzo 2003 SPAZIO E GEOMETRIA VERBALE (a cura di Elisabetta Contardo e Elisabetta Pronsati) Esercitazione su F5.1 P: sarebbe ottimale a livello di scuola dell obbligo, fornire dei concetti
Lezione 5:10 Marzo 2003 SPAZIO E GEOMETRIA VERBALE (a cura di Elisabetta Contardo e Elisabetta Pronsati) Esercitazione su F5.1 P: sarebbe ottimale a livello di scuola dell obbligo, fornire dei concetti
Matematica generale CTF
 Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Corrispondenze e funzioni
 Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
Categoria Student Per studenti degli ultimi due anni della scuola secondaria di secondo grado
 Categoria Student Per studenti degli ultimi due anni della scuola secondaria di secondo grado. Risposta A). Il triangolo ABC ha la stessa altezza del triangolo AOB ma base di lunghezza doppia (il diametro
Categoria Student Per studenti degli ultimi due anni della scuola secondaria di secondo grado. Risposta A). Il triangolo ABC ha la stessa altezza del triangolo AOB ma base di lunghezza doppia (il diametro
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
1. Distribuzioni campionarie
 Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 3 e 6 giugno 2013 - di Massimo Cristallo - 1. Distribuzioni campionarie
Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 3 e 6 giugno 2013 - di Massimo Cristallo - 1. Distribuzioni campionarie
Siamo così arrivati all aritmetica modulare, ma anche a individuare alcuni aspetti di come funziona l aritmetica del calcolatore come vedremo.
 DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
GEOMETRIA DELLE MASSE
 1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
Cenni di geografia astronomica. Giorno solare e giorno siderale.
 Cenni di geografia astronomica. Tutte le figure e le immagini (tranne le ultime due) sono state prese dal sito Web: http://www.analemma.com/ Giorno solare e giorno siderale. La durata del giorno solare
Cenni di geografia astronomica. Tutte le figure e le immagini (tranne le ultime due) sono state prese dal sito Web: http://www.analemma.com/ Giorno solare e giorno siderale. La durata del giorno solare
Capitolo 4.2. Analisi tecnica: Fibonacci
 1 Capitolo 4.2 Analisi tecnica: Fibonacci 0 Contenuti ANALISI TECNICA: FIBONACCI L analisi di Fibonacci mira a identificare i potenziali livelli di supporto e di resistenza futuri basati sui trend dei
1 Capitolo 4.2 Analisi tecnica: Fibonacci 0 Contenuti ANALISI TECNICA: FIBONACCI L analisi di Fibonacci mira a identificare i potenziali livelli di supporto e di resistenza futuri basati sui trend dei
OSCURI PREDATORI DI LUCE
 OSCURI PREDATORI DI LUCE LA CADUTA DI EUCLIDE IN UN BUCO NERO PAOLO DULIO DIPARTIMENTO DI MATEMATICA DI COSA PARLIAMO Ricerca e applicazioni I protagonisti di un viaggio fantastico Geometria dello spazio-tempo
OSCURI PREDATORI DI LUCE LA CADUTA DI EUCLIDE IN UN BUCO NERO PAOLO DULIO DIPARTIMENTO DI MATEMATICA DI COSA PARLIAMO Ricerca e applicazioni I protagonisti di un viaggio fantastico Geometria dello spazio-tempo
Moto circolare uniforme
 Moto circolare uniforme 01 - Moto circolare uniforme. Il moto di un corpo che avviene su una traiettoria circolare (una circonferenza) con velocità (in modulo, intensità) costante si dice moto circolare
Moto circolare uniforme 01 - Moto circolare uniforme. Il moto di un corpo che avviene su una traiettoria circolare (una circonferenza) con velocità (in modulo, intensità) costante si dice moto circolare
Progressioni numeriche Successione di Fibonacci e sezione aurea
 Progressioni numeriche Successione di Fibonacci e sezione aurea Progetto Matematica e Statistica - Progetto Lauree Scientifiche Loredana Caso 1 Successioni numeriche 2 Una successione numerica è una sequenza
Progressioni numeriche Successione di Fibonacci e sezione aurea Progetto Matematica e Statistica - Progetto Lauree Scientifiche Loredana Caso 1 Successioni numeriche 2 Una successione numerica è una sequenza
Il mistero dei muoni: perché arrivano sulla terra e cosa c entra la relatività del tempo e dello spazio?
 Il mistero dei muoni: perché arrivano sulla terra e cosa c entra la relatività del tempo e dello spazio? Carlo Cosmelli, Dipartimento di Fisica, Sapienza Università di Roma Abbiamo un problema, un grosso
Il mistero dei muoni: perché arrivano sulla terra e cosa c entra la relatività del tempo e dello spazio? Carlo Cosmelli, Dipartimento di Fisica, Sapienza Università di Roma Abbiamo un problema, un grosso
LOCUZIONI AL MONDO. Il mistero di ogni persona (22/4/2013 24/4/2013) Testi tradotti dai messaggi originali pubblicati sul sito Locutions to the World
 LOCUZIONI AL MONDO Il mistero di ogni persona (22/4/2013 24/4/2013) Testi tradotti dai messaggi originali pubblicati sul sito Locutions to the World 2 Sommario 1. La decisione della SS. Trinità al tuo
LOCUZIONI AL MONDO Il mistero di ogni persona (22/4/2013 24/4/2013) Testi tradotti dai messaggi originali pubblicati sul sito Locutions to the World 2 Sommario 1. La decisione della SS. Trinità al tuo
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria).
 Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
Soluzione degli esercizi sul moto rettilineo uniformemente accelerato
 Liceo Carducci Volterra - Classe 3 a B Scientifico - Francesco Daddi - 8 novembre 00 Soluzione degli esercizi sul moto rettilineo uniformemente accelerato Esercizio. Un corpo parte da fermo con accelerazione
Liceo Carducci Volterra - Classe 3 a B Scientifico - Francesco Daddi - 8 novembre 00 Soluzione degli esercizi sul moto rettilineo uniformemente accelerato Esercizio. Un corpo parte da fermo con accelerazione
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI
 APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
Esercizi sul moto rettilineo uniformemente accelerato
 Liceo Carducci Volterra - Classe 3 a B Scientifico - Francesco Daddi - 8 novembre 010 Esercizi sul moto rettilineo uniformemente accelerato Esercizio 1. Un corpo parte da fermo con accelerazione pari a
Liceo Carducci Volterra - Classe 3 a B Scientifico - Francesco Daddi - 8 novembre 010 Esercizi sul moto rettilineo uniformemente accelerato Esercizio 1. Un corpo parte da fermo con accelerazione pari a
13. Campi vettoriali
 13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
Dimostrare alla Scuola media: dal perché al rigore spontaneamente
 (Maria Cantoni, gennaio 2013). Un lavoro che viene da lontano e che continua oggi. Dimostrare alla Scuola media: dal perché al rigore spontaneamente Costruzione dei triangoli in prima media. Prima dei
(Maria Cantoni, gennaio 2013). Un lavoro che viene da lontano e che continua oggi. Dimostrare alla Scuola media: dal perché al rigore spontaneamente Costruzione dei triangoli in prima media. Prima dei
f(x) = 1 x. Il dominio di questa funzione è il sottoinsieme proprio di R dato da
 Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Le frasi sono state mescolate
 Roma o Venezia? 1 Questo percorso ti aiuterà a capire che cosa sia e come si costruisca un testo argomentativo Nella prossima pagina troverai un testo in cui ad ogni frase corrisponde un diverso colore.
Roma o Venezia? 1 Questo percorso ti aiuterà a capire che cosa sia e come si costruisca un testo argomentativo Nella prossima pagina troverai un testo in cui ad ogni frase corrisponde un diverso colore.
1 Gli effetti della forza di Coriolis
 LA FORZA DI CORIOLIS di Giulio Mazzolini 2012 1 Gli effetti della forza di Coriolis È un effetto noto che i venti nell emisfero nord deviano sempre verso destra, invece nell emisfero sud deviano sempre
LA FORZA DI CORIOLIS di Giulio Mazzolini 2012 1 Gli effetti della forza di Coriolis È un effetto noto che i venti nell emisfero nord deviano sempre verso destra, invece nell emisfero sud deviano sempre
La trigonometria prima della trigonometria. Maurizio Berni
 La trigonometria prima della trigonometria Maurizio Berni 9 maggio 2010 Negli istituti tecnici agrari la trigonometria viene affrontata: nella seconda classe in Disegno e Topografia (risoluzione di triangoli
La trigonometria prima della trigonometria Maurizio Berni 9 maggio 2010 Negli istituti tecnici agrari la trigonometria viene affrontata: nella seconda classe in Disegno e Topografia (risoluzione di triangoli
Nascita e morte delle stelle
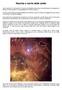 Nascita e morte delle stelle Se la materia che componeva l universo primordiale fosse stata tutta perfettamente omogenea e diffusa in modo uguale, non esisterebbero né stelle né pianeti. C erano invece
Nascita e morte delle stelle Se la materia che componeva l universo primordiale fosse stata tutta perfettamente omogenea e diffusa in modo uguale, non esisterebbero né stelle né pianeti. C erano invece
Consideriamo due polinomi
 Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Alla ricerca del rettangolo più bello
 Alla ricerca del rettangolo più bello Livello scolare: biennio Abilità interessate Individuare nel mondo reale situazioni riconducibili alla similitudine e descrivere le figure con la terminologia specifica.
Alla ricerca del rettangolo più bello Livello scolare: biennio Abilità interessate Individuare nel mondo reale situazioni riconducibili alla similitudine e descrivere le figure con la terminologia specifica.
2. Un teorema geniale e divertente anche per la scuola elementare
 051-056 BDM 56 Maurizi imp 21.5.2008 11:49 Pagina 51 II. Didattica 2. Un teorema geniale e divertente anche per la scuola elementare Lorella Maurizi 1 51 Ho proposto ai bambini di una classe quinta della
051-056 BDM 56 Maurizi imp 21.5.2008 11:49 Pagina 51 II. Didattica 2. Un teorema geniale e divertente anche per la scuola elementare Lorella Maurizi 1 51 Ho proposto ai bambini di una classe quinta della
Capitolo 25: Lo scambio nel mercato delle assicurazioni
 Capitolo 25: Lo scambio nel mercato delle assicurazioni 25.1: Introduzione In questo capitolo la teoria economica discussa nei capitoli 23 e 24 viene applicata all analisi dello scambio del rischio nel
Capitolo 25: Lo scambio nel mercato delle assicurazioni 25.1: Introduzione In questo capitolo la teoria economica discussa nei capitoli 23 e 24 viene applicata all analisi dello scambio del rischio nel
di Frederic Moyersoen Giocatori: 3-10 Età: a partire dagli 8 anni Durata: circa 30 minuti
 di Frederic Moyersoen Giocatori: 3-10 Età: a partire dagli 8 anni Durata: circa 30 minuti Contenuto: 44 Carte percorso, 27 Carte azione, 28 Carte oro, 7 Cercatori d oro, 4 Sabotatori. Idea del gioco I
di Frederic Moyersoen Giocatori: 3-10 Età: a partire dagli 8 anni Durata: circa 30 minuti Contenuto: 44 Carte percorso, 27 Carte azione, 28 Carte oro, 7 Cercatori d oro, 4 Sabotatori. Idea del gioco I
I Solidi Regolari??-??- 2001
 I Solidi Regolari??-??- 2001 Cosa sono i Solidi Platonici 1 I Solidi Platonici sono solidi convessi delimitati da facce costitute da poligoni regolari tutti uguali tra loro. Un Solido di questo genere
I Solidi Regolari??-??- 2001 Cosa sono i Solidi Platonici 1 I Solidi Platonici sono solidi convessi delimitati da facce costitute da poligoni regolari tutti uguali tra loro. Un Solido di questo genere
1. Particolari terne numeriche e teorema di PITAGORA. 2. Le terne pitagoriche 3. Applicazioni i idel teorema di Pitagora.
 TEOREMA DI PITAGORA Contenuti 1. Particolari terne numeriche e teorema di PITAGORA. Le terne pitagoriche 3. Applicazioni i idel teorema di Pitagora Competenze 1. Sapere il significato di terna pitagorica
TEOREMA DI PITAGORA Contenuti 1. Particolari terne numeriche e teorema di PITAGORA. Le terne pitagoriche 3. Applicazioni i idel teorema di Pitagora Competenze 1. Sapere il significato di terna pitagorica
lo 2 2-1 - PERSONALIZZARE LA FINESTRA DI WORD 2000
 Capittol lo 2 Visualizzazione 2-1 - PERSONALIZZARE LA FINESTRA DI WORD 2000 Nel primo capitolo sono state analizzate le diverse componenti della finestra di Word 2000: barra del titolo, barra dei menu,
Capittol lo 2 Visualizzazione 2-1 - PERSONALIZZARE LA FINESTRA DI WORD 2000 Nel primo capitolo sono state analizzate le diverse componenti della finestra di Word 2000: barra del titolo, barra dei menu,
Le funzioni continue. A. Pisani Liceo Classico Dante Alighieri A.S. 2002-03. A. Pisani, appunti di Matematica 1
 Le funzioni continue A. Pisani Liceo Classico Dante Alighieri A.S. -3 A. Pisani, appunti di Matematica 1 Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato
Le funzioni continue A. Pisani Liceo Classico Dante Alighieri A.S. -3 A. Pisani, appunti di Matematica 1 Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato
Le strategie di promozione della lettura messe in atto dalla. biblioteca comunale di Soriano nel Cimino risultano abbastanza
 CAPITOLO QUARTO ANALISI DEI SERVIZI DI PROMOZIONE PER UNA VALUTAZIONE DEI BENEFICI 1. Premessa Le strategie di promozione della lettura messe in atto dalla biblioteca comunale di Soriano nel Cimino risultano
CAPITOLO QUARTO ANALISI DEI SERVIZI DI PROMOZIONE PER UNA VALUTAZIONE DEI BENEFICI 1. Premessa Le strategie di promozione della lettura messe in atto dalla biblioteca comunale di Soriano nel Cimino risultano
I filosofi greci del IV secolo a.c. come Platone e Aristotele ritenevano che le stelle fossero oggetti celesti eterni e immutabili, che ruotavano
 Corso di Astronomia I filosofi greci del IV secolo a.c. come Platone e Aristotele ritenevano che le stelle fossero oggetti celesti eterni e immutabili, che ruotavano attorno alla Terra con orbite circolari.
Corso di Astronomia I filosofi greci del IV secolo a.c. come Platone e Aristotele ritenevano che le stelle fossero oggetti celesti eterni e immutabili, che ruotavano attorno alla Terra con orbite circolari.
La propagazione delle onde luminose può essere studiata per mezzo delle equazioni di Maxwell. Tuttavia, nella maggior parte dei casi è possibile
 Elementi di ottica L ottica si occupa dello studio dei percorsi dei raggi luminosi e dei fenomeni legati alla propagazione della luce in generale. Lo studio dell ottica nella fisica moderna si basa sul
Elementi di ottica L ottica si occupa dello studio dei percorsi dei raggi luminosi e dei fenomeni legati alla propagazione della luce in generale. Lo studio dell ottica nella fisica moderna si basa sul
CONTINUITÀ E DERIVABILITÀ Esercizi proposti. 1. Determinare lim M(sinx) (M(t) denota la mantissa di t)
 CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
IL LATO OSCURO DELL UNIVERSO dov e` la materia che non vediamo? Elena Zucca. INAF - Osservatorio Astronomico di Bologna
 IL LATO OSCURO DELL UNIVERSO dov e` la materia che non vediamo? Elena Zucca INAF - Osservatorio Astronomico di Bologna Ma l Universo è costituito solo da materia luminosa? La forza di gravità Galileo
IL LATO OSCURO DELL UNIVERSO dov e` la materia che non vediamo? Elena Zucca INAF - Osservatorio Astronomico di Bologna Ma l Universo è costituito solo da materia luminosa? La forza di gravità Galileo
IGiochidiArchimede-SoluzioniBiennio 22 novembre 2006
 PROGETTO OLIMPII I MTEMTI U.M.I. UNIONE MTEMTI ITLIN SUOL NORMLE SUPERIORE IGiochidirchimede-Soluzioniiennio novembre 006 Griglia delle risposte corrette Problema Risposta corretta E 4 5 6 7 8 9 E 0 Problema
PROGETTO OLIMPII I MTEMTI U.M.I. UNIONE MTEMTI ITLIN SUOL NORMLE SUPERIORE IGiochidirchimede-Soluzioniiennio novembre 006 Griglia delle risposte corrette Problema Risposta corretta E 4 5 6 7 8 9 E 0 Problema
Usando il pendolo reversibile di Kater
 Usando il pendolo reversibile di Kater Scopo dell esperienza è la misurazione dell accelerazione di gravità g attraverso il periodo di oscillazione di un pendolo reversibile L accelerazione di gravità
Usando il pendolo reversibile di Kater Scopo dell esperienza è la misurazione dell accelerazione di gravità g attraverso il periodo di oscillazione di un pendolo reversibile L accelerazione di gravità
Corso di fotografia 27-29-31 maggio 2014 Scuola di Como Daniela Lietti, Michela Prest, Carlo Pozzoni
 Il corso di fotografia è stato suddiviso in tre incontri distinti: Corso di fotografia 27-29-31 maggio 2014 Scuola di Como Daniela Lietti, Michela Prest, Carlo Pozzoni Il primo è servito a consentirci
Il corso di fotografia è stato suddiviso in tre incontri distinti: Corso di fotografia 27-29-31 maggio 2014 Scuola di Como Daniela Lietti, Michela Prest, Carlo Pozzoni Il primo è servito a consentirci
Esercizio 1 Dato il gioco ({1, 2, 3}, v) con v funzione caratteristica tale che:
 Teoria dei Giochi, Trento, 2004/05 c Fioravante Patrone 1 Teoria dei Giochi Corso di laurea specialistica: Decisioni economiche, impresa e responsabilità sociale, A.A. 2004/05 Soluzioni degli esercizi
Teoria dei Giochi, Trento, 2004/05 c Fioravante Patrone 1 Teoria dei Giochi Corso di laurea specialistica: Decisioni economiche, impresa e responsabilità sociale, A.A. 2004/05 Soluzioni degli esercizi
Analisi e diagramma di Pareto
 Analisi e diagramma di Pareto L'analisi di Pareto è una metodologia statistica utilizzata per individuare i problemi più rilevanti nella situazione in esame e quindi le priorità di intervento. L'obiettivo
Analisi e diagramma di Pareto L'analisi di Pareto è una metodologia statistica utilizzata per individuare i problemi più rilevanti nella situazione in esame e quindi le priorità di intervento. L'obiettivo
Gli strumenti della geografia
 Gli strumenti della geografia La geografia studia lo spazio, cioè i tanti tipi di luoghi e di ambienti che si trovano sulla Terra. La geografia descrive lo spazio e ci spiega anche come è fatto, come vivono
Gli strumenti della geografia La geografia studia lo spazio, cioè i tanti tipi di luoghi e di ambienti che si trovano sulla Terra. La geografia descrive lo spazio e ci spiega anche come è fatto, come vivono
UNA LEZIONE SUI NUMERI PRIMI: NASCE LA RITABELLA
 UNA LEZIONE SUI NUMERI PRIMI: NASCE LA RITABELLA Tutti gli anni, affrontando l argomento della divisibilità, trovavo utile far lavorare gli alunni sul Crivello di Eratostene. Presentavo ai ragazzi una
UNA LEZIONE SUI NUMERI PRIMI: NASCE LA RITABELLA Tutti gli anni, affrontando l argomento della divisibilità, trovavo utile far lavorare gli alunni sul Crivello di Eratostene. Presentavo ai ragazzi una
Funzioni funzione dominio codominio legge argomento variabile indipendente variabile dipendente
 Funzioni In matematica, una funzione f da X in Y consiste in: 1. un insieme X detto dominio di f 2. un insieme Y detto codominio di f 3. una legge che ad ogni elemento x in X associa uno ed un solo elemento
Funzioni In matematica, una funzione f da X in Y consiste in: 1. un insieme X detto dominio di f 2. un insieme Y detto codominio di f 3. una legge che ad ogni elemento x in X associa uno ed un solo elemento
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE
 LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
ISTITUTO COMPRENSIVO CARLOTTA ASCHIERI Scuola media Anno scolastico 2006-2007. matematica e informatica classe 2 D
 ISTITUTO COMPRENSIVO CARLOTTA ASCHIERI Scuola media Anno scolastico 2006-2007 matematica e informatica classe 2 D PRESENTAZIONE Durante l anno scolastico 2006 2007 la nostra classe, nell ambito dell organizzazione
ISTITUTO COMPRENSIVO CARLOTTA ASCHIERI Scuola media Anno scolastico 2006-2007 matematica e informatica classe 2 D PRESENTAZIONE Durante l anno scolastico 2006 2007 la nostra classe, nell ambito dell organizzazione
Statistica e biometria. D. Bertacchi. Variabili aleatorie. V.a. discrete e continue. La densità di una v.a. discreta. Esempi.
 Iniziamo con definizione (capiremo fra poco la sua utilità): DEFINIZIONE DI VARIABILE ALEATORIA Una variabile aleatoria (in breve v.a.) X è funzione che ha come dominio Ω e come codominio R. In formule:
Iniziamo con definizione (capiremo fra poco la sua utilità): DEFINIZIONE DI VARIABILE ALEATORIA Una variabile aleatoria (in breve v.a.) X è funzione che ha come dominio Ω e come codominio R. In formule:
Le curve ellittiche sono un gioiello della matematica. Sono state studiate per secoli per la loro bellezza e importanza.
 Come fare soldi con le curve ellittiche L. Göttsche Le curve ellittiche sono un gioiello della matematica. Sono state studiate per secoli per la loro bellezza e importanza. È difficile spiegare la bellezza
Come fare soldi con le curve ellittiche L. Göttsche Le curve ellittiche sono un gioiello della matematica. Sono state studiate per secoli per la loro bellezza e importanza. È difficile spiegare la bellezza
Qui cade sua altezza
 Qui cade sua altezza Silvia Sbaragli N.R.D. Bologna DFA, SUPSI Locarno (Svizzera) Pubblicato in: Sbaragli S. (2010). Qui cade sua altezza. La Vita Scolastica. 18, 25-27. Nell insegnamento della matematica
Qui cade sua altezza Silvia Sbaragli N.R.D. Bologna DFA, SUPSI Locarno (Svizzera) Pubblicato in: Sbaragli S. (2010). Qui cade sua altezza. La Vita Scolastica. 18, 25-27. Nell insegnamento della matematica
Lezioni di Matematica 1 - I modulo
 Lezioni di Matematica 1 - I modulo Luciano Battaia 16 ottobre 2008 Luciano Battaia - http://www.batmath.it Matematica 1 - I modulo. Lezione del 16/10/2008 1 / 13 L introduzione dei numeri reali si può
Lezioni di Matematica 1 - I modulo Luciano Battaia 16 ottobre 2008 Luciano Battaia - http://www.batmath.it Matematica 1 - I modulo. Lezione del 16/10/2008 1 / 13 L introduzione dei numeri reali si può
www.andreatorinesi.it
 La lunghezza focale Lunghezza focale Si definisce lunghezza focale la distanza tra il centro ottico dell'obiettivo (a infinito ) e il piano su cui si forma l'immagine (nel caso del digitale, il sensore).
La lunghezza focale Lunghezza focale Si definisce lunghezza focale la distanza tra il centro ottico dell'obiettivo (a infinito ) e il piano su cui si forma l'immagine (nel caso del digitale, il sensore).
L infinito nell aritmetica. Edward Nelson Dipartimento di matematica Università di Princeton
 L infinito nell aritmetica Edward Nelson Dipartimento di matematica Università di Princeton Poi lo condusse fuori e gli disse: . E soggiunse:
L infinito nell aritmetica Edward Nelson Dipartimento di matematica Università di Princeton Poi lo condusse fuori e gli disse: . E soggiunse:
IGiochidiArchimede--Soluzionibiennio
 PROGETTO OLIMPIADI DI MATEMATICA U.M.I. UNIONE MATEMATICA ITALIANA MINISTERO DELLA PUBBLICA ISTRUZIONE SCUOLA NORMALE SUPERIORE IGiochidiArchimede--Soluzionibiennio 17 novembre 2010 Griglia delle risposte
PROGETTO OLIMPIADI DI MATEMATICA U.M.I. UNIONE MATEMATICA ITALIANA MINISTERO DELLA PUBBLICA ISTRUZIONE SCUOLA NORMALE SUPERIORE IGiochidiArchimede--Soluzionibiennio 17 novembre 2010 Griglia delle risposte
risulta (x) = 1 se x < 0.
 Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Lezione 10: Il problema del consumatore: Preferenze e scelta ottimale
 Corso di Scienza Economica (Economia Politica) prof. G. Di Bartolomeo Lezione 10: Il problema del consumatore: Preferenze e scelta ottimale Facoltà di Scienze della Comunicazione Università di Teramo Scelta
Corso di Scienza Economica (Economia Politica) prof. G. Di Bartolomeo Lezione 10: Il problema del consumatore: Preferenze e scelta ottimale Facoltà di Scienze della Comunicazione Università di Teramo Scelta
INdAM QUESITI A RISPOSTA MULTIPLA
 INdAM Prova scritta per il concorso a 40 borse di studio, 2 borse aggiuntive e a 40 premi per l iscrizione ai Corsi di Laurea in Matematica, anno accademico 2011/2012. Piano Lauree Scientifiche. La prova
INdAM Prova scritta per il concorso a 40 borse di studio, 2 borse aggiuntive e a 40 premi per l iscrizione ai Corsi di Laurea in Matematica, anno accademico 2011/2012. Piano Lauree Scientifiche. La prova
Dimensione di uno Spazio vettoriale
 Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
1.6 Che cosa vede l astronomo
 1.6 Che cosa vede l astronomo Stelle in rotazione Nel corso della notte, la Sfera celeste sembra ruotare attorno a noi. Soltanto un punto detto Polo nord celeste resta fermo; esso si trova vicino a una
1.6 Che cosa vede l astronomo Stelle in rotazione Nel corso della notte, la Sfera celeste sembra ruotare attorno a noi. Soltanto un punto detto Polo nord celeste resta fermo; esso si trova vicino a una
SCHEDA M MOSAICI CLASSIFICARE CON LA SIMMETRIA
 SCHEDA M MOSAICI CLASSIFICARE CON LA SIMMETRIA Qui sotto avete una griglia, che rappresenta una normale quadrettatura, come quella dei quaderni a quadretti; nelle attività che seguono dovrete immaginare
SCHEDA M MOSAICI CLASSIFICARE CON LA SIMMETRIA Qui sotto avete una griglia, che rappresenta una normale quadrettatura, come quella dei quaderni a quadretti; nelle attività che seguono dovrete immaginare
Una sperimentazione. Probabilità. Una previsione. Calcolo delle probabilità. Nonostante ciò, è possibile dire qualcosa.
 Una sperimentazione Probabilità Si sta sperimentando l efficacia di un nuovo farmaco per il morbo di Parkinson. Duemila pazienti partecipano alla sperimentazione: metà di essi vengono trattati con il nuovo
Una sperimentazione Probabilità Si sta sperimentando l efficacia di un nuovo farmaco per il morbo di Parkinson. Duemila pazienti partecipano alla sperimentazione: metà di essi vengono trattati con il nuovo
N. 4 I ludi geometrici di Leonardo da Vinci Un gioco per avvicinarsi al concetto di area franco ghione, daniele pasquazi
 N. 4 I ludi geometrici di Leonardo da Vinci Un gioco per avvicinarsi al concetto di area franco ghione, daniele pasquazi Tra i molteplici interessi scientifici di Leonardo non dobbiamo dimenticare la matematica.
N. 4 I ludi geometrici di Leonardo da Vinci Un gioco per avvicinarsi al concetto di area franco ghione, daniele pasquazi Tra i molteplici interessi scientifici di Leonardo non dobbiamo dimenticare la matematica.
GIROSCOPIO. Scopo dell esperienza: Teoria fisica. Verificare la relazione: ω p = bmg/iω
 GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
Energia potenziale elettrica e potenziale. In queste pagine R indicherà una regione in cui è presente un campo elettrostatico.
 Energia potenziale elettrica e potenziale 0. Premessa In queste pagine R indicherà una regione in cui è presente un campo elettrostatico. 1. La forza elettrostatica è conservativa Una o più cariche ferme
Energia potenziale elettrica e potenziale 0. Premessa In queste pagine R indicherà una regione in cui è presente un campo elettrostatico. 1. La forza elettrostatica è conservativa Una o più cariche ferme
Quando troncare uno sviluppo in serie di Taylor
 Quando troncare uno sviluppo in serie di Taylor Marco Robutti October 13, 2014 Lo sviluppo in serie di Taylor di una funzione è uno strumento matematico davvero molto utile, e viene spesso utilizzato in
Quando troncare uno sviluppo in serie di Taylor Marco Robutti October 13, 2014 Lo sviluppo in serie di Taylor di una funzione è uno strumento matematico davvero molto utile, e viene spesso utilizzato in
Si sa che la via più breve tra due punti è la linea retta. Ma vi siete mai chiesti, Qual è la via più breve tra tre punti? o tra quattro punti?
 Dov'è Moriart? Cerchiamo la via più breve con Mathcad Potete determinare la distanza più breve da tre punti e trovare Moriart? Si sa che la via più breve tra due punti è la linea retta. Ma vi siete mai
Dov'è Moriart? Cerchiamo la via più breve con Mathcad Potete determinare la distanza più breve da tre punti e trovare Moriart? Si sa che la via più breve tra due punti è la linea retta. Ma vi siete mai
Matematica 1 - Corso di Laurea in Ingegneria Meccanica
 Matematica 1 - Corso di Laurea in Ingegneria Meccanica Esercitazione su massimi e minimi vincolati 9 dicembre 005 Esercizio 1. Considerare l insieme C = {(x,y) R : (x + y ) = x } e dire se è una curva
Matematica 1 - Corso di Laurea in Ingegneria Meccanica Esercitazione su massimi e minimi vincolati 9 dicembre 005 Esercizio 1. Considerare l insieme C = {(x,y) R : (x + y ) = x } e dire se è una curva
Ciao!! Un cielo stellato così come lo puoi vedere con i tuoi occhi. Il cielo visto da un potente telescopio molto lontano dalle città
 1 Ciao!! Quando guardi il cielo ogni volta che si fa buio, se è sereno, vedi tanti piccoli punti luminosi distribuiti nel cielo notturno: le stelle. Oggi si apre l immaginario Osservatorio per guardare...
1 Ciao!! Quando guardi il cielo ogni volta che si fa buio, se è sereno, vedi tanti piccoli punti luminosi distribuiti nel cielo notturno: le stelle. Oggi si apre l immaginario Osservatorio per guardare...
B. Vogliamo determinare l equazione della retta
 Risoluzione quesiti ordinamento Quesito N.1 Indicata con α la misura dell angolo CAB, si ha che: 1 Area ( ABC ) = AC AB sinα = 3 sinα π 3 sinα = 3 sinα = 1 α = Il triangolo è quindi retto in A. La misura
Risoluzione quesiti ordinamento Quesito N.1 Indicata con α la misura dell angolo CAB, si ha che: 1 Area ( ABC ) = AC AB sinα = 3 sinα π 3 sinα = 3 sinα = 1 α = Il triangolo è quindi retto in A. La misura
Ulteriori problemi di fisica e matematica
 Facoltà di Medicina e Chirurgia Università degli Studi di Firenze Agosto 2010 Ulteriori problemi di fisica e matematica Giovanni Romano Perché un raggio di luce proveniente dal Sole e fatto passare attraverso
Facoltà di Medicina e Chirurgia Università degli Studi di Firenze Agosto 2010 Ulteriori problemi di fisica e matematica Giovanni Romano Perché un raggio di luce proveniente dal Sole e fatto passare attraverso
Classe seconda scuola primaria
 Classe seconda scuola primaria Il percorso di seconda cerca di approfondire le differenze tra le principali proprietà delle figure geometriche solide, in particolare il cubo, e di creare attività di osservazione
Classe seconda scuola primaria Il percorso di seconda cerca di approfondire le differenze tra le principali proprietà delle figure geometriche solide, in particolare il cubo, e di creare attività di osservazione
Forze come grandezze vettoriali
 Forze come grandezze vettoriali L. Paolucci 23 novembre 2010 Sommario Esercizi e problemi risolti. Per la classe prima. Anno Scolastico 2010/11 Parte 1 / versione 2 Si ricordi che la risultante di due
Forze come grandezze vettoriali L. Paolucci 23 novembre 2010 Sommario Esercizi e problemi risolti. Per la classe prima. Anno Scolastico 2010/11 Parte 1 / versione 2 Si ricordi che la risultante di due
~ Copyright Ripetizionando - All rights reserved ~ http://ripetizionando.wordpress.com STUDIO DI FUNZIONE
 STUDIO DI FUNZIONE Passaggi fondamentali Per effettuare uno studio di funzione completo, che non lascia quindi margine a una quasi sicuramente errata inventiva, sono necessari i seguenti 7 passaggi: 1.
STUDIO DI FUNZIONE Passaggi fondamentali Per effettuare uno studio di funzione completo, che non lascia quindi margine a una quasi sicuramente errata inventiva, sono necessari i seguenti 7 passaggi: 1.
L analisi dei dati. Capitolo 4. 4.1 Il foglio elettronico
 Capitolo 4 4.1 Il foglio elettronico Le più importanti operazioni richieste dall analisi matematica dei dati sperimentali possono essere agevolmente portate a termine da un comune foglio elettronico. Prenderemo
Capitolo 4 4.1 Il foglio elettronico Le più importanti operazioni richieste dall analisi matematica dei dati sperimentali possono essere agevolmente portate a termine da un comune foglio elettronico. Prenderemo
Un gioco con tre dadi
 Un gioco con tre dadi Livello scolare: biennio Abilità interessate Costruire lo spazio degli eventi in casi semplici e determinarne la cardinalità. Valutare la probabilità in diversi contesti problematici.
Un gioco con tre dadi Livello scolare: biennio Abilità interessate Costruire lo spazio degli eventi in casi semplici e determinarne la cardinalità. Valutare la probabilità in diversi contesti problematici.
MATEMATICA DEL DISCRETO elementi di teoria dei grafi. anno acc. 2009/2010
 elementi di teoria dei grafi anno acc. 2009/2010 Grafi semplici Un grafo semplice G è una coppia ordinata (V(G), L(G)), ove V(G) è un insieme finito e non vuoto di elementi detti vertici o nodi di G, mentre
elementi di teoria dei grafi anno acc. 2009/2010 Grafi semplici Un grafo semplice G è una coppia ordinata (V(G), L(G)), ove V(G) è un insieme finito e non vuoto di elementi detti vertici o nodi di G, mentre
Rilevazione degli apprendimenti. Anno Scolastico 2006 2007 PROVA DI MATEMATICA. Scuola Secondaria di II grado. Classe Terza Tipo A. Codici. Scuola:...
 Ministero della Pubblica Istruzione Rilevazione degli apprendimenti Anno Scolastico 2006 2007 PROVA DI MATEMATICA Scuola Secondaria di II grado Classe Terza Tipo A Codici Scuola:..... Classe:.. Studente:.
Ministero della Pubblica Istruzione Rilevazione degli apprendimenti Anno Scolastico 2006 2007 PROVA DI MATEMATICA Scuola Secondaria di II grado Classe Terza Tipo A Codici Scuola:..... Classe:.. Studente:.
Traduzione e adattamento a cura di Gylas per Giochi Rari
 Traduzione e adattamento a cura di Gylas per Giochi Rari Versione 1.0 Luglio 2001 NOTA. La presente traduzione non sostituisce in alcun modo il regolamento originale del gioco; il presente documento è
Traduzione e adattamento a cura di Gylas per Giochi Rari Versione 1.0 Luglio 2001 NOTA. La presente traduzione non sostituisce in alcun modo il regolamento originale del gioco; il presente documento è
Codici ed affreschi. Questa chiesa rupestre merita un approfondimento e una pubblicazione monografica.
 Codici ed affreschi. Alcuni studiosi della storia dell arte hanno accennato alla possibilità di uno stretto contatto tra codici miniati ed affreschi. Qui presentiamo un caso significativo: un particolare
Codici ed affreschi. Alcuni studiosi della storia dell arte hanno accennato alla possibilità di uno stretto contatto tra codici miniati ed affreschi. Qui presentiamo un caso significativo: un particolare
Costruite un grafo che rappresenti la situazione del torneo (in modo che siano rappresentate le squadre e le partite). Che tipo di grafo ottenete?
 IL TORNEO DI CALCIO Avete un gruppo di sei squadre che devono sfidarsi in un torneo di calcio. Il torneo deve essere circolare e di sola andata, cioè ogni squadra deve giocare una partita contro ciascuna
IL TORNEO DI CALCIO Avete un gruppo di sei squadre che devono sfidarsi in un torneo di calcio. Il torneo deve essere circolare e di sola andata, cioè ogni squadra deve giocare una partita contro ciascuna
matematica probabilmente
 IS science centre immaginario scientifico Laboratorio dell'immaginario Scientifico - Trieste tel. 040224424 - fax 040224439 - e-mail: lis@lis.trieste.it - www.immaginarioscientifico.it indice Altezze e
IS science centre immaginario scientifico Laboratorio dell'immaginario Scientifico - Trieste tel. 040224424 - fax 040224439 - e-mail: lis@lis.trieste.it - www.immaginarioscientifico.it indice Altezze e
Calcolo delle probabilità
 Calcolo delle probabilità Laboratorio di Bioinformatica Corso A aa 2005-2006 Statistica Dai risultati di un esperimento si determinano alcune caratteristiche della popolazione Calcolo delle probabilità
Calcolo delle probabilità Laboratorio di Bioinformatica Corso A aa 2005-2006 Statistica Dai risultati di un esperimento si determinano alcune caratteristiche della popolazione Calcolo delle probabilità
Capitolo II. La forma del valore. 7. La duplice forma in cui si presenta la merce: naturale e di valore.
 Capitolo II La forma del valore 7. La duplice forma in cui si presenta la merce: naturale e di valore. I beni nascono come valori d uso: nel loro divenire merci acquisiscono anche un valore (di scambio).
Capitolo II La forma del valore 7. La duplice forma in cui si presenta la merce: naturale e di valore. I beni nascono come valori d uso: nel loro divenire merci acquisiscono anche un valore (di scambio).
