Capitolo 3 Flussaggio Stazionario di una Valvola Formula 1
|
|
|
- Leonzio Gianmarco Guidi
- 8 anni fa
- Visualizzazioni
Transcript
1 Capitolo 3 Flussaggio Stazionario di una Valvola Formula Introduzione al problema In questa simulazione si vuole verificare il comportamento del fluido nel passaggio attraverso una valvola motoristica ad alte prestazioni. Lo studio della miglior geometria di condotti e valvole, e soprattutto la ricerca delle prestazioni in questo campo sono stati studiati da molto tempo grazie ai banchi di flussaggio stazionari, ovvero grazie a simulazioni sperimentali che prevedevamo l utilizzo di testate reali o di manichini che ne riproducevano le geometrie, allo scopo si far passare un flusso stazionario per verificare caratteristiche quali il coefficiente di efflusso e la capacità di realizzare moti organizzati nel cilindro (Swirl e Tumble). I problemi principali legati alla simulazione sperimentale erano tuttavia notevoli, e legati soprattutto all incapacità di misurare le grandezze volute nei punti esatti in cui la teoria indicava di misurarle: questo ha portato all adozione d approssimazioni che risultano essere la causa principale degli errori riscontrati poi nei risultati finali: per esempio, nel caso di simulazione in aspirazione, si approssimava la pressione sulla valvola con la pressione nel cilindro non potendo porre un trasduttore proprio a ridosso della valvola stessa. L utilizzo della CFD in questo campo presenta quindi vantaggi molto importanti in quanto permette di estrarre le grandezze necessarie nei punti esatti in cui esse dovrebbero essere misurate nella realtà, per cui indagare il flusso attorno alla valvola o la pressione che si ha in tale zona non è più un problema. L obiettivo di questa simulazione è proprio quello di riprodurre una prova di flussaggio stazionario ricavando i parametri più significativi per la motoristica, ovvero il Coefficiente d Efflusso della valvola e l intensità del voltice di Tumble che si genera nel cilindro. Per quanto riguarda la geometria fornita, essa è data da un semicilindro completo di valvola di aspirazione e condotto. Si tratta quindi dello stesso assemblato che si disporrebbe nel caso di una simulazione sperimentale. Per simmetria, il modello può essere studiato in una sola delle sue metà estendendo poi i risultati anche sulla restante parte del pezzo reale.
2 Per poter analizzare in modo completo la fase di aspirazione, e per tracciare i grafici di coefficiente d efflusso e di intensità del vortice di tumble, la geometria di cui si dispone è rappresentata da differenti modelli con differenti valori di alzata della valvola. In tal modo, impostando il flussaggio su ognuno, è possibile ricostruire il comportamento del fluido durante tutta l alpirazione. In particolare, le alzate di cui si dispone sono: 2 mm 4 mm 6 mm 8 mm 10 mm 12 mm 14 mm 16 mm Queste verranno indagate in modo completo al fine di ottenere una simulazione il più possibile esplicativa del comportamento reale del componente. 3.2 Generazione della mesh e controllo Y+ Per quanto riguarda la generazione della mesh necessaria al calcolo, dato che si dispone di differenti geometrie date dalle differenti alzate della valvola, che comunque risultano essere molto simili tra
3 di loro, è possibile cercare di ottimizzare una mesh riferita ad una geometria significativa per poi utilizzarla come base per la creazione delle altre griglie di calcolo. In particolare, si è scelto come geometria significativa quella corrispondente ad una alzata di 6mm in quanto questo risulta un valore intermedio tra alzata minima e massima. Naturalmente, per ogni geometria verrà effettuato un controllo ed eventualmente si cercherà di ottimizzare in modo particolare eventuali problemi che possono insorgere. Inizialmente, il primo obiettivo risulta quello di realizzare una meshatura particolarmente curata per quanto riguarda i layer in parete. Uno dei parametri fondamentali che determinano la bontà di una mesh, infatti, è il valore delle Y+ in parete, che dipendono direttamente dall altezza delle celle a ridosso delle superfici solide. Il metodo utilizzato, infatti, non è in grado di risolvere correttamente il substrato viscoso dello strato limite, per cui è necessario realizzare un primo strato di celle tali da inglobarlo completamente. Il controllo viene fatto direttamente sul valore fornito dal software per le Y+, che deve essere almeno maggiore di 30 e preferibilmente inferiore a 100. È stata quindi realizzata una mesh avente un numero di celle di volume non eccessivamente grande per non pesare sul costo computazionale, sulla quale si è curato però in modo particolare gli strati di celle a ridosso delle superfici. Con tale geometria è stata condotta la prima simulazione volta proprio a ricercare la miglior configurazione dei layer superficiali, dato che, infittendo poi la mesh di volume, questi non vengono, comunque, modificati. Nelle immagini seguenti riportiamo alcune viste per visualizzare i risultati.
4
5
6 3.3 Parametri utilizzati nella simulazione In merito alle grandezze che verranno utilizzate in tutta la trattazione, come il Coefficiente di Efflusso e la Velocità Angolare del Vortice di Tumble, vogliamo precisare come è stato possibile estrarre direttamente dal software i valori finali numerici, senza dover effettuare alcun calcolo esterno alla simulazione. Per quanto riguarda la teoria, sia Coefficiente d Efflusso che Tumble presentano trattazioni che permettono di trovare i valori trovati applicando semplici formule basate su alcune semplificazioni ed ipotesi. Tali ipotesi in particolare risultano spesso abbastanza grossolane, come per esempio il caso del vortice di tumble, per il quale si ipotizza un moto pressoché rigido attorno ad un asse ben fissato: questo non rispecchia ovviamente la realtà dove le condizioni di funzionamento sono ben più complesse e la riduzione ad un solo movimento rigido è sicuramente restrittiva. In ogni caso, per questa simulazione così come per le simulazioni sperimentali al banco di flussaggio, tale teoria è ampliamente adottata, per cui anche noi la assumeremo come buona per la nostra simulazione numerica. Per quanto riguarda il Coefficiente d Efflusso, la sua definizione risulta essere il rapporto tra portata reale che attraversa la valvola e portata ideale che si potrebbe misurare dall attraversamento di un ugello ideale nelle stesse condizioni di geometria e differenza di pressione. Abbiamo quindi: La portata reale in kg/s è quella fornita e misurata dalla simulazione. La portata ideale è invece calcolabile dalle condizioni di geometria e pressione che si registrano nel caso reale, per cui si ha: Dove ρ è la densità totale in ingresso all ugello, A l area minima di passaggio, a la velocità del suono totale calcolata dalle condizioni di ingresso, e Φ è la funzione di pressione, calcolata a sua volta come:
7 Nel nostro caso avremo naturalmente come valore di p 1 il valore della pressione ill ingresso del condotto, e quindi la pressione atmosferica, e come p 2 il valore di pressione media misurata sull area di passaggio della valvola. Per quanto riguarda invece il calcolo della Velocità del Tumble, è stato necessario definire una funzione apposita, basata sulla teoria trovata in bibliografia. La velocità angolare del vortice di Tumble viene in questo caso considerata come velocità angolare di un movimento rigido attorno ad un asse fisso, e viene calcolato come rapporto tra flusso della quantità di moto e flusso del momento di inerzia come segue. È quindi necessario definire una funzione apposita (nel nostro caso abbiamo preferito, per un miglior controllo, definire due differenti funzioni per numeratore e denominatore della funzione) per poi effettuare una sommatoria sulle celle interessate. In particolare, proprio per definire tali celle, è stato necessario definire un Treshold comprendente le celle che, considerando il fatto che il cilindro è di provenienza Formula 1, potevano interessare la corsa totale del motore, stimata a partire dall alesaggio in circa 40 mm. Il modello è stato quindi traslato in verticale in modo da far coincidere il centro del sistema di riferimento (e quindi l asse di rotazione del Tumble) esattamente al centro del cilindro e a metà della corsa, ed il treshold è stato definito raccogliendo le celle il cui centroide cadeva ad una distanza verticale compresa tra 20 mm e -20 mm dall origine degli assi.
8 Grazie a questa operazione è stato possibile definire le celle interessate al moto di Tumble, e quindi le celle sulle quali era necessario impostare il calcolo della funzione. Grazie a Starccm+ è stato quindi possibile definire le Field Functions d interesse, relative sia a grandezze impostate che a grandezze monitorate nella simulazione, per cui è stato possibile calcolare in modo automatico il valore di ogni parametro ad ogni iterazione e su questo realizzare plot di evoluzione e criteri di convergenza. 3.4 Ricerca della Convergenza di mesh Una volta ottenuto un buon risultato per quanto riguarda i valori delle Y+, è possibile indagare varie meshature caratterizzate da differenti dimensioni delle celle, per verificare la convergenza di mesh, ovvero il numero minimo di celle oltre il quale i risultati non sono più condizionati dalla mesh stessa. Tale valore sarà quello adottato poi anche per le altre alzate. Come detto, le differenti meshature influenzano solamente la mesh di volume e non i layer superficiali: questo è fondamentale in quanto permette di mantenere praticamente inalterati i risultati ottenuti sulle Y+. La scelta fatta è stata quella di partire da meshature piuttosto grossolane caratterizzate da un numero di celle poco elevato, per poi salire progressivamente fino ad un valore massimo indicativo di oltre il quale il costo computazionale comincia ad essere troppo elevato, rispetto alla potenza di calcolo disponibile.
9 Sono state quindi generate differenti meshature partendo da quella avente un numero di celle totali pari a circa 45000, con incrementi di alla volta. Il confronto e la graficazione dei parametri di interesse della simulazione permetteranno di scegliere la mesh più adeguata per procedere. Naturalmente, per poter effettuare un confronto alla pari, è necessario definire dei criteri di convergenza sensati e soprattutto comuni a tutti i casi che si vogliono analizzare. Come noto, Starccm+ permette di definire criteri di convergenza sia sulle grandezze prettamente numeriche, quali i residui sulle equazioni di calcolo, ma anche criteri di convergenza basati sulle grandezze ingegneristiche d interesse per la simulazione. Tale possibilità è stata naturalmente sfruttata in questa prova, applicando tutta una serie di criteri anche abbastanza spinti al fine di ottenere un confronto quanti mai selettivo. La convergenza è quindi verificata se sono verificate le seguenti condizioni: Mass Flow Inlet > Asintotico; 0,0005 Kg/s in 100 iterazioni successive Mass Flow Outlet > Asintotico; 0,0005 Kg/s in 100 iterazioni successive Mass Flow SectionPlane > Asintotico; 0,0005 Kg/s in 100 iterazioni successive Valve Area Averaged Pressure > Asintotico; 10 Pa in 100 iterazioni successive Omega Tumble > Asintotico; 0,01 /s in 100 iterazioni successive Coefficiente d Efflusso > Asintotico; 0,0001 in 100 iterazioni successive. A questo punto non resta che raccogliere per ogni simulazione i dati finali d interesse e confrontarne l andamento al variare del numero d elementi adottati per la mesh. Elementi Iterazioni CPU iterazione [s] CPU totale [s] , , , , , , Elementi Portata IN [kg/s] Portata OUT [kg/s] Portata VALV [kg/s] , , , , , , , , , , , , , , , , , , Elementi Press.Valvola Coeff.Efflusso Omega Tumble
10 [Pa] ,17 0, , ,42 0, , ,01 0, , ,68 0, , ,05 0, , ,04 0, ,7924 Di seguito riportiamo i grafici per i risultati ottenuti in modo da rendere più chiara la tendenza dei valore in base al numero di elementiadottati Iterazioni CPU iterazione [s]
11 CPU totale [s] ,1070 0,1080 Portata IN [kg/s] ,1090 0,1100 0,1110 0,1120 0,1130 0,1140 0,1150 0,1150 0,1140 0,1130 0,1120 0,1110 0,1100 0,1090 0,1080 0,1070 Portata OUT [kg/s]
12 0,1150 Portata VALV [kg/s] 0,1140 0,1130 0,1120 0,1110 0,1100 0,1090 0, Press.Valvola [Pa] ,2105 0,2100 0,2095 0,2090 0,2085 0,2080 0,2075 0,2070 0,2065 Coeff.Efflusso
13 Omega Tumble 460, , , , , , , , , , Dai confronti sui risultati ottenuti si può concludere che la geometria a circa elementi risulta essere quella che è in grado di offrire i risultati più attendibili. Se, infatti, si tiene conto dei grafici relativi a pressione sulla valvola, portate, e coefficiente d efflusso, i valori sono pressoché stabili rispetto alle mesh con un numero di elementi maggiore. Per quanto riguarda il valore dell omega Tumble, questo subisce ancora variazioni vistore, ma il metodo utilizzato per il suo calcolo è sicuramente meno affidabile nei risultati rispetto ai valori ottenuti per gli altri monitoraggi. Valutando anche l andamento rispetto a tempi di calcolo e numero di passi, la mesh a elementi è sicuramente più conveniente di quella a in quanto, pur fornendo risultati praticamente confrontabili, permette un numero di iterazioni minore e soprattutto un tempo necessario alle singole iterazioni pari a 10,9 s contro gli oltre 13 della mesh più fitta. Alla luce di quanto detto, scegliamo la mesh a elementi come modello per la valutazione di tutte le altre alzate.
14 3.5 Simulazione completa alle varie alzate Come anticipato, per verificare il comportamento del gruppo valvole durante tutta la fase di aspirazione, è necessario effettuare le simulazioni per differenti valori di alzata: i risultati ottenuti per ognuna consentiranno di realizzare curve indicative durante tutta la fase di apertura delle valvole. Per quanto riguarda questo caso, le alzate scelte per la valutazione dei parametri relativi a Coefficiente d Efflusso e Velocità angolare del Vortice di Tumble sono: 2 mm 4 mm 6 mm 8 mm 10 mm 12 mm 14 mm 16 mm In particolar modo, per problemi dovuti alla geometria importata, non è stato possibile utilizzare il comodo comando di Replace Surface presente in Star Ccm+ che permette di sostituire geometrie che, se presentano differenze non particolarmente accentuate, vengono automaticamente riconosciute dal software per cui tutti i settagli relativi alla divisione in Regions, alla meshatura, ed addirittura la soluzione stessa vengono direttamente riscalati sulla nuova geometria. Tutto questo non è stato possibile per problemi dovuti proprio al riconoscimento della superficie importata: è stato necessario quindi importare ogni caso analizzato e costruire la mesh secondo i principi ottimizzati nella fase iniziale di ricerca della convergenza di mesh. A tal proposito, come preannunciato, è stata scelta la mesh con circa elementi in quanto si è dimostrata la prima ad avere risultati praticamente invariati rispetto alle meshature più fitte e teoricamente più precise. Per ogni geometria sono state impostate le stesse condizioni al contorno e gli stessi criteri di convergenza, presi direttamente dalle simulazioni per la ricerca della convergenza di mesh, in modo da ottenere casi tra loro analoghi che permettono un confronto reale. In particolare, di ognuno dei casi studiati sono stati valutati il Coefficiente di Efflusso calcolato direttamente dal software grazie alle funzioni inserite manualmente, e l evoluzione del vortice di Tumble sia da un punto di vista teorico, valutando cioè la velocità angolare dello stesso secondo la legge precedentemente spiegata, sia da un punto di vista visivo, valutando come i vettori velocità si disponevano nel piano di simmetria della geometria (che è piano di mezzeria del cilindro), e nel piano costruito appositamente in modo da tagliare più o meno nella metà la valvola di aspirazione. Riportiamo quindi nei capitoli seguenti i risultati ottenuti.
15 3.5.1 Andamento del Coefficiente d Efflusso Per quanto riguarda il Coefficiente d Efflusso, una volta aver inserito le funzioni necessarie al suo calcolo secondo la teoria motoristica più diffusa, è stato possibile generare un report che potesse fornire per ogni iterazione il valore calcolato per questo parametro. Grazie a questo è stato possibile anche creare un Criterio di Covergenza asintotico abbastanza stretto per la valutazione della simulazione. Per ogni caso studiato è stato estratto quindi il valore finale calcolato, ovvero il valore relativo all ultima iterazione effettuata, considerato praticamente stabile in quanto il criterio di convergenza impostato prevedeva una variazione massima di 0,0001 in 100 passi successivi. Grazie alle simulazioni alle differenti alzate è stato quindi possibile raccogliere i dati per generare un grafico che mostrasse l andamento del Coefficiente di Efflusso durante tutta la fase di apertura delle valvole. La successiva fase di chiusura che completa l aspirazione sarà ovviamente simmetrica rispetto al caso analizzato. Sintetizzando i risultati in un grafico abbiamo ottenuto, Alzata [mm] Coefficiente di Efflusso 2 0, , , , , , , , ,35 Coefficiente di Efflusso 0,3 0,25 0,2 0,15 0,1 0, Alzata [mm]
16 Com è possibile notare, l andamento del Coefficiente di Efflusso è in linea rispetto al tipico andamento previsto per le valvole di aspirazione di un motore a combustione interna. L ottimizzazione dei condotti e la loro geometria particolarmente efficiente che evita il più possibile di avere perdite nella fase di aspirazione fa si inoltre che il suo valore possa salire rapidamente e possa mantenersi alto per buona parte della fase di apertura valvole, a conferma del livello prestazionale del motore analizzato. Dato che il nostro calcolo è stato effettuato prendendo come riferimento la semiarea del cilindro, è possibile calcolare anche l Area Efficace che ne deriva semplicemente dalla relazione: Graficando ancora una volta i risultati ottenuti per una migliore leggibilità si ottiene l andamento in figura, che come ovvio ricalca quello del Coefficiente di Efflusso, dato che l area di riferimento adottata è costante per ogni caso analizzato. Alzata [mm] Area Efficace [mm 2 ] 2 23, , , , , , , , Area Efficace [mm2] Alzata [mm]
17 3.5.2 Andamento del Vortice di Tumble Per quanto riguarda il Moto di Tumble nel cilindro, invece, è stato adottato come preannunciato sia il metodo di valutazione classico che prevede il calcolo della velocità angolare come rapporto tra flusso della quantità di moto e flusso del momento d inerzia, sia il metodo visivo andando a verificare l evoluzione del vortice rispetto alla fase d aspirazione plottando direttamente i vettori velocità su due piani di cui il primo è quello di simmetria del cilindro, ed il secondo è stato creato in modo da essere circa nella mezzeria della valvola. Per quanto riguarda i valori ottenuti per la velocità angolare, occorre precisare ancora una volta che la teoria alla base del calcolo di tale parametro presenta notevoli approssimazioni tra le quali per esempio il fatto che il vortice sia assunto come un movimento rigido attorno ad un asse fisso nel centro del cilindro. Tale assunzione è ovviamente molto limitante, per cui i risultati che ne derivano sono spesso soggetti a variabilità che risulta essere inevitabile. Riportiamo in ogni caso i valori ottenuti, graficandoli ancora una volta rispetto alle alzate oggetto della simulazione. Alzata [mm] Omega Tumble [1/s] 2 105, , , , , , , , Omega Tumble [1/s] Alzata [mm] Il software ci permette inoltre di plottare i vettori velocità direttamente su piani di riferimento. Questa è stata la base per la valutazione visiva del voltice di tumble e della sua evoluzione.
18 Riportiamo quindi le immagini ottenute in sequenza sia del piano di simmetria della geometria, sia del piano appositamente realizzato a cavallo della valvola. Le immagini si riferiscono, per ogni alzata, al piano della valvola sopra e al piano di simmetria del cilindro, sotto.
19 ALZATA 2 mm
20 ALZATA 4 mm
21 ALZATA 6 mm
22 ALZATA 8 mm
23 ALZATA 10 mm
24 ALZATA 12 mm
25 ALZATA 14 mm
26 ALZATA 16 mm
27 Dall analisi delle immagini alle differenti alzate è possibile verificare come il vortice venga alimentato mano a mano che la fase di aspirazione avanza, ed in questa operazione fondamentale risulta essere la conformazione dei condotti di ingresso e il posizionamento dela valvola rispetto al cilindro. L obiettivo è infatti quello di generare un vortice il più intenso possibile in modo da avere il miglior mescolamento tra l aria e il combustibile che formano la carica in ingresso. Tutto questo è fondamentale soprattutto nella fase di aspirazione e nella prima fase di compressione. Dopo questo momento, infatti, il pistone che torna a muoversi verso il PMS tende a schiacciare il vortice e quindi in parte a contrastarlo, per cui è fondamentale riuscire a realizzare un vortice il più intenso possibile quando le valvole di aspirazione sono aperte, in modo che questa turbolenza benefica al mescolamento e alla successiva combustione si protragga e si mantenga il più possibile nel cilindro. Per questo motivo, l analisi CFD dei moti nel cilindro e l ottimizzazione delle geometrie di condotti e valvole risulta fondamentale per ottenere ottimi risultati. ezio85@inwind.it
28
29
30
Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R
 Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
IL RISPARMIO ENERGETICO E GLI AZIONAMENTI A VELOCITA VARIABILE L utilizzo dell inverter negli impianti frigoriferi.
 IL RISPARMIO ENERGETICO E GLI AZIONAMENTI A VELOCITA VARIABILE L utilizzo dell inverter negli impianti frigoriferi. Negli ultimi anni, il concetto di risparmio energetico sta diventando di fondamentale
IL RISPARMIO ENERGETICO E GLI AZIONAMENTI A VELOCITA VARIABILE L utilizzo dell inverter negli impianti frigoriferi. Negli ultimi anni, il concetto di risparmio energetico sta diventando di fondamentale
Usando il pendolo reversibile di Kater
 Usando il pendolo reversibile di Kater Scopo dell esperienza è la misurazione dell accelerazione di gravità g attraverso il periodo di oscillazione di un pendolo reversibile L accelerazione di gravità
Usando il pendolo reversibile di Kater Scopo dell esperienza è la misurazione dell accelerazione di gravità g attraverso il periodo di oscillazione di un pendolo reversibile L accelerazione di gravità
e-dva - eni-depth Velocity Analysis
 Lo scopo dell Analisi di Velocità di Migrazione (MVA) è quello di ottenere un modello della velocità nel sottosuolo che abbia dei tempi di riflessione compatibili con quelli osservati nei dati. Ciò significa
Lo scopo dell Analisi di Velocità di Migrazione (MVA) è quello di ottenere un modello della velocità nel sottosuolo che abbia dei tempi di riflessione compatibili con quelli osservati nei dati. Ciò significa
CONTROLLO IN TENSIONE DI LED
 Applicazioni Ver. 1.1 INTRODUZIONE CONTROLLO IN TENSIONE DI LED In questo documento vengono fornite delle informazioni circa la possibilità di pilotare diodi led tramite una sorgente in tensione. La trattazione
Applicazioni Ver. 1.1 INTRODUZIONE CONTROLLO IN TENSIONE DI LED In questo documento vengono fornite delle informazioni circa la possibilità di pilotare diodi led tramite una sorgente in tensione. La trattazione
GIROSCOPIO. Scopo dell esperienza: Teoria fisica. Verificare la relazione: ω p = bmg/iω
 GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
SPC e distribuzione normale con Access
 SPC e distribuzione normale con Access In questo articolo esamineremo una applicazione Access per il calcolo e la rappresentazione grafica della distribuzione normale, collegata con tabelle di Clienti,
SPC e distribuzione normale con Access In questo articolo esamineremo una applicazione Access per il calcolo e la rappresentazione grafica della distribuzione normale, collegata con tabelle di Clienti,
Parte I. Prima Parte
 Parte I Prima Parte Capitolo 1 Introduzione generale 1.1 Il problema dell assegnazione Corsi-Borsisti Il problema dell assegnazione delle borse dei corsi ai vari studenti può essere riassunto nei punti
Parte I Prima Parte Capitolo 1 Introduzione generale 1.1 Il problema dell assegnazione Corsi-Borsisti Il problema dell assegnazione delle borse dei corsi ai vari studenti può essere riassunto nei punti
ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE P.N.I. 2004
 ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
Esame sezione Brevetti 2003-2004 Prova Pratica di meccanica
 Esame sezione Brevetti 2003-2004 Prova Pratica di meccanica OGGETVO: Brevettazione dl un perfezionamento riguardante I pressatori per mescolatori dl gomma Egregio dottore, Le invio una breve relazione
Esame sezione Brevetti 2003-2004 Prova Pratica di meccanica OGGETVO: Brevettazione dl un perfezionamento riguardante I pressatori per mescolatori dl gomma Egregio dottore, Le invio una breve relazione
Effetto reddito ed effetto sostituzione.
 . Indice.. 1 1. Effetto sostituzione di Slutsky. 3 2. Effetto reddito. 6 3. Effetto complessivo. 7 II . Si consideri un consumatore che può scegliere panieri (x 1 ; ) composti da due soli beni (il bene
. Indice.. 1 1. Effetto sostituzione di Slutsky. 3 2. Effetto reddito. 6 3. Effetto complessivo. 7 II . Si consideri un consumatore che può scegliere panieri (x 1 ; ) composti da due soli beni (il bene
Analisi e diagramma di Pareto
 Analisi e diagramma di Pareto L'analisi di Pareto è una metodologia statistica utilizzata per individuare i problemi più rilevanti nella situazione in esame e quindi le priorità di intervento. L'obiettivo
Analisi e diagramma di Pareto L'analisi di Pareto è una metodologia statistica utilizzata per individuare i problemi più rilevanti nella situazione in esame e quindi le priorità di intervento. L'obiettivo
INTEGRATORE E DERIVATORE REALI
 INTEGRATORE E DERIVATORE REALI -Schemi elettrici: Integratore reale : C1 R2 vi (t) R1 vu (t) Derivatore reale : R2 vi (t) R1 C1 vu (t) Elenco componenti utilizzati : - 1 resistenza da 3,3kΩ - 1 resistenza
INTEGRATORE E DERIVATORE REALI -Schemi elettrici: Integratore reale : C1 R2 vi (t) R1 vu (t) Derivatore reale : R2 vi (t) R1 C1 vu (t) Elenco componenti utilizzati : - 1 resistenza da 3,3kΩ - 1 resistenza
13. Campi vettoriali
 13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
Anno 4 Grafico di funzione
 Anno 4 Grafico di funzione Introduzione In questa lezione impareremo a disegnare il grafico di una funzione reale. Per fare ciò è necessario studiare alcune caratteristiche salienti della funzione che
Anno 4 Grafico di funzione Introduzione In questa lezione impareremo a disegnare il grafico di una funzione reale. Per fare ciò è necessario studiare alcune caratteristiche salienti della funzione che
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
APPLICATION SHEET Luglio
 Indice 1. Descrizione dell applicazione 2. Applicazione - Dati 3. Selezione del prodotto e dimensionamento 4. Soluzione Motovario 1. Descrizione dell applicazione Gli schermi per campi da cricket fanno
Indice 1. Descrizione dell applicazione 2. Applicazione - Dati 3. Selezione del prodotto e dimensionamento 4. Soluzione Motovario 1. Descrizione dell applicazione Gli schermi per campi da cricket fanno
Politecnico di Bari I Facoltà di Ingegneria Corso di Laurea Specialistica in Ingegneria Meccanica ENERGIA EOLICA
 Politecnico di Bari I Facoltà di Ingegneria Corso di Laurea Specialistica in Ingegneria Meccanica ENERGIA EOLICA turbine eoliche ad asse verticale VAWT A.A. 2008/09 Energie Alternative Prof.B.Fortunato
Politecnico di Bari I Facoltà di Ingegneria Corso di Laurea Specialistica in Ingegneria Meccanica ENERGIA EOLICA turbine eoliche ad asse verticale VAWT A.A. 2008/09 Energie Alternative Prof.B.Fortunato
L ANALISI ABC PER LA GESTIONE DEL MAGAZZINO
 L ANALISI ABC PER LA GESTIONE DEL MAGAZZINO È noto che la gestione del magazzino è uno dei costi nascosti più difficili da analizzare e, soprattutto, da contenere. Le nuove tecniche hanno, però, permesso
L ANALISI ABC PER LA GESTIONE DEL MAGAZZINO È noto che la gestione del magazzino è uno dei costi nascosti più difficili da analizzare e, soprattutto, da contenere. Le nuove tecniche hanno, però, permesso
Corso di Componenti e Impianti Termotecnici LE RETI DI DISTRIBUZIONE PERDITE DI CARICO LOCALIZZATE
 LE RETI DI DISTRIBUZIONE PERDITE DI CARICO LOCALIZZATE 1 PERDITE DI CARICO LOCALIZZATE Sono le perdite di carico (o di pressione) che un fluido, in moto attraverso un condotto, subisce a causa delle resistenze
LE RETI DI DISTRIBUZIONE PERDITE DI CARICO LOCALIZZATE 1 PERDITE DI CARICO LOCALIZZATE Sono le perdite di carico (o di pressione) che un fluido, in moto attraverso un condotto, subisce a causa delle resistenze
Capitolo 13: L offerta dell impresa e il surplus del produttore
 Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Massimo Rundo Politecnico di Torino Dipartimento Energia Fluid Power Research Laboratory
 La simulazione delle pompe oleodinamiche Massimo Rundo Politecnico di Torino Dipartimento Energia Fluid Power Research Laboratory Politecnico di Torino Dipartimento Energia Macchine a fluido Laboratorio
La simulazione delle pompe oleodinamiche Massimo Rundo Politecnico di Torino Dipartimento Energia Fluid Power Research Laboratory Politecnico di Torino Dipartimento Energia Macchine a fluido Laboratorio
f(x) = 1 x. Il dominio di questa funzione è il sottoinsieme proprio di R dato da
 Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
1. Scopo dell esperienza.
 1. Scopo dell esperienza. Lo scopo di questa esperienza è ricavare la misura di tre resistenze il 4 cui ordine di grandezza varia tra i 10 e 10 Ohm utilizzando il metodo olt- Amperometrico. Tale misura
1. Scopo dell esperienza. Lo scopo di questa esperienza è ricavare la misura di tre resistenze il 4 cui ordine di grandezza varia tra i 10 e 10 Ohm utilizzando il metodo olt- Amperometrico. Tale misura
Automazione Industriale (scheduling+mms) scheduling+mms. adacher@dia.uniroma3.it
 Automazione Industriale (scheduling+mms) scheduling+mms adacher@dia.uniroma3.it Introduzione Sistemi e Modelli Lo studio e l analisi di sistemi tramite una rappresentazione astratta o una sua formalizzazione
Automazione Industriale (scheduling+mms) scheduling+mms adacher@dia.uniroma3.it Introduzione Sistemi e Modelli Lo studio e l analisi di sistemi tramite una rappresentazione astratta o una sua formalizzazione
Calcolo del Valore Attuale Netto (VAN)
 Calcolo del Valore Attuale Netto (VAN) Il calcolo del valore attuale netto (VAN) serve per determinare la redditività di un investimento. Si tratta di utilizzare un procedimento che può consentirci di
Calcolo del Valore Attuale Netto (VAN) Il calcolo del valore attuale netto (VAN) serve per determinare la redditività di un investimento. Si tratta di utilizzare un procedimento che può consentirci di
Sez. J.1 Sistemi e tecnologie ad aria compressa, di ausilio alla produzione SISTEMI DI RAFFREDDAMENTO TUBI VORTEX FRIGID-X TM VORTEX TUBE
 Sez. J.1 Sistemi e tecnologie ad aria compressa, di ausilio alla produzione SISTEMI DI RAFFREDDAMENTO DC COOLING TUBI VORTEX FRIGID-X TM VORTEX TUBE Documentazione non registrata, soggetta a modifiche
Sez. J.1 Sistemi e tecnologie ad aria compressa, di ausilio alla produzione SISTEMI DI RAFFREDDAMENTO DC COOLING TUBI VORTEX FRIGID-X TM VORTEX TUBE Documentazione non registrata, soggetta a modifiche
I processi di tempra sono condotti sul manufatto finito per generare sforzi residui di compressione in superficie. Vengono sfruttate allo scopo
 I processi di tempra sono condotti sul manufatto finito per generare sforzi residui di compressione in superficie. Vengono sfruttate allo scopo diverse metodologie. 1 La tempra termica (o fisica) si basa
I processi di tempra sono condotti sul manufatto finito per generare sforzi residui di compressione in superficie. Vengono sfruttate allo scopo diverse metodologie. 1 La tempra termica (o fisica) si basa
Slide Cerbara parte1 5. Le distribuzioni teoriche
 Slide Cerbara parte1 5 Le distribuzioni teoriche I fenomeni biologici, demografici, sociali ed economici, che sono il principale oggetto della statistica, non sono retti da leggi matematiche. Però dalle
Slide Cerbara parte1 5 Le distribuzioni teoriche I fenomeni biologici, demografici, sociali ed economici, che sono il principale oggetto della statistica, non sono retti da leggi matematiche. Però dalle
Il concetto di valore medio in generale
 Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Approccio intermedio fra i precedenti
 Modelli usati per simulare il sistema respiratorio Ingegneria Biomedica Anno Accademico 2008-0909 Tommaso Sbrana Un modello è una rappresentazione di un oggetto o di un fenomeno che ne riproduce alcune
Modelli usati per simulare il sistema respiratorio Ingegneria Biomedica Anno Accademico 2008-0909 Tommaso Sbrana Un modello è una rappresentazione di un oggetto o di un fenomeno che ne riproduce alcune
LE FINESTRE E L ISOLAMENTO ACUSTICO
 LE FINESTRE E L ISOLAMENTO ACUSTICO Roberto Malatesta. William Marcone Ufficio Tecnico (giugno 2008) LA PROTEZIONE DAL RUMORE DEGLI EDIFICI, LA NORMATIVA NAZIONALE La maggior sensibilità delle persone
LE FINESTRE E L ISOLAMENTO ACUSTICO Roberto Malatesta. William Marcone Ufficio Tecnico (giugno 2008) LA PROTEZIONE DAL RUMORE DEGLI EDIFICI, LA NORMATIVA NAZIONALE La maggior sensibilità delle persone
Dimensione di uno Spazio vettoriale
 Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Giovanni Schgör (g.schgor)
 Giovanni Schgör (g.schgor) BATTERIE E PANNELLI SOLARI 10 March 2009 La batteria Dopo gli articoli (1) (2) sulla modellizzazione dei pannelli solari, si vuole analizzare il comportamento di questi nella
Giovanni Schgör (g.schgor) BATTERIE E PANNELLI SOLARI 10 March 2009 La batteria Dopo gli articoli (1) (2) sulla modellizzazione dei pannelli solari, si vuole analizzare il comportamento di questi nella
Simulazioni accoppiate 1D-3D per scenari d incendio
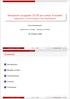 Simulazioni accoppiate 1D-3D per scenari d incendio Applicazione a tunnel stradali e linee metropolitane Luca Iannantuoni Dipartimento di Energia - Politecnico di Milano 29 Ottobre 2009 Luca Iannantuoni
Simulazioni accoppiate 1D-3D per scenari d incendio Applicazione a tunnel stradali e linee metropolitane Luca Iannantuoni Dipartimento di Energia - Politecnico di Milano 29 Ottobre 2009 Luca Iannantuoni
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI
 APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
GEOMETRIA DELLE MASSE
 1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
Indice di rischio globale
 Indice di rischio globale Di Pietro Bottani Dottore Commercialista in Prato Introduzione Con tale studio abbiamo cercato di creare un indice generale capace di valutare il rischio economico-finanziario
Indice di rischio globale Di Pietro Bottani Dottore Commercialista in Prato Introduzione Con tale studio abbiamo cercato di creare un indice generale capace di valutare il rischio economico-finanziario
VALORE DELLE MERCI SEQUESTRATE
 La contraffazione in cifre: NUOVA METODOLOGIA PER LA STIMA DEL VALORE DELLE MERCI SEQUESTRATE Roma, Giugno 2013 Giugno 2013-1 Il valore economico dei sequestri In questo Focus si approfondiscono alcune
La contraffazione in cifre: NUOVA METODOLOGIA PER LA STIMA DEL VALORE DELLE MERCI SEQUESTRATE Roma, Giugno 2013 Giugno 2013-1 Il valore economico dei sequestri In questo Focus si approfondiscono alcune
Teoria delle code. Sistemi stazionari: M/M/1 M/M/1/K M/M/S
 Teoria delle code Sistemi stazionari: M/M/1 M/M/1/K M/M/S Fabio Giammarinaro 04/03/2008 Sommario INTRODUZIONE... 3 Formule generali di e... 3 Leggi di Little... 3 Cosa cerchiamo... 3 Legame tra N e le
Teoria delle code Sistemi stazionari: M/M/1 M/M/1/K M/M/S Fabio Giammarinaro 04/03/2008 Sommario INTRODUZIONE... 3 Formule generali di e... 3 Leggi di Little... 3 Cosa cerchiamo... 3 Legame tra N e le
Verranno descritti di seguito brevemente gli algoritmi di calcolo utilizzati per l interpretazione nei tre metodi inseriti all interno del programma.
 3. Teoria Verranno descritti di seguito brevemente gli algoritmi di calcolo utilizzati per l interpretazione nei tre metodi inseriti all interno del programma. 3.1 Metodo convenzionale (metodo del tempo
3. Teoria Verranno descritti di seguito brevemente gli algoritmi di calcolo utilizzati per l interpretazione nei tre metodi inseriti all interno del programma. 3.1 Metodo convenzionale (metodo del tempo
Il riduttore di focale utilizzato è il riduttore-correttore Celestron f/ 6.3.
 LE FOCALI DEL C8 Di Giovanni Falcicchia Settembre 2010 Premessa (a cura del Telescope Doctor). Il Celestron C8 è uno Schmidt-Cassegrain, ovvero un telescopio composto da uno specchio primario concavo sferico
LE FOCALI DEL C8 Di Giovanni Falcicchia Settembre 2010 Premessa (a cura del Telescope Doctor). Il Celestron C8 è uno Schmidt-Cassegrain, ovvero un telescopio composto da uno specchio primario concavo sferico
I documenti di www.mistermanager.it. Gli ingredienti per l allenamento per la corsa LE RIPETUTE
 I documenti di www.mistermanager.it Gli ingredienti per l allenamento per la corsa LE RIPETUTE Le Ripetute sono una delle forme di allenamento che caratterizzano i corridori più evoluti, in quanto partono
I documenti di www.mistermanager.it Gli ingredienti per l allenamento per la corsa LE RIPETUTE Le Ripetute sono una delle forme di allenamento che caratterizzano i corridori più evoluti, in quanto partono
PRINCIPI FONDAMENTALI...
 QUALITA DEL SERVIZIO 1) PREMESSA... 2 2) PRINCIPI FONDAMENTALI... 2 2.1) EFFICIENZA NEL SERVIZIO... 2 2.2) CONTINUITÀ... 2 2.3) IMPARZIALITÀ DI TRATTAMENTO... 3 2.4) SALUTE, SICUREZZA ED AMBIENTE... 3
QUALITA DEL SERVIZIO 1) PREMESSA... 2 2) PRINCIPI FONDAMENTALI... 2 2.1) EFFICIENZA NEL SERVIZIO... 2 2.2) CONTINUITÀ... 2 2.3) IMPARZIALITÀ DI TRATTAMENTO... 3 2.4) SALUTE, SICUREZZA ED AMBIENTE... 3
GMG s.n.c. di Moretti Massimo & c. via XX settembre n 15 48024 Massa Lombarda (RA Tel/fax 0545 82966
 Oggetto: progetto stampante solida per materiali ceramici Punti da rispettare 1) apparato a controllo numerico per formare oggetti tridimensionali in materiali sinterizzabili ad alta temperatura 2) sviluppo
Oggetto: progetto stampante solida per materiali ceramici Punti da rispettare 1) apparato a controllo numerico per formare oggetti tridimensionali in materiali sinterizzabili ad alta temperatura 2) sviluppo
TECNICA DELLE COSTRUZIONI: PROGETTO DI STRUTTURE LE FONDAZIONI
 LE FONDAZIONI Generalità sulle fondazioni Fondazioni dirette Plinti isolati Trave rovescia Esecutivi di strutture di fondazione Generalità Le opere di fondazione hanno il compito di trasferire le sollecitazioni
LE FONDAZIONI Generalità sulle fondazioni Fondazioni dirette Plinti isolati Trave rovescia Esecutivi di strutture di fondazione Generalità Le opere di fondazione hanno il compito di trasferire le sollecitazioni
Anno 2014. Rapporto ambientale
 Anno 2014 Rapporto ambientale 1 ANNO 2014 Nell anno 2005 la SITI TARGHE S.r.l. ha ottenuto la certificazione ambientale secondo la norma internazionale ISO 14001:2004, rinnovata nel 2008, nel 2011 e nel
Anno 2014 Rapporto ambientale 1 ANNO 2014 Nell anno 2005 la SITI TARGHE S.r.l. ha ottenuto la certificazione ambientale secondo la norma internazionale ISO 14001:2004, rinnovata nel 2008, nel 2011 e nel
ALLEGATO 1 Analisi delle serie storiche pluviometriche delle stazioni di Torre del Lago e di Viareggio.
 ALLEGATO 1 Analisi delle serie storiche pluviometriche delle stazioni di Torre del Lago e di Viareggio. Per una migliore caratterizzazione del bacino idrologico dell area di studio, sono state acquisite
ALLEGATO 1 Analisi delle serie storiche pluviometriche delle stazioni di Torre del Lago e di Viareggio. Per una migliore caratterizzazione del bacino idrologico dell area di studio, sono state acquisite
risulta (x) = 1 se x < 0.
 Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Rapporto ambientale Anno 2012
 Rapporto ambientale Anno 2012 Pagina 1 di 11 1 ANNO 2012 Nell anno 2005 la SITI TARGHE srl ha ottenuto la certificazione ambientale secondo la norma internazionale ISO 14001:2004, rinnovata nel 2008 e
Rapporto ambientale Anno 2012 Pagina 1 di 11 1 ANNO 2012 Nell anno 2005 la SITI TARGHE srl ha ottenuto la certificazione ambientale secondo la norma internazionale ISO 14001:2004, rinnovata nel 2008 e
Consideriamo due polinomi
 Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Capitolo 2. Operazione di limite
 Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
COSTRUIAMO UN AEROMODELLO 3D 4
 COSTRUIAMO UN AEROMODELLO 3D 4 Con i comandi che abbiamo visto fina ad ora dovreste essere in grado di costruire da soli le ali del modello (ovviamente fatene una sola e poi specchiatela), basta trasformare
COSTRUIAMO UN AEROMODELLO 3D 4 Con i comandi che abbiamo visto fina ad ora dovreste essere in grado di costruire da soli le ali del modello (ovviamente fatene una sola e poi specchiatela), basta trasformare
ROI, WACC e EVA: strumenti di pianificazione economico finanziaria Di : Pietro Bottani Dottore Commercialista in Prato
 Articolo pubblicato sul n 22 / 2004 di Amministrazione e Finanza edito da Ipsoa. ROI, WACC e EVA: strumenti di pianificazione economico finanziaria Di : Pietro Bottani Dottore Commercialista in Prato Premessa
Articolo pubblicato sul n 22 / 2004 di Amministrazione e Finanza edito da Ipsoa. ROI, WACC e EVA: strumenti di pianificazione economico finanziaria Di : Pietro Bottani Dottore Commercialista in Prato Premessa
Compressori volumetrici a) Compressori alternativi
 Compressori volumetrici a) Compressori alternativi Il parametro fondamentale per la valutazione di un compressore alternativo è l efficienza volumetrica: η v = (Portata volumetrica effettiva) / (Volume
Compressori volumetrici a) Compressori alternativi Il parametro fondamentale per la valutazione di un compressore alternativo è l efficienza volumetrica: η v = (Portata volumetrica effettiva) / (Volume
La pista del mio studio Riflettiamo sulla pista. Guida per l insegnante
 Riflettiamo sulla pista Guida per l insegnante Obiettivi educativi generali Compito di specificazione - possiede capacità progettuale - è in grado di organizzare il proprio tempo e di costruire piani per
Riflettiamo sulla pista Guida per l insegnante Obiettivi educativi generali Compito di specificazione - possiede capacità progettuale - è in grado di organizzare il proprio tempo e di costruire piani per
VERIFICHE PERIODICHE DEL MANTENIMENTO DI REQUISITI IMPIANTISTICI ED IGIENICO AMBIENTALI IN SALA OPERATORIA.
 VERIFICHE PERIODICHE DEL MANTENIMENTO DI REQUISITI IMPIANTISTICI ED IGIENICO AMBIENTALI IN SALA OPERATORIA. Esperienza relativa ai controlli eseguiti dal 2008 al 2012 Statistica basata su 5 anni di validazioni
VERIFICHE PERIODICHE DEL MANTENIMENTO DI REQUISITI IMPIANTISTICI ED IGIENICO AMBIENTALI IN SALA OPERATORIA. Esperienza relativa ai controlli eseguiti dal 2008 al 2012 Statistica basata su 5 anni di validazioni
V= R*I. LEGGE DI OHM Dopo aver illustrato le principali grandezze elettriche è necessario analizzare i legami che vi sono tra di loro.
 LEGGE DI OHM Dopo aver illustrato le principali grandezze elettriche è necessario analizzare i legami che vi sono tra di loro. PREMESSA: Anche intuitivamente dovrebbe a questo punto essere ormai chiaro
LEGGE DI OHM Dopo aver illustrato le principali grandezze elettriche è necessario analizzare i legami che vi sono tra di loro. PREMESSA: Anche intuitivamente dovrebbe a questo punto essere ormai chiaro
IL DIMENSIONAMENTO DEGLI IMPIANTI IDROSANITARI Miscelatori e riduttori di pressione
 FOCUS TECNICO IL DEGLI IMPIANTI IDROSANITARI Miscelatori e riduttori di pressione CRITERI DI CALCOLO DELLA PORTATA DI PROGETTO Lo scopo principale del dimensionamento di una rete idrica è quello di assicurare
FOCUS TECNICO IL DEGLI IMPIANTI IDROSANITARI Miscelatori e riduttori di pressione CRITERI DI CALCOLO DELLA PORTATA DI PROGETTO Lo scopo principale del dimensionamento di una rete idrica è quello di assicurare
Casi concreti PREMESSA casi concreti completa e dettagliata documentazione nessun caso concreto riportato è descritto più di una volta
 Casi concreti La pubblicazione dei casi concreti ha, come scopo principale, quello di dare a tante persone la possibilità di essere informate della validità della consulenza individuale e indipendente
Casi concreti La pubblicazione dei casi concreti ha, come scopo principale, quello di dare a tante persone la possibilità di essere informate della validità della consulenza individuale e indipendente
S-TRAINER v.1.00 Esempio d uso
 S-TRAINER v.1.00 Esempio d uso S-TRAINER v.1.00, ovvero il software per la pianificazione e la gestione dell allenamento sportivo. Andiamo a scoprire le potenzialità di questo nuovo software ideato da
S-TRAINER v.1.00 Esempio d uso S-TRAINER v.1.00, ovvero il software per la pianificazione e la gestione dell allenamento sportivo. Andiamo a scoprire le potenzialità di questo nuovo software ideato da
~ Copyright Ripetizionando - All rights reserved ~ http://ripetizionando.wordpress.com STUDIO DI FUNZIONE
 STUDIO DI FUNZIONE Passaggi fondamentali Per effettuare uno studio di funzione completo, che non lascia quindi margine a una quasi sicuramente errata inventiva, sono necessari i seguenti 7 passaggi: 1.
STUDIO DI FUNZIONE Passaggi fondamentali Per effettuare uno studio di funzione completo, che non lascia quindi margine a una quasi sicuramente errata inventiva, sono necessari i seguenti 7 passaggi: 1.
LA MASSIMIZZAZIONE DEL PROFITTO ATTRAVERSO LA FISSAZIONE DEL PREZZO IN FUNZIONE DELLE QUANTITÀ
 LA MASSIMIZZAZIONE DEL PROFITTO ATTRAVERSO LA FISSAZIONE DEL PREZZO IN FUNZIONE DELLE QUANTITÀ In questa Appendice mostreremo come trovare la tariffa in due parti che massimizza i profitti di Clearvoice,
LA MASSIMIZZAZIONE DEL PROFITTO ATTRAVERSO LA FISSAZIONE DEL PREZZO IN FUNZIONE DELLE QUANTITÀ In questa Appendice mostreremo come trovare la tariffa in due parti che massimizza i profitti di Clearvoice,
LEGGE DI STEVIN (EQUAZIONE FONDAMENTALE DELLA STATICA DEI FLUIDI PESANTI INCOMPRIMIBILI) z + p / γ = costante
 IDRAULICA LEGGE DI STEVIN (EQUAZIONE FONDAMENTALE DELLA STATICA DEI FLUIDI PESANTI INCOMPRIMIBILI) z + p / γ = costante 2 LEGGE DI STEVIN Z = ALTEZZA GEODETICA ENERGIA POTENZIALE PER UNITA DI PESO p /
IDRAULICA LEGGE DI STEVIN (EQUAZIONE FONDAMENTALE DELLA STATICA DEI FLUIDI PESANTI INCOMPRIMIBILI) z + p / γ = costante 2 LEGGE DI STEVIN Z = ALTEZZA GEODETICA ENERGIA POTENZIALE PER UNITA DI PESO p /
Generalità sulle elettropompe
 Generalità sulle elettropompe 1) Introduzione Ne esistono diverse tipologie ma si possono inizialmente suddividere in turbopompe e pompe volumetriche. Le prime sono caratterizzate da un flusso continuo
Generalità sulle elettropompe 1) Introduzione Ne esistono diverse tipologie ma si possono inizialmente suddividere in turbopompe e pompe volumetriche. Le prime sono caratterizzate da un flusso continuo
Progetto di simulazione molecolare per il corso di Complementi di algoritmi A.A. 2005-06
 Progetto di simulazione molecolare per il corso di Complementi di algoritmi A.A. 2005-06 13 febbraio 2006 1 Descrizione Il progetto si compone delle seguenti fasi: 1. caricamento di soluzioni in formato
Progetto di simulazione molecolare per il corso di Complementi di algoritmi A.A. 2005-06 13 febbraio 2006 1 Descrizione Il progetto si compone delle seguenti fasi: 1. caricamento di soluzioni in formato
Nell esempio verrà mostrato come creare un semplice documento in Excel per calcolare in modo automatico la rata di un mutuo a tasso fisso conoscendo
 Nell esempio verrà mostrato come creare un semplice documento in Excel per calcolare in modo automatico la rata di un mutuo a tasso fisso conoscendo - la durata del mutuo in anni - l importo del mutuo
Nell esempio verrà mostrato come creare un semplice documento in Excel per calcolare in modo automatico la rata di un mutuo a tasso fisso conoscendo - la durata del mutuo in anni - l importo del mutuo
Come valutare le caratteristiche aerobiche di ogni singolo atleta sul campo
 Come valutare le caratteristiche aerobiche di ogni singolo atleta sul campo Prima di organizzare un programma di allenamento al fine di elevare il livello di prestazione, è necessario valutare le capacità
Come valutare le caratteristiche aerobiche di ogni singolo atleta sul campo Prima di organizzare un programma di allenamento al fine di elevare il livello di prestazione, è necessario valutare le capacità
6.5. Risultati simulazioni sistema rifiuti e riscaldamento
 Capitolo 6 Risultati pag. 301 6.5. Risultati simulazioni sistema rifiuti e riscaldamento Come già detto nel paragrafo 5.8, i risultati riportati in questo paragrafo fanno riferimento alle concentrazione
Capitolo 6 Risultati pag. 301 6.5. Risultati simulazioni sistema rifiuti e riscaldamento Come già detto nel paragrafo 5.8, i risultati riportati in questo paragrafo fanno riferimento alle concentrazione
Calcolatori Elettronici A a.a. 2008/2009
 Calcolatori Elettronici A a.a. 2008/2009 PRESTAZIONI DEL CALCOLATORE Massimiliano Giacomin Due dimensioni Tempo di risposta (o tempo di esecuzione): il tempo totale impiegato per eseguire un task (include
Calcolatori Elettronici A a.a. 2008/2009 PRESTAZIONI DEL CALCOLATORE Massimiliano Giacomin Due dimensioni Tempo di risposta (o tempo di esecuzione): il tempo totale impiegato per eseguire un task (include
CHIUSURE di MAGAZZINO di FINE ANNO
 CHIUSURE di MAGAZZINO di FINE ANNO Operazioni da svolgere per il riporto delle giacenze di fine esercizio Il documento che segue ha lo scopo di illustrare le operazioni che devono essere eseguite per:
CHIUSURE di MAGAZZINO di FINE ANNO Operazioni da svolgere per il riporto delle giacenze di fine esercizio Il documento che segue ha lo scopo di illustrare le operazioni che devono essere eseguite per:
2.0 Gli archivi. 2.1 Inserire gli archivi. 2.2 Archivio Clienti, Fornitori, Materiali, Noleggi ed Altri Costi. Impresa Edile Guida all uso
 2.0 Gli archivi All interno della sezione archivi sono inserite le anagrafiche. In pratica si stratta di tutti quei dati che ricorreranno costantemente all interno dei documenti. 2.1 Inserire gli archivi
2.0 Gli archivi All interno della sezione archivi sono inserite le anagrafiche. In pratica si stratta di tutti quei dati che ricorreranno costantemente all interno dei documenti. 2.1 Inserire gli archivi
1 Serie di Taylor di una funzione
 Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
Modulo 2. Domanda aggregata e livello di produzione
 Modulo 2 Domanda aggregata e livello di produzione Esercizio. In un sistema economico privo di settore pubblico, la funzione di consumo è: C = 200 + 0.8Y; gli investimenti sono I= 50. a) Qual è il livello
Modulo 2 Domanda aggregata e livello di produzione Esercizio. In un sistema economico privo di settore pubblico, la funzione di consumo è: C = 200 + 0.8Y; gli investimenti sono I= 50. a) Qual è il livello
Laboratorio di Fisica 3 Ottica 2. Studenti: Buoni - Giambastiani - Leidi Gruppo: G09
 Laboratorio di Fisica 3 Ottica 2 Studenti: Buoni - Giambastiani - Leidi Gruppo: G09 24 febbraio 2015 1 Lunghezza d onda di un laser He-Ne 1.1 Scopo dell esperienza Lo scopo dell esperienza è quello di
Laboratorio di Fisica 3 Ottica 2 Studenti: Buoni - Giambastiani - Leidi Gruppo: G09 24 febbraio 2015 1 Lunghezza d onda di un laser He-Ne 1.1 Scopo dell esperienza Lo scopo dell esperienza è quello di
INVERTER DI STRINGA POWER ONE AURORA: Dimensionamento del generatore fotovoltaico con Aurora Designer
 INVERTER DI STRINGA POWER ONE AURORA: Dimensionamento del generatore fotovoltaico con Aurora Designer INDICE Cap. 1 Il configuratore Aurora Designer 1 Cap. 2 Ottimizzazione del dimensionamento del generatore
INVERTER DI STRINGA POWER ONE AURORA: Dimensionamento del generatore fotovoltaico con Aurora Designer INDICE Cap. 1 Il configuratore Aurora Designer 1 Cap. 2 Ottimizzazione del dimensionamento del generatore
Studio di una funzione ad una variabile
 Studio di una funzione ad una variabile Lo studio di una funzione ad una variabile ha come scopo ultimo quello di pervenire a un grafico della funzione assegnata. Questo grafico non dovrà essere preciso
Studio di una funzione ad una variabile Lo studio di una funzione ad una variabile ha come scopo ultimo quello di pervenire a un grafico della funzione assegnata. Questo grafico non dovrà essere preciso
INTRODUZIONE I CICLI DI BORSA
 www.previsioniborsa.net 1 lezione METODO CICLICO INTRODUZIONE Questo metodo e praticamente un riassunto in breve di anni di esperienza e di studi sull Analisi Tecnica di borsa con specializzazione in particolare
www.previsioniborsa.net 1 lezione METODO CICLICO INTRODUZIONE Questo metodo e praticamente un riassunto in breve di anni di esperienza e di studi sull Analisi Tecnica di borsa con specializzazione in particolare
G3. Asintoti e continuità
 G3 Asintoti e continuità Un asintoto è una retta a cui la funzione si avvicina sempre di più senza mai toccarla Non è la definizione formale, ma sicuramente serve per capire il concetto di asintoto Nei
G3 Asintoti e continuità Un asintoto è una retta a cui la funzione si avvicina sempre di più senza mai toccarla Non è la definizione formale, ma sicuramente serve per capire il concetto di asintoto Nei
Idrostatica Correnti a pelo libero (o a superficie libera) Correnti in pressione. Foronomia
 Idrostatica Correnti a pelo libero (o a superficie libera) Correnti in pressione Foronomia In idrostatica era lecito trascurare l attrito interno o viscosità e i risultati ottenuti valevano sia per i liquidi
Idrostatica Correnti a pelo libero (o a superficie libera) Correnti in pressione Foronomia In idrostatica era lecito trascurare l attrito interno o viscosità e i risultati ottenuti valevano sia per i liquidi
Nuova funzione di ricerca del sito WIKA.
 Nuova funzione di ricerca del sito WIKA. Il sito WIKA dispone ora di una funzione di ricerca completamente riprogettata. Essa è uno strumento particolarmente importante in quanto deve fornire al navigatore
Nuova funzione di ricerca del sito WIKA. Il sito WIKA dispone ora di una funzione di ricerca completamente riprogettata. Essa è uno strumento particolarmente importante in quanto deve fornire al navigatore
4 Dispense di Matematica per il biennio dell Istituto I.S.I.S. Gaetano Filangieri di Frattamaggiore EQUAZIONI FRATTE E SISTEMI DI EQUAZIONI
 119 4 Dispense di Matematica per il biennio dell Istituto I.S.I.S. Gaetano Filangieri di Frattamaggiore EQUAZIONI FRATTE E SISTEMI DI EQUAZIONI Indice degli Argomenti: TEMA N. 1 : INSIEMI NUMERICI E CALCOLO
119 4 Dispense di Matematica per il biennio dell Istituto I.S.I.S. Gaetano Filangieri di Frattamaggiore EQUAZIONI FRATTE E SISTEMI DI EQUAZIONI Indice degli Argomenti: TEMA N. 1 : INSIEMI NUMERICI E CALCOLO
Statistica. Lezione 6
 Università degli Studi del Piemonte Orientale Corso di Laurea in Infermieristica Corso integrato in Scienze della Prevenzione e dei Servizi sanitari Statistica Lezione 6 a.a 011-01 Dott.ssa Daniela Ferrante
Università degli Studi del Piemonte Orientale Corso di Laurea in Infermieristica Corso integrato in Scienze della Prevenzione e dei Servizi sanitari Statistica Lezione 6 a.a 011-01 Dott.ssa Daniela Ferrante
Aspettative, Produzione e Politica Economica
 Aspettative, Produzione e Politica Economica In questa lezione: Studiamo gli effetti delle aspettative sui livelli di spesa e produzione. Riformuliamo il modello IS-LM in un contesto con aspettative. Determiniamo
Aspettative, Produzione e Politica Economica In questa lezione: Studiamo gli effetti delle aspettative sui livelli di spesa e produzione. Riformuliamo il modello IS-LM in un contesto con aspettative. Determiniamo
ControlloCosti. Cubi OLAP. Controllo Costi Manuale Cubi
 ControlloCosti Cubi OLAP I cubi OLAP Un Cubo (OLAP, acronimo di On-Line Analytical Processing) è una struttura per la memorizzazione e la gestione dei dati che permette di eseguire analisi in tempi rapidi,
ControlloCosti Cubi OLAP I cubi OLAP Un Cubo (OLAP, acronimo di On-Line Analytical Processing) è una struttura per la memorizzazione e la gestione dei dati che permette di eseguire analisi in tempi rapidi,
Siamo così arrivati all aritmetica modulare, ma anche a individuare alcuni aspetti di come funziona l aritmetica del calcolatore come vedremo.
 DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
FIRESHOP.NET. Gestione della distinta base & della produzione. www.firesoft.it
 FIRESHOP.NET Gestione della distinta base & della produzione www.firesoft.it Sommario SOMMARIO Introduzione... 3 Definire la distinta base di un articolo... 5 Utilizzare la distinta base diretta... 8 Utilizzare
FIRESHOP.NET Gestione della distinta base & della produzione www.firesoft.it Sommario SOMMARIO Introduzione... 3 Definire la distinta base di un articolo... 5 Utilizzare la distinta base diretta... 8 Utilizzare
www.andreatorinesi.it
 La lunghezza focale Lunghezza focale Si definisce lunghezza focale la distanza tra il centro ottico dell'obiettivo (a infinito ) e il piano su cui si forma l'immagine (nel caso del digitale, il sensore).
La lunghezza focale Lunghezza focale Si definisce lunghezza focale la distanza tra il centro ottico dell'obiettivo (a infinito ) e il piano su cui si forma l'immagine (nel caso del digitale, il sensore).
Capitolo 25: Lo scambio nel mercato delle assicurazioni
 Capitolo 25: Lo scambio nel mercato delle assicurazioni 25.1: Introduzione In questo capitolo la teoria economica discussa nei capitoli 23 e 24 viene applicata all analisi dello scambio del rischio nel
Capitolo 25: Lo scambio nel mercato delle assicurazioni 25.1: Introduzione In questo capitolo la teoria economica discussa nei capitoli 23 e 24 viene applicata all analisi dello scambio del rischio nel
Il polo magnetico: simulazione nel tempo
 Corso di Elettrotecnica Industriale Professore Paolo Di Barba Il polo magnetico: simulazione nel tempo Anno Accademico 2013/2014 Lo scopo dell esercizio è quello di valutare l andamento del campo magnetico
Corso di Elettrotecnica Industriale Professore Paolo Di Barba Il polo magnetico: simulazione nel tempo Anno Accademico 2013/2014 Lo scopo dell esercizio è quello di valutare l andamento del campo magnetico
SISTEMI MULTIAGENTE. Esercizio
 Esercizio SISTEMI MULTIAGENTE Nello studio dei sistemi dinamici complessi la simulazione al computer ha un ruolo importante dal momento che presenta molti vantaggi rispetto ai metodi sperimentali più tradizionali;
Esercizio SISTEMI MULTIAGENTE Nello studio dei sistemi dinamici complessi la simulazione al computer ha un ruolo importante dal momento che presenta molti vantaggi rispetto ai metodi sperimentali più tradizionali;
Tecniche di Prototipazione. Introduzione
 Tecniche di Prototipazione Introduzione Con il termine prototipo si intende il primo esempio di un prodotto che deve essere sviluppato e che consente di poter effettuare considerazioni preliminari prima
Tecniche di Prototipazione Introduzione Con il termine prototipo si intende il primo esempio di un prodotto che deve essere sviluppato e che consente di poter effettuare considerazioni preliminari prima
ENERGIA DA OLI VEGETALI
 PROGETTO 012 ENERGIA DA OLI VEGETALI IMPIANTO DI PRODUZIONE DI ENERGIA ELETTRICA TRAMITE DIESEL GENSET ALIMENTATO AD OLIO DI PALMA Prove effettuate nell anno 2009 1 Scopo del documento Riportare i risultati
PROGETTO 012 ENERGIA DA OLI VEGETALI IMPIANTO DI PRODUZIONE DI ENERGIA ELETTRICA TRAMITE DIESEL GENSET ALIMENTATO AD OLIO DI PALMA Prove effettuate nell anno 2009 1 Scopo del documento Riportare i risultati
LA RETTA. Retta per l'origine, rette orizzontali e verticali
 Retta per l'origine, rette orizzontali e verticali LA RETTA Abbiamo visto che l'equazione generica di una retta è del tipo Y = mx + q, dove m ne rappresenta la pendenza e q il punto in cui la retta incrocia
Retta per l'origine, rette orizzontali e verticali LA RETTA Abbiamo visto che l'equazione generica di una retta è del tipo Y = mx + q, dove m ne rappresenta la pendenza e q il punto in cui la retta incrocia
Prese d aria supersoniche [1-14]
![Prese d aria supersoniche [1-14] Prese d aria supersoniche [1-14]](/thumbs/29/13842101.jpg) Politecnico di Milano Facoltà di Ingegneria Industriale Corso di Laurea in Ingegneria Aerospaziale Insegnamento di Propulsione Aerospaziale Anno accademico 2011/12 Capitolo 4 sezione a2 Prese d aria supersoniche
Politecnico di Milano Facoltà di Ingegneria Industriale Corso di Laurea in Ingegneria Aerospaziale Insegnamento di Propulsione Aerospaziale Anno accademico 2011/12 Capitolo 4 sezione a2 Prese d aria supersoniche
Forze come grandezze vettoriali
 Forze come grandezze vettoriali L. Paolucci 23 novembre 2010 Sommario Esercizi e problemi risolti. Per la classe prima. Anno Scolastico 2010/11 Parte 1 / versione 2 Si ricordi che la risultante di due
Forze come grandezze vettoriali L. Paolucci 23 novembre 2010 Sommario Esercizi e problemi risolti. Per la classe prima. Anno Scolastico 2010/11 Parte 1 / versione 2 Si ricordi che la risultante di due
GUIDA AL CALCOLO DEI COSTI DELLE ATTIVITA DI RICERCA DOCUMENTALE
 GUIDA AL CALCOLO DEI COSTI DELLE ATTIVITA DI RICERCA DOCUMENTALE L applicazione elaborata da Nordest Informatica e disponibile all interno del sito è finalizzata a fornirvi un ipotesi dell impatto economico
GUIDA AL CALCOLO DEI COSTI DELLE ATTIVITA DI RICERCA DOCUMENTALE L applicazione elaborata da Nordest Informatica e disponibile all interno del sito è finalizzata a fornirvi un ipotesi dell impatto economico
ISTRUZIONI PER LA GESTIONE BUDGET
 ISTRUZIONI PER LA GESTIONE BUDGET 1) OPERAZIONI PRELIMINARI PER LA GESTIONE BUDGET...1 2) INSERIMENTO E GESTIONE BUDGET PER LA PREVISIONE...4 3) STAMPA DIFFERENZE CAPITOLI/BUDGET.10 4) ANNULLAMENTO BUDGET
ISTRUZIONI PER LA GESTIONE BUDGET 1) OPERAZIONI PRELIMINARI PER LA GESTIONE BUDGET...1 2) INSERIMENTO E GESTIONE BUDGET PER LA PREVISIONE...4 3) STAMPA DIFFERENZE CAPITOLI/BUDGET.10 4) ANNULLAMENTO BUDGET
Controllo di Gestione - Guida Operativa
 Controllo di Gestione - Guida Operativa Il modulo software di Controllo di Gestione, meglio denominato Monitoraggio e Controllo del piano degli obiettivi permette di monitorare, durante l esercizio, gli
Controllo di Gestione - Guida Operativa Il modulo software di Controllo di Gestione, meglio denominato Monitoraggio e Controllo del piano degli obiettivi permette di monitorare, durante l esercizio, gli
Corso di Informatica Generale (C. L. Economia e Commercio) Ing. Valerio Lacagnina Rappresentazione in virgola mobile
 Problemi connessi all utilizzo di un numero di bit limitato Abbiamo visto quali sono i vantaggi dell utilizzo della rappresentazione in complemento alla base: corrispondenza biunivoca fra rappresentazione
Problemi connessi all utilizzo di un numero di bit limitato Abbiamo visto quali sono i vantaggi dell utilizzo della rappresentazione in complemento alla base: corrispondenza biunivoca fra rappresentazione
