Caterina Fenu, Giuseppe Rodriguez
|
|
|
- Aurora Fiori
- 6 anni fa
- Visualizzazioni
Transcript
1 Grafo, Giuseppe Rodriguez Dipartimento di Matematica e Informatica, Università di Cagliari viale Merello 92, Cagliari (Dip. in collab. con Michele Marchesi e Roberto Tonelli Ingegneria Elettrica e Elettronica, Univ. degli Studi di Cagliari) Due giorni di Algebra Lineare Numerica Genova, Febbraio 2012 (Universitá degli Studi di Cagliari) 16 Febbraio / 39
2 Grafi Un grafo è formalmente una coppia di insiemi G = (V, E) dove: Grafo V è un insieme finito numerabile che rappresentiamo con l insieme {1,..., n} i cui elementi vengono chiamati nodi; E è un insieme di coppie {(i, j) V V } i cui elementi vengono chiamati archi. Se (i, j) E allora diremo che il nodo i e il nodo j sono adiacenti. Se l insieme E è costituito da coppie ordinate diremo che il grafo è orientato, non orientato altrimenti. (Universitá degli Studi di Cagliari) 16 Febbraio / 39
3 Esempi Esempi di grafi: Grafo Grafo non orientato Grafo orientato (Universitá degli Studi di Cagliari) 16 Febbraio / 39
4 Nodi connessi e grafi connessi Grafo Un cammino è una sequenza di archi {(i 1, i 2 ),..., (i n 1, i n )}. Se il grafo è orientato si parla di cammino orientato. Un cammino orientato che inizia e termina con lo stesso nodo si chiama ciclo. Grafo non orientato: due nodi i e j si dicono connessi se esiste un cammino che porta da i a j o viceversa. Se ogni coppia di nodi è connessa allora il grafo è detto connesso. Grafo orientato: due nodi i e j si dicono fortemente connessi se esiste un cammino orientato che porta da i a j e se questo cammino orientato esiste per ogni coppia di nodi allora il grafo è detto fortemente connesso. Due nodi i e j si dicono invece debolmente connessi se esiste un cammino che porta da i a j nel quale ogni arco può essere percorso nel suo verso o nel verso opposto. Se ogni coppia di nodi è debolmente connessa allora il grafo è detto debolmente connesso. (Universitá degli Studi di Cagliari) 16 Febbraio / 39
5 Reti complesse Grafo Cos è una rete complessa? Non esiste una definizione precisa. Una possibile scelta è quella di definire una rete complessa come un grafo in cui è presente almeno una delle seguenti caratteristiche: Scale-free (power law degree distribution) Small world Highly clustered. (Universitá degli Studi di Cagliari) 16 Febbraio / 39
6 Esempi Esempi di : Grafo Interazioni tra proteine Interazioni tra neuroni (Universitá degli Studi di Cagliari) 16 Febbraio / 39
7 Esempi Esempi di grafi che non sono : Grafo Reticolo regolare Rete completamente random (Universitá degli Studi di Cagliari) 16 Febbraio / 39
8 Matrice di incidenza Grafo Ad ogni rete complessa può essere associata una matrice di incidenza definita nel modo seguente: A ij = { w se l arco tra il nodo i e il nodo j esiste e ha peso w 0 se il nodo i e il nodo j non sono connessi Lo studio delle proprietà di una rete può essere affrontato analizzando la sua matrice di incidenza che ha, infatti, caratteristiche diverse a seconda del grafo considerato. In genere le matrici di incidenza non sono presentano particolari strutture ma un elemento comune a tutte è la sparsità. (Universitá degli Studi di Cagliari) 16 Febbraio / 39
9 Grafo Con il termine metrica denotiamo un indicatore numerico che rappresenti una proprietà della rete. Dal punto di vista numerico è interessante implementare degli algoritmi efficienti che ne consentano il calcolo a partire dalla matrice di incidenza. Due questioni rilevanti sono legate alle : determinare i nodi più importanti; determinare quanto è facile passare da un nodo all altro. (Universitá degli Studi di Cagliari) 16 Febbraio / 39
10 Grafo Grado di un nodo Il grado di un nodo è dato dal numero di nodi adiacenti ad esso. Se la Rete non è orientata allora deg(i) = n A(i, j) oppure deg(i) = j=1 j i n A(j, i) j=1 j i Se la Rete è orientata per ogni nodo possiamo considerare gli archi in uscita oppure gli archi in entrata: deg out(i) = n A(i, j) e deg in(i) = j=1 j i n A(j, i) j=1 j i (Universitá degli Studi di Cagliari) 16 Febbraio / 39
11 Distanza Grafo La distanza tra due nodi è il cammino più breve che li collega (geodetica). Se due nodi non sono connessi si pone per convenzione una distanza pari a infinito. Per effettuare il calcolo, bisogna prendere in considerazione le potenze della matrice di incidenza, infatti Quindi: [A k ] ij = n di cammini di lunghezza k che collegano i e j dist(i, j) = min{k : (A k ) ij 0} i j (Universitá degli Studi di Cagliari) 16 Febbraio / 39
12 Grafo Subgraph centrality La subgraph centrality indica l importanza di un nodo in base al numero di sottografi a cui partecipa. Per fare questo si sommano i cammini chiusi quel nodo penalizzando quelli di maggiore lunghezza. In formule: SC(i) = k=0 [A k ] ii k! = [e A ] ii (Universitá degli Studi di Cagliari) 16 Febbraio / 39
13 Grafo Indice di Hub e di Authority Un nodo è un hub se punta a nodi considerati importanti e un nodo è un authority se è uno di questi nodi importanti. Si ha quindi una definizione ricorsiva: Un nodo ha un alto indice di hub se punta a nodi che hanno un alto indice di authority e un nodo ha un alto indice di authority se viene puntato da nodi che hanno un alto indice di hub. (Universitá degli Studi di Cagliari) 16 Febbraio / 39
14 Algoritmo HITS Grafo Questo algoritmo si basa su un metodo iterativo. Ad ogni nodo i vengono assegnati due pesi non negativi: un peso di authority x i e un peso di hub y i a cui viene assegnato un valore iniziale arbitrario diverso da zero. I valori sono incrementati poi nel seguente modo: x (k) i = j:(j,i) E y (k 1) j e y (k) i = j:(i,j) E x (k) j I pesi vengono poi normalizzati in modo che i vettori x = [x 1,..., x n ] e y = [y 1,..., y n ] abbiano norma unitaria. (Universitá degli Studi di Cagliari) 16 Febbraio / 39
15 Algoritmo HITS In notazione matriciale si ha: Grafo cioè x (k) = A T y (k 1) e y (k) = Ax (k) x (k) = c k A T Ax (k 1) e y (k) = c kaa T y (k 1) Quindi, l algoritmo HITS è il metodo delle potenze applicato alle matrici A T A e AA T e i vettori contenenti gli indici di authority e gli indici di hub sono gli autovettori dominanti di queste matrici, rispettivamente. (Universitá degli Studi di Cagliari) 16 Febbraio / 39
16 Grafo Grafo Power low degree distribution Una rete è scale-free se la distribuzione dei gradi dei suoi nodi segue una legge di potenza, cioè la frazione F (k) dei nodi che hanno grado k si comporta come F (k) ck p dove c è una costante di normalizzazione e p è un parametro il cui valore, in genere, varia tra -2 e -3. (Universitá degli Studi di Cagliari) 16 Febbraio / 39
17 Grafo Loglog scale Grafo d min = 0 d max = p = 2.27 R = 0.98 (Universitá degli Studi di Cagliari) 16 Febbraio / 39
18 Grafo Grafo Diametro e Distanza media Il diametro di una rete è definito come la massima distanza tra due nodi nella rete, cioè diam(g) = max dist(i, j) i,j V La distanza media è la media delle distanze al variare delle coppie di nodi connessi: l(g) = 1 N dove C = {(i, j) : dist(i, j) < }. (i,j) C dist(i, j) (Universitá degli Studi di Cagliari) 16 Febbraio / 39
19 Grafo Effetto small-world Grafo Si dice che una rete presenta un effetto small-world se il valore di l(g) cresce al più come log n. Modello di una rete small-world: (Universitá degli Studi di Cagliari) 16 Febbraio / 39
20 Grafo Indice di Clustering Grafo È la media degli indici di clustering di tutti i nodi clust(g) = 1 n n C(i) i=1 dove C(i) è la probabilità che due nodi connessi a uno stesso nodo siano a loro volta connessi tra loro. C(i) = t i (A + A T ) 3 ii = T i 2[deg tot(i) (deg tot(i) 2[A 2 ] ii )] (Universitá degli Studi di Cagliari) 16 Febbraio / 39
21 Grafo Grafo Indice di Estrada È definito come la somma delle subgraph centralities di ogni nodo: n [ EE(G) = e A ] = Traccia ( e A) = ii n i=1 i=1 e λ i (Universitá degli Studi di Cagliari) 16 Febbraio / 39
22 Grafo I moderni sistemi software sono composti da svariate unità elementari, chiamate moduli, legate tra loro in modo da svolgere specifici compiti. In particolare, nei sistemi object-oriented (OO) i moduli sono le classi e il legame tra loro è dato da relazioni quali ereditarietà o dipendenza. Recentemente lo studio di tali sistemi software ha potuto beneficiare della teoria delle. (Universitá degli Studi di Cagliari) 16 Febbraio / 39
23 Netbeans Grafo Il sistema software preso in considerazione è Netbeans. Questo sistema è scritto in Java e le sue classi sono contenute in file sorgenti chiamati Compilation Units (CU). La maggior parte delle CU contiene soltanto una classe e solo una piccola percentuale ne contiene più di una. Lo scopo del lavoro in corso è quello di verificare il diffondersi di bug all interno del sistema e dare quindi una misura della fallibilità del software. (Universitá degli Studi di Cagliari) 16 Febbraio / 39
24 Software graphs Grafo Il vantaggio di utilizzare un sistema software quale Netbeans sta nel fatto che sia il codice sorgente di numerose versioni sia i dati riguardanti i bug sono completamente disponibili. In particolare, le informazioni sui bug sono date a livello di CU ed è quindi naturale associare al sistema software una rete complessa nel modo seguente: i nodi sono le CU la CU i e la CU j sono connesse con un arco orientato se nella seconda è presente una classe che dipende o che eredita i moduli dalla prima. (Universitá degli Studi di Cagliari) 16 Febbraio / 39
25 Software graphs Grafo È in corso un lavoro di analisi su un insieme di reti corrispondenti a diversi parti del software con un numero di nodi variabile: da un minimo di 2 nodi (un arco) a un massimo di nodi ( archi). È allora facile vedere come la scelta del giusto algoritmo sia cruciale nell analisi di queste reti. (Universitá degli Studi di Cagliari) 16 Febbraio / 39
26 Problemi Grafo La rete è orientata (la matrice non è simmetrica); Sono presenti dei nodi disconnessi ( 10%); Sono presenti dei cicli. (Universitá degli Studi di Cagliari) 16 Febbraio / 39
27 Hub e di Authority Grafo HITS [Kleinberg, 1999] HITS esponenziale [Farahat et al., 2006] Consiste nell applicare l algoritmo HITS sostituendo la matrice A con la matrice ( e A I ) Hub centrality e Authority centrality [Benzi et al., submitted] Consiste nel calcolare le subgraph centralities della matrice [ 0 ] A A T 0 cioè la matrice di adiacenza associata al grafo bipartito. (Universitá degli Studi di Cagliari) 16 Febbraio / 39
28 Risultati numerici Nodi: 12 Archi:18 Grafo Grafo associato alla matrice Grafo bipartito associato alla matrice (Universitá degli Studi di Cagliari) 16 Febbraio / 39
29 Risultati numerici Grafo Hub Metodo HITS Exp HITS Hub centr Authority Metodo HITS Exp HITS Auth centr (Universitá degli Studi di Cagliari) 16 Febbraio / 39
30 Risultati numerici Nodi: 17 Archi:14 Grafo Grafo associato alla matrice Grafo bipartito associato alla matrice (Universitá degli Studi di Cagliari) 16 Febbraio / 39
31 Risultati numerici Grafo Hub Metodo HITS Exp HITS Hub centr Authority Metodo HITS Exp HITS Auth centr (Universitá degli Studi di Cagliari) 16 Febbraio / 39
32 Grafo Algoritmo base Distanza media Burning algorithm Dijkstra s algorithm (Universitá degli Studi di Cagliari) 16 Febbraio / 39
33 Burning algorithm Grafo Consta di due passi: Riordinare i nodi in ordine topologico, cioè in modo che (i, j) E i < j. Trovare la distanza minima tramite un pulling algorithm, cioè calcolando le distanze minime a ritroso fino ad arrivare al nodo considerato. (Universitá degli Studi di Cagliari) 16 Febbraio / 39
34 Dijkstra s algorithm Grafo Consiste nel dividere i nodi in due gruppi: quelli permanenti e quelli temporanei. I nodi permanenti sono quelli per cui la distanza è stata calcolata e quelli temporanei sono i nodi per i quali bisogna calcolarla. Per un dato nodo i si inizializza un vettore d con valori uguali a infinito. Si percorre poi la rete a partire dal nodo i seguendo ogni arco esistente. Qundo si arriva al nodo j, si sostuisce il valore di d(j) con il numero di passi effettuati per arrivare a quel nodo e si etichetta il nodo j come permanente. Alla fine del calcolo nel vettore d saranno memorizzate le distanze dal nodo i a tutti gli altri nodi. Per ottenere tutte le distanze si devono considerare tutti i nodi uno per volta. (Universitá degli Studi di Cagliari) 16 Febbraio / 39
35 Risultati numerici Grafo Distanza media Nodi Archi l(g) 1 l(g) 2 Time 1 Time , 48 2, 48 0, 25 0, , 55 2, 55 1, 37 0, , 16 3, 16 6, 84 0, , 63 3, 63 17, 6 1, , 35 4, , 69 3, (Universitá degli Studi di Cagliari) 16 Febbraio / 39
36 Approssimazione tramite formule di quadratura Grafo Supponiamo di volere trovare delle approssimazioni per la forma quadratica v T f (A)v Se A è simmetrica consideriamo la sua fattorizzazione spettrale A = QΛQ T, dove Q è una matrice n n contenente gli autovettori di A e Λ è una matrice diagonale contenente gli autovalori di A. Allora si ha: n v T f (A)v = v T Qf (Λ)Q T 2 v = f (λ i )w i i=1 dove w = Q T v. Questa somma può essere interpretata come un integrale di Stieltjes v T f (A)v = λn λ 1 f (λ)dµ(λ) (1) (Universitá degli Studi di Cagliari) 16 Febbraio / 39
37 Approssimazione tramite formule di quadratura Grafo Questo integrale può essere approssimato mediante una formula di quadratura del tipo Si ha: λn λ 1 f (λ)dµ(λ) = N M w j f (s j ) + v k f (z k ) + R[f ]. j=1 M = 0 per la regola di Gauss; k=1 M = 1 (z 1 = λ 1 oppure z 1 = λ n ) per la regola di Gauss-Radau; M = 2 (z 1 = λ 1 e z 2 = λ n ) per la regola di Gauss-Lobatto. Sotto opportune ipotesi sulla funzione f, le formule di quadratura forniscono delle approssimazioni per difetto e/o per eccesso per l integrale (1). (Universitá degli Studi di Cagliari) 16 Febbraio / 39
38 Metodo di bidiagonalizzazione di Lanczos Grafo Per esempio, supponiamo di voler calcolare l elemento di posto (i, j) di f (A) tramite la formula di Gauss allora la forma quadratica prende la forma [Golub and Meurant, 2010] e T i f (A)e j = N w j f (s j ) = e1 T f (J N )e 1 j=1 dove α 1 β 1 β 1 α 2 β 2 J N = β N 2 α N 1 β N 1 β N 1 α N (Universitá degli Studi di Cagliari) 16 Febbraio / 39
39 Grafo GRAZIE (Universitá degli Studi di Cagliari) 16 Febbraio / 39
Introduzione ai grafi. Introduzione ai grafi p. 1/2
 Introduzione ai grafi Introduzione ai grafi p. 1/2 Grafi Un grafo G é costituito da una coppia di insiemi (V,A) dove V é detto insieme dei nodi e A é detto insieme di archi ed é un sottinsieme di tutte
Introduzione ai grafi Introduzione ai grafi p. 1/2 Grafi Un grafo G é costituito da una coppia di insiemi (V,A) dove V é detto insieme dei nodi e A é detto insieme di archi ed é un sottinsieme di tutte
Introduzione ai grafi
 TFA A048 Anno Accademico 2012-13 Outline Cenni storici sui grafi Nozioni introduttive: cammini, connessione, alberi, cicli Cammini di costo minimo Origini storiche La nascita della teoria dei grafi risale
TFA A048 Anno Accademico 2012-13 Outline Cenni storici sui grafi Nozioni introduttive: cammini, connessione, alberi, cicli Cammini di costo minimo Origini storiche La nascita della teoria dei grafi risale
Appunti del corso di Informatica 1 (IN110 Fondamenti) 7 Grafi e alberi: introduzione
 Università di Roma Tre Dipartimento di Matematica e Fisica Corso di Laurea in Matematica Appunti del corso di Informatica (IN0 Fondamenti) Grafi e alberi: introduzione Marco Liverani (liverani@mat.uniroma.it)
Università di Roma Tre Dipartimento di Matematica e Fisica Corso di Laurea in Matematica Appunti del corso di Informatica (IN0 Fondamenti) Grafi e alberi: introduzione Marco Liverani (liverani@mat.uniroma.it)
GRAFI. Cosa sono Grafi non orientati Grafi orientati Grafi pesati Alberi Automi!
 G R A F I 1 GRAFI Cosa sono Grafi non orientati Grafi orientati Grafi pesati Alberi Automi! 2 cip: cip: Pallogrammi Pallogrammi GRAFI: cosa sono I grafi sono una struttura matematica fondamentale: servono
G R A F I 1 GRAFI Cosa sono Grafi non orientati Grafi orientati Grafi pesati Alberi Automi! 2 cip: cip: Pallogrammi Pallogrammi GRAFI: cosa sono I grafi sono una struttura matematica fondamentale: servono
Reti Complesse Biologiche
 Reti Complesse Biologiche Corso di Modelli di Sistemi Biologici II Università di Roma Sapienza Anno Accademico 2008/2009 Fabrizio De Vico Fallani, PhD Dipartimento di Fisiologia Umana e Farmacologia fabrizio.devicofallani@uniroma1.it
Reti Complesse Biologiche Corso di Modelli di Sistemi Biologici II Università di Roma Sapienza Anno Accademico 2008/2009 Fabrizio De Vico Fallani, PhD Dipartimento di Fisiologia Umana e Farmacologia fabrizio.devicofallani@uniroma1.it
Gestione della produzione e della supply chain Logistica distributiva
 Gestione della produzione e della supply chain Logistica distributiva Paolo Detti Dipartimento di Ingegneria dell Informazione e Scienze Matematiche Università di Siena Convergenza dell algoritmo Se non
Gestione della produzione e della supply chain Logistica distributiva Paolo Detti Dipartimento di Ingegneria dell Informazione e Scienze Matematiche Università di Siena Convergenza dell algoritmo Se non
Cammini minimi fra tutte le coppie
 Capitolo 12 Cammini minimi fra tutte le coppie Consideriamo il problema dei cammini minimi fra tutte le coppie in un grafo G = (V, E, w) orientato, pesato, dove possono essere presenti archi (ma non cicli)
Capitolo 12 Cammini minimi fra tutte le coppie Consideriamo il problema dei cammini minimi fra tutte le coppie in un grafo G = (V, E, w) orientato, pesato, dove possono essere presenti archi (ma non cicli)
Possibile applicazione
 p. 1/4 Assegnamento Siano dati due insiemi A e B entrambi di cardinalità n. Ad ogni coppia (a i,b j ) A B è associato un valore d ij 0 che misura la "incompatibilità" tra a i e b j, anche interpretabile
p. 1/4 Assegnamento Siano dati due insiemi A e B entrambi di cardinalità n. Ad ogni coppia (a i,b j ) A B è associato un valore d ij 0 che misura la "incompatibilità" tra a i e b j, anche interpretabile
Esercizi Capitolo 11 - Strutture di dati e progettazione di algoritmi
 Esercizi Capitolo 11 - Strutture di dati e progettazione di algoritmi Alberto Montresor 19 Agosto, 2014 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore
Esercizi Capitolo 11 - Strutture di dati e progettazione di algoritmi Alberto Montresor 19 Agosto, 2014 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore
POSHMAP. Il social network made in Italy dedicato alla moda. Sara Longo, Social Media Mining
 POSHMAP Il social network made in Italy dedicato alla moda 1 2 Il social media Poshmap è una piattaforma nella quale poter condividere gli scatti con le proprie scelte di stile: ogni utente può caricare
POSHMAP Il social network made in Italy dedicato alla moda 1 2 Il social media Poshmap è una piattaforma nella quale poter condividere gli scatti con le proprie scelte di stile: ogni utente può caricare
Problemi, istanze, soluzioni
 lgoritmi e Strutture di Dati II 2 Problemi, istanze, soluzioni Un problema specifica una relazione matematica tra dati di ingresso e dati di uscita. Una istanza di un problema è formata dai dati di un
lgoritmi e Strutture di Dati II 2 Problemi, istanze, soluzioni Un problema specifica una relazione matematica tra dati di ingresso e dati di uscita. Una istanza di un problema è formata dai dati di un
UNIVERSITÀ DEGLI STUDI ROMA TRE Collegio Didattico in Ingegneria Informatica corso di Ricerca operativa 2. Esercizi sul problema dell assegnamento
 UNIVERSITÀ DEGLI STUDI ROMA TRE Collegio Didattico in Ingegneria Informatica corso di Ricerca operativa Esercizi sul problema dell assegnamento Richiami di Teoria Ricordiamo che, dato un grafo G=(N,A),
UNIVERSITÀ DEGLI STUDI ROMA TRE Collegio Didattico in Ingegneria Informatica corso di Ricerca operativa Esercizi sul problema dell assegnamento Richiami di Teoria Ricordiamo che, dato un grafo G=(N,A),
Universita degli Studi di Ancona - Facolta di Ingegneria Laurea in Ing. Elettronica (VO) Ing. Informatica e Automatica - Ing. delle Telecomunicazioni
 Universita degli Studi di Ancona - Facolta di Ingegneria Laurea in Ing. Elettronica (VO) Ing. Informatica e Automatica - Ing. delle Telecomunicazioni ANALISI NUMERICA - Primo Parziale - TEMA A (Prof. A.M.Perdon)
Universita degli Studi di Ancona - Facolta di Ingegneria Laurea in Ing. Elettronica (VO) Ing. Informatica e Automatica - Ing. delle Telecomunicazioni ANALISI NUMERICA - Primo Parziale - TEMA A (Prof. A.M.Perdon)
Appunti su Indipendenza Lineare di Vettori
 Appunti su Indipendenza Lineare di Vettori Claudia Fassino a.a. Queste dispense, relative a una parte del corso di Matematica Computazionale (Laurea in Informatica), rappresentano solo un aiuto per lo
Appunti su Indipendenza Lineare di Vettori Claudia Fassino a.a. Queste dispense, relative a una parte del corso di Matematica Computazionale (Laurea in Informatica), rappresentano solo un aiuto per lo
Analisi interazione domanda/offerta: modelli di assegnazione
 Corso di Laurea Ingegneria Civile e Ambientale - AA Corso di: Fondamenti di Trasporti Lezione: Analisi interazione domanda/offerta: modelli di assegnazione Giuseppe Inturri Università di Catania Dipartimento
Corso di Laurea Ingegneria Civile e Ambientale - AA Corso di: Fondamenti di Trasporti Lezione: Analisi interazione domanda/offerta: modelli di assegnazione Giuseppe Inturri Università di Catania Dipartimento
Corso di elettrotecnica Materiale didattico: i grafi
 Corso di elettrotecnica Materiale didattico: i grafi A. Laudani 12 ottobre 2005 I grafi costituiscono uno strumento matematico che permette di descrivere e schematizzare una grande varietà di problemi
Corso di elettrotecnica Materiale didattico: i grafi A. Laudani 12 ottobre 2005 I grafi costituiscono uno strumento matematico che permette di descrivere e schematizzare una grande varietà di problemi
Analisi interazione domanda/offerta: modelli di assegnazione
 Corso di Laurea Ingegneria Civile - AA 1112 Corso di: Fondamenti di Trasporti Lezione: Analisi interazione domanda/offerta: modelli di assegnazione Giuseppe Inturri Università di Catania Dipartimento di
Corso di Laurea Ingegneria Civile - AA 1112 Corso di: Fondamenti di Trasporti Lezione: Analisi interazione domanda/offerta: modelli di assegnazione Giuseppe Inturri Università di Catania Dipartimento di
AMPL Problemi su Reti
 Dipartimento di Matematica Università di Padova Corso di Laurea Informatica Outline Problemi su Reti Cammino Minimo Molti problemi di ottimizzazione combinatoria possono essere modellati ricorrendo ai
Dipartimento di Matematica Università di Padova Corso di Laurea Informatica Outline Problemi su Reti Cammino Minimo Molti problemi di ottimizzazione combinatoria possono essere modellati ricorrendo ai
Introduzione. Il routing permette la comunicazione tra due nodi differenti anche se non sono collegati direttamente
 Routing Introduzione Il livello 3 della pila ethernet ha il compito di muovere i pacchetti dalla sorgente attraversando più sistemi Il livello di network deve quindi: Scegliere di volta in volta il cammino
Routing Introduzione Il livello 3 della pila ethernet ha il compito di muovere i pacchetti dalla sorgente attraversando più sistemi Il livello di network deve quindi: Scegliere di volta in volta il cammino
Corso di Perfezionamento
 Programmazione Dinamica 1 1 Dipartimento di Matematica e Informatica Università di Camerino 15 febbraio 2009 Tecniche di Programmazione Tecniche di progettazione di algoritmi: 1 Divide et Impera 2 Programmazione
Programmazione Dinamica 1 1 Dipartimento di Matematica e Informatica Università di Camerino 15 febbraio 2009 Tecniche di Programmazione Tecniche di progettazione di algoritmi: 1 Divide et Impera 2 Programmazione
Corso di Laurea in Matematica Analisi Numerica (1 mod., 6 crediti, 48 ore, a.a , lez.3)
 Docente: Marco Gaviano (e-mail:gaviano@unica.it) Corso di Laurea in Matematica Analisi Numerica (1 mod., 6 crediti, 48 ore, a.a. 2014-2015, lez.3) 1 Analisi Numerica 1 mod. a.a. 2014-2015, Lezione n.3
Docente: Marco Gaviano (e-mail:gaviano@unica.it) Corso di Laurea in Matematica Analisi Numerica (1 mod., 6 crediti, 48 ore, a.a. 2014-2015, lez.3) 1 Analisi Numerica 1 mod. a.a. 2014-2015, Lezione n.3
Ricerca Operativa. G. Liuzzi. Lunedí 20 Aprile 2015
 1 Lunedí 20 Aprile 2015 1 Istituto di Analisi dei Sistemi ed Informatica IASI - CNR Rilassamento di un problema Rilassare un problema di Programmazione Matematica vuol dire trascurare alcuni (tutti i)
1 Lunedí 20 Aprile 2015 1 Istituto di Analisi dei Sistemi ed Informatica IASI - CNR Rilassamento di un problema Rilassare un problema di Programmazione Matematica vuol dire trascurare alcuni (tutti i)
Polinomio di Taylor del secondo ordine per funzioni di due variabili
 Esercitazioni del 15 aprile 2013 Polinomio di Taylor del secondo ordine per funzioni di due variabili Sia f : A R 2 R una funzione di classe C 2. Fissato un p unto (x 0, y 0 A consideriamo il seguente
Esercitazioni del 15 aprile 2013 Polinomio di Taylor del secondo ordine per funzioni di due variabili Sia f : A R 2 R una funzione di classe C 2. Fissato un p unto (x 0, y 0 A consideriamo il seguente
La forma normale di Schur
 La forma normale di Schur Dario A Bini, Università di Pisa 30 ottobre 2013 Sommario Questo modulo didattico contiene risultati relativi alla forma normale di Schur, alle sue proprietà e alle sue applicazioni
La forma normale di Schur Dario A Bini, Università di Pisa 30 ottobre 2013 Sommario Questo modulo didattico contiene risultati relativi alla forma normale di Schur, alle sue proprietà e alle sue applicazioni
Problemi di Flusso: Il modello del Trasporto
 Problemi di Flusso: Il modello del rasporto Andrea Scozzari a.a. 2014-2015 April 27, 2015 Andrea Scozzari (a.a. 2014-2015) Problemi di Flusso: Il modello del rasporto April 27, 2015 1 / 25 Problemi su
Problemi di Flusso: Il modello del rasporto Andrea Scozzari a.a. 2014-2015 April 27, 2015 Andrea Scozzari (a.a. 2014-2015) Problemi di Flusso: Il modello del rasporto April 27, 2015 1 / 25 Problemi su
Flusso a Costo Minimo
 Sapienza Università di Roma - Dipartimento di Ingegneria Informatica, Automatica e Gestionale Flusso a Costo Minimo Docente: Renato Bruni bruni@dis.uniroma.it Corso di: Ottimizzazione Combinatoria Dal
Sapienza Università di Roma - Dipartimento di Ingegneria Informatica, Automatica e Gestionale Flusso a Costo Minimo Docente: Renato Bruni bruni@dis.uniroma.it Corso di: Ottimizzazione Combinatoria Dal
Problema del trasporto
 p. 1/1 Problema del trasporto Supponiamo di avere m depositi in cui è immagazzinato un prodotto e n negozi che richiedono tale prodotto. p. 1/1 Problema del trasporto Supponiamo di avere m depositi in
p. 1/1 Problema del trasporto Supponiamo di avere m depositi in cui è immagazzinato un prodotto e n negozi che richiedono tale prodotto. p. 1/1 Problema del trasporto Supponiamo di avere m depositi in
Metodi iterativi per sistemi lineari
 Generare una successione di vettori Metodi iterativi per sistemi lineari convergente alla soluzione del sistema Convergenza in norma Costruzione di un metodo iterativo Per una qualche norma vettoriale
Generare una successione di vettori Metodi iterativi per sistemi lineari convergente alla soluzione del sistema Convergenza in norma Costruzione di un metodo iterativo Per una qualche norma vettoriale
Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006. Matematica 2 (Analisi)
 Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006 Matematica 2 (Analisi) Nome:................................. N. matr.:.................................
Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006 Matematica 2 (Analisi) Nome:................................. N. matr.:.................................
Claudio Arbib Università di L Aquila. Ricerca Operativa. Reti di flusso
 Claudio Arbib Università di L Aquila Ricerca Operativa Reti di flusso Sommario Definizioni di base Flusso di un campo vettoriale Divergenza Integrale di Gauss-Greene Flusso in una rete Sorgenti, pozzi
Claudio Arbib Università di L Aquila Ricerca Operativa Reti di flusso Sommario Definizioni di base Flusso di un campo vettoriale Divergenza Integrale di Gauss-Greene Flusso in una rete Sorgenti, pozzi
3x 2 = 6. 3x 2 x 3 = 6
 Facoltà di Scienze Statistiche, Algebra Lineare 1 A, GParmeggiani LEZIONE 7 Sistemi lineari Scrittura matriciale di un sistema lineare Def 1 Un sistema di m equazioni ed n incognite x 1, x 2, x n, si dice
Facoltà di Scienze Statistiche, Algebra Lineare 1 A, GParmeggiani LEZIONE 7 Sistemi lineari Scrittura matriciale di un sistema lineare Def 1 Un sistema di m equazioni ed n incognite x 1, x 2, x n, si dice
Problema del cammino minimo
 Algoritmi e Strutture di Dati II Problema del cammino minimo Un viaggiatore vuole trovare la via più corta per andare da una città ad un altra. Possiamo rappresentare ogni città con un nodo e ogni collegamento
Algoritmi e Strutture di Dati II Problema del cammino minimo Un viaggiatore vuole trovare la via più corta per andare da una città ad un altra. Possiamo rappresentare ogni città con un nodo e ogni collegamento
UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Studi in Ingegneria Informatica Ricerca Operativa 1 Seconda prova intermedia 17 giugno 2013
 A UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Studi in Ingegneria Informatica Ricerca Operativa Seconda prova intermedia 7 giugno 0 Nome: Cognome: Matricola: Orale /06/0 ore aula N Orale 0/07/0 ore aula N
A UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Studi in Ingegneria Informatica Ricerca Operativa Seconda prova intermedia 7 giugno 0 Nome: Cognome: Matricola: Orale /06/0 ore aula N Orale 0/07/0 ore aula N
Algoritmi e Strutture Dati
 Algoritmi e Strutture Dati Capitolo 13 Cammini minimi: Algoritmo di Dijkstra (*) (ACM in grafi diretti e non diretti senza archi di peso negativo) Punto della situazione Algoritmo basato sull ordinamento
Algoritmi e Strutture Dati Capitolo 13 Cammini minimi: Algoritmo di Dijkstra (*) (ACM in grafi diretti e non diretti senza archi di peso negativo) Punto della situazione Algoritmo basato sull ordinamento
GRAFI. fig.1 - GRAFI (1) Si avvisa il lettore che certe definizioni che verranno date differiscono da quelle presenti in letteratura.
 GRAFI 1. Definizioni, terminologia, esempi e applicazioni (1) Un grafo orientato (o diretto o di-grafo) G è una coppia (V,E) dove V è un insieme non vuoto ed E una relazione binaria su V, E V V, ossia
GRAFI 1. Definizioni, terminologia, esempi e applicazioni (1) Un grafo orientato (o diretto o di-grafo) G è una coppia (V,E) dove V è un insieme non vuoto ed E una relazione binaria su V, E V V, ossia
Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari
 Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari Antonio Lanteri e Cristina Turrini UNIMI - 2016/2017 Antonio Lanteri e Cristina Turrini (UNIMI - 2016/2017 Elementi di Algebra Lineare
Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari Antonio Lanteri e Cristina Turrini UNIMI - 2016/2017 Antonio Lanteri e Cristina Turrini (UNIMI - 2016/2017 Elementi di Algebra Lineare
Sistemi lineari. Lorenzo Pareschi. Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara
 Sistemi lineari Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
Sistemi lineari Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
Algoritmi e Strutture Dati
 Introduzione ai grafi Grafi: Definizione e Algoritmi di visita Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino A.A. 2007/08 Introduzione ai
Introduzione ai grafi Grafi: Definizione e Algoritmi di visita Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino A.A. 2007/08 Introduzione ai
1) Codici convoluzionali. 2) Circuito codificatore. 3) Diagramma a stati e a traliccio. 4) Distanza libera. 5) Algoritmo di Viterbi
 Argomenti della Lezione 1) Codici convoluzionali 2) Circuito codificatore 3) Diagramma a stati e a traliccio 4) Distanza libera 5) Algoritmo di Viterbi 1 Codici convoluzionali I codici convoluzionali sono
Argomenti della Lezione 1) Codici convoluzionali 2) Circuito codificatore 3) Diagramma a stati e a traliccio 4) Distanza libera 5) Algoritmo di Viterbi 1 Codici convoluzionali I codici convoluzionali sono
NORMA DI UN VETTORE. Una NORMA VETTORIALE su R n è una funzione. : R n R +
 NORMA DI UN VETTORE Una NORMA VETTORIALE su R n è una funzione. : R n R + {0}, che associa ad ogni vettore x R n di componenti x i, i = 1,..., n, uno scalare in modo che valgano le seguenti proprietà:
NORMA DI UN VETTORE Una NORMA VETTORIALE su R n è una funzione. : R n R + {0}, che associa ad ogni vettore x R n di componenti x i, i = 1,..., n, uno scalare in modo che valgano le seguenti proprietà:
CENTRALITA nella RETE
 CENTRALITA nella RETE Nozione di Centralità Nozione introdotta dai sociologi nel dopoguerra (Bavelas 1948) L ipotesi è che la centralità strutturale sia un elemento in grado di motivare l importanza di
CENTRALITA nella RETE Nozione di Centralità Nozione introdotta dai sociologi nel dopoguerra (Bavelas 1948) L ipotesi è che la centralità strutturale sia un elemento in grado di motivare l importanza di
Grafi diretti. Un grafo diretto (o grafo orientato) G è una coppia (V,E) dove. V è u n i n s i e m e d i nodi (o vertici);
 Algoritmi e Strutture di Dati II 2 Grafi diretti Un grafo diretto (o grafo orientato) G è una coppia (V,E) dove V è u n i n s i e m e d i nodi (o vertici); E µ V V è u n i n s i e m e d i archi. Denotiamo
Algoritmi e Strutture di Dati II 2 Grafi diretti Un grafo diretto (o grafo orientato) G è una coppia (V,E) dove V è u n i n s i e m e d i nodi (o vertici); E µ V V è u n i n s i e m e d i archi. Denotiamo
2.3 Cammini ottimi. E. Amaldi Fondamenti di R.O. Politecnico di Milano 1
 . Cammini ottimi E. Amaldi Fondamenti di R.O. Politecnico di Milano .. Cammini minimi e algoritmo di Dijkstra Dato un grafo orientato G = (N, A) con una funzione di costo c : A c ij R e due nodi s e t,
. Cammini ottimi E. Amaldi Fondamenti di R.O. Politecnico di Milano .. Cammini minimi e algoritmo di Dijkstra Dato un grafo orientato G = (N, A) con una funzione di costo c : A c ij R e due nodi s e t,
Minimo albero di copertura
 apitolo 0 Minimo albero di copertura efinizione 0.. ato un grafo G = (V, E) non orientato e connesso, un albero di copertura di G è un sottoinsieme T E tale che il sottografo (V, T ) è un albero libero.
apitolo 0 Minimo albero di copertura efinizione 0.. ato un grafo G = (V, E) non orientato e connesso, un albero di copertura di G è un sottoinsieme T E tale che il sottografo (V, T ) è un albero libero.
Grafi: definizioni e visite
 Grafi: definizioni e visite Grafi (non orientati) Grafo (non orientato): G = (V, E) V = nodi (o vertici) E = archi fra coppie di nodi distinti. Modella relazioni fra coppie di oggetti. Parametri della
Grafi: definizioni e visite Grafi (non orientati) Grafo (non orientato): G = (V, E) V = nodi (o vertici) E = archi fra coppie di nodi distinti. Modella relazioni fra coppie di oggetti. Parametri della
LEZIONE 12. v = α 1 v α n v n =
 LEZIONE 12 12.1. Combinazioni lineari. Definizione 12.1.1. Sia V uno spazio vettoriale su k = R, C e v 1,..., v n V vettori fissati. Un vettore v V si dice combinazione lineare di v 1,..., v n se esistono
LEZIONE 12 12.1. Combinazioni lineari. Definizione 12.1.1. Sia V uno spazio vettoriale su k = R, C e v 1,..., v n V vettori fissati. Un vettore v V si dice combinazione lineare di v 1,..., v n se esistono
Domini di funzioni di due variabili. Determinare i domini delle seguenti funzioni di due variabili (le soluzioni sono alla fine del fascicolo):
 UNIVERSITA DEGLI STUDI DI SALERNO C.d.L. in INGEGNERIA GESTIONALE Esercizi di Ricerca Operativa Prof. Saverio Salerno Corso tenuto nell anno solare 2009 I seguenti esercizi sono da ritenersi di preparazione
UNIVERSITA DEGLI STUDI DI SALERNO C.d.L. in INGEGNERIA GESTIONALE Esercizi di Ricerca Operativa Prof. Saverio Salerno Corso tenuto nell anno solare 2009 I seguenti esercizi sono da ritenersi di preparazione
Parte V: Rilassamento Lagrangiano
 Parte V: Rilassamento Lagrangiano Tecnica Lagrangiana Consideriamo il seguente problema di Programmazione Lineare Intera: P 1 min c T x L I Ax > b Cx > d x > 0, intera in cui A = matrice m x n C = matrice
Parte V: Rilassamento Lagrangiano Tecnica Lagrangiana Consideriamo il seguente problema di Programmazione Lineare Intera: P 1 min c T x L I Ax > b Cx > d x > 0, intera in cui A = matrice m x n C = matrice
AUTOMA A STATI FINITI
 Gli Automi Un Automa è un dispositivo, o un suo modello in forma di macchina sequenziale, creato per eseguire un particolare compito, che può trovarsi in diverse configurazioni più o meno complesse caratterizzate
Gli Automi Un Automa è un dispositivo, o un suo modello in forma di macchina sequenziale, creato per eseguire un particolare compito, che può trovarsi in diverse configurazioni più o meno complesse caratterizzate
Grafi e reti di flusso
 Grafi e reti di flusso Molti problemi di ottimizzazione sono caratterizzati da una struttura di grafo: in molti casi questa struttura emerge in modo naturale, in altri nasce dal particolare modo in cui
Grafi e reti di flusso Molti problemi di ottimizzazione sono caratterizzati da una struttura di grafo: in molti casi questa struttura emerge in modo naturale, in altri nasce dal particolare modo in cui
Il valore di flusso che si ottiene è
 1) Si consideri un insieme di piste da sci e di impianti di risalita. Lo si modelli con un grafo orientato che abbia archi di due tipi: tipo D (discesa e orientato nel senso della discesa) e tipo R (risalita
1) Si consideri un insieme di piste da sci e di impianti di risalita. Lo si modelli con un grafo orientato che abbia archi di due tipi: tipo D (discesa e orientato nel senso della discesa) e tipo R (risalita
Una breve introduzione all implementazione in C di algoritmi su grafo
 Una breve introduzione all implementazione in C di algoritmi su grafo A cura di Gianmaria Leo Introduzione La lezione è un introduzione a concetti e strumenti che permettono l implementazione di algoritmi
Una breve introduzione all implementazione in C di algoritmi su grafo A cura di Gianmaria Leo Introduzione La lezione è un introduzione a concetti e strumenti che permettono l implementazione di algoritmi
Elementi di Algebra Lineare Spazi Vettoriali
 Elementi di Algebra Lineare Spazi Vettoriali Antonio Lanteri e Cristina Turrini UNIMI - 2015/2016 Antonio Lanteri e Cristina Turrini (UNIMI - 2015/2016) Elementi di Algebra Lineare 1 / 37 index Spazi vettoriali
Elementi di Algebra Lineare Spazi Vettoriali Antonio Lanteri e Cristina Turrini UNIMI - 2015/2016 Antonio Lanteri e Cristina Turrini (UNIMI - 2015/2016) Elementi di Algebra Lineare 1 / 37 index Spazi vettoriali
Catene di Markov. 8 ottobre 2009
 Catene di Markov 8 ottobre 2009 Definizione 1. Si dice catena di Markov (finita) un sistema dotato di un numero finito n di stati {1, 2,..., n} che soddisfi la seguente ipotesi: la probabilità che il sistema
Catene di Markov 8 ottobre 2009 Definizione 1. Si dice catena di Markov (finita) un sistema dotato di un numero finito n di stati {1, 2,..., n} che soddisfi la seguente ipotesi: la probabilità che il sistema
Algoritmo basato su cancellazione di cicli
 Algoritmo basato su cancellazione di cicli Dato un flusso ammissibile iniziale, si costruisce una sequenza di flussi ammissibili di costo decrescente. Ciascun flusso è ottenuto dal precedente flusso ammissibile
Algoritmo basato su cancellazione di cicli Dato un flusso ammissibile iniziale, si costruisce una sequenza di flussi ammissibili di costo decrescente. Ciascun flusso è ottenuto dal precedente flusso ammissibile
INFORMATICA AA Università degli Studi di Ferrara Facoltà di Scienze MM FF NN Corso di Laurea in «Scienze e Tecnologie per i Beni Culturali»
 Università degli Studi di Ferrara Facoltà di Scienze MM FF NN Corso di Laurea in «Scienze e Tecnologie per i Beni Culturali» AA 010-011 INFORMATICA Prof. Giorgio Poletti giorgio.poletti@unife.it Grafi
Università degli Studi di Ferrara Facoltà di Scienze MM FF NN Corso di Laurea in «Scienze e Tecnologie per i Beni Culturali» AA 010-011 INFORMATICA Prof. Giorgio Poletti giorgio.poletti@unife.it Grafi
UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Studi in Ingegneria Informatica Ricerca Operativa 1 Seconda prova intermedia 20 giugno 2014
 A Ricerca Operativa 1 Seconda prova intermedia Un tifoso di calcio in partenza da Roma vuole raggiungere Rio De Janeiro per la finale del mondiale spendendo il meno possibile. Sono date le seguenti disponibilità
A Ricerca Operativa 1 Seconda prova intermedia Un tifoso di calcio in partenza da Roma vuole raggiungere Rio De Janeiro per la finale del mondiale spendendo il meno possibile. Sono date le seguenti disponibilità
Introduzione al Metodo agli Elementi Finiti (FEM) (x, y) Γ Tale formulazione viene detta Formulazione forte del problema.
 Introduzione al Metodo agli Elementi Finiti (FEM) Consideriamo come problema test l equazione di Poisson 2 u x 2 + 2 u = f(x, y) u = f y2 definita su un dominio Ω R 2 avente come frontiera la curva Γ,
Introduzione al Metodo agli Elementi Finiti (FEM) Consideriamo come problema test l equazione di Poisson 2 u x 2 + 2 u = f(x, y) u = f y2 definita su un dominio Ω R 2 avente come frontiera la curva Γ,
Raccolta di esercizi di Calcolo Numerico Prof. Michela Redivo Zaglia
 Raccolta di esercizi di Calcolo Numerico Prof. Michela Redivo Zaglia Nota Bene: Gli esercizi di questa raccolta sono solo degli esempi. Non sono stati svolti né verificati e servono unicamente da spunto
Raccolta di esercizi di Calcolo Numerico Prof. Michela Redivo Zaglia Nota Bene: Gli esercizi di questa raccolta sono solo degli esempi. Non sono stati svolti né verificati e servono unicamente da spunto
Integrazione numerica
 Integrazione numerica Lucia Gastaldi DICATAM - Sez. di Matematica, http://lucia-gastaldi.unibs.it Indice 1 Formule di quadratura semplici e composite Formule di quadratura Grado di precisione Formule di
Integrazione numerica Lucia Gastaldi DICATAM - Sez. di Matematica, http://lucia-gastaldi.unibs.it Indice 1 Formule di quadratura semplici e composite Formule di quadratura Grado di precisione Formule di
«Sciente e Tecnologie dei Beni Culturali»
 5 Informatica CdS in «Sciente e Tecnologie dei Beni Culturali» AA 2014-2015 Mini-sito dell insegnamento: http://www.unife.it/scienze/beni.culturali/insegnamenti/informatica Prof. Giorgio Poletti giorgio.poletti@unife.it
5 Informatica CdS in «Sciente e Tecnologie dei Beni Culturali» AA 2014-2015 Mini-sito dell insegnamento: http://www.unife.it/scienze/beni.culturali/insegnamenti/informatica Prof. Giorgio Poletti giorgio.poletti@unife.it
UNIVERSITÀ di ROMA TOR VERGATA
 UNIVERSITÀ di ROMA TOR VERGATA Corso di PS-Probabilità P.Baldi Tutorato 9, 19 maggio 11 Corso di Laurea in Matematica Esercizio 1 a) Volendo modellizzare l evoluzione della disoccupazione in un certo ambito
UNIVERSITÀ di ROMA TOR VERGATA Corso di PS-Probabilità P.Baldi Tutorato 9, 19 maggio 11 Corso di Laurea in Matematica Esercizio 1 a) Volendo modellizzare l evoluzione della disoccupazione in un certo ambito
LEZIONE 3. a + b + 2c + e = 1 b + d + g = 0 3b + f + 3g = 2. a b c d e f g
 LEZIONE 3 3.. Matrici fortemente ridotte per righe. Nella precedente lezione abbiamo introdotto la nozione di soluzione di un sistema di equazioni lineari. In questa lezione ci poniamo il problema di descrivere
LEZIONE 3 3.. Matrici fortemente ridotte per righe. Nella precedente lezione abbiamo introdotto la nozione di soluzione di un sistema di equazioni lineari. In questa lezione ci poniamo il problema di descrivere
Osservazione. Convergenza dei metodi di Gauss-Seidel e di Jacobi. Condizioni sufficienti per la convergenza. Definizione
 Osservazione Convergenza dei metodi di Gauss-Seidel e di Jacobi Fallimento dei metodi. (Es. Gauss- Seidel Condizioni sufficienti; teoremi di localizzazione degli autovalori; dimostrazione di convergenza
Osservazione Convergenza dei metodi di Gauss-Seidel e di Jacobi Fallimento dei metodi. (Es. Gauss- Seidel Condizioni sufficienti; teoremi di localizzazione degli autovalori; dimostrazione di convergenza
Elementi di Algebra e di Matematica Discreta Numeri interi, divisibilità, numerazione in base n
 Elementi di Algebra e di Matematica Discreta Numeri interi, divisibilità, numerazione in base n Cristina Turrini UNIMI - 2016/2017 Cristina Turrini (UNIMI - 2016/2017) Elementi di Algebra e di Matematica
Elementi di Algebra e di Matematica Discreta Numeri interi, divisibilità, numerazione in base n Cristina Turrini UNIMI - 2016/2017 Cristina Turrini (UNIMI - 2016/2017) Elementi di Algebra e di Matematica
MATRICI E SISTEMI LINEARI
 1 Rappresentazione di dati strutturati MATRICI E SISTEMI LINEARI Gli elementi di una matrice, detti coefficienti, possono essere qualsiasi e non devono necessariamente essere omogenei tra loro; di solito
1 Rappresentazione di dati strutturati MATRICI E SISTEMI LINEARI Gli elementi di una matrice, detti coefficienti, possono essere qualsiasi e non devono necessariamente essere omogenei tra loro; di solito
Soluzione. (a) L insieme F 1 e linearmente indipendente; gli insiemi F 2 ed F 3 sono linearmente
 1. Insiemi di generatori, lineare indipendenza, basi, dimensione. Consideriamo nello spazio vettoriale R 3 i seguenti vettori: v 1 = (0, 1, ), v = (1, 1, 1), v 3 = (, 1, 0), v 4 = (3, 3, ). Siano poi F
1. Insiemi di generatori, lineare indipendenza, basi, dimensione. Consideriamo nello spazio vettoriale R 3 i seguenti vettori: v 1 = (0, 1, ), v = (1, 1, 1), v 3 = (, 1, 0), v 4 = (3, 3, ). Siano poi F
Grafi (orientati): cammini minimi
 Grafi (orientati): cammini minimi Una breve presentazione Definizioni Sia G=(V,E) un grafo orientato con costi w sugli archi. Il costo di un cammino π= è dato da: Un cammino minimo tra
Grafi (orientati): cammini minimi Una breve presentazione Definizioni Sia G=(V,E) un grafo orientato con costi w sugli archi. Il costo di un cammino π= è dato da: Un cammino minimo tra
II Università degli Studi di Roma
 Versione preliminare gennaio TOR VERGATA II Università degli Studi di Roma Dispense di Geometria. Capitolo 3. 7. Coniche in R. Nel Capitolo I abbiamo visto che gli insiemi di punti P lineare di primo grado
Versione preliminare gennaio TOR VERGATA II Università degli Studi di Roma Dispense di Geometria. Capitolo 3. 7. Coniche in R. Nel Capitolo I abbiamo visto che gli insiemi di punti P lineare di primo grado
2.3.3 Cammini ottimi nei grafi senza circuiti
 .. Cammini ottimi nei grafi senza circuiti Sia un grafo G = (N, A) orientato senza circuiti e una funzione di costo che assegna un valore c ij R ad ogni arco (i, j) A circuito Proprietà I nodi di un grafo
.. Cammini ottimi nei grafi senza circuiti Sia un grafo G = (N, A) orientato senza circuiti e una funzione di costo che assegna un valore c ij R ad ogni arco (i, j) A circuito Proprietà I nodi di un grafo
2. Risolvere con il metodo di eliminazione di Gauss con pivoting parziale il seguente sistema lineare:
 Esercizi sui metodi diretti per la risoluzione di sistemi lineari 1. Data la matrice 1 0 2 1 3 1 5 2 1 determinare la sua fattorizzazione P LR. Risolvere il sistema Ax = b con b = (3, 5, 6) T mediante
Esercizi sui metodi diretti per la risoluzione di sistemi lineari 1. Data la matrice 1 0 2 1 3 1 5 2 1 determinare la sua fattorizzazione P LR. Risolvere il sistema Ax = b con b = (3, 5, 6) T mediante
Esempi. non. orientato. orientato
 Definizione! Un grafo G = (V,E) è costituito da un insieme di vertici V ed un insieme di archi E ciascuno dei quali connette due vertici in V detti estremi dell arco.! Un grafo è orientato quando vi è
Definizione! Un grafo G = (V,E) è costituito da un insieme di vertici V ed un insieme di archi E ciascuno dei quali connette due vertici in V detti estremi dell arco.! Un grafo è orientato quando vi è
Modello dei grafi casuali
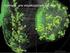 RETI CASUALI Modello dei grafi casuali Un grafo casuale è un grafo con N nodi connessi da n archi, scelti casualmente tra tutte le possibili combinazioni di collegamenti On Random Graphs, Erdos and Renyi,
RETI CASUALI Modello dei grafi casuali Un grafo casuale è un grafo con N nodi connessi da n archi, scelti casualmente tra tutte le possibili combinazioni di collegamenti On Random Graphs, Erdos and Renyi,
Macchine sequenziali. Automa a Stati Finiti (ASF)
 Corso di Calcolatori Elettronici I Macchine sequenziali Prof. Roberto Canonico Università degli Studi di Napoli Federico II Dipartimento di Ingegneria Elettrica e delle Tecnologie dell Informazione Corso
Corso di Calcolatori Elettronici I Macchine sequenziali Prof. Roberto Canonico Università degli Studi di Napoli Federico II Dipartimento di Ingegneria Elettrica e delle Tecnologie dell Informazione Corso
PROCESSI STOCASTICI 1: ESERCIZI
 PROCESSI STOCASTICI 1: ESERCIZI (1) ESERCIZIO: Date P e Q matrici stocastiche, dimostrare che la matrice prodotto P Q è una matrice stocastica. Dedurre che la potenza P n e il prodotto P 1 P 2 P n sono
PROCESSI STOCASTICI 1: ESERCIZI (1) ESERCIZIO: Date P e Q matrici stocastiche, dimostrare che la matrice prodotto P Q è una matrice stocastica. Dedurre che la potenza P n e il prodotto P 1 P 2 P n sono
REGRESSIONE E CORRELAZIONE
 REGRESSIONE E CORRELAZIONE Nella Statistica, per studio della connessione si intende la ricerca di eventuali relazioni, di dipendenza ed interdipendenza, intercorrenti tra due variabili statistiche 1.
REGRESSIONE E CORRELAZIONE Nella Statistica, per studio della connessione si intende la ricerca di eventuali relazioni, di dipendenza ed interdipendenza, intercorrenti tra due variabili statistiche 1.
1 Schemi alle differenze finite per funzioni di una variabile
 Introduzione In questa dispensa vengono forniti alcuni elementi di base per la soluzione di equazioni alle derivate parziali che governano problemi al contorno. A questo scopo si introducono, in forma
Introduzione In questa dispensa vengono forniti alcuni elementi di base per la soluzione di equazioni alle derivate parziali che governano problemi al contorno. A questo scopo si introducono, in forma
Alberi di copertura. Mauro Passacantando. Dipartimento di Informatica Largo B. Pontecorvo 3, Pisa
 Alberi di copertura Mauro Passacantando Dipartimento di Informatica Largo B. Pontecorvo, Pisa mpassacantando@di.unipi.it M. Passacantando TFA 0/ - Corso di Ricerca Operativa Università di Pisa / 9 Definizioni
Alberi di copertura Mauro Passacantando Dipartimento di Informatica Largo B. Pontecorvo, Pisa mpassacantando@di.unipi.it M. Passacantando TFA 0/ - Corso di Ricerca Operativa Università di Pisa / 9 Definizioni
Geometria per il TFA grafi e reti
 Universita di Roma Tre Geometria per il TFA grafi e reti Francesca MEROLA merola@mat.uniroma3.it http://ricerca.mat.uniroma3.it/users/merola/ Internet map 1024 by The Opte Project roadmap esempi di grafi
Universita di Roma Tre Geometria per il TFA grafi e reti Francesca MEROLA merola@mat.uniroma3.it http://ricerca.mat.uniroma3.it/users/merola/ Internet map 1024 by The Opte Project roadmap esempi di grafi
Metodi matematici per il calcolo di grandezze caratteristiche nell analisi di reti complesse
 19/06/2015 Metodi matematici per il calcolo di grandezze caratteristiche nell analisi di reti complesse Carlo Sau Sommario 1. Introduzione... 3 2. Generalità e principali metriche delle reti... 3 3. Fattorizzazione
19/06/2015 Metodi matematici per il calcolo di grandezze caratteristiche nell analisi di reti complesse Carlo Sau Sommario 1. Introduzione... 3 2. Generalità e principali metriche delle reti... 3 3. Fattorizzazione
Programmazione Lineare Intera: Piani di Taglio
 Programmazione Lineare Intera: Piani di Taglio Andrea Scozzari a.a. 2014-2015 April 22, 2015 Andrea Scozzari (a.a. 2014-2015) Programmazione Lineare Intera: Piani di Taglio April 22, 2015 1 / 23 Programmazione
Programmazione Lineare Intera: Piani di Taglio Andrea Scozzari a.a. 2014-2015 April 22, 2015 Andrea Scozzari (a.a. 2014-2015) Programmazione Lineare Intera: Piani di Taglio April 22, 2015 1 / 23 Programmazione
Algoritmi e strutture dati
 Algoritmi e Strutture Dati Cammini minimi Definizioni Sia G = (V,E) un grafo orientato pesato sugli archi. Il costo di un cammino π = è dato da: Un cammino minimo tra una coppia di
Algoritmi e Strutture Dati Cammini minimi Definizioni Sia G = (V,E) un grafo orientato pesato sugli archi. Il costo di un cammino π = è dato da: Un cammino minimo tra una coppia di
11.4 Chiusura transitiva
 6 11.4 Chiusura transitiva Il problema che consideriamo in questa sezione riguarda il calcolo della chiusura transitiva di un grafo. Dato un grafo orientato G = hv,ei, si vuole determinare il grafo orientato)
6 11.4 Chiusura transitiva Il problema che consideriamo in questa sezione riguarda il calcolo della chiusura transitiva di un grafo. Dato un grafo orientato G = hv,ei, si vuole determinare il grafo orientato)
Appunti di matematica per le Scienze Sociali Parte 1
 Appunti di matematica per le Scienze Sociali Parte 1 1 Equazioni 1.1 Definizioni preliminari 1.1.1 Monomi Si definisce monomio ogni prodotto indicato di fattori qualsiasi, cioè uguali o diseguali, numerici
Appunti di matematica per le Scienze Sociali Parte 1 1 Equazioni 1.1 Definizioni preliminari 1.1.1 Monomi Si definisce monomio ogni prodotto indicato di fattori qualsiasi, cioè uguali o diseguali, numerici
+1 i j i = j i = j 1 1 i j 2 Il problema di PL associato alla scelta della migliore strategia per te è quindi il seguente: min z
 Esercizio 1. Considera il seguente gioco. Tu e il tuo avversario potete scegliere un intero tra 1 e. Se il numero x che hai scelto è minore di quello y del tuo avversario, allora tu vinci un euro, a meno
Esercizio 1. Considera il seguente gioco. Tu e il tuo avversario potete scegliere un intero tra 1 e. Se il numero x che hai scelto è minore di quello y del tuo avversario, allora tu vinci un euro, a meno
Simulazioni e Metodi Montecarlo Cercano gli stati fondamentali di sistemi complessi non risolubili analiticamente e le loro proprietà analoghi per
 Simulazioni e Metodi Montecarlo Cercano gli stati fondamentali di sistemi complessi non risolubili analiticamente e le loro proprietà analoghi per molti versi al problema del commesso viaggiatore lasciano
Simulazioni e Metodi Montecarlo Cercano gli stati fondamentali di sistemi complessi non risolubili analiticamente e le loro proprietà analoghi per molti versi al problema del commesso viaggiatore lasciano
Terzo allenamento. Olimpiadi Italiane di Informatica - Selezione territoriale
 Terzo allenamento Olimpiadi Italiane di Informatica - Selezione territoriale Luca Chiodini luca@chiodini.org - l.chiodini@campus.unimib.it 22 marzo 2016 Programma 1. Lettura di un problema tratto dalle
Terzo allenamento Olimpiadi Italiane di Informatica - Selezione territoriale Luca Chiodini luca@chiodini.org - l.chiodini@campus.unimib.it 22 marzo 2016 Programma 1. Lettura di un problema tratto dalle
Risoluzione di sistemi lineari sparsi e di grandi dimensioni
 Risoluzione di sistemi lineari sparsi e di grandi dimensioni Un sistema lineare Ax = b con A R n n, b R n, è sparso quando il numero di elementi della matrice A diversi da zero è αn, con n α. Una caratteristica
Risoluzione di sistemi lineari sparsi e di grandi dimensioni Un sistema lineare Ax = b con A R n n, b R n, è sparso quando il numero di elementi della matrice A diversi da zero è αn, con n α. Una caratteristica
LEZIONE 2. ( ) a 1 x 1 + a 2 x a n x n = b, ove a j, b R sono fissati.
 LEZIONE 2 2 Sistemi di equazioni lineari Definizione 2 Un equazione lineare nelle n incognite x, x 2,, x n a coefficienti reali, è un equazione della forma (2 a x + a 2 x 2 + + a n x n = b, ove a j, b
LEZIONE 2 2 Sistemi di equazioni lineari Definizione 2 Un equazione lineare nelle n incognite x, x 2,, x n a coefficienti reali, è un equazione della forma (2 a x + a 2 x 2 + + a n x n = b, ove a j, b
Note per il corso di Geometria e algebra lineare 2009-10 Corso di laurea in Ing. Elettronica e delle Telecomunicazioni
 Note per il corso di Geometria e algebra lineare 009-0 Corso di laurea in Ing. Elettronica e delle Telecomunicazioni Spazi di n-uple e matrici. I prodotti cartesiani RR R e RRR R 3, costituiti dalle coppie
Note per il corso di Geometria e algebra lineare 009-0 Corso di laurea in Ing. Elettronica e delle Telecomunicazioni Spazi di n-uple e matrici. I prodotti cartesiani RR R e RRR R 3, costituiti dalle coppie
La notazione usata è quella usuale nel caso scalare, ed è estesa al caso generale. Consideriamo una forma quadratica:
 . SU ALCUNI OPERAORI DI DERIVAZIONE Alcune operazioni tipiche dell analisi matematica hanno un diretto riscontro in termini matriciali. Consideriamo ad esempio una forma lineare: f() l l + l +..l n n ;
. SU ALCUNI OPERAORI DI DERIVAZIONE Alcune operazioni tipiche dell analisi matematica hanno un diretto riscontro in termini matriciali. Consideriamo ad esempio una forma lineare: f() l l + l +..l n n ;
LEZIONE 4. { x + y + z = 1 x y + 2z = 3
 LEZIONE 4 4.. Operazioni elementari di riga. Abbiamo visto, nella precedente lezione, quanto sia semplice risolvere sistemi di equazioni lineari aventi matrice incompleta fortemente ridotta per righe.
LEZIONE 4 4.. Operazioni elementari di riga. Abbiamo visto, nella precedente lezione, quanto sia semplice risolvere sistemi di equazioni lineari aventi matrice incompleta fortemente ridotta per righe.
Il determinante. Calcolo del determinante di matrici particolari. matrici di ordine 2: sia. a11 a A = allora
 Calcolo del determinante di matrici particolari matrici di ordine 2: sia allora Esempio. [ ] a11 a A = 12, a 21 a 22 det A = a 11 a 22 a 21 a 12. Calcolare il determinante di [ ] 1 2 A =. 3 4 matrici di
Calcolo del determinante di matrici particolari matrici di ordine 2: sia allora Esempio. [ ] a11 a A = 12, a 21 a 22 det A = a 11 a 22 a 21 a 12. Calcolare il determinante di [ ] 1 2 A =. 3 4 matrici di
Figura 1: 1) Si scriva la formulazione del problema come problema di PLI (con un numero minimo di vincoli) e la matrice dei vincoli.
 ESERCIZIO 1 Sia dato il grafo orientato in Figura 1. Si consideri il problema di flusso a 1 2 4 Figura 1: costo minimo su tale grafo con b 1 = 4 b 2 = 2 b = b 4 = e c 12 = 2 c 1 = 4 c 14 = 1 c 2 = 1 c
ESERCIZIO 1 Sia dato il grafo orientato in Figura 1. Si consideri il problema di flusso a 1 2 4 Figura 1: costo minimo su tale grafo con b 1 = 4 b 2 = 2 b = b 4 = e c 12 = 2 c 1 = 4 c 14 = 1 c 2 = 1 c
Makespan con set-up dipendenti dalla sequenza. 1/s jk /C max
 Makespan con set-up dipendenti dalla sequenza 1/s jk /C max 1/s jk /C max Un tempo di riattrezzaggio (set-up) s jk è richiesto fra il processamento di j e quello di k. In questo caso, C max dipende dalla
Makespan con set-up dipendenti dalla sequenza 1/s jk /C max 1/s jk /C max Un tempo di riattrezzaggio (set-up) s jk è richiesto fra il processamento di j e quello di k. In questo caso, C max dipende dalla
Similitudine (ortogonale) e congruenza (ortogonale) di matrici.
 Lezione del 4 giugno. Il riferimento principale di questa lezione e costituito da parti di: 2 Forme bilineari, quadratiche e matrici simmetriche associate, 3 Congruenza di matrici simmetriche, 5 Forme
Lezione del 4 giugno. Il riferimento principale di questa lezione e costituito da parti di: 2 Forme bilineari, quadratiche e matrici simmetriche associate, 3 Congruenza di matrici simmetriche, 5 Forme
Rappresentazione dei numeri interi in un calcolatore
 Corso di Calcolatori Elettronici I A.A. 2012-2013 Rappresentazione dei numeri interi in un calcolatore Prof. Roberto Canonico Università degli Studi di Napoli Federico II Dipartimento di Ingegneria Elettrica
Corso di Calcolatori Elettronici I A.A. 2012-2013 Rappresentazione dei numeri interi in un calcolatore Prof. Roberto Canonico Università degli Studi di Napoli Federico II Dipartimento di Ingegneria Elettrica
Autovalori ed autovettori di una matrice
 Autovalori ed autovettori di una matrice Lucia Gastaldi DICATAM http://www.ing.unibs.it/gastaldi/ Indice 1 Definizioni di autovalori ed autovettori Autovalori ed autovettori 2 Metodo delle potenze 3 Calcolo
Autovalori ed autovettori di una matrice Lucia Gastaldi DICATAM http://www.ing.unibs.it/gastaldi/ Indice 1 Definizioni di autovalori ed autovettori Autovalori ed autovettori 2 Metodo delle potenze 3 Calcolo
A m n B n p = P m p. 0 1 a b c d. a b. 0 a 0 c Il risultato e lo stesso solo nel caso in cui c = 0 e a = d.
 Matematica II, 220404 Il prodotto di matrici e un operazione parziale che prende in entrata una matrice A ed una matrice B, tali che il numero delle colonne di A sia uguale al numero delle righe di B,
Matematica II, 220404 Il prodotto di matrici e un operazione parziale che prende in entrata una matrice A ed una matrice B, tali che il numero delle colonne di A sia uguale al numero delle righe di B,
età (anni) manutenzione (keuro) ricavato (keuro)
 .6 Cammini minimi. Determinare i cammini minimi dal nodo 0 a tutti gli altri nodi del seguente grafo, mediante l algoritmo di Dijkstra e, se applicabile, anche mediante quello di Programmazione Dinamica.
.6 Cammini minimi. Determinare i cammini minimi dal nodo 0 a tutti gli altri nodi del seguente grafo, mediante l algoritmo di Dijkstra e, se applicabile, anche mediante quello di Programmazione Dinamica.
