= = 4 5.
|
|
|
- Prospero Casali
- 5 anni fa
- Visualizzazioni
Transcript
1 n.a. discreti Esempio 54 Dieci carte vengono suddivise in due scatole U 1 e U 2 di 5 carte ciascuna. Nella scatola U 1 vi sono solo carte vincenti mentre nella scatola U 2 vi sono 3 carte vincenti e 2 perdenti. Si sceglie a caso una delle due scatole e da essa si e ettuano estrazioni con restituzione (all infinito). Indicando con H l evento la scatola scelta è U 1 e con E i l evento la i-esima carta estratta è vincente, i =1, 2...,, calcolare a) la probabilità dell evento E 1 ; b) la probabilità dell evento nelle prime due estrazioni vi è una (e una sola) carta vincente ; c) il valore atteso del numero aleatorio Y = numero di estrazioni sino ad ottenere una carta vincente. P (E 1 )= ; = ; E(Y )= ;. Soluzione. Si ha P (E 1 )=P(E 1^ ) = P (E 1^(H_H c )) = P (E 1 H)P (H)+P (E 1 H c )P (H c )= Inoltre = = 4 5. = P (E 1 E c 2 _ Ec 1 E 2)=P (E 1 E c 2 )+P (Ec 1 E 2). G. Sanfilippo - CdP pag. 233
2 n.a. discreti Osserviamo che gli eventi E i, condizionatamente ad H, sono stocasticamente indipendenti, pertanto si ha P (E 1 E c 2 )=P (E 1E c 2 H)P (H) +P (E 1E c 2 Hc )P (H c )= = P (E 1 H 1 )P (E c 2 H)P (H) +P (E 1 H c )P (E c 2 Hc )P (H c )= = 3 25 E facile verificare che P (E 1 E c 2 )=P(Ec 1 E 2) (gli eventi E i sono scambiabili), quindi = Osserviamo che P (Y =1 H) =1, e P (Y = n H) =0, n > 1 ; inoltre P (Y = n H c )= n 1, n 1. 5 Pertanto, E(Y )= P +1 n=1 np (Y = n) = = P +1 n=1 n[p (Y = n H)P (H) +P (Y = n Hc )P (H c )] = = P +1 n=1 n n = = 8 6 = 4 3. Piu in generale, posto p 1 =1, p 2 = 3 5,sihaY H G(p 1), Y H c G(p 2 ) e E(Y )=E(Y H)P (H) +E(Y H c )P (H c )= p 1 2 p 2 Nota. Il numero aleatorio Y non ha una distribuzione geometrica, bensì la sua distribuzione è una mistura di due distribuzioni geometriche. G. Sanfilippo - CdP pag. 234
3 n.a. discreti Esercizio 27 (Distribuzione di Pascal 19 ) Data una successione di eventi E 1,E 2,...,E n,..., indipendenti ed equiprobabili, con P (E i )=p, q =1 p, siat k il numero aleatorio di prove fino al k-esimo successo, con k 2 N. Osserviamo che X è un numero aleatorio discreto, infatti T k 2{k, k +1,k+2,...}. Verificare che oppure che P (T k = n) = n 1 p k q n k, n = k, k +1,k+2,... k 1 P (T k = k + h) = k + h 1 p k q h,h=1, 2, 3,... k 1 Il numero aleatorio T k ha una distribuzione di Pascal di parametri k, p. Esempio 55 (Problema della ripartizione della posta) Sia data una successione di eventi E 1,E 2,...,E n,..., indipendenti ed equiprobabili, con P (E i ) = p. Calcolare la probabilità dell evento A k,m di ottenere k successi prima di m insuccessi. Osserviamo che si verificano k successi prima di m insuccessi se e solo se il k-esimo successo non si verifica dopo la k + m 1-esima prova, cioè A k,m =(T k = k) _ (T k = k +1)_ _(T k = k + m 1), G. Sanfilippo - CdP pag. 235
4 dove T k è il numero aleatorio di prove sino al k esimo successo. Pertanto n.a. discreti P (A k,m )=P (T k = k) +P (T k = k +1)+ + P (T k = k + m 1) = = k 1 p k q 0 + k 1 k k + m 2 p k q p k q m 1 = k 1 k 1 k+m X 1 n=k n 1 p k q n k. k 1 Immaginiamo due giocatori A, B che mettono in palio un montepremi di 64 euro e fanno la seguente gara. Si lancia una moneta, se esce Testa, il giocatore A ottiene 1 punto, altrimenti, se esce Croce, il giocatore B ottiene 1 punto. Si lancia nuovamente la moneta sino a quando uno dei due giocatori raggiunge un punteggio pari a 6. Vince il montepremi il giocatore che per prima raggiunge 6 punti. Supponiamo che il gioco si interrompe con il punteggio di 5 a 3 per il giocatore A. Come andrebbe suddiviso equamente il premio tra i due giocatori? Per stabilire la ripartizione equa osserviamo che se il gioco continuasse ancora il giocatore A vincerebbe se egli facesse un punto prima che il giocatore B facesse 3 punti. La probabilità di G. Sanfilippo - CdP pag. 236
5 ottenere 1 successo prima di 3 insuccessi è data da n.a. discreti = P (E 1 _ E c 1 E 2 _ E c 1 E 2cE 3 )= = 7 8. La ripartizione equa consiste nel suddividere la posta in 8 parti delle quali 7 andrebbero ad A e 1 andrebbe a B. Considerato che la posta in gioco è di 64 euro, ad A andrebbero 56 parti e a B 8 parti. G. Sanfilippo - CdP pag. 237
6 Distribuzione di Poisson n.a. discreti Si dice che un numero aelatorio X ha una distribuzione di Poisson 20 di parametro 2 R +,esiindica X P( ), se valgono le seguenti condizioni, con 1) X 2 N 0 = {0, 1, 2, 3,...,n,...}; 2) P (X = n) =p n = n n! e, 8 n 2 N 0. Si ha P 1n=0 p n = P 1 n=0 n n! e = e P 1n=0 n n! = e e =1. La distribuzione di Poisson di parametro può essere utilizzata come approssimazione di una distribuzione binomiale di parametri (n, p) quando n tende a infinito e p è piccolo, purchè il prodotto np si mantenga costante e pari a.intalcasosihache Bin(n, p) =)P( ), = np. 20 S.D. Poisson, Ricerche sulla probabilità dei giudizi in materia criminale e civile, 1837 G. Sanfilippo - CdP pag. 238
7 n.a. discreti Per tale motivo la distribuzione di Poisson si usa in una grande varietà di applicazioni, ad esempio (sotto certe condizioni) si utilizza come distribuzione di probabilità di un n.a. X che rappresenta 1. il num. di telefonate che giungono ad un centralino in un giorno; 2. il num. di clienti che si presentano ad uno sportello in una mattina; 3. il num. di automobili che transitano ad un casello autostradale in un mese; 4. il num. di particelle emesse da un corpo radioattivo in un periodo di tempo fissato; 5. il num. di errori di stampa in una pagina di un libro Una delle prime applicazioni si ebbe nell esercito prussiano, per valutare la probabilità, molto piccola, che un soldato dell esercito morisse in seguito ad un calcio di cavallo 21. Osserviamo che, sotto certe ipotesi, la distribuzione Binomiale si può approssimare con la distribuzione di Poisson. In riferimento al num. di errori di stampa in una pagina di un libro, possiamo supporre che ci sia una piccola probabilità p che una singola lettera di un testo venga sbagliata. Inoltre se consideriamo gli eventi E i = l i-esima lettera è sbagliata, indipendenti ed equiprobabili allora il numero aleatorio di errori in una pagina può essere approssimato con un numero 21 Ladislaus Bortkiewicz, The law of small numbers, 1898 G. Sanfilippo - CdP pag. 239
8 aleatorio con distribuzione di Poisson con parametro numero di lettere che formano una singola pagina. n.a. discreti = np, dove n rappresenta il Approssimazione della Distribuzione Binomiale con una Distribuzione di Poisson Consideriamo una successione S 1, S 2,...,S n,... di numeri aleatori con distribuzione binomiale con lo stesso valore atteso,cioès n Bin(n, p n ) con n p n = 22. In questo modo ad ogni prova la probabilità di successo p n al crescere di n diventa sempre più piccola e i successi diventano eventi rari. Si ha lim P (S n = k) = n!1 k k! e 8k 2 N 0 Infatti lim n!1 P (S n = h) =lim n!1 n h ( n ) h (1 n )n h = n(n 1) (n h+1) =lim n!1 h! ( n ) h (1 n ) n (1 n ) h = h h! e. Pertanto: B(n, n )! n!1 P( ), cioè sotto certe condizioni (n grande e p piccolo ) la distribuzione Binomiale si può approssimare con la distribuzione di Poisson Si considera la successione a partire dai valori di n per i quali si ha p n = n < 1 23 Piu in generale si può dimostrare che data una successione di numeri aleatori {X n}n con Xn avente distribuzione binomiale di parametri n, pn e con limn!1 npn = = costante allora la successione {Xn}n converge in distribuzione a un numero aleatorio X con distribuzione di Poisson di parametro,cioèxn 7! d X con X P ( ). G. Sanfilippo - CdP pag. 240
9 Previsione e Varianza Si ha n.a. discreti E(X) = P 1 n=0 np n = P 1 n=0 n n n! e = = P 1 n=0 n n 1 n! e = P 1 n=1 n 1 (n 1)! e = 1=, E(X 2 )= P 1 i=0 n 2 p n = = 2 +, Var(X) = =. Nella distribuzione di Poisson la previsione e la varianza coincidono. Infatti si ha E(X) =var(x) = Tale risultato è ragionevole se consideriamo X come approssimazione di una distribuzione binomiale di parametri (n, p), pern grande, p piccolo e = np. Infattisiha = np ' np(1 p). G. Sanfilippo - CdP pag. 241
10 n.a. discreti Esempio 56 Il numero aleatorio X di telefonate che arrivano ad un centralino in un dato giorno ha una distribuzione di Poisson di parametro >0. Sapendo che il numero medio di arrivi nel giorno considerato è pari a 10, calcolare la probabilità dell evento A = arrivano al più 2 telefonate e dell evento (2.5 apple X < 3.5). Inoltre, supposto che siano arrivate almeno 2 telefonate (evento B), calcolare la probabilità che siano arrivate al più 3 telefonate (evento C). P (A) = P (2.5 apple X<3.5) = = Poichè E(X) =10si ha X P(10). Quindi P (A) = P (X apple 2) = P (X =0)+P (X =1)+P (X =2)= 10 = 0 e 10 0! e 10 1! e 10 2! =61e 10 ' Inoltre Infine, P (2.5 apple X<3.5) = P (X =3)= 103 e 10 3! = = P (C B) =P (X apple 3 X 2) = P (X=2_X=3) P (X 2) = P (X=2)+P (X=3) 1 P (X<2) = = ! e ! e e ! 101 e 10 1! = e 10 = (e 10 1) =' G. Sanfilippo - CdP pag. 242
11 n.a. discreti Esempio 57 In una città esiste un parco autobus costituito da 1000 unità. Da considerazioni statistiche si sa che in media il numero di autobus guasti che si osservano ogni mattina è pari a 2. Indichiamo con X il numero aleatorio di autobus guasti in una mattina specifica. Se, per ogni i =1, 2,...,1000, definiamo l evento E i = l i-mo autobus è difettoso, possiamo ritenere gli E i equiprobabili e indipendenti, con p = P (E i ).SihaX B(1000,p). Calcolare p. Inoltre calcolare P (X > 1) utilizzando opportune approssimazioni. Esempio 58 Consideriamo un esperimento che consiste nel contare il numero di particelle emesse da un grammo di materiale radioattivo in un secondo. Se sappiamo che mediamente vengono emesse 2 particelle, come possiamo approssimare la probabilità che non siano emesse più di 3 particelle? ' Esempio 59 Si supponga che il numero aleatorio delle richieste, al secondo, che pervengono ad un elaboratore possa essere descritto da una distribuzione di Poisson con =10richieste per secondo. Qual è la probabilità con cui nessuna richiesta arrivi all elaboratore in un secondo? Qual è la probabilità che l elaboratore riceva non più di 15 richieste in un secondo? In base alle ipotesi si ha P (X = h) = 10h h! e 10 h =0, 1, 2,... G. Sanfilippo - CdP pag. 243
12 da cui n.a. discreti P (X =0) = e 10 = e poi P (X apple 15) = e 10 15X x=0 10 x x! = G. Sanfilippo - CdP pag. 244
CALCOLO DELLE PROBABILITA - 13 Aprile 2011 CdL in STAD, SIGAD - docente: G. Sanfilippo
 Cognome e Nome: Matricola CdS CALCOLO DELLE PROBABILITA - 13 Aprile 211 CdL in STAD, SIGAD - docente: G Sanfilippo Motivare dettagliatamente le risposte su fogli allegati e scrivere le risposte negli appositi
Cognome e Nome: Matricola CdS CALCOLO DELLE PROBABILITA - 13 Aprile 211 CdL in STAD, SIGAD - docente: G Sanfilippo Motivare dettagliatamente le risposte su fogli allegati e scrivere le risposte negli appositi
Distribuzione di Poisson
 Distribuzione di Poisson Si dice che un numero aelatorio X ha una distribuzione di Poisson 9 di parametro 2 R +,esiindica X P( ), se valgono le seguenti condizioni, con ) X 2 N 0 = {0,, 2, 3,...,n,...};
Distribuzione di Poisson Si dice che un numero aelatorio X ha una distribuzione di Poisson 9 di parametro 2 R +,esiindica X P( ), se valgono le seguenti condizioni, con ) X 2 N 0 = {0,, 2, 3,...,n,...};
Vettori Aleatori discreti
 Vettori Aleatori discreti Un vettore aleatorio X =(X,X 2,...,X n ) si dice discreto se esiste un insieme finito o numerabile C R n tale che P (X = x) >, 8x 2 C, P (X = x) =, 8x /2 C, dove, ponendo x =(x,...,x
Vettori Aleatori discreti Un vettore aleatorio X =(X,X 2,...,X n ) si dice discreto se esiste un insieme finito o numerabile C R n tale che P (X = x) >, 8x 2 C, P (X = x) =, 8x /2 C, dove, ponendo x =(x,...,x
Estrazioni senza restituzione da un urna di composizione incognita. P(E i)=
 Estrazioni senza restituzione da un urna di composizione incognita. Consideriamo n estrazioni senza restituzione da un urna contenente N palline, di cui r sono bianche, con r incognito. Introdotta la partizione
Estrazioni senza restituzione da un urna di composizione incognita. Consideriamo n estrazioni senza restituzione da un urna contenente N palline, di cui r sono bianche, con r incognito. Introdotta la partizione
Cognome e Nome:... Matricola... CdS...
 Cognome e me: Matricola CdS CALCOLO DELLE PROBABILITA - 7 Giugno CdS in STAD, SIGAD - docente: G Sanfilippo Motivare dettagliatamente le risposte su fogli allegati e scrivere le risposte negli appositi
Cognome e me: Matricola CdS CALCOLO DELLE PROBABILITA - 7 Giugno CdS in STAD, SIGAD - docente: G Sanfilippo Motivare dettagliatamente le risposte su fogli allegati e scrivere le risposte negli appositi
Statistica Inferenziale
 Statistica Inferenziale Prof. Raffaella Folgieri Email: folgieri@mtcube.com aa 2009/2010 Riepilogo lezione 3 Abbiamo visto: Definizione di partizione di Teorema di Bayes Definizione di variabile aleatoria
Statistica Inferenziale Prof. Raffaella Folgieri Email: folgieri@mtcube.com aa 2009/2010 Riepilogo lezione 3 Abbiamo visto: Definizione di partizione di Teorema di Bayes Definizione di variabile aleatoria
ES.2.2. Consideriamo un esperimento statistico definito da un insieme Ω di risultati possibili. Una partizione finita di Ω è una sequenza di K eventi
 ES22 1 Variabili aleatorie discrete Consideriamo un esperimento statistico definito da un insieme Ω di risultati possibili Una partizione finita di Ω è una sequenza di K eventi A 1, A 2 A k A K necessari
ES22 1 Variabili aleatorie discrete Consideriamo un esperimento statistico definito da un insieme Ω di risultati possibili Una partizione finita di Ω è una sequenza di K eventi A 1, A 2 A k A K necessari
Alcune v.a. discrete notevoli
 Alcune v.a. discrete notevoli Variabile aleatoria Bernoulliana Il risultato X di un esperimento aleatorio può essere classificato nel modo che segue: successo oppure insuccesso. Indichiamo: Successo =
Alcune v.a. discrete notevoli Variabile aleatoria Bernoulliana Il risultato X di un esperimento aleatorio può essere classificato nel modo che segue: successo oppure insuccesso. Indichiamo: Successo =
! X (92) X n. P ( X n X ) =0 (94)
 Convergenza in robabilità Definizione 2 Data una successione X 1,X 2,...,X n,... di numeri aleatori e un numero aleatorio X diremo che X n tende in probabilità a X escriveremo X n! X (92) se fissati comunque
Convergenza in robabilità Definizione 2 Data una successione X 1,X 2,...,X n,... di numeri aleatori e un numero aleatorio X diremo che X n tende in probabilità a X escriveremo X n! X (92) se fissati comunque
Foglio di esercizi 3-29 Marzo 2019 Probabilità e statistica Ingegneria Meccanica Alessandro Ciallella
 Foglio di esercizi 3-29 Marzo 209 Probabilità e statistica Ingegneria Meccanica Alessandro Ciallella Esercizio. Una compagnia aerea dispone di un aereo da 20 posti e di uno da 0 posti. Poiché si sa che
Foglio di esercizi 3-29 Marzo 209 Probabilità e statistica Ingegneria Meccanica Alessandro Ciallella Esercizio. Una compagnia aerea dispone di un aereo da 20 posti e di uno da 0 posti. Poiché si sa che
Esercizi. 2. [Conteggio diretto] Due dadi vengono lanciati in successione. a) Qual è la probabilità che la somma dei due risultati faccia 7?
![Esercizi. 2. [Conteggio diretto] Due dadi vengono lanciati in successione. a) Qual è la probabilità che la somma dei due risultati faccia 7? Esercizi. 2. [Conteggio diretto] Due dadi vengono lanciati in successione. a) Qual è la probabilità che la somma dei due risultati faccia 7?](/thumbs/94/122023687.jpg) 1 E. Vitali Matematica (Scienze Naturali) Esercizi 1. [Conteggio diretto] Quattro ragazzi, A, B, C e D, dispongono di due biglietti per il teatro e decidono di tirare a sorte chi ne usufruirà. a) Qual
1 E. Vitali Matematica (Scienze Naturali) Esercizi 1. [Conteggio diretto] Quattro ragazzi, A, B, C e D, dispongono di due biglietti per il teatro e decidono di tirare a sorte chi ne usufruirà. a) Qual
Probabilità 1, laurea triennale in Matematica I prova scritta sessione estiva a.a. 2008/09
 Probabilità, laurea triennale in Matematica I prova scritta sessione estiva a.a. 2008/09. Due roulette regolari vengono azionate più volte; sia T il numero di volte che occorre azionare la prima roulette
Probabilità, laurea triennale in Matematica I prova scritta sessione estiva a.a. 2008/09. Due roulette regolari vengono azionate più volte; sia T il numero di volte che occorre azionare la prima roulette
Calcolo delle Probabilità 16 Giugno 2016, C.d.L. STAD, UNIPA
 Calcolo delle Probabilità 6 Giugno 206, C.d.L. STAD, UNIPA Prova intera esercizi, 2, 3, 4, 5, 6. Tempo 2 h 45 minuti. Esercizio risolto correttamente vale 5.5 punti. Seconda Prova in itinere esercizi 4,
Calcolo delle Probabilità 6 Giugno 206, C.d.L. STAD, UNIPA Prova intera esercizi, 2, 3, 4, 5, 6. Tempo 2 h 45 minuti. Esercizio risolto correttamente vale 5.5 punti. Seconda Prova in itinere esercizi 4,
Esercitazione del 04/06/2015 Probabilità e Statistica Foglio 14
 Esercitazione del 0/06/05 Probabilità e Statistica Foglio David Barbato Esercizio. Ci sono 0 monetine di cui 5 con due teste, con due croci e regolari una moneta regolare ha una faccia testa e una faccia
Esercitazione del 0/06/05 Probabilità e Statistica Foglio David Barbato Esercizio. Ci sono 0 monetine di cui 5 con due teste, con due croci e regolari una moneta regolare ha una faccia testa e una faccia
CALCOLO DELLE PROBABILITÀ
 CALCOLO DELLE PROBABILITÀ - gennaio 000 Elettronici: nn. 4 Informatici: nn. 6. Un lotto contiene pezzi buoni ed un solo pezzo difettoso. Si effettuano tre estrazioni senza restituzione, e sia E i = pezzo
CALCOLO DELLE PROBABILITÀ - gennaio 000 Elettronici: nn. 4 Informatici: nn. 6. Un lotto contiene pezzi buoni ed un solo pezzo difettoso. Si effettuano tre estrazioni senza restituzione, e sia E i = pezzo
Esercitazione del 03/06/2014 Probabilità e Statistica
 Esercitazione del 03/06/2014 Probabilità e Statistica David Barbato Esercizio 1. Sia (X i ) i N una successione di variabili aleatorie i.i.d. con distribuzione geometrica di parametro p = 1 2. Sia Y i
Esercitazione del 03/06/2014 Probabilità e Statistica David Barbato Esercizio 1. Sia (X i ) i N una successione di variabili aleatorie i.i.d. con distribuzione geometrica di parametro p = 1 2. Sia Y i
Scrivere su ogni foglio NOME e COGNOME. Le risposte devono essere giustificate sui fogli protocollo e riportate nel foglio RISPOSTE.
 CORSO DI CALCOLO DELLE PROBABILITÀ o modulo - PROVA d esame del 9/02/200 - Laurea Quadriennale in Matematica - Prof. Nappo Scrivere su ogni foglio NOME e COGNOME. Le risposte devono essere giustificate
CORSO DI CALCOLO DELLE PROBABILITÀ o modulo - PROVA d esame del 9/02/200 - Laurea Quadriennale in Matematica - Prof. Nappo Scrivere su ogni foglio NOME e COGNOME. Le risposte devono essere giustificate
P (0 semafori rossi) = 0,05 P (1 semaforo rosso) = 0,20 P (2 semafori rossi) = 0,25 P (3 semafori rossi) = 0,35 P (4 semafori rossi) = 0,15
 ESERCITAZIONE : ROBABILITA, VARIABILI CASUALI, BINOMIALE ESERCIZIO N. Una donna che si reca al lavoro in macchina ha osservato che il seguente modello è un approssimato modello probabilistico per il numero
ESERCITAZIONE : ROBABILITA, VARIABILI CASUALI, BINOMIALE ESERCIZIO N. Una donna che si reca al lavoro in macchina ha osservato che il seguente modello è un approssimato modello probabilistico per il numero
P (A) = P (B) = P (A ^ B) = P (A _ B) = P (A _ A c B)= P ([A _ B] ^ [A c _ B c ]) =
![P (A) = P (B) = P (A ^ B) = P (A _ B) = P (A _ A c B)= P ([A _ B] ^ [A c _ B c ]) = P (A) = P (B) = P (A ^ B) = P (A _ B) = P (A _ A c B)= P ([A _ B] ^ [A c _ B c ]) =](/thumbs/60/44901085.jpg) Esercizio 7 2 Un esperimento consiste nel lanciare una moneta e nell estrarre una pallina da un urna contenente 4 palline numerate da 1 a 4. Consideriamo gli eventi: A = Esce Testa, B = Si estrae la pallina
Esercizio 7 2 Un esperimento consiste nel lanciare una moneta e nell estrarre una pallina da un urna contenente 4 palline numerate da 1 a 4. Consideriamo gli eventi: A = Esce Testa, B = Si estrae la pallina
V.C. UNIFORME. 1 n. con funzione di probabilità associata: MODA(X): la distribuzione Uniforme è zeromodale.
 V.C. UNIFORME La v.c. discreta UNIFORME descrive il modello probabilistico dell equiprobabilità. I valori della v.c.u. sono dati dai primi n numeri naturali: x = 1, 2,, (n-1), n con funzione di probabilità
V.C. UNIFORME La v.c. discreta UNIFORME descrive il modello probabilistico dell equiprobabilità. I valori della v.c.u. sono dati dai primi n numeri naturali: x = 1, 2,, (n-1), n con funzione di probabilità
Probabilità classica. Distribuzioni e leggi di probabilità. Probabilità frequentista. Probabilità soggettiva
 Probabilità classica Distribuzioni e leggi di probabilità La probabilità di un evento casuale è il rapporto tra il numero dei casi favorevoli ed il numero dei casi possibili, purchè siano tutti equiprobabili.
Probabilità classica Distribuzioni e leggi di probabilità La probabilità di un evento casuale è il rapporto tra il numero dei casi favorevoli ed il numero dei casi possibili, purchè siano tutti equiprobabili.
CP110 Probabilità: Esame 4 luglio Testo e soluzione
 Dipartimento di Matematica, Roma Tre Pietro Caputo 2011-12, II semestre 4 luglio, 2012 CP110 Probabilità: Esame 4 luglio 2012 Testo e soluzione 1. (6 pts) Una scatola contiene 10 palline numerate da 1
Dipartimento di Matematica, Roma Tre Pietro Caputo 2011-12, II semestre 4 luglio, 2012 CP110 Probabilità: Esame 4 luglio 2012 Testo e soluzione 1. (6 pts) Una scatola contiene 10 palline numerate da 1
VARIABILI ALEATORIE Una moneta equilibrata viene lanciata più volte. Qual è la probabilità che al 6 lancio:
 VARIABILI ALEATORIE. Una moneta equilibrata viene lanciata più volte. Qual è la probabilità che al lancio: a) si abbia testa per la prima volta? b) Si sia avuto testa almeno una volta? c) Si sia avuta
VARIABILI ALEATORIE. Una moneta equilibrata viene lanciata più volte. Qual è la probabilità che al lancio: a) si abbia testa per la prima volta? b) Si sia avuto testa almeno una volta? c) Si sia avuta
Costruzione di macchine. Modulo di: Progettazione probabilistica e affidabilità. Marco Beghini. Lezione 3: Variabili aleatorie discrete notevoli
 Costruzione di macchine Modulo di: Progettazione probabilistica e affidabilità Marco Beghini Lezione 3: Variabili aleatorie discrete notevoli Esperimenti binari ripetuti o esperimenti bernoulliani (Bernoulli
Costruzione di macchine Modulo di: Progettazione probabilistica e affidabilità Marco Beghini Lezione 3: Variabili aleatorie discrete notevoli Esperimenti binari ripetuti o esperimenti bernoulliani (Bernoulli
Corso di Statistica. Distribuzioni di probabilità per variabili casuali discrete. Prof.ssa T. Laureti a.a
 Corso di Statistica Distribuzioni di probabilità per variabili casuali discrete Prof.ssa T. Laureti a.a. 2013-2014 1 Variabili casuale di Bernoulli La v.c. di Bernoulli trae origine da una prova nella
Corso di Statistica Distribuzioni di probabilità per variabili casuali discrete Prof.ssa T. Laureti a.a. 2013-2014 1 Variabili casuale di Bernoulli La v.c. di Bernoulli trae origine da una prova nella
PROBABILITÀ I. a.a. 2011/2012 DIARIO DELLE LEZIONI
 PROBABILITÀ I. a.a. 2011/2012 DIARIO DELLE LEZIONI Settimana 5-9 marzo. Elementi di analisi combinatoria (vedasi capitolo I del Ross). Integrazioni: triangolo di Tartaglia, dimostrazione diretta della
PROBABILITÀ I. a.a. 2011/2012 DIARIO DELLE LEZIONI Settimana 5-9 marzo. Elementi di analisi combinatoria (vedasi capitolo I del Ross). Integrazioni: triangolo di Tartaglia, dimostrazione diretta della
Esercizi svolti di statistica. Gianpaolo Gabutti
 Esercizi svolti di statistica Gianpaolo Gabutti (gabuttig@hotmail.com) 1 Introduzione Questo breve documento contiene lo svolgimento di alcuni esercizi di statistica da me svolti durante la preparazione
Esercizi svolti di statistica Gianpaolo Gabutti (gabuttig@hotmail.com) 1 Introduzione Questo breve documento contiene lo svolgimento di alcuni esercizi di statistica da me svolti durante la preparazione
Esercizi: fascicolo 4
 Esercizi: fascicolo 4 Esercizio 1 Dimostrare le seguenti proprietà (1), (2) e (3): (1) X 1 = 0 X 0; (2) X L 1 (Ω, P ), λ R λx 1 = λ X 1 ; (3) X, Y L 1 (Ω, P ) X + Y 1 X 1 + Y 1. Esercizio 2 Si estraggono
Esercizi: fascicolo 4 Esercizio 1 Dimostrare le seguenti proprietà (1), (2) e (3): (1) X 1 = 0 X 0; (2) X L 1 (Ω, P ), λ R λx 1 = λ X 1 ; (3) X, Y L 1 (Ω, P ) X + Y 1 X 1 + Y 1. Esercizio 2 Si estraggono
Statistica, a.a. 2010/2011 Docente: D. Dabergami Lezione 4
 X N(m ; s ) f X x 1 e π σ xμ σ σ 0 m F X x x 1 π σ e tμ σ dt 1 0.5 EX μ VarX σ m La distribuzione normale permette di modellizzare moltissimi fenomeni aleatori (ad esempio misure di ogni genere), serve
X N(m ; s ) f X x 1 e π σ xμ σ σ 0 m F X x x 1 π σ e tμ σ dt 1 0.5 EX μ VarX σ m La distribuzione normale permette di modellizzare moltissimi fenomeni aleatori (ad esempio misure di ogni genere), serve
SOLUZIONI DEL 2 0 TEST DI PREPARAZIONE ALLA 1 a PROVA INTERMEDIA
 SOLUZIONI DEL 0 TEST DI PREPARAZIONE ALLA 1 a PROVA INTERMEDIA Esercizio 0.1 Una moneta non truccata viene lanciata 10 volte. Calcolare la probabilità che non esca mai testa. Quale risulta la probabilità
SOLUZIONI DEL 0 TEST DI PREPARAZIONE ALLA 1 a PROVA INTERMEDIA Esercizio 0.1 Una moneta non truccata viene lanciata 10 volte. Calcolare la probabilità che non esca mai testa. Quale risulta la probabilità
Statistica ARGOMENTI. Calcolo combinatorio
 Statistica ARGOMENTI Calcolo combinatorio Probabilità Disposizioni semplici Disposizioni con ripetizione Permutazioni semplici Permutazioni con ripetizioni Combinazioni semplici Assiomi di probabilità
Statistica ARGOMENTI Calcolo combinatorio Probabilità Disposizioni semplici Disposizioni con ripetizione Permutazioni semplici Permutazioni con ripetizioni Combinazioni semplici Assiomi di probabilità
CP110 Probabilità: Esame 2 luglio Testo e soluzione
 Dipartimento di Matematica, Roma Tre Pietro Caputo 212-13, II semestre 2 luglio, 213 CP11 Probabilità: Esame 2 luglio 213 Testo e soluzione 1. (6 pts Due mazzi di carte francesi vengono uniti e mischiati.
Dipartimento di Matematica, Roma Tre Pietro Caputo 212-13, II semestre 2 luglio, 213 CP11 Probabilità: Esame 2 luglio 213 Testo e soluzione 1. (6 pts Due mazzi di carte francesi vengono uniti e mischiati.
3 4 t t t 1. 5 k = 6. p(k) = 2
 PROVE D'ESAME DI CCP, A.A. 2013/2014 12/06/2014 (1) Sia A un mazzo di 16 carte, contenente le carte di valore da 1 a 8 sia di cuori che di quadri. (a) Quanti sono i sottoinsiemi di 10 carte di A? (b) Quanti
PROVE D'ESAME DI CCP, A.A. 2013/2014 12/06/2014 (1) Sia A un mazzo di 16 carte, contenente le carte di valore da 1 a 8 sia di cuori che di quadri. (a) Quanti sono i sottoinsiemi di 10 carte di A? (b) Quanti
Esercizi di Calcolo delle Probabilità
 Esercizi di Calcolo delle Probabilità Versione del 1/05/005 Corso di Statistica Anno Accademico 00/05 Antonio Giannitrapani, Simone Paoletti Calcolo delle probabilità Esercizio 1. Un dado viene lanciato
Esercizi di Calcolo delle Probabilità Versione del 1/05/005 Corso di Statistica Anno Accademico 00/05 Antonio Giannitrapani, Simone Paoletti Calcolo delle probabilità Esercizio 1. Un dado viene lanciato
, B con probabilità 1 4 e C con probabilità 1 4.
 Laurea triennale in MATEMATICA, Corso di PROBABILITÀ Prof. L. Bertini - G. Nappo - F. Spizzichino Esonero del 0.06.00 N.B. Scrivere le soluzioni degli esercizi su questi fogli giustificando brevemente
Laurea triennale in MATEMATICA, Corso di PROBABILITÀ Prof. L. Bertini - G. Nappo - F. Spizzichino Esonero del 0.06.00 N.B. Scrivere le soluzioni degli esercizi su questi fogli giustificando brevemente
P ( X n X > ɛ) = 0. ovvero (se come distanza consideriamo quella euclidea)
 10.4 Convergenze 166 10.4.3. Convergenza in Probabilità. Definizione 10.2. Data una successione X 1, X 2,...,,... di vettori aleatori e un vettore aleatorio X aventi tutti la stessa dimensione k diremo
10.4 Convergenze 166 10.4.3. Convergenza in Probabilità. Definizione 10.2. Data una successione X 1, X 2,...,,... di vettori aleatori e un vettore aleatorio X aventi tutti la stessa dimensione k diremo
CALCOLO DELLE PROBABILITÀ - 9 giugno 1998 Scrivere le risposte negli appositi spazi Motivare dettagliatamente le risposte su fogli allegati
 CALCOLO DELLE PROBABILITÀ - 9 giugno 1998 1. Dati gli eventi A,B,C, ognuno dei quali implica il successivo, e tali che P (A) è metà della probabilità di B, che a sua volta ha probabilità metà di quella
CALCOLO DELLE PROBABILITÀ - 9 giugno 1998 1. Dati gli eventi A,B,C, ognuno dei quali implica il successivo, e tali che P (A) è metà della probabilità di B, che a sua volta ha probabilità metà di quella
MATEMATICA E STATISTICA CORSO A SCIENZE BIOLOGICHE MOLECOLARI ESERCITAZIONE
 MATEMATICA E STATISTICA CORSO A SCIENZE BIOLOGICHE MOLECOLARI ESERCITAZIONE 5-3-09 ES1-Se la probabilità di colpire un bersaglio è 1/5 e rimane tale ad ogni tentativo, calcola la probabilità che, sparando
MATEMATICA E STATISTICA CORSO A SCIENZE BIOLOGICHE MOLECOLARI ESERCITAZIONE 5-3-09 ES1-Se la probabilità di colpire un bersaglio è 1/5 e rimane tale ad ogni tentativo, calcola la probabilità che, sparando
Esami di Calcolo delle Probabilitá del 9 Giugno 2010
 Candidato/a................................................ Corso di Laurea.......................................... Esami di Calcolo delle Probabilitá del Giugno 00 É fatto assoluto divieto di usare
Candidato/a................................................ Corso di Laurea.......................................... Esami di Calcolo delle Probabilitá del Giugno 00 É fatto assoluto divieto di usare
Esercitazione del 16/04/2019 Istituzioni di Calcolo delle Probabilità
 Esercitazione del 6/04/09 Istituzioni di Calcolo delle Probabilità David Barbato Nozioni di riepilogo con esercizi Distribuzione di una funzione di una variabile aleatoria discreta. Sia X una variabile
Esercitazione del 6/04/09 Istituzioni di Calcolo delle Probabilità David Barbato Nozioni di riepilogo con esercizi Distribuzione di una funzione di una variabile aleatoria discreta. Sia X una variabile
Distribuzione Binomiale
 Statistica e analisi dei dati Data: 2 Maggio 2016 Distribuzione Binomiale Docente: Prof. Giuseppe Boccignone Scriba: Nicoló Pisaroni 1 Conteggi e tempi di attesa Consideriamo il seguente schema, facendo
Statistica e analisi dei dati Data: 2 Maggio 2016 Distribuzione Binomiale Docente: Prof. Giuseppe Boccignone Scriba: Nicoló Pisaroni 1 Conteggi e tempi di attesa Consideriamo il seguente schema, facendo
Calcolo delle probabilità (3/7/2001) (Ing. Elettronica, Informatica, Telecomunicazioni - Latina)
 Calcolo delle probabilità (3/7/00). La distribuzione di probabilità di un numero aleatorio X non negativo soddisfa la condizione P (X > x + y X > y) = P (X > x), x > 0, y > 0. Inoltre la previsione di
Calcolo delle probabilità (3/7/00). La distribuzione di probabilità di un numero aleatorio X non negativo soddisfa la condizione P (X > x + y X > y) = P (X > x), x > 0, y > 0. Inoltre la previsione di
Statistica Applicata all edilizia: alcune distribuzioni di probabilità
 Statistica Applicata all edilizia: Alcune distribuzioni di probabilità E-mail: orietta.nicolis@unibg.it 23 marzo 2010 Indice Distribuzioni di probabilità discrete 1 Distribuzioni di probabilità discrete
Statistica Applicata all edilizia: Alcune distribuzioni di probabilità E-mail: orietta.nicolis@unibg.it 23 marzo 2010 Indice Distribuzioni di probabilità discrete 1 Distribuzioni di probabilità discrete
Calcolo delle Probabilità e Statistica Matematica Fisciano, 10/1/2012
 Fisciano, 10/1/2012 Esercizio 1 Un esperimento consiste nel generare a caso un vettore di interi (x 1, x 2, x 3, x 4 ), dove x i {1, 2, 3, 4, 5, 6} i. (i) Si individui lo spazio campionario, determinandone
Fisciano, 10/1/2012 Esercizio 1 Un esperimento consiste nel generare a caso un vettore di interi (x 1, x 2, x 3, x 4 ), dove x i {1, 2, 3, 4, 5, 6} i. (i) Si individui lo spazio campionario, determinandone
CP210 Introduzione alla Probabilità: Esonero 1
 Dipartimento di Matematica, Roma Tre Pietro Caputo 018-19, II semestre 9 aprile, 019 CP10 Introduzione alla Probabilità: Esonero 1 Cognome Nome Matricola Firma Nota: 1. L unica cosa che si può usare durante
Dipartimento di Matematica, Roma Tre Pietro Caputo 018-19, II semestre 9 aprile, 019 CP10 Introduzione alla Probabilità: Esonero 1 Cognome Nome Matricola Firma Nota: 1. L unica cosa che si può usare durante
Metodi Matematici Probabilità e Statistica. Correzione Compitino del
 Metodi Matematici Probabilità e Statistica Correzione Compitino del.4.04 nota: Una sola risposta è esatta. 4 punti per una risposta esatta, -2 per una sbagliata, 0 per una non data. Gli esercizi sono divisi
Metodi Matematici Probabilità e Statistica Correzione Compitino del.4.04 nota: Una sola risposta è esatta. 4 punti per una risposta esatta, -2 per una sbagliata, 0 per una non data. Gli esercizi sono divisi
Matematica e Statistica per Scienze Ambientali
 per Scienze Ambientali Variabili aleatorie - Appunti 1 1 Dipartimento di Matematica Sapienza, Università di Roma Roma, Gennaio 2013 Variabili aleatorie Un numero aleatorio è un esempio di variabile aleatoria.
per Scienze Ambientali Variabili aleatorie - Appunti 1 1 Dipartimento di Matematica Sapienza, Università di Roma Roma, Gennaio 2013 Variabili aleatorie Un numero aleatorio è un esempio di variabile aleatoria.
Due variabili aleatorie X ed Y si dicono indipendenti se comunque dati due numeri reali a e b si ha. P {X = a, Y = b} = P {X = a}p {Y = b}
 Due variabili aleatorie X ed Y si dicono indipendenti se comunque dati due numeri reali a e b si ha P {X = a, Y = b} = P {X = a}p {Y = b} Una variabile aleatoria χ che assume i soli valori 1, 2,..., n
Due variabili aleatorie X ed Y si dicono indipendenti se comunque dati due numeri reali a e b si ha P {X = a, Y = b} = P {X = a}p {Y = b} Una variabile aleatoria χ che assume i soli valori 1, 2,..., n
CP110 Probabilità: Esame 13 settembre Testo e soluzione
 Dipartimento di Matematica, Roma Tre Pietro Caputo 2011-12, II semestre 13 settembre, 2012 CP110 Probabilità: Esame 13 settembre 2012 Testo e soluzione 1. (6 pts) Una scatola contiene 10 palline, 8 bianche
Dipartimento di Matematica, Roma Tre Pietro Caputo 2011-12, II semestre 13 settembre, 2012 CP110 Probabilità: Esame 13 settembre 2012 Testo e soluzione 1. (6 pts) Una scatola contiene 10 palline, 8 bianche
Probabilità condizionate
 Probabilità condizionate Dati due eventi E ed H, con H φ, si definisce evento condizionato il seguente ente logico a tre valori E H = vero falso indeterminato se E ed H sono entrambi veri se E è falso
Probabilità condizionate Dati due eventi E ed H, con H φ, si definisce evento condizionato il seguente ente logico a tre valori E H = vero falso indeterminato se E ed H sono entrambi veri se E è falso
Esercitazione del 04/06/2015 Probabilità e Statistica Foglio 13
 Esercitazione del 04/06/2015 Probabilità e Statistica Foglio 13 David Barbato Approssimazioni normali. Theorem 1 (Teorema del limite centrale). Siano X 1,..., X n variabili aleatorie indipendenti ed identicamente
Esercitazione del 04/06/2015 Probabilità e Statistica Foglio 13 David Barbato Approssimazioni normali. Theorem 1 (Teorema del limite centrale). Siano X 1,..., X n variabili aleatorie indipendenti ed identicamente
CP110 Probabilità: Esonero 1. Testo e soluzione
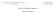 Dipartimento di Matematica, Roma Tre Pietro Caputo 2011-12, II semestre 10 aprile, 2012 CP110 Probabilità: Esonero 1 Testo e soluzione 1. (8 punti) Un urna contiene palline bianche, palline rosse e 6 palline
Dipartimento di Matematica, Roma Tre Pietro Caputo 2011-12, II semestre 10 aprile, 2012 CP110 Probabilità: Esonero 1 Testo e soluzione 1. (8 punti) Un urna contiene palline bianche, palline rosse e 6 palline
Numero Aleatorio Semplice
 Numero Aleatorio Semplice Dati n eventi E 1,E 2,,E n ed n numeri reali 1, 2,, n si definisce numero aleatorio semplice la seguente quantità: X = 1 E 1 + 2 E 2 + + n E n (45) Al variare in tutti i modi
Numero Aleatorio Semplice Dati n eventi E 1,E 2,,E n ed n numeri reali 1, 2,, n si definisce numero aleatorio semplice la seguente quantità: X = 1 E 1 + 2 E 2 + + n E n (45) Al variare in tutti i modi
Esercizi di Probabilità - Matematica Applicata a. a aprile 2014
 Esercizi di Probabilità - Matematica Applicata a. a. 2013-3014 db 1 aprile 2014 1 Funzione di ripartizione Si dice funzione di ripartizione o funzione cumulativa delle frequenze di una variabile casuale
Esercizi di Probabilità - Matematica Applicata a. a. 2013-3014 db 1 aprile 2014 1 Funzione di ripartizione Si dice funzione di ripartizione o funzione cumulativa delle frequenze di una variabile casuale
Lezioni da Matematica I Calcolo differenziale, Algebra lineare, Probabilità e statistica G. Aletti & G. Naldi & L. Pareschi
 Lezioni da Matematica I Calcolo differenziale, Algebra lineare, Probabilità e statistica G. Aletti & G. Naldi & L. Pareschi http://www.ateneonline.it/naldi matematica McGraw-Hill Capitolo 12, Modelli Probabilistici
Lezioni da Matematica I Calcolo differenziale, Algebra lineare, Probabilità e statistica G. Aletti & G. Naldi & L. Pareschi http://www.ateneonline.it/naldi matematica McGraw-Hill Capitolo 12, Modelli Probabilistici
Materiale didattico per il corso di Statistica I Quarta esercitazione SOLUZIONI
 Materiale didattico per il corso di Statistica I Quarta esercitazione SOLUZIONI Claudia Furlan 1 Anno Accademico 2006-2007 1 Ringrazio Carlo Gaetan, Nicola Sartori e Aldo Solari per il materiale, aggiunte
Materiale didattico per il corso di Statistica I Quarta esercitazione SOLUZIONI Claudia Furlan 1 Anno Accademico 2006-2007 1 Ringrazio Carlo Gaetan, Nicola Sartori e Aldo Solari per il materiale, aggiunte
L assegnazione è coerente? SÌ NO. A e B sono stocasticamente indipendenti? SÌ NO
 CALCOLO DELLE PROBABILITÀ - gennaio 00 Scrivere le risposte negli appositi spazi Motivare dettagliatamente le risposte su fogli allegati Nuovo Ordinamento esercizi -4. Vecchio Ordinamento esercizi -6..
CALCOLO DELLE PROBABILITÀ - gennaio 00 Scrivere le risposte negli appositi spazi Motivare dettagliatamente le risposte su fogli allegati Nuovo Ordinamento esercizi -4. Vecchio Ordinamento esercizi -6..
b = 1 2σ 3. La lunghezza di una barra è un numero aleatorio X con densità della forma 0, x 0, 0 < x 1 a = 1 F (x) = 2 2x 1 x2
 CALCOLO DELLE PROBABILITÀ E STATISTICA - 0 gennaio 2002 Informatica (N.O.) (Canali 4) esercizi -4 Vecchio Ordinamento esercizi -6. Da un lotto contenente 4 pezzi buoni e 2 difettosi si estraggono senza
CALCOLO DELLE PROBABILITÀ E STATISTICA - 0 gennaio 2002 Informatica (N.O.) (Canali 4) esercizi -4 Vecchio Ordinamento esercizi -6. Da un lotto contenente 4 pezzi buoni e 2 difettosi si estraggono senza
C = {C 1 = A B c H, C 2 = A c B H, C 3 = A B c H c, C 4 = A c B H c } ; P (C 1 ) = 21/100, P (C 2 ) = 9/100, P (C 3 ) = 49/100, P (C 4 ) = 21/100.
 CALCOLO DELLE PROBABILITÀ - 20 gennaio 2007 Motivare dettagliatamente le risposte su fogli allegati Elettronica: Es.1 4. Nettuno: Es.1 3. 1. Si effettuano due estrazioni con restituzione da un lotto contenente
CALCOLO DELLE PROBABILITÀ - 20 gennaio 2007 Motivare dettagliatamente le risposte su fogli allegati Elettronica: Es.1 4. Nettuno: Es.1 3. 1. Si effettuano due estrazioni con restituzione da un lotto contenente
Teorema del limite centrale TCL Questo importante teorema della statistica inferenziale si applica a qualsiasi variabile aleatoria che sia combinazion
 Teorema del limite centrale TCL Questo importante teorema della statistica inferenziale si applica a qualsiasi variabile aleatoria che sia combinazione lineare di N variabili aleatorie le cui funzioni
Teorema del limite centrale TCL Questo importante teorema della statistica inferenziale si applica a qualsiasi variabile aleatoria che sia combinazione lineare di N variabili aleatorie le cui funzioni
0.1 P(A n ) Quindi stiamo cercando n che soddisfa la seguente relazione: n + 180
 Esercizio 1 Alcuni ingegneri civili ritengono che il peso in tonnellate che un braccio di ponte può sopportare senza avere cedimenti strutturali possa descriversi mediante una variabile aleatoria Y con
Esercizio 1 Alcuni ingegneri civili ritengono che il peso in tonnellate che un braccio di ponte può sopportare senza avere cedimenti strutturali possa descriversi mediante una variabile aleatoria Y con
Esercitazione # 3. Trovate la probabilita che in 5 lanci di un dado non truccato il 3 si presenti
 Statistica Matematica A Esercitazione # 3 Binomiale: Esercizio # 1 Trovate la probabilita che in 5 lanci di un dado non truccato il 3 si presenti 1. mai 2. almeno una volta 3. quattro volte Esercizio #
Statistica Matematica A Esercitazione # 3 Binomiale: Esercizio # 1 Trovate la probabilita che in 5 lanci di un dado non truccato il 3 si presenti 1. mai 2. almeno una volta 3. quattro volte Esercizio #
Lezione 12. Statistica. Alfonso Iodice D Enza Università degli studi di Cassino. Lezione 12. A. Iodice.
 discrete uniforme Bernoulli Poisson Statistica Alfonso Iodice D Enza iodicede@unicas.it Università degli studi di Cassino () Statistica 1 / 56 Outline discrete uniforme Bernoulli Poisson 1 2 discrete 3
discrete uniforme Bernoulli Poisson Statistica Alfonso Iodice D Enza iodicede@unicas.it Università degli studi di Cassino () Statistica 1 / 56 Outline discrete uniforme Bernoulli Poisson 1 2 discrete 3
CP110 Probabilità: Esonero 1. Testo e soluzione
 Dipartimento di Matematica, Roma Tre Pietro Caputo 2009-2010, II semestre 1 aprile, 2010 CP110 Probabilità: Esonero 1 Testo e soluzione 1. (7 pt Una scatola contiene 15 palle numerate da 1 a 15. Le palle
Dipartimento di Matematica, Roma Tre Pietro Caputo 2009-2010, II semestre 1 aprile, 2010 CP110 Probabilità: Esonero 1 Testo e soluzione 1. (7 pt Una scatola contiene 15 palle numerate da 1 a 15. Le palle
Esercizi settimana 5. Esercizi applicati. Esercizio 1. Si considerino tre monete truccate, ognuna con probabilità 2 3
 1 Esercizi settimana 5 Esercizi applicati Esercizio 1. Si considerino tre monete truccate, ognuna con probabilità 3 di ottenere testa. Se scegliete la prima moneta vincete 10 punti se esce testa e punti
1 Esercizi settimana 5 Esercizi applicati Esercizio 1. Si considerino tre monete truccate, ognuna con probabilità 3 di ottenere testa. Se scegliete la prima moneta vincete 10 punti se esce testa e punti
Inferenza nel caso di un conteggio 21-2
 21-1 Inferenza nel caso di un conteggio 21-2 Quando il risultato di un esperimento o di uno studio osservazionale è un conteggio, la distribuzione di riferimento da impiegare (salvo evidenti violazioni)
21-1 Inferenza nel caso di un conteggio 21-2 Quando il risultato di un esperimento o di uno studio osservazionale è un conteggio, la distribuzione di riferimento da impiegare (salvo evidenti violazioni)
SOLUZIONI DEL 1 0 TEST DI PREPARAZIONE ALLA 1 a PROVA INTERMEDIA
 SOLUZIONI DEL 1 0 TEST DI PREPARAZIONE ALLA 1 a PROVA INTERMEDIA 1 Esercizio 0.1 Dato P (A) = 0.5 e P (A B) = 0.6, determinare P (B) nei casi in cui: a] A e B sono incompatibili; b] A e B sono indipendenti;
SOLUZIONI DEL 1 0 TEST DI PREPARAZIONE ALLA 1 a PROVA INTERMEDIA 1 Esercizio 0.1 Dato P (A) = 0.5 e P (A B) = 0.6, determinare P (B) nei casi in cui: a] A e B sono incompatibili; b] A e B sono indipendenti;
Corso di Istituzioni di Matematiche con Elementi di Statistica. anno accademico 2015/2016 corso A-L (G. Gaeta & N. Bressan)
 Corso di Istituzioni di Matematiche con Elementi di Statistica anno accademico 215/216 corso A-L (G. Gaeta & N. Bressan) Esercizi Foglio 9 (Funzioni aleatorie; distribuzioni di probabilita ) Esercizio
Corso di Istituzioni di Matematiche con Elementi di Statistica anno accademico 215/216 corso A-L (G. Gaeta & N. Bressan) Esercizi Foglio 9 (Funzioni aleatorie; distribuzioni di probabilita ) Esercizio
Calcolo delle Probabilità 2
 Prova d esame di Calcolo delle Probabilità 2 Maggio 2006 Sia X una variabile aleatoria distribuita secondo la densità seguente ke x 1 x < 0 f X (x) = 1/2 0 x 1. 1. Determinare il valore del parametro reale
Prova d esame di Calcolo delle Probabilità 2 Maggio 2006 Sia X una variabile aleatoria distribuita secondo la densità seguente ke x 1 x < 0 f X (x) = 1/2 0 x 1. 1. Determinare il valore del parametro reale
P (T + H)P (H) P (T + H)P (H) + P (T + H)P ( H) 0.95P (H) 0.95P (H) (1 P (H)) ragionevole screening su popolazione a rischio
 Test per HIV T + = test positivo ; T = test negativo H = presenza di HIV Test sensibile: P (T + H) = 0.95 possibilità di falsi risultati P (T H) = 1 0.95 = 0.05 P (T + H) = 0.05 (supponiamo) calcoliamo
Test per HIV T + = test positivo ; T = test negativo H = presenza di HIV Test sensibile: P (T + H) = 0.95 possibilità di falsi risultati P (T H) = 1 0.95 = 0.05 P (T + H) = 0.05 (supponiamo) calcoliamo
Prove di Statistica e Analisi Numerica
 Prove di Statistica e Analisi Numerica Lorenzo Barone 12 novembre 2010 1 Testi delle prove Calcolo delle Probabilità Prova scritta del 21/12/2004 1. In un magazzino ci sono mele provenienti da due campi
Prove di Statistica e Analisi Numerica Lorenzo Barone 12 novembre 2010 1 Testi delle prove Calcolo delle Probabilità Prova scritta del 21/12/2004 1. In un magazzino ci sono mele provenienti da due campi
X = X 1 + X 2 +... + X n. dove. 1 se alla i-esima prova si ha un successo 0 se alla i-esima prova si ha un insuccesso. X i =
 PIU DI UNA VARIABILE CASUALE Supponiamo di avere n variabili casuali, X 1, X 2,..., X n. Le n variabili casuali si dicono indipendenti se e solo se P(X 1 x 1 X 2 x 2... X n x n ) = = P(X 1 x 1 ) P(X 2
PIU DI UNA VARIABILE CASUALE Supponiamo di avere n variabili casuali, X 1, X 2,..., X n. Le n variabili casuali si dicono indipendenti se e solo se P(X 1 x 1 X 2 x 2... X n x n ) = = P(X 1 x 1 ) P(X 2
Esercizi su variabili discrete: binomiali e ipergeometriche
 CORSO DI CALCOLO DELLE PROBABILITÀ E STATISTICA Esercizi su variabili discrete: binomiali e ipergeometriche Es1 Due squadre di rugby si sfidano giocando fra loro varie partite La squadra che vince 4 partite
CORSO DI CALCOLO DELLE PROBABILITÀ E STATISTICA Esercizi su variabili discrete: binomiali e ipergeometriche Es1 Due squadre di rugby si sfidano giocando fra loro varie partite La squadra che vince 4 partite
TEST n La funzione di ripartizione di una variabile aleatoria:
 TEST n. 1 1. Un esperimento consiste nell estrarre successivamente, con reimmissione nel mazzo, due carte da un mazzo di 52 carte. Individuare la probabilità di estrarre due assi. A 0.0059 B 0.0044 C 0.0045
TEST n. 1 1. Un esperimento consiste nell estrarre successivamente, con reimmissione nel mazzo, due carte da un mazzo di 52 carte. Individuare la probabilità di estrarre due assi. A 0.0059 B 0.0044 C 0.0045
1. Siano A, E eventi incompatibili, e sia B E, con P (A) = 1 5, P (B) = 3 10, P (E) = 1 2.
 CALCOLO DELLE PROBABILITA - 5 gennaio 005 Ing. Elettronica : 4, Nettuno :. Siano A, E eventi incompatibili, e sia B E, con P (A) = 5, P (B) = 0, P (E) =. Dimostrare che tale assegnazione è coerente, determinando
CALCOLO DELLE PROBABILITA - 5 gennaio 005 Ing. Elettronica : 4, Nettuno :. Siano A, E eventi incompatibili, e sia B E, con P (A) = 5, P (B) = 0, P (E) =. Dimostrare che tale assegnazione è coerente, determinando
X Vincita (in euro) Tabella 1: Vincite
 Cognome e Nome:....................................... Matricola............. CdS............. CALCOLO DELLE PROBABILITA - 9 Giugno 1 CdS in STAD, SIGAD - docente: G. Sanfilippo Motivare dettagliatamente
Cognome e Nome:....................................... Matricola............. CdS............. CALCOLO DELLE PROBABILITA - 9 Giugno 1 CdS in STAD, SIGAD - docente: G. Sanfilippo Motivare dettagliatamente
Esercizi - Fascicolo IV
 Esercizi - Fascicolo IV Esercizio Una compagnia di assicurazioni emette una polizza che pagherà n euro se l evento E si verificherà entro un anno. Se la compagnia stima che l evento E si verificherà entro
Esercizi - Fascicolo IV Esercizio Una compagnia di assicurazioni emette una polizza che pagherà n euro se l evento E si verificherà entro un anno. Se la compagnia stima che l evento E si verificherà entro
Statistica Inferenziale
 Statistica Inferenziale Prof. Raffaella Folgieri Email: folgieri@mtcube.com aa 2009/2010 Riepilogo lezione 1 Abbiamo visto: Definizioni di statistica, statistica inferenziale, probabilità (interpretazione
Statistica Inferenziale Prof. Raffaella Folgieri Email: folgieri@mtcube.com aa 2009/2010 Riepilogo lezione 1 Abbiamo visto: Definizioni di statistica, statistica inferenziale, probabilità (interpretazione
Esercizi di Probabilità e Statistica
 Esercizi di Probabilità e Statistica Samuel Rota Bulò 2 aprile 200 Funzioni di v.a., Media e Varianza Esercizio Calcolare la media delle distribuzioni binomiale, e quella di Poisson. Di quest ultima calcolare
Esercizi di Probabilità e Statistica Samuel Rota Bulò 2 aprile 200 Funzioni di v.a., Media e Varianza Esercizio Calcolare la media delle distribuzioni binomiale, e quella di Poisson. Di quest ultima calcolare
Distribuzioni di probabilità
 > Note Distribuzioni di probabilità filename: distribuzioni.mws version: 2.0 tested: Maple V Release 6.02 on Windows 2000 date: 15 marzo 2003 author: Claudio Marsan Liceo Cantonale di Mendrisio Via Agostino
> Note Distribuzioni di probabilità filename: distribuzioni.mws version: 2.0 tested: Maple V Release 6.02 on Windows 2000 date: 15 marzo 2003 author: Claudio Marsan Liceo Cantonale di Mendrisio Via Agostino
Modelli descrittivi, statistica e simulazione
 Modelli descrittivi, statistica e simulazione Master per Smart Logistics specialist Roberto Cordone (roberto.cordone@unimi.it) Statistica inferenziale Cernusco S.N., giovedì 18 febbraio 2016 (9.00/13.00)
Modelli descrittivi, statistica e simulazione Master per Smart Logistics specialist Roberto Cordone (roberto.cordone@unimi.it) Statistica inferenziale Cernusco S.N., giovedì 18 febbraio 2016 (9.00/13.00)
Numero di successi su n prove
 Numero di successi su n prove Risultati possibili lanciando, volte una moneta. numero di volte in cui esce croce... (,) 0. 0 0 0..... numero di volte in cui esce testa Figura : I risultati favorevoli all
Numero di successi su n prove Risultati possibili lanciando, volte una moneta. numero di volte in cui esce croce... (,) 0. 0 0 0..... numero di volte in cui esce testa Figura : I risultati favorevoli all
Statistica descrittiva I. La frequenza
 Statistica descrittiva I. La frequenza Supponiamo di ripetere n volte un esperimento che può dare esito 0 o 1, il numero di uni su n ripetizioni è detto frequenza di 1: f 1,n = #{esperimenti con esito
Statistica descrittiva I. La frequenza Supponiamo di ripetere n volte un esperimento che può dare esito 0 o 1, il numero di uni su n ripetizioni è detto frequenza di 1: f 1,n = #{esperimenti con esito
CALCOLO DELLE PROBABILITA - 14 Gennaio 2015 CdL in STAD, SIGAD
 Cognome e Nome:....................................... Matricola............. CdS............. CALCOLO DELLE PROBABILITA - 4 Gennaio 5 CdL in STAD, SIGAD Motivare dettagliatamente le risposte su fogli
Cognome e Nome:....................................... Matricola............. CdS............. CALCOLO DELLE PROBABILITA - 4 Gennaio 5 CdL in STAD, SIGAD Motivare dettagliatamente le risposte su fogli
Variabili aleatorie discrete. Giovanni M. Marchetti Statistica Capitolo 5 Corso di Laurea in Economia
 Variabili aleatorie discrete Giovanni M. Marchetti Statistica Capitolo 5 Corso di Laurea in Economia 2015-16 1 / 45 Variabili aleatorie Una variabile aleatoria è simile a una variabile statistica Una variabile
Variabili aleatorie discrete Giovanni M. Marchetti Statistica Capitolo 5 Corso di Laurea in Economia 2015-16 1 / 45 Variabili aleatorie Una variabile aleatoria è simile a una variabile statistica Una variabile
P(X > 0) = P(X 1 = 1) + P(X 1 = 1, X 2 = 1, X 3 = 1) =
 1 Esercizi settimana 3 Esercizio 1. Un urna contiene 8 palline bianche, 4 nere e rosse. Si assuma di vincere e ogni volta che si estragga una pallina nera, si perda 1e per ogni pallina bianca e non succeda
1 Esercizi settimana 3 Esercizio 1. Un urna contiene 8 palline bianche, 4 nere e rosse. Si assuma di vincere e ogni volta che si estragga una pallina nera, si perda 1e per ogni pallina bianca e non succeda
Variabili casuali (1, T ) 1+0=1 1/16 (1 T ) 1 1/16 (1, C) 1+1=2 1/16 (1 C) 1 1/16 (1, T ) 9+0=9 1/16 (9, C) 9+1=10 1/16
 Variabili casuali Soluzione Es.. Lo spazio campionario Ω è costituito da tutti gli accoppiamenti asso e T o C e nove con T o C quindi 4*2 +4*2 = 6 coppie di valori: Ω = {, T,, T,, T, T,, C,, C,, C,, C,,
Variabili casuali Soluzione Es.. Lo spazio campionario Ω è costituito da tutti gli accoppiamenti asso e T o C e nove con T o C quindi 4*2 +4*2 = 6 coppie di valori: Ω = {, T,, T,, T, T,, C,, C,, C,, C,,
UNIVERSITÀ di ROMA TOR VERGATA
 UNIVERSITÀ di ROMA TOR VERGATA Corso di Laurea Magistrale in Scienze della Nutrizione Umana Corso di Statistica Medica, anno 205- P.Baldi Lista di esercizi 5, 8 febbraio 20. Esercizio Si fanno 25 estrazioni
UNIVERSITÀ di ROMA TOR VERGATA Corso di Laurea Magistrale in Scienze della Nutrizione Umana Corso di Statistica Medica, anno 205- P.Baldi Lista di esercizi 5, 8 febbraio 20. Esercizio Si fanno 25 estrazioni
Matematica II: Calcolo delle Probabilità e Statistica Matematica
 Matematica II: Calcolo delle Probabilità e Statistica Matematica ELT A-Z Docente: dott. F. Zucca Esercitazione # 3 1 Distribuzione di Bernoulli e Distribuzione Binomiale Esercizio 1 Sia n un intero maggiore
Matematica II: Calcolo delle Probabilità e Statistica Matematica ELT A-Z Docente: dott. F. Zucca Esercitazione # 3 1 Distribuzione di Bernoulli e Distribuzione Binomiale Esercizio 1 Sia n un intero maggiore
ES.2.3. è pari ad 1. Una variabile aleatoria X che assume valori su tutta la retta si dice distribuita
 ES.2.3 1 Distribuzione normale La funzione N(x; µ, σ 2 = 1 e 1 2( x µ σ 2 2πσ 2 si chiama densità di probabilità normale (o semplicemente curva normale con parametri µ e σ 2. La funzione è simmetrica rispetto
ES.2.3 1 Distribuzione normale La funzione N(x; µ, σ 2 = 1 e 1 2( x µ σ 2 2πσ 2 si chiama densità di probabilità normale (o semplicemente curva normale con parametri µ e σ 2. La funzione è simmetrica rispetto
2. Introduzione alla probabilità
 . Introduzione alla probabilità Carla Seatzu, 8 Marzo 008 Definizioni preliminari: Prova: è un esperimento il cui esito è aleatorio Spazio degli eventi elementari: è l insieme Ω di tutti i possibili esiti
. Introduzione alla probabilità Carla Seatzu, 8 Marzo 008 Definizioni preliminari: Prova: è un esperimento il cui esito è aleatorio Spazio degli eventi elementari: è l insieme Ω di tutti i possibili esiti
) la sua densità discreta sarà della forma. p X (0) = 1 2, p X(1) = 1 2,
 Esercizi settimana 6 Esercizi applicati Esercizio. Siano X e Y due v.a. discrete indipendenti tali che X B(, ) e Y B(, ), n 0. (i) Si calcoli la legge di X + Y ; (ii) Si calcoli la legge di X Y ; (iii)
Esercizi settimana 6 Esercizi applicati Esercizio. Siano X e Y due v.a. discrete indipendenti tali che X B(, ) e Y B(, ), n 0. (i) Si calcoli la legge di X + Y ; (ii) Si calcoli la legge di X Y ; (iii)
Primi elementi di Probabilità
 Primi elementi di Probabilità Sergio Polidoro Dipartimento di Matematica, Università di Bologna In queste dispense vengono introdotte le nozioni di valore atteso e di varianza per variabili aleatorie discrete
Primi elementi di Probabilità Sergio Polidoro Dipartimento di Matematica, Università di Bologna In queste dispense vengono introdotte le nozioni di valore atteso e di varianza per variabili aleatorie discrete
Esercizi settimana 4. Esercizi applicati. Esercizio 1. Si considerino tre monete truccate, ognuna con probabilità 2 3
 1 Esercizi settimana Esercizi applicati Esercizio 1. Si considerino tre monete truccate, ognuna con probabilità 3 di ottenere testa. Se scegliete la prima moneta vincete 10 punti se esce testa e punti
1 Esercizi settimana Esercizi applicati Esercizio 1. Si considerino tre monete truccate, ognuna con probabilità 3 di ottenere testa. Se scegliete la prima moneta vincete 10 punti se esce testa e punti
CP110 Probabilità: Esame 5 giugno Testo e soluzione
 Dipartimento di Matematica, Roma Tre Pietro Caputo 21-11, II semestre 5 giugno, 212 CP11 Probabilità: Esame 5 giugno 212 Testo e soluzione 1. (6 pts) Sette biglietti numerati da 1 a 7 vengono distribuiti
Dipartimento di Matematica, Roma Tre Pietro Caputo 21-11, II semestre 5 giugno, 212 CP11 Probabilità: Esame 5 giugno 212 Testo e soluzione 1. (6 pts) Sette biglietti numerati da 1 a 7 vengono distribuiti
Esercitazione 4 del corso di Statistica (parte 2)
 Esercitazione 4 del corso di Statistica (parte ) Dott.ssa Paola Costantini Febbraio Esercizio n. Il tempo di percorrenza del treno che collega la stazione di Roma Termini con l aeroporto di Fiumicino è
Esercitazione 4 del corso di Statistica (parte ) Dott.ssa Paola Costantini Febbraio Esercizio n. Il tempo di percorrenza del treno che collega la stazione di Roma Termini con l aeroporto di Fiumicino è
