Metodi statistici per la ricerca sociale Capitolo 11. Regressione Multipla e Correlazione
|
|
|
- Albano Mosca
- 5 anni fa
- Visualizzazioni
Transcript
1 Metodi statistici per la ricerca sociale Capitolo 11. Regressione Multipla e Correlazione Alessandra Mattei Dipartimento di Statistica, Informatica, Applicazioni (DiSIA) Università degli Studi di Firenze mattei@disia.unifi.it LM 88 SOCIOLOGIA E RICERCA SOCIALE A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 1 / 70
2 Relazioni Multivariate Lo studio di un fenomeno collettivo richiede in genere la rilevazione, su ogni singola unità statistica, di molteplici caratteri che devono a essere analizzati simultaneamente Analisi delle relazioni che intercorrono tra le variabili che caratterizzano il fenomeno Variabili di controllo A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 2 / 70
3 Variabili di controllo Obiettivo: Studiare l associazione tra una variabile Y e una variabile X 1 Studiare l associazione tra Y e X 1 controllando per le altre variabili: Come cambia l associazione tra X 1 e Y tenendo conto della presenza di altre variabili? Controllare (aggiustare) per altre variabili significa rimuovere l influenza di tali variabili fissando il loro valore Studi sperimentali: I fattori di controllo (di stratificazione) sono fissati dallo sperimentatore e mantenuti costanti Studi osservazionali: Raggruppare unità con valori uguali (o simili) delle variabili di controllo A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 3 / 70
4 Variabili di controllo: Esempi Esempio 1: Studio sperimentale Obiettivo: Valutare l effetto della dimensione delle classi in asili sul punteggio a un test cognitivo Unità di analisi: Insegnante Variabile esplicativa di interesse (Trattamento): Classe piccola (13-17 bambini) versus classe regolare (22-25 bambini) Variabile di controllo (Fattore di stratificazione): Asilo Variabile risultato (variabile al livello di classe): media dei punteggi al test cognitivo dei bambini della classe a cui un insegnante è assegnato Esempio 2: Studio osservazionale Studio della relazione tra reddito e gli anni di istruzione Il reddito può essere influenzato dal genere Variabile di controllo: Genere Si può controllare per il genere analizzando l associazione tra il reddito e gli anni di istruzione separatamente per ogni livello della variabile di controllo A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 4 / 70
5 Il modello di regressione lineare multipla I dati consistono di n osservazioni su una variabile dipendente (risposta), Y, e k variabili esplicative X 1,..., X k Osservazione Risposta Variabili esplicative u i Y i x i1 x i2 x ik 1 y 1 x 11 x 12 x 1k 2 y 2 x 21 x 22 x 2k 3 y 3 x 31 x 32 x 3k n y n x n1 x n2 x nk A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 5 / 70
6 Performance delle scuole elementari u i y i x i1 x i2 x i3 u i y i x i1 x i2 x i u = Scuola elementare (n = 24) Y = Indice di performance accademiche della scuola X 1 = Dimensione media di classe X 2 = Percentuale di insegnanti di ruolo X 3 = Percentuale di studenti le cui famiglie hanno un reddito al di sotto della soglia di povertà A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 6 / 70
7 Performance delle scuole elementari Ŷ i = x i1 Ŷ i = x i2 Indice di performance della scuola Indice di performance della scuola Dimensione media di classe Percentuale insegnanti di ruolo A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 7 / 70
8 Performance delle scuole elementari: Diagramma a dispersione tridimensionale Indice di performance della scuola Percentuale insegnanti di ruolo Dimensione media di classe A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 8 / 70
9 Il modello di regressione lineare multipla Le osservazioni y 1,..., y i,..., y n sono realizzazioni di variabili aleatorie Y 1,..., Y i,..., Y n Normali indipendenti aventi media che è funzione lineare delle variabili esplicative X 1,..., X k, e varianza costante indipendentemente dal valore delle variabili esplicative X 1,..., X k : Per i = 1,..., n Y i X i1 = x i1,... X ik = x ik N(β 0 + β 1 x i1 + + β k x ik, σ 2 ) indipendenti Quindi, per ogni i = 1,..., n e E (Y i X i1 = x i1,... X ik = x ik ) = β 0 + β 1 x i1 + + β k x ik Var(Y i X i = x i ) = σ 2 (ipotesi di omoschedasticità) A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 9 / 70
10 Il modello di regressione lineare multipla: Assunzioni Assunzione 1. Per ogni unità i = 1,..., n Y i = β 0 + β 1 x i1 + β 2 x i2 + + β k x ik + ɛ i Assunzione 2. Gli errori ɛ i, i = 1,..., n, sono variabili aleatorie indipendenti aventi media nulla e varianza costante indipendentemente dal valore delle variabili esplicative X 1,..., X k : Per i = 1,..., n ɛ i N(0, σ 2 ) indipendenti A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 10 / 70
11 Il modello di regressione lineare multipla Esempio: Performance delle scuole elementari Ê (Y i X i1 = x i1, X i2 = x i2 ) = x i x i2 Indice di performance della scuola Percentuale insegnanti di ruolo Dimensione media di classe A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 11 / 70
12 Interpretazione dei coefficienti di regressione Modello di regressione lineare multipla Y i = β 0 + β 1 x i1 + + β k x ik + ɛ i i = 1,..., n I parametri di regressione β 1,..., β k sono chiamati coefficienti di regressione parziale Il parametro β 0 (constante) rappresenta il valore atteso della variabile risposta Y per X 1 = X 2 = = X k = 0 E (Y i X i1 = 0, X i2 = 0,..., X ik = 0) = β 0 + β β k 0 = β 0 Il parametro β j (coefficiente di regressione parziale) descrive come la variabile risposta Y varia in media per ogni incremento unitario della variabile esplicativa X j quando tutte le altre variabili sono tenute costanti La grandezza della variazione non dipende dai valori a cui sono fissate le altre variabili esplicative Il parametro β j rappresenta l effetto (il contributo) della variabile esplicativa X j controllando per le altre variabili A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 12 / 70
13 Interpretazione dei coefficienti di regressione Esempio: Performance delle scuole elementari Y i = β 0 + β 1 x i1 + β 2 x i2 + ɛ i Ŷ i = β 0 + β 1 x i1 + β 2 x i2 = x i x i2 Le performance attese di scuole elementari con dimensione media di classe nulla e percentuale di insegnanti di ruolo pari a zero sono Per un incremento unitario della dimensione media di classe le performance attese delle scuole elementari diminuiscono di 2.31 punti, fissato il valore della percentuale di insegnanti di ruolo, ossia controllando per la percentuale di insegnanti di ruolo Per un incremento unitario nella percentuale di insegnanti di ruolo, le performance delle scuole elementari aumentano in media di 0.58 punti, fissato il valore della dimensione media di classe, ossia controllando per dimensione media di classe A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 13 / 70
14 Interpretazione dei coefficienti di regressione Esempio: Performance delle scuole elementari Ŷ i = β 0 + β 1 x i1 + β 2 x i2 = x i x i2 Indice di performance della scuola Percentuale insegnanti di ruolo Dimensione media di classe A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 14 / 70
15 Interpretazione dei coefficienti di regressione: Regressioni parziali Esempio: Performance delle scuole Ŷ i = x i x i2 = x i1 se x x i1 se x x i1 se x2 = 70 (a) = 80 (b) = 90 (c) Indice di performance della scuola (c) (b) (a) Dimensione media di classe A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 15 / 70
16 Interpretazione dei coefficienti di regressione: Regressioni parziali Esempio: Performance delle scuole Ŷ i = xi x i2 = x i2 se x x i2 se x x i2 se x1 = 16 (a) = 20 (b) = 24 (c) Indice di performance della scuola (a) (b) (c) Percentuale insegnanti di ruolo A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 16 / 70
17 Stima puntuale dei coefficienti di regressione Il metodo dei minimi quadrati Il metodo dei minimi quadrati consiste nel ricercare quei valori di β 0, β 1,..., β k che rendono minima la funzione G(β 0, β 1,..., β k ) = Valori Teorici n i=1 ŷ i = β 0 + β 1 x i1 + + β k x ik (y i β 0 β 1 x i1 β k x ik ) 2 i = 1,..., n I valori teorici sono i valori di Y forniti dal modello di regressione stimata in corrispondenza dei valori osservati x i1,..., x ik, i = 1,..., n La funzione di regressione stimata fornisce una stima della media di Y al variare di X 1,..., X k Residui di regressione ê i = y i ŷ i = y i β 0 β 1 x i1 β k x ik i = 1,..., n A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 17 / 70
18 Valori teorici e residui di regressione Esempio: Performance delle scuole elementari Ŷ i = β 0 + β 1 x i1 + β 2 x i2 = x i x i2 Scuola x 1 x 2 y i ŷ i ê i Ŷ 10 = = ê 24 = Y 24 Ŷ24 = = 73.3 ( ) = 0.20 A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 18 / 70
19 Alcune proprietà Il valore atteso della variabile risposta in corrispondenza dei valori (x 1,..., x k ) è y β 0 + β 1 x β k x k = y La somma (media) dei valori teorici è uguale alla somma (media) dei valori osservati n i=1 ŷ i = n i=1 y i ŷ = 1 n La somma dei residui è uguale a zero ê ê n = n i=1 n i=1 ŷ i = 1 n ê i = 0 n i=1 y i = y A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 19 / 70
20 Esempio: Performance delle scuole elementari Ŷ i = β 0 + β 1 x i1 + β 2 x i2 = x i x i2 x 1 = = x 2 = = y = = β 0 + β 1 x 1 + β 2 x 2 = = y Indice di performance della scuola Percentuale insegnanti di ruolo i=1 ŷ i = = Dimensione media di classe 24 y i i=1 e 24 i=1 ê i = 0 A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 20 / 70
21 Scomposizione della somma dei quadrati Somma dei Somma dei Somma dei Quadrati = Quadrati della + Quadrati degli Totale Regressione Errori n i=1 (y i y) 2 = n i=1 (ŷ i y) 2 + (y i ŷ i ) 2 n i=1 A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 21 / 70
22 Scomposizione della somma dei quadrati Somma dei Quadrati Totale Devianza Totale TSS = n i=1 (y i y) 2 = n i=1 y 2 i n y 2 Somma dei Quadrati di Regressione Devianza di Regressione (Devianza Spiegata): Devianza dei valori teorici RSS = n i=1 (ŷ i y) 2 Somma dei Quadrati dei Residui Devianza Residua SSE = n i=1 (y i ŷ i ) 2 = n i=1 (ê i ) 2 A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 22 / 70
23 Indice di determinazione multipla R 2 = RSS TSS = 1 SSE TSS Indica la proporzione di variabilità totale di Y spiegata dalla variabili esplicative X 1,..., X k attraverso il modello di regressione R 2 non dipende dall unità di misura delle variabili 0 R 2 1 R 2 = 0 (RSS = 0 e SSE = TSS) ŷ i = β 0 + β 1 x i1 + + β k x ik = β 0 = y per ogni i R 2 = 1 (RSS = TSS e SSE = 0): tutti i residui sono nulli (il modello passa per tutti i punti campionari) R 2 NON può diminuire se si aggiungono variabili esplicative R 2 R 2 YX j per ogni j = 1,..., k A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 23 / 70
24 Indice di determinazione multipla Esempio: Performance delle scuole elementari Scuola y i ŷ i (y i ȳ) 2 (ŷ i ȳ) 2 êi Totale A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 24 / 70
25 Indice di determinazione multipla Esempio: Performance delle scuole elementari TSS = RSS = SSE = TSS = = = RSS + SSE R 2 = RSS TSS = = R 2 = 1 SSE TSS = = = L 89.4% della variabilità totale delle performance delle scuole è spiegata dal modello di regressione lineare Si noti che R 2 = > R 2 Y,X 1 = e R 2 = > R 2 Y,X 2 = A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 25 / 70
26 Coefficiente di correlazione multipla Il coefficiente di correlazione multipla è il coefficiente di correlazione campionario tra i valori osservati della variabile risposta e i valori teorici R = r Y, Ŷ = s Y,Ŷ s Y sŷ n (y i ȳ) (ŷ i ŷ) i=1 = n n (y i ȳ) 2 (ŷ i ŷ) 2 i=1 i=1 0 R 1 Si può dimostrare che R = + (R 2 ) A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 26 / 70
27 Coefficiente di correlazione multipla Esempio: Performance delle scuole elementari Scuola y i ŷ i (y i ȳ) 2 (ŷ i ȳ) 2 êi Totale A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 27 / 70
28 Coefficiente di correlazione multipla Esempio: Performance delle scuole elementari R = r Y, Ŷ = = R = + R 2 = = A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 28 / 70
29 Indice di determinazione multipla corretto R 2 Adjusted = 1 SSE/(n k 1) TSS/(n 1) R 2 Adjusted R2 Introducendo una nuova variabile esplicativa nel modello R 2 Adjusted può aumentare o diminuire a seconda di quanto si riduce la somma dei quadrati dei residui (SSE) Può assumere valori negativi A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 29 / 70
30 Indice di determinazione multipla corretto Esempio: Performance delle scuole elementari Quindi TSS = RSS = SSE = n = 24 k = 2 R 2 Adjusted /(24 2 1) = /(24 1) = = = Modello R 2 RAdjusted 2 Solo x Solo x x 2 + x A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 30 / 70
31 Stima della varianza degli errori s 2 = SSE n k 1 = ê ê2 n n k 1 = n i=1 ê2 i n k 1 = n i=1 ê2 i gdl È uno stimatore non distorto della varianza degli errori σ 2 Errore Standard di regressione s = s 2 n i=1 = ê2 i n k 1 s è una misura della variabilità degli scostamenti dei valori osservati dai valori teorici: misura la dispersione media dello stimatore intorno al suo valore atteso A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 31 / 70
32 Stima della varianza degli errori Esempio: Performance delle scuole elementari e Quindi s 2 = Ŷ i = β 0 + β 1 x i1 + β 2 x i2 = x i x i2 SSE = n = 24 SSE n k 1 = = e s = s 2 = = 3.44 A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 32 / 70
33 Stimatori dei minimi quadrati Nel modello di regressione multipla le caratteristiche della popolazione che interessa studiare sono i coefficienti β 0, β 1,..., β k Indichiamo con B 0, B 1,..., B k gli stimatori dei minimi quadrati Il valori assunti da B 0, B 1,..., B k in corrispondenza di un particolare campione sono detto stime dei minimi quadrati dei coefficienti di regressione β 0, β 1,..., β k : β 0, β 1,..., β k = stime dei minimi quadrati dei coefficienti di regressione β 0, β 1,..., β k Gli stimatori dei minimi quadrati hanno buone proprietà: Sono stimatori non distorti con varianza minima nella classe degli stimatori corretti di un certo tipo A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 33 / 70
34 Inferenza per i parametri del modello di regressione B j N (β j, var( B j )) B j β j e.s.( B N (0, 1) j ) dove e.s.( B j ) = j = 0, 1,..., k var( B j ) = σ 2 c jj errore standard dello stimatore B j. dove B j β j ê.s.( B j ) t n k 1 ê.s.( B j ) = s 2 c jj s 2 = SSE n k 1 = n i=1 ê2 i n k 1 = n i=1 (y i ŷ i ) 2 n k 1 j = 0, 1,..., k A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 34 / 70
35 Intervalli di confidenza per i coefficienti di regressione Fissato il livello di confidenza 1 α IC 1 α (β j ) = [ β j t n k 1 (α/2) ê.s.( B j ); β j + t n k 1 (α/2) ê.s.( B j )] dove t n k 1 (α/2) è tale che Pr ( t α/2,n k 1 < t n k 1 < t α/2,n k 1 ) = 1 α A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 35 / 70
36 Intervalli di confidenza per i coefficienti di regressione Esempio: Performance delle scuole elementari Variabile Stima Errore Standard Constante Dimensione di classe Percentuale insegnanti di ruolo Errore standard di regressione s = 3.44 con 21 gdl Fissato il livello di confidenza 1 α = 0.95, t 21 (0.025) = IC 0.95 (β 0 ) = [ ; ] = [51.08; 99.34] IC 0.95 (β 1 ) = [ ; ] = [ 2.77; 1.85] IC 0.95 (β 2 ) = [ ; ] = [0.33; 0.83] A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 36 / 70
37 Verifica di ipotesi su un singolo parametro Per j = 0, 1,..., k H 0 β j = 0 versus H a β j 0 Statistica Test T = B j ê.s.( B j ) t n k 1 Sotto H 0 Regione di rifiuto al livello di significatività α RC α T t (n k 1),α/2 o T t (n k 1),α/2 Utilizzo del p value = 2 [1 Pr (t n k 1 T oss ; H 0 )] Se NON è rifiutata l ipotesi nulla H 0 β j = 0, allora si conclude che il coefficiente di regressione β j non è statisticamente diverso da zero al livello di significatività α: i dati suggeriscono che non esiste una associazione (parziale) tra Y e X j A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 37 / 70
38 Verifica di ipotesi Esempio: Performance delle scuole elementari Variabile Stima Errore Standard Constante Dimensione di classe Percentuale insegnanti di ruolo Errore standard di regressione s = 3.44 con 21 gdl Fissato il livello di significatività α = 0.05, t 21 (0.025) = T β1 oss = β Toss β0 0 = ê.s.( B 0 ) = = 6.48 β 1 ê.s.( B 1 ) = 2.31 β2 = Toss = 0.22 β 2 ê.s.( B 2 ) = = 4.83 Si ha evidenza al livello del 5% che le performance delle scuole elementari siano associate con la dimensione di classe, controllando per la percentuale di insegnanti di ruolo Si ha evidenza al livello del 5% che le performance delle scuole elementari siano associate con la percentuale di insegnanti di ruolo, controllando per la dimensione di classe A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 38 / 70
39 Intervalli di confidenza e verifica di ipotesi Ipotesi. Per j = 0, 1,..., k H 0 β j = 0 versus H a β j 0 Regione critica al livello di significatività α RC α = t t n k 1 (α/2) oppure t t n k 1 (α/2) Calcolato il valore osservato della statistica test T β j oss = H 0 β j = 0 se T β j oss RC α Fissato il livello di confidenza 1 α β j ± t n k 1 (α/2) ê.s.( B j ) β j ê.s.( B j ) si rifiuta L intervallo di confidenza include lo zero? No il parametro è significativamente diverso da zero: il valore osservato della statistica test appartiene alla regione critica Si il parametro NON è significativamente diverso da zero: il valore osservato della statistica test NON appartiene alla regione critica A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 39 / 70
40 Stimatore della risposta media: E[Y i X i1 = x 1,..., X ik = x k ] Ŷ x = B 0 + B 1 x B k x k Correttezza E (Ŷx ) = β 0 + β 1 x + + β k x k Varianza e errore Standard di Ŷ x 1,...,x k Var (Ŷx 1,...,x k ) e.s. (Ŷx 1,...,x k ) = Var (Ŷx 1,...,x k ) La varianza e l errore standard dello stimatore della risposta media, Ŷ x 1,...,x k, dipende da σ2 (la varianza degli errori del modello di regressione) Stimatore della varianza e dell errore standard dello stimatore di Ŷ x 1,...,x k Var (Ŷx 1,...,x k ) ê.s. (Ŷx 1,...,x k ) = Var ( Ŷ x 1,...,x k ) Intervallo di confidenza al livello di confidenza del (1 α) IC 1 α (E[Y i X i1 = x 1,..., X ik = x k ]) = Ŷx 1,...,x k ± t n k 1,α/2ê.s. (Ŷx 1,...,x k ) A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 40 / 70
41 Previsione Previsione Ŷ P x 1,...,x k = B 0 + B 1 x B k x k Varianza e errore Standard di Ŷ x 1,...,x k Var (Ŷ P x1,...,x ) e.s. (Ŷ P x k 1,...,x ) = k Var (Ŷ P x1,...,x ) k La varianza e l errore standard dello stimatore Ŷ P x1,...,x, dipende da σ 2 k (la varianza degli errori del modello di regressione) Stimatore della varianza e dell errore standard dello stimatore di Ŷ P x1,...,x k Var (Ŷ P x1,...,x ) ê.s. (Ŷ P x k 1,...,x ) = Var (Ŷ P k x1,...,x ) k Intervallo di confidenza al livello di confidenza del (1 α) IC 1 α (Y P x1,...,x ) = Ŷ P x k 1,...,x ± t k n k 1,α/2 ê.s. (Ŷ P x1,...,x ) k A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 41 / 70
42 Esempio: Performance delle scuole elementari x 1 = 20 e x 2 = 80 Ŷ i = β 0 + β 1 x i1 + β 2 x i2 = x i x i2 Stima della risposta media e previsione: Ŷ x 1,x 2 = ŶP x 1,x 2 = = Stima dell errore standard dello stimatore della risposta media e della previsione ê.s. (Ŷx 1,x 2 ) = P ê.s. (Ŷx1,x ) = Intervallo di confidenza al livello di confidenza del (1 α) = 0.95 IC 1 α (E[Y i X i1 = 20, X 2i = 80]) = ± = (73.754; ) Intervallo di previsione al livello di confidenza del (1 α) = 0.95 IC 1 α (Y P x1,x ) = ± = (67.938; ) 2 A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 42 / 70
43 Il test F Il test F è una procedura per verificare ipotesi riguardanti uno o più coefficienti di regressione Obiettivo: verificare l ipotesi che due o più parametri siano congiuntamente pari a zero Tale ipotesi sottintende che le variabili esplicative corrispondenti ai parametri supposti nulli non sono utili a spiegare la relazione lineare con la variabile dipendente Y A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 43 / 70
44 Il test F per valutare l influenza complessiva delle variabili esplicative Y i = β 0 + β 1 x i1 + β 2 x i2 + + β k x ik + ɛ i Ipotesi H 0 β 1 = β 2 = = β k = 0 versus H a Almeno un β j 0 Oppure, equivalentemente Statistica test j = 1,..., k H 0 Correlazione multipla nella popolazione = 0 versus H a Correlazione multipla nella popolazione > 0 F = R 2 /k (1 R 2 )/(n k 1) F k,(n k 1) Sotto H 0 A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 44 / 70
45 La distribuzione F Fisher F(1, 21) F(2, 50) F(10, 50) F(5, 50) F(2, 21) F(3, 21) F(5, 200) F(5, 30) F(5, 10) F gdl1,gdl 2 0 E[F gdl1,gdl 2 ] = gdl 2 /(gdl 2 2) A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 45 / 70
46 Il test F α = Livello di significatività del test Regione critica di livello α RC α F f k,(n k 1) (α) dove f k,(n k 1) (α) Pr(F gdl1,gdl 2 f k,(n k 1) (α)) = α p value = Pr(F gdl1,gdl 2 F oss ; H 0 ) α p value f α (gdl 1, gdl 2 ) F oss A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 46 / 70
47 Il test F Esempio: Performance delle scuole elementari Ipotesi: H 0 β 1 = β 2 = 0 versus H a β 1 0 o β 2 0 Scomposizione della somma dei quadrati Fonte di Variabilità Simbolo SQ GdL Regressione RSS k = 2 Residua SSE n k 1 = = 21 Totale TSS n 1 = 24 1 = 23 Valore osservato della statistica test R /2 = F oss = ( )/21 = α = 0.05 f 2,21 (0.05) = Regione critica di livello α = 0.05: RC 0.05 = F F oss = > = f 2,21 (0.05) I dati mostrano evidenza contro H 0 al livello di significatività del 5% p value = Pr(F 2, ; H 0 ) = A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 47 / 70
48 La statistica test F come rapporto tra medie dei quadrati Si dimostra che F = F = RSS/k SSE/(n k 1) = RMS MSE R 2 /k (1 R 2 )/(n k 1) = Media dei quadrati di regressione Media dei quadrati dei residui Tavola di Analisi della Varianza (Tavola ANOVA) Fonte di Somma dei Media dei Statistica Variabilità quadrati GdL quadrati F p value Regressione RSS k RMS RMS/MSE p value Residua SSE n k 1 MSE Totale TSS n 1 TMS A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 48 / 70
49 Tavola di Analisi della Varianza (Tavola ANOVA) Esempio: Performance delle scuole elementari Fonte di Somma dei Media dei Statistica Variabilità quadrati GdL quadrati F oss p value Regressione Residua Totale F oss = = A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 49 / 70
50 Modelli di regressione a confronto Modello esteso Y i = β 0 + β 1 x i1 + + β h x ih + + β k x ik + ɛ i versus Modell ridotto Y i = β 0 + β 1 x i1 + + β h x ih + ɛ i Oppure, equivalentemente, H 0 β h+1 = β h+2 = = β k = 0 versus H a Almeno un uguaglianza in H 0 è falsa A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 50 / 70
51 Modelli di regressione a confronto Esempio: Performance delle scuole elementari Y = Indice di performance accademiche della scuola X 1 = Dimensione media di classe X 2 = Percentuale di insegnanti di ruolo X 3 = Percentuale di studenti le cui famiglie hanno un reddito al di sotto della soglia di povertà Quindi Ossia M e Y i = β 0 + β 1 x i1 + β 2 x i2 + β 3 x i3 + ɛ i versus M r Y i = β 0 + β 1 x i1 + ɛ i H 0 β 2 = β 3 = 0 versus H a β 2 0 oppure β 3 0 A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 51 / 70
52 Modelli di regressione a confronto Valori teorici ŷ ie = β 0 + β 1 x i1 + + β h x ih + + β k x ik e ŷ ir = β 0 + β 1 x i1 + + β h x ih Somma dei quadrati degli errori Modello Esteso Modello Ridotto SSE e = n (y i ŷ ie ) 2 con gdl e = n k 1 i=1 SSE r = n (y i ŷ ir ) 2 con gdl r = n h 1 i=1 Indice di determinazione multipla R 2 e = 1 SSE e TSS e R 2 r = 1 SSE r TSS SSE r SSE e e R 2 r R 2 e e gdl r = n h 1 > gdl e = n k 1 A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 52 / 70
53 Modelli di regressione a confronto Statistica Test F = (SSE r SSE e )/(gdl r gdl e ) = (SSE r SSE e )/(k h) SSE e /gdl e SSE e /(n k 1) F = (R2 e R 2 r )/(gdl r gdl e ) (1 R 2 e )/gdl e = (R2 e R 2 r )/(k h) (1 R 2 e )/(n k 1) dove gdl r gdl e = k h = numero di termini aggiuntivi presenti nel modello esteso (numero di parametri posti a zero sotto H 0 ) Sotto l ipotesi nulla F F (gdlr gdl e),gdl e = F k h,n k 1 Regione di rifiuto al livello di significatività α: RC α F f k h,(n k 1) (α) p value = Pr(F k h,n k 1 F oss ; H 0 ) A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 53 / 70
54 Modelli di regressione a confronto Esempio: Performance delle scuole elementari Ipotesi M e Y i = β 0 + β 1 x i1 + β 2 x i2 + β 3 x i3 + ɛ i versus M r Y i = β 0 + β 1 x i1 + ɛ i H 0 β 2 = β 3 = 0 versus H a β 2 0 oppure β 3 0 Statistica test F F oss = = Modello SSE GdL R 2 Ridotto Esteso Totale ( )/(22 20) /20 ( )/(22 20) ( )/20 = / /20 = 14.3 = / /20 = 14.3 A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 54 / 70
55 Modelli di regressione a confronto Esempio: Performance delle scuole elementari Regione critica al livello di significatività α = 0.05: RC 0.05 F f 2,20 (0.05) = 3.49 F oss = 14.3 > 3.49 I dati mostrano evidenza contraria all ipotesi nulla al livello di significatività del 5%: Al livello di significatività del 5% il modello esteso è preferibile al modello ridotto p value p value = Pr(F 2, ; H 0 ) = A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 55 / 70
56 Modelli di regressione a confronto Esempio: Performance delle scuole elementari Ipotesi M e Y i = β 0 + β 1 x i1 + β 2 x i2 + β 3 x i3 + ɛ i versus M r Y i = β 0 + β 1 x i1 + β 2 x i2 + ɛ i Statistica test F F oss = H 0 β 3 = 0 versus H a β 3 0 Modello SSE GdL R 2 Ridotto Esteso Totale ( )/(21 20) /20 = /20 = 3.05 Regione critica al livello di significatività α = 0.05: RC 0.05 F f 1,20(0.05) = 4.35 F oss = 3.05 < 4.35 I dati non mostrano evidenza contraria all ipotesi nulla al livello di significatività del 5%: Al livello di significatività del 5% il modello ridotto è preferibile al modello esteso p value = Pr(F 1, ; H 0) = A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 56 / 70
57 Relazione tra la statistica test F e la statistica test T H 0 β j = 0 versus H a β j 0 j = 0, 1,..., k Statistica Test B j F = ( ê.s.( B j ) ) t 2 n k 1 F 1,(n k 1) Regione critica di livello α 2 = (T ) 2 F 1,n k 1 Sotto H 0 RC α F f 1,(n k 1) (α) = t 2 (n k 1) (α/2) p value Pr(F 1,n k 1 F oss ; H 0 ) = Pr (t n k 1 T oss o t n k 1 T oss ; H 0 ) A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 57 / 70
58 Test F e Test T Esempio: Performance delle scuole elementari H 0 β 3 = 0 versus H a β 3 0 Errore Variabile Stima Standard t p value Constante Dimensione media di classe Percentuale insegnanti di ruolo Percentuale studenti poveri Errore standard di regressione s = 3.28 con 20 gdl Fissato il livello di significatività α = 0.05, t 20(0.025) = F 1,20(0.05) = 4.35 = (2.086) 2 = t 2 20(0.025) F β 3 oss = (T β 3 oss) 2 = ( ) = ( 1.75) 2 = 3.05 p value = Pr(F 1, ; H 0) = Un procedimento analogo può essere applicato per gli altri coefficienti A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 58 / 70
59 Test F e test T nel modello di regressione lineare semplice Y i = β 0 + β 1 x i1 + ɛ i1 Errore Variabile Stima Standard t p value Constante Dimensione media di classe Errore standard di regressione s = con 22 gdl Fonte di Somma dei Media dei Statistica Variabilità quadrati GdL quadrati F p value Regressione Residua Totale F oss = = = ( 8.742)2 = T 2 A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 59 / 70
60 Modelli di regressione a confronto: Modello Esteso versus Modello Nullo Ipotesi M e Y i = β 0 + β 1 x i1 + + β k x ik + ɛ i versus M r Y i = β 0 + ɛ i H 0 β 1 = = β k = 0 versus H a Almeno un uguaglianza in H 0 è falsa Statistica test F = (SSE r SSE e )/(k h) SSE e /(n k 1) Modello SSE GdL Ridotto TSS n 1 Esteso SSE n k 1 Regione critica al livello di significatività α = RC α p value = Pr(F k,n k 1 F oss ; H 0 ) RSS/k SSE/(n k 1) = RMS MSE F k,n k 1 Sotto H 0 F f k,n k 1 (α) A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 60 / 70
61 Modello Esteso versus Modello Nullo Esempio: Performance delle scuole elementari Sistema di ipotesi M e Y i = β 0 + β 1 x i1 + β 2 x i2 + ɛ i versus M r Y i = β 0 + ɛ i Statistica test H 0 β 1 = β 2 = 0 versus H a β 1 0 oppure β 2 0 F oss = (SSE r SSE e )/(k h) = SSE e /(n k 1) oppure... Modello SSE GdL Ridotto Esteso Totale ( )/(2 0) /21 = A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 61 / 70
62 Modello Esteso versus Modello Nullo Esempio: Performance delle scuole elementari Tavola ANOVA F oss = Fonte di Somma dei Media dei Statistica Variabilità quadrati GdL quadrati F oss p value Regressione Residua Totale RSS/k ( )/(2 0) = = SSE e /(n k 1) / = Regione critica al livello di significatività α = 0.05 RC 0.05 F f 2,21 (0.05) = F oss > 3.467: I dati mostrano evidenza contraria all ipotesi nulla al livello di significatività del 5%. p value p value = Pr(F 2, ; H 0 ) = A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 62 / 70
63 Interazione tra variabili (Effetti di secondo ordine) Esiste interazione tra due variabili esplicative quantitative se l associazione tra la variabile risposta Y e ciascuna delle due variabili cambia al variare del valore dell altra variabile esplicativa Termine di interazione = prodotto tra le due variabili (prodotto incrociato) Esempio Y i = β 0 + β 1 x i1 + β 2 x i2 + β 3 x i1 x i2 + ɛ i Y i = (β 0 + β 2 x i2 ) + (β 1 + β 3 x i2 ) x i1 + ɛ i Y i = (β 0 + β 1 x i1 ) + (β 2 + β 3 x i1 ) x i2 + ɛ i La variazione attesa in Y per un incremento unitario di X 1 dipende dal valore di X 2. Analogamente la variazione attesa in Y per un incremento unitario di X 2 dipende dal valore di X 1 A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 63 / 70
64 Interpretazione dei coefficienti di regressione Esempio: Performance delle scuole elementari Ŷ i = β0 + β 1 x i1 + β 2 x i2 + β 3 x i1 x i2 = x i x i x i1 x i2 β 0 = = performance attese in scuole con dimensione media di classe zero e percentuale di insegnanti di ruolo zero β 1 = 1.15: Per le scuole in cui la percentuale di insegnanti di ruolo è zero, un incremento unitario nella dimensione media di classe implica un incremento atteso nelle performance medie di 1.15 punti β 2 = 1.37: Per le scuole in cui la dimensione media di classe è zero, un incremento unitario della percentuale di insegnanti di ruolo implica un incremento atteso nelle performance medie di 1.37 punti β 3 = 0.04: l associazione parziale tra le performance delle scuole e la dimensione media di classe varia di 0.04 punti per ogni incremento unitario della percentuale di insegnanti di ruolo ovvero l associazione parziale tra le performance delle scuole e la percentuale di insegnanti di ruolo varia di 0.04 punti per ogni incremento unitario della dimensione media di classe A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 64 / 70
65 Interpretazione dei coefficienti di regressione Esempio: Performance delle scuole elementari Ŷ = x i xi x i1 xi2 Quindi x i1 se x2 = 70 (a) x i1 se x2 = 80 (b) x i1 se x2 = 90 (c) Indice di performance della scuola (c) (b) (a) Dimensione media di classe A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 65 / 70
66 Interpretazione dei coefficienti di regressione Esempio: Performance delle scuole elementari Ŷ = x i xi x i1 xi2 Quindi x i2 se x1 = 16 (a) x i2 se x1 = 20 (b) x i2 se x1 = 24 (c) Indice di performance della scuola (a) (b) (c) Percentuale insegnanti di ruolo A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 66 / 70
67 Verifica di ipotesi per il termine di interazione Per la verifica di ipotesi su un termine di interazione si procede in modo analogo alla verifica di ipotesi su un singolo coefficiente del modello di regressione Esempio: Y i = β 0 + β 1 x i1 + β 2 x i2 + β 3 x i1 x i2 + ɛ i Ipotesi H 0 β 3 = 0 versus H a β 3 0 Statistica Test B 3 T = ê.s.( B 3 ) t n k 1 k = 3 Sotto H 0 Regione critica al livello α: RC α T oss t n 3 1,α/2 o T oss t n 3 1,α/2 Se l evidenza contro l ipotesi nulla (ossia a favore della presenza di in termine di interazione tra due variabili esplicative) è debole in genere si preferisce eliminare il termine di interazione e considerare un modello con solo gli effetti principali delle due variabili Se l evidenza contro l ipotesi nulla (ossia a favore della presenza di in termine di interazione tra due variabili esplicative) è forte, allora è opportuno mantenere sia il termine di interazione sia gli effetti principali delle due variabili A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 67 / 70
68 Esempio: Performance delle scuole elementari Errore Variabile Stima Standard t p value Constante Dimensione media di classe Percentuale insegnanti di ruolo Interazione Errore standard di regressione s = con 20 gdl Fonte di Somma dei Media dei Statistica Variabilità quadrati GdL quadrati F p value Regressione Residua Totale Il termine di interazione non è significativamente diverso da zero Notare la perdita di significatività degli effetti principali delle due variabili rispetto al modello senza interazione a causa di un elevata correlazione tra le variabili esplicative e la loro interazione: r X1,X 1 X 2 = 0.906, r X2,X 1 X 2 = A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 68 / 70
69 Variabili esplicative centrate rispetto alla media Esempio: Performance delle scuole elementari Quindi Y i = β 0 + β 1 (x i1 x 1) + β 2 (x i2 x 2) + β 3 (x i1 x 1) (x i2 x 2) + ɛ i x 1 = e x 2 = Errore Variabile Stima Standard t p value Constante Dimensione media di classe centrata rispetto alla sua media Percentuale insegnanti di ruolo centrata rispetto alla sua media Interazione Errore standard di regressione s = con 20 gdl A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 69 / 70
70 Variabili esplicative centrate rispetto alla media Esempio: Performance delle scuole elementari β 0 = = performance attese in scuole con dimensione media di classe e percentuale di insegnanti di ruolo zero pari alle loro medie (x 1 = e x 2 = 80.33, rispettivamente) β 1 = 2.26: Per le scuole in cui la percentuale di insegnanti di ruolo è pari alla media, x 2 = 80.33, un incremento unitario nella dimensione media di classe (centrata) determina una riduzione attesa nelle performance medie di 2.26 punti β 2 = 0.55: Per le scuole in cui la dimensione media di classe è pari alla media, x 1 = 19.42, un incremento unitario della percentuale di insegnanti di ruolo (centrata), implica un incremento atteso nelle performance medie di 0.55 punti β 3 = 0.04: uguale al modello con variabili non centrate Gli errori standard dei coefficienti di regressione parziali associati alle variabili esplicative (centrate) sono più simili a quelli del modello senza interazione Le stime degli effetti principali sono più significativi A. Mattei (Università di Firenze) Metodi statistici per la ricerca sociale 70 / 70
Metodi statistici per la ricerca sociale Capitolo 13. Combinare regressione e ANOVA: predittori categoriali e quantitativi
 Metodi statistici per la ricerca sociale Capitolo 13. Combinare regressione e ANOVA: predittori categoriali e quantitativi Alessandra Mattei Dipartimento di Statistica, Informatica, Applicazioni (DiSIA)
Metodi statistici per la ricerca sociale Capitolo 13. Combinare regressione e ANOVA: predittori categoriali e quantitativi Alessandra Mattei Dipartimento di Statistica, Informatica, Applicazioni (DiSIA)
Metodi statistici per la ricerca sociale Capitolo 12. Confronto fra gruppi: L analisi della varianza (ANOVA)
 Metodi statistici per la ricerca sociale Capitolo 12. Confronto fra gruppi: L analisi della varianza (ANOVA) Alessandra Mattei Dipartimento di Statistica, Informatica, Applicazioni (DiSIA) Università degli
Metodi statistici per la ricerca sociale Capitolo 12. Confronto fra gruppi: L analisi della varianza (ANOVA) Alessandra Mattei Dipartimento di Statistica, Informatica, Applicazioni (DiSIA) Università degli
Statistica. Capitolo 12. Regressione Lineare Semplice. Cap. 12-1
 Statistica Capitolo 1 Regressione Lineare Semplice Cap. 1-1 Obiettivi del Capitolo Dopo aver completato il capitolo, sarete in grado di: Spiegare il significato del coefficiente di correlazione lineare
Statistica Capitolo 1 Regressione Lineare Semplice Cap. 1-1 Obiettivi del Capitolo Dopo aver completato il capitolo, sarete in grado di: Spiegare il significato del coefficiente di correlazione lineare
1. variabili dicotomiche: 2 sole categorie A e B
 Variabile X su scala qualitativa (due categorie) modello di regressione: variabili quantitative misurate almeno su scala intervallo (meglio se Y è di questo tipo e preferibilmente anche le X i ) variabili
Variabile X su scala qualitativa (due categorie) modello di regressione: variabili quantitative misurate almeno su scala intervallo (meglio se Y è di questo tipo e preferibilmente anche le X i ) variabili
Metodi Statistici per la Ricerca Sociale: Formulario
 Metodi Statistici per la Ricerca Sociale: Formulario Attenzione. Il Formulario contiene una selezione delle formule. Le formule non riportate sono supposte note Associazione tra variabili categoriche Misure
Metodi Statistici per la Ricerca Sociale: Formulario Attenzione. Il Formulario contiene una selezione delle formule. Le formule non riportate sono supposte note Associazione tra variabili categoriche Misure
Capitolo 12 La regressione lineare semplice
 Levine, Krehbiel, Berenson Statistica II ed. 2006 Apogeo Capitolo 12 La regressione lineare semplice Insegnamento: Statistica Corso di Laurea Triennale in Ingegneria Gestionale Facoltà di Ingegneria, Università
Levine, Krehbiel, Berenson Statistica II ed. 2006 Apogeo Capitolo 12 La regressione lineare semplice Insegnamento: Statistica Corso di Laurea Triennale in Ingegneria Gestionale Facoltà di Ingegneria, Università
s a Inferenza: singolo parametro Sistema di ipotesi: : β j = β j0 H 1 β j0 statistica test t confronto con valore t o p-value
 Inferenza: singolo parametro Sistema di ipotesi: H 0 : β j = β j0 H 1 : β j β j0 statistica test t b j - b s a jj j0 > t a, 2 ( n-k) confronto con valore t o p-value Se β j0 = 0 X j non ha nessuna influenza
Inferenza: singolo parametro Sistema di ipotesi: H 0 : β j = β j0 H 1 : β j β j0 statistica test t b j - b s a jj j0 > t a, 2 ( n-k) confronto con valore t o p-value Se β j0 = 0 X j non ha nessuna influenza
Metodi statistici per l economia (Prof. Capitanio) Slide n. 10. Materiale di supporto per le lezioni. Non sostituisce il libro di testo
 Metodi statistici per l economia (Prof. Capitanio) Slide n. 10 Materiale di supporto per le lezioni. Non sostituisce il libro di testo 1 REGRESSIONE LINEARE Date due variabili quantitative, X e Y, si è
Metodi statistici per l economia (Prof. Capitanio) Slide n. 10 Materiale di supporto per le lezioni. Non sostituisce il libro di testo 1 REGRESSIONE LINEARE Date due variabili quantitative, X e Y, si è
La regressione lineare semplice
 La regressione lineare semplice Il modello di regressione lineare semplice - 1 y = β 0 + βx + ε 10 8 Una retta nel piano Variabile Y 6 4 2 0 0 1 2 3 4 Variabile X 1 Il modello di regressione lineare semplice
La regressione lineare semplice Il modello di regressione lineare semplice - 1 y = β 0 + βx + ε 10 8 Una retta nel piano Variabile Y 6 4 2 0 0 1 2 3 4 Variabile X 1 Il modello di regressione lineare semplice
Statistica multivariata Donata Rodi 17/10/2016
 Statistica multivariata Donata Rodi 17/10/2016 Quale analisi? Variabile Dipendente Categoriale Continua Variabile Indipendente Categoriale Chi Quadro ANOVA Continua Regressione Logistica Regressione Lineare
Statistica multivariata Donata Rodi 17/10/2016 Quale analisi? Variabile Dipendente Categoriale Continua Variabile Indipendente Categoriale Chi Quadro ANOVA Continua Regressione Logistica Regressione Lineare
Metodi statistici per la ricerca sociale Capitolo 15. Regressione logistica: modellare variabili risposta categoriali
 Metodi statistici per la ricerca sociale Capitolo 15. Regressione logistica: modellare variabili risposta categoriali Alessandra Mattei Dipartimento di Statistica, Informatica, Applicazioni (DiSIA) Università
Metodi statistici per la ricerca sociale Capitolo 15. Regressione logistica: modellare variabili risposta categoriali Alessandra Mattei Dipartimento di Statistica, Informatica, Applicazioni (DiSIA) Università
Nel modello omoschedastico la varianza dell errore non dipende da i ed è quindi pari a σ 0.
 Regressione [] el modello di regressione lineare si assume una relazione di tipo lineare tra il valore medio della variabile dipendente Y e quello della variabile indipendente X per cui Il modello si scrive
Regressione [] el modello di regressione lineare si assume una relazione di tipo lineare tra il valore medio della variabile dipendente Y e quello della variabile indipendente X per cui Il modello si scrive
Metodi statistici per la ricerca sociale Capitolo 7. Confronto tra Due Gruppi Esercitazione
 Metodi statistici per la ricerca sociale Capitolo 7. Confronto tra Due Gruppi Esercitazione Alessandra Mattei Dipartimento di Statistica, Informatica, Applicazioni (DiSIA) Università degli Studi di Firenze
Metodi statistici per la ricerca sociale Capitolo 7. Confronto tra Due Gruppi Esercitazione Alessandra Mattei Dipartimento di Statistica, Informatica, Applicazioni (DiSIA) Università degli Studi di Firenze
Regressione Lineare Semplice e Correlazione
 Regressione Lineare Semplice e Correlazione 1 Introduzione La Regressione è una tecnica di analisi della relazione tra due variabili quantitative Questa tecnica è utilizzata per calcolare il valore (y)
Regressione Lineare Semplice e Correlazione 1 Introduzione La Regressione è una tecnica di analisi della relazione tra due variabili quantitative Questa tecnica è utilizzata per calcolare il valore (y)
Metodi statistici per la ricerca sociale Capitolo 12. Confronto fra gruppi: L analisi della varianza. Esercitazione
 Metodi statistici per la ricerca sociale Capitolo 12. Confronto fra gruppi: L analisi della varianza Esercitazione Alessandra Mattei Dipartimento di Statistica, Informatica, Applicazioni (DiSIA) Università
Metodi statistici per la ricerca sociale Capitolo 12. Confronto fra gruppi: L analisi della varianza Esercitazione Alessandra Mattei Dipartimento di Statistica, Informatica, Applicazioni (DiSIA) Università
Metodi statistici per la ricerca sociale Capitolo 13. Combinare regressione e ANOVA: predittori categoriali e quantitativi Esercitazione
 Metodi statistici per la ricerca sociale Capitolo 13. Combinare regressione e ANOVA: predittori categoriali e quantitativi Esercitazione Alessandra Mattei Dipartimento di Statistica, Informatica, Applicazioni
Metodi statistici per la ricerca sociale Capitolo 13. Combinare regressione e ANOVA: predittori categoriali e quantitativi Esercitazione Alessandra Mattei Dipartimento di Statistica, Informatica, Applicazioni
Correlazione e regressione
 Correlazione e regressione Correlazione 1 Come posso determinare il legame tra due o più variabili? Correlazione COEFFICIENTE DI CORRELAZIONE (r di Pearson) massimo consumo di ossigeno e prestazione nelle
Correlazione e regressione Correlazione 1 Come posso determinare il legame tra due o più variabili? Correlazione COEFFICIENTE DI CORRELAZIONE (r di Pearson) massimo consumo di ossigeno e prestazione nelle
Metodi statistici per la ricerca sociale Capitolo 9. Regressione Lineare e Correlazione Esercitazione
 Metodi statistici per la ricerca sociale Capitolo 9. Regressione Lineare e Correlazione Esercitazione Alessandra Mattei Dipartimento di Statistica, Informatica, Applicazioni (DiSIA) Università degli Studi
Metodi statistici per la ricerca sociale Capitolo 9. Regressione Lineare e Correlazione Esercitazione Alessandra Mattei Dipartimento di Statistica, Informatica, Applicazioni (DiSIA) Università degli Studi
L'analisi bivariata (analisi della varianza e correlazione) Prof. Stefano Nobile. Corso di Metodologia della ricerca sociale
 L'analisi bivariata (analisi della varianza e correlazione) Prof. Stefano Nobile Corso di Metodologia della ricerca sociale L analisi della varianza (ANOVA) La tecnica con cui si esplorano le relazioni
L'analisi bivariata (analisi della varianza e correlazione) Prof. Stefano Nobile Corso di Metodologia della ricerca sociale L analisi della varianza (ANOVA) La tecnica con cui si esplorano le relazioni
Regressione & Correlazione
 Regressione & Correlazione Monia Ranalli Ranalli M. Dipendenza Settimana # 4 1 / 20 Sommario Regressione Modello di regressione lineare senplice Stima dei parametri Adattamento del modello ai dati Correlazione
Regressione & Correlazione Monia Ranalli Ranalli M. Dipendenza Settimana # 4 1 / 20 Sommario Regressione Modello di regressione lineare senplice Stima dei parametri Adattamento del modello ai dati Correlazione
LM 88 SOCIOLOGIA E RICERCA SOCIALE. Metodi Statistici per la Ricerca Sociale. Regressione lineare e correlazione
 LM 88 SOCIOLOGIA E RICERCA SOCIALE Metodi Statistici per la Ricerca Sociale Regressione lineare e correlazione 1. Su un campione di individui sono rilevati i caratteri X (peso in Kg) e Y (altezza in cm),
LM 88 SOCIOLOGIA E RICERCA SOCIALE Metodi Statistici per la Ricerca Sociale Regressione lineare e correlazione 1. Su un campione di individui sono rilevati i caratteri X (peso in Kg) e Y (altezza in cm),
STATISTICA. Esercitazione 5
 STATISTICA Esercitazione 5 Esercizio 1 Ad un esame universitario sono stati assegnati in modo casuale due compiti diversi con i seguenti risultati: Compito A Compito B Numero studenti 102 105 Media dei
STATISTICA Esercitazione 5 Esercizio 1 Ad un esame universitario sono stati assegnati in modo casuale due compiti diversi con i seguenti risultati: Compito A Compito B Numero studenti 102 105 Media dei
Test F per la significatività del modello
 Test F per la significatività del modello Per verificare la significatività dell intero modello si utilizza il test F Si vuole verificare l ipotesi H 0 : β 1 = 0,, β k = 0 contro l alternativa che almeno
Test F per la significatività del modello Per verificare la significatività dell intero modello si utilizza il test F Si vuole verificare l ipotesi H 0 : β 1 = 0,, β k = 0 contro l alternativa che almeno
Variabili indipendenti qualitative. In molte applicazioni si rende necessario l introduzione di un fattore a due o più livelli.
 Variabili indipendenti qualitative Di solito le variabili nella regressione sono variabili continue In molte applicazioni si rende necessario l introduzione di un fattore a due o più livelli Ad esempio:
Variabili indipendenti qualitative Di solito le variabili nella regressione sono variabili continue In molte applicazioni si rende necessario l introduzione di un fattore a due o più livelli Ad esempio:
per togliere l influenza di un fattore es.: quoziente di mortalità = morti / popolazione
 Rapporti statistici di composizione la parte rispetto al tutto percentuali di derivazione per togliere l influenza di un fattore es.: quoziente di mortalità = morti / popolazione di frequenza (tassi) rapporti
Rapporti statistici di composizione la parte rispetto al tutto percentuali di derivazione per togliere l influenza di un fattore es.: quoziente di mortalità = morti / popolazione di frequenza (tassi) rapporti
STATISTICA A K (60 ore)
 STATISTICA A K (60 ore) Marco Riani mriani@unipr.it http://www.riani.it Richiami sulla regressione Marco Riani, Univ. di Parma 1 MODELLO DI REGRESSIONE y i = a + bx i + e i dove: i = 1,, n a + bx i rappresenta
STATISTICA A K (60 ore) Marco Riani mriani@unipr.it http://www.riani.it Richiami sulla regressione Marco Riani, Univ. di Parma 1 MODELLO DI REGRESSIONE y i = a + bx i + e i dove: i = 1,, n a + bx i rappresenta
lezione 4 AA Paolo Brunori
 AA 2016-2017 Paolo Brunori dove eravamo arrivati - abbiamo individuato la regressione lineare semplice (OLS) come modo immediato per sintetizzare una relazione fra una variabile dipendente (Y) e una indipendente
AA 2016-2017 Paolo Brunori dove eravamo arrivati - abbiamo individuato la regressione lineare semplice (OLS) come modo immediato per sintetizzare una relazione fra una variabile dipendente (Y) e una indipendente
STATISTICA MULTIVARIATA SSD MAT/06
 Università degli studi di Ferrara Dipartimento di Matematica A.A. 2018/2019 I semestre STATISTICA MULTIVARIATA SSD MAT/06 LEZIONE 4 - Questioni di analisi e applicazione della regressione lineare Pratica
Università degli studi di Ferrara Dipartimento di Matematica A.A. 2018/2019 I semestre STATISTICA MULTIVARIATA SSD MAT/06 LEZIONE 4 - Questioni di analisi e applicazione della regressione lineare Pratica
Esercitazione 5 Sta/s/ca Aziendale
 Esercitazione 5 Sta/s/ca Aziendale David Aristei 12 maggio 2015 Si è interessa/ ad analizzare le determinan/ a livello aziendale della produ>vità del lavoro (PL, in migliaia di euro per dipendente) di
Esercitazione 5 Sta/s/ca Aziendale David Aristei 12 maggio 2015 Si è interessa/ ad analizzare le determinan/ a livello aziendale della produ>vità del lavoro (PL, in migliaia di euro per dipendente) di
Regressione lineare semplice
 Regressione lineare semplice Prof. Giuseppe Verlato Sezione di Epidemiologia e Statistica Medica, Università di Verona Statistica con due variabili var. nominale, var. nominale: gruppo sanguigno - cancro
Regressione lineare semplice Prof. Giuseppe Verlato Sezione di Epidemiologia e Statistica Medica, Università di Verona Statistica con due variabili var. nominale, var. nominale: gruppo sanguigno - cancro
R - Esercitazione 6. Andrea Fasulo Venerdì 22 Dicembre Università Roma Tre
 R - Esercitazione 6 Andrea Fasulo fasulo.andrea@yahoo.it Università Roma Tre Venerdì 22 Dicembre 2017 Il modello di regressione lineare semplice (I) Esempi tratti da: Stock, Watson Introduzione all econometria
R - Esercitazione 6 Andrea Fasulo fasulo.andrea@yahoo.it Università Roma Tre Venerdì 22 Dicembre 2017 Il modello di regressione lineare semplice (I) Esempi tratti da: Stock, Watson Introduzione all econometria
STATISTICA. Regressione-3 L inferenza per il modello lineare semplice
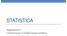 STATISTICA Regressione-3 L inferenza per il modello lineare semplice Regressione lineare: GRAFICO DI DISPERSIONE & & analisi residui A. Valutazione preliminare se una retta possa essere una buona approssimazione
STATISTICA Regressione-3 L inferenza per il modello lineare semplice Regressione lineare: GRAFICO DI DISPERSIONE & & analisi residui A. Valutazione preliminare se una retta possa essere una buona approssimazione
Il modello di regressione lineare multipla. Il modello di regressione lineare multipla
 Introduzione E la generalizzazione del modello di regressione lineare semplice: per spiegare il fenomeno d interesse Y vengono introdotte p, con p > 1, variabili esplicative. Tale generalizzazione diventa
Introduzione E la generalizzazione del modello di regressione lineare semplice: per spiegare il fenomeno d interesse Y vengono introdotte p, con p > 1, variabili esplicative. Tale generalizzazione diventa
Statistica economica
 Statistica economica a.a. 013/14 Dr. Luca Secondi 10.a. Output tipico di un modello di regressione lineare multipla 1 Le analisi basate sul modello di regressione prevedono la stima dei coefficienti associati
Statistica economica a.a. 013/14 Dr. Luca Secondi 10.a. Output tipico di un modello di regressione lineare multipla 1 Le analisi basate sul modello di regressione prevedono la stima dei coefficienti associati
Esercizi di statistica
 Esercizi di statistica Test a scelta multipla (la risposta corretta è la prima) [1] Il seguente campione è stato estratto da una popolazione distribuita normalmente: -.4, 5.5,, -.5, 1.1, 7.4, -1.8, -..
Esercizi di statistica Test a scelta multipla (la risposta corretta è la prima) [1] Il seguente campione è stato estratto da una popolazione distribuita normalmente: -.4, 5.5,, -.5, 1.1, 7.4, -1.8, -..
Tecniche di sondaggio
 SMID a.a. 2005/2006 Corso di Statistica per la Ricerca Sperimentale Tecniche di sondaggio 24/1/2006 Nomenclatura Indicheremo con P una popolazione, con N la sua numerosità, con k la sua etichetta e con
SMID a.a. 2005/2006 Corso di Statistica per la Ricerca Sperimentale Tecniche di sondaggio 24/1/2006 Nomenclatura Indicheremo con P una popolazione, con N la sua numerosità, con k la sua etichetta e con
Il modello di regressione (VEDI CAP 12 VOLUME IEZZI, 2009)
 Il modello di regressione (VEDI CAP 12 VOLUME IEZZI, 2009) Quesito: Posso stimare il numero di ore passate a studiare statistica sul voto conseguito all esame? Potrei calcolare il coefficiente di correlazione.
Il modello di regressione (VEDI CAP 12 VOLUME IEZZI, 2009) Quesito: Posso stimare il numero di ore passate a studiare statistica sul voto conseguito all esame? Potrei calcolare il coefficiente di correlazione.
Università del Piemonte Orientale Corso di Laurea in Medicina e Chirurgia. Corso di Statistica Medica. Correlazione. Regressione Lineare
 Università del Piemonte Orientale Corso di Laurea in Medicina e Chirurgia Corso di Statistica Medica Correlazione Regressione Lineare Corso di laurea in medicina e chirurgia - Statistica Medica Correlazione
Università del Piemonte Orientale Corso di Laurea in Medicina e Chirurgia Corso di Statistica Medica Correlazione Regressione Lineare Corso di laurea in medicina e chirurgia - Statistica Medica Correlazione
Esercitazione del
 Esercizi sulla regressione lineare. Esercitazione del 21.05.2013 Esercizio dal tema d esame del 13.06.2011. Si consideri il seguente campione di n = 9 osservazioni relative ai caratteri ed Y: 7 17 8 36
Esercizi sulla regressione lineare. Esercitazione del 21.05.2013 Esercizio dal tema d esame del 13.06.2011. Si consideri il seguente campione di n = 9 osservazioni relative ai caratteri ed Y: 7 17 8 36
CORSO DI STATISTICA (parte 1) - ESERCITAZIONE 6
 CORSO DI STATISTICA (parte 1) - ESERCITAZIONE 6 Dott.ssa Antonella Costanzo a.costanzo@unicas.it Esercizio 1. Associazione, correlazione e dipendenza tra caratteri In un collettivo di 11 famiglie è stata
CORSO DI STATISTICA (parte 1) - ESERCITAZIONE 6 Dott.ssa Antonella Costanzo a.costanzo@unicas.it Esercizio 1. Associazione, correlazione e dipendenza tra caratteri In un collettivo di 11 famiglie è stata
Lezione 18. Statistica. Alfonso Iodice D Enza Università degli studi di Cassino. Lezione 18. A. Iodice
 Statistica Alfonso Iodice D Enza iodicede@unicas.it Università degli studi di Cassino () Statistica 1 / 45 Outline 1 2 3 4 5 () Statistica 2 / 45 Modello di In molte applicazioni il ruolo delle variabili
Statistica Alfonso Iodice D Enza iodicede@unicas.it Università degli studi di Cassino () Statistica 1 / 45 Outline 1 2 3 4 5 () Statistica 2 / 45 Modello di In molte applicazioni il ruolo delle variabili
Lezione 15. L analisi della Varianza (ANOVA): i disegni entro i sogetti e misti. Argomenti della lezione: Disegni entro i soggetti
 Lezione 15 L analisi della Varianza (ANOVA): i disegni entro i sogetti e misti Argomenti della lezione: Disegni entro i soggetti Disegni misti Effect size e potenza Disegni entro i soggetti Gli stessi
Lezione 15 L analisi della Varianza (ANOVA): i disegni entro i sogetti e misti Argomenti della lezione: Disegni entro i soggetti Disegni misti Effect size e potenza Disegni entro i soggetti Gli stessi
Confronto fra gruppi: il metodo ANOVA. Nicola Tedesco (Statistica Sociale) Confronto fra gruppi: il metodo ANOVA 1 / 23
 Confronto fra gruppi: il metodo ANOVA Nicola Tedesco (Statistica Sociale) Confronto fra gruppi: il metodo ANOVA 1 / 23 1 Nella popolazione, per ciascun gruppo la distribuzione della variabile risposta
Confronto fra gruppi: il metodo ANOVA Nicola Tedesco (Statistica Sociale) Confronto fra gruppi: il metodo ANOVA 1 / 23 1 Nella popolazione, per ciascun gruppo la distribuzione della variabile risposta
Università del Piemonte Orientale Corso di Laurea in Medicina e Chirurgia. Corso di Statistica Medica. Correlazione. Regressione Lineare
 Università del Piemonte Orientale Corso di Laurea in Medicina e Chirurgia Corso di Statistica Medica Correlazione Regressione Lineare Corso di laurea in medicina e chirurgia - Statistica Medica Correlazione
Università del Piemonte Orientale Corso di Laurea in Medicina e Chirurgia Corso di Statistica Medica Correlazione Regressione Lineare Corso di laurea in medicina e chirurgia - Statistica Medica Correlazione
Corso di Laurea: Numero di Matricola: Esame del 31 maggio 2018 Tempo consentito: 120 minuti
 Corso di Laurea: Numero di Matricola: Esame del 31 maggio 2018 Tempo consentito: 120 minuti Professor Paolo Vitale Anno Accademico 2017-8 UdA, Scuola d Economia Domanda 1 [6 punti]. (a) La multi-collineartità
Corso di Laurea: Numero di Matricola: Esame del 31 maggio 2018 Tempo consentito: 120 minuti Professor Paolo Vitale Anno Accademico 2017-8 UdA, Scuola d Economia Domanda 1 [6 punti]. (a) La multi-collineartità
L Analisi della Varianza ANOVA (ANalysis Of VAriance)
 L Analisi della Varianza ANOVA (ANalysis Of VAriance) 1 Concetti generali: Confronto simultaneo tra più di due popolazioni, esempi... La analisi della varianza estende il confronto a p gruppi con p>2.
L Analisi della Varianza ANOVA (ANalysis Of VAriance) 1 Concetti generali: Confronto simultaneo tra più di due popolazioni, esempi... La analisi della varianza estende il confronto a p gruppi con p>2.
Sommario. 2 I grafici Il sistema di coordinate cartesiane Gli istogrammi I diagrammi a torta...51
 Sommario 1 I dati...15 1.1 Classificazione delle rilevazioni...17 1.1.1 Esperimenti ripetibili (controllabili)...17 1.1.2 Rilevazioni su fenomeni non ripetibili...18 1.1.3 Censimenti...19 1.1.4 Campioni...19
Sommario 1 I dati...15 1.1 Classificazione delle rilevazioni...17 1.1.1 Esperimenti ripetibili (controllabili)...17 1.1.2 Rilevazioni su fenomeni non ripetibili...18 1.1.3 Censimenti...19 1.1.4 Campioni...19
Metodi Statistici per il Management
 Metodi Statistici per il Management Statistica Multivariata I Simone Borra - Roberto Rocci Introduzione e obiettivi La statistica multivariata si occupa di analizzare e studiare in modo simultaneo un set
Metodi Statistici per il Management Statistica Multivariata I Simone Borra - Roberto Rocci Introduzione e obiettivi La statistica multivariata si occupa di analizzare e studiare in modo simultaneo un set
Università del Piemonte Orientale Specializzazioni di area sanitaria Statistica Medica
 Università del Piemonte Orientale Specializzazioni di area sanitaria Statistica Medica Regressione Lineare e Correlazione Argomenti della lezione Determinismo e variabilità Correlazione Regressione Lineare
Università del Piemonte Orientale Specializzazioni di area sanitaria Statistica Medica Regressione Lineare e Correlazione Argomenti della lezione Determinismo e variabilità Correlazione Regressione Lineare
IL CONFRONTO TRA LE VARIANZE DI DUE POPOLAZIONI
 IL CONFRONTO TRA LE VARIANZE DI DUE POPOLAZIONI Perchè confrontare le varianze stimate in due campioni? Torniamo all'esempio dei frinosomi Per poter applicare il test t avevamo detto che le varianze, e
IL CONFRONTO TRA LE VARIANZE DI DUE POPOLAZIONI Perchè confrontare le varianze stimate in due campioni? Torniamo all'esempio dei frinosomi Per poter applicare il test t avevamo detto che le varianze, e
Anova e regressione. Andrea Onofri Dipartimento di Scienze Agrarie ed Ambientali Universitá degli Studi di Perugia 22 marzo 2011
 Anova e regressione Andrea Onofri Dipartimento di Scienze Agrarie ed Ambientali Universitá degli Studi di Perugia 22 marzo 2011 Nella sperimentazione agronomica e biologica in genere è normale organizzare
Anova e regressione Andrea Onofri Dipartimento di Scienze Agrarie ed Ambientali Universitá degli Studi di Perugia 22 marzo 2011 Nella sperimentazione agronomica e biologica in genere è normale organizzare
Politecnico di Milano - Scuola di Ingegneria Industriale. II Prova in Itinere di Statistica per Ingegneria Energetica 7 Luglio 2011
 Politecnico di Milano - Scuola di Ingegneria Industriale II Prova in Itinere di Statistica per Ingegneria Energetica 7 Luglio 2011 c I diritti d autore sono riservati. Ogni sfruttamento commerciale non
Politecnico di Milano - Scuola di Ingegneria Industriale II Prova in Itinere di Statistica per Ingegneria Energetica 7 Luglio 2011 c I diritti d autore sono riservati. Ogni sfruttamento commerciale non
Esercitazioni di Statistica Dott.ssa Cristina Mollica
 Esercitazioni di Statistica Dott.ssa Cristina Mollica cristina.mollica@uniroma.it Regressione Esercizio. Siano dati i seguenti valori per le due variabili X ed Y: 4 5 3 5 3 3 Con riferimento al modello
Esercitazioni di Statistica Dott.ssa Cristina Mollica cristina.mollica@uniroma.it Regressione Esercizio. Siano dati i seguenti valori per le due variabili X ed Y: 4 5 3 5 3 3 Con riferimento al modello
Indice. Prefazione. 4 Sintesi della distribuzione di un carattere La variabilità Introduzione La variabilità di una distribuzione 75
 00PrPag:I-XIV_prefazione_IAS 8-05-2008 17:56 Pagina V Prefazione XI 1 La rilevazione dei fenomeni statistici 1 1.1 Introduzione 1 1.2 Caratteri, unità statistiche e collettivo 1 1.3 Classificazione dei
00PrPag:I-XIV_prefazione_IAS 8-05-2008 17:56 Pagina V Prefazione XI 1 La rilevazione dei fenomeni statistici 1 1.1 Introduzione 1 1.2 Caratteri, unità statistiche e collettivo 1 1.3 Classificazione dei
Corso in Statistica Medica
 Corso in Statistica Medica Introduzione alle tecniche statistiche di elaborazione dati Regressione e correlazione Dott. Angelo Menna Università degli Studi di Chieti G. d Annunziod Annunzio Anno Accademico
Corso in Statistica Medica Introduzione alle tecniche statistiche di elaborazione dati Regressione e correlazione Dott. Angelo Menna Università degli Studi di Chieti G. d Annunziod Annunzio Anno Accademico
Università di Pavia Econometria. Richiami di Statistica. Eduardo Rossi
 Università di Pavia Econometria Richiami di Statistica Eduardo Rossi Università di Pavia Campione casuale Siano (Y 1, Y 2,..., Y N ) variabili casuali tali che le y i siano realizzazioni mutuamente indipendenti
Università di Pavia Econometria Richiami di Statistica Eduardo Rossi Università di Pavia Campione casuale Siano (Y 1, Y 2,..., Y N ) variabili casuali tali che le y i siano realizzazioni mutuamente indipendenti
PROBABILITÀ ELEMENTARE
 Prefazione alla seconda edizione XI Capitolo 1 PROBABILITÀ ELEMENTARE 1 Esperimenti casuali 1 Spazi dei campioni 1 Eventi 2 Il concetto di probabilità 3 Gli assiomi della probabilità 3 Alcuni importanti
Prefazione alla seconda edizione XI Capitolo 1 PROBABILITÀ ELEMENTARE 1 Esperimenti casuali 1 Spazi dei campioni 1 Eventi 2 Il concetto di probabilità 3 Gli assiomi della probabilità 3 Alcuni importanti
lezione n. 6 (a cura di Gaia Montanucci) Verosimiglianza: L = = =. Parte dipendente da β 0 e β 1
 lezione n. 6 (a cura di Gaia Montanucci) METODO MASSIMA VEROSIMIGLIANZA PER STIMARE β 0 E β 1 Distribuzione sui termini di errore ε i ε i ~ N (0, σ 2 ) ne consegue : ogni y i ha ancora distribuzione normale,
lezione n. 6 (a cura di Gaia Montanucci) METODO MASSIMA VEROSIMIGLIANZA PER STIMARE β 0 E β 1 Distribuzione sui termini di errore ε i ε i ~ N (0, σ 2 ) ne consegue : ogni y i ha ancora distribuzione normale,
Statistica Applicata all edilizia: il modello di regressione
 Statistica Applicata all edilizia: il modello di regressione E-mail: orietta.nicolis@unibg.it 27 aprile 2009 Indice Il modello di Regressione Lineare 1 Il modello di Regressione Lineare Analisi di regressione
Statistica Applicata all edilizia: il modello di regressione E-mail: orietta.nicolis@unibg.it 27 aprile 2009 Indice Il modello di Regressione Lineare 1 Il modello di Regressione Lineare Analisi di regressione
Premessa: la dipendenza in media
 Premessa: la dipendenza in media Supponiamo di avere K diversi livelli di un fattore che potrebbero influire su una determinata variabile. Per esempio supponiamo di domandarci se la diversificazione (intesa
Premessa: la dipendenza in media Supponiamo di avere K diversi livelli di un fattore che potrebbero influire su una determinata variabile. Per esempio supponiamo di domandarci se la diversificazione (intesa
Data Mining. Prova parziale del 20 aprile 2017: SOLUZIONE
 Università degli Studi di Padova Corso di Laurea Magistrale in Informatica a.a. 2016/2017 Data Mining Docente: Annamaria Guolo Prova parziale del 20 aprile 2017: SOLUZIONE ISTRUZIONI: La durata della prova
Università degli Studi di Padova Corso di Laurea Magistrale in Informatica a.a. 2016/2017 Data Mining Docente: Annamaria Guolo Prova parziale del 20 aprile 2017: SOLUZIONE ISTRUZIONI: La durata della prova
Presentazione dell edizione italiana
 1 Indice generale Presentazione dell edizione italiana Prefazione xi xiii Capitolo 1 Una introduzione alla statistica 1 1.1 Raccolta dei dati e statistica descrittiva... 1 1.2 Inferenza statistica e modelli
1 Indice generale Presentazione dell edizione italiana Prefazione xi xiii Capitolo 1 Una introduzione alla statistica 1 1.1 Raccolta dei dati e statistica descrittiva... 1 1.2 Inferenza statistica e modelli
Esercizio 2: voto e ore dedicate allo studio
 La seguente tabella riporta il voto riportato da 10 studenti all esame di Statistica Sociale e il numero di ore di lezione non seguite dallo studente (il corso prevede 30 ore di lezione). Ci si chiede
La seguente tabella riporta il voto riportato da 10 studenti all esame di Statistica Sociale e il numero di ore di lezione non seguite dallo studente (il corso prevede 30 ore di lezione). Ci si chiede
Presentazione dell edizione italiana Prefazione xix Ringraziamenti xxii Glossario dei simboli xxiii
 Sommario Presentazione dell edizione italiana Prefazione xix Ringraziamenti xxii Glossario dei simboli xxiii xv Parte I Statistica descrittiva 1 Capitolo 1 Introduzione 3 Perché studiare statistica? 4
Sommario Presentazione dell edizione italiana Prefazione xix Ringraziamenti xxii Glossario dei simboli xxiii xv Parte I Statistica descrittiva 1 Capitolo 1 Introduzione 3 Perché studiare statistica? 4
ECONOMETRIA: Laboratorio I
 ECONOMETRIA: Laboratorio I Luca De Angelis CLASS - Università di Bologna Programma Laboratorio I Valori attesi e varianze Test di ipotesi Stima di un modello lineare attraverso OLS Valore atteso Data una
ECONOMETRIA: Laboratorio I Luca De Angelis CLASS - Università di Bologna Programma Laboratorio I Valori attesi e varianze Test di ipotesi Stima di un modello lineare attraverso OLS Valore atteso Data una
TECNICHE DI ANALISI DEI DATI
 TECNICE DI ANALISI DEI DATI AA 08/09 PRO. V.P. SENESE Questi materiali sono disponibili per tutti gli studenti al seguente indirizzo: https://goo.gl/xy5fr Seconda Università di Napoli (SUN) Dipartimento
TECNICE DI ANALISI DEI DATI AA 08/09 PRO. V.P. SENESE Questi materiali sono disponibili per tutti gli studenti al seguente indirizzo: https://goo.gl/xy5fr Seconda Università di Napoli (SUN) Dipartimento
Esame di Statistica A-Di Prof. M. Romanazzi
 1 Università di Venezia Esame di Statistica A-Di Prof. M. Romanazzi 25 Maggio 2015 Cognome e Nome..................................... N. Matricola.......... Valutazione Il punteggio massimo teorico di
1 Università di Venezia Esame di Statistica A-Di Prof. M. Romanazzi 25 Maggio 2015 Cognome e Nome..................................... N. Matricola.......... Valutazione Il punteggio massimo teorico di
Casa dello Studente. Casa dello Studente
 Esercitazione - 14 aprile 2016 ESERCIZIO 1 Di seguito si riporta il giudizio (punteggio da 0 a 5) espresso da un gruppo di studenti rispetto alle diverse residenze studentesche di un Ateneo: a) Si calcolino
Esercitazione - 14 aprile 2016 ESERCIZIO 1 Di seguito si riporta il giudizio (punteggio da 0 a 5) espresso da un gruppo di studenti rispetto alle diverse residenze studentesche di un Ateneo: a) Si calcolino
Corso di Psicometria Progredito
 Corso di Psicometria Progredito 5. La correlazione lineare Gianmarco Altoè Dipartimento di Pedagogia, Psicologia e Filosofia Università di Cagliari, Anno Accademico 2013-2014 Sommario 1 Tipi di relazione
Corso di Psicometria Progredito 5. La correlazione lineare Gianmarco Altoè Dipartimento di Pedagogia, Psicologia e Filosofia Università di Cagliari, Anno Accademico 2013-2014 Sommario 1 Tipi di relazione
STATISTICA (2) ESERCITAZIONE Dott.ssa Antonella Costanzo
 STATISTICA (2) ESERCITAZIONE 7 11.03.2014 Dott.ssa Antonella Costanzo Esercizio 1. Test di indipendenza tra mutabili In un indagine vengono rilevate le informazioni su settore produttivo (Y) e genere (X)
STATISTICA (2) ESERCITAZIONE 7 11.03.2014 Dott.ssa Antonella Costanzo Esercizio 1. Test di indipendenza tra mutabili In un indagine vengono rilevate le informazioni su settore produttivo (Y) e genere (X)
PROCEDURE/TECNICHE DI ANALISI / MISURE DI ASSOCIAZIONE A) ANALISI DELLA VARIANZA
 PROCEDURE/TECNICHE DI ANALISI / MISURE DI ASSOCIAZIONE A) ANALISI DELLA VARIANZA PROCEDURA/TECNICA DI ANALISI DEI DATI SPECIFICAMENTE DESTINATA A STUDIARE LA RELAZIONE TRA UNA VARIABILE NOMINALE (ASSUNTA
PROCEDURE/TECNICHE DI ANALISI / MISURE DI ASSOCIAZIONE A) ANALISI DELLA VARIANZA PROCEDURA/TECNICA DI ANALISI DEI DATI SPECIFICAMENTE DESTINATA A STUDIARE LA RELAZIONE TRA UNA VARIABILE NOMINALE (ASSUNTA
Analisi della varianza
 Analisi della varianza Prof. Giuseppe Verlato Sezione di Epidemiologia e Statistica Medica, Università di Verona ANALISI DELLA VARIANZA - 1 Abbiamo k gruppi, con un numero variabile di unità statistiche.
Analisi della varianza Prof. Giuseppe Verlato Sezione di Epidemiologia e Statistica Medica, Università di Verona ANALISI DELLA VARIANZA - 1 Abbiamo k gruppi, con un numero variabile di unità statistiche.
REGISTRO DELLE LEZIONI*
 UNIVERSITÀ DEGLI STUDI DI GENOVA Dipartimento di Matematica Corso di laurea in Statistica matematica e trattamento informatico dei dati Nome: Statistica Inferenziale codice: 483847 codice padre (se ins.
UNIVERSITÀ DEGLI STUDI DI GENOVA Dipartimento di Matematica Corso di laurea in Statistica matematica e trattamento informatico dei dati Nome: Statistica Inferenziale codice: 483847 codice padre (se ins.
Richiami di inferenza statistica Strumenti quantitativi per la gestione
 Richiami di inferenza statistica Strumenti quantitativi per la gestione Emanuele Taufer Inferenza statistica Parametri e statistiche Esempi Tecniche di inferenza Stima Precisione delle stime Intervalli
Richiami di inferenza statistica Strumenti quantitativi per la gestione Emanuele Taufer Inferenza statistica Parametri e statistiche Esempi Tecniche di inferenza Stima Precisione delle stime Intervalli
Richiami di inferenza statistica. Strumenti quantitativi per la gestione. Emanuele Taufer
 Richiami di inferenza statistica Strumenti quantitativi per la gestione Emanuele Taufer Inferenza statistica Inferenza statistica: insieme di tecniche che si utilizzano per ottenere informazioni su una
Richiami di inferenza statistica Strumenti quantitativi per la gestione Emanuele Taufer Inferenza statistica Inferenza statistica: insieme di tecniche che si utilizzano per ottenere informazioni su una
Statistica. Alfonso Iodice D Enza
 Statistica Alfonso Iodice D Enza iodicede@gmail.com Università degli studi di Cassino () Statistica 1 / 24 Outline 1 2 3 4 5 () Statistica 2 / 24 Dipendenza lineare Lo studio della relazione tra caratteri
Statistica Alfonso Iodice D Enza iodicede@gmail.com Università degli studi di Cassino () Statistica 1 / 24 Outline 1 2 3 4 5 () Statistica 2 / 24 Dipendenza lineare Lo studio della relazione tra caratteri
Contenuti: Capitolo 14 del libro di testo
 Test d Ipotesi / TIPICI PROBLEMI DI VERIFICA DI IPOTESI SONO Test per la media Test per una proporzione Test per la varianza Test per due campioni indipendenti Test di indipendenza Contenuti Capitolo 4
Test d Ipotesi / TIPICI PROBLEMI DI VERIFICA DI IPOTESI SONO Test per la media Test per una proporzione Test per la varianza Test per due campioni indipendenti Test di indipendenza Contenuti Capitolo 4
Prefazione Ringraziamenti dell'editore Il sito web dedicato al libro Test online: la piattaforma McGraw-Hill Education Guida alla lettura
 INDICE GENERALE Prefazione Ringraziamenti dell'editore Il sito web dedicato al libro Test online: la piattaforma McGraw-Hill Education Guida alla lettura XI XIV XV XVII XVIII 1 LA RILEVAZIONE DEI FENOMENI
INDICE GENERALE Prefazione Ringraziamenti dell'editore Il sito web dedicato al libro Test online: la piattaforma McGraw-Hill Education Guida alla lettura XI XIV XV XVII XVIII 1 LA RILEVAZIONE DEI FENOMENI
1.1 Obiettivi della statistica Struttura del testo 2
 Prefazione XV 1 Introduzione 1.1 Obiettivi della statistica 1 1.2 Struttura del testo 2 2 Distribuzioni di frequenza 2.1 Informazione statistica e rilevazione dei dati 5 2.2 Distribuzioni di frequenza
Prefazione XV 1 Introduzione 1.1 Obiettivi della statistica 1 1.2 Struttura del testo 2 2 Distribuzioni di frequenza 2.1 Informazione statistica e rilevazione dei dati 5 2.2 Distribuzioni di frequenza
Analisi della varianza
 1. 2. univariata ad un solo fattore tra i soggetti (between subjects) 3. univariata: disegni fattoriali 4. univariata entro i soggetti (within subjects) 5. : disegni fattoriali «misti» L analisi della
1. 2. univariata ad un solo fattore tra i soggetti (between subjects) 3. univariata: disegni fattoriali 4. univariata entro i soggetti (within subjects) 5. : disegni fattoriali «misti» L analisi della
LEZIONI DI STATISTICA MEDICA
 LEZIONI DI STATISTICA MEDICA Lezione n.12 - Test statistico Sezione di Epidemiologia & Statistica Medica Università degli Studi di Verona IPOTESI SCIENTIFICA Affermazione che si può sottoporre a verifica
LEZIONI DI STATISTICA MEDICA Lezione n.12 - Test statistico Sezione di Epidemiologia & Statistica Medica Università degli Studi di Verona IPOTESI SCIENTIFICA Affermazione che si può sottoporre a verifica
Argomenti della lezione:
 Lezione 7 Argomenti della lezione: La regressione semplice Il modello teorico Il calcolo dei parametri Regressione lineare Esamina la relazione lineare tra una o più variabili esplicative (o indipendenti,
Lezione 7 Argomenti della lezione: La regressione semplice Il modello teorico Il calcolo dei parametri Regressione lineare Esamina la relazione lineare tra una o più variabili esplicative (o indipendenti,
Analisi della regressione multipla
 Analisi della regressione multipla y = β 0 + β 1 x 1 + β 2 x 2 +... β k x k + u 2. Inferenza Assunzione del Modello Classico di Regressione Lineare (CLM) Sappiamo che, date le assunzioni Gauss- Markov,
Analisi della regressione multipla y = β 0 + β 1 x 1 + β 2 x 2 +... β k x k + u 2. Inferenza Assunzione del Modello Classico di Regressione Lineare (CLM) Sappiamo che, date le assunzioni Gauss- Markov,
Esercizi su Regressione e Connessione
 Esercizi su Regressione e Connessione Stefano Cabras 31 marzo 2009 Sommario Questa serie di esercizi è principalmente incentrata sulla regressione e la connessione, tuttavia in alcuni esercizi le soluzioni
Esercizi su Regressione e Connessione Stefano Cabras 31 marzo 2009 Sommario Questa serie di esercizi è principalmente incentrata sulla regressione e la connessione, tuttavia in alcuni esercizi le soluzioni
Regressione multipla
 Regressione multipla L obiettivo è costruire un modello probabilistico per spiegare la variabile y tramite più di una variabile indipendente x 1, x 2,..., x k. Esempio: Per un efficiente progettazione
Regressione multipla L obiettivo è costruire un modello probabilistico per spiegare la variabile y tramite più di una variabile indipendente x 1, x 2,..., x k. Esempio: Per un efficiente progettazione
lezione 5 AA Paolo Brunori
 AA 2016-2017 Paolo Brunori dove eravamo arrivati - le stime OLS ci consentono di approssimare linearmente la relazione fra una variabile dipendente (Y) e una indipendente (X) - i parametri stimati su un
AA 2016-2017 Paolo Brunori dove eravamo arrivati - le stime OLS ci consentono di approssimare linearmente la relazione fra una variabile dipendente (Y) e una indipendente (X) - i parametri stimati su un
3.1 Classificazione dei fenomeni statistici Questionari e scale di modalità Classificazione delle scale di modalità 17
 C L Autore Ringraziamenti dell Editore Elenco dei simboli e delle abbreviazioni in ordine di apparizione XI XI XIII 1 Introduzione 1 FAQ e qualcos altro, da leggere prima 1.1 Questo è un libro di Statistica
C L Autore Ringraziamenti dell Editore Elenco dei simboli e delle abbreviazioni in ordine di apparizione XI XI XIII 1 Introduzione 1 FAQ e qualcos altro, da leggere prima 1.1 Questo è un libro di Statistica
Cognome e Nome:... Corso di laurea:...
 Statistica - corso base Prof. B. Liseo Prova di esame dell 8 gennaio 201 Cognome e Nome:................................................................... Corso di laurea:.......................................................................
Statistica - corso base Prof. B. Liseo Prova di esame dell 8 gennaio 201 Cognome e Nome:................................................................... Corso di laurea:.......................................................................
Statistica. Alfonso Iodice D Enza
 Statistica Alfonso Iodice D Enza iodicede@unicas.it Università degli studi di Cassino () Statistica 1 / 33 Outline 1 2 3 4 5 6 () Statistica 2 / 33 Misura del legame Nel caso di variabili quantitative
Statistica Alfonso Iodice D Enza iodicede@unicas.it Università degli studi di Cassino () Statistica 1 / 33 Outline 1 2 3 4 5 6 () Statistica 2 / 33 Misura del legame Nel caso di variabili quantitative
Il modello di regressione
 Il modello di regressione Capitolo e 3 A M D Marcello Gallucci Milano-Bicocca Lezione: II Concentti fondamentali Consideriamo ora questa ipotetica ricerca: siamo andati in un pub ed abbiamo contato quanti
Il modello di regressione Capitolo e 3 A M D Marcello Gallucci Milano-Bicocca Lezione: II Concentti fondamentali Consideriamo ora questa ipotetica ricerca: siamo andati in un pub ed abbiamo contato quanti
CHEMIOMETRIA. CONFRONTO CON VALORE ATTESO (test d ipotesi) CONFRONTO DI VALORI MISURATI (test d ipotesi) CONFRONTO DI RIPRODUCIBILITA (test d ipotesi)
 CHEMIOMETRIA Applicazione di metodi matematici e statistici per estrarre (massima) informazione chimica (affidabile) da dati chimici INCERTEZZA DI MISURA (intervallo di confidenza/fiducia) CONFRONTO CON
CHEMIOMETRIA Applicazione di metodi matematici e statistici per estrarre (massima) informazione chimica (affidabile) da dati chimici INCERTEZZA DI MISURA (intervallo di confidenza/fiducia) CONFRONTO CON
Indipendenza, Dipendenza e interdipendenza
 Indipendenza, Dipendenza e interdipendenza In analisi bivariata la tabella di contingenza consente di esaminare congiuntamente due variabili consente di rilevare le relazioni esistenti tra le variabili
Indipendenza, Dipendenza e interdipendenza In analisi bivariata la tabella di contingenza consente di esaminare congiuntamente due variabili consente di rilevare le relazioni esistenti tra le variabili
Regressione lineare. Lo studio della relazione lineare tra due variabili. X e Y caratteri entrambi quantitativi. variabile dipendente
 Regressione lineare Se la correlazione misura l intensità e il segno del legame lineare tra due variabili, l obiettivo delle tecniche di regressione è, invece, quello di individuare il tipo di relazione
Regressione lineare Se la correlazione misura l intensità e il segno del legame lineare tra due variabili, l obiettivo delle tecniche di regressione è, invece, quello di individuare il tipo di relazione
Metodologie Quantitative
 Metodologie Quantitative Regressione Lineare Nozioni di base M Q Marco Perugini Milano-Bicocca 1 I COMUNICAZIONE MERCOLEDI 11 NOVEMBRE NON CI SARA LEZIONE DI MQ Concetti base Con l analisi di regressione
Metodologie Quantitative Regressione Lineare Nozioni di base M Q Marco Perugini Milano-Bicocca 1 I COMUNICAZIONE MERCOLEDI 11 NOVEMBRE NON CI SARA LEZIONE DI MQ Concetti base Con l analisi di regressione
Cognome e Nome:... Matricola e corso di laurea:...
 Statistica - corso base Prof. B. Liseo Prova di esame dell 8 gennaio 2014 Cognome e Nome:................................................................... Matricola e corso di laurea:...................................................
Statistica - corso base Prof. B. Liseo Prova di esame dell 8 gennaio 2014 Cognome e Nome:................................................................... Matricola e corso di laurea:...................................................
Indice. centrale, dispersione e forma Introduzione alla Statistica Statistica descrittiva per variabili quantitative: tendenza
 XIII Presentazione del volume XV L Editore ringrazia 3 1. Introduzione alla Statistica 5 1.1 Definizione di Statistica 6 1.2 I Rami della Statistica Statistica Descrittiva, 6 Statistica Inferenziale, 6
XIII Presentazione del volume XV L Editore ringrazia 3 1. Introduzione alla Statistica 5 1.1 Definizione di Statistica 6 1.2 I Rami della Statistica Statistica Descrittiva, 6 Statistica Inferenziale, 6
Argomenti della lezione:
 Lezione 13 L analisi della Varianza (ANOVA): il modello lineare Argomenti della lezione: Modello lineare Disegni a una via L Analisi della Varianza (ANOVA): Esamina differenze tra le medie di due o più
Lezione 13 L analisi della Varianza (ANOVA): il modello lineare Argomenti della lezione: Modello lineare Disegni a una via L Analisi della Varianza (ANOVA): Esamina differenze tra le medie di due o più
Regressione lineare multipla CORSO DI ANALISI DEI DATI Anno Accademico 2009/2010, I ciclo
 Regressione lineare multipla CORSO DI ANALISI DEI DATI Anno Accademico 2009/2010, I ciclo 1 Controllo di ipotesi sui parametri In questo contesto risulta necessario avvalersi dell assunzione di normalita
Regressione lineare multipla CORSO DI ANALISI DEI DATI Anno Accademico 2009/2010, I ciclo 1 Controllo di ipotesi sui parametri In questo contesto risulta necessario avvalersi dell assunzione di normalita
