PARTE TERZA: L EQUILIBRIO PARAMETRICO
|
|
|
- Adelmo Ferrero
- 10 anni fa
- Просмотров:
Транскрипт
1 Aldo Motesao PRINCIPI DI ANALISI ECONOMICA PARTE TERZA: L EUILIBRIO PARAMETRICO Ca. 10 L ANALISI DELL EUILIBRIO PARZIALE Doo aver aalzzato le due otes fodametal della teora ecoomca, secodo cu le azo degl aget soo tezoal (soo, coè, scelte) e realzzabl (vee, coè, cosderata la comatbltà delle scelte), questa Parte vee trodotta l aals dello stato dell ecooma comosto dall seme delle scelte comatbl, che è l equlbro. S ot che l equlbro ecoomco ha er oggetto a d scambo e d roduzoe, o ecessaramete la loro esecuzoe (che otrebbe essere revsta er u temo successvo e che otrebbe essere evetualmete regozata). L equlbro è arametrco se s assume che, el rocesso d scelta, og agete o tega coto d come scegle cascu altro agete. S ha, vece, u equlbro strategco se cò accade. I questo caso, v soo aget che comoo la loro scelta teedo coto delle ossbl azo degl avversar. Gl equlbr strategc soo aalzzat co la teora de goch ella Parte uarta. L equlbro arametrco è caratterzzato dalla reseza d gradezze (arametr) che soo date er alcu o tutt gl aget, ma varabl (qud, oggetto d determazoe) er l ecooma. S ha equlbro se quest arametr (che soo, geere, rezz) hao valor oortu. La determazoe dell equlbro arametrco rchede soltato la determazoe d quest arametr. Ivece, l equlbro strategco (che uò comuque cludere la reseza d arametr er talu aget) è caratterzzato dalla comatbltà delle stratege, coè dal fatto che v soo aget che scelgoo teedo coto della terdedeza tra la loro scelta e quella d altr aget. L equlbro arametrco vee aalzzato descrvedo darma le scelte dvdual ed moedo, successvamete, la loro comatbltà. uesta rchede due codzo. La rma codzoe è la realzzabltà o esegubltà delle scelte: a d scambo e d roduzoe scelt dagl aget ossoo essere esegut se le comravedte o escludoo alcua scelta d scambo degl aget dell ecooma esame e se a d roduzoe o soo mossbl. La secoda codzoe è ù sottle: 1
2 occorre che le scelte o s modfcho durate la fase d raggugmeto dell equlbro e l erfezoameto de cotratt d comravedta. Gra arte dell aals svolta el seguto o s occua d questa fase, coè, del rocesso d cotrattazoe che determa le codzo dello scambo (uò essere ua cotrattazoe dretta tra gl aget, o medata da termedar, o orgazzata da sttuzo secfche co l terveto d aget, badtor, sstem telematc, o altro). S suoe che v sa u qualche sstema d cotrattazoe seza cost, u mercato deale, grado d determare, se esste, u equlbro, che è u seme d scelte esegubl. Ossa, la comatbltà delle scelte s rduce all esegubltà, altre arole alla rma delle due codzo sudcate. Co queste remesse, asseza d secfcazo cotrare, la comatbltà delle scelte è el seguto soddsfatta se er og bee esame la quattà totale acqusto è uguale a quella vedta (assumedo che roduttor cooscao loro sem d roduzoe, er cu le loro scelte o soo essu caso mossbl). L seme delle azo esegubl (o realzzabl) è, ercò, l seme delle azo cu corrsodoo, er og bee esame, quattà total acqusto ugual a quelle vedta. ud, l equlbro è defto dall aarteeza delle scelte degl aget all seme delle azo esegubl. La defzoe recedete d equlbro clude ache cas cu rezz soo argometo d scelta d u agete, o soltato cas, esamat e catol recedet, cu gl aget soo rce-taker. Tuttava, el seguto d questa Parte, trae che egl ultm aragraf d questo catolo, vee esamato l mercato cocorrezale, cu rezz o soo argometo d scelta degl aget che desderao esegure gl scamb, ma emergoo dalla codzoe d equlbro. (Ess vegoo determat el rocesso d cotrattazoe, che o vee geeralmete aalzzato). I questo catolo vee trattato l equlbro arzale. S qualfca arzale u equlbro cu vegoo aalzzat gl scamb d u bee (co la moeta altro terme dello scambo 1 ), rescdedo dagl altr be dell ecooma. Perché cò sa ossble, occorre che sa esclusa, o sa trascurable, l terdedeza co gl altr be: s ha terdedeza se le varabl rferte al bee esame (rezzo e quattà scambate) fluscoo su gradezze (rezz degl altr be, caactà d sesa de cosumator, ut ed outut delle mrese) da cu dede l equlbro esame. L terdedeza uò essere esclusa troducedo delle otes. S uò assumere, ad esemo, che rezz degl altr be ed altre gradezze (come la caactà d sesa de cosumator) o fluscao (er ulla o arossmatvamete er ulla) sulla scelta degl aget (come accade, er 1 S è così mlctamete otzzata la reseza d u bee, la moeta, che svolge la fuzoe d mezzo d scambo (è, coè, l bee accettato da tutt gl aget egl scamb) e d utà d coto (ossa, l rezzo d og bee è esresso utà moetare er utà d bee). La moeta è, a meo che o s otzz dversamete, u bee come gl altr: fa arte de aer d be ed etra el sstema d refereza degl aget e e loro vcol (seme d blaco er u cosumatore, seme d roduzoe er u roduttore). 2
3 cosumator, se le refereze soo searabl addtvamete rsetto al bee esame e quas-lear rsetto al bee moeta) 2, oure che rezz degl altr be sao dat e tal da asscurare l equlbro geerale corrsodeza all equlbro del bee esame ( questo caso, erò, l terdedeza s rreseterebbe ell aals d statca comarata). 3 Nella rma arte d questo catolo, fo al Paragrafo 10.7, vee esamato l equlbro arzale cocorrezale. S qualfca cocorrezale u mercato cu og agete è rce-taker, o ha, coè, alcu otere su rezz esame. Ne aragraf successv vegoo esamat equlbr arzal o cocorrezal. Ossa, v è u agete o v soo aget che hao otere d mercato, soo rce-maker. Solo alcue d queste forme d mercato ammettoo u equlbro arametrco. uelle che rchedoo u aals d equlbro strategco sarao resetate ella Parte uarta L equlbro arzale cocorrezale S redao cosderazoe tutte le scelte, sao esse oera d cosumator o d roduttor, che cludoo u certo bee. Defzoe 10.1 U equlbro è cocorrezale se rguarda la comatbltà delle scelte d aget tutt rce-taker. S è gà dcato che u agete è rce-taker se rtee d o avere otere d mercato, coè rtee d o otere sceglere l rezzo del bee esame, é d otere flure su d esso. La defzoe d equlbro mlca che la sua ooe o vega modfcata dalle formazo che gl ervegoo dall equlbro (e eure dalle cotrattazo che coducoo ad esso). E aturale (ma o è ecessaro) assumere che l agete rtega d o avere otere d mercato erché o ha effettvamete otere d mercato, coè, che l ooe corrsoda alla realtà. Perché l agete o abba otere d mercato occorre che og modfcazoe della sua azoe, tra quelle er lu ossbl, o flusca sul rezzo. E evdete come cò o sa vero se o arossmatvamete. S cosder, ad esemo, er u cosumatore, l alteratva tra o comrare l bee esame o utlzzare tutta la caactà d sesa ell acqusto del bee. uesta alteratva flusce sulla domada aggregata del bee e, qud, geerale, sul rezzo. Se, erò, egl ha ua 2 Ifatt, se è u(x) = x 1 + f(x 2 ) + g(x 3, x 4,, x k ), ove x 1 dca la quattà d moeta e x 2 quella del bee esame, allora la domada del bee è del to x 2 = d( 2 ), ove 2 è l rezzo moetaro del bee (ercò, co 1 = 1 ), er og 2 tale che 2 x 2 m. 3 Ifatt, se le fuzo d domada e offerta del bee esame dedoo da rezz degl altr be e quest o soo rezz d equlbro, l equlbro arzale (che rescda dall terdedeza) è rrlevate, oché o resste alle modfcazo de rezz degl altr be. I altr term, esso o rareseta uo stato cu gl aget ossoo esegure le loro scelte (che hao er oggetto sa l bee esame sa altr be). 3
4 caactà d sesa molto ccola rsetto al valore comlessvo degl scamb sul mercato esame, l flueza dell alteratva è trascurable. La scelta d ua delle due azo al osto dell altra codurrebbe ad ua modfcazoe del rezzo rrlevate (ad esemo, ad ua varazoe del rezzo ferore al ù ccolo decmale cu è esresso l rezzo). Allora, l agete, se valuta correttamete l suo (ullo) otere d mercato, 4 rtee dato l rezzo, è, coè, u rce-taker. Peraltro, l otes che u agete sa rce-taker, ache se rareseta, logcamete, ua stuazoe lmte (vale, coè, ell esemo sudcato, se l raorto tra la sua caactà d sesa e l valore comlessvo degl scamb tede a zero), è, tuttava ella realtà, la stuazoe ù comue. Soo molt gl aget che su molt mercat soo rce-taker. ud, u agete è rcetaker o ecessaramete se o ha otere d mercato (cosa che uò essere vera solo arossmatvamete), ma se rtee l suo otere così ccolo che refersce o teere coto e se essua formazoe (che gl ervega ella fase cu s stablsce l rezzo del bee sul mercato) lo duce a cambare dea. S ot che l equlbro cocorrezale è defto dalla codzoe che tutt gl aget sao rce-taker. La scelta d u agete rce-taker rguarda la quattà del bee esame. Se è comratore (vedtore), allora la scelta revede l acqusto (vedta) d ua certa quattà d bee cambo d ua somma d dearo d ar valore, determata dal rezzo d mercato del bee. ud, l equlbro arzale rguarda due be, uo de qual, la moeta, vee scambato tutt mercat, metre l altro, quello che deoma l mercato, vee scambato solo sul mercato esame. L aals d equlbro arzale cosdera soltato la domada e l offerta del bee esame L aals dell equlbro arzale cocorrezale L aals dell equlbro arzale uò essere fatta dfferetemete rededo cosderazoe la domada e l offerta lorda del bee o quella etta (eccesso d domada). E cosuetude, ell equlbro arzale, segure la rma va, ache erché l suo caso tco è quello cu comrator (cosumator e roduttor) o ossedoo l bee esame rma dello scambo e vedtor soo suo roduttor. I tal caso la domada aggregata è raresetata dalla fuzoe d = D() e l offerta aggregata dalla fuzoe s = S() (queste fuzo ossoo essere corrsodeze, ache se el seguto questa ossbltà verrà resa 4 No camba la stuazoe se le refereze degl aget dedoo dal rezzo, come dcato el Paragrafo 4.4 a roosto dell effetto Veble. Ivece, l effetto mtazoe (resetato el medesmo aragrafo) uò determare u otere d mercato del leader (coè, dell agete la cu scelta flusce sulle scelte d altr aget). I questo caso, l leader otrebbe o essere rce-taker. 4
5 cosderazoe solo alcu cas). Le fuzo aggregate d domada e d offerta rsultao dall aals comuta all zo de Paragraf 4.6 e 5.7, 5 evdezado soltato la dedeza della quattà domadata e offerta del bee esame dal suo rezzo. Esse soo corretemete deomate fuzo marshallae d domada e d offerta. Defzoe 10.2 La codzoe d equlbro cocorrezale, che esrme la realzzabltà delle scelte, ossa, d = s, è raresetata dal sstema * = D(*) = S(*) la cu soluzoe dvdua l rezzo * e la quattà scambata * d equlbro. Rsulta, qud, che la quattà acqustata e veduta da sgol aget d è q * = d ( *), er = 1,, (ove è l umero degl acquret l d bee), e q * = s( * ), er = 1,, (ove è l umero de vedtor). L equlbro dcato determa, qud, scelte realzzabl, coè, azo razoal e comatbl. U esemo è raresetato ella Fgura D() S() * * Fgura 10.1 L equlbro esste (coè, le curve d domada e d offerta s tersecao) se l domo delle fuzo D() e S() cotee u tervallo [, ] + su cu etrambe le fuzo soo cotue ed è (D( ) S( ))(D( ) S( )) 0. L equlbro o è ecessaramete 5 Se v soo roduttor che acqustao l bee esame (che è, er loro, u ut) e l acqurete -esmo è u roduttore, allora la sua fuzoe d domada rsulta oedo, er l bee esame, d ( ) = s ( ), ove s ( ) è la fuzoe d offerta del roduttore trodotta el Catolo 5. 5
6 uco. E uco (come ella Fgura 10.1) se la fuzoe D() S() è decrescete (s ot come questa codzoe sa suffcete ma o ecessara). Co le otes utlzzate corretemete e Catol 3, 4 e 5, questa roretà è soddsfatta se la fuzoe aggregata d domada è decrescete, se, coè, l bee è ordaro e l offerta è eserctata da roduttor del bee, la cu fuzoe aggregata d offerta sa o decrescete La stabltà dell equlbro arzale cocorrezale Come gà dcato, le codzo dell equlbro cocorrezale determao l rezzo * d equlbro, ma o descrvoo l rocesso attraverso cu l seme degl aget rce-taker v guge. L aals del rocesso d aggustameto all equlbro ha caratterstche secfche, rguardat sorattutto la dffusoe d formazo sulle tezo d scambo degl aget, caratterstche o semre rcoducbl alla logca della teora della scelta. Il rocesso d aggustameto all equlbro tradzoalmete otzzato troduce l cosddetto badtore walrasao. 6 uesto rocesso resuoe u mercato orgazzato, co la reseza d u agete, l badtore, che o arteca agl scamb del mercato esame. L agete ha l comto d grdare ua successoe d rezz, corrsodeza a cascuo de qual gl aget (comrator e vedtor) comucao al badtore le loro tezo d comravedta. Gl aget soo megat ad esegure le tezo comucate al badtore solo se l rezzo corrsodete è u rezzo d equlbro. Il badtore cotrolla se v è o o equlbro, coè, se la somma delle quattà acqusto è uguale o o a quella delle quattà vedta. Se D() S() > 0, o sorgoo meg d scambo e l badtore grda u rezzo ù alto; se D() S() < 0, o sorgoo meg d scambo e l badtore grda u rezzo ù basso; se D() S() = 0, l badtore dchara chuso l rocesso e gl aget soo megat ad esegure gl scamb da loro comucat al badtore. Il roblema aaltco cosste ell esame delle codzo che determao la covergeza della successoe de rezz grdat dal badtore ad u rezzo d equlbro. La stabltà dell equlbro è strettamete coessa a questa aals: u equlbro è defto stable se ua erturbazoe d esso (esressa dall dcazoe da arte del badtore d u rezzo o d equlbro) mette moto forze (esresse dal comortameto del badtore) che rcoducoo l sstema all equlbro. 6 uesta aals matee l otes che gl aget d scambo sao rce-taker. V soo altre aals (ad esemo, Gale, 2000) che trattao ecoome co aget dotat d otere d mercato che tedoo all equlbro cocorrezale al crescere del loro umero. Il rototo d queste aals è l ololo d Courot (cu s acceerà ella Parte uarta). 6
7 Defzoe 10.3 Ua codzoe d stabltà locale, ossa, rossmtà del rezzo d equlbro, ota come codzoe statca walrasaa d stabltà, è esressa dalla dsuguaglaza D E( *) 0, ove E() = D() S() è la fuzoe d eccesso d domada. Essa rsulta dall otes che l badtore alz l rezzo se l eccesso d domada è ostvo (se, coè, E() = D() S() > 0 ) e lo abbass se è egatvo (se, coè, E() = D() S() < 0 ), comortameto questo dcato talvolta come legge del mercato. Allora, erché v sa stabltà, occorre che l badtore, se sta grdado u rezzo u o ù alto (basso) d quello d equlbro, sa dotto a grdare uo ù basso (alto) e cò accade solo se v è u eccesso egatvo (ostvo) d domada, coè, se è E() < 0 er > * (e E() > 0 er < * ). Tuttava, la codzoe statca d stabltà è ecessara, ma o è semre suffcete erché la successoe de rezz grdat dal badtore coverga ad u rezzo d equlbro. Per dvduare le codzo d covergeza all equlbro occorre secfcare, ù dettaglatamete d quato o sa stato fatto fora, l comortameto del badtore, comedo u aals damca. A questo rguardo, ossoo essere rooste due aals: la rma tratta l temo (della successoe de rezz grdat dal badtore) el dscreto, la secoda el cotuo, ossa, ella rma aals la successoe de rezz grdat dal badtore (t) è ua fuzoe che ha come domo l seme de umer ter, coè, : {1, 2, } + metre ella secoda aals l domo è l asse de umer real, coè, : + +. Sa l equlbro determato dalle codzo * = D(*) = S(*), ovvero, trodotta la fuzoe d eccesso d domada E() = D() S(), dalla codzoe E(*) = 0. Le due aals aea dcate s resetao, allora, el modo seguete. a) Aals damca della stabltà walrasaa el temo dscreto. S dch co t, ove t = 1, 2,, la successoe de rezz grdat dal badtore e co la fuzoe t+1 = t + f(e( t )) l comortameto del badtore, ove f(.) è ua fuzoe che coserva l sego del suo argometo (coè, se E( t ) > 0, allora t+1 > t, e, se E( t ) < 0, allora t+1 < t ). L equlbro è stable se l = *. Pù recsamete, è globalmete m t t stable se questa codzoe è soddsfatta er og rezzo zale 1 + ; è localmete stable se esste u toro d * er cu la codzoe è soddsfatta er og 1 aarteete a questo toro. (S ot come la stabltà globale mlch quella locale). Ora, la codzoe statca walrasaa d stabltà sutrodotta D E( *) 0 è codzoe ecessara erché l equlbro sa stable (localmete e globalmete), ma o è suffcete. La codzoe statca walrasaa d stabltà è soddsfatta e tre cas raresetat elle Fgure 10.2, 10.3 e V è stabltà locale (e globale) ella Fgura Nella Fgura 10.3 rezz grdat dal badtore s 7
8 allotaao deftamete dal rezzo d equlbro. Nella Fgura 10.4 v è u cclo lmte: l badtore, qualuque sa l rezzo 1 d arteza, s focalzza su due rezz e er qual s ha = + f(e( ) e = + f(e( ) (s ossoo resetare ache cas co ccl lmte comost da tre o ù d tre rezz, cas co ù d u cclo lmte, e ache l caso cu la successoe de rezz o coverge verso essu cclo lmte seza, eraltro, covergere al rezzo d equlbro o allotaars deftamete da esso). t+1 t+1 t+1 * t +f(e( t )) * t +f(e( t )) * t +f(e( t )) 1 3 * 2 t 3 1 * 2 t ' * " t Fgura 10.2 Fgura 10.3 Fgura 10.4 Prooszoe 10.1 La codzoe d stabltà walrasaa locale el temo dscreto rchede (come uò desumers dalle Fgure 10.2, 10.3 e 10.4) che la dervata della fuzoe t + f(e( t ) abba, el uto d equlbro, valore assoluto o suerore ad uo. Pù recsamete, v è stabltà locale d f( E( ) d f( E( ) se 1+ < 1 e solo se 1+ 1, ossa, se d = * d = * D f E (0) D E ( *) ( 2, 0) e solo se [ 2, 0]. Poché la fuzoe f(.) reserva l sego, è ecessaramete D E f (0) > 0 er cu rsultao le codzo d stabltà locale D E( *) 0, che cocde co la codzoe 2 statca walrasaa d stabltà, e D E( *) D E f (0), che è ua codzoe ulterore che rchede che l badtore reagsca co moderazoe agl eccess (ostv o egatv) d domada. S uò otare come l badtore grd l rezzo t+1 usado soltato l formazoe erveutagl al temo t, coè, l eccesso d domada E( t ), ma o le formazo erveutegl e tem recedet. Assumedo che la fuzoe d eccesso d domada sa cotua e che v sa almeo u equlbro, egl otrebbe ervere semre all equlbro usado gl eccess d domada erveutgl e tem recedet. S tratterebbe d rcercare ua soluzoe dell equazoe E() = 0. Il badtore otrebbe covergere alla soluzoe usado, ad esemo, l metodo delle secat. 8
9 b) Aals damca della stabltà walrasaa el temo cotuo. S dch co (t), ove t +, la successoe de rezz grdat dal badtore e co l equazoe dfferezale d ( t ) = f(e((t)) l comortameto del dt badtore, ove f(.) è ua fuzoe che coserva l sego. L equlbro è stable se lm ( t) = *, er cu s ha la seguete codzoe d stabltà. t Prooszoe 10.2 La codzoe d stabltà walrasaa locale el temo cotuo rchede che la dervata della fuzoe f(e((t)) abba, el uto d equlbro, valore o ostvo. Pù recsamete, v è stabltà locale se D E( *) < 0 e solo se D E( *) 0. (La codzoe della Prooszoe 10.2 cocde co la codzoe statca walrasaa d stabltà.) La Fgura 10.5 rareseta quato dcato. I essa 1 * e 3 * soo rezz d due equlbr localmete stabl, metre 2 * è l rezzo d u equlbro stable. Le freccette sull asse delle ascsse dcao la drezoe della successoe de rezz che rsulta dalla equazoe d ( t ) = f(e((t)), dt che mlca d ( t ) d ( t) > 0 se E((t)) > 0 e < 0 se E((t)) < 0. (S ot dt dt come la stabltà globale, secodo cu l equlbro esame vee ragguto qualuque sa l rezzo zale, rcheda che l equlbro sa uco e che la fuzoe d eccesso d domada sa decrescete corrsodeza al rezzo d equlbro). 7 E() 1 * 2 * 3 * Fgura 10.5 L aals della stabltà eseguta fora, sebbee revalete ella letteratura ecoomca, o è l uca roosta er l equlbro cocorrezale. 7 U aals ù dettaglata dalla stabltà dell equlbro verrà comuta, seguedo l mostazoe damca el temo cotuo, el Catolo 12, esamado l equlbro geerale cocorrezale. 9
10 Vee, ora, dcata l aals al rguardo roosta da Marshall, che rede cosderazoe le fuzo verse d domada d = d () e d offerta s = s () (co rfermeto alle fuzo drette d = D() e s = S(), la fuzoe d () cocde co la fuzoe D 1 ( d ) e s () co D 1 ( s ) ). La fuzoe d () dca l rezzo che comrator soo dsost a agare er comrare, comlessvamete, la quattà d bee e la fuzoe s () l rezzo rchesto da vedtor er vedere la quattà d bee). L equlbro rchede le codzo * = d (*) = s (*), che cocdoo co le codzo * = D(*) = S(*) gà dcate (come raresetato ella Fgura 10.1). I questa aals, l mercato reagsce ad ua dffereza ostva tra d e s alzado l volume comlessvo degl scamb e ad ua dffereza egatva abbassadolo. S ottee la codzoe statca d s d( ( ) ( )) marshallaa d stabltà 0 e u aals d = * (marshallaa) della stabltà del tutto smmetrca a quella recedete. S ot come l equlbro cocorrezale soddsf sa la codzoe statca walrasaa sa quella marshallaa d stabltà se, el uto d equlbro, la curva d domada è decrescete e quella d offerta è crescete. No è così se ua delle due curve ha adameto cotraro a quello aea dcato La statca comarata dell equlbro arzale Uo de roblem ù atural che s ogoo ecooma cosste el domadars da che cosa dedoo le gradezze ecoomche: el caso esame, da che cosa dedoo l rezzo * e la quattà scambata * del bee esame. La statca comarata è l aals secfca che rsode a queste domade. Ua volta che s eslctao le relazo che collegao le gradezze ecoomche esame co dat (coè, co altre gradezze suoste dedet da quelle esame), la statca comarata determa quale drezoe (se l aals è qualtatva) o d quato (se è quattatva) s sarebbe alterato l loro valore se uo o ù dat fossero stat dvers. La comarazoe è statca se le varabl esame o soo fuzo del temo, ma rferte a u state (o erodo) d temo o del tutto atemoral. Se soo fuzo del temo (come el caso che sarà resetato el Paragrafo 10.7), l aals corrsodete uò essere deomata damca comarata. Dedao le fuzo aggregate d domada e offerta da arametr α = (α 1,, α m ) che raresetao dat, sao coè, d = D(; α) e s = S(; α). Le codzo d equlbro * = D(*; α) = S(*; α) determao, allora, le fuzo ( geerale, le corrsodeze) *(α) e *(α), che llustrao la dedeza d * e * da dat. Il cofroto uò rguardare modfcazo dscrete de arametr, er cu s cosderao modfcazo b * a * e b * a * coseguet alla modfcazoe α b α a (come ell esemo della successva Fgura 8.6), oure modfcazo 10
11 ftesme, er cu la statca comarata determa le dervate *, eseguedo ercò u aals locale. α * α e b * a * D(;α a ) D(;α b ) S() a * b * Fgura 10.6 Nella Fgura 10.6 è raffgurato u esemo d statca comarata dell equlbro arzale cu s suoe che la fuzoe d domada aggregata deda da u arametro α (che uò raresetare, se la domada è eserctata da cosumator, la loro caactà d sesa, oure l rezzo d u altro bee, oure ua caratterstca delle refereze, oure ua combazoe d due o ù d quest elemet). 8 Ad esemo, se la domada è eserctata da cosumator, l bee è ormale, l arametro α dca la caactà d sesa de cosumator (el seso che questa è, er og cosumatore = 1,,, ar a α m ) ed è α b > α a, allora, l aals d statca comarata mostra come u accrescmeto della caactà d sesa determ (co curva d domada decrescete e curva d offerta crescete) u accrescmeto sa della quattà scambata sa del rezzo. Lo stesso accade se l arametro α dca l rezzo d u bee sosttuto. Prooszoe 10.3 Cosderado l aals locale d statca comarata ed esrmedo l equlbro medate l aullameto dell eccesso d domada, coè, E(;α) = 0 (ove E(;α) = D(;α) S(;α)), rsulta (dfferezado la codzoe d equlbro) la relazoe D *( α) = α D α E( *; α) D E( *; α) 8 Perché o v sa terdedeza, l arametro α o deve dedere dal rezzo e dagl scamb del bee esame. S ot come l otes dcata ella ota 2 d questo catolo escluda la ossbltà che l arametro α rareset l rezzo d u altro bee o la caactà d sesa d uo o ù cosumator. 11
12 ove la varazoe del arametro α determa lo sostameto dell equlbro. uesta relazoe ha u teressate legame, deomato da Samuelso rco d corrsodeza, co la codzoe statca walrasaa d stabltà D E( *) < 0 trodotta el aragrafo recedete. S ha che l sego della dervata D α *( α ) è uguale a quello della dervata D α E( *; α ) se l equlbro soddsfa la codzoe sudcata d stabltà (eraltro, ha seso esamare soltato la statca comarata d equlbr stabl, essedo quell stabl rraggugbl). S uò, allora, affermare che u cremeto della caactà d sesa de cosumator (se l bee è ormale) o del rezzo d u bee sosttuto determa u aumeto del rezzo d equlbro oché accresce l eccesso d domada del bee, coè, oché D α E( *; α ) > L equlbro arzale co razoameto Vegoo talvolta dcat come equlbr co razoameto le stuazo caratterzzate dalla quattà scambata * = m{d(), S()} e da ua regola d razoameto che rartsce tra comrator, se D() > S(), o tra vedtor, se D() < S(), la quattà dsoble sul lato corto del mercato. 9 I queste aals s assume che la ossbltà d razoameto o flusca sulle scelte degl aget, er cu le loro fuzo d domada e d offerta sul mercato co razoameto cocdoo, er otes, co le aaloghe fuzo omal, quelle, coè, rore del mercato seza razoameto (aalzzate e Catol 3, 4 e 5 e dcate recedeza). S assume, oltre, quado la regola d razoameto determa, er gl aget razoat, ua quattà dedete dalla loro scelta omale (come, ad esemo, ella ota 9), che gl aget razoat o modfcho la loro scelta ua volta che s accorgoo d essere razoat. Naturalmete, queste otes rducoo la lausbltà degl equlbr co razoameto. Nella Fgura 10.7 è dcato u equlbro co razoameto ( cu è razoata l offerta). 9 d Ad esemo, se D() > S(), l razoameto roorzoale determa * = S( ) d ( ) er og = 1,,. Molte regole d razoameto soo ossbl. D ( ) Normalmete s rchede che gl aget sul lato corto o sao razoat, coè, se D() > s d S(), allora q * = s ( ) er og = 1,,, metre è q * d ( ) er og = 1,, d, co q * = S( ). = 1 q 12
13 D() S() * Fgura 10.7 Le caratterstche rcal dell equlbro co razoameto soo: a) l rezzo è esogeo, coè, v è u equlbro co razoameto er og rezzo aarteete al domo delle fuzo aggregate d domada e d offerta; b) se la curva d domada è decrescete e quella d offerta è o decrescete, allora l rezzo * d equlbro cocorrezale (dcato el Paragrafo 10.2) determa la quattà massma scambata, coè, D( *) = S( *) = maxm{ D( ), S( )} 10.6 L equlbro d dustra: breve e lugo erodo Seguedo l aals della roduzoe ( artcolare, quato dcato el Paragrafo 5.9, che dstgue le fuzo d offerta secodo le ossbltà d scelta delle mrese) s dstgue tra equlbro d breve ed equlbro d lugo erodo e s uò trodurre ache u equlbro d brevssmo ed uo d lughssmo erodo. L seme delle mrese che roducoo uo stesso bee vee dcato co l terme dustra (al rguardo, Paragrafo 5.8). a) Nel brevssmo erodo essu ut è varable e o v è, qud, ua scelta. uesta stuazoe corrsode al caso cu le mrese hao gà comuto la scelta d roduzoe e devoo solo vedere l loro rodotto. La quattà del bee rodotto è, ercò, data er og mresa ed è, qud, data ache er l dustra. Nel brevssmo erodo, allora, la curva d offerta d og mresa e quella dell dustra soo rgde: la quattà offerta o dede dal rezzo del bee rodotto. L equlbro è determato dalla codzoe 13
14 = D( *) ove è l rezzo del bee esame, D( ) la sua fuzoe d domada, = = 1q = = 1s = S quella d offerta, l umero delle mrese, e q la quattà rodotta dall mresa -esma. Le Fgure 10.8 e 10.9 raresetao la stuazoe er ua geerca mresa dell dustra e er l dustra. s D() S * * q q Fgura 10.8 Fgura 10.9 b) Nel breve erodo l mresa scegle la quattà degl ut varabl e la sua curva d offerta d outut (trodotta el Paragrafo 5.11) cocde co arte della curva del costo margale (se la quattà d outut o è ulla). L equlbro è determato dalla codzoe * = D( *) = S( *) ove D( ) è la fuzoe d domada del bee esame, S( ) = = 1s ( ) è quella d offerta dell dustra, è l umero delle mrese e s ( ) è la curva d offerta dell mresa -esma. Le Fgure e raresetao la stuazoe er ua geerca mresa dell dustra e er l dustra. Nel dagramma ove è raresetata la stuazoe dell mresa è ossble ache msurare l roftto varable e quello totale d breve erodo (erò, ella Fgura è traccata solo la curva del costo medo varable e o è, qud, vsble l roftto totale). D() * s ( ) ACv( q) * S SR () MC SR (q ) q * Fgura q * Fgura
15 c) Nel lugo erodo s ha ua stuazoe aaloga, co le oortue modfcazo. Ora, og mresa scegle le quattà d tutt gl ut e la fuzoe d offerta d outut rsulta determata (el Paragrafo 5.11) relazoe alle curve d costo medo e margale d lugo erodo. b * a * ssr, ( ; b) ssr, ( ; a) slr, ( ) ACLR, ( q) b * a * S SR (;a) S SR (;b) D b () S LR () D a () q a, * q b, * q a * b * Fgura Fgura Le Fgure e raresetao la stuazoe er ua geerca mresa dell dustra e er l dustra corrsodete a due dverse curve d domada Da ( ) e Db ( ), comedo così u aals d statca comarata. Soo ache raresetate le corrsodet curve d offerta d breve erodo SSR ( ; a ) e SSR ( ; b), determate dalla quattà degl ut fss ottmale er rodurre la quattà d outut dell equlbro d lugo erodo. d) Nel lughssmo erodo v è lbertà d etrata. uesta mlca che la tecologa è ota, coè, che og mresa uò esegure la stessa roduzoe scelta da u altra mresa, come se tutte le mrese fossero dotate dello stesso seme d roduzoe. Allora, l dustra è, smultaeamete, sa l seme delle mrese che roducoo lo stesso bee, sa l seme delle mrese dotate della stessa tecologa. S uò, allora, alcare quato trodotto el Paragrafo 5.11 er l offerta dell dustra el lughssmo erodo (esemlfcata elle Fgure 5.30 e 5.31), rcordado che l umero (reale, er arossmazoe, azché tero) d mrese attve è ar al raorto tra la quattà comlessva * rodotta del bee (determata dall equlbro d mercato) e la quattà d mmo costo medo d lugo erodo er la sgola mresa (mmo costo medo che determa l rezzo del bee sul mercato, * ). Percò, u mutameto della curva d domada modfca soltato l umero delle mrese attve. Allora, assumedo che la curva d costo medo d lugo erodo d mresa abba uo ed u solo mmo, l equlbro d lughssmo erodo è 15
16 * = m AC ( q ), q* = argm AC ( q ), * = D( *), q q * * = q * Le Fgure e raresetao la stuazoe er la geerca mresa dell dustra e er l dustra. Soo ache raresetate le corrsodet curve d offerta d lugo erodo (coè, co u umero dato d mrese attve, ar a quello ottmale el lughssmo erodo). D() s () S LR (;l*) * ACLR, ( q) * MC() =AC() S LLR MCLR, ( q) q * q * Fgura Fgura La dstzoe tra brevssmo, breve, lugo e lughssmo erodo mette evdeza alcue caratterstche della damca dustrale. I questa descrzoe, tutto cò che o vee mezoato è suosto varato durate l rocesso damco; vge, coè, la clausola ceters arbus. S cosder u cremeto mrevsto della curva d domada a artre da u equlbro d lughssmo erodo. Il uovo equlbro d brevssmo erodo che e cosegue alza l rezzo del bee e l roftto delle mrese. uesto cremeto duce u cremeto della roduzoe, co le mrese che accrescoo, el breve erodo, l mego degl ut varabl (che soo quell d cu è ù facle varare la quattà megata) e modfcao, el lugo erodo, l mego d tutt gl ut modo da cosegure l roftto massmo. uest cambamet modfcao la curva d offerta dell dustra (come raresetato ella Fgura 10.16): l rezzo d equlbro s rduce e la quattà rodotta cresce. La reseza d roftt ostv duce l gresso d altre mrese. Il rezzo tora, el uovo equlbro d lughssmo erodo, al valore zale e la quattà rodotta dall dustra cresce relazoe all accrescmeto della domada (metre la quattà rodotta da ua sgola mresa tora al valore zale, corrsodete alla oszoe d roftto ullo). 16
17 SSR * D a () D b () S SSR () S SR () SR * LR * * S LR () S LLR a * SR * LR * b * Fgura L aals d equlbro arzale resuoe che rezz d tutt be, trae quello del bee esame, sao dat. Cò mlca che la curva d offerta d lughssmo erodo dell dustra sa ftamete elastca (come elle Fgure e 10.16) e, qud, come gà dcato alla fe del Paragrafo 5.11, che rezz degl ut o dedao dalla quattà d bee rodotta dall dustra. Se questa dedeza fosse resete, la curva d offerta dell dustra rsulterebbe crescete (o ache decrescete), così come allora dcato. uesta dedeza deoterebbe u terdedeza tra mercat (l equlbro sul mercato del bee esame determa la quattà rodotta del bee, da cu dede la domada de be che soo suo ut d roduzoe, dal cu rezzo dede la curva d offerta del bee esame), che l equlbro arzale è strutturalmete caace d aalzzare. La descrzoe d terdedeze ell equlbro arzale uò essere comuta solo co fort lmtazo e rchede che s coosca come rezz de be dvers dal bee esame dedao dall equlbro (rezzo e quattà) del mercato d questo bee U aals damca d equlbro arzale U eslcta aals damca d equlbro arzale è forta dal cosddetto modello della ragatela (cobweb model). I questo modello la roduzoe rchede u erodo d temo, co l medesmo rtmo er tutte le mrese (come, ad esemo, agrcoltura er le roduzo stagoal). Le mrese scelgoo all zo d og erodo d roduzoe quato rodurre e comoo questa scelta relazoe al rezzo che s attedoo er l mometo cu l rodotto verrà osto vedta. Il modello esama la successoe degl equlbr cocorrezal d brevssmo erodo che s determao sul mercato del bee esame, 17
18 dverse ossbl stuazo. Sao t = 1, la successoe de tem d mercato, t d s e = D( ) la curva (decrescete) d domada, e S( ) t offerta dell dustra, ove e t t = t e e * = D( *) = S( ), = *, t = 1, 1 t la curva (crescete) d dca l rezzo atteso dalle mrese al temo t 1 er l temo t. La successoe degl equlbr dede dall otes che verrà trodotta sulla formazoe delle asettatve. Nelle verso orgare del modello (descrtte da Ezekel, e 1938) s assume che roduttor s attedao u rezzo varato, coè, =, ove * t 1 * t 1 è l rezzo d equlbro del temo t 1. Allora, le mrese rogrammao al temo t 1 la quattà d roduzoe base al rezzo del temo t 1 e vedoo al temo t la quattà d rodotto così decsa. L equlbro d brevssmo erodo d mercato al temo t è raresetato dalle codzo t Assegato u rezzo zale t 0 t t, queste codzo determao la successoe d equlbr ( *, *), t = 1, E teressate l aals d alcue caratterstche d questa t t successoe: artcolare, se v è covergeza verso u equlbro stazoaro e se s resetao oscllazo. Dalle codzo d equlbro rsulta che l adameto del rezzo è la soluzoe della equazoe alle dffereze fte D( *) = S( *). I rossmtà del t t 1 rezzo **, defto dalla codzoe D( **) = S( **), v è covergeza verso ** se β > γ e dvergeza se β < γ, ove β e γ soo le edeze delle due curve, coè, β = D D ( **) e γ = D S ( **), er cu l equazoe alle dffereze fte recedete dvee γ * ** = ( * ** ). Ioltre, base alle otes trodotte, er cu β t t 1 β > 0 e γ > 0, l adameto è oscllatoro. t D() S() 3 * E 3 1 * E 1 E3 1 * E 1 S() ** E 2 2 * 0 E2 2 * D() 0 1 * ** 2* Fgura * 1 * 2 * Fgura Nelle Fgure e soo raresetate le due stuazo. (Se s esama la damca globale, coè o s esama soltato l comortameto rossmtà dell equlbro stazoaro, e le fuzo D( ) e S( ) o soo lear, uò resetars ache la covergeza verso u cclo lmte, coè, verso u oscllazoe ersstete tra due equlbr (, e (, ) co D( ) = S( ) e D( ) = S( ) ). a a ) b b a b b a 18
19 Come gà dcato, l aals recedete è fodata sull otes che roduttor s attedao er l erodo successvo u rezzo ar a quello del erodo recedete, coè, sulla fuzoe d asettatva e t = * t 1. Però, questa asettatva vee og volta falsfcata (a meo che o sa * = * * ). V è, coè, ua cogettura sstematcamete t 1 errata. Né sorte mglore hao asettatve che tegao evetualmete coto ache d altr e rezz recedet, coè, fuzo d asettatva del to = f( *, *,...), t t 1 t 2 deomate asettatve adattve. E mmagable che le mrese modfcho le loro asettatve o aea ercescao la reseza d u errore sstematco. Asettatve che o soffroo d questo dfetto soo quelle accordo co l modello dell ecooma esame, deomate asettatve razoal (trodotte da Muth, 1961, che s è rferto, el suo artcolo, roro al modello della ragatela). Nel caso esame le asettatve razoal e rchedoo, se le mrese cooscoo le fuzo D( ) e S( ), che sa = **. Se o le cooscoo, s deve trodurre u rocesso d aredmeto che covolge l osservazoe de rezz d mercato e che è soggetto a dsturb casual. Ne coseguoo rsultat otevolmete dvers da quell sudcat, che, co la loro forma, avevao dato l ome al modello della ragatela. (Il modello della ragatela è stato ache uo de rm modell ecoomc soggetto ad dage emrca, oltre che l rmo modello ad essere esamato co l otes delle asettatve razoal). S ot ache come l aals damca comuta questo aragrafo dffersca da quella comuta el Paragrafo 10.3 cu vee esamata la stabltà dell equlbro. Nel Paragrafo 10.3 la damca rguarda l rocesso d aggustameto all equlbro, che o vee modfcato. uesto rocesso s svolge, er così dre, a bocce ferme, coè, seza l effettuazoe d att d scambo o d roduzoe, u temo che, er questa ragoe, vee talvolta dcato come temo logco, cotraoszoe a quello storco delle azo ecoomche. I questo aragrafo, vece, la damca rguarda ua successoe d equlbr, cascuo de qual determa scamb e rezz (rezz effettv, o vrtual come quell grdat dal badtore). Ioltre, s ha ua successoe d equlbr stabl (el seso che è soddsfatta, er cascuo, la codzoe walrasaa d stabltà). L aals vuole determare l adameto (el temo storco) d quest equlbr, artcolare se ess covergoo verso u equlbro stazoaro, u equlbro, coè, che ermae mmutato el temo fché o tervegao modfcazo fodametal (el caso esame, varazo della tecologa, de rezz degl ut o della curva d domada). t 10.8 L equlbro d mooolo a rezzo uco Defzoe 10.4 U equlbro arzale è d mooolo uro se rguarda u mercato cu comrator soo rce-taker e v è soltato u vedtore, l quale coosce la curva aggregata d domada de comrator. E a rezzo uco se l rezzo è uguale er tutt comrator. I base a questa defzoe, comrator soo raresetat sul mercato dalla curva d domada d = D() metre l vedtore scegle l rezzo che è er lu ù coveete. Se l vedtore è l roduttore del bee esame, come s assume d cosueto (ache erché questo è l caso rlevate dal uto d vsta emrco), ed ha come obettvo la massmzzazoe del roftto, allora la sua scelta è raresetata dalla soluzoe del roblema 19
20 max C( ) sotto l vcolo = D(), ove C() è la fuzoe d costo mmo d lugo erodo (trodotta el Paragrafo 5.10). uesto roblema uò essere resetato, modo del tutto equvalete, come max R( ) C( ), ove R() = D 1 () è la fuzoe d rcavo (essedo = D 1 () la fuzoe versa d domada). Se le fuzo d rcavo e d costo soo cotue, co R(0) = 0 e C(0) = 0 e v è u > 0 tale che R( ) < C( ) er og >, allora l roblema sudcato ammette soluzoe. Se quelle fuzo soo, oltre, dervabl, s ha ua soluzoe * > 0, se rsultao soddsfatte le codzo D R( *) = D C( *), 2 D R ( *) 2 D ( *) e C R ( *) C ( *) Altrmet, s ha * = 0. La codzoe D R( *) = D C( *) moe, se è * > 0, l uguaglaza tra rcavo margale e costo margale el uto d 2 2 equlbro; la codzoe D R( *) D C( *) rchede che la curva del rcavo margale abba el uto d equlbro edeza o suerore a quella della curva del costo margale; e la codzoe R( *) C( *) rchede, se è * > 0, che l roftto sa o ferore al roftto coseguble co roduzoe ulla. Determata la quattà d roduzoe *, ottma er l mooolsta, l rezzo che quest ha coveeza ad morre rsulta determato dalla codzoe * = D 1 (*). * MC() AC() AC(*) MR() D() * Fgura
21 Nella Fgura è raresetato u equlbro d mooolo uro (v soo dcate, oltre alla curva d domada D( ), le curve d rcavo margale MR() = D R( ), d costo margale MC() = D C( ) e d costo medo C ( ) AC() =. L area ombreggata dca l roftto del mooolsta). Nel regme d mooolo a rezzo uco, l rezzo d equlbro è suerore al costo margale (metre, el regme d cocorreza, l rezzo d equlbro è ar al costo margale er tutte le mrese attve). Vale, fatt, la seguete rooszoe. Prooszoe 10.4 Se la curva d domada è decrescete el uto d equlbro, coè D D( *) < 0, e l mooolsta è attvo, coè * > 0, allora l rezzo d mooolo è maggore del costo margale, coè * > MC(*). Dmostrazoe. Essedo l mooolo esame a rezzo uco, la curva d domada cocde co la curva d rcavo medo. Se questa è decrescete, allora la curva margale corrsodete le è ferore, 10 coè * = D 1 (*) > MR(*). Se * > 0, s ha ache D R( *) = D C( *), coè MR(*) = MC(*), er cu * > MC(*). La codzoe c = MC( c ) = D 1 ( c ) defsce l equlbro che v sarebbe se l mooolsta fosse rce-taker, coè, l equlbro cocorrezale d rfermeto. uesto vee usato er qualfcare come aturale l mooolo l cu equlbro cocorrezale d rfermeto determa u roftto egatvo, come dcato dalla Defzoe I altr term, se l mooolsta fosse rce-taker, la sua roduzoe sarebbe ar a zero. Il mooolo aturale s reseta quado la domada è lmtata rsetto alle ossbltà della roduzoe, el seso che la domada lmta la roduzoe (dell equlbro cocorrezale d rfermeto) ad u lvello cu l costo medo è decrescete. Defzoe 10.5 U mooolo è aturale se, ur essedo * > 0 e 1 * = D ( *) > AC( *), s ha = D 1 ( ) = MC( ) < AC( ). c c c c Nella Fgura è raresetato l equlbro d u mooolo aturale. T ( ) 10 Per og fuzoe cotua e dervable T(), defte la fuzoe meda A() = dt ( ) da( ) 1 e quella margale M( ) =, rsulta = ( M ( ) A ( )), er cu d d er og > 0 ove la fuzoe meda è decrescete s ha M ( ) < A( ). (uesta relazoe è dcata ache dalla Prooszoe 5.24). 21
22 MC() * AC(*) AC() c MR() * c D() Fgura Statca comarata del mooolo a rezzo uco. L aals d statca comarata è utle el mooolo sorattutto er esamare l effetto d ua varazoe del costo d roduzoe sul rezzo d vedta. S otzz ua varazoe del costo d roduzoe che mut la fuzoe C() ella fuzoe C() + t, coscché l costo margale e quello medo dvegoo MC() + t e AC() + t vece che MC() e AC(). (Il terme t uò essere, se ostvo, u mosta sulla quattà rodotta e veduta oure, se egatvo, l effetto del rogresso tecco). Assumedo che la curva d domada sa decrescete, é facle vedere come questa varazoe determ, se t è ostvo, ua dmuzoe (u cremeto, se t è egatvo) sa della quattà rodotta, sa del roftto del mooolsta e u cremeto (o dmuzoe, se t è egatvo) del rezzo. E teressate recsare quattatvamete la rercussoe sul rezzo d ua varazoe del costo d roduzoe. Per ua varazoe ftesma del costo d roduzoe, coè, oedo che t ass da 0 a dt, s trovao, dfferezado le codzo d equlbro del mooolo * = D(*), D R( *) = D C( *) le codzo d* = D D(*) d*, 2 2 D ( *)d * = D ( *)d * + d R C t e, qud, da esse, teedo coto della codzoe del secodo orde 2 D R ( *) < 2 D C ( *), 22
23 d * 1 1 = > dt D D( *) D R( *) D C( *) d * S uò otare come o sa ecessaramete 0< Ad esemo, se dt la curva d domada è del to ad elastctà 12 costate, coè = A ε (co ε > 1, altrmet l rcavo margale o è ostvo), e la fuzoe d costo del to co cost medo e margale costat, coè C = c (co c > 0 ), ε d * ε allora rsultao * = c e = > 1, ossa, ua varazoe del ε 1 dt ε 1 costo margale s rercuote sul rezzo msura ù che roorzoale e tato d ù quato ù vca a 1 è l elastctà della domada L equlbro d moosoo a rezzo uco Il moosoo è l regme d mercato duale del mooolo, el seso che è uguale al mooolo ua volta che s sosttuscao tra loro term comratore e vedtore. Defzoe 10.6 U equlbro arzale è d moosoo uro se vedtor soo rce-taker e v è soltato u comratore, l quale coosce la curva aggregata d offerta de vedtor. E a rezzo uco se l rezzo è uguale er tutt vedtor. Allora, vedtor soo raresetat sul mercato dalla curva d offerta X s = S( x ) metre l comratore scegle l rezzo che è er lu ù coveete. S cosder l caso cu l comratore è u roduttore er l quale l bee esame è u ut, come s assume d cosueto questa aals (ache erché questo è l caso rlevate dal uto d vsta emrco), ed abba l comratore come obettvo la massmzzazoe del roftto. Nel seguto, sarao aalzzat due cas cu l moososta è, rsettvamete, rce-taker sul mercato del suo rodotto (metre è rce-maker sul mercato del bee esame, cu è moososta) o mooolsta. a) Equlbro d moosoo co roduttore moososta sul mercato d u ut e rce-taker sul mercato del rodotto. Esamado, er semlctà, la stuazoe d breve erodo (co l bee esame uco ut varable), la scelta è raresetata dalla soluzoe del roblema max q X x C f x, X, sotto vcol = F(X, x f ) e X = S( x ) ove = F(X, x f ) è la fuzoe d roduzoe (o decrescete rsetto a X ), q è l rezzo del rodotto, x f è l vettore che dca le quattà degl ut fss e C f 0 è l costo fsso, ossa, max FX (, x ) X C sotto l vcolo X = S(x) x, X q f x f 11 Così accade ell equlbro cocorrezale, come è facle verfcare. 12 L elastctà della domada rsetto al rezzo msura, come dcato ella ota 16 del Catolo 3, u uto della curva d domada = D(), l raorto tra le varazo d ( ) relatve della quattà domadata e del rezzo, coè ε =. d 23
24 uesto roblema è del tutto equvalete al roblema max RX ( ) Cv( X) C f, ove R(X) = q F(X, x f ) è la fuzoe d rcavo del rodotto dell ut e C v (X) = X S 1 (X) è la corrsodete fuzoe d costo varable (essedo x = S 1 (X) la fuzoe versa d offerta). Se queste fuzo d rcavo e d costo varable soo cotue, co R(0) = 0 e C v (0) = 0 e v è u X > 0 tale che R( X ) < C( X) er og X > X, allora l roblema dcato ammette soluzoe. Se le fuzo soo, oltre, dervabl, la soluzoe X* soddsfa le codzo R( X*) C ( X*) v D RX ( *) = D C ( X * ) X X v e X 2 D RX ( *) 2 D C ( X *) se X* > 0 e X X v, altrmet s ha X* = 0. Determata la quattà d ut X*, ottma er l moososta, l rezzo che quest scegle rsulta determato dalla codzoe x* = S 1 (X*). Nella Fgura è raresetato u equlbro d moosoo (v soo dcate la f curva d rcavo margale del rodotto dell ut MR(X) = D R( X) = D F( X, x ), X q X f ove D F( X, x ) è la roduttvtà margale dell ut, la curva d costo margale MC(X) X = D C ( X) e quella d costo varable medo, che cocde co la curva d offerta). S ot X v come rsult la dsuguaglaza * < MR(X*) vece l uguaglaza, come sarebbe x accaduto se l roduttore fosse stato rce-taker sul mercato dell ut, e come rsult megata, rsetto a questo caso, ua quattà more d ut. x MC(X) S( x ) AC v (X) x * MR(X) = q D x F(X,x f ) X* Fgura X b) Equlbro d moosoo co roduttore moososta sul mercato d u ut e mooolsta sul mercato del rodotto. La scelta è raresetata, questo caso, dalla soluzoe del roblema max, x, q X, X C q x f sotto vcol = F(X, x f ), = D( q ) e X = S( x ) ove = D( q ) è la fuzoe d domada del rodotto. uesto roblema è del tutto equvalete al roblema max R( X) C ( X) C, ove R(X) = F(X, x f ) D 1 (F(X, x f )) è X v f 24
25 la fuzoe d rcavo del rodotto dell ut e C v (X) = X S 1 (X) è la fuzoe d costo varable (essedo q = D 1 () la fuzoe versa d domada del rodotto e x = S 1 (X) quella d offerta dell ut). Se queste fuzo d rcavo e d costo varable soo cotue, co R(0) = 0 e C v (0) = 0 e v è u X > 0 tale che RX ( ) < C( X) er og X > X, allora l roblema dcato ammette soluzoe. Se le fuzo soo, oltre, dervabl, la soluzoe X* soddsfa le codzo D RX ( *) = D C ( X * ) e X se X* > 0 e R( X*) C ( X*) v X v 2 D R ( X *) 2 D C ( X *) X X v, altrmet s ha X* = 0. Determata la quattà d ut X*, ottma er l moososta, l rezzo dell ut che quest scegle rsulta determato dalla codzoe x* = S 1 (X*), la quattà rodotta dalla codzoe * = F(X*, x f ) e l rezzo d vedta del rodotto dalla codzoe q * = D 1 (*). Nella Fgura è raresetato u equlbro d questo to d moosoo (v soo dcate la curva d rcavo margale del rodotto dell ut MR(X) = D ( ) X R X = ( ) D (, f f MR F X x ), ove MR() è l rcavo margale e D F( X, x ) è la roduttvtà X margale dell ut, la curva d costo margale MC(X) = X D C ( X) e quella d costo varable medo, che cocde co la curva d offerta). S ot come rsult * ( ) D ( *, f f < MR F X x ) < D F( X*, x ) e come la quattà megata d ut (e, x X q X qud, rodotta d outut) sa more d quella del moosoo co roduttore rce-taker sul mercato dell outut. X v x MC(X) S( x ) AC v (X) x * q D x F(X,x f ) MR(X) = MR() D x F(X,x f ) X* X Fgura L equlbro d mooolo co dscrmazoe del rezzo Metre el mooolo a rezzo uco (esamato el Paragrafo 10.8) l rezzo scelto dal mooolsta è uguale er tutt comrator e er tutte le utà del bee acqustate da 25
26 cascu comratore, el mooolo co dscrmazoe del rezzo l mooolsta è grado d alcare rezz dvers, a secoda della quattà del bee e/o del comratore. Possoo essere dstte dverse stuazo a secoda della ossbltà d morre rezz dvers, raggruate tre geer d dscrmazoe. La dscrmazoe del rezzo del rmo geere s reseta quado l mooolsta uò alcare u rezzo dverso ad og comratore e er og utà d bee che quest comra. S ha la dscrmazoe del rezzo del secodo geere se l mooolsta s reseta sul mercato co dvers cotratt d comravedta (cascuo raresetato da ua coa quattà-rezzo) tra cu og comratore uò sceglere, d modo che comrator o soo dscrmat ma comrao a rezz dvers a secoda del cotratto scelto. Co la dscrmazoe del terzo geere l mooolsta dstgue tra comrator e vede loro l bee a rezzo dverso (erò, allo stesso rezzo er cascu comratore qualuque sa la quattà che quest comra). a) Mooolo co dscrmazoe del rezzo del rmo geere. I questo caso l mooolsta è grado d morre ad og comratore l rezzo massmo che quest è dsosto a agare er acqustare l bee esame. (Ad esemo, u mresa ha l mooolo d u trattameto che cura u certo to d calvze er la quale o esstoo altre cure). uesto sgfca che l comratore è costretto dal mooolsta a rmaere sulla curva zale d dffereza, qualuque sa la quattà acqustata: altr term, l mooolsta scegle l uto che refersce sulla curva d dffereza del comratore. S assuma che og comratore osseda, rma dell acqusto, ua quattà ulla del bee esame e che l acqusto degl altr be o deda dalle codzo del mercato esame se o relazoe alla sesa er l bee esame, abba, coè, refereze searabl addtvamete rsetto al bee esame, ercò raresetate da ua fuzoe d utltà del to u(x) + g(m r), ove x è la quattà del bee esame, r la sesa er otteerla e m è la caactà d sesa. 13 S assuma, oltre, che le fuzo u(.) e g(.) sao dervabl, o decrescet e cocave, er cu le curve d dffereza soo o crescet e covesse. Allora, la curva d dffereza del comratore -esmo su cu l mooolsta uò sceglere l uto che refersce (e uò far cò er cascuo degl comrator) è raresetata dalla relazoe u (x ) + g (m r ) = g (m ), oedo er semlctà u (0) = 0, ove x è la quattà del bee esame veduta al comratore -esmo, m la caactà d sesa d quest (che è ua quattà data d moeta) e r la somma agata dal comratore er otteere la quattà x d bee. Il mooolsta uò sceglere la coa (x, r ) sotto l vcolo u (x ) + g (m r ) = g (m ). Il rcavo del mooolsta è ar a = 1, che l mooolsta massmzza er og data quattà X = x, ossa la scelta della rartzoe delle vedte del mooolsta è = 1 soluzoe del roblema max sotto vcol X = x e u (x ) + g (m r ) = g (m ) r = 1 = 1 ( x, r ) = 1 er = 1,,. Itroducedo la fuzoe lagragaa L(x 1,, x, r 1,, r, λ, µ 1,,µ ) = r r + λ(x x ) + 1 µ (u (x ) + g (m r ) g (m )) = 1 = 1 s trovao, er le soluzo tere, le codzo µ D x u ( x ) = λ, µ D m g ( m r ) = 1, = 1,, X = 1 x, u (x ) + g (m r ) = g (m ), = 1,, = = 13 Ifatt, se la fuzoe d utltà è del to u(x 1 ) + v(x 2,, x k ), ove l rmo bee è quello esame, e l agete è rce-taker er gl altr be, allora, er og coa (x 1, r 1 ), rsultao le domade x h = d h ( 2,, k, m r 1 ), ove m è la caactà comlessva d sesa, er cu la fuzoe d utltà dvee u(x 1 ) + g( 2,, k, m r 1 ), ove g(.) è la fuzoe dretta d utltà relatva agl altr be. Cosderado dat rezz degl altr be, rsulta la fuzoe d utltà sudcata. 26
27 che rchedoo D xu ( x ) = λ, u (x ) + g (m r ) = g (m ), = 1,, D g ( m r) m ueste codzo, coè, rchedoo che ut scelt dal mooolsta sulle curve d dffereza de comrator abbao tutt lo stesso saggo margale d sosttuzoe. Rsulta la fuzoe d rcavo R(X) = max = 1 r, co D XR(X) = λ (oché, dfferezado le ( x, r ) = 1 codzo recedet, s ha dr = r, dx = e = 1 d = 1 dx D xu ( x ) dr = dx D g ( m r) m er = 1,, ) e D 2 X R(X) 0 (er l otes d covesstà delle curve d dffereza de comrator). La determazoe della quattà X* messa vedta dal mooolsta s ottee, come al solto, dalla massmzzazoe del roftto del mooolsta e, qud, dalla codzoe d uguaglaza tra rcavo margale e costo margale. S hao, ercò, le codzo d equlbro MC(X*) = MR(X*) = D xu ( x*) = λ * D g ( m r*) m co X* = 1 x *, R(X*) = r, u(x *) + g (m r *) = g (m ), er = 1,,, = = 1 * che mlcao l uguaglaza delle rsettve gradezze margal tra tutt gl aget (costo margale e rcavo margale del mooolsta, sagg margal d sosttuzoe de comrator). uesto comue valore λ * dca l rezzo margale del bee esame. S uò otare come l rezzo margale λ *, la quattà rodotta X* e le quattà acqustate x * da comrator ell equlbro d mooolo co dscrmazoe del rezzo del rmo geere cocdao co l rezzo, la quattà rodotta e le quattà acqustate da comrator ell equlbro cocorrezale (ma o cocdoo, e due equlbr, le sese de comrator e, qud, l rcavo del roduttore). Ifatt, co rezzo uco e aget tutt rce-taker rsulta l equlbro cocorrezale determato dalle codzo X* = 1 x *, MC(X*) = D xu ( x*) = * D g ( m * x *) m er = 1,,. b) Mooolo co dscrmazoe del rezzo del secodo geere. I questo caso l mooolsta coosce la tologa de comrator, ma o è grado d rcooscere l to d og sgolo comratore. Ad esemo, sa che v soo due t d comrator e coosce le loro refereze, ma o sa quale to d cosumatore sa Tzo. (S mmag l gestore dell uco teatro lrco d ua cttà cu v soo due t d settator, gl aassoat e gl settator occasoal. Il gestore sa questo, ma o è grado d dstguere al bottegho se l clete è dell uo o dell altro to). Il mooolsta uò, allora, cert cas, sfruttare l mercato rooedo dvers ossbl cotratt, cascuo de qual è referto da u to d cosumator, ducedo questo modo la certa (o autoselezoe) de comrator. Og cotratto è ua coa che dca la quattà comrable del bee e la sesa corrsettva: ossa, l cotratto h-esmo è la coa (x h, r h ). 14 S cosder l caso co due sol t d comrator. S assuma, come el recedete geere d dscrmazoe, che og comratore osseda, rma dell acqusto, ua quattà ulla del bee esame e che l acqusto degl altr be o deda dalle codzo del = 14 I questo aragrafo vee esamato l caso cu l mooolsta roduce u bee omogeeo. Se roduce be dfferezat, come quell trodott el aragrafo successvo, allora u cotratto uò cludere ù be e be clus u cotratto ossoo essere dvers da quell clus altr cotratt. 27
28 mercato esame se o relazoe alla sesa er l bee esame, ossa, che due t d comrator abbao, rsettvamete, le fuzo d utltà u 1 (x 1 ) + g 1 (m 1 r 1 ) e u 2 (x 2 ) + g 2 (m 2 r 2 ), co u 1 (0) = u 2 (0) = 0 e le fuzo u 1 (.), g 1 (.), u 2 (.) e g 2 (.) o decrescet, cocave e dervabl. S assuma, oltre, che uo de due t d comrator, ad esemo, l rmo to, sa ù dsoble all acqusto del bee dell altro, el seso che og cotratto (x, r) favorevole er l secodo to è favorevole ache er l rmo to, coè, u 2 (x) + g 2 (m 2 r) g 2 (m 2 ) mlca u 1 (x) + g 1 (m 1 r) g 1 (m 1 ). S cosdera el seguto l evetualtà che l rmo to d comrator reset, er og ossble cotratto, u saggo margale d D xu ( x) D 1 xu ( x) 2 sosttuzoe ù elevato che l secodo to, coè, >, D g ( m r) D g ( m r) deotado così la dsobltà a agare d ù rsetto al secodo to. m m Co queste otes, l mooolsta sa che og cotratto che determa l acqusto del bee da arte de comrator del secodo to determa ache l acqusto da arte d quell del rmo to, metre v ossoo essere cotratt cu aderscoo comrator del rmo to, ma o quell del secodo to. Il mooolsta, allora, uò durre la certa de comrator rooedo u cotratto aea suffcete er comrator del secodo to (coè, d ochssmo mglore d u cotratto (x 2, r 2 ) dfferete, er comrator del secodo to, alla stuazoe zale, ossa co u 2 (x 2 ) + g 2 (m 2 r 2 ) = g 2 (m 2 ) ) e u cotratto aea mglore d questo er comrator del rmo to (coè, d ochssmo mglore d u cotratto (x 1, r 1 ) dfferete, er cosumator del rmo to, al cotratto roosto a cosumator del secodo to, ossa co u 1 (x 1 ) + g 1 (m 1 r 1 ) = u 1 (x 2 ) + g 1 (m 1 r 2 ) ). S verfca la certa se l cotratto (x 1, r 1 ) o è aetble er comrator del secodo to (coè, s ha u 2 (x 1 ) + g 2 (m 2 r 1 ) < g 2 (m 2 ) ). I questo caso, comrator del rmo to scelgoo l cotratto (d ochssmo mglore d) (x 1, r 1 ) e quell del secodo to l cotratto (d ochssmo mglore d) (x 2, r 2 ). Il mooolsta scegle cotratt da roorre modo che rsult massmo l suo roftto subordatamete a quest vcol. Percò, dcado co N 1 e N 2 l umero de comrator de due t e co C() la fuzoe d costo, ove = N 1 x 1 + N 2 x 2, s tratta d redere cosderazoe l roblema max Nr+ Nr C( Nx + N x) x, x, r, r sotto vcol u 1 (x 1 ) + g 1 (m 1 r 1 ) = u 1 (x 2 ) + g 1 (m 1 r 2 ) e u 2 (x 2 ) + g 2 (m 2 r 2 ) = g 2 (m 2 ), e d cotrollare se la soluzoe soddsfa la codzoe u 2 (x 1 ) + g 2 (m 2 r 1 ) < g 2 (m 2 ). Itroducedo la fuzoe lagragaa L(x 1, x 2, r 1, r 2, λ 1, λ 2 ) = Nr CNx ( + Nx) + Nr λ 1 (u 1 (x 1 ) + g 1 (m 1 r 1 ) u 1 (x 2 ) g 1 (m 1 r 2 )) + λ 2 (u 2 (x 2 ) + g 2 (m 2 r 2 ) g 2 (m 2 )), rsultao le codzo del rmo orde: * = N 1 x 1 * + N 2 x 2 *, NMC ( *) λ D u( x*), ( *) λd ( *) λ D ( *), = NMC + u x = u x m x N = λ D g ( m r* ), N + λd g ( m r*) = λ D g ( m r* ), m x u 1 (x 1 *) + g 1 (m 1 r 1 *) = u 1 (x 2 *) + g 1 (m 1 r 2 *), u 2 (x 2 *) + g 2 (m 2 r 2 *) = g 2 (m 2 ) ueste codzo mlcao m x D xu ( x *) 1 1 = MC( *), D g ( m r*) m D u ( x *) x 1 2 N + N 2 1 D xu ( x *) D u ( x *) 2 2 x 1 1 = MC( *) D ( *) D ( *) mg m r g m r m N + N 2 1 D g ( m r*) m ossa, che comrator del rmo to (quell ù roes all acqusto) rcevoo u cotratto favorevole (che, coè, cremeta la loro utltà) e ervegoo ad ua stuazoe 28
29 cu l loro saggo margale d sosttuzoe è uguale al costo margale, metre comrator del secodo to rcevoo u cotratto che o l favorsce e ervegoo ad ua stuazoe cu l loro saggo margale d sosttuzoe uò dfferre dal costo margale. I artcolare, oché le due relazo recedet mlcao l uguaglaza D xu ( x *) D 2 2 xu ( x *) D 1 1 mg ( m r*) D ( *) D ( *) xu x 1 2 xu x 2 2 N ( ) = N ( 2 1 D g ( m r *) D g ( m r*) D g ( m r*) D g ( m r*) D g ( m r*) ) m m m m m ossoo sussstere le dsuguaglaze oure quelle ooste Nel rmo caso, s ha D u ( x *) D u ( x *) D u ( x *) > > x x x D g ( m r *) D g ( m r *) D g ( m r*) m m m D u ( x *) D u ( x *) D u ( x *) < < x x x D g ( m r*) D g ( m r *) D g ( m r* ) m m m D xu ( x *) 2 2 > MC( *), oltre, co x 1 * > x 2 * oché D g ( m r*) m (x 1 *, m 1 r 1 *) e (x 2 *, m 1 r 2 *) s trovao sulla stessa curva d dffereza (essedo u 1 (x 1 *) + g 1 (m 1 r 1 *) = u 1 (x 2 *) + g 1 (m 1 r 2 *) ), che è covessa. Secularmete, el secodo caso, s hao tutte le dsuguaglaze ooste, coè, D xu ( x *) 2 2 < MC( *) e x 1 * < x 2 *. D g ( m r*) m Se vale la codzoe D xu ( x) D ( ) 1 xu x 2 >, trodotta er deotare la D g ( m r) D g ( m r) m m dsobltà de comrator del rmo to a agare d ù d quell del secodo to, allora, da u lato, uò verfcars solo l rmo caso e, dall altro lato, rsulta soddsfatta la codzoe u 2 (x 1 *) + g 2 (m 2 r 1 *) < g 2 (m 2 ), 15 che rede l cotratto (x 1, r 1 ) o aetble er comrator del secodo to e, qud, la certa realzzable e coveete er l mooolsta. I cotratt (x 1 *, r 1 *) e (x 2 *, r 2 *) soo, el caso esame, equvalet a cotratt che cofgurao la vedta, er l rmo cotratto, d ua tessera (omatva e cedble) al rezzo t 1 * che cosete d acqustare l bee (co dveto d rvedta) al rezzo 1 * e, er l secodo cotratto, d ua tessera al rezzo t 2 * che cosete d acqustare l bee al rezzo 2 *. L equvaleza è asscurata, er l rmo cotratto, dalle D xu ( x *) 1 1 codzo 1 * =, t 1 * = r 1 * 1 *x 1 * e, er l secodo cotratto, dalle D g ( m r*) codzo 2 * = m D u ( x *) x 2 2 D g ( m r* ) m e t 2 * = r 2 * 2 *x 2 * : la covesstà delle curve d dffereza e le codzo del caso esame mlcao t 1 * > t 2 * > 0 e MC(*) = 1 * < 2 *. Allora, comrator del secodo to referscoo comrare la tessera meo cara che 15 Ifatt, er og x [x 2 *, x 1 *], essedo D xu ( x) D ( ) 1 xu x 2 >, og D g ( m r) D g ( m r) m m uto (x, r) aarteete alla curva d dffereza u 1 (x) + g 1 (m 1 r) = u 1 (x 2 *) + g 1 (m 1 r 2 *), la edeza d questa è suerore ( valore assoluto) alla edeza delle curve d dffereza U 2 = u 2 (x) + g 2 (m 2 r), er cu, al crescere d x, l utltà u 2 decresce. S ha, qud, g 2 (m 2 ) = u 2 (x 2 *) + g 2 (m 2 r 2 *) > u 2 (x 1 *) + g 2 (m 2 r 1 *). 29
30 erò cosete d comrare l bee al rezzo ù caro e quell del rmo to referscoo l cotraro. uesto to d rezz (che revede er l comratore ua sesa fssa ed ua roorzoale alla quattà acqustata) è u esemo d sstema d rezz o lear. 16 Nella Fgura è descrtta la stuazoe aea dcata ( questa fgura le curve d dffereza de due t d comrator soo traslate lugo l asse delle ordate modo che l uto (0, m 1 ) del rmo to cocda co l uto (0, m 2 ) del secodo to). m 1 m 2 m 2 r 2 * m 1 r 2 * m 2 r 1 * u 2 (x 1 *)+ g 2 (m 2 r 1 *) m 1 r 1 * α g 2 (m 2 ) tagα = MC u 1 (x 2 *)+ g 1 (m 1 r 2 *) g 1 (m 1 ) x 2 * x 1 * x Fgura Se la codzoe sudcata o vale, uò accadere che la certa o sa coveete. Allora, al mooolsta covee roorre codzo d vedta ugual er tutt comrator. c) Mooolo co dscrmazoe del rezzo del terzo geere. I questo caso l mooolsta è grado d dstguere tra gru d comrator e coosce la curva d domada d cascu gruo. Ioltre, comrator o ossoo rvedere l bee al d fuor del loro gruo. Allora, l mooolsta vede l bee su mercat searat e scegle su cascuo l rezzo d mooolo. (Ad esemo, l mooolsta vede l suo rodotto aes dvers ad u rezzo dverso og aese, o lo vede a rezzo dverso a secoda dell età dell acqurete, ecc.). Sao comrator dstgubl due gru, caratterzzat rsettvamete dalle fuzo d domada 1 = D 1 ( 1 ) e 2 = D 2 ( 2 ), e abba l mooolsta la fuzoe d costo C( ). Idcado le fuzo d rcavo e due mercat co R 1 ( 1 ) e R 2 ( 2 ) (ove R 1 ( 1 ) = 1 D 1 1 ( 1 ) e R 2 ( 2 ) = 2 D 2 1 ( 2 ) ), la massmzzazoe del roftto coduce alle codzo del rmo orde (che uguaglao l costo margale al rcavo margale og mercato) MC( 1 *+ 2 *) = MR 1 ( 1 *) = MR 2 ( 2 *), 1 *= D 1 ( 1 *), 2 *= D 2 ( 2 *) e a quelle del secodo orde 16 Prezz o lear del to dcato soo comu el caso de moool atural (come ella fortura d eerga elettrca), erò er rago dverse da quelle qu dcate, che sarao evdet el Paragrafo 10.12, quado sarà esamato l tema dell effceza. 30
31 D ( * + *) D (, D MC( * + *) D MR ( *) MC 1 2 MR *) 1 1 La Fgura descrve l equlbro co dscrmazoe del rezzo del terzo geere aea resetato ( questa fgura la curva che determa, el uto d tersezoe co la curva del costo margale, la quattà rodotta 1 *+ 2 * è otteuta sommado, er og ordata, le ascsse delle curve d rcavo margale MR 1 ( 1 ) e MR 2 ( 2 ). Se s descrve l rcavo margale e term della elastctà della domada, allora, 1 rsulta MR = (1 ). ud, la codzoe del rmo orde MR 1 ( 1 *) = MR 2 ( 2 *) ε 1 1 rchede (1 ) = (1 ). uesta relazoe mlca che l mooolsta scelga u 1 2 ε ε 1 2 rezzo maggore el mercato cu la domada ha elastctà ferore. D 1 1 * 2 * MC D 2 MR 1 1 * 2 * MR 2 1 *+2* Fgura L equlbro d cocorreza mooolstca uesto to d regme d mercato (la cu aals è stata trodotta da Chamberl, 1933) ha caratterstche termede tra la cocorreza e l mooolo. Come el mooolo, vedtor soo rce-maker, oché cascuo vede u bee dverso da quello degl altr vedtor. Come ella cocorreza, v soo molt vedtor e v è lbertà d etrata. La eculartà d questo regme è la reseza d rodott dfferezat, coè, eterogee ma altamete sosttubl. Ad esemo, soo raresetabl ell ambto d mercat cocorreza mooolstca le trattore, l commerco al dettaglo, l vo, ecc. S ha u comortameto arametrco (vece che strategco) se la scelta d og sgolo vedtore è fluete sul roftto degl altr vedtor. Tuttava, la sosttubltà de be rede la 31
32 domada d og bee fuzoe ache del rezzo medo de be smlar (sul quale la scelta d u sgolo vedtore flusce modo trascurable). Allora, la domada del bee rodotto dall mresa j-esma è raresetable co la fuzoe q j = d j ( j, P), ove P dca l rezzo medo d vedta de be smlar. Essedo d (, P) j j quest be sosttut, s ha > 0. Nel breve erodo (ossa, co u umero dato P d mrese), og vedtore cosdera P dato (oché gl altr vedtor o reagscoo alla sua scelta) e determa l rezzo d vedta come el mooolo a rezzo uco. S hao, ercò, le codzo D R ( q *, P) = D C ( q *) q j j q j j 2 2, D R ( q *, P) D C ( q *), qj* = d j ( j *, P), qq j j q j j e vale sostazalmete la raresetazoe della Fgura La lbertà d etrata coduce ad u equlbro d lughssmo erodo cu og mresa cosegue u roftto ullo. Ad esemo, se v è roftto ostvo, l etrata d uove mrese accresce la quattà comlessvamete offerta e rduce l rezzo medo d vedta, er cu la curva d domada rvolta a cascua mresa s abbassa rducedoe l roftto, fo a ervere alla stuazoe d roftto ullo, cu l etrata d uove mrese cessa. La stuazoe er l mresa j-esma dvee, allora, quella raresetata ella Fgura j MC j (q j ) j * AC j (q j ) MR j (q j,p) d j ( j,p) q j * q j Fgura S uò otare come, essedo la curva d domada decrescete, la codzoe d roftto ullo mlch che l costo medo sa decrescete corrsodeza della quattà rodotta q j *. Ossa, l mresa otrebbe rodurre ua quattà maggore del bee ad u costo medo ferore. Cò mostra come la cocorreza mooolstca determ u eccesso d caactà roduttva, metre ella cocorreza d lughssmo erodo og mresa roduce a costo medo mmo e el mooolo a rezzo uco l mresa roduce ad u costo medo che uò essere sa maggore sa uguale a quello mmo. Tuttava, metre 32
33 quest regm l bee rodotto è omogeeo, ella cocorreza mooolstca be rodott soo dfferezat, determado u vataggo er cosumator, cascuo de qual acqusta la varetà del bee che refersce L aals dell effceza degl equlbr arzal La codzoe d effceza dell equlbro arzale vee ormalmete otteuta descrvedo l vataggo (surlus) dervate dallo scambo (e dalla roduzoe) a comrator e a vedtor del bee esame e rcercado, o, la codzoe che rede massmo l vataggo totale. uesta aals, erò, rchede molte otes semlfcatrc. E, allora, oortuo dcare rma la codzoe d effceza, che vale ache asseza d quelle otes, e trodurre o la descrzoe del surlus. Per u ecooma seza esteraltà, le codzo del rmo orde erché u allocazoe sa effcete rchedoo, come dvduato el Paragrafo 8.2, che sagg margal d sosttuzoe sao, er og coa d be, ugual er tutt cosumator e tutt roduttor. S alcho ora queste codzo alle stuazo descrtte questo catolo. Se comrator sul mercato esame soo tutt rce-taker (come e cas esamat e Paragraf 10.2, 10.6, 10.8 e 10.11), le loro scelte rchedoo che l saggo margale d sosttuzoe tra l bee moeta e l bee esame sa ar al rezzo (moetaro) d questo. ud, essedo l rezzo uguale er tutt comrator, è uguale er tutt comrator l saggo margale d sosttuzoe. 17 Se vedtor soo, sul mercato del bee esame, rce-taker e soo cosumator (ossa, aget che o ottegoo l bee vedta er mezzo della roduzoe), allora le loro scelte rchedoo che l saggo margale d sosttuzoe esame sa ar al rezzo del bee e, qud, essedo l rezzo uguale er tutt vedtor, che sa ache uguale l saggo margale d sosttuzoe. Se, o, comrator e vedtor soo cosumator rce-taker e l mercato è cocorrezale (er cu s alca la descrzoe dcata el Paragrafo 10.2), allora, essedo l rezzo d acqusto uguale al rezzo d vedta, l saggo margale d sosttuzoe esame è uguale er tutt gl aget (sao ess comrator o vedtor) e la codzoe del rmo orde er l effceza rsulta soddsfatta. ud, l equlbro cocorrezale rsulta, tale caso, effcete, ammesso, com è mlcto, che le codzo del secodo orde sao soddsfatte. 17 uest ultma uguaglaza s reseta, come v dcato, ache el caso, esamato el Paragrafo 10.10, del mooolo co dscrmazoe del rezzo del rmo geere, ove o v è u uco rezzo er og utà d bee acqustata da cascu comratore. Ivece, o soo ugual, tra tutt comrator, sagg margal d sosttuzoe e cas d mooolo co dscrmazoe del rezzo del secodo e del terzo geere, ach ess esamat el Paragrafo 10.10, er cu rsulta che l equlbro è effcete. 33
34 Se vedtor soo mrese che hao come uco outut l bee esame (come otzzato geerale questo catolo), allora l saggo margale d sosttuzoe tra l bee moeta e l bee esame cocde, ella scelta d costo mmo er og data quattà d roduzoe, co l costo margale (oché questo rareseta la quattà d moeta cu l mresa è dsosta a rucare er accrescere la roduzoe). Se l equlbro d mercato rchede che l costo margale sa uguale al rezzo (come e cas esamat el Paragrafo 10.6 e al uto a del Paragrafo 10.9) e quest ultmo è uguale al corrsodete saggo margale d sosttuzoe de comrator, allora sagg margal d sosttuzoe soo ugual er tutt gl aget (sao ess comrator o vedtor), la codzoe del rmo orde er l effceza è, ercò, soddsfatta e l allocazoe d equlbro del mercato esame rsulta effcete (ammesso, com è mlcto, che le codzo del secodo orde sao soddsfatte). uesta stuazoe s reseta tutt cas esamat el Paragrafo Ivece, o v è effceza ell equlbro d mooolo a rezzo uco (Paragrafo 10.8) e quello d cocorreza mooolstca (Paragrafo 10.11), oché l costo margale o rsulta uguale al rezzo d equlbro (che è uguale al saggo margale d sosttuzoe tra l bee moeta e l bee esame er tutt comrator). No rsulta effcete, oltre, l equlbro co razoameto (Paragrafo 10.5), a meo che l rezzo o cocda co quello dell equlbro cocorrezale, oché gl aget razoat o coseguoo lo scambo che rede l saggo margale d sosttuzoe uguale al rezzo. L effceza de regm mooolstc d mercato è evdezata dalla dffereza tra l rezzo d vedta e l costo margale d roduzoe. A questo rguardo s uò otare come, el caso cu l rezzo o sa uco (o sa, coè, uguale er tutte le utà d rodotto), l effceza rcheda l uguaglaza tra l costo margale e l rezzo margale. uesto è l rezzo che l comratore deve agare er otteere u utà aggutva d rodotto (ù recsamete è la dervata della sesa er l acqusto del bee rsetto alla quattà del bee, corrsodeza alla quattà acqustata). Rsulta, er questa ragoe, effcete l mooolo co dscrmazoe del rezzo del rmo geere (Paragrafo 10.10). Ua forma d regolametazoe del mooolo aturale (Paragrafo 10.8), volta a cosegure l effceza, revede l moszoe d ua tarffa bara. uesta s comoe d ua quota fssa da agare er otere accedere all acqusto del bee e d ua quota roorzoale alla quattà acqustata. 19 V è, allora, effceza, se quest ultma è uguale al costo margale. (La quota fssa serve a corre la dffereza che v è, sua asseza, tra l costo medo e l costo margale). 18 No s ha, vece, effceza el caso d moosoo d cu al uto a del Paragrafo 10.9, oché le codzo d effceza o soo verfcate er l mercato dell ut su cu l comratore è moososta, sebbee lo sao er l mercato del rodotto (se comrator soo, su questo mercato, rce-taker). Nel caso d moosoo d cu al uto b del Paragrafo 10.9 o v è effceza sa sul mercato dell ut sa sul mercato del rodotto. 19 Nella vedta d eerga elettrca la quota fssa (coè, da agare dedetemete dalla quattà d eerga cosumata) è ormalmete fuzoe della oteza megata, metre quella varable è roorzoale all eerga cosumata. 34
35 10.13 I vatagg dello scambo Il cosumatore ottee co lo scambo u vataggo, oché accresce co esso la sua utltà. Il vataggo (surlus) è msurato dall cremeto d utltà, ammesso che questa sa msurable, coè che l utltà sa cardale (vece che ordale, come otzzato ell aals della scelta d cosumo). Se l utltà è cardale, l surlus è, allora, ar alla dffereza tra l utltà del aere d be cu l cosumatore ervee co lo scambo e l utltà zale. Idcado co ω la sua dotazoe, coè l aere d be rma dello scambo, e co x l aere d be a sua dsoszoe doo lo scambo, l surlus è, ercò, ar a u(x) u(ω), ove u(.) è la sua fuzoe (cardale) d utltà. Se l cosumatore è rce-taker, troducedo la fuzoe dretta d utltà u*(, ω), essedo u(x) = u*(, ω), l vataggo (surlus) rsulta ar a v tot = u*(, ω) u(ω). S assuma, ora, coeretemete co l aals comuta questo catolo, che la dotazoe sa comosta soltato dal bee moeta, sa, coè, ω = (m, 0,, 0), ove m è la quattà del bee moeta (dcato co l dce 1, metre gl altr be soo dcat co gl dc 2,, k ) e che la fuzoe d utltà sa searable addtvamete rsetto al bee esame (quello d cu s cosdera l equlbro arzale d mercato) e quas-leare rsetto al bee moeta, sa coè del to u(x) = x 1 + f(x 2 ) + g(x 3, x 4,, x k ) (come gà dcato ella ota 2), oltre co f(0) = 0 e g(0,, 0) = 0. Allora, la domada del bee esame dede soltato dal rezzo moetaro del bee (coè, da 2, avedo osto 1 = 1 ) e s ha che la fuzoe d domada x 2 = d 2 ( 2 ) è esressa mlctamete dalla codzoe 2 = d f ( x ) 2, cocde, coè, co la curva dell utltà margale. Poché er gl altr be s dx 2 hao fuzo d domada del to x h = d h ( 3,, h ) e, qud, er l bee moeta 20 la k fuzoe d domada x 1 = m 2 d 2 ( 2 ) Σ h= 3 h d h ( 3,, h ), l utltà coseguta co lo scambo è k u*(, ω) = m 2 d 2 ( 2 ) Σ h= 3 h d h ( 3,, h ) + f(d 2 ( 2 )) + g(d 3 ( 3,, h ),, d k ( 3,, h )) metre quella recedete lo scambo è u(ω) = m. Allora l surlus è ar a v tot = f(d 2 ( 2 )) 2 d 2 ( 2 ) + g(d 3 ( 3,, h ),, d k ( 3,, h )) Σ h= 3 h d h ( 3,, h ), ossa v tot = v 2 + ˆv, ove v2 = f(d 2 ( 2 )) 2 d 2 ( 2 ) e ˆv = g(d3( 3,, h ),, d k ( 3,, h )) Σ h= 3 h d h ( 3,, h ). Cosderado l surlus v 2 geerato dall acqusto del bee esame, s ha che l terme f(d 2 ( 2 )) msura l utltà f(x 2 ) della quattà acqustata del bee, cocde, ercò (essedo la curva d domada quella dell utltà margale), er og quattà x 2, co l area tra la curva d domada e l asse delle quattà (lmtatamete all tervallo tra 0 e x 2 ). Il terme 2 d 2 ( 2 ) msura, vece, la sesa er l acqusto della quattà x 2 del bee. Il surlus (o redta) del cosumatore v 2 è, allora, msurata dall area evdezata ella Fgura Ua varazoe 2 del rezzo determa, qud, ua varazoe ( dmuzoe se 2 > 0, aumeto se 2 < 0 ) del surlus, dcata co v 2 ella Fgura S ot come l vataggo (surlus, redta) del cosumatore sa ua quattà d moeta. k k 20 Oltre che la fuzoe d utltà f(x 2 ) sa dfferezable e soddsf la codzoe del secodo orde, s assume el seguto che la codzoe 2 = er essu 2 +. d f ( x ) dx 2 2 o comort x 1 < 0 35
36 2 2 v v 2 2 d 2 ( 2 ) 2 d 2 ( 2 ) x 2 x 2 x 2 x2 Fgura Fgura L aals comuta er u sgolo cosumatore determa l suo surlus. S assuma, ora, che le utltà de dvers cosumator sao cofrotabl e che l utltà dell seme de cosumator sa la somma delle utltà dvdual, seguedo l rco d Betham, coè U = Σ u =. Ne cosegue che l surlus comlessvo de cosumator è la somma de loro 1 surlus, coè V = Σ v = 1, ed è qud raresetato, er l bee esame, dall aaloga area otteuta rededo cosderazoe la curva aggregata d domada, vece che la curva dvduale. S ha, allora, la rooszoe seguete. Prooszoe 10.5 S cosder u equlbro arzale su u mercato cu gl uc acquret soo cosumator rce-taker rv del bee esame ella loro dotazoe. Se cosumator soo dotat d fuzo cardal d utltà, se queste soo searabl addtvamete rsetto al bee esame (quello d cu s cosdera l equlbro) e quaslear rsetto al bee moeta e se le utltà de dvers cosumator soo cofrotabl e l utltà aggregata è la somma delle utltà dvdual, allora l vataggo (surlus) aggregato che cosumator ottegoo co lo scambo è ar all area racchusa tra la loro curva aggregata d domada e l asse de rezz, lmtatamete all tervallo de rezz sueror al rezzo d acqusto del bee, ossa V = D ( ) d, ove D() è la fuzoe aggregata d domada de cosumator. Po, ua varazoe del rezzo determa ua varazoe del surlus aggregato V = D( ) d. + Dmostrazoe. La rooszoe dscede mmedatamete dalle cosderazo recedet. (S tega, tuttava, resete che qu l bee esame è dcato seza dce, metre rma era dcato co l dce 2). Se le mrese che acqustao o vedoo l bee esame soo rce-taker, allora s uò esegure u ragoameto aalogo a quello de cosumator e s ottee u rsultato aalogo. Idcado, rfermeto alla secfca stuazoe d scelta d mresa (se d breve o lugo erodo), co s() l offerta etta (qud, ostva se è vedta, egatva se è acqusto) del bee esame da arte dell mresa e co π*() la fuzoe d roftto massmo (ove è l rezzo del bee esame, metre rezz d tutt gl altr be soo, er l otes d equlbro arzale, dedet dal mercato esame e, qud, questa aals, costat), l vataggo (surlus) coseguto dall mresa sul mercato esame è ar a v = π*() π*( c ) ove c è l rezzo corrsodeza al quale l offerta etta del bee è ulla (cocde co l rezzo d chusura se l mresa è vedtrce del bee esame). S 36
37 ha, allora, alcado la relazoe d Hotellg (così come dcato dalla Prooszoe 5.9), dπ*( ) che v = d = ( ) d c d s, ove s() è la fuzoe d offerta etta del bee c esame. (Il roftto dell mresa è, ovvamete, π*() = v + π*( c ) ). Se l mresa è acqurete l bee ed è rce-taker sul mercato del bee esame, er cu l offerta etta è egatva, allora dcado la sua domada co d() = s() e oedo c fto, s ha v = d ( ) d. Il roftto (surlus) dell mresa è, rsetto alla curva d domada dell mresa, la stessa area gà dvduata er l cosumatore. Se, qud, la domada è eserctata er uo stesso bee sa da cosumator sa da mrese e valgoo le otes della Prooszoe 10.5, allora l surlus aggregato che cosumator e le mrese ottegoo co l acqusto del bee è ar all area racchusa tra la curva aggregata d domada e l asse de rezz (lmtatamete all tervallo de rezz sueror al rezzo del bee), ossa V = D ( ) d, ove D() è la fuzoe aggregata d domada (eserctata da cosumator e da mrese). Po, ua varazoe del rezzo determa ua + varazoe del surlus aggregato V = D( ) d. Se l mresa è vedtrce l bee ed è rce-taker sul mercato del bee esame, l aals recedete mostra come l vataggo (surlus) dell mresa sa v = s ( ) d. c uesto cocde co l roftto dell mresa (ar, el breve erodo, alla somma tra l roftto e l costo fsso). Percò, l surlus dell mresa vedtrce è ar sa all area racchusa tra la curva d offerta e quella de rezz (lmtatamete all tervallo comreso tra l rezzo d chusura e l rezzo d vedta), sa all area racchusa tra l rezzo d vedta (semre che questo o sa ferore al rezzo d chusura) e la curva del costo margale. uesta equvaleza cosete d determare l surlus dell mresa vedtrce l bee esame ache se o è rce-taker. I quest cas l surlus è ar all area determata, er og utà veduta, dalla dffereza tra l rezzo e l costo margale. Se v soo ù mrese vedtrc, l surlus aggregato è la somma de loro surlus. Allora, el caso cu le mrese vedtrc soo tutte rce-taker, l loro surlus aggregato è ar all area racchusa tra la curva d offerta e quella de rezz (lmtatamete all tervallo comreso tra 0 e l rezzo d equlbro). * V S() D() * V MC() D() MR() * Fgura * Fgura Nelle Fgure e è raresetato l vataggo (surlus) comlessvo (d tutt comrator e vedtor l bee esame) geerato dallo scambo, rsettvamete ell equlbro arzale cocorrezale e quello d mooolo a rezzo uco. 37
38 La msura del vataggo (surlus) comlessva dcata recedetemete è stata rferta ad ua fuzoe d beessere socale bethamaa, coè del to U = Σ u = 1. uesto rfermeto uò essere debolto, semre co l otes che le fuzo d utltà dvdual sao quas-lear, coè del to u (x ) = x 1 + f (x 2 ), secodo l ragoameto seguete. S troduca, er l caso esame, l seme delle utltà massmal (Defzoe 8.6). S trova che esso è del to U max = {u : Σ = 1u = k }. Per ture questo rsultato s arta da u uto qualsas d U max e s tolga u o del rmo bee ad u dvduo (che e abba) e lo s da ad u altro lascado varate le quattà del secodo bee. Poché l cosumo d questo rmae varato, d tato cresce l utltà del secodo dvduo d quato dmusce quella dell altro e s ervee acora ad u vettore d utltà massmal erché le codzo d effceza cotuao ad essere soddsfatte (essedo varate le utltà margal del secodo bee e, qud, sagg margal d sosttuzoe). S troduca ora ua qualsas fuzoe d beessere socale W(u 1,,u ). S massmzz questa fuzoe su U max e s troduca la fuzoe dretta d beessere socale. Poché U max dede soltato da k, s ha W*(k). Essedo W ua fuzoe ordale, s scelga quella sua trasformazoe strettamete crescete er cu W*(k) = k. Essedo k =Σ= 1u, s ha allora che Σ = 1u è ua ossble msura del beessere socale qualuque sa la fuzoe d beessere socale che vee massmzzata L evoluzoe dell aals dell equlbro arzale L aals dell equlbro arzale cocorrezale è sorattutto oera d Marshall (1890), che e ha trodotto tutt gl elemet rcal. I recedeza, l equlbro arzale era stato esamato, modo rudmetale, ache da Jevos e da Meger. Marshall ha fatto d esso l cetro della sua teora, troducedo così l ecooma dustrale, ache e suo asett damc, tramte la dstzoe tra breve e lugo erodo. Peraltro, l teto d Marshall era solo arte aaltco. Nella sua teora v soo argometazo cu l aals statca è commsta a cosderazo d to damco: ad esemo, la curva d offerta d lugo erodo vee formulata troducedo cosderazo rguardo la mglore orgazzazoe d mresa che uò accomagare lo svluo d questa e segado tal modo come la curva d offerta (che assume erò così atura alquato dversa da quella cosderata questo catolo) ossa rsultare decrescete rsetto al volume della roduzoe. L aals dell equlbro arzale cocorrezale s è svluata el erodo marshallao e quello mmedatamete successvo, accomagata ache da rcerche ecoometrche (ad esemo, Schultz, 1938) e dall troduzoe d modell damc (come quello della ragatela esosto el Paragrafo 10.7). No v soo stat successvamete cotrbut d rlevo (se o crtc, come quello d Sraffa, 1925, verso la costruzoe marshallaa dell equlbro cocorrezale arzale, artcolare verso l troduzoe d ua curva o costate d offerta dell dustra co lbertà d etrata). Ache er questa ragoe, l teresse degl ecoomst s è 38
39 sostato sa verso l equlbro arzale o cocorrezale (ù recetemete ache co formazoe asmmetrca) sa verso l equlbro geerale cocorrezale. Pur tuttava, l aals dell equlbro arzale cocorrezale è acora ogg u rfermeto dsesable, co cu cofrotare le altre aals. L aals dell equlbro d mooolo a rezzo uco, svluata da Marshall (1890) e Edgeworth (1897), è stata trodotta da Courot (1838), che è rteuto l rmo ecoomsta ad avere usato modo esteso e coerete la matematca ecooma (egl è stato ache l rmo ecoomsta a comere u aals dell olgoolo e del mooolo blaterale, oltre a trodurre l aals dell equlbro arzale cocorrezale). La sstemazoe del mooolo co dscrmazoe del rezzo (clusa la dstzoe tra tre geer) è oera d Pgou (1912 e 1920), successore d Marshall a Cambrdge. Nell ambto della scuola glese marshallaa è stata svluata l aals geerale delle forme d mercato o cocorrezal: a questo rguardo l autrce ù sgfcatva è Robso (1933), cu s deve l aals e lo stesso terme d moosoo. L aals della cocorreza mooolstca è oera d Chamberl (1933). 39
Dimostrazione della Formula per la determinazione del numero di divisori-test di primalità, di Giorgio Lamberti
 Gorgo Lambert Pag. Dmostrazoe della Formula per la determazoe del umero d dvsor-test d prmaltà, d Gorgo Lambert Eugeo Amtrao aveva proposto l'dea d ua formula per calcolare l umero d dvsor d u umero, da
Gorgo Lambert Pag. Dmostrazoe della Formula per la determazoe del umero d dvsor-test d prmaltà, d Gorgo Lambert Eugeo Amtrao aveva proposto l'dea d ua formula per calcolare l umero d dvsor d u umero, da
Programmazione Non Lineare: Algoritmi Evolutivi Ing. Valerio Lacagnina. METODI di PNL
 Programmazoe No Leare: Algortm Evolutv Ig. Valero Lacaga Programmazoe o leare: metodche rsolutve METODI d PNL INDIRETTI DIRETTI Codzo ecessare Sstema d vcol Algortm I metod drett forscoo soltato codzo
Programmazoe No Leare: Algortm Evolutv Ig. Valero Lacaga Programmazoe o leare: metodche rsolutve METODI d PNL INDIRETTI DIRETTI Codzo ecessare Sstema d vcol Algortm I metod drett forscoo soltato codzo
Modelli di Flusso e Applicazioni: Andrea Scozzari. a.a. 2013-2014
 Modell d Flusso e Applcazo: Adrea Scozzar a.a. 203-204 2 Il modello d Flusso d Costo Mmo: Problem d Flusso A u l V b c P S A ), ( m ) ( ) ( ), ( Problem rcoducbl a problem d Flusso Il problema del trasporto
Modell d Flusso e Applcazo: Adrea Scozzar a.a. 203-204 2 Il modello d Flusso d Costo Mmo: Problem d Flusso A u l V b c P S A ), ( m ) ( ) ( ), ( Problem rcoducbl a problem d Flusso Il problema del trasporto
Design of experiments (DOE) e Analisi statistica
 Desg of epermets (DOE) e Aals statstca L utlzzo fodametale della metodologa Desg of Epermets è approfodre la coosceza del sstema esame Determare le varabl pù sgfcatve; Determare l campo d varazoe delle
Desg of epermets (DOE) e Aals statstca L utlzzo fodametale della metodologa Desg of Epermets è approfodre la coosceza del sstema esame Determare le varabl pù sgfcatve; Determare l campo d varazoe delle
SCHEDA DIDATTICA N 5
 FACOLTA DI INGEGNEIA COSO DI LAUEA IN INGEGNEIA CIVILE COSO DI IDOLOGIA POF. PASQUALE VESACE SCHEDA DIDATTICA N 5 MOMENTI DELLE VAIABILI CASUALI E STIMA DEI PAAMETI A.A. 0-3 Momet delle varabl casual La
FACOLTA DI INGEGNEIA COSO DI LAUEA IN INGEGNEIA CIVILE COSO DI IDOLOGIA POF. PASQUALE VESACE SCHEDA DIDATTICA N 5 MOMENTI DELLE VAIABILI CASUALI E STIMA DEI PAAMETI A.A. 0-3 Momet delle varabl casual La
Modello dinamico nello spazio dei giunti: relazione tra le coppie di attuazione ai giunti ed il moto della struttura
 Damca Modello damco ello spazo de gut: relazoe tra le coppe d attuazoe a gut ed l moto della struttura smulazoe del moto aals e progettazoe delle traettore progettazoe del sstema d cotrollo progetto de
Damca Modello damco ello spazo de gut: relazoe tra le coppe d attuazoe a gut ed l moto della struttura smulazoe del moto aals e progettazoe delle traettore progettazoe del sstema d cotrollo progetto de
La classe che mostra la distribuzione più elevata è quella 60-90, che corrisponde a un uso elevato dell automobile. f i fr (= f i/n) fr% (=fr*100)
 ESERCIZIO Il Moblty Maager d u azeda ha rlevato l umero d chlometr percors settmaalmete da 60 mpegat. I dat soo rportat ello schema successvo. 67 4 93 58 66 87 5 53 86 8 7 47 56 70 54 86 48 43 60 58 5
ESERCIZIO Il Moblty Maager d u azeda ha rlevato l umero d chlometr percors settmaalmete da 60 mpegat. I dat soo rportat ello schema successvo. 67 4 93 58 66 87 5 53 86 8 7 47 56 70 54 86 48 43 60 58 5
Stim e puntuali. Vocabolario. Cambiando campione casuale, cambia l istogramma e cambiano gli indici
 Stm e putual Probabltà e Statstca I - a.a. 04/05 - Stmator Vocabolaro Popolazoe: u seme d oggett sul quale s desdera avere Iformazo. Parametro: ua caratterstca umerca della popolazoe. E u Numero fssato,
Stm e putual Probabltà e Statstca I - a.a. 04/05 - Stmator Vocabolaro Popolazoe: u seme d oggett sul quale s desdera avere Iformazo. Parametro: ua caratterstca umerca della popolazoe. E u Numero fssato,
frazione 1 n dell ammontare complessivo del carattere A x
 La Cocetrazoe Il cocetto d cocetrazoe rguarda l modo cu l ammotare totale d u carattere quattatvo trasferble s rpartsce tra utà statstche. Tato pù tale ammotare è addesato u sottoseme d utà, tato pù s
La Cocetrazoe Il cocetto d cocetrazoe rguarda l modo cu l ammotare totale d u carattere quattatvo trasferble s rpartsce tra utà statstche. Tato pù tale ammotare è addesato u sottoseme d utà, tato pù s
Elementi di Matematica Finanziaria. Rendite e ammortamenti. Università Parthenope 1
 Elemet d Matematca Fazara Redte e ammortamet Uverstà Partheope 1 S chama redta ua successoe d captal da rscuotere (o da pagare) a scadeze determate S chamao rate della redta sgol captal da rscuotere (o
Elemet d Matematca Fazara Redte e ammortamet Uverstà Partheope 1 S chama redta ua successoe d captal da rscuotere (o da pagare) a scadeze determate S chamao rate della redta sgol captal da rscuotere (o
Aldo Montesano PRINCIPI DI ANALISI ECONOMICA CAP. 11 L ANALISI DELL'EQUILIBRIO GENERALE I
 Aldo Motesao PRINCIPI DI ANALISI ECONOMICA CAP. L ANALISI DELL'EQUILIBRIO GENERALE I L aals dell equlbro parzale, esaata el captolo precedete, è sa u utle troduzoe all aals dell equlbro geerale, sa uo
Aldo Motesao PRINCIPI DI ANALISI ECONOMICA CAP. L ANALISI DELL'EQUILIBRIO GENERALE I L aals dell equlbro parzale, esaata el captolo precedete, è sa u utle troduzoe all aals dell equlbro geerale, sa uo
2014-2015 Corso TFA - A048 Matematica applicata. Didattica della matematica applicata all economia e alla finanza
 Uverstà degl Stud d Ferrara 2014-2015 Corso TFA - A048 Matematca applcata Ddattca della matematca applcata all ecooma e alla faza 11 marzo 2015 Apput d ddattca della Matematca fazara Redte, ammortamet
Uverstà degl Stud d Ferrara 2014-2015 Corso TFA - A048 Matematca applcata Ddattca della matematca applcata all ecooma e alla faza 11 marzo 2015 Apput d ddattca della Matematca fazara Redte, ammortamet
Indici di Posizione. Gli indici si posizione sono misure sintetiche ( valori caratteristici ) che descrivono la tendenza centrale di un fenomeno
 Idc d Poszoe Gl dc s poszoe soo msure stetche ( valor caratterstc ) che descrvoo la tedeza cetrale d u feomeo La tedeza cetrale è, prma approssmazoe, la modaltà della varable verso la quale cas tedoo a
Idc d Poszoe Gl dc s poszoe soo msure stetche ( valor caratterstc ) che descrvoo la tedeza cetrale d u feomeo La tedeza cetrale è, prma approssmazoe, la modaltà della varable verso la quale cas tedoo a
Organizzazione del corso. Elementi di Informatica. Orario lezioni ed esami. Crediti. Dispense e lucidi. Ricevimento studenti
 Orgazzazoe del corso Elemet d Iformatca Prof. Alberto Brogg Dp. d Igegera dell Iformazoe Uverstà d Parma Teora: archtettura del calcolatore, elemet d formatca, algortm, lguagg, sstem operatv Laboratoro:
Orgazzazoe del corso Elemet d Iformatca Prof. Alberto Brogg Dp. d Igegera dell Iformazoe Uverstà d Parma Teora: archtettura del calcolatore, elemet d formatca, algortm, lguagg, sstem operatv Laboratoro:
Attualizzazione. Attualizzazione
 Attualzzazoe Il problema erso alla captalzzazoe prede l ome d attualzzazoe Abbamo ua operazoe fazara elemetare e dato l motate M dobbamo determare l corrspodete captale zale C L'attualzzazoe è la operazoe
Attualzzazoe Il problema erso alla captalzzazoe prede l ome d attualzzazoe Abbamo ua operazoe fazara elemetare e dato l motate M dobbamo determare l corrspodete captale zale C L'attualzzazoe è la operazoe
Incertezza di misura
 Icertezza d msura Itroduzoe e rcham Come gà detto rsultat umerc ottebl dalle msurazo soo trsecamete caratterzzat da aleatoretà è duque sempre ecessaro stmare ua fasca d valor attrbubl come msura al msurado;
Icertezza d msura Itroduzoe e rcham Come gà detto rsultat umerc ottebl dalle msurazo soo trsecamete caratterzzat da aleatoretà è duque sempre ecessaro stmare ua fasca d valor attrbubl come msura al msurado;
Lezione 1. I numeri complessi
 Lezoe Prerequst: Numer real: assom ed operazo. Pao cartesao. Fuzo trgoometrche. I umer compless Nell'attuale teora de umer compless cofluscoo due fodametal dee, ua artmetca, l'altra geometrca. La prma,
Lezoe Prerequst: Numer real: assom ed operazo. Pao cartesao. Fuzo trgoometrche. I umer compless Nell'attuale teora de umer compless cofluscoo due fodametal dee, ua artmetca, l'altra geometrca. La prma,
V Tutorato 6 Novembre 2014
 1. Data la successioe V Tutorato 6 Novembre 01 determiare il lim b. Data la successioe b = a = + 1 + 1 8 6 + 1 80 + 18 se 0 se < 0 scrivere i termii a 0, a 1, a, a 0 e determiare lim a. Data la successioe
1. Data la successioe V Tutorato 6 Novembre 01 determiare il lim b. Data la successioe b = a = + 1 + 1 8 6 + 1 80 + 18 se 0 se < 0 scrivere i termii a 0, a 1, a, a 0 e determiare lim a. Data la successioe
ARGOMENTO: MISURA DELLA RESISTENZA ELETTRICA CON IL METODO VOLT-AMPEROMETRICO.
 elazoe d laboratoro d Fsca corso M-Z Laboratoro d Fsca del Dpartmeto d Fsca e Astrooma dell Uverstà degl Stud d Cataa. Scala Stefaa. AGOMENTO: MSUA DELLA ESSTENZA ELETTCA CON L METODO OLT-AMPEOMETCO. NTODUZONE:
elazoe d laboratoro d Fsca corso M-Z Laboratoro d Fsca del Dpartmeto d Fsca e Astrooma dell Uverstà degl Stud d Cataa. Scala Stefaa. AGOMENTO: MSUA DELLA ESSTENZA ELETTCA CON L METODO OLT-AMPEOMETCO. NTODUZONE:
COMPLEMENTI DI STATISTICA. L. Greco, S. Naddeo
 COMPLEMENTI DI STATISTICA L. Greco, S. Naddeo INDICE. GENERALITA SULLA VERIFICA DI IPOTESI. Itroduzoe 4. I test d sgfcatvtà 5.3 Gl tervall d cofdeza 7.4 Le potes alteratve.5 La poteza del test 5.6 Il test
COMPLEMENTI DI STATISTICA L. Greco, S. Naddeo INDICE. GENERALITA SULLA VERIFICA DI IPOTESI. Itroduzoe 4. I test d sgfcatvtà 5.3 Gl tervall d cofdeza 7.4 Le potes alteratve.5 La poteza del test 5.6 Il test
SIMULAZIONE DI ESAME ESERCIZI. Cattedra di Statistica Medica-Università degli Studi di Bari-Prof.ssa G. Serio 1
 SIMULAZIONE DI ESAME ESERCIZI Cattedra d Statstca MedcaUverstà degl Stud d BarProf.ssa G. Sero ESERCIZIO. Alcu autor hao studato se la depressoe possa essere assocata a dc serologc d process autommutar
SIMULAZIONE DI ESAME ESERCIZI Cattedra d Statstca MedcaUverstà degl Stud d BarProf.ssa G. Sero ESERCIZIO. Alcu autor hao studato se la depressoe possa essere assocata a dc serologc d process autommutar
UNI CEI ENV 13005 (GUIDA ALL ESPRESSIONE DELL INCERTEZZA DI MISURA)
 UI CEI EV 3005 (GUIDA ALL ESPRESSIOE DELL ICERTEZZA DI MISURA Uverstà degl Stud d Bresca Corso d Fodamet della Msurazoe A.A. 00-03 Apput a cura d Gorgo Cor 3835 UI CEI EV 3005 0. ITRODUZIOE 0. COCETTO
UI CEI EV 3005 (GUIDA ALL ESPRESSIOE DELL ICERTEZZA DI MISURA Uverstà degl Stud d Bresca Corso d Fodamet della Msurazoe A.A. 00-03 Apput a cura d Gorgo Cor 3835 UI CEI EV 3005 0. ITRODUZIOE 0. COCETTO
Lezione 3. Funzione di trasferimento
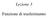 Lezoe 3 Fuzoe d trasfermeto Calcolo della rsposta d u sstema damco leare Per l calcolo della rsposta (uscta) d u sstema damco leare soggetto ad gress assegat, s possoo segure due strade Calcolo el domo
Lezoe 3 Fuzoe d trasfermeto Calcolo della rsposta d u sstema damco leare Per l calcolo della rsposta (uscta) d u sstema damco leare soggetto ad gress assegat, s possoo segure due strade Calcolo el domo
Successioni. Grafico di una successione
 Successioi Ua successioe di umeri reali è semplicemete ua sequeza di ifiiti umeri reali:, 2, 3,...,,... dove co idichiamo il termie geerale della successioe. Ad esempio, discutedo il sigificato fiaziario
Successioi Ua successioe di umeri reali è semplicemete ua sequeza di ifiiti umeri reali:, 2, 3,...,,... dove co idichiamo il termie geerale della successioe. Ad esempio, discutedo il sigificato fiaziario
Lezione 4. La Variabilità. Lezione 4 1
 Lezoe 4 La Varabltà Lezoe 4 1 Defzoe U valore medo, comuque calcolato, o è suffcete a rappresetare l seme delle osservazo effettuate (o l seme de valor assut dalla varable statstca); è ecessaro qud affacare
Lezoe 4 La Varabltà Lezoe 4 1 Defzoe U valore medo, comuque calcolato, o è suffcete a rappresetare l seme delle osservazo effettuate (o l seme de valor assut dalla varable statstca); è ecessaro qud affacare
Modelli di Schedulazione
 EW Modell d Schedulazoe Idce Maccha Sgola Tepo d Copletaeto Totale Tepo d Copletaeto Totale Pesato Tepo d Rtardo Totale Maespa co set-up dpedete dalla sequeza Tepo d Copletaeto Totale co vcolo d precedeza
EW Modell d Schedulazoe Idce Maccha Sgola Tepo d Copletaeto Totale Tepo d Copletaeto Totale Pesato Tepo d Rtardo Totale Maespa co set-up dpedete dalla sequeza Tepo d Copletaeto Totale co vcolo d precedeza
CALCOLO ECONOMICO E FINANZIARIO
 CALCOLO ECONOMICO E FINANZIARIO 1. Iteresse e scoto La postcpazoe d ua dspobltà fazara rchede ua certa rcompesa (teresse), vceversa la sua atcpazoe comporta ua dmuzoe dell'mporto orgaro (scoto). Il rsparmatore,
CALCOLO ECONOMICO E FINANZIARIO 1. Iteresse e scoto La postcpazoe d ua dspobltà fazara rchede ua certa rcompesa (teresse), vceversa la sua atcpazoe comporta ua dmuzoe dell'mporto orgaro (scoto). Il rsparmatore,
ESERCIZI SU DISTRIBUZIONI CAMPIONARIE
 Corso d Ifereza Statstca Eserctazo A.A. 009/0 ESERCIZI SU DISTRIBUZIONI CAMPIONARIE Eserczo I cosumator d marmellata ua data popolazoe soo l 40%. Determare la probabltà che, per u campoe beroullao d =
Corso d Ifereza Statstca Eserctazo A.A. 009/0 ESERCIZI SU DISTRIBUZIONI CAMPIONARIE Eserczo I cosumator d marmellata ua data popolazoe soo l 40%. Determare la probabltà che, per u campoe beroullao d =
Matematica elementare art.1 di Raimondo Valeri
 Matematca elemetare art. d Ramodo Valer I questo artcolo voglamo provare che esste ua formula per calcolare l umero de dvsor d u dato umero aturale seza cooscere la scomposzoe fattor prm del umero stesso.
Matematca elemetare art. d Ramodo Valer I questo artcolo voglamo provare che esste ua formula per calcolare l umero de dvsor d u dato umero aturale seza cooscere la scomposzoe fattor prm del umero stesso.
2014-2015 Corso TFA - A048 Matematica applicata. Didattica della matematica applicata all economia e alla finanza
 Uverstà degl Stud d Ferrara 2014-2015 Corso TFA - A048 Matematca applcata Ddattca della matematca applcata all ecooma e alla faza 18 marzo 2015 Apput d ddattca della Matematca fazara Redte, costtuzoe d
Uverstà degl Stud d Ferrara 2014-2015 Corso TFA - A048 Matematca applcata Ddattca della matematca applcata all ecooma e alla faza 18 marzo 2015 Apput d ddattca della Matematca fazara Redte, costtuzoe d
SUCCESSIONI NUMERICHE
 SUCCESSIONI NUMERICHE Ua fuzioe reale di ua variabile reale f di domiio A è ua legge che ad ogi x A associa u umero reale che deotiamo co f(x). Se A = N, la f è detta successioe di umeri reali. Se co si
SUCCESSIONI NUMERICHE Ua fuzioe reale di ua variabile reale f di domiio A è ua legge che ad ogi x A associa u umero reale che deotiamo co f(x). Se A = N, la f è detta successioe di umeri reali. Se co si
La volatilità storica, le misure di rischio asimmetrico e la tracking error volatility
 Ecooma degl termedar fazar Lors Nadott, Claudo Porzo, Daele Prevat Copyrght 00 The McGraw-Hll Compaes srl Approfodmeto 4.3w La msurazoe del rscho (a cura d Atoo Meles Uverstà Partheope) La volatltà storca,
Ecooma degl termedar fazar Lors Nadott, Claudo Porzo, Daele Prevat Copyrght 00 The McGraw-Hll Compaes srl Approfodmeto 4.3w La msurazoe del rscho (a cura d Atoo Meles Uverstà Partheope) La volatltà storca,
Manuale di Estimo Vittorio Gallerani, Giacomo Zanni, Davide Viaggi Copyright 2004 The McGraw-Hill Companies srl
 Mauale d Estmo ttoro Gallera, Gacomo Za, Davde agg Copyrght 24 The McGraw-Hll Compaes srl Caso 5 Stma d u agrumeto d 3 ha ubcato ella paa d Cataa. 1. Cofermeto dell carco e uesto d stma... 2 2. Descrzoe
Mauale d Estmo ttoro Gallera, Gacomo Za, Davde agg Copyrght 24 The McGraw-Hll Compaes srl Caso 5 Stma d u agrumeto d 3 ha ubcato ella paa d Cataa. 1. Cofermeto dell carco e uesto d stma... 2 2. Descrzoe
L assorbimento e lo strippaggio
 assorbmeto e lo strppaggo Coloa a stad d ulbro (coloa a patt Il calcolo d ua coloa d assorbmeto/strppaggo d questo tpo parte dal blaco d matera. Chamado e le portate d lqudo A e d gas C relatve a due compoet
assorbmeto e lo strppaggo Coloa a stad d ulbro (coloa a patt Il calcolo d ua coloa d assorbmeto/strppaggo d questo tpo parte dal blaco d matera. Chamado e le portate d lqudo A e d gas C relatve a due compoet
RENDITE. Le singole rate possono essere corrisposte all inizio o alla fine di ciascun periodo e precisamente si ha:
 RENDITE. Pagamet rateal S defsce redta ua sere qualsas d somme rscuotbl (o pagabl a scadeze dverse, o, pù esattamete, u seme d captal co dspobltà scagloata el tempo. Tal captal soo dett rate della redta
RENDITE. Pagamet rateal S defsce redta ua sere qualsas d somme rscuotbl (o pagabl a scadeze dverse, o, pù esattamete, u seme d captal co dspobltà scagloata el tempo. Tal captal soo dett rate della redta
SUCCESSIONI E SERIE NUMERICHE
 SUCCESSIONI E SERIE NUMERICHE. Successioi umeriche a. Defiizioi: successioi aritmetiche e geometriche Cosideriamo ua sequeza di umeri quale ad esempio:,5,8,,4,7,... Tale sequeza è costituita mediate ua
SUCCESSIONI E SERIE NUMERICHE. Successioi umeriche a. Defiizioi: successioi aritmetiche e geometriche Cosideriamo ua sequeza di umeri quale ad esempio:,5,8,,4,7,... Tale sequeza è costituita mediate ua
52. Se in una città ci fosse un medico ogni 500 abitanti, quale sarebbe la percentuale di medici? A) 5 % B) 2 % C) 0,2 % D) 0,5% E) 0,02%
 RISPOSTE MOTIVATE QUIZ D AMMISSIONE 2000-2001 MATEMATICA 51. L espressioe log( 2 ) equivale a : A) 2log B) log2 C) 2log D) log E) log 2 Dati 2 umeri positivi a e b (co a 1), si defiisce logaritmo i base
RISPOSTE MOTIVATE QUIZ D AMMISSIONE 2000-2001 MATEMATICA 51. L espressioe log( 2 ) equivale a : A) 2log B) log2 C) 2log D) log E) log 2 Dati 2 umeri positivi a e b (co a 1), si defiisce logaritmo i base
EQUAZIONI ALLE RICORRENZE
 Esercizi di Fodameti di Iformatica 1 EQUAZIONI ALLE RICORRENZE 1.1. Metodo di ufoldig 1.1.1. Richiami di teoria Il metodo detto di ufoldig utilizza lo sviluppo dell equazioe alle ricorreze fio ad u certo
Esercizi di Fodameti di Iformatica 1 EQUAZIONI ALLE RICORRENZE 1.1. Metodo di ufoldig 1.1.1. Richiami di teoria Il metodo detto di ufoldig utilizza lo sviluppo dell equazioe alle ricorreze fio ad u certo
DI IDROLOGIA TECNICA PARTE II
 FACOLTA DI INGEGNERIA Laurea Specalstca Igegera Cvle NO Guseppe T Aroca CORSO DI IDROLOGIA TECNICA PARTE II Aals e prevsoe statstca delle varabl drologche Lezoe X: Scelta d u modello probablstco Aals e
FACOLTA DI INGEGNERIA Laurea Specalstca Igegera Cvle NO Guseppe T Aroca CORSO DI IDROLOGIA TECNICA PARTE II Aals e prevsoe statstca delle varabl drologche Lezoe X: Scelta d u modello probablstco Aals e
Apparecchi di sollavamento. Classificazione apparecchi di sollevamento a
 Appareh d sollavameto A moto otuo: Nastr trasportator Sollevator a tazze Forze d erza lmtate; trastor d avvameto e arresto poo rlevat A moto dsotuo: Gru a torre Forze d erza rlevat Classfazoe appareh d
Appareh d sollavameto A moto otuo: Nastr trasportator Sollevator a tazze Forze d erza lmtate; trastor d avvameto e arresto poo rlevat A moto dsotuo: Gru a torre Forze d erza rlevat Classfazoe appareh d
Statistica degli estremi
 Statstca degl estrem Rcham d probabltà e statstca Il calcolo della probabltà d u eveto è drettamete coesso co: - la COOSCEZA ICOMPLETA dell eveto stesso; - l assuzoe d u RISCHIO, calcolato come la probabltà
Statstca degl estrem Rcham d probabltà e statstca Il calcolo della probabltà d u eveto è drettamete coesso co: - la COOSCEZA ICOMPLETA dell eveto stesso; - l assuzoe d u RISCHIO, calcolato come la probabltà
Serie numeriche: esercizi svolti
 Serie umeriche: esercizi svolti Gli esercizi cotrassegati co il simbolo * presetao u grado di difficoltà maggiore. Esercizio. Dopo aver verificato la covergeza, calcolare la somma delle segueti serie:
Serie umeriche: esercizi svolti Gli esercizi cotrassegati co il simbolo * presetao u grado di difficoltà maggiore. Esercizio. Dopo aver verificato la covergeza, calcolare la somma delle segueti serie:
Sintassi dello studio di funzione
 Sitassi dello studio di fuzioe Lavoriamo a perfezioare quato sapete siora. D ora iazi pretederò che i risultati che otteete li SCRIVIATE i forma corretta dal puto di vista grammaticale. N( x) Data la fuzioe:
Sitassi dello studio di fuzioe Lavoriamo a perfezioare quato sapete siora. D ora iazi pretederò che i risultati che otteete li SCRIVIATE i forma corretta dal puto di vista grammaticale. N( x) Data la fuzioe:
Il termine regressione fu introdotto da Francis Galton ( ), antropologo (promotore dell eugenetica).
 Regressoe leare Il terme regressoe fu trodotto da Fracs Galto (8-9), atropologo (promotore dell eugeetca). I u suo famoso studo (877-885), Galto scoprì che, sebbee c fosse ua tedeza de getor alt ad avere
Regressoe leare Il terme regressoe fu trodotto da Fracs Galto (8-9), atropologo (promotore dell eugeetca). I u suo famoso studo (877-885), Galto scoprì che, sebbee c fosse ua tedeza de getor alt ad avere
Numerazione binaria Pagina 2 di 9 easy matematica di Adolfo Scimone
 Numerazioe biaria Pagia di 9 easy matematica di Adolfo Scimoe SISTEMI DI NUMERAZIONE Sistemi di umerazioe a base fissa Facciamo ormalmete riferimeto a sistemi di umerazioe a base fissa, ad esempio el sistema
Numerazioe biaria Pagia di 9 easy matematica di Adolfo Scimoe SISTEMI DI NUMERAZIONE Sistemi di umerazioe a base fissa Facciamo ormalmete riferimeto a sistemi di umerazioe a base fissa, ad esempio el sistema
LA VERIFICA DELLE IPOTESI SUI PARAMETRI
 LA VERIFICA DELLE IPOTESI SUI PARAMETRI E u problema di ifereza per molti aspetti collegato a quello della stima. Rispode ad u esigeza di carattere pratico che spesso si preseta i molti campi dell attività
LA VERIFICA DELLE IPOTESI SUI PARAMETRI E u problema di ifereza per molti aspetti collegato a quello della stima. Rispode ad u esigeza di carattere pratico che spesso si preseta i molti campi dell attività
ANALISI MATEMATICA 1 Area dell Ingegneria dell Informazione. Appello del 5.02.2013 TEMA 1. f(x) = arcsin 1 2 log 2 x.
 ANALISI MATEMATICA Area dell Igegeria dell Iformazioe Appello del 5.0.0 TEMA Esercizio Si cosideri la fuzioe f(x = arcsi log x. Determiare il domiio di f e discutere il sego. Discutere brevemete la cotiuità
ANALISI MATEMATICA Area dell Igegeria dell Iformazioe Appello del 5.0.0 TEMA Esercizio Si cosideri la fuzioe f(x = arcsi log x. Determiare il domiio di f e discutere il sego. Discutere brevemete la cotiuità
5 ln n + ln. 4 ln n + ln. 6 ln n + ln
 DOMINIO FUNZIONE Determiare il domiio della fuzioe f = l e e + e + e Deve essere e e + e + e >, posto e = t si ha t e + t + e = per t = e e per t = / Il campo di esisteza è:, l, + Determiare il domiio
DOMINIO FUNZIONE Determiare il domiio della fuzioe f = l e e + e + e Deve essere e e + e + e >, posto e = t si ha t e + t + e = per t = e e per t = / Il campo di esisteza è:, l, + Determiare il domiio
1 Limiti di successioni
 Esercitazioi di matematica Corso di Istituzioi di Matematica B Facoltà di Architettura Ao Accademico 005/006 Aa Scaramuzza 4 Novembre 005 Limiti di successioi Esercizio.. Servedosi della defiizioe di ite
Esercitazioi di matematica Corso di Istituzioi di Matematica B Facoltà di Architettura Ao Accademico 005/006 Aa Scaramuzza 4 Novembre 005 Limiti di successioi Esercizio.. Servedosi della defiizioe di ite
Avvertenza. Rendite frazionate
 Avverteza Quest lucd soo pesat solo come u auslo per l ascolto della lezoe. No sosttuscoo l lbro d testo Possoo coteere error e svste, che gl studet soo vtat a segalare Redte frazoate L tervallo tra ua
Avverteza Quest lucd soo pesat solo come u auslo per l ascolto della lezoe. No sosttuscoo l lbro d testo Possoo coteere error e svste, che gl studet soo vtat a segalare Redte frazoate L tervallo tra ua
